光学第二章习题
《应用光学》第2章课后答案全文

12. 由两个透镜组成的一个倒像系统,设第一组透镜的焦距 为f1′,第二组透镜的焦距为f2′,物平面位于第一组透镜 的物方焦面上,求该倒像系统的垂轴放大率。
解:
1
1
1
1
F2
1
1
第一组透镜
第二组透镜
1
第二组透镜
13. 由两个同心的反射球面(二球面球心重合)构成的光学系 统,按照光线反射的顺序第一个反射球面是凹的,第二个 反射球面是凸的,要求系统的像方焦点恰好位于第一个反 射球面的顶点,求两个球面的半径r1,r2和二者之间的间隔 d之间的关系。
B′
面,如图示.
l ′ = 2f′
4 试用作图法对位于空气中的正透镜组( f 0 )分别求 下列不同物距的像平面位置.
l = −f′
B
……
F
F′
A
H H′
像平面在像 空间无限远 处.
l′=∞
4 试用作图法对位于空气中的正透镜组( f 0 )分别求 下列不同物距的像平面位置.
l f' 2
B′
r1 无穷远物点
r2
r1/2
最终像点
11 2
l2 l2 r2
l2
l2
2 r2
(l2l2 )
14. 假定显微镜物镜由相隔20mm的两个薄透镜组构成,物平 面和像平面之间的距离为180mm,放大率β=-10×,要求近 轴光线通过二透镜组时的偏角Δu1和Δu2相等,求二透镜 组的焦距。
y n1u1 u1 10
l = −f′
B
……
F′
F
H H′
A
像平面在像 空间无限远 处.
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平面位置.
应用光学习题(第二章)

个面对不晕像点。
n2 n2 n 1 l2 r2 r2 n2 n n2 n2 l2 r2 n 1r2 n2
1 n n 1 n 1 r1 - r2 r1 r2 n n n 由于 d始终都是大于零的,所 以r1 r2 (由于 r1 0,r2 0,且 r1 r2,该透镜为负弯月型透 镜)
1 n2
S1
S1与S2重合,所以 r2 l2 l2
d l1 l2
n
r1
C1 l2 l2 l1 r2 l1
C2
n1 n1 1 n 而 l1 r1 r1 n1 n 1 n d r1 r2 n
b. 同心球面透镜 物像点重合且位于两个 球面的共同曲率中心 C1,C 2点上Leabharlann 所以编号出处
2_004
P193_7
什么是不晕透镜?当透 镜成无球差点实像点时 ,应采用 什么样的结构形式 ?
答: ( 1)所谓不晕透镜,是轴 上物点单色光成像时, 不产生球差的透镜
(2) 由于不晕条件,物象点 在透镜的同一侧,所以 不晕透镜 分为两种情况:一种是 实物成虚像,而另一种 是虚物成实像。 该题中得到实像点时, 采用的就是虚物成实像 的形式(会聚光入射) r1 0,r2 0 a. 正弯月单透镜 r1 r2 r1 r2,所以第一个面对球心 C 1点在 C2点的左边
,S2,S 同心球面透镜构成不晕 透镜C ( ,S1,S1 2 C1 2)
n1 1
1 n2
C1 C2
n
r1 l1 l1 r2 l2 l2
,S2与S2重合 S1,S1 d r1 r2
编号
出处
2_005
课后习题试题

物理光学作业习题第一章光波的基本性质(1)作业习题1、试说明下列各组光波表达式所代表的偏振态。
⑴Ex=Eo sin(ωt-kz),Ey=Eo cos(ωt-kz)⑵Ex=Eo cos(ωt-kz),Ey=Eo cos(ωt-kz+π)4⑶Ex=Eo sin(ωt-kz),Ey=-Eo sin(ωt-kz)2、试证明:频率相同,振幅不同的右旋与左旋圆偏振光能合成一椭圆偏振光。
3、把一根截面是矩形的玻璃棒(折射率为1.5)弯成马蹄形,如图所示。
矩形宽为d,弯曲部分是一个圆,内半径是R。
光线从一个端面正入射。
欲使光线从另一端面全部出射,R/d应等于多少?4、若入射光线是线偏振光,入射角为︒45,其振动面与入射面间的夹角为︒45。
试证:这时空气和玻璃的分界面上,反射光仍然是线偏振光,并求其振动面和入射面间的夹角α以及振r动面的旋转方向。
5、欲使线偏振光的激光束通过红宝石棒时,在棒的端面上没有反射损失,则棒端面对棒轴倾角α应取何值?光束入射角φ1等于多少?入射光的振动方向如何?已知红宝石的折射率为n=1.76。
光束在棒内沿棒轴方向传播。
6、 试证明琼斯矢量⎥⎦⎤⎢⎣⎡∆i Be A 表示的椭圆偏振光,其主轴与X 轴夹角为21tan —1⎪⎭⎫ ⎝⎛-∆22cos 2B A AB (2)讨论习题1、 如图用棱镜是光束方向改变,要求光束垂直于棱镜表面射出,入射光是平行于纸面振动的H e —N e 激光(波长λ=3628Å)。
问,入射角φi 等于多少时,透射光为最强?并由此计算此棱镜底角α应磨成多少??已知棱镜材料的折射率n=1.52。
若入射光是垂直纸面振动的H e —N e 激光束,则能否满足反射损失小于1%的要求?2、 下图是激光技术中用以选择输出波长的方法之一。
它是利用在入射面内振动的光,在布鲁斯特角入射时反射光强为零,以及布鲁斯特角的值与波长有关的这些事实,使一定波长的光能以最低损耗通过三棱镜而在腔内产生振荡,其余波长的光则因损耗大而被抑制不能振荡,从而达到选择输出波长的目的。
光学第二章习题解答

∆y = y2 − y1 ≈ 2 f ′
λ
b
− f′
λ
b
= f′
λ
b
∆y ⋅ b 0.02 × 0.885 ɺ λ= = = 5900 A f′ 300
(2)波长为 波长为0.1nm的x射线时,相邻最小值间的距离为 射线时, 波长为 的 射线时
′λ 300 × 0.1×10−9 f ∆y = = 0.02 b −6 −4 = 1.5 × 10 m = 1.5 × 10 cm
主焦点
还有次焦点: 还有次焦点:± f ′ /3,
± f ′ /5, ± f ′ / 7⋯
故:光强极大值出现在轴上 1/3m,1/5m,1/7m……1/(2k+1)m等处 , , 等处
2.6 波长为 的点光源波带片成一个像点,该波带 波长为λ的点光源波带片成一个像点 的点光源波带片成一个像点, 个透明奇数半波带(1, , )。另外 有100个透明奇数半波带 ,3,5 ……199)。另外 个透明奇数半波带 )。 100个不透明偶数半波带。比较用波带片换上同样焦 个不透明偶数半波带。 个不透明偶数半波带 距和口径的透镜时像点的强度比I: 距和口径的透镜时像点的强度比 :I0 解:(1) 只有 ) 只有100个透明奇数半波带透过 个透明奇数半波带透过
∵
θ3 < θ 2
∴
二级和三级光谱部分重叠 二级和三级光谱部分重叠
2.14 用波长为 用波长为589nm的单色光照射一衍射光栅, 的单色光照射一衍射光栅 的单色光照射一衍射光栅, 其光谱的中央最大值和第二十级主最大值之间的衍 射角为15 10′。试求该光栅1cm内的缝数是多少? 15° cm内的缝数是多少 射角为15°10′。试求该光栅 cm内的缝数是多少? 解: 由光栅方程 d sin θ = jλ
工程光学习题参考答案第二章理想光学系统
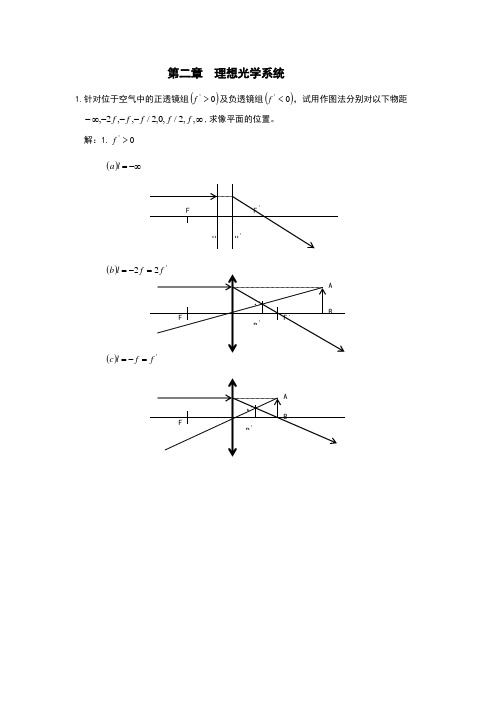
第二章 理想光学系统1.针对位于空气中的正透镜组()0'>f 及负透镜组()0'<f ,试用作图法分别对以下物距 ∞---∞-,,2/,0,2/,,2,f f f f f ,求像平面的位置。
解:1.0'>f ()-∞=l a()'2f l b -=()f f l c =-=()/f l d -=()0=l e()/f l f =')(f f l g -=='22)(f f l h -==+∞=l i )(2.0'<f -∞=l a )(l b )(=l c =)(/)(f l d -=0 el(=)f=l2/ (f)()fg=l(=h)ll i)(+∞=2. 已知照相物镜的焦距f’=75mm,被摄景物位于(以F 点为坐标原点)=x ,2,4,6,8,10,m m m m m -----∝-处,试求照相底片应分别放在离物镜的像方焦面多远的地方。
解: (1)x= -∝ ,xx ′=ff ′ 得到:x ′=0 (2)x ′= (3)x ′= (4)x ′= (5)x ′=(6)x ′=3.设一系统位于空气中,垂轴放大率*-=10β,由物面到像面的距离(共轭距离)为7200mm , 物镜两焦点间距离为1140mm 。
求该物镜焦距,并绘出基点位置图。
解:∵ 系统位于空气中,f f -='10''-===ll y y β 由已知条件:1140)('=+-+x f f7200)('=+-+x l l解得:mm f 600'= mm x 60-=4.已知一个透镜把物体放大*-3投影到屏幕上,当透镜向物体移近18mm 时,物体将被放大*-4,试求透镜的焦距,并用图解法校核之。
解:方法一:31'11-==l l β ⇒ ()183321'1--=-=l l l ①42'22-==l l β ⇒ 2'24l l -= ② 1821+-=-l l ⇒ 1821-=l l ③ '/1/1/11'1f l l =-'/1/1/12'2f l l =-将①②③代入④中得 mm l 2702-= mm l 1080'2-= ∴ mm f 216'=方法二: 311-=-=x fβ 422-=-=x fβ ⇒ mm f 216-= 1812=-x x方法三: 12)4)(3(21''=--==∆∆=ββαnn x x2161812'-=⨯=∆x''fx -=β143''''2'121=+-=∆=+-=-∴fx fx x ββ mm x f 216''=∆=∴5.一个薄透镜对某一物体成实像,放大率为⨯-1,今以另一个薄透镜紧贴在第一个透镜上,则见像向透镜方向移动,放大率为原先的3/4倍,求两块透镜的焦距为多少 解:⇒ 2'21'1/1/1/1/1l l l l -=- ④6.有一正薄透镜对某一物成倒立的实像,像高为物高的一半,今将物面向物体移近100mm , 则所得像与物同大小,求该正透镜组的焦距。
光学课件全部习题

解:三列平面波的复振幅分别为
选z=0平面
~ E1 = A1e i ( − k sin θx + k cosθz ) = A1e − ik sin θx ~ ikz E2 = A2 e = 2 A1
~ E3 = A3e i ( k sin θx + k cosθz ) = A1e ik sin θx
~ ~* ~ ~ ~ ~* ~* ~* I = EE = ( E1 + E2 + E3 )( E1 + E2 + E3 )
wwwwenku1comview9c970f097eb60a1分布a2sinkz221有三列在xz平面内传播的同频率单色平面波其振幅分别为a1a2a3传播方向如图求xy平面上的光强分布可设三列波在坐标原点初相均为0
第二章部分典型习题答案
2h1 +
λ1
2
= m1λ1
2h1 +
λ2
2
= m2 λ2
2h2 + 2h2 +
λ1
2
kλ1 = (k + 1)λ2
= (m1 + k )λ1 = (m2 + k + 1)λ2
980λ1 = 981λ2
λ2
2
λ1 = 589.6nm λ1 = 589nm
第四章部分典型习题答案
4.10 单色平面波垂直照射图示的衍射屏,图中标出的是该处到轴上场点 的光程,屏中心到场点的光程为ro,阴影区为不透光区.试用矢量图解 法求场点的光强与波自由传播时该场点的光强的比值.
2
2
I = 5I F
r0 + λ r0 + λ / 4
1 A= 2 AF 4
工程光学第二版习题答案(李湘宁_贾志宏)

丝,问其通过球面的共轭像在何处?当入射高度
h=10mm,实际光线的像方截距为多少?与高斯像面的距离
为多少?
解:
8、一球面镜半径 r=-100mm, 求 = 0 , -0.1 , -0.2 , -1 ,1 , 5, 10,∝时的物距像距。
第 4 页 共 29 页
解:( 1)
东北石油大学测控 09 级工程光学期末复习资料
解:
100mm,则所得像与物
6.希望得到一个对无限远成像的长焦距物镜,焦距 系统最后一面到像平面的距离 (工作距) 为 并画出光路图。
解:
=1200mm,由物镜顶点到像面的距离 L=700 mm,由 ,按最简单结构的薄透镜系统考虑, 求系统结构,
7.一短焦距物镜,已知其焦距为 系统结构。
35 mm,筒长 L=65 mm,工作距 , 按最简单结构的薄透镜系统考虑,求
3.一光学系统由一透镜和平面镜组成,如图
3-29 所示,平面镜 MM与透镜光轴垂直交于 D 点,透镜前方
离平面镜 600 mm有一物体 AB,经透镜和平面镜后,所成虚像
至平面镜的距离为 150 mm,且像高为
物高的一半,试分析透镜焦距的正负,确定透镜的位置和焦距,并画出光路图。
解:平面镜成 β =1 的像,且分别在镜子两侧,物像虚实相反 级工程光学期末复习资料
第六章习题
1.如果一个光学系统的初级子午彗差等于焦宽(),则
应等于多少?
解:
2.如果一个光学系统的初级球差等于焦深
(),则
应为多少? 解:
3. 设计一双胶合消色差望远物镜,
和火石玻璃 F2(
,
面的曲率半径。
解:
,采用冕牌玻璃 K9 (
解:设一个气泡在中心处,另一个在第二面和中心之间。
《光学教程》(姚启钧)第二章 光的衍射

3. 惠更斯-菲涅耳原理(1818)
菲涅耳对惠更斯原理的改进: 给不同次波赋予相应的相位和振幅,并将次波的干涉 叠加性引入惠更斯原理,得到衍射的定量表达式。
波面S上每个面元dS都是次波源,次波在p点引起振动的振幅与面积dS成正 比,与距离r成反比,且与倾角有关。
A(Q) K ( ) dE( P) dS r
相应的振动相位依次为:
a1 a2 a3 a4 ...... ak ak 1
f1,f1+,f1+2, f1+3,…f1+(k-1),f1+k。
对于轴上光源点 S 和轴上场点 P ,设圆孔恰好分 为 k 个半波带,则有
~ i 1 E1 a1e ~ i 1 E2 a2e ~ i 1 2 E3 a3e
次波中心Q 的光振幅 Q点在p 点引起的 光波振幅 倾斜因子 次波中心附 近的小面元
d · r S Q S(波面)
次波中心 设初相为零
n
dE(p) · p
观 察 点
倾斜因子K()的特点
A(Q) K ( ) dE( p) C dS cos(kr t ) r
0, K K max K ( ) , K 0 2
2
1mm 1000 mm 1000 mm 4 6 1000 mm 1000 mm 500 10 mm
2
半径为0.5mm的圆屏挡住的波带数为:
j
'
0.5mm 1000mm 1000mm 1 1000mm 1000mm 500 106 mm
又:
( h r0 , R)
2 2
R rk (r0 h)
《光学教程》(姚启钧)课后习题解答

《光学教程》(姚启钧)习题解答第一章光的干涉1、波长为的绿光投射在间距为的双缝上,在距离处的光屏500nm d 0.022cm 180cm 上形成干涉条纹,求两个亮条纹之间的距离。
若改用波长为的红光投射到此700nm 双缝上,两个亮纹之间的距离为多少?算出这两种光第2级亮纹位置的距离。
解:1500nmλ= 7011180500100.4090.022r y cm d λ-∆==⨯⨯= 改用2700nmλ=7022180700100.5730.022r y cm d λ-∆==⨯⨯= 两种光第二级亮纹位置的距离为:21220.328y y y cm∆=∆-∆=2、在杨氏实验装置中,光源波长为,两狭缝间距为,光屏离狭缝的640nm 0.4mm 距离为,试求:⑴光屏上第1亮条纹和中央亮纹之间的距离;⑵若P 点离中50cm 央亮纹为问两束光在P 点的相位差是多少?⑶求P 点的光强度和中央点的强0.1mm 度之比。
解:⑴ 7050640100.080.04r y cm d λ-∆==⨯⨯=⑵由光程差公式210sin yr r d dr δθ=-==0224y dr πππϕδλλ∆==⋅=⑶中央点强度:204I A=P 点光强为:221cos4I A π⎛⎫=+ ⎪⎝⎭01(10.8542I I =+=3、把折射率为的玻璃片插入杨氏实验的一束光路中,光屏上原来第5级亮条纹1.5所在的位置变为中央亮条纹,试求插入的玻璃片的厚度。
已知光波长为7610m-⨯ 解:,设玻璃片的厚度为1.5n =d由玻璃片引起的附加光程差为:()1n dδ'=- ()15n d λ-=()7645561061061010.5d m cm n λ---==⨯⨯=⨯=⨯-4、波长为的单色平行光射在间距为的双缝上。
通过其中一个缝的能500nm 0.2mm 量为另一个的倍,在离狭缝的光屏上形成干涉图样,求干涉条纹间距和条纹250cm 的可见度。
物理光学与应用光学习题解第二章
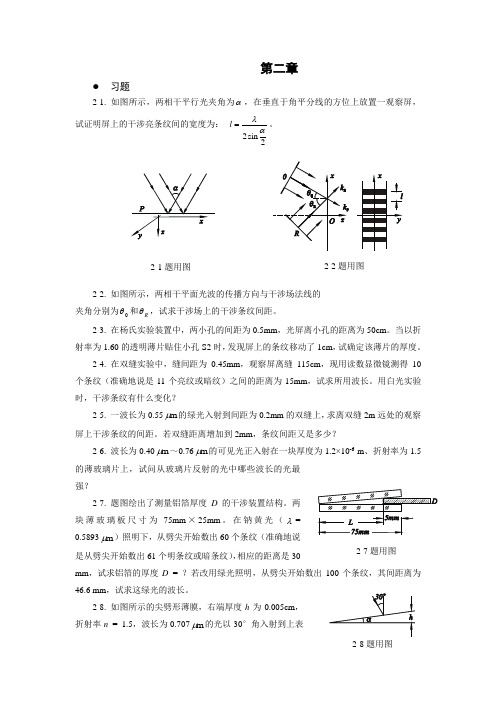
第二章习题2-1. 如图所示,两相干平行光夹角为α,在垂直于角平分线的方位上放置一观察屏,试证明屏上的干涉亮条纹间的宽度为: 2sin2αλ=l 。
2-2. 如图所示,两相干平面光波的传播方向与干涉场法线的 夹角分别为0θ和R θ,试求干涉场上的干涉条纹间距。
2-3. 在杨氏实验装置中,两小孔的间距为0.5mm ,光屏离小孔的距离为50cm 。
当以折射率为1.60的透明薄片贴住小孔S2时,发现屏上的条纹移动了1cm ,试确定该薄片的厚度。
2-4. 在双缝实验中,缝间距为0.45mm ,观察屏离缝115cm ,现用读数显微镜测得10个条纹(准确地说是11个亮纹或暗纹)之间的距离为15mm ,试求所用波长。
用白光实验时,干涉条纹有什么变化?2-5. 一波长为0.55m μ的绿光入射到间距为0.2mm 的双缝上,求离双缝2m 远处的观察屏上干涉条纹的间距。
若双缝距离增加到2mm ,条纹间距又是多少?2-6. 波长为0.40m μ~0.76m μ的可见光正入射在一块厚度为1.2×10-6 m 、折射率为1.5的薄玻璃片上,试问从玻璃片反射的光中哪些波长的光最强?2-7. 题图绘出了测量铝箔厚度D 的干涉装置结构。
两块薄玻璃板尺寸为75mm ×25mm 。
在钠黄光(λ=0.5893m μ)照明下,从劈尖开始数出60个条纹(准确地说是从劈尖开始数出61个明条纹或暗条纹),相应的距离是30mm ,试求铝箔的厚度D = ?若改用绿光照明,从劈尖开始数出100个条纹,其间距离为46.6 mm ,试求这绿光的波长。
2-8. 如图所示的尖劈形薄膜,右端厚度h 为0.005cm ,折射率n = 1.5,波长为0.707m μ的光以30°角入射到上表2-1题用图2-2题用图2-7题用图2-8题用图面,求在这个面上产生的条纹数。
若以两块玻璃片形成的空气尖劈代替,产生多少条条纹?2-9. 利用牛顿环干涉条纹可以测定凹曲面的曲率半径,结构如图所示。
光学教程第二版习题答案(一至七章)

∴ d1
=
h1 − h2 tan u1′
= 1.5 −1 0.015
= 33.33mm
tan u2 ′ = tan u2
+
h2 f 2′
= 0.015 +
1 = 0.011
− 250
∴d2
=
h2 − h3 tan u2 ′
1 − 0.9 =
0.011
= 9.091mm
2-13 一球形透镜,直径为 40mm,折射率为 1.5,求其焦距和主点位置。
= −200mm
lH
= dϕ2 ϕ
= 50 × 5 = −100mm − 2.5
2-11
有三个透镜,
f1′
= 100mm,
f2′
= 50mm,
f
′
3
=
−50mm,其间隔 d1
= 10mm,
d 2 = 10mm ,设该系统处于空气中,求组合系统的像方焦距。
解:设 h1 = 100mm, u1 = 0 ,则:
tan u3′
= tan u3 +
h3 f3′
= 2.8 +
62 − 50
= 1.56
∴组合系统的像方焦距为:
f
′=
h1 tan u3′
100 =
1.56
= 64.1mm
2-12
一个三 片型望远镜 系统,已知
f
′
1
= 100mm,
f
′
2
=
−250mm ,
f
′
3
= 800mm,入
射平行光在三个透镜上的高度分别为: h1 = 1.5mm, h2 = 1mm , h3 = 0.9mm ,试求合成
工程光学基础 习题参考答案-第二章_02

3、设一系统位于空气中, 设一系统位于空气中,垂轴放大 率 β = −10 × , 由物面到像面的距离 (共轭距) 共轭距)为 7200mm,物镜两焦点 间距离为 1140mm。求该物镜焦距, 求该物镜焦距, 并绘出基点位置图。 并绘出基点位置图。 解: 由公式 β = − x' f = − (2-4) , f' x
f 2 ' = −240mm
8、一短焦距物镜 一短焦距物镜, 焦距物镜,已知其焦距为 35mm,筒长 L=65mm,工作距离 l k ' = 50mm ,按 最简单结构的薄透镜系统考虑, 最简单结构的薄透镜系统考虑,求系统结构。 求系统结构。 解: (仿照 (仿照 P32 P32 例 2) 利用正切计算法,设 h1 = 100mm ,有公式:
1 1 1 d (2-33) = + − f ' f1 ' f 2 ' f1 ' f 2 '
f1 ' f 2 ' nr1 r2 f ' = − f = − ∆ = ( n − 1)[n( r − r ) + ( n − 1)d ] 2 1 1 Φ = f ' − dr2 l ' = H n( r2 − r1 ) + ( n − 1)d − dr1 l = H n( r2 − r1 ) + ( n − 1)d
xx' = ff ' = − f ' 2 ∴ x' = − f2 x
代入数据得:
x = −∞, x' = 0.5625mm x = −10m, x' = 0.703mm x = −6m, x' = 0.9375mm x = −4m, x' = 1.406mm x = −2m, x' = 2.813mm
光学课后习题解答

当j=9时,
扎一—3/8 nm
19
所以,在390~760nm的可见光中,从玻璃片上反射最强的光波波长为
423.5 nm,480 nm,553.8 nm,654.5 nm.
12.迈克耳孙干涉仪的反射镜M2移动0.25mm时,看到条纹移过的数目为909个,设光为垂直入射,求所
17.9cm,纸厚0.036mm,求光波的波长。
11.波长为400Ll760nm的可见光正射在一块厚度为1.2×10-6m,折射率为1.5玻璃片上,试问从玻璃片反
射的光中哪些波长的光最强.
解:依题意,反射光最强即为增反膜的相长干涉,则有:
=2n2d =(2j1)-
4n2d2j 1
,=4n2d = 4 1.5 1.2 10^ = 7200nm
用光源的波长。
解:根据课本59页公式可知,迈克耳孙干涉仪移动每一条条纹相当h的变化为:
现因
N =909所对应的h为
2 0.25
909
13.迈克耳孙干涉仪平面镜的面积为4×4c∏t观察到该镜上有20个条纹。当入射光的波长为589nm时,
两镜面之间的夹角为多大?
解:因为S
又因为
所以
2
解:
Δ)
(1)由公式
r°
/ =扎
d
A「0
-y二
50__5_2
6.4 10 =8.0 10 cm
得
d
=0.4
(2)由课本第
20页图1-2
的几何关系可知
r2-r1dsid tan "^=0.04^=0.8 10
2222八'
I=AA22 A1A2cos=4A CoS
(3)由公式2得
光学第二章习题补充

光学第二章习题2.15 根据反射定律推导球面反射镜的物像距公式和焦距公式。
2.16 一凹面镜半径为50cm ,物体放置在何处时可产生放大两倍的像?2.17 将水注入杯中,杯底看起来向上升高了1cm ,水的折射率为4/3,求杯中水的深度。
2.8 一薄透镜折射率为1.500,光焦度为500D ,将其浸入折射率为1.502的液体中时,其光焦度为多少?2.19 一个玻璃球,折射率为n ,半径为R ,置于空气之中,11=n ,5.121=='n n ,12='n 求:(1)物在无限远时经过球成像于何处?(2)物在球面前2R 处时,经球成像于何处,大小如何 ?(3)如果物体是个指向球面的小箭头,问在(2)的条件下成像后箭头指向何方?2.20 一束平行光轴的近轴光线入射到如图所示的玻璃球上,玻璃球半径为R ,折射率为5.1,其后半球面渡上了铝反射膜,光线最后会聚于一点,求汇聚点的位置。
2.21 已知如图所示的薄透镜对于近轴光线成像而言相当于一个半径为cm 30的凹面反射镜,该薄透镜后球面半径为cm 5,且后表面渡上了铝反射膜,求其前球面的半径。
2.22 凸透镜和凹透镜的焦距分别为20.0cm 和40.0cm ,在之右40.0cm ,傍轴小物放在之左30.0cm ,求它的像。
2.23 凸透镜焦距为10cm ,凹透镜焦距为4cm ,两个透镜相距12cm 。
已知物在凸透镜左边20cm 处,求像的位置和横向放大率。
2.24 薄透镜的折射率为1.5,光焦度为5.00D ,将它浸入某液体,光焦度变为-1.00D 。
求液体的折射率。
2.25 屏幕方在距物100cm 远处,二者之间放一凸透镜。
当前后移动透镜时,我们发现透镜有两个位置可以使物成像在屏幕上。
测得这两个位置之间的距离为20cm 。
求这两个位置到幕的距离和透镜的焦距以及两个像的横向放大率。
2.26 有两块玻璃薄透镜分别为凸透镜和凹透镜,其表面的球面曲率半径均为10cm 。
《光学教程》(姚启钧)课后习题解答

《光学教程》(姚启钧)课后习题解答 - 百度文库《光学教程》(姚启钧)习题解答第一章光的干涉1 、波长为的绿光投射在间距为的双缝上,在距离处的光屏上形成干涉条纹,求两个亮条纹之间的距离。
若改用波长为的红光投射到此双缝上,两个亮纹之间的距离为多少?算出这两种光第2 级亮纹位置的距离。
解:改用两种光第二级亮纹位置的距离为:2 、在杨氏实验装置中,光源波长为,两狭缝间距为,光屏离狭缝的距离为,试求:⑴光屏上第 1 亮条纹和中央亮纹之间的距离;⑵若 P 点离中央亮纹为问两束光在 P 点的相位差是多少?⑶求 P 点的光强度和中央点的强度之比。
解:⑴⑵由光程差公式⑶中央点强度:P 点光强为:3 、把折射率为的玻璃片插入杨氏实验的一束光路中,光屏上原来第 5 级亮条纹所在的位置变为中央亮条纹,试求插入的玻璃片的厚度。
已知光波长为解:,设玻璃片的厚度为由玻璃片引起的附加光程差为:4 、波长为的单色平行光射在间距为的双缝上。
通过其中一个缝的能量为另一个的倍,在离狭缝的光屏上形成干涉图样,求干涉条纹间距和条纹的可见度。
解:由干涉条纹可见度定义:由题意,设,即代入上式得5 、波长为的光源与菲涅耳双镜的相交棱之间距离为,棱到光屏间的距离为,若所得干涉条纹中相邻亮条纹的间隔为,求双镜平面之间的夹角。
解:由菲涅耳双镜干涉条纹间距公式6 、在题 1.6 图所示的劳埃德镜实验中,光源 S 到观察屏的距离为,到劳埃德镜面的垂直距离为。
劳埃德镜长,置于光源和屏之间的中央。
⑴若光波波长,问条纹间距是多少?⑵确定屏上可以看见条纹的区域大小,此区域内共有几条条纹?(提示:产生干涉的区域 P 1 P 2 可由图中的几何关系求得)解:由图示可知:①②在观察屏上可以看见条纹的区域为 P 1 P 2 间即,离屏中央上方的范围内可看见条纹。
7 、试求能产生红光()的二级反射干涉条纹的肥皂膜厚度。
已知肥皂膜折射率为,且平行光与法向成 30 0 角入射。
光学 第二章 习题

第二章习题1、选择题:2008.在菲涅耳圆屏衍射的几何阴影中心处( )(A)永远是个亮点,其强度只与入射光强有关。
(B)永远是个亮点,其强度随着圆屏的大小而变。
(C)有时是亮点,有时是暗点。
2014.一波长为500nm的单色平行光,垂直射到0.02cm宽的狭缝上,在夫琅禾费衍射花样中心两旁第二条暗纹之间的距离为3mm,则所用透镜的焦距为()(A)60mm (B)60cm (C)30mm (D)30cm2026.一个衍射光栅宽为3cm,以波长为600nm的光照射,第二级主极大出现于衍射角为300处。
则光栅的总刻度线数为(A)1.25*104 (B)2.5*104 (C)6.25*103 (D)9.48*103 2028.X 射线投射在间距为d的平行点阵面的晶体中,试问发生布拉格晶体衍射的最大波长为多少?(A)d/4 (B)d/2 (C)d (D)2d2128. 菲涅尔圆孔衍射实验表明,几何光学是波动光学在一定条件下的近似,如果从圆孔露出来的波面对所考察的点作出的的半波带的数目为K,这种条件下可表达成:()(A)衍射波级数K~0;(B)衍射波级数K=1;(C)衍射波级数K〉1;(D)衍射波级数K〉〉1。
2129. 用半波带法研究菲涅尔圆孔的衍射的结果说明,圆孔轴线上的P点的明暗决定于:()(A)圆孔的大小;(B)圆孔到P点的距离;(C)半波带数目的奇偶;(D)圆孔半径与波长的比值。
2130 用半波带法研究菲涅尔圆孔衍射时,圆孔线上P点的明暗决定于:()(A)圆孔的直径;(B)光源到圆孔的距离;(C)圆孔到P的距离;(D)圆孔中心和边缘光线到P点的光程差。
2131 一波带片主焦点的光强约为入射光强的400倍,则波带片的开带数为:()(A)10;(B)20;(C)40;(D)100。
2132 在夫琅和费单缝衍射中,当入射光的波长变大时,中央零级条纹:()(A)宽度变小;(B)宽度变大;(C)宽度不变;(D)颜色变红。
物理光学-第二章(仅)习题

物理光学习题库——光的干涉部分一、选择题1. 下列哪一个干涉现象不属于分振幅干涉?A. 薄膜干涉B.迈克尔逊干涉C.杨氏双缝干涉D.马赫-曾德干涉2. 平行平板的等倾干涉图样定域在A. 无穷远B.平板上界面C.平板下界面D.自由空间3. 在双缝干涉试验中,两条缝的宽度原来是相等的,若其中一缝的宽度略变窄,则A.干涉条纹间距变宽B. 干涉条纹间距变窄C.不再发生干涉现象D. 干涉条纹间距不变,但原来极小处强度不再为04. 在杨氏双缝干涉实验中,相邻亮条纹和相邻暗条纹的间隔与下列的哪一种因素无关?A.光波波长B.屏幕到双缝的距离C. 干涉级次D. 双缝间隔5. 一束波长为λ的单色光从空气中垂直入射到折射率为n的透明薄膜上,要使反射光得到干涉加强,薄膜厚度应为A.λ/4B.λ/4nC. λ/2D. λ/2n6. 在白炽灯入射的牛顿环中,同级圆环中相应于颜色蓝到红的空间位置是A.由里向外B.由外向里C. 不变D. 随机变化7. 一个光学平板玻璃A与待测工件B之间形成空气劈尖,用波长为500nm的单色光垂直照明,看到的反射光干涉条纹弯曲部分的顶点恰好与其右边条纹的直线部分的切线相切,则工件的上表面缺陷是A.不平处为凸起,最大高度为250nmB.不平处为凸起,最大高度为500nmC.不平处为凹槽,最大高度为250nmD. 不平处为凹槽,最大高度为500nm8. 在单色光照明下,轴线对称的杨氏干涉双孔装置中,单孔屏与双孔屏的间距为1m,双孔屏与观察屏的间距为2m,装置满足远场、傍轴近似条件,屏上出现对比度K=0.1的等间隔干涉条纹,现将双孔屏沿横向向上平移1mm,则A. 干涉条纹向下平移2mmB. 干涉条纹向上平移2mmC. 干涉条纹向上平移3mmD. 干涉条纹不移动9. F-P腔内间距h增加时,其自由光谱范围ΔλA. 恒定不变B. 增加C. 下降D. =010. 把一平凸透镜放在平玻璃板上,构成牛顿环装置,当平凸透镜慢慢向上平移时,由反射光形成的牛顿环A. 向中心收缩,条纹间隔不变B. 向中心收缩,环心呈明暗交替变化C. 向外扩张,环心呈明暗交替变化D. 向外扩张,条纹间隔变大11. 在迈克尔逊干涉仪的一条光路中,垂直光线方向放入折射率为n、厚度为h的透明介质片,放入后,两路光束光程差的改变量为A. 2(n-1)hB. 2nhC. nhD. (n-1)h12. 在楔形平板的双光束干涉实验中,下列说法正确的是A. 楔角越小,条纹间隔越宽;B. 楔角一定时,照射波长越长,条纹间隔越宽C. 局部高度变化越大,条纹变形越严重D. 形成的干涉属于分波前干涉13. 若把牛顿环装置(都是用折射率为1.52的玻璃制成的)由空气搬入折射率为1.33的水中,则干涉条纹会A. 不变B. 变密集C.变稀疏D.不确定14. 若想观察到非定域干涉条纹,则应选择A. 单色扩展光源B.单色点光源C.15. 将一金属丝置于两块玻璃平板之间,构成如图所示的结构,当在A点施加一个均匀增加的力F时,下列说法正确的是A.条纹间隔逐渐增大B.条纹数量逐渐变多C.干涉条纹级次D.条纹向级次低的方向移动16. 由A、B两只结构相同的激光器发出的激光具有非常接近的强度、波长及偏振方向,这两束激光A. 相干B.不相干C.可能相干D.无法确定17. 下列干涉现象不属于分振幅干涉的是A. 薄膜干涉B.迈克尔逊干涉C. 马赫-增德尔干涉D.菲涅尔双棱镜干涉18. 有关平行平板的多光束干涉,下列说法正确的是A. 干涉形成的条件是在平板的内表面镀增透膜B.透射场的特点是在全亮的背景上得到极细锐的暗纹C.膜层的反射率越低,透射场的亮纹越细锐D. 透射场亮纹的光强等于入射光强19.镀于玻璃表面的单层增透膜,为了使增透效果好,膜层材料的折射率应该()A.大于玻璃折射率B.等于玻璃折射率C.介于玻璃折射率与空气折射率之间D. 等于空气折射率E. 小于空气折射率二、填空题1. 干涉条纹对比度表达式为,其取值范围是,两列相干简谐波叠加时,两列波的振幅比为1:3时,则干涉条纹对比度为。
2023年大学_《光学》(赵凯华钟锡华著)课后习题答案下载

2023年《光学》(赵凯华钟锡华著)课后习题答案
下载
《光学》(赵凯华钟锡华著)内容简介
绪论
第一章几何光学
第二章波动光学基本原理
第三章干涉装置光场的时空相干性
第四章衍射光栅
第五章傅里叶变换光学
第六章全息照相
第七章光在晶体中的传播
第八章光的吸收、色散和散射
第九章光的量子性激光
《光学》(赵凯华钟锡华著)目录
《光学(上下)》分上、下两册。
上册主要内容:几何光学、波动光学基本原理、干涉装置和光场的`时空相干性。
下册主要内容:衍射光栅、傅里叶变换光学、全息照相、光在晶体中的传播、光的吸收、色散和散射、光的量子性和激光。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章习题一、选择题:2008.在菲涅耳圆屏衍射的几何阴影中心处( B )(A)永远是个亮点,其强度只与入射光强有关。
(B)永远是个亮点,其强度随着圆屏的大小而变。
(C)有时是亮点,有时是暗点。
2014.一波长为500nm的单色平行光,垂直射到0.02cm宽的狭缝上,在夫琅禾费衍射花样中心两旁第二条暗纹之间的距离为3mm,则所用透镜的焦距为( D )(A)60mm (B)60cm (C)30mm (D)30cm2026.一个衍射光栅宽为3cm,以波长为600nm的光照射,第二级主极大出现于衍射角为300处。
则光栅的总刻度线数为A(A)1.25*104 (B)2.5*104 (C)6.25*103 (D)9.48*1032028.X 射线投射在间距为d的平行点阵面的晶体中,试问发生布拉格晶体衍射的最大波长为多少?D(A)d/4 (B)d/2 (C)d (D)2d2128. 菲涅尔圆孔衍射实验表明,几何光学是波动光学在一定条件下的近似,如果从圆孔露出来的波面对所考察的点作出的的半波带的数目为K,这种条件下可表达成:( D )(A)衍射波级数K~0;(B)衍射波级数K=1;(C)衍射波级数K〉1;(D)衍射波级数K〉〉1。
2129. 用半波带法研究菲涅尔圆孔的衍射的结果说明,圆孔轴线上的P点的明暗决定于:(C )(A)圆孔的大小;(B)圆孔到P点的距离;(C)半波带数目的奇偶;(D)圆孔半径与波长的比值。
2130 用半波带法研究菲涅尔圆孔衍射时,圆孔线上P点的明暗决定于:(D )(A)圆孔的直径;(B)光源到圆孔的距离;(C)圆孔到P的距离;(D)圆孔中心和边缘光线到P点的光程差。
2131 一波带片主焦点的光强约为入射光强的400倍,则波带片的开带数为:( A )(A)10;(B)20;(C)40;(D)100。
2132 在夫琅和费单缝衍射中,当入射光的波长变大时,中央零级条纹:(B )(A)宽度变小;(B)宽度变大;(C)宽度不变;(D)颜色变红。
2135 从光栅衍射光谱中你看出哪种可见光衍射比较显著?(A )(A)红光;(B)黄光;(C)绿光;(D)紫光。
2136 在光栅衍射实验中,为了得到较多的谱线,应该:( B )(A)适当减小光栅常数d;(B)适当增加光栅常数d;(C)适当减少缝数N;(D)适当增加缝数N。
2137 在光栅衍射实验中,若只增加光栅的缝数N,将会改变衍射图中的:(C )(A)干涉主最大的位置;(B)单缝衍射中亮纹内的谱线数;(C)光谱线的亮度和宽度;(D)光谱线的亮度和位置。
2138 若白光照射到衍射光栅上,在某一级光谱中,偏离中心最远的光的颜色是:( A )(A)红;(B)黄;(C)蓝;(D)紫。
2139 为了增加光栅衍射的分辨本领,可以:( C )(A)减小缝的宽度;(B)减小光栅常数;(C)增加缝数;(D)增加光的波长。
3140 NaCl晶体的晶格常数为0.28nm,用波长为1.40?的伦琴射线照射晶面,转动晶体出现第二级衍射条纹的偏向角φ为:( D )(A)30度;(B)40度;(C)50度;(D)60度。
2141 NaCl晶体的晶格常数为0.28nm,用x射线照射晶面,第二级光谱的掠射角为1度,则x射线的波长为:( A )(A)0.049?;(B)0.025?; (C) 2.8?;(D)1.4?。
二、填空题:1002.衍射可分为菲涅耳衍射和夫琅禾费衍射两大类。
1014.光的衍射条件是障碍物的限度和波长可比拟。
1133. 光波的波长为λ的单色光,通过线度为l的障碍物时,只有当_________________才能观察到明显的衍射现象。
1134. 惠更斯-菲涅尔原理是在惠更斯原理基础上,进一步考虑了_次波的干涉,补充和发展了惠更斯原理二建立起来的。
1135. 在菲涅尔圆孔衍射中,单色点光源距圆孔为R,光波波长为λ,半径为ρ的圆孔露出的波面对在轴线上的距圆孔无限远处可作的半波带数为1136. 在菲涅尔圆孔衍射中,圆孔半径为6 mm,波长为600nm的平行单色光垂直通过圆孔,在圆孔的轴线上距圆孔6 m处可作___10_____个半波带。
1137. 在菲涅尔圆孔衍射中,入射光的强度为I0,在轴线上P点的光程差为λ/2时,P点的光强与入射光强的比为1138. 在菲涅尔圆孔衍射中,入射光的振幅为A,在轴线上P点恰好作出一个半波带,该点的光强为2a1139. 在夫琅禾费单缝衍射中,缝宽为a,在衍射角为方向θ,狭缝边缘与中心光线的光程差为.。
1140. 在夫琅禾费单缝衍射中,缝宽为a,波长为λ,在衍射角为方向θ,狭缝两边缘光波的位相差为。
1141. 在夫琅禾费单缝衍射中,缝宽为a,波长为λ,在观察屏上出现暗纹的条件,有衍射角θ可表示为.(k=1,2,3等)。
1142. 夫琅禾费双缝衍射是与单缝衍射和双缝衍射的总效果,其光强表达式中, (sinu/u)^2 _是单缝衍射因子,(cos&/2)^2是双缝干涉因子。
1143. 光栅衍射是夫琅禾费单缝衍射和多缝干涉的总效果,单缝衍射因子是(sinu/u)^2 _,多缝干涉因子是(cos&/2)^21144. 光栅衍射实验中,光栅常数为a+b,缝数为N,两相邻主最大之间有N-1个最小,两相邻次最小中有N-2 个最大1145. 在光栅衍射实验中,光栅常数为d,能观察到衍射条纹的最大波长为。
d1146. 光栅衍射的第三级缺级,则光栅常数与缝宽之比为3;还有第6,9,12……级主级大缺级。
1147. 光栅常数为2.5×10-4 cm的光栅,它的第一级和第四级谱线的分辨本领分别为12000和48000。
1148. 波长为λ的平行单色光垂直这是到半径为a的圆孔上所产生的衍射,中心亮斑称爱里斑,它的角半径为1149. 强激光从激光器孔径为d的输出窗射向月球,得到直径为D的光斑。
如果激光器的孔径是2d,则月球上的光斑直径是D/2。
1150. 直径为2 mm的氦氖激光束(λ=633 nm),西欧那个地面射向月球,已知月球到地面的建立为3.76×105 km,则在月球上得到的光斑直径为2.90*105m。
三、简答题:3026.什么是光的衍射?.答:光绕过障碍物偏离直线传播而进入几何阴影,并在屏幕上出现光强分布不均匀的现象3027.明显产生衍射现象的条件是什么?答:障碍物的线度和光的波长可以比拟。
3028.惠更斯-菲涅耳原理是怎样表述的?8.答:障碍物的线度和光的波长可以比拟3029.衍答:障碍物的线度和光的波长可以比拟。
:衍射分菲涅耳衍射和夫琅禾费衍射两大类。
3030.什么叫半波带?答:由任何相邻两带的对应部分所发出的次波到达P点时的光程差都为半个波长(即相位相反)而分成的环形带。
3031.为什么圆屏几何影子的中心永远有光?答:由于圆屏衍射。
3032.夫琅禾费单缝衍射有哪些明显特征?答:中央有一条特别明亮的亮条纹,两侧排列着一些强度较小的亮条纹,相邻的亮条纹之间有一条暗条纹;两侧的亮条纹是等宽的,而中央亮条纹的宽度为其他亮条纹的两倍3033.什么是艾里斑?答:在夫琅禾费圆孔衍射图样的中央,光强占总光强的84%的亮斑。
3034.艾里斑的半角宽度为多少?答:艾里斑的半角宽度为:3035.艾里斑的线半径怎样计算?答:艾里斑的线半径为:3036.干涉和衍射有什么关系?3037.光栅的光谱线在什么情况下缺级?在什么情况下重叠?计算题:答:当 d 是 b 的倍数时,光栅的光谱线发生缺级。
光栅的光谱线发生重叠的条件是:。
四、4003.波长为546.1 nm 的平行光垂直地射在1 mm 宽的缝上,若将焦距为100 cm 的透镜紧贴于缝的后面,并使光聚焦到屏上,试问衍射图样的中央到⑴ 第一最大值;⑵第一最小值;⑶ 第三最小值的距离分别为多少?.解:4005.请按以下要求设计一块光栅:① 使波长600 nm 的第二级谱线的衍射角小于30°,并能分辨其0.02 nm 的波长差;② 色散尽可能大;③ 第三级谱线缺级。
则该光栅的缝数、光栅常量、缝宽和总宽度分别是多少?用这块光栅总共能看到600 nm 的几条谱线?解:4013.钠光通过宽为0.2mm的狭缝后,投射到与缝相距300cm的照相版上,所得的第二最小距离为0.885cm,则钠光的波长为多少?若改用波长为0.1nm的X射线作此实验,则版上的这两个最小值之间的距离是多少?解:(1)强度为最小值的点满足:第二最小的距离为:(2)4018.一平面透射光栅的光栅常数d=1.5mm,宽度D=3cm,一束准单色光以300角射到光栅上,已知光栅后透镜只能接受衍射角小于600角的衍射光,在透镜后焦面上接受衍射光谱。
试求:(1).在第一级光谱中能否分辨波长为500nm和500.01nm的两条相邻谱线?(2).最多能收到第几级光谱?能分辨的最小波长间隔是多少?.解:(1)光栅的分辨本领入射光中所含双线的波长差为0.01nm<0.025nm,故第一级光谱不能分辨该双线。
(2)平行光斜入射时,对于与入射线在法线同侧的衍射线所满足的光栅方程为将==300,=600代入上式,得最大光谱级次为故最多能观察到第4级光谱,在第4级能分辨的最小波长间距为继续阅读。
