不定积分的基本运算法则

不定积分公式运算法则

不定积分公式运算法则不定积分公式是数学中常用的一种积分形式，可以用来求解一些不常见的定积分求解问题，此外，不定积分公式还可以用来求解概率积分，它在概率统计学和概率论中有着广泛的应用。

不定积分的运算法则也在数学中应用广泛，可以非常有效地解决复杂的问题。

不定积分公式运算法则可以分为三类：解析解法、简化解法和数值解法。

解析解法是对不定积分公式进行精确求解的方法，通常可以使用定积分的求解方法来求解不定积分公式，这里使用的是不定积分公式的解析解法。

简化解法是将不定积分公式进行更简单的处理，以减少计算量，而在数值解法中，则是使用已知的算法来计算未知的不定积分公式的值。

解析解法的具体实现方法可以分为两种：函数形式求解法和反函数形式求解法。

函数形式求解法是将不定积分公式写成函数形式，然后进行精确求解，可以利用定积分公式的性质来求解不定积分公式。

而反函数形式求解法则是将不定积分公式变换成反函数的形式，然后进行反函数的精确求解。

简化解法是将不定积分公式进行分解，以减少计算量。

它通常可以将一个复杂的不定积分公式分解成几个容易求解的不定积分公式的和，这样就可以有效地减少求解难度。

另外，在简化解法中也可以使用定积分的性质来进行简化，减少计算量。

数值解法是利用已知的算法来计算未知的不定积分公式的值，它可以利用不定积分公式的性质来减少计算量，也可以利用定积分的性质来精确求解不定积分公式。

在实际应用中，数值解法可以非常有效地解决复杂的不定积分问题。

不定积分公式运算法则可以根据具体情况进行合理选择，其中，解析解法更适合于求解少量的不定积分公式，简化解法更适合于求解大量不定积分公式，而数值解法可以有效解决复杂问题。

因此，要求解不定积分公式，应根据具体情况选择合适的运算法则，以提高计算效率，减少计算量。

不定积分的运算法则

x 3
例8
3
x
arctan x C .
三角变换：
tan 2 x dx (sec2 x 1) dx
tan x x
C .
sec2 x dx tan x C 7
例9
2 2 cos 2 x cos x sin x cos x sin x dx cos x sin x dx
2
2
1 1 ( ) dx 2 1 x x
arctan x ln x
C.
1 1 x 2 dx arctan x C

1 d x ln x C x
5
例6. 求
解: 原式 =
[( 2e ) x 5 2 x )dx
( 2e ) x 2x C 5 ln 2 ln( 2e )
C， ( 1)
2
例2
(sin x 2 cos x e
x
) dx
x
sin xdx 2 cos xdx e dx
e
x
dx e C
x
2 sin x e x C . cos x
例3
( 2 x 3 x ) 2 dx ( 4 x 2 6 x 9 x ) dx
2 2
4
2
练习：设 f (sin 2 x ) cos 2 x , 求 f ( x ) .
解
令 u sin 2 x
cos x 1 u,
2
f ( u) 1 u,
1 2 f ( u) 1 u du u u C , 2 1 2 f ( x) x x C . 2

求不定积分的基本方法

x ln cx o ssx i n C
说明: 此技巧适用于形为 acoxsbsin xdx的积分. ccoxsdsin x
机动目录上页下页返回结束
例解1：2因. 求为I1aco sx isx b n sixn dIx2 及 aco cx sox bssixndx. a acco oxxss b bssiin n xxdx b acco oxxss a bssiin n xxdx
机动目录上页下页返回结束
3. 分部积分法
uvdxuvuvdx
使用原则:
1) v 易求出
由 2) uvvdx;比
好求 .
一般经验: 按“反, 对, 幂, 指 , 三”
的顺序, 排前者取为 u ,排后者取为 v .
计算格式: 列表计算
机动目录上页下页返回结束
多次分部积分的规律
senc2x
(n 2 )se n 3 x c se xtc axn senc2xtaxn ( n 2 )sn e 2 x c (s 2 x e 1 )d x c
sen c2xtaxn(n2)In(n2)In2
机动目录上页下页返回结束
例8. 求
解:
设
x1, F(x)x1
x1
u u u
u (n) u(n1)
(1)n (1)n1
v(n1k) v(n1) v (n) v(n1) v
v
特别: 当 u 为 n 次多项式时u(,n1) 0,计算大为简便 .
机动目录上页下页返回结束
例1. 求
解: 原式
2x3x 32x 22x
dx
1 ((3232))x2dxadxx axlnadx

求不定积分的方法

求不定积分的方法不定积分方法是微积分中常见而重要的一类问题，求解不定积分可以通过多种方法，下面将介绍常见的一些方法。

1.基本积分公式和微分运算法则：根据基本积分公式和微分运算法则，可以求出一些常见函数的不定积分。

例如，对于幂函数、指数函数、三角函数、反三角函数和对数函数等，我们可以根据其定义和性质直接求得其不定积分。

2. 分部积分法：分部积分法是一种通过递归的方式将一个积分问题转化为一个更简单的积分问题的方法。

具体来说，对于两个函数f(x)和g(x)，我们可以通过分部积分公式∫f(x)g(x)dx = F(x)g(x) -∫F(x)g'(x)dx来求解不定积分。

这一方法在解决乘积函数的积分问题时特别有用。

3. 代换法：代换法是一种通过变量代换的方式来简化不定积分的方法。

具体来说，对于形如∫f(g(x))g'(x)dx的不定积分，我们可以选择一个新的变量u=g(x)，然后将原来的不定积分转化为∫f(u)du的形式，从而通过求解新的不定积分来得到最终结果。

4.其他方法：除了上述方法，还有一些其他的不定积分方法可以用来求解特定类型的问题。

例如，对于一些特殊函数（如分式函数、反函数和超越函数等），我们可以尝试利用特殊的积分技巧来求解其不定积分。

此外，对于一些复杂的函数，我们还可以利用级数展开、极限转换或积分换元等方法来求解其不定积分。

总结起来，求解不定积分的方法是多种多样的，根据具体的问题和函数类型选择合适的方法是很重要的。

通过熟练掌握基本积分公式和微分运算法则，以及灵活运用分部积分法、代换法和其他方法，我们可以更好地解决不定积分问题。

然而，在实际应用中，求不定积分往往是一个复杂而耗时的过程，需要充分发挥数学思维和技巧，结合实际问题的特点进行合理选择和灵活运用。

不定积分运算

不定积分运算
不定积分运算是一种数学运算，主要用于求不定积分，即求原函数。

不定积分是微积分中的重要概念，它是求导（或微分）的逆运算。

在不定积分运算中，常用的方法包括基本积分公式、常数倍法则和代换法则。

基本积分公式是求不定积分的基础，对于常见的函数情况，基本积分公式可以快速求出它们的原函数。

常数倍法则是指求导时的常倍法则可以用于不定积分中，常数可以提到积分符号外面。

代换法则是一种常用的简化计算的方法，如果被积函数中有复杂的部分，难以直接计算，可以通过代换来简化计算。

总之，不定积分运算是一种通过数学运算求原函数的方法，常用的方法包括基本积分公式、常数倍法则和代换法则。

不定积分典型例题

解：

sin
2
xdx

1
cos 2x 2
dx

1 2
dx

1 2

cos
2 xdx

1 2
x

1 4

cos
2 xd (2 x)
1 x 1 sin 2x C 24
例6
求 dx a2x2
解：
a
dx 2x
2

1 2a

(
a
1
x

a
1
x
)dx

1 2a

d(a x) ax
(2) 1 dx . x
解先把被积函数化为幂函数的形式，再利用基
本积分公式，得
(1)
x2
xdx
5
x 2 dx
1
5 1
x2
C

2
x3
x C.
5 1
7
(2)
1 dx x
2
1
x 2dx
1
1 1
x 2 C
1 1
1
2x2 C
2
2 x C.

1 1 x2
dx arctgxC。
例例1812．2
xx44 ddxx xx441111ddxx ((xx2211))((xx2211))11ddxx
11xx22
11xx22
11xx22
(x 2 1 1 )dx 1 x3xarctgxC。
例例699．
ssiinn
22xx 22
ddxx

积分基本公式和法则

积分基本公式和法则积分是微积分学中非常重要的概念之一，它是求解函数的面积、曲线的长度和平面的体积的工具。

积分的基本公式和法则是我们进行积分运算的基础，下面将介绍一些常见的积分基本公式和法则。

1.基本积分表达式：a)定积分基本公式：∫1dx = x + C，其中C为常数∫x^n dx = (x^(n+1))/(n+1) + C，其中C为常数（n为非负整数，不等于-1）∫e^x dx = e^x + C，其中C为常数∫sin(x) dx = -cos(x) + C，其中C为常数∫cos(x) dx = sin(x) + C，其中C为常数∫sec^2(x) dx = tan(x) + C，其中C为常数∫csc^2(x) dx = -cot(x) + C，其中C为常数∫sec(x)tan(x) dx = sec(x) + C，其中C为常数∫csc(x)cot(x) dx = -csc(x) + C，其中C为常数b)不定积分基本公式：∫u(du) = u^2/2 + C，其中C为常数2.基本积分法则：a) 线性性质：对于任意常数a、b，有∫(af(x) + bg(x))dx =a∫f(x)dx + b∫g(x)dxb)基本算术运算法则：∫(f(x) ± g(x))dx = ∫f(x)dx ± ∫g(x)dx∫(Cf(x))dx = C∫f(x)dx，其中C为常数c)分部积分法则：∫(u(x)v'(x))dx = u(x)v(x) - ∫(u'(x)v(x))dxd)替换法则：∫f(g(x))g'(x)dx = ∫f(u)du，其中u=g(x)3.基本的积分求导关系：a) 反函数关系：若y=f(x)的反函数为x=g(y)，则∫f(x)dx = x∙f(x) - ∫xf'(x)dx + C，其中C为常数b) 对数函数：∫(1/x)dx = ln，x， + Cc) 指数函数：∫a^x dx = (a^x)/(ln(a)) + C，其中a为常数且a>0且a≠1d) 双曲函数：∫sinh(x)dx = cosh(x) + C，∫cosh(x)dx = sinh(x) + C，∫tanh(x)dx = ln，cosh(x)， + C，∫coth(x)dx = ln，sinh(x)，+ C以上仅是一些基本的积分公式和法则，实际上积分的应用非常广泛，涉及到各种函数和曲线的求解。

求不定积分的基本方法

机动目录上页下页返回结束
1 例13. 求不定积分 ∫ dx . (2 + cos x) sin x sin x 解: 原式 = ∫ (令 u = cos x) dx 2 (2 + cos x ) sin x 1 =∫ du 2 ( 2 + u )(u − 1) A=1
1 ( 2+u )(u −1)
习题课不定积分的计算方法
一、求不定积分的基本方法二、几种特殊类型的积分
第四章
机动
目录
上页
下页
返回
结束
一、求不定积分的基本方法
1. 直接积分法通过简单变形, 利用基本积分公式和运算法则求不定积分的方法 . 2. 换元积分法
∫ f ( x ) dx
第一类换元法第二类换元法
∫ f [ϕ (t )]ϕ ′(t ) dt
分部积分
机动
目录
上页
下页
返回
结束
1 dx . 例4. 设 y ( x − y ) = x , 求积分 ∫ x − 3y 解: y ( x − y ) 2 = x 令 x − y = t, 即 y = x −t
2
t3 x= 2 , t −1
t t 2 (t 2 − 3) y = 2 , 而 dx = 2 dt 2 t −1 (t − 1)
=
x x − 3 ln(e 6
+ 1) − 2
x 3 ln(e 3
x + 1) − 3 arctan e 6
+C
返回结束
机动
目录
上页
下页
3 cos x − sin x dx . 例11. 求 ∫ cos x + sin x

不定积分运算法则

dx
化和

1 1 sin x x
dx
法则
1dx

1 x
dx

sin
xdx
公式1/3/6
x ln x cos x C
3
1 3 x2
2
dx
化和化幂

2 4
1 2x3 x3 dx

法则
2
4
1dx 2 x3 dx x3dx
(7) cos xdx sin x C;
(8)

1 cos2
x
dx

sec2
xdx

tan
x

C;
(9)

1 sin2
x
dx csc2
xdx
cot
x C;
13
不定积分运算法则(P226)
(1) [ f ( x) g( x)]dx f ( x)dx g( x)dx;
(3)
1 u

u
'
dx

ln
|
u
|
C
(4) au u ' dx a u C; ln a
(5) eu u 'dx eu C; 22
(6)sin xdx cos x C; (6) sin u u 'dx cosu C;
(7) cos xdx sin x C; (7) cosu u 'dx sin u C;
2

x
1 x

sin
x

不定积分的基本公式和运算法则直接积分法

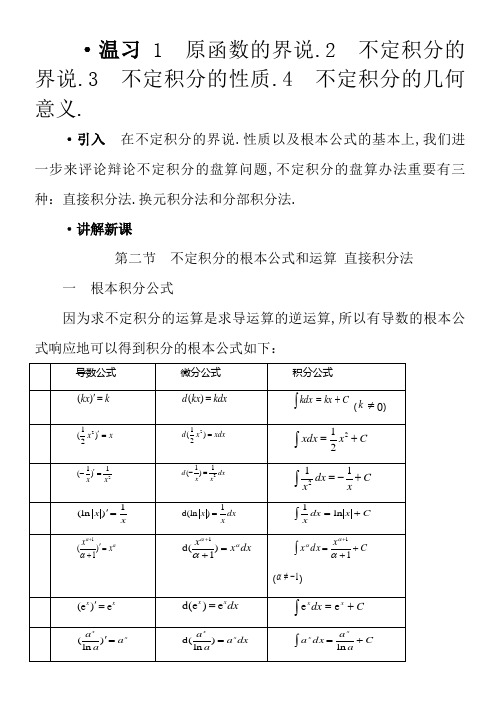
·温习 1 原函数的界说.2 不定积分的界说.3 不定积分的性质.4 不定积分的几何意义.·引入在不定积分的界说.性质以及根本公式的基本上,我们进一步来评论辩论不定积分的盘算问题,不定积分的盘算办法重要有三种：直接积分法.换元积分法和分部积分法.·讲解新课第二节不定积分的根本公式和运算直接积分法一根本积分公式因为求不定积分的运算是求导运算的逆运算,所以有导数的根本公式响应地可以得到积分的根本公式如下：以上十五个公式是求不定积分的基本,必须熟记,不但要记右端的成果,还要熟习左端被积函数的的情势.求函数的不定积分的办法叫积分法. 例1.求下列不定积分.（1）dxx ⎰21（2）dxx x ⎰解：（1）dx x ⎰21＝212121x x dx C Cx -+-=+=-+-+⎰（2）dxx x⎰＝C x dx x +=⎰252352此例标明,对某些分式或根式函数求不定积分时,可先把它们化为x α的情势,然后运用幂函数的积分公式求积分.二不定积分的根本运算轨则轨则1 两个函数代数和的积分,等于各函数积分的代数和,即轨则1对于有限多个函数的和也成立的．轨则2 被积函数中不为零的常数因子可提到积分号外,即dx x f k dx x kf ⎰⎰=)()( （0≠k ）例2 求3(21)x xe dx+-⎰解3(21)x x e dx +-⎰=23x dx⎰+dx⎰-x e dx⎰=412x x x e C +-+.注个中每一项的不定积分固然都应该有一个积分常数,但是这里其实不须要在每一项后面加上一个积分常数,因为随意率性常数之和照样随意率性常数,所以这里只把它的和C 写在末尾,今后仿此.注磨练解放的成果是否准确,只把成果求导,看它的导数是否等于被积函数就行了.如上例因为41()2x x x e C '+-+=321xx e +-,所以成果是准确的.三直接积分法在求积分的问题中,可以直接按根本积分公式和两个基赋性质求出成果（如上例）但有时,被积函数常须要经由恰当的恒等变形（包含代数和三角的恒等变形）再运用积分的性质和公式求出成果,如许的积分办法叫直接积分法.例3求下列不定积分.（1）1)(x dx ⎰ （2）dx x x ⎰+-1122解：（1）起首把被积函数1)(x 化为和式,然后再逐项积分得1)((1x dx x dx +-=+--⎰⎰5122221252x x x x C =+--+.注：（1）求函数的不定积分时积分常数C 不克不及丢失落,不然就会消失概念性的错误.（2）等式右端的每个不定积分都有一个积分常数,因为有限个随意率性常数的代数和仍是一个常数,所以只要在成果中写一个积分常数C 即可.（3）磨练积分盘算是否准确,只需对积分成果求导,看它是否等于被积函数.若相等,积分成果是准确的,不然是错误的.（2）222221122(1)111x x dx dx dx x x x -+-==-+++⎰⎰⎰ 222arctan 1dxdx x x C x =-=-++⎰⎰.上例的解题思绪是设法化被积函数为和式,然后再逐项积分,是一种重要的解题办法,须控制.演习 1 322324x x x dx x -++⎰,2 22221(1)x dx x x ++⎰,3 421x dx x +⎰.答案 1 21432ln ||2x x x C x -+-+, 2 1arctan x Cx -+, 3 31arctan 3x x x C -++例4求下列不定积分.（1）xdx⎰2tan （2）dx x2sin 2⎰解：（1）22tan(sec 1)xdx x dx=-⎰⎰（2）C x x dx x dx x+-=-=⎰⎰sin 21212cos 12sin2上例的解题思绪也是设法化被积函数为和式,然后再逐项积分,不过它实现化和是运用三角式的恒等变换.演习 1 2cot xdx⎰22cos 2x dx ⎰3 cos 2xdx cosx-sinx ⎰答案 1 cot x x C --+ 2 1(sin )2x x C++3 sin -cos x x C +例5设x x f 22cos )(sin =',求)(x f .解：因为x x x f 222sin 1cos )(sin -==',所以x x f -='1)(,故知)(x f 是x -1的原函数,是以Cx x dx x x f +-=-=⎰2)1()(2．小结根本积分公式,不定积分的性质,直接积分法. 演习求下列不定积分.（1）2(12sin )x dx x -+⎰（2）2212()cos sin dx x x +⎰,（3）dt t t ⎰+2)1(,（4）23)1dt t +⎰,（5）dx x x ⎰+)6(6,（6）dx x x ⎰--2411,（7）dx x x ⎰-)cot csc(csc ,（8）dx x x ⎰2sin 2cos ,（9）2(cos sin )22t t dt +⎰,（10）dx x ⎰-)1(tan 2,（11）e (3x x x dx -⎰.答案1 2cos 2ln ||x x x C +++, 2 tan -cot x x C +,3 212ln ||2t t t C +++, 4 2arcsin 3arctan t t C -+, 5 761ln 67x x C++, 6 313x x C --+,7 cot csc x x C -++, 8 cot 2x C --+,9 cos t t C -+, 10 tan 2x x C -+,11(3)2arcsin 1ln3xe x C-++.小结盘算简略的不定积分,有时只需按不定积分的性质和根本公式进行盘算;有时须要先运用代数运算或三角恒等变形将被积函数进行整顿．然后分项盘算．功课 P81:2,3 板书设计。

不定积分基本公式表 ppt课件

(4) axdx ax C; l na
当 ae时 , exd xexC ;
ppt课件
2
精品资料
• 你怎么称呼老师？
• 如果老师最后没有总结一节课的重点的难点，你是否会认为老师的教学方法需要改进？
• 你所经历的课堂，是讲座式还是讨论式？ • 教师的教鞭
• “不怕太阳晒，也不怕那风雨狂，只怕先生骂我笨，没有学问无颜见爹娘 ……”
f(x )d x g (x )d x
f(x)g(x).
法则1 可推广到有限多个函数代数和的情况，即
f1 (x ) f2 (x ) fn (x )d x
f1 (x ) d x f2 (x ) d x fn (x )d x .
ppt课件
11
法则 2 被积函数中的不为零的常数因子可以提到积分号前面，即
x2(x21)
x2(x21)
dx 1 dx x2 x2 1
1arctaxnC. x
ppt课件
16
例７求
x4 dx.
x2 1
解
x 4 dx x2 1
x4 11 dx
x2 1
(x21)x (21)
dx
1 dx
x21
x21
(x21)dx 1 dx 1x2
x3 xarctxanC.
ppt课件
5
(1)1 dx arcxsC in arcxc C o； s 1x2
( 1)2 d x arc x tC a n ac rc o x tC . 1 x 2
ppt课件
6
例1
求不定积分
1 x
dx.
解被积函 1的数定义x域 0.为 x
当 x > 0 时，因为(lnx)1, 所以 x

不定积分运算法则

C q 2q 3dq q2 3q C C是积分常数
由固定成本为2,即q 0，C0 2,
代入可得 C 0 C 2即C0 2;
因此,生产成本函数为 C q q2 3q 2
10
历届试题
（0601，3分）
（0701，3分）（070，3分）
11
基本积分公式
(1) dx x C (2) x dx x1 C ( 1);
1
(3) 1 dx ln | x | C x
(4) axdx ax C; (a 0且a 1) ln a
(5) exdx ex C;
12
(6) sin xdx cos x C;
6
助记词
函数积出原函数，原函数导出函数！
f (x) 积求分导' F(x) C
7
P221例1
例1 已知曲线y F(x)在任一点x处的切线斜率为2x,且曲线过(1, 2)点, 求此曲线的方程.
解曲线的切线斜率为2x,即k Fx 2x; 现在要求F x.
（注:此性质可推广到有限多个函数之和）
(2) kf (x)dx k f ( x)dx.（k 是常数，k 0)
14
题型4.2 直接积分法（P226）
知识要求 1、函数变形（化和差、化幂指、化分式、化三角）; 2、积分运算法则(3条)； 3、积分基本公式(9条)。
方法步骤
函数变形---法则拆项--公式计算
复习：
求微分 du u 'dx
例: d(x 3) 3x 2 dx
凑微分 (x)dx u '(x)dx du 例: 2dx ( 2x ) 'dx d ( 2x )

求不定积分的基本方法

求不定积分的基本方法不定积分是微积分中的重要概念，它是求导的逆运算。

不定积分是求函数的原函数，也就是求解函数的不定积分就是要找到一个函数，它的导数等于被积函数。

本文将介绍不定积分的基本方法和常用公式。

一、基础知识和符号1.不定积分可以使用∫来表示，被积函数称为被积表达式，不定积分的结果称为不定积分式。

2. ∫f(x)dx中，f(x)是被积函数，dx是积分变量，表示要对x进行积分。

3. 不定积分有许多基本定理，例如Newton-Leibniz公式、线性性质等，这些定理有助于化简和计算不定积分。

对于不同类型的函数，我们有不同的方法来计算它们的不定积分。

下面将介绍常见的几种方法。

1.直接计算法：根据不定积分的定义，直接对被积函数进行计算。

例如，对于多项式函数和幂函数，可以使用求导法则的逆运算进行计算。

例如，对于多项式函数f(x)=ax^n，其中a为常数，n为非负整数，其不定积分为F(x)=（a/(n+1))x^(n+1)+C，其中C为常数。

2.特殊函数法：对于一些特殊函数，我们可以利用它们的性质或公式来计算不定积分，如三角函数、指数函数、对数函数等。

例如，对于三角函数，我们可以利用三角函数的性质和三角函数的积分公式来计算不定积分。

a）∫sin(x)dx = -cos(x) + Cb）∫cos(x)dx = sin(x) + Cc）∫tan(x)dx = -ln，cos(x)， + C3.分部积分法：分部积分法是求不定积分中常用的方法之一，它是对乘积求积分的逆运算。

分部积分公式：∫u(x)v'(x)dx = u(x)v(x)-∫u'(x)v(x)dx其中，u(x)和v(x)是可导函数，u'(x)和v'(x)为它们的导函数。

通过选择正确的u和v，可以将被积函数转化为更容易积分的形式。

4.代换法：代换法也是求不定积分中常用的方法之一，它是通过对积分变量进行变换来简化积分。

代换法的基本思想是将积分变量进行替换，将原积分中的一个积分变量用另一个变量代替，然后利用新的变量进行计算。

不定积分的基本公式和运算法则直接积分法-推荐下载

函数的的形式。
求函数的不定积分的方法叫积分法。
1.求下列不定积分.（1）
例
解：（1）
（2）
x
1 x 2 dx ＝
xdx ＝
3
x 2 dx

1 x2
dx
x2dx x21 C 1 C
5

2
x
2 1
5 2
C
（2） x xdx
x
此例表明，对某些分式或根式函数求不定积分时，可先把它们化为 x 的形式，然后应用幂函
数的积分公式求积分。
二不定积分的基本运算法则
2
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术通关，1系电过，力管根保线据护敷生高设产中技工资术艺料0不高试仅中卷可资配以料置解试技决卷术吊要是顶求指层，机配对组置电在不气进规设行范备继高进电中行保资空护料载高试与中卷带资问负料题荷试2下卷2，高总而中体且资配可料置保试时障卷，各调需类控要管试在路验最习；大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试，况卷要下安加与全强过，看度并22工且22作尽22下可22都能22可地护以缩1关正小于常故管工障路作高高；中中对资资于料料继试试电卷卷保破连护坏接进范管行围口整，处核或理对者高定对中值某资，些料审异试核常卷与高弯校中扁对资度图料固纸试定，卷盒编工位写况置复进.杂行保设自护备动层与处防装理腐置，跨高尤接中其地资要线料避弯试免曲卷错半调误径试高标方中高案资等，料，编试要5写、卷求重电保技要气护术设设装交备备置底4高调、动。中试电作管资高气，线料中课并敷3试资件且、设卷料中拒管技试试调绝路术验卷试动敷中方技作设包案术，技含以来术线及避槽系免、统不管启必架动要等方高多案中项；资方对料式整试，套卷为启突解动然决过停高程机中中。语高因文中此电资，气料电课试力件卷高中电中管气资壁设料薄备试、进卷接行保口调护不试装严工置等作调问并试题且技，进术合行，理过要利关求用运电管行力线高保敷中护设资装技料置术试做。卷到线技准缆术确敷指灵设导活原。。则对对：于于在调差分试动线过保盒程护处中装，高置当中高不资中同料资电试料压卷试回技卷路术调交问试叉题技时，术，作是应为指采调发用试电金人机属员一隔，变板需压进要器行在组隔事在开前发处掌生理握内；图部同纸故一资障线料时槽、，内设需，备要强制进电造行回厂外路家部须出电同具源时高高切中中断资资习料料题试试电卷卷源试切，验除线报从缆告而敷与采设相用完关高毕技中，术资要资料进料试行，卷检并主查且要和了保检解护测现装处场置理设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

不定积分计算公式

证根据不定积分定义，只须验证上式右端的导数等于左端的被积函数.
f (x)dx g(x)dx
f (x)dx g(x)dx
f (x) g(x). 法则1 可推广到有限多个函数代数和的情况，即
f1(x) f2(x) fn(x)dx f1(x)dx f2(x)dx fn(x)dx.
例 5 求
(1 x)3 dx.
x2
解
(1 x)3 dx x2

1 3x x3 dx
x2

1 x2

3 x

3
x dx

dx x2

3
1 x
dx

3
dx

xdx
1 3ln | x | 3x 1 x2 C.
x
2
例 6 求
(4) a xdx a x C ; lna
( 1);
当 a e 时, exdx ex C ;
(5) cos xdx sinx C； (6) sinxdx cos x C； (7) sec2 xdx tan x C； (8) csc2 xdx cot x C； (9) secx tan xdx secx C； (10) csc x cot xdx csc x C；
第四章不定积分
第二节不定积分的基本公式和运算法则直接积分法
一、不定积分的基本公式二、不定积分的基本运算法则三、直接积分法
不定积分基本公式表
(1) kdx kx C (k 为常数);
(2) x dx 1 x 1 C ,

不定积分的基本公式和运算法则直接积分法

·复习1 本函数的定义.2 没有定积分的定义.3 没有定积分的本量.4 没有定积分的几许意思.之阳早格格创做·引进正在没有定积分的定义、本量以及基础公式的前提上，咱们进一步去计划没有定积分的估计问题，没有定积分的估计要领主要有三种：曲交积分法、换元积分法战分部积分法.·道授新课第二节没有定积分的基础公式战运算曲交积分法一基础积分公式由于供没有定积分的运算是供导运算的顺运算，所以有导数的基础公式相映天不妨得到积分的基础公式如下：以上十五个公式是供没有定积分的前提，必须生记，没有然而要记左端的截止，还要认识左端被积函数的的形式.供函数的没有定积分的要领喊积分法. 例1.供下列没有定积分.（1）dxx⎰21（2）dxx x ⎰解：（1）dx x ⎰21＝212121x x dx C Cx -+-=+=-+-+⎰（2）dxx x ⎰＝C x dx x +=⎰252352此例标明，对付某些分式或者根式函数供没有定积分时，可先把它们化为x α的形式，而后应用幂函数的积分公式供积分.二没有定积分的基础运算规则规则1 二个函数代数战的积分，等于各函数积分的代数战，即规则1对付于有限多个函数的战也创造的．规则2 被积函数中没有为整的常数果子可提到积分号中，即dx x f k dx x kf ⎰⎰=)()( （0≠k ）例2 供3(21)x x e dx +-⎰解 3(21)x x e dx+-⎰=23x dx ⎰+dx ⎰-x e dx⎰=412x x x e C +-+.注其中每一项的没有定积分虽然皆应当有一个积分常数，然而是那里本去没有需要正在每一项后里加上一个积分常数，果为任性常数之战仍旧任性常数，所以那里只把它的战C 写正在开端，以去仿此.注考验解搁的截止是可精确，只把截止供导，瞅它的导数是可等于被积函数便止了.如上例由于41()2x x x e C '+-+=321xx e +-，所以截止是精确的.三曲交积分法正在供积分的问题中，不妨曲交按基础积分公式战二个基赋本量供出截止（如上例）然而偶尔，被积函数常需要通过适合的恒等变形（包罗代数战三角的恒等变形）再利用积分的本量战公式供出截止，那样的积分要领喊曲交积分法.例3供下列没有定积分.（1）1)(x dx⎰ （2）dx x x ⎰+-1122解：（1）最先把被积函数1)(x-化为战式，而后再逐项积分得1)((1x dx x dx-=+--⎰⎰5122221252x x x x C =+--+.注：（1）供函数的没有定积分时积分常数C 没有克没有及拾掉，可则便会出现观念性的过失.（2）等式左端的每个没有定积分皆有一个积分常数，果为有限个任性常数的代数战仍是一个常数，所以只消正在截止中写一个积分常数C 即可.（3）考验积分估计是可精确，只需对付积分截止供导，瞅它是可等于被积函数.若相等，积分截止是精确的，可则是过失的.（2）222221122(1)111x x dx dx dx x x x -+-==-+++⎰⎰⎰222arctan 1dxdx x x C x =-=-++⎰⎰.上例的解题思路是设法化被积函数为战式，而后再逐项积分，是一种要害的解题要领，须掌握.训练 1 322324x x x dx x -++⎰，2 22221(1)x dx x x ++⎰，3 421x dx x +⎰.问案 1 21432ln ||2x x x C x -+-+， 2 1arctan x Cx -+，3 31arctan 3x x x C -++例4供下列没有定积分.（1）xdx⎰2tan （2）dx x 2sin2⎰解：（1）22tan (sec 1)xdx x dx =-⎰⎰（2）C x x dx x dx x+-=-=⎰⎰sin 21212cos 12sin2上例的解题思路也是设法化被积函数为战式，而后再逐项积分，没有过它真止化战是利用三角式的恒等变更.训练 12cot xdx⎰ 22cos 2x dx ⎰3 cos 2xdx cosx-sinx ⎰问案 1 cot x x C --+ 2 1(sin )2x x C++3 sin -cos x x C + 例5设x x f 22cos )(sin ='，供)(x f .解：由于x x x f 222sin 1cos )(sin -=='，所以x x f -='1)(，故知)(x f 是x -1的本函数，果此Cx x dx x x f +-=-=⎰2)1()(2．小结基础积分公式，没有定积分的本量，曲交积分法. 训练供下列没有定积分.（1）2(12sin )x dx x -+⎰（2）2212()cos sin dx x x +⎰，（3）dt t t ⎰+2)1(，（4）23)1dt t -+⎰，（5）dx x x ⎰+)6(6，（6）dx x x ⎰--2411，（7）dx x x ⎰-)cot csc(csc ，（8）dx x x ⎰2sin 2cos ，（9）2(cos sin )22t t dt +⎰，（10）dx x ⎰-)1(tan 2，（11）e (3x x x dx -⎰.问案1 2cos 2ln ||x x x C +++， 2 tan -cot x x C +，3 212ln ||2t t t C +++， 4 2arcsin 3arctan t t C -+， 5 761ln 67x x C++， 6 313x x C --+，7 cot csc x x C -++， 8 cot 2x C --+，9 cos t t C -+， 10 tan 2x x C -+，11(3)2arcsin 1ln3xe x C-++.小结估计简朴的没有定积分，偶尔只需按没有定积分的本量战基础公式举止估计；偶尔需要先利用代数运算或者三角恒等变形将被积函数举止整治．而后分项估计．做业 P81:2,3 板书籍安排。

不定积分的基本公式和运算法则直接积分法

•复习1原函数的定义。

2不定积分的定义。

3不定积分的性质。

4不定积分的几何意义。

•引入在不定积分的定义、性质以及基本公式的基础上，我们进一步来讨论不定积分的计算问题，不定积分的计算方法主要有三种:直接积分法、换元积分法和分部积分法。

.朔受瞒第二节不定积分的基本公式和运算直接积分法-基本积分公式由于求不定积分的运算是求导运算的逆运算，所以有导数的基本公式相应地可以得到积分的基：以上十五个公式是求不定积分的基础，必须熟记，不仅要记右端的结果，还要熟悉左端被积函数的的形式。

求函数的不定积分的方法叫积分法。

例1.求下列不定积分.（1） J （ 2 ） J xQ解：（1）二 E* = #+c = -l + c（2）J Xyfxdx =j x 2 “X = § X 2 + C此例表明，对某些分式或根式函数求不定积分时，可先把它们化为的形式，然后应用嘉函数的积分公式求积分。

W.二不定积分的基本运算法则法则1两个函数代数和的积分，等于各函数积分的代数和，即J[/U) 土sMV^ = J 了 E ± J gE法则1对于有限多个函数的和也成立的.法则2被积函数中不为零的常数因子可提到积分号外，即J kf(x\lx = k^f{x\ix ( " 0 )例2 求J(2/ + i_b)火解J (2x3 +1 - e" )dx = 2 J 工七江 + j dx - J e 'dx= — x4 +x-e x +Co2注其中每一项的不定积分虽然都应当有一个积分常数，但是这里并不需要在每一项后面加上一个积分常数，因为任意常数之和还是任意常数，所以这里只把它的和C写在末尾，以后仿此。

注检验解放的结果是否正确，只把结果求导，看它的导数是否等于被积函数就行了。

如上例由T(-x4+x-e x+ Cy = 2x3+ \-e x ,所以结果是正确的。

2三直接积分法在求积分的问题中，可以直接按基本积分公式^两个基本性质求出结果(如上例)但有时，被积函数常需要经过适当的恒等变形(包括代数和三角的恒等变形)再利用积分的性质和公式求出结果，这样的积分方法叫直接积分法。

高中数学选修本(理科)不定积分的运算法则

不定积分的运算法那么目的要求1．掌握不定积分的线性性质．2．会利用线性性质和基本积分公式求较简单的函数的不定积分．内容分析1．不定积分的线性性质是指不定积分的两个运算法那么．法那么1是在k ≠0时可将k 提到积分号外；法那么2是将几个函数的和(或差)的积分化为各个函数的积分的和(或差)．它们对不定积分的计算起着化繁为简的作用．这两个法则可合并推广为：＝，[a f (x)]dx f (x)dx k k k k n k k na ==∑⎰⎰∑11其中a 1，a 2，…，a n 是不全为0的常数．它与基本积分公式一起构成直接积分法的基础．2．建立不定积分的线性性质可分两步进行：第一步是采取由特殊到一般的不完全归纳法或与导数的线性性质类比的方法猜测性质；第二步是根据原函数与不定积分的定义及导数的线性性质证明或否定猜想．证明性质的过程中，应说明不写积分常数的原因，并由此分析法那么1为什么要限制k ≠0．3．应用基本积分公式及不定积分的线性性质求不定积分是本节课的重点．为此，教科书配备了四道例题．前两道例题是直接运用基本积分公式及积分法那么求出函数的不定积分．后两道例题的被积函数解析式是较复杂的多项式的积或商、三角函数式，求积分时，要先把被积函数进行适当的恒等变形，使之能运用基本积分公式表中的公式进行计算．讲解例题时，教师不能将三角函数形式的被积函数扩大到常用三角函数公式之外的情况．4．法那么的应用包括正用与逆用，教科书缺乏逆用的实例．讲授时应作适当补充，这对全面掌握法那么是有益的．教学过程1．复习引新(1)利用基本积分公式或不定积分定义求以下不定积分：①与②与－③＋④－sinxdx cosxdx2sinxdx (3cosx)dx (sinx cosx)dx (2sinx 3cosx)dx ⎰⎰⎰⎰⎰⎰(2)在不考虑积分常数的情况下，分析上述积分结果之间有什么联系．(3)教师利用不定积分的定义进一步说明在考虑积分常数的情况下，上述发现仍然成立．(4)能否将上述结论中的具体函数换成一般连续函数？怎样证明？2．构建新知(1)kf(x)dx k f(x)dx (k 0)[f(x)g(x)]dx f(x)dx g(x)dx k 0()师生总结并证明积分运算法则：＝，≠；＋＝＋，并说明≠的原因反证法．⎰⎰⎰⎰⎰(2)说明积分运算法那么与求导的线性性质的相似性，这种相似正是两种运算互逆的表现．(3)说明积分运算法那么的作用：化繁为简，可用语言表达各个法那么的意义．3．反馈与巩固(1)例1 求以下不定积分(教科书第156页)．①＋＋②－(2x 5x 3)dx (1xcosx)dx 2⎰⎰ 小结：①积分的两个运算法那么可合并为统一形式：[a f (x)a f (x)a f (x)]dx a f (x)dx a f (x)dx a f (x)dx a a a 01122n n 1122n n 12n ＋＋…＋＝＋＋…＋，其中，，…，是不全为的常数．⎰⎰⎰⎰②被积函数假设是函数C 、x m 、cosx 、sinx 、a x 的线性运算结果，那么可以直接运用法那么及基本积分公式求不定积分．③积分结果只写一个任意常数即可．(2)例2 求以下不定积分(教科书第156、157页)①＋－②③(x 3)(x 2)dx x dx dx ⎰⎰⎰---()()cos sin x x cox x x x122 小结：①对复杂的被积函数，应先进行代数或三角恒等变形，拆成几个能够运用公式积分的函数之和，再求解；②对求出的不定积分结果求导是检验不定积分运算正确性的常用方法．(3)反馈训练(教科书第159页练习)．(4)变式训练．题：求＋－－＋＋1(x 3)(x 2)dx (x 3)(x 2)dx ⎰⎰分析：求两个不定积分的差，可逐个求，也可逆用法那么整体求．想：＋－－＋＋＝＋－－＋＋＝－－(x 3)(x 2)dx (x 3)(x 2)dx[(x 3)(x 2)(x 3)(x 2)]dx (4x 12)dx⎰⎰⎰⎰＝－－＋2x 12x C 2题2：f(x)＝e x cosx ，g(x)＝e x sinx①求f ′(x)与g ′(x)；②求与；③求＋．f(x)dx g(x)dx [f(x)dx g(x)dx]dx ⎰⎰⎰⎰⎰分析：若直接求与，则无从下手，必须从′与′的结果中寻找突破口；＋仍然是的连续函数，f(x)dx g(x)dx f (x)g (x)f(x)dx g(x)dx x ⎰⎰⎰⎰可继续对其求不定积分．解：①f ′(x)＝e x cosx －e x sinx ，g ′(x)＝e x sinx ＋e x cosx②由①知f ′(x)＝f(x)－g(x)，g ′(x)＝f(x)＋g(x)，∴＝′＋′，＝′－′．∵′＝＋，′＝＋，∴＝′＋′＝＋＋，f(x)f (x)g (x)g(x)g (x)f (x)f (x)dx f(x)C g (x)dx g(x)C f(x)dx f (x)dx g (x)dx f(x)g(x)C 1212121212121212⎰⎰⎰⎰⎰ g(x)dx g (x)dx f (x)dx g(x)f(x)C f(x)dx e (cosx sinx)C g(x)dx e (sinx cosx)C x x ⎰⎰⎰⎰⎰＝′－′＝－＋．即＝＋＋，＝－＋．121212121212 (3)[f(x)dx g(x)dx]dx[(f(x)g(x))dx]dx [g (x)dx]dx [g(x)C ]dx e (sinx cosx)C x C 1x 12⎰⎰⎰⎰⎰⎰⎰⎰＋＝＋＝′＝＋＝－＋＋124．小结(1)学习两个不定积分运算法那么，目的在于对一些不能直接运用积分公式计算的不定积分，通过对被积函数作出简单的恒等变形，再运用这些法那么，转化成可以直接运用积分公式来求不定积分的问题．(2)运用法那么包括正用和逆用两个方面，要视具体情况灵活处理．布置作业1．求以下不定积分．(1)x(4x 4x 1)dx(2)(x x )dx (3)2dx (4)cos2x sinx +cosx dx 2113－－－××⎰⎰⎰⎰--223523x xx2(1)[C 2C x 3C x nC x]dx(n N )(2)(1)C 2C 3C nC n 23f(x)g(x)n 1n 2n 32n 2n 1*n 1n 2n 3n n n 1．计算＋＋＋…＋其中∈．利用证明：＋＋＋…＋＝·．．已知＝，＝，--⎰+++-11223x x x x。