辅助圆 (解题精讲
2024年中考数学总复习第一部分考点精讲第六单元圆微专题辅助圆问题

图①
微专题 辅助圆问题
情形2:∠C为锐角
动点轨迹:如图②,点C在以点O为圆心,圆心角为360°-2α 的优弧 AB 上运动(不含A,B两点);
图②
微专题 辅助圆问题
情形3:∠C为钝角
动点轨迹:如图③,点C在以点O为圆心,圆心角为(360°-2α) 的劣弧 AB上运动(不含A,B两点).
解:这四个点所在的圆如解
例7题图
图所示.
例7解题图
【判断依据】__圆__内__接__四__边__形__的__对__角__互__补______.
微专题 辅助圆问题
二阶 利用辅助圆求最值 方法一 点圆最值(2021.10、17,2020.17)
方法解读
已知平面内一定点D和⊙O,点E为⊙O上一动点,设点O与点D 之间的距离为d,⊙O的半径为r.
微专题 辅助圆问题
(2)异侧型:如图③,由点A,B,C,D构成的四边形中,若∠D +∠B=180°,则A,B,C,D四点共圆,∠A+∠C=180°.
提示:可用反证法证明 图③
微专题 辅助圆问题
例6 如图,在Rt△ABC中,∠ACB=90°,点D为平面内一点,
∠ADC=∠BAC,过点C作CD的垂线,
ห้องสมุดไป่ตู้
微专题 辅助圆问题
位置关系 点D在⊙O内
点D在⊙O上
点D在⊙O外
图示
DE的最大值 此时点E的位置
DE的最小值
d+r
2r
d+r
连接DO并延长交⊙O于点E
r-d
0
d-r
此时点E的位置 连接OD并延长 点E与点D重合 连接OD交⊙O
2024中考压轴题05 圆的综合(5题型+解题模板+技巧精讲)(原卷版)

压轴题05圆的综合目录题型一切线的判定题型二圆中求线段长度题型三圆中的最值问题题型四圆中的阴影部分面积题型五圆中的比值(相似)问题下图为二次函数图象性质与几何问题中各题型的题型一切线的判定解题模板:技巧:有切点,连半径,证垂直(根据题意,可以证角为90°,如已有90°角,可以尝试证平行) 没切点,作垂直,证半径(通常为证全等,也可以通过计算得到与半径相等)【例1】1.(2023-四川攀枝花-中考真题)如图,AB 为O 的直径,如果圆上的点D 恰使ADC B ∠=∠,求证:直线CD 与O 相切.【变式1-1】(2023-辽宁-中考真题)如图,ABC 内接于O ,AB 是O 的直径,CE 平分ACB ∠交O 于点E ,过点E 作EF AB ∥,交CA 的延长线于点F .求证:EF 与O 相切;【变式1-2】(2023-辽宁-中考真题)如图,AB 是O 的直径,点C E ,在O 上,2CAB EAB ∠=∠,点F 在线段AB 的延长线上,且AFE ABC ∠=∠.(1)求证:EF与O相切;(2)若41sin5BF AFE=∠=,,求BC的长.【变式1-3】(2023-湖北鄂州-中考真题)如图,AB为O的直径,E为O上一点,点C为EB的中点,过点C作CD AE⊥,交AE的延长线于点D,延长DC交AB的延长线于点F.(1)求证:CD是O的切线;题型二圆中求线段长度解题模板:【例2】(2023-西藏-中考真题)如图,已知AB为O的直径,点C为圆上一点,AD垂直于过点C的直线,交O于点E,垂足为点D,AC平分BAD∠.(1)求证:CD 是O 的切线; (2)若8AC =,6BC =,求DE 的长.【变式2-1】(2023-内蒙古-中考真题)如图,AB 是⊙O 的直径,E 为⊙O 上的一点,点C 是AE 的中点,连接BC ,过点C 的直线垂直于BE 的延长线于点D ,交BA 的延长线于点P .(1)求证:PC 为⊙O 的切线;(2)若PC =,10PB =,求BE 的长.【变式2-2】(2023-辽宁大连-中考真题)如图1,在O 中,AB 为O 的直径,点C 为O 上一点,AD 为CAB ∠的平分线交O 于点D ,连接OD 交BC 于点E .(1)求BED ∠的度数;(2)如图2,过点A 作O 的切线交BC 延长线于点F ,过点D 作DG AF ∥交AB 于点G .若AD =4DE =,求DG 的长.【变式2-3】(2023-湖北恩施-中考真题)如图,ABC 是等腰直角三角形,90ACB ∠=︒,点O 为AB 的中点,连接CO 交O 于点E ,O 与AC 相切于点D .(1)求证:BC是O的切线;(2)延长CO交O于点G,连接AG交O于点F,若AC FG的长.题型三圆中的最值问题解题模板:技巧精讲:1、辅助圆模型【例3】(2023-湖南长沙-三模)如图1:在O 中,AB 为直径,C 是O 上一点,3,4AC BC ==.过O 分别作OH BC ⊥于点H ,OD AC ⊥于点D ,点E 、F 分别在线段BC AC 、上运动(不含端点),且保持90EOF ∠=︒.(1)OC =______;四边形CDOH 是______(填矩形/菱形/正方形); CDOH S =四边形______; (2)当F 和D 不重合时,求证:OFD OEH ∽;(3)⊙在图1中,P 是CEO 的外接圆,设P 面积为S ,求S 的最小值,并说明理由;⊙如图2:若Q 是线段AB 上一动点,且1QAQB n =∶∶,90EQF ∠=︒,M 是四边形CEQF 的外接圆,则当n 为何值时,M 的面积最小?最小值为多少?请直接写出答案.【变式3-1】(2023-安徽-模拟预测)如图,半圆的直径4AB =,弦CD AB ∥,连接,,,AC BD AD BC .(1)求证:ADC BCD △≌△;(2)当ACD 的面积最大时,求CAD ∠的度数.【变式3-2】(2023-四川-中考真题)如图1,已知线段AB ,AC ,线段AC 绕点A 在直线AB 上方旋转,连接BC ,以BC 为边在BC 上方作Rt BDC ,且30DBC ∠=︒.(1)若=90BDC ∠︒,以AB 为边在AB 上方作Rt BAE △,且90AEB ∠=︒,30EBA ∠=︒,连接DE ,用等式表示线段AC 与DE 的数量关系是 ;(2)如图2,在(1)的条件下,若DE AB ⊥,4AB =,2AC =,求BC 的长;(3)如图3,若90BCD ∠=︒,4AB =,2AC =,当AD 的值最大时,求此时tan CBA ∠的值.【变式3-3】(2023-陕西西安-模拟预测)【问题情境】如图1,在ABC 中,120A ∠=︒,AB AC =,BC =ABC 的外接圆的半径值为______; 【问题解决】如图2,点P 为正方形ABCD 内一点,且90BPC ∠=︒,若4AB =,求AP 的最小值; 【问题解决】如图3,正方形ABCD 是一个边长为的书展区域设计图,CE 为大门,点E 在边BC 上,CE =,点P 是正方形ABCD 内设立的一个活动治安点,到B 、E 的张角为120︒,即120BPE ∠=︒,点A 、D 为另两个固定治安点,现需在展览区域内部设置一个补水供给点Q ,使得Q 到A 、D 、P 三个治安点的距离和最小,试求QA QD QP ++的最小值.(结果精确到0.1m 1.7≈,214.3205≈)题型四 圆中的阴影部分面积【例4】(2024-西藏拉萨-一模)如图,等腰ABC 的顶点A ,C 在O 上, BC 边经过圆心0且与O 交于D 点,30B ∠=︒.(1)求证:AB 是O 的切线; (2)若6AB =,求阴影部分的面积【变式4-1】(2023-陕西西安-一模)如图,正六边形ABCDEF 内接于O .(1)若P 是CD 上的动点,连接BP ,FP ,求BPF ∠的度数;(2)已知ADF △的面积为O 的面积.【变式4-2】(2023-浙江衢州-中考真题)如图,在Rt ABC △中,90,ACB O ∠=︒为AC 边上一点,连结OB .以OC 为半径的半圆与AB 边相切于点D ,交AC 边于点E .(1)求证:BC BD =.(2)若,2OB OA AE ==.⊙求半圆O 的半径.⊙求图中阴影部分的面积.【变式4-3】(2023-辽宁阜新-中考真题)如图,AB 是O 的直径,点C ,D 是O 上AB 异侧的两点,DE CB ⊥,交CB 的延长线于点E ,且BD 平分ABE ∠.(1)求证:DE 是O 的切线.(2)若60ABC ∠=︒,4AB =,求图中阴影部分的面积.【变式4-4】(2023-山东枣庄-中考真题)如图,AB 为O 的直径,点C 是AD 的中点,过点C 做射线BD 的垂线,垂足为E .(1)求证:CE 是O 切线;(2)若34BE AB ==,,求BC 的长;(3)在(2)的条件下,求阴影部分的面积(用含有π的式子表示).题型五 圆中的比值(相似)问题 技巧精讲:【例5】(2024-陕西西安-模拟预测)如图,AB 为O 的直径, 点 D 为O 上一点, 过点 B 作O 切线交AD 延长线于点 C ,CE 平分ACB ∠,CE BD ,交于F .(1)求证:BE BF =;(2)若O 半径为2,3sin 5A =,求DF 的长度. 【变式5-1】(2023-湖南湘西-二模)如图,AB 是O 的直径,点C ,D 在O 上,AD 平分CAB ∠,交BC 于点E ,连接BD .(1)求证:BED ABD △△.(2)当3tan 4ABC ∠=,且10AB =时,求线段BD 的长.(3)点G 为线段AE 上一点,且BG 平分ABC ∠,若GE =,3BG =,求CE 的长.【变式5-2】(2024-陕西西安-一模)如图,AB 是O 的直径CD 与O 相切于点C ,与BA 的延长线交于点D ,连接BC ,点E 在线段OB 上,过点E 作BD 的垂线交DC 的延长线于点F ,交BC 于点G .(1)求证:FC FG =;(2)若220AO AD ==,点E 为OB 的中点,求GE 的长.【变式5-3】(2024-陕西西安-一模)如图,AB 是O 的直径,点D 在直径AB 上(D 与,A B 不重合),CD AB ⊥且CD AB =,连接CB ,与O 交于点F ,在CD 上取一点E ,使EF 与O 相切.(1)求证:EF EC =;(2)若D 是OA 的中点,4AB =,求BF 的长.一、解答题1.(2024-云南-模拟预测)如图,四边形ABCD 内接于O ,对角线AC 是O 的直径,过点C 作AC 的垂线交AD 的延长线于点E ,F 为CE 的中点,连接BD ,DF ,BD 与AC 交于点P .(1)求证:DF 是O 的切线;(2)若45DPC ∠=︒,228PD PB +=,求AC 的长.2.(2024-湖北黄冈-模拟预测)如图,PO 平分APD ∠,PA 与⊙O 相切于点A ,延长AO 交PD 于点C ,过点O 作OB PD ⊥,垂足为B .(1)求证:PB 是⊙O 的切线;(2)若⊙O 的半径为4,5OC =,求PA 的长.3.(2024-江苏淮安-模拟预测)如图,已知直线l 与O 相离,OA l ⊥于点A ,交O 于点 P ,点 B 是O 上一点,连接BP 并延长,交直线l 于点 C ,使得AB AC =.(1)判断直线AB 与O 的位置关系并说明理由;(2)4PC OA ==,求线段 PB 的长.4.(2024-四川凉山-模拟预测)如图,CD 是O 的直径,点P 是CD 延长线上一点,且AP 与O 相切于点A ,弦AB CD ⊥于点F ,过D 点作DE AP ⊥于点E .(1)求证:∠∠EAD FAD =;(2)若4PA =,2PD =,求O 的半径和DE 的长.5.(2024-四川凉山-模拟预测)如图,在Rt ABC △中,90ACB ∠=︒,以AC 为直径的O 交AB 于点D ,E 为BC 的中点,连接DE 并延长交AC 的延长线于点F .(1)求证:DE 是O 的切线;(2)若30A ∠=︒,3DF =,求CE 长.6.(2024-山东泰安-一模)如图,AB CD ,是O 的两条直径,过点C 的O 的切线交AB 的延长线于点E ,连接AC BD ,.(1)求证:ABD CAB ∠=∠;(2)若B 是OE 的中点,12AC =,求O 的半径.7.(2024-福建南平-一模)如图1,点D 是ABC 的边AB 上一点.AD AC =,CAB α∠=,O 是BCD △的外接圆,点E 在DBC 上(不与点C ,点D 重合),且90CED α∠=︒-.(1)求证:ABC 是直角三角形;(2)如图2,若CE 是⊙O 的直径,且2CE =,折线ADF 是由折线ACE 绕点A 顺时针旋转α得到. ⊙当30α=︒时,求CDE 的面积;⊙求证:点C ,D ,F 三点共线.8.(2023-四川甘孜-中考真题)如图,在Rt ABC △中,=90ABC ∠︒,以BC 为直径的O 交AC 边于点D ,过点C 作O 的切线,交BD 的延长线于点E .(1)求证:=DCE DBC ∠∠;(2)若=2AB ,=3CE ,求O 的半径.9.(2023-湖北黄石-中考真题)如图,AB 为O 的直径,DA 和O 相交于点F ,AC 平分DAB ∠,点C 在O 上,且CD DA ⊥,AC 交BF 于点P .(1)求证:CD 是O 的切线;(2)求证:2AC PC BC ⋅=;(3)已知23BC FP DC =⋅,求AF AB的值.10.(2023-辽宁鞍山-中考真题)如图,四边形ABCD 内接于O ,AB 为O 的直径,过点D 作DF BC ⊥,交BC 的延长线于点F ,交BA 的延长线于点E ,连接BD .若180EAD BDF ∠+∠=︒.(1)求证:EF 为O 的切线.(2)若10BE =,2sin 3BDC ∠=,求O 的半径.11.(2023-湖南湘西-中考真题)如图,点D ,E 在以AC 为直径的O 上,ADC ∠的平分线交O 于点B ,连接BA ,EC ,EA ,过点E 作EH AC ⊥,垂足为H ,交AD 于点F .(1)求证:2AE AF AD =⋅;(2)若sin 5ABD AB ∠==,求AD 的长. 12.(2023-辽宁沈阳-中考真题)如图,AB 是O 的直径,点C 是O 上的一点(点C 不与点A ,B 重合),连接AC 、BC ,点D 是AB 上的一点,AC AD =,BE 交CD 的延长线于点E ,且BE BC =.(1)求证:BE 是O 的切线;(2)若O 的半径为5,1tan 2E =,则BE 的长为______ .13.(2023-黑龙江大庆-中考真题)如图,AB 是O 的直径,点C 是圆上的一点,CD AD ⊥于点D ,AD 交O 于点F ,连接AC ,若AC 平分DAB ∠,过点F 作FG AB ⊥于点G ,交AC 于点H ,延长AB ,DC 交于点E .(1)求证:CD 是O 的切线;(2)求证:AF AC AE AH ⋅=⋅;(3)若4sin 5DEA ∠=,求AH FH的值.14.(2023-四川雅安-中考真题)如图,在Rt ABC △中,90ABC ∠=︒,以AB 为直径的O 与AC 交于点D ,点E 是BC 的中点,连接BD ,DE .(1)求证:DE 是O 的切线;(2)若2DE =,1tan 2BAC ∠=,求AD 的长;(3)在(2)的条件下,点P 是O 上一动点,求PA PB +的最大值.15.(2023-辽宁营口-中考真题)如图,在ABC 中,AB BC =,以BC 为直径作O 与AC 交于点D ,过点D 作DE AB ⊥,交CB 延长线于点F ,垂足为点E .(1)求证:DF 为O 的切线;(2)若3BE =,4cos 5C =,求BF 的长.。
初中数学竞赛精品标准教程及练习66辅助圆

初中数学竞赛精品标准教程及练习66辅助圆辅助圆是数学竞赛中一个重要的几何概念,在初中数学竞赛中也有相应的考察。
辅助圆是指在解决一个几何问题时,引入一个与原图形相关的圆,通过利用圆的性质来简化问题或推导出解决问题的关键步骤。
在这篇文章中,我们将介绍一些常见的辅助圆构造和应用,并通过练习题来帮助读者更好地理解和应用辅助圆的方法。
一、辅助圆的定义和性质辅助圆有以下几个关键性质:1.辅助圆的圆心和半径与原图形的一些关键元素有关;2.通过辅助圆,我们可以推导出一些关键的几何关系;3.辅助圆一般是在原图形的内部或外部构造的。
二、辅助圆的常见构造和应用1.内切圆和外接圆辅助圆中最常见的是内切圆和外接圆的构造。
当我们在几何问题中遇到一个三角形时,我们可以构造三角形的内切圆和外接圆来帮助我们解决问题。
内切圆是指与三角形的三边都相切的圆,其圆心与三角形内心重合,半径为内切圆半径。
我们可以利用内切圆的性质来简化问题,比如求三角形的面积、周长和角度等。
外接圆是指与三角形的三个顶点都在同一圆上的圆,其圆心为三角形的外心,半径为外接圆半径。
通过外接圆的性质,我们可以简化问题,比如求三角形的面积、周长和角度等。
2.相切圆和割圆除了内切圆和外接圆,我们还可以构造其他的辅助圆来解决问题。
相切圆是指与图形的其中一边或一些点相切的圆,通过相切圆的性质,我们可以求出一些关键的几何关系。
割圆是指与图形相交于一点,并且与图形的一些边相切的圆,通过割圆的构造和性质,我们可以推导出一些几何关系。
3.切线圆和中位线圆除了上述常见的辅助圆外,还有一些其他类型的辅助圆。
切线圆是指与图形的一些边相切的圆,并且与图形的其他边都有公共点。
中位线圆是指与图形的一条中位线相切的圆,通过中位线圆的构造,我们可以得到一些关键的几何关系。
三、辅助圆的练习题1.【例题】在三角形ABC中,角BAC=60°,O为三角形的内心。
设OC与AB的交点为D,求证:BD=AB-BD。
精心构造辅助圆,解决问题少困难

精心构造辅助圆 解决问题少困难圆是几何中具有美学价值的一种图形,不仅曲线光滑圆润,美丽迷人,是美好象征的化身,而且几何性质众多,在解决诸多数学问题中,显示出非常重要的作用,有圆的参与,将会使一个比较困难的问题简单起来,所以,在解决一些与圆有关的问题中,要深入挖掘圆的信息,精心构造辅助圆,利用圆的几何性质和圆的方程,发挥出圆的价值,让这些问题迎刃而解,实现“精心构造辅助圆,解决问题少困难”的理想目标.一、利用方程,构造圆在平面上涉及动点轨迹的问题中,直接求解问题比较困难时,可以先考虑建立直角坐标系,特别是有垂直条件与对称条件时,就更要考虑解析法,求出动点的轨迹方程,如果满足圆方程的结构特点,就可以构造圆,让圆的几何性质闪耀光彩,使问题得到解决.例1. (2016届北京西城期末理科)如图,正方形ABCD 的边长为6,点E ,F 分别在边AD ,BC 上,且2DE AE =,2CF BF =.如果对于常数λ,在正方形ABCD 的四条边上,有且只有6个不同的点P 使得=PE PF λ⋅成立,那么λ的取值范围是( )(A )(0,7)(B )(4,7)(C )(0,4)(D )(5,16)- 图1解:以D 为坐标原点,DC 所在直线建立直角坐标系,设点(,)P x y ,则点(0,4),(6,4)E F ,所以(0,4),=(6-x,4-y)PE x y PF =--,由=PE PF λ⋅得动点P 的轨迹方程是:22(3)(4)9x y λ-+-=+,所以动点P 的轨迹是一个以(3,4)为圆心, 9λ+为半径的圆,所以“在正方形ABCD 的四条边上,有且只有6个不同的点P 使得=PE PF λ⋅成立”等价于“圆与正方形四条边有且仅有6个不同交点”,当且仅当3913λ<+<,解得:04λ<<,所以选C.评析:通过解析法揭穿了动点P 的几何意义,为实现问题的转化起到了桥梁作用,通过几何背景的分析,抽象代数特征,促使问题圆满解决,其间,由代数方程,构造了一个圆,将原问题转化为直线与圆的位置关系讨论,从而建立起了不等式,实现了向量问题坐标化,几何问题代数化的转化目标.从而减少了解题的困难程度. 例2.直线:(2)l y k x =+与曲线2:465C y x x =----有且仅有两个不同公共点.求实数k 的取值范围.解:由曲线2:465C y x x =----的方程可以构造出半圆:22(3)(+4)4x y -+=且4y ≤-. E FD P C A BE FD P C A B x y 图2如图所示:要使直线l 与曲线C 有且仅有2个公共点,则需AB AC k k k <≤其中AB 为半圆的切线,(1,4)C -,半圆的圆心到直线:(2)l y k x =+的距离是2342202372,211k kd k k ++-±==⇒=+由图可知:20237=21AB k --,43AC k =- 所以实数k 的取值范围是202374(,]213--- 评析:解决本题的关键是由曲线C 的方程构造半圆,然后由图形抽象代数条件,完全回避了探究较复杂的一元二次方程在区间[1,5]上有两个不等实根的条件.所以在解决解析几何的问题时,一定要分析曲线方程的结构特点,抓住构造几何图形的机会,将会让图形闪耀光辉.相关问题:1.(2019届北京昌平区高三上期末理科)设点12,F F 分别为椭圆22:195x y C +=的左、右焦点,点P 是椭圆上任意一点,若使得12PF PF m ⋅=成立的点恰好是4个,则实数m 的值可以是( ) BA .B .C .5D .8 2.(2019届北京西城区高三上期末理科) 设双曲线22: 13y C x -=的左焦点为F ,右顶点为A . 若在双曲线C 上,有且只有2个不同的点P 使得=PF PA λ⋅成立,则实数λ的取值范围是____. (-2,0)二、利用定义,构造圆圆的定义是:在平面内到定点的距离等于定长的点的集合叫做圆.即动点满足一定点和一定长的轨迹可以生成圆,在解决问题的过程中,如能构造出这样的几何条件,就可以构造辅助圆,将原问题转化为圆的问题求解,可能使复杂问题简单化.例3. 设直线:,圆,若在圆C 上存在两点,在直线 上存在一点M ,使得,则的取值范围是( )A. [18,6]-B. [652,652]-+C. [16,4]-D. [652,652]---+解:考虑极端情形:当,MP MQ 是圆C 的切线时,如果此时的M 点轨迹与直线有公共点,那 么对于,MP MQ 不都是圆C 的切线时,都能在直线上存在符合条件的M 点.所以“在圆C 上存 在两点,在直线上存在一点M ,使得”等价于“当,MP MQ 是圆C 的切线时,M 点的轨迹与直线有公共点”.而当,MP MQ 是圆C 的切线时,易证:四边形MPCQ 是正方形,所 以MC 的长是定值2,且C 为定点,因此,动点M 的轨迹是以C 为圆心,2为半径的圆, C 123l 340x y a 22 (2)2C x y :,P Q l 90PMQ a l l ,P Q l 90PMQ l AD C B即M 点的轨迹方程是22(2)4x y -+=,直线2164a ≤⇒-≤≤,所以选C.评析:根据极端性原理,抓住几何条件构造点M 的圆轨迹是解决本题的关键,而构造圆的关键在于构造定值(即半径)与配套的定点(即圆心),所以在解决解析几何问题时,要时刻关注定值的出现于定点的出现,特别是在解决有关椭圆、双曲线问题中,要紧扣椭圆、双曲线定义,关注定值的相关信息与定点的相关信息.例4.过点(1,2)P --作圆22:(3)(4)1C x y -+-=的两切线,PA PB ,其中,,A B 为切点,求直线AB 的方程.解:由圆的切线性质可知:=PA PB ,所以由圆的定义可知:,A B 在以PA 为直径,P 为圆心的圆上,=PA PB =于是可得圆P 的方程:22(1)(2)52x y +++=,将圆C 的方程与圆P 的方程相减可得公共弦AB 所在的直线方程为:812710x y +-=评析:本题的解决中利用了等长线段构造辅助圆,从而出现了两圆公共弦的大好时机.具有一个公共定点的等长线段的另一个端点在一个圆上,这就是圆定义的灵活运用,在解决问题中要注意这些信息.相关问题:已知椭圆C: 22143x y +=的左右焦点分别是12,F F ,点P 是椭圆C 上的动点,N 是线段1F P 的延长线上一点,点M 是2NPF ∠的平分线上一点,且20PM F M ⋅=,直线:34150l x y --=与x 轴、y 轴交点分别为,A B ,求ABM ∆面积的最大值. 1258三、利用垂直,构造圆圆有一个重要性质是:直径上的圆周角是直角.反过来说,直角三角形的直角顶点在以斜边为直径,斜边中点为圆心的圆上,这显然是一个真命题.这也是构造辅助圆的依据,所以当垂直条件出现时,要注意辅助圆的构造,可能使原问题转化为圆的问题,从而获得解题思路. 例5. 已知圆和两点,,若圆上存在点,使得,则的最大值为( )A .7B .6C .5D .4解:由于,所以可以构造一个圆:点P 在以AB 为直径的圆上,记此圆为圆O ,点P 又在圆C 上,所以“圆上存在点,使得”等价于“圆O 与圆C 有公共点”, 所以1146m CO m m -≤≤+⇒≤≤,所以的最大值为6.选B.评析:从垂直条件出发,构造了一个辅助圆,实现了将原问题转化为两圆位置关系的转化目标,使问题轻松获解,其间表现出辅助圆的重要作用. l ()()22:341C x y -+-=(),0A m -()(),00B m m >C P 90APB ∠=m 90APB ∠=C P 90APB ∠=m例6.过点(0,4)P 的直线l 交椭圆22:14x C y +=于不同两点,A B (A 在PB 之间),O 为坐标原点.当90PAO ∠=,求直线l 的斜率.解:按照通常用到的方法,将直角用斜率之积为-1或用向量的数量积为0写出坐标关系,再用直线与曲线联立,出韦达定理,代入求值.但是在直角中不涉及,A B 两点坐标,只涉及A 点的坐标,所以直曲联立与韦达定理不好使.基于此,需要变换思路,由直角构造圆,点A 在PO 为直径的圆上,于是得到下列解法:设00(,)A x y ,则2200(2)4x y +-=,220044x y +=,消去0x 得:002,23y y ==-(舎),0x =l的斜率是24k -=24k -== 评析:由此题的解答可见:由垂直条件构造辅助圆是构造方程的主要依据,这种方法仅是直曲联立用韦达定理方法的补充,不能迷信它.比如将本题的条件90PAO ∠=改为90AOB ∠=,就没有必要构造辅助圆了,直接用斜率之积为-1或用向量的数量积为0,写出坐标关系,直曲联立出韦达定理,代入求值比较简单.相关问题:设点P 是双曲线22:1169x y C -=上一点,12,F F 是双曲线C 的左右焦点,且120PF PF ⋅=,求点P 到x 轴的距离. 95四、利用换元,构造圆由于圆的方程是特殊的二元二次方程,特殊性表现在两个方面:一是没有两元的交叉项,二是两元的二次项系数相等。
初数-构造辅助圆解题教法解析

■七 口工 思路: .1 ADCB^AFCB ADAB^ADAF InllSlll FD=BD=FB zDBF=60° zCBD=30° izUlE^ Example
在平面直角坐标系中,已知A (-3, 0) , B (1, 0),点P
在y轴上,且4ABP为直角三角形,NAPB=90° .请问满
足条件的点P有几个?并求出它们的坐标.
思路:作以AB为直径的圆,P在圆 与y轴的交点上,根据圆的定义和 勾股定理即可求P坐标
例题 Example
二、作三角形的外接 园
总结:直角三角形斜边即为直角三 角形外接圆半径
求证:ZCPO=ZDPO.
思路:切线长定理可知,OA^AP,
AM±OP,可得AM2=OM・MP,由
相交弦定理可知CM.MD=AM. MB, 因此可得CM.MD=OM.MP,所以C、
圆,由CO=BO即
Example
三、运用四点共圆的判定方法构造辅助 国 (不在11月月考范围内)
总结:若四边形A5CD的一组对边A3、DC的延长线相交于居
LilI心角关系定理:同B0或等国中, “知一推二”
周角定理及推论
1 .圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
2 .推论1:同弧或等弧所对的圆周角相等.
3 .推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
4 .推论3:如果三角形一条边上的中线等于这条边的一半,那么这个三角形是直角
思路:连DF, EF,寻找PD、PE、PF之间的
・关系,证明△PDF-Z\PFE,而发现P、D、B、
中考复习讲义:三种构造辅助圆解题的模型

中考热点:三种构造辅助圆解题的模型一、问题导读“圆”是一个完美的图形,在初中数学中具有丰富内容,其中大部分是与角度相关性质,如在圆周角中能轻易找到,等角和直角并与圆心角联系也比较紧密,通过在图形中构造辅助圆往往能获得意想不到的效果,如果题目中出现了以下条件:三点及三点以上到同一点距离相等,作辅助圆;同一侧有相等的角,或者需要构造出相等的角时,作辅助圆;若一个四边形的一组对角互补,则它的四个顶点共圆.在这些情况下,借助圆去解决一些问题都是非常好的一个选择,下面举例说明这三种构造辅助圆解题的模型应用。
二、典例精析类型1 根据共端点等线段模型,根据圆的定义构造圆1.如图,已知OA=OB=OC,且∠AOB=k∠BOC,则∠ACB是∠BAC的()A.k/2倍 B.k倍 C.2k D.1/k【分析】由OA=OB=OC,得到A,B,C在以O为圆心的同一个圆上,则∠AOB=2∠ACB,∠BOC=2∠BAC,而∠AOB=k∠BOC,即可得到∠ACB=k∠BAC.【解答】∵OA=OB=OC,∴A,B,C在以O为圆心的同一个圆上,如图,∴∠AOB=2∠ACB,∠BOC=2∠BAC,而∠AOB=k∠BOC,即2∠ACB=k2∠BAC,∴∠ACB=k∠BAC.故选:B.2.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E 为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是()A.1.5 B.1.2 C.2.4 D.以上都不对【分析】先依据勾股定理求得AB的长,然后依据翻折的性质可知PF=FC,故此点P在以F为圆心,以2为半径的圆上,依据垂线段最短可知当FP⊥AB时,点P到AB的距离最短,然后依据题意画出图形,最后,利用相似三角形的性质求解即可.【解答】如图所示:当PE∥AB.在Rt△ABC中,∵∠C=90°,AC=6,BC=8,∴由勾股定理可求得AB=10,由翻折的性质可知:PF=FC=2,∠FPE=∠C=90°.∵PE∥AB,∴∠PDB=90°.由垂线段最短可知此时FD有最小值.又∵FP为定值,∴PD有最小值.又∵∠A=∠A,∠ACB=∠ADF,∴△AFD∽△ABC.∴AF/AB=DF/BC,即4/10=DF/8,解得:DF=3.2.∴PD=DF﹣FP=3.2﹣2=1.2.故选:B.3.如图2所示,在凸四边形ABCD中,AB=BC=BD,∠ABC=80°,则∠ADC的度数为____度【解析】∵AB=BC=BD,得到A,C,D在以B为圆心的同一个圆上,∴∠ACD=1/2∠ABD, ∠DAC=1/2∠DBC,∵∠ABC=∠ABD +∠DBC =80°,∴∠ACD+∠DAC=1/2∠ABD+1/2∠DBC=1/2(∠ABD+∠DBC)= 1/2×80°=40°,∴∠ADC=180°﹣(∠DAC+∠ACD)=180°﹣40°=140°.故答案为:140.4. 如图,在四边形ABCD中,AB=AC=AD,若∠BAC=25°,∠CAD=75°,则∠BDC=度,∠DBC=_____度.【解析】法一:∵AB=AC=AD,∴点B,C,D在以A为圆心的圆上,∵∠BAC=25°,∴∠BDC=1/2∠BAC=12.5°,∵∠CAD=75°,∴∠DBC=1/2∠CAD=37.5°.故答案为:12.5,37.5.法二:∵AB=AC=AD,∴∠ADB=∠ABD,∠ACB=∠ABC,∠ADC=∠ACD,∵∠BAC=25°,∠CAD=75°,∴∠ACB=(180°﹣25°)÷2=77.5°,∠DAB=∠DAC+∠CAB=100°,∠ADC=∠ACD=(180°﹣75°)÷2=52.5°,∴∠ADB=(180°﹣100°)÷2=40°,∴∠BDC=∠ADC﹣∠ADB=52.5°﹣40°=12.5°,∠DCB=∠DCA+∠ACB=52.5°+77.5°=130°,∴∠DBC=180°﹣∠DCB﹣∠BDC=180°﹣130°﹣12.5°=37.5°.∴∠BDC=12.5°,∠DBC=37.5°.类型2 直角模型,依据直径所对的圆周角是直角,构造三角形的外接圆解题5. 如图所示,矩形ABCG与矩形CDEF全等,点BCD在一条直线上,∠APE的顶点P在线段BD上移动,使得∠APE为直角的点P的个数是_____个.【分析】∵∠APE的顶点P在线段BD上移动,且∠APE为直角,∴点P也在以AE为直径的⊙O的圆上运动;∴以AE为直径作⊙O,⊙O与BD的交点即为所求.【解答】∵点BCD在一条直线上,∠APE的顶点P在线段BD上移动,∠APE为直角,∴点P在以AE为直径的⊙O的圆上运动,∴点P就是⊙O与BD的交点,由图示知,BD与⊙O有2个交点.故答案为:2.【点评】本题主要考查了圆周角定理:直径所对的圆周角是直角.解答该题时,采用了“数形结合”的数学思想.6. 已知:如图,直尺的宽度为2,A、B两点在直尺的一条边上,AB=6,C、D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C、D两点之间的距离为_____.【分析】由∠ACB=∠ADB=90°,根据90°的圆周角所对的弦是直径,可得A,B,C,D 在以AB为直径的圆上,C,D即是此圆与直尺的交点,设E为AB中点,可得EC是半径为3,然后作EF⊥CD交CD于F,根据垂径定理可得:CD=2CF,然后由勾股定理求得CF的长,继而求得答案.【解答】设E为AB中点,∵∠ACB=∠ADB=90°,∴A,B,C,D在以AB为直径的圆上,连接DE,CE,则CE=DE=1/2AB=3,作EF⊥CD交CD于F,∴CD=2CF,∵AB∥CD,∴EF=2,在Rt△CFE和Rt△DFE中,CF=√5,∴CD=2√5.故答案为:2√5.【点评】此题考查了圆周角定理,垂径定理以及勾股定理等知识.此题拿度适中,解题的关键是由∠ACB=∠ADB=90°,根据90°的圆周角所对的弦是直径,得到A,B,C,D 在以AB为直径的圆上.7. 已知Rt△ABC中,AC=5,BC=12,∠ACB=90°,P是AB边上的动点(与点A、B不重合),Q是BC边上的动点(与点B、C不重合)(1)如图,当PQ∥AC,且Q为BC的中点时,求线段CP的长;(2)当PQ与AC不平行时,△CPQ可能为直角三角形吗?若有可能,请求出线段CQ的长的取值范围;若不可能,请说明理由.【分析】(1)根据平行线等分线段定理得到点P是斜边的中点,再直角三角形斜边上的中线等于斜边的一半,要求线段CP的长,只需根据勾股定理求得AB的长.(2)若PQ与AC不平行,则要使△CPQ成为直角三角形.只需保证∠CPQ=90°.根据直径所对的圆周角是直角,则分析以CQ为直径的圆和斜边AB的公共点的情况:一是半圆和AB相切;二是半圆和AB相交.首先求得相切时CQ的值,即可进一步求得相交时CQ 的范围.【解答】(1)在Rt△ABC中∠ACB=90°,AC=5,BC=12,∴AB=13;∵Q是BC的中点,∴CQ=QB;又∵PQ∥AC,∴AP=PB,即P是AB的中点,∴Rt△ABC中,CP=13/2.(2)当AC与PQ不平行时,只有∠CPQ为直角,△CPQ才可能是直角三角形.以CQ为直径作半圆D,①当半圆D与AB相切时,设切点为M,连接DM,则DM⊥AB,且AC=AM=5,∴MB=AB﹣AM=13﹣5=8;设CD=x,则DM=x,DB=12﹣x;在Rt△DMB中,DB=DM+MB,即(12﹣x)=x+8,解之得x=10/3,∴CQ=2x=20/3;即当CQ=20/3且点P运动到切点M位置时,△CPQ为直角三角形.②当20/3<CQ<12时,半圆D与直线AB有两个交点,当点P运动到这两个交点的位置时,△CPQ为直角三角形③当0<CQ<20/3时,半圆D与直线AB相离,即点P在AB边上运动时,均在半圆D外,∠CPQ<90°,此时△CPQ不可能为直角三角形.∴当20/3≤CQ<12时,△CPQ可能为直角三角形.8.已知平面直角坐标系中两定点A(-1,0),B(4,0),抛物线y=ax+bx-2过点A,B,顶点为C,点P(m,n)为抛物线上一点,其中n<0.(1)求抛物线的解析式和顶点C的坐标;(2)当∠APB为钝角时,求m的取值范围.【分析】(1)利用待定系数法求出解析式,再利用x=0得出y的值即可得出C点坐标.(2)因为AB为直径,所以当抛物线上的点P在⊙C的内部时,满足∠APB为钝角,进而得出m的取值范围;]解:(1) (1)∵抛物线y=ax+bx﹣2(a≠0)过点A,B,∴a-b-2=0, 16a+4b-2=0,解得:a=1/2, b=-3/2,∴抛物线的解析式为:y=1/2x﹣3/2x﹣2,当x=0时,y=﹣2,∴C(0,﹣2);(2)∵A(-1,0),B(4,0),抛物线与y轴的交点D的坐标为(0,-2),如图,抛物线的对称轴与x轴的交点为M(3/2,0),∵AD=1+2=5,AB=(4+1) =25,BD=4+2=16+4=20,则AD+BD=AB,由勾股定理的逆定理,知△ABD是直角三角形,∠ADB=90°,以M为圆心,以MA为半径作圆,则☉M经过点D,则☉M内抛物线上的所有的点都可以是P点,且使∠APB为钝角,根据抛物线及圆的对称性,☉M与抛物线的另一个交点坐标为(3,-2),则满足条件的m的取值范围为:-1<m<0或3<m<4.类型3 四点共圆模型(1)若一个四边形的一组对角互补,则它的四个顶点共圆;(2)动点对定线段所张的角为定值.9. 如图2,在平面直角坐标系xOy中,点A的坐标为(0,m),点B的坐标为(0,n),其中m>n>0.点P为x轴正半轴上的一个动点,当∠APB达到最大时,直接写出此时点P的坐标________.【解析】当以AB为弦的圆与x轴正半轴相切时,对应的∠APB最大,根据垂径定理和勾股定理即可求解.当以AB为弦的圆与x轴正半轴相切时,作CD⊥y轴,连接CP、CB.∵A的坐标为(0,m),点B的坐标为(0,n),10. 在平面直角坐标系中,已知点A(4,0)、B(﹣6,0),点C是y轴上的一个动点,当∠BCA=45°时,点C的坐标为_____.【分析】如解答图所示,构造含有90°圆心角的⊙P,则⊙P与y轴的交点即为所求的点C.注意点C有两个.【解答】设线段BA的中点为E,∵点A(4,0)、B(﹣6,0),∴AB=10,E(﹣1,0).(1)如答图1所示,过点E在第二象限作EP⊥BA,且EP=1/2AB=5,则易知△PBA为等腰直角三角形,∠BPA=90°,PA=PB=5√2;以点P为圆心,PA(或PB)长为半径作⊙P,与y轴的正半轴交于点C,∵∠BCA为⊙P的圆周角,∴∠BCA=1/2∠BPA=45°,即则点C即为所求.过点P作PF⊥y轴于点F,则OF=PE=5,PF=1,在Rt△PFC中,PF=1,PC=5√2,由勾股定理得:CF=7,∴OC=OF+CF=5+7=12,∴点C坐标为(0,12);(2)如答图2所示,在第3象限可以参照(1)作同样操作,同理求得y轴负半轴上的点C坐标为(0,﹣12).综上所述,点C坐标为(0,12)或(0,﹣12).故答案为:(0,12)或(0,﹣12).【点评】本题难度较大.由45°的圆周角联想到90°的圆心角是解题的突破口,也是本题的难点所在.11. 已知△ABC是等腰直角三角形,AC=BC=2,D是边AB上一中点,将△CAD绕C逆时针向旋α得到△CEF,其点E是点A的对应点,点F是点D的对应点.DF与AE交于点M;当α从90°变化到180°时,点M运动的路径长为______.【分析】先证明A、D、M、C四点共圆,得到∠CMF=∠CAD=45°,即可推出点M在以AC 为直径的⊙O上,运动路径是弧CD,利用弧长公式即可解决问题.【解答】∵CA=CE,CD=CF,∴∠CAE=∠CEA,∠CDF=∠CFD∵∠ACD=∠ECF,∴∠ACE=∠DCF,∵2∠CAE+∠ACE=180°,2∠CDF+∠DCF=180°,∴∠CAE=∠CDF,∴A、D、M、C四点共圆,∴∠CMF=∠CAD=45°,∴∠CMD=180°﹣∠CMF=135°.(补充:不用四点共圆的方法:由△OAC∽△ODM,推出△AOD∽△COM,推出∠OCM=∠OAD,即可证明∠CMF=∠CDM+∠DCM=∠CAO+∠OAD=∠CAD=45°)∵O是AC中点,连接OD、CM.∵AD=DB,CA=CB,∴CD⊥AB,∴∠ADC=90°,∵A、D、M、C四点共圆,∴当α从90°变化到180°时,点M在以AC为直径的⊙O上,运动路径是弧CD,【点评】本题考查几何变换综合题、等腰直角三角形的性质、平行线的判定和性质、弧长公式、四点共圆等知识,解题的关键是发现A、D、M、C四点共圆,最后一个问题的关键,正确探究出点M的运动路径,记住弧长公式,属于中考压轴题.三、总结提升圆是我们初中阶段学习的唯一一个曲线图形,除了它本身的基本性质和计算常被考察到以外,还可以用作辅助线。
辅助圆解线段长度问题

辅助圆解线段长度问题
在数学中,辅助圆是指用来解决特定问题的辅助构造圆。
对于线段长度问题,我们可以使用辅助圆来帮助我们求解。
假设我们要求解两条平行线段AB和CD的长度,而且它们之间没有直接的测量方法。
我们可以通过构造辅助圆来间接地求解这个问题。
首先,我们可以选择其中一条线段(假设为AB)作为辅助圆的直径。
然后,我们以点A为圆心,在辅助圆上绘制一条弧,使得该弧与线段CD相交于一点。
再以点B为圆心,绘制一条与第一条弧相切且与线段CD相交的弧。
接下来,我们连接第一条弧与第二条弧的交点,连接这个交点与线段CD的两个端点,得到一个与线段CD同样长度的线段。
因为弧的长度与弦的长度相等,所以这个线段就是我们所要求的。
通过辅助圆的构造,我们可以间接地求解线段长度问题,即使没有直接的测量手段。
这种方法在许多几何问题中都十分有用,特别是在缺乏直接度量手段的情况下。
总结起来,辅助圆是用来解决线段长度问题的一种方法。
通过构造辅助圆,可以间接地求解线段长度,无需直接测量。
这种方法在数学几何学中被广泛应用,为我们解决各种问题提供了有力的工具。
模型24 辅助圆系列最值模型(解析版)-中考数学解题大招复习讲义
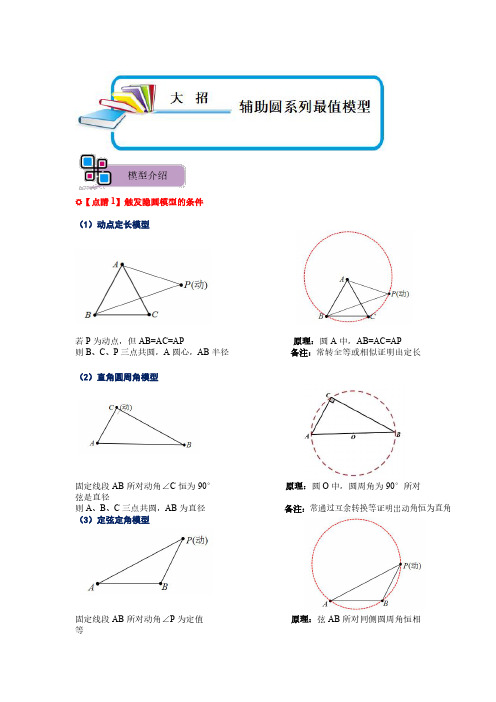
模型介绍【点睛1】触发隐圆模型的条件(1)动点定长模型若P为动点,但AB=AC=AP原理:圆A中,AB=AC=AP则B、C、P三点共圆,A圆心,AB半径备注:常转全等或相似证明出定长(2)直角圆周角模型固定线段AB所对动角∠C恒为90°原理:圆O中,圆周角为90°所对弦是直径则A、B、C三点共圆,AB为直径备注:常通过互余转换等证明出动角恒为直角(3)定弦定角模型固定线段AB所对动角∠P为定值原理:弦AB所对同侧圆周角恒相等则点P 运动轨迹为过A 、B 、C 三点的圆备注:点P 在优弧、劣弧上运动皆可(4)四点共圆模型①若动角∠A+动角∠C=180°原理:圆内接四边形对角互补则A 、B 、C 、D 四点共圆备注:点A 与点C 在线段AB 异侧(5)四点共圆模型②固定线段AB 所对同侧动角∠P=∠C原理:弦AB 所对同侧圆周角恒相等则A 、B 、C 、P 四点共圆备注:点P 与点C 需在线段AB 同侧【点睛2】圆中旋转最值问题条件:线段AB 绕点O 旋转一周,点M 是线段AB 上的一动点,点C 是定点(1)求CM 最小值与最大值(2)求线段AB 扫过的面积(3)求ABC S △最大值与最小值作法:如图建立三个同心圆,作OM ⊥AB ,B 、A 、M 运动路径分别为大圆、中圆、小圆 结论:①CM 1最小,CM 3最大②线段AB 扫过面积为大圆与小圆组成的圆环面积③ABC S △最小值以AB 为底,CM 1为高;最大值以AB 为底,CM 2为高例题精讲考点一:定点定长构造隐圆【例1】.如图,已知AB =AC =AD ,∠CBD =2∠BDC ,∠BAC =44°,则∠CAD 的度数为.解:∵AB =AC =AD ,∴B ,C ,D 在以A 为圆心,AB 为半径的圆上,∴∠CAD =2∠CBD ,∠BAC =2∠BDC ,∵∠CBD =2∠BDC ,∠BAC =44°,∴∠CAD =2∠BAC =88°.故答案为:88°变式训练【变式1-1】.如图所示,四边形ABCD 中,DC ∥AB ,BC =1,AB =AC =AD =2.则BD 的长为()A .B .C .D .解:以A 为圆心,AB 长为半径作圆,延长BA 交⊙A 于F ,连接DF .∵DC ∥AB ,∴=,∴DF =CB =1,BF =2+2=4,∵FB 是⊙A 的直径,∴∠FDB =90°,∴BD ==.故选:B .【变式1-2】.如图,点A,B的坐标分别为A(4,0),B(0,4),C为坐标平面内一点,BC=2,点M为线段AC的中点,连接OM,OM的最大值为.解:∵C为坐标平面内一点,BC=2,∴点C的运动轨迹是在半径为2的⊙B上,如图,取OD=OA=4,连接OD,∵点M为线段AC的中点,∴OM是△ACD的中位线,∴OM=,∴OM最大值时,CD取最大值,此时D、B、C三点共线,此时在Rt△OBD中,BD==4,∴CD=2+4,∴OM的最大值是1+2.故答案为:1+2.考点二:定弦定角构造隐圆【例2】.如图,在△ABC中,BC=2,点A为动点,在点A运动的过程中始终有∠BAC=45°,则△ABC面积的最大值为.解:如图,△ABC的外接圆⊙O,连接OB、OC,∵∠BAC=45°,∴∠BOC=2∠BAC=2×45°=90°,过点O作OD⊥BC,垂足为D,∵OB=OC,∴BD=CD=BC=1,∵∠BOC=90°,OD⊥BC,∴OD=BC=1,∴OB==,∵BC=2保持不变,∴BC边上的高越大,则△ABC的面积越大,当高过圆心时,最大,此时BC边上的高为:+1,∴△ABC的最大面积是:×2×(+1)=+1.故答案为:+1.变式训练【变式2-1】.如图,P是矩形ABCD内一点,AB=4,AD=2,AP⊥BP,则当线段DP最短时,CP=.解:以AB为直径作半圆O,连接OD,与半圆O交于点P′,当点P与P′重合时,DP 最短,则AO=OP′=OB=AB=2,∵AD=2,∠BAD=90°,∴OD=2,∠ADO=∠AOD=∠ODC=45°,∴DP′=OD﹣OP′=2﹣2,过P′作P′E⊥CD于点E,则P′E=DE=DP′=2﹣,∴CE=CD﹣DE=+2,∴CP′=.故答案为:2.【变式2-2】.如图,边长为4的正方形ABCD外有一点E,∠AEB=90°,F为DE的中点,连接CF,则CF的最大值为.解:如图,以AB为直径作圆H,∵∠AEB=90°,∴点E在这个⊙H上,延长DC至P,使CD=PC,连接BE,EH,PH,过H作HM⊥CD于M,∵EF=DF,CD=PC,∴CF=PE,Rt△AEB中,∵H是AB的中点,∴EH=AB=2,Rt△PHM中,由勾股定理得:PH===2,∵PE≤EH+PH=2+2,当P,E,H三点共线时,PE最大,CF最大,∴CF的最大值是+1考点三:对角互补构造隐圆【例3】.如图,在矩形ABCD中,AB=3,BC=5,点E在对角线AC上,连接BE,作EF⊥BE,垂足为E,直线EF交线段DC于点F,则=__________.解:如图,连接BF,取BF的中点O,连接OE,OC.∵四边形ABCD是矩形,EF⊥BE,∴四边形EFCB对角互补,∴B,C,F,E四点共圆,∴∠BEF=∠BCF=90°,AB=CD=3,BC=AD=5,∵OB=OF,∴OE=OB=OF=OC,∴B,C,F,E四点在以O为圆心的圆上,∴∠EBF=∠ECF,∴tan∠EBF=tan∠ACD,∴==变式训练【变式3-1】.如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ACD=30°,AD=2,E是AC的中点,连接DE,则线段DE长度的最小值为.解:∵∠BAD=∠BCD=90°,∴A、B、C、D四点共圆,且BD为直径,取BD中点O,则圆心为点O,连接AO、CO,取AO中点F,连接EF,DF,∵∠ACD=30°,∴∠AOD=60°,∵OA=OD,∴△OAD为等边三角形,∴OA=OD=OC=AD=2,∴∠AFD=90°,则DF=,∵EF是△AOC的中位线,∴EF=OC=1,在△DEF中,DF﹣EF≤DE,∴当D、E、F三点共线时,DE取到最小,最小值为.∴DE的最小值为.【变式3-2】.如图,正方形ABCD的边长为2,点E是BC边上的一动点,点F是CD上一点,且CE=DF,AF、DE相交于点O,BO=BA,则OC的值为.解:如图∵四边形ABCD是正方形,∴AD=DC,∠ADF=∠ECD=∠ABC=90°,∵DF=CE,∴△ADF≌△DCE,∴∠DAF=∠EDC,∵∠EDC+∠ADO=90°,∴∠DAF+∠ADO=90°,∴∠AOD=90°,∴四边形ABEO对角互补,∴A、B、E、O四点共圆,取AE的中点K,连接BK、OK,作OM⊥CD于M.则KB=AK=KE=OK,∵BA=BO,∴∠BAO=∠BOA=∠AEB=∠DEC,∵AB=DC,∠ABE=∠DCE,∠AEB=∠DEC,∴△ABE≌△DCE,∴BE=EC=1,∴DF=EC=FC=1,∴DE==,∵△DFO∽△DEC,∴==,∴==,∴OD=,OF=,∵•DO•OF=•DF•OM,∴OM=,∴MF==,∴CM=1+=,在Rt△OMC中,OC==,故答案为.实战演练1.如图,在平面直角坐标系中,点A、B的坐标分别为(﹣3,0)、(0,4),以点A为圆心,以AB长为半径画弧交x轴上点C,则点C的坐标为()A.(5,0)B.(2,0)C.(﹣8,0)D.(2,0)或(﹣8,0)解:∵点A、B的坐标分别为(﹣3,0)、(0,4),∴OA=3,OB=4,∴AB==5,∴AC′=5,AC=5,∴C′点坐标为(2,0);C点坐标为(﹣8,0).故选:D.2.如图,在矩形ABCD中,已知AB=3,BC=4,点P是BC边上一动点(点P不与B,C 重合),连接AP,作点B关于直线AP的对称点M,则线段MC的最小值为()A.2B.C.3D.解:连接AM,∵点B和M关于AP对称,∴AB=AM=3,∴M在以A圆心,3为半径的圆上,∴当A,M,C三点共线时,CM最短,∵AC=,AM=AB=3,∴CM=5﹣3=2,故选:A.3.如图,在矩形ABCD中,AB=8,BC=6,点P在矩形的内部,连接PA,PB,PC,若∠PBC=∠PAB,则PC的最小值是()A.6B.﹣3C.2﹣4D.4﹣4解:∵四边形ABCD是矩形,∴∠ABC=90°,∴∠ABP+∠PBC=90°,∵∠PBC=∠PAB,∴∠PAB+∠PBA=90°,∴∠APB=90°,∴点P在以AB为直径的圆上运动,设圆心为O,连接OC交⊙O于P,此时PC最小,∵OC===2,∴PC的最小值为2﹣4,故选:C.4.如图所示,∠MON=45°,Rt△ABC,∠ACB=90°,BC=6,AC=8,当A、B分别在射线OM、ON上滑动时,OC的最大值为()A.12B.14C.16D.14解:如图,在Rt△ABC中,由勾股定理得AB=,在AB的下方作等腰直角△AQB,∠AQB=90°,作BH⊥QC于H,∴点O在以点Q为圆心,QB为半径的圆上,∵∠AQB+∠ACB=180°,∴点A、C、B、Q共圆,∴∠BCQ=∠BAQ=45°,∴BH=CH=3,在Rt△BQH中,由勾股定理得QH=4,∴CQ=7,当点C、Q、O共线时,OC最大,∴OC的最大值为OQ+CQ=5+7=12,故选:A.5.如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为.解:∵AB=AC=AD,∴B,C,D在以A为圆心,AB为半径的圆上,∴∠CAD=2∠CBD,∠BAC=2∠BDC,∵∠CBD=2∠BDC,∠BAC=44°,∴∠CAD=2∠BAC=88°.故答案为:88°.6.如图示,A,B两点的坐标分别为(﹣2,0),(3,0),点C在y轴上,且∠ACB=45°,则点C的坐标为.解:在x轴的上方作等腰直角△ABF,FB=FA,∠BAF=90°,以F为圆心,FA为半径作⊙F交y轴于C,连接CB,CA.∵∠ACB=∠AFB=45°,∵B(﹣2,0),A(3,0),△ABF是等腰直角三角形,∴F(,),FA=FB=FC=,设C(0.m),则()2+(﹣m)2=()2,解得m=6或﹣1(舍弃)∴C(0,6),根据对称性可知C′(0,﹣6)也符合条件,综上所述,点C的坐标为(0,6)或(0,﹣6).故答案为(0,6)或(0,﹣6).7.如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB+∠PBA=90°,则线段CP长的最小值为2.解:∵∠PAB+∠PBA=90°,∴∠APB=90°,∴P在以AB为直径的圆周上(P在△ACB内部),连接OC,交⊙O于P,此时CP的值最小,如图,∵AB=6,∴OB=3,∵BC=4,∴由勾股定理得:OC=5,∴CP=5﹣3=2,故答案为:2.8.在△ABC中,AB=4,∠C=45°,则AC+BC的最大值为.解:过点B作BD⊥AC于点D,∵∠C=45°,∴△BCD为等腰直角三角形,∴BD=CD,设BD=CD=a,延长AC至点F,使得CF=a,∵tan∠AFB==,作△ABF的外接圆⊙O,过点O作OE⊥AB于点E,则AE=AB=2,∠AOE=∠AFB,∴tan∠AOE=,∴OE=4,OA==,∴+BC=(AC+BC)=(AC+CF)=≤(OA+OF),∴+BC的最大值为×=4.故答案为:.9.如图,等边△ABC中,AB=6,点D、点E分别在BC和AC上,且BD=CE,连接AD、BE交于点F,则CF的最小值为.解:如图,∵△ABC是等边三角形,∴AB=BC=AC,∠ABC=∠BAC=∠BCE=60°,∵BD=CE,∴△ABD≌△BCE(SAS)∴∠BAD=∠CBE,又∵∠AFE=∠BAD+∠ABE,∴∠AFE=∠CBE+∠ABE=∠ABC,∴∠AFE=60°,∴∠AFB=120°,∴点F的运动轨迹是O为圆心,OA为半径的弧上运动(∠AOB=120°,OA=2),连接OC交⊙O于N,当点F与N重合时,CF的值最小,最小值=OC﹣ON=4﹣2=2.故答案为2.10.如图,正方形ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D 出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,则线段DP的最小值为.解:如图:,∵动点F,E的速度相同,∴DF=AE,又∵正方形ABCD中,AB=2,∴AD=AB,在△ABE和△DAF中,,∴△ABE≌△DAF,∴∠ABE=∠DAF.∵∠ABE+∠BEA=90°,∴∠FAD+∠BEA=90°,∴∠APB=90°,∵点P在运动中保持∠APB=90°,∴点P的路径是一段以AB为直径的弧,设AB的中点为G,连接CG交弧于点P,此时CP的长度最小,AG=BG=AB=1.在Rt△BCG中,DG===,∵PG=AG=1,∴DP=DG﹣PG=﹣1即线段DP的最小值为﹣1,故答案为:﹣1.11.如图,四边形ABCD 中,∠ABC =∠ACD =∠ADC =45°,△DBC 的面积为8,则BC 长为.解:如图,作DH ⊥BC 交BC 的延长线于H ,取CD 的中点O ,连接OA ,OB .∵DH ⊥BH ,∴∠DHC =90°,∴四边形DACH 对角互补,∴A ,C ,H ,D 四点共圆,∵∠DAC =90°,CO =OD ,∴OA =OD =OC =OH ,∴A ,C ,H ,D 四点在以O 为圆心的圆上,∵AC =AD ,∴∠CHA =∠AHD =45°,(没有学习四点共圆,可以这样证明:过点A 作AM ⊥DH 于M ,过点A 作AN ⊥BH 于N ,证明△AMD ≌△ANC ,推出AM =AN ,推出AH 平分∠MHN 即可)∵∠ABC =45°,∴∠BAH =90°,∴BA =AH ,∵∠BAH =∠CAD =90°,∴∠BAC =∠HAD ,∵AC =AD ,AB =AH ,∴△BAC ≌△HAD (SAS ),∴BC =DH ,∴S △BCD =×BC ×DH =×BC 2=16,∴BC =4或﹣4(舍弃),故答案为4.12.已知:在△ABC中,AB=AC=6,∠B=30°,E为BC上一点,BE=2EC,DE=DC,∠ADC=60°,则AD的长.解:连接AE,过点A作AH⊥BC于H点,在Rt△ABH中,∵∠B=30°,∴AH=AB=3.利用勾股定理可得BH=3,根据等腰三角形性质可知CH=BH=3,BC=6.∴CE=BC=2.∴HE=CH﹣CE=.在Rt△AHE中,由勾股定理可求AE=2.所以AE=CE,∠CAE=∠ACB=30°,所以∠AEB=60°=∠ADC,∴四边形AECD对角互补,∴点A、D、C、E四点共圆,∴∠ADE=∠ACE=30°,所以∠CDE=∠ADC﹣∠ADE=30°.∵DE=DC,∴∠DEC=75°.∴∠AED=120°﹣75°=45°.过点A作AM⊥DE于M点,则AM=AE=.在Rt△AMD中,∠ADM=30°,∴AD=2AM=.故答案为2.13.如图,在正方形ABCD中,AD=6,点E是对角线AC上一点,连接DE,过点E作EF ⊥ED,连接DF交AC于点G,将△EFG沿EF翻折,得到△EFM.连接DM.交EF于点N.若AF=2.则△EMN的面积是.解:如图,取DF的中点K,连接AK,EK.连接GM交EF于H.∵四边形ACD是正方形,∴AD=AB=6,∠DAB=90°,AB∥CD,∠DAC=∠CAB=45°,∵DE⊥EF,∴∠DEF=∠DAF=90°,∴四边形AFED对角互补,∴A,F,E,D四点共圆,∵DK=KF,∴KA=KD=KF=KE,∴∠DFE=∠DAE=45°,∴∠EDF=∠EFD=45°,∴DE=EF,∵AF=2,AD=6,∴DF==2,∴DE=DF=2,∵AF∥CD,∴==,∴FG=FM=,∴GM=FM=,∴FH=GH=HM=,∵EF⊥GM,∴GH=HM=,∴EH=EF﹣FH=2﹣=,∵MH∥DE,∴===,∴EN=EH=,=•EN•MH=••=.∴S△ENM故答案为.14.如图,在正方形ABCD中,AD=8,点E是对角线AC上一点,连接DE,过点E作EF ⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB的中点,则FM=,=.解:∵将△EFG沿EF翻折,得到△EFM,∴FG=FM,∵四边形ABCD是正方形,∴AB∥CD,∴△AGF∽△CGD,∴,∵点F是AB的中点,∴AF=CD,∴,∵AD=8,∴AF=4,∴DF==4,∴FM=FG=;∵AC是正方形ABCD的对角线,∴∠CAD=45°,∵EF⊥DE,∴∠DEF=90°=∠BAD,∴∠BAD+∠DEF=180°,∴点A,D,E,F四点共圆,∴∠DFE=∠DAC=45°,∴∠EDF=45°,∴DE=EF=DF=2,连接GM,交EF于P,由折叠知,PG=PM,GM⊥EF,∵DE⊥EF,∴GM∥DE,∴△FPG∽△FED,∴,∴PF=EF=,∴PE=EF﹣PF=,∵GM∥DE,∴△MPN∽△DEN,∴,∴,∴EN=PE=,在Rt△DEN中,,故答案为:;.15.如图,在矩形ABCD中,AB=6,AD=8,点E,F分别是边CD,BC上的动点,且∠AFE=90°(1)证明:△ABF∽△FCE;(2)当DE取何值时,∠AED最大.(1)证明:∵四边形ABCD是矩形,∴∠B=∠C=90°,∵∠AFE=90°,∴∠AFB+∠EFC=90°,∵∠EFC+∠FEC=90°,∴∠AFB=∠FEC,∴△ABF∽△FCE.(2)取AE的中点O,连接OD、OF.∵∠AFE=∠ADE=90°(对角互补),∴A、D、E、F四点共圆,∴∠AED=∠AFD,∴当⊙O与BC相切时,∠AFD的值最大,易知BF=CF=4,∵△ABF∽△FCE,∴=,∴=,∴EC=,∴DE=DC﹣CE=6﹣=.∴当DE=时,∠AED的值最大.16.如图,将两张等腰直角三角形纸片OAB和OCD放置在平面直角坐标系中,点O(0,0),A(0,4).将Rt△OCD绕点O顺时针旋转,连接AC,BD,直线AC与BD相交于点P.(1)求证:AP⊥BP;(2)若点Q为OA的中点,求PQ的最小值.(1)证明:∵△OAB和△OCD都是等腰直角三角形,∴OA=OB,OC=OD,∠AOB=∠COD=90°,∴∠AOC+∠COB=∠COB+∠BOD=90°,∴∠AOC=∠BOD,在△AOC和△BOD中,,∴△AOC≌△BOD(SAS),∴∠OAC=∠OBD,∵△OAB是等腰直角三角形,∴∠OAB+∠OBA=90°,∴∠OAC+∠CAB+∠ABO=90°,∴∠OBD+∠CAB+∠ABO=90°,∴∠APB=90°,∴AP⊥BP;(2)解:如图,∵AP⊥BP,∴点P在以AB为直径的圆E上运动,由点圆最值可得,当P,Q,E三点共线,且点P在EQ的延长线上时,PQ最小,∵△OAB是等腰直角三角形,A(0,4),∴OA=OB=4,∴AB=OA=4,∵E是AB的中点,Q是OA的中点,∴QE=OB=2,∵PE是圆E的半径,∴PE=AB=2,∴PQ=PE﹣QE=2﹣2,∴PQ的最小值为2﹣2.17.(1)【学习心得】于彤同学在学习完“圆”这一章内容后,感觉到一些几何问题如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.例如:如图1,在△ABC中,AB=AC,∠BAC=90°,D是△ABC外一点,且AD=AC,求∠BDC的度数.若以点A为圆心,AB为半径作辅助⊙A,则点C、D必在⊙A上,∠BAC是⊙A的圆心角,而∠BDC是圆周角,从而可容易得到∠BDC=45°.(2)【问题解决】如图2,在四边形ABCD中,∠BAD=∠BCD=90°,∠BDC=25°,求∠BAC的度数.(3)【问题拓展】如图3,如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是﹣1.解:(1)如图1,∵AB=AC,AD=AC,∴以点A为圆心,AB为半径作圆A,点B、C、D必在⊙A上,∵∠BAC是⊙A的圆心角,而∠BDC是圆周角,∴∠BDC=∠BAC=45°,故答案是:45;(2)如图2,取BD的中点O,连接AO、CO.∵∠BAD=∠BCD=90°,∴点A、B、C、D共圆,∴∠BDC=∠BAC,∵∠BDC=25°,∴∠BAC=25°,(3)如图3,在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,在△ABE和△DCF中,,∴△ABE≌△DCF(SAS),∴∠1=∠2,在△ADG和△CDG中,,∴△ADG≌△CDG(SAS),∴∠2=∠3,∴∠1=∠3,∵∠BAH+∠3=∠BAD=90°,∴∠1+∠BAH=90°,∴∠AHB=180°﹣90°=90°,取AB的中点O,连接OH、OD,则OH=AO=AB=1,在Rt△AOD中,OD===,根据三角形的三边关系,OH+DH>OD,∴当O、D、H三点共线时,DH的长度最小,最小值=OD﹣OH=﹣1.(解法二:可以理解为点H是在Rt△AHB,AB直径的半圆上运动当O、H、D三点共线时,DH长度最小)故答案为:﹣1.18.如图,已知抛物线y=ax2+bx+6(a≠0)的图象与x轴交于点A(﹣2,0)和点B(6,0),与y轴交于点C,点D为抛物线的顶点.(1)求抛物线的表达式及顶点D的坐标;(2)如图①,连接BC,点P是线段BC上方抛物线上一动点,若△PBC的面积为12,求点P的坐标;(3)如图②,已知⊙B的半径为2,点Q是⊙B上一个动点,连接AQ,DQ,求DQ+AQ 的最小值.解:(1)令x=0,则y=6,C(0,6),∵A(﹣2,0),B(6,0),∴设抛物线的表达式为y=a(x﹣6)(x+2)(a≠0),当x=0时,y=﹣12a=6,解得a=﹣,抛物线的表达式为y=﹣(x﹣6)(x+2)=﹣x2+2x+6,∵y=﹣x2+2x+6=﹣(x﹣2)2+8,∴顶点D的坐标为(2,8);(2)由(1)知,C(0,6),设直线BC的表达式为y=kx+t,将点B、C的坐标代入得6k+t=0,,解得,∴直线BC的表达式为y=﹣x+6;如图,过点P作PH∥y轴交BC于点H,连接PB,PC,设P(x,﹣x2+2x+6),则H(x,﹣x+6)(0<x<6),∴PH=﹣x2+2x+6﹣(﹣x+6)=﹣x2+3x,∵△PBC的面积为12,∴OB•PH=×6×(﹣x2+3x)=12,即﹣x2+3x=4,解得x=2或x=4,∴点P的坐标为(2,8)或(4,6);(3)如图,取点E(5.5,0),∴BE=0.5,∵AB=8,BQ=2,∴AB:BQ=4:1,∵BE=0.5,BQ=2,∴BQ:BE=4:1,∵∠ABQ=∠QBE,∴△ABQ∽△QBE,∴AQ:QE=BQ:BE=4:1,即QE=AQ,∴DQ+AQ=DQ+QE,由两点间线段最短可知,当点D,Q,E三点共线时,DQ+QE最小,最小值为DE,∴DE==.即DQ+AQ的最小值为:.19.模型分析如图在△ABC中,AD⊥BC于点D,其中∠BAC为定角,AD为定值,我们称该模型为定角定高模型.问题:随着点A的运动,探究BC的最小值(△ABC面积的最小值).(1)当∠BAC=90°时(如图①):第一步:作△ABC的外接圈⊙O;第二步:连接OA;第三步:由图知AO≥AD,当AO=AD时,BC取得最小值.(2)当∠BAC<90°时(如图②):第一步:作△ABC的外接圆⊙O;第二步:连接OA,OB,OC,过点O作OE⊥BC于点E:第三步:由图知AO+OE≥AD,当AO+OE=AD时,BC取得最小值.那么∠BAC>90°呢?结论:当AD过△ABC的外接圆圆心O(即AB=AC)时,BC取得最小值,此时△ABC的面积最小当∠BAC<90°时,请根据【模型分析】(2)中的做法将下面证明过程补充完整.求证:当AD过△ABC的外接圆圆心O(即AB=AC)时,BC取得最小值,此时△ABC 的面积最小.证明:如解图,作△ABC的外接圆⊙O,连接OA,OB,OC,过点O作OE⊥BC于点E,设⊙O的半径为r,∠BOE=∠BAC=α,AD=h,∴BC=2BE=2OB•sinα=2r•sinα,∵sinα为定值,∴要使BC最小,只需…自主探究:我们知道了当AD过△ABC的外接圆圆心O(即AB=AC)时,△ABC的面积取得最小值,那么要使△ABC的周长取得最小值,需要满足什么条件呢?模型分析:证明:如图1,作△ABC的外接圆⊙O,连接OA,OB,作OE⊥BC于E,设⊙O的半径为r,AD=h,∴BC=2BE=2CE,∵=,∴∠BOC=2∠BAC=2α,∵OB=OC,∴∠BOE=∠BOC=α,∴OE=OB•cosα=r•cosα,∵OA+OE≥AD,∴r+r•cosα≥h,∴r≥,∵BE=OB•sinα=r•sinα,∴BC=2BE=2r•sinα,∴当r最小时,BC最小,∴当r=时,BC=;最小自主探究:解:如图2,延长CB知E,使BE=AB,延长BC至F,使CF=AC,∴AB+BC+AC=BE+BC+CF=EF,∠AEB=∠EAB,∠CAF=∠AFC,∴∠ABC=2∠EAB,∠ACB=2∠CAF,∵∠ABC+∠ACB=180°﹣∠BAC=180°﹣α,∴2∠EAB+2∠CAF=180°﹣α,∴∠EAF+∠CAF=90°﹣,∴∠EAF=∠EAF+∠CAF+∠BAC=90°+,作△AEF的外接圆O,作OH⊥EF于H,连接OA,OE,OF,在优弧EF上任取一点G (不在E和点F处),连接EG,FG,∴∠G=180°﹣∠EFA=90﹣,同理上可得:∠EOH=∠G=90°﹣,∴∠OEH=90°﹣∠EOH=,∴OH=r•sin,EF=2EH=2r•cos,∵OH+AD≤OA,∴r•sin+h≤r,∴(1﹣sin)r≥h,∴r≥,∴r=,最小∴EF=,最小∴△ABC的周长最小值为:.20.如图,抛物线y=ax2+x+c与x轴交于A,B两点(点B在点A左侧),与y轴交于点C,直线y=kx+b经过点A,C,且OA=2OC=4.(1)求抛物线的解析式;(2)点E为AC上方抛物线上一动点,过点E作EF∥y轴交AC于点F,求线段EF的最大值;(3)在(2)的结论下,若点G是x轴上一点,当∠CGF的度数最大时,求点G的坐标.解:(1)∵OA=2OC=4,∴A(4,0),C(0,2),将A(4,0),C(0,2)代入y=ax2+x+c,∴,解得,∴y=﹣x2+x+2;(2)将点A(4,0),C(0,2)代入y=kx+b,∴,解得,∴y=﹣x+2,设E(t,﹣t2+t+2),则F(t,﹣t+2),∴EF=﹣t2+t+2+t﹣2=﹣t2+2t=﹣(t﹣2)2+2,当t=2时,EF的最大值为2;(3)∵t=2,∴E(2,3),F(2,1),设G(x,0),作△CFG的外接圆M,设圆M的半径为r,当圆M与x轴相切时,∠CGF最大,此时M(x,r),∵MC=MF=r,∴x2+(r﹣2)2=r2,(2﹣x)2+(1﹣r)2=r2,解得x=4﹣,∴G(4﹣,0).。
正弦定理辅助圆

正弦定理辅助圆正弦定理是解三角形问题中的一种重要定理,它为三角形的边与角之间的关系提供了一个有效的计算方法。
而辅助圆则是在使用正弦定理解题时常用的一种方法,通过构造一个以某一边为直径的圆来辅助求解问题。
辅助圆的构造方法如下:设已知三角形的边长分别为a,b,c,而三个对应的角分别为A,B,C。
我们以边a为直径构造一个圆,将其划分为两个相等的弧,记为弧BC。
根据圆的性质可知,弧BC对应的圆心角为2A。
在画出辅助圆之后,我们可以使用正弦定理来得出以下结果:1. 正弦定理形式:a/sinA = b/sinB = c/sinC在辅助圆中,以边a作为直径,可得出∠BAC对应的弧对应的圆心角为2A,那么可以得出:c/2r = sinA (r为圆的半径)2. 辅助圆半径和三角形周长关系:三角形的周长c = 2πr根据辅助圆的构造,可知辅助圆的直径与三角形的一条边a相等,即直径为2r。
所以周长为直径的圆的周长,即2πr。
3. 余弦定理角形式的转化关系:在三角形中,设∠BAC=A,∠ACB=B,∠ABC=C,边长分别为a,b,c,可得出余弦定理角形式:cosA = (b² + c² - a²) / (2bc)cosB = (c² + a² - b²) / (2ca)cosC = (a² + b² - c²) / (2ab)将正弦定理形式的a/sinA = b/sinB代入,可得出:cosA = (b² + c² - a²) / (2bc) = 2(sinBsinC + cosBcosC) - 1这个转化关系也常常在解三角形问题时使用,将余弦定理转化为正弦定理形式的等式。
在求解三角形问题时,我们可以根据正弦定理和辅助圆的方法来构造方程,进一步计算出所求解的角度和边长。
通过辅助圆的引入,我们可以更加简洁地使用正弦定理,提高解题的效率。
初中几何关于动点运动的辅助圆的构造技巧讲解
Part 4
课程总结
圆周角定理: 直径所对的圆周角为90°,90°的圆周角所对的弦是直径
下次课见
对应练习
如图,Rt△ABC中,∠ACB=90∘,∠CAB=60∘,AB=4,点P是BC边上的动点,过点c作 直线AP的垂线,垂足为Q,当点P从点C运动到点B时,点Q的运动路径长为___.
Q
常 见 构 造 情 景(2)正方形中的十字
已知正方形ABCD,点EF分别为 BC,CD上的动点,连接AF,BF交 于点G,AE=BF。
AA''
A
AA
NN
CC C
BBB N
对应练习
如图,在Rt△ABC中,∠B=60∘,BC=3,D为BC边上的三等分点,BD=2CD,E为AB 边上一动点,将△DBE沿DE折叠到△DB′E的位置,连接AB′,则线段AB′的最小值 为:___.
对应练习
(桂林中考题)如图,正方形OABC的边长为2,以O为圆心,EF为直径的半圆经过 点A,连接AE,CF相交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点
2.如何构造辅助圆? 先找运动的直角, 再找直角所对的固定边
常 见 构 造 情 景(1)图中已知垂直
已知正方形ABCD,点G为对角线BD 上的一动点,连接AG,过点B作 BH⊥直线AG于点H。
则点H的轨迹为:以AB为直径的圆上 的一段弧AB
经典例题
如图,正方形ABCD的边长是2,点P从点D出发沿DB向点B运动,至点B停止运动,连接 AP,过点B作BH垂直于直线AP于点H,在点P运动过程中,点H所走过的路径长是( )
动的一个动点,连接EF,将△AEF沿EF折叠,点A落在点G处,在运动的过程中, 点G运动的路径长为:
精编初中数学几何证明--辅助圆专题讲解探究

精编初中数学几何证明--辅助圆专题讲解探究在几何证明中,困难的并不在于题目,而在于辅助线.在初二学习全等系列的知识点过程中,我们带着学生学习了很多种的辅助线,比如倍长中线、截长补短等.而在学习完圆之后,我们又遇到了新的问题,如做弦的垂线,连接半径,连接直径等.这些的辅助线对于中档的学生都是可以解决的,但我们有没有遇到作出一个圆的辅助线?这也是今天要讲的专题--辅助圆.“辅助圆”通常活跃于各校模拟试题,因难度系数大,学生不易接受,所以得分率一直都很低.因其考点新颖,有创新又不失难度,所以在近几年的江苏中考中也开始陆续出现了关于“辅助圆”的辅助线问题.那么下面我就来对“辅助圆”问题说说自己的一些看法.出现“辅助圆”的情况在我总结来看无外乎就是线段最值、存在唯一点、点的运动等. 那下面我就按照如下几点来探究“辅助圆”出现的一般情况.一线段最值线段最值分类相对较多,我们单独来看看什么时候需要我们作出相对的辅助圆的情况.Ⅰ.折叠中的线段最值1.(成都中考)如图,在边长为 2 的菱形 ABCD 中,∠A=60°,M 是AD 边的中点,N 是 AB 边上一动点,将△AMN 沿 MN 所在直线翻折得到△A¢MN,连接A¢C,则A¢C长度的最小值是.〖分析〗△AMN 沿MN 所在直线翻折过程中,始终都保持着MA=MA’,即 A 点的运动轨迹满足于圆的基本概念,则 A 点的运动轨迹是以 M 为圆心,MA 为半径的一个圆,则A¢C的最小值即转化到点 C 到⊙M 的上的最小值问题,这时就可以得到A¢C 最小值是 CM—半径,求出 CM 的长即可,如下图.2.(无锡惠山区二模)如图,在 Rt△ABC 中,∠B=60°,BC=3,D 为 BC 边上的三等分点,BD=2CD,E 为A B 边上一动点,将△DBE 沿D E 折叠到△D B¢E 的位置,连接A B¢,则线段A B¢的最小值为.〖分析〗△DBE 沿 DE 折叠过程中,与上题一样,始终满足于 DB=D B¢,与 1 相似,即作出辅助圆⊙D,以 D 为圆心,DB 为半径的圆.A 为圆外一点,求AB’的最小值即用 AD—半径即可,如下图.Ⅱ.圆轨迹中的线段最值3.(无锡惠山区一模)在平面直角坐标系中,O 为坐标原点,以 A(4,3)为圆心,1 为半径作圆.P 点为圆上一动点,连结 OP.点 B 为 OP 的中点,点 C 坐标为(2,0),求B C 的取值范围.〖分析〗点 P 的运动轨迹是圆,B 为 OP 中点,随着 P 的运动而运动,则根据“瓜豆原理”,B 的运动轨迹也是一个圆.我们需要确定的是 B 所在圆的圆心及半径,则就可以解出此题.为 确定圆心,则连接 OA ,取 OA 中点 Q .连接 BQ ,BQ= 1 AP = 1 ,则 B 的运动轨迹是以 Q 2 2 1 为圆心, 2为半径的圆.再求出 CB 的最大和最小值=CQ ±半径即可.(如下图)4.(无锡外国语中学一模)如图,点 O 在线段 AB 上,OA=1,OB=3,以 O 为圆心,OA 长为半径作圆 O .点 M 在圆 O 上运动,连接 MB ,以 MB 为腰作等腰 Rt △MBC ,使 ∠MBC=90°,M .B .C 三点为逆时针顺序,连接 A C ,则 A C 长的取值范围是 .〖分析〗点M 的运动轨迹是圆,点 C 是由 BM 旋转 90°得出,则根据“瓜豆原理”初步确定点C 的运动轨迹也是一个圆.我们需要确定的是 B 所在圆的圆心及半径,则就可以解出此题.为确定圆心,连接 OM,将 OM 也绕着点 B 旋转 90°,确定O¢,连接O¢C .易证△BOM≌△BO¢C ,得出OM =O¢C =1 ,则可得出点 C 的运动轨迹是以O¢为圆心,1 为半径的圆.再求出AC 的最大和最小值= AO¢±半径即可.(如下图)Ⅲ.直角三角形中的辅助圆5.(江阴校级一模)如图,在等腰直角三角形 ABC 中,∠ABC=90°,AB=BC=2,P 是△ABC 所在平面内一点,且满足P A⊥PB,则P C 的取值范围为.〖分析〗因为∠APB=90°,由 90°所对的弦是直径得出,构造⊙O.以 AB 中点 O 为圆心,1 为半径作圆,则 P 是在⊙O 上运动,确定 CP 的最小值为 OC—半径即可.(如下图)6.(无锡天一中学二模)如图, E, F 是正方形 ABCD 的边 AD 上两个动点,满足AE=DF.连接 CF 交 BD 于点 G,连接 BE 交 AG 于点 H.若正方形的边长为 2,则线段 DH 长度的最小值是.〖分析〗因为 AE=DF,易得△ABE≌△ DCF、△AGD≌△ CGD,则∠ ABE= ∠ GAD=∠ DCF.因为∠ GAD+∠ BAH=90 °,所以∠ BAH+ ∠ ABE=90°,所以∠AHB=90°.则点 H 是在以 AB 为直径的圆上运动.确定 DH 的最小值为 OD—半径即可.(如下图)Ⅳ.定弦、定角中的辅助圆7.(无锡滨湖区期中考试)如图,在正方形 ABCD,AB= 2 ,若点 P 满足 PD=2,且∠BPD=90°,请求出 AP 的长.〖分析〗因为∠BAD=∠BPD=90°,则可认为 B、A、P、D 四点是在以 BD 为直径的圆上,设BD 的中点为 O,则如图,共圆.得到∠BDA=∠APB=45°,得出∠DPE=45°,则在 Rt△PED 中,得出 DE=PE= ,在 Rt△AED 中,AD= 2 ,得出 AE= ,则可得AP= 6- .如下图即可.8.(威海中考)如图,△ABC 为等边三角形,AB=2,若P为△ABC 内一动点,且满足∠PAB=∠ACP,则线段P B 长度的最小值.〖分析〗因为△ABC 为等边三角形,满足∠PAB=∠ACP,则可确定∠APC=120°,而∠APC 所对的边恒定为 AC,且长度为定值,则由圆周角的性质可以得出 P 点的运动轨迹是一个弧,点P 是在△APC 的外接圆上运动,确定 BP 的最小值为 OB—半径即可.(如下图)这也是我们定弦定角定理的一般模型.9.(无锡惠山区二模)如图,已知A、B 是半径为2的⊙O 上的两动点,以A B 为直角边在⊙O 内作等腰R t△ABC,∠B=90°,连接O C,则O C 的最小值为.〖分析〗因为△ABC 为等腰 Rt△,则∠BCA=45°为定值,延长 BC 交⊙O 于点 D,则∠ACD=135°,连接 AD.因为∠ B=90°,则AD 为⊙O 的直径,即 AD=4 为定值,则满足于上述例 7 的定弦定角定理模型,可分析得出点 C 是在一个圆上运动,则需要找圆心.设圆心为O¢,因为∠ACD=135°,则其所对的圆心角∠AO¢D =90°,则O¢是在⊙O 上,半径O¢D=2 .连接O¢C ,则当O¢、O、C 三点共线的时候,OC 的值最小,为2 2-2 .(如下图)二证明角度关系或求值Ⅰ.角度的倍数关系1.(江苏学大教师月考)如图,AB=AC=AD,如果∠DAC 是∠CAB 的 k 倍,那么∠DBC 是∠BDC 的()倍A.k B.2k C.3k D.不能确定〖分析〗因为 AB=AC=AD,则 B、C、D 三点可以看成是在以点 A 为圆心,AB 为半径的圆上.则∠DBC 与∠CAD 是同弧所对的圆周角和圆心角,∠BDC 与∠CAB 是同弧所对的圆周角和圆心角.∠DAC 是∠CAB 的 k 倍,则∠DBC 也是∠BDC 的 k 倍.Ⅱ.角度求值问题2.(2015 年无锡惠山区校级月考)已知在正方形 ABCD 中,两顶点 A、B 分别在平面直角坐标系的 x 轴、y 轴的正半轴上滑动,点 C 点 D 在第一象限,点 E 为正方形 ABCD 的对称中心,连结 OE,证明 OE 平分角∠ AOB.〖分析〗因为∠AOB=∠AEB=90°,则可以说明 A、O、B、E 四点共圆,以 AB 的中点O¢为圆心,O¢A 为半径的圆.这种有一组对角为 90°的四边形称为损矩形,即可采用四点共圆的技巧去解决.很明显,∠EBA 与∠AOE 是同弧所对的圆周角,则∠EBA=∠AOE=45°,即可说明 OE 平分角∠ AOB.(如下图)Ⅲ.角度最值问题3.(2015 年南京市校级月考)如图,O 是半径为 2,AB、CD 是互相垂直的两条直径,点P 是O 上任意一点,过点 P 作 PM⊥AB 于 M,P N⊥CD 于 N,点 Q 是 MN 的中点,当点 P 沿着圆周从 D 运动到点 C 时,t an∠QCN 的最大值为.〖分析〗因为 PM⊥AB,PN⊥CD,则四边形 MONP 为矩形,得到对角线MN=OP=2.说明 OQ 的长度恒定为 1,确定点 Q 是在以 O 为圆心, 1 为半径的圆上,则当 CQ 与圆相切时,即是∠ QCO 最大, tan∠QCN 的值最大.(如下图)三最值存在问题Ⅰ.线段范围1.(2011 年河池中考)如图,在 Rt△ABC 中,∠ABC=90°,A B=3 ,B C=4 ,P是BC 边上的动点.设 BP=x,若能在 AC 边上找到一点 Q,使∠BQP=90 °,则 x 的取值范围是.〖分析〗因为∠ABC=90 °,则由直径所对的圆周角等于 90 °,得出以 BP 为直径的圆与线段 AC 有交点,得出题目的解题技巧.则当⊙O 与 AC 相切时,x 的值最小,当点 P 到达 C 点时,x 的值最大.(如下图)2.(2015 年无锡外国语二模)在平面直角坐标系中,已知△AOB 是等边三角形,点 A 的坐标是(4,0),点 B 在第一象限,若 N 为直线y=-x-2 上一点,过 B 作直线 l⊥x 轴,在 l 上是否存在一点 M,使得∠OMA=2∠ONA,且这样的点 N 有且只有一个.若存在,请直接写出点 M 的坐标;若不存在,请说明理由.〖分析〗因为题目中满足∠OMA=2∠ONA,在图中我们可以看出以 M 为圆心,OM 为半径的圆正好满足于此条件,则可以理解为辅助圆.若这样的点 N 有且只有一个,则说明⊙M与直线y=-x-2 相切即可,同时也要注意图形的对称性,M 存在另外一个点,与图中的 M 点关于x 轴对称即可.(如左图)Ⅱ.路程长或面积问题3.(2015 年无锡惠山区校级月考)如图,矩形 OABC 的边 OA、OC 分别在 x 轴、y 轴上,点 B 的坐标为(7,3),点 E 在边 AB 上,且 AE=1,已知点 P 为y 轴上一动点,连接EP ,过点 O 作直线 E P 的垂线段,垂足为点 H ,在点 P 从点 F (0,程中,点 H 的运动路径长为.25 )运动到原点 O 的过 4〖分析〗因为∠APB=90°,且 OE 为定长,则点 H 在以 OE 为直径的圆上运动. 点 P 由 点 F 为起点, O 为终点运动, 则点 H 的运动轨迹是一段弧, 圆心角为∠ OO ¢H ,则求出∠ OO ¢H 的度数即可,而∠ OO ¢H =2 ∠ OEF ,求出∠ OEF 的度数即可.(如下图)4.(2015 年无锡外国语月考)如图,圆 O 的半径为 2,弦 AB=2,点 P 为优弧 AB 上一动点,BC ⊥BP 交直线 P A 于点 C ,则△ABC 的最大面积为 .〖分析〗因为 BC 半径为 2,弦AB=2,则∠P=30°,BC⊥BP,则∠C=60°.因为∠C=60°,且AB=2,则可以得出点 C 是在△ABC 的外接圆上运动,也可以理解为我们上面讲解的定弦定角定理.要使得△ABC 的面积最大,则 C 到AB 的距离最大,如下图即可.在辅助圆方面还需要学生多多的做练习,理解我们出现辅助圆的情况的一般要求,同时具体情况具体分析,需要学生具有很强的临场发挥能力,这部分的知识点活跃在模拟考试及中考中,还是需要学生能理解掌握,方便与学生能运用技巧性方法去解决实际困难问题.。
初中数学-构造辅助圆解题教法解析

教法解析
内容简介
Contents
教学内容分析 学生情况分析 教学设计思想 知识点回顾 典例分析
教学内容分析
【教学内容分析】
本节课的授课内容是学完《圆》后, 作为对学生能力提升的一个引申和补充的 内容,也属于构造辅助线的一种。
直线形 直线型辅助线
曲线形
圆 辅助圆
学生情况分析
教学设计思想
例题 Example
一、利用圆的定义添补辅助圆 1.直接用定义 2.间接用定义:共斜边的等腰直角三角形
例题 Example
一、利用圆的定义构造辅助圆 总结:需要多条共端点等线段时,
可以利用圆定义构造辅助圆
在平面直角坐标系中,一次函数y=-2x的图象与反比例函数
y
k x
的图象的一个交点为A(-1,n).
如图,在△ABC中,高BE、CF相交于H,且
∠BHC=135°,G为△ABC内的一点,且GB=GC,
∠BGC=3∠A,连结HG,求证:HG平分∠BHF.
思路:经计算可得∠A=45°,△ABE, △BFH皆为等腰直角三角形,只需证 ∠GHB=∠GHF=22.5°.
由∠BGC=3∠A=135°=∠BHC,得B、G、 H、C四点共圆,由∠ sin∠B
二、作三角形的外接圆
总结:三角形中涉及到倒角的题目, 可以考虑构造三角形外接圆
在△ABC中,AD是BC边的中线,且∠B+∠CAD=90°.
试判断△ABC的形状,并加以证明.
思路:由需要倒角而想到构造外接 圆,根据90°进而确定直径,结合 垂径定理推论,分类讨论后即可得 到答案
BC
(3) 在图 2 中,固定 △AOB ,将△COD 绕点O 旋转,直接写出 PM 的最大值.
省时省力的辅助圆

2022年7月下半月㊀解法探究㊀㊀㊀㊀省时省力的辅助圆◉山东省滕州市滕南中学㊀郭效萍1引言圆是初中阶段学习的重要图形,它的一些性质,例如,同弧所对的圆周角相等,半圆所对的圆周角是直角,直径是圆中最长的弦等,给解决问题带来极大的方便.在解答有关几何问题时,并不是图形中出现圆才利用圆的性质,有时需要构造一个辅助圆,然后利用圆的性质解答,这是解决几何问题的基本方法之一.2利用圆的集合定义构造辅助圆从集合的角度定义:圆是平面内到定点距离等于定长的点的集合.根据这个定义可以得到,当几个点到同一点的距离相等时,则这几点一定在同一个圆上.这样构造辅助圆,解答时不仅能利用题中的已知条件,而且可以利用圆的一些性质.例1㊀如图1,在四边形A B C D 中,A B =A C =A D ,若øB AC =25ʎ,øC AD =75ʎ,分别求øB D C 和øD B C 的度数.图1㊀㊀㊀图2解法1:(普通方法)ȵA B =A C =A D ,ʑøA D B =øA B D ,㊀øA C B =øA B C ,㊀øA D C =øA C D .ȵøB A C =25ʎ,øC A D =75ʎ,ʑøA C B =(180ʎ-25ʎ)ː2=77.5ʎ,㊀øD A B =øD A C +øC A B =100ʎ,㊀øA D C =øA C D =(180ʎ-75ʎ)ː2=52.5ʎ.ʑøA D B =(180ʎ-100ʎ)ː2=40ʎ.ʑøB D C =øA D C -øA D B=52.5ʎ-40ʎ=12.5ʎ,㊀øD C B =øD C A +øA C B=52.5ʎ+77.5ʎ=130ʎ.ʑøD B C =180ʎ-øD C B -øB D C=180ʎ-130ʎ-12.5ʎ=37.5ʎ.解法2:(构造辅助圆的方法)由A B =A C =A D ,得点B ,C ,D 在以A 为圆心,以A D 为半径的圆上,如图2.由øB A C =25ʎ,得øB D C =12øB A C =12.5ʎ.由øC A D =75ʎ,得øD B C =12øC A D =37.5ʎ.点评:比较上面两种方法可以发现,构造辅助圆后,解决过程明显简洁.这里主要利用了圆周角定理及其推论:同弧所对的圆周角相等,等弧所对的圆周角也相等.这是因为这些圆周角都等于它所对的圆心角的一半.3利用圆周角定理的推论构造辅助圆因为90ʎ的圆周角所对的弦是直径,所以当直角三角形的斜边一定时,直角顶点一定在以斜边为直径的圆上运动.此时构造辅助圆,可以确定直角顶点的运动轨迹.例2㊀如图3所示,矩形A B C G (A B <B C )与矩形C D E F 全等,点B ,C ,D 在一条直线上,øA P E 的顶点P 在线段B D 上移动,使得øA P E 为直角的点P 的个数是.图3㊀㊀㊀图4解析:如图4所示,根据90ʎ的圆周角所对的弦是直径,当øA P E 为直角时,点P 应在以A E 为直径的☉O 上.又因为点B ,C ,D 在同一条直线上,øA P E的顶点P 在线段B D 上移动,所以点P 就是☉O 与B D 的交点.由图4可知,B D 与☉O 有2个交点.故答案为:2.点评:本题确定点的方法使用的是交轨法,即从每一个条件出发确定一个点的轨迹,两个点的轨迹的交点就是符合题意的点.本题两个点的轨迹分别是一条直线和一个圆.4利用一个角对定线段所张的角度为定值构造辅助圆㊀㊀当一个角对固定长度的线段所张开的角度为定值时,角的顶点的运动轨迹为一个圆,此时可以作辅助圆,这条定线段为辅助圆的弦,这个角为圆周角.此时可以利用圆的相关性质解答问题.例3㊀如图5,点A 与点B 的坐标分别是(1,0),(5,0),点P 是该直角坐标系内的一个动点.(1)使øA P B =30ʎ的点P 有个.(2)若点P 在y 轴上,且øA P B =30ʎ,求满足条件的点P 的坐标.57Copyright ©博看网. All Rights Reserved.解法探究2022年7月下半月㊀㊀㊀(3)当点P 在y 轴上移动时,øA P B 是否有最大值?若有,求点P 的坐标,并说明此时øA P B 最大的理由;若没有,请说明理由.图5㊀㊀㊀图6解析:(1)如图6,以A B 为边,在第一象限内作等边三角形A B C ,以点C 为圆心,A C 为半径作☉C ,交y 轴于点P 1,P 2.在优弧A P 1B 上任取一点P ,则øA P B =12øA C B =12ˑ60ʎ=30ʎ.所以使øA P B =30ʎ的点P 有无数个.(2)①当点P 在y 轴的正半轴上时,过点C 作C G ʅA B ,垂足为点G ,如图6.由点A (1,0),B (5,0),得O A =1,O B =5,则A B =4.由点C 为圆心,C G ʅA B ,得A G =B G =12A B =2.则O G =O A +A G =3.由әA B C 是等边三角形,得A C =B C =A B =4.则C G =A C 2-A G 2=42-22=23.于是点C 的坐标为(3,23).过点C 作C D 垂直于y 轴,垂足为点D ,连接C P 2,如图6.由点C (3,23),得C D =3,O D =23.由点P 1,P 2是☉C 与y 轴的交点,得øA P 1B =øA P 2B =30ʎ.由C P 2=C A =4,C D =3,得D P 2=42-32=7.由点C 为圆心,C D ʅP 1P 2,得P 1D =P 2D =7,从而P 2(0,23-7),P 1(0,23+7).②当点P 在y 轴的负半轴上时,同理可得:点P 3(0,-23-7),P 4(0,-23+7).综上所述,满足条件的点P 的坐标为(0,23-7),(0,23+7),(0,-23-7),(0,-23+7).图7(3)如图7,当过点A ,B 的☉E 与y 轴相切于点P 时,øA P B 最大.理由:可证øA P B =øA E H ,当øA P B 最大时,øA E H 最大.由s i n øA E H =2A E知,当A E最小即P E 最小时,øA E H 最大.所以当圆与y 轴相切时,øA P B 最大.①当点P 在y 轴的正半轴上时,连接E A ,作E H ʅx 轴,垂足为点H ,如图7.由☉E 与y 轴相切于点P ,得P E ʅO P .由E H ʅA B ,O P ʅO H ,得øE P O =øP O H =øE H O =90ʎ.则四边形O P E H 是矩形,O P =E H ,P E =O H =3,得E A =3.由øE HA =90ʎ,AH =2,E A =3,得E H =E A 2-AH 2=32-22=5,则O P =5,则点P (0,5).②当点P 在y 轴的负半轴上时也符合题意,此时点P (0,-5).综上所述,存在满足条件的点P ,其坐标为(0,5),(0,-5).点评:解答第(3)小题时,体现了转化的思想,即由øA P B 转化为øA E H ,由øA E H 转化为2A E,由2A E转化为A E ,再由A E 转化为P E ,由P E 转化为直线与圆相切.5利用作辅助圆求最值圆外一定点与圆上各点连接而成的所有线段中,有一条最短线段和最长线段,这两条线段都在过圆心与圆外一点的直线上,如图8所示,最长线段是P A ,最短线段是P B .利用这一点,可以求与圆有关的线段的最值.图8㊀图9㊀图10例4㊀如图9,R t әA B C 中,A B ʅB C ,A B =6,B C =4,P 是әA B C 内部的一个动点,且满足øP A B =øP B C ,则线段C P 长的最小值为.解析:如图10,由øA B C =90ʎ,得øA B P +øP B C =90ʎ.又øP A B =øP B C ,则øB A P +øA B P =90ʎ,即øA P B =90ʎ,则点P 在以A B 为直径的☉O 上.连接O C 交☉O 于点P ,此时P C 最小.在R t әB C O 中,øO B C =90ʎ,B C =4,O B =3,则O C =O B 2+B C 2=5,P C =O C -O P =5-3=2.因此P C 的最小值为2.点评:几何中求最值的情况包括:(1)利用轴对称求线段和的最小值;(2)利用勾股定理求曲面上或不同平面上两点之间的最短距离;(3)利用三角形相似解决系数不为1的线段和最小值问题;(4)利用直径是圆中最长的弦解决与圆有关的线段的最值.几何问题中作辅助线的方法比较多,如作垂线㊁平行线㊁连接㊁延长㊁倍长中线㊁旋转三角形等,但作辅助圆这种作铺助线的方法容易被忽略.上述四个实例分别从四个不同的角度阐释了在什么情况下需要作辅助圆,如何作辅助圆,作辅助圆后如何利用辅助圆,以期对学生突破几何学习有所帮助.W67Copyright ©博看网. All Rights Reserved.。
3.最值问题之辅助圆(轨迹)

几何最值问题之辅助圆(轨迹)最值问题的必要条件是至少有一个动点,因为是动态问题,所以才会有最值.在将军饮马问题中,折点P 就是那个必须存在的动点.并且它的运动轨迹是一条直线,解题策略就是作端点关于折点所在直线的对称即可.当然,动点的运动轨迹是可以变的,比如P 点轨迹也可以是一个圆,就有了第二类最值问题——辅助圆.在这类题目中,题目很少直接告诉我们动点轨迹是个圆,也很少把这个圆画出来,因此,结合题目给的条件,分析出动点的轨迹图形,将是我们面临的最大的问题.若已经确定了动点的轨迹圆,接下来求最最值的问题就会变得简单了,比如:如下图,A 为圆外一点,在圆上找一点P 使得P A 最小.当然,也存在耿直的题目直接告诉动点轨迹是个圆的 确定共圆的方法有几种,①到定点的距离等于定长②共斜边的直角三角形,定角对定弦③对角互补的四边形 ④同侧内角相等的八字形1.如图,已知圆C 的半径为3,圆外一定点O 满足OC =5,点P 为圆C 上一动点,经过点O 的直线l 上有两点A 、B ,且OA =OB ,∠APB =90°,l 不经过点C ,则AB 的最小值为________.【分析】连接OP ,根据△APB 为直角三角形且O 是斜边AB 中点,可得OP 是AB 的一半,若AB 最小,则OP 最小即可.连接OC ,与圆C 交点即为所求点P ,此时OP 最小,AB 也取到最小值.Alll一、从圆的定义构造圆圆的定义:平面内到定点的距离等于定值的所有点构成的集合.构造思路:若动点到平面内某定点的距离始终为定值,则其轨迹是圆或圆弧.2.如图,在边长为2的菱形ABCD 中,∠A =60°,M 是AD 边的中点,N 是AB 边上的一动点,将△AMN 沿MN 所在直线翻折得到△A ’MN ,连接A ’C ,则A ’C 长度的最小值是__________.【分析】考虑△AMN 沿MN 所在直线翻折得到△A ’MN ,可得MA ’=MA =1,所以A ’轨迹是以M 点为圆心,MA 为半径的圆弧.连接CM ,与圆的交点即为所求的A ’,此时A ’C 的值最小.构造直角△MHC ,勾股定理求CM ,再减去A ’M 即可.A'NMABCDA'NMABCDDCBA MN A'H A'N MA BCD3.如图,在Rt △ABC 中,∠C =90°,AC =6,BC =8,点F 在边AC 上,并且CF =2,点E 为边BC 上的动点,将△CEF 沿直线EF 翻折,点C 落在点P 处,则点P 到边AB 距离的最小值是__________.【分析】考虑到将△FCE 沿EF 翻折得到△FPE ,可得P 点轨迹是以F 点为圆心,FC 为半径的圆弧.过F 点作FH ⊥AB ,与圆的交点即为所求P 点,此时点P 到AB 的距离最小.由相似先求FH ,再减去FP ,即可得到PH .ABCEFPABCEFPB4.如图,已知等边△ABC的边长为8,点P是AB边上的一个动点(与点A、B不重合).直线l是经过点P的一条直线,把△ABC沿直线l折叠,点B的对应点是点B’.当PB=6时,在直线l变化过程中,求△ACB’面积的最大值.【分析】考虑l是经过点P的直线,且△ABC沿直线l折叠,所以B’轨迹是以点P为圆心,PB为半径的圆弧.考虑△ACB’面积最大,因为AC是定值,只需B’到AC距离最大即可.过P作作PH⊥AC交AC于H点,与圆的交点即为所求B’点,先求HB’,再求面积.5.如图,矩形ABCD 中,AB =4,BC =8,P 、Q 分别是直线BC 、AB 上的两个动点,AE =2,△AEQ 沿EQ 翻折形成△FEQ ,连接PF 、PD ,则PF +PD 的最小值是_________.【分析】F 点轨迹是以E 点为圆心,EA 为半径的圆,作点D 关于BC 对称点D ’,连接PD ’,PF +PD 化为PF +PD ’.连接ED ’,与圆的交点为所求F 点,与BC 交点为所求P 点,勾股定理先求ED ‘,再减去EF 即可.Q ABC DEFPD'PFE DCBAQ二、定边对直角知识回顾:直径所对的圆周角是直角.构造思路:一条定边所对的角始终为直角,则直角顶点轨迹是以定边为直径的圆或圆弧. 图形释义:若AB 是一条定线段,且∠APB =90°,则P 点轨迹是以AB 为直径的圆.6.已知正方形ABCD 边长为2,E 、F 分别是BC 、CD 上的动点,且满足BE =CF ,连接AE 、BF ,交点为P 点,则PD 的最小值为_________.【分析】由于E 、F 是动点,故P 点也是动点,因而存在PD 最小值这样的问题,那P 点轨迹如何确定?考虑BE =CF ,易证AE ⊥BF ,即在运动过程中,∠APB =90°,故P 点轨迹是以AB 为直径的圆.连接OC ,与圆的交点即为P 点,再通过勾股定理即可求出PC 长度.思路概述:分析动点形成原理,通常“非直即圆”(不是直线就是圆),接下来可以寻找与动点相关有无定直线与定角.ABEFABCDPF7.如图,E 、F 是正方形ABCD 的边AD 上的两个动点,满足AE =DF ,连接CF 交BD 于点G ,连接BE 交AG 于点H ,若正方形边长为2,则线段DH 长度的最小值是________.【分析】根据条件可知:∠DAG =∠DCG =∠ABE ,易证AG ⊥BE ,即∠AHB =90°,所以H 点轨迹是以AB 为直径的圆弧当D 、H 、O 共线时,DH 取到最小值,勾股定理可求.HGAB CDEFαααHGABCDE F8.如图,Rt △ABC 中,AB ⊥BC ,AB =6,BC =4,P 是△ABC 内部的一个动点,且满足∠P AB =∠PBC ,则线段CP 长的最小值是_________.【分析】∵∠PBC +∠PBA =90°,∠PBC =∠P AB , ∴∠P AB +∠PBA =90°, ∴∠APB =90°,∴P 点轨迹是以AB 为直径的圆弧.当O 、P 、C 共线时,CP 取到最小值,勾股定理先求OC ,再减去OP 即可.9.如图, AB 是半圆O 的直径,点C 在半圆O 上,AB =5,AC =4.D 是弧BC 上的一个动点,连接AD ,过点C 作CE ⊥AD 于E ,连接BE .在点D 移动的过程中,BE 的最小值为 .【分析】E 是动点,E 点由点C 向AD 作垂线得来,∠AEC =90°,且AC 是一条定线段,所以E 点轨迹是以AC 为直径的圆弧.PABCCCB当B 、E 、M 共线时,BE 取到最小值.连接BC ,勾股定理求BM ,再减去EM 即可.10.如图,在Rt △ABC 中,∠ACB =90°,BC =4,AC =10,点D 是AC 上的一个动点,以CD 为直径作圆O ,连接BD 交圆O 于点E ,则AE 的最小值为_________.【分析】连接CE ,由于CD 为直径,故∠CED =90°,考虑到CD 是动线段,故可以将此题看成定线段CB 对直角∠CEB .BB取CB 中点M ,所以E 点轨迹是以M 为圆心、CB 为直径的圆弧.连接AM ,与圆弧交点即为所求E 点,此时AE值最小,22AE AM EM =−==.11.如图,正方形ABCD 的边长为4,动点E 、F 分别从点A 、C 同时出发,以相同的速度分别沿AB 、CD 向终点B 、D 移动,当点E 到达点B 时,运动停止,过点B 作直线EF 的垂线BG ,垂足为点G ,连接AG ,则AG 长的最小值为 .【分析】首先考虑整个问题中的不变量,仅有AE =CF ,BG ⊥EF ,但∠BGE 所对的BE 边是不确定的.GF EDCB A重点放在AE =CF ,可得EF 必过正方形中心O 点,连接BD ,与EF 交点即为O 点.∠BGO 为直角且BO 边为定直线,故G 点轨迹是以BO 为直径的圆.记BO 中点为M 点,当A 、G 、M 共线时,AG 取到最小值,利用Rt △AOM 勾股定理先求AM ,再减去GM 即可.12.如图,正方形ABCD 的边长是4,点E 是AD 边上一动点,连接BE ,过点A 作AF ⊥BE 于点F ,点P 是AD 边上另一动点,则PC +PF 的最小值为________.【分析】∠AFB =90°且AB 是定线段,故F 点轨迹是以AB 中点O 为圆心、AB 为直径的圆.AB C DE F GABCDE FP考虑PC +PF 是折线段,作点C 关于AD 的对称点C ’,化PC +PF 为PC ’+PF ,当C ’、P 、F 、O 共线时,取到最小值.13.如图,在Rt △ABC 中,∠ACB =90°,∠B =30°,AB =4,D 是BC 上一动点,CE ⊥AD 于E ,EF ⊥AB 交BC 于点F ,则CF 的最大值是_________.【分析】∠AEC =90°且AC 为定值,故E 点轨迹是以AC 为直径的圆弧.考虑EF ⊥AB ,且E 点在圆上,故当EF 与圆相切的时候,CF 取到最大值.F EDCBAB连接OF ,易证△OCF ≌△OEF ,∠COF =30°,故CF 可求.三、定边对定角在“定边对直角”问题中,依据“直径所对的圆周角是直角”,关键性在于寻找定边、直角,而根据圆周角定理:同圆或等圆中,同弧或等弧所对的圆周角都相.定边必不可少,而直角则可一般为定角.例如,AB 为定值,∠P 为定角,则A 点轨迹是一个圆.当然,∠P 度数也是特殊角,比如30°、45°、60°、120°,下分别作对应的轨迹圆. 若∠P =30°,以AB 为边,同侧构造等边三角形AOB ,O 即为圆心.若∠P =45°,以AB 为斜边,同侧构造等腰直角三角形AOB ,O 即为圆心.BB若∠P =60°,以AB 为底,同侧构造顶角为120°的等腰三角形AOB ,O 即为圆心.若∠P =120°,以AB 为底,异侧为边构造顶角为120°的等腰三角形AOB ,O 即为圆心.14.如图,等边△ABC 边长为2,E 、F 分别是BC 、CA 上两个动点,且BE =CF ,连接AE 、BF ,交点为P 点,则CP 的最小值为________.【分析】由BE =CF 可推得△ABE ≌△BCF ,所以∠APF =60°,但∠APF 所对的边AF 是变化的.EFCBAP60°EF CBAP所以考虑∠APB =120°,其对边AB 是定值.所以如图所示,P 点轨迹是以点O 为圆心的圆弧.(构造OA =OB 且∠AOB =120°)当O 、P 、C 共线时,可得CP 的最小值,利用Rt △OBC 勾股定理求得OC ,再减去OP 即可.15.如图,△ABC 为等边三角形,AB =2,若P 为△ABC 内一动点,且满足∠P AB =∠ACP ,则线段PB 长度的最小值为_________.120°EF CBAP 120°MOP ABCF E120°ABCP【分析】由∠P AB =∠ACP ,可得∠APC =120°,后同上例题.16.在△ABC 中,AB =4,∠C =60°,∠A >∠B ,则BC 的长的取值范围是________. 【分析】先作图,如下条件不多,但已经很明显,AB 是定值,∠C =60°,即定边对定角.故点C 的轨迹是以点O 为圆心的圆弧.(作AO =BO 且∠AOB =120°)题意要求∠A >∠B ,即BC >AC ,故点C 的轨迹如下图.当BC 为直径时,BC 取到最大值,考虑∠A 为△ABC 中最大角,故BC 为最长边,BC >AB =4.无最小值.4ABC 60°17.如图,AB 是圆O 的直径,M 、N 是弧AB (异于A 、B )上两点,C 是弧MN 上一动点,∠ACB 的角平分线交圆O 于点D ,∠BAC 的平分线交CD 于点E ,当点C 从点M 运动到点N 时,则C 、E 两点的运动路径长的比是_______.【分析】分别考虑C 、E 两点的轨迹,C 点轨迹上是弧MCN ,其对应圆心角为∠MON ,半径为OM (或ON ).再考虑E 点轨迹,考虑到CE 、AE 都是角平分线,所以连接BE ,BE 平分∠ABC ,可得:∠AEB =135°.考虑到∠AEB 是定角,其对边AB 是定线段,根据定边对定角,所以E 点轨迹是个圆,考虑到∠ADB =90°,所以D 点即为圆心,DA 为半径.E 点轨迹所对的圆心角为∠MDN ,是∠MON 的一半,所以C 、E 两点轨迹圆半径之比为1:根号2,圆心角之比为2:1,所以弧长比值为根号2.ABAA。
巧用辅助圆,妙解几何题

巧用协助圆,妙解几何题在一些数学题中,看似与圆毫没关系可是用惯例的解题方法却没法解决问题,而经过题中的某些条件结构协助圆,运用圆的知识进行解答,常常就会使题目简单化,进而使难题水到渠成 .本文联合一些实例,探析怎样巧用协助圆妙解几何题.一、几何问题中的求线段长度求线段的长度是初中数学比较常有的问题.该问题的惯例解法是经过做垂直线建立直角三角形进而运用勾股定理或是巧用面积公式 .可是在一些问题中,经过直接作出垂线,常常会使图形更为复杂,进而不可以成功解题例 1 如下图,在四边形ABCD 中, AD // BC ,已知BC CD AC 23,AB6.则BD.分析经过题干中的条件BC CD AC ,我们能够想到以 C 为圆心, BC 为半径作圆.依据圆的性质:直径对应的圆周角为直角,能够延伸BC 交于⊙ C 于点 E ,连结 DE ,如图所示,此时V BDE 为直角三角形. Q AD // BC,AB DE 6 ,由勾股定理得BD42 BD.点拨依据题干中的线段相等,进而建立协助圆,接着利用圆的性质进行解题.此中需要注意的是,固然协助圆能做出,可是要想解题,就要对圆的性质有一个深刻的理解.二、几何问题中的求角的度数求角的度数问题一般都是以三角形为载体,该问题的惯例解法是利用三角函数的知识去解答,可是因为初中数学只学习了一些特别的三角函数值且在直角三角形的载体中.当遇到一般的三角形,此时学生常常会无能为力例 2如下图,在VABC中,此中 AB AC,BD是ABC 的均分线,BD AD BC,则 A.分析由题意得,本题要求的是 A ,因为本题见告随意一个角的大小且V ABC 也不是直角三角形,所以运用三角函数的知识是很难解答该题的.由题干中BD均分ABC ,可得ABD DBC .作 V ABC 的外接圆,如下图.依据圆的性质可得,AD DE .因为四边形 ABED 为内接四边形,所以ABC EDC C,所以2C DEB ,DE EC .因为BD AD BC BE EC且AD DE EC,所以BE BD .因为DEB BDE2C,在 VBDE中,DEB BDE DBE180,即41C 180,得 C40 .在 VABC 中,A ABC C180,得C2A 100.点拨本题是依据角均分线进而想到画出三角形的外接圆,而后找出各角之间的关系进行解答的 .所以,在求解角的度数时,要充足运用协助圆,找出相等的角,最后经过运用三角形内角和为180 列出式子求解.此类题型的难点在于,怎样画出协助圆.三、几何问题中的求最值求最值的问题在中考取是常有问题,其一般的思路就是设未知数,而后找寻关系列出函数表达式,即可解答出 .固然解题思路清楚,可是此类题型的难点就是在怎样将条件整合起来,找出其之间的关系,例 3如下图,在 RtV ABC 中,BAC 30 ,AB 2 3,动点P、Q分别在AB、AC 上,CPQ 90 ,则 CQ min.分析经过审题后,感觉CQ 就是独立的,没法向已知条件上靠,独一能够用的就是CPQ90,可是没法运用勾股定理,因为三条边都是未知的.可是经过认真审题,从条件 CPQ 90 出发,能够想到圆的直径对应的圆周角为直角此时能够试试看,看画出辅助圆对解题有无帮助.经过图能够看出,要想CQ 最小,AB与⊙O 要相切.此时就能够依据OP AB,OP OC,可得APQ30,此时设PQ OQ OP OC r,3r AC cos30 gAB 3 ,解得r1,所以CQ min 2 .点拨依据题干中条件画出协助圆,借助圆的性质:圆心到切点之间的线段最短是解答本题重点,可见协助圆对题目的综合剖析起了很大的作用.此中需要特别注意的是,当题中给出直角时不可以单单的只想到勾股定理也要联想到圆.综上所述,在解答几何问题时,如若发现运用惯例方法不可以解决问题或是解决过程比较繁琐,此时能够经过认真审题,发掘题干中与圆有联系的条件,进而做出协助圆进行剖析解题 .因为做出协助圆的重点就是擅长捕获题干的细节之处,这对学生的要求比较高,所以学生要在此后的学习中勤总结.。
绝杀中考压轴题:“辅助圆模型”
辅助圆模型1 . 共端点,等线段模型分析:(1)若有共端点的三条等线段,可思考构造辅助圆。
一般来说,构造辅助圆是为了利用圆的性质来解决角度问题。
例子:如图,△ABC和△ACD都是等腰三角形,AB=AC,AC=AD,连接BD。
求证:∠1+∠2=90°。
证明:利用模型构造辅助圆,∵AB=AC,∴∠ABC=∠2,∵∠BAC=2∠1,∴2∠2+2∠1=180°,∴∠1+∠2=90°。
方法二:利用模型构造辅助圆,延长CA交圆于点E,联结BE,∵CA是直径,∴∠EBC=90°。
∴∠E+∠2=90°,∵∠1=∠E,∴∠1+∠2=90°针对训练:如图,△ABC为等腰三角形,AB=AC,在△ABC的外侧作直线AP,点B与点D关于AP轴对称,连接BD、CD,CD与AP交于点E。
求证:∠1=∠2。
提示:可知AD=AB=AC,构造辅助圆可知关键的相等关系,∠1=2∠BDC,∠BDC=∠EBD,∠2=2∠BDC,∠1=∠2。
模型2. 直角三角形共斜边模型分析:共斜边的两个直角三角形,同侧或异侧,都有四点共圆,再根据圆周角定理得到角度相等,完成角度等量关系的代替,是证明角相等的思路之一。
例子:如图,AD、BE、CF为△ABC的三条高,H为垂心,求证:∠ADF=∠ADE。
证明:利用模型,可知B、C、E、F四点共圆,∴∠FBE=∠FCE,B、D、H、F四点共圆,∴∠ADF=∠FBE,D、C、E、H四点共圆,∴∠ADE=∠FCE,∴∠ADF=∠ADE。
针对训练:如图,已知△ABC中,AH是高,AT是角平分线,且TD⊥AB,TE⊥AC。
求:∠AHD=∠AHE。
提示:利用模型可知,A、D、T、E四点共圆,且AT为直径,联结OH,∵AH⊥BC,∴△ATH是直角三角形。
∴OH=1/2AT(O是AT中点),∴点H在圆上,∵AT是角平分线,TD⊥AB,TE⊥AC。
∴△ATD≌△ATE,∴AD=AE,∴∠AHD=∠AHE。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5、如图,在等腰梯形ABCD中,AB∥CD,AB=998,CD=1001,AD=1999,点P在线段AD上,满足条件得∠BPC=90°得点P得个数为()
A、0B.1C.21D.不小于3得整数
(全国初中数学联赛题)
三·四点共圆
1·若有一个四边形对角互补,则四边形得四个顶点四点共圆。
【例3】如图;已知H就是△ABC三条高得交点,连结DF,DE,EF,求证:H就是△DEF得内心。
6。如图,AD、BE就是锐角三角形得两条高,S△ABC=18,S△DEC=2,则COSC等于( )
A.3B、C.D.
8。如图,已知△ABC中,AH就是高,AT就是角平分线,且TD⊥AB,TE⊥AC。
求证:(1)∠AHD=∠AHE;(2)(陕西省竞赛题)
1在凸四边形ABCD得BC边上取两点E,F,E比F离B更近,如果∠BAE=CDF∠EAF=∠FDE证明:∠FAC=∠EDB
5五点共圆(7456)
【例7】如图,已知在凸四边形ABCDE中,∠BAE=3,BC=CD=DE,且∠BCD=∠CDE=.求证:∠BAC=∠CAD=∠DAK,
(全国初中数学联赛题)
课外训练
A组
1.如图,正方形ABCD得中心为O,面积为1989cm2,P为正方形内一点,且∠OPB=45°,PA:PB=5:14,则PB得长为、
2如图在ABC中,AB=AC,D就是BC边上任意一点就是C点关于直线AD得对称点,B与AD交与P试问当D在BC(除BC中点外)上运动时,AD·AP得值有何变化?请加以证明。
3等边ABC中,D,E分别就是BC,CA边上得点,且BD=CE=CD。连接BE,CD交于P,证明:CP垂直AD。
3.运用四点共圆得判定方法:(1)若一个四边形得一组对角互补,则它得四个顶点共圆。
(2)同底同侧张等角得三角形,各顶点共圆。
(3)若四边形ABCD得对角线相交于P,且PA·PC=PB·PD,则它得四个顶点共圆.
(4)若四边形ABCD得一组对边AB、DC得延长线相交于P,且PA·PB=PC·PD,则它得四个顶点共圆、
2.如图,在△ABC中,AB=AC=2,BC边上有100个不同得点Pl、P2,…P100,记(i=1,2,…100),则=.
3。设△ABC三边上得高分别为AD、BE、CF,且其垂心H不与任一顶点重合,则由点A、B、C、D、E、F、H中某四点可以确定得圆共有()
A.3个B。4个C、5个D。6个
(2000年太原市竞赛题)
变式练习:如图,直线AB与AC与⊙O分别相切于B、C,P为圆上一点,P到AB、AC得距离分别为4cm、6cm,那么P到BC得距离为.
(全国初中数学联赛题)
思路点拨连DF,EF,寻找PD、PE、PF之间得关系,证明△PDF∽△PFE,而发现P、D、B、F与P、E、C、F分别共圆,突破角就是解题得关键.
第二十五讲辅助圆
在处理平面几何中得许多问题时,常需要借助于圆得性质,问题才得以解决。
而我们需要得圆并不存在(有时题设中没有涉及圆;有时虽然题设涉及圆,但就是此圆并不就是我们需要用得圆),这就需要我们利用已知条件,借助图形把需要得实际存在得圆找出来,添补辅助圆得常见方法1。利用圆得定义添补辅助圆;2、作三角形得外接圆;
【例4】如图,在△ABC中,高BE、CF相交于H,且∠BHC=135°,G为△ABC内得一点,且GB=GC,∠BGC=3∠A,连结HG,求证:HG平分∠BHF、
思路点拨经计算可得∠A=45°,△ABE,△BFH皆为等腰直角三角形,只需证∠GHB=∠GHF=22。5°.
由∠BGC=3∠A=135°=∠GHC,得B、G、H、C四点共圆,运用圆中角转化灵活得特点证明.
【例题求解】
一·利用圆得定义添加辅助圆
【例1】如图,若PA=PB,∠APB=2∠ACB,AC与PB交于点P,且PB=4,PD=3,则AD·DC等于( )
A.6B.7C.12D、16
思路点拨作出以P点为圆心、PA长为半径得圆,为相交弦定理得应用创设了条件、
注:到一个定点等距离得几个点在同一个圆上,这就是利用圆得定义添辅助圆得最基本方法.
注:许多直线形问题借助辅助圆,常能降低问题得难度,使问题获得简解、巧解或新解.
变式练习:已知等腰三角形ABC,AB=AC,AD垂直BC于D,DE垂直AC于E,F就是DE中点,求证:AF垂直于BE。
3把被证共圆得四点两两连成相交得两条线段,若能证明它们各自被交点分成得两线段之积相等,即可肯定这四点共圆;
【例5】如图,P就是⊙O外一点,PA与PB就是⊙O得切线,A,B为切点,PO与AB交于点M,过M任作⊙O得弦CD.求证:∠CPO=∠DPO.
4把被证共圆得四点两两连结并延长相交得两线段,若能证明自交点至一线段两个端点所成得两线段之积等于自交点至另一线段两端点所成得两线段之积,即可肯定这四点也共圆.
【例6】如图,P就是⊙O外一点,PA切⊙O于A,PBC就是⊙O得割线,AD⊥PO于D、求证:、
思路点拨因所证比例线段不就是对应边,故不能通过判定△PBD与△PCD相似证明.PA2=PD·PO=PB·PC,B、C、O、D共圆,这样连OB,就得多对相似三角形,以此达到证明得目得.
注:四点共圆既就是一类问题,又就是平面几何中一个重要得证明方法,它与证明三角形全等与相似三角形有着同等重要得地位,这就是因为,某四点共圆,不但与这四点相联系得条件集中或转移,而且可直接运.用圆得性质为解题服务.
变式练习:如图,已知OA=OB=OC,且∠AOB=∠BOC,则∠ACB就是∠BAC得()
A、倍B.就AB=AC,任意延长CA到P,再延长AB到Q,使AP=BQ,求证:△ABC得外心O与A,P,Q四点共圆、
思路点拨先作出△ABC得外心O,连PO、OQ,将问题转化为证明角相等、
注:圆具有丰富得性质:(1)圆得对称性;
(2)等圆或同圆中不同名称量得转化;
(3)与圆相关得角;(4)圆中比例线段.
适当发现并添出辅助圆,就为圆得丰富性质得运用创造了条件,由于图形得复杂性,有时在图中并不需画出圆,可谓“图中无圆,心中有圆”、
2·同底同侧有相等顶角得三角形,则各顶点四点共圆(若能证明其两顶角为直角,即可肯定这四个点共圆,且斜边上两点连线为该圆直径。)
