Excel矩阵运算
excel的矩阵运算

excel的矩阵运算在Excel中进行矩阵运算,可以使用数组公式和一些特定的函数来实现。
以下是一些关于在Excel中进行矩阵运算的方法和步骤:1.矩阵加法和减法:假设你有两个矩阵A和B,它们位于Excel的不同区域,例如A1:C3和E1:G3。
你可以使用数组公式来进行矩阵的加法和减法。
* 矩阵加法:选择一个空白的区域,例如I1:K3,输入公式=A1:C3+E1:G3,然后按Ctrl+Shift+Enter组合键。
这将计算矩阵A和B的和,并将结果显示在选定的区域中。
* 矩阵减法:选择一个空白的区域,例如I1:K3,输入公式=A1:C3-E1:G3,然后按Ctrl+Shift+Enter组合键。
这将计算矩阵A减去矩阵B的结果,并将结果显示在选定的区域中。
2.矩阵乘法:在Excel中,可以使用MMULT函数来进行矩阵乘法。
假设你有两个矩阵A和B,它们位于Excel的不同区域,例如A1:C3和E1:G3。
以下是使用MMULT函数进行矩阵乘法的步骤:* 选择一个空白的区域,例如I1:K3。
* 输入公式=MMULT(A1:C3, E1:G3),然后按Enter键。
这将计算矩阵A和B的乘积,并将结果显示在选定的区域中。
3.矩阵的逆和转置:在Excel中,可以使用MINVERSE函数来计算矩阵的逆矩阵,使用TRANSPOSE函数来计算矩阵的转置。
以下是使用这些函数的步骤:* 逆矩阵:选择一个空白的区域,例如I1:K3,输入公式=MINVERSE(A1:C3),然后按Ctrl+Shift+Enter组合键。
这将计算矩阵A的逆矩阵,并将结果显示在选定的区域中。
* 转置矩阵:选择一个空白的区域,例如I1:K3,输入公式=TRANSPOSE(A1:C3),然后按Enter键。
这将计算矩阵A 的转置,并将结果显示在选定的区域中。
Excel 矩阵运算及引用

利用Excel中函数进行矩阵运算实验一、实验目的与要求了解Excel的函数应用并能够利用Excel进行常用的矩阵运算。
掌握以Excel 中的几个主要矩阵运算函数的功能,即MDETERM:用于计算矩阵行列式的值;MINVERSE:用于求解某个可逆矩阵的逆矩阵;MMULT:用于计算两个矩阵的乘积,进行两个矩阵的乘法时必须确保第一个乘积矩阵的列等于第二个乘积矩阵的行;TRANSPOSE:用来求解矩阵的转置或用于Excel中行列的互换。
二、实验内容及步骤1.矩阵的数乘用一个数乘以一个矩阵,必须将该数与矩阵的每一个元素相乘。
将单元格B3中的数字乘以矩阵A,只需在单元格B10中输入公式“=$B$3*B5”(注意:单元格B3必须采用绝对引用,及固定单元格),然后将其复制到B10:D12区域(利用自拖功能也可以实现),最终结果见下表:矩阵的数乘2.矩阵的加法具有相同行列的两个矩阵才能相加。
要进行矩阵的加法,只需将两个矩阵相同行、列的元素相加,即可得到新的矩阵。
如下图,要将矩阵A和B相加,只需在单元格G4中输入公式“=A4+D4”,并将其复制到G4:H8区域(利用自拖功能也可以实现),就可得到最终结果。
矩阵的相加3.矩阵的转置对矩阵E进行转置,首先选中打算放置输出结果的整个单元格区域F4:H7,然后选择“插入-函数”,在“查找与引用”或“全部”函数中选择函数“TRANSPOSE”。
在“函数参数”的对话框中输入“A4:D6”,同时按住[Ctrl]+[Shift]+[Enter]键,最终得到下列结果。
矩阵转置也可以利用复制,选择性粘贴中选择转置即可得到上述结果。
4、矩阵相乘做法一:进行矩阵乘法必须保证第一个乘积矩阵的列等于第二个乘积矩阵的行。
首先选中打算放置输出结果的整个单元格区域A9:D10,然后选择“插入-函数”,在“数学与三角”或“全部”函数中选择函数“MMULT”。
在“函数参数”的对话框中分别输入第一个数组“A4:C5”和第二个数组“E4:H6”,同时按住[Ctrl]+[Shift]+[Enter]键,最终得到下列结果。
用Excel进矩阵计算

用Excel进行矩阵计算一、Excel的数组、数组名和矩阵函数的设置1矩阵不是一个数,而是一个数组。
在Excel里,数组占用一片单元域,单元域用大括号表示,例如{A1:C3},以便和普通单元域A1:C3相区别。
设置时先选定单元域,同时按Shift+Ctrl+Enter键,大括弧即自动产生,数组域得以确认。
2Excel的一个单元格就是一个变量,一片单元域也可以视为一组变量。
为了计算上的方便,一组变量最好给一个数组名。
例如A={A1:C3}、B={E1:G3}等。
数组名的设置步骤是:选定数组域,点“插入”菜单下的“名称”,然后选择“定义”,输入数组名如A或B等,单击“确定”即可。
3矩阵函数是Excel进行矩阵计算的专用模块。
常用的矩阵函数有MDETERM(计算一个矩阵的行列式)、MINVERSE(计算一个矩阵的逆矩阵)、MMULT(计算两个矩阵的乘积)、SUMPRODUCT(计算所有矩阵对应元素乘积之和)……函数可以通过点击“=”号,然后用键盘输入,可以通过点击“插入”菜单下的“函数”,或点击fx图标,然后选择“粘贴函数”中相应的函数输入。
二、矩阵的基本计算数组计算和矩阵计算有很大的区别,我们用具体例子说明。
已知A={3 -2 5,6 0 3,1 5 4},B={2 3 -1,4 1 0,5 2 -1},将这些数据输入Excel相应的单元格,可设置成图1的形状,并作好数组的命名,即第一个数组命名为A,第二个数组命名为B。
计算时先选定矩阵计算结果的输出域,3×3的矩阵,输出仍是3×3个单元格,然后输入公式,公式前必须加上=号,例如=A +B、=A-B、=A*B等。
A+B、A-B数组运算和矩阵运算没有区别,“=A*B”是数组相乘计算公式,而“=MMULT(A,B)”则是矩阵相乘计算公式,“=A/B”是数组A除数组B的计算公式,而矩阵相除是矩阵A 乘B的逆矩阵,所以计算公式是“=MMULT(A,MINVERSE(B))”。
Excel中矩阵的运算

nxn方阵对应行列式的值第二步,选中A4单元格,在“插入”菜单中选中“函数”菜单项:第三步,在打开的“函数”对话框中,选中“MDETERM”函数如图2,并按“确定”按钮:第四步,在弹出的对话框中输入矩阵所在的地址,按确定即得到行列式的值。
矩阵求和已知第二步,在A5单元格中输入公式:=A1+El,按回车,这时A5中显示数字7;第三步,选中A5单元格,移动鼠标至其右下角,鼠标形状变为黑色十字时,按下鼠标左键往右拖至C5,B5和C5中分别显示一3.3。
同样的方法选中A5:C5,往下拖至A7:C7,便得到A+B的值。
矩阵求逆第一步,在A1:C3中输入矩阵A;第二步。
选中A5:C7,“插入”→“函数”→“MINVERSE”→“确定”:第三步,在“array”项中输入A1:C3,按F2,同时按CTRL+SHIFF+ENTER即可如图6。
5矩阵转置第一步,在Al:C3中输入矩阵A,并选中;第二步,“编辑”→“复制”;第三步,选中A5,“编辑”→“选择性粘贴”→“转置”→确定”。
矩阵求秩6.1矩阵秩的概念定义设A是mxn矩阵,从A中任取k行k列(k≤min(m,n)),由这些行、列相交处的元素按原来的次序所构成的阶行列式,称为矩阵A的一个k阶子行列式,简称k阶子式。
定义矩阵A的所有不为零的子式的最高阶数r称为矩阵A的秩,记作r(A),即r(A)=r。
6.2矩阵秩的数学求法6.2.1行列式法:即定义从矩阵的最高阶子式算起,计算出不等于零的子式的最高阶数r,此r即为该矩阵的秩。
6.2.2行初等变换法:用初等行变换化矩阵为阶梯形矩阵,此阶梯形矩阵非零行的行数r就是该矩阵的秩。
6.3利用EXCEL求矩阵秩方法一,根据矩阵秩的定义,可以求所有不为零子式的最高阶数。
求矩阵A的秩.显然A是4x4矩阵,4为其所有子式的最高阶数。
先求IAI的值,若|A|不为零,则矩阵A的秩为4。
若|A|为零,求所有阶数为3的子式的值。
若存在阶数为3的子式的值不为零,则矩阵A的秩为3,否则继续求所有阶数为2的子式的值,依次类推。
excel中矩阵的计算
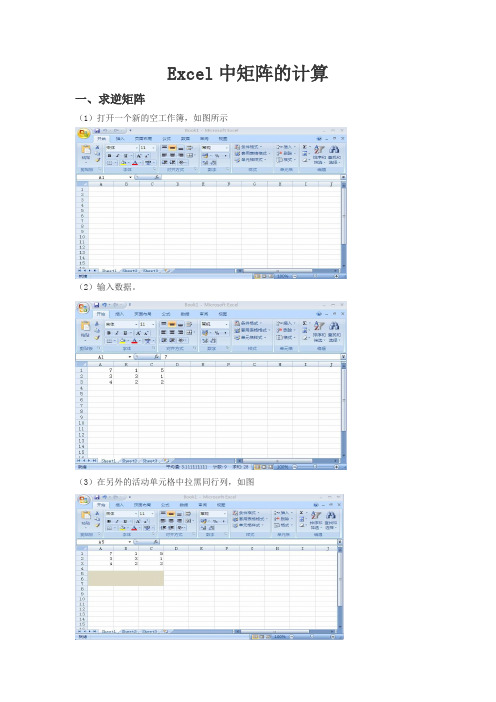
Excel中矩阵的计算一、求逆矩阵(1)打开一个新的空工作簿,如图所示(2)输入数据。
(3)在另外的活动单元格中拉黑同行列,如图(4)点击“公式”-fx,点击“数学与三角函数”(5)点击求逆矩阵的函数键MINVERSE(6)点击确定,输入原数据所在块的第一个数据的行列 ,加“:”,输入最后一个数据的行列(7) 点击确定后,计算后会返回一个值(8)按F2,然后CRTL+SHIFT+ENTER,就会显示出一个三行三列的矩阵,即原矩阵的逆矩阵二、其他:矩阵法解方程组Excel的数组、数组名和矩阵函数的设置矩阵不是一个数,而是一个数组。
在Excel里,数组占用一片单元域,单元域用大括号表示,例如{A1:C3},以便和普通单元域A1:C3相区别。
设置时先选定单元域,同时按Shift+Ctrl+Enter键,大括弧即自动产生,数组域得以确认。
Excel的一个单元格就是一个变量,一片单元域也可以视为一组变量。
为了计算上的方便,一组变量最好给一个数组名。
例如A={A1:C3}、B={E1:G3}等。
具体操作1、数组名的设置。
选定数组域,点“插入”菜单下的“名称”,然后选择“定义”,输入数组名如A或B等,单击“确定”即可。
或是:选定要命名的单元格,点右键——“命名单元格区域”出现下图即可“命名A”;选定要命名的单元格,点右键——“命名单元格区域”出现下图即可“命名B”;如:已知A={3 -2 5,6 0 3,1 5 4},B={2 3 -1,4 1 0,5 2 -1},将这些数据输入Excel 相应的单元格,可设置成图1的形状,并作好数组的命名,即第一个数组命名为A,第二个数组命名为B。
2、矩阵函数是Excel进行矩阵计算的专用模块。
常用的矩阵函数有:MDETERM(计算一个矩阵的行列式)MINVERSE(计算一个矩阵的逆矩阵)MMULT(计算两个矩阵的乘积)SUMPRODUCT(计算所有矩阵对应元素乘积之和)TRANSPOSE(计算矩阵的转置矩阵)……函数可以通过点击“=”号,然后用键盘输入,可以通过点击“插入”菜单下的“函数”;或点击fx图标,然后选择“粘贴函数”中相应的函数输入。
excel计算矩阵相关运算的教程

excel计算矩阵相关运算的教程
在Excel中输入好数据以后多数情况下需要统计数据,其中有关矩阵的计算较为常用,下面是由店铺分享的excel计算矩阵相关运算的教程,希望对你有用。
excel计算矩阵相关运算的教程:
矩阵相关运算步骤1:输入初始矩阵到单元格中后,选中该矩阵区域,然后复制,右键粘贴,选择“转置”即可。
如附图所示。
使用MDETERM 函数计算矩阵行列式的值
矩阵相关运算步骤2:如果有一个m×n阶的矩阵A,设|A|级该矩阵对应行列式的值。
这里使用上面矩阵转置的矩阵为示例数据。
输入该公式后,发现返回的是非法数据警告,原因在于行列式的值必须符合行列式的规则,行数和列数必须相等,所以计算矩阵行列式的值的前提是该矩阵为方阵。
矩阵相关运算步骤3:如附图所示,计算方阵对应行列式的值就ok了。
利用MINVERSE函数求矩阵的逆矩阵
矩阵相关运算步骤4:注意只有方阵才有逆矩阵,所以该矩阵必须是一个n阶方阵。
在单元格中输入“=MINVERSE(数组)”回车即可得到该矩阵的逆阵。
演示如附图所示。
矩阵相关运算步骤5:步骤1所示的附图并没有计算出逆阵,而是返回了一个#NUM!,原因在于如果矩阵可逆,则|A|不会等于0,也就是说行列式的值为0的矩阵没有逆阵,由于示例的矩阵行列式的值为0,所以不存在可逆阵。
附图为存在可逆阵的一个示例。
注:公式必须你数组公式输入,然后按下F2,再按 Ctrl+Shift+Enter。
excel 计算i矩阵 剑法

Excel计算矩阵剑法I. 概述在现代社会中,信息技术的快速发展给我们的生活带来了诸多便利。
而Excel作为一款常用的办公软件,除了常见的数据处理和图表制作,还可以进行复杂的矩阵运算。
本文将介绍如何使用Excel进行矩阵剑法的计算,以及剑法在矩阵运算中的应用。
II. Excel中的矩阵运算在Excel中,我们可以利用数组公式来进行矩阵运算。
我们需要将矩阵数据输入到Excel的单元格中,然后使用公式来进行运算。
下面以矩阵加法为例,介绍如何在Excel中进行矩阵运算。
1. 矩阵数据输入假设我们有两个3×3的矩阵A和B,我们将矩阵A的数据输入到单元格A1:C3,矩阵B的数据输入到单元格E1:G3。
2. 使用数组公式进行运算在单元格I1中输入公式{=A1:C3+B1:D3},然后按下Ctrl+Shift+Enter,Excel会自动将该公式转换为数组公式,并计算出A矩阵和B矩阵的和,结果将显示在单元格I1:K3中。
III. 矩阵剑法的概念矩阵剑法是一种基于矩阵的加减乘除运算的特殊技巧,它可以帮助我们在进行矩阵运算时更加高效地操作数据。
下面将介绍矩阵剑法的一些基本概念和运算规则。
1. 矩阵的加法对于两个同型矩阵A和B,它们的和记作C=A+B,其中C的每个元素都等于A和B对应位置元素的和。
在Excel中,我们可以使用数组公式来进行矩阵的加法运算,如上文所示。
2. 矩阵的减法与加法类似,矩阵的减法也可以使用数组公式在Excel中进行运算。
两个矩阵A和B的差记作C=A-B,其中C的每个元素都等于A和B 对应位置元素的差。
3. 矩阵的乘法矩阵的乘法是一种较为复杂的运算,对于矩阵A(m×n)和B(n×p),它们的乘积C=A*B是一个m×p的矩阵,C的每个元素都等于A的对应行和B的对应列的乘积之和。
在Excel中进行矩阵乘法时,我们可以使用SUMPRODUCT函数或者数组公式来实现。
EXCEL中的数组公式与矩阵运算

EXCEL中的数组公式与矩阵运算在Excel这个日常办公软件中,数组公式和矩阵运算可能是许多用户比较陌生的概念,但它们却是一些高效操作和复杂计算的利器。
通过灵活运用数组公式和矩阵运算,你可以快速处理大量数据,进行复杂的逻辑运算,实现更高效的工作流程。
什么是数组公式?数组公式是Excel中的一种特殊公式,能够同时处理多个数值,而不是单个数值。
通过数组公式,你可以在一个单元格中计算多个数值,实现更复杂的计算逻辑。
要输入数组公式,你可以在输入完公式后,按下Ctrl+Shift+Enter,而不是单纯的Enter键。
使用数组公式的一个常见场景是在一列或一行数据中查找特定条件下的数值,或者对多个数据进行汇总计算。
比如,你可以利用数组公式在一个范围内查找符合条件的数值并将其相加,而不需要编写复杂的多个公式。
如何进行矩阵运算?矩阵运算是一种在Excel中进行复杂计算的方法,特别适用于涉及多个数据集合的情况。
通过矩阵运算,你可以快速进行大量数据的计算和分析,而无需逐个单元格操作。
在Excel中,你可以使用矩阵函数,如MMULT(矩阵乘法)、MINVERSE(矩阵求逆)、TRANSPOSE(矩阵转置)等,来进行矩阵运算。
这些函数可以帮助你高效地进行线性代数运算,处理复杂的数据关系。
实际案例演示让我们通过一个简单的实际案例来演示数组公式和矩阵运算在Excel中的应用。
假设你有两个矩阵A和B,你想要计算它们的乘积。
你可以使用MMULT函数来实现这一计算,将两个矩阵相乘得到最终结果。
{=MMULT(A1:B2,C1:D2)}在这个公式中,A1:B2和C1:D2分别代表两个矩阵的范围。
通过输入这个数组公式,你可以得到两个矩阵的乘积结果,而无需逐个单元格进行计算。
通过灵活运用数组公式和矩阵运算,你可以在Excel中更高效地处理数据,实现复杂的计算逻辑。
无论是查找特定条件下的数据,还是进行大规模数据的分析,都可以通过这些功能轻松实现。
高级数据处理技巧利用Excel的数组函数进行矩阵运算

高级数据处理技巧利用Excel的数组函数进行矩阵运算高级数据处理技巧——利用Excel的数组函数进行矩阵运算在现代数据分析和处理中,矩阵运算是一个非常重要的概念。
矩阵运算可以帮助我们简化复杂的数据处理过程,并更高效地进行数值计算和统计分析。
而Excel作为广泛使用的电子表格软件,提供了强大的数组函数,使得我们能够轻松地进行矩阵运算。
本文将介绍一些高级数据处理技巧,通过利用Excel的数组函数,来进行矩阵运算。
无论是求矩阵的转置、相乘、求逆,还是进行特征值分解和奇异值分解,Excel都可以轻松胜任。
下面将分别介绍各种运算和使用对应的Excel数组函数的方法。
一、矩阵转置矩阵的转置是指将矩阵的行和列交换位置,得到一个新的矩阵。
在Excel中,我们可以使用TRANSPOSE函数来实现矩阵的转置操作。
具体操作如下:1. 将要进行转置的矩阵数据输入到Excel中的某个区域。
2. 在需要转置结果的位置输入函数"=TRANSPOSE(矩阵区域)"。
3. 按下回车键,即可得到转置后的矩阵结果。
这样,我们就可以方便地实现矩阵的转置操作。
二、矩阵相乘在数据处理中,矩阵相乘是常见的操作,它有助于我们进行矩阵的乘法运算和线性变换等。
在Excel中,我们可以使用MMULT函数来实现矩阵的相乘操作。
具体操作如下:1. 将要相乘的两个矩阵数据输入到Excel中的不同区域。
2. 在需要相乘结果的位置输入函数"=MMULT(矩阵1, 矩阵2)"。
3. 按下回车键,即可得到相乘后的矩阵结果。
通过使用MMULT函数,我们可以方便地实现矩阵相乘的运算,并得到运算结果。
三、矩阵求逆求矩阵的逆是在数据处理和统计分析中常用的操作之一。
通过求矩阵的逆,我们可以解线性方程组、进行参数估计等。
在Excel中,我们可以使用MINVERSE函数来实现矩阵的求逆操作。
具体操作如下:1. 将要求逆的矩阵数据输入到Excel中的某个区域。
EXCEL进行矩阵计算
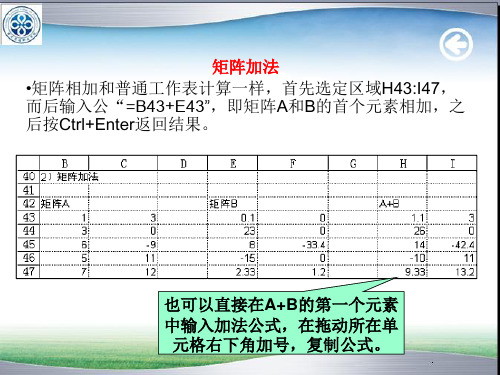
也可以直接在A+B的第一个元素 中输入加法公式,在拖动所在单 元格右下角加号,复制公式。
矩阵转置 •矩阵转置在Excel中通过函数Transpose完成,操作方法是 首先选定结果区域,而后在公式栏中输入“=Transpose(原 始矩阵)”,结果区域要根据原始矩阵的大小设定,如原始矩 阵为4行3列,则选定的结果区域需为3行4列方可返回全部转 置结果,由于Transpose函数属于数组函数,在输入公式后 需同按Ctrl+Shift+Enter键返回,结果将以花括号标识,代表 此函数为数组运算结果:
也可以用选择性粘贴,选转置选项。
矩阵乘法 •矩阵乘法在Excel中通过函数MMult完成,操作方法是首先 选定结果区域,而后在公式栏中输入“=MMult(矩阵A,矩阵 B)”,结果区域要根据原始矩阵的大小设定,如原始矩阵分 别为2行2列和2行3列,则选定的结果区域需为2行3列方可返 回全部结果,即要求矩阵A的列数等于矩阵B的行数。由于 MMult函数属于数组函数,在输入公式后需同按 Ctrl+Shift+Enter键返回,数组运算结果:
矩阵逆运算 •矩阵求逆在Excel中通过函数MInverse完成,操作方法是先 选定结果区域,而后在公式栏输入“=MInverse (原始矩阵)”, 结果区域要根据原始矩阵大小设定,如原始矩阵为4行4列, 则选定的结果区域需为4行4列方可返回全部结果。由于 MInverse函数属于数组函数,输入公式后按Ctrl+Shift
运用Excel矩阵运算

1 Excel 进行矩阵运算 1.1 Excel 的矩阵定义矩阵不是一个数,而是一个数组。
为方便计算,最好对矩阵命名。
矩阵命名的步骤是:选定数组域(矩阵所占的单元格),点“插入”菜单下的“名称”,然后选择“定义”,输入A 或B 等,单击“确定”即可。
则矩阵命名为A 或B 。
1.2 Excel 的常用矩阵函数Excel 常用矩阵函数有:MDETERM(array)(计算一数组所代表的矩阵的行列式的值)、MINVERSE(array)(计算一数组所代表的矩阵的逆矩阵)和 MMULT(arrayl ,rray2)(计算两个数组矩阵的乘积)。
函数运用有三种方法:(1)通过在编辑栏输入“=”号,输入函数名称;(2)通过点击“插入”菜单下的“函数”,选择“函数类别”的“数学与三角函数”;(3)点击工具栏图标x f ,然后选择“插入函数”中相应的函数。
1.3用Excel 进行矩阵转置输入要转置的矩阵,选定该矩阵复制,选定存放结果的第一个单元格,点鼠标右键点 “选择性粘贴”命令,在选择性粘贴对话框,选中“转置”复选框,单击确定即可。
1.4 用Excel 进行矩阵相乘矩阵相乘是运用函数MMULT(A ,B),其方法如下: (1) 输入矩阵A 、B ,要求A 的列数与B 的行数相等;(2) 在空白区选择一存放相乘结果矩阵D 的区域,与D 矩阵行数和列数相同; (3) 保持该区域为选中状态,选择“插入”菜单中的“fx 函数”,打开插入函数窗口,在窗口中选择“数学与三角函数”中的MMULT 函数,单击确定。
(4) 在函数参数窗口,在Array1中输入A , Array2中输入B ,按 “Ctrl+Shift+Enter ”,特别注意,不能直接按回车键,必须按住“Ctrl ”‘Shift ”后再按回车键,运行得出AB 相乘的结果D 矩阵。
1.5 用Excel 进行矩阵求逆应用矩阵函数“MINVERSE(array)”进行矩阵求逆。
Excel在矩阵中的计算演示

Excel矩阵计算演示Excel中除了基于纯量的计算函数外,同时还有许多矩阵运算函数,通过这些这些函数,可以直观、快速的完成一些复杂的计算。
本例将全面介绍如何在工作表中进行矩阵运算。
【Summary】1、矩阵转置Excel函数:=Transpose(原矩阵)2、矩阵乘法,A、B矩阵相乘Excel函数:=MMult(矩阵A,矩阵B)3、求逆矩阵Excel函数:=MInverse (原矩阵)4、求矩阵行列式的值Excel函数:=MDETERM(矩阵)5、以上函数均有两种操作方法:一是直接在公示栏输入以上相应公式;二是选择“插入→函数→常用函数”,然后选择相应函数即可。
【矩阵类型】矩阵的基本类型包括行向量、列向量和矩阵,这些形式在工作表中都可以得到直观地展现,如:【矩阵和纯量的算术运算】矩阵和纯量的运算要求矩阵中的每个元素和纯量一一运算,在工作表中只需将该纯量设定为绝对引用后通过Ctrl+Enter即可完成计算,如C29为纯量,C31:E33为3*3矩阵,将二者相乘只需选定结果区域后选择矩阵的第一个元素C31和纯量C29相乘,而后将C29设定为绝对应用,即$C$29,之后按Ctrl+Enter,即在选定区域中返回计算结果:【矩阵加法】矩阵相加和普通工作表计算一样,首先选定区域H43:I47,而后输入公式“=B43+E43”,即矩阵A和B的首个元素相加,之后按Ctrl+Enter返回结果。
【矩阵转置】矩阵转置在Excel中通过函数Transpose完成,操作方法是首先选定结果区域,而后在公式栏中输入“=Transpose(原始矩阵)”,结果区域要根据原始矩阵的大小设定,如原始矩阵为4行3列,则选定的结果区域需为3行4列方可返回全部转置结果,由于Transpose函数属于数组函数,在输入公式后需同按Ctrl+Shift+Enter键返回,结果将以花括号标识,代表此函数为数组运算结果:返回结果如下:【矩阵乘法】矩阵乘法在Excel中通过函数MMult完成,操作方法是首先选定结果区域,而后在公式栏中输入“=MMult(矩阵A,矩阵B)”,结果区域要根据原始矩阵的大小设定,如原始矩阵分别为2行2列和2行3列,则选定的结果区域需为2行3列方可返回全部结果,即要求矩阵A的列数等于矩阵B的行数。
excel 判断矩阵

在Excel中,你可以使用一些内置的函数和公式来创建和操作矩阵。
然而,Excel本身并不直接支持矩阵运算,例如矩阵乘法、矩阵逆或行列式计算等。
这些复杂的矩阵运算需要更高级的数学软件,如MATLAB或Python的NumPy库。
不过,你可以在Excel中创建一个矩阵,并使用一些基本的函数进行操作。
例如,你可以使用数组公式来创建一个矩阵,并使用SUM、AVERAGE等函数来计算矩阵的元素之和或平均值。
如果你想在Excel中进行更复杂的矩阵运算,你可能需要使用VBA宏或者第三方的Excel插件。
下面是一个在Excel中创建和操作矩阵的简单例子:
1. 打开Excel,在A1单元格中输入“1”,在B1单元格中输入“2”,在C1单元格中输入“3”。
然后,在D1、E1和F1中分别输入“4”、“5”和“6”。
这样你就创建了一个3x2的矩阵。
2. 如果你想计算这个矩阵的所有元素之和,你可以在另一个单元格中输入`=SUM(A1:F1)`并按Enter键。
这将会返回36,这是这个矩阵所有元素之和。
3. 如果你想计算矩阵的平均值,你可以在另一个单元格中输入`=AVERAGE(A1:F1)`并按Enter键。
这将会返回6,这是这个矩阵所有元素之平均值。
以上就是一些基本的操作。
但如果你需要进行更复杂的矩阵运算,可能需要考虑使用更专业的数学软件或编程语言。
第七节 用excel进行矩阵的简单运算

一、Excel矩阵计算
• 快速生成单位矩阵
– 应用R1C1引用样式 。工具》选项》常规》 “R1C1 引用样式” 前打“√”。
– F5键,会弹出“定位”功能窗口,输入 “R1C1:R42C42”,单击确定,所需区域即被选中。
– 利用IF函数自动生成单位矩阵。直接输入 “=if(row()=column(),1,0)”,然后按 “shift+Ctrl+Enter”,完成单位矩阵。
第七章 关 联
一、Excel矩阵计算
• 矩阵的转置、行列式、相乘、逆矩阵
– 通常用复制-选择性粘贴-转置,或 transpose( )可以实现转置功能。
– 矩阵的行列式语法:MDETERM(array) – 数组的矩阵乘积语法:MMULT(array1,
array2) – 求逆矩阵语法:MINVERSE(array)
第ห้องสมุดไป่ตู้章 关 联
• 一列数据,想把它放到矩阵式的对角线 上。
• =A1:A10*(ROW(A1:A10)=COLUMN(A:J)) 输入公式后,选定10行10列,一起按下 三键。
第七章 关 联
二、河南省2002和2007投入产出 表中投入产出模型的运算
• 直接消耗系数矩阵A的计算(P180)
A QXˆ 1
• 一、Excel矩阵计算 • 二、河南省2002和2007投入产出表中投
入产出模型的运算
第七章 关 联
一、Excel矩阵计算
• 矩阵数组的定义
– 一个单元格就是一个变量,一片单元域也可以视为一组变量, 称为数组。数组可以进行定义。如A={A1:C3}、B={E1:G3} 等。
– 数组名的设置步骤:选定数组域,单击“插入”菜单,选择 “名称”项中的“定义”命令,输入数组名,单击“确定” 按钮即可。
excel矩阵的乘法

excel矩阵的乘法Excel矩阵的乘法在Excel中,矩阵的乘法是一种常用的操作,它可以用来计算两个矩阵相乘的结果。
矩阵的乘法涉及到行、列、元素等概念,下面将详细介绍矩阵乘法的相关知识。
1. 什么是矩阵?矩阵是由数个数按照行列排列成的矩形阵列。
在Excel中,我们可以用二维表格来表示矩阵,其中每个单元格的值就是矩阵中的一个元素。
2. 矩阵的乘法原理矩阵的乘法是指将一个矩阵的每一行与另一个矩阵的每一列进行对应元素的乘法,并将结果进行累加得到新的矩阵。
3. 矩阵乘法的规则矩阵乘法的规则如下:- 第一个矩阵的列数必须等于第二个矩阵的行数;- 乘积矩阵的行数等于第一个矩阵的行数,列数等于第二个矩阵的列数;- 乘法的顺序不可交换,即A*B与B*A的结果一般不相同。
4. 矩阵乘法的操作步骤矩阵乘法的操作步骤如下:- 在Excel中,输入两个矩阵,并确定它们的大小;- 在乘积矩阵的对应单元格中,输入乘法公式,使用SUMPRODUCT函数实现对应元素的乘法和累加;- 拖动公式填充整个乘积矩阵。
5. 矩阵乘法的示例下面以一个示例来说明矩阵乘法的具体操作。
假设有两个矩阵A和B,它们的大小分别为3行2列和2行4列。
在Excel中,我们可以按照行列的方式输入矩阵A和B,如下所示:矩阵A:1 23 45 6矩阵B:7 8 9 1011 12 13 14接下来,我们需要创建乘积矩阵C,其大小为3行4列。
在C1单元格中输入以下公式:=SUMPRODUCT(A1:B1,$A$4:$B$5)然后,拖动公式填充整个乘积矩阵C。
最终,得到的乘积矩阵C如下所示:C:29 32 35 3865 72 79 86101 112 123 1346. 矩阵乘法的应用矩阵乘法在Excel中有广泛的应用,尤其在数据分析和数学建模方面。
例如,可以用矩阵乘法来计算多个变量的线性关系,进行矩阵的特征值和特征向量计算等。
总结:通过以上介绍,我们了解了Excel中矩阵乘法的原理、规则和操作步骤。
Excel高级技巧使用数组公式进行复杂数据提取和汇总计算及矩阵运算

Excel高级技巧使用数组公式进行复杂数据提取和汇总计算及矩阵运算Excel作为一种强大的电子表格工具,不仅可以进行基础的数据输入和计算,还提供了许多高级技巧来处理复杂的数据操作。
本文将介绍如何使用数组公式来进行复杂数据的提取和汇总计算,以及如何进行矩阵运算。
一、数组公式的基本概念在Excel中,数组公式是一种特殊的公式,用于处理多个数据区域。
它可以对多个数据进行一次性的计算,并将结果返回到一个单元格中。
数组公式通常使用大括号{}括起来,并且在输入时需要按下Ctrl+Shift+Enter来确认。
二、使用数组公式进行数据提取数组公式在实际应用中最常见的用途之一是进行数据的提取。
假设我们有一个包含学生成绩的表格,其中包括学生的姓名、科目和成绩。
我们要提取某个学生的所有科目成绩。
首先,我们需要创建一个新的空白单元格,用于存放提取结果。
然后,我们使用数组公式来进行数据提取。
假设学生姓名存放在A列,科目存放在B列,成绩存放在C列,在空白单元格D1中输入以下数组公式:=IF($A$2:$A$10="小明",$B$2:$B$10 & ":" & $C$2:$C$10,"")上述数组公式的含义是,如果A列中的单元格等于"小明",则将B列和C列的单元格合并,并将结果返回到空白单元格中。
通过按下Ctrl+Shift+Enter,数组公式将应用到整个数据区域,并将提取结果显示在空白单元格中。
三、使用数组公式进行数据汇总计算除了数据的提取,数组公式还可以用于进行数据的汇总计算。
假设我们有一个销售数据表格,其中包括产品名称、销售额和销售数量。
我们要计算每个产品的销售总额。
首先,我们需要创建一个新的表格,用于存放汇总结果。
然后,我们使用数组公式来进行数据汇总计算。
假设产品名称存放在A列,销售额存放在B列,销售数量存放在C列,在汇总表格的A列中输入所有的产品名称,在B列中输入以下数组公式:=SUM(IF($A$2:$A$100="产品1",$B$2:$B$100*$C$2:$C$100,0))上述数组公式的含义是,如果A列中的单元格等于"产品1",则将B列和C列的对应单元格相乘,然后求和。
excel矩阵运算大全

excel矩阵运算大全第 1 章 Excel-矩阵的求逆、转置与相乘1.1 SUMSQ(A1,B1) A1和B1各自平方后求和 1.2 TRANSPOSE函数TRANSPOSE函数的功能是求矩阵的转置矩阵。
公式为 = TRANSPOSE(array)式中,Array―需要进行转置的数组或工作表中的单元格区域。
函数TRANSPOSE必须在某个区域中以数组公式的形式输入,该区域的行数和列数分别与array的列数和行数相同。
步骤:(1)选取存放转置矩阵结果的单元格区域。
(2)单击工具栏上的【粘贴函数】按钮,在【粘贴函数】对话框中选取函数TRANSPOSE,在该函数对话框中输入(可用鼠标拾取)单元格A2:C5,按“Crtl+Shift+Enter”组合键,即得转置矩阵。
利用TRANSPOSE函数可以把工作表中的某些行(或列)排列的数据转换成列(或行)排列的数据。
例如,由于工作需要,要把工作表中的某些行数据改为列数据,若一个一个地改动数据,将是很麻烦也很费时的,而利用TRANSPOSE函数则可以很轻松地进行这项工作。
但需要注意的是,利用TRANSPOSE函数对行(列)数据进行转换,则无法单独修改其中转换单元格区域中的某单元格的数据。
1.3 MINVERSE函数MINVERSE函数的功能是返回矩阵的逆矩阵。
公式为 = MINVERSE(array)式中,array―具有相等行列数的数值数组或单元格区域。
MINVERSE函数的使用方法与TRANSPOSE函数是一样的。
在求解线性方程组时,常常用到MINVERSE函数。
1.4 MMULT函数MMULT函数的功能是返回两数组的矩阵乘积。
结果矩阵的行数与 array1 的行数相同,列数与 array2 的列数相同。
公式为= MMULT(array1?array2)式中array1? array2―要进行矩阵乘法运算的两个数组。
array1的列数必须与 array2 的行数相同,而且两个数组中都只能包含数值。
excel数组和矩阵运算

excel数组和矩阵运算一、基本运算自然对数ln(x),对数log(x,底数),指数exp(x),幂函数^阶乘fact(x),双阶乘factdouble,排列permut,组合combin取整int,截断取舍trunc,四舍五入round连乘product,求和sum二、数组运算在Excel里,数组占用一片单元域,单元域用大括号表示,例如{A1:C3}。
设置时先选定输出单元域(必须也是一样大小单元,单个单元格只能显示一个数字),同时按Shift+Ctrl+Enter键,大括弧即自动产生,数组域得以确认。
用花括号{}表示数组。
如{10,20,30;40,50,60}。
数组的各个元素间用逗号与分号分隔,分号表示的是数组的行分隔。
可以进行加、减、乘、除、乘方、开方等运算例如乘方,输入=A1:B4^2,按ctrl+shift+enter例如相乘,输入=A1:B4*D1:E4,按ctrl+shift+enterSUMPRODUCT(array1,array2,array3...):计算所有矩阵的相应元素的乘积之和。
SUMSQ(array),平方和。
等价于公式={sum(A1:B4^2)}SUMXMY2(array_x, array_y),返回两个数组中对应数值之差的平方和,(A-B)^2SUMX2PY2(array_x, array_y),返回两个数组中对应平方和的和,A^2+B^2SUMX2MY2(array_x, array_y),返回两个数组中对应平方差的和,A^2-B^2三、矩阵运算进行矩阵加、减、乘、求逆、转置等。
矩阵加法和减法与数组的加法和减法表达式相同。
它也是“=A+B”和“=A-B”MMULT(array1,array2):计算两个矩阵的乘积;按ctrl+shift+enter。
例如:=MMULT(A,B)MINVERSE(array):计算矩阵的逆矩阵;按ctrl+shift+enterTRANSPOSE(array),转置矩阵,按ctrl+shift+enterMDETERM(array):计算矩阵的行列式;例如:mdeterm(A1:B2) 矩阵除法,A乘以B的逆矩阵,xB=A,有x=A除以B=MMULT(A,MINVERSE(B))。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Excel矩阵计算
目前有很多软件可进行矩阵运算,特别是Matlab,其矩阵运算功能尤为强大。
但这些专业软件所占空间很大,价格昂贵。
其实Excel就有矩阵运算功能,虽然比不上专业软件,但不比一些数学小软件差多少。
下面把从网上搜集到的一些有关利用Excel进行矩阵计算的资料整理如下:
资料一:
(1)数组和矩阵的定义
矩阵不是一个数,而是一个数组。
在Excel里,数组占用一片单元域,单元域用大括号表示,例如{A1:C3},以便和普通单元域A1:C3相区别。
设置时先选定单元域,同时按Shift+Ctrl+Enter键,大括弧即自动产生,数组域得以确认。
一个单元格就是一个变量,一片单元域也可以视为一组变量。
为了计算上的方便,一组变量最好给一个数组名。
例如A={A1:C3}、
B={E1:G3}等。
数组名的设置步骤是:选定数组域,单击“插入”菜单,选择“名称”项中的“定义”命令,输入数组名,单击“确定”按钮即可。
更简单的命名办法为:选择数组域,单击名称框,直接输入名称就行了。
矩阵函数是Excel进行矩阵计算的专用模块。
用“插入”-“函数”命令打开“粘贴函数”对话框(如图11),选中函数分类栏中的“数学与三角函数”,在右边栏常用的矩阵函数有:MDETERM--计算一个矩阵的行列式;MINVERSE--计算一个矩阵的逆矩阵;MMULT--计算两个矩阵的乘积; SUMPRODUCT--计算所有矩阵对应元素乘积之和。
(2)矩阵的基本计算
数组计算和矩阵计算有很大的区别,比如下面这个例子中,A和B都是定义好的数组,因为这两个数组都是3×3的,输出结果也是3×3个单元格。
计算时先选定矩阵计算结果的输出域,为3×3的单元格区域,然后输入公式。
如果输入“=A+B”或“=A-B”,计算结果是数组对应项相加或相减,输入“=A*B”表示数组A和B相乘,输入“=A/B”表示数组A 除数组B。
如果要进行矩阵计算,就要用到相应的矩阵函数。
矩阵相加、相减与数组的加减表达形式是一样的,也是“=A+B”和“=A-B”,表示矩阵相乘可以输入“=MMULT(A,B)”,而矩阵相除是矩阵A乘B 的逆矩阵,所以计算公式是“=MMULT(A,MINVERSE(B))”。
公
式输入后,同时按Shift+Ctrl+Enter键得到计算结果。
对于更复杂的
矩阵计算,可以采用分步计算
资料二:
矩阵转置!
通常用复制-选择性粘贴-转置,或transpose( )可以实现转置功能!
资料三:
矩阵运算函数
1.MDETERM
用途:返回一个数组的矩阵行列式的值。
语法:MDETERM(array)
参数:Array是一个行列数相等的数值数组。
Array可以是单元
格区域,例如A1:C3;或是一个数组常量,如
{1,2,3;4,5,6;7,8,9};也可以是区域或数组常量的名称。
矩阵行列式的值多用于求解多元联立方程。
实例:如果A1=1、A2=2、B1=3、B2=4,则公
式“=MDETERM(A1:B2)”返回-2。
2.MINVERSE
用途:返回数组矩阵的逆距阵。
语法:MINVERSE(array)
参数:Array是具有相等行列数的数值数组,它可以是单元格区域,例如A1:C3;也可以是常数数组如
{1,2,3;4,5,6;7,8,9};或者是两者的名称。
实例:公式“=MINVERSE({4,-1;2,0})”返回
{0,0.5;-1,2};=MINVERSE({1,2,1;3,4,-1;0,2,0})返回{0.25,0.25,-0.75;0,0,0.5;0.75,-0.25,-0.25}。
3.MMULT
用途:返回两数组的矩阵乘积。
结果矩阵的行数与array1的行数
相同,矩阵的列数与array2的列数相同。
语法:MMULT(array1,array2)
参数:Array1和array2是要进行矩阵乘法运算的两个数
组。
Array1的列数必须与array2的行数相同,而且两个数组中都只
能包含数值。
Array1和array2可以是单元格区域、数组常数或引
用。
实例:公式“=MMULT({1,2;2,3},{3,4;4,5})”返回11。
