上海市各区2018届九年级中考二模数学试卷精选汇编:二次函数专题
上海市各区2017-2018届九年级中考二模数学试卷精选汇编:函数综合运用及其他

上海市各区2018届九年级中考二模数学试卷精选汇编函数综合运用专题宝山区、嘉定区22、有一座抛物线拱型桥,在正常水位时,水面BC 的宽为10米,拱桥的最高点D 到水面BC 的距离DO 为4米,点O 是BC 的中点,如图5,以点O 为原点,直线BC 为x 轴,建立直角坐标系xOy .(1)求该抛物线的表达式;(2)如果水面BC 上升3米(即3=OA )至水面EF ,点E 在点F 的左侧, 求水面宽度EF 的长.22.解:(1)根据题意:该抛物线的表达式为:b ax y +=2………………1分 ∵该抛物线最高点D 在y 轴上,4=DO ,∴点D 的坐标为)4,0(………1分 ∵10=BC ,点O 是BC 的中点 ∴点B 的坐标为)0,5(- ∴254-=a ,4=b …2分 ∴抛物线的表达式为:42542+-=x y …………………1分 (2)根据题意可知点E 、点F 在抛物线42542+-=x y 上,EF ∥BC ……1分∵3=OA ∴点E 、点F 的横坐标都是3,…1分∴点E 坐标为)3,25(-……………1分 , 点F 坐标为)3,25(……1分∴5=EF (米)……………1分 答水面宽度EF 的长为5米.长宁区22.(本题满分10分,第(1)小题5分,第(2)小题5分)某旅游景点的年游客量y (万人)是门票价格x (元)的一次函数,其函数图像如下图. (1)求y 关于x 的函数解析式;(2)经过景点工作人员统计发现:每卖出一张门票所需成本为20元.那么要想获得年利润11500万元,且门票价格不得高于230元,该年的门票价格应该定为多少元?22.(本题满分10分,第(1)小题5分,第(2)小题5分)解:(1)设)0(≠+=k b kx y ,函数图像过点(200,100), (50,250) (1分)代入解析式得:⎩⎨⎧=+=+25050100200b k b k (2分)解之得:⎩⎨⎧=-=3001b k (1分)所以y 关于x 的解析式为:300+-=x y (1分) (2)设门票价格定为x 元,依题意可得:11500)300)(20(=+--x x (2分) 整理得: 0175003202=+-x x 解之得:x =70或者x =250(舍去) (2分) 答:门票价格应该定为70元. (1分)崇明区22.(本题满分10分,第(1)、(2)小题满分各5分)温度通常有两种表示方法:华氏度(单位:℉)与摄氏度(单位:℃),已知华氏度数y 与摄氏度数x 之间是一次函数关系,下表列出了部分华氏度与摄氏度之间的对应关系:(1)选用表格中给出的数据,求y 关于x 的函数解析式;(2)有一种温度计上有两个刻度,即测量某一温度时左边是摄氏度,右边是华氏度,那么在多少摄氏度时,温度计上右边华氏度的刻度正好比左边摄氏度的刻度大56?22.(本题满分10分,每小题5分)(1)解:设(0)y kx b k =+≠ ………………………………………………1分把0x =,32y =;35x =,95y =代入,得323595b k b =⎧⎨+=⎩ ……………1分解得9532k b ⎧=⎪⎨⎪=⎩ ……………………………………………………………………2分∴y 关于x 的函数解析式为9325y x =+ ……………………………………1分 (2)由题意得:932565x x +=+ ………………………………………………4分解得30x = …………………………………………………1分 ∴在30摄氏度时,温度计右边华氏度的刻度正好比左边摄氏度的刻度大56奉贤区22.(本题满分10分,第(1)小题满分4分,第(2)小题满分6分)某学校要印刷一批艺术节的宣传资料,在需要支付制版费100元和每份资料0.3元印刷费的前提下,甲、乙两个印刷厂分别提出了不同的优惠条件.甲印刷厂提出:所有资料的印刷费可按9折收费;乙印刷厂提出:凡印刷数量超过200份的,超过部分的印刷费可按8折收费.(1)设该学校需要印刷艺术节的宣传资料x 份,支付甲印刷厂的费用为y 元,写出y 关于x 的函数关系式,并写出它的定义域;(2)如果该学校需要印刷艺术节的宣传资料600份,那么应该选择哪家印刷厂比较优惠? 22、(1)0.27100(0)y x x =+>; (2)乙;黄浦区22.(本题满分10分)今年1月25日,上海地区下了一场大雪.这天早上王大爷去买菜,他先去了超市,发现蔬菜普遍涨价了,青菜、花菜和大白菜这两天的价格如下表.王大爷觉得超市的菜不够新鲜,所以他又去了菜市场,他花了30元买了一些新鲜菠菜,他跟卖菜阿姨说:“你今天的菠菜比昨天涨了5元/斤。
上海市各区2018届中考数学二模试卷精选汇编压轴题专题(有答案)
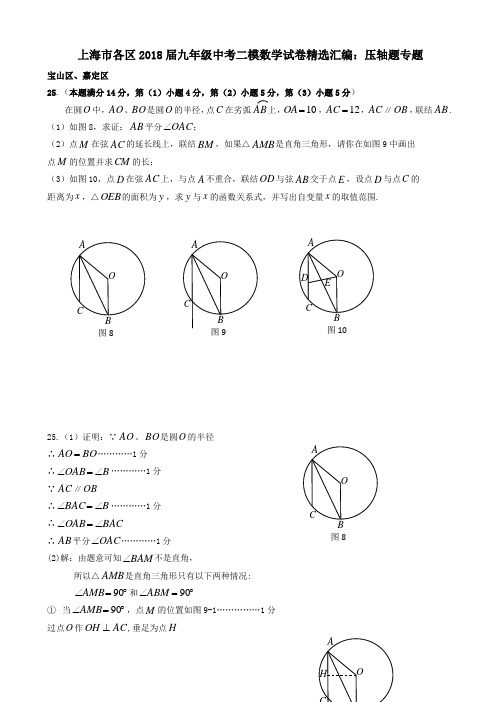
上海市各区2018届九年级中考二模数学试卷精选汇编:压轴题专题宝山区、嘉定区25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)在圆O 中,AO 、BO 是圆O 的半径,点C 在劣弧AB 上,10=OA,12=AC ,AC ∥OB ,联结AB . (1)如图8,求证:AB 平分OAC ∠;(2)点M 在弦AC 的延长线上,联结BM ,如果△AMB 是直角三角形,请你在如图9中画出 点M 的位置并求CM 的长;(3)如图10,点D 在弦AC 上,与点A 不重合,联结OD 与弦AB 交于点E ,设点D 与点C 的 距离为x ,△OEB 的面积为y ,求y 与x 的函数关系式,并写出自变量x 的取值范围.25.(1)证明:∵AO 、BO 是圆O 的半径 ∴BO AO =…………1分 ∴B OAB ∠=∠…………1分 ∵AC ∥OB∴B BAC ∠=∠…………1分 ∴BAC OAB ∠=∠∴AB 平分OAC ∠…………1分 (2)解:由题意可知BAM ∠不是直角,所以△AMB 是直角三角形只有以下两种情况:︒=∠90AMB 和︒=∠90ABM① 当︒=∠90AMB ,点M 的位置如图9-1……………1分 过点O 作AC OH ⊥,垂足为点H图8图10图8∵OH 经过圆心 ∴AC HC AH 21== ∵12=AC ∴6==HC AH 在Rt △AHO 中,222OA HO AH =+ ∵10=OA ∴8=OH∵AC ∥OB ∴︒=∠+∠180OBM AMB ∵︒=∠90AMB ∴︒=∠90OBM ∴四边形OBMH 是矩形 ∴10==HM OB∴4=-=HC HM CM ……………2分 ②当︒=∠90ABM ,点M 的位置如图9-2 由①可知58=AB ,552cos =∠CAB 在Rt △ABM 中,552cos ==∠AM AB CAB∴20=AM8=-=AC AM CM ……………2分综上所述,CM 的长为4或8.说明:只要画出一种情况点M 的位置就给1分,两个点都画正确也给1分. (3)过点O 作AB OG ⊥,垂足为点G 由(1)、(2)可知,CAB OAG ∠=∠sin sin 由(2)可得:55sin =∠CAB ∵10=OA ∴52=OG ……………1分 ∵AC ∥OB ∴ADOBAE BE =……………1分 又BE AE -=58,x AD -=12,10=OB ∴xBEBE -=-121058 ∴x BE -=22580 ……………1分∴52225802121⨯-⨯=⨯⨯=xOG BE y ∴xy -=22400……………1分自变量x 的取值范围为120<≤x ……………1分图10长宁区25.(本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)在圆O 中,C 是弦AB 上的一点,联结OC 并延长,交劣弧AB 于点D ,联结AO 、BO 、AD 、BD . 已知圆O 的半径长为5 ,弦AB 的长为8.(1)如图1,当点D 是弧AB 的中点时,求CD 的长; (2)如图2,设AC =x ,y S S OBDACO=∆∆,求y 关于x 的函数解析式并写出定义域; (3)若四边形AOBD 是梯形,求AD 的长.25.(本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分) 解:(1)∵OD 过圆心,点D 是弧AB 的中点,AB =8, ∴OD ⊥AB ,421==AB AC (2分) 在Rt △AOC 中,︒=∠90ACO Θ,AO =5, ∴322=-=AC AO CO (1分)5=OD Θ,2=-=∴OC OD CD (1分)(2)过点O 作OH ⊥AB ,垂足为点H ,则由(1)可得AH =4,OH =3 ∵AC =x ,∴|4|-=x CH在Rt △HOC 中,︒=∠90CHO Θ,AO =5, ∴258|4|322222+-=-+=+=x x x HC HO CO , (1分)∴525882+-⋅-=⋅=⋅==∆∆∆∆∆∆x x x x OD OC BC AC S S S S S S y OBD OBC OBC ACO OBD ACO O AC DBO BA C DBAOxx x x 5402582-+-= (80<<x ) (3分)(3)①当OB //AD 时, 过点A 作AE ⊥OB 交BO 延长线于点E ,过点O 作OF ⊥AD ,垂足为点F , 则OF =AE , AE OB OH AB S ABO ⋅=⋅=∆2121Θ ∴OF OB OH AB AE ==⋅=524 在Rt △AOF 中,︒=∠90AFO Θ,AO =5, ∴5722=-=OF AO AF ∵OF 过圆心,OF ⊥AD ,∴5142==AF AD . (3分) ②当OA //BD 时, 过点B 作BM ⊥OA 交AO 延长线于点M ,过点D 作DG ⊥AO ,垂足为点G , 则由①的方法可得524==BM DG , 在Rt △GOD 中,︒=∠90DGO Θ,DO =5, ∴5722=-=DG DO GO ,518575=-=-=GO AO AG , 在Rt △GAD 中,︒=∠90DGA Θ,∴622=+=DG AG AD ( 3分)综上得6514或=AD 崇明区25.(本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)如图,已知ABC △中,8AB =,10BC =,12AC =,D 是AC 边上一点,且2AB AD AC =⋅,联结BD ,点E 、F 分别是BC 、AC 上两点(点E 不与B 、C 重合),AEF C ∠=∠,AE 与BD 相交于点G . (1)求证:BD 平分ABC ∠;(2)设BE x =,CF y =,求y 与x 之间的函数关系式; (3)联结FG ,当GEF △是等腰三角形时,求BE 的长度.25.(满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)(第25题图)A BCDGEF(备用图)ABCD(1)∵8AB =,12AC = 又∵2AB AD AC =g ∴163AD =∴16201233CD =-= ……………………………1分 ∵2AB AD AC =g ∴AD AB AB AC= 又∵BAC ∠是公共角 ∴ADB ABC △∽△ …………………………1分 ∴ABD C =∠∠,BD ADBC AB= ∴203BD =∴BD CD = ∴DBC C =∠∠ ………………………1分 ∴ABD DBC =∠∠ ∴BD 平分ABC ∠ ………………………1分 (2)过点A 作AH BC ∥交BD 的延长线于点H∵AH BC ∥ ∴16432053AD DH AH DC BD BC ==== ∵203BD CD ==,8AH = ∴163AD DH == ∴12BH = ……1分 ∵AH BC ∥ ∴AH HG BE BG = ∴812BG x BG -= ∴128xBG x =+…1分 ∵BEF C EFC =+∠∠∠ 即BEA AEF C EFC +=+∠∠∠∠ ∵AEF C =∠∠ ∴BEA EFC =∠∠ 又∵DBC C =∠∠∴BEG CFE △∽△ ……………………………………………………………1分∴BE BGCF EC= ∴12810x x x y x +=-∴228012x x y -++= …………………………………………………………1分(3)当△GEF 是等腰三角形时,存在以下三种情况:1° GE GF = 易证23GE BE EF CF == ,即23x y =,得到4BE = ………2分 2° EG EF = 易证BE CF =,即x y =,5BE =-+…………2分 3° FG FE = 易证 32GE BE EF CF == ,即32x y =3BE =-+ ………2分奉贤区25.(本题满分14分,第(1)小题满分5分,第(2)小题满分5分,第(3)小题满分4分)已知:如图9,在半径为2的扇形AOB 中,∠AOB=90°,点C 在半径OB 上,AC 的垂直平分线交OA 于点D ,交弧AB 于点E ,联结BE 、CD .(1)若C 是半径OB 中点,求∠OCD 的正弦值; (2)若E 是弧AB 的中点,求证:BC BO BE ⋅=2;(3)联结CE ,当△DCE 是以CD 为腰的等腰三角形时,求CD 的长.图9备用图ABO备用图ABO黄浦区25.(本题满分14分)如图,四边形ABCD中,∠BCD=∠D=90°,E是边AB的中点.已知AD=1,AB=2.(1)设BC=x,CD=y,求y关于x的函数关系式,并写出定义域;(2)当∠B=70°时,求∠AEC的度数;(3)当△ACE为直角三角形时,求边BC的长.25. 解:(1)过A作AH⊥BC于H,————————————————————(1分)由∠D=∠BCD=90°,得四边形ADCH为矩形.在△BAH 中,AB =2,∠BHA =90°,AH =y ,HB =1x -,所以22221y x =+-,——————————————————————(1分) 则()22303y x x x =-++<<.———————————————(2分)(2)取CD 中点T ,联结TE ,————————————————————(1分) 则TE 是梯形中位线,得ET ∥AD ,ET ⊥CD .∴∠AET =∠B =70°. ———————————————————————(1分) 又AD =AE =1,∴∠AED =∠ADE =∠DET =35°. ——————————————————(1分) 由ET 垂直平分CD ,得∠CET =∠DET =35°,————————————(1分) 所以∠AEC =70°+35°=105°. ——————————————————(1分)(3)当∠AEC =90°时,易知△CBE ≌△CAE ≌△CAD ,得∠BCE =30°, 则在△ABH 中,∠B =60°,∠AHB =90°,AB =2,得BH =1,于是BC =2. ——————————————————————(2分)当∠CAE =90°时,易知△CDA ∽△BCA ,又2224AC BC AB x =-=-,则2241174AD CAx x AC CBx -±=⇒=⇒=-(舍负)—————(2分) 易知∠ACE <90°.所以边BC 的长为2或117+.——————————————————(1分)金山区25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5 分)如图9,已知在梯形ABCD 中,AD ∥BC ,AB =DC =AD =5,3sin 5B =,P 是线段BC 上 一点,以P 为圆心,PA 为半径的⊙P 与射线AD 的另一个交点为Q ,射线PQ 与射线CD 相交于点E ,设BP =x .(1)求证△ABP ∽△ECP ;(2)如果点Q 在线段AD 上(与点A 、D 不重合),设△APQ 的面积为y ,求y 关于x 的函数关系式,并写出定义域; (3)如果△QED 与△QAP 相似,求BP 的长.25.解:(1)在⊙P 中,PA =PQ ,∴∠PAQ =∠PQA ,……………………………(1分)∵AD ∥BC ,∴∠PAQ =∠APB ,∠PQA =∠QPC ,∴∠APB =∠EPC ,……(1分) ∵梯形ABCD 中,AD ∥BC ,AB =DC ,∴∠B =∠C ,…………………………(1分) ∴△APB ∽△ECP .…………………………………………………………(1分) (2)作AM ⊥BC ,PN ⊥AD ,∵AD ∥BC ,∴AM ∥PN ,∴四边形AMPN 是平行四边形,∴AM =PN ,AN =MP .………………………………………………………(1分) 在Rt △AMB 中,∠AMB =90°,AB =5,sinB =35, ∴AM =3,BM =4,∴PN =3,PM =AN =x -4,……………………………………(1分) ∵PN ⊥AQ ,∴AN =NQ ,∴AQ = 2x -8,……………………………………(1分) ∴()1128322y AQ PN x =⋅⋅=⋅-⋅,即312y x =-,………………………(1分) 定义域是1342x <<.………………………………………………………(1分) (3)解法一:由△QED 与△QAP 相似,∠AQP =∠EQD ,①如果∠PAQ =∠DEQ ,∵△APB ∽△ECP ,∴∠PAB =∠DEQ ,又∵∠PAQ =∠APB ,∴∠PAB =∠APB ,∴BP =BA =5.………………………(2分)ABCD图9备用图②如果∠PAQ =∠EDQ ,∵∠PAQ =∠APB ,∠EDQ =∠C ,∠B =∠C ,∴∠B =∠APB ,∴ AB =AP ,∵AM ⊥BC ,∴ BM =MP =4,∴ BP =8.………(2分) 综上所述BP 的长为5或者8.………………………………………………(1分) 解法二:由△QAP 与△QED 相似,∠AQP =∠EQD , 在Rt △APN 中,AP PQ ===∵QD ∥PC ,∴EQ EPQD PC=, ∵△APB ∽△ECP ,∴AP EPPB PC=,∴AP EQ PB QD =, ①如果AQ EQ QP QD =,∴AQ AP QP PB =x=,解得5x =………………………………………………………………………(2分) ②如果AQ DQ QP QE =,∴AQ PBQP AP==解得8x =………………………………………………………………………(2分) 综上所述BP 的长为5或者8.…………………………………………………(1分)静安区25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分) 如图,平行四边形ABCD 中,已知AB =6,BC =9,31cos =∠ABC .对角线AC 、BD 交于点O .动点P 在边AB 上,⊙P 经过点B ,交线段PA 于点E .设BP = x .(1) 求AC 的长;(2) 设⊙O 的半径为y ,当⊙P 与⊙O 外切时, 求y 关于x 的函数解析式,并写出定义域; (3) 如果AC 是⊙O 的直径,⊙O 经过点E , 求⊙O 与⊙P 的圆心距OP 的长.25.(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分) 解:(1)作AH ⊥BC 于H ,且31cos =∠ABC ,AB =6, A 第25题图B P OC DE · 第25题备用图ABOCDDA · POE那么2316cos =⨯=∠⋅=ABC AB BH …………(2分) BC =9,HC =9-2=7,242622=-=AH , ……………………(1分) 9493222=+=+=HC AH AC ﹒ ………(1分)(2)作OI ⊥AB 于I ,联结PO , AC =BC =9,AO =4.5 ∴∠OAB =∠ABC ,∴Rt △AIO 中, 31cos cos ==∠=∠AO AI ABC IAO∴AI =1.5,IO =2322=AI ……………………(1分) ∴PI =AB -BP -AI =6-x -1.5=x -29, ……………………(1分) ∴Rt △PIO 中,41539481918)29()23(2222222+-=+-+=-+=+=x x x x x OI PI OP ……(1分) ∵⊙P 与⊙O 外切,∴y x x x OP +=+-=415392 ……………………(1分) ∴y =x x x x x x -+-=-+-153364214153922…………………………(1分) ∵动点P 在边AB 上,⊙P 经过点B ,交线段PA 于点E .∴定义域:0<x ≤3…………(1分) (3)由题意得:∵点E 在线段AP 上,⊙O 经过点E ,∴⊙O 与⊙P 相交 ∵AO 是⊙O 半径,且AO >OI ,∴交点E 存在两种不同的位置,OE =OA =29① 当E 与点A 不重合时,AE 是⊙O 的弦,OI 是弦心距,∵AI =1.5,AE =3, ∴点E 是AB 中点,321==AB BE ,23==PE BP ,3=PI , IO =23 3327)23(32222==+=+=IO PI OP ……………………(2分)② 当E 与点A 重合时,点P 是AB 中点,点O 是AC 中点,2921==BC OP ……(2分) ∴33=OP 或29. 闵行区25.(本题满分14分,其中第(1)小题4分,第(2)、(3)小题各5分)如图,已知在Rt △ABC 中,∠ACB = 90o,AC =6,BC = 8,点F 在线段AB 上,以点B 为圆心,BF 为半径的圆交BC 于点E ,射线AE 交圆B 于点D (点D 、E 不重合).(1)如果设BF = x ,EF = y ,求y 与x 之间的函数关系式,并写出它的定义域;第25题图(2)(2)如果»»2EDEF =,求ED 的长; (3)联结CD 、BD ,请判断四边形ABDC 是否为直角梯形?说明理由.25.解:(1)在Rt △ABC 中,6AC =,8BC =,90ACB ∠=o∴10AB =.……………………………………………………………(1分) 过E 作EH ⊥AB ,垂足是H , 易得:35EH x =,45BH x =,15FH x =.…………………………(1分) 在Rt △EHF 中,222223155EF EH FH x x ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭,∴(08)y x x =<<.………………………………………(1分+1分) (2)取»ED的中点P ,联结BP 交ED 于点G ∵»»2EDEF =,P 是»ED 的中点,∴»»»EP EF PD ==. ∴∠FBE =∠EBP =∠PBD .∵»»EPEF =,BP 过圆心,∴BG ⊥ED ,ED =2EG =2DG .…………(1分) 又∵∠CEA =∠DEB ,∴∠CAE =∠EBP =∠ABC .……………………………………………(1分)又∵BE 是公共边,∴BEH BEG ∆∆≌.∴35EH EG GD x ===.在Rt △CEA 中,∵AC = 6,8BC =,tan tan AC CECAE ABC BC AC∠=∠==, ∴66339tan 822CE AC CAE ⨯⨯=⋅∠===.……………………………(1分) (备用图)CBA (第25题图)CBEF DADEBACF∴9169782222BE =-=-=.……………………………………………(1分) ∴6672125525ED EG x ===⨯=.……………………………………(1分)(3)四边形ABDC 不可能为直角梯形.…………………………………(1分)①当CD ∥AB 时,如果四边形ABDC 是直角梯形, 只可能∠ABD =∠CDB = 90o. 在Rt △CBD 中,∵8BC =, ∴32cos 5CD BC BCD =⋅∠=, 24sin 5BD BC BCD BE =⋅∠==. ∴321651025CD AB ==,328153245CE BE -==; ∴CD CEAB BE≠. ∴CD 不平行于AB ,与CD ∥AB 矛盾.∴四边形ABDC 不可能为直角梯形.…………………………(2分) ②当AC ∥BD 时,如果四边形ABDC 只可能∠ACD =∠CDB = 90o. ∵AC ∥BD ,∠ACB = 90o, ∴∠ACB =∠CBD = 90o . ∴∠ABD =∠ACB +∠BCD > 90o. 与∠ACD =∠CDB = 90o矛盾.∴四边形ABDC 不可能为直角梯形.…………………………(2分)普陀区25.(本题满分14分)已知P 是O ⊙的直径BA 延长线上的一个动点,P ∠的另一边交O ⊙于点C 、D ,两点位于AB 的上方,AB =6,OP m =,1sin 3P =,如图11所示.另一个半径为6的1O ⊙经过点C 、D ,圆心距1OO n =.(1)当6m =时,求线段CD 的长;(2)设圆心1O 在直线AB 上方,试用n 的代数式表示m ;(3)△1POO 在点P 的运动过程中,是否能成为以1OO 为腰的等腰三角形,如果能,试求出此时n 的值;如果不能,请说明理由.DEBACFDC25.解:(1)过点O 作OH ⊥CD ,垂足为点H ,联结OC .在Rt △POH 中,∵1sin 3P =,6PO =,∴2OH =. ········· (1分) ∵AB =6,∴3OC =. ······················ (1分)由勾股定理得 CH = ····················· (1分)∵OH ⊥DC ,∴2CD CH == ················ (1分) (2)在Rt △POH 中,∵1sin 3P =, PO m =,∴3mOH =. ········ (1分) 在Rt △OCH 中,2293m CH ⎛⎫- ⎪⎝⎭=. ················ (1分)在Rt △1O CH 中,22363m CH n ⎛⎫-- ⎪⎝⎭=. ·············· (1分)可得 2236933m m n ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭=,解得23812n m n -=. ········· (2分)(3)△1POO 成为等腰三角形可分以下几种情况:● 当圆心1O 、O 在弦CD 异侧时①1OP OO =,即m n =,由23812n n n-=解得9n =. ········· (1分)即圆心距等于O ⊙、1O ⊙的半径的和,就有O ⊙、1O ⊙外切不合题意舍去.(1分)②11O P OO =n =,解得23m n =,即23n 23812n n -=,解得n ·········· (1分) ● 当圆心1O 、O 在弦CD 同侧时,同理可得 28132n m n-=.∵1POO ∠是钝角,∴只能是m n =,即28132n n n-=,解得n . ·· (2分)综上所述,n .青浦区25.(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分)如图9-1,已知扇形MON,∠MON=90o,点B在弧MN上移动,联结BM,作OD⊥BM,垂足为点D,C为线段OD上一点,且OC=BM,联结BC并延长交半径OM于点A,设OA= x,∠COM的正切值为y.(1)如图9-2,当AB⊥OM时,求证:AM =AC;(2)求y关于x的函数关系式,并写出定义域;(3)当△OAC为等腰三角形时,求x的值.25.解:(1)∵OD⊥BM,AB⊥OM,∴∠ODM =∠BAM=90°.··········(1分)∵∠ABM +∠M =∠DOM +∠M,∴∠ABM =∠DOM.·········(1分)∵∠OAC=∠BAM,OC =BM,∴△OAC≌△ABM,······················(1分)∴AC =AM.·························(1分)(2)过点D作DE//AB,交OM于点E.················(1分)∵OB=OM,OD⊥BM,∴BD=DM.················(1分)∵DE//AB,∴=MD MEDM AE,∴AE=EM,∵OM,∴AE=)12x.················(1分)∵DE//AB,∴2==OA OC DMOE OD OD,···················(1分)∴2=DM OAOD OE,∴=y(0<≤x·················(2分)(3)(i)当OA=OC时,∵111222===DM BM OC x,O MNDCBA图9-1ONDCBA图9-2NMO备用图在Rt △ODM中,==OD =DM y OD,1=x=x=x .(2分) (ii )当AO =AC 时,则∠AOC =∠ACO ,∵∠ACO >∠COB ,∠COB =∠AOC ,∴∠ACO >∠AOC ,∴此种情况不存在. ····················· (1分) (ⅲ)当CO =CA 时,则∠COA =∠CAO=α,∵∠CAO >∠M ,∠M =90α︒-,∴α>90α︒-,∴α>45︒,∴290α∠=>︒BOA ,∵90∠≤︒BOA ,∴此种情况不存在. ·· (1分)松江区25.(本题满分14分,第(1)小题4分,第(2)小题每个小题各5分)如图,已知Rt △ABC 中,∠ACB =90°,BC =2,AC =3,以点C 为圆心、CB 为半径的圆交AB 于点D ,过点A 作AE ∥CD ,交BC 延长线于点E.(1)求CE 的长;(2)P 是 CE 延长线上一点,直线AP 、CD 交于点Q.① 如果△ACQ ∽△CPQ ,求CP 的长;② 如果以点A 为圆心,AQ 为半径的圆与⊙C 相切,求CP 的长.25.(本题满分14分,第(1)小题4分,第(2)小题每个小题各5分) 解:(1)∵AE ∥CD∴BC DC BE AE=…………………………………1分 ∵BC=DC∴BE=AE …………………………………1分 设CE =x(第25题图)CBA DE(备用图)CBADECBA DE则AE =BE =x +2 ∵ ∠ACB =90°, ∴222AC CE AE +=即229(2)x x +=+………………………1分 ∴54x =即54CE =…………………………………1分 (2)①∵△ACQ ∽△CPQ ,∠QAC>∠P∴∠ACQ=∠P …………………………………1分 又∵AE ∥CD ∴∠ACQ=∠CAE∴∠CAE=∠P ………………………………1分 ∴△ACE ∽△PCA ,…………………………1分 ∴2AC CE CP =⋅…………………………1分 即2534CP =⋅ ∴365CP =……………………………1分 ②设CP =t ,则54PE t =- ∵∠ACB =90°,∴AP ∵AE ∥CD ∴AQ ECAP EP=……………………………1分5545454t t ==--∴AQ =1分若两圆外切,那么1AQ == 此时方程无实数解……………………………1分CBA DEPQ若两圆内切切,那么2595t AQ +== ∴21540160t t -+= 解之得2041015t ±=………………………1分又∵54t >∴2041015t +=………………………1分徐汇区25. 已知四边形ABCD 是边长为10的菱形,对角线AC 、BD 相交于点E ,过点C 作CF ∥DB 交AB 延长线于点F ,联结EF 交BC 于点H . (1)如图1,当EF BC ⊥时,求AE 的长;(2)如图2,以EF 为直径作⊙O ,⊙O 经过点C 交边CD 于点G (点C 、G 不重合),设AE 的长为x ,EH 的长为y ;① 求y 关于x 的函数关系式,并写出定义域;③ 联结EG ,当DEG ∆是以DG 为腰的等腰三角形时,求AE 的长.杨浦区25、(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分)如图9,在梯形ABCD中,AD//BC,AB=DC=5,AD=1,BC=9,点P为边BC上一动点,作PH⊥DC,垂足H在边DC上,以点P为圆心PH为半径画圆,交射线PB于点E.(1)当圆P过点A时,求圆P的半径;(2)分别联结EH和EA,当△ABE△CEH时,以点B为圆心,r为半径的圆B与圆P相交,试求圆B的半径r的取值范围;(3)将劣弧沿直线EH翻折交BC于点F,试通过计算说明线段EH和EF的比值为定值,并求出此定值。
上海市各区2018届最新中考二模数学分类汇编:函数综合运用(含答案)

上海市各区2018届九年级中考二模数学试卷精选汇编函数综合运用专题宝山区、嘉定区22、有一座抛物线拱型桥,在正常水位时,水面BC 的宽为10米,拱桥的最高点D 到水面BC 的距离DO 为4米,点O 是BC 的中点,如图5,以点O 为原点,直线BC 为x 轴,建立直角坐标系xOy . (1)求该抛物线的表达式;(2)如果水面BC 上升3米(即3=OA )至水面EF ,点E 在点F 的左侧, 求水面宽度EF 的长.22.解:(1)根据题意:该抛物线的表达式为:b ax y +=2………………1分 ∵该抛物线最高点D 在y 轴上,4=DO ,∴点D 的坐标为)4,0(………1分 ∵10=BC ,点O 是BC 的中点 ∴点B 的坐标为)0,5(- ∴254-=a ,4=b …2分 ∴抛物线的表达式为:42542+-=x y …………………1分 (2)根据题意可知点E 、点F 在抛物线42542+-=x y 上,EF ∥BC ……1分 ∵3=OA ∴点E 、点F 的横坐标都是3,…1分∴点E 坐标为)3,25(-……………1分 , 点F 坐标为)3,25(……1分∴5=EF (米)……………1分 答水面宽度EF 的长为5米.长宁区22.(本题满分10分,第(1)小题5分,第(2)小题5分)某旅游景点的年游客量y (万人)是门票价格x (元)的一次函数,其函数图像如下图. (1)求y 关于x 的函数解析式;(2)经过景点工作人员统计发现:每卖出一张门票所需成本为20元.那么要想获得年利润11500万元,且门票价格不得高于230元,该年的门票价格应该定为多少元?22.(本题满分10分,第(1)小题5分,第(2)小题5分)xy图5D E C OBF A解:(1)设)0(≠+=k b kx y ,函数图像过点(200,100), (50,250) (1分)代入解析式得:⎩⎨⎧=+=+25050100200b k b k (2分)解之得:⎩⎨⎧=-=3001b k (1分)所以y 关于x 的解析式为:300+-=x y (1分) (2)设门票价格定为x 元,依题意可得:11500)300)(20(=+--x x (2分) 整理得: 0175003202=+-x x 解之得:x =70或者x =250(舍去) (2分) 答:门票价格应该定为70元. (1分)崇明区22.(本题满分10分,第(1)、(2)小题满分各5分)温度通常有两种表示方法:华氏度(单位:℉)与摄氏度(单位:℃),已知华氏度数y 与摄氏度数x 之间是一次函数关系,下表列出了部分华氏度与摄氏度之间的对应关系:摄氏度数x (℃) … 0 … 35 … 100 … 华氏度数y (℉)…32…95…212…(1)选用表格中给出的数据,求y 关于x 的函数解析式;(2)有一种温度计上有两个刻度,即测量某一温度时左边是摄氏度,右边是华氏度,那么在多少摄氏度时,温度计上右边华氏度的刻度正好比左边摄氏度的刻度大56? 22.(本题满分10分,每小题5分)(1)解:设(0)y kx b k =+≠ ………………………………………………1分把0x =,32y =;35x =,95y =代入,得323595b k b =⎧⎨+=⎩……………1分解得9532k b ⎧=⎪⎨⎪=⎩ ……………………………………………………………………2分∴y 关于x 的函数解析式为9325y x =+ ……………………………………1分 (2)由题意得:932565x x +=+ ………………………………………………4分 解得30x = …………………………………………………1分∴在30摄氏度时,温度计右边华氏度的刻度正好比左边摄氏度的刻度大56奉贤区22.(本题满分10分,第(1)小题满分4分,第(2)小题满分6分)某学校要印刷一批艺术节的宣传资料,在需要支付制版费100元和每份资料0.3元印刷费的前提下,甲、乙两个印刷厂分别提出了不同的优惠条件.甲印刷厂提出:所有资料的印刷费可按9折收费;乙印刷厂提出:凡印刷数量超过200份的,超过部分的印刷费可按8折收费.(1)设该学校需要印刷艺术节的宣传资料x 份,支付甲印刷厂的费用为y 元,写出y 关于x 的函数关系式,并写出它的定义域;(2)如果该学校需要印刷艺术节的宣传资料600份,那么应该选择哪家印刷厂比较优惠? 22、(1)0.27100(0)y x x =+>; (2)乙;黄浦区22.(本题满分10分)今年1月25日,上海地区下了一场大雪.这天早上王大爷去买菜,他先去了超市,发现蔬菜普遍涨价了,青菜、花菜和大白菜这两天的价格如下表.王大爷觉得超市的菜不够新鲜,所以他又去了菜市场,他花了30元买了一些新鲜菠菜,他跟卖菜阿姨说:“你今天的菠菜比昨天涨了5元/斤。
【初三英语试题精选】2018上海市各区中考二模数学试卷精选汇编:二次函数专题

2018上海市各区中考二模数学试卷精选汇编:二次函数专
题
上海市各区1,0)、C(3,0)在抛物线上
∴ ,解得( 2分)
∴抛物线的表达式为,顶点D的坐标是(1,-4)( 2分)(2)∵A(0,-3),C(3,0),D(1,-4)∴ ,,
∴ ∴ ( 2分)
∴ (1分)
(3)∵ ,,
∴△CAD∽△AOB,∴
∵OA=OC,∴
∴ ,即( 1分)
若以O、P、C为顶点的三角形与△ABC相似,且△ABC为锐角三角形
则也为锐角三角形,点P在第四象限
由点C(3,0),D(1,-4)得直线CD的表达式是,设()过P作PH⊥OC,垂足为点H,则,
①当时,由得,
∴ ,解得,∴ (2分)
②当时,由得,
∴ ,解得,∴ ( 2分)
综上得或
崇明区
24.(本题满分12分,第(1)、(2)、(3)小题满分各4分)
已知抛物线经过点、、.
(1)求抛物线的解析式;
(2)联结AC、BC、AB,求的正切值;
(3)点P是该抛物线上一点,且在第一象限内,过点P作交轴。
上海市各区2018届中考数学二模试卷精选汇编选择题专题

上海市各区2018届九年级中考二模数学试卷精选汇编 选择题专题 宝山区、嘉定区一、选择题:(本大题共6题,每题4分,满分24分)1.下列说法中,正确的是(▲)(A )0是正整数; (B )1是素数; (C )22是分数; (D )722是有理数. 2.关于x 的方程022=--mx x 根的情况是(▲) (A )有两个不相等的实数根; (B )有两个相等的实数根;(C )没有实数根; (D )无法确定.3. 将直线x y 2=向下平移2个单位,平移后的新直线一定不经过的象限是(▲)(A )第一象限; (B )第二象限; (C )第三象限; (D )第四象限.4. 下列说法正确的是(▲)(A )一组数据的中位数一定等于该组数据中的某个数据;(B )一组数据的平均数和中位数一定不相等;(C )一组数据的众数可以有几个;(D )一组数据的方差一定大于这组数据的标准差.5.对角线互相平分且相等的四边形一定是(▲)(A )等腰梯形; (B )矩形; (C )菱形; (D )正方形.6.已知圆1O 的半径长为cm 6,圆2O 的半径长为cm 4,圆心距cm O O 321=,那么圆1O 与圆2O 的位置关系是(▲)(A )外离; (B )外切; (C )相交; (D )内切.1. D2. A3. B4. C5. B6. C长宁区一、选择题(本大题共6题, 每题4分, 满分24分)【每题只有一个正确选项, 在答题纸相应题号的选项上用2B 铅笔正确填涂】1.函数12-=x y 的图像不经过( ▲ )(A ) 第一象限; (B ) 第二象限; (C ) 第三象限; (D ) 第四象限.2.下列式子一定成立的是( ▲ )(A ) a a a 632=+; (B )428x x x =÷;(C ) a a 121=; (D )6321)(aa -=--. 3.下列二次根式中,2的同类二次根式是( ▲ )(A )4; (B )x 2; (C )92; (D )12. 4.已知一组数据2、x 、8、5、5、2的众数是2,那么这组数据的中位数是( ▲ )(A ) 3.5; (B ) 4; (C ) 2; (D )6.5.5.已知圆A 的半径长为4,圆B 的半径长为7,它们的圆心距为d ,要使这两圆没有公共点,那么d 的值可以取( ▲ )(A ) 11; (B ) 6; (C ) 3; (D )2.6.已知在四边形ABCD 中,AD //BC ,对角线AC 、BD 交于点O ,且AC =BD ,下列四个命题中真命题是( ▲ )(A ) 若AB =CD ,则四边形ABCD 一定是等腰梯形;(B ) 若∠DBC =∠ACB ,则四边形ABCD 一定是等腰梯形;(C ) 若ODCO OB AO =,则四边形ABCD 一定是矩形; (D ) 若AC ⊥BD 且AO =OD ,则四边形ABCD 一定是正方形.一、选择题:(本大题共6题,每题4分,满分24分)1.B ; 2.D ; 3.C ; 4.A ; 5.D ; 6.C .崇明区一、选择题(本大题共6题,每题4分,满分24分)1.8的相反数是…………………………………………………………………………………( ▲ )(A)18; (B)8; (C)18-; (D)8-.2.下列计算正确的是 …………………………………………………………………………( ▲ )(A)=; (B)23a a a +=; (C)33(2)2a a =; (D)632a a a ÷=.3.今年3月12日,某学校开展植树活动,某植树小组20名同学的年龄情况如下表:。
2018届中考数学上海市各区二模试卷专题汇编七【二次函数题】含答案解析

2018届中考数学上海市各区二模试卷 专题汇编七【二次函数题】宝山区、嘉定区24.(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分) 已知平面直角坐标系(如图7),直线的经过点和点.(1)求、的值;(2)如果抛物线经过点、,该抛物线的顶点为点,求的值; (3)设点在直线上,且在第一象限内,直线与轴的交点为点,如果,求点的坐标.24.解:(1) ∵直线的经过点∴……………………1分∴………………………………1分∵直线的经过点∴……………………1分xOy mx y +=)0,4(-A )3,(n B m n c bx x y ++=2A B P ABP ∠sin Q mx y +=mx y +=y D DOB AQO ∠=∠Q mx y +=)0,4(-A 04=+-m 4=m mx y +=)3,(n B 34=+n 图7∴…………………………………………1分 (2)由可知点的坐标为∵抛物线经过点、 ∴∴,∴抛物线的表达式为…………………1分 ∴抛物线的顶点坐标为……………1分∴,,∴∴……………………………………1分∴∴…………………………………………1分(3)过点作轴,垂足为点,则∥轴∵, ∴△∽△1-=n B )3,1(-c bx x y ++=2A B ⎩⎨⎧=+-=+-310416c b c b 6=b 8=c c bx x y ++=2862++=x x y 862++=x x y )1,3(--P 23=AB 2=AP 52=PB 222PB BP AB =+︒=∠90PAB PB AP ABP =∠sin 1010sin =∠ABP Q x QH ⊥H QH y DOB AQO ∠=∠QBO OBD ∠=∠OBD QBO∴……………1分 ∵直线与轴的交点为点∴点的坐标为, 又,∴,……………1分 ∵∴, ∵∥轴∴∴∴ ……………………………………1分 即点的纵坐标是 又点在直线上 点的坐标为……………1分 长宁区24.(本题满分12分,第(1)小题4分,第(2)小题3分,第(3)小题5分)OB DBQB OB =4+=x y y D D )4,0(4=OD 10=OB 2=DB 25=QB 24=DQ 23=AB 28=AQ 24=DQ QH y AQ ADQH OD =28244=QH 8=QH Q 8Q 4+=x y Q )8,4(如图在直角坐标平面内,抛物线与y 轴交于点A ,与x 轴分别交于点B (-1,0)、点C (3,0),点D 是抛物线的顶点.(1)求抛物线的表达式及顶点D 的坐标; (2)联结AD 、DC ,求的面积;(3)点P 在直线DC 上,联结OP ,若以O 、P 、C 为顶点的三角形与△ABC 相似,求点P 的坐标.24.(本题满分12分,第(1)小题4分,第(2)小题3分,第(3)小题5分)解:(1) 点B (-1,0)、C (3,0)在抛物线上 ∴,解得 ( 2分)32-+=bx ax y ACD ∆32-+=bx ax y ⎩⎨⎧=-+=--033903b a b a ⎩⎨⎧-==21ba 备用图第24题图∴抛物线的表达式为,顶点D 的坐标是(1,-4) ( 2分) (2)∵A (0,-3),C (3,0),D (1,-4) ∴,,∴ ∴ ( 2分)∴(1分)(3)∵,, ∴△CAD ∽△AOB ,∴∵OA=OC , ∴∴,即 ( 1分) 若以O 、P 、C 为顶点的三角形与△ABC 相似 ,且△ABC 为锐角三角形 则也为锐角三角形,点P 在第四象限由点C (3,0),D (1,-4)得直线CD 的表达式是,设() 过P 作PH ⊥OC ,垂足为点H ,则,①当时,由得,∴,解得, ∴(2分) ②当时,由得,322--=x x y 23=AC 52=CD 2=AD 222AD AC CD +=︒=∠90CAD .32232121=⨯⨯=⋅⋅=∆AD AC S ACD ︒=∠=∠90AOB CAD 2==AO ACBO AD OAB ACD ∠=∠︒=∠90AOC ︒=∠=∠45OCA OAC ACD OCA OAB OAC ∠+∠=∠+∠BCD BAC ∠=∠POC ∆62-=x y )62,(-t t P 30<<t t OH =t PH 26-=ABC POC ∠=∠ABC POC ∠=∠tan tan BO AOOH PH =326=-t t 56=t )518,56(1-P ACB POC ∠=∠145tan tan tan =︒=∠=∠ACB POC 1=OH PH∴,解得,∴ ( 2分) 综上得或 崇明区24.(本题满分12分,第(1)、(2)、(3)小题满分各4分) 已知抛物线经过点、、.(1)求抛物线的解析式; (2)联结AC 、BC 、AB ,求的正切值;(3)点P 是该抛物线上一点,且在第一象限内,过点P 作交轴于点,当点在点的上方,且与相似时,求点P 的坐标.126=-t t2=t )2,2(2-P )518,56(1-P )2,2(2-P24.(本题满分12分,每小题4分)解:(1)设所求二次函数的解析式为,………………………1分将(,)、(,)、(,)代入,得解得………2分所以,这个二次函数的解析式为……………………………1分(2)∵(,)、(,)、(,)∴,,∴∴………………………………………………………2分∴……………………………………………2分(3)过点P作,垂足为H设,则∵(,)∴,∵∴当△APG与△ABC相似时,存在以下两种可能:1°则即∴解得………………………1分∴点的坐标为……………………………………………………1分2°则即∴解得…………………………1分∴点的坐标为……………………………………………………1分奉贤区24.(本题满分12分,每小题满分各4分)已知平面直角坐标系(如图8),抛物线为直线,过点C作直线的垂线,垂足为点E,联结DC、BC.(1)当点C(0,3)时,①求这条抛物线的表达式和顶点坐标;②求证:∠DCE=∠BCE;(2)当CB平分∠DCO时,求的值.黄浦区24.(本题满分12分)已知抛物线经过点A (1,0)和B (0,3),其顶点为D.(1)求此抛物线的表达式; (2)求△ABD 的面积;(3)设P 为该抛物线上一点,且位于抛物线对称轴 右侧,作PH ⊥对称轴,垂足为H ,若△DPH 与△AOB 相 似,求点P 的坐标.24. 解:(1)由题意得:,———————————————————(2分) 解得:,—————————————————————————(1分)所以抛物线的表达式为. ——————————————(1分) (2)由(1)得D (2,﹣1),———————————————————(1分) 作DT ⊥y 轴于点T,则△ABD 的面积=.————————(3分)2y x bx c =++013b cc =++⎧⎨=⎩43b c =-⎧⎨=⎩243y x x =-+()11124131211222⨯⨯-⨯⨯-⨯+⨯=(3)令P.————————————————(1分)由△DPH 与△AOB 相似,易知∠AOB=∠PHD=90°,所以或,————————————(2分) 解得:或,所以点P 的坐标为(5,8),.————————————————(1分)金山区24.(本题满分12分,每小题4分)平面直角坐标系xOy 中(如图8),已知抛物线经过点A (1,0)和B (3,0),与y 轴相交于点C ,顶点为P .(1)求这条抛物线的表达式和顶点P 的坐标; (2)点E 在抛物线的对称轴上,且EA=EC , 求点E 的坐标;(3)在(2)的条件下,记抛物线的对称轴为 直线MN ,点Q 在直线MN 右侧的抛物线 上,∠MEQ=∠NEB ,求点Q 的坐标.()()2,432p pp p -+>243132p p p -++=-2431123p p p -++=-5p =73p =78,39⎛⎫- ⎪⎝⎭2y x bx c =++24.解:(1)∵二次函数的图像经过点A (1,0)和B (3,0),∴,解得:,.……………………………(2分)∴这条抛物线的表达式是…………………………………(1分) 顶点P 的坐标是(2,-1).………………………………………………(1分)(2)抛物线的对称轴是直线,设点E 的坐标是(2,m ).…(1分)根据题意得:m=2,…(2分)∴点E 的坐标为(2,2).…………………………………………………(1分)(3)解法一:设点Q 的坐标为,记MN 与x 轴相交于点F . 作QD ⊥MN ,垂足为D ,则,………………………(1分) ∵∠QDE=∠BFE=90°,∠QED=∠BEF ,∴△QDE ∽△BFE ,…………………(1分)∴,∴,解得(不合题意,舍去),.……………………………(1分) ∴,点E 的坐标为(5,8).…………………………………………(1分) 解法二:记MN 与x 轴相交于点F .联结AE ,延长AE 交抛物线于点Q ,2y x bx c =++10930b c b c ++=⎧⎨++=⎩4b =-3c =243y x x =-+243y x x =-+2x ==2(,43)t t t -+2DQ t =-2243241DE t t t t =-+-=-+DQ DEBF EF =224112t t t --+=11t =25t =5t =∵AE=BE , EF ⊥AB ,∴∠AEF=∠NEB ,又∵∠AEF=∠MEQ ,∴∠QEM=∠NEB ,………………………………(1分)点Q 是所求的点,设点Q 的坐标为, 作QH ⊥x 轴,垂足为H ,则QH=,OH=t ,AH=t-1,∵EF ⊥x 轴,∴EF ∥QH ,∴,∴,………(1分)解得(不合题意,舍去),.……………………………………(1分) ∴,点E 的坐标为(5,8).…………………………………………(1分) 静安区24.(本题满分12分,第(1)小题满分4分,第(2)小题满分4分,第(3)小题满分4分)在平面直角坐标系xOy 中,已知点B (8,0)和点C (9,).抛物线(a ,c 是常数,a ≠0)经过点B 、C ,且与x 轴的另一交点为A .对称轴上有一点M ,满足MA=MC . (1) 求这条抛物线的表达式; (2) 求四边形ABCM 的面积;(3) 如果坐标系内有一点D ,满足四边形ABCD且AD//BC ,求点D 的坐标.24.(本题满分12分,第(1)小题4分,第(2)小题4解:(1)由题意得:抛物线对称轴,即. …………(1分)点B (8,0)关于对称轴的对称点为点A (0,0)∴, …………(1分)2(,43)t t t -+243t t -+EF AF QH AH =221431t t t =-+-11t =25t =5t =3-c ax ax y +-=82a ax 28-=4=x 0=c将C (9,-3)代入,得…………………………(1分)∴抛物线的表达式:…………………………(1分) (2)∵点M 在对称轴上,∴可设M (4,y )又∵MA=MC ,即∴, 解得y=-3, ∴M (4,-3) …………………(2分)∵MC//AB 且MC ≠AB, ∴四边形ABCM 为梯形,, AB=8,MC=5,AB 边上的高h = yM = 3∴(3) 将点B (8,0)和点C (9,﹣3)代入可得,解得 由题意得,∵AD//BC,∴,…(1分)又∵AD 过(0,0),DC=AB=8, 设D(x,-3x), …………………………(1分)解得(不合题意,舍去),…………………………(1分)∴∴点D 的坐标.……………………(1分)axax y 82-=31-=a xx y 38312+-=22MC MA =2222)3(54++=+y y 2393)58(21)(21=⨯+⨯=⨯+=MH MC AB S bkx y BC +=⎩⎨⎧-=+=+3908b k b k ⎩⎨⎧=-=243b k 3-=BC k 3-=AD k x y AD 3-=2228)33()9(=+-+-x x 11=x 5132=x 5393-=-=x y )539,513(-闵行区24.(本题满分12分,其中每小题各4分) 如图,已知在平面直角坐标系xOy 中,抛物线点A 和点B (1,0),与y 轴相交于点C (0,3(1)求抛物线的解析式和顶点D 的坐标; (2)求证:∠DAB=∠ACB ;(3)点Q 在抛物线上,且△ADQ 是以AD 为 底的等腰三角形,求Q 点的坐标.24.解:(1)把B (1,0)和C (0,3)代入中,得,解得.……………………………………(2分)∴抛物线的解析式是:.……………………………(1分)∴顶点坐标D (-1,4).……………………………………………(1分)(2)令,则,,,∴A (-3,0)∴,∴∠CAO=∠OCA .…………………………………(1分)22y ax x c=-+22y ax x c=-+9603a c c ++=⎧⎨=⎩13a c =-⎧⎨=⎩223y x x =--+0y =2230x x --+=13x =-21x =3OA OC ==(第24题图)在中,.………………………………(1分)∵,,,∴,;∴,是直角三角形且,∴,又∵∠DAC 和∠OCB 都是锐角,∴∠DAC=∠OCB .…………………(1分) ∴,即.……………………………………………………(1分)(3)令,且满足,,0),,4)∵是以AD 为底的等腰三角形,∴,即,化简得:.………………………………………………(1分)由,……………………………………………………(1分)解得,.Rt BOC ∆1tan 3OB OCB OC ∠==AC=DC=AD =2220AC DC +=220AD =222AC DC AD +=ACD ∆90ACD ∠=1tan 3DC DAC AC ∠==DAC CAO BCO OCA ∠+∠=∠+∠DAB ACB ∠=∠(Q x )y 223y x x =--+(3A -(1D -ADQ ∆22QD QA =2222(3)(1)(4)x y x y ++=++-220x y -+=222023x y y x x -+=⎧⎨=--+⎩11x y ⎧=⎪⎪⎨⎪=⎪⎩22x y ⎧=⎪⎪⎨⎪=⎪⎩∴点Q 的坐标是,.…(2分) 普陀区24.(本题满分12分) 如图10,在平面直角坐标系中,直线与轴、轴分别相交于点、,并与抛物线的对称轴交于点,抛物线的顶点是点.(1)求和的值;(2)点是轴上一点,且以点、、为顶点的三角形与△相似,求点的坐标;(3)在抛物线上是否存在点:它关于直线的对称点恰好在轴上.如果存在,直接写出点的坐标,如果不存在,试说明理由. 24.解:(1) 由直线经过点,可得. (1分)由抛物线的对称轴是直线,可得. (1分)⎝⎭⎝⎭图10 xy1 1O∵直线与轴、轴分别相交于点、,∴点的坐标是,点的坐标是. (2分)∵抛物线的顶点是点,∴点的坐标是. (1分)∵点是轴上一点,∴设点的坐标是.∵△BCG 与△BCD 相似,又由题意知,,∴△BCG 与△相似有两种可能情况: (1分)①如果,那么,解得,∴点的坐标是. (1分)②如果,那么,解得,∴点的坐标是. (1分)综上所述,符合要求的点有两个,其坐标分别是和 .(3)点的坐标是或. (2分+2分)青浦区24.(本题满分12分,第(1)、(2)、(3)小题,每小题4分)已知:如图8,在平面直角坐标系xOy 中,抛物线的图像与x 轴交于点A (3,0),与y 轴交于点B ,顶点C 在直线上,将抛物线沿射线AC 的方向平移,当顶点C 恰好落在y 轴上的点D 处时,点B 落在点E 处.23y ax bx =++2x =(1)求这个抛物线的解析式;(2)求平移过程中线段BC 所扫过的面积;(3)已知点F 在x 轴上,点G 在坐标平面内,且以点C 、E 、F 、G 为顶点的四边形是矩形,求点F 的坐标. .24.解:(1)∵顶点C 在直线上,∴,∴. (1分)将A (3,0)代入,得, (1分)解得,. (1分)∴抛物线的解析式为. (1分)(2)过点C 作CM ⊥x 轴,CN ⊥y 轴,垂足分别为M 、N .∵=,∴C (2,). (1分)∵,∴∠MAC=45°,∴∠ODA=45°, ∴.(1分)∵抛物线与y 轴交于点B ,∴B (0,),∴.(1分)2x =22=-=bx a 4=-b a 23y ax bx =++933=0++a b 1=a 4=-b 243=-+y x x 243=-+y x x ()221=--x 1-1==CM MA 3==OD OA 243=-+y x x 36=BD∵抛物线在平移的过程中,线段BC 所扫过的面积为平行四边形BCDE 的面积,∴. (1分)(3)联结CE.∵四边形是平行四边形,∴点是对角线与的交点, 即 .(i )当CE 为矩形的一边时,过点C 作,交轴于点,设点,在中,,即,解得 ,∴点 (1分)同理,得点(1分)(ii )当CE 为矩形的对角线时,以点为圆心,长为半径画弧分别交轴于点、,可得、(2分)综上所述:满足条件的点有,,),.松江区24.(本题满分12分,每小题各4分)如图,已知抛物线y=ax2+bx 的顶点为C (1,),P 是抛物线上位于第一象限内的一点,直线OP 交该抛物线对称轴于点B ,直线CP 交x 轴于点A . (1)求该抛物线的表达式;(2)如果点P 的横坐标为m ,试用m 的代数式表示线段BC 的长; (3)如果△ABP 的面积等于△ABC 的面积,求点P 坐标.12262122==⨯⨯⋅=⨯=BCDEBCDSSBD CN BCDE O CE BD OE OC ==1CF CE⊥x 1F 1F a (,0)1Rt OCF 22211=OF OC CF +22(2)5a a =-+52a =152F (,0)252F (-,0)O OC x 3F 4F 34=OF OF OC ==3F )4F ()152F (,0)252F (-,0)3F )4F ()1-24.(本题满分12分,每小题各4分) 解:(1)∵抛物线y=ax2+bx 的顶点为C (1,) ∴ .......................................2分 解得: .......................................1分 ∴抛物线的表达式为:y=x2-2x ; (1)(2)∵点P 的横坐标为m ,∴P 的纵坐标为:m2-2m……………………………1分令BC 与x 轴交点为M ,过点P 作PN ⊥x 轴,垂足为点N∵P 是抛物线上位于第一象限内的一点,∴PN= m2-2m ,ON=m ,O M=1由得………………………1分∴ BM=m-2…………………………………………………1分∵ 点C 的坐标为(1,),∴ BC= m-2+1=m-1………………………………………1分(3)令P(t ,t2-2t) ………………………………………………1分△ABP 的面积等于△ABC 的面积∴AC=AP1-112a b b a +=-⎧⎪⎨-=⎪⎩12a b =⎧⎨=-⎩PN BM ON OM =221m m BMm -=1-(第24题图)过点P 作PQ ⊥BC 交BC 于点Q∴CM=MQ=1∴t2-2t=1 …………………………………………………1分∴(舍去)………………………………1分∴ P 的坐标为()……………………………………1分徐汇区24. 如图,已知直线与轴、轴分别交于点、,抛物线过点、,且与轴交于另一个点.(1)求该抛物线的表达式;(2)点是线段上一点,过点作直线∥轴交该抛物线于点,当四边形是平行四边形时,求它的面积;(3)联结,设点是该抛物线上的一点,且满足,求点的坐标.1t =1t =1122y x =-+x y B C 212y x bx c=-++B C x A M BC M l y N OMNC AC D DBA CAO ∠=∠D杨浦区24、(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分)如图8,在平面直角坐标系中,抛物线于X轴交于点A、B,于y轴交于点C,直线经过点A、C,点P为抛物线上位于直线AC上方的一个动点。
上海市各区2018届中考数学二模试卷精选汇编填空题专题

上海市各区2018届九年级中考二模数学试卷精选汇编 填空题专题宝山区、嘉定区二、填空题(本大题共12题,每题4分,满分48分) 7.计算:=4 ▲ .8.一种细菌的半径是00000419.0米,用科学记数法把它表示为 ▲ 米. 9. 因式分解:=-x x 42 ▲ .10.不等式组⎩⎨⎧>+≤-063,01x x 的解集是 ▲ .11.在一个不透明的布袋中装有2个白球、8个红球和5个黄球,这些球除了颜色不同之外,其余均相同.如果从中随机摸出一个球,摸到黄球的概率是 ▲ . 12.方程23=+x 的根是 ▲ .13.近视眼镜的度数y (度)与镜片焦距x (米)呈反比例,其函数关系式为xy 120=.如果近似眼镜镜片的焦距3.0=x 米,那么近视眼镜的度数y 为 ▲ . 14.数据1、2、3、3、6的方差是 ▲ .15.在△ABC 中,点D 是边BC 的中点,=,=,那么=AD ▲ (用、表示). 16.如图1,在矩形ABCD 中,点E 在边CD 上,点F 在对角线BD 上,5:2:=DE DF ,BD EF ⊥,那么=∠ADB tan ▲ .17.如图2,点A 、B 、C 在圆O 上,弦AC 与半径OB 互相平分,那么AOC ∠度数为 ▲ 度. 18.如图3,在△ABC 中,5==AC AB ,6=BC ,点D 在边AB 上,且︒=∠90BDC .如果△ACD 绕点A 顺时针旋转,使点C 与点B 重合,点D 旋转至点1D ,那么线段1DD 的长为 ▲ .7. 2 8. 64.1910-⨯ 9. (4)x x - 10. 21x -<≤图2A BCD图3图111. 1312. 1x = 13. 400 14. 2.8 15. 2a b +r r16. 2 17. 120° 18. 4225长宁区二、填空题(本大题共12题, 每题4分, 满分48分) 【在答题纸相应题号后的空格内直接填写答案】 7. 计算:=--︒0)3(30sin ▲ . 8. 方程6+=-x x 的解是 ▲ .9. 不等式组⎪⎩⎪⎨⎧≥-<+-1)12(303x x 的解集是 ▲ .10.已知反比例函数xky =的图像经过点(-2017,2018),当0>x 时,函数值y 随 自变量x 的值增大而 ▲ .(填“增大”或“减小”)11.若关于x 的方程032=--m x x 有两个相等的实数根,则m 的值是 ▲ . 12.在形状为等腰三角形、圆、矩形、菱形、直角梯形的5张纸片中随机抽取一张,抽到中心对称图形的概率是 ▲ .13.抛物线522++=mx mx y 的对称轴是直线 ▲ . 14.小明统计了家里3月份的电话通话清单,按通话时间画出频数分布直方图(如图所示),则通话时间不足10分钟的 通话次数的频率是 ▲ .15.如图,在四边形ABCD 中,点E 、F 分别是边AB 、AD 的中点,BC =15,CD =9,EF =6,∠AFE =50°,则∠ADC 的度数为 ▲ .16.如图,在梯形ABCD 中,AB //CD ,∠C=90°,BC =CD =4,52=AD , 若=,=,用a 、b 表示= ▲ . 17.如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做半高三角形.已知直角三角形ABC 是半高三角形,且斜边5=AB ,则它的周长等于 ▲ . 18.如图,在矩形ABCD 中,对角线BD 的长为1,点P 是线段BD上的一点,联结CP ,将△BCP 沿着直线CP 翻折,若点B 落在 边AD 上的点E 处,且EP //AB ,则AB 的长等于 ▲ .第14题图 A DEF第15题图 第16题图 DCBA 第18题图AB CD二.填空题:(本大题共12题,满分48分) 7.21-; 8.2-=x ; 9.3>x ; 10.增大; 11.43-=m ; 12.53; 13.1-=x ;14.7.0;15.︒140; 16.→→-a b 21; 17.255或535++; 18.215-.崇明区二、填空题(本大题共12题,每题4分,满分48分) 7.因式分解:29x -= ▲ .8.不等式组1023x x x -<⎧⎨+>⎩的解集是 ▲ .9.函数12y x =-的定义域是 ▲ . 103=的解是 ▲ .11.已知袋子中的球除颜色外均相同,其中红球有3个,如果从中随机摸得1个红球的概率为18,那么袋子中共有 ▲ 个球.12.如果关于x 的方程240x x k +-=有两个相等的实数根,那么实数k 的值是 ▲ . 13.如果将抛物线221y x x =+-向上平移,使它经过点(1,3)A ,那么所得新抛物线的表达式是▲ .14.某校组织了主题为“共建生态岛”的电子小报作品征集活动,先从中随机抽取了部分作品,按,,,A B C D 四个等级进行评分,然后根据统计结果绘制了如下两幅不完整的统计图,那么此次抽取的作品中等级为B 的作品数为 ▲ .15.已知梯形ABCD ,AD BC ∥,2BC AD =,如果AB a =,AC b =,那么DA = ▲ . (用,a b 表示).16.如图,正六边形ABCDEF 的顶点B 、C 分别在正方形AGHI 的边AG 、GH 上,如果4AB =,那么CH 的长为 ▲ .17.在矩形ABCD 中,5AB =,12BC =,点E 是边AB 上一点(不与A 、B 重合),以点A 为圆心,AE 为半径作A ⊙,如果C ⊙与A ⊙外切,那么C ⊙的半径r 的取值范围是 ▲ .18.如图,ABC △中,90BAC ∠=︒,6AB =,8AC =,点D 是BC 的中点,将ABD △沿AD 翻折得到AED △,联结CE ,那么线段CE 的长等于 ▲ .(第14题图)HDCIFGE (第18题图)DCBAE二、填空题:(本大题共12题,每题4分,满分48分)7.(3)(3)x x +-; 8.31x -<<; 9.2x ≠; 10.8x =; 11.24; 12.4-; 13.22y x x =+; 14.48;15.1122a b -; 16.6-; 17.813r <<; 18.145. 奉贤区 7.计算:=-aa 211 . 8.如果822=-b a ,且4=+b a ,那么b a -的值是 . 9.方程242=-x 的根是 . 10.已知反比例函数)0(≠=k xky ,在其图像所在的每个象限内,y 的值随x 的值增大而减 小,那么它的图像所在的象限是第 象限.11.如果将抛物线22y x =平移,使平移后的抛物线顶点坐标为(1,2),那么所得新抛物线的表达式是 .12.将6本相同厚度的书叠起来,它们的高度是9厘米.如果将这样相同厚度的书叠起来的高度是42厘米,那么这些书有 本.13.从1,2,3,4,5,6,7,8这八个数中,任意抽取一个数,这个数恰好是合数的概率是. 14.某校为了了解学生双休日参加社会实践活动的情况,随机抽取了100名学生进行调查,并绘成如图3所示的频数分布直方图.已知该校共有1000名学生,据此估计,该校双休日参加社会实践活动时间在2~2.5小时之间的学生数大约是全体学生数的 (填百分数) . 15.如图4,在梯形ABCD 中,AD //BC ,BC=2AD ,E 、F 分别是边AD 、BC 的中点,设a AD =, =,那么EF 等于 (结果用、的线性组合表示). 16.如果一个矩形的面积是40,两条对角线夹角的正切值是34,那么它的一条对角线长是 . 17.已知正方形ABCD ,AB =1,分别以点A 、C 为圆心画圆,如果点B 在圆A 外,且圆A与圆C 外切,那么圆C 的半径长r 的取值范围是 .18.如图5,将△ABC 的边AB 绕着点A 顺时针旋转)900(︒<<︒αα得到AB ’,边AC 绕着点A 逆时针旋转)900(︒<<︒ββ得到AC ’,联结B ′C ′.当︒=+90βα时,我们称△A B ′C ′ 是△ABC 的“双旋三角形”.如果等边△ABC 的边长为a ,那么它的“双旋三角形”的面 积是 (用含a 的代数式表示). 人数 AB ′二、填空题: 7、12a ; 8、2; 9、4; 10、一三; 11、22(1)2y x =-+; 12、28; 13、38; 14、28%; 15、12a b +; 16、10; 171r << 18、214a黄浦区 7= . 8.因式分解:212x x --= . 9.方程1x +=的解是 .10.不等式组12031302x x ⎧->⎪⎪⎨⎪-≤⎪⎩的解集是 .11.已知点P 位于第三象限内,且点P 到两坐标轴的距离分别为2和4,若反比例函数图像经过点P ,则该反比例函数的解析式为 .12.如果一次函数的图像经过第一、二、四象限,那么其函数值y 随自变量x 的值的增大而 . (填“增大”或“减小”)13.女生小琳所在班级共有40名学生,其中女生占60%.现学校组织部分女生去市三女中参观,需要从小琳所在班级的女生当中随机抽取一名女生参加,那么小琳被抽到的概率是 . 14.已知平行四边形相邻两个内角相差40°,则该平行四边形中较小内角的度数是 . 15.半径为1的圆的内接正三角形的边长为 .16.如图,点D 、E 分别为△ABC 边CA 、CB 上的点,已知DE ∥AB ,且DE 经过△ABC 的重心,设CA a =, CB b =,则DE = .(用a 、b 表示)17.如图,在四边形ABCD 中,902624ABC ADC AC BD ∠=∠=︒==,,,M 、N 分别是AC 、BD 的中点,则线段MN 的长为 .18.如图,将矩形ABCD 沿对角线AC 折叠,使点B 翻折到点E 处,如果DE ∶AC =1∶3,那么AD ∶AB = .图4A B DFE CBC二、填空题:(本大题共12题,每题4分,满分48分)71; 8.()()34x x +-; 9.2; 10.166x <≤; 11.8y x =; 12.减小; 13.124; 14.70; 1516.2233b a -.; 17.5; 18∶1. 金山区7.因式分解:2a a -= ▲ . 8.函数y =的定义域是 ▲ .9.方程21xx =-的解是 ▲ . 10.一次函数2y x =-+的图像不经过第 ▲ 象限.11.有一枚材质均匀的正方体骰子,它的六个面上分别有1点、2点、…、6点的标记,掷这枚骰子,向上一面出现的点数是素数的概率是 ▲ . 12.如果关于x 的一元二次方程240x x k -+=有两个不相等的实数根,那么k 的取值范围是 ▲ .13.如果梯形的中位线长为6,一条底边长为8,那么另一条底边长等于 ▲ . 14.空气质量指数,简称AQI ,如果AQI 在0~50空 气质量类别为优,在51~100空气质量类别为良, 在101~150空气质量类别为轻度污染,按照某市最 近一段时间的AQI 画出的频数分布直方图如图3 所示,已知每天的AQI 都是整数,那么空气质量 类别为优和良的天数占总天数的百分比为 ▲ %. 15.一辆汽车在坡度为1:2.4的斜坡上向上行驶130米,那么这辆汽车的高度上升了 ▲ 米.16.如果一个正多边形的中心角等于30°,那么这个正多边形的边数是 ▲ . 17.如果两圆的半径之比为3:2,当这两圆内切时圆心距为3,那么当这两圆相交时,圆心距d 的的取值范围是 ▲ .图318.如图4,Rt △ABC 中,∠C =90°,AC =6,BC =8,D 是AB 的中点,P 是直线BC 上一点,把△BDP 沿PD 所在的直线翻折后,点B 落在点Q 处,如果QD ⊥BC , 那么点P 和点B 间的距离等于 ▲ .二.填空题:(本大题共12题,满分48分)7.()1a a -; 8.2x ≥; 9.2x =; 10.三; 11.12; 12.4k <; 13.4; 14.80; 15.50; 16.12; 17.3d 15<<; 18.52或10. 静安区二、填空题:(本大题共12题,每题4分,满分48分) 【在答题纸相应题号后的空格内直接填写答案】 7.32)2(a a ⋅ = ▲ .8.分解因式:=+-xy y x 4)(2▲ . 9.方程组⎩⎨⎧=-=+62,3x y y x 的解是 ▲ .10.如果4-x x 有意义,那么x 的取值范围是 ▲ .11.如果函数x a y 12--=(a 为常数)的图像上有两点),1(1y 、),31(2y ,那么函数值1y ▲ 2y .(填“<”、“=”或“>”)12.为了解植物园内某种花卉的生长情况,在一片约有3000株此类花卉的园地内,随机抽测了200株的高度作为样本,统计结果整理后列表如下:(每组数据可包括最低值,不包括最高值)厘米的约为 ▲ 株.13.从1,2,3,4,5,6,7,8,9中任取一个数,这个数即是奇数又是素数的概率是 ▲ .14.如图,在△ABC中,点G 是重心,过点G 作DE ∥BC ,分别交AB 、AC 于点D 、E .已知b CBa AB ==, ,那么AE = ▲ .(用向量表示). 15.如图,已知⊙O 中,直径AB 平分弦CD ,且交CD 于点E , 如果OE =BE ,那么弦CD 所对的圆心角是 ▲ 度.16.已知正多边形的边长为a ,且它的一个外角是其内角的一半,那么此正图4AB E DCG·第14题图多边形的边心距是 ▲ .(用含字母a 的代数式表示). 17.在平面直角坐标系中,如果对任意一点(a ,b ),规定两种变换:),(),(b a b a f --=,),(),(a b b a g -=,那么[]=-)2,1(f g ▲ .18.等腰△ABC 中,AB =AC ,它的外接圆⊙O 半径为1,如果线段OB 绕点O 旋转90°后可与线段OC 重合,那么∠ABC 的余切值是 ▲ .7、54a . 8、2)(y x +. 9、⎩⎨⎧=-=41y x . 10、x > 4. 11、>. 12、960.13、31. 14、b a 3232-. 15、120. 16、a 23. 17、(2,1). 18、12±. 闵行区二、填空题:(本大题共12题,每题4分,满分48分) 7.计算:21+2-= ▲ .8.在实数范围内分解因式:243x -= ▲ . 91的解是 ▲ .10.已知关于x 的方程230x x m --=没有实数根,那么m 的取值范围是 ▲ .11.已知直线(0)y kx b k =+≠与直线13y x =-平行,且截距为5,那么这条直线的解析式为 ▲ .12.一个十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当小杰过马路时,恰巧是绿灯的概率是 ▲ .13.已知一个40个数据的样本,把它分成6组,第一组到第四组的频数分别是10、5、7、6,第五组的频率是0.1,那么第六组的频数是 ▲ .14.如图,已知在矩形ABCD 中,点E 在边AD 上,且AE = 2ED .设B A a =u u r r ,BC b =uu u r r ,那么CE =uu u r▲ (用a r 、b r的式子表示).15.如果二次函数2111y a x b x c =++(10a ≠,1a 、1b 、1c 是常数)与2222y a x b x c =++(20a ≠,2a 、2b 、2c 是常数)满足1a 与2a 互为相反数,1b 与2b 相等,1c 与2c 互为倒数,那么称这两个函数为“亚旋转函数”.请直接写出函数232y x x =-+-的“亚旋转函数”为 ▲ .16.如果正n 边形的中心角为2α,边长为5,那么它的边心距为 ▲ .(用锐角α的三角比表示) 17.如图,一辆小汽车在公路l 上由东向西行驶,已知测速探头M 到公路l 的距离MN 为9米,测得此车从点A 行驶到点B 所用的时间为0.6秒,并测得点A 的俯角为30o,点B 的俯角为60o.那么此车从A 到B 的平均速度为 ▲ 米/秒.1.732≈1.414≈) 18.在直角梯形ABCD 中,AB // CD ,∠DAB = 90o,AB = 12,DC = 7,5cos 13ABC ∠=,点E 在线段AD 上,将△ABE 沿BE 翻折,点A 恰巧落在对角线BD 上点P 处,那么PD = ▲ .AB DCEDCMl二、填空题:(本大题共12题,每题4分,满分48分)7.5; 8.2x x -(; 9.1x =; 10.94m <-; 11.153y x =-+; 12.512; 13.8; 14.13a b -r r ; 15.2132y x x =+-; 16.5cot 2α(或52tan α); 17.17.3; 18.12. 普陀区7.计算:xy x 3122⋅= ▲ . 8.方程x 的根是 ▲ .9.大型纪录片《厉害了,我的国》上映25天,累计票房约为402700000元,成为中国纪录电影票房冠军.402700000用科学记数法表示是 ▲ .10.用换元法解方程312122=+-+x x x x 时,如果设y xx =+21,那么原方程化成以y 为“元”的方程是 ▲ . 11.已知正比例函数的图像经过点M (2-)、),(11y x A 、),(22y x B ,如果21x x <,那么1y ▲ 2y .(填“>”、“=”、“<”)12.已知二次函数的图像开口向上,且经过原点,试写出一个符合上述条件的二次函数的解析式: ▲ .(只需写出一个)13.如果一个多边形的内角和是720,那么这个多边形的边有 ▲ 条.14.如果将“概率”的英文单词 probability 中的11个字母分别写在11张相同的卡片上,字面朝下随意放在桌子上,任取一张,那么取到字母b 的概率是 ▲ .15.2018年春节期间,反季游成为出境游的热门,中国游客青睐的目的地仍主要集中在温暖的东南亚地区.据调查发现2018年春节期间出境游约有700万人,游客目的地分布情况的扇形图如图3所示,从中可知出境游东南亚 地区的游客约有 ▲ 万人.16. 如图4,在梯形ABCD 中,BC AD //,AD BC 3=,点E 、F 分别是边AB 、CD 的中点.设=,b DC =,那么向量EC 用向量a 、b 表示是 ▲ .17. 如图5,矩形ABCD 中,如果以AB 为直径的⊙O 沿着BC 滚动一周,点B 恰好与点C 重合,那么ABBC的值等于 ▲ .(结果保留两位小数)A东南亚欧美澳新16% 港澳台 15%韩日 11%其他13%图318. 如图6,在平面直角坐标系xOy 中,△ABC 的顶点A 、C 在坐标轴上,点B 的坐标是(22).将△ABC沿x 轴向左平移得到△111A B C ,点1B 落在函数6y x =-的图像上.如果此时四边形11AA C C 的面积等于552,那么点1C 的坐标是 ▲ .二、填空题:(本大题共12题,每题4分,满分48分)青浦区7.计算:32()=a a ÷- ▲ . 8.因式分解:24=a a - ▲ . 9.函数y 的定义域是 ▲ .010.不等式组1020.x x +≥⎧⎨->⎩,的整数解是 ▲ .11.关于x 的方程=2(1)ax x a +≠的解是 ▲ . 12.抛物线2(3)+1y x =-的顶点坐标是 ▲ .13.掷一枚材质均匀的骰子,掷得的点数为合数的概率是 ▲ .14.如果点1P (2,1y )、2P (3,2y )在抛物线2+2y x x =-上,那么1y ▲ 2y .(填“>”、 “<”或 “=”) 15.如图2,已知在平行四边形ABCD 中,E 是边AB 的中点,F 在边AD 上,且AF ︰FD=2︰1,如果AB a =,BC b =,那么EF = ▲ .16.如图3,如果两个相似多边形任意一组对应顶点P 、P '所在的直线都经过同一点O ,且有(0)OP k OP k '=⋅≠,那么我们把这样的两个多边形叫位似多边形,点O 叫做位似中心.已知ABC ∆与A B C '''∆是关于点O 的位似三角形,3OA OA '=,则ABC ∆与A B C '''∆的周长之比是 ▲ .17.如图4,在△ABC 中,BC=7,AC=,tan 1C =,点P 为AB 边上一动点(点P 不与点B 重合),以点P 为圆心,PB 为半径画圆,如果点C 在圆外,那么PB 的取值范围是 ▲ .18.已知,在Rt △ABC 中,∠C =90°,AC =9, BC =12,点D 、E 分别在边AC 、BC 上,且7.323x y ; 8. 3x =; 9. 810027.4⨯ ; 10. 32=-yy ; 11.>;12. 2y x =等; 13.6; 14.112; 15.315; 16.b a212+;17.3.14;18.(5-211). yxOABC图 6 A B CDEF图 4BCDO A 图5CD ︰CE =3︰4.将△CDE 绕点D 顺时针旋转,当点C 落在线段DE 上的点F 处时,BF恰好是∠ABC 的平分线,此时线段CD 的长是 ▲ .二、填空题:7.a ; 8.()4-a a ; 9.3≥-x ; 10.101、、-; 11. 21-a ; 12.(3,1); 13.13; 14.>; 15.2132-b a ; 16.1︰3; 17.3508<<PB ; 18.6. 松江区7.因式分解:34a a - = ▲ . 8x =的根是 ▲ . 9.函数32x y x-=的定义域是 ▲ . 10.已知方程240x x m -+=有两个不相等的实数根,则m 的取值范围是 ▲ . 11.把抛物线22y x =-向左平移1个单位,则平移后抛物线的表达式为 ▲ . 12.函数y kx b =+的图像如图所示,则当0y <时,x 的取值范围是 ▲ .13.一枚质地均匀的正方体骰子的六个面上分别刻有1到6的点数,随机投掷这枚骰子,那么向上一面的点数为合数的概率是 ▲ .14.某区有4000名学生参加学业水平测试,从中随机抽取500名,对测试成绩进行了统计,统计结果见下表:那么根据上述数据可以估计该区这次参加学业水平测试成绩小于60分的有 ▲ 人.15. 如图,在△ABC 中,D 是AB 的中点,E 是AC 上一点,且AE =2EC ,如果AB a =uuu r r ,AC b =uuu r r ,那么DE uuu r=▲ .(用a r 、b r表示).图3A BCDEF 图2图4POP'ACDE (第15题图)B(第12题图)(第18题图)ADCB16.一个正n 边形的一个内角等于它的中心角的2倍,则n =▲ .17.平面直角坐标系xoy 中,若抛物线2y ax =上的两点A 、B 满足OA =OB ,且1tan 2OAB ∠=,则称线段AB 为该抛物线的通径.那么抛物线212y x =的通径长为 ▲ . 18.如图,已知平行四边形ABCD 中,AC =BC ,∠ACB =45°,将三角形ABC 沿着AC 翻折,点B 落在点E 处,联结DE ,那么DEAC的值为 ▲ . 二、填空题:(本大题共12题,每题4分,满分48分)7. (2)(2)a a a +-; 8. 2x =; 9. 0x ≠; 10. 4m <; 11.22(1)y x =-+;12. 1x <-; 13. 13; 14. 120; 15. 1223a b -+r r ;1 .徐汇区 7. 函数12y x =-的定义域是 8. 在实数范围内分解因式:22x y y -=9. 2=的解是 10. 不等式组2672x x -≥⎧⎨+>-⎩的解集是11. 已知点1(,)A a y 、2(,)B b y 在反比例函数3y x=的图像上,如果0a b <<,那么1y 与2y 的大小关系是1y 2y12. 抛物线2242y x x =+-的顶点坐标是13. 四张背面完全相同的卡片上分别写有0.3227四个实数,如果将卡片字面 朝下随意放在桌子上,任意取一张,那么抽到有理数的概率为14. 在ABC ∆中,点D 在边BC 上,且:1:2BD DC =,如果设AB a =,AC b =,那么BD 等于 (结果用a 、b 的线性组合表示)15. 如图,为了解全校300名男生的身高情况,随机抽取若干男生进行身高测量,将所得数据(精确到1cm )整理画出频数分布直方图(每组数据含最低值,不含最高值),估计该校男生的身高在170cm ~175cm 之间的人数约有 人16. 已知两圆相切,它们的圆心距为3,一个圆的半径是4,那么另一个圆的半径是17. 从三角形(非等腰三角形)一个顶点引出一条射线与对边相交,该顶点与该交点间的线段把这个三角形分割成两个小三角形,如果其中一个小三角形是等腰三角形,另一个与原三角形相似,那么我们把这条线段叫做这个三角形的完美分割线,如图,在ABC ∆中,1DB =,2BC =,CD 是ABC ∆的完美分割线,且ACD ∆是以CD 为底边的等腰三角形,则CD 的长为18. 如图,在Rt ABC ∆中,90C ∠=︒,5AB =,3BC =,点P 、Q 分别在边BC 、AC 上,PQ ∥AB ,把PCQ ∆绕点P 旋转得到PDE ∆(点C 、Q 分别与点D 、E 对应),点D 落在线段PQ 上,若AD 平分BAC ∠,则CP 的长为二. 填空题7. 2x ≠ 8. (y x x + 9. 7x = 10. 93x -<≤-11. > 12. (1,4)-- 13. 3414. 1133b a -r r15. 72 16. 1或7 17. 3218. 2 杨浦区二、填空题(本大题共12题,每题4分,满分48分) 【请将结果直接填入答题纸的相应位置上】 7、计算: 8、当时,化简:=9、函数中,自变量x 的取值范围是10、如果反比例函数 的图像经过点的值等于11、三人中至少有两人性别相同的概率是 12、25位同学10秒钟跳绳的成绩汇总如下表:那么跳绳次数的中位数是13、李明早上骑自行车上学,中途因道路施工推车步行了一段路,到学校共用时15分钟,如果他骑自行车的平均速度是每分钟250米,推车步行的平均速度是每分钟80米,他家离学校的路程是2900米,设他推车步行的时间为x分钟,那么可列出的方程是14、四边形ABCD中,向量=15、若正n边形的内角和为1400,则边数n为16、如图3,△ABC中,∠A=800,∠B=400,BC的垂直平分线交AB于点D,联结DC,如果AD=2,BD=6那么△ADC的周长为17、如图4,正△ABC的边长为2,点A、B的半径为的圆上,点C在圆内,将正△ABC绕点A逆时针旋转,当点C第一次落在圆上时,旋转角的正切值是18、当关于X的一元二次方程有实数根,且其中一个根为另一个根的2倍时,称之为“倍根方程”,如果关于X的一元二次方程是“倍根方程”,那么m的值为。
上海市各区2018届九年级中考二模数学试卷精选汇编:计算题专题

x 2 x2 4x 4 x 2
先化简,再求值:
x
x2
x2
,其中 x
4
2 2.
19.解:原式
x+2 x2
x2
x
2
x2
·················································(3 分) ( x 2) x 2
x
1
·····································································(2 分)
( 6 分)
=2 3 1 2 3 3 ———————————————————————— ( 2 分)
=4—————————————————————————————(
2 分)
金山区
1
计算: tan45o 2sin 60o 122
2
1. 2
3
19.解:原式 = 1 2
2 3 4 ……………………………………………(
计算:
18
2018
( cot 45 )
0
1
2 3 ( 3) (sin 30 ) .
解:原式 = 3 2 ( 1)2018 ( 3
2 ) 1 ( 1 ) 1 …………………( 5 分) 2
=3 2 1 3 2 1 2
…………………………( 3 分)
=2 2 3
…………………………………( 2 分)
第 3页共 4页
x2x2
x
1 .
··············································································(1 分)
上海市各区2018届中考二模数学分类汇编_选择题专题(含答案)

市各区2018届九年级中考二模数学试卷精选汇编选择题专题宝山区、嘉定区一、选择题:(本大题共6题,每题4分,满分24分) 1.下列说法中,正确的是(▲)(A )0是正整数; (B )1是素数; (C )22是分数; (D )722是有理数. 2.关于x 的方程022=--mx x 根的情况是(▲)(A )有两个不相等的实数根; (B )有两个相等的实数根; (C )没有实数根; (D )无法确定.3. 将直线x y 2=向下平移2个单位,平移后的新直线一定不经过的象限是(▲) (A )第一象限; (B )第二象限; (C )第三象限; (D )第四象限.4. 下列说确的是(▲)(A )一组数据的中位数一定等于该组数据中的某个数据; (B )一组数据的平均数和中位数一定不相等; (C )一组数据的众数可以有几个;(D )一组数据的方差一定大于这组数据的标准差. 5.对角线互相平分且相等的四边形一定是(▲)(A )等腰梯形; (B )矩形; (C )菱形; (D )正方形.6.已知圆1O 的半径长为cm 6,圆2O 的半径长为cm 4,圆心距cm O O 321=,那么圆1O 与圆2O 的位置关系是(▲)(A )外离; (B )外切; (C )相交; (D )切.1. D2. A3. B4. C5. B6. C长宁区一、选择题(本大题共6题, 每题4分, 满分24分)【每题只有一个正确选项, 在答题纸相应题号的选项上用2B 铅笔正确填涂】 1.函数12-=x y 的图像不经过( ▲ )(A ) 第一象限; (B ) 第二象限; (C ) 第三象限; (D ) 第四象限. 2.下列式子一定成立的是( ▲ )(A ) a a a 632=+; (B )428x x x =÷;(C ) aa 121=; (D )6321)(aa-=--. 3.下列二次根式中,2的同类二次根式是( ▲ ) (A )4; (B )x 2; (C )92; (D )12. 4.已知一组数据2、x 、8、5、5、2的众数是2,那么这组数据的中位数是( ▲ ) (A ) 3.5; (B ) 4; (C ) 2; (D )6.5.5.已知圆A 的半径长为4,圆B 的半径长为7,它们的圆心距为d ,要使这两圆没有公共点, 那么d 的值可以取( ▲ )(A ) 11; (B ) 6; (C ) 3; (D )2.6.已知在四边形ABCD 中,AD //BC ,对角线AC 、BD 交于点O ,且AC =BD , 下列四个命题中真命题是( ▲ )(A ) 若AB =CD ,则四边形ABCD 一定是等腰梯形; (B ) 若∠DBC =∠ACB ,则四边形ABCD 一定是等腰梯形; (C ) 若ODCOOB AO =,则四边形ABCD 一定是矩形; (D ) 若AC ⊥BD 且AO =OD ,则四边形ABCD 一定是正方形. 一、选择题:(本大题共6题,每题4分,满分24分) 1.B ; 2.D ; 3.C ; 4.A ; 5.D ; 6.C .崇明区一、选择题(本大题共6题,每题4分,满分24分)1.8的相反数是…………………………………………………………………………………( ▲ )(A)18; (B)8;(C)18-;(D)8-.2.下列计算正确的是 …………………………………………………………………………( ▲ )(A)+=;(B)23a a a +=;(C)33(2)2a a =;(D)632a a a ÷=.3.今年3月12日,某学校开展植树活动,某植树小组20名同学的年龄情况如下表:那么这20名同学年龄的众数和中位数分别是……………………………………………( ▲ )(A)15,14;(B)15,15;(C)16,14;(D)16,15.4.某美术社团为练习素描,他们第一次用120元买了若干本相同的画册,第二次用240元在同一家商店买与上一次相同的画册,这次商家每本优惠4元,结果比上次多买了20本.求第一次买了多少本画册?设第一次买了x 本画册,列方程正确的是 ………………………( ▲ ) (A)120240420x x -=+; (B)240120420x x -=+;(C)120240420x x -=-;(D)240120420x x-=-. 5.下列所述图形中,既是轴对称图形又是中心对称图形的是 ……………………………( ▲ )(A) 等边三角形;(B) 平行四边形;(C) 菱形;(D) 正五边形.6.已知ABC △中,D 、E 分别是AB 、AC 边上的点,DE BC ∥,点F 是BC 边上一点,联结AF 交DE 于点G ,那么下列结论中一定正确的是 ………………………………………( ▲ )(A)EG FGGD AG=; (B)EG AEGD AD=; (C)EG AGGD GF=; (D)EG CFGD BF=. 一、选择题:(本大题共6题,每题4分,满分24分)1.D ; 2.B ; 3.B ; 4.A ; 5.C ; 6.D.奉贤区1.下列二次根式中,与a 是同类二次根式的是()(A )2a ; (B )a 2; (C )a 4; (D )a +4.2.某班要推选学生参加学校的“诗词达人”比赛,有7名学生报名参加班级选拔赛,他们的选拔赛成绩各不相同,现取其中前3名参加学校比赛.小红要判断自己能否参加学校比赛,在知道自己成绩的情况下,还需要知道这7名学生成绩的()(A )众数; (B )中位数; (C )平均数; (D )方差.3.下列四个不等式组中,其中一个不等式组的解集在数轴上的正确表示如图1所示,这个不等式组是()(A )⎩⎨⎧->≥;,32x x (B )⎩⎨⎧-<≤;,32x x (C )⎩⎨⎧-<≥;,32x x (D )⎩⎨⎧->≤.32x x ,4.如果将直线l 1:22-=x y 平移后得到直线l 2:x y 2=,那么下列平移过程正确的是() (A )将l 1向左平移2个单位; (B )将l 1向右平移2个单位; (C )将l 1向上平移2个单位; (D )将l 1向下平移2个单位. 5.将一把直尺和一块含30°和60°角的三角板ABC 按如图2所 示的位置放置,如果∠CDE =40°,那么∠BAF 的大小为() (A )10°; (B )15°; (C )20°; (D )25°.6.直线AB 、CD 相交于点O ,射线 OM 平分∠AOD ,点P 在射线OM 上(点P 与点O 不重 合),如果以点P 为圆心的圆与直线AB 相离,那么圆P 与直线CD 的位置关系是() (A )相离; (B )相切; (C )相交; (D )不确定. 一、选择题:1、C ;2、B ;3、D ;4、C ;5、A ;6、A ;黄浦区一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】 1.下列实数中,介于23与32之间的是( ) (A )2;(B )3;(C )227; (D )π.图1图22.下列方程中没有实数根的是( ) (A )210x x +-=; (B )210x x ++=; (C )210x -=;(D )20x x +=.3.一个反比例函数与一个一次函数在同一坐标平面的图像如图示,如果其中的反比例函数解析式为ky x=,那么该一次函数可能的解析式是( ) (A )y kx k =+; (B )y kx k =-; (C )y kx k =-+;(D )y kx k =--.4.一个民营企业10名员工的月平均工资如下表,则能较好反映这些员工月平均工资水平的是( )(工资单位:万元) (A )平均数;(B )中位数;(C )众数;(D )标准差.5.计算:AB BA +=u u u r u u u r( ) (A )AB u u u r;(B )BA u u u r ; (C )0r;(D )0.6.下列命题中,假命题是( )(A )如果一条直线平分弦和弦所对的一条弧,那么这条直线经过圆心,并且垂直于这条弦; (B )如果一条直线平分弦所对的两条弧,那么这条直线经过圆心,并且垂直于这条弦; (C )如果一条直线经过圆心,并且平分弦,那么该直线平分这条弦所对的弧,并且垂直于这条弦; (D )如果一条直线经过圆心,并且垂直弦,那么该直线平分这条弦和弦所对的弧.一、选择题(本大题6小题,每小题4分,满分24分)1.A ;2.B ;3.B ;4.B ;5.C ;6.C .金山区1.下列各数中,相反数等于本身的数是(▲)(A )1-; (B )0; (C )1; (D )2. 2.单项式32a b 的次数是(▲)(A )2; (B )3 (C )4; (D )5.3.如果将抛物线22y x =-向上平移1个单位,那么所得新抛物线的表达式是(▲)(A )()221y x =-+; (B )()221y x =--; (C )221y x =--; (D )221y x =-+.4.如果一组数据1,2,x ,5,6的众数为6,则这组数据的中位数为(▲) (A )1; (B )2 (C )5; (D )6. 5.如图1,□ABCD 中,E 是BC 的中点,设AB a =u u u r r ,AD b =u u u r r,那么向量AE u u u r 用向量a r 、b r表示为(▲)(A )12a b +r r ;(B )12a b -r r ;(C )12a b -+r r ;(D )12a b --r r .6.如图2,∠AOB=45°,OC 是∠AOB 的角平分线,PM ⊥OB , 垂足为点M ,PN ∥OB ,PN 与OA 相交于点N ,那么PMPN的值等于( ▲ )(A )12; (B ; (C ; (D一、选择题:(本大题共6题,每题4分,满分24分)1.B ; 2.C ; 3.D ; 4.C ; 5.A ; 6.B .静安区一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个是正确的,选择正确项的代号并填涂在答题纸的相应位置上】 1.下列实数中,有理数是 (A )2; (B )21; (C )34; (D )4. 2.下列方程中,有实数根的是(A )x x -=-1;(B )01)2(2=-+x ; (C )012=+x ;(D )034=-+-x x .3.如果b a >,0<m ,那么下列不等式中成立的是 (A) bm am >; (B) mbm a >; (C) m b m a +>+; (D) m b m a +->+-.4.如图,AB //CD ,直线EF 分别交AB 、CD 于点E 、F ,EG 平分∠BEF ,图1MN A BC图2PABEDC G 第4题图F如果∠EFG =64°,那么∠EGD 的大小是(A) 122°; (B) 124°; (C) 120°; (D) 126°.5.已知两组数据:a 1,a 2,a 3,a 4,a 5和a 1-1,a 2-1,a 3-1,a 4-1,a 5-1, 下列判断中错误的是(A) 平均数不相等,方差相等; (B) 中位数不相等,标准差相等; (C) 平均数相等,标准差不相等; (D) 中位数不相等,方差相等. 6.下列命题中,假命题是(A )两组对角分别相等的四边形是平行四边形;(B )有一条对角线与一组邻边构成等腰三角形的平行四边形是菱形; (C )一组邻边互相垂直,两组对边分别平行的四边形是矩形; (D )有一组邻边相等且互相垂直的平行四边形是正方形.闵行区一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确选项的代号并填涂在答题纸的相应位置上】1.在下列各式中,二次单项式是 (A )21x +;(B )213xy ;(C )2xy ;(D )21()2-.2.下列运算结果正确的是 (A )222()a b a b +=+; (B )2323a a a +=; (C )325a a a ⋅=;(D )112(0)2a a a-=≠. 3.在平面直角坐标系中,反比例函数(0)ky k x=≠图像在每个象限y 随着x 的增大而减小,那么它的图像的两个分支分别在 (A )第一、三象限; (B )第二、四象限; (C )第一、二象限;(D )第三、四象限. 4.有9名学生参加校民乐决赛,最终成绩各不相同,其中一名同学想要知道自己是否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的 (A )平均数;(B )中位数;(C )众数;(D )方差.5.已知四边形ABCD 是平行四边形,下列结论中不正确的是 (A )当AB = BC 时,四边形ABCD 是菱形; (B )当AC ⊥BD 时,四边形ABCD 是菱形; (C )当∠ABC = 90o 时,四边形ABCD 是矩形;(D )当AC = BD 时,四边形ABCD 是正方形.6.点A 在圆O 上,已知圆O 的半径是4,如果点A 到直线a 的距离是8,那么圆O 与直线a 的位置关系可能是(A )相交; (B )相离; (C )相切或相交; (D )相切或相离. 一、选择题:(本大题共6题,每题4分,满分24分) 1.C ;2.C ;3.A ;4.B ;5.D ;6.D .普陀区1. 下列计算中,错误的是 ························· (▲) (A )120180=; (B )422=-; (C )2421=; (D )3131=-.2.下列二次根式中,最简二次根式是 ···················· (▲) (A )a 9; (B )35a ; (C )22b a +; (D )21+a . 3.如果关于x 的方程022=++c x x 没有实数根,那么c 在2、1、0、3-中取值是 (▲) (A )2; (B ); (C )0; (D )3-.4.如图1,已知直线CD AB //,点E 、F 分别在AB 、CD 上,CFE ∠:EFB ∠3=:4,如果40B ∠=o ,那么BEF ∠= ······························ (▲) (A )20o ; (B )40o ; (C )60o ; (D )80o .5. 自1993年起,联合国将每年的3月22日定为“世界水日”,宗旨是唤起公众的节水意识,加强水资源保护.某校在开展“节约每一滴水”的活动中,从初三年级随机选出20名学生统计出各自家庭一个月的节约用水量,有关数据整理如下表.ABCDFE图1100.580.560.540.5图1这组数据的中位数和众数分别是 ······················ (▲) (A )1.2,1.2; (B )1.4,1.2; (C )1.3,1.4; (D )1.3,1.2.6. 如图2,已知两个全等的直角三角形纸片的直角边分别为a 、b )(b a ≠,将这两个三角形的一组等边重合,拼合成一个无重叠的几何图形,其中轴对称图形有 ············ (▲) (A )3个; (B )4个; (C )5个; (D )6个.一、选择题:(本大题共6题,每题4分,满分24分)1.(B); 2.(C);3.(A); 4.(C); 5.(D); 6.(B).青浦区一、选择题:(本大题共6题,每题4分,满分24分)[每小题只有一个正确选项,在答题纸相应题号的选项上用2B 铅笔正确填涂] 1.下列实数中,有理数是( ▲) (A ;(B )2.1g;(C )π;(D )135.2.下列方程有实数根的是( ▲ )(A )4+2=0x ; (B 1-; (C )2+21=0x x -;(D )111x x x =--. 3.已知反比例函数1y x=,下列结论正确的是( ▲ ) (A )图像经过点(-1,1);(B )图像在第一、三象限;(C )y 随着x 的增大而减小; (D )当1x >时,1y <. 4.用配方法解方程241=0x x -+,配方后所得的方程是( ▲ )(A )2(2)=3x -; (B )2(+2)=3x ; (C )2(2)=3x --;(D )2(+2)=3x -. 5. “a 是实数,20a ≥”这一事件是( ▲ )(A )不可能事件; (B )不确定事件; (C )随机事件; (D )必然事件. 6. 某校40名学生参加科普知识竞赛(竞赛分数都是整数),竞赛成绩的频数分布直方图如图1所示,成绩的中位数落在( ▲ ) (A )50.5~60.5分; (B )60.5~70.5分; (C )70.5~80.5分; (D )80.5~90.5分.图2CBA(第6题图)一、选择题:1.B ; 2.C ; 3.B ; 4.A ; 5.D ; 6.C .松江区一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】 1(A(B(C(D 2.下列运算正确的是(▲) (A )532x x x =+;(B )532x x x =⋅; (C )235()x x =;(D )623x x x ÷=.3.下列图形中,既是中心对称又是轴对称图形的为(▲) (A )正三角形; (B )等腰梯形;(C )平行四边形; (D )菱形.4.关于反比例函数2y x=,下列说法中错误的是(▲) (A )它的图像是双曲线; (B )它的图像在第一、三象限; (C )y 的值随x 的值增大而减小;(D )若点(a ,b )在它的图像上,则点(b ,a )也在它的图像上.5.将一组数据中的每一个数都加上1得到一组新的数据,那么下列四个统计量中,值保持不变的是(▲) (A )方差;(B )平均数;(C )中位数;(D )众数.6.如图,在△ABC 中,∠C =90°,AC =3,BC =4,⊙B 的半径为1,已知⊙A 与直线BC 相交,且与⊙B 没有公共点,那么⊙A 的半径可以是(▲)(A )4; (B )5; (C )6;(D )7.一、选择题:(本大题共6题,每题4分,满分24分)1.B; 2.B; 3. D; 4. C; 5. A; 6. D;徐汇区一. 选择题1. 下列算式的运算结果正确的是( )A. 326m m m ⋅=B. 532m m m ÷=(0m ≠)C. 235()m m --=D. 422m m m -=2. 直线31y x =+不经过的象限是( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 如果关于x 的方程210x +=有实数根,那么k 的取值围是( )A. 0k >B. 0k ≥C. 4k >D. 4k ≥4. 某射击选手10次射击成绩统计结果如下表,这10次成绩的众数、中位数分别是( )A. 8、8B. 8、8.5C. 8、9D. 8、105. 如果一个正多边形角和等于1080°,那么这个正多边形的每一个外角等于( )A. 45°B. 60°C. 120°D. 135°6. 下列说法中,正确的个数共有( )(1)一个三角形只有一个外接圆(2)圆既是轴对称图形,又是中心对称图形(3)在同圆中,相等的圆心角所对的弧相等(4)三角形的心到该三角形三个顶点距离相等A. 1个B. 2个C. 3个D. 4个1. B2. D3. D4. B5. A6. C浦区一、选择题(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个现象是正确的,选择正确项的代号并填涂在答题纸上相应位置上】1、下列各数中是无理数的是 ( )(A ) (B )1. (C )半径为1cm 的圆周长 (D )2、下列运算正确的是 ( )(A)(B)(C)(D)3、若,则下列不等式中一定成立的是()(A)x (B)(C)(D)4、某校120名学生某一周用于阅读课外书籍的时间的频率分布直方图如图1所示,其中阅读时间是8-10小时的组频数和组频率分别是()(A)15和0.125 (B)15和0.25 (C)30和0.125 (D)30和0.255、下列图形是中心对称图形的是()6、如图2,半径为1的圆O1和半径为3的圆O2相切,如果半径为2的圆与圆O1和圆O2都相切,那么这样的圆的个数是()(A) 1 (B)2 (C)3 (D)4CBADBC。
上海市各区2018届九年级中考二模数学试卷精选汇编:压轴题专题

24 OF
5
∴ AF
AO 2 OF 2 7 5
14
∵ OF 过圆心, OF⊥ AD,∴ AD 2AF
. ( 3 分)
5
②当 OA// BD 时, 过点 B 作 BM⊥OA 交 AO 延长线于点 M ,过点 D 作 DG⊥ AO,垂足为点 G,
则由①的方法可得
∴ GO DO 2
DG DG 2
24
BM
, 在 Rt△ GOD 中,
∴ OH 8 ∴ AMB
OBM 180
C
M
B
图 9-1
∵ AMB 90 ∴ OBM 90
∴四边形 OBMH 是矩形
∴ OB HM 10
∴ CM HM HC 4 …………… 2 分
②当 ABM 90 ,点 M 的位置如图 9-2 由①可知 AB 8 5 , cos CAB 2 5
5 在 Rt△ ABM 中, cos CAB AB 2 5
22 x
∴yΒιβλιοθήκη 1 BE OG180 5
25
2
2 22 x
∴ y 400 …………… 1 分 22 x
自变量 x 的取值范围为 0 x 12 …………… 1 分
长宁区
25.(本题满分 14 分,第( 1)小题 4 分,第( 2)小题 4 分,第( 3)小题 6 分) 在圆 O 中, C是弦 AB 上的一点,联结 OC 并延长,交劣弧 AB 于点 D,联结 AO、 BO、 AD、 BD. 已知圆 O 的半径长为 5 ,弦 AB 的长为 8.
5
7
7
, AG AO GO 5
5
5
DGO 18
,
5
90 ,DO=5,
在 Rt△ GAD中,
上海市各区2018届中考数学二模试卷精选汇编二次函数专

上海市各区2018届九年级中考二模数学试卷精选汇编:二次函数专题宝山区、嘉定区24.(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分) 已知平面直角坐标系xOy (如图7),直线m x y +=的经过点)0,4(-A 和点)3,(n B . (1)求m 、n 的值;(2)如果抛物线c bx x y ++=2经过点A 、B ,该抛物线的顶点为点P ,求ABP ∠si n 的值;(3)设点Q 在直线m x y +=上,且在第一象限内,直线m x y +=与y 轴的交点为点D ,如果DOB AQO ∠=∠,求点Q 的坐标.24.解:(1) ∵直线m x y +=的经过点)0,4(-A∴04=+-m ……………………1分∴4=m ………………………………1分∵直线m x y +=的经过点)3,(n B ∴34=+n ……………………1分∴1-=n …………………………………………1分(2)由可知点B 的坐标为)3,1(-∵抛物线c bx x y ++=2经过点A 、B ∴⎩⎨⎧=+-=+-310416c b c b∴6=b , 8=c∴抛物线c bx x y ++=2的表达式为862++=x x y …………………1分∴抛物线862++=x x y 的顶点坐标为)1,3(--P ……………1分∴23=AB ,2=AP ,52=PB∴222PB BP AB =+图7∴︒=∠90PAB ……………………………………1分∴PB AP ABP =∠sin ∴1010sin =∠ABP …………………………………………1分(3)过点Q 作x QH ⊥轴,垂足为点H ,则QH ∥y 轴 ∵DOB AQO ∠=∠,QBO OBD ∠=∠∴△OBD ∽△QBO ∴OBDBQB OB =……………1分 ∵直线4+=x y 与y 轴的交点为点D ∴点D 的坐标为)4,0(,4=OD又10=OB ,2=DB∴25=QB ,24=DQ ……………1分∵23=AB∴28=AQ ,24=DQ ∵QH ∥y 轴 ∴AQADQH OD = ∴28244=QH ∴8=QH ……………………………………1分 即点Q 的纵坐标是8又点Q 在直线4+=x y 上点Q 的坐标为)8,4(……………1分长宁区24.(本题满分12分,第(1)小题4分,第(2)小题3分,第(3)小题5分)如图在直角坐标平面内,抛物线32-+=bx ax y 与y 轴交于点A ,与x 轴分别交于点B (-1,0)、点C (3,0),点D 是抛物线的顶点.(1)求抛物线的表达式及顶点D 的坐标; (2)联结AD 、DC ,求ACD ∆的面积;(3)点P 在直线DC 上,联结OP ,若以O 、P 、C 为顶点的三角形与△ABC 相似,求点P 的坐标.24.(本题满分12分,第(1)小题4分,第(2)小题3分,第(3)小题5分) 解:(1) 点B (-1,0)、C (3,0)在抛物线32-+=bx ax y 上∴⎩⎨⎧=-+=--033903b a b a ,解得⎩⎨⎧-==21b a ( 2分)∴抛物线的表达式为322--=x x y ,顶点D 的坐标是(1,-4) ( 2分) (2)∵A (0,-3),C (3,0),D (1,-4) ∴23=AC ,52=CD ,2=AD∴222AD AC CD += ∴︒=∠90CAD ( 2分) ∴.32232121=⨯⨯=⋅⋅=∆AD AC S ACD (1分) (3)∵︒=∠=∠90AOB CAD ,2==AOACBO AD , ∴△CAD ∽△AOB ,∴OAB ACD ∠=∠∵OA =OC ,︒=∠90AOC ∴︒=∠=∠45OCA OAC∴ACD OCA OAB OAC ∠+∠=∠+∠,即BCD BAC ∠=∠ ( 1分) 若以O 、P 、C 为顶点的三角形与△ABC 相似 ,且△ABC 为锐角三角形 则POC ∆也为锐角三角形,点P 在第四象限由点C (3,0),D (1,-4)得直线CD 的表达式是62-=x y ,设)62,(-t t P (30<<t ) 过P 作PH ⊥OC ,垂足为点H ,则t OH =,t PH 26-=①当ABC POC ∠=∠时,由ABC POC ∠=∠tan tan 得BO AO OH PH =,∴326=-t t ,解得56=t , ∴)518,56(1-P (2分)备用图 第24题图②当ACB POC ∠=∠时,由145tan tan tan =︒=∠=∠ACB POC 得1=OHPH ,∴126=-tt,解得2=t ,∴)2,2(2-P ( 2分) 综上得)518,56(1-P 或)2,2(2-P 崇明区24.(本题满分12分,第(1)、(2)、(3)小题满分各4分)已知抛物线经过点(0,3)A 、(4,1)B 、(3,0)C . (1)求抛物线的解析式;(2)联结AC 、BC 、AB ,求BAC ∠的正切值;(3)点P 是该抛物线上一点,且在第一象限内,过点P 作PG AP ⊥交y 轴于点G ,当点G在点A 的上方,且APG △与ABC △相似时,求点P 的坐标.24.(本题满分12分,每小题4分)解:(1)设所求二次函数的解析式为2(0)y ax bx c a =++≠,………………………1分将A (0,3)、B (4,)、C (3,0)代入,得 1641,930,3.a b c a b c c ++=⎧⎪++=⎨⎪=⎩解得12523a b c ⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩………2分所以,这个二次函数的解析式为215322y x x =-+ ……………………………1分(2)∵A (0,3)、B (4,)、C (3,0)∴AC =BC =AB =∴222AC BC AB +=∴90ACB =︒∠ ………………………………………………………2分∴13BC tan BAC AC ===∠ ……………………………………………2分 (3)过点P 作PH y ⊥轴,垂足为H设P 215(,3)22x x x -+,则H 215(0,3)22x x -+ ∵A (0,3) ∴21522AH x x =-,PH x = ∵90ACB APG ==︒∠∠∴当△APG 与△ABC 相似时,存在以下两种可能: 1° PAG CAB =∠∠ 则13tan PAG tan CAB ==∠∠ 即13PH AH = ∴2115322x x x =- 解得11x = ………………………1分 ∴点P 的坐标为(11,36) ……………………………………………………1分 2° PAG ABC =∠∠ 则3tan PAG tan ABC ==∠∠ 即3PH AH = ∴231522x x x =- 解得173x = …………………………1分 ∴点P 的坐标为1744(,)39……………………………………………………1分 奉贤区 24.(本题满分12分,每小题满分各4分)已知平面直角坐标系xOy (如图8),抛物线)0(3222>++-=m m mx x y 与x 轴交于点A、B(点A在点B左侧),与y轴交于点C,顶点为D,对称轴为直线,过点C作直线的垂线,垂足为点E,联结DC、BC.(1)当点C(0,3)时,①求这条抛物线的表达式和顶点坐标;②求证:∠DCE=∠BCE;(2)当CB平分∠DCO时,求m的值.黄浦区24.(本题满分12分)已知抛物线2y x bx c =++经过点A (1,0)和B (0,3),其顶点为D . (1)求此抛物线的表达式; (2)求△ABD 的面积;(3)设P 为该抛物线上一点,且位于抛物线对称轴 右侧,作PH ⊥对称轴,垂足为H ,若△DPH 与△AOB 相 似,求点P 的坐标.24. 解:(1)由题意得:013b c c =++⎧⎨=⎩,———————————————————(2分)解得:43b c =-⎧⎨=⎩,—————————————————————————(1分)所以抛物线的表达式为243y x x =-+. ——————————————(1分) (2)由(1)得D (2,﹣1),———————————————————(1分) 作DT ⊥y 轴于点T , 则△ABD 的面积=()11124131211222⨯⨯-⨯⨯-⨯+⨯=.————————(3分)(3)令P ()()2,432p p p p -+>.————————————————(1分)由△DPH 与△AOB 相似,易知∠AOB =∠PHD =90°,所以243132p p p -++=-或2431123p p p -++=-,————————————(2分)解得:5p =或73p =,所以点P 的坐标为(5,8),78,39⎛⎫-⎪⎝⎭.————————————————(1分)金山区24.(本题满分12分,每小题4分)平面直角坐标系xOy 中(如图8),已知抛物线2y x bx c =++经过点A (1,0)和B (3,0),与y 轴相交于点C ,顶点为P .(1)求这条抛物线的表达式和顶点P 的坐标; (2)点E 在抛物线的对称轴上,且EA =EC ,求点E 的坐标;(3)在(2)的条件下,记抛物线的对称轴为直线MN ,点Q 在直线MN 右侧的抛物线 上,∠MEQ =∠NEB ,求点Q 的坐标.24.解:(1)∵二次函数2y x bx c =++的图像经过点A (1,0)和B (3,0),∴10930b c b c ++=⎧⎨++=⎩,解得:4b =-,3c =.……………………………(2分)∴这条抛物线的表达式是243y x x =-+…………………………………(1分)顶点P 的坐标是(2,-1).………………………………………………(1分)(2)抛物线243y x x =-+的对称轴是直线2x =,设点E 的坐标是(2,m ).…(1分)根据题意得:=解得:m=2,…(2分) ∴点E 的坐标为(2,2).…………………………………………………(1分) (3)解法一:设点Q 的坐标为2(,43)t t t -+,记MN 与x 轴相交于点F .图8作QD ⊥MN ,垂足为D ,则2DQ t =-,2243241DE t t t t =-+-=-+………………………(1分) ∵∠QDE=∠BFE=90°,∠QED=∠BEF ,∴△QDE ∽△BFE ,…………………(1分)∴DQ DEBF EF=,∴224112t t t --+=, 解得11t =(不合题意,舍去),25t =.……………………………(1分) ∴5t =,点E 的坐标为(5,8).…………………………………………(1分)解法二:记MN 与x 轴相交于点F .联结AE ,延长AE 交抛物线于点Q ,∵AE=BE , EF ⊥AB ,∴∠AEF=∠NEB ,又∵∠AEF=∠MEQ ,∴∠QEM=∠NEB ,………………………………(1分)点Q 是所求的点,设点Q 的坐标为2(,43)t t t -+, 作QH ⊥x 轴,垂足为H ,则QH =243t t -+,OH =t ,AH =t -1, ∵EF ⊥x 轴,∴EF ∥QH ,∴EF AFQH AH=,∴221431t t t =-+-,………(1分) 解得11t =(不合题意,舍去),25t =.……………………………………(1分) ∴5t =,点E 的坐标为(5,8).…………………………………………(1分)静安区24.(本题满分12分,第(1)小题满分4分,第(2)小题满分4分,第(3)小题满分4分)在平面直角坐标系xOy 中,已知点B (8,0)和点C (9,3-).抛物线c ax ax y +-=82(a ,c 是常数,a ≠0)经过点B 、C ,且与x 轴的另一交点为A .对称轴上有一点M ,满足MA =MC .(1) 求这条抛物线的表达式; (2) 求四边形ABCM 的面积;(3) 如果坐标系内有一点D ,满足四边形ABCD且AD //BC ,求点D 的坐标.24.(本题满分12分,第(1)小题4分,第(2)小题4解:(1)由题意得:抛物线对称轴aax 28-=,即4=x . …………(1分) 点B (8,0)关于对称轴的对称点为点A (0,0)∴0=c , …………(1分)将C (9,-3)代入ax ax y 82-=,得31-=a …………………………(1分)∴抛物线的表达式:x x y 38312+-=…………………………(1分) (2)∵点M 在对称轴上,∴可设M (4,y ) 又∵MA =MC ,即22MCMA =∴2222)3(54++=+y y , 解得y =-3, ∴M (4,-3) …………………(2分) ∵MC //AB 且MC ≠AB , ∴四边形ABCM 为梯形,,AB =8,MC =5,AB 边上的高h = y M = 3 ∴2393)58(21)(21=⨯+⨯=⨯+=MH MC AB S(3) 将点B (8,0)和点C (9,﹣3)代入b kx y BC += 可得⎩⎨⎧-=+=+3908b k b k ,解得⎩⎨⎧=-=243b k 由题意得,∵AD //BC , 3-=BC k ∴3-=AD k ,x y AD 3-=又∵AD 过(0,0),DC =AB =8,设D (x ,-3x ) 2228)33()9(=+-+-x x , …………………………(1分) 解得11=x (不合题意,舍去), 5132=x …………………………(1分)∴5393-=-=x y ∴点D 的坐标)539,513(-.……………………(1分)闵行区 24.(本题满分12分,其中每小题各4分)如图,已知在平面直角坐标系xOy 中,抛物线22y ax x c =-+与x 轴交于 点A 和点B (1,0),与y 轴相交于点C (0,3).(1)求抛物线的解析式和顶点D 的坐标; (2)求证:∠DAB=∠ACB ;(3)点Q 在抛物线上,且△ADQ 是以AD 为 底的等腰三角形,求Q 点的坐标.24.解:(1)把B (1,0)和C (0,3)代入22y ax x c =-+中,得9603a c c ++=⎧⎨=⎩,解得13a c =-⎧⎨=⎩.……………………………………(2分)∴抛物线的解析式是:223y x x =--+.……………………………(1分) ∴顶点坐标D (-1,4).……………………………………………(1分) (2)令0y =,则2230x x --+=,13x =-,21x =,∴A (-3,0)∴3OA OC ==,∴∠CAO =∠OCA .…………………………………(1分)在Rt BOC ∆中,1tan 3OB OCB OC ∠==.………………………………(1分)∵AC =DC =AD =, ∴2220AC DC +=,220AD =;∴222AC DC AD +=,ACD ∆是直角三角形且90ACD ∠=,∴1tan 3DC DAC AC ∠==,又∵∠DAC 和∠OCB 都是锐角,∴∠DAC =∠OCB .…………………(1分) ∴DAC CAO BCO OCA ∠+∠=∠+∠,即DAB ACB ∠=∠.……………………………………………………(1分) (3)令(Q x ,)y 且满足223y x x =--+,(3A -,0),(1D -,4)∵ADQ ∆是以AD 为底的等腰三角形,∴22QD QA =,即2222(3)(1)(4)x y x y ++=++-,化简得:220x y -+=.………………………………………………(1分) 由222023x y y x x -+=⎧⎨=--+⎩,……………………………………………………(1分)解得11x y ⎧=⎪⎪⎨⎪=⎪⎩,22x y ⎧=⎪⎪⎨⎪=⎪⎩.∴点Q的坐标是⎝⎭,⎝⎭.…(2分) 普陀区24.(本题满分12分)如图10,在平面直角坐标系xOy 中,直线3y kx =+与x 轴、y 轴分别相交于点A 、B ,并与抛物线21742y x bx =-++的对称轴交于点()2,2C ,抛物线的顶点是点D . (1)求k 和b 的值;(2)点G 是y 轴上一点,且以点B 、C 、G 为顶点的三角形与△BCD 相似,求点G 的坐标;(3)在抛物线上是否存在点E :它关于直线AB 的对称点F 恰好在y 轴上.如果存在,直接写出点E 的坐标,如果不存在,试说明理由.24.解:(1) 由直线3y kx =+经过点()2,2C ,可得12k =-. ··········· (1分)由抛物线21742y x bx =-++的对称轴是直线2x =,可得1b =. ····· (1分) (2) ∵直线132y x =-+与x 轴、y 轴分别相交于点A 、B ,∴点A 的坐标是()6,0,点B 的坐标是()0,3. ············ (2分)∵抛物线的顶点是点D ,∴点D 的坐标是92,2⎛⎫ ⎪⎝⎭. ·········· (1分) ∵点G 是y 轴上一点,∴设点G 的坐标是()0,m . ∵△BCG 与△BCD 相似,又由题意知,GBC BCD ∠=∠,∴△BCG 与△BCD 相似有两种可能情况: ·············· (1分) ①如果BG BC CB CD =2,解得1m =,∴点G 的坐标是()0,1. (1分)②如果BG BC CD CB =,那么352m -,解得12m =,∴点G 的坐标是10,2⎛⎫ ⎪⎝⎭. (1分)图10xy 11 O综上所述,符合要求的点G 有两个,其坐标分别是()0,1和10,2⎛⎫ ⎪⎝⎭.(3)点E 的坐标是91,4⎛⎫- ⎪⎝⎭或92,2⎛⎫ ⎪⎝⎭. ················· (2分+2分) 青浦区24.(本题满分12分,第(1)、(2)、(3)小题,每小题4分)已知:如图8,在平面直角坐标系xOy 中,抛物线23y ax bx =++的图像与x 轴交于点A (3,0),与y 轴交于点B ,顶点C 在直线2x =上,将抛物线沿射线AC 的方向平移,当顶点C 恰好落在y 轴上的点D 处时,点B 落在点E 处. (1)求这个抛物线的解析式;(2)求平移过程中线段BC 所扫过的面积;(3)已知点F 在x 轴上,点G 在坐标平面内,且以点C 、E 、F 、G 为顶点的四边形是矩形,求点F 的坐标. .24.解:(1)∵顶点C 在直线2x =上,∴22=-=bx a,∴4=-b a .····· (1分) 将A (3,0)代入23y ax bx =++,得933=0++a b , ······ (1分) 解得1=a ,4=-b . ···················· (1分) ∴抛物线的解析式为243=-+y x x . ············· (1分) (2)过点C 作CM ⊥x 轴,CN ⊥y 轴,垂足分别为M 、N .∵243=-+y x x =()221=--x ,∴C (2,1-). ········ (1分)∵1==CM MA ,∴∠MAC =45°,∴∠ODA =45°,∴3==OD OA . ······················ (1分) ∵抛物线243=-+y x x 与y 轴交于点B ,∴B (0,3),∴6=BD . ······················· (1分) ∵抛物线在平移的过程中,线段BC 所扫过的面积为平行四边形BCDE 的面积,∴12262122==⨯⨯⋅=⨯=BCDEBCDSSBD CN . ······· (1分)(3)联结CE .∵四边形BCDE 是平行四边形,∴点O 是对角线CE 与BD 的交点, 即OE OC ==(i )当CE 为矩形的一边时,过点C 作1CF CE ⊥,交x 轴于点1F ,设点1F a (,0),在1Rt OCF 中,22211=OF OC CF +, 即 22(2)5a a =-+,解得 52a =,∴点152F (,0) ·········· (1分) 同理,得点252F (-,0) ······················ (1分) (ii )当CE 为矩形的对角线时,以点O 为圆心,OC 长为半径画弧分别交x 轴于点 3F 、4F ,可得34=OF OF OC ==3F )、4F ()· (2分) 综上所述:满足条件的点有152F (,0),252F (-,0),3F )),4F (). 松江区24.(本题满分12分,每小题各4分)如图,已知抛物线y=ax 2+bx 的顶点为C (1,1-),P 是抛物线上位于第一象限内的一点,直线OP 交该抛物线对称轴于点B ,直线CP 交x 轴于点A . (1)求该抛物线的表达式;(2)如果点P 的横坐标为m ,试用m 的代数式表示线段BC 的长; (3)如果△ABP 的面积等于△ABC 的面积,求点P 坐标.24.(本题满分12分,每小题各4分)解:(1)∵抛物线y=ax 2+bx 的顶点为C (1,1-)∴ 112a b b a+=-⎧⎪⎨-=⎪⎩ …………………………………2分(第24题图)解得:12a b =⎧⎨=-⎩ …………………………………1分∴抛物线的表达式为:y=x 2-2x ;…………………………1分 (2)∵点P 的横坐标为m ,∴P 的纵坐标为:m 2-2m ……………………………1分 令BC 与x 轴交点为M ,过点P 作PN ⊥x 轴,垂足为点N ∵P 是抛物线上位于第一象限内的一点, ∴PN = m 2-2m ,ON =m ,O M =1由PN BMON OM=得221m m BM m -=………………………1分 ∴ BM =m -2…………………………………………………1分 ∵ 点C 的坐标为(1,1-),∴ BC= m -2+1=m -1………………………………………1分(3)令P (t ,t 2-2t ) ………………………………………………1分 △ABP 的面积等于△ABC 的面积 ∴AC =AP过点P 作PQ ⊥BC 交BC 于点Q ∴CM =MQ =1∴t 2-2t =1 …………………………………………………1分∴1t =+1t =-1分∴ P 的坐标为(1+)……………………………………1分 徐汇区24. 如图,已知直线122y x =-+与x 轴、y 轴分别交于点B 、C ,抛物线212y x bx c =-++ 过点B 、C ,且与x 轴交于另一个点A .(1)求该抛物线的表达式;(2)点M 是线段BC 上一点,过点M 作直线l ∥y 轴 交该抛物线于点N ,当四边形OMNC 是平行四边形时, 求它的面积;(3)联结AC ,设点D 是该抛物线上的一点,且满足DBA CAO ∠=∠,求点D 的坐标.杨浦区24、(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分)如图8,在平面直角坐标系中,抛物线于X轴交于点A、B,于y轴交于点C,直线经过点A、C,点P为抛物线上位于直线AC上方的一个动点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长宁区
24.(本题满分 12 分,第( 1)小题 4 分,第( 2)小题 3 分,第( 3)小题 5 分)
如图在直角坐标平面内,抛物线 y ax2 bx 3与 y 轴交于点 A,与 x 轴分别交于点
B( - 1, 0)、点 C(3, 0),点 D 是抛物线的顶点 . ( 1)求抛物线的表达式及顶点 D 的坐标; ( 2)联结 AD、 DC,求 ACD 的面积; ( 3)点 P 在直线 DC上,联结 OP,若以 O、P、C 为顶点的三角形与△ ABC相似,求点 P 的坐标.
∴△ CAD∽△ AOB,∴ ACD OAB
∵OA=OC, AOC 90 ∴ OAC OCA 45
∴ OAC OAB OCA ACD ,即 BAC BCD
若以 O、 P、 C为顶点的三角形与△ ABC相似 ,且△ ABC为锐角三角形
则 POC 也为锐角三角形,点 P 在第四象限
( 1 分) ( 1 分)
上海市各区 2018 届九年级中考二模数学试卷精选汇编:二次函数专题
宝山区、嘉定区
24.( 本题满分 12 分,第( 1)小题 4 分,第( 2)小题 4 分,第( 3)小题 4 分 )
已知平面直角坐标系 xOy (如图 7),直线 y x m 的经过点 A( 4,0) 和点 B (n,3) . (1)求 m 、 n 的值; (2)如果抛物线 y x 2 bx c 经过点 A 、 B ,该抛物线的顶点为点 P ,求 sin ABP 的
∴ n 1 ………………………………………… 1 分 (2 )由可知点 B 的坐标为 ( 1,3)
∵抛物线 y x 2 bx c 经过点 A 、 B 16 4b c 0
∴
1b c 3 ∴ b 6, c 8 ∴抛物线 y x 2 bx c 的表达式为 y x 2 6x 8 ………………… 1 分 ∴抛物线 y x 2 6x 8 的顶点坐标为 P( 3, 1) …………… 1 分 ∴ AB 3 2 , AP 2 , PB 2 5 ∴ AB 2 BP 2 PB 2 ∴ PAB 90 …………………………………… 1 分
解:( 1)设所求二次函数的解析式为 y ax2 bx c(a 0) ,……………………… 1 分
将 A ( 0 , 3 )、 B ( 4 ,)、 C ( 3 , 0 )代入,得
16a 4b c 1, 9a 3b c 0, c 3.
1 a
2
解得 b
5
……… 2 分
2
c3
所以,这个二次函数的解析式为
6
6 18
, ∴ P1( , )
t
5
55
②当 POC ACB 时 ,由 tan POC tan ACB
∴ 6 2t 1 ,解得 t 2 ,∴ P2 (2, 2) t
综上得
6 P1( ,ຫໍສະໝຸດ 18) 或 P2( 2,2)
55
崇明区
tan 45
( 2 分)
1 得 PH 1 ,
OH ( 2 分)
24.(本题满分 12 分,第 (1) 、 (2) 、 (3) 小题满分各 4 分) 已知抛物线经过点 A(0, 3) 、 B (4,1) 、 C (3, 0) .
( 2 分) ( 2 分)
(2)∵ A( 0, - 3), C( 3, 0),D( 1, - 4) ∴ AC 3 2 , CD 2 5 , AD 2
∴ CD 2 AC 2 AD 2 ∴ CAD 90
( 2 分)
∴ S ACD
1 AC AD
2
1 32 2
2 3.
(3)∵ CAD
AOB 90 , AD AC 2 , BO AO
∴点 D 的坐标为 (0,4) , OD 4
又 OB 10 , DB 2
∴ QB 5 2 , DQ 4 2 …………… 1 分
∵ AB 3 2 ∴ AQ 8 2 , DQ ∵ QH ∥ y 轴
42
∴ OD AD QH AQ
∴ 4 42 QH 8 2
∴ QH 8 …………………………………… 1 分 即点 Q 的纵坐标是 8 又点 Q 在直线 y x 4 上 点 Q 的坐标为 ( 4,8) …………… 1 分
值;
(3)设点 Q 在直线 y x m 上,且在第一象限内, 直线 y x m 与 y 轴的交点为点 D ,
y
如果 AQO DOB ,求点 Q 的坐标 .
O
x
图7
24.解:( 1) ∵直线 y x m 的经过点 A( 4,0) ∴ 4 m 0 …………………… 1 分
∴ m 4 ……………………………… 1 分 ∵直线 y x m 的经过点 B(n,3) ∴ n 4 3 …………………… 1 分
y
1 x2
5 x3
22
( 2)∵ A ( 0 , 3 )、 B ( 4 ,)、 C ( 3 , 0 )
由点 C( 3,0), D( 1, - 4)得直线 CD 的表达式是 y 2x 6 ,设 P(t,2t 6) ( 0 t 3 )
过 P 作 PH⊥ OC,垂足为点 H,则 OH t , PH 6 2t
①当 POC
ABC 时,由 tan POC tan ABC 得 PH
OH
AO , BO
6 2t
∴
3 ,解得 t
第 24 题图
备用图
24. (本题满分 12 分,第( 1)小题 4 分,第( 2)小题 3 分,第( 3)小题 5 分)
解:( 1) 点 B(- 1, 0)、 C( 3,0)在抛物线 y ax2 bx 3上
ab3 0
a1
∴
,解得
9a 3b 3 0
b2
∴抛物线的表达式为 y x 2 2x 3 ,顶点 D 的坐标是( 1, - 4)
(1)求抛物线的解析式; (2)联结 AC、BC、 AB,求 BAC 的正切值; (3)点 P 是该抛物线上一点, 且在第一象限内, 过点 P 作 PG AP 交 y 轴于点 G ,当点 G
在点 A 的上方,且 △ APG 与 △ ABC 相似时,求点 P 的坐标.
y
A
B
O
C
x
(第 24 题图)
24.( 本题满分 12 分,每小题 4 分 )
∴ sin ABP AP PB
∴ sin ABP
10
………………………………………… 1 分
10
(3)过点 Q 作 QH x 轴,垂足为点 H ,则 QH ∥ y 轴
∵ AQO DOB , OBD QBO
∴△ OBD ∽△ QBO
∴ OB
DB
…………… 1 分
QB OB
∵直线 y x 4 与 y 轴的交点为点 D
