七年级数学有理数混合运算练习(附答案)
(完整版)有理数混合运算经典习题含答案.doc

(完整版)有理数混合运算经典习题含答案.doc有理数的混合运算习题一.选择题1. 计算 ( 2 5)3 ()A.1000B.- 1000C.30D.- 302. 计算 2 32( 2 32 ) ( )A.0B.- 54C.- 72D.- 183. 计算1 ( 5)( 155)5A.1B.25C.- 5D.354. 下列式子中正确的是()A. 24 ( 2)2 ( 2)3B. ( 2)324 ( 2)2 C.24 ( 2)3 ( 2) 2 D. ( 2)2( 3)3245.24 ( 2) 2 的结果是()A.4B.- 4C.2D. - 26. 如果 a 10,(b 3)2 0 ,那么b1 的值是()aA. -2B.- 3C.- 4D.4二 .填空题1.有理数的运算顺序是先算,再算,最算;如果有括号,那么先算。
2.一个数的 101 次幂是负数,则这个数是。
7.20.9 5.6 1.7 。
4. 22( 1)3。
5. (6) (7) 5。
13136.2( 1)11。
7. (7 3) ( 7)。
72 2488. ( 50)(21 )。
5 10三 .计算题、 ( 3)2 21 (2 ) 4( 1 )( 1 )( 1.5) 4 12.75 ( 5 1 )2 3 5 2 3 4 28 ( 5)634 5 ( 1)3( 2) ( 5) ( 4.9) 0.6 256( 10)25 ( 2( 5)3( 3)25 ( 6) ( 4) 2 ( 8)5521( 6 ) ( 12)( 16 50 3 2) ( 2)( 6) 8 ( 2) 3 ( 4) 2 5 4725( 1 ) 2 1 ( 22 2 )11997(1 0.5)13 [ 32( 2) 2 2]2 2 333314(1 0.5)1[2 ( 3)2]( 81) ( 2.25) ( 4) 16 ( 3 )2 ( 2 1) 039 4 352[ 4 (1 0.2 1) ( 2)]( 5) ( 3 6)( 7) ( 3 6) 12 ( 3 6)57775( 4) 20.25 ( 5) ( 4) 3( 3) 21 ) 32 2 134 1 ( )(1 9614 328238( 8) ( 7.2) ( 2.5) 5 ;7.8 ( 8.1) 019.65 ( 1 2) 4 ( 2 1) 7127 5 40.25 ( 5) 4 (13 11 1 1) () ( 3 ) ( 1 ) 34( ) 225 52 422四、 1、已知 x 2y 3 0, 求 2 1 x5y 4xy 的值。
(完整版)七年级有理数混合运算(附答案)

有理数混合运算1.下列计算①()330-=--;②()()11135=-+-;③()4223=-÷-;④()55154-=⨯---,其中正确的个数是( ) A 、1个 B 、2个 C 、3个 D 、4个2.下列各式运算结果为负数的是( )A 、532⨯- B 、()5312⨯- C 、()5132⨯- D 、()1532-⨯-3.判断题(1)()()5152125-=-÷=⨯-÷ ( ) (2)()313125431254-=⨯+-=⨯-- ( )(3)()()()138212733-=---=--⨯- ( )(4)()()()[]842812842812=+-÷-=-÷+-÷- ( ) (5)()()100105222=-=-⨯ ( )4.计算(1)()3316⨯÷-; (2)212--; (3)()325.1-⨯-;(4)2234⨯-; (5)()()48352-⨯+⨯-; (6)()⎪⎭⎫⎝⎛---21435420;(7)()322212÷-⨯-; (8)22388⎪⎭⎫ ⎝⎛⨯-;(9)()()33751-÷--; (10)⎪⎭⎫⎝⎛-⨯⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛-9153153;(11)()⎪⎭⎫⎝⎛-⨯--⨯-253112232;5.列式计算 (1)21与31-的和的平方; (2)2-的立方减去3-的倒数的差;(3)已知甲数为23-,乙数比甲数的平方的2倍少21,求乙数。
6.拓展提高(1)已知有理数满足01331=-+++-c b a ,求()2011c b a ⨯⨯的值;(2)已知a 、b 互为相反数,c 、d 互为倒数,x 的平方等于4,试求()()()200920102d c b a x d c x ⨯-+++⨯⨯- 的值。
有理数除法 一. 判断。
1. 如果两数相除,结果为正,则这两个数同正或同负。
七年级数学有理数的混合运算配套练习及答案

2.7有理数的混合运算(一)一、基础训练1.有理数混合运算顺序,先 ,再 ,最后 ,如果有 先进行 . 2.计算:(1) ()()232-⨯-⎡⎤⎣⎦= (2) ()2232-⨯-= (3) 1155-÷⨯= (4) 223---= 二、典型例题 例1计算: ()()331122416⎛⎫--÷-⨯- ⎪⎝⎭分析:减号把算式分为两段,在这两段上分别先乘方,再乘除,然后把所得结果相加减.例2计算: ()()2232121131131323744⎧⎫⎡⎤⎪⎪⎛⎫⎛⎫⎛⎫-⨯-÷-+⨯--⨯-÷⎢⎥⎨⎬ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎪⎪⎣⎦⎩⎭分析:有多重括号的混合运算一般先去小括号,再去中括号,最后去大括号.三、拓展提升1. 计算:666666666666+++++ 分析:合并同类项得666⨯.2. 已知a 与b 互为相反数,c 与d 互为倒数,且()210x +=,试求()()200920083x a b cd ++--的值.分析: a +b =0,cd =1,x =-1四、课后作业 1.计算:(1) ()()230332--÷⨯- (2) ()148121549-÷⨯÷-(3) ()221.25 3.20.5233⎛⎫⨯-÷-÷ ⎪⎝⎭ (4) 724987⎛⎫-÷⨯- ⎪⎝⎭(5) ()1535126-⨯-÷⎡⎤⎣⎦ (6) ()112143223232⎛⎫-⨯--÷ ⎪⎝⎭(7) ()21832845-÷--⨯ (8) ()()()222322323⨯-+-⨯+-+(9)()222234113332322⎡⎤⎛⎫⎛⎫⎛⎫-⨯-÷----⨯-⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎝⎭⎣⎦2.当整数n 为 数时, ()11n-=-; 若n 是正整数时,则()()111nn +-+-=3.已知a =2,b =-3,c =1,则代数式222a ba ac c--+=2.7有理数的混合运算(一) 一、基础训练1.乘方,乘除,加减,括号,括号内的运算 2.(1)36 (2)-36 (3)125- (4)-7 二、典型例题 例1 8 例2114三、拓展提升 1. 76 2. -2 四、课后作业 1.(1)24 (2)1615(3)9 (4)16 (5)6 (6)-7 (7)-64 (8)49 (9)- 7 2.奇,0 3.52.7有理数的混合运算(二)一、基础训练1.计算:(1) ()2255--÷-=(2) ()()23250.06-⨯-⨯=(3) 221122⎡⎤⎛⎫⎛⎫---÷- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦=2.若()2110x y ++-=,则20082009x y +=二、典型例题 例1 7778812⎛⎫⎛⎫-÷- ⎪ ⎪⎝⎭⎝⎭分析: 乘法有分配律,而除法没有分配律,通常把除数化成一个数进行计算.例2 7115117115912636369126⎛⎫⎛⎫-+÷-÷-+⎪ ⎪⎝⎭⎝⎭分析:用乘法的分配律,并利用71151912636⎛⎫-+÷ ⎪⎝⎭与17115369126⎛⎫÷-+ ⎪⎝⎭互为倒数简化计算.三、拓展提升1. 若()22210ab b -+-=, 求()()()()()()1111112220082008ab a b a b a b +++⋅⋅⋅+++++++.2. 31x =-则代数式2311n n x x x x x -++++⋅⋅⋅++=四、课后作业 1.计算: (1) 1111321523411⎛⎫⎛⎫⨯-÷-⨯ ⎪ ⎪⎝⎭⎝⎭ (2) ()()()3232320.110-+---⨯-(3) 5255524757123⎛⎫÷-+⨯-÷ ⎪⎝⎭ (4) ()22418222893⎛⎫⎛⎫-⨯--÷ ⎪ ⎪⎝⎭⎝⎭(5) ()233310.110.22334⎡⎤÷+÷----+--⎣⎦(6) 621847255559⎛⎫⎛⎫⎛⎫-÷---- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(7) 2222227195777⎛⎫⎛⎫⎛⎫-⨯-+⨯--⨯- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ (8) ()()()2352121720.25832⎛⎫-⨯--÷-- ⎪⎝⎭⨯+-⨯-2.(1)问题:你能比较20092008和20082009的大小吗?为了解决这个问题,写出它的一般形式,即比较1n n+和()1nn +的大小(n 是正整数),然后我们从分析n =1、2、3…这些简单情况入手,从中发现规律,经过归纳,猜想出结论.通过计算,比较下列各组数的大小(在横线上填“>”“=”或“<”).21 12,32 23,43 34,54 45,65 56,…(2)从第(1)题结果经过归纳,可以猜想出1n n +和()1nn +的大小关系是什么?(3)根据上面的归纳猜想,尝试比较20092008和20082009的大小.2.7有理数的混合运算(二) 一、基础训练1.(1)-1 (2)-30 (3)-1 2. 2 二、典型例题 例1 -3 例2 242425三、拓展提升 1.200920102. n 为奇数时值为0,n 为偶数时值为1 四、课后作业1.(1)225- (2)-7 (3)512- (4)18 (5)995 (6)6245(7)-22 (8)-12.(1)< < > > > (2) 1n n +>()1nn +(3n ≥且n 是正整数) (3)20092008>20082009。
初一七年级数学有理数混合运算专题练习及答案
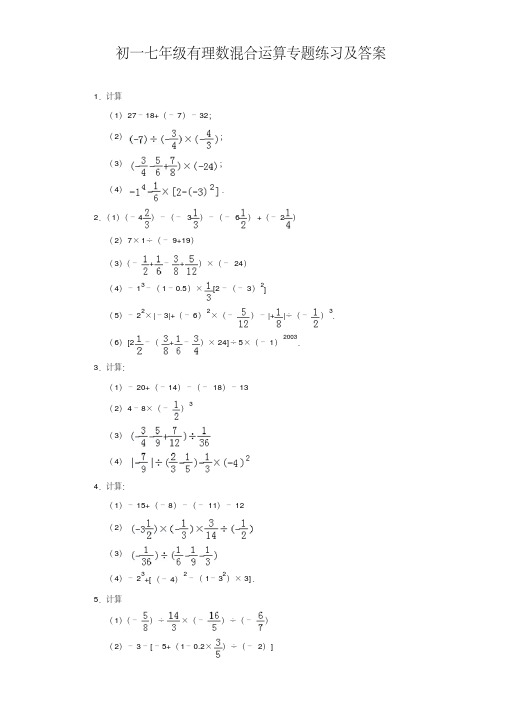
( 5)
|
( 6)
.
40.计算: ( 1) 12﹣(﹣ 18) +(﹣ 7)﹣ 15; ( 2)(﹣ 8)+4÷(﹣ 2); ( 3)(﹣ 10)÷(﹣ )× 5;
( 4) [1 ﹣( 1﹣ 0.5× ) ] ×[2 ﹣(﹣ 3)2] .
41.计算 ( 1) 23﹣ 17﹣(﹣ 7) +(﹣ 16) ( 2)(﹣ 4)+|﹣ 8|+(﹣ 3) 3﹣(﹣ 3) ( 3)﹣ 24÷( 2 )2﹣ 3 ×(﹣ )
)
2
]
.
26.计算下列各式: ( 1)
( 2)
.
27.计算 ( 1)(﹣ 3 )﹣(﹣ 2 )﹣(﹣ 2 )﹣( +1.75)﹣(﹣ 1 )
( 2)﹣ 4×(﹣ 2 )﹣ 6×(﹣ 2 ) +17×(﹣ 2 )﹣ 19 ÷
( 3)﹣ 12+
×
[﹣
2
2+
(﹣
3)
2×(﹣
2) +(﹣ 3) ]÷(﹣
)2
;
( 3)
;
( 4)
;
( 5)
;
( 6)(﹣ 2)3﹣ 2×(﹣ 3) +|2﹣ 5|﹣(﹣ 1) 2010. 34.计算:
( 1) 13+5×(﹣ 2)﹣(﹣ 4)÷(﹣ 8);
( 2) ÷(﹣ 2 )﹣ ×(﹣ 1 ) +0.75 ;
( 3) [1 ﹣( + ﹣
)×(﹣
2)
3
]÷(﹣
3);
( 4)﹣ 24﹣ [3+0.4 ÷(
( 3)(﹣ )×(﹣ 1 )÷(﹣ 2 )
( 4)﹣ 10+8÷(﹣ 2)3﹣(﹣ 2)2×(﹣ 3)
人教版七年级有理数的混合运算练习题40道(带答案)

人教版七年级有理数的混合运算练习题40道(带答案)有理数的混合运算专题训练以下是一些有理数的混合运算题目,需要按照以下顺序进行运算:1.先乘方,再乘除,最后加减;2.同级运算,从左到右进行;3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行。
1.1241/141 + (-) + (+) + (-) + 2/先算括号内的正负号,得到-1,然后按照顺序进行运算,得到2/3.2.(-81) ÷ (-2.25) × (-) ÷ 16先算括号内的正负号,得到正,然后按照顺序进行运算,得到9.3.11 + (-22) - 3 × (-11)按照顺序进行运算,得到56.4.(+12) × (-) - 15 × (-1)按照顺序进行运算,得到-3.5.(-) × [-32 × (-)2 - 2]先算括号内的正负号,得到正,然后按照顺序进行运算,得到64.6.(-23) ÷ (-4)3先算括号内的正负号,得到正,然后按照顺序进行运算,得到-1/8.7.12 ÷ [(-)2 - 8]先算括号内的正负号,得到-6,然后按照顺序进行运算,得到-2.8.[(-2)2 × (-3)] × (-)先算括号内的正负号,得到正,然后按照顺序进行运算,得到6.9.[(-0.5)-] × (-6)先算括号内的正负号,得到正,然后按照顺序进行运算,得到3.10.|-| × (-) ÷ 2先算绝对值,得到0,然后按照顺序进行运算,得到0.11.-2² - (-2)² - 2³ + (-2)³先算括号内的正负号,得到-8,然后按照顺序进行运算,得到0.12.(-6)² - (-3)² ÷ (-1/2)³ × (-3)先算括号内的正负号,得到正,然后按照顺序进行运算,得到-108.13.-(-1)¹⁹⁹⁷ - (1 - 0.5) × 3 ÷ (-12)¹⁴先算括号内的正负号,得到正,然后按照顺序进行运算,得到-1.14.(-1)³ - (-8½) × 4/17 + (-3)³ ÷ [(-2)⁵ + 5]先算括号内的正负号,得到-1,然后按照顺序进行运算,得到-2.5.15.-10 + 8 ÷ (-2)² - (-4) × (-3)先算括号内的正负号,得到正,然后按照顺序进行运算,得到-4.16.-49 + 2 × (-3)² + (-6) ÷ (-1/9)先算括号内的正负号,得到正,然后按照顺序进行运算,得到-47.17.-14 + (1 - 0.5) × 1/3 × [2 × (-3)²]先算括号内的正负号,得到正,然后按照顺序进行运算,得到-10.18.[(-1/2)² - 3 × 3/4] ÷ 1/5先算括号内的正负号,得到-7/16,然后按照顺序进行运算,得到-8.75.19.5 × (-6) - (-4)² ÷ (-8)先算括号内的正负号,得到正,然后按照顺序进行运算,得到-25.20.(-2)² - 2 × [(-3)² ÷ (-4)] + (-5) × (-4)²先算括号内的正负号,得到正,然后按照顺序进行运算,得到-82.21.(7/12 - 5/6 + 3/4) × (-12) ÷ 6先算括号内的正负号,得到-1,然后按照顺序进行运算,得到2.22.(-7) ÷ 6 + (-5)³ - 3 ÷ (-2)³先算括号内的正负号,得到-125/8,然后按照顺序进行运算,得到-51.875.23.(-)² + (-)(-2)先算括号内的正负号,得到正,然后按照顺序进行运算,得到-2.24.-42 × [(-7) ÷ 6] + (-5)³ - 3 ÷ (-2)³先算括号内的正负号,得到-35,然后按照顺序进行运算,得到-124.875.25.6 - (-12) ÷ (-2)²先算括号内的正负号,得到正,然后按照顺序进行运算,得到2.26.(-5) ÷ (-1/2)²先算括号内的正负号,得到正,然后按照顺序进行运算,得到-20.27.42 × (-2/3) + (-4) ÷ 0.25按照顺序进行运算,得到-94.最终答案:1.2/32.93.564.-35.646.-1/87.-28.69.310.011.012.-10813.-114.-2.515.-416.-4717.-1018.-8.7519.-2520.-8221.222.-51.87523.-224.-124.87525.226.-2027.-941.删除明显有问题的段落,文章内容不完整,无法进行改写。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级数学有理数混合运算练习一、计算题1.计算. (1)3351 (1)()48624-+÷- (2)3221113()(2)(2)()(3)()222⨯---÷+-⨯-÷- (3)2419(5)25-⨯- (4)43510.712(15)0.7(15)9494⨯+⨯-+⨯+⨯- (5)2111315()1(2)(5)223114-⨯-⨯÷⨯-÷- (6)31002111132(2)()(1)3(3)82--++⨯-+-⨯-- 2.计算. (1)()()50.750.34-÷÷-. (2)()349731221⎛⎫⎛⎫⨯⨯- ⎪ ⎪⎝⎭⎝-÷⎭- . (3)()11150.6 1.75232⎛⎫-⨯-⨯÷- ⎪⎝⎭. (4)3777148128⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+--+-÷- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦. 3.计算 (1)4512117621⎛⎫⎛⎫⎛⎫÷÷ ⎪ ⎪ ⎪⎝⎭⎝-⎭⎝-⎭-. (2)()14812649⎛⎫-÷⨯-÷ ⎪⎝⎭. (3)11111345660⎛⎫⎛⎫-+-÷- ⎪ ⎪⎝⎭⎝⎭. 4.用简便方法计算(1)()()()11.2548220⎛⎫+⨯-⨯- ⎪⎭⨯-⎝. (2)()532.465⎛⎫⎛⎫-⨯-⨯+ ⎪ ⎪⎝⎭⎝⎭. (3)()312461014313⎛⎫⎛⎫⎛⎫⨯+⨯-⨯- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭-.(4)()()()()181201250.0012-⎛⎫⨯⨯⨯⨯ ⎪--⎭-⎝ . (5)513160522++-+⎡⎤⎛⎫⎛⎫⎛⎫-⨯ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦. (6)341000.70.03105⎛⎫-⨯--+ ⎪⎝⎭. (7)1314414⎛⎫-⨯ ⎪⎝⎭. 5.计算(1)()1481341()1139⎛⎫⎛⎫⨯÷- -÷+⎝-⎪ ⎪⎭⎝⎭. (2)()453251⎡⎤⎛⎫⎛⎫÷÷- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣-⎦-. (3)157136918⎛⎫⎛⎫-+÷- ⎪ ⎪⎝⎭⎝⎭. 6.计算下列各题 (1) 5.3 3.2 2.5 5.7--+-- (2)1111513 4.522552---+-+ (3)()()31117 6.2580.7522424⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎛⎫+-+⎭--+--+ ⎪⎝⎭. 7.计算下列各题. (1)23113()()0425÷-+÷-21171[21(37)3]73222⨯-⨯÷ (2)254[4()(0.4)()]31425⨯-+-÷-10911(0.1258)5⨯÷⨯ 8.计算 (1)222183(2)(6)()3-+⨯-+-÷- (2)221124[(5)()0.8]5255⎧⎫----⨯-÷⎨⎬⎩⎭(3)3223731(25)(1)()()(0.1)940.1-⨯--⨯---÷- 9.计算(1)222302(3)(1)(1)---⨯--- (2)2211(0.51)()[2(3)]3---⨯-⨯--(3)23225(3)(2)()52--⨯-+-⨯ (4)2223[(4)7]()2--÷- (5)321424(3)(3)263⨯--+--- (6)214(8.1)2(16)45549-÷⨯÷---÷ (7)2521(1)(1)(0.5)32-----+- (8)222247111()()(6)()36322-÷-÷-⨯- 10.计算. (1)11(3)()333-⨯÷-⨯ (2)777()()9912-÷- (3)232412[(3)]()(3)2()42743--⨯-+-÷⨯-+ (4)2222213 1.20.3()(3)3-⨯÷--⨯- 11.计算:(1)521315.565772-+--; (2)111()(24)8612--⨯-; (3)1111115()133()555-⨯--⨯-⨯-; (4)20192311917(1)5()5-+÷--⨯-;(5)20182110.2(20)(2)4---⨯-+-; (6)2233[5(10.6)(3)]5---+-⨯÷-.12.计算:1332(3) 2.195(4)7.81(4).3843-+++-++-13.计算:(1)6133()(1)()15245-÷---⨯;(2)115322()22-÷⨯--÷-; (3)112(3)12()64⨯-+⨯+.14.计算: (1)223193451[()2]1543-⨯-+⨯--; (2)20182151[(5)()0.8]33--⨯-÷-+.参考答案1.答案:解:(1)原式735(24)(24)(24) 486=⨯--⨯-+⨯-42920 =-+-53=-(2)原式1113()(2)()(3)4 842=⨯---⨯+-⨯-⨯31166828 =-++=(3)原式1 (20)(5)25=-+⨯-1(20)(5)(5)25=-⨯-+⨯-14 10099.55=-=(4) 原式7135111 ()(15)() 109944 =⨯++-⨯+7(15)3 5=+-⨯21(45)5=+-343.5=-(5)原式11134144() 26115525 =⨯⨯⨯⨯⨯-=-(6)原式213(8)()1398=-+⨯-+-⨯283()() 398 =-+-+-67172=-解析:2.答案:(1)2.(2)3-.(3)1135,(4)123-.解析:3.答案:(1)162121-;(2)83;(3)7-.解析:4.答案:(1)81-.(2)1.2.(3)6-.(4)0.004-.(5)19-.(6)37.(7)5 597 -.解析:5.答案:(1)()14131418931⎛⎫⎛⎫⎛⎫÷+⨯-÷-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 44138113914=-⨯⨯⨯ 7221077=-=-. (2)()124535⎡⎤⎛⎫⎛⎫-÷-÷- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 124525=-÷⨯ 2453545=-⨯⨯=-. (3)157136918⎛⎫⎛⎫-+÷- ⎪ ⎪⎝⎭⎝⎭ ()15718369⎛⎫=-+⨯- ⎪⎝⎭ ()()()157181818368=⨯--⨯-+⨯- 615145=-+-=-.解析:6.答案:(1)11.7-.(2)253-. (3)3-. 解析:7.答案:解:(1)23113()()0425÷-+÷-21171[21(37)3]73222⨯-⨯÷ 1(8)016=⨯-+-2222272[21()]73227⨯-⨯⨯ 21222221[()]27311=---⨯ 21(8)2=--- 1642=-- 164.2=- (2)254[4()(0.4)()]31425⨯-+-÷-10911(0.1258)5⨯÷⨯1452256()314545=-⨯+⨯⨯9[(0.1258)0.125]÷⨯⨯ 5561()(1)3258=-+⨯÷⨯ (23)8=-+⨯8.=解析:8.答案:解:(1)原式16434(6)9=-+⨯+-÷ 641254=-+-106=-.(2)原式11427[4(25)]22555=---⨯-÷ 145[4(1)]2527=----⨯ 145(41)2527=-+⨯ 5163=-+ 12=- (3)原式3231691(10)()(10)()91610=---⨯--÷- 10001100(1000)=-+-⨯-10001100000=-++99001.=解析:9.答案:解:(1)原式491(1)49112=--⨯--=--+=-.(2)原式111()()(29)23=---⨯-⨯-1711(7)1.666=--⨯-=-+= (3)原式45229(8)727225255=-⨯-+⨯=+= (4)原式34(1649)()3()44.43=-÷-=-⨯-= (5)原式124(3)24()246=⨯-+⨯-+4(27)43⨯---2743227421.=--++-=- (6)原式81441(45)109916=-⨯⨯⨯---19981010=-=-(7)原式8191(1)3136 4444=---+=+-+=(8)原式1113636364=÷⨯⨯111136.36364144=⨯⨯⨯=解析:10.答案:(1)9(2)-4(3)0(4)-145解析:11.答案:(1)解:原式521(36)(15.55)10100772=--+-=-+=(2)解:原式111(242424)(342)3 8612=-⨯-⨯-⨯=---=(3)解:原式1111 (5133)()5()1155=-+-⨯-=⨯-=-(4)解:原式114 191725363512555 =--+⨯=-+=-.(5)解:原式1111(20)41(20)41(1)44 4520=---⨯-+=--⨯-+=---+=(6)解:原式331 9[5(1)]559 =---+-⨯⨯119(5)925 =---+-1195925=-+-+164225=-解析:12.答案:解:原式12[(3)(4)](2.197.81)33=-+-++33[5(4)]84++-58108 =-++55 22.88 =+=解析:13.答案:(1)解:原式623846()2 534555=-⨯-+⨯=+=(2)解:原式3131 52(2)548 2244 =-⨯-⨯-=-+=.(3)解:原式1161212623164=-+⨯+⨯=-++=-.解析:14.答案:解:(1)原式431625(8)1549=-⨯+⨯-2031638 3494=-+⨯-⨯204633=-+-111.3=-;(2) 原式194 1[(5)]3255 =--⨯-⨯+194 1()355 =--⨯-+11(1)3=--⨯-113=-+2.3=-.解析:。
