数学北师大版九年级上册菱形 的判断
北师大版九年级数学上册教学课件:1.1菱形的性质与判定 (共36张PPT)

拓展点一
拓展点二
拓展点三
拓展点一
拓展点二
拓展点三
拓展点二 菱形判定方法的综合应用 例2 (2016· 沈阳)如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连 接DE.求证:
(1)∠CEB=∠CBE; (2)四边形BCED是菱形. 分析:(1)欲证明∠CEB=∠CBE,只要证明∠CEB=∠ABD, ∠CBE=∠ABD即可. (2)先证明四边形BCED是平行四边形,再根据BC=BD即可判定.
分析:根据AB=AD及AE为∠BAD的平分线可得出∠1=∠2,从而证 得△BAE≌△DAE,这样就得出四边形ABED为平行四边形,然后根据 菱形的判定定理即可得出结论.
知识点一
知识点二
知识点三
证明:如图,∵AE平分∠BAD, ∴∠1=∠2. ∵AB=AD,AE=AE, ∴△BAE≌△DAE.∴BE=DE. ∵AD∥BC,∴∠2=∠3=∠1. ∴AB=BE. ∴AB=BE=DE=AD. ∴四边形ABED是菱形.
1识点二
知识点三
知识点一 菱形的定义 有一组邻边相等的平行四边形叫做菱形. 名师解读 几何中的定义都有两重性:一是可作为一条性质,二是 可作为一条判定. (1)根据菱形的定义,判断一个四边形是菱形必须同时具备两个 条件: ①四边形是平行四边形; ②四边形有一组邻边相等. (2)由菱形的定义可知,一个四边形是菱形,则具有如下性质: ①菱形是平行四边形; ②菱形有一组邻边相等.
知识点一
知识点二
知识点三
例2 (2016· 淮安)已知:如图,在菱形ABCD中,点E,F分别为边 CD,AD的中点,连接AE,CF,求证:△ADE≌△CDF. 分析:由菱形的性质得出AD=CD,由中点的定义证出DE=DF,由 SAS证明△ADE≌△CDF即可. 证明:∵四边形ABCD是菱形, ∴AD=CD, ∵点E,F分别为边CD,AD的中点, ∴AD=2DF,CD=2DE,∴DE=DF,
菱形的性质与判定第1课时

重点难点 细解读 观察以下由火柴棒摆成的图形:
议一议:(1)三个图形都是平行四边形吗?
(2)与图1相比,图2与图3有什么共同特边形中,如果内角大小保持不变,仅
改变边的长度,请仔细观察和思考,在这变化过程
中,哪些关系没变?哪些关系变了?
平行四边形 邻边相等
菱形
如果改变了边的长度,使两邻边相等,那么 这个平行四边形成为怎样的四边形?
(C) 对角相等
(D) 邻角互补
2、已知菱形的周长是12cm,那么它的
边长是__3_c_m__.
3、如下图:菱形ABCD中∠BAD=60
度,则∠ABD=__6_0__0 __.
D
A
4、菱形的两条对角线长分别为 6cm和8cm,则菱形的边长是(C )
O
C
B
A.10cm B.7cm C. 5cm D.4cm
菱形
有一组邻边相等的平行四边形叫菱形.
判断一个四边形是菱形 应满足的两个条件:
(1)是平行四边形 (2)是有一组邻边相等
有一组邻边相等的 四边形一定是菱形?
注意:
有一组邻边相等的四 边形未必是菱形
我可不是 菱形哟^-^
菱形的性质……
具有平行四边形所有的性质
菱形还有一些特殊的性质?
小组 活动
∴OB=OD(菱形的对角线互相平分)
在等腰三角形ABD中
∵OB=OD ∴AO⊥BD
即 AC⊥BD
菱形 的性质
定理:每一条对角线 平分一组对角
菱形是特殊的平行四边形,具有平行 四边形的所有性质. 定理:菱形的四条边都相等
定理:菱形的对角线互相垂直
AB=BC=CD=AD AO⊥BD
应用能力 巧提高
1 菱形的性质与判定 数学北师大版九年级上册

—— 探究新知 ——
观察平行四边形图形的变化,你有什么发现?
菱形的定义: 有一组邻边相等的平行四边形 叫做菱形.
下面几幅图片中都含有一些平行四边形, 观察这些平行四边形,你能发现它们有什么样 的共同特征?
你能举出一些生活中菱形的例子吗?与同伴交流。
知AB=5cm,AO=4cm,求 BD 的长.
A
【选自教材P4页 随堂练习】
∵四边形ABCD 是菱形,
∴BD=2BO= 2×3=6(菱形的对角线
D
互相平分).
O
B
∴BD 的长为 6 cm.
C
2.已知:如图,在菱形ABCD 中,∠BAD=2∠B.求证: △ABC是等边三角形. 【选自教材P4页 习题1.1 第1题】
A
C′
D
由题意可知,OC=OC′,CD=C′D,CE=C′E.
又∵AD∥BC,∠EOC=∠DOC′,
∴△COE≌△C′OD,即 EC=C′D.
B
又∵C′D=CD,∴C′D=CD=EC=C′E,
O
E
C
∴四边形 CDC′E 是菱形.
课堂小结
菱形的定义 有一组邻边相等的平行四边形是菱形.
菱形的判定定理 对角线互相垂直的平行四边形是菱形. 四边相等的四边形是菱形.
A
∴BD是线段 AC 的垂直平分线 ∴BA = BC ∴四边形 ABCD 是菱形(菱形定义)
B C
O D
定理 对角线互相垂直的平行四边形是菱形.
∵四边形 ABCD 是平行四边形,
AC⊥BD,
A
∴四边形 ABCD是菱形。
B C
北师大版初中数学九年级上册1.1菱形的性质与判定(教案)

4.培养学生的数据分析观念:在解决与菱形相关的问题时,培养学生对数据的敏感度,学会从数据中发现规律,培养数据分析素养。
5.培养学生的团队合作意识:在小组讨论、合作探究中,提高学生的沟通能力和团队协作能力,为学生的终身学习奠定基础。
4.菱形的周长与面积的计算。
5.实际应用:利用菱形性质解决相关问题。
二、核心素养目标
本节课的核心素养目标主要包括以下几方面:
1.培养学生的几何直观:通过观察、操作、探究菱形的性质,使学生能够发展空间观念和几何直觉,提高解决几何问题的能力。
2.发展学生的逻辑推理能力:在学习菱形的判定过程中,引导学生运用逻辑思维,通过演绎推理和合情推理,掌握严谨的证明方法。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与菱形相关的实际问题。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作。比如,使用直尺和量角器来构造一个菱形,并观察其性质。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
-菱形的周长与面积的计算:掌握计算公式,能够解决相关问题。
-举例:给出具体的菱形图形,指导学生如何计算周长和面积。
2.教学难点
-对角线垂直平分性质的证明:学生需要理解并掌握证明过程中的每一步逻辑。
-举例:在黑板上逐步展示证明过程,解释为什么对角线互相垂直且平分是菱形的必要充分条件。
-菱形判定方法的灵活运用:学生需要能够根据不同题目的特点选择合适的判定方法。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解菱形的基本概念。菱形是四条边相等的四边形,它在几何图形中有着特殊的地位。它是平面几何中的一种重要图形,具有独特的性质和应用。
北师大版九年级上册菱形的性质与判定讲义

北师大版九年级上册菱形的性质与判定讲义要点一、菱形的定义有一组邻边相等的平行四边形叫做菱形.要点二、菱形的性质菱形除了具有平行四边形的一切性质外,还有一些特殊性质:1、.菱形的四条边都相等;2、菱形的两条对角线相互垂直,并且每一条对角线平分一组对角.3、菱形也是轴对称图形,有两条对称轴〔对角线所在的直线〕,对称轴的交点就是对称中心.菱形的面积:〔1〕一种是平行四边形的面积公式:底×高〔2〕另一种是两条对角线乘积的一半要点三、菱形的判定菱形的判定方法有三种:1.定义:有一组邻边相等的平行四边形是菱形.2.对角线相互垂直的平行四边形是菱形.3.四条边相等的四边形是菱形.典型例题:例1、以下四边形中不一定为菱形的是〔〕A. 对角线相等的平行四边形B. 对角线平分一组对角的平行四边形C. 对角线相互垂直的平行四边形D. 用两个全等的等边三角形拼成的四边形【答案】A【解析】A. 对角线相等的平行四边形是矩形而不一定是菱形;B. 对角线平分一组对角的平行四边形是菱形;C. 对角线相互垂直的平行四边形是菱形;D. 用两个全等的等边三角形拼成的四边形四条边形等是菱形;例2、菱形的一个内角为60°,较短的一条对角线长4,那么菱形的周长为_____________。
【答案】16【解析】菱形有一个内角为60°,那么较短对角线与菱形的一组邻边构成一个等边三角形,∴可得边长为4,那么菱形周长为16.【点睛】此题主要考察菱形的性质和等边三角形的判定的运用,难度不大,关键熟练掌握假定菱形有一个内角为60°,那么较短对角线与菱形的一组邻边构成一个等边三角形. 例3、菱形的两条对角线长区分是14cm 和20cm ,那么它的面积为__.【答案】140cm 2【解析】∵菱形的面积等于对角线乘积的一半,∴面积S=12×14×20=140(cm 2). 例4、如下图,在菱形ABCD 中,AC =8,BD =10.求:(1)AB 的长.(2)菱形ABCD 的面积.解:(1)∵ 四边形ABCD 是菱形.∴ AC ⊥BD ,AO =12AC ,OB =12BD . 又∵ AC =8,BD =10.∴ AO =12×8=4,OB =12×10=5. 在Rt △ABO 中,222AB OA OB =+(2)由菱形的性质可知: 118104022S AC BD ==⨯⨯=菱形ABCD . 例5、菱形的两条对角线长为6和8,那么菱形的边长为________.解:设该菱形为ABCD ,对角线相交于O ,AC =8,BD =6,由菱形性质知:AC 与BD 相互垂直平分,例6、菱形ABCD 中,∠A ∶∠B =1∶5,假定周长为8,那么此菱形的初等于( ).A.21B.4C.1D.2【答案】C ;提示:由题意,∠A =30°,边长为2,菱形的初等于12×2=1. 例7、如图,在ABCD 中,对角线AC ,BD 相交于点O ,AB =5,AC =6,BD =8.〔1〕求证:四边形ABCD 是菱形;〔2〕过点A 作AH ⊥BC 于点H ,求AH 的长.【答案】(1)证明见地析(2) 245【解析】试题剖析:〔1〕由平行四边形的对角线相互平分失掉△AOB 的两条边OA 、OB 的长度,那么依据勾股定理的逆定理判定∠AOB=90°,即平行四边形的对角线相互垂直平分,故四边形ABCD是菱形.〔2〕依据菱形的不变性,用不同方法求面积:平行四边形的面积=菱形的面积,可求解.试题解析:〔1〕证明:∵在ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8,∴AO=AC=3,BO=BD=4,∵AB=5,且32+42=52,∴AO2+BO2=AB2,∴△AOB是直角三角形,且∠AOB=90°,∴AC⊥BD,∴四边形ABCD是菱形;〔2〕解:如下图:∵四边形ABCD是菱形,∴BC=AB=5,∵S△ABC=AC•BO=BC•AH,∴×6×4=×5×AH,解得:AH=.例8、在四边形ABCD中,AB//CD,∠B=∠D.〔1〕求证:四边形ABCD为平行四边形;〔2〕假定点P为对角线AC上的一点,PE⊥AB于E,PF⊥AD于F,且PE=PF,求证:四边形ABCD是菱形.【解析】试题剖析:〔1〕依据平行线的性质战争行四边形的判定证明即可;〔2〕依据角平分线的性质和菱形的判定证明即可.试题解析:〔1〕∵AB∥CD,∴∠DCA=∠BAC,在△ADC与△ABC中,∴△ADC≌△ABC〔AAS〕,∴AB=DC,∵AB ∥CD ,∴四边形ABCD 为平行四边形;〔2〕∵四边形ABCD 为平行四边形,∴∠DAB=∠DCB ,∵PE ⊥AB 于E ,PF ⊥AD 于F ,且PE=PF ,∴∠DAC=∠BAC=∠DCA=∠BCA ,∴AB=BC ,∴四边形ABCD 是菱形.课后习题:1.在以下说法中,菱形对角线不具有的性质是 ( )A. 对角线相互垂直;B. 对角线所在的直线是对称轴;C. 对角线相等;D. 对角线相互平分.【解析】菱形的对角线相互垂直平分,菱形是轴对称图形,每一条对角线所在的直线就是菱形的一条对称轴, 应选C.2.如图,在菱形ABCD 中,对角线AC 、BD 相交于点O ,E 为AB 的中点,且OE=2,那么菱形ABCD 的周长为〔 〕A. 12B. 16C. 8D. 4【解析】试题解析:∵四边形ABCD 为菱形,∴AC ⊥BD ,AB=BC=CD=DA ,∴△AOB 为直角三角形.∵OE=2,且点E 为线段AB 的中点,∴AB=2OE=4.C 菱形ABCD =4AB=4×4=16.应选B .3.菱形的周长为40cm ,两条对角线之比3:4,那么菱形面积为〔 〕A. 96cm 2B. 48cm 2C. 24cm 2D. 12cm 2【答案】A如图,设3AO xcm = , 4BO xcm = .∵菱形的周长为40cm ,有勾股定理得, ()()2223410x x += , 21=1216=96cm 2S ∴⨯⨯菱形 ,应选A. 4.菱形的一个内角为60°,较短的一条对角线长4,那么菱形的周长为_____________。
北师大版九年级数学上册第一章四边形2菱形的判定

弧,得到两弧的交点C,连接BC,CD,就得到了一个四边形,如图.
(1)猜一猜,这是什么四边形?
(菱形)
(2)根据画图,你还有其他方法能判定此四边形的形状吗?
小组合作试着进行证明. (四边相等的四边形是菱形)
证明:因为AB=AD,AB=BC,所以AD=BC . 又因为
AB=CD,所以四边形ABCD为平行四边形.
九年级北师上册
第2课时
菱形的判定
1、通过阅读课本理解菱形的判定条件及其证明,并能利用
这两个定理解决一些简单的问题,发展推理能力和运算
能力.
2、经历实际操作,探索菱形判定定理的证明过程,发展合情
推理能力和初步的演绎推理的能力.
3、经历运用几何符号和图形描述命题的条件和结论的过程,建立
初步的符号感,发展抽象思维,培养抽象能力.
2.用一长一短两根细木条,在它们的中点处固定一颗小钉,做成
一个可以转动的十字,四周围上一根橡皮筋.
(平行四边形;对
①做成了一个什么形状的四边形?理由是什么? 角线互相平分)
②转动木条,满足什么条件时这个四边形变成菱形? (木条互相垂直)
③根据活动过程试着猜想满足什么条件时可以说明一个
平行四边形是菱形. (对角线互相垂直)
又因为AB=AD,所以平行四边形ABCD为菱形
小组展示
越展越优秀
提疑惑:你有什么疑惑?
教师讲评
【知识点】菱形的判定
①菱形定义:有一组邻边相等的平行四边形是菱形(平行四边形
+一组邻边相等=菱形).
②对角线互相垂直的平行四边形是菱形.
几何语言:如图,∵AC⊥BD,四边形 ABCD 是平行四边形,
∴平行四边形 ABCD 是菱形.
新北师大版九年级上菱形的判定

A
B
还有其它 的方法吗? 菱形
平行四边形
探究(一)
用一长一短两根细 木条,在它们的中点处固 定一个小钉,做成一个可 以转动的十字,四周围上 一根橡皮筋,做成一个四 边形.转动木条,这个四边 形什么时候变成菱形?
猜想
猜想一:对角线互相垂直的平行四边形是菱形
判定一:对角线互相垂直的平行四形 D 是菱形
D
O
OA=OC,EF⊥AC. B
F (3)利用四边相等,你会吗?
C
思考
老师说下列三个图形都是菱形,你相信吗?
3 4 3
3
3
┍
5
4
5
4
4
有一组邻边相等的平 行四边形叫做菱形
5 5
对角线互相垂直的平行 四边形是菱形
5 5
有四条边相等的四边形是菱形。
证明:∵ AE∥BF ∴∠CAD=∠ACB ∵AC平分∠BAD ∴ ∠CAD= ∠BAC ∴ ∠ACB= ∠BAC ∴AB=BC 同理可证 AB=AD
∴OA=OC
又∵ AC ⊥ BD; ∴BA=BC
A
O
C
(线段垂直平分线上的点到线段两 个端点的距离相等)
B
∴ ABCD是菱形 (有一组邻边相等的平行四边形叫做菱形).
菱形
平行四边形
探究(二)
情境:李芳同学先画两条
等长的线段AB、AD,然后分 别以B、D为圆心,AB为半径 画弧,得到两弧的交点C,连 接BC、CD,就得到了一个四 A 边形,猜一猜,这是什么四边 形?
D C
B
猜想二:四边相等的四边形是菱形
判定二:四边相等的四边形是菱形
D
已知:在四边形ABCD中有 AB=BC=CD=AD 求证:四边形ABCD是一个菱形
北师大版九年级数学上册知识点

北师大版九年级数学(上)册知识点1、菱形的性质与判定①菱形的定义:一组邻边相等的平行四边形叫做菱形。
②菱形的性质:•具有平行四边形的性质,且四条边都相等,两条对角线互相垂直平分,每一条对角线平分一组对角。
••菱形是轴对称图形,每条对角线所在的直线都是对称轴。
•••③菱形的判别方法:•一组邻边相等的平行四边形是菱形。
••对角线互相垂直的平行四边形是菱形。
••四条边都相等的四边形是菱形。
•2、矩形的性质与判定①矩形的定义:有一个角是直角的平行四边形叫矩形。
矩形是特殊的平行四边形。
②矩形的性质:具有平行四边形的性质,且对角线相等,四个角都是直角。
(矩形是轴对称图形,有两条对称轴)③矩形的判定:•有一个内角是直角的平行四边形叫矩形(根据定义)。
••对角线相等的平行四边形是矩形。
••四个角都相等的四边形是矩形。
•④推论:直角三角形斜边上的中线等于斜边的一半。
3、正方形的性质与判定①正方形的定义:一组邻边相等的矩形叫做正方形。
②正方形的性质:正方形具有平行四边形、矩形、菱形的一切性质。
(正方形是轴对称图形,有两条对称轴)③正方形常用的判定:•有一个内角是直角的菱形是正方形;••邻边相等的矩形是正方形;••对角线相等的菱形是正方形;••对角线互相垂直的矩形是正方形。
•④正方形、矩形、菱形和平行边形四者之间的关系⑤梯形定义:•一组对边平行且另一组对边不平行的四边形叫做梯形。
••两条腰相等的梯形叫做等腰梯形。
••一条腰和底垂直的梯形叫做直角梯形。
•⑥等腰梯形的性质:•等腰梯形同一底上的两个内角相等,对角线相等。
••同一底上的两个内角相等的梯形是等腰梯形。
••三角形的中位线平行于第三边,并且等于第三边的一半。
••夹在两条平行线间的平行线段相等。
••在直角三角形中,斜边上的中线等于斜边的一半•第二章一元二次方程1、认识一元二次方程•只含有一个未知数的整式方程,且都可以化为ax2+bx+c=0•(a、b、c为常数,a≠0)的形式,这样的方程叫一元二次方程。
北师大版九年级数学上册1.1菱形的性质与判定重难点题型总结
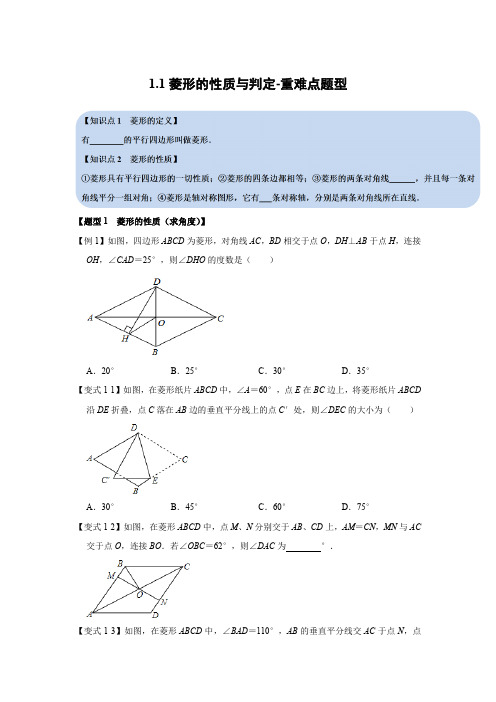
1.1菱形的性质与判定-重难点题型【题型1 菱形的性质(求角度)】【例1】如图,四边形ABCD为菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=25°,则∠DHO的度数是()A.20°B.25°C.30°D.35°【变式1-1】如图,在菱形纸片ABCD中,∠A=60°,点E在BC边上,将菱形纸片ABCD 沿DE折叠,点C落在AB边的垂直平分线上的点C′处,则∠DEC的大小为()A.30°B.45°C.60°D.75°【变式1-2】如图,在菱形ABCD中,点M、N分别交于AB、CD上,AM=CN,MN与AC 交于点O,连接BO.若∠OBC=62°,则∠DAC为°.【变式1-3】如图,在菱形ABCD中,∠BAD=110°,AB的垂直平分线交AC于点N,点M 为垂足,连接DN ,则∠CDN 的大小是 .【题型2 菱形的性质(求长度)】【例2】如图,在菱形ABCD 中,BC =10,点E 在BD 上,F 为AD 的中点,FE ⊥BD ,垂足为E ,EF =4,则BD 长为( )A .8B .10C .12D .16【变式2-1】如图四边形ABCD 为菱形,点E 为BC 的中点,点F 在CD 上,若∠DAB =60°,∠DF A =2∠EAB ,AD =4,则CF 的长为( )A .45B .45√3C .65D .85 【变式2-2】如图,在菱形ABCD 中,AB =13cm ,AC =24cm ,E ,F 分别是CD 和BC 的中点,连接EF 并延长与AB 的延长线相交于点G ,则EG 的长度为 cm .【变式2-3】如图,在菱形ABCD 中,AB =BD ,点E ,F 分别在BC ,CD 边上,且CE =DF ,BF 与DE 交于点G ,若BG =3,DG =5,则CD = .【题型3 菱形的性质(等积法)】【例3】如图,菱形ABCD 的对角线AC ,BD 交于点O .过O 作OE ⊥AB 于点E .延长EO 交CD 于点F ,若AC =8,BD =6,则EF 的值为( )A .5B .125C .245D .485【变式3-1】如图,在菱形ABCD 中,对角线AC 、BD 交于点O ,且AC =6,BD =8,过A 点作AE 垂直BC ,交BC 于点E ,则BE CE 的值为( )A .512B .725C .718D .524【变式3-2】如图,在菱形ABCD 中,AB =10,AC =16,过点D 作DE ⊥BA ,交BA 的延长线于点E ,则线段DE 的长为 .【变式3-3】如图,在菱形ABCD中,∠ADC=120°,AB=3,点E在BC上,且BE=2EC,BF⊥AE,垂足为F,则BF的值为.【题型4 菱形的判定(选择条件)】【例4】在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD.若要使四边形ABCD为菱形,则可以添加的条件是()A.∠AOB=60°B.AC⊥BD C.AC=BD D.AB⊥BC【变式4-1】已知平行四边形ABCD,下列条件:①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.其中能使平行四边形ABCD是菱形的有()A.①③B.②③C.③④D.①②③【变式4-2】如图,在▱ABCD中,M,N是BD上两点,BM=DN,连接AM,MC,CN,NA,添加一个条件,使四边形AMCN是菱形,这个条件是()A.OM=12AC B.MB=MO C.BD⊥AC D.∠AMB=∠CND【变式4-3】如图,在△ABC中,点D、E、F分别在边AB、BC、CA上,且DE∥CA,DF ∥BA,下列四种说法:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是菱形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果AB=AC,那么四边形AEDF是菱形.其中,正确的有.(只填写序号)【题型5 菱形的判定(证明题)】【例5】如图,在▱ABCD中,点E、F在对角线BD上,BE=DF.(1)求证:四边形AECF是平行四边形;(2)若BD平分∠ABC,求证:四边形AECF是菱形.【变式5-2】已知:如图,在四边形ABCD中,AB∥DC,对角线AC、BD交于点O,过点C作CE⊥CD交AB的延长线于点E,联结OE,OC=OE.(1)求证:OE=12AC;(2)如果DB平分∠ADC,求证:四边形ABCD是菱形.【变式5-3】如图,在平行四边形ABCD中,E,F是对角线BD上的点,且BE=DF,连接AE,CF.(1)求证△ADE≌△CBF;(2)连接AF,CE,若AB=AD,求证:四边形AFCE是菱形.【变式5-3】如图,在平行四边形ABCD中,点O是BC的中点,连接DO并延长,交AB 延长线于点E,连接BD,EC.(1)求证:四边形BECD是平行四边形;(2)若∠A=50°,则当∠ADE=°时,四边形BECD是菱形.【题型6 菱形的判定与性质综合(最值问题)】【例6】如图,已知菱形ABCD的边长为6,点M是对角线AC上的一动点,且∠ABC=120°,则MA+MB+MD的最小值是()A.3√3B.3+3√3C.6+√3D.6√3【变式6-1】如图,菱形ABCD的边长为2√3,∠ABC=60°,点E、F在对角线BD上运动,且EF=2,连接AE、AF,则△AEF周长的最小值是()A.4B.4+√3C.2+2√3D.6【变式6-2】如图所示,四边形ABCD中,AC⊥BD于点O,AO=CO=4,BO=DO=3,点P为线段AC上的一个动点.过点P分别作PM⊥AD于点M,作PN⊥DC于点N.连接PB,在点P运动过程中,PM+PN+PB的最小值等于.【变式6-3】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.(1)证明不论E、F在BC、CD上如何滑动,总有BE=CF;(2)当点E、F在BC、CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.【题型7 菱形的判定与性质综合(多结论问题)】【例7】如图,▱ABCD中,对角线AC、BD相交于点O,AD=12AC,M、N、P分别是OA、OB、CD的中点,下列结论:①CN⊥BD;②MN=NP;③四边形MNCP是菱形;④ND平分∠PNM.其中正确的有()A.1 个B.2 个C.3 个D.4 个【变式7-1】如图,平行四边形ABCD中,对角线AC,BD交于点O,BD=2AD,E,F,G 分别是OC,OD,AB的中点.下列结论正确的是()①EG=EF;②△EFG≌△GBE;③FB平分∠EFG;④EA平分∠GEF;⑤四边形BEFG是菱形.A.③⑤B.①②④C.①②③④D.①②③④⑤【变式7-2】如图,在菱形ABCD中,∠A=60°,E、F分别是AB,AD的中点,DE、BF 相交于点G,连接BD,CG.有下列结论:①∠BGD=120°;②BG+DG=CG;③△BDF ≌△CGB;④S菱形ABCD=AB2;⑤2DE=√3DC;⑥BF=BC,正确结论的有()个.A.1B.2C.3D.4【变式7-3】如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:①∠DBC=60°:②△AED≌△DFB;③GC与BD一定不垂直;④∠BGE 的大小为定值.其中结论正确的是()A.①②③B.①②④C.①③④D.②③④【题型8 菱形的判定与性质综合(动点问题)】【例8】如图,在菱形ABCD 中,AB =5cm ,∠ADC =120°,点E 、F 同时由A 、C 两点出发,分别沿AB 、CB 方向向点B 匀速移动(到点B 为止),点E 的速度为1cm /s ,点F 的速度为2cm /s ,经过t 秒△DEF 为等边三角形,则t 的值为( )A .34B .43C .32D .53 【变式8-1】如图,菱形ABCD 中,∠BAD =60°,AB =8,对角线AC ,BD 交于点O ,E 是线段OC 上一动点,F 是射线AD 上一动点,若∠BEF =120°,则在点E 运动的过程中,EF 长度为整数的个数有( )A .6个B .5个C .4个D .3个【变式8-2】如图,▱ABCD 的对角线AC 、BD 相交于点O .AB =10,AC =12,BD =16.(1)求证:▱ABCD 是菱形;(2)若点P 是对角线BD 上一动点(不与点B 、D 重合),PE ⊥AB 于点E ,PF ⊥AD 于点F ,PE +PF 是否为定值?若是,求出这个定值;若不是,请说明理由.【变式8-3】如图1,四边形ABCD 为菱形,对角线AC ,BD 相交于点O ,点E 为OC 上的动点.(1)当AD =AE 时,OE =1,OD =5,求菱形ABCD 的面积;(2)如图2,当OE =OD 时,过点A 作CD 的垂线,垂足为F ,交ED 延长线于点G ,求证:GE=√2AO.。
北师版九年级数学上册 1.1.1第1节 菱形的性质与判定

)B
A.78° B.75° C.60°
D.45°
10.如图,在菱形ABCD中,对角线AC与BD相交于点O, AB=5,AC=6.过D点作DE∥AC交BC的延长线于点E. (1)求△BDE的周长; (2)点P为线段BC上的点,连结PO并延长交AD于点Q. 求证:BP=DQ.
解:(1)∵四边形ABCD是菱形 ∴AB=AD=BC=5,AD=BC,AC⊥BD.
点点对接
解:(1)由已知可得:∠EBC=∠EDC, 又AB∥DC, ∴∠APD=∠EDC, ∠APD=∠EBC;
(2)点P运动到AB的中点时,
理由是:
连接DB. ∵∠DAB=60°,AD=AB, ∴△ABD是等边三角形, 而P是AB边的中点, ∴DP⊥AB,
6.菱形的周长是40cm,两邻角的比是1∶2,则较短的对 角线长是 10 cm.
情景导入
定义:有一组邻边相等的平行四边形是菱形。
平行四边形
一组邻边相等
菱形
邻边 是
相等
两 垂直
新识探究
生活中的菱形,菱形在日常生活中也很常见,请你举例。
新识探究
我们可以通过折纸,剪纸的方法得到菱形,将一 张长方形的纸对折,再对折,然后沿图中的虚线剪一 下,打开即可。
新识探究
观察得到的菱形,并思考:
=4cm,OB
AB·DH,
点点对接
例2:如图,在菱形ABCD中,P是AB上的一个动点(不 与A、B重合),连接DP交对角线AC于E,连接EB.(1 )求证:∠APD=∠EBC;(2)若∠DAB=60°,试问P点 运动到什么位置时,△ADP的面积等于菱形ABCD面积的 ?为1 什么?
4
解析:(1)先证△BCE≌△DCE,得∠EBC=∠EDC,再由 AB∥CD得∠APD=∠EDC;(2)连接BD,
九年级数学上册第1章例说菱形的判定(北师大版)

例说菱形的判定
菱形,是四边相等的四边形,这是菱形的定义,要判断一个四边形是不是菱形,除用定义判断,还可用其它等价条件。
1. 证明四边形的四条边相等
例1 已知:如图1,C是线段BD上一点,和都是等边三角形,R、F、G、H分别是四边形ABDE各边的中点。
求证:四边形RFGH是菱形。
证明:连结AD、BE
因为和都是等边三角形
所以
故四边形RFGH是菱形
2. 邻边相等的平行四边形一定是菱形
例2 已知:如图2,在等腰梯形ABCD中,AD//BC,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点。
求证:四边形MENF是菱形。
证明:因为E是BM的中点,N是BC的中点,F是CM的中点
3. 对角线互相垂直的平行四边形是菱形
例3 已知:如图3,梯形ABCD中,AD//BC,对角线,M、N为底边BC的三等分点,且BC=3AD,AM与BD交于点G,AC与DN交于点H。
求证:四边形AGHD是菱形。
证明:因为BC=3AD
M、N是BC的三等分点
又1= 2
所以四边形AGHD是平行四边形
又,所以四边形AGHD是菱形。
4. 对角线互相垂直平分的四边形是菱形
例4 已知:如图4,中,BAC的平分线交BC于点D,E是AB上一点,且AE=AC,EF//BC交AD于点F。
求证:四边形CDEF是菱形。
证明:连结CE交AD于点O
因为AC=AE
所以为等腰三角形因为AO平分CAE
所以,且OC=OE 因为EF//CD,
所以1= 2
所以OF=OD
于是CE垂直平分DF
所以四边形CDEF是菱形总结以上,得到下表。
1.1第2课时菱形的判定+课件-2024-2025学年北师大版数学九年级上册

检 ∴AB2=132=169,AO2+OB2=122+52=169,
测
∴AB2=AO2+OB2,
∴△AOB为直角三角形,∠AOB=90°. ∴AC,BD互相垂直,
图1-1-21
又∵四边形ABCD是平行四边形,∴▱ABCD是菱形.
谢 谢 观 看!
数学 九年级 上册 北师版
第 一
特殊平行四边形
章
1 第2课时 菱形的判定
-
第2课时 菱形的判定
探究与应用
课堂小结与检测
探
探究一 菱形的判定定理1
究 与
[启发猜想]
应 根据菱形的定义,有一组邻边相等的平行四边形是菱形可以
用
判定一个平行四边形是菱形.想一想除了菱形的定义之外,
对角线满足什么条件时可以判定一个平行四边形是菱形?
线垂直.
探
应用三 通过折纸制作菱形
究 与
例3 小颖通过折纸得到一个菱形,其做法如下:如图1-1-18,
应 先将一张长方形的纸对折、再对折,然后沿图中的虚线剪
用
下,将纸展开,就得到了一个菱形.你能说说小颖这样做的道
理吗?
图1-1-18
探 解:小颖这样做的道理是:
究
与 方法1:根据折叠可知,小颖剪下来的四边形的四条边相等,根据定
应用
计算与证明
定义法 对角线垂直法 四边相等法
课 [检测]
堂
小 1.如图1-1-19,四边形ABCD是平行四边形,AC与BD相交于点
结 与
O,添加一个条件: 答案不唯一,如AB=BC , 可使四边形ABCD
检 成为菱形.
测
图1-1-19
课 2.如图1-1-20所示,已知△ABC,AB=AC,将△ABC沿边BC翻转,
北师大版数学九年级上册优秀教学案例:1.1菱形的性质与判定

二、教学目标
(一)知识与技能
1.让学生掌握菱形的定义及其性质,能够运用菱形的性质解决一些简单的问题。
3.教师总结学生提出的问题,引出本节课的主题:“菱形的性质与判定”。
(二)讲授新知
1.教师引导学生观察菱形的图形,引导学生发现菱形的定义及其性质。
2.教师通过几何画板等工具,演示菱形的性质,如对角线互相垂直平分、四边相等等。
3.教师引导学生理解菱形的判定方法,如对角线互相垂直平分且四边相等的四边形为菱形。
(三)学生小组讨论
1.教师将学生分成若干小组,每组学生共同探讨菱形的性质和判定方法。
2.教师设计小组讨论任务,如绘制菱形、验证菱形性质等,培养学生的团队协作能力。,提高学生的沟通能力。
(四)总结归纳
1.教师引导学生对自己的学习过程进行反思,总结菱形的性质和判定方法。
2.问题导向,培养学生独立思考能力:教师在教学过程中提出一系列具有挑战性的问题,引导学生进行思考、探究。学生通过独立思考、解决问题,提高了自己的逻辑思维能力和独立解决问题的能力。
3.小组合作,培养团队协作精神:教师将学生分成若干小组,进行合作学习。学生在小组内共同探讨菱形的性质和判定方法,分享学习心得,既培养了学生的团队协作能力,又提高了学生的沟通能力。
4.教育学生学会关爱集体,培养学生的团队协作精神。
三、教学策略
(一)情景创设
1.教师通过向学生展示生活中的菱形实例,如珠宝、瓷砖等,让学生感受到菱形的美感,激发学生学习菱形的兴趣。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章特殊平行四边形1.1.1菱形的性质一、教学目标1、知识与技能:经历菱形的性质的探究过程,熟练掌握菱形的两条特有的性质。
2、过程与方法:(1)经历菱形的性质的探究过程,培养学生的动手实验、观察推理的意识,发展学生的形象思维和逻辑推理能力.(2)根据菱形的性质进行简单的证明,培养学生的逻辑推理能力和演绎能力.3、情感态度:在探究菱形的性质的活动中获得成功的体验,通过运用菱形的性质,锻炼克服困难的意志,建立自信心.二、教学重难点教学重点:菱形性质的探求.教学难点:菱形性质的探求和应用.三、教具学具准备教具准备:多媒体矩形纸片直尺(或三角板)四、教学过程:(一)情境引入多媒体展示:生活中的菱形板书:菱形的性质(二)探索新知1、定义运用多媒体动态地展示将平行四边形的一边进行平移,即由平行四边形变菱形的过程。
学生活动:思考、交流、在老师指导下、归纳菱形的定义板书:一、菱形的定义:强调:菱形(1)是平行四边形;(2)一组邻边相等.2、探索性质(1).做一做下面我们一起做一个菱形将一个矩形的纸对折两次,沿图中虚线剪下,再打开(同桌互相帮助)(2).小组讨论。
引导学生从边、角、线及对称性方面进行探讨。
问题:1、从边来看(位置关系与数量关系)?2、从角来看(对角,邻角间有什么关系)?3、从对角线来看(位置关系与数量关系)?4、对角线分得的每组对角有什么关系?5、菱形是中心图形吗?如果是,对称中心在哪里?6、 菱形是轴对称图形吗?如果是,那么它有几条对称轴?对称轴在哪里?对称轴之间有什么位置关系?(学生可能先大胆猜想或根据问题的提示,进而通过折叠、旋转各自手中菱形来推理验证自己的猜想,对于学生可能出现的合情的方法,老师应给予鼓励与肯定。
) (3)小组交流成果,概括菱形的性质1、菱形边的性质。
2、菱形角的性质。
3、菱形的对角线的性质。
4、菱形对称性。
教师强调,并板书:二、菱形的性质:(让学生动手操作后,有意识地利用自己的知识储备进行合理的研究,并合情地做出猜想.最后学由生口头表述性质,如所用的语言表述不恰当时及时给予纠正。
)(三)、例题精讲教师活动:屏幕呈现例题,指导学生观看问题,并点评解题思路及过程,最后屏幕呈现详细解题过程,供学生参考。
例1:如图,在菱形ABCD 中,∠BAD=2∠B ,试求出∠B 的度数,并说明△ABC 是等边三角形解:(1)在菱形ABCD 中,∠B+∠BAD=180°(两条线平行,同旁内角互补)又∵∠BAD=2∠B ∴∠B=60°(2)在菱形ABCD 中,AB=BC (菱形的四条边都相等) 又∵∠B=60°7 D5 O42 83 C A1 6B∴△ABC 是等边三角形(一个角为60º的等腰三角形是等边三角形)例2:如图,已知菱形ABCD 的对角线AC=8cm ,BD=6cm,求这个菱形的周长。
解:∵AC=8cm ,BD=6cm∴AO=4cm, BO=3cm (菱形的对角线互相平分) ∴AB=5cm(勾股定理)∴菱形ABCD 的周长=4AB=20cm(菱形的四条边都相等) (四)知识检测,学习反馈学生活动:完成屏幕上展示的练习,并每题由一名学生来说出答案及原因。
教师活动:屏幕展示练习:1、对于以下图形(1)矩形(2)等边三角形(3)平行四边形(4)菱形(5)圆(6)线段, 既是轴对称图形又是中心对称图形的有( D ) A 、1个 B 、2个 C 、3个 D 、4个2、已知菱形的两条对角线长分别是10和24,则菱形的周长为__52___。
3、 如图,在菱形ABCD 中,AB=5cm, AO=4cm ,求这一菱形的周长与两条对角线的长度。
解:这一菱形的周长=4AB=4×5=20cm 对角线AC=2AO=2×4=8cm∵BO=3cm(勾股定理)∴BD=2BO=2×3=6cm (五)、课堂小结 这堂课你学到了什么?1、菱形的定义:一组邻边相等的平行四边形叫做菱形。
2、菱形的性质: (1)、菱形边的性质。
(2)、菱形角的性质。
(3)、菱形的对角线的性质。
(4)、菱形对称性。
3、应用:1.1.2菱形的判定一、教学目标:经历菱形的判定方法的探究过程,掌握菱形的三种判定方法.OD A BCDABCO二、教学重点:菱形判定方法的探究.三、教学难点:菱形判定方法的探究及灵活运用.四、教学过程:活动1、引入新课,激发兴趣1、复习(1)菱形的定义:一组邻边相等的平行四边形是菱形。
(2)菱形的性质1 菱形的两组对边分别平行,四条边都相等;性质2 菱形的两组对角分别相等,邻角互补;性质3 菱形的两条对角线互相平分,菱形的两条对角线互相垂直,且每一条对角线平分一组对角。
2、导入(1)如果一个四边形是一个平行四边形,则只要再有什么条件就可以判定它是一个菱形?依据是什么?根据菱形的定义可知:一组邻边相等的平行四边形是菱形.所以只要再有一组邻边相等的条件即可.(2)要判定一个四边形是菱形,除根据定义判定外,还有其它的判定方法吗?活动2、探究与归纳菱形的第二个判定方法【问题牵引】用一长一短两根细木条,在它们的中点处固定一个小钉子,做成一个可转动的十字架,四周围上一根橡皮筋,做成一个四边形。
问: 任意转动木条,这个四边形总有什么特征?你能证明你发现的结论吗?继续转动木条,观察什么时候橡皮筋周围的四边形变成菱形?你能证明你的猜想吗?学生猜想:对角线互相垂直的平行四边形是菱形。
教师提问:这个命题的前提是什么?结论是什么?学生用几何语言表示命题如下:已知:在□ABCD中,对角线AC⊥BD,ODCBA求证:□ABCD是菱形。
分析:我们可根据菱形的定义来证明这个平行四边形是菱形,由平行四边形的性质得到BO=DO,由∠AOB=∠AOD=90º及AO=AO,得ΔAOB≌ΔAOD,可得到AB=AD (或根据线段垂直平分线性质定理,得到AB=AD) ,最后证得□ABCD是菱形。
【归纳定理】通过探究和进一步证明可以归纳得到菱形的第二个判定方法(判定定理1):对角线互相垂直的平行四边形是菱形。
提示:此方法包括两个条件——(1)是一个平行四边形;(2)两条对角线互相垂直。
对角线互相垂直且平分的四边形是菱形。
活动3、菱形第二个判定方法的应用例3 如图,如图,□ABCD的对角线AC、BD相交于点O,且AB=5,AO=4,BO=3,求证:□ABCD是菱形。
思路点拨:由于平行四边形对角线互相平分,构成了△ABO是一个三角形,•而AB=5,AO=4,BO=3,由勾股定理的逆定理可知∠AOB=90°,证出对角线互相垂直,这样可利用菱形第二个判定方法证得。
活动4、探究与归纳菱形的第三个判定方法【操作探究】过程: 先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,提问:观察画图的过程,你能说明得到的四边形为什么是菱形吗?你能得到什么结论?学生观察思考后,展开讨论,指出该四边形四条边相等,即有两组对边相等,它首先是一个平行四边形,又有一组邻边相等,根据菱形定义即可判定该四边形是菱形。
得出从一般的四边形直接判定菱形的方法:四边相等的四边形是菱形。
学生进行几何论证,教师规范学生的证明过程。
【归纳定理】从一般的四边形直接判定菱形的方法(判定定理2):四边相等的四边形是菱形。
活动5、菱形第三个判定方法的应用如图,顺次连接矩形ABCD 各边的中点,得到四边形EFGH ,求证:四边形EFGH 是菱形。
思路点拨:方法一,由中点联想到连接矩形对角线BD 、AC ,可得AC=BD 。
利用三角形中位线等于底边的一半,证明EF=FG=GH=EH 。
根据判定定理,所以四边形EFGH 是菱形。
方法二:通过证明图中四个Rt △全等,得到EF=FG=GH=EH 。
活动6、随堂练习练习1:判断下列说法是否正确?为什么? (1)对角线互相垂直的四边形是菱形; (2)对角线互相垂直平分的四边形是菱形;(3)对角线互相垂直,且有一组邻边相等的四边形是菱形; (4)两条邻边相等,且一条对角线平分一组对角的四边形是菱形. 练习2:填空。
如图:□ABCD 的对角线AC 与BD 相交于点O , (1)若AB=AD ,则□ABCD 是 形; (2)若AC=BD ,则□ABCD 是 形; (3)若∠ABC 是直角,则□ABCD 是 形; (4)若∠BAO=∠DAO ,则□ABCD 是 形。
活动7、评价和反思1、通过探究,本节课你得到了哪些结论?有什么认识?2、菱形的判定方法有哪些?2.1矩形的性质与判定一、教学目标:1. 知识与技能:经历并了解矩形判定方法的探索过程,使学生逐步掌握说理的基本方BCD AO法;掌握矩形的判定方法,能根据判定方法进行初步运用。
2. 过程与方法:在探索判定方法的过程中发展学生的合理推理意识、主动探究的习惯,在画矩形的过程中,培养学生动手实践能力,积累数学活动经验。
3. 情感态度与价值观:激发学生学习数学的热情,培养学生勇于探索的精神和独立思考合作交流的良好习惯,体验数学活动来源于生活又服务于生活,提高学生的学习兴趣。
通过与他人的合作,培养学生的合作意识和团队精神。
二、教学重点与难点:教学重点:探索矩形的判定方法、突破方法:为了突出重点,以学生自主探索、合作交流为主,提出问题,让学生动眼观察,动脑猜想,动手验证,进而掌握矩形的判定方法。
教学难点:判定方法的理解和初步运用,突破方法采用教师引导和学生合作的教学方法,及化归的数学思想。
三、教具准备:教师:三角板、圆规学生:三角板、圆规、白纸四、教学过程(一)自学导纲1、创设情境导入新课师:请同学们观察教室的门窗是什么形状?工人师傅在制作这些门窗时,是怎样验证它们是矩形的?大家想不想知道?本节老师将带领大家一起探讨这一问题。
(板书课题 20.2 矩形的判定)2、出示导纲,学生自学师:请同学们自学教材P107,独立完成下列问题导纲知识性问题1~4。
(二)合作互动探究新知1、师:哪们同学愿意将你自学的成果展示给大家,其他同学注意倾,看有没有与自己不同的在方。
生、汇报师:大家完成的很好,请猜想它是真命题还是假命题?你能证明一下你的猜想吗?请同学们用圆规和直尺画对角线相等的平行四边形,并与同桌交流一下,这是个什么图形?生:汇报师:这像个矩形,如何用逻辑推理的方法验证,请同学们小组合作,讨论验证。
生:小组合作交流师:请同学们说说你的证明过程(学生回答) 你们为什么想到用这种方法?通过动手操作和逻辑推理明白它是个真命题,我们把它做为矩形的判定定理1(板书定理1)判定定理1 对角线相等的平行四边形是矩形。
2、用几何符号应怎样表示?3 、刚才我们验证了猜想1,那么猜想2呢?还请同学们小组之间相互交流讨论合作完成导纲探究性问题3。
