八年级数学上册压轴题专题练习
八年级上册数学压轴题精选

八年级上册数学压轴题精选一、整数运算1. 求解下列算式:(1)$(-5) \times (-8) = ?$(2)$7 \div (-3) = ?$二、分数运算1. 求解下列算式:(1)$\frac{2}{3} + \frac{1}{4} = ?$(2)$\frac{5}{6} - \frac{1}{3} = ?$三、代数式化简1. 将下列代数式化简为最简形式:(1)$2x - (3x + 4) =$?(2)$\frac{3}{4}(x-1) - \frac{1}{2}(2x-3) =$?四、方程解求1. 求解下列一元一次方程:(1)$2x + 5 = 13$(2)$\frac{3x}{2} - 1 = 7$五、图形计算1. 计算下列图形的周长和面积:(1)矩形的长为5cm,宽为3cm。
(2)正方形的边长为8cm。
六、比例与相似1. 求解下列比例:(1)$\frac{4}{5} = \frac{12}{x}$ (2)$\frac{2}{3} = \frac{x}{9}$ 七、平面几何1. 判断下列命题的真假:(1)直角三角形的两条直角边的平方和等于斜边的平方。
(2)等腰三角形的两条底边相等。
八、统计与概率1. 求解下列问题:(1)一筐中有红球12个,蓝球18个,随机摸出一个求红球的概率。
(2)甲、乙两个班级的学生人数分别是45人和50人,从两个班级任意抽取一个学生,求乙班学生被抽中的概率。
以上是八年级上册数学压轴题精选。
通过掌握这些题目类型,学生们可以对课本中重要的数学知识点进行巩固和提升。
希望同学们能够通过认真解答这些题目,提高自己的数学水平。
八年级上册数学 全册全套试卷专题练习(解析版)

八年级上册数学全册全套试卷专题练习(解析版)一、八年级数学全等三角形解答题压轴题(难)1.在四边形ABCD 中,E 为BC 边中点.(Ⅰ)已知:如图,若AE 平分∠BAD,∠AED=90°,点F 为AD 上一点,AF=AB.求证:(1)△ABE≌AFE;(2)AD=AB+CD(Ⅱ)已知:如图,若AE 平分∠BAD,DE 平分∠ADC,∠AED=120°,点F,G 均为AD上的点,AF=AB,GD=CD.求证:(1)△GEF 为等边三角形;(2)AD=AB+12BC+CD.【答案】(Ⅰ)(1)证明见解析;(2)证明见解析;(Ⅱ)(1)证明见解析;(2)证明见解析.【解析】【分析】(Ⅰ)(1)运用SAS证明△ABE≌AFE即可;(2)由(1)得出∠AEB=∠AEF,BE=EF,再证明△DEF≌△DEC(SAS),得出DF=DC,即可得出结论;(Ⅱ)(1)同(Ⅰ)(1)得△ABE≌△AFE(SAS),△DGE≌△DCE(SAS),由全等三角形的性质得出BE=FE,∠AEB=∠AEF,CE=GE,∠CED=∠GED,进而证明△EFG是等边三角形;(2)由△EFG 是等边三角形得出GF=EE=BE=12BC ,即可得出结论. 【详解】(Ⅰ)(1)∵AE 平分∠BAD ,∴∠BAE=∠FAE ,在△ABE 和△AFE 中, AB AF BAE FAE AE AE ⎪∠⎪⎩∠⎧⎨===,∴△ABE ≌△AFE (SAS ),(2)∵△ABE ≌△AFE ,∴∠AEB=∠AEF ,BE=EF ,∵E 为BC 的中点,∴BE=CE ,∴FE=CE ,∵∠AED=∠AEF+∠DEF=90°,∴∠AEB+∠DEC=90°,∴∠DEF=∠DEC ,在△DEF 和△DEC 中,FE CE DEF DEC DE DE ⎪∠⎪⎩∠⎧⎨===,∴△DEF ≌△DEC (SAS ),∴DF=DC ,∵AD=AF+DF ,∴AD=AB+CD ;(Ⅱ)(1)∵E 为BC 的中点,∴BE=CE=12BC , 同(Ⅰ)(1)得:△ABE ≌△AFE (SAS ),△DEG ≌△DEC (SAS ),∴BE=FE ,∠AEB=∠AEF ,CE=GE ,∠CED=∠GED ,∵BE=CE ,∴FE=GE ,∵∠AED=120°,∠AEB+∠CED=180°-120°=60°,∴∠AEF+∠GED=60°,∴∠GEF=60°,∴△EFG 是等边三角形,(2)∵△EFG是等边三角形,∴GF=EF=BE=12 BC,∵AD=AF+FG+GD,∴AD=AB+CD+12 BC.【点睛】本题考查了全等三角形的判定与性质、等边三角形的判定与性质等知识;熟练掌握等边三角形的判定与性质,证明三角形全等是解题的关键.2.如图,在△ABC中,∠ABC为锐角,点D为直线BC上一动点,以AD为直角边且在AD 的右侧作等腰直角三角形ADE,∠DAE=90°,AD=AE.(1)如果AB=AC,∠BAC=90°.①当点D在线段BC上时,如图1,线段CE、BD的位置关系为___________,数量关系为___________②当点D在线段BC的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.(2)如图3,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.探究:当∠ACB多少度时,CE⊥BC?请说明理由.【答案】(1)①垂直,相等.②都成立,理由见解析;(2)45°,理由见解析【解析】【分析】(1)①根据∠BAD=∠CAE,BA=CA,AD=AE,运用“SAS”证明△ABD≌△ACE,根据全等三角形性质得出对应边相等,对应角相等,即可得到线段CE、BD之间的关系;②先根据“SAS”证明△ABD≌△ACE,再根据全等三角形性质得出对应边相等,对应角相等,即可得到①中的结论仍然成立;(2)先过点A作AG⊥AC交BC于点G,画出符合要求的图形,再结合图形判定△GAD≌△CAE,得出对应角相等,即可得出结论.【详解】(1):(1)CE与BD位置关系是CE⊥BD,数量关系是CE=BD.理由:如图1,∵∠BAD=90°-∠DAC,∠CAE=90°-∠DAC,∴∠BAD=∠CAE.又 BA=CA,AD=AE,∴△ABD≌△ACE (SAS)∴∠ACE=∠B=45°且 CE=BD.∵∠ACB=∠B=45°,∴∠ECB=45°+45°=90°,即 CE⊥BD.故答案为垂直,相等;②都成立,理由如下:∵∠BAC=∠DAE=90°,∴∠BAC+∠DAC=∠DAE+∠DAC,∴∠BAD=∠CAE,在△DAB与△EAC中,AD AEBAD CAEAB AC⎧⎪∠∠⎨⎪⎩===∴△DAB≌△EAC,∴CE=BD,∠B=∠ACE,∴∠ACB+∠ACE=90°,即CE⊥BD;(2)当∠ACB=45°时,CE⊥BD(如图).理由:过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,∵∠ACB=45°,∠AGC=90°﹣∠ACB,∴∠AGC=90°﹣45°=45°,∴∠ACB=∠AGC=45°,∴AC=AG,在△GAD与△CAE中,AC AGDAG EACAD AE⎧⎪∠∠⎨⎪⎩===∴△GAD≌△CAE,∴∠ACE=∠AGC=45°,∠BCE=∠ACB+∠ACE=45°+45°=90°,即CE⊥B C.3.如图1,在等边△ABC中,E、D两点分别在边AB、BC上,BE=CD,AD、CE相交于点F.(1)求∠AFE的度数;(2)过点A作AH⊥CE于H,求证:2FH+FD=CE;(3)如图2,延长CE至点P,连接BP,∠BPC=30°,且CF=29CP,求PFAF的值.(提示:可以过点A作∠KAF=60°,AK交PC于点K,连接KB)【答案】(1)∠AFE=60°;(2)见解析;(3)75【解析】【分析】(1)通过证明BCE CAD≌得到对应角相等,等量代换推导出60AFE∠=︒;(2)由(1)得到60AFE∠=︒,CE AD=则在Rt AHF△中利用30°所对的直角边等于斜边的一半,等量代换可得;(3)通过在PF上取一点K使得KF=AF,作辅助线证明ABK和ACF全等,利用对应边相等,等量代换得到比值.(通过将ACF顺时针旋转60°也是一种思路.)【详解】(1)解:如图1中.∵ABC为等边三角形,∴AC=BC,∠BAC=∠ABC=∠ACB=60°,在BCE和CAD中,60BE CDCBE ACDBC CA=⎧⎪∠=∠=︒⎨⎪=⎩,∴BCE CAD≌(SAS),∴∠BCE=∠DAC,∵∠BCE+∠ACE=60°,∴∠DAC+∠ACE=60°,∴∠AFE=60°.(2)证明:如图1中,∵AH ⊥EC,∴∠AHF=90°,在Rt△AFH中,∵∠AFH=60°,∴∠FAH=30°,∴AF=2FH,∵EBC DCA≌,∴EC=AD,∵AD=AF+DF=2FH+DF,∴2FH+DF=EC.(3)解:在PF上取一点K使得KF=AF,连接AK、BK,∵∠AFK=60°,AF=KF,∴△AFK为等边三角形,∴∠KAF=60°,∴∠KAB=∠FAC,在ABK和ACF中,AB ACKAB ACFAK AF=⎧⎪∠=∠⎨⎪=⎩,∴ABK ACF≌(SAS),BK CF=∴∠AKB=∠AFC=120°,∴∠BKE=120°﹣60°=60°,∵∠BPC=30°,∴∠PBK=30°,∴29BK CF PK CP===,∴79PF CP CF CP=-=,∵45()99 AF KF CP CF PK CP CP CP ==-+=-=∴779559CPPFAF CP== .【点睛】掌握等边三角形、直角三角形的性质,及三角形全等的判定通过一定等量代换为本题的关键.4.综合与实践:我们知道“两边及其中一边的对角分别对应相等的两个三角形不一定全等”.但是,乐乐发现:当这两个三角形都是锐角三角形时,它们会全等.(1)请你用所学知识判断乐乐说法的正确性.如图,已知ABC∆、111A B C∆均为锐角三角形,且11AB A B=,11BC B C=,1C C∠=∠.求证:111ABC A B C∆∆≌.(2)除乐乐的发现之外,当这两个三角形都是______时,它们也会全等.【答案】(1)见解析;(2)钝角三角形或直角三角形.【解析】【分析】(1)过B作BD⊥AC于D,过B1作B1D1⊥B1C1于D1,得出∠BDA=∠B1D1A1=∠BDC=∠B1D1C1=90°,根据SAS证△BDC≌△B1D1C1,推出BD=B1D1,根据HL证Rt△BDA≌Rt△B1D1A1,推出∠A=∠A1,根据AAS推出△ABC≌△A1B1C1即可.(2)当这两个三角形都是直角三角形时,直接利用HL即可证明;当这两个三角形都是钝角三角形时,与(1)同理可证.【详解】(1)证明:过点B作BD AC⊥于D,过1B作1111B D A C⊥于1D,则11111190BDA B D A BDC B D C∠=∠=∠=∠=︒.在BDC∆和111B D C∆中,1C C ∠=∠,111BDC B D C ∠=∠,11BC B C =,∴111BDC B D C ∆∆≌,∴11BD B D =.在Rt BDA ∆和111Rt B D A ∆中,11AB A B =,11BD B D =,∴111Rt Rt (HL)BDA B D A ∆∆≌,∴1A A ∠=∠.在ABC ∆和111A B C ∆中,1C C ∠=∠,1A A ∠=∠,11AB A B =,∴111(AAS)ABC A B C ∆∆≌.(2)如图,当这两个三角形都是直角三角形时,∵11AB A B =,11BC B C =,190C C ∠==∠︒.∴Rt ABC ∆≌111Rt A B C ∆(HL );∴当这两个三角形都是直角三角形时,它们也会全等;如图,当这两个三角形都是钝角三角形时,作BD ⊥AC ,1111B D A C ⊥,与(1)同理,利用AAS 先证明111BDC B D C ∆∆≌,得到11BD B D =,再利用HL 证明111Rt Rt BDA B D A ∆∆≌,得到1A A ∠=∠,再利用AAS 证明111ABC A B C ∆∆≌;∴当这两个三角形都是钝角三角形时,它们也会全等;故答案为:钝角三角形或直角三角形.【点睛】本题考查了全等三角形的性质和判定的应用,主要考查学生的推理能力.解题的关键是熟练掌握证明三角形全等的方法.5.如图,A (0,4)是直角坐标系y 轴上一点,动点P 从原点O 出发,沿x 轴正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.(1)若AB∥x轴,如图1,求t的值;(2)设点A关于x轴的对称点为A′,连接A′B,在点P运动的过程中,∠OA′B的度数是否会发生变化,若不变,请求出∠OA′B的度数,若改变,请说明理由.(3)如图2,当t=3时,坐标平面内有一点M(不与A重合)使得以M、P、B为顶点的三角形和△ABP全等,请直接写出点M的坐标.【答案】(1)4;(2)∠OA′B的度数不变,∠OA′B=45 ,理由见解析;(3)点M的坐标为(6,﹣4),(4,7),(10,﹣1)【解析】【分析】(1)利用等腰直角三角形的性质以及平行线的性质,可证明△AOP为等腰直角三角形,从而求得答案;(2)根据对称的性质得:PA=PA'=PB,由∠PAB+∠PBA=90°,结合三角形内角和定理即可求得∠OA'B=45°;(3)分类讨论:分别讨论当△ABP≌△MBP、△ABP≌△MPB、△ABP≌△MPB时,点M的坐标的情况;过点M作x轴的垂线、过点B作y轴的垂线,利用等腰直角三角形的性质及全等三角形的判定和性质求得点M的坐标即可.【详解】(1)∵AB∥x轴,△APB为等腰直角三角形,∴∠PAB=∠PBA=∠APO=45°,∴△AOP为等腰直角三角形,∴OA=OP=4.∴t=4÷1=4(秒),故t的值为4.(2)如图2,∠OA′B的度数不变,∠OA′B=45°,∵点A 关于x 轴的对称点为A ′,∴PA =PA ',又AP =PB ,∴PA =PA '=PB ,∴∠PAA '=∠PA 'A ,∠PBA '=∠PA 'B ,又∵∠PAB +∠PBA =90°,∴∠PAA '+∠PA 'A +∠PA 'B +∠PBA '=180()PAB PBA ∠∠︒-+180=︒-90°=90°,∴∠AA 'B =45°,即∠OA 'B =45°;(3)当t =3时,M 、P 、B 为顶点的三角形和△ABP 全等, ①如图3,若△ABP ≌△MBP ,则AP =PM ,过点M 作MD ⊥OP 于点D ,∵∠AOP =∠PDM ,∠APO =∠DPM ,∴△AOP ≌△MDP (AAS ),∴OA =DM =4,OP =PD =3,∴M 的坐标为:(6,-4).②如图4,若△ABP ≌△MPB ,则AB PM =,过点M 作M E ⊥x 轴于点E ,过点B 作BG ⊥x 轴于点G ,过点B 作BF ⊥y 轴于点F ,∵△APB 为等腰直角三角形,则△MPB 也为等腰直角三角形,∴∠BAP =∠MPB=45︒,PA PB =∵139023∠+∠=︒=∠+∠,∴12∠=∠∴Rt AOP Rt PGB ≅∴34BG OP PG AO ====,∵BG ⊥x 轴BF ,⊥y 轴∴四边形BGOF 为矩形,∴3OP BG ==,则431AF OA OF =-=-=347BF OG OP PG ==+=+=在Rt ABF 和Rt PME 中∠BAF =45︒+1∠,∠MPE =45︒+2∠,∴∠BAF =∠MPE∵AB PM =∴Rt ABF Rt PME ≅∴71ME BF PE AF ====,∴M 的坐标为:(4,7),③如图5,若△ABP ≌△MPB ,则AB PM =,过点M 作M E ⊥x 轴于点D ,过点B 作BG ⊥x 轴于点E ,过点B 作BF ⊥y 轴于点F ,∵△APB 为等腰直角三角形,则△MPB 也为等腰直角三角形,∴∠BAP =∠MPB=45︒,PA PB =∵139023∠+∠=︒=∠+∠,∴12∠=∠∴Rt AOP Rt PEB ≅∴34BE OP PE AO ====,∵BE ⊥x 轴BF ,⊥y 轴∴四边形BEOF 为矩形,∴3OP BG ==,则431AF OA OF =-=-=347BF OE OP PE ==+=+=在Rt ABF 和Rt PMD 中∵BF ⊥y 轴∴42∠=∠∵42ABF PMD ∠∠∠+=∠+∴ABF PMD ∠∠=∵AB PM =∴Rt ABF Rt PMD ≅∴17MD AF PD BF ====,∴M 的坐标为:(10,﹣1).综合以上可得点M 的坐标为:(6,﹣4),(4,7),(10,﹣1).【点睛】本题考查了等腰三角形的性质,全等三角形的判定和性质,矩形的判定和性质,第(3)小题要注意分类讨论,作此类型的题要结合图形,构建适当的辅助线,寻找相等的量才能得出结论.二、八年级数学 轴对称解答题压轴题(难)6.已知:AD 是ABC ∆的高,且BD CD =.(1)如图1,求证:BAD CAD ∠=∠;(2)如图2,点E 在AD 上,连接BE ,将ABE ∆沿BE 折叠得到'A BE ∆,'A B 与AC 相交于点F ,若BE=BC ,求BFC ∠的大小;(3)如图3,在(2)的条件下,连接EF ,过点C 作CG EF ⊥,交EF 的延长线于点G ,若10BF =,6EG =,求线段CF 的长.图1. 图2. 图3.【答案】(1)见解析,(2)BFC ∠=60(3)8=CF .【解析】【分析】(1)根据等腰三角形三线合一,易得AB=AC ,BAD CAD ∠=∠;(2)在图2中,连接CE ,可证得BCE ∆是等边三角形,60BEC ∠= ,30BED ∠=且由折叠性质可知1'2ABE A BE ABF ∠=∠=∠,可得BFC FAB ABF ∠=∠+∠ ()2BAD ABE =∠+∠ 260BED =∠=;(3)连接CE ,过点E 分别作EH AB ⊥于点H ,EM BF ⊥于点M ,EN AC ⊥于点N ,可证得Rt BEM Rt CEN ∆≅∆,BM CN =,BF FM CF CN -=+,可得线段CF 的长.【详解】解:(1)证明:如图1,AD BC ⊥,BD CD =AB AC ∴=BAD CAD ∴∠=∠;图1(2)解:在图2中,连接CEED BC ⊥,BD CD = BE CE ∴= 又BE BC = BE CE BC ∴== BCE ∴∆是等边三角形60BEC ∴∠= 30BED ∴∠=由折叠性质可知1'2ABE A BE ABF ∠=∠=∠ 2ABF ABE ∴∠=∠ 由(1)可知2FAB BAE ∠=∠ BFC FAB ABF ∴∠=∠+∠ ()2BAD ABE =∠+∠ 223060BED =∠=⨯=图2(3)解:连接CE ,过点E 分别作EH AB ⊥于点H ,EM BF ⊥于点M ,EN AC ⊥于点N'ABE A BE ∠=∠,BAD CAD ∠=∠ EM EH EN ∴==AFE BFE ∴∠=∠ 又60BFC ∠= 60AFE BFE ∴∠=∠=在Rt EFM ∆中,906030FEM ∠=-= 2EF FM ∴=令FM m =,则2EF m = 62FG EG EF m ∴=-=-同理12FN EF m ==,2124CF FG m ==-在Rt BEM ∆和Rt CEN ∆中,EM EN =,BE CE = Rt BEM Rt CEN ∴∆≅∆ BM CN ∴=BF FM CF FN ∴-=+ 10124m m m ∴-=-+解得1m = 8CF ∴=图3故答案为(1)见解析,(2)BFC ∠= 60(3)8CF =.【点睛】本题考查翻折的性质,涉及角平分线的性质、等腰三角形的性质和判定、等边三角形的判定和性质、含30度角的直角三角形、全等三角形的判定和性质等知识点,属于较难的题型.7.如图,ABC 中,A ABC CB =∠∠,点D 在BC 所在的直线上,点E 在射线AC 上,且AD AE =,连接DE .(1)如图①,若35B C ∠=∠=︒,80BAD ∠=︒,求CDE ∠的度数;(2)如图②,若75ABC ACB ∠=∠=︒,18CDE ∠=︒,求BAD ∠的度数;(3)当点D 在直线BC 上(不与点B 、C 重合)运动时,试探究BAD ∠与CDE ∠的数量关系,并说明理由.【答案】(1)40°;(2)36°;(3)∠BAD 与∠CDE 的数量关系是2∠CDE=∠BAD .【解析】【分析】(1)根据等腰三角形的性质得到∠BAC=110°,根据等腰三角形的性质和三角形的外角的性质即可得到结论;(2)根据三角形的外角的性质得到∠E=75°-18°=57°,根据等腰三角形的性质和三角形的外角的性质即可得到结论;(3)设∠ABC=∠ACB=y°,∠ADE=∠AED=x°,∠CDE=α,∠BAD=β,分3种情况:①如图1,当点D在点B的左侧时,∠ADC=x°-α,②如图2,当点D在线段BC上时,∠ADC=y°+α,③如图3,当点D在点C右侧时,∠ADC=y°-α,根据这3种情况分别列方程组即,解方程组即可得到结论.【详解】(1)∵∠B=∠C=35°,∴∠BAC=110°,∵∠BAD=80°,∴∠DAE=30°,∵AD=AE,∴∠ADE=∠AED=75°,∴∠CDE=∠AED-∠C=75°−35°=40°;(2)∵∠ACB=75°,∠CDE=18°,∴∠E=75°−18°=57°,∴∠ADE=∠AED=57°,∴∠ADC=39°,∵∠ABC=∠ADB+∠DAB=75°,∴∠BAD=36°.(3)设∠ABC=∠ACB=y°,∠ADE=∠AED=x°,∠CDE=α,∠BAD=β①如图1,当点D在点B的左侧时,∠ADC=x°﹣α∴y x ay x aβ⎧=+⎨=-+⎩①②,①-②得,2α﹣β=0,∴2α=β;②如图2,当点D在线段BC上时,∠ADC=y°+α∴y x ay a xβ⎧=+⎨+=+⎩①②,②-①得,α=β﹣α,∴2α=β;③如图3,当点D在点C右侧时,∠ADC=y°﹣α∴180180y a xx y aβ︒︒⎧-++=⎨++=⎩①②,②-①得,2α﹣β=0,∴2α=β.综上所述,∠BAD与∠CDE的数量关系是2∠CDE=∠BAD.【点睛】考核知识点:等腰三角形性质综合运用.熟练运用等腰三角形性质和三角形外角性质,分类讨论分析问题是关键.8.(1)问题发现:如图1, ABC 和ADE 均为等边三角形,点B D E 、、在同一直线上,连接.CE①求证: BD CE =; ②求BEC ∠的度数.(2)拓展探究:如图2, AB C 和ADE 均为等腰直角三角形,90BAC DAE ∠=∠=︒,点B D E 、、在同一直线上AF ,为ADE 中DE 边上的高,连接.CE①求BEC ∠的度数:②判断线段AF BE CE 、、之间的数量关系(直接写出结果即可).()3解决问题:如图3,AB 和ADE 均为等腰三角形,BAC DAE n ∠=∠=,点B D E 、、在同一直线上,连接CE .求AEC ∠的度数(用含n 的代数式表示,直接写出结果即可).【答案】(1)①证明见解析;②60°;(2)①90°;②BE =CE+2AF ;(3)∠AEC =90°+12n ︒. 【解析】【分析】(1)根据等边三角形的性质得AB=AC,AD=AE, ∠DAE=∠BAC=60°,根据SAS 进一步证明△BAD ≌△CAE,依据其性质可得 BD CE =,再根据对应角相等求出BEC ∠的度数;(2)根据等腰直角三角形的性质得AB=AC,AD=AE, ∠DAE=∠BAC=90°,根据SAS 进一步证明△BAD ≌△CAE ,根据对应角相等求出BEC ∠的度数;因为DE=2AF,BD=EC,结合线段的和差关系得出结论;(3)根据等腰三角形的性质得AB=AC,AD=AE, ∠DAE=∠BAC=n °,根据SAS 进一步证明△BAD ≌△CAE ,根据对应角相等求出得出∠ADB=BEC ∠的度数,结合内角和用n 表示∠ADE 的度数,即可得出结论.【详解】(1)①∵△ABC 和△ADE 均为等边三角形(如图1),∴ AB=AC ,AD=AE ,∠BAC=∠DAE=60°,∴ ∠BAC-∠DAC=∠DAE-∠DAC ,∴ ∠BAD=∠CAE.∴ △BAD ≌△CAE (SAS )∴ BD=CE.② 由△CAE ≌△BAD ,∴ ∠AEC=∠ADB=180°-∠ADE=120°.∴ ∠BEC=∠AEC-∠AED=120°-60°=60°.(2)①∵△ABC 和△ADE 均为等腰直角三角形(如图2),∴ AB=AC ,AD=AE ,∠ADE=∠AED=45°,∵∠BAC=∠DAE=90°,∴∠BAC-∠DAC=∠DAE-∠DAC,∴∠BAD=∠CAE.∴△BAD≌△CAE(SAS).∴ BD=CE,∠AEC=∠ADB=180°-∠ADE=135°. ∴∠BEC=∠AEC-∠AED=135°-45°=90°.② BE=CE+2AF.(3)如图3:∠AEC=90°+12n︒,理由如下,∵△ABC和△ADE均为等腰直角三角形,∴ AB=AC,AD=AE,∠ADE=∠AED=n°,∴∠BAC-∠DAC=∠DAE-∠DAC,∴∠BAD=∠CAE.∴△BAD≌△CAE(SAS).∴∠AEC=∠ADB=180°-∠ADE=180°-1801809022n n.∴∠AEC=90°+12n︒.【点睛】本题考查等边三角形、等腰直角三角形的性质及旋转型三角形全等,掌握全等常见模型及由特殊到一般找出解题规律是解答此题的关键.9.(1)操作:如图,在已知内角度数的三个三角形中,请用直尺从某一顶点画一条线段,把原三角形分割成两个等腰三角形,并在图中标注相应的角的度数(2)拓展,△ABC中,AB=AC,∠A=45°,请把△ABC分割成三个等腰三角形,并在图中标注相应的角的度数.(3)思考在如图所示的三角形中∠A=30°.点P和点Q分别是边AC和BC上的两个动点.分别连接BP和PQ把△ABC分割成三个三角形.△ABP,△BPQ,△PQC若分割成的这三个三角形都是等腰三角形,求∠C的度数所有可能值直接写出答案即可.【答案】(1)见解析;(2)见解析;(3)∠C所有可能的值为10°、20°、25°,35°、40°、50°、80°、100°.【解析】【分析】(1)在图1、图2、图3中,分别作AB、AB、BC的垂直平分线,根据垂直平分线的性质及外角的性质求出各角度数即可;(2)分别作AB、BC的垂直平分线,交于点O,连接OA、OB、OC可得三角形OAB、OAC、OBC为等腰三角形,根据等腰三角形的性质及外角性质求出各角度数即可;(3)分PB=PA、AB=AP、BA=BP时,PB=PQ、BP=BQ、QB=QP,PQ=QC、PC=QC、PQ=PC等10种情况,根据等腰三角形的性质分别求出∠C的度数即可.【详解】(1)在图1、图2、图3中,分别作AB、AB、BC的垂直平分线,如图1,∵∠ABC=23°,∠BAC=90°,∴∠C=90°-23°=67°,∵MN垂直平分AB,∴BD=AD,∴△ABD是等腰三角形,∴∠BAD=∠ABC=23°,∴∠ADC=2∠ABC=46°,∵∠BAC=90°,∴∠DAC=∠BAC-∠BAD=67°,∴∠DAC=∠C,∴△DAC是等腰三角形,同理:图2中,∠ADC=46°,∠DAC=88°,∠C=46°,△ABD和△ACD是等腰三角形,图3中,∠BCD=23°,∠ADC=46°,∠ACD=46°,△BCD和△ACD是等腰三角形.(2)作AB、BC的垂直平分线,交于点O,连接OA、OB、OC,∵点O是三角形垂直平分线的交点,∴OA=OB=OC,∴△OAB、△OAC、△OBC是等腰三角形,∵AB=AC,∠BAC=45°,∴∠ABC=∠ACB=67.5°,∴AD是BC的垂直平分线,∴∠BAD=∠CAD=22.5°,∴∠OBA=∠OAB=22.5°,∠OCA=∠OAC=22.5°,∴∠OBC=∠OCB=45°.(3)①如图,当PB=PA,PB=PQ,PQ=CQ时,∵∠A=30°,PB=PQ,∴∠ABP=∠A=30°,∴∠APB=120°,∵PB=PQ,PQ=CQ,∴∠PQB=∠PBQ,∠C=∠CPQ,∴∠PBQ=2∠C,∴∠APB=∠PBQ+∠C=3∠C=120°,解得:∠C=40°.②如图,当PB=PA,PB=BQ,PQ=CQ时,∴∠PQB=2∠C,∠PQB=∠BPQ,∴∠PBQ=180°-2∠PQB=180°-4∠C,∴180°-4∠C+∠C=120°,解得:∠C=20°,③如图,当PA=PB,BQ=PQ,CQ=CP时,∵∠PQC=2∠PBQ,∠PQC=12(180°-∠C),∴∠PBQ=14(180°-∠C),∴14(180°-∠C)+∠C=120°,解得:∠C=100°.④如图,当PA=PB,BQ=PQ,PQ=CP时,∵∠PQC=∠C=2∠PBQ,又∵∠C+∠PBQ=120°,∴∠C=80°;⑤如图,当AB=AP,BP=BQ,PQ=QC时,∵∠A=30°,∴∠APB=12(180°-30°)=75°,∵BP=BQ,PQ=CQ,∴∠BPQ=∠BQP,∠QPC=∠QCP,∴∠BQP=2∠C,∴∠PBQ=180°-4∠C,∴∠C+180°-4∠C=75°,解得:∠C=35°.⑥如图,当AB=AP,BQ=PQ,PC=QC时,∴∠PQC=2∠PBC,∠PQC=12(180°-∠C),∴∠PBC=14(180°-∠C),∴14(180°-∠C)+∠C=75°,解得:∠C=40°.⑦如图,当AB=AP,BQ=PQ,PC=QP时,∵∠C=∠PQC=2∠PBC,∠C+∠PQC=75°,∴∠C=50°;⑧当AB=AP,BP=PQ,PQ=CQ时,∵AB=BP ,∠A=30°,∴∠ABP=∠APB=75°,又∵∠PBQ=∠PQB=2∠C ,且有∠PBQ+∠C=180°-30°-75°=75°,∴3∠C=75°,∴∠C=25°;⑨当AB=BP ,BP=PQ ,PQ=CQ 时,∵AB=BP ,∴∠BPA=∠A=30°,∵∠PBQ=∠PQB=2∠C ,∴2∠C+∠C=30°,解得:∠C=10°.⑩当AB=BP ,BQ=PQ ,PQ=CQ 时,∴∠PQC=∠C=2∠PBQ ,∴12∠C+∠C=30°, 解得:∠C=20°.综上所述:∠C 所有可能的值为10°、20°、25°,35°、40°、50°、80°、100°.【点睛】本题考查复杂作图及等腰三角形的性质,熟练掌握等腰三角形的性质是解题关键.10.已知:在平面直角坐标系中,A 为x 轴负半轴上的点,B 为y 轴负半轴上的点.(1)如图1,以A 点为顶点、AB 为腰在第三象限作等腰Rt ABC ∆,若2OA =,4OB =,试求C 点的坐标;(2)如图2,若点A 的坐标为()23,0-,点B 的坐标为()0,m -,点D 的纵坐标为n ,以B 为顶点,BA 为腰作等腰Rt ABD ∆.试问:当B 点沿y 轴负半轴向下运动且其他条件都不变时,整式2253m n +-化,请说明理由; (3)如图3,E 为x 轴负半轴上的一点,且OB OE =,OF EB ⊥于点F ,以OB 为边作等边OBM ∆,连接EM 交OF 于点N ,试探索:在线段EF 、EN 和MN 中,哪条线段等于EM 与ON 的差的一半?请你写出这个等量关系,并加以证明.【答案】(1) C(-6,-2);(2)不发生变化,值为3-;(3)EN=12(EM-ON),证明见详解. 【解析】【分析】 (1)作CQ ⊥OA 于点Q,可以证明AQC BOA ≅,由QC=AD,AQ=BO,再由条件就可以求出点C 的坐标;(2)作DP ⊥OB 于点P ,可以证明AOB BPD ≅,则有BP=OB-PO=m-(-n)=m+n 为定值,从而可以求出结论2253m n +-的值不变为3-.(3)作BH ⊥EB 于点B ,由条件可以得出∠1=30°,∠2=∠3=∠EMO=15°,∠EOF=∠BMG=45°,EO=BM,可以证明ENO BGM ≅,则GM=ON,就有EM-ON=EM-GM=EG ,最后由平行线分线段成比例定理就可得出EN=12(EM-ON).【详解】(1)如图(1)作CQ ⊥OA 于Q,∴∠AQC=90°, ∵ABC △为等腰直角三角形,∴AC=AB,∠CAB=90°, ∴∠QAC+∠OAB=90°,∵∠QAC+∠ACQ=90°,∴∠ACQ=∠BAO,又∵AC=AB,∠AQC=∠AOB,∴AQC BOA ≅(AAS),∴CQ=AO,AQ=BO,∵OA=2,OB=4,∴CQ=2,AQ=4,∴OQ=6,∴C(-6,-2).(2)如图(2)作DP ⊥OB 于点P ,∴∠BPD=90°,∵ABD △是等腰直角三角形,∴AB=BD,∠ABD=∠ABO+∠OBD=90°,∵∠OBD+∠BDP=90°,∴∠ABO=∠BDP ,又∵AB=BD,∠AOB=∠BPD=90°,∴AOB BPD ≅∴AO=BP ,∵BP=OB -PO=m-(-n)=m+n, ∵A ()23,0-,∴OA=3∴m+n=23∴当点B 沿y 轴负半轴向下运动时,AO=BP=m+n=23∴整式2253m n +-3-(3)()12EN EM ON =- 证明:如图(3)所示,在ME 上取一点G 使得MG=ON,连接BG 并延长,交x 轴于H.∵OBM 为等边三角形,∴BO=BM=MO,∠OBM=∠OMB=∠BOM=60°,∴EO=MO,∠EBM=105°,∠1=30°,∵OE=OB,∴OE=OM=BM,∴∠3=∠EMO=15°,∴∠BEM=30°,∠BME=45°,∵OF⊥EB,∴∠EOF=∠BME,∴ENO BGM ≅,∴BG=EN,∵ON=MG,∴∠2=∠3,∴∠2=15°,∴∠EBG=90°,∴BG=12EG, ∴EN=12EG, ∵EG=EM-GM, ∴EN=12(EM-GM), ∴EN=12(EM-ON). 【点睛】 本题考查了等腰直角三角形的性质,等边三角形的性质,等腰三角形的性质,三角形的外角与内角的关系,全等三角形的判定与性质,平行线分线段成比例定理的运用.三、八年级数学整式的乘法与因式分解解答题压轴题(难)11.一个四位数,记千位上和百位上的数字之和为x ,十位上和个位上的数字之和为y ,如果x y =,那么称这个四位数为“和平数”.例如:1423,14x =+,23y =+,因为x y =,所以1423是“和平数”.(1)直接写出:最小的“和平数”是 ,最大的“和平数”是 ;(2)将一个“和平数”的个位上与十位上的数字交换位置,同时,将百位上与千位上的数字交换位置,称交换前后的这两个“和平数”为一组“相关和平数”.例如:1423与4132为一组“相关和平数”求证:任意的一组“相关和平数”之和是1111的倍数.(3)求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的倍数的所有“和平数”;【答案】(1)1001,9999;(2)见详解;(3)2754和4848【解析】【分析】(1)根据和平数的定义,即可得到结论;(2)设任意的两个“相关和平数”为abcd,badc(a,b,c,d分别取0,1,2, (9)a≠0,b≠0),于是得到abcd badc+=1100(a+b)+11(c+d)=1111(a+b),即可得到结论.(3)设这个“和平数”为abcd,于是得到d=2a,a+b=c+d,b+c=12k,求得2c+a=12k,即a=2、4,6,8,d=4、8、12(舍去)、16(舍去);①、当a=2,d=4时,2(c+1)=12k,得到c=5则b=7;②、当a=4,d=8时,得到c=4则b=8,于是得到结论;【详解】解:(1)由题意得,最小的“和平数”1001,最大的“和平数”9999,故答案为:1001,9999;(2)设任意的两个“相关和平数”为abcd,badc(a,b,c,d分别取0,1,2,…,9且a≠0,b≠0),则abcd badc+=1100(a+b)+11(c+d)=1111(a+b);即两个“相关和平数”之和是1111的倍数.(3)设这个“和平数”为abcd,则d=2a,a+b=c+d,b+c=12k,∴2c+a=12k,即a=2、4,6,8,d=4、8、12(舍去)、16(舍去),①当a=2,d=4时,2(c+1)=12k,可知c+1=6k且a+b=c+d,∴c=5则b=7,②当a=4,d=8时,2(c+2)=12k,可知c+2=6k且a+b=c+d,∴c=4则b=8,综上所述,这个数为:2754和4848.【点睛】本题考查了因式分解的应用,正确的理解新概念和平数”是解题的关键.12.阅读理解:把两个相同的数连接在一起就得到一个新数,我们把它称为“连接数”,例如:234234,3939…等,都是连接数,其中,234234称为六位连接数,3939称为四位连接数.(1)请写出一个六位连接数 ,它 (填“能”或“不能”)被13整除.(2)是否任意六位连接数,都能被13整除,请说明理由.(3)若一个四位连接数记为M ,它的各位数字之和的3倍记为N ,M ﹣N 的结果能被13整除,这样的四位连接数有几个?【答案】(1)证明见解析(2)abcabc 能被13整除(3)这样的四位连接数有1919,2525,3131,一共3个【解析】分析:(1)根据六位连接数的定义可知123123为六位连接数,再将123123进行因数分解,判断得出它能被13整除;(2)设abcabc 为六位连接数,将abcabc 进行因数分解,判断得出它能被13整除; (3)设xyxy 为四位连接数,用含x 、y 的代数式表示M 与N ,再计算M ﹣N ,然后将13M N -表示为77x +7y +3413x y +,根据M ﹣N 的结果能被13整除以及M 与N 都是1~9之间的整数,求得x 与y 的值,即可求解.详解:(1)123123为六位连接数;∵123123=123×1001=123×13×77,∴123123能被13整除;(2)任意六位连接数都能被13整除,理由如下:设abcabc 为六位连接数.∵abcabc =abc ×1001=abc ×13×77,∴abcabc 能被13整除;(3)设xyxy 为四位连接数,则M =1000x +100y +10x +y =1010x +101y ,N =3(x +y +x +y )=6x +6y ,∴M ﹣N =(1010x +101y )﹣(6x +6y )=1004x +95y ,∴13M N -=10049513x y +=77x +7y +3413x y +.∵M ﹣N 的结果能被13整除,∴3413x y +是整数.∵3x +4y 取值范围大于3小于63,所以能被13整除的数有13,26,39,52,∴x =1,y =9;x =2,y =5;x =3,y =1;x =8,y =7;x =9,y =3;x =5,y =6;x =6,y =2;满足条件的四位连接数的3131,2525,6262,9393,8787,5656,1919共7个. 点睛:本题考查了因式分解的应用,整式的运算,理解“连接数”的定义是解题的关键.13.阅读下列材料:利用完全平方公式,可以将多项式2(0)ax bx c a ++≠变形为2()a x m n ++的形式, 我们把这样的变形方法叫做多项式2ax bx c ++的配方法.运用多项式的配方法及平方差公式能对一些多项式进行分解因式.例如:21124x x ++=222111111()()2422x x ++-+ =21125()24x +- =115115()()2222x x +++-=(8)(3)x x ++ 根据以上材料,解答下列问题: (1)用多项式的配方法将281x x +-化成2()x m n ++的形式;(2)下面是某位同学用配方法及平方差公式把多项式2340x x --进行分解因式的解答过程:老师说,这位同学的解答过程中有错误,请你找出该同学解答中开始出现错误的地方,并用“ ”标画出来,然后写出完整的、正确的解答过程:(3)求证:x ,y 取任何实数时,多项式222416x y x y +--+的值总为正数.【答案】(1)2(4)17x +- ;(2)(5)(8)x x +-;(3)见解析【解析】试题分析:(1)根据配方法,可得答案;(2)根据配方法,可得平方差公式,再根据平方差公式,可得答案;(3)根据交换律、结合率,可得完全平方公式,根据完全平方公式,可得答案. 试题解析:解:(1)281x x +-=2228441x x ++--=2(4)17x +-(2)2340x x -- =222333()()40222x x -+-- =23169()24x --=313313()()2222x x -+-- =(5)(8)x x +- (3)证明:222416x y x y +--+=22214411x x y y -++-++=22(1)(2)11x y -+-+∵2(1)x -≥0,2(2)y -≥0,∴22(1)(2)110x y -+-+>.∴x ,y 取任何实数时,多项式222416x y x y +--+的值总是正数.点睛:本题考查了配方法,利用完全平方公式:a 2±2ab +b 2=(a ±b )2配方是解题关键.14.仔细阅读下面例题,解答问题:例题:已知二次三项式2x 4x m -+有一个因式是()x 3+,求另一个因式以及m 的值. 解:设另一个因式为()x n +,得()()2x 4x m x 3x n -+=++则()22x 4x m x n 3x 3n -+=+++ {n 34m 3n +=-∴=.解得:n 7=-,m 21=-∴另一个因式为()x 7-,m 的值为21-问题:仿照以上方法解答下面问题:已知二次三项式22x 3x k +-有一个因式是()2x 5-,求另一个因式以及k 的值.【答案】()4,x + 20.【解析】【分析】根据例题中的已知的两个式子的关系,二次三项式2x 4x m -+的二次项系数是1,因式是()x 3+的一次项系数也是1,利用待定系数法求出另一个因式.所求的式子22x 3x k +-的二次项系数是2,因式是()2x 5-的一次项系数是2,则另一个因式的一次项系数一定是1,利用待定系数法,就可以求出另一个因式.【详解】解:设另一个因式为()x a +,得()()22x 3x k 2x 5x a +-=-+则()222x 3x k 2x 2a 5x 5a +-=+-- {2a 535a k -=∴-=-解得:a 4=,k 20=故另一个因式为()x 4+,k 的值为20【点睛】正确读懂例题,理解如何利用待定系数法求解是解本题的关键.15.由多项式的乘法:(x +a)(x +b)=x 2+(a +b)x +ab ,将该式从右到左使用,即可得到用“十字相乘法”进行因式分解的公式:x 2+(a +b)x +ab =(x +a)(x +b).实例 分解因式:x 2+5x +6=x 2+(2+3)x +2×3=(x +2)(x +3).(1)尝试 分解因式:x 2+6x +8;(2)应用 请用上述方法解方程:x 2-3x -4=0.【答案】(1) (x+2)(x +4);(2) x =4或x =-1.【解析】【分析】(1)类比题干因式分解方法求解可得;(2)利用十字相乘法将左边因式分解后求解可得.【详解】(1)原式=(x+2)(x +4);(2)x 2-3x -4=(x -4)(x +1)=0,所以x -4=0或x +1=0,即x =4或x =-1.【点睛】本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.四、八年级数学分式解答题压轴题(难)16.已知分式A=2344(1)11a a a a a -++-÷--. (1) 化简这个分式;(2) 当a >2时,把分式A 化简结果的分子与分母同时..加上3后得到分式B ,问:分式B 的值较原来分式A 的值是变大了还是变小了?试说明理由.(3) 若A 的值是整数,且a 也为整数,求出符合条件的所有a 值的和.【答案】(1)22a A a +=-;(2)变小了,理由见解析;(3)符合条件的所有a 值的和为11.【解析】分析:(1)分解因式,再通分化简.(2)用作差法比较二者大小关系.(3)先分离常数,再尝试让分子能被分母整除.详解: (1)A =2344111a a a a a -+⎛⎫+-÷ ⎪--⎝⎭=()()()2113211a a a a a -+--÷--=22a a +-. (2)变小了,理由如下:()()()()()()()()21522512212121a a a a a a A B a a a a a a ++-+-++-=-==-+-+-+ . ∵a >2 ∴a -2>0,a+1>0,∴()()1221A B a a -=-+>0,即A >B (3) 24122a A a a +==+-- 根据题意,21,2,4a -=±±± 则a =1、0、-2、3、4、6, 又1a ≠ ∴0+(-2)+3+4+6=11 ,即:符合条件的所有a 值的和为11.点睛:比较大小的方法:(1)作差比较法:0a b a b ->>;0a b a b -<⇒<(a b ,可以是数,也可以是一个式子)(2)作商比较法:若a >0,b >0,且1a b >,则a >b ;若a <0,b <0,且1a b>,则a <b .17.为进一步落实《中华人民共和国民办教育促进法》,某市教育局拿出了b 元资金建立民办教育发展基金会,其中一部分作为奖金发给了n 所民办学校.奖金分配方案如下:首先将n 所民办学校按去年完成教育、教学工作业绩(假设工作业绩均不相同)从高到低,由1到n 排序,第1所民办学校得奖金b n元,然后再将余额除以n 发给第2所民办学校,按此方法将奖金逐一发给了n 所民办学校.(1)请用n 、b 分别表示第2所、第3所民办学校得到的奖金; (2)设第k 所民办学校所得到的奖金为k a 元(1k n ≤≤),试用k 、n 和b 表示k a (不必证明);(3)比较k a 和1k a +的大小(k=1,2 ,……,1n -),并解释此结果关于奖金分配原则的实际意义.【答案】(1)211()(1)b b a b n n n n =-⨯=- ,23111()(1)(1)b b a b n n n n n =-⨯-=-; (2)11(1)k k b a n n-=- ; (3)1k k a a +> .奖金分配的实际意义:名次越靠后,奖金越少.【解析】【试题分析】(1)根据第1所民办学校得奖金b n 元,然后再将余额除以n 发给第2所民办学校,得:22311111()(1),()(1)(1).bb b b a b a b n n n n n n n n n=-⨯=-=-⨯-=- (2)根据(1)中的两个式子,11(1)k k b a n n -=- ; (3)11(1)k k b a n n -=-,+11(1)k k b a n n=-,则1111+121111111(1)(1)(1)1(1)(1)(1)0k k k k k k k b b b b b a a n n n n n n n n n n n n----⎡⎤-=---=---=-⋅⋅=-⋅>⎢⎥⎣⎦,则+1k k a a >.奖金分配的实际意义:名次越靠后,奖金越少.【试题解析】(1)根据题意得:22311111()(1),()(1)(1).bb b b a b a b n n n n n n n n n=-⨯=-=-⨯-=- (2)根据(1)中的两个式子,11(1)k k b a n n -=- (3)11(1)k k b a n n -=-,+11(1)k k b a n n=-,则1111+121111111(1)(1)(1)1(1)(1)(1)0k k k k k k k b b b b b a a n n n n n n n n n n n n----⎡⎤-=---=---=-⋅⋅=-⋅>⎢⎥⎣⎦,则+1k k a a >.奖金分配的实际意义:名次越靠后,奖金越少.【方法点睛】本题目是一道分式的实际应用问题,第一个问题有难度,依据奖金的分配规则,写出23a a 、 的表达式;第二问在第一问的基础上,找出规律,直接写出k a 的表达式即可;第三问用作差法比较两个分式的大小,若差为正数,则被减数大于减数;若差为0,则被减数等于减数;若差为负数,则被减数小于减数.18.京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的23;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成. (1)求甲、乙两队单独完成这项工程各需多少天? (2)已知甲队每天的施工费用为8.4万元,乙队每天的施工费用为5.6万元.工程预算的施工费用为500万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.【答案】(1)甲队单独完成需60天,乙队单独完成这项工程需要90天;(2)工程预算的施工费用不够,需追加预算4万元.【解析】【分析】(1)设甲单独完成这项工程所需天数,表示出乙单独完成这项工程所需天数及各自的工作效率.根据工作量=工作效率×工作时间列方程求解;(2)根据题意,甲乙合作工期最短,所以须求合作的时间,然后计算费用,作出判断.【详解】(1)解:设乙队单独完成这项工程需要x 天,则甲队单独完成需要2x 3填; 403012x x 3+= 解得:x 90=经检验,x =90是原方程的根. 则22x 906033=⨯=(天) 答:甲、乙两队单独完成这项工程分别需60天和90天.(2)设甲、乙两队合作完成这项工程需要y 天,则有y (160+190)=1. 解得y =36. 需要施工费用:36×(8.4+5.6)=504(万元).∵504>500.∴工程预算的施工费用不够用,需追加预算4万元.19.某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程。
人教版八年级上册数学 期末专题《压轴题专练》(含答案)

人教版八年级上册数学期末专题《压轴题专练》1.如图 1,在Rt△ABC 中,∠ACB=90°,D 是AB 上一点,且∠ACD=∠B ;(1)求证:CD⊥AB ,并指出你在证明过程中应用了哪两个互逆的真命题;(2)如图 2,若AE 平分∠BAC ,交CD 于点F ,交BC 于E .求证:∠AEC=∠CFE ;(3)如图 3,若E 为BC 上一点,AE 交CD 于点F ,BC=3CE ,AB=4AD ,△ABC 、△CEF 、△ADF 的面积分别为S 、S 、 △CEF △ABC S ,且S =36,则S ﹣S = .(仅填结果) △ADF △ABC △CEF 2.已知△ABC 的面积是 60,请完成下列问题:△ADF (1)如图 1,若AD 是△ABC 的BC 边上的中线,则△ABD 的面积_______△ACD 的面积(填“>”“<”或“=”)(2)如图 2,若CD 、BE 分别是△ABC 的AB 、AC 边上的中线,求四边形ADOE 的面积可以用如下方法:连接AO ,由 AD=DB 得:S =S ,同理 :S =S ,设 S =x ,S =y ,则S =x ,S =y 由题意得:S = S =30,S = S △AEO △ADO △BDO △CEO △AEO △ADO △CEO △BDO△ABE △ABC △ADC =30,可列方程组为: ,解得_______,通过解这个方程组可得四边形ADOE 的面积为_______.△ABC (3)如图 3,AD :DB=1:3,CE :AE=1:2,请你计算四边形ADOE 的面积,并说明理由.3.阅读下列材料:某同学遇到这样一个问题:如图1,在△ABC 中,AB=AC,BD 是△ABC 的高.P 是BC 边上一点,PM,PN 分别与直线AB ,AC 垂直,垂足分别为点M,N.求证:BD=PM+PN .他发现,连接AP ,有S =S +S ,即 △ACP .由AB=AC,可得BD=PM+PN .△ABC △ABP 他又画出了当点P 在CB 的延长线上,且上面问题中其他条件不变时的图形,如图 2 所示.他猜想此时BD ,PM ,PN 之 间的数量关系是:BD=PN-PM .请回答:(1)请补全以下该同学证明猜想的过程;证明:连接AP .∵, ∴.∵AB=AC ,∴BD=PN-PM.(2)参考该同学思考问题的方法,解决下列问题:在△ABC中,AB=AC=BC,BD是△ABC的高.P是△ABC所在平面上一点,PM,PN,PQ分别与直线AB,AC,BC垂直,垂足分别为点M,N,Q.①图3,若点P在△ABC的内部,则BD,PM,PN,PQ之间的数量关系是:;②②若点P在如图4 所示位置,利用图4 探究得出此时BD,PM,PN,PQ之间数量关系是: .4.如图1,在平面直角坐标系中,已知A(a,0),B(b,3),C(4,0),且满足(a+b)2+|a﹣b+6|=0,线段AB 交y 轴于F 点.(1)求点A、B 的坐标;(2)点D 为y 轴正半轴上一点,若ED∥AB,且AM,DM 分别平分∠CAB,∠ODE,如图 2,求∠AMD的度数;(3)如图 3,(也可以利用图1)①求点F 的坐标;②坐标轴上是否存在点P,使得△ABP 和△ABC的面积相等?若存在,求出P 点坐标;若不存在,请说明理由.5.问题情境:如图1,在直角三角形ABC 中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);特例探究:如图2,∠MAN=90°,射线AE 在这个角的内部,点B、C 在∠MAN的边AM、AN 上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;归纳证明:如图3,点B,C 在∠MAN的边AM、AN 上,点E,F 在∠MAN内部的射线AD 上,∠1、∠2分别是△ABE、△CAF 的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;拓展应用:如图4,在△ABC中,AB=AC,AB>BC.点D 在边BC 上,CD=2BD,点E、F 在线段AD 上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为.6.如图,AD是△ABC的角平分线,点F,E分别在边AC,AB上,且FD=BD.(1)求证:∠B+∠AFD=180°;(2)如果∠B+2∠DEA=180°,探究线段AE,AF,FD之间满足的等量关系,并证明.7.(1)如图(1)在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:DE=BD+CE;(2)如图(2)将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请给出证明;若不成立,请说明理由.8.如图1,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.(1)直接写出∠AFC的度数:60°;(2)请你判断并写出FE与FD之间的数量关系;(3)如图2,在△ABC中,如果∠ACB不是直角,而(1)中的其它条件不变,试判断线段A E、CD与AC之间的数量关系并说明理由.9.已知点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M,N分别是射线AE,AF上的点,且PM=PN.(1)如图1,当点M在线段AB上,点N在线段AC的延长线上时,求证:BM=CN;(2)在(1)的条件下,直接写出线段AM,AN与AC之间的数量关系________;(3)如图2,当点M在线段AB的延长线上,点N在线段AC上时,若AC:PC=2:1,且PC=4,求四边形ANPM的面积.10.(1)如图1,△ABC中,作∠ABC、∠ACB的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F.①求证:OE=BE;②若△ABC的周长是25,BC=9,试求出△AEF的周长;(2)如图2,若∠ABC的平分线与∠ACB外角∠ACD的平分线相交于点P,连接AP,试探求∠BAC与∠PAC的数量关系式.11.观察发现:如图1,OP平分∠MON,在OM,ON上分别取OA,OB,使OA=OB,再在OP上任取一点D,连接AD,BD.请你猜想AD与BD之间的数量关系,并说明理由.拓展应用:如图2,在△ABC中,∠ACB是直角,∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F,请你写出FE与FD之间的数量关系,并说明理由.12.如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?7.(1)如图(1)在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:DE=BD+CE;(2)如图(2)将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请给出证明;若不成立,请说明理由.8.如图1,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.(1)直接写出∠AFC的度数:60°;(2)请你判断并写出FE与FD之间的数量关系;(3)如图2,在△ABC中,如果∠ACB不是直角,而(1)中的其它条件不变,试判断线段A E、CD与AC之间的数量关系并说明理由.9.已知点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M,N分别是射线AE,AF上的点,且PM=PN.(1)如图1,当点M在线段AB上,点N在线段AC的延长线上时,求证:BM=CN;(2)在(1)的条件下,直接写出线段AM,AN与AC之间的数量关系________;(3)如图2,当点M在线段AB的延长线上,点N在线段AC上时,若AC:PC=2:1,且PC=4,求四边形ANPM的面积.10.(1)如图1,△ABC中,作∠ABC、∠ACB的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F.①求证:OE=BE;②若△ABC的周长是25,BC=9,试求出△AEF的周长;(2)如图2,若∠ABC的平分线与∠ACB外角∠ACD的平分线相交于点P,连接AP,试探求∠BAC与∠PAC的数量关系式.11.观察发现:如图1,OP平分∠MON,在OM,ON上分别取OA,OB,使OA=OB,再在OP上任取一点D,连接AD,BD.请你猜想AD与BD之间的数量关系,并说明理由.拓展应用:如图2,在△ABC中,∠ACB是直角,∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F,请你写出FE与FD之间的数量关系,并说明理由.12.如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?。
人教版八年级上册数学期末动点问题压轴题专题训练(含答案)

人教版八年级上册数学期末动点问题压轴题专题训练1.如图,△ABC是等边三角形,点D是边BC上一个动点(点D不与点B,C重合),连接AD,点E在边AC的延长线上,且DA=DE.(1)求证:△BAD=△EDC:(2)用等式表示线段CD,CE,AB之间的数量关系,并证明.2.如图,已知△ ABC是边长为10cm的等边三角形,点F为AC的中点,动点D,E同时从A,B两点出发,分别沿AB,BC匀速运动,其中点D运动的速度是1cm/s,点E运动的速度是2cm/s,设运动时为t 秒.(1)当t为何值时,△ AFD与△ CFE全等;(2)当t为何值时,△ BDE为直角三角形.3.已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作等边△ADE(顶点A、D、E按逆时针方向排列),连接CE.(1)如图1,当点D在边BC上时,求证:△BD=CE,△AC=CE+CD;(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CE+CD是否成立?若不成立,请写出AC、CE、CD之间存在的数量关系,并说明理由.4.在等边△ABC中,(1)如图1,P,Q是BC边上两点,AP=AQ,△BAP=20°,求△AQB的度数;(2)点P,Q是BC边上的两个动点(不与B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.△依题意将图2补全;△求证:P A=PM.5.如图,在三角形ABC中,D是射线BC上一动点.(1)如图1,点D在BC边上(不与点B,C重合),△ 按要求作图:分别过点D作DE BA∥交边AB于点F;∥交边AC于点E,作DF CA△ 在△的条件下,判断△EDF与△A的数量关系,并说明理由;(2)如图2,若点D在BC的延长线上,DF CA∥,△EDF=△A,试判断DE与BA的位置关系,并说明理由.6.如图1,等腰Rt△ABC中,△BAC=90°,AB=AC,D,E分别是AC和BC上的动点,BD△AE,垂足为F.(1)求证△CAE=△ABD;(2)连接DE,满足△AEB=△DEC,求证:BD=DE+AE;(3)点G在BD的延长线上,连接EG,满足△AEB=△GEC,试写出AE,EG,BG之间的数量关系,并证明.7.已知:如图,ABC是边长为6cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P,Q两点停止运动,设点P的运动时间为()s t,解答下列各问题:(1)ABC的面积为多少?△是等边三角形?(2)当t为何值时,PBQ△是直角三角形时,求t的值.(3)当PBQA a,将点A向右平移b个单位得到点B,其中a,b满足8.如图△所示,点A的坐标为(0,)+-=.a b50(2)如图△,坐标轴上有两个动点P ,Q ,点P 从A 点出发沿y 轴负方向以每秒1个单位长度的速度运动,点Q 从O 点出发以每秒2个单位长度的速度沿x 轴正方向运动,点P 、Q 同时出发,点P 到达O 点时整个运动结束.设运动时间为t 秒,问t 为何值时,使得12OBP BOQ S S =△△?并求出此时点P 和点Q 的坐标; (3)如图△所示,点F 为x 轴上一点,作△BOF 的平分线OG ,且OG △FB ,垂足为G ,△AOB 的平分线OE 与射线FB 交于点E ,求△E 的度数.9.如图,在平面直角坐标系中,点A ,B 的坐标分别为(a ,0),(b ,0),且a ,b 满足()23-20a b ++=.现同时将点A ,B 分别向左平移2个单位,再向上平移2个单位,得到点A ,B 的对应点C ,D ,连接AC ,BD ,CD .(1)直接写出A ,B 两点的坐标为:A ___________, B ___________.(2)若点P 是线段AC 上的一个动点,Q 是线段CD 的中点,连接PQ ,PO ,当点P 在线段AC 上移动时(不与点A ,C 重合),请找出PQD ∠,OPQ ∠,POB ∠的数量关系,并证明你的结论.(3)在坐标轴上是否存在点M ,使三角形MAD 的面积与三角形ACD 的面积相等?若存在,请求出点M 的坐标;若不存在,试说明理由.10.已知:直线AD BC ∥,动点P 在直线EF 上运动,探究ADP ,DPC ∠,BCP ∠之间的关系.(1)【问题发现】若25ADP ∠=︒,35BCP ∠=︒,求DPC ∠的度数.(2)【结论猜想】当点P 在线段AB 上时,猜想ADP ,DPC ∠,BCP ∠三个角之间的数量关系,并说明理(3)【拓展延伸】若点P 在射线AE 上或者在射线BF 上时(不包括端点),试着探究ADP ,DPC ∠,BCP ∠之间的关系是否会发生变化,请挑选一种情形画出图形,写出结论,并说明理由.11.ABC 中,70C ∠=︒,点D ,E 分别是ABC 边AC ,BC 上的点,点P 是一动点,令1PDA ∠=∠,2PEB ∠=∠,DPE α∠=∠.初探:(1)如图1,若点P 在线段AB 上,且60α∠=︒,则12∠+∠=_____________; (2)如图2,若点P 在线段AB 上运动,则△1,△2,α∠之间的关系为_____________; (3)如图3,若点P 在线段AB 的延长线上运动,则△1,△2,α∠之间的关系为_____________; 再探:(4)如图4,若点P 运动到ABC 的内部,写出此时△1,△2,α∠之间的关系,并说明理由.12.如图,AB 、CD 被AC 所截,AB CD ∥,△CAB =108°,点P 为直线AB 上一动点(不与点A 重合),连CP ,作△ACP 和△DCP 的平分线分别交直线AB 于点E 、F .(1)当点P 在点A 的右侧时△若△ACP =36°,则此时CP 是否平分△ECF ,请说明理由. △求△ECF 的度数.(2)在点P 运动过程中,直接写出△APC 与△AFC 之间的数量关系.(1)求证:AB CD ∥;(2)如图2,若3ABE EBF ∠=∠,120BFD ∠=︒,试求CDFBDF∠∠的值;(3)如图3,若H 是直线CD 上一动点(不与D 重合),BI 平分HBD ∠,则EBI ∠与BHD ∠的数量关系为______.14.如图1,在△ABC 中,BO AC ⊥于点O ,3,1AO BO OC ===,过点A 作AH BC ⊥于点H ,交BO 于点P .(1)求线段OP 的长度;(2)连接OH ,求证:点O 到△AHC 的两边距离相等;(3)如图2,若点D 为AB 的中点,点M 为线段BO 延长线上一动点,连接MD ,过点D 作DN DM ⊥交线段OA 延长线于N 点,则BDM ADN S S ∆∆-的值是否发生改变,如改变,求出该值的变化范围;若不改变,求该式子的值.15.在ABC 中,BAC ABC ∠>∠,三个内角的平分线交于点O .(1)填空:如图1,若80BCA ∠=︒,则BOA ∠的大小为________度;(3)如图2,CO 的延长线交AB 于点E ,点M 是AB 边上的一动点(不与点E 重合),过点M 作MN CE ⊥于点N ,请探索AMN ∠、ABC ∠、BAC ∠三者之间的数量关系.16.如图1,CE 平分ACD ∠,AE 平分BAC ∠,90EAC ACE ∠+∠=︒(1)请判断AB 与CD 的位置关系并说明理由;(2)如图2,在(1)的结论下,当90E ∠=︒保持不变,移动直角顶点E ,使MCE ECD ∠=∠,当直角顶点E 点移动时,问BAE ∠与MCD ∠是否存在确定的数量关系?(3)如图3,在(1)的结论下,P 为线段AC 上一定点,点Q 为直线CD 上一动点,当点Q 在射线CD 上运动时(点C 除外),CPQ CQP ∠+∠与BAC ∠有何数量关系?17.如图,在△ABC 中,D 为AB 的中点,AB =AC =10cm ,BC =8cm ,动点P 从点B 出发,沿BC 方向以每秒3cm 的速度向点C 运动;同时动点Q 从点C 出发,沿CA 方向以每秒3cm 的速度向点A 运动,运动时间是t 秒.(1)在运动过程中,当点C 位于线段PQ 的垂直平分线上时,求出t 的值;(2)在运动过程中,是否存在某一时刻t ,使△BPD 和△CQP 全等,若存在,求出t 的值.若不存在,请说明理由.18.如图,△ABC是边长是12cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:(1)当点Q到达点C时,PQ与AB的位置关系如何?请说明理由.(2)在点P与点Q的运动过程中,△BPQ是否能成为等边三角形?若能,请求出t,若不能,请说明理由.(3)则当t为何值时,△BPQ是直角三角形?2,0,以线段OA为边在第四象限内作等边AOB,点C 19.如图,在平面直角坐标系中,点A的坐标为()OC>,连接BC,以线段BC为边在第四象限内作等边CBD,连接DA.为x轴正半轴上一动点()2(1)求证:OBC ABD≌;(2)是否存在点C,使得ACD△为直角三角形.若存在,请求出点C的坐标;若不存在,请说明理由;(3)是否存在点C,使得ACD△为等腰三角形.若存在,请求出AC的长;若不存在,请说明理由.B-(0,4)点4(6,)A -.(1)如图1,动点P 从点B 出发,以每秒2个单位长度的速度沿BA 方向运动,同时动点Q 从点O 出发,以每秒3个单位长度的速度沿y 轴向上运动,当点P 运动到点A 时,P 、Q 同时停止运动,设点P 运动时间为t 秒.用含t 的式子表示P ,Q 两点的坐标.(2)如图2,点D 为线段OA (端点除外)上某一点,当点D 在线段上运动时,过点D 作直线EF 交x 轴正半轴于E ,交直线AB 于F ,,EOD AFD ∠∠的平分线相交于点N ,若ODF α∠=,请用含α的式子表示ONF ∠的大小,并说明理由.答案1. (2)AB =CD +CE 2.(1)103t =(2)t =2或53.(2)AC+CD =CE ,4.(1)80°5.(1);△△EDF =△A , (2)DE BA ∥,6. (3)BG =AE +EG ,7.(1)2cm (2)3 (3)2或48.(1)(0,2)A ,(3,2)B (2)65t =,点0,54P ⎛⎫ ⎪⎝⎭,12,05Q ⎛⎫ ⎪⎝⎭ (3)△E =45°9.(1)(−3,0);(2,0)(2)△DQP +△QPO +△BOP =360°; (3)(0,163)或(0,−43)或(−8,0)或(2,0)10.(1)60°;(2)△DPC =△ADP +△PCB(3)△PCB =△DPC +△ADP ;或△ADP =△DPC +△PCB11.(1)130︒;(2)1270α∠+∠=︒+∠; (3)1270α∠-∠=︒+∠; (4)12430α∠+∠=︒-∠,12.(1)△平分,;△36°(2)当点P 在点E 的右侧时,2APC AFC ∠=∠;当点P 、点E 在点A 的左侧,点F 在点A 的右侧时,2180AFC APC ∠+∠=︒;当点P 、点E 、点F 均在点A 的左侧时, 2180AFC APC ∠-∠=︒.13. (2)4(3)△BHD =2△EBI 或△EBI =90°-12△BHD14.(1)OP =1;(3)不变,9415.(1)130(3)2360AMN ABC BAC ∠=∠-∠+︒或2AMN BAC ABC ∠=∠-∠16.(1)平行,(2)存在,1902BAE MCD ∠+∠=︒(3)BAC PQC QPC ∠=∠+∠17.(1)43t = (2)当1t =时,△BPD △△CQP18.(1)PQ 与AB 垂直,(2)能,当4s t =时,△BPQ 是等边三角形(3) 2.4s t =或6s t =,△BPQ 是直角三角形19. (2)C (4,0)(3)不存在,20.(1)P (2t ,-4),Q (0,3t ); (2)12ONF α∠=,。
八年级上册压轴题数学考试试卷含答案

八年级上册压轴题数学考试试卷含答案一、压轴题1.如图,在ABC ∆中,90,,8ACB AC BC AB cm ∠=︒==,过点C 做射线CD ,且//CD AB ,点P 从点C 出发,沿射线CD 方向均匀运动,速度为3/cm s ;同时,点Q 从点A 出发,沿AB 向点B 匀速运动,速度为1/cm s ,当点Q 停止运动时,点P 也停止运动.连接,PQ CQ ,设运动时间为()()08t s t <<.解答下列问题:(1)用含有t 的代数式表示CP 和BQ 的长度; (2)当2t =时,请说明//PQ BC ;(3)设BCQ ∆的面积为()2S cm ,求S 与t 之间的关系式.解析:(1)CP=3t ,BQ=8-t ;(2)见解析;(3)S=16-2t . 【解析】 【分析】(1)直接根据距离=速度⨯时间即可; (2)通过证明PCQ BQC ≅,得到∠PQC=∠BCQ,即可求证;(3)过点C 作CM⊥A B ,垂足为M ,根据等腰直角三角形的性质得到CM=AM=4,即可求解.【详解】解:(1)CP=3t ,BQ=8-t ; (2)当t=2时,CP=3t=6,BQ=8-t=6 ∴CP=BQ ∵CD ∥AB ∴∠PCQ=∠BQC 又∵CQ=QC ∴PCQ BQC ≅∴∠PQC=∠BCQ ∴PQ∥BC(3)过点C 作CM⊥AB,垂足为M∵AC=BC,CM⊥AB ∴AM=118422AB =⨯=(cm ) ∵AC=BC,∠ACB=90︒ ∴∠A=∠B=45︒ ∵CM⊥AB ∴∠AMC=90︒ ∴∠ACM=45︒ ∴∠A=∠ACM ∴CM=AM=4(cm ) ∴118t 416222BCQSBQ CM t ==⨯-⨯=- 因此,S 与t 之间的关系式为S=16-2t . 【点睛】此题主要考查列代数式、全等三角形的判定与性质、平行线的判定、等腰三角形的性质,熟练掌握逻辑推理是解题关键.2.已知AB //CD ,点E 是平面内一点,∠CDE 的角平分线与∠ABE 的角平分线交于点F . (1)若点E 的位置如图1所示.①若∠ABE =60°,∠CDE =80°,则∠F = °; ②探究∠F 与∠BED 的数量关系并证明你的结论;(2)若点E 的位置如图2所示,∠F 与∠BED 满足的数量关系式是 .(3)若点E 的位置如图3所示,∠CDE 为锐角,且1452E F ∠≥∠+︒,设∠F =α,则α的取值范围为 .解析:(1)①70;②∠F =12∠BED ,证明见解析;(2)2∠F+∠BED =360°;(3)3045α︒≤<︒【解析】 【分析】(1)①过F 作FG//AB ,利用平行线的判定和性质定理得到∠DFB=∠DFG+∠BFG=∠CDF+∠ABF ,利用角平分线的定义得到∠ABE+∠CDE=2∠ABF+2∠CDF=2(∠ABF+∠CDF ),求得∠ABF+∠CDF=70︒,即可求解; ②分别过E 、F 作EN//AB ,FM//AB ,利用平行线的判定和性质得到∠BED=∠ABE+∠CDE ,利用角平分线的定义得到∠BED=2(∠ABF+∠CDF ),同理得到∠F=∠ABF+∠CDF ,即可求解;(2)根据∠ABE 的平分线与∠CDE 的平分线相交于点F ,过点E 作EG ∥AB ,则∠BEG+∠ABE=180°,因为AB ∥CD ,EG ∥AB ,所以CD ∥EG ,所以∠DEG+∠CDE=180°,再结合①的结论即可说明∠BED 与∠BFD 之间的数量关系;(3)通过对1452E F ∠≥∠+︒的计算求得30α≥︒,利用角平分线的定义以及三角形外角的性质求得45α<︒,即可求得3045α︒≤<︒. 【详解】(1)①过F 作FG//AB ,如图:∵AB ∥CD ,FG ∥AB , ∴CD ∥FG ,∴∠ABF=∠BFG ,∠CDF=∠DFG , ∴∠DFB=∠DFG+∠BFG=∠CDF+∠ABF , ∵BF 平分∠ABE , ∴∠ABE=2∠ABF , ∵DF 平分∠CDE , ∴∠CDE=2∠CDF ,∴∠ABE+∠CDE=2∠ABF+2∠CDF=2(∠ABF+∠CDF )=60︒+80︒=140︒, ∴∠ABF+∠CDF=70︒, ∴∠DFB=∠ABF+∠CDF=70︒, 故答案为:70; ②∠F=12∠BED , 理由是:分别过E 、F 作EN//AB ,FM//AB ,∵EN//AB ,∴∠BEN=∠ABE ,∠DEN=∠CDE , ∴∠BED=∠ABE+∠CDE ,∵DF 、BF 分别是∠CDE 的角平分线与∠ABE 的角平分线, ∴∠ABE=2∠ABF ,∠CDE=2∠CDF , 即∠BED=2(∠ABF+∠CDF );同理,由FM//AB ,可得∠F=∠ABF+∠CDF , ∴∠F=12∠BED ; (3)2∠F+∠BED=360°. 如图,过点E 作EG ∥AB , 则∠BEG+∠ABE=180°,∵AB ∥CD ,EG ∥AB , ∴CD ∥EG ,∴∠DEG+∠CDE=180°,∴∠BEG+∠DEG=360°-(∠ABE+∠CDE ), 即∠BED=360°-(∠ABE+∠CDE ), ∵BF 平分∠ABE , ∴∠ABE=2∠ABF , ∵DF 平分∠CDE , ∴∠CDE=2∠CDF ,∠BED=360°-2(∠ABF+∠CDF ), 由①得:∠BFD=∠ABF+∠CDF , ∴∠BED=360°-2∠BFD , 即2∠F+∠BED=360°;(3)∵1452E F ∠≥∠+︒,∠F =α,∴2452αα≥+︒,解得:30α≥︒, 如图,∵∠CDE 为锐角,DF 是∠CDE 的角平分线, ∴∠CDH=∠DHB 190452<⨯︒=︒, ∴∠F <∠DHB 45<︒,即45α<︒, ∴3045α︒≤<︒, 故答案为:3045α︒≤<︒. 【点睛】本题考查了平行线的性质、角平分线的定义以及三角形外角性质的应用,在解答此题时要注意作出辅助线,构造出平行线求解.3.现给出一个结论:直角三角形斜边的中线等于斜边的一半;该结论是正确的,用图形语言可以表示为:如图1在ABC ∆中,90︒∠=C ,若点D 为AB 的中点,则12CD AB =. 请结合上述结论解决如下问题:已知,点P 是射线BA 上一动点(不与A,B 重合)分别过点A,B 向直线CP 作垂线,垂足分别为E,F,其中Q 为AB 的中点(1)如图2,当点P 与点Q 重合时,AE 与BF 的位置关系____________;QE 与QF 的数量关系是__________(2)如图3,当点P 在线段AB 上不与点Q 重合时,试判断QE 与QF 的数量关系,并给予证明.(3)如图4,当点P 在线段BA 的延长线上时,此时(2)中的结论是否成立?请画出图形并写出主要证明思路.解析:(1)AE//BF;QE=QF ;(2)QE=QF ,证明见解析;(3)结论成立,证明见解析. 【解析】 【分析】(1)根据AAS 得到AEQ BFQ ∆≅∆,得到AEQ BFQ ∠=∠、QE=QF ,根据内错角相等两直线平行,得到AE//BF ;(2)延长EQ 交BF 于D ,根据AAS 判断得出AEQ BDQ ∆≅∆,因此EQ DQ =,根据直角三角形斜边的中线等于斜边的一半即可证明;(3)延长EQ 交FB 的延长于D ,根据AAS 判断得出AEQ BDQ ∆≅∆,因此EQ DQ =,根据直角三角形斜边的中线等于斜边的一半即可证明. 【详解】(1)AE//BF ;QE=QF (2)QE=QF证明:延长EQ 交BF 于D ,,AE CP BF CP ⊥⊥//AE BF ∴AEQ BDQ ∴∠=∠AQE BQD AEQ BDQ AQ BQ ∠=∠⎧⎪∠=∠⎨⎪=⎩, AEQ BDQ ∴∆≅∆EQ DQ ∴=90BFE ︒∠=QE QF ∴=(3)当点P 在线段BA 延长线上时,此时(2)中结论成立 证明:延长EQ 交FB 的延长于D 因为AE//BF所以AEQ BDQ ∠=∠AQE BQD AEQ BDQ AQ BQ ∠=∠⎧⎪∠=∠⎨⎪=⎩AEQ BDQ ∴∆≅∆EQ=QF90BFE ︒∠=QE QF ∴=【点睛】本题考查了三角形全等的判定方法:AAS ,平行线的性质,根据P 点位置不同,画出正确的图形,找到AAS 的条件是解决本题的关键.4.已知:如图1,直线//AB CD ,EF 分别交AB ,CD 于E ,F 两点,BEF ∠,DFE ∠的平分线相交于点K . (1)求K ∠的度数;(2)如图2,BEK ∠,DFK ∠的平分线相交于点1K ,问1K ∠与K ∠的度数是否存在某种特定的等量关系?写出结论并证明;(3)在图2中作1BEK ∠,1DFK ∠的平分线相交于点2K ,作2BEK ∠,2DFK ∠的平分线相交于点3K ,依此类推,作n BEK ∠,n DFK ∠的平分线相交于点1n K +,请用含的n 式子表示1n K ∠+的度数.(直接写出答案,不必写解答过程)解析:(1)90︒;(2)12K K ∠∠=,证明见解析;(3)111902n n K ∠++=⨯︒ 【解析】 【分析】(1) 过 K 作KG ∥AB ,交 EF 于 G ,证出//AB CD ∥KG ,得到BEK EKG ∠∠=,GKF KFD ∠∠=,根据角平分线的性质及平行线的性质得到()2180BEK DFK ∠∠+=,即可得到答案;(2)根据角平分线的性质得到1112BEK KEK KEB ∠∠∠==,1112KFK DFK DFK ∠∠∠==,根据90BEK KFD ∠∠+=求出1145KEK KFK ∠∠+=,根据()()111180K KEF EFK KEK KFK ∠∠∠∠∠=-+-+求出答案;(3)根据(2)得到规律解答即可. 【详解】(1) 过 K 作KG ∥AB ,交 EF 于 G ,∵//AB CD , ∴//AB CD ∥KG ,BEK EKG ∠∠∴=,GKF KFD ∠∠=,EK ,FK 分别为BEF ∠与EFD ∠的平分线,BEK FEK ∠∠∴=,EFK DFK ∠∠=,∵//AB CD ,180BEK FEK EFK DFK ∠∠∠∠∴+++=,()2180BEK DFK ∠∠∴+=,90BEK DFK ∠∠∴+=,则 90EKF EKG GKF ∠∠∠=+=;(2) 12K K ∠∠=, 理由为:BEK ∠,DFK ∠的平分线相交于点1K , 1112BEK KEK KEB ∠∠∠∴==,1112KFK DFK DFK ∠∠∠==, 180BEK FEK EFK DFK ∠∠∠∠+++=,即 ()2180BEK KFD ∠∠+=,90BEK KFD ∠∠∴+=,1145KEK KFK ∠∠∴+=,()()11118045K KEF EFK KEK KFK ∠∠∠∠∠∴=-+-+=, 12K K ∠∠∴=;(3)由(2)知90K ∠=;1119022K K ∠∠==⨯同理可得2112K K ∠∠==14K ∠1904=⨯, ∴111902n n K ∠++=⨯. 【点睛】此题考查平行线的性质:两直线平行,内错角相等;平行公理的推论:平行于同一直线的两直线平行;角平分线的性质;(3)是难点,注意总结前两问的做题思路得到规律进行解答. 5.Rt △ABC 中,∠C =90°,点D 、E 分别是△ABC 边AC 、BC 上的点,点P 是一动点.令∠PDA =∠1,∠PEB =∠2,∠DPE =∠α.(1)若点P 在线段AB 上,如图(1)所示,且∠α=60°,则∠1+∠2= ;(2)若点P 在线段AB 上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为 ; (3)若点P 运动到边AB 的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由;(4)若点P 运动到△ABC 形外,如图(4)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.解析:(1)150°;(2)∠1+∠2=90°+α;(3)∠1=90°+∠2+α,理由详见解析;(4)∠2=90°+∠1-α,理由详见解析 【解析】 【分析】(1)先用平角的得出,∠CDP=180°-∠1,∠CEP=180°-∠2,最后用四边形的内角和即可; (2)同(1)方法即可;(3)利用平角的定义和三角形的内角和即可得出结论; (4)利用三角形的内角和和外角的性质即可得出结论. 【详解】解:(1) ∵∠1+∠CDP=180°, ∴∠CDP=180°-∠1,同理:∠CEP=180°-∠2,根据四边形的内角和定理得,∠CDP+∠DPE+∠CEP+∠C=360°,∵∠C=90°,∴180°-∠1+α+180°-∠2+90°=360°,∴∠1+∠2=90°+α=90°+60°=150°,故答案为:150;(2) ∵∠1+∠CDP=180°,∴∠CDP=180°-∠1,同理:∠CEP=180°-∠2,根据四边形的内角和定理得,∠CDP+∠DPE+∠CEP+∠C=360°,∵∠C=90°,∴180°-∠1+α+180°-∠2+90°=360°,∴∠1+∠2=90°+α,故答案为:∠1+∠2=90°+α;(3)∠1=90°+∠2+∠α.理由如下:如图3,设DP与BE的交点为F,∵∠2+∠α=∠DFE,∠DFE+∠C=∠1,∴∠1=∠C+∠2+∠α=90°+∠2+∠α.(4)∠2=90°+∠1-∠α,理由如下:如图4,设PE与AC的交点为G,∵∠PGD=∠EGC,∴∠α+180°-∠1=∠C+180°-∠2,∴∠2=90°+∠1-∠α.故答案为∠2=90°+∠1-∠α.【点睛】此题是三角形综合题,主要考查了四边形的内角和,三角形的内角和,三角形的外角的性质,平角的定义,解本题的关键是将∠1,∠2,α转化到一个三角形或四边形中,是一道比较简单的中考常考题.6.已知ABC,P 是平面内任意一点(A、B、C、P 中任意三点都不在同一直线上).连接PB、PC,设∠PBA=s°,∠PCA=t°,∠BPC=x°,∠BAC=y°.(1)如图,当点 P 在ABC 内时,①若 y=70,s=10,t=20,则 x=;②探究 s、t、x、y 之间的数量关系,并证明你得到的结论.(2)当点 P 在ABC 外时,直接写出 s、t、x、y 之间所有可能的数量关系,并画出相应的图形.解析:(1)①100;②x=y+s+t;(2)见详解.【解析】【分析】(1)①利用三角形的内角和定理即可解决问题;②结论:x=y+s+t.利用三角形内角和定理即可证明;(2)分6种情形分别求解即可解决问题.【详解】解:(1)①∵∠BAC=70°,∴∠ABC+∠ACB=110°,∵∠PBA=10°,∠PCA=20°,∴∠PBC+∠PCB=80°,∴∠BPC=100°,∴x=100,故答案为:100.②结论:x=y+s+t.理由:∵∠A+∠ABC+∠ACB=∠A+∠PBA+∠PCA+∠PBC+∠PCB=180°,∠PBC+∠PCB+∠BPC=180°,∴∠A+∠PBA+∠PCA=∠BPC,∴x=y+s+t.(2)s、t、x、y之间所有可能的数量关系:如图1:s+x=t+y;如图2:s+y=t+x;如图3:y=x+s+t;如图4:x+y+s+t=360°;如图5:t=s+x+y;如图6:s=t+x+y;【点睛】本题考查三角形的内角和定理,三角形的外角的性质等知识,解题的关键是学会用分类讨论的思想思考问题.7.如图,△ABC是等边三角形,△ADC与△ABC关于直线AC对称,AE与CD垂直交BC的延长线于点E,∠EAF=45°,且AF与AB在AE的两侧,EF⊥AF.(1)依题意补全图形.(2)①在AE上找一点P,使点P到点B,点C的距离和最短;②求证:点D到AF,EF的距离相等.解析:(1)详见解析;(2)①详见解析;②详见解析.【解析】【分析】(1)本题考查理解题意能力,按照题目所述依次作图即可.(2)①本题考查线段和最短问题,需要通过垂直平分线的性质将所求线段转化为其他等量线段之和,以达到求解目的.②本题考查垂直平分线的判定以及全等三角形的证明,继而利用角的平分线性质即可得出结论.【详解】(1)补全图形,如图1所示(2)①如图2,连接BD,P为BD与AE的交点∵等边△ACD,AE⊥CD∴PC=PD,PC+PB最短等价于PB+PD最短故B,D之间直线最短,点P即为所求.②证明:连接DE,DF.如图3所示∵△ABC,△ADC是等边三角形∴AC=AD,∠ACB=∠CAD=60°∵AE⊥CD∴∠CAE=12∠CAD=30°∴∠CEA=∠ACB﹣∠CAE=30°∴∠CAE=∠CEA∴CA=CE∴CD垂直平分AE∴DA=DE∴∠DAE=∠DEA∵EF⊥AF,∠EAF=45°∴∠FEA=45°∴∠FEA=∠EAF∴FA=FE,∠FAD=∠FED∴△FAD≌△FED(SAS)∴∠AFD=∠EFD∴点D到AF,EF的距离相等.【点睛】本题第一问作图极为重要,要求对题意有较深的理解,同时对于垂直平分线以及角平分线的定义要清楚,能通过题目文字所述转化为考点,信息转化能力需要多做题目加以提升.8.在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以每分钟1米的速度由A向B和由C向A爬行,其中一只蜗牛爬到终点时,另一只也停止运动,经过t分钟后,它们分别爬行到D、E处,请问:(1)如图1,在爬行过程中,CD和BE始终相等吗,请证明?(2)如果将原题中的“由A向B和由C向A爬行”,改为“沿着AB和CA的延长线爬行”,EB与CD交于点Q,其他条件不变,蜗牛爬行过程中∠CQE的大小保持不变,请利用图2说明:∠CQE=60°;(3)如果将原题中“由C向A爬行”改为“沿着BC的延长线爬行,连接DE交AC于F”,其他条件不变,如图3,则爬行过程中,证明:DF=EF解析:(1)相等,证明见解析;(2)证明见解析;(3)证明见解析.【解析】【分析】(1)先证明△ACD≌△CBE,再由全等三角形的性质即可证得CD=BE;(2)先证明△BCD≌△ABE,得到∠BCD=∠ABE,求出∠DQB=∠BCQ+∠CBQ=∠ABE+∠CBQ=180°-∠ABC,∠CQE=180°-∠DQB,即可解答;(3)如图3,过点D作DG∥BC交AC于点G,根据等边三角形的三边相等,可以证得AD=DG=CE;进而证明△DGF和△ECF全等,最后根据全等三角形的性质即可证明.【详解】(1)解:CD和BE始终相等,理由如下:如图1,AB=BC=CA,两只蜗牛速度相同,且同时出发,∴CE=AD,∠A=∠BCE=60°在△ACD与△CBE中,AC=CB,∠A=∠BCE,AD=CE∴△ACD≌△CBE(SAS),∴CD=BE,即CD和BE始终相等;(2)证明:根据题意得:CE=AD,∵AB=AC,∴AE=BD,∴△ABC是等边三角形,∴AB=BC,∠BAC=∠ACB=60°,∵∠EAB+∠ABC=180°,∠DBC+∠ABC=180°,∴∠EAB=∠DBC,在△BCD和△ABE中,BC=AB,∠DBC=∠EAB,BD=AE∴△BCD≌△ABE(SAS),∴∠BCD=∠ABE∴∠DQB=∠BCQ+∠CBQ=∠ABE+∠CBQ=180°-∠ABC=180°-60°=120°,∴∠CQE=180°-∠DQB=60°,即CQE=60°;(3)解:爬行过程中,DF始终等于EF是正确的,理由如下:如图,过点D作DG∥BC交AC于点G,∴∠ADG=∠B=∠AGD=60°,∠GDF=∠E,∴△ADG为等边三角形,∴AD=DG=CE,在△DGF和△ECF中,∠GFD=∠CFE,∠GDF=∠E,DG=EC∴△DGF≌△EDF(AAS),∴DF=EF.【点睛】本题主要考查了全等三角形的判定与性质和等边三角形的性质;题弄懂题中所给的信息,再根据所提供的思路寻找证明条件是解答本题的关键.9.如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点 P 在线段 AB 上以1/cm s的速度由点 A 向点 B 运动,同时,点 Q 在线段 BD 上由点 B 向点 D 运动.它们运动的时间为t(s).(1)若点 Q 的运动速度与点 P 的运动速度相等,当t=1 时,△ACP 与△BPQ 是否全等,请说明理由,并判断此时线段 PC 和线段 PQ 的位置关系;(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他cm s,是否存在实数x,使得△ACP 与△BPQ 全等?若条件不变.设点 Q 的运动速度为x/存在,求出相应的x、t的值;若不存在,请说明理由.解析:(1)全等,垂直,理由详见解析;(2)存在,11t x =⎧⎨=⎩或232t x =⎧⎪⎨=⎪⎩【解析】【分析】(1)在t =1的条件下,找出条件判定△ACP 和△BPQ 全等,再根据全等三角形的性质和直角三角形的两个锐角互余的性质,可证∠CPQ= 90°,即可判断线段 PC 和线段 PQ 的位置关系;(2)本题主要在动点的条件下,分情况讨论,利用三角形全等时对应边相等的性质进行解答即可.【详解】(1)当t=1时,AP= BQ=1, BP= AC=3,又∠A=∠B= 90°,在△ACP 和△BPQ 中,{AP BQA B AC BP=∠=∠=∴△ACP ≌△BPQ(SAS).∴∠ACP=∠BPQ ,∴∠APC+∠BPQ=∠APC+∠ACP = 90*.∴∠CPQ= 90°,即线段PC 与线段PQ 垂直;(2)①若△ACP ≌△BPQ ,则AC= BP ,AP= BQ ,34t t xt =-⎧⎨=⎩解得11t x =⎧⎨=⎩; ②若△ACP ≌△BQP ,则AC= BQ ,AP= BP ,34xt t t =⎧⎨=-⎩解得:232t x =⎧⎪⎨=⎪⎩ 综上所述,存在11t x =⎧⎨=⎩或232t x =⎧⎪⎨=⎪⎩使得△ACP 与△BPQ 全等. 【点睛】本题主要考查三角形全等与动点问题,熟练掌握三角形全等的性质与判定定理,是解决本题的关键.10.阅读并填空:如图,ABC 是等腰三角形,AB AC =,D 是边AC 延长线上的一点,E 在边AB 上且联接DE 交BC 于O ,如果OE OD ,那么CD BE =,为什么?解:过点E 作EF AC 交BC 于F所以ACB EFB ∠=∠(两直线平行,同位角相等)D OEF ∠=∠(________)在OCD 与OFE △中()________COD FOE OD OED OEF ⎧∠=∠⎪=⎨⎪∠=∠⎩所以OCD OFE △≌△,(________)所以CD FE =(________)因为AB AC =(已知)所以ACB B =∠∠(________)所以EFB B ∠=∠(等量代换)所以BE FE =(________)所以CD BE =解析:见解析【解析】【分析】先根据平行线的性质,得到角的关系,然后证明OCD OFE △≌△,写出证明过程和依据即可.【详解】解:过点E 作//EF AC 交BC 于F ,∴ACB EFB ∠=∠(两直线平行,同位角相等),∴D OEF ∠=∠(两直线平行,内错角相等),在OCD 与OFE △中()()()COD FOE OD OED OEF ⎧∠=∠⎪=⎨⎪∠=∠⎩对顶角相等已知已证, ∴OCD OFE △≌△,(ASA )∴CD FE =(全等三角形对应边相等)∵AB AC =(已知)∴ACB B =∠∠(等边对等角)∴EFB B ∠=∠(等量代换)∴BE FE =(等角对等边)∴CD BE =;【点睛】本题考查了全等三角形的判定和性质,平行线的性质,解题的关键是由平行线的性质正确找到证明三角形全等的条件,从而进行证明.11.在△ABC 中,已知∠A =α.(1)如图1,∠ABC 、∠ACB 的平分线相交于点D .①当α=70°时,∠BDC 度数= 度(直接写出结果);②∠BDC 的度数为 (用含α的代数式表示);(2)如图2,若∠ABC 的平分线与∠ACE 角平分线交于点F ,求∠BFC 的度数(用含α的代数式表示).(3)在(2)的条件下,将△FBC 以直线BC 为对称轴翻折得到△GBC ,∠GBC 的角平分线与∠GCB 的角平分线交于点M (如图3),求∠BMC 的度数(用含α的代数式表示).解析:(1)(1)①125°;②1902α︒+,(2)1BFC 2α∠=;(3)1BMC 904α︒∠=+ 【解析】【分析】(1)①由三角形内角和定理易得∠ABC+∠ACB=110°,然后根据角平分线的定义,结合三角形内角和定理可求∠BDC ;②由三角形内角和定理易得∠ABC+∠ACB=180°-∠A ,采用①的推导方法即可求解; (2)由三角形外角性质得BFC FCE FBC ∠=∠-∠,然后结合角平分线的定义求解; (3)由折叠的对称性得BGC BFC ∠=∠,结合(1)②的结论可得答案.【详解】解:(1)①∵12DBC ∠=∠ABC ,∠DCB =12∠ACB , ∴∠BDC =180°﹣∠DBC ﹣∠DCB=180°﹣12(∠ABC +∠ACB ) =180°﹣12(180°﹣70°) =125° ②∵12DBC ∠=∠ABC ,∠DCB =12∠ACB , ∴∠BDC =180°﹣∠DBC ﹣∠DCB=180°﹣12(∠ABC +∠ACB ) =180°﹣12(180°﹣∠A ) =90°+12∠A =90°+12α. 故答案分别为125°,90°+12α. (2)∵BF 和CF 分别平分∠ABC 和∠ACE ∴1FBC ABC 2∠=∠,1FCE ACE 2∠=∠, ∴BFC FCE FBC ∠=∠-∠=11(ACE ABC)A 22∠-∠=∠即1BFC 2α∠=. (3)由轴对称性质知:1BGC BFC 2α∠=∠=, 由(1)②可得1BMC 90BGC 2∠=︒+∠, ∴1BMC 904α∠=︒+. 【点睛】 本题考查三角形中与角平分线有关的角度计算,熟练掌握三角形内角和定理,以及三角形的外角性质是解题的关键.12.在等腰ABC ∆中,AB AC =,AE 为BC 边上的高,点D 在ABC ∆的外部且60CAD ∠=,AD AC =,连接BD 交直线AE 于点F ,连接FC .(1)如图①,当120BAC ∠<时,求证:BF CF =;(2)如图②,当40BAC ∠=时,求AFD ∠的度数;(3)如图③,当120BAC ∠>时,求证:CF AF DF =+.解析:(1)见解析;(2)60AFD ∠=;(3)见解析【解析】【分析】(1)根据等腰三角形三线合一的性质,可得AE 垂直平分BC ,F 为垂直平分线AE 上点,即可得出结论;(2)根据(1)的结论可得AE 平分∠BAC ,∠BAF=20°,由AB=AC=AD ,推出40ABD ADB ∠=∠=,根据外角性质可得AFD BAF ABF ∠=∠+∠计算即可;(3)在CF 上截取CM=DF ,连接AM ,证明△ACM ≌△ADF (SAS ),进而证得△AFM 为等边三角形即可.【详解】(1)证明:∵AE 为等腰△ABC 底边BC 上的高线,AB=AC ,AE BC ∴⊥,∠AEB=∠AEC=90°,BE=CE ,∴AE 垂直平分BE ,F 在AE 上,BF CF ∴=;(2) ,AB AC AD AC ==,AB AD ∴=,100BAD BAC CAD ∠=∠+∠=,40ABD ADB ∴∠=∠=,由(1)知,AE 平分∠BAC ,20BAF CAF ∴∠=∠=,60AFD BAF ABF ∴∠=∠+∠=,故答案为:60°;(3) 在CF 上截取CM=DF ,连接AM ,由(1)可知,∠ABC=∠ACB ,∠FBC =∠FCB ,ABF ACF ∴∠=∠,AB AC AD ==,ABF D ∴∠=∠,ACF D ∴∠=∠,在△ACM 和△ADF 中,AC AD ACM ADF CM DF =⎧⎪∠=∠⎨⎪=⎩∴△ACM ≌△ADF (SAS ),,AF AM FAD MAC ∴=∠=∠,60FAM DAC ∴∠=∠=,∴△AFM 为等边三角形,FM AF ∴=,CF FM MC AF DF ∴=+=+.【点睛】本题考查了等腰三角形的性质,垂直平分线的性质,三角形全等的判定和性质,等边三角形的判定和性质,掌握三角形全等的判定和性质是解题的关键.13.如图1,在等边△ABC 中,E 、D 两点分别在边AB 、BC 上,BE =CD ,AD 、CE 相交于点F .(1)求∠AFE 的度数;(2)过点A 作AH ⊥CE 于H ,求证:2FH +FD =CE ;(3)如图2,延长CE 至点P ,连接BP ,∠BPC =30°,且CF =29CP ,求PF AF的值. (提示:可以过点A 作∠KAF =60°,AK 交PC 于点K ,连接KB )解析:(1)∠AFE =60°;(2)见解析;(3)75【解析】【分析】(1)通过证明 BCE CAD ≌ 得到对应角相等,等量代换推导出60AFE ∠=︒; (2)由(1)得到60AFE ∠=︒,CE AD = 则在Rt AHF △ 中利用30°所对的直角边等于斜边的一半,等量代换可得;(3)通过在PF 上取一点K 使得KF =AF ,作辅助线证明ABK 和ACF 全等,利用对应边相等,等量代换得到比值.(通过将ACF 顺时针旋转60°也是一种思路.)【详解】(1)解:如图1中.∵ABC 为等边三角形,∴AC =BC ,∠BAC =∠ABC =∠ACB =60°,在BCE 和CAD 中,60BE CD CBE ACD BC CA =⎧⎪∠=∠=︒⎨⎪=⎩, ∴ BCE CAD ≌(SAS ),∴∠BCE =∠DAC ,∵∠BCE +∠ACE =60°,∴∠DAC +∠ACE =60°,∴∠AFE =60°.(2)证明:如图1中,∵AH ⊥EC ,∴∠AHF =90°,在Rt △AFH 中,∵∠AFH =60°,∴∠FAH =30°,∴AF =2FH ,∵ EBC DCA ≌,∴EC =AD ,∵AD =AF +DF =2FH +DF ,∴2FH +DF =EC .(3)解:在PF 上取一点K 使得KF =AF ,连接AK 、BK ,∵∠AFK =60°,AF =KF ,∴△AFK 为等边三角形,∴∠KAF =60°,∴∠KAB =∠FAC ,在ABK 和ACF 中,AB AC KAB ACF AK AF =⎧⎪∠=∠⎨⎪=⎩, ∴ ABK ACF ≌(SAS ),BK CF =∴∠AKB =∠AFC =120°,∴∠BKE =120°﹣60°=60°,∵∠BPC =30°,∴∠PBK =30°, ∴29BK CF PK CP ===, ∴79PF CP CF CP =-=, ∵45()99AF KF CP CF PK CP CP CP ==-+=-=∴779559CP PF AF CP == . 【点睛】掌握等边三角形、直角三角形的性质,及三角形全等的判定通过一定等量代换为本题的关键.14.在ABC 中,AB AC =,D 是直线AB 上一点,E 在直线BC 上,且DE DC =. (1)如图1,当D 在AB 上,E 在CB 延长线上时,求证:EDB ACD ∠=∠;(2)如图2,当ABC 为等边三角形时,D 是BA 的延长线上一点,E 在BC 上时,作//EF AC ,求证:BE AD =;(3)在(2)的条件下,ABC ∠的平分线BF 交CD 于点F ,连AF ,过A 点作AH CD ⊥于点H ,当30EDC ∠=︒,6CF =时,求DH 的长度.解析:(1)见解析;(2)见解析;(3)3【解析】【分析】(1)根据等腰三角形的性质和外角的性质即可得到结论;(2)过E 作EF ∥AC 交AB 于F ,根据已知条件得到△ABC 是等边三角形,推出△BEF 是等边三角形,得到BE=EF ,∠BFE=60°,根据全等三角形的性质即可得到结论; (3)连接AF ,证明△ABF ≌△CBF ,得AF=CF ,再证明DH=AH=12CF=3. 【详解】解:(1)∵AB=AC ,∴∠ABC=∠ACB ,∵DE=DC ,∴∠E=∠DCE ,∴∠ABC-∠E=∠ACB-∠DCB ,即∠EDB=∠ACD ;(2)∵△ABC 是等边三角形,∴∠B=60°,∴△BEF 是等边三角形,∴BE=EF ,∠BFE=60°,∴∠DFE=120°,∴∠DFE=∠CAD ,在△DEF 与△CAD 中,EDF DCA DFE CAD DE CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△DEF ≌△CAD (AAS ),∴EF=AD ,∴AD=BE ;(3)连接AF ,如图3所示:∵DE=DC ,∠EDC=30°,∴∠DEC=∠DCE=75°,∴∠ACF=75°-60°=15°,∵BF 平分∠ABC ,∴∠ABF=∠CBF ,在△ABF 和△CBF 中,AB BC ABF CBF BF BF =⎧⎪∠=∠⎨⎪=⎩, △ABF ≌△CBF (SAS ),∴AF=CF ,∴∠FAC=∠ACF=15°,∴∠AFH=15°+15°=30°,∵AH ⊥CD ,∴AH=12AF=12CF=3, ∵∠DEC=∠ABC+∠BDE ,∴∠BDE=75°-60°=15°,∴∠ADH=15°+30°=45°,∴∠DAH=∠ADH=45°,∴DH=AH=3.【点睛】本题考查了全等三角形的判定与性质,等腰三角形和直角三角形的性质,三角形的外角的性质,等边三角形的判定和性质,证明三角形全等是解决问题的关键.15.在Rt ABC 中,90ACB ∠=︒,30A ∠=︒,BD 是ABC 的角平分线,DE AB ⊥于点E .(1)如图1,连接EC ,求证:EBC 是等边三角形;(2)如图2,点M 是线段CD 上的一点(不与点,C D 重合),以BM 为一边,在BM 下方作60BMG ∠=︒,MG 交DE 延长线于点G .求证:AD DG MD =+;(3)如图3,点N 是线段AD 上的点,以BN 为一边,在BN 的下方作60BNG ∠=︒,NG 交DE 延长线于点G .直接写出ND ,DG 与AD 数量之间的关系.解析:(1)证明见解析;(2)证明见解析;(3)结论:AD DG ND =-,证明见解析.【解析】【分析】(1)先根据直角三角形的性质得出60ABC ∠=︒,再根据角平分线的性质可得CD ED =,然后根据三角形的判定定理与性质可得BC BE =,最后根据等边三角形的判定即可得证;(2)如图(见解析),延长ED 使得DF MD =,连接MF ,先根据直角三角形的性质、等边三角形的判定得出MDF ∆是等边三角形,再根据等边三角形的性质、角的和差得出,,F MDB MF MD FMG DMB ∠=∠=∠=∠,然后根据三角形全等的判定与性质、等量代换即可得证;(3)如图(见解析),参照题(2),先证HDN ∆是等边三角形,再根据等边三角形的性质、角的和差得出,,H NDG NH ND HNB DNG ∠=∠=∠=∠,然后根据三角形全等的判定与性质、等量代换即可得证.【详解】(1)3,090A ACB ∠=︒∠=︒9060ABC A ∴∠=︒-∠=︒ BD 是ABC ∠的角平分线,DE AB ⊥CD ED ∴=在BCD ∆和BED ∆中,CD ED BD BD =⎧⎨=⎩()BCD BED HL ∴∆≅∆BC BE ∴=EBC ∴∆是等边三角形;(2)如图,延长ED 使得DF MD =,连接MF3,090A ACB ∠=︒∠=︒,BD 是ABC ∠的角平分线,DE AB ⊥60,ADE BDE AD BD ∴∠=∠=︒=60,18060MDF ADE MDB ADE BDE ∴∠=∠=︒∠=︒-∠-∠=︒MDF ∴∆是等边三角形,60MF DM F DMF ∴=∠=∠=︒60BMG ∠=︒DMF DM B M G G D M G ∴∠+∠=+∠∠,即FMG DMB ∠=∠在FMG ∆和DMB ∆中,60F MDB MF MD FMG DMB ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩()FMG DMB ASA ∴∆≅∆GF BD ∴=,即DF DG BD +=AD DF DG MD DG ∴=+=+即AD DG MD =+;(3)结论:AD DG ND =-,证明过程如下:如图,延长BD 使得DH ND =,连接NH由(2)可知,60,18060,ADE HDN ADE BDE AD BD ∠=︒∠=︒-∠-∠=︒= HDN ∴∆是等边三角形,60NH ND H HND ∴=∠=∠=︒60BNG ∠=︒HND BND BND BNG ∠+∠=+∠∴∠,即N HNB D G ∠=∠在HNB ∆和DNG ∆中,60H NDG NH ND HNB DNG ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩()HNB DNG ASA ∴∆≅∆HB DG ∴=,即DH BD DG +=ND AD DG ∴+=即AD DG ND =-.【点睛】本题考查了直角三角形的性质、等边三角形的判定与性质、三角形全等的判定定理与性质等知识点,较难的是题(2)和(3),通过作辅助线,构造一个等边三角形是解题关键.二、选择题16.下列判断正确的是( )A .3a 2bc 与bca 2不是同类项B .225m n 的系数是2 C .单项式﹣x 3yz 的次数是5D .3x 2﹣y +5xy 5是二次三项式解析:C【解析】【分析】根据同类项的定义,单项式和多项式的定义解答.【详解】A .3d 2bc 与bca 2所含有的字母以及相同字母的指数相同,是同类项,故本选项错误.B .225m n 的系数是25,故本选项错误. C .单项式﹣x 3yz 的次数是5,故本选项正确.D .3x 2﹣y +5xy 5是六次三项式,故本选项错误.故选C .【点睛】本题考查了同类项,多项式以及单项式的概念及性质.需要学生对概念的记忆,属于基础题.17.如图,已知线段AB 的长度为a ,CD 的长度为b ,则图中所有线段的长度和为( )A .3a+bB .3a-bC .a+3bD .2a+2b解析:A【解析】【分析】依据线段AB 长度为a ,可得AB=AC+CD+DB=a ,依据CD 长度为b ,可得AD+CB=a+b ,进而得出所有线段的长度和.【详解】∵线段AB 长度为a ,∴AB=AC+CD+DB=a ,又∵CD 长度为b ,∴AD+CB=a+b ,∴图中所有线段的长度和为:AB+AC+CD+DB+AD+CB=a+a+a+b=3a+b ,故选A .【点睛】本题考查了比较线段的长度和有关计算,主要考查学生能否求出线段的长度和知道如何数图形中的线段. 18.已知max {}2,,x x x 表示取三个数中最大的那个数,例如:当x =9时,max {}{}22,,max 9,9,9x x x ==81.当max {}21,,2x x x =时,则x 的值为( ) A .14- B .116 C .14 D .12解析:C【解析】【分析】利用max {}2,,x x x 的定义分情况讨论即可求解. 【详解】解:当max{}21,,2x x x =时,x ≥0 x 12,解得:x =14x x >x 2,符合题意; ②x 2=12,解得:x =22x x >x 2,不合题意; ③x =12x x >x 2,不合题意;故只有x =14时,max }21,2x x =. 故选:C .【点睛】此题主要考查了新定义,正确理解题意分类讨论是解题关键.19.当x 取2时,代数式(1)2x x -的值是( ) A .0B .1C .2D .3 解析:B【解析】【分析】把x 等于2代入代数式即可得出答案.【详解】解:根据题意可得:把2x =代入(1)2x x -中得: (1)21==122x x -⨯, 故答案为:B.【点睛】本题考查的是代入求值问题,解题关键就是把x 的值代入进去即可.20.地球与月球的平均距离为384 000km ,将384 000这个数用科学记数法表示为( ) A .3.84×103B .3.84×104C .3.84×105D .3.84×106 解析:C【解析】【分析】科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.【详解】试题分析:384 000=3.84×105.故选C .【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.21.﹣3的相反数是( )A .13-B .13C .3-D .3解析:D【解析】【分析】相反数的定义是:如果两个数只有符号不同,我们称其中一个数为另一个数的相反数,特别地,0的相反数还是0.【详解】根据相反数的定义可得:-3的相反数是3.故选D.【点睛】本题考查相反数,题目简单,熟记定义是关键.22.已知a+b=7,ab=10,则代数式(5ab+4a+7b)+(3a–4ab)的值为()A.49 B.59C.77 D.139解析:B【解析】【分析】首先去括号,合并同类项将原代数式化简,再将所求代数式化成用(a+b)与ab表示的形式,然后把已知代入即可求解.【详解】解:∵(5ab+4a+7b)+(3a-4ab)=5ab+4a+7b+3a-4ab=ab+7a+7b=ab+7(a+b)∴当a+b=7,ab=10时原式=10+7×7=59.故选B.23.宁波港处于“一带一路”和长江经济带交汇点,地理位置得天独厚.全年货物吞吐量达9.2亿吨,晋升为全球首个“9亿吨”大港,并连续8年蝉联世界第一宝座.其中9.2亿用科学记数法表示正确的是()A.B.C.D.解析:A【解析】因为科学记数法的表达形式为:,所以9.2亿用科学记数法表示为:,故选A.点睛:本题主要考查科学记数法的表达形式,解决本题的关键是要熟练掌握科学记数法的表达形式.24.下列判断正确的是()A.有理数的绝对值一定是正数.B.如果两个数的绝对值相等,那么这两个数相等.C.如果一个数是正数,那么这个数的绝对值是它本身.D.如果一个数的绝对值是它本身,那么这个数是正数.解析:C【解析】试题解析:A∵0的绝对值是0,故本选项错误.B∵互为相反数的两个数的绝对值相等,故本选项正确.C如果一个数是正数,那么这个数的绝对值是它本身.D∵0的绝对值是0,故本选项错误.故选C.25.一个角是这个角的余角的2倍,则这个角的度数是()A.30B.45︒C.60︒D.75︒解析:C【解析】【分析】设这个角为α,先表示出这个角的余角为(90°-α),再列方程求解.【详解】解:根据题意列方程的:2(90°-α)=α,解得:α=60°.故选:C.【点睛】本题考查余角的概念,关键是先表示出这个角的余角为(90°-α).26.某地冬季某天的天气预报显示气温为﹣1℃至8℃,则该日的最高与最低气温的温差为()A.﹣9℃B.7℃C.﹣7℃D.9℃解析:D【解析】【分析】这天的温差就是最高气温与最低气温的差,列式计算.【详解】解:该日的最高与最低气温的温差为8﹣(﹣1)=8+1=9(℃),故选:D.【点睛】本题主要考查有理数的减法法则:减去一个数等于加上这个数的相反数,这是需要熟记的内容.27.下列调查中,适宜采用全面调查的是()A.对现代大学生零用钱使用情况的调查B.对某班学生制作校服前身高的调查C.对温州市市民去年阅读量的调查D.对某品牌灯管寿命的调查解析:B【解析】【分析】。
初中数学八年级上册压轴题专项练习(解析版)

八年级上册数学压轴题专题练习(解析版)一、压轴题1.如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点 P在线段 AB上以1cm/s的速度由点 A向点 B运动,同时,点 Q在线段 BD上由点 B向点 D运动.它们运动的时间为t(s).(1)若点 Q的运动速度与点 P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段 PC和线段 PQ的位置关系;(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点 Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.2.在Rt ABC中,∠ACB=90︒,∠A=30︒,BD是ABC的角平分线,DE⊥AB于点E.(1)如图1,连接EC,求证:EBC是等边三角形;(2)如图2,点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM下方作∠BMG=60︒,MG交DE延长线于点G.求证:AD=DG+MD;(3)如图3,点N是线段AD上的点,以BN为一边,在BN的下方作∠BNG=60︒,NG交DE延长线于点G.直接写出ND,DG与AD数量之间的关系.3.在《经典几何图形的研究与变式》一课中,庞老师出示了一个问题:“如图1,等腰直角三角形的三个顶点分别落在三条等距的平行线l1,l2,l3上,∠BAC=90︒,且每两条平行线之间的距离为1,求AB的长度”.在研究这道题的解法和变式的过程中,同学们提出了很多想法:(1)小明说:我只需要过B、C向l1作垂线,就能利用全等三角形的知识求出AB的长.(2)小林说:“我们可以改变ABC的形状.如图2,AB=AC,∠BAC=120︒,且每两条平行线之间的距离为1,求AB的长.”(3)小谢说:“我们除了改变ABC的形状,还能改变平行线之间的距离.如图3,等边三角形ABC三个顶点分别落在三条平行线l1,l2,l3上,且l1与l2之间的距离为1,l2与l3之间的距离为2,求AB的长、”请你根据3位同学的提示,分别求出三种情况下AB的长度.4.在ABC中,AB=AC,D是直线AB上一点,E在直线BC上,且DE=DC.(1)如图1,当D在AB上,E在CB延长线上时,求证:∠EDB=∠ACD;(2)如图2,当ABC为等边三角形时,D是BA的延长线上一点,E在BC上时,作EF//AC,求证:BE=AD;(3)在(2)的条件下,∠ABC的平分线BF交CD于点F,连AF,过A点作AH⊥CD于点H,当∠EDC=30︒,CF=6时,求DH的长度.5.(阅读材科)小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若∠BAC=∠DAE,AB=AC,AD=AE,则△ABD≌△ACE.(材料理解)(1)在图1中证明小明的发现.(深入探究)(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:①BD=EC;②∠BOC=60°;③∠AOE=60°;④EO=CO,其中正确的有.(将所有正确的序号填在横线上).(延伸应用)(3)如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.6.阅读下面材料,完成(1)-(3)题.数学课上,老师出示了这样一道题:如图1,已知等腰△ABC中,AB=AC,AD为BC边上的中线,以AB为边向AB左侧作等边△ABE,直线CE与直线AD交于点F.请探究线段EF、AF、DF之间的数量关系,并证明.同学们经过思考后,交流了自已的想法:小明:“通过观察和度量,发现∠DFC的度数可以求出来.”小强:“通过观察和度量,发现线段DF和CF之间存在某种数量关系.”小伟:“通过做辅助线构造全等三角形,就可以将问题解决.”......老师:“若以AB为边向AB右侧作等边△ABE,其它条件均不改变,请在图2中补全图形,探究线段EF、AF、DF三者的数量关系,并证明你的结论.”(1)求∠DFC的度数;(2)在图1中探究线段EF、AF、DF之间的数量关系,并证明;(3)在图2中补全图形,探究线段EF、AF、DF之间的数量关系,并证明.7.(1)填空①把一张长方形的纸片按如图①所示的方式折叠,EM,FM为折痕,折叠后的C点落在B 1M或B1M的延长线上,那么EMF的度数是________;②把一张长方形的纸片按如图②所示的方式折叠,B点与M点重合,EM,FM为折痕,折叠后的C点落在A1M或A1M的延长线上,那么EMF的度数是_______.(2)解答:①把一张长方形的纸片按如图③所示的方式折叠,EM,FM为折痕,折叠后的C点落在B1M或B1M的延长线上左侧,且EMF80,求C1MB1的度数;②把一张长方形的纸片按如图④所示的方式折叠,B点与M点重合,EM,FM为折痕,折叠后的C点落在A1M或A1M的延长线右侧,且EMF60,求C1MA1的度数.(3)探究:把一张四边形的纸片按如图⑤所示的方式折叠,EB,FB为折痕,设ABC,EBF,A1BC1,求,,之间的数量关系.8.已知ABC和ADE都是等腰三角形,AB AC,AD AE,DAE BAC.(初步感知)(1)特殊情形:如图①,若点D,E分别在边AB,AC上,则DB__________EC.(填>、<或=)(2)发现证明:如图②,将图①中的ADE绕点A旋转,当点D在ABC外部,点E 在ABC内部时,求证:DB EC.(深入研究)(3)如图③,ABC和ADE都是等边三角形,点C,E,D在同一条直线上,则∠CDB的度数为__________;线段CE,BD之间的数量关系为__________.(4)如图④,ABC和ADE都是等腰直角三角形,∠BAC=∠DAE=90︒,点C、D、E在同一直线上,AM为ADE中DE边上的高,则∠CDB的度数为__________;线段AM,BD,CD之间的数量关系为__________.(拓展提升)(5)如图⑤,ABC和ADE都是等腰直角三角形,∠BAC=∠DAE=90︒,将ADE绕点A逆时针旋转,连结BE、CD.当AB=5,AD=2时,在旋转过程中,△ABE与ADC的面积和的最大值为__________.9.直角三角形ABC中,∠ACB=90︒,直线l过点C.(1)当AC=BC时,如图1,分别过点A和B作AD⊥直线l于点D,BE⊥直线l于点E,ACD与△CBE是否全等,并说明理由;(2)当AC=8cm,BC=6cm时,如图2,点B与点F关于直线l对称,连接BF、CF,点M是AC上一点,点N是CF上一点,分别过点M、N作MD⊥直线l于点D,NE⊥直线l于点E,点M从A点出发,以每秒1cm的速度沿A→C路径运动,终点为C,点N从点F出发,以每秒3cm的速度沿F→C→B→C→F路径运动,终点为F,点M,N同时开始运动,各自达到相应的终点时停止运动,设运动时间为t秒,当△CMN为等腰直角三角形时,求t的值.10.已知:ABC中,过B点作BE⊥AD,∠ACB=90︒,AC=BC.(1)如图1,点D在BC的延长线上,连AD,作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC 于F,连DE,问BD与CF有何数量关系,并加以证明;(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC=3MC,请直接写出DB的值.BC11.(1)在等边三角形ABC中,①如图①,D,E分别是边AC,AB上的点且AE=CD,BD与EC交于点F,则∠BFE的度数是度;②如图②,D,E分别是边AC,BA延长线上的点且AE=CD,BD与EC的延长线交于点F,此时∠BFE的度数是度;(2)如图③,在△ABC中,AC=BC,∠ACB是锐角,点O是AC边的垂直平分线与BC的交点,点D,E分别在AC,OA的延长线上,AE=CD,BD与EC的延长线交于点F,若∠ACB=α,求∠BFE的大小.(用含α的代数式表示).12.已知ABC,P是平面内任意一点(A、B、C、P中任意三点都不在同一直线上).连接 PB、PC,设∠PBA=s°,∠PCA=t°,∠BPC=x°,∠BAC=y°.(1)如图,当点 P在ABC内时,①若 y=70,s=10,t=20,则 x=;②探究 s、t、x、y之间的数量关系,并证明你得到的结论.(2)当点 P在ABC外时,直接写出 s、t、x、y之间所有可能的数量关系,并画出相应的图形.13.Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.(1)若点P在线段AB上,如图(1)所示,且∠α=60°,则∠1+∠2=;(2)若点P在线段AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为;(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由;(4)若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.14.探索发现:11111111 =1-;=-;=-……1⨯222⨯3233⨯434根据你发现的规律,回答下列问题:(1)11=,=;n⨯(n+1)4⨯5111⋅+++1⨯22⨯33⨯4+1n⨯(n+1)(2)利用你发现的规律计算:(3)利用规律解方程:111112x-1 ++++=x(x+1)(x+1)(x+2)(x+2)(x+3)(x+3)(x+4)(x+4)(x+5)x(x+5) 15.数学活动课上,老师出了这样一个题目:“已知:MF⊥NF于F,点A、C分别在NF和MF上,作线段AB和CD(如图1),使∠FAB-∠MCD=90︒.求证:AB//CD”.(1)聪聪同学给出一种证明问题的辅助线:如图2,过A作AG//FM,交CD于G.请你根据聪聪同学提供的辅助线(或自己添加其它辅助线),给出问题的证明.(2)若点E在直线CD下方,且知∠BED=30︒,直接写出∠ABE和∠CDE之间的数量关系.16.现给出一个结论:直角三角形斜边的中线等于斜边的一半;该结论是正确的,用图形语言可以表示为:如图1在∆ABC中,∠C=90︒,若点D为AB的中点,则CD=请结合上述结论解决如下问题:1AB.2已知,点P是射线BA上一动点(不与A,B重合)分别过点A,B向直线CP作垂线,垂足分别为E,F,其中Q为AB的中点(1)如图2,当点P与点Q重合时,AE与BF的位置关系____________;QE与QF的数量关系是__________(2)如图3,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明.(3)如图4,当点P在线段BA的延长线上时,此时(2)中的结论是否成立?请画出图形并写出主要证明思路.17.在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.(1)如图,当点D在BC延长线上移动时,若∠BAC=40°,则∠ACE=,∠DCE=,BC、DC、CE之间的数量关系为;(2)设∠BAC=α,∠DCE=β.①当点D在BC延长线上移动时,α与β之间有什么数量关系?请说明理由;②当点D在直线BC上(不与B,C两点重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.(3)当CE∥AB时,若△ABD中最小角为15°,试探究∠ACB的度数(直接写出结果,无需写出求解过程).18.阅读材料并完成习题:在数学中,我们会用“截长补短”的方法来构造全等三角形解决问题.请看这个例题:如图1,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若AC=2cm,求四边形ABCD的面积.解:延长线段CB到E,使得BE=CD,连接AE,我们可以证明△BAE≌△DAC,根据全等三角形的性质得AE=AC=2,∠EAB=∠CAD,则∠EAC=∠EAB+∠BAC=∠DAC+∠BAC=∠BAD=90°,得S四边形ABCD =S△ABC+S△ADC=S△ABC+S△ABE=S△AEC,这样,四边形ABCD的面积就转化为等腰直角三角形EAC面积.(1)根据上面的思路,我们可以求得四边形ABCD的面积为 cm2.(2)请你用上面学到的方法完成下面的习题.如图2,已知FG=FN=HM=GH+MN=2cm,∠G=∠N=90°,求五边形FGHMN的面积.19.(1)如图1,ABC和DCE都是等边三角形,且B,C,D三点在一条直线上,连接AD,BE相交于点P,求证:BE=AD.(2)如图2,在BCD中,若∠BCD<120︒,分别以BC,CD和BD为边在BCD外部作等边ABC,等边△CDE,等边BDF,连接AD、BE、CF恰交于点P.①求证:AD=BE=CF;②如图2,在(2)的条件下,试猜想PB,PC,PD与BE存在怎样的数量关系,并说明理由.20.阅读并填空:如图,ABC是等腰三角形,AB=AC,D是边AC延长线上的一点,E在边AB上且联接DE交BC于O,如果OE OD,那么CD=BE,为什么?解:过点E作EF AC交BC于F所以∠ACB=∠EFB(两直线平行,同位角相等)∠D=∠OEF(________)在OCD与△OFE中⎧∠COD=∠FOE(________)⎪⎨OD=OE⎪∠D=∠OEF⎩所以△OCD≌△OFE,(________)所以CD=FE(________)因为AB=AC(已知)所以∠ACB=∠B(________)所以∠EFB=∠B(等量代换)所以BE=FE(________)所以CD=BE【参考答案】***试卷处理标记,请不要删除一、压轴题⎧t=2⎧t=1⎪1.(1)全等,垂直,理由详见解析;(2)存在,⎨或⎨3x=1x=⎩⎪2⎩【解析】【分析】(1)在t =1的条件下,找出条件判定△ACP和△BPQ全等,再根据全等三角形的性质和直角三角形的两个锐角互余的性质,可证∠CPQ= 90°,即可判断线段 PC和线段 PQ的位置关系;(2)本题主要在动点的条件下,分情况讨论,利用三角形全等时对应边相等的性质进行解答即可.【详解】(1)当t=1时,AP= BQ=1, BP= AC=3,又∠A=∠B= 90°,在△ACP和△BPQ中,AP=BQ{∠A=∠BAC=BP∴△ACP≌△BPQ(SAS).∴∠ACP=∠BPQ ,∴∠APC+∠BPQ=∠APC+∠ACP = 90*.∴∠CPQ= 90°,即线段PC与线段PQ垂直;(2)①若△ACP ≌△BPQ ,则AC= BP ,AP= BQ ,⎧3=4-t ⎨t =xt⎩解得⎨⎧t =1;x =1⎩②若△ACP ≌△BQP ,则AC= BQ ,AP= BP ,⎧3=xt ⎨t =4-t⎩⎧t =2⎪解得:⎨3x =⎪⎩2⎧t =2⎧t =1⎪综上所述,存在⎨或⎨3使得△ACP 与△BPQ 全等.x =1x =⎩⎪⎩2【点睛】本题主要考查三角形全等与动点问题,熟练掌握三角形全等的性质与判定定理,是解决本题的关键.2.(1)证明见解析;(2)证明见解析;(3)结论:AD =DG -ND ,证明见解析.【解析】【分析】(1)先根据直角三角形的性质得出∠ABC =60︒,再根据角平分线的性质可得CD =ED ,然后根据三角形的判定定理与性质可得BC =BE ,最后根据等边三角形的判定即可得证;(2)如图(见解析),延长ED 使得DF =MD ,连接MF ,先根据直角三角形的性质、等边三角形的判定得出∆MDF 是等边三角形,再根据等边三角形的性质、角的和差得出∠F =∠MDB ,MF =MD ,∠FMG =∠DMB ,然后根据三角形全等的判定与性质、等量代换即可得证;(3)如图(见解析),参照题(2),先证∆HDN 是等边三角形,再根据等边三角形的性质、角的和差得出∠H =∠NDG ,NH =ND ,∠HNB =∠DNG ,然后根据三角形全等的判定与性质、等量代换即可得证.【详解】(1)∠ACB =90︒,∠A =30︒∴∠ABC =90︒-∠A =60︒BD 是∠ABC 的角平分线,DE ⊥AB∴CD =ED⎧CD=ED在∆BCD和∆BED中,⎨BD=BD⎩∴∆BCD≅∆BED(HL)∴BC=BE∴∆EBC是等边三角形;(2)如图,延长ED使得DF=MD,连接MF∠ACB=90︒,∠A=30︒,BD是∠ABC的角平分线,DE⊥AB∴∠ADE=∠BDE=60︒,AD=BD∴∠MDF=∠ADE=60︒,∠MDB=180︒-∠ADE-∠BDE=60︒∴∆MDF是等边三角形∴MF=DM,∠F=∠DMF=60︒∠BMG=60︒∴∠DMF+∠DMG=∠BMG+∠DMG,即∠FMG=∠DMB⎧∠F=∠MDB=60︒⎪在∆FMG和∆DMB中,⎨MF=MD⎪∠FMG=∠DMB⎩∴∆FMG≅∆DMB(ASA)∴GF=BD,即DF+DG=BD∴AD=DF+DG=MD+DG即AD=DG+MD;(3)结论:AD=DG-ND,证明过程如下:如图,延长BD使得DH=ND,连接NH由(2)可知,∠ADE=60︒,∠HDN=180︒-∠ADE-∠BDE=60︒,AD=BD ∴∆HDN是等边三角形∴NH=ND,∠H=∠HND=60︒∠BNG=60︒∴∠HND+∠BND=∠BNG+∠BND,即∠HNB=∠DNG⎧∠H=∠NDG=60︒⎪在∆HNB和∆DNG中,⎨NH=ND⎪∠HNB=∠DNG⎩∴∆HNB≅∆DNG(ASA)∴HB =DG ,即DH +BD =DG∴ND +AD =DG即AD =DG -ND .【点睛】本题考查了直角三角形的性质、等边三角形的判定与性质、三角形全等的判定定理与性质等知识点,较难的是题(2)和(3),通过作辅助线,构造一个等边三角形是解题关键.3.(1)5;(2)【解析】【分析】(1)分别过点B ,C 向l 1作垂线,交l 1于M ,N 两点,证明△ABM ≌△CAN ,得到AM=CN ,AN=BM ,即可得出AB ;(2)分别过点B ,C 向l 1作垂线,交l 1于点P ,Q 两点,在l 1上取M ,N 使∠AMB=∠CNA=120°,证明△AMB ≌△CAN ,得到CN=AM ,再通过△PBM 和△QCN 算出PM 和NQ 的值,得到AP ,最后在△APB 中,利用勾股定理算出AB 的长;(3)在l 3上找M 和N ,使得∠BNC=∠AMC=60°,过B 作l 3的垂线,交l 3于点P ,过A 作l 3的垂线,交l 3于点Q ,证明△BCN ≌△CAM ,得到CN=AM ,在△BPN 和△AQM 中利用勾股定理算出NP 和AM ,从而得到PC ,结合BP 算出BC 的长,即为AB.【详解】解:(1)如图,分别过点B ,C 向l 1作垂线,交l 1于M ,N 两点,由题意可得:∠BAC=90°,∵∠NAC+∠MAB=90°,∠NAC+∠NCA=90°,∴∠MAB=∠NCA ,在△ABM 和△CAN 中,221221;(3)33⎧∠AMB =∠CNA ⎪⎨∠MAB =∠NCA ,⎪AB =AC ⎩∴△ABM ≌△CAN (AAS ),∴AM=CN=2,AN=BM=1,∴AB=22+12=5;(2)分别过点B,C向l1作垂线,交l1于P,Q两点,在l1上取M,N使∠AMB=∠CNA=120°,∵∠BAC=120°,∴∠MAB+∠NAC=60°,∵∠ABM+∠MAB=60°,∴∠ABM=∠NAC,在△AMB和△CNA中,⎧∠AMB=∠CNA⎪⎨∠ABM=∠NAC,⎪AB=AC⎩∴△AMB≌△CNA(AAS),∴CN=AM,∵∠AMB=∠ANC=120°,∴∠PMB=∠QNC=60°,∴PM=11 BM,NQ=NC,22∵PB=1,CQ=2,设PM=a,NQ=b,∴a2+12=4a2,b2+22=4b2,解得:a=323,b=,332⎛23⎫43=∴CN=AM=22+ ,⎪3⎪3⎝⎭∴AB=AP2+BP2=(AM+PM)2+BP2=221;3(3)如图,在l3上找M和N,使得∠BNC=∠AMC=60°,过B作l3的垂线,交于点P,过A作l3的垂线,交于点Q,∵△ABC是等边三角形,∴BC=AC,∠ACB=60°,∴∠BCN+∠ACM=120°,∵∠BCN+∠NBC=120°,∴∠NBC=∠ACM,在△BCN和△CAM中,⎧∠BNC=∠CMA⎪⎨∠NBC=∠MAC,⎪BC=AC⎩∴△BCN≌△CAM(AAS),∴CN=AM,BN=CM,∵∠PBN=90°-60°=30°,BP=2,∴BN=2NP,在△BPN中,BP2+NP2=BN2,即22+NP2=4NP2,解得:NP=23,3∵∠AMC=60°,AQ=3,∴∠MAQ=30°,∴AM=2QM,在△AQM中,AQ2+QM2=AM2,即32+QM2=4QM2,解得:QM=3,∴AM=23=CN,∴PC=CN-NP=AM-NP=在△BPC中,BP2+CP2=BC2,43,3⎛43⎫221即BC=BP2+CP2=22+ ,=⎪3⎪3⎝⎭2∴AB=BC=221.3【点睛】本题考查了全等三角形的判定和性质,平行线之间的距离,等腰三角形的性质,等边三角形的性质以及勾股定理,解题的关键是利用平行线构造全等三角形,再利用全等三角形的性质以及勾股定理求解.4.(1)见解析;(2)见解析;(3)3【解析】【分析】(1)根据等腰三角形的性质和外角的性质即可得到结论;(2)过E作EF∥AC交AB于F,根据已知条件得到△ABC是等边三角形,推出△BEF是等边三角形,得到BE=EF,∠BFE=60°,根据全等三角形的性质即可得到结论;(3)连接AF,证明△ABF≌△CBF,得AF=CF,再证明DH=AH=【详解】解:(1)∵AB=AC,∴∠ABC=∠ACB,∵DE=DC,∴∠E=∠DCE,∴∠ABC-∠E=∠ACB-∠DCB,即∠EDB=∠ACD;(2)∵△ABC是等边三角形,∴∠B=60°,∴△BEF是等边三角形,∴BE=EF,∠BFE=60°,∴∠DFE=120°,∴∠DFE=∠CAD,在△DEF与△CAD中,1CF=3.2⎧∠EDF=∠DCA⎪⎨∠DFE=∠CAD,⎪DE=CD⎩∴△DEF≌△CAD(AAS),∴EF=AD,∴AD=BE;(3)连接AF,如图3所示:∵DE=DC,∠EDC=30°,∴∠DEC=∠DCE=75°,∴∠ACF=75°-60°=15°,∵BF平分∠ABC,∴∠ABF=∠CBF,在△ABF和△CBF中,⎧AB=BC⎪⎨∠ABF=∠CBF,⎪BF=BF⎩△ABF≌△CBF(SAS),∴AF=CF,∴∠FAC=∠ACF=15°,∴∠AFH=15°+15°=30°,∵AH⊥CD,∴AH=11AF=CF=3,22∵∠DEC=∠ABC+∠BDE,∴∠BDE=75°-60°=15°,∴∠ADH=15°+30°=45°,∴∠DAH=∠ADH=45°,∴DH=AH=3.【点睛】本题考查了全等三角形的判定与性质,等腰三角形和直角三角形的性质,三角形的外角的性质,等边三角形的判定和性质,证明三角形全等是解决问题的关键.5.(1)证明见解析;(2)①②③;(3)∠A+∠C=180°.【解析】【分析】(1)利用等式的性质得出∠BAD=∠CAE,即可得出结论;(2)同(1)的方法判断出△ABD≌△ACE,得出BD=CE,再利用对顶角和三角形的内角和定理判断出∠BOC=60°,再判断出△BCF≌△ACO,得出∠AOC=120°,进而得出∠AOE=60°,再判断出BF<CF,进而判断出∠OBC>30°,即可得出结论;(3)先判断出△BDP是等边三角形,得出BD=BP,∠DBP=60°,进而判断出△ABD≌△CBP (SAS),即可得出结论.【详解】(1)证明:∵∠BAC=∠DAE,∴∠BAC+∠CAD=∠DAE+∠CAD,∴∠BAD=∠CAE,在△ABD和△ACE中,⎧AB=AC⎪⎨∠BAD=∠CAE,⎪AD=AE⎩∴△ABD≌△ACE;(2)如图2,∵△ABC和△ADE是等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=60°,∴∠BAD=∠CAE,在△ABD和△ACE中,⎧AB=AC⎪⎨∠BAD=∠CAE,⎪AD=AE⎩∴△ABD≌△ACE,∴BD=CE,①正确,∠ADB=∠AEC,记AD与CE的交点为G,∵∠AGE=∠DGO,∴180°-∠ADB-∠DGO=180°-∠AEC-∠AGE,∴∠DOE=∠DAE=60°,∴∠BOC=60°,②正确,在OB上取一点F,使OF=OC,∴△OCF是等边三角形,∴CF=OC,∠OFC=∠OCF=60°=∠ACB,∴∠BCF=∠ACO,∵AB=AC,∴△BCF≌△ACO(SAS),∴∠AOC=∠BFC=180°-∠OFC=120°,∴∠AOE=180°-∠AOC=60°,③正确,连接AF,要使OC=OE,则有OC=∵BD=CE,∴CF=OF=1 CE,21BD,2∴OF=BF+OD,∴BF<CF,∴∠OBC>∠BCF,∵∠OBC+∠BCF=∠OFC=60°,∴∠OBC>30°,而没办法判断∠OBC大于30度,所以,④不一定正确,即:正确的有①②③,故答案为①②③;(3)如图3,延长DC至P,使DP=DB,∵∠BDC=60°,∴△BDP是等边三角形,∴BD=BP,∠DBP=60°,∵∠BAC=60°=∠DBP,∴∠ABD=∠CBP,∵AB=CB,∴△ABD≌△CBP(SAS),∴∠BCP=∠A,∵∠BCD+∠BCP=180°,∴∠A+∠BCD=180°.【点睛】此题考查三角形综合题,等腰三角形的性质,等边三角形的性质,全等三角形的判定和性质,构造等边三角形是解题的关键.6.(1)60°;(2)EF=AF+FC,证明见解析;(3)AF=EF+2DF,证明见解析.【解析】【分析】(1)可设∠BAD=∠CAD=α,∠AEC=∠ACE=β,在△ACE中,根据三角形内角和可得2α+60+2β=180°,从而有α+β=60°,即可得出∠DFC的度数;(2)在EC上截取EG=CF,连接AG,证明△AEG≌△ACF,然后再证明△AFG为等边三角形,从而可得出EF=EG+GF=AF+FC;(3)在AF上截取AG=EF,连接BG,BF,证明方法类似(2),先证明△ABG≌△EBF,再证明△BFG为等边三角形,最后可得出结论.【详解】解:(1)∵AB=AC,AD为BC边上的中线,∴可设∠BAD=∠CAD=α,又△ABE为等边三角形,∴AE=AB=AC,∠EAB=60°,∴可设∠AEC=∠ACE=β,在△ACE中,2α+60°+2β=180°,∴α+β=60°,∴∠DFC=α+β=60°;(2)EF=AF+FC,证明如下:∵AB=AC,AD为BC边上的中线,∴AD⊥BC,∴∠FDC=90°,∵∠CFD=60°,则∠DCF=30°,∴CF=2DF,在EC上截取EG=CF,连接AG,又AE=AC,∴∠AEG=∠ACF,∴△AEG≌△ACF(SAS),∴∠EAG=∠CAF,AG=AF,又∠CAF=∠BAD,∴∠EAG=∠BAD,∴∠GAF=∠BAD+∠BAG=∠EAG+∠BAG=∠60°,∴△AFG为等边三角形,∴EF=EG+GF=AF+FC,即EF=AF+FC;(3)补全图形如图所示,结论:AF=EF+2DF.证明如下:同(1)可设∠BAD=∠CAD=α,∠ACE=∠AEC=β,∴∠CAE=180°-2β,∴∠BAE=2α+180°-2β=60°,∴β-α=60°,∴∠AFC=β-α=60°,又△ABE为等边三角形,∴∠ABE=∠AFC=60°,∴由8字图可得:∠BAD=∠BEF,在AF上截取AG=EF,连接BG,BF,又AB=BE ,∴△ABG ≌△EBF (SAS ),∴BG =BF ,又AF 垂直平分BC ,∴BF=CF ,∴∠BFA=∠AFC=60°,∴△BFG 为等边三角形,∴BG=BF ,又BC ⊥FG ,∴FG=BF=2DF ,∴AF =AG +GF =BF +EF =2DF +EF .【点睛】本题考查了全等三角形的判定和性质、等边三角形的性质、等腰三角形的性质等知识,解决问题的关键是常用辅助线构造全等三角形,属于中考常考题型.7.90︒,45︒;20︒,30︒;a +γ=2β,a -γ=2β.【解析】【分析】(1)①如图①知∠EMC 1=11∠BMC 1,∠C 1MF =∠C 1MC 得22∠EMF =1(∠BMC 1+∠C 1MC )可求出解.2111∠ABC 1,∠C 1BF =∠C 1BC 得∠EBF =(∠ABC 1+∠C 1BC )可222②由图②知∠EBA 1=求出解.(2)①由图③折叠知∠CMF =∠FMC 1,∠BME =∠EMB 1,可推出(∠BMC -∠EMF )-∠EMF =∠C 1MB 1,即可求出解.②由图④中折叠知∠CMF =∠C 1MF ,∠ABE =∠A 1BE ,可推出290︒-60︒+∠A 1MC 1=90︒,即可求出解.(3)如图⑤-1、⑤-2中分别由折叠可知,a -β=β-γ、a -β=β+γ,即可求得()a +γ=2β、a -γ=2β.【详解】解:(1)①如图①中,11∠EMC 1=∠BMC 1,∠C 1MF =∠C 1MC ,22∴∠EMF =∠EMC 1+∠C 1MF =故答案为90︒.②如图②中,11(∠BMC 1+∠C 1MC )=⨯180︒=90︒,2211∠EBA 1=∠ABC 1,∠C 1BF =∠C 1BC ,22∴∠EBF =∠EBC 1+∠C 1BF =故答案为45︒.(2)①如图③中由折叠可知,11(∠ABC 1+∠C 1BC )=⨯90︒=45︒,22∠CMF =∠FMC 1,∠BME =∠EMB 1,∠C 1MF +∠EMB 1-∠EMF =∠C 1MB 1,∴∠CMF +∠BME -∠EMF =∠C 1MB 1,∴(∠BMC -∠EMF )-∠EMF =∠C 1MB 1,∴180︒-80︒=∠C 1MB 1=20︒;②如图④中根据折叠可知,∠CMF =∠C 1MF ,∠ABE =∠A 1BE ,︒2∠CMF +2∠ABE +∠AMC =90,11︒∴2(∠CMF +∠ABE )+∠AMC 11=90,(∴2(90∴290︒-∠EMF +∠A 1MC 1=90︒,︒)-60︒+∠A 1MC 1=90︒,)︒∴∠AMC =30;11(3)如图⑤-1中,由折叠可知,a -β=β-γ,∴a +γ=2β;如图⑤-2中,由折叠可知,a -β=β+γ,∴a -γ=2β.【点睛】本题考查了图形的变换中折叠属全等变换,图形的角度及边长不变及一些角度的计算问题,突出考查学生的观察能力、思维能力以及动手操作能力,本题是代数、几何知识的综合运用典型题目.8.(1)=;(2)证明见解析;(3)60°,BD=CE;(4)90°,AM+BD=CM ;(5)7【解析】【分析】(1)由DE ∥BC ,得到DB EC =,结合AB=AC ,得到DB=EC ;AB AC(2)由旋转得到的结论判断出△DAB≌△EAC,得到DB=CE;(3)根据等边三角形的性质和全等三角形的判定定理证明△DAB≌△EAC,根据全等三角形的性质求出结论;(4)根据全等三角形的判定和性质和等腰直角三角形的性质即可得到结论;(5)根据旋转的过程中△ADE的面积始终保持不变,而在旋转的过程中,△ADC的AC始终保持不变,即可.【详解】[初步感知](1)∵DE∥BC,∴DB EC=,AB AC∵AB=AC,∴DB=EC,故答案为:=,(2)成立.理由:由旋转性质可知∠DAB=∠EAC,在△DAB和△EAC中⎧AD=AE⎪⎨∠DAB=∠EAC,⎪AB=AC⎩∴△DAB≌△EAC(SAS),∴DB=CE;[深入探究](3)如图③,设AB,CD交于O,∵△ABC和△ADE都是等边三角形,∴AD=AE,AB=AC,∠DAE=∠BAC=60°,∴∠DAB=∠EAC,在△DAB和△EAC中⎧AD=AE⎪⎨∠DAB=∠EAC,⎪AB=AC⎩∴△DAB≌△EAC(SAS),∴DB=CE,∠ABD=∠ACE,∵∠BOD=∠AOC,∴∠BDC=∠BAC=60°;(4)∵△DAE 是等腰直角三角形,∴∠AED=45°,∴∠AEC=135°,在△DAB 和△EAC 中⎧AD =AE⎪⎨∠DAB =∠EAC,⎪AB =AC⎩∴△DAB ≌△EAC (SAS ),∴∠ADB=∠AEC=135°,BD=CE ,∵∠ADE=45°,∴∠BDC=∠ADB-∠ADE=90°,∵△ADE 都是等腰直角三角形,AM 为△ADE 中DE 边上的高,∴AM=EM=MD ,∴AM+BD=CM ;故答案为:90°,AM+BD=CM ;【拓展提升】(5)如图,由旋转可知,在旋转的过程中△ADE 的面积始终保持不变,△ADE 与△ADC 面积的和达到最大,∴△ADC 面积最大,∵在旋转的过程中,AC 始终保持不变,∴要△ADC 面积最大,∴点D 到AC 的距离最大,∴DA ⊥AC ,∴△ADE 与△ADC 面积的和达到的最大为2+故答案为7.【点睛】此题是几何变换综合题,主要考查了旋转和全等三角形的性质和判定,旋转过程中面积变化分析,解本题的关键是三角形全等的判定.9.(1)全等,理由见解析;(2)t=3.5秒或5秒1×AC×AD=5+2=7,2【解析】【分析】(1)根据垂直的定义得到∠DAC=∠ECB ,利用AAS 定理证明△ACD ≌△CBE ;(2)分点F 沿C→B 路径运动和点F 沿B→C 路径运动两种情况,根据等腰三角形的定义列出算式,计算即可;【详解】解:(1)△ACD 与△CBE 全等.理由如下:∵AD ⊥直线l ,∴∠DAC+∠ACD=90°,∵∠ACB=90°,∴∠BCE+∠ACD=90°,∴∠DAC=∠ECB ,在△ACD 和△CBE 中,⎧∠ADC =∠CEB⎪⎨∠DAC =∠ECB,⎪CA =CB⎩∴△ACD ≌△CBE (AAS );(2)由题意得,AM=t ,FN=3t ,则CM=8-t ,由折叠的性质可知,CF=CB=6,∴CN=6-3t ,点N 在BC 上时,△CMN 为等腰直角三角形,当点N 沿C→B 路径运动时,由题意得,8-t=3t-6,解得,t=3.5,当点N 沿B→C 路径运动时,由题意得,8-t=18-3t ,解得,t=5,综上所述,当t=3.5秒或5秒时,△CMN 为等腰直角三角形;【点睛】本题考查的是全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理,灵活运用分情况讨论思想是解题的关键.10.(1)见详解,(2)BD =2CF ,证明见详解,(3)【解析】【分析】(1)欲证明BF =AD ,只要证明∆BCF ≅∆ACD 即可;(2)结论:BD =2CF .如图2中,作EH ⊥AC 于H .只要证明∆ACD ≅∆EHA ,推出CD =AH ,EH =AC =BC ,由∆EHF ≅∆BCF ,推出CH 2.3=CF 即可解决问题;(3)利用(2)中结论即可解决问题;【详解】(1)证明:如图1中,BE⊥AD于E,∴∠AEF=∠BCF=90︒,∠AFE=∠CFB,∴∠DAC=∠CBF,BC=AC,∴∆BCF≅∆ACD(AAS),∴BF=AD.(2)结论:BD=2CF.理由:如图2中,作EH⊥AC于H.∠AHE=∠ACD=∠DAE=90︒,∴∠DAC+∠ADC=90︒,∠DAC+∠EAH=90︒,∴∠ADC=∠EAH,AD=AE,∴∆ACD≅∆EHA,∴CD=AH,EH=AC=BC,CB=CA,∴BD=CH,∠EHF=∠BCF=90︒,∠EFH=∠BFC,EH=BC,∴∆EHF≅∆BCF,∴FH=FC,∴BD=CH=2CF.(3)如图3中,作EH⊥AC于交AC延长线于H.∠AHE=∠ACD=∠DAE=90︒,∴∠DAC+∠ADC=90︒,∠DAC+∠EAH=90︒,∴∠ADC=∠EAH,AD=AE,∴∆ACD≅∆EHA,∴CD=AH,EH=AC=BC,CB=CA,∴BD=CH,∠EHM=∠BCM=90︒,∠EMH=∠BMC,EH=BC,∴∆EHM≅∆BCM,∴MH=MC,∴BD=CH=2CM.AC=3CM,设CM=a,则AC=CB=3a,BD=2a,∴DB2a2==.BC3a3【点睛】本题考查三角形综合题、全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.另外对于类似连续几步的综合题,一般前一步为后一步提供解题的条件或方法.11.(1)①60°;②60°;(2)∠BFE =α.【解析】【分析】(1)①先证明△ACE≌△CBD得到∠ACE=∠CBD,再由三角形外角和定理可得∠BFE=∠CBD+∠BCF;②先证明△ACE≌△CBD得∠ACE=∠CBD=∠DCF,再由三角形外角和定理可得∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA;(2)证明△AEC≌△CDB得到∠E=∠D,则∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α.【详解】(1)如图①中,∵△ABC是等边三角形,∴AC=CB,∠A=∠BCD=60°,∵AE=CD,∴△ACE≌△CBD,∴∠ACE=∠CBD,∴∠BFE=∠CBD+∠BCF=∠ACE+∠BCF=∠BCA=60°.故答案为60.(2)如图②中,∵△ABC是等边三角形,∴AC=CB,∠A=∠BCD=60°,∴∠CAE=∠BCD=′120°∵AE=CD,∴△ACE≌△CBD,∴∠ACE=∠CBD=∠DCF,∴∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA=60°.故答案为60.(3)如图③中,∵点O是AC边的垂直平分线与BC的交点,∴OC=OA,∴∠EAC=∠DCB=α,∵AC=BC,AE=CD,∴△AEC≌△CDB,∴∠E=∠D,∴∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α.【点睛】本题综合考查了三角形全等以及三角形外角和定理.12.(1)①100;②x=y+s+t;(2)见详解.【解析】【分析】(1)①利用三角形的内角和定理即可解决问题;②结论:x=y+s+t.利用三角形内角和定理即可证明;(2)分6种情形分别求解即可解决问题.【详解】解:(1)①∵∠BAC=70°,∴∠ABC+∠ACB=110°,∵∠PBA=10°,∠PCA=20°,∴∠PBC+∠PCB=80°,∴∠BPC=100°,∴x=100,故答案为:100.②结论:x=y+s+t.理由:∵∠A+∠ABC+∠ACB=∠A+∠PBA+∠PCA+∠PBC+∠PCB=180°,∠PBC+∠PCB+∠BPC=180°,∴∠A+∠PBA+∠PCA=∠BPC,∴x=y+s+t.(2)s、t、x、y之间所有可能的数量关系:如图1:s+x=t+y;如图2:s+y=t+x;如图3:y=x+s+t;如图4:x+y+s+t=360°;如图5:t=s+x+y;如图6:s=t+x+y;【点睛】本题考查三角形的内角和定理,三角形的外角的性质等知识,解题的关键是学会用分类讨论的思想思考问题.13.(1)150°;(2)∠1+∠2=90°+α;(3)∠1=90°+∠2+α,理由详见解析;(4)∠2=90°+∠1-α,理由详见解析【解析】【分析】(1)先用平角的得出,∠CDP=180°-∠1,∠CEP=180°-∠2,最后用四边形的内角和即可;(2)同(1)方法即可;(3)利用平角的定义和三角形的内角和即可得出结论;(4)利用三角形的内角和和外角的性质即可得出结论.【详解】解:(1)∵∠1+∠CDP=180°,∴∠CDP=180°-∠1,同理:∠CEP=180°-∠2,根据四边形的内角和定理得,∠CDP+∠DPE+∠CEP+∠C=360°,∵∠C=90°,∴180°-∠1+α+180°-∠2+90°=360°,∴∠1+∠2=90°+α=90°+60°=150°,故答案为:150;(2)∵∠1+∠CDP=180°,∴∠CDP=180°-∠1,同理:∠CEP=180°-∠2,根据四边形的内角和定理得,∠CDP+∠DPE+∠CEP+∠C=360°,∵∠C=90°,∴180°-∠1+α+180°-∠2+90°=360°,∴∠1+∠2=90°+α,故答案为:∠1+∠2=90°+α;(3)∠1=90°+∠2+∠α.理由如下:如图3,设DP与BE的交点为F,∵∠2+∠α=∠DFE,∠DFE+∠C=∠1,∴∠1=∠C+∠2+∠α=90°+∠2+∠α.(4)∠2=90°+∠1-∠α,理由如下:如图4,设PE 与AC 的交点为G ,∵∠PGD =∠EGC ,∴∠α+180°-∠1=∠C +180°-∠2,∴∠2=90°+∠1-∠α.故答案为∠2=90°+∠1-∠α.【点睛】此题是三角形综合题,主要考查了四边形的内角和,三角形的内角和,三角形的外角的性质,平角的定义,解本题的关键是将∠1,∠2,α转化到一个三角形或四边形中,是一道比较简单的中考常考题.14.(1)【解析】【分析】(1)根据简单的分式可得,相邻两个数的积的倒数等于它们的倒数之差,即可得到和1111n -,-;(2);(3)见解析.45n n +1n +114⨯51n ⨯(n +1)(2)根据(1)规律将乘法写成减法的形式,可以观察出前一项的减数等于后一项的被减数,因此可得它们的和.(3)首先利用(2)的和的结果将左边化简,再利用分式方程的解法求解即可.【详解】111111=-=-,解:(1);n (n +1)n n +14⨯545故答案为1111-,-45n n +111111+-+-+22334+111n -=1-= ;n n +1n +1n +1(2)原式=1-1111-+-+(3)已知等式整理得:x x +1x +1x +2112x -1-=所以,原方程即:,x x +5x (x +5)方程的两边同乘x (x +5),得:x +5﹣x =2x ﹣1,解得:x =3,检验:把x =3代入x (x +5)=24≠0,∴原方程的解为:x =3.【点睛】+112x -1-=x +4x +5x (x +5)本题主要考查学生的归纳总结能力,关键在于根据简单的数的运算寻找规律,是考试的热点.15.(1)见解析;(2)∠ABE -∠CDE =30︒【解析】(1)根据聪聪提供的辅助线作法进行证明,先由平行线的性质得:∠AGC=∠MCD,∠F+∠GAF=90︒,再证明∠MCD=∠BAG,可得结论;(2)根据平行线的性质和三角形的外角性质可得结论.【详解】解:(1)证明:如图2,过A作AG//FM,交CD于G,∴∠AGC=∠MCD,∠F+∠GAF=90︒,FN⊥FM,∴∠F=90︒,∴∠GAF=90︒,∠FAB-∠MCD=90︒,∴∠FAB-∠GAF=∠MCD=∠BAG,∴AB//CD;(2)解:∠ABE-∠CDE=30︒,理由如下:如图3,AB//CD,∴∠BPD=∠ABE,∠BPD=∠CDE+∠BED,∠BED=30︒,∴∠BPD-∠CDE=30︒,∴∠ABE-∠CDE=30︒.。
八年级数学上册压轴题 期末复习试卷专题练习(解析版)
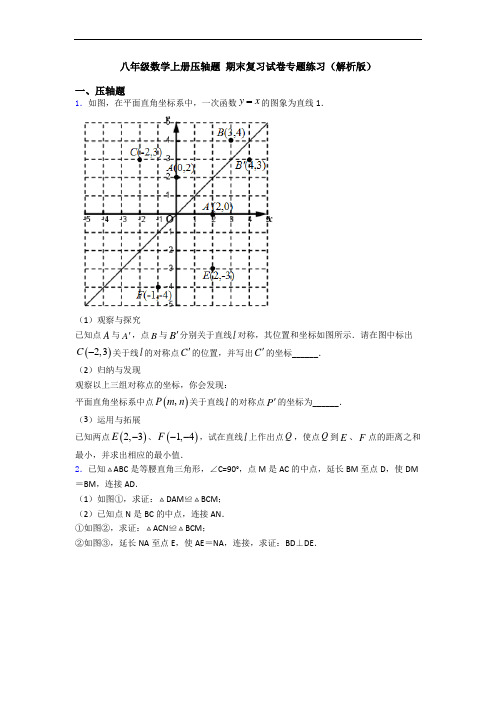
八年级数学上册压轴题 期末复习试卷专题练习(解析版)一、压轴题1.如图,在平面直角坐标系中,一次函数y x =的图象为直线1.(1)观察与探究已知点A 与A ',点B 与B '分别关于直线l 对称,其位置和坐标如图所示.请在图中标出()2,3C -关于线l 的对称点C '的位置,并写出C '的坐标______.(2)归纳与发现观察以上三组对称点的坐标,你会发现:平面直角坐标系中点()P m n ,关于直线l 的对称点P '的坐标为______. (3)运用与拓展已知两点()2,3E -、()1,4F --,试在直线l 上作出点Q ,使点Q 到E 、F 点的距离之和最小,并求出相应的最小值.2.已知ABC 是等腰直角三角形,∠C=90°,点M 是AC 的中点,延长BM 至点D ,使DM =BM ,连接AD .(1)如图①,求证:DAM ≌BCM ; (2)已知点N 是BC 的中点,连接AN . ①如图②,求证:ACN ≌BCM ;②如图③,延长NA 至点E ,使AE =NA ,连接,求证:BD ⊥DE .3.如图,直线l1:y1=﹣x+2与x轴,y轴分别交于A,B两点,点P(m,3)为直线l1上一点,另一直线l2:y2=12x+b过点P.(1)求点P坐标和b的值;(2)若点C是直线l2与x轴的交点,动点Q从点C开始以每秒1个单位的速度向x轴正方向移动.设点Q的运动时间为t秒.①请写出当点Q在运动过程中,△APQ的面积S与t的函数关系式;②求出t为多少时,△APQ的面积小于3;③是否存在t的值,使△APQ为等腰三角形?若存在,请求出t的值;若不存在,请说明理由.4.如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段BC,使BA=BC,连接AC(1)如图1,求C点坐标;(2)如图2,若P点从A点出发沿x轴向左平移,连接BP,作等腰直角BPQ,连接CQ,当点P在线段OA上,求证:PA=CQ;(3)在(2)的条件下若C、P,Q三点共线,直接写出此时∠APB的度数及P点坐标5.如图,直线11 2y x b=-+分别与x轴、y轴交于A,B两点,与直线26y kx=-交于点()C4,2.(1)b= ;k= ;点B坐标为;(2)在线段AB上有一动点E,过点E作y轴的平行线交直线y2于点F,设点E的横坐标为m,当m为何值时,以O、B、E、F为顶点的四边形是平行四边形;(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得P,Q,A,B四个点能构成一个菱形.若存在,直接写出所有符合条件的Q点坐标;若不存在,请说明理由.6.如图,在平面直角坐标系中,直线y=2x+4与x轴交于点A,与y轴交于点B,过点B 的另一条直线交x轴正半轴于点C,且OC=3.图1 图2 (1)求直线BC 的解析式;(2)如图1,若M 为线段BC 上一点,且满足S △AMB =S △AOB ,请求出点M 的坐标; (3)如图2,设点F 为线段AB 中点,点G 为y 轴上一动点,连接FG ,以FG 为边向FG 右侧作正方形FGQP ,在G 点的运动过程中,当顶点Q 落在直线BC 上时,求点G 的坐标; 7.某校七年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究.(1)如图1,在△ABC 中,∠ABC 与∠ACB 的平分线交于点P ,∠A =64°,则∠BPC = ;(2)如图2,△ABC 的内角∠ACB 的平分线与△ABC 的外角∠ABD 的平分线交于点E .其中∠A =α,求∠BEC .(用α表示∠BEC );(3)如图3,∠CBM 、∠BCN 为△ABC 的外角,∠CBM 、∠BCN 的平分线交于点Q ,请你写出∠BQC 与∠A 的数量关系,并说明理由;(4)如图4,△ABC 外角∠CBM 、∠BCN 的平分线交于点Q ,∠A=64°,∠CBQ ,∠BCQ 的平分线交于点P ,则∠BPC= ゜,延长BC 至点E ,∠ECQ 的平分线与BP 的延长线相交于点R ,则∠R= ゜.8.在平面直角坐标系xOy 中,对于点(,)P a b 和点(,)Q a b ',给出如下定义:若1,(2),(2)b a b b a -≥⎧=<⎩'⎨当时当时,则称点Q 为点P 的限变点.例如:点(2,3)的限变点的坐标是(2,2),点(2,5)--的限变点的坐标是(2,5)-,点(1,3)的限变点的坐标是(1,3).(1)①点3,1)-的限变点的坐标是________;②如图1,在点(2,1)A -、(2,1)B 中有一个点是直线2y =上某一个点的限变点,这个点是________;(填“A ”或“B ”)(2)如图2,已知点(2,2)C --,点(2,2)D -,若点P 在射线OC 和OD 上,其限变点Q 的纵坐标b '的取值范围是b m '≥或b n '≤,其中m n >.令s m n =-,直接写出s 的值. (3)如图3,若点P 在线段EF 上,点(2,5)E --,点(,3)F k k -,其限变点Q 的纵坐标b '的取值范围是25b '-≤≤,直接写出k 的取值范围.9.(1)问题发现:如图1,△ACB 和△DCE 均为等边三角形,点A 、D 、E 在同一直线上,连接BE .①请直接写出∠AEB 的度数为_____;②试猜想线段AD 与线段BE 有怎样的数量关系,并证明;(2)拓展探究:图2, △ACB 和△DCE 均为等腰三角形,∠ACB =∠DCE =90°,点A 、D 、E 在同-直线上, CM 为△DCE 中DE 边上的高,连接BE ,请判断∠AEB 的度数线段CM 、AE 、BE 之间的数量关系,并说明理由.10.学习了三角形全等的判定方法(即“SAS ”、“ASA ”、“AAS ”、“SSS ”)和直角三角形全等的判定方法(即“HL ”)后,我们继续对“两个三角形满足两边的其中一边的对角对应相等”的情形进行研究. (初步思考)我们不妨将问题用符号语言表示为:在△DEF 中,AC =DF ,BC =EF ,∠B =∠E ,然后,对∠B 进行分类,可分为“∠B 是直角、钝角、锐角”三种情况进行探究. (深入探究)第一种情况:当∠B 是直角时,△ABC ≌△DEF .(1)如图①,在△ABC 和△DEF 中,AC =DF ,BC =EF ,∠B =∠E =90°,根据______,可以知道Rt △ABC ≌Rt △DEF .第二种情况:当∠B 是钝角时,△ABC ≌△DEF .(2)如图②,在△ABC 和△DEF 中,AC =DF ,BC =EF ,∠B =∠E ,且∠B 、∠E 都是钝角.求证:△ABC ≌△DEF .第三种情况:当∠B 是锐角时,△ABC 和△DEF 不一定全等.(3)在△ABC 和△DEF 中,AC =DF ,BC =EF ,∠B =∠E ,且∠B 、∠E 都是锐角.请你用直尺在图③中作出△DEF ,使△DEF 和△ABC 不全等,并作简要说明.11.问题情景:数学课上,老师布置了这样一道题目,如图1,△ABC 是等边三角形,点D 是BC 的中点,且满足∠ADE =60°,DE 交等边三角形外角平分线于点E .试探究AD 与DE 的数量关系.操作发现:(1)小明同学过点D 作DF ∥AC 交AB 于F ,通过构造全等三角形经过推理论证就可以解决问题,请您按照小明同学的方法确定AD 与DE 的数量关系,并进行证明.类比探究:(2)如图2,当点D 是线段BC 上任意一点(除B 、C 外),其他条件不变,试猜想AD 与DE 之间的数量关系,并证明你的结论.拓展应用:(3)当点D 在线段BC 的延长线上,且满足CD =BC ,在图3中补全图形,直接判断△ADE 的形状(不要求证明).12.在Rt ABC 中,ACB =∠90°,30A ∠=︒,点D 是AB 的中点,连结CD .(1)如图①,BC 与BD 之间的数量关系是_________,请写出理由;(2)如图②,若P 是线段CB 上一动点(点P 不与点B 、C 重合),连结DP ,将线段DP绕点D逆时针旋转60°,得到线段DF,连结BF,请猜想BF,BP,BD三者之间的数量关系,并证明你的结论;(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图③中补全图形,并直接写出BF,BP,BD三者之间的数量关系.【参考答案】***试卷处理标记,请不要删除一、压轴题1.(1) (3,-2);(2) (n,m);(3)图见解析,点Q到E、F点的距离之和最小值为210【解析】【分析】(1)根据题意和图形可以写出C'的坐标;(2)根据图形可以直接写出点P关于直线l的对称点的坐标;(3)作点E关于直线l的对称点E',连接E'F,根据最短路径问题解答.【详解】(1)如图,C'的坐标为(3,-2),故答案为(3,-2);P m n,关于直线l的对称点P'的坐标为(n,m),(2)平面直角坐标系中点()故答案为(n,m);(3)点E关于直线l的对称点为E'(-3,2),连接E'F角直线l于一点即为点Q,此时点Q到E、F点的距离之和最小,即为线段E'F,∵E'F()[]221(3)2(4)210 =---+--=⎡⎤⎣⎦,∴点Q到E、F点的距离之和最小值为210.【点睛】此题考查轴对称的知识,画关于直线的对称点,最短路径问题,勾股定理关键是找到点的对称点,由此解决问题.2.(1)见解析;(2)①见解析;②见解析【解析】【分析】(1)由点M是AC中点知AM=CM,结合∠AMD=∠CMB和DM=BM即可得证;(2)①由点M,N分别是AC,BC的中点及AC=BC可得CM=CN,结合∠C=∠C和BC=AC 即可得证;②取AD中点F,连接EF,先证△EAF≌△ANC得∠NAC=∠AEF,∠C=∠AFE=90°,据此知∠AFE=∠DFE=90°,再证△AFE≌△DFE得∠EAD=∠EDA=∠ANC,从而由∠EDB=∠EDA+∠ADB=∠EAD+∠NAC=180°-∠DAM即可得证.【详解】解:(1)∵点M是AC中点,∴AM=CM,在△DAM和△BCM中,∵AM CMAMD CMBDM BM=⎧⎪∠=∠⎨⎪=⎩,∴△DAM≌△BCM(SAS);(2)①∵点M是AC中点,点N是BC中点,∴CM=12AC ,CN=12BC , ∵△ABC 是等腰直角三角形, ∴AC=BC , ∴CM=CN ,在△BCM 和△ACN 中,∵CM CN C C BC AC =⎧⎪∠=∠⎨⎪=⎩, ∴△BCM ≌△ACN (SAS ); ②证明:取AD 中点F ,连接EF ,则AD=2AF , ∵△BCM ≌△ACN , ∴AN=BM ,∠CBM=∠CAN , ∵△DAM ≌△BCM ,∴∠CBM=∠ADM ,AD=BC=2CN , ∴AF=CN ,∴∠DAC=∠C=90°,∠ADM=∠CBM=∠NAC , 由(1)知,△DAM ≌△BCM , ∴∠DBC=∠ADB , ∴AD ∥BC , ∴∠EAF=∠ANC , 在△EAF 和△ANC 中,AE AN EAF ANC AF NC =⎧⎪∠=∠⎨⎪=⎩, ∴△EAF ≌△ANC (SAS ), ∴∠NAC=∠AEF ,∠C=∠AFE=90°, ∴∠AFE=∠DFE=90°, ∵F 为AD 中点, ∴AF=DF , 在△AFE 和△DFE 中,AF DF AFE DFE EF EF =⎧⎪∠=∠⎨⎪=⎩, ∴△AFE ≌△DFE (SAS ), ∴∠EAD=∠EDA=∠ANC ,∴∠EDB=∠EDA+∠ADB=∠EAD+∠NAC=180°-∠DAM=180°-90°=90°, ∴BD ⊥DE . 【点睛】本题是三角形的综合问题,解题的关键是掌握中点的性质、等腰直角三角形的性质、全等三角形的判定与性质等知识点. 3.(1)b=72;(2)①△APQ 的面积S 与t 的函数关系式为S=﹣32t +272或S=32t ﹣272;②7<t <9或9<t <11,③存在,当t 的值为3或9+或9﹣或6时,△APQ 为等腰三角形. 【解析】分析:(1)把P (m ,3)的坐标代入直线1l 的解析式即可求得P 的坐标,然后根据待定系数法即可求得b ;(2)根据直线2l 的解析式得出C 的坐标,①根据题意得出9AQ t =-,然后根据12P S AQ y =⋅即可求得APQ 的面积S 与t 的函数关系式;②通过解不等式273322t -<或327 3.22t -<即可求得7<t <9或9<t <11.时,APQ 的面积小于3;③分三种情况:当PQ =PA 时,则()()()2222(71)032103,t -++-=++-当AQ =PA 时,则()()222(72)2103,t --=++-当PQ =AQ 时,则()222(71)03(72)t t -++-=--, 即可求得.详解:解;(1)∵点P (m ,3)为直线l 1上一点, ∴3=−m +2,解得m =−1, ∴点P 的坐标为(−1,3), 把点P 的坐标代入212y x b =+ 得,()1312b =⨯-+, 解得72b =; (2)∵72b =; ∴直线l 2的解析式为y =12x +72, ∴C 点的坐标为(−7,0),①由直线11:2l y x =-+可知A (2,0),∴当Q 在A . C 之间时,AQ =2+7−t =9−t , ∴11273(9)32222S AQ yP t t =⋅=⨯-⨯=-; 当Q 在A 的右边时,AQ =t −9, ∴11327(9)32222S AQ yP t t ;=⋅=⨯-⨯=- 即△APQ 的面积S 与t 的函数关系式为27322S t =-或327.22S t =- ②∵S <3, ∴273322t -<或327 3.22t -< 解得7<t <9或9<t <11. ③存在;设Q (t −7,0),当PQ =PA 时,则()()()2222(71)032103,t -++-=++-∴22(6)3t -=,解得t =3或t =9(舍去), 当AQ =PA 时,则()()222(72)2103,t --=++-∴2(9)18,t -=解得9t =+9t =- 当PQ =AQ 时,则()222(71)03(72)t t -++-=--,∴22(6)9(9)t t -+=-, 解得t =6.故当t 的值为3或9+9-6时,△APQ 为等腰三角形.点睛:属于一次函数综合题,考查了一次函数图象上点的坐标特征,待定系数法求函数解析式,等腰三角形的性质以及三角形的面积,分类讨论是解题的关键.4.(1)(1,-4);(2)证明见解析;(3)()135,1,0APB P ︒∠= 【解析】【分析】(1)作CH ⊥y 轴于H ,证明△ABO ≌△BCH ,根据全等三角形的性质得到BH=OA=3,CH=OB=1,求出OH ,得到C 点坐标;(2)证明△PBA ≌△QBC ,根据全等三角形的性质得到PA=CQ ;(3)根据C 、P ,Q 三点共线,得到∠BQC=135°,根据全等三角形的性质得到∠BPA=∠BQC=135°,根据等腰三角形的性质求出OP ,得到P 点坐标.【详解】解:(1)作CH ⊥y 轴于H ,则∠BCH+∠CBH=90°,因为AB BC ⊥,所以.∠ABO+∠CBH=90°,所以∠ABO=∠BCH ,在△ABO 和△BCH 中,ABO BCH AOB BHC AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩ABO BCH ∴∆≅∆:BH=OA=3,CH=OB=1,:OH=OB+BH=4,所以C 点的坐标为(1,-4);(2)因为∠PBQ=∠ABC=90°,,PBQ ABQ ABC ABQ PBA QBC ∴∠-=∠-∠∴∠=∠在△PBA 和△QBC 中,BP BQ PBA QBC BA BC =⎧⎪∠=∠⎨⎪=⎩PBA QBC ∴∆≅∆:.PA=CQ ;(3) ()135,1,0APB P ︒∠= BPQ ∆是等腰直角三角形,:所以∠BQP=45°,当C 、P ,Q 三点共线时,∠BQC=135°,由(2)可知,PBA QBC ∴∆≅∆;所以∠BPA=∠BQC=135°,所以∠OPB=45°,所以.OP=OB=1,所以P 点坐标为(1,0) .【点睛】本题考查的是全等三角形的判定和性质、三角形的外角的性质,掌握全等三角形的判定定理和性质定理是解题的关键.5.(1)4;2;(0,4);(2)125m =或285m =;(3)存在.Q点坐标为()-,()4,()0,4-或()5,4. 【解析】【分析】(1)根据待定系数法,将点C (4,2)代入解析式可求解;(2)设点E (m ,142m +),F (m ,2m -6),得()154261022EF m m m =-+--=-,由平行四边形的性质可得BO =EF =4,列出方程即可求解;(3)分两种情况讨论,由菱形的性质按照点平移的坐标规律,先确定P 点坐标,再确定O 点坐标即可求解.【详解】解:(1)(1)∵直线y 2=kx -6交于点C (4,2),∴2=4k -6,∴k =2, ∵直线212y x b =-+过点C (4,2), ∴2=-2+b ,∴b =4, ∴直线解析式为:212y x b =-+,直线解析式为y 2=2x -6, ∵直线212y x b =-+分别与x 轴、y 轴交于A ,B 两点, ∴当x =0时,y =4,当y =0时,x =8,∴点B (0,4),点A (8,0),故答案为:4;2;(0,4)(2)∵点E 在线段AB 上,点E 的横坐标为m , ∴1,42E m m ⎛⎫-+ ⎪⎝⎭,(),26F m m -, ∴()154261022EF m m m =-+--=-. ∵四边形OBEF 是平行四边形,∴EF BO =, ∴51042m -=, 解得:125m =或285m =时, ∴当125m =或285m =时,四边形OBEF 是平行四边形.(3)存在.此时Q 点坐标为()-,()4,()0,4-或()5,4.理由如下:假设存在.以P ,Q ,A ,B 为顶点的菱形分两种情况:①以AB 为边,如图1所示.因为点()8,0A ,()0,4B ,所以45AB =.因为以P ,Q ,A ,B 为顶点的四边形为菱形,所以AP AB =或BP BA =.当AP AB =时,点()845,0P -或()845,0+;当BP BA =时,点()8,0P -. 当()845,0P -时,()8458,04Q --+,即()45,4-; 当()845,0P +时,()8458,04Q +-+,即()45,4; 当()8,0P -时,()880,004Q -+-+-,即()0,4-.②以AB 为对角线,对角线的交点为M ,如图2所示.可得5AP =,点P 坐标为()3,0.因为以P ,Q ,A ,B 为顶点的四边形为菱形,所以点Q 坐标为()5,4.综上可知:若点P 为x 轴上一点,则在平面直角坐标系中存在一点Q ,使得P ,Q ,A ,B 四个点能构成一个菱形,此时Q 点坐标为()45,4-,()45,4,()0,4-或()5,4.【点睛】本题是一次函数综合题,利用待定系数法求解析式,平行四边形的性质,菱形的性质,利用分类讨论思想解决问题是本题的关键. 6.(1)443y x =-+;(2)612(,)55M ;(3)23(0,)7G 或(0,-1)G 【解析】【分析】(1)求出点B ,C 坐标,再利用待定系数法即可解决问题;(2)结合图形,由S △AMB =S △AOB 分析出直线OM 平行于直线AB ,再利用两直线相交建立方程组求得交点M 的坐标;(3)分两种情形:①当n >2时,如图2-1中,点Q 落在BC 上时,过G 作直线平行于x 轴,过点F ,Q 作该直线的垂线,垂足分别为M ,N .求出Q (n-2,n-1).②当n <2时,如图2-2中,同法可得Q (2-n ,n+1),代入直线BC 的解析式解方程即可解决问题.【详解】解:(1)∵直线y=2x+4与x 轴交于点A ,与y 轴交于点B ,∴A (-2,0),B (0,4),,又∵OC=3,∴C (3,0),设直线BC 的解析式为y=kx+b ,将B 、C 的坐标代入得: 304k b b +=⎧⎨=⎩, 解得:434k b ⎧=-⎪⎨⎪=⎩,∴直线BC 的解析式为443y x =-+; (2)连接OM ,∵S △AMB =S △AOB ,∴直线OM 平行于直线AB ,故设直线OM 解析式为:2y x =,将直线OM 的解析式与直线BC 的解析式联立得方程组2443y x y x =⎧⎪⎨=-+⎪⎩, 解得:65125x y ⎧=⎪⎪⎨⎪=⎪⎩故点612(,)55M ; (3)∵FA=FB ,A (-2,0),B (0,4),∴F (-1,2),设G (0,n ),①当n >2时,如图2-1中,点Q 落在BC 上时,过G 作直线平行于x 轴,过点F ,Q 作该直线的垂线,垂足分别为M ,N .∵四边形FGQP 是正方形,易证△FMG ≌△GNQ ,∴MG=NQ=1,FM=GN=n-2,∴Q (n-2,n-1),∵点Q 在直线443y x =-+上, ∴41(2)43n n -=--+, ∴23=7n , ∴23(0,)7G . ②当n <2时,如图2-2中,同法可得Q (2-n ,n+1),∵点Q 在直线443y x =-+上, ∴4+1(2)43n n =--+, ∴n=-1,∴(0,-1)G . 综上所述,满足条件的点G 坐标为23(0,)7G 或(0,-1)G 【点睛】 本题属于一次函数综合题,考查了待定系数法,三角形的面积,全等三角形的判定和性质,正方形的性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.7.(1) 122°;(2)12BEC α∠=;(3)01902BQC A ;(4)119,29 ; 【解析】【分析】(1)根据三角形的内角和角平分线的定义;(2)根据三角形的一个外角等于与它不相邻的两个内角的和,用A ∠与1∠表示出2∠,再利用E ∠与1∠表示出2∠,于是得到结论;(3)根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出EBC ∠与ECB ∠,然后再根据三角形的内角和定理列式整理即可得解;(4)根据(1),(3)的结论可以得出∠BPC 的度数;根据(2)的结论可以得到∠R 的度数.【详解】解:(1)BP 、CP 分别平分ABC ∠和ACB ∠,12PBC ABC ∴∠=∠,12PCB ACB ∠=∠, 180()BPC PBC PCB ∴∠=︒-∠+∠11180()22ABC ACB =︒-∠+∠, 1180()2ABC ACB =︒-∠+∠, 1(180180)2A =︒-︒-∠, 1180902A =-︒+︒∠, 9032122,故答案为:122︒;(2)如图2示,CE 和BE 分别是ACB ∠和ABD ∠的角平分线,112ACB ∴∠=∠,122ABD ∠=∠, 又ABD ∠是ABC ∆的一外角,ABD A ACB ∴∠=∠+∠,112()122A ABC A ∴∠=∠+∠=∠+∠, 2∠是BEC ∆的一外角,112111222BEC A A α∴∠=∠-∠=∠+∠-∠=∠=; (3)1()2QBC A ACB ∠=∠+∠,1()2QCB A ABC ∠=∠+∠, 180BQC QBC QCB ∠=︒-∠-∠,11180()()22A ACB A ABC =︒-∠+∠-∠+∠, 11180()22A A ABC ACB =︒-∠-∠+∠+∠, 结论1902BQC A ∠=︒-∠. (4)由(3)可知,119090645822BQCA , 再根据(1),可得180()BPCPBC PCB 1118022QBC QCB1180902Q 118090582 119;由(2)可得:11582922R Q ;故答案为:119,29.【点睛】本题考查了三角形的外角性质与内角和定理,熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.8.(1)①()3,1;②B ;(2)3s =;(3)59k ≤≤. 【解析】【分析】(1)利用限变点的定义直接解答即可;(2)先利用逆推原理求出限变点(2,1)A -、(2,1)B 对应的原来点坐标,然后把原来点坐标代入到2y =,满足解析式的就是答案; (3)先OC OD ,的关系式,再求出点P 的限变点Q 满足的关系式,然后根据图象求出m n ,的值,从而求出s 即可;(4)先求出线段EF 的关系式,再求出点P 的限变点Q 所满足的关系式,根据图像求解即可.【详解】解:(1)①∵32a =,∴11b b ==-=',∴坐标为:()3,1,故答案为:()3,1; ②∵对于限变点来说,横坐标保持不变,∴限变点(2,1)A -对应的原来点的坐标为:()2,1-或()21--,, 限变点(2,1)B 对应的原来点的坐标为:()2,2,∵()2,2满足2y =,∴这个点是B ,故答案为:B ;(2)∵点C 的坐标为(2,2)--,∴OC 的关系式为:()0y x x =≤,∵点D 的坐标为(2,2)-,∴OD 的关系式为:()0y x x =-≥,∴点P 满足的关系式为:()()00x x y x x ≤⎧⎪=⎨->⎪⎩, ∴点P 的限变点Q 的纵坐标满足的关系式为: 当2x ≥时:1b x '=--,当02x <<时:b x x '=-=,当0x ≤时,b x x '==-,图像如下:通过图象可以得出:当2x ≥时,3b '≤-,∴3n =-, 当2x <时,0b '≥,∴0m =, ∴()033s m n =-=--=;(3)设线段EF 的关系式为:()022y ax c a x k k =+≠-≤≤>-,,, 把(2,5)E --,(,3)F k k -代入得:253a c ka c k -+=-⎧⎨+=-⎩,解得:13a c =⎧⎨=-⎩, ∴线段EF 的关系式为()322y x x k k =--≤≤>-,, ∴线段EF 上的点P 的限变点Q 的纵坐标满足的关系式4(2)|3|3(22)x xb x x x -⎧'=⎨-=--<⎩,图象如下:当x =2时,b ′取最小值,b '=2﹣4=﹣2,当b '=5时,x ﹣4=5或﹣x +3=5,解得:x =9或x =﹣2,当b ′=1时,x ﹣4=1,解得:x =5,∵ 25b '-≤≤,∴由图象可知,k 的取值范围时:59k ≤≤.【点睛】本题主要考查了一次函数的综合题,解答本题的关键是熟练掌握新定义“限变点”,解答此题还需要掌握一次函数的图象与性质以及最值的求解,此题有一定的难度.9.(1)①60°;②AD=BE.证明见解析;(2)∠AEB =90°;AE=2CM+BE ;理由见解析.【解析】【分析】(1)①由条件△ACB 和△DCE 均为等边三角形,易证△ACD ≌△BCE ,从而得到:AD=BE ,∠ADC=∠BEC .由点A ,D ,E 在同一直线上可求出∠ADC ,从而可以求出∠AEB 的度数.②由△ACD ≌△BCE ,可得AD=BE ;(2)首先根据△ACB 和△DCE 均为等腰直角三角形,可得AC=BC ,CD=CE ,∠ACB=∠DCE=90°,据此判断出∠ACD=∠BCE ;然后根据全等三角形的判定方法,判断出△ACD ≌△BCE ,即可判断出BE=AD ,∠BEC=∠ADC ,进而判断出∠AEB 的度数为90°;根据DCE=90°,CD=CE ,CM ⊥DE ,可得CM=DM=EM ,所以DE=DM+EM=2CM ,据此判断出AE=BE+2CM .【详解】(1)①∵∠ACB=∠DCE ,∠DCB=∠DCB ,∴∠ACD=∠BCE ,在△ACD 和△BCE 中,AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACD≌△BCE,∴AD=BE,∠CEB=∠ADC=180°−∠CDE=120°,∴∠AEB=∠CEB−∠CED=60°;②AD=BE.证明:∵△ACD≌△BCE,∴AD=BE.(2)∠AEB=90°;AE=2CM+BE;理由如下:∵△ACB和△DCE均为等腰直角三角形,∠ACB =∠DCE= 90°,∴AC = BC, CD = CE,∠ACB =∠DCB =∠DCE-∠DCB,即∠ACD = ∠BCE,∴△ACD≌△BCE,∴AD = BE,∠BEC = ∠ADC=135°.∴∠AEB =∠BEC-∠CED =135°- 45°= 90°.在等腰直角△DCE中,CM为斜边DE上的高,∴CM =DM= ME,∴DE = 2CM.∴AE = DE+AD=2CM+BE.【点睛】本题考查了等边三角形的性质、等腰直角三角形的性质、三角形全等的判定与性质等知识,解题时需注意运用已有的知识和经验解决相似问题.10.(1)HL;(2)见解析;(3)如图②,见解析;△DEF就是所求作的三角形,△DEF 和△ABC不全等.【解析】【分析】(1)根据直角三角形全等的方法“HL”证明;(2)过点C作CG⊥AB交AB的延长线于G,过点F作FH⊥DE交DE的延长线于H,根据等角的补角相等求出∠CBG=∠FEH,再利用“角角边”证明△CBG和△FEH全等,根据全等三角形对应边相等可得CG=FH,再利用“HL”证明Rt△ACG和Rt△DFH全等,根据全等三角形对应角相等可得∠A=∠D,然后利用“角角边”证明△ABC和△DEF全等;(3)以点C为圆心,以AC长为半径画弧,与AB相交于点D,E与B重合,F与C重合,得到△DEF与△ABC不全等;(4)根据三种情况结论,∠B不小于∠A即可.【详解】(1)在直角三角形中一条斜边和一条直角边对应相等的两个直角三角形全等运用的是HL.(2)证明:如图①,分别过点C、F作对边AB、DE上的高CG、FH,其中G、H为垂足.∵∠ABC、∠DEF都是钝角∴G、H分别在AB、DE的延长线上.∵CG⊥AG,FH⊥DH,∴∠CGA=∠FHD=90°.∵∠CBG=180°-∠ABC,∠FEH=∠180°-∠DEF,∠ABC=∠DEF,∴∠CBG =∠FEH .在△BCG 和△EFH 中,∵∠CGB =∠FHE ,∠CBG =∠FEH ,BC =EF ,∴△BCG ≌△EFH .∴CG =FH .又∵AC =DF .∴Rt △ACG ≌△DFH .∴∠A =∠D .在△ABC 和△DEF 中,∵∠ABC =∠DEF ,∠A =∠D ,AC =DF ,∴△ABC ≌△DEF .(3)如图②,△DEF 就是所求作的三角形,△DEF 和△ABC 不全等.【点睛】本题是三角形综合题,主要考查了全等三角形的判定与性质,应用与设计作图,熟练掌握三角形全等的判定方法是解题的关键,阅读量较大,审题要认真仔细.11.(1)AD =DE ,见解析;(2)AD =DE ,见解析;(3)见解析,△ADE 是等边三角形,【解析】【分析】(1)根据题意,通过平行线的性质及等边三角形的性质证明ADF EDC ∆∆≌即可得解; (2)根据题意,通过平行线的性质及等边三角形的性质证明AFD DCE ∆∆≌即可得解; (3)根据垂直平分线的性质及等边三角形的判定定理进行证明即可.【详解】(1)如下图,数量关系:AD =DE .证明:∵ABC ∆是等边三角形∴AB =BC ,60B BAC BCA ∠∠∠︒===∵DF ∥AC∴BFD BAC ∠∠=,∠BDF =∠BCA∴60B BFD BDF ∠∠∠︒===∴BDF ∆是等边三角形,120AFD ∠︒=∴DF =BD∵点D 是BC 的中点∴BD =CD∴DF =CD∵CE 是等边ABC ∆的外角平分线∴120DCE AFD ∠︒∠==∵ABC ∆是等边三角形,点D 是BC 的中点∴AD ⊥BC∴90ADC ∠︒=∵60BDF ADE ∠∠︒==∴30ADF EDC ∠∠︒==在ADF ∆与EDC ∆中AFD ECD DF CDADF EDC ∠∠⎧⎪⎨⎪∠∠⎩=== ∴()ADF EDC ASA ∆∆≌∴AD =DE ;(2)结论:AD =DE .证明:如下图,过点D 作DF ∥AC ,交AB于F∵ABC ∆是等边三角形∴AB =BC ,60B BAC BCA ∠∠∠︒===∴BFD BAC BDF BCA∠∠∠∠=,=∴60B BFD BDF∠∠∠︒===∴BDF∆是等边三角形,120AFD∠︒=∴BF=BD∴AF=DC∵CE是等边ABC∆的外角平分线∴120DCE AFD∠︒∠==∵∠ADC是ABD∆的外角∴60ADC B FAD FAD∠∠∠︒∠=+=+∵60ADC ADE CDE CDE∠∠∠︒∠=+=+∴∠FAD=∠CDE在AFD∆与DCE∆中AFD DCEAF CDFAD EDC∠∠⎧⎪⎨⎪∠∠⎩===∴()AFD DCE ASA∆∆≌∴AD=DE;(3)如下图,ADE∆是等边三角形.证明:∵BC CD=∴AC CD=∵CE平分ACD∠∴CE垂直平分AD∴AE=DE∵60ADE∠=︒∴ADE∆是等边三角形.【点睛】本题主要考查了等边三角形的性质及判定,三角形全等的判定及性质,平行线的性质,垂直平分线的性质等相关内容,熟练掌握三角形综合解决方法是解决本题的关键. 12.(1)BC BD=,理由见解析;(2)BF BP BD+=,证明见解析;(3)BF BP BD+=.【解析】(1)利用含30的直角三角形的性质得出12BC AB =,即可得出结论; (2)同(1)的方法得出BC BD =进而得出BCD ∆是等边三角形,进而利用旋转全等模型易证DCP DBF ∆≅∆,得出CP BF =即可解答;(3)同(2)的方法得出结论.【详解】解:(1)90ACB ∠=︒,30A ∠=︒,60CBA ∴∠=︒,12BC AB =, 点D 是AB 的中点,BC BD ∴=,故答案为:BC BD =;(2)BF BP BD +=,理由:90ACB ∠=︒,30A ∠=︒,60CBA ∴∠=︒,12BC AB =, 点D 是AB 的中点,BC BD ∴=,DBC ∴∆是等边三角形,60CDB ∴∠=︒,DC DB =,线段DP 绕点D 逆时针旋转60︒,得到线段DF ,60PDF ∴∠=︒,DP DF =,CDB PDB PDF PDB ∴∠-∠=∠-∠,CDP BDF ∴∠=∠,在DCP ∆和DBF ∆中, DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩,DCP DBF ∴∆≅∆,CP BF ∴=,CP BP BC +=,BF BP BC ∴+=,BC BD =,BF BP BD ∴+=;(3)如图③,BF BD BP =+,理由:90ACB ∠=︒,30A ∠=︒,60CBA ∴∠=︒,12BC AB =, 点D 是AB 的中点,BC BD ∴=,DBC ∴∆是等边三角形,60CDB ∴∠=︒,DC DB =,线段DP 绕点D 逆时针旋转60︒,得到线段DF ,60PDF ∴∠=︒,DP DF =,CDB PDB PDF PDB ∴∠+∠=∠+∠,CDP BDF ∴∠=∠,在DCP ∆和DBF ∆中, DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩,DCP DBF ∴∆≅∆,CP BF ∴=,CP BC BP =+,BF BC BP ∴=+,BC BD =,BF BD BP ∴=+.【点睛】 此题是三角形综合题,主要考查了含30的直角三角形的性质,等边三角形的判定,全等三角形的判定和性质,旋转的性质,解本题的关键是判断出DCP DBF ∆≅∆,是一道中等难度的中考常考题.。
(完整版)八年级数学上册压轴题专题练习

(完整版)八年级数学上册压轴题专题练习-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN1、已知点O 为等边ABC ∆内一点,0110=∠AOB ,α=∠BOC ,以OC 为一边作等边OCD ∆,连接AD 。
(1)当0150=α时,试判断AOD ∆的形状,并说明理由。
(2)探究:当α为多少度时,AOD ∆为等腰三角形。
2、(1)如图1:点E 在正方形ABCD 的边上,BF ⊥AE 于点F,DG ⊥AE 于点G ,求证:△ADG ≌△BAF(2)如图2:已知AB=AC ,∠1=∠2=∠BAC, 求证:△ABE ≌△CAF (3)如图3:在等腰三角形ABC 中,AB=AC,AB>BC ,点D 在边BC 上,CD=2BD ,点E 、F 在线段AD 上,∠1=∠2=∠BAC,若△ABC 的面积为9,则△ABE 与△CDF 的面积的和是多少。
图1 图2 图33、.问题背景,请你证明以上三个命题;① 如图1,在正三角形ABC 中,N 为BC 边上任一点,CM 为正三角形外角∠ACK 的平分线,若∠ANM=60°,则AN=NM② 如图2,在正方形ABCD 中,N 为BC 边上任一点,CM 为正方形外角∠DCK 的平分线,若∠ANM=90°,则AN=NMOABCD③ 如图3,在正五边形ABCDE 中,N 为BC 边上任一点,CM 为正五边形外角∠DCK 的平分线,若∠ANM=108°,则AN=NM4、已知点C 为线段AB 上一点,分别以AC 、BC 为边在线段AB 同侧作△ACD 和△BCE ,且CA=CD ,CB=CE ,∠ACD=∠BCE ,直线AE 与BD 交于点F ,(1)如图1,若∠ACD=60°,则∠AFB= ;如图2,若∠ACD=90°,则∠AFB= ;如图3,若∠ACD=120°,则∠AFB= ;(2)如图4,若∠ACD=α,则∠AFB= (用含α的式子表示); (3)将图4中的△ACD 绕点C 顺时针旋转任意角度(交点F 至少在BD 、AE 中的一条线段上),变成如图5所示的情形,若∠ACD=α,则∠AFB 与α的有何数量关系并给予证明.提示:始终证明DCB ACE ∆≅∆5.如图,已知D 为AB 的中点,AB=AC=10厘米,BC=8厘米,点D 为AB 的中点。
(新)八年级上册数学各种类型典型压轴题练习试题全汇编

(新)八年级上册数学典型压轴题练习试题汇编一、压轴(1) 选填题 (一)多结论证明1.如图,AD 是△ABC 的中线,E ,F 分别是AD 和AD 延长线上的点,且DE =DF ,连接BF ,CE ,下列说法:①CE =BF ;②△ABD 和△ACD 面积相等;③BF ∥CE ;④△BDF ≌△CDE ,其中正确的有( )A .1个B .2个C .3个D .4个FBAC2.如图,在△ABC 中,AB =AC ,∠BAC =90°,BD 平分∠ABC 交AC 于D ,AE ⊥BD 于E ,CF ∥AE 交BD 的延长线于F ;给出四个结论:①∠ACF =12∠ABC ;②CF =12BD ;③BE =2AE +DF ;④CF =AE +DE ,其屮正确的结论有( )A .1个B .2个C .1个D .2个AC3.如图,在Rt △ABC 中,AB =CB ,BO ⊥AC ,把△ABC 折叠,使AB 落在AC 上,点B 与AC 上的点E 重合,展开后,折痕AD 交BO 于点F ,连接DE ,EF ,下列四个结论:①AB =2BD ;②图中有4对全等三角形;③若将△DEF 沿EF 折叠,则点D 一定不会落在AC 上;④BD =BF ,其中正确的是( )A .①②③④B .②③④C .①③④D .②④DBC4.如图,在△ABC 中,∠BAC =90°,AD 是高,BE 是中线,CF 是角平分线,CF 交AD 于点G ,交BE 于点H ,下列说法:①△ABE 的面积=△BCE 的面积;②∠AFG =∠AGF ;③∠FAG =2∠ACF ;④BH =CH ,其中正确的是( )A .①②③④B .①②③C .②④D .①③5.如图,Rt △ACB 中,∠ACB =90°,△ABC 的角平分线AD 、BE 相交于点P ,过P 作PF ⊥AD 交BC 的延长线于点F ,交AC 于点H ,则下列结论:①∠APB =135°;②BF =BA ;③PH =PD ;④连接CP ,CP 平分∠ACB ,其中正确的是( )A .①②③B .①②④C .①③④D .①②③④DC6.如图,△ABC 中,∠ABC =45°,AD ⊥BC 于D 点,BE ⊥AC 于E 点,AD 与BE 交于点F ,连接CF ,DE ,下列结论:①AC =BF ;②∠BED =45°;③BE =AE +2DC ;④若∠ABF =30°,则BF CFAB=1, 其中正确结论的序号是()A .①②③B .①②③④C .①③④D .①③④DABC(二)几何计算7.如图,在△ABC 中,∠BAC =∠BCA =44°,M 为△ABC 内一点,且∠MCA =30°,∠MAC =16°,则∠BMC 的度数为( )A .120°;B .126°C .144°D .150°BCA8.如图,设△ABC 和△CDE 都是等边三角形,若∠AEB =70°,则∠EBD 的度数是( )A .115°B .20°C .125°D .130°DC9.如图,△ABC 中,点D 是BC 上一点,已知∠DAC =30°,∠DAB =75°,CE 平分∠ACB 交AB 于点E 、连DE ,则∠DEC =( )A .10°B .15°C .20°D .25°BACD10.在△ABC 和△BDE 中,点C 在边BD 上,边AC 交边BE 于点F .若AC =BD ,AB =ED ,BC =BE ,则∠ACB 等于( )A .∠EDBB .∠BEDC .12∠AFB C .2∠ABFBADC11.如图,已知△ABC 的面积为8cm 2,BP 为∠ABC 的角平分线,AP 垂直BP 于点P ,则△PBC 的面积为( )A .3.5B .3.9C .4D .4.2DACB12.已知:四边形ABCD 中,对角线BD 平分∠ABC ,∠ACB =72°,∠ABC =50°,并且∠BAD +∠CAD =180°,那么∠BDC 的度数为________.DAB(三)多解与画图13.在△ABC 中,AC =BC ,∠ACB =90°,CE 是过C 点的一条直线,AD ⊥CE 于D ,BE ⊥CE 于E ,DE =4cm ,AD =2cm ,则BE =( )A . 2cmB . 2cmC .6cm 或2cmD .6cm14.△ABC 中,AD 是高,∠BAD =60°,∠CAD =20°,AE 平分∠BAC ,则∠EAD 的度数为____________. 15.如图,在平面直角坐标系中,点A (12,6),∠ABO =90°,一动点从点 B 出发以2厘米/秒的速度沿射线BO 运动,点D 在y 轴上,D 点随着C 点运动而运动,且始终保持OA =C D .当点C 经过_____秒时,△OAB 与△OCD 全等.16.已知△ABC 中,AB =AC ,BD ⊥AC 于D ,AC =2BD ,则∠BAC =______.17.如图,在△ABC 中,AB =BC ,∠ABC =100°,边BA 绕点B 顺时针旋转m °(0<m <180)得到线段BD ,连接AD ,D C .若△ADC 为等腰三角形,则m 所有可能的取值是________.DAC18.如图,等腰Rt △ABC 中,∠ACB =90°将线段AB 绕点A 逆时针旋转,旋转后B 点的对应点为D ,连接C D .若AB ∥CD ,则∠CAD 的度数是_______.CA B19.D 为等腰Rt △ABC 斜边BC 上一点(不与B 、C 童合),DE ⊥BC 于点D ,交直线BA 于点E ,作∠EDF =45°,DF 交AC 于F ,连接EF ,BD =nDC ,当n =________时,△DEF 为等腰直角三角形.20.在平面直角坐标系中,已知A (0,2),B (2,0),若在坐标轴上取点C ,使△ABC 为等腰三角形,满足条件的点C 的个数是( )A .6B .7C .8D .9(四)最值问题21.如图,在△ABC 中,∠C =90°,AC =BC =6,D 为AB 的中点,点E ,F 分别在AC ,BC 边上运动(点E不与点A 、C 重合)且保持∠EDF =90°,连接EF ,在此运动过程中,S △CEF 的最大值为______.FA CBE22.如图,在四边形ABCD 中,∠A =∠C =90°,∠ABC =α,在AB 、BC 上分别一点E 、F ,使△DEF 的周长最小,此时,∠EDF =( )A .αB .90°-αC .2D .180°-2αDBF23.如图,P 为∠AOB 内一定点,M ,N 分别是射线OA ,OB 上一点,当△PMN 周长最小时,∠MPN =110°,则∠AOB =( )A .35°B .40°C .45°D .50°O24.如图,在等腰△ABC 中,AB =AC =5,∠ACB =75°,AD ⊥BC 于D ,点M ,N 分别是线段AB ,线段AD 上的动点,则MN +BN 的最小值是( )A .3BC .4.5D .6AD25.如图,OE 是等边△AOB 的中线,OB =4,C 是直线OE 上一动点,以AC 为边在直线AC 下方作等边△ACD ,连接ED ,下列说法正确的是( )A .ED 的最小值是2B .ED 的最小值是1C .ED 有最大值D .ED 没有最大值也没有最小值D26.如图,AD 为等边△ABC 的高,E ,F 分别为线段AD 、AC 上的动点,且AE =CF ,当BF +CE 取得最小值时,∠AFB =( )A .112.5°B .105°C .90°D .82.5°DABC27.如图,等腰△ABC 底边BC 的长为4cm ,面积是12cm 2,腰AB 的垂直平分线EF 交AC 于点F ,若D 为BC 边上的中点,M 为线段EF 上一动点,则△BDM 的周长最小值为_______.B28.如图,在Rt △ABC 中,∠ACB =90°,∠A =30°.若点M ,N 分别是线段AB ,AC 上两个动点,BC =4,则MC +MN 的最小值为_____.BCAN二、压轴(2)几何合题29.在△ABC 中,AB =AC ,CD 为AB 边上的高 (1)如图1,求证;∠BAC =2∠BCD ;(2)如图2.∠ACD 的平分线CE 交AB 于E ,过E 作EF ⊥BC 于F ,EF 与CD 交点G .若ED =m ,BD =n ,含有m 、n 的代式表示△EGC 的面积.图2图1FBBCA CA30.射线AE 为△ABC 的外角平分线,点P 为射线AE 上不与A 点重合的一个动点. (1)如图1,若BP 平分∠ABC ,且∠ACB =30°,则∠APB =______;(直接写出结果) (2)如图1,求证:不论P 在何处,总有AB +AC <PB +PC ;(3)如图2,若点P 在AE 上,作PM ⊥BA 交BA 的延长线于M 点,且∠BPC =∠BAC ,求AC ABAM-的值.图1图2BBE31.如图,Rt △ACB 中,∠ACB =90°,AB =BC ,E 点为射线CB 上一动点,连接AE ,作AF ⊥AE 且AF =AE(1)如图1,过F 点作FD ⊥AC 交AC 于D 点,求证:EC +CD =DF ;(2)如图2,连接BF 交AC 于G 点,若AGCG=3求证:E 点为BC 的中点; (3)E 点在射线CB 上,连接BF 与直线AC 交于G 点,若43BC BE =,则AGCG=________.图1图2BFBF32.如图,在等腰△ABC 中,AC =BC ,D ,E 分别为AB ,BC 上一点,∠CDE =∠A. (1)如图1,若BC =BD ,求证:CD =DE ;(2)如图2,过点C 作CH ⊥DE ,垂足为点H ,若CD =BD ,EH =1,求DE -BE 的值.图1图2AABCBC33.已知△ABC 中,AC =B C .(1)如图1,分别过A ,B 作AM ⊥BC ,BN ⊥AC ,垂足分别为M ,N ,AM 与BN 相交于点P ,求证:AP =BP . (2)如图2,分别在AC 的右侧、BC 的左侧作等边△ACE 和等边△BCD ,AE 与BD 相交于点F ,连接CF 并延长交AB 于点G 求证:点G 是AB 的中点;(3)在(2)的条件中,当∠ACE 的大小发生变化时,设直线CD 与直线AE 相交于点H .直接写出: 当∠ACB =_______度时,使得AH =C D .图2图1DEABC C34.如图1,已知等腰△ABC 中,AB =AC ,AD 为BC 边上的中线,以AB 为边向外作等边△ABE ,直线CE 与直线AD 交于点F .(1)若AF =10,DF =3,试求EF 的长;(2)若以AB 为边向内作等边△ABE ,其它条件均不改变,用尺规作图补全图2(保留作图痕迹),并直接写出EF ,AF ,DF 三者的数量关系____________.图1图2EBC ACA35.已知:在△ABC 中,∠B =60°,D ,F 分别为AB ,BC 上的点,且AF ,CD 交于点F . (1)如图1,若AE ,CD 为△ABC 的角平分线; ①求证:∠AFC =120°;②若AD =6,CE =4,求AC 的长;(2)如图2,若∠FAC =∠FCA =30°,求证:AD =CE .图2图1AACBCB36.如图,等腰△ABC 中,∠ACB =90°,AC =BC ,D 为AB 上一点. (1)如图1,若AD =AC ,且BE ⊥CD 于点E . ①求∠BCD 的度数;②求CDBE的值; (2)如图2,若F 为CD 上一点,且在线段BC 的垂直平分线上,∠BCD =15°,求证:AF =B C.图2图1BCCAA35.已知:在△ABC 中,∠B =60°,D ,E 分别为AB ,BC 上的点,且AE ,CD 交于点F . (1)如图1,若AE ,CD 为ABC 的角平分线; ①求证:∠AFC =120°;②若AD =6,CE =4,求AC 的长; (2)如图2,若∠FAC =∠FCA =30°,求证:AD =CE .FDECABFDB EC A36.如图,等腰△ABC 中,∠ACB =90°,AC =BC ,D 为AB 上一点. (1)如图1,若AD =AC ,且BE ⊥CD 于点E .①求∠BCD 的度数;②求BECD的值;(2)如图2,若F 为CD 上一点,且在线段BC 上垂直平分线上,∠BCD =15°,求证:AF =BC .A C DE BBFD AC37.(1)如图1,△ABC 中,∠BAC =90°,AB =BC ,直线m 经过点A ,BD ⊥m ,CE ⊥m ,垂足分别为D ,E ,求证:DE =BD +CE ;(2)如图2,将(1)中的条件改为:在△ABC 中,AB =AC ,D ,A ,E 三点都在直线m 上,并且满足∠BDA =∠AEC =∠BAC ,求证:DE =BD +CE ;(3)如图3,D ,E 是D ,A ,E 三点所在直线m 上的两动点(D ,A ,E 三点互不重合),点F 为∠BAC 平分线上的一点,且△ABF 和△ACF 均为等边三角形,连接BD ,CE .若∠BDA =∠AEC =∠BAC ,求证:△DEF 为等边三角形.D AE mCBD A mE CBB FCmEA D38.等腰Rt △ABC 中,CA =CB ,∠ACB =90°,点O 是AB 的中点. (1)如图1,求证:CO =BO ;(2)如图2,点M 在边AC 上,点N 在BC 的延长线上,MN -AM =CN ,求∠MON 的度数; (3)如图3,AD ∥BC ,OD ∥AC ,AD 与OD 交于点D ,Q 是OB 的中点,连接CQ ,DQ ,试判断线段CQ 与DQ 的关系,并给出证明.B O A CNMCA O B39.在△ABC 中,BD 为∠ABC 的平分线. (1)如图1,∠C =2∠DBC ,∠A =60°,求证:△ABC 为等边三角形; (2)如图2,若∠A =2∠C ,BC =8,AB =4.8,求AD 的长度;(3)如图3,若∠ABC =2∠ACB ,∠ACB 的平分线OC 与BD 相交于点O ,且OC =AB ,求∠A 的度数.DCB ACDB AB CODA40.在△ABC 中,∠ACB =90°.(1)如图1,点B 与点D 关于直线AC 对称,连接AD ,点E ,F 分别是线段CD ,AB 上的点(点E 不与点D ,C 重合),且∠AEF =∠ABC ,∠ABC =2∠CAE ,求证:BF =DE ; (2)如图2,若AC =BC ,BD ⊥AD ,连接DC ,求证:∠ADC =45°;(3)如图3,若AC =BC ,点D 在AB 的延长线上,以DC 为斜边作等腰直角△DCE ,过直角顶点E 作EF ⊥AC 于点F ,求证:点F 是AC 的中点.DECBF AACDBDBECF A41.在等腰△ABC 中,∠BAC =90°,AB =AC ,点P 为AC 上一点,M 为BC 上一点. (1)若AM ⊥BP 于点E .①如图1,BP 为△ABC 的角平分线,求证:PA =PM ; ②如图2,BP 为△ABC 的中线,求证:BP =AM +MP ;(2)如图3,若点N 在AB 上,AN =CP ,AM ⊥PN ,求AMPN的值.MEPCB A EPMABCNPMABC42.如图,Rt △ABC 中,∠ACB =90°,AC =BC .F 为BC 延长线上一点,连接AF ,BD ⊥AF 于点D ,BD 与AC 交于点E 点. (1)求证:CE =CF ;(2)如图2,若M 为AB 的中点,N 为AE 的中点,P 为BF 的中点,连接MN ,PN ,求∠MNP 的度数;(3)如图3,以AB 为边作Rt △AHB ,∠AHB =90°,过点C 作CG ⊥BH 于G ,若AH =2,CG =5,请直接写出BH 的长为 .ED FCBAPENMA BCFDABC三、压轴(3)代几综合题43.如图1,在平面直角坐标系中,A (a ,0),B (b ,0),050101022=++-+b a b a ,点C 在y 轴正半轴上.(1)求证:OA =OB ;(2)已知:BD ⊥AC 于D ,DE 平分∠BDC ,交y 轴于点E ,求点E 的坐标;(3)如图2,当∠OAC =60°,且OC =35,点M 为x 轴负半轴上一动点,以CM 为边,在CM 的右侧作等边△CMN ,连接ON ,当ON 最短时,求ON 的长度.44.如图1,直线AB 分别交x 轴,y 轴于A ,B 两点,OC 平分∠AOB 交AB 于点C ,点D 为线段AB 上一点,过D 作DE ∥OC 交y 轴于点E .已知AO =m ,BO =n ,且m ,n 满足0236122=-++-m n n n .(1)求A ,B 两点的坐标;(2)若点D 为AB 的中点,求OE 的长;(3)如图2,若点P (x ,-2x +6)为直线AB 在x 轴下方的一点,点E 是y 轴正半轴上的一动点,以E 为直角顶点作等腰直角△PEF ,使点F 在第一象限,且F 点的横,纵坐标始终相等,求点P 的坐标.45.如图,直线AB 交x 轴于点A (a ,0),交y 轴于点B (0,b ),且a ,b 满足0)5(2=-++a b a .(1)点A 的坐标为 ,点B 的坐标为 ;(2)如图1,若点C 的坐标为(-3,-2),且BE ⊥AC 于点E ,OD ⊥OC 交BE 的延长线于点D ,试求出点D 的坐标;(3)如图2,M ,N 分别为OA ,OB 边上的点,OM =ON ,OP ⊥AN 交AB 于点P ,过点P 作PG ⊥BM 交AN 的延长线于点G ,请写出线段AG ,OP 与PG 之间的数量关系,并证明你的结论.46.如图,在平面直角坐标系中,A (8,0),点B 在第一象限,△OAB 为等边三角形,OC ⊥AB ,垂足为C .(1)直接写出点C 的横坐标;(2)作点C 关于y 轴的对称点D ,连DA 交OB 于点E ,求OE 的长;(3)P 为y 轴上一动点,连接PA ,以PA 为边在PA 所在直线的下方作等边△PAH ,当OH 最短时,求点H 的横坐标.47.平面直角坐标系中,点A (a ,0),点B (0,b ),已知a ,b 满足++-+b a b a 882232=0. (1)求点A ,点B 的坐标;(2)如图1,点E 为线段OB 上一点,连接AE ,过A 作AF ⊥AE ,且AF =AE ,连接BF 交x 轴于于点D ,若点D (-1,0),求点E 的坐标;(3)在(2)条件下,如图2,过E 作EH ⊥OB 交AB 于点H ,点M 是射线EH 上一点(点M 不在线段EH 上),连接MO ,作∠MON =45°,ON 交线段BA 的延长线于点N ,连接MN ,探究线段MN 与OM 的关系.48.在平面直角坐标系中,点A (0,a ),B (b ,0)分别在y 轴与x 轴正半轴上,满足0)16(2=-+-ab b a(1)a = ,b = ,∠OAB 的度数是 ;(2)如图1,已知C (0,1),在第一象限内存在点D ,CD 交AB 于E ,AE 为△ACD 的中线,3=∆ACD S ,求点D 的坐标;(3)如图2,已知P (2,0),连接PA ,在AB 上有一点F ,满足∠APB =∠OPF ,连接OF ,请给出三条线段PA ,PF ,FO 之间的数量关系,并证明你的结论.三、压轴(3)代几综合题43.如图1,在平面直角坐标系中,A (a ,0)、B (b ,0),a 2+b 2-10a +10b +50=0,点C 在y 轴正半轴上.(1)求证:OA =OB ;(2)已知:BD ⊥AC 于D ,DE 平分∠BDC ,交y 轴于点E ,求点E 的坐标;(3)如图2,当∠OAC =60º,且OC =53,点M 为x 轴负半轴上一动点,以CM 为边,在CM 的右侧作等边△CMN ,连接ON ,当ON 最短时,求ON 长度.图1 图244.如图1,直线AB 分别交x 轴,y 轴于A ,B 两点,OC 平分∠AOB 交AB 于点C ,点D 为线段AB 上一点,过D 作DE ∥OC 交y 轴于点E ,已知AO =m ,BO =n ,且m ,n 满足0236122=-++-m n n n ;(1)求A ,B 两点的坐标;(2)若点D 为AB 的中点,求OE 的长?(3)如图2,若点P (x ,-2x +6)为直线AB 在x 轴下方的一点,点E 是y 轴正半轴上的一动点,以E 为直角顶点作等腰直角△PEF ,使点F 在第一象限,且F 点的横,纵坐标始终相等,求点P 的坐标?图1 图245.如图,直线AB 交x 轴点A (a ,0),交y 轴于点B (0,b ),且a ,b 满足()052=-++a b a .(1)点A 的坐标为 ,点B 的坐标为 ;(2)如图1,若点C 的坐标为(-3,-2),且BE ⊥AC 于点E ,OD ⊥OC 交BE 的延长线于点D ,试求点D 的坐标;(3)如图2,M ,N 分别为OA ,OB 边上的点,OM =ON ,OP ⊥AN 交AB 与点P ,过点P 作PG ⊥BM 交AN 的延长线于点G ,请写出线段AG ,OP 与PG 之间的数量关系,并证明你的结论.图1 图246. 如图,在平面直角坐标系中,A (8,0),点B 在第一象限,△OAB 为等边三角形,OC ⊥AB ,垂足为点C .(1)直接写出点C 的横坐标 ;(2)作点C 关于y 轴的对称点D ,连DA 交OB 于点E ,求OE 的长;(3)P 为y 轴上的一动点,连接PA ,以PA 为边在PA 所在直线的下方作等边△PAH .当OH 最短时,求点H 的坐标.47.平面直角坐标系中,点A (a ,0),点B (0,b ),已知a 、b 满足0328822=++-+b a b a ; (1)求点A 、点B 的坐标;(2)如图1,点E 为线段OB 上一点,连接AE ,过A 作AF ⊥AE ,且AF =AE ,连接BF 交x 轴于点D ,若点D (1-,0),求点E 的坐标;(3)在(2)的条件下,如图2,过E 作EH ⊥OB 交AB 于H ,点M 是射线EH 上一点(点M 不在线段EH 上),连接MO ,作∠MON =45°,ON 交线段BA 的延长线于点N ,连接MN ,探究线段MN 与OM 的关系.图1图248.在平面直角坐标系中,点A (0,a ),点B (b ,0)分别在y 轴和x 轴正半轴上,满足()0162=-+-ab b a .(1)a = ,b = ,∠OAB 的度数是 ;(2)如图1,已知C (0,1),在第一象限内存在点D ,CD 交AB 于E ,AE 为△ACD 的中线,S △ACD =3,求点D 的坐标;(3)如图2,已知P (2,0),连接PA ,在AB 上有一点F ,满足∠APB =∠OPF ,连接OF ,情给出三条线段PA ,PF ,FO 之间的数量关系,并证明你的结论.图1图249.如图,已知A (a ,0)、B (0,b ),且a ,b 满足:0328822=++++b a b a .D 为第一象限内一点,连接BD ,连接AD 交y 轴于C 点,且AC =CD (1)求A 、B 点坐标;(2)如图1,若20=ABD S △,求D 点坐标;(3)如图2,过B 作BE ⊥y 轴,且BE =2OC ,连接AE ,问线段AE 和BD 有何数量和位置关系,请证明你的结论.图1图250.如图,已知A (-a ,0)、B (a ,0),点P 为第二象限内一动点,但始终保持PA = a ,∠PAB 的平分线AE 与线段PB 的垂直平分线CD 交于点D ,作DF ⊥AB 于点F . (1)若P 点坐标为(-2,2),求点C 的坐标 (2)求点D 的横坐标(用a 表示)(3)当点P 运动到某一位置时,恰好点C 落在y 轴上,直接写出CDCE=图1图251.已知,点A (0,a )、B (b ,0)、C (c ,0),其中a =|x +2|+|1-x |,且x 满足点(x +1,2x -1)关于x 轴对称的点在第一象限,b 、c 满足|3b +9|+(c +4)2=0.(1)如图1,在△AOC 内有一点D ,连AD 并延长交OC 于点P ,点E 在AC 上,且∠AED =∠AOD ,∠PDE =∠PDO ,若CE =2,求①△AOC 的周长;②OPCP 的值(2)如图2,点M 在线段AB 上(不与A ,B 重合)移动,过点A 作NA ⊥AB 于A ,且∠MON =45°,探究线段AN 、BM 、MN 之间的数量关系并证明你的结论。
人教版八年级数学上册期中考试压轴题专题复习题(含答案)

人教版八年级数学上册期中考试压轴题专题复习题1、在△ABC中,AB=BC,△ABC≌△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点,观察并猜想线段EA1与FC有怎样的数量关系?并证明你的结论.2、两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.求证:(1)△ABE≌△ACD;(2)DC⊥BE.3、如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.(1)若∠C=40°,求∠BAD的度数;(2)若AC=5,DC=4,求△ABC的周长.4、如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;(2)若B、C在DE的两侧(如图所示),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.5、如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.(1)求∠CBE的度数;(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.6、如图,△ABC为等腰直角三角形,点D是边BC上一动点,以AD为直角边作等腰直角△ADE,分别过A、E点向BC边作垂线,垂足分别为F、G.连接BE.(1)证明:BG=FD;(2)求∠ABE的度数.7、如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.(1)求证:OM=ON.(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.8、如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.(1)点D在边AB上时,证明:AB=FA+BD;(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请画出图形并直接写出正确结论.9、如图,△ABC中,∠ACB=90°,AC=BC,将△ABC绕点C逆时针旋转角α.(0°<α<90°)得到△A1B1C1,连接BB1.设CB1交AB于D,A1B1分别交AB、AC于E、F.(1)在图中不再添加其它任何线段的情况下,请你找出一对全等的三角形,并加以说明(△ABC 与△A1B1C1全等除外);(2)当△BB1D是等腰三角形时,求α.10、CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:①如图1,若∠BCA=90°,∠α=90°,则BE CF;(填“>”,“<”或“=”);EF,BE,AF三条线段的数量关系是:.②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件,使①中的两个结论仍然成立,并证明两个结论成立.(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想并证明.11、在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧..作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,当点D在线段BC上,如果∠BAC=90º,则∠BCE= º.(2)设∠BAC=α,∠BCE=β.①如图2,当点D在线段BC上移动,则α、β之间有怎样的数量关系?请说明理由;②当点D在直线BC上移动,则α、β之间有怎样的数量关系?请画出图形,并直接写出你的结论.12、在△ABC中,∠C>∠B,AE平分∠BAC,F为射线AE上一点(不与点E重合),且FD⊥BC 于D;(1)如果点F与点A重合,且∠C=50°,∠B=30°,如图1,求∠EFD的度数;(2)如果点F在线段AE上(不与点A重合),如图2,问∠EFD与∠C﹣∠B有怎样的数量关系?并说明理由.(3)如果点F在△ABC外部,如图3,此时∠EFD与∠C﹣∠B的数量关系是否会发生变化?请说明理由.13、如图,△ABC是等边三角形,AB=6,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.(1)当∠BQD=30°时,求AP的长;(2)证明:在运动过程中,点D是线段PQ的中点;(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.14、问题背景:如图1:在四边形ABC 中,AB=AD,∠BAD=120∘,∠B=∠ADC=90∘.E,F 分别是BC,CD 上的点。
八年级数学上册压轴题 期末复习试卷测试卷(含答案解析)

八年级数学上册压轴题期末复习试卷测试卷(含答案解析)一、压轴题1.在平面直角坐标系中,点A、B在坐标轴上,其中A(0,a)、B(b,0)满足:222110a b a b--++-=.(1)直接写出A 、B 两点的坐标;(2)将线段AB平移到CD,点A的对应点为C(-3,m),如图(1)所示.若SΔABC=16,求点D 的坐标;(3)平移线段AB到CD,若点C、D也在坐标轴上,如图(2)所示,P为线段AB上一动点(不与A、B重合),连接OP,PE平分∠OPB,交x轴于点M,且满足∠BCE=2∠ECD.求证:∠BCD=3(∠CEP-∠OPE).2.已知ABC是等腰直角三角形,∠C=90°,点M是AC的中点,延长BM至点D,使DM =BM,连接AD.(1)如图①,求证:DAM≌BCM;(2)已知点N是BC的中点,连接AN.①如图②,求证:ACN≌BCM;②如图③,延长NA至点E,使AE=NA,连接,求证:BD⊥DE.3.如图,直线l1:y1=﹣x+2与x轴,y轴分别交于A,B两点,点P(m,3)为直线l1上一点,另一直线l2:y2=12x+b过点P.(1)求点P坐标和b的值;(2)若点C是直线l2与x轴的交点,动点Q从点C开始以每秒1个单位的速度向x轴正方向移动.设点Q的运动时间为t秒.①请写出当点Q 在运动过程中,△APQ 的面积S 与t 的函数关系式;②求出t 为多少时,△APQ 的面积小于3;③是否存在t 的值,使△APQ 为等腰三角形?若存在,请求出t 的值;若不存在,请说明理由.4.如图,在ABC ∆中,90,,8ACB AC BC AB cm ∠=︒==,过点C 做射线CD ,且//CD AB ,点P 从点C 出发,沿射线CD 方向均匀运动,速度为3/cm s ;同时,点Q 从点A 出发,沿AB 向点B 匀速运动,速度为1/cm s ,当点Q 停止运动时,点P 也停止运动.连接,PQ CQ ,设运动时间为()()08t s t <<.解答下列问题:(1)用含有t 的代数式表示CP 和BQ 的长度;(2)当2t =时,请说明//PQ BC ;(3)设BCQ ∆的面积为()2S cm ,求S 与t 之间的关系式.5.如图,已知A(3,0),B(0,-1),连接AB ,过B 点作AB 的垂线段BC ,使BA=BC ,连接AC(1)如图1,求C 点坐标;(2)如图2,若P 点从A 点出发沿x 轴向左平移,连接BP ,作等腰直角BPQ ,连接CQ ,当点P 在线段OA 上,求证:PA=CQ ;(3)在(2)的条件下若C 、P ,Q 三点共线,直接写出此时∠APB 的度数及P 点坐标6.(1)在等边三角形ABC中,①如图①,D,E分别是边AC,AB上的点且AE=CD,BD与EC交于点F,则∠BFE的度数是度;②如图②,D,E分别是边AC,BA延长线上的点且AE=CD,BD与EC的延长线交于点F,此时∠BFE的度数是度;(2)如图③,在△ABC中,AC=BC,∠ACB是锐角,点O是AC边的垂直平分线与BC的交点,点D,E分别在AC,OA的延长线上,AE=CD,BD与EC的延长线交于点F,若∠ACB=α,求∠BFE的大小.(用含α的代数式表示).7.在平面直角坐标系xOy中,若P,Q为某个矩形不相邻的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.图1为点P,Q的“相关矩形”的示意图.已知点A的坐标为(1,2).(1)如图2,点B的坐标为(b,0).①若b=﹣2,则点A,B的“相关矩形”的面积是;②若点A,B的“相关矩形”的面积是8,则b的值为.(2)如图3,点C在直线y=﹣1上,若点A,C的“相关矩形”是正方形,求直线AC的表达式;(3)如图4,等边△DEF的边DE在x轴上,顶点F在y轴的正半轴上,点D的坐标为(1,0).点M的坐标为(m,2),若在△DEF的边上存在一点N,使得点M,N的“相关矩形”为正方形,请直接写出m的取值范围.8.阅读下面材料,完成(1)-(3)题.数学课上,老师出示了这样一道题:如图1,已知等腰△ABC中,AB=AC,AD为BC边上的中线,以AB为边向AB左侧作等边△ABE,直线CE与直线AD交于点F.请探究线段EF、AF、DF之间的数量关系,并证明.同学们经过思考后,交流了自已的想法:小明:“通过观察和度量,发现∠DFC的度数可以求出来.”小强:“通过观察和度量,发现线段DF和CF之间存在某种数量关系.”小伟:“通过做辅助线构造全等三角形,就可以将问题解决.”......老师:“若以AB为边向AB右侧作等边△ABE,其它条件均不改变,请在图2中补全图形,探究线段EF、AF、DF三者的数量关系,并证明你的结论.”(1)求∠DFC的度数;(2)在图1中探究线段EF、AF、DF之间的数量关系,并证明;(3)在图2中补全图形,探究线段EF 、AF 、DF 之间的数量关系,并证明.9.(阅读材科)小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若∠BAC =∠DAE ,AB =AC ,AD =AE ,则△ABD ≌△ACE .(材料理解)(1)在图1中证明小明的发现.(深入探究)(2)如图2,△ABC 和△AED 是等边三角形,连接BD ,EC 交于点O ,连接AO ,下列结论:①BD =EC ;②∠BOC =60°;③∠AOE =60°;④EO =CO ,其中正确的有 .(将所有正确的序号填在横线上).(延伸应用)(3)如图3,AB =BC ,∠ABC =∠BDC =60°,试探究∠A 与∠C 的数量关系.10.如图,在边长为2的等边三角形ABC 中,D 点在边BC 上运动(不与B ,C 重合),点E 在边AB 的延长线上,点F 在边AC 的延长线上,AD DE DF ==. (1)若30AED ∠=︒,则ADB =∠______.(2)求证:BED CDF △≌△.(3)试说明点D 在BC 边上从点B 至点C 的运动过程中,BED 的周长l 是否发生变化?若不变,请求出l 的值,若变,请求出l 的取值范围.11.在《经典几何图形的研究与变式》一课中,庞老师出示了一个问题:“如图1,等腰直角三角形的三个顶点分别落在三条等距的平行线1l ,2l ,3l 上,90BAC ∠=︒,且每两条平行线之间的距离为1,求AB 的长度”.在研究这道题的解法和变式的过程中,同学们提出了很多想法:(1)小明说:我只需要过B 、C 向1l 作垂线,就能利用全等三角形的知识求出AB 的长. (2)小林说:“我们可以改变ABC 的形状.如图2,AB AC =,120BAC ∠=︒,且每两条平行线之间的距离为1,求AB 的长.”(3)小谢说:“我们除了改变ABC 的形状,还能改变平行线之间的距离.如图3,等边三角形ABC 三个顶点分别落在三条平行线1l ,2l ,3l 上,且1l 与2l 之间的距离为1,2l 与3l 之间的距离为2,求AB 的长、”请你根据3位同学的提示,分别求出三种情况下AB 的长度.12.在Rt ABC 中,ACB =∠90°,30A ∠=︒,点D 是AB 的中点,连结CD .(1)如图①,BC 与BD 之间的数量关系是_________,请写出理由;(2)如图②,若P 是线段CB 上一动点(点P 不与点B 、C 重合),连结DP ,将线段DP 绕点D 逆时针旋转60°,得到线段DF ,连结BF ,请猜想BF ,BP ,BD 三者之间的数量关系,并证明你的结论;(3)若点P 是线段CB 延长线上一动点,按照(2)中的作法,请在图③中补全图形,并直接写出BF ,BP ,BD 三者之间的数量关系.【参考答案】***试卷处理标记,请不要删除一、压轴题1.(1)A (0,3),B (4,0);(2)D (1,-265);(3)见解析【解析】【分析】(1)根据非负数的性质求解;(2)如图1中,设直线CD交y轴于E.首先求出点E的坐标,再求出直线CD的解析式以及点C坐标,利用平移的性质得到点D坐标;(3)如图2中,延长AB交CE的延长线于M.利用平行线的性质以及三角形的外角的性质求证;【详解】(1)∵222110a b a b--++-=,∴220,2110a b a b--=+-=,∴2202110a ba b--=⎧⎨+-=⎩,∴34ab=⎧⎨=⎩,∴A(0,3),B(4,0);(2)如图1中,设直线CD交y轴于E.∵CD//AB,∴S△ACB=S△ABE,∴12AE×BO=16,∴12×AE×4=16,∴AE=8,∴E(0,-5),设直线AB的解析式为y=kx+b,将点A(0,3),(4,0)代入解析式中得:343kb⎧=-⎪⎨⎪=⎩,∴直线AB的解析式为y=334x-+,∵AB//CD , ∴直线CD 的解析式为y=34x c -+, 又∵点E (0,-5)在直线CD 上,∴c=5,即直线CD 的解析式为y=354x --, 又∵点C (-3,m )在直线CD 上,∴m=115, ∴C (-3, 115), ∵点A (0,3)平移后的对应点为C (-3,115), ∴直线AB 向下平移了265个单位,向左平移了3个单位, 又∵B (4,0)的对应点为点D ,∴点D 的坐标为(1,-265); (3)如图2中,延长AB 交CE 的延长线于点M .∵AM ∥CD ,∴∠DCM=∠M ,∵∠BCE=2∠ECD ,∴∠BCD=3∠DCM=3∠M ,∵∠M=∠PEC-∠MPE ,∠MPE=∠OPE ,∴∠BCD=3(∠CEP-∠OPE ).【点睛】考查了非负数的性质、平行线的性质、三角形的外角的性质、一次函数的应用等知识,解题关键是灵活运用所学知识解决问题,学会添加常用辅助线,利用平行线的性质解决问题.2.(1)见解析;(2)①见解析;②见解析【解析】【分析】(1)由点M是AC中点知AM=CM,结合∠AMD=∠CMB和DM=BM即可得证;(2)①由点M,N分别是AC,BC的中点及AC=BC可得CM=CN,结合∠C=∠C和BC=AC 即可得证;②取AD中点F,连接EF,先证△EAF≌△ANC得∠NAC=∠AEF,∠C=∠AFE=90°,据此知∠AFE=∠DFE=90°,再证△AFE≌△DFE得∠EAD=∠EDA=∠ANC,从而由∠EDB=∠EDA+∠ADB=∠EAD+∠NAC=180°-∠DAM即可得证.【详解】解:(1)∵点M是AC中点,∴AM=CM,在△DAM和△BCM中,∵AM CMAMD CMBDM BM=⎧⎪∠=∠⎨⎪=⎩,∴△DAM≌△BCM(SAS);(2)①∵点M是AC中点,点N是BC中点,∴CM=12AC,CN=12BC,∵△ABC是等腰直角三角形,∴AC=BC,∴CM=CN,在△BCM和△ACN中,∵CM CNC CBC AC=⎧⎪∠=∠⎨⎪=⎩,∴△BCM≌△ACN(SAS);②证明:取AD中点F,连接EF,则AD=2AF,∵△BCM≌△ACN,∴AN=BM,∠CBM=∠CAN,∵△DAM≌△BCM,∴∠CBM=∠ADM,AD=BC=2CN,∴AF=CN,∴∠DAC=∠C=90°,∠ADM=∠CBM=∠NAC ,由(1)知,△DAM ≌△BCM ,∴∠DBC=∠ADB ,∴AD ∥BC ,∴∠EAF=∠ANC ,在△EAF 和△ANC 中,AE AN EAF ANC AF NC =⎧⎪∠=∠⎨⎪=⎩,∴△EAF ≌△ANC (SAS ),∴∠NAC=∠AEF ,∠C=∠AFE=90°,∴∠AFE=∠DFE=90°,∵F 为AD 中点,∴AF=DF ,在△AFE 和△DFE 中,AF DF AFE DFE EF EF =⎧⎪∠=∠⎨⎪=⎩,∴△AFE ≌△DFE (SAS ),∴∠EAD=∠EDA=∠ANC ,∴∠EDB=∠EDA+∠ADB=∠EAD+∠NAC=180°-∠DAM=180°-90°=90°,∴BD ⊥DE .【点睛】本题是三角形的综合问题,解题的关键是掌握中点的性质、等腰直角三角形的性质、全等三角形的判定与性质等知识点.3.(1)b=72;(2)①△APQ 的面积S 与t 的函数关系式为S=﹣32t +272或S=32t ﹣272;②7<t <9或9<t <11,③存在,当t 的值为3或9+或9﹣或6时,△APQ 为等腰三角形.【解析】分析:(1)把P (m ,3)的坐标代入直线1l 的解析式即可求得P 的坐标,然后根据待定系数法即可求得b ;(2)根据直线2l 的解析式得出C 的坐标,①根据题意得出9AQ t =-,然后根据12P S AQ y =⋅即可求得APQ 的面积S 与t 的函数关系式;②通过解不等式273322t -<或327 3.22t -<即可求得7<t <9或9<t <11.时,APQ 的面积小于3;③分三种情况:当PQ =PA 时,则()()()2222(71)032103,t -++-=++-当AQ =PA 时,则()()222(72)2103,t --=++-当PQ =AQ 时,则()222(71)03(72)t t -++-=--,即可求得.详解:解;(1)∵点P (m ,3)为直线l 1上一点,∴3=−m +2,解得m =−1,∴点P 的坐标为(−1,3),把点P 的坐标代入212y x b =+ 得,()1312b =⨯-+, 解得72b =; (2)∵72b =; ∴直线l 2的解析式为y =12x +72,∴C 点的坐标为(−7,0),①由直线11:2l y x =-+可知A (2,0),∴当Q 在A . C 之间时,AQ =2+7−t =9−t , ∴11273(9)32222S AQ yP t t =⋅=⨯-⨯=-; 当Q 在A 的右边时,AQ =t −9, ∴11327(9)32222S AQ yP t t ;=⋅=⨯-⨯=- 即△APQ 的面积S 与t 的函数关系式为27322S t =-或327.22S t =- ②∵S <3, ∴273322t -<或327 3.22t -< 解得7<t <9或9<t <11. ③存在;设Q (t −7,0),当PQ =PA 时,则()()()2222(71)032103,t -++-=++-∴22(6)3t -=,解得t =3或t =9(舍去), 当AQ =PA 时,则()()222(72)2103,t --=++-∴2(9)18,t -=解得9t =+9t =- 当PQ =AQ 时,则()222(71)03(72)t t -++-=--,∴22(6)9(9)t t -+=-, 解得t =6.故当t 的值为3或9+9-6时,△APQ 为等腰三角形.点睛:属于一次函数综合题,考查了一次函数图象上点的坐标特征,待定系数法求函数解析式,等腰三角形的性质以及三角形的面积,分类讨论是解题的关键.4.(1)CP=3t,BQ=8-t;(2)见解析;(3)S=16-2t.【解析】【分析】(1)直接根据距离=速度⨯时间即可;(2)通过证明PCQ BQC≅,得到∠PQC=∠BCQ,即可求证;(3)过点C作CM⊥AB,垂足为M,根据等腰直角三角形的性质得到CM=AM=4,即可求解.【详解】解:(1)CP=3t,BQ=8-t;(2)当t=2时,CP=3t=6,BQ=8-t=6∴CP=BQ∵CD∥AB∴∠PCQ=∠BQC又∵CQ=QC∴PCQ BQC≅∴∠PQC=∠BCQ∴PQ∥BC(3)过点C作CM⊥AB,垂足为M∵AC=BC,CM⊥AB∴AM=118422AB=⨯=(cm)∵AC=BC,∠ACB=90︒∴∠A=∠B=45︒∵CM⊥AB∴∠AMC=90︒∴∠ACM=45︒∴∠A=∠ACM∴CM=AM=4(cm ) ∴118t 416222BCQ S BQ CM t ==⨯-⨯=- 因此,S 与t 之间的关系式为S=16-2t .【点睛】 此题主要考查列代数式、全等三角形的判定与性质、平行线的判定、等腰三角形的性质,熟练掌握逻辑推理是解题关键.5.(1)(1,-4);(2)证明见解析;(3)()135,1,0APB P ︒∠= 【解析】【分析】(1)作CH ⊥y 轴于H ,证明△ABO ≌△BCH ,根据全等三角形的性质得到BH=OA=3,CH=OB=1,求出OH ,得到C 点坐标;(2)证明△PBA ≌△QBC ,根据全等三角形的性质得到PA=CQ ;(3)根据C 、P ,Q 三点共线,得到∠BQC=135°,根据全等三角形的性质得到∠BPA=∠BQC=135°,根据等腰三角形的性质求出OP ,得到P 点坐标.【详解】解:(1)作CH ⊥y 轴于H ,则∠BCH+∠CBH=90°,因为AB BC ⊥,所以.∠ABO+∠CBH=90°,所以∠ABO=∠BCH ,在△ABO 和△BCH 中,ABO BCH AOB BHC AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩ABO BCH ∴∆≅∆:BH=OA=3,CH=OB=1,:OH=OB+BH=4,所以C 点的坐标为(1,-4);(2)因为∠PBQ=∠ABC=90°,,PBQ ABQ ABC ABQ PBA QBC ∴∠-=∠-∠∴∠=∠在△PBA 和△QBC 中,BP BQ PBA QBC BA BC =⎧⎪∠=∠⎨⎪=⎩PBA QBC ∴∆≅∆:.PA=CQ ;(3) ()135,1,0APB P ︒∠= BPQ ∆是等腰直角三角形,:所以∠BQP=45°,当C 、P ,Q 三点共线时,∠BQC=135°,由(2)可知,PBA QBC ∴∆≅∆;所以∠BPA=∠BQC=135°,所以∠OPB=45°,所以.OP=OB=1,所以P 点坐标为(1,0) .【点睛】本题考查的是全等三角形的判定和性质、三角形的外角的性质,掌握全等三角形的判定定理和性质定理是解题的关键.6.(1)①60°;②60°;(2)∠BFE =α.【解析】【分析】(1)①先证明△ACE ≌△CBD 得到∠ACE=∠CBD ,再由三角形外角和定理可得∠BFE=∠CBD+∠BCF ;②先证明△ACE ≌△CBD 得∠ACE=∠CBD=∠DCF ,再由三角形外角和定理可得∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA ;(2)证明△AEC ≌△CDB 得到∠E=∠D ,则∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α.【详解】(1)如图①中,∵△ABC 是等边三角形,∴AC=CB ,∠A=∠BCD=60°,∵AE=CD ,∴△ACE ≌△CBD ,∴∠ACE=∠CBD ,∴∠BFE=∠CBD+∠BCF=∠ACE+∠BCF=∠BCA=60°.故答案为60.(2)如图②中,∵△ABC是等边三角形,∴AC=CB,∠A=∠BCD=60°,∴∠CAE=∠BCD=′120°∵AE=CD,∴△ACE≌△CBD,∴∠ACE=∠CBD=∠DCF,∴∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA=60°.故答案为60.(3)如图③中,∵点O是AC边的垂直平分线与BC的交点,∴OC=OA,∴∠EAC=∠DCB=α,∵AC=BC,AE=CD,∴△AEC≌△CDB,∴∠E=∠D,∴∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α.【点睛】本题综合考查了三角形全等以及三角形外角和定理.7.(1)①6;②5或﹣3;(2)直线AC的表达式为:y=﹣x+3或y=x+1;(3)m的取值范围为﹣3≤m≤﹣323m≤3.【解析】【分析】(1)①由矩形的性质即可得出结果;②由矩形的性质即可得出结果;(2)过点A(1,2)作直线y=﹣1的垂线,垂足为点G,则AG=3求出正方形AGCH的边长为3,分两种情况求出直线AC的表达式即可;(3)由题意得出点M在直线y=2上,由等边三角形的性质和题意得出OD=OE=12DE=1,EF=DF=DE=2,得出OF OD①当点N在边EF上时,若点N与E重合,点M,N的“相关矩形”为正方形,则点M的坐标为(﹣3,2)或(1,2);若点N与F重合,点M,N的“相关矩形”为正方形,则点M的坐标为(﹣2);得出m的取值范围为﹣3≤m≤﹣或2﹣≤m≤1;②当点N在边DF上时,若点N与D重合,点M,N的“相关矩形”为正方形,则点M 的坐标为(3,2)或(﹣1,2);若点N与F重合,点M,N的“相关矩形”为正方形,则点M的坐标为(22);得出m的取值范围为2≤m≤3或2﹣≤m≤1;即可得出结论.【详解】解:(1)①∵b=﹣2,∴点B的坐标为(﹣2,0),如图2﹣1所示:∵点A的坐标为(1,2),∴由矩形的性质可得:点A,B的“相关矩形”的面积=(1+2)×2=6,故答案为:6;②如图2﹣2所示:由矩形的性质可得:点A,B的“相关矩形”的面积=|b﹣1|×2=8,∴|b﹣1|=4,∴b=5或b=﹣3,故答案为:5或﹣3;(2)过点A(1,2)作直线y=﹣1的垂线,垂足为点G,则AG=3,∵点C在直线y=﹣1上,点A,C的“相关矩形”AGCH是正方形,∴正方形AGCH的边长为3,当点C在直线x=1右侧时,如图3﹣1所示:CG=3,则C(4,﹣1),设直线AC的表达式为:y=kx+a,则214k ak a=+⎧⎨-=+⎩,解得;13ka=-⎧⎨=⎩,∴直线AC的表达式为:y=﹣x+3;当点C在直线x=1左侧时,如图3﹣2所示:CG=3,则C(﹣2,﹣1),设直线AC的表达式为:y=k′x+b,则212k bk b=+⎧⎨-=-+''⎩,解得:k1 b1=⎧⎨='⎩,∴直线AC的表达式为:y=x+1,综上所述,直线AC的表达式为:y=﹣x+3或y=x+1;(3)∵点M的坐标为(m,2),∴点M在直线y=2上,∵△DEF是等边三角形,顶点F在y轴的正半轴上,点D的坐标为(1,0),∴OD=OE=12DE=1,EF=DF=DE=2,∴OF=3OD=3,分两种情况:如图4所示:①当点N在边EF上时,若点N与E重合,点M,N的“相关矩形”为正方形,则点M的坐标为(﹣3,2)或(1,2);若点N与F重合,点M,N的“相关矩形”为正方形,则点M的坐标为(﹣2+3,2)或(2﹣3,2);∴m的取值范围为﹣3≤m≤﹣2+3或2﹣3≤m≤1;②当点N在边DF上时,若点N与D重合,点M,N的“相关矩形”为正方形,则点M的坐标为(3,2)或(﹣1,2);若点N与F重合,点M,N的“相关矩形”为正方形,则点M的坐标为(2﹣3,2)或(﹣2+3,2);∴m的取值范围为2﹣3≤m≤3或﹣1≤m≤﹣2+3;综上所述,m的取值范围为﹣3≤m≤﹣2+3或2﹣3≤m≤3.【点睛】此题主要考查图形与坐标综合,解题的关键是熟知正方形的性质、一次函数的图像与性质及新定义的应用.8.(1)60°;(2)EF=AF+FC,证明见解析;(3)AF=EF+2DF,证明见解析.【解析】【分析】(1)可设∠BAD=∠CAD=α,∠AEC=∠ACE=β,在△ACE中,根据三角形内角和可得2α+60+2β=180°,从而有α+β=60°,即可得出∠DFC的度数;(2)在EC上截取EG=CF,连接AG,证明△AEG≌△ACF,然后再证明△AFG为等边三角形,从而可得出EF=EG+GF=AF+FC;(3)在AF上截取AG=EF,连接BG,BF,证明方法类似(2),先证明△ABG≌△EBF,再证明△BFG为等边三角形,最后可得出结论.【详解】解:(1)∵AB=AC,AD为BC边上的中线,∴可设∠BAD=∠CAD=α,又△ABE为等边三角形,∴AE=AB=AC,∠EAB=60°,∴可设∠AEC=∠ACE=β,在△ACE中,2α+60°+2β=180°,∴α+β=60°,∴∠DFC=α+β=60°;(2)EF=AF+FC,证明如下:∵AB=AC,AD为BC边上的中线,∴AD⊥BC,∴∠FDC=90°,∵∠CFD=60°,则∠DCF=30°,∴CF=2DF,在EC上截取EG=CF,连接AG,又AE=AC,∴∠AEG=∠ACF,∴△AEG≌△ACF(SAS),∴∠EAG=∠CAF,AG=AF,又∠CAF=∠BAD,∴∠EAG=∠BAD,∴∠GAF=∠BAD+∠BAG=∠EAG+∠BAG=∠60°,∴△AFG为等边三角形,∴EF=EG+GF=AF+FC,即EF=AF+FC;(3)补全图形如图所示,结论:AF=EF+2DF.证明如下:同(1)可设∠BAD =∠CAD =α,∠ACE =∠AEC =β,∴∠CAE =180°-2β,∴∠BAE =2α+180°-2β=60°,∴β-α=60°,∴∠AFC=β-α=60°,又△ABE 为等边三角形,∴∠ABE=∠AFC=60°,∴由8字图可得:∠BAD =∠BEF ,在AF 上截取AG =EF ,连接BG ,BF ,又AB=BE ,∴△ABG ≌△EBF (SAS ),∴BG =BF ,又AF 垂直平分BC ,∴BF=CF ,∴∠BFA=∠AFC=60°,∴△BFG 为等边三角形,∴BG=BF ,又BC ⊥FG ,∴FG=BF=2DF ,∴AF =AG +GF =BF +EF =2DF +EF .【点睛】本题考查了全等三角形的判定和性质、等边三角形的性质、等腰三角形的性质等知识,解决问题的关键是常用辅助线构造全等三角形,属于中考常考题型.9.(1)证明见解析;(2)①②③;(3)∠A +∠C =180°.【解析】【分析】(1)利用等式的性质得出∠BAD=∠CAE ,即可得出结论;(2)同(1)的方法判断出△ABD ≌△ACE ,得出BD=CE ,再利用对顶角和三角形的内角和定理判断出∠BOC=60°,再判断出△BCF ≌△ACO ,得出∠AOC=120°,进而得出∠AOE=60°,再判断出BF <CF ,进而判断出∠OBC >30°,即可得出结论;(3)先判断出△BDP 是等边三角形,得出BD=BP ,∠DBP=60°,进而判断出△ABD ≌△CBP (SAS ),即可得出结论.【详解】(1)证明:∵∠BAC=∠DAE ,∴∠BAC+∠CAD=∠DAE+∠CAD ,∴∠BAD=∠CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩=== , ∴△ABD ≌△ACE ;(2)如图2,∵△ABC 和△ADE 是等边三角形,∴AB=AC ,AD=AE ,∠BAC=∠DAE=60°,∴∠BAD=∠CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩=== , ∴△ABD ≌△ACE ,∴BD=CE ,①正确,∠ADB=∠AEC ,记AD 与CE 的交点为G ,∵∠AGE=∠DGO ,∴180°-∠ADB-∠DGO=180°-∠AEC-∠AGE ,∴∠DOE=∠DAE=60°,∴∠BOC=60°,②正确,在OB 上取一点F ,使OF=OC ,∴△OCF 是等边三角形,∴CF=OC ,∠OFC=∠OCF=60°=∠ACB ,∴∠BCF=∠ACO ,∵AB=AC ,∴△BCF ≌△ACO (SAS ),∴∠AOC=∠BFC=180°-∠OFC=120°,∴∠AOE=180°-∠AOC=60°,③正确,连接AF ,要使OC=OE ,则有OC=12CE , ∵BD=CE , ∴CF=OF=12BD , ∴OF=BF+OD ,∴BF <CF , ∴∠OBC >∠BCF ,∵∠OBC+∠BCF=∠OFC=60°,∴∠OBC >30°,而没办法判断∠OBC 大于30度,所以,④不一定正确,即:正确的有①②③,故答案为①②③;(3)如图3,延长DC 至P ,使DP=DB ,∵∠BDC=60°,∴△BDP 是等边三角形,∴BD=BP ,∠DBP=60°,∵∠BAC=60°=∠DBP ,∴∠ABD=∠CBP ,∵AB=CB ,∴△ABD ≌△CBP (SAS ),∴∠BCP=∠A , ∵∠BCD+∠BCP=180°,∴∠A+∠BCD=180°.【点睛】此题考查三角形综合题,等腰三角形的性质,等边三角形的性质,全等三角形的判定和性质,构造等边三角形是解题的关键.10.(1)90°;(2)证明见解析;(3)变化,234l +≤<.【解析】【分析】(1)由等边三角形的性质可得∠ABC=∠ACB=60°,由等腰三角形的性质可求DAE=∠DEA=30°,由三角形内角和定理可求解;(2)根据等腰三角形的性质,可证得∠CDF=∠DEA 和∠EDB=∠DFA ,由此可利用“ASA”证明全等;(3)根据全等三角形的性质可得l =2+AD ,根据AD 的取值范围即可得出l 的取值范围.【详解】解:(1)∵△ABC 是等边三角形,∴AB=AC=BC=2,∠ABC=∠ACB=60°,∵AD=DE∴∠DAE=∠DEA=30°,∴∠ADB=180°-∠BAD-∠ABD=90°,故答案为:90°;(2)∵AD=DE=DF ,∴∠DAE=∠DEA ,∠DAF=∠DFA ,∵∠DAE+∠DAF=∠BAC=60°,∴∠DEA+∠DFA=60°,∵∠ABC=∠DEA+∠EDB=60°,∴∠EDB=∠DFA ,∵∠ACB=∠DFA+∠CDF=60°,∴∠CDF=∠DEA ,在△BDE 和△CFD 中∵CDF DEA DE DF EDB DFA ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△BDE ≌△CFD (ASA )(3)∵△BDE ≌△CFD ,∴BE=CD ,∴l =BD+BE+DE=BD+CD+AD=BC+AD=2+AD ,当D 点在C 或B 点时,AD=AC=AB=2,此时B 、D 、E 三点在同一条直线上不构成三角形,2+AD=4;当D 点在BC 的中点时,∵AB=AC ,∴BD=112BC =,AD ==此时22l AD =+=综上可知24l +≤<.【点睛】本题考查全等三角形的性质和判定,勾股定理,等边三角形的性质,等腰三角形的性质,三角形内角和定理.(1)掌握等腰三角形等边对等角是解决此问的关键;(2)中注意角之间的转换;(3)中注意临界点是否可取.11.(123【解析】【分析】(1)分别过点B ,C 向l 1作垂线,交l 1于M ,N 两点,证明△ABM ≌△CAN ,得到AM=CN,AN=BM ,即可得出AB ;(2)分别过点B ,C 向l 1作垂线,交l 1于点P ,Q 两点,在l 1上取M ,N 使∠AMB=∠CNA=120°,证明△AMB ≌△CAN ,得到CN=AM ,再通过△PBM 和△QCN 算出PM 和NQ 的值,得到AP ,最后在△APB 中,利用勾股定理算出AB 的长;(3)在l 3上找M 和N ,使得∠BNC=∠AMC=60°,过B 作l 3的垂线,交l 3于点P ,过A 作l 3的垂线,交l 3于点Q ,证明△BCN ≌△CAM ,得到CN=AM ,在△BPN 和△AQM 中利用勾股定理算出NP 和AM ,从而得到PC ,结合BP 算出BC 的长,即为AB.【详解】解:(1)如图,分别过点B ,C 向l 1作垂线,交l 1于M ,N 两点,由题意可得:∠BAC=90°,∵∠NAC+∠MAB=90°,∠NAC+∠NCA=90°,∴∠MAB=∠NCA ,在△ABM 和△CAN 中,===AMB CNA MAB NCA AB AC ∠∠⎧⎪∠∠⎨⎪⎩,∴△ABM ≌△CAN (AAS ),∴AM=CN=2,AN=BM=1,∴AB=22251=+;(2)分别过点B ,C 向l 1作垂线,交l 1于P ,Q 两点,在l 1上取M ,N 使∠AMB=∠CNA=120°,∵∠BAC=120°,∴∠MAB+∠NAC=60°,∵∠ABM+∠MAB=60°,∴∠ABM=∠NAC ,在△AMB 和△CNA 中,===AMB CNA ABM NAC AB AC ∠∠⎧⎪∠∠⎨⎪⎩,∴△AMB ≌△CNA (AAS ),∴CN=AM ,∵∠AMB=∠ANC=120°, ∴∠PMB=∠QNC=60°,∴PM=12BM ,NQ=12NC , ∵PB=1,CQ=2,设PM=a ,NQ=b , ∴2221=4a a +,2222=4b b +,解得:3=3a ,23=3b , ∴CN=AM=222323⎛⎫+ ⎪ ⎪⎝⎭=43, ∴AB=22AP BP +=()22AM PM BP ++=2213;(3)如图,在l 3上找M 和N ,使得∠BNC=∠AMC=60°,过B 作l 3的垂线,交于点P ,过A 作l 3的垂线,交于点Q ,∵△ABC 是等边三角形,∴BC=AC ,∠ACB=60°,∴∠BCN+∠ACM=120°,∵∠BCN+∠NBC=120°,∴∠NBC=∠ACM ,在△BCN 和△CAM 中,BNC CMA NBC MAC BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCN ≌△CAM (AAS ),∴CN=AM ,BN=CM ,∵∠PBN=90°-60°=30°,BP=2,∴BN=2NP ,在△BPN 中,222BP NP BN +=,即22224NP NP +=,解得:NP=233, ∵∠AMC=60°,AQ=3,∴∠MAQ=30°,∴AM=2QM ,在△AQM 中,222AQ QM AM +=,即22234QM QM +=,解得:QM=3,∴AM=23=CN ,∴PC=CN-NP=AM-NP=43, 在△BPC 中,BP 2+CP 2=BC 2,即BC=22224322123BP CP ⎛⎫+=+= ⎪ ⎪⎝⎭, ∴AB=BC=221.【点睛】本题考查了全等三角形的判定和性质,平行线之间的距离,等腰三角形的性质,等边三角形的性质以及勾股定理,解题的关键是利用平行线构造全等三角形,再利用全等三角形的性质以及勾股定理求解.12.(1)BC BD =,理由见解析;(2)BF BP BD +=,证明见解析;(3)BF BP BD +=.【解析】【分析】(1)利用含30的直角三角形的性质得出12BC AB =,即可得出结论; (2)同(1)的方法得出BC BD =进而得出BCD ∆是等边三角形,进而利用旋转全等模型易证DCP DBF ∆≅∆,得出CP BF =即可解答;(3)同(2)的方法得出结论.【详解】解:(1)90ACB ∠=︒,30A ∠=︒,60CBA ∴∠=︒,12BC AB =, 点D 是AB 的中点,BC BD ∴=,故答案为:BC BD =;(2)BF BP BD +=,理由:90ACB ∠=︒,30A ∠=︒,60CBA ∴∠=︒,12BC AB =, 点D 是AB 的中点,BC BD ∴=,DBC ∴∆是等边三角形,60CDB ∴∠=︒,DC DB =,线段DP 绕点D 逆时针旋转60︒,得到线段DF ,60PDF ∴∠=︒,DP DF =,CDB PDB PDF PDB ∴∠-∠=∠-∠,CDP BDF ∴∠=∠,在DCP ∆和DBF ∆中, DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩,DCP DBF ∴∆≅∆,CP BF ∴=,CP BP BC +=,BF BP BC ∴+=,BC BD =,BF BP BD ∴+=;(3)如图③,BF BD BP =+,理由:90ACB ∠=︒,30A ∠=︒,60CBA ∴∠=︒,12BC AB =, 点D 是AB 的中点, BC BD ∴=,DBC ∴∆是等边三角形,60CDB ∴∠=︒,DC DB =,线段DP 绕点D 逆时针旋转60︒,得到线段DF ,60PDF ∴∠=︒,DP DF =,CDB PDB PDF PDB ∴∠+∠=∠+∠,CDP BDF ∴∠=∠,在DCP ∆和DBF ∆中,DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩,DCP DBF ∴∆≅∆,CP BF ∴=,CP BC BP =+,BF BC BP ∴=+,BC BD =,BF BD BP ∴=+.【点睛】此题是三角形综合题,主要考查了含30的直角三角形的性质,等边三角形的判定,全等三角形的判定和性质,旋转的性质,解本题的关键是判断出DCP DBF ∆≅∆,是一道中等难度的中考常考题.。
八年级上册数学典型压轴题专项训练含答案解析

八年级上册数学典型压轴题专项训练(附答案)1.问题背景:如图1:在四边形ABC中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由;实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进.1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.2.【问题提出】学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.【初步思考】我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=D F,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.【深入探究】第一种情况:当∠B是直角时,△ABC≌△DEF.(1)如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据,可以知道Rt△ABC≌Rt△DEF.第二种情况:当∠B是钝角时,△ABC≌△DEF.(2)如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是钝角,求证:△ABC≌△DEF.第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.(3)在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)(4)∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,若,则△ABC≌△DEF.3.有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形,你能办到吗?请画示意图说明剪法.我们有多少种剪法,图1是其中的一种方法:定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种)(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值;4.如图,△ABC中,AB=AC,∠A=36°,称满足此条件的三角形为黄金等腰三角形.请完成以下操作:(画图不要求使用圆规,以下问题所指的等腰三角形个数均不包括△ABC)(1)在图1中画1条线段,使图中有2个等腰三角形,并直接写出这2个等腰三角形的顶角度数分别是度和度;(2)在图2中画2条线段,使图中有4个等腰三角形;(3)继续按以上操作发现:在△ABC中画n条线段,则图中有个等腰三角形,其中有个黄金等腰三角形..在等腰直角三角形ABC中,∠BAC=90°,AB=AC,直线MN过点A且MN∥BC,过点B 为一锐角顶点作Rt△BDE,∠BDE=90°,且点D在直线MN上(不与点A重合),如图1,DE与AC交于点P,易证:BD=DP.(无需写证明过程)(1)在图2中,DE与CA延长线交于点P,BD=DP是否成立?如果成立,请给予证明;如果不成立,请说明理由;(2)在图3中,DE与AC延长线交于点P,BD与DP是否相等?请直接写出你的结论,无需证明.6.如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.7.【问题情境】张老师给爱好学习的小军和小俊提出这样一个问题:如图1,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为G,可以证得:PD=GF,PE=CG,则PD+PE=CF.【变式探究】如图3,当点P在BC延长线上时,其余条件不变,求证:PD-PE=CF. 8.在图1、图2、图3、图4中,点P在线段BC上移动(不与B、C重合),M在BC的延长线上.(1)如图1,△ABC和△APE均为正三角形,连接CE.①求证:△ABP≌△ACE.②∠ECM的度数为°.(2)①如图2,若四边形ABCD和四边形APEF均为正方形,连接CE.则∠ECM的度数为°.②如图3,若五边形ABCDF和五边形APEGH均为正五边形,连接CE.则∠ECM的度数为°.(3)如图4,n边形ABC…和n边形APE…均为正n边形,连接CE,请你探索并猜想∠ECM的度数与正多边形边数n的数量关系(用含n的式子表示∠ECM的度数),并利用图4(放大后的局部图形)证明你的结论.9、如图,在△ABC中,点D为边BC的中点,过点A作射线AE,过点C作CF⊥AE于点F,过点B作BG⊥AE于点G,连接FD并延长,交BG于点H(1)求证:DF=DH;(2)若∠CFD=120°,求证:△DHG为等边三角形.10、已知两等边△ABC,△DEC有公共的顶点C。
八年级上册数学压轴题试题及答案解答_

八年级上册数学压轴题试题及答案解答_一、压轴题1.对x y 、定义一种新运算T ,规定:()()(),2T x y mx ny x y =++(其中mn 、均为非零常数).例如:()1,133T m n =+.(1)已知()()1,10,0,28T T -==.①求mn 、的值; ②若关于p 的不等式组()()2,244,32T p p T p p a ⎧->⎪⎨-≤⎪⎩恰好有3个整数解,求a 的取值范围; (2)当22x y ≠时,()(),,T x y T y x =对任意有理数,x y 都成立,请直接写出mn 、满足的关系式.学习参考:①()a b c ab ac +=+,即单项式乘以多项式就是用单项式去乘多项式的每一项,再把所得的结果相加;②()()a b m n am an bm bn ++=+++,即多项式乘以多项式就是用一个多项式的每一项去乘另一个多项式的每一项,再把所得的结果相加.解析:(1)①11m n =⎧⎨=⎩;②42≤a <54;(2)m=2n 【解析】【分析】(1)①构建方程组即可解决问题;②根据不等式即可解决问题;(2)利用恒等式的性质,根据关系式即可解决问题.【详解】解:(1)①由题意得()088m n n ⎧--=⎨=⎩,解得11m n =⎧⎨=⎩, ②由题意得()()()()222424432464p p p p p p p p a ⎧+-+->⎪⎨+-+-≤⎪⎩, 解不等式①得p >-1.解不等式②得p≤1812a -, ∴-1<p≤1812a -, ∵恰好有3个整数解,∴2≤1812a -<3.∴42≤a <54;(2)由题意:(mx+ny )(x+2y )=(my+nx )(y+2x ),∴mx 2+(2m+n )xy+2ny 2=2nx 2+(2m+n )xy+my 2,∵对任意有理数x ,y 都成立,∴m=2n .【点睛】本题考查一元一次不等式、二元一次方程组、恒等式等知识,解题的关键是学会用转化的思想思考问题,属于中考常考题型.2.已知AB //CD ,点E 是平面内一点,∠CDE 的角平分线与∠ABE 的角平分线交于点F . (1)若点E 的位置如图1所示.①若∠ABE =60°,∠CDE =80°,则∠F = °;②探究∠F 与∠BED 的数量关系并证明你的结论;(2)若点E 的位置如图2所示,∠F 与∠BED 满足的数量关系式是 .(3)若点E 的位置如图3所示,∠CDE 为锐角,且1452E F ∠≥∠+︒,设∠F =α,则α的取值范围为 .解析:(1)①70;②∠F =12∠BED ,证明见解析;(2)2∠F+∠BED =360°;(3)3045α︒≤<︒ 【解析】【分析】(1)①过F 作FG//AB ,利用平行线的判定和性质定理得到∠DFB=∠DFG+∠BFG=∠CDF+∠ABF ,利用角平分线的定义得到∠ABE+∠CDE=2∠ABF+2∠CDF=2(∠ABF+∠CDF ),求得∠ABF+∠CDF=70︒,即可求解; ②分别过E 、F 作EN//AB ,FM//AB ,利用平行线的判定和性质得到∠BED=∠ABE+∠CDE ,利用角平分线的定义得到∠BED=2(∠ABF+∠CDF ),同理得到∠F=∠ABF+∠CDF ,即可求解;(2)根据∠ABE 的平分线与∠CDE 的平分线相交于点F ,过点E 作EG ∥AB ,则∠BEG+∠ABE=180°,因为AB ∥CD ,EG ∥AB ,所以CD ∥EG ,所以∠DEG+∠CDE=180°,再结合①的结论即可说明∠BED 与∠BFD 之间的数量关系;(3)通过对1452E F ∠≥∠+︒的计算求得30α≥︒,利用角平分线的定义以及三角形外角的性质求得45α<︒,即可求得3045α︒≤<︒.【详解】(1)①过F作FG//AB,如图:∵AB∥CD,FG∥AB,∴CD∥FG,∴∠ABF=∠BFG,∠CDF=∠DFG,∴∠DFB=∠DFG+∠BFG=∠CDF+∠ABF,∵BF平分∠ABE,∴∠ABE=2∠ABF,∵DF平分∠CDE,∴∠CDE=2∠CDF,∴∠ABE+∠CDE=2∠ABF+2∠CDF=2(∠ABF+∠CDF)=60︒+80︒=140︒,∴∠ABF+∠CDF=70︒,∴∠DFB=∠ABF+∠CDF=70︒,故答案为:70;②∠F=12∠BED,理由是:分别过E、F作EN//AB,FM//AB,∵EN//AB,∴∠BEN=∠ABE,∠DEN=∠CDE,∴∠BED=∠ABE+∠CDE,∵DF、BF分别是∠CDE的角平分线与∠ABE的角平分线,∴∠ABE=2∠ABF,∠CDE=2∠CDF,即∠BED=2(∠ABF+∠CDF);同理,由FM//AB,可得∠F=∠ABF+∠CDF,∴∠F=12∠BED;(3)2∠F+∠BED=360°.如图,过点E作EG∥AB,则∠BEG+∠ABE=180°,∵AB ∥CD ,EG ∥AB ,∴CD ∥EG ,∴∠DEG+∠CDE=180°,∴∠BEG+∠DEG=360°-(∠ABE+∠CDE ),即∠BED=360°-(∠ABE+∠CDE ),∵BF 平分∠ABE ,∴∠ABE=2∠ABF ,∵DF 平分∠CDE ,∴∠CDE=2∠CDF ,∠BED=360°-2(∠ABF+∠CDF ),由①得:∠BFD=∠ABF+∠CDF ,∴∠BED=360°-2∠BFD ,即2∠F+∠BED=360°;(3)∵1452E F ∠≥∠+︒,∠F =α, ∴2452αα≥+︒,解得:30α≥︒,如图,∵∠CDE 为锐角,DF 是∠CDE 的角平分线,∴∠CDH=∠DHB 190452<⨯︒=︒, ∴∠F <∠DHB 45<︒,即45α<︒,∴3045α︒≤<︒,故答案为:3045α︒≤<︒.【点睛】本题考查了平行线的性质、角平分线的定义以及三角形外角性质的应用,在解答此题时要注意作出辅助线,构造出平行线求解.3.(1)如图1,ABC 和DCE 都是等边三角形,且B ,C ,D 三点在一条直线上,连接AD ,BE 相交于点P ,求证:BE AD =.(2)如图2,在BCD 中,若120BCD ∠<︒,分别以BC ,CD 和BD 为边在BCD 外部作等边ABC ,等边CDE △,等边BDF ,连接AD 、BE 、CF 恰交于点P . ①求证:AD BE CF ==;②如图2,在(2)的条件下,试猜想PB ,PC ,PD 与BE 存在怎样的数量关系,并说明理由.解析:(1)详见解析;(2)①详见解析;②PB PC PD BE ++=,理由详见解析【解析】【分析】(1)根据等边三角形的性质得出BC=AC ,CE=CD ,∠ACB=∠DCE=60°,进而得出∠BCE=∠ACD ,判断出BCE ACD ≌(SAS ),即可得出结论;(2)①同(1)的方法判断出≌ACD BCE (SAS ),ABD CBF ≌(SAS ),即可得出结论; ②先判断出∠APB=60°,∠APC=60°,在PE 上取一点M ,使PM=PC ,证明CPM △是等边三角形, 进而判断出PCD MCE ≌(SAS ),即可得出结论.【详解】(1)证明:∵ABC 和DCE 都是等边三角形,∴BC=AC ,CE=CD ,∠ACB=∠DCE=60°,∴∠ABC+∠ACE=∠DCE+∠ACE ,即∠BCE=∠ACD ,∴BCE ACD ≌(SAS ),∴BE=AD ;(2)①证明:∵ABC 和DCE 是等边三角形,∴AC=BC ,CD=CE ,∠ACB=∠DCE=60°,∴∠ACB+∠BCD=∠DCE+∠BCD ,即∠ACD=∠BCE ,∴≌ACD BCE (SAS ),∴AD=BE ,同理:ABD CBF ≌(SAS ),∴AD=CF ,即AD=BE=CF ;②解:结论:PB+PC+PD=BE,理由:如图2,AD与BC的交点记作点Q,则∠AQC=∠BQP,ACD BCE,由①知,≌∴∠CAD=∠CBE,在ACQ中,∠CAD+∠AQC=180°-∠ACB=120°,∴∠CBE+∠BQP=120°,在BPQ中,∠APB=180°-(∠CBE+∠BQP)=60°,∴∠DPE=60°,同理:∠APC=60°,∴∠=︒∠CPD=120°,60,CPE在PE上取一点M,使PM=PC,△是等边三角形,∴CPM==,∠PCM=∠CMP=60°,∴CP CM PM∴∠CME=120°=∠CPD,△是等边三角形,∵CDE∴CD=CE,∠DCE=60°=∠PCM,∴∠PCD=∠MCE,≌(SAS),∴PCD MCE∴PD=ME,∴BE=PB+PM+ME=PB+PC+PD.【点睛】此题是三角形综合题,主要考查了三角形的内角和定理,等边三角形的性质和判定,全等三角形的判定和性质,构造出全等三角形是解本题的关键.4.阅读材料并完成习题:在数学中,我们会用“截长补短”的方法来构造全等三角形解决问题.请看这个例题:如图1,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若AC=2cm,求四边形ABCD的面积.解:延长线段CB到E,使得BE=CD,连接AE,我们可以证明△BAE≌△DAC,根据全等三角形的性质得AE=AC=2,∠EAB=∠CAD,则∠EAC=∠EAB+∠BAC=∠DAC+∠BAC=∠BAD=90°,得S四边形ABCD =S △ABC +S △ADC =S △ABC +S △ABE =S △AEC ,这样,四边形ABCD 的面积就转化为等腰直角三角形EAC 面积.(1)根据上面的思路,我们可以求得四边形ABCD 的面积为 cm 2.(2)请你用上面学到的方法完成下面的习题.如图2,已知FG=FN=HM=GH+MN=2cm ,∠G=∠N=90°,求五边形FGHMN 的面积. 解析:(1)2;(2)4【解析】【分析】(1)根据题意可直接求等腰直角三角形EAC 的面积即可;(2)延长MN 到K ,使NK=GH ,连接FK 、FH 、FM ,由(1)易证FGH FNK ≌,则有FK=FH ,因为HM=GH+MN 易证FMK FMH ≌,故可求解. 【详解】(1)由题意知21=22ABC ADC ABC ABE AEC ABCD AC S SS S S S =+=+==四边形, 故答案为2;(2)延长MN 到K ,使NK=GH ,连接FK 、FH 、FM ,如图所示:FG=FN=HM=GH+MN=2cm ,∠G=∠N=90°,∴∠FNK=∠FGH=90°,∴FGH FNK ≌, ∴FH=FK ,又FM=FM ,HM=KM=MN+GH=MN+NK ,∴FMK FMH ≌,∴MK=FN=2cm ,∴12=242FGH HFM MFN FMK FGHMN S SS S S MK FN =++=⨯⋅=五边形. 【点睛】本题主要考查全等三角形的性质与判定,关键是根据截长补短法及割补法求面积的运用.5.已知:MN ∥PQ ,点A ,B 分别在MN ,PQ 上,点C 为MN ,PQ 之间的一点,连接CA ,CB .(1)如图1,求证:∠C=∠MAC+∠PBC ;(2)如图2,AD ,BD ,AE ,BE 分别为∠MAC ,∠PBC ,∠CAN ,∠CBQ 的角平分线,求证:∠D+∠E=180°;(3)在(2)的条件下,如图3,过点D 作DA 的垂线交PQ 于点G ,点F 在PQ 上,∠FDA=2∠FDB ,FD 的延长线交EA 的延长线于点H ,若3∠C=4∠E ,猜想∠H 与∠GDB 的倍数关系并证明.解析:(1)见解析;(2)见解析;(3)猜想:∠H= 3∠GDB ,证明见解析.【解析】【分析】(1)作辅助线:过C 作EF ∥MN ,根据平行的传递性可知这三条直线两两平行,由平行线的性质得到内错角相等∠MAC=∠ACF ,∠BCF=∠PBC ,再进行角的加和即可得出结论;(2)根据角平分线线定理得知11,22MAD MAC NAE NAC ∠=∠∠=∠,利用平角为180°得到∠DAE=90°,同理得90DBE ∠=︒,再根据四边形内角和180°,得出结论;(3)由(1)(2)中的结论进行等量代换得到3∠ADB=2∠E ,并且两角的和为180°,由此得到两个角的度数分别为72°和108°,利用角的和与差得到∠HDA=36°,∠H=54°,由此得到倍数关系. 【详解】(1)如图:过C 作EF ∥MN ,∵MN ∥PQ , ∴MN ∥EF ∥PQ ,∴∠MAC=∠ACF ,∠BCF=∠PBC ,∴∠ACF+∠BCF=∠MAC+∠PBC ,即∠ACB=∠MAC+∠PBC .(2)∵AD ,AE 分别为∠MAC ,∠CAN 的角平分线,∴11,22MAD MAC NAE NAC ∠=∠∠=∠, ∴11118090222MAD NAE MAC NAC ∠+∠=∠+∠=⨯︒=︒,于是∠DAE=90°同理可得:90PBD QBE ∠+∠=︒,由(1)可得:∵ 180D E MAD PBD NAE QBE ∠+∠=∠+∠+∠+∠=︒.(3)猜想:∠H= 3∠GDB.理由如下:由(1)可知:2()2C MAC PBC MAD PBD ADB ∠=∠+∠=∠+∠=∠, ∵3∠C=4∠E ,∴6∠ADB=4∠E ,∴3∠ADB=2∠E ,∵∠ADB+∠E=180°,∴∠ADB=72°,∠E=108°,∵DG ⊥DA ,∴∠GDB=18°,∵∠FDA=2∠FDB ,∴∠ADF=144°,∴∠HDA=36°,∵DA ⊥AE ,∴∠H=54°,∴∠H=3∠GDB .【点睛】考查平行线中角度的关系,学生要熟悉掌握平行线的性质以及角平分线定理,结合角的和与差进行计算,本题的关键是平行线的性质.6.在△ABC 中,已知∠A =α.(1)如图1,∠ABC 、∠ACB 的平分线相交于点D .求∠BDC 的大小(用含α的代数式表示);(2)如图2,若∠ABC 的平分线与∠ACE 的平分线交于点F ,求∠BFC 的大小(用含α的代数式表示);(3)在(2)的条件下,将△FBC 以直线BC 为对称轴翻折得到△GBC ,∠GBC 的平分线与∠GCB 的平分线交于点M (如图3),求∠BMC 的度数(用含α的代数式表示).解析:(1)∠BDC =90°+2α;(2)∠BFC =2α;(3)∠BMC =90°+4α.【解析】【分析】 (1)由三角形内角和可求∠ABC +∠ACB =180°﹣α,由角平分线的性质可求∠DBC +∠BCD =12(∠ABC +∠ACB )=90°﹣2α,由三角形的内角和定理可求解;(2)由角平分线的性质可得∠FBC =12∠ABC ,∠FCE =12∠ACE ,由三角形的外角性质可求解; (3)由折叠的性质可得∠G =∠BFC =2α,方法同(1)可求∠BMC =90°+2G ∠,即可求解.【详解】解:(1)∵∠A =α,∴∠ABC +∠ACB =180°﹣α,∵BD 平分∠ABC ,CD 平分∠ACB ,∴∠DBC =12∠ABC ,∠BCD =12∠ACB , ∴∠DBC +∠BCD =12(∠ABC +∠ACB )=90°﹣2α, ∴∠BDC =180°﹣(∠DBC +∠BCD )=90°+2α; (2)∵∠ABC 的平分线与∠ACE 的平分线交于点F ,∴∠FBC =12∠ABC ,∠FCE =12∠ACE , ∵∠ACE =∠A +∠ABC ,∠FCE =∠BFC +∠FBC ,∴∠BFC =12∠A =2α; (3)∵∠GBC 的平分线与∠GCB 的平分线交于点M , ∴方法同(1)可得∠BMC =90°+2G ∠, ∵将△FBC 以直线BC 为对称轴翻折得到△GBC ,∴∠G =∠BFC =2α, ∴∠BMC =90°+4α. 【点睛】此题考查三角形的内角和定理,三角形的外角等于与它不相邻的两个内角的和,角平分线的性质定理,折叠的性质.7.在△ABC 中,AB =AC ,D 是直线BC 上一点,以AD 为一条边在AD 的右侧作△ADE ,使AE =AD ,∠DAE =∠BAC ,连接CE .(1)如图,当点D 在BC 延长线上移动时,若∠BAC =40°,则∠ACE = ,∠DCE = ,BC 、DC 、CE 之间的数量关系为 ;(2)设∠BAC =α,∠DCE =β.①当点D 在BC 延长线上移动时,α与β之间有什么数量关系?请说明理由; ②当点D 在直线BC 上(不与B ,C 两点重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.(3)当CE∥AB时,若△ABD中最小角为15°,试探究∠ACB的度数(直接写出结果,无需写出求解过程).解析:(1)70°,40°,BC+DC=CE;(2)①α=β;②当点D在BC上移动时,α=β或α+β=180°;(3)∠ACB=60°.【解析】【分析】(1)证△BAD≌△CAE,推出∠B=∠ACE,根据三角形外角性质和全等三角形的性质求出即可;(2)①证△BAD≌△CAE,推出∠B=∠ACE,根据三角形外角性质求出即可;②分三种情况:(Ⅰ)当D在线段BC上时,证明△ABD≌△ACE(SAS),则∠ADB=∠AEC,∠ABC=∠ACE,推出∠DAE+∠DCE=180°,即α+β=180°;(Ⅱ)当点D在线段BC反向延长线上时,α=β,同理可证明△ABD≌△ACE(SAS),则∠ABD=∠ACE,推出∠BAC=∠DCE,即α=β;(Ⅲ)当点D在线段BC的延长线上时,由①得α=β;(3)当点D在线段BC的延长线上或在线段BC反向延长线上移动时,α=β,由CE∥AB,得∠ABC=∠DCE,推出∠ABC=∠BAC,易证∠ABC=∠ACB=∠BAC,则△ABC是等边三角形,得出∠ACB=60°;当D在线段BC上时,α+β=180°,由CE∥AB,得∠ABC+∠DCE=180°,推出∠ABC=∠BAC,易证∠ABC=∠ACB=∠BAC,则△ABC是等边三角形,得出∠ACB=60°.【详解】(1)如图1所示:∵∠DAE=∠BAC,∴∠DAE+∠CAD=∠BAC+∠CAD,∴∠BAD=∠CAE.在△BAD和△CAE中,AB ACBAD CAE AD AE=⎧⎪∠=∠⎨⎪=⎩,∴△BAD≌△CAE(SAS),∴∠ACE=∠B12=(180°﹣40°)=70°,BD=CE,∴BC+DC=CE.∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,∴∠BAC=∠DCE.∵∠BAC=40°,∴∠DCE=40°.故答案为:70°,40°,BC+DC=CE;(2)①当点D在线段BC的延长线上移动时,α与β之间的数量关系是α=β.理由如下:∵∠DAE=∠BAC,∴∠DAE+∠CAD=∠BAC+∠CAD,∴∠BAD=∠CAE.在△BAD和△CAE中,AB ACBAD CAE AD AE=⎧⎪∠=∠⎨⎪=⎩,∴△BAD≌△CAE(SAS),∴∠B=∠ACE.∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,∴∠BAC=∠DCE.∵∠BAC=α,∠DCE=β,∴α=β;②分三种情况:(Ⅰ)当D在线段BC上时,α+β=180°,如图2所示.理由如下:同理可证明:△ABD≌△ACE(SAS),∴∠ADB=∠AEC,∠ABC=∠ACE.∵∠ADC+∠ADB=180°,∴∠ADC+∠AEC=180°,∴∠DAE+∠DCE=180°.∵∠BAC=∠DAE=α,∠DCE=β,∴α+β=180°;(Ⅱ)当点D在线段BC反向延长线上时,α=β,如图3所示.理由如下:同理可证明:△ABD≌△ACE(SAS),∴∠ABD=∠ACE.∵∠ACE=∠ACD+∠DCE,∠ABD=∠ACD+∠BAC,∴∠ACD+∠DCE=∠ACD+∠BAC,∴∠BAC=∠DCE.∵∠BAC=α,∠DCE=β,∴α=β;(Ⅲ)当点D在线段BC的延长线上时,如图1所示,α=β;综上所述:当点D在BC上移动时,α=β或α+β=180°;(3)∠ACB=60°.理由如下:∵当点D在线段BC的延长线上或在线段BC反向延长线上移动时,α=β,即∠BAC=∠DCE.∵CE∥AB,∴∠ABC=∠DCE,∴∠ABC=∠BAC.∵AB=AC,∴∠ABC=∠ACB=∠BAC,∴△ABC是等边三角形,∴∠ACB=60°;∵当D在线段BC上时,α+β=180°,即∠BAC+∠DCE=180°.∵CE∥AB,∴∠ABC+∠DCE=180°,∴∠ABC=∠BAC.∵AB=AC,∴∠ABC=∠ACB=∠BAC,∴△ABC是等边三角形,∴∠ACB=60°;综上所述:当CE∥AB时,若△ABD中最小角为15°,∠ACB的度数为60°.【点睛】本题是三角形综合题目,考查了全等三角形的判定与性质、等腰三角形的性质、等边三角形的判定与性质、平行线的性质、三角形的外角性质和多边形内角和等知识.本题综合性强,熟练掌握全等三角形的判定与性质是解题的关键.8.已知,如图1,直线l2⊥l1,垂足为A,点B在A点下方,点C在射线AM上,点B、C 不与点A重合,点D在直线11上,点A的右侧,过D作l3⊥l1,点E在直线l3上,点D的下方.(1)l2与l3的位置关系是;(2)如图1,若CE平分∠BCD,且∠BCD=70°,则∠CED=°,∠ADC=°;(3)如图2,若CD⊥BD于D,作∠BCD的角平分线,交BD于F,交AD于G.试说明:∠DGF=∠DFG;(4)如图3,若∠DBE=∠DEB,点C在射线AM上运动,∠BDC的角平分线交EB的延长线于点N,在点C的运动过程中,探索∠N:∠BCD的值是否变化,若变化,请说明理由;若不变化,请直接写出比值.解析:(1)互相平行;(2)35,20;(3)见解析;(4)不变,1 2【解析】【分析】(1)根据平行线的判定定理即可得到结论;(2)根据角平分线的定义和平行线的性质即可得到结论;(3)根据角平分线的定义和平行线的性质即可得到结论;(4)根据角平分线的定义,平行线的性质,三角形外角的性质即可得到结论.【详解】解:(1)直线l2⊥l1,l3⊥l1,∴l2∥l3,即l2与l3的位置关系是互相平行,故答案为:互相平行;(2)∵CE平分∠BCD,∴∠BCE=∠DCE=12BCD,∵∠BCD=70°,∴∠DCE=35°,∵l2∥l3,∴∠CED=∠DCE=35°,∵l2⊥l1,∴∠CAD=90°,∴∠ADC=90°﹣70°=20°;故答案为:35,20;(3)∵CF平分∠BCD,∴∠BCF=∠DCF,∵l2⊥l1,∴∠CAD=90°,∴∠BCF+∠AGC=90°,∵CD⊥BD,∴∠DCF+∠CFD=90°,∴∠AGC=∠CFD,∵∠AGC=∠DGF,∴∠DGF=∠DFG;(4)∠N:∠BCD的值不会变化,等于12;理由如下:∵l2∥l3,∴∠BED=∠EBH,∵∠DBE=∠DEB,∴∠DBE=∠EBH,∴∠DBH=2∠DBE,∵∠BCD+∠BDC=∠DBH,∴∠BCD+∠BDC=2∠DBE,∵∠N+∠BDN=∠DBE,∴∠BCD+∠BDC=2∠N+2∠BDN,∵DN平分∠BDC,∴∠BDC=2∠BDN,∴∠BCD=2∠N,∴∠N:∠BCD=12.【点睛】本题考查了三角形的综合题,三角形的内角和定理,三角形外角的性质,平行线的判定和性质,角平分线的定义,正确的识别图形进行推理是解题的关键.9.某校七年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究.(1)如图1,在△ABC 中,∠ABC 与∠ACB 的平分线交于点P ,∠A =64°,则∠BPC = ;(2)如图2,△ABC 的内角∠ACB 的平分线与△ABC 的外角∠ABD 的平分线交于点E .其中∠A =α,求∠BEC .(用α表示∠BEC );(3)如图3,∠CBM 、∠BCN 为△ABC 的外角,∠CBM 、∠BCN 的平分线交于点Q ,请你写出∠BQC 与∠A 的数量关系,并说明理由;(4)如图4,△ABC 外角∠CBM 、∠BCN 的平分线交于点Q ,∠A=64°,∠CBQ ,∠BCQ 的平分线交于点P ,则∠BPC= ゜,延长BC 至点E ,∠ECQ 的平分线与BP 的延长线相交于点R ,则∠R= ゜.解析:(1) 122°;(2)12BEC α∠=;(3)01902BQC A ;(4)119,29 ; 【解析】【分析】 (1)根据三角形的内角和角平分线的定义; (2)根据三角形的一个外角等于与它不相邻的两个内角的和,用A ∠与1∠表示出2∠,再利用E ∠与1∠表示出2∠,于是得到结论;(3)根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出EBC ∠与ECB ∠,然后再根据三角形的内角和定理列式整理即可得解;(4)根据(1),(3)的结论可以得出∠BPC 的度数;根据(2)的结论可以得到∠R 的度数.【详解】解:(1)BP 、CP 分别平分ABC ∠和ACB ∠,12PBC ABC ∴∠=∠,12PCB ACB ∠=∠, 180()BPC PBC PCB ∴∠=︒-∠+∠11180()22ABC ACB =︒-∠+∠, 1180()2ABC ACB =︒-∠+∠, 1(180180)2A =︒-︒-∠,1180902A =-︒+︒∠, 9032122,故答案为:122︒; (2)如图2示,CE 和BE 分别是ACB ∠和ABD ∠的角平分线,112ACB ∴∠=∠,122ABD ∠=∠, 又ABD ∠是ABC ∆的一外角,ABD A ACB ∴∠=∠+∠, 112()122A ABC A ∴∠=∠+∠=∠+∠, 2∠是BEC ∆的一外角,112111222BEC A A α∴∠=∠-∠=∠+∠-∠=∠=; (3)1()2QBC A ACB ∠=∠+∠,1()2QCB A ABC ∠=∠+∠, 180BQC QBC QCB ∠=︒-∠-∠,11180()()22A ACB A ABC =︒-∠+∠-∠+∠, 11180()22A A ABC ACB =︒-∠-∠+∠+∠, 结论1902BQC A ∠=︒-∠. (4)由(3)可知,119090645822BQC A , 再根据(1),可得180()BPCPBC PCB 1118022QBC QCB 1180902Q 118090582119;由(2)可得:115829 22R Q;故答案为:119,29.【点睛】本题考查了三角形的外角性质与内角和定理,熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.10.(概念认识)如图①,在∠ABC中,若∠ABD=∠DBE=∠EBC,则BD,BE叫做∠ABC的“三分线”.其中,BD是“邻AB三分线”,BE是“邻BC三分线”.(问题解决)(1)如图②,在△ABC中,∠A=70°,∠B=45°,若∠B的三分线BD交AC于点D,则∠BDC= °;(2)如图③,在△ABC中,BP、CP分别是∠ABC邻AB三分线和∠ACB邻AC三分线,且BP⊥CP,求∠A的度数;(延伸推广)(3)在△ABC中,∠ACD是△ABC的外角,∠B的三分线所在的直线与∠ACD的三分线所在的直线交于点P.若∠A=m°,∠B=n°,直接写出∠BPC的度数.(用含 m、n的代数式表示)解析:(1)85或100;(2)45°;(3)23m或13m或23m+13n或13m-13n或13n-13m【解析】【分析】(1)根据题意可得B的三分线BD有两种情况,画图根据三角形的外角性质即可得BDC∠的度数;(2)根据BP 、CP 分别是ABC ∠邻AB 三分线和ACB ∠邻AC 三分线,且BP CP ⊥可得135ABC ACB ,进而可求A ∠的度数;(3)根据B 的三分线所在的直线与ACD ∠的三分线所在的直线交于点P .分四种情况画图:情况一:如图①,当BP 和CP 分别是“邻AB 三分线”、“邻AC 三分线”时;情况二:如图②,当BP 和CP 分别是“邻BC 三分线”、“邻CD 三分线”时;情况三:如图③,当BP 和CP 分别是“邻BC 三分线”、“邻AC 三分线”时;情况四:如图④,当BP 和CP 分别是“邻AB 三分线”、“邻CD 三分线”时,再根据A m ∠=︒,B n ∠=︒,即可求出BPC ∠的度数.【详解】解:(1)如图,当BD 是“邻AB 三分线”时,701585BD C; 当BD 是“邻BC 三分线”时,7030100BD C;故答案为:85或100;(2)BP CP , 90BPC ∴∠=︒,90PBC PCB , 又BP 、CP 分别是ABC ∠邻AB 三分线和ACB ∠邻AC 三分线, 23PBC ABC ,23PCB ACB ∠=∠, ∴229033ABC ACB , 135ABCACB , 在ABC ∆中,180A ABC ACB ∠+∠+∠=︒180()45A ABC ACB . (3)分4种情况进行画图计算:情况一:如图①,当BP 和CP 分别是“邻AB 三分线”、“邻AC 三分线”时,2233BPC A m ; 情况二:如图②,当BP 和CP 分别是“邻BC 三分线”、“邻CD 三分线”时,1133BPC A m ; 情况三:如图③,当BP 和CP 分别是“邻BC 三分线”、“邻AC 三分线”时,21213333BPC A ABC m n ; 情况四:如图④,当BP 和CP 分别是“邻AB 三分线”、“邻CD 三分线”时,①当m n >时,11113333BPC A ABC m n ∠=∠-∠=-; ②当m n <时,11113333P ABC A n m ∠=∠-∠=-. 【点睛】本题考查了三角形的外角性质,解决本题的关键是掌握三角形的外角性质.注意要分情况讨论.11.已知ABC,P 是平面内任意一点(A、B、C、P 中任意三点都不在同一直线上).连接 PB、PC,设∠PBA=s°,∠PCA=t°,∠BPC=x°,∠BAC=y°.(1)如图,当点 P 在ABC 内时,①若 y=70,s=10,t=20,则 x=;②探究 s、t、x、y 之间的数量关系,并证明你得到的结论.(2)当点 P 在ABC 外时,直接写出 s、t、x、y 之间所有可能的数量关系,并画出相应的图形.解析:(1)①100;②x=y+s+t;(2)见详解.【解析】【分析】(1)①利用三角形的内角和定理即可解决问题;②结论:x=y+s+t.利用三角形内角和定理即可证明;(2)分6种情形分别求解即可解决问题.【详解】解:(1)①∵∠BAC=70°,∴∠ABC+∠ACB=110°,∵∠PBA=10°,∠PCA=20°,∴∠PBC+∠PCB=80°,∴∠BPC=100°,∴x=100,故答案为:100.②结论:x=y+s+t.理由:∵∠A+∠ABC+∠ACB=∠A+∠PBA+∠PCA+∠PBC+∠PCB=180°,∠PBC+∠PCB+∠BPC=180°,∴∠A+∠PBA+∠PCA=∠BPC,∴x=y+s+t.(2)s、t、x、y之间所有可能的数量关系:如图1:s+x=t+y;如图2:s+y=t+x;如图3:y=x+s+t;如图4:x+y+s+t=360°;如图5:t=s+x+y;如图6:s=t+x+y;【点睛】本题考查三角形的内角和定理,三角形的外角的性质等知识,解题的关键是学会用分类讨论的思想思考问题.12.如图,△ABC是等边三角形,△ADC与△ABC关于直线AC对称,AE与CD垂直交BC 的延长线于点E,∠EAF=45°,且AF与AB在AE的两侧,EF⊥AF.(1)依题意补全图形.(2)①在AE上找一点P,使点P到点B,点C的距离和最短;②求证:点D到AF,EF的距离相等.解析:(1)详见解析;(2)①详见解析;②详见解析.【解析】【分析】(1)本题考查理解题意能力,按照题目所述依次作图即可.(2)①本题考查线段和最短问题,需要通过垂直平分线的性质将所求线段转化为其他等量线段之和,以达到求解目的.②本题考查垂直平分线的判定以及全等三角形的证明,继而利用角的平分线性质即可得出结论.【详解】(1)补全图形,如图1所示(2)①如图2,连接BD,P为BD与AE的交点∵等边△ACD,AE⊥CD∴PC=PD,PC+PB最短等价于PB+PD最短故B,D之间直线最短,点P即为所求.②证明:连接DE,DF.如图3所示∵△ABC,△ADC是等边三角形∴AC=AD,∠ACB=∠CAD=60°∵AE⊥CD∴∠CAE=12∠CAD=30°∴∠CEA=∠ACB﹣∠CAE=30°∴∠CAE=∠CEA∴CA=CE∴CD垂直平分AE∴DA=DE∴∠DAE=∠DEA∵EF⊥AF,∠EAF=45°∴∠FEA=45°∴∠FEA=∠EAF∴FA=FE,∠FAD=∠FED∴△FAD≌△FED(SAS)∴∠AFD=∠EFD∴点D到AF,EF的距离相等.【点睛】本题第一问作图极为重要,要求对题意有较深的理解,同时对于垂直平分线以及角平分线的定义要清楚,能通过题目文字所述转化为考点,信息转化能力需要多做题目加以提升.13.阅读并填空:如图,ABC是等腰三角形,AB AC=,D是边AC延长线上的一点,E在边AB上且联接DE交BC于O,如果OE OD,那么CD BE=,为什么?解:过点E 作EF AC 交BC 于F所以ACB EFB ∠=∠(两直线平行,同位角相等)D OEF ∠=∠(________)在OCD 与OFE △中()________COD FOE OD OED OEF ⎧∠=∠⎪=⎨⎪∠=∠⎩所以OCD OFE △≌△,(________)所以CD FE =(________)因为AB AC =(已知)所以ACB B =∠∠(________)所以EFB B ∠=∠(等量代换)所以BE FE =(________)所以CD BE =解析:见解析【解析】【分析】先根据平行线的性质,得到角的关系,然后证明OCD OFE △≌△,写出证明过程和依据即可.【详解】解:过点E 作//EF AC 交BC 于F ,∴ACB EFB ∠=∠(两直线平行,同位角相等),∴D OEF ∠=∠(两直线平行,内错角相等),在OCD 与OFE △中()()()COD FOE OD OED OEF ⎧∠=∠⎪=⎨⎪∠=∠⎩对顶角相等已知已证,∴OCD OFE △≌△,(ASA )∴CD FE =(全等三角形对应边相等)∵AB AC =(已知)∴ACB B =∠∠(等边对等角)∴EFB B ∠=∠(等量代换)∴BE FE =(等角对等边)∴CD BE =;【点睛】本题考查了全等三角形的判定和性质,平行线的性质,解题的关键是由平行线的性质正确找到证明三角形全等的条件,从而进行证明.14.如图,若要判定纸带两条边线a ,b 是否互相平行,我们可以采用将纸条沿AB 折叠的方式来进行探究.(1)如图1,展开后,测得12∠=∠,则可判定a//b ,请写出判定的依据_________; (2)如图2,若要使a//b ,则1∠与2∠应该满足的关系是_________;(3)如图3,纸带两条边线a ,b 互相平行,折叠后的边线b 与a 交于点C ,若将纸带沿11A B (1A ,1B 分别在边线a ,b 上)再次折叠,折叠后的边线b 与a 交于点1C ,AB//11A B ,137BB AC ==,,求出1A C 的长.解析:(1)内错角相等,两直线平行;(2)∠1+2∠2=180°;(3)4或10【解析】【分析】(1)根据平行线的判定定理,即可得到答案;(2)由折叠的性质得:∠3=∠4,若a ∥b ,则∠3=∠2,结合三角形内角和定理,即可得到答案;(3)分两种情况:①当B 1在B 的左侧时,如图2,当B 1在B 的右侧时,如图3,分别求出1A C 的长,即可得到答案.【详解】(1)∵12∠=∠,∴a ∥b (内错角相等,两直线平行),故答案是:内错角相等,两直线平行;(2)如图1,由折叠的性质得:∠3=∠4,若a ∥b ,则∠3=∠2,∴∠4=∠2,∵∠2+∠4+∠1=180°,∴∠1+2∠2=180°,∴要使a ∥b ,则1∠与2∠应该满足的关系是:∠1+2∠2=180°.故答案是:∠1+2∠2=180°;(3)①当B 1在B 的左侧时,如图2,∵AB//11A B ,a ∥b ,∴AA 1=BB 1=3,∴1A C =AC- AA 1=7-3=4;②当B 1在B 的右侧时,如图3,∵AB//11A B ,a ∥b ,∴AA 1=BB 1=3,∴1A C =AC+AA 1=7+3=10.综上所述:1A C =4或10.【点睛】本题主要考查平行线的判定和性质定理,折叠的性质以及三角形的内角和定理,掌握“平行线间的平行线段长度相等”是解题的关键.15.如图1,在等边△ABC 中,E 、D 两点分别在边AB 、BC 上,BE =CD ,AD 、CE 相交于点F .(1)求∠AFE 的度数;(2)过点A 作AH ⊥CE 于H ,求证:2FH +FD =CE ;(3)如图2,延长CE 至点P ,连接BP ,∠BPC =30°,且CF =29CP ,求PF AF的值. (提示:可以过点A 作∠KAF =60°,AK 交PC 于点K ,连接KB ) 解析:(1)∠AFE =60°;(2)见解析;(3)75【解析】【分析】(1)通过证明 BCE CAD ≌ 得到对应角相等,等量代换推导出60AFE ∠=︒; (2)由(1)得到60AFE ∠=︒,CE AD = 则在Rt AHF △ 中利用30°所对的直角边等于斜边的一半,等量代换可得;(3)通过在PF 上取一点K 使得KF =AF ,作辅助线证明ABK 和ACF 全等,利用对应边相等,等量代换得到比值.(通过将ACF 顺时针旋转60°也是一种思路.)【详解】(1)解:如图1中.∵ABC 为等边三角形,∴AC =BC ,∠BAC =∠ABC =∠ACB =60°,在BCE 和CAD 中,60BE CD CBE ACD BC CA =⎧⎪∠=∠=︒⎨⎪=⎩,∴ BCE CAD ≌(SAS ),∴∠BCE =∠DAC ,∵∠BCE +∠ACE =60°,∴∠DAC +∠ACE =60°,∴∠AFE =60°.(2)证明:如图1中,∵AH ⊥EC ,∴∠AHF =90°,在Rt △AFH 中,∵∠AFH =60°,∴∠FAH =30°,∴AF =2FH ,∵ EBC DCA ≌,∴EC =AD ,∵AD =AF +DF =2FH +DF ,∴2FH +DF =EC .(3)解:在PF 上取一点K 使得KF =AF ,连接AK 、BK ,∵∠AFK =60°,AF =KF ,∴△AFK 为等边三角形,∴∠KAF =60°,∴∠KAB =∠FAC ,在ABK 和ACF 中,AB AC KAB ACF AK AF =⎧⎪∠=∠⎨⎪=⎩,∴ ABK ACF ≌(SAS ),BK CF =∴∠AKB =∠AFC =120°,∴∠BKE =120°﹣60°=60°,∵∠BPC =30°,∴∠PBK =30°, ∴29BK CF PK CP ===, ∴79PF CP CF CP =-=, ∵45()99AF KF CP CF PK CP CP CP ==-+=-=∴779559CPPFAF CP== .【点睛】掌握等边三角形、直角三角形的性质,及三角形全等的判定通过一定等量代换为本题的关键.二、选择题16.购买单价为a元的物品10个,付出b元(b>10a),应找回()A.(b﹣a)元B.(b﹣10)元C.(10a﹣b)元D.(b﹣10a)元解析:D【解析】【分析】根据题意知:花了10a元,剩下(b﹣10a)元.【详解】购买单价为a元的物品10个,付出b元(b>10a),应找回(b﹣10a)元.故选D.【点睛】本题考查了列代数式,能读懂题意是解答此题的关键.17.如果一个角的补角是130°,那么这个角的余角的度数是()A.30°B.40°C.50°D.90°解析:B【解析】【分析】直接利用互补的定义得出这个角的度数,进而利用互余的定义得出答案.【详解】解:∵一个角的补角是130︒,∴这个角为:50︒,∴这个角的余角的度数是:40︒.故选:B.【点睛】此题主要考查了余角和补角,正确把握相关定义是解题关键.18.已知max}2,x x表示取三个数中最大的那个数,例如:当x=9时,max}}22,max,9x x==81.当max}21,2x x=时,则x的值为()A.14-B.116C.14D.12解析:C 【解析】【分析】利用max }2,x x 的定义分情况讨论即可求解.【详解】解:当max }21,2x x =时,x ≥012,解得:x =14>x >x 2,符合题意;②x 2=12,解得:x =2x >x 2,不合题意;③x =12x >x 2,不合题意;故只有x =14时,max }21,2x x =.故选:C .【点睛】此题主要考查了新定义,正确理解题意分类讨论是解题关键.19 =( )A .1B .2C .3D .4 解析:B【解析】【分析】根据算术平方根的概念可得出答案.【详解】解:根据题意可得:,故答案为:B.【点睛】本题考查算术平方根的概念,解题关键在于对其概念的理解.20.当x 取2时,代数式(1)2x x -的值是( )A .0B .1C .2D .3 解析:B【解析】【分析】把x 等于2代入代数式即可得出答案.【详解】解:根据题意可得:把2x =代入(1)2x x -中得: (1)21==122x x -⨯, 故答案为:B.【点睛】本题考查的是代入求值问题,解题关键就是把x 的值代入进去即可.21.有理数a ,b 在数轴上的对应点的位置如图所示,则下列各式成立的是( )A .a >bB .﹣ab <0C .|a |<|b |D .a <﹣b 解析:D【解析】【分析】根据各点在数轴上的位置得出a 、b 两点到原点距离的大小,进而可得出结论.【详解】解:∵由图可知a <0<b ,∴ab <0,即-ab >0又∵|a |>|b |,∴a <﹣b .故选:D .【点睛】本题考查的是数轴,熟知数轴上两点间的距离公式是解答此题的关键.22.下列每对数中,相等的一对是( )A .(﹣1)3和﹣13B .﹣(﹣1)2和12C .(﹣1)4和﹣14D .﹣|﹣13|和﹣(﹣1)3解析:A【解析】【分析】根据乘方和绝对值的性质对各个选项进行判断即可.【详解】A.(﹣1)3=﹣1=﹣13,相等;B.﹣(﹣1)2=﹣1≠12=1,不相等;C.(﹣1)4=1≠﹣14=﹣1,不相等;D. ﹣|﹣13|=﹣1≠﹣(﹣1)3=1,不相等.故选A.23.在223,2,7-四个数中,属于无理数的是( ) A .0.23 B 3 C .2- D .227【解析】【分析】根据无理数为无限不循环小数、开方开不尽的数、含π的数判断即可.【详解】0.23是有限小数,是有理数,不符合题意,是开方开不尽的数,是无理数,符合题意,-2是整数,是有理数,不符合题意,227是分数,是有理数,不符合题意,故选:B.【点睛】本题考查无理数概念,无理数为无限不循环小数、开方开不尽的数、含π的数,熟练掌握无理数的定义是解题关键.24.如果﹣2xy n+2与 3x3m-2y 是同类项,则|n﹣4m|的值是()A.3 B.4 C.5 D.6解析:C【解析】【分析】同类项要求相同字母上的次数相同,由此求出m,n,代入即可求解.【详解】解:∵﹣2xy n+2与 3x3m-2y 是同类项,∴3m-2=1,n+2=1,解得:m=1,n=-1,∴|n﹣4m|=|-1-4|=5,故选C.【点睛】本题考查了同类项的概念,属于简单题,熟悉概念和列等式是解题关键.25.某厂准备加工500个零件,在加工了100个零件后,引进了新机器,使得每天的工作效率是原来的两倍,结果共用了6天完成了任务,若设该厂原来每天加工x个零件,则由题意可列出方程()A.1005006 2x x+=B.1005006 x2x+=C.1004006 2x x+=D.1004006 x2x+=解析:D【分析】根据共用6天完成任务,等量关系为:用老机器加工100个零件用的时间+用新机器加工400套用的时间=6即可列出方程.【详解】设该厂原来每天加工x 个零件, 根据题意得:1004006x 2x+= 故选:D .【点睛】此题考查了由实际问题抽象出分式方程,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.26.如图,已知直线//a b ,点,A B 分别在直线,a b 上,连结AB .点D 是直线,a b 之间的一个动点,作//CD AB 交直线b 于点C,连结AD .若70ABC ︒∠=,则下列选项中D ∠不可能取到的度数为()A .60°B .80°C .150°D .170°解析:A【解析】【分析】 延长CD 交直线a 于E .由∠ADC =∠AED +∠DAE ,判断出∠ADC >70°即可解决问题.【详解】解:延长CD 交直线a 于E .∵a ∥b ,∴∠AED =∠DCF ,∵AB ∥CD ,∴∠DCF =∠ABC =70°,。
数学八年级上册 压轴题 期末复习试卷专题练习(word版

数学八年级上册 压轴题 期末复习试卷专题练习(word 版一、压轴题1.如图,以直角三角形AOC 的直角顶点O 为原点,以OC ,OA 所在直线为轴和轴建立平面直角坐标系,点A (0,a ),C (b ,0)满足a 6b 80-+-=. (1)a = ;b = ;直角三角形AOC 的面积为 .(2)已知坐标轴上有两动点P ,Q 同时出发,P 点从C 点出发以每秒2个单位长度的速度向点O 匀速移动,Q 点从O 点出发以每秒1个单位长度的速度向点A 匀速移动,点P 到达O 点整个运动随之结束.AC 的中点D 的坐标是(4,3),设运动时间为t 秒.问:是否存在这样的t ,使得△ODP 与△ODQ 的面积相等?若存在,请求出t 的值;若不存在,请说明理由.(3)在(2)的条件下,若∠DOC =∠D CO ,点G 是第二象限中一点,并且y 轴平分∠GOD .点E 是线段OA 上一动点,连接接CE 交OD 于点H ,当点E 在线段OA 上运动的过程中,探究∠GOD ,∠OHC ,∠ACE 之间的数量关系,并证明你的结论(三角形的内角和为180).2.如图1所示,直线:5L y mx m =+与x 轴负半轴,y 轴正半轴分别交于A 、B 两点.(1)当OA OB =时,求点A 坐标及直线L 的解析式.(2)在(1)的条件下,如图2所示,设Q 为AB 延长线上一点,作直线OQ ,过A 、B 两点分别作AM OQ ⊥于M ,BN OQ ⊥于N ,若17AM =,求BN 的长. (3)当m 取不同的值时,点B 在y 轴正半轴上运动,分别以OB 、AB 为边,点B 为直角顶点在第一、二象限内作等腰直角OBF ∆和等腰直角ABE ∆,连接EF 交y 轴于P 点,如图3.问:当点B 在y 轴正半轴上运动时,试猜想PB 的长是否为定值?若是,请求出其值;若不是,说明理由.3.如图,在△ABC中,AB=AC=18cm,BC=10cm,AD=2BD.(1)如果点P在线段BC上以2cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等,经过2s后,△BPD与△CQP是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?4.如图,直线11 2y x b=-+分别与x轴、y轴交于A,B两点,与直线26y kx=-交于点()C4,2.(1)b= ;k= ;点B坐标为;(2)在线段AB上有一动点E,过点E作y轴的平行线交直线y2于点F,设点E的横坐标为m,当m为何值时,以O、B、E、F为顶点的四边形是平行四边形;(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得P,Q,A,B四个点能构成一个菱形.若存在,直接写出所有符合条件的Q点坐标;若不存在,请说明理由.5.问题背景:(1)如图1,已知△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:DE=BD+CE.拓展延伸:(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC.请写出DE、BD、CE三条线段的数量关系.(不需要证明)实际应用:(3)如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(-2,0),点A的坐标为(-6,3),请直接写出B点的坐标.6.在平面直角坐标系中点A(m−3,3m+3),点 B(m,m+4)和 D(0,−5),且点 B 在第二象限.(1)点B 向平移单位,再向下平移(用含m 的式子表达)单位可以与点A 重合;(2)若点B 向下移动 3 个单位,则移动后的点B 和点A 的纵坐标相等,且有点 C(m−2,0).①则此时点A、B、C 坐标分别为、、.②将线段AB 沿y 轴负方向平移n 个单位,若平移后的线段AB 与线段CD 有公共点,求n 的取值范围.③当m<−1 式,连接AD,若线段AD 沿直线AB 方向平移得到线段BE,连接DE 与直线y=−2 交于点F,则点F 坐标为.(用含m 的式子表达)7.如图,已知△ABC 中,AB=AC=10cm ,BC=8cm ,点D 为AB 的中点.如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动. (1)若点Q 的运动速度与点P 的运动速度相等,经过1s 后,BP= cm ,CQ= cm . (2)若点Q 的运动速度与点P 的运动速度相等,经过1s 后,△BPD 与△CQP 是否全等,请说明理由;(3)若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使△BPD 与△CQP 全等?(4)若点Q 以(3)中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿△ABC 三边运动,求经过多长时间点P 与点Q 第一次相遇?8.如图,在平面直角坐标系中,直线AB 经过点A (32,32)和B (23,0),且与y 轴交于点D ,直线OC 与AB 交于点C ,且点C 的横坐标为3. (1)求直线AB 的解析式;(2)连接OA ,试判断△AOD 的形状;(3)动点P 从点C 出发沿线段CO 以每秒1个单位长度的速度向终点O 运动,运动时间为t 秒,同时动点Q 从点O 出发沿y 轴的正半轴以相同的速度运动,当点Q 到达点D 时,P ,Q 同时停止运动.设PQ 与OA 交于点M ,当t 为何值时,△OPM 为等腰三角形?求出所有满足条件的t 值.9.如图已知ABC 中,,8B C AB AC ∠=∠==厘米,6BC =厘来,点D 为AB 的中点.如果点P 在线段BC 上以每秒2厘米的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动,设运动时间为t (秒).(1)用含t 的代数式表示线段PC 的长度;(2)若点,P Q 的运动速度相等,经过1秒后,BPD △与CQP 是否全等,请说明理由; (3)若点,P Q 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP 全等?(4)若点Q 以(3)中的运动速度从点C 出发,点v 以原来的运动速度从点B 同时出发,都顺时针沿三边运动,求经过多长时间,点P 与点Q 第一次在ABC 的哪条边上相遇?10.在Rt ABC 中,90ACB ∠=︒,30A ∠=︒,BD 是ABC 的角平分线,DE AB ⊥于点E .(1)如图1,连接EC ,求证:EBC 是等边三角形;(2)如图2,点M 是线段CD 上的一点(不与点,C D 重合),以BM 为一边,在BM 下方作60BMG ∠=︒,MG 交DE 延长线于点G .求证:AD DG MD =+;(3)如图3,点N 是线段AD 上的点,以BN 为一边,在BN 的下方作60BNG ∠=︒,NG 交DE 延长线于点G .直接写出ND ,DG 与AD 数量之间的关系.11.如图,直线l 1的表达式为:y=-3x+3,且直线l 1与x 轴交于点D ,直线l 2经过点A ,B ,直线l 1,l 2交于点C . (1)求点D 的坐标; (2)求直线l 2的解析表达式; (3)求△ADC 的面积;(4)在直线l 2上存在异于点C 的另一点P ,使得△ADP 与△ADC 的面积相等,求点P 的坐标.12.在等腰Rt△ABC中,AB=AC,∠BAC=90°(1)如图1,D,E是等腰Rt△ABC斜边BC上两动点,且∠DAE=45°,将△ABE绕点A逆时针旋转90后,得到△AFC,连接DF①求证:△AED≌△AFD;②当BE=3,CE=7时,求DE的长;(2)如图2,点D是等腰Rt△ABC斜边BC所在直线上的一动点,连接AD,以点A为直角顶点作等腰Rt△ADE,当BD=3,BC=9时,求DE的长.【参考答案】***试卷处理标记,请不要删除一、压轴题t=时,使得△ODP与△ODQ的面积相等;(3)1.(1)6;8;24;(2)存在 2.4∠GOD+∠ACE=∠OHC,见解析【解析】【分析】(1)利用非负性即可求出a,b即可得出结论,即可求出△ABC的面积;(2)先表示出OQ,OP,利用那个面积相等,建立方程求解即可得出结论;(3)先判断出∠OAC=∠AOD,进而判断出OG∥AC,即可判断出∠FHC=∠ACE,同理∠FHO=∠GOD,即可得出结论.【详解】--=,解:(1) 解:(1)∵a6b80∴a-6=0,b-8=0,∴a=6,b=8,∴A(0,6),C(8,0);∴S △ABC=6×8÷2=24,故答案为(0,6),(8,0); 6;8;24 (2) ∵114222ODQ D S OQ x t t ∆=⋅=⋅⋅= 11(82)312322ODP D S OP y t t ∆=⋅=⋅-⋅=- 由2123t t =-时, 2.4t =∴存在 2.4t =时,使得△ODP 与△ODQ 的面积相等 (3) )∴2∠GOA+∠ACE=∠OHC ,理由如下: ∵x 轴⊥y 轴,∴∠AOC=∠DOC+∠AOD=90° ∴∠OAC+∠ACO=90° 又∵∠DOC=∠DCO ∴∠OAC=∠AOD ∵y 轴平分∠GOD ∴∠GOA=∠AOD ∴∠GOA=∠OAC ∴OG ∥AC ,如图,过点H 作HF ∥OG 交x 轴于F , ∴HF ∥AC ∴∠FHC=∠ACE 同理∠FHO=∠GOD , ∵OG ∥FH , ∴∠GOD=∠FHO ,∴∠GOD+∠ACE=∠FHO+∠FHC 即∠GOD+∠ACE=∠OHC , ∴2∠GOA+∠ACE=∠OHC . ∴∠GOD+∠ACE=∠OHC .【点睛】此题是三角形综合题,主要考查了非负性的性质,三角形的面积公式,角平分线的定义,平行线的性质,正确作出辅助线是解本题的关键. 2.(1)5y x =+;(2)223)PB 的长为定值52【解析】 【分析】(1)先求出A 、B 两点坐标,求出OA 与OB ,由OA= OB ,求出m 即可;(2)用勾股定理求AB ,再证AMO OBN ∆≅∆,BN=OM ,由勾股定理求OM 即可;(3)先确定答案定值,如图引辅助线EG ⊥y 轴于G ,先证AOB EBG ∆≅∆,求BG 再证BFP GEP ∆≅∆,可确定BP 的定值即可.【详解】(1)对于直线:5L y mx m =+. 当0y =时,5x =-. 当0x =时,5y m =.()5,0A ∴-,()0,5B m .OA OB =.55m ∴=. 解得1m =.∴直线L 的解析式为5y x =+.(2)5OA =,17AM =.∴由勾股定理,2222OM OA AM =-=.180AOM AOB BON ∠+∠+∠=︒. 90AOB ∠=︒.90AOM BON ∴∠+∠=︒. 90AOM OAM ∠+∠=︒. BON OAM ∴∠=∠. 在AMO ∆与OBN ∆中, 90BON OAM AMO BNO OA OB ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩. ()AMO OBN AAS ∴∆≅∆. 22BN OM ∴==..(3)如图所示:过点E 作EG y ⊥轴于G 点.AEB ∆为等腰直角三角形,AB EB ∴=90ABO EBG ∠+∠=︒.EG BG ⊥,90GEB EBG ∴∠+∠=︒. ABO GEB ∴∠=∠. AOB EBG ∴∆≅∆.5BG AO ∴==,OB EG = OBF ∆为等腰直角三角形, OB BF ∴=BF EG ∴=.BFP GEP ∴∆≅∆.1522BP GP BG ∴===.【点睛】本题考查求解析式,线段的长,判断定值问题,关键是掌握求坐标,利用条件OA= OB ,求OM ,用勾股定理求AB ,再证AMO OBN ∆≅∆,构造 AOB EBG ∆≅∆,求BG ,再证BFP GEP ∆≅∆.3.(1)①△BPD 与△CQP 全等,理由见解析;②当点Q 的运动速度为125cm /s 时,能够使△BPD 与△CQP 全等;(2)经过90s 点P 与点Q 第一次相遇在线段AB 上相遇. 【解析】 【分析】(1)①由“SAS”可证△BPD ≌△CQP ;②由全等三角形的性质可得BP=PC=12BC=5cm ,BD=CQ=6cm ,可求解; (2)设经过x 秒,点P 与点Q 第一次相遇,列出方程可求解. 【详解】解:(1)①△BPD 与△CQP 全等, 理由如下:∵AB =AC =18cm ,AD =2BD , ∴AD =12cm ,BD =6cm ,∠B =∠C , ∵经过2s 后,BP =4cm ,CQ =4cm , ∴BP =CQ ,CP =6cm =BD , 在△BPD 和△CQP 中,BD CP B C BP CQ =⎧⎪∠=∠⎨⎪=⎩, ∴△BPD ≌△CQP (SAS ),②∵点Q 的运动速度与点P 的运动速度不相等, ∴BP ≠CQ ,∵△BPD 与△CQP 全等,∠B =∠C ,∴BP=PC=12BC=5cm,BD=CQ=6cm,∴t=52,∴点Q的运动速度=612552=cm/s,∴当点Q的运动速度为125cm/s时,能够使△BPD与△CQP全等;(2)设经过x秒,点P与点Q第一次相遇,由题意可得:125x﹣2x=36,解得:x=90,点P沿△ABC跑一圈需要181810232++=(s)∴90﹣23×3=21(s),∴经过90s点P与点Q第一次相遇在线段AB上相遇.【点睛】本题考查了全等三角形的判定和性质,等腰三角形的性质,一元一次方程的应用,掌握全等三角形的判定是本题的关键.4.(1)4;2;(0,4);(2)125m=或285m=;(3)存在.Q点坐标为()-,()4,()0,4-或()5,4.【解析】【分析】(1)根据待定系数法,将点C(4,2)代入解析式可求解;(2)设点E(m,142m+),F(m,2m-6),得()154261022EF m m m=-+--=-,由平行四边形的性质可得BO=EF=4,列出方程即可求解;(3)分两种情况讨论,由菱形的性质按照点平移的坐标规律,先确定P点坐标,再确定O 点坐标即可求解.【详解】解:(1)(1)∵直线y2=kx-6交于点C(4,2),∴2=4k-6,∴k=2,∵直线212y x b=-+过点C(4,2),∴2=-2+b,∴b=4,∴直线解析式为:212y x b =-+,直线解析式为y 2=2x -6, ∵直线212y x b =-+分别与x 轴、y 轴交于A ,B 两点, ∴当x =0时,y =4,当y =0时,x =8,∴点B (0,4),点A (8,0),故答案为:4;2;(0,4)(2)∵点E 在线段AB 上,点E 的横坐标为m ,∴1,42E m m ⎛⎫-+ ⎪⎝⎭,(),26F m m -, ∴()154261022EF m m m =-+--=-. ∵四边形OBEF 是平行四边形,∴EF BO =,∴51042m -=, 解得:125m =或285m =时, ∴当125m =或285m =时,四边形OBEF 是平行四边形. (3)存在.此时Q 点坐标为()45,4-,()45,4,()0,4-或()5,4.理由如下:假设存在.以P ,Q ,A ,B 为顶点的菱形分两种情况:①以AB 为边,如图1所示.因为点()8,0A ,()0,4B ,所以45AB =.因为以P ,Q ,A ,B 为顶点的四边形为菱形,所以AP AB =或BP BA =.当AP AB =时,点()845,0P -或()845,0+;当BP BA =时,点()8,0P -.当()845,0P -时,()8458,04Q --+,即()45,4-; 当()845,0P +时,()8458,04Q +-+,即()45,4; 当()8,0P -时,()880,004Q -+-+-,即()0,4-.②以AB 为对角线,对角线的交点为M ,如图2所示.可得5AP =,点P 坐标为()3,0.因为以P ,Q ,A ,B 为顶点的四边形为菱形,所以点Q 坐标为()5,4.综上可知:若点P 为x 轴上一点,则在平面直角坐标系中存在一点Q ,使得P ,Q ,A ,B 四个点能构成一个菱形,此时Q 点坐标为()45,4-,()45,4,()0,4-或()5,4.【点睛】本题是一次函数综合题,利用待定系数法求解析式,平行四边形的性质,菱形的性质,利用分类讨论思想解决问题是本题的关键.5.(1)证明见解析;(2)DE =BD +CE ;(3)B(1,4)【解析】【分析】(1)证明△ABD ≌△CAE ,根据全等三角形的性质得到AE=BD ,AD=CE ,结合图形解答即可;(2)根据三角形内角和定理、平角的定义证明∠ABD=∠CAE ,证明△ABD ≌△CAE ,根据全等三角形的性质得到AE=BD ,AD=CE ,结合图形解答即可;(3)根据△AEC ≌△CFB ,得到CF=AE=3,BF=CE=OE-OC=4,根据坐标与图形性质解答.【详解】(1)证明:∵BD ⊥直线m ,CE ⊥直线m ,∴∠ADB =∠CEA =90°∵∠BAC =90°∴∠BAD +∠CAE =90°∵∠BAD +∠ABD =90°∴∠CAE=∠ABD∵在△ADB和△CEA中ABD CAEADB CEAAB CA∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ADB≌△CEA(AAS)∴AE=BD,AD=CE∴DE=AE+AD=BD+CE即:DE=BD+CE(2)解:数量关系:DE=BD+CE理由如下:在△ABD中,∠ABD=180°-∠ADB-∠BAD,∵∠CAE=180°-∠BAC-∠BAD,∠BDA=∠AEC,∴∠ABD=∠CAE,在△ABD和△CAE中,ABD CAEBDA AECAB CA∠∠⎧⎪∠∠⎨⎪⎩===∴△ABD≌△CAE(AAS)∴AE=BD,AD=CE,∴DE=AD+AE=BD+CE;(3)解:如图,作AE⊥x轴于E,BF⊥x轴于F,由(1)可知,△AEC≌△CFB,∴CF=AE=3,BF=CE=OE-OC=4,∴OF=CF-OC=1,∴点B的坐标为B(1,4).【点睛】本题考查的是全等三角形的判定和性质、坐标与图形性质,掌握全等三角形的判定定理和性质定理是解题的关键.6.(1)左;3;(1-2m);(2)①(-4,0);(-1,0)(-3,0);②当平移后的线段AB 与线段CD 有公共点时,1913n≤≤;③ F9(,2)12m--.【解析】【分析】(1)根据平面直角坐标系中点的平移计算方法即可得解(2)①根据B 点向下平移后,点B 和点A 的纵坐标相等得到等量关系,可求出m 的值,从而求出A 、B 、C 三点坐标;②过 C 作 CK 垂直 x 轴交 AB 于 K 点过 B 做 BM 垂直 x 轴于 M 点,设出K 点坐标,作 KH ⊥BM 与 H 点,表示出H 点坐标,然后利用面积关系ABM AKM BKM S S S ∆∆∆=+求出距离;当 B '在线段 CD 上时,BB '交 x 轴于 M 点,过 B '做 B 'E ⊥OD ,利用S △COD = S △OB'C + S △OB'D ,求出n 的值,从而求出n 的取值范围;③通过坐标平移法用m 表示出E 点的坐标,利用D 、E 两点坐标表示出直线DE 的函数关系式,令y=﹣2,求出x 的值即可求出F 点坐标.【详解】解:(1)根据平移规律可得:B 向左平移;m -(m -1)=3,所以平移3个单位;m+4-(3m+3)=1-2m ,所以再向下平移(1-2m )个单位;故答案为:左;3;(1-2m )(2)①点 B 向下移动 3 个单位得:B (m ,m+1)∵移动后的点 B 和点 A 的纵坐标相等∴m+1=3m+3∴m=﹣1∴A (-4,0);B (-1,0);C (-3,0);②如图 1,过 C 作 CK 垂直 x 轴交 AB 于 K 点过 B 做 BM 垂直 x 轴于 M 点,设 K 点坐标为(-3,a )M 点坐标为(-1,0)作 KH ⊥BM 与 H 点,H 点坐标为(-1,a )AM=3,BM=3,KC=a,KH=2∵ABM AKM BKM S S S ∆∆∆=+ ∴222AM BM KC AM KHBM⨯⨯⨯=+ ∴33323222a⨯⨯⨯=+解得:1a =,∴当线段 AB 向下平移 1 个单位时,线段 AB 和 CD 开始有交点,∴ n ≥ 1,当 B'在线段 CD 上时,如图 2BB'交 x 轴于 M 点,过 B'做 B'E⊥OD,B'M=n-3,B'E=1,OD=5,OC=3∵ S△COD = S△OB'C + S△OB'D∴'' 222 CO OD CO B M OD B E ⨯⨯⨯=+∴353(3)51 222n⨯⨯-⨯=+解得:193n=,综上所述,当平移后的线段 AB 与线段 CD 有公共点时,1913n≤≤.③∵A(m−3,3m+3), B(m,m+4) D(0,−5)且AD 沿直线 AB 方向平移得到线段BE,∴E点横坐标为:3E点纵坐标为:﹣5+m+4-(3m+3)=﹣4-2m∴E(3,﹣4-2m),设DE:y=kx+b,把D(0,﹣5),E(3,﹣4-2m)代入y=kx+b∴3k+b=42mb=5⎧⎨⎩﹣-﹣∴1-2mk=3b=-5⎧⎪⎨⎪⎩,∴y=12mx53--,把y=﹣2代入解析式得:﹣2=12mx53--,x=912m-,∴F9(,2) 12m--.【点睛】本题考查平面直角坐标系中点的平移计算及一次函数解析式求法,解题关键在于理解掌握平面直角坐标系中点平移计算方法以及用待定系数法求函数解析式方法的应用.7.(1)BP=3cm,CQ=3cm;(2)全等,理由详见解析;(3)154;(4)经过803s点P与点Q第一次相遇.【解析】【分析】(1)速度和时间相乘可得BP、CQ的长;(2)利用SAS可证三角形全等;(3)三角形全等,则可得出BP=PC,CQ=BD,从而求出t的值;(4)第一次相遇,即点Q第一次追上点P,即点Q的运动的路程比点P运动的路程多10+10=20cm的长度.【详解】解:(1)BP=3×1=3㎝,CQ=3×1=3㎝(2)∵t=1s,点Q的运动速度与点P的运动速度相等∴BP=CQ=3×1=3cm,∵AB=10cm,点D为AB的中点,∴BD=5cm.又∵PC=BC﹣BP,BC=8cm,∴PC=8﹣3=5cm,∴PC=BD又∵AB=AC,∴∠B=∠C ,在△BPD 和△CQP 中,PC BD B C BP CQ =⎧⎪∠=∠⎨⎪=⎩∴△BPD ≌△CQP(SAS)(3)∵点Q 的运动速度与点P 的运动速度不相等,∴BP 与CQ 不是对应边,即BP≠CQ∴若△BPD ≌△CPQ ,且∠B=∠C ,则BP=PC=4cm ,CQ=BD=5cm ,∴点P ,点Q 运动的时间t=433BP =s , ∴154Q CQ V t ==cm/s ; (4)设经过x 秒后点P 与点Q 第一次相遇. 由题意,得154x=3x+2×10, 解得80x=3 ∴经过803s 点P 与点Q 第一次相遇. 【点睛】本题考查动点问题,解题关键还是全等的证明和利用,将动点问题视为定点问题来分析可简化思考过程.8.(1)y+2;(2)△AOD 为直角三角形,理由见解析;(3)t =23. 【解析】【分析】(1)将点A 、B 的坐标代入一次函数表达式:y =kx +b ,即可求解;(2)由点A 、O 、D 的坐标得:AD 2=1,AO 2=3,DO 2=4,故DO 2=OA 2+AD 2,即可求解; (3)点C,1),∠DBO =30°,则∠ODA =60°,则∠DOA =30°,故点C1),则∠AOC =30°,∠DOC =60°,OQ =CP =t ,则OP =2﹣t .①当OP =OM 时,OQ =QH +OH,即2(2﹣t )+12(2﹣t )=t ,即可求解;②当MO =MP 时,∠OQP =90°,故OQ =12O P ,即可求解;③当PO =PM 时,故这种情况不存在. 【详解】解:(1)将点A、B的坐标代入一次函数表达式:y=kx+b得:33=2023k bk b⎧+⎪⎨⎪=+⎩,解得:3 =32kb⎧⎪⎨⎪=⎩-,故直线AB的表达式为:y=﹣3x+2;(2)直线AB的表达式为:y=﹣3x+2,则点D(0,2),由点A、O、D的坐标得:AD2=1,AO2=3,DO2=4,故DO2=OA2+AD2,故△AOD为直角三角形;(3)直线AB的表达式为:y=﹣3x+2,故点C(3,1),则OC=2,则直线AB的倾斜角为30°,即∠DBO=30°,则∠ODA=60°,则∠DOA=30°故点C(3,1),则OC=2,则点C是AB的中点,故∠COB=∠DBO=30°,则∠AOC=30°,∠DOC=60°,OQ=CP=t,则OP=OC﹣PC=2﹣t,①当OP=OM时,如图1,则∠OMP=∠MPO=12(180°﹣∠AOC)=75°,故∠OQP=45°,过点P作PH⊥y轴于点H,则OH=12OP=12(2﹣t),由勾股定理得:PH=32(2﹣t)=QH,OQ=QH+OH=32(2﹣t)+12(2﹣t)=t,解得:t=23;②当MO=MP时,如图2,则∠MPO=∠MOP=30°,而∠QOP=60°,∴∠OQP=90°,故OQ=12OP,即t=12(2﹣t),解得:t=23;③当PO=PM时,则∠OMP=∠MOP=30°,而∠MOQ=30°,故这种情况不存在;综上,t=2323.【点睛】本题考查等腰三角形的性质、一次函数解析式、勾股定理、含30°的角的直角三角形的性质等知识点,还利用了方程和分类讨论的思想,综合性较强,难度较大,解题的关键是学会综合运用性质进行推理和计算.9.(1)6-2t;(2)全等,理由见解析;(3)83;(4)经过24s后,点P与点Q第一次在ABC的BC边上相遇【解析】【分析】(1)根据题意求出BP,由PC=BC-BP,即可求得;(2)根据时间和速度的关系分别求出两个三角形中,点运动轨迹的边长,由∠B=∠C,利用SAS判定BPD△和CQP全等即可;(3)根据全等三角形的判定条件探求边之间的关系,得出BP=PC,再根据路程=速度×时间公式,求点P的运动时间,然后求点Q的运动速度即得;(4)求出点P 、Q 的路程,根据三角形ABC 的三边长度,即可得出答案.【详解】(1)由题意知,BP=2t ,则PC=BC-BP=6-2t ,故答案为:6-2t ;(2)全等,理由如下:∵p Q V V =,t=1,∴BP=2=CQ ,∵AB=8cm ,点D 为AB 的中点,∴BD=4(cm ),又∵PC=BC-BP=6-2=4(cm ),在BPD △和CQP 中BD PC B C BP CQ =⎧⎪∠=∠⎨⎪=⎩∴BPD △≌CQP (SAS )故答案为:全等.(3)∵p Q V V ≠,∴BP CQ ≠,又∵BPD △≌CPQ ,∠B=∠C ,∴BP=PC=3cm ,CQ=BD=4cm ,∴点,P Q 运动时间322BP t ==(s ), ∴48332Q CQ V t===(cm/s ), 故答案为:83;(4)设经过t 秒时,P 、Q 第一次相遇,∵2/p V cm s =,8/3Q V cm s =, ∴2t+8+8=83t ,解得:t=24此时点Q 走了824643⨯=(cm ),∵ABC 的周长为:8+8+6=22(cm ),∴6422220÷=,∴20-8-8=4(cm ),经过24s 后,点P 与点Q 第一次在ABC 的BC 边上相遇,故答案为:24s ,在 BC 边上相遇.【点睛】考查了全等三角形的判定和性质,路程,速度,时间的关系,全等三角形中的动点问题,动点的追及问题,熟记三角形性质和判定,熟练掌握全等的判定依据和动点的运动规律是解题的关键,注意动点中追及问题的方向.10.(1)证明见解析;(2)证明见解析;(3)结论:AD DG ND =-,证明见解析.【解析】【分析】(1)先根据直角三角形的性质得出60ABC ∠=︒,再根据角平分线的性质可得CD ED =,然后根据三角形的判定定理与性质可得BC BE =,最后根据等边三角形的判定即可得证;(2)如图(见解析),延长ED 使得DF MD =,连接MF ,先根据直角三角形的性质、等边三角形的判定得出MDF ∆是等边三角形,再根据等边三角形的性质、角的和差得出,,F MDB MF MD FMG DMB ∠=∠=∠=∠,然后根据三角形全等的判定与性质、等量代换即可得证;(3)如图(见解析),参照题(2),先证HDN ∆是等边三角形,再根据等边三角形的性质、角的和差得出,,H NDG NH ND HNB DNG ∠=∠=∠=∠,然后根据三角形全等的判定与性质、等量代换即可得证.【详解】(1)3,090A ACB ∠=︒∠=︒9060ABC A ∴∠=︒-∠=︒ BD 是ABC ∠的角平分线,DE AB ⊥CD ED ∴=在BCD ∆和BED ∆中,CD ED BD BD =⎧⎨=⎩()BCD BED HL ∴∆≅∆BC BE ∴=EBC ∴∆是等边三角形;(2)如图,延长ED 使得DF MD =,连接MF3,090A ACB ∠=︒∠=︒,BD 是ABC ∠的角平分线,DE AB ⊥60,ADE BDE AD BD ∴∠=∠=︒=60,18060MDF ADE MDB ADE BDE ∴∠=∠=︒∠=︒-∠-∠=︒MDF ∴∆是等边三角形,60MF DM F DMF ∴=∠=∠=︒60BMG ∠=︒DMF DM B MGG DM G∴∠+∠=+∠∠,即FMG DMB∠=∠在FMG∆和DMB∆中,60F MDBMF MDFMG DMB∠=∠=︒⎧⎪=⎨⎪∠=∠⎩()FMG DMB ASA∴∆≅∆GF BD∴=,即DF DG BD+=AD DF DG MD DG∴=+=+即AD DG MD=+;(3)结论:AD DG ND=-,证明过程如下:如图,延长BD使得DH ND=,连接NH由(2)可知,60,18060,ADE HDN ADE BDE AD BD∠=︒∠=︒-∠-∠=︒= HDN∴∆是等边三角形,60NH ND H HND∴=∠=∠=︒60BNG∠=︒HND BND BNDBNG∠+∠=+∠∴∠,即NHNB D G∠=∠在HNB∆和DNG∆中,60H NDGNH NDHNB DNG∠=∠=︒⎧⎪=⎨⎪∠=∠⎩()HNB DNG ASA∴∆≅∆HB DG∴=,即DH BD DG+=ND AD DG∴+=即AD DG ND=-.【点睛】本题考查了直角三角形的性质、等边三角形的判定与性质、三角形全等的判定定理与性质等知识点,较难的是题(2)和(3),通过作辅助线,构造一个等边三角形是解题关键.11.(1)(1,0);(2)362y x -=;(3)92;(4)(6,3). 【解析】【分析】 (1)由题意已知l 1的解析式,令y=0求出x 的值即可;(2)根据题意设l 2的解析式为y=kx+b ,并由题意联立方程组求出k ,b 的值;(3)由题意联立方程组,求出交点C 的坐标,继而即可求出S △ADC ;(4)由题意根据△ADP 与△ADC 底边都是AD ,面积相等所以高相等,△ADC 高就是点C 到AD 的距离进行分析计算.【详解】解:(1)由y=-3x+3,令y=0,得-3x+3=0,∴x=1,∴D (1,0);(2)设直线l 2的解析表达式为y=kx+b ,由图象知:x=4,y=0;x=3,y =32-,代入表达式y=kx+b , ∴40332k b k b +⎧⎪⎨+-⎪⎩==, ∴326k b ⎧⎪⎨⎪-⎩==, ∴直线l 2的解析表达式为362y x -=; (3)由33362y x y x ⎪-+-⎧⎪⎨⎩==,解得23x y ⎧⎨⎩-==, ∴C (2,-3),∵AD=3, ∴331922ADC S =⨯⨯-=; (4)△ADP 与△ADC 底边都是AD ,面积相等所以高相等,△ADC 高就是点C 到直线AD 的距离,即C 纵坐标的绝对值=|-3|=3,则P 到AD 距离=3,∴P 纵坐标的绝对值=3,点P 不是点C ,∴点P 纵坐标是3,∵y=1.5x-6,y=3,∴1.5x-6=3,解得x=6,所以P (6,3).【点睛】本题考查的是一次函数图象的性质以及三角形面积的计算等有关知识,熟练掌握求一次函数解析式的方法以及一次函数图象的性质和三角形面积的计算公式是解题的关键.12.(1)①见解析;②DE =297;(2)DE 的值为 【解析】【分析】(1)①先证明∠DAE =∠DAF ,结合DA =DA ,AE =AF ,即可证明;②如图1中,设DE =x ,则CD =7﹣x .在Rt △DCF 中,由DF 2=CD 2+CF 2,CF =BE =3,可得x 2=(7﹣x )2+32,解方程即可;(2)分两种情形:①当点E 在线段BC 上时,如图2中,连接BE .由△EAD ≌△ADC ,推出∠ABE =∠C =∠ABC =45°,EB =CD =5,推出∠EBD =90°,推出DE 2=BE 2+BD 2=62+32=45,即可解决问题;②当点D 在CB 的延长线上时,如图3中,同法可得DE 2=153.【详解】(1)①如图1中,∵将△ABE 绕点A 逆时针旋转90°后,得到△AFC ,∴△BAE ≌△CAF ,∴AE =AF ,∠BAE =∠CAF ,∵∠BAC =90°,∠EAD =45°,∴∠CAD +∠BAE =∠CAD +∠CAF =45°,∴∠DAE =∠DAF ,∵DA =DA ,AE =AF ,∴△AED ≌△AFD (SAS );②如图1中,设DE =x ,则CD =7﹣x .∵AB =AC ,∠BAC =90°,∴∠B =∠ACB =45°,∵∠ABE =∠ACF =45°,∴∠DCF =90°,∵△AED ≌△AFD (SAS ),∴DE =DF =x ,∵在Rt △DCF 中, DF 2=CD 2+CF 2,CF =BE =3,∴x 2=(7﹣x )2+32,∴x =297, ∴DE =297; (2)∵BD =3,BC =9,∴分两种情况如下:①当点E 在线段BC 上时,如图2中,连接BE .∵∠BAC=∠EAD=90°,∴∠EAB=∠DAC,∵AE=AD,AB=AC,∴△EAB≌△DAC(SAS),∴∠ABE=∠C=∠ABC=45°,EB=CD=9-3=6,∴∠EBD=90°,∴DE2=BE2+BD2=62+32=45,∴DE=35;②当点D在CB的延长线上时,如图3中,连接BE.同理可证△DBE是直角三角形,EB=CD=3+9=12,DB=3,∴DE2=EB2+BD2=144+9=153,∴DE=317,综上所述,DE的值为35或317.【点睛】本题主要考查旋转变换的性质,三角形全等的判定和性质以及勾股定理,添加辅助线,构造旋转全等模型,是解题的关键.。
(完整版)八年级数学上册压轴题专题练习

1、已知点O 为等边ABC ∆内一点,0110=∠AOB ,α=∠BOC ,以OC 为一边作等边OCD ∆,连接AD 。
(1)当0150=α时,试判断AOD ∆的形状,并说明理由。
(2)探究:当α为多少度时,AOD ∆为等腰三角形。
2、(1)如图1:点E 在正方形ABCD 的边上,B F ⊥AE 于点F,DG ⊥AE 于点G ,求证:△ADG ≌△BAF(2)如图2:已知AB=AC ,∠1=∠2=∠BAC, 求证:△ABE ≌△CAF(3)如图3:在等腰三角形ABC 中,AB=AC,AB>BC ,点D 在边BC 上,CD=2BD ,点E 、F 在线段AD 上,∠1=∠2=∠BAC,若△ABC 的面积为9,则△ABE 与△CDF 的面积的和是多少。
图1 图2 图33、.问题背景,请你证明以上三个命题;① 如图1,在正三角形ABC 中,N 为BC 边上任一点,CM 为正三角形外角∠ACK 的平分线,若∠ANM=60°,则AN=NM② 如图2,在正方形ABCD 中,N 为BC 边上任一点,CM 为正方形外角∠DCK 的平分线,若∠ANM=90°,则AN=NM③ 如图3,在正五边形ABCDE 中,N 为BC 边上任一点,CM 为正五边形外角∠DCK 的平分线,若∠ANM=108°,则AN=NM O A B C D4、已知点C 为线段AB 上一点,分别以AC 、BC 为边在线段AB 同侧作△ACD 和△BCE ,且CA=CD ,CB=CE ,∠ACD=∠BCE ,直线AE 与BD 交于点F ,(1)如图1,若∠ACD=60°,则∠AFB= ;如图2,若∠ACD=90°,则∠AFB= ;如图3,若∠ACD=120°,则∠AFB= ;(2)如图4,若∠ACD=α,则∠AFB= (用含α的式子表示);(3)将图4中的△ACD 绕点C 顺时针旋转任意角度(交点F 至少在BD 、AE 中的一条线段上),变成如图5所示的情形,若∠ACD=α,则∠AFB 与α的有何数量关系?并给予证明.提示:始终证明DCB ACE ∆≅∆5.如图,已知D 为AB 的中点,AB=AC=10厘米,BC=8厘米,点D 为AB 的中点。
八年级上册压轴题数学考测试卷含答案

八年级上册压轴题数学考测试卷含答案一、压轴题1.如图,在ABC ∆中,90,,8ACB AC BC AB cm ∠=︒==,过点C 做射线CD ,且//CD AB ,点P 从点C 出发,沿射线CD 方向均匀运动,速度为3/cm s ;同时,点Q 从点A 出发,沿AB 向点B 匀速运动,速度为1/cm s ,当点Q 停止运动时,点P 也停止运动.连接,PQ CQ ,设运动时间为()()08t s t <<.解答下列问题:(1)用含有t 的代数式表示CP 和BQ 的长度;(2)当2t =时,请说明//PQ BC ;(3)设BCQ ∆的面积为()2S cm ,求S 与t 之间的关系式.解析:(1)CP=3t ,BQ=8-t ;(2)见解析;(3)S=16-2t .【解析】【分析】(1)直接根据距离=速度⨯时间即可;(2)通过证明PCQ BQC ≅,得到∠PQC=∠BCQ,即可求证; (3)过点C 作CM⊥A B ,垂足为M ,根据等腰直角三角形的性质得到CM=AM=4,即可求解.【详解】解:(1)CP=3t ,BQ=8-t ;(2)当t=2时,CP=3t=6,BQ=8-t=6∴CP=BQ∵CD ∥AB∴∠PCQ=∠BQC又∵CQ=QC∴PCQ BQC ≅∴∠PQC=∠BCQ∴PQ∥BC(3)过点C 作CM⊥AB,垂足为M∵AC=BC,CM⊥AB∴AM=118422AB=⨯=(cm)∵AC=BC,∠ACB=90︒∴∠A=∠B=45︒∵CM⊥AB∴∠AMC=90︒∴∠ACM=45︒∴∠A=∠ACM∴CM=AM=4(cm)∴118t4162 22BCQS BQ CM t ==⨯-⨯=-因此,S与t之间的关系式为S=16-2t.【点睛】此题主要考查列代数式、全等三角形的判定与性质、平行线的判定、等腰三角形的性质,熟练掌握逻辑推理是解题关键.2.(1)在等边三角形ABC中,①如图①,D,E分别是边AC,AB上的点且AE=CD,BD与EC交于点F,则∠BFE的度数是度;②如图②,D,E分别是边AC,BA延长线上的点且AE=CD,BD与EC的延长线交于点F,此时∠BFE的度数是度;(2)如图③,在△ABC中,AC=BC,∠ACB是锐角,点O是AC边的垂直平分线与BC的交点,点D,E分别在AC,OA的延长线上,AE=CD,BD与EC的延长线交于点F,若∠ACB=α,求∠BFE的大小.(用含α的代数式表示).解析:(1)①60°;②60°;(2)∠BFE =α.【解析】【分析】(1)①先证明△ACE≌△CBD得到∠ACE=∠CBD,再由三角形外角和定理可得∠BFE=∠CBD+∠BCF;②先证明△ACE≌△CBD得∠ACE=∠CBD=∠DCF,再由三角形外角和定理可得∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA;(2)证明△AEC≌△CDB得到∠E=∠D,则∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α.【详解】(1)如图①中,∵△ABC是等边三角形,∴AC=CB,∠A=∠BCD=60°,∵AE=CD,∴△ACE≌△CBD,∴∠ACE=∠CBD,∴∠BFE=∠CBD+∠BCF=∠ACE+∠BCF=∠BCA=60°.故答案为60.(2)如图②中,∵△ABC是等边三角形,∴AC=CB,∠A=∠BCD=60°,∴∠CAE=∠BCD=′120°∵AE=CD,∴△ACE≌△CBD,∴∠ACE=∠CBD=∠DCF,∴∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA=60°.故答案为60.(3)如图③中,∵点O 是AC 边的垂直平分线与BC 的交点,∴OC=OA ,∴∠EAC=∠DCB=α,∵AC=BC ,AE=CD ,∴△AEC ≌△CDB ,∴∠E=∠D ,∴∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α.【点睛】本题综合考查了三角形全等以及三角形外角和定理.3.已知//,MN GH 在Rt ABC 中,90,30ACB BAC ∠=︒∠=︒,点A 在MN 上,边BC 在GH 上,在Rt DEF △中,90,DFE ∠=︒边DE 在直线AB 上,45EDF ∠=︒; (1)如图1,求BAN ∠的度数;(2)如图2,将Rt DEF △沿射线BA 的方向平移,当点F 在M 上时,求AFE ∠度数; (3)将Rt DEF △在直线AB 上平移,当以A D F 、、为顶点的三角形是直角三角形时,直接写出FAN ∠度数.解析:(1)60°;(2)15°;(3)30°或15°【解析】【分析】(1)利用两直线平行,同旁内角互补,得出90CAN ∠=︒,即可得出结论; (2)先利用三角形的内角和定理求出AFD ∠,即可得出结论;(3)分90DAF ∠=︒和90AFD ∠=︒两种情况求解即可得出结论.【详解】解:(1)//MN GH ,180ACB NAC ∴∠+∠=︒,90ACB ∠=︒,90CAN ∴∠=︒,30BAC ∠=︒,9060BAN BAC ∴∠=︒-∠=︒;(2)由(1)知,60BAN ∠=︒,45EDF ∠=︒,18075AFD BAN EDF ∴∠=︒-∠-∠=︒,90DFE ∠=︒,15AFE DFE AFD ∴∠=∠-∠=︒;(3)当90DAF ∠=︒时,如图3,由(1)知,60BAN ∠=︒,30FAN DAF BAN ∴∠=∠-∠=︒;当90AFD ∠=︒时,如图4,90DFE ∠=︒,∴点A ,E 重合,45EDF ∠=︒,45DAF ∴∠=︒,由(1)知,60BAN ∠=︒,15FAN BAN DAF ∴∠=∠-∠=︒,即当以A 、D 、F 为顶点的三角形是直角三角形时,FAN ∠度数为30或15︒.【点睛】此题是三角形综合题,主要考查了平行线的性质,三角形的内角和定理,角的和差的计算,求出60BAN ∠=︒是解本题的关键.4.在我们认识的多边形中,有很多轴对称图形.有些多边形,边数不同对称轴的条数也不同;有些多边形,边数相同但却有不同数目的对称轴.回答下列问题:(1)非等边的等腰三角形有________条对称轴,非正方形的长方形有________条对称轴,等边三角形有___________条对称轴;(2)观察下列一组凸多边形(实线画出),它们的共同点是只有1条对称轴,其中图1-2和图1-3都可以看作由图1-1修改得到的,仿照类似的修改方式,请你在图1-4和图1-5中,分别修改图1-2和图1-3,得到一个只有1条对称轴的凸五边形,并用实线画出所得的凸五边形;(3)小明希望构造出一个恰好有2条对称轴的凸六边形,于是他选择修改长方形,图2中是他没有完成的图形,请用实线帮他补完整个图形;(4)请你画一个恰好有3条对称轴的凸六边形,并用虚线标出对称轴.解析:(1)1,2,3;(2)答案见解析;(3)答案见解析;(4)答案见解析.【解析】【分析】(1)根据等腰三角形的性质、矩形的性质以及等边三角形的性质进行判断即可;(2)中图1-2和图1-3都可以看作由图1-1修改得到的,在图1-4和图1-5中,分别仿照类似的修改方式进行画图即可;(3)长方形具有两条对称轴,在长方形的右侧补出与左侧一样的图形,即可构造出一个恰好有2条对称轴的凸六边形;(4)在等边三角形的基础上加以修改,即可得到恰好有3条对称轴的凸六边形.【详解】解:(1)非等边的等腰三角形有1条对称轴,非正方形的长方形有2条对称轴,等边三角形有3条对称轴,故答案为1,2,3;(2)恰好有1条对称轴的凸五边形如图中所示.(3)恰好有2条对称轴的凸六边形如图所示.(4)恰好有3条对称轴的凸六边形如图所示.5.如图,在ABC ∆中,AC BC =,90ACB ∠=︒,点D 为ABC ∆内一点,且BD AD =.(1)求证:CD AB ⊥;(2)若15CAD ∠=︒,E 为AD 延长线上的一点,且CE CA =.①求BDC ∠的度数.②若点M 在DE 上,且DC DM =,请判断ME 、BD 的数量关系,并说明理由. ③若点N 为直线AE 上一点,且CEN ∆为等腰∆,直接写出CNE ∠的度数.解析:(1)证明见解析;(2)①120BDC ∠=︒;②ME BD =,理由见解析;③ 7.5°或15°或82.5°或150°【解析】【分析】(1)利用线段的垂直平分线的性质即可证明;(2)①利用SSS 证得△ADC ≌△BDC ,可求得∠ACD=∠BCD=45°,∠CAD=∠CBD=15°,即可解题;②连接MC ,易证△MCD 为等边三角形,即可证明△BDC ≌△EMC 即可解题;③分EN=EC 、EN=CN 、CE=CN 三种情形讨论,画出图形,利用等腰三角形的性质即可求解.【详解】(1)∵CB=CA ,DB=DA ,∴CD 垂直平分线段AB ,∴CD ⊥AB ;(2)①在△ADC 和△BDC 中,BC AC CD CD BD AD =⎧⎪=⎨⎪=⎩,∴△ADC ≌△BDC (SSS ),∴∠ACD=∠BCD=12∠BCA=45°,∠CAD=∠CBD=15°, ∴∠BDC=180︒-45°-15°=120°;②结论:ME=BD ,理由:连接MC ,∵AC BC =,90ACB ∠=︒,∴∠CAB=∠CBA=45°,∵∠CAD=∠CBD=15°,∴∠DBA=∠DAB=30°,∴∠BDE=30°+30°=60°,由①得∠BDC=120°,∴∠CDE=60°,∵DC=DM ,∠CDE=60°,∴△MCD 为等边三角形,∴CM=CD ,∵EC=CA=CB ,∠DMC=60°,∴∠E=∠CAD=∠CBD=15°,∠EMC=120°,在△BDC 和△EMC 中,15120CBD E BDC EMC CD CM ∠=∠=︒⎧⎪∠=∠=︒⎨⎪=⎩,∴△BDC ≌△EMC (AAS ),∴ME=BD ;③当EN=EC 时,∠1152EN C ︒==7.5°或∠2EN C =180152︒-︒=82.5°; 当EN=CN 时,∠3EN C =180215︒-⨯︒=150°;当CE=CN 时,点N 与点A 重合,∠CNE=15°,所以∠CNE 的度数为7.5°或15°或82.5°或150°.【点睛】本题考查了全等三角形的判定和性质、等边三角形的判定和性质、等腰三角形的性质和判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考压轴题.6.某校七年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究.(1)如图1,在△ABC 中,∠ABC 与∠ACB 的平分线交于点P ,∠A =64°,则∠BPC = ;(2)如图2,△ABC 的内角∠ACB 的平分线与△ABC 的外角∠ABD 的平分线交于点E .其中∠A =α,求∠BEC .(用α表示∠BEC );(3)如图3,∠CBM 、∠BCN 为△ABC 的外角,∠CBM 、∠BCN 的平分线交于点Q ,请你写出∠BQC 与∠A 的数量关系,并说明理由; (4)如图4,△ABC 外角∠CBM 、∠BCN 的平分线交于点Q ,∠A=64°,∠CBQ ,∠BCQ 的平分线交于点P ,则∠BPC= ゜,延长BC 至点E ,∠ECQ 的平分线与BP 的延长线相交于点R ,则∠R= ゜.解析:(1) 122°;(2)12BEC α∠=;(3)01902BQC A ;(4)119,29 ; 【解析】【分析】 (1)根据三角形的内角和角平分线的定义;(2)根据三角形的一个外角等于与它不相邻的两个内角的和,用A ∠与1∠表示出2∠,再利用E ∠与1∠表示出2∠,于是得到结论;(3)根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出EBC ∠与ECB ∠,然后再根据三角形的内角和定理列式整理即可得解;(4)根据(1),(3)的结论可以得出∠BPC 的度数;根据(2)的结论可以得到∠R 的度数.【详解】解:(1)BP 、CP 分别平分ABC ∠和ACB ∠,12PBC ABC ∴∠=∠,12PCB ACB ∠=∠, 180()BPC PBC PCB ∴∠=︒-∠+∠11180()22ABC ACB =︒-∠+∠, 1180()2ABC ACB =︒-∠+∠, 1(180180)2A =︒-︒-∠, 1180902A =-︒+︒∠, 9032122,故答案为:122︒;(2)如图2示,CE 和BE 分别是ACB ∠和ABD ∠的角平分线,112ACB ∴∠=∠,122ABD ∠=∠, 又ABD ∠是ABC ∆的一外角,ABD A ACB ∴∠=∠+∠,112()122A ABC A ∴∠=∠+∠=∠+∠, 2∠是BEC ∆的一外角,112111222BEC A A α∴∠=∠-∠=∠+∠-∠=∠=; (3)1()2QBC A ACB ∠=∠+∠,1()2QCB A ABC ∠=∠+∠, 180BQC QBC QCB ∠=︒-∠-∠,11180()()22A ACB A ABC =︒-∠+∠-∠+∠, 11180()22A A ABC ACB =︒-∠-∠+∠+∠, 结论1902BQC A ∠=︒-∠. (4)由(3)可知,119090645822BQCA , 再根据(1),可得180()BPCPBC PCB 1118022QBC QCB 1180902Q 118090582119;由(2)可得:11582922R Q ;故答案为:119,29.【点睛】本题考查了三角形的外角性质与内角和定理,熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.7.在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以每分钟1米的速度由A向B和由C向A爬行,其中一只蜗牛爬到终点时,另一只也停止运动,经过t分钟后,它们分别爬行到D、E处,请问:(1)如图1,在爬行过程中,CD和BE始终相等吗,请证明?(2)如果将原题中的“由A向B和由C向A爬行”,改为“沿着AB和CA的延长线爬行”,EB与CD交于点Q,其他条件不变,蜗牛爬行过程中∠CQE的大小保持不变,请利用图2说明:∠CQE=60°;(3)如果将原题中“由C向A爬行”改为“沿着BC的延长线爬行,连接DE交AC于F”,其他条件不变,如图3,则爬行过程中,证明:DF=EF解析:(1)相等,证明见解析;(2)证明见解析;(3)证明见解析.【解析】【分析】(1)先证明△ACD≌△CBE,再由全等三角形的性质即可证得CD=BE;(2)先证明△BCD≌△ABE,得到∠BCD=∠ABE,求出∠DQB=∠BCQ+∠CBQ=∠ABE+∠CBQ=180°-∠ABC,∠CQE=180°-∠DQB,即可解答;(3)如图3,过点D作DG∥BC交AC于点G,根据等边三角形的三边相等,可以证得AD=DG=CE;进而证明△DGF和△ECF全等,最后根据全等三角形的性质即可证明.【详解】(1)解:CD和BE始终相等,理由如下:如图1,AB=BC=CA,两只蜗牛速度相同,且同时出发,∴CE=AD,∠A=∠BCE=60°在△ACD与△CBE中,AC=CB,∠A=∠BCE,AD=CE∴△ACD≌△CBE(SAS),∴CD=BE,即CD和BE始终相等;(2)证明:根据题意得:CE=AD,∵AB=AC,∴AE=BD,∴△ABC是等边三角形,∴AB=BC,∠BAC=∠ACB=60°,∵∠EAB+∠ABC=180°,∠DBC+∠ABC=180°,∴∠EAB=∠DBC,在△BCD和△ABE中,BC=AB,∠DBC=∠EAB,BD=AE∴△BCD≌△ABE(SAS),∴∠BCD=∠ABE∴∠DQB=∠BCQ+∠CBQ=∠ABE+∠CBQ=180°-∠ABC=180°-60°=120°,∴∠CQE=180°-∠DQB=60°,即CQE=60°;(3)解:爬行过程中,DF始终等于EF是正确的,理由如下:如图,过点D作DG∥BC交AC于点G,∴∠ADG=∠B=∠AGD=60°,∠GDF=∠E,∴△ADG为等边三角形,∴AD=DG=CE,在△DGF和△ECF中,∠GFD=∠CFE,∠GDF=∠E,DG=EC∴△DGF≌△EDF(AAS),∴DF=EF.【点睛】本题主要考查了全等三角形的判定与性质和等边三角形的性质;题弄懂题中所给的信息,再根据所提供的思路寻找证明条件是解答本题的关键.8.阅读并填空:如图,ABC 是等腰三角形,AB AC =,D 是边AC 延长线上的一点,E 在边AB 上且联接DE 交BC 于O ,如果OE OD ,那么CD BE =,为什么?解:过点E 作EF AC 交BC 于F所以ACB EFB ∠=∠(两直线平行,同位角相等)D OEF ∠=∠(________)在OCD 与OFE △中()________COD FOE OD OED OEF ⎧∠=∠⎪=⎨⎪∠=∠⎩所以OCD OFE △≌△,(________)所以CD FE =(________)因为AB AC =(已知)所以ACB B =∠∠(________)所以EFB B ∠=∠(等量代换)所以BE FE =(________)所以CD BE =解析:见解析【解析】【分析】先根据平行线的性质,得到角的关系,然后证明OCD OFE △≌△,写出证明过程和依据即可.【详解】解:过点E 作//EF AC 交BC 于F ,∴ACB EFB ∠=∠(两直线平行,同位角相等),∴D OEF ∠=∠(两直线平行,内错角相等),在OCD 与OFE △中()()()COD FOE OD OED OEF ⎧∠=∠⎪=⎨⎪∠=∠⎩对顶角相等已知已证, ∴OCD OFE △≌△,(ASA )∴CD FE =(全等三角形对应边相等)∵AB AC =(已知)∴ACB B =∠∠(等边对等角)∴EFB B ∠=∠(等量代换)∴BE FE =(等角对等边)∴CD BE =;【点睛】本题考查了全等三角形的判定和性质,平行线的性质,解题的关键是由平行线的性质正确找到证明三角形全等的条件,从而进行证明.9.在△ABC 中,已知∠A =α.(1)如图1,∠ABC 、∠ACB 的平分线相交于点D .①当α=70°时,∠BDC 度数= 度(直接写出结果);②∠BDC 的度数为 (用含α的代数式表示);(2)如图2,若∠ABC 的平分线与∠ACE 角平分线交于点F ,求∠BFC 的度数(用含α的代数式表示).(3)在(2)的条件下,将△FBC 以直线BC 为对称轴翻折得到△GBC ,∠GBC 的角平分线与∠GCB 的角平分线交于点M (如图3),求∠BMC 的度数(用含α的代数式表示). 解析:(1)(1)①125°;②1902α︒+,(2)1BFC 2α∠=;(3)1BMC 904α︒∠=+ 【解析】【分析】(1)①由三角形内角和定理易得∠ABC+∠ACB=110°,然后根据角平分线的定义,结合三角形内角和定理可求∠BDC ;②由三角形内角和定理易得∠ABC+∠ACB=180°-∠A ,采用①的推导方法即可求解; (2)由三角形外角性质得BFC FCE FBC ∠=∠-∠,然后结合角平分线的定义求解; (3)由折叠的对称性得BGC BFC ∠=∠,结合(1)②的结论可得答案.【详解】解:(1)①∵12DBC ∠=∠ABC ,∠DCB =12∠ACB , ∴∠BDC =180°﹣∠DBC ﹣∠DCB =180°﹣12(∠ABC +∠ACB ) =180°﹣12(180°﹣70°) =125° ②∵12DBC ∠=∠ABC ,∠DCB =12∠ACB , ∴∠BDC =180°﹣∠DBC ﹣∠DCB =180°﹣12(∠ABC +∠ACB ) =180°﹣12(180°﹣∠A ) =90°+12∠A =90°+12α. 故答案分别为125°,90°+12α. (2)∵BF 和CF 分别平分∠ABC 和∠ACE ∴1FBC ABC 2∠=∠,1FCE ACE 2∠=∠, ∴BFC FCE FBC ∠=∠-∠=11(ACE ABC)A 22∠-∠=∠ 即1BFC 2α∠=. (3)由轴对称性质知:1BGC BFC 2α∠=∠=, 由(1)②可得1BMC 90BGC 2∠=︒+∠, ∴1BMC 904α∠=︒+. 【点睛】 本题考查三角形中与角平分线有关的角度计算,熟练掌握三角形内角和定理,以及三角形的外角性质是解题的关键.10.探究:如图①,在△ABC中,∠ACB=90°,CD⊥AB于点D,若∠B=30°,则∠ACD 的度数是度;拓展:如图②,∠MCN=90°,射线CP在∠MCN的内部,点A、B分别在CM、CN上,分别过点A、B作AD⊥CP、BE⊥CP,垂足分别为D、E,若∠CBE=70°,求∠CAD的度数;应用:如图③,点A、B分别在∠MCN的边CM、CN上,射线CP在∠MCN的内部,点D、E在射线CP上,连接AD、BE,若∠ADP=∠BEP=60°,则∠CAD+∠CBE+∠ACB=度.解析:探究:30;(2)拓展:20°;(3)应用:120【解析】【分析】(1)利用直角三角形的性质依次求出∠A,∠ACD即可;(2)利用直角三角形的性质直接计算得出即可;(3)利用三角形的外角的性质得出结论,直接转化即可得出结论.【详解】(1)在△ABC中,∠ACB=90°,∠B=30°,∴∠A=60°,∵CD⊥AB,∴∠ADC=90°,∴∠ACD=90°﹣∠A=30°;故答案为:30,(2)∵BE⊥CP,∴∠BEC=90°,∵∠CBE=70°,∴∠BCE=90°﹣∠CBE=20°,∵∠ACB=90°,∴∠ACD=90°﹣∠BCE=70°,∵AD⊥CP,∴∠CAD=90°﹣∠ACD=20°;(3)∵∠ADP是△ACD的外角,∴∠ADP=∠ACD+∠CAD=60°,同理,∠BEP=∠BCE+∠CBE=60°,∴∠CAD+∠CBE+∠ACB=∠CAD+∠CBE+∠ACD+∠BCE=(∠CAD+∠ACD)+(∠CBE +∠BCE )=120°,故答案为120.【点睛】此题是三角形的综合题,主要考查了直角三角形的性质,三角形的外角的性质,垂直的定义,解本题的关键是充分利用直角三角形的性质:两锐角互余,是一道比较简单的综合题.11.(1)填空①把一张长方形的纸片按如图①所示的方式折叠,EM ,FM 为折痕,折叠后的C 点落在1B M 或1B M 的延长线上,那么EMF ∠的度数是________;②把一张长方形的纸片按如图②所示的方式折叠,B 点与M 点重合,EM ,FM 为折痕,折叠后的C 点落在1A M 或1A M 的延长线上,那么EMF ∠的度数是_______. (2)解答:①把一张长方形的纸片按如图③所示的方式折叠,EM ,FM 为折痕,折叠后的C 点落在1B M 或1B M 的延长线上左侧,且80EMF ∠=︒,求11C MB ∠的度数; ②把一张长方形的纸片按如图④所示的方式折叠,B 点与M 点重合,EM ,FM 为折痕,折叠后的C 点落在1A M 或1A M 的延长线右侧,且60EMF ∠=︒,求11C MA ∠的度数.(3)探究:把一张四边形的纸片按如图⑤所示的方式折叠,EB ,FB 为折痕,设ABC α∠=︒,EBF β∠=︒,11A BC γ∠=︒,求α,β,γ之间的数量关系. 解析:90︒,45︒;20︒,30︒;2a γβ+=,2a γβ-=.【解析】【分析】(1)①如图①知1112EMC BMC ∠=∠,1112C MF C MC ∠=∠得 ()1112EMF BMC C MC ∠=∠+∠可求出解. ②由图②知111111,22EBA ABC C BF C BC ∠=∠∠=∠得()1112EBF ABC C BC ∠=∠+∠可求出解.(2)①由图③折叠知11,CMF FMC BME EMB ∠=∠∠=∠,可推出11()BMC EMF EMF C MB ∠-∠-∠=∠,即可求出解.②由图④中折叠知11,CMF C MF ABE A BE ∠=∠∠=∠,可推出()112906090A MC ︒︒︒-+∠=,即可求出解.(3)如图⑤-1、⑤-2中分别由折叠可知,a ββγ-=-、a ββγ-=+,即可求得 2a γβ+=、2a γβ-=.【详解】解:(1)①如图①中,1112EMC BMC ∠=∠,1112C MF C MC ∠=∠, ()1111111800229EMF EMC C MF BMC C MC ︒︒∴∠=∠+∠=∠⨯=+∠=, 故答案为90︒. ②如图②中,111111,22EBA ABC C BF C BC ∠=∠∠=∠, ()111111904522EBF EBC C BF ABC C BC ︒︒∴∠=∠+∠=∠+∠=⨯=, 故答案为45︒.(2)①如图③中由折叠可知,11,CMF FMC BME EMB ∠=∠∠=∠,1111C MF EMB EMF C MB ∠+∠-∠=∠,11CMF BME EMF C MB ∴∠+∠-∠=∠,11()BMC EMF EMF C MB ∴∠-∠-∠=∠,111808020C MB ︒︒︒∴-=∠=;②如图④中根据折叠可知,11,CMF C MF ABE A BE ∠=∠∠=∠,112290CMF ABE A MC ︒∠+∠+∠=,112()90CMF ABE A MC ︒∴∠+∠+∠=,()1129090EMF AMC ︒︒∴-∠+∠=,()112906090AMC ︒︒︒∴-+∠=, 1130A MC ︒∴∠=;(3)如图⑤-1中,由折叠可知,a ββγ-=-,2a γβ∴+=;如图⑤-2中,由折叠可知,a ββγ-=+,2a γβ∴-=.【点睛】本题考查了图形的变换中折叠属全等变换,图形的角度及边长不变及一些角度的计算问题,突出考查学生的观察能力、思维能力以及动手操作能力,本题是代数、几何知识的综合运用典型题目.12.已知在△ABC 中,AB =AC ,射线BM 、BN 在∠ABC 内部,分别交线段AC 于点G 、H . (1)如图1,若∠ABC =60°,∠MBN =30°,作AE ⊥BN 于点D ,分别交BC 、BM 于点E 、F .①求证:∠1=∠2;②如图2,若BF =2AF ,连接CF ,求证:BF ⊥CF ;(2)如图3,点E 为BC 上一点,AE 交BM 于点F ,连接CF ,若∠BFE =∠BAC =2∠CFE ,求ABFACF S S 的值.解析:(1)①见解析;②见解析;(2)2【解析】【分析】(1)①只要证明∠2+∠BAF =∠1+∠BAF =60°即可解决问题;②只要证明△BFC ≌△ADB ,即可推出∠BFC =∠ADB =90°;(2)在BF 上截取BK =AF ,连接AK .只要证明△ABK ≌CAF ,可得S △ABK =S △AFC ,再证明AF =FK =BK ,可得S △ABK =S △AFK ,即可解决问题;【详解】(1)①证明:如图1中,∵AB=AC,∠ABC=60°∴△ABC是等边三角形,∴∠BAC=60°,∵AD⊥BN,∴∠ADB=90°,∵∠MBN=30°,∠BFD=60°=∠1+∠BAF=∠2+∠BAF,∴∠1=∠2②证明:如图2中,在Rt△BFD中,∵∠FBD=30°,∴BF=2DF,∵BF=2AF,∴BF=AD,∵∠BAE=∠FBC,AB=BC,∴△BFC≌△ADB,∴∠BFC=∠ADB=90°,∴BF⊥CF(2)在BF上截取BK=AF,连接AK.∵∠BFE=∠2+∠BAF,∠CFE=∠4+∠1,∴∠CFB =∠2+∠4+∠BAC ,∵∠BFE =∠BAC =2∠EFC ,∴∠1+∠4=∠2+∠4∴∠1=∠2,∵AB =AC ,∴△ABK ≌CAF ,∴∠3=∠4,S △ABK =S △AFC ,∵∠1+∠3=∠2+∠3=∠CFE =∠AKB ,∠BAC =2∠CEF ,∴∠KAF =∠1+∠3=∠AKF ,∴AF =FK =BK ,∴S △ABK =S △AFK , ∴ABF AFC S 2S ∆∆=. 【点睛】本题考查全等三角形的判定和性质、等边三角形的性质、等腰三角形的判定和性质、直角三角形30度角性质等知识,解题的关键是能够正确添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.13.在《经典几何图形的研究与变式》一课中,庞老师出示了一个问题:“如图1,等腰直角三角形的三个顶点分别落在三条等距的平行线1l ,2l ,3l 上,90BAC ∠=︒,且每两条平行线之间的距离为1,求AB 的长度”.在研究这道题的解法和变式的过程中,同学们提出了很多想法:(1)小明说:我只需要过B 、C 向1l 作垂线,就能利用全等三角形的知识求出AB 的长. (2)小林说:“我们可以改变ABC 的形状.如图2,AB AC =,120BAC ∠=︒,且每两条平行线之间的距离为1,求AB 的长.”(3)小谢说:“我们除了改变ABC 的形状,还能改变平行线之间的距离.如图3,等边三角形ABC 三个顶点分别落在三条平行线1l ,2l ,3l 上,且1l 与2l 之间的距离为1,2l 与3l 之间的距离为2,求AB 的长、”请你根据3位同学的提示,分别求出三种情况下AB 的长度.解析:(1)5;(2)2213;(3)2213【解析】【分析】 (1)分别过点B ,C 向l 1作垂线,交l 1于M ,N 两点,证明△ABM ≌△CAN ,得到AM=CN ,AN=BM ,即可得出AB ;(2)分别过点B ,C 向l 1作垂线,交l 1于点P ,Q 两点,在l 1上取M ,N 使∠AMB=∠CNA=120°,证明△AMB ≌△CAN ,得到CN=AM ,再通过△PBM 和△QCN 算出PM 和NQ 的值,得到AP ,最后在△APB 中,利用勾股定理算出AB 的长;(3)在l 3上找M 和N ,使得∠BNC=∠AMC=60°,过B 作l 3的垂线,交l 3于点P ,过A 作l 3的垂线,交l 3于点Q ,证明△BCN ≌△CAM ,得到CN=AM ,在△BPN 和△AQM 中利用勾股定理算出NP 和AM ,从而得到PC ,结合BP 算出BC 的长,即为AB.【详解】解:(1)如图,分别过点B ,C 向l 1作垂线,交l 1于M ,N 两点,由题意可得:∠BAC=90°,∵∠NAC+∠MAB=90°,∠NAC+∠NCA=90°,∴∠MAB=∠NCA ,在△ABM 和△CAN 中,===AMB CNA MAB NCA AB AC ∠∠⎧⎪∠∠⎨⎪⎩,∴△ABM ≌△CAN (AAS ),∴AM=CN=2,AN=BM=1,∴AB=22251=+;(2)分别过点B ,C 向l 1作垂线,交l 1于P ,Q 两点,在l 1上取M ,N 使∠AMB=∠CNA=120°,∵∠BAC=120°,∴∠MAB+∠NAC=60°,∵∠ABM+∠MAB=60°,∴∠ABM=∠NAC ,在△AMB 和△CNA 中,===AMB CNA ABM NAC AB AC ∠∠⎧⎪∠∠⎨⎪⎩,∴△AMB ≌△CNA (AAS ),∴CN=AM ,∵∠AMB=∠ANC=120°,∴∠PMB=∠QNC=60°,∴PM=12BM ,NQ=12NC , ∵PB=1,CQ=2,设PM=a ,NQ=b , ∴2221=4a a +,2222=4b b +,解得:3=3a ,23=3b , ∴CN=AM=222323⎛⎫+ ⎪ ⎪⎝⎭=433, ∴AB=22AP BP +=()22AM PM BP ++=2213;(3)如图,在l 3上找M 和N ,使得∠BNC=∠AMC=60°,过B 作l 3的垂线,交于点P ,过A 作l 3的垂线,交于点Q ,∵△ABC 是等边三角形,∴BC=AC ,∠ACB=60°,∴∠BCN+∠ACM=120°,∵∠BCN+∠NBC=120°,∴∠NBC=∠ACM ,在△BCN 和△CAM 中,BNC CMA NBC MAC BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCN ≌△CAM (AAS ),∴CN=AM ,BN=CM ,∵∠PBN=90°-60°=30°,BP=2,∴BN=2NP ,在△BPN 中,222BP NP BN +=,即22224NP NP +=,解得:NP=233, ∵∠AMC=60°,AQ=3,∴∠MAQ=30°,∴AM=2QM ,在△AQM 中,222AQ QM AM +=,即22234QM QM +=,解得:QM=3,∴AM=23=CN ,∴PC=CN-NP=AM-NP=433, 在△BPC 中,BP 2+CP 2=BC 2,即BC=222243221233BP CP ⎛⎫+=+= ⎪ ⎪⎝⎭, ∴AB=BC=2213.【点睛】本题考查了全等三角形的判定和性质,平行线之间的距离,等腰三角形的性质,等边三角形的性质以及勾股定理,解题的关键是利用平行线构造全等三角形,再利用全等三角形的性质以及勾股定理求解.14.已知,在平面直角坐标系中,(42,0)A ,(0,42)B ,C 为AB 的中点,P 是线段AB 上一动点,D 是线段OA 上一点,且PO PD =,DE AB ⊥于E .(1)求OAB ∠的度数;(2)当点P 运动时,PE 的值是否变化?若变化,说明理由;若不变,请求PE 的值. (3)若45OPD ∠=︒,求点D 的坐标.解析:(1)45°;(2)PE 的值不变,PE=4,理由见详解;(3)D(828-,0).【解析】【分析】(1)根据(42,0)A ,(0,2)B ,得△AOB 为等腰直角三角形,根据等腰直角三角形的性质,即可求出∠OAB 的度数;(2)根据等腰直角三角形的性质得到∠AOC=∠BOC=45°,OC ⊥AB ,再证明△POC ≌△DPE ,根据全等三角形的性质得到OC=PE ,即可得到答案;(3)证明△POB ≌△DPA ,得到PA=OB=2,DA=PB ,进而得OD 的值,即可求出点D 的坐标.【详解】(1)(42,0)A ,(0,42)B ,∴OA=OB=2∵∠AOB=90°,∴△AOB 为等腰直角三角形,∴∠OAB=45°;(2)PE 的值不变,理由如下:∵△AOB 为等腰直角三角形,C 为AB 的中点,∴∠AOC=∠BOC=45°,OC ⊥AB ,∵PO=PD ,∴∠POD=∠PDO ,∵D 是线段OA 上一点,∴点P 在线段BC 上,∵∠POD=45°+∠POC ,∠PDO=45°+∠DPE ,∴∠POC=∠DPE ,在△POC 和△DPE 中,90POC DPE OCP PED PO PD ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,∴△POC ≅△DPE(AAS),∴OC=PE ,∵OC=12AB=12×42×2=4, ∴PE=4;(3)∵OP=PD , ∴∠POD=∠PDO=(180°−45°)÷2=67.5°,∴∠APD=∠PDO−∠A=22.5°,∠BOP=90°−∠POD=22.5°,∴∠APD=∠BOP ,在△POB 和△DPA 中,OBP PAD BOP APD OP PD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△POB ≌△DPA(AAS),∴PA=OB=42,DA=PB ,∴DA=PB=42×2-42=8-42,∴OD=OA−DA=42-(8-42)=828-,∴点D 的坐标为(828-,0).【点睛】本题主要考查等腰直角三角形的性质,三角形全等的判定与性质定理,图形与坐标,掌握等腰直角三角形的性质,是解题的关键.15.如图,ABC ∆在平面直角坐标系中,60BAC ∠=︒,()0,43A ,8AB =,点B 、C 在x 轴上且关于y 轴对称.(1)求点C 的坐标;(2)动点P 以每秒2个单位长度的速度从点B 出发沿x 轴正方向向终点C 运动,设运动时间为t 秒,点P 到直线AC 的距离PD 的长为d ,求d 与t 的关系式;(3)在(2)的条件下,当点P 到AC 的距离PD 为33AP ,作ACB ∠的平分线分别交PD 、PA 于点M 、N ,求MN 的长.解析:(1)C (4,0);(2)433d t =;(3)103MN =【解析】【分析】(1)根据对称的性质知ABC ∆为等边三角形,利用直角三角形中30度角的性质即可求得答案;(2)利用面积法可求得AC PD PC OA ⋅=⋅,再利用坐标系中点的特征即可求得答案; (3)利用(2)的结论求得2BP =,利用角平分线的性质证得ABO CBQ ∆∆≌,求得3CQ AO ==43QN =,再利用直角三角形中30度角的性质即可求得答案.【详解】(1)∵点B 、C 关于y 轴对称, ∴12OB OC BC ==, ∴AB AC =,∵60BAC ∠=︒,∴ABC ∆为等边三角形,∴8AB BC AC ===, ∴142OC BC ==, ∴点C 的坐标为:()4,0C ;(2)连接AP ,∵1122APC S AC PD PC OA ∆=⋅=⋅, ∴AC PD PC OA ⋅=⋅,∵()0,43A ,∴43OA =,∵2BP t =,∴82PC t =-,∵8AC =,∴433PC OA PD t AC⋅==-, 即:433d t =-;(3)∵点P 到AC 的距离为33,∴43333d t =-=,∴1t =,∴2BP =,延长CN 交AB 于点Q ,过点N 作NE x ⊥轴于点E ,连接PQ 、BN ,∵CQ 为ACB ∠的角平分线,ABC ∆为等边三角形,∴1302BCQ ACB ∠=∠=︒,CQ AB ⊥, ∵1302BAO BAC ∠=∠=︒,AB BC =, ∴ABO CBQ ∆∆≌,∴CQ AO ==设2QN a =,在Rt CNE ∆中,30QCB ∠=︒,∴112)22NE CN a a ===, ∵ABP ABN BPN S S S ∆∆∆=+, ∴111222BP OA AB QN BP NE ⋅=⋅+⋅,∴1112822)222a a ⨯⨯=⨯⨯+⨯⨯,∴a =∴7QN =, ∵60ACB ∠=︒,90PDC ∠=︒,∴30DPC ∠=︒,∵30BCQ ∠=︒,∴PM CM =,在Rt CDM ∆中,90MDC ∠=︒,30MCD ∠=︒, ∴12MD MC =,∴12MD PM =,PD =∴PM CM ==,∴MN CQ QN CM =--==【点睛】本题是三角形综合题,涉及的知识有:含30度直角三角形的性质,全等三角形的判定与性质,外角性质,角平分线的性质,等边三角形的判定和性质,坐标与图形性质,熟练掌握性质及定理、灵活运用面积法求线段的长是解本题的关键.二、选择题16.近年来,国家重视精准扶贫,收效显著.据统计约有65 000 000人脱贫,把65 000 000用科学记数法表示,正确的是()A.0.65×108B.6.5×107C.6.5×108D.65×106解析:B【解析】分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正数;当原数的绝对值小于1时,n是负数.详解:65 000 000=6.5×107.故选B.点睛:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.17.我国古代《易经》一书中记载了一种“结绳计数”的方法,一女子在从右到左依次排列的绳子上打结,满六进一,用来记录采集到的野果数量,下列图示中表示91颗的是()A.B.C.D.解析:B【解析】【分析】由于从右到左依次排列的绳子上打结,满六进一,所以从右到左的数分别进行计算,然后把它们相加即可得出正确答案.【详解】解:A、5+3×6+1×6×6=59(颗),故本选项错误;B、1+3×6+2×6×6=91(颗),故本选项正确;C、2+3×6+1×6×6=56(颗),故本选项错误;D、1+2×6+3×6×6=121(颗),故本选项错误;故选:B.【点睛】本题是以古代“结绳计数”为背景,按满六进一计数,运用了类比的方法,根据图中的数学列式计算;本题题型新颖,一方面让学生了解了古代的数学知识,另一方面也考查了学生的思维能力.18 =( )A .1B .2C .3D .4解析:B【解析】【分析】根据算术平方根的概念可得出答案.【详解】解:根据题意可得:,故答案为:B.【点睛】本题考查算术平方根的概念,解题关键在于对其概念的理解.19.当x 取2时,代数式(1)2x x -的值是( ) A .0B .1C .2D .3 解析:B【解析】【分析】把x 等于2代入代数式即可得出答案.【详解】解:根据题意可得:把2x =代入(1)2x x -中得: (1)21==122x x -⨯, 故答案为:B.【点睛】本题考查的是代入求值问题,解题关键就是把x 的值代入进去即可.20.如图,直线AB ⊥直线CD ,垂足为O ,直线EF 经过点O ,若35BOE ∠=,则FOD ∠=( )A .35°B .45°C .55°D .125°解析:C【解析】【分析】 根据对顶角相等可得:BOE AOF ∠=∠,进而可得FOD ∠的度数.【详解】解:根据题意可得:BOE AOF ∠=∠,903555FOD AOD AOF ∴∠=∠-∠=-=.故答案为:C.【点睛】本题考查的是对顶角和互余的知识,解题关键在于等量代换.21.将连续的奇数1、3、5、7、…、,按一定规律排成如表:图中的T 字框框住了四个数字,若将T 字框上下左右移动,按同样的方式可框住另外的四个数, 若将T 字框上下左右移动,则框住的四个数的和不可能得到的数是( ) A .22B .70C .182D .206解析:D【解析】【分析】根据题意设T 字框第一行中间数为x ,则其余三数分别为2x -,2x +,10x +, 根据其相邻数字之间都是奇数,进而得出x 的个位数只能是3或5或7,然后把T 字框中的数字相加把x 代入即可得出答案.【详解】设T 字框第一行中间数为x ,则其余三数分别为2x -,2x +,10x +2x -,x ,2x +这三个数在同一行∴x 的个位数只能是3或5或7∴T 字框中四个数字之和为()()()2210410x x x x x +-++++=+A .令41022x += 解得3x =,符合要求;B .令41070x += 解得15x =,符合要求;C .令410182x +=解得43x =,符合要求;D .令410206x +=解得49x =,因为47, 49, 51不在同一行,所以不符合要求. 故选D.【点睛】本题考查的是列代数式,规律型:数字的变化类,一元一次方程的应用,解题关键是把题意理解透彻以及找出其规律即可.22.一周时间有604800秒,604800用科学记数法表示为( )A .2604810⨯B .56.04810⨯C .66.04810⨯D .60.604810⨯ 解析:B【解析】【分析】科学记数法的表示形式为10n a ⨯的形式,其中110,a n ≤<为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值1>时,n 是正数;当原数的绝对值1<时,n 是负数.【详解】604800的小数点向左移动5位得到6.048,所以数字604800用科学记数法表示为56.04810⨯,故选B .【点睛】本题考查科学记数法的表示方法.科学记数法的表示形式为10n a ⨯的形式,其中110,a n ≤<为整数,表示时关键要正确确定a 的值以及n 的值.23.如图是小明制作的一张数字卡片,在此卡片上可以用一个正方形圈出44⨯个位置的16个数(如1,2,3,4,8,9,10,11,15,16,17,18,22,23,24,25).若用这样的正方形圈出这张数字卡片上的16个数,则圈出的16个数的和不可能为下列数中的( )A .208B .480。
人教版八年级上册数学期末动点问题压轴题专题训练(含解析)

人教版八年级上册数学期末动点问题压轴题专题训练(1)当时,点C 的坐标为 .(2)动点A 在运动的过程中,试判断发生变化,请说明理由.(3)当时,在坐标平面内是否存在一点若存在,请直接写出点P 的坐标;若不存在,请说明理由.(1)如图1,当点在边上时.①求证:;②求证:;(2)如图2,当点在边的延长线上时,其他条件不变,请写出2a =3a =D BC ABD ACE ≌△△BC DC CE =+D BC(1)请直接写出点A 和点B 的坐标;(2)请判断的形状并说明理由;(3)下列结论:①四边形为定值.请选择一个正确的结论并说明理由.(1)求证:;(2)求的面积;(3)点M ,N 分别是线段,上的动点,连接,求的最小值.DEF OEDF OEF DFE ∠+∠CD CE =CDE BC BD MN 12MN DN +(1)求出点的坐标.(2)求证:.(3)数学活动小组进行深入探究后发现变,你同意这个说法吗?请说明理由B OD BC =(1)如图①,请找出图中与相等的角,并说明理由;(2)如图②,交轴于点,过点作轴于点,求证:平分;(3)如图③,若,点在轴正半轴移动,且,取,连交轴OAB ∠BC x M C CD x ⊥,2D AM CD =AD BAC ∠()3,0A B y OB OA >()0,3P CP x边三角形,使其与点在直线的两侧,与直线相交于点(点与点A 不重合),连接.(1)如图,当时,①求证:;②在点A 运动的过程中,的度数是否会发生改变?如果会请说明理由,如果不会请求出的度数;(2)在点A 运动的过程中,试探究线段,,之间的数量关系.11.在平面直角坐标系中,点在轴的正半轴上,点在第一象限,,.(1)如图1,求证:是等边三角形;(2)如图1,若点M 为y 轴正半轴上一动点,以为边作等边三角形,连接并延长交轴于点,求证:;(3)如图2,若,,点为的中点,连接、交于,请问、与之间有何数量关系,并证明你的结论.12.在平面直角坐标系中,点A 为y 轴正半轴上一点,点B 为x 轴上一动点,连接ABD C AB DC l E E EB 120BAC ∠<︒ABE ACE =∠∠DCB ∠DCB ∠EA EB ED A y B OB AB =150BOP ∠=︒OAB BM BMN NA x P 2AP AO =BC BO ⊥BC BO =D CO AC DB E AE BE CE,以为腰作等腰,.(1)如图1,点B 在x 轴负半轴上,点C 的坐标是,直接写出点A 和点B 的坐标;(2)如图2,点B 在x 轴负半轴上,交x 轴于点D ,若平分.且点C 的纵坐标是,求线段的长;(3)如图3,点B 在x 轴正半轴上,以为边在左侧作等边,连接,,若,且,求的面积.13.等腰直角中,,,,点、分别是轴,轴上两个动点,直角边交轴于点,斜边交轴于点.(1)如图1,已知点的横坐标为,直接写出点的坐标;(2)如图2,若点为轴上的固定点,且,当点在轴正半轴运动时,分别以、为直角边在第一、二象限作等腰直角和等腰直角,连接交轴于点,问当点在轴的正半轴上运动时,的长度是否变化?若变化请说明理由;若不变化,请求出的长度.14.在平面直角坐标系中,点为坐标原点,点、分别位于轴和轴AB AB Rt ABC △90BAC ∠=︒(2,2)-AC BD ABC ∠3-BD BC BC BCE EO CO 60COE ∠=︒8CO =AOC ABC 90BAC ∠=︒AB AC =ABC C ∠=∠B A x y AC x D BC y E C 2-A A x ()6,0A -B y OB AB BOD ABC CD y P B y BP BP O ()6,0B -()0,6A x y上,连接,交轴于点.(1)求点的坐标;(2)动点从出发以个单位/秒的速度沿轴向终点运动,连接,将线段绕着点逆时针旋转后得到线段,与为对应点.连接、,为的面积,用含的式子表示;(3)在()的条件下,连接,过点作于,交轴于,交于,若,求点的坐标.15.如图①,在中,,现有一动点,从点出发,沿着三角形的边运动,回到点停止,速度为,设运动时间为秒.(1)如图①,当的面积等于面积的一半时,求的值:(2)如图②,点在边上,点在边上,在的边上,若另外有一个动点与点同时从点出发,沿着边运动,回到点停止.在两点运动过程中的某一时刻,以为顶点的三角形恰好与全等,求点的运动速度.16.如图,在平面直角坐标系中,,点在轴正半轴上,.AB CA AB ⊥x C C P B 2x C AP AP A 90︒AQ P Q PQ CQ S PCQ △t S 2BQ A AH BQ ⊥G x H PQ AC M :2:1APM AQM S S = H Rt ABC △90,12cm,16cm,20cm B AB BC AC ∠=︒===P A AB BC CA →→A 2cm /s t ABP ABC t D BC 4cm CD =E AC 5cm,,3cm CE ED BC ED =⊥=ABC Q P A AC CB BA →→A ,,A P Q EDC △Q ()0,9A B x 45OAB ∠=︒(1)求出点坐标;(2)动点从点出发,以每秒个单位长度的速度沿轴正半轴运动,同时点从点出发,以相同速度沿轴向左运动,连接,过点作交直线于点,连接,设点的运动时间为,请用含的式子表示的面积;(3)在(2)的条件下,直线与直线交于点,当时,求点坐标.17.已知中,,过点的直线交轴于,其中是方程组的解,(1)求的值(2)动点从点出发,沿线段以每秒1个单位的速度运动,运动时间为秒;请用含的式子表示线段的长度;并直接写出此时的取值范围;(3)在(2)的条件下,当为何值时,直线与直线互相垂直.18.在平面直角坐标系中,O 为坐标原点,直线交x 轴的正半轴于点A ,交y 轴的B P O 1y Q B x PQ O OG PQ ⊥AB G PG P t t OPG PQ AB H 72OPG S =△H AOB OA OB a ==A AM x (),0M b ,a b 3830a b a b +=⎧⎨+=⎩,a b P A AO t t OP t t BP AM AB(1)如图1求的长;(2)如图2动点E 在第二象限,点E 的坐标为,连接,,请写出面积s 与t 的关系;(3)在(2)的条件下,如图3点F 在第一象限,连接、、,,连接,当,求的值.OD (,)t m DE OE ODE FE FD FA 30ADF ∠=FE FA =EB 12,4EBO ODA ODA EFA EOB ∠=∠∠+∠=∠t m +参考答案:1.(1)(2)动点A 在运动的过程中,的值不变,(3)或或【分析】本题考查全等三角形判定及性质.(1)根据题意过点C 作轴于点,证明出,利用全等性质即可得到本题答案;(2)由(1)得,利用全等性质及点坐标表示线段长即可得到本题答案;(3)根据题意分3种情况讨论P 点位置,利用全等三角形性质及判定即可得到本题答案.【详解】(1)解:如下图,过点C 作轴于点E ,则,,∵是等腰直角三角形,∴,∴,∴.在和中,∴(AAS ),∵,∴,∴,∴;(2)解:动点A 在运动的过程中,的值不变.理由如下:(2,3)-+c d (4,)1-(3,2)--(2,1)-CE y ⊥E ACE BAO ≌ACE BAO ≌CE y ⊥CEA AOB ∠=∠ABC ,90AC BA BAC =∠︒=90ACE CAE BAO CAE ∠+∠=︒=∠+∠ACE BAO ∠=∠ACE △BAO CEA AOB ACE BAOAC BA ∠=∠⎧⎪∠=∠⎨⎪=⎩ACE BAO ≌(0,1),(0,2)B A -12BO AE AO CE ====,123OE =+=2,3C -()+c d由(1)知,,∵,,∴,∴,∴,又∵点C 的坐标为,∴,即的值不变;(3)解:存在一点P ,使与全等,符合条件的点P 的坐标是或或,分为三种情况讨论:①如下图,过点P 作轴于点E ,则,∴,∴,在和中,,∴(AAS ),∴,∴,即点P 的坐标是,②如下图,过点C 作轴于点M ,过点P 作轴于点E ,ACE BAO ≌(0,1)B (0,)A a -1,BO AE AO CE a ====1OE a =+(,1)C a a --(,)c d 11c d a a +=--=-+c d PAB ABC (4,)1-(3,2)--(2,1)-PE x ⊥90PBA AOB PEB ∠=∠=∠=︒90,90EPB PBE PBE ABO ∠+∠=︒∠+∠=︒EPB ABO ∠=∠PEB △BOA △EPB OBA PEB BOA PB BA ∠=∠⎧⎪∠=∠⎨⎪=⎩PEB BOA △≌△1,3PE BO EB AO ====314OE =+=(4,)1-CM x ⊥PE x ⊥则.∵,∴,∴,∴,∴,在和中,,∴(AAS ),∴.∵,∴,即点P 的坐标是;③如下图,过点P 作轴于点E ,则.∵,∴,∴,90CMB PEB ∠=∠=︒CAB PAB △≌△45,PBA CBA BC BP ∠=∠=︒=90CBP ∠=︒90,90MCB CBM CBM PBE ∠+∠=︒∠+∠=︒MCB PBE ∠=∠CMB BEP △MCB EBP CMB BEP BC PB ∠=∠⎧⎪∠=∠⎨⎪=⎩CMB BEP △≌△,PE BM CM BE ==3,4),10C B -((,)2,413PE OE BE BO ==-=-=(3,2)--PE x ⊥90BEP BOA ∠=∠=︒CAB PBA △≌△,90AB BP CAB ABP =∠=∠=︒90,90ABO PBE PBE BPE ∠+∠=︒∠+∠=︒∴.在和中,,∴(AAS ),∴,∴,即点P 的坐标是,综上所述,符合条件的点P 的坐标是或或.2.(1)①见解析;②见解析;(2),见解析【分析】本题主要考查了等边三角形,全等三角形.(1)①根据等边三角形的性质得出,,,根据得出,从而说明三角形全等;②根据全等的性质得出,然后根据即得;(2)根据等边三角形的性质得出,,,根据得出,从而说明,根据全等的性质得出,然后根据即得.【详解】(1)证明:①∵和是等边三角形,∴,,.∴,∴.在和中,,∴;②∵,ABO BPE ∠=∠BOA △PEB △ABO BPE BOA PEB BA PB ∠=∠⎧⎪∠=∠⎨⎪=⎩BOA PEB △≌△1,3PE BO BE OA ====312OE BE BO =-=-=(2,1)-(4,)1-(3,2)--(2,1)-BC CD CE +=AB AC =AD AE =60BAC DAE ∠=∠=︒BAC DAC DAE DAC ∠-∠=∠-∠BAD EAC ∠=∠BD CE =BC BD CD =+AB AC =AD AE =60BAC DAE ∠=∠=︒BAC DAC DAE DAC ∠+∠=∠+∠BAD EAC ∠=∠ABD ACE ≌△△BD CE =+=BC CD BD ABC ADE V 60BAC DAE ∠=∠=︒AB BC AC ==AD DE AE ==BAC DAC DAE DAC ∠-∠=∠-∠BAD CAE ∠=∠ABD △ACE △AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩()SAS ABD ACE △≌△ABD ACE ≌△△∵,,∴,∴是等腰直角三角形,即∵点D 是线段中点,∴,,(0,6)A (6,0)B 6O A O B ==AOB ∠AB OD AB ⊥12OD AD AB ==∠∵,,∴在中,∵在(1)中已求出根据翻折可知:、∴N 点关于的对称点H 在根据对称性有:∴,∴是等边三角形,∵N 点关于的对称点是点H ,3BD =30CBD ∠=︒DG Rt BDG △12DG BD =CE CD =11BDC BKC △BE BK DBC KBC ∠=∠60BDK DBC KBC ∠=∠+∠=︒BDK BE NH如图,,即:,在中,PNC DNC∠=∠24PNC αβ∠==2αβ=MCN DCM DCN x β∠=∠+∠=+MCN △180MCN DCN NMC ∠+∠+∠=2180x βαα+++=︒3180x βα++=︒解得:,.II.当点在线段上时,如图,,,即:,在中,,,即:联立得:,解得:,此时:,不合题意舍去;III .当点在线段上时,如图,,52550x βα=︒⎧⎪=︒⎨⎪=︒⎩∴5DCM ∠=︒N PD 180PNC DNC ∠+∠=︒∴24180αβ+=︒290αβ+=︒∴MCN DCM DCN x β∠=∠+∠=+ CMN PCN MCN CMN x βα∠=∠+∠=++∴4180PCN NDC x βαβ∠+∠=+++=︒5180x βα++=︒2602905180x x ααββα+=︒⎧⎪+=︒⎨⎪++=︒⎩11.2526.2537.5x βα=︒⎧⎪=︒⎨⎪=︒⎩11.2526.5PCN DCN ∠=︒<∠=︒N DM PNC DNC ∠=∠【详解】(1)解:过点B 作轴于点D ,∵,∴,∵轴,∴,∵,∴,∴,在和中,,∴,∴,∵,∴;(2)解:∵,∴,∴,∵轴,∴,∴,∴,在和中,BD y ⊥()()6,0,0,3A C -6,3OA OC ==BD y ⊥90BCD CBD ∠+∠=︒90ACB ∠=︒90BCD ACO ∠+∠=︒ACO CBD ∠=∠ACO △CBD △90AOC CDB ACO CBDAC BC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩≌ACO CBD 6,3OA CD OC BD ====()0,3C ()3,3B -90ACB ∠=︒90BCF ∠=︒90CBF F ∠+∠=︒BE y ∥90AEF ∠=︒90CAD F ∠+∠=︒CAD CBF ∠=∠CAD CBF V∴,∴,∵,∴∴.【点睛】本题主要考查了三角形综合,折叠的性质,全等三角形的判定和性质,角平分线的性质,解题的关键是掌握全等三角形的判定方法,全等三角形对应边相等,对应角相等;折叠前后对应角相等;角平分线上的点到两边距离相等.7.(1)(2)见解析(3)的度数总是保持不变,理由见解析【分析】本题考查了全等三角形的性质与判定,等腰三角形的性质,坐标与图形;(1)根据等腰三角形的性质解答即可;(2)根据等式的性质得出,进而利用证明与全等,进而解答即可;(3)根据全等三角形的性质得出,进而利用平角的定义解答即可.【详解】(1)解:如图所示,过作轴于,()Rt Rt HL EFO EFN ≌FN FO =(),0F t FO t=-2FG HG t +=-()2,0-COD ∠BAC OAD ∠=∠SAS BAC OAD AOD ABO ∠=∠A AE x ⊥E),点C 是的中点,,D 作轴于点F ,,,4=AB 114222AB ==⨯=DF x ⊥90DFO =︒90FDO DOF +∠=︒),的坐标为,关于x 轴的对称点,则的坐标为,交x 轴于点,则为定值,此时的周长最小.作轴于点Q ,114222AB '==⨯=M '()0,2M '''M ''M AM ''P PAM C AM AP ''=+ AM 'PAM '△()4,4A -AQ y ⊥对于(3),作轴,先证明,可得,再得出,进而得出,根据等腰直角三角形的性质和判定即可得出答案.【详解】(1).理由:,;(2)证明:如图②中,延长交的延长线于点..∵,,,.,即.垂直平分,平分.(3)的长度不变,.理由:如图③中,过点作轴于点...CH y ⊥≌CHB BOA △△,3===CH BO BH OA 3==OA OP ==OB PH CH OAB OBC ∠=∠90,90OAB OBA OBC OBA ∠+∠=∠+∠=︒︒ OAB OBC ∴∠=∠AB CD T ,90,90,AD CD ADT T BAM BCT BAM ⊥∴∠=∴∠+∠=∴∠=∠︒︒ BC BA ===90CB T A B M ∠∠︒()CBT ABM ASA ∴≌△△CT AM ∴=2,2AM CD CT CD =∴= CD DT =,AD CT AD ⊥∴ CT ,AC AT AD ∴=∴BAC ∠OQ 3OQ =C CH y ⊥H 90,90CHB BOA HBC HCB ∴∠=∠=∴∠+∠=︒︒90,90,ABC OBA HBC HCB OBA ∠=∴∠+∠=︒︒∴∠=∠..,..,.【点睛】本题主要考查了全等三角形的性质和判定,同角的余角相等,线段垂直平分线的性质,等腰直角三角形的性质和判定等,构造辅助线是解题的关键.10.(1)①见解析;②不变,(2)或【分析】(1)①根据垂直平分线的性质得出,再由等边对等角及各角之间的数量关系求解即可;②设与交于点M ,根据等边三角形的性质及各角之间的关系得出,即可求解;(2)分两种情况进行分析:当时,当时,分别利用全等三角形的判定和性质及等边三角形的判定和性质分析求解即可.【详解】(1)证明:①点A 、E 在线段的垂直平分线l 上,∴,∴,∴,即;②在点A 运动的过程中,的度数不变,理由如下:如图,设与交于点M ,(),CB AB CHB BOA AAS =∴ ≌△△,3∴===CH BO BH OA ()()3,0,0,3,3A P OA OP ∴== ,BH OP OB PH CH ∴=∴==90,45CHP CPH OPQ ∠=∴∠=∠=︒︒ 90,45∠=∴∠=︒=︒∠ POQ OQP OPQ 3OQ OP ∴==30DCB ∠=︒ED EB EA =+EB ED EA=+AC AB EC EB ==,AB CD 260ECB ∠=︒120BAC ∠<︒120BAC ∠>︒BC ,AC AB EC EB ==,ABC ACB EBC ECB ∠∠∠∠==ABC EBC ACB EBC ∠∠∠∠-=-ABE ACE ∠∠=DCB ∠AB CD∵是等边三角形,∴ ,∴,∴,∴,∴,∴,∵,∴,即;(2)当时,在上截取,连接,∵,∴,由(1)得直线,,∴,∴是等边三角形,∴ ,∴,即,ABD ,60AB AD BAD ∠==︒AD AC =ADC ACE ∠∠=,ABE ADC EBC ECB ∠∠∠∠==,180,180AMD EMB BED ABE EMB BAD ADC AMD ∠∠∠∠∠∠∠∠==︒--=︒--60BED BAD ∠∠==︒,EBC ECB BED EBC ECB ∠∠∠∠∠+==260ECB ∠=︒30DCB ∠=︒120BAC ∠<︒ED EF EA =AF ED DF EF =+ED DF EA =+l BC ⊥30DCB ∠=︒903060AED ∠=︒-︒=︒AEF 60,EAF BAD AE AF ∠∠==︒=–EAF BAF BAD BAF ∠∠∠∠=-BAE DAF ∠∠=∴,∴,∵,∴;当时,如图所示在上截取,连接,∵,∴,由(1)得直线,,,∴,∴F 是等边三角形,∴,∴,∴,∴,∴,∵,∴;综上可得:或.【点睛】题目主要考查线段垂直平分线的性质,全等三角形的判定和性质,等边三角形的判定和性质等,理解题意,作出相应辅助线是解题关键,同时注意进行分类讨论.11.(1)见解析(2)见解析(3),证明见解析【分析】(1)根据有一个角是的等腰三角形是等边三角形可得结论;(SAS)BAE DAF ≌ EB DF =ED DF EA =+ED EB EA =+120BAC ∠>︒EB EF EA =AF EB BF EF =+EB BF EA =+l BC ⊥30DCB ∠=︒BE BC =903060AEB AEC ∠∠==︒-︒=︒AE 60,EAF BAD AE AF ∠∠==︒=–EAF DAF BAD DAF ∠∠∠∠-=EAD BAF ∠∠=(SAS)BAF DAE ≌ BF ED =EB BF EA =+EB ED EA =+ED EB EA =+EB ED EA =+AE BE CE =+60︒(2)根据证明,得,由8字形可得,最后由含角的直角三角形的性质可得结论;(3)如图2,在上截取,先证,方法是根据题意得到三角形为等边三角形,三角形为等腰直角三角形,确定出度数,根据,且,得到度数,进而确定出为,再由,得到,再由,且夹角,利用得到三角形与三角形全等,利用全等三角形的对应边相等得到,得到三角形为等边三角形,得到,由,等量代换即可得证.【详解】(1)解:证明:,,,,是等边三角形;(2)证明:由(1)知:是等边三角形,,是等边三角形,,,,,,,,,,,,SAS MBO NBA ≌OMB ANB ∠∠=60FAM FBN ∠∠==︒30︒AC AG CE =60AEB ∠=︒ABO BOC ABD ∠AB BC =150ABC ∠=︒BAE ∠AEB ∠60︒AG CE =AE CG =AB CB =BAC BCA ∠=∠SAS BCG BAE BG BE =BEG BE EG =AE EG AG =+150BOP ∠=︒ 90AOP ︒=∠60AOB ∴∠=︒OB AB = OAB ∴ OAB 60ABO ∴∠=︒BMN BM BN ∴=60MBN ∠=︒MBO NBA ∴∠=∠AB OB = (SAS)MBO NBA ∴△≌△OMB ANB ∴∠=∠AFM BFN ∠=∠ 60FAM FBN ∴∠=∠=︒60OAP FAM ∠=∠=︒ 90AOP ︒=∠30APO ∴∠=︒;(3),理由如下:如图2,在上截取,连接,,即,,,,为的中点,平分,即,,,,,,,在和中,,,,为等边三角形,,.【点睛】本题是三角形综合题,考查了等腰直角三角形的性质和判定,等边三角形的性质和判定,全等三角形的判定和性质,以及含角的直角三角形的性质,添加辅助线.12.(1),2AP AO ∴=AE BE CE =+AC AG EC =BG AG EG CE EG +=+AE CG =BC BO ⊥ BC BO =90OBC ∴∠=︒D CO BD ∴OBC ∠45CBD OBD ∠=∠=︒60ABO ∠=︒ 105ABD ∴∠=︒150ABC ∠=︒AB OB BC == 15BAC BCA ∴∠=∠=︒154560AEB ∴∠=︒+︒=︒ABE CBG AB CB BAE BCG AE CG =⎧⎪∠=∠⎨⎪=⎩(SAS)ABE CBG ∴△≌△BG BE ∴=BEG ∴△BE EG ∴=AE AG EG CE BE ∴=+=+30︒()02A ,()40B -,∴,∵∴,∵,∴,,90ADC BOA ∠=︒=∠90CAD BAO ABO ∠+∠=︒=∠CAD ABO ∠=∠(2,2)C -2CD =2OD =∴,,∴,;(2)解:如图2,作轴,交轴于,交的延长线于,∴,∵平分,∴,,,∴,∴,∵,∴,∵,∴,∴,∵,,∴,∴,∴的长为6;(3)解:∵为等边三角形,∴,,如图3,在上截取,使,连接,2AO CD ==4BO AD AO OD ==+=()02A ,()40B -,CM x ⊥x N BA M 90BNM BNC ∠=︒=∠BD ABC ∠MBN CBN ∠=∠BN BN =90BNM BNC ∠=︒=∠()ASA MBN CBN ≌3MN CN ==∥CM AO ACM CAO ∠=∠90CAO BAO ABD BAO ∠+∠=︒=∠+∠CAO ABD ∠=∠ACM ABD ∠=∠AC AB =90MAC DAB ∠=︒=∠()ASA ACM ABD ≌6BD CM CN MN ==+=BD BCE BE CE =60BEC EBC ECB ∠=∠=∠=︒OC OF OF OE =EF∴是等边三角形,∴,∴∵,∴,∴,OEF OE EF =60OEF ∠=︒=∠OEF BEF BEC ∠-∠=∠-∠OE EF =BEO CEF ∠=∠()SAS BEO CEF ≌OBE FCE ∠=∠13.(1)(2)【分析】(1)如图①,过作 轴于, 证明可得从而可得答案;(2)如图①,过点作 轴于点.证明 ,可得 ,再证明,从而可得: .【详解】(1)解: 如图①,过作 轴于,∴,∵,∴,∴,∵,∴.∴,,∴,∴,故答案为 : .(2)的长度不变,理由如下:如图②, 过点作 轴于点.()0,23BP =C CF y ⊥F ,ACF BAO ≌CF AO =C CE y ⊥E CBE BAO ≌,6CE BO BE AO ===CPE DPB ≌3BP EP ==C CF y ⊥F 90,90CFA AOB ACF CAF ∠=∠=︒∠+∠=︒90BAC ∠=︒90CAF OAB ∠+∠=︒ACF OAB ∠=∠AC AB =()AAS ACF BAO ≌CF AO =2c x =- 2CF AO ==()0,2A ()0,2BP C CE y ⊥E∵ ,∴∵∴ .∵90ABC ∠=︒90CBE ABO ∠+∠=︒90BAO ABO ∠+∠=︒CBE BAO ∠=∠90CEB AOB ∠=∠=∵,∴,在和中,90BAC PAQ ∠=∠=︒BAP CAQ ∠=∠BAP △CAQ AB AQ =⎧∴四边形为正方形,∴,过作于点,∵AOCN 6OA CN OC ===T TL CN ⊥L AH BQ⊥AOH TLQ ≌∴,解得;②当点在上,点∴,解得;3AP DE cm AQ EC ===,352x =103x =cm/s P AB 5AP EC cm AQ ==,532x =65x =cm/s∴点P 的路程为∴点P 的路程为3AP ED AQ EC ===,AB +1216205AQ =++-=4543x =5AP EC cm AQ ==,AB +1216203AQ =++-=4345x =从出发,以每小时从出发,以相同速度沿,①当在线段上时,P O Q B OQ ∴=AP =t P AO,等腰,,设,,为的一个外角,RO PO ∴=∴POR 45R BAO ∴∠=∠=︒QPO α∠=45RPQ α∴∠=︒-QON BOG α∠==∠ABO ∠ OBG,,,,90HTA ∴∠=︒45HAT OAB ∠=∠=︒45HAT AHT ∴∠=∠=︒HT AT ∴=由(1)知,,则,∵直线与直线互相垂直,∴,()1.0M -1OM =BP AM 90MNB ∠=︒。
专题5.4 行程问题与销售利润问题(压轴题专项讲练)-2024-2025学年八年级数学上册压轴题专项

专题5.4 行程问题与销售利润问题【典例1】一艘轮船在相距90千米的甲、乙两地之间匀速航行,从甲地到乙地顺流航行用6小时,逆流航行比顺流航行多用4小时.(1)求该轮船在静水中的速度和水流速度;(2)若在甲、乙两地之间建立丙码头,使该轮船从甲地到丙地和从乙地到丙地所用的航行时间相同,问甲、丙两地相距多少千米?(1)设该轮船在静水中的速度是x 千米/小时,水流速度是y 千米/小时,根据路程=速度×时间,即可得出关于x ,y 的二元一次方程组,解之即可得出结论;(2)设甲、丙两地相距a 千米,则乙、丙两地相距(90−a )千米,根据时间=路程÷速度,即可得出关于a 的一元一次方程,解之即可得出结论.解:(1)设该轮船在静水中的速度是x 千米/小时,水流速度是y 千米/小时, 依题意,得:{6(x +y)=90(6+4)(x −y)=90,解得:{x =12y =3,答:该轮船在静水中的速度是12千米/小时,水流速度是3千米/小时; (2)设甲、丙两地相距a 千米,则乙、丙两地相距(90−a )千米, 依题意,得:a 12+3=90−a 12−3,解得:a =2254,答:甲、丙两地相距2254千米.1.(2023春·全国·七年级专题练习)A市到B市的航线长1200km,一架飞机从A市顺风飞往B市需2小时30分,从B市逆风飞往A市需3小时20分.求飞机的速度与风速.2.(2023春·全国·七年级专题练习)桥长1000米,现有一列匀速行驶的货车从桥上通过,测得货车从上桥到完全过桥共用了60秒,而整个货车在桥上的时间是40秒,求货车的长度和速度.3.(2023春·浙江·七年级专题练习)从甲地到乙地有一段上坡路与一段平路,如果保持上坡路每小时走3千米,平路每小时走4千米,下坡路每小时走5千米,那么从甲地到乙地需0.9小时,从乙地到甲地需0.7小时。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、已知点0为等边ABC内一点,AOB 1100, BOC ,以0C为一边作等边OCD,连接AD。
(1 )当1500时,试判断AOD的形状,并说明理由。
(2)探究:当为多少度时,AOD为等腰三角形。
2、(1)如图1:点E在正方形ABCD的边上,BF丄AE于点F,DG丄AE于点G 求证:△ ADG ◎△ BAF
(2)如图2:已知AB=AC / 1 = / 2=Z BAC,求证:△ ABE^A CAF
(3)如图3:在等腰三角形ABC中,AB=AC,AB>BC点D在边BC上,CD=2BD点E、F在线段AD上,/仁/2=Z BAC,若厶ABC的面积为9,则厶ABE-与^ CDF的面积的和是多少。
图1 图2 图3
3、.问题背景,请你证明以上三个命题;
①如图1,在正三角形ABC中,N为BC边上任一点,CM为正三角形外角/ ACK的平分线, 若/ ANM=60,则AN=NM
②如图2,在正方形ABCD中,N为BC边上任一点,CM为正方形外角/ DCK的平分线,若
/ ANM=90 ,贝U AN=NM
③如图3,在正五边形ABCDE中,N为BC边上任一点,CM为正五边形外角/ DCK的平分线,若/ ANM=10° ,贝U AN=NM
图 1 图2
4、已知点C 为线段AB 上一点,分别以 AC 、BC 为边在线段AB 同侧作△ ACD 和厶BCE , 且 CA=CD , CB=CE ,/ ACD= / BCE ,直线 AE 与 BD 交于点 F ,
(1) _________________________________________ 如图 1,若/ ACD=60 ° 则/ AFB= ;如图 2,若/ ACD=90 ° 则/
AFB= _______ ;如图 3,若/ ACD=120 ° 则/ AFB= _____________ ;
(2) 如图4,若/ ACD= a,则/ AFB= ____________________ (用含a 的式子表示);
(3) 将图4中的△ ACD 绕点C 顺时针旋转任意角度(交点 F 至少在BD 、AE 中的一条线 段上),变成如图5所示的情形,若/ ACD= a,则/ AFB 与a 的有何数量关系?并给予证明.
提示:始终证明
ACE DCB 圏 團
迟 E
F D B 图
5
C 砂 图斗
5. 如图,已知D为AB的中点,AB=AC=10厘米,BC=8厘米,点D为AB的中点。
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA 上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,与是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使与全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿三边运动,求经过多长时间点P与点Q第一次在的哪条边上相遇?
(3)当点Q的运动速度为多少时,存在某一时刻,使DPQ为等边三角形,请求出点Q的运动
速度和时间t的值。
6
、在ABC 中,AB
600得到线段BD。
AC, BAC(00600),将线段BC绕点B逆时针旋转
(1) 如图1, 直接写出ABD的大小。
(用含的式子表示)
(2) 如图2, BCE1500, ABE90°, 判断ABE的形状并加以证明。
(3) 在(2)
的条件
下,连接DE,若DEC450,求的值。
B C
7、如图, ABD 和 ACE 都是等边三角形, DC 和BE 交于0,连接OA
(1) 求证:BE DC
(2) 求 BOD 的度数
(3) 求证:0A 平分 DOE
8、如图,AB=BC , AD=DE ,且AB 丄BC , AD 丄DE , CG 丄DB 的延长线于点 G ,
的延长线于点 F ,求证:CG+EF=DB
EF
丄
DB
形成一个 AMN ,贝U AMN 的周长为
10、数学课上,李老师出示了如下框中的题目.在等边三角形
ABC 中,点E 在AB 上,点 D 在CB 的延长线上,且ED = EC ,如图,试确定线段 AE 与DB 的大小关系,并说明理由.小 敏与同
桌小聪讨论后,进行了如下解答: (1 )特殊情况,探索结论当点 E 为AB 的中点时,如图①,确定线段 AE 与DB 的大小关 系,请你直接写出结论: AE _______ DB (填“〉”,“V”或“=”).
(2)特例启发,解答题目解:题目中,AE 与DB 的大小关系是:AE ___________ DB (填“〉”,
“V”或“=”).理由如下:如图②,过点 E 作EF // BC ,交AC 于点F .(请你完成以 下解答过程) (3 )拓展结论,设计新题在等边三角形 ABC 中,点E 在直线AB 上,点D 在直线BC 上, 且ED = EC .若△ ABC 的边长为1, AE = 2,求CD 的长(请你直接写出结果).①②
9、如图,△ ABC 是等边三角形,△ BDC 是等腰三角形 个60度角,角的两边分别交 AB 、AC 于M , N , 间的关系并说明理由。
(2)若厶ABC 的周长为2, 射线AB,CA 上的点,其他条件不变,请直接写出 ,BD=CD, / BDC=120 °,以 D 为顶点作一 连接MN 。
( 1)探究线段 BM,MN,NC 之 求厶AMN 的周长(3)若点M , N 分别是 BM,MN,NC 之间的数量关系
变式填空题:如图,等边 ABC 的边长为2 , BDC 是顶角 BDC 120°的等腰三角形, 以D 为顶点作一个60°的角,角的两边分别交
AB 于点M , 交AC 于点N ,连接MN ,
11、如图,在△ ABC中,AB=AC,CD丄AB于点D,CD=BD,BE 平分/ ABC,点H是BC边上的中点,连接DH,交BE于点G,连接CG.
(1)求证:△ ADC ◎△ FDB ;
(2)求证:CE=1/2BF ;
(3)判断△ ECG的形状,并证明你的结论.
12、(1)如图(1),已知:在厶ABC中,/ BAC = 90°, AB=AC,直线m经过点A, BD 丄直线m, CE丄直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ ABC中,AB=AC , D、A、E三点都在直线m 上,并且有/ BDA= / AEC= / BAC=,其中为任意锐角或钝角•请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由•
(3)拓展与应用:如图(3), D、E是D、A、E三点所在直线m上的两动点(D、A、E 三点互不重合),点F为/ BAC平分线上的一点,且△ ABF和厶ACF均为等边三角形,连接BD、CE,若/ BDA= / AEC= / BAC,试判断厶DEF 的形状•
C 區]3)。
