伯努利实验指导
伯努利方程实验

一,实验目的及要求1.通过定性分析实验,提高动态水力学中许多水力现象的实验分析能力;2.通过定量测量实验,可以进一步掌握增压管中流体力学的能量转换特性,验证流体总流量恒定的伯努利方程,掌握测压管头线的实验测量技巧和绘制方法。
二,实验内容与方法1.定性分析实验(1)确认相同静态液体的测压管的头线是水平线。
实验表明,在阀门完全关闭并稳定后,每个压力计管液位的连接线均为水平线。
此时,滑动标尺的读数值为水在流动前的总能量头。
(2)观察不同流量下某段液压元件的变化规律。
(3)验证动态水压力是否根据均匀流段上的静水压力规则分布。
(4)遵守过程中总能量斜率线的变化规律。
(5)观察压力计头线的变化规律。
(6)沿管道的压力分布是通过使用压力计的头线来判断的。
2.定量分析实验-伯努利方程验证和测压管头线测量分析实验实验方法和步骤:在恒定流量的情况下,改变流量两次,一次打开阀门很大,以至于1号测量管的液位接近可读范围内的最低点。
流量稳定后,测量并记录每个压力测量管的液位读数,并同时测量并记录实验流量。
三,数据处理及结果要求1.记录相关信息,实验常数,实验数据记录和结果计算:有关详细信息,请参见实验报告书2.结果要求(1)定性分析实验中回答有关问题(2)计算速度头和总头(3)在上述结果的最大流量下绘制总压头线和压强计压头线四,注意事项1.应注意每次循环供水实验:必须将测得的水倒回到原始实验设备的水桶中,以保持自循环供水(在以下实验中不会提示此注意事项)。
2.稳压缸内的气腔越大,稳压效果越好。
但是,稳压缸的水位必须淹没连接管的入口,以避免连接管的进气口,否则,有必要拧松稳压缸的排气螺钉以提高水位。
圆筒;如果调压罐的水位高于排气螺钉的开口,则表明存在空气泄漏,需要进行检查和处理。
3.传感器与压力稳定缸之间的连接管应确保通气畅通,并且水不能进入连接管和进气口,否则应将其清除。
4.智能数显流量计启动后需要预热3〜5分钟。
伯努利方程实验
实验二柏努利方程实验一、实验目的1、熟悉流体流动中各种能量和压头的概念及其相互转换关系,在此基础上,掌握柏努利方程;2、观察流速变化的规律;3、观察各项压头变化的规律。
二、实验装置实验设备由玻璃管、测压管、活动测压头、水槽、循环水泵等组成。
活动测压头的小管端部封闭。
管身开有小孔,小孔位置与玻璃管中心线平齐,小管又与测压管相通,转动活动测压头就可以测量动、静压头。
管路分成四段,由大小不同的两种规格的玻璃管所组成,管段2的内径约为24mm,其余部分的内径约为13mm。
第四段的位置比第三段低5cm,准确的数值标注在设备上,阀A供调节流量之用。
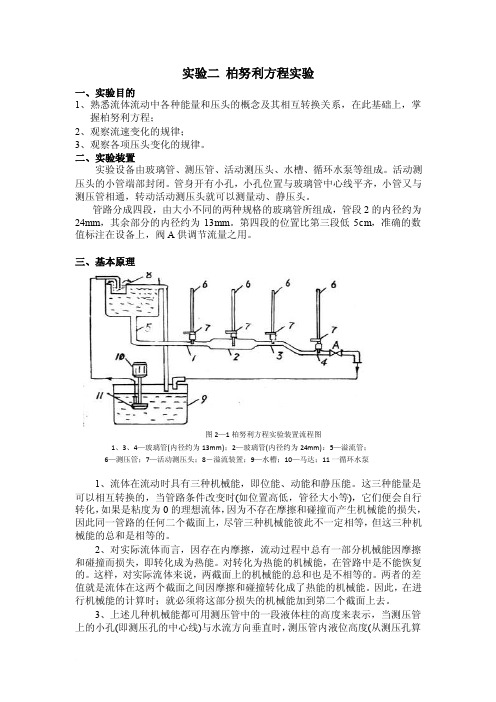
三、基本原理图2—1柏努利方程实验装置流程图1、3、4—玻璃管(内径约为13mm);2—玻璃管(内径约为24mm):5—溢流管;6—测压管;7—活动测压头;8-溢流装置;9—水槽;10—马达;11一循环水泵1、流体在流动时具有三种机械能,即位能、动能和静压能。
这三种能量是可以相互转换的,当管路条件改变时(如位置高低,管径大小等),它们便会自行转化,如果是粘度为0的理想流体,因为不存在摩擦和碰撞而产生机械能的损失,因此同一管路的任何二个截面上,尽管三种机械能彼此不一定相等,但这三种机械能的总和是相等的。
2、对实际流体而言,因存在内摩擦,流动过程中总有一部分机械能因摩擦和碰撞而损失,即转化成为热能。
对转化为热能的机械能,在管路中是不能恢复的。
这样,对实际流体来说,两截面上的机械能的总和也是不相等的。
两者的差值就是流体在这两个截面之间因摩擦和碰撞转化成了热能的机械能。
因此,在进行机械能的计算时;就必须将这部分损失的机械能加到第二个截面上去。
3、上述几种机械能都可用测压管中的一段液体柱的高度来表示,当测压管上的小孔(即测压孔的中心线)与水流方向垂直时,测压管内液位高度(从测压孔算起)即为静压头,它反映测压点处液体压强大小。
当测压孔由与水流方向垂直方位转为正对水流方向时,测压管内液位将因此上升,所增加的液位高度即为测压孔处液体的动压头,它反映出该点水流动能的大小。
伯努利方程实验

实验四伯努利方程实验一、实验目的1、观察流体流经伯努利方程试验管的能量转化情况,对实验中出现的现象进行分析,加深对伯努利方程的理解;2、掌握一种测量流体流速的原理;3、验证静压原理。
二、实验仪器装置如图1所示图1 伯努利方程仪1.水箱及潜水泵2.上水管3.溢流管4.整流栅5.溢流板6.定压水箱7.实验细管8. 实验粗管9.测压管10.调节阀11.接水箱12.量杯13.回水管14.实验桌三、实验步骤1、关闭调节阀,打开进水阀门,启动水泵,待定压水箱接近放满时,适度打开调节阀,排净管路和测压管中的空气;2、关闭调节阀,调节进水阀门,使定压水箱溢流板有一定溢流;3、测出位置水头,并记录位置水头和试验管测试截面的内径;4、打开调节阀至一定开度,待液流稳定,且检查定压水箱的水位恒定后,测读伯努利方程试验管四个截面上测压管的液柱高度;5、改变调节阀的开度,在新工况下重复步骤4;6、关闭调节阀,测读伯努利方程试验管上各个测压管的液柱高度,记下数据。
可以观察到各测压管中的水面与定压水箱的水面相平,以此验证静压原理;7、实验结束,关闭水泵。
四、数据处理实验数据填入表1表1 实验记录表1、计算出伯努利方程试验管各测试截面的相应能量损失水头和压强水头,填写在表中。
速度水头:22gV=总水头-测压管水头压强水头:P=测压管水头-位置水头能量损失水头:wh=静水头-总水头五、思考题1、为什么能量损失是沿着流动的方向增大的?2、为什么在实验过程中要保持定压水箱中有溢流?3、测压管工作前为什么要排尽管路中的空气?其测量的是绝对压力还是表压力?。
伯努利方程实验报告

伯努利方程实验报告一、实验目的1.了解伯努利方程的基本原理;2.掌握伯努利方程的实验方法和实验技巧;3.学会通过实验验证伯努利方程。
二、实验原理P + 1/2ρv² + ρgh = 常数其中,P表示流体的压强,ρ表示流体的密度,v表示流体的速度,g表示重力加速度,h表示流体的高度。
根据伯努利方程,当流体在静止状态时,速度较大,压力较小;当流体通过狭窄的管道流动时,速度较小,压力较大。
通过这些规律,我们可以用实验验证伯努利方程。
三、实验步骤1.准备实验器材:一台水泵、一根直径较大的圆柱形管道和一根直径较小的管道、一个流体压力计、一根导管。
2.将大直径的管道与小直径的管道垂直连接,使其构成一个导管系统。
3.打开水泵,通过水泵将流体注入导管系统。
4.使用流体压力计测量不同位置的流体压力,并记录在实验记录表中。
5.同时,使用流体压力计测量不同位置的流体速度,并记录在实验记录表中。
6.根据伯努利方程计算不同位置的常数,并记录在实验记录表中。
7.分析实验数据,验证伯努利方程。
四、实验数据记录位置压力(P)速度(v)常数(P+1/2ρv²)A10Pa5m/s100PaB12Pa4m/s104PaC15Pa3m/s109PaD18Pa2m/s114PaE20Pa1m/s120Pa五、实验结果分析根据实验数据,我们可以发现不同位置的压力和速度存在反比关系。
当速度增加时,压力减小;当速度减小时,压力增加。
这符合伯努利方程的预测。
六、实验结论通过本次实验我们验证了伯努利方程的基本原理。
在导管系统中,速度较大的地方,压力较小;而速度较小的地方,压力较大。
伯努利方程在描述流体运动时具有很高的准确性。
七、实验心得通过这次实验,我对伯努利方程有了更深刻的理解。
实验过程中我们利用了流体压力计等仪器进行了测量,结果也和理论预期相符合。
实验中还要注意流体的稳定性,以及仪器的准确性。
此外,在记录实验数据时,要注意数据的准确性和仪器的精度。
伯努利原理的小实验

伯努利原理的小实验实验题目:伯努利原理实验实验目的:通过实验观察和验证伯努利原理,并认识流体力学中的压强和流速之间的关系。
实验原理:伯努利原理表明在不可压缩流体中,当流速增加时,压强会降低;当流速减小时,压强会增加。
实验材料和仪器:1.一段透明的塑料管;2.水龙头;3.测压装置(例如压力计);4.输送水的水泵(可选)。
实验步骤:1.将透明的塑料管固定在水平放置的支架上,保证管子两端都露出一段距离。
2.使一端伸入水龙头水流中,另一端露出管外面。
3.打开水龙头,让水直流通过管子。
4.在管子的不同位置,使用压力计测量压强。
可以选择几个不同位置分别测量,例如在水流的中间位置、靠近水龙头的位置、离水龙头较远的位置。
5.记录每个位置的压力测量结果和对应的高度差。
6.关闭水龙头,观察压力计指针的变化。
实验注意事项:1.实验时要小心操作,以免发生意外。
2.记录实验数据时要准确,可以多次测量求平均值。
实验结果和分析:在实验过程中,我们可以观察到以下现象和结果:1.在不同位置测量的压力结果会不同。
一般来说,在水流较快的位置,压力会较低;而在水流较慢的位置,压力会较高。
2.通过对比实验数据,我们可以发现,水流速度和压力之间存在着反比关系。
流速越快,压力越低;流速越慢,压力越高。
通过实验结果和分析,我们可以得出结论:实验观察结果与伯努利原理相吻合。
当流体流速增大时,流体的压强会减小;当流体流速减小时,流体的压强会增加。
这一结论符合伯努利原理的描述。
伯努利原理在实际生活和工程中有着广泛的应用。
例如,汽车的运动速度和发动机发送的空气流速之间的关系、翅膀形状和飞机升力之间的关系等都可以通过伯努利原理加以解释和研究。
通过这个小实验,我们不仅能够深入理解伯努利原理,还能够更好地了解流体力学的基本原理。
伯努利方程实验

伯努利方程实验一、实验目的和要求1.通过定性分析实验,提高对动水力学诸多水力现象的实验分析能力;2.通过定量测量实验,进一步掌握有压管流中动水力学的能量转换特性,验证流体恒定总流的伯努利方程,掌握测压管水头线的实验测量技能与绘制方法。
二、实验内容与方法1.定性分析实验(1)验证同一静止液体的测压管水头线是根水平线。
阀门全关,稳定后,实验显示各测压管的液面连线是一根水平线。
而这时的滑尺读数值就是水体在流动前所具有的总能头。
(2)观察不同流速下,某一断面上水力要素变化规律。
(3)验证均匀流断面上,动水压强按静水压强规律分布。
(4)观察沿流程总能坡线的变化规律。
(5)观察测压管水头线的变化规律。
(6)利用测压管水头线判断管道沿程压力分布。
2.定量分析实验——伯努利方程验证与测压管水头线测量分析实验实验方法与步骤:在恒定流条件下改变流量2次,其中一次阀门开度大到使⑲号测管液面接近可读数范围的最低点,待流量稳定后,测记各测压管液面读数,同时测记实验流量。
三、数据处理及成果要求1. 记录有关信息及实验常数、实验数据记录及结果计算:详见实验报告册2.成果要求(1) 回答定性分析实验中的有关问题(2) 计算流速水头和总水头(3) 绘制上述成果中最大流量下的总水头线和测压管水头线四、注意事项1.各自循环供水实验均需注意:计量后的水必须倒回原实验装置的水斗内,以保持自循环供水(此注意事项后述实验不再提示)。
2.稳压筒内气腔越大,稳压效果越好。
但稳压筒的水位必须淹没连通管的进口,以免连通管进气,否则需拧开稳压筒排气螺丝提高筒内水位;若稳压筒的水位高于排气螺丝口,说明有漏气,需检查处理。
3.传感器与稳压筒的连接管要确保气路通畅,接管及进气口均不得有水体进入,否则需清除。
4.智能化数显流量仪开机后需预热3~5分钟。
伯努利方程实验
二、伯努利方程实验一、实验目的1、验证流体定常流的伯努利方程;2、通过对有压管路定常流体实验分析,进一步掌握有压管流中流体能量转换的规律。
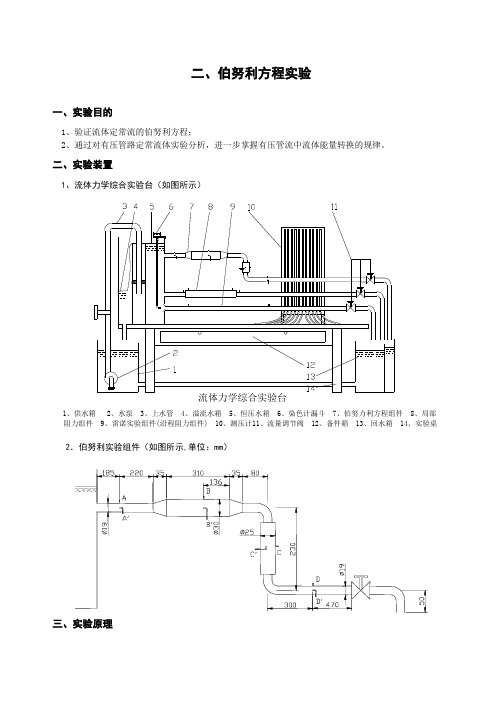
二、实验装置1、流体力学综合实验台(如图所示)流体力学综合实验台1、供水箱2、水泵3、上水管4、溢流水箱5、恒压水箱6、染色计漏斗7、伯努力利方程组件8、局部阻力组件 9、雷诺实验组件(沿程阻力组件) 10、测压计11、流量调节阀 12、备件箱 13、回水箱 14、实验桌2.伯努利实验组件(如图所示,单位:mm)三、实验原理1、伯努利方程在实验管路中沿水流方向取n 个过水截面。
可以列出进口截面(1)至截面(i)的能量方程式(i=2,3,.....,,n)W i hg g p Z g g p Z i i i -+++=++12222111νρνρ选好基准面,从已设置的各截面的测压管中读出g pZ ρ+值,测出通过管路的流量,即可计算出截面平均流速ν及动压g 22ν,从而可得到各截面测管水头和总水头。
对于无黏性流体来说其各项水头之和(即总水头)是不变的,是一个常数。
对于黏性流体来说,各项水头不但可以有变化,或互相转化,而且总水头也必然不,沿流向降低。
2、毕托管测量流速最简单的毕托管是一根弯成90°的开口细管,弯管开口一侧正对流向,流体进入管后,上升一定高度后,速度变为零。
它与同一断面的测压管高度的高度差为h ,可得到流速为u g h =或中c 称为毕托管的流速系数,一般条件下,c=0.97-0.99,在本实验中取1。
对于固定汾丘里管,它的仪器常数为常数。
四、实验方法与步骤1、熟悉实验台结构,及各开关阀门的位置及作用。
用手捏各测点塑料管,观察测压管水面起伏的方式,分清各测压点与各测压管的对应关系。
2、打开水泵开关,向水箱充水,将恒压水箱5充满,并向溢流水箱4溢流,保持水泵开启状态,保证恒压水箱5始终满水状态。
3、检查流量调节阀11开关情况。
在流量调节阀11完全关闭状态下,检查所有测压管水面是否平齐。
伯努利实验仪实验指导书

化学工程实验仪器系列产品CEA—F02型伯努利实验仪实验指导书北京新华教仪科贸有限公司一、实验目的流动流体所具有的总能量是由各种形式的能量所组成,并且各种形式的能量之间又可相互转换。
当流体在导管内作定常流动时,在导管的各截面之间的各种形式机械能的变化规律,可由机械能衡算基本方程来表达。
这些规律对于解决流体流动过程的管路计算、流体压强、流速与流量的测量,以及流体输送等问题,都有着十分重要的作用。
本实验采用一种称之为伯努利试验仪的装置,实验观察不可压缩流体在导管内流动时的各种形式机械能的相互转化现象,并验证机械能衡算方程(伯努利方程)。
通过实验,加深对流体流动过程基础本原理的理解。
二、实验原理对于不可压缩流体,在导管内作定常流动,系统与环境又无功的交换时,若以单位质量流体为衡算基准,则对确定的系统即可列出机械能衡算方程:f h u p gZu p gZ ∑+++=++222221112121ρρJ ·kg 1- (1)若以单位重量流体为计算基准时,则又可表达为fHgu gp Z gu g p Z ∑+++=++2222222111ρρ m 液柱 (2)式中 Z ——流体的位压头,m 液柱; p ——流体的压强,Pa ;u ——流体的平均流速,m ·s 1-;ρ——流体密度,kg ·m 3-;f h ∑——流动系统内因阻力造成的能量损失,J ·kg 1-;f H ∑——流动系统内因阻力造成的压头损失,m 液柱。
下标1和2分别为系统的进口和出口两个截面。
不可流体的机械能衡算方程,应用于各种具体情况下可作适当简化,例如: (1)当流体为理想液体时,于是式(1)和(2)可简化为222221112121u p gZu p gZ ++=++ρρ J ·kg1- (3)gu gp Z gu gp Z 2222222111++=++ρρ m 液柱 (4)该式即为伯努利(Bernoulli )方程。
伯努利方程实验实验报告

伯努利⽅程实验实验报告伯努利⽅程实验⼀、实验⽬的:1.通过实验,加深对伯努利⽅程式及能量之间转换的了解。
2.观察⽔流沿程的能量变化,并了解其⼏何意义。
3.了解压头损失⼤⼩的影响因素。
⼆、实验原理:在流体流动过程中,⽤带⼩孔的测压管测量管路中流体流动过程中各点的能量变化。
当测压管的⼩孔正对着流体的流动⽅向时,此时测得的是管路中各点的动压头和静压头的总和,即以单位质量流体为衡算基来研究流体流动的能量守恒与转化规律。
对于不可压缩流体,在导管内作稳态流动时,则对确定的系统即可列出机械能衡算⽅程:∑+++=+++f e h pgZ p u Z ρωρ222212112u 2g当测压管的⼩孔垂直于流体的流动⽅向时,此时测得的是管路中各点的静压头的值,即。
将在同⼀流量下测得的hA 、hB 值描在坐标上,可以直观看出流速与管径的关系。
⽐较不同流量下的hA 值,可以直观看出沿程的能量损失,以及总能量损失与流量、流速的关系。
通过hB 的关系曲线,可以得出在突然扩⼤、突然缩⼩处动能与静压能的转换。
三.实验装置四.实验步骤1.将低位槽灌有⼀定数量的蒸馏⽔,关闭离⼼泵出⼝上⽔阀及实验测试导管出⼝流量调节阀和排⽓阀、排⽔阀,打开回⽔阀和循环⽔阀⽽后启动离⼼泵。
2.逐步开⼤离⼼泵出⼝上⽔阀当⾼位槽溢流管有液体溢流后,利⽤流量调节阀出⽔的流量。
3.流体稳定后读取并记录各点数据。
4.关⼩流量调节阀重复步骤。
5.分析讨论流体流过不同位置处的能量转换关系并得出结果。
6.关闭离⼼泵,实验结束。
五.实验注意事项:1.测记压头读数时,必须保持⽔位恒定。
2.注意测压管内⽆⽓泡时,⽅可开始读数。
3.测压管液⾯有波动时,读数取平均值为宜。
4.阀门开关要缓慢,否则影响实验结果。
六.数据处理d A=14mm , d B=28mm, d C=d D=14mm,Z D=125mm七.误差分析(1)不同流量时的动能⽐较。
同⼀管径下,流量⼤时,动能较⼤。
(2)同⼀流量时不同管径上动能⽐较。
伯努利方程实验

伯努利方程实验一、目的和要求1、 熟悉流体流动中各种能量和压头的概念及其相互转换关系,在此基础上,掌握柏努利方程;2、 观察流速变化的规律;3、观察各项压头变化的规律。
二、实验原理1、流体在流动中具有三种机械能:位能、动能、静压能。
当管路条件如管道位置高低、管径大小等发生变化时,这三种机械能就会相应改变以及相互转换。
2、如图所示,不可压缩流体在导管中做稳态流动,由界面1-1’流入,经粗细不同或位置高低不同的管道,由截面2-2’流出:以单位质量流体为基准,机械能衡算式为:式中:u l 、u 2一分别为液体管道上游的某截面和下游某截面处的流速,m /s ;P 1、P 2一分别为流体在管道上游截面和下游截面处的压强,Pa ;z l 、z 2一分别为流体在管道上游截面和下游截面中心至基准水平的垂直距离,m; ρ一流体密度,Kg /m 3; g 一重力加速度,m /s 2; ∑h f 一流体两截面之间消耗的能量,J /Kg 。
3、∑h f 是流体在流动过程中损失的机械能,对于实际流体,由于存在内摩擦,流体在流动中总有一部分机械能随摩擦和碰撞转化为热能损耗(不能恢复),因此各截面上的机械能总和不相等,两者之差就是流体在这两截面之间流动时损失的机械能。
4、对于理想流体(实际上并不存在真正的理想流体,而是一种假设,对解决工程实际问题有重要意义),不存在因摩擦而产生的机械能损失,因此在管内稳定流动时,若无外加能量,得伯努利方程:22112212 22u p u p z g z g ρρ++=++式②表示1kg 理想流体在各截面上所具有的总机械能相等,但各截面上每一种形式的机械能并不一定相等,各种形式的机械能可以相互转换。
式①时伯努利方程的引伸,习惯上也称为伯努利方程(工程伯努利方程)。
5、流体静止,此时得到静力学方程式:121221 () p p z g z g P P gh ρρρ+=+=+或式③所以流体静止状态仅为流动状态一种特殊形式。
伯努利方程实验

伯努利方程实验1.目的:1.通过实验加深对伯努利方程和能量转换的理解。
2.观察沿流的能量变化并了解其几何意义。
3.了解影响头部损失的因素。
2,实验原理:在流体流动过程中,使用带小孔的压力计测量管道中流体流动过程中每个点的能量变化。
当测压管的孔口面向流体的流动方向时,测量管道中每个点的动压和静压之和,即基于单位质量流体研究流体流动的能量守恒和转换规律。
对于不可压缩的流体,当它在管道中稳定流动时,可以列出所确定系统的机械能平衡方程:速度和管道直径之间的关系可以直接从在相同流量下测量的HA和Hb坐标中看出率。
比较不同流速下的HA值,可以看到沿途的能量损失以及总能量损失与流速和速度之间的关系。
动能和静压能之间的转换可以从Hb的关系曲线获得。
3,实验装置4.实验步骤1.在低位水箱中注入一定量的蒸馏水,关闭离心泵的出水阀以及实验管出口处的流量控制阀,排气阀和排水阀。
,打开回水阀和循环水阀,然后启动离心泵。
2.逐渐打开离心泵的出口供水阀。
当高位水箱的溢流管中有液体溢流时,请使用流量控制阀调节水流量。
3.流体稳定后读取并记录每个点的数据。
4.调低流量控制阀并重复上述步骤。
5.分析并讨论流过不同位置的流体的能量转换关系,并得出结果。
6.关闭离心泵,实验结束。
5,注意事项:1.在测量和记录压头读数时,保持水位恒定。
2.仅当压力测量管中没有气泡时才能开始读数。
3.当测压管的液位波动时,平均读数是合适的。
4.阀门应缓慢打开和关闭,否则会影响实验结果。
6,数据处理转换实验数据表流量(L / h)200350500压力压力压力测试点标记(mmh2o)(mmh2o)(mmh2o)93.2388.72 83.52 91.0187.84 77.73 94.0389.33 89.32 89.4683.12 82,01 89.1585.54 74.78 91.8389.14 89.02 85.7474.62 63.63 89.1279.73 74.68 Da = 14mm,DB = 28mm,DC = DD = 14mm,ZD = 125mm测试点标记91.0193.232.2233.889.4694.03 4.5734.389.832.6834.585。
伯努利方程实验指导

伯努利定律實驗(Bernoulli ’s Law Experiment)胡裕民 編寫 一. 實驗目的:1. 驗證在風洞(wind tunnel)中的總壓力P tot 為定值。
2. 驗證伯努利定律(Bernoulli ’s Law)。
3. 固定氣流速率下量測F W 、F a 與α的函數關係。
二. 原理介紹:1738年瑞士物理學家Daniel Bernoulli (1700-1782)在所發表的“Hydrodynamic ”一書中首次提出伯努利方程式—說明流體(fluid)的速度、壓力以及高度之間的關係。
此伯努利方程式的提出被視為往後氣體動力學研究的開端。
一理想的流體在流線型的流動(laminar flow)中,會滿足下列的伯努利方程式:t tan cons gy v 21P 2st =++ρρ (1)其中P st 、ρ、v 、y 分別為流體的靜態(static)壓力、密度、速度以及高度。
在大約相同高度下,eq.1可簡化表示為:t tan cons P v 21P tot 2st ≈=+ρ (2)此說明在一樣高度下,總壓力P tot 無論在何處均相同。
在本實驗中,風洞沿著氣體流動方向的截面積(cross-section area)逐漸地減少。
氣體流動時由於不可壓縮性(incompressibility),因此不同截面積處的流動速率將不同,此可由連續方程式(equation of continuity)來表示:A v A v 0⋅=⋅ (3)將eq.3代入eq.2可得:00A v 2A P ⋅⋅=⋅∆ρ (4)其中ΔP = P tot -P st ,ΔP 稱之為動態壓力(ΔP = P tot -P st )。
本實驗第一部分是利用風洞裝置來量測不同位置(亦即有不同的截面積)處的壓力,驗證在一樣高度下,總壓力P tot 無論在何處均相同;並驗證在eq.(4)中A P ⋅∆為一常數,亦即驗證伯努利定律(Bernoulli ’s Law)。
伯努利方程实验

伯努利方程实验一、实验目的:1. 验证流体静压原理;2. 通过观察流体在管道中的运动规律,加深对伯努利方程能量意义的理解;3. 验证管道流动中,摩擦损失与流速平方成正比关系;4. 验证毕托管的测速原理。
二、实验原理:1. 1. 在流体静止时,等压面是水平面,自由波面也是水平面。
在重力势能函数的微分 dW= -gdz 时,有dp = -ρgdz ,即等压与等高程同在。
2. 2. 对于一个恒定的不可压缩管流中,在流动方向上的两个渐变流段,流体的能量关系有伯努利方程给出:22111222121222l P v P v z z h ggααγγ-++=+++3. 管道内的摩擦损失与流体流速的关系服从达西公式:212()2l L v h d g λζ-=+∑212()2l L v h d g λζ-=+∑4. 4. 毕托管能测量出来流滞止点(全压)和管测点(静压)之压力差h v ,于是测点流速可由下式确定:u = 式中;φ1。
三、实验装置伯努利方程仪由玻璃管、活动测头、测压管、上水槽和循环水泵等部分组成。
活动测头的小管底部封闭,管身开有小孔。
小孔中心位置与玻璃管中心平齐,小管与玻璃测压管相通,用小扳手转动活动测头,就可以测量流体的静动压水头。
由于玻璃管前后直径不同(管道直径经测量标注的管段上),位置也有高低,测点有前有后,可以十分方便地测量出不同流速下不同管段的位能、压力能和动能的数值,去验证伯努利方程的结论.实验装置图附后. 四、实验方法:1. 测点静压水头的涸量; 开动循环水泵,将出口阀门A 关闭,这时观察各测压管内自由液面的高度,记录在表格中。
观察在转动活动测头对,自由液面有无变化。
如果发现各测点自由波面高度不相等,或者发现转动活动测头时自由液面发生变化,应试图找出产生误差的原因、并作出记录。
各测点静压水头的数据记录在表1中。
2. 验证摩擦损失与流速平方成正比(达西公式);使各测头的小孔对准来流方向,然后打开出口阀门A(不全开,保持小流量)。
伯努利方程实验实验报告

一、实验目的1. 深入理解伯努利方程的基本原理及其在流体力学中的应用。
2. 通过实验验证伯努利方程的适用性,并观察流体在流动过程中能量转换的现象。
3. 掌握流速、流量、压强等流体力学基本参数的测量方法。
4. 分析不同条件下流体流动特性的变化。
二、实验原理伯努利方程描述了在不可压缩、定常流动条件下,流体在任意两点之间的能量守恒关系。
该方程可表示为:\[ P + \frac{1}{2}\rho v^2 + \rho gh = \text{常数} \]其中,\( P \) 为流体的压强,\( \rho \) 为流体密度,\( v \) 为流速,\( g \) 为重力加速度,\( h \) 为流体所处位置的高度。
三、实验装置实验装置主要包括:1. 实验管道:选用不同内径的管道,以便观察不同条件下流体流动特性的变化。
2. 测压管:用于测量流体在管道各点的压强。
3. 流量计:用于测量流体流量。
4. 计时器:用于测量流体通过实验管道的时间。
四、实验步骤1. 将实验管道连接好,并确保管道内无气泡。
2. 打开水源,调节流量,使流体在管道内稳定流动。
3. 在实验管道的不同位置安装测压管,并记录各测点的压强值。
4. 使用流量计测量流体流量,并记录数据。
5. 计时器记录流体通过实验管道的时间,计算流速。
6. 根据实验数据,计算各测点的能量值,并绘制能量分布图。
五、实验结果与分析1. 在实验管道内,不同位置的压强值存在差异,符合伯努利方程的预测。
2. 随着管道内径的减小,流速增大,压强减小,符合能量守恒定律。
3. 在管道的局部收缩或扩张处,流速和压强变化较大,符合能量转换现象。
4. 通过实验验证了伯努利方程在流体力学中的适用性。
六、结论1. 伯努利方程在流体力学中具有重要的应用价值,可描述流体在流动过程中的能量转换关系。
2. 通过实验验证了伯努利方程的适用性,并观察到了流体在流动过程中的能量转换现象。
3. 实验结果表明,流速、流量、压强等流体力学基本参数之间存在着密切的联系。
水力学试验指导书
实验一伯努利方程实验一、实验目的1.验证流体恒定总流的能量方程;2.通过对动水力学诸多水力现象的实验分析研讨,进一步掌握有压管流中动水力学的能量转换特征;3.掌握流速、流量、压强等动水力学水力要素的实验测量技能。
二、实验属性综合性试验。
本实验涉及的《工程流体力学》课程知识是综合性的。
内容有:流体力学相似性原理和因次分析、流体力学连续性方程、能量方程及动量方程等。
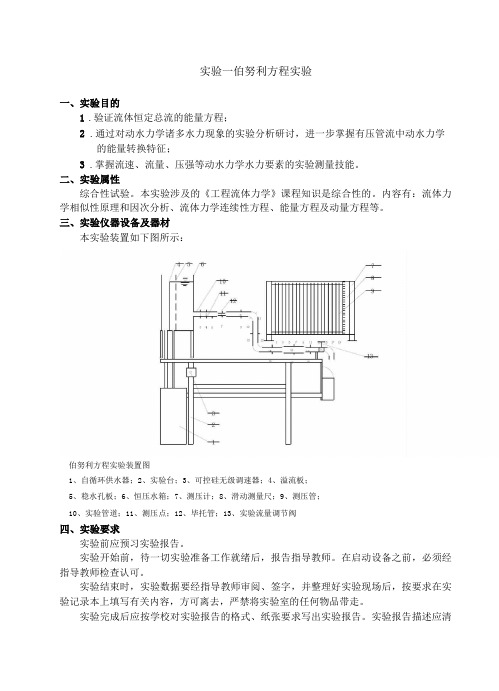
三、实验仪器设备及器材本实验装置如下图所示:伯努利方程实验装置图1、自循环供水器;2、实验台;3、可控硅无级调速器;4、溢流板;5、稳水孔板;6、恒压水箱;7、测压计;8、滑动测量尺;9、测压管;10、实验管道;11、测压点;12、毕托管;13、实验流量调节阀四、实验要求实验前应预习实验报告。
实验开始前,待一切实验准备工作就绪后,报告指导教师。
在启动设备之前,必须经指导教师检查认可。
实验结束时,实验数据要经指导教师审阅、签字,并整理好实验现场后,按要求在实验记录本上填写有关内容,方可离去,严禁将实验室的任何物品带走。
实验完成后应按学校对实验报告的格式、纸张要求写出实验报告。
实验报告描述应清楚、肯定,语言通顺,用语专业、准确;结构严谨、层次清晰。
实验报告数据观察细致,记录及时、准确、真实,外文、符号、公式准确,使用统一规定的名词和符号。
实验报告的内容要求:1.实验名称;2.实验目的;3.实验原理;4.实验装置;5.实验步骤;6.实验原始数据;7.实验数据处理及结果;8.思考题分析。
五、实验原理在实验管路中沿管内水流方向取n个过水断面。
可以列出进口断面(1)至另一断面(i)的能量方程(i=1, 2, 3,……,n)“p av2r p av2,Z + 1 + -1-1 Z + i- + -i—― + h1丫 2 g i丫 2 g w(j)取a = a =……a =1选好基准面,从已设置的各断面的测压管中读出Z + p值,测出1 2 n yav2 八,一一,一一、一,一一通过管路的流量,即可计算出断面平均流速V及q―,从而即可得到各断面测管水头和总2g水头。
伯努利实验

(2)能量方程实验
首先,关闭阀门,测定能量方程实验四组测压管的 液体高度,记下各测压管的读数(填入表1)。
其次,调节阀门至小开开度,测定能量方程实验管 的四组截面测压管的液面高度。之后,改变阀门至中开、 大开开度,重复上述实验,并分别记下各测压管的读数 表1 (填入表1)。
表2
毕托管方法 能量方程实验管上的四组测压管的任一组都相当
一个毕托管,可测得管内的任意一点的流体点速度。
由于本实验台将总压管置于能量方程实验管的轴线, 所以,测得的动压头代表了轴心处的最大流速。毕托 管求点速度公式为:
u 2gh
式中:u—毕托管测点处的流速; Δh—毕托管总压水头与静压水头差(即总水头与 测压管水头差,Δh =H单–H双)。
之后,可根据该截面轴心处的最大速度与平均流 速的关系求出所在截面的平均流速(结果记入表3)。具 体为:层流,V=0.5umax;湍流,V=0.8umax。
表3
Ⅰ
(4)验证伯努利方程
表4
hw13 截 面 阀 门 状 态
小 开 中 开 大 开 各截面总水头Hi(m) 1—2 3—4 5—6 7—8 各截面间水头损失 hLi j(m) 1—3 1—5 1—7 3—5 3—7 5—7
能量方程实验
一、实验目的
(1)观察流体经能量方程(又称伯努利方程)实验管 时的能量转化情况,并对实验中出现的现象进行分析, 从而加深对能量方程的理解;
(2)掌握量杯测平均流速和毕托管测流速的方法;
(3)验证伯努利方程。
伯努利实验指导

流体实验华北电力大学目录实验一不可压缩流体恒定流能量方程(伯诺里方程)实验 (2)实验二雷诺实验 (5)实验三管道沿程阻力实验 (7)伯努利方程实验一、实验目的和要求1. 通过定性分析实验,提高对动水力学诸多水力现象的实验分析能力;2. 通过定量测量实验,进一步掌握有压管流中动水力学的能量转换特性,验证流体恒定总流的伯努利方程,掌握测压管水头线的实验测量技能与绘制方法;二、实验装置1.实验装置简图实验装置及各部分名称如图1所示。
321513246789111315110121465415161711139735191719181011121314789图1 伯努利方程实验装置图1. 自循环供水器2. 实验台3. 可控硅无级调速器 3. 溢流板 5. 稳水孔板 6. 恒压水箱 7. 实验管道 8. 测压点①~○19 9. 弯针毕托管 10. 测压计 11. 滑动测量尺 12. 测压管①~○19 13. 实验流量调节阀 14.回水漏斗 15. 稳压筒 16.传感器 17. 智能化数显流量仪2.装置说明(1) 流量测量——智能化数显流量仪智能化数显流量仪系统包括实验管道内配套流量计、稳压筒15、高精密传感器16和智能化数显流量仪17(含数字面板表及A/D 转换器)。
该流量仪为管道式瞬时流量仪,测量精度一级。
流量仪的使用方法,需先排气调零,待水箱溢流后,间歇性全开、全关管道出水阀13数次,排除连通管内气泡。
再全关阀13,待稳定后将流量仪调零。
测流量时,水流稳定后,流量仪所显示的数值即为瞬时流量值。
(2) 测流速——弯针管毕托管151617弯针管毕托管用于测量管道内的点流速。
为减小对流场的干扰,本装置中的弯针直径为φ1.6⨯1.2 mm (外径⨯内径)。
实验表明只要开孔的切平面与来流方向垂直,弯针管毕托管的弯角从90︒~180︒均不影响测流速精度,如图2所示。
(3) 本仪器测压点有两种: 1) 毕托管测压点,图1中标号为①、⑥、⑧、○12、○14、○16、○18(后述加*表示),与测压计的测压管连接后,用以测量毕托管探头对准点的总水头值,近似替代所在断面的平均总水头值,可用于定性分析,但不能用于定量计算;2) 普通测压点,图1中标号为②、③、④、⑤、⑦、⑨、⑩、○11、○13、○15、○17、○19,与测压计的测压管连接后,用以测量相应测点的测压管水头值。
伯努利实验指导书

伯努利方程实验指导书一、实验目的1、掌握流体流动中各种能量或压头的定义及其相互转化关系,加深对Bernoulli方程(能量方程)的理解,加深对流动过程中能量损失的了解;2、观察静压头、位压头、动压头相互转换的规律。
3、掌握流速、流量、压强等流动参量的实验测量技能。
二、基本原理1.不可压缩流体在管内作稳定流动时,由于管路条件的变化,会引起流动过程中三种机械能(位能、动能、静压能)的相应改变及相互转换。
对理想流体在系统内任一截面处,虽然三种能量不一定相等,但能量之和是守恒的。
2.对于实际流体,由于存在内摩擦,流体在流东时总有一部分机械能损耗。
3.以上机械能均可用测压管中的液柱高度表示。
当测压孔正对流体流动方向时测压管中的液柱高度为动压头和静压头之和,测压孔处流体的位压头由测压孔的几何高度确定。
三、实验装置图实验测试导管的结构尺寸见图二中标绘四、实验的操作方法1.将低位槽灌有一定数量的蒸馏水,关闭离心泵出口调节阀门及实验测试导管出口调节阀门而后启动离心泵。
2.逐步开大离心泵出口调节阀当高位槽溢流管有液体溢流后,调节导管出口调节阀为全开位置。
3.流体稳定后读取A、B、C、D截面静压头和冲压头并记录数据。
4.关小导管出口调节阀重复上述步骤。
5.分析讨论流体流过不同位置处的能量转换关系并得出结果。
6.关闭离心泵,实验结束。
五、使用设备时应注意的事项1.不要将离心泵出口调节阀开得过大以免使水流冲击到高位槽外面,同时导致高位槽液面不稳定。
2.当导管出口调节阀开大应检查一下高位槽内的水面是否稳定,当水面下降时应适当开大泵出口调节阀。
3.导管出口调节阀须缓慢地关小以免造成流量突然下降测压管中的水溢出管外。
4.注意排除实验导管内的空气泡。
5.离心泵不要空转和出口阀门全关的条件下工作。
六、观察现象及实验结果实验分析:(以009实验装置为例)A截面的直径14mm;B截面的直径28mm;C截面、D截面的直径14mm;以桌面为零基准面ZD =0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
流体实验华北电力大学目录实验一不可压缩流体恒定流能量方程(伯诺里方程)实验 (2)实验二雷诺实验 (5)实验三管道沿程阻力实验 (7)伯努利方程实验一、实验目的和要求1. 通过定性分析实验,提高对动水力学诸多水力现象的实验分析能力;2. 通过定量测量实验,进一步掌握有压管流中动水力学的能量转换特性,验证流体恒定总流的伯努利方程,掌握测压管水头线的实验测量技能与绘制方法;二、实验装置1.实验装置简图实验装置及各部分名称如图1所示。
321513246789111315110121465415161711139735191719181011121314789图1 伯努利方程实验装置图1. 自循环供水器2. 实验台3. 可控硅无级调速器 3. 溢流板 5. 稳水孔板 6. 恒压水箱 7. 实验管道 8. 测压点①~○19 9. 弯针毕托管 10. 测压计 11. 滑动测量尺 12. 测压管①~○19 13. 实验流量调节阀 14.回水漏斗 15. 稳压筒 16.传感器 17. 智能化数显流量仪2.装置说明(1) 流量测量——智能化数显流量仪智能化数显流量仪系统包括实验管道内配套流量计、稳压筒15、高精密传感器16和智能化数显流量仪17(含数字面板表及A/D 转换器)。
该流量仪为管道式瞬时流量仪,测量精度一级。
流量仪的使用方法,需先排气调零,待水箱溢流后,间歇性全开、全关管道出水阀13数次,排除连通管内气泡。
再全关阀13,待稳定后将流量仪调零。
测流量时,水流稳定后,流量仪所显示的数值即为瞬时流量值。
(2) 测流速——弯针管毕托管151617弯针管毕托管用于测量管道内的点流速。
为减小对流场的干扰,本装置中的弯针直径为φ1.6⨯1.2 mm (外径⨯内径)。
实验表明只要开孔的切平面与来流方向垂直,弯针管毕托管的弯角从90︒~180︒均不影响测流速精度,如图2所示。
(3) 本仪器测压点有两种: 1) 毕托管测压点,图1中标号为①、⑥、⑧、○12、○14、○16、○18(后述加*表示),与测压计的测压管连接后,用以测量毕托管探头对准点的总水头值,近似替代所在断面的平均总水头值,可用于定性分析,但不能用于定量计算;2) 普通测压点,图1中标号为②、③、④、⑤、⑦、⑨、⑩、○11、○13、○15、○17、○19,与测压计的测压管连接后,用以测量相应测点的测压管水头值。
(4) 测点⑥*、⑦所在喉管段直径为d 2,测点○16*、○17所在扩管段直径为d 3,其余直径均为d 1。
3.基本操作方法(1)测压管与稳压筒的连通管排气。
打开开关供水,使水箱充水,待水箱溢流,间歇性全开、全关管道出水阀13数次,直至连通管及实验管道中无气泡滞留即可。
再检查调节阀关闭后所有测压管水面是否齐平,如不平则需查明故障原因(例连通管受阻、漏气或夹气泡等)并加以排除,直至调平。
(2)恒定流操作。
全开调速器,此时水箱保持溢流,阀门13开度不变情况下,实验管道出流为恒定流。
(3)非恒定流操作。
调速器开、关过程中,水箱6无溢流情况下,实验管道出流为非恒定流。
(4)流量测量。
实验流量用阀13调节,记录智能化数显流量仪的流量值。
三、实验原理1.伯努利方程。
在实验管路中沿管内水流方向取n 个过水断面,在恒定流动时,可以列出进口断面(1)至另一断面(i )的伯努利方程式(i =2,3…,n )221111w122i i i i i p p z z h g g g gααρρ-++=+++v v取α1=α2=αn …=1,选好基准面,从已设置的各断面的测压管中读出pz gρ+值,测出通过管路的流量,即可计算出断面平均流速v 及22g αv ,从而可得到各断面测管水头和总水头。
2.过流断面性质。
均匀流或渐变流断面流体动压强符合静压强的分布规律,即u u9090~180u迎流面开小孔管端封闭图2 弯针管毕托管类型在同一断面上pz C gρ+=,但在不同过流断面上的测压管水头不同,1212p p z z g g ρρ+≠+;急变流断面上p z C gρ+≠。
四、实验内容与方法1.定性分析实验(1) 验证同一静止液体的测压管水头线是根水平线。
阀门全关,稳定后,实验显示各测压管的液面连线是一根水平线。
而这时的滑尺读数值就是水体在流动前所具有的总能头。
(2) 观察不同流速下,某一断面上水力要素变化规律。
以测点⑧*、⑨所在的断面为例,测管⑨的液面读数为该断面的测压管水头。
测管⑧*连通毕托管,显示测点的总水头。
实验表明,流速越大,水头损失越大,水流流到该断面时的总水头越小,断面上的势能亦越小。
(3) 验证均匀流断面上,动水压强按静水压强规律分布。
观察测点②和③,尽管位置高度不同,但其测压管的液面高度相同,表明pz C gρ+=。
(4) 观察沿流程总能坡线的变化规律。
加大开度,使接近最大流量,若稳定后各测管水位如图3所示,图中A-A为管轴线。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19A AA水箱液面图3 测压管水位示例纵观带毕托管的测点①*、⑥*、⑧*、○12*、○14*、○16*、○18*的测管水位(实验时可加入雷诺实验用的红色水,使这些管呈红色,如图3中以较深颜色表示的测压管),可见各测管的液面沿流程是逐渐降低而没有升高的,表明总能量沿流程只会减少,不会增加,能量损失是不可能逆转的。
(5) 观察测压管水头线的变化规律。
总变化规律:纵观测压点②、④、⑤、⑦、⑨、○13、○15、○17、○19的测压管水位,可见沿流程有升也有降,表明测压管水头线沿流程可升也可降。
沿程水头损失:从②、④、⑤点可看出沿程水头损失的变化规律,等径管道上,距离相等,沿程损失相同。
势能与动能的转换:以测点⑤、⑦、⑨为例,测点所在流段上高程相等,管径先收缩后扩大,流速由小增大再减小。
测管⑤到测管⑦的液位发生了陡降,表明水流从测点⑤断面流到测点⑦断面时有部分压力势能转化成了流速动能。
而测管⑦到测管⑨测管水位回升了,这正和前面相反,说明有部分动能又转化成了压力势能。
这就清楚验证了动能和势能之间是可以互相转化的,因而是可逆的。
位能和压能的转换:以测点⑨与○15所在的两断面为例,由于二断面的流速水头相等,测点⑨的位能较大,压能(测管液位离管轴线的高度)很小,而测点○15的位能很小,压能却比⑨点大,这就说明了水流从测点⑨断面流到测点○15断面的过程中,部分位能转换成了压能。
(6) 利用测压管水头线判断管道沿程压力分布。
测压管水头线高于管轴线,表明该处管道处于正压下;测压管水头线低于管轴线,表明该处管道处于负压下,出现了真空。
高压和真空状态都容易使管道破坏。
实验显示(参图3),测点⑦的测管液面低于管轴线,说明该处管段承受负压(真空);测压管⑨的液位高出管轴线,说明该处管段承受正压。
2. 定量分析实验——伯努利方程验证与测压管水头线测量分析实验实验方法与步骤:在恒定流条件下改变流量2次,其中一次阀门开度大到使○19号测管液面接近可读数范围的最低点,待流量稳定后,测记各测压管液面读数,同时测记实验流量(毕托管测点供演示用,不必测记读数)。
实验数据处理与分析参考第五部分内容。
五、数据处理及成果要求1.记录有关信息及实验常数实验设备名称: 实验台号:_________ 实 验 者:______________________ 实验日期:_________ 均匀段d 1= ⨯10-2m 喉管段d 2= ⨯10-2m 扩管段d 3= ⨯10-2m (基准面选在标尺的零点上) 2.实验数据记录及计算结果表1 管径记录表测点编号 ①* ②③ ④ ⑤ ⑥* ⑦ ⑧* ⑨ ⑩○11 ○12* ○13 ○14* ○15 ○16* ○17 ○18* ○19 管径d /10-2m注:(1).测点6、7所在断面内径为d 2,测点16、17为d 3,余均为d 1。
(2).标“*”者为毕托管测点(测点编号见图1)。
(3).测点2、3为直管均匀流段同一个断面上的两个测压点,10、11位弯管非均匀流段同一断面上的两个测点。
表2 测压管水头h i ,流量测记表(其中ii i p h z gρ=+,单位10-2m ,i 为测点编号) 实验次数 h 2h 3h 4h 5h 7h 9h 10h 11 h 13 h 15 h 17 h 19q V /(10-6m 3/s)12表3 计算数值表 (1) 流速水头管径d /10-2m111V q V t ==201.3/(10-6m 3/s) 222V q V t ==/(10-6m 3/s)A /10-4m 2 v /(10-2m/s)22g v/10-2m A /10-4m 2 v /(10-2m/s)22g v/10-2m(2) 总水头H i (其中22i i i i p H z g gαρ=++v ,单位10-2m ,i 为测点编号) 实验次数 H 2 H 4 H 5 H 7 H 9 H 13 H 15 H 17 H 19 V q/(10-6m 3/s)1 23.成果要求(1) 回答定性分析实验中的有关问题。
(2) 计算流速水头和总水头。
见表3(3) 绘制上述成果中最大流量下的总水头线和测压管水头线。
(轴向尺寸参见图4,总水头线和测压管水头线可以绘在图4上)/mm404060604013510010019516016080100200300400500100200300400500600700800900100011001200/mm 501514042567131113101289171916180图4 绘制测压管水头线坐标图六、分析思考题1.测压管水头线和总水头线的变化趋势有何不同?为什么? 2.阀门开大,使流量增加,测压管水头线有何变化?为什么?3.由毕托管测量的总水头线与按实测断面平均流速绘制的总水头线一般都有差异,试分析其原因。
4.为什么急变流断面不能被选作能量方程的计算断面?七、注意事项1.各自循环供水实验均需注意:计量后的水必须倒回原实验装置的水斗内,以保持自循环供水(此注意事项后述实验不再提示)。
2. 稳压筒内气腔越大,稳压效果越好。
但稳压筒的水位必须淹没连通管的进口,以免连通管进气,否则需拧开稳压筒排气螺丝提高筒内水位;若稳压筒的水位高于排气螺丝口,说明有漏气,需检查处理。
3.传感器与稳压筒的连接管要确保气路通畅,接管及进气口均不得有水体进入,否则需清除。
4.智能化数显流量仪开机后需预热3~5分钟。
雷诺实验一、实验目的和要求1. 观察层流、湍流的流态及其转换过程;2. 测定临界雷诺数,掌握园管流态判别准则;3. 学习应用量纲分析法进行实验研究的方法,确定非圆管流的流态判别准数。
