第四章 对称密码体制
对称密码体制和非对称密码体制

对称密码体制和⾮对称密码体制⼀、对称加密 (Symmetric Key Encryption)对称加密是最快速、最简单的⼀种加密⽅式,加密(encryption)与解密(decryption)⽤的是同样的密钥(secret key)。
对称加密有很多种算法,由于它效率很⾼,所以被⼴泛使⽤在很多加密协议的核⼼当中。
⾃1977年美国颁布DES(Data Encryption Standard)密码算法作为美国数据加密标准以来,对称密码体制迅速发展,得到了世界各国的关注和普遍应⽤。
对称密码体制从⼯作⽅式上可以分为分组加密和序列密码两⼤类。
对称加密算法的优点:算法公开、计算量⼩、加密速度快、加密效率⾼。
对称加密算法的缺点:交易双⽅都使⽤同样钥匙,安全性得不到保证。
此外,每对⽤户每次使⽤对称加密算法时,都需要使⽤其他⼈不知道的惟⼀钥匙,这会使得发收信双⽅所拥有的钥匙数量呈⼏何级数增长,密钥管理成为⽤户的负担。
对称加密算法在分布式⽹络系统上使⽤较为困难,主要是因为密钥管理困难,使⽤成本较⾼。
⽽与公开密钥加密算法⽐起来,对称加密算法能够提供加密和认证却缺乏了签名功能,使得使⽤范围有所缩⼩。
对称加密通常使⽤的是相对较⼩的密钥,⼀般⼩于256 bit。
因为密钥越⼤,加密越强,但加密与解密的过程越慢。
如果你只⽤1 bit来做这个密钥,那⿊客们可以先试着⽤0来解密,不⾏的话就再⽤1解;但如果你的密钥有1 MB⼤,⿊客们可能永远也⽆法破解,但加密和解密的过程要花费很长的时间。
密钥的⼤⼩既要照顾到安全性,也要照顾到效率,是⼀个trade-off。
分组密码:也叫块加密(block cyphers),⼀次加密明⽂中的⼀个块。
是将明⽂按⼀定的位长分组,明⽂组经过加密运算得到密⽂组,密⽂组经过解密运算(加密运算的逆运算),还原成明⽂组,有 ECB、CBC、CFB、OFB 四种⼯作模式。
序列密码:也叫流加密(stream cyphers),⼀次加密明⽂中的⼀个位。
2019信息网络安全专业技术人员继续教育(信息安全技术)习题及答案

信息安全技术第一章概述第二章基础技术一、判断题1.加密技术和数字签名技术是实现所有安全服务的重要基础。
(对)2.对称密码体制的特征是:加密密钥和解密密钥完全相同,或者一个密钥很容易从另ー个密钥中导出。
(对)3.对称密钥体制的对称中心服务结构解决了体制中未知实体通信困难的问题。
(错)4.公钥密码体制算法用一个密钥进行加密,!而用另一个不同但是有关的密钥进行解密。
(对)5.公钥密码体制有两种基本的模型:一种是加密模型,另一种是解密模型(错)6.Rabin体制是基于大整数因子分解问题的,是公钥系统最具典型意义的方法。
(错)7.对称密码体制较之于公钥密码体制具有密钥分发役有安全信道的限制,可实现数字签名和认证的优点。
(错)8.国密算法包括 SM2,SM3和SM4. (对)9.信息的防篡改、防删除、防插入的特性称为数据完整性保护。
(对)10.Hash函数的输人可以是任意大小的消息,其输出是一个长度随输入变化的消息摘要。
(错)11.数字签名要求签名只能由签名者自己产生。
(对)12、自主访问控制(DAC)是基于对客体安全级别与主体安全级别的比较来进行访问控制的。
(错)13.基于角色的访问控制(RBAC)是基于主体在系统中承担的角色进行访问控制,而不是基于主体的身份。
(对)二、多选题1.公钥密码体制与以前方法的区别在于()。
A.基于数学函数而不是替代和置换B、基于替代和置换C.是非对称的,有两个不同密钥D.是对称的,使用一个密钥2.公钥密码的优势体现在()方面。
A.密钥交换B.未知实体间通信C.服务D.认证服务3.以下属于非对称算法的是()。
A.RSAB.DSAC.AESD.ECC4.密钥生命周期过程包括( )A.密钥生成B.密钥分发;C.密钥存储D.密钥使用与更新汽'tE.密钥销毁5.下列关于密码模块的描述正确的是()。
A.是硬件、软件、固件或其组合B.实现了经过验证的安全功能C.包括密码算法和密钥生成等过程D.在一定的密码系统边界之外实现6.访问控制的基本要素包括()。
对称密码体制

实例二:对压缩文档解密
• 任务描述:
李琳同学在电脑里备份了一份文档,当时 出于安全考虑,所以加了密码,时间久了,密 码不记得了。请帮李琳同学找回密码。
实例二:对压缩文档解密
• 任务分析:
WinRAR对文档的加密方式属于对称性加 密,即加密和解密的密码相同,这种文档的解 密相对来说比较简单,网上有很多专用工具, 可以实现密码的硬解。
推荐:RAR Password Unlocker
实例二:对压缩文档解密
• 操作步骤:
– (1)启动软件; – (2)打开加密的文件; – (3)单击“STRAT”按钮,开始解密; – (4)弹出结果对话框,找到密码。
实例三:Office文档加密
• 操作步骤:
– (1)启动word;
– (2)文件——另存为;
走进加密技术
对称密码体制
知识回顾
• 密码技术的发展经历了三个阶段
• 1949年之前 密码学是一门艺术 (古典密码学) • 1949~1975年 密码学成为科学 • 1976年以后 密码学的新方向
传 统 加 密 方 法
(现代密码学)
——公钥密码学
密码体制
• 密码体制也叫密码系统,是指能完整地解
决信息安全中的机密性、数据完整性、认
小结
对称密码体制 对称密码体制也称为单钥体制、私钥体制或对 称密码密钥体制、传统密码体制或常规密钥密码体 制。 主要特点是:加解密双方在加解密过程中使用 相同或可以推出本质上等同的密钥,即加密密钥与 解密密钥相同,基本原理如图所示。
– (3)文件类型为:2003-07文档; – (4)单击“工具”选择“常规选项”; – (5)设置文档打开密码,存盘。
实例四:Office文档解密
第04章 密码学原理

57 10 63 14
49 2 55 6
41 59 47 61
33 51 39 53
25 43 31 45
17 35 23 37
9 27 15 29
1 19 7 21
58 11 62 13
50 3 54 5
42 60 46 28
34 52 38 20
26 44 30 12
18 36 22 4
第4章 网络安全密码学基本理论
密码学是一门研究信息安全保护的科学。它最早可追溯到 几千年前,主要用于军事和外交通信。随着网络与信息技术的 发展,密码学的应用不再局限于军事、政治、外交领域,而是 逐步应用于社会各个领域,例如电子商务、个人安全通信、网 络安全管理等。 密码学的发展可大致划分为四个阶段:
第4章 网络安全密码学基本理论 第一个阶段:从古代到1949年。该时期的密码学没有数学
第4章 网络安全密码学基本理论 4.1.2 密码学基本概念
密码学,是保护明文的秘密以防止攻击者获知的科学。
密码分,析学是在不知道密钥的情况下识别出明文的科学。
明文,是指需要采用密码技术进行保护的消息。
密文,是指用密码技术处理“明文”后的结果,通常称为加
密消息。
第4章 网络安全密码学基本理论
将明文变换成密文的过程称作加密(encryption)。 其逆过程,即由密文恢复出原明文的过程称作解密
道交换密钥,以保证发送消息或接收消息时能够有供使用的密钥。
第4章 网络安全密码学基本理论
加密
解密
明文
密文
密文
明文
图4-1 私钥密码体制原理示意图
第4章 网络安全密码学基本理论 密钥分配和管理是极为重要的问题。 为了保证加密消息的安全,密钥分配必须使用安全途径, 例如由专门人员负责护送密钥给接收者。 同时,消息发送方和接收方都需要安全保管密钥,防止非 法用户读取。 另外的问题是密钥量。由于加密和解密使用同一个密钥, 因此,与不同的接收者进行加密通信时,需要有几个不同的密
第四章 密码学基础1

混乱:
指明文、密钥和密文之间的统计关系尽可能
复杂,使得攻击者无法理出三者的相互依赖 关系。
s-p网络的轮函数包括3个变换:代换、 置换、密钥混合。
4.3.2 DES数据加密标准
1 算法简介
数据加密标准(Data Encryption Standard,DES) 是使用 最广泛的密码系统。1973年美国国家标准局征求国家 密码标准文字,IBM公司于1974年提交,于1977年被 采纳为DES。 DES出现后20年间,在数据加密方面发挥了不可替代的 作用。20世纪90年代后,随着技术的发展,密钥长度 偏短,DES不断传出被破译的进展情况。1998年12月 美国国家标准局不再用DES作为官方机密,推荐为一般 商业应用,于2001年11月发布了高级加密标准 (AES)。
字母表是循环的,Z后面的是A,能定义替换
表,即密钥。 明文:a b c d e f g h I j k l m n o p q r s t uvwxyz 密文: D E F G H I J K L M N O P Q R S T U VWXYZABC
Caesar算法能用如下公式表示: C=E(3,m)=(m+3) mod 26 如果对字母表中的每个字母用它之后的第k个 字母来代换,而不是固定其后面第3个字母, 则得到了一般的Caesar算法: C=E(k,m)=(m+k) mod 26
如果加密、解密用不同的密钥,是非对 称加密。图解
Ek1(P)=C
Dk2(C)=P Dk2(Ek1(P))=P
4.1.3密码的分类 1按应用技术分:
手工密码 机械密码 电子机内乱密码
通过电子电线,程序进行逻辑运算,以少量制乱
第四章-公钥密码体制

• 推论: p素数,a是任意整数,则: ap a mod p
– M kφ(n)+1=M mod n
RSA算法举例(1)
p = 53,q = 61,n = pq = 3233, φ(n)=52x60 = 3120 令d = 791,则e = 71 令m = RE NA IS SA NC E 即m = 1704 1300 0818 1800 1302 0426 170471 mod 3233 = 3106,…, C = 3106 0100 0931 2691 1984 2927
欧拉定理
• 证明: • R={x1,x2,…,x(n)}为所有小于n且与n互素的正整数,考虑集 合 • S={(ax1mod n), (ax2mod n),…, (ax(n) mod n)} • (aximod n)与n互素 • (aximod n)两两不等: • (aximod n) = (axjmod n) ximod n = xjmod n • S有(n)个元素 • 故S也是所有小于n且与n互素的正整数,因此S=R,从而 xi=(aximod n)((axi)) mod n • (a(n) xi) mod n • 注意到xi 与n互素,从而得到结论.
费马(Fermat)定理
• 若p是素数,a是正整数,且gcd(a,p)=1,则ap1≡1mod p • 证明:考虑集合{1,2,…,p-1},对每个数乘以a,得到 集合{a mod p,2a mod p,…,(p-1)a mod p},对于p, 后者两两不同且都在1与p-1之间,因此两个集合相 同,于是:
【软考继续教育-应用密码学】14-17对称密码体制(1-4)

24 6 4 20 37 45 56 36
1 21 26 13 47 33 34 29
5 10 8 2 55 48 53 32
图5-24 置换选择1
密钥(48位)
图5-25 置换选择2
41
循环左移位
轮 1 序 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
移 位 数
1
1
2
17
CBC模式
18
CBC模式的特点
同一个明文分组重复出现时产生不同的密文分 组 加密函数的输入是当前的明文分组和前一个密 文分组的异或;对每个分组使用相同的密钥。 将明文分组序列的处理连接起来了。每个明文 分组的加密函数的输入与明文分组之间不再有 固定的关系 有助于将CBC模式用于加密长消息
输出(64位)
图5-17 逆初始置换(IP-1)
34
Li Ri 1
Ri Li 1 F ( Ri 1 , K i )
R16 R15
L16 L15 F ( R15 , K16 )
35
输入(32位)
输入(32位,来自于S盒)
32 4 8 12 16 20 24 28
1 5 9 13 17 21 25 29
8 7 6 5 4 3 2 1
48 47 46 45 44 43 42 41
16 15 14 13 12 11 10 9
56 55 54 53 52 51 50 49
24 23 22 21 20 19 18 17
64 63 62 61 60 59 58 57
32 31 30 29 28 27 26 25
2
2
2
2
2
对称密码体制
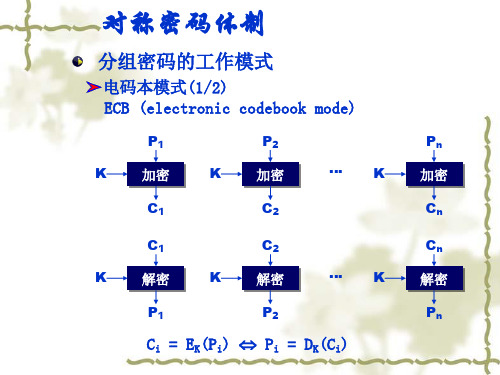
分组密码的工作模式
电码本模式(1/2) ECB (electronic codebook mode)
P1 K 加密
P2
K
加密
…K
Pn 加密
C1
C2
Cn
C1 K 解密
C2
K
解密
…K
Cn 解密
P1
P2
Pn
Ci = EK(Pi) Pi = DK(Ci)
对称密码体制
分组密码的工作模式
电码本模式(2/2) ECB特点
对称密码体制
分组密码的工作模式
密码反馈模式(2/6)
加密:Ci =Pi(EK(Si)的高j位) Si+1=(Si<<j)|Ci
V1
Shift register 64-j bit |j bit
64
Shift register 64-j bit |j bit
64
Cn-1 Shift register 64-j bit |j bit
对称密码体制
分组密码的工作模式
密码反馈模式(6/6) Pi=Ci(EK(Si)的高j位) 因为: Ci=Pi(EK(Si)的高j位)
则: Pi=Pi(EK(Si)的高j位) (EK(Si)的高j位) =Pi 0 = Pi
CFB的特点 ❖分组密码流密码 ❖没有已知的并行实现算法 ❖隐藏了明文模式 ❖需要共同的移位寄存器初始值V1 ❖对于不同的消息,V1必须唯一 ❖误差传递:一个单元损坏影响多个单元
对称密码体制
分组密码的工作模式
密码分组链接模式(3/3)
CBC特点 ❖没有已知的并行实现算法 ❖能隐藏明文的模式信息 ❖需要共同的初始化向量V1 ❖相同明文不同密文 ❖初始化向量V1可以用来改变第一块 ❖对明文的主动攻击是不容易的 ❖信息块不容易被替换、重排、删除、重放 ❖误差传递:密文块损坏两明文块损坏 ❖安全性好于ECB ❖适合于传输长度大于64位的报文,还可以进行用 户鉴别,是大多系统的标准如 SSL、IPSec
现代密码学教程

()
(7) 差分分析是一种攻击迭代密码体制的选择明文攻击方法,所以,对于 和 都有一
定的攻击效果。
()
(8) 线性分析实际上是一种已知明文攻击方法。
()
(9) 通过 类似, 也存在弱密钥,但其弱密钥数量少于 的弱密钥数。 ( )
(10) 算法是可逆的,即可以用相同的算法进行加密和解密。
()
(11) 因为 密码算法采用 结构,所以具有加解密相似的特征。 ( )
,并且
,
,
,求 。
(8) 请给出一个 完全类问题的例子。
第四章 分组密码
1.
(1)
判在分断组题密码中,分组或密钥越长意味着安全性越高,因此,在实际应用中应选用分组和
密钥都长的分组密钥算法。
()
(2) 分组密码一般采用简单的、安全性弱的加密算法进行多轮迭代运算,使得安全性增强。
一般来说,分组密码迭代轮数越多,密码分析越可困难。
计算机网络的普及和发展。
()
(5) 年后,美国数据加密标准( )的公布使密码学的研究公开,从而开创了现
代密码学的新纪元,是密码学发展史上的一次质的飞跃。
()
(6) 现代密码系统的安全性不应取决于不易改变的算法,而应取决于可随机改变的密钥。
()
(7) 能经受住选择明文攻击的密码体制就能经受住已知明文攻击。 ( )
第五章 序列密码
1(. 1)判断序题列密码(又称流密码)是属于对称密码体制。
()
(2) 序列密码的加解密钥是由种子密钥生成的,而种子密钥的长度是由需加密的明文长
度决定。
()
(3) 利用反馈移位寄存器来生成序列密码的密钥的过程中,反馈移位寄存器的初始值是
由种子密钥决定的。
密码体制的分类方法

密码体制是指用于保护信息安全的加密和解密方法。
根据不同的分类标准,可以将密码体制分为以下几类:
对称密码体制(Symmetric Cryptography):也称为私钥密码体制,加密和解密使用相同的密钥。
常见的对称密码算法有DES、AES和IDEA等。
对称密码体制具有加密速度快的优点,但需要确保密钥的安全性。
公钥密码体制(Public Key Cryptography):也称为非对称密码体制,加密和解密使用不同的密钥,其中一个密钥是公开的,称为公钥,另一个密钥是私有的,称为私钥。
常见的公钥密码算法有RSA、Diffie-Hellman和椭圆曲线密码等。
公钥密码体制具有密钥分发方便的优点,但加密和解密速度较慢。
哈希函数(Hash Function):哈希函数是一种将任意长度的输入数据转换为固定长度的输出数据的算法。
常见的哈希函数有MD5、SHA-1和SHA-256等。
哈希函数主要用于数据完整性校验和数字签名等应用。
数字签名(Digital Signature):数字签名是一种用于验证数据的真实性、完整性和来源的密码技术。
它使用私钥对数据进行加密,生成数字签名,然后使用公钥对数字签名进行解密和验证。
随机数生成(Random Number Generation):随机数生成是密码体制中重要的组成部分,用于生成安全的密钥和初始化向量。
随机数生成器应具有高度随机性和不可预测性。
这些分类方法是根据密码体制的核心原理和使用方式进行的。
不同类型的密码体制在不同的应用场景中具有各自的优势和适用性。
在实际应用中,常常根据具体需求选择合适的密码体制进行数据保护和安全通信。
信息安全概论第四章公钥密码体制

14
Diffie-Hellman密钥交换算法 密钥交换算法
Diffie和Hellman在其里程碑意义的文章中, 虽然给出了密码的思想,但是没有给出真正意 义上的公钥密码实例,也既没能找出一个真正 带陷门的单向函数 然而,他们给出单向函数的实例,并且基于此 提出Diffie-Hellman密钥交换算法
13
常用的公开密钥算法
公钥算法的种类很多,具有代表性的三种密码: 公钥算法的种类很多,具有代表性的三种密码: 基于整数分解难题(IFP)的算法体制 基于整数分解难题(IFP)的算法体制(RSA) 基于离散对数难题(DLP)算法体制 基于离散对数难题(DLP)算法体制(ElGamal) 基于椭圆曲线离散对数难题( ECDLP ) 的算法体制 基于椭圆曲线离散对数难题 ( ECDLP) (ECC)
3
4.1 公钥密码体制的基本原理
对称算法的不足
(1)密钥管理量的困难 传统密钥管理:两两分别用一个密钥时, 传统密钥管理:两两分别用一个密钥时,则n个用户需 C(n,2)=n(n-1)/2个密钥 当用户量增大时, 个密钥, 要C(n,2)=n(n-1)/2个密钥,当用户量增大时,密钥空 间急剧增大。 间急剧增大。如: n=100 时, C(100,2)=4,995 n=5000时 n=5000时, C(5000,2)=12,497,500 (2)密钥必须通过某一信道协商,对这个信道的安全 密钥必须通过某一信道协商, 性的要求比正常的传送消息的信道的安全性要高
7
公开密钥密码的重要特性
加密与解密由不同的密钥完成 Y: X: Y = EKU(X) X = DKR(Y) = DKR(EKU(X))
加密: X 解密: Y
知道加密算法,从加密密钥得到解密密钥在计算上 , 是不可行的 两个密钥中任何一个都可以用作加密而另一个用 作解密(不是必须的) X = DKR(EKU(X))
安徽工程大学 信息安全原理及应用 第4讲 对称密钥密码体制

流密码的研究现状
在保密强度要求高的场合如大量军事密码系统,仍多采用 流密码,美军的核心密码仍是“一次一密”的流密码体制。鉴 于流密码的分析和设计在军事和外交保密通信中有重要价值, 流密码的设计基本上都是保密的,国内外少有专门论述流密码 学的著作,公开的文献也不多。尽管如此,由于流密码长度可 灵活变化,且具有运算速度快、密文传输中没有差错或只有有 限的错误传播等优点,目前仍是国际密码应用的主流,而基于 伪随机序列的流密码是当今最通用的密码系统。
❖ 目前密钥流生成器大都是基于移位寄存器的。因为移位寄存 器结构简单,易于实现且运行速度快。这种基于移位寄存器 的密钥流序列称为移位寄存器序列。
密钥流生成器
❖ 一个反馈移位寄存器由两部分组成:移位寄存器和反馈函数, 构 成一个密钥流生成器。 每次输出一位,移位寄存器中所有位都右 移一位,新的最左端的位根据寄存器中其它位计算得到。移位寄 存器输出的一位常常是最低有效位。
密钥发生器 种子 k
明文流 m i
明文流m i 加密算法E
密钥流 k i 密钥流 发生器
密文流 c i
安全通道 密钥 k
解密算法D
密钥流 发生器
明文流m i
密钥流 k i
图1 同步流密码模型
内部状态 输出函数
内部状态 输出函数
密钥发生器 种子 k
k
密文流 c i
k
图2 自同步流密码模型
明文流 m i
c(x)
f
*(x)
xn
f
(1) x
c0xn
c1xn1
... cn1x cn
称作是LFSR的特征多项式。cn0称之为非奇异LFSR。
密钥流生成器 y (1) i SR 1
2对称密码体制

2011-12-10
15
1997 年 DESCHALL 小 组 经 过 近 4 个 月 的 努 力 , 通 过 Internet搜索了 × 1016 个密钥,找出了DES的密钥, 恢 搜索了3× 个密钥, 找出了 的密钥, 搜索了 的密钥 复出了明文。 复出了明文。 1998年5月美国 年 月美国 月美国EFF(electronics frontier foundation) 宣布,他们以一台价值20万美元的计算机改装成的专用解 宣布,他们以一台价值 万美元的计算机改装成的专用解 密机, 小时破译了56 比特密钥的 比特密钥的DES。 密机,用56小时破译了 小时破译了 。
2011-12-10
14
DES首次被批准使用五年,并规定每隔五年由美国国 首次被批准使用五年, 首次被批准使用五年 家保密局作出评估, 家保密局作出评估,并重新批准它是否继续作为联邦加密 标准。最近的一次评估是在1994年1月,美国已决定 标准。最近的一次评估是在 年 月 美国已决定1998年 年 12月以后将不再使用 月以后将不再使用DES。因为按照现有的技术水平,采 月以后将不再使用 。因为按照现有的技术水平, 用不到几十万美元的设备,就可破开 密码体制。 用不到几十万美元的设备,就可破开DES密码体制。目前 密码体制 的新标准是AES,它是由比利时的密码学家Joan Daemen和 ,它是由比利时的密码学家 的新标准是 和 Vincent Rijmen设计的分组密码 设计的分组密码—Rijndael(荣代尔)。 设计的分组密码 (荣代尔)。
置换选择pc1循环移位置换选择pc2置换选择pc2置换选择164比特201492731子密钥产生器?给出每次迭代加密用的子密钥ki子密钥产生器框图密钥64bit置换选择1pc1除去第816?64位8个校验位201492732置换选择2pc2ci28bitdi28bit循环左移ti1bit循环左移ti1bitki57494133251791585042342618102595143352719113605044366355473931231576254463830221466153453729211352820124置换选择1pc1迭代次数12345678循环左移位位数11222222左循环移位位数2014927331417112415328156211023191242681672720132415231374755304051453348444939563453464250362932置换选择2pc2迭代次数910111213141516循环左移位数12222221201492734des的安全性?穷举攻击分析穷举攻击就是对所有可能的密钥逐个进行脱密测试直到找到正确密钥为止的一种攻击方法方法
对称密码体制

对称密码体制对称密码体制是一种有效的信息加密算法,它尝试在满足基本安全约束的同时提供最大的加密强度和性能。
它是最常用的信息加密类型之一,甚至在金融机构、政府机构、企业以及个人之间都被广泛使用。
对称密码体制通过使用单个密钥(称为“秘密密钥”)来确保信息的安全传输和接收,而无需在发送方和接收方之间共享保密信息。
这一密钥的特点在于,既可以用来加密信息,也可以用于解密信息。
由于秘密密钥是由发送方和接收方共同拥有,因此不需要额外的通信,也无需额外的身份验证。
在使用对称密码体制时,发送方必须在发送数据之前将其加密,而接收方则必须使用相同的密钥对数据进行解密,以此来识别发送方。
然而,有一种特殊情况除外,即发送方可以使用密钥来加密消息,而接收方可以使用相同的密钥来解密消息,而无需在发送方和接收方之间共享信息。
在实际使用中,对称密码体制有三种形式:数据加密标准(DES)、高级加密标准(AES)和哈希密码(HMAC)。
其中,DES是一种最常用的对称密码体制,它采用了比较古老的56位密钥来加密数据,并且它的加密强度受到比较严格的限制。
而AES是一种更新的,比DES更安全的对称加密算法,它使用128位或256位密钥,并且可以提供更强的安全性和性能。
最后,HMAC是一种哈希加密算法,它使用128位或256位密钥来确保信息的完整性和真实性,同时也可以使用相同的密钥来加密和解密数据。
对称密码体制是一种有效的信息加密算法,它在满足基本安全约束的同时还能提供最大的加密强度和最高的性能。
它是最常用的信息加密类型之一,甚至在金融机构、政府机构、企业以及个人之间都被广泛使用,并且有三种形式:数据加密标准(DES)、高级加密标准(AES)和哈希密码(HMAC),可以满足各种要求。
其中,AES可以提供更高的安全性和性能,而HMAC可以确保信息的完整性和真实性,因此在实际应用中,对称密码体制也被广泛应用。
对称密码体制在许多领域都有着广泛的应用,尤其是在安全传输方面。
物联网安全技术第4章 物联网认证机制

T , M Nonce
Checksum
SK
EP
E TNonce , K PK EP
T E X T1 PK CA T E X T2 PK EP
CA 认证中心
EP 外部组织 Mote 传感节点 PK 公钥 SK 私钥 TEXT 签名文本 E 密文 K 会话密钥
16
4.3.3 基于ECC公钥算法的用户强 认证协议
18
第四章 物联网认证机制
4.1 物联网认证机制的安全目标及分类 4.2 基于对称密码体制的认证协议 4.3 基于非对称密码体制的认证协议 4.4 µTESL广播认证协议 4.5 基于中国剩余定理的广播认证协议
19
4.4.1 µTESL广播认证协议
µTESLA广播认证协议
µTESLA主要用于提供点到多的广播认证,其 基本思想是通过对认证密钥的延迟分发而引入非对称 认证方式。
普通高等教育 物联网工程类规划教材
物联网安全技术
第四章 物联网认证机制
4.1 物联网认证机制的安全目标及分类 4.2 基于对称密码体制的认证协议 4.3 基于非对称密码体制的认证协议 4.4 µTESL广播认证协议 4.5 基于中国剩余定理的广播认证协议
2
4.1 物联网认证机制的安全目标及分类
物联网认证机制的安全目标
MAC4=HMAC-SHA256(MIK,NB)
CompareMAC4 ? = MAC3 If:MAC4=MAC3
则节点B完成对节点A的鉴别, 将MEK保存为与A的会话密钥。
10
4.2.2 基于分组密码算法的双向 认证协议
基于分组密码算法的双向认证协议
认证之前,节点A应具备身份标识IDA和预共享密钥KP, 节点B应具备身份标识IDB和预共享密钥KP。
密码学

1.密码体制分类:1)对称密码体制(密钥必须完全保密、加密与解密密钥相同,或可由其中一个很容易推出另一个,又称秘密密钥、单钥、传统密码体制,包括分组密码和序列密码)优点:加解密速度较快,有很高的数据吞吐率;使用的密钥相对较短;密文的长度与明文长度相同;缺点:密钥分发需要安全通道;密钥量大,难于管理;难以解决不可否认问题。
2)非对称密码体制(使用两个密钥,一个是对外公开的公钥,一个是必须保密的私钥,不能由公钥推出私钥,又称双钥或公开密钥密码体制)优点:密钥的分发相对容易;密钥管理简单;可以有效地实现数字签名。
缺点:与对称密码体制相比,非对称密码体制加解密速度较慢;同等安全强度下,非对称密码体制要求的密钥位数要多一些;密文的长度往往大于明文长度。
2.AES与DES对比:1)相似处:二者的圈(轮)函数都是由3层构成:非线性层、线性混合层、子密钥异或,只是顺序不同;AES的子密钥异或对应于DES中S盒之前的子密钥异或;AES的列混合运算的目的是让不同的字节相互影响,而DES中F函数的输出与左边一半数据相加也有类似的效果;AES的非线性运算是字节代换,对应于DES中唯一的非线性运算S盒;行移位运算保证了每一行的字节不仅仅影响其它行对应的字节,而且影响其他行所有的字节,这与DES中置换P相似。
2)不同之处:AES的密钥长度(128位192位256位)是可变的,而DES的密钥长度固定为56位;DES是面向比特的运算,AES是面向字节的运算;AES的加密运算和解密运算不一致,因而加密器不能同时用作解密器,DES 则无此限制。
3.Hash函数:也称散列、哈希、杂凑函数等,是一个从消息空间到像空间的不可逆映射;可将任意长度的输入经过变换得到固定长度的输出;是一种具有压缩特性的单向函数。
性质:1)H可应用于任意长度的消息2)H产生定长的输出3)对任意给定的消息x,计算H(x)较容易,用硬件和软件均可实现4)单向性5)抗弱碰撞性6)抗强碰撞性应用:数字签名;生成程序或者文档的数字指纹;用于安全传输和存储口令特点:1)输入数字串与输出数字串具有唯一的对应关系;输入数字串中2)任何变化会导致输出数字串也发生变化;从输出数字串不能够反求出输入数字串。
对称密码体制的原理

对称密码体制的原理
对称密码体制是指使用相同的密钥进行加密和解密的密码算法。
其原理基于异或运算和分组加密算法。
在对称密码体制中,发送方和接收方之间共享一个密钥,该密钥被用来对数据进行加密和解密。
加密使用密钥对数据进行加密,解密则使用相同的密钥对数据进行解密。
密钥的加密和解密使用异或运算,即将要加密或解密的数据与密钥进行异或运算,得到一个新的比特序列,该比特序列作为新的密钥,再次用于加密或解密。
分组加密算法是将数据分成若干组,每组数据使用密钥进行加密,从而实现数据的安全性。
常用的分组加密算法有 DES、3DES、AES 等。
对称密码体制具有高效、安全、易于实现等优点,被广泛运用于网络通信、电子邮件等领域。
继续教育信息安全技术题库及答案

网络信息安全题库及答案一判断题第二章物理内存1、信息网络的物理安全要从环境和设备两个角度来考虑(对)2、计算机场地可以选择在公共区域人流量比较大的地方(错)3、计算机场地可以选择在化工生产车间附件(错)4、计算机场地在正常情况下温度保持在职18至此28摄氏度。
(对)5、机房供电线路和动力、照明用电可以用同一线路(错)6、只要手干净就可以直接触摸或者擦拨电路组件,不必有进一步的措施(错)7、备用电路板或者元器件、图纸文件必须存放在防静电屏蔽袋内,使用时要远离静电敏感器件。
(对)8、屏蔽室是一个导电的金属材料制成的大型六面体,能够抑制和阻挡电磁波在空气中传播。
(对)9、屏蔽室的拼接、焊接工艺对电磁防护没有影响。
(错)10、由于传输的内容不同,电力结可以与网络线同槽铺设。
(错)11、接地线在穿越墙壁、楼板和地坪时应套钢管或其他非金属的保护套管,钢管应与接地线做电气连通。
(对)12、新添设备时应该先给设备或者部件做上明显标记,最好是明显的无法除去的标记,以防更换和方便查找赃物。
(对)13、TEMPEST技术,是指在设计和生产计算机设备时,就对可能产生电磁辐射的元器件、集成电路、连接线、显示器等采取防辐射措施,从而达到减少计算机信息泄露的最终目的。
(对)14、机房内的环境对粉尘含量没有要要求。
(错)15、防电磁辐射的干扰技术,是指把干扰器发射出来的电磁波和计算机辐射出来的电磁波混合在一起,以掩盖原泄露信息的内容和特征等,使窃密者即使截获这一混合信号也无法提取其中的信息。
(对)16、有很高使用价值或很高机密程度的重要数据应采用加密等方法进行保护。
(对)17、纸介资料废弃应用碎纸机粉碎或焚毁。
(对)第三章容灾与数据备份1、灾难恢复和容灾具有不同的含义。
(错)2、数据备份按数据类型划分可以分成系统数据备份和用户数据备份。
(对)3、对目前大量的数据备份来说,磁带是应用得最广的介质。
(对)4、增量备份是备份从上次进行完全备份后更改的全部数据文件。
信息安全导论(4-2_密码基础-对称密码)

16
9 11 13 15
8
1 3 5 7
8
DES算法的整体结构——Feistel结 构
2. 按下述规则进行16次迭 代,即
Li R i-1 R i Li-1 f ( Ri 1 , Ki )
Li-1
Ri-1 ki
1≤i≤16 这里 是对应比特的模2加, f是一个函数(称为轮函 数); 16个长度为48比特的子密钥 Ki(1≤i≤16)是由密钥k 经密钥编排函数计算出来 的.
特串,每个6比特,B=B1B2B3B4B5B6B7B8.
15
分组密码的轮函数
S盒代换:6入4出,查表
8个S盒S1……S8. 每个S盒是一个固定的 4*16阶矩阵,其元素取0~15之间的整数. 输入6比特b1b2b3b4b5b6,输出如下 1) b1b6两个比特确定了S盒的行 2) b2b3b4b5四个比特确定了S盒的列 3) 行、列确定的值即为输出
16
S1 14 0 4 15 15 3 0 13 10 13 13 1 7 12 10 3 2 14 4 11 12 10 9 4 4 13 1 6 13 1 7 2 4 15 1 12 1 13 14 8 0 7 6 10 13 8 6 15 12 11 2 8 1 15 14 3 11 0 4 11 2 15 11 1 13 7 14 8 8 4 7 10 9 0 4 13 14 11 9 0 4 2 1 12 10 4 15 2 2 11 11 13 8 13 4 14 1 4 8 2 14 7 11 1 14 9 9 0 3 5 0 6 1 12 11 7 15 2 5 12 14 7 13 8 4 8 1 7 2 15 13 4 6 15 10 3 6 3 8 6 0 6 12 10 7 4 10 1 9 7 2 9 15 4 12 1 6 10 9 4 15 2 6 9 11 2 4 15 3 4 15 9 6 15 11 1 10 7 13 14 2 12 8 5 0 9 3 4 15 3 12 10 11 13 2 1 3 8 13 4 15 6 3 8 9 0 7 13 11 13 7 2 6 9 12 15 8 1 7 10 11 7 14 8 8 1 11 7 S2 4 14 1 2 9 12 5 11 7 0 8 6 13 8 1 15 2 7 1 4 5 0 9 15 13 1 0 14 12 3 15 5 9 5 6 12 2 1 12 7 12 5 2 14 8 2 3 5 3 15 12 0 3 13 4 1 9 5 6 0 3 6 10 9 13 10 6 12 7 14 12 3 5 12 14 11 15 10 5 9 4 14 10 7 7 12 8 15 14 11 13 0 12 6 9 0 11 12 5 11 11 1 5 12 13 3 6 10 14 0 1 6 5 2 0 14 5 0 15 3 0 9 3 5 4 11 10 5 12 10 2 7 0 9 3 4 7 11 13 0 10 15 5 2 0 14 3 5 5 11 2 14 2 15 14 2 4 14 8 2 14 8 0 5 5 3 11 8 6 8 9 3 12 9 5 6 10 5 15 9 8 1 7 12 15 9 4 14 9 6 14 3 11 8 6 13 1 6 2 12 7 2 8 1117 3 10 15 5 10 6 12 11 6 12 9 3 12 11 7 14 5 9 3 10 9 5 10 0 0 3 5 6 7 8 0 13
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
为0010。
x5 x0 10
x5 x4 x3 x2 x1 x0 10 11 0 0
(y3 , y2, y1 , y0)=(0,0,1,0)
列号 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
行号
0
14 4 13 1 2 15 11 8 3 10 6 12 5 9 0 7
密钥空间足够大,尽可能消除弱密钥,从而使所有密钥 同等概率,以防穷举密钥攻击。今后一段时间内,128 比特密钥应该是足够安全的。
算法要足够复杂,充分实现明文与密钥的扩散和混淆, 没有简单关系可循,要能抵抗各种已知的攻击,如差分 攻击和线性攻击等;另外,还要求有较高的非线性阶数。
软硬件实现性
软件实现的要求:尽量使用适合编程的子块和简 单的运算。子块的长度能自然地适应软件编程, 如8、16、32比特等;最好是用处理器的基本运 算,如加法、乘法、移位等。
际使用中的许多分组密码,如DES、IDEA等,所 用的置换只不过是上述置换集的一个很小的子集。
分组密码的算法实质:是在密钥的控 制下,能从一个足够大和足够好的置换 子集中简单而迅速地选出一个置换,用 来对当前输入的明文数字组进行加密变 换。
(2)设计的算法应满足的要求
安全性:
分组长度足够大,使不同明文分组的个数足够多,防止 明文穷举攻击法。新算法标准一般要求 n=128bit。
输出64比特密文数据
图4.7 DES加密算法框图
4.2.1.1初始置换IP和初始逆置换IP-1
将64比特明文数据用初始置换IP进行置换操 作,得到一个乱序的64比特明文分组,进行16轮 完全类似的迭代运算后,用初始逆置换IP-1进行置 换操作,产生密文数据组。置换表中数字表示将 64比特数据组中在该数字所在位置的比特置换为 该数字表示的位置的比特。初始置换IP和初始逆 置换IP-1如表4.1所示:
4.2.1 DES加密过程
DES是分组长度为64比特 的分组密码算法,密钥长度 也是64比特,其中每8比特 有一位奇偶校验位,因此有 效密钥长度为56比特。DES 算法是公开的,其安全性依 赖于密钥的保密程度。DES 结构框图如图4.7。
输入64比特明文数据 初始置换IP
在密钥控制下16轮迭代 交换左右32比特 初始逆置换IP-1
一轮SP网络加密过程:
X i1
S——替换
P——置换
Xi
图4.6 一轮SP网络加密过程
4.2 数据加密标准 DES
数据加密标准 (Data Encryption Standard) 是至今为止使用最为广泛的加密算法。IBM 提交 了他们研制的一种密码算法,在经过大量的公开 讨论之后于1977年1月15日被正式批准为美国联邦 信息处理标准,即FIPS-46,同年7月15日开始生 效。1999年颁发新标准, DES只能用于(历史)遗 留系统和3DES的使用。
LDi
K’i RD
i
图4.5 一轮Feistel网络解密过程
解密: RDi-1 = LDi ; RDi = LDi-1⊕F(RDi-1,Ki)
(2)SP网络结构
每一轮的输入首选被一个由子密钥控制的可逆函 数S作用,然后再对所得结果用置换P作用。S和P被分 别称为混淆层和扩散层,起混淆和扩散的作用。
与子密钥的异或运算
将选择扩展运算的48 比特输出数据与子 密钥(48比特)进行异或。
与子密钥的异或运算实质上是对明文的 代换操作。
选择压缩运算:
将输入的48比特数据自左至右分成8组,每组为6 比特。然后输入8个S盒,每个S盒为一非线性代换, 有4比特输出,如图3.9所示。
S1 S2
48比特寄存器
初始逆置换IP-1
40 8 48 16 56 24 64 32 39 7 47 15 55 23 63 31 38 6 46 14 54 22 62 30 37 5 45 13 53 21 61 29 36 4 44 12 52 20 60 28 35 3 43 11 51 19 59 27 34 2 42 10 50 18 58 26 33 1 41 9 49 17 57 25
将明文消息划分成长度为n的组(x0,x1,…,xn-1),每
组分别在密钥K=(k0,k1,…,km-1) 的控制下变换成等
长的输出数字序列 (y0,y1,…,yn-1) ,加密函数是
E:Vn×K→Vn ,其中Vn 是n维矢量空间,K为密钥空
间。
密 k (k0 , , km1 )
密钥 k= (k0 , , km1 )
我们在第二章介绍经典密码算法中使用的加密 技术能不能达到混淆和扩散的作用?
迭代密码是实现混淆和扩散原则的一 种有效的方法。合理选择的轮函数经 过若干次迭代后能够提供必要的混淆
和扩散。
2、分组密码的一般结构
分组密码的结构一般可以分为两种:
(1)Feistel网络结构
(2)SP网络结构
我们将DES作为对称密码的研究对象, DES算法是基于Feistel网络结构,所以本 次授课内容重点在于该网络结构工作原理 的研究。
第四章 对称密码体制
本章内容:
分组密码的一般原理
工作方式 一般结构
DES算法的描述 分组密码的工作模式
4.1 分组密码原理
对称密码体制根据对明文的加密方式的不同 而分为分组密码和流密码。分组密码先按一定 长度(如64字节、128字节等)对明文进行分组, 以组为单位加/解密;流密码则不进行分组,而 是按位加密。
硬件实现的要求:加密和解密应具有相似性;尽 量采用标准的组件结构,以便能适应于在超大规 模集成电路中实现。
(3)两个基本设计方法
混淆(confusion):使得密文的统计特性与密钥的 取值之间的关系尽量复杂,必须让明文的每个比特 影响到密文的许多比特的取值。
扩散(Diffusion):明文的统计结构被扩散消失到密 文的长程统计特性,使得明文和密文之间的统计关 系尽量复杂。
个比特位。这说明IP和IP-1互逆。
4.2.1.2 一轮迭代变换
迭代变换是DES算法的核心部分,如图4.8所示。 在每轮开始将输入的64比特数据分成左、右长度相等 的两半,将右半部分原封不动地作为本轮输出的64比 特数据的左半部分,同时对右半部分进行一系列的变 换,即用轮函数作用右半部分,然后将所得结果(32 比特数据)与输入数据的左半部分进行逐位异或,将 所得数据作为本轮输出的64比特数据的右半部分。
Li-1(32比特)
Ri-1(32比特) 选择扩展运算E 48比特寄存器
48比特寄存器 选择压缩运算S 32比特寄存器
置换运算P
子密钥Ki(48比特)
轮函数F
Li(32比特)
Li=Ri-1
Ri(32比特)
Ri=Li-1⊕F(Ri-1,Ki)
图4.8 DES的一轮迭代
选择扩展运算
将输入的32比特数据,根据变换表扩展为48 比特的输出数据,变换表如下:
用 算法简洁:容易通过分析算法而知道算法抗各种攻
击的能力,也有助于设计高强度的算法。
Feistel的解密算法:
以密文分组作为算法的输入,但以相反的次序使用子 密钥,即第一轮使用 ,K第l 二轮使用 ,K直l1 至L轮使用 。 单K轮1 解密过程如图4.5所示:
K1
RDi-
LDi-
1
1
⊕
第i
F
轮
分组密码系统对不同的组采用同样的密 钥来进行加/解密。流密码的基本思想是利用 动态的密钥流进行加密/解密。
k
x1
y1
┇
┇
无记忆元件
xm
ym
分组密码(y=ek(x))
k
xi
…
······
yi
内部记忆元件
流密码(yi=
e
z
)( x
i
i
)
图4.1 分组密码和流密码的加密
1、 分组密码设计原理
(1)原理
图4.3 Feistel网络
L0
第1轮
⊕
明文(2w位) F
F
…
R0 K1
Ri-1 Ki
…
…
第n轮
Ln-1
⊕
Ln Ln+1
F 密文(2w位)
Rn-1 Kn
Rn Rn+1
单轮加密运算:
网络中每轮的运算基本相同:每轮中都对数据的左 半部分进行代换,方法是先对右边一半数据应用轮函 数,然后将输出的数据与左半部分进行异或。轮函数 的结构一直不变 ,但作为控制参数的每轮子密钥一般 不同。代换完成后,再做一次置换操作交换左右两半 数据。运算过程如图4.4。
LEi-1
第i轮 ⊕
REi-1
F
Ki
LEi
REi
图4.4 一轮Feistel网络加密过程
加密: LEi = REi-1;REi = LEi-1⊕F(REi-1,Ki)
安全性以及软、硬件实现速度: 分组长度 密钥长度 循环次数 子密钥算法:子密钥算法越复杂则安全性越高 轮函数:轮函数越复杂则安全性越高。 快速的软件实现:算法经常被镶嵌在应用程序中使
6比特 S3 S4 S5 S6 S7 S8 选择函数组
4比特
32比特寄存器
图4.9 选择压缩运算S
对每个盒Si,6比特输入中的第1和第6比特组成 的二进制数确定Si 的行,中间 4 位二进制数用来确 定Si的列。Si中相应行、列位置的十进制数的 4 位 二进制数表示作为输出。图4.10表示DES的S1-盒的
(1)Feistel网络结构
工作过程:一个分组长度为n(偶数)比特 的L轮Feistel网络的加密过程如下。给定明文P,
将P分成左边和右边长度相等的两半并分别记为L0
和R0,进行L轮完全类似的迭代运算后,再将左边 和右边长度相等的两半合并产生密文分组,第i轮
