实验四噪声图像的复原
全变差正则化模型的噪声图像复原算法

全变差正则化模型的噪声图像复原算法全变差正则化模型的噪声图像复原算法摘要:噪声图像复原是数字图像处理领域的重要任务之一。
在实际应用中,图像往往会受到各种噪声的干扰,降低图像质量和视觉效果。
全变差正则化模型是一种常用的图像复原方法,它通过最小化图像的总变差来以很好地去除噪声。
本文将介绍全变差正则化模型的基本原理和算法,并结合具体的噪声图像复原实例进行实验,验证全变差正则化模型的有效性和性能。
一、引言随着图像传感器和图像采集设备的不断进步,数字图像的应用越来越广泛。
然而,由于各种原因,如信号传输过程中的干扰、传感器质量问题等,图像往往会受到不同程度的噪声污染。
图像上的噪声会扭曲图像的细节和轮廓,降低图像的清晰度和质量。
图像复原是指通过对噪声图像进行处理,恢复原始图像的过程。
在图像复原的方法中,全变差正则化模型被广泛应用。
全变差正则化模型的基本思想是通过最小化图像的总变差来达到去噪的目的。
总变差描述了图像的边缘平滑度,对图像中的高频噪声具有较强的抑制作用。
因此,全变差正则化模型能够有效地去除噪声,提升图像的质量和细节。
二、全变差正则化模型的原理全变差正则化模型的核心思想是通过最小化图像的总变差来降低噪声的影响。
图像的总变差是指图像中相邻像素间的灰度差的绝对值之和。
设图像为$u(x, y)$,则总变差$TV(u)$可以定义为:$$TV(u)=\sum_{x, y}|\nabla u(x, y)|$$其中,$\nabla u(x, y)=(\frac{\partial u}{\partial x}, \frac{\partial u}{\partial y})$是图像在$(x, y)$处的梯度。
全变差正则化模型的优化目标是最小化如下的能量函数:$$\min_u\{E(u) + \lambda TV(u)\}$$其中,$E(u)$表示图像的损失函数,$\lambda$是正则化参数,用于调节总变差的重要性。
全变差正则化模型的求解通常采用迭代算法,如次梯度法、投影梯度法等。
噪声及复原

实验报告实验题目:图像噪声污染及图像复原处理问题描述:复原的目的是在预定义的意义上改善给定的图像,图像复原大部分是客观的处理,复原通过使用退化现象的先验知识试图重建或恢复一副退化的图像。
而模拟噪声的行为和影响的能力是图像复原的核心,故在本次试验中我先对图像使用函数imnoise 来进行噪声污染,并比较分析了高斯噪声、椒盐噪声、乘性噪声以及泊松噪声的污染效果。
随后,我分别运用大小为77 的中值滤波和S max 的自适应中值滤波对仅有噪声污染的图像进行复原处理,并比较分析了两种方法的效果。
方法简述:本次试验采用imnoise 函数来噪声污染一幅图像,其基本语法为:g=imnoise(f,type,parameters)其中f 为输入图像,type 指噪声类型,parameters 是均值方差等各种参数(依噪声类型的不同其意义有所不同)。
函数imnoise 在给图像添加噪声之前,将图像转换为范围[0,1]内的double 类图像。
实验中我分别用函数g1=imnoise(f,'speckle',0.04);g2=imnoise(f,'salt & pepper',0.05);g3=imnoise(f,'poisson');g4=imnoise(f,'gaussian',0,0.05);对图像进行了乘性噪声污染,椒盐噪声污染,泊松噪声污染以及高斯噪声污染,其结果见图(5-1)。
并对高斯噪声添加语句取不同的参数,比较分析其均值及方差对噪声污染强度的影响,其结果见图(5-2)。
随后,我分别运用f1=medfilt2(g,[7 7],'symmetric');f2=adpmedian(g,7);对一副被椒盐噪声污染的图像进行了复原处理,其结果见图(5-3)实验结果及分析:图(5-1)各种噪声污染对比程序:f = imread('C:\Documents and Settings\pomo\桌面\a.jpg'); g1=imnoise(f,'speckle',0.04);g2=imnoise(f,'salt & pepper',0.05);g3=imnoise(f,'poisson');g4=imnoise(f,'gaussian',0,0.05);subplot(2,2,1);imshow(g1),title('乘性噪声');subplot(2,2,2);imshow(g2),title('椒盐噪声');subplot(2,2,3);imshow(g3),title('泊松噪声');subplot(2,2,4);imshow(g4),title('高斯噪声');图(5-2)其中(a)为均值为0,方差为0.01的高斯噪声分析:噪声均值一定时,方差越大,噪声污染程度越严重;同样的噪声均值越大,噪声污染程度越轻,而且当均值为0时,不管方差取什么,结果都达不到污染的效果。
图像中的噪声及其复原方法的比较研究

图像中的噪声及其复原方法的比较研究司洋【摘要】In the process of obtaining images, there are various factors influencing imaging system leading the image quality lower, so image restoration technology is the model tending to be degradation of the handling and using for contrary to restore the original image. In this paper, we focus on the noise factors of the image quality degradation and study on reduction of image acquisition in common Gaussian white noise and a Salt and Pepper Noise.We experiments in the ways of image noise reduction filtering algorithms and wavelet threshold of noise reduction methods for simulation, and they compared with the double methods of noise reduction in one picture. Finally, we come to the conclusion.%图像降噪作为图像预处理的必要步骤,在图像处理中有着重要的意义。
由于在获取图像的过程中,成像系统受到各种因素的影响,会导致图像质量的降低,图像复原技术就是趋向于将退化模型化并用相反的处理来恢复原图像。
图像去噪与复原

图像去噪与复原第一章引言图像去噪与复原是图像处理领域的重要研究方向之一,它的目标是通过技术手段提升图像质量,使得图像更加清晰、真实。
在实际应用中,图像往往会受到各种噪声的干扰,如受损、模糊、噪点等,因此图像去噪与复原的研究对于图像重建、物体检测、医学图像分析等领域具有重要意义。
第二章图像去噪技术图像去噪是图像复原的基础步骤之一,其主要目的是消除图像中的噪声干扰,提高图像的质量。
在图像去噪技术中,常用的方法有线性滤波器、非线性滤波器等。
2.1 线性滤波器线性滤波器是一种简单而常用的图像去噪方法,它将图像中的每个像素按照一定的权重进行加权平均,从而减少噪声的影响。
常用的线性滤波器有均值滤波器、中值滤波器等。
2.2 非线性滤波器非线性滤波器是一种更加复杂的图像去噪方法,它通过对图像进行非线性处理,来提高图像的质量。
常用的非线性滤波器有小波变换滤波器、双边滤波器等。
第三章图像复原技术图像复原是基于已受损图像的重建过程,对于恢复图像的细节和特征具有重要作用。
在图像复原技术中,常用的方法有最小均方误差估计、基于插值的复原等。
3.1 最小均方误差估计最小均方误差估计是一种常用的图像复原方法,它通过建立图像受损与原图像之间的关系模型,利用最小均方误差准则来估计原图像,从而恢复图像的细节和特征。
3.2 基于插值的复原基于插值的复原是一种通过对已知图像进行插值运算,来恢复图像的细节和特征的方法。
常用的插值算法有最近邻插值、双线性插值、双三次插值等。
第四章图像去噪与复原的应用图像去噪与复原的技术在实际应用中有着广泛的应用前景。
在医学图像处理中,图像去噪与复原可以用于提升图像质量,从而帮助医生更准确地进行疾病诊断。
在电影特效制作中,图像去噪与复原可以提高影片的画面质量,使得观众获得更好的视觉体验。
此外,图像去噪与复原的技术还可以应用于安全监控、图像检索、无人驾驶等领域。
第五章图像去噪与复原的挑战与展望图像去噪与复原的研究依然面临着一些挑战。
维纳滤波复原实验报告

维纳滤波复原实验报告一、实验介绍维纳滤波是一种常用的图像复原技术,可以通过提供滤波器来降低图像的噪声和估计原始图像。
本次实验旨在通过使用维纳滤波器来复原被噪声污染的图像。
二、实验方法1. 实验准备首先需要准备一个带有噪声的图像作为输入图像,以及一个用作参考的干净图像。
通过加载图像,可以将两幅图像转换为灰度图像来简化处理。
2. 维纳滤波器的建立维纳滤波器可以通过以下公式来构建:H(u, v) = \frac{1}{H(u, v)} \cdot \frac{{ F(u, v) ^2}}{{ F(u, v) ^2 + S_n(u, v)}} 其中,H(u, v)是滤波器的频域函数,F(u, v)是输入图像的傅里叶变换,S_n(u, v)是噪声功率谱。
通过计算输入图像的傅里叶变换,以及噪声功率谱,可以根据上述公式来生成维纳滤波器。
3. 图像复原将输入图像通过傅里叶变换转换到频域,然后与维纳滤波器相乘,最后再进行傅里叶反变换,即可得到复原后的图像。
三、结果与讨论在实验中,我们使用了一幅被高斯噪声污染的图像作为输入图像,并使用了一个无噪声的参考图像。
通过对输入图像进行傅里叶变换,我们得到了输入图像的频域表示。
接着,根据输入图像和参考图像的功率谱,我们生成了对应的维纳滤波器。
最后,我们将输入图像通过傅里叶变换转换到频域,然后与维纳滤波器相乘,再进行傅里叶反变换,得到了复原后的图像。
实验结果显示,通过应用维纳滤波器,最终得到的复原图像与参考图像相比较为接近,且噪声得到了明显的减少。
这证明了维纳滤波的有效性和可行性。
然而,维纳滤波也存在一些限制。
由于维纳滤波是一种线性滤波方法,当输入图像中存在较大的模糊或失真时,滤波器可能无法恢复出清晰的图像。
此外,既有的维纳滤波器还无法处理复杂的噪声类型,如椒盐噪声或周期性噪声。
四、实验总结本次实验通过使用维纳滤波器来复原被噪声污染的图像,展示了维纳滤波的效果和限制。
维纳滤波是一种常用的图像复原技术,能够有效地降低图像噪声并估计原始图像。
图像的复原处理 数字图像处理南昌大学

实验报告七姓名:胡文松学号: 6103413007 班级:生物医学工程131实验日期: 2016.05.18实验成绩:实验题目:图像的复原处理一.实验目的(1)熟悉常见的噪声及其概率密度函数。
(2)熟悉在实际应用中比较重要的图像复原技术,学会用MATLAB复原函数对退化图像进行复原处理。
二.实验原理运动模糊的产生景物与相机之间的相对运动通常会使相机所成的像存在运动模糊。
对于线性移不变模糊,退化图像u0可以写成,u0=h*u+n,其中h为模糊核,*表示卷积,n为加性噪声。
维纳滤波图像复原用于复原由于PSF以及可能的加性噪声卷积退化的图像I,该算法利用图像和噪声的相关矩阵,从估计图像与真实图像之间的最小均方误差意义上来说是最佳的。
在没有噪声的情况下,维纳滤波器退化成理想的逆滤波器。
约束最小二乘方滤波复原用于复原由于PSF以及可能的加性噪声退化的图像,在保持图像平滑的条件下,该算法在估计图像和实际图像间的最小二乘方误差的意义上来说是最佳的。
三.实验内容及结果(1)选择图像fig606a.jpg,对其分别加入高斯噪声,均匀噪声和椒盐噪声,显示原始图像和噪声图像,及每个图片相对应的直方图。
(2)选择图像i_camera.bmp,对其使用运动模糊处理,再在模糊图像中加入高斯噪声,使用winner滤波和约束最小二乘方滤波对其进行去退化处理,比较效果,显示原始图像和复原图像。
源程序和结果:I=imread('fig606a.jpg');I=rgb2gray(I);subplot(2,4,1);imshow(I);title('灰度图像');I2=imnoise(I,'salt & pepper',0.05);I3=imnoise(I,'gaussian',0.1);%I4=I+(rand(1,length(256))-0.5)*0.2;noise=0.1*randn(size(I));I4=imadd(I,im2uint8(noise));I4=imnoise(I,'speckle',0.05);%均匀噪声subplot(2,4,2);imshow(I2);title('加入椒盐噪声:');subplot(2,4,3);imshow(I3);title('加入高斯噪声:');subplot(2,4,4);imshow(I4);title('加入均匀噪声:');subplot(2,4,5);imhist(I);title('原图直方图');subplot(2,4,6);imhist(I2);title('椒盐噪声直方图');subplot(2,4,7);imhist(I3);title('高斯噪声直方图');subplot(2,4,8);imhist(I4);title('均匀噪声直方图');四.结果分析从实验结果可知:1)对图像进行不同的加噪,图像的直方图有所改变,其中高斯噪声的加入改变最大,均匀噪声的影响最小。
数字图像处理实验报告4

数字图像处理与分析实验报告学院:班级:姓名:学号:实验四图像复原一、实验目的1. 了解图象退化的几种原因2. 掌握对相应退化原因的复原方法二、实验内容1. 使用函数fspecial( )和imfilter( )模拟产生退化图象2. 使用平滑滤波器和维纳滤波器复原图象三、实验步骤1. 加性噪声退化图象(1)先用imnoise( )函数给图象加噪声,如对图象增加高斯白噪声x=imread(‘cameraman.tif’);x=imnoi se(x,’gaussian’)得到图像:(2)使用平滑滤波器对其进行滤波h=fspecial(‘average’)y=imfilter(x,h);得到图像:(3)使用维纳滤波器进行处理w=wiener2(x) %注意:维纳滤波要求为灰度图像!得到图像:2. 使用演示程序比较各种滤波器的效果:nrfiltdemo3.运动退化图像(1)使用fspecial( )和imfilter( )模拟产生运动退化图象相应的程序如下:I = imread('C:\Documents and Settings\Administrator\桌面\1.BMP');figure;imshow(I);title('Original Image');LEN = 31;THETA = 15;PSF = fspecial('motion',LEN,THETA); % create PSFBlurred = imfilter(I,PSF,'circular','conv'); % blur the imagefigure;imshow(Blurred);title('Blurred Image');得到图像:(2)使用维纳滤波器进行处理wnr1=deconvwnr(Blurred,PSF);figure;imshow(wnr1);title('Restored, True PS');四、实验总结本次实验的目的就是了解图像退化的几种原因,比如性噪声,通过对图像添加高斯噪声对图像进行退化,在图像退化以后再对图像进行恢复。
(完整word版)数字图像处理实验 ——图像恢复

数字图像处理实验——图像恢复班级:信息10—1姓名:张慧学号:36实验四、图像复原一、实验目的1了解图像退化原因与复原技术分类化的数学模型;2熟悉图像复原的经典与现代方法;3热练掌握图像复原的应用;4、通过本实验掌握利用MATLAB编程实现数字图像的图像复原。
二、实验原理:图像复原处理是建立在图像退化的数学模型基础上的,这个退化数学模型能够反映图像退化的原因。
图像的退化过程可以理解为施加于原图像上的运算和噪声两者联合作用的结果,图像退化模型如图1所示,可以表示为:g ( x, y ) H [ f ( x, y )] n( x, y ) f ( x, y )h( x, y ) n( x, y) (1)图1 图像退化模型(1)在测试图像上产生高斯噪声lena图-需能指定均值和方差;并用滤波器(自选)恢复图像;噪声是最常见的退化因素之一,也是图像恢复中重点研究的内容,图像中的噪声可定义为图像中不希望有的部分。
噪声是一种随机过程,它的波形和瞬时振幅以及相位都随时间无规则变化,因此无法精确测量,所以不能当做具体的处理对象,而只能用概率统计的理论和方法进行分析和处理。
本文中研究高斯噪声对图像的影响及其去噪过程。
①高斯噪声的产生:所谓高斯噪声是指它的概率密度函数服从高斯分布(即正态分布)的一类噪声。
一个高斯随机变量z的PDF可表示为:P(z)()22x pz u2σ-⎡⎤-⎢⎥⎣⎦(2)其中z代表灰度,u是z的均值,σ是z的标准差。
高斯噪声的灰度值多集中在均值附近。
图2 高斯函数可以通过不同的算法用matlab 来产生高斯噪声。
②高斯噪声对信号的影响噪声影响图像处理的输入、采集、处理的各个环节以及输出结果的全过程,在图像中加高斯噪声通常会使图像变得模糊并且会出现细小的斑点,使图像变得不清晰。
③去除高斯噪声的一些方法去除高斯噪声的方法有直方图变换,低通滤波,高通滤波,逆滤波,维纳滤波,中值滤波等。
本文应用高斯平滑滤波进行去噪处理。
《数字图像处理A》图像复原与重建实验

《数字图像处理A》图像复原与重建实验一、实验目的图像的降噪与复原既在日常生活中拥有广泛的应用场景,又是数字图像处理领域的经典应用。
本实验首先对特定图像进行添加噪声和模糊,然后再使用经典的算法对噪声退化图像进行复原和重建。
通过该实验,进一步理解图像降噪和复原的基本原理,巩固图像处理基本操作的同时,提升对图像降噪和复原的理解和掌握。
二、实验内容1.利用matlab实现对特定图像添加高斯噪声和运动模糊。
2.使用逆滤波对退化图像进行处理。
3.使用常数比进行维纳滤波。
4.使用自相关函数进行维纳滤波。
三、实验原理1. 图像退化模型在一般情况下图像的退化过程可建模为一个退化函数和一个噪声项,对一幅图像f(x,y)进行处理,产生退化图像g(x,y),如下所示,其中η(x,y)是噪声项,H则是源图像的退化函数。
g(x,y)=H[f(x,y)]+η(x,y)2. 图像的噪声模型图像的噪声模型分为空间域噪声模型(通过噪声的概率密度函数对噪声进行描述)和频率域噪声模型(由噪声的傅里叶性质进行描述)两种类型。
在本实验中,我们采用的是空间噪声的经典噪声模型高斯噪声,高斯噪声模型的概率分布函数如下所示,其中σ是标准差,μ是期望。
p(z)=√2πσ−(x−μ)22σ2⁄3. 图像模糊图像模糊是一种常见的主要的图像退化过程。
场景和传感器两者导致的模糊可以通过空间域和频率域低通滤波器来建模。
而另一种常见的退化模型是图像获取时传感器和场景之间的均匀线性运动生成的图像模糊。
本实验的模糊模型采用的则是运动模糊,该模糊可以通过工具箱函数fspecial进行建模。
1.带噪声退化图像的复原在图像复原中经典的方法包括两种,分别是直接逆滤波和维纳滤波。
其中,直接逆滤波的复原模型如下所示,其中G(u,v)表示退化图像的傅里叶变换,H(u,v)则表示退化函数。
除了直接逆滤波之外,更为常见的是使用维纳滤波对退化图像进行复原,复原模型如教材100页4.7节所示。
数码相机性能测评 实验四 噪声及色彩还原性测试
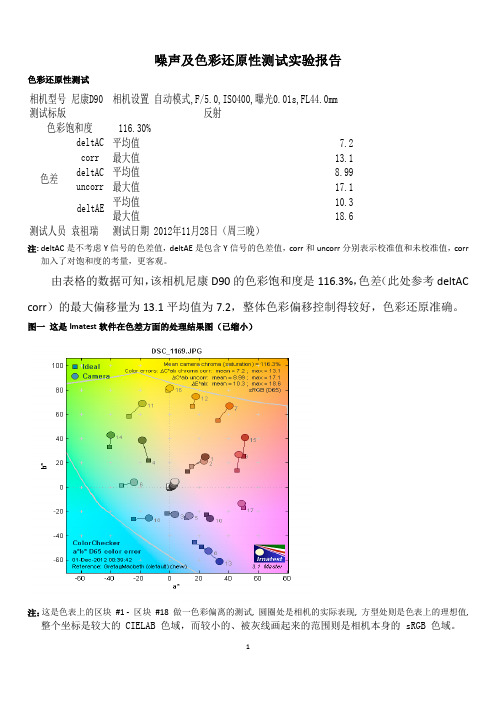
噪声及色彩还原性测试实验报告色彩还原性测试相机型号尼康D90相机设置自动模式,F/5.0,ISO400,曝光0.01s,FL44.0mm测试标版116.30%平均值7.2最大值13.1平均值8.99最大值17.1平均值10.3最大值18.6测试人员袁祖瑞测试日期2012年11月28日(周三晚)反射色彩饱和度色差deltAC corr deltACuncorrdeltAE注: deltAC 是不考虑Y 信号的色差值,deltAE 是包含Y 信号的色差值,corr 和uncorr 分别表示校准值和未校准值,corr 加入了对饱和度的考量,更客观。
由表格的数据可知,该相机尼康D90的色彩饱和度是116.3%,色差(此处参考deltAC corr )的最大偏移量为13.1平均值为7.2,整体色彩偏移控制得较好,色彩还原准确。
图一 这是Imatest 软件在色差方面的处理结果图(已缩小)注:这是色表上的区块 #1 - 区块 #18 做一色彩偏离的测试, 圆圈处是相机的实际表现, 方型处则是色表上的理想值, 整个坐标是较大的 CIELAB 色域,而较小的、被灰线画起来的范围则是相机本身的 sRGB 色域。
图二这是软件在色彩偏移对照方面的处理结果图注:如下图所示,在每个方格中的最外层区域Zone1原本的色块,里边两层Zone2和Zone3是标明的理想值。
在Zone 1 和Zone 2 之间, 主要是用来比较曝光的误差。
Zone 3 代表色彩的理想值, 比较Zone 1 及Zone 3 可以知道在色彩上的偏移情况。
注:在白平衡的误差上, 我们主要是HSV 色彩模式中的彩度值( 上图褐色数值), 以及Kelvin 的色温值( 上图蓝色数值) 以及Mireds( Mireds = 10^6 /(Degrees Kelvin) ) 表示。
比较上图中的各方格的区域Zone1和Zone2,发现亮度接近,说明该相机的曝光误差小。
实验四噪声图像的复原

实验四噪声图像的复原1、运动模糊与维纳滤波1.实验方式通过对图像添加运动模糊模拟实际拍照的延时效应,并且利用维纳滤波方式对图像进行滤波,观察维纳滤波对运动模糊的过滤效果,并对照其他几种滤波方式对运动模糊的影响。
实验代码:close all;clear all;clc;i=imread('E:\Matlabimage\book.jpg');I=rgb2gray(i);I = im2double(I);LEN = 21;THETA = 11;PSF = fspecial('motion', LEN, THETA);blurred = imfilter(I, PSF, 'conv', 'circular');wnr2 = deconvwnr(blurred, PSF);subplot(2,2,1);imshow(i);title('原图')subplot(2,2,2);imshow(I);title('灰度图')subplot(2,2,3);imshow(blurred);title('运动模糊图像')subplot(2,2,4);imshow(wnr2);title('恢复图像')代码解释:程序首先读取一幅JPG格式的彩色图片,然后将此图片转化为双精度灰度图片,然后产生运动模糊算子PSF,其中参数LEN和THETA表示摄像物体逆时针方向一THETA方向运动了LEN个像素,并且通过imfilter实现运动模糊效果,将返回的结果放入blurred,然后通过deconvwnr实现滤波,并将滤波前后的图像显示出来。
实验结果:几种滤波方式对运动模糊的滤除效果对比:运动模糊+维纳滤波:运动模糊+中值滤波:运动模糊+平均值滤波由对比结果可知维纳滤波对运动模糊有很好的处理效果。
2、利用MATLAB实现频域滤波的程序1、频域sobel滤波实验根据公式设计高通或低通滤波器对图像进行处理,并观察频域滤波的效果实验代码:close all;clear all;clc;f=imread('cameraman.tif');F=fft2(f); %对图像进行傅立叶变换%对变换后图像进行对数变化,并对其坐标平移,使其中心化S=fftshift(log(1+abs(F)));S=gscale(S); %将频谱图像标度在0-256的范围内figure,imshow(S) %显示频谱图像h=fspecial('sobel'); %产生空间‘sobel’模版figure;freqz2(h) %查看相应频域滤波器的图像PQ=paddedsize(size(f)); %产生滤波时所需大小的矩阵H=freqz2(h,PQ(1),PQ(2)); %产生频域中的‘sobel’滤波器H1=ifftshift(H); %重排数据序列,使得原点位于频率矩阵的左上角figure,imshow(abs(H),[]),title('abs(H)'); %以图形形式显示滤波器figure,imshow(abs(H1),[]),title('abs(H1)');gs=imfilter(double(f),h); %用模版h进行空域滤波gf=dftfilt(f,H1); %用滤波器对图像进行频域滤波figure,imshow(gs,[]),title('gs');figure,imshow(gf,[]),title('gf');figure,imshow(abs(gs),[]),title('abs(gs)');figure,imshow(abs(gf),[]),title('abs(gf)');代码解释:程序先读入一幅灰度图像,然后进行傅里叶变换,在对变换后的图像进行对数变换改变频谱F的幅度范围,然后对变化后的图像进行平移,将低频部分移到频谱中心,再将频谱转化为双精度显示出来,然后利用fspecial函数产生sobel模板然后显示出频域滤波器的图像,再利用paddedsize产生滤波器所需要的矩阵,再利用此滤波器产生频域的sobel滤波器,然后绘出此频域滤波器,然后再分别对同一幅图像进行空域滤波与频域滤波,并将滤波后的图像显示出来对比滤波效果。
图像退化与复原

一.实验名称:图像退化与复原二.实验目的1.了解光电图像的退化原因;2.掌握和理解基本的噪声模型,并能对图像进行加噪处理;3.了解点扩展函数(PSF)与光学传递函数(OTF)的关系,熟悉几种经典的退化模型的模拟试验和 OTF 估计方法;4.熟悉和掌握几种经典的图像复原方法与其基本原理;5.能熟练利用 MATLAB 或 C/C++工具进行图像的各种退化处理,并能编程实现退化图像的复原。
三.实验原理光电成像系统出现图像退化的过程是复杂多变的,为了研究的需要,通常情况下都把退化简化为化为一个线性移不变过程,见下图 1 所示。
图 1 光电图像退化与复原原理图因此,在空域中退化过程可以表示如下:g f h(1)(x,y)(x,y)(x,y)(x,y)只有加性噪声不存在情况下,退化过程可以模型化如下表达式:g f(2)(x,y)(x,y)(x,y)其频域表达式为:u (3)v v=(,)+(),)G,(F u v N u针对这种退化图像的复原,除了周期噪声以外,通常都可以采用空间域滤波的方法进行图像复原,此时图像复原与图像增强几乎是没有区别的。
常见的空间域滤波方法有均值滤波器和统计排序滤波器。
当退化图像存在线性移不变退化时,图像的复原不能采用简单空间域滤波器来实现,要实现线性移不变退化图像的复原,必须知道退化系统的退化函数,即点扩展函数(x,y)h 。
在点扩展函数已知的情况下,常见图像复原方法有逆滤波和维纳滤波两种。
在考虑噪声的情况下,逆滤波的原理可以表示如下:()()()()()()G u,v N u,v F u,v F u,v H u,v H u,v(4)通常情况下,()N u,v 是未知的,因此即使知道退化模型也不能复原图像。
此外,当,H u v 的任何元素为零或者值很小时,,/,N u v H u v 的比值决定着复原的结果,从而导致图像复原结果出现畸变。
对于这种情况,通常采用限制滤波频率使其难以接近原点值,从而减少遇到零值的可能性。
图像处理中的图像去噪与复原技术研究

图像处理中的图像去噪与复原技术研究摘要:近些年来,随着数码相机和智能手机的广泛应用,图像处理技术也得以迅速发展。
然而,大多数摄影师或普通用户在拍摄时难免会遇到一些噪点或模糊影像的问题。
为了解决这些问题,图像去噪与复原技术逐渐显露出重要性。
本文将重点介绍图像处理中的图像去噪与复原技术,包括基于滤波器的去噪方法、基于深度学习的图像复原技术等。
1. 引言现代图像处理技术已经成为了许多领域如医学、电影制作、安防监控等的重要组成部分。
然而,由于不可控的拍摄环境、相机传感器的限制以及图像传输过程中的干扰等原因,所得的图像经常受到噪点和失真的影响。
因此,如何通过图像处理技术去除这些噪点并恢复图像的清晰度成为了重要的研究方向。
2. 图像去噪技术图像去噪技术是图像处理中一个重要的研究方向,目标是通过处理图像中的噪点,使图像更清晰、更具信息量。
一种常见的去噪方法是基于滤波器的方法,包括均值滤波、中值滤波和高斯滤波等。
这些方法通过对图像进行滤波操作,去除图像中的高频噪声,从而实现图像去噪的效果。
此外,还有一些基于局部邻域像素的非线性滤波方法,如双边滤波和NL-Means算法。
这些方法利用图像中的局部相似性来平衡滤波效果,进一步提升图像去噪的质量。
另外,随着深度学习技术的发展,越来越多的研究开始将深度学习应用于图像处理中的去噪问题。
深度学习方法通过构建卷积神经网络,利用大量的标注数据来学习图像去噪的模型。
与传统方法相比,深度学习方法具有更强大的学习能力,能够更好地去噪图像并保持图像的细节信息。
近年来,基于深度学习的图像去噪方法在图像处理领域取得了显著的突破。
3. 图像复原技术图像复原技术是一种通过恢复被噪声或失真破坏的图像,使其尽可能接近原始图像的过程。
常见的图像复原技术包括盲去卷积、超分辨率重建以及图像修复等。
盲去卷积是一种旨在解决由于传感器模糊或运动模糊导致的图像模糊问题的方法。
它通过估计图像的模糊核和图像本身,从而恢复原始图像的清晰度。
实验四 图像恢复技术

实验三 图像恢复技术一、 实验目的掌握退化图像中常见噪声模型及参数估计方法;加深对几种常用的图像复原方法的理解;通过Matlab 开发环境实现参数维纳滤波器复原图像。
二、 实验内容1. 对各种常见噪声模型进行仿真实现;2. 把仿真噪声加入纯净图像上形成退化图像,让后对噪声进行参数估计,并与原设定参数进行比较以衡量估计的准确性;3. 仿真几种常见噪声,并用参数维纳滤波器方法进行图像复原; 4. 观察复原效果,并进行仔细讨论。
三、 知识要点与范例1. 图像恢复退化模型图像恢复问题可以分为两大类:1) 假定系统退化函数H 为恒等算子,而只考虑环境噪声引起退化的情况; 2) 同时考虑H 和环境噪声 。
2. 噪声模型对噪声的行为和效果进行仿真的能力是图像恢复处理中的重点。
除了周期噪声,通常假定噪声与象素坐标无关。
Matlab 噪声仿真函数为:g = imnoise (f, type, parameters);常见的噪声(高斯、椒盐噪声)的仿真实例如下: g = imnoise (f, ‘gaussian ’, m, var);g = imnoise (f,’salt & pepper ’, d); (where ’d ’ represents the noise density). 3. 产生具有某种固定分布的空间随机噪声.MATLAB 中两个常用的随机分布产生函数是:rand (均匀分布噪声), randn (标准正态分布噪声)f(x,y)n(x,y)的最优估计 退化过程恢复过程(,)f x y空间随机噪声是有各自的PDF 或 CDF 所决定的。
除了有上面所讲的immoise 噪声产生函数外, 具有某种规定 CDF 的大部分随机噪声都可由均匀分布的随机量(这里用w 表示)通过某个随机数产生方程来生成。
也就是说,给定w ~ (0,1), 具有某个确定分布F z 的随机变量z 可以通过解如下方程获得:z = F z -1(w). 如:变量z 满足如下Rayleigh 分布:2()/1for z ()0for <z a bz ea F z a --⎧- ≥ ⎪=⎨⎪⎩ 则:z a =+, 这个方程也通常叫做随机数产生方程 (RNGE)。
数字图像处理实验四

数字图像处理实验四图像复原一、实验目的了解matlab有关图像复原的操作,如图像的读写,显示,加噪声,去噪声等。
二、实验要求1、使用不同模糊化方法对图像Lena进行模糊处理,对原图像及模糊化图像进行比较(注明模糊化的类型),并保存模糊图像。
(此题中所用的图像和保存的图像在Images文件夹中)I = imread('lena.tif'); %读入图像subplot(221);imshow(I);title('原始图像');H=fspecial('motion',30,45); %运动模糊PSFMotionBlur=imfilter(I,H); %卷积imwrite(MotionBlur,'运动模糊.tif'); %保存运动模糊图像subplot(222);imshow(MotionBlur);title('运动模糊图像');H=fspecial('disk',10); %圆盘状模糊PSFbulrred=imfilter(I,H);imwrite(bulrred,'圆盘状模糊.tif'); %保存圆盘状模糊图像subplot(223);imshow(bulrred);title('圆盘状模糊图像');H=fspecial('unsharp'); %钝化模糊PSFSharpened=imfilter(I,H);imwrite(Sharpened,'钝化模糊.tif'); %保存钝化模糊图像subplot(224);imshow(Sharpened);title('钝化模糊图像');原始图像运动模糊图像圆盘状模糊图像钝化模糊图像2、对图像Lena添加不同类型的噪声,对原图像及噪声图像进行比较(注明加入噪声的类型,及噪声参数),并保存噪声图像。
图像复原实验

数字图像处理实验报告1 - 图像复原学生姓名:学号:实验时间:地点:指导教师:一、实验目的运用理论知识,在MA TLAB环境下对图像复原技术进行实验验证,学习算法实现的科学方法,增强对算法及其效果的感性认识。
(1)对图像进行复原处理。
调用MA TLAB中的图像复原函数,编写MA TLAB程序,实现对图像的复原。
(2)C++编程,利用双线性插值将照片放大。
二、实验内容要求:以下实验采用学生本人的照片作为处理对象。
(1)利用MA TLAB做图像复原实验。
实验方法和步骤如下:选择一幅完好的照片,进行退化处理,然后对退化后的图像进行复原,并对不同参数的复原结果进行比较。
(2)用VC++编写程序,采用邻近差值和双线性插值两种方法,将图像放大到原来的 1.5倍, 并存储为res0.yuv 和res1.yuv。
三、实验结果(1)①先对图像进行模糊处理,用matlab中fspecial函数产生motion滤波器,然后对灰度图像进行滤波即可得到。
再用deconvwnr函数对图像进行维纳滤波可的如下结果(程序代码详见附录1.1):由此可见滤波效果并不是很明显,其中一个原因就是要取合适的len、theta参数是很困难的,所以导致模糊效果不是很好。
②先对图像进行模糊处理,用matlab中fspecial函数产生motion滤波器,然后对灰度图像进行滤波即可得到。
在对图像加高斯噪声,用imnoise函数。
再用deconvwnr函数对图像进行维纳滤波可见不同参数情况下的滤波情况如下(程序代码详见附录1.2):由此可见,平滑滤波不一定总是能带来很好的效果,如果图像过于模糊,平滑滤波就会导致图像过于平滑,就会使得图像高频分量也就是边缘轮廓十分的不明显。
③先对图像进行模糊处理,用matlab中fspecial函数产生motion滤波器,然后对灰度图像进行滤波即可得到。
在对图像加高斯噪声,用imnoise函数。
再用deconvblind函数对图像进行盲滤波可见不同参数情况下的滤波情况如下(程序代码详见附录1.3):(2)采用双线性插值法对所给图像实现长和宽分别1.5倍的放大。
图像噪声处理与复原

数字图像处理实验报告专业班级:学生姓名:学号:指导老师:实验四图像噪声处理与复原1 实验目的1.掌握噪声模拟和图像滤波函数的使用方法2.了解图像复原的Matlab实现方法2 实验内容A)模糊与噪声<i>对图像‘flowers.tif’分别采用运动PSF和均值滤波PSF进行模糊。
<ii>在上述模糊图像上再添加噪声B)维纳滤波复原<i>使用维纳滤波复原函数deconvwnr复原无噪声模糊图像。
<ii>*使用维纳滤波复原函数deconvwnr复原模糊噪声图像。
<iii>*设置信噪比和相关函数的维纳滤波复原。
clear all;close all;I=imread(' F22.jpg');figure(1);imshow(I);title('原始图像');I=I(10+[1:256],222+[1:256],:); %剪切图像figure(2);subplot(3,3,1);imshow(I);title('截取部分原始图像');len=30; %运动位移theta=10; %运动角度PSF=fspecial('motion',len,theta);blurred=imfilter(I,PSF,'circular','conv');subplot(3,3,2);imshow(blurred); title('模糊图像');%%%%%%%% 维纳滤波复原%%%%%%wnr1=deconvwnr(blurred,PSF); %真实PSFsubplot(3,3,3);imshow(wnr1);title('真实PSF 复原图像');%非真实PSFwnr2=deconvwnr(blurred,fspecial('motion',2*len,theta));subplot(3,3,4);imshow(wnr2);title('非真实PSF 复原图像');%非真实PSFwnr3=deconvwnr(blurred,fspecial('motion',len,2*theta));subplot(3,3,5);imshow(wnr3);title('非真实PSF 复原图像');%使用维纳滤波复原函数deconvwnr 复原模糊噪声图像noise=0.1*randn(size(I));BlurredNoisy=imadd(blurred,im2uint8(noise));subplot(3,3,6);imshow(BlurredNoisy);title('增加模糊噪声图像');wnr4=deconvwnr(BlurredNoisy,PSF);subplot(3,3,7);imshow(wnr4);title('增加模糊噪声真实PSF 复原图像');%设置信噪比的复原结果NSR=sum(noise(:).^2)/sum(im2double(I(:)).^2); %计算信噪比wnr5=deconvwnr(BlurredNoisy,PSF,NSR);subplot(3,3,8);imshow(wnr5);title('设置信噪比的复原图像');%设置自相关函数的复原结果NP=abs(fftn(noise)).^2; %噪声能量谱密度NCORR=fftshift(real(ifftn(NP))); %噪声自相关函数IP=abs(fftn(im2double(I))).^2; %图像能量谱密度ICORR=fftshift(real(ifftn(IP))); %图像自相关函数wnr6=deconvwnr(BlurredNoisy,PSF,NCORR,ICORR);subplot(3,3,9);imshow(wnr6);title('设置自相关函数的复原图像');%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% figure(3);subplot(2,2,1);I=imread('F22.jpg');imshow(I)H=fspecial('motion',50,45); %运动PSPmotionblur=imfilter(I,H);subplot(2,2,2);imshow(motionblur)H=fspecial('disk',10); %均值滤波PSPaverageblur=imfilter(I,H);subplot(2,2,3);imshow(averageblur);J=imnoise(motionblur,'salt & pepper');subplot(2,2,4);imshow(J);%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%3、实验仪器1计算机;2 MA TLAB程序;3移动式存储器(软盘、U盘等)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验四噪声图像的复原
-、运动模糊与维纳滤波
1•实验方式
通过对图像添加运动模糊模拟实际拍照的延时效应,并且利用维纳滤波方式对图像进行滤波,观察维纳滤波对运动模糊的过滤效果,并对照其他几种滤波方式对运动模糊的影响。
实验代码:
close all;clear all;clc;
i=imread('E:\Matlabimage\book.jpg');
匸rgb2gray(i);
I = im2double(l);
LEN = 21;
THETA = 11;
PSF = fspecial('motion', LEN, THETA);
blurred = imfilter(I, PSF, 'conv', 'circular');
wnr2 = dec onvwn r(blurred, PSF);
subplot(2,2,1);imshow(i);title('原图')
subplot(2,2,2);imshow(l);title('灰度图') subplot(2,2,3);imshow(blurred);title('运动模糊图像') subplot(2,2,4);imshow(wnr2);title('恢复图像')
代码解释:程序首先读取一幅JPG格式的彩色图片,然后将此图片转化为双精
度灰度图片,然后产生运动模糊算子PSF,其中参数LEN和THETA表示摄像物体逆时针方向一THETA方向运动了LEN个像素,并且通过imfilter实现运动模糊效果,将返回的结果放入blurred,然后通过deconvwnr实现滤波,并将滤波前后的图像显示出来。
实验结果:
欢迎下载 2 二、利用MATLAB 实现频域滤波的程序
1、频域sobel 滤波
实验根据公式设计高通或低通滤波器对图像进行处理,并观察频域滤波的效果 实验代码:
close all;clear all;clc;
f=imread('camerama n.tif);
F=fft2(f); %对图像进行傅立叶变换
%对变换后图像进行对数变化,并对其坐标平移,使其中心化
%将频谱图像标度在0-256的范围内
%显示频谱图像
%产生空间‘ sobe '模版
%查看相应频域滤波器的图像 %产生滤波时所需大小的矩阵
S=fftshift(log(1+abs(F)));
S=gscale(S); figure,imshow(S) h=fspecial('sobel'); figure;freqz2(h) PQ=paddedsize(size (f));
几种滤波方式对运动模糊的滤除效果对比:
运动模糊+维纳滤波: 运动模糊+中值滤波:
运动模糊+平均值滤波
由对比结果可知维纳滤波对运动模糊有很好的处理效果。
H=freqz2(h,PQ(1),PQ(2)); %产生频域中的‘ sobe'滤波器
H仁ifftshift(H); %重排数据序列,使得原点位于频率矩阵的左上角
figure,imshow(abs(H),[]),title('abs(H)'); % 以图形形式显示滤波器
figure,imshow(abs(H1),[]),title('abs(H1)');
gs=imfilter(double(f),h); %用模版h进行空域滤波
gf=dftfilt(f,H1); %用滤波器对图像进行频域滤波
figure,imshow(gs,[]),title('gs');
figure,imshow(gf,[]),title('gf);
figure,imshow(abs(gs),[]),title('abs(gs)'); figure,imshow(abs(gf),[]),title('abs(gf)');
代码解释:程序先读入一幅灰度图像,然后进行傅里叶变换,在对变换后的图像进行对数变换改变频谱F的幅度范围,然后对变化后的图像进行平移,将低频部分移到频谱中心,再将频谱转化为双精度显示出来,然后利用fspecial函数产生sobel模板然后显示出频域滤波器的图像,再利用paddedsize产生滤波器所需要的矩阵,再利用此滤波器产生频域的sobel滤波器,然后绘出此频域滤波器,然
后再分别对同一幅图像进行空域滤波与频域滤波,并将滤波后的图像显示出来对比滤波效果。
实验结果:
变换后的频谱:频域滤波器图像
:
频域sobel滤波器:
'j :- d k *• -、.•弐亠山、总L kJ | 口
平移后的滤波器:
欢迎下载4
空域滤波结果: 频域滤波结果:
欢迎下载 5
实验结论:由实验结果可知空域滤波与频域滤波结果相似,可以分别出图
像中具有一定特征的图像的一部分,并且对滤波后的图像取振幅可以用于图像的 边沿提取和锐化
2、高斯高通滤波:
说明:利用高斯高通滤波器对图像进行处理,并分析高斯高通滤波器对图像的影 响。
实验代码:
f=imread('eight.tif); %读取图片
PQ=paddedsize(size(f)); %产生滤波时所需大小的矩阵 D0=0.05*PQ(1); %设定高斯高通滤波器的阈值
H=hpfilte('gaussia n',PQ(1),PQ(2),D0);
% 产生高斯高通滤波器 g=dftfilt(f,H);
%对图像进行滤波 figure,imshow(f)
% 显示原图像 figure,imshow(g,[]) %显示滤波后图像
代码解释:实验先读入一幅灰度图像,然后产生滤波矩阵和阈值,在对图像进行 高斯高
通滤波,再将滤波后的图像显示出来,观察滤波效果。
对空域滤波后的图像振幅: 频域滤波后的振幅:
实验结果:
原图: 实验结论:由实验结果可知图像经过高
斯高通滤波器后颜色更加均衡,图像 物体边沿产生了白色光晕,突出了图像轮廓,有利于图像中物体轮廓信息的提取。
几种不同频域滤波结果的对比:
理想低通(阈值:100): 理想高通(阈值:10):
咼斯咼通滤波后:
巴特沃斯低通: 巴特沃斯高通:
对比可以看出不同的高通和低通滤波器对图像的影响不同并且滤波后的图像使得原图像的一些特征更加突出,颜色对比也更加鲜明。
三、实验心得
通过这次实验我了解了运动模糊和维纳滤波,并且了解到维纳滤波对运动模糊有非常好的处理效果,,频率滤波器对图像也有很大影响,sobel和高斯高通使得图像边沿更加突出,其他频率滤波器也是的图像不同部分的对比更加突出,并且处理结果不同,我们在应用中要根据不同的环境选择不同的频率滤波器对图像进行处理,以达到最好的处理结果。
