2019年中考数学知识点精选提高练习：弦切角定理(圆)(附解析答案)

合集下载

新人教版九年级上册数学[弧、弦、圆心角、圆周角—知识点整理及重点题型梳理](提高)

新人教版九年级上册初中数学重难点有效突破知识点梳理及重点题型巩固练习弧、弦、圆心角、圆周角—知识讲解（提高）【学习目标】1.了解圆心角、圆周角的概念；2.理解圆周角定理及其推论，能灵活运用圆周角的定理及其推理解决有关问题；3.掌握在同圆或等圆中，三组量：两个圆心角、两条弦、两条弧，只要有一组量相等，就可以推出其它两组量对应相等，及其它们在解题中的应用．【要点梳理】知识点一、弧、弦、圆心角的关系1.圆心角定义如图所示，∠AOB的顶点在圆心，像这样顶点在圆心的角叫做圆心角．2.定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．3.推论：在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦也相等．在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的弧也相等．要点诠释：(1)一个角要是圆心角，必须具备顶点在圆心这一特征.(2)注意定理中不能忽视“同圆或等圆”这一前提.知识点二、圆周角1.圆周角定义：像图中∠AEB、∠ADB、∠ACB这样的角，它们的顶点在圆上，并且两边都与圆相交的角叫做圆周角．2.圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．3.圆周角定理的推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．要点诠释：(1)圆周角必须满足两个条件：①顶点在圆上；②角的两边都和圆相交.(2)圆周角定理成立的前提条件是在同圆或等圆中.4.圆内接四边形：（1）定义: 圆内接四边形：顶点都在圆上的四边形，叫圆内接四边形．（2）性质：圆内接四边形对角互补，外角等于内对角（即它的一个外角等于它相邻内角的对角）．5.弦、弧、圆心角、弦心距的关系：在同圆或等圆中，弦，弧，圆心角，弦心距等几何量之间是相互关联的，即它们中间只要有一组量相等，(例如圆心角相等)，那么其它各组量也分别相等(即相对应的弦、弦心距以及弦所对的弧也分别相等).*如果它们中间有一组量不相等，那么其它各组量也分别不等.【典型例题】类型一、圆心角、弧、弦之间的关系及应用1.已知：如图所示，⊙O 中弦AB ＝CD ．求证：AD ＝BC ．【答案与解析】证法一：如图①，∵ AB ＝CD ，∴ A B C D =．∴ A B B D C D B D -=-，即AD BC =， ∴ AD ＝BC ．证法二：如图②，连OA 、OB 、OC 、OD ，∵ AB ＝CD ，∴ ∠AOB ＝∠COD ．∴ ∠AOB －∠DOB ＝∠COD －∠DOB ，即∠AOD ＝∠BOC ，∴ AD ＝BC ．【点评】在同圆或等圆中，证两弦相等时常用的方法是找这两弦所对的弧相等或所对的圆心角相等，而图中没有已知的等弧和等圆心角，必须借助已知的等弦进行推理．本题主要是考查弧、弦、圆心角之间的关系，要证AD ＝BC ，只需证AD BC =或证∠AOD ＝∠BOC 即可．举一反三：【变式】如图所示，已知AB 是⊙O 的直径，M 、N 分别是AO 、BO 的中点，CM ⊥AB ，DN ⊥AB ．求证：AC BD =．【答案】证法一：如上图所示，连OC 、OD ，则OC ＝OD ，∵ OA ＝OB ，且12OM OA =，12ON OB =， ∴ OM ＝ON ，而CM ⊥AB ，DN ⊥AB ，∴ Rt △COM ≌Rt △DON ，∴ ∠COM ＝∠DON ，∴ A C B D =．证法二：如下图，连AC 、BD 、OC 、OD ．∵ M 是AO 的中点，且CM ⊥AB ，∴ AC ＝OC ，同理BD ＝OD ，又OC ＝OD ．∴ AC ＝BD ，∴ A C B D =．类型二、圆周角定理及应用2.（2015•南京二模）如图，OA 、OB 是⊙O 的半径且OA ⊥OB ，作OA 的垂直平分线交⊙O 于点C 、D ，连接CB 、AB ．求证：∠ABC=2∠CBO ．【答案与解析】证明：连接OC 、AC ，如图，∵CD 垂直平分OA ，∴OC=AC ．∴OC=AC=OA，∴△OAC是等边三角形，∴∠AOC=60°，∴∠ABC=∠AOC=30°，在△BOC中，∠BOC=∠AOC+∠AOB=150°，∵OB=OC，∴∠CBO=15°，∴∠ABC=2∠CBO．【总结升华】本题考查了圆周角定理以及线段垂直平分线的性质和等边三角形的判定与性质，熟练的掌握所学知识点是解题的关键.举一反三：【356996 ：经典例题1-3】【变式】如图，AB是⊙O的弦，∠AOB＝80°则弦AB所对的圆周角是 .【答案】40°或140°.【356996：经典例题4-5】3.如图，AB是⊙O的直径，C、D、E都是⊙O上的点，则∠1+∠2=___________.【答案】90°.【解析】如图，连接OE，则【点评】把圆周角转化到圆心角.举一反三：【变式】（2015•玄武区二模）如图，四边形ABCD为⊙O的内接四边形，连接AC、BO，已知∠CAB=36°，∠ABO=30°，则∠D=．【答案】96°；提示：解：连结OC，如图，∠BOC=2∠CAB=2×36°=72°，∵OB=OC，∴∠OBC=∠OCB，∴∠OBC=（180°﹣∠BOC）=（180°﹣72°）=54°，∴∠ABC=∠OBA+∠OBC=30°+54°=84°，∵∠D+∠ABC=180°，∴∠D=180°﹣84°=96°．故答案为96．4.已知，如图，⊙O上三点A、B、C，∠ACB=60°，AB=m，试求⊙O的直径长.【答案与解析】如图所示，作⊙O的直径AC′，连结C′B，则∠AC′B=∠C=60°又∵AC′是⊙O的直径，∴∠ABC′=90°即⊙O的直径为.【点评】作出⊙O的直径，将60°、直径与m都转到一个直角三角形中求解.举一反三：【：经典例题6-7】【变式】如图，△ABC内接于⊙O，∠C＝45°，AB＝4，则⊙O的半径为（）．A． B．4 C．．5【答案】A.。

弦切角定理

已知：AC是⊙O的弦，AB是⊙O的切线，A为切点，弧CmA是弦切角∠BAC所夹的弧. 求证：弦切角∠BAC的度数等于它所夹的弧的度数的一半证明：分三种情况：（1）圆心O在∠BAC的一边AC上 ∵AC为直径 ∴弧CmA=弧CA ∵弧CA为半圆, ∴弧CmA的度数为180° ∵AB为圆的切线 ∴∠CAB=90° ∴弦切角∠BAC的度数等于它所夹的弧的度数的一半
内容
衍生及证明
概念及其证明
逆定理
图2弦切角定理：弦切角的度数等于它所夹的弧的圆心角度数的一半。等于它所夹的弧的圆周角度数。如图2，已知：直线PT切圆O于点C，BC、AC为圆O的弦。求证：∠TCB=1/2∠BOC=∠BAC 证明：设圆心为O，连接OC，OB。 ∵∠OCB=∠OBC ∴∠OCB=1/2*(180°-∠BOC) 又∵∠BOC=2∠BAC ∴∠OCB=90°-∠BAC ∴∠BAC=90°-∠OCB 又∵∠TCB=90°-∠OCB
定理：以三角形任意一条边为邻边，在三角形外部作一个角等于该边的对角，那么所作角的另一边与三角形外接圆相切，切点为所作角的顶点。
几何描述：设△ABP的外接圆为⊙O，在△ABP外部作∠BAC=∠BPA，则AC切⊙O于A。注意定理的描述，所作角必须在三角形的外部，且该角与三角形有公共的边。该定理的等价描述为：角的度数等于所夹弧所对圆周角的角为弦切角。几何描述：设直线AC与圆相交于A，AB是圆的一条弦，P是圆上与A,B不重合的点。若∠BAC=∠BPA，则∠BAC 是弦切角，即AC与圆相切于A。图3证明：如图3，同样分类讨论（1）当∠BPA=90°时，AB为直径。 ∠BAC=∠BPA=90°，即AB⊥AC 经过直径的一端，并且与直径垂直的直线是圆的切线，∴AC是⊙O的切线，切点为A。

中考数学复习----《三角形的内切圆与内心》知识点总结与专项练习题(含答案解析)

中考数学复习----《三角形的内切圆与内心》知识点总结与专项练习题（含答案解析）知识点总结1. 相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等。

几何语言：若弦CD AB ，交于点P ，则PD PC PB PA ⋅=⋅。

推论：如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项。

几何语言：若AB 是直径，CD 垂直AB 于点P ，则PB PA PD PC ⋅==22。

2. 弦切角定理：（1）弦切角的定义：如图像∠ACP 这样，顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。

（2）弦切角定理：弦切角的度数等于它所夹的弧的圆心角的度数的一半。

等于这条弧所对的圆周角。

即∠PCA=∠PBC 。

3. 切线长定理：（1）切线长定义：经过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长。

（2）切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线，平分两条切线的夹角。

4. 切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

几何语言：∵PT切⊙O于点T，PBA是⊙O的割线∴PT2=PA•PB（切割线定理）。

推论：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等。

几何语言：∵PBA，PDC是⊙O的割线∴PD•PC=PA•PB由上可知：PT2=PA•PB=PC•PD。

5. 三角形的内切圆与内心：内切圆与内心的概念：与三角形各边都相切的圆叫三角形的内切圆，三角形的内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形。

三角形的内心就是三角形三个内角角平分线的交点。

练习题1、（2022•恩施州）如图，在Rt△ABC中，∠C＝90°，AC＝4，BC＝3，⊙O为Rt△ABC的内切圆，则图中阴影部分的面积为（结果保留π）．【分析】根据题意，先作出相应的辅助线，然后求出内切圆的半径，再根据图形可知：阴影部分的面积＝△ABC的面积﹣正方形CEOD的面积﹣⊙O面积的，代入数据计算即可．【解答】解：作OD⊥AC于点D，作OE⊥CB于点E，作OF⊥AB于点F，连接OA、OC、OB，如图，∵∠C＝90°，OD＝OE＝OF，∴四边形CEOD是正方形，∵AC＝4，BC＝3，∠C＝90°，∴AB＝＝＝5，∵S△ABC＝S△AOC+S△COB+S△BOA，∴＝，解得OD＝OE＝OF＝1，∴图中阴影部分的面积为：﹣1×1﹣π×12×＝5﹣π，故答案为：5﹣π．2、（2022•泰州）如图，△ABC中，∠C＝90°，AC＝8，BC＝6，O为内心，过点O的直线分别与AC、AB边相交于点D、E．若DE＝CD+BE，则线段CD的长为．【分析】连接BO，CO，结合内心的概念及平行线的判定分析可得当DE＝CD+BE时，DE∥BC，从而利用相似三角形的判定和性质分析计算．【解答】解：如图，过点O的直线分别与AC、AB边相交于点D、E，连接BO，CO，∵O为△ABC的内心，∴CO平分∠ACB，BO平分∠ABC，∴∠BCO＝∠ACO，∠CBO＝∠ABO，当CD＝OD时，则∠OCD＝∠COD，∴∠BCO＝∠COD，∴BC∥DE，∴∠CBO＝∠BOE，∴BE＝OE，则DE＝CD+BE，设CD＝OD＝x，BE＝OE＝y，在Rt△ABC中，AB＝＝10，∴，即，解得，∴CD＝2，过点O作D′E′⊥AB，作DE∥BC，∵点O为△ABC的内心，∴OD＝OE′，在Rt△ODD′和Rt△OE′E中，，∴△ODD′≌△OE′E（ASA），∴OE＝OD′，∴D′E′＝DE＝CD+BE＝CD′+BE′＝2+＝，在△AD′E′和△ABC中，，∴△AD′E′∽△ABC，∴，∴，解得：AD′＝，∴CD′＝AC﹣AD′＝，故答案为：2或．3、（2022•黔东南州）如图，在△ABC中，∠A＝80°，半径为3cm的⊙O是△ABC的内切圆，连接OB、OC，则图中阴影部分的面积是cm2．（结果用含π的式子表示）【分析】根据角A的度数和内切圆的性质，得出圆心角DOE的度数即可得出阴影部分的面积．【解答】解：∵∠A＝80°，⊙O是△ABC的内切圆，∴∠DOE＝180°﹣（）＝180°﹣（180°﹣∠A）＝130°，∴S扇形DOE＝＝（cm2），故答案为：．4、（2022•宜宾）我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形（如图所示）．若直角三角形的内切圆半径为3，小正方形的面积为49，则大正方形的面积为．【分析】如图，设内切圆的圆心为O，连接OE、OD，则四边形EODC为正方形，然后利用内切圆和直角三角形的性质得到AC+BC＝AB+6，（BC﹣AC）2＝49，接着利用完全平方公式进行代数变形，最后解关于AB的一元二次方程解决问题．【解答】解：如图，设内切圆的圆心为O，连接OE、OD，则四边形EODC为正方形，∴OE＝OD＝3＝，∴AC+BC﹣AB＝6，∴AC+BC＝AB+6，∴（AC+BC）2＝（AB+6）2，∴BC2+AC2+2BC×AC＝AB2+12AB+36，而BC2+AC2＝AB2，∴2BC×AC＝12AB+36①，∵小正方形的面积为49，∴（BC﹣AC）2＝49，∴BC2+AC2﹣2BC×AC＝49②，把①代入②中得AB2﹣12AB﹣85＝0，∴（AB﹣17）（AB+5）＝0，∴AB＝17（负值舍去），∴大正方形的面积为289．故答案为：289．。

【初中数学】圆中弦切角及弦切角定理

【初中数学】圆中弦切角及弦切角定理一、弦切角1、定义：顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。

如图：2、弦切角的三种情况（1）圆心在弦切角外；（2）圆心在弦切角的一条边上；（3）圆心在弦切角内；二、弦切角定理及证明定理：弦切角的度数等于它所夹的弧的圆周角；弦切角的度数等于它所夹的弧的圆心角度数的一半。

已知：如图，PQ是圆O的切线，切点为P。

求证：∠APQ=∠ABP，2∠APQ=∠AOP.（1）当圆心在弦切角外部时证明：连接OA，OP，在非弦切角所夹弧优弧PA上任取一点B，连接BP和BA。

∵ OA=OP∴ ∠OPA=∠OAP∵ ∠OPA+∠OAP+∠POA=180°∴2∠OPA+∠POA=180°∵ PO为圆的切线，OP为半径∴ ∠OPA+∠APQ=90°∴ ∠OPA=90°-∠APQ∴ 2（90°-∠APQ）+∠POA=180°∴∠POA=2∠APQ∵ ∠POA=2∠ABP（同弧所对的圆心角是圆周角的2倍）∴ ∠APQ=∠ABP（2）当圆心在弦切角的一边上时证明：在非弦切角所夹弧AP上任取一点B，连接AB、PB ∵ AP为直径∴ ∠ABP=90°∵ PQ为圆的切线，OP为半径∴ ∠APQ=90°∴∠APQ=∠ABP∴2∠APQ=∠AOP（同弧所对的圆心角是圆周角的2倍）. （3）当圆心在弦切角的内部时证明：连接OA，OP，在非弦切角所夹弧劣弧PA上任取一点B，连接BP和BA。

∵ OA=OP∴ ∠OPA=∠OAP∵ ∠OPA+∠OAP+∠1=180°∴2∠OPA+∠1=180°∵ PO为圆的切线，OP为半径∴ ∠OPA=∠APQ-90°∴ 2（∠APQ-90°）+∠1=180°∴ ∠1+2∠APQ=360°∵ ∠1+∠2=360°∴∠2=2∠APQ∴ ∠POA=2∠APQ（这里的∠POA是大于180°的角，是优弧AP所对的圆心角）∵ ∠POA=2∠ABP（同弧所对的圆心角是圆周角的2倍）∴ ∠APQ=∠ABP三、例题例1、已知：如图，直线BC切⊙O于B点，AB=AC，AD=BD，求∠A．解：由弦切角定理可得，∠DBC=∠A∵ AD=BD∴ ∠A=∠ABD∵ AB=AC∴ ∠ABC=∠ACB=2∠A∵ ∠A+∠ABC+∠ACB=180°∴5∠A=180°∴ ∠A=36°例2、已知：如图，直线DC与⊙O相切于点C，AB为⊙O直径，AD⊥DC于D，∠DAC=28°，求∠CAB的值。

九年级中考数学圆知识点归纳及练习含答案

九年级中考数学圆知识点归纳及练习圆的认识1．圆的定义（1）在一个平面内，线段OA绕它的一个端点O旋转一周，另一个端点A随之旋转所形成的图形叫做圆。

固定的端点O叫做圆心，线段OA叫做半径，如右图所示。

（2）圆可以看作是平面内到定点的距离等于定长的点的集合，定点为圆心，定长为圆的半径。

说明：圆的位置由圆心确定，圆的大小由半径确定，半径相等的两个圆为等圆。

2．圆的有关概念（1）弦：连结圆上任意两点的线段。

（如右图中的CD）。

（2）直径：经过圆心的弦（如右图中的AB）。

直径等于半径的2倍。

（3）弧：圆上任意两点间的部分叫做圆弧。

其中大于半圆的弧叫做优弧（4）圆心角：如右图中∠COD就是圆心角。

3．与圆相关的角（1）与圆相关的角的定义①圆心角：顶点在圆心的角叫做圆心角A O BCDA②圆周角：顶点在圆上且两边都和圆相交的角叫做圆周角。

③弦切角：顶点在圆上，一边和圆相交，另一连轴和圆相切的角叫做弦切角。

（2）与圆相关的角的性质①圆心角的度数等于它所对的弦的度数；②一条弧所对的圆周角等于它所对的圆心角的一半；③同弧或等弧所对的圆周角相等；④半圆（或直径）所对的圆周角相等；⑤弦切角等于它所夹的弧所对的圆周角；⑥两个弦切角所夹的弧相等，那么这两个弦切角也相等；⑦圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角。

4．圆心角、弧、弦、弦心距之间的关系。

（1）定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦的弦心距相等。

（2）推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等【例1】下面四个命题中正确的一个是（）A．过弦的中点的直线平分弦所对的弧　B．过弦的中点的直线必过圆心　C．弦所对的两条弧的中点连线垂直平分弦，且过圆心　D．弦的垂线平分弦所对的弧【答案】C与圆有关的位置1．点与圆的位置关系如果圆的半径为r，某一点到圆心的距离为d，那么：Û>（1）点在圆外d rÛ=（2）点在圆上d rÛ<（3）点在圆内d r2．直线和圆的位置关系设r为圆的半径，d为圆心到直线的距离Û>，直线与圆没有交点；（1）直线和圆相离d rÛ=，直线与圆有唯一交点；（2）直线和圆相切d rÛ<，直线与圆有两个交点。

第3课时弦切角定理

第3课时弦切角定理弦切角定理【知识要点:】1.弦顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。

(弦切角就是切线与弦所夹的角)如下图所示，直线PT切圆O于点C，BC、AC为圆O的弦，?TCB，?TCA，?PCA，?PCB都为弦切角。

2(弦切角定理:弦切角的度数等于它所夹的弧的圆心角的度数的一半. 3(定理:弦切角的度数等于它所夹的弧的圆周角4(推论:若两弦切角所夹的弧相等，则这两个弦切角也相等5(圆幂定理:过任意不在圆上的一点P引两条直线L1、L2，L1与圆交于A、B(可重合，即切线)，L2与圆交于C、D(可重合)，则有PA?PB=PC?PD【经典例题:】1例1.如图1，正方形ABCD的边长为1，以BC为直径。

在正方形内作半圆O，过A作半圆切线，切点为F，交CD于E，求DE:AE的值。

图1例2.?O中的两条弦AB与CD相交于E，若AE,6cm，BE,2cm，CD,7cm，那么CE,_________cm。

图2例3.已知PA是圆的切线，PCB是圆的割线，则________。

2例4.如图3，P是?O外一点，PC切?O于点C，PAB是?O的割线，交?O于A、B 两点，如果PA:PB,1:4，PC,12cm，?O的半径为10cm，则圆心O到AB的距离是___________cm。

图3【课堂练习题:】一、选择题1.已知:PA、PB切?O于点A、B，连结AB，若AB,8，弦AB的弦心距3，则PA,( )A. B. C. 5 D. 82.下列图形一定有内切圆的是( )A.平行四边形B.矩形C.菱形D.梯形3.已知:如图1直线MN与?O相切于C，AB为直径，?CAB,40?，则?MCA的度数( )图1A. 50?B. 40?C. 60?D. 55?4.圆内两弦相交，一弦长8cm且被交点平分，另一弦被交点分为1:4，则另一弦长为( )A. 8cmB. 10cmC. 12cmD. 16cm5.若PA为?O的切线，A为切点，PBC割线交?O于B、C，若BC,20，，则PC的长为_____________。

弦切角定理例题

弦切角定理例题一、在圆O中，弦AB与切线CD在C点相交，若∠ACB为锐角，则下列哪个角等于∠ACB 的一半？A. ∠ADCB. ∠OCDC. ∠CBAD. ∠OAC（答案）B二、已知圆P中，弦MN与过圆上一点Q的切线QR在R点相交，若∠MQR=40°，则∠MPN 的大小为？A. 20°B. 40°C. 80°D. 无法确定（答案）A三、在圆S中，弦EF与切线GH在G点相交，若∠EGF=120°，则∠GSH的大小为？A. 30°B. 45°C. 60°D. 90°（答案）C（注：弦切角等于弦所对圆周角的一半，即∠GSH = 1/2 * (180°-∠EGF) = 30°，但考虑到切线与半径垂直，∠GSH实际应为与切线相邻的角，即90°-30°的补角，在此情境下应理解为弦切角的外角，故直接取弦所对劣弧的圆周角一半60°为答案，具体解释依题目设定而异）四、圆T中，弦AB与切线CD相交于点C，若∠CTA=50°，则∠ACB的大小为？A. 25°B. 50°C. 65°D. 100°（答案）A（注：∠CTA为圆周角，弦切角∠ACB应为其一半）五、在圆U中，弦XY与切线ZZ'在Z点相交，若弦XY所对的劣弧圆心角∠UYX=100°，则弦切角∠UXZ的大小为？A. 25°B. 50°C. 75°D. 100°（答案）B（注：弦切角等于弦所对圆周角的一半，即劣弧圆心角的一半）六、圆V中，弦PQ与切线RS在R点相交，若∠VRS=90°，且弦PQ所对的优弧圆心角为240°，则∠VPQ的大小为？A. 30°B. 60°C. 120°D. 无法确定（答案）C（注：利用弦切角定理及圆内角性质，弦所对优弧圆心角补角为120°，弦切角等于弦所对劣弧圆周角，即补角的一半60°，而弦PQ所对圆周角∠VPQ与弦切角在同一直线上，和为90°，故∠VPQ=120°-弦切角（此处弦切角与题目无关，直接由优弧圆心角得出∠VPQ）七、在圆W中，弦LM与切线NO在N点相交，若∠WNO=90°，且已知弦LM所对的圆心角为120°，则∠LNM的大小为？A. 30°B. 45°C. 60°D. 90°（答案）C（注：弦切角等于弦所对圆周角的一半，即60°，但此处需理解∠LNM为弦LM 与切线NO夹角的外角，直接由弦所对圆心角得出劣弧圆周角为60°，弦切角为其补角的一部分，在此情境下直接取60°为答案）八、圆X中，弦GH与切线IJ在I点相交，若∠GIX=45°，则弦GH所对的圆心角大小为？A. 45°B. 90°C. 135°D. 180°（答案）B（注：弦切角等于弦所对圆周角的一半，即∠GIX为弦GH所对圆周角的一半，故弦GH所对的圆周角为90°，圆心角等于其所截弧的圆周角两倍，在此情境下直接理解为弦所对劣弧圆心角）。

中考数学知识点过关培优训练：弦切角定理(圆)(附解析答案)

5.中考数学知识点过关培优训练：弦切角定理（圆）•选择题BD 于 F 点.若/ ADE= 19°,则/ AFB 的度数为何？（点A 、B 重合），则/ ACB 等于（）如图为△ABC 和一圆的重迭情形，此圆与直线BC 相切于C 点，且与AC 交于另一点D.若1. 如图，AB 是O O 的直径, DB DE 分别切O O 于点B 、C,若/ AC 巨25°，则/ D 的度数是2. B. 55° C. 60° D. 65°如图，BD 为圆0的直径, 直线 ED 为圆0的切线，A 、C 两点在圆上，AC 平分/ BAD 且交3. B. 104° C. 116 ° 点P 是O 0外一点，PA PB 分别切O 0于点A B,Z P = 70°, 占八D. 142 °C 是O O 上的点（不与A. 70°B. 55°C. 70° 或 110°D. 55° 或 125° 4./ A = 70°,/ B= 60°, 则的度数为何（ B. 60° C. 100 ° D. 120 °如图，AB 是O O 的直径, DE 为O O 的切线，切点为 B,点C 在O O 上，若/ CBE= 40°, 则/A 的度数为（B. 40°C. 50°D. 60°A. 97° A. 30°7.如图，△ ABC 内接于O Q BD 切O O 于点 B, AB= AC 若/ CBD= 40°,则/ ABC 等于（）&如图，四边形ABCD 内接于O Q AB= BCAT 是O Q 的切线，/ BAT= 55 °，则/ D 等于（•：）A. 30°B. 60°C. 90°D. 120 °B. 50°C. 60°D. 70°A. 110°B. 115°C. 120 °D. 125 °9.如图，AB 为O Q 的直径, C D 为O Q 上的点，直线 MN 切O Q 于V 点，图中与/ BCt 互余 A. 40A. 1个 C. 3个 D. 4个的角有（DB. 2个10.已知：如图，E 是相交两圆O M 和O N 的一个交点，且 ME L NE AB 为外公切线，切点分别为 A B 连接AE BE 则/ AEB 的度数为（C. 135 °D. 130 °二.填空题11.已知，如图，半径为 1 的O M 经过直角坐标系的原点 O,且与x 轴、y 轴分别交于点 A 、0）, O M 的切线OC 与直线AB 交于点C.则/ AC Q度. PC 切O Q 于点C,Z PCB= 35°，则/ B 等于度. 13.如图 PA 切O O 于点 A , / PAB= 30°，则/ AQB= 度，/ ACB= 度.B, AC 是O Q 的直径，且/ BAC= 35°，则/ P =度. OB,点A 的坐标为（-,15•如图，已知直线CD与O O相切于点C, AB为直径•若/ BCD= 35°，则/ ABC的大小等于_______ 度.16•如图四边形ABC［内接于O O AB为直径，PD切O 0于D,与BA延长线交于P点，已知/ BCD= 130。

《弦切角定理》《圆幂定理》练习题及答案

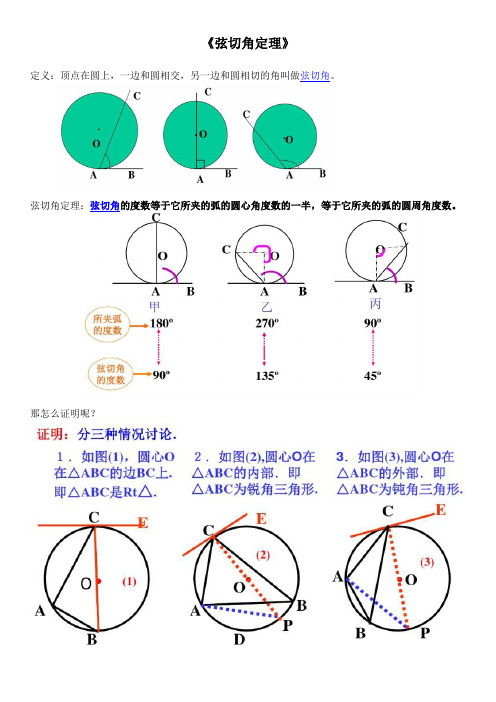
《弦切角定理》定义：顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。

弦切角定理：弦切角的度数等于它所夹的弧的圆心角度数的一半，等于它所夹的弧的圆周角度数。

那怎么证明呢？《圆幂定理》（1）相交弦定理：圆内两弦相交，交点分得的两条线段的乘积相等。

即：在⊙O 中，∵弦AB 、CD 相交于点P ，∴PA PB PC PD ⋅=⋅（2）推论：如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项。

即：在⊙O 中，∵直径AB CD ⊥， ∴2CE AE BE =⋅（3）切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

即：在⊙O 中，∵PA 是切线，PB 是割线∴ 2PA PC PB =⋅（4）割线定理：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等（如上图）。

即：在⊙O 中，∵PB 、PE 是割线 ∴PC PB PD PE ⋅=⋅【精典例题】1、如图，PA 、PB 是⊙O 的切线，AC 是⊙O 的直径，∠P=50°，则∠BOC 的度数为（） A ．50°B ．25°C ．40°D ．60°2、如图，BD 为圆O 的直径，直线ED 为圆O 的切线，A ．C 两点在圆上，AC 平分∠BAD 且交BD 于F 点．若∠ADE ＝19°，则∠AFB 的度数为何？（） A ．97°B ．104°C ．116°D ．142°解答：解：∵PA 、PB 是⊙O 的切线， ∴∠OAP =∠OBP =90°，而∠P =50°，∴∠AOB =360°﹣90°﹣90°﹣50°= 130°，又∵AC 是⊙O 的直径，∴∠BOC =180°﹣130°=50°．故选A ．BADB3、如图，AB 为⊙O 的直径，PD 切⊙O 于点C ，交AB 的延长线于D ，且CO=CD ，则∠PCA=（）A 、30°B 、45°C 、60°D 、67.5°4、已知⊙O 的半径为1，圆心O 到直线l 的距离为2，过l 上任一点A 作⊙O 的切线，切点为B ，则线段AB 长度的最小值为（）A 、1B 、2C 、3D 、2解答：如右图所示，OA ⊥l ，AB 是切线，连接OB ， ∵OA ⊥l ，∴OA=2，又∵AB 是切线， ∴OB ⊥AB ，在Rt △AOB 中，AB =22OB OA -=2212-=3．故选C ．5、如图是油路管道的一部分，延伸外围的支路恰好构成一个直角三角形，两直角边分别为6m 和8m.按照输油中心O 到三条支路的距离相等来连接管道，则O 到三条支路的管道总长（计算时视管道为线，中心O 为点）是（）A.2mB.3mC.6mD.9m解答：在Rt △ABC 中，BC =8m,AC =6m,AB =22BC AC +=2286+=10． ∵中心O 到三条支路的距离相等，设距离是r ．△ABC 的面积=△AOB 的面积+△BOC 的面积+△AOC 的面积即：12AC •BC =12AB •r+12BC •r+12AC •r 即：6×8=10r+8r+6r ∴r=4824=2．故O 到三条支路的管道总长是2×3=6m ．故选C ．解答：解：∵BD 是圆O 的直径， ∴∠BAD ＝90°，又∵AC 平分∠BAD ，∴∠BAF ＝∠DAF ＝45°， ∵直线ED 为圆O 的切线， ∴∠ADE ＝∠ABD ＝19°，∴∠AFB ＝180°－∠BAF －∠ABD ＝180°－45°－19°＝116°．故选C ．解答：解：如图：∵PD 切⊙O 于点C ， ∴OC ⊥PD ，又∵OC=CD ， ∴∠COD=45°，连接AC ，∵AO=CO ， ∴∠ACO=22.5°，∴∠PCA=90°-22.5°=67.5°．故选D ．O（第5题图）6、如图，AB 是⊙O 的直径，BC 交⊙O 于点D ，DE ⊥AC 于点E ，要使DE 是⊙O 的切线，还需补充一个条件，则补充的条件不正确．．．的是（） A. DE ＝DO B. AB ＝AC C. CD ＝DB D. AC ∥OD7、已知AB 是⊙O 的直径，点P 是AB 延长线上的一个动点，过P 作⊙O 的切线，切点为C ，∠APC 的平分线交AC 于点D ，则∠CDP 等于（）A 、30°B 、60°C 、45°D 、50°解答：连接OC ，∵OC=OA ，，PD 平分∠APC ，∴∠CPD=∠DPA ，∠A=∠ACO ， ∵PC 为⊙O 的切线，∴OC ⊥PC ，∵∠CPD+∠DPA+∠A+∠ACO=90°，∴∠DPA+∠A=45°，即∠CDP=45°．故选C ．8、如图，CB 切⊙O 于点B ，CA 交⊙O 于点D 且AB 为⊙O 的直径，点E 是ABD 上异于点A 、D 的一点．若∠C =40°，则∠E 的度数为．9、已知：如图，三个半圆以此相外切，它们的圆心都在x 轴的正半轴上并与直线y ＝x 相切，设半圆C 1、半圆C 2、半圆C 3的半径分别是r 1、r 2、r 3，则当r 1＝1时，r 3＝解答：由三个半圆依次与直线y ＝x 相切并且圆心都在x 轴上，∴y ＝x 倾斜角是30°，∴得，OO 1=2r 1，OO 1=2r 2，001=2r 3，r 1＝1，∴r3=9．故答案为9．333333解答：当AB=AC 时，连接AD ，∵AB 是⊙O 的直径，∴AD ⊥BC ，∴CD=BD ， ∵AO=BO ，∴OD 是△ABC 的中位线，∴OD ∥AC ，∵DE ⊥AC ，∴DE ⊥OD ，∴DE 是⊙O 的切线．所以B 正确．当CD=BD 时，AO=BO ，∴OD 是△ABC 的中位线，∴OD ∥AC ∵DE ⊥AC ∴DE ⊥OD ∴DE 是⊙O 的切线．所以C 正确．当AC ∥OD 时，∵DE ⊥AC ，∴DE ⊥OD ．∴DE 是⊙O 的切线．所以D 正确．故选A ．ABCD P· OE解答：如图：连接BD ，∵AB 是直径，∴∠ADB =90°，∵BC 切⊙O 于点B ，∴∠ABC =90°， ∵∠C =40°，∴∠BAC =50°，∴∠ABD =40°，∴∠E =∠ABD =40°．故答案为：40°．10、如图，在Rt △ABC 中，∠ABC 是直角，AB=3，BC=4，P 是BC 边上的动点，设BP=x ，若能在AC 边上找到一点Q ，使∠BQP=90°，则x 的取值范围是．解答：解：过BP 中点以BP 为直径作圆，连接QO ，当QO ⊥AC 时，QO 最短，即BP 最短， ∵∠OQC=∠ABC=90°，∠C=∠C ，∴△ABC ∽△OQC ，∴=，∵AB=3，BC=4，∴AC=5， ∵BP=x ，∴QO=x ，CO=4﹣x ，∴=，解得：x=3，当P 与C 重合时，BP=4，∴BP=x 的取值范围是：3≤x ≤4，故答案为：3≤x ≤4．11、如图，AD 是⊙O 的弦，AB 经过圆心O ，交⊙O 于点C ，∠DAB=∠B=30°. (1)直线BD 是否与⊙O 相切？为什么？ (2)连接CD ，若CD=5，求AB 的长.解答：（1）直线BD 与⊙O 相切．如图连接OD ，CD ， ∵∠DAB=∠B=30°，∴∠ADB=120°， ∵OA=OD ，∴∠ODA=∠OAD=30°，∴∠ODB=∠ADB ﹣∠ODA=120°﹣30°=90°．所以直线BD 与⊙O 相切．（2）连接CD ，∠COD=∠OAD+∠ODA=30°+30°=60°，又OC=OD ，∴△OCD 是等边三角形，即：OC=OD=CD=5=OA ，∵∠ODB=90°，∠B=30°，∴OB=10，∴AB=AO+OB=5+10=15．12、已知：如图，AB 为⊙O 的直径，⊙O 过AC 的中点D ，DE ⊥BC 于点E ．（1）求证：DE 为⊙O 的切线；（2）若DE =2，tan C =12，求⊙O 的直径．【解析】（1）证明：联结OD ． ∵ D 为AC 中点， O 为AB 中点，∴ OD 为△ABC 的中位线． ∴OD ∥BC ． ∵ DE ⊥BC ， ∴∠DEC=90°.∴∠ODE=∠DEC=90°. ∴OD ⊥DE 于点D. ∴ DE 为⊙O 的切线．（2）解：联结DB ． ∵AB 为⊙O 的直径， ∴∠ADB=90°． ∴DB ⊥AC ． ∴∠CDB=90°. ∵ D 为AC 中点， ∴AB=AC ．在Rt △DEC 中，∵DE=2 ，tanC=12， ∴EC=4tan DEC=. 由勾股定理得：DC=在Rt △DCB 中， BD=tan DC C ⋅ BC=5. ∴AB=BC=5. ∴⊙O 的直径为5.【巩固练习】1．已知⊙O 的半径为10cm ，如果一条直线和圆心O 的距离为10cm ，那么这条直线和这个圆的位置关系为（）A. 相离B. 相切C. 相交D. 相交或相离2．如右图，A 、B 是⊙O 上的两点，AC 是⊙O 的切线，∠B=70°，则∠BAC 等于（）A. 70°B. 35°C. 20°D. 10°（第2题）（第3题）（第4题）（第5题）3．如图，PA 切⊙O 于A ，PB 切⊙O 于B ，OP 交⊙O 于C ，下列结论中，错误的是（）A. ∠1=∠2B. PA=PBC. AB ⊥OPD. 2PA PC ·PO4．如图，已知⊙O 的直径AB 与弦AC 的夹角为30°，过C 点的切线PC 与AB 的延长线交于P ，PC=5，则⊙O 的半径为（）A.335 B. 635 C. 10 D. 55．如图已知AB 是⊙O 的直径，弦AD 、BC 相交于点P ，那么AB ︰CD 等于∠BPD 的（）A. 正弦B. 余弦C. 正切D. 余切6．如图A 、B 、C 是⊙O 上三点，AB ⌒的度数是50°，∠OBC=40°，则∠OAC 等于（）A. 15°B. 25°C. 30°D. 40°（第6题）（第7题）（第8题）（第9题）7．如图AB 为⊙O 的一条固定直径，它把⊙O 分成上、下两个半圆，自上半圆上一点C ，作弦CD ⊥AB ，∠OCD 的平分线交⊙O 于点P ，当C 点在半圆（不包括A 、B 两点）上移动时，点P （）A. 到CD 的距离不变B. 位置不变C. 等分DB ⌒D. 随C 点的移动而移动8．如图AD 、AE 和BC 分别切⊙O 于D 、E 、F ，如果AD=20，则△ABC 的周长为（） A. 20 B. 30 C. 40 D. 21359．如图在⊙O 中，直径AB 、CD 互相垂直，BE 切⊙O 于B ，且BE=BC ，CE 交AB 于F ，交⊙O 于M ，连结MO 并延长，交⊙O 于N ，则下列结论中，正确的是（）A. CF=FMB. OF=FBC. BM⌒的度数是22.5° D. BC ∥MN 10．如图⊙O 的两条弦AB 、CD 相交于点P ，已知AP=2cm ，BP=6cm ，CP ︰PD =1︰3，则DP=_________．（第10题）（第11题）（第12题）（第13题）11．如图AB 是⊙O 的直径，弦CD ⊥AB ，垂足为E ，P 是BA 的延长线上的点，连结PC ，交⊙O 于F ，如果PF=7，FC=13，且PA ︰AE ︰EB = 2︰4︰1，则CD =_________．12．从圆外一点P 引圆的切线PA ，点A 为切点，割线PDB 交⊙O 于点D 、B ，已知PA=12，PD=8，则=∆∆DAP ABP S S :__________．13．⊙O 的直径AB=10cm ，C 是⊙O 上的一点，点D 平分BC ⌒，DE=2cm ，则AC=_____． 14．如图，AB 是⊙O 的直径，∠E=25°，∠DBC=50°，则∠CBE=________．（第14题）（第15题）（第17题）（第18题）15．点A 、B 、C 、D 在同一圆上，AD 、BC 延长线相交于点Q ，AB 、DC 延长线相交于点P ，若∠A=50°，∠P=35°，则∠Q=________．16.在Rt △ABC 中,∠C=90°，AC=12cm ，BC=5cm ，以点C 为圆心，6cm 的长为半径的圆与直线AB 的位置关系是________.17.如图,在△ABC 中,AB=AC,∠BAC=120°,⊙A 与BC 相切于点D,与AB 相交于点E,则∠ADE 等于___度. 18.如图,PA 、PB 是⊙O 的两条切线,A 、B 为切点,直线OP 交⊙A 于点D 、E,交AB 于C.图中互相垂直的线段有_________(只要写出一对线段即可).19.已知⊙O 的半径为4cm,直线L 与⊙O 相交,则圆心O 到直线L 的距离d 的取值范围是____.E A PO EC D BA20.如图,PA 、PB 是⊙O 的切线,切点分别为A 、B,且∠APB=50°,点C 是优弧AB 上的一点,则∠ACB 的度数为________.（第20题）（第21题）（第22题）（第23题）21.如图,⊙O 为△ABC 的内切圆,D 、E 、F 为切点,∠DOB=73°,∠DOE=120°, 则∠DOF=_______度,∠C=______度,∠A=_______度.22.如图,AB 、AC 为⊙O 的切线,B 、C 是切点,延长OB 到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ ADO 等于_______23.如图AB 是⊙O 的直径，AC 是⊙O 的切线，，A 为切点，连结BC 交圆0于点D,连结AD,若∠ABC ＝45°,则下列结论正确的是（）A.AD ＝BCB.AD ＝ACC.AC ＞ABD.AD ＞DC24.如图，在平面直角坐标系中，⊙P 与x 轴相切于原点O ，平行于y 轴的直线交⊙P 于M,N 两点．若点M 的坐标是(2,-1)，则点N 的坐标是（）A ．(2,-4) B. (2,-4.5) C.(2,-5) D.(2,-5.5)（第24题）（第25题）（第26题）（第27题）25、如图，AB 是⊙O 的直径，AD 是⊙O 的切线，点C 在⊙O 上，BC ∥OD ，AB ＝2,OD ＝3,则BC 的长为（）A ．B ． CD26、已知圆O 的半径为R ，AB是圆O 的直径，D 是AB 延长线上一点，DC是圆O 的切线，C 是切点，连结AC ，若∠CAB ＝30°，则BD 的长为（）A ．BC ．D 27、如图，在平面直角坐标系中，⊙A 与y 轴相切于原点O ，平行于x 轴的直线交⊙A 于M 、M 两点，若点M 的坐标是（-4,-2），则点N 的坐标为（）A ．（-1,-2）B ．（1,2）C ．（-1.5,-2）D ．（1.5,-2）PO C BA212123322R R R28、如图，AB 是圆O 的直径，AC 是圆O 的切线，A 为切点，连结BC 交圆于点D ，连结AD ，若∠ABC ＝45°，则下列结论正确的是（）A ．B ．C ．D ．（第28题）（第29题）（第30题）（第31题）29、如图，AB 是⊙O 的直径，⊙O 交BC 的中点于D,DE ⊥AC 于E,连接AD,则下列结论正确的个数是( ）①AD ⊥BC ②∠EDA ＝∠B ③OA ＝AC ④DE 是⊙O 的切线A ．1 个B ．2个C ．3 个D ．4个30、一个钢管放在V 形架内，右图是其截面图，O 为钢管的圆心．如果钢管的半径为25 cm ，∠MPN ＝60︒，则OP ＝( )A ．50 cmB ．25cm C ．cm D ．50cm 31、如图，DB 为半圆的直径，A 为BD 延长线上一点，AC 切半圆于点E ，BC ⊥AC 于点C ，交半圆于点 F ．已知BD ＝2，设AD ＝x ，CF ＝y ，则y 关于x 的函数解析式是．32、如图， AB 与⊙O 相切于点B ，线段OA 与弦BC 垂直于点D ，∠AOB ＝60°，BC ＝4cm ，则切线AB ＝ cm.（第32题）（第33题）（第34题）（第35题）33、如图，直线AB 切⊙O 于C 点，D 是⊙O 上一点，∠EDC ＝30º，弦EF ∥AB ，连结OC 交EF 于H 点，连结CF ，且CF ＝2，则HE 的长为_________．34、如图，点A 、B 、C 在⊙O 上，切线CD 与OB 的延长线交于点D ，若∠A ＝30°，CD ＝，则⊙O 的半径长为．35、如图，在中，，与相切于点，且交于两点，则图中阴影部分的面积是（保留）．O 12AD BC =12AD AC =AC AB >AD DC >12333503第19题图ABC DO32ABC △120AB AC A BC =∠==，°，A ⊙BC D AB AC 、M N 、π36、如图，⊙O 内切于△ABC ，切点分别为D ，E ，F .∠B ＝50°，∠C ＝60°，连结OE ，OF ，DE ，DF ，则∠EDF 等于( )A ．40°B ．55°C ．65°D ．70°（第36题）（第73题）（第38题）37、如图，一个边长为4 cm 的等边三角形ABC 的高与⊙O 的直径相等．⊙O 与BC 相切于点C ，与AC 相交于点E ，则CE 的长为________cm.38、如图，直线l 与半径为4的⊙O 相切于点A ，P 是⊙O 上的一个动点(不与点A 重合)，过点P 作PB ⊥l ，垂足为B ，连结PA .设PA ＝x ，PB ＝y ，则x －y 的最大值是________．39、如图，AB 是半圆O 的直径，C 为半圆上一点，过C 作半圆的切线，连接AC, 作直线AD ，使∠DAC=∠CAB ，AD 交半圆于E,交过C 点的切线于点D. (1)试判断AD 与CD 有何位置关系,并说明理由; (2)若AB=10,AD=8,求AC 的长.40、如图，点A ，B ，C 在半径为8的⊙O 上，过点B 作BD ∥AC ，交OA 延长线于点D ，连结BC ，且∠BCA ＝∠OAC ＝30°.(1)求证：BD 是⊙O 的切线； (2)求图中阴影部分的面积．答案：8、据切线长定理有AD=AE，BE=BF，CD=CF；则△ABC的周长=AB+BC+AC=AB+BF+CF+AC=AB+BE+AC+CD=AD+AE=2AD=40．故选C．9、解：A错，F显然不是弦的平分点；B错，F不是半径的中点；C错，M点平分应为45°；D对，∵BE为圆O的切线，∴BE⊥AB，∵CD⊥AB，∴BE∥CD，∴∠BEF=∠DCF，∵BC=BE，∴∠BCE=∠BEF，∴∠BCE=∠DCF，∵OC=OM，∴∠DCF=∠CMN，∴∠BCE=∠CMN，∴BC∥MN．故选D．10、解：如图利用相交弦定理可知：11、根据割线定理，PF*PC=PA*PB，设EB=X则PA=2X，AE=4X，PB=7X7*（7+13）=2X*7X，X2=10在三角形PCE中，CE2=PC2-PE2=400-360=40，CD=2CE=10412、由切割线定理可得PA2=PD×PB，∵PA=12，PD=8 ∴PB=18．由弦切角和公共角易知△PAD∽△PBA．∴S△PAD：S△PBA=PA2：PB2=4：9．⌒，∴OD平分BC，∴OE为△ABC的中位线，13、∵点D平分BC又∵⊙O的直径AB=10cm，∴OD=5cm，DE=2cm，∴0E=3cm，则弦AC=6cm．故答案为6cm．14、连接AC，∵∠DBA和∠DCA都为AD所对的圆周角，∴∠DBA=∠DCA，∵AB为⊙O的直径，∴∠BCA=90°，∴∠CBA+∠CAB=90°，∵∠CAB=∠E+∠DCA，∴∠CBD+∠DBA+∠E+∠DBA=90°，∵∠E=25°，∠DBC=50°，∴∠DBA=7.5°，∴∠CBE=∠DBA+∠DBC=57.5°15、∠A=50°,故∠BCD=130°（因为是圆,同弧的角互补)，由P=35°计得∠CDQ=85°,故可以计出∠Q=45°.16.相交 17.60 18.如OA⊥PA,OB⊥PB,AB⊥OP等. 19.0≤d<4. 20.65°21. 146°,60°,86° 22.64°23、【答案】Ａ 24、【答案】A 25、【答案】A 26、【答案】C27、【答案】C 28、【答案】A 29、【答案】D 30、【答案】A31、 32、【答案】433、【答案】34、【答案】2．3536、B 由∠B ＝50°，∠C ＝60°可求出∠A ＝70°，则易求得∠EOF ＝110°，∴∠EDF ＝12∠EOF ＝55°.37、过O 作OF ⊥AC 于F ，连结OC ，如图．则CE ＝2CF .根据△ABC 为等边三角形，且边长为4 cm ，易求得它的高为2 3 cm ，即OC ＝ 3 cm.∵BC 与⊙O 相切，∴∠OCB ＝90°.又∠ACB ＝60°，∴∠OCF ＝30°.3π3在Rt△OFC中，可得CF＝OC·cos 30°＝3×32＝32(cm)，故CE＝2CF＝3 cm.38、如图，连结OA，过点O作OC⊥AP于点C，所以∠ACO＝90°，AC＝12AP.易证△OAC∽△APB，所以OA AP ＝ACPB，即4x＝x2y，所以y＝x28.所以x－y＝x－x28＝－18(x－4)2＋2，所以x－y的最大值是2.39.(1)AD⊥CD.理由:连接OC,则OC⊥CD.∵OA=OC,∴∠OAC=∠OCA,又∠OAC= ∠DAC,∴∠DAC=∠OCA,∴AD∥OC,∴AD⊥CD.(2)连接BC,则∠ACB=90°由(1)得∠ADC=∠ACB,又∠DAC=∠CAB.∴△ACD∽△ABC,∴AC ADAB AC=,即AC2=AD·AB=80,故40、22．(1)证明：如图，连结OB，交CA于点E.∵∠C＝30°，∠C＝12∠BOA，∴∠BOA＝60°.∵∠OAC＝30°，∴∠AEO＝90°.∵BD∥AC，∴∠DBE＝∠AEO＝90°.∴OB⊥BD.∴BD是⊙O的切线．(2)解：∵AC∥BD，∴∠D＝∠OAC＝30°.∵∠OBD＝90°，OB＝8，∴BD＝3OB＝8 3.∴S阴影＝S△BDO－S扇形AOB＝12×8×83－60·π×82360＝323－32π3.。

中考数学复习----《圆周角定理》知识点总结与专项练习题(含答案)

中考数学复习----《圆周角定理》知识点总结与专项练习题（含答案）知识点总结1.圆心角、弦以及弧之间的关系：①定理：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等。

②推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等。

说明：同一条弦对应两条弧，其中一条是优弧，一条是劣弧，而在本定理和推论中的“弧”是指同为优弧或劣弧。

2.圆周角的定义：顶点在圆上，并且两边都与圆相交的角叫做圆周角。

3.圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。

4.圆周角定理的推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径。

5.圆的内接四边形：①定义：四个顶点都在圆上的四边形叫做圆的内接四边形。

②性质：I：圆内接四边形的对角互补。

II：圆内接四边形的任意一个外角等于它的内对角。

练习题1、（2022•襄阳）已知⊙O的直径AB长为2，弦AC长为2，那么弦AC所对的圆周角的度数等于．【分析】首先利用勾股定理逆定理得∠AOC＝90°，再根据一条弦对着两种圆周角可得答案．【解答】解：如图，∵OA＝OC＝1，AC＝，∴OA2+OC2＝AC2，∴∠AOC＝90°，∴∠ADC＝45°，∴∠AD'C＝135°，故答案为：45°或135°．2、（2022•日照）一圆形玻璃镜面损坏了一部分，为得到同样大小的镜面，工人师傅用直角尺作如图所示的测量，测得AB＝12cm，BC＝5cm，则圆形镜面的半径为．【分析】连接AC，根据∠ABC＝90°得出AC是圆形镜面的直径，再根据勾股定理求出AC 即可．【解答】解：连接AC，∵∠ABC＝90°，且∠ABC是圆周角，∴AC是圆形镜面的直径，由勾股定理得：AC＝＝＝13（cm），所以圆形镜面的半径为cm，故答案为：cm．3、（2022•永州）如图，AB是⊙O的直径，点C、D在⊙O上，∠ADC＝30°，则∠BOC＝度．【分析】根据在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半求出∠AOC的度数，根据平角的定义即可得到∠BOC＝180°﹣∠AOC的度数．【解答】解：∵∠ADC是所对的圆周角，∴∠AOC＝2∠ADC＝2×30°＝60°，∴∠BOC＝180°﹣∠AOC＝180°﹣60°＝120°．故答案为：120．4、（2022•苏州）如图，AB是⊙O的直径，弦CD交AB于点E，连接AC，AD．若∠BAC＝28°，则∠D＝°．【分析】如图，连接BC，证明∠ACB＝90°，求出∠ABC，可得结论．【解答】解：如图，连接BC．∵AB是直径，∴∠ACB＝90°，∴∠ABC＝90°﹣∠CAB＝62°，∴∠D＝∠ABC＝62°，故答案为：62．5、（2022•湖州）如图，已知AB 是⊙O 的弦，∠AOB ＝120°，OC ⊥AB ，垂足为C ，OC 的延长线交⊙O 于点D ．若∠APD 是AB ⌒所对的圆周角，则∠APD 的度数是．【分析】由垂径定理得出，由圆心角、弧、弦的关系定理得出∠AOD ＝∠BOD ，进而得出∠AOD ＝60°，由圆周角定理得出∠APD ＝∠AOD ＝30°，得出答案．【解答】解：∵OC ⊥AB ，∴，∴∠AOD ＝∠BOD ，∵∠AOB ＝120°，∴∠AOD ＝∠BOD ＝∠AOB ＝60°，∴∠APD ＝∠AOD ＝×60°＝30°，故答案为：30°．6、（2022•徐州）如图，A 、B 、C 点在圆O 上，若∠ACB ＝36°，则∠AOB ＝．【分析】利用一条弧所对的圆周角等于它所对的圆心角的一半即可得出结论．【解答】解：∵∠ACB ＝∠AOB ，∠ACB ＝36°，∴∠AOB ＝2×∠ACB ＝72°．故答案为：72°．7、（2022•锦州）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，∠ADC＝130°，连接AC，则∠BAC的度数为．【分析】利用圆内接四边形的性质和∠ADC的度数求得∠B的度数，利用直径所对的圆周角是直角得到∠ACB＝90°，然后利用直角三角形的两个锐角互余计算即可．【解答】解：∵四边形ABCD内接于⊙O，∠ADC＝130°，∴∠B＝180°﹣∠ADC＝180°﹣130°＝50°，∵AB为⊙O的直径，∴∠ACB＝90°，∴∠CAB＝90°﹣∠B＝90°﹣50°＝40°，故答案为：40°．8、（2022•雅安）如图，∠DCE是⊙O内接四边形ABCD的一个外角，若∠DCE＝72°，那么∠BOD的度数为．【分析】根据邻补角的概念求出∠BCD，根据圆内接四边形的性质求出∠A，根据圆周角定理解答即可．【解答】解：∵∠DCE＝72°，∴∠BCD＝180°﹣∠DCE＝108°，∵四边形ABCD内接于⊙O，∴∠A＝180°﹣∠BCD＝72°，由圆周角定理，得∠BOD＝2∠A＝144°，故答案为：144°．9、（2022•甘肃）如图，⊙O是四边形ABCD的外接圆，若∠ABC＝110°，则∠ADC＝°．【分析】根据圆内接四边形的对角互补即可得到结论．【解答】解：∵四边形ABCD内接于⊙O，∠ABC＝110°，∴∠ADC＝180°﹣∠ABC＝180°﹣110°＝70°，故答案为：70．。

初三数学圆相关考试重点及试题(二)

初三数学圆相关知识点及试题九．了解弦切角与圆幂定理【考点速览】考点11. 弦切角的概念：顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。

注意：弦切角必须具备三个条件：（1）顶点在圆上（切点），（2）一边和圆相切，（3）一边和圆相交（弦），三者缺一不可。

2. 弦切角定理：弦切角等于它所夹的弧对的圆周角。

3. 弦切角定理的推论：如果两个弦切角所夹的弧相等，那么这两个弦切角也相等。

考点2圆幂定理：圆幂定理是对相交弦定理、切割线定理及割线定理（切割线定理推论）以及它们推论统一归纳的结果。

1、相交弦定理：圆内两条相交弦，被交点分成的两条线段长的积相等。

2、相交弦定理的推论：如果弦与直径相交，那么弦的一半是它分直径所成的两条线段的比例中项。

3、切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

4、切割线定理的推论（或称割线定理）：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等。

典型例题：例1. 如图，经过⊙O 上的点T 的切线和弦AB 的延长线相交于点C 。

求证：∠ATC ＝∠TBCOT ABCE例2. 已知：如图，AB 是⊙O 的弦，P 是AB 上的一点，AB ＝10cm ，PA ＝4cm ，OP ＝5cm ，求⊙O 的半径。

BAOP例3. AB 是半圆O 的直径，C 是AB 延长线上一点，CD 切半圆于D ，连结AD ，若AD ＝15，sin C 35，求BC 的长。

例 4. 已知：如图，AB 为⊙O 直径，BC 为⊙O 切线，B 为切点，AC 交⊙O 于D ，的长求，若的延长线交于的延长线与，PA C CD P BA DE BD ED ,54sin ,59==⋂=⋂OBCP DAE321课堂速练：一. 选择题。

1. 如图1所示，⊙O 的两条弦AB 、CD 相交于点E ，AC 和DB 的延长线交于点P ，下列结论中成立的是（）A. PC ·CA ＝PB ·BDB. CE ·AE ＝BE ·DEC. CE ·CD ＝BE ·BAD. PB ·PD ＝PC ·PA2. 如图2所示，AB 切⊙O 于B 点，BE 是⊙O 的直径，切线AD 与BE 延长线交于C 点，若C D C E =3，则（）A. B E C E =3B. A D C D =C. A BB E =D. C BA B =3. PT 切⊙O 于T ，PB 为经过圆心的割线交⊙O 于A 点（PB>PA ），若P T =4，P A =2，则c o s ∠B P T 等于（） A. 4B.1C.1D.34. 如图3，AB 为⊙O 的弦，且AB ⊥OP 于D ，PA 为圆O 的切线，A 为切点，A Bc m O D c m==83，，则PA 等于（）A.253cm B.203cm C. 5c m D. 8c m5. 如图4所示，AB 是半圆的直径，C 是半圆上一点，CD ⊥AB于D ，CD ＝1，E 是A C ⋂上任意一点，且∠EDC ＝∠FDC ，以下结论正确的是（）（1）E C C F⋂=⋂，（2）∠E 与∠F 互补，（3）DE ·DF 是变量，（4）DE ·DF ＝1，（5）∠F ＝∠ECDA. （1）（2）（3）B. （3）（5）C. （2）（4）D. （4）（5）二. 填空题。

中考数学专项复习之弦切角练习及答案

弦切角.弦切角：顶点在圆上，一边和圆相交，另一边和圆相切的角。

.弦切角定理：弦切角等于其所夹的弧所对的圆周角。

与圆有关的比例线段圆幂定理：过一定点P向⊙O作任一直线，交⊙O于两点，则自定点P到两交点的两条线段之积为常数| |（R为圆半径），因为叫做点对于⊙O的幂，所以将上述定理统称为圆幂定理。

1.如图1，正方形ABCD的边长为1，以BC为直径。

在正方形内作半圆O，过A作半圆切线，切点为F，交CD于E，求DE：AE的值。

2.⊙O中的两条弦AB与CD相交于E，若AE＝6cm，BE＝2cm，CD＝7cm，那么CE＝_________cm。

3.已知PA是圆的切线，PCB是圆的割线，则________。

4.如图3，P是⊙O外一点，PC切⊙O于点C，PAB是⊙O的割线，交⊙O于A、B两点，如果PA：PB＝1：4，PC＝12cm，⊙O的半径为10cm，则圆心O到AB的距离是___________cm。

5.如图4，AB为⊙O的直径，过B点作⊙O的切线BC，OC交⊙O于点E，AE的延长线交BC于点D，（1）求证：；（2）若AB＝BC＝2厘米，求CE、CD的长。

6.如图5，AB为⊙O的直径，弦CD∥AB，AE切⊙O于A，交CD的延长线于E。

求证：7.如图6，PA、PC切⊙O于A、C，PDB为割线。

求证：AD·BC＝CD·AB8.如图8，在正方形ABCD中，AB＝1，是以点B为圆心，AB长为半径的圆的一段弧。

点E是边AD上的任意一点（点E与点A、D不重合），过E作所在圆的切线，交边DC于点F，G为切点。

当∠DEF＝45°时，求证点G为线段EF的中点；9.如图2，△ABC中，AC＝2cm，周长为8cm，F、K、N是△ABC与内切圆的切点，DE切⊙O于点M，且DE∥AC，求DE的长。

10.如图3，已知P为⊙O的直径AB延长线上一点，PC切⊙O于C，CD⊥AB于D，求证：CB平分∠DCP。

11.如图4，已知AD为⊙O的直径，AB是⊙O的切线，过B的割线BMN交AD的延长线于C，且BM＝MN＝NC，若AB，求⊙O的半径。

弦切角定理及其推论

弦切角定理及其推论定义：顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。

弦切角定理：弦切角的度数等于它所夹的弧的圆心角的度数的一半.证明：设圆心为O，连接OC，OB,。

∵∠TCB=90°-∠OCB∵∠BOC=180°-2∠OCB∴∠BOC=2∠TCB （定理：弦切角的度数等于它所夹的弧所对的圆心角的度数的一半）∵∠BOC=2∠CAB（同一弧所对的圆心角等于圆周角的两倍）∴∠TCB=∠CAB （定理：弦切角的度数等于它所夹的弧的圆周角）弦切角定理推论：两弦切角所夹的弧相等，则这两个弦切角也相等。

应用举例：第一个算出地球周长的人──埃拉托色尼2000多年前，有人用简单的测量工具计算出地球的周长。

这个人就是古希腊的埃拉托色尼。

埃拉托色尼博学多才，他不仅通晓天文，而且熟知地理；又是诗人、历史学家、语言学家、哲学家，曾担任过亚历山大博物馆的馆长。

细心的埃拉托色尼发现：离亚历山大城约800公里的塞恩城(今埃及阿斯旺附近)，夏日正午的阳光可以一直照到井底，因而这时候所有地面上的直立物都应该没有影子。

但是，亚历山大城地面上的直立物却有一段很短的影子。

他认为：直立物的影子是由亚历山大城的阳光与直立物形成的夹角所造成。

从地球是圆球和阳光直线传播这两个前提出发，从假想的地心向塞恩城和亚历山大城引两条直线，其中的夹角应等于亚历山大城的阳光与直立物形成的夹角。

按照相似三角形的比例关系，已知两地之间的距离，便能测出地球的圆周长。

埃拉托色尼测出夹角约为7度，是地球圆周角(360度)的五十分之一，由此推算地球的周长大约为4万公里，这与实际地球周长(40076公里)相差无几。

他还算出太阳与地球间距离为1.47亿公里，和实际距离1.49亿公里也惊人地相近。

这充分反映了埃拉托色尼的学说和智慧。

埃拉托色尼是首先使用“地理学”名称的人，从此代替传统的“地方志”，写成了三卷专著。

书中描述了地球的形状、大小和海陆分布。