祁县中学高三10月月考
祁县某校高三年级数学试题及答案)
祁县某校高三年级10月月考 (数学)一、选择题1. 设集合M={x|y=ln(4−x)},N={x|0≤x≤5},则M∩N=()A.{x|0<x≤5}B.{x|0≤x<4}C.{x|4≤x<5}D.{x|4<x≤5}2. 设p:a∈(−∞,−5],q:函数f(x)=x2−ax在(1,+∞)上单调递增,则下列说法正确的是()A.p是q的充分条件但不是必要条件B.p是q的必要条件但不是充分条件C.p是q的充要条件D.p既不是q的充分条件也不是q的必要条件3. 函数f(x)=ln(x+2)√2−x的定义域为()A.(2,+∞)B.(−2,2)C.(−∞,−2)D.(−∞,2)4. 已知角α的顶点在坐标原点,始边在x轴正半轴上,终边在直线y=3x上,则2cos2α−1=()A.35B.−45C.45D.−355. 已知命题p:∃x0∈R,sinx0<1;命题q:∃x0∈R,sinx0+cosx0=√2.则下列命题中的真命题是()A.p∧qB.(¬p)∧qC.p∧(¬q)D.¬(p∨q)6. 函数f(x)=2ln|x|2x+2−x的大致图象为( )A.B.C.D.7. 已知a,b,c∈(0,+∞),a=5+log14a,b+12b=3,c+4c=4,则()A.b<a<cB.a<c<bC.c<a<bD.c<b<a8. 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π2)的部分图象如图所示,则下列说法中正确的是()A.f(x)的最小正周期为2πB.f(x)=2sin(12x−π3)C.点(10π3,0)是f(x)图象的一个对称中心D.直线x=2π是f(x)图象的一条对称轴9. 今年第6号台风“烟花”于2021年7月25日12时30分前后登陆舟山普陀区.如图,A点正北方向的C市受到台风侵袭,一艘船从A点出发前去实施救援,以24nmile/ℎ的速度向正北航行,在A处看到S岛在船的北偏东15∘方向,船航行34ℎ后到达B处,在B处看到S岛在船的北偏东45∘方向.此船从A点到C市航行过程中距离S岛的最近距离为()A.9√2nmileB.9(√2−1)nmileC.9(√3−1)nmileD.9(√3−√2)nmile10. 将函数f(x)=−2sin2x的图象向右平移π6个单位长度后,再将得到的图象上各点的横坐标变为原来的2倍,纵坐标不变,得到函数g(x)的图象,则下列区间是g(x)的一个单调递减区间的为()A.[−4,−2]B.[−1,−12] C.[−7,−6] D.[6,8]11. 已知函数f(x)=√x+1在[a,b]上的值域为[a+2−m,b+2−m],其中a≠b,则实数m的取值范围是()A.(34,1] B.(34,+∞) C.(14,1] D.[34,1]12. 已知函数f(x)=ln(x2+1)+e x+e−x,则不等式f(lnx)−f(1)<0的解集为()A.(1e ,+∞) B.(0,e) C.(0,1e)∪(1,e) D.(1e,e)二、填空题已知函数f(x)=x3−2x2+x,则曲线y=f(x)在点(2,f(2))处的切线方程为________.有以下三个条件:①定义域不是R;②在(−1,1)上单调递增;③是周期函数.写出一个同时满足以上三个条件的函数:f(x)=_______.若存在x∈[0,1],使得3x+13x≥7m+1成立,则实数m的取值范围是________.在△ABC中,内角A,B,C的对边分别为a,b,c,若b,a,c成等差数列,c+a=2acos2B2+12b,且a=2,则△ABC的面积为________.三、解答题已知a∈R,命题p:不等式e x+4e x≥a的解集为R;命题q:f(x)={(3a−1)x+4a,x<1−x+1,x≥1’是定义在R上的减函数.若“p且q”为假命题,“p或q”为真命题,求a的取值范围.已知函数f(x)=√3sinωx−cosωx(ω>0)图象的相邻两条对称轴间的距离为π2(1)若f(x)=1,求x的值;(2)将f(x)的图象向左平移m(m>0)个单位长度,所得图象与函数y=2cos2x的图象重合,求实数m的最小值.已知某公司生产的一新款手机的年固定成本为350万元,设该公司一年内共生产这种手机x万部并全部销售完,且每万部的销售收入为600万元,生产这种手机每年需另投入成本R(x)万元,且当0<x<40时,R(x)=10x(x+10),当x≥40时,R(x)=601x+40000x−6550.(1)写出年利润W(万元)关于年产量x(万部)的函数解析式(年利润=年销售收入-年成本)(2)年产量为多少万部时,该公司所获年利润最大?最大年利润是多少?在锐角△ABC中,角A,B,C所对的边分别为a,b,c,√3cosC+sinC=√3b且a=1(1)求△ABC的外接圆的半径;(2)求2b−c的取值范围.已知函数f(x)=2x+mx+lnx(m∈R)(1)若x=1是f(x)的极值点,求m的值并判断x=1是f(x)的极大值点还是极小值点;(2)若函数g(x)=f(x)−2mx在[1,2]上单调递增,求m的取值范围.已知函数f(x)=lnx+ax+2(a∈R)(1)讨论f(x)的单调性;(2)若a≥1,讨论函数g(x)=f(x)−x2−2的零点个数.参考答案与试题解析祁县某校高三年级10月月考 (数学)一、选择题1.【答案】B【考点】交集及其运算【解析】此题暂无解析【解答】B2.【答案】A【考点】必要条件、充分条件与充要条件的判断【解析】此题暂无解析【解答】A3.【答案】B【考点】函数的定义域及其求法【解析】此题暂无解析【解答】B4.【答案】B【考点】直线的倾斜角任意角的三角函数二倍角的余弦公式【解析】此题暂无解析【解答】B5.【答案】A【考点】全称命题与特称命题逻辑联结词“或”“且”“非”【解析】此题暂无解析【解答】A6.【答案】A【考点】函数的图象【解析】此题暂无解析【解答】A7.【答案】D【考点】指数式、对数式的综合比较【解析】此题暂无解析【解答】D8.【答案】C【考点】由y=Asin(ωx+φ)的部分图象确定其解析式正弦函数的对称性【解析】此题暂无解析【解答】C9.【答案】C【考点】解三角形的实际应用【解析】此题暂无解析【解答】C10.【答案】D【考点】函数y=Asin(ωx+φ)的图象变换正弦函数的单调性【解析】此题暂无解析【解答】D11.【答案】A【考点】函数的值域及其求法已知函数的单调性求参数问题【解析】此题暂无解析【解答】A12.【答案】D【考点】利用导数研究函数的单调性其他不等式的解法【解析】此题暂无解析【解答】D二、填空题【答案】5x−y−8=0【考点】利用导数研究曲线上某点切线方程【解析】此题暂无解析【解答】5x−y−8=0【答案】tanx(答案不唯一)【考点】函数的定义域及其求法函数的值域及其求法函数的单调性及单调区间周期函数【解析】此题暂无解析【解答】tanx(答案不唯一)【答案】(−∞,13]【考点】不等式恒成立问题基本不等式【解析】此题暂无解析【解答】(−∞,13]【答案】√3【考点】等差数列的性质正弦定理余弦定理【解析】此题暂无解析【解答】√3三、解答题【答案】解:因为e x +4e ≥2√e x ⋅4e=4,不等式e x+4e≥a 的解集为R ,所以a ≤4,即命题p 为真时,a ≤4.因为函数f (x )={(3a −1)x +4a,x <1−x +1,x ≥1是定义在R 上的减函数,所以{3a −1<0,3a −1+4a ≥−1+1解得17≤a <13,即命题q 为真时,实数a 的取值范围为[17,13).因为"p 且q "为假命题,“p 或q ”为真命题,所以p,q 一真一假.若p 真q 假,可得a ∈(−∞,17)∪[13,4],若p 假q 真,可得a ∈⌀ .故实数a 的取值范围是(−∞,17)∪[13,4]. 【考点】复合命题及其真假判断 基本不等式函数单调性的判断与证明 【解析】 此题暂无解析 【解答】 解:因为e x +4e x≥2√e x ⋅4ex =4,不等式e x+4ex ≥a 的解集为R ,所以a ≤4,即命题p 为真时,a ≤4.因为函数f (x )={(3a −1)x +4a,x <1−x +1,x ≥1是定义在R 上的减函数,所以{3a −1<0,3a −1+4a ≥−1+1解得17≤a <13,即命题q 为真时,实数a 的取值范围为[17,13).因为"p 且q "为假命题,“p 或q ”为真命题,所以p,q 一真一假.若p 真q 假,可得a ∈(−∞,17)∪[13,4],若p 假q 真,可得a ∈⌀ .故实数a 的取值范围是(−∞,17)∪[13,4]. 【答案】解:(1)f (x )=√3sinωx −cosωx =2(√32sinωx −12cosωx)=2sin (ωx −π6).因为f (x )图象的相邻两条对称轴间的距离为π2, 所以f (x )的最小正周期为π. 所以2πω=π,ω=2所以f (x )=2sin (2x −π6).令f (x )=1,可得2sin (2x −π6)=1,2x −π6=2kπ+π6或2kπ+5π6,k ∈Z,即x =kπ+π6或x =kπ+π2,k ∈Z .(2)将f (x )的图象向左平移m (m >0)个单位长度, 得到y =2sin (2x +2m −π6)的图象,所得图象与函数y =2cos2x 的图象重合, 所以2m −π6=2kπ+π2,k ∈Zm =kπ+π3,k ∈Z. ,因为m >0,所以当k =0时,m 取得最小值,且最小值为π3. 【考点】函数y=Asin (ωx+φ)的图象变换由y=Asin (ωx+φ)的部分图象确定其解析式 正弦函数的图象 【解析】 此题暂无解析 【解答】解:(1)f (x )=√3sinωx −cosωx =2(√3sinωx −1cosωx)=2sin (ωx −π6).因为f (x )图象的相邻两条对称轴间的距离为π2, 所以f (x )的最小正周期为π.所以2πω=π,ω=2所以f (x )=2sin (2x −π6).令f (x )=1,可得2sin (2x −π6)=1,2x −π6=2kπ+π6或2kπ+5π6,k ∈Z,即x =kπ+π6或x =kπ+π2,k ∈Z .(2)将f (x )的图象向左平移m (m >0)个单位长度, 得到y =2sin (2x +2m −π6)的图象, 所得图象与函数y =2cos2x 的图象重合, 所以2m −π6=2kπ+π2,k ∈Zm=kπ+π3,k∈Z. ,因为m>0,所以当k=0时,m取得最小值,且最小值为π3.【答案】解:(1)当0<x<40时,W(x)=600x−10x(x+10)−350=−10x2+500x−350;当x≥40时,W(x)=600x−(601x+40000x −6550)−350=−(x+40000x)+6200,W(x)={−10x2+500x−350,0<x<40−(x+40000x)+6200,x≥40(2)若0<x<40,W(x)=−10(x−25)2+5900当x=25时,W(x)max=5900,若x≥40,W(x)=−(x+40000x)+6200≤6200−2√40000=5800当且仅当x=40000x,即x=200时,W(x)max=5800,∴年产量为25万部时,该公司所获年利润最大,最大年利润是5900万元.【考点】分段函数的应用基本不等式在最值问题中的应用函数最值的应用根据实际问题选择函数类型【解析】此题暂无解析【解答】解:(1)当0<x<40时,W(x)=600x−10x(x+10)−350=−10x2+500x−350;当x≥40时,W(x)=600x−(601x+40000x −6550)−350=−(x+40000x)+6200,∴W(x)={−10x2+500x−350,0<x<40−(x+40000x)+6200,x≥40.(2)若0<x<40,W(x)=−10(x−25)2+5900,当x=25时,W(x)max=5900,若x≥40,W(x)=−(x+40000x)+6200≤6200−2√40000=5800,当且仅当x=40000x,即x=200时,W(x)max=5800,∴年产量为25万部时,该公司所获年利润最大,最大年利润是5900万元.【答案】解:(1)由√3cosC+sinC=√3b且a=1可得a(√3cosC+sinC)=√3b,根据正弦定理可得√3sinB=√3sinAcosC+sinCsinA.∵A+B+C=π,∴sinB=sin(A+C),代人得√3sinAcosC+√3cosAsinC=√3sinAcosC+sinCsinA,∴√3cosAsinC=sinCsinA.∵0<C<π2,∴sinC≠0,∴tanA=√3,又∵0<A<π2,∴A=π3,设△ABC的外接圆的半径为R,由正弦定理可得2R=asinA=2√33,解得R=√33.(2)由(1)可知2R=2√33,∴2b−c=2×2√33sinB−2√33sinC=4√33sinB−2√33sin(2π3−B)=4√33sinB−√33sinB−cosB=√3sinB−cosB=2sin(B−π6).∵△ABC为锐角三角形,∴{0<B<π2,0<2π3−B<π2,即π6<B<π2,则0<B−π6<π3,0<2sin(B−π6)<√3,即2b−c的取值范围是(0,√3).【考点】正弦定理两角和与差的正弦公式【解析】此题暂无解析【解答】解:(1)由√3cosC+sinC=√3b且a=1可得a(√3cosC+sinC)=√3b,根据正弦定理可得√3sinB=√3sinAcosC+sinCsinA.∵A+B+C=π,∴sinB=sin(A+C),代人得√3sinAcosC+√3cosAsinC=√3sinAcosC+sinCsinA,∴√3cosAsinC=sinCsinA.∵0<C<π2,∴sinC≠0,∴tanA=√3,又∵0<A<π2,∴A=π3,设△ABC的外接圆的半径为R,由正弦定理可得2R=asinA =2√33,解得R=√33.(2)由(1)可知2R=2√33,∴2b−c=2×2√33sinB−2√33sinC=4√33sinB−2√33sin(2π3−B)=4√33sinB−√33sinB−cosB=√3sinB−cosB=2sin(B−π6).∵△ABC为锐角三角形,∴{0<B<π2,0<2π3−B<π2,即π6<B<π2,则0<B−π6<π3,0<2sin(B−π6)<√3,即2b−c的取值范围是(0,√3).【答案】解:(1)由题可知f(x)的定义域为(0,+∞),f′(x)=2−mx2+1x,x∈(0,+∞).因为x=1是f(x)的极值点,所以f′(1)=0,即2−m+1=0,解得m=3,当m=3时,f′(x)=2−3x2+1x=(x−1)(2x+3)x2,令f′(x)=0,可得x=1,当x∈(0,1)时f′(x)<0,f(x)单调递减,当x∈(1,+∞)时,f′(x)>0,f(x)单调递增,所以x=1是f(x)的极小值点.(2)由题可知g(x)=2x+lnx−mx(x>0),g′(x)=2+1x+mx2(x>0).因为g(x)在[1,2]上单调递增,所以g′(x)≥0在[1,2]上恒成立,即2+1x+mx2≥0在[1,2]上恒成立,所以m≥−2x2−x在[1,2]上恒成立,所以m≥(−2x2−x)max,x∈[1,2].因为在[1,2]上,(−2x2−x)max=−2×12−1=−3所以m≥−3,即m的取值范围是[−3,+∞).【考点】利用导数研究函数的极值利用导数研究函数的单调性【解析】此题暂无解析【解答】解:(1)由题可知f(x)的定义域为(0,+∞),f′(x)=2−mx2+1x,x∈(0,+∞).因为x=1是f(x)的极值点,所以f′(1)=0,即2−m+1=0,解得m=3,当m=3时,f′(x)=2−3x2+1x=(x−1)(2x+3)x2,令f′(x)=0,可得x=1,当x∈(0,1)时f′(x)<0,f(x)单调递减,当x∈(1,+∞)时,f′(x)>0,f(x)单调递增,所以x=1是f(x)的极小值点.(2)由题可知g(x)=2x+lnx−mx(x>0),g′(x)=2+1x+mx2(x>0).因为g(x)在[1,2]上单调递增,所以g′(x)≥0在[1,2]上恒成立,即2+1x+mx2≥0在[1,2]上恒成立,所以m≥−2x2−x在[1,2]上恒成立,所以m≥(−2x2−x)max,x∈[1,2].因为在[1,2]上,(−2x2−x)max=−2×12−1=−3所以m≥−3,即m的取值范围是[−3,+∞).【答案】解:(1)由题可知f′(x)=1x+a(x>0).当a≥0时,f′(x)>0,所以f(x)在(0,+∞)上单调递增,当a<0时,令f′(x)=0,可得x=−1a当x∈(0,−1a)时f′(x)>0,f(x)单调递增,当x∈(−1a,+∞)时f′(x)<0,f(x)单调递减.综上:当a≥0时f(x)在(0,+∞)上单调递增;当a<0时f(x)在(0,−1a )上单调递增,在(−1a,+∞)上单调递减.(2)由题可知g(x)=f(x)−x2−2=lnx+ax−x2g′(x)=1x−2x+a=−2x2+ax+1x,x>0令−2x02+ax0+1=0,解得x0=a+√a2+84(负值舍去).因为在(0,x0)上,g′(x)>0,g(x)单调递增,在(x0,+∞)上,g′(x)<0,g(x)单调递减,所以g(x)max=g(x0).当a=1时,x0=1,g(x)max=g(1)=0,此时g(x)只有一个零点1.当a>1时,x0=a+√a2+84>1,g(1)=a−1>0.令ℎ(x)=lnx−x+1,则ℎ′(x)=1x −1=1−xx所以当x∈(0,1)时,ℎ′(x)>0,ℎ(x)单调递增,当x∈(1,+∞)时,ℎ′(x)<0,ℎ(x)单调递减,所以ℎ(x)≤ℎ(1)=0,即lnx≤x−1.因为g(12a )=ln12a−14a2+12<12a−1−14a2+12=−14(1a−1)2−14<0g(2a)=ln2a−2a2<2a−1−2a2=−2(a−1)2−1<0所以g(x)在(12a,1)和(1,2a)上各有一个零点.综上可得:当a=1时,g(x)的零点个数为1,当a>1时,g(x)的零点个数为2.【考点】利用导数研究函数的单调性利用导数研究与函数零点有关的问题【解析】此题暂无解析【解答】解:(1)由题可知f′(x)=1x+a(x>0).当a≥0时,f′(x)>0,所以f(x)在(0,+∞)上单调递增,当a<0时,令f′(x)=0,可得x=−1a当x∈(0,−1a)时f′(x)>0,f(x)单调递增,当x∈(−1a,+∞)时f′(x)<0,f(x)单调递减.综上:当a≥0时f(x)在(0,+∞)上单调递增;当a<0时f(x)在(0,−1a)上单调递增,在(−1a,+∞)上单调递减.(2)由题可知g(x)=f(x)−x2−2=lnx+ax−x2g′(x)=1x−2x+a=−2x2+ax+1x,x>0令−2x02+ax0+1=0,解得x0=a+√a2+84(负值舍去).因为在(0,x0)上,g′(x)>0,g(x)单调递增,在(x0,+∞)上,g′(x)<0,g(x)单调递减,所以g(x)max=g(x0).当a=1时,x0=1,g(x)max=g(1)=0,此时g(x)只有一个零点1.当a>1时,x0=a+√a2+84>1,g(1)=a−1>0.令ℎ(x)=lnx−x+1,则ℎ′(x)=1x−1=1−xx所以当x∈(0,1)时,ℎ′(x)>0,ℎ(x)单调递增,当x∈(1,+∞)时,ℎ′(x)<0,ℎ(x)单调递减,所以ℎ(x)≤ℎ(1)=0,即lnx≤x−1.因为g(12a)=ln12a−14a2+12<12a−1−14a2+12=−14(1a−1)2−14<0g(2a)=ln2a−2a2<2a−1−2a2=−2(a−12)2−12<0所以g(x)在(12a,1)和(1,2a)上各有一个零点.综上可得:当a=1时,g(x)的零点个数为1,当a>1时,g(x)的零点个数为2.。
祁县第一中学2018-2019学年上学期高三数学10月月考试题

9. 已知一元二次不等式 f(x)<0 的解集为{x|x<﹣1 或 x> },则 f(10x)>0 的解集为( A.{x|x<﹣1 或 x>﹣lg2} C.{x|x>﹣lg2} B.{x|﹣1<x<﹣lg2}
D.{x|x<﹣lg2}
第 1 页,共 17 页
10.函数 y=2|x|的定义域为[a,b],值域为[1,16],当 a 变动时,函数 b=g(a)的图象可以是(
座号_____
姓名__________
分数__________
的焦点重合,则 m 的值等于(
3. Sn 是等差数列{an}的前 n 项和,若 3a8-2a7=4,则下列结论正确的是( A.S18=72 C.S20=80 4. 已知 P(x,y)为区域 ( A.6 ) B.0 C.2
x
D.2
5. 设函数 f x e 取值范围是( A.
由图可得 A(a,﹣a),B(a,a),
第 6 页,共 17 页
由 ∴A(2,﹣2),
,得 a=2.
化目标函数 z=2x﹣y 为 y=2x﹣z, ∴当 y=2x﹣z 过 A 点时,z 最大,等于 2×2﹣(﹣2)=6. 故选:A. 5. 【答案】D 【解析】
考 点:函数导数与不等式.1 【思路点晴】本题主要考查导数的运用,涉及划归与转化的数学思想方法.首先令 f x 0 将函数变为两个函 数 g x e 范围. 6. 【答案】D 【解析】解:命题 p:∃x∈R,cosx≥a,则 a≤1. 下列 a 的取值能使“¬p”是真命题的是 a=2. 故选;D. 7. 【答案】C 【解析】解:不等式(m+1)x2﹣(m﹣1)x+3(m﹣1)<0 对一切 x∈R 恒成立, 即(m+1)x2﹣(m﹣1)x+3(m﹣1)<0 对一切 x∈R 恒成立 若 m+1=0,显然不成立 若 m+1≠0,则 解得 a .
山西省晋中祁县中学校高三英语10月月考试题

山西省晋中市祁县中学校2020届高三英语10月月考试题满分:150分第一部分阅读理解(满分60分)第一节(共15小题;每小题3分,满分45分)阅读下列短文,从每题所给的A、B、C和D 四个选项中,选出最佳选项。
AMake a five-minute film and win!Do you love the summer holidays but hate being bored? Then why don't you enter the Film Street Summer Shorts Competition by making a short film this summer with your family and friends?What you have to doTo enter the competition, you have to make a short film that around 5 minutes long(It can be shorter but not longer!) on a digital camera, or mobile phone.AwardsThe best short film entered into our competition will be shown in Film Street 's Cinema and you 'll win a Cineworld Cinemas pass for yourself and there more for other members of your film crew. If you have a Cineworld Cinemas pass, you can watch as many films as you like for a year, for free, at any Cineworld Cinema!Rules.We can't show films that tell others about either your, or any other kids',name or address..We can't show films that hurt, harm or insult(侮辱)other people..We can't show films that have bad language.Copyright ChecklistGetting permission to use someone else's work in your film can be expensive, so check your film to make sure that:.Your film is original and you haven't copied someone else..There are no scenes of branding on shop signs, books,magazines or CDs..There are no scenes of someone else's artwork.Address and DatePost your finished film on tape,CD or DVD by Monday,October1st,2007 to:Unit 6,Third Floor, The Bond180-182 Fazeley Street; BirminghamSo what's stopping you? Start making your Film Street Summer Short now!21、Who is the passage written for .A.actorsB.teachersC.childrenD.parents22、From the third paragraph, we can learn that_______.A.the competition is held by Cineworld CinemasB.the winner can watch films for free for one year at any Cineworld CinemaC.the winner’s film will be paid for his short filmD.the winner’s short film can be shown in any cinema23、The unde rlined part "original" is closest in meaning to “_________”.A.good for childrenB.made by yourselfC.full of exciting momentsD.interesting enoughBLuciano Baietti, a retired school headmaster from Italy, holds the Guinness record for the most university degrees. The 70-year-old currently has 15 bachelors or。
山西省晋中市祁县中学届高三历史上学期10月月考试题复习班

山西省晋中市祁县中学2021届高三历史上学期10月月考试题(复习班)第I卷(选择题)一、选择题(共32小题,每小题1.5分,共计48分。
在每小题列出的四个选项中,只有一项是最佳选项)1.周初,《牧誓》和《大浩》上皆称诸侯曰“友邦君”,是君臣之分亦未全定也。
逮克殷践奄,灭国数十,而新建之国皆其功臣、昆弟、甥舅,本周之臣子;由是天子之尊,非复诸侯之长,而为诸侯之君。
这一变化表明周王室( )A.强化了中央对地方的管理 B.借助了宗族势力维系统治C.借鉴了殷商地方管理模式 D.明确了同地方的隶属关系2.秦朝统一后,对原属燕国的辽西走廊和辽东地区采取设置郡县、开辟交通等措施,这与其统治中原内地的措施并无不同,且是同时进行的,增修燕之北长城与修筑北方的长城也没有区别。
这些措施的施行意在( )A.建立大一统的国家 B.强化国家文化认同C.消除地方割据隐患 D.协调区域经济发展3.唐朝前期设立政事堂作为宰相议事处所,凡遇军国大事,皆由政事堂会议商议决定,经皇帝批准后,以诏令形式颁布执行。
当时所有以皇帝诏敕形式颁行的政府诏令,既须皇帝画敕,又须中书、门下两省共同认可,并经政事堂盖印,否则便不具有合法性。
由此可知 ( ) A.朝议制度减少了君主的决策失误B.政事堂会议形成了民主政治的雏形C.皇帝与宰相的权力都受到了限制D.独立于皇权之外的决策机构已形成4.《后汉书》中出现了许多诸如“家世州郡”、“家世衣冠”、“世仕州郡”、“世吏两千石”、“家世两千石”的话语,这在关于西汉历史的史料中是很少出现的。
东汉时期的这一现象反映了( )A.中央和地方存在着尖锐的矛盾 B.门阀士族的政治作用显著提高C.血缘宗族力量制约了专制皇权 D.豪强势力推动了国家政权发展5.如表反映的是明代内阁大臣在阁年限统计情况。
这种状况( )C.说明了内阁辅助作用不大D促进了官吏队伍的年轻化6.黑格尔说,大海邀请人类从事征服和掠夺,但同时也鼓励人类追求利润,从事商业……平凡的土地和平原流域把人类束缚在土地上,而大海却挟着人类超越了那些思想和行动的有限圈子。
2020届山西省晋中市祁县中学高三上学期10月月考检测语文试题及答案

绝密★启用前山西省晋中市祁县中学2020届高三年级上学期10月月考检测语文试题2019年10月第Ⅰ卷阅读题一、现代文阅读(36分)(一)论述类文本阅读(9分,每小题3分)阅读下面的文字,完成1-3题。
先秦儒家已形成比较立体、丰富的生态伦理思想。
这种思想首先体现为“乐”。
孔子非常擅长在观察自然现象时对自身社会经验进行审视和升华,自然之道和其处世之道在某个合适的时间节点产生共鸣,从而引发孔子深层的思考,其生态情怀也在类似的体悟中逐渐浓厚。
认知自然、体验自然、进而体悟人生哲理,让孔子得出“知者乐水,仁者乐山”这样的结论。
由“乐”而生“畏”。
孔子说:“天何言哉?四时行焉,百物生焉。
天何言哉!”在孔子看来,四季的轮回、万物的生长都有其运行轨迹和规律,这种力量非人力所能干涉,孔子对自然的敬畏之情也在这种感慨中毕现。
荀子则认为:“天行有常,不为尧存,不为桀亡。
”既然这种“常”的力量如此强大,非人力所能改变,聪明的做法就是顺应这种力量并对之合理利用,即荀子所讲的“制天命而用之”。
那么,该如何“制”呢?荀子较为强调见微知著、因循借力、顺时守天、因地制宜。
这种总结比起孔子体验式思维多了些理性,已试图对联系自然与人类社会的“道”进行理性阐释和总结。
在此基础上,“推人及物”的思想就产生了。
“人皆有不忍人之心”是孟子生态道德的基础,“不忍心”推广于自然万物就成了推人及物的生态道德。
如果说“老吾老以及人之老,幼吾幼以及人之幼,……故推恩足以保四海,不推恩无以保妻子”是简单适用于人类社会的推恩思维,是简单的换位思考、推己及人,那么,孟子的“亲亲而仁民,仁民而爱物”则已拓展为推人及物了。
荀子也说:“物也者,大共名也……推而别之,别则有别,至于无别然后至。
”他认为自然万物有着千丝万缕的联系,有共性,有同质性;同时,根据某种特质,又可在共性的基础上区分差异,剥离出异质性。
这种异质性基础上的同质性是推人及物的逻辑基石。
在生态实践中,先秦儒者非常强调“时禁”与适度消费。
祁县高中2018-2019学年上学期高三数学10月月考试题

祁县高中2018-2019学年上学期高三数学10月月考试题 班级__________ 座号_____ 姓名__________ 分数__________一、选择题(本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的.)1. 某几何体的三视图如图所示,则该几何体为( )A .四棱柱B .四棱锥C .三棱台D .三棱柱2. 已知集合},052|{2Z x x x x M ∈<+=,},0{a N =,若∅≠N M ,则=a ( ) A .1- B . C .1-或 D .1-或2-3. 已知直线l的参数方程为1cos sin x t y t αα=+⎧⎪⎨=⎪⎩(t 为参数,α为直线l 的倾斜角),以原点O 为极点,x 轴正半轴为极轴建立极坐标系,圆C 的极坐标方程为4sin()3πρθ=+,直线l 与圆C 的两个交点为,A B ,当||AB 最小时,α的值为( )A .4πα=B .3πα=C .34πα=D .23πα=4. 已知,y 满足不等式430,35250,1,x y x y x -+≤⎧⎪+-≤⎨⎪≥⎩则目标函数2z x y =+的最大值为( )A .3B .132C .12D .15 5. 正方体的内切球与外接球的半径之比为( ) A.B.C.D.6. 已知变量与正相关,且由观测数据算得样本平均数,,则由该观测的数据算得的线性回归方程可能是( ) ABCD7. 设集合{}|||2A x R x =∈≤,{}|10B x Z x =∈-≥,则A B =( )A.{}|12x x <≤B.{}|21x x -≤≤C. {}2,1,1,2--D. {}1,2【命题意图】本题考查集合的概念,集合的运算等基础知识,属送分题.8. 若当R x ∈时,函数||)(x a x f =(0>a 且1≠a )始终满足1)(≥x f ,则函数3||log x x y a =的图象大致是 ( )【命题意图】本题考查了利用函数的基本性质来判断图象,对识图能力及逻辑推理能力有较高要求,难度中等.9. 若变量x ,y 满足:,且满足(t+1)x+(t+2)y+t=0,则参数t 的取值范围为( )A .﹣2<t <﹣B .﹣2<t ≤﹣C .﹣2≤t ≤﹣D .﹣2≤t <﹣10.函数()f x 在定义域R 上的导函数是'()f x ,若()(2)f x f x =-,且当(,1)x ∈-∞时,'(1)()0x f x -<,设(0)a f =,b f =,2(log 8)c f =,则( )A .a b c <<B .a b c >>C .c a b <<D .a c b <<11.已知双曲线C :22221x y a b-=(0a >,0b >),以双曲线C 的一个顶点为圆心,为半径的圆被双曲线C 截得劣弧长为23a π,则双曲线C 的离心率为( )A .65B .5C .5D .512.已知全集为R ,集合{}|23A x x x =<->或,{}2,0,2,4B =-,则()R A B =ð( )A .{}2,0,2-B .{}2,2,4-C .{}2,0,3-D .{}0,2,4二、填空题(本大题共4小题,每小题5分,共20分.把答案填写在横线上)13.如图,在棱长为的正方体1111D ABC A B C D -中,点,E F 分别是棱1,BC CC 的中点,P 是侧面11BCC B 内一点,若1AP 平行于平面AEF ,则线段1A P 长度的取值范围是_________.14.函数()x f x xe =在点()()1,1f 处的切线的斜率是 .15.不等式0<1﹣x 2≤1的解集为 .16.当下社会热议中国人口政策,下表是中国人民大学人口预测课题组根据我过2000年第五次人口普查预测年份 2030 2035 2040 2045 2050 年份代号t 1 2 3 4 5 所占比例y6865626261的线性回归方程为附:回归直线的斜率和截距的最小二乘估计公式分别为: =, =﹣.三、解答题(本大共6小题,共70分。
山西省晋中市祁县中学校2020届高三地理10月月考试题
山西省晋中市祁县中学校2020届高三地理10月月考试题本试卷分为选择题和非选择题两部分,考试时间90分钟,满分100分第I卷(选择题)一、选择题(共28小题,每小题1.5分,共计42分。
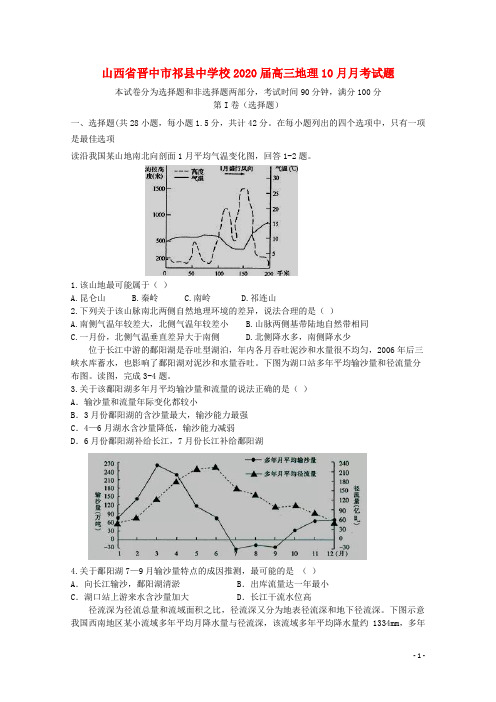
在每小题列出的四个选项中,只有一项是最佳选项读沿我国某山地南北向剖面1月平均气温变化图,回答1-2题。
1.该山地最可能属于()A.昆仑山B.秦岭C.南岭D.祁连山2.下列关于该山脉南北两侧自然地理环境的差异,说法合理的是()A.南侧气温年较差大,北侧气温年较差小B.山脉两侧基带陆地自然带相同C.一月份,北侧气温垂直差异大于南侧D.北侧降水多,南侧降水少位于长江中游的鄱阳湖是吞吐型湖泊,年内各月吞吐泥沙和水量很不均匀,2006年后三峡水库蓄水,也影响了鄱阳湖对泥沙和水量吞吐。
下图为湖口站多年平均输沙量和径流量分布图。
读图,完成3-4题。
3.关于该鄱阳湖多年月平均输沙量和流量的说法正确的是()A.输沙量和流量年际变化都较小B.3月份鄱阳湖的含沙量最大,输沙能力最强C.4—6月湖水含沙量降低,输沙能力减弱D.6月份鄱阳湖补给长江,7月份长江补给鄱阳湖4.关于鄱阳湖7—9月输沙量特点的成因推测,最可能的是()A.向长江输沙,鄱阳湖清淤 B.出库流量达一年最小C.湖口站上游来水含沙量加大 D.长江干流水位高径流深为径流总量和流域面积之比,径流深又分为地表径流深和地下径流深。
下图示意我国西南地区某小流域多年平均月降水量与径流深,该流域多年平均降水量约1334mm,多年平均实际蒸发量约920mm,地表和地下多年平均径流深合计约为757mm。
据此完成5-6题。
5. 该流域5月较4月降水量明显增加,而径流深增加缓慢,与此不相关的是()A. 3、4月地表较为干燥B. 前期地下溶孔裂隙处于非饱和状态C. 4、5月农业用水较多D. 流域内植被茂盛,水流汇聚速度慢6. 若不考虑人类因素,下列有关该流域的说法正确的是()A. 有流域外地下径流汇入B. 有流域外地表径流汇入C.该流域水资源总量减少D. 流域内地表水下渗严重下图为亚洲东部及太平洋地区某时刻近地面等压线图(单位:hPa),读图回答7-9题。
山西省祁县中学2016届高三10月月考数学(理)试卷

祁县中学2015—2016学年高三10月月考数学理科试题一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.“p 或q 是假命题”是“非p 为真命题”的( ) A .充分而不必要条件 B .必要而不充分条件C .充要条件D .既不充分也不必要条件2.已知集合⎭⎬⎫⎩⎨⎧≥--=031x x xA ,⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+-==)4(log 21x y x B ,则=B A C R )(( )A. φ B .{}3 C .{}43<≤x x D .{}41<<x x3.函数f(x)的图象向右平移一个单位长度,所得图象与xy e =关于y 轴对称,则f(x)=( )A.1+x e B. 1-x e C. 1+-x e D. 1--x e4.若存在正数x 使2()1x x a -<成立,则a 的取值范围是( )A.(,)-∞+∞ B .(2,)-+∞ C. (0,)+∞ D .(1,)-+∞ 5.由曲线1=xy 及直线2,==y x y 围成的平面图形的面积是( )A.87B. 2ln 23-C.2ln 23+D.825 6.已知函数1)391ln()(2+-+=x x x f ,则=+)21(lg )2(lg f f ( )A .1-B .0C .1D .27.函数ππln cos 22y x x ⎛⎫=-<< ⎪⎝⎭的图象是( )8.若函数32)(2++-=x x x f ,则)(x f 的单调递增区间是( )A. []1,1- B .)1,(-∞ C. []3,1 D. ),1(+∞9.已知函数)3(log )(22a ax x x f +-=在区间[)+∞,2上是增函数,则实数a 的取值范围是( )A. (]4,∞- B .(],44- C. (],24- D . (][)∞+⋃-∞-,,24 10.已知函数)(ln )(ax x x x f -=有两个极值点,则实数a 的取值范围是( )A .)0,(-∞B .)21,0(C . )1,0(D .),0(+∞11.设函数3y x =与22xy -=的图象的交点为00()x y ,,则0x 所在的区间是( ) A .(01), B .(12),C .(23),D .(34),12. 设定义在R 上的函数)(x f 是最小正周期为π2的偶函数,)('x f 是)(x f 的导函数,当],0[π∈x 时,1)(0<<x f ;当),0(π∈x 且2π≠x 时,0)(')2(>-x f x π,则函数x x f y sin )(-=在]2,2[ππ-∈x 上的零点个数为( )A .2B .4 C.5 D. 8二、填空题:本大题共4小题,每小题5分,共20分.将答案填在答题卡中的横线上.13.设ax x f x ++=)110lg()(是偶函数,x x bx g 24)(-=是奇函数,那么b a +的值是_______14.函数()f x 对于任意实数x 满足条件()()12f x f x +=,若()15,f =-则()()5f f =_______ .15.设曲线*)(1N n xy n ∈=+在点)1,1(处的切线与x 轴的交点的横坐标为n x ,令n n x a lg =,则9921a a a +++ 的值为_______ .16.已知,给出以下四个命题:xx(1)若,则;(2)直线是函数图象的一条对称轴;(3)在区间上函数是增函数;(4)函数的图象可由的图象向右平移个单位而得到.其中正确命题的序号为_______ .三、解答题:本大题共6小题,共70分. 解答应写出文字说明、证明过程或演算步骤. 17.(本大题满分10分)已知锐角ABC ∆中,内角C B A 、、的对应边分别为c b a 、、,且 C b c B c b A a sin )2(sin )2(sin 2-+-= (1)求角A 的大小;(2)求C B cos cos 2+的取值范围 18.(本大题满分12分)若函数431)(23+-+=bx ax x x f 在2-=x 和1=x 处取的极值. (1)求函数()f x 的解析式;(2)讨论方程()f x k =实数解的个数.19. (本大题满分12分)已知是定义在上的偶函数,且时,.(1)求,;(2)求函数的表达式;(3)若,求的取值范围.20.(本小题满分12分)已知集合{}⎭⎬⎫⎩⎨⎧<+--=<+--=0)1(2,0)]13()[2(2a x a x xB a x x x A (1)当B A a 时,求2=; (2)求使A B ⊆的实数a 的取值范围。
山西省祁县中学高三数学10月月考试题 文

祁县中学2015---2016学年高三10月月考数学(文科)试题一.选择题(本大题共有12个小题,每小题5分,共60分)1.已知集合P={x ∈N|1≤x ≤10},集合Q={x ∈R|06--2=x x },则P ∩Q 等于( )A.{2}B.{1,2}C. {2,3}D.{3} 2.若函数)2(),3,0[)1(xf x f 则的定义域为+的定义域为( )A .[1,8]B .[1,4)C .[0,2)D .[0,2]3. 函数3)(5-+=x x x f 的零点落在的区间是( )A .[]1,0B .[]2,1C .[]3,2D .[]4,34.已知10.20.7321.5, 1.3,()3a b c -===,则,,a b c 的大小为 ( )A.c a b <<B. c b a <<C. a b c <<D. a c b <<5.在R 的定义运算: ⎝⎛c a bc ad d b -=⎪⎪⎭⎫,若不等式 ⎝⎛+-11a x 12≥⎪⎪⎭⎫-x a 对任意实数x 恒成立,则实数a 的最大值为( )A .21-B .23- C .21 D .236. 下列判断错误..的是( )A .“22bm am <”是“a < b ”的充分不必要条件B .命题“01,23≤--∈∀x x R x ”的否定是“ 01,23>--∈∃x x R x ”C .若f (x)是定义在R 上的奇函数,且f (x+2)也为奇函数,则f (x)是以4为周期的周期函数.D .若q p Λ为假命题, 则p, q 均为假命题7若把函数x x y 2sin -2cos 3=的图象向右平移0)(>m m 个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是( )A .π3 B .12π C .π6 D .5π6 8.函数f(x)=ln(4+3x -x 2)的单调递减区间是( ) A.),(∞+23 B.),(23-∞ C.),(41- D. ),(423 9. 函数1ln --=x e y x的图象大致是( )10. 若定义在R 上的函数)(-)1()(x f x f x f y =+=满足满足,且当]1,1[-∈x 时,2)(x x f =,函数⎩⎨⎧≤>=1,21),1-(log )(3x x x x g x ,则函数)(-)()(x g x f x h =在区间]5,5[-内的零点的个数为( )A .6 B. 7 C. 8 D. 911. 已知函数()f x 是定义在实数集R 上得不恒为零的偶函数,且对任意实数x 都有(1)(1)()xf x x f x +=+,则5()2f =( )A .0 B.12C.1D.5212. 设()f x 是R 上的偶函数,对任意x R ∈,都有(2)(2),f x f x -=+且当[2,0]x ∈-时,1()()1,(2,6]2x f x =--若在区间内关于x 的方程()log (2)0(1)a f x x a -+=>恰有3个不同的实数根,则a 的取值范围是( )A .(1,2)B .(2,)+∞ C. D.二.填空题13.已知:()()110p x m x m -+--<;:1223q x <<,若q 是p 的充分不必要条件, 则实数m 的取值范围是___________________。
2020届山西省晋中市祁县中学高三上学期10月月考检测物理试题及答案

绝密★启用前山西省晋中市祁县中学2020届高三年级上学期10月月考检测物理试题2019年10月一、单选题(本大题共8小题,共32.0分)1.一物体在几个力的共同作用下通过一段位移,其中恒力、做功分别为、,下列说法正确的是( )A. 这两个力大小一定不相等B. 比做的功多C. 这两个力做的总功为14 JD. 可能比大2.一物体从某一行星表面竖直向上抛出不计空气阻力。
时抛出,位移随时间变化的图象如图所示,则A. 该物体上升的时间为5sB. 该行星表面的重力加速度为C. 该物体被抛出时的初速度为D. 该物体落到行星表面时的速度为3.弹簧发生形变时,其弹性势能的表达式为,其中k是弹簧的劲度系数,x是形变量如图,一质量为m物体位于一直立的轻弹簧上方h高度处,该物体从静止开始落向弹簧设弹簧的劲度系数为k,则物块的最大动能为弹簧发生的形变在弹性限度内( )A.mghB.C. D.4.如图所示,一同学用双手手未画出水平对称地用力将两长方体课本夹紧,且同时以加速度a竖直向上匀加速捧起已知课本A质量为m,课本B质量为2m,手垂直课本的作用力大小为F,书本A、B之间动摩擦因数为用整体法与隔离法可分析出此过程中,书A受到书B施加的摩擦力大小为( )A. FB.C.D.5、如图所示,质量为M的小车放在光滑水平面上,小车上用细线悬吊一质量为m的小球,M>m,用一力F水平向右推小球,使小球和车一起以加速度a向右运动时,细线与竖直方向成α角,细线的拉力为T。
若用一力F′水平向左拉小车,使小球和车一起以加速度a′向左运动时,细线与竖直方向也成α角,细线的拉力为T′。
则A、a′=a,T′=TB、a′>a,T′=TC、a′<a,T′>TD、aʹ<a,T′<T6、关于曲线运动,下说法中正确的是 ( )A.在恒力作用下,物体不可以做曲线运动B. 曲线运动的加速度可以为零C. 曲线运动一定是变速运动D. 物体做曲线运动,动能一定会发生变化7、我国的“神舟”系列航天飞船的成功发射和顺利返回,显示了我国航天事业取得的巨大成就已知地球的质量为M,引力常量为G,飞船的质量为m,设飞船绕地球做匀速圆周运动的轨道半径为r,则A. 飞船在此轨道上的运行速率为。
山西省晋中市祁县中学校2020届高三语文10月月考试题

山西省晋中市祁县中学校2020届高三语文10月月考试题第Ⅰ卷阅读题一、现代文阅读(36分)(一)论述类文本阅读(9分,每小题3分)阅读下面的文字,完成1-3题。
先秦儒家已形成比较立体、丰富的生态伦理思想。
这种思想首先体现为“乐”。
孔子非常擅长在观察自然现象时对自身社会经验进行审视和升华,自然之道和其处世之道在某个合适的时间节点产生共鸣,从而引发孔子深层的思考,其生态情怀也在类似的体悟中逐渐浓厚。
认知自然、体验自然、进而体悟人生哲理,让孔子得出“知者乐水,仁者乐山"这样的结论。
由“乐"而生“畏”。
孔子说:“天何言哉?四时行焉,百物生焉。
天何言哉!"在孔子看来,四季的轮回、万物的生长都有其运行轨迹和规律,这种力量非人力所能干涉,孔子对自然的敬畏之情也在这种感慨中毕现.荀子则认为:“天行有常,不为尧存,不为桀亡。
"既然这种“常”的力量如此强大,非人力所能改变,聪明的做法就是顺应这种力量并对之合理利用,即荀子所讲的“制天命而用之"。
那么,该如何“制"呢?荀子较为强调见微知著、因循借力、顺时守天、因地制宜。
这种总结比起孔子体验式思维多了些理性,已试图对联系自然与人类社会的“道”进行理性阐释和总结。
在此基础上,“推人及物"的思想就产生了。
“人皆有不忍人之心”是孟子生态道德的基础,“不忍心”推广于自然万物就成了推人及物的生态道德。
如果说“老吾老以及人之老,幼吾幼以及人之幼,……故推恩足以保四海,不推恩无以保妻子"是简单适用于人类社会的推恩思维,是简单的换位思考、推己及人,那么,孟子的“亲亲而仁民,仁民而爱物”则已拓展为推人及物了。
荀子也说:“物也者,大共名也……推而别之,别则有别,至于无别然后至."他认为自然万物有着千丝万缕的联系,有共性,有同质性;同时,根据某种特质,又可在共性的基础上区分差异,剥离出异质性。
这种异质性基础上的同质性是推人及物的逻辑基石。
2021届山西省晋中市祁县中学高三上学期10月月考数学(理)试题(复习班)

2021届山西省晋中市祁县中学高三上学期10月月考数学(理科)试题一、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1、若函数22log(23)y x x=--的定义域,值域分别是,M N,则=NMCR)(( )A、[1,3]-B、(1,3)-C、(0,3]D、[)3,+∞2、复数iziz-=+=θθsin,cos21,则21zz-的最大值为()A、5B、5C、6D、63、已知实数a满足01a<<,则”21x-<”是函数2()log(23)af x x x=+-单调递减的( )A、充分不必要条件B、必要不充分条件C、充要条件D、既不充分也不必要条件4、已知非零向量,m n满足35=m n,1cos,5=m n.若()t⊥+n m n,则实数t的值为( )A、35-B、38C、3-D、35、曲线e xy=,e xy-=和直线1x=围成的图形面积是( )A、1e e--B、1e e-+C、1e e2---D、1e e2-+-6、用火柴棒按如图的方法搭三角形:按图示的规律搭下去,则第100个图形所用火柴棒数为( )A、401B、201C、402D、2027、已知在ABC△中,点M在边BC上,且2BC CM=-,点E在边AC上,且12AE EC=,则向量EM=( )A、1123AC AB+B、1162AC AB+C、1126AC AB+D、1362AC AB+8、已知数列{}n a的首项为2,且数列{}n a满足111nnnaaa+-=+,数列{}n a的前n项的和为n S,则1008S等于( )A 、504B 、294C 、294-D 、504-9、若将函数2sin 2y x =的图像向左平移π12个单位长度,则平移后图象的对称轴为( ) A 、 ππ26k x =-(Z)k ∈B 、ππ26k x =+(Z)k ∈C.、ππ212k x =-(Z)k ∈D 、ππ212k x =+(Z)k ∈10、ABC △的内角,,A B C 的对边分别为,,a b c 22cos c b A +=,则角B 的大小为( ) A 、π6B 、π3C 、2π3D 、5π611、已知非零向量AB 与AC 满足()0AB AC BC ABAC⋅=+且3BC AB =,则ABC △为( )A 、等腰非等边三角形B 、直角三角形C 、等边三角形D 、三边均不相等的三角形12、已知对任意实数x 都有()()'2e xf x f x -=,()01f =-,若()()1f x k x >-恒成立,则k 的取值范围是( ) A 、()1,+∞B 、323,4e 2⎛⎫ ⎪⎝⎭C 、121,4e ⎛⎫ ⎪⎝⎭D 、3214e ⎛⎫ ⎪⎝⎭,二、填空题(每小题5分,共20分)13、已知函数()f x 的定义域为[]0,2,则()()21f xg x x =-的定义域为14、已知sin 1si ())n(αβαβ+=-,-=725-,则tan tan αβ= 15、已知函数1()cos 2(2)sin 2f x m x m x =+-,其中12m ≤≤.若函数()f x 的最大值 记为()g m ,则()g m 的最小值为16、已知函数3()33333x xf x x x -=--+-+,若22(3)(1)6f a f b +-=,则的最大值是17、(本题10分)在公差不为0的等差数列{}n a 中,841,,a a a 成等比数列,数列{}n a 的前10项和为45.(1)求数列{}n a 的通项公式;(2)若11+=n n n a a b ,数列{}n b 的前n 项和为n T ,求n T .2()2cos ()214f x x x π=-+(1)求函数f x ()的最小正周期及对称轴方程; (2)若不等式2)(2<-<-m x f 在,42x ππ⎡⎤∈⎢⎥⎣⎦上恒成立,求实数m 的取值范围.19、(本题12分)设等差数列{}n a 的公差为d ,点(,)n n a b 在函数()2xf x =的图象上(*N n ∈).(1)若12a =-,点87(,4)a b 在函数()f x 的图象上,求数列{}n a 的前n 项和n S ; (2)若11a =,函数()f x 的图象在点22(,)a b 处的切线在x 轴上的截距为12ln 2-,求数列n n a b ⎧⎫⎨⎬⎩⎭的前n 项和n T .20、(本题12分)设函数()e cos xf x a x =+,其中R a ∈. (1)已知函数()f x 为偶函数,求a 的值; (2)若1a =,证明:当0x >时,()2f x >;(3)若()f x 在区间[]0,π内有两个不同的零点,求a 的取值范围.21、(本题12分)在①(2)sin (2)sin 2sin ab A b a Bc C +++= ②sin cos a A a C =-,③ABC △的面积)(43222c b a S ABC -+=∆这三个条件中任选一个,补充在下面的问题中,作为问题的条件,再解答这个问题在ABC △中,角,,A B C 的对边分别是,,a b c ,若c =,且_______,探究ABC △的周长l 是否存在最大值?若存在,求出l 的最大值;若不存在,说明理由。
山西省祁县中学高三地理10月月考试题新人教版

2013届高三10月月考试题第I卷(选择题,共66分)一、选择题(0每题给出的四个选项中有一个以上是正确的,将正确的选项填在后面的答题卡上,选错、漏选均不得分。
)钓鱼岛全称“钓鱼台群岛”,它由钓鱼岛、黄尾岛、赤尾岛、南小岛、北小岛、大南小岛、大北小岛和飞濑岛等岛屿组成,总面积约7平方公里,是我国固有领土。
其大致位置:东经123°,北纬26°。
我国福建福州经度:119°18′E 纬度:26°4′N,完成5-6题。
1.钓鱼岛与福州的距离大约是A.190km B.390km C.590km D.790km2.6月22日,当北京天安门广场上人民英雄纪念碑影子最短时,太阳位于钓鱼岛的A.东南B.西南C.东北 D.西北3地理教学中经常用一些示意图来表示地理现象的发生与变化。
下列四图中能够正确表示地理现象发生与变化的是()A.①②B.③④ C.②③ D.①④某科考队结束了两个月的海上考察,于4月21日返回到P地。
图3为P地所在区域当日某时地面形势图。
读图回答4~6题。
4.此时可能出现连续性降水的地方是( )A.①B.②C.③D.④5.在科学考察中,利用遥感技术可以( )A.获取卫星云图 B.查询地理数据C.选择考察路线 D.对科考船实时导航6.科考队出发日P地昼长为11小时,返回到P地时,P地当日的昼长约为( )A.10小时 B.11小时C.13小时 D.14小时图3是2012年4月18日8时—4月19日8时我国部分地区降水分布示意图。
读图回答7~8题。
7.形成图示地区降水的主要原因是( )A.高压脊控制B.锋面活动C.反气旋过境 D.热带气旋影响8.若图示降水持续多日,最易发生洪涝的地区是( )A.江汉平原 B.四川盆地C.珠江三角洲 D.长江三角洲C.强对流降雨天气D.沙尘暴天气读亚洲部分地区四个季度平均气温分布图,回答9~10题。
9.据图5气温分布状况判断,四幅图由第一季度到第四季度的正确排序是( )A.①→②→③→④B.①→②→④→③C.③→④→②→①D.③→①→②→④10.下列气候统计图中,反映了图5中K城市气候特征的是( )A B C D图6图3为东非高原基塔莱和多多马的降水资料及两地之间游牧路线示意图。
山西省晋中市祁县中学校2020届高三物理10月月考试题

山西省晋中市祁县中学校2020届高三物理10月月考试题一、单选题(本大题共8小题,共32。
0分)1.一物体在几个力的共同作用下通过一段位移,其中恒力、做功分别为、,下列说法正确的是( )A。
这两个力大小一定不相等 B. 比做的功多C。
这两个力做的总功为14 J D。
可能比大2.一物体从某一行星表面竖直向上抛出不计空气阻力。
时抛出,位移随时间变化的图象如图所示,则A。
该物体上升的时间为5sB。
该行星表面的重力加速度为C。
该物体被抛出时的初速度为D. 该物体落到行星表面时的速度为3.弹簧发生形变时,其弹性势能的表达式为,其中k是弹簧的劲度系数,x是形变量如图,一质量为m物体位于一直立的轻弹簧上方h高度处,该物体从静止开始落向弹簧设弹簧的劲度系数为k,则物块的最大动能为弹簧发生的形变在弹性限度内( )A.mghB.C. D。
4.如图所示,一同学用双手手未画出水平对称地用力将两长方体课本夹紧,且同时以加速度a竖直向上匀加速捧起已知课本A质量为m,课本B质量为2m,手垂直课本的作用力大小为F,书本A、B之间动摩擦因数为用整体法与隔离法可分析出此过程中,书A受到书B施加的摩擦力大小为()A. FB. C。
D.5、如图所示,质量为M的小车放在光滑水平面上,小车上用细线悬吊一质量为m的小球,M>m,用一力F 水平向右推小球,使小球和车一起以加速度a向右运动时,细线与竖直方向成α角,细线的拉力为T。
若用一力F′水平向左拉小车,使小球和车一起以加速度a′向左运动时,细线与竖直方向也成α角,细线的拉力为T′。
则A、a′=a,T′=TB、a′>a,T′=TC、a′<a,T′>TD、aʹ<a,T′<T6、关于曲线运动,下说法中正确的是()A.在恒力作用下,物体不可以做曲线运动B。
曲线运动的加速度可以为零C。
曲线运动一定是变速运动D. 物体做曲线运动,动能一定会发生变化7、我国的“神舟"系列航天飞船的成功发射和顺利返回,显示了我国航天事业取得的巨大成就已知地球的质量为M,引力常量为G,飞船的质量为m,设飞船绕地球做匀速圆周运动的轨道半径为r,则A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
祁县中学高三10月月考数学(文科)试题一.选择题(本大题共有12个小题,每小题5分,共60分)1.已知集合P={x ∈N|1≤x ≤10},集合Q={x ∈R|06--2=x x },则P ∩Q 等于( )A.{2}B.{1,2}C.{2,3}D.{3} 2.若函数)2(),3,0[)1(x f x f 则的定义域为+的定义域为( )A .[1,8]B .[1,4)C .[0,2)D .[0,2]3. 函数3)(5-+=x x x f 的零点落在的区间是( )A .[]1,0B .[]2,1C .[]3,2D .[]4,3 4.已知10.20.7321.5, 1.3,()3a b c -===,则,,a b c 的大小为 ( )A.c a b <<B. c b a <<C. a b c <<D. a c b << 5.在R 的定义运算: ⎝⎛c a bc ad d b -=⎪⎪⎭⎫,若不等式 ⎝⎛+-11a x 12≥⎪⎪⎭⎫-x a 对任意实数x 恒成立,则实数a 的最大值为( )A .21-B .23- C .21 D .236. 下列判断错误..的是( ) A .“22bm am <”是“a < b ”的充分不必要条件B .命题“01,23≤--∈∀x x R x ”的否定是“ 01,23>--∈∃x x R x ”C .若f (x)是定义在R 上的奇函数,且f (x+2)也为奇函数,则f (x)是以4为周期的周期函数.D .若q p Λ为假命题, 则p, q 均为假命题7若把函数x x y 2sin -2cos 3=的图象向右平移0)(>m m 个单位长度后,所得到的图象关于y轴对称,则m 的最小值是( )A .π3 B .12π C .π6 D .5π68.函数f(x)=ln(4+3x -x 2)的单调递减区间是( )A.),(∞+23B.),(23-∞C.),(41- D. ),(4239. 函数1ln --=x e y x的图象大致是( )10. 若定义在R 上的函数)(-)1()(x f x f x f y =+=满足满足,且当]1,1[-∈x 时,2)(x x f =,函数⎩⎨⎧≤>=1,21),1-(log )(3x x x x g x ,则函数)(-)()(x g x f x h =在区间]5,5[-内的零点的个数为( )A .6 B. 7 C. 8 D. 911. 已知函数()f x 是定义在实数集R 上得不恒为零的偶函数,且对任意实数x 都有(1)(1)()xf x x f x +=+,则5()2f =( )A .0 B.12C.1D.5212. 设()f x 是R 上的偶函数,对任意x R ∈,都有(2)(2),f x f x -=+且当[2,0]x ∈-时,1()()1,(2,6]2x f x =--若在区间内关于x 的方程()log (2)0(1)a f x x a -+=>恰有3个不同的实数根,则a 的取值范围是( )A .(1,2)B .(2,)+∞C .3(1,4)D .3(4,2)二.填空题13.已知:()()110p x m x m -+--<;:1223q x <<,若q 是p 的充分不必要条件, 则实数m 的取值范围是___________________。
14. 在△ABC 中,已知113cos ,cos(),07142A A B B A π=-=<<<,则角B = 。
15. 已知tan(π-α)=3 , 则1sin cos αα=__________. 16.给出一列三个命题:①函数c bx x x x f ++=||)(为奇函数的充要条件是0=c ; ②若函数)lg()(2a ax x x f -+=的值域是R ,则0,4≥-≤a a 或;③若函数)1(-=x f y 是偶函数,则函数)(x f y =的图象关于直线0=x 对称.其中正确的命题序号是三、解答题(.解答应写出文字说明,证明过程或演算步骤) 17.已知函数]4,161[,log )(4∈=x x x f 的值域为集合A ,关于x 的不等式)(2)21(3R a x a x ∈>+的解集为B ,集合}015|{≥+-=x xx C ,集合}121|{-<≤+=m x m x D )0(>m (1)若AUB=B,求实数a 的取值范围; (2)若C D ⊆,求实数m 的取值范围.18.已知()f x 是定义在R 上的偶函数,且0x ≥时,12()log (1)f x x =+.(1)求(0)f ,(1)f -; (2)求函数()f x 的表达式;(3)若(1)(3)0f a f a ---<,求a 的取值范围.19.函数)sin()(ϕω+=x A x f (0>A ,0>ω,2πϕ<)的一段图象如图所示.(1)求函数()y f x =的解析式; (2)将函数()y f x =的图象向右平移4π个单位,得到)(x g y =的图象,求函数 )()()(x g x f x h +=的图象的对称轴和对称中心.20. 已知函数321()(1) 1.32a f x x x a x =+--+ (1)若曲线()y f x =在点(2,(2))f 处的切线与直线610x y ++=平行,求出这条切线的方程;(2)当0a >时,求:①讨论函数()f x 的单调区间;②对任意的1x <-,恒有()1f x <,求实数a 的取值范围. 21. 已知 f(x)=2cos 2x+√3sin2x(1)求函数()f x 的最小正周期及单调增区间;(2)在∆ABC 中,c b a ,,分别是角C B A ,,的对边,且3)(=C f ,1=c ,32=ab ,且b a >,求a,b 的值.22、已知函数,ln )(xax x f -=g (x )=f (x )+ax ﹣6lnx ,其中a ∈R .(Ⅰ)讨论f (x )的单调性;(Ⅱ)若g (x )在其定义域内为增函数,求正实数a 的取值范围;(Ⅲ)设函数h (x )=x 2﹣mx+4,当a=2时,若∃x 1∈(0,1),∀x 2∈[1,2],总有 g (x 1)≥h (x 2)成立,求实数m 的取值范围.上学期高三期中考试数学(文科)参考答案一.选择题:DCBBD DDDCA AD 二、填空题:13.2331-≤≤m ; 14. 3π=B ; 15..-10316.1.2三、解答题:解:(1)因为14>,所以)(x f 在]4,161[上,单调递增,所以=A )]4(),161([f f ]1,2[-=,--------------------------2分又由)(2)21(3R a x a x ∈>+可得:x a x 22)3(>+-即:x a x >--3,所以4a x -<,所以)4,(aB --∞=,--------------------------4分又B B A = 所以可得:B A ⊆,--------------------------5分所以14>-a,所以4-<a 即实数a 的取值范围为)4,(--∞.--------------------------6分 (2)因为015≥+-x x ,所以有015≤+-x x ,所以21≤<-x ,所以]5,1(-=C ,--------------------8分对于集合C m x m x D ⊆-<≤+=}121|{有:①当121-≥+m m 时,即20≤<m 时∅=D ,满足C D ⊆.--------------------10分 ②当121-<+m m 时,即2>m 时∅≠D ,所以有:⎩⎨⎧≤-->+51211m m 32≤<-⇒m ,又因为2>m ,所以32≤<⇒m --------------------13分 综上:由①②可得:实数m 的取值范围为]3,0(.--------------------14分 18.解:-----------12分21.解:(1)22()(2cos ,3)(1,sin 2)2cos 3sin 2f x m n x x x x =⋅=⋅=+ ---2分cos 213sin 22sin(2)16x x x π=++=++------4分 ∴函数()f x 的最小周期22T ππ== -----5分由得)(22622-2Z k k x k ∈+≤+≤πππππ:单调增区间为Z k k k ∈⎥⎦⎤⎢⎣⎡+,6,3-ππππ ----------6分(2)31)62sin(2)(=++=πC C f ∴1)62sin(=+πCC 是三角形内角,∴262ππ=+C 即:6π=C -------8分∴232cos 222=-+=ab c a b C 即:722=+b a . -------9分 将32=ab 代入可得:71222=+aa ,解之得:432或=a ∴23或=a ,∴32或=b ---- --11分b a >,∴2=a ,3=b . -------12分19.解:(1)由题图知A =2,π=T ,于是22==Tπω, 将x y 2sin 2=的图象向左平移12π个单位长度,得)2sin(2ϕ+=x y 的图象. 于是6122ππϕ=⨯=,∴)62sin(2)(π+=x x f . …………………6分(2)依题意得⎪⎭⎫ ⎝⎛+-=⎥⎦⎤⎢⎣⎡+-=62cos 26)4(2sin 2)(πππx x x g . ……………8分故=+=)()(x g x f y )62sin(2π+x ⎪⎭⎫ ⎝⎛+-62cos 2πx )122sin(22π-=x .…10分由2122πππ+=-k x ,得)(,2247Z k k x ∈+=ππ. 由ππk x =-122,得)(,224Z k k x ∈+=ππ. ∴)(x h 的对称轴为)(,2247Z k k x ∈+=ππ, 对称中心为)(,0,224Z k k ∈⎪⎭⎫⎝⎛+ππ -22.解:(1)2()1f x ax x a '=+-+,得切线斜率为(2)33k f a '==+ ---------2分 据题设,6k =-,所以3a =-,故有(2)3f = ----------------------------3分所以切线方程为(2)6(2),y f x -=--即6150x y +-= - -----------------------4分(2)①)1)(1()1)(1(1)(2aa x x a a ax x a x ax x f --+=+-+=+-+=/ 若102a <<,则11a a -<-,可知函数()f x 的增区间为1(,)a a --∞和(1,)-+∞, 减区间为1(,1)a a-- -----------------6分若12a =,则21()(1)02f x x '=+≥,可知函数()f x 的增区间为(,)-∞+∞;------------7分若12a >,则11a a ->-,可知函数()f x 的增区间为(,1)-∞-和1(,)a a-+∞, 减区间为1(1,)a a-- -------------------------------------9分②当102a <<时,据①知函数()f x 在区间1(,)a a --∞上递增,在区间1(,1)a a--上递减, 所以,当1x <-时,max 1()()a f x f a -=,故只需1()1a f a-<, 即32222(1)(1)(1)032a a a a a a---+-< 显然1a ≠,变形为22111032a a a a -+-<,即2140a a -<,解得1142a << ---------11分当12a ≥时,据①知函数()f x 在区间(,1)-∞-上递增,则有2132)1(-)(+=<a f x f 只需12132≤+a ,解得1324a ≤≤. ----------13分综上,正实数a的取值范围是1344a <≤ --------------------------------------------14分。
