2014数字信号处理第三章作业 (1)
数字信号处理教程课后习题及答案

分析:已知边界条件,如果没有限定序列类型(例如因果序列、反因果序列等), 则递推求解必须向两个方向进行(n ≥ 0 及 n < 0)。
解 : (1) y1 (0) = 0 时, (a) 设 x1 (n) = δ (n) ,
按 y1 (n) = ay1 (n − 1) + x1 (n) i) 向 n > 0 处递推,
10
T [ax1(n)+ bx2 (n)] =
n
∑
[ax1
(n
)
+
bx2
(n
)]
m = −∞
T[ax1(n) + bx2(n)] = ay1(n) + by2(n)
∴ 系统是线性系统
解:(2) y(n) =
[x(n )] 2
y1(n)
= T [x1(n)] = [x1(n)] 2
y2 (n) = T [x2 (n)] = [x2 (n)] 2
β α
n +1
β α β =
n +1− N −n0
N−
N
α −β
y(n) = Nα n−n0 ,
(α = β )
, (α ≠ β )
如此题所示,因而要分段求解。
2 .已知线性移不变系统的输入为 x( n ) ,系统的单位抽样响应
为 h( n ) ,试求系统的输出 y( n ) ,并画图。
(1)x(n) = δ (n)
当n ≤ −1时 当n > −1时
∑ y(n) = n a −m = a −n
m=−∞
1− a
∑ y(n) =
−1
a−m =
数字信号处理第三章习题答案

x1(n)
x2(n)
(b)
y (n)
(c)
(a) x1(n) (b) x2 (n)
(c) y(n) x1(n) x2 (n)
5.如果X(k)=DFT[ x(n)],证明DFT的初值定理
x(0)
1
N 1
X (k)
N k0
证明 由IDFT定义式
x(n)
1 N
N 1
1, 0 n 4 x2 (n) 1, 5 n 9 作图表示 x1(n) 、 x2 (n) 和 y(n) x1(n) ,x2 (n)
循环卷积区间长度L=10。
解 x1(n) 、 x2 (n) 和 y(n) x1(n) x2 (n) 分别如题3解图
(a)、(b)、(c)所示。
2
N
2
N
k) k)
N] 2 ,k 2]
0,1,L
,N
1
1 e j0N
或
X7 (k)
1
e
j (0
2 N
k
)
,k
0,1,L
,N
1
(9) 解法一
x9 (n)
cos(0n)RN
(n)
1 [e 2
j0n
e
] j0n
N 1
X9 (k) x9 (n)WNkn n0
fl(n)长度为27,f(n)长度为20.前面已推出二者的关系为
f (n) fl (n 20m) R20 (n) m
只有在如上周期延拓序列中无混叠的点上,才满足f(n)=fl(n),所以
f (n) fl (n) x(n) y(n), 7 n 19
数字信号处理(方勇)第三章习题答案

数字信号处理(方勇)第三章习题答案3-1 画出)5.01)(25.01()264.524.14)(379.02()(211211------+--+--=z zz z z z z H 级联型网络结构。
解:23-2 画出112112(23)(465)()(17)(18)z z z H z z z z --------+=--+级联型网络结构。
解:()x n ()y n 243-3 已知某三阶数字滤波器的系统函数为1211252333()111(1)(1)322z z H z z z z -----++=-++,试画出其并联型网络结构。
解:将系统函数()H z 表达为实系数一阶,二阶子系统之和,即:()H z 11122111111322z z z z ----+=+-++ 由上式可以画出并联型结构如题3-3图所示:)题3-3图3-4 已知一FIR 滤波器的系统函数为121()(10.70.5)(12)H z z z z ---=-++,画出该FIR 滤波器的线性相位结构。
解: 因为121123()(10.70.5)(12)1 1.30.9H z zz z z z z ------=-++=+-+,所以由第二类线性相位结构画出该滤波器的线性相位结构,如题3-4图所示:()x n 1-1-1z -题3-4图3-5 已知一个FIR 系统的转移函数为:12345()1 1.25 2.75 2.75 1.23H z z z z z z -----=+--++求用级联形式实现的结构流图并用MATLAB 画出其零点分布及其频率响应曲线。
解: 由转移函数可知,6=N ,且)(n h 偶对称,故为线性相位系统,共有5个零点,为5阶系统,因而必存在一个一阶系统,即1±=z 为系统的零点。
而最高阶5-z 的系数为+1,所以1-=z 为其零点。
)(z H 中包含11-+z 项。
所以:11()()(1)H z H z z -=+。
数字信号处理 重点习题(1-5章)

数字信号处理 重点习题(1-5章)第一章5.设系统分别用下面的差分方程描述, x(n)与y(n)分别表示系统输入和输出, 判断系统是否是线性非时变的。
(6)y(n)=x(n2)(7)y(n)= (8)y(n)=x(n)sin(ωn)6.给定下述系统的差分方程, 试判定系统是否是因果稳定系统, 并说明理由。
(3) y(n)= x(k) (5) y(n)=e x(n)13.有一连续信号x a(t)=cos(2πft+),式中,f =20 Hz,=π/2。
(1)求出x a(t)的周期;(2)用采样间隔T=0.02 s对x a(t)进行采样,试写出采样信号 的表达式;(3) 画出对应 的时域离散信号(序列)x(n)的波形, 并求出x(n)的周期。
14. 已知滑动平均滤波器的差分方程为(1)求出该滤波器的单位脉冲响应;(2)如果输入信号波形如题14图所示,试求出y(n)并画出它的波形。
第二章3.线性时不变系统的频率响应(频率响应函数)H(e jω)=|H(e jω)|e jθ(ω), 如果单位脉冲响应h(n)为实序列,试证明输入x(n)=A cos(ω0n+)的稳态响应为10.若序列h(n)是实因果序列, 其傅里叶变换的实部如下式:H R(e jω)=1+cosω,求序列h(n)及其傅里叶变换H(e jω)。
18.已知,分别求:(1) 收敛域0.5<|z|<2对应的原序列x(n);(2)收敛域|z|>2对应的原序列x(n)。
24.已知线性因果网络用下面差分方程描述: y(n)=0.9y(n-1)+x(n)+0.9x(n-1),(1)求网络的系统函数H(z)及单位脉冲响应h(n);(2) 写出网络频率响应函数H(e jω)的表达式, 并定性画出其幅频特性曲线; (3) 设输入x(n)=e jω0n, 求输出y(n)。
28.若序列h(n)是因果序列, 其傅里叶变换的实部如下式:,求序列h(n)及其傅里叶变换H(e jω).29.若序列h(n)是因果序列, h(0)=1, 其傅里叶变换的虚部为,求序列h(n)及其傅里叶变换H(e jω)。
数字信号处理课后习题答案(全)1-7章

x(n)=-δ(n+2)+δ(n-1)+2δ(n-3)
h(n)=2δ(n)+δ(n-1)+ δ(n-2)
由于
x(n)*δ(n)=x(n)
1
x(n)*Aδ(n-k)=Ax(n-k)
2
故
第 1 章 时域离散信号和时域离散系统
y(n)=x(n)*h(n)
=x(n)*[2δ(n)+δ(n-1)+ δ(n-2) 1 2
(5) 系统是因果系统, 因为系统的输出不取决于x(n)的未来值。 如果
|x(n)|≤M, 则|y(n)|=|ex(n)|≤e|x(n)|≤eM,
7. 设线性时不变系统的单位脉冲响应h(n)和输入序列x(n)如题7图所示,
要求画出y(n)输出的波形。
解: 解法(一)采用列表法。
y(n)=x(n)*h(n)=
0≤m≤3
-4≤m≤n
非零区间如下:
第 1 章 时域离散信号和时域离散系统
根据非零区间, 将n分成四种情况求解: ① n<0时, y(n)=0
② 0≤n≤3时, y(n)= ③ 4≤n≤7时, y(n)= ④ n>7时, y(n)=0
1=n+1
n
1=8-m n0
3
mn4
第 1 章 时域离散信号和时域离散系统
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器, 延时器是线性非时变系统, 下面证明。 令输入为
输出为
x(n-n1)
y′(n)=x(n-n1-n0) y(n-n1)=x(n-n1-n0)=y′(n) 故延时器是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n-n0)+bx2(n-n0) =aT[x1(n)]+bT[x2(n)]
数字信号处理课后第三章习题答案

1 e j 0 N
2 j(0 k ) N 1 e
k 0, 1, , N 1
(8) 解法一
直接计算:
1 j 0 n x8 (n) sin(0 n) RN (n) [e e j 0 n ] R N ( n ) 2j
X 8 (n)
n 0
N 1
kn x8 (n)WN
k 0, 1, , N 1
(4)
X (k ) WNkn
n 0
m1
π j ( m1) k 1 WNkm N e 1 WNk
π sin mk N R (k ) N π sin k N
第3章
离散傅里叶变换(DFT)及其快速算法 (FFT)
所以
DFT[ X (n)] X (n)W
n 0
N 1
N 1
kn N
N 1 mn kn x(m)WN WN n 0 m 0
N 1
n ( m k ) x(m)WN m 0 n 0
N 1
第3章
由于
离散傅里叶变换(DFT)及其快速算法 (FFT)
第3章
离散傅里叶变换(DFT)及其快速算法 (FFT)
(10) 解法一
X (k )
n 0
N 1
kn nWN
k 0, 1, , N 1
上式直接计算较难, 可根据循环移位性质来求解X(k)。 因为x(n)=nRN(n), 所
以
x(n)-x((n-1))NRN(n)+Nδ(n)=RN(n) 等式两边进行DFT, 得到
1 [e j0 n e j0 n ] e 2 j n 0
数字信号处理习题第三章

第3章频域中的离散时间信号3.16 求下面每个序列的DTFT:(a) x1[n]=αnμ[n−1],|α|<1(b) x2[n]=nαnμ[n],|α|<1(e) x5[n]= αnμ[−n−1],|α|>1答案:(a)X1(e jω)=∑αn e−jωn∞n=1=∑(αe−jω)n=∞n=1∑(αe−jω)n−1=αe−jω1−αe−jω∞n=0(b)X2(e jω)=j dX(e jω)dω=j ddω(11−αe−jω)=αe−jω(1−αe−jω)2(e)X5(e jω)=∑αn e−jωn=∑α−m e jωm=∑α−m e jωm−1=∞m=0∞m=1−1n=−∞e jωα−e jω3.17 求下面每个序列的DTFT:(a) xa[n]= μ[n+2]−μ[n−3](b) xb[n]=αn(μ[n−1]− μ[n−4]),|α|<1(c) xc[n]= 2nαnμ[n],|α|<1答案:(a)设μ[n]的DTFT变换为:μ(e jω)=11−e−jω+∑πδ(ω+2kπ)∞k=−∞Xa(e jω)=(e j2ω−e−j3ω)μ(e jω)=(e j2ω−e−j3ω)[11−e−jω+∑πδ(ω+2kπ)]∞k=−∞(b)设x[n]= αnμ[n],|α|<1,其DTFT变换为:X(e jω)=11−αe−jωXb (e jω)=e−jωX(e jω)−e−j4ωX(e jω)=e−jω−e−j4ω1−αe−jω(c)xc[n]= 2nαnμ[n]=2(n+1)αnμ[n]−2αnμ[n],|α|<1X C (e jω)=2(1−αe−jω)2−21−αe−jω=2αe−jω(1−αe−jω)23.21 求下面每个DTFT的逆DTFT:(a) Xa (e jω)=∑δ(ω+2πk)∞k=−∞(b) Xb (e jω)=e jω(1−e jωN)1−e jω(c) Xc (e jω)=1+2∑cosωιNι=0(d) Xd (e jω)=−αe−jω(1−αe−jω)2,|α|<1答案:(a) xa [n]=12π∫δ(ω)e jωn∞−∞dω=1(b ) X b (e jω)=e jω(1−e jωN )1−e jω=e jω∑ejωnN−1n=0 令m =−n X(ejω)=∑e−jωm −N+1m=0 x[n]={1,−(N −1)≤n ≤00,其他X b (e jω)=e jω∑e−jωm−N+1m=0=e jωX(e jω) X b [n]=x[n+1]={1,−N ≤n ≤−10,其他(c )X c (e jω)=1+2∑cosωιN ι=0=2+∑e−jωιN ι=−N , x c [n]={3,n =01,0<|n |<N 0,其他(d )X 0(e jω)=11−αe −jω x o [n]=αn μ[n]X d (ejω)=−αe −jω(1−αe −jω)2=dX0(e jω)dωx d [n]=n x o [n]=nαn μ[n]3.26 X (e jω)是实序列x[n]的DTFT 。
数字信号处理(方勇)第三章习题答案
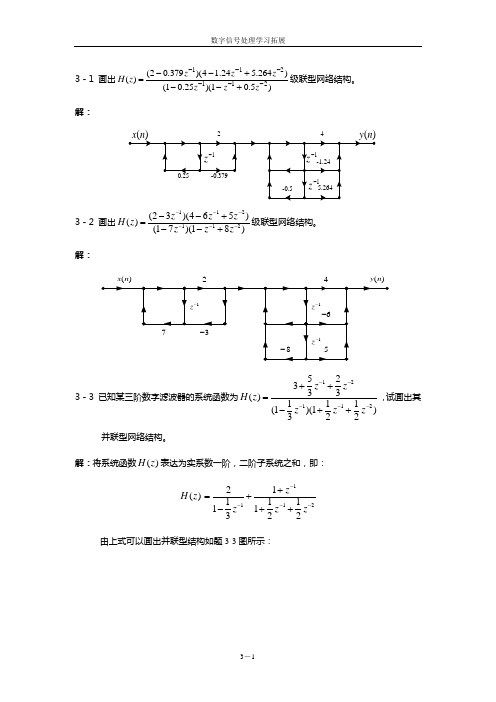
3-1 画出)5.01)(25.01()264.524.14)(379.02()(211211------+--+--=z zz zzzz H 级联型网络结构。
解:243-2 画出112112(23)(465)()(17)(18)z z zH z z zz--------+=--+级联型网络结构。
解:()x n ()y n 243-3 已知某三阶数字滤波器的系统函数为1211252333()111(1)(1)322zzH z z zz-----++=-++,试画出其并联型网络结构。
解:将系统函数()H z 表达为实系数一阶,二阶子系统之和,即:()H z 11122111111322z zzz----+=+-++由上式可以画出并联型结构如题3-3图所示:)题3-3图3-4 已知一FIR 滤波器的系统函数为121()(10.70.5)(12)H z z z z ---=-++,画出该FIR滤波器的线性相位结构。
解: 因为121123()(10.70.5)(12)1 1.30.9H z z z z z z z ------=-++=+-+,所以由第二类线性相位结构画出该滤波器的线性相位结构,如题3-4图所示:()x n 1-1-1z -题3-4图3-5 已知一个FIR 系统的转移函数为:12345()1 1.25 2.75 2.75 1.23H z zzzzz-----=+--++求用级联形式实现的结构流图并用MATLAB 画出其零点分布及其频率响应曲线。
解: 由转移函数可知,6=N ,且)(n h 偶对称,故为线性相位系统,共有5个零点,为5阶系统,因而必存在一个一阶系统,即1±=z 为系统的零点。
而最高阶5-z 的系数为+1,所以1-=z 为其零点。
)(z H 中包含11-+z 项。
所以:11()()(1)H z H z z -=+。
1()H z 为一四阶子系统,设12341()1H z bz cz bz z ----=++++,代入等式,两边相等求得12341()10.2530.25H z z z z z ----=+-++,得出系统全部零点,如图3-5(b )所示。
数字信号处理 刘顺兰第三章完整版习题解答

数字信号处理刘顺兰第三章完整版习题解答一、题目解答1. 题目利用时域抽样、频域抽样、零填充、插值法等,实现信号的变换。
1.1 时域抽样时域抽样是指将一个连续时间信号在时间轴上的等间隔位置上进行采样,可以得到一个离散时间信号。
时域抽样的原理是,将时间轴上的信号按照一定的时间间隔进行采样,每个采样点的振幅值就是该点对应的连续时间信号的振幅值。
时域抽样可以通过以下步骤进行实现:1.假设连续时间信号为x(t),采样频率为Fs(采样频率是指每秒采样的次数),采样间隔为Ts(采样间隔是指相邻两个采样点之间的时间间隔)。
2.根据采样频率和采样间隔,计算出采样点数N:N =Fs * T,其中T为采样时长。
为Ts。
4.在每段的中点位置进行采样,得到N个采样点。
5.将N个采样点按照时域顺序排列,即可得到离散时间信号。
1.2 频域抽样频域抽样是指将一个连续频谱信号在频率轴上的等间隔位置上进行采样,可以得到一个离散频谱信号。
频域抽样的原理是,将频率轴上的信号按照一定的频率间隔进行采样,每个采样频率点上的能量值就是该频率点对应的连续频谱信号的能量值。
频域抽样可以通过以下步骤进行实现:1.假设连续频谱信号为X(f),采样频率为Fs(采样频率是指每秒采样的次数),采样间隔为Δf(采样间隔是指相邻两个采样频率点之间的频率间隔)。
2.根据采样频率和采样间隔,计算出采样点数N:N =Fs / Δf,其中Δf为采样频率点之间的频率间隔。
为Δf。
4.在每段的中点位置进行采样,得到N个采样频率点。
5.将N个采样频率点按照频域顺序排列,即可得到离散频谱信号。
1.3 零填充零填充是指在信号的末尾添加一些零值样本,使得信号的长度变长。
零填充的原理是,通过增加信号的长度,可以在时域和频域上提高信号的分辨率,从而更精确地观察信号的特征。
零填充可以通过以下步骤进行实现:1.假设原始信号为x(n),长度为N。
2.计算需要填充的长度L,L > 0。
吉大14秋学期《数字信号处理》在线作业一答案

C.双线性变换是一种分段线性变换
D.以上说法都不对
?
正确答案:ACD
6.以下对双线性变换的描述中正确的是( )
A.双线性变换是一种非线性变换
B.双线性变换可以用来进行数字频率与模拟频率间的变换
C.双线性变换把s平面的左半平面单值映射到z平面的单位圆内
A.连续非周期信号的频谱为周期连续函数
B.连续周期信号的频谱为周期连续函数
C.离散非周期信号的频谱为周期连续函数
D.离散周期信号的频谱为周期连续函数
?
正确答案:ABD
三,判断题
1.采样频率fs=5000Hz,DFT的长度为2000,其谱线间隔为2.5Hz。
A.错误
B.正确
?
正确答案:B
2.时间抽取法FFT对两个经时间抽取的N/2点离散序列X(2r)和X(2r+1)做DFT,并将结果相加,就得一个N点DFT。
C.并联型
D.频率抽样型
?
正确答案:ABC
9.下面关于IIR滤波器设计说法错误的是( )
A.双线性变换法的优点是数字频率和模拟频率成线性关系
B.冲激响应不变法无频率混叠现象
C.冲激响应不变法不适合设计高通滤波器
D.双线性变换法只适合设计低通、带通滤波器
?
正确答案:ABD
10.下面说法中不正确的是()
D.以上说法都不对
?
正确答案:ABC
7.下面说法中不正确的是( )
A.连续非周期信号的频谱为非周期连续函数
B.连续周期信号的频谱为非周期连续函数
C.离散非周期信号的频谱为非周期连续函数
D.离散周期信号的频谱为非周期连续函数
数字信号处理答案第三章

= = =
0 0 1 j 2πn e 10 , n = 1, 2, . . . , k. 2
3.3
(a) X1 (z ) = = = = The ROC is (b)
1 3 ∞ 0
1 1 ( )n z −n − 1 ( )n z −n + 3 2 n=−∞ n=0 1
1 −1 1− 3 z
+ +
1 ( )n z n − 1 2 n=0 1 − 1, 1− 1 2z −1 2 z)
∞
1
1−1 −1 3zFra bibliotek(1 −
5 6 1 −1 )(1 3z
< |z | < 2. X2 (z ) = = = 1 ( )n z −n − 2n z −n 3 n=0 n=0 1 1−
1 −1 3z ∞ ∞
nan cosw0 nz −n nan ejw0 n + e−jw0 n −n z 2 60
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher. For the exclusive use of adopters of the book Digital Signal Processing, Fourth Edition, by John G. Proakis and Dimitris G. Manolakis. ISBN 0-13-187374-1.
数字信号处理习题集(1-3章)

第一章数字信号处理概述简答题:1.在A/D变换之前和D/A变换之后都要让信号通过一个低通滤波器,它们分别起什么作用?答:在A/D变化之前让信号通过一个低通滤波器,是为了限制信号的最高频率,使其满足当采样频率一定时,采样频率应大于等于信号最高频率2倍的条件。
此滤波器亦称位“抗折叠”滤波器。
在D/A变换之后都要让信号通过一个低通滤波器,是为了滤除高频延拓谱,以便把抽样保持的阶梯形输出波平滑化,故友称之为“平滑”滤波器。
判断说明题:2.模拟信号也可以与数字信号一样在计算机上进行数字信号处理,自己要增加一道采样的工序就可以了。
()答:错。
需要增加采样和量化两道工序。
3.一个模拟信号处理系统总可以转换成功能相同的数字系统,然后基于数字信号处理理论,对信号进行等效的数字处理。
()答:受采样频率、有限字长效应的约束,与模拟信号处理系统完全等效的数字系统未必一定能找到。
因此数字信号处理系统的分析方法是先对抽样信号及系统进行分析,再考虑幅度量化及实现过程中有限字长所造成的影响。
故离散时间信号和系统理论是数字信号处理的理论基础。
第二章 离散时间信号与系统分析基础一、连续时间信号取样与取样定理计算题:1.过滤限带的模拟数据时,常采用数字滤波器,如图所示,图中T 表示采样周期(假设T 足够小,足以防止混迭效应),把从)()(t y t x 到的整个系统等效为一个模拟滤波器。
(a ) 如果kHz T rad n h 101,8)(=π截止于,求整个系统的截止频率。
(b )对于kHz 201=,重复(a )的计算。
解 (a )因为当0)(8=≥ωπωj e H rad 时,在数 — 模变换中)(1)(1)(Tj X T j X T e Y a a j ωω=Ω= 所以)(n h 得截止频率8πω=c对应于模拟信号的角频率c Ω为8π=ΩT c因此Hz Tf c c 6251612==Ω=π 由于最后一级的低通滤波器的截止频率为Tπ,因此对T 8π没有影响,故整个系统的截止频率由)(ωj eH 决定,是625Hz 。
数字信号处理第三章习题解答

(4)在频带宽度不变的情况下,将频率分辨率提高一倍的N值。
解:
(1)已知
(2)
(3)
(4)频带宽度不变就意味着采样间隔T不变,应该使记录时间扩大一倍为0.04s实现频率分辨率提高一倍(F变为原来的1/2)
18.我们希望利用 长度为N=50的FIR滤波器对一段很长的数据序列进行滤波处理,要求采用重叠保留法通过DFT来实现。所谓重叠保留法,就是对输入序列进行分段(本题设每段长度为M=100个采样点),但相邻两段必须重叠V个点,然后计算各段与 的L点(本题取L=128)循环卷积,得到输出序列 ,m表示第m段计算输出。最后,从 中取出B个,使每段取出的B个采样点连接得到滤波输出 。
————第三章————
离散傅里叶变换DFT
3.1 学习要点
3.1.1DFT的定义、DFT与Z变换(ZT)、傅里叶变换(FT)的关系及DFT的物理意义
1.DFT的定义
设序列 为有限长序列,长度为 ,则定义 的 点离散傅立叶变换为
(3.1)
的 点离散傅立叶逆变换为
(3.2)
其中, , 成为DFT变换区间长度。
学习DFT的性质时,应与傅里叶变换的性质对照学习,要搞清两者的主要区别。我们知道,傅里叶变换将整个时域作为变换区间,所以在其性质中,对称性以原点为对称点,序列的移动范围无任何限制。
然而,DFT是对有限长序列定义的一种变换,也就是说,DFT变换区间为 。这一点与傅立叶变换截然不同,由于 及 区间在DFT变换区间以外,所以讨论对称性时,不能再以原点作为对称点,而是以 点作为对称点。为了区别于无限长共轭对称序列,用 和 分别表示有限长(或圆周)共轭对称序列和共轭反对称序列。其定义为
即 隐含周期性,周期为 。
数字信号处理答案 唐向宏

第二章 2-1:(1)
(3) 或者
(6) 2-4:(1)
(3) 2-5: 2-9:(1) 2-12:
(2) (3)
2-16:
第三章 3-1:(1)
(3) (5) 3-4:
3-8:(1) (2)
3-10:
3-11:
3-17: 3-19 已知有限长序列, , N=10 试求(1);(2);(3); 解:, **** ,
**** 1) 2) 3) 3-20:(1) ;(2) 解: 同理可得 3-24:已知x(n)和y(n)为实有限长序列,若, ,试求以下两种情况的,以及 和: (1);(2) 解:的实部傅里叶变换对应于共轭对称分量,虚部的傅里叶变换对应于 共轭反对称分量。 (1) (2)
3-25:解:记 r(n)长度为20,圆周卷积与线性卷积关系 只有在如上周期延拓序列中无混叠的点才满足r(n)=rl(n) 所以 3-26:(1)
(2) (3) (4)
10. 已知两个有限长序列:x(n)={1, 2, 3, 4, 0, 0, 0}0,h(n)={-1, -1, -1, -1, -1, 1, 1}0。
求x(n)⑦h(n)。 m 01
23 4 5 6
f(n)= x(n)⑦h(n)
x(m) 1 2 3 4 0 0 0
h(m) -1 -1 -1 -1 -1 1 1
“数字信号处理”课程 习题答案
第一章 1-3:(1) 非周期 (2)周期 N=10 (3)周期 N=2 1-11:N4=N0+N2 N5=N1+N3 1-13:(1)能恢复原始信号 (2)不能 (3)能 1-14:(1) T=0.02s (2)fs=100
(3) (4) x(n)=xa(nT)=2cos(100πn+π/2) N=1 1-17:(c):{-2 5 0 -1}B1B 1-22:(1)线性 (2)线性 (3)线性 1-23:(1)时变 (2)时变 (3)时不变 1-24:(1)非因果 (2)非因果 (3)因果(n0>0);非因果(n0<0) 1-25:(1)稳定 (2)稳定 (3)稳定 1-26:(1)因果不稳定 (2)非因果稳定 1-27:y(n)=x(n)*h1(n)*[h1(n)+h2(n)]
数字信号处理课后答案+第3章(高西全丁美玉第三版)

故
N [δ( k ) − 1] X (k ) = k 1 − WN
k = 1, 2, ⋯, N − 1
当k=0时, 可直接计算得出X(0)为
N ( N − 1) X ( 0) = ∑ n ⋅ W = ∑ n = 2 n=0 n =0
N −1 0 N N −1
这样, X(k)可写成如下形式:
N ( N − 1) 2 X (k ) = −N k 1 − W N , k =0 k = 1, 2, ⋯ , N − 1
解法二 由DFT共轭对称性可得同样结果。 因为
x9 (n) = cos(ω 0 n) ⋅ R N (n) = Re[ x 7 (n)]
1 * X 9 (k ) = X 7e (k ) = [ X 7 (k ) + X 7 ( N − k )] 2
jω 0 N − jω 0 N 1 1− e 1− e = + 2π 2π 2 j(ω0 − k ) − j(ω0 + ) k N N 1 − e 1− e
=
1− e
−j
2π (m−k ) N N 2π (m−k ) N
1− e
−j
N = 0
k =m k≠m
0≤k≤N-1
(6) X (k ) = ∑ cos
n =0
N −1
1 2π kn mn ⋅ WN = (e 2 N n =0
∑
N −1
j
2π mn N
+e
-j
2π 2π mn - j kn N )e N
1 x ( 0) = N
∑ X (k )
n = 0, 1, ⋯ , N − 1
1 x( n) = N
数字信号处理 答案 第三章

解: x1 ( n) 和 x2 (n) 的图形如图 P3.7_1 所示:
3.8 图 P3.8 表示一个 4 点序列 x( n) 。 (1)绘出 x( n) 与 x( n) 的线性卷积结果的图形。 (2)绘出 x( n) 与 x( n) 的 4 点循环卷积结果的图形。 (3)绘出 x( n) 与 x( n) 的 8 点循环卷积结果的图形,并将结果与(1)比较,说明线性卷积与循环卷 积之间的关系。
j [(2π k /10) + (π /10)]
={
3.7
N ,k=m或 k=−m 2 0,其 他
图 P3.7 表示的是一个有限长序列 x( n) ,画出 x1 ( n) 和 x2 (n) 的图形。 (1) x1 ( n) = x ⎡ ⎣( n − 2 ) ⎤ ⎦ 4 R4 (n)
(2) x2 ( n) = x ⎡ ⎣( 2 − n ) ⎤ ⎦ 4 R4 (n)
解: (1) X ( k )
= ∑ δ (n)WNnk = δ (0) = 1, 0 ≤ k ≤ N − 1
n=0
N −1
(2) X ( k ) =
∑ δ [(n − n )]
n =0 0
N −1
N
RN (n)WNnk = WNn0 k , 0 ≤ k ≤ N − 1
(3) (4)
X (k ) = ∑ a W
− jω N
−j
N ω 2
j
N ω 2
−j
N ω 2
⎛N ⎞ sin ⎜ ω ⎟ N −1 ) ⎝ 2 ⎠ e− j 2 ω = sin
ω
2
⎛N ⎞ sin ⎜ ω ⎟ ⎝ 2 ⎠ , ϕ (ω ) = − N − 1 ω | X (e jω ) |= ω 2 sin 2
2014数字信号处理第三章作业 (1)
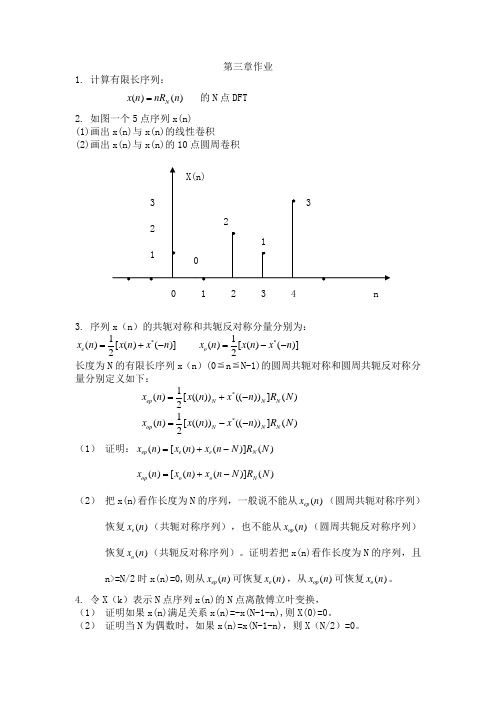
第三章作业1. 计算有限长序列:()()N x n nR n = 的N 点DFT2. 如图一个5点序列x(n)(1)画出x(n)与x(n)的线性卷积(2)画出x(n)与x(n)的10点圆周卷积3. 序列x (n )的共轭对称和共轭反对称分量分别为:*1()[()()]2e x n x n x n =+- *1()[()()]2o x n x n x n =-- 长度为N 的有限长序列x (n )(0≦n ≦N-1)的圆周共轭对称和圆周共轭反对称分量分别定义如下: *1()[(())(())]()2ep N N N x n x n x n R N =+- *1()[(())(())]()2op N N N x n x n x n R N =-- (1) 证明:()[()()]()ep e e N x n x n x n N R N =+-()[()()]()op o o N x n x n x n N R N =+-(2) 把x(n)看作长度为N 的序列,一般说不能从()ep x n (圆周共轭对称序列)恢复()e x n (共轭对称序列),也不能从()op x n (圆周共轭反对称序列)恢复()o x n (共轭反对称序列)。
证明若把x(n)看作长度为N 的序列,且n>=N/2时x(n)=0,则从()ep x n 可恢复()e x n ,从()op x n 可恢复()o x n 。
4. 令X (k )表示N 点序列x(n)的N 点离散傅立叶变换,(1) 证明如果x(n)满足关系x(n)=-x(N-1-n),则X(0)=0。
(2) 证明当N 为偶数时,如果x(n)=x(N-1-n),则X (N/2)=0。
0 1 2 3 4n5.频谱分析的模拟信号以8kHz被抽样,计算了512个抽样的DFT,试确定频谱抽样的频率间隔,并证明之。
6.已知x(n)是2N点的实序列(0≦n≦2N-1),其DFT为X(k)=DFT[x(n)],请用一个N点DFT运算来计算此X(k).。
数字信号处理第三章离散傅里叶变换(DFT)及其快速算法(FFT)

周期
2
s、fs N
分辨率
2
N
fs N
返回
回到本节
DFT和DFS之间的关系:
周期延拓
取主值
有限长序列
周期序列
主值区序列
有限长序列 x(n) n 0,1, 2, M 1
周期序列 xN (n) x(n mN ) x((n))N m 0 n0 N 1 n mN n0 ((n))N n0
四种傅立叶变换
离散傅立叶变换(DFT)实现了信号首次在频域 表示的离散化,使得频域也能够用计算机进行处理。 并且这种DFT变换可以有多种实用的快速算法。使信 号处理在时、频域的处理和转换均可离散化和快速 化。因而具有重要的理论意义和应用价值,是本课程 学习的一大重点。
本节主要介绍
3.1.1 DFT定义 3.1.2 DFT与ZT、FT、DFS的关系 3.1.3 DFT的矩阵表示
• X(k)为x(n)的傅立叶变换 X (e j ) 在区间 [0, 2 ]上的N
点等间隔采样。这就是DFT的物理意义。
j ImZ
2பைடு நூலகம்3
4
5 6
1 2
N
k=0 ReZ
7 (N-1)
DFT与z变换
X(ejω)
X(k)
0
o
2
0
N 1 k
DFT与DTFT变换
回到本节
变量
、f k
之间的某种变换关系.
• 所以“时间”或“频率”取连续还是离 散值,就形成各种不同形式的傅里叶变换 对。
3.1 离散傅里叶变换的定义及物理意义
时间域
t:连续
模拟域
数字信号处理习题及解答

数字信号处理习题及解答
第一章 离散时间信号与离散时间系统
4 解答
数字信号处理习题及解答
第二章 Z变换及离散时间系统分析 1
数字信号处理习题及解答
第二章 Z变换及离散时间系统分析 1 解答
数字信号处理习题及解答
第二章 Z变换及离散时间系统分析 1 解答
数字信号处理习题及解答
第二章 Z变换及离散时间系统分析 2
7
(1) X(ej0) x(n)6
n3
(2)
πX (ej)d x(0 )2π4π
π
7
(3) X (ejπ) x(n)ejn ( 1 )nx(n)2
n
n 3
数字信号处理习题及解答
第三章 信号的傅里叶变换 2 试求如下序列的傅里叶变换: (1) x1(n)=δ(n-3)
(2) x2(n)1 2δ(n1)δ(n)1 2δ(n1)
11 a 2 ac 2ac o o s s
F[x T o(n) ]jIm X(e [j]jIm 1a [1 ej]jIm 1a [1 ej1 1 a ae ejj ]
1a 2a s2a i cno s
数字信号处理习题及解答
第三章 信号的傅里叶变换 4 已知长度为N=10的两个有限长序列:
1 0≤ x1(n)0 5≤
故系统是非时变系统。 由于
T[ax1(n)+bx2(n)]=[ax1(n)+bx2(n)]2 ≠aT[x1(n)]+bT[x2(n)] =ax21(n)+bx22(n)
因此系统是非线性系统。
数字信号处理习题及解答
第一章 离散时间信号与离散时间系统
2 给定下述系统的差分方程, 试判定系统是否是因果稳定系统, 并说明理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章作业
1. 计算有限长序列:
()()N x n nR n = 的N 点DFT
2. 如图一个5点序列x(n)
(1)画出x(n)与x(n)的线性卷积
(2)画出x(n)与x(n)的10点圆周卷积
3. 序列x (n )的共轭对称和共轭反对称分量分别为:
*1()[()()]2e x n x n x n =+- *1()[()()]2
o x n x n x n =-- 长度为N 的有限长序列x (n )(0≦n ≦N-1)的圆周共轭对称和圆周共轭反对称分量分别定义如下: *1()[(())(())]()2
ep N N N x n x n x n R N =+- *1()[(())(())]()2
op N N N x n x n x n R N =-- (1) 证明:()[()()]()ep e e N x n x n x n N R N =+-
()[()()]()op o o N x n x n x n N R N =+-
(2) 把x(n)看作长度为N 的序列,一般说不能从()ep x n (圆周共轭对称序列)
恢复()e x n (共轭对称序列),也不能从()op x n (圆周共轭反对称序列)恢复()o x n (共轭反对称序列)。
证明若把x(n)看作长度为N 的序列,且n>=N/2时x(n)=0,则从()ep x n 可恢复()e x n ,从()op x n 可恢复()o x n 。
4. 令X (k )表示N 点序列x(n)的N 点离散傅立叶变换,
(1) 证明如果x(n)满足关系x(n)=-x(N-1-n),则X(0)=0。
(2) 证明当N 为偶数时,如果x(n)=x(N-1-n),则X (N/2)=0。
0 1 2 3 4
n
5.频谱分析的模拟信号以8kHz被抽样,计算了512个抽样的DFT,试确定频谱抽样的频率间隔,并证明之。
6.已知x(n)是2N点的实序列(0≦n≦2N-1),其DFT为X(k)=DFT[x(n)],请用一个N点DFT运算来计算此X(k).。
