《圆锥的体积》圆柱与圆锥PPT教材课件
合集下载
《圆柱和圆锥——圆柱的体积》数学教学PPT课件(3篇)

V=sh
S h
教学新知
教学新知
试一试:一个圆柱形零件,底面半径是5厘米,高是8厘米。 这个零件的体积是多少立方厘米?
V=sh=5²π×8=628(cm³)
教学新知
练一练:
1.计算圆柱的体积。(单位:cm)
V=sh=4²π×8=401.92(cm³) V=sh=3²π×6=169.56(cm³)
V=sh=1.5²π×0.5×2=7.065(m³)
8.两个底面积相等的圆柱,一个高是4.5分米,体积是81立方分米。另 一个高是3分米,它的体积是多少立方分米?
s=V1÷h1=81÷4.5=18(dm²) V2=sh2=18×3=54(m³)
课堂练习
9.把3个高相等、底面半径都是10厘米的圆柱形盒子叠放在 一起,如图 所示,拿走1个盒子,表面积就减少314平方厘米。每个盒子的体积是 多少立方厘米?
个近似的长方体。拼成的长方体的底面积等于圆柱的(底面积), 高就是圆柱的( 高 )。 (2)用字母V表示圆柱的体积,S表示圆柱的底面积,h表示圆柱的高, 圆柱的体积公式可以写成(V=sh)。 (3)一个圆柱的底面积是0.6平方分米,高是3.5分米,体积是(2.1)立 方分米。
课后习题
2.—根木料如图所示,求这根木料的体积。(单位:m)
2.一根圆柱形木料,底面周长是62.8厘米,高是50厘米。这根木料的体 积是多少?
r=C÷2π=62.8÷6.28=10(cm) V=sh=10²π×50=15700(cm³)
教学新知
例一:完成下面的表格。
底面积/m2
高/m
体积/m3
圆 柱
0.6
1.2
0.25
3
0.72 0.75
《圆柱与圆锥——圆锥的体积》数学教学PPT课件(2篇)

等底等高
等底等高
等底等高
等底等高
等底等高
等底等高
等底等高
等底等高
等底等高
等底等高
等底等高
等底等高
通过实验我知道了:圆柱 的体积等于和它等底等高 的圆锥的体积的 3 倍。
圆柱体的体积是与它等底等高的圆锥体体积的3倍,圆锥体的体积是与 它等底等高的圆柱体体积的三分之一。 那么圆锥体积的计算公式: 圆锥体积=底面积×高×13
V=1/3sh=1/3×3.6×2=2.4(m³) h=2.4÷4÷2=0.3(m)
8.将一个底面直径是20cm,高为10cm的金属圆锥体,全部浸没在直径 是40cm的圆柱形水槽中,水槽水面会升高多少cm?
V=1/3sh=1/3×100×3.14×10=3140/3(cm³) h=V÷s=3140/3÷20²÷3.14=5/6(cm)
2.把一个底面直径是2分米,高是3分米的圆柱体削成一个最大 的圆锥体削去(6.28)立方分米。
3.一个圆柱体和一个圆锥体的底面积和体积分别相等,已知圆 柱体的高6厘米,那么圆锥体的高是 ( 18 )厘米。
课后习题
4.等底等高的圆柱和圆锥的体积相差16立方米,这个圆柱的
体积是(24)立方米,圆锥的体积是( 8 )立方米。
装满一车沙,卸后沙堆成—个高是5米的圆锥形,它的底面积是多
少平方米?
V长方体=4×1.5×4=24(m³)
S=V长方体÷h÷1/3=14.4(m²)
2.—堆圆锥形黄沙,底面周长是25.12米,高1.5米,每立方米的黄沙重
1.5吨。这堆沙重多少吨?
V=⅓sh=⅓×(25.12÷6.28)²×3.14×1.5=25.12(m³)
V圆柱=sh=3²×3.14×5=141.3(dm³)
人教版六年级数学下册第三单元《圆柱与圆锥》课件共10个精品课件

柱的底面直径与高的比。
πd=h d :h = 1 :π
课堂总结
通过这节课的学习, 你有什么收获?
义务教育人教版六年级下册
第3单元 圆柱与圆锥 1.圆 柱
第 5 课时 圆柱的体积
复习导入
填空。 圆柱的侧面积=( 底面周长×高 ) 圆柱的表面积=( 侧面积+底面积×2 ) 长方体的体积=( 长×宽×高 ) 正方体的体积=(棱长×棱长×棱长)
底面 侧面
圆柱的底面都 是圆,并且大 小一样。
底面 圆柱的侧面是曲面。
哪个圆柱比较高?为什么?
底面 O
侧面 高
底面 O 侧面 高
底面 O
底面
圆柱两个底面之间的距离叫做高, 圆柱有无数条高。
动手操作: 如果把一张长方形的硬纸贴在木棒上,快速转
动木棒,想一想,转出来的是什么形状?
转动起来像一个圆柱。
8cm
要解决这个问题,就
是要计算什么?
10cm
杯子的容积
10cm
杯子的底面积: 杯子的容积:
8cm
3.14×(8÷2)2
50.24×10
=3.14×42
=502.4 (cm3 )
=3.14×16
=502.4 (mL)
=50.24 (cm2 )
答:因为502.4大于498,所以杯子能 装下这袋牛奶。
(长方体)
(正方体 )
( 圆柱 )
课堂总结
通过这节课的学习, 你有什么收获?
义务教育人教版六年级下册
第3单元 圆柱与圆锥 1.圆 柱
第 2 课时 圆柱的认识(2)
复习导入
圆柱由哪几部分组成? 有什么特征?
上、下底面:圆 侧面:曲面
探究新知
圆柱和圆锥的体积
长方体的底面积等于圆柱体的底面积 长方体的高等于圆柱体的高
长方体的体积=长×宽×高 圆柱的体积=底面积×高 V=Sh V=πr ² h
20厘米 25厘米
20)2=314(cm2) (1)水桶的底面积:3.14×( 2 3 (2)水桶的容积: 314×25=7850(cm )
4分米 10分米
把一个棱长是6厘米的正方体木 块,加工成一个最大的圆锥体, 圆锥的体积是多少立方厘米?
0.8米
求各圆柱的 体积。
0.5分米
求下面各圆柱的体积。
1、底面半径3cm,高5cm。 2、底面直径8m,高10m。 3、底面周长25.12dm,高2dm。
圆柱体积=底面积
高
圆柱体积=底面积
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积= 底面积
高
高
圆柱体积=底面积 圆锥体积= 底面积
高
高
1 3
圆柱与圆锥的体积之间有什么关系?
等底等高圆锥体积是圆柱体积的三分之一 等底底面周 长31.4米,高15米,这个玻璃罩的容积 是多少立方米?(玻璃厚度忽略不计)
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
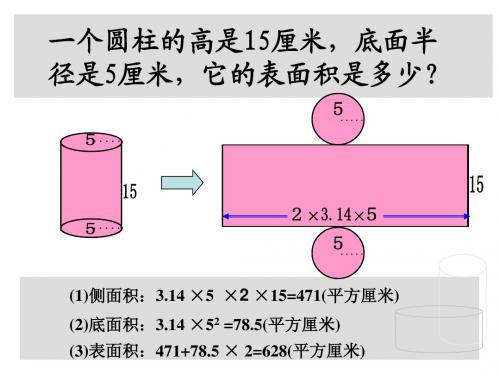
一个圆柱的高是15厘米,底面半 径是5厘米,它的表面积是多少?
圆柱和圆锥的体积

01
02
03
底面形状相同
圆柱和圆锥的底面都是圆 形。
高与底面垂直
圆柱和圆锥的高都与底面 垂直,且都位于底面的中 心。
侧面展开图相似
圆柱和圆锥的侧面展开图 都是长方形或扇形。
圆柱和圆锥的体积关系公式
圆柱体积公式
$V_{cylinder} = pi r^2 h$
圆锥体积公式
$V_{cone} = frac{1}{3} pi r^2 h$
这个公式是由圆的面积公式和高度相 乘得到的。
圆柱体积公式的推导
首先,我们知道圆的面积公式是:A = πr²。 然后,将这个公式乘以高度h,得到圆柱体的体积公式:V = πr²h。
02 圆锥的体积
圆锥体积的定义
圆锥体积是指圆锥所占空间的大小。 圆锥体积可以通过底面积和高来计算。
圆锥体积的公式
圆锥体积的公式为:V = (1/3)πr²h,其中r为底面半径,h为高。
圆柱和圆锥的体积
contents
目录
• 圆柱的体积 • 圆锥的体积 • 圆柱和圆锥的体积关系 • 圆柱和圆锥的体积的应用
01 圆柱的体积
圆柱体积的定义
01
圆柱体积是指圆柱体所占空间的 大小。
02
圆柱体积是高度和底面积的乘积 。
圆柱体积的公式
圆柱体积的公式是:V = πr²h,其中r 是Байду номын сангаас面半径,h是高。
体积关系
$V_{cylinder} = 3V_{cone}$
圆柱和圆锥体积关系的证明
证明方法一:利用几何图形推导
1. 将圆锥的底面平放在桌面上, 使其与桌面紧密接触。
2. 将圆锥的侧面展开成扇形, 并连接扇形的弧边与圆锥的顶点。
苏教版六年级下册数学《圆柱的体积》圆柱和圆锥PPT(第3课时)

教学新知
例二:计算圆柱的表面积。(单位:cm)(π取3.14)
S=2π×0.8+2π≈11.304 S=2π×0.5×3.5+2π×0.5²≈12.56
教学新知
例三:一个圆柱形油桶,底面直径是0.6米,高是1米。做这个油桶至少 需要铁皮多少平方米?(得数保留两位小数)
S=2π×0.3×1+2π×0.3²≈2.45(㎡)
能想到一些什么? (2)全部浸入,水面上升9厘米,你又能想到什么?怎样
计算出这个圆钢的体积? (3)这题还可以怎样思考?
教学新知
例一:一个圆柱形水桶的容积是80立方分米,里面装了2/5的水。 已知它的底面积是10平方分米,里面水的深度是多少?
【讲解】根据“水桶的容积是80立方分米”和“里 面装了 2/5的水”这两个条件,我们可以求出水桶 内水的体积,然后用水的体积除以水桶底面积得出 水桶内水的深度。 80× =32(立方分米)……水桶内水的体积 32÷10=3.2(分米)……水桶平均剖成两片,其中一片如图所示。(单位:厘米) (1)剖面面积是多少平方厘米? (2)这片木料的表面积和体积各是多少?
(1)S1=20×12=240(cm²) (2)S2=πrh+πr²+S1=3.14×6×20+3.14×6²+240=792.84(cm²)
V=1/2S3h=1/2×3.14×6²×20=1130.4(cm³)
课后习题
7.把一根长2.4米的圆柱形状的木料锯成4段,表面积增加了 0.18平方米。
这根木料原来的体积是多少立方米?
S=0.18÷6=0.03(m²)
V=sh=0.03×2.4=0.072(m³)
8.一个圆柱高4厘米,底面半径是2厘米。如果将它的底面平均分成若干份,
圆柱圆锥圆台体积和表面积.ppt

1
1
A.4
B.2
3 C. 6
3 D. 4
[答案] D
[解析]
三棱锥B1-ABC的高h=3,底面积S=S△ABC=
3 4
×12= 43,
则VB1-ABC=13Sh=13×
43×3=
3 4.
5.若一圆柱与圆锥的高相等,且轴截面面积也相等,那
么圆柱与圆锥的体积之比为( )
A.1
1 B.2
3
3
C. 2
D.4
例题解析
命题方向 多面体与旋转体的面积
【例1】圆台的上、下底面半径分别是10 cm和20 cm,它的侧 面展开图的扇环的圆心角是180°,那么圆台的表面积是多少?
命题方向 多面体的体积
[例 2] 长方体相邻三个面的面积分别为 2、3、6 求它的
体积.
[解析] 设长方体的长、宽、高分别为a、b、c则有
据条件得到
1 2
πl2=2π,解得母线长l=2,2πr=πl=2π,r=1所以
该圆锥的体积为:V圆锥=13Sh=13×
22-12π=
3 3 π.
[点评] 本题主要考查空间几何体的体积公式和侧面展开 图.审清题意,所求的为体积,不是其他的量,分清图形在 展开前后的变化;其次,对空间几何体的体积公式要记准记 牢,属于中低档题.
[解析]
三棱台ABC-A1B1C1的上、下底面积之比为4:9.连接 A1B、BC1和AC1,把棱台分为三个棱锥B-A1B1C1,C1- ABC,A1-ABC1.则这三个棱锥体积之比为________.
[答案] 4:9:6
[解析] 如图,设三棱锥B-A1B1C1,C1-ABC,A1- ABC1体积分别为V1、V2、V3,又设棱台的高为h,上、下底面 积分别为S1、S2.依题意,得
人教版《圆柱与圆锥》(完美版)PPT课件1

解答此类题的关键是明确长方形的长(宽)或 正方形的边长等于圆柱的底面周长,根据公式 C=2πr 或C=πd求出圆的周长,然后与长方形 的长(宽)或正方形的边长进行比较即可确定 答案。
规范解答:选择①和B、②和A或②和C都恰好 能做成圆柱形的盒子。
1.把圆柱的侧面沿高展开,得到一个(长方形),它 的长等于圆柱底面的(周长),宽等于圆柱的 ( 高 )。
思路分析:塔的顶端呈圆锥形,求塔的顶端的体积就
是求圆锥的体积。计算时先根据公式S底=π
求
出圆锥的底面积,再根据公式V
求出圆锥的体
积。
规范解答::圆锥的底面积: 3.14×(18.84÷3.14÷2)²
=3.14×9 =28.26(m²) 圆锥的体积:
×28.26×6 =2×28.26 =56.52(m³) 答:塔的顶端的体积是 56.52立方米。
20×2×3.14×60+202×3.14=8792(cm²) 答:做这个水桶至少需要8792平方厘米铁皮。
例3 一根钢管,长50厘米,外圆直径是10厘米, 钢管厚2cm(如下图)。铸造这样一根钢管需要 钢材多少立方厘米?
思路分析:求铸造这样一根钢管需要钢材的体积, 就是用大圆柱的体积减去中空的小圆柱的体积。
思路分析:瓶子正放和倒放时的容积与饮料的体积不
变,所以瓶子空余部分的容积相等。因此,饮料瓶的
容积就相当于一个高为(20+4)cm 的圆柱形容器的
容积,可推知饮料体积占瓶子容积的
,即
480mL的
。
确定瓶中饮料的体积占瓶子容积的几分之几是解答
此题的关键。
规范解答:20+4=24(cm) 480× =400(mL) 答:瓶内现有饮料400毫升。
3.一个内半径是10cm的饮料瓶里,饮料的高度为 4cm,把瓶盖拧紧倒置放平,无水部分是圆柱形, 高度为16cm,这个瓶子的容积是多少?
《圆锥的体积》圆柱与圆锥PPT课件2 (共17张PPT)

圆 锥 在 生 活 中 的 应 用
圆 锥 在 生 活 中 的 应 用
努 力 吧 !
说说下列各图是由哪些图形组成的。
计算下面各圆锥的体积.
3dm 3.6m 8dm 8cm 12cm
s 9m
2
1Hale Waihona Puke V=3sh1 × 19 × 12 = 76 (立方厘米) 3
答:这个零件的体积是76立方厘米。
1 2 3.14 2 1.5 3 3 6.28 (米 )
答:这堆小麦的体积是6.28立方米.
一个圆锥形零件,它的底面直径是10厘 米,高是3厘米,这个零件的体积是多少 立方厘米?
1 2 3.14 (10 2) 3 3
78.(厘米 5 )
3
答:这堆零件的体积是78.5立方厘米.
一堆大米,近似于圆锥形,量得 底面周长是9.42厘米,高5厘米。 它的体积是多少立方厘米?
把一个棱长是6厘米的正方体木块, 加工成一个最大圆锥体,圆锥的体 积是多少立方厘米?
• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •
挫折的名言 1、 我觉得坦途在前,人又何必因为一点小障碍而不走路呢?——鲁迅 2、 “不耻最后”。即使慢,弛而不息,纵会落后,纵会失败,但一定可以达到他所向的目标。——鲁迅 3、 故天将降大任于是人也,必先苦其心志,劳其筋骨,饿其体肤,空乏其身,行拂乱其所为,所以动心忍性,曾益其所不能。 战胜挫折的名言 1、卓越的人一大优点是:在不利与艰难的遭遇里百折不饶。——贝多芬 2、每一种挫折或不利的突变,是带着同样或较大的有利的种子。——爱默生 3、我以为挫折、磨难是锻炼意志、增强能力的好机会。——邹韬奋 4、斗争是掌握本领的学校,挫折是通向真理的桥梁。——歌德 激励自己的座右铭 1、 请记得,好朋友的定义是:你混的好,她打心眼里为你开心;你混的不好,她由衷的为你着急。 2、 要有梦想,即使遥远。 3、 努力爱一个人。付出,不一定会有收获;不付出,却一定不会有收获,不要奢望出现奇迹。 4、 承诺是一件美好的事情,但美好的东西往往不会变为现实。 工作座右铭 1、 不积跬步,无以至千里;不积小流,无以成江海。——《荀子劝学》 2、 反省不是去后悔,是为前进铺路。 3、 哭着流泪是怯懦的宣泄,笑着流泪是勇敢的宣言。 4、 路漫漫其修远兮,吾将上下而求索。——屈原《离骚》 5、 每一个成功者都有一个开始。勇于开始,才能找到成功的路。 国学经典名句 1、知我者,谓我心忧,不知我者,谓我何求。(诗经王风黍离) 2、人而无仪,不死何为。 (诗经风相鼠) 3、言者无罪,闻者足戒。 (诗经大序) 4、他山之石,可以攻玉。 (诗经小雅鹤鸣) 5、投我以桃,报之以李。 (诗经大雅抑) 6、天作孽,犹可违,自作孽,不可活。(尚书) 7、满招损,谦受益。 (尚书大禹谟) 青春座右铭 1、爱的力量大到可以使人忘记一切,却又小到连一粒嫉妒的沙石也不能容纳。 2、把手握紧,什么也没有;把手伸开,你就拥有了一切。 3、不在打击面前退缩,不在困难面前屈服,不在挫折面前低头,不在失败面前却步。勇敢前进! 4、当你能飞的时候就不要放弃飞。 5、当你能梦的时候就不要放弃梦。 激励向上人生格言 1、实现自己既定的目标,必须能耐得住寂寞单干。 2、世界会向那些有目标和远见的人让路。 3、为了不让生活留下遗憾和后悔,我们应该尽可能抓住一切改变生活的机会。 4、无论你觉得自己多么的不幸,永远有人比你更加不幸。 5、无论你觉得自己多么的了不起,也永远有人比你更强。 6、打击与挫败是成功的踏脚石,而不是绊脚石。 激励自己的名言 1、忍别人所不能忍的痛,吃别人所别人所不能吃的苦,是为了收获得不到的收获。 2、销售是从被别人拒绝开始的。 3、好咖啡要和朋友一起品尝,好机会也要和朋友一起分享。 4、生命之灯因热情而点燃,生命之舟因拼搏而前行。 5、拥有梦想只是一种智力,实现梦想才是一种能力。 6、有识有胆,有胆有识,知识与胆量是互相促进的。 7、体育锻炼可以(有时可以迅速)使人乐观(科学实验证明)。 8、勤奋,机会,乐观是成功的三要素。(注意:传统观念认为勤奋和机会是成功的要素,但是经过统计学和成功人士的分析得出,乐观是成功的第三要素) 9、自信是人格的核心。 10、获得的成功越大,就越令人高兴。
圆锥ppt课件

在工程设计中的应用
圆锥在工程设计中也有着广泛的 应用,例如桥梁的设计、隧道的
设计等。
圆锥的形状和性质在工程设计中 有着重要的意义,例如圆锥的稳
定性、抗压性等。
圆锥在水利工程、土木工程等领 域也有着实际的应用,例如在设 计水坝、大坝等工程时,需要考
虑圆锥形的结构稳定性。
05
圆锥的相关公式与定理
圆锥的母线
利用手工绘制圆锥的草图
绘制底面
使用圆规和直尺,绘制出一个 圆形作为圆锥的底面。
连接底面和侧面
使用直尺或曲线板,将侧面与 底面平滑连接起来,得到圆锥 的草图。
准备工具
准备好纸、笔、圆规、直尺等 手工绘图工具。
绘制侧面
以底面圆心为顶点,用直尺绘 制出一个等腰三角形,作为圆 锥的侧面。
调整草图
可以使用橡皮等工具对草图进 行修改和调整,使其更加符合 要求。
圆锥的侧面积可以通过公式 S = πrl 来计算,其 中 r 是底面半径,l 是母线长度。
侧面积公式的推导
侧面积公式是由圆的周长公式和圆锥的侧面展开 图推导而来的。
3
侧面积的应用
圆锥的侧面积在几何学、工程、艺术等领域都有 广泛的应用。
圆锥的全面积
全面积公式
圆锥的全面积可以通过公式 S_total = πrl + πr² 来计算,其中 r 是底面半径,l 是母线长度。
06
圆锥的绘制方法
利用几何软件绘制圆锥
确定底面半径
首先需要确定圆锥的底面半径,可以使用几何软件中的测 量工具进行测量。
绘制圆
在几何软件中,选择画圆工具,并确定圆心和半径,绘制 出一个圆形。
绘制圆锥
选择画三角形工具,以圆心为顶点,绘制出一个等腰三角 形,然后选择“合并形状”工具,将三角形与圆形进行合 并,得到圆锥的侧面。
苏教版六年级下册数学《圆柱的体积》圆柱和圆锥PPT(第2课时)

(打结处大约用彩带15厘米) (1)S=2πrh+2πr²=2×3.14×15×20+2×3.14×15²=3297(cm²)
(2)l=4h+4d+15=4(20+30)+15=215cm
教学新知
练一练:一个用塑料薄膜覆盖的蔬菜大棚,长15米,横截面是一个半径 2米的半圆形。
(1)搭建这个大棚大约要用多少 平方米的塑料薄膜?
(1)V=sh=4²π×3.5=175.84(m³) 175.84m³=175.84t (2)S=2πrh+πr²=2×3.14×4×3.5+3.14×4²=138.16(m²)
教学新知
试一试:一个圆柱形蛋糕盒,底面半径是15厘米,高是20厘米。 (1)做这个蛋糕盒大约要用硬纸板多少平方厘米? (2)用彩带捆扎这个蛋糕盒(如下图),至少需要彩带多少厘米?
18.84dm
2m
282.6cm² 157cm³
244.92dm² 282.6dm³
37.68m² 15.7m³
教学新知
算一算:一个圆柱形油桶,从里面量,底面直径是40厘米,高是50厘米。 (1)它的容积是多少升? (2)如果1升柴油重0.85千克,这个油桶可装柴油多少千克? (3)做这样一个油桶,至少需要铁皮多少平方分米?(得数保留一位
教学新知
思考: (1)把圆钢竖着拉出水面8厘米,水面下降了 4厘米,你
能想到一些什么? (2)全部浸入,水面上升9厘米,你又能想到什么?怎样
计算出这个圆钢的体积? (3)这题还可以怎样思考?
教学新知
例一:一个圆柱形水桶的容积是80立方分米,里面装了2/5的水。 已知它的底面积是10平方分米,里面水的深度是多少?
教学新知
(2)l=4h+4d+15=4(20+30)+15=215cm
教学新知
练一练:一个用塑料薄膜覆盖的蔬菜大棚,长15米,横截面是一个半径 2米的半圆形。
(1)搭建这个大棚大约要用多少 平方米的塑料薄膜?
(1)V=sh=4²π×3.5=175.84(m³) 175.84m³=175.84t (2)S=2πrh+πr²=2×3.14×4×3.5+3.14×4²=138.16(m²)
教学新知
试一试:一个圆柱形蛋糕盒,底面半径是15厘米,高是20厘米。 (1)做这个蛋糕盒大约要用硬纸板多少平方厘米? (2)用彩带捆扎这个蛋糕盒(如下图),至少需要彩带多少厘米?
18.84dm
2m
282.6cm² 157cm³
244.92dm² 282.6dm³
37.68m² 15.7m³
教学新知
算一算:一个圆柱形油桶,从里面量,底面直径是40厘米,高是50厘米。 (1)它的容积是多少升? (2)如果1升柴油重0.85千克,这个油桶可装柴油多少千克? (3)做这样一个油桶,至少需要铁皮多少平方分米?(得数保留一位
教学新知
思考: (1)把圆钢竖着拉出水面8厘米,水面下降了 4厘米,你
能想到一些什么? (2)全部浸入,水面上升9厘米,你又能想到什么?怎样
计算出这个圆钢的体积? (3)这题还可以怎样思考?
教学新知
例一:一个圆柱形水桶的容积是80立方分米,里面装了2/5的水。 已知它的底面积是10平方分米,里面水的深度是多少?
教学新知
圆锥的ppt课件

圆锥的特性
01
02
03
圆锥的底面
圆锥的底面是一个圆,其 半径为r,圆心角为θ。
圆锥的高
圆锥的高是从顶点到圆心 的距离,记作h。
圆锥的母线
圆锥的母线是与底面圆的 边缘相切的线段,其长度 为l。
圆锥的应用
圆锥在几何学中的应用
圆锥是几何学中一个重要的基本图形,常用于研究几何性质和定理,如勾股定 理、射影定理等。
圆锥的底面展开图
圆锥的底面展开图是一个圆 这个圆的半径等于圆锥的底面半径
这个圆的周长等于圆锥底面的周长
圆锥展开图的应用
圆锥展开图在制作工艺品中应用广泛
圆锥展开图可以帮助我们理解圆锥的 几何性质和特点
通过圆锥展开图可以计算圆锥的母线 长和底面周长
05
圆锥的绘制方法
利用几何画板绘制圆锥
打开几何画板软件,选择“绘 图”菜单中的“圆锥”命令。
圆锥的母线
母线定义
圆锥的母线是从顶点到底面边缘的连线段。
母线长度
母线的长度等于从顶点到底面的垂直距离,即 l = h + r。
母线与底面半径关系
母线长度 l 与底面半径 r 的关系可以用公式 l = r + h 来表示。
03
圆锥的体积和表面积
圆锥的体积
圆锥体积的定义
圆锥体积是指圆锥所占空间的 大小。
展开后是一个扇形,扇形的半径等于 圆锥的母线长度。
侧面积
圆锥的侧面积等于展开后的扇形面积,即 S = (1/2) × l × r,其中 l 是母线长度,r 是底面半径 。
侧面积与底面周长关系
侧面积 S 与底面周长 C 的关系可以用公式 S = C × h / (2π) 来表示。
圆柱与圆锥ppt模版课件

圆锥的体积
圆锥的体积计算公式为:V = (1/3) * π * r^2 * h,其中r是 底面半径,h是圆锥的高。
圆锥的体积由底面圆的面积和 高度共同决定,与斜高无关。
圆锥的体积随底面半径和高的 增大而增大。
圆锥的斜高与底面半径关系
圆锥的斜高计算公式为:l = sqrt(r^2 + h^2),其中r是底面
饮料瓶、帽子和灯罩等。
02 圆柱的几何性质
圆柱的表面积
01
02
03
04
圆柱的表面积由两个底面和一 个侧面组成。
底面是一个圆形,其面积为π × r^2,其中r是底面半径。
侧面是一个矩形,其面积为2 × π × r × h,其中h是圆柱的
高。
因此,圆柱的表面积A = 2 × π × r^2 + 2 × π × r × h。
当圆锥的高固定时,母线随底面半径的增大而增大;当底面半径固定时,母线随高 的增大而增大。
04 圆柱与圆锥的相互关系
圆柱与圆锥的相似性
01
02
03
定义相似
如果一个圆柱和一个圆锥 的底面直径与高之比相等, 则它们是相似的。
面积相似
相似圆柱和圆锥的底面面 积之比等于它们的半径平 方之比,而侧面积之比等 于它们的半径之比。
度。
圆柱与圆锥的应用场景
建筑学
圆柱和圆锥在建筑设计中有广 泛的应用,如柱子、穹顶和拱
门。
工程学
在机械工程中,圆柱和圆锥用 于制造各种零件和结构,如轴 承、齿轮和螺母。
自然界
自然界中存在许多圆柱和圆锥 形状的物体,如树木、植物和 动物的身体结构。
日常生活
在日常生活中,我们经常接触 到圆柱和圆锥形状的物品,如
《圆锥的体积》圆柱与圆锥PPT优秀课件4

打谷场上,有一个近似于圆锥的小麦堆, 测得底面半径是2米,高是1.5米。你能计算出 这堆小麦的体积吗?
1 2 3.14 2 1.5 3
6.28 (米 )
3
答:这堆小麦的体积是6.28立方米。
一个圆锥形零件,它的底面直径是10厘 米,高是3厘米,这个零件的体积是多少 立方厘米?
1 2 3.14 (10 2) 3 3
高,底面积是相等的吗?
下面我们用刚才比较过的圆锥体 和圆柱体再来做一个实验:
当圆柱体和圆锥体既 不等底也不等高时, 圆锥体体积还是圆柱 体体积的三分之一吗?
圆锥的体积V等于和它等底等高 的圆柱体积的三分之一
V圆柱=sh
1 V锥=3
sh
判断下面的说法是不是正确。
1 (1)圆锥的体积等于圆柱体积的 。( X ) 3
答:这个零件的体积是76立方厘米。
一堆大米,近似于圆锥形,量得 底面周长是9.42厘米,高5厘米。 它的体积是多少立方厘米?
有一根底面直径是6厘米,长是15厘米的圆 柱形钢材,要把它削成与最大的圆锥形零件。 要削去钢材多少立方厘米?
6厘米
15厘米
把一个棱长是6厘米的正方体木块, 加工成一个最大圆锥体,圆锥的体 积是多少立方厘米?
圆锥的体积
Hale Waihona Puke 这堆小麦的体 积是多少呢?
圆锥的体积 怎么求呢?
现在我们把他们放大后再 来做个实验:
第一次
第二次
第三次
圆锥的体积正好等于与它等底等高的圆柱体积的三分之一
(即Ⅴ锥= sh)
1 3
这里也有一个圆锥体和一个圆柱体,请 仔细观察一下:
比一比:
这个圆锥体的高,底面积,和圆柱体的
《圆柱的体积》PPT课件

面测量得到的。)
8cm
杯子的容积。
杯子的容积: 50.24 ×10 =502.4(cm3)
10cm
杯子的底面积: 3.14 ×(8÷2)2
=3.14 ×16 =50.24(cm2)
=502.4(mL) 牛奶的体积: 240×2=480(mL) 502.4>480 答:杯子能装下2袋这样的牛奶。
课堂练习
小明和妈妈出去游玩,带了一个圆柱形保温壶,从里 面量底面直径是8cm,高是15cm。如果两人游玩期间 要喝1L水,带这壶水够喝吗?
保温壶的底面积:
3.14×(8÷2)2 =3.14×16 =50.24(cm2)
保温壶的容积:
50.24×15=753.6(cm3) =0.7536(L)
1L>0.7536L
答:带这壶水不够喝。
课堂练习
一根圆柱形木料底面直径是0.4m,长5m。如果做一张 课桌用去木料0.02m3,这根木料最多能做多少张课桌?
木料的体积:
3.14×(0.4÷2)2×5 =3.14×0.2 =0.628(m3)
“退一”法。
0.628÷0.02=31.4(张)
答:这根木料最多能做31张课桌。
已知底面直径和高求圆柱体积。 V=π(d2 )2h =3.14×(1÷2)2×10 =7.85(立方米) 答:挖出的土有7.85立方米。
探究新知
下图的杯子能不能装下2袋这样的牛奶?(数据是从杯子 里面测量得到的。)
思考:
8cm
1.已知什么?
10cm
2.要求什么?
3.要注意什么?
探究新知
下图的杯子能不能装下2袋这样的牛奶?(数据是从杯子里
)
于土的高度有关。
两个花坛的体积
人教版小学数学六年级下册《第三单元圆柱与圆锥:3.圆柱的体积》PPT1

169.56立方分米。
判断:
1、圆柱的体积比表面积大。( ) ×
2、等底等高的正方体、长方体和圆柱,它们的体积
都相等。( √ )
3、一个圆柱的底面半径扩大到原来的3倍,体积也
4、体积相等的两个圆柱不一定是等底等高。(√ )
扩到原来的3倍。( × )
判断:
5、高不变,圆柱体的底面积越大,它的体积就
人教版六年级数学下册第三单元
圆柱的体积练习课
知识回顾:
圆柱的体积公式是怎样推导出来的?
转化
长方体的体积= 底面积 × 高 圆柱的体积= V
底面积 S
圆柱体积计算公式是:
V
×
高 h
已知圆柱的底面积和高,怎样求圆柱的体积?
V=s×h
已知圆柱的体积和高,怎样求圆柱的底面积?
s=V÷h
已知圆柱的体积和底面积,怎样求圆柱的高?
越大。( √ )
6、圆柱体的高越长,它的体积越大。( × ) 7、圆柱体的底面直径和高可以相等。(√ )
巩固练习:
将一个棱长为6分米的正方 体钢材熔铸成底面半径为1 分米的圆柱体,这个圆柱有 多长?(得数保留整数)
思考:正方体与熔铸成的圆柱体体积有什么关系? 正方体的体积:6×6×6=216(dm3) 圆柱的长:216÷(3.14×1×1) =216÷3.14 ≈69(分米)
=18×3 =54(dm3)
答:它的体积是54dm3。
练一练:
把一个棱长6分米的正方体木块切削成一个体积最 大的圆柱体,这个圆柱的体积是多少立方分米?
d 2 思考:圆柱的直径和高 V ( ) h 2 是正方体的什么? =3.14×(6÷2)2×6 =3.14×32×6 3) =169.56 ( dm 答:这个圆柱的体积是
判断:
1、圆柱的体积比表面积大。( ) ×
2、等底等高的正方体、长方体和圆柱,它们的体积
都相等。( √ )
3、一个圆柱的底面半径扩大到原来的3倍,体积也
4、体积相等的两个圆柱不一定是等底等高。(√ )
扩到原来的3倍。( × )
判断:
5、高不变,圆柱体的底面积越大,它的体积就
人教版六年级数学下册第三单元
圆柱的体积练习课
知识回顾:
圆柱的体积公式是怎样推导出来的?
转化
长方体的体积= 底面积 × 高 圆柱的体积= V
底面积 S
圆柱体积计算公式是:
V
×
高 h
已知圆柱的底面积和高,怎样求圆柱的体积?
V=s×h
已知圆柱的体积和高,怎样求圆柱的底面积?
s=V÷h
已知圆柱的体积和底面积,怎样求圆柱的高?
越大。( √ )
6、圆柱体的高越长,它的体积越大。( × ) 7、圆柱体的底面直径和高可以相等。(√ )
巩固练习:
将一个棱长为6分米的正方 体钢材熔铸成底面半径为1 分米的圆柱体,这个圆柱有 多长?(得数保留整数)
思考:正方体与熔铸成的圆柱体体积有什么关系? 正方体的体积:6×6×6=216(dm3) 圆柱的长:216÷(3.14×1×1) =216÷3.14 ≈69(分米)
=18×3 =54(dm3)
答:它的体积是54dm3。
练一练:
把一个棱长6分米的正方体木块切削成一个体积最 大的圆柱体,这个圆柱的体积是多少立方分米?
d 2 思考:圆柱的直径和高 V ( ) h 2 是正方体的什么? =3.14×(6÷2)2×6 =3.14×32×6 3) =169.56 ( dm 答:这个圆柱的体积是
六年级数学下册《圆柱和圆锥的认识》课件

定积分法
使用定积分求出圆锥的体积公式,再代入底面半径和高度即可求得圆锥的体积。
圆台的定义和特征
定义
圆台是由一个上底面半径、下底面半径、高和侧面 组成的几何图形。
特征
圆台的侧面是一个梯形,底面圆的半径和高度可确 定圆台的大小。
实际应用
圆台广泛应用于生活中的各种容器和建筑结构中, 比如灯罩和教堂尖顶。
圆锥广泛应用于生活中的各种容器和建筑结构中,比如冰淇淋蛋筒和火车车头。
圆锥的表面积求解方法
公式法
使用圆锥的侧面积公式和底面积公式相加即可求得 圆锥的表面积。
展开图法
将圆锥展开成一个弓形,在弓形的开端加上一个扇 形即可得到圆锥的展开图,再利用展开图计算圆锥 的表面积。
圆锥的体积求解方法
底面积法
使用底面积公式和三角形面积公式计算圆锥的体积。
公式法
使用圆台的体积公式即可求得圆台的体积。
几何体分解法
可以将圆台分解为一个圆锥和一个圆柱,分别计算 它们的体积后相加即可得到圆台的体积。
圆柱与圆锥的差异和联系
相同点
• 都有底面和侧面 • 表面积和体积的计算方法类似 • 都广泛应用于实际生活和工程中
不同点
• 底面形状不同:圆柱底面为圆形,圆锥底面 为圆形或椭圆形
交通锥标志
交通锥一般用于道路施工和事故现场,图标通常设 计成圆锥形,用以提醒司机注意交通安全。
数学思维拓展:解决圆柱和圆锥问题的 策略
1
抽象转化法
将题目抽象成一些基本的几何图形,然后利用几何图形的相似、等量关系等解题。
2
代数运算法
当几何图形较为复杂时,可以将某些参 一个圆锥的底面半径为5cm,高为12cm,它 的表面积是多少?
圆柱和圆锥的学习方法和技巧
使用定积分求出圆锥的体积公式,再代入底面半径和高度即可求得圆锥的体积。
圆台的定义和特征
定义
圆台是由一个上底面半径、下底面半径、高和侧面 组成的几何图形。
特征
圆台的侧面是一个梯形,底面圆的半径和高度可确 定圆台的大小。
实际应用
圆台广泛应用于生活中的各种容器和建筑结构中, 比如灯罩和教堂尖顶。
圆锥广泛应用于生活中的各种容器和建筑结构中,比如冰淇淋蛋筒和火车车头。
圆锥的表面积求解方法
公式法
使用圆锥的侧面积公式和底面积公式相加即可求得 圆锥的表面积。
展开图法
将圆锥展开成一个弓形,在弓形的开端加上一个扇 形即可得到圆锥的展开图,再利用展开图计算圆锥 的表面积。
圆锥的体积求解方法
底面积法
使用底面积公式和三角形面积公式计算圆锥的体积。
公式法
使用圆台的体积公式即可求得圆台的体积。
几何体分解法
可以将圆台分解为一个圆锥和一个圆柱,分别计算 它们的体积后相加即可得到圆台的体积。
圆柱与圆锥的差异和联系
相同点
• 都有底面和侧面 • 表面积和体积的计算方法类似 • 都广泛应用于实际生活和工程中
不同点
• 底面形状不同:圆柱底面为圆形,圆锥底面 为圆形或椭圆形
交通锥标志
交通锥一般用于道路施工和事故现场,图标通常设 计成圆锥形,用以提醒司机注意交通安全。
数学思维拓展:解决圆柱和圆锥问题的 策略
1
抽象转化法
将题目抽象成一些基本的几何图形,然后利用几何图形的相似、等量关系等解题。
2
代数运算法
当几何图形较为复杂时,可以将某些参 一个圆锥的底面半径为5cm,高为12cm,它 的表面积是多少?
圆柱和圆锥的学习方法和技巧
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
V圆柱=sh
V=
1 3
sh
打谷场上,有一个近似于圆锥的小麦堆, 测得底面半径是2米,高是1.5米。你能计算出 这堆小麦的体积吗?
答:这堆小麦的体积是6.28立方米.
感谢您的阅读! 为了便于学习和使用,本文 档下载后内容可随意修改调 整及打印,欢迎下载!
一个圆锥形零件,它的底面直径是10厘 米,高是3厘米,这个零件的体积是多少 立方厘米?
说说下列各图是由哪些图形组成的。
计算下面各圆锥的体积.
3dm 12cm
3.6m 8dm 8cm
V=31 sh
1 3
×19×12=76(立方厘米)
答:这个零件的体积是76立方厘米。
一堆大米,近似于圆锥形,量得 底面周长是9.42厘米,高5厘米。 它的体积是多少立方厘米?
把一个棱长是6厘米的正方体木块, 加工成一个最大圆锥体,圆锥的体 积是多少立方厘米?
答:这堆零件的体积是78.5立方厘米.
一、填空: 用字12、 、母圆圆表锥柱示的体是体积(积 的V==13(与13 s和13h它×(底)等面。底积等×高高))的,圆 锥的体积相等。
3、一个圆柱和一个圆锥等底等高,圆柱 的体积是3立方分米,圆锥的体积是(1 ) 立方分米。
4、一个圆锥的底面积是12平方厘米,高 是6厘米,体积是(24 )立
只有一条
底面 有一个底面,是圆形
丰收的喜悦
这堆小麦的体 积是多少呢?
圆锥的体积 怎么求呢?
准备等底等高的圆柱形容器和 圆锥形容器各一个.
将圆锥形容器装满沙,再倒入圆柱 形容器,看几次能倒满.
圆锥的体积V等于和它等底等高 的圆柱体积的三分之一
二、判断:
1、圆锥的体积等于圆柱体积的1/3。
( ×)
2、圆柱的体积大于与它等底等高的圆
锥体的体积。
( √)
3、圆锥的高是圆柱高的3倍,它们的体
积一定相等。
( ×)
4、一根圆柱形木料,把它加工成最大
的圆锥,削去部分的体积和圆锥的体积
比是2:1。
( √)
圆 锥 在 生 活 中 的 应 用
圆 锥 在 生 活 中 的 应 用
复习:
1、圆柱体积的计算公式是什么?
圆柱的体积=底面积×高
V柱=S底h
2、圆柱的特征是什么?
两个底相等
说出圆柱和圆锥各部分的名称及特征:
高 有无数条
侧面 展开后是长方形或正方形
底面 有两个底面,是相等的圆形
圆柱的体积公式用字母表示是( V=s h )。如果已知d=6厘
米,h=10厘米。那么圆柱的体积是(282.6)立方厘米。如果已知 c=6.28分米,h=5分米。那么圆柱的体积是(15.7 )立方分米。
