PPK初始过程能力研究
过程能力研究(CPK PPK)

基础统计学
Minitab简介
Improve
测量系统分析
Y的表现水平
及目标 确定改进目标
Control
流程能力 -2-
Six sigma GB Training-V3.0
目
录
流程能力介绍 计数型流程能力 计量型流程能力 流程能力指数 短期/长期流程能力分析 流程能力练习
流程能力 -3-
Six sigma GB Training-V3.0
0
1σ
2σ 3σ
4σ
5σ
6σ
流程能力 -21-
Six sigma GB Training-V3.0
尾部面积是多少?
µ 2.5
SL
我们从Z表获得尾 部的面积...…或者 我们可以使用 Minitab!
−5σ −4σ −3σ −2σ −1σ
0
1σ
2σ 3σ
4σ
5σ
6σ
流程能力 -22-
Six sigma GB Training-V3.0
最终结果物
-明确反映当前Process的短期及长期流程能力的报告书
流程能力 -6-
Six sigma GB Training-V3.0
什么导致缺陷? 额外的波动源于:
− − −
制造流程和测量系统 供给的材料波动 不合理的过窄的规格 (为了强化的设计,比顾客的要求更窄)
不适当的设计容限
不稳定的部 件和材料
正态分布
−3σ
−2σ
−1σ
0 Avg
1σ
2σ
3σ
-3
-2
-1
Z
平均 = 50 标准偏差 = 10
1
2
3
流程能力 -20-
Cpk_与Ppk_两种过程能力指数的对比分析研究

Cpk 与Ppk 两种过程能力指数的对比分析研究1摘 要:在进行统计质量控制的时候,工序能力指数Cpk(Index of Process Capability)与过程能力指数Ppk(Index of Process Performance)是评价过程及改进方向和目标的重要指标,但在实际操作过程中,Cpk 和Ppk 容易被混淆。
本文通过两种指标的定义及计算过程的比较,分析其差异,并利用SPC(Statistical Process Control)统计过程控制软件中这两个指标的应用范围情况进行了示例说明,更为直观地显示了它们的联系与区别。
关键词:Cpk(工序能力指数); Ppk(过程能力指数); SPC(统计过程控制)中图分类号:O291. 引言质量管理中数理统计的理论和方法非常重要[1]。
由于每天生产产品的质量,如工件的厚度、表面粗糙度等不断变动的缘故,为了加工出厚度均匀、粗糙度一致的工件,即使对加工环境的温度、湿度,对切削时的进刀量等操作条件做出严格的规定,实际生产出来的产品质量仍然存在波动。
而且上面所列出的加工条件固定不变也是难以办到的事,这些加工条件也存在着一定程度的波动,因此工序质量在各种影响因素制约下,呈现波动特性。
统计方法能够对这些波动的状况及其相互关系进行定量分析,是监控、改进产品质量非常有用的工具。
工序与过程能力指数在质量控制中越来越频繁地使用。
近来随着生产力的高度发展,对产品质量和服务质量的要求不断提高,不合格品率越来越低,而与其对应的过程能力指数要求越来越大。
这反映了生产能力的进步、不合格品率下降、经济效益的提高。
过程能力性能指数Ppk 是在美国克莱斯勒、福特和通用这三大汽车公司制定的QS-9000标准提出的,与过程能力指数Cpk 并列,共称为量度过程的参数[2]。
Cpk 主要用于周期性的过程评价,而Ppk 则用于实时过程性能研究和初始过程能力评估。
目前我国许多企业日常计算的是Ppk,而不少人却误认为是Cpk,于是基本概念的错误带来认识上的混淆。
过程能力分析CPK PPK

2010-03-04
2010-03-04
分析用控制图的控 制中心及控制限是 变化的
2010-03-04
2010-03-04
• 组内过程能力:也即潜在的过程能力 (Cpk),考察的是稳定状态下即仅存在普 通原因变异的过程能力,它考察的是组内 波动,所使用估计参数:过程平均值 (X)-子 组内标准差; • 整体能力:也指整体过程能力(Ppk),不 仅考察组内的变异,而且还考虑组间的变 异,可适用于非稳定状态的过程。所使用 的估计参数:过程平均值 (X)-整体标准差; 2010-03-04
2010-03-04
十一、CPK换算成PPM的计算方式---excel算法
STANDARDIZE(x,mean,standard_dev) ---返回标准正态分布的标准化域值,记作z x:需要进行规范化的数值(规格上、下限) mean:数据分布的算术平均值 standard_dev:数据分布的标准偏差
Cp的评级标准及处理: 等级 A+ A B C D Cp值 Cp≥1.67 1.33≤Cp≤1.67 1.00≤Cp≤1.33 0.67≤Cp≤1.00 Cp≤0.67 处理原则 无缺点。可考虑降低成本。 状态良好维持现状。 改进为A级。 制程不良较多,须提升能力。 制程能力太差,应考虑重新整改设计制程。
过程能力分析
CPK PPK PPM的计算及理解
2010-03-04
2010-03-04
2010-03-04
2010-03-04
• • • • • • • •
2010-03-04
USL:规格上限 LSL:规格下限 SL:规格中心值 T:规格总容差( USL- LSL ) UCL:控制上限(control) LCL:控制下限 CL:实际中心值 σ:标准差 ---也叫标准偏差,就是方差 开平方根, 方差=【(x1-x)^2+(x2x)^2+…+(xn-x)^2】/( n-1 )
PPK初始过程能力研究
174.18 174.17 174.25 174.23 174.16 174.20
0.48
0.40
0.30
0.60
0.30
0.30
3
1.02
*
4
0.73
*
5
0.58
*
6
0.48
*
7
0.42
0.08
8
0.37
0.14
9
0.34
0.18
10
0.31
0.22
1.连续取样
2.组容<7时没有极差下控制限
●Ppk = Min (
USL-X 3σ
D4 3.27 2.57 2.28 2.11 2.00 1.92 1.86 1.82 1.78
X-LSL 3σ
d2 )≥1.67
10-21-07 10-21-08
=Min
1.84
1.85 ) =
1.84
10-21-03 10-21-04 10-21-05 10-21-06 10-21-07 10-21-08
173.90 174.20 174.32 174.48 174.02 174.26
174.32 174.18 174.26 174.12 174.32 174.02
174.38 174.32 174.10 174.02 174.48 174.22 174.08 173.92 174.14 174.02 174.40 174.02 173.98 174.02 173.88 174.22 174.32 174.08 174.32
871.0
870.5
870.9
871.2
0.40
0.46
0.42
过程能力研究(process capability study)

过程能力研究(process capability study)概述过程能力研究旨在分析稳定过程某一质量特性输出对其公差要求的满足程度,该研究结果以指数形式给出,这样的指数称为过程能力指数( PCI)。
过程能力指数是将过程的变异与公差相比较而得出的,虽然专家学者已经提出了为数众多的过程能力指数,但常用的仅有少数的几个。
适用场合·当过程处于统计受控时;·当过程输出服从正态分布时;·当测量过程是在多大程度上满足需求时;C p 和C pk 和P p·当较为关注极小化过程超出公差而导致的不合格情形,相对而言,并不过分强调极小化过程均值相对于目标值的偏移。
C pm 和C pmk·当较为关注极小化过程均值相对于目标值的偏移情形,相对而言,并不过分强调极小化过程超出公差而导致的不合格。
实施步骤1用控制图确定过程处于统计受控状态,如果不受控就不要再做下去。
2用正态概率图或适合的检验确定过程是否服从正态分布。
此时,若有统计软件以及统计学家的建议将会事半功倍。
如果过程不服从正态分布,不要继续往下做了,可以参考“注意事项”提及的处理办法。
3确定过程均值的估计量ˆμ,也即是控制图上的中心线:如果用X 控制图,则X ˆμ=;如果用单值控制图(X 图),则X ˆμ=。
4确定X ˆσ,即估计过程标准差。
该标准差是有全部样本数据计算得到的总标准差。
首选方法:由方差开方计算而得:X ˆs σ==其中,m 为样本含量。
统计软件和电子计算器通常就是使用这个公式来计算X ˆσ的。
有时把它称为总体( Overall)或者长期(Long-term)标准差。
备选方法:利用控制图计算。
对于单值控制图,直接使用单值控制图计算表中的X ˆσ (图表5.27)。
对于X-R 控制图,可利用下式计算得到:X 2R d ˆσ=÷其中,d 2可以查表A.2。
此时得到的X ˆσ称为组间(Within)或者短期(Short-term)标准差。
初始过程能力分析报告 PPK
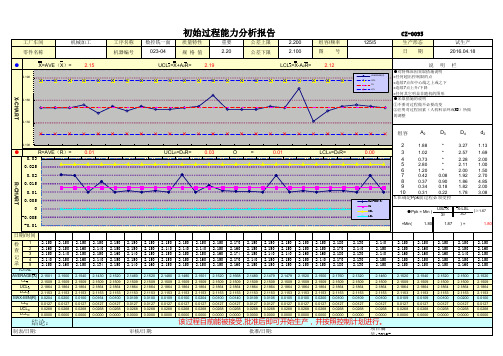
1 2 3 4 5 TOTAL AVERAGE(X) CLX UCLX LCLX MAX-MIN(R) CLR UCLR LCLR
制表/日期:
X-CHART ● R-CHART 检 查 记 录
2.130
组容
2.100
A2
1.88
D3
*
D4
3.27 2.57 2.28 2.11 2.00 1.92 1.86 1.82 1.78
2.170 2.160 2.174 2.170 2.160
2.1668 2.1509 2.1864 2.1153 0.0140 0.0127 0.0268 0.0000
2.150 2.150 2.150 2.140 2.150
2.1480 2.1509 2.1864 2.1153 0.0109 0.0127 0.0268 0.0000
初始过程能力分析报告
工厂车间 零件名称 ● X=AVE(X)=
2.190
CZ-0095
2.200 2.100 LCLX=X-A2R= 组容/频率 图 2.12
AVERAGE(X)
机械加工
工序名称 机器编号
数控铣一面 023-04
质量特性 规 格 值 2.19
重要 2.20
公差上限 公差下限
125/5
2.150 2.150 2.140 2.150 2.160
2.1500 2.1509 2.1864 2.1153 0.0200 0.0127 0.0268 0.0000
2.150 2.160 2.150 2.160 2.150
2.1540 2.1509 2.1864 2.1153 0.0100 0.0127 0.0268 0.0000
初始过程能力研究结果要求

初始过程能力研究结果要求
初始过程能力研究的结果要求主要取决于你的组织或项目的具体需求。
一般来说,以下是一些关键的结果要求:
1.过程能力指数(Cpk/Ppk):这是衡量过程能力最常用的指标。
Cpk代表稳定过程的能力,而Ppk 代表潜在过程能力。
这两个指数都表示过程满足规格要求的能力。
通常,Cpk/Ppk值应大于或等于1.33,以满足大部分组织的需求。
2.过程输出分布:理解过程输出的分布对于了解过程行为至关重要。
这可能涉及到收集和分析大量数据,以了解过程输出的平均值、标准差、偏度和峰度等统计量。
3.异常和偏差的识别:在初始过程能力研究中,应识别并理解任何异常或偏差。
这可能涉及到使用控制图或其他统计工具来识别过程的不稳定或异常行为。
4.过程改进建议:根据研究结果,可能需要提出一些过程改进建议。
这可能包括更改过程参数、改进工具和设备、重新设计产品或服务等。
5.风险评估:评估过程风险也是初始过程能力研究的一个重要部分。
这可能涉及到识别可能影响过程输出的潜在因素,并评估这些因素对过程稳定性和性能的影响。
6.文档化:所有的研究结果和建议都应被详细记录并妥善保存。
这可能包括研究报告、数据表、控制图、改进建议等。
请注意,这些只是一些常见的结果要求,具体的要求可能会因组织、行业或项目的不同而有所不同。
因此,在进行初始过程能力研究时,应明确你的具体需求,并确保你的研究结果能够满足这些需求。
初始过程能力研究计划

初始过程能力研究计划
说明:计算P P K指数并采取下列措施:
1、稳定过程:
(1)P P K≥1.67
该过程可能满足客户的要求,批准后,开始生产并按照已批准的控制计划进行。
(2)1.33≤P P K≤1.67
该过程可能不满足客户的要求,生产批准后,从开始生产就对特性加以重视,直至实际的C PK≥1.33为止
(3)P P K<1.33
该过程没有达到满足客户要求的标准,必须优先进行过程改进,过程改进形成纠正措施计划文件,通常要求增加检验或试验,直到C PK达到1.33为止,用于这些临时措施的修订过的计划必须由客户评审认可.
2、非稳定过程:
根据不稳定的性质,该过程可能不满足顾客的要求,应识别和分析特殊的原因,并尽可能消除,采用100%的检验并增加SPC取样直到当前的Cpk达到1.33
或Ppk达到1.67为止,或者到客户满意为止.
必须优先进行过程改进并成形成纠正措施计划文件,用于这些临时措施的修订
过程和控制.
3、对于初始过程能力研究,在计算Ppk时,为取得足够数据,除按控制计划(CP)抽样外,需要按Ppk计算要求另外抽取足够样本(100PCS)来测试相关
特性。
(注:文件素材和资料部分来自网络,供参考。
请预览后才下载,期待你的好评与关注。
)。
CPK过程能力分析

- 名称不同:Cpk是过程能力指数,Ppk是过程性能指数.
- 实施时机不同:Cpk一般是量产时实施,Ppk一般试生产时实施. 我们默认为稳定状态下连续抽样表征了量产的状况,所以新飞通目前 采取了在试产阶段控制Cpk的方式
12
600.4 599.6 600.0 600.8 600.4
13
599.4 599.0 598.4 599.0 599.6
14
598.8 599.2 599.6 598.6 599.8
5
6
598.8 598.8 599.8 599.2 599.4
600.0 600.2 600.2 599.6 599.0
案例-步骤4
用 ppm表示实际DATA脱离规格的程度。
案例-步骤4
只考虑工程的群内变动显示正态分布时,数据表现为 脱离规格的预想 ppm
案例-步骤4
对所有DATA的变动值来显示正态分布时, DATA表现脱离规格的预测 ppm
提高过程能力的思路
常犯的错误或常见问题
✓ 工艺过程不处于稳定状态,有异常发生时进行过程 性能分析
✓ 样本数量太少 ,不具备代表意义
✓ 有明显因为各种特殊原因导致的明显有问题的数 据,没做剔除而保留下来,影响了整体分析的结果
✓ 对计算结果的意义不了解,没有制定很好的改善 措施
回顾与讨论
过程能力分析的前提条件是什么? CP与CPK,PP与PPK之间的区别是什么? CPK与PPK之间的区别是什么? CP>1.67而 CPK<1.0的时候,应该如何处理? CP<1.0的时候,又该如何处理
PPK初始过程能力研究报告表
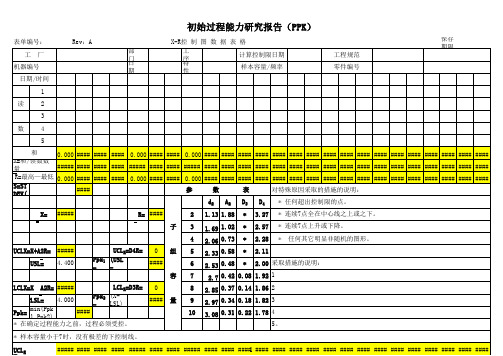
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
AVG.
研究评定:由以上计算结果可知PPK= ##### >1.67,初始能力指数足够.若批准,开始生产并按照已批准的控制计划进行.
说明:试生产时前期质量部连续取样125件对产品特性进行测量并记录结果,提交前期质量科长审批签字后存档,下发至相关责任单位,并将结果反馈至项目经理。
2
1.13 1.88 1.69 1.02 2.06 0.73 2.33 0.58 2.53 0.48
Ppk1= (USL-X)/3δ s= ####
2.7 0.42 0.08 1.92 1 2.85 0.37 0.14 1.86 2 2.97 0.34 0.18 1.82 3 3.08 0.31 0.22 1.78 4 5。
初始过程能力研究报告(PPK)
表单编号: 工 厂 Rev:A 部 日 门 期 X-R控 制 图 数 据 表 格 工 特 序 性 计算控制限日期 样本容量/频率 工程规范 零件编号 保存期限 3年
机器编号 日期/时间 1 读 2 3 数 4 5 和
0.000 #### #### #### 0.000 #### #### 0.000 #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### ####
X=和/读数数量 ##### #### #### #### ##### #### #### ##### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### R=最高—最低 0.000 #### #### #### 0.000 #### #### 0.000 #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### S=STDEV(C6:V10)=δ s= #### 参 数 d2 X= ##### R= #### 子 2 3 4 UCLX=X+A2R= USL= ##### 4.400 UCLR=D4R= 0 组 5 6 容 LCLX=X A2R= ##### 4.000 LCLR=D3R= 0 量 7 8 9 10 A2 表 D3 * * * * * D4 3.27 2.57 2.28 2.11 2.00 采取措施的说明: 对特殊原因采取的措施的说明: * 任何超出控制限的点。 * 连续7点全在中心线之上或之下。 * 连续7点上升或下降。 * 任何其它明显非随机的图形。
初始过程研究

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载初始过程研究地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容初始过程研究说明:确保由顾客或供方设定安全、主要、关键或重要特性的过程能力在可接受水平,确定在零件提交前可计量(可测数值)地进行评价。
具体要求:项目管理职责:管理和评价初始过程能力研究,以确保满足下列期望(已提交级别为基础)初始过程研究·在提交前,所有顾客或供应商确定的特殊特性必须验证在可接受的水平;·必须使用变量性数据;·在研究前必须完成MSA(测量系统分析); eq \o(\s\up 7(* ),\s\do 3( 必))·收集并分析数据,使用X-R控制图(一种对极差和变量进行分析、统计的统计图表)是很重要的;·至少包含100个数据的25个子组.过程研究·过程研究的结果基于正态分布的数据,稳定过程·参考SPC(统计过程控制)手册·如果在提交时过程不稳定和能力达不到,供应商必须提供过渡控制计划和纠正措施计划·过程能力或表现的指标如Cpk、Ppk或其他,要达成一致特殊特性:由顾客或供应商确定的,在装配、形状、功能、耐久性、可靠性和/或安全性(包括政府法规)方面影响到顾客满意度的要求。
必须包括在设计记录和控制计划中;供应商必须在他们使用的所有文件上表明特殊特性;所有特殊特性必须经过研究且CPK和PPK≥1.67;如果行动计划不需要;Cpk和/或Ppk≥1.33≤1.67时可能要求改进;指数<1.33---与顾客联系对研究结果评审;P.I.S.T和P.I.P.C均为100%;如果不是,要产生工作计划来达到100%;可接受指标不能满足时要采取策略;过程不能改进时供应商必须与顾客联系;必须提交纠正措施和过度控制计划(100%检查);\必须持续减少变差,直到Cpk/Ppk>1.33和接到批准。
初始过程能力研究报告-PPK

初始过程能力研究报告-PPK1. 引言1.1 研究背景与意义随着全球经济一体化的推进,市场竞争日益激烈,企业对产品和过程的质量要求也在不断提高。
初始过程能力(Process Performance Index, PPK)作为衡量生产过程稳定性的重要指标,是企业在生产初期就确保产品质量,降低成本,提高竞争力的关键。
在我国,许多企业在初始过程能力方面仍存在不足,导致生产效率低下,资源浪费严重。
因此,深入研究初始过程能力PPK,对提高我国制造业的整体水平具有重要的现实意义。
1.2 研究目的与内容本研究旨在探讨初始过程能力PPK的评估与改进方法,以期为企业提供有效的过程优化策略。
研究内容主要包括:PPK的定义与计算方法、应用领域、评估指标与标准、评估流程与步骤以及改进策略等。
通过案例分析,验证所提出方法的有效性,为企业提供实际操作指导。
2. 初始过程能力PPK概述2.1 PPK的定义与计算方法PPK(Process Performance Index)即过程性能指数,是衡量初始过程能力的一个重要参数。
它是通过对过程数据的统计分析得出的,反映了过程输出满足规格要求的程度。
PPK的计算基于过程均值和标准差,其公式如下:[ PPK = ]其中,USL(Upper Specification Limit)为规格上限,LSL(Lower Specification Limit)为规格下限,σ(sigma)为过程标准差。
PPK的取值范围为0到1,PPK值越大,表示过程能力越强,过程输出满足规格要求的概率越高。
通常,PPK值在0.67以上被认为是过程能力良好。
2.2 PPK的应用领域PPK在制造业中有着广泛的应用,主要表现在以下几个方面:1.新产品开发:在新产品开发阶段,通过计算PPK值,可以评估过程能力是否满足设计要求,从而为产品的设计和生产提供依据。
2.过程改进:通过对PPK值的监测,可以发现过程中的问题,指导企业进行过程改进,提高产品质量。
Cpk_与Ppk_两种过程能力指数的对比分析研究[1]
![Cpk_与Ppk_两种过程能力指数的对比分析研究[1]](https://img.taocdn.com/s3/m/98cfcf39376baf1ffc4fad01.png)
Cpk 与Ppk 两种过程能力指数的对比分析研究1摘要:在进行统计质量控制的时候,工序能力指数Cpk(Index of Process Capability)与过程能力指数Ppk(Index of Process Performance)是评价过程及改进方向和目标的重要指标,但在实际操作过程中,Cpk 和Ppk 容易被混淆。
本文通过两种指标的定义及计算过程的比较,分析其差异,并利用SPC(Statistical Process Control)统计过程控制软件中这两个指标的应用范围情况进行了示例说明,更为直观地显示了它们的联系与区别。
关键词:Cpk(工序能力指数);Ppk(过程能力指数);SPC(统计过程控制)中图分类号:O291. 引言质量管理中数理统计的理论和方法非常重要[1]。
由于每天生产产品的质量,如工件的厚度、表面粗糙度等不断变动的缘故,为了加工出厚度均匀、粗糙度一致的工件,即使对加工环境的温度、湿度,对切削时的进刀量等操作条件做出严格的规定,实际生产出来的产品质量仍然存在波动。
而且上面所列出的加工条件固定不变也是难以办到的事,这些加工条件也存在着一定程度的波动,因此工序质量在各种影响因素制约下,呈现波动特性。
统计方法能够对这些波动的状况及其相互关系进行定量分析,是监控、改进产品质量非常有用的工具。
工序与过程能力指数在质量控制中越来越频繁地使用。
近来随着生产力的高度发展,对产品质量和服务质量的要求不断提高,不合格品率越来越低,而与其对应的过程能力指数要求越来越大。
这反映了生产能力的进步、不合格品率下降、经济效益的提高。
过程能力性能指数Ppk 是在美国克莱斯勒、福特和通用这三大汽车公司制定的QS-9000标准提出的,与过程能力指数Cpk 并列,共称为量度过程的参数[2]。
Cpk 主要用于周期性的过程评价,而Ppk 则用于实时过程性能研究和初始过程能力评估。
目前我国许多企业日常计算的是Ppk,而不少人却误认为是Cpk,于是基本概念的错误带来认识上的混淆。
CMK CPK PPK 之间有什么区别

CMK CPK PPK 之间有什么区别一、CMK设备过程能力指数:研究的对象是设备,表现为某设备加工某零件,在某公差情况下的加工一致性,无偏移的设备能力CM,有偏移的设备能力指数是CMK,汽车行业,加工关键尺寸,要求CM≥2,CMK≥1.67;二、PPK初始过程能力指数:抽样方法,稳定情况下连续抽样30件以上,抽样方法和计算公式和CMK一模一样,汽车行业,做PPAP文件是,提交的是PPK,而不是CPK,很多人会将该概念搞混;汽车行业关键尺寸要求PPK≥1.67,重要尺寸要求PPK≥1.33;三、CPK过程能力指数:抽样方法,稳定情况下间隔抽样,可以是每2小时抽5件,也可以每天抽2件,根据需要和研究的对象自己定,与PPK的区别是抽样方法即研究的对象有不同,计算公式有点差异(均值、方差)。
Ppk、Cpk区别及计算编辑本段简介PPK是SPC中控制图中用来计算工序性能或叫过程性能的指数。
PP(Performance Indies of Process):定义为不考虑过程有无偏移时,容差范围除以过程性能,一般表达式为:Pp性能指数公式ppk:是指考虑过程有特殊原因引起的偏差时,样本数据的过程性能。
ppk是spc第二版中提到的新内容。
(该指数仅用来与Cp及Cpk对比,或/和Cp、Cpk一起去度量和确认一段时间内改进的优先次序)CPU:稳定过程的上限能力指数,定义为容差范围上限除以实际过程分布宽度上限:CPL:稳定过程的下限能力指数,定义为容差范围下限除以实际过程分布宽度下限。
其实,公式中的K是定义分布中心μ与公差中心M的偏离度,μ与M的偏离为ε=| M-μ| 关于Cpk与Ppk的关系,这里引用TS16949中PPAP手册中的一句话:“当可能得到历史的数据或有足够的初始数据来绘制控制图时(至少100个个体样本),可以在过程稳定时计算Cpk。
对于输出满足规格要求且呈可预测图形的长期不稳定过程,应该使用Ppk。
”编辑本段Ppk、Cpk区别及计算Ppk、Cpk区别及计算Cpk = Cp * ( 1 - |Ca|),PPK是过程性能指数,也可表示初始能力指数,它和CPK的计算方式是一样的,只是利用的标准差的估计值不同,通常相对而言CPK会比PPK的值大.1、首先我们先说明Pp、Cp两者的定义及公式Cp(Capability Indies of Process):稳定过程的能力指数,定义为容差宽度除以过程能力,不考虑过程有无偏移,一般表达式为:Pp(Performance Indies of Process):过程性能指数,定义为不考虑过程有无偏移时,容差范围除以过程性能,一般表达式为:(该指数仅用来与Cp及Cpk对比,或/和Cp、Cpk一起去度量和确认一段时间内改进的优先次序)CPU:稳定过程的上限能力指数,定义为容差范围上限除以实际过程分布宽度上限,一般表达式为:CPL:稳定过程的下限能力指数,定义为容差范围下限除以实际过程分布宽度下限,一般表达式为:2、现在我们来阐述Cpk、Ppk的含义Cpk:这是考虑到过程中心的能力(修正)指数,定义为CPU与CPL的最小值。
过程能力指数Cp与Cpk 过程绩效指数Pp与Ppk

USL LSL Cp= 6
其中, USL是质量特性的规格上限,LSL是质量特性的规格下限,σ是质量特性 实际值计算出的标准差 当Cp<1时,说明过程能力不足 当1≤Cp<1.33时,说明过程能力尚可 当1.33≤Cp<1.67时,说明过程能力充足 当Cp≥1.67时,说明过程能力富余
则是从过程长期的总波动来考虑过程满足质量要求的程度。
Pp, Ppk的计算与Cp,Cpk的计算类似
USL LSL Pp= 6s
USL x x LSL , Ppk=min 3 s 3 s
其中,s是样本的标准差, x 是所有测量值的均值 样本标准差s=
x
n i 1
其中,μ是过程输出的均值
过程能力指数Cp与Cpk
当Cpk<1时,说明过程能力不足 当1≤Cpk<1.33时,说明程能力尚可
当1.33≤Cpk<1.67时,说明过程能力充足 当Cpk≥1.67时,说明过程能力富余
过程绩效指数Pp与Ppk
Cp,Cpk反映的是短期内过程输出满足产品质量要求的程度,而Pp,Ppk
过程能力
过程能力是处于稳定生产状态下过程的实际加工能力,它
是衡量过程波动的一种标志。
如果一个过程仅受到随机因素的影响,且产品的质量特性
均值和波动都能基本保持稳定,则称该过程处于统计控制 状态。只有当过程处于统计控制状态,对过程能力的分析 才是有意义的。
过程能力指数Cp与Cpk
过程的潜在能力指数Cp
i
x
2
n 1
过程能力指数Cp与Cpk
过程能力指数Cpk
Cpk: Complex Process Capability index
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
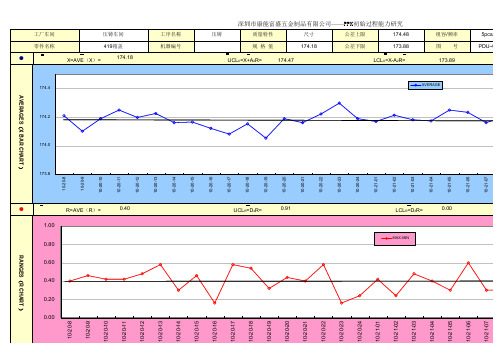
419箱盖
工厂车间 零件名称 ●
174.48
公差上限
尺寸
质量特性
压铸
压铸车间
深圳市康能富盛五金制品有限公司——PPK初始过程能力研究
RANGES(R CHART )
10-20-8 10-20-9 10-20-10 10-20-11 10-20-12 10-20-13 10-20-14 10-20-15 10-20-16 10-20-17 10-20-18 10-20-19 10-20-20 10-20-21 10-20-22 10-20-23 10-20-24 10-21-01 10-21-02 10-21-03 10-21-04 10-21-05 10-21-06 10-21-07
871.0
871.1
870.8
870.8
870.6
870.4
870.8
870.3
870.9
870.8
871.1
871.5
870.9
870.8
871.1
174.21 174.10 174.19 174.25 174.20 174.22 174.16 174.16 174.12 174.08 174.15 174.05 174.19 174.16 174.22 174.30 174.19 174.17 174.21
173.98 173.90 174.44 174.26 174.16 173.88 174.30 174.22 174.22 173.86 174.32 173.98 174.22 174.22 174.46 174.36 174.22 174.26 174.08
174.18 174.18 174.08 174.44 174.00 174.24 174.22 174.10 174.10 174.00 174.06 173.92 174.30 174.32 174.08 174.26 174.20 174.32 174.18
3
1.02
*
4
0.73
*
5
0.58
*
6
0.48
*
7
0.42
0.08
8
0.37
0.14
9
0.34
0.18
10
0.31
0.22
1.连续取样
2.组容<7时没有极差下控制限
●Ppk = Min (
USL-X 3σ
D4 3.27 2.57 2.28 2.11 2.00 1.92 1.86 1.82 1.78
X-LSL 3σ
174.18 174.17 174.25 174.23 174.16 174.20
0.48
0.40
0.30
0.60
0.30
0.30
d2 )≥1.67
10-21-07 10-21-08
=Min
1.84
1.85 ) =
1.84
10-21-03 10-21-04 10-21-05 10-21-06 10-174.32 174.48 174.02 174.26
174.32 174.18 174.26 174.12 174.32 174.02
0.00
RANGES(R CHART )
0.20
0.40
0.60
0.80
MAX-MIN
UCL
1.00
0.00
LCLR=D3R=
0.91
UCLR=D4R=
0.40
R=AVE(R)=
●
10-20-8 10-20-9 10-20-10 10-20-11 10-20-12 10-20-13 10-20-14 10-20-15 10-20-16 10-20-17 10-20-18 10-20-19 10-20-20 10-20-21 10-20-22 10-20-23 10-20-24 10-21-01 10-21-02 10-21-03 10-21-04 10-21-05 10-21-06 10-21-07
173.8
AVERAGES(X BAR CHART )
LCL
174.0
174.2
174.4
AVERAGE
5pcs/连续 PDU-419X
组容/频率 图号
173.89
LCLX=X-A2R=
174.47
UCLX=X+A2R=
174.18
X=AVE(X)=
173.88
公差下限
174.18
规格值
工序名称 机器编号
10-20-8 10-20-9 10-20-10 10-20-11 10-20-12 10-20-13 10-20-14 10-20-15 10-20-16 10-20-17 10-20-18 10-20-19 10-20-20 10-20-21 10-20-22 10-20-23 10-20-24 10-21-01 10-21-02 10-21-03 10-21-04 10-21-05 10-21-06 10-21-07
174.18 174.24 174.02 174.14 174.14 174.46 174.00 174.38 174.08 174.44 174.12 174.24 174.02 173.92 174.32 174.26 174.08 174.28 174.22
174.32 173.86 174.30 174.38 174.20 174.32 174.20 174.20 174.06 174.08 173.86 174.10 174.42 174.32 174.36 174.38 174.12 173.90 174.26
日期班次
1
检
2
查
记
3
录
4
5
TOTAL
AVERAGE
MAX-MIN
10-20-8 10-20-9 10-20-10 10-20-11 10-20-12 10-20-13 10-20-14 10-20-15 10-20-16 10-20-17 10-20-18 10-20-19 10-20-20 10-20-21 10-20-22 10-20-23 10-20-24 10-21-01 10-21-02
说明栏 ●对特殊原因采取措施说明
UCLx *任何超出控制限的点
*连续7点在中心线之上或之下
*连续7点上升/下降
CL x *任何其它明显非随机的图形
●采取措施的说明
①不要对过程做不必要改变
LCLx
②注明对过程因素(人机料法环 或MS)所做的调整
10-21-08
UCLR CL R
组容
A2
D3
2
1.88
*
174.38 174.24 174.38 174.38 174.20 174.22
174.22 174.32 174.20 173.88 174.10 174.18
174.08 173.92 174.08 174.30 174.16 174.32
870.9
870.9
871.2
871.2
870.8
871.0
174.38 174.32 174.10 174.02 174.48 174.22 174.08 173.92 174.14 174.02 174.40 174.02 173.98 174.02 173.88 174.22 174.32 174.08 174.32
871.0
870.5
870.9
871.2
0.40
0.46
0.42
0.42
0.48
0.58
0.30
0.46
0.16
0.58
0.54
0.32
0.44
0.40
0.58
0.16
0.24
0.42
0.24
制表/日 期:
审核/日 期:
有限公司——PPK初始过程能力研究
10-21-07 10-21-08
5pcs/连续 PDU-419XG
生产形态 日期
2017/10/22
