升余弦滚降滤波器设计
滚降滤波器

%设置参量,采用八倍采样速率,滚降系数为0 0.25 0.5 1 Fd=1;Fs=8;Delay=3;R=[0 0.25 0.5 1];%建立升余弦滚降滤波器for i=1:4[yf,tf]=rcosine(Fd,Fs,'fir',R(i),Delay);%画图得到升余弦滚降滤波器波形figure(i)subplot(2,2,1)plot(yf);grid;xlabel('Time');ylabel('Amplitude');title('升余弦滚降滤波器');%输入随机序列x=randint(100,1)*2-1;%原始输入信号为+1,-1码xt=zeros(1,800);xt(1:8:end)=x;y=filter(yf,tf,xt);yt=y((size(yf)+1)/2:8:end);%画出原始信号波形subplot(2,2,2);stem(x(1:40));title('原始信号')%画出将原始信号内插后通过升余弦滚降滤波器后的输出subplot(2,2,3)plot(y(1:100));title('滤波后输出')grid;%画出将图6抽取后的输出波形subplot(2,2,4);stem(yt(1:40));grid;title('抽取后输出')end1.2.3.4.从图中可以看到,当α=0时,就是理想奈奎斯特滤波器,此时的传输带宽是理想奈奎斯特滤波器的最小带宽,但当α>0 时,系统传输带宽就超过了奈奎斯特最小带宽,这时码率速率Rs 就小于小于 2 倍带宽,如果解调器在每个码元间隔内仅做一次采样,那么会因为采样点太少而不能可靠恢复模拟波形,产生失真。
但是数字通信系统不需要恢复模拟波形,只需要在取样时刻无码间串扰就行,而升余弦系列滤波器在取样时刻具有无码间串扰特性。
因此,仍符合奈奎斯特第一准则,它所实现的频谱效率要比理论最高效率下降一个滚降系数а 倍。
实验一升余弦滚降系统及眼图
实验一升余弦滚降系统及眼图、实验目的1. 理解无码间串扰系统的原理;2. 理解升余弦滚降系统的工作原理;3. 理解眼图的工作原理及实现方法。
、实验仪器及软件电脑、MATLAB7.0软件三、实验原理1. 无码间串扰系统若想消除码间串扰,应有a n h k n T s t00 (1-1)n k由于a n是随机的,要想通过各项相互抵消使码间串扰为0是不行的,这就需要对h t的波形提出要求,如果相邻码元的前一个码元的波形到达后一个码元抽样判决时刻时已经衰减到0,如图1-1(a)所示的波形,就能满足要求。
但这样的波形不易实现,因为实际中的h t波形有很长的“拖尾”,也正是由于每个码元拖尾"造成对相邻码元的串扰,但只要让它在t0 T s,t0 2T s等后面码元抽样判决时刻上正好为0,就能消除码间串扰,如图1-1(b)所示。
这也是消除码间串扰的基本思想。
著名的奈奎斯特第一准则就给出了无码间串扰时基带传输特性应满足的频率条件:(1-2)图1-1消除码间串扰显然,满足式(1-2)的系统H 并不是唯一的,容易想到的一种就是H 为一个理想低通滤波器。
2. 升余弦滚降系统理想低通特性的基带系统具有最大的频带利用率。
但实际上理想低通系统在应用中存在两个问题: 是实现极为困难,二是理想的冲击响应h t 的“拖尾”很长,衰减很慢,当定时存在偏差时,可能出现严重的码间串扰。
实际使用中常采用升余弦频谱特性的系统,其系统传输特性如下:T s ,0其中, 称为滚降系数。
其单位冲激响应为sin t T s cos g 一tT s yl 43. 眼图一个实际的基带传输系统尽管经过了十分精心的设计,但要 使其传输特性完全符合理想情况是非常困难的,甚至是不可能的。
码间干扰问题与发送滤波器特性、信道特性、接收滤波器特性等 因素有关,因而计算由于这些因素所引起的误码率就非常困难, 尤其在信道特性不能完全确知的情况下,甚至得不到一种合适的 定量分析方法。
高性能升余弦滤波器设计

H i h Pe f r a c ie Co i e Fi e sg g r o m n e Ra s sn l r De i n t
HEN a E L n L U n —k n WANG a¨ C I Big u h Hu
, ,Biblioteka ( e at e t f o u i t n& If m t n n i eig 1 .D p r n o mm nc i a m C ao no a o e g er , r i n n
转化和升余弦滤波器 的 A I SC前端设计。第 2节 阐 述成形滤波与 C D理论 , 3 S 第 节介绍设计方法与流
程 , 4节 总结全 文 。 第
其优 良的性能被广泛应用 。利用 C oi S it 2 理 论 n c g a n i Dg n i (S ) C D 表示定点数并且实现高效的移 一 加运算和实 2 1 成形 滤波 器 . 现定点数乘法可以极 大减低硬件资源… , 利用滤波 用冲激响应表示 ,yu t N qi 准则 可以叙述为具有 s 器邻近抽头系数的特点进行相 同项的合并共享可进
ascl dC o i Sg i t C D)a d cm o u l al a nc i D g ( S e n n i n o m n sb—s u tr saigm d r sd t i po ete t c e h r o eaeu e o m rv r u n h
运算 的高效精简 , 运用 C R L代码实现补码与 C D 、T S
1 引 言
在数字移动通信 系统中脉冲成形滤波器在减少 码 间干扰影 响 的 同时 , 能 够 减 少 调制 带 宽 和 抑 制 还 频带外的扩散 , 其中升余弦( a eC s e 滤波器以 R i oi ) s n
升余弦滚降滤波器的作用

升余弦滚降滤波器的作用升余弦滚降滤波器(Raised Cosine Rolloff Filter)是一种常用的数字通信系统中的滤波器。
它的作用是用于调整信号的带宽,以减小信号的带外泄漏,并且在频域上具有平滑的过渡特性。
升余弦滚降滤波器通常用于调制和解调过程中,特别是在正交幅度调制(QAM)和正交频分多路复用(OFDM)系统中,以提高系统的性能和抗干扰能力。
在数字通信系统中,信号经过调制传输到信道中,会受到各种噪声和干扰的影响,导致信号的失真和误差。
升余弦滚降滤波器可以对信号进行预处理,使其在通过传输信道之前具有更好的性能。
具体来说,升余弦滚降滤波器可以起到以下几个方面的作用:1. 带宽控制:升余弦滚降滤波器可以调整信号的带宽,限制信号的频谱分布在所需的范围内。
通过控制滤波器的参数,可以实现信号的带宽压缩或展宽,以适应不同的传输需求。
2. 频谱形状控制:升余弦滚降滤波器在频域上具有平滑的过渡特性,可以减小信号在过渡频段上的幅度变化。
这样可以有效地减小信号的带外泄漏,降低对其他信号的干扰。
3. 抗多径干扰:在无线通信系统中,信号会经过多条路径传播到接收端,导致多径干扰。
升余弦滚降滤波器可以通过控制滤波器的时域特性,使信号在时域上具有较长的冲激响应,从而减小多径干扰的影响。
4. 时频特性匹配:在正交调制和解调过程中,升余弦滚降滤波器可以用于匹配发送端和接收端的时频特性。
通过在发送端和接收端都使用相同的滤波器,可以保持信号的相干性,提高系统的传输效率和可靠性。
升余弦滚降滤波器在数字通信系统中具有广泛的应用。
在正交幅度调制(QAM)系统中,升余弦滚降滤波器常用于发送端对数字信号进行调制,以及接收端对接收到的信号进行解调。
在正交频分多路复用(OFDM)系统中,升余弦滚降滤波器用于子载波的生成和接收端的信号处理。
此外,升余弦滚降滤波器还可以应用于其他数字通信系统中,如调幅、调频和调相等。
总结起来,升余弦滚降滤波器在数字通信系统中起到了带宽控制、频谱形状控制、抗多径干扰和时频特性匹配等作用。
bpsk调制 升余弦 相关解调

BPSK调制、升余弦和相关解调是数字通信中常见的调制和解调技术。
本文将从理论和实际应用的角度介绍这三个主题,以帮助读者更好地理解和应用这些技术。
一、BPSK调制1. BPSK调制是一种基带调制技术,全称为二进制相移键控调制(Binary Phase Shift Keying)。
它通过改变载波信号的相位来传输数字信息。
具体来说,当数字为0时,载波信号的相位不变;当数字为1时,载波信号的相位反转180度。
这样就可以在相位上进行二进制编码。
2. BPSK调制的优点是简单直观,适用于频谱效率要求不高的情况。
在实际应用中,BPSK调制常用于低速数据传输、卫星通信和短波通信等场景。
3. 在无线传感网中,由于节点之间的距离较近、数据传输速率较低,可以采用BPSK调制来实现简单可靠的通信。
二、升余弦滚降滤波器1. 在数字通信中,为了尽可能减小传输信号的带宽,减小信道间的干扰,常常采用升余弦滚降滤波器(R本人sed Cosine Filter)来进行信号的滤波和调制。
2. 升余弦滚降滤波器的频率响应在频率为0附近有较好的抑制作用,可以有效地控制信号的带宽。
其滚降特性也能够减小信号在频率间隔内的干扰,提高信号的抗干扰能力。
3. 实际应用中,升余弦滚降滤波器常用于QPSK、16QAM等多种调制方式,尤其适用于要求频谱效率高、抗干扰能力强的场景。
三、相关解调1. 相关解调是指在接收端利用发送端已知的信号来解调接收到的信号。
通过计算接收信号和已知信号的相关性,可以还原发送信号。
2. 相关解调在数字通信中有着广泛的应用,特别是在多路径传输、信道干扰较大的高速数据传输场景中效果明显。
相对于其他解调方法,相关解调在抗噪声和多径干扰方面有明显的优势。
3. GPS定位系统中采用的CDMA技术就采用了相关解调的原理,来实现对传输信号的解调和定位。
BPSK调制、升余弦滚降滤波器和相关解调是数字通信领域中重要的技术手段,它们在不同的场景中发挥着重要的作用。
升余弦滚降课设报考

移动通信设计题目:C语言实现升余弦滚降信号的匹配接收班级:08通信B姓名:谭洋学号:0815232015指导老师:陈东华一、 设计原理余弦特性滚降的传输函数可表示为相应的h(t)为式中,α为滚降系数,用于描述滚降程度。
它定义为 其中,fN - 奈奎斯特带宽,f ∆ - 超出奈奎斯特带宽的扩展量当α=1时,即为升余弦频谱特性,这时H(ω)可表示为其单位冲激响应为:二、实现程序程序如下:#include <math.h>#include <stdio.h>#define pi 3.141592653589793/* 本函数实现滚降特性函数,升余弦滤波器说明:fs/fd 必须为整数,fd 为信号采样频率,fs 为滤波器采样频率 当函数返回0时为正常返回,为-1时为异常返回*/int rcosine(float fd,float fs,float rcs[]) /* 函数(升余弦滤波器)返回0为正常返回,-1为异常返回 */{int k,n;float kf,nf;nf=fs/fd; n=int(nf);if(nf!=n) return(-1); /* 当fs/fd 不是整数时异常返回 */ for(k=0; k<3*n; k++)⎪⎪⎪⎩⎪⎪⎪⎨⎧+≥+<≤--+-<≤=S S S S S S S S T T T T T T T T H παωπαωπαωπαπαωω)1(,0)1()1()],(2sin 1[2)1(0,)(()222sin /cos //14/S S S S t T t T h t t T t T παππα=⋅-/Nf f α∆=⎪⎪⎩⎪⎪⎨⎧>≤+=s s s s T T T T H πωπωωω2,02),2cos 1(2)(2241cos sin )(s s s s T t T t T t T t t h -∙=πππ{ kf=k-3*n;if(kf==-n) rcs[k]=0;else{ nf=kf/n; kf=pi*nf;rcs[k]=(sin(kf)/kf)*(cos(kf/2)/(1-nf*nf));}rcs[6*n-k]=rcs[k];}rcs[3*n]=1.0;return(0); /* 当fs/fd是整数时正常返回 */ }void main( ){ int flag,i;static float rcs[200];flag=rcosine(0.6,12.0,rcs);if(flag==0)for(i=0;i<200;i++)printf("%.4f\t",rcs[i]);else printf("\n\n error!");scanf("%d",&i);}三、测试结果程序运行结果如下图:由上图可看出程序运行结果即为升余弦滚降特性曲线的离散点。
平方根升余弦滚降FIR数字滤波器的设计

平方根升余弦滚降FIR数字滤波器的设计张维良郭兴波潘长勇杨知行(清华大学电子工程系微波与数字通信国家重点实验室,北京100084)摘要:本文采用本地查找算法,根据不同的误差准则设计了一系列平方根升余弦滚降FIR滤波器,并且在基带传输系统中对FIR滤波器进行了性能仿真,得出了在对称度准则下设计的FIR滤波器具有较好的性能的结论。
关键词:数字滤波器;平方根升余弦滚降滤波器;本地查找算法;奈奎斯特第一准则;基带传输系统;眼图一、引言数字FIR滤波器由于其严格的线性相位特性,在许多应用领域都显示了强大的生命力。
近来,针对FIR滤波器的重要应用意义,不少学者对FIR滤波器的设计以及硬件实现进行了广泛的研究,研究内容包括FIR滤波器系数的简化、FIR滤波器结构的改进、可编程FIR滤波器的设计[1~5]。
本文在前人研究的基础之上,设计了一系列平方根升余弦滚降FIR滤波器,并根据其应用特点做了一些性能分析。
设计一个高效的适合在硬件中实现的FIR滤波器必须解决以下3个问题。
第一个问题是在硬件资源有限的情况下如何最简单有效地表示滤波器的系数。
在硬件实现过程中,由于受硬件资源的限制,通常滤波器的系数只能取8位左右,这种有限精度系数的误差对滤波器的性能影响非常大。
设计FIR滤波器算法必须解决的第二个问题是如何衡量不同的系数表示方法的情况下滤波器的性能,也就是滤波器性能衡量的准则。
第三个问题是采用何种算法用来找到最优的滤波器,所谓最优是指在某一个滤波器性能衡量准则下,滤波器的误差最小。
目前,已经有一些文献[1~5]提到了上面3个问题,针对第一个问题,FIR滤波器系数在硬件中可以有许多的表示方法,比如SD(Signed Digit)、CSD(Canonic Signed Dig-it)等[6]。
滤波器性能衡量的准则跟具体的应用有关,比较通用的误差衡量准则有2种:第一种是最大误差最小化准则,就是使滤波器幅度频率响应在一定的频率范围内满足最大误差最小;第二种误差准则是均方误差准则,就是使得滤波器的时域响应的误差的均方值最小,这种误差准则较好地衡量了滤波器带来的信噪比损失。
根升余弦滚降滤波器的作用

根升余弦滚降(Root Raised Cosine Rolloff)滤波器是一种常用的数字通信系统中的滤波器,主要用于控制信号的带宽和抑制多径干扰。
根升余弦滚降滤波器的作用可以分为以下几个方面:
信号带宽控制:根升余弦滚降滤波器可以调整信号的带宽,使其适应特定的通信系统要求。
滤波器可以限制信号的频谱,确保信号在传输过程中不会出现过多的频谱重叠,从而减小干扰和误码率。
频域形状控制:根升余弦滚降滤波器的频域响应呈现出余弦函数的形状,这种形状具有平滑的特性。
滤波器的频域响应控制了信号的频谱形状,可以有效地减小带内和带外干扰,提高系统的抗干扰性能。
多径干扰抑制:在无线通信系统中,多径传播会导致信号在接收端出现多个时延不同的副本,这会导致码间干扰和符号间干扰。
根升余弦滚降滤波器的特性可以降低多径干扰的影响,通过对信号的时域和频域特性进行控制,可以使接收端更好地恢复原始信号,减小误码率。
根升余弦滚降滤波器在数字通信系统中起着重要作用,它可以控制信号的带宽,抑制干扰,降低多径干扰的影响,从而提高系统的性能和可靠性。
升余弦滤波器参数

升余弦滤波器参数
1. 抽样率(Sampling Rate):
抽样率是指连续信号经过模数转换器转换成离散信号的频率。
对于升余弦滤波器来说,抽样率通常是基带信号的两倍。
2. 带宽扩展系数(Bandwidth Expansion Factor):
3. 滚降系数(Roll-off Factor):
滚降系数衡量了滤波器频率特性的陡峭程度。
它决定了滤波器在通带和阻带之间的过渡带的宽度。
滚降系数的取值范围通常为0到1,其中0表示滤波器频率特性非常陡峭,1表示滤波器频率特性非常平缓。
4. 滤波器长度(Filter Length):
滤波器长度是指滤波器的时间或采样点数。
滤波器长度的选择通常是根据系统需求和计算复杂性来确定的。
滤波器长度较长可以提供更好的滤波性能,但会增加计算复杂性。
除了以上参数,升余弦滤波器还有一些其他的设计要点:
5.滤波器类型:
6.相位响应:
7.窗函数:
窗函数可用于调整升余弦滤波器的频率响应特性。
常用的窗函数包括矩形窗、汉宁窗、汉明窗等。
选择合适的窗函数可以改善滤波器的频率响应。
8.频域设计:
总结:
升余弦滤波器的参数包括抽样率、带宽扩展系数、滚降系数和滤波器长度等。
除了这些参数,滤波器类型、相位响应、窗函数和频域设计等也是设计滤波器时需要考虑的要点。
通过合理选择参数和设计要点,可以实现升余弦滤波器的优化设计,提高数字通信系统的传输性能。
升余弦应用
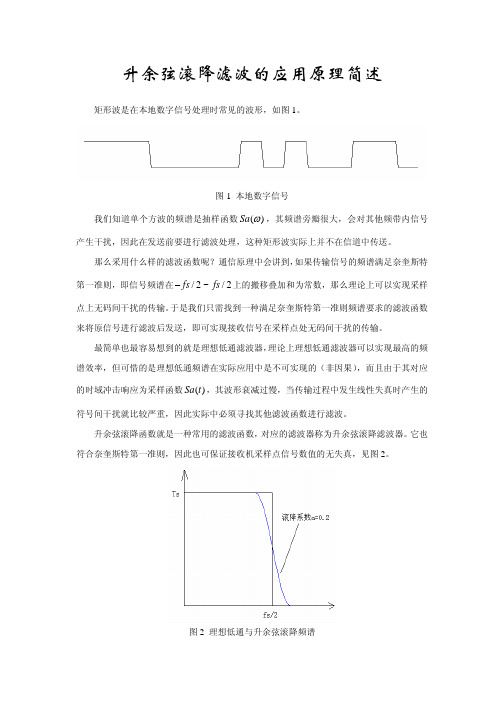
升余弦滚降滤波的应用原理简述矩形波是在本地数字信号处理时常见的波形,如图1。
图1 本地数字信号我们知道单个方波的频谱是抽样函数()Sa ω,其频谱旁瓣很大,会对其他频带内信号产生干扰,因此在发送前要进行滤波处理,这种矩形波实际上并不在信道中传送。
那么采用什么样的滤波函数呢?通信原理中会讲到,如果传输信号的频谱满足奈奎斯特第一准则,即信号频谱在上的搬移叠加和为常数,那么理论上可以实现采样点上无码间干扰的传输。
于是我们只需找到一种满足奈奎斯特第一准则频谱要求的滤波函数来将原信号进行滤波后发送,即可实现接收信号在采样点处无码间干扰的传输。
/2~/2fs fs −最简单也最容易想到的就是理想低通滤波器,理论上理想低通滤波器可以实现最高的频谱效率,但可惜的是理想低通频谱在实际应用中是不可实现的(非因果),而且由于其对应的时域冲击响应为采样函数,其波形衰减过慢,当传输过程中发生线性失真时产生的符号间干扰就比较严重,因此实际中必须寻找其他滤波函数进行滤波。
()Sa t 升余弦滚降函数就是一种常用的滤波函数,对应的滤波器称为升余弦滚降滤波器。
它也符合奈奎斯特第一准则,因此也可保证接收机采样点信号数值的无失真,见图2。
图2 理想低通与升余弦滚降频谱升余弦滚降滤波器是可实现的,并且其时域波形的“拖尾”衰减较快,如图3,从而降低了可能的符号间的串扰,因此在实际通信系统中一般采用升余弦滚降滤波器代替理想低通滤波器对信号进行成形滤波。
这一过程称为“基带成形滤波”。
图2 升余弦滚降频谱信号与理想低通信号的时域波形比较升余弦滚降滤波器的这种优点是以频谱效率的降低为代价的,滚降系数а影响着频谱效率。
а越小,频谱效率就越高,当a=0时,升余弦频谱信号退化为抽样函数,а过小时,升余弦滚降滤波器的设计和实现比较困难(a=0时无法实现),符号间干扰也较大,a越大,升余弦频谱信号拖尾越小,符号间干扰越小,不过频谱效率就越低,因为超出fs/2部分的频谱多了。
升余弦滤波器原理

升余弦滤波器原理在与舍友的深夜畅谈中,对于项⽬中升余弦滤波器的使⽤技巧收获颇丰,分享如下(感谢舍友):聊天背景:我的⼯作:我做的是基带通信同步部分的硬件实现,作为收端的第⼀环,同步⼀开始便是添加⼀个根升余弦滤波器,“好事成双”,发端的最后⼀环也会添加⼀个⼀模⼀样的根升余弦滤波器(发端为了调满幅,系数和收端的会稍有不同,但呈倍数关系)。
舍友的⼯作:舍友做的是收端的信道估计与均衡的原理分析,但不同于⼀般的信道估计,导师对他的要求是将收发两端的滤波器也考虑在内。
那么信道的频响函数就成了H = H_filter_sender * H_channel * H_filter_receiver。
这也是他⼯作的难处所在。
我的疑惑:两⼈的⼯作的共同点便是都使⽤到了根升余弦滤波器,那么这两个滤波器到底是⽤来做什么的呢?以往在做⼯程实现时并没有考虑太多,⽽实验室师兄让我注意到了在发端有⼀个和咱收端相同的滤波器,两个根升余弦滤波器⼀乘,根没了,只剩下⼀个升余弦滤波器。
且对OFDM的同步来说,此滤波器可通过对单载波调制的同步头上采样⽽获得和⽤OFDM调制的数据部分相同的采样速率。
细究下来,如此设计的原因⼀定不⽌是调节采样速率这么简单,况且在⾃然界“对称”也被公认为⼀种美的结构,那这两对共⽣的滤波器⾝上有哪些简洁的⼯程美呢?舍友答疑:如此设计⼀⽯三鸟,⼤呼妙哉!1,发端的根升余弦滤波器主要起到脉冲成形的作⽤:在对原始01数据进⾏编码调制后数据仍是为数不多的⼏个离散状态,BPSK为1和-1两种状态,QPSK也是1和-1两种状态(只是⽐BPSK多了两个映射象限),16QAM则为±1,±2,±3这6状态。
这些存在于时域的波形在时域上反应出来就是⼀个⼜⼀个⽅波,⼤佬傅⾥叶告诉我们,⽅波的组成是由近乎⽆限⾼的⾼频分量组成的,⽽这在通信系统中是物理不可实现的。
升余弦滚降滤波器以具有余弦函数性质的频域响应代替了⽅形频响,将⾼频的⽅波“滚降”到物理可实现的余弦波形,即起到了⼀个低通滤波器的作⽤。
升余弦滚降系统可以看成是一个的低通和一个的函数的叠加

最佳基带系统
收发总传输函数满足抽样点无失真条件,且收发
匹配
G f GT f GR f GR f GT f *
幅频特性
相|频G特R性 f || GT f |
• 线性相位:收发分配
• 例如 G f | G f | e j2 ft0 ,可以设计
k
抽样点无失真传输
满足时域条件
g 0 1, g mTs 0, m 0
或频域条件
G f k / Ts Ts
k
的g(t)即满足抽样点无失真传输条件。
注:这里g(t)是发送成形、信道、接收滤波器共同形 成的。
抽样点无失真传输
满足
可以看见:
由于NRZ是时宽有限信号,其频谱无限,因此 经过带限系统输出信号与原信号不同。
• 滤波器带宽越宽,输出信号与输入信号越接近。
B=0.5/Ts
2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
0
1
2
3
4
5
6
7
8
B=1/Ts
1.5
1
0.5
0
-0.5
-1
-1.5
0
1
2
3
4
5
6
7
8
B=2/Ts
最佳抽样时刻:张开最大时刻
最佳判决门限电平:中央横轴
定时误差的灵敏度:斜边的斜 率。越陡越灵敏,对定时要求 越高
信号畸变范围:垂直高度
过零点畸变范围:水平宽度
噪声容限:抽样时刻眼睛张开 高度的一半。噪声超过此值即 出错。
信号和系统-时移定理升余弦滚降滤波

约束条件的证明
信号与系统习题讨论
当t≤0时
L [f( t t0 ) ]0 f() e s ( t0 )d 0 t0f() e s ( t0 )d
∵在[0,-t0]内f(t)=0
∴ L [ f( t t 0 ) ] 0 f() e s ( t 0 ) d 0 f() e s e s 0 d t F ( s ) e s 0t
什么要用它?它在数字通信系统中起什么作用? 3. 怎样实现升余弦滚降滤波,时域?频域?
问题的分析
数字通信系统框图
信号与系统习题讨论
升余弦滚降滤波的作用
信号与系统习题讨论
我们可以看到升余弦滚降滤波在数字通信系统 中用于信号的成形,为什么信号要成形?为什么选择 成形信号为升余弦滚降信号?
我们已经看到,信号成形是在数字信号被调 制之前。对于一般的数字信号,都是方波形式的, 已调信号的频谱如下图:
F(s)L[t(1)u(t1)L][t(1)u(t)L][t(tu)L][u(t)s]121s
信号与系统习题讨论
第二个问题 数字通信系统中的 升余弦滚降滤波
问题的出现
信号与系统习题讨论
思考题: 如何用时域方法实现升余弦滚降滤波?
引发的疑问: 1. 数字通信系统的整体框架是什么样的? 2. 数字通信系统中何处使用升余弦滚降滤波?为
信号和系统-时移定理升余弦滚降滤波
• •
约束条件的证明
信号与系统习题讨论
当t≥0时
L [f( t t0 ) ] 0 t 0f() e s ( t0 )d 0 f() e s ( t0 )d
∵在[-t0,0]内f(t)=0
∴ L [ f( t t 0 ) ] 0 f() e s ( t 0 ) d 0 f() e s e s 0 d t F ( s ) e s 0t
根升余弦滤波器 系数

根升余弦滤波器系数根升余弦滤波器是一种常用的数字信号处理滤波器,他具有正交性和频率响应衰减幅度较小的特点,能够有效地提取出信号中的有效信息。
而其核心之一便是系数的选取。
一、根升余弦滤波器的结构及工作原理根升余弦滤波器是基于根升余弦函数(Root raised cosine function)设计出的一种带通滤波器,其结构由一个低通滤波器和一个恒定系数的全通滤波器组成。
根升余弦滤波器将原始信号进行采样,经过低通滤波器得到基带信号,通过乘以一定系数解决码间干扰,再通过全通滤波器进行频率偏移和相位矫正,最终得到一个带通的数字信号。
二、系数的选取系数的选取直接影响到根升余弦滤波器性能的好坏。
一般而言,系数的定义包括滚降因子(rolloff factor)、长度、抽样因子(sampling factor)、截止频率(cutoff frequency)等。
这些参数的设定应根据滤波器系统的具体特点和性能要求进行调整。
2.1 滚降因子滚降因子是指滤波器在通过其时,频率回归到直流的下降速度。
一般地,它决定了滤波器频率响应在理想低通滤波器上方的衰减速度。
滚降因子越大,频带外的能量越小,对群延迟的影响也越小,但其通带内的带宽越窄,故难以满足高数据速率的调制要求;反之,滚降因子越小,通带内的信息传输能力越好,但频带外的能量也越多,会对系统的可靠性产生影响。
2.2 长度长度通常决定滤波器的时间分辨率和频率分辨率。
长度越大,分辨率越高,但对运算量要求也就越大,且滤波器的群延迟也会相应增加。
2.3 抽样因子抽样因子决定了滤波器的采样率及其带宽。
若在符号间距离内发生一个倒谷,则当抽样因子为1/2的正交滤波器时,无法得到正确的符号,即会产生码间干扰。
故一般在设计滤波器时,抽样因子应尽量小,但也要考虑到抗码间干扰的作用。
2.4 截止频率截止频率指的是根升余弦滤波器的通带和阻带的分界线,通过调整截止频率,可以细致调整其频率响应。
同时,阻带的边缘频率应根据信号处理系统的要求进一步调整,以提高滤波器的过渡特性和幅度响应的平直性。
升余弦滤波器

升余弦滤波器
2010/05/05 4:09 P.M.
发送数字信号时,通常需要成型滤波器对数字信号0或1进行成型滤波。
最常用的一种就是升余弦弦滤波器(RCF),因为它能够消除符号间干扰(ISI)。
其频域响应为
其中,r为滚降系数(r=0时即为理想低通滤波器brickwall filter,现实中不可实现。
),T为输入符号的符号周期。
其时域冲击响应为
可见,上式可以用来计算滤波器的系数,这样就可以构造出升余弦滤波器。
Matlab中通过命令rcosfir,就可以得到滤波器的系数。
但,实际中,接收端也需要一个低通滤波器(与发送端用到的原因不同)。
因此我们在发送端和接收端的低通滤波器都采用根升余弦滤波器(RRCF)。
升余弦滚降滤波器设计

实验 三 升余弦滚降和根升余弦滚降滤波器设计 一、实验目的
1.掌握升余弦滚降滤波器设计原理和设计方法; 2.掌握根升余弦滚降滤波器设计原理和设计方法; 二、实验原理
1. 定义h (t )为升余弦脉冲成型函数。
h (t ) 升余弦函数定义如下
2
2
2
sin()cos(
)
()14c
c
c
t
t
h t t
c
T
T
t
T
T παππα
=
⋅
-,
对应的频谱为:
2. 定义h r (t )为根升余弦脉冲成型函数。
h r (t ) 根升余弦函数定义如下
222sin((1))4cos((1)
()14c
c
c
r c t
t
t
h t t c T
T
T
t T T παα
π
απα-++=
⎛
⎫ ⎪- ⎪⎝⎭
,
对应的频谱为: 三、实验内容
1.已知通带码元截止频率为fc,其码元周期为Tc ,以频率为fs 对升余弦脉冲成型函数h (t )和h (t-Tc )抽样,设计它的数字滤波器。
要求此系统延时m 个码
元,每码元采样k次。
2.已知通带码元截止频率为fc,其码元周期为Tc,以频率为fs对根升余弦脉冲成型函数hr(t)和hr(t-Tc)抽样,设计它的数字滤波器。
要求此系统延时m个码元,每码元采样k次。
四、方案设计和实现步骤
五、仿真结果
六、分析和结论
七、参考文献
八、程序附录。
【doc】基于Simulink的滚升余弦滤波器的实现和性能分析

基于Simulink的滚升余弦滤波器的实现和性能分析第28卷第1期2012年1月昆明冶金高等专科学校JournalofKunmingMetallurgyCollegeV01.28No.1Jan.2012doi:10.3969/j.issn.1009—0479.2012.01.012基于Simulink的滚升余弦滤波器的实现和性能分析崔黎,高飞(云南民族大学电气信息工程学院,云南昆明650031)摘要:基于Matlab/Simulink平台,给出了滚升余弦滤波器和眼图的具体实现方法及流程.以FIR滤波器为基本模块构造了滚升余弦滤波器基本模型,并通过改变滚降系数对滚升余弦滤波器的性能作出分析,验证了方案的可行性.关键词:滚升余弦滤波器;FIR;眼图;Simulink中图分类号:TN713文献标识码:A文章编号:1009—0479一(2012)O1—0053—04 ThePerformanceAnalysisofImplementingRaisedCosineFIR DigitalFiltersBasedonSimulinkCUlLi.GAOFei(SchoolofElectronicsandInformationEngineering,YunnanUniversityofNationalities,Ku nming650031,China)Abstract:BasedonSimulinkplatform,thispaperoffersaspecificmethodandprocessforimpl ementingtheRaisedCosineFIRDigitalFiltersandEyeDiagram.TakingFIRdigitalfilterasabasicblock,thean- thorsestablishthebasicmodelofRaisedCosineFIRDigitalFilters,analyzetheperformanceo fitbychangingrollofffactorsandfinallyverifyitsfeasibility.Keywords:raisedcosineFIRdigitalfilters;FIR;eyediagram;simulink0引言在现代数字通信中,基带信号的频谱范围都是比较宽的,为了让信号在带限的信道中传输,需要在发送端把信号经过成形滤波器进行带限,因此就会引入码间串扰.为了使误码率足够小,必须最大限度地减小码间干扰,只要求特定时刻的波形幅值无失真的传送,而不必要求整个波形无失真.存在着一类无码间串扰时域函数,且具有滚升余弦频率特性,幅频响应缓慢,在工程上易于近似实现.常用的奈奎斯特类型(在采样时刻无码间串扰)传输函数日(是滚升余弦滤波器.滚升余弦滤波器是基带信号调制与解调中降低码间串扰的基本单元.本文实现滚升余弦滤波器仿真模型的思想为:首先输入信号,采样完成后进入滚升余弦滤波器进行滤波,再通过示波器接收并观察波形.本文基于Simulink仿真平台,从模块窗口选择对应模块对滚升余弦滤波器进行了设计,仿真和结果分析,其重点在于输入波形的采样,FIR滤波器构造滚升余弦滤波器及眼图的实现.1基于Simulink滚升余弦滤波器的设计思想1.1方案设计概述1.1.1滚升余弦滤波器基本模型构造根据滚升余弦滤波器的特性,设计了一个基带传输系统,如图1所示.收稿日期:2011—03—11作者简介:崔黎(1983一),女,湖北天门人,硕士研究生,主要研究方向为无线传感器网络技术.昆明冶金高等专科学校2012年1月根据图1所示,我们可以在Simulink模块库中找到基本的模块,构造一个基带传输模型,然后观察这个模型的性能及结果.1.1.2系统各个子模块介绍i输入信号卜1采样1—1『一1眼图图1基带传输系统框图通过以上已经设计好的模型,在模块库中找到以下模块来构造整个系统:随机整数信号发生器(randomintegergenerator):用于生成随机输入信号;单极性转化为双极性模块(unipolartobipolarcon?verter):将输入波形由单极性转化为双极性波形;采样模块(upsample):对输入波形进行采样;离散数字滤波器(discretefilter):通过此模块构造滚升余弦滤波器,然后对波形进行滤波;示波器(scope):观察输入输出波形,并进行比较;眼图(discrete—timeeyediagramscope):观察输出波形的码间串扰情况.1.2关键模块的具体实现1.2.1通过FIR滤波器模块设计滚升余弦滤波器模块滚升余弦滤波器时域表达式是一个无穷阶数的系数的FIR滤波器,可以运用Matlab通信工具箱中提供的设计滚升余弦滤波器的函数rcosine.当rcosine用于计算FIR滤波器时,根据设计选项的不同,可以得到同样结果的采样序列.函数rcosine用于计算FIR滤波器时的用法如下: Bum=rcosine(,F,fir/norma1.r,delay)上式中,'fir/normal'用于FIR滚升余弦滤波器设计;r是滚降系数,r取值在[0,1];F为输人数字序列的采样率,即码元速率;为滤波器采样率,F必须是的正整数倍;delay是输入到响应峰值之间的时延(单位是码元时隙数).通过Matlab作出一组滚升余弦滤波器的冲激响应,滚降系数为0.5,0.75,1,并通过F 丌求出其幅频特性,其实现代码如下.clc;clearall;closeall;echooff;tic;k=10;m=4;beta=[0.500.751.00];forii=1:length(beta)h=rcos(k,m,beta(ii));in=zeros(1,101);in(11)=1;out(ii,:)=conv(in,h);endt=0:0.1:10;figure;plot(t,out(1,1:101),ir一t,out(2,1:101),bo一t,out(3,1:101),k+一;gridon;xlabel(Time');ylabel(Amplitude');title(impulseResponseofRcosine');legend(Roll—Off=0.50.Roll—Off=0.75Roll—Off=1.00';simulation—time=toc于是就可以调用FIR滤波器,通过对其各个参数的设置实现滚升余弦滤波器.首先,在Simulink模块库浏览器的界面找到DiscreteFIRFilter模块,通过输入函数rcosine,使之改变为滚升余弦滤波器.具体模块参数设置如图2所示.于是,由FIR滤波器模块得到了滚升余弦滤波器的实际模块,如图3所示.第l期崔黎,高飞:基于Simulink的滚升余弦滤波器的实现和性能分析551.2.2眼图模块的实现在工程上,为了便于观察接受波形中的码间串扰情况,可在采样判决设备的输人端口处将已恢复的采样时钟作为同步,用示波器观察该端口的接收波形.利用示波管显示的暂时记忆特性,在示波管上显示出多个时隙内接收信号的重叠波形团,成为眼图.调用眼图模块.调节眼图模块的参数如下:每个数据采样点数设置为10,每次扫描显示的符号个数设置为2,这样眼图可以显示2个符号时间宽度;显示所保留的扫描波形轨迹数,可以设为默认值;每次显示的新轨迹数也可以设置为默认值;眼图模块可以同时显示同相支路和正交支路上的眼图,这里我们选择in-phaseonly选项.图4所示为眼图模块.2滚升余弦滤波器的实现~豁黼曛箍谨整%zi#撼靠黪#热~|~豫琳m毒.誊-廿.魏漆晒鳓l蓐毋簟誊襄霉l韵蓐尊鳓躏瓣滴媾靳薛舔静壤毒霉Il绱尊瓣如嚣毒善参德靠箍罐蕾鬣.每獭媾鼍霉弧餐晦|燎嘲蠼秣毒霉酶媾鹫毛舔蠹|螨确誊填赫鼍鬻氆羲聱晦警鼍醯蠢嘲诵警囊蕊嘛酗协馥锚罐篝誊≯雌如藿鹰旗每鹇墓嘲翻螭謦确嚏尊嘲|毫霉耋l 雠瞧鹭..№n瞪|.蔓薯||童曩毒薯≯.|曩:誊蠢|--Coefficitgou?ee:lI)ialoz瑚∞ersll精u脚er邑t0rc0掌ffieient:zcoEine《li爵fiz/normal0嚣i》Initlal鲁ta~eg:Sa~aletime1fozinhezited》:一i菌函二量囊图2滚升余弦滤波器参数设置Simulink是Matlab提供的实现动态系统建模和仿真的一个软件包,是Matlab的一个重要组成部分,甚?譬筹盏喜线建装?=『——_萼五线性,连续时间系统,离散时间系统混合系统建模,且}—————————一『系统可以是多进程的.Simulink通过自带的模块库为用户DisoreteFIRFiher2提供多种多样的基本功能模块,用户可以直接调用这些模块.因此,用户使用Simulink进行系统建模十分方便.在模型结构设计好的基础上,用Simulink建立模型的具体操作步骤为:(1)启动Simulink模块库浏览窗口.(2)新建一个空白模型.为此,点击浏览器工具栏上的"新建"按钮或用鼠标左键点击"File—New—Mod一图3滚升余弦滤波器模块Disorete—TimeEyeDiagramSoope图4眼图模块el",便打开一个空白模型窗口.在Simulink里模型是保存在模型文件里的,新建一个空白模型也就是新建了一个空白的模型文件,模型文件的后缀名为.mdl.(3)在模块库浏览窗口中找到所需的模块.(4)分别将所需的各个模块从库里拖曳到空白的模型窗口,这时Simulink会在模型窗口复制出这些模块.(5)将用户界面中的模块排列好,并把它们用连接线连接起来.注意模块的输入端只能和模块的输出端相连接,调节相应的参数便得到可以进行仿真的模型.按照上述方法,运用已经设计好的滚升余弦滤波器模块和眼图模块,建立仿真模型观察滚升余弦滤波器的输出波形,眼图以及功率谱,设计模型如图5所示.56昆明冶金高等专科学校2012年1月DiagramSoope3图5滚升余弦滤波器与眼图的设计模型其设计模型具体参数调节如下:设系统仿真步进为1e一4s,采样间隔为1e一3s 的2元整数(0,1),并将其转化为双极性的(一1,1),然后通过将基带数据的采样速率升高为10000次/s,其输出为冲激脉冲形式的数据序列,再通过滚降系数为0.75的滚升余弦滤波器,滤波器延时时间为3个数据时隙,即30个滤波采样间隔.滤波器输出降低到1/4倍采样速率,使送入频谱仪的采样率为25007欠/s,这样频谱仪显示的频率范围是0~1250Hz.使送入通信模块库中的眼图显示模块.由于滚升余弦滤波器存在延迟,为了使滤波器输出波形对应于输人数据脉冲,将输人数据延迟3O个采样时间间隔,以示波器对比显示滤波器输入输出波形.模型建好,参数调节好以后,在模型窗口上部的菜单栏上用鼠标左键点击"Simulation---~Start"开始仿真,双击示波器即可得到示波器图形.仿真结果的输入输出波形,功率频谱和眼图如图6~l0所示.为了衡量不同误差准则情况下设计的滚升余弦滤波器的性能,根据图1的基带传输系统,在图2中调节滚降系数,然后对滚升余弦滤波器的性能做了仿真,以作为滤波器性能比较的参考.在滚降系数r=0,r=0.75两种情况下,对波形和功率谱作如下比较.图7,8和图9,10分别为当r:0.75,r=0时的幅度频率响应的功率频谱及眼图,其中图7,9幅度频率响应特性图的横坐标为频率,纵坐标为响应频率的功率;图10为有码间串扰的眼图.对于滚降系数改变对码间串扰消除的优劣性,当r=0时码间串扰严重,眼图不明显,图中所有仿真的波形没有重叠而是分散的;当r=0.75时基本无码间串扰,眼图十分清晰,图中所有仿真波形基本重叠在一起.以上2种情况的对比,说明通过调节滚降系数可以消除码间串扰.黼图6滤波器输入输出波形∞褂频率/kHz时间/ms图7滚降系数r=0.75的功率频谱图8滚降系数r=0.75的眼图频率/kHz-兰;;釜主;兰一时间/ms图9滚降系数r=0的功率频谱图10滚降系数r=0的眼图(下转第72页)加:2mOm加72昆明冶金高等专科学校2012年1月计手段,针对不同商业广告的需要,对商业摄影的创意与手段进行不断创新.商业摄影师需要不断地扩展创意,在研究中创造出有效而又时尚的商业摄影模式,以便于快捷准确地传达产品的信息.参考文献:[1]薄久夫.商品广告摄影[M].北京:中国摄影出版社,1995.[2]张雄,蒋烨,刘永健.现代广告摄影[M].长沙:湖南人民出版社,2009.[3]桑塔格.论摄影[M].黄灿然,译.上海:上海译文出版社,2010.[4]陈志宏.现代商业广告摄影的审美和鉴赏思辨[J].时代文学,2007(2):102—103[5]玄光社编辑部.商品摄影完全攻略[M].陈丝纶,译.北京:中国青年出版社,2010[6]邸贵玉.现代广告摄影创意及其创作[J].影像技术,2011(2):30—31.(上接第56页),,,[责任编辑:贾朝光]3结语本文讨论了数字通信中基带成形滤波器和匹配滤波器所采用的滚升余弦滤波器的设计方法,以及如何通过Simulink模块进行仿真.通过对滚降系数的调节,对比了有码间串扰及无码间串扰,深入探讨了用FIR滤波器实现滚升余弦滤波器的方法及其正确性和有效性,同时也通过眼图观察了滚升余弦滤波器消除码间串扰的效果.在设计滤波器时要权衡考虑的问题:滚降系数越大,尾随脉冲就越短(这就意味着旁瓣电平幅度小),旁瓣幅度小使得输出信号对定时误差的敏感度较小.当r=1时定时误差仍然可能导致码间串扰,引起检测性能的下降,但已不如r=0严重了,这是因为r=1时的旁瓣电平小于r=O的旁瓣电平.另外,滤波器的滚降系数越小则超量带宽就越小,这允许在提高信号传输速率的同时增加使用系统的用户数,其代价是尾随脉冲长,旁瓣电平大,因此对定时误差的敏感度就高.参考文献:[1]徐平平,宋铁成.BernardSklar.数字通信——基础与应用[M].2版,叶芝慧,译.北京:电子工业出版社,2002.[2]邵玉斌.Matlab/Simulink通信系统建模与仿真实例分析[M].北京:清华大学出版社,2008.[3]陈杰.MA TLAB宝典[M].北京:电子工业出版社,2007.[4]徐明远,邵玉斌.MATLAB仿真在通信与电子工程中的应用[M].西安:西安电子科技大学出版社,2005.[5]张维良,郭兴波,潘长勇,等.平方根升余弦滚降FIR数字滤波器的设计[J].电讯技术,2002(6):51—55.[6]刘睿强,景新幸.一种升余弦成形滤波器的设计[J].现代电子技术,2006(13):51—55.[7]王亚飞,许淑芳.直扩系统中FIR数字升余弦滤波器的设计与实现[J].桂林电子科技大学,2007,27(4):267—270.[8]文安平.平方根升余弦滚降数字滤波器的设计与实现[J].信息技术,2005(9):58—60.[9]高飞,汪皓.基于MATLAB的"信号与系统"仿真实验及其性能分析[J].云南民族大学,2001,10(1):266—269[责任编辑:贾朝光】。
c语言生成根升余弦滤波器

c语言生成根升余弦滤波器(实用版)目录1.介绍升余弦滤波器2.讲解 C 语言生成升余弦滤波器的方法3.演示如何使用 C 语言生成根升余弦滤波器4.分析根升余弦滤波器的性能5.总结正文升余弦滤波器是一种常用的数字滤波器,其特性是在通带内具有恒定的增益,而在阻带内则有较大的衰减。
这种滤波器可以用于信号处理、数据通信等领域,能够有效地抑制信号中的干扰和噪音。
在 C 语言中,我们可以使用一些特定的函数来生成升余弦滤波器。
在这里,我们将介绍如何使用 C 语言生成根升余弦滤波器。
首先,我们需要了解根升余弦滤波器的参数。
这些参数包括滚降因子、滤波器阶数和过采样率。
滚降因子决定了滤波器的滚降程度,滤波器阶数决定了滤波器的通带和阻带宽度,过采样率则决定了滤波器的分辨率。
在 C 语言中,我们可以使用以下步骤来生成根升余弦滤波器:1.定义滤波器的参数,包括滚降因子、滤波器阶数和过采样率。
2.使用 rcos 函数计算升余弦滤波器的脉冲响应。
3.使用滤波器设计函数,如 comm.raisedcosinetransmitfilter 或comm.raisedcosinefilter,来生成滤波器的系数。
下面是一个简单的示例,演示如何使用 C 语言生成根升余弦滤波器:```c#include <stdio.h>#include <math.h>#include <communications.h>int main() {// 定义滤波器参数double roll_off = 0.25; // 滚降因子int order = 19; // 滤波器阶数int oversampling_rate = 8; // 过采样率// 计算升余弦滤波器的脉冲响应double *pulse_response = (double *)malloc(order *sizeof(double));rcos(roll_off, order, pulse_response);// 生成滤波器系数double *filter_coefficients = (double *)malloc(order *sizeof(double));comm.raisedcosinetransmitfilter(pulse_response, order, oversampling_rate, filter_coefficients);// 输出滤波器系数printf("Filter coefficients:");for (int i = 0; i < order; i++) {printf("%lf ", filter_coefficients[i]);}// 释放内存free(pulse_response);free(filter_coefficients);return 0;}```上述代码首先计算了升余弦滤波器的脉冲响应,然后使用comm.raisedcosinetransmitfilter 函数生成了滤波器的系数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验 三 升余弦滚降和根升余弦滚降滤波器设计
一、实验目的
1.掌握升余弦滚降滤波器设计原理和设计方法; 2.掌握根升余弦滚降滤波器设计原理和设计方法; 二、实验原理
1. 定义h (t )为升余弦脉冲成型函数。
h (t ) 升余弦函数定义如下
2
2
2
sin()cos(
)
()14c
c
c
t
t
h t t
c
T
T
t T παππα
=
⋅
-,
对应的频谱为:
10||111()(1cos((||)))
||2
10||22222c
c c c c
c
c
Tc f H f f f f T
T T T T
T
T
α
αα
α
αα
π-⎧
≤≤⎪
⎪⎪--+⎪
=+-<≤
⎨⎪⎪+⎪>
⎪⎩
2. 定义h r (t )为根升余弦脉冲成型函数。
h r (t ) 根升余弦函数定义如下
2
2sin((1))4cos((1)
()14c
c
c
r c t
t
t
h t t c T
T
T
t T παα
π
απα-++=
⎛⎫
⎪- ⎪⎝
⎭,
对应的频谱为:
10||11()||10||2222c
r c
c
c
f H f f f T
T
T
T
α
α
α
α
-⎧
≤≤
⎪-+=<≤
+⎪>
⎪⎩
三、实验内容
1.已知通带码元截止频率为fc,其码元周期为Tc ,以频率为fs 对升余弦脉
冲成型函数h (t )和h (t-Tc )抽样,设计它的数字滤波器。
要求此系统延时m 个码元,
每码元采样k次。
2.已知通带码元截止频率为fc,其码元周期为Tc,以频率为fs对根升余弦脉冲成型函数hr(t)和hr(t-Tc)抽样,设计它的数字滤波器。
要求此系统延时m个码元,每码元采样k次。
四、方案设计和实现步骤
五、仿真结果
六、分析和结论
七、参考文献
八、程序附录。
