第三章╲t点群、空间群和晶体结构
简述晶体结构与空间点阵之间的关系

简述晶体结构与空间点阵之间的关系晶体结构是指由原子、离子或分子按照一定的规律排列而形成的固体结构。
而空间点阵则是描述晶体结构的数学模型,用来表示晶体中原子、离子或分子的排列方式和间距。
晶体结构与空间点阵之间存在着密切的关系,下面将从晶体结构和空间点阵的定义、表示方法以及它们之间的关系三个方面来进行阐述。
一、晶体结构的定义和表示方法晶体结构是指由原子、离子或分子按照一定的规律排列而形成的固体结构。
在晶体中,原子、离子或分子之间的排列方式是非常有序的,各个粒子之间有着固定的位置关系和间距。
晶体结构可以通过实验方法如X射线衍射等来确定,也可以通过理论计算和模拟方法来推测。
晶体结构的表示方法主要有两种,一种是晶体结构的几何图形表示,另一种是用数学模型表示。
几何图形表示主要通过晶体的晶面、晶胞和晶格来描述晶体的结构。
晶面是晶体表面上的一个平面,晶胞是晶体中的最小重复单元,晶格是由相邻晶胞的重复堆积形成的一个无限延伸的空间网格。
数学模型表示主要是通过空间点阵来描述晶体的结构。
二、空间点阵的定义和表示方法空间点阵是一种数学模型,用来描述晶体中原子、离子或分子的排列方式和间距。
空间点阵是由一系列的基矢量和晶胞参数来表示的。
基矢量是一组线性无关的矢量,它们的线性组合可以表示出空间中的任意矢量。
晶胞参数包括晶胞的长度、角度和对称操作元素等。
空间点阵可以分为离散点阵和连续点阵两种。
离散点阵是指晶体中的原子、离子或分子按照一定的规律在空间中离散排列的情况,如简单立方晶体、体心立方晶体和面心立方晶体等。
连续点阵是指晶体中的原子、离子或分子在空间中连续排列的情况,如钻石晶体和金属晶体等。
三、晶体结构与空间点阵的关系晶体结构与空间点阵之间存在着密切的关系。
晶体结构可以通过空间点阵来描述和表示。
在晶体中,原子、离子或分子按照一定的规律排列,形成了一种具有周期性的结构。
这种周期性的结构可以通过空间点阵的平移操作来表示,即晶体结构是由空间点阵的平移操作所生成的。
点群空间群和晶体结构介绍

交换律,即
ai ·bj=bj ·ai
两个群的直接积G以 G G AGB 表示:
G G AG B {a1b1, a1b2 ,...a1bm ,...a2bm ,...anbm}
G是n×m阶群。群的直接积是扩大群的一种最简单的方法。
子群、母群及生殖元素
子群:若群GA的全部元素是群G中的元素,并且两者的结合律 相同,称GA是群G的子群,而G是群GA的母群。如果对称元素GA和 GB能够得到G的全部对称元素,则称这两个对称元素为群G中的两 个生殖元素(Generating Element).
立方系各晶类的投影图
在(e)所示:在投影面上{111)位置4个3轴,单胞3个轴为4次轴, 过单胞3个轴两两构成3个镜面及6个{110}的镜面。一般位置点的等 效点系共有48个点。
5种点群中(e) 是该晶系的全对称点群。从这5种点群可以看 到立方晶系不一定有4次轴,例如点群(a) 和(b) 就没有4次轴。另 外,立方晶系并不一定总是具有最高的对称性,例如四方晶系的 点群D4h-4/mmm(16阶)和六方晶系的点群D6h-6/mmm(24阶)就 比立方晶系的点群T-23(12阶)的对称性高。
上述的两种导出方法有一个共同的缺点,就是导出点群后, 还要再确定每一种点群分属于哪一种晶系。
C)用推导7种晶系的方法也可以推导出32种点群。对每一种晶 系在保证晶系的对称性不变的前提下,加入可能的对称操 作,这种导出方法的优点在于使点群与晶系的关系十分明 确。
下面将用这种方法导出32种点群。 在导出点群时应该注意到在每一个点群中都有主导生
群的阶数相等。
在极射投影时,点群中所有对称操作都经过投影基圆中心。
3.3点群的推导方法
通过对晶体外形的研究,人们发现共有32种晶态,每一种晶态 对应着一种点群。可以用不同方法导出32种点群。
第三章晶系及空间群(PDF)

四方
一个4次轴
三方
一个3次轴
(菱形)
正交
三个互相垂直的2次轴或 对称面或它们的组合
单斜
2、m、2/m
三斜
1、-1
晶胞形状
a=b=c, ===90° a=b≠c, ==90º, =120° a=b≠c, ===90° 与六方相同 a=b=c, ==≠90° a≠b≠c, ===90°
相结构基础及研究方法
Fundamental of Phase Structure and its methods
第三章:晶系及空间群
•主讲人:陈 骏 •冶金与生态工程学院 物理化学系
单位晶胞及其选取
选取单位晶胞的原则
要求选取晶胞最能反映该点阵的对称 性,选取晶胞的原则为:
1)选取的平行六面体应反映出点阵的 最高对称性; 2)平行六面体内的棱和角相等的数目 应最多; 3)当平行六面体的棱边夹角存在直角 时,直角数目应最多; 4)在满足上述条件的情况下,晶胞应 具有最小的体积。 5)重复单位原点的选择一定程度上取 决于个人爱好;通常选择原子或离子 在边、角、中心等特殊位置,易于画 出单位,及想象整个结构;
• 晶胞有六个参量,轴长和轴间夹角。 这六个参量称为晶胞参数。因为晶胞 能够决定整个点阵,所以这些量又称 为点阵参数。
所选取的晶胞需满足晶体空间点阵的两个条件: 周期性条件和对称性条件。
晶胞和晶胞参数
晶系
六方 三方晶系中菱形单胞
如何理解菱形单胞?
晶系名称 特征对称
立方 六方
四个3次轴 一个6次轴
可能对 称元素
无 无 2,m
方向 Z
1,1 2,m,2/m 222,mm2,mmm
无, 2, 底对角 4,4,4/m,422,
2.2.3点群和空间群

该图形显然具有一个对称中心
因此 3 次倒转轴相当于 1 条 3 次旋转轴加上一个对称中心
3 3i
4 次倒转轴
相当于旋转90后再对中 心反演而图形不变。
这是一个独立的对称操 作。它既没有 4 次旋转 轴也没有对称中心,不 能分解成其他基本对称 要素的组合。
注意这里的 2、6、4、 8 这四个点是不存在的, 也是过渡点。
对称面
对称面是一个假想的平面,相应 的对称操作为对此平面的反映。对 称面就像一面镜子,把物体的两个 相同的部分以互成镜像反映的关系 联系起来。 垂直于对称面作任意直线,位于 直线两侧等距离的两点是性质完全 相同的对应点 晶体中如果存在有对称面,则必 定通过晶体的几何中心并将晶体分 为互成镜像反映的两个相同部分 在结晶学中,对称面一般用符号 “m” 表示。
倒转轴
倒转轴是一种复合对称 要素,由一根假想的直线 和在此直线上的一个定点 组成。相应的对称操作是 绕此直线旋转一定角度以 及对此定点的倒反。 根据晶体对称轴定律,倒 转轴也只有 1 次、2 次、 3 次、4 次和 6 次 5 种
倒反类倒转轴 中,只有 4 次倒转轴是一个独立的基本对称操
点群:在宏观晶体中存在的所有对称要素都必定 通过晶体的中心,因此不论如何进行对称操作,晶
体中至少有一个点是不变的,因此对称型也称为点
群。32点群
特征对称元素与7 大晶系
在32晶体学点群中,某些点群均含有一种相同的对称元素, 这样的对称元素叫做特征对称元素。
根据相应的对称性特征,晶体结构可以分为 7 类, 称为 7 大晶系。这 7 大晶系按对称程度增加的次序
在旋转操作中,使物体复原所需的最小旋转角 称为基转角。轴次 n 可以写成
点群空间群和晶体结构

点群空间群和晶体结构晶体是由原子、分子或离子组成的固态物质。
在结晶过程中,这些粒子以一种有序的方式排列,形成了晶体的特定结构。
晶体结构的研究是固体科学的重要分支之一,可以帮助我们理解固体的物理、化学性质以及它们在各种应用中的作用。
点群是空间中对称性的一种表示方式。
点群描述了一个结构中的元素在一组操作下保持不变的方式。
这些操作可以是旋转、翻转或镜像。
常见的点群包括旋转群、镜面群和反演群。
每个点群由一组操作组成,这些操作在结构中的每个点上施加时,都可以保持结构的不变性。
点群对于确定晶体结构的对称性非常重要,因为它可以帮助我们预测晶体的物理性质,例如电学性、磁学性、光学性等。
空间群是点群在三维空间中的扩展。
它描述了一个晶体结构在所有操作下的对称性。
空间群由点群以及平移操作组成。
平移操作使得结构在空间中移动,形成了无穷多的平行结构。
这些平行结构可以通过空间群中的平移操作进行描述。
空间群的数量非常庞大,目前已知有230个不同的空间群。
每个空间群都有一个唯一的编号和名称,用于标识它的对称性。
晶体结构是晶体中离子、原子或分子的排列方式。
不同的晶体结构由不同的元素组成,以及不同的点群和空间群类型。
它们可以由晶体学的X射线衍射实验来确定。
X射线衍射会产生一种特殊的模式,称为衍射图样。
通过对衍射图样进行分析,可以确定出晶体中的原子或离子的位置,从而推断出晶体的结构。
晶体结构是固体科学的基础,它们在材料科学、化学、凝聚态物理学等领域中有着广泛的应用。
通过对晶体结构的研究,可以优化材料的性能,设计新型材料,解释物质的性质,并探索新的应用领域。
总而言之,点群、空间群和晶体结构是固体晶体学中的重要概念。
它们描述了晶体的对称性以及晶体中原子、离子或分子的排列方式。
通过对晶体结构的研究,我们可以了解晶体物质的性质和行为,并为材料科学和应用领域提供基础性的知识。
晶体点群、空间群简要归纳

晶体点群、空间群简要归纳本⽂只是很简要的归纳,具体内容还请见李新征⽼师群论书和其在蔻享的群论课。
另外推荐肖瑞春⽼师科学⽹博客的这篇博⽂,介绍了群论及后续的学习:若研究中涉及群论和物理性质相关,其中陈纲的《晶体物理学基础》书特别好,易懂,将主动变换和被动变换等分析得特别清晰,不过此书太厚,注意⽤到什么学什么,⽤minimized的知识来科研,否则被导师批评...1.对称操作、对称元素对称操作:保持系统不变的操作。
对称元素:它是⼀个⼏何实体,对称操作可以依据对称元素施⾏对称操作。
对称元素可以是点、直线、⾯等。
2.点群:1)定义:三维实正交群O(3)群的有限⼦群物理理解:实际上点群是实际的物理系统在三维空间的⼀些对称操作的集合。
这些对称操作会保持⼀个点不动。
2)点群分类第⼀类点群:只包含纯转动元素的点群。
第⼆类点群:点群中,除了纯转动元素,还包含转动反演元素的点群。
因为点群是O(3)群的⼦群,⽽O(3)群中有固有转动和⾮固有转动。
3)点群的性质{()}性质1:点群这个集合可以写成C k(2π/n)、IC k′2π/n′的形式,其中n,→k′,n′取有限个⽅向和值;C k(2π/n)是绕→k轴转2π/n⾓的操作。
性质2:设G是点群,K是G的纯转动部分,由于纯转动部分的乘积以及逆元必属于这个纯转动部分,所以K也是G的纯转动⼦群,即K=G∩SO(3)∘.点群G与其有限⼦群K的关系有以下三种可能的情况:1.G=K, 即点群只包含纯转动操作;称为第⼀类点群。
2.若点群G中除了纯转动操作,还包含纯空间反演操作I, 则可以通过G=K∪IK得到这种情况对应的第⼆类点群。
3.若点群G中除了纯转动操作,且G中不包含纯反演操作I时 , 此第⼆类点群G⼀定与⼀个第⼀类G+同构,其中,G+=K∪K+, ⽽K+定义为:K+={Ig∣g∈G,但g∉K}根据这⾥的第3点,可以知道构造这种情况对应的第⼆类点群的⽅法:根据⼀个已知的第⼀类点群K∪K+,即可以构造⼀个第⼆类点群K∪I K+.还可以证明K必须是K∪K+的不变⼦群,其阶数是K∪K+的⼀半。
晶体结构空间群点群

(二)点群、单形及空间群点群:晶体可能存在的对称类型。
通过宏观对称要素在一点上组合运用而得到。
只能有32种对称类型,称32种点群表1- 3 32种点群及所属晶系*2/m表示其对称面与二次轴相垂直,/表示垂直的意思。
其余类推同一晶系晶体可为不同点群的原因:阵点上原子组合情况不同。
如错误!未找到引用源。
,对称性降低,平行于六面体面的对称面不存在,4次对称轴也不存在。
理想晶体的形态―单形和聚形:单形:由对称要素联系起来的一组同形等大晶面的组合。
32种对称型总共可以导出47种单形,如错误!书签自引用无效。
,错误!书签自引用无效。
,错误!书签自引用无效。
所示聚形:属于同一晶类的两个或两个以上的单形聚合而成的几何多面体。
大量的晶体形态是由属于同一晶类的单形聚合而成的封闭一定空间的几何多面体,如单形四方柱与平行双面形成了四方柱体的真实晶体形态空间群:描述晶体中原子通过宏观和微观对称要素组合的所有可能方式。
属于同一点群的晶体可因其微观对称要素的不同而分属不同的空间群,空间群有230种,见教材中表1- 4国际通用的空间群符号及其所代表的意义为:P:代表原始格子以及六方底心格子(六方底心格子为三方晶系和六方晶系所共有)。
F:代表面心格子。
I:代表体心格子。
C:代表(001)底心格子(即与z轴相交的平行六面体两个面中心与八个角顶有相当的构造单位配布)。
A:代表(100)底心格子(即与x轴相交的平行六面体两个面中心与八个角顶有相当的构造单位配布)。
R:代表三方原始格子。
其它符号:意义与前述相同表1- 4 晶体的空间群、点群、晶系、晶族一览表续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4点群符号m 43m2晶 系 等轴晶系 晶 族高级晶族/k/174/stu/content/1.1.3.2.htm。
点群、空间群和晶体结构介绍

群是某些具有相互联系规律的一些元素的组合,群的元素可 以是字母、数字、对称操作、点阵等。
任何一个群都应具有以下4个基本性质:
封闭性(Closure)
群G的n个不等效元素中,任两个元素组合或一个同类元素自 身组合都是群中的一个元素。
群中所有元素都遵循组合律,但组合次序不能变。
有唯一的单位元素(E)。它和群中任何一个元素的组合是元素 本身。 群中每一个元素,必有一个相应的逆元素(Inverse Element) 使得两者相乘为其本身。 以一个4次对称轴C4的全部操作所构成的群G来说明4个基本性 质。 两个独立群的直接积 设有两个独立群 GA和GB,其中GA是n阶群,GB是m阶群。两个 群中除了恒等元素外,没有其它共有元素,两个群的元素间相乘有 ai · bj=bj · ai 交换律,即 两个群的直接积G以 G G A G B 表示:
立方系各晶类的投影图
在(e)所示:在投影面上{111)位置4个3轴,单胞3个轴为4次轴, 过单胞3个轴两两构成3个镜面及6个{110}的镜面。一般位置点的等 效点系共有48个点。 5种点群中(e) 是该晶系的全对称点群。从这5种点群可以看 到立方晶系不一定有4次轴,例如点群(a) 和(b) 就没有4次轴。另 外,立方晶系并不一定总是具有最高的对称性,例如四方晶系的 点群D4h-4/mmm(16阶)和六方晶系的点群D6h-6/mmm(24阶)就 比立方晶系的点群T-23(12阶)的对称性高。
这两种类型的对称操作正是描述整个晶体结构对称性的基本操作。 图 (a)是正交点阵的阵 点 上 放 上 对 称 性 为 C2vmm2 的物体的空间群的俯 视图。
(a)正交晶系的Pmm2空间群
图中画出单胞的轮廓,原点选在左上角,a轴指向页底,b 轴指向右, c 轴从页面指出来。以圆圈排列来表示它的对称性 ,在左边的图中每个阵点的对称性用一般位置点的等效点系表 示。其中每一个圆圈既可以代表晶体中单个原子,也可以代表 原子集团。在右边的图上给出对称元素的配置。在原点有一个 沿 c 方向的2次轴和 2个镜面 (用粗线表示 )。 P- 初基点阵, mm2基本操作。非基本操作(附加的2次轴和镜面)未表示。
点群和空间群ppt课件

❖ 经过严格证明可以得出,晶体中可能存在230种空间群,任 何一种晶体的微观结构属于且只属于230种空间群之一。
50
点群与空间群的关系
晶体外形的对称性仅有32个点群,而晶体结构的对称性却有320
种空间群。晶体外形的对称性是晶体结构对称性的反映。 属于同一点群的晶体不一定属于同一空间群。换言之,空间群
59
60
61
62
63
64
重要对称元素的书写与图形记号
65
5
3
3
5
1
1
4
6
2
4
6 2
19
20
(3) 6 象转轴——实际上就是3度转轴+对称面(m)
5 5
3
3
1
1
2
6
2
4
6
4
21
22
(3) 4 象转轴
3
1 2
2
3
1 4
4
23
24
结论: 晶体的宏观对称性中有以下八种基本的对称
操作:1,2,3,4,6,1, m, 4 。 这些基本的操
作组合起来,就可以得到32种不包括平移的宏观 操作类型。
12
二、中心反演(中心反映)
1.中心反演
如图所示,有对称心i,晶体中
iA
任一点A过中心 i 连线Ai并延长到A',
使Ai = A' i, A与A'是等同点, i点称
A
为对称心。
2.表示方式
x, y, z
(1)熊夫利符号表示——i;
x, y,z
(2)国际符号表示—— 1
山东大学结晶化学课件第三章 第四节

1空间群:晶体结构具有空间点阵式的周期性结构,点阵结构的空间对称操作群称为空间群空间群的推引:1890年,俄国科学家E.S.Fedorov(费多洛夫)完成了230个空间群 的推引工作,使晶体结构的几何理论得到较完整的发展.230个空间 群又称费多洛夫群,反映了晶体几何属性上的对称性.2• 晶体的微观对称元素有以下七类:1、旋转轴:1,2,3,4,6 2、反映面:m 3、对称中心:1 (i) 4、反轴:4 5、螺旋轴:21,31,32,41,42,43,61,62,63,64,65 6、滑移面:a,b,c,n,d 7、平移 平移这七类对称元素在空间的组合所表现出的对称性的集合即为空间群,它 反映了晶体微观结构的全部对称性,描述了无限晶格空间结构的对称性。
3•空间群与点群的同形关系¾空间群是把点群的对称性应用于无限的空间点阵,再 考虑到可能的平移对称性,螺旋轴和滑移面而得到的。
•晶体外形所具有的宏观对称元素,在微观晶体结构中,加入平移成分,可以表现为不同的微观对称元素。
因此,属于同一点群的晶体,可以 可以表现为不同的微观对称元素。
因此,属于同 点群的晶体,可以 属于不同的空间群。
属于同一宏观点群的所有空间群,称为与该点群 同形的空间群.从某一点群出发而得到的种种可能的微观对称类型– 空间 群时,相应对称元素之间的角度关系是与该点群相同的。
4•空间群的国际符号空间群的国际符号由两部分构成,第一个大写字母表示点 阵格子类型,第 部分标明空间群的特征对称元素,其定 阵格子类型,第二部分标明空间群的特征对称元素,其定 向和符号形式与点群相同,但增加了螺旋轴和滑移面。
如 果空间群的微观对称元素用相应的宏观对称元素取代,则 得到晶体的点群。
得到晶体的点群 ¾对称元素选取的一般原则: 1、反映面 反映面m 2、滑移面a,b,c,n,d 3、旋转轴 旋转轴 4、螺旋轴(尽量采用比较对称的写法,如I222=I21212,I2221=I212121。
点群空间群和晶体结构

点群空间群和晶体结构
一、点群
点群是模拟物体在实际应用中的一种常用方法,它可以使用离散的点
来模拟物体的形状,形成空间网格。
它比传统三维建模技术更易于实现,
更少的信息就可以获得一个物体的完整几何描述。
点群可以被用来快速创建几何模型,而且可以利用点的位置和位置关
系来描述一个物体的形状特征,例如法向量和曲率,这对于计算机视觉、
求解机器人运动规划任务等都是非常有用的信息。
点群技术也被用来提取
复杂物体的特征,比如可以通过计算点群中局部点的法向量和曲率等特征
来识别物体的形状。
点群技术的另一个重要应用是三维重构,也就是把两个点群之间的关
系映射为3D模型,这样可以根据点群之间的变换关系或者任意点群之间
的距离来精确恢复模型的几何形状和位置变换。
点群技术的另一个作用就是可以将点群视为物体制作模型的基础构件,如通过点群文件可以构建3D打印、CAD和CAM模型。
二、空间群
空间群是由含有三维空间元素的群体组成的,是用来描述三维物体的
空间结构的一种技术。
空间群可以帮助科学家和工程师深入理解物体的表
面结构,从而更好地控制物体的生长和变化。
铁电第三章群论铁电体的晶体结构

空间点阵
这些阵点在空间呈周期性规则排列并具有完全相 同的周围环境,这种由它们在三维空间规则排列 的阵列称为空间点阵,简称点阵。
晶胞
具有代表性的基本单元(最小平行六面体)作 为点阵的组成单元,称为晶胞。将晶胞作三维
的重复堆砌就构成了空间点阵。
晶体结构与点阵
晶体结构和空间点阵的区别
空间点阵是晶体中质点排列的几何学抽象,用以描 述和分析晶体结构的周期性和对称性,由于各阵点 的周围环境相同,它只能有14种类型
晶体结构则是晶体中实际质点(原子、离子或分子) 的具体排列情况,它们能组成各种类型的排列,因此, 实际存在的晶体结构是无限的。
晶胞选取的原则
同一空间点阵可因选取方式不同而得到不相同的晶胞
晶胞选取的原则
选取的平行六面体应反映出点阵的最高对称性; 平行六面体内的棱和角相等的数目应最多; 当平行六面体的棱边夹角存在直角时,直角数目应最多; 当满足上述条件的情况下,晶胞应具有最小的体积。
四方晶体绕中心轴转90或90的整数倍后, 晶体自身重合;六角晶体绕中心轴转60 或60的整数倍后,晶体自身重合.
12/26/2019
3
对称性和对称操作
12/26/2019
4
晶体的对称性是由其内部格子结构所决 定的,它不仅与晶体的结构有密切关系, 而且也于晶体的力学、电学、光学以及 压电铁电性质等有密切关系。
分数坐标,不对称单位
12/26/2019
6
原子排列的作用
原子排列
组织
性能
固态物质的内部结构是了解掌握材料性能的基础,才 能从内部找到改善和发展新材料的途径。
物质:气态,液态,固态 固态物质:晶体,非晶体
晶体:原子在空间呈有规则地长程有序排列; 非晶体:原子排列没有长程有序。
空间群与晶体

本次您浏览到是第十四页,共二十七页。
我们从正方点阵出发介绍.点群与晶体结构对称 性 比如的正关方系体有48个对称操作:
沿着立方轴转π/2,π,3π/2,有
3个立方轴,共9种 沿着面对角线转π,有6条面对角线,共6种 沿着体对角线转2π/3,4π/3,有4条体对角线,共8
其中由于3、6次象转操作可分解为反演操作(m) +旋转操作(3、6)
所以点式操作只有8个独立操 作,1,2,3,4,6和 。
。
本次您浏览到是第十三页,共二十七页。
现在,我们来介绍点对称操作的集合所构成的点群 晶体学点群共有32种,称为32种晶体学点群,简
称32种点群。
为什么晶体学点群有32种而不是更多或更少 ?
。与空间操作相对应的对称操作要素只能存在于无 限的结构中,而不能存在于有限的晶体中。
包括了这些与平移有关的操作之后,晶体的对称运 动可以全部分类成230个对称操作群,称晶体空间 群,也称空间群。
本次您浏览到是第二十页,共二十七页。
如果考虑实际晶体的某些物理性质,则不仅有空间 位置上的对称特征,而且会有物理性质上的对称特 征.例如,磁性有南北两极,电荷有正负两类,自旋 有上下两态等等.这些具有相反两种状态的性质,可 以用反对称操作来描述.
我们再看一个n滑移的例子.如图6,1所示,滑移面 垂直于c方向,轨迹为(x,y,s)滑移量为(a+b)/2 ,则其对’(x,y,z)点的操作为
本次您浏览到是第十九页,共二十七页。
应该注意,与点阵、螺旋轴、滑移面对应的对称操 作,空间上的每一点都移动了,具有这种性质的操 作称空间操作。因为空间操作直接与晶体微观结构 的周期性相联系,故也称微观对称操作,其阶为∞
第03章 晶体结构_02

• 对任意倒格矢和正格矢:
都有如下关系式,其中括号内是一个整数。
• 由于倒晶格的倒晶格是正晶格,fcc的倒晶格是bcc,bcc的倒晶格
是fcc,hcp的倒晶格是hcp(相对正晶格转动30)。
41
两个定理
• 如果
有周期性
,它就可以做如下傅里叶展开,
其中的求和对所用的倒格矢,其展开系数定义为:
• 如果
surface orientations
48
49
布里渊区(Brillouin zone)
• 倒空间的Wigner-Seitz元胞称为(第一)布里渊区; • 下图展示重要结构的布里渊区(点总是指k=0点); • 对于fcc,X点指区边界在[001]方向的点,K指[110],L指[111]。
Brillouin zones and special k points for the (a) primitive cubic (pc), (b) fcc。
2
半导体:晶体结构
• Bravais晶格的格点由下式产生:
• 两维晶格及其元胞取法:
3
半导体:晶体结构
• 晶体结构由晶格和依附于每个格点上的构成单元(building block, 或 base)组成。
• 总的来讲,有
4
半导体:晶体结构
• 元胞可以有多种取法:
• 最反映Bravais晶格对称性的一种:Wigner-Seitz(WS)胞:
7. 合金半导体
• 不同半导体混合后,会出现三种情况: 1. 不相溶,将会形成团簇,或相分离,也可形成缺陷; 2. 形成有序(周期)结构,称为超晶格; 3. 形成随机合金。
• 随机合金:对于
,在任意给定的原子位置上,找到Ge
材料分析方法-3 微观对称性-空间群-实际晶体结构
•
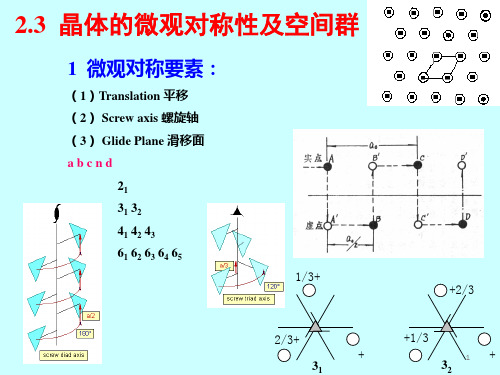
LiFeO2(Li1/2Fe1/2) O
•
CaF2结构:
•
NaYF4 (Na1/2Y1/2)F2
(Li1/2Fe1/2) O
33
(2)多元化合物的原子有序-无序转变:
离子排列的有序化,产生离子位置的分离,简单的结构类 型变成复杂的晶体结构
• 阳离子配置图:Na+离子占据CaF2 结构一半的顶角位置(棱上)和 5/6的面心位置 ;U5+离子占据其 余1/6的面心位置(体心)和1/2的 顶角位置。
32点群:点对称操作群
根据特征对称要素归属为7种晶系
7种晶系
晶格类型P,I,F,A,B,C,R
14种布拉菲点阵
32个点群+平移操作(螺旋轴,滑移面)
230空间群
2.4 实际晶体结构
1,铁素体铁-Fe:体心立方点阵,空间群:Im3m(229号),每个 单胞包括2个阵点:(0,0,0)点群 m3m;(1/2,1/2,1/2)。
• 有序化,四方体心结构,晶胞参数 沿c轴较CaF2结构增大一倍。
34
黄铜矿(Cu1/2Fe1/2)S
• 立方硫化锌结构。 • 有序化,Fe原子占据立方硫化锌
结构1/2的顶角位置,1/2面心位 置(体心),Cu原子占据立方硫 化锌结构其余1/2的顶角位置(棱 上),1/2面心位置(底心) • 四方体心结构,晶胞参数沿c轴较 ZnS结构增大一倍。
重复点数:一套等效点系在一个单位晶胞中所拥有的等效 点系的数目。重复点数与原始点在晶胞中所处的位置有关, 该点的对称称为点位置的对称性。如原始点处在某个(些) 对称要素位置上,则得到的等效点系位置被称为特殊等效点 系位置;反之,处在一般位置上(点对称为1),则称为一 般等效点系位置。
物理化学第3章 晶体结构
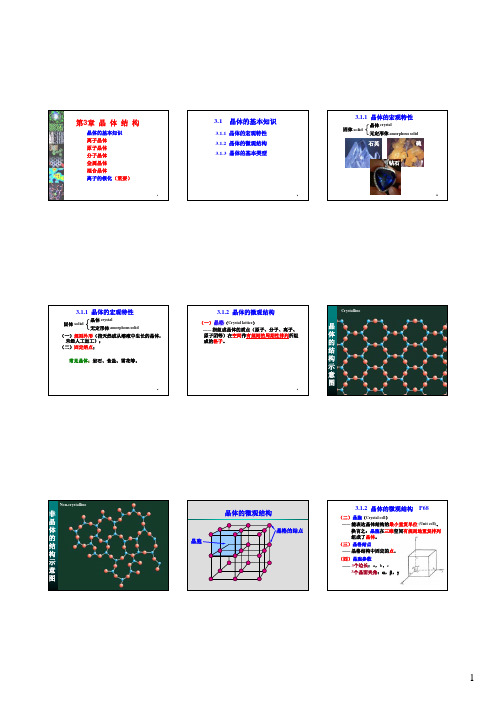
离子的极化
-+ -+ - + -+ - +
27
3
(一)影响离子极化的因素
(1)离子的正电荷越多,半径越小,离子的极化作用 越强。
(2)当离子电荷相同,半径相近时,不同外层电子构 型的离子极化作用大小为: (18、18+2、2电子构型)> 9-17电子构型 > 8电子构型
Cu+ Ag+ Au+
Li+
的
与另3个C以共价键结合,
层 状
并有大π键 (离域键); 层与层之间:
高价卤化物的熔点比低价的更低:
FeCl3 (306℃) < FeCl2 (672℃); SnCl4 (-33℃) < SnCl2 (246℃);
结
以分子间力结合
3.7.2 离子极化对物质结构和性质的影响
构
22
23
24
3.7.1 离子的极化作用和变形性
简单立方
体心立方
面心立方
10
立方晶系的3种晶胞
简单立方
体心立方
面心立方
Slide 11 of 35
3.1.3 晶体的基本类型 (重要)
—— 按占据晶格结点的粒子种类及 质点互相间作用力划分为4类晶体
晶体类型 离子晶体 原子晶体 分子晶体 金属晶体
例
NaCl 金刚石
干冰 Na、Fe
占据结点的质点 阴离子、阳离子
21
离子晶体的“反常”现象
石墨的结构特点
(1)溶解度:KI和AgI的在水中的溶解度差异很大。
石
每层内:
(2)熔点: ⅡA族元素的氯化物的熔点顺序:
3.7 离子的极化(重要)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
附图1
在图中没有标出对称元素的投影,因为 任何方向都可以是1次轴,故不能标出它的位 置。投影图中的一般位置点的等效点只有一 个点,因为经对称操作后这个点仍在原来位 置。 2) 如果物体有 1(E) 和ቤተ መጻሕፍቲ ባይዱ1(i) 对称操作,这个点 群是2阶的:{E,i}或{1,1}。点群的熊夫利斯 符号是 Ci ,国际简略符号是 1 ,即点群的符号 是 Ci-1 。这个点群的生殖对称元素是 1 ,生殖 矩阵就是反演操作的变换矩阵。这种点群的极 射投影图如附图 l(b) 所示:在图中心标出对称 中心。一般位置点的等效点系是一个在上半球 ( 用 ● 表示 ) ,另一个在下半球 ( 用 ○ 表示 ) 的 2 个 等效点。
群是某些具有相互联系规律的一些元素的组合,群的元素可 以是字母、数字、对称操作、点阵等。
任何一个群都应具有以下4个基本性质:
封闭性(Closure)
群G的n个不等效元素中,任两个元素组合或一个同类元素自 身组合都是群中的一个元素。
群中所有元素都遵循组合律,但组合次序不能变。
有唯一的单位元素(E)。它和群中任何一个元素的组合是元素 本身。 群中每一个元素,必有一个相应的逆元素(Inverse Element) 使得两者相乘为其本身。 以一个4次对称轴C4的全部操作所构成的群G来说明4个基本性 质。 两个独立群的直接积 设有两个独立群 GA和GB,其中GA是n阶群,GB是m阶群。两个 群中除了恒等元素外,没有其它共有元素,两个群的元素间相乘有 ai · bj=bj · ai 交换律,即 两个群的直接积G以 G G A G B 表示:
除了上述两种点群,我们不可能再 增加任何对称操作而使物体仍属于三斜 晶系,所以,属于三斜晶系的晶类只有 两种。 Ci-1 点群的对称操作最多 ( 不严 格地说它具有最高的对称性 ) ,称这种
点群为该晶系的全对称点群。
附图1
从上述两种点群的极射投影再一次说明在投影图上一般位置 的正规点系的数目和点群具有对称操作的数目相同,即与点群 的阶数相同。
3.2点群的描述及图示
一组变换矩阵表示
点 极射投影 群 该点群所有元素的极射投影以及一般位置点的正规点系
(Regular Point System,RPS)的极射投影。 一般位置点指不处在对称元素上的点;正规点系是指某一点 经过点群所有对称操作导出的全部点的集合。 一般位置点的正规点系的总点数(又称等效位置点数)和点 群的阶数相等。 在极射投影时,点群中所有对称操作都经过投影基圆中心。
立方系各晶类的投影图
在(e)所示:在投影面上{111)位置4个3轴,单胞3个轴为4次轴, 过单胞3个轴两两构成3个镜面及6个{110}的镜面。一般位置点的等 效点系共有48个点。 5种点群中(e) 是该晶系的全对称点群。从这5种点群可以看 到立方晶系不一定有4次轴,例如点群(a) 和(b) 就没有4次轴。另 外,立方晶系并不一定总是具有最高的对称性,例如四方晶系的 点群D4h-4/mmm(16阶)和六方晶系的点群D6h-6/mmm(24阶)就 比立方晶系的点群T-23(12阶)的对称性高。
C)用推导7种晶系的方法也可以推导出32种点群。对每一种晶 系在保证晶系的对称性不变的前提下,加入可能的对称操 作,这种导出方法的优点在于使点群与晶系的关系十分明 确。 下面将用这种方法导出32种点群。
在导出点群时应该注意到在每一个点群中都有主导生 殖对称元素,群内其它对称元素可以由主导生殖对称元素 组合增殖生成。如果由一组矩阵表示点群,则生殖对称元 素的变换矩阵就是点群的生成矩阵。
三斜晶系
三斜晶系单胞的棱长及其夹角不受任何限制。它可能的对称 操作是1(C1)或1 (i)。这晶系可以有2个点群。 1) 如果物体只有一个1(C1)恒等操作,它所属的点群是1阶 的{C1)或{1}。其熊夫利斯符号是C1,国际简略符号是l,即点 群符号是C1-1。 这种点群符号和其对称操作符号相同。因为C1-1 点群只有 一种单一对称操作,所以,尽管点群符号和对称操作符号相 同也不会引起混乱。这种点群的生殖对称元素就是 C1(E),生 殖矩阵就是恒等操作的变换矩阵。这种点群的极射投影图如 附图1(a)所示。
材料结构与性能
授课教师:刘胜新 (18课时)
第三章点群、空间群和晶体结构
引言
群(Group)是某些具有相互联系规律的元素的组合.晶体对称 操作符合一定规律的组合,这种群即是对称群(Symmetry Group )。晶体外形是一个有限对称图象,对其进行对称操作时,至少 保持一点不动,即这些操作是点对称操作,它们组成点对称群, 称为点群(Point Group)。 讨论点对称操作有哪些可能的组合方式,并对晶体做进一步划分。 3.1 群的概念和基本性质
G G AG B {a1b1 , a1b2 ,...a1bm ,...a2bm ,...anbm}
群的直接积是扩大群的一种最简单的方法。 G是n×m阶群。
子群、母群及生殖元素
子群:若群GA的全部元素是群G中的元素,并且两者的结合律 相同,称GA是群G的子群,而G是群GA的母群。如果对称元素GA和 GB能够得到 G的全部对称元素,则称这两个对称元素为群 G中的两 个生殖元素(Generating Element).
3.3点群的推导方法
通过对晶体外形的研究,人们发现共有32种晶态,每一种晶态 对应着一种点群。可以用不同方法导出32种点群。 A)从五种循环群1(C1)、2(C2)、3(C3)、4(C4)、6(C6)开始,再在 每种循环群上加进各种新的对称操作,最终导出32种点群。 例如: 在垂直于循环群对称轴的方向加上 2次对称轴;在垂直于循环 轴的方向或包含循环轴加上镜面;用非真旋转轴代替真旋转轴等。 用这些操作或者这些操作的某一种组合可能会得出一些新的点群。
B) 首先找出仅由真旋转构成的所有群,这种纯旋转结晶学点群 共有11种。然后在这11种点群的基础上,把每一种都加上反演对 称操作,又获得11种点群。由这11种中心对称点群,又可以找出 与11种纯旋转点群不同的10种非中心对称子群,最后导出了32种 点群,是一种最快和最好的方法。
上述的两种导出方法有一个共同的缺点,就是导出点群后, 还要再确定每一种点群分属于哪一种晶系。
