全等三角形培优讲义之令狐文艳创作
小升初讲义数学共16讲之令狐文艳创作

令狐文艳创作目录令狐文艳第1讲前言第一章丰富的图形世界第2讲生活中的立体图形第3讲展开与折叠第4讲截与看几何体第5讲平面图形与基本的推理第6讲直线、线段、射线、角第二章有理数第7讲数怎么不够用了第8讲数轴第9讲绝对值第10讲有理数的加法第11讲有理数的减法第12讲有理数的加减混合运算第13讲有理数的乘法第14讲有理数的除法第15讲有理数的乘方第16讲有理数的混合运算第1讲前言数学:人类离不开;人人都能学会!一、走进数学世界宇宙之大(海王星、流星雨),粒子之微(铍原子、氯化钠晶体结构),火箭之速(火箭),化工之巧(陶瓷),地球之变(陨石坑),生物之谜(青蛙),日用之繁(杯子、表),大千世界,天上人间,无处不有数学的贡献,让我们共同走进数学世界,去领略一下数学的风采,体会数学的魅力。
1.大自然的鬼斧神工使几何图形的对称美成了造型艺术、建筑美学的基础。
雪花的对称性就是大自然的杰作。
晶体(如冰糖)的表面对称极为精巧,并由此内含着深刻的物理性质。
在人类赖以生存的建筑群中,小到衣物装饰,大到房屋建筑、路面铺设,几乎处处都有美丽的对称性装饰,古代皇宫中壁画的边饰等无不含有极为壮丽的对称美,以至亡国之君李煜在身受软禁之际,还深情怀恋昔日的“雕阑玉砌应犹在”。
2.天工造物,每每使人惊叹不已;生物进化提示的规律,有时几个世纪也难以洞悉其中的奥秘。
蜂房的构造,大概最令人折服的实例之一。
18世纪初,法国学者马拉尔琪实测了蜂房底部菱形,得出令人惊异而有趣得结论:拼成蜂房底部的每个菱形的蜡板,钝角都是109°28ˊ,锐角都是70°32ˊ。
瑞士数学家克尼格经过精心计算,结果更令人震惊:建造同样体积且用料最省的蜂房,菱形的两角应是109°26ˊ与70°34ˊ,与实测仅差2分。
人们对蜜蜂出类拔萃的“建筑术”赞叹万分之余,无人去理会这不起眼的“2分”。
不料蜜蜂却不买克尼格的账,冷酷的科学事实后来去判断错方是克尼格。
初二超经典相似三角形模型分析大全之令狐文艳创作

相似三角形模型分析大全一、令狐文艳二、相似三角形判定的基本模型认识(一)A字型、反A字型(斜A字型)(平行)(不平行)(二)8字型、反8字型BCBC(蝴蝶型)(平行)(不平行)(三)母子型(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景(五)一线三直角型:(六)双垂型:三、相似三角形判定的变化模型旋转型:由A 字型旋转得到。
8字型拓展CB EDA共享性GA BCEF一线三等角的变形一线三直角的变形第二部分 相似三角形典型例题讲解 母子型相似三角形:例1:如图,梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于点O ,BE ∥CD 交CA 延长线于E .求证:OE OA OC ⋅=2. 例2:已知:如图,△ABC 中,点E 在中线AD 上,ABC DEB ∠=∠.求证:(1)DADE DB ⋅=2; (2)DAC DCE ∠=∠.B例3:已知:如图,等腰△ABC 中,AB =AC ,AD ⊥BC 于D ,CG ∥AB ,BG 分别交AD 、AC 于E 、F .求证:EG EF BE⋅=2.相关练习:1、如图,已知AD 为△ABC 的角平分线,EF 为AD 的垂直平分线.求证:FC FB FD⋅=2.2、已知:AD 是Rt △ABC 中∠A 的平分线,∠C=90°,EF 是AD 的垂直平分线交AD 于M ,EF 、BC 的延长线交于一点N 。
求证:(1)△AME ∽△NMD; (2)ND 2=NC ·NB3、已知:如图,在△ABC 中,∠ACB=90°,CD ⊥AB 于D ,E 是AC 上一点,CF ⊥BE 于F 。
求证:EB ·DF=AE ·DB4.在∆ABC 中,AB=AC ,高AD 与BE 交于H ,EF BC ⊥,垂足为F ,延长AD 到G ,使DG=EF ,M 是AH 的中点。
求证:∠=︒GBM 905.已知:如图,在Rt △ABC 中,∠C =90°,BC =2,AC =4,P 是斜边AB 上的一个动点,PD ⊥AB ,交边AC 于点D (点D 与点A 、C 都不重合),E 是射线DC 上一点,且∠EPD =∠A .设A 、P 两点的距离为x ,△BEP 的面积为y .(1)求证:AE =2PE ;(2)求y 关于x 的函数解析式,并写出它的定义域;D E(3)当△BEP 与△ABC 相似时,求△BEP 的面积. 双垂型:1、如图,在△ABC 中,∠A=60°,BD 、CE 分别是AC 、AB 上的高求证:(1)△ABD ∽△ACE ;(2)△ADE ∽(3)BC=2ED2、如图,已知锐角△ABC ,AD 、CE 分别是BC 、AB 边上的高,△ABC 和△BDE 的面积分别是27和3,DE=62,求:点B 到直线AC 的距离。
全等三角形培优讲义

全等三角形常见辅助线作法【知识导图】思维模式是全等变换中的“对折”.2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是 全等变换中的“旋转”.3)遇到角平分线,可以自角平分线上的某一点向角的两边作垂线, 利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理.4)过图形上某一点作特定的平分线, 构造全等三角形,利用的思维模式是全等变换中的 “平移”或“翻转折叠”5)截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长, 是之与特定线段相等, 再利用三角形全等的有关性质加以说明. 这种作法,适合于证明线段的和、差、倍、分等类的题目.特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利 用三角形面积的知识解答.第二部分:例题剖析、倍长中线(线段)造全等概念三边之和大于等于第三边稳定性与三角形有关的线段中线角平分线高三角形内角和定理 三角形与三角形有关的角三角形的外角性质直角三角形判定多边形及其内角和【导学】全等三 角形第一部分:知 识点回顾—常见辅助线的作法 有以下几种:1) 遇到等腰三角形,可作底边 上的高,利用 “三线合一” 的性质解题,精准诊查已知,如图△ABC 中,AB=5, AC=3,贝忡线AD 的取值范围是 E 、F 分别在 AB AC 上, DEL DF , D 是中点,试比较 BE+CF 与 EF 的大小.例1、( “希望杯”试题) 例2、如图,△ ABC 中, 例3、如图,△ ABC 中, BD=DC=AC E 是DC 的中点,求证: AD 平分/ BAE.二、截长补短 1、如图, 2、如图, ABC 中,AB=2AC AD 平分 BAC ,且 AD=BD 求证:CD L A(B AC// BD,EA,EB 分别平分/ CAB,/ DBA CD 过点 E ,求证;AB = AC B已知在VABC 内, BAC 60 , C求证P B > P A .例2如图,在厶ABC 的边上取两点 D 、E ,且BD=CE 求证:AB+AC>AD+AE. 四、借助角平分线造全等1、如图,已知在△ ABC 中,/ B=60°, △ ABC 的角平分线 AD,CE 相交于点O,求证:OE=OD2、如图,△ ABC 中,AD 平分/ BAC DGL BC 且平分 BC, DE! AB 于 E, DF L AC 于 F.(1)说明 BE=CF 的理由;(2)如果 AB=a , AC=b ,求 AE 、 BE 的长.五、旋转例1正方形ABCD 中 , E 为BC 上的一点,F 为CD 上的一点,BE+DF=EF / EAF 的度数.FC如图,340° , P , Q例1 ADABC 的角平分线,直线MN L AD 于为MN 上一点,△ ABC 周长记为P A , △ EBC 周长记为F B .求例2如图,ABC是边长为3的等边三角形,BDC是等腰三角形,且BDC 1200,以D为顶点做一个600角,使其两边分别交AB于点M,交AC于点N,连接MN贝U AMN的周长为_________________ 例3设点E、F分别在正方形ABCD的边BC CD上滑动且保持/ EAF=4f,AP± EF 于点P,(1) 求证:AP=AB ( 2)若AB=5,求厶ECF的周长。
中考数学高频考点之令狐文艳创作

高频命题点令狐文艳一、选择题、填空题常考点1、相反数、绝对值、倒数①相反数:a 的相反数为a -(解题时找其数字一样,符号不一样的) ②绝对值:(0)0(0)(0)a a a a a a >⎧⎪==⎨⎪-<⎩ ③倒数:ab 的倒数为b a ,倒数等于本身的数为±1(解题时找符号一样,分子、分母颠倒的)性质:①实数a 、b 互为相反数⇔0a b +=;②实数a 、b 互为倒数⇔1ab =2、科学记数法:10n a ⨯⑴确定a :110a ≤<;⑵确定n :①当原数≥10时,n 等于原数的整数位数减去1;②当0<原数<1时,n 是负整数,n 的绝对值等于原数中左起第一个非零数前零的个数(含整数位数的零)。
3、幂的运算①同底数幂相乘:m n m n a a a +⋅=; ②同底数幂相除:m n m n a a a -÷=; ③幂的乘方:()()m n mn n m a a a ==④积的乘方:()n n n ab a b =; ⑤零次幂:01(0)a a =≠;⑥负整数次幂:1n na a -=4、整式运算①合并同类项:字母和指数不变,系数相加减;②幂的运算:(同3; ④平方差公式:22()()a b a b a b +-=-,完全平方公式:222()2a b a ab b ±=±+。
5、因式分解(1)方法:①提公因式法:()pa pb pc p a b c ++=++;②公式法22222:()():2()a b a b a b a ab b a b ⎧-=+-⎨±+=±⎩平方差公式逆用完全平方公式逆用 (2)步骤:一提二套三检查6、二次根式⑴性质:①2(0)a a =≥a =(同1-②)。
==先将二次根式化为最简二次根式,再将被开方数相同的二次根式进行合并。
7、不等式组解法及解集表示⑴、解法步骤:去分母,移项,合并同类项,系数化为1.⑵、注意事项:①不等式两边同时除以或乘以一个负数,不等号要改变方向;②求不等式组的解集有两种方法:第一种,口诀法:同大取大,同小取小,大小小大取中间,小小大大去不了;第二种,数形结合法:用数轴表示;③边界:有等号用实心圆点,无等号用空心圆圈;方向:大于向右,小于向左.8、函数自变量取值范围(1)分式:分母不能为0;(2)二次根式:被开方数大于等于0;(3)分式+二次根式:分母不能为0和被开方数大于等于0.9、利用平行线的性质计算角度性质:两直线平行,同位角相等,内错角相等,同旁内角互补.考法:结合余角、补角、对顶角、内错角以及三角形内角和、内外角关系等知识考查.10、利用圆周角定理及推论求角度定理:一条弧多对的圆周角等于它所对的圆心角的一半。
初二数学三角形专题练习1之令狐文艳创作

三角形、令狐文艳★★★主要知识点:1.三角形的分类三角形按边分类可分为_______和______(等边三角形是等腰三角形的特殊情况);按角分类可分为______、_______和_______,2.一般三角形的性质(1)角与角的关系:三个内角的和等于___°;三个外角的和等于___;一个外角等于和它不相邻的两个内角之和,并且大于任何—个和它不相邻的内角,____________。
(2)边与边的关系:三角形中任两边之和大于第三边,任两边之差小于第三边。
(3)边与角的大小对应关系:在一个三角形中,__边对等角;等角对等____。
(4)三角形的主要线段的性质(见下表):3. 几种特殊三角形的特殊性质A CB 第 8 题 (1)等腰三角形的特殊性质:①等腰三角形的两个_____角相等;②等腰三角形_______、_____中线和______是同一条线段,三线合一;这条线段所在的直线是等腰三角形的对称轴。
(2)等边三角形的特殊性质:①等边三角形每个内角都等于___°。
②三线合一(3)直角三角形的特殊性质:①直角三角形的两个锐角互为___角; ②直角三角形斜边上的中线等于斜边的一半。
③s=21ab(a 、b 分别为两直角边)或S △ = 21a h ( h 是a 边上的高 )4. 三角形的面积一般三角形:S △ = 21a h ( h 是a 边上的高 ) 例1: (基础题) 如图,AC //DF , GH 是截线. ∠CBF =40°, ∠BHF =80°.求∠HBF , ∠BFP , ∠BED .∠BEF 的度数例2: (基础题)①在△ABC 中,已知∠B = 40°,∠C = 80°,则∠A = (度)②如图,△ABC 中,∠A = 60°,∠C = 50°,则外角∠CBD = 。
③已知,在△ABC 中, ∠A + ∠B = ∠C ,那么△ABC 的形状为()A 、直角三角形B 、钝角三角形C 、锐角三角形H P GF EDC B AD B A第 14 题D 、以上都不对④下列长度的三条线段能组成三角形的是( )A.3cm ,4cm ,8cmB.5cm ,6cm ,11cmC.5cm ,6cm ,10cmD.3cm ,8cm ,12cm⑤如果一个三角形的三边长分别为x ,2,3,那么x 的取值范围是。
九年级数学培优教程整理篇(全)之令狐文艳创作

第1讲二次根式的性质和运算令狐文艳考点·方法·破译1.了解二次根式、最简二次根式、同类二次根式的定义,能准确进行辨析;2.掌握二次根式有关性质,并能熟练运用性质进行化简;3.会根据二次根式的性质挖掘题中隐含条件,求参数的值(或取值范围).经典·考题·赏板【例1】(荆州)下列根式中属最简二次根式的是()【解法指导】判断式子是否为最简二次根式的条件有两点:①被开方式中不能含分母;②被开方式中不能有可开尽方的数或式子. B中含分母,C、D含开方数4、9,故选A.【变式题组】1.⑴(中山)下列根式中不是最简二次根式的是()式是()A.①,② B.③,④C.①,③D.①,④【例2】(黔东南)方程x-=,当y>0时,m480的取值范围是()A.0<m<1 B.m≥2C.m<2 D.m≤2【解法指导】本题属于两个非负数的代数和问题,隐含两个代数式均为0的结论.由题意得4x-8=0,x-y-m=0.化为y=2-m,则2-m>0,故选C.【变式题组】2.(宁波)若实数x、y2y=,则xy的(0值是__________.3.(荆门)若2=+,则x-y的值为x y()()A.- 1 B.1C.2 D.3有意义的x的取值范围是4.(鄂州)使代数式4x-()A.x>3 B.x≥3C.x>4 D.x≥3且x≠45.(怀化)22(4)0--=,则a-b-c=________.a c是同类二次根式的是【例3】下列二次根式中,与()AD【解法指导】判断几个二次根式是否为同类二次根式应先把它们都化为最简二次根式,再看被开方数是否一样. A.=; B.不能化简;C.=;D==.故本题应选D.【变式题组】6.如果最简二次根式是同类二次根式,则a =________.7.在下列各组根式中,是同类二次根式的是( ) A.和.和8.已知最简二次根式b是同类二次根式,则a =_______,b =______.【例4】下列计算正确的是( ) A=4= C= D.(11+=【解法指导】正确运用二次根式的性质①2(0)a a =≥;②(0)0(0)(0)a a a a a a ⎧⎪===⎨⎪-⎩><;③0,0)a b =≥≥;④0,0)b a =≥> 进行化简计算,并能运用乘法公式进行计算.A 、B 中的项不能合并.D.2(111+-=-=-.故本题应选C.【变式题组】9. (聊城)下列计算正确的是( ) A .= B =C3= D 3=-10.计算:200720074)(4⋅=_____________11.22-=_____________12.(济宁)已知a ) A .a B .-a C .-1 D .013.已知a >b >0,a +b =6,则的值为( )A .2B .2CD .12【例5】已知xy >0,化简二次根式的正确结果为( )AC .D .【解法指导】先要判断出y <0,再根据xy >0知x <0.故原式=选D.【变式题组】14.已知a 、b 、c 为△AB C 三边的长,则化简a b c --+_______.15.观察下列分母有理化的计算:=,==一规律计算:1)2006+⋅=_________.16.已知,则0<x <1,则=_________.【例6】(辽宁)⑴先化简吗,再求值:11()b a b b a a b ++++,其中a =b =⑵已知x =,y =值为________.【解法指导】对于⑴,先化简代数式再代入求值;对于⑵,根据已知数的特征求xy 、x +y 的值,再代入求值.【解】⑴原式=22()()()()ab a a b b a b a bab a b ab a b ab+++++==++,当12a =,12b =时,ab =1,a +b⑵由题意得:xy =1,x +y =10, 10199=-.【变式题组】17.(威海)先化简,再求值:(a +b )2+(a -b)(2a +b)-3a 2,其中2a =--2b =.18.(黄石)已知a 是4的小数部分,那么代数式22224()()442a a a a a a a a a+-+⋅-+++的值为________. 【例7】已知实数x 、y 满足(2008x y =,则3x 2-2y 2+3x -3y -2007的值为( )A .-2008B .2008C .-1D .1【解法指导】对条件等式作类似于因式分解的变形,找出a 、b 的关系,再代入求值.解:∵(2008x y =,∴(x =y =(y =x =,由以上两式可得x =y .∴(2008x =, 解得x 2=2008,所以3x 2-2y 2+3x -3y -2007=3x 2-2x 2+3x -3x -2007=x 2-2007=1,故选D.【变式题组】19.若a >0,b >0,且=,求的值.演练巩固·反馈提高 01.若4m =,则估计m 的值所在的范围是( )A .1<m <2B .2<m <3C .3<m <4D .4<m <5 02n 的最大值为( )A .12B .11C .8D .303.(黄石)下列根式中,不是..最简二次根式的是( )04.(贺州)下列根式中,不是最简二次根式的是( )05.下列二次根式中,是最简二次根式的是( )06.(常德)设a =20, b =(-3)2,c =11()2d -=, 则a 、b 、c 、d 、按由小到大的顺序排列正确的是( )A .c <a <d <bB .b <d <a <cC .a <c <d <bD .b <c <a <d07.(十堰)下列运算正确的是( )A==C .21)31=-D 53=-08.如果把式子(1a -根号外的因式移入根号内,化简的结果为( )A..09.(徐州)如果式子2x -化简的结果为2x -3,则x 的取值范围是( )A .x ≤1B .x ≥2C .1≤x ≤2D .x >010.(怀化)函数y =中自变量的取值范围是________.11.(湘西)对于任意不相等的两个数a ,b ,定义一种运算a ※b =32=-那么12※4=________.12.(荆州)先化简,再求值:22321121a a a a a a -+÷-+-,其中a =13.(广州)先化简,再求值:((6)a a a a +--,其中12a =.培优升级·奥赛检测01.(凉山州)已知一个正数的平方根是3x -2和5x +6,则这个数是________.02.已知a 、b 是正整数,且满足是整数,则这样的有序数对(a ,b )共有________对.03.(全国竞赛)设a =,则5432322a a a a a a a+---+=-________. 04.(全国竞赛)设x =,a 是x 的小数部分,b 是x 的小数部,则a 3+b 3+3ab =________.05.(重庆竞赛)已知2y =,则x 2+y 2=________.06.(全国竞赛)已知1a =,a =,2a =,那么a 、b 、c 的大小关系是( )A .a <b <cB .b <a <cC .c <b <aD .c <a <b 07.(武汉联赛)已知y =(x ,y 均为实数),则y 的最大值与最小值的差为( )A3B .3C 3D 08.(全国竞赛)已知非零实数a 、b 满足24242a b a -++=,则a +b 等于( )A .-1B .0C .1D .209.(全国竞赛) ) A .5-B .1C .5D .110.已知0(0,0)x y x y -=>>,则的值为( )A .13B .12C .23D .3411.已知152a b c +-=-,求a +b +c 的值.12.已知9+9-a 和b ,求ab-3a +4b +8的值.第2讲 二次根式的化简与求值考点·方法·破译1.会灵活运用二次根式的运算性质化简求值.2.会进行二次根式的有理化计算,会整体代入求值及变形求值.3.会化简复合二次根式,会在根式范围内分解因式. 经典·考题·赏板【例1】(河北竞赛)已知2=,那么__________ 【解法指导】通过平方或运用分式性质,把已知条件和待求式的被开方数都用1x x+表示或化简变形.解:两边平方得,124x x ++=,12x x+= ,两边同乘以x 得,212x x+= ,∵2315x x x++=,29111x x x++=,∴原式【变式题组】1.若14aa +=(0<a <1=________2.=)A .1a a-B .1a a-C .1a a+D .不能确定【例2】(全国初中数学联赛)满足等式=2003的正整数对(x ,y )的个数是( )A .1B .2C .3D .4【解法指导】对条件等式作类似于因式分解的变形,将问题转化为求不定方程的正整数解.解:可化为0=,∴0=∵0>,∴0=,则xy =2003,且2003是质数,∴正整数对(x ,y )的个数有2对,应选B .【变式题组】3.若a >0,b >0,且=,求的值.1)a =<<,求代数式22632x x x x x x +-+÷-. 【解法指导】视x -2,x 2-4x为整体,把=平方,移项用含a 的代数式表示x -2,x 2-4x ,注意0<a <1的制约.解:平方得,12x a a =++,∴12x a a -=+,2221442x x a a-+=++, 222142x x a a -=+-,∴化简原式=(3)(2)(2)3x x x x x x +---+ =2211()1()211()a a a a a a a a a a a ++-+-=++--【变式题组】4.(武汉)已知32x x +=+,求代数式35(2)242x x x x -÷----的值. 5.(五羊杯竞赛)已知1m =,1n =,且22(714)(367)8m m a n n -+--=,则a 的值等于( )A .-5B .5C .-9D .9【例4】(全国竞赛)如图,点A 、C 都在函数0)y x =>的图像上,点B 、D 都在x 轴上,且使得△OAB 、△BCD 都是等边三角形,则点D 的坐标为________.【解法指导】解:如图,分别过点A 、C 作x 轴的垂线,垂足分别为E 、F .设OE=a ,BF=b ,则a ,CF,所以,点A 、C 的坐标为(a)、 (2a +bb),所以2(2)a b =+=a b ⎧=⎪⎨=⎪⎩因此,点D 的坐标为(,0) 【变式题组】6.(邵阳)阅读下列材料,然后回答问题.在进行二次根式化简时,我们有时会碰上如1323235+,,一样的式子,其实我们还可以将其进一步化简:335333535=⨯⨯=; (一) 36333232=⨯⨯=; (二)()()()131313132132-=-+-⨯=+; (三)以上这种化简的步骤叫做分母有理化,132+还可以用以下方法化简: ()()()13131313131313131322-=+-+=+-=+-=+; (四) (1)请你用不同的方法化简352+; ①参照(三)试得:352+=_____________________________;(要有简化过程) ②参照(四)试得:352+=_____________________________;(要有简化过程) (22n +++【例5】(五羊杯竞赛)设a 、b 、c 、d为正实数,a <b ,c <d ,bc >ad ,有一个三角形的三边长分别为,.【解法指导】虽然不能用面积公式求三角形面积(为什么?)a 、c 为直角边的直角三角形的斜边,从构造图形入手,将复杂的根式计算转化为几何问题加以解决.解:如图,作长方形ABCD ,使AB =b -a ,AD =c ,延长DA 至E ,使DE =d ,延长DC 至F ,使DF=b ,连结EF 、FB 、EB ,则BF=,EF=,BE =,从而知△BEF 就是题设的三角形,而S △BEF =S长方形ABCD +S △BCF +S △ABE -S △DEF =(b -a )c +12(d -c )(b -a )-12bd =12(bc -ad )【变式题组】7.(北京竞赛)已知a 、b 均为正数,且a +b =2,求U =演练巩固·反馈提高01.已知x =,y =,那么代数式值为__________02.设1a =,则32312612a a a +--=( )A .24B .25C .10D .12 03.(天津)计算2001200019991)1)1)2001--+=__________04.(北京竞赛)若有理数x 、y 、z 满足1()2x y z =++,则2()x yz -=__________ 05.(北京竞赛)正数m 、n 满足430m n +-==__________ 06.(河南竞赛)若1x =,则32(2(15x x x -++的值是( ) A .2B .4C .6D .807.已知实数a 满足2000a a -=,那么22000a -的值是( )A .1999B .2000C .2001D .200208.设a =b =c =a 、b 、c 之间的大小关系是( )A .a <b <cB .c <b <aC .c <a <bD .a <c <b09.已知1x = 培优升级·奥赛检测01.(信利杯竞赛)已知1x =+,那么2111242x x x +-=+--__________025==__________03.(江苏竞赛)已知(2002x y =,则2234x xy y --6658x y --+=__________04.(全国联赛)7x =,则x =__________05.(T 1杯联赛) 已知x =,y =,那么22y x x y +=__________06.(武汉选拔赛)如果a b +=,a b -=3333b c b c +=-,那么333a b c -的值为( )A ..2001C .1D .007.(绍兴竞赛)当x =时,代数式32003(420052001)x x --的值是( ) A .0B .-1C .1D .20032-08.(全国联赛)设a 、b 、c 为有理数,且等式a +=成立,则29991001abc ++的值是( )A .1999B .2000C .2001D .不能确定09.计算:(1(2(34947+++ (4)10.已知实数a 、b 满足条件1b a b a -=<,化简代数式11()(1)a b a b ---,将结果表示成不含b 的形式.11.已知21(0)a x aa +=> 12.(奥林匹克竞赛)已知自然数x 、y 、z 满足等式0=,求x +y +z 的值.第3讲 一元二次方程的解法考点·方法·破译1.掌握一元二次方程根的定义并能应用根的定义解题;2.掌握一元二次方程的四种解法,并能灵活应用各种解法解方程;3.会应用一元二次方程解实际应用题。
人教版小学数学四年级下册三角形的特性说课稿之令狐文艳创作

人教版小学数学四年级下册令狐文艳《三角形的特性》说课稿鹿泉区李村镇闫同小学高丽巍各位评委、老师:大家好。
今天我给大家说课的题目是《三角形的特性》,下面我就教材分析、学情分析、教学方法、学习方法、教具准备、教学过程设计、教学反思七个方面说这节课。
一、教材分析1、教学内容分析本节课是人教版四年级下册第五章《三角形》第一节的内容《三角形的特性》,主要学习三角形的定义以及三角形的特性,并学会在三角形内画高。
2.本节课在教材中所处的地位和作用《三角形的特性》是本章第一节第一课时的内容,是学习本章内容的基础,只有熟练掌握三角形的特性,才能更好的学习后面三角形的分类及三角形的内角和。
3.本节课教学重点及难点分析教学重点:认识三角形,知道三角形的特性,会在三角形内画高。
教学难点:理解三角形高和底的含义,会在三角形内画高。
4.本节课教学目标分析(1)通过动手操作和观察比较,使学生认识三角形,知道三角形的特性及三角形高和底的含义,会在三角形内画高。
(2)通过实验,使学生知道三角形的稳定性及其在生活中的应用。
(3)培养学生观察、操作的能力和应用数学知识解决实际问题的能力。
(4)体验数学与生活的联系,培养学生学习数学的兴趣。
二、学情分析1.学生原有知识水平分析四年级学生已经学习了长方形、正方形的相关知识,了解了长方形、正方形的特性,建立了基本的几何形体概念,具备学习本节课的知识基础。
2.学生认知水平分析小学四年级的学生具有初步的几何形体观念和逻辑思维能力,能够探索和解决简单的实际问题,具备了学习本节课的认知能力。
3.学习需要分析小学四年级的学生具有较强的好奇心,学习了长方形、正方形等四边形的相关特性后,他们迫切想知道生活中常见的三角形有那些特性,本课时的展开将极大的满足他们的好奇心。
三、教学方法从学生现有的知识水平和认知规律出发,为了更好的突出重点,化解难点,在教学过程中,主要体现以下教学方法:1.巧设疑问,体现两“主”教师通过设疑,激发学生兴趣,并营造学习新知识的良好氛围,指明观察方向,发挥教师的主导作用。
北师大九年级数学(上)之令狐文艳创作

第一章证明(二)3令狐文艳三角形有关性质、定理及反证法3 知识要点3易错易混点4典型例题4学习自评5线段的垂直平分线与角平分线7知识要点7易错易混点7典型例题8学习自评9第二章一元二次方程13一元二次方程13知识要点13易错易混点13典型例题13学习自评14解一元二次方程的方法17知识要点17易错易混点18典型例题18学习自评19一元二次方程的应用21知识要点21易错易混点21典型例题21学习自评22第三章证明(三)25平行四边形25知识要点25易错易混点25典型例题25学习自评26特殊平行四边形28知识要点28易错易混点28典型例题28学习自评30第四章试图与投影33视图的特点与画法错误!未定义书签。
知识要点33易错易混点33典型例题34学习自评35平行投影与中心投影错误!未定义书签。
知识要点错误!未定义书签。
易错易混点错误!未定义书签。
典型例题错误!未定义书签。
学习自评错误!未定义书签。
第五章反比例函数39反比例函数及其图像与性质39知识要点39易错易混点40典型例题40学习自评40反比例函数的应用44知识要点44易错易混点44典型例题44学习自评44第六章频率与概率49频率与概率的关系49知识要点49易错易混点49典型例题49学习自评49用试验的方法求概率50知识要点50易错易混点50典型例题50学习自评50第一章证明(二)三角形有关性质、定理及反证法知识要点三角形的性质与判定:序号必记项目必记知识必记内容巧记方法1 公理三角形全等的判定公理三边对应相等的两个三角形全等两边及夹角对应相等的两个三角形全等;两角及其夹边对应相等的两个三角形全等SSSSASASA2 定理三角形全等的判定定理两角及其中一角的对边对应相等的两个三角形全等AAS3 公理三角形全等的性质全等三角形的对应边相等、对应角相等4 定理等腰三角形的性质的推论等腰三角形的两个底角相等等边对等角5 定理等腰三角形的判定定理等腰三角形顶角的平分线、底边上的中线底边上的高互相重合“三线合一”6 定理等边三角形的判定定理有一个角等于60°的等腰三角形是等边三角形7 定理有一个角等于30°的直角三角形的性质在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半8 定理等边三角形的判定定理三个角都相等的三角形是等边三角形等角对等边9 定理勾股定理直角三角形两条直角边的平方和等于斜边的平方符号语言:若∠C=90°,则c2=a2+b21 0 概念互逆定理如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理称为互逆定理1 1 定理勾股定理的逆定理如果三角形的两边的平方和等于第三边的平方,那么这个三角形为直角三角形符号语言若,则a2+b2=c2,∠C=90°。
全等三角形判定的综合应用之令狐文艳创作

授课教案一.热身训练 1.如图1,若△ABC ≌△ADE ,∠EAC=35°,则∠BAD=______度.2.如图2,AB ∥CD ,AD ∥BC ,OE=OF,图中全等三角形共有______对3.已知:如图3,∠ABC =∠DEF ,AB =DE ,要说明△ABC ≌△DEF (1)若以“SAS ”为依据,还须添加的一个条件为______.(2)若以“ASA ”为依据,还须添加的一个条件为______.(3)若以“AAS ”为依据,还须添加的一个条件为______.4.如图4,在△ABC 中,∠C =90°,AD 平分∠BAC ,DE ⊥AB 于E ,则△_____≌△_____.5.如图5,AB=CD ,AD=BC ,O 为BD 中点,过O 点作直线与DA ︒=∠60ADB ,EO=10,则∠DBC=,FO=.二.知识梳理 1. 判定和性质判定方法:边角边(SAS )、角边角(ASA )角角边(AAS )、边边边(SSS ) 性 质:对应边相等,对应角相等,对应中线相等,对应高相等,对应角平分线相等 注:① 判定两个三角形全等必须有一组边对应相等;② 全等三角形面积相等.2.证题的思路:⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧)找任意一边()找两角的夹边(已知两角)找夹已知边的另一角()找已知边的对角()找已知角的另一边(边为角的邻边)任意角(若边为角的对边,则找已知一边一角)找第三边()找直角()找夹角(已知两边AAS ASA ASA AAS SAS AAS SSS HL SAS三.典型例题例1.已知:如图AC=BD ,∠CAB=∠DBA 。
求证:∠CAD=∠DBC 。
分析:由已知,再加上一组公共边等,可以得到△ABC 与△BAD 等,再由等量公理可得证。
例2. 已知,如图,HI ∥BC ,JI ∥AB 。
求证:△BIH ≌△IBJ用角边角公理可证明。
三角函数与解三角形之令狐文艳创作

课程标题 三角函数与解三角形令狐文艳(一) 主要知识: 三角函数的定义域、值域及(二)主要方法:1.求三角函数的定义域实质就是解三角不等式(组).一般可用三角函数的图象或三角函数线确定三角不等式的解.列三角不等式,既要考虑分式的分母不能为零;偶次方根被开方数大于等于零;对数的真数大于零及底数大于零且不等于1,又要考虑三角函数本身的定义域;2.求三角函数的值域的常用方法:1、化为求sin()y A x B ωϕ=++的值域;sin cos y a x b x c =++,引入辅助角(cos ϕϕϕ==,化为)y x c ϕ=++求解方法同类型。
2、化为关于sin x (或cos x )的二次函数式;2sin sin y a x b x c =++,设sin t x =,化为二次函数2y at bt c =++在[1,1]t ∈-上的最值求之;周期问题一般将函数式化为()y Af x ωϕ=+(其中()f x 为三角函数,0ω>).①y=sinx 图象的对称中心(k π,0), 对称轴x=k π+2π;y=cosx 呢?(自己给出)②y=tanx图象的对称中心(2k π,0)(二)主要方法: 1、函数sin()y A x ωϕ=+(0,0)A ω>>的单调增区间可由2222k x k πππωϕπ-+≤+≤+解出,单调减区间可由32222k x k πππωϕπ+≤+≤+解出; 周期2T Wπ=2、函数cos()y A x ωϕ=+(0,0)A ω<>的单调减区间可由22k x k πωϕππ≤+≤+解出,单调增区间呢。
(自己导出) 周期2T W π=3、函数tan()y A x ωϕ=+(0,0)A ω<>的单调增区间可由22k x k πππωϕπ-≤+≤+解出。
(无增区间,重点掌握) 周期T W π=课堂练习:1.已知函数()b a x x a x a x f ++--=2cos sin 322cos 的定义域为0,2π⎡⎤⎢⎥⎣⎦,值域为[]5,1-,求常数,a b 的值 (化为求sin()y A x B ωϕ=++的值域).2、函数3sin(2)3y x π=-的单调递减区间是3、函数()tan 4f x x π⎛⎫=+ ⎪⎝⎭的单调增区间为 2、函数()2cos (sin cos )1f x x x x =-+,x R ∈.(Ⅰ)求函数()f x 的最小正周期;(Ⅱ)求函数()f x 在区间π3π84⎡⎤⎢⎥⎣⎦,上的最小值和最大值.(化为求sin()y A x B ωϕ=++的值域). 3、函数22()cos 2cos 2xf x x =-的一个单调增区间是4、若函数21()sin 2f x x =-()x R ∈,则()f x 是.A 最小正周期为π2的奇函数 .B 最小正周期为π的奇函数.C 最小正周期为2π的偶函数 .D 最小正周期为π的偶函数5、函数sin cos sin cos y x x x x =++的最大值6、当函数213sin cos 22y x a x a =+--的最大值为1时,求a 的值. 7、函数()1cos cos 22f x x x=-的最大值是8、已知函数2π()2sin 24f x x x⎛⎫=+- ⎪⎝⎭,ππ42x ⎡⎤∈⎢⎥⎣⎦,.(1)求()f x 的最大值和最小值;(2)f (x )的最小正周期。
人教版八年级数学培优竞赛之令狐文艳创作

目录令狐文艳第1讲全等三角形的性质与判定(P2----11) 第2讲角平分线的性质与判定(P12----16)第3讲轴对称及轴对称变换(P17----24)第4讲等腰三角形(P25----36)第5讲等边三角形(P37----42)第6讲实数(P43----49)第7讲变量与函数(P50----54)第8讲一次函数的图象与性质(P55----63)第9讲一次函数与方程、不等式(P64----68)第10讲一次函数的应用(P69----80)第11讲幂的运算(P81----86)第12讲整式的乘除((P87----93)第13讲因式分解及其应用(P94----100)第14讲分式的概念•性质与运算(P101----108)第15讲分式的化简求值与证明(P109----117)第16讲分式方程及其应用(P118----125)第17讲反比例函数的图像与性质(P126----138)第18讲反比例函数的应用(P139----146)第19讲勾股定理(P147-----157)第20讲平行四边形(P158-----166)第21讲菱形矩形(P167-----178)第22讲正方形(P179-----189)第23讲梯形(P190-----198)第24讲数据的分析(P199-----209)模拟测试一模拟测试二模拟测试三第01讲全等三角形的性质与判定考点·方法·破译B AC D E F 1.能够完全重合的两个三角形叫全等三角形.全等三角形的形状和大小完全相同;2.全等三角形性质:①全等三角形对应边相等,对应角相等;②全等三角形对应高、角平分线、中线相等;③全等三角形对应周长相等,面积相等;3.全等三角形判定方法有:SAS ,ASA ,AAS ,SSS ,对于两个直角三角形全等的判定方法,除上述方法外,还有HL 法;4.证明两个三角形全等的关键,就是证明两个三角形满足判定方法中的三个条件,具体分析步骤是先找出两个三角形中相等的边或角,再根据选定的判定方法,确定还需要证明哪些相等的边或角,再设法对它们进行证明;5..证明两个三角形全等,根据条件,有时能直接进行证明,有时要证的两个三角形并不全等,这时需要添加辅助线构造全等三角形,构造全等三角形常用的方法有:平移、翻折、旋转、等倍延长线中线、截取等等.经典·考题·赏析【例1】如图,AB ∥EF ∥DC ,∠ABC =90°,AB =CD ,那么图中有全等三角形( )A .5对B .4对C .3对D .2对 【解法指导】从题设题设条件出发,首先找到比较明显的一对全等三角形,并由此推出结论作为下面有用的条件,从而推出第二对,第三对全等三角形.这种逐步推进的方法常用到.解:⑴∵AB ∥EF ∥DC ,∠ABC =90. ∴∠DCB =90.在△ABC 和△DCB 中AB DC ABC DCBBC CB =⎧⎪=⎨⎪=⎩∠∠∴△ABC ≌∴△DCB (SAS ) ∴∠A =∠D⑵在△ABE 和△DCE 中A D AED DECAB DC =⎧⎪=⎨⎪=⎩∠∠∠∠∴△ABE ≌∴△DCE ∴BE =CE⑶在Rt △EFB 和Rt △EFC 中∴Rt △EFB ≌Rt △EFC (HL )故选C .【变式题组】A F C E DB 01.(天津)下列判断中错误的是( )A .有两角和一边对应相等的两个三角形全等B .有两边和一角对应相等的两个三角形全等C .有两边和其中一边上的中线对应相等的两个三角形全等D .有一边对应相等的两个等边三角形全等02.(丽水)已知命题:如图,点A 、D 、B 、E 在同一条直线上,且AD =BE ,∠A =∠FDE ,则△ABC ≌△DEF .判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件使它成为真命题,并加以证明.03.(上海)已知线段AC 与BD 相交于点O , 连接AB 、DC ,E 为OB 的中点,F 为OC 的中点,连接EF (如图所示). ⑴添加条件∠A =∠D ,∠OEF =∠OFE ,求证:AB =DC ; ⑵分别将“∠A =∠D ”记为①,“∠OEF =∠OFE ”记为②,“AB =DC ”记为③,添加①、③,以②为结论构成命题1;添加条件②、③,以①为结论构成命题 2.命题1是______命题,命题2是_______命题(选择“真”或“假”填入空格).【例2】已知AB =DC ,AE =DF ,CF =FB . 求证:AF =DE .【解法指导】想证AF =DE ,首先要找出AF 和DE 所在的三角形.AF 在△AFB 和△AEF 中,而DE 在△CDE 和△DEF 中,因而只需证明△ABF ≌△DCE 或△AEF ≌△DFE 即可.然后再根据已知条件找出证明它们全等的条件.证明:∵FB =CE ∴FB +EF =CE +EF ,即BE =CF在△ABE 和△DCF 中,AB DC AE DFBE CF =⎧⎪=⎨⎪=⎩∴△ABE ≌△DCF (SSS ) ∴∠B =∠C 在△ABF 和△DCE中,AB DC B C BF CE =⎧⎪=⎨⎪=⎩∠∠∴△ABF ≌△DCE ∴AF =DE【变式题组】01.如图,AD 、BE 是锐角△ABC 的高,相交于点O ,若BO =AC ,BC =7,CD =2,则AO 的长为( )A .2B .3C .4D .5A B C D O F E A C E F B D02.如图,在△ABC 中,AB =AC ,∠BAC =90°,AE 是过A 点的一条直线,AE ⊥CE 于E ,BD ⊥AE 于D ,DE =4cm ,CE =2cm ,则BD =__________.03.(北京)已知:如图,在△ABC 中,∠ ACB =90°,CD ⊥AB 于点D ,点E 在AC 上,CE =BC ,过点E 作AC 的垂线,交CD 的延长线于点F . 求证:AB =FC .【例3】如图①,△ABC ≌△DEF ,将△ABC和△DEF 的顶点B 和顶点E 重合,把△DEF 绕点B 顺时针方向旋转,这时AC 与DF 相交于点O .⑴当△DEF 旋转至如图②位置,点B (E )、C 、D 在同一直线上时,∠AFD 与∠DCA 的数量关系是________________;⑵当△DEF 继续旋转至如图③位置时,⑴中的结论成立吗?请说明理由_____________.【解法指导】⑴∠AFD =∠DCA⑵∠AFD =∠DCA 理由如下:由△ABC ≌△DEF ,∴AB =DE ,BC =EF , ∠ABC =∠DEF , ∠BAC =∠EDF ∴∠ABC -∠FBC =∠DEF -∠CBF , ∴∠ABF =∠DECAE第1题图 A B CD E B C DO第2题图 A FE C BDB (E ) OC F 图③ DA在△ABF 和△DEC中,AB DE ABF DECBF EC =⎧⎪=⎨⎪=⎩∠∠ ∴△ABF ≌△DEC ∠BAF =∠DEC ∴∠BAC -∠BAF =∠EDF -∠EDC , ∴∠FAC =∠CDF ∵∠AOD =∠FAC +∠AFD =∠CDF +∠DCA∴∠AFD =∠DCA【变式题组】01.(绍兴)如图,D 、E 分别为△ABC 的AC 、BC 边的中点,将此三角形沿DE 折叠,使点C 落在AB 边上的点P 处.若∠CDE =48°,则∠APD 等于( )A .42°B .48°C .52°D .58°02.如图,Rt △ABC 沿直角边BC 所在的直线向右平移得到△DEF ,下列结论中错误的是( )A .△ABC ≌△DEFB .∠DEF =90°.EC =CF 03.一张长方形纸片沿对角线剪开,得到两种三角形纸片,再将这两张三角形纸片摆成如下图形式,使点B 、F 、C 、D 在同一条直线上.⑴求证:AB ⊥ED ;⑵若PB =BC ,找出图中与此条件有关的一对全等三角形,并证明.【例4】(第21届江苏竞赛试题)已知,如图,BD 、CE 分别是△ABC 的边A C 和AB 边上的高,点P 在BD 的延长线,E FB AC D G 第2题图BP =AC ,点Q 在CE 上,CQ =AB. 求证:⑴AP =AQ ;⑵AP ⊥AQ【解法指导】证明线段或角相等,也就是证线段或角所在的两三角形全等.经观察,证AP =AQ ,也就是证△APD 和△AQE ,或△APB 和△QAC 全等,由已知条件BP =AC ,CQ =AB ,应该证△APB ≌△QAC ,已具备两组边对应相等,于是再证夹角∠1=∠2即可. 证AP ⊥AQ ,即证∠PAQ =90°,∠PAD +∠QAC =90°就可以.证明:⑴∵BD 、CE 分别是△ABC 的两边上的高, ∴∠BDA =∠CEA =90°,∴∠1+∠BAD =90°,∠2+∠BAD =90°,∴∠1=∠2.在△APB 和△QAC 中,2AB QC BP CA =⎧⎪=⎨⎪=⎩∠1∠∴△APB ≌△QAC ,∴AP =AQ⑵∵△APB ≌△QAC ,∴∠P =∠CAQ , ∴∠P +∠PAD =90° ∵∠CAQ +∠PAD =90°,∴AP ⊥AQ【变式题组】01.如图,已知AB =AE ,∠B =∠E ,BA =ED ,点F 点,求证:AF ⊥CD .02在墙上,梯子顶端距地面的垂直距离MA 为am 的倾斜角为75墙上,此时梯子顶端距地面的垂直距离NB 为斜角为45°,这间房子的宽度是( )A .2a b m +B .2a b m -C .bmD .am03.如图,已知五边形ABCDE 中,∠ ABC =∠AED =90°,AB=CD =AE =BC +DE =2,则五边形ABCDE 的面积为__________A ECB A 75° C45° B NM第2题图 第3题图 D2 1 A B C P Q E F D演练巩固·反馈提高01.(海南)已知图中的两个三角形全等,则∠α度数是( )A .72°B .60°C .58°D .50°02.如图,△ACB ≌△A /C /B /,∠BCB =30°,则∠ACA 的度数是( )A .20°B .30°C .35°D .40°03.(牡丹江)尺规作图作∠AOB 的平分线方法如下:以O 为圆心,任意长为半径画弧交OA 、OB 于C 、D ,再分别以点C 、D 为圆心,以大于12CD 长为半径画弧,两弧交于点P ,作射线OP ,由作法得△OCP≌△ODP 的根据是( )A .SASB .ASAC .AASD .SSS04.(江西)如图,已知AB =AD ,那么添加下列一个条件后,仍无法判定△ABC ≌△ADC 的是( )A . CB =CDB .∠BAC =∠DAC05.有两块不同大小的等腰直角三角板△和△,将它们的一个锐角顶点放在一起,将它们的一个锐角顶点放在一起,如图,当A 、B 、D 不在一条直线上时,下面的结论不正确的是( )A . △ABE ≌△CBDB . ∠ABE =∠CBDC . ∠ABC =∠EBD =45°D . AC ∥BE06.如图,△ABC 和共顶点A ,AB =AE ,∠1=∠2,∠B =∠E .BC 交AD 于M ,DE 交AC 于N ,小华说:“一定有第1题图 aαc c a 50°b 72° 58°△ABC ≌△AED .”小明说:“△ABM ≌△AEN .”那么( )A . 小华、小明都对B . 小华、小明都不对C . 小华对、小明不对D .小华不对、小明对07.如图,已知AC =EC , BC =CD ,AB =ED ,如果∠BCA =119°,∠ACD =98°,那么∠ECA 的度数是___________. 08.如图,△ABC ≌△ADE ,BC 延长线交DE 于F ,∠B =25°,∠ACB =105°,∠DAC =10°,则∠DFB 的度数为_______. 09.如图,在Rt △ABC 中,∠C =90°, DE ⊥AB 于D , BC =BD .10.如图,BA ⊥AC , CD ∥AB . BC =DE ,且BC ⊥DE ,若AB =2,CD =6,则AE =_____.11.如图, AB =CD , AB ∥CD . BC =12cm ,同时有P 、Q 两只蚂蚁从点C 出发,沿CB 方向爬行,P 的速度是0.1cm /s , Q 的速度是0.2cm /s . 求爬行时间t 为多少时,△APB ≌△QDC .12.如图, △ABC 中,∠BCA =90°,AC =BC ,AE 是BC 边上的中线,过C 作CF ⊥AE ,垂足为F ,过B 作BD ⊥BC 交CF 的延长线于D .⑴求证:AE =CD ; ⑵若AC =12cm , 求BD 的长. 13.(吉林)如图,AB =AC ,AD ⊥BC 于点D ,AD 等于AE ,AB 平分∠DAE 交DE 于点F ,请你写出图中三对全等三角形,并选取其中一对加以证明.14.如图,将等腰直角三角板ABC 的直角顶点C 放在直线l 上,从另两个顶点A 、BD AC .Q P. BD B A CEF A EB F D CA E FB D C分别作l 的垂线,垂足分别为D 、E .⑴找出图中的全等三角形,并加以证明;⑵若DE =a ,求梯形DABE 的面积.(温馨提示:补形法) 15.如图,AC ⊥BC , AD ⊥BD , AD =BC ,CE⊥AB ,DF ⊥AB ,垂足分别是E 、F .求证:CE =DF .16.我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等,那么在什么情况下,它们会全等?⑴阅读与证明:对于这两个三角形均为直角三角形,显然它们全等;对于这两个三角形均为钝角三角形,可证明它们全等(证明略);对于这两个三角形均为锐角三角形,它们也全等,可证明如下;已知△ABC 、△A 1B 1C 1均为锐角三角形,AB =A 1B 1,BC =B 1C 1,∠C =∠C 1.求证:△ABC ≌△A 1B 1C 1.(请你将下列证明过程补充完整)⑵归纳与叙述:由⑴可得一个正确结论,请你写出这个结论.培优升级·奥赛检测01.如图,在△ABC 中,AB =AC ,E 、F 分别是AB 、AC 上的点,且AE =AF ,BF 、CE 相交于点O ,连接AO 并延长交BC 于点D ,则图中全等三角形有( )A .4对B .5对C .6对D .7对A B C D A 1 B 1C 1D 1 F 第6题图 2 1 A B CE N M 3 2 1 A D E B CF A D E CO AEOB FC D第1题图 B 第2题图 第3题图AE FC D B A E B C02.如图,在△ABC 中,AB =AC ,OC =OD ,下列结论中:①∠A =∠B ②DE =CE ,③连接DE , 则OE 平分∠AOB ,正确的是( )A .①②B .②③C .①③D .①②③03.如图,A 在DE 上,F 在AB 上,且AC =CE , ∠1=∠2=∠3, 则DE 的长等于()A .DCB . BCC . ABD .AE +AC04.下面有四个命题,其中真命题是( )A .两个三角形有两边及一角对应相等,这两个三角形全等B .两边和第三边上的高对应相等的两个三角形全等C . 有一角和一边对应相等的两个直角三角形全等D . 两边和第三边上的中线对应相等的两个三角形全等 05.在△ABC 中,高AD 和BE 所在直线相交于H 点,且BH =AC ,则∠ABC =_______.06.如图,EB 交AC 于点M , 交FC 于点D , AB 交FC 于点N ,∠E =∠F =90°,∠B =∠C , AE =AF . 给出下列结论:①∠1=∠2;②BE =CF ; ③△ACN ≌△ABM ; ④CD =DB ,其中正确的结论有___________.(填序号)07.如图,AD 为在△ABC 的高,E 为AC 上一点,BE 交AD 于点F ,且有BF =AC ,FD =CD .⑴求证:BE ⊥AC ;⑵若把条件“BF =AC ”和结论“BE ⊥AC ”互换,这个命题成立吗?证明你的判定. 08.如图,D 为在△ABC 的边BC 上一点,且CD =AB ,∠BDA =∠BAD ,AE 是△ABD 的中线.求证:AC =2AE .09.如图,在凸四边形ABCD 中,E 为△ACD 内一点,满足AC=AD ,AB =AE , ∠BAE +∠BCE =90°, ∠BAC =∠EAD .求证:∠CED =90°.10.(沈阳)将两个全等的直角三角形ABC 和DBE 按图①方式摆放,其中∠ACB =∠AB E D CA B C D E DEB =90°,∠A =∠D =30°,点E 落在AB 上,DE 所在直线交AC 所在直线于点F .⑴求证:AF +EF =DE ;⑵若将图①中△DBE 绕点B 顺时针方向旋转角α,且0°<α<60°,其他条件不变,请在图②中画出变换后的图形,并直接写出(1)中结论是否仍然成立;⑶若将图①中△DBE 绕点B 按顺时针方向旋转角β,且60°<β<180°,其他条件不变,如图③你认为(1)中结论还成立吗?若成立,写出证明过程;若不成立,请写出此时AF 、EF 与DE 之间的关系,并说明理由。
全等三角形的讲义整理讲义之令狐文艳创作

令狐文艳令狐文艳全等三角形令狐文艳专题一 全等三角形的性质【知识点1】能够完全重合的两个三角形叫做全等三角形。
(两个三角形全等是指两个三角形的大小和形状完全一样,与他们的位置没有关系。
)【知识点2】两个三角形重合在一起,重合的顶点叫做对应顶点;重合的边叫做 对应边;重合的角叫做对应角。
【例题1】如图,已知图中的两个三角形全等,填空:(1)AB 与是对应边,BC 与是对应边, CA 与是对应边;(2)∠A 与是对应角,∠ABC 与是对应角, ∠BAC与是对应角DABC【方法总结】在两个全等三角形中找对应边和对应角的方法。
(1)有公共边的,公 共边一定是对应边;(2)有公共角的,公共角一定是对应角;(3)有对顶角的,对顶角是对应角;(4)在两个全等三角形中,最长的边对最长的边,最短的边对最短的边,最大的角对最大的角,最小的角对最小的角。
【练习1】 如图,图中有两对三角形全等,填空: (1)△BOD ≌; (2)△ACD ≌.【知识点3】 全等三角形的对应边相等,对应角相等。
(由定义还可知道,全等三角形的周长相等,面积相等,对应边上的中线和高相等,对应角的角平分线相等)【例题2】 (海南省中考卷第5题)已知图2中的两个三角形全等,则∠α度数是()A.72°B.60°C.58°D.50°【例题3】(清远)如图,若111ABC A B C △≌△,且11040A B ∠=∠=°,°,则1C ∠=.【练习2】 如图,ACBA CB '''△≌△,BCB ∠'=30°,则ACA '∠的度数为( )A20° B.30°C.35° D.40°【练习3】如图,△ABD 绕着点B 沿顺时针方向旋转90°到△EBC ,且∠ABD=90°。
(1)△ABD 和△EBC 是否全等?如果全等,请指出对应边与对应角。
初中数学教学案例分析之令狐文艳创作

初中数学教学案例分析令狐文艳课题:探索三角形全等的条件(一)一、教学设计:1 学习方式:对于全等三角形的研究,实际是平面几何中对封闭的两个图形关系研究的第一步。
它是两个三角形间最简单,最常见的关系。
它不仅是学习后面知识的基础,并且是证明线段相等、角相等以及两线互相垂直、平行的重要依据。
因此必须熟练地掌握全等三角形的判定方法,并且灵活的应用。
为了使学生更好地掌握这一部分内容,遵循启发式教学原则,用设问形式创设问题情景,设计一系列实践活动,引导学生操作、观察、探索、交流、发现、思维,使学生经历从现实世界抽象出几何模型和运用所学内容,解决实际问题的过程,真正把学生放到主体位置。
2 学习任务分析:充分利用教科书提供的素材和活动,鼓励学生经历观察、操作、推理、想象等活动,发展学生的空间观念,体会分析问题、解决问题的方法,积累数学活动经验。
培养学生有条理的思考,表达和交流的能力,并且在以直观操作的基础上,将直观与简单推理相结合,注意学生推理意识的建立和对推理过程的理解,能运用自己的方式有条理的表达推理过程,为以后的证明打下基础。
3 学生的认知起点分析:学生通过前面的学习已了解了图形的全等的概念及特征,掌握了全等图形的对应边、对应角的关系,这为探究三角形全等的条件做好了知识上的准备。
另外,学生也具备了利用已知条件作三角形的基本作图能力,这使学生能主动参与本节课的操作、探究成为可能。
4 教学目标:(1)学生在教师引导下,积极主动地经历探索三角形全等的条件的过程,体会利用操作、归纳获得数学结论的过程。
(2)掌握三角形全等的“边边边”、“边角边”、“角边角”、“角角边”的判定方法,了解三角形的稳定性,能用三角形的全等解决一些实际问题。
(3)培养学生的空间观念,推理能力,发展有条理地表达能力,积累数学活动经验。
5 教学的重点与难点:重点:三角形全等条件的探索过程是本节课的重点。
从设置情景提出问题,到动手操作,交流,直至归纳得出结论,整个过程学生不仅得到了两个三角形全等的条件,更重要得是经历了知识的形成过程,体会了一种分析问题的方法,积累了数学活动经验,这将有利于学生更好的理解数学,应用数学。
《全等三角形》培优题型全集之令狐文艳创作
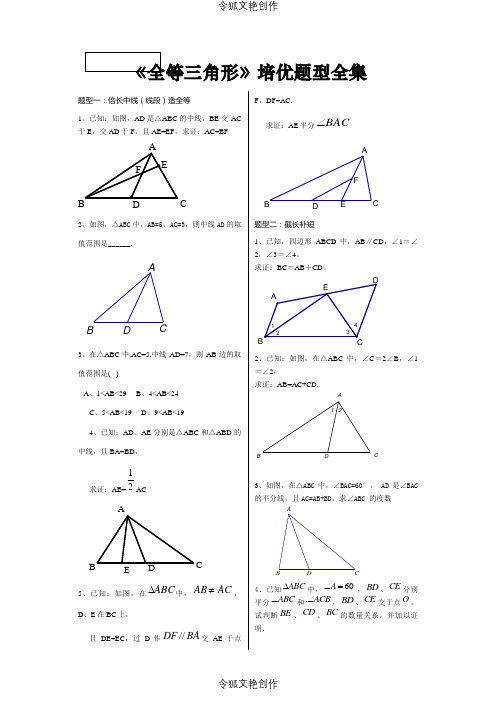
《全等三角形》培优题型全集题型一:倍长中线(线段)造全等1、已知:如图,AD是△ABC的中线,BE交AC于E,交AD于F,且 AE=EF,求证:AC=BFC2、如图,△ABC中,AB=5,AC=3,则中线AD的取值范围是______.D CBA3、在△ABC中,AC=5,中线AD=7,则AB边的取值范围是( )A、1<AB<29B、4<AB<24C、5<AB<19D、9<AB<194、已知:AD、AE分别是△ABC和△ABD的中线,且BA=BD,求证:AE=21ACCE5、已知:如图,在ABC∆中,ACAB≠,D、E在BC上,且DE=EC,过D作BADF//交AE于点F,DF=AC.求证:AE平分BAC∠ABFD E C题型二:截长补短1、已知,四边形ABCD中,AB∥CD,∠1=∠2,∠3=∠4。
求证:BC=AB+CD。
2、已知:如图,在△ABC中,∠C=2∠B,∠1=∠2,求证:AB=AC+CD.3、如图,在△ABC中,∠BAC=60°, AD是∠BAC的平分线,且AC=AB+BD,求∠ABC 的度数D CBA4、已知ABC∆中,60A∠=,BD、CE分别平分ABC∠和.ACB∠,BD、CE交于点O,试判断BE、CD、BC的数量关系,并加以证明.D CBA12DOECBA题型三:角平分线上的点向角两边引垂线段1、如图,在四边形ABCD中,BC>BA,AD=CD,求证:∠BAD+∠C=180°DCBA2、如图,四边形ABCD中,AC平分∠BAD,CE ⊥AB于E,AD+AB=2AE,则∠B与∠ADC互补,为什么?3、如图,△ABD和△ACD,BD=CD,∠ABD=∠ACD,求证AD平分∠BAC.4、已知,AB>AD,∠1=∠2,CD=BC。
求证:∠ADC+∠B=180°。
图九21CBAD5、如图,在△ABC中∠A BC,∠A CB的外角平分线相交于点P,求证:AP是∠BAC的角平分线图十一4321ABC6、如图,∠B=∠C=90°,AM平分∠DAB,DM 平分∠ADC。
全等三角形证明过程步骤练习之令狐文艳创作

全等三角形训练令狐文艳一、知识点填空(1)能够的两个图形叫做全等形,能够的两个三角形叫做全等三角形.(2)把两个全等的三角形重合到一起,重合的顶点叫做,重合的边叫做,重合的角叫做.(3)全等三角形的边相等,全等三角形的角相等.(4)对应相等的两个三角形全等(边边边或).(5)两边和它们的对应相等的两个三角形全等(边角边或).(6)两角和它们的对应相等的两个三角形全等(角边角或).(7)两角和其中一角的对应相等的两个三角形全等(角角边或).(8)和一条对应相等的两个直角三角形全等(斜边、直角边或).(9)角的上的点到角的两边的距离相等.2.如图,图中有两对三角形全等,填空: (1)△CDO≌,其中,CD的对应边是,A BCDEODO的对应边是,OC的对应边是;(2)△ABC≌,∠A的对应角是,∠B的对应角是,∠ACB的对应角是.3. 如图,OA⊥AC,OB⊥BC,填空:(1)利用“角的平分线上的点到角的两边的距离相等”,已知=,可得=;(2)利用“角的内部到角两边距离相等的点在角的平分线上”,已知=,可得=;4.如图,AB⊥AC,DC⊥DB,填空:(1)已知AB=DC,利用可以判定△ABO≌△DCO;(2)已知AB=DC,∠BAD=∠CDA,利用可以判△ABD≌△DCA;(3)已知AC=DB,利用可以判定△ABC≌△DCB;(4)已知AO=DO,利用可以判定△ABO≌△DCO;(5)已知AB=DC,BD=CA,利用可以判定△ABD≌△DCA.二、推理填空,完成下面的证明过程:5. 如图,OA=OC,OB=OD.求证:AB∥DC.ABDO12OA BC证明:在△ABO和△CDO中,∴△ABO≌△CDO().∴∠A=.∴AB∥DC(相等,两直线平行).6. 如图,AB∥DC,AE⊥BD,CF⊥BD,BF=DE.求证:△ABE≌△CDF.证明:∵AB∥DC,∴∠1=.∵AE⊥BD,CF⊥BD,∴∠AEB=.∵BF=DE,∴BE=.在△ABE和△CDF中,∴△ABE≌△CDF().7.如图,点B、E、C、F在同一直线上,且AB=DE,AC=DF,BE=CF,求证:ΔABC≌ΔDEF。
关于三角形的全部公式之令狐文艳创作

勾股定理:直角三角形中,直角边的平方和等于斜边的平方。
c^2=a^2+b^2 .
令狐文艳
正弦定理:
a/sinA=b/sinB=c/sinC=2R (R是外接圆的半径)
余弦定理:
a^2=b^2+c^2-2bccosA
b^2=a^2+c^2-2accosB
c^2=a^2+b^2-2abcosC
面积公式:
1.海伦公式△ABC中三边为a,b,c。
p=(a+b+c)/
2.
S(abc)=√[p(p-a)(p-b)(p-c)]即已知三角形三边求面积的海伦公式。
2.已知三角形底a,高h,则S=ah/2
3.已知三角形两边a,b,这两边夹角C,则S=absinC/2
4.设三角形三边分别为a、b、c,内切圆半径为r
则三角形面积=(a+b+c)r/2
5.设三角形三边分别为a、b、c,外接圆半径为r
则三角形面积=abc/4r
6.已知三角形三边a、b、c,则S=√{1/4[c^2a^2-
((c^2+a^2-b^2)/2)^2]}
7.三阶行列式求面积
| a b 1 |
S△=1/2 * | c d 1 |
| e f 1 |
(注意上式最后取绝对值。
)
| a b 1 |
| c d 1 |
| e f 1 |
为三阶行列式,直角坐标系内坐标A(a,b),B(c,d), C(e,f)。
三角形的周长:
L=a+b+c
三角形内角和公式:
∠A+∠B+∠C=180°。
与三角形的角有关模型之令狐文艳创作

与三角形有关的角
令狐文艳
基础知识点回顾:
1、三角形的内角:三角形的内角和为180°;
2、三角形的外角:三角形一边与另一边延长线组成的角;
三角形外角定理:三角形的一个外角等于与它不相邻的两个内角的和。
知识讲解概览:
1、“8”字模型
2、飞镖模型
3、内外角平分线模型
一、“8”字模型与飞镖模型
(1)“8”字模型
如图,线段 AB与CD相交于点O,连接A、C,连接B、D,则有∠A+∠C=∠B+∠D
(2)飞镖模型
如图,则有∠A+∠B+∠C=∠ADC
例1:下图是一个五角星,求∠A+∠B+∠C+∠D+∠E的大小。
例2:如下图,BE平分∠ABC,DE平分∠ADC,BE与AD相交于点G,BC与DE相交于点H。
求证:2∠E=∠A+∠C。
二、内外角平分线问题
(1)内角平分线+内角平分线
如图,在△ABC 中,点P 是∠ABC 和∠ACB 角平分线的交点,
则∠P=90°+21
∠A
(2)内角平分线+外角平分线
如图,在△ABC 中,点P 是∠ABC 和外角∠ACD 角平分线的交
点,则∠P=21
∠A
(3)外角平分线+外角平分线
如图,在△ABC 中,点P 是∠ABC 和外角∠ACB 角平分线的交
点,则∠P=90°-21
∠A
例3:在△ABC 中,AD ⊥BC ,AE 平分∠BAC ,AG ⊥AE ,CG 是外角∠ACF 的平分线,若∠G -∠DAE =60°,则∠ACB=。
三角形折叠问题之令狐文艳创作

专题:折叠问题中的角度运算令狐文艳学习目标学习重难点(2006•宿迁)如图,将矩形ABCD 沿AE 折叠,若∠BAD ′=30°,则∠AED ′等于( )A. 30°B. 45°C. 60°D. 75°如图将六边形ABCDEF 沿着直线GH 折叠,使点A 、B 落在六边形CDEFGH 的内部,则下列结论一定正确的是( )A. ∠1+∠2=900°-2(∠C+∠D+∠E+∠F )B. ∠1+∠2=1080°-2(∠C+∠D+∠E+∠F )C. ∠1+∠2=720°-(∠C+∠D+∠E+∠F )D.∠1+∠2=360°-(∠C+∠D+∠E+∠F ) 1 2如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=A. 40°B. 30°C. 20°D. 10°已知△ABC是一张三角形的纸片.(1)如图①,沿DE 折叠,使点A落在边AC上点A′的位置,∠DA′E与∠1的之间存在怎样的数量关系?为什么?(2)如图②所示,沿DE折叠,使点A落在四边形BCED的内部点A′的位置,∠A、∠1与∠2之间存在怎样的数量关系?为什么?(3)如图③,沿DE折叠,使点A落在四边形BCED的外部点A′的位置,∠A、∠1与∠2之间存在怎样的数量关系?为什么?已知,如图,把△ABC纸片沿OE折叠,当点A落在四边形BCDE的内部时,则∠A与∠1+∠2之间有一种数量关系:2∠A=∠1+∠2始终保持不变,为什么?.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,(1)设∠AED的度数为x,∠ADE的度数为y,那么∠1、∠2的度数分别是多少?(用含有x或y的代数式表示)(2)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律,并说明理由.折一折,想一想,如图所示,在△ABC中,将纸片一角折叠,使点C落在△ABC内一点C′上,若∠1=40°,∠2=30°.(1)求∠C的度数;(2)试通过第(1)问,直接写出∠1、∠2、∠C三者之间的关系.如图(1),△ABC是一个三角形的纸片,点D、E分别是△ABC边上的两点;研究(1):若沿直线DE折叠,则∠BDA′与∠A的关系是∠BDA′=2∠A;研究(2):若折成图2的形状,猜想∠BDA′,∠CEA′和∠A关系,并说明理由;研究(3):若折成图3的形状,猜想∠BDA′,∠CEA′和∠A的关系,并说明理由.图1、图2、图3、如图①,把△ABC纸片沿DE折叠,使点A落在四边形BCED内部点A′的位置,通过计算我们知道:2∠A=∠1+∠2.请你继续探索:(1)如果把△ABC纸片沿DE 折叠,使点A落在四边形BCED的外部点A′的位置,如图②,此时∠A与∠1、∠2之间存在什么样的关系?为什么?请说明理由.(2)如果把四边形ABCD沿EF 折叠,使点A、D落在四边形BCFE的内部A′、D′的位置,如图③,你能求出∠A、∠D、∠1与∠2之间的关系吗?(直接写出关系式即可)三角形纸片ABC中,∠A=55°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),则∠1+∠2的度数为度..如图,已知四边形ABCD,∠C=72°,∠D=81°.沿EF折叠四边形,使点A、B分别落在四边形内部的点A′、B′处,求∠1+∠2的大小.(2013•宁夏)如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于()21.(2006•武汉)(北师大版)将五边形纸片ABCDE按如图方式折叠,折痕为AF,点E、D 分别落在E′、D′,已知∠AFC=76°,则∠CFD′等于()(2006•梅州)如图,在平面内,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF等于()如图,把△ABC沿线段DE折叠,使点A落在点F处,BC∥DE;若∠B=50°,则∠BDF的度数为()如图,把一张长方形纸片ABCD,沿EF折叠后,ED′与BC的交点为G,点D,C分别落在D′,C′的位置上.若∠EFG=55°,则∠1等于()将一条两边沿互相平行的纸带按如图折叠.设∠1=x°,则∠α的度数为()将长方形ABCD沿折痕EF折叠,使CD落在GH的位置,若∠FGH=55°,则∠HEF=()如图,一个宽度相等的纸条按如图所示方法折叠一下,则∠1=()如图,D、E分别为△ABC的边AB、AC上的点,DE∥BC,将△ABC沿线段DE折叠,使点A落在BC 上的点F处,若∠B=55°,则∠BDF的度数为()如图所示,将一张长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置上,ED′的延长线与BC的交点为G.若∠EFG=80°,则∠BFC′的度数为()如图a是长方形纸带,∠DEF=24°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数()如图a是长方形纸带,∠DEF=24°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE 的度数()如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为()如图,将长方形ABCD沿对角线BD折叠,使点C恰好落在如图C′的位置,若∠DBC=15°,则∠ABC′=()一张长方形纸条折成如图的形状,如果∠1=130°,∠2=()如图:将一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,ED′的延长线与BC交于点G.若∠EFG=55°,则∠1=()如图,已知长方形ABCD,我们按如下步骤操作可以得到一个特定角:(1)以点A所在直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于E;(2)将纸片展平后,再一次折叠纸片,以E所在直线为折痕,使点A落在BC上,折痕EF交AD于F,则∠AEF的度数86.如图,将纸片△ABC沿着DE折叠压平,且∠1+∠2=72°,则∠A=()如图,把△ABC纸片沿DE折叠,当点A落在四边形BCED的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是()如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为()一个宽度相等纸条,按如图所示的方式折叠一下,已知∠3=120°,则∠1的度数为()如图,把一张长方形纸条折叠后,若∠AOB′=70°,则∠OGC的度数为()如图,∠A=60°,∠B=70°,将纸片的一角折叠,使点C落在△ABC内,若∠2=80°,则∠1的度数为()如图(1)是长方形纸带,∠DEF=α,将纸带沿EF折叠成图(2),再沿BF折叠成图(3),则图(3)中的∠CFE的度数是()如图,生活中,将一个宽度相等的纸条按右图所示折叠一下,如果∠1=140°,那么∠2的度数为()如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B =()如图,一张长方形纸条沿AB折叠,如果∠1=124°,那么∠2的度数是()如图,把长方形ABCD沿EF对折后使两部分重合,若∠AEF=110°,则∠1=()如图,一张三角形纸片△ABC,沿DE折叠使得顶点C落在边AB上,若DE∥AB,∠A=45°,则∠ADC的度数是()如图所示,把一个三角形纸片ABC顶角向内折叠3次之后,3个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是()(2012•石家庄二模)如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为()如图,正方形纸片ABCD的边长为8,将其沿EF折叠,则图中①②③④四个三角形的周长之和为()如图,将五边形ABCDE沿AE对折到如图的位置,其中∠AEC=72°,则∠CED′=()如图,在△ABC中,∠A=35°,在平面内沿直线DE将△ABC折叠后,量得∠BDA′=110°,那么∠CEA′的度数为()(2009•莱芜)如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠AED′等于().如图,已知△ABC中,∠BAC=140°,现将△ABC进行折叠,使顶点B、C均与顶点A重合,求∠DAE的度数.。
全等三角形全套练习题之令狐文艳创作

全等三角形令狐文艳一、全等三角形1、定义:能够完全重合的两个三角形叫做全等三角形。
特征:形状相同、大小相等、完全重合。
一个三角形经过平移、翻折、旋转可以得到它的全等形。
平移、翻折、旋转前后的图形全等。
2、全等三角形的表示:“全等”用“≌”表示,“∽”表示两图形的形状相同,“=”表示大小相等,读作“全等于”。
注意:记两三角形全等时,通常把表示对应顶点的字母写在对应位置上。
全等三角形的对应元素:对应顶点,对应边,对应角3、全等三角形的性质(1)全等三角形的对应边相等、对应角相等。
(2)全等三角形的周长相等、面积相等。
(3)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
4、全等三角形的判定(1)边边边:三边对应相等的两个三角形全等(可简写成“SSS”)(2)边角边:两边和它们的夹角对应相等两个三角形全等(可简写成“SAS”)(3)角边角:两角和它们的夹边对应相等的两个三角形全等(可简写成“ASA”)(4)角角边:两角和其中一角的对边对应相等的两个三角形全等(可简写成“AAS”)(5)斜边、直角边:斜边和一条直角边对应相等的两个直角三角形全等(可简写成“HL”)5、证明两个三角形全等的基本思路:二、角的平分线1、(性质)角的平分线上的点到角的两边的距离相等。
2、(判定)角的内部到角的两边的距离相等的点在角的平分线上。
三、学习全等三角形应注意的问题(1)要正确区分“对应边”与“对边”,“对应角”与“对角”的不同含义;(2)表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;(3)“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等;(4)时刻注意图形中的隐含条件,如“公共角”、“公共边”、“对顶角”。
(一)三角形全等的判定一(SSS)F E D CBA 1.如图,AB =AD ,CB =CD .△ABC 与△ADC 全等吗?为什么?2.如图,C 是AB 的中点,AD =CE ,CD =BE . 求证△ACD ≌△CBE .3.如图,点B ,E ,C ,F 在一条直线上,AB=DE ,AC=DF ,BE=CF .求证∠A=∠D .4.已知,如图,AB=AD ,DC=CB .求证:∠B=∠D.5.如图,AD =BC ,AB =DC ,DE =BF.求证:BE =DF.(二) 三角形全等的判定二(SAS )1.如图,AC 和BD 相交于点O ,OA=OC ,OB=OD .求证DC ∥AB .2.如图,△ABC ≌△A B C ''',AD ,A D ''分别是△ABC ,△A B C '''的对应边上的中线,AD 与A D ''有什么关系?证明你的结论.3.如图,已知AC ⊥AB ,DB ⊥AB ,AC =BE ,AE =BD ,试猜想线段CE 与DE 的大小与位置关系,并证明你的结论.4.已知:如图,AD ∥BC ,AD=CB ,求证:△ADC ≌△CBA .5.已知:如图AD ∥BC ,AD=CB ,AE=CF 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形常见辅助线作法
令狐文艳
【知识导图】
【导学】全等三角形 第一部分:知识点回顾 常见辅助线的
作法有以下几种:
1)
遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”.
2)
遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转”.
3)
遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理.
4)
过图形上某一点作特定的平分线,构造全等三角形,利用
精准诊查
概念
三边之和大于等于第三边稳定性
与三角形有关的线段
高
中线角平分线
与三角形有关的角
三角形内角和定理三角形的外角
直角三角形
性质判定
多边形及其内角和
三角形
令狐文艳
令狐文艳
040C ∠=,P ,Q
分别在BC ,CA 上,并且AP ,BQ 分别是
BAC ∠,ABC ∠的角平分线。
求证:BQ+AQ=AB+BP
4、如图,在四边形ABCD 中,BC >BA,AD =CD ,BD 平分ABC ∠,
求证: 0
180
=∠+∠C A
5、如图在△ABC 中,AB >AC ,∠1=∠2,P 为AD 上任意一点,求证;AB-AC >PB-PC 应用:
三、平移变换
例1 AD 为△ABC 的角平分线,直线MN ⊥AD 于A.E 为MN 上一点,△ABC 周长记为A P ,△EBC 周长记为B P .求证B P >A P .
例 2 如图,在△ABC 的边上取两点D 、E ,且BD=CE ,求证:AB+AC>AD+AE. 四、借助角平分线造全等
1、如图,已知在△ABC 中,∠B=60°,△ABC 的角平分线AD,CE 相交于点O ,求证:OE=OD
2、如图,△ABC 中,AD 平分∠BAC ,DG ⊥BC 且平分BC ,DE ⊥AB 于E ,DF ⊥AC 于F.
(1)说明BE=CF 的理由;(2)如果AB=a ,AC=b ,求AE 、BE 的长. 五、旋转
O E
D
C
B
A
D
C
B
A
令狐文艳
,请你判断线段BE 与CD 的关
F
D A
A
C B
B
C
O
令狐文艳
【课后作业】
1.如图,在△ABC 中,∠ACB =90°,AC =BC ,直线l 经过顶点C ,过A 、B 两点分别作l 的垂线AE 、BF ,E 、F 为垂足.
(1)当直线l 不与底边AB 相交时,求证:EF =AE +BF . (2)如图,将直线l 绕点C 顺时针旋转,使l 与底边AB
交于点D ,请你探究直线l 在如下位置时,EF 、AE 、
BF 之间的关系.
①AD >BD ;②AD =BD ;③AD <BD .
2.如图3,Rt △ABC 中,∠ACB=90°,AC=BC ,AD ⊥CD ,BF ⊥CD ,AB 交CD 于E. 求证:DF=CD-AD.
3.如图,已知AC=BC ,∠ACB=90°,D 为AB 上任意一点,AE ⊥CD 延长线于E ,BF ⊥CD 于F.求证:EF=BF-AE.
4.如图,在△ABC 中,AC ⊥BC,AC=BC,D 为AB 上一点,AF ⊥CD 交CD 的延长线于F ,BE ⊥CD 于E.求证:EF=BE —AF
5.如图,AD 为△ABC 的中线,∠ADB 和∠ADC 的平分线分别交AB 、AC 于点E 、F .求证:BE+CF >EF .
A
C
F D
E B。
