不确定度评定报告
检定证书测量不确定度评定报告样本数字压力计
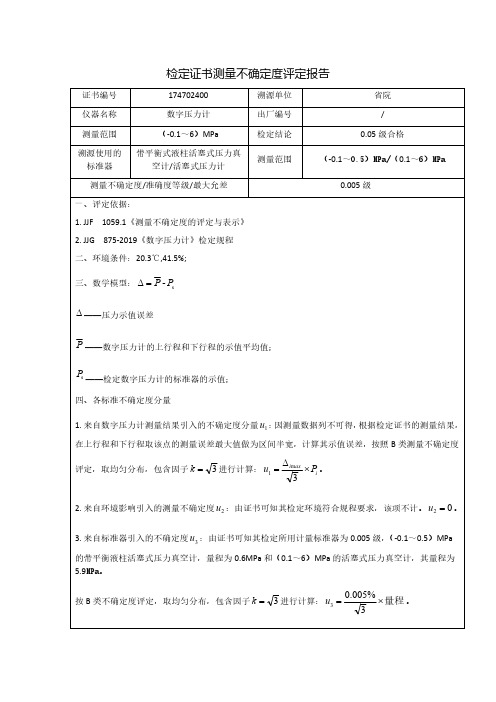
检定证书测量不确定度评定报告证书编号174702400溯源单位省院仪器名称数字压力计出厂编号/测量范围(-0.1~6)MPa 检定结论0.05级合格溯源使用的标准器带平衡式液柱活塞式压力真空计/活塞式压力计测量范围(-0.1~0.5)MPa/(0.1~6)MPa测量不确定度/准确度等级/最大允差0.005级一、评定依据:1.JJF 1059.1《测量不确定度的评定与表示》2.JJG875-2019《数字压力计》检定规程二、环境条件:20.3℃,41.5%;三、数学模型:s-P P =∆∆——压力示值误差P ——数字压力计的上行程和下行程的示值平均值;s P ——检定数字压力计的标准器的示值;四、各标准不确定度分量1.来自数字压力计测量结果引入的不确定度分量1u :因测量数据列不可得,根据检定证书的测量结果,在上行程和下行程取该点的测量误差最大值做为区间半宽,计算其示值误差,按照B 类测量不确定度评定,取均匀分布,包含因子3=k 进行计算:i axi P u ⨯∆=3m 1。
2.来自环境影响引入的测量不确定度2u :由证书可知其检定环境符合规程要求,该项不计。
02=u 。
3.来自标准器引入的不确定度3u :由证书可知其检定所用计量标准器为0.005级,(-0.1~0.5)MPa 的带平衡液柱活塞式压力真空计,量程为0.6MPa 和(0.1~6)MPa 的活塞式压力真空计,其量程为5.9MPa。
按B 类不确定度评定,取均匀分布,包含因子3=k 进行计算:量程⨯=3%005.03u 。
cu 1u 3u 五、合成标准不确定度根据不确定度的传播率,数字压力计示值误差的相对不确定度公式计算如下:2322222212c 31u c u c u c u ++=各分量不相关,相关系数为1,计算结果见表1:表1测量不确定度计算结果标准器示值/MPa 正行程平均值/MPa 反行程平均值/MPa /MPa /MPa MPa U (k =2)/MPa U r (k =2)/%FS -0.08-0.0802-0.08020.000120.000020.000120.00030.004-0.04-0.0401-0.04010.000060.000020.000060.00020.002-0.02-0.0201-0.02010.000060.000020.000060.00020.00200.00000.0000/0.000170.000170.00040.00610.99990.99990.000060.000170.000180.00040.0062 2.0000 2.00000.000000.000170.000170.00040.0063 3.0001 3.00020.000120.000170.000210.00050.0074 4.0003 4.00040.000230.000170.000290.00060.0095 5.0004 5.00060.000350.000170.000390.00080.01366.00056.00050.000290.000170.000340.00070.011六、扩展不确定度数字压力计的扩展不确定度U=ku c (k =2)计算结果见表1;用满量程的百分数表示见表1。
不确定度评定报告-耐压测试仪

耐电压测试仪示值误差校准结果的不确定度评定一、耐电压测试仪电压示值误差校准结果的不确定度评定1、 概述1.1 测量依据:JJG795-2004《耐电压测试仪检定规程》。
1.2 测量环境:环境温度(20±5)℃,相对湿度≤75%RH ,交流电源电压(220±2.2)V 。
1.3 测量标准:AN2001耐压测试仪校验装置,测量范围:交直流电压:0.500-1.000-10.000kV ;交直流电流:0.500-20.00-200.00mA ;电压持续时间:0.01-999.99s 。
1.4 被测对象:型号规格为WB2672A 的耐电压测试仪的交流电压部份。
1.5 测量过程:将耐电压测试仪的高端和低端分别与耐压测试仪校验装置的高压输入和公共回路瑞分别对接,采用直接测量法,由耐压测试仪校验装置直接读取测试仪实际输出电压值。
1.6 评定结果的使用:符合上述条件的测量结果,一般可直接使用本不确定度的评定方法。
2、 数字模型ΔV=V x -V N式中:ΔV ——被测耐压仪的电压示值误差(kV );V x ——被测耐压仪的电压示值(kV );V N ——耐压测试仪校验装置的电压示值(kV )。
3、 标准不确定的评定3.1 标准不确定度u(V x )的评定输入量V x 的标准不确定度u(V x )主要是由被测耐压仪电压的测量重复性引起的,可通过连续测量列,采用A 类方法进行评定。
对一台耐压仪,选择5.00kV 点,连续测量10次,得到如表1所示的一列数据:表1被测耐压仪5.00kV 电压点的测量平均值为:1222.511==∑=ni xi x U n U (kV)按照贝塞尔公式可得单次实验标准差:0027.090000676.01)V V()V (12==--=∑=n s ni x xix (kV)自由度 ν(V x ) = n -1=10-1=93.2 标准不确定度u (V N )的评定输入量U n 的标准不确定度u (V N )主要是由耐压测试仪校验装置本身误差引起的,可以采用B 类方法进行评定。
测量不确定度评估报告

测量不确定度评估报告1.识别测量不确定度的来源在医学实验室中构成测量不确定度的4个主要分量主要包括“检验过程不精密度”、“校准品赋值的不确定度”、“样品影响分量”和“其它检验影响分量”。
我们参考CNAS-GL05:2011《测量不确定度要求的实施指南》和CNAS-TRL-001:2012《医学实验室―测量不确定度的评定与表达》的要求,制定了测量不确定度评定程序,评估了本科室申报的定量项目的测量不确定度。
由于在医学实验室中“样品影响分量”和“其它检验影响分量”的不确定度难以估计,故我们只评估了前两个分量的不确定度。
2.目标不确定度2.1 确定的检验程序在正式启用前,实验室应为每个测量程序确定目标不确定度,即规定每个测量程序的测量不确定度性能要求。
2.2 检验科每个测量程序的目标不确定度由各实验室确定。
2.3 各实验室在确定目标不确定度时可以基于生物变异、国内外专家组的建议、管理准则或当地医学界的判断。
根据应用要求,对不同水平的测量结果可以确定一个或多个目标不确定度。
2.4目标不确定度如下:2.4.1临床化学项目将TEa(国家标准(GB/T20470-2006)、卫生部临床检验中心室间质量评价标准)作为目标扩展不确定度。
2.4.2血液学项目,将TEa(行业标准WS/T406-2012)指标作为目标扩展不确定度。
3.确立输出量与输入量之间的数学模型若输出量为Y(被测量值),输入量X的估计值为xi,则被测量与各输入量之间的函数关系为Y=f(x1,x2,x3,x4…);由于在医学实验室中“样品影响分量”和“其它检验影响分量”的不确定度难以估计,故只对前两个分量的不确定进行评估。
4测量不确定度的计算4.1 A类评估:检验过程不精密度评估样本使用高低2个水平的室内质控品作为实验用样本。
计算本室2水平质控品的日间精密度。
计算批间变异系数CV。
=批间u 批间CV4.2 B 类评估:校准品赋值的不确定度评估信息来源于厂商提供的校准品溯源性文件。
流量积算仪不确定度评定报告

流量积算仪不确定度评定报告一、引言流量积算仪是用于测量流体的流量的仪器设备。
在工业生产和科学实验中,准确测量流体的流量对于保证生产质量和准确分析实验数据至关重要。
然而,由于流量积算仪本身的特性和外界环境的影响,流量测量结果存在一定的不确定度。
本报告旨在评定流量积算仪的不确定度,为用户提供可靠的测量结果。
二、流量积算仪的不确定度来源1. 仪器本身的不确定度:流量积算仪的制造工艺和精度会对测量结果产生影响。
具体来说,仪器的测量范围、灵敏度、稳定性等参数会影响测量结果的准确性和可重复性。
2. 外界环境的不确定度:流量积算仪在使用过程中会受到温度、压力、湿度等环境因素的影响。
这些因素会导致流体的物理性质发生变化,从而影响测量结果的准确性。
3. 操作人员的不确定度:操作人员的技术水平和经验也会对测量结果产生一定的影响。
不同的操作人员可能会有不同的操作习惯和误差来源,从而导致测量结果的差异。
三、流量积算仪不确定度评定方法1. 重复性实验法:通过多次重复测量同一流体的流量,计算测量结果的标准差,可以评定仪器的重复性误差。
较小的标准差表示仪器的重复性较好。
2. 校准方法:将流量积算仪与已知标准流量仪器进行比较,计算测量结果与标准值的偏差,可以评定仪器的准确性。
3. 不确定度分析方法:根据测量结果和仪器的技术参数,利用统计学方法计算出仪器测量结果的不确定度。
常用的方法有不确定度传递法、蒙特卡洛模拟法等。
四、不确定度评定结果根据以上评定方法,我们对某型号流量积算仪进行了不确定度评定。
经过多次重复测量和与标准流量仪器的对比,得出以下评定结果:1. 流量积算仪的重复性误差较小,标准差为0.05%。
2. 流量积算仪的准确性误差在允许范围内,与标准流量仪器的偏差为0.2%。
3. 综合考虑仪器本身的特性和外界环境的影响,我们计算得出流量积算仪的测量结果不确定度为0.3%。
五、不确定度控制和改进措施根据以上评定结果,我们可以采取以下措施来控制和改进流量积算仪的不确定度:1. 加强对操作人员的培训和质量管理,提高操作人员的技术水平和操作规范性,减小人为误差的影响。
工业铂电阻温度计—不确定度评定报告

工业铂电阻测量结果不确定度评定一、测量过程简述:1、测量依据:根据国家JJG229-2010《工业铂、铜热电阻检定规程》。
2、测量环境条件:温度19.8℃,湿度32.0%RH 。
3、测量标准:二等标准铂电阻温度计。
4、被测对象:工业铂热电阻。
5、评定方法:用二等铂电阻温度计队工业用的铂电阻进行检定,以水的沸点100℃为例利用比较法对该点测量结果进行不确定度评定。
二、评定的数学模型:()()()**∆•+=t t x t dt dR R dt dR R R /// 式中: Rt —t 温度时被测热电阻的实际电阻值;Rx —t 温度附近x ℃时被测热电阻测得的电阻值;()t dt dR /—t 温度时被测热电阻随温度的变化率;()*t dt dR /—t 温度时标准铂电阻温度计电阻随温度的变化率; ()****-=∆∆x t R R R R —; R t *—t 温度时标准温度计的电阻值;R x *—x ℃时标准铂电阻温度计的电阻值;三、各输入量的标准不确定度的评定标准不确定度u (R x )记作u (x )由5个不确定度分量构成1、二等标准铂电阻温度计引入的标准不确定度()1x u 的评定在0℃时,根据检定规程规定,Rtp 的检定周期不稳定性为1.9mk ,属正态分布,k =2,则:mk mk x u 95.029.1)(1==同理,100℃时,根据检定规程规定,Rtp 的检定周期不稳定性为1.9mk ,属正态分布,k =2,则:mk mk x u 95.029.1)(1== 2、恒温槽带来的不确定度()2x u0℃制冷恒温槽制冷恒温槽的扩展不确定度()06.02=x u ℃,k =2不确定度区间的半宽:30mk 0.03℃℃/206.0===a认为均匀分布,则3=k ()mk mk k a x u 32.173302===估计()()1.022=∆x u x u ,则自由度()502=x v 。
布氏硬度计测量不确定度评定报告

编号:BQDD1902014布氏硬度计的测量不确定度评定编制:审核:批准:布氏硬度计的测量不确定度评定1. 目的本文件用于布氏硬度计校准过程中,测量设备、人员、环境条件的等因素引起的不确定度评定,使计量人员能够准确、有效地评定通用卡尺的测量结果不确定度。
2. 适用范围本文件适用于实验室所有布氏硬度计的测量结果不确定度评定。
3. 引用文件GJB 3756-1999《测量不确定度表示与评定》 JJG 150-2005《金属布氏硬度计》4. 测量方法(依据JJG 150-2005《金属布氏硬度计》)布氏硬度计的示值误差采用标准硬度块进行校准,校准点的分布,对于不同的标尺,使用对应的标准硬度块进行重复性测量。
下面针对不同标尺示值误差的测量不确定度进行评定。
5. 数学模型 数学模型%100⨯-=HHH δ 式中:δ 被校硬度计的示值误差; H —硬度计示值的算术平均值; H —硬度块的标准值; 6. 不确定度传播律由于输入量H 和H 彼此独立不相关,则不确定度传播律为: )()()(2222212H H u c u c u c +=δ式中:)(H u —标准硬度块引入的标准不确定度;)(H u —硬度计自身引入的标准不确定度;)(δu c—示值误差的合成标准不确定度。
灵敏系数11=c ,12-=c 。
7. 计算标准不确定度分量7.1 标准硬度块引入的标准不确定度)(H u标准硬度块引入的标准不确定度主要来源于标准硬度块证书给出的标准不确定度,根据证书给出的扩展不确定度a ,包含因子k=2,计算得出;7.2硬度计引入的标准不确定度)(H u硬度计引入的标准不确定度主要包括硬度计示值重复性引入的标准不确定度和测量装置测量分辨力引入的标准不确定度。
7.2.1硬度计示值重复性引入的标准不确定度)(1H u ;在一台硬度计上,用硬度块连续测量10次,得出试验标准差,在实际测量中,在重复条件下连续测量5次,则由重复性引入的标准不确定度为:533.2)(1SnSH du n==7.2.2压痕测量装置估读误差引入的标准不确定度)(2H u布氏硬度计压痕测量装置读数显微镜的分度值c 为0.01,估读误差为±1/5,其硬度值的影响为2倍压痕直径关系,看作均匀分布,压痕测量误差引入的标准不确定度为:%100352%1005/2)(2⨯=⨯=dck d c H u 7.2.3硬度计引入的标准不确定度)(H u 为: )()()(2221H H H u u u +=因各分量独立不相关,所以硬度计示值的合成不确定度为:)()(22H H u uu c+=9. 扩展不确定度U :取置信因子k=2 U =k u c。
高温试验不确定度评定报告

高温试验不确定度评定报告一、 测量方法及测量依据1.过程概述: 1.1方法及评定依据JJF 1059.1-2012测量不确定度评定与表示;GB/T 2423.2-2008 《电工电子产品环境试验 第2部分:试验方法 试验B:高温》。
1.2 环境条件 室温。
1.3 检测程序设定温度变化速率为1℃/min ,在温度试验箱降温过程中,利用温控器对温度变化的感应,通过温控器的通断,控制电路的通断,透过氖灯的发亮和熄灭,读出瞬间温度试验箱的温度值。
二、 测量结果不确定度的主要来源及数学模型1.测量结果不确定度的主要来源 (1) 测量重复性; (2) 校准不确定度; (3) 空间分布不确定度。
2.数学模型考虑到影响测量不确定度的因素后,其数学模型为),,,(21N X X X f Y其中Y ——被测量(输出量)X ——影响量(输入量)三、 各输入量标准不确定度的评定1. 测量重复性X 1标准不确定度的评定对同一样品进行10次重复测量,测得结果数据如下表:测量结果为十次测量的平均值,测试过程中随机效应导致的不确定度为()()4077.01U 12=--==∑=n S Ni iσσσσ2. 高低温箱校准证书不确定度U =0.2℃,置信因子k=2,所以由检定仪器所引起的相对不确定度为0.1=22.0)(F U 1rel =3. 空间分布不确定度80℃时温度均匀度为0.7℃,置信因子k=2,所以由空间分布所引起的相对不确定度为35.020.7=)(F U 3rel =四、 合成标准不确定度=++=)()()(22122F U F U U y U rel rel c σ0.5465五、 扩展不确定度扩展不确定度U 由合成标准不确定度uc 乘包含因子k 得到,按公式)(*y U k U c =取置信因子k=2,扩展不确定度U=1.0931(℃)六、 结果报告高温试验(94.08±1.0931)℃,k=2。
钢直尺测量结果不确定度评定

1 概述 1.1 测量方法: 依据 JJG1—1999《钢直尺检定规程》。 1.2 环境条件:温度(20±2)℃,相对湿度≤85%RH 。 1.3 测量标准:三等金属线纹尺 1.4 测量对象:1000mm 钢直尺最大允许示值误差为±0.20mm。 1.5 测量过程 钢直尺测量时,将放置在检定台上的钢直尺和三等标准金属线纹尺调至平行,并使 两尺的首端(零位)对准,然后在三等标准金属线纹尺上直接读出被测尺的示值误差。 1.6 评定结果的使用 在符合上述条件下的测量结果,一般可参照使用本不确定度的评定方法。 2 数学模型 △L=△е 式中:△L—钢直尺的示值误差; △е—钢直尺在三等金属线纹尺上对应的偏差读数值。 3 输入量△е的标准不确定度分量的评定
u (e3 )
L a 3
0.006mm
第 1 页 共 3 页
单位 mm
测量点
200 0.001
400 0.002
600 0.003
800 0.005
1000 0.006
u (e3 )
3.4 三等金属线纹尺和钢直尺线膨胀系数存在不确定度, 当温度偏离标准温度 20℃引起 的标准不确定度分项 u (e4 ) 的评定(采用 B 类方法进行评定) 由于三 等金属线纹尺和钢直尺的线膨胀系数,钢直尺的线膨胀系数分别在 αs= (16.5±1)×10-6/℃和α=(11.5±1)×10-6/℃范围内分布,两者线膨胀系数中心值差为△α 应在(5±2)×10-6/℃范围内服从三角分布,该三角分布半宽 α为 2×10-6/℃,包含因子 κ 取 6 ,L 以 1000mm 代入,△t 以 2℃代入,得
不确定度来源 校准钢直尺时人眼分辨率 标准金属线纹尺示值误差 温度偏离标准温度 被校准钢直尺和标准金属线纹尺线 膨胀系数的不确定度 被校准钢直尺和标准金属线纹尺两 者温度差
不确定度评定报告-导热系数

导热系数不确定度评定报告1、概述1.1 测量依据:GB/T 10294-2008 绝热材料稳态热阻及有关特性的测定防护热板法。
1.2 测量方法:按照GB/T 8813-2020 要求,裁切规定尺寸试样,在样品两边紧贴不同温度的金属板,当温度稳定后,测量样品两面的温度差,通过公式计算导热系数。
1.3 测量工具和仪器设备:平板导热仪:温度误差±0.5,导热板温度分别为15℃&35℃游标卡尺:测量范围150mm,精度0.01mm,最大允许误差±0.05mm。
1.4 被测对象:300mm*300mm*25mm 方形试样1.5 环境条件:温度(23±2)℃,湿度(50±10)%,调节6h1.6 评定日期: 2022.9.20-27.2、建立模型:γ=φd2A(T1−T2)∗β其中γ为导热系数,φ为平均加热功率,d为样品平均厚度,A为计量面积,双试件装置需乘以2,T1为试件热面平均温度,T2为冷面平均温度,β为设备修正系数,由厂商给出(0.96)。
3.不确定度来源分析公式共包含6个参数,其中修正系数为设备厂商给出,暂不考虑其影响。
其中平均加热功率(φ)的不确定度来源主要是:(1)设备功率误差引入的不确定度分量;(2)功率稳定性和均匀性引入的不确定度分量其中样品厚度(d)测量的不确定度来源主要是:(1)随机因素重复性测量引入的不确定度分量;(2)游标卡尺校准引入的不确定度分量;(3)游标卡尺误差波动引入的不确定度分量;其中计量面积(A)测量的不确定度来源主要是:(1)设备磨损误差引入的不确定度分量(可忽略);(2)样品变形引入的不确定度分量;其中试件平均温度(T1、T2)测量的不确定度来源主要是:(1)设备误差引入的不确定度分量;(2)温度板均匀性引入的不确定度分量;4.不确定度量化:4.1:平均加热功率的不确定度,根据校准报告的热流参数校准结果和日常检测经验(导热系数不大于0.1时),其波动不超过±1%,均匀分布,k =√3Uφ-rel=1%/√3=0.57%4.2样品厚度D:1.随机因素引入的不确定度分量,采用A 类方法重复性测量进行评定。
不确定度报告
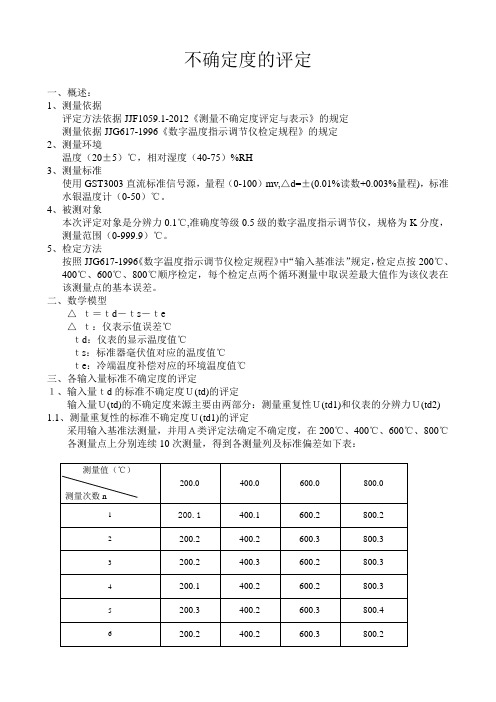
不确定度的评定一、概述:1、测量依据评定方法依据JJF1059.1-2012《测量不确定度评定与表示》的规定测量依据JJG617-1996《数字温度指示调节仪检定规程》的规定2、测量环境温度(20±5)℃,相对湿度(40-75)%RH3、测量标准使用GST3003直流标准信号源,量程(0-100)mv,△d=±(0.01%读数+0.003%量程),标准水银温度计(0-50)℃。
4、被测对象本次评定对象是分辨力0.1℃,准确度等级0.5级的数字温度指示调节仪,规格为K分度,测量范围(0-999.9)℃。
5、检定方法按照JJG617-1996《数字温度指示调节仪检定规程》中“输入基准法”规定,检定点按200℃、400℃、600℃、800℃顺序检定,每个检定点两个循环测量中取误差最大值作为该仪表在该测量点的基本误差。
二、数学模型△t=td-ts-te△t:仪表示值误差℃td:仪表的显示温度值℃ts:标准器毫伏值对应的温度值℃te:冷端温度补偿对应的环境温度值℃三、各输入量标准不确定度的评定1、输入量td的标准不确定度U(td)的评定输入量U(td)的不确定度来源主要由两部分:测量重复性U(td1)和仪表的分辨力U(td2) 1.1、测量重复性的标准不确定度U(td1)的评定采用输入基准法测量,并用A类评定法确定不确定度,在200℃、400℃、600℃、800℃各测量点上分别连续10次测量,得到各测量列及标准偏差如下表:采用B类评定法评定不确定度,由仪表分辨力b导致的示值误差区间半宽为a=b/2, 均匀分布,包含因子K= 3 ,因此U(td2)=0.05/K=0.05/ 3 =0.029℃输入量的不确定度U(td)=u2(td1)+u2(td2)200℃:U(td)=(0.045)2+(0.029)2=0.054℃400℃:U(td)=(0.040)2+(0.029)2 =0.049℃600℃:U(td)=(0.033)2+(0.029)2=0.044℃800℃:U(td)=(0.047)2+(0.029)2=0.055℃2、输入量ts的标准不确定度U(ts)的评定输入量ts的标准不确定度主要来自直流标准信号源的误差,采用B类方法评定,其误差分布按均匀分布考虑K= 3 ,△d=±(0.01%读数+0.003%量程):200℃:△d=±(0.01%×8.138+0.003%×100)/0.040=0.095℃, U(ts)=0.095/ 3 =±0.055℃400℃:△d=±(0.01%×16.397+0.003%×100)/0.0425=0.109℃,U(ts)=0.109/ 3 =±0.063℃600℃:△d=±(0.01%×24.905+0.003%×100)/0.0425=0.129℃,U(ts)=0.129/ 3 =±0.075℃800℃:△d=±(0.01%×33.275+0.003%×100)/0.041=0.154℃,U(ts)=0.154/ 3 =±0.089℃3、输入量te的标准不确定度U(te)的评定输入量te的标准不确定度来自标准水银温度计的修正值.,采用B类方法评定,其误差分布按正态分布考虑K=2.58由所用二等标准水银温度计检定证书查得(20.2℃)修正值△t=-0.03℃,则U(te) =-0.03℃/2.58=0.012℃四、合成标准不确定度Uc的评定由于td和ts、te彼此相对独立,所以合成标准不确定度可按下式计算:Uc=u2(td)+u2(ts)+ u2(te)200℃:Uc=(0.054)2+(0.055)2+(0.012)2 =0.078℃400℃:Uc=(0.049)2+(0.063)2+(0.012)2=0.081℃600℃:Uc=(0.044)2+(0.075)2+(0.012)2=0.088℃800℃:Uc=(0.055)2+(0.089)2+(0.012)2=0.105℃五、扩展不确定度U取包含因子k=2,则扩展不确定度U=k×Uc200℃:U=2×0.078=0.156℃400℃:U=2×0.081=0.162℃600℃:U=2×0.088=0.176℃800℃:U=2×0.105=0.210℃六、结论根据JJG617-1996《数字温度指示调节仪检定规程》的规定,在本单位现有仪器设备的技术条件下,用GST3003直流标准信号源作为标准器,按输入基准法对配K型热电偶、测量范围(0-999.9)℃、分辨力0.1℃、准确度等级0.5级的数字温度指示调节仪检定时,其扩展不确定度为:200℃:U≈0.16℃400℃:U≈0.16℃600℃:U≈0.18℃800℃:U≈0.21℃置信概率为95%,包含因子k=2,扩展不确定度不大于最大允许误差的1/5。
一般工作压力表测量不确定度评定7篇

一般工作压力表测量不确定度评定7篇篇1一、引言在现代企业中,员工的工作压力逐渐成为关注的焦点。
为了更好地了解员工的工作压力状况,本文采用一般工作压力表对某企业员工进行测量,并对其不确定度进行评定。
二、测量方法与数据采集本次测量采用一般工作压力表,该量表包含多个维度,如工作量、时间压力、人际关系等,以全面评估员工的工作压力。
在数据采集过程中,我们向企业员工发放问卷,要求他们根据自身实际情况进行填写。
共收集到有效问卷200份,为后续的数据分析提供了基础。
三、数据处理与分析1. 数据清洗:对收集到的数据进行清洗,去除无效、重复或极端值,确保数据的准确性和可靠性。
2. 描述性统计:对数据进行描述性统计,包括平均数、标准差、最大值和最小值等,以了解员工工作压力的整体状况。
3. 信效度检验:通过信效度检验,验证测量工具的可靠性和有效性。
结果表明,一般工作压力表在本样本中具有良好的信效度。
4. 维度分析:对工作压力表的各个维度进行独立样本t检验,以了解不同维度上员工工作压力的差异。
结果表明,不同维度上员工的工作压力存在显著差异。
四、不确定度评定不确定度评定是评估测量结果可靠性的重要环节。
本文采用方差分析法对一般工作压力表测量结果的不确定度进行评定。
首先,计算各维度得分的方差,然后根据方差的大小评估不确定度。
结果表明,一般工作压力表各维度得分的方差较小,说明测量结果具有较好的稳定性。
五、结论与建议通过本次测量与不确定度评定,我们得出以下结论:企业员工在工作压力方面存在显著差异,不同维度上员工的工作压力有所不同。
同时,一般工作压力表在本样本中具有良好的信效度,测量结果具有较好的稳定性。
针对以上结论,我们提出以下建议:企业应关注员工在工作压力方面的差异,针对不同维度采取相应的管理措施,以降低员工的工作压力。
同时,企业可定期使用一般工作压力表对员工进行测量,以监控员工工作压力的变化,并及时调整管理策略。
此外,员工也应积极关注自身的工作压力状况,适时调整工作态度和行为,以保持身心健康。
测量不确定度评定报告

测量不确定度评定报告1、评定目的识别实验室定量项目检测结果不确定度的来源,明确评定方法,给临床检测结果提供不确定度依据。
2、评定依据CNAS-GL05《测量不确定度要求的实施指南》JJF1059-1999《测量不确定度评定和表示》CNAS—CL01《检测和校准实验室能力认可准则》3、测量不确定度评定流程测量不确定度评定总流程见图一。
图一测量不确定度评定总流程4、测量不确定度评定方法4.1建立数学模型4.1.1数学模型根据检验工作原理和程序建立,即确定被测量Y(输出量)与影响量(输入量)X1,X2,…,X N间的函数关系f来确定,即:Y=f(X1,X2,…,X N)建立数学模型时应说明数学模型中各个量的含义和计量单位。
必须注意,数学模型中不能进入带有正负号(±)的项。
另外,数学模型不是唯一的,若采用不同测量方法和不同测量程序,就可能有不同的数学模型。
4.1.2计算灵敏系数偏导数Y/x i=c i称为灵敏系数。
有时灵敏系数c i可由实验测定,即通过变化第i个输入量x i,而保持其余输入量不变,从而测定Y的变化量。
4.2不确定度来源分析测量过程中引起不确定度来源,可能来自于:a、对被测量的定义不完整;b、复现被测量定义的方法不理想;c、取样的代表性不够,即被测量的样本不能完全代表所定义的被测量;d、对测量过程受环境影响的认识不周全或对环境条件的测量和控制不完善;e、对模拟式仪器的读数存在人为偏差(偏移);f、测量仪器的计量性能(如灵敏度、鉴别力阈、分辨力、死区及稳定性等)的局限性;g、赋予计量标准的值或标准物质的值不准确;h、引入的数据和其它参量的不确定度;i、与测量方法和测量程序有关的近似性和假定性;j、在表面上完全相同的条件下被测量在重复观测中的变化。
4.3标准不确定度分量评定4.3.1A类评定--对观测列进行统计分析所作的评估a对输入量X I进行n次独立的等精度测量,得到的测量结果为:x1,x2,…x n。
测量过程不确定度评定报告

外径千分尺测量阀杆Ø35外径不确定度评定报告1.概述1.1测量依据:按图PFF78-35-02阀杆尺寸进行测量。
1.2环境条件:常温,相对湿度<35%RH 。
1.3测量设备:(25-50)mm 外径千分尺,在其测量范围内最大示值误差为±0.004mm 。
1.4被测对象:外径为025.0087.035--mm 的阀杆。
材料为12Cr13,α1=10.3×10-6/℃。
1.5测量方法:用外径千分尺直接测量。
2. 测量模型:由于对象内径值可以直接在内径千分尺上直接测量 故:L=L S -L S (δα·Δt +αs ·δt)L---被测内孔的测定内径;L S ---内径千分尺对内孔内径的测量值。
δα—被测内孔线膨胀系数与内径千分尺线膨胀系数之差。
Δt — 被测内孔温度对参考温度20℃的偏差,取±10℃。
αs — 内径千分尺线膨胀系数,取11.5×10-6/℃。
δt — 被测内孔温度与内径千分尺温度之差,取±1℃。
3.灵敏系数该数学模型是透明箱模型,必须逐一计算灵敏系数:1 ≈ ∂ ∂)Δ1(=t s t αD S δαδLs f C --= ;t S s αδD s αf C -== ∂ ∂=-35×1㎜℃=-3.5×104µm ℃;δαD f C S t t -=Δ=Δ ∂ ∂=-35×1×10-6㎜/℃=-0.035µm/℃δαf C δα ∂ ∂/==-Ds Δt=-35×10㎜℃=-3.5×105µm ℃ t δf C t δ ∂ ∂/==-Ds αs=-35×11.5×10-6㎜/℃=-0.402µm /℃4.计算各分量标准不确定度4.1外径千分尺示值误差引入的分量u(L S )根据外径千分尺检定规程,在其测量范围内最大示值误差e=±0.004mm在半宽度为区间内,以均匀分布,则u(L S)= 4/1.732 =2.4μm;4.2被测主轴线膨胀系数不准确引入的分量u(αS)由于被测主轴线膨胀系数α1= 10.4×10-6/℃是给定的,是一个常数,故 u(αS)= 0 ,4.3测量环境偏离标准温度20℃引入的分量u(Δt)测量环境偏离标准温度20℃的偏差为±10℃,在半宽为10℃范围内,以等概率分布(均匀分布)。
不确定度评定报告

b为工作曲线的斜率
c为样品中元素的浓度
由最小二乘法回归线性函数,得:
C式:Ii=0.2915+4.3606Ci,r=0.717157;
Mn式:Ii=0.2304+2.8389Ci,r=0.735686.
被测量C的标准不确定度为:
式中:
n=2×3=6, =0.0051
= =0.4605%,
电火花直读光谱仪测定低合金钢中碳和锰测量结果不确定评定报告
一、目的
由于测量误差的存在,使得被测量的真值难以确定,只能得到一个被测量的近似量和一个用于表示近似度的误差范围,即测量不确定度。通过对测量结果不确定度的评估,以让客户了解测量结果是否符合特定需求,确定测量数据之可信及真实程度。
二、范围
适用于万基钢管(秦皇岛)有限公司金属材料实验室中电火花直读光谱仪测量C和Mn测量结果不确定度的评定。
-0.0022
2.5×10-9,2.89×10-8,
4.84×10-8
Mn
1.84
5.4519,5.4586,
5.4514
-0.00207,0.00463,
-0.00257
4.3×10-6,2.15×10-5,
6.59×10-6
YSBS 20140a-5
C
0.908
4.2557,4.2544,
4.2426
0.2532
0.2535
0.2531
0.2528
0.2527
0.2529
0.000519
0.000212
= 0.00155
= 0.00084
2、控样修正引起的不确定度分量
同样控样修正引入的不确定度分量包括其化学值不确定度(B类),修正时,重复激发引入的不确定(A类)。
不确定度评定报告_2

不确定度评定报告1.测量方法由标准晶振输出频标信号,输入到通用计数器中,在通用计数器上显示读数。
2.数学模型 数学模型A=A S +δ式中: A —频率计上显示的频率值 A S —参考频率标准值;δ—被测与参考频标频率的误差。
3.输入量的标准不确定度3.1 标准晶振引入的标准不确定度, 用B 类标准不确定度评定。
标准晶振的频率准确度为±2×10-10, 即当被测频率为10MHz 时, 区间半宽为a =10×106×2×10-9=2×10-2Hz, 在区间内认为是均匀分布, 则标准不确定度为()s A u =a/k =1.2×10-2Hz()=rel s A u 1.2×10-2/107=1.2×10-93.2被测通用计数器的测量重复性引入的标准不确定度分量u(δ2)u(δ2)来源于被测通用计数器的测量重复性, 可通过连续测量得到测量列, 采用A 类方式进行评定。
对一台通用计数器10MHz 连续测量10次, 得到测量列9999999.6433.9999999.6446.9999999.6448、9999999.6437、9999999.6435.9999999.6428、9999999.6446.9999999.6437、9999999.6457、9999999.6451Hz 。
由测量列计算得算术平均值 ∑==ni i f n f 11=9999999.6442Hz,标准偏差 ()Hz n ffs ni i00091.0121=--=∑=标准不确定度分量u(δ3)=0.00091/=0.00029Hzu(δ3)rel =2.9×10-114 合成标准不确定度评定 主要标准不确定度汇总表不确定度来源(i x )i a i k ()i u x标准晶振引入的标准不确定度()rel s A u 2×10-3Hz 31.2×10-10 通用计数器引入的标准不确定度分量()1δu2.5×10-2Hz31.5×10-9被测石英晶体振荡器测量重复性()rel u 2δ0.00091Hz 12.9×10-11输入量AS 、δ1.δ2相互独立, 所以合成标准不确定度为u c (A)= 922212105.1)()()(-⨯=++δδu u A u S5 扩展不确定度评定 取k=2, 则 扩展不确定度为U rel =k ×u c =2×1.5×10-9=3×10-96测量不确定度报告f =f0(1±3×10-9)Hz, k=2不确定度评定报告1.测量方法由标准晶振输出频标信号,输入到通用计数器中,在通用计数器上显示读数。
测量不确定度评定报告

测量不确定度评定报告一、引言二、测量方法和装置本次测量使用的方法是直线测量法,采用直尺和游标卡尺进行测量。
直线测量法是一种简单有效的测量方法,在工程和科学领域得到广泛应用。
1.人为误差测量1:30.2cm测量2:30.1cm测量3:30.3cm根据三次测量结果的平均值,得到被测量值为30.2cm。
通过测量结果的离散程度,可评估人为误差的大小。
2.仪器误差仪器误差是由于测量仪器本身的不准确性而引起的。
在使用直尺和游标卡尺进行测量时,需要考虑到仪器的刻度精度和读数精度。
本次测量中,直尺和游标卡尺的刻度间距分别为0.1cm和0.01cm。
根据仪器的刻度间距,可以评估测量结果在刻度内的不确定度。
例如,如果测量结果位于两个刻度之间,不确定度可以评估为刻度间距的一半。
3.环境影响环境因素如温度、湿度等的变化会对测量结果产生一定的影响。
在本次测量中,环境温度保持相对稳定,湿度变化较小,因此可以忽略环境影响对测量结果的不确定度。
四、测量不确定度评定五、灵敏度分析和建议灵敏度分析用于评估测量结果对误差的敏感程度,从而提供改进测量方法和装置的建议。
1.人为误差的影响2.仪器误差的影响根据前述的仪器误差评估,本次测量结果对仪器误差的敏感程度较高。
为了减小仪器误差对测量结果的影响,可以考虑使用更精密的测量仪器,如数字卡尺等,降低仪器误差。
六、结论本次测量的不确定度评定结果为0.1cm。
测量结果对人为误差的敏感程度较低,对仪器误差的敏感程度较高。
改进测量方法和装置可降低仪器误差对测量结果的影响。
不确定度评定

不确定度评定报告对KJMZ-2011-0272报告各项测量结果进行不确定度评估1.煤中分析水分测量不确定度评定依据JJF1059-1999《测量不确定度评定与表示》和GB/T212-2008《煤的工业分析方法》,用空气干燥法对煤的水分进行测量。
1.1检测环境条件室内温度(20±5)℃,相对湿度≤45%,无影响检测工作的振动冲击、气流冲击,无强电磁干扰。
水分测定数据如下:皿重:(g)16.2340,15.3826试样重:(g) 1.0000, 1.0000干燥后重:(g)17.2287,16.3371水分重:(g)0.0053,0.0055水分含量:M ad% 0.53, 0.55平均值:M ad% 0.541.2被测量说明1.2.1测量程序称量瓶质量----称取1g左右煤样,称准至0.0002g--105℃-110℃干燥箱干燥至恒重—称量---计算1.2.2计算公式Mad=m1/m×100%中式:m1--干燥后失去的质量gm—试样质量gM ad—空气干燥基水分%1.3不确定度源分析水分测定值不确定度主要来自a)A类不确定度(测量重复性)b)试样称量c)干燥后的质量称量d)质量恒定1.4不确定度组分评定1.4.1A类不确定u=S(X)=)1-()-(1=21 n n XXni=0.011.4.2B类不确定a)试样质量m试样称量误差0.0002g按均匀发布转化为标准不确定度:U(m)=0.0002/√3=0.0001154gb) 干燥后失去的质量m1干燥后称量误差0.0002g按均匀发布转化为标准不确定度:U(m1)=0.0002/3=0.0001154gc)质量恒定此煤样水分测定值0.54%,不需进行检查性干燥,可不考虑质量恒定的不确定度。
1.5合成标准不确定度合成标准不确定度相对不确定度=)(+)(22Aad u Aad u B A =0.029绝对不确定度:u (c )=0.54ⅹ0.029=0.016 1.扩展不确定度 扩展因子K=1.96水分测量值Mad 的扩展不确定度: U (Mad )=0.016ⅹ1.96=0.03 结果表述:此煤样水分测定结果为:(0.54±0.03)%2.煤中空干基灰分测量不确定度评定依据JJF1059-1999《测量不确定度评定与表示》和GB/T212-2008《煤的工业分析方法》,用缓慢法对煤的灰分进行测量。
不确定度评定报告

实验室计量器具不确定度的评定摘要不确定度论的基础思想是否定真值。
否定真值就是否定客观,这就否定了认识(测得值)的客观标准。
于是就否定了认识与客观存在的差别(误差),也就否定了准确度(误差范围)。
测量学就是研究如何得到真值的学问,否定真值的可认识性,也就否定了测量学自身。
计量学的物质基础是体现单位制的基准和代表基准工作的各等级标准。
各种标准的量值,就是各种层次的相对真值;否定真值,也就否定了计量。
关键词:不确定度误差砝码评定引言在测量过程中,各项误差合成后得到的总极限误差称为测量的不确定度,他是表示由于测量过程中各项误差影响而使测量结果不能肯定的误差范围。
测量误差=测量值-真值,测量值>真值,为正差;测量值<真值,为负差。
由于我们习惯了测量误差这个概念,现在提出测量不确定度,确实理解起来比较困难。
测量不确定度目前在各种资料上给出的解释不尽相同,但本质都是相同的。
我们可以这样简单的理解:测量误差为一个确定值(尽管被测量真值是一个未知量),而不确定度是被测量真值所处一个范围的评定或由于测量误差致使测量结果不能肯定的程度。
(这是我个人理解所得,上课的时候也是这样教学生的)由ISO、IEC、BIPM、IFCC、IUPAC、IUPAP、OIML七个国际组织共同组成国际测量不确定度工作组,在1NC-1(1980)建议书的基础上,起草制定了《测量不确定度表示指南》(GUM)。
1993年,GUM以7个国际组织的名义正式由ISO颁布实施,并在1995年作了修订。
为了贯彻GUM在我国的实施,由全国法制计量委员会委托中国计量科学研究院起草制定了国家计量技术规范《测量不确定度评定与表示》(JJF1059-1999)。
该规范原则上等同GUM的基本内容,作为我国统一准则对测量结果及其质量进行评定、表示和比较。
第一章测量不确定度的原理国家计量技术规范《测量不确定度评定与表示》(JJF1059-1999)中,对测量不确定度定义为:表征合理地赋予被测量之值的分散性,与测量结果相联系的参数。
数字式万用表不确定度评定

数字式万用表测量不确定度评定报告(一) 交流电压示值误差测量结果的不确定度评定 1.概述1.1 测量依据:JJG (航天)35-1999《交流数字电流表检定规程》、JJG (航天)34-1999《交流数字电压表检定规程》、JJG 598-1989《直流数字电流表试行检定规程》、JJG 315-1983《直流数字电压表试行检定规程》、JJG 724-1991《直流数字式欧姆表检定规程》。
1.2 测量环境条件:环境温度(20±5) ℃,相对湿度(40-80)%RH。
1.3 测量标准:XF30A*型多功能校准仪,准确度等级:0.05级。
1.4 被测对象:数字式万用表,型号:17B ,多档位,量程,功能量程 分辨率 精确度交流电压(40~500Hz )400.0mV 0.1mV 3.0%+34.000V 0.001V 40.00V 0.01V 400.0V 0.1V 1000V1V1.5 测量过程:选用多功能校准仪作为标准,采用标准源法,即通过标准源和被检万用表的读数,从而达到测量示值误差的目的。
2. 数学模型ΔV= V X 1 - V X 2ΔV ---被检表电压示值误差;V X 1---被检表示值最佳估计值;V X 2—标准表读数; 式中:传播系数即灵敏系数,分别求偏导数则c1=1,c2=-1。
3. 不确定度分量3.1重复性测量引入的不确定度分量u(V X 1)不确定度分量u(V X 1) 主要是被检万用表交流电压档的测量重复性引起,采用A 类方法评定。
考虑到在重复性的条件下所得到的测量列的分散性包含了电压源的稳定度、调节细度、人员操作等随机分量所引起的不确定度,故不另作分析。
对一台万用表交流电压档的100V 点,连续独立测量10次,每次均重新调整零位,得到测量值如下:(单位:V )其算术平均值为:V X 1=∑==ni xi n x 11=99.432V ≈99.43V单次测量的实验标准差按贝塞尔计算公式:()2111∑=--=ni i x x n S =0.182V则标准不确定度为:u(V X 1) =S ≈0.182V 3.2 标准器准确度引起的不确定度分量u (V X 2 )标准不确定度分量u(V X 2)主要由标准源准确度引起,采用B 类方法进行评定。
酸度计不确定度评定报告

2015年度陕西省计量技术机构“酸度量值比对”不确定度评定报告2015年10月,陕西省计量技术机构“酸度量值比对”工作正式开展。
主持此次比对的单位为陕西省质量技术监督局。
参加比对单位是全省9个市级法定技术机构和1个计量授权检定机构。
比对使用的仪器是由上海仪电科学仪器股份有限公司提供的型号为PHS-3E 的数显酸度计,仪器测量范围:0.00~14.00pH ;0~±1999mV ;0~99.9℃。
仪器编号为600710N0015050024,使用E-301F 型复合电极一支。
量值比对仪器的检定方法采用直接比对法。
量值比对仪器的检定依据:JJG119-2005《实验室pH (酸度)计》计量检定规程。
酸度计的测量不确定度分析1.1 酸度计电计pH 示值误差测量的不确定度分析电计示值测量不确定度主要是测量时使用的标准器的不确定度和示值的重复性不确定度或量化误差(最小分辨率)引起的不确定度两项构成。
(1)数学模型电计示值误差服从公式(1):s pH pH d -= (1)式中:d 为示值误差;pH 为被测量电计示值;pH s 为pH 计检定仪示值。
由于pH 与pH s 相互独立,则: 1=∂∂pHd ,1-=∂∂s pH d 故:)()()(22s pH u pH u d u += (2)(2)各分量的标准不确定度a )测量标准器的标准不确定度)(s pH u测量时采用酸度计检定仪,有效期内的检定证书给出的pH 示值误差为+0.009pH 。
考虑为均匀分布,则其pH 值标准不确定度为pH pH pH u s 0026.032009.0)(== b )电计示值测量的重复性标准不确定度)(pH u计算电计示值测量的标准不确定度)(pH u ,实测结果表明:单次测量的标准偏差:00.0)(=pH s ,因而应该考虑量化误差,即分辨力导致的)(量pH u 。
0.01级的pH ,其分辨率力为0.01pH ,考虑为均匀分布,则有pH H pH u pH u 0029.032p 01.0)()(===量 (3)合成不确定度pH pH u pH u d u u s c 0152.00029.00026.0)()()(2222=+=+==(4)扩展不确定度取包含因子2=k ,pH k u U c 0304.020152.0=⨯=⨯=1.2 电计mV 值示值误差测量不确定度分析(1)数学模型电计mV 值示值误差服从以下公式s x V V d -= (3)式中:d 为示值误差:x V 为被测量电计mV 示值;s V 为mV 计检定仪示值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
不确定度评定报告
1、测量方法
由标准晶振输出频标信号,输入到通用计数器中,在通用计数器上显示读数。
2、数学模型 数学模型
A=A S +δ
式中:A —频率计上显示的频率值
A S —参考频率标准值;
δ—被测与参考频标频率的误差。
3、输入量的标准不确定度
3.1 标准晶振引入的标准不确定度()s A u ,用B 类标准不确定度评定。
标准晶振的频率准确度为±2×10-10,即当被测频率为10MHz 时,区间半宽为a =10×106×2×10-9=2×10-2Hz ,在区间内认为是均匀分布,则标准不确定度为
()s A u =a/k =1.2×10-2Hz
()=rel s A u 1.2×10-2/107=1.2×10-9
3.2被测通用计数器的测量重复性引入的标准不确定度分量u(δ2)
u(δ2)来源于被测通用计数器的测量重复性,可通过连续测量得到测量列,采用A 类方式进行评定。
对一台通用计数器10MHz 连续测量10次,得到测量列9999999.6433、9999999.6446、9999999.6448、9999999.6437、9999999.6435、9999999.6428、9999999.6446、9999999.6437、9999999.6457、9999999.6451Hz 。
由测量列计算得
算术平均值 ∑==n
i i f n f 1
1=9999999.6442Hz,
标准偏差 ()
Hz n f
f
s n
i i
00091.01
2
1
=--=
∑=
标准不确定度分量u(δ3)=0.00091/=0.00029Hz
u(δ3)rel =2.9×10-11
4 合成标准不确定度评定 主要标准不确定度汇总表
不确定度来源(i x )
i a i k ()i u x
标准晶振引入的标准不确定度()rel s A u 2×10-3Hz 3
1.2×10-10 通用计数器引入的标准不确定度分量()1δu
2.5×10-2Hz
3
1.5×10-9
被测石英晶体振荡器测量重复性
()rel u 2δ
0.00091Hz 1
2.9×10-11
输入量A S 、δ1、δ2相互独立,所以合成标准不确定度为
u c (A)= 922212105.1)()()(-⨯=++δδu u A u S
5 扩展不确定度评定 取k=2,则 扩展不确定度为
U rel =k ×u c =2×1.5×10-9=3×10-9
6测量不确定度报告
f =f 0(1±3×10-9)Hz ,k=2
不确定度评定报告
1、测量方法
由标准晶振输出频标信号,输入到通用计数器中,在通用计数器上显示读数。
2、数学模型
数学模型
A=A S +δ
式中:A —频率计上显示的频率值
A S —参考频率标准值;
δ—被测与参考频标频率的误差。
3、输入量的标准不确定度
3.1 标准晶振引入的标准不确定度()s A u ,用B 类标准不确定度评定。
标准晶振的频率准确度为±2×10-10,即当被测频率为10MHz 时,区间半宽为a =10×106×2×10-10=2×10-3Hz ,在区间内认为是均匀分布,则标准不确定度为
()s A u =a/k =1.2×10-3Hz
()=rel s A u 1.2×10-3/107=1.2×10-10
3.2由通用计数器时基不准引入的标准不确定度分量()1δu ,用B 类标准不确定度评定。
计数器的时基所选的闸门时间τ=10s 时,它的不确定度取决于晶振。
晶振给出值的相对频率准确度为±ττf f /∆,
()1δu =
1010
105.13
105.2)()
(--⨯=⨯=
∆=
=k
f f f f u u τ
τ
τ
ττ
τ
3.3 被测通用计数器的测量重复性引入的标准不确定度分量u(δ2)
u(δ2)来源于被测通用计数器的测量重复性,可通过连续测量得到测量列,采用A 类方式进行评定。
对一台通用计数器10MHz 连续测量10次,得到测量列9999999.64308、9999999.64313、9999999.64312、9999999.64315、9999999.64321、9999999.64319、9999999.64323、9999999.64320、9999999.64328、9999999.64322。
由测量列计算得
算术平均值 ∑==n
i i f n f 1
1=9999999.64318Hz,
标准偏差 ()
Hz n f
f
s n
i i
00006.01
2
1
=--=
∑=
标准不确定度分量u(δ3)=0.00006/=0.000019Hz
u(δ3)rel =1.9×10-12
4 合成标准不确定度评定 主要标准不确定度汇总表
不确定度来源(i x )
i a i k ()i u x
标准晶振引入的标准不确定度()rel s A u 2×10-3Hz 3
1.2×10-10 通用计数器引入的标准不确定度分量()1δu
2.5×10-3Hz
3
1.5×10-10
被测石英晶体振荡器测量重复性
()rel u 2δ
0.00006Hz 1
1.9×10-12
输入量A S 、δ1、δ2相互独立,所以合成标准不确定度为
u c (A)= 10222121093.1)()()(-⨯=++δδu u A u S
5 扩展不确定度评定 取k=2,则 扩展不确定度为
U rel =k ×u c =2×1.93×10-3=4×10-10
6测量不确定度报告
f =f 0(1±4×10-10)Hz ,k=2。
