函数单调性极值最值与凹凸性拐点_1
高等数学函数的单调性和凹凸性

连续曲线 y ? f ( x) 的拐点.
y
y ? x4
例如 ,
o
x
(2) 若 f ??( x0 ) 不存在 ,点 ( x0 , f ( x0 )) 也可能
是连续曲线 y ? f ( x ) 的拐点 .
y
例如 ,
o
25x
注意 改变凹凸性的点只可能是二阶导数为零及二阶 导数不存在的点 .
判断曲线的凹凸性和拐点的步骤:
x2
?
2,
3
对应
y1
(0,1)
(
2
3
,
11
27
)
?
1,
y2
?
2
11 27
3) 列表判别
3
x (?? ,0)
0
(0,
2 3
)
2
3
(
2 3
,
?
?
)
y?? ? 0 ? 0 ?
y凹
1
凸 11
27
凹
故该曲线在
(??
, 0)
及
(
2
3
,
?
?
) 上向上凹 , 在(0,
2) 上
3
向上凸
, 点(0,1)及
(2
3
,
11 27
1 (1 , 2)
0?
2 (2, ? ? ) 0?
f (x)
2
1
y
故
的单调增区间为
(??
, 1), (2, ? ? );
2
1
的单调减区间为 (1 , 2).
o 12 x
11
练习 确定 f ( x ) ? ( x ? 1) ?3 x 2 的单调区间 .
4.4-5 函数的单调性,极最值,凹凸性,拐点
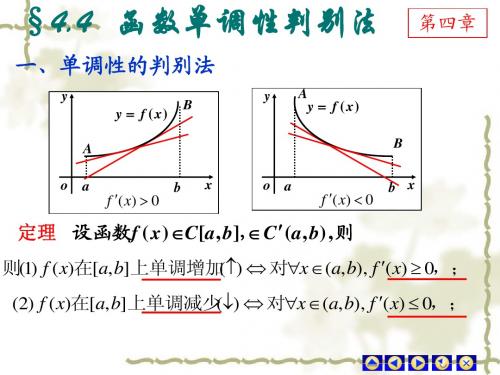
例4 求下列函数的最值
(1) y 3 ( x 2 2 x ) 2 x 0,3 4( x 1) ( x ) 解 f 33 x 2 2 x 而 令f x) 0,得驻点 x 1, x 0,2是不可导点 ( 由于f (1) 1, f ( 2) 0, f (0) 0, f ( 3) 3 9
内的所有 x 0及f x不存在的点 找出 a, b f (一般有限个) :
x 1 , x 2 , , x k ;在f a , f x 1 , f x 2 , , f x k , f b 中 选取出最大最小 ,
即为f x 在a, b上的M, m.
若 f ( x0 ) f ( x0 ) f ( x0 ) 0,f
( 4)
( x0 ) 0, 则如何?
(1).若 f ( x0 ) f ( x0 ) f ( 2n1) ( x0 ) 0,f
则f ( x)在x0处取极值 .
( 2n)
( x0 ) 0,
x
f (x) f (x)
故
( , 1)
1
0
(1 , 2)
2 0 1
( 2 , )
y
2
(2 , ); 的单调减(单减)区间 为 (1 , 2).
的单调增(单增)区间为 ( , 1) ,
2 1
o
1 2
x
说明:
1) 单调区间的分界点除驻点外,也可是导数不存在的点.
例如,
y y 3 x2
f ( x0 ) f ( x) f ( x0 ) f ( x0 )( x x0 ) ( x x0 ) 2 o ( x x0 ) 2 2!
函数的凹凸性和拐点

函数的凹凸性和拐点
函数的凹凸性和拐点是微积分中的重要概念,用于研究函数图像的形态和性质。
下面
将分别对凹凸性和拐点进行详细介绍。
一、凹凸性
在数学中,一个函数在某一区间上的凹凸性是指函数图像在该区间上是向上凸或向下凸。
几何上,一个曲线在某点处向上凸表明曲线凹向上方,而向下凸则表明曲线凹向下方。
凹凸性的判断方法是通过函数的二阶导数来进行。
如果函数的二阶导数大于零,则函
数在该点处向上凸;反之,如果函数的二阶导数小于零,则函数在该点处向下凸。
函数的图像如果是向上凸的,则可以将其形容为“形如碗状”,反之则形容为“形如
山状”或“钩状”。
在具体的分析中,凹凸性可作为确定函数的最值和极值的重要参考。
二、拐点
拐点是指函数图像上的一点,该点处曲线的凹凸性发生变化。
在拐点之前,函数图像
呈现一种凹凸性,而在拐点之后,则呈现相反的凹凸性。
因此,拐点也被称为凹凸性变化点。
拐点的判断方法是通过函数的二阶导数进行判断。
如果函数在某一点处的二阶导数发
生了从正数变成负数,或从负数变成正数的变化,则该点即为拐点。
在实际分析中,拐点
可用于确定函数的折线形态,以及确定函数的最值和极值。
综上所述,函数的凹凸性和拐点是微积分中的重要概念,用于研究函数图像的性质和
形态。
凹凸性可以帮助我们更好地理解函数的最值和极值,而拐点则可以帮助我们确定函
数的折线形态,以及确定函数的最值和极值。
在实际运用中,我们应该结合具体问题进行
分析,寻找函数的凹凸性和拐点,以便更好地解决问题。
函数的凹凸性与拐点

课程思政
课程思政:奥运精神 播放视频《谷爱凌自由式滑雪夺冠》
播放视频
曲线的凹凸性正如滑雪运动员在跳台上滑过的优美曲线。北京2022 年冬奥会自由式滑雪女子大跳台决赛,中国选手谷爱凌在最后一跳中 首次跳出了1620的超高难度,夺得金牌! 赛后,谷爱凌表示,采取超 高难度动作,想要挑战自己,并不是为了赢对手,展示自己的体育精 神。谷爱凌希望自己的精神,让大家能够体会体育精神,做到打破和 突破,成就最好的自己。我们在学习和生活中也应该向她学习不屈不 挠的奥运精神,突破自己,展现自我。
凹的
99
2凹凸性的定理 练习2 求函数y x4的凹凸性
1100
谢谢观看
2凹凸性的定理
定理 设函数 y f (x) 在 (a,b)内有二阶导数。 那么(1)若在 (a,b) 内 f (x) 0,则曲线在 (a,b) 内上凹。 (2)若在 (a,b) 内 f (x) 0,则曲线在 (a,b)内下凹。
7
2凹凸性的定理
拐点:如果点P的两侧,函数的凹凸性不一样,那么 这样的点P叫做函数的拐点。
8
2凹凸性的定理
例2 求曲线 y 3x4 4x3 1的拐点及凹、凸的区间
解: D : (,)
y 12x3 令y 0,
12x2 , 得 x1
0,
y x2
36x(x 2. 3
2). 3
x
(,0)
0
(0, 23)
2 3
(
2 3
,)
f (x)
00Biblioteka 拐点拐点f (x)
凹的
0,1 凸的
(2,11) 3 27
曲线的凹凸性与拐点
数学教研室
目录
CONTENT
3.3 单调性与凹凸性

例5、 判断曲线 f (x)
1 9
x2
解: f (x) 在定义域 Df (
2 11 f (x) 9 x 3 3 x2
3 x 的凹凸性及拐点。 , ) 内连续,
2 21 f (x) 9 9 3 x5
2 9
(1
1 )
3 x5
0
x
1
(x 0) (x 0)
以 x 1、x 0 划分定义域得:
例4、 确定函数 f (x) 2x3 9x2 12x 3 的单调区间。 解: f (x) 在定义域 Df ( , ) 内连续,
f (x) 6x2 18x 12 6(x 1)(x 2) 0 x1 1 x2 2 以 x1 1、x2 2划分定义域得:
Df ( ,1) 1 ( 1 ,2 ) 2 (2, ) f (x)
单调区间
定义: 若函数在某区间内单调增,称该区间为函数的单调增区间。
减
减
单调增区间、单调减区间统称为单调区间。
问题: 如何确定函数的单调区间
首要任务是确定函数单调性的分界点。
单调性分界点只可能产生于: 驻点 与不可导点处
方法: 用驻点及不可导点划分函数定义域, 在各个开区间内确定
导数的正负,从而确定单调区间。
(1) 当 f (x0 ) 0 时, x0 为 f (x) 的极小值点; (2) 当 f (x0 ) 0 时, x0 为 f (x) 的极大值点。
例3、 求函数 f (x) 3x x3 的极值。
解: 函数 f (x) 在其定义域 ( , ) 内连续,
f (x) 3 3x2 3(1 x)(1 x) 0 x1 f (x) 6x f ( 1) 6 0 f (1) 6 0
函数的单调性与曲线的凹凸性

2) 如果函数在某驻点两边导数同号, 则不改变函数的单调性 . 例如,
例2. 证明 证: 令
时, 成立不等式
且
证
从而
因此
证明
二、曲线的凹凸与拐点
定义 . 设函数 在区间 I 上连续 ,
(1) 若恒有 图形是凹的;
(2) 若恒有
图形是凸的 . 连续曲线上有切线的凹凸分界点 称为拐点 .
则称
则称
的凹凸区间及拐点.
2) 求拐点可疑点坐标
令
得
3) 列表判别
对应
凹
故该曲线在
及
向上凸 , 点 ( 0 , 1 ) 及
凸
凹
上向上凹, 均为拐点.
内容小结
1. 可导函数单调性判别
2.曲线凹凸与拐点的判别
在 I 上单调递增 在 I 上单调递减
+
–
拐点 — 连续曲线上有切线的凹凸分界点
思考与练习
1. 设在 或
拐点
定理2.(凹凸判定法)设函数 在区间I 上有二阶导数
(1) 在 I 内
则 f (x) 在 I 内图形是凹的 ;
(2) 在 I 内 证:
则 f (x) 在 I 内图形是凸的 . 利用一阶泰勒公式可得
两式相加
说明 (1) 成立; (2) 证毕
例3. 判断曲线 解:
的凹凸性.
故曲线
在
上是向上凹的.
说明:
1) 若在某点二阶导数为 0 , 在其两侧二阶导数不变号, 则曲线的凹凸性不变 .
2) 根据拐点的定义及上述定理, 可得拐点的判别法如下:
若曲线
或不存在,
但
在 两侧异号, 则点
是曲线
的一个拐点.
函数的凹凸性与极值点

函数的凹凸性与极值点函数的凹凸性和极值点是微积分中重要的概念。
通过研究函数的凹凸性和极值点,我们可以更加深入地理解函数的性质,进而应用于许多实际问题的求解中。
本文将详细介绍函数的凹凸性和极值点。
一、凹凸性的定义首先我们来定义函数的凹凸性。
假设函数f(x)在区间I上可导,若对于任意的x1、x2∈I且x1<x2,有f'(x1)<f'(x2),则称函数f(x)在区间I上是凹函数;若对于任意的x1、x2∈I且x1<x2,有f'(x1)>f'(x2),则称函数f(x)在区间I上是凸函数。
凹凸函数很类似于水果篮中的凹凸形状,凹函数可以想象成篮子底部向上凹陷,而凸函数则相反,底部向下凸起。
函数凹凸性的变化有助于我们分析函数的增减性、拐点等特性。
二、凹凸性与导数的关系函数的凹凸性与函数的导数密切相关。
如果函数f(x)在区间I上连续,那么f'(x)的正负性与函数的凹凸性有以下关系:1. 如果f'(x)在区间I上单调递增,那么f(x)在区间I上是凹函数;2. 如果f'(x)在区间I上单调递减,那么f(x)在区间I上是凸函数;3. 若f''(x)存在且在区间I上恒大于零,那么f(x)在区间I上是凸函数;4. 若f''(x)存在且在区间I上恒小于零,那么f(x)在区间I上是凹函数。
通过对函数的导数进行研究,我们可以得到函数的凹凸性质。
这为我们进一步分析函数的特点提供了重要的线索。
三、极值点的定义与判定接着我们来回顾一下极值点的定义。
对于函数f(x),如果存在某一点x0,使得在x0的某个邻域内,f(x0)是函数的最大值或最小值,则称x0是函数f(x)的极值点。
对于可导的函数f(x),我们可以通过导数来判断函数的极值点:1. 若f'(x0) = 0,且f''(x0)存在,则x0是函数f(x)的驻点。
2. 若f'(x0) = 0,且f''(x0) > 0,则x0是函数f(x)的极小值点。
函数的凹凸性与拐点
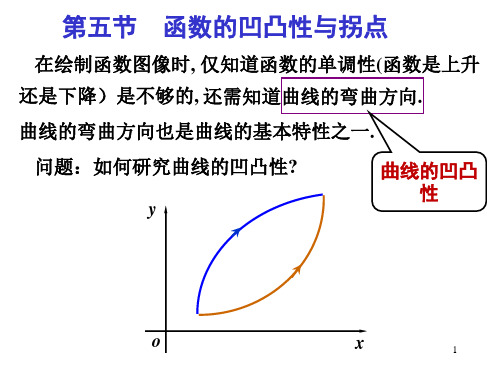
o
y
x0
x
(2) 若 x ( x0 , x0 ) 时, f ( x) 0 ,
x ( x0 , x0 ) 时, f ( x) 0 , o
x0
x
则 x0 为极小值点;
(3) 如果在上述两个区间内 f ( x) 同号,则x0 不是极值点.
极值点是函数单调性发生改变的点, 即为单调区间 的分界点.
f ( x1 x2 )
凹(上2 凹、下凸)
o x1 x1 x2 x2
2
xo
f ( x1 x2 ) 2
y f (x)
f ( x1 ) f ( x2 ) 2
凸 (下凹、上凸)
x1 x1 x2 x2
x
2
图形上任意弧段位于 所张弦的下方:凹
图形上任意弧段位于 所张弦的上方:凸
f ( x1 x2 ) f (x1) f (x2 ) . f ( x1 x2 ) f (x1) f (x2 ) .
令y 0,
得
x1
0,
x2
2. 3
3
x
(,0)
0
(0, 2 3)
2 3
(23 ,)
f ( x)
0
0
f ( x) 拐点
拐点
f (x)的凹区间为(, 0), ( 2 , +)
凸区间为 [0, 2] 3
3
拐点:(0,1),(2 3 ,1127).
11
例3 求曲线 y (x 1) 3 x2 的凹凸区间与拐点.
y
拐点 非拐点
12
例3 求曲线 y (x 1) 3 x2 的凹凸区间与拐点.
函数的凹凸性与拐点

图1函数的单调性可用函数的一阶导函数来判定,对于同样的递增函数有着不同的增法,如向上凸的增或凹的增,那么对于这两种不同的增法我们如何刻画呢?一、曲线的凹凸与拐点1.曲线的凹凸定义和判定法从图1可以看出曲线弧ABC 在区间()c a ,内是向下凹入的,此时曲线弧ABC 位于该弧上任一点切线的上方;曲线弧CDE 在区间()b c ,内是向上凸起的,此时曲线弧CDE 位于该弧上任一点切线的下方.关于曲线的弯曲方向,我们给出下面的定义:定义1 如果在某区间内的曲线弧位于其任一点切线的上方,那么此曲线弧叫做在该区间内是凹的;如果在某区间内的曲线弧位于其任一点切线的下方,那么此曲线弧叫做在该区间内是凸的.例如,图1中曲线弧ABC 在区间()c a ,内是凹的,曲线弧CDE 在区间()b c ,内是凸的. 由图1还可以看出,对于凹的曲线弧,切线的斜率随x 的增大而增大;对于凸的曲线弧,切线的斜率随x 的增大而减小.由于切线的斜率就是函数()x f y =的导数,因此凹的曲线弧,导数是单调增加的,而凸的曲线弧,导数是单调减少的.由此可见,曲线()x f y =的凹凸性可以用导数()x f '的单调性来判定.而()x f '的单调性又可以用它的导数,即()x f y =的二阶导数()x f ''的符号来判定,故曲线()x f y =的凹凸性与()x f ''的符号有关.由此提出了函数曲线的凹凸性判定定理:定理1 设函数()x f y =在()b a ,内具有二阶导数.(1)如果在()b a ,内,()x f ''>0,那么曲线在()b a ,内是凹的;(2)如果在()b a ,内,()x f ''<0,那么曲线在()b a ,内是凸的. x y o ()y f x =A B x yo ()y f x =A B图2例1 判定曲线3x y =的凹凸性.2.拐点的定义和求法定义2 连续曲线上凹的曲线弧和凸的曲线弧的分界点叫做曲线的拐点. 定理2(拐点存在的必要条件) 若函数()x f 在0x 处的二阶导数存在,且点()()00,x f x 为曲线()x f y =的拐点,则().00=''x f我们知道由()x f ''的符号可以判定曲线的凹凸.如果()x f ''连续,那么当()x f ''的符号由正变负或由负变正时,必定有一点0x 使()0x f ''=0.这样,点()()00,x f x 就是曲线的一个拐点.因此,如果()x f y =在区间()b a ,内具有二阶导数,我们就可以按下面的步骤来判定曲线()x f y =的拐点:(1) 确定函数()x f y =的定义域;(2) 求()x f y ''='';令()x f ''=0,解出这个方程在区间()b a ,内的实根;(3) 对解出的每一个实根0x ,考察()x f ''在0x 的左右两侧邻近的符号.如果()x f ''在0x 的左右两侧邻近的符号相反,那么点()()00,x f x 就是一个拐点,如果()x f ''在0x 的左右两侧邻近的符号相同,那么点()()00,x f x 就不是拐点.例2 求曲线233x x y -=的凹凸区间和拐点.解 (1)函数的定义域为()+∞∞-,;(2)()1666,632-=-=''-='x x y x x y ;令0=''y ,得1=x ;(3)列表考察y ''的符号(表中“∪”表示曲线是凹的,“∩” 表示曲线是凸的): x()1,∞- 1 ()+∞,1 y ''- 0 + 曲线y ∩ 拐点 ()2,1- ∪由上表可知,曲线在()1,∞-内是凸的,在()+∞,1内是凹的;曲线的拐点为()2,1-.例3 已知点(1,3)为曲线32y ax bx =+的拐点,求,a b的值。
函数的单调性与曲线的凹凸性

则称曲线 y f ( x) 在 I 上是凹的.
类似地,可给出曲线是凸的定义,若上式中不等 号反向,则称曲线 y f ( x) 在 I 上是凸的.
直接利用定义来判别曲线的凹凸性是比较困难的, 下面利用二阶导数来判别曲线的凹凸性.
x2
的凹凸性.
(详细解答过程可参见课本 P108)
例 3.4.8 判别曲线 y x3 的凹凸性. (详细解答过程可参见课本 P109)
3、拐点的定义
在例 3.4.8 中,点(0,0)是曲线由凸变凹的分界点, 称为曲线的拐点.
一般地,连续曲线 y f ( x) 上凹弧与凸弧的分界点 称为曲线的拐点.
x2 2
,
令 y 0 得拐点可疑点 : x 1 , x 1 (横坐标 )
x
( , 1)
1
0
(1, 1)
1
(1, )
y
y
0
凸的
凹的
拐点
拐点
凹的
曲线 y e
x2 2
: 在 ( , 1) 及 (1, ) 内为凹的 ,
在 (1, 1)内为凸的 .
当 x 0 时, f ( x) 0 , (,0] 上单调减少;
当 0 x 时, f ( x) 0 , [0, ] 上单调增加;
[0, ). 单调区间为( ,0],
注意:学习课本例 3 与例 4 之间的一段话
例 3.4.4 确定函数 f ( x) (2x 5) x
2、曲线凹凸性的判定
定理 3.4.3 设 f ( x) 在区间 I 上具有二阶导数 . (1)若在区间 I 上, f ( x) 0 ,则曲线 y f ( x) 是凹的; (2)若在区间 I 上, f ( x) 0 ,则曲线 y f ( x) 是凸的.
函数的凹凸性与拐点
得证.
15
不等式证明的方法:
1、拉格朗日中定理;
2、函数的单调性、极值; 3、函数的凹凸性;
16
作业:
P 3 134
17
爱是什么? 一个精灵坐在碧绿的枝叶间沉思。 风儿若有若无。 一只鸟儿飞过来,停在枝上,望着远处将要成熟的稻田。 精灵取出一束黄澄澄的稻谷问道:“你爱这稻谷吗?” “爱。” “为什么?” “它驱赶我的饥饿。” 鸟儿啄完稻谷,轻轻梳理着光润的羽毛。 “现在你爱这稻谷吗?”精灵又取出一束黄澄澄的稻谷。 鸟儿抬头望着远处的一湾泉水回答:“现在我爱那一湾泉水,我有点渴了。” 精灵摘下一片树叶,里面盛了一汪泉水。 鸟儿喝完泉水,准备振翅飞去。 “请再回答我一个问题,”精灵伸出指尖,鸟儿停在上面。 “你要去做什么更重要的事吗?我这里又稻谷也有泉水。” “我要去那片开着风信子的山谷,去看那朵风信子。” “为什么?它能驱赶你的饥饿?” “不能。” “它能滋润你的干渴?” “不能。”爱是什么? 一个精灵坐在碧绿的枝叶间沉思。 风儿若有若无。 一只鸟儿飞过来,停在枝上,望着远处将要成熟的稻田。 精灵取出一束黄澄澄的稻谷问道:“你爱这稻谷吗?” “爱。” “为什么?” “它驱赶我的饥饿。” 鸟儿啄完稻谷,轻轻梳理着光润的羽毛。 “现在你爱这稻谷吗?”精灵又取出一束黄澄澄的稻谷。 鸟儿抬头望着远处的一湾泉水回答:“现在我爱那一湾泉水,我有点渴了。” 精灵摘下一片树叶,里面盛了一汪泉水。 鸟儿喝完泉水,准备振翅飞去。 “请再回答我一个问题,”精灵伸出指尖,鸟儿停在上面。 “你要去做什么更重要的事吗?我这里又稻谷也有泉水。” “我要去那片开着风信子的山谷,去看那朵风信子。” “为什么?它能驱赶你的饥饿?” “不能。” “它能滋润你的干渴?” “不能。”
函数单调性极值最值与凹凸性拐点1

解
f
(
x)
2
(
x
1
2) 3
( x 2)
3
当x 2时, f ( x)不存在. 但函数f ( x)在该点连续.
当x 2时,f ( x) 0;
M
当x 2时,f ( x) 0.
f (2) 1为f ( x)的极大值.
三、小结
极值是函数的局部性概念:极大值可能小于极小 值,极小值可能大于极大值.
(1) 求导数 f ( x);
(2) 求驻点,即方程 f (x) 0的根;导数不存在的点
(3)这些点将定义域分成若 干区间并判断 f '(x)符号 (4) 求极值.
例1 求出函数 f ( x) x3 3x2 9x 5 的极值. 解 f ( x) 3x2 6x 9 3( x 1)(x 3) 令 f ( x) 0, 得驻点 x1 1, x2 3. 列表讨论
当2 x 时, f ( x) 0, 在[2,)上单调增加;
单调区间为 (,1], [1,2],[2,).
例3 确定函数 f ( x) 3 x2 的单调区间.
解 D : (,).
f ( x) 2 , 33 x
( x 0)
当x 0时,导数不存在.
y 3 x2
当 x 0时,f ( x) 0, 在(,0]上单调减少;
利用泰勒公式]
练习题答案
一、1、(,1],[3,)单调增加,[1,3] 单调减少; 2、增加,(,1],[1,) 3、(,1],[1,) ;[1,0),(0,1];(,1],(0,1].
二、1、在(,0),(0, 1],[1,) 内单调减少, 2
在[1 ,1]上单调增加; 2
2、在(, 2 a],[a,)内单调增加, 3
34 函数的单调性、凹凸性与极值

(2)求拐点的方法
方法: 设函数f ( x )在 x0的邻域内二阶可导, 且 f ′′( x0 ) = 0, 则有:
1) x0 两近旁f ′′( x )变号, 点( x0 , f ( x0 ))为拐点;
2) x0 两近旁f ′′( x )不变号, 点( x0 , f ( x0 ))不是拐点.
例9 求曲线 y = 3 x 4 − 4 x 3 + 1 的拐点及凹、凸的区间. 解 易见函数的定义域为 ( −∞ ,+∞ ),
定理4 (第一充分条件) 设函数 f ( x ) 在点 x0 的某个邻域内连续并且 可导(导数 f ′( x0 ) 也可以不存在), (1)如果在点 x0的左邻域内 f ′( x ) > 0; 在点 x0的右 邻域内 f ′( x ) < 0, 则 f ( x ) 在 x0 处取得极大值 f ( x0 ); (2)如果在点 x0的左邻域内 f ′( x ) < 0; 在点 x0的右 邻域内 f ′( x ) > 0, 则 f ( x ) 在 x0 处取得极小值 f ( x0 ); (3)如果在点 x0的邻域内, 在 x0处没有极值.
例3
2 3 y = x 讨论函数 的单调区间.
解 Q D : ( −∞ ,+∞ ).
y′ = 32 ( x ≠ 0), 3 x 当 x = 0 时, 导数不存在.
当 x < 0时,y′ < 0,
∴ 在 ( −∞ , 0]上单调减少;
当 x > 0时,y′ > 0,
∴ 在 [0, +∞ )上单调增加;
向上凸:图形 上任意弧段位 于所张弦的上 方
定义 设 f ( x ) 在区间 I 内连续,
x1 + x 2 f ( x1 ) + f ( x 2 ) ∀x1 , x2 ∈ I , 恒有 f ( )< , 2 2 则称 f ( x ) 在 I 上的图形是(向上)凹的. x1 + x 2 f ( x1 ) + f ( x 2 ) ∀x1 , x2 ∈ I , 恒有 f ( )> , 2 2
微分学中函数的凹凸性与拐点

微分学中函数的凹凸性与拐点微分学是数学中一个重要的分支,通过研究函数的变化率和曲线的特征,可以帮助我们更好地理解数学和物理问题。
其中,函数的凹凸性和拐点是微分学中的两个重要概念,它们可以帮助我们分析函数的性质和图像的特点。
一、函数的凹凸性函数的凹凸性表示的是函数曲线的弯曲程度。
具体来说,若函数$y=f(x)$在区间$I$上连续且在$I$上有可导的二阶导数,则函数$f(x)$在该区间的凹凸性可通过二阶导数的正负性进行判断。
1. 凹函数与凸函数函数$f(x)$在区间$I$上是凹函数,当且仅当对于区间$I$上的任意两个不同的实数$x_1,x_2$以及介于它们之间的任意实数$t \in (0,1)$,有以下不等式成立:$$f(tx_1 + (1-t)x_2) \ge tf(x_1) + (1-t)f(x_2)$$即曲线的下方比直线连接处更低。
而函数$f(x)$在区间$I$上是凸函数,则是指对于区间$I$上的任意两个不同的实数$x_1,x_2$以及介于它们之间的任意实数$t \in (0,1)$,有以下不等式成立:$$f(tx_1 + (1-t)x_2) \le tf(x_1) + (1-t)f(x_2)$$即曲线的下方比直线连接处更高。
2. 判定凹凸性的方法通过计算函数的二阶导数可以判断函数的凹凸性。
若函数$f(x)$在区间$I$上连续并且两阶可导,且对于区间$I$上任意$x$,有$f''(x)>0$,则函数$f(x)$在区间$I$上是凹的;若对于区间$I$上任意$x$,有$f''(x)<0$,则函数$f(x)$在区间$I$上是凸的。
二、函数的拐点函数的拐点是指函数曲线由凸转为凹,或由凹转为凸的点。
具体来说,若函数$y=f(x)$在区间$I$上连续且在$I$上有可导的二阶导数,则函数$f(x)$在该区间的拐点可以通过二阶导数的变号来判断。
1. 判定拐点的方法通过计算函数的二阶导数的符号变化可以判断函数的拐点。
函数的极值与拐点

函数的极值与拐点函数的极值与拐点是数学中常见的概念,它们与函数的变化趋势密切相关。
通过研究函数在某个区间上的增减性、单调性以及二阶导数的符号等,我们可以确定函数的极值点和拐点。
本文将详细讨论函数的极值与拐点的定义、判定方法及其在实际问题中的应用。
一、函数的极值首先,我们来定义函数的极值。
对于函数f(x),如果在某个点x=a 处,存在一个邻域,使得在这个邻域内,函数值f(x)小于或大于f(a),那么我们称f(a)为函数的极大值或极小值,简称极值。
极大值和极小值的统称为极值。
那么如何判定函数的极值呢?我们给出以下定理:定理1:若函数f(x)在[a,b]上连续,在(a,b)内可导,且在(x=a)和(x=b)处的导数值不为0,则:1. 当导数恒大于0时,函数在[a,b]上单调递增,且在x=a处取得极小值,x=b处取得极大值;2. 当导数恒小于0时,函数在[a,b]上单调递减,且在x=a处取得极大值,x=b处取得极小值。
以上定理提供了一种判定函数极值的方法,但并不是所有函数的极值都可以通过导数来求解。
对于二次函数、三次函数等特殊函数,可以通过求解导数为0的方程来找到极值点。
二、函数的拐点接下来,我们来定义函数的拐点。
对于函数f(x),如果在某个点x=a处,左极限f(a-)和右极限f(a+)存在且相等,且在该点左右两侧函数的凹凸性改变,那么我们称a为函数的拐点。
如何判定函数的拐点呢?我们给出以下定理:定理2:若函数f(x)在[a,b]上连续,在(a,b)内二阶可导,则:1. 当二阶导数f''(x)恒大于0时,函数在[a,b]上凹,且拐点位于(a,b)内;2. 当二阶导数f''(x)恒小于0时,函数在[a,b]上凸,且拐点位于(a,b)内;3. 当二阶导数f''(x)为0时,函数存在可能的拐点。
以上定理意味着,函数的凹凸性与二阶导数的符号有直接关系。
通过求解二阶导数为0的方程,我们可以找到可能的拐点,然后进一步确定拐点是否存在。
函数的单调性与极值、最值

THANKS FOR WATCHING
感谢您的观看
金融问题
在投资组合理论中,凹凸性可以用来描述投资组合的风险和回报之间的关系。投资者可以根据自己的风 险承受能力和投资目标,选择合适的投资组合策略。
05 函数的拐点
函数拐点定义
函数拐点是指函数图像上凹凸 性发生变化的点,即函数的一 阶导数在该点为零或不存在的 点。
在数学上,函数拐点的定义是 函数在某点的二阶导数为零的 点,即$f''(x)=0$。
最值的求法
代数法
通过求导数、找驻点、判断单调性等方法来求解 最值。
无穷区间法
利用极限的思想,将函数在无穷区间上的最值转 化为有限区间上的最值。
几何法
通过函数图像,直观地观察函数的最大值和最小 值。
最值在实际问题中的应用
01
优化问题
在生产、运输、分配等实际问题 中,常常需要通过求解最值来达 到最优解。
定义法
通过比较任意两点之间的函数值来判断函数的单调性。如 果任意两点之间的函数值都满足增减性条件,则函数在该 区间内单调。
图像法
通过观察函数的图像来判断函数的单调性。如果在图像上 随着$x$的增大,$y$的值也增大(或减小),则函数在该 区间内单调递增(或递减)。
Hale Waihona Puke 单调性在实际问题中的应用单调性与最值
单调性与优化问题
在解决优化问题时,可以利用函数的单调性来找到最优解。例如,在求解最大值或最小值 问题时,可以利用函数的单调性来确定搜索区间,从而缩小搜索范围,提高求解效率。
02 函数的极值
函数极值的定义
极值点
函数在某点的值比其邻近点的值大或小的点。
极大值
函数在某点的值比其左侧邻近点的值大,比 其右侧邻近点的值小。
单调性.凹凸性.极值与最值

f (x) 0, x I
在 I 上单调递增 在 I 上单调递减
+
f (x) 0, x I
–
拐点 — 连续曲线上有切线的凹凸分界点
机动 目录 上页 下页 返回 结束
三、函数的极值及其求法
定义:
在其中当
时,
(1)
则称 为 的极大点 ,
称 为函数的极大值 ;
x 1
(x 1)2
函数曲线在定义域 -1,+ 内上凹.
例2. 判断曲线
的凹凸性.
y
解: y 4x3,
故曲线
在
上是向上凹的. o x
说明:
1) 若在某点二阶导数为 0 , 在其两侧二阶导数不变号,
则曲线的凹凸性不变 .
2) 根据拐点的定义及上述定理, 可得拐点的判别法如下:
若曲线
或不存在,
证明 y x sin x,x (, ) y' 1 cos x 0, x (, )
且y仅在离散点x 2k (k N )等于0,
y x sin x是单调增函数,
例2. 确定函数
的单调区间.
解: f (x) 6x2 18x 12 6(x 1)(x 2)
当 x 1 时, f ( x) f (1) 0,
即 x 1时,2 x 3 1 x
例5 证明:方程 xex =2在(0,1)内有且仅有一个实根
证明 设f (x) xex -2,因f (x)在[0,1]上连续, 且f (0) 2 0, f (1) e 2 0.由零值定理,
(3) 以(2)中所找点为分界点,将定义域分割成部分区间, 判断在每一区间上导数的符号,由定理得出结论。
函数的拐点与极值的判断

拐点与极值的联系
拐点和极值都是函数图像上的点,具有特定的几何意义。 拐点和极值都是函数的一阶导数在该点附近的行为发生变化的表现。 拐点和极值在某些情况下是相互关联的,例如在单峰函数中,拐点通常位于极值点附近。 判断拐点和极值的方法通常需要使用导数或二阶导数,并分析其符号变化。
社会科学:拐点 与极值可以用于 研究社会现象的 变化趋势,如人 口增长、经济发 展等,为政策制 定提供科学依据。
感谢观看
汇报人:XX
02
函数的极值判断
极值的定义
极值点:函数在 某点的值大于或 小于其邻近点的 值
极值:函数在极 值点处的函数值
局部极值:在一 定区间内函数达 到最大或最小值 的点
全局极值:在整 个定义域内函数 达到最大或最小 值的点
极值的判断方法
判断导数:导数等于0的点可能是极值点
判断二阶导数:二阶导数大于0的点是极小值点,二阶导数小于0的点是极大值点
拐点与极值的区别
定义不同:拐点是函数图像上凹 凸的分界点,而极值是函数在某 点的值大于或小于其邻近点的值。
判断方法不同:拐点的判断需要 考察函数的一阶导数和二阶导数, 而极值的判断需要考察函数的一 阶导数。
添加标题
添加标题
添加标题
添加标题
性质不同:拐点不一定是极值点, 但极值点一定是拐点。
应用场景不同:拐点常用于研究 函数的凹凸性,而极值常用于研 究函数的最大值和最小值。
判断一阶导数的符号变化:如果在某点的左侧导数大于0,右侧导数小于0,则该点为 极大值点,反之则为极小值点 判断函数值:如果在某点的左侧函数值大于右侧函数值,则该点为极大值点,反之则为 极小值点
极值的Байду номын сангаас质
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10 1、 y ; 3 2 4x 9x 6x 2 2、 y 3 ( 2 x a )(a x ) 3、 y x sin 2 x .
a ( 0 );
三、证明下列不等式: 1、当 x 0 时,1 x ln( x 1 x 2 ) 1 x 2 ; 2、当 x 4 时,2 x x 2 ; 1 3 3、若 x 0 ,则sin x x x . 6 四、方程 ln x ax (a 0) 有几个实根.
练习题
一、填空题: 1、函数 y 2 x 3 6 x 2 18 x 7 单调区间为________ _____________. 2x 2、函数 y 在区间[-1,1]上单调________, 2 1 x 在_________上单调减. 2 2 3、函数 y x ln x 的单调区间为____________, 单减区间为_____________.
二、单调区间求法
问题:如上例,函数在定义区间上不是单调的, 但在各个部分区间上单调.
定义:若函数在其定义域的某个区间内是单调 的,则该区间称为函数的单调区间. 导数等于零的点和不可导点,可能是单调区间 的分界点. 方法: 用方程 f ( x ) 0的根及 f ( x ) 不存在的点
来划分函数 f ( x )的定义区间 , 然后判断区间内导 数的符号.
思考题
若 f (0) 0 ,是否能断定 f ( x ) 在原点的 充分小的邻域内单调递增?
思考题解答
不能断定.
1 2 x 2 x sin , x 0 例 f ( x) x 0, x0
1 f (0) lim (1 2 x sin ) 1 0 x 0 x 1 1 但 f ( x ) 1 4 x sin 2 cos , x x x0
k k 3、在[ , ]上单调增加, 2 2 3 k k 在[ , ] 上单调减少,( k 0,1, 2, ) . 2 3 2 2 1 四、(1)a 时没有实根; e 1 (2) 0 a 时有两个实根; e xe 1 (3)a 时只有 一个实根. e
极小值 f ( 3) 22.
f ( x ) x 3 3 x 2 9 x 5图形如下
M
m
定理3(第二充分条件)设 f ( x ) 在x0 处具有二阶导数, 且 f ' ( x0 ) 0 , f '' ( x0 ) 0 , 那末 f '' ( x0 ) 0 时, 函数 f ( x ) 在x0 处取得极大值; (1)当 '' (2)当 f ( x0 ) 0 时, 函数 f ( x ) 在x0 处取得极小值.
所以,函数 f ( x ) 在x0 处取得极大值.同理可证(2).
例2 求出函数 f ( x ) x 3 3 x 2 24 x 20 的极值. 解
f ( x ) 3 x 2 6 x 24 3( x 4)( x 2)
x2 2.
令 f ( x ) 0, 得驻点 x1 4,
解 y e x 1. 又 D : ( ,).
在( ,0)内, y 0,
函数单调减少;
在(0,)内, y 0,
函数单调增加 .
注意:函数的单调性是一个区间上的性质,要用 导数在这一区间上的符号来判定,而不能用一 点处的导数符号来判别一个区间上的单调性.
练习题答案
[ 一、1、( ,1], [ 3, ) 单调增加, 1,3] 单调减少; 2、增加,( ,1], [1, ) 3、( ,1] ,[1, ) ;[ 1,0 ), ( 0,1]; ( , 1], ( 0,1]. 1 二、1、在( ,0), ( 0, ], [1,) 内单调减少, 2 1 在[ ,1]上单调增加; 2 2 2、在( , a ], [a ,) 内单调增加, 3 2 在[ 3 a , a ] 上单调减少;
f ( x ) 0, 在[1,2]上单调减少;
当2 x 时, f ( x ) 0, 在[2,)上单调增加;
单调区间为 ( ,1], [1,2], [ 2, ).
例3
确定函数 f ( x ) 3 x 2 的单调区间.
解 D : ( , ).
函数极值及其求法
一、函数极值的定义 二、函数极值的求法 三、小结 思考题
一、函数极值的定义
y
y f ( x)
ax
y
1
o
x2
x3
x4
x5
x6
b
x
y
o
x0
x
o
x0
x
定义 设函数f ( x )在区间(a , b )内有定义, x0是
(a , b )内的一个点, 如果存在着点x0的一个邻域, 对于这邻域内的 任何点x ,除了点x0外, f ( x ) f ( x0 )均成立, 就称 f ( x0 )是函数f ( x )的一个极大值; 如果存在着点x0的一个邻域, 对于这邻域内的 任何点x ,除了点x0外, f ( x ) f ( x0 )均成立, 就称 f ( x0 )是函数f ( x )的一个极小值.
例2 确定函数 f ( x ) 2 x 3 9 x 2
12 x 3的单调区间.
解 D : ( , ).
f ( x ) 6 x 2 18 x 12 6( x 1)( x 2)
解方程f ( x ) 0 得, x1 1, x2 2.
当 x 1时, f ( x ) 0, 在(,1]上单调增加; 当1 x 2时,
函数单调性的判定法
一、单调性的判别法 二、单调区间求法
三、小结 思考题
一、单调性的判别法
y
y f ( x)
A
B
y
A y f ( x)
B
oaf ( x源自) 0bxo a
f ( x ) 0
b x
定理 设函数 y f ( x )在[a, b]上连续,在( a, b )内可 导(1) . 如果在( a, b )内f ( x ) 0,那末函数 y f ( x ) 在[a, b]上单调增加; ( 2) 如果在( a, b )内 f ( x ) 0, 那末函数 y f ( x ) 在[a, b]上单调减少.
注意:区间内个别点导数为零,不影响区间的单调性.
y x 3 , y x 0 0, 但在( ,)上单调增加. 例如,
例4 当x 0时, 试证x ln(1 x )成立.
x . 证 设f ( x ) x ln(1 x ), 则 f ( x ) 1 x
f ( x )在[0,)上连续, 且(0,)可导,f ( x ) 0,
( x ) 3 x 2 6 x 9 3( x 1)( x 3) f
令 f ( x ) 0, 得驻点 x1 1, x2 3. 列表讨论
x
f ( x )
f ( x)
( ,1) 1
(1,3)
3
0
极 小 值
( 3, )
0
极 大 值
极大值 f (1) 10,
f ( x2 ) f ( x1 ). y f ( x )在[a , b]上单调增加 .
若在(a , b)内, ( x ) 0, 则 f ( ) 0, f
f ( x2 ) f ( x1 ). y f ( x )在[a , b]上单调减少.
例1 讨论函数y e x x 1的单调性.
点 注意: 可导函数 f ( x ) 的极值点必定是它的驻 , 但函数的驻点却不一定 是极值点.
y x 3 , y x 0 0, 例如,
但x 0不是极值点.
定理2(第一充分条件)
(1)如果 x ( x0 , x0 ), 有 f ' ( x ) 0;而 x ( x0 , x0 ) , x 有 f ' ( x ) 0 ,则 f ( x )在 处取得极大值. (2)如果 x ( x0 , x0 ), 有 f ' ( x ) 0;而 x ( x0 , x0 ) f ' ( x ) 0 ,则 f ( x )在x0 处取得极小值. 有 ' (3)如果当 x ( x0 , x0 ) 及 x ( x0 , x0 ) 时, f ( x ) 符号相同,则 f ( x ) 在 x0 处无极值.
a, 五、设 f ( x ) 在[a, b ]上连续,在( b )内 f ( x ) ,试证 x x 明:对于[a, b ]上任意两 1 , 2 有 x1 x 2 f ( x1 ) f ( x 2 ) f( ) [提示:方法(1) 2 2 f ( x ) 0 , f ( x ) 单增;方法(2) f ( x ) 0 , 利用泰勒公式]
在[0,)上单调增加; f (0) 0,
当x 0时,x ln(1 x ) 0, 即 x ln(1 x ).
三、小结
单调性的判别是拉格朗日中值定理的重要应用. 定理中的区间换成其它有限或无限区间,结论 仍然成立. 应用:利用函数的单调性可以确定某些方程实 根的个数和证明不等式.
函数的极大值与极小值统称为极值,使函数取得 极值的点称为极值点.
二、函数极值的求法
定理1(必要条件) 设 f ( x ) 在点 x0 处具有导数,且 在 x0 处取得极值,那末必定 f ' ( x0 ) 0 . 定义 使导数为零的点即方程 f ( x ) 0 的实根)叫 (
做函数 f ( x ) 的驻点.
(1) f ( x0 ) lim f ( x0 x ) f ( x0 ) 0, 证
