单因素方差分析与多重比较
数据多重比较法

单因素方差分析单因素方差分析也称作一维方差分析。
它检验由单一因素影响的一个(或几个相互独立的)因变量由因素各水平分组的均值之间的差异是否具有统计意义。
还可以对该因素的若干水平分组中哪一组与其他各组均值间具有显著性差异进行分析,即进行均值的多重比较。
One-Way ANOVA过程要求因变量属于正态分布总体。
如果因变量的分布明显的是非正态,不能使用该过程,而应该使用非参数分析过程。
如果几个因变量之间彼此不独立,应该用Repeated Measure过程。
[例子]调查不同水稻品种百丛中稻纵卷叶螟幼虫的数量,数据如表5-1所示。
表5-1 不同水稻品种百丛中稻纵卷叶螟幼虫数数据保存在“DATA5-1.SAV”文件中,变量格式如图5-1。
图5-1分析水稻品种对稻纵卷叶螟幼虫抗虫性是否存在显著性差异。
1)准备分析数据在数据编辑窗口中输入数据。
建立因变量“幼虫”和因素水平变量“品种”,然后输入对应的数值,如图5-1所示。
或者打开已存在的数据文件“DATA5-1.SAV”。
2)启动分析过程点击主菜单“Analyze”项,在下拉菜单中点击“Compare Means”项,在右拉式菜单中点击“0ne-Way ANOVA”项,系统打开单因素方差分析设置窗口如图5-2。
图5-2 单因素方差分析窗口3)设置分析变量因变量:选择一个或多个因子变量进入“Dependent List”框中。
本例选择“幼虫”。
因素变量:选择一个因素变量进入“Factor”框中。
本例选择“品种”。
4)设置多项式比较单击“Contrasts”按钮,将打开如图5-3所示的对话框。
该对话框用于设置均值的多项式比较。
图5-3 “Contrasts”对话框定义多项式的步骤为:均值的多项式比较是包括两个或更多个均值的比较。
例如图5-3中显示的是要求计算“1.1×mean1-1×mean2”的值,检验的假设H0:第一组均值的1.1倍与第二组的均值相等。
方差分析(单因素、多因素方差分析)

单因素方差分析1.基本理解方差分析:是一种利用实验获取数据并进行分析的统计方法,经常用于研究不同效应对指定实验的影响是否显著。
方差分析用于检验连续型随机变量在三及以上分类数据不同水平上的差异情况。
方差分析包括:单因素方差分析、多元素方差分析、多元方差分析、协方差分析、重复测量方差分析。
在问卷数据中:单因素方差分析使用较多。
单因素方差分析:用于检验单个因素取不同水平是某因变量的均值是否有显著的变化,也可进一步用于因变量均值的多重比较(检验某些水平下的实验结果具体区别于其他水平的显著差异)。
图1检验步骤2.单因素方差分析操作步骤操作步骤第一步:首先将数据导入spss中并进行赋值后,点击分析、比较平均值、单因素ANOVA检验。
图2单因素方差分析第一步操作步骤第二步:进入图中对话框后将需检验的变量放入因变量列表中,在因子中放入分类变量,点击事后比较勾选假定等方差(LSD),不假定等方差(塔姆黑泥T2)点击继续。
图3单因素方差分析事后比较勾选3.当因素方差分析结果后点击线性进入图中下方选项框、勾选描述、方差齐性检验点击继续、确定。
图4单因素方差分析选项勾选然后单因素方差分析的描述、方差齐性、假设检验就出来了。
图5单因素方差分析结果单因素方差分析事后两两比较结果。
图6事后比较结果4.结果整理将首先将描述统计的结果粘贴复制到Excel表格中进行整理,保留均值和标准差及前面的内容,后在后面加入ANOVA表中的F和p值,将整理好的两两比较结果粘贴到表格的最后,最后将整理好的结果粘贴到Word文档中进行整理。
可参考图中结果整理。
(注:一般在看结果时首先看ANOVA表的结果,看显著情况,显著(p<0.05)看方差齐性检验的结果,若方差齐性检验的结果方差齐(p>0.05),然后再看事后比较的结果,方差齐看LSD,方差不齐看塔姆黑泥的结果,同样差异的显著看事后比较每行对应的显著性(若p<0.05,代表比较的对象显著。
单因素试验

• 同时考虑如下 Cr2 个假设的检验问题,
H
ij 0
: i
j ,i
j, i,
j
1,2,
,r .
•
样本均值
yi
应是
i
的很好估计,若
H
ij 0
为真,
yi y j
不应过大,过大就应拒绝
H
ij 0
.
5.效应模型
在单因子试验中,对水平 A1, A2 , , Ar 的选择方式有二种: •r 个水平 A1, A2 , , Ar 是特定的,如四个玉米品种,现要
3.单因素试验的方差分析
设 A 表示欲考察的因素,它的 r个不同水平,对应
的作指若标干视次作重复r 试个验总:体nX1,1n, X2 ,2.,....n.Xr .r(. 每可个等水重平复下也,可我不们等
重复),同一水平的
的一个样本:X i1, X i2 ,
ni 个结果,就是这个总体
...X ini .
0
H
1:
2 a
0
若拒绝
H
0
,就意味着
2 a
>0,从而认定
A
的随机效应存
在显著差异,
2 a
愈大,此种差异就愈大。
在方差分析中,总平方和的分解和检验的统计量都
与固定效应完全一样,只是各平方和的含义略有差别。
谢谢! 请老师和同学们指正!
如今我们选用不平衡设计,即A1, A2, A3, A4分别制作
了7,5,6,6个样品,共有24个样品等待测试。
2.单因素试验举例——随机化
• 这里一次测试就是一次试验,试验次序要随机化。
因子 A 的水平
试验编号
A1
单因素的方差分析和LSR法多重比较Excel表格计算

1、划分变异原因总变异=处理间变异+区组间变异+误差变异2、列出试验结果并初步计算,求处理和T,区组和T ,和总和T。
3、分解并计算各项平方和、自由度(1)求平方和n (区组)=4k (处理)=6矫正数39609.37501257.631099.3855.46102.79(2)求各项自由度235使用说明:①使用前请详细阅读文档为娱乐学习之用,处理及区组均为10个,作中的蓝字为使用者填入,其他如工作表、格式及果给予重视,如为“不能反映处理间效应”或“一、单因素随机化完全区组设计的方差分析2=nkT C =k 2i i=11n A SS C T ∙==∑-==∑=C SS T B -n 1j 2j .k 1=--=SS SS SS SS B A T e ==1-nk T f =-=1f k A =-=1n f B --=)1)(1(n k f e n n 2ij i=1j=1x T SS C ==∑∑-3155、进行F检验64(2)求F值32.092.70(3)查F表(4)检验由表中F值和F临界值相比较得知:①否定H01,差异极显著2②接受H02,区组间差异不显著1结论:该项试验结果能极显著反映处理间的效应。
已知k=65种 , n=41.30893 3.16 4.351.3089 4.14 5.69②4 3.25 4.461.3089 4.25 5.84③5 3.31 4.551.3089 4.33 5.95④6 3.36 4.611.3089 4.40 6.03⑤0#VALUE!#VALUE! 1.3089#VALUE!#VALUE!⑥二、邓肯(Duncan)多重极差法(LSR法),a有2、3……等(1)求LSR(1)H 01:α1=α2=…=αH 02;β1=β2=…=β=1-nk T f =-=1f k A =-=1n f B =--=)1)(1(n k f e ==22/e A A S S F 22e /=B B F S S =X S =0#VALUE!#VALUE! 1.3089#VALUE!#VALUE!⑦0#VALUE!#VALUE! 1.3089#VALUE!#VALUE!⑧细阅读统计学有关资料,按照相关要求进行完善,同时建议按照统计学示例进行验算;②本之用,处理及区组均为10个,作者不承担由使用该文档而产生的法律责任,如不赞同,请删除;③文者填入,其他如工作表、格式及公式等内容请勿非专业改动或删除;④在输入数据后请对方差分析结为“不能反映处理间效应”或“不能接受”,多重比较已无意义,请核对原始数据。
方差分析中的多重比较

XD
XC
XB
XE
XA
7.5* 5.0
[应用心理学专业必修课
心理统计学
淮北煤师院教育学院 李怀龙]
Email:lihlong@
13
Psychology Statistics
X 从结果看, 在X D与X E, D与X A 两对差数之间差异是 显著的。因此可以说数学老师当班主任与地理老师 当班主任对学生数学成绩有不同的影响;物理老师 当班主任与地理老师当班主任对学生数学成绩有不 同的影响。 对例8.3进行方差分析时,F > F0.05 , 只是在整体上 得出了不同科目教师当班主任对学生有显著影响的 结论。而通过多重比较法进一步地明确告诉我们哪 些科目的教师在这方面的影响显著。
[应用心理学专业必修课 心理统计学 淮北煤师院教育学院 李怀龙] Email:lihlong@ 14
PsychoLeabharlann ogy Statistics2、N-K法(q检验) 、 检验) 法 检验
例8.3 为研究不同科目的教师当班主任,对学生某一学科的 学习是否有影响。把40名学生随机分派到5名教不同科 目的班主任负责的班级中,经过一段时间以后对这40名 学生进行数学考试,结果见下表。用方差分析的方法检 验5组不同班主任的学生数学成绩是否有显著差异。(其 中,A表示班主任教数学,B表示班主任教语文,C表示 班主任教生物,D表示班主任教地理,E表示班主任教物 理)。
[应用心理学专业必修课
心理统计学
淮北煤师院教育学院 李怀龙]
Email:lihlong@
1
Psychology Statistics
第三讲-方差分析与多重比较-

比值越小,两者越接近,即处理间的差异
与处理内的差异差不多,说明处理间差异不
显著。反之,差异显著。
F 通过查F表判断: dft(1) dfe(2)
F> F0.05=? F0.01=?
F> > F0.01 p<< 0.01
例1:将4个不同药厂生产的阿司匹林片用崩解仪 法进行片剂释放度的测定,每个样品进行5次实验, 以释放63%所需时间的对数值作为指标问4个药 厂生产的片剂释放度是否有差异?
方差分析可以帮助我们掌握客观 规律的主要矛盾或技术关键,是科学 研究工作的一个十分重要的工具。
二、方差分析的基本原理
• 重复数相等的几个均数的比较
符号:
nn knk knn k k
xxiijj xxijij x为ij 表中所有观测数据之和
ii11 jij111 jii111j1j1
作用:检验多个总体均值是否相等
• 在前面讲了两个样本平均数差异 显著性检验,所用的一般为t检验。 • t检验可判断两组数据平均数的差 异显著性。
• 而方差分析可以同时判断多组数 据平均数(样本≥3)之间的差异显著性。
当然,在多组数据的平均数之间做比较 时,可以在平均数的所有对之间做t检验。但 这样做会提高工作量和显著水平的概率,因 而是不可取的。
1.10 0.57 0.77 0.88 0.83 6.178 1.787 2.971 3.914 14.85
解: dfT=kn-1=4×5-1=19
dft=k-1=4-1=3 dfe=dfT-dft=19-3=16
n nnk kn1 i
nk kn
( x(
ij11 ji11
xjikj 1ij(xixj))2i 2nxi1n)12jjikkn11 ((ijxknk1x11ij(jikxj 1iijj(xx)i2xjxx )ii ))2x22 )i2ni1nnkk1 iijnjnkkk1111(((x(xxixiijij xxx))2)222x)2
常用的多重比较方法

常用的多重比较方法
在数据分析和统计学中,常用的多重比较方法包括以下几种:
1. 方差分析中的多重比较方法:用于比较多个组或处理之间的均值差异,包括Tukey's HSD(Tukey's Honestly Significant Difference)、Bonferroni校正和Scheffé法等。
2. 多重t检验:用于比较两个或多个样本均值是否有显著差异,通常用于独立样本或配对样本之间的比较。
3. 多重相关分析:用于比较多个变量之间的相关性,包括Pearson相关系数、Spearman等级相关系数等。
4. 多重回归分析:用于比较多个自变量对因变量的影响程度,可以进行变量选择和模型比较。
5. 多重比例比较:用于比较不同组别之间的比例差异,包括卡方检验和Fisher 精确检验等。
以上仅列举了常见的一些多重比较方法,具体选择何种方法应根据研究问题、数据类型和假设情况等综合考虑。
此外,需要注意的是,在进行多重比较时,需要
进行多重校正,以控制因进行多个比较而增加的类型I错误的风险。
SPSS如何实现多个条件的多重比较

SPSS如何实现多个条件的多重比较在使用SPSS进行数据分析时,我们常常需要进行多个条件下的多重比较。
SPSS提供了一些简单的策略来实现这一目标。
下面将介绍一些常见的方法。
1. 单因素方差分析(One-way ANOVA)如果我们有一个自变量(组别)和一个因变量(数值型),并且希望比较多个组之间的均值差异,我们可以使用单因素方差分析。
在SPSS中,选择“分析”菜单下的“一元方差分析”选项。
然后将因变量移至“因变量”框中,将自变量移至“因子”框中。
点击“选项”,勾选“描述性统计”和“多重比较”。
2. 重复测量方差分析(Repeated Measures ANOVA)在某些情况下,我们可能有多个因变量,并且希望比较这些因变量在多个时间点或条件下的均值差异。
这时可以使用重复测量方差分析。
在SPSS中,选择“分析”菜单下的“一元方差分析”选项。
在“因变量”框中选择所有的因变量,将自变量(时间点或条件)移至“因子”框中。
点击“选项”,勾选“描述性统计”和“多重比较”。
3. 多元方差分析(Multivariate ANOVA)在某些情况下,我们可能有多个自变量,并且想要比较这些自变量在多个因变量上的均值差异。
这时可以使用多元方差分析。
在SPSS中,选择“分析”菜单下的“一元方差分析”选项。
在“因变量”框中选择所有的因变量,将自变量移至“因子”框中。
点击“选项”,勾选“描述性统计”和“多重比较”。
4. 进一步的多重比较分析除了上述方法,SPSS还提供了更多的多重比较分析方法,如LSD(最小显著差异法)、Bonferroni法、Tukey法等。
这些方法可在上述分析的结果中找到。
需要注意的是,在进行多重比较时,我们应该根据实际情况选择最适合的方法。
在选择方法时,应综合考虑样本大小、数据分布和研究假设等因素。
以上就是在SPSS中实现多个条件的多重比较的一些基本方法。
希望对您有帮助!。
duncan 多重范围检验步骤

Duncan多重范围检验(Duncan's Multiple Range Test)是一种用于统计分析中进行多重比较的方法。
这种方法是由美国统计学家Duncan于1955年提出的,用于确定在多组样本中是否存在显著差异。
在统计学和实验设计中,多重范围检验被广泛应用于比较各组平均值的差异,从而确定这些差异是否具有统计学意义。
Duncan多重范围检验步骤包括以下几个主要步骤:1. 数据收集:需要收集一组样本数据,这些数据通常是实验数据或观测数据,可以是定量数据或定性数据。
2. 单因素方差分析(One-way ANOVA):在进行Duncan多重范围检验之前,通常需要先进行单因素方差分析。
单因素方差分析用于确定各组之间的平均值是否存在显著差异。
如果经过方差分析后确定了组间存在显著差异,则可以进行后续的Duncan多重范围检验。
3. 计算平均值:对于方差分析中确定了显著差异的组别,需要计算各组的平均值。
4. 计算Duncan检验统计值:Duncan多重范围检验的关键是计算每对组别之间的检验统计值。
这些统计值用于确定各组之间的差异是否具有统计学意义。
5. 比较各组平均值:将计算得到的各组平均值进行比较,根据Duncan检验统计值和显著水平,确定各组之间的差异是否显著。
6. 结论:根据Duncan多重范围检验的结果,得出各组之间的比较结论,确定那些组之间存在显著差异,对实验结果进行解读和评价。
Duncan多重范围检验是一种常用的多重比较方法,适用于对多组样本进行比较,特别是在实验设计和统计分析中具有重要的应用价值。
在实际应用中,需要遵循上述步骤进行操作,并根据计算结果进行科学合理的结论推断。
对于Duncan多重范围检验步骤的具体操作,需要注意以下几点:1. 数据收集在进行Duncan多重范围检验之前,首先需要收集一组样本数据。
这些数据可以是实验数据或观测数据,涉及到不同组的样本数据,可以是定量数据也可以是定性数据。
单因素方差分析与多重比较

▪ 因素的不同水平(不同总体)下,各观察值之间的差异 ▪ 比如,不同行业之间的被投诉次数之间的差异 ▪ 这种差异可能是由于抽样的随机性所造成的,也可能
是由于行业本身所造成的,后者所形成的误差是由系
统性因素造成的,称为系统误差
方差分析的基本思想和原理
(两类方差)
1. 数据的误差用平方和(sum of squares)表示,称 为方差
单因素方差分析与 多重比较
§3.1 方差分析引论
一. 方差分析及其有关术语 二. 方差分析的基本思想和原理 三. 方差分析的基本假定 四. 问题的一般提法
什么是方差分析(ANOVA)?
(analysis of variance)
1. 检验多个总体均值是否相等
▪ 通过分析观察数据的误差判断各总体均值是否
=115.9295
构造检验的统计量
(计算水平项平方和 SSA)
1. 各组平均值 xi (i 1,2,, k)
平均值 的离差平方和
x 与总
2. 反映各总体的样本均值之间的差异程度,又称组
间平方和
3. 该平方和既包括随机误差,也包括系统误差
4. 计算公式为
k
SSA
ni
k
xi x 2 ni xi x 2
统计量F
2. 当H0为真时,二者的比值服从分子自由度为
这种差异也可能是由于抽样的随机性所造成的
2. 需要有更准确的方法来检验这种差异是否显著, 也就是进行方差分析
所以叫方差分析,因为虽然我们感兴趣的是均值, 但在判断均值之间是否有差异时则需要借助于方差
这个名字也表示:它是通过对数据误差来源的分析 判断不同总体的均值是否相等。因此,进行方差分 析时,需要考察数据误差的来源。
最新SPSS单因素方差分析步骤

spss教程:单因素方差分析用来测试某一个控制变量的不同水平是否给观察变量造成显著差异和变动。
方差分析前提:不同水平下,各总体均值服从方差相同的正态分布。
所以方差分析就是研究不同水平下各个总体的均值是否有显著的差异。
统计推断方法是计算F统计量,进行F检验,总的变异平方和 SST,控制变量引起的离差SSA(Between Group离差平方和),另一部分随机变量引起的SSE(组内Within Group离差平方和),SST=SSA+SSE。
方法/步骤1.计算检验统计量的观察值和概率P_值:Spss自动计算F统计值,如果相伴概率P小于显著性水平a,拒绝零假设,认为控制变量不同水平下各总体均值有显著差异,反之,则相反,即没有差异。
2.方差齐性检验:控制变量不同水平下各观察变量总体方差是否相等进行分析。
采用方差同质性检验方法(Homogeneity of variance),原假设“各水平下观察变量总体的方差无显著差异,思路同spss两独立样本t检验中的方差分析”。
图中相伴概率0.515大于显著性水平0.05,故认为总体方差相等。
趋势检验:趋势检验可以分析随着控制变量水平的变化,观测变量值变化的总体趋势是怎样的,线性变化,二次、三次等多项式。
趋势检验可以帮助人们从另一个角度把握控制变量不同水平对观察变量总体作用的程度。
图中线性相伴概率为0小于显著性水平0.05,故不符合线性关系。
3.多重比较检验:单因素方差分析只能够判断控制变量是否对观察变量产生了显著影响,多重比较检验可以进一步确定控制变量的不同水平对观察变量的影响程度如何,那个水平显著,哪个不显著。
常用LSD、S-N-K方法。
LSD方法检测灵敏度是最高的,但也容易导致第一类错误(弃真)增大,观察图中结果,在LSD项中,报纸与广播没有显著差异,但在别的方法中,广告只与宣传有显著差异。
4. 相似性子集:由图可知,划分的子集结果是一样的。
通常在相似性子集划分时多采用S-N-K 方法的结论。
第三章_单因素方差分析与多重比较精品

第三章_单因素方差分析与多重比较精品单因素方差分析是统计学中用于比较不同组之间差异的一种方法。
通过对多个组进行方差分析,可以确定是否有统计上显著的差异存在。
然而,在进行多组比较时,会面临多个比较中出现误差增加的问题。
因此,多重比较技术被提出,用于解决这个问题。
首先,我们来了解单因素方差分析。
单因素方差分析是通过比较不同组之间的方差差异来确定是否存在显著的组间差异。
在进行单因素方差分析时,我们需要计算组内的平均平方差(MSW)和组间的平均平方差(MSB),然后计算F值,再通过比较F值与临界F值来确定差异是否显著。
然而,当进行多组比较时,会遇到一种被称为多重比较问题的情况。
多重比较问题是指在进行多次比较时,由于进行多个比较而增加了整体犯错的可能性。
举例来说,如果我们进行了十次不同组的比较,每次比较的显著性水平设定为0.05,那么整体犯错的概率就会增加到0.50,即有一半的可能性会发生错误。
为了解决多重比较问题,研究人员引入了多重比较技术。
多重比较技术有多种方法,其中一种常用的方法是泰基法(Tukey's method)。
泰基法通过比较不同组之间的均值差异来确定哪些组之间存在显著差异。
具体而言,泰基法计算了每对组之间的均值差异,并利用一个修正的显著水平来设置显著性门限。
只有当两组之间的均值差异超过这个门限时,才被认为是显著的。
除了泰基法外,还有其他多重比较方法,例如邓肯多重范围检验(Duncan's multiple range test)和奥内尔法(Bonferroni method)。
这些方法各有优点和局限性,研究人员可以根据实际情况选择最适合的方法。
在使用多重比较技术时,需要注意以下几点。
首先,选择适当的显著性水平是非常重要的。
不同的显著性水平会对结果产生不同的影响。
其次,在进行多次比较时,应该考虑调整显著性水平,以控制整体的犯错率。
此外,还需要根据实际问题选择合适的多重比较方法,以便获得可靠的结果。
单因素方差分析与多重比较

单因素方差分析单因素方差分析也称作一维方差分析。
它检验由单一因素影响的一个(或几个相互独立的)因变量由因素各水平分组的均值之间的差异是否具有统计意义。
还可以对该因素的若干水平分组中哪一组与其他各组均值间具有显著性差异进行分析,即进行均值的多重比较。
One-Way ANOVA过程要求因变量属于正态分布总体。
如果因变量的分布明显的是非正态,不能使用该过程,而应该使用非参数分析过程。
如果几个因变量之间彼此不独立,应该用Repeated Measure过程。
[例子]调查不同水稻品种百丛中稻纵卷叶螟幼虫的数量,数据如表5-1所示。
表5-1 不同水稻品种百丛中稻纵卷叶螟幼虫数从复水稻品种1 2 3 4 51 41 33 38 37 312 39 37 35 39 343 40 35 35 38 34 数据保存在“DATA5-1.SAV”文件中,变量格式如图5-1。
图5-1分析水稻品种对稻纵卷叶螟幼虫抗虫性是否存在显著性差异。
1)准备分析数据在数据编辑窗口中输入数据。
建立因变量“幼虫”和因素水平变量“品种”,然后输入对应的数值,如图5-1所示。
或者打开已存在的数据文件“DATA5-1.SAV”。
2)启动分析过程点击主菜单“Analyze”项,在下拉菜单中点击“Compare Means”项,在右拉式菜单中点击“0ne-Way ANOVA”项,系统打开单因素方差分析设置窗口如图5-2。
图5-2 单因素方差分析窗口3)设置分析变量因变量:选择一个或多个因子变量进入“Dependent List”框中。
本例选择“幼虫”。
因素变量:选择一个因素变量进入“Factor”框中。
本例选择“品种”。
4)设置多项式比较单击“Contrasts”按钮,将打开如图5-3所示的对话框。
该对话框用于设置均值的多项式比较。
图5-3 “Contrasts”对话框定义多项式的步骤为:均值的多项式比较是包括两个或更多个均值的比较。
例如图5-3中显示的是要求计算“1.1×mean1-1×mean2”的值,检验的假设H0:第一组均值的1.1倍与第二组的均值相等。
第三章_单因素方差分析与多重比较

第三章_单因素方差分析与多重比较1.引言在统计学中,方差分析是一种用于比较不同组之间差异的方法。
它可以帮助我们确定不同因素之间是否存在显著差异,以及哪些因素对结果有重要影响。
在实际应用中,我们常常需要使用单因素方差分析,即只考虑一种因素对结果的影响。
本章将介绍单因素方差分析的基本原理和方法,以及如何进行多重比较来进一步分析不同组之间的差异。
2.单因素方差分析的基本原理在单因素方差分析中,我们假设只有一个因素对结果有影响,而其他因素对结果没有影响。
我们通过计算组内变异和组间变异来判断不同组之间是否存在显著差异。
组内变异表示同一组内部个体之间的差异,而组间变异表示不同组之间的差异。
如果组间变异显著大于组内变异,则可以认为不同组之间存在显著差异。
为了进行单因素方差分析,我们需要满足以下几个前提条件:1)样本来自正态分布总体;2)各个组的方差相等;3)各个组的观测值之间相互独立。
3.单因素方差分析的步骤单因素方差分析的步骤通常包括以下几个步骤:1)建立假设:根据实际问题,我们需要建立相应的零假设和备择假设。
零假设通常表示不同组之间没有显著差异,而备择假设表示不同组之间存在显著差异。
2)计算统计量:根据计算公式,计算组内平方和和组间平方和,进而计算F值。
3)判断显著性:根据给定的显著性水平,查表或计算P值,判断F 值是否显著。
4)做出结论:根据显著性检验的结果,决定是否接受零假设,进而得到结论。
4.多重比较在单因素方差分析中,如果我们得到了显著的F值,说明不同组之间存在差异,但是并不能告诉我们具体是哪些组之间存在差异。
这时候,我们可以进行多重比较来进一步分析不同组之间的差异。
多重比较可以帮助我们确定哪些组之间存在显著差异,以及差异的大小。
常用的多重比较方法包括Bonferroni法、Tukey法和Duncan法等。
这些方法都可以通过计算置信区间来确定差异的显著性。
多重比较的步骤通常包括以下几个步骤:1)计算均值差异:首先计算不同组之间的均值差异,可以通过计算置信区间来确定差异的显著性。
单因素方差分析

单因素方差分析(ANOVA):两两比较检验Post-Hoc选项详解添加时间:2014-5-5分享到:0One-Way ANOVA:两两比较检验后,务必进行Post Hoc检验,也称事后分析,或称为两两比较分析。
但具体算法有很多种,各自有哪些差别呢?一旦确定均值间存在差值,两两范围检验和成对多重比较就可以确定哪些均值存在差值了。
范围检验识别彼此间没有差值的同类均值子集。
成对多重比较检验每一对均值之间的差分,并得出一个矩阵,其中星号指示在 0.05 的 alpha 水平上的组均值明显不同。
一、假定方差齐性Tukey's 真实显著性差异检验、Hochberg’s GT2、Gabriel 和Scheffé 是多重比较检验和范围检验。
其他可用的范围检验为 Tukey 的 b、S-N-K (Student-Newman-Keuls)、Duncan、R-E-G-W F(Ryan-Einot-Gabriel-Welsch F 检验)、R-E-G-W Q(Ryan-Einot-Gabriel-Welsch 范围检验)和 Waller-Duncan。
可用的多重比较检验为 Bonferroni、Tukey's 真实显著性差异检验、Sidak、Gabriel、Hochberg、Dunnett、Scheffé 和 LSD(最小显著性差异)。
详细剖析• 最小显著差法(LSD). 使用 t 检验执行组均值之间的所有成对比较。
对多个比较的误差率不做调整。
LSD法侧重于减少第二类错误,此法精度较差,易把不该判断为显著的差异错判为显著,敏感度最高。
LSD法的使用:在进行试验设计时就确定各处理只是固定的两个两个相比,每个处理平均数在比较中只比较一次。
例如,在一个试验中共有4个处理,设计时已确定只是处理1与处理2、处理3与处理4(或1与3、2与4;或1与4、2与3)比较,而其它的处理间不进行比较。
因为这种比较形式实际上不涉及多个均数的极差问题,所以不会增大犯I型错误的概率。
方差分析与邓肯多重比较
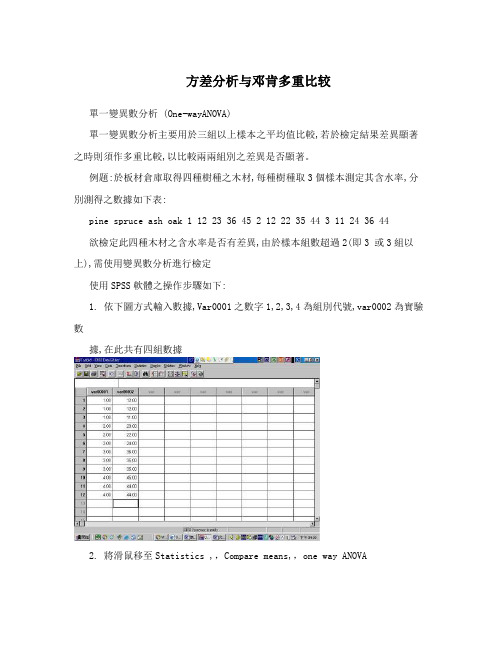
方差分析与邓肯多重比较單一變異數分析 (One-wayANOVA)單一變異數分析主要用於三組以上樣本之平均值比較,若於檢定結果差異顯著之時則須作多重比較,以比較兩兩組別之差異是否顯著。
例題:於板材倉庫取得四種樹種之木材,每種樹種取3個樣本測定其含水率,分別測得之數據如下表:pine spruce ash oak 1 12 23 36 45 2 12 22 35 44 3 11 24 36 44欲檢定此四種木材之含水率是否有差異,由於樣本組數超過2(即3 或3組以上),需使用變異數分析進行檢定使用SPSS軟體之操作步驟如下:1. 依下圖方式輸入數據,Var0001之數字1,2,3,4為組別代號,var0002為實驗數據,在此共有四組數據2. 將滑鼠移至Statistics ,,Compare means,,one way ANOVA3.var0001設為Factor,var0002設為dependent list4.點選Post Hoc,,勾選Duncan,,continue5. 點選 OK,即進行檢測6.結果如下:若差異顯著則Sig值大於0.05,表示各組間差異不顯著若差異顯著則Sig值小於0.057. 此時須看Duncan之比較結果如上之結果資料整理如下:在此可見比較結果將各組數據由小至大分為四各階層,各組樣本分別屬於不同之階層,比較結果可以下表方式呈現其結果:組別平均值 Duncan比較結果 1 11.67 A2 23.00 B3 35.33 C4 44.33 DDuncan比較結果可用ABCD….或abcd….表示,若各組樣本所標示之英文字母不同則表示差異顯著。
於表格下方須註明字母所代表之義意為何。
您好:本篇文章是精心制作,值得下载收藏,,但下面两页是无用的,请跳过阅读吧。
您好:本篇文章是精心制作,值得下载收藏,,但下面两页是无用的,请跳过阅读吧。
您好:本篇文章是精心制作,值得下载收藏,,但下面两页是无用的,请跳过阅读吧。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单因素方差分析单因素方差分析也称作一维方差分析。
它检验由单一因素影响的一个(或几个相互独立的)因变量由因素各水平分组的均值之间的差异是否具有统计意义。
还可以对该因素的若干水平分组中哪一组与其他各组均值间具有显著性差异进行分析,即进行均值的多重比较。
One-Way ANOVA过程要求因变量属于正态分布总体。
如果因变量的分布明显的是非正态,不能使用该过程,而应该使用非参数分析过程。
如果几个因变量之间彼此不独立,应该用Repeated Measure过程。
[例子]调查不同水稻品种百丛中稻纵卷叶螟幼虫的数量,数据如表5-1所示。
表5-1 不同水稻品种百丛中稻纵卷叶螟幼虫数从复水稻品种1 2 3 4 51 41 33 38 37 312 39 37 35 39 343 40 35 35 38 34 数据保存在“DATA5-1.SAV”文件中,变量格式如图5-1。
图5-1分析水稻品种对稻纵卷叶螟幼虫抗虫性是否存在显著性差异。
1)准备分析数据在数据编辑窗口中输入数据。
建立因变量“幼虫”和因素水平变量“品种”,然后输入对应的数值,如图5-1所示。
或者打开已存在的数据文件“DATA5-1.SAV”。
2)启动分析过程点击主菜单“Analyze”项,在下拉菜单中点击“Compare Means”项,在右拉式菜单中点击“0ne-Way ANOVA”项,系统打开单因素方差分析设置窗口如图5-2。
图5-2 单因素方差分析窗口3)设置分析变量因变量:选择一个或多个因子变量进入“Dependent List”框中。
本例选择“幼虫”。
因素变量:选择一个因素变量进入“Factor”框中。
本例选择“品种”。
4)设置多项式比较单击“Contrasts”按钮,将打开如图5-3所示的对话框。
该对话框用于设置均值的多项式比较。
图5-3 “Contrasts”对话框定义多项式的步骤为:均值的多项式比较是包括两个或更多个均值的比较。
例如图5-3中显示的是要求计算“1.1×mean1-1×mean2”的值,检验的假设H0:第一组均值的1.1倍与第二组的均值相等。
单因素方差分析的“0ne-Way ANOVA”过程允许进行高达5次的均值多项式比较。
多项式的系数需要由读者自己根据研究的需要输入。
具体的操作步骤如下:① 选中“Polynomial”复选项,该操作激活其右面的“Degree”参数框。
② 单击Degree参数框右面的向下箭头展开阶次菜单,可以选择“Linear”线性、“Quadratic”二次、“Cubic”三次、“4th”四次、“5th”五次多项式。
③ 为多项式指定各组均值的系数。
方法是在“Coefficients”框中输入一个系数,单击Add按钮,“Coefficients”框中的系数进入下面的方框中。
依次输入各组均值的系数,在方形显示框中形成—列数值。
因素变量分为几组,输入几个系数,多出的无意义。
如果多项式中只包括第一组与第四组的均值的系数,必须把第二个、第三个系数输入为0值。
如果只包括第一组与第二组的均值,则只需要输入前两个系数,第三、四个系数可以不输入。
可以同时建立多个多项式。
一个多项式的一组系数输入结束,激话“Next”按钮,单击该按钮后“Coefficients”框中清空,准备接受下一组系数数据。
如果认为输入的几组系数中有错误,可以分别单击“Previous”或“Next”按钮前后翻找出错的一组数据。
单击出错的系数,该系数显示在编辑框中,可以在此进行修改,修改后单击“Change”按钮在系数显示框中出现正确的系数值。
当在系数显示框中选中一个系数时,同时激话“Remove”按钮,单击该按钮将选中的系数清除。
④单击“Previous”或“Next”按钮显示输入的各组系数检查无误后,按“Continue”按钮确认输入的系数并返回到主对话框。
要取消刚刚的输入,单击“Cancel”按钮;需要查看系统的帮助信息,单击“Help”按钮。
本例子不做多项式比较的选择,选择缺省值。
5)设置多重比较在主对话框里单击“Post Hoc”按钮,将打开如图5-4所示的多重比较对话框。
该对话框用于设置多重比较和配对比较。
方差分析一旦确定各组均值间存在差异显著,多重比较检测可以求出均值相等的组;配对比较可找出和其它组均值有差异的组,并输出显著性水平为0.95的均值比较矩阵,在矩阵中用星号表示有差异的组。
图5-4 “Post Hoc Multiple Comparisons”对话框(1)多重比较的选择项:①方差具有齐次性时(Equal Variances Assumed),该矩形框中有如下方法供选择:LSD (Least-significant difference) 最小显著差数法,用t检验完成各组均值间的配对比较。
对多重比较误差率不进行调整。
Bonferroni (LSDMOD) 用t检验完成各组间均值的配对比较,但通过设置每个检验的误差率来控制整个误差率。
Sidak 计算t统计量进行多重配对比较。
可以调整显著性水平,比Bofferroni方法的界限要小。
Scheffe对所有可能的组合进行同步进入的配对比较。
这些选择项可以同时选择若干个。
以便比较各种均值比较方法的结果。
R-E-G-WF (Ryan-Einot-Gabriel-Welsch F) 用F检验进行多重比较检验。
R-E-G-WQ (Ryan-Einot-Gabriel-Welsch range test) 正态分布范围进行多重配对比较。
S-N-K(Student-Newmnan-Keuls) 用Student Range分布进行所有各组均值间的配对比较。
如果各组样本含量相等或者选择了“Harmonic average of all groups”即用所有各组样本含量的调和平均数进行样本量估计时还用逐步过程进行齐次子集(差异较小的子集)的均值配对比较。
在该比较过程中,各组均值从大到小按顺序排列,最先比较最末端的差异。
Tukey(Tukey's,honestly signicant difference) 用Student-Range统计量进行所有组间均值的配对比较,用所有配对比较误差率作为实验误差率。
Tukey's-b用“stndent Range”分布进行组间均值的配对比较。
其精确值为前两种检验相应值的平均值。
Duncan (Duncan's multiple range test) 新复极差法(SSR),指定一系列的“Range”值,逐步进行计算比较得出结论。
Hochberg's GT2用正态最大系数进行多重比较。
Gabriel用正态标准系数进行配对比较,在单元数较大时,这种方法较自由。
Waller-Dunca用t统计量进行多重比较检验,使用贝叶斯逼近。
Dunnett指定此选择项,进行各组与对照组的均值比较。
默认的对照组是最后一组。
选择了该项就激活下面的“ControlCategory”参数框。
展开下拉列表,可以重新选择对照组。
“Test”框中列出了三种区间分别为:•“2-sides” 双边检验;•“<Control” 左边检验•“>Conbo1”“右边检验。
②方差不具有齐次性时(Equal Varance not assumed),检验各均数间是否有差异的方祛有四种可供选择:Tamhane's T2, t检验进行配对比较。
Dunnett's T3,采用基于学生氏最大模的成对比较法。
Games-Howell,Games-Howell比较,该方法较灵活。
Dunnett's C,采用基于学生氏极值的成对比较法。
③ Significance 选择项,各种检验的显著性概率临界值,默认值为0.05,可由用户重新设定。
本例选择“LSD”和“Duncan”比较,检验的显著性概率临界值0.05。
6) 设置输出统计量单击“Options”按钮,打开“Options”对话框,如图5-5所示。
选择要求输出的统计量。
并按要求的方式显示这些统计量。
在该对话框中还可以选择对缺失值的处理要求。
各组选择项的含义如下:图5-5输出统计量的设置“Statistics”栏中选择输出统计量:Descriptive,要求输出描述统计量。
选择此项输出观测量数目、均值、标准差、标准误、最小值、最大值、各组中每个因变量的95%置信区间。
Fixed and random effects, 固定和随机描述统计量Homogeneity-of-variance,要求进行方差齐次性检验,并输出检验结果。
用“Levene lest ”检验,即计算每个观测量与其组均值之差,然后对这些差值进行一维方差分析。
Brown-Forsythe 布朗检验Welch,韦尔奇检验Means plot,即均数分布图,根据各组均数描绘出因变量的分布情况。
“Missing Values”栏中,选择缺失值处理方法。
Exclude cases analysis by analysis选项,被选择参与分析的变量含缺失值的观测量,从分析中剔除。
Exclude cases listwise选项,对含有缺失值的观测量,从所有分析中剔除。
以上选择项选择完成后,按“Continue”按钮确认选择并返回上一级对话框;单击“Cancel”按钮作废本次选择;单击“Help”按钮,显示有关的帮助信息。
本例子选择要求输出描述统计量和进行方差齐次性检验,缺失值处理方法选系统缺省设置。
6)提交执行设置完成后,在单因素方差分析窗口框中点击“OK”按钮,SPSS就会根据设置进行运算,并将结算结果输出到SPSS结果输出窗口中。
7) 结果与分析输出结果:表5-2描述统计量,给出了水稻品种分组的样本含量N、平均数Mean、标准差Std.Deviation、标准误Std.Error、95%的置信区间、最小值和最大值。
表5-3为方差齐次性检验结果,从显著性慨率看,p>0.05,说明各组的方差在a=0.05水平上没有显著性差异,即方差具有齐次性。
这个结论在选择多重比较方法时作为一个条件。
表5-4方差分析表:第1栏是方差来源,包括组间变差“Between Groups”;组内变差“Within Groups”和总变差“Total”。
第2栏是离差平方和“Sum of Squares”,组间离差平方和87.600,组内离差平方和为24.000,总离差平方和为111.600,是组间离差平方和与组内离差平方和相加之和。
第3栏是自由度df,组间自由度为4,组内自由度为10;总自由度为14。
第4栏是均方“Mean Square”,是第2栏与第3栏之比;组间均方为21.900,组内均方为2.400。
