第四讲格点图形面积的计算

合集下载

格点法求面积的公式

面积计算公式：皮克公式:格点多边形面积=多边形一周的格点数÷2+多边形内部格点数-1
设格点多边形的面积为s，它各边上格点的个数和为x。

格点多边形，其内部都只有一个格点，它们的面积与各边上格点的个数和的对应关系如下表，请写出s与x之间的关系式。

格点的起源
格点问题起源于以下两个问题的研究：
1、狄利克雷除数问题，即求x>1时D2（x）=区域{1≤u≤x，1≤v≤x，uv≤x}上的格点数。

1849年，狄利克雷证明了D2（x）=xlnx+（2ν一1）x+△（x），这里ν为欧拉常数，△（x）=O（x0.5）。

这一问题的目的是要求出使余项估计△（x）=O（x）成立的又的下确界θ0。

2、圆内格点问题，设x>1，A2（x）=圆内μ+ν≤x上的格点数。

高斯证明了A2（x）=πx+R（x），这里R（x）=O（x^1/2）,求使余项估计R（x）=O（x）成立的λ的下确界α的问题，称之为圆内格点问题或高斯圆问题。

高斯小学奥数四年级下册含答案第04讲_格点图形面积计算

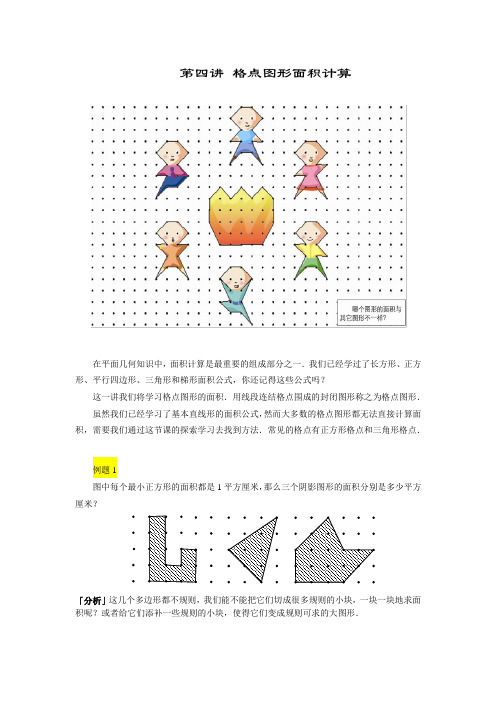
第四讲格点图形面积计算在平面几何知识中，面积计算是最重要的组成部分之一．我们已经学过了长方形、正方形、平行四边形、三角形和梯形面积公式，你还记得这些公式吗？这一讲我们将学习格点图形的面积．用线段连结格点围成的封闭图形称之为格点图形．虽然我们已经学习了基本直线形的面积公式，然而大多数的格点图形都无法直接计算面积，需要我们通过这节课的探索学习去找到方法．常见的格点有正方形格点和三角形格点．例题1图中每个最小正方形的面积都是1平方厘米，那么三个阴影图形的面积分别是多少平方厘米？「分析」这几个多边形都不规则，我们能不能把它们切成很多规则的小块，一块一块地求面积呢？或者给它们添补一些规则的小块，使得它们变成规则可求的大图形．练习1图中相邻两格点间的距离均为1厘米，那么阴影图形的面积分别是多少平方厘米？通过例1中的第1小题我们学会了将大块不规则图形“分割”成许多规则的图形，这种方法称为“分割法”；但是不一定每个图形都很容易分割，第2小题我们学会了把不好算的图形“添补”成规则的大图形，计算时用大图形的面积减去空白部分的面积，这种方法称为“添补法”．分割法，正所谓“大事化小”，把不规则的大图形化为规则的小图形．添补法则正好相反，是“以小见大”，把不规则图形周围添上规则的小图形，使总面积便于计算．使用割、补法的时候，一般应该从图形的顶点出发，尽量沿着格线划分，以便与小方格的面积找到联系或者利用垂直等性质．接下来我们用分割、添补的方法计算一下三角形格点图形的面积．例题2下图是一个三角形点阵，其中能连出的最小等边三角形的面积为1平方厘米．那么这五个图形的面积分别为多少平方厘米？「分析」前三个图是可以直接计算的，④、⑤是无法直接计算的，试着用分割、添补的方法解决吧！我们发现：如果一个三角形的两边都沿三角形格线方向，并且分别是最短线段的m 倍和n 倍，那么这个三角形的面积就是最小等边三角形面积的m n 倍．练习2下图是一个三角形点阵，其中能连出的最小等边三角形的面积为1平方厘米．那么这四个图形的面积分别为多少平方厘米？要计算格点图形的面积，我们只需要应用合适的方法，数一下要求的图形占了几个单位面积即可．当单位面积不为1时，我们就要格外小心了，千万不能在数完后再乘单位面积！对于复杂的格点图形，使用割补法一定能计算面积．但是割补法有时显得有些繁琐，有没有更简单明了的方法呢？那么我们接下来看一个简单快捷的方法．例如，我们要计算如下图的格点多边形的面积（假设最小的正方形面积是1）．我们可以用割补的方法求出图形的面积，现在还有另一种方法，从格点数入手．围成阴影部分的边线，经过了一些格点．这些边界上的格点叫做边界格点，一共有12个；格点图形还完全盖住了一些格点，这些图形内部的格点叫做内部格点，一共有1个．一般的，在最小正方形面积为1的正方形网格中，我们有：这样，按公式计算：122116÷+-=，我们就得出图中阴影部分的面积了．例题3 如图，相邻两格点间的距离均为1厘米，求阴影部分的面积？「分析」尝试着用格点图形面积公式计算一下把！先数数边界格点、内部格点分别有多少个呢？练习3如图，每一个最小正方形的面积都是2，阴影部分的面积是多少？类似地，在最小正三角形面积为1的三角形网格中，三角形格点图形也有面积计算公式：仔细比较这两个公式，可以发现：三角形格点的公式正好是正方形格点公式的2倍．大家想一下，为什么是这样呢？例题4如图，每个最小等边三角形的面积都是1平方厘米．阴影部分的面积是多少平方厘米？「分析」尝试着用格点图形面积公式计算一下把！先数数边界格点、内部格点分别有多少个呢？练习4如图，每个最小等边三角形的面积都是1平方厘米，阴影部分的面积是多少平方厘米？例题5如图，每一个最小正方形的面积都是3平方厘米．阴影部分的面积是多少平方厘米？「分析」试着比较分割法、添补法、公式法，这三个方法哪个更合适呢？例题6（1）左图中每个最小正三角形的面积是2平方厘米．阴影部分面积是多少平方厘米？（2）右图中每个最小正三角形的面积是4平方厘米．阴影部分面积是多少平方厘米？「分析」试着比较分割法、添补法、公式法，这三个方法哪个更合适呢？对于大部分格点图形而言，分割法和添补法都可以用来求面积．对于特殊的格点图形，如果不易分割，可以试试添补；如果不易添补，可以试试分割．如果用分割法和添补法都不易解决，那么格点公式就派上用场了！在使用格点公式时，有以下几点需要注意：（1）注意是正方形格点还是三角形格点；（2）按照顺序来数边界格点和内部格点；（3）用格点公式计算出来的不是面积，而是最小的正方形或正三角形的面积的倍数．看似这一讲的题目不是很难，怎么保证计算的准确性呢？如果你用分割法计算面积，不妨再用添补法验算一下．如果你用割补法计算面积，不妨再用格点公式算一算．用不同方法得到的都是同样的结果，基本上就不会出错了．课堂内外几何的起源古埃及人聚居在尼罗河附近，以在河边的农田耕作为生．可是尼罗河每隔一段时间会泛滥，河水涌上岸，把河边的农田淹没，冲毁农田的边界．所以，每次河水泛滥后，埃及人都要重新划分农田的范围和界限．埃及人在划分土地时，发现很多不同形状的农田，都可以分割为几块较细小的三角形农田，例：1块长方形农田2块大小相同的三角形农田1块梯形农田3块三角形农田这些不同形状的农田，其实就是不同的几何图形；把农田分割为几块较细小的农田，即是把几何图形分割．原来古埃及人是研究几何图形的先锋呢！作业1. 如图，每相邻两个格点的距离都是1，那么两个阴影图形的面积分别是________、________．2. 下图中三角形点阵所能连出的最小正三角形面积为1，图中两个图形的面积分别是________、________．3. 如图，最小正三角形的面积是4平方厘米，那么阴影部分的面积是________平方厘米．4. 右图中，每个最小正方形面积为2，则图中阴影部分的面积是________．5. 下图三角形点阵所能连出的最小正三角形面积为2，图形的面积是_________．第四讲格点图形面积计算1. 例题1答案：7平方厘米；5平方厘米；11平方厘米详解：如图所示，用分割法、添补法．三个图形的面积分别是：4111127⨯+⨯+⨯=平方厘米； 4⨯⨯÷32⨯⨯÷2. 例题2答案：6；12；4；7；9详解：①：326⨯=平方厘米；②：4312⨯=平方厘米；③：224⨯=平方厘米；3. 例题3答案：6.5平方厘米详解：内部格点：3个，边界格点：9个．面积=3921 6.5+÷-=平方厘米．4. 例题4答案：34平方厘米详解：内部格点：7个；边界格点：22个．面积：7222234⨯+-=平方厘米．5.例题5答案：19.5平方厘米；31.5平方厘米④： ⑤： 121212+17⨯+⨯+⨯= 或：441313137⨯-⨯-⨯-⨯= 2339⨯+= 或：441212139⨯-⨯-⨯-⨯=详解：可以分割、添补，也可以用公式法：（1）内部格点：4个；边界格点：7个．面积：()7241319.5÷+-⨯=平方厘米；（2）内部格点：8个；边界格点：7个．面积：()7281331.5÷+-⨯=平方厘米．6. 例题6答案：28平方厘米；56平方厘米详解：可以分割、添补，也可以用公式法：（1）内部格点：4个；边界格点：8个．面积：()4282228⨯+-⨯=平方厘米；（2）内部格点：3个；边界格点：10个．面积：()32102456⨯+-⨯=平方厘米．7. 练习1答案：3平方厘米；10平方厘米详解：如图，分别用分割法、添补法．8. 练习2答案：12；20；5；18 详解：①：3412⨯=平方厘米； ②：直接数，每层4个，共5层，4520⨯=9. 练习3答案：13 简答：内部格点：1个，边界格点：13个．面积=()11321213+÷-⨯=．10. 练习4答案：17平方厘米简答：内部格点：1个；边界格点：17个．面积：1217217⨯+-=平方厘米． ③： ④：1112125⨯+⨯+⨯= 122312818⨯+⨯+⨯+=11.作业1答案：6；6.5简答：可用分割或添补法完成．12.作业2答案：7；12简答：使用割补法分别计算．13.作业3答案：56简答：大正三角形的面积是254100⨯=平方厘米，利用添补法可得．14.作业4答案：29简答：综合利用分割法与添补法．也可以用正方形格点图形面积公式计算．注意每个最小正方形面积是2．15.作业5答案：44简答：综合利用分割法与添补法．也可以用三角形格点图形面积公式计算．注意每个最小正三角形面积是2．。

格点面积公式推导过程

格点面积公式推导过程
一、格点面积公式的基本概念
格点面积公式乃是指将实际曲线投影到平面上，运用数学方法计算出该曲线的面积，其实就是把曲线分成若干个小矩形，积分计算的一种变形。

二、格点面积公式的推导过程
1、由定义可知，格点面积公式是假设曲线投影到平面上的投影
面积，那么用以下坐标轴可表示出该投影平面：
(x,y)，其中x表示投影后的曲线横坐标值，y表示投影后的曲
线纵坐标值。

2、设定格点矩形横纵坐标分别为（x1,y1）和（x2,y2），分别为x和y轴上格点下标，假设格点之间的距离为Δx和Δy，定义Δx = x2-x1;Δy = y2-y1，即每个格点矩形的面积为：
S=Δx*Δy
3、假设曲线投影到平面上，把曲线进行分段，每段投影的坐标
均可以用（x,y）表示，当曲线投影到平面上时，x1≤x≤x2,y1≤y
≤y2，由此可以知道曲线投影到平面上的面积就是所有格点矩形的面积之和：
S = ΣΔx*Δy
4、将等差数列求和公式代入本公式可以得到：
S=Δx*Δy*n
其中n表示格点矩形的个数，即曲线投影到平面上的分段点个数，
因此可得格点面积公式：
S=Δx*Δy*n
三、结论
根据上述推导得出，格点面积公式是把实际曲线投影到平面上，运用数学方法计算出该曲线的面积，公式为：S=Δx*Δy*n，其中n 表示格点矩形的个数。

七年级下数学拓展课——数格点算面积

当我听别人讲解某些数学问题时，常觉得很难理解，甚至不可能理解。这时便想，是否可以将问题化简些呢﹖往往，在终于弄清楚之后，实际上，它只是一个更简单的问题。
——希尔伯特
再见！
的格点数，那么有 S 2 N L 2
A
即：格点多边形面积等于图形内部所包含
格点数的2倍与周界上格点数的和减去2．
C
B
B
(a)
巩固：
1、求下列格点多边形的面积(每相邻三个点“∵”或“∴” 成面积为1的等边三角形)．
⑴
⑵
⑶
⑷
2、把同一个三角形的三条边分别5等分、7等分(如图1，图2)，然
后适当连接这些等分点，便得到了若干个面积相等的小三角形．已知图1中阴影部分面积是294平方分米，那么图2中阴影部分的面积是______平方分米．
D
添补法：把不规则图形周围添
补上规则的小图形转化一个规
则的大图形，使总面积便于计
算。
（1）求下列多边形的面积
（2）不妨设S---格点多边形的面积，N--多边形内部的格点数，L--它的边上的格点数，那么S、N、L三者之间有没有关系呢？
图形序号 S N L
① 104
② 2.5 1 5
③
42 6
S、N、L三者之间有怎样的关系呢？
二、探究格点多边形的面积S与内部、边上格点数(N、 L)的关系
活动五猜想N=4、5、…、10、…的格点多边形中S与L 之间的关系活动六归纳总结：格点多边形中S与L之间的关系
S N L 1 2
通过上面的探究，我们发现，这种格点多边形的面积计算起来很方便，只要数一下图形边线上的格点的数目及图形内部的格点的数目，就可用公式算出。

《数格点算面积》课件

实例三：三角形格点算面积
总结词
通过三角形格点计算面积的方法
详细描述
三角形格点算面积是通过数三角形的底和高以及格点数来计算面积的一种方法。首先，确定三角形格点的底和高，然后数格点的数量，最后将格点数乘以底和高的乘积的一半即可得到面积。
04
数格点算面积的应用场景
土地测量与规划
土地面积测量
通过数格点的方法，可以快速准确地测量土地面积，为土地规划
计和成本预算提供依据。
室内装修设计
在室内装修设计中，通过数格点算面积的方法可以精确计算出各个区域的面积，为材料选择和预
算制定提供参考。
房地产销售
在房地产销售过程中，利用数格点算面积的方法可以精确计算出房屋的建筑面积和使用面积，为
购房者提供准确信息。
05
数格点算面积的注意事项与技巧
格点选取的原则与技巧
专业的地理信息系统软件，具有强大的数据处理和分析功能。
QGIS
开源的地理信息系统软件，适用于各种操作系统。
GRASS GIS
同样是一款开源的地理信息系统软件，具有广泛的用途和强大的功能。
06
总结与展望
数格点算面积的重要性和意义
数学教育意义
通过数格点算面积的练习，有助于培养学生的逻辑思维和空间想象力，提高他们的数学素养。
数格点算面积的原理
原理
基于格点的可数性和均匀性，通过将平面图形划分为若干个小正方形，然后数出这些小正方形中的格点数，最后根据格点数和正方形面积的对应关系计算出整个图形的面积。
应用
数格点算面积的方法在数学、物理、工程等领域都有广泛的应用，如计算几何形状的面积、求解微积分问题等。
03
数格点算面积的实例分析

格点面积

4、右图是一个方格网，计算阴影部分的面积．
D
A
F
1cm C 1cm
EB
竞赛题选讲
补：如图是一个5×5的网格, 每个小方格的面积都是1,阴影部分是类似数字"2"的图形,那么阴影部分的面积是多少?(2013希望杯初赛)
哥哥说：“我的地一圈只有15棵树，而弟弟的地一圈有17棵树，弟弟的面积大！”
皮（毕）克定理：
若一个格点多边形内部有N个格点，它的边界上有L个格点，则它的面积为：
(周界格点数÷2+内部格点数－1） ×单位正方形面积
补：求下图中格点多边形的面积（每相邻四个点围成的小方格的面积为1平方厘米）。
19
求格点图形面积的方法：
一、直接求二、分块求三、大减小
1、分成相同小块 2、分成学过的图形
1、如图，每相邻三个点所形成的三角形都是面积为1的等边三角形，计算 ABC的面积．
A
C B
2、求下列格点多边形的面积(每相邻三个点“∵”或“∴”形成面积为1的等边三角形)．
3、把大正三角形每边八等分，组成如右图所示的三角形网．如果大三角形的面积是128，求图中粗线所围成的三角形的面积．
高
米
底 6厘米平行四边形面积=底×高
1 厘米
1厘米2厘米 Βιβλιοθήκη 底3 厘高米
下底 5厘米 (2+5)×3÷2=10.5平方厘米
梯形面积=（上底+下底）×高÷2
1 厘米
1厘米
3 厘
高
米
底 5厘米 3×5÷2=7.5平方厘米三角形面积=底×高÷2
组一：（正方形格点）
2、如图，计算各个格点多边形的面积

正方形格点面积公式

正方形格点面积公式
正方形格点面积公式是指一个正方形的面积可以用其边长的平方
除以2表示。

在计算正方形面积的过程中，我们可以使用不同的公式，例如正方形的面积可以使用边长乘以自身来计算，也可以使用对角线
的平方除以2来计算。

这些公式的计算方式都十分简单，但是在实际
应用中需要根据不同场景和需求灵活选择。

对于正方形格点面积，我们可以将其看作由若干个单位正方形组
成的图形。

每个单位正方形的面积为1，因此正方形格点面积所包含的单位正方形数量即为其面积的大小。

也就是说，一个边长为n的正方
形格点面积为n的平方。

此外，正方形格点面积公式在计算面积时还需要考虑格点的特殊
性质。

由于每个格点处都有一个坐标值，因此我们可以通过在坐标系
中标出正方形各个顶点的坐标值来计算正方形格点面积。

例如，当一
个正方形的顶点坐标分别为（x1，y1）、（x1，y2）、（x2，y2）和
（x2，y1）时，该正方形的面积可以用公式（x2 - x1）*（y2 - y1）
来计算。

总之，正方形格点面积公式简单易用，是计算正方形面积的常见
方法之一。

无论是在学习中还是在实际运用中，都具有一定的实用性
和价值。

【详解】四年级下第04讲_格点图形面积计算

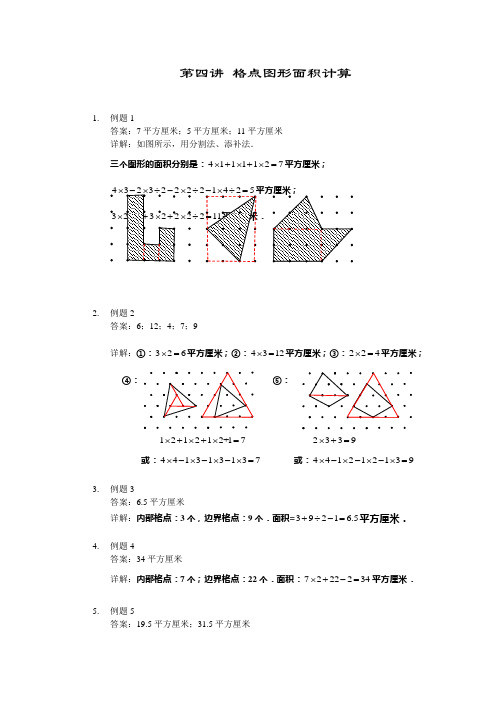
第四讲格点图形面积计算1. 例题1答案：7平方厘米；5平方厘米；11平方厘米详解：如图所示，用分割法、添补法．三个图形的面积分别是：4111127⨯+⨯+⨯=平方厘米； 4⨯⨯÷32⨯⨯÷2. 例题2答案：6；12；4；7；9详解：①：326⨯=平方厘米；②：4312⨯=平方厘米；③：224⨯=平方厘米；3. 例题3答案：6.5平方厘米详解：内部格点：3个，边界格点：9个．面积=3921 6.5+÷-=平方厘米．4. 例题4答案：34平方厘米详解：内部格点：7个；边界格点：22个．面积：7222234⨯+-=平方厘米．5.例题5答案：19.5平方厘米；31.5平方厘米④： ⑤： 121212+17⨯+⨯+⨯= 或：441313137⨯-⨯-⨯-⨯= 2339⨯+= 或：441212139⨯-⨯-⨯-⨯=详解：可以分割、添补，也可以用公式法：（1）内部格点：4个；边界格点：7个．面积：()7241319.5÷+-⨯=平方厘米；（2）内部格点：8个；边界格点：7个．面积：()7281331.5÷+-⨯=平方厘米．6. 例题6答案：28平方厘米；56平方厘米详解：可以分割、添补，也可以用公式法：（1）内部格点：4个；边界格点：8个．面积：()4282228⨯+-⨯=平方厘米；（2）内部格点：3个；边界格点：10个．面积：()32102456⨯+-⨯=平方厘米．7. 练习1答案：3平方厘米；10平方厘米详解：如图，分别用分割法、添补法．8. 练习2答案：12；20；5；18 详解：①：3412⨯=平方厘米； ②：直接数，每层4个，共5层，4520⨯=9. 练习3答案：13 简答：内部格点：1个，边界格点：13个．面积=()11321213+÷-⨯=．10. 练习4答案：17平方厘米简答：内部格点：1个；边界格点：17个．面积：1217217⨯+-=平方厘米． ③： ④：1112125⨯+⨯+⨯= 122312818⨯+⨯+⨯+=11.作业1答案：6；6.5简答：可用分割或添补法完成．12.作业2答案：7；12简答：使用割补法分别计算．13.作业3答案：56简答：大正三角形的面积是254100⨯=平方厘米，利用添补法可得．14.作业4答案：29简答：综合利用分割法与添补法．也可以用正方形格点图形面积公式计算．注意每个最小正方形面积是2．15.作业5答案：44简答：综合利用分割法与添补法．也可以用三角形格点图形面积公式计算．注意每个最小正三角形面积是2．。

格点与面积

有N=4，L=7，则用粗线围成图形的面积为：（4+7 -1)×1=6.5(平方厘米)
方法二：如下图，先求出粗实线外格点内的图形的面积，有①=3÷2=1.5，
②=2÷2=1，③=2÷2=1，④=2÷2=1，⑤=2÷2=l，⑥=2÷2=1，还有三个小正方形，所以粗实线外格点内的图形面积为1.5+l+1+1+1+1+3=9.5，而整个格点阵所围成的图形的面积为16，所以粗线围成的图形的面积为：16-9.5=6.5平方厘米．
··········
····· ·····
··········
··········
1．如图6-1，每一个小方格的面积都是l平方厘米，那么用粗线围成的图形的面积是多少平方厘米?
【分析与解】方法一：正方形格点阵中多边形面积公式：（N+L -1)×单位正方形面积，其中N为图形内格点数，L为图形周界上格点数．
3.求下列各个格点多边形的面积.
4、如果每个小正方形的面积是1平方厘米，那么下图中五角星的面积是多少平方厘米？
5、用9个钉子钉成相互间隔为1厘米的正方阵(如右图).如果用一根皮筋将适当的三个钉子连结起来就得到一个三角形,这样得到的三角形中,面积等于1平方厘米的三角形的个数有多少?
1.______(面积单位).
3、下图中的每个正方形的面积都是1，那么图中这只狗所占的图形的面积是多少？
4.将图中的图形分割成面积相等的三块.
5、如下图（a），计算这个格点多边形的面积
6、如下图，计算下列各格点多边形的面积，统计每个图形周界上的格点数与图形内包含的格点数.
1、求下图中格点多边形的面积（每相邻四个点围成的小方格的面积为1平方厘米）。
2.右图中,其中每相邻的三点“∴”或“∵”所形成的三角形都是面积为1的等边三角形,试计算四边形ABCD的面积.

巧用“格点”算面积 - ME博客—数学教师博客群,教育博客,教 …

巧用“格点”算面积
请你算一算下面各图的面积：（为了计算的方便，我们把图中相邻两个点之间的距离看作是1个长度单位，把相邻4个点连线后得到的正方形的面积看成是1个面积单位。

）
这里一共有6张图，估计大家利用计算公式可以很方便地算出图1和图3的面积。

图1面积长×宽：7×3=21，图3面积长×宽÷2：5×4÷2=10。

但其它的几张图就不能直接算了。

你有没有发现，这些图都是画在格点图上的，利用这些格点，我们就可以很轻松地算出所有图形的面积了。

格点面积=内部格点数+周界格点数÷2－1。

还是拿图1和图3举例。

图1面积：12＋20÷2－1=21；图3面积：7＋8÷2－1=10。

计算的结果和我们刚才用面积计算公式的结果是一样的。

那你现在是不是也可以用这个新的公式来算算其它几张图的面积了呢？
哈哈，其实这个新公式并不是我的发明，它的名字叫“毕克定理”。

利用该公式计算格点面积时，不必考虑这是一个什么图形，而是直接利用它就可以算出各种图形的面积了。

是不是很方便啊？。

格点与面积

③ ⑤①
④
利用拼补:
5×5 = 25 4× (2×3÷2 )= 12 25 －12 = 13
利用分割:
4× (3×2÷2 )= 12 1× 1 = 1 12+1= 13
例5.图中有三个正方形,分别计算正方形①、
正方形② 和正方形③的面积;并观察三个正方形的面积之间有什么关系
思考:三个正方形面积
由水平线和垂直线相交而成的方格纸中, 水平线和垂直线的交点称面积为相格等点的每个小正方形称为面积单位
每个小正方形的边长称为
一个单位长度
这是一个面积单位
这都是单位长度
注意: 单位长度必
须是由水平线或垂直线连接而成。
长
宽图一
高图二底
高图三底
上底高
下底图四
格点与面积
求长方形面积？
长方形面积长宽
三角形面积底高 2
平行四边形面积底高
梯形面积 (上底下底)高 2
例2.计算图中三角形的面积.
长方形的面积为: 45 20
②
①
④
③
三角形①的面积为: 24 2 4
三角形②的面积为: 23 2 3
三角形③的面积为: 25 2 5
所以三角形④的面积为:
20 - (4+3+5 )= 20 - 12 = 8
③ ①
正方形①的面积: 2×2＝ 4 正方形②的面积: 2×2＝ 4
正方形③的面积:
②
4× (2×2÷2) ＝ 8
思考:三个正方形面积关系
正方形①的面积+正方形②的面积＝正方形③的面积:
分割是把要求的图形分割成几个基本图形,分别来求面积,然后相加.

格点求面积公式(一)

格点求面积公式(一)
格点求面积公式
1. 矩形格点面积公式
对于平面上的矩形格点区域，面积可以通过格点的个数来计算，
公式如下：
Area=(n+1)×(m+1)
其中，n表示矩形格点区域的纵向格点数，m表示矩形格点区域的横向格点数。

例子：假设有一个长为3，宽为4的矩形格点区域，即n=2，m=3。

根据公式计算可得：
Area=(2+1)×(3+1)=9
所以，该矩形格点区域的面积为9个格点。

2. 正方形格点面积公式
对于平面上的正方形格点区域，面积也可以通过格点的个数来计算，公式如下：
Area=(n+1)2
其中，n表示正方形格点区域的边长。

例子：假设有一个边长为5的正方形格点区域，即n=4。

根据公式计算可得：
Area=(4+1)2=25
所以，该正方形格点区域的面积为25个格点。

3. 三角形格点面积公式
对于平面上的三角形格点区域，面积同样可以通过格点的个数来计算，公式如下：
Area=(n+1)×(m+1)
2
其中，n表示三角形格点区域的高度（即底边上的格点数），m表示三角形格点区域的宽度（即最长斜边上的格点数）。

例子：考虑一个高度为3，宽度为4的三角形格点区域，即n=2，m=3。

根据公式计算可得：
$Area = = = $
所以，该三角形格点区域的面积为个格点。

以上就是几种常见的格点求面积公式，根据不同形状的格点区域，我们可以利用相应的公式来计算其面积。

正方形格点面积公式

正方形格点面积公式
正方形格点面积公式是指由正方形边界内部的格点组成的正方形
的面积。

在平面直角坐标系中，我们可以用数学语言来表示这一面积
公式。

假设正方形的边长为a，则其内部共有(a-1)个正方形，其中边
长为1的正方形共有a×a个。

因此，正方形格点面积公式可以表示为：(a-1)²+a² = 2a²-2a+1
这个公式的由来可以通过计数方法来理解。

我们可以把正方形边
界内的格点看作是坐标平面中的整数点，因为它们的坐标为(a, b)，
其中a与b都是整数。

在正方形的边界上各有a个格点，因此正方形
上的格点数量为4a-4。

由于四个角上的点被计算了两次，所以我们需
要减去4，得到正方形边界内部的点的数量2a-2。

因此，若正方形的
内部共有(a-1)个正方形，则正方形内部的点的数量为2a-2+a^2-1，即
2a^2-2a。

然而，需要注意的是，正方形的四个角也被计算了两次，所
以必须再加上1个点，即得到上述的公式。

在实际应用中，正方形格点面积公式可用于计算正方形网格的面积。

例如，当我们需要确定一块土地的面积时，可以先将其划分成若
干个小正方形，然后使用上述公式计算每个正方形的面积，再将所有
小正方形的面积相加即可得到该土地的面积。

此外，该公式还可用于
计算物体的体积等其他方面。

格点算面积

NL
13 23 33 ……
S值
3 2 5 2 7 2
…
当N等于 0时S值
1 2 1 2 1 2
当N等于0时 S与L之间关
系式
S L2 2
S L2 2
S L2 2
…
在N=0基础之上增
加多少
1
2
3
现S与N、L 之间的关系
S L2 1 2
S L22 2
S L23 2
…
结论
S L2N 2
NL
2、如图,如果每相邻的三个点构成的等边三角形的面积为1,那么还能用皮克公式来计算格点多边形的面积吗
当N等于0 当N等于0 在N=0基础之现S与N、L 时S与N之时S值上增加多少之间的关系
间关系式
5
S L2
3
2
2
2
7
S L2
3
2
2
2
9
S L2
3
2
2
2
…
…
1
2
3
S L2 1 2
S L22 2
S L23 2
…
结论
S L2N 2
NL
16 26 36 ……
S 当N等于当N等于在N=0基础现S与N、L
第一阶段：课前准备知识预备：格点多边形
格点多边形：方格网中的每个交点叫做格点如右图中的点A、 B、C、D、E… ,每一个小方格的边长是1个单位长度即是每个小正方形的面积为1如右图阴影正方形.
如果一个多边形的所有顶点都在格点上,那么这个多边形叫做格点多边形如图中的多边形 ABCDE
B
C
…
讨论结果
当N=0时S与L之间的关系式为：

格点多边形的面积计算

格点多边形的面积计算
格点多边形是指由若干个在平面上排列的格点构成的封闭图形。

计算格点多边形的面积可以使用格点计数法。

首先，我们需要找到格点多边形内部的所有整数坐标点。

这可以通过扫描整个多边形内部的每个格点来实现。

如果一个格点被多边形边界所覆盖，则该点为内部点；否则为外部点。

接下来，我们需要计算多边形和每个内部点之间的三角形面积。

可以通过计算每个三角形的底和高来实现。

三角形的底可以是一个格点到多边形的一个边界的垂线，而高是从该垂线下的格点到多边形另一条边的距离。

最后，将所有三角形的面积加起来即可得到格点多边形的面积。

需要注意的是，如果多边形边缘上有格点，则需要使用半格来计算面积。

也就是说，半个格点的面积应该被计算在多边形内部。

以上就是格点多边形的面积计算方法。

使用这种方法可以得到准确的结果，但需要花费较多的时间和计算量。

第四讲 格点图形面积的计算

格点法求面积的公式

高斯小学奥数四年级下册含答案第04讲_格点图形面积计算

格点面积公式推导过程

七年级下数学拓展课——数格点算面积

《数格点算面积》课件

格点面积

正方形格点面积公式

【详解】四年级下第04讲_格点图形面积计算

格点与面积

巧用“格点”算面积 - ME博客—数学教师博客群,教育博客,教 …

格点与面积

格点求面积公式(一)

正方形格点面积公式

格点算面积

格点多边形的面积计算

第四讲格点图形面积的计算