规划计算题整理教学内容
土地利用规划计算题以及答案

土地利用规划计算题以及答案1、某地预测到规划期末人口将达到90万,人均粮食占有量500 kg,蔬菜占有量160kg,预测到2010年本地粮食作物平均播种单产将达到15000kg/hm2,蔬菜平均播种单产将达到30000kg/hm2,该地区的农作物复种指数为2,城市化水平将达到65%,如果规划年将粮食作物和经济作物(蔬菜除外)播种面积调整到8:2,村镇和城市人均占地指标分别为100m2和80m2,试测算该地规划年耕地和居民点用地需求量各是多少?解答如下:求耕地需求量:粮食用地=(总人口×人均粮食占有量)/(粮食播种单产×复种指数)=(90万人×500kg/人)/(15000kg/hm2×2)=1.5万hm2经济作物用地=(1.5×2)/8=0.375万hm2蔬菜用地=(总人口×人均蔬菜占有量)/(蔬菜播种单产×复种指数)=(90万人×160kg/人)/(30000kg/hm2×2)=0.24万hm2因此,规划年耕地需求量=粮食用地+经济作物用地+蔬菜用地=1.5万hm2+0.375万hm2+0.24万hm2=2.115万hm2求居民点用地城市居民点用地=(总人口×城市化水平×人均用地指标)=90万人×65%×80m2/人=0.468万hm2村镇居民点用地=(村镇总人口×人均用地指标)=90万人×35%×100m2/人=0.315万hm2因此,居民点用地=城市居民点用地+村镇居民点用地=0.783万hm22、某地2001年末总人口为116万、该地垦殖率为36.56%,预测规划期内人口年自然增长率4.5‰、年机械增长率为16‰,人均粮食占有量420kg,人均蔬菜占有量160kg,预测到2010年本地粮食作物平均播种单产将达到15000kg/ha,蔬菜平均播种单产将达到30000kg/ha,规划期内由外地调入粮食15万t,调出蔬菜10万t,该地区的粮食复种指数为2,蔬菜复种指数为3.5,城市化水平将达到62%,如果规划年将经济作物(蔬菜除外)用地面积调整到耕地总面积的11.13%,村镇和城市人均占地指标分别为124m2和96m2,试测算该地规划年:(1)该地规划期末总人口、城市人口和村镇人口(6分);P总人口=P2001×(1+年机械增长率+自然增长率)规划期年限=116×(1+4.5‰+16‰)(2010-2001)=139.2435万人P城市人口=139.2435×62%=86.3310万人P村镇人口=139.2435×38%=52.9125万人(2)耕地需求量(6分);粮食用地需求量=(规划目标年总人口×人均粮食占有量-调入粮食量)/(粮食播种单产×复种指数)=(139.2435万人×420kg/人-15000kg)/(15000kg/hm2×2)=19493.59hm2蔬菜用地=(总人口×人均蔬菜占有量+调出量)/(蔬菜播种单产×复种指数)=(139.2435万人×160kg/人+10000kg)/(30000kg/hm2×3.5)=2121.90hm2由于经济作物用地占耕地总面积的11.13%,因此,蔬菜用地和粮食用地占耕地总面积的88.87%.因此,规划年耕地需求量=(粮食用地+蔬菜用地)/88.87%=(19493.59hm2+2121.90hm2)/88.87%=24322.5948hm2(3)居民点用地需求量(4分)城市居民点用地=(城市总人口×人均占用地指标)=86.3310万人×96m2/人=9287.776hm2村镇居民点用地=(村镇总人口×人均占用地指标)=52.9125万人×124m2/人=6561.15hm2因此,居民点用地=城市居民点用地+村镇居民点用地=15848.926 hm2(4)规划年人均土地和人均耕地指标(2分)规划年人均土地=(规划目标年耕地总面积/垦殖率)/规划目标年总人口=(24322.5948hm2/36.56%)/139.2435万人=0.7167亩/人规划年人均耕地=(规划目标年耕地总面积)/规划目标年总人口=(24322.5948hm2)/139.2435万人=0.2620亩/人3、下表为某县2000—2010年土地利用综合平衡表,请用所学知识完成下列各题:(1)填空题表—1各类土地综合平衡表单位:hm2类型基期面积土地利用类型期内减少耕地园地林地牧草地城镇村用地交通用地水域未利用地耕地41203800601301545352510320园地550460205 302010590林地54210500181442牧草地2101801015 530城镇村用地6146020101050086114交通用地32650 10268122001010126水域1560101040150060未利用地18580131220861630155规划面积81073990573698248633338156661937期内增加19011319868133138 6631(2)填空题表—2土地利用结构表用地类型基期年规划年面积%面积%耕地412050.28%399049.22%园地550 6.78%5737.07%林地542 6.69%6988.61%牧草地210 2.59%248 3.06%城镇村用地6147.57%6337.81%交通用地326 4.02%338 4.17%水域156019.24%156619.32%未利用地185 2.28%610.75%土地总面积8107100%8107100%4、(此题数字和老师给的不符仅供参考方法).下表为某县2000—2010年土地利用综合平衡表,请用所学知识完成下列各题:(1)填空题表—1各类土地综合平衡表单位:hm2类型基期面积土地利用类型期内减少耕地园地林地牧草地城镇村用地交通用地水域未利用地耕地51204850501201535251510270园地510440105202010570林地64210600181442牧草地3123006612城镇村用地9146020101080086114交通用地5205010208124001010120水域1860101040180060未利用地18080101020861630150规划面积100585040540770368909519185161838期内增加190100170681091195131838备注:农作物播种面积为10000hm2。
规划问题的教学例题

规划问题的教学例题例1 某工厂在计划期内要安排I、II两种产品生产。
生产单位产品所需的设备台时及A,B两种原材料的消耗以及资源的限制如表1-1所示另外,工厂每生产一单位I可以获利50元,每生产一单位II可以获利100元,问工厂应分别生产多少单位产品I和产品II,才能获利最多?例 2 货物托运问题某公司拟用集装箱托运甲、乙两种货物,这两种货物每件的体积、重量,可获利润以及托运限制如表1-2且甲种货物最多托运4件,问两种货物各托运多少件,可获利最大。
例3 投资场所的选择某公司计划在市区的东、南、西、北四个区建立销售门面,拟议中有10个位置Ai(i=1,2, (10)可供选择,考虑到各个地区居民消费水平以及居民的居住密度,规定在东区A1,A2,A3三个点中至少选择两个;在西区A4,A5两个点中至少选择一个;在南区A6,A7两个点中至少选择一个;在北区A8,A9,A10三个点中至少选择2个。
另外,投资总额不能超过720万元,问应该选择哪几家销售点,可使得年利润为最大?例4 固定成本问题高压容器公司制造小、中、大三种尺寸的金属容器,所用资源为金属板、劳动力和机器设备,制造一个容器的各种资源的数量如表1-3所示不考虑固定费用,每种容器出售一只的利润分别为4万元,5万元,6万元,可使用的金属板有500t,劳动力有300人/月,机器有100台/月。
例5 路灯照度问题在一条20m宽的道路两侧,分别安装了一只2kw和一只3kw的路灯,它们离地面的高度分别为5m和6m。
在漆黑的夜晚,当两只路灯开启时,两只路灯连线路面上最暗的点和最亮的点在哪里?如果3kw路灯的高度可以在3m到9m之间变化,如何使得路面上最暗和最亮的点的位置?如果两只路灯的高度均可以在3m到9m之间变化,结果将如何?例6 某部门有三个生产同一产品的工厂(产地),生产的产品运往四个销售点(销地)出售,各个工厂的生产量、各销地的销量(单位:吨)、从各个工厂到各个销售点的单位运价(元/吨)如下表,研究如何调运才能使得总运费最小。
数学学习计划模板汇总10篇_1

数学学习计划模板汇总10篇数学学习计划篇1一、复习的主要内容1、熟练地数出数量在20以内的物体的个数,会区分几个和第几个,掌握数的顺序和大小,掌握10以内各数的组成,会读、写0――20各数。
2、初步知道加、减法的含义和加减法算式中各部分部分名称,初步知道加法和减法的关系,比较熟练地计算一位数的加法和10以内的减法。
3、初步学会根据加、减法的含义和算法解决一些简单的实际问题。
4、认识符号“=”“<”“>”,会使用这些符号表示数的大小。
5、直观认识长方体、正方体、圆柱、球、长方形、正方形、三角形和圆。
6、初步了解分类的方法,会进行简单的分类。
7、初步了解钟表,会认识整时和半时。
8、认真作业、书写整洁的良好习惯。
9、通过实践活动体验数学与日常生活的密切联系。
二、复习的重、难点重点:主要放在数与数的运算这一块内容中。
难点:加减混合的看图列式应用题、钟面的认识。
三、复习的主要目标1、引导学生主动整理知识,回顾自己的学习过程和收获,逐步养成回顾和反思的习惯。
2、通过总复习使学生在本学期学习到的知识系统化。
巩固所学的知识,对于缺漏的知识进行加强。
3、通过形式多样化的复习充分调动学生的学习积极性,让学生在生动有趣复习活动中经历、体验、感受数学学习的乐趣。
4、有针对性的辅导,帮助学生树立数学学习信心,使每个学生都得到不同程度的进一步发展。
5、培养学生的良好审题、书写、检查作业的学习习惯。
四、复习措施根据本班学生掌握知识的实际情况制定以下措施:1、将学生的零散知识集中起来,使知识纵成行、横成片,形成互相联系的知识网络。
2、采用变换练习的方式,开展游戏活动等多种方式调动学生的学习积极性。
3、加强对10以内口算加减法的练习和20以内的进位加法的练习。
4、加强对中下等生进行个别辅导五、复习时间安排1、回顾与反思本学期的学习情况(1课时)2、0—20各数的认识及相应的加减运算(2课时)3、分类(1课时)4、认识物体和图形(1课时)5、认识钟表(2课时)6、期末练习试卷3份(3课时)数学学习计划篇2一、指导思想依据新课程标准的要求,联系本册教材资料和学生自身实际,灵活、简便、愉快地进行复习。
初一学生的计划书怎么写

初一学生的计划书怎么写一、整理规划时间,确定要学习的内容在开始前,整理出可利用的时间,清楚自己在的空闲时间生活习惯。
在此前提下,以每一天为单位,制定学习计划。
接下来,梳理自身学习情况,找出最需要提高,合理分配复习和预习时间,有针对性地制定假期学习计划。
每天有效学习时间最好保持在4—5个小时。
根据自己的情况合理的规划一下,寒假中要做到既不睡懒觉,也不要开夜车。
习惯比聪明更重要!按照计划来,每天坚持!二、复习上学期内容,攻克薄弱环节把寒假分为复习和预习两个阶段,前段时间主要是复习,在此基础上留一个星期的时间对下学期内容进行预习。
今年的寒假假期较短,目标不宜太大、复习范围不宜太广。
如果想真正有收获,就不能贪多!适宜重点攻克薄弱学科、或学科中的重点内容。
(我的数学可重点复习第二章和第三章,我这两章基础都能掌握,不过在分析应用上还需要改进,寒假的时候适合做些应用的分析题,帮助提高。
英语可将平时的上课内容拿来复习,记忆一些固定的用法和常用搭配,可把上学期的教材全解做为复习的工具书。
把上学期的课文从开始再复习下,有些需要记忆的东西一定要记住。
比如每单元的单词及其拼写和固定搭配和固定句式及语法知识。
)三、预习下学期课程将下学期的课程提前预习一下,掌握各重要科目(语文、数学、英语)下学期的重难点。
预习的过程中碰到的不懂的问题要及时做记录,等到开学的时候可询问老师。
(数学要提前预习前2章,英语要预习前四单元)四、时间安排表早上8:00起床之后刷牙漱口洗脸吃早饭;8:30合理安排30分钟大声朗读背诵英语课文,听一些英语听力。
听读是培养英语语感最好的方法。
听读的材料可以是上学期的英语教材,也可把下学期教材预习;9:00做寒假作业先做数学。
因为早上头脑是最清醒的,数学逻辑思维比较强,所以先做数学的作业;10:00开始休息15分钟,学了一个小时也该舒展舒展筋骨了,因此利用这15分钟的时间充分休息,也活动活动;10:20—11:20做英语寒假作业,给自己每天定一个目标。
规划求解的例子和练习

规划问题求解三、规划求解及应用1、线性规划问题线性规划的一般形式,线性规划可以找到全局的最优解。
例4:某公司生产和销售两种产品,两种产品各生产一个单位需要工时3小时和7小时,用电量4千瓦和5千瓦,需要原材料9公斤和4公斤。
公司可提供的工时为300小时,可提供的用电量为250千瓦,可提供的原材料为420公斤。
两种产品的单位利润分别为200元和210元。
该公司怎样安排两种产品的生产量,所获得的利润最大。
操作步骤:(1)建立数学模型(2)在EXCEL中输入模型,注意:用颜色区分不同功能的单元格,可以不做这样的修饰。
输入模型的参考原则:围绕数据建立模型;约束的左侧表达式和右侧表达式,最好同行和同列;行和列的总和应该靠近行和列;左向右,从上往下输入模型;可以使用颜色、影印等来区别参数和模型中的变量。
(3)在E3中输入公式:=SUMPRODUCT(C3:D3,$C$7:$D$7),复制到e5;e6 在C8中输入公式:=SUMPRODUCT(C6:D6*C7:D7)说明:SUMPRODUCT(C3:D3,$C$7:$D$7)等价于c3*c7+d3*d7(4)选择“工具”菜单的规划求解:①设置目标单元格②设置可变单元格;③设置约束条件;④设置非负数条件。
(5)单击“求解”,单击“确定”。
(6)拓展训练:为了了解利润随着产量的变化,可以制作模拟运算表:使用序列填充产生数据B13:B23;C12:M12①在B12中输入公式:=C8②选中B12:M23区域,选择“数据”菜单的模拟运算表,在“输入引用行的单元格”中输入$C$7,在“输入引用列的单元格”中输入$D$7,单击“确定”。
③利用数据产生三维曲面图形。
操作技巧见课堂操作。
2、非线性规划问题例5:某公司生产和销售两种产品,两种产品各生产一个单位需要工时3小时和7小时,用电量4千瓦和5千瓦,需要原材料9公斤和4公斤。
公司可提供的工时为300,可提供的用电量为250千瓦,可提供的原材料为420公斤。
初三数学学习计划10篇

初三数学学习计划10篇初三数学学习计划1一、复习目标:(1)使所学知识系统化、结构化、让学生将三年的数学知识连成一个有机的整体,更利于学生理解;(2)精讲多练,巩固基础知识,掌握基本技能;(3)抓好方法教学,引导学生归纳、总结解题的方法,适应各种题型变化;(4)做好综合题训练,提高学生综合运用知识分析问题的能力。
二、复习方法与措施:1、挖掘教材,夯实基础,重视对基础知识的理解和基本方法的指导通过将近3年的学习,学生已经掌握了一定基础知识、基本方法和基本技能,但对教材的理解是零碎的、解题规律的探究是肤浅的。
因此,在组织学生进行总复习的时候,首先引导学生系统梳理教材、构建知识结构,让各种概念、公理、定理、公式、常用结论及解题方法技巧,都能在学生的头脑中再现。
例如:分式的化简求值,学生应想到分解因式的方法、提公因式法、公式法等,证明三角形全等马上想到全等三角形的所有判定。
教学中,要立足课本,充分挖掘和发挥教材例、习题的潜在功能,引导学生归纳、整理教材中的基础知识、基本方法,使之形成结构。
例如:课本上课题学习等。
坚决克服那种重难题、重技巧、轻课本、轻基础的做法。
2、抓好教材中例题、习题的归类、变式的教学。
在数学复习课教学中,挖掘教材中的例题、习题等的功能,是大面积提高教学质量的需要。
因此在复习中根据教学的目的、教学重点和学生实际,引导学生对相关的例题进行分析、归类,总结解题规律,提高复习效率。
对具有可变性的例习题,引导学生进行变式训练,使学生从多方面感知数学的方法、提高学生综合分析问题、解决问题的能力。
3、强化训练,注重应用,发展能力数学教学的最终目的,是培养学生创新意识、应用意识,及综合能力。
教师可以自觉地、有目的地加以培养。
这样,就可以大大地加快数学能力的形成和发展,使各种思维方法合理、简捷,最大限度地发挥学生创造性能力。
分析近几年来各省市的中考能力题:在学生已有的基础上,可以通过阅读理解,推理分析,总结规律,归纳其结论;联系实际,注重应用,培养探索、发现、创新能力是中考命题必然趋势。
小学四年级数学上册教学计划4篇

小学四年级数学上册教学计划4篇(一)学问与技能:1、熟悉计数单位“十万”“百万”“千万”“亿”“十亿”“百亿”“千亿”,熟悉自然数,把握十进制计数法,会依据数级读、写亿以内和亿以上的数,会依据要求用“四舍五入”法求一个数的近似数。
体会和感受大数在日常生活中的应用,进一步培育数感。
2、会笔算三位数乘两位数的乘法、除数是两位数的除法,会进展相应的乘、除法估算和验算。
3、会口算两位数乘一位数(积在100以内)和几百几十乘一位数,整十数除整十数、整十数除几百几十数。
4、熟悉直线、射线和线段,知道它们的区分;熟悉常见的几种角,会比拟角的大小,会用量角器量出角的度数,能按指定度数画角。
5、熟悉垂线、平行线,会用直尺、三角板画垂线和平行线;把握平行四边形和梯形的特征。
6、结合生活情境和探究活动学习图形的有关学问,进展空间观念。
7、了解不同形式的”条形统计图,学会简洁的数据分析,进一步体会统计在现实生活中的作用。
(二)过程与方法1、经受从实际生活中发觉问题、提出问题、解决问题的过程,体会数学在日常生活中的作用,初步形成综合运用数学学问解决问题的力量。
2、初步了解运筹的思想,培育从生活中发觉数学问题的意识,初步形成观看、分析及推理的力量。
(三)情感态度价值观1、体会学习数学的乐趣,提高学习数学的兴趣,建立学好数学的信念。
2、养成仔细作业、书写干净的良好习惯。
重点:大数的熟悉,三位数乘两位数,除数是两位数的除法,角的度量,以及平行四边形和梯形的熟悉。
难点:1、亿以内数的读法及写法,培育学生的数感。
2、使学生把握乘法的估算方法。
3、使学生理解垂直与平行的概念,会用直尺、三角尺画垂线和平行线。
4、让学生熟悉两种复式条形统计图,能依据统计图提出并答复简洁的问题,能发觉信息并进展简洁的数据分析。
5、使学生通过简洁的事例,初步体会运筹思想和对策论方法在解决实际问题中的应用。
教学措施篇二1、在教学中,充分发挥学生的主体性作用,在学好根底学问的前提下,鼓舞学生提出不同的问题,大胆质疑,努力创新。
土地利用规划计算题以及答案

1、某地预测到规划期末人口将达到90万,人均粮食占有量500 kg,蔬菜占有量160 kg,预测到2 010年本地粮食作物平均播种单产将达到15000kg/hm2,蔬菜平均播种单产将达到30000kg/hm2,该地区的农作物复种指数为2,城市化水平将达到65%,如果规划年将粮食作物和经济作物(蔬菜除外)播种面积调整到8:2,村镇和城市人均占地指标分别为100m2和80m2,试测算该地规划年耕地和居民点用地需求量各是多少?解答如下:求耕地需求量:粮食用地=(总人口×人均粮食占有量)/(粮食播种单产×复种指数)=(90万人×500kg/人)/(15000 kg/hm2×2)=1.5万hm2经济作物用地=(1.5×2)/8=0.375万hm2蔬菜用地=(总人口×人均蔬菜占有量)/(蔬菜播种单产×复种指数)=(90万人×160kg/人)/(30000 kg/hm2×2)=0.24万hm2因此,规划年耕地需求量=粮食用地+经济作物用地+蔬菜用地=1.5万hm2+0.375万hm2+0.24万hm2=2.115万hm2求居民点用地城市居民点用地=(总人口×城市化水平×人均用地指标)=90万人×65%×80 m2/人=0.468万hm2村镇居民点用地=(村镇总人口×人均用地指标)=90万人×35%×100 m2/人=0.315万hm2因此,居民点用地=城市居民点用地+村镇居民点用地=0.783万hm22、某地2001年末总人口为116万、该地垦殖率为36.56%,预测规划期内人口年自然增长率4.5‰、年机械增长率为16‰,人均粮食占有量420 kg,人均蔬菜占有量160 kg,预测到2010年本地粮食作物平均播种单产将达到15000kg/ha,蔬菜平均播种单产将达到30000kg/ha,规划期内由外地调入粮食15万t,调出蔬菜10万t,该地区的粮食复种指数为2,蔬菜复种指数为3.5,城市化水平将达到62%,如果规划年将经济作物(蔬菜除外)用地面积调整到耕地总面积的11.13%,村镇和城市人均占地指标分别为124m2和96m2,试测算该地规划年:(1)该地规划期末总人口、城市人口和村镇人口(6分);P总人口=P2001×(1+年机械增长率+自然增长率)规划期年限=116×(1+4.5‰+16‰)(2010-2001)=139.2435万人P城市人口=139.2435×62%=86.3310万人P村镇人口=139.2435×38%=52.9125万人(2)耕地需求量(6分);粮食用地需求量=(规划目标年总人口×人均粮食占有量-调入粮食量)/(粮食播种单产×复种指数)=(139.2435万人×420kg/人-15000 kg)/(15000 kg/hm2×2)=19493.59hm2蔬菜用地=(总人口×人均蔬菜占有量+调出量)/(蔬菜播种单产×复种指数)=(139.2435万人×160kg/人+10000 kg)/(30000 kg/hm2×3.5)=2121.90hm2由于经济作物用地占耕地总面积的11.13%,因此,蔬菜用地和粮食用地占耕地总面积的88.87%. 因此,规划年耕地需求量=(粮食用地+蔬菜用地)/ 88.87%=(19493.59hm2 +2121.90hm2 )/ 88.87%=24322.5948hm2(3)居民点用地需求量(4分)城市居民点用地=(城市总人口×人均占用地指标)=86.3310万人×96 m2/人=9287.776hm2村镇居民点用地=(村镇总人口×人均占用地指标)=52.9125万人×124 m2/人=6561.15hm2因此,居民点用地=城市居民点用地+村镇居民点用地=15848.926 hm2(4)规划年人均土地和人均耕地指标(2分)规划年人均土地=(规划目标年耕地总面积/垦殖率)/规划目标年总人口=(24322.5948hm2/36.56%)/139.2435万人=0.7167亩/人规划年人均耕地=(规划目标年耕地总面积)/规划目标年总人口=(24322.5948hm2)/139.2435万人=0.2620亩/人3、下表为某县2000—2010年土地利用综合平衡表,请用所学知识完成下列各题:(1)填空题表—1各类土地综合平衡表单位:hm2类型基期面积土地利用类型期内减少耕地园地林地牧草地城镇村用地交通用地水域未利用地耕地4120 3800 60 130 15 45 35 25 10 320 园地550 460 20 5 30 20 10 5 90 林地542 10 500 18 14 42 牧草地210 180 10 15 5 30 城镇村用地614 60 20 10 10 500 8 6 114 交通用地326 50 10 26 8 12 200 10 10 126 水域1560 10 10 40 1500 60 未利用地185 80 13 12 20 8 6 16 30 155 规划面积8107 3990 573 698 248 633 338 1566 61 937 期内增加190 113 198 68 133 138 66 31(2)填空题表—2 土地利用结构表用地类型基期年规划年面积% 面积%耕地4120 50.28% 3990 49.22%园地550 6.78% 573 7.07%林地542 6.69% 698 8.61%牧草地210 2.59% 248 3.06%城镇村用地614 7.57% 633 7.81%交通用地326 4.02% 338 4.17%水域1560 19.24% 1566 19.32%未利用地185 2.28% 61 0.75%土地总面积8107 100% 8107 100%4、(此题数字和老师给的不符仅供参考方法).下表为某县2000—2010年土地利用综合平衡表,请用所学知识完成下列各题:(1)填空题表—1各类土地综合平衡表单位:hm2类型基期面积土地利用类型期内减少耕地园地林地牧草地城镇村用地交通用地水域未利用地耕地5120 4850 50 120 15 35 25 15 10 270园地510 440 10 5 20 20 10 5 70林地642 10 600 18 14 42牧草地312 300 6 6 12城镇村用地914 60 20 10 10 800 8 6 114交通用地520 50 10 20 8 12 400 10 10 120水域1860 10 10 40 1800 60未利用地180 80 10 10 20 8 6 16 30 150规划面积10058 5040 540 770 368 909 519 1851 61 838期内增加190 100 170 68 109 119 51 31 838备注:农作物播种面积为10000 hm2。
土地利用规划计算题以及答案

评价指标
Ⅰ
Ⅱ
Ⅲ
指标平均值
年均耕地粮食单产 P1
636.95
625.63
620.36
627.6467
年均耕地油料单产 P2
131.34
135
142
136.1133
年均耕地价值产投比 P3
2.19
2.10
3.06
2.4500
年均耕地纯收入 P4
1238.42 1275.99 2148.61 1554.3400
评价指标 方案 I
方案 II
方案 III
P1
12.1779
11.9614
11.8607
P2
11.5792
11.9018
12.5190
P3
10.7265
10.2857
14.9878
P4
9.5610
9.8510
16.5880
P5
12.2008
10.7699
13.0293
P6
9.7570
11.9439
14.2991
牧草地 城镇村用地 交通用地 水域
期内减少 未利用地
耕地
4120
苏教版三年级上册数学教学计划(四篇)

苏教版三年级上册数学教学计划(四篇)一、教学内容:本册教材在前四册教学的根底上,依据《数学课程标准》关于第一学段内容标准的要求和这套教材的整体编写规划,在“数与代数”“空间与图形”“统计与概率”“实践活动”四个领域安排了如下内容:1、数与代数⑴10000以内数的熟悉、读写和大小的比拟。
整千数加减整千数(和不超过10000)的口算,整千数加整百数及相应的减法的口算。
⑵两位数除以一位数(每一位都能整除)的口算,两位数除以一位数的笔算和估算,除法的验算。
⑶两位数加减两位数(加法中和不超过100)的口算,整百数加整百数(和超过1000)及相应的减法的口算。
⑷整百数乘一位数的口算,三位数乘一位数的笔算和估算。
⑸分数的初步熟悉(把一个物体或一个图形看作“1”),两个同分母分数以及分子都是1的两个异分母分数的大小比拟。
简洁的同分母分数加减计算。
⑹千克和克的熟悉,千克和克的互化。
⑺24时记时法的熟悉。
2、空间与图形⑴长方形和正方形的特征。
⑵周长的含义,长方形和正方形的周长计算。
⑶物体的正面、侧面和上面的熟悉。
⑷由三个一样的正方体摆成的物体的正面、侧面、上面的视图。
3、统计与概率⑴对可能性大小的熟悉。
⑵用画“正”字的方法收集整理数据。
⑶简洁的条形统计图。
4、实践活动⑴农村新貌:在供应的农村情境中提出并解决有关乘除计算的实际问题。
⑵称一称:使用适宜的称量工具称出一些水果、蔬菜等物体的重量及体重。
⑶周末一天的安排:用24时记时法安排周末一天的活动,并解决有关的实际问题。
⑷周长是多少:围绕周长问题进展制作、拼摆、测量计算以及估量等数学活动。
⑸摸牌和下棋:在摸牌和下棋活动中体会事情发生的可能性的大小。
二、教学目标:1、数与代数。
⑴通过对教具的观看、在计数器上拨珠,并联系实际加深对千和千位的熟悉,初步熟悉一万和万位,熟悉万以内的数位挨次表,能结合详细情境理解四位数的意义,把握四位数的组成。
把握10000以内数的读写方法。
能用10000以内的数表示日常生活中的一些事物,并进展沟通。
环境规划复习重点计算题.docx
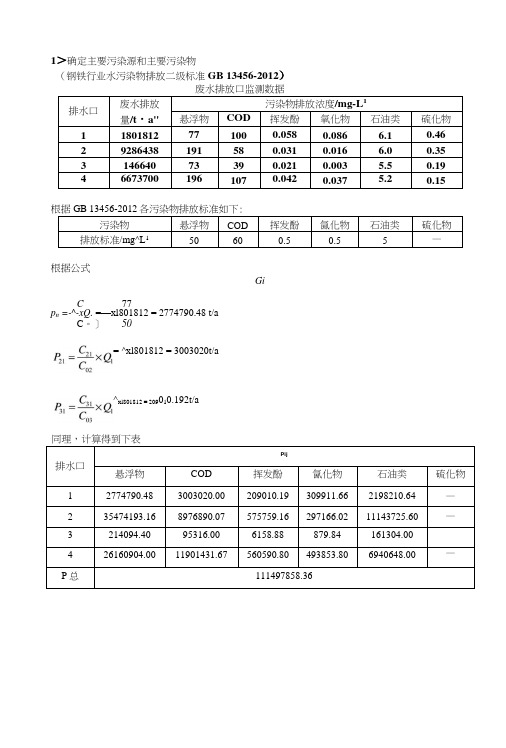
1>确定主要污染源和主要污染物(钢铁行业水污染物排放二级标准GB 13456-2012)废水排放口监测数据排水口废水排放量/t・a"污染物排放浓度/mg-L1悬浮物COD挥发酚氧化物石油类硫化物11801812771000.0580.086 6.10.46 29286438191580.0310.016 6.00.35 314664073390.0210.003 5.50.19 466737001961070.0420.037 5.20.15根据GB 13456-2012各污染物排放标准如下:污染物悬浮物COD 挥发酚氤化物石油类硫化物排放标准/mg^L150 60 0.5 0.5 5 —根据公式GiC77p n =-^-xQ. =—xl801812 = 2774790.48 t/aC。
]50^xl801812 = 209010.192t/a同理,计算得到下表排水口Pij悬浮物COD 挥发酚氤化物石油类硫化物1 2774790.48 3003020.00 209010.19 309911.66 2198210.64 —2 35474193.16 8976890.07 575759.16 297166.02 11143725.60 —3 214094.40 95316.00 6158.88 879.84 161304.004 26160904.00 11901431.67 560590.80 493853.80 6940648.00 —P总111497858.36= ^xl801812 = 3003020t/a根据表格可知:对于污染源K2〉K4>K1>K3,所以主要污染源为第2污染源;对于污染物K1>K2>K5>K3>K4,所以主耍污染物为悬浮物。
2、某水域经五次监测溶解氧的浓度:5.6mg/L, 6.1mg/L, 4.5mg/L, 4.8mg/L, 5.8mg/L,用内梅罗法计算溶解氧的统计浓度值是4・95mg/LPn亦=4.5加g/厶(由于溶解氧越高,水体越干净,因此选择溶解氧最低值作为Pn和)(5・6 + 6・1 + 4・5 + 4・8 + 5・8)徳/厶=5.36卿/厶方法一:根据地表水环境质量标准(GB 3838-2002),选用溶解氧第II类标准5. = 6mg / L导专“75max5 晋二晋= 0.8931内=J«nJ2+(U)2 = J0.8932; 0.752 = ° 825p内=1内xSj = 0.825 x 6加g IL- 4.9 5 mg / L即:溶解氧的统计浓度为4.95mg / L方法二卩内=(竝J+(几_w_ LxD408 50x5000t / m 2 • d408X1X106 50x5000x24x3600g / m 2 •s = 0.0189g / m 2c = c° +QLuH0.0189x50 >2x750 )= 0.0116m 5 / L3、试按下表给定的数据计算某处的大气质量指数,分别采用单因子环境质量指 数,均值型,加评价因子 飘尘so 2NO X CO 日均浓度/mg*m 30.22 0.32 0.13 5.20 评价标准 0.25 0.25 0.15 6.70 计权系数0.20.50.2 0.1飘尘2豊嚨加(2)均值型综合质量指数:1 "1/均=—工厶=—(0.88 + 1.28 + 0.87 + 0.78) = 0.9525ni=\ 4 (3)加权型综合质量指数:/=£ 比厶=0.2x0.88 + 0.5x1.28 + 0.2x0.87 + 0」x0.78 = 1.068 /=! (4)内梅罗多因子环境质量指数:G = I 均=0.9525= 1.1284、已知某工业位于一山谷地区,计算的混合高度h=750m,该地区长50m,宽 5km,上风向风速为2m/s, SO2的本地浓度为0.011mg/L o 该地区建成后的计划 燃煤量为8000t/d,煤的含硫量约为3%, SO?的转化率为85%,试用单箱模型估 计该地区的S02浓度。
小学六年级数学教学计划4篇

小学六年级数学教学计划4篇一、根本状况分析:本年级学生有学生47人,其中男生有25人,女生有22人。
从总体上看,学生数学力量相对欠缺,数学根底不够扎实,学校热忱一般,大多数学生上课能用心听讲,仔细思索问题,积极主动地发言,提出不同的看法,能按时完成作业。
反响比拟慢的也不少,一道特别简洁的计算题,你给他讲一遍不会,再讲一遍还是不会,连续讲一遍仍旧不会。
二、教学内容本册教学内容分为五大板快:(一)、数与运算。
1.其次单元。
2.第四单元。
(二)、空间与图形。
1.第一单元。
2.第三单元。
3.第六单元。
(三)、统计与概率。
第五单元。
(四)综合应用:数学与体育、生活中的数。
(五)整理与复习。
三、教学目的和要求:1、通过观看、操作等活动熟悉圆及圆的对称性,熟悉到同一个圆中半径、直径、半径和直径的关系,体会圆的本质特征及圆心和半径的作用,会用圆规画圆。
结合详细情境,通过动手试验、拼摆操作等实践活动,探究并把握圆的周长和面积的计算方法,体会的思想。
结合观赏与绘制图案的过程,体会圆在图案设计中的应用,能用圆规设计简洁的图案,感受图案的美,进展想象力和制造力。
2、在详细情境中理解或的意义,加深对百分数意义的理解。
能利用百分数的有关学问或运用方程解决一些实际问题,提高解决实际问题的力量,感受百分数与日常生活的亲密联系。
3、经受运用平移、旋转或作轴对称图形进展图案设计的过程,能敏捷运用平移、旋转和轴对称在方格纸上设计图案;结合观赏和设计漂亮的图案,感受图形世界的奇妙。
4、经受从详细情境中抽象出比的过程,理解比的意义及其与除法、分数的关系。
在实际情境中,体会化简比的必要性,会运用商不变的性质和分数的根本性质化简比。
能运用比的意义,解决根据肯定的比进展安排的实际问题,进一步体会比的意义,提高解决问题的力量,感受比在生活中的广泛应用。
5、熟悉复式条形统计图和复式折线统计图,感受复式条形统计图和折线统计图的特点。
能依据需要选择复式条形统计图、复式折线统计图有效地表示数据。
物流系统规划与设计部分计算与案例整理

3 53 4一、计算题——从至表、最邻近法、交叉中值法选址、贪婪取走启发式算法选址①从至表(课本P141) 定量关联法: (1)从至表法例:某物流中心有5个作业区域,作业区域间的流量如下表。
试用从至表法,做出该物流中心的布局方案设计。
该物流中心的物流分析从至表如下图所示:作业区域到达区域1 2 3 4 5 起始 出发 区域15 10 2 3 2 8 9 7 3 12 17 46 5Ⅰ选取具有最大流量的成对作业区3和5,进入布局图Ⅱ分别计算未进入布局图的作业区域(1,2,4)与已进入布局图的作业区域(3,5)间的流量和和,选择与已经入作业区3和5间流量和最大的作业区2,进入布局图,构成三角形Ⅲ分别计算未进入布局图的作业区域(1,4)与已进入布局图的作业区域(2,3,5)间的流量和,选择与已进入作业区2,3,5间流量和最大的作业区1,进入布局图,插入三角形内部,形成四个三角形。
作业区域 3 5 合计1 10 32 8 7 4 0 6 13 15 6作业区域 2 3 5合计 1 5 10 3 4 0 0 618 621717 8 7②最邻近法(—此例是不对称的距离矩阵,考试时考对称的,也会指定配送中心—) ——从任意一个城市开始,在每一步取离当前所在城市最近的尚未到过的城市作为下 一个城市,若这样的城市不止一个,则任取其中一个,直至走遍所有的城市,最 后回到开始出发的城市。
例题:假设某一车辆需到四个城市送货,城市之间的距离见表。
请问如何选择路线?③交叉中值法选址交叉中值模型: nZ=min ∑W i {|Xi-Xs|+|Yi-Ys |} i=1式中 Wi ——与第i 个点对应的权重(例如需求) Xi 、Yi ——第i 个需求点的坐标 Xs 、Ys ——服务设施点的坐标 n ——需求点的总数目求解步骤:确定中值 → 确定横坐标(从左至右计算权重和,直至大于等于中值/从右至距离1 2 3 4 1 8 5 6 2 6 8 5 3 7 9 5 4 9 7 8 解答:1 2 3 4 则最短路径为:1→3→4→2→1 总路程:233→4→2→1→3 总路程:23 4→2→1→3→4 总路程:23 86 57 6 9 985 7 8 5左计算权重和,直至大于等于中值)→ 确定从坐标(从上至下计算权重和, 直至大于等于中值/从下至上计算权重和,直至大于等于中值)例题:一个报刊连锁公司想在一个地区开设一个新的报刊零售点,主要的服务对象是附近的5个住宿小区的居民,他们是新开设报刊零售点的主要顾客源。
理财规划师三计算题归纳

例:张先生购买了一套总价100万的新房,首付20万,贷款80万,利率为6%,期限为20年。
• 如果采用等额本息方式,每月还款额为多少?第一个月所还本金为多少?第一个月所还利息为多少?一共还了多少本金?一共还了多少利息?张先生在还款5年之后,还有多少本金未还?还了多少本金?还了多少利息?• 如果采用等额本金法,第一个月还了多少本金?第一个月还了多少利息?一共还了多少本金?一共还了多少利息?等额本息法下:PMT=5731.45第一个月所还利息=800000×6%/12=4000第一个月所还本金=5731.45-4000=1731.45一共还的本金=800000一共还的利息=5371.45×240-800000=575548五年后还剩未还本金=679197五年内一共所还的本金=120803五年内一共还的利息=223084等额本金法下:第一个月还的本金=800000/240=3333.33第一个月所还利息=800000×6%/12=4000一共应还本金=800000一共应还利息=3333.33×0.005(利息)×(240+239+ (1)=3333.33×0.005×(240+1)×240÷2=482000等差数列=(首项+末项)*项数除以2假定:贷款20万元,期限20年,年利率为10%。
1.计算等额本息还款法下每年还款额?还款总额为多少?所还利息总额为多少?2.计算等额本金条件下第一年的还款额?还款总额为多少?所还利息总额?等额本息还款法下:每年还款额:23492所还利息总额为多少:269839还款总额为多少:269839+200000=469839等额本金还款法下:第一年的还款额:30000本金=200000/20=10000利息=200000×10%=20000所还利息总额:10000×10%×20 ×(1+20)/2=210000还款总额为多少:210000+200000=410000例:王先生年收入为10万元,预计收入每年增加3%,每年的储蓄比例为40%,目前有存款2万元,打算5年后买房,假设王先生的投资报酬率为10%。
2024年小学四年级数学教学复习工作计划例文(3篇)

2024年小学四年级数学教学复习工作计划例文一、复习指导原则:1、巩固知识体系,消除知识盲点。
对教材内容进行全面梳理,明确知识点的相互关系,通过基础复习和练习,强化记忆,深化理解,使学生能将所学知识转化为稳定的个人知识能力,实现从感性理解到理性认知的提升。
2、增强解题灵活性,提升实际问题解决能力。
在复习和练习中,引导学生对知识进行分类和整合,找出知识间的联系和解题规律,构建完整的知识框架,以达到灵活运用知识解决实际问题、提升应用数学的能力。
3、在复习过程中,注重引导学生形成有效的学习方法,培养数学感和逻辑思维能力,促进学生逻辑推理能力的发展。
4、培养学生的良好学习习惯,如认真做题、仔细检查,塑造良好的数学情感态度。
二、复习方式:采用分类复习、综合复习与完成复习提纲相结合的方式进行。
三、复习目标:1、进一步巩固对万级、亿级数的认识,掌握十进制计数法,熟练使用“万”、“亿”单位表示大数及近似数、改写等,建立完整的整数概念认知结构。
2、进一步熟练掌握除数为两位数的除法,提升计算器使用技能,加深对计算器功能的理解。
3、理解直线、射线和线段的特性,熟悉角的概念,能准确画出平行线和垂线,进一步发展空间观念。
4、通过复习,能掌握统计的基本知识和方法,能根据给定数据制作统计图并分析结果。
5、提升综合运用数学知识解决实际问题的能力,通过解决实际问题,进一步体验数学的应用价值。
6、通过复习过程,回顾和整理学期学习内容,激发主动学习的意愿,增强反思意识和能力。
四、复习策略:1、教授有效的复习技巧,进行全面、系统的单元复习,重点内容进行强化复习。
复习后进行检测,以评估学习效果。
设计多样化的复习作业,注重层次性、综合性、趣味性和开放性,及时批改,及时补缺。
2、强化计算和理解能力的训练,采用互动式复习方法,如学生出题、抢答、抽查和互批作业,激发学习兴趣。
3、对基础较好的学生,主要在课堂上提升其能力;对基础较弱的学生,采取课堂引导与课后辅导相结合的方式,通过“一帮一”模式,鼓励学生共同进步,同时争取家长的配合,激发他们的学习动力,确保每天的任务能及时完成。
初三数学寒假班课程规划

初三数学寒假班课程规划一、课程背景和目标数学是一门重要的学科,也是初中阶段的一个重要科目。
通过冬季假期的学习和巩固,可以帮助学生夯实数学基础,提高数学解题能力,为下学期的学习打下坚实的基础。
本次初三数学寒假班课程旨在帮助学生复习和巩固初三上学期所学的数学知识,同时引导学生培养数学思维能力和解题技巧,为下学期的学习打好基础。
二、学习内容和进度安排1. 第一周:复习整数、分数和小数的计算、性质及应用- 复习整数的加减乘除及应用,- 复习分数和小数的计算,学习分数和小数的化简及比较大小;- 复习分数和小数的四则运算(加减乘除),学习四则运算的运用;- 复习分数的关系和大小的比较。
2. 第二周:复习代数式、方程式和不等式的运算和解法- 复习代数式的运算,包括同类项合并、因式分解等;- 复习方程式的解法,包括等式的化简、配方法及分式方程的解法;- 复习不等式的解法,包括一元一次不等式的解法和不等式组的解法。
3. 第三周:复习平面图形的性质、几何变换和计算题- 复习平面图形的性质,包括直线、角、面积、周长等基本概念;- 复习几何变换,包括平移、旋转、对称等;- 复习平面图形的计算题,包括图形的面积和周长的计算。
4. 第四周:复习统计与概率知识- 复习统计:包括数据的收集整理、频数表的制作、统计图的绘制等;- 复习概率:包括随机事件的概念、概率的计算、事件间的关系等。
5. 第五周:综合复习、答疑和练习- 对前几周学习的内容进行综合复习,巩固知识;- 针对学生的问题和难点进行答疑;- 提供相关的练习题和试题,帮助学生巩固知识,并了解应试技巧。
三、教学方法和手段1. 授课方式:课堂讲解、示范、讨论和答疑相结合,灵活运用多媒体教学手段,例如投影仪、电子白板等。
2. 合作学习:鼓励学生之间互相合作,共同解决问题,培养学生的团队合作意识和解决问题的能力。
3. 实践和应用:适当安排实际问题的解决和应用题目,让学生将数学知识和解题技巧应用到实际生活中。
示范课教师个人计划

示范课教师个人计划一、课题示范课教学二、教学目标1. 让学生对本堂课的知识点有透彻的理解,能够准确地运用相关知识解决问题。
2. 激发学生对本学科的兴趣,培养他们积极主动的学习态度。
3. 锻炼学生的思维能力,提高他们的课堂参与度和团队协作能力。
三、教学重点&难点1. 重点本堂课的核心知识点,例如在数学示范课中,某个特定的定理及其应用就是重点。
这部分知识是构建后续知识体系的基石,所以必须让学生熟练掌握。
2. 难点一些比较抽象或者容易混淆的概念,像在语文示范课里,对文言文特殊句式的理解和辨析就可能是难点。
这需要通过多种教学方法让学生逐步攻克。
四、教学方法1. 讲授法直接向学生讲解知识点,确保把基础概念、原理等准确无误地传授给学生。
例如在讲解历史事件时,把事件的背景、经过、影响等清晰地讲述。
2. 讨论法提出有争议或者值得探讨的问题,让学生分组讨论。
比如在政治课上,提出关于社会现象的不同观点,让学生讨论并阐述自己的理由。
3. 演示法对于一些操作性强或者比较直观的内容,通过演示让学生更好地理解。
例如在物理课上演示实验过程。
五、教学过程1. 课程导入我会先讲一个有趣的小故事或者提出一个引人入胜的问题。
比如说在英语示范课上,我可以先讲一个关于英语国家文化习俗的有趣故事,像英国人喝茶的特殊习惯。
然后问学生们是否想了解更多英语国家独特的文化现象,从而引出本堂课要学习的英语单词和短语,这些单词和短语都和文化习俗相关。
2. 知识讲解用通俗易懂的语言讲解知识点。
如果是生物课,在讲解细胞结构的时候,我会把细胞比作一个小工厂,细胞核是厂长室,线粒体是动力车间等。
然后通过画图、举例等方式让学生深入理解每个部分的功能。
3. 互动环节把学生分成小组,给每个小组一个和知识点相关的小任务。
比如在地理示范课上,让小组讨论本地的地形地貌对气候的影响。
我会说:“同学们,现在你们就是小小地理学家啦,咱们这个小组讨论一下咱们这儿的地形地貌对气候有啥影响呀?大家可以从你们平时感受到的天气情况出发哦。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
和可覆盖需求点 i 的设
1
1,2,3
1,2,3
2
1,2,4,5
1,2,4,5
3
1,3,41,3,442,3,4,6,7
2,3,4,6,7
5
2,5,6
2,5,6
6
4,5,6
4,5,6
7
4,7
4,7
因为 ={2,3,4,6,7},| |=5 为最大,故首先 =4。因无容量约束,指派
主要的日常费用是他们员工完成任务过程中的运输费用。因此,用城
市距离进行考虑,要求新的办公室到各个合作伙伴之间运输的运输费
用最小。1)请确定一个新办公室的地址,用笛卡尔坐标来表达相应 结果。2)如果由于该地区的人口稀少,城市还没有达到一定的规模, 可以用欧几米德距离进行计算,新办公室又得在哪里投建?请比较两
2,3,4,6,7 归村落 4 服务。
此时 N={1,5},M={1,2,3,5,6,7};则更新候选点服务范围,见表 2.10.2。
2.10.2 更新后的候选点服务范围
精品文档
精品文档
村落号
1
1
1,2,3
2
1,5
3
1
4
5
5
2,5,6
6
5
7 因为 ={1,5}=N,恰好满足条件。则 =2。 综上所述,银行需要 2 台自动取款机,分别至于村落号为 2 和 4 的位置,2 号为 1,5 村落服务,4 号为 2,3,4,6,7 村落服务。
要点: 1. 明确 N,M, , 含义; 2. 分析正确后, 可参照 直接写出,无需再看网络图; 3. 熟悉最少点覆盖启发式算法的步骤,考虑是否有容量约束。
解:【集合覆盖模型】
区域中需求点集合 N={1,2,3,4,5,6,7}; ATM 取款机设施候选点集合 M={1,2,3,4,5,6,7}; 由网络图确定候选设施点 j 可覆盖的需求点集合 施节点的集合 ,见表 2.10.1。
精品文档
精品文档
费用结果保留三位小数得最优解为 X=5.5767,y=4.010,H=13.456
1 n
n
x j , y0( 0 )
j 1
1 n
n j 1
yj
,即
精品文档
,仓库到各生产地的距离 。
精品文档
直线距离为 =
目标函数运输总费用 H=
,其中
根据下列进行迭代:
=,
,=
直到运费无法减小。
用 MATLAB 进行编码:
运行结果得,迭代 78 次得到最优解。 其中选址坐标为(5.6235,4.9918),最小运费为 H=13.4550。 或由 EXCEL 迭代得,结果如图
12.一台机器工具小制造商要迁址,并确定了两个地区以供选择。 A 地的年固定成本为 800000 元,可变成本为 14000 元/台;B 地的年 固定成本为 920000 元,可变成本为 13000 元/台。产品最后售价为 17000 元/台。
(1) 当产量为多少时,两地的总成本相等? (2) 当产量处于什么范围时,A 地优于 B 地?当产量处于什么 范围时,B 地优于 A 地?
由
EXCEL
迭代得,结果如图
精品文档
精品文档
费用结果保留四位小数得最优解为 x=7.6257,y=7.6047,此时费用最小为 H=62.1020 (3)比较两次结果可知欧基米德中的费用小于笛卡尔距离,因直线距离是<直 角距离,因此用欧基米德距离更为精确。直角距离比较适合于城区范围内的选址, 欧基米德距离比较适合于远距离的选址。
|
4
3
3
4
3
3
4
2
5
11
2
5
7
2
7
2
2
7
11
4
11
11
4
11
14
1
12
7
1
12
可得
为偶数,即 均在第六个、第七个点之间。 ,
(2)设初始点为(
)有题意得,阿基米德距离为
=
,
目标函数 H(运输总费用)=
,
利用不动点算法,取一个初始的迭代点( , )=(8,7),此时 =62.51
令=
,
,=
=
=62.14
11. —个临时帮助服务中心计划在一个大城市的郊外开设一个新
的办公室。在经过一定的精简之后,该公司有 5 个大的合作伙伴。在
一个以 km 为单位的笛卡尔坐标系中,它们的坐标分别为:(4,4),
(4,11),(7 ,2),(11,11), (14,7)。它们的服务需求量的权重分
别为:wl=3,w2=2,w3=2,w4=4,w5=1。对于该服务中心来说,
精品文档
第二章 设施选址
10.一家银行准备在某县的农村地区投放一批 ATM 自动取款机, 以方便农村的用户取款。该农村地区的村落座落情况和相对距离如图 2.13 所示。为了能确保任一村的人都可以在 20 分钟之内到达自动取 款机取款,银行需要多少台自动取款机?它们的位置又在哪里?
图 2.13 村落座落情况和相对距离
13.利用表 2.8 所示的因素评分,以最大综合得分为基础,建模 分析应选择地点 A、B、C 中的哪一个?
精品文档
精品文档
表 2.8 因素评分表
解:权重矩阵设为 W,则 三个位置的因素评分作为 3 行构成因素矩阵 S。
可得综合加权矩阵 E=S*W=
。
可知 E(A)> E(B)> E(C)。即选择 A 点。
次结果,分析它们之间的关系。
要点:1. 补充交叉中值模型知识点
精品文档
精品文档
关键句:将 n 点需求的选址问题转化为
精品文档
点需求的选址问题。
精品文档
2.笛卡尔距离即直角距离,欧基米德距离即直线距离; 3.重心法:初始化+迭代公式+Excel/C 编程/matlab 编程迭代+迭代终止条件 解:(1)设新办公室的地址的坐标为(x,y),给题目已知的 5 个点编号 1~5。 由于笛卡尔距离 =| - |+| - |。 则目标函数为时总运输距离 H 最短。
14.一个玩具制造商在全国的五个地区生产玩具,原材料将从一个
新的中心仓库运出,而此仓库的地点还有待确定。运至各地的原材料
数量相同,已建立一个坐标城,各地的坐标位置如表 2.9 所示。请确
定中心仓库的坐标位置。
表 2.9 各地的坐标位置
解:设仓库的坐标为(
为 ,因运至各地的原材料数量相同,故可设
初始解: x0( 0 )
解:答:设 x 为之制造商的年产量 A 地,总成本 C(A)=800000+14000x B 地,总成本 C(B)=920000+13000x
1)若两地成本相等,则 C(A)=C(B) 解得:x=120
2)若 A 地优于 B 地,则 C(A)<C(B),因此得 0<x<120 同理,当 x>120 时,B 地优于 A 地。
