二次函数图形变换综合压轴题
二次函数综合压轴题(含答案)

二次函数综合压轴题(含答案)1.如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(﹣2,0),点C(8,0),与y轴交于点A.(1)求二次函数y=ax2+bx+4的表达式;(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N 作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;(3)连接OM,在(2)的结论下,求OM与AC的数量关系.2.如图,在平面直角坐标系中,抛物线y=x2﹣x﹣与x轴交于A、B 两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.(1)求直线AE的解析式;(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD 上的一点,求KM+MN+NK的最小值;(3)点G是线段CE的中点,将抛物线y=x2﹣x﹣沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.3.如图所示,在平面直角坐标系中xOy中,抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.(1)求A、B两点的坐标及抛物线的对称轴;(2)求直线l的函数表达式(其中k、b用含a的式子表示);(3)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为,求a的值;(4)设P是抛物线对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.4.如图,已知抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),C(0,3)点M、N为抛物线上的动点,过点M作MD∥y轴,交直线BC于点D,交x轴于点E.(1)求二次函数y=ax2+bx+c的表达式;(2)过点N作NF⊥x轴,垂足为点F,若四边形MNFE为正方形(此处限定点M在对称轴的右侧),求该正方形的面积;(3)若∠DMN=90°,MD=MN,求点M的横坐标.5.如图,直线y=﹣x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣x2+bx+c经过点A,B.(1)求点B的坐标和抛物线的解析式;(2)M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.①点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;②点M在x轴上自由运动,若三个点M,P,N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”.请直接写出使得M,P,N三点成为“共谐点”的m的值.6.如图,抛物线y=﹣x2+x+2与x轴交于点A,B,与y轴交于点C.(1)试求A,B,C的坐标;(2)将△ABC绕AB中点M旋转180°,得到△BAD.①求点D的坐标;②判断四边形ADBC的形状,并说明理由;(3)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请直接写出所有满足条件的P点的坐标;若不存在,请说明理由.7.如图,抛物线y=ax2+bx﹣a﹣b(a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为y=x+.(1)求该抛物线的函数关系式与C点坐标;(2)已知点M(m,0)是线段OA上的一个动点,过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点,当m为何值时,△BDE恰好是以DE为底边的等腰三角形?(3)在(2)问条件下,当△BDE恰好是以DE为底边的等腰三角形时,动点M 相应位置记为点M′,将OM′绕原点O顺时针旋转得到ON(旋转角在0°到90°之间);i:探究:线段OB上是否存在定点P(P不与O、B重合),无论ON如何旋转,始终保持不变,若存在,试求出P点坐标;若不存在,请说明理由;ii:试求出此旋转过程中,(NA+NB)的最小值.8.如图,抛物线y=ax2+bx﹣2的对称轴是直线x=1,与x轴交于A,B两点,与y轴交于点C,点A的坐标为(﹣2,0),点P为抛物线上的一个动点,过点P 作PD⊥x轴于点D,交直线BC于点E.(1)求抛物线解析式;(2)若点P在第一象限内,当OD=4PE时,求四边形POBE的面积;(3)在(2)的条件下,若点M为直线BC上一点,点N为平面直角坐标系内一点,是否存在这样的点M和点N,使得以点B,D,M,N为顶点的四边形是菱形?若存在上,直接写出点N的坐标;若不存在,请说明理由.【温馨提示:考生可以根据题意,在备用图中补充图形,以便探究】9.如图甲,直线y=﹣x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.(1)求该抛物线的解析式;(2)在该抛物线的对称轴上是否存在点M,使以C,P,M为顶点的三角形为等腰三角形?若存在,请直接写出所符合条件的点M的坐标;若不存在,请说明理由;(3)当0<x<3时,在抛物线上求一点E,使△CBE的面积有最大值(图乙、丙供画图探究).10.如图,抛物线y=ax2+bx+c(a≠0)与直线y=x+1相交于A(﹣1,0),B(4,m)两点,且抛物线经过点C(5,0).(1)求抛物线的解析式;(2)点P是抛物线上的一个动点(不与点A、点B重合),过点P作直线PD⊥x轴于点D,交直线AB于点E.①当PE=2ED时,求P点坐标;②是否存在点P使△BEC为等腰三角形?若存在请直接写出点P的坐标;若不存在,请说明理由.11.如图所示,顶点为(,﹣)的抛物线y=ax2+bx+c过点M(2,0).(1)求抛物线的解析式;(2)点A是抛物线与x轴的交点(不与点M重合),点B是抛物线与y轴的交点,点C是直线y=x+1上一点(处于x轴下方),点D是反比例函数y=(k>0)图象上一点,若以点A,B,C,D为顶点的四边形是菱形,求k的值.12.如图,在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点C,抛物线y=﹣x2+bx+c经过A、C两点,与x轴的另一交点为点B.(1)求抛物线的函数表达式;(2)点D为直线AC上方抛物线上一动点;①连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为S1,△BCE 的面积为S2,求的最大值;②过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF中的某个角恰好等于∠BAC的2倍?若存在,求点D的横坐标;若不存在,请说明理由.13.如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).(1)请直接写出B、C两点的坐标及抛物线的解析式;(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE=∠OCD?(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,请求出t的值.14.如图,抛物线y=a(x﹣1)(x﹣3)与x轴交于A,B两点,与y轴的正半轴交于点C,其顶点为D.(1)写出C ,D 两点的坐标(用含a 的式子表示);(2)设S △BCD :S △ABD =k ,求k 的值;(3)当△BCD 是直角三角形时,求对应抛物线的解析式.15.如图,是将抛物线y=﹣x 2平移后得到的抛物线,其对称轴为直线x=1,与x 轴的一个交点为A (﹣1,0),另一个交点为B ,与y 轴的交点为C .(1)求抛物线的函数表达式;(2)若点N 为抛物线上一点,且BC ⊥NC ,求点N 的坐标;(3)点P 是抛物线上一点,点Q 是一次函数y=x +的图象上一点,若四边形OAPQ 为平行四边形,这样的点P 、Q 是否存在?若存在,分别求出点P ,Q 的坐标;若不存在,说明理由.16.如图,已知抛物线y=ax 2+2x +c 与y 轴交于点A (0,6),与x 轴交于点B (6,0),点P 是线段AB 上方抛物线上的一个动点.(1)求这条抛物线的表达式及其顶点坐标;(2)当点P 移动到抛物线的什么位置时,使得∠PAB=75°,求出此时点P 的坐标;(3)当点P 从A 点出发沿线段AB 上方的抛物线向终点B 移动,在移动中,点P 的横坐标以每秒1个单位长度的速度变动,与此同时点M 以每秒1个单位长度的速度沿AO 向终点O 移动,点P ,M 移动到各自终点时停止,当两个动点移动t秒时,求四边形PAMB的面积S关于t的函数表达式,并求t为何值时,S有最大值,最大值是多少?17.如图1,抛物线C1:y=x2+ax与C2:y=﹣x2+bx相交于点O、C,C1与C2分别交x轴于点B、A,且B为线段AO的中点.(1)求的值;(2)若OC⊥AC,求△OAC的面积;(3)抛物线C2的对称轴为l,顶点为M,在(2)的条件下:①点P为抛物线C2对称轴l上一动点,当△PAC的周长最小时,求点P的坐标;②如图2,点E在抛物线C2上点O与点M之间运动,四边形OBCE的面积是否存在最大值?若存在,求出面积的最大值和点E的坐标;若不存在,请说明理由.18.如图,抛物线y=﹣x2+bx+c与直线AB交于A(﹣4,﹣4),B(0,4)两点,直线AC:y=﹣x﹣6交y轴于点C.点E是直线AB上的动点,过点E作EF ⊥x轴交AC于点F,交抛物线于点G.(1)求抛物线y=﹣x2+bx+c的表达式;(2)连接GB,EO,当四边形GEOB是平行四边形时,求点G的坐标;(3)①在y轴上存在一点H,连接EH,HF,当点E运动到什么位置时,以A,E,F,H为顶点的四边形是矩形?求出此时点E,H的坐标;②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求AM+CM它的最小值.19.如图1,抛物线y=x2+bx+c经过A(﹣2,0)、B(0,﹣2)两点,点C 在y轴上,△ABC为等边三角形,点D从点A出发,沿AB方向以每秒2个单位长度的速度向终点B运动,设运动时间为t秒(t>0),过点D作DE⊥AC于点E,以DE为边作矩形DEGF,使点F在x轴上,点G在AC或AC的延长线上.(1)求抛物线的解析式;(2)将矩形DEGF沿GF所在直线翻折,得矩形D'E'GF,当点D的对称点D'落在抛物线上时,求此时点D'的坐标;(3)如图2,在x轴上有一点M(2,0),连接BM、CM,在点D的运动过程中,设矩形DEGF与四边形ABMC重叠部分的面积为S,直接写出S与t之间的函数关系式,并写出自变量t的取值范围.20.如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x轴正半轴于点B(4,0),与过A点的直线相交于另一点D(3,),过点D作DC ⊥x轴,垂足为C.(1)求抛物线的表达式;(2)点P在线段OC上(不与点O、C重合),过P作PN⊥x轴,交直线AD 于M,交抛物线于点N,连接CM,求△PCM面积的最大值;(3)若P是x轴正半轴上的一动点,设OP的长为t,是否存在t,使以点M、C、D、N为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.21.如图,已知抛物线y=ax2+c过点(﹣2,2),(4,5),过定点F(0,2)的直线l:y=kx+2与抛物线交于A、B两点,点B在点A的右侧,过点B作x轴的垂线,垂足为C.(1)求抛物线的解析式;(2)当点B在抛物线上运动时,判断线段BF与BC的数量关系(>、<、=),并证明你的判断;(3)P为y轴上一点,以B、C、F、P为顶点的四边形是菱形,设点P(0,m),求自然数m的值;(4)若k=1,在直线l下方的抛物线上是否存在点Q,使得△QBF的面积最大?若存在,求出点Q的坐标及△QBF的最大面积;若不存在,请说明理由.22.如图1,经过原点O的抛物线y=ax2+bx(a≠0)与x轴交于另一点A(,0),在第一象限内与直线y=x交于点B(2,t).(1)求这条抛物线的表达式;(2)在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.23.抛物线y=ax2+bx+3经过点A(1,0)和点B(5,0).(1)求该抛物线所对应的函数解析式;(2)该抛物线与直线y=x+3相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线PM∥y轴,分别与x轴和直线CD交于点M、N.①连结PC、PD,如图1,在点P运动过程中,△PCD的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;②连结PB,过点C作CQ⊥PM,垂足为点Q,如图2,是否存在点P,使得△CNQ与△PBM相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.24.如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(﹣4,0)、B(0,3),抛物线y=﹣x2+2x+1与y轴交于点C.(1)求直线y=kx+b的函数解析式;(2)若点P(x,y)是抛物线y=﹣x2+2x+1上的任意一点,设点P到直线AB 的距离为d,求d关于x的函数解析式,并求d取最小值时点P的坐标;(3)若点E在抛物线y=﹣x2+2x+1的对称轴上移动,点F在直线AB上移动,求CE+EF的最小值.25.如图1,在平面直角坐标系xOy中,抛物线C:y=ax2+bx+c与x轴相交于A,B两点,顶点为D(0,4),AB=4,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C′.(1)求抛物线C的函数表达式;(2)若抛物线C′与抛物线C在y轴的右侧有两个不同的公共点,求m的取值范围.(3)如图2,P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P 在抛物线C′上的对应点P′,设M是C上的动点,N是C′上的动点,试探究四边形PMP′N能否成为正方形?若能,求出m的值;若不能,请说明理由.26.如图,抛物线y=x2+bx+c经过点B(3,0),C(0,﹣2),直线l:y=﹣x ﹣交y轴于点E,且与抛物线交于A,D两点,P为抛物线上一动点(不与A,D重合).(1)求抛物线的解析式;(2)当点P在直线l下方时,过点P作PM∥x轴交l于点M,PN∥y轴交l于点N,求PM+PN的最大值.(3)设F为直线l上的点,以E,C,P,F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.27.如图1,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.(1)求抛物线的函数表达式;(2)若点D是y轴上的一点,且以B,C,D为顶点的三角形与△ABC相似,求点D的坐标;(3)如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别交于点F,G,试探究当点H 运动到何处时,四边形CHEF的面积最大,求点H的坐标及最大面积;(4)若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y 轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.28.在平面直角坐标系xOy中,抛物线y=ax2+bx+c与y轴交于点C,其顶点记为M,自变量x=﹣1和x=5对应的函数值相等.若点M在直线l:y=﹣12x+16上,点(3,﹣4)在抛物线上.(1)求该抛物线的解析式;(2)设y=ax2+bx+c对称轴右侧x轴上方的图象上任一点为P,在x轴上有一点A(﹣,0),试比较锐角∠PCO与∠ACO的大小(不必证明),并写出相应的P点横坐标x的取值范围.(3)直线l与抛物线另一交点记为B,Q为线段BM上一动点(点Q不与M重合),设Q点坐标为(t,n),过Q作QH⊥x轴于点H,将以点Q,H,O,C为顶点的四边形的面积S表示为t的函数,标出自变量t的取值范围,并求出S可能取得的最大值.29.如图①,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C 作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.(1)填空:b=,c=;(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;(3)在x轴下方,该二次函数的图象上是否存在点M,使△PQM是以点P为直角顶点的等腰直角三角形?若存在,请求出运动时间t;若不存在,请说明理由;(4)如图②,点N的坐标为(﹣,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.30.如图,已知抛物线y=ax2﹣2ax﹣9a与坐标轴交于A,B,C三点,其中C (0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l 与射线AC,AB分别交于点M,N.(1)直接写出a的值、点A的坐标及抛物线的对称轴;(2)点P为抛物线的对称轴上一动点,若△PAD为等腰三角形,求出点P的坐标;(3)证明:当直线l绕点D旋转时,+均为定值,并求出该定值.31.如图,抛物线y=x2+bx+c与x轴交于点A(﹣2,0),交y轴于点B(0,).直线y=kx过点A与y轴交于点C,与抛物线的另一个交点是D.(1)求抛物线y=x2+bx+c与直线y=kx的解析式;(2)设点P是直线AD下方的抛物线上一动点(不与点A、D重合),过点P作y轴的平行线,交直线AD于点M,作DE⊥y轴于点E.探究:是否存在这样的点P,使四边形PMEC是平行四边形?若存在请求出点P的坐标;若不存在,请说明理由;(3)在(2)的条件下,作PN⊥AD于点N,设△PMN的周长为m,点P的横坐标为x,求m与x的函数关系式,并求出m的最大值.32.如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0),C(3,0),D(3,4),以A为顶点的抛物线y=ax2+bx+c过点C,动点P从点A出发,以每秒个单位的速度沿线段AD向点D运动,运动时间为t秒,过点P作PE ⊥x轴交抛物线于点M,交AC于点N.(1)直接写出点A的坐标,并求出抛物线的解析式;(2)当t为何值时,△ACM的面积最大?最大值为多少?(3)点Q从点C出发,以每秒1个单位的速度沿线段CD向点D运动,当t为何值时,在线段PE上存在点H,使以C,Q,N,H为顶点的四边形为菱形?33.如图(1),在平面直角坐标系中,矩形ABCO,B点坐标为(4,3),抛物线y=x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y 轴交于E点,与抛物线y=x2+bx+c交于第四象限的F点.(1)求该抛物线解析式与F点坐标;(2)如图(2),动点P从点C出发,沿线段CB以每秒1个单位长度的速度向终点B运动;同时,动点M从点A出发,沿线段AE以每秒个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.①问EP+PH+HF是否有最小值?如果有,求出t的值;如果没有,请说明理由.②若△PMH是等腰三角形,请直接写出此时t的值.34.如图,已知:在平面直角坐标系中,直线l与y轴相交于点A(0,m)其中m<0,与x轴相交于点B(4,0).抛物线y=ax2+bx(a>0)的顶点为F,它与直线l相交于点C,其对称轴分别与直线l和x轴相交于点D和点E.(1)设a=,m=﹣2时,①求出点C、点D的坐标;②抛物线y=ax2+bx上是否存在点G,使得以G、C、D、F四点为顶点的四边形为平行四边形?如果存在,求出点G的坐标;如果不存在,请说明理由.(2)当以F、C、D为顶点的三角形与△BED相似且满足三角形FAC的面积与三角形FBC面积之比为1:3时,求抛物线的函数表达式.35.如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)、B(3,0).(1)求b、c的值;(2)如图1直线y=kx+1(k>0)与抛物线第一象限的部分交于D点,交y轴于F点,交线段BC于E点.求的最大值;(3)如图2,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB.问在直线BC下方的抛物线上是否存在点Q,使得△QMB与△PMB的面积相等?若存在,求出点Q的坐标;若不存在,请说明理由.36.已知二次函数y=ax2+bx﹣2的图象与x轴交于A、B两点,与y轴交于点C,点A的坐标为(4,0),且当x=﹣2和x=5时二次函数的函数值y相等.(1)求实数a、b的值;(2)如图1,动点E、F同时从A点出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.①是否存在某一时刻t,使得△DCF为直角三角形?若存在,求出t的值;若不存在,请说明理由.②设△DEF与△ABC重叠部分的面积为S,求S关于t的函数关系式;37.如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+n与x轴、y 轴分别交于B、C两点,抛物线y=ax2+bx+3(a≠0)过C、B两点,交x轴于另一点A,连接AC,且tan∠CAO=3.(1)求抛物线的解析式;(2)若点P是射线CB上一点,过点P作x轴的垂线,垂足为H,交抛物线于Q,设P点横坐标为t,线段PQ的长为d,求出d与t之间的函数关系式,并写出相应的自变量t的取值范围;(3)在(2)的条件下,当点P在线段BC上时,设PH=e,已知d,e是以y为未知数的一元二次方程:y2﹣(m+3)y+(5m2﹣2m+13)=0(m为常数)的两个实数根,点M在抛物线上,连接MQ、MH、PM,且.MP平分∠QMH,求出t值及点M的坐标.38.在平面直角坐标系中,抛物线y=ax2﹣5ax+4a与x轴交于A、B(A点在B 点的左侧)与y轴交于点C.(1)如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;(2)如图2,点P为第四象限抛物线上一点,连接PC,若∠BCP=2∠ABC时,求点P的横坐标;(3)如图3,在(2)的条件下,点F在AP上,过点P作PH⊥x轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=﹣4a,连接KB并延长交抛物线于点Q,求PQ的长.39.如图,抛物线y=﹣x2﹣2x+3 的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.(1)求A,B,C三点的坐标.(2)点M为线段AB上一点(点M不与点A,B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PMNQ的周长最大时,求△AEM的面积.(3)在(2)的条件下,当矩形PMNQ的周长最大时,连结DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=2DQ,求点F的坐标.40.如图,抛物线y=ax2﹣2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A坐标为(4,0).(1)求该抛物线的解析式;(2)抛物线的顶点为N,在x轴上找一点K,使CK+KN最小,并求出点K的坐标;(3)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;(4)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D 的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.参考答案与试题解析1.如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(﹣2,0),点C(8,0),与y轴交于点A.(1)求二次函数y=ax2+bx+4的表达式;(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N 作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;(3)连接OM,在(2)的结论下,求OM与AC的数量关系.【考点】HF:二次函数综合题.【分析】(1)由B、C的坐标,利用待定系数法可求得抛物线解析式;(2)可设N(n,0),则可用n表示出△ABN的面积,由NM∥AC,可求得,则可用n表示出△AMN的面积,再利用二次函数的性质可求得其面积最大时n 的值,即可求得N点的坐标;(3)由N点坐标可求得M点为AB的中点,由直角三角形的性质可得OM=AB,在Rt△AOB和Rt△AOC中,可分别求得AB和AC的长,可求得AB与AC的关系,从而可得到OM和AC的数量关系.【解答】解:(1)将点B,点C的坐标分别代入y=ax2+bx+4可得,解得,∴二次函数的表达式为y=﹣x2+x+4;(2)设点N的坐标为(n,0)(﹣2<n<8),则BN=n+2,CN=8﹣n.∵B(﹣2,0),C(8,0),∴BC=10,在y=﹣x2+x+4中令x=0,可解得y=4,∴点A(0,4),OA=4,∴S=BN•OA=(n+2)×4=2(n+2),△ABN∵MN∥AC,∴,∴==,∴,∵﹣<0,∴当n=3时,即N(3,0)时,△AMN的面积最大;(3)当N(3,0)时,N为BC边中点,∵MN∥AC,∴M为AB边中点,∴OM=AB,∵AB===2,AC===4,∴AB=AC,∴OM=AC.【点评】本题为二次函数的综合应用,涉及待定系数法、平行线分线段成比例、三角形的面积、二次函数的性质、直角三角形的性质、勾股定理等知识.在(1)中注意待定系数法的应用,在(2)中找到△AMN和△ABN的面积之间的关系是解题的关键,在(3)中确定出AB为OM和AC的中间“桥梁”是解题的关键.本题考查知识点较多,综合性较强,难度适中.2.如图,在平面直角坐标系中,抛物线y=x2﹣x﹣与x轴交于A、B 两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.(1)求直线AE的解析式;(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD 上的一点,求KM+MN+NK的最小值;(3)点G是线段CE的中点,将抛物线y=x2﹣x﹣沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.【考点】HF:二次函数综合题.【分析】(1)抛物线的解析式可变形为y=(x+1)(x﹣3),从而可得到点A 和点B的坐标,然后再求得点E的坐标,设直线AE的解析式为y=kx+b,将点A和点E的坐标代入求得k和b的值,从而得到AE的解析式;(2)设直线CE的解析式为y=mx﹣,将点E的坐标代入求得m的值,从而得到直线CE的解析式,过点P作PF∥y轴,交CE与点F.设点P的坐标为(x,x2﹣x﹣),则点F(x,x﹣),则FP=x2+x.由三角形的面积公式得到△EPC的面积=﹣x2+x,利用二次函数的性质可求得x 的值,从而得到点P的坐标,作点K关于CD和CP的对称点G、H,连接G、H交CD和CP与N、M.然后利用轴对称的性质可得到点G和点H的坐标,当点O、N、M、H在条直线上时,KM+MN+NK有最小值,最小值=GH;(3)由平移后的抛物线经过点D,可得到点F的坐标,利用中点坐标公式可求得点G的坐标,然后分为QG=FG、QG=QF,FQ=FQ三种情况求解即可.【解答】解:(1)∵y=x2﹣x﹣,∴y=(x+1)(x﹣3).∴A(﹣1,0),B(3,0).当x=4时,y=.∴E(4,).设直线AE的解析式为y=kx+b,将点A和点E的坐标代入得:,解得:k=,b=.∴直线AE的解析式为y=x+.(2)设直线CE的解析式为y=mx﹣,将点E的坐标代入得:4m﹣=,解得:m=.∴直线CE的解析式为y=x﹣.过点P作PF∥y轴,交CE与点F.设点P的坐标为(x,x2﹣x﹣),则点F(x,x﹣),则FP=(x﹣)﹣(x2﹣x﹣)=x2+x.∴△EPC的面积=×(x2+x)×4=﹣x2+x.∴当x=2时,△EPC的面积最大.∴P(2,﹣).如图2所示:作点K关于CD和CP的对称点G、H,连接G、H交CD和CP 与N、M.∵K是CB的中点,∴k(,﹣).∴tan∠KCP=.∵OD=1,OC=,∴tan∠OCD=.∴∠OCD=∠KCP=30°.∴∠KCD=30°.∵k是BC的中点,∠OCB=60°,∴OC=CK.∴点O与点K关于CD对称.∴点G与点O重合.∴点G(0,0).∵点H与点K关于CP对称,∴点H的坐标为(,﹣).∴KM+MN+NK=MH+MN+GN.当点O、N、M、H在条直线上时,KM+MN+NK有最小值,最小值=GH.∴GH==3.∴KM+MN+NK的最小值为3.(3)如图3所示:∵y′经过点D,y′的顶点为点F,∴点F(3,﹣).∵点G为CE的中点,∴G(2,).∴FG==.∴当FG=FQ时,点Q(3,),Q′(3,).当GF=GQ时,点F与点Q″关于y=对称,∴点Q″(3,2).当QG=QF时,设点Q1的坐标为(3,a).由两点间的距离公式可知:a+=,解得:a=﹣.∴点Q1的坐标为(3,﹣).综上所述,点Q的坐标为(3,)或′(3,)或(3,2)或(3,﹣).【点评】本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数的解析式、轴对称最短路径问题、等腰三角形的定义和性质,找到KM+MN+NK取得最小值的条件是解答问题(2)的关键;分为QG=FG、QG=QF,FQ=FQ三种情况分别进行计算是解答问题(3)的关键.3.如图所示,在平面直角坐标系中xOy中,抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.(1)求A、B两点的坐标及抛物线的对称轴;(2)求直线l的函数表达式(其中k、b用含a的式子表示);(3)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为,求a的值;(4)设P是抛物线对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.。
中考数学——二次函数的综合压轴题专题复习含答案解析

中考数学——二次函数的综合压轴题专题复习含答案解析一、二次函数1.在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C(0,3),顶点为G.(1)求抛物线和直线AC的解析式;(2)如图,设E(m,0)为x轴上一动点,若△CGE和△CGO的面积满足S△CGE=S△CGO,求点E的坐标;(3)如图,设点P从点A出发,以每秒1个单位长度的速度沿x轴向右运动,运动时间为ts,点M为射线AC上一动点,过点M作MN∥x轴交抛物线对称轴右侧部分于点N.试探究点P在运动过程中,是否存在以P,M,N为顶点的三角形为等腰直角三角形?若存在,求出t的值;若不存在,请说明理由.【答案】(1)抛物线解析式为:y=﹣x2+2x+3;直线AC解析式为:y=3x+3;(2)点E 坐标为(1,0)或(﹣7,0);(3)存在以P,M,N为顶点的三角形为等腰直角三角形,t的值为或或.【解析】【分析】(1)用待定系数法即能求出抛物线和直线AC解析式.(2)△CGE与△CGO虽然有公共底边CG,但高不好求,故把△CGE构造在比较好求的三角形内计算.延长GC交x轴于点F,则△FGE与△FCE的差即为△CGE.(3)设M的坐标(e,3e+3),分别以M、N、P为直角顶点作分类讨论,利用等腰直角三角形的特殊线段长度关系,用e表示相关线段并列方程求解,再根据e与AP的关系求t 的值.【详解】(1)∵抛物线y=ax2+bx+c过点A(-1,0),B(3,0),C(0,3),, 解得:,∴抛物线解析式为:y=-x2+2x+3,设直线AC解析式为y=kx+3,∴-k+3=0,得:k=3,∴直线AC解析式为:y=3x+3.(2)延长GC交x轴于点F,过G作GH⊥x轴于点H,∵y=-x2+2x+3=-(x-1)2+4,∴G(1,4),GH=4,∴S△CGO=OC•x G=×3×1=,∴S△CGE=S△CGO=×=2,①若点E在x轴正半轴上,设直线CG:y=k1x+3,∴k1+3=4 得:k1=1,∴直线CG解析式:y=x+3,∴F(-3,0),∵E(m,0),∴EF=m-(-3)=m+3,∴S△CGE=S△FGE-S△FCE=EF•GH-EF•OC=EF•(GH-OC)=(m+3)•(4-3)=,∴=2,解得:m=1,∴E的坐标为(1,0).②若点E在x轴负半轴上,则点E到直线CG的距离与点(1,0)到直线CG距离相等,即点E到F的距离等于点(1,0)到F的距离,∴EF=-3-m=1-(-3)=4,解得:m=-7 即E(-7,0),综上所述,点E坐标为(1,0)或(-7,0).(3)存在以P,M,N为顶点的三角形为等腰直角三角形,设M(e,3e+3),则y N=y M=3e+3,①若∠MPN=90°,PM=PN,如图2,过点M作MQ⊥x轴于点Q,过点N作NR⊥x轴于点R,∵MN∥x轴,∴MQ=NR=3e+3,∴Rt△MQP≌Rt△NRP(HL),∴PQ=PR,∠MPQ=∠NPR=45°,∴MQ=PQ=PR=NR=3e+3,∴x N=x M+3e+3+3e+3=7e+6,即N(7e+6,3e+3),∵N在抛物线上,∴-(7e+6)2+2(7e+6)+3=3e+3,解得:e1=-1(舍去),e2=−,∵AP=t,OP=t-1,OP+OQ=PQ,∴t-1-e=3e+3,∴t=4e+4=,②若∠PMN=90°,PM=MN,如图3,∴MN=PM=3e+3,∴x N=x M+3e+3=4e+3,即N(4e+3,3e+3),∴-(4e+3)2+2(4e+3)+3=3e+3,解得:e1=-1(舍去),e2=−,∴t=AP=e-(-1)=−+1=,③若∠PNM=90°,PN=MN,如图4,∴MN=PN=3e+3,N(4e+3,3e+3),解得:e=−,∴t=AP=OA+OP=1+4e+3=,综上所述,存在以P,M,N为顶点的三角形为等腰直角三角形,t的值为或或.【点睛】本题考查了待定系数法求函数解析式,坐标系中三角形面积计算,等腰直角三角形的性质,解一元二次方程,考查了分类讨论和方程思想.第(3)题根据等腰直角三角形的性质找到相关线段长的关系是解题关键,灵活运用因式分解法解一元二次方程能简便运算.2.如图,抛物线y=x2﹣mx﹣(m+1)与x轴负半轴交于点A(x1,0),与x轴正半轴交于点B(x2,0)(OA<OB),与y轴交于点C,且满足x12+x22﹣x1x2=13.(1)求抛物线的解析式;(2)以点B为直角顶点,BC为直角边作Rt△BCD,CD交抛物线于第四象限的点E,若EC =ED,求点E的坐标;(3)在抛物线上是否存在点Q,使得S△ACQ=2S△AOC?若存在,求出点Q的坐标;若不存在,说明理由.【答案】(1)y=x2﹣2x﹣3;(2)E 113+113+3)点Q的坐标为(﹣3,12)或(2,﹣3).理由见解析.【解析】【分析】(1)由根与系数的关系可得x1+x2=m,x1•x2=﹣(m+1),代入x12+x22﹣x1x2=13,求出m1=2,m2=﹣5.根据OA<OB,得出抛物线的对称轴在y轴右侧,那么m=2,即可确定抛物线的解析式;(2)连接BE、OE.根据直角三角形斜边上的中线等于斜边的一半得出BE=12CD=CE.利用SSS证明△OBE≌△OCE,得出∠BOE=∠COE,即点E在第四象限的角平分线上,设E点坐标为(m,﹣m),代入y=x2﹣2x﹣3,求出m的值,即可得到E点坐标;(3)过点Q作AC的平行线交x轴于点F,连接CF,根据三角形的面积公式可得S△ACQ=S△ACF.由S△ACQ=2S△AOC,得出S△ACF=2S△AOC,那么AF=2OA=2,F(1,0).利用待定系数法求出直线AC的解析式为y=﹣3x﹣3.根据AC∥FQ,可设直线FQ的解析式为y=﹣3x+b,将F(1,0)代入,利用待定系数法求出直线FQ的解析式为y=﹣3x+3,把它与抛物线的解析式联立,得出方程组22333y x xy x⎧=--⎨=-+⎩,求解即可得出点Q的坐标.【详解】(1)∵抛物线y=x2﹣mx﹣(m+1)与x轴负半轴交于点A(x1,0),与x轴正半轴交于点B(x2,0),∴x1+x2=m,x1•x2=﹣(m+1),∵x12+x22﹣x1x2=13,∴(x1+x2)2﹣3x1x2=13,∴m2+3(m+1)=13,即m2+3m﹣10=0,解得m1=2,m2=﹣5.∵OA<OB,∴抛物线的对称轴在y轴右侧,∴m=2,∴抛物线的解析式为y=x2﹣2x﹣3;(2)连接BE、OE.∵在Rt△BCD中,∠CBD=90°,EC=ED,∴BE=12CD=CE.令y=x2﹣2x﹣3=0,解得x1=﹣1,x2=3,∴A(﹣1,0),B(3,0),∵C(0,﹣3),∴OB =OC ,又∵BE =CE ,OE =OE ,∴△OBE ≌△OCE (SSS ),∴∠BOE =∠COE ,∴点E 在第四象限的角平分线上,设E 点坐标为(m ,﹣m ),将E (m ,﹣m )代入y =x 2﹣2x ﹣3,得m =m 2﹣2m ﹣3,解得m =1132±, ∵点E 在第四象限,∴E 点坐标为(113+,﹣113+); (3)过点Q 作AC 的平行线交x 轴于点F ,连接CF ,则S △ACQ =S △ACF .∵S △ACQ =2S △AOC ,∴S △ACF =2S △AOC ,∴AF =2OA =2,∴F (1,0).∵A (﹣1,0),C (0,﹣3),∴直线AC 的解析式为y =﹣3x ﹣3.∵AC ∥FQ ,∴设直线FQ 的解析式为y =﹣3x +b ,将F (1,0)代入,得0=﹣3+b ,解得b =3,∴直线FQ 的解析式为y =﹣3x +3.联立22333y x x y x ⎧=--⎨=-+⎩, 解得11312x y =-⎧⎨=⎩,2223x y =⎧⎨=-⎩, ∴点Q 的坐标为(﹣3,12)或(2,﹣3).【点睛】本题是二次函数综合题,其中涉及到一元二次方程根与系数的关系,求二次函数的解析式,直角三角形的性质,全等三角形的判定与性质,二次函数图象上点的坐标特征,三角形的面积,一次函数图象与几何变换,待定系数法求直线的解析式,抛物线与直线交点坐标的求法,综合性较强,难度适中.利用数形结合与方程思想是解题的关键.3.已知如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与点A重合),过点P作PD∥y 轴交直线AC于点D.(1)求抛物线的解析式;(2)求点P在运动的过程中线段PD长度的最大值;(3)△APD能否构成直角三角形?若能请直接写出点P坐标,若不能请说明理由;(4)在抛物线对称轴上是否存在点M使|MA﹣MC|最大?若存在请求出点M的坐标,若不存在请说明理由.【答案】(1)y=x2﹣4x+3;(2)94;(3)点P(1,0)或(2,﹣1);(4)M(2,﹣3).【解析】试题分析:(1)把点A、B的坐标代入抛物线解析式,解方程组得到b、c的值,即可得解;(2)求出点C的坐标,再利用待定系数法求出直线AC的解析式,再根据抛物线解析式设出点P的坐标,然后表示出PD的长度,再根据二次函数的最值问题解答;(3)①∠APD是直角时,点P与点B重合,②求出抛物线顶点坐标,然后判断出点P为在抛物线顶点时,∠PAD是直角,分别写出点P的坐标即可;(4)根据抛物线的对称性可知MA=MB,再根据三角形的任意两边之差小于第三边可知点M为直线CB与对称轴交点时,|MA﹣MC|最大,然后利用待定系数法求出直线BC的解析式,再求解即可.试题解析:解:(1)∵抛物线y=x2+bx+c过点A(3,0),B(1,0),∴93010b cb c++=⎧⎨++=⎩,解得43bc=-⎧⎨=⎩,∴抛物线解析式为y=x2﹣4x+3;(2)令x=0,则y=3,∴点C(0,3),则直线AC的解析式为y=﹣x+3,设点P(x,x2﹣4x+3).∵PD∥y轴,∴点D(x,﹣x+3),∴PD=(﹣x+3)﹣(x2﹣4x+3)=﹣x2+3x=﹣(x﹣32)2+94.∵a=﹣1<0,∴当x=32时,线段PD的长度有最大值94;(3)①∠APD是直角时,点P与点B重合,此时,点P(1,0),②∵y=x2﹣4x+3=(x ﹣2)2﹣1,∴抛物线的顶点坐标为(2,﹣1).∵A(3,0),∴点P为在抛物线顶点时,∠PAD=45°+45°=90°,此时,点P(2,﹣1).综上所述:点P(1,0)或(2,﹣1)时,△APD能构成直角三角形;(4)由抛物线的对称性,对称轴垂直平分AB,∴MA=MB,由三角形的三边关系,|MA﹣MC|<BC,∴当M、B、C三点共线时,|MA﹣MC|最大,为BC的长度,设直线BC的解析式为y=kx+b(k≠0),则3k bb+=⎧⎨=⎩,解得:33kb=-⎧⎨=⎩,∴直线BC的解析式为y=﹣3x+3.∵抛物线y=x2﹣4x+3的对称轴为直线x=2,∴当x=2时,y=﹣3×2+3=﹣3,∴点M (2,﹣3),即,抛物线对称轴上存在点M(2,﹣3),使|MA﹣MC|最大.点睛:本题是二次函数综合题,主要利用了待定系数法求二次函数解析式,二次函数的最值问题,二次函数的对称性以及顶点坐标的求解,(2)整理出PD的表达式是解题的关键,(3)关键在于利用点的坐标特征作出判断,(4)根据抛物线的对称性和三角形的三边关系判断出点M的位置是解题的关键.4.如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.(1)求抛物线的解析式和直线AC的解析式;(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.【答案】(1)抛物线解析式为y=﹣x2+2x+3;直线AC的解析式为y=3x+3;(2)点M的坐标为(0,3);(3)符合条件的点P的坐标为(73,209)或(103,﹣139),【解析】分析:(1)设交点式y=a(x+1)(x-3),展开得到-2a=2,然后求出a即可得到抛物线解析式;再确定C(0,3),然后利用待定系数法求直线AC的解析式;(2)利用二次函数的性质确定D的坐标为(1,4),作B点关于y轴的对称点B′,连接DB′交y轴于M,如图1,则B′(-3,0),利用两点之间线段最短可判断此时MB+MD的值最小,则此时△BDM的周长最小,然后求出直线DB′的解析式即可得到点M的坐标;(3)过点C作AC的垂线交抛物线于另一点P,如图2,利用两直线垂直一次项系数互为负倒数设直线PC的解析式为y=-13x+b,把C点坐标代入求出b得到直线PC的解析式为y=-13x+3,再解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩==得此时P点坐标;当过点A作AC的垂线交抛物线于另一点P时,利用同样的方法可求出此时P点坐标.详解:(1)设抛物线解析式为y=a(x+1)(x﹣3),即y=ax2﹣2ax﹣3a,∴﹣2a=2,解得a=﹣1,∴抛物线解析式为y=﹣x2+2x+3;当x=0时,y=﹣x2+2x+3=3,则C(0,3),设直线AC的解析式为y=px+q,把A(﹣1,0),C(0,3)代入得3p qq-+=⎧⎨=⎩,解得33pq=⎧⎨=⎩,∴直线AC的解析式为y=3x+3;(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点D的坐标为(1,4),作B点关于y轴的对称点B′,连接DB′交y轴于M,如图1,则B′(﹣3,0),∵MB=MB′,∴MB+MD=MB′+MD=DB′,此时MB+MD的值最小,而BD的值不变,∴此时△BDM的周长最小,易得直线DB′的解析式为y=x+3,当x=0时,y=x+3=3,∴点M的坐标为(0,3);(3)存在.过点C作AC的垂线交抛物线于另一点P,如图2,∵直线AC的解析式为y=3x+3,∴直线PC的解析式可设为y=﹣13x+b,把C(0,3)代入得b=3,∴直线PC的解析式为y=﹣13x+3,解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩==,解得3xy=⎧⎨=⎩或73209xy⎧=⎪⎪⎨⎪=⎪⎩,则此时P点坐标为(73,209);过点A作AC的垂线交抛物线于另一点P,直线PC的解析式可设为y=﹣x+b,把A(﹣1,0)代入得13+b=0,解得b=﹣13,∴直线PC的解析式为y=﹣13x﹣13,解方程组2231133y x xy x⎧-++⎪⎨--⎪⎩==,解得1xy=-⎧⎨=⎩或103139xy⎧=⎪⎪⎨⎪=-⎪⎩,则此时P点坐标为(103,﹣139).综上所述,符合条件的点P的坐标为(73,209)或(103,﹣139).点睛:本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求函数解析式,理解两直线垂直时一次项系数的关系,通过解方程组求把两函数的交点坐标;理解坐标与图形性质,会运用两点之间线段最短解决最短路径问题;会运用分类讨论的思想解决数学问题.5.已知,点M 为二次函数2()41y x b b =--++图象的顶点,直线5y mx =+分别交x 轴正半轴,y 轴于点,A B .(1)如图1,若二次函数图象也经过点,A B ,试求出该二次函数解析式,并求出m 的值. (2)如图2,点A 坐标为(5,0),点M 在AOB ∆内,若点11(,)4C y ,23(,)4D y 都在二次函数图象上,试比较1y 与2y 的大小.【答案】(1)2(2)9y x =--+,1m =-;(2)①当102b <<时,12y y >;②当12b =时,12y y =;③当1425b <<时,12y y < 【解析】 【分析】 (1)根据一次函数表达式求出B 点坐标,然后根据B 点在抛物线上,求出b 值,从而得到二次函数表达式,再根据二次函数表达式求出A 点的坐标,最后代入一次函数求出m 值.(2)根据解方程组,可得顶点M 的纵坐标的范围,根据二次函数的性质,可得答案. 【详解】(1)如图1,∵直线5y mx =+与y 轴交于点为B ,∴点B 坐标为(0,5)又∵(0,5)B 在抛物线上,∴25(0)41b b =--++,解得2b =∴二次函数的表达式为2(2)9y x =--+ ∴当0y =时,得15=x ,21x =- ∴(5,0)A代入5y mx =+得,550m +=,∴1m =-(2)如图2,根据题意,抛物线的顶点M 为(,41)b b +,即M 点始终在直线41y x =+上,∵直线41y x =+与直线AB 交于点E ,与y 轴交于点F ,而直线AB 表达式为5y x =-+解方程组415y xy x=+⎧⎨=-+⎩,得45215xy⎧=⎪⎪⎨⎪=⎪⎩∴点421(,)55E,(0,1)F∵点M在AOB∆内,∴45b<<当点,C D关于抛物线对称轴(直线x b=)对称时,1344b b-=-,∴12b=且二次函数图象的开口向下,顶点M在直线41y x=+上综上:①当12b<<时,12y y>;②当12b=时,12y y=;③当1425b<<时,12y y<.【点睛】本题考查二次函数与一次函数的综合应用,难度系数大同学们需要认真分析即可.6.如图,在平面直角坐标系中有抛物线y=a(x﹣2)2﹣2和y=a(x﹣h)2,抛物线y=a (x﹣2)2﹣2经过原点,与x轴正半轴交于点A,与其对称轴交于点B;点P是抛物线y=a(x﹣2)2﹣2上一动点,且点P在x轴下方,过点P作x轴的垂线交抛物线y=a(x﹣h)2于点D,过点D作PD的垂线交抛物线y=a(x﹣h)2于点D′(不与点D重合),连接PD′,设点P的横坐标为m:(1)①直接写出a的值;②直接写出抛物线y=a(x﹣2)2﹣2的函数表达式的一般式;(2)当抛物线y=a(x﹣h)2经过原点时,设△PDD′与△OAB重叠部分图形周长为L:①求PDDD'的值;②直接写出L与m之间的函数关系式;(3)当h为何值时,存在点P,使以点O、A、D、D′为顶点的四边形是菱形?直接写出h 的值.【答案】(1)①12;②y =212x ﹣2x ; (2)①1;②L =2(22)(02)21(221)4(24)2m m m m π⎧+<⎪⎨-++<<⎪⎩…; (3)h =±3 【解析】 【分析】(1)①将x =0,y =0代入y =a (x ﹣2)2﹣2中计算即可;②y =212x ﹣2x ; (2)将(0,0)代入y =a (x ﹣h )2中,可求得a =12,y =12x 2,待定系数法求OB 、AB 的解析式,由点P 的横坐标为m ,即可表示出相应线段求解;(3)以点O 、A 、D 、D ′为顶点的四边形是菱形,DD ′=OA ,可知点D 的纵坐标为2,再由AD =OA =4即可求出h 的值. 【详解】解:(1)①将x =0,y =0代入y =a (x ﹣2)2﹣2中, 得:0=a (0﹣2)2﹣2, 解得:a =12; ②y =212x ﹣2x ;. (2)∵抛物线y =a (x ﹣h )2经过原点,a =12; ∴y =12x 2, ∴A (4,0),B (2,﹣2),易得:直线OB 解析式为:y =﹣x ,直线AB 解析式为:y =x ﹣4 如图1,222111,2,,,(,0),(,),,222P m m m D m m E m F m m D m m '⎛⎫⎛⎫⎛⎫--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,①221122,222PD m m m m DD m '⎛⎫=--== ⎪⎝⎭PD 2m 1DD 2m'∴== ②如图1,当0<m ≤2时,L =OE +EF +OF =2(22)m m m m ++=+,当2<m <4时,如图2,设PD ′交x 轴于G ,交AB 于H ,PD 交x 轴于E ,交AB 于F ,则222111,2,,,(,0),(,4),,222P m m m D m m E m F m m D m m '⎛⎫⎛⎫⎛⎫--- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭, 2211(4)23422PF m m m m m ⎛⎫=---=-+- ⎪⎝⎭,2222322m 22,PG m 22m 2422FH PH PF ===-+-=-+ ∵DD ′∥EGEG PE DD PD '∴=,即:EG •PD =PE •DD ′,得:EG •(2m )=(2m ﹣12m 2)•2m ∴EG =2m ﹣12m 2,EF =4﹣m ∴L =EG +EF +FH +GH =EG +EF +PG2212242222m m m m ⎛⎫=-+-+-+ ⎪ ⎪⎝⎭221m (221)m 42+=-+++ 2(22)m(0m 2)21m (221)m 4(2m 4)L ⎧+<⎪∴=⎨+-+++<<⎪⎩…;(3)如图3,∵OADD ′为菱形 ∴AD =AO =DD ′=4, ∴PD =2,23PA =23h ∴=±【点睛】本题是二次函数综合题,考查了待定系数法求函数解析式,菱形的性质,抛物线的平移等,解题时要注意考虑分段函数表示方法.7.如图,抛物线y =ax 2+bx ﹣1(a ≠0)交x 轴于A ,B (1,0)两点,交y 轴于点C ,一次函数y =x +3的图象交坐标轴于A ,D 两点,E 为直线AD 上一点,作EF ⊥x 轴,交抛物线于点F (1)求抛物线的解析式;(2)若点F 位于直线AD 的下方,请问线段EF 是否有最大值?若有,求出最大值并求出点E 的坐标;若没有,请说明理由;(3)在平面直角坐标系内存在点G ,使得G ,E ,D ,C 为顶点的四边形为菱形,请直接写出点G 的坐标.【答案】(1)抛物线的解析式为y=13x2+23x﹣1;(2)4912,(12,72);(3)点G的坐标为(2,1),(﹣2,﹣2﹣1),2,2﹣1),(﹣4,3).【解析】【分析】(1)利用待定系数法确定函数关系式;(2)由函数图象上点的坐标特征:可设点E的坐标为(m,m+3),点F的坐标为(m,1 3m2+23m﹣1),由此得到EF=﹣13m2+13m+4,根据二次函数最值的求法解答即可;(3)分三种情形①如图1中,当EG为菱形对角线时.②如图2、3中,当EC为菱形的对角线时,③如图4中,当ED为菱形的对角线时,分别求解即可.【详解】解:(1)将y=0代入y=x+3,得x=﹣3.∴点A的坐标为(﹣3,0).设抛物线的解析式为y=a(x﹣x1)(x﹣x2),点A的坐标为(﹣3,0),点B的坐标为(1,0),∴y=a(x+3)(x﹣1).∵点C的坐标为(0,﹣1),∴﹣3a=﹣1,得a=13,∴抛物线的解析式为y=13x2+23x﹣1;(2)设点E的坐标为(m,m+3),线段EF的长度为y,则点F的坐标为(m,13m2+23m﹣1)∴y=(m+3)﹣( 13m2+23m﹣1)=﹣13m2+13m+4即y=-13(m﹣12) 2+4912,此时点E的坐标为(12,72);(3)点G的坐标为(2,1),(﹣2,﹣2﹣1),2,2﹣1),(﹣4,3).理由:①如图1,当四边形CGDE为菱形时.∴EG 垂直平分CD ∴点E 的纵坐标y =132-+=1, 将y =1带入y =x +3,得x =﹣2. ∵EG 关于y 轴对称, ∴点G 的坐标为(2,1);②如图2,当四边形CDEG 为菱形时,以点D 为圆心,DC 的长为半径作圆,交AD 于点E ,可得DC =DE ,构造菱形CDEG 设点E 的坐标为(n ,n +3), 点D 的坐标为(0,3)∴DE =22(33)n n ++-=22n ∵DE =DC =4, ∴22n =4,解得n 1=﹣22,n 2=22.∴点E 的坐标为(﹣22,﹣22+3)或(22,22+3) 将点E 向下平移4个单位长度可得点G ,点G 的坐标为(﹣22,﹣22﹣1)(如图2)或(22,22﹣1)(如图3)③如图4,“四边形CDGE 为菱形时,以点C 为圆心,以CD 的长为半径作圆,交直线AD 于点E ,设点E 的坐标为(k ,k +3),点C 的坐标为(0,﹣1). ∴EC =22(0)(31)k k -+++=22816k k ++. ∵EC =CD =4, ∴2k 2+8k +16=16, 解得k 1=0(舍去),k 2=﹣4. ∴点E 的坐标为(﹣4,﹣1) 将点E 上移1个单位长度得点G . ∴点G 的坐标为(﹣4,3).综上所述,点G 的坐标为(2,1),(﹣22,﹣22﹣1),(22,22﹣1),(﹣4,3).【点睛】本题考查二次函数综合题、轴对称变换、菱形的判定和性质等知识,解题的关键是学会利用对称解决最值问题,学会用分类讨论的思想思考问题,属于中考压轴题.8.已知抛物线2(5)6y x m x m =-+-+-. (1)求证:该抛物线与x 轴总有交点;(2)若该抛物线与x 轴有一个交点的横坐标大于3且小于5,求m 的取值范围;(3)设抛物线2(5)6y x m x m =-+-+-与y 轴交于点M ,若抛物线与x 轴的一个交点关于直线y x =-的对称点恰好是点M ,求m 的值.【答案】(1)证明见解析;(2)1?<?m?3<;(3)56m m ==或 【解析】 【分析】(1)本题需先根据判别式解出无论m 为任何实数都不小于零,再判断出物线与x 轴总有交点.(2)根据公式法解方程,利用已有的条件,就能确定出m 的取值范围,即可得到结果. (3)根据抛物线y=-x 2+(5-m )x+6-m ,求出与y 轴的交点M 的坐标,再确定抛物线与x 轴的两个交点关于直线y=-x 的对称点的坐标,列方程可得结论. 【详解】(1)证明:∵()()()222454670b ac m m m ∆=-=-+-=-≥ ∴抛物线与x 轴总有交点.(2)解:由(1)()27m ∆=-,根据求根公式可知,方程的两根为:257m m x ()-±-=即1216x x m =-=-+, 由题意,有 3<-m 6<5+1<?m 3∴<(3)解:令 x = 0, y =6m -+ ∴ M (0,6m -+)由(2)可知抛物线与x 轴的交点为(-1,0)和(6m -+,0), 它们关于直线y x =-的对称点分别为(0 , 1)和(0, 6m -), 由题意,可得:6166m m m 或-+=-+=- 56m m ∴==或 【点睛】本题考查对抛物线与x 轴的交点,解一元一次方程,解一元一次不等式,根的判别式,对称等,解题关键是熟练理解和掌握以上性质,并能综合运用这些性质进行计算.9.如图,菱形ABCD 的边长为20cm ,∠ABC =120°,对角线AC ,BD 相交于点O ,动点P 从点A 出发,以4cm /s 的速度,沿A →B 的路线向点B 运动;过点P 作PQ ∥BD ,与AC 相交于点Q ,设运动时间为t 秒,0<t <5.(1)设四边形PQCB 的面积为S ,求S 与t 的关系式;(2)若点Q 关于O 的对称点为M ,过点P 且垂直于AB 的直线l 交菱形ABCD 的边AD (或CD )于点N ,当t 为何值时,点P 、M 、N 在一直线上?(3)直线PN 与AC 相交于H 点,连接PM ,NM ,是否存在某一时刻t ,使得直线PN 平分四边形APMN 的面积?若存在,求出t 的值;若不存在,请说明理由. 【答案】(1) S=﹣231003t +0<t <5); (2) 307;(3)见解析. 【解析】 【分析】(1)如图1,根据S=S △ABC -S △APQ ,代入可得S 与t 的关系式;(2)设PM=x ,则AM=2x ,可得3,计算x 的值,根据直角三角形30度角的性质可得3AM=AO+OM ,列方程可得t 的值;(3)存在,通过画图可知:N 在CD 上时,直线PN 平分四边形APMN 的面积,根据面积相等可得MG=AP ,由AM=AO+OM ,列式可得t 的值. 【详解】解:(1)如图1,∵四边形ABCD 是菱形, ∴∠ABD=∠DBC=12∠ABC=60°,AC ⊥BD , ∴∠OAB=30°, ∵AB=20,∴OB=10,3 由题意得:AP=4t ,∴PQ=2t ,AQ=23t , ∴S=S △ABC ﹣S △APQ , =11··22AC OB PQ AQ -, =111020322322t t ⨯⨯-⨯⨯ , =﹣23t 2+1003(0<t <5); (2)如图2,在Rt △APM 中,AP=4t , ∵点Q 关于O 的对称点为M , ∴OM=OQ , 设PM=x ,则AM=2x , ∴AP=3x=4t , ∴x=3, ∴AM=2PM=3, ∵AM=AO+OM ,∴3=103+103﹣23t ,t=307; 答:当t 为307秒时,点P 、M 、N 在一直线上; (3)存在,如图3,∵直线PN 平分四边形APMN 的面积, ∴S △APN =S △PMN ,过M 作MG ⊥PN 于G ,∴11··22PN AP PN MG = , ∴MG=AP ,易得△APH ≌△MGH ,∴3,∵AM=AO+OM ,同理可知:3﹣3,3333t ,t=3011. 答:当t 为3011秒时,使得直线PN 平分四边形APMN 的面积.【点睛】考查了全等三角形的判定与性质,对称的性质,三角形和四边形的面积,二次根式的化简等知识点,计算量大,解答本题的关键是熟练掌握动点运动时所构成的三角形各边的关系.10.已知,抛物线y =﹣x 2+bx +c 经过点A (﹣1,0)和C (0,3). (1)求抛物线的解析式;(2)在抛物线的对称轴上,是否存在点P ,使PA +PC 的值最小?如果存在,请求出点P 的坐标,如果不存在,请说明理由;(3)设点M 在抛物线的对称轴上,当△MAC 是直角三角形时,求点M 的坐标.【答案】(1)223y x x =-++;(2)当PA PC +的值最小时,点P 的坐标为()1,2;(3)点M 的坐标为()1,1、()1,2、81,3⎛⎫ ⎪⎝⎭或21,3⎛⎫- ⎪⎝⎭. 【解析】 【分析】()1由点A 、C 的坐标,利用待定系数法即可求出抛物线的解析式;()2连接BC 交抛物线对称轴于点P ,此时PA PC +取最小值,利用二次函数图象上点的坐标特征可求出点B 的坐标,由点B 、C 的坐标利用待定系数法即可求出直线BC 的解析式,利用配方法可求出抛物线的对称轴,再利用一次函数图象上点的坐标特征即可求出点P 的坐标;()3设点M 的坐标为()1,m ,则22CM (10)(m 3)=-+-,()22AC [01](30)10=--+-=,()22AM [11](m 0)=--+-,分AMC 90∠=o 、ACM 90∠=o 和CAM 90∠=o 三种情况,利用勾股定理可得出关于m 的一元二次方程或一元一次方程,解之可得出m 的值,进而即可得出点M 的坐标. 【详解】解:()1将()1,0A -、()0,3C 代入2y x bx c =-++中, 得:{103b c c --+==,解得:{23b c ==,∴抛物线的解析式为223y x x =-++.()2连接BC 交抛物线对称轴于点P ,此时PA PC +取最小值,如图1所示.当0y =时,有2230x x -++=, 解得:11x =-,23x =,∴点B 的坐标为()3,0.Q 抛物线的解析式为2223(1)4y x x x =-++=--+, ∴抛物线的对称轴为直线1x =.设直线BC 的解析式为()0y kx d k =+≠, 将()3,0B 、()0,3C 代入y kx d =+中, 得:{303k d d +==,解得:{13k d =-=,∴直线BC 的解析式为3y x =-+. Q 当1x =时,32y x =-+=,∴当PA PC +的值最小时,点P 的坐标为()1,2.()3设点M 的坐标为()1,m ,则22(10)(3)CM m =-+-,()22[01](30)10AC =--+-=()22[11](0)AM m =--+-分三种情况考虑:①当90AMC ∠=o 时,有222AC AM CM =+,即22101(3)4m m =+-++,解得:11m =,22m =,∴点M 的坐标为()1,1或()1,2;②当90ACM ∠=o 时,有222AM AC CM =+,即224101(3)m m +=++-,解得:83m =, ∴点M 的坐标为81,3⎛⎫⎪⎝⎭;③当90CAM ∠=o 时,有222CM AM AC =+,即221(3)410m m +-=++,解得:23m =-, ∴点M 的坐标为21,.3⎛⎫- ⎪⎝⎭综上所述:当MAC V 是直角三角形时,点M 的坐标为()1,1、()1,2、81,3⎛⎫⎪⎝⎭或21,.3⎛⎫- ⎪⎝⎭【点睛】本题考查待定系数法求二次(一次)函数解析式、二次(一次)函数图象的点的坐标特征、轴对称中的最短路径问题以及勾股定理,解题的关键是:()1由点的坐标,利用待定系数法求出抛物线解析式;()2由两点之间线段最短结合抛物线的对称性找出点P 的位置;()3分AMC 90∠=o 、ACM 90∠=o 和CAM 90∠=o 三种情况,列出关于m 的方程.11.如图,直线y =﹣x +4与x 轴交于点B ,与y 轴交于点C ,抛物线y =﹣x 2+bx +c 经过B ,C 两点,与x 轴另一交点为A .点P 以每秒2个单位长度的速度在线段BC 上由点B 向点C 运动(点P 不与点B 和点C 重合),设运动时间为t 秒,过点P 作x 轴垂线交x 轴于点E ,交抛物线于点M .(1)求抛物线的解析式;(2)如图①,过点P 作y 轴垂线交y 轴于点N ,连接MN 交BC 于点Q ,当12MQ NQ =时,求t 的值;(3)如图②,连接AM 交BC 于点D ,当△PDM 是等腰三角形时,直接写出t 的值. 【答案】(1)y =﹣x 2+3x +4;(2)t 的值为12;(3)当△PDM 是等腰三角形时,t =1或t ﹣1. 【解析】 【分析】(1)求直线y=-x+4与x 轴交点B ,与y 轴交点C ,用待定系数法即求得抛物线解析式. (2)根据点B 、C 坐标求得∠OBC=45°,又PE ⊥x 轴于点E ,得到△PEB 是等腰直角三角形,由PB =求得BE=PE=t ,即可用t 表示各线段,得到点M 的横坐标,进而用m 表示点M 纵坐标,求得MP 的长.根据MP ∥CN 可证MPQ NCQ V V ∽,故有12MP MQ NC NQ ==,把用t 表示的MP 、NC 代入即得到关于t 的方程,求解即得到t 的值. (3)因为不确定等腰△PDM 的底和腰,故需分3种情况讨论:①若MD=MP ,则∠MDP=∠MPD=45°,故有∠DMP=90°,不合题意;②若DM=DP ,则∠DMP=∠MPD=45°,进而得AE=ME ,把含t 的式子代入并解方程即可;③若MP=DP ,则∠PMD=∠PDM ,由对顶角相等和两直线平行内错角相等可得∠CFD=∠PMD=∠PDM=∠CDF 进而得CF=CD .用t 表示M 的坐标,求直线AM 解析式,求得AM 与y 轴交点F 的坐标,即能用t 表示CF 的长.把直线AM 与直线BC 解析式联立方程组,解得x 的值即为点D 横坐标.过D 作y 轴垂线段DG ,得等腰直角△CDG ,用DG 即点D 横坐标,进而可用t 表示CD 的长.把含t 的式子代入CF=CD ,解方程即得到t 的值. 【详解】(1)直线y =﹣x +4中,当x =0时,y =4 ∴C (0,4)当y =﹣x +4=0时,解得:x =4 ∴B (4,0)∵抛物线y =﹣x 2+bx +c 经过B ,C 两点 ∴1640004b c c -++=⎧⎨++=⎩ 解得:34b c =⎧⎨=⎩∴抛物线解析式为y =﹣x 2+3x +4(2)∵B (4,0),C (0,4),∠BOC =90° ∴OB =OC∴∠OBC =∠OCB =45° ∵ME ⊥x 轴于点E ,PBt ∴∠BEP =90°∴Rt △BEP 中,2PE sin PBE PB ∠==∴BE PE t ==, ∴4M P P x x OE OBBE t y PE t ===﹣=﹣,== ∵点M 在抛物线上∴2243445M y t t t t +++=﹣(﹣)(﹣)=﹣, ∴24MP MP y y t t +=﹣=﹣ , ∵PN ⊥y 轴于点N∴∠PNO =∠NOE =∠PEO =90° ∴四边形ONPE 是矩形 ∴ON =PE =t ∴NC =OC ﹣ON =4﹣t ∵MP ∥CN ∴△MPQ ∽△NCQ ∴12MP MQ NC NQ == ∴24142t t t -+=-解得:12142t t =,=(点P 不与点C 重合,故舍去) ∴t 的值为12(3)∵∠PEB =90°,BE =PE ∴∠BPE =∠PBE =45° ∴∠MPD =∠BPE =45°①若MD =MP ,则∠MDP =∠MPD =45° ∴∠DMP =90°,即DM ∥x 轴,与题意矛盾 ②若DM =DP ,则∠DMP =∠MPD =45° ∵∠AEM =90° ∴AE =ME∵y =﹣x 2+3x +4=0时,解得:x 1=﹣1,x 2=4 ∴A (﹣1,0)∵由(2)得,x M =4﹣t ,ME =y M =﹣t 2+5t ∴AE =4﹣t ﹣(﹣1)=5﹣t ∴5﹣t =﹣t 2+5t解得:t 1=1,t 2=5(0<t <4,舍去)③若MP =DP ,则∠PMD =∠PDM如图,记AM 与y 轴交点为F ,过点D 作DG ⊥y 轴于点G ∴∠CFD =∠PMD =∠PDM =∠CDF ∴CF =CD∵A (﹣1,0),M (4﹣t ,﹣t 2+5t ),设直线AM 解析式为y =ax +m ∴()2045a m a t m t t -+=⎧⎨-+=-+⎩ 解得:a tm t =⎧⎨=⎩ , ∴直线AM :y tx t += ∴F (0,t ) ∴CF =OC ﹣OF =4﹣t ∵tx +t =﹣x +4,解得:41tx t -=+, ∴41D x tt DG -=+==, ∵∠CGD =90°,∠DCG =45° ∴)2421t CD DG t -+==,∴)2441t t t -+﹣ 解得:21t =﹣综上所述,当△PDM 是等腰三角形时,t =1或21t =﹣. 【点睛】本题考查了二次函数的图象与性质,解二元一次方程组和一元二次方程,等腰直角三角形的性质,相似三角形的判定和性质,涉及等腰三角形的分类讨论,要充分利用等腰的性质作为列方程的依据.12.已知,如图,抛物线2(0)y ax bx c a =++≠的顶点为(1,9)M ,经过抛物线上的两点(3,7)A --和(3,)B m 的直线交抛物线的对称轴于点C .(1)求抛物线的解析式和直线AB 的解析式.(2)在抛物线上,A M 两点之间的部分(不包含,A M 两点),是否存在点D ,使得2DAC DCM S S ∆∆=?若存在,求出点D 的坐标;若不存在,请说明理由.(3)若点P 在抛物线上,点Q 在x 轴上,当以点,,,A M P Q 为顶点的四边形是平行四边形时,直接写出满足条件的点P 的坐标.【答案】(1)抛物线的表达式为:228y x x =-++,直线AB 的表达式为:21y x =-;(2)存在,理由见解析;点P (6,16)-或(4,16)--或(17,2)+或(17,2).【解析】 【分析】(1)二次函数表达式为:y=a (x-1)2+9,即可求解; (2)S △DAC =2S △DCM ,则()()()()()21112821139112222DAC C A S DH x x x x x x =-=-++-++=--⨯V ,,即可求解;(3)分AM 是平行四边形的一条边、AM 是平行四边形的对角线两种情况,分别求解即可. 【详解】解:(1)二次函数表达式为:()219y a x =-+, 将点A 的坐标代入上式并解得:1a =-, 故抛物线的表达式为:228y x x =-++…①, 则点()3,5B ,将点,A B 的坐标代入一次函数表达式并解得: 直线AB 的表达式为:21y x =-; (2)存在,理由:二次函数对称轴为:1x =,则点()1,1C , 过点D 作y 轴的平行线交AB 于点H ,设点()2,28D x x x -++,点(),21H x x -,∵2DAC DCM S S ∆∆=, 则()()()()()21112821139112222DAC C A S DH x x x x x x =-=-++-++=--⨯V , 解得:1x =-或5(舍去5), 故点()1,5D -;(3)设点(),0Q m 、点(),P s t ,228t s s =-++, ①当AM 是平行四边形的一条边时,点M 向左平移4个单位向下平移16个单位得到A ,同理,点(),0Q m 向左平移4个单位向下平移16个单位为()4,16m --,即为点P , 即:4m s -=,6t -=,而228t s s =-++, 解得:6s =或﹣4, 故点()6,16P -或()4,16--; ②当AM 是平行四边形的对角线时,由中点公式得:2m s +=-,2t =,而228t s s =-++, 解得:17s =±故点()17,2P 或()17,2;综上,点()6,16P -或()4,16--或()17,2或()17,2. 【点睛】本题考查的是二次函数综合运用,涉及到一次函数、平行四边形性质、图形的面积计算等,其中(3),要注意分类求解,避免遗漏.13.已知矩形ABCD 中,AB =5cm ,点P 为对角线AC 上的一点,且AP =25cm .如图①,动点M 从点A 出发,在矩形边上沿着A B C →→的方向匀速运动(不包含点C ).设动点M 的运动时间为t (s ),APM ∆的面积为S (cm ²),S 与t 的函数关系如图②所示: (1)直接写出动点M 的运动速度为 /cm s ,BC 的长度为 cm ;(2)如图③,动点M 重新从点A 出发,在矩形边上,按原来的速度和方向匀速运动.同时,另一个动点N 从点D 出发,在矩形边上沿着D C B →→的方向匀速运动,设动点N 的运动速度为()/v cm s .已知两动点M 、N 经过时间()x s 在线段BC 上相遇(不包含点C ),动点M 、N 相遇后立即停止运动,记此时APM DPN ∆∆与的面积为()()2212,S cm S cm . ①求动点N 运动速度()/v cm s 的取值范围;②试探究12S S ⋅是否存在最大值.若存在,求出12S S ⋅的最大值并确定运动速度时间x 的值;若不存在,请说明理由.【答案】(1)2,10;(2)①2/6/3cm s v cm s ≤<;②当154x =时,12S S ⋅取最大值2254. 【解析】 【分析】(1)由题意可知图像中0~2.5s 时,M 在AB 上运动,求出速度,2.5~7.5s 时,M 在BC 上运动,求出BC 长度;(2)①分别求出在C 点相遇和在B 点相遇时的速度,取中间速度,注意C 点相遇时的速度不能取等于;②过M 点做MH ⊥AC ,则125MH CM ==得到S 1,同时利用12()PAD CDM ABM N ABCD S S S S S S ∆∆∆+=---(N )矩形=15,得到S 2,再得到12S S ⋅关于x 的二次函数,利用二次函数性质求得最大值 【详解】(1)5÷2.5=2/cm s ;(7.5-2.5)×2=10cm (2)①解:在C 点相遇得到方程57.5v= 在B 点相遇得到方程152.5v= ∴5=7.515=2.5vv⎧⎪⎪⎨⎪⎪⎩解得 23=5v v ⎧=⎪⎨⎪⎩。
二次函数与几何综合压轴题(原卷版)-2024年中考数学

二次函数与几何综合压轴题几乎所有的地方都把二次函数与几何综合压轴题作为中考压轴题。
1.(2023·青海·中考真题)如图,二次函数2y x bx c =−++的图象与x 轴相交于点A 和点()1,0C ,交y 轴于点()0,3B .(1)求此二次函数的解析式;(2)设二次函数图象的顶点为P ,对称轴与x 轴交于点Q ,求四边形AOBP 的面积(请在图1中探索); (3)二次函数图象的对称轴上是否存在点M ,使得△AMB 是以AB 为底边的等腰三角形?若存在,请求出满足条件的点M 的坐标;若不存在,请说明理由(请在图2中探索).2.(2023·内蒙古·中考真题)如图,在平面直角坐标系中,抛物线2y x bx c =−++与x 轴的交点分别为A 和()10B ,(点A 在点B 的左侧),与y 轴交于点()0,3C ,点P 是直线AC 上方抛物线上一动点.(1)求抛物线的解析式;(2)如图1,过点P 作x 轴平行线交AC 于点E ,过点P 作y 轴平行线交x 轴于点D ,求PE PD +的最大值及点P 的坐标;(3)如图2,设点M 为抛物线对称轴上一动点,当点P ,点M 运动时,在坐标轴上确定点N ,使四边形PMCN 为矩形,求出所有符合条件的点N 的坐标.3.(2023·海南·中考真题)如图1,抛物线2y x bx c =++交x 轴于A ,()3,0B 两点,交y 轴于点()0,3C −.点P 是抛物线上一动点.(1)求该抛物线的函数表达式;(2)当点P 的坐标为()1,4−时,求四边形BACP 的面积;(3)当动点P 在直线BC 上方时,在平面直角坐标系是否存在点Q ,使得以B ,C ,P ,Q 为顶点的四边形是矩形?若存在,请求出点Q 的坐标;若不存在,请说明理由;(4)如图2,点D 是抛物线的顶点,过点D 作直线DH y ∥轴,交x 轴于点H ,当点P 在第二象限时,作直线PA ,PB 分别与直线DH 交于点G 和点I ,求证:点D 是线段IG 的中点.4.(2023·西藏·中考真题)在平面直角坐标系中,抛物线2y x bx c =−++与x 轴交于()30A −,,()10B ,两点,与y 轴交于点C .(1)求抛物线的解析式;(2)如图甲,在y 轴上找一点D ,使ACD 为等腰三角形,请直接写出点D 的坐标;(3)如图乙,点P 为抛物线对称轴上一点,是否存在P 、Q 两点使以点A ,C ,P ,Q 为顶点的四边形是菱形?若存在,求出P 、Q 两点的坐标,若不存在,请说明理由.5.(2023·四川甘孜·中考真题)已知抛物线2y x bx c =++与x 轴相交于()10A −,,B 两点,与y 轴相交于点()03C −,.(1)求b ,c 的值;(2)P 为第一象限抛物线上一点,PBC 的面积与ABC 的面积相等,求直线AP 的解析式;(3)在(2)的条件下,设E 是直线BC 上一点,点P 关于AE 的对称点为点P ′,试探究,是否存在满足条件的点E ,使得点P ′恰好落在直线BC 上,如果存在,求出点P ′的坐标;如果不存在,请说明理由.6.(2023·四川达州·中考真题)如图,抛物线2y ax bx c ++过点()()()1,0,3,,00,3A B C −.(1)求抛物线的解析式;(2)设点P 是直线BC 上方抛物线上一点,求出PBC 的最大面积及此时点P 的坐标;(3)若点M 是抛物线对称轴上一动点,点N 为坐标平面内一点,是否存在以BC 为边,点B C M N 、、、为顶点的四边形是菱形,若存在,请直接写出点N 的坐标;若不存在,请说明理由.7.(2023·四川巴中·中考真题)在平面直角坐标系中,抛物线2(0)y ax bx c a ++≠经过点(1,0)A −和(0,3)B ,其顶点的横坐标为1.(1)求抛物线的表达式.(2)若直线x m =与x 轴交于点N ,在第一象限内与抛物线交于点M ,当m 取何值时,使得AN MN +有最大值,并求出最大值.(3)若点P 为抛物线2(0)y ax bx c a ++≠的对称轴上一动点,将抛物线向左平移1个单位长度后,Q 为平移后抛物线上一动点.在(2)的条件下求得的点M ,是否能与A 、P 、Q 构成平行四边形?若能构成,求出Q 点坐标;若不能构成,请说明理由.8.(2023·四川眉山·中考真题)在平面直角坐标系中,已知抛物线2y ax bx c ++与x 轴交于点()()3,0,1,0A B −两点,与y 轴交于点()0,3C ,点P 是抛物线上的一个动点.(1)求抛物线的表达式;(2)当点P 在直线AC 上方的抛物线上时,连接BP 交AC 于点D .如图1.当PD DB的值最大时,求点P 的坐标及PD DB 的最大值; (3)过点P 作x 轴的垂线交直线AC 于点M ,连接PC ,将PCM △沿直线PC 翻折,当点M 的对应点'M 恰好落在y 轴上时,请直接写出此时点M 的坐标.9.(2023·四川内江·中考真题)如图,在平面直角坐标系中,抛物线2y ax bx c ++与x 轴交于()4,0B ,()2,0C −两点.与y 轴交于点()0,2A −.(1)求该抛物线的函数表达式;(2)若点P 是直线AB 下方抛物线上的一动点,过点P 作x 轴的平行线交AB 于点K ,过点P 作y 轴的平行线交x 轴于点D ,求与12PK PD +的最大值及此时点P 的坐标; (3)在抛物线的对称轴上是否存在一点M ,使得MAB △是以AB 为一条直角边的直角三角形:若存在,请求出点M 的坐标,若不存在,请说明理由.10.(2023·湖北黄冈·中考真题)已知抛物线212y x bx c =−++与x 轴交于,(4,0)A B 两点,与y 轴交于点(0,2)C ,点P 为第一象限抛物线上的点,连接,,,CA CB PB PC .(1)直接写出结果;b =_____,c =_____,点A 的坐标为_____,tan ABC ∠=______;(2)如图1,当2PCB OCA ∠=∠时,求点P 的坐标; (3)如图2,点D 在y 轴负半轴上,OD OB =,点Q 为抛物线上一点,90QBD ∠=°,点E ,F 分别为BDQ △的边,DQ DB 上的动点,QE DF =,记BE QF +的最小值为m . ①求m 的值;②设PCB 的面积为S ,若214S m k =−,请直接写出k 的取值范围.11.(2023·湖北武汉·中考真题)抛物线21:28=−−C y x x 交x 轴于,A B 两点(A 在B 的左边),交y 轴于点C .(1)直接写出,,A B C 三点的坐标;(2)如图(1),作直线()04=<<x t t ,分别交x 轴,线段BC ,抛物线1C 于,,D E F 三点,连接CF .若BDE 与CEF △相似,求t 的值;(3)如图(2),将抛物线1C 平移得到抛物线2C ,其顶点为原点.直线2y x =与抛物线2C 交于,O G 两点,过OG 的中点H 作直线MN (异于直线OG )交抛物线2C 于,M N 两点,直线MO 与直线GN 交于点P .问点P 是否在一条定直线上?若是,求该直线的解析式;若不是,请说明理由.12.(2023·湖南郴州·中考真题)已知抛物线24y ax bx ++与x 轴相交于点 1,0A ,()4,0B ,与y 轴相交于点C .(1)求抛物线的表达式;(2)如图1,点P 是抛物线的对称轴l 上的一个动点,当PAC △的周长最小时,求PAPC的值; (3)如图2,取线段OC 的中点D ,在抛物线上是否存在点Q ,使1tan 2QDB ∠=若存在,求出点Q 的坐标;若不存在,请说明理由.且与直线:1l y x =−−交于D E 、两点(点D 在点E 的右侧),点M 为直线l 上的一动点,设点M 的横坐标为t .(1)求抛物线的解析式.(2)过点M 作x 轴的垂线,与拋物线交于点N .若04t <<,求NED 面积的最大值.(3)抛物线与y 轴交于点C ,点R 为平面直角坐标系上一点,若以B C M R 、、、为顶点的四边形是菱形,请求出所有满足条件的点R 的坐标.在此抛物线上,其横坐标分别为,2(0)m m m >,连接AP ,AQ .(1)求此抛物线的解析式.(2)当点Q 与此抛物线的顶点重合时,求m 的值.(3)当PAQ ∠的边与x 轴平行时,求点P 与点Q 的纵坐标的差.(4)设此抛物线在点A 与点P 之间部分(包括点A 和点P )的最高点与最低点的纵坐标的差为1h ,在点A 与点Q 之间部分(包括点A 和点Q )的最高点与最低点的纵坐标的差为2h .当21h h m −=时,直接写出m 的值.15.(2023·青海西宁·中考真题)如图,在平面直角坐标系中,直线l 与x 轴交于点()6,0A ,与y 轴交于点()0,6B −,抛物线经过点A ,B ,且对称轴是直线1x =.(1)求直线l 的解析式; (2)求抛物线的解析式;(3)点P 是直线l 下方抛物线上的一动点,过点P 作PC x ⊥轴,垂足为C ,交直线l 于点D ,过点P 作PM l ⊥,垂足为M .求PM 的最大值及此时P 点的坐标.16.(2023·湖南·中考真题)如图,二次函数2y x bx c =++的图象与x 轴交于A ,B 两点,与y 轴交于C 点,其中()10B ,,()0,3C .(1)求这个二次函数的表达式;(2)在二次函数图象上是否存在点P ,使得PAC ABC S S =△△?若存在,请求出P 点坐标;若不存在,请说明理由;(3)点Q 是对称轴l 上一点,且点Q 的纵坐标为a ,当QAC △是锐角三角形时,求a 的取值范围.17.(2023·辽宁营口·中考真题)如图,抛物线()210y ax bx a +−≠与x 轴交于点 1,0A 和点B ,与y 轴交于点C ,抛物线的对称轴交x 轴于点()3,0D ,过点B 作直线l x ⊥轴,过点D 作DE CD ⊥,交直线l 于点E .(1)求抛物线的解析式;(2)如图,点P 为第三象限内抛物线上的点,连接CE 和BP 交于点Q ,当57BQ PQ =时.求点P 的坐标; (3)在(2)的条件下,连接AC ,在直线BP 上是否存在点F ,使得DEF ACD BED ∠=∠+∠?若存在,请直接写出点F 的坐标;若不存在,请说明理由.18.(2023·湖南湘西·中考真题)如图(1),二次函数25y ax x c =−+的图像与x 轴交于()4,0A −,(),0B b 两点,与y 轴交于点()0,4C −.(1)求二次函数的解析式和b 的值.(2)在二次函数位于x 轴上方的图像上是否存在点M ,使13BOM ABC S S =△△?若存在,请求出点M 的坐标;若不存在,请说明理由.(3)如图(2),作点A 关于原点O 的对称点E ,连接CE ,作以CE 为直径的圆.点E ′是圆在x 轴上方圆弧上的动点(点E ′不与圆弧的端点E 重合,但与圆弧的另一个端点可以重合),平移线段AE ,使点E 移动到点E ′,线段AE 的对应线段为A E ′′,连接E C ′,A A ′,A A ′的延长线交直线E C ′于点N ,求AA CN′的值.19.(2023·辽宁盘锦·中考真题)如图,抛物线23y ax bx ++与x 轴交于点()10A −,,()30B ,,与y 轴交于点C .(1)求抛物线的解析式.(2)如图1,点Q 是x 轴上方抛物线上一点,射线QM x ⊥轴于点N ,若QM BM =,且4tan 3MBN ∠=,请直接写出点Q 的坐标.(3)如图2,点E 是第一象限内一点,连接AE 交y 轴于点D ,AE 的延长线交抛物线于点P ,点F 在线段CD 上,且CF OD =,连接FA FE BE BP ,,,,若AFE ABE S S =△△,求PAB 面积.20.(2023·重庆·中考真题)如图,在平面直角坐标系中,抛物线22y ax bx ++过点()1,3,且交x 轴于点()1,0A −,B 两点,交y 轴于点C .(1)求抛物线的表达式;(2)点P 是直线BC 上方抛物线上的一动点,过点P 作PD BC ⊥于点D ,过点P 作y 轴的平行线交直线BC 于点E ,求PDE △周长的最大值及此时点P 的坐标;(3)在(2)中PDE △周长取得最大值的条件下,将该抛物线沿射线CB M 为平移后的抛物线的对称轴上一点.在平面内确定一点N ,使得以点A ,P ,M ,N 为顶点的四边形是菱形,写出所有符合条件的点N 的坐标,并写出求解点N 的坐标的其中一种情况的过程.21.(2023·四川广安·中考真题)如图,二次函数2y x bx c =++的图象交x 轴于点A B ,,交y 轴于点C ,点B 的坐标为()1,0,对称轴是直线=1x −,点P 是x 轴上一动点,PM x ⊥轴,交直线AC 于点M ,交抛物线于点N .(1)求这个二次函数的解析式.(2)若点P 在线段AO 上运动(点P 与点A 、点O 不重合),求四边形ABCN 面积的最大值,并求出此时点P 的坐标.(3)若点P 在x 轴上运动,则在y 轴上是否存在点Q ,使以M 、N C Q 、、为顶点的四边形是菱形?若存在,请直接写出所有满足条件的点Q 的坐标;若不存在,请说明理由.22.(2023·湖北十堰·中考真题)已知抛物线28y ax bx ++过点()4,8B 和点()8,4C ,与y 轴交于点A .(1)求抛物线的解析式;(2)如图1,连接,AB BC ,点D 在线段AB 上(与点,A B 不重合),点F 是OA 的中点,连接FD ,过点D 作DE FD ⊥交BC 于点E ,连接EF ,当DEF 面积是ADF △面积的3倍时,求点D 的坐标;(3)如图2,点P 是抛物线上对称轴右侧的点,(),0H m 是x 轴正半轴上的动点,若线段OB 上存在点G (与点,O B 不重合),使得GBP HGP BOH ∠=∠=∠,求m 的取值范围.23.(2023·四川·中考真题)如图1,在平面直角坐标系中,已知二次函数24y ax bx ++的图象与x 轴交于点()2,0A −,()4,0B ,与y 轴交于点C .(1)求抛物线的解析式;(2)已知E 为抛物线上一点,F 为抛物线对称轴l 上一点,以B ,E ,F 为顶点的三角形是等腰直角三角形,且90BFE ∠=°,求出点F 的坐标; (3)如图2,P 为第一象限内抛物线上一点,连接AP 交y 轴于点M ,连接BP 并延长交y 轴于点N ,在点P 运动过程中,12OM ON +是否为定值?若是,求出这个定值;若不是,请说明理由.24.(2023·黑龙江绥化·中考真题)如图,抛物线21y ax bx c =++的图象经过(6,0)A −,(2,0)B −,(0,6)C 三点,且一次函数6y kx =+的图象经过点B .(1)求抛物线和一次函数的解析式.(2)点E ,F 为平面内两点,若以E 、F 、B 、C 为顶点的四边形是正方形,且点E 在点F 的左侧.这样的E ,F 两点是否存在?如果存在,请直接写出所有满足条件的点E 的坐标:如果不存在,请说明理由.(3)将抛物线21y ax bx c =++的图象向右平移8个单位长度得到抛物线2y ,此抛物线的图象与x 轴交于M ,N 两点(M 点在N 点左侧).点P 是抛物线2y 上的一个动点且在直线NC 下方.已知点P 的横坐标为m .过点P 作PD NC ⊥于点D .求m 为何值时,12CD PD +有最大值,最大值是多少?25.(2023·四川德阳·中考真题)已知:在平面直角坐标系中,抛物线与x 轴交于点(4,0)A −,(2,0)B ,与y 轴交于点(0,4)C −.(1)求抛物线的解析式;(2)如图1,如果把抛物线x 轴下方的部分沿x 轴翻折180°,抛物线的其余部分保持不变,得到一个新图象.当平面内的直线6y kx =+与新图象有三个公共点时,求k 的值; (3)如图2,如果把直线AB 沿y 轴向上平移至经过点D ,与抛物线的交点分别是E ,F ,直线BC 交EF 于点H ,过点F 作FG CH ⊥于点G ,若DF HG=F 的坐标.26.(2023·辽宁锦州·中考真题)如图,抛物线2y bx c ++交x 轴于点()1,0A −和B ,交y 轴于点(C ,顶点为D .(1)求抛物线的表达式;(2)若点E 在第一象限内对称右侧的抛物线上,四边形ODEB 的面积为E 的坐标;(3)在(2)的条件下,若点F 是对称轴上一点,点H 是坐标平面内一点,在对称轴右侧的抛物线上是否存在点G ,使以E ,F ,G ,H 为顶点的四边形是菱形,且60EFG ∠=°,如果存在,请直接写出点G 的坐标;如果不存在,请说明理由.27.(2023·辽宁鞍山·中考真题)如图1,抛物线253y ax x c =++经过点()3,1,与y 轴交于点()0,5B ,点E 为第一象限内抛物线上一动点.(1)求抛物线的解析式.(2)直线243y x =−与x 轴交于点A ,与y 轴交于点D ,过点E 作直线EF x ⊥轴,交AD 于点F ,连接BE .当BE DF =时,求点E 的横坐标.(3)如图2,点N 为x 轴正半轴上一点,OE 与BN 交于点M .若OE BN =,3tan 4BME ∠=,求点E 的坐标.28.(2023·辽宁丹东·中考真题)抛物线24y ax bx +−与x 轴交于点()4,0A −,()2,0B ,与y 轴交于点C .(1)求抛物线的表达式;(2)如图,点D 是抛物线上的一个动点,设点D 的横坐标是()42m m −<<,过点D 作直线DE x ⊥轴,垂足为点E ,交直线AC 于点F .当D ,E ,F 三点中一个点平分另外两点组成的线段时,求线段DF 的长;(3)若点P 是抛物线上的一个动点(点P 不与顶点重合),点M 是抛物线对称轴上的一个点,点N 在坐标平面内,当四边形CMPN 是矩形邻边之比为1:2时,请直接写出点P 的横坐标.。
中考数学总复习《二次函数综合压轴题》专项提升练习(附答案)

中考数学总复习《二次函数综合压轴题》专项提升练习(附答案)学校:___________班级:___________姓名:___________考号:___________1.已知,如图,抛物线y=ax2+bx−8与x轴交于A、B两点,与y轴交于点C,OA=6,OB=43点P为x轴下方的抛物线上一点.(1)求抛物线的函数表达式;(2)连接AP、CP,求四边形AOCP面积的最大值;(3)若点P到AB和AC两边的距离相等,求点P的坐标.2.在平面直角坐标系中,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C.过点D(−52,34),且顶点P的坐标为(−1,3).(1)求二次函数的解析式;(2)如图1,若点M是二次函数图象上的点,且在直线CD的上方.连接MC,MD求△MCD面积的最大值;(3)如图2,设点Q是抛物线对称轴上的一点,连接QC,将线段QC绕点Q逆时针旋转90°,点C的对应点为F,连接PF交抛物线于点E,请直接写出点E的坐标.3.在平面直角坐标系中,已知点A(3,3)、B(6,0),AC⊥x轴,垂足为点C,直线y=12x与抛物线y=−14x2+2x相交于点O、D过x轴正半轴上的任意一点P作y轴的平行线PE交射线OA于点E.(1)求点D的坐标;(2)设点P的横坐标为a a≠3求以点A、B、C、E为顶点的四边形的面积S与a的函数关系式;(3)设直线PE交射线OD于点F交抛物线于点Q以FQ为一边在FQ的右边作矩形FQMN若FN=32且矩形FQMN与△AOB重叠部分为轴对称图形求出a的取值范围.4.在平面直角坐标系中设直线l的解析式为:y=kx+m(k、m为常数且.k≠0) 当直线l与一条曲线有且只有一个公共点时我们称直线l与这条曲线“相切” 这个公共点叫做“切点”.(1)求直线l:y=−x+6与双曲线y=9x的切点坐标;(2)已知一次函数y1=2x二次函数y2=x2+1是否存在二次函数y3=ax2+bx+c其图象经过点(−3,2)使得直线y1=2x与y2=x2+1,y3=ax2+bx+c都相切于同一点? 若存在求出y3的解析式;若不存在请说明理由;(3)已知直线l1:y=k1x+m1(k1≠0)直线l2:y2=k2x+m2(k2≠0)是抛物线y=−x2+2x+2的两条切线当l1与l2的交点P的纵坐标为4时试判断k1⋅k2是否为定值并说明理由.5.如图在平面直角坐标系中点O为坐标原点抛物线y=512x2−136x−2与x轴的交点分别为点A B与y轴的交点为点C.(1)求直线BC解析式;(2)点P为第四象限的抛物线上一点连接PB、PC当PB=PC时求点P的坐标;(3)在(2)的条件下连接OP点M在y轴的负半轴上连接MP∠OMP=∠CBP N为OM的中点点Q 在OP上连接MQ、NQ,MQ交抛物线于点R当MQ=2NQ时求R点的横坐标.6.如图在平面直角坐标系中抛物线y=ax2+bx+c(a≠0)若抛物线与x轴交于B(4,0)C(−2,0)两点与y轴交于点A(0,−2).(1)求该抛物线的函数表达式;(2)如图1 若点E是直线CA下方的抛物线上一点过点E作EF∥AB交x轴于点F且EF=√5求点E的横坐标;(3)如图2 点M在点B的正下方连接CM交抛物线于点N直线BN交对称轴于点P作PQ∥CM交射线BM于点Q求BQ的大小.7.如图在平面直角坐标系xOy中已知直线y=−x−3与x轴交于点A与y轴交于点C过A C两点的抛物线y=ax2+bx+c与x轴交于另一点B(1,0)抛物线对称轴为直线l.(1)求抛物线的解析式;(2)点M为直线AC下方抛物线上一点当△MAC的面积最大时求点M的坐标;(3)点P是抛物线上的点过点P作l的垂线垂足为D E是l上的点.要使得以P D E为顶点的三角形与△BOC全等请求出点P点E的坐标;8.如图抛物线y=−x2+bx+c与x轴相交于A B两点与y轴交于点C抛物线的对称轴交x轴于点D.已知A(−1,0),C(0,3).(1)求抛物线的解析式;(2)在抛物线的对称轴上有一点P使得|PB−PC|的值最大求此点P的坐标;(3)点M为该抛物线的顶点直线MD⊥x轴于点D在直线MD上是否存在点N使点N到直线MC的距离等于点N到点A的距离?若存在求出点N的坐标;若不存在请说明理由;9.在平面直角坐标系中点O为坐标原点抛物线y=ax2+x+6交x轴负半轴于A交正半轴于B交y 轴于C OB=OC.(1)求抛物线的解析式;(2)如图1 点P是第三象限抛物线上一点连接BP交y轴于点D设点P横坐标为t线段CD长为d求d与t的函数关系;(3)如图2 在(2)的条件下过点C作BP的垂线交x轴于点F垂足为点G E为CF上一点连接BE 若BE=BD∠BEG=2∠PBA求点P坐标.10.如图1 在平面直角坐标系中O为坐标原点AD为等腰直角△ABC底边BC上的高抛物线y=a(x−2)2+4的顶点为点A且经过B C两点B C两点在x轴上.(1)求该抛物线的解析式;(2)如图2 点E为抛物线上位于直线AC上方的一点过点E作EN⊥x轴交直线AC于点N求线段EN的长度最大值及此时点E的坐标;(3)如图2 点M(5,b)是抛物线上的一点点P为对称轴上一动点在(2)的条件下当线段EN的长度最大时求PE+PM的最小值.11.抛物线y=ax2−2ax−3a(a>0)与x轴交于A B两点(点A在点B的左边)与y轴交于点C.(1)求抛物线的对称轴;(2)求证:不论a取何值函数图象必过两个定点;(3)如图若OB=OC点P是直线BC(不与B C重合)上一动点过点P作x轴的垂线交抛物线于M点连接CM将△PCM沿CM对折如果点P的对应点N恰好落在y轴上求此时点P的坐标.12.已知抛物线y=a(x+6)(x−2)经过点(0,2)交x轴于点A和点B(点A在点B的左侧)抛物线的顶点为D对称轴DE交x轴于点E连接EC.(1)直接写出a的值点A的坐标;(2)若点M是抛物线对称轴DE上的点当△MCE是等腰三角形时求点M的坐标;(3)点P是抛物线上的动点连接PC、PE将△PCE沿CE所在的直线对折点P落在坐标平面内的点P′处.直接写出点P′恰好落在直线AD上时点P的横坐标.13.综合与探究如图1 抛物线y=ax2+bx+4与x轴交于A(−4,0)B(3,0)两点与y轴交于点C连接AC BC现将△ABC沿x轴向右平移至△A′B′C′线段A′C′与线段BC交于点E与抛物线交于点F.(1)求出抛物线和直线BC的函数表达式;(2)当线段FE的长度最大时求此时点F的坐标;(3)如图2 连接OC′将△OA′C′沿着A′C′翻折得到△O′A′C′是否存在某一时刻使得点O′恰好在抛物线上若存在请直接写出此时平移的距离;若不存在请说明理由.14.如图1 已知二次函数y=ax2+bx+c(a b c为常数且a≠0)的图像与x轴交于A B两点(A 点在B点左侧)与y轴交于点C(0,3)且其函数表达式可以变形为y=a(x+1)(x−3)的形式.已知点P为该抛物线在第一象限内的一动点设其横坐标为m.(1)求出点A点B的坐标和该二次函数的表达式;(2)连接BC过点P作PQ⊥x轴于点Q交BC于点N直线AP交y轴于点M连接MN.①求出直线AP的函数表达式(用含有m的代数式表示);②设四边形MNQO的面积为S求S关于m的函数关系式并求S的最大值;(3)如图2 若直线l为该二次函数图像的对称轴交x轴于点H直线AP BP分别交直线l于点E F.在点P运动的过程中HF+HE是否为定值?若是请求出该定值;若不是请说明理由.15.在平面直角坐标系中关于x的二次函数y=ax2+bx+c(a b c为常数且a<0)与x轴交于两个不同的点A(x1,0)B(x2,0)(x1<x2)与y轴交于点C抛物线的顶点为M.(1)如图1 已知a=−1b=2c=3.①求此二次函数图象的顶点M的坐标;②点E是x轴正半轴上的一个动点过点E作直线PE⊥x轴交抛物线于点P交直线BC于点F.当点E在线EF求此时点P的坐标.段OB上运动时(不与点O B重合)恰有线段PF=12(2)如图2 当c=0时点P是抛物线对称轴左侧图像上任意一点过点P作PE⊥x轴于点E连接MP交y轴于点Q连接EQ MB.则EQ MB有怎样的位置关系?说明理由.16.如图抛物线的顶点坐标为(2,−3)与y轴交于点C(0,1).(1)求抛物线的解析式;(2)求点A B的坐标及线段AB的长;(3)求△ABC的外接圆⊙D的半径;(4)若(3)中的⊙D交抛物线的对称轴于M N两点(点M在点N的上方)在对称轴右边的抛物线上有一动点P连接PM PN PC线段PC交弦MN于点G.若PC把图形PMCN(指圆弧MCN和线段PM PN组成的图形)分成两部分当这两部分面积之差等于4时求出点P的坐标.17.如图在平面直角坐标系中抛物线y=12x2−32x−2与x轴分别交于点A点B与y轴交于点C.(1)如图1 连接AC直接写出sin∠ACO的值;(2)如图2 连接BC.点G(1,a)在抛物线上连接CG、BG若异于点G的点H也在抛物线上且S△BCH= S△BCG求点H的坐标;(3)如图3 若直线y=mx+n与抛物线交于点P Q连接AP交y轴正半轴于点M连接AQ交y轴负半轴于点N若OM⋅ON=32求4m+n的值.18.如图1 已知二次函数图象与y轴交点为C(0,3)其顶点为D(1,2).(1)求二次函数的表达式;(2)直线CD与x轴交于M现将线段CM上下移动若线段CM与二次函数的图象有交点求CM向上和向下平移的最大距离;(3)若将(1)中二次函数图象平移使其顶点与原点重合然后将其图象绕O点顺时针旋转90°得到抛物线G如图2所示直线y=−x+2与G交于A B两点P为G上位于直线AB左侧一点求ΔABP面积最大值及此时点P的坐标.19.如图在平面直角坐标系中抛物线y=ax2+bx+4(a≠0)经过点(−1,6)与x轴交于点A(−4,0)B 两点与y轴交于点C.(1)求抛物线的解析式;(2)点P是直线AC上方抛物线上一动点过点P作PD∥y轴交AC于点D求PD的最大值及此时点P的坐标;个单位长度得到新抛物线y′新抛物线y′的对称轴交x轴于点M点N是直(3)将该抛物线沿x轴向右平移52线AC上一点在平面内确定一点K使得以C,M,N,K为顶点的四边形是以CN为边的菱形写出所有符合条件的点K的坐标并写出求解点K坐标的其中一种情况的过程.20.如图抛物线y=x2+bx+c与x轴交于A(1,0)B两点与y轴交于点C(0,3).(1)求该抛物线的解析式;(2)如图(1)点P是线段BC上的一动点过点P作PQ∥y轴交抛物线于点Q连接CQ若CQ平分∠OCB求点P的坐标;(3)如图(2)过A B C三点作⊙I直线y=t(t>3)交⊙I于点M N交抛物线于点E F.若EM+FN=MN求t的值参考答案:1.(1)y =x 2+143x −8 (2)51(3)P (56,−4112)【分析】(1)利用待定系数法求解即可;(2)如图所示 连接AC 过点P 作PD ⊥x 轴交AC 于D 先求出直线AC 的解析式 设P (t,t 2+143t −8) 则D (t,−43t −8) 则PD =−t 2−6t 求出S △APC 的最大值 再由S 四边形AOCP =S △ACP +S △AOC 可知当S △APC最大时 S 四边形AOCP 最大 由此即可得到答案;(3)如图所示 取点E 使其坐标为(4,0) 连接AC 、CE 取CE 中点F 连接AF 先证明AE =AC 进而得到AF 平分∠CAE 则直线AF 上的点到AC AB 的距离相等 由此即可知点P 即为直线AF 与抛物线的交点 据此求解即可.【详解】(1)解:∵OA =6∵A (−6,0)∵可设抛物线解析式为y =a (x +6)(x −43)又∵当x =0时 y =−8 即C (0,−8)∵6×(−43)a =−8 ∵a =1∵抛物线解析式为y =(x +6)(x −43)=x 2+143x −8;(2)解:如图所示 连接AC 过点P 作PD ⊥x 轴交AC 于D 设直线AC 的解析式为y =kx +b 1∵{−6k +b 1=0b 1=−8∵{k =−43b 1=−8∵直线AC 的解析式为y =−43x −8设P(t,t2+143t−8)则D(t,−43t−8)∵PD=−43t−8−(t2+143t−8)=−t2−6t∵S△APC=S△APD+S△CPD=12PD⋅(x P−x A)+12PD⋅(x C−x P)=12PD⋅(x C−x A)=3PD=−3(t+3)2+27∵−3<0∵当t=−3时S△APC最大最大为27∵S四边形AOCP=S△ACP+S△AOC∵S四边形AOCP=S△ACP+24∵当S△APC最大时S四边形AOCP最大最大为27+24=51;(3)解:如图所示取点E使其坐标为(4,0)连接AC、CE取CE中点F连接AF∵A(−6,0)C(0,−8)∠AOC=90°∵AE=10,AC=√OA2+OC2=10∵AC=AE∵F是CE的中点∵AF平分∠CAE∵直线AF上的点到AC AB的距离相等设直线AF的解析式为y=k1x+b2∵{−6k1+b2=0 2k1+b2=−4∵{k1=−12 b2=−3∵直线AF的解析式为y=−12x−3联立{y=−12x−3y=x2+14x3−8得6x2+31x−30=0解得{x=56y=−4112或{x=−6y=0(舍去)∵点P的坐标为(56,−4112).【点睛】本题主要考查了二次函数的综合一次函数与几何综合角平分线的性质等腰三角形的性质与判定勾股定理等等正确作出辅助线是解题的关键.2.(1)y=−x2−2x+2(2)12564(3)(−2,2)或(−1,3)【分析】(1)用待定系数法即可求解;(2)由△MCD面积=S△MHD+S△MHC即可求解;(3)①当点Q在点C的下方时证明△QNF≌△CQH(AAS)得到CG=2−t=QN QH=1=FN则点F(t−3,t+1)求出直线PF的表达式进而求解;②当点Q在点C的上方时同理可得:点F′的坐标为(t−3,t−1)进而求解.【详解】(1)解:设抛物线的表达式为:y=a(x−ℎ)2+k则y=a(x+1)2+3将点C的坐标代入上式并得:34=a(−52+1)2+3解得:a=−1故抛物线的表达式为:y =−(x +1)2+3=−x 2−2x +2 即y =−x 2−2x +2;(2)解:由抛物线的表达式知 点C (0,2)如图1 过点M 作MH∥y 轴交CD 于点H设直线CD 的表达式为:y =sx +t则{34=−52s +t t =2解得{s =12t =2 故直线CD 的表达式为:y =12x +2 设点M(m,−m 2−2m +2) 点H(m,12m +2) 则△MCD 面积=S △MHD +S △MHC =12MH ×(x C −x D )=12×[(−m 2−2m +2)−(12m +2)]×52 =−54(m 2+52m) ∵ −54<0 故函数由最大值当m =−54时 △MCD 面积的最大值为12564;(3)设点Q(−1,t) 如图2①当点Q 在点C 的下方时过点Q 作x 轴的平行线交y 轴于点H 交过点F 与y 轴的平行线于点N∵∠FQN +∠QFN =90°∴∠QFF =∠CQH∵∠N =∠CHQ =90°∴△QNF ≌△CQH (AAS )∴CH =2−t =QN∴点F(t −3,t +1)设直线FP 的表达式为:y =px +q则{3=−p +q t +1=p(t −3)+q解得{p =1q =4 故直线PF 的表达式为:y =x +4②联立直线PE 与抛物线的:{y =x +4y =−x 2−2x +2解得:{x =−2y =2(不合题意的值已舍去) 即点E(−2,2);②当点Q 在点C 的上方时同理可得:点F′的坐标为(t −3,t +1)由点P F ′的坐标得:直线PF ′的表达式为y =x +4 同情况①故点E(−2,2);当点F 与点E 重合时 也符合题意综上 点E 的坐标为(−2,2)或(−1,3).【点睛】本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质和旋转的性质;会利用三角形全等的知识解决线段相等的问题;会解一元二次方程;理解坐标与图形性质.3.(1)D(6,3)(2)S ={9−32a (0<a <3)3a −92(a >3)(3)a =3−√3或a =94或3≤a <4【分析】(1)联立两个函数解析式解方程组即可;(2)先求解直线OA 的解析式为y =x 可得点E(a,a) 再分两种情况讨论即可;(3)分情况讨论:①如图 当a <3 且FQ =FN 时 矩形FQMN 与△AOB 重叠部分为轴对称图形 ②如图 当AC 为矩形FQMN 的对称轴时 矩形FQMN 与△AOB 重叠部分为轴对称图形 ③如图 当PQ 与AC 重合时 矩形FQMN 与△AOB 重叠部分为等腰直角三角形 是轴对称图形 ④如图 当点F 为直线OD 与AB 的交点时 可得当3≤a <4时 矩形FQMN 与△AOB 重叠部分为等腰直角三角形 是轴对称图形 从而可得答案.【详解】(1)解:联立y =12x 和y =−14x 2+2x 得{x =0,y =0 或{x =6y =3∵点D(6,3).(2)设直线OA 的解析式为y =kx∵点A(3,3)∴3k =3 解得k =1∴直线OA 的解析式为y =x .∵点P 的横坐标为a,PE ∥y 轴 且交射线OA 于点E∴点E(a,a).当0<a <3时 如图S =S △OAB −S △OCE =12×6×3−12×3a =9−32a . 当a >3时 如图S =S △OBE −S △OAC =12×6a −12×3×3=3a −92. 综上 S ={9−32a (0<a <3)3a −92(a >3); (3)①如图 当a <3 且FQ =FN 时 矩形FQMN 与△AOB 重叠部分为轴对称图形∵FQ=FN∴−14a2+2a−12a=32解得a=3±√3其中a=3+√3不满足a<3∴a=3−√3.②如图当AC为矩形FQMN的对称轴时矩形FQMN与△AOB重叠部分为轴对称图形此时∴32=2(3−a)解得a=94.③如图当PQ与AC重合时矩形FQMN与△AOB重叠部分为等腰直角三角形是轴对称图形此时a=3.④如图当点F为直线OD与AB的交点时∵点A(3,3),B(6,0)∵AB所在的直线方程为y=−x+6联立y=−x+6和y=12x解得x=4.∴当3≤a<4时矩形FQMN与△AOB重叠部分为等腰直角三角形是轴对称图形综上 a 的取值范围是a =3−√3或a =94或3≤a <4. 【点睛】本题考查的是利用二次函数的图象与性质 列二次函数关系式 矩形的性质 轴对称图形的性质 一元二次方程的解法 清晰的分类讨论 熟练的运用数形结合的方法解题是关键.4.(1)切点坐标为(3,3)(2)y 3=12x 2+x +12(3)k 1⋅k 2是定值【分析】(1)联立直线和双曲线解析式得到关于x 的一元二次方程 由相切的定义得出x 的值 解之可得;(2)联立{y =2x y =x 2+1可得切点为(1,2) 从而得出y 3=ax 2+bx +c 经过点(−3,2) (1,2) 利用待定系数法得出y 3=ax 2+2ax +2−3a 联立{y =ax 2+2ax +2−3a y =2x 得:ax 2+(2a −2)x +2−3a =0 利用Δ=0得出a =12 b =1 c =12 即可得解;(3)由l 1与l 2的交点P 的纵坐标为4 可令P(t ,4) 则直线l 1:y =k 1x −k 1t +4 直线 l 2:y 2=k 2x −k 2t +4 联立{y =k 1x −k 1t +4y =−x 2+2x +2得:x 2+(k 1−2)x −k 1t +2=0 由直线l 1:y =k 1x +m 1(k 1≠0)是抛物线y =−x 2+2x +2的切线 可得Δ=k 12+(4t −4)k 1−4=0 同理可得:k 22+(4t −4)k 2−4=0 从而得出k 1,k 2为x 2+(4t −4)x −4=0的两根 最后由一元二次方程根与系数的关系即可得出答案.【详解】(1)解:联立{y =−x +6y =9x得:x 2−6x +9=0 解得:x =3∴切点坐标为(3,3);(2)解:∵直线y 1=2x 与二次函数y 2=x 2+1相切∴联立{y =2x y =x 2+1得:x 2−2x +1=0 解得:x =1∴切点为(1,2)∵ y 1=2x 与y 2=x 2+1,y 3=ax 2+bx +c 都相切于同一点∴ y 3=ax 2+bx +c 经过点(−3,2)∴{a +b +c =29a −3b +c =2解得:{b =2a c =2−3a∴y 3=ax 2+2ax +2−3a联立{y =ax 2+2ax +2−3a y =2x得:ax 2+(2a −2)x +2−3a =0 ∴Δ=(2a −2)2−4×a ×(2−3a )=4a 2−8a +4−8a +12a 2=16a 2−16a +4=(4a −2)2=0 解得:a =12 ∴b =2a =1∴ y 3的解析式为:y 3=12x 2+x +12; (3)解:k 1⋅k 2是定值理由如下:∵ l 1与l 2的交点P 的纵坐标为4∴令P(t ,4)∴直线l 1:y =k 1x +m 1=k 1t +m 1=4 直线 l 2:y 2=k 2x +m 2=k 2t +m 2=4∴m 1=4−k 1t∴直线l 1:y =k 1x −k 1t +4 直线 l 2:y 2=k 2x −k 2t +4联立{y =k 1x −k 1t +4y =−x 2+2x +2得:x 2+(k 1−2)x −k 1t +2=0 ∵直线l 1:y =k 1x +m 1(k 1≠0)是抛物线y =−x 2+2x +2的切线∴Δ=(k 1−2)2−4×1×(2−k 1t )=k 12−4k 1+4−8+4k 1t =k 12+(4t −4)k 1−4=0同理可得:k 22+(4t −4)k 2−4=0∴ k 1,k 2为x 2+(4t −4)x −4=0的两根∴k 1⋅k 2=−4.【点睛】本题是二次函数综合题 考查了新定义 二次函数的性质 一元二次方程的根与系数的关系等知识 解题的关键是理解题意 学会构建方程组解决问题 属于中考压轴题.5.(1)y =13x −2(2)P (4,−4)(3)0或5−√2655【分析】(1)令抛物线y =0 x =0 求出点B C 的坐标 设直线BC 的解析式为y =kx +b (k ≠0) 代入点B C 的坐标 即可求解;(2)由题意得△PBC 是等腰三角形 即点P 在过点B C 的BC 中点且垂直于直线BC 的直线上 求出点B C的中点坐标 设点P (a,512a 2−136a −2) 利用勾股定理即可求出a 的值 求出符合点点P 特征的点即可;(3)过点P 作PF ⊥x 轴 垂足为点F 根据(2)的结论结合已知分别证明△PFO,△PBC,△OPM 是等腰直角三角形 利用等腰直角三角形的性质求出点M 的坐标 进而得到N 点的坐标 求出直线OP 的解析式 设点Q (b,−b ) 利用两点间距离公式结合MQ =2NQ 求出点Q 的坐标 再求出直线MQ 的解析式 联立抛物线即可求解.【详解】(1)解:在抛物线y =512x 2−136x −2中 令x =0 则y=−2∴C (0,−2)令y =0 则512x 2−136x −2=0 即5x 2−26x −24=0解得:x 1=6,x 2=−45 ∵点B 在x 轴的正半轴∴B (6,0)设直线BC 的解析式为y =kx +b (k ≠0) 代入点B C 的坐标 得{−2=b 0=6k +b解得:{b =−2k =13∴直线BC 的解析式为y =13x −2;(2)解:设点P (a,512a 2−136a −2) ∵ PB =PC ∴PB 2=PC 2 即(a −6)2+(512a 2−136a −2)2=a 2+(512a 2−136a −2+2)2整理得:a 2+2a −24=0解得:a =4或a =−6(舍去 不符合题意)当a =4时∴P (4,−4);(3)解:如图 过点P 作PF ⊥x 轴 垂足为点F由(2)知点P(4,−4)∴PF=OF=4∴△PFO是等腰直角三角形∴∠POF=∠POM=45°∵PC=√(4−0)2+[(−4)−(−2)]2=2√5,BC=√(0−6)2+(−2−0)2=2√10又PC2+PB2=BC2∴△PBC是等腰直角三角形∴∠BPC=90°,∠CBP=∠PCB=45°∵∠OMP=∠CBP∴∠OMP=45°∴△OPM是等腰直角三角形∴OP=MP∴OP=√42+(−4)2=4√2=MP∴OM=√OP2+MP2=8∵点M在y轴的负半轴上∴点M(0,−8)∵N为OM的中点∴N(0,−4)设直线OP的解析式为y=k′x(k′≠0)将P(4,−4)代入得−4=4k′解得k′=−1∴直线OP的解析式为y=−x设Q(b,−b)∵MQ=2NQ∴√b2+(−b+8)2=2√b2+(−b+4)2∴b=0或b=83当b=0时此时点Q与点O重合∴MQ与抛物线交点在y轴上∴点R的横坐标为0当b=83时设直线MQ的解析式为y=sx+t将点Q(83,−83)M(0,−8)代入得{−8=t−83=83s+t解得{s=2t=−8∵直线MQ的解析式为y=2x−8联立直线MQ与抛物线y=512x2−136x−2得{y=2x−8y=512x2−136x−2解得{x=5+√2655y=2√2655+2(舍去不符合题意)或{x=5−√2655y=2−2√2655∵此时MQ交抛物线于点R的横坐标为5−√2655综上点R的横坐标为0或5−√2655.【点睛】本题考查二次函数的图象及性质一次函数解析式熟练掌握二次函数的图象及性质等腰直角三角形的判定及性质直角三角形的性质用待定系数法求函数的解析式是解题的关键.6.(1)y=14x2−12x−2(2)点E的横坐标为1−√5(3)BQ=92【分析】(1)将B(4,0)C(−2,0)A(0,−2)代入抛物线解析式得到{16a+4b+c=04a−2b+c=0c=−2求出a、b、c的值即可得出答案;(2)先利用待定系数法求出直线AB 的解析式为:y =12x −2 设点E 的坐标为(e ,14e 2−12e −2)(−2<e <0) 从而求出直线EF 的解析式为:y =12x +14e 2−e −2 进而得出F (2e +4−12e 2,0) 表示出EF =√[e −(2e +4−12e 2)]2+(14e 2−12e −2)2=√5(14e 2−12e −2)2=√5 解方程即可得出答案;(3)设点M 的坐标为(4,m)(m <0) 待定系数法求出直线CM 的解析式为:y =m6x +m3 联立{y =m6x +m 3y =14x 2−12x −2得出N (12+2m 3,m2+9m9) 再利用待定系数法求出直线BN 的解析式为:y =m+96x −2m+183 从而得出P (1,−m−92) 利用待定系数法求出直线PQ 的解析式为y =m 6x −4m+276从而得出Q (4,−92) 即可得解. 【详解】(1)解:∵ 抛物线y =ax 2+bx +c (a ≠0)与x 轴交于B(4,0) C(−2,0)两点 与y 轴交于点A(0,−2)∴{16a +4b +c =04a −2b +c =0c =−2解得:{a =14b =−12c =−2∴抛物线的解析式为y =14x 2−12x −2; (2)解:设直线AB 的解析式为:y =k 1x +b 1 将A(0,−2) B(4,0)代入直线得:{0=4k 1+b 1b 1=−2解得:{k 1=12b 1=−2∴直线AB 的解析式为:y =12x −2 ∵点E 是直线CA 下方的抛物线上一点∴设点E 的坐标为(e ,14e 2−12e −2)(−2<e <0)∵EF ∥AB∴设直线EF 的解析式为:y =12x +b 2∴14e 2−12e −2=12e +b 2∴b 2=14e 2−e −2∴直线EF 的解析式为:y =12x +14e 2−e −2令y =0 则12x +14e 2−e −2=0 解得:x =2e +4−12e 2∴F (2e +4−12e 2,0)∴EF =√[e −(2e +4−12e 2)]2+(14e 2−12e −2)2=√(e −2e −4+12e 2)2+(14e 2−12e −2)2=√(12e 2−e −4)2+(14e 2−12e −2)2=√[2(14e 2−12e −2)]2+(14e 2−12e −2)2=√4(14e 2−12e −2)2+(14e 2−12e −2)2=√5(14e 2−12e −2)2∵EF =√5∴√5(14e 2−12e −2)2=√5∴(14e 2−12e −2)2=1 ∴14e 2−12e −2=1或14e 2−12e −2=−1 ∵点E 是直线CA 下方的抛物线上一点∴14e 2−12e −2<0 ∴14e 2−12e −2=−1 ∴e 2−2e −4=0解得:e =1+√5或e =1−√5∵−2<e <0 ∴e =1−√5∴点E 的横坐标为1−√5; (3)解:∵点M 在点B 的正下方 ∴设点M 的坐标为(4,m)(m <0) 设直线CM 的解析式为y =k 2x +b 2将C(−2,0) M(4,m)代入解析式得:{0=−2k 2+b 2m =4k 2+b 2解得:{k 2=m6b 2=m 3∴直线CM 的解析式为:y =m 6x +m3联立{y =m 6x +m 3y =14x 2−12x −2整理得:3x 2−(6+2m )x −(24+4m )=0∴(x +2)(3x −12−2m )=0解得:x 1=−2 ∴点N 的横坐标为12+2m 3纵坐标为y =12+2m36⋅m +m 3=12+2m 18⋅m +m 3=18m+2m 218=m 2+9m9∴N (12+2m 3,m 2+9m 9)设直线BN 的解析式为:y =k 3x +b 3 将B(4,0) N (12+2m 3,m 2+9m9)代入解析式得:{0=4k 3+b 3m 2+9m9=12+2m 3k 3+b 3解得:{k 3=m+96b 3=−2m+183∴直线BN 的解析式为:y =m+96x −2m+183∵抛物线的解析式为y =14x 2−12x −2 ∴对称轴为直线x =−−122×14=1∴点P 的横坐标为1 纵坐标为y =m+96×1−2m+183=−3m−276=−m−92∴P (1,−m −92) ∵PQ ∥CM∴设直线PQ 的解析式为y =m 6x +b 4∴−m −92=m6×1+b 4 解得:b 4=−4m−276∴直线PQ 的解析式为y =m6x −4m+276∵作PQ ∥CM 交射线BM 于点Q ∴点Q 的横坐标为4 纵坐标为y =m 6×4−4m+276=−92∴Q (4,−92)∴BQ =0−(−92)=92.【点睛】本题考查了二次函数综合题 待定系数法求二次函数解析式 一次函数解析式 二次函数综合—线段问题 勾股定理求两点之间的距离等知识点 熟练掌握以上知识点并灵活运用 采用数形结合的思想是解此题的关键. 7.(1)y =x 2+2x −3 (2)M (−32,−154)(3)P 点坐标为(−4,5)或(2,5)或(−2,−3)或(0,−3) E(−1,6)或(−1,4)或(−1,−6)或(−1,0)【分析】(1)先求出A,C 的坐标 进而利用待定系数法求出二次函数解析式即可;(2)过点M 作MF 垂直于x 轴交AC 于点F 设M (x,x 2+2x −3) F(x,−x −3) 则MF =(−x −3)−(x 2+2x −3)=−x 2−3x 由S △AMC =12MF ×|x C −x A |即可求解;(3)抛物线对称轴为直线x=−1.∠PDE =∠BOC OB =1 OC =3.设P (x,x 2+2x −3) 则D (−1,x 2+2x −3) 分两种情况当PD =OC DE =OB 时 △PDE ≌△COB 此时|−1−x |=3 当PD =OB DE =OC 时 △EDP ≌△COB 此时|−1−x |=1 求解即可. 【详解】(1)解:把x =0代入y =−x −3得y=−3; 把y =0代入y =−x −3得x =−3. ∴A(−3,0) C(0,−3).∵抛物线y =ax 2+bx +c 经过A,C,B 三点∴{9a −3b +c =0a +b +c =0c =−3解得{a =1b =2c =−3.∴抛物线的解析式为y =x 2+2x −3;(2)过点M 作MF 垂直于x 轴交AC 于点F 设M (x,x 2+2x −3) 则F(x,−x −3) 则MF =(−x −3)−(x 2+2x −3)=−x 2−3xS △AMC =12MF ×|x C −x A |= 12(−x 2−3x )×3=−32(x +32)2+278∴当x =−32时 S △AMC 最大 此时y =x 2+2x −3=−154. ∴当M 坐标为(−32,−154)时 S △AMC 取得最大值.(3)∵y =x 2+2x −3=(x +1)2−4 ∵抛物线对称轴为直线x=−1. ∵过点P 作l 的垂线 垂足为D ∵∠PDE =∠BOC =90° ∵C(0,−3),A (−3,0) ∵B (1,0)∵OB =1 OC =3.设P (x,x 2+2x −3) 则D (−1,x 2+2x −3) 当PD =OC DE =OB 时 此时|−1−x |=3 解得x =−4或x =2. ∵P 点坐标为(−4,5)或(2,5)∵DE =OB =1∴E(−1,6)或(−1,4). 当PD =OB DE =OC 时 此时|−1−x |=1 解得x =−2或x =0. ∵P 点坐标为(−2,−3)或(0,−3)∵DE =3∴E(−1,−6)或(−1,0).综上:P 点坐标为(−4,5)或(2,5)或(−2,−3)或(0,−3) E(−1,6)或(−1,4)或(−1,−6)或(−1,0).【点睛】本题考查了二次函数求解析式 二次函数的性质 三角形全等的性质 最值问题等 熟练掌握各知识点 能准确作出辅助线 并结合图形列出相应关系式是解题的关键. 8.(1)y =−x 2+2x +3 (2)P (1,6)(3)存在点N 满足要求 点N 坐标为(1,−4+2√6)或(1,−4−2√6)【分析】本题考查了待定系数法求二次函数表达式 二次函数的图像与性质及二次函数与一次函数综合 (1)用待定系数法求二次函数表达式;(2)根据抛物线特征得出当A,C,P 三点共线时 |PA −PC |最大 求出直线AC 的解析式为y =3x +3 即可求出结论;(3)设直线MC 与x 轴交于点E 过点N 作NQ ⊥MC 于Q 先求出直线MC 的解析式为y =x +3 证出MQ =NQ =√22MN 设点N (1,n ) 根据NQ 2=AN 2列方程并解方程即可解决.【详解】(1)解:∵抛物线y =−x 2+bx +c 经过A (−1,0),C (0,3)两点∴{−1−b +c =0c =3解得:{b =2c =3∴该抛物线的解析式为y =−x 2+2x +3;(2)解:由抛物线的对称性得 点B 关于抛物线对称轴的对称点是点A∴PA =PB∴|PB −PC |=|PA −PC |∴当A,C,P 三点共线时 |PA −PC |最大如图 连接AC 并延长AC 交抛物线的对称轴于点P设直线AC 的解析式为y =kx +d 把A (−1,0),C (0,3)代入得:{−k +d =0d =3解得:{k =3d =3∴直线AC 的解析式为y =3x +3 ∵抛物线的对称轴为直线x =−2−2=1当x =1时 ∴点P (1,6);(3)存在N 满足条件 理由如下:∵抛物线y =−x 2+2x +3与x 轴交于A 、B 两点 ∴点A (−1,0)∵y =−x 2+2x +3=−(x −1)2+4∴顶点M 为(1,4) ∵点M 为(1,4) 点C (0,3) ∴直线MC 的解析式为:y =x +3如图 设直线MC 与x 轴交于点E 过点N 作NQ ⊥MC 于Q∴点E (−3,0)∴DE =4=MD ∴∠NMQ =45°∵NQ⊥MC∴∠NMQ=∠MNQ=45°∴MQ=NQ∴MQ=NQ=√22MN设点N(1,n)∵点N到直线MC的距离等于点N到点A的距离∴NQ=AN∴NQ2=AN2∴(√22MN)2=AN2即(√22|4−n|)2=4+n2∴n2+8n−8=0∴n=−4±2√6∴存在点N满足要求点N坐标为(1,−4+2√6)或(1,−4−2√6).9.(1)y=−13x2+x+6(2)d=−2t(3)P(−4,−103)【分析】(1)先令x=0求出点C坐标再根据已知可得点B的坐标运用待定系数法即可求出抛物线解析式;(2)由(1)可得点B的坐标设P(t,−13t2+t+6)运用待定系数法求得直线PB的解析式为y=−13(t+3)x+2(t+3)进而求出D(0,2t+6)即可求得答案;(3)找点F关于原点的对称点F′连接CF′过点F′作F′K⊥GE于K根据已知先证△COF≌△BOD得OF= OD再证∠F′CK=2∠PBA进而证得△CF′K≌△EBG得F′K=BG再证△F′FK≌△BFG可得F′F=BF OB=3OF进而求出点D的坐标运用待定系数法求出直线BD的解析式再求出直线BD与抛物线的交点P的坐标.【详解】(1)解:∵抛物线y=ax2+x+6交y轴于点C∴C(0,6)∴OC=6∵OB=OC∴B(6,0)∵ B (6,0)在抛物线y =ax 2+x +6上∴ 0=36a +6+6∴ a =−13∴ y =−13x 2+x +6.(2)∵点P 是第三象限抛物线上一点∴ P (t,−13t 2+t +6)设直线PB 的解析式为y =kx +b (k ≠0)∴ {6k +b =0kt +b =−13t 2+t +6∴ {k =−13(t +3)b =2(t +3)∴直线PB 的解析式为y =−13(t +3)x +2(t +3).令x =0 得y =2(t +3)=2t +6∴ D (0,2t +6)∴ CD =6−(2t +6)=−2t∵线段 CD 长为 d∴ d =−2t ;(3)解:找点F 关于原点的对称点F ′ 连接CF ′ 过点F ′作F ′K ⊥GE 于K∵ CG ⊥BP OB ⊥OC∴ ∠COF =∠BOD =90°∵ OC =OB∴ △COF ≌△BOD∴ CF =BD∵点F 关于原点的对称点F ′∴∠FCO=∠F′CO OF=OF′∴∠F′CK=2∠PBA∵∠BEG=2∠PBA∴∠F′CK=∠BEG∵F′K⊥CG∴△CF′K≌△EBG∴F′K=BG∵F′K⊥CG∴∠FKF′=∠FGB=90°∵∠F′FK=∠BFG∴△F′FK≌△BFG∴F′F=BF∴OB=3OF∴OD=OF=13OB=2∴D(0,−2)设直线BD的解析式是y=mx+n∴{−2=0×m+n0=8m+n∴{m=1 3n=−2∴直线BD的解析式是y=13x−2∵点P在直线BD上也在抛物线y=−13x2+x+6上∴{y=13x−2y=−13x2+x+6∴{x=−4y=−103∴P(−4,−103);【点睛】本题考查了二次函数的综合题熟练掌握二次函数图像上点的坐标特征二次函数的性质中心对称的性质全等三角形的判定和性质等知识添加正确的辅助线是解题的关键.10.(1)y=−14x2+x+3(2)1(3)5√174【分析】(1)先确定点A的坐标为(2,4)再结合等腰直角三角形的性质可得C(6,0)然后运用待定系数法即可解答;(2)先用待定系数法可得AC的函数解析式为y=−x+6设E(t,−14t2+t+3)N(t,−t+6)则EN=−14t2+2t−3然后化成顶点式求最值即可;(3)先确定点M(5,74)过点E作AD的对称点E′(0,3)连接E′M交AD于点P此时PE+PM最短时M(5,74)最后运用勾股定理即可解答.【详解】(1)解:∵AD为等腰直角△ABC底边BC上的高y=a(x−2)2+4的顶点为点A ∵A的坐标为(2,4)∵AD=4∵AD为等腰直角△ABC底边BC上的高∵CD=AD=4∵C(6,0).把C(6,0)代入y=a(x−2)2+4解得:a=−14∵抛物线的解析式为y=−14(x−2)2+4即y=−14x2+x+3.(2)解:设直线AC的函数解析式为y=kx+b ∵A(2,4),C(6,0)∵AC的函数解析式为y=−x+6.设E(t,−14t2+t+3)EN=−14t2+t+3−(−t+6)=−14t2+2t−3=−14(t−4)2+1∵当t=4时EN最大为1∵E(4,3).(3)解:∵M(5,b)在抛物线y =−14(x −2)2+4上∵M (5,74).∵AD 是此抛物线的对称轴∵过点E 作AD 的对称点E ′(0,3) 连接E ′M 交AD 于点P 此时PE +PM 最短 M (5,74);∵PE +PM 最短=E ′M =√(0−5)2+(3−74)2=5√174. 【点睛】本题主要考查了二次函数与几何的综合 求函数解析 求函数最值等知识点 灵活运用相关知识成为解题的关键.11.(1)x =1; (2)(3,0) (−1,0);(3)点P 的坐标为(3−√2,−√2)或(3+√2,√2).【分析】(1)本题根据抛物线y =ax 2+bx +c(a ≠0)的对称轴公式为x =−b2a 即可解题.(2)本题根据抛物线公式可整理为y =a (x 2−2x −3)=a (x −3)(x +1) 即可解题.(3)本题由(2)得到点B 的坐标 利用OB =OC 求得点C 的坐标 推出a 值 得到抛物线解析式 设直线BC 的解析式为y =kx −3 利用待定系数法求出直线BC 的解析式 设点P (m,m −3) 则M (m,m 2−2m −3) 根据过点P 作x 轴的垂线交抛物线于M 点 分以下两种情况讨论 当P 在M 的上方时 当P 在M 的下方时 根据这两种情况分析得到PM = CP 并对应的建立等式求解 即可解题.【详解】(1)解:∵抛物线解析式为y =ax 2−2ax −3a (a >0)∴抛物线的对称轴为x =−−2a2a =1;(2)解:∵抛物线解析式为y =ax 2−2ax −3a (a >0)整理可得y =a (x 2−2x −3)=a (x −3)(x +1)∴不论a 取何值 函数图象必过(3,0) (−1,0);(3)解:由(2)可知 点B 的坐标为(3,0)∴OB =3∵ OB =OC∴OC =3∴点C 的坐标为(0,−3) 且−3a =−3 即a =1∴抛物线解析式为y=x2−2x−3设直线BC的解析式为y=kx−3将(3,0)代入解析式有3k−3=0解得k=1∴直线BC的解析式为y=x−3设点P(m,m−3)则M(m,m2−2m−3)当P在M的上方时则PM=−m2+3m∵△PCM沿CM对折如果点P的对应点N恰好落在y轴上∴∠PCM=∠NCM∵PM∥y轴∴∠NCM=∠PMC∴∠PCM=∠PMC∴PC=PM∴√2m=−m2+3m整理得:m2+(√2−3)m=0解得:m1=0(不合题意舍去)则点P的坐标为(3−√2,−√2);当P在M的下方时则PM=m2−3m同理可得:√2m=m2−3m整理得:m2−(√2+3)m=0解得:m1=0(不合题意舍去)则点P的坐标为(3+√2,√2);综上所述点P的坐标为(3−√2,−√2)或(3+√2,√2).【点睛】本题考查了二次函数与一次函数综合折叠的性质二次函数的图象和性质待定系数法求函数解析式 勾股定理表示两点间的距离 等腰三角形性质 熟练掌握折叠的性质 结合分类讨论的数学思想 即可解题.12.(1)a =−16(2)(−2,−2)或(−2,4)或(−2,2√2)或(−2,−2√2)(3)−13−√2412或−13+√2412.【分析】本题主要考查了二次函数的应用 等腰三角形 全等三角形等几何图形等知识点 熟练运用数形结合利用几何关系寻找等量关系是解题的关键.(1)将点C 坐标代入抛物线解析式即可解答;(2)分三种情况:当ME =MC 、CE =CM 、EM =CE 时 然后利用等腰三角形的性质即可解答;(3)先判断出△PQE≌△P ′Q ′E (AAS )得出PQ =P ′Q ′、EQ =EQ ′ 进而得出P ′Q ′=n ,EQ ′=QE =m +2 确定出点P ′(n −2,2+m) 将点P ′的坐标代入直线AD 的解析式中和点P 代入抛物线解析式中 联立方程组求解即可.【详解】(1)解:∵抛物线y =a (x +6)(x −2)过点(0,2)∵2=a (0+6)(0−2) a =−16.(2)解:∵a =−16 ∵抛物线的解析式为y =−16(x +6)(x −2)=−16(x +2)2+83 ∵抛物线的对称轴为直线x =−2;∵E(−2,0)∵C(0,2)∵OC =OE =2∵CE =√2OC =2√2∵△CME 是等腰三角形∵①当ME =MC 时∵∠ECM =∠CED =45°∵∠CME =90°∵M(−2,2);②当CE =CM 时。
二次函数压轴题(带详细答案)

二次函数压轴题强化训练(带详细答案)一.解答题(共30小题)1.(2016•深圳模拟)已知:如图,在平面直角坐标系xOy中,直线与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.(1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式;(2)若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;(3)设抛物线的对称轴与直线BC的交点为T,Q为线段BT上一点,直接写出|QA﹣QO|的取值范围.2.(2015•枣庄)如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(,)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC为直角三角形时点P的坐标.3.(2007•玉溪)如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在y轴上.(1)求m的值及这个二次函数的关系式;(2)P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于点E,设线段PE的长为h,点P的横坐标为x,求h与x之间的函数关系式,并写出自变量x的取值范围;(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.4.(2013•凉山州)如图,抛物线y=ax2﹣2ax+c(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.(1)求抛物线的解析式;(2)抛物线的对称轴l在边OA(不包括O、A两点)上平行移动,分别交x轴于点E,交CD于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值,并直接判断△PCM 的形状;若不存在,请说明理由.5.(2009•綦江县)如图,已知抛物线y=a(x﹣1)2+3(a≠0)经过点A(﹣2,0),抛物线的顶点为D,过O作射线OM∥AD.过顶点平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连接BC.(1)求该抛物线的解析式;(2)若动点P从点O出发,以每秒1个长度单位的速度沿射线OM运动,设点P运动的时间为t(s).问当t为何值时,四边形DAOP分别为平行四边形,直角梯形,等腰梯形?(3)若OC=OB,动点P和动点Q分别从点O和点B同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC和BO运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t(s),连接PQ,当t为何值时,四边形BCPQ的面积最小?并求出最小值及此时PQ的长.6.(2013•天水)如图1,已知抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)两点.(1)求抛物线的解析式;(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m 的值及点D的坐标;(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出所有满足△POD∽△NOB的点P坐标(点P、O、D分别与点N、O、B对应).7.(2014•河南)如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(5,0)两点,直线y=﹣x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.(1)求抛物线的解析式;(2)若PE=5EF,求m的值;(3)若点E′是点E关于直线PC的对称点,是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.8.(2013•德州)如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.(1)求抛物线的解析式;(2)若点P是第二象限内抛物线上的动点,其横坐标为t,①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.9.(2013•河南)如图,抛物线y=﹣x2+bx+c与直线y=x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3,).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.(1)求抛物线的解析式;(2)若点P的横坐标为m,当m为何值时,以O、C、P、F为顶点的四边形是平行四边形?请说明理由.(3)若存在点P,使∠PCF=45°,请直接写出相应的点P的坐标.10.(2013•重庆)如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).(1)求直线BC与抛物线的解析式;(2)若点M是抛物线在x轴下方图象上的一动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标.11.(2013•徐州)如图,二次函数y=x2+bx﹣的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.(1)请直接写出点D的坐标:;(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED 与正方形ABCD重叠部分的面积;若不存在,请说明理由.12.(2013•泰安)如图,抛物线y=x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A,B,且B点的坐标为(2,0).(1)求该抛物线的解析式.(2)若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值.(3)若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.13.(2014•广元)如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=,A(3,0),D(﹣1,0),E(0,3).(1)求抛物线的解析式及顶点B的坐标;(2)求证:CB是△ABE外接圆的切线;(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围.14.(2014•成都)如图,已知抛物线y=(x+2)(x﹣4)(k为常数,且k>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣x+b与抛物线的另一交点为D.(1)若点D的横坐标为﹣5,求抛物线的函数表达式;(2)若在第一象限内的抛物线上有点P,使得以A,B,P为顶点的三角形与△ABC相似,求k的值;(3)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A 出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?15.(2014•南宁)在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A,B两点,点A在点B的左侧.(1)如图1,当k=1时,直接写出A,B两点的坐标;(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D 的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k 的值;若不存在,请说明理由.16.(2013•防城港)如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).(1)求点B,C的坐标;(2)判断△CDB的形状并说明理由;(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.17.(2014•重庆)如图,抛物线y=﹣x2﹣2x+3 的图象与x轴交于A、B两点(点A在点B 的左边),与y轴交于点C,点D为抛物线的顶点.(1)求A、B、C的坐标;(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PMNQ的周长最大时,求△AEM的面积;(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=2DQ,求点F的坐标.18.(2014•钦州)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.(1)求该抛物线的解析式;(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH 相似?若存在,求出此时m的值;若不存在,请说明理由.19.(2014•昆明)如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A (﹣2,0)、B(4,0)两点,与y轴交于点C.(1)求抛物线的解析式;(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标.20.(2013•恩施州)如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB 沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).(1)求直线BD和抛物线的解析式.(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.21.(2013•毕节地区)如图,抛物线y=ax2+b与x轴交于点A、B,且A点的坐标为(1,0),与y轴交于点C(0,1).(1)求抛物线的解析式,并求出点B坐标;(2)过点B作BD∥CA交抛物线于点D,连接BC、CA、AD,求四边形ABCD的周长;(结果保留根号)(3)在x轴上方的抛物线上是否存在点P,过点P作PE垂直于x轴,垂足为点E,使以B、P、E为顶点的三角形与△CBD相似?若存在请求出P点的坐标;若不存在,请说明理由.22.(2014•德州)如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.(1)求抛物线的解析式;(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.23.(2014•吉林)如图①,直线l:y=mx+n(m<0,n>0)与x,y轴分别相交于A,B两点,将△AOB绕点O逆时针旋转90°得到△COD,过点A,B,D的抛物线P叫做l的关联抛物线,而l叫做P的关联直线.(1)若l:y=﹣2x+2,则P表示的函数解析式为;若P:y=﹣x2﹣3x+4,则l 表示的函数解析式为.(2)求P的对称轴(用含m,n的代数式表示);(3)如图②,若l:y=﹣2x+4,P的对称轴与CD相交于点E,点F在l上,点Q在P的对称轴上.当以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标;(4)如图③,若l:y=mx﹣4m,G为AB中点,H为CD中点,连接GH,M为GH中点,连接OM.若OM=,直接写出l,P表示的函数解析式.24.(2013•武汉)如图,点P是直线l:y=﹣2x﹣2上的点,过点P的另一条直线m交抛物线y=x2于A、B两点.(1)若直线m的解析式为y=﹣x+,求A,B两点的坐标;(2)①若点P的坐标为(﹣2,t).当PA=AB时,请直接写出点A的坐标;②试证明:对于直线l上任意给定的一点P,在抛物线上能找到点A,使得PA=AB成立.(3)设直线l交y轴于点C,若△AOB的外心在边AB上,且∠BPC=∠OCP,求点P的坐标.25.(2013•遂宁)如图,抛物线y=x2+bx+c与x轴交于点A(2,0),交y轴于点B(0,).直线y=kx过点A与y轴交于点C,与抛物线的另一个交点是D.(1)求抛物线y=x2+bx+c与直线y=kx的解析式;(2)设点P是直线AD上方的抛物线上一动点(不与点A、D重合),过点P作y轴的平行线,交直线AD于点M,作DE⊥y轴于点E.探究:是否存在这样的点P,使四边形PMEC 是平行四边形?若存在请求出点P的坐标;若不存在,请说明理由;(3)在(2)的条件下,作PN⊥AD于点N,设△PMN的周长为l,点P的横坐标为x,求l与x的函数关系式,并求出l的最大值.26.(2013•舟山)如图,在平面直角坐标系xOy中,抛物线y=(x﹣m)2﹣m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.(1)当m=2时,求点B的坐标;(2)求DE的长?(3)①设点D的坐标为(x,y),求y关于x的函数关系式?②过点D作AB的平行线,与第(3)①题确定的函数图象的另一个交点为P,当m为何值时,以A,B,D,P为顶点的四边形是平行四边形?27.(2006•重庆)已知:m、n是方程x2﹣6x+5=0的两个实数根,且m<n,抛物线y=﹣x2+bx+c 的图象经过点A(m,0)、B(0,n).(1)求这个抛物线的解析式;(2)设(1)中抛物线与x轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;(3)P是线段OC上的一点,过点P作PH⊥x轴,与抛物线交于H点,若直线BC把△PCH 分成面积之比为2:3的两部分,请求出P点的坐标.28.(2015•阜新)如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).(1)求抛物线的函数表达式;(2)若点P在抛物线上,且S△AOP=4S BOC,求点P的坐标;(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.29.(2014•白银)如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2﹣3向右平移一个单位后得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.(1)求点M、A、B坐标;(2)连接AB、AM、BM,求∠ABM的正切值;(3)点P是顶点为M的抛物线上一点,且位于对称轴的右侧,设PO与x正半轴的夹角为α,当α=∠ABM时,求P点坐标.30.(2014•宿迁)如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过点A,B,C三点的圆与y轴的另一个交点为D.(1)如图1,已知点A,B,C的坐标分别为(﹣2,0),(8,0),(0,﹣4);①求此抛物线的表达式与点D的坐标;②若点M为抛物线上的一动点,且位于第四象限,求△BDM面积的最大值;(2)如图2,若a=1,求证:无论b,c取何值,点D均为定点,求出该定点坐标.二次函数压轴题强化答案一.解答题(共30小题)1.(2016•深圳模拟)已知:如图,在平面直角坐标系xOy中,直线与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.(1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式;(2)若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;(3)设抛物线的对称轴与直线BC的交点为T,Q为线段BT上一点,直接写出|QA﹣QO|的取值范围.【考点】二次函数综合题.【专题】压轴题;开放型.【分析】(1)点A的坐标是纵坐标为0,得横坐标为8,所以点A的坐标为(8,0);点B的坐标是横坐标为0,解得纵坐标为6,所以点B的坐标为(0,6);由题意得:BC是∠ABO的角平分线,所以OC=CH,BH=OB=6∵AB=10,∴AH=4,设OC=x,则AC=8﹣x由勾股定理得:x=3∴点C的坐标为(3,0)将此三点代入二次函数一般式,列的方程组即可求得;(2)求得直线BC的解析式,根据平行四边形的性质,对角相等,对边平行且相等,借助于三角函数即可求得;(3)如图,由对称性可知QO=QH,|QA﹣QO|=|QA﹣QH|.当点Q与点B重合时,Q、H、A三点共线,|QA﹣QO|取得最大值4(即为AH的长);设线段OA的垂直平分线与直线BC的交点为K,当点Q与点K重合时,|QA﹣QO|取得最小值0.【解答】解:(1)点C的坐标为(3,0).(1分)∵点A、B的坐标分别为A(8,0),B(0,6),∴可设过A、B、C三点的抛物线的解析式为y=a(x﹣3)(x﹣8).将x=0,y=6代入抛物线的解析式,得.(2分)∴过A、B、C三点的抛物线的解析式为.(3分)(2)可得抛物线的对称轴为直线,顶点D的坐标为,设抛物线的对称轴与x轴的交点为G.直线BC的解析式为y=﹣2x+6.4分)设点P的坐标为(x,﹣2x+6).解法一:如图,作OP∥AD交直线BC于点P,连接AP,作PM⊥x轴于点M.∵OP∥AD,∴∠POM=∠GAD,tan∠POM=tan∠GAD.∴,即.解得.经检验是原方程的解.此时点P的坐标为.(5分)但此时,OM<GA.∵,∴OP<AD,即四边形的对边OP与AD平行但不相等,∴直线BC上不存在符合条件的点P(6分)解法二:如图,取OA的中点E,作点D关于点E的对称点P,作PN⊥x轴于点N.则∠PEO=∠DEA,PE=DE.可得△PEN≌△DEG.由,可得E点的坐标为(4,0).NE=EG=,ON=OE﹣NE=,NP=DG=.∴点P的坐标为.(5分)∵x=时,,∴点P不在直线BC上.∴直线BC上不存在符合条件的点P.(6分)(3)|QA﹣QO|的取值范围是.(8分)(如点K处),此时OK=AK,则|QA﹣QO|=0,当Q在OA的垂直平分线上与直线BC的交点时,当Q在AH的延长线与直线BC交点时,此时|QA﹣QO|最大,直线AH的解析式为:y=﹣x+6,直线BC的解析式为:y=﹣2x+6,联立可得:交点为(0,6),∴OQ=6,AQ=10,∴|QA﹣QO|=4,∴|QA﹣QO|的取值范围是:0≤|QA﹣QO|≤4.【点评】此题考查了二次函数与一次函数以及平行四边形的综合知识,解题的关键是认真识图,注意数形结合思想的应用.2.(2015•枣庄)如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(,)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC为直角三角形时点P的坐标.【考点】二次函数综合题.【专题】几何综合题;压轴题.【分析】(1)已知B(4,m)在直线y=x+2上,可求得m的值,抛物线图象上的A、B两点坐标,可将其代入抛物线的解析式中,通过联立方程组即可求得待定系数的值.(2)要弄清PC的长,实际是直线AB与抛物线函数值的差.可设出P点横坐标,根据直线AB和抛物线的解析式表示出P、C的纵坐标,进而得到关于PC与P点横坐标的函数关系式,根据函数的性质即可求出PC的最大值.(3)当△PAC为直角三角形时,根据直角顶点的不同,有三种情形,需要分类讨论,分别求解.【解答】解:(1)∵B(4,m)在直线y=x+2上,∴m=4+2=6,∴B(4,6),∵A(,)、B(4,6)在抛物线y=ax2+bx+6上,∴,解得,∴抛物线的解析式为y=2x2﹣8x+6.(2)设动点P的坐标为(n,n+2),则C点的坐标为(n,2n2﹣8n+6),∴PC=(n+2)﹣(2n2﹣8n+6),=﹣2n2+9n﹣4,=﹣2(n﹣)2+,∵PC>0,∴当n=时,线段PC最大且为.(3)∵△PAC为直角三角形,i)若点P为直角顶点,则∠APC=90°.由题意易知,PC∥y轴,∠APC=45°,因此这种情形不存在;ii)若点A为直角顶点,则∠PAC=90°.如答图3﹣1,过点A(,)作AN⊥x轴于点N,则ON=,AN=.过点A作AM⊥直线AB,交x轴于点M,则由题意易知,△AMN为等腰直角三角形,∴MN=AN=,∴OM=ON+MN=+=3,∴M(3,0).设直线AM的解析式为:y=kx+b,则:,解得,∴直线AM的解析式为:y=﹣x+3 ①又抛物线的解析式为:y=2x2﹣8x+6 ②联立①②式,解得:x=3或x=(与点A重合,舍去)∴C(3,0),即点C、M点重合.当x=3时,y=x+2=5,∴P1(3,5);iii)若点C为直角顶点,则∠ACP=90°.∵y=2x2﹣8x+6=2(x﹣2)2﹣2,∴抛物线的对称轴为直线x=2.如答图3﹣2,作点A(,)关于对称轴x=2的对称点C,则点C在抛物线上,且C(,).当x=时,y=x+2=.∴P2(,).∵点P1(3,5)、P2(,)均在线段AB上,∴综上所述,△PAC为直角三角形时,点P的坐标为(3,5)或(,).【点评】此题主要考查了二次函数解析式的确定、二次函数最值的应用以及直角三角形的判定、函数图象交点坐标的求法等知识.3.(2007•玉溪)如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在y轴上.(1)求m的值及这个二次函数的关系式;(2)P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于点E,设线段PE的长为h,点P的横坐标为x,求h与x之间的函数关系式,并写出自变量x的取值范围;(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.【考点】二次函数综合题.【专题】压轴题.【分析】(1)因为直线y=x+m过点A,将A点坐标直接代入解析式即可求得m的值;设出二次函数的顶点式,将(3,4)代入即可;(2)由于P和E的横坐标相同,将P点横坐标代入直线和抛物线解析式,可得其纵坐标表达式,h即为二者之差;根据P、E在二者之间,所以可知x的取值范围是0<x<3;(3)先假设存在点P,根据四边形DCEP是平行四形的条件进行推理,若能求出P点坐标,则证明存在点P,否则P点不存在.【解答】解:(1)∵点A(3,4)在直线y=x+m上,∴4=3+m.∴m=1.设所求二次函数的关系式为y=a(x﹣1)2.∵点A(3,4)在二次函数y=a(x﹣1)2的图象上,∴4=a(3﹣1)2,∴a=1.∴所求二次函数的关系式为y=(x﹣1)2.即y=x2﹣2x+1.(2)设P、E两点的纵坐标分别为y P和y E.∴PE=h=y P﹣y E=(x+1)﹣(x2﹣2x+1)=﹣x2+3x.即h=﹣x2+3x(0<x<3).(3)存在.解法1:要使四边形DCEP是平行四边形,必需有PE=DC.∵点D在直线y=x+1上,∴点D的坐标为(1,2),∴﹣x2+3x=2.即x2﹣3x+2=0.解之,得x1=2,x2=1(不合题意,舍去)∴当P点的坐标为(2,3)时,四边形DCEP是平行四边形.解法2:要使四边形DCEP是平行四边形,必需有BP∥CE.设直线CE的函数关系式为y=x+b.∵直线CE经过点C(1,0),∴0=1+b,∴b=﹣1.∴直线CE的函数关系式为y=x﹣1.∴得x2﹣3x+2=0.解之,得x1=2,x2=1(不合题意,舍去)∴当P点的坐标为(2,3)时,四边形DCEP是平行四边形.【点评】此题考查了用待定系数法求函数解析式以及函数图象上点的坐标特征,结合图形有利于解答;(3)是一道存在性问题,有一定的开放性,需要先假设点P存在,然后进行验证计算.4.(2013•凉山州)如图,抛物线y=ax2﹣2ax+c(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.(1)求抛物线的解析式;(2)抛物线的对称轴l在边OA(不包括O、A两点)上平行移动,分别交x轴于点E,交CD于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值,并直接判断△PCM 的形状;若不存在,请说明理由.【考点】二次函数综合题.【专题】压轴题.【分析】(1)将A(3,0),C(0,4)代入y=ax2﹣2ax+c,运用待定系数法即可求出抛物线的解析式;(2)先根据A、C的坐标,用待定系数法求出直线AC的解析式,进而根据抛物线和直线AC的解析式分别表示出点P、点M的坐标,即可得到PM的长;(3)由于∠PFC和∠AEM都是直角,F和E对应,则若以P、C、F为顶点的三角形和△AEM 相似时,分两种情况进行讨论:①△PFC∽△AEM,②△CFP∽△AEM;可分别用含m的代数式表示出AE、EM、CF、PF的长,根据相似三角形对应边的比相等列出比例式,求出m的值,再根据相似三角形的性质,直角三角形、等腰三角形的判定判断出△PCM的形状.【解答】解:(1)∵抛物线y=ax2﹣2ax+c(a≠0)经过点A(3,0),点C(0,4),∴,解得,∴抛物线的解析式为y=﹣x2+x+4;(2)设直线AC的解析式为y=kx+b,∵A(3,0),点C(0,4),∴,解得,∴直线AC的解析式为y=﹣x+4.∵点M的横坐标为m,点M在AC上,∴M点的坐标为(m,﹣m+4),∵点P的横坐标为m,点P在抛物线y=﹣x2+x+4上,∴点P的坐标为(m,﹣m2+m+4),∴PM=PE﹣ME=(﹣m2+m+4)﹣(﹣m+4)=﹣m2+4m,即PM=﹣m2+4m(0<m<3);(3)在(2)的条件下,连结PC,在CD上方的抛物线部分存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似.理由如下:由题意,可得AE=3﹣m,EM=﹣m+4,CF=m,若以P、C、F为顶点的三角形和△AEM 相似,情况:①P点在F上,PF=﹣m2+m+4﹣4=﹣m2+m.若△PFC∽△AEM,则PF:AE=FC:EM,即(﹣m2+m):(3﹣m)=m:(﹣m+4),∵m≠0且m≠3,∴m=.∵△PFC∽△AEM,∴∠PCF=∠AME,∵∠AME=∠CMF,∴∠PCF=∠CMF.在直角△CMF中,∵∠CMF+∠MCF=90°,∴∠PCF+∠MCF=90°,即∠PCM=90°,∴△PCM为直角三角形;②P点在F下,PF=4﹣(﹣m2+m+4)=m2﹣m若△PFC∽△AEM,则PF:AE=FC:EM,即(m2﹣m):(3﹣m)=m:(﹣m+4),∵m≠0且m≠3,∴m=(不合题意舍去).∵∠CFP=90°,∴∠CPM=∠CFP+FCM>90°,∴△CPM为钝角三角形;③若△CFP∽△AEM,则CF:AE=PF:EM,即m:(3﹣m)=(﹣m2+m):(﹣m+4),∵m≠0且m≠3,∴m=1.∵△CFP∽△AEM,∴∠CPF=∠AME,∵∠AME=∠CMF,∴∠CPF=∠CMF.∴CP=CM,∴△PCM为等腰三角形.综上所述,存在这样的点P使△PFC与△AEM相似.此时m的值为或1,△PCM为直角三角形或等腰三角形.【点评】此题是二次函数的综合题,其中涉及到运用待定系数法求二次函数、一次函数的解析式,矩形的性质,相似三角形的判定和性质,直角三角形、等腰三角形的判定,难度适中.要注意的是当相似三角形的对应边和对应角不明确时,要分类讨论,以免漏解.5.(2009•綦江县)如图,已知抛物线y=a(x﹣1)2+3(a≠0)经过点A(﹣2,0),抛物线的顶点为D,过O作射线OM∥AD.过顶点平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连接BC.(1)求该抛物线的解析式;(2)若动点P从点O出发,以每秒1个长度单位的速度沿射线OM运动,设点P运动的时间为t(s).问当t为何值时,四边形DAOP分别为平行四边形,直角梯形,等腰梯形?(3)若OC=OB,动点P和动点Q分别从点O和点B同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC和BO运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t(s),连接PQ,当t为何值时,四边形BCPQ的面积最小?并求出最小值及此时PQ的长.【考点】二次函数综合题.【专题】压轴题.【分析】(1)将A的坐标代入抛物线y=a(x﹣1)2+3(a≠0)可得a的值,即可得到抛物线的解析式;(2)易得D的坐标,过D作DN⊥OB于N;进而可得DN、AN、AD的长,根据平行四边形,直角梯形,等腰梯形的性质,用t将其中的关系表示出来,并求解可得答案;(3)根据(2)的结论,易得△OCB是等边三角形,可得BQ、PE关于t的关系式,将四边形的面积用t表示出来,进而分析可得最小值及此时t的值,进而可求得PQ的长.【解答】解:(1)∵抛物线y=a(x﹣1)2+3(a≠0)经过点A(﹣2,0),∴0=9a+3,∴a=﹣(1分)∴二次函数的解析式为:y=﹣x2+x+;(3分)(2)①∵D为抛物线的顶点,∴D(1,3),过D作DN⊥OB于N,则DN=3,AN=3,∴AD==6,∴∠DAO=60°.(4分)∵OM∥AD,①当AD=OP时,四边形DAOP是平行四边形,∴OP=6,∴t=6(s).(5分)②当DP⊥OM时,四边形DAOP是直角梯形,过O作OH⊥AD于H,AO=2,则AH=1(如果没求出∠DAO=60°可由Rt△OHA∽Rt△DNA (求AH=1)∴OP=DH=5,t=5(s)(6分)③当PD=OA时,四边形DAOP是等腰梯形,易证:△AOH≌△DPP′,∴AH=CP,∴OP=AD﹣2AH=6﹣2=4,∴t=4(s)综上所述:当t=6、5、4时,对应四边形分别是平行四边形、直角梯形、等腰梯形;(7分)(3)由(2)及已知,∠COB=60°,OC=OB,△OCB是等边三角形则OB=OC=AD=6,OP=t,BQ=2t,∴OQ=6﹣2t(0<t<3)过P作PE⊥OQ于E,则PE=t(8分)∴S BCPQ=×6×3×(6﹣2t)×t=(t﹣)2+(9分)当t=时,四边形BCPQ的面积最小值为.(10分)∴此时OQ=3,OP=,OE=;。
二次函数60道压轴题型专项训练(12大题型)(原卷版)—2024-2025学年九年级数学上册(浙教)

二次函数60道压轴题型专项训练(12大题型)【题型目录】压轴题型一 二次函数的图象与性质压轴题压轴题型二 二次函数与各项系数符号压轴题压轴题型三 根据二次函数的对称性求值压轴题型四 二次函数的平移压轴题压轴题型五 二次函数与坐标轴交点压轴题压轴题型六 二次函数的应用(销售、增长率等问题)压轴题型七 二次函数的应用(图形运动、拱桥、投球等问题)压轴题型八 二次函数中的存在性问题压轴题型九 二次函数与一次函数压轴题压轴题型十 二次函数的翻折问题压轴题型十一 二次函数最值问题压轴题型十二 二次函数的综合【压轴题型一 二次函数的图象与性质压轴题】1.(2024·浙江嘉兴·二模)已知直线3y x =--与抛物线2()4=--y x m 对称轴左侧部分的图象有且只有一个交点,则m 的取值范围是( )A .54m £B .54m £或74m =C .1m £D .1m £或54m =2.(2024·浙江宁波·二模)已知二次函数2y x bx c =++的图象与x 轴只有一个公共点,且当x a =和x a n =+时函数值都为m ,则m 与n 的等量关系为 .3.(2024·浙江杭州·一模)已知二次函数()()13y a x x =--的图像过点()4,m ,(),p n (1)当1m =时,求a 的值;(2)若>>0m n ,求p 的取值范围;(3)求证:0>am an +.4.(2024·浙江杭州·一模)已知二次函数2(2)3(0)y m x m =-->的图象与x 轴交于点(,0),(,0)A a B b .(1)当3a =-时,求b 的值.(2)当0a b <<时,求m 的取值范围.(3)若(1,),(1,)P a p Q b q ++两点也都在此函数图象上,求证:0p q +>.5.(2024·浙江杭州·一模)在平面直角坐标系中,点(1,)m 和(3,)n 都在二次函数2y ax bx =+(0,,¹a a b 是常数)的图象上.(1)若6==-m n ,求该二次函数的表达式和函数图象的对称轴.(2)若1a =-,m n <,求b 的取值范围.(3)已知点()()()1231,,2,,4,y y y -也都在该二次函数图象上,若0mn <且a<0,试比较123y y y ,,的大小,并说明理由.【压轴题型二 二次函数与各项系数符号压轴题】1.(23-24九年级上·浙江杭州·阶段练习)抛物线()20y ax bx c a =++¹的顶点为(12)D -,,与x 轴的一个交点A 在点(30)-,和(20)-,之间,其部分图象如图,则以下结论:①0abc <;②若方程20ax bx c m ++-=没有实数根,则2m >;③320b c +<;④图象上有两点()11,P x y 和()22,Q x y ,若12x x <且122x x +<-,则一定有12y y >;正确的是( )A .4个B .3个C .2个D .1个2.(20-21九年级上·浙江·期末)抛物线2y ax bx c =++(a ,b ,c 为常数,且0a ¹)经过点()1,0-和()0m ,;且12m <<,当1x <-时,y 随着x 的增大而减小.下列结论:①0abc >;②0a b +>③若点()13,A y -,点()23,B y 都在抛物线上,则12y y <;④()10a m b -+=;⑤若1c £-,则244b ac a -£.其中结论正确的是.3.(23-24九年级上·浙江杭州·期中)在二次函数223(0)y x tx t =-+>中.(1)若函数图象的顶点在x 轴上,求t 的值.(2)若点(,)t s 在抛物线上,令q t s =+,求证:134q £.(3)如果(2,)A m a -,()4,B b ,(,)C m a 都在这个二次函数图象上,且3a b <<,求m 的取值范围.4.(2024·云南昆明·二模)在平面直角坐标系中,抛物线()24430y mx mx m m =-+->与x 轴的交点为A ,B .(1)求抛物线的对称轴及顶点坐标;(2)若 1,m =当 3t x t +≤≤时,函数最小值为 2-,求t 的值;(3)横、纵坐标都是整数的点叫做整点.若抛物线在点 A ,B 之间的部分与线段 AB 所围成的区域内(包括边界)恰有10个整点,求m 的取值范围.5.(23-24九年级下·北京·阶段练习)已知抛物线()20y ax bx c a =++>,(1)若抛物线过点()()35m m -,,,,求抛物线的对称轴;(2)已知点()()()()0112042y x y y n -,,,,,,,在抛物线上,其中121x -<<-,若存在1x 使1y n >,试比较012y y y ,,的大小关系.【压轴题型三 根据二次函数的对称性求值】1.(2024·山东淄博·二模)二次函数2y ax bx c =++(a ,b ,c 是常数,0a ¹)的自变量x 与函数值y 的部分对应值如下表:x…2-1-012…2y ax bx c=++…tm2-2-n…且当12x =-时,与其对应的函数值0y >,有下列结论:①函数图象的顶点在第四象限内;②2-和3是关于x 的方程2ax bx c t ++=的两个根;③36m n +<-,其中正确的结论个数是( )A .0个B .1个C .2个D .3个2.(23-24九年级上·安徽芜湖·期中)已知二次函数2y ax bx c =++的图像过点(1,0)A -和(0,1)C .(1)若此抛物线的对称轴是直线12x =,点C 与点P 关于直线12x =对称,则点P 的坐标是 .(2)若此抛物线的顶点在第一象限,设t a b c =++,则t 的取值范围是 .3.(2024·云南曲靖·二模)已知抛物线²y ax bx c =++(a ,b ,c 为常数,0a ¹)(1)若20a b -=,4-+=a b c ,求此抛物线的顶点坐标;(2)在(1)的条件下,抛物线经过点()0,2,将抛物线²y ax bx c =++的图象0x <的部分向下平移h (h 为正整数)个单位长度,平移后的图象恰好与x 轴有2个交点,若点1(,)S m n y -与点2(,)Q m y 在平移后的抛物线上(点S ,Q 不重合),且点S 与点 Q 关于对称轴对称,求代数式22281244m mn n n h -+-+的值.4.(23-24九年级上·北京朝阳·期中)在平面直角坐标系xOy 中,点()1,m ,()4,n 在抛物线()20y ax bx c a =++>上.设抛物线的对称轴为直线x t =.(1)若30a b +=.比较,,m n c 的大小关系,并说明理由;(2)点()00),1(x m x ¹在抛物线上,若m c n <<,求t 及0x 的取值范围.5.(23-24九年级上·北京西城·期中)已知点()11,M x y ,()22,N x y 在抛物线()220y ax bx a =++>的图象上,设抛物线的对称轴为x t =.(1)若()2,1M -,()8,1N -,则t =_______;(2)当12x =-,223x <<时,都有122y y >>,求t 的取值范围.【压轴题型四 二次函数的平移压轴题】1.(2024·河北邯郸·二模)我们把横、纵坐标都是整数的点称为整点,如图,抛物线1C :224y x x =-++与()22:C y x m =-(m 是常数)围成的封闭区域(边界除外)内整点的个数不能是( )A .1个B .2个C .3个D .4个2.(2024·福建·模拟预测)定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形OABC 中,点()02A ,,点()20C ,,则互异二次函数()2y x m m =--与正方形OABC 有交点时m 的最大值和最小值的差为3.(2024·广东广州·二模)在平面直角坐标系中,将过点()2,1-的抛物线211:4C y x bx =-+(b 为常数)向右平移m 个单位(0m >),再向上平移n 个单位(0n ³)得到新的抛物线2C ,其顶点为E .(1)求点E 的坐标;(用含m ,n 的式子表示)(2)若抛物线2C 与坐标轴有且只有两个公共点,求满足条件的点E 的纵坐标;(3)当1n =时,抛物线2C 与x 轴交于A 、B 两点,与y 轴交于点D ,且当02x ££时,对抛物线1C 上的任意一点P ,在抛物线2C 上总存在一点Q ,使得点P ,Q 的纵坐标相等,探究下列问题:①求m 的取值范围;②若存在一点F ,满足DF AF BF ==,求点F 的纵坐标的取值范围.4.(2024·内蒙古赤峰·二模)小爱同学学习二次函数后,对函数()21y x =--进行了探究.在经历列表、描点、连线步骤后,得到如图的函数图象.请根据函数图象,回答下列问题:(1)观察探究:①至少写出该函数的两条性质;②直接写出方程()211x --=-的解;③直接写出方程()21x a --=有四个实数根时a 的取值范围.(2)延伸思考:将函数()21y x =--的图象经过怎样的平移可得到函数()21213y x =---+的图象?写出平移过程,并直接写出当123y <£时,自变量x 的取值范围.5.(2024·山东济南·二模)已知抛物线1C :26y x mx m =--+交x 轴于点A ,B ,交y 轴于点C .(1)如图1,当点A 坐标为()30-,时,求抛物线的解析式;(2)在(1)的条件下,点D 是第二象限内抛物线上的一点,连接BD ,若BD 将四边形ABCD 平分成面积相等的两部分,求点D 的横坐标;(3)如图2,EFH V 为等边三角形,点F ,H 在x 轴上,且点E 的坐标为()06,,将抛物线1C :26y x mx m =--+向右平移m 个单位,再向下平移6m 个单位后得到新的抛物线2C ,若2C 与等边EFH V 三边恰有四个交点,求m 的取值范围.【压轴题型五 二次函数与坐标轴交点压轴题】1.(2024·浙江杭州·一模)已知抛物线2y ax bx =+与2y bx ax =+的交点为A ,与x 轴的交点分别为B ,C ,点A ,B ,C 的横坐标分别为1x ,2x ,3x ,且1230x x x ¹.若0a b +<,20a b +>,则下列说法正确的是( )A .231x x x <<B .321x x x <<C .213x x x <<D .312x x x <<2.(2023·浙江绍兴·中考真题)在平面直角坐标系xOy 中,一个图形上的点都在一边平行于x 轴的矩形内部(包括边界),这些矩形中面积最小的矩形称为该图形的关联矩形.例如:如图,函数()2(2)03y x x =-££的图象(抛物线中的实线部分),它的关联矩形为矩形OABC .若二次函数()21034y x bx c x =++££图象的关联矩形恰好也是矩形OABC ,则b =.3.(23-24九年级上·浙江杭州·期中)已知抛物线()230y ax ax c a =++¹与y 轴交于点A .(1)当1a =,2c =,求该抛物线与x 轴交点坐标;(2)若1a =,点(),P m n 在二次函数抛物线23y ax ax c =++的图象上,且0n c ->,试求m 的值;(3)若点A 的坐标是()0,1,当2c c -<时,抛物线与x 轴只有一个公共点,求a 的取值范围.4.(22-23九年级上·浙江湖州·期末)在书本阅读材料中提到利用几何画板可以探索函数2y ax bx c =++的系数a ,b ,c 与图像的关系.如图1,在几何画板软件中绘制一个二次函数的图像的具体步骤如下:步骤一:在直角坐标系内的x 轴上取任意三个点A (A 不在原点),B ,C ,度量三个点的横坐标,分别记为a ,b ,c ;步骤二:绘制函数2y ax bx c =++;步骤三:任意移动A ,B ,C 三点的位置,发现抛物线的开口方向、大小、位置会发生变化.问题:如图2,将点A 移动到点()1,0-的位置.(1)若点B 移动到点()4,0-,请求出此时抛物线的对称轴;(2)在点B ,C 移动的过程中,且满足AB AC =,是否存在某一位置使得抛物线与x 轴只有一个交点,若存在,请求出此时点B 的坐标,若不存在,请说明理由.5.(22-23九年级上·浙江杭州·期末)已知二次函数2(0)y ax bx c a =++>的图象经过点(1,1)A -和(2,4)B .(1)求a ,b 满足的关系式;(2)当自变量x 的值满足12x -££时,y 随x 的增大而增大,求a 的取值范围;(3)若函数图象与x 轴无交点,求2a b +的取值范围.【压轴题型六 二次函数的应用(销售、增长率等问题)】1.(2024·天津红桥·三模)某服装店试销一种成本为每件60元的服装,规定试销期间每件服装的销售单价不低于成本,且获得的利润不得高于成本的45%.经试销发现,销售量y (件)与销售单价x (元)符合一次函数关系120y x =-+.有下列结论:①销售单价可以是90元;②该服装店销售这种服装可获得的最大利润为891元;③销售单价有两个不同的值满足该服装店销售这种服装获得的利润为500元,其中,正确结论的个数是( )A .0B .1C .2D .32.(2021·江苏连云港·中考真题)某快餐店销售A 、B 两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A 种快餐的利润,同时提高每份B 种快餐的利润.售卖时发现,在一定范围内,每份A 种快餐利润每降1元可多卖2份,每份B 种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是 元.3.(2024·四川德阳·三模)“端午节”吃粽子是中国传统习俗,在端午节来临前,某超市购进一种品牌粽子,每盒进价是40元,并规定每盒售价不得少于50元,日销售量不低于350盒,根据以往销售经验发现,当每盒定价为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒,设每盒售价为x 元,日销售量为P 盒.(1)当60x =时,P 等于______;(2)当每盒售价定为多少元时,日销售利润W (元)最大?最大利润是多少?(3)小强说:“当日销售利润最大时,日销售额不是最大.”小红说:“当日销售利润不低于8000元时,每盒售价x 的范围为6080x ££.”你认为他们的说法正确吗?4.(22-23八年级下·浙江杭州·期中)某商店进购一商品,第一天每件盈利(毛利润)10元,销售500件.(1)第二、三天该商品十分畅销.销售量持续走高.在售价不变的基础上,第二、三天的销售量达到605件,求第二、三天的日平均增长率;(2)经市场调查发现,在进货价不变的情况下,若每件涨价1元,日销量将减少20件.①现要保证每天总毛利润6000元,同时又要使顾客得到实惠,则每件应张价多少元?②现需按毛利润的10%交纳各种税费,人工费每日按销售量每件支出0.9元,水电房租费每日102元,若剩下的每天总纯利润要达到5100元,则每件涨价应为多少?5.(2023·湖北省直辖县级单位·一模)某销售卖场对一品牌商品的销售情况进行了调查,已知该商品的进价为每件3元,每周的销售量y (件)与售价x (元/件)(x 为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:x (元/件)456y (件)1000095009000(1)求y 关于x 的函数关系式(不求自变量的取值范围);(2)在销售过程中要求销售单价不低于成本价,且不高于15元/件.若某一周该商品的销售量不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?(3)抗疫期间,该商场这种商品的售价不大于15元/件时,每销售一件商品便向某慈善机构捐赠整数m 元()15m ££,捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请直接写出整数m 的值.【压轴题型七 二次函数的应用(图形运动、拱桥、投球等问题)】1.(22-23九年级上·浙江台州·期末)以初速度v (单位:m/s )从地面竖直向上抛出小球,从抛出到落地的过程中,小球的高度h (单位:m )与小球的运动时间t (单位:s )之间的关系是24.9h vt t =-.现将某弹性小球从地面竖直向上抛出,初速度为9.8m/s ,经过a 秒后,将第二个相同材质的小球从地面以初速度4.9m/s 竖直上抛.若两球能在空中相遇,则a 的取值范围为( )A .34a <<B .12a <<C .324a <<D 2a <<2.(23-24九年级上·浙江湖州·期末)如图,乒乓球桌桌面是长 2.7m AB =,宽 1.5m AD =的矩形,E F ,分别是AB 和CD 的中点,在E ,F 处设置高0.15m HE =的拦网.一次运动员在AD 端发球,在P 点击打乒乓球后经过桌面O 点反弹后的运行路径近似二次项系数427a =-的抛物线的一部分.已知本次发球反弹点O 在到桌面底边AD 的距离为0.1m ,到桌面侧边AB 的距离为0.1m 处.若乒乓球沿着正前方飞行(垂直于BC ),此时球在越过拦网时正好比拦网上端GH 高0.1m ,则乒乓球落在对面的落点Q 到拦网EF 的距离为 m ;若乒乓球运行轨迹不变,飞行方向从O 点反弹后飞向对方桌面,落点Q 在距离BC 为0.2m 的Q 点处,此时QC 的长度为 m .3.(2023·浙江杭州·模拟预测)已知点(2,2)A -和点(4,)B n -在抛物线2(0)y ax a =¹上.(1)求a 的值及点B 的坐标;(2)点P 在y 轴上,且ABP V 是以AB 为直角边的三角形,求点P 的坐标;(3)将抛物线2(0)y ax a =¹向右并向下平移,记平移后点A 的对应点为A ¢,点B 的对应点为B ¢,若四边形ABB A ¢¢为正方形,求此时抛物线的表达式.4.(22-23九年级上·天津河西·期末)如图所示,在ABC V 中,90B Ð=°,5cm AB =,7cm BC =,点P 从点A 开始沿AB 边向点B 以1cm /s 的速度运动,点Q 从点B 开始沿BC 边向点C 以2cm /s 的速度运动.P 、Q 分别从A 、B 同时出发,当P 、Q 两点中有一点停止运动时,则另一点也停止运动.设运动的时间为s t .(0)t ≥(1)当t 为何值时,PQ 的长度等于5cm ;(2)求出V BPQ S 关于t 的函数解析式,计算P 、Q 出发几秒时,V BPQ S 有最大值,并求出这个最大面积?5.(23-24九年级上·浙江温州·期中)如图,抛物线2y x bx c =-++与x 轴交于点()3,0A -、()1,0B ,与y 轴交于点C .(1)求抛物线的表达式.(2)已知点D 为y 轴上一点,点D 关于直线AC 的对称点为1D .①当点1D 刚好落在第二象限的抛物线上时,求出点D 的坐标.②点P 在抛物线上(点P 不与点A 、点C 重合),连接PD ,1PD ,1DD ,是否存在点P ,使1PDD △为等腰直角三角形?若存在,请求出点P 的坐标;若不存在,请说明理由.【压轴题型八 二次函数中的存在性问题】1.(2024·浙江宁波·一模)新定义:若一个点的横纵坐标之和为6,则称这个点为“和谐点”.若二次函数22y x x c =-+(c 为常数)在13-<<的图象上存在两个“和谐点”,则c 的取值范围是( )A .2574c <<B .2544c <<C .11c -<<D .2504c <<2.(23-24九年级上·浙江温州·期中)图1是洞头深门大桥,其桥底呈抛物线,以O 为原点,OA 所在直线为x 轴建立平面直角坐标系(如图2所示),桥面CB ∥OA ,其抛物线解析式为()218020320y x =--+,抛物线上点A 离桥面距离22AB =米,若存在一点E 使得38CE CB =,则点E 到抛物线的距离ED = 米.3.(2024·浙江宁波·模拟预测)如图,一次函数y =的图象与坐标轴交于点A 、B ,抛物线2y x bx c =++的图象经过A 、B 两点.(1)求二次函数的表达式;(2)若点P 为抛物线上一动点,在直线AB 上方是否存在点P 使PAB V 的面积最大?若存在,请求出PAB V 面积的最大值及点P 的坐标,请说明理由.4.(23-24九年级上·黑龙江伊春·期末)如图,已知抛物线22y ax x c =-+与直线y kx b =+都经过(0,3)A -、(3,0)B 两点,该抛物线的顶点为.(1)求此抛物线和直线AB 的表达式;(2)设直线AB 与该抛物线的对称轴交于点E ,在射线EB 上是否存在一点M ,过M 作x 轴的垂线交抛物线于点N ,使点M ,N ,C ,E 是平行四边形的四个顶点?若存在,直接写出点M 的坐标;若不存在,说明理由;5.(22-23九年级上·浙江温州·期中)如图,直线212y x =-+与x 轴交于点C ,与y 轴交于点B ,抛物线23103y ax x c =++经过B C ,两点,与x 轴交于另一点A ,点E 是直线BC 上方抛物线上的一动点,过E 作EF y ∥轴交x 轴于点F ,交直线BC 于点M .(1)求抛物线的解析式;(2)求线段EM 的最大值;(3)在(2)的条件下,连接AM ,点Q 是抛物线对称轴上的动点,在抛物线上是否存在点P ,使得以P Q A M ,,,为顶点的四边形为平行四边形?如果存在,请直接写出P 点坐标;如果不存在,请说明理由.【压轴题型九 二次函数与一次函数压轴题】1.(2024·浙江杭州·一模)二次函数21y x bx c =++(b ,c 是常数)过()2,0-,()0m ,两个不重合的点,一次函数2y x d =+过()0m ,和二次函数的顶点,则m 的值为( )A .﹣1B .0C .1D .22.(23-24九年级上·浙江绍兴·期末)二次函数2(,,y ax bx c a b c =++为常数,且0)ab ¹经过()()11,0,,0x ,一次函数y a x c =+经过()2,0x ,一次函数y b x c =+经过()3,0x .已知1254,1x m x m -<<-<<+,31n x n <<+,其中,m n 为整数,则m n +的值为 .3.(2024·浙江舟山·三模)已知一次函数5y x =-的图象与x 轴,y 轴分别交于点A ,B ,将点A 向左平移4个单位,得到点A ¢,且点A ¢恰好在二次函数23y ax bx =+-(a 、b 是常数,0a ¹)图象的对称轴上.(1)用含a 的代数式表示b .(2)求证:二次函数与一次函数图象交于一个定点,并求出该点的坐标.(3)若二次函数图象与线段AB 恰有一个公共点,结合函数图象,求a 的取值范围.4.(23-24九年级上·浙江宁波·期末)如图,在平面直角坐标系xOy 中,一次函数121y x =+的图象与二次函数22y x ax b =++的图象相交于A ,B 两点,点A 坐标为()1m -,,点B 坐标为()25,.(1)求m 的值以及二次函数的解析式.(2)根据图象,直接写出当1y >2y 时x 的取值范围.(3)若将二次函数向上平移t 个单位长度后,得到的图象与x 轴没有交点,求t 的取值范围.5.(2023·浙江金华·三模)如图,一次函数()00b y x b a b a=-+>>,与坐标轴交于A ,B 两点,以A 为顶点的抛物线过点B ,过点B 作y 轴的垂线交该抛物线另一点于点D ,以AB ,AD 为边构造ABCD Y ,延长BC 交抛物线于点E .(1)若2a b ==,如图1.①求该抛物线的表达式.②求点E 的坐标.(2)如图2,请问BE AB 是否为定值,若是,请求出该定值;若不是,请说明理由.【压轴题型十 二次函数的翻折问题】1.(22-23九年级上·浙江湖州·期末)抛物线223y x x =-++与y 轴交于点C ,过点C 作直线l 垂直于y 轴,将抛物线在y 轴右侧的部分沿直线l 翻折,其余部分保持不变,组成图形G ,点()1,M m y ,()21,N m y +为图形G 上两点,若12y y >,则m 的取值范围是( )A .102m £<B 1m <<C m <<D 12m <<2.(2023江苏南通·模拟预测)如图,将二次函数2y x m =-(其中0m >)的图象在x 轴下方的部分沿x 轴翻折,图象的其余部分保持不变,形成新的图象记为1y ,另有一次函数2y x =+的图象记为2y ,若1y 与2y 恰有两个交点时,则m 的范围是 .3.(2024·浙江·模拟预测)如图,抛物线22(0)y x x m m =-++>与y 轴交于A 点,其顶点为D .直线122y x m =--分别与x 轴、y 轴交于B 、C 两点,与直线AD 相交于E 点.(1)求A 、D 的坐标(用m 的代数式表示);(2)将ACE V 沿着y 轴翻折,若点E 的对称点P 恰好落在抛物线上,求m 的值;(3)抛物线22(0)y x x m m =-++>上是否存在一点P ,使得以P 、A 、C 、E 为顶点的四边形是平行四边形?若存在,求此抛物线的解析式;若不存在,请说明理由.4.(23-24九年级上·浙江绍兴·期中)如图,在平面直角坐标系中,将二次函数223y x x =--在x 轴上方的图象沿x 轴翻折到x 轴下方,图象的其余部分不变,将这个组合的图象记为M .(1)若直线12y x n =+与图象M 恰好有3个交点.求n 的值.(2)若直线12y x n =+与图象M 恰好有2个交点.求n 的取值范围.5.(2023·浙江杭州·二模)已知二次函数2420y mx mx m m =-+-¹(),且与x 轴交于不同点M 、N .(1)若二次函数图象经过点30A (,),①求二次函数的表达式和顶点坐标;②将抛物线在05x ££之间的那部分函数图象沿直线5x =翻折,将抛物线翻折前后的这两部分合记为图象F ,若直线y kx n =+过点151C (,),且与图象F 恰有两个交点,求n 的取值范围;(2)若0m <,当4MN £时,求实数m 的取值范围.【压轴题型十一 二次函数最值问题】1.(2024·浙江温州·二模)已知二次函数222y x x -=+, 当0x t ££时,函数最大值为M ,最小值为N .若5M N =,则t 的值为 ( )A .0.5B .1.5C .3D .42.(2023·浙江杭州·模拟预测)已知二次函数()2211y ax b x =--+(a ,b 为常数且0a >),当21x -££-时,y 随x 的增大而增大,则ab 的最大值为 .3.(2024·浙江嘉兴·三模)已知二次函数 23y x bx =++的图象经过点()()()12,,,43A x n B x t C -,,.(1)求二次函数的函数表达式;(2)当 212x x -=时,①若 0nt £,求 t n -的取值范围;②设直线AB 的函数表达式为y kx m =+,求m 的最大值.4.(2024·浙江宁波·模拟预测)已知二次函数214y x bx c =-++的图象经过原点O 和点()8,0A t +,其中0t ³.(1)当0=t 时.①求y 关于x 的函数解析式;求出当x 为何值时,y 有最大值?最大值为多少?②当x a =和x b =时()a b ¹,函数值相等,求a 的值.(2)当0t >时,在08x ££范围内,y 有最大值18,求相应的t 和x 的值.5.(23-24九年级上·浙江湖州·期末)设二次函数2y ax bx c =++(a b c ,,均为常数,且0a ¹).已知函数值y 和自变量x 的部分对应取值如下表所示:x L3-2-1-01L y L n 5a -n a-4a L (1)若1a =.①求二次函数的表达式,并写出顶点坐标;②已知点()1,m y 与()23,m y -都在该二次函数图象上,且12y y ³,请求出1y 的最小值.(2)将该二次函数图象向右平移k (02k <<)个单位,若平移后的二次函数图象在20x -££的范围内有最小值为3116a -,求k 的值.【压轴题型十二 二次函数的综合】1.(22-23九年级上·浙江宁波·阶段练习)如图,抛物线218333y x x =+-与x 轴交于点A 和点B 两点,与y 轴交于点C ,D 点为抛物线上第三象限内一动点,当2180ACD ABC Ð+Ð=°时,点D 的坐标为( )A .(8,3)--B .(,)--1673C .(6,7)--D .(5,8)--2.(23-24九年级上·浙江金华·期末)定义:若x ,y 满足:24x y k =+,24y x k =+(k 为常数)且x y ¹,则称点(),M x y 为“好点”.(1)若()5,P m 是“好点”,则m .(2)在32x -<<的范围内,若二次函数23y x x c =-+的图象上至少存在一个“好点”,则c 的取值范围为 .3(2024·浙江温州·二模)在平面直角坐标系中,已知抛物线()2233y mx m x m =--+-(m 是常数,且0m ¹)经过点()2,4,且与y 轴交于点A ,其对称轴与x 轴交于点B .(1)求出二次函数的表达式.(2)垂直于y 轴的直线l 与抛物线交于点(),P a p 和(),Q b q ,与直线AB 交于点(),c n ,若a c b <<,直接写出a b c ++的取值范围.(3)当13x t =-,2x t =,33x t =+时,对应的函数值分别为1y ,2y ,3y .求证:123454y y y ++³.4.(23-24九年级下·浙江宁波·期中)如图,已知抛物线21:4C y x =,()01F ,,点()11,A x y ,()22,B x y 为抛物线上第一象限内的两点,且满足FA FB ^,以FA FB 、为边向右作矩形FAPB ,若P 点纵坐标为5.(1)求12y y +的值;(2)求12x x 的值;(3)求矩形FAPB 的面积.5.(21-22九年级上·浙江·周测)如图,在平面直角坐标系中,抛物线24y ax bx =++交y 轴于点A ,交x 轴于点()6,0B -和点()2,0C ,连接AB 、AQ 、BQ ,BQ 与y 轴交于点N .(1)求抛物线表达式;(2)点713Q æöç÷èø,,点M 在x 轴上,点E 在平面内,若BME AOM V V ≌,且四边形ANEM 是平行四边形.①求点E 的坐标;②设射线AM 与BN 相交于点P ,交BE 于点H ,将BPH V 绕点B 旋转一周,旋转后的三角形记为11BPH △,求11BP 的最小值.。
2023年九年级数学中考专题:二次函数综合压轴题(相似三角形问题)(含简单答案)
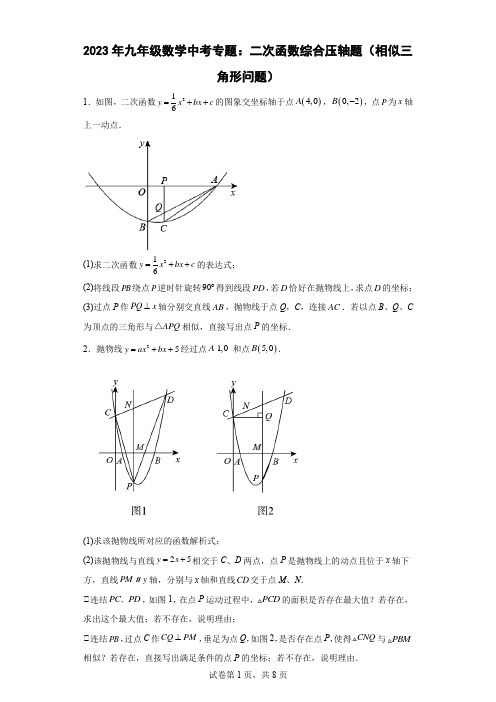
2023年九年级数学中考专题:二次函数综合压轴题(相似三角形问题)1.如图,二次函数216y x bx c =++的图象交坐标轴于点()4,0A ,()0,2B -,点P 为x 轴上一动点.(1)求二次函数216y x bx c =++的表达式; (2)将线段PB 绕点P 逆时针旋转90︒得到线段PD ,若D 恰好在抛物线上,求点D 的坐标; (3)过点P 作PQ x ⊥轴分别交直线AB ,抛物线于点Q ,C ,连接AC .若以点B 、Q 、C 为顶点的三角形与APQ △相似,直接写出点P 的坐标. 2.抛物线25y ax bx =++经过点1,0A 和点()5,0B .(1)求该抛物线所对应的函数解析式;(2)该抛物线与直线25y x =+相交于C 、D 两点,点P 是抛物线上的动点且位于x 轴下方,直线PM y ∥轴,分别与x 轴和直线CD 交于点M 、N .①连结PC PD 、,如图1,在点P 运动过程中,PCD 的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;①连结PB ,过点C 作CQ PM ⊥,垂足为点Q ,如图2,是否存在点P ,使得CNQ 与PBM 相似?若存在,直接写出满足条件的点P 的坐标;若不存在,说明理由.3.已知抛物线24y ax ax b =-+与x 轴交于A ,B 两点,(A 在B 的左侧),与y 轴交于C ,若OB OC =,且03C (,).(1)求抛物线的解析式;(2)设抛物线的顶点为D ,点P 在抛物线的对称轴上,且APD ACB ∠=∠,求点P 的坐标; (3)在抛物线上是否存在一点M ,过M 作MN x ⊥轴于N ,以A 、M 、N 为顶点的三角形与AOC ∆相似,若存在,求出所有符合条件的M 点坐标,若不存在,请说明理由. 4.如图.在平面直角坐标系中.抛物线212y x bx c =++与x 轴交于A 、B 两点,与y 轴交于点C .点A 的坐标为()1,0-,点C 的坐标为()0,2-.已知点(),0E m 是线段AB 上的动点(点E 不与点A ,B 重合).过点E 作PE x ⊥轴交抛物线于点P ,交BC 于点F .(1)求该抛物线的表达式;(2)若:1:2EF PF =,请求出m 的值;(3)是否存在这样的m ,使得BEP △与ABC 相似?若存在,求出此时m 的值;若不存在,请说明理由;(4)当点E 运动到抛物线对称轴上时,点M 是x 轴上一动点,点N 是抛物线上的动点,在运动过程中,是否存在以C 、B 、M 、N 为顶点的四边形是平行四边形?若不存在,请说明理由;若存在,请直接写出点M 的坐标.5.如图,二次函数212y x bx c =-++图像交x 轴于点A ,B (A 在B 的左侧),与y 轴交于点(0,3)C ,CD y ⊥轴,交抛物线于另一点D ,且5CD =,P 为抛物线上一点,PE y轴,与x 轴交于E ,与BC ,CD 分别交于点F ,G .(1)求二次函数解析式;(2)当P 在CD 上方时,是否存在点P ,使得以C ,P ,G 为顶点的三角形与FBE 相似,若存在,求出CPG △与FBE 的相似比,若不存在,说明理由.(3)点D 关于直线PC 的对称点为D ,当点D 落在抛物线的对称轴上时,此时点P 的坐标为________.6.如图,抛物线22y ax bx =++与x 轴交于点A ,B ,与y 轴交于点C ,已知A ,B 两点坐标分别是(1,0)A ,(4,0)B -,连接,AC BC .(1)求抛物线的表达式;(2)将ABC ∆沿BC 所在直线折叠,得到DBC ∆,点A 的对应点D 是否落在抛物线的对称轴上?若点D 在对称轴上,请求出点D 的坐标;若点D 不在对称轴上,请说明理由;(3)若点P 是抛物线位于第二象限图象上的一动点,连接AP 交BC 于点Q ,连接BP ,BPQ ∆的面积记为1S ,ABQ ∆的面积记为2S ,求12S S 的值最大时点P 的坐标. 7.已知,二次函数23y ax bx =+-的图象与x 轴交于A ,B 两点(点A 在点B 的左边),与y 轴交于C 点,点A 的坐标为()1,0-,且OB OC =.(1)求二次函数的解析式;(2)当04x ≤≤时,求二次函数的最大值和最小值分别为多少?(3)设点C '与点C 关于该抛物线的对称轴对称.在y 轴上是否存在点P ,使PCC '△与POB 相似,且PC 与PO 是对应边?若存在,求出点P 的坐标;若不存在,请说明理由.8.已知菱形OABC 的边长为5,且点(34)A ,,点E 是线段BC 的中点,过点A ,E 的抛物线2y ax bx c =++与边AB 交于点D ,(1)求点E 的坐标;(2)连接DE ,将BDE △沿着DE 翻折痕.①当B 点的对应点B '恰好落在线段AC 上时,求点D 的坐标;①连接OB ,BB ',若BB D '△与BOC 相似,请直接写出此时抛物线二次项系数=a ______. 9.如图,抛物线22(0)y ax x c a =-+≠与x 轴交于A 、()3,0B 两点,与y 轴交于点()0,3C -,抛物线的顶点为D .(1)求抛物线的解析式;(2)已知点M 是x 轴上的动点,过点M 作x 轴的垂线交抛物线于点G ,是否存在这样的点M ,使得以点A 、M 、G 为顶点的三角形与BCD △相似,若存在,请求出点M 的坐标;若不存在,请说明理由.(3)在直线BC 下方抛物线上一点P ,作PQ 垂直BC 于点Q ,连接CP ,当CPQ 中有一个角等于ACO ∠时,求点P 的坐标.10.如图,抛物线顶点D 在x 轴上,且经过(0,3)-和(4,3)-两点,抛物线与直线l 交于A 、B 两点.(1)直接写出抛物线解析式和D 点坐标;(2)如图1,若()03A ,-,且 94ABDS =,求直线l 解析式; (3)如图2,若90ADB ∠=︒,求证:直线l 经过定点,并求出定点坐标.11.如图1,已知抛物线2=23y x x --与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,连接BC ,点P 是线段BC 下方抛物线上一动点,过点P 作∥PE BC ,交x 轴于点E ,连接OP 交BC 于点F .(1)直接写出点A ,B ,C 的坐标以及抛物线的对称轴; (2)当点P 在线段BC 下方抛物线上运动时,求BFPE取到最小值时点P 的坐标; (3)当点P 在y 轴右边抛物线上运动时,过点P 作PE 的垂线交抛物线对称轴于点G ,是否存在点P ,使以P 、E 、G 为顶点的三角形与①AOC 相似?若存在,来出点P 的坐标;若不存在,请说明理由.12.如图,抛物线212ax ax b =-+y 经过()1,0A -,32,2C ⎛⎫⎪⎝⎭两点,与x 轴交于另一点B .(1)求此抛物线的解析式;(2)若抛物线的顶点为M ,点P 为线段OB 上一动点(不与点B 重合),点Q 在线段MB 上移动,且2PM MQ MB =⋅,设线段OP x =,2MQ y =,求2y 与x 的函数关系式,并直接写出自变量x 的取值范围;并直接写出PM APPQ BQ-的值;(3)在同一平面直角坐标系中,两条直线x m =,x n =分别与抛物线交于点E ,G ,与(2)中的函数图象交于点F ,.H 问四边形EFHG 能否为平行四边形?若能,求m ,n 之间的数量关系;若不能,请说明理由.13.已知抛物线213222y x x =-++交x 轴于A 、B 两点,A 在B 的左边,交y 轴于点C .(1)求抛物线顶点的坐标;(2)如图1,若10,2E ⎛⎫- ⎪⎝⎭,P 在抛物线上且在直线AE 上方,PQ AE ⊥于O ,求PQ 的最大值;(3)如图2,点(),3D a (32a <)在抛物线上,过A 作直线交抛物线于第四象限另一点F ,点M 在x 轴上,以M 、B 、D 为顶角的三角形与AFB △相似,求点M 的坐标. 14.如图,抛物线23y ax bx =+-与x 轴交于点()1,0A 、()3,0B ,与y 轴交于点C ,联结AC 、BC .(1)求该抛物线的表达式及顶点D 的坐标;(2)如果点P 在抛物线上,CB 平分ACP ∠,求点P 的坐标:(3)如果点Q 在抛物线的对称轴上,DBQ 与ABC 相似.求点Q 的坐标.15.如图,抛物线23y ax x c =-+与x 轴交于(4,0)A -,B 两点,与y 轴交于点(0,4)C ,点D 为x 轴上方抛物线上的动点,射线OD 交直线AC 于点E ,将射线OD 绕点O 逆时针旋转45︒得到射线OP ,OP 交直线AC 于点F ,连接DF .(1)求抛物线的解析式; (2)当点D 在第二象限且34DE EO =时,求点D 的坐标; (3)当ODF △为直角三角形时,请直接写出点D 的坐标.16.如图①,抛物线与x 轴交于A ,B 两点,与y 轴交于点C (0,3),顶点为D (4,-1),对称轴与直线BC 交于点E ,与x 轴交于点F .(1)求二次函数的解析式;(2)点M 在第一象限抛物线的对称轴上,若点C 在BM 的垂直平分线上,求点M 的坐标; (3)如图①,过点E 作对称轴的垂线在对称轴的右侧与抛物线交于点H ,x 轴上方的对称轴上是否存在一点P ,使以E ,H ,P 为顶点的三角形与EFB △相似,若存在,求出P点坐标;若不存在,请说明理由.17.如图,在平面直角坐标系xOy 中,已知抛物线2y ax x c =++经过()2,0A -,()0,4B 两点,直线3x =与x 轴交于点C .(1)求a ,c 的值;(2)经过点O 的直线分别与线段AB ,直线3x =交于点D ,E ,且BDO △与OCE △的面积相等,求直线DE 的解析式;(3)P 是抛物线上位于第一象限的一个动点,在线段OC 和直线3x =上是否分别存在点F ,G ,使B ,F ,G ,P 为顶点的四边形是以BF 为一边的矩形?若存在,求出点F的坐标;若不存在,请说明理由.18.如图1,抛物线2y ax bx c =++与x 轴交于A ,B (点A 在点B 左侧),与y 轴负半轴交于C ,且满足2OA OB OC ===.(1)求抛物线的解析式;(2)如图2,D 为y 轴负半轴上一点,过D 作直线l 垂直于直线BC ,直线l 交抛物线于E ,F 两点(点E 在点F 右侧),若3DF DE =,求D 点坐标; (3)如图3,点M 为抛物线第二象限部分上一点,点M ,N 关于y 轴对称,连接MB ,P 为线段MB 上一点(不与M 、B 重合),过P 点作直线x t =(t 为常数)交x 轴于S ,交直线NB 于Q ,求QS PS -的值(用含t 的代数式表示).参考答案:1.(1)211266y x x =-- (2)()3,1D -或()8,10D -(3)点P 的坐标为()011-,或()10,.2.(1)265y x x =-+ (2)37,24⎛⎫- ⎪⎝⎭或()3,4-3.(1)243y x x =-+ (2)()2,2P 或()2,2-(3)存在符合条件的M 点,且坐标为:110(3M ,7)9-,()26,15M ,38(3M ,5)9-4.(1)213222y x x =--; (2)2m =;(3)存在,m 的值为0或3;(4)存在,M 点的坐标为()7,0或()1,0M 或⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭.5.(1)215322y x x =-++;(2)存在点P ,使得以C ,P ,G 为顶点的三角形与FBE 相似,CPG △与FBE 的相似比为2或25;(3)P 点横坐标55.6.(1)213222y x x =--+(2)点D 不在抛物线的对称轴上, (3)(2,3)-7.(1)2=23y x x --(2)函数的最大值为5,最小值为4- (3)存在,(0,9)P -或9(0,)5P -8.(1)13(2)2E , (2)①11(4)2D ,或23(4)6D ,;①47-9.(1)2=23y x x --(2)()0,0,()6,0,8,03⎛⎫ ⎪⎝⎭,10,03⎛⎫⎪⎝⎭(3)57,24⎛⎫- ⎪⎝⎭或者315,24⎛⎫- ⎪⎝⎭10.(1)()2324y x =--,()2,0D (2)334y x =-或1534y x =- (3)证明见解析,定点坐标为423⎛⎫- ⎪⎝⎭,11.(1)A (﹣1,0),B (3,0),C (0,﹣3),对称轴为直线x =1(2)当t =32时,BF PE 最小,最小值为47,此时P (32,﹣154).(3)存在,点P 的坐标为(2,﹣3)12.(1)211322y x x =-++(2)22150322y x x x =-+≤<(),PM AP PQ BQ -的值为0 (3)m 、n 之间的数量关系是2(1)m n m +=≠13.(1)(32,258)答案第3页,共3页(3)(2,0)或(-5,0)或13,07⎛⎫ ⎪⎝⎭或2205⎛⎫- ⎪⎝⎭,14.(1)2=+43y x x --,(21)D , (2)111639⎛⎫ ⎪⎝⎭,- (3)(2,−2)或12,3⎛⎫ ⎪⎝⎭15.(1)234y x x =--+(2)(1,6)D -或(3,4)D -(3)(3,4)-或(0,4)或2⎫⎪⎪⎝⎭或2⎫⎪⎪⎝⎭16.(1)21234y x x =-+(2)(4,3(3)存在P 1)或(4,1),使以E ,H ,P 为顶点的三角形与EFB △相似,17.(1)12a =-,4c = (2)23y x =- (3)存在这样的点F ,点F 的坐标为(2,0)或18.(1)2122y x =- (2)()0,1D -或190,8D ⎛⎫- ⎪⎝⎭, (3)24QS PS t -=-+。
2023年九年级数学中考专题:二次函数综合压轴题(特殊三角形问题)(含简略答案)

(1)求直线 的解析式;
(2)如图1,点 是直线 下方抛物线上的一点,连接 ,当 的面积最大时,连接 ,设 分别是线段 上的点,且 ,求四边形 的面积;
(3)如图2,点 是线段 的中点,将抛物线 沿 轴正方向平移得到新抛物线 , 经过点 , 的顶点为 ,在新抛物线 的对称轴上,是否存在点 ,使得 为等腰三角形?若存在,写出点 的坐标;若不存在,请说明理由.
(3)若点Q是上述抛物线上一点,且满足∠ABQ=2∠ABC,求满足条件的点Q的坐标.
11.如图,在平面直角坐标系中,已知抛物线 与直线 相交于 , 两点,其中 , .
(1)求该抛物线的函数表达式;
(2)点 为直线 下方抛物线上的任意一点,连接 , ,求 面积的最大值;
(3)在抛物线对称轴上找一点 ,使点 , , 三点构成的图形是直角三角形,求点 的坐标.
(2)当△PBC的面积最大时,求P点的坐标.
(3)在X轴上是否存在点N,使△NBC是等腰三角形,若存在直接写出所有符合条件的点N的坐标,若不存在说明理由
8.如图,直线 交 轴于点 ,交 轴于点B,抛物线 的顶点为 ,且经过点 .
(1)求该抛物线所对应的函数表达式;
(2)点 是抛物线上的点, 是以 为直角边的直角三角形,请直接写出点 的坐标.
13.如图,抛物线 经过 , 两点,且与 轴交于点 ,点 是抛物线的顶点,抛物线的对称轴 交 轴于点 ,连接 .
(1)求经过 三点的抛物线的函数表达式;
(2)点 在该抛物线的对称轴上,若 是以 为直角边的直角三角形,求点 的坐标;
(3)若 为 的中点,过点 作 轴于点 , 为抛物线上一动点, 为 轴上一动点, 为直线 上一动点,当以 、 、 、 为顶点的四边形是正方形时,请求出点 的坐标.
【中考数学压轴题专题突破04】二次函数中的几何变换问题

【中考压轴题专题突破】二次函数中的几何变换问题1.如图,已知二次函数y=ax2+bx+c(a,b,c是常数,且a>0)的图象经过点A(3,6),并与x轴相交于B、C两点(点B在点C右侧),且S△ABC=12,∠ACB=45°.(1)求二次函数的解析式;(2)若D是线段AC上一点,且以D、O、C为顶点的三角形与△ABC相似,求点D的坐标;(3)设直线y=1为直线l,将二次函数的图象在直线l下方的部分沿直线l翻折到直线l的上方,图象其余的部分不变,得到一个新图象,问是否存在与新图象恰有三个不同公共点且平行于AC的直线?若存在,请求出所有符合条件的直线的解析式;若不存在,请说明理由.2.已知二次函数y=ax2﹣2ax+c(a<0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,直线BC与它的对称轴交于点F,且CF:FB=1:3.(1)求A、B两点的坐标;(2)若△COB的内心I在对称轴上,求这个二次函数的关系式;(3)在(2)的条件下,Q(m,0)是x轴上一点,过点Q作y轴的平行线,与直线BC 交于点M,与抛物线交于点N,连接CN,将△CMN沿直线CN翻折,M的对应点为M′,是否存在点Q,使得M′恰好落在y轴上?若存在,求出点Q的坐标;若不存在,请说明理由.3.已知二次函数y=ax2+4x+c(a≠0)的图象是经过y轴上点C(0,2)的一条抛物线,顶点为A,对称轴是经过点H(2,0)且平行于y轴的一条直线.点P是对称轴上位于点A 下方的一点,连接CP并延长交抛物线于点B,连接CA、AB.(1)求这个二次函数的表达式及顶点A的坐标;(2)当∠ACB=45°时,求点P的坐标;(3)将△CAB沿CB翻折后得到△CDB,问点D能否恰好落在坐标轴上?若能,求点P 的坐标,若不能,说明理由.4.小明在课外学习时遇到这样一个问题:定义:如果二次函数y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2(a2≠0,a2,b2,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”.求函数y=﹣x2+3x﹣2的“旋转函数”.小明是这样思考的:由函数y=﹣x2+3x﹣2可知,a1=﹣1,b1=3,c1=﹣2,根据:a1+a2=0,b1=b2,c1+c2=0,求出a2、b2、c2,就能确定这函数的“旋转函数”.请参考小明的方法解决下面问题:(1)写出函数y=﹣x2+3x﹣2的“旋转函数”;(2)若函数y=﹣x2+mx﹣2与y=x2﹣2nx+n互为“旋转函数”,求(m+n)2018;(3)已知函数y=﹣的图象与x轴交于点A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1、B1、C1,试证明经过点A1、B1、C1的二次函数与函数y=﹣互为“旋转函数”.5.如图,在平面直角坐标系中,点A为二次函数y=﹣x2+4x﹣1图象的顶点,图象与y轴交于点C,过点A并与AC垂直的直线记为BD,点B、D分别为直线与y轴和x轴的交点,点E是二次函数图象上与点C关于对称轴对称的点,将一块三角板的直角顶点放在A点,绕点A旋转,三角板的两直角边分别与线段OD和线段OB相交于点P、Q两点.(1)点A的坐标为,点C的坐标为.(2)求直线BD的表达式.(3)在三角板旋转过程中,平面上是否存在点R,使得以D、E、P、R为顶点的四边形为菱形?若存在,直接写出P、Q、R的坐标;若不存在请说明理由.6.把二次函数y=x2+bx+c的图象沿y轴向下平移3个单位长度,再沿x轴向左平移1个单位长度后,得抛物线M,其顶点恰好落在y轴上点(0,﹣1).【解决问题】请直接写出抛物线M的函数表达式,并求b、c的值.【探索研究】小明在抛物线M上任意找了一个点P(m,n),以点P为圆心,OP长为半径画圆,他观察发现所画出的圆与过点(0,﹣2)且平行于x轴的直线相切,请判断他的发现是否正确?并说明理由.【理解应用】将抛物线M的图象绕原点O顺时针旋转90°得抛物线N,C为抛物线N上一动点,点Q 的坐标为(1,﹣1)、直接写出△OCQ周长的最小值.【中考压轴题专题突破】二次函数中的几何变换问题参考答案与试题解析1.解:(1)如图1中,作AE⊥x轴于E.∵A(3.6),S△ABC=12,∴×BC×6=12,∴BC=4,∵∠ACB=45°,∴CE=AE=6,∴BE=2,∴B(1,0),C(﹣3,0),∵二次函数经过A、B、C三点,∴解得,∴抛物线的解析式为y=x2+x﹣.(2)如图2中,由(1)可知B(1,0),C(﹣3,0),A(3,6)∴BC=4,AC=6,①当△DOC∽△ABC时,有=,即=,∴DC=,过D作DM⊥x轴于M,则△CDE是等腰直角三角形,∴CE=DE=,OE=,∴D(,).②当△ODC∽△ABC时,有=,即=,∴CD=,同理可得D(﹣2,1),综上所述点D坐标为(﹣2,1)或(,).(3)如图3中,∵直线AC的解析式为y=x+3,设所求直线的解析式为y=x+m,①设直线l:y=1与抛物线的左边的交点为P,则过P平行AC的直线与新图象有3个不同公共点,令y=1,则x2+x﹣=1,交点x=﹣1,∴P(﹣1﹣,1),代入y=x+m得m=2+,∴y=x+2+.②设l下方部分翻折后的抛物线为L,则与AC平行且和L相切的直线也符合条件,∵L的解析式为y=﹣(x+1)2+4,∴由消去y得x2+4x+2m﹣7=0,由题意△=0,∴16﹣4(2m﹣7)=0,∴m=,∴直线为y=x+,综上所述返回条件的直线的解析式为y=x+2+或y=x+.2.解:(1)由题意画出草图,如图1,在二次函数y=ax2﹣2ax+c中,对称轴为直线x=﹣=1,则OH=1,∵FH∥OC,∴==,∴HB=3,∴B(4,0),由抛物线的对称性知A(﹣2,0),∴A(﹣2,0),B(4,0);(2)如图2,△COB的内心I在对称轴上,∵对称轴为x=1,∴I(1,1),过点I作IM⊥OC于M,作IN⊥BC于N,则∠IMC=∠INC=90°,IM=IN,∵IC=IC,∴△CMI≌△CNI(HL),∴CN=CM=c﹣1,同理,△BIH≌△BIN(HL),∴BN=BH=3,∴BC=CN+BN=c+2,在Rt△OCB中,OC2+OB2=BC2,即c2+42=(c+2)2,解得,c=3,将点B(4,0)代入y=ax2﹣2ax+3中,得,16a﹣8a+3=0,解得,a=﹣,∴y=﹣x2+x+3;(3)如图3,点M'落在y轴上时,过点M作MH⊥y轴于H,则HM∥OB,∴△CHM∽△COB,∴==,由翻折可知,MC=M'C,∠M'CN=∠MCN,∵MN∥y轴,∴∠M'CN=∠MNC,∴∠MCN=∠MNC,∴MC=MN,将B(4,0)代入y=kx+3,得,k=﹣,∴yBC=﹣x+3,∵Q(m,0),∴M(m,﹣m+3),N(m,﹣m2+m+3),①当点N在点M上方时,CM=NM=﹣m2+m,HM=m,∵=,∴=,解得,m1=0(舍去),m2=,∴Q(,0);②当点N在点M下方时,CM=NM=﹣(﹣m2+m),HM=m,∵=,∴﹣=,解得,m1=0(舍去),m2=,∴Q(,0);综上所述,Q的坐标为(,0)或(,0).3.解:(1)由抛物线的对称性可知,抛物线的图象经过点(0,2)和点(4,2),则,解得,∴y=﹣x2+4x+2,∴当x=2时,y=6,∴点A的坐标是(2,6);(2)如图1,过点C作CE⊥AH,过点P作PF⊥AC于F,则CE=2,AE=4,AC=,∵∠AFP=∠AEC=90°,∠F AP=∠EAC,∴△AFP∽△AEC,∴,∵∠FCP=45°,∴CF=PF.设CF=PF=m,则AF=2m,∴m+2m=2,m=.∴,∴PH=,∴P(2,);(3)①当点D落在x轴的正半轴上时,如图2,CD=AC=,又∵OC=2,∴OD=4,由对称性可知AP=PD,设PH=m,则AP=PD=6﹣m,在Rt△DPH中,有PH2+HD2=PD2,即m2+22=(6﹣m)2,解得,∴;②当点D落在y轴的负半轴上时,如图3,CD=AC=,由对称性可知∠DCP=∠ACP,又∵AH∥OC,∴∠DCP=∠APC,∴∠APC=∠ACP,∴,∴,∴;③当点D落在x轴的负半轴上时,如图4,CD=AC=,又∵OC=2,∴OD=4,∴DH=AP=6,连接AD,∴直线CH是线段AD的中垂线,又点P在直线AH上,∴点P与点H重合,∴P3(2,0).综上所述,点P的坐标为:、、P3(2,0).4.解:(1)由y=﹣x2+3x﹣2函数可知a1=﹣1,b1=3,c1=﹣2.由a1+a2=0,b1=b2,c1+c2=0,得a2=1,b2=3,c2=2.函数y=﹣x2+3x﹣2的“旋转函数”为y=x2+3x+2;(2)由y=﹣x2+mx﹣2与y=x2﹣2nx+n互为“旋转函数“,得﹣2n=m,﹣2+n=0.解得n=2,m=﹣3.当m=2,n=﹣3时,(m+n)2018=(2﹣3)2018=(﹣1)2018=1;(3)∵当y=0时,﹣(x+1)(x﹣4)=0,解得x=﹣1,x=4,∴A(﹣1,0),B(4,0).当x=0时,y=﹣×(﹣4)=2,即C(0,2).由点A,B,C关于原点的对称点分别是A1,B1,C1,得A1(1,0),B1(﹣4,0),C1(0,﹣2).设过点A1,B1,C1的二次函数y=ax2+bx+c,将A1,B1,C1代入,得,解得,过点A1,B1,C1的二次函数y=x2+x﹣2.y=﹣(x+1)(x﹣4)=﹣x2+x+2函数可知a1=﹣,b1=,c1=2.由a1+a2=0,b1=b2,c1+c2=0,得a2=,b2=,c2=﹣2.y=﹣(x+1)(x﹣4)的“旋转函数”为y=x2+x﹣2.∴经过点A1,B1,C1的二次函数与函数y=﹣(x+1)(x﹣4)互为“旋转函数”.5.解:(1)y=﹣x2+4x﹣1图象的顶点x=﹣=2,y==3,∴点A的坐标为(2,3),当x=0时,y=﹣1,∴点C的坐标为(0,﹣1);(2)直线AC的解析式是y=2x﹣1,过点A并与AC垂直的直线记为BD,k,∴直线BD的表达式为:;(3)存在.菱形DERP时,P1(8﹣,0),Q1(0,),R1(4﹣,﹣1);菱形DREP时,P2(,0),Q2(0,),R2(,,﹣1).6.解:【解决问题】∵平移后的抛物线M,顶点为(0,﹣1),a=∴抛物线M的函数表达式为:y=x2﹣1根据平移规则,抛物线M向上平移3个单位长度,向右平移1个单位长度得原抛物线∴原抛物线函数表达式为:y=(x﹣1)2﹣1+3=x2﹣x+∴b=﹣,c=.【探索研究】小明的判断正确,理由如下:∵过点(0,﹣2)且平行于x轴的直线即直线y=﹣2∴过点P作P A⊥直线y=﹣2于点A,如图1∵点P(m,n)在抛物线M上∴n=m2﹣1∴OP2=m2+n2=m2+(m2﹣1)2=m2+m4﹣m2+1=m4+m2+1=(m2+1)2∵P A=n﹣(﹣2)=m2﹣1+2=m2+1∴OP=P A∴直线y=﹣2与⊙P相切【理解应用】如图2,抛物线M旋转后得到的抛物线N开口向右,顶点为(﹣1,0)作直线x=﹣2,过点C作CD⊥直线x=﹣2于点D,过点Q作QE⊥直线x=﹣2于点E 由【探索研究】可知,CD=CO∴CO+CQ=CD+CQ∴当D、C、Q在同一直线上时,CO+CQ=CD+CQ=EQ最小∵Q(1,﹣1)∴OQ=,EQ=1﹣(﹣2)=3∴C△OCQ=CO+CQ+OQ,最小值为EQ+OQ=3+故答案为:3+。
搞定二次函数压轴100题(含详解)

搞定二次函数压轴100题1. 若二次函数y=a1x2+b1x+c1的图象记为C1,其顶点为A,二次函数y=a2x2+b2x+c2的图象记为C2,其顶点为B,且满足点A 在C2上,点B在C1上,则称这两个二次函数互为“伴侣二次函数”.(1)一个二次函数的“伴侣二次函数”有个;(2)①求二次函数y=x2+3x+2与x轴的交点;②求以上述交点为顶点的二次函数y=x2+3x+2的“伴侣二次函数”.(3)试探究a1与a2满足的数量关系.2. 已知二次函数y=x2+2bx+c(b,c为常数).(1)当b=1,c=−3时,求二次函数在−2≤x≤2上的最小值;(2)当c=3时,求二次函数在0≤x≤4上的最小值;(3)当c=4b2时,若在自变量x的值满足2b≤x≤2b+3的情况下,与其对应的函数值y的最小值为21,求此时二次函数的解析式.3. 如图,已知二次函数图象的顶点坐标为(2,0),直线y=x+1与二次函数的图象交于A、B两点,其中点A在y轴上.(1)二次函数的解析式为y=;(2)证明点不在(1)中所求的二次函数的图象上;(3)若C为线段AB的中点,过C点作轴于E点,CE与二次函数的图象交于D点.①y轴上存在点K,使以K、A、D、C为顶点的四边形是平行四边形,则K点的坐标是;②二次函数的图象上是否存在点P,使得?若存在,求出P点坐标;若不存在,请说明理由.x和直线y= 4. 二次函数y=x2+px+q的顶点M是直线y=−12x+m的交点.(1)若直线y=x+m过点D(0,−3),求M点的坐标及二次函数y=x2+px+q的解析式;(2)试证明无论m取任何值,二次函数y=x2+px+q的图象与直线y=x+m总有两个不同的交点;(3)在(1)的条件下,若二次函数y=x2+px+q的图象与yx上求异于轴交于点C,与x的右交点为A,试在直线y=−12 M的点P,使P在△CMA的外接圆上.5. 已知二次函数y=−x2+bx+c+1.(1)当b=1时,求这个二次函数的对称轴方程;(2)若c=−14b2−2b,问:b为何值时,二次函数的图象与x轴相切;(3)若c=0,二次函数的图象与x轴交于点A(x1,0),B(x2,0),且x1<x2,与y轴的正半轴交于点M,以AB为直径的半圆恰好经过点M,二次函数的对称轴l与x轴、直线BM、直线AM分别相交于点D,E,F且满足DEEF =13,求二次函数的表达式.6. 如图,已知二次函数y=−x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连接BC.(1)求该二次函数的解析式及点M的坐标;(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC 的边界),求m的取值范围;(3)点P是直线AC上的动点,若以点P,点C,点M构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).7. 已知二次函数y=−x2+bx+c的图象经过点P(0,1)与Q(2,−3).(1)求此二次函数的解析式;(2)若点A是第一象限内该二次函数图象上一点,过点A作x轴的平行线交二次函数图象于点B,分别过点B、A作x轴的垂线,垂足分别为C、D,且所得四边形ABCD恰为正方形.①求正方形的ABCD的面积;②联结PA、PD,PD交AB于点E,求证:△PAD∽△PEA.8. 如图,在直角坐标系中,O为坐标原点,二次函数y=x2+mx+ 2的图象与x轴的正半轴交于点A,与y轴的正半轴交于点B,且OA:OB=1:2.设此二次函数图象的顶点为D.(1)求这个二次函数的解析式;(2)将△OAB绕点A顺时针旋转90∘后,点B落到点C的位置.将上述二次函数图象沿y轴向上或向下平移后经过点C.请直接写出点C的坐标和平移后所得图象的函数解析式;(3)设(2)中平移后所得二次函数图象与y轴的交点为B1,顶点为D1.点P在平移后的二次函数图象上,且满足△PBB1的面积是△PDD1面积的2倍,求点P的坐标.9. 如图,已知二次函数y=−x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连接BC.(1)求该二次函数的解析式及点M的坐标;(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;(3)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).10. 已知二次函数y=mx2+nx+p图象的顶点横坐标是2,与x轴交于A(x1,0),B(x2,0),x1<0<x2,与y轴交于点C,O为坐标原点,tan∠CAO−tan∠CBO=1.(1)求证:n+4m=0;(2)求m,n的值;(3)当p>0且二次函数图象与直线y=x+3仅有一个交点时,求二次函数的最大值.11. 如图,直线y=5x+5交x轴于点A,交y轴于点C,过A,C两点的二次函数y=ax2+4x+c的图象交x轴于另一点B.(1)求二次函数的解析式;(2)连接BC,点N是线段BC上的动点,作ND⊥x轴交二次函数的图象于点D,求线段ND长度的最大值;(3)若点H为二次函数y=ax2+4x+c图象的顶点,点M(4,m)是该二次函数图象上一点,在x轴,y轴上分别找点F,E,使四边形HEFM的周长最小,求出点F,E的坐标.,当x=0和x=2时,12. 已知二次函数y=(t+1)x2+2(t+2)x+32函数值相等.(1)求二次函数的表达式.(2)若一次函数y=kx+6的图象与二次函数的图象都经过点A(−3,m),求m和k的值.(3)设二次函数的图象与x轴交于点B,C(点B在点C的左侧),将二次函数的图象在点B,C间的部分(含点B和点C)向左平移n(n>0)个单位长度后得到的图象记为G,同时将2中得到的直线y=kx+6向上平移n个单位长度.请结合图象回答:当平移后的直线与图象G有公共点时,n的取值范围是多少?13. 已知二次函数y=x2−2ax−2a−6(a为常数,a≠0).(1)求证:该二次函数的图象与x轴有两个交点;(2)设该二次函数的图象与x轴交于点A(−2,0)和点B,与y轴交于点C,线段BC的垂直平分线l与x轴交于点D.①求点D的坐标;②设点P是抛物线上的一个动点,点Q是直线l上的一个动点.以点B,D,P,Q为顶点的四边形是否可能为平行四边形?若能,直接写出点Q的坐标.14. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(−1,0),B(4,0),C(0,2)三点.(1)求该二次函数的解析式;(2)点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O 是坐标原点),求点D的坐标;(3)点P是该二次函数图象上位于一象限上的一动点,连接PA 分别交BC,y轴于点E,F,若△PEB,△CEF的面积分别为S1,S2,求S1−S2的最大值.15. 已知二次函数y=(t−4)x2−(2t−5)x+4在x=0与x=5的函数值相等.(1)求二次函数的解析式;(2)若二次函数的图象与x轴交于A,B两点(A在B左侧),与y轴交于点C,一次函数y=kx+b经过B,C两点,求一次函数的表达式;(3)在(2)的条件下,过动点D(0,m)作直线l∥x轴,其中m>−2.将二次函数图象在直线l下方的部分沿直线l向上翻折,其余部分保持不变,得到一个新图象M.若直线y=kx+b与新图象M恰有两个公共点,请直接写出m的取值范围.),A(5,0),16. 已知二次函数y=ax2+bx+c的图象经过点P(0,−52 B(1,0).(1)求该二次函数的解析式;(2)点C在该二次函数的图象上,当△ABC的面积为12时,求点C坐标;(3)在(2)的条件下,求△ABC外接圆圆心点D的坐标.17. 如图,直线y=5x+5交x轴于点A,交y轴于点C,过A,C两点的二次函数y=ax2+4x+c的图象交x轴于另一点B.(1)求二次函数的表达式;(2)连接BC,点N是线段BC上的动点,作ND⊥x轴交二次函数的图象于点D,求线段ND长度的最大值;(3)若点H为二次函数y=ax2+4x+c图象的顶点,点M(4,m)是该二次函数图象上一点,在x轴、y轴上分别找点F,E,使四边形HEFM的周长最小,求出点F,E的坐标.18. 如图1,一次函数y=kx+k与二次函数y=kx2+kx(k>0)交于A,B两点,二次函数图象的顶点为P.(1)写出三条与系数k无关的一次函数与二次函数共有的结论.(2)当k为何值时,△AOP为等边三角形?(3)若一次函数y=kx+k的图象与二次函数y=kx2+2kx的图象交于点C,D,与y轴交于点F,如图2,某数学学习小组探究k=1时得出以下结论,其中正确结论的序号有.①AF=BF;②点C是BF的黄金分割点;③AFAD =√5+12;④△CFO与△ADO的面积相等.(4)在(3)中,若去掉k=1,以上正确的结论还成立吗?若成立,请选择两个加以说明.19. 如图,顶点为P(4,−4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M,N关于点P对称,连接AN,ON.(1)求该二次函数的关系式.(2)若点A的坐标是(6,−3),求△ANO的面积.(3)当点A在对称轴l右侧的二次函数图象上运动时,请解答下列问题:①证明:∠ANM=∠ONM;②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标,如果不能,请说明理由.20. 对于二次函数y=x2−3x+2和一次函数y=−2x+4,把y=t(x2−3x+2)+(1−t)(−2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E,现有点A(2,0)和抛物线E上的点B(−1,n),请完成下列任务:(1)【尝试】(1)当t=2时,抛物线y=t(x2−3x+2)+(1−t)(−2x+4)的顶点坐标为;(2)判断点A是否在抛物线E上;(3)求n的值.(2)【发现】通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线E总过定点,坐标为.(3)【应用】(1)二次函数y=−3x2+5x+2是二次函数y=x2−3x+2和一次函数y=−2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由;(2)以AB为边作矩形ABCD,使得其中一个顶点落在y轴上;若抛物线E经过A,B,C,D其中的三点,求出所有符合条件的t的值.与y=x2−mx−21. 已知关于x的二次函数y=x2−mx+m2+12m2+2,这两个二次函数图象中的一条与x轴交于A、B两个不同2的点.(1)试判断哪个二次函数的图象经过A、B两点(写出判断过程);(2)若A点坐标为(−1,0),求点B的坐标;(3)在(2)的条件下,设点C是抛物线上的一点,且△ABC的面积为10,直接写出点C的坐标.22. 已知二次函数y=x2+bx+c(b,c为常数)的图象经过点A(1,0)与点C(0,−3),其顶点为P.(1)求二次函数的解析式;(2)若Q为对称轴上的一点,且QC平分∠PQO,求Q点坐标;(3)当m≤x≤m+1时,y的取值范围是−4≤y≤2m,求m 的值.23. 如图,在直角坐标系中,O为原点.点A在x轴的正半轴上,点B在y轴的正半轴上,tan∠OAB=2.二次函数y=x2+mx+2的图象经过点A,B,顶点为D.(1)求这个二次函数的解析式;(2)将△OAB绕点A顺时针旋转90∘后,点B落到点C的位置.将上述二次函数图象沿y轴向上或向下平移后经过点C.请直接写出点C的坐标和平移后所得图象的函数解析式;(3)设(2)中平移后所得二次函数图象与y轴的交点为B1,顶点为D1.点P在平移后的二次函数图象上,且满足△PBB1的面积是△PDD1面积的2倍,求点P的坐标.24. 在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(−3,0),B(0,−3)两点,二次函数y=x2+mx+n 的图象经过点A.(1)求一次函数y=kx+b的解析式;(2)若二次函数y=x2+mx+n图象的顶点在直线AB上,求m,n的值;(3)当−3≤x≤0时,二次函数y=x2+mx+n的最小值为−4,求m,n的值.在x=0和x=2时25. 已知二次函数y=(t+1)x2+2(t+2)x+32的函数值相等.(1)求二次函数的解析式;(2)若一次函数y=kx+6的图象与二次函数的图象都经过点A(−3,m),求m和k的值;(3)设二次函数的图象与x轴交于点B,C(点B在点C的左侧),将二次函数的图象在点B,C间的部分(含点B和点C)向左平移n(n>0)个单位后得到的图象记为G,同时将(2)中得到的直线y=kx+6向上平移n个单位.请结合图象回答:当平移后的直线与图象G有公共点时,n的取值范围.26. 如图,在平面直角坐标系中,点A,C的坐标分别为(−1,0),(0,−√3),点B在x轴上.已知某二次函数的图象经过A,B,C 三点,且它的对称轴为直线x=1,点P为直线BC下方的二次函数图象上的一个动点(点P与B,C不重合),过点P作y轴的平行线交BC于点F.(1)求该二次函数的解析式;(2)若设点P的横坐标为m,用含m的代数式表示线段PF的长;(3)求△PBC面积的最大值,并求此时点P的坐标.27. 如图,已知二次函数y=ax2+bx+c的图象经过A(−1,0),B(3,0),N(2,3)三点,且与y轴交于点C.(1)求这个二次函数的解析式,并写出顶点M及点C的坐标;(2)若直线y=kx+d经过C,M两点,且与x轴交于点D.试证明四边形CDAN是平行四边形;(3)点P是这个二次函数的对称轴上一动点,请探索:是否存在这样的点P,使以点P为圆心的圆经过A,B两点,并且与直线CD相切?如果存在,请求出点P的坐标;如果不存在,请说明理由.28. 如图,已知在平面直角坐标系xOy中,二次函数y=−x2+mx+n的图象经过点A(3,0),B(m,m+1),且与y轴相交于点C.(1)求这个二次函数的解析式并写出其图象顶点D的坐标;(2)求∠CAD的正弦值;(3)设点P在线段DC的延长线上,且∠PAO=∠CAD,求点P 的坐标.x2+bx+c的图象29. 如图,在平面直角坐标系中,二次函数y=−14与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(−4,0).(1)求该二次函数的表达式及点C的坐标;(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图象上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.(1)求S的最大值;(2)在点F的运动过程中,当点E落在该二次函数图象上时,请直接写出此时S的值.30. 已知二次函数y1=x2−2x−3及一次函数y2=x+m.(1)求该二次函数图象的顶点坐标以及它与x轴的交点坐标;(2)将该二次函数图象在x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分不变,得到一个新图象.请你在图中画出这个新图象,并求出新图象与直线y2=x+m有三个不同公共点时m的值;(3)当0≤x≤2时,函数y=y1+y2+(m−2)x+3的图象与x轴有两个不同的公共点,求m的取值范围.31. 如图,已知二次函数y=ax2−4x+c的图象与坐标轴交于点A(−1,0)和点B(0,−5).(1)求该二次函数的解析式;(2)已知该函数图象的对称轴上存在一点P,使得△ABP的周长最小.请求出点P的坐标.32. 如图,二次函数y=ax2+bx+c的图象经过点A(−1,0),B(4,0),C(−2,−3),直线BC与y轴交于点D,E为二次函数图象上任一点.(1)求这个二次函数的表达式;(2)若点E在直线BC的上方,过点E分别作BC和y轴的垂线,交直线BC于不同的两点F,G(F在G的左侧),求△EFG的周长的最大值;(3)是否存在点E,使得△EDB是以BD为直角边的直角三角形,如果存在,求点E的坐标;如果不存在,请说明理由.x+3的图象33. 已知平面直角坐标系xOy(如图),一次函数y=34x的图象上,且MO=与y轴交于点A,点M在正比例函数y=32MA.二次函数y=x2+bx+c的图象经过点A、M.(1)求线段AM的长;(2)求这个二次函数的解析式;(3)如果点B在y轴上,且位于点A下方,点C在上述二次函数x+3的图象上,且四边形的图象上,点D在一次函数y=34ABCD是菱形,求点C的坐标.34. 如图,二次函数y=a(x2−2mx−3m2)(其中a,m为常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B左侧),与y轴交于点C(0,−3),点D在二次函数图象上,且CD∥AB,连接AD;过点A作射线AE交二次函数于点E,使AB 平分∠DAE.(1)当a=1时,求点D的坐标;(2)证明:无论a,m取何值,点E在同一直线上运动;(3)设该二次函数图象顶点为F,试探究:在x轴上是否存在点P,使以PF,AD,AE为边构成的三角形是以AE为斜边的直角三角形?如果存在,请用含m的代数式表示点P的横坐标;如果不存在,请说明理由.m+1(m为常数).35. 已知:二次函数y=x2−mx+34(1)若这个二次函数的图象与x轴只有一个公共点A,且A点在x轴的正半轴上.①求m的值;②四边形AOBC是正方形,且点B在y轴的负半轴上,现将这个二次函数的图象平移,使平移后的函数图象恰好经过B,C 两点,求平移后的图象对应的函数解析式;m+1的最小值(2)当0≤x≤2时,求函数y=x2−mx+34(用含m的代数式表示).36. 如图,在平面直角坐标系xOy中,将二次函数y=x2−1的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.(1)求N的函数表达式;(2)设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A,B,求PA2+PB2的最大值;(3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数.x2+bx+c的图象经过点A(−3,6),并与x轴37. 已知二次函数y=12交于点B(−1,0)和点C,与y轴交于点E,顶点为P,对称轴与x 轴交于点D.(1)求这个二次函数的解析式;(2)连接CP,△DCP是什么特殊形状的三角形?并加以说明;(3)点Q是第一象限的抛物线上一点,且满足∠QEO=∠BEO,求出点Q的坐标.38. 如图,二次函数y=ax2+bx+c的图象经过点A(−1,0),B(4,0),C(−2,−3),直线BC与y轴交于点D,E为二次函数上任一点.(1)求这个二次函数的解析式;(2)若点E在直线BC的上方,过E分别作BC和y轴的垂线,交直线BC于不同的两点F,G(F在G的左侧),求△EFG周长的最大值;(3)是否存在点E,使得△EDB是以BD为直角边的直角三角形,如果存在,求点E的坐标;如果不存在,请说明理由.39. 已知关于x的二次函数y=x2+(k2−3k−4)x+2k的图象与x轴从左到右分别交于A,B两点,且这两点关于原点对称.(1)求k的值;(2)在(1)的条件下,若反比例函数y=m的图象与二次函数xy=x2+(k2−3k−4)x+2k的图象从左到右交于Q,R,S三点,且点Q的坐标为(−1,−1),点R(x R,y R),S(x S,y S)中的纵坐标y R,y S分别是一元二次方程y2+my−1=0的解,求四边形AQBS的面积S;四边形AQBS(3)在(1),(2)的条件下,在x轴下方是否存在二次函数y=x2+(k2−3k−4)x+2k图象上的点P使得S△PAB=2S△RAB,若存在,求出点P的坐标;若不存在,请说明理由.40. 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,−4).(1)求出图象与轴的交点A,B的坐标;S△MAB,若(2)在二次函数的图象上是否存在点P,使S△PAB=54存在,求出P点的坐标;若不存在,请说明理由;(3)将二次函数的图象在轴下方的部分沿轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y= x+b(b<1)与此图象有两个公共点时,的取值范围.41. 下图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,−4).(1)求出图象与x轴的交点A,B的坐标.S△MAB?若存(2)在二次函数的图象上是否存在点P,使S△PAB=54在,求出P点的坐标;若不存在,请说明理由.(3)将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b(b<1)与此图象有两个公共点时,b 的取值范围.42. 已知二次函数y=ax2+bx+c的图象经过A(1,0),B(3,0),C(0,−3).(1)求此二次函数的解析式以及顶点D的坐标;(2)如图①,过此二次函数抛物线图象上一动点P(m,n)(0<m<3)作y轴平行线,交直线BC于点E,是否存在一点P,使线段PE的长最大?若存在,求出PE长的最大值;若不存在,说明理由.(3)如图②,过点A作y轴的平行线交直线BC于点F,连接DA,DB,四边形OAFC沿射线CB方向运动,速度为每秒1个单位长度,运动时间为t秒,当点C与点F重合时立即停止运动,求运动过程中四边形OAFC与四边形ADBF重叠部分面积S的最大值.梅花香自苦寒来),点F(0,1)在y轴上,43. 二次函数的顶点在原点O,经过点A(1,14直线y=−1与y轴交于点H.(1)求二次函数的解析式;(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=−1交于点M,求证:FM平分∠OFP;(3)当△FPM是等边三角形时,求P点的坐标.44. 如图,已知二次函数图象的顶点坐标为D(1,1),直线y=kx+m的图象与该二次函数的图象交于A,C两点,且A(0,2),直线与x轴的交点为B,满足sin∠ABO=√5,点P是线段AC上一动点,5且不与A,C两点重合,PG∥y轴交抛物线于点G.(1)求k,m和这个二次函数的解析式;(2)点E是直线BC与抛物线对称轴的交点,当△PGE∽△AOB 时,求点P的坐标;时,另外一点F在抛物线上,当S△ACF=S△ACG时,(3)若PG=2116求点F的坐标.45. 如图,△ABC是以BC为底边的等腰三角形,点A,C分别是一次x+3的图象与y轴、x轴的交点,点B在二次函数函数y=−34x2+bx+c的图象上,且该二次函数图象上存在一点D,使y=18四边形ABCD能构成平行四边形.(1)试求b,c的值,并写出该二次函数的解析式;(2)动点P从A到D,同时动点Q从C到A都以每秒1个单位的速度运动,问:①当P运动到何处时,△APQ是直角三角形?②当P运动到何处时,四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?46. 如图,二次函数y=x2+px+q(p<0)的图象与x轴交于A,B.两点,与y轴交于点C(0,−1),△ABC的面积为54(1)求该二次函数的解析式;(2)过y轴上的一点M(0,m)作y轴的垂线,若该垂线与△ABC 的外接圆有公共点,求m的取值范围;(3)在该二次函数的图象上是否存在点D,使四边形ACBD为直角梯形?若存在,求出点D的坐标;若不存在,请说明理由.47. 如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).(1)求a,b的值;(2)点C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6).写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.48. 如图,三角形ABC是以BC为底边的等腰三角形,点A,C分别x+3的图象与y轴、x轴的交点,点B在二是一次函数y=−34x2+bx+c的图象上,且该二次函数图象上存在一次函数y=18点D使四边形ABCD能构成平行四边形.(1)试求b,c的值,并写出该二次函数表达式;(2)动点P从A到D,同时动点Q从C到A都以每秒1个单位的速度运动,问:①当P运动到何处时,有PQ⊥AC?②当P运动到何处时,四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?49. 如图,已知二次函数y=12x2+bx+c的图象经过点A(3,6),并与x轴交于点B(1,0)和点C.(1)求二次函数的解析式及点C的坐标;(2)若D为线段AC上一点,且以D,O,C为顶点的三角形与△ABC相似,求点D的坐标;(3)设直线y=1为直线l,将该二次函数的图象在直线l下方的部分沿直线l翻折到直线l上方,图象的其余部分不变,得到一个新图象.是否存在与新图象恰有三个不同公共点且平行于AC 的直线?若存在,请求出所有符合条件的直线的解析式;若不存在,请说明理由.50. 已知二次函数y=ax2−2ax+c(a<0)的最大值为4,且抛物线过点(72,−94).点P(t,0)是x轴上的动点,抛物线与y轴的交点为C,顶点为D.(1)求该二次函数的解析式及顶点D的坐标;(2)求∣PC−PD∣的最大值及对应的点P的坐标;(3)设Q(0,2t)是y轴上的动点,若线段PQ与函数y=a∣x∣2−2a∣x∣+c的图象只有一个公共点,求t的取值.51. 如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(−2,0),点C(8,0),与y轴交于点A.(1)求二次函数y=ax2+bx+4的表达式;(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;(3)连接OM,在(2)的结论下,求OM与AC的数量关系.52. 如图,三角形ABC是以BC为底边的等腰三角形,点A,C分别x+3的图象与y轴,x轴的交点,点B在二是一次函数y=−34x2+bx+c的图象上,且该二次函数图象上存在一次函数y=18点D使四边形ABCD为平行四边形.(1)试求b,c的值,并写出该二次函数表达式;(2)动点P从A到D,同时动点Q从C到A都以每秒1个单位的速度运动,问:①当P运动到何处时,有PQ⊥AC?②当P运动到何处时,四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?53. 已知关于x的二次函数y=x2+(k2−3k−4)x+2k的图象与x轴分别交于A,B两点(点A在点B左侧),且这两点关于原点对称.(1)求k的值.的图象与二次函数(2)在(1)的条件下,若反比例函数y=mxy=x2+(k2−3k−4)x+2k的图象从左到右分别交于Q,R,S三点,且点Q的坐标为(−1,−1),点R(x R,y R),S(x S,y S)的纵坐标y R,y S分别是一元二次方程y2+my−1=0的解,求四边形AQBS的面积.(3)在(1)(2)的条件下,在x轴下方的二次函数y=x2+ (k2−3k−4)x+2k的图象上是否存在点P,使得S△PAB=2S△RAB?若存在,求出点P坐标;若不存在,请说明理由.54. 如图,二次函数y=ax2−6ax+4a+3的图象与y轴交于点A,点B是x轴上一点,其坐标为(1,0),连接AB,tan∠ABO=2.(1)则点A的坐标为,a=;(2)过点A作AB的垂线与该二次函数的图象交于另一点C,求点C的坐标;(3)连接BC,过点A作直线l交线段BC于点P,设点B,点C 到l的距离分别为d1,d2,求d1+d2的最大值.55. 二次函数y=ax2+bx+4的图象与x轴交于两点A,B,与y轴交于点C,且A(−1,0),B(4,0).(1)求此二次函数的表达式.(2)如图1,抛物线的对称轴m与x轴交于点E,CD⊥m,垂足,0),动点N在线段DE上运动,连接CF,为点D,点F(−76CN,FN,若以点C,D,N为顶点的三角形与△FEN相似,求点N的坐标.(3)如图2,点M在抛物线上,且点M的横坐标是1,点P为抛物线上一动点,若∠PMA=45∘,求点P的坐标.56. 在平面直角坐标系中,O为坐标原点,一次函数y=ax+b的图象与二次函数y=ax2+bx的图象交于点A,B.其中a,b均为非零实数.(1)当a=b=1时,求AB的长;(2)当a>0时,请用含a,b的代数式表示△AOB的面积;(3)当点A的横坐标小于点B的横坐标时,过点B作x轴的垂线,垂足为Bʹ.若二次函数y=ax2+bx的图象的顶点在反比例函的图象上,请用含a的代数式表示△BBʹA的面积.数y=ax57. 如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(3,0),B(−1,0),C(0,−3),顶点为D.(1)求这个二次函数的解析式及顶点坐标;(2)在y轴上找一点P(点P与点C不重合),使得∠APD= 90∘,求点P坐标;(3)在(2)的条件下,将△APD沿直线AD翻折,得到△AQD,求点Q坐标.58. 已知:二次函数y=ax2+bx+6(a≠0)的图象与x轴交于A、B两点(点A在点B的左侧),点A、点B的横坐标是方程x2−4x−12=0的两个根.(1)求出该二次函数的表达式及顶点坐标;(2)如图,连接AC、BC,点P是线段OB上一个动点(点P不与点O、B重合),过点P作PQ∥AC交BC于点Q,当△CPQ的面积最大时,求点P的坐标.59. 如图,二次函数y=−x2+bx+c的图象与x轴交于点B(−3,0),与y轴交于点C(0,−3).(1)求直线BC及二次函数的解析式;(2)设抛物线的顶点为D,与x轴的另一个交点为A.点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标;(3)连接CD,求∠OCA与∠OCD两角和的度数.60. 如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数x刻画.y=−x2+4x刻画,斜坡可以用一次函数y=12(1)请用配方法求二次函数图象的最高点P的坐标;(2)小球的落点是A,求点A的坐标;(3)连接抛物线的最高点P与点O,A得△POA.求△POA的面积;。
近三年二次函数压轴题(带详解答案)

近三年全国二次函数压轴题(带详解答案)一.解答题(共40小题)1.如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.(1)求二次函数的表达式;(2)在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P 的坐标;(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.2.如图,抛物线y=ax2﹣x﹣2(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).(1)求抛物线的解析式;(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.3.已知抛物线y=a(x﹣1)2+3(a≠0)与y轴交于点A(0,2),顶点为B,且对称轴l1与x轴交于点M(1)求a的值,并写出点B的坐标;(2)有一个动点P从原点O出发,沿x轴正方向以每秒2个单位的速度运动,设运动时间为t秒,求t为何值时PA+PB最短;(3)将此抛物线向右平移所得新的抛物线与原抛物线交于点C,且新抛物线的对称轴l2与x轴交于点N,过点C作DE∥x轴,分别交l1,l2于点D、E,若四边形MDEN是正方形,求平移后抛物线的解析式.4.如图,在平面直角坐标系xOy,已知二次函数y=﹣x2+bx的图象过点A(4,0),顶点为B,连接AB、BO.(1)求二次函数的表达式;(2)若C是BO的中点,点Q在线段AB上,设点B关于直线CQ的对称点为B',当△OCB'为等边三角形时,求BQ的长度;(3)若点D在线段BO上,OD=2DB,点E、F在△OAB的边上,且满足△DOF 与△DEF全等,求点E的坐标.5.如图,已知抛物线y=ax2+bx+c过点A(﹣3,0),B(﹣2,3),C(0,3),其顶点为D.(1)求抛物线的解析式;(2)设点M(1,m),当MB+MD的值最小时,求m的值;(3)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值;(4)若抛物线的对称轴与直线AC相交于点N,E为直线AC上任意一点,过点E 作EF∥ND交抛物线于点F,以N,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由.6.如图1,已知二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为﹣,直线l的解析式为y=x.(1)求二次函数的解析式;(2)直线l沿x轴向右平移,得直线l′,l′与线段OA相交于点B,与x轴下方的抛物线相交于点C,过点C作CE⊥x轴于点E,把△BCE沿直线l′折叠,当点E 恰好落在抛物线上点E′时(图2),求直线l′的解析式;(3)在(2)的条件下,l′与y轴交于点N,把△BON绕点O逆时针旋转135°得到△B′ON′,P为l′上的动点,当△PB′N′为等腰三角形时,求符合条件的点P的坐标.7.如图,抛物线y=x2+x+c与x轴的负半轴交于点A,与y轴交于点B,连结AB,点C(6,)在抛物线上,直线AC与y轴交于点D.(1)求c的值及直线AC的函数表达式;(2)点P在x轴正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.①求证:△APM∽△AON;②设点M的横坐标为m,求AN的长(用含m的代数式表示).8.如图1,在平面直角坐标系中,O是坐标原点,抛物线y=﹣x2﹣x+8与x轴正半轴交于点A,与y轴交于点B,连接AB,点M,N分别是OA,AB的中点,Rt△CDE≌Rt△ABO,且△CDE始终保持边ED经过点M,边CD经过点N,边DE与y轴交于点H,边CD与y轴交于点G.(1)填空:OA的长是,∠ABO的度数是度;(2)如图2,当DE∥AB,连接HN.①求证:四边形AMHN是平行四边形;②判断点D是否在该抛物线的对称轴上,并说明理由;(3)如图3,当边CD经过点O时,(此时点O与点G重合),过点D作DQ∥OB,交AB延长线上于点Q,延长ED到点K,使DK=DN,过点K作KI∥OB,在KI上取一点P,使得∠PDK=45°(点P,Q在直线ED的同侧),连接PQ,请直接写出PQ的长.9.如图,抛物线y=ax2+bx+c(a≠0)与直线y=x+1相交于A(﹣1,0),B(4,m)两点,且抛物线经过点C(5,0).(1)求抛物线的解析式;(2)点P是抛物线上的一个动点(不与点A、点B重合),过点P作直线PD⊥x 轴于点D,交直线AB于点E.①当PE=2ED时,求P点坐标;②是否存在点P使△BEC为等腰三角形?若存在请直接写出点P的坐标;若不存在,请说明理由.10.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与y轴交与点C(0,3),与x轴交于A、B两点,点B坐标为(4,0),抛物线的对称轴方程为x=1.(1)求抛物线的解析式;(2)点M从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点N从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,设△MBN的面积为S,点M运动时间为t,试求S与t的函数关系,并求S的最大值;(3)在点M运动过程中,是否存在某一时刻t,使△MBN为直角三角形?若存在,求出t值;若不存在,请说明理由.11.如图,某日的钱塘江观潮信息如图:按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离s(千米)与时间t (分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点A(0,12),点B坐标为(m,0),曲线BC可用二次函数s=t2+bt+c(b,c是常数)刻画.(1)求m的值,并求出潮头从甲地到乙地的速度;(2)11:59时,小红骑单车从乙地出发,沿江边公路以0.48千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为0.48千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度v=v0+(t ﹣30),v0是加速前的速度).12.如图,在平面直角坐标系xOy中,已知A,B两点的坐标分别为(﹣4,0),(4,0),C(m,0)是线段A B上一点(与A,B点不重合),抛物线L1:y=ax2+b1x+c1(a<0)经过点A,C,顶点为D,抛物线L2:y=ax2+b2x+c2(a<0)经过点C,B,顶点为E,AD,BE的延长线相交于点F.(1)若a=﹣,m=﹣1,求抛物线L1,L2的解析式;(2)若a=﹣1,AF⊥BF,求m的值;(3)是否存在这样的实数a(a<0),无论m取何值,直线AF与BF都不可能互相垂直?若存在,请直接写出a的两个不同的值;若不存在,请说明理由.13.如图,抛物线y=﹣x2+x+2与x轴交于点A,B,与y轴交于点C.(1)试求A,B,C的坐标;(2)将△ABC绕AB中点M旋转180°,得到△BAD.①求点D的坐标;②判断四边形ADBC的形状,并说明理由;(3)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请直接写出所有满足条件的P点的坐标;若不存在,请说明理由.14.如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(﹣1,0)、B(4,0)、C(0,2)三点.(1)求该二次函数的解析式;(2)点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O是坐标原点),求点D的坐标;(3)点P是该二次函数图象上位于第一象限上的一动点,连接PA分别交BC、y 轴于点E、F,若△PEB、△CEF的面积分别为S1、S2,求S1﹣S2的最大值.15.抛物线y=4x2﹣2ax+b与x轴相交于A(x1,0),B(x2,0)(0<x1<x2)两点,与y轴交于点C.(1)设AB=2,tan∠ABC=4,求该抛物线的解析式;(2)在(1)中,若点D为直线BC下方抛物线上一动点,当△BCD的面积最大时,求点D的坐标;(3)是否存在整数a,b使得1<x1<2和1<x2<2同时成立,请证明你的结论.16.如图1,抛物线C1:y=x2+ax与C2:y=﹣x2+bx相交于点O、C,C1与C2分别交x轴于点B、A,且B为线段AO的中点.(1)求的值;(2)若OC⊥AC,求△OAC的面积;(3)抛物线C2的对称轴为l,顶点为M,在(2)的条件下:①点P为抛物线C2对称轴l上一动点,当△PAC的周长最小时,求点P的坐标;②如图2,点E在抛物线C2上点O与点M之间运动,四边形OBCE的面积是否存在最大值?若存在,求出面积的最大值和点E的坐标;若不存在,请说明理由.17.已知,抛物线y=ax2+bx+3(a<0)与x轴交于A(3,0)、B两点,与y轴交于点C,抛物线的对称轴是直线x=1,D为抛物线的顶点,点E在y轴C点的上方,且CE=.(1)求抛物线的解析式及顶点D的坐标;(2)求证:直线DE是△ACD外接圆的切线;=S△ACD,求点P的坐标;(3)在直线AC上方的抛物线上找一点P,使S△ACP(4)在坐标轴上找一点M,使以点B、C、M为顶点的三角形与△ACD相似,直接写出点M的坐标.18.如图,在平面直角坐标系中,抛物线y=x2﹣x﹣与x轴交于A、B 两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.(1)求直线AE的解析式;(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;(3)点G是线段CE的中点,将抛物线y=x2﹣x﹣沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.19.如图,抛物线y=ax2+bx﹣2与x轴交于A、B两点,与y轴交于C点,已知A (3,0),且M(1,﹣)是抛物线上另一点.(1)求a、b的值;(2)连结AC,设点P是y轴上任一点,若以P、A、C三点为顶点的三角形是等腰三角形,求P点的坐标;(3)若点N是x轴正半轴上且在抛物线内的一动点(不与O、A重合),过点N 作NH∥AC交抛物线的对称轴于H点.设ON=t,△ONH的面积为S,求S与t 之间的函数关系式.20.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B 两点,与y轴交于点C,且OA=2,OB=8,OC=6.(1)求抛物线的解析式;(2)点M从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时,点N从B出发,在线段BC上以每秒1个单位长度的速度向C点运动,当其中一个点到达终点时,另一个点也停止运动,当△MBN存在时,求运动多少秒使△MBN的面积最大,最大面积是多少?(3)在(2)的条件下,△MBN面积最大时,在BC上方的抛物线上是否存在点P,使△BPC的面积是△MBN面积的9倍?若存在,求点P的坐标;若不存在,请说明理由.21.如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0).与y 轴交于点C(0,3).(1)求抛物线的解析式;(2)点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值;(3)点D为抛物线对称轴上一点.①当△BCD是以BC为直角边的直角三角形时,求点D的坐标;②若△BCD是锐角三角形,求点D的纵坐标的取值范围.22.已知抛物线y=x2+bx﹣3(b是常数)经过点A(﹣1,0).(1)求该抛物线的解析式和顶点坐标;(2)P(m,t)为抛物线上的一个动点,P关于原点的对称点为P'.①当点P'落在该抛物线上时,求m的值;②当点P'落在第二象限内,P'A2取得最小值时,求m的值.23.如图,抛物线y=﹣x2+bx+c与x轴分别交于A(﹣1,0),B(5,0)两点.(1)求抛物线的解析式;(2)在第二象限内取一点C,作CD垂直X轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由.24.如图,已知抛物线y=ax2+bx+c(a≠0)的图象的顶点坐标是(2,1),并且经过点(4,2),直线y=x+1与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.(1)求抛物线的解析式;(2)证明:圆C与x轴相切;(3)过点B作BE⊥m,垂足为E,再过点D作DF⊥m,垂足为F,求BE:MF 的值.25.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.26.如图,已知抛物线y=﹣x2﹣x+2与x轴交于A、B两点,与y轴交于点C (1)求点A,B,C的坐标;(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.27.如图1,抛物线y=ax2+(a+3)x+3(a≠0)与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.(1)求a的值和直线AB的函数表达式;(2)设△PMN的周长为C1,△AEN的周长为C2,若=,求m的值;(3)如图2,在(2)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接E′A、E′B,求E′A+E′B的最小值.28.在平面直角坐标系中,已知抛物线y=x2+bx+c的顶点M的坐标为(﹣1,﹣4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.(1)填空:b=,c=,直线AC的解析式为;(2)直线x=t与x轴相交于点H.①当t=﹣3时得到直线AN(如图1),点D为直线AC下方抛物线上一点,若∠COD=∠MAN,求出此时点D的坐标;②当﹣3<t<﹣1时(如图2),直线x=t与线段AC,AM和抛物线分别相交于点E,F,P.试证明线段HE,EF,FP总能组成等腰三角形;如果此等腰三角形底角的余弦值为,求此时t的值.29.如图,抛物线y=ax2﹣(2a+1)x+b的图象经过(2,﹣1)和(﹣2,7)且与直线y=kx﹣2k﹣3相交于点P(m,2m﹣7).(1)求抛物线的解析式;(2)求直线y=kx﹣2k﹣3与抛物线y=ax2﹣(2a+1)x+b的对称轴的交点Q的坐标;(3)在y轴上是否存在点T,使△PQT的一边中线等于该边的一半?若存在,求出点T的坐标;若不存在请说明理由.30.如图,抛物线经过A(﹣1,0),B(5,0),C(0,)三点.(1)求抛物线的解析式;(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.31.如图,已知二次函数的图象M经过A(﹣1,0),B(4,0),C(2,﹣6)三点.(1)求该二次函数的解析式;(2)点G是线段AC上的动点(点G与线段AC的端点不重合),若△ABG与△ABC相似,求点G的坐标;(3)设图象M的对称轴为l,点D(m,n)(﹣1<m<2)是图象M上一动点,当△ACD的面积为时,点D关于l的对称点为E,能否在图象M和l上分别找到点P、Q,使得以点D、E、P、Q为顶点的四边形为平行四边形?若能,求出点P的坐标;若不能,请说明理由.32.如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A 在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.(1)求抛物线的解析式;(2)判断直线l与⊙E的位置关系,并说明理由;(3)动点P在抛物线上,当点P到直线l的距离最小时.求出点P的坐标及最小距离.33.如图,抛物线y=﹣x2+6x交x轴正半轴于点A,顶点为M,对称轴MB交x 轴于点B.过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.(1)求点A,M的坐标.(2)当BD为何值时,点F恰好落在该抛物线上?(3)当BD=1时①求直线MF的解析式,并判断点A是否落在该直线上.②延长OE交FM于点G,取CF中点P,连结PG,△FPG,四边形DEGP,四边形OCDE的面积分别记为S1,S2,S3,则S1:S2:S3=.34.如图1,二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于点C.若tan∠ABC=3,一元二次方程ax2+bx+c=0的两根为﹣8、2.(1)求二次函数的解析式;(2)直线l绕点A以AB为起始位置顺时针旋转到AC位置停止,l与线段BC交于点D,P是AD的中点.①求点P的运动路程;②如图2,过点D作DE垂直x轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在l运动过程中,∠EPF的大小是否改变?请说明理由;(3)在(2)的条件下,连结EF,求△PEF周长的最小值.35.如图,在平面直角坐标系中,抛物线y=a(x﹣1)2+4与x轴交于点A、B两点,与y轴交于点C,且点B的坐标为(3,0),点P在这条抛物线上,且不与B、C两点重合.过点P作y轴的垂线与射线BC交于点Q,以PQ为边作Rt△PQF,使∠PQF=90°,点F在点Q的下方,且QF=1.设线段PQ的长度为d,点P的横坐标为m.(1)求这条抛物线所对应的函数表达式.(2)求d与m之间的函数关系式.(3)当Rt△PQF的边PF被y轴平分时,求d的值.(4)以OB为边作等腰直角三角形OBD,当0<m<3时,直接写出点F落在△OBD的边上时m的值.36.某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足下列关系式:y=.(1)李明第几天生产的粽子数量为420只?(2)如图,设第x天每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价﹣成本)(3)设(2)小题中第m天利润达到最大值,若要使第(m+1)天的利润比第m 天的利润至少多48元,则第(m+1)天每只粽子至少应提价几元?37.如图,已知抛物线y=﹣(x2﹣7x+6)的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.(1)用配方法将抛物线的解析式化为顶点式:y=a(x﹣h)2+k(a≠0),并指出顶点M的坐标;(2)在抛物线的对称轴上找点R,使得CR+AR的值最小,并求出其最小值和点R的坐标;(3)以AB为直径作⊙N交抛物线于点P(点P在对称轴的左侧),求证:直线MP是⊙N的切线.38.若关于x的二次函数y=ax2+bx+c(a>0,c>0,a,b,c是常数)与x轴交于两个不同的点A(x1,0),B(x2,0)(0<x1<x2),与y轴交于点P,其图象顶点为点M,点O为坐标原点.(1)当x1=c=2,a=时,求x2与b的值;(2)当x1=2c时,试问△ABM能否为等边三角形?判断并证明你的结论;(3)当x1=mc(m>0)时,记△MAB,△PAB的面积分别为S1,S2,若△BPO∽△PAO,且S1=S2,求m的值.39.如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,顶点M 关于x轴的对称点是M′.(1)求抛物线的解析式;(2)若直线AM′与此抛物线的另一个交点为C,求△CAB的面积;(3)是否存在过A,B两点的抛物线,其顶点P关于x轴的对称点为Q,使得四边形APBQ为正方形?若存在,求出此抛物线的解析式;若不存在,请说明理由.40.已知点A(﹣2,n)在抛物线y=x2+bx+c上.(1)若b=1,c=3,求n的值;(2)若此抛物线经过点B(4,n),且二次函数y=x2+bx+c的最小值是﹣4,请画出点P(x﹣1,x2+bx+c)的纵坐标随横坐标变化的图象,并说明理由.二次函数压轴题参考答案与试题解析一.解答题(共40小题)1.如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.(1)求二次函数的表达式;(2)在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P 的坐标;(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.【专题】16 :压轴题.【分析】(1)代入A(1,0)和C(0,3),解方程组即可;(2)求出点B的坐标,再根据勾股定理得到BC,当△PBC为等腰三角形时分三种情况进行讨论:①CP=CB;②BP=BC;③PB=PC;(3)设AM=t则DN=2t,由AB=2,得BM=2﹣t,S△MNB=×(2﹣t)×2t=﹣t2+2t,运用二次函数的顶点坐标解决问题;此时点M在D点,点N在对称轴上x轴上方2个单位处或点N在对称轴上x轴下方2个单位处.【解答】解:(1)把A(1,0)和C(0,3)代入y=x2+bx+c,解得:b=﹣4,c=3,∴二次函数的表达式为:y=x2﹣4x+3;(2)令y=0,则x2﹣4x+3=0,解得:x=1或x=3,∴B(3,0),∴BC=3,点P在y轴上,当△PBC为等腰三角形时分三种情况进行讨论:如图1,①当CP=CB时,PC=3,∴OP=OC+PC=3+3或OP=PC﹣OC=3﹣3∴P1(0,3+3),P2(0,3﹣3);②当BP=BC时,OP=OB=3,∴P3(0,﹣3);③当PB=PC时,∵OC=OB=3∴此时P与O重合,∴P4(0,0);综上所述,点P的坐标为:(0,3+3)或(0,3﹣3)或(0,﹣3)或(0,0);(3)如图2,设A运动时间为t,由AB=2,得BM=2﹣t,则DN=2t,∴S△MNB=×(2﹣t)×2t=﹣t2+2t=﹣(t﹣1)2+1,即当M(2,0)、N(2,2)或(2,﹣2)时△MNB面积最大,最大面积是1.【点评】本题是二次函数的综合题型,其中涉及到运用待定系数法求二次函数,等腰三角形的性质,轴对称的性质等知识,运用数形结合、分类讨论及方程思想是解题的关键.2.如图,抛物线y=ax2﹣x﹣2(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).(1)求抛物线的解析式;(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.【专题】16 :压轴题;35 :转化思想.【分析】方法一:(1)该函数解析式只有一个待定系数,只需将B点坐标代入解析式中即可.(2)首先根据抛物线的解析式确定A点坐标,然后通过证明△ABC是直角三角形来推导出直径AB和圆心的位置,由此确定圆心坐标.(3)△MBC的面积可由S=BC×h表示,若要它的面积最大,需要使h取△MBC最大值,即点M到直线BC的距离最大,若设一条平行于BC的直线,那么当该直线与抛物线有且只有一个交点时,该交点就是点M.方法二:(1)略.(2)通过求出A,B,C三点坐标,利用勾股定理或利用斜率垂直公式可求出AC ⊥BC,从而求出圆心坐标.(3)利用三角形面积公式,过M点作x轴垂线,水平底与铅垂高乘积的一半,得出△MBC的面积函数,从而求出M点.【解答】方法一:解:(1)将B(4,0)代入抛物线的解析式中,得:0=16a﹣×4﹣2,即:a=;∴抛物线的解析式为:y=x2﹣x﹣2.(2)由(1)的函数解析式可求得:A(﹣1,0)、C(0,﹣2);∴OA=1,OC=2,OB=4,即:OC2=OA•OB,又:OC⊥AB,∴△OAC∽△OCB,得:∠OCA=∠OBC;∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,∴△ABC为直角三角形,AB为△ABC外接圆的直径;所以该外接圆的圆心为AB的中点,且坐标为:(,0).(3)已求得:B(4,0)、C(0,﹣2),可得直线BC的解析式为:y=x﹣2;设直线l∥BC,则该直线的解析式可表示为:y=x+b,当直线l与抛物线只有一个交点时,可列方程:x+b=x2﹣x﹣2,即:x2﹣2x﹣2﹣b=0,且△=0;∴4﹣4×(﹣2﹣b)=0,即b=﹣4;∴直线l:y=x﹣4.所以点M即直线l和抛物线的唯一交点,有:,解得:即M(2,﹣3).过M点作MN⊥x轴于N,S△BMC=S梯形OCMN+S△MNB﹣S△OCB=×2×(2+3)+×2×3﹣×2×4=4.方法二:(1)略.(2)∵y=(x﹣4)(x+1),∴A(﹣1,0),B(4,0).C(0,﹣2),∴K AC==﹣2,K BC==,∴K AC×K BC=﹣1,∴AC⊥BC,∴△ABC是以AB为斜边的直角三角形,△ABC的外接圆的圆心是AB的中点,△ABC的外接圆的圆心坐标为(,0).(3)过点M作x轴的垂线交BC′于H,∵B(4,0),C(0,﹣2),∴l BC:y=x﹣2,设H(t,t﹣2),M(t,t2﹣t﹣2),∴S=×(H Y﹣M Y)(B X﹣C X)=×(t﹣2﹣t2+t+2)(4﹣0)=﹣t2+4t,△MBC∴当t=2时,S有最大值4,∴M(2,﹣3).【点评】考查了二次函数综合题,该题的难度不算太大,但用到的琐碎知识点较多,综合性很强.熟练掌握直角三角形的相关性质以及三角形的面积公式是理出思路的关键.3.已知抛物线y=a(x﹣1)2+3(a≠0)与y轴交于点A(0,2),顶点为B,且对称轴l1与x轴交于点M(1)求a的值,并写出点B的坐标;(2)有一个动点P从原点O出发,沿x轴正方向以每秒2个单位的速度运动,设运动时间为t秒,求t为何值时PA+PB最短;(3)将此抛物线向右平移所得新的抛物线与原抛物线交于点C,且新抛物线的对称轴l2与x轴交于点N,过点C作DE∥x轴,分别交l1,l2于点D、E,若四边形MDEN是正方形,求平移后抛物线的解析式.【专题】16 :压轴题.【分析】(1)利用待定系数法即可解决问题;(2)如图1中,作点A关于x轴的对称点A′,连接BA′交x轴于P,点P即为所求.(3)如图2中,设抛物线向右平移后的解析式为y=﹣(x﹣m)2+3.想办法用m表示点C的坐标,分两种情形,利用待定系数法即可解决问题;【解答】解:(1)把A(0,2)代入抛物线的解析式可得,2=a+3,∴a=﹣1,∴抛物线的解析式为y=﹣(x﹣1)2+3,∴抛物线的顶点B坐标为(1,3).(2)如图1中,作点A关于x轴的对称点A′,连接BA′交x轴于P,点P即为所求.∵A′(0,﹣2),B(1,3),∴直线A′B的解析式为y=5x﹣2,∴P(,0),∴t==时,PA+PB最短(3)如图2中,设抛物线向右平移后的解析式为y=﹣(x﹣m)2+3.由,解得x=,∴点C的横坐标,∵MN=m﹣1,四边形MDEN是正方形,∴C(,m﹣1),把点C的坐标代入y=﹣(x﹣1)2+3,得到m﹣1=﹣+3,解得m=3或﹣5(舍弃),∴移后抛物线的解析式为y=﹣(x﹣3)2+3.当点C在x轴下方时,C(,1﹣m),把点C的坐标代入y=﹣(x﹣1)2+3,得到1﹣m=﹣+3,解得m=7或﹣1(舍弃),∴移后抛物线的解析式为y=﹣(x﹣7)2+3.【点评】本题考查二次函数综合题、待定系数法、正方形的性质、轴对称最短问题等知识,解题的关键是学会利用轴对称解决最短问题,学会利用参数解决问题,属于中考压轴题.4.如图,在平面直角坐标系xOy,已知二次函数y=﹣x2+bx的图象过点A(4,0),顶点为B,连接AB、BO.(1)求二次函数的表达式;(2)若C是BO的中点,点Q在线段AB上,设点B关于直线CQ的对称点为B',当△OCB'为等边三角形时,求BQ的长度;(3)若点D在线段BO上,OD=2DB,点E、F在△OAB的边上,且满足△DOF 与△DEF全等,求点E的坐标.【专题】16 :压轴题.【分析】(1)利用待定系数法求二次函数的表达式;(2)先求出OB和AB的长,根据勾股定理的逆定理证明∠ABO=90°,由对称计算∠QCB=60°,利用特殊的三角函数列式可得BQ的长;(3)因为D在OB上,所以F分两种情况:i)当F在边OA上时,ii)当点F在AB上时,当F在边OA上时,分三种情况:①如图2,过D作DF⊥x轴,垂足为F,则E、F在OA上,②如图3,作辅助线,构建△OFD≌△EDF≌△FGE,③如图4,将△DOF沿边DF翻折,使得O恰好落在AB边上,记为点E,当点F在OB上时,过D作DF∥x轴,交AB于F,连接OF与DA,依次求出点E的坐标即可.【解答】解:(1)将点A的坐标代入二次函数的解析式得:﹣×42+4b=0,解得b=2,∴二次函数的表达式为y=﹣x2+2x.(2)∵y=﹣x2+2x=﹣(x﹣2)2+2,∴B(2,2),抛物线的对称轴为x=2.如图1所示:由两点间的距离公式得:OB==2,BA==2.∵C是OB的中点,∴OC=BC=.∵△OB′C为等边三角形,∴∠OCB′=60°.又∵点B与点B′关于CQ对称,∴∠B′CQ=∠BCQ=60°.∵OA=4,OB=2,AB=2,∴OB2+AB2=OA2,∴∠OBA=90°.在Rt△CBQ中,∠CBQ=90°,∠BCQ=60°,BC=,∴tan60°=,∴BQ=CB=×=.(3)分两种情况:i)当F在边OA上时,①如图2,过D作DF⊥x轴,垂足为F,∵△DOF≌△DEF,且E在线段OA上,∴OF=FE,由(2)得:OB=2,∵点D在线段BO上,OD=2DB,∴OD=OB=,∵∠BOA=45°,∴cos45°=,∴OF=OD•cos45°==,则OE=2OF=,∴点E的坐标为(,0);②如图3,过D作DF⊥x轴于F,过D作DE∥x轴,交AB于E,连接EF,过E 作EG⊥x轴于G,∴△BDE∽△BOA,∴=,∵OA=4,∴DE=,∵DE∥OA,∴∠OFD=∠FDE=90°,∵DE=OF=,DF=DF,∴△OFD≌△EDF,同理可得:△EDF≌△FGE,∴△OFD≌△EDF≌△FGE,∴OG=OF+FG=OF+DE=+=,EG=DF=OD•sin45°=,∴E的坐标为(,);③如图4,将△DOF沿边DF翻折,使得O恰好落在AB边上,记为点E,过B作BM⊥x轴于M,过E作EN⊥BM于N,由翻折的性质得:△DOF≌△DEF,∴OD=DE=,∵BD=OD=,∴在Rt△DBE中,由勾股定理得:BE==,则BN=NE=BE•cos45°=×=,OM+NE=2+,BM﹣BN=2﹣,∴点E的坐标为:(2+,2﹣);ii)当点F在AB上时,过D作DF∥x轴,交AB于F,连接OF与DA,∵DF∥x轴,∴△BDF∽△BOA,∴,由抛物线的对称性得:OB=BA,∴BD=BF,则∠BDF=∠BFD,∠ODF=∠AFD,∴OD=OB﹣BD=BA﹣BF=AF,则△DOF≌△DAF,∴E和A重合,则点E的坐标为(4,0);综上所述,点E的坐标为:(,0)或(,)或(2+,2﹣)或(4,0).。
2023年九年级数学中考专题:二次函数综合压轴题(特殊四边形问题)(含简单答案)

12.如图,在平面直角坐标系中,抛物线 与x轴交于 两点,过点 的直线 与该抛物线交于另一点 ,且点 的横坐标为 .动点 在该抛物线上,其横坐标为 ,且点 不与 重合.作点 关于 轴的对称点 ,过点 作 轴的垂线交直线 于点 ,以 、 为一组邻边作矩形 .
(3) , ,
14.(1) ,
(2) ,
(3)
(4)点Q的坐标为 , , ,
15.(1)抛物线解析式为 ,顶点坐标为
(2) 或
(3)在直线 存在一点 ,
16.(1)抛物线的解析式为 ;
(2) 的最大值为 ;此时,点 ;
(3)满足条件的点P有4个,坐标分别为 或 或 或 .
17.(1)
(2)
(3)存在, 或 或
9.如图,抛物线 与x轴交于A, 两点,与y轴交于点C,一次函数 经过点B,C,点P是抛物线上的动点,过点P作 轴,垂足为Q,交直线 于点D.
(1)求抛物线的解析式及点A的坐标;
(2)当点P位于直线 上方且 面积最大时,求线段 的长;
(3)在平面直角坐标系中,以P,D,O,C为顶点的四边形是平行四边形,请直接写出符合条件点P的坐标.
18.综合与探究
如图1(注意:图1与图2完全相同)所示,抛物线 经过点 和点 ,与 轴的另一个交点为 ,与 轴相交于点 .
(1)求抛物线的函数图1中探究)
(3)设点 在 轴上,点 在抛物线上,要使以点 , , , 为顶点的四边形是平行四边形,请直接写出所有满足条件的点 的坐标.(请在图2中探究)
18.(1)
(2)
(3)P点坐标为: 、 、
(1)求抛物线 的解析式;
二次函数与几何图形综合(压轴题)-含答案
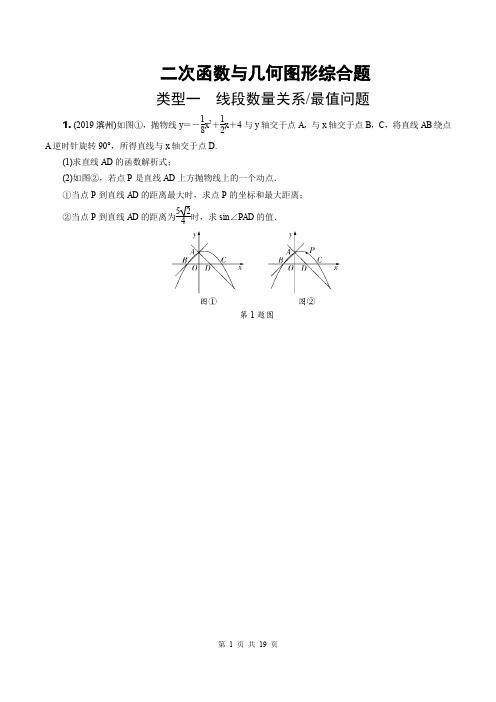
二次函数与几何图形综合题类型一 线段数量关系/最值问题1. (2019滨州)如图①,抛物线y =-18x 2+12x +4与y 轴交于点A ,与x 轴交于点B ,C ,将直线AB 绕点A 逆时针旋转90°,所得直线与x 轴交于点D .(1)求直线AD 的函数解析式;(2)如图②,若点P 是直线AD 上方抛物线上的一个动点. ①当点P 到直线AD 的距离最大时,求点P 的坐标和最大距离; ②当点P 到直线AD 的距离为524时,求sin ∠P AD 的值.第1题图2. 如图,直线y =x +2与抛物线y =ax 2+bx +6相交于A (12,52)和B (4,c ).(1)求抛物线的解析式;(2)点P 是直线AB 上的动点,设点P 的横坐标为n ,过点P 作PC ⊥x 轴,交抛物线于点C ,交x 轴于点M .①当点P 在线段AB 上运动时(点P 不与点A ,B 重合),是否存在这样的点P ,使线段PC 的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;②点P 在直线AB 上自由移动,当点C 、P 、M 中恰有一点是其他两点所连线段的中点时,请直接写出n 的值.第2题图类型二面积数量关系/最值问题1. (2019成华区一诊)如图,抛物线经过原点O,与x轴交于点A(-4,0),且经过点B(4,8).(1)求抛物线的解析式;(2)设直线y=kx+4与抛物线两交点的横坐标分别为x1,x2(x1<x2),当1x2-1x1=22时,求k的值;(3)连接OB,点P为x轴下方抛物线上一动点,过点P作OB的平行线交直线AB于点C,连接OC、OP,当S△POC∶S△BOC=1∶2时,求点P的坐标.第1题图2. (2019武侯区一诊)如图,在平面直角坐标系中,直线y =mx +3与抛物线交于点A (9,-6),与y 轴交于点B ,抛物线的顶点C 的坐标是(4,-11).(1)分别求该直线和抛物线的函数表达式;(2)D 是抛物线上位于对称轴左侧的点,若△ABD 的面积为812,求点D 的坐标;(3)在y 轴上是否存在一点P ,使∠APC =45°?若存在,求出满足条件的点P 的坐标;若不存在,请说明理由.类型三特殊三角形存在性问题1. (2019武侯区二诊)如图,抛物线y=x2+(m+2)x+4的顶点C在x轴正半轴上,直线y=x+2与抛物线交于A,B两点(点A在点B的左侧).(1)求抛物线的函数表达式;(2)点P是抛物线上一点,若S△P AB=2S△ABC,求点P的坐标;(3)将直线AB上下平移,平移后的直线y=x+t与抛物线交于A′、B′两点(A′在B′的左侧),当以点A′、B′、(2)中第二象限的点P为顶点的三角形是直角三角形时,求t的值.类型四特殊四边形存在性问题1. (2019高新区二诊)如图,在同一直角坐标系中,抛物线C1:y=ax2-2x-3与抛物线C2:y=x2+mx +n关于y轴对称,C2与x轴交于A、B两点,其中点A在点B的左侧,交y轴于点D.(1)求A、B两点的坐标;(2)过抛物线C2:y=x2+mx+n在第三象限上的一点P,作PF⊥x轴于点F,交AD于点E,若E关于PD的对称点E′恰好落在y轴上,求P点的坐标;(3)在抛物线C1上是否存在一点G,在抛物线C2上是否存在一点Q,使得以A、B、G、Q四点为顶点的四边形是平行四边形?若存在,求出G、Q两点的坐标;若不存在,请说明理由.类型五相似三角形问题1.(2019金牛区一诊)如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.(1)求抛物线的解析式和顶点C的坐标;(2)连接AD、CD,若点E为抛物线上一动点(点E与顶点C不重合),当△ADE与△ACD面积相等时,求点E的坐标;(3)若点P为抛物线上一动点(点P与顶点C不重合),过点P向CD所在的直线作垂线,垂足为点Q,以P、C、Q为顶点的三角形与△ACH相似时,求点P的坐标.第1题图备用图参考答案类型一 线段数量关系/最值问题1. 解:(1)抛物线y =-18x 2+12x +4,令x =0,可得A 点的坐标为(0,4),令y =0,可得B 点的坐标为(-4,0),C 点的坐标为(8,0). 易得直线AB 的函数解析式为y =x +4, ∵OA =OB , ∴∠BAO =45°.又∵直线AD 由直线AB 逆时针旋转90°而来, ∴∠BAD =90°,∴∠OAD =45°,△OAD 为等腰直角三角形, ∴OD =OA =4,D (4,0),易得直线AD 的函数解析式为y =-x +4;(2)①如解图①,过点P 作PE ⊥x 轴交AD 于点E ,PF ⊥AD 于点F ,第1题解图①易得△PEF 为等腰直角三角形, ∴PF =22PE , ∴当PE 取得最大值时,PF 取得最大值, 设P (x ,-18x 2+12x +4),则E (x ,-x +4),∴PE =-18x 2+12x +4-(-x +4)=-18x 2+32x =-18(x -6)2+92,∴当x =6时,PE 有最大值92,此时PF 有最大值924,∴当x =6时,-18x 2+12x +4=52,∴当点P 到直线AD 的距离最大时,点P 的坐标为(6,52),最大距离为924;②如解图②,连接AP ,过点P 作PE ⊥x 轴,交AD 于点E ,PF ⊥AD 于点F ,当点P 到AD 的距离为524时,PF =524,则此时PE =2PF =52,将PE =52代入PE =-18(x -6)2+92中,解得x 1=10,x 2=2,∴此时点P 的坐标为(10,-72)或(2,92),当点P 的坐标为(2,92)时,AP =22+(92-4)2=172,∴sin ∠P AD =524172=53434;当点P 的坐标为(10,-72)时,AP =102+(-72-4)2=252,∴sin ∠P AD =PF AP =524252=210.综上,sin ∠P AD 的值是53434或210.第1题解图②2. 解:(1)∵B (4,c )在直线y =x +2上, ∴c =6,则B (4,6),∵A (12,52),B (4,6)在抛物线y =ax 2+bx +6上,∴⎩⎪⎨⎪⎧14a +12b +6=5216a +4b +6=6., 解得⎩⎪⎨⎪⎧a =2b =-8,故抛物线的解析式为y =2x 2-8x +6; (2)①存在.设点P 的坐标为(n ,n +2)(12<n <4),则点C 的坐标为(n ,2n 2-8n +6),∴PC =(n +2)-(2n 2-8n +6)=-2n 2+9n -4=-2(n -94)2+498.∵-2<0,12<n <4,∴当n =94时,线段PC 的长取得最大值498.② n 的值为5±212或17±1298.【解法提示】设P 的坐标为(n ,n +2),则点C 的坐标为(n ,2n 2-8n +6),易知抛物线与x 轴交点坐标为(1,0),(3,0),直线与x 轴交点坐标为(-2,0).(Ⅰ)若M 点为PC 的中点,此时n <-2或1<n <3,则PM =CM ,即n +2=-(2n 2-8n +6),整理得2n 2-7n +8=0,此方程没有实数解;(Ⅱ)若P 点为CM 的中点,此时,n >4或-2<n <12,则PM =PC ,CM =2PM ,即2n 2-8n +6=2(n +2),整理得n 2-5n +1=0,解得n 1=5+212,n 2=5-212,n 1,n 2均满足条件;(Ⅲ)若C 点为PM 的中点,此时12<n <1或3<n <4,则PC=CM ,PM =2CM ,即n +2=2(2n 2-8n +6),整理得4n 2-17n +10=0,解得n 1=17+1298,n 2=17-1298,n 1,n 2均满足条件.综上所述,n 的值为5±212或17±1298.类型二 面积数量关系/最值问题1. 解:(1)∵抛物线经过原点O , ∴设抛物线的解析式为y =ax 2+bx ,把点A (-4,0),B (4,8)代入,得⎩⎪⎨⎪⎧16a -4b =016a +4b =8,解得⎩⎪⎨⎪⎧a =14b =1,∴抛物线的解析式为y =14x 2+x ;(2)联立⎩⎪⎨⎪⎧y =14x 2+xy =kx +4,消去y ,得14x 2+(1-k )x -4=0,∴x 1+x 2=4(k -1),x 1x 2=-16,∵1x 2-1x 1=22, ∴(x 1+x 2)2-4x 1x 2(x 1x 2)2=12, 即16(k -1)2+64256=12, 解得k =3或k =-1,经检验都符合题意,∴k 的值为3或-1;(3)∵OB ∥PC ,S △POC ∶S △BOC =1∶2,∴PC ∶OB =1∶2,∵B (4,8),∴OB =45,直线OB 的解析式为y =2x ,∴PC =25,设点P 的坐标为(a ,14a 2+a )(-4<a <0),直线PC 的解析式为y =2x +t , 把P (a ,14a 2+a )代入y =2x +t ,整理得t =14a 2-a , ∴直线PC 的解析式为y =2x +14a 2-a , 易得直线AB 的解析式为y =x +4,联立⎩⎪⎨⎪⎧y =x +4y =2x +14a 2-a , 解得x =4+a -14a 2, ∴PC =5(x C -x P )=5×(4+a -14a 2-a )=25, 解得a =22(舍去)或a =-22,将a =-22代入抛物线的解析式,得y =14×(-22)2-22=2-22, ∴点P 的坐标为(-22,2-22).2. 解:(1)把点A (9,-6)代入y =mx +3中,得m =-1,∴直线的函数表达式为y =-x +3;∵抛物线的顶点C 的坐标是(4,-11)且过点A (9,-6),设抛物线的函数表达式为y =a (x -4)2-11,∴a (9-4)2-11=-6,解得a =15,∴抛物线的函数表达式为y =15(x -4)2-11=15x 2-85x -395; (2)设点D 的横坐标为n .∵抛物线对称轴为直线x =4,∴分两种情况讨论①当0<n <4时,如解图①,过点D 作x 轴的垂线交直线AB 于点E ,则D (n ,15n 2-85n -395),E (n ,-n +3), ∴DE =-n +3-(15n 2-85n -395)=-15n 2+35n +545, ∴S △ABD =S △BDE +S △ADE =12DE ·(x E -x B )+12DE ·(x A -x E ) =12DE ·(x A -x B )=12(-15n 2+35n +545)×9=812, 解得n 1=3-352(不合题意,舍去),n 2=3+352(不合题意,舍去);第2题解图①②当n <0时,如解图②,过点D 作x 轴的垂线交直线AB 于点E ,S △ABD =S △ADE -S △BDE =12DE ·(x A -x E )-12DE ·(x B -x E )=12DE ·(x A -x B )=12(-15n 2+35n +545)×9=812, 解得n 1=3-352,n 2=3+352(不合题意,舍去). 当n =3-352时,y =15×(3-352)2-85×3-352-395=35-152. ∴D (3-352,35-152);第2题解图②(3)在y 轴上存在一点P ,使∠APC =45°,如解图③,分别过点C 、A 作y 轴、x 轴的平行线,两线交于点G ,则∠CGA =90°,∵A 、C 的坐标分别为(9,-6),(4,-11),∴点G 的坐标为(4,-6).∴GA =GC =5.作以G 为圆心,GA 的长度为半径的圆,交y 轴于点P ,P ′,连接AP 、CP 、AP ′、P ′C ,此时∠APC =∠AP ′C =12∠CGA =45°, ∴GP =5.设点P 的坐标为(0,k ),过点G 作GH ⊥y 轴于点H ,则H (0,-6).在Rt △PGH 中,PH 2+HG 2=PG 2,即(k +6)2+42=52,解得k 1=-3,k 2=-9,∴P (0,-3),P ′(0,-9).第2题解图③类型三 特殊三角形存在性问题1. 解:(1)∵抛物线的顶点C 在x 轴的正半轴上,∴4ac -b 24a =16-(m +2)24=0, 解得m =2或-6,∵顶点在x 轴正半轴上,∴-m +22>0.解得m <-2, ∴m =-6,∴抛物线的函数表达式为y =x 2-4x +4;(2)如解图①,过点C 作抛物线的对称轴,交直线AB 于点D ,由y =x 2-4x +4得抛物线的对称轴是直线x =2,则D (2,4),DC =4.在点D 上方的抛物线的对称轴上取一点E ,使DE =2DC ,则E (2,12).连接AE ,BE ,则S △ABE =2S △ABC .过点E (2,12)作直线AB 的平行线交抛物线于点P 1,P 2,此时满足S △P AB =S △ABE =2S △ABC .设直线P 1P 2的函数表达式为y =x +k ,∵点E (2,12)在直线P 1P 2上,∴2+k =12,∴k =10.∴直线P 1P 2的函数表达式为y =x +10.联立⎩⎪⎨⎪⎧y =x +10y =x 2-4x +4, 解得⎩⎪⎨⎪⎧x 1=-1y 1=9或⎩⎪⎨⎪⎧x 2=6y 2=16, 综上所述,满足条件的点P 的坐标为(-1,9),(6,16);第1题解图①(3)设A ′(x 1,y 1),B ′(x 2,y 2),显然,∠P A ′B ′≠90°.①如解图②,当∠A ′B ′P =90°时,过点B ′作直线MN ∥y 轴,A ′M ⊥MN 于点M ,PN ⊥MN 于点N , ∵直线A ′B ′的解析式是y =x +t ,∴∠B ′A ′M =45°,∴△A ′B ′M 和△PB ′N 都是等腰直角三角形,∴PN =NB ′,∴x 2+1=9-y 2,即x 2+y 2=8,联立⎩⎪⎨⎪⎧x 2+y 2=8y 2=x 2+t , 解得⎩⎨⎧x 2=4-12ty 2=4+12t , 将点(4-12t ,4+12t )代入抛物线的函数表达式,得4+12t =(4-12t )2-4×(4-12t )+4. 解得 t 1=0,t 2=10(此时点A ′与点P 重合,舍去);第1题解图②如解图③,若∠A′PB′=90°,过点P作EF∥y轴,A′E⊥EF于E,B′F⊥EF于点F,则△A′EP∽△PFB′,∴A′EPE=PFB′F.∴x1+19-y1=y2-9x2+1.∴x1x2+(x1+x2)+1=9(y1+y2)-y1y2-81,令x2-4x+4=x+t,即x2-5x+4-t=0,则x1+x2=5,x1x2=4-t,y1+y2=(x1+t)+(x2+t)=x1+x2+2t=5+2t,y1y2=(x1+t)(x2+t)=x1x2+t(x1+x2)+t2=t2+4t+4,∴(4-t)+5+1=9(5+2t)-(t2+4t+4)-81,整理得t2-15t+50=0,解得t1=5,t2=10(此时A′与P重合,舍去),综上,t的值为0或5.第1题解图③类型四特殊四边形存在性问题1. 解:(1)∵C1、C2关于y轴对称,∴C1与C2的交点一定在y轴上,且C1与C2的形状,大小均相同,∴a=1,n=-3,∴C1的对称轴为直线x=1,∴C2的对称轴为直线x=-1,∴m=2,∴C 1的函数表达式为y =x 2-2x -3,C 2的函数表达式为y =x 2+2x -3=0,在C 2的函数表达式y =x 2+2x -3中,当y =0可得x 2+2x -3=0,解得x =-3或x =1,∴A (-3,0),B (1,0);(2)根据题意可得点D 的坐标为(0,-3),设直线AD 的表达式为y =kx +b .把(0,-3)和(-3,0)代入到y =kx +b 中得⎩⎪⎨⎪⎧b =-3-3k +b =0, 解得⎩⎪⎨⎪⎧b =-3k =-1, ∴直线AD 的表达式为y =-x -3,设P (a ,a 2+2a -3),则E (a ,-a -3),则PE =-a -3-(a 2+2a -3)=-a 2-3a ,根据对称可得四边形PEDE ′是菱形,则DE ′=PE =-a 2-3a , 如解图,过点P 作PG ⊥y 轴于点G ,∵ED ∥PE ′,ED 所在直线斜率k =-1∴∠E ′=∠AEF =45°,GE ′=-a ,PG =GE ′.在Rt △PGE ′中,根据勾股定理得:PE ′=-2a ,根据菱形性质可得:PE ′=DE ′, ∴-2a =-a 2-3a ,解得a =2-3,∴P (2-3,2-42);第1题解图(3)存在.∵AB 的中点为(-1,0),且点G 在抛物线C 1上,点Q 在抛物线C 2上,∴AB 只能为平行四边形的一边,∴GQ ∥AB 且GQ =AB ,由(1)可知AB =1-(-3)=4,∴GQ =4,设G (t ,t 2-2t -3),则Q (t +4,t 2-2t -3)或(t -4,t 2-2t -3),①当Q (t +4,t 2-2t -3)时,则t 2-2t -3=(t +4)2+2(t +4)-3,解得t =-2,∴t 2-2t -3=4+4-3=5,∴G (-2,5),Q (2,5);②当Q (t -4,t 2-2t -3)时,则t 2-2t -3=(t -4)2+2(t -4)-3,解得t =2,∴t 2-2t -3=4-4-3=-3,∴G (2,-3),Q (-2,-3),综上可知,存在满足条件的点G 、Q ,其坐标为G (-2,5),Q (2,5)或G (2,-3),Q (-2,-3).类型五 相似三角形问题1. 解:(1)把点A 、B 、D 的坐标分别代入抛物线的解析式中得:⎩⎪⎨⎪⎧a +b +c =09a -3b +c =0c =3,解得⎩⎪⎨⎪⎧a =-1b =-2c =3,∴抛物线的解析式为y =-x 2-2x +3,∴抛物线的对称轴为直线x =-b 2a=-1, ∴点C 的坐标为(-1,4);(2)如解图①,过点C 作CE ∥AD 交抛物线于点E ,交y 轴于点T ,则△ADE 与△ACD 面积相等,直线AD 过点D ,设其解析式为y =mx +3,将点A 的坐标代入得:0=-3m +3,解得m =1,则直线AD 的解析式为y =x +3,∵CE ∥AD ,设直线CE 的解析式为y =x +n ,将点C 的坐标代入上式得:4=-1+n ,解得n =5,则直线CE 的解析式为y =x +5,则点T 的坐标为(0,5),联立⎩⎪⎨⎪⎧y =-x 2-2x +3y =x +5, 解得x =-1或x =-2(x =-1为点C 的横坐标),即点E 的坐标为(-2,3);在y 轴取一点H ′,使DT =DH ′=2,过点H ′作直线E ′E ″∥AD ,则△ADE ′和△ADE ″都与△ACD 面积相等,同理可得直线E ′E ″的解析式为y =x +1,联立⎩⎪⎨⎪⎧y =-x 2-2x +3y =x +1, 解得x =-3±172, ∴点E ″、E ′的坐标分别为(-3+172,-1+172)、(-3-172,-1-172), 综上,满足要求的点E 的坐标为(-2,3)或(-3+172,-1+172)或(-3-172,-1-172);第1题解图①(3)如解图②,设点P 的坐标为(m ,n ),则n =-m 2-2m +3,把点C 、D 的坐标代入一次函数的解析式y =kx +b 得:⎩⎪⎨⎪⎧4=-k +b b =3, 解得⎩⎪⎨⎪⎧k =-1b =3, 即直线CD 的解析式为y =-x +3,由(1)得,直线AD 的解析式为y =x +3,∴AD ⊥CD ,而直线PQ ⊥CD ,故直线PQ 的解析式中的k 值与直线AD 的解析式中的k 值相同, 同理可得直线PQ 的解析式为y =x +(n -m ),联立⎩⎪⎨⎪⎧y =-x +3y =x +(n -m ), 解得x =3+m -n 2, 即点Q 的坐标为(3+m -n 2,3-m +n 2), 则PQ 2=(m -3+m -n 2)2+(n -3-m +n 2)2=(m +n -3)22=12(m +1)2·m 2, 同理可得:PC 2=(m +1)2[1+(m +1)2],AH =2,CH =4,则AC =25, 当△ACH ∽△CPQ 时,PC PQ =AC CH =52,即4PC 2=5PQ 2,整理得3m 2+16m +16=0,解得m =-4或m =-43, ∴点P 的坐标为(-4,-5)或(-43,359); 当△ACH ∽△PCQ 时,同理可得,点P 的坐标为(-23,359)或(2,-5), 综上所述,点P 的坐标为(-4,-5)或(-43,359)或(-23,359)或(2,-5).。
二次函数综合压轴题

二次函数综合压轴题一、题目描述给定二次函数y=ax2+bx+c,其中a eq0,试回答以下问题:1.当a>0时,二次函数的图像开口向上还是向下?2.当a<0时,二次函数的图像开口向上还是向下?3.求二次函数的顶点坐标,并判断顶点是函数的最大值还是最小值。
4.求二次函数的对称轴方程。
二、问题解答1. 当 a>0 时,二次函数的图像开口向上还是向下?当a>0时,二次函数的图像开口向上。
这是因为二次函数的开口方向与二次系数 a 的正负有关系。
2. 当 a<0 时,二次函数的图像开口向上还是向下?当a<0时,二次函数的图像开口向下。
和前一问的解释类似,当二次系数 a为负数时,二次函数的图像将向下方向打开。
3. 求二次函数的顶点坐标,并判断顶点是函数的最大值还是最小值。
二次函数的顶点坐标可以通过求解顶点的横坐标公式 $x=-\\frac{b}{2a}$ 和代入得出的y坐标来求得。
顶点坐标即为二次函数的最值点。
考虑二次函数y=ax2+bx+c,代入公式可得 $x=-\\frac{b}{2a}$。
将 x 的值代入原方程,即可求得对应的 y 值。
若 a>0,则二次函数的图像开口向上,顶点为函数的最小值;若 a<0,则二次函数的图像开口向下,顶点为函数的最大值。
4. 求二次函数的对称轴方程。
二次函数的对称轴是过顶点的垂直线。
对称轴方程可以通过将顶点的横坐标公式 $x=-\\frac{b}{2a}$ 代入直线方程的一般形式 $x=\\frac{b}{2a}$ 得到。
对称轴方程为 $x=\\frac{b}{2a}$。
三、总结本文简要介绍了二次函数的相关概念和性质,通过回答一系列问题对其进行了深入探讨。
我们得知,当二次系数 a 的正负不同时,二次函数的图像开口方向、顶点的性质和对称轴方程都会有所不同。
希望通过本文的解答,能够对二次函数的相关问题有更深入的理解。
2024年 九年级数学中考复习 二次函数与图形面积综合压轴题 专题训练(含答案)

(1)求抛物线的解析式;(2)当点P在直线AD上方时,求2.已知二次函数y=ax2线的顶点为D.(1)求此二次函数解析式;(2)连接DC、BC、DB,判断(3)在对称轴右侧抛物线上找一点出点P的坐标及此时四边形(1)求抛物线的解析式及其对称轴;(2)点D、E是直线x=1上的两个动点,且DE=1,点D 周长的最小值.(3)点P为抛物线上一点,连接CP,直线CP把四边形CBPA 的坐标.(1)求这个二次函数的表达式.(2)连接PO、PC,并把边形POP′C为菱形?若存在,请求出此时点(1)求抛物线的解析式;(2)点P为抛物线对称轴上一动点,(3)在(2)条件下,是否存在点出点M的横坐标;若不存在,请说明理由.(1)求抛物线的解析式;(2)设点P的横坐标是x,△(1)求抛物线的解析式;(2)在抛物线上是否存在点M,使∠ABC=∠BCM,如果存在,求在,说明理由;(3)若D是抛物线第二象限上一动点,过点D作DF⊥x轴于点交于E点,求△ABE的面积.(1)求该抛物线的解析式;(2)如图1,若线段DE将△AOC分成面积比为1:3两部分,,求点(3)如图2,连接OP,是否存在点P,使得∠OPD=2∠CAO,若存在,若不存在,请说明理由.(1)求直线BC的表达式.(2)点E是直线BC下方抛物线上一动点,当△BCE的面积最大时,求点(1)请直接写出点A,B,C的坐标;(2)点P(m,n)(0<m<6)在抛物线上,当m取何值时,△PBC面积的最大值.(3)点F是抛物线上的动点,作FE∥AC交x轴于点E,是否存在点为顶点的四边形是平行四边形?若存在,请写出所有符合条件的点请说明理由.(1)求该抛物线的解析式及对称轴;(2)若过点B的直线与抛物线相交于另一点D,当∠ABD=∠BAC(3)在(2)的条件下,当点D在x轴下方时,连接AD,此时在S△ABD,请直接写出所有符合条件的点P的坐标.点P,使S△BDP=23(1)求抛物线的解析式.(2)将△AOC沿AB方向平移到△PMN.①如图2,若PM经过点C,PN与x轴交于点Q,求S△PCQ的值.S△AOC②如图3,直线y=1x与抛物线AB段交于点D,与直线AB交于点E,当顶点2上移动时,求△MPN与△OBD公共部分面积的最大值.13.如图,已知抛物线y=ax2+bx+c经过点A(−3,0),C(0,4)两点,且与x轴的另一个交点为B,对称轴为直线x=−1.(1)求抛物线的表达式;(2)已知点M是抛物线对称轴上一点,当△MBC的周长最小时,求M点的坐标.(3)D是第二象限内抛物线上的动点,设点D的横坐标为m,求四边形ABCD面积S的最大值及此时D点的坐标;(4)若点P在抛物线对称轴上,是否存在点P,使以点B,C,P为顶点的三角形是等腰三角形?若存在,请求出P点的坐标;若不存在,请说明理由.14.如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(−1,0),B(4,0),C(0,4)三点.(1)求抛物线的解析式及顶点D的坐标:(2)在抛物线的对称轴上探求一点M的坐标,使得点M到点A、点C的距离之和最小;(3)在直线BC上方的抛物线上探求一点P,使得△PBC的面积最大,并求出△PBC的面积的最大值.(1)求该抛物线的函数解析式;(2)点P(m,n)(0<m<6)在抛物线上,当m取何值时,△PBC面积的最大值;(3)在(2)中△PBC面积取最大值的条件下,点M是抛物线对称轴上的一点,在抛物线上确定一点N,使得以A P M N为顶点的四边形是平行四边形,请直接写出所有符及此时点F的坐标.17.如图抛物线y=ax2+bx+c经过点A(−1,0),点C(0,3),且OB=OC.(1)求抛物线的解析式及其对称轴;(2)点D、E是直线x=1上的两个动点,且DE=1,点D在点E的上方,求四边形ACDE的周长的最小值;(3)点P为抛物线上一点,连接CP,直线CP把四边形CBPA的面积分为3:5两部分,求点P 的坐标.18.如图,在平面直角坐标系中,抛物线y=x2+bx+c经过A(−1,0)、C(0,−3)两点,且与x轴交于另一点B(点B在点A右侧).(1)求抛物线的解析式;(2)若点M是线段BC上一动点,过点M的直线ED平行y轴交x轴于点D,交抛物线于点E,求△BCE面积的最大值及此时点M的坐标;(3)在(2)的条件下:当△BCE的面积取得最大值时,在x轴上是否存在这样的点P,使得以点M,B,P为顶点的三角形是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.19.如图,抛物线y=ax2+bx−6与x轴交于A(−2,0),B(6,0),交y轴于点C,点P是线段BC下方抛物线上一动点,过点P作PQ∥AC交BC于点Q,连接AQ,OQ,PA,PB.(1)求抛物线的函数解析式;(2)求△AOQ周长的最小值;(3)假设△PAQ与△PBQ的面积分别为S1,S2,且S=S1+S2,求S的最大值.20.如图1,抛物线y=x2+bx+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.(1)求抛物线的解析式;(2)若点M是抛物线上的动点,当A、C两点到直线BM的距离相等时,求直线BM的解析式;(3)已知点D、F在抛物线上,点D的横坐标为m(−3<m<−1),点F的横坐标为m+1.过点D作x轴的垂线交直线AC于点M,过点F作x轴的垂线交直线AC于点N.①如图2,连接DF,求四边形DFNM面积的最大值及此时点D的坐标;②如图3连接AD和FC,试探究△ADM与△CFN的面积之和是否为定值吗?若是,请求出来;若不是,请说明理由.参考答案把A,D的坐标代入得{−k+3k+所以直线AD的解析式为y=过点P作x轴的垂线,分别交∵P、D、C构成以PC为底边的等腰三角形,∴点D在PC的垂直平分线上,∴点C与点P关于对称轴直线x=∵C(0,3)∴点P的坐标为(2,3),∵S=S△DCP+S△CBP,四边形PBCD11∴A′C′=32+22=13,∴CD+AE=A′D+DC′,则当A′小,四边形ACDE的周长的最小值= =10+1+A′D+DC′=10+1+A′C′10+1+13;直线CP把四边形CBPA的面积分为又∵S△PCB:S△PCA=12EB则BE:AE=3:5或5:3,则AE=52或32,即:点E的坐标为(32,0)或((3)过点P作PQ∥y轴交BC于点∴PF⊥y轴,∵二次函数y=x2−2x−3的图像与当y=0时,得y=x2−2x−3=5.解:(1)根据题意,得{0=−(−1)2−b+c0=−32+3b+c,解得{b=2c=3,∴抛物线解析式为:y=∴∠OPH=∠POH=45°,∴OH=PH,设M(m,−m2+2m+3),则设直线BC的解析式为:y {0=3k+b3=b,解得{k=−1b=3,∴直线BC的解析式为:y∴PQ =−16x 2+56x +4−(−12x +4∴y =12×BO ×PQ =12×(−16x 2+即y =−23x 2+163x(3)解:y=0时,12x2−x−4解得x1=−2,x2=4,∴A(−2,0),故AB=4−(−2)记过点A、B、D的圆的圆心为点则点G在线段AB的垂直平分线上,故可设同理,点G在线段DE的垂直平分线上,8.(1)解:∵抛物线y=∴{0=16a−4b+20=a+b+2,设点M的坐标为(n,0),则OM=−n,MC 在Rt△MOC中,∵OM2+OC2=MC2,∴(−n)2+22=(n+4)2,解得n=−32,∴M(−3,0),∴OC OM =ODPD,即OC⋅PD=OM⋅OD,设P(t,−12t2−32t+2)(−4<t<0),∴2(−12t2−32t+2)=32(−t),设点E的坐标为(∴EF=2m−4−(233由(1)知B(6,0),∴OB=6∴−1+5 22=a+32,解得∴点P的坐标为(−②当AP为平行四边形的对角线时,如图.∴−1+a2=3+522,解得∴点P的坐标为③当AM为平行四边形的对角线时,如图.∴−1+32=a+522,解得∴点P的坐标为(−综上,点P的坐标为设直线BC为y=kx+b({0=6k+bb=−6,解得{k=1b=−6,∴直线BC为y=x−6,根据三角形的面积,当平行于直线此时,△PBC的面积最大,设F(a,12a2−2a−6).当点F在x轴下方时,∵C(0,−6),即OC=6,a2−2a−6=−6,∴12解得a1=0(舍去),a2=4,∴F(4,−6).当点F在x轴的上方时,令y=6,设BD与AC的交点为点E,∵∠ABD=∠BAC,∴AE=BE,∵直线x=−1垂直平分AB,∴点E在直线x=−1上,∵∠ABD=∠BAC,∴BD∥AC,∵直线AC的解析式为y=34x+3∴可设直线BD的解析式为y=把B(2,0)代入y=34x+m中得0∴符合题意的直线解析式为y=∴F (m,34m−32),∴PF =|−38m 2−34m +3−(34m−∴S △BDP =12PF ⋅(x B −x D )=12×∴|−38m 2−32m +92|=3,∴−38m 2−32m +92=3或−38m 2−32m ∴m 2+4m−4=0或m 2+4m−20②当4≤a≤6时,S=S△PEF=12EF⋅PF=12(a−32a+3)(−a+=14a2−3a+913.解:(1)∵抛物线(3)过点D 作DG ⊥x 轴交设点D 的横坐标为m ,∴D (m,−43m 2−83m +4),∴DF =−43m 2−83m +4−(∵四边形ABCD 的面积=∴S △ADC =12×AG ×DF +(4)存在,理由如下:14.(1)解:由题意,设该抛物线的解析式为将C(0,4)代入,得4=−4a∴该二次函数的解析式为∵y=−x2+3x+4=−(∴顶点坐标为D(32,254);(2)解:∵该抛物线的对称轴为直线故直线BC与坐标轴的交点即为点设直线BC的解析式为:将B(6,0),C(0,−6)解得:{b=−6k=1,∴直线BC的解析式为:∴M (−1,−1),EM =6,设F (m ,m 2−4m ),则N (m ∴FN =m−(m 2−4m )=−m ∵S 1=12FN (x B −x G ),S 2=∴S 1S 2=FNEM =−m 2+5m6=−16(m ∴当m =52时,S 1S 2的最大值为由(2)得,当ME最大时,∴DO=DB=DM=3 2∵∠BDM=90°,x2−2x−6交y轴于点∵抛物线y=12∴C(0,−6)∴OB=OC=6,∠BOC=90°∴∠BCO=45°∵O、O′关于直线BC对称∴BC与OO′互相垂直平分∴四边形BOCO′是正方形,∵PQ∥AC。
二次函数与图像压轴题及参考答案

二次函数与图像1、如图,在平面直角坐标系中,开口向上的抛物线与x 轴交于A B 、两点,D 为抛物线的顶点,O 为坐标原点.若OA OB OA OB <、()的长分别是方程2430x x -+=的两根,且45DAB ∠=°.(1)求抛物线对应的二次函数解析式;(2)过点A 作AC AD ⊥交抛物线于点C ,求点C 的坐标; (3)在(2)的条件下,过点A 任作直线l 交线段CD 于点P ,求C D 、到直线l 的距离分别为12d d 、,试求12d d +的最大值.2、如图所示,已知抛物线21y x =-与x 轴交于A 、B 两点,与y 轴交于点C .(1)求A 、B 、C 三点的坐标.(2)过点A 作AP ∥CB 交抛物线于点P ,求四边形ACBP 的面积.(3)在x 轴上方的抛物线上是否存在一点M ,过M 作MG ⊥x 轴于点G ,使以A 、M 、G三点为顶点的三角形与∆PCA 相似.若存在,请求出M 点的坐标;否则,请说明理由.3、已知抛物线)0(2≠++=a c bx ax y 与x 轴交于不同的两点A (x 1,0)和B (x 2,0),与y 轴的正半轴交于点C 。
如果21x x 、 是方程062=--x x 的两个根(21x x <),且△ABC 的面积为215。
(1)求此抛物线的解析式;(2)求直线AC 和BC 的解析式;(3)如果P 是线段AC 上的一个动点(不与点A 、C 重合),过点P 作直线m y =(m 为常数),与直线BC 交于点Q ,则在x 轴上是否存在点R ,使得以PQ 为一腰的△PQR 为等腰直角三角形?若存在,求出点R 的坐标;若不存在,请说明理由。
4.如图,抛物线y= –12x 2+bx +c 与x 轴分别相交于点A (–2,0)、B (4,0),与y 轴交于点C ,顶点为点P .(1)求抛物线的解析式;(2)动点M 、N 从点O 同时出发,都以每秒1个单位长度的速度分别在线段OB 、OC 上向点B 、C 方向运动,过点M 作x 轴的垂线交BC 于点F ,交抛物线于点H . ①当四边形OMHN 为矩形时,求点H 的坐标;②是否存在这样的点F ,使△PFB 为直角三角形?若存在,求出点F 的坐标;若不存在,请说明理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数图形变换综合压轴题
1、在平面直角坐标系xoy中,抛物线y=mx2-2mx-3(m≠0)与x轴交于A(3,0),B两点.
(1)求抛物线的表达式及点B的坐标.
(2)当-2<x<3时的函数图像记为G,求此时函数y的取值范围.
(3)在(2)的条件下,将图像G在x轴上方的部分沿x轴翻折,图像G的其余部分保持不变,得到一个新图像M.若经点C(4,2)的直线y=kx+b(k≠0)与图像M在第三象限内有两个公共过点,结合图像求b的取值范围.
2、已知关于x 的一元二次方程0132=-+-k x x 有实数根,k 为正整数.
(1)求k 的值;
(2)当此方程有两个不为0的整数根时,将关于x 的二次函数132-+-=k x x y 的图象向下平移2个单
位,求平移后的函数图象的解析式;
(3)在(2)的条件下,将平移后的二次函数图象位于y 轴左侧的部分沿x 轴翻折,图象的其余部分保
持不变,得到一个新的图象G .当直线5y x b =+与图象G 有3个公共点时,请你直接写出b 的取值范围.
3、已知:抛物线C1:y=ax +4ax+4a-5的顶点为P,与x 轴相交于A,B 两点(点A 在点B 的左边),点B 的横坐标是1
(1)求抛物线的解析式和顶点坐标;
(2)将抛物线沿x 轴翻折,再向右平移,平移后的抛物线C2的顶点为M ,当点P ,M 关于点B 成中心对称时,求平移后的抛物线C2的解析式;
(3)直线y=-5
3x+m 与抛物线C1,C2的对称轴分别交于点E,F ,设由点E ,P ,F ,M 构成的四边形的面积为S ,试用含m 的代数式表示S 。
4、将抛物线沿c1:y=-x2+沿x轴翻折,得拋物线c2,如图所示.
(1)请直接写出拋物线c2的表达式.
(2)现将拋物线C1向左平移m个单位长度,平移后得到的新抛物线的顶点为M,与x轴的交点从左到右依次为A,B;将抛物线C2向右也平移m个单位长度,平移后得到的新抛物线的顶点为N,与x轴交点从左到右依次为D,E.
①当B,D是线段AE的三等分点时,求m的值;
②在平移过程中,是否存在以点A,N,E,M为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由.
5、将抛物线沿c1:y=-x2+沿x轴翻折,得拋物线c2,如图所示.
(1)请直接写出拋物线c2的表达式.
(2)现将拋物线C1向左平移m个单位长度,平移后得到的新抛物线的顶点为M,与x轴的交点从左到右依次为A,B;将抛物线C2向右也平移m个单位长度,平移后得到的新抛物线的顶点为N,与x轴交点从左到右依次为D,E.
①当B,D是线段AE的三等分点时,求m的值;
②在平移过程中,是否存在以点A,N,E,M为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由.。
