规律探索型
专题06 整式中规律探索的三种考法(解析版)-2024年常考压轴题攻略(7年级上册人教版)

专题06整式中规律探索的三种考法类型一、单项式规律性问题例.如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点.若青蛙从数1这点开始跳,第1次跳到数3那个点,如此,则经2015次跳后它停的点所对应的数为()A.5B.3C.2D.1【答案】C【分析】先根据题意,求出前几次跳到的点的位置,发现这是一个循环,按照3、5、2、1成一个循环,再用解循环问题的方法求解.【详解】解:按照题意,第一次在1这个点,下一次就跳到3,再下一次跳到5,再下一次跳到2,2是偶数了,就逆时针跳一个点,又回到了1这个点,发现这是一个循环,3、5、2、1是一个循环,÷ ,20154=5033∴最后到2这个点.故选:C.【点睛】本题考查找规律,解题的关键是通过前几个数发现这是一个循环问题,利用解循环问题的方法求解.【变式训练1】按上面数表的规律.得下面的三角形数表:【点睛】本题考查了数字的变化类,找出数字的变化规律是解题的关键.类型三、图形类规律探索例.根小棒,搭2020个这样的小正方形需要小棒()根.A.8080B.6066C.6061D.6060【答案】C【分析】通过归纳与总结得出规律:每增加1个正方形,火柴棒的数量增加3根,由此求出第n个图形时需要火柴的根数的代数式,然后代入求值即可.【详解】解:搭2个正方形需要4+3×1=7根火柴棒;搭3个正方形需要4+3×2=10根火柴棒;搭n个这样的正方形需要4+3(n﹣1)=3n+1根火柴棒;∴搭2020个这样的正方形需要3×2020+1=6061根火柴棒;故选C.【点睛】本题考查了图形规律型:图形的变化.解题的关键是发现各个图形的联系,找出其中的规律,有一定难度,要细心观察总结.【变式训练1】下列每一个图形都是由一些同样大小的三角形按一定的规律排列组成的,其中第①个图形中有5个小三角形,第②个图形中有10个小三角形,第③个图形中有16个小三角形,按此规律,则第⑨个图中小三角形的个数是()A.69B.73C.77D.83【答案】B【分析】根据已知图形得出第⑨个图形中三角形的个数的特点,据此可得答案.【详解】解:∵第①个图形中三角形的个数5=1+2×(1-1),第②个图形中三角形的个数10=5+2×1+3,第③个图形中三角形的个数16=5+2×2+3+4,第④个图形中三角形的个数23=5+2×3+3+4+5,第⑤个图形中三角形的个数31=5+2×4+3+4+5+6,……【答案】57【分析】根据每个图形增加三角形的个数,找到规律即可.【详解】解:第1个图形中一共有1个三角形,第2个图形中一共有1+4=5个三角形,第3个图形中一共有1+4+4=9个三角形,…,第n个图形中三角形的个数是1+4(n﹣1)=(4n﹣3)个,当n=15时,4n﹣3=4×15﹣3=57.故答案为:57.【点睛】本题考查了图形的变化规律,解题关键是通过图形数量的变化发现规律,并应用规律解决问题.课后训练20192020)a a -。
初中数学中规律探索型问题的类型与解题方法

初中数学中规律探索型问题的类型与解题方法关键词:初中数学规律探索型问题类型解题方法
规律探索型问题是中考中的必考知识点,我们把规律探索型问题也称为归纳猜想型问题,其特点是这样的:给出一组具有某种特定关系的数、式、图形;或是给出与图形有关的操作变化过程;或是给出某一具体的问题情境,要求通过观察分析推理,探究其中蕴含的规律,进而归纳或猜想出一般性的结论.规律探索型问题包括三类问题:数字类规律探索问题、图形类规律探索问题、点的坐标类规律探索问题.
一、数字类规律探索问题
1.解题思路
解答数字类规律探索问题,应在读懂题意、领会问题实质的前提下进行,或分类归纳,或整体归纳,得出的规律要具有一般性,而不是一些只适合于部分数据的“规律”.
2.例题展示
3.例题分析
二、图形类规律探索问题
1.解题思路
解答图形类规律探索问题,要注意分析图形特征和图形变换规律,一要合理猜想,二要加以实际验证.
2.例题展示
3.例题分析
针对几何图形的规律探索题,首先要仔细观察、分析图形,从中发现图形的变化特点,再将图形的变化以数或式的形式表示出来,从而得出图形的变化规律.如果图形的变化具有周期性,就要先确定循环周期及一个循环周期内图形的变化特点,然后用所求总数除以循环周期,得到余数,进而使所求问题得以解决.
本题就是一个典型的规律性问题,由AB为边长为2的等边三角形ABC的高,利用三线合一得到B为BC的中点,求出BB的长,利用勾股定理求出AB的长,进而求出S,同理求出S,依此类推,得到S.。
中考数学重难点突破专题一:规律探索型问题试题(含答案)

精品基础教育教学资料,仅供参考,需要可下载使用!专题一 规律探索问题类型1 数字规律1.甲、乙、丙三位同学进行报数游戏,游戏规则为:甲报1,乙报2,丙报3,再甲报4,乙报5,丙报6,…依次循环反复下去,当报出的数为2020时游戏结束,若报出的数是偶数,则该同学得1分.当报数结束时甲同学的得分是__337__分.解析:甲报的数中第一个数为1,第2个数为1+3=4,第3个数为1+3×2=7,第4个数为1+3×3=10,…,第n 个数为1+3(n -1)=3n -2,3n -2=2020,则n =674,甲报出了674个数,一奇一偶,所以偶数有674÷2=337个,得337分.2.如图,给正五边形的顶点依次编号为1,2,3,4,5,若从某一顶点开始,沿五边形的边顺时针行走,顶点编号是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第10次“移位”,则他所处顶点的编号为__3__.3.(2017·六盘水)计算1+4+9+16+25+…的前29项的和是__8555__.解析:12+22+32+42+52+…+292+…+n 2=0×1+1+1×2+2+2×3+3+3×4+4+4×5+5+…(n -1)n +n=(1+2+3+4+5+…+n)+[0×1+1×2+2×3+3×4+…+(n -1)n]=n (n +1)2+{13(1×2×3-0×1×2)+13(2×3×4-1×2×3)+13(3×4×5-2×3×4)+…+13[(n -1)·n·(n +1)-(n -2)·(n -1)·n]}=n (n +1)2+13[(n -1)·n·(n +1)]=n (n +1)(2n +1)6, ∴当n =29时,原式=29×(29+1)×(2×29+1)6=8555. 类型2 图形规律4.(2017·天水)观察下列的“蜂窝图”则第n 个图案中的“”的个数是__3n +1__.(用含有n 的代数式表示)5.(2017·临沂)将一些相同的“○“按如图所示摆放,观察每个图形中的“○“的个数,若第n 个图形中“○“的个数是78,则n 的值是( B )A .11B .12C .13D .14解:第1个图形有1个小圆;第2个图形有1+2=3个小圆;第3个图形有1+2+3=6个小圆;第4个图形有1+2+3+4=10个小圆;第n 个图形有1+2+3+…+n =n (n +1)2个小圆;∵第n 个图形中“○“的个数是78,∴78=n (n +1)2,解得:n 1=12,n 2=-13(不合题意舍去).6.(2017·德州)观察下列图形,它是把一个三角形分别连接这个三角形三边的中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,…将这种做法继续下去(如图2,图3…),则图6中挖去三角形的个数为( C )A .121B .362C .364D .729解:图1挖去中间的1个小三角形,图2挖去中间的(1+3)个小三角形,图3挖去中间的(1+3+32)个小三角形,…则图6挖去中间的(1+3+32+33+34+35)个小三角形,即图6挖去中间的364个小三角形,类型3 坐标变化规律7.在平面直角坐标系中,对于平面内任一点(a ,b),若规定以下三种变换:①△(a ,b)=(-a ,b);②○(a ,b)=(-a ,-b);③Ω(a ,b)=(a ,-b),按照以上变换例如:△(○(1,2))=(1,-2),则○(Ω(3,4))等于__(-3,4)__.8.(2017·衢州)如图,正△ABO 的边长为2,O 为坐标原点,A 在x 轴上,B 在第二象限,△ABO 沿x 轴正方向作无滑动的翻滚,经一次翻滚后得到△A 1B 1O ,则翻滚3次后点B的对应点的坐标是__(5,3)__,翻滚2017次后AB 中点M 经过的路径长为 (134633+896)π .解析:如图作B 3E ⊥x 轴于E ,易知OE =5,B 3E =3,∴B 3(5,3),观察图象可知三次一个循环,一个循环点M 的运动路径为120·π·3180+120π·1180+120π·1180=(23+43)π,∵2017÷3=672…1,∴翻滚2017次后AB 中点M 经过的路径长为672·(23+43)π+233π=(134633+896)π.9.(2017·菏泽)如图,AB ⊥y 轴,垂足为B ,将△ABO 绕点A 逆时针旋转到△AB 1O 1的位置,使点B 的对应点B 1落在直线y =-33x 上,再将△AB 1O 1绕点B 1逆时针旋转到△A 1B 1O 2的位置,使点O 1的对应点O 2落在直线y =-33x 上,依次进行下去…若点B 的坐标是(0,1),则点O 12的纵坐标为__(-9-93,9+33)__.解:观察图象可知,O 12在直线y =-33x 时,OO 12=6·OO 2=6(1+3+2)=18+63, ∴O 12的横坐标=-(18+63)·cos30°=-9-93,O 12的纵坐标=12OO 12=9+33,∴O 12(-9-93,9+33). 10.定义:直线l 1与l 2相交于点O ,对于平面内任意一点M ,点M 到直线l 1、l 2的距离分别为p 、q ,则称有序实数对(p ,q)是点M 的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是( C )A .2B .3C .4D .5解析:如图,∵到直线l 1的距离是l 的点在与直线l 1平行且与l 1的距离是1的两条平行线a 1、a 2上,到直线l 2的距离为2的点在与直线l 2平行且与l 2的距离是2的两条平行线b 1、b 2上,∴“距离坐标”是(1,2)的点是M 1,M 2,M 3,M 4,一共4个.11.(2017·绍兴模拟)在平面直角坐标系中,对图形F 给出如下定义:如图形F 上的所有点都在以原点为顶点的角的内部或边界上,在所有满足条件的角中,其度数的最小值称为图形的坐标角度.例如,图中的矩形ABCD 的坐标角度是90°.现将二次函数y =ax 2(1≤a ≤3)的图象在直线y =1下方的部分沿直线y =1向上翻折,则所得图形的坐标角度α的取值范围是( B )A .30°≤α≤60°B .60°≤α≤90°C .90°≤α≤120°D .120°≤α≤150°12.(2017·昆山二模)赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,若这四个全等直角三角形的两条直角边分别平行于x 轴和y 轴,大正方形的顶点B 1,C 1,C 2,C 3,…,C n 在直线y =-12x +72上,顶点D 1,D 2,D 3,…,D n 在x 轴上,则第n 个阴影小正方形的面积为__(23)2n -2__.解:设第n 个大正方形的边长为a n ,则第n 个阴影小正方形的边长为55a n,当x =0时,y =-12x +72=72,∴72=55a 1+52a 1,∴a 1= 5.∵a 1=a 2+12a 2,∴a 2=235,同理可得:a 3=23a 2,a 4=23a 3,a 5=23a 4,…,∴a n =(23)n -1a 1=5(23)n -1,∴第n 个阴影小正方形的面积为(55a n )2=[(23)n -1]2=(23)2n -2.。
中考规律探索型问题及答案

规 律 探1.如图,下面是按照一定规律画岀的“数形图”,经观察可以发现:图A 比图A i 多岀2个“树枝”比图A 多岀4个“树枝”,图A 比图A 3多岀8个“树枝”,……,照此规律,图A 比图A2多岀“树枝”()D. 124【答案】C的代数式表示)OQQG O 0-O 0 0 5第1个图形 第2个图形0 Q0 0 0 0 90 0 O0 Q Q 9 0 Qoo oo • a C 殆彷0 4 0 0 0O第3个图形第4个图形【答案】n(n 1) 4或n 2 n 4 3.观察下列算式:2① 1 X 3 - 2 = 3 - 4 = -1 ② 2 X 4 - 3 2 = 8 - 9 = -1③ 3 X 5 - 4 2 = 15 - 16 = -1④ _________________________6.观察下面的变形规律:1 1 1 11 1 11----- =1 — — • ------------ = — — — • -------- =———1 2 223233434解答下面的问题:2.将一些半径相同的小圆按如图所示的规律摆放,请仔细观察,第 n 个图形有个小圆 (用含n(1 )请你按以上规律写出第 4个算式; 2)把这个规律用含字母的式子表示出来;(3)你认为(2)中所写岀的式子一定成立吗?并说明理由. 【答案】解:⑴4 6 5224 25 1 ;2⑵答案不唯一.如n n 2 n 11 ;2 2 2⑶ n n 2 n 1 n 2n n 2n 11.4. 观察上面的图形,它们是按一定规律排列的,依照此规律,第 【答案】155. 先找规律,再填数: 22n n2n 1【答案】11006____ 个图形共有120个8.如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答(1) _______________________________ 表中第8行的最后一个数是 ___________________ ,它是自然数 的平方,第8行共有 ____________________________ 个数;(2) ______________________________________________ 用含n 的代数式表示:第 n 行的第一个数是 _____ ,最后一个数是 _____________________________________________ ,第n 行共有____________ 个 数;(3)求第n 行各数之和.【解】(1) 64,8,15;(2) (n 1)2 1,n 2,2n 1;(3)第2行各数之和等于 3X 3 ;第3行各数之和等于 5X 7;第4行各数之和等于 7 X 7-13 ;类似的,第n(1 )若n 为正整数,请你猜想n(n 1)(2) (3) 证明你猜想的结论; 1 .求和: 丄+…+3 42009 2010【答案】 1(1)(2) 证明:n 1 n(n 1)n n(n 1)n 1 n n(n 1)1 n(n 1)(3) 原式=1+…+42009 2010 2010200920107.设 S ,=1g 丄,S 2=1厶 12 22 22丄,X3232■V …,S.=1 A4 n(n【答案】S n1 1~~2n=[1S= (用含n 的代数式表示,其中2n1 1 k 1 [1 占2 2 A 1 爲]2 21 n(n 1)1 n(n1 1 1 ‘ S =(1厂)+(1 厂)+(1 厂尸…+(1n(n 1))2小n 2n n 1接下去利用拆项法1 n(n 1)即可求和.n 1设 S .. .3则行各数之和等于(2n 1)(n2 n 1) = 2 n3 3n2 3n 1.「、 2 32012上乙“ _ 人— 2 3 2012 — 2 3 4 2013 e. — — 2013八9.求 1+2+2+2+…+2 的值,可令 S=1+2+2+2+…+2 ,则 2S=2+2+2+2+…+2,因此 2S- S=2 - 1.仿照以上推理,计算出1+5+52+53+…+5 2012的值为( )选C.个小正方形。
第40课 探索型问题

基础自测
1.(2010· 湛江)观察下列算式:31=3, 32=9, 33=27, 34=81, 35= 243, 36=729, 37=2187, 38=6561,……,通过观察,用你所 发现的规律确定32010的个位数字是( B ) A.3 B.9 C.7 D.1 解析:通过观察可知规律:幂的个位数字是3,9,7,1,3,9,7,1, ……,所以2010除以4,得余数是2,幂的个位数字是9.
求出所有符合条件的点P的坐标;若
不存在,请说明理由.
5 解:(1)设经过点A(0,6),B(2,0),C(7, )的抛物线的解析式 2 2+bx+c, 为y=ax c=6, 1 则有 4a+2b+c=0, 解得a= ,b=-4,c=6. 2 5 49a+7b+c= , 2 ∴此抛物线的解析式为 y=x2-4x+6.
后对猜想的结论进行证明.这类题主要考查解题者的发散
思维和所学基本知识的应用能力.
3.存在探索型问题:指在一定条件下需探索发现某种数学 关系是否存在的问题.解题时一般是先对结论作肯定存 在的假设,然后由此肯定的假设出发,结合已知条件进 行推理论证.若导出矛盾,则否定先前假设;若推出合 理的结论,则说明假设正确,由此得出问题的结论.
[难点正本 疑点清源]
1.按探索对象分类 按探索对象的不同,探索题可分为条件探索题和结论探索题, 即执果索因和执因导果. 2.按探索方法分类 (1)直观探索法,对所学的新知识的思维迁移,进行发现,这种 方法多用于图形性质的发现; (2)归纳探索法,让读者对某些单个的、特殊的事物进行分析比 较,从中总结出规律性的东西,从而进行发现; (3)类比探索法,把所要解决的新问题和与之有关的问题进行分 类比较,发现它们之间的共同特点和规律.
中考一轮复习--专题五 规律探索题

(3)通过对简单、特殊情况的观察,再推广到一般情况.
2.规律探究的基本原则:
(1)遵循类推原则,项找项的规律,和找和的规律,差找差的规律,积
找积的规律.
(2)遵循有序原则,从特殊开始,从简单开始,先找3个,发现规律,再
验证运用规律.
类型一
类型二
类型三
类型一 数式的变化规律
例1(2019·安徽)观察以下等式:
∴S5= =-1-a,
4
∴S6=-S5-1=a.
1
1
∴S7= = =S1,
6
故此规律为 6 个一循环,
∵2 018÷6=336 余 2,
1+
∴S2 018=- .
1
2
3
4
5
6
7
4.(2018·黑龙江龙东区)如图,已知等边△ABC的边长是2,以BC边上
的高AB1为边作等边三角形,得到第一个等边△AB1C1;再以等边
(2)∵2 020÷3=673…1,∴需要小正方形674个,大正方形673个.
1
2
3
4
5
6
7
7.图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上
面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.
将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有
n(n + 1)
圆圈的个数为1+2+3+…+n= 2 .如果图3和图4中的圆圈各有13
为
.
类型一
类型二
类型三
分析:(1)观察图形,结合已知条件,得出将基本图每复制并平移一
次,特征点增加5个,由此得出图4中特征点的个数为17+5=22个,进
探索图形规律的方法总结

探索图形规律的方法总结一、规律探索型问题的分类1、数式规律通常给定一些数字、代数式、等式或不等式,然后猜想其中蕴含的规律,反映了由特殊到一般的数学方法,考查了学生的分析、归纳、抽象、概括能力。
一般解法是先写出数式的基本结构,然后通过横比(比较同一等式中不同部分的数量关系)或纵比(比较不同等式间相同位置的数量关系)找出各部分的特征,改写成要求的格式。
猜想归纳是解决这类问题的有效方法,通过对已给出的材料和信息对研究的对象进行观察、实验、比较、归纳和分析综合,作出符合一定规律与事实的推测性想象,从而发现一般规律。
它是发现和认识规律的重要手段。
平时的教学不能局限于课本,可以设计一些猜想性、类比性的活动,让学生经历一个观察、试验等活动过程,在活动中通过对大量特殊情形的观察猜想出一般情形的结论,从而探索事物的内在规律。
2、图形规律根据一组相关图形的变化规律,从中总结图形变化所反映的规律。
解决这类图形规律问题的方法有两种,一种是数图形,将图形转化成数字规律,再用数字规律的解决问题,一种是通过图形的直观性,从图形中直接寻找规律。
图案、图表具有直观、形象、简明,包含的信息量多等特点,解决此类问题需要把“形”转化为“数”,考查学生数形结合的数学思想。
二、规律探索型问题常用解法1、抓住条件中的变与不变找数学规律的题目,都会涉及到一个或者几个变化的量。
所谓找规律,多数情况下,是指变量的变化规律。
所以,抓住了变量,就等于抓住了解决问题的关键。
而这些变量通常按照一定的顺序给出,揭示的规律,常常包含着事物的序列号。
如:一组按规律排列的式子:,,,,…(),其中第7个式子是,第个式子是(为正整数)。
分子和分母的底数没变,变化的是符号及它们的指数,再把变量和序列号放在一起加以比较,就很容易发现其中的奥秘。
2、化繁为简,形转化为数有些题目看上去很大、图形很复杂,实际上,关键性的内容并不多。
对题目做一番认真地分析,去粗取精,取伪存真,把其中主要的、关键的内容抽出来,题目的难度就会大幅度降低,问题也就容易解决了。
中考数学复习指导:探索规律型问题归类解析

探索规律型问题归类解析探索规律型问题是历年中考数学试题中的重要题型之一,其特点是给出一组变化了的数字、式子、表格、图形等,要求学生通过观察、归纳、猜想、验证、类比,探求其内在规律.1.通用的解题策略解答规律型问题一般要从特殊情况入手→探索发现规律→综合归纳→猜想得出结论→验证结论.这种“特殊——一般——特殊”的解题模式,体现了总结归纳的数学思想,也正是人们认识新事物的一般过程.具体来说,就是先写出开头几个数式的基本结构,然后通过横比或纵比找出各部分的特征,写出符合要求的结果.例1 如图1,房间地面的图案是用大小相同的黑、白正方形镶嵌而成.图中,第1个黑色“L”形由3个正方形组成,第2个黑色“L”形由7个正方形组成,…那么组成第6个黑色“L”形的正方形个数是( )(A)22 (B)23 (C)24 (D)25解析从特例入手:如图1.纵比正方形的个数3,7,11,15中,后一个数比前一个大4(即相邻两数的差为4),猜想与4有关.横比3与1,7与2,11与3,15与4之间有何关系?联想到与4有关,故改写为:3=4×1-1,7=4×2-1.11=4×3-1,15=4×4-1.猜想组成第6个黑色L形的正方形个数是4 ×6-1=23个.故选B.点评考察相邻两数的差(或商)是探究数字规律的常用手段.常见的类型有:相邻两数的差(或商)相等或成倍数关系,相邻两数的差相等与商相等交替出现等.2.关注特殊数列(1)斐波那契数列:1,1,2,3,5,8,13,21…(其规律为:从第三项开始,每一项都等于前两项之和);(2)平方数数列:1,4,9,16,25,36…(其规律为:n2,即每一项都等于项数的平方).例2 有一组数:1,2,5,10,17,26…请观察这组数的构成规律,用你发现的规律确定第8个数为_______.解析规律为:n2+1(n=0,1,2…).答案:50.点评此类题要注意n2,n2+1,n2-1等(3)三角形数列:1,3,6,10,15,21,…(其规律为1+2+3+…+n)例3 世界上著名的莱布尼茨三角形如图2所示,则排在第10行从左边数第3个位置上的数是:( )(A)(B)(C)(D)解析从第3行起,从左边数第3位置上的数分别为,,,,…它们的分母可分别改写为:1×3,3×4,6×5,10×6,15×7,21×8,…,而1,3,6,10,15,21,…,正是三角形数,故答案为:.选B.(4)杨辉三角形,杨辉三角形斜边上1以外的各数,都等于它“肩上”的两数之和,如图3.(5)与等差等比数列有关的数列.如例1中3,7,11,15…就是一个等差数列.例4 数字解密:第一个数是3=2+1,第二个数是5=3+2,第三个数是9=5+4,第四个数是17=9+8,……观察并猜想第六个数应是_______.解析第二个加数1,2,4,8…规律为2n(为一等比数列,也要关注这一数列),第一个加数2,3,5,9…比第二个加数大1.所以第六个数为(25+1)+25=65.例5 一组按规律排列的数:…请你推断第9个数是________.解析这列数的分母为2,3,4,5,6…的平方数,分子形成二阶等差数列,依次相差2,4,6,8…故第9个数分子为1+2+4+6+8+10+12+14+16=73,分母为100,故答案为.(6)与循环有关的问题例6 让我们轻松一下,做一个数字游戏:第一步:取一个自然数n1=5,计算n12+1得a1;第二步:算出a1的各位数字之和得n2,计算n22+1得a3;第三步:算出a2的各位数字之和得n3,再计算n32+1得a3;……依此类推,则a2008=_______.解析根据题意可算出a1=26,a2=65,a3=122,a4=26,a5=65,a6=122,…发现每3个数就出现一次循环.所以由2008=669×3+1,可得a2008=a1=26.点评一列数由某m个数循环出现组成,可依据同余等值(由n=p·m+r得a n=a r)实施转换.(7)分奇数项偶数项的问题例7 一组按规律排列的式子:,…(a b≠0),其中第7个式子是________,第n个式子是_(n为正整数).解析6的指数2,5,8,11…,相邻两数差为3,是等差数列,其规律为3n-1;再注意到奇数项为负,偶数项为正,则第n个式子为第七个式子为3.特殊数列的迁移例8 把数字按如图4所示排列起来,从上开始,依次为第一行、第二行、第三行、…,中间用虚线围的一列,从上至下依次为1.5.13.25.…,则第10个数为_______.解析1 中间框出的一列数的规律为:第n个数为1+4+8+12+…+4(n-1).所以第10个数为1+4+8+12+…+36=.解析2 用虚线圈出的一列数1,5,13,25可改写为:02+12,12+22,22+32,32+42,猜想第10个数为92+102=181.点评此列数可看成是平方数数列的迁移.例9 图5中是与杨辉三角有类似性质的三角形数垒.a,b,c,d是相邻两行的前四个数,那么当a=8时,c=_______,d=_______.解析除两边外,中间的每个数等于肩上两数的和.答案:9;32.点评此列数可看成是杨辉三角形的迁移.4.关注中考新题型例10 观察图6所示表格,依据表格数据排列的规律,数2008在表格中出现的次数共有_______次.解析从特例入手,通过扩充表格可得:数1,2,3,4,5,6,7,8,9,10出现次数分别为1,2,2,3,2,4,2,4,3,4.出现的次数恰为给定数的所有因数的个数,而2008的因数为1,2,4,8,251,502,1004,2008等8个.故答案为8.点评本例中新产生的数为自然数的倍数,因此,其出现的次数与其因数的多少有关,仔细观察便会发现,其出现次数就是给定数所有因数的个数,本题规律的隐蔽性较强,因而有一定的难度.。
专题5 规律探索型问题

,摆放第三个“7”字图形得顶点F2,依此类推,…,摆
放第n个“7”字图形得顶点Fn-1,…,则顶点F2019的坐
标为
6062 5
5
,405
5
.
【解析】(1)12 ;(2)过 C 作 CM⊥y 轴于 M,过 M1 作 M1N⊥x 轴,过
F 作 FN1⊥x 轴.根据勾股定理易证得 BD= 22+12 = 5 ,CM=
=13
,∴FN1=6 5 5
,∴AN1=3 5 5
,∴ON1=OA+AN1=2 5 5
+3 5 5
=5
5 5
,∴F(5 5 5
,6
5 5
),
同理,F1(8 5 5
,7
5 5
),即(1×35+5
5 ,6+5 1
5 ),F2(115 5 ,
85 5
),即(2×35+5
5 ,6+5 2
5 ),F3(145 5 ,105 5 ),即
(2)写出你猜想的第n个等式:________(用含n的等式表 示),并证明.
解:(1)第 6 个等式为:121 =16 +616 ; (2)2n2-1 =n1 +n(2n1-1) . 证明:∵右边n1 +n(2n1-1) =n2(n2-n1-+11) =2n2-1 =左边.∴等式成立.
【思路方法】数式规律题的解题方法: 第一步:给已知等式标序数; 第二步:观察等式的每一项与序数(1,2,3,…,n)之 间的关系(平方、乘积); 第三步:将等式拆分,每一项用含序数的式子表示出 来.
专题5 规律探索型问题
专题解读
规律探索型问题指的是给出一组具有某种特定关系 的数、式、图形,或是给出与图形有关的操作变化过 程,或某一具体的问题情境,要求通过观察分析推理 ,探究其中蕴含的规律,进而归纳或猜想出一般性的 结论.主要思想方法是从特殊到一般的归纳猜想法. 常见类型有“数式规律”“图形规律”等题型.
第33章 规律探索型问题

第三十三章 规律探索型问题12.(2012山东省滨州,12,3分)求1+2+22+23+…+22012的值,可令S=1+2+22+23+…+22012,则2S=2+22+23+24+…+22013,因此2S ﹣S=22013﹣1.仿照以上推理,计算出1+5+52+53+…+52012的值为( )A .52012﹣1B .52013﹣1C .D .【解析】设S=1+5+52+53+…+52012,则5S=5+52+53+54+…+52013,因此,5S ﹣S=52013﹣1, S=.【答案】选C .【点评】本题考查同底数幂的乘法,以及类比推理的能力.两式同时乘以底数,再相减可得s的值. (2012广东肇庆,15,3)观察下列一组数:32,54,76,98,1110,…… ,它们是按一定规律排列的,那么这一组数的第k 个数是 ▲ .【解析】通过观察不难发现,各分数的分子与分母均相差1,分子为连续偶数,分母为连续奇数. 【答案】122 k k【点评】本题是一道规律探索题目,考查了用代数式表示一般规律,难度较小.18. ( 2012年四川省巴中市,18,3)观察下列面一列数:1,-2,3,-4,5,-6,…根据你发现的规律,第2012个数是___________【解析】观察知: 下列面一列数中,它们的绝对值是连续正整数,第2012个数的绝对值是2012,值偶数项是负数,故填-2012. 【答案】-2012【点评】本题是找规律的问题,确定符号是本题的难点.20.(2012贵州省毕节市,20,5分)在下图中,每个图案均由边长为1的小正方形按一定的规律堆叠而成,照此规律,第10个图案中共有 个小正方形。
解析:观察图案不难发现,图案中的正方形按照从上到下成奇数列排布,写出第n个图案的正方形的个数,然后利用求和公式写出表达式,再把n=10代入进行计算即可得解.答案:解:第1个图案中共有1个小正方形,第2个图案中共有1+3=4个小正方形,第3个图案中共有1+3+5=9个小正方形,…,第n个图案中共有1+3+5+…+(2n-1)=2)121(-+nn=n2个小正方形,所以,第10个图案中共有102=100个小正方形.故答案为:100.点评:本题是对图形变化规律的考查,根据图案从上到下的正方形的个数成奇数列排布,得到第n个图案的正方形的个数的表达式是解题的关键.18.(2012贵州六盘水,18,4分)图7是我国古代数学家杨辉最早发现的,称为“杨辉三角形”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角形”中有许多规律,如它的每一行的数字正好对应了()na b+(n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如222()2a b a ab b+=++展开式中的系数1、2、1恰好对应图中第三行的数字;再入,33223()33a b a a b ab b+=+++展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出4()a b+的展开式.4()a b+=▲ .分析:该题属规律型,通过观察可发现第五行的系数是:1、4、6、4、1,再根据例子中字母的排列规律即得到答案.解答:解:由题意,4432234()464a b a a b a b ab b+=++++,故填432234464a ab a b ab b++++.点评:本题考查了数字的变化规律,从整体观察还要考虑字母及字母指数的变化规律,从而得到答案.17. (2012山东莱芜, 17,4分) 将正方形ABCD 的各边按如图所示延长,从射线AB 开始,分别在各射线上标记点321,,A A A ….,按此规律,则点A 2012在射线上. 【解析】根据表格中点的排列规律,可以得到点的坐标是每16个点排列的位置一循环, 2012=16×125+12,所以点A 2012所在的射线和点12A 所在的直线一样。
掌握探索规律方法 培养创新思维能力

掌握探索规律方法培养创新思维能力近年来,探索规律的题目成为中考数学的热点之一,目的是考查学生观察、分析、探索、类比、归纳、总结、创新实践的能力。
规律探索型问题是根据已知条件或题目中所提供的若干个特例,通过观察、分析、归纳出来题目所给信息中所蕴含的本质规律或特征。
1、图案变化规律探究型【例1】(2012 b 贵州毕节)在下图中,每个图案均由边长为1的小正方形按一定的规律堆叠而成,照此规律,第10个图案中共有个小正方形。
【分析】第1个图案,小正方形有1=12个;第2个图案,边长为1的小正方形有4=22个;第3个图案,边长为1的小正方形有9=32个;第4个图案,边长为1的小正方形有16=42个,……,所以,第10个图案中共有102=100边长为1的小正方形。
【答案】100。
【例2】(2012 b 深圳市)如图,这是由边长为1的等边三角形摆出的一系列图形,按这种方式摆下去,则第n个图形的周长是=。
【分析】第(1)个图案,周长=3=1+2;第(2)个图案,周长=4=2+2;第(3)个图案,周长=5=3+2;第(4)个图案,周长是=6=4+2,……,所以,第个n图案,周长= n+2【答案】 n+22. 数字变化规律猜想型【例3】(2012 b 大庆)已知12=1,112=121,1112=12321,…,则依据上述规律,111111112的计算结果中,从左向右数第12个数字是.【分析】根据平方后的结果的规律,从左向右依次是从1开始的连续的自然数再逐渐减小至1,且中间的自间的自然数与底数的1的个数相同,根据此规律可得:12=1, 112=121,1112=12321,…111111112=123456787654321,所以,第12个数字是4. 【答案】4.【例4】(2012 b 赤峰)将分数67化为小数是0.8.57142.,则小数点后第2012位上的数是.【分析】∵67化为小数是0.8.57142.,∴2012÷6=335(组)…2(个);所以小数点后面第2012位上的数字是:5;【答案】5.【例5】(2012 b 江苏扬州)大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是2013,则m 的值是()a. 43b. 44c. 45d. 46【分析】观察规律,分裂成的数都是奇数,且第一个数是底数乘以与底数相邻的前一个数的积再加上1,奇数的个数等于底数,∵23=3+5,33=7+9+11,43=13+15+17+19,…∴m3分裂后的第一个数是m(m-1)+1,共有m个奇数,∵45×(45-1)+1=1981,46×(46-1)+1=2071,∴第2013个奇数是底数为45的数的立方分裂后的一个奇数,∴m=45. 【答案】c.3. 几何变化规律归纳型【例6】(2012 b 贵阳)如图,在△aba1中,∠b=20°,ab=a1b,在a1b上取一点c,延长aa1到a2,使得a1a2=a1c;在a2c上取一点d,延长a1a2到a3,使得a2a3=a2d;…,按此做法进行下去,∠an的度数为8002n-1.【分析】先根据等腰三角形的性质求出∠ba1a的度数,再根据三角形外角的性质及等腰三角形的性质分别求出∠ca2a1,∠da3a2及∠ea4a3的度数,找出规律即可得出∠an的度数.∵在△aba1中,∠b=20°,ab=a1b,∴∠ba1a=1800-∠b2=1800-2002=80°,∵a1a2=a1c,∠ba1a是△a1a2c的外角,∴∠ca2a1=∠ba1a2=8002=40°;同理可得,∠da3a2=20°,∠ea4a3=10°,∴∠an=8002n-1. 【答案】8002n-14、数列变化规律探索型【例7】(2012 b 四川省自贡市)一质点p从距原点1个单位的m点处向原点方向跳动,第一次跳动到om的中点m3处,第二次从m3跳到om3的中点m2处,第三次从点m2跳到om2的中点m1处,如此不断跳动下去,则第n次跳动后,该质点到原点o的距离为()a.1n2b.12n-1c.(12)n+1d.12n【分析】根据题意,得第一次跳动到om的中点m3处,即在离原点的12处,第二次从m3点跳动到m2处,即在离原点的(12)2处,则跳动n次后,即跳到了离原点的12n处.【答案】d【例8】(2012 ?偊b 辽宁省鞍山市)如图,在△abc中,∠acb=90°,∠a=60°,ac=a,作斜边ab边中线cd,得到第一个三角形acd;de⊥bc于点e,作rt△bde斜边db上中线ef,得到第二个三角形def;依此作下去…则第n个三角形的面积等于3a222n.【分析】∵∠acb=90°,cd(转下页)图像的平移与反函数王荃梅(正宁县山河初中甘肃正宁745300)在反函数的教学中,我们往往遇到与平移有关的反函数的问题,多数同学对这个问题理解存在一定问题,本文就这个问题进行探讨与大家一起学习。
中考数学总复习第40课 探索型问题

- b =1,
2a
a=-1,
∴ -b2=1, 解得 b=2.
4a
即当顶点坐标为(1,1)时,a=-1.
- b =m, 2a
a=- 1 ,
当顶点坐标为 (m ,m ),m ≠0
时,
-b2=m , 4a
解得
b=2.
m
∴a 与 m 之间的关系式是:a=-m1 或 am+1=0.]
(2)∵a≠0,
∴y=ax2+bx=a
专题解读
1.探索型问题: 探索是人类认识客观世界过程中最生动,最活跃的思维活 动.探索问题主要考查学生探究、发现、总结问题的能力,主 要包括: (1)规律探索型问题; (2)结论探索型问题; (3)存在性探索型问题; (4)动态探索型问题. 2.解答探索型问题的注意事项: 由于探索型问题的题型新颖,综合性强,思维能力要求高,结 构独特,因此解题时并无固定模式,它要求解题者具有较扎实 的基本功,较强的观察力,丰富的想象力及综合分析问题的能 力.解题时要注意问题情境,注重思维的严密性,注意寻找问 题解决的切入口.有时也可采用以下方法来寻找突破口:(1)利 用特殊值(特殊点,特殊数量,特殊线段等)进行归纳,概括;(2) 反演推理法(反证法);(3)分类讨论法;(4)类比猜想法.
3,4 3
3,
-2 P2 3
3,4 3
3
;当∠PAO=90°时,P3
34 9
3,4 3
3 ;当∠POA=90°时,
-16 3,4 3
P4 9
3.
名师点拨
存在性探索问题是运用几何计算进行探索的综合型 问题,要注意相关的条件,可以先假设结论成立,然后通 过计算求相应的值,再作存在性的判断.
【预测演练 3】 如图 40-7,在△ABC 中,AB=AC=10 cm,BC=12 cm, 点 D 是 BC 边的中点.点 P 从点 B 出发,以 a(cm/s)(a>0)的速度沿 BA 匀速向点 A 运动;点 Q 同时以 1 cm/s 的速度从点 D 出发,沿 DB 匀 速向点 B 运动,其中一个动点到达端点时,另一个动点也随之停止运 动,设它们运动的时间为 t(s). (1)若 a=2,△BPQ∽△BDA (点 P 与点 D 对应),求 t 的值; (2)设点 M 在边 AC 上,四边形 PQCM 为平行四边形. ①若 a=5,求 PQ 的长; 2 ②是否存在实数 a,使得点 P 在∠ACB 的平分线上?若存在,请求 出 a 的值;若不存在,请说明理由.
2020年中考数学一轮专项复习——规律探索(含答案)

2020年中考数学一轮专项复习——规律探索中考备考攻略规律探索型问题是根据已知条件或题干所提供的若干特例,通过观察、类比、归纳,发现题目所蕴含的数字或图形的本质规律与特征的一类探索性问题.纵观宜宾近五年中考,往往以选择题、填空题形式出现,这类问题在素材的选取、文字的表述、题型的设计等方面都比较新颖.其目的是考查收集、分析数据、处理信息的能力.所以规律探索型问题备受命题专家的青睐,逐渐成为中考数学的热门考题.规律探索型问题是指在一定条件下,探索发现有关数学对象所具有的规律性或不变性的问题,它往往给出了一组变化了的数、式子、图形或条件,要求通过阅读、观察、分析、猜想来探索规律.它体现了“特殊到一般”的数学思想方法,既考查分析、解决问题能力,也考查观察、联想、归纳能力以及探究能力和创新能力.题型可涉及填空题、选择题或解答题.中考重难点突破数与式变化规律【典例1】(2019·达州中考)a 是不为1的有理数,我们把11-a 称为a 的差倒数,如2的差倒数为11-2=-1,-1的差倒数11-(-1)=12.已知a 1=5,a 2是a 1的差倒数,a 3是a 2的差倒数,a 4是a 3的差倒数,…,依此类推,a 2 019的值是( )A .5B .-14C .43D .451.一组按规律排列的多项式:a +b ,a 2-b 3,a 3+b 5,a 4-b 7,…,其中第10个式子是( )A. a 10+b 19 B .a 10-b 19 C .a 10-b 17 D .a 10-b 212.有一组数:12,35,510,717,926,…,请观察它们的构成形式,用你发现的规律写出第n (n 为正整数)个数: .3.已知:1+112+122=112,1+122+132=116,1+132+142=1112,…,根据此规律1+192+1102= .4.(2019·自贡中考)阅读下列材料:小明为了计算1+2+22+…+22 017+22 018的值,采用以下方法:设S=1+2+22+…+22 017+22 018,①则2S=2+22+…+22 018+22 019.②②-①,得2S-S=S=22 019-1.∴S=1+2+22+…+22 017+22 018=22 019-1.请仿照小明的方法解决以下问题:(1)1+2+22+…+29=;(2)3+32+…+310=;(3)求1+a+a2+…+a n的和(a>0,n是正整数,请写出计算过程).点阵变化规律【典例2】如图,在一个三角点阵中,从上向下数有无数多行,其中各行点数依次为2、4、6、…、2n、…,若前n行点数和为930,则n=()A.29B.30C.31D.325.将全体正奇数排成一个三角形数阵:13 57911131517192123252729………………根据以上排列规律,数阵中第25行的第20个数是()A.639B.637C.635D.633循环排列规律【典例3】观察下列图形,并判断照此规律从左向右第2 018个图形是()A B C D6.如图是一列用若干根火柴棒摆成的由正方形组成的图案.(1)完成下表的填空:正方形个数 1 2 3 4 5 6 … 火柴棒根数4710131619…(2)某同学用若干根火柴棒按如图的方式摆图案,摆完了第1个后,摆第2个,接着摆第3个,第4个,…,当他摆完第n 个图案时剩下了20根火柴棒,要刚好摆完第(n +1)个图案还差2根.问最后摆的图案是第几个图案?图形生长变化规律【典例4】(2019·内江中考)如图,将△ABC 沿着过BC 的中点D 的直线折叠,使点B 落在AC 边上的B 1处,称为第一次操作,折痕DE 到AC 的距离为h 1;还原纸片后,再将△BDE 沿着过BD 的中点D 1的直线折叠,使点B 落在DE 边上的B 2处,称为第二次操作,折痕D 1E 1到AC 的距离记为h 2;按上述方法不断操作下去……经过第n 次操作后得到折痕D n -1E n -1,到AC 的距离记为h n .若h 1=1,则h n 的值为( )A .1+12n -1 B .1+12nC .2-12n -1 D .2-12n7.(2019·广元中考)如图,过点A 0(0,1)作y 轴的垂线交直线l :y =33x 于点A 1,过点A 1作直线l 的垂线,交y 轴于点A 2,过点A 2作y 轴的垂线交直线l 于点A 3,…,这样依次下去,得到△A 0A 1A 2、△A 2A 3A 4、△A 4A 546、…,其面积分别记为S 1、S 2、S 3、…,则S 100为( )A .⎝⎛⎭⎫332100B .(33)100C .33×4199D .33×2395与坐标有关的规律【典例5】如图,已知A 1(1,0),A 2(1,1),A 3(-1,1),A 4(-1,-1),A 5(2,-1),…,则点A 2018的坐标为 .8.(2019·攀枝花中考)正方形A 1B 1C 1A 2、A 2B 2C 2A 3、A 3B 3C 3A 4、…按如图所示的方式放置,点A 1、A 2、A 3、…和点B 1、B 2、B 3、…分别在直线y =kx +b (k >0)和x 轴上.已知点A 1(0,1),点B 1(1,0),则点C 5的坐标是 .中考备考过关1.某校数学课外小组,在坐标纸上为学校的一块空地设计植树方案如下:第k 棵树种植在点P k (x k ,y k )处,其中x 1=1,y 1=1,当k ≥2时,⎩⎨⎧x k =x k -1+1-5⎝⎛⎭⎫⎣⎡⎦⎤k -15-⎣⎡⎦⎤k -25,y k =y k -1+⎣⎡⎦⎤k -15-⎣⎡⎦⎤k -25,[a]表示非负实数a 的整数部分,如[2.6]=2,[0.2]=0.按此方案,第2 019棵树种植点的坐标为( )A .(5,2 019)B .(6,2 020)C .(3,403)D .(4,404)2.正方形A 1B 1C 1O 、A 2B 2C 2C 1、A 3B 3C 3C 2、…按如图所示的方式放置,点A 1、A 2、A 3、…和点C 1、C 2、C 3、…分别在直线y =kx +b (k >0)和x 轴上,已知B 1(1,1),B 2(3,2),则点B n 的坐标是 .,(第2题图)) ,(第3题图))3. 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳记数”.如图,一位妇女在从右到左依次排列的绳子上打结,满六进一,用来记录采集到的野果数量,由图可知,她一共采集到的野果数量为 个.4.(2019·广安中考)如图,在平面直角坐标系中,点A 1的坐标为(1,0),以OA 1为直角边作Rt △OA 1A 2,并使∠A 1OA 2=60°;再以OA 2为直角边作Rt △OA 2A 3,并使∠A 2OA 3=60°;再以OA 3为直角边作Rt △OA 3A 4,并使∠A 3OA 4=60°……按此规律进行下去,则点A 2 019的坐标为 .5.符号“f ”表示一种运算,它对一些数的运算结果如下:(1)f (1)=0,f (2)=1,f (3)=2,f (4)=3,…;(2)f ⎝⎛⎭⎫12=2,f ⎝⎛⎭⎫13=3,f ⎝⎛⎭⎫14=4,f ⎝⎛⎭⎫15=5,…. 利用以上规律计算:f ⎝⎛⎭⎫12 019-f (2 019)= .6.用同样大小的黑色棋子按如图所示的方式摆图形,按照这样的规律摆下去,则第n 个图形需棋子 枚(用含n 的代数式表示).7.观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2 019个图形共有 个○.8.如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着-5、-2、1、9,且任意相邻四个台阶上数的和都相等.尝试 (1)问前4个台阶上数的和是多少? (2)问第5个台阶上的数x 是多少?应用 求从下到上前31个台阶上数的和;发现 试用含k (k 为正整数)的式子表现出数“1”所在的台阶数.9.观察: 11×2=1-12,12×3=12-13,13×4=13-14,….解答下面的问题:(1)若n 为正整数,请你猜想1n ×(n +1)= ;(2)若n 为正整数,请你猜想11×2+12×3+13×4+…+1n ×(n +1)= ;(3)若x -1+(xy -2)2=0,求1xy +1(x +1)(y +1)+1(x +2)(y +2)+…+1(x +2 017)(y +2 017)的值.10.一列火车自A 城驶往B 城,沿途有n 个车站(包括起点站A 和终点站B ),该列火车挂有一节邮政车厢,行驶时需要在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该站的邮包一个,还要装上该站发给后面行程中每个车站的邮包一个.例如,当列车停靠在第x 个车站时,邮政车厢上需要卸下已经通过的(x -1)个车站发给该站的邮包(x -1)个,还要装上后面行程中要停靠的(n -x )个车站的邮包(n -x )个.(1)根据题意,完成下表:车站序号 在第x 个车站启程时邮政车厢上的邮包总个数1 n -12 (n -1)-1+(n -2)=2(n -2)3 2(n -2)-2+(n -3)=3(n -3)4 3(n -3)-3+(n -4)=4(n -4)5 … … n 0(2)根据上表写出列车在第x 个车站启程时,邮政车厢上共有的邮包个数y (用x 、n 表示); (3)当n =18时,列车在第几个车站启程时邮车上的邮包个数最多?参考答案中考重难点突破数与式变化规律【典例1】(2019·达州中考)a 是不为1的有理数,我们把11-a 称为a 的差倒数,如2的差倒数为11-2=-1,-1的差倒数11-(-1)=12.已知a 1=5,a 2是a 1的差倒数,a 3是a 2的差倒数,a 4是a 3的差倒数,…,依此类推,a 2 019的值是( D )A .5B .-14C .43D .45【解析】∵a 1=5,a 2=11-a 1=11-5=-14,a 3=11-a 2=11-⎝⎛⎭⎫-14=45,a 4=11-a 3=11-45=5,…,∴数列以5、-14、45三个数依次不断循环.∵2 019÷3=673,∴a 2 019=a 3=45.1.一组按规律排列的多项式:a +b ,a 2-b 3,a 3+b 5,a 4-b 7,…,其中第10个式子是( B )A .a 10+b 19B .a 10-b 19C .a 10-b 17D .a 10-b 212.有一组数:12,35,510,717,926,…,请观察它们的构成形式,用你发现的规律写出第n (n 为正整数)个数:2n -1n 2+1W. 3.已知:1+112+122=112,1+122+132=116, 1+132+142=1112,…,根据此规律1+192+1102= 1190 W. 4.(2019·自贡中考)阅读下列材料:小明为了计算1+2+22+…+22 017+22 018的值,采用以下方法: 设S =1+2+22+…+22 017+22 018,① 则2S =2+22+…+22 018+22 019.② ②-①,得2S -S =S =22 019-1.∴S =1+2+22+…+22 017+22 018=22 019-1. 请仿照小明的方法解决以下问题: (1)1+2+22+…+29= ; (2)3+32+…+310= ;(3)求1+a +a 2+…+a n 的和(a >0,n 是正整数,请写出计算过程).解:(1)210-1;(2)311-12; (3)设S =1+a +a 2+…+a n ,①则aS =a +a 2+a 3+…+a n +a n +1.②②-①,得(a -1)S =a n +1-1.∴S =a n +1-1a -1,即1+a +a 2+…+a n =an +1-1a -1.点阵变化规律【典例2】如图,在一个三角点阵中,从上向下数有无数多行,其中各行点数依次为2、4、6、…、2n 、…,若前n 行点数和为930,则n =( B )A .29B .30C .31D .32【解析】设前n 行的点数和为S ,则S =2+4+6+…+2n =(2n +2)n2=n (n +1). 若S =930,则n (n +1)=930,即(n +31)(n -30)=0,∴n 1=-31(不合题意,舍去),n 2=30.5.将全体正奇数排成一个三角形数阵:1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 … … … … … …根据以上排列规律,数阵中第25行的第20个数是( A ) A .639 B .637 C .635 D .633循环排列规律【典例3】观察下列图形,并判断照此规律从左向右第2 018个图形是( B )A B C D【解析】根据题意可知前面4个笑脸循环出现,因为2 018÷4=504……2,所以第2 018个图形是循环出现到第2个图形.6.如图是一列用若干根火柴棒摆成的由正方形组成的图案.(1)完成下表的填空:正方形个数 1 2 3 4 5 6 … n火柴棒根数4 7 10 13 16 19 … 3n +1(2)某同学用若干根火柴棒按如图的方式摆图案,摆完了第1个后,摆第2个,接着摆第3个,第4个,…,当他摆完第n 个图案时剩下了20根火柴棒,要刚好摆完第(n +1)个图案还差2根.问最后摆的图案是第几个图案?解:(1)见上表;(2)由3(n +1)+1=22,解得n =6. ∴这位同学最后摆的图案是第7个图案.图形生长变化规律【典例4】(2019·内江中考)如图,将△ABC 沿着过BC 的中点D 的直线折叠,使点B 落在AC 边上的B 1处,称为第一次操作,折痕DE 到AC 的距离为h 1;还原纸片后,再将△BDE 沿着过BD 的中点D 1的直线折叠,使点B 落在DE 边上的B 2处,称为第二次操作,折痕D 1E 1到AC 的距离记为h 2;按上述方法不断操作下去……经过第n 次操作后得到折痕D n -1E n -1,到AC 的距离记为h n .若h 1=1,则h n 的值为( C )A .1+12n -1 B .1+12nC .2-12n -1 D .2-12n【解析】根据相似三角形的性质,对应高的比等于相似比,得出h 2=1+12h 1,依次得出h 3、h 4、…、h n ,再对h n 进行计算变形即可.,7.(2019·广元中考)如图,过点A 0(0,1)作y 轴的垂线交直线l :y =33x 于点A 1,过点A 1作直线l 的垂线,交y 轴于点A 2,过点A 2作y 轴的垂线交直线l 于点A 3,…,这样依次下去,得到△A 0A 1A 2、△A 2A 3A 4、△A 4A 546、…,其面积分别记为S 1、S 2、S 3、…,则S 100为( D )A .⎝⎛⎭⎫332100B .(33)100C .33×4199D .33×2395与坐标有关的规律【典例5】如图,已知A 1(1,0),A 2(1,1),A 3(-1,1),A 4(-1,-1),A 5(2,-1),…,则点A 2018的坐标为 (505,505) .【解析】根据各个点(点A 1和第四象限内的点除外)分别位于象限的角平分线上,逐步探索出下标和各点坐标之间的关系,根据规律推出点A 2 018的坐标.通过观察可得序号是4的倍数的点在第三象限,由2 018÷4=504……2,得点A 2 018在第一象限,其横、纵坐标都为(2 018-2)÷4+1=505.,8.(2019·攀枝花中考)正方形A 1B 1C 1A 2、A 2B 2C 2A 3、A 3B 3C 3A 4、…按如图所示的方式放置,点A 1、A 2、A 3、…和点B 1、B 2、B 3、…分别在直线y =kx +b (k >0)和x 轴上.已知点A 1(0,1),点B 1(1,0),则点C 5的坐标是 (47,16) W.中考备考过关1.某校数学课外小组,在坐标纸上为学校的一块空地设计植树方案如下:第k 棵树种植在点P k (x k ,y k )处,其中x 1=1,y 1=1,当k ≥2时,⎩⎨⎧x k =x k -1+1-5⎝⎛⎭⎫⎣⎡⎦⎤k -15-⎣⎡⎦⎤k -25,y k =y k -1+⎣⎡⎦⎤k -15-⎣⎡⎦⎤k -25,[a]表示非负实数a 的整数部分,如[2.6]=2,[0.2]=0.按此方案,第2 019棵树种植点的坐标为( D )A .(5,2 019)B .(6,2 020)C .(3,403)D .(4,404)2.正方形A 1B 1C 1O 、A 2B 2C 2C 1、A 3B 3C 3C 2、…按如图所示的方式放置,点A 1、A 2、A 3、…和点C 1、C 2、C 3、…分别在直线y =kx +b (k >0)和x 轴上,已知B 1(1,1),B 2(3,2),则点B n 的坐标是 (2n -1,2n -1) W.,(第2题图)) ,(第3题图))3. 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳记数”.如图,一位妇女在从右到左依次排列的绳子上打结,满六进一,用来记录采集到的野果数量,由图可知,她一共采集到的野果数量为 1 838 个.4.(2019·广安中考)如图,在平面直角坐标系中,点A 1的坐标为(1,0),以OA 1为直角边作Rt △OA 1A 2,并使∠A 1OA 2=60°;再以OA 2为直角边作Rt △OA 2A 3,并使∠A 2OA 3=60°;再以OA 3为直角边作Rt △OA 3A 4,并使∠A 3OA 4=60°……按此规律进行下去,则点A 2 019的坐标为 (-22 017,22 0173) W.5.符号“f ”表示一种运算,它对一些数的运算结果如下:(1)f (1)=0,f (2)=1,f (3)=2,f (4)=3,…;(2)f ⎝⎛⎭⎫12=2,f ⎝⎛⎭⎫13=3,f ⎝⎛⎭⎫14=4,f ⎝⎛⎭⎫15=5,…. 利用以上规律计算:f ⎝⎛⎭⎫12 019-f (2 019)= 1 W.6.用同样大小的黑色棋子按如图所示的方式摆图形,按照这样的规律摆下去,则第n 个图形需棋子 (3n +1) 枚(用含n 的代数式表示).7.观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第 2 019个图形共有 6 058 个○.8.如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着-5、-2、1、9,且任意相邻四个台阶上数的和都相等.尝试 (1)问前4个台阶上数的和是多少? (2)问第5个台阶上的数x 是多少?应用 求从下到上前31个台阶上数的和;发现 试用含k (k 为正整数)的式子表现出数“1”所在的台阶数.解:尝试 (1)由题意,得-5-2+1+9=3,故前4个台阶上的数字的和是3; (2)由题意,得-2+1+9+x =3,所以x =-5;应用 由题意知台阶上的数从下到上每4个循环,因为31÷4=7……3,所以7×3+1-2-5=15, 即从下到上前31个台阶上数的和是15. 发现 “1”所在的台阶数为4k -1.9.观察: 11×2=1-12,12×3=12-13,13×4=13-14,….解答下面的问题:(1)若n 为正整数,请你猜想1n ×(n +1)= ;(2)若n 为正整数,请你猜想11×2+12×3+13×4+…+1n ×(n +1)= ;(3)若x -1+(xy -2)2=0,求1xy +1(x +1)(y +1)+1(x +2)(y +2)+…+1(x +2 017)(y +2 017)的值.解:(1)1n -1n +1;(2)1-1n +1;[原式=1-12+12-13+13-14+…+1n -1n +1=1-1n +1.](3)∵x -1+(xy -2)2=0,∴x -1=0,xy -2=0, 解得x =1,y =2.则原式=11×2+12×3+13×4+…+12 018×2 019=1-12 019=2 018 2 019.10.一列火车自A城驶往B城,沿途有n个车站(包括起点站A和终点站B),该列火车挂有一节邮政车厢,行驶时需要在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该站的邮包一个,还要装上该站发给后面行程中每个车站的邮包一个.例如,当列车停靠在第x个车站时,邮政车厢上需要卸下已经通过的(x-1)个车站发给该站的邮包(x-1)个,还要装上后面行程中要停靠的(n-x)个车站的邮包(n-x)个.(1)根据题意,完成下表:(2(3)当n=18时,列车在第几个车站启程时邮车上的邮包个数最多?解:(1)见上表;(2)y=x(n-x);(3)当n=18时,y=x(18-x)=-x2+18x=-(x-9)2+81.当x=9时,y取最大值,所以列车在第9个车站启程时,邮政车厢上的邮包个数最多.。
专题一 规律探索型问题
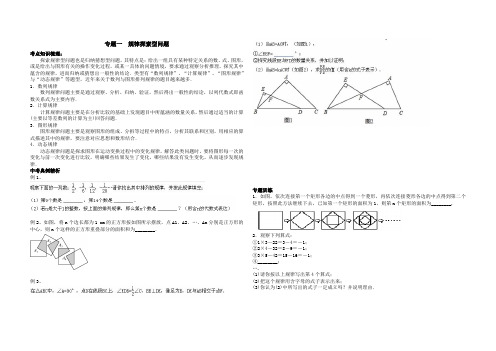
专题一规律探索型问题考点知识梳理:探索规律型问题也是归纳猜想型问题,其特点是:给出一组具有某种特定关系的数、式、图形,或是给出与图形有关的操作变化过程,或某一具体的问题情境,要求通过观察分析推理,探究其中蕴含的规律,进而归纳或猜想出一般性的结论.类型有“数列规律”、“计算规律”、“图形规律”与“动态规律”等题型,近年来关于数列与图形排列规律的题目越来越多.1.数列规律数列规律问题主要是通过观察、分析、归纳、验证,然后得出一般性的结论,以列代数式即函数关系式为主要内容.2.计算规律计算规律问题主要是在分析比较的基础上发现题目中所蕴涵的数量关系,然后通过适当的计算(主要以等差数列的计算为主)回答问题.3.图形规律图形规律问题主要是观察图形的组成、分拆等过程中的特点,分析其联系和区别,用相应的算式描述其中的规律,要注意对应思想和数形结合.4.动态规律动态规律问题是探求图形在运动变换过程中的变化规律,解答此类问题时,要将图形每一次的变化与前一次变化进行比较,明确哪些结果发生了变化,哪些结果没有发生变化,从而逐步发现规律.中考典例精析例1、例2、如图,将n个边长都为1 cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积和为________.例3、专题训练1.如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去,已知第一个矩形的面积为1,则第n个矩形的面积为________.2.观察下列算式:①1×3-22=3-4=-1;②2×4-32=8-9=-1;③3×5-42=15-16=-1;④________;….(1)请你按以上规律写出第4个算式;(2)把这个规律用含字母的式子表示出来;(3)你认为(2)中所写出的式子一定成立吗?并说明理由.3.在平面直角坐标系中,一蚂蚁从原点O 出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.(1)填写下列各点的坐标:A1(______,______), A3(______,______),A12(______,______); (2)写出点A4n 的坐标(n 是正整数);(3)指出蚂蚁从点A100到点A101的移动方向.4.在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x 轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点,…,则边长为8的正方形内部的整点的个数为_____(第4题) (第10题) (第11题)5、如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.6、7、在右表中,我们把第i 行第j 列的数记为a i ,j (其中i ,j 都是不大于5的正整数),对于表中的每个数a i ,j ,规定如下:当i≥j 时,a i ,j =1;当i <j 时,a i ,j =0.例如:当i=2,j=1时,a i ,j =a 2,1=1.按此规定,a 1,3=____;表中的25个数中,共有____个1;计算a 1,1•a i ,1+a 1,2•a i ,2+a 1,3•a i ,3+a 1,4•a i ,4+a 1,5•a i ,5的值为____9.甲、乙、丙、丁四位同学围成一圈依序循环报数,规定:①甲、乙、丙、丁首次报出的数依次为1、2、3、4,接着甲报5,乙报6……按此规律,后一位同学报出的数比前一位同学报出的数大1.当报到的数是50时,报数结束; ②若报出的数为3的倍数,则报该数的同学需拍手一次. 在此过程中,甲同学需拍手的次数为____________.10.如图为手的示意图,在各个手指间标记字母A ,B ,C ,D.请你按图中箭头所指方向(即A →B →C →D →C →B →A →B →C →…的方式)从A 开始数连续的正整数1,2,3,4,…,当数到12时,对应的字母是________;当字母C 第201次出现时,恰好数到的数是________;当字母C 第2n +1次出现时(n 为正整数),恰好数到的数是________.(用含n 的代数式表示)11.如图是圆心角为30°,半径分别是1、3、5、7、…的扇形组成的图形,阴影部分的面积依次记为S1、S2、S3、…,则S50=________.(结果保留π)12、如图所示,在x 轴的正半轴上依次截取OA 1=A 1A 2=A 2A 3=A 3A 4=A 4A 5…,过A 1、A 2、A 3、A 4、A 5…分别作x 轴的垂线与反比例函数的图象交于点P 1、P 2、P 3、P 4、P 5…,并设△OA 1P 1、△A 1A 2P 2、△A 2A 3P 3…面积分别为S 1、S 2、S 3…,按此作法进行下去,则S n 的值为 ______(n 为正整数).(第12题) (第13题)13、如图,n +1个上底、两腰皆为1,下底长为2的等腰梯形的下底均在同一直线上,设四边形P1M1N1N2的面积为S1,四边形P2M2N2N3的面积为S2,…,四边形PnMnNnNn +1的面积为Sn ,通过逐一计算S1,S2,…,可得Sn =________.14、如图,在平面直角坐标系中,线段OA 1=1,OA 1与x 轴的夹角为30°,线段A 1A 2=1,A 2A 1⊥OA 1,垂足为A 1;线段A 2A 3=1,A 3A 2⊥A1A 2,垂足为A 2;线段A 3A 4=1,A 4A 3⊥A2A 3,垂足为A 3;…按此规律,点A 2012的坐标为________(第14题) (第20题)15、如图,一串有趣的图案按一定的规律排列,请仔细观察,按此规律第2010个图案是A .B.C .D .16.A .3B .9C .7D .117、18、如图,将边长为a 的正六边形A 1A 2A 3A 4A 5A 6在直线l 上由图1的位置按顺时针方向向右作无滑动滚动,当A 1第一次滚动到图2位置时,顶点A 1所经过的路径的长为( )19、请先观察下列算式,再填空:32-12=8×1,52-32=8×2. ①72-52=8×_____; ②92-(_____)2=8×4; ③(_____)2-92=8×5;④132-(_____)2=8×_____; …(1)通过观察归纳,你知道上述规律的一般形式吗?请把你的猜想写出来. (2)你能运用本章所学的平方差公式来说明你的猜想的正确性吗?20、在课本的阅读材料中,介绍了一个第七届国际数学教育大会的会徽.它的主题图案是由一连串如图所示的直角三角形演化而成的.设其中的第一个直角三角形OA 1A 2是等腰三角形,且OA 1=A 1A 2=A 2A 3=A 3A 4=…=A 8A 9=1,(1)请你先计算图中的线段OA 7,OA 8,OA 9的长,再猜想OA n 的长 (2)若∠A n-1OA n 是第一个小于15°的角,求n 的值.(备选数据:Sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)中考演练1.(2012年广东肇庆)观察下列一组数:23,45,67,89,…,它们是按一定规律排列的,那么这一组数的第k个数是________.2.(2012年湖南株洲)一组数据为:x ,-2x 2,4x 2,-8x 2,…,观察其规律,推断第n 个数据应为______. 3.(2011年浙江)如图Z4-2,下面是按照一定规律画出的“树形图”,经观察可以发现:图A 2比图A 1多出2个“树枝”, 图A 3比图A 2多出4个“树枝”, 图A 4比图A 3多出8个“树枝”,…,照此规律,图A 6比图A 2多出“树枝”()图Z4-2A .28个B .56个C .60个D .124个4.(2012年山东)求1+2+22+23+…+22 012的值,可令S =1+2+22+23+…+22 012,则2S =2+22+23+24+…+22 013,因此,2S -S =22 013-1.仿照以上推理,计算出1+5+52+53+…+52 012的值为( )A .52 012-1B .52 013-1 C.52 013-14 D.52 012-145.(2012年贵州毕节)在图Z4-3中,每个图案均由边长为1的小正方形按一定的规律堆叠而成,照此规律,第10个图案中共有______个小正方形.图Z4-3图Z4-46.(2011年湖南常德)先找规律,再填数: 11+12-1=12,13+14-12=112,15+16-13=130,17+18-14=156,…… 则12 011+12 012-________=12 011×2 012. 7.(2012年河北)某数学活动小组的20位同学站成一列做报数游戏,规则是:从前面第一位同学开始,每位同学依次报自己顺序的倒数加1,第1位同学报⎝ ⎛⎭⎪⎫11+1,第2位同学报⎝ ⎛⎭⎪⎫12+1……这样得到的20个数的积为________________.8.(2010年浙江嵊州)如图Z4-4,平面内有公共端点的六条射线OA ,OB ,OC ,OD ,OE ,OF ,从射线OA 开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,…,则“17”在射线__________上;“2 007”在射线____________上.9.(2012年云南)观察图Z4-5的图形的排列规律(其中▲、■、★分别表示三角形、正方形、五角星).若第一个图形是三角形,则第18个图形是________________(填图形名称).▲■★■▲★▲■★■▲★▲……图Z4-510.(2011年广东湛江)已知:A 23=3×2=6,A 35=5×4×3=60,A 45=5×4×3×2=120,A 46=6×5×4×3=360,…,观察前面的计算过程,寻找计算规律计算A 37=_______________(直接写出计算结果),并比较A 310________A 410(填“>”或“<”或“=”). 11.(2012年广东汕头)观察下列等式:第1个等式:a 1=11×3=12×⎝ ⎛⎭⎪⎫1-13; 第2个等式:a 2=13×5=12×⎝ ⎛⎭⎪⎫13-15;第3个等式:a 3=15×7=12×⎝ ⎛⎭⎪⎫15-17; 第4个等式:a 4=17×9=12×⎝ ⎛⎭⎪⎫17-19;……请解答下列问题:(1)按以上规律列出第5个等式:a 5=______=______;(2)用含有n 的代数式表示第n 个等式:a n =______=______(n 为正整数); (3)求a 1+a 2+a 3+a 4+…+a 100的值.12.(2010年浙江宁波)18世纪瑞士数学家欧拉证明了简单多面体中顶点数V 、面数F 、棱数E 之间存在的一个有趣的关系式,被称为欧拉公式.请你观察图Z4-6中的几种简单多面体模型,解答下列问题: (1)根据上面的多面体模型,完成表格中的空格:你发现顶点数V 、面数F 、棱数E 之间存在的关系式是______________;(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是__________;(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱.设该多面体外表面三角形的个数为x 个,八边形的个数为y 个,求x +y 的值.。
3.1字母表示数--探索规律

如何解决规律探索型?难易度:★★★★关键词:规律探索答案:探索图案中的变化规律问题,一般是从第1个图案开始,数出第1、第2、第3、第4个图案中图形的个数,然后根据所得出的数字去发现其中存在的变化规律,然后用字母表示出一般规律即可.【举一反三】典例:观察下列图形:它们是按一定规律排列的,依照此规律,第20个图形共有个★.思路导引:通过观察各个图形的规律可发现:第1个图形中★的个数为3;第2个图形中★的个数为3+3=3×2=6;第3个图形中★的个数为3+3+3=3×3=9;第4个图形中★的个数为3+3+3+4=3×4=12;…;第n个图形中★的个数为3n.所以第20个图形中★的个数为3×20=60.标准答案:60如何用字母表示数进行规律计算?难易度:★★★★关键词:列代数式答案:在用字母表示一组数据的运算时,一定要抓住核心的部分,找出对应的数据,横向、纵向、首项、末项之间进行比对,从而找出其变化的规律,再用字母表示出来。
【举一反三】典例:观察下列各式:12+1=1×2,22+2=2×3,32+3=3×4,……第6个式子是______,第9个式子是______,请你将猜想到的规律用自然数表示出来_______思路导引:一般来说,此类问题一定要仔细观察,在观察时,把每一组数据对应比较,找出变化前后的特点。
12+1=1×2,22+2=2×3,32+3=3×4把每一行的每一个数据对应比较,就会发现第一个数都是平方,第一个数从1开始,依次递加1;第二个数与第一个数字相同,只是没有平方;等号后的两数以乘积相连,两数差1。
以此分析,第六个式子为62+6=6×7,第九个式子为92+9=9×10;标准答案:62+6=6×7;92+9=9×10;n2+n=n(n+1)如何用字母表示一个多位数?难易度:★★★★关键词:列代数式答案:我们表示数时,一般采用的是下进制。
规律探索型问题

为
.
【点评】本题是对图形变化规律的考查,查出前三 个图形的火柴棒的根数,并观察出后一个图形比前 一个图形多6根火柴棒是解题的关键.
考点4 数形结合猜想型问题
【例 4】(2012·益阳)观察图形,解答问题:
(1)按下表已填写的形式填写表中的空格:
考点4 数形结合猜想型问题
解:(1)填表如下:
考点4 数形结合猜想型问题
A. 2010
B. 2012
C. 2014
D. 2016
4.(2012·绍兴) 在一条笔直的公路边,有一些树和路灯,每相 邻的两盏灯之间有 3 棵树,相邻的树与树,树与灯间的距离 是 10m,如图,第一棵树左边 5 cm 处有一个路牌,则从此路
牌起向右 510m~550m 之间树与灯的排列顺序是 ( B )
第①个图有 2 个相同的小正方形,2=1×2; 第②个图有 6 个相同的小正方形,6=2×3;
答第③题个模图板有 12 个16.相探同索的小数正量方规形律,1题2=常3×用4;的方法
第④个图有 20 个相同的小正方形,20=4×5;…… 按此规律,第○n 个图有 n(n+1)个相同的小正方形. (3)首先分析题意,找到规律,并进行推导得出答案. 观察分析可得: 第 1 个图有 1 个圆; 第 2 个图由 7 个圆组成,7=1+6; 第 3 个图由 19 个圆组成,19=1+6+2×6;…… 故第 9 个图由 1+6+2×6+3×6+…+8×6 =1+(1+2+3+…+8)×6=217 个圆组成.
答题模板 探索数量规律题常用的方法
答题思路
第一步:审题,仔细观察图形并找到相应的规律; 第二步:化形为数,相当于找出数列的前若干项; 第三步:考察相邻两项的差异,再根据这些项或项中某
初中数学专题规律探索型问题课件

(三)猜想数值结果
当一些条件改变的前提下,结果的数值不变,或者其变 化规律呈现出某种特征时,可以猜想在新的条件下,数 值仍然不变,或者仍然按照原来的特征变化,依此猜想 到结果的数值。
例如:1、如图,在梯形ABCD中AB∥CD,AB=b,CD=a,E为AD边上 的一点,EF∥AB,且EF交BC于点F,某同学在研究这一问题时, 发现如下事实: (1)当DE/AE=1时,有EF=(a+b)/2;
(2)当DE/AE=2时,有EF=(a+2b)/3;
(3)当DE/AE=3时,有EF=(a+3b)/4;
当DE/AE=k时,参照上述结论,请你猜想用k表示EF的一般结论,并 证明之
(四)阅读理解型探究规律
阅读理解类型的问题和一般试题相比较,不仅考察学生对 数学知识的理解水平,而且考察学生的阅读能力,因而试 题的篇幅较长,信息量较大。
黄店镇中学九年级数学组 王志海
规律探索型问题:就是对材料信息的加工
提炼和运用,从而得出数学概念和规律,或者将 实际问题抽象为数学问题,建立数学模型的一类 问题。 对规律归纳和发现能反映出一个人的应用数 学、发展数学和进行数学创新的意识和能力。求 解规律探索型问题要求学生有敏锐的观察力,能 从特殊的情况出发,经过周密的思考,全面的分 析,去推得一般的结论。这类试题意在检测解题 者驾驭数学的创新意识和才能,因此,成为了这 几年的热点内容。
2
3
…
N
探索问题。
若你是一家餐厅的大堂经理,由你负责在一个宽 敞明亮的大厅里组织一次规模盛大的西式冷餐会,你 会选择哪种餐桌的摆法? 说明:新颖的问题可以立刻吸引学生的注意力,我们 需要的是等待学生讨论后的完美答案。因此要一步步 加大题目的开放性,不仅在探索过程中培养了学生的 创造能力,也使之对数学的生活化和生活的数学化都 有较好的体验。
规律探索性问题(含解析)

规律探索性问题第一部分 讲解部分一.专题诠释规律探索型题是根据已知条件或题干所提供的若干特例,通过观察、类比、归纳,发现题目所蕴含的数字或图形的本质规律与特征的一类探索性问题。
这类问题在素材的选取、文字的表述、题型的设计等方面都比较新颖新。
其目的是考查学生收集、分析数据,处理信息的能力。
所以规律探索型问题备受命题专家的青睐,逐渐成为中考数学的热门考题。
二.解题策略和解法精讲规律探索型问题是指在一定条件下,探索发现有关数学对象所具有的规律性或不变性的问题,它往往给出了一组变化了的数、式子、图形或条件,要求学生通过阅读、观察、分析、猜想来探索规律.它体现了“特殊到一般”的数学思想方法,考察了学生的分析、解决问题能力,观察、联想、归纳能力,以及探究能力和创新能力.题型可涉及填空、选择或解答.。
三.考点精讲 考点一:数与式变化规律通常根据给定一列数字、代数式、等式或者不等式,然后写出其中蕴含的一般规律,一般解法是先写出数式的基本结构,然后通过比较各式子中相同的部分和不同的部分,找出各部分的特征,改写成要求的规律的形式。
例1. 有一组数:13,25579,,101726,请观察它们的构成规律,用你发现的规律写出第n (n 为正整数)个数为 .分析:观察式子发现分子变化是奇数,分母是数的平方加1.根据规律求解即可. 解答:解:21211211⨯-=+; 23221521⨯-=+; 252311031⨯-=+;272411741⨯-=+; 219251265+⨯-=;…; ∴第n (n 为正整数)个数为2211n n -+. 点评:对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.此题的规律为:分子变化是奇数,分母是数的平方加1. 例2(2010广东汕头)阅读下列材料:1×2 =31(1×2×3-0×1×2), 2×3 = 31(2×3×4-1×2×3),3×4 = 31(3×4×5-2×3×4),由以上三个等式相加,可得1×2+2×3+3×4= 31×3×4×5 = 20. 读完以上材料,请你计算下列各题:(1) 1×2+2×3+3×4+···+10×11(写出过程);(2) 1×2+2×3+3×4+···+n ×(n +1) = ______________; (3) 1×2×3+2×3×4+3×4×5+···+7×8×9 = ______________.分析:仔细阅读提供的材料,可以发现求连续两个正整数积的和可以转化为裂项相消法进行简化计算,从而得到公式)1(433221+⨯++⨯+⨯+⨯n n[])1()1()2)(1()321432()210321(31+--++++⨯⨯-⨯⨯+⨯⨯-⨯⨯⨯=n n n n n n )2)(1(31++=n n n ;照此方法,同样有公式: )2()1(543432321+⨯+⨯++⨯⨯+⨯⨯+⨯⨯n n n [])2()1()1()3()2()1()43215432()32104321(41+⨯+⨯⨯--+⨯+⨯+⨯++⨯⨯⨯-⨯⨯⨯+⨯⨯⨯-⨯⨯⨯=n n n n n n n n )3)(2)(1(41+++=n n n n . 解:(1)∵1×2 = 31(1×2×3-0×1×2), 2×3 =31(2×3×4-1×2×3), 3×4 = 31(3×4×5-2×3×4),…10×11 =31(10×11×12-9×10×11), ∴1×2+2×3+3×4+···+10×11=31×10×11×12=440.(2))2)(1(31++n n n .(3)1260.点评:本题通过材料来探索有规律的数列求和公式,并应用此公式进行相关计算.本题系初、高中知识衔接的过渡题,对考查学生的探究学习、创新能力及综合运用知识的能力都有较高的要求.如果学生不掌握这些数列求和的公式,直接硬做,既耽误了考试时间,又容易出错.而这些数列的求和公式的探索,需要认真阅读材料,寻找材料中提供的解题方法与技巧,从而较为轻松地解决问题.例3(2010山东日照,19,8分)我们知道不等式的两边加(或减)同一个数(或式子)不等号的方向不变.不等式组是否也具有类似的性质?完成下列填空:一般地,如果⎩⎨⎧>>dc b a ,那么a +c b +d .(用“>”或“<”填空)你能应用不等式的性质证明上述关系式吗?分析:可以用不等式的基本性质和不等式的传递性进行证明。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、下列图案是由边长为单位长度的小正方形按一定的规律拼接 而成。依此规律,第5个图案中小正方形的个数为____4_1____。
3、按如下规律摆放三角形:
则第(4)堆三角形的个数为___1__4________; 第(n)堆三角形的个数为____3__n_+_2_____
中考真题 09中考.doc
22
3
3
3 3 3 3 …
44
(1)猜想并写出第n个等式; 【猜想】
(2)证明你写出的等式的正确性. 【证】
题型二:关于图形规律问题
1、为庆祝“六、一”儿童节,某幼儿园举行用火柴棒摆“金鱼” 比赛.如图所为(A ) A、2+6n ,B、8+6n , C、4+4n , D、8n
题型三:关于数形结合规律问题
1、柜台上放着一堆罐头,它们摆放在的形状见右 图:
第一层有2×3听罐头; 第二层有3×4听罐头; 第三层有4×5听罐头。 根据这堆罐头排列规律,第n(n为正整数)层有 __ n2+_3_n+_2 ____听罐头(用含n的式子表示)
2、意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有 这样一组数:1,1,2,3,5,8,13,…,
1、观察一列数2,4,8,16,32,---,发现从第二项 开始,每一项与前一项之比是一个常数,这个常数是_2___; 根据此规律,如果an(n为正整数)表示这个数列的第n 项,那么
a18 =_2_1_8__,an=______2_n___。
(1)如果欲求 1 3 32 33 320的值,可令
其中从第三个数起,每一个数都等于它前面两上数的和。现以这 组数中的各个数作为正方形的长度构造如下正方形:
...
11 2
3
5
再分别依次从左到右取2个、3个、4个、5个,正方形拼成如下矩
形并记为①、②、③、④.相应矩形的周长如下表所示:
序号 ① ② 周长 6 10
③④ 16 26
若按此规律继续作矩形,则序号为⑩的矩形周长是____ _4_6_6 。
规律探索型
题型一:关于代数规律问题
1、有一组数:1,2,5,10,17,26,……,请观察这组数的构
成规律,用你发现的规律确定第8个数为 50
.
2、把正整数1,2,3,4,5,……,按如下规律排列:
1 2,3, 4,5,6,7, 8,9,10,11,12,13,14,15,
…………
2n-1
按此规律,可知第n行有 个正整数.
s 1 3 32 33 320 (1)
将(1)式两边同乘以 3,得
由(_2_3 ()_2用s _) 式_由_3 减特_ _去3 殊_2 _到 (_1_)3 一式_3 _ 般,_得3 _的4 _s _方 __法_3 __2 ___知__s1 _:若__数_12_列((_23_)2a_11_,_a_21_,)a_3__ an ,
若 10 b120b,符合前面式 则 a子 b的 _1_ 09规 __律 _。 _, _
a
a
5. 1121, 2131, 3141,.... 33 44 55
请你将发现的规律用含自然数n(n≥1)的等式表示出
来 n 1 (n1) .1
n2
n2
中考真题
(09安徽)17.观察下列等式:
1 1 1 1 2 2 2 2
观察图中的规律,求出第10个黑色梯形的面积
S4
S3 S2 S1 0 1 3 5 7 9 11 13
图6
S10=__7_6_______
3、填在下面三个田字格内的数有相同的规律,根据此规律, C = 1_08__.
13 5 20
35 7 56
5A BC
从第二项开始每一项与 前一项之比的常数为 q,
则an 常数
q
_a_1_q_n_1__(用含 1, 那么 a1 a 2
a1a,3q, n的代a数n 式_a表_1_(示_q_n_),_如_1_果)__这(用个含
a1
,
q
,
n
的代数式表示 )
q 1
2、如图6,∠AOB=450,过OA到点O的距离分别为 1,3,5,7,9,11,----的点作OA的垂线与OB相 交,得到并标出一组黑色梯形,它们的面积分别为 S1、S2、S3、S4---
3、一个巴尔末的中学教师成功地从光谱数据,95,1126,
25, 21
36, 32
---中得到巴尔末公式,从而打开了光谱奥秘的大门,请你按照这
种规律,写出第n(n≥1)个数据是___________________.
解(: n2)2或(n2)2 n(n4) (n2)24
4、已 2知 222 : 2, 33323,44424, 55525 , 3 3 8 8 15 15 24 24
