矩形截面惯性矩附抗弯截面系数
实心、空心及圆环形惯性矩与抗弯截面系数

梁的强度条件
1. 纯弯曲梁的最大弯曲正应力:
(1) 等截面直梁,中性轴为横截面对称轴
Wz——抗弯截面系数
(2) 中性轴不是横截面对称轴,且材料拉压强度不相等
(3) 利用正应力的强度条件可以对梁进行三种不同形式的强度计算:
(a) 校核强度
(b) 选择截面尺寸或型钢号
(c) 确定许可荷载
2. 横力弯曲的梁
注意:
(1) 一般的梁,其强度主要受到按正应力的强度条件控制,所以在选择梁的截面尺寸或确定许可荷载时,都先按正应力强度条件进行计算,然后按切应力强度条件校核。
(2) 在弯矩为最大的横截面上距中性轴最远点处有最大正应力;在剪力为最大的横截面的中性轴上各点处有最大切应力。
轴惯性矩及抗弯截面系数
(1) 实心矩形的惯性矩及抗弯截面系数
(2) 空心矩形的惯性矩及抗弯截面系数
(3) 实心圆截面的惯性矩及抗弯截面系数
(4) 空心圆截面的惯性矩
三角形
bh
惯性矩IIx1 bh^3/4
Ix bh^3/36
Ix2 bh^3/16 抗弯截面系数W
Wx1 bh^2/24 Wx2 bh^2/12。
抗扭截面系数 抗弯截面系数

抗扭截面系数抗弯截面系数
抗扭截面系数抗弯截面系数如下:
抗扭截面系数:Wt=Ip/r(Wt为抗扭截面系数,Ip为横截面的极惯性矩,r为截面半径)
抗弯截面系数:Wz=Iz/y(Wz为抗弯截面系数,Iz为横截面对z轴惯性矩,y为截面离圆心最大值)
在横截面距圆心为ρ处取一微面积dA,该微面积上的内力为τdA,对圆心的力矩为ρ*τdA,在整个横截面积分得横截面上的内力系对圆心之矩,这就是横截面上的扭矩T。
T=∫ρ*τdA又有τp=Gρdφ/dx,将T代入其中的T=Gdφ/dx*∫ρ²dA,令
Ip=∫ρ²dA,代入化简得τmax=T*r/Ip令Wt=Ip/r,即为抗扭截面系数的来由。
对于中性轴为横截面的对称轴,最大拉、压应力相等,都为
σ=My/Iz。
令Wz=Iz/y即得抗弯截面系数。
扩展资料:以上公式都为在平面假设的基础上导出的。
试验结果表明,只有对等直圆轴,平面假设才成立,所以这些公式只适用于等直圆轴。
对于圆截面沿周线缓慢变化的小锥度圆锥周,也可以近似的应用这些公式。
实心轴:Ip=πd⁴/32,Wt=Ip*2/d=πd³/16,Iz=πd⁴/64,Wz=πd³/32空心轴:α=d/D,Wt=πD⁴(1-α⁴)/32,Wz=πD³(1-α⁴)/32。
常见截面的惯性矩和抗弯截面系数

常见截面惯性矩和抗弯截面系数自动计算 简介本文档主要介绍:工程常见截面的截面惯性矩、抗弯截面系数,主要包括矩形、矩形管、圆形、圆管、椭圆、椭圆管、六边形、花键的截面惯性矩、抗弯截面系数公式及公式自动求值方法。
理论依据根据材料力学,抗弯截面系数W X 与截面惯性矩I X 的关系公式如下: 的距离离中性为,其中轴X最远点截面上W max maxy y I X X 。
下面一一列出前述各形状截面的公式和wxMaxima 计算机自动求值算式。
矩形矩形截面如下图所示。
平行于X 轴的矩形边长为b ,平行于Y 轴的矩形边长为h ,矩形截面相对于X 轴的截面惯性矩公式为:123bh I X = 其相对于X 轴的抗弯截面系数公式为:6212W 23max bh h bh y I X X === 下面为wxMaxima 计算机自动求值算式,将下面的内容复制进wxMaxima 软件的空白区域,将数值修改为与工程实际情况相符合的数值,然后点击菜单栏的“单元”→“对单元进行求值”,即可得到想要的结果:/*矩形的截面惯性矩和抗弯截面系数计算*//*设置软件输出结果为数值*/if numer#false then numer:true else numer:true;b:38;h:130;Ix:1/12*b*h^3;Wx:1/6*b*h^2;/*作用在截面上的弯矩*/M:109874;/*弯矩在截面上产生的应力*/σ:M/Wx;矩形管矩形管截面如下图所示。
平行于X 轴的内部矩形边长为b ,平行于Y 轴的内部矩形边长为h ,平行于X 轴的外部矩形边长为B ,平行于Y 轴的外地部矩形边长为H ,矩形管截面相对于X 轴的截面惯性矩公式为:1212-123333bh BH bh BH I X -== 其相对于X 轴的抗弯截面系数公式为:hbh BH h bh BH y I X X 6212W 3333max -=-== /*矩形管的截面惯性矩和抗弯截面系数计算*//*设置软件输出结果为数值*/if numer#false then numer:true else numer:true;b:38;h:130;Ix:(B*H^3-b*h^3)/12;Wx:(B*H^3-b*h^3)/6/H;/*作用在截面上的弯矩*/M:109874;/*弯矩在截面上产生的应力*/σ:M/Wx;圆形圆形截面如下图所示。
抗弯截面系数及惯性矩公式大全

抗弯截面系数及惯性矩公式大全
梁的强度条件
1. 纯弯曲梁的最大弯曲正应力:
(1) 等截面直梁,中性轴为横截面对称轴
Wz——抗弯截面系数
(2) 中性轴不是横截面对称轴,且材料拉压强度不相等
(3) 利用正应力的强度条件可以对梁进行三种不同形式的强度计算:
(a) 校核强度
(b) 选择截面尺寸或型钢号
(c) 确定许可荷载
2. 横力弯曲的梁
注意:
(1) 一般的梁,其强度主要受到按正应力的强度条件控制,所以在选择梁的截面尺寸或确定许可荷载时,都先按正应力强度条件进行计算,然后按切应力强度条件校核。
(2) 在弯矩为最大的横截面上距中性轴最远点处有最大正应力;在剪力为最大的横截面的中性轴上各点处有最大切应力。
轴惯性矩及抗弯截面系数
(1) 实心矩形的惯性矩及抗弯截面系数
(2) 空心矩形的惯性矩及抗弯截面系数
(3) 实心圆截面的惯性矩及抗弯截面系数
(4) 空心圆截面的惯性矩。
惯性矩、静矩、截面抵抗矩计算

惯性矩和对Y轴的惯性矩。
y
解:
100
1)求出A1和A2分别对自身形心 2
轴的惯性矩
0
I x1
b1h13 12
100 203 12
66.67 103
100
A1 •Ⅱ•ຫໍສະໝຸດ A2Ⅰx1
xc a2 30 x
Ix2
b2h23 12
20 100 3 12
16.67 105
2 0
2)求对整个截面形心X轴的惯性矩
截面对x轴的惯性矩:
I x y2dA
量纲:L4 y
A
截面对y轴的惯性矩: I y x2dA
A
注意:
1)同一截面对不同的轴惯性 矩不同;
2)惯性矩永远为正值;
x
dA
y r
x
3)惯性矩的单位为m4;
2、惯性半径(回转半径)
截面对x轴的惯性半径: ix I x / A 截面对y轴的惯性半径: iy I y / A
二、常见截面的惯性矩和惯性半径
形心轴:通过截面形心的坐标轴 ➢ 矩形截面对于其对称轴(即形心轴)x,y的惯性矩。
y
对x轴的惯性矩
x
Ix
1 12
bh3
h 对y轴的惯性矩:
b
Iy
1 12
hb3
➢ 矩形截面对于其对称轴(即形心轴)x,y的惯性半径。
y
对x轴的惯性半径
x
h
ix
Ix A
1/12bh3 h
截面的几何性质
知识点:截面惯性矩和静矩的计算 一、截面惯性矩的定义及计算 二、常见截面的惯性矩和惯性半径 三、组合截面的概念 四、惯性矩的平行移轴公式 五、静矩的概念及公式 六、常见截面的静矩
各种截面下极惯性矩
面
32
抗扭截面系数
Wt
IP R
α d D
b
h z
y
D d
z y
2.组合图形
W 称为抗弯截面系数
I y I yC a2 A I z I zC b2 A
I yz I yC zC abA
I y I yi
I z I zi
I yz I yizi
(1)两平行轴中,必须有一轴为形心轴,截面对任意两平行轴 的惯性矩间的关系,应通过平行的形心轴惯性矩来换算;
(2)截面图形对所有平行轴的惯性矩中,以对通过形心轴的惯 性矩最小.
6、惯性矩与极惯性矩的关系:
z
I p
2dA
A
( y2 z2 )dA
A
y
dA
y2dA z2dA I z I y
o
A
A
z
y
图形对任一对相互垂直的坐标系的惯性矩之和恒等于此图形对该两轴交点的极惯性矩。
四、惯性半径(Radius of gyration of the area)
iy
Iy A
iz
Iz A
组合图形1两平行轴中必须有一轴为形心轴截面对任意两平行轴的惯性矩间的关系应通过平行的形心轴惯性矩来换算
各种截面下惯性矩,极惯性矩
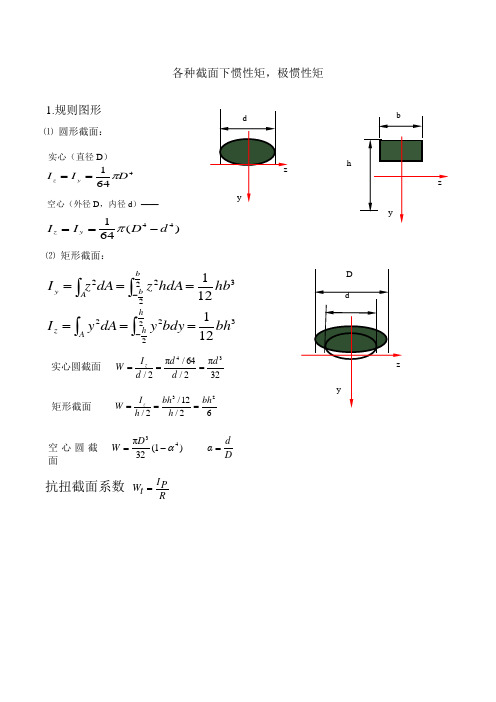
1.规则图形
d
⑴ 圆形截面:
实心(直径 D)
Iz
Iy
1 D4
64
空心(外径 D,内径 d)——
Iz
Iy
1 (D4
64
d 4)
⑵ 矩形截面:
z y
I y
z2dA
A
b
2 b
2
z 2 hdA
1 12
抗弯截面系数和惯性矩计算公式

梁的强度条件
1.纯弯曲梁的最大弯曲正应力:
(1)等截面直梁,中性轴为横截面对称轴
Wz——抗弯截面系数
(2)中性轴不是横截面对称轴,且材料拉压强度不相等
(3)利用正应力的强度条件可以对梁进行三种不同形式的强度计算:
(a)校核强度
(b)选择截面尺寸或型钢号
(c)确定许可荷载
2.横力弯曲的梁
注意:
(1)一般的梁,其强度主要受到按正应力的强度条件控制,所以在选择梁的截面尺寸或确定许可荷载时,都先按正应力强度条件进行计算,然后按切应力强度条件校核。
(2)在弯矩为最大的横截面上距中性轴最远点处有最大正应力;在剪力为最大的横截面的中性轴上各点处有最大切应力。
轴惯性矩及抗弯截面系数
(1)实心矩形的惯性矩及抗弯截面系数
(2)空心矩形的惯性矩及抗弯截面系数
(3)实心圆截面的惯性矩及抗弯截面系数
(4)空心圆截面的惯性矩。
常用截面惯性矩与截面系数的计算
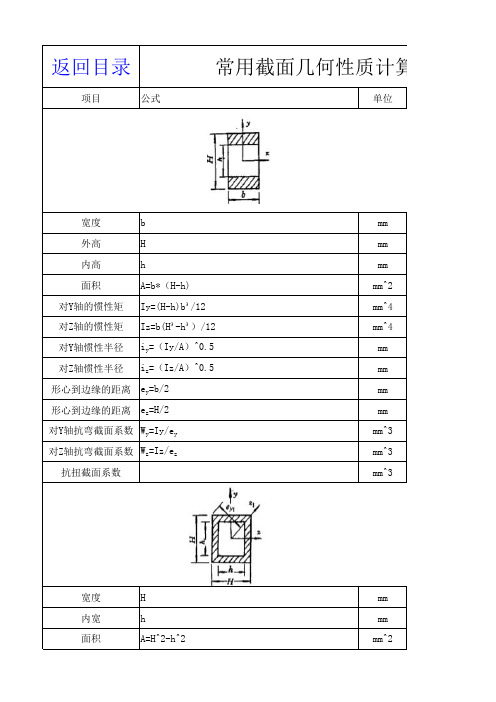
常用截面几何性质计算返回目录项目公式单位宽度b mm外高H mm内高h mm面积A=b*(H-h)mm^2对Y轴的惯性矩Iy=(H-h)b³/12mm^4对Z轴的惯性矩Iz=b(H³-h³)/12mm^4对Y轴惯性半径i y=(Iy/A)^0.5mm对Z轴惯性半径i z=(Iz/A)^0.5mm形心到边缘的距离e y=b/2mm形心到边缘的距离e z=H/2mm对Y轴抗弯截面系数W y=Iy/e y mm^3对Z轴抗弯截面系数W z=Iz/e z mm^3抗扭截面系数mm^3宽度H mm内宽h mm面积A=H^2-h^2mm^2对Y轴的惯性矩Iy=(H^4-h^4)/12mm^4对Z轴的惯性矩Iz=(H^4-h^4)/12mm^4对Y轴惯性半径i y=(Iy/A)^0.5mm 对Z轴惯性半径i z=(Iz/A)^0.5mm 形心到边缘的距离e y=H/2mm 形心到边缘的距离e z=H/2mm 形心到边缘的距离e z1=0.707*H mm 对Y轴抗弯截面系数W y=Iy/e y mm^3对Z轴抗弯截面系数W z=Iz/e z mm^3对Z轴抗弯截面系数W z1=Iz/e z mm^3抗扭截面系数mm^3宽度a mm直径d mm面积A=a^2-Pi*d^2/4mm^2对Y轴的惯性矩Iy=a^4/12-Pi*d^4/64mm^4对Z轴的惯性矩Iz=a^4/12-Pi*d^4/64mm^4对Y轴惯性半径i=(Iy/A)^0.5mm 对Z轴惯性半径i=(Iz/A)^0.5mm 形心到边缘的距离e y=a/2mm 形心到边缘的距离e z=a/2mm 对Y轴抗弯截面系数W y=Iy/e y mm^3对Z轴抗弯截面系数W z=Iz/e z mm^3抗扭截面系数mm^3a=0,三角形顶宽a mm底宽b mm高h mm面积A=h*(a+b)/2mm^2对Y轴的惯性矩mm^4对Z轴的惯性矩Iz=h^3*(a^2+4*a*b+b^2)/36/(a+b)mm^4对Y轴惯性半径mm 对Z轴惯性半径iz=(Iz/A)^0.5mm 形心到边缘的距离e y1=h*(2*a+b)/(a+b)/3mm 形心到边缘的距离e y2=h*(a+2*b)/(a+b)/3mm 对底边抗弯截面系数W z1=Iz/e y1mm^3对顶边抗弯截面系数W z2=Iz/e y2mm^3抗扭截面系数mm^3正多边形边数n边长a mm 外接圆半径R=a/2/sin(180°/n)mm 内接圆半径r=a/2/sin(180°/n)mm 面积A=n*R^2*sin(2*Pi/n)/2mm^2惯性矩I=A*(6*R^2-a^2)/24mm^4对Y轴惯性半径i=(I/A)^0.5mm形心到底边的距离e y=r mm 形心到顶边的距离e y1=R mm 对底边抗弯截面系数W z=I/R/cos(Pi/n)mm^3对顶点抗弯截面系数W z1=I/R mm^3抗扭截面系数mm^3宽度a mm直径d mm面积A=a^2-Pi*d^2/4mm^2对Y轴的惯性矩Iy=a^4/12-Pi*d^4/64mm^4对Z轴的惯性矩Iz=a^4/12-Pi*d^4/64mm^4对Y轴惯性半径i=(Iy/A)^0.5mm 对Z轴惯性半径i=(Iz/A)^0.5mm 形心到边缘的距离e y=a/2mm 形心到边缘的距离e z=a/2mm 对Y轴抗弯截面系数W y=Iy/e y mm^3对Z轴抗弯截面系数W z=Iz/e z mm^3抗扭截面系数mm^3外径D mm内径d mm面积A=Pi*(D^2-d^2)/4mm^2惯性矩I=Pi*(D^4-d^4)/64mm^4惯性半径i=(Iz/A)^0.5mm 形心到边缘的距离e=D/2mm 抗弯截面系数W=I/e mm^3抗扭截面系数Wt=Pi*D^3(1-(d/D)^4)/16mm^3外径D mm内径d mm面积A=Pi*(D^2-d^2)/8mm^2对Y轴的惯性矩Iy=Pi*(D^4-d^4)/128mm^4对Z轴的惯性矩Iz=0.00686*(D^4-d^4)-0.0177*D^2*d^2*(D-d)/(D+d mm^4对Y轴惯性半径i y=(Iy/A)^0.5mm 对Z轴惯性半径i z=(Iz/A)^0.5mm 形心到边缘的距离e y=2*(D^2+D*d+d^2)/3*Pi*(D+d)mm 形心到边缘的距离e z=D/2mm 对Y轴抗弯截面系数W y=Pi*D^3*(1-d^4/D^4)/64mm^3对顶点的抗弯截面系数W z=Iz/(D/2-e y)mm^3对底边的抗弯截面系数W z1=Iz/e y mm^3抗扭截面系数mm^3直径d mm宽度b mm深度t mm面积A=Pi*d^2/4-b*t mm^2对Y轴的惯性矩Iy=Pi*d^4/64-t*b^3/12mm^4对Z轴的惯性矩Iz=Pi*d^4/64-b*t*(d-t)^2/4mm^4对Y轴惯性半径i y=(Iy/A)^0.5mm 对Z轴惯性半径i z=(Iz/A)^0.5mm 形心到边缘的距离e y=d/2mm 形心到边缘的距离e z=d/2mm 对Y轴抗弯截面系数W y=Iy/e y mm^3对Z轴抗弯截面系数W z=Iz/e z mm^3抗扭截面系数mm^3直径d mm宽度b mm深度t mm面积A=Pi*d^2/4-2*b*t mm^2对Y轴的惯性矩Iy=Pi*d^4/64-t*b^3/6mm^4对Z轴的惯性矩Iz=Pi*d^4/64-b*t*(d-t)^2/2mm^4对Y轴惯性半径i y=(Iy/A)^0.5mm 对Z轴惯性半径i z=(Iz/A)^0.5mm 形心到边缘的距离e y=d/2mm 形心到边缘的距离e z=d/2mm 对Y轴抗弯截面系数W y=Iy/e y mm^3对Z轴抗弯截面系数W z=Iz/e z mm^3抗扭截面系数mm^3直径d mm支架d1mm面积A=Pi*d^2/4-d1*d mm^2对Y轴的惯性矩Iy=Pi*d^4*(1-1.69*d1/d)/64mm^4对Z轴的惯性矩Iz=Pi*d^4*(1-1.69*d1^3/d^3)/64mm^4对Y轴惯性半径i y=(Iy/A)^0.5mm 对Z轴惯性半径i z=(Iz/A)^0.5mm 形心到边缘的距离e y=d/2mm 形心到边缘的距离e z=d/2mm 对Y轴抗弯截面系数W y=Iy/e y mm^3对Z轴抗弯截面系数W z=Iz/e z mm^3抗扭截面系数mm^3宽度B mm宽度b mm高度H mm高度h mm面积A=B*H+b*h mm^2对Z轴的惯性矩Iz=(B*H^3+b*h^3)/12mm^4对Z轴惯性半径i z=(Iz/A)^0.5mm 形心到边缘的距离e z=H/2mm 对Z轴抗弯截面系数W z=Iz/e z mm^3抗扭截面系数mm^3宽度B mm宽度a mm高度H mm高度d mm面积A=B*H+b*h mm^2对Z轴的惯性矩Iz=mm^4对Z轴惯性半径i z=(Iz/A)^0.5mm 形心到边缘的距离e y=d/2mm 形心到边缘的距离e z=d/2mm 对Y轴抗弯截面系数W y=Iy/e y mm^3对Z轴抗弯截面系数W z=Iz/e z mm^3抗扭截面系数mm^3宽度B mm宽度a mm205214 4533.375 7642.7109384.6026074495.9760858861010 453.3375 764.271093810102020。
实心、空心及圆环形惯性矩与抗弯截面系数

梁的强度条件
1. 纯弯曲梁的最大弯曲正应力:
(1) 等截面直梁,中性轴为横截面对称轴
Wz——抗弯截面系数
(2) 中性轴不是横截面对称轴,且材料拉压强度不相等
(3) 利用正应力的强度条件可以对梁进行三种不同形式的强度计算:
(a) 校核强度
(b) 选择截面尺寸或型钢号
(c) 确定许可荷载
2. 横力弯曲的梁
注意:
(1) 一般的梁,其强度主要受到按正应力的强度条件控制,所以在选择梁的截面尺寸或确定许可荷载时,都先按正应力强度条件进行计算,然后按切应力强度条件校核。
(2) 在弯矩为最大的横截面上距中性轴最远点处有最大正应力;在剪力为最大的横截面的中性轴上各点处有最大切应力。
轴惯性矩及抗弯截面系数
(1) 实心矩形的惯性矩及抗弯截面系数
(2) 空心矩形的惯性矩及抗弯截面系数
(3) 实心圆截面的惯性矩及抗弯截面系数
(4) 空心圆截面的惯性矩
计算公式编辑
常见截面的惯性矩公式
矩形
b*h^3/12 其中:b—宽;h—高
三角形
b*h^3/36 其中:b—底长;h—高
圆形
π*d^4/64 其中:d—直径
圆环形
π*D^4*(1-α^4)/64; α=d/D 其中:d—内环直径;D—外环直径。
【最新精选】抗弯截面系数和惯性矩计算公式

【最新精选】抗弯截面系数和惯性矩计算公式梁的强度条件1. 纯弯曲梁的最大弯曲正应力:(1) 等截面直梁,中性轴为横截面对称轴Wz ——抗弯截面系数(2) 中性轴不是横截面对称轴,且材料拉压强度不相等(3) 利用正应力的强度条件可以对梁进行三种不同形式的强度计算:(a) 校核强度(b) 选择截面尺寸或型钢号(c) 确定许可荷载2. 横力弯曲的梁注意:(1) 一般的梁,其强度主要受到按正应力的强度条件控制,所以在选择梁的截面尺寸或确定许可荷载时,都先按正应力强度条件进行计算,然后按切应力强度条件校核。
(2) 在弯矩为最大的横截面上距中性轴最远点处有最大正应力;在剪力为最大的横截面的中性轴上各点处有最大切应力。
轴惯性矩及抗弯截面系数(1) 实心矩形的惯性矩及抗弯截面系数(2) 空心矩形的惯性矩及抗弯截面系数(3) 实心圆截面的惯性矩及抗弯截面系数(4) 空心圆截面的惯性矩【附加总结类文档一篇,不需要的朋友可以下载后编辑删除,谢谢】2015年文化馆个人工作总结在XXXX年X月,本人从XXXX学院毕业,来到了实现我梦想的舞台--XX区文化馆工作。
在这里我用艰辛的努力,勤劳的付出,真诚而认真地工作态度认真的做好自身的每一项文化馆相关工作,取得了较为良好的工作业绩。
随着一场场活动的成功举办、一台台戏剧的成功出演,在这个带有着梦想和希望的舞台上,转眼之间我已在这里渡过了XX年的青春事业,我亦与舞台共同成长,逐步由一名青涩的毕业生,历练成为了今天的XXX。
梦想在于不断坚持,未来的旅途在于不断的前进,在这个承载着梦的舞台上,我持以坚定的信心和丰富的工作能力与工作经验,一步一步超前迈进着。
下面我将自身XX年来的工作能力情况总结如下:一、一专多能服务1、高端学识水平。
本人于XXXX年XX月毕业于XXXX大学XX专业。
随后于XXXX年X月进入XX区文化馆从事XX工作,至今已有XX年的时间。
在本人从事文化馆XX工作的XX年里,我始终坚持积极探索、勤奋学习,做到辅助教学与实际工作相长,坚定与时俱进的思想理念,努力攻克各项困难,将提高效益型,能力型的工作绩效作为自己的奋斗目标,并在自身的素质方面进行了坚持不懈的强化与提高。
抗弯截面系数和惯性矩计算公式

抗弯截面系数和惯性矩计算公式
(总3页)
--本页仅作为文档封面,使用时请直接删除即可--
--内页可以根据需求调整合适字体及大小--
梁的强度条件
1. 纯弯曲梁的最大弯曲正应力:
(1) 等截面直梁,中性轴为横截面对称轴
Wz——抗弯截面系数
(2) 中性轴不是横截面对称轴,且材料拉压强度不相等
(3) 利用正应力的强度条件可以对梁进行三种不同形式的强度计算:
(a) 校核强度
(b) 选择截面尺寸或型钢号
(c) 确定许可荷载
2. 横力弯曲的梁
注意:
(1) 一般的梁,其强度主要受到按正应力的强度条件控制,所以在选择梁的截面尺寸或确定许可荷载时,都先按正应力强度条件进行计算,然后按切应力强度条件校核。
(2) 在弯矩为最大的横截面上距中性轴最远点处有最大正应力;在剪力为最大的横截面的中性轴上各点处有最大切应力。
轴惯性矩及抗弯截面系数
(1) 实心矩形的惯性矩及抗弯截面系数
(2) 空心矩形的惯性矩及抗弯截面系数
(3) 实心圆截面的惯性矩及抗弯截面系数
(4) 空心圆截面的惯性矩。
实心、空心及圆环形惯性矩与抗弯截面系数

梁的强度条件1. 纯弯曲梁的最大弯曲正应力:(1) 等截面直梁,中性轴为横截面对称轴% =见归/ W zWz――抗弯截面系数故由IB得M^JW z<\a\(2) 中性轴不是横截面对称轴,且材料拉压强度不相等则6昨至汰」拉仲许用应力”:皿航< 0」压缩许用应力(3) 利用正应力的强度条件可以对梁进行三种不同形式的强度计算:(a) 校核强度(b) 选择截面尺寸或型钢号(c) 确定许可荷载2. 横力弯曲的梁另还要满足对于寻截面克梁,则有:b——中性轴处截面之宽度"(1) 一般的梁,其强度主要受到按正应力的强度条件控制,所以在选择梁的截面尺寸或确定许可荷载时,都先按正应力强度条件进行计算,然后按切应力强度条件校核。
(2) 在弯矩为最大的横截面上距中性轴最远点处有最大正应力;在剪力为最大的横截面的中性轴上各点处有最大切应力。
I. 1- ' —=2也1(单位为HIlHld 或廿)忱际 6 (2)空心矩形的惯性矩及抗弯截面系数iy轴惯性矩及抗弯截面系数 (1)实心矩形的惯性矩及抗弯截面系数 (1)实心竝形的惯性悲及抗弯截面系数 1 对中性轴二的抗弯截面系数:BH 3 bh 3HB 3 hb 312 IT - bl 6H 2 ? 2p~ = y~ + zr Tr(3)实心圆截面的惯性矩及抗弯截面系数(4)空心圆截面的惯性矩计算公式编辑常见截面的惯性矩公式矩形b*hA3/12其中:b—宽;h —咼三角形b*hA3/36其中:b 底长;h 咼圆形n *dA4/64其中: d—直径圆环形n *D A4*(1 - a人4)/64;a =d/M中:d —内环直径;D —外环直径。
【最新精选】抗弯截面系数和惯性矩计算公式

【最新精选】抗弯截面系数和惯性矩计算公式梁的强度条件1. 纯弯曲梁的最大弯曲正应力:(1) 等截面直梁,中性轴为横截面对称轴Wz ——抗弯截面系数(2) 中性轴不是横截面对称轴,且材料拉压强度不相等(3) 利用正应力的强度条件可以对梁进行三种不同形式的强度计算:(a) 校核强度(b) 选择截面尺寸或型钢号(c) 确定许可荷载2. 横力弯曲的梁注意:(1) 一般的梁,其强度主要受到按正应力的强度条件控制,所以在选择梁的截面尺寸或确定许可荷载时,都先按正应力强度条件进行计算,然后按切应力强度条件校核。
(2) 在弯矩为最大的横截面上距中性轴最远点处有最大正应力;在剪力为最大的横截面的中性轴上各点处有最大切应力。
轴惯性矩及抗弯截面系数(1) 实心矩形的惯性矩及抗弯截面系数(2) 空心矩形的惯性矩及抗弯截面系数(3) 实心圆截面的惯性矩及抗弯截面系数(4) 空心圆截面的惯性矩【附加总结类文档一篇,不需要的朋友可以下载后编辑删除,谢谢】2015年文化馆个人工作总结在XXXX年X月,本人从XXXX学院毕业,来到了实现我梦想的舞台--XX区文化馆工作。
在这里我用艰辛的努力,勤劳的付出,真诚而认真地工作态度认真的做好自身的每一项文化馆相关工作,取得了较为良好的工作业绩。
随着一场场活动的成功举办、一台台戏剧的成功出演,在这个带有着梦想和希望的舞台上,转眼之间我已在这里渡过了XX年的青春事业,我亦与舞台共同成长,逐步由一名青涩的毕业生,历练成为了今天的XXX。
梦想在于不断坚持,未来的旅途在于不断的前进,在这个承载着梦的舞台上,我持以坚定的信心和丰富的工作能力与工作经验,一步一步超前迈进着。
下面我将自身XX年来的工作能力情况总结如下:一、一专多能服务1、高端学识水平。
本人于XXXX年XX月毕业于XXXX大学XX专业。
随后于XXXX年X月进入XX区文化馆从事XX工作,至今已有XX年的时间。
在本人从事文化馆XX工作的XX年里,我始终坚持积极探索、勤奋学习,做到辅助教学与实际工作相长,坚定与时俱进的思想理念,努力攻克各项困难,将提高效益型,能力型的工作绩效作为自己的奋斗目标,并在自身的素质方面进行了坚持不懈的强化与提高。
抗弯截面系数

截面抵抗矩之相礼和热创作(1):截面抵抗矩(W)就是截面对其形心轴惯性矩与截面上最远点至形心轴距离的比值.次要用来计算弯矩作用下截面最外边的正应力.工程实践中最稀有的弯曲成绩是横力弯曲,横截面上不但有正应力,而且还有切应力.由于切应力的作用,横截面发生翘曲,立体假设不再成立.但进一步的理论分析证明,对于跨长与截面高度比l/h>5 的长梁利用公式δ=My/I 来计算其横力弯曲的正应力,所得结果偏差甚微,充足满足工程实践必要.其中W=I/y,W称为抗弯截面系数(又称为截面抵抗矩).由于横力弯曲时,梁的弯矩随截面地位变更,Mmax所在截面称为风险截面,最大弯曲正应力发生在弯矩最大的截面上,且离中心轴最远处,该处为风险点.中和轴的确定1)找出达到极限弯矩时截面的中和轴.中和轴分为弹性中和轴和塑性中和轴.弹性形态下的中和轴:整个截面关于经此轴线的截面面积矩为0.横截面在此轴线弯曲正应力为0.(中和轴初始定义即为构件弯曲后某一截面的长度没有改变即为没有正应力或者说轴力)(和形心的定义同等,一样平常状况下中和轴即为形心的一条轴线)截面面积矩:指弹性形态下截面各微元面积与各微元至中和轴距离乘积的积分.单位mm.指弹性形态下中和轴一侧截面的面积矩,次要用于计算截面上恣意点的剪切应力值.塑性形态下的中和轴:塑性中和轴为构件截面面积中分线,该中和轴两边的面积相称.2)弹性形态下截面抵抗矩:如本文扫尾定义.其意义在于在弹性形态下计算某一构件断面地位最晦气地位的最大应力,该地位应力满足则此地位截面满足计算要求;塑性形态下截面塑性抵抗矩:分别求两正面积对中和轴的面积矩,面积矩之和即为塑性截面模量,也称为塑性抵抗矩.经常运用截面抗弯系数公式矩形截面抵抗矩W=bh^2/6圆形截面的抵抗矩W=πd^3/32圆环截面抵抗矩:W=π(D^4-d^4)/(32D).稀有截面面积、形心和惯性矩抗弯系数公式稀有图形的面积、形心和惯性矩序图形面积形心位置惯性矩(形心轴)号123 4 5 6。
抗弯截面系数

截面抵御矩之公保含烟创作(1):截面抵御矩(W)就是截面对其形心轴惯性矩与截面上最远点至形心轴间隔的比值.主要用来计算弯矩作用下截面最外边的正应力.工程实际中最罕见的弯曲问题是横力弯曲,横截面上不只有正应力,而且还有切应力.由于切应力的作用,横截面发作翘曲,平面假定不再成立.但进一步的实际剖析证明,关于跨长与截面高度比l/h>5 的长梁应用公式δ=My/I 来计算其横力弯曲的正应力,所得后果误差甚微,足够满足工程实际需要.其中W=I/y,W称为抗弯截面系数(又称为截面抵御矩).由于横力弯曲时,梁的弯矩随截面位置变卦,Mmax所在截面称为危险截面,最年夜弯曲正应力发作在弯矩最年夜的截面上,且离中心轴最远处,该处为危险点.中和轴确实定1)找出到达极限弯矩时截面的中和轴.中和轴分为弹性中和轴和塑性中和轴.弹性状态下的中和轴:整个截面关于经此轴线的截面面积矩为0.横截面在此轴线弯曲正应力为0.(中和轴初始定义即为构件弯曲后某一截面的长度没有改动即为没有正应力或许说轴力)(和形心的定义一致,一般情况下中和轴即为形心的一条轴线)截面面积矩:指弹性状态下截面各微元面积与各微元至中和轴间隔乘积的积分.单元mm.指弹性状态下中和轴一侧截面的面积矩,主要用于计算截面上任意点的剪切应力值.塑性状态下的中和轴:塑性中和轴为构件截面面积平分线,该中和轴两边的面积相等.2)弹性状态下截面抵御矩:如本文扫尾定义.其意义在于在弹性状态下计算某一构件断面位置最倒霉位置的最年夜应力,该位置应力满足则此位置截面满足计算要求;塑性状态下截面塑性抵御矩:辨别求两正面积对中和轴的面积矩,面积矩之和即为塑性截面模量,也称为塑性抵御矩.常常使用截面抗弯系数公式矩形截面抵御矩W=bh^2/6圆形截面的抵御矩W=πd^3/32圆环截面抵御矩:W=π(D^4-d^4)/(32D).罕见截面面积、形心和惯性矩抗弯系数公式罕见图形的面积、形心和惯性矩序图形面积形心位置惯性矩(形心轴)号123 4 5 6。
抗弯截面系数

截面抵抗矩之羊若含玉创作(1):截面抵抗矩(W)就是截面临其形心轴惯性矩与截面上最远点至形心轴距离的比值.主要用来盘算弯矩作用下截面最外边的正应力.工程实际中最罕有的弯曲问题是横力弯曲,横截面上不但有正应力,并且还有切应力.由于切应力的作用,横截面产生翘曲,平面假设不再成立.但进一步的理论剖析证明,对于跨长与截面高度比l/h>5 的长梁应用公式δ=My/I 来盘算其横力弯曲的正应力,所得成果误差甚微,足够知足工程实际需要.其中W=I/y,W称为抗弯截面系数(又称为截面抵抗矩).由于横力弯曲时,梁的弯矩随截面位置变更,Mmax所在截面称为危险截面,最大弯曲正应力产生在弯矩最大的截面上,且离中心轴最远处,该处为危险点.中和轴的确定1)找出达到极限弯矩时截面的中和轴.中和轴分为弹性中和轴和塑性中和轴.弹性状态下的中和轴:整个截面关于经此轴线的截面面积矩为0.横截面在此轴线弯曲正应力为0.(中和轴初始界说即为构件弯曲后某一截面的长度没有转变即为没有正应力或者说轴力)(和形心的界说一致,一般情况下中和轴即为形心的一条轴线)截面面积矩:指弹性状态下截面各微元面积与各微元至中和轴距离乘积的积分.单位mm.指弹性状态下中和轴一侧截面的面积矩,主要用于盘算截面上任意点的剪切应力值.塑性状态下的中和轴:塑性中和轴为构件截面面积平分线,该中和轴双方的面积相等.2)弹性状态下截面抵抗矩:如本文开首界说.其意义在于在弹性状态下盘算某一构件断面位置最晦气位置的最大应力,该位置应力知足则此位置截面知足盘算要求;塑性状态下截面塑性抵抗矩:分离求两正面积对中和轴的面积矩,面积矩之和即为塑性截面模量,也称为塑性抵抗矩.经常使用截面抗弯系数公式矩形截面抵抗矩W=bh^2/6圆形截面的抵抗矩W=πd^3/32圆环截面抵抗矩:W=π(D^4-d^4)/(32D).罕有截面面积、形心和惯性矩抗弯系数公式罕有图形的面积、形心和惯性矩序图形面积形心位置惯性矩(形心轴)号1234 5 6。
抗弯截面系数

截面抵抗矩之五兆芳芳创作(1):截面抵抗矩(W)就是截面对其形心轴惯性矩与截面上最远点至形心轴距离的比值.主要用来计较弯矩作用下截面最外边的正应力.工程实际中最罕有的弯曲问题是横力弯曲,横截面上不但有正应力,并且还有切应力.由于切应力的作用,横截面产生翘曲,平面假定不再成立.但进一步的理论阐发证明,对于跨长与截面高度比l/h>5 的长梁利用公式δ=My/I 来计较其横力弯曲的正应力,所得结果误差甚微,足够满足工程实际需要.其中W=I/y,W称为抗弯截面系数(又称为截面抵抗矩).由于横力弯曲时,梁的弯矩随截面位置变更,Mmax所在截面称为危险截面,最大弯曲正应力产生在弯矩最大的截面上,且离中心轴最远处,该处为危险点.中和轴的确定1)找出达到极限弯矩时截面的中和轴.中和轴分为弹性中和轴和塑性中和轴.弹性状态下的中和轴:整个截面关于经此轴线的截面面积矩为0.横截面在此轴线弯曲正应力为0.(中和轴初始定义即为构件弯曲后某一截面的长度没有改动即为没有正应力或说轴力)(和形心的定义一致,一般情况下中和轴即为形心的一条轴线)截面面积矩:指弹性状态下截面各微元面积与各微元至中和轴距离乘积的积分.单位mm.指弹性状态下中和轴一侧截面的面积矩,主要用于计较截面上任意点的剪切应力值.塑性状态下的中和轴:塑性中和轴为构件截面面积平分线,该中和轴两边的面积相等.2)弹性状态下截面抵抗矩:如本文开头定义.其意义在于在弹性状态下计较某一构件断面位置最倒霉位置的最大应力,该位置应力满足则此位置截面满足计较要求;塑性状态下截面塑性抵抗矩:辨别求两正面积对中和轴的面积矩,面积矩之和即为塑性截面模量,也称为塑性抵抗矩.经常使用截面抗弯系数公式矩形截面抵抗矩W=bh^2/6圆形截面的抵抗矩W=πd^3/32圆环截面抵抗矩:W=π(D^4-d^4)/(32D).罕有截面面积、形心和惯性矩抗弯系数公式罕有图形的面积、形心和惯性矩序图形面积形心位置惯性矩(形心轴)号123 4 5 6。
