第02章质点运动定律

合集下载

练习册第2章《质点力学的运动定律守恒定律》答案（1）

练习册第2章《质点⼒学的运动定律守恒定律》答案（1）第2章质点⼒学的运动定律守恒定律⼀、选择题1(C)，2(E)，3(D)，4(C)，5(C)，6(B)，7(C)，8(C)，9(B)，10(C)，11(D)，12(A)，13(D)⼆、填空题(1). ω2=12rad/s ，A=0.027J (2). 290J (3). 3J (4). 18 N ·s(5). j t i t 2323+ (SI) (6). 16 N ·s ， 176 J (7). 16 N ·s ，176 J (8). M k l /0，Mknm M Ml +0(9). j i5- (10).2m v ，指向正西南或南偏西45°三、计算题1. 已知⼀质量为m 的质点在x 轴上运动，质点只受到指向原点的引⼒的作⽤，引⼒⼤⼩与质点离原点的距离x 的平⽅成反⽐，即2/x k f -=，k 是⽐例常数．设质点在 x =A 时的速度为零，求质点在x =A /4处的速度的⼤⼩．解：根据⽜顿第⼆定律x m t x x m t m xk f d d d d d d d d 2vv v v =?==-= ∴ ??-=-=4/202d d ,d d A Ax mx kmx x k v v v v vk mAA A m k 3)14(212=-=v ∴ )/(6mA k =v2. 质量为m 的⼦弹以速度v 0⽔平射⼊沙⼟中，设⼦弹所受阻⼒与速度反向，⼤⼩与速度成正⽐，⽐例系数为Ｋ，忽略⼦弹的重⼒，求：(1) ⼦弹射⼊沙⼟后，速度随时间变化的函数式； (2) ⼦弹进⼊沙⼟的最⼤深度．解：(1) ⼦弹进⼊沙⼟后受⼒为－Ｋv ，由⽜顿定律tmK d d vv =- ∴ ??=-=-v v v v vv 0d d ,d d 0t t m K t m K∴ mKt /0e -=v v(2) 求最⼤深度解法⼀： t xd d =vt x mKt d ed /0-=vt x m Kt txd e d /000-?=v∴ )e 1()/(/0mKt K m x --=vK m x /0m ax v =解法⼆： x m t x x m t m K d d )d d )(d d (d d vvv v v ===- ∴ v d K mdx -=v v d d 000m a x ??-=K mx x∴ K m x /0m ax v =3. ⼀物体按规律x ＝ct 3在流体媒质中作直线运动，式中c 为常量，t 为时间．设媒质对物体的阻⼒正⽐于速度的平⽅，阻⼒系数为k ，试求物体由x ＝0运动到x ＝l 时，阻⼒所作的功．解：由x ＝ct 3可求物体的速度： 23d d ct tx==v 物体受到的阻⼒⼤⼩为： 343242299x kc t kc k f ===v ⼒对物体所作的功为：=W W d =-lx x kc 03432d 9 =7273732l kc -4. ⼀质量为2 kg 的质点，在xy 平⾯上运动，受到外⼒j t i F 2244-= (SI)的作⽤，t = 0时，它的初速度为j i430+=v (SI)，求t = 1 s 时质点的速度及受到的法向⼒n F .解： j t i m F a 2122/-==t a d /d v = ∴ t j t i d )122(d 2-=v=?vv vd ?-t t j t i 02d )122(∴ j t i t 3042-=-v vj t i t j t i t )44()23(42330-++=-+=v v当t = 1 s 时， i51=v 沿x 轴故这时， j a a y n12-==j a m F n n24-== (SI)5.⼀辆⽔平运动的装煤车，以速率v 0从煤⽃下⾯通过，每单位时间内有质量为m 0的煤卸⼊煤车．如果煤车的速率保持不变，煤车与钢轨间摩擦忽略不计，试求：(1) 牵引煤车的⼒的⼤⼩；(2) 牵引煤车所需功率的⼤⼩；(3) 牵引煤车所提供的能量中有多少转化为煤的动能？其余部分⽤于何处？解：(1) 以煤车和?t 时间内卸⼊车内的煤为研究对象，⽔平⽅向煤车受牵引⼒F 的作⽤，由动量定理： 000)(v v M t m M t F -+=?? 求出： 00v m F = (2) 2000v v m F P ==(3) 单位时间内煤获得的动能： 2021v m E K =单位时间内牵引煤车提供的能量为 P E ===21/E E K 50％即有50％的能量转变为煤的动能，其余部分⽤于在拖动煤时不可避免的滑动摩擦损耗．6.⼀链条总长为l ，质量为m ，放在桌⾯上，并使其部分下垂，下垂⼀段的长度为a ．设链条与桌⾯之间的滑动摩擦系数为µ．令链条由静⽌开始运动，则(1)到链条刚离开桌⾯的过程中，摩擦⼒对链条作了多少功？(2)链条刚离开桌⾯时的速率是多少？解：(1)建⽴如图坐标.某⼀时刻桌⾯上全链条长为y ,则摩擦⼒⼤⼩为 g lym f µ=摩擦⼒的功 ??--==0d d al al f y gy lmy f W µ=22al y lmg-µ =2)(2a l lmg--µ(2)以链条为对象，应⽤质点的动能定理 ∑W ＝222121v v m m - 其中 ∑W = W P ＋W f ，v 0 = 0 W P =?la x P d =la l mg x x l mg la 2)(d 22-=? 由上问知 la l mg W f 2)(2--=µal -a-a1)(22)(v m a l l mg l a l mg =---µ得 []21222)()(a l a l lg ---=µv7. 如图所⽰，在中间有⼀⼩孔O 的⽔平光滑桌⾯上放置⼀个⽤绳⼦连结的、质量m = 4 kg 的⼩块物体．绳的另⼀端穿过⼩孔下垂且⽤⼿拉住．开始时物体以半径R 0 = 0.5 m 在桌⾯上转动，其线速度是4 m/s ．现将绳缓慢地匀速下拉以缩短物体的转动半径．⽽绳最多只能承受 600 N 的拉⼒．求绳刚被拉断时，物体的转动半径R 等于多少？解：物体因受合外⼒矩为零，故⾓动量守恒．设开始时和绳被拉断时物体的切向速度、转动惯量、⾓速度分别为v 0、J 0、ω0和v 、J 、ω．则ωωJ J =00 ①因绳是缓慢地下拉，物体运动可始终视为圆周运动．①式可写成R mR R mR //20020v v =整理后得： v v /00R R =②物体作圆周运动的向⼼⼒由绳的张⼒提供 R m F /2v = 1分再由②式可得： 3/12020)/(F mR R v =当F = 600 N 时，绳刚好被拉断，此时物体的转动半径为R = 0.3 m8.设两个粒⼦之间相互作⽤⼒是排斥⼒，其⼤⼩与粒⼦间距离r 的函数关系为3r k f =，k 为正值常量，试求这两个粒⼦相距为r 时的势能．（设相互作⽤⼒为零的地⽅势能为零．）解：两个粒⼦的相互作⽤⼒ 3r k f =已知f ＝0即r ＝∞处为势能零点, 则势能∞∞∞=?==r r P P r r kW E d d 3r f)2(2r k =1. 汽车发动机内⽓体对活塞的推⼒以及各种传动部件之间的作⽤⼒能使汽车前进吗？使汽车前进的⼒是什么⼒？参考解答：汽车发动机内⽓体对活塞的推⼒以及各种传动部件之间的作⽤⼒都是汽车系统的内⼒，内⼒只会改变内部各质点的运动状态，不会改变系统的总动量，所以不能使汽车前进。

第02章--质点运动定律

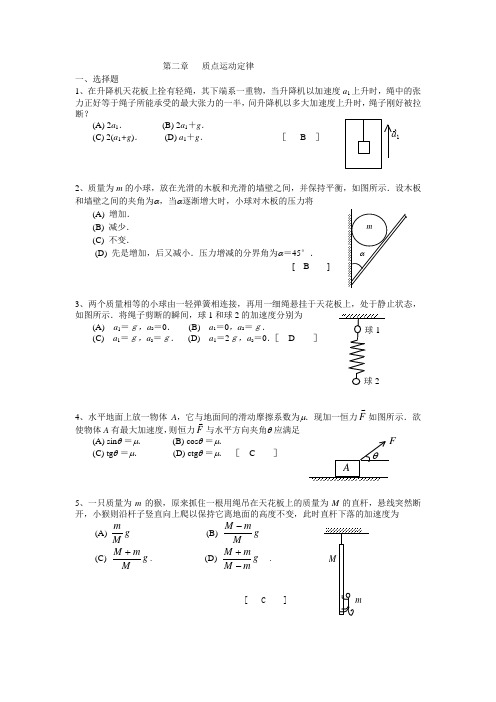
第二章质点运动定律一、选择题1、在升降机天花板上拴有轻绳，其下端系一重物，当升降机以加速度a 1上升时，绳中的张力正好等于绳子所能承受的最大张力的一半，问升降机以多大加速度上升时，绳子刚好被拉断？(A) 2a 1． (B) 2a 1＋g ．(C) 2(a 1+g )． (D) a 1＋g ．［ B ］2、质量为m 的小球，放在光滑的木板和光滑的墙壁之间，并保持平衡，如图所示．设木板和墙壁之间的夹角为α，当α逐渐增大时，小球对木板的压力将 (A) 增加．(B) 减少．(C) 不变． (D) 先是增加，后又减小．压力增减的分界角为α＝45°． [ B ]3、两个质量相等的小球由一轻弹簧相连接，再用一细绳悬挂于天花板上，处于静止状态，如图所示．将绳子剪断的瞬间，球1和球2的加速度分别为(A) a 1＝ｇ，a 2＝0． (B) a 1＝0，a 2＝ｇ． (C) a 1＝ｇ，a 2＝ｇ． (D) a 1＝2ｇ，a 2＝0．［ D ］4、水平地面上放一物体A ，它与地面间的滑动摩擦系数为μ．现加一恒力F如图所示．欲使物体A 有最大加速度，则恒力F与水平方向夹角θ 应满足(A) sin θ ＝μ． (B) cos θ ＝μ． (C) tg θ ＝μ． (D) ctg θ ＝μ．［ C ］5、一只质量为m 的猴，原来抓住一根用绳吊在天花板上的质量为M 的直杆，悬线突然断开，小猴则沿杆子竖直向上爬以保持它离地面的高度不变，此时直杆下落的加速度为(A) g M m (B) g M m M - (C)g M m M +. (D) g mM mM -+ .[ C ]a 16、如图所示，质量为m 的物体A 用平行于斜面的细线连结置于光滑的斜面上，若斜面向左方作加速运动，当物体开始脱离斜面时，它的加速度的大小为(A) g sin θ． (B) g cos θ．(C) g ctg θ． (D) g tg θ．［ C ］7、如图所示，一轻绳跨过一个定滑轮，两端各系一质量分别为m 1和m 2的重物，且m 1>m 2．滑轮质量及轴上摩擦均不计，此时重物的加速度的大小为a ．今用一竖直向下的恒力gm F =代替质量为m 1的物体，可得质量为m 2的重物的加速度为的大小a ′，则(A) a ′= a (B) a ′> a(C) a ′< a (D) 不能确定. ［ B ］8、质量分别为m 1和m 2的两滑块A 和B 通过一轻弹簧水平连结后置于水平桌面上，滑块与桌面间的摩擦系数均为μ，系统在水平拉力F 作用下匀速运动，如图所示．如突然撤消拉力，则刚撤消后瞬间，二者的加速度a A 和a B 分别为(A) a A =0 , a B =0. (B) a A >0 , a B <0.(C) a A <0 , a B >0. (D) a A <0 , a B =0.［ D ］9、质量为m 的物体自空中落下，它除受重力外，还受到一个与速度平方成正比的阻力的作用，比例系数为k ，k 为正值常量．该下落物体的收尾速度(即最后物体作匀速运动时的速度)将是(A)k mg . (B) kg2 . (C) gk . (D) gk . ［ A ］10、质量分别为m 和M 的滑块A 和B ，叠放在光滑水平桌面上，如图所示．A 、B 间静摩擦系数为μs ，滑动摩擦系数为μk ，系统原处于静止．今有一水平力作用于A 上，要使A 、B 不发生相对滑动，则应有(A) F ≤μs mg ． (B) F ≤μs (1+m /M )mg ． (C) F ≤μs (m+M )mg ． (D) F ≤MmM mgk +μ．［ B ］11、如图所示，用一斜向上的力F(与水平成30°角)，将一重为G 的木块压靠在竖直壁面上，如果不论用怎样大的力F ，都不能使木块向上滑动，则说明木块与壁面间的静摩擦系数μ的大小为(A) .21≥μ (B) 31≥μ. (C) 3≥μ. (D) 32≥μ. ［ B ］12、一辆汽车从静止出发，在平直公路上加速前进的过程中，如果发动机的功率一定，阻力大小不变，那么，下面哪一个说法是正确的？(A) 汽车的加速度是不变的． (B) 汽车的加速度不断减小． (C) 汽车的加速度与它的速度成正比．(D) 汽车的加速度与它的速度成反比．［ B ］13、升降机内地板上放有物体A ，其上再放另一物体B ，二者的质量分别为M A 、M B ．当升降机以加速度a 向下加速运动时(a <g )，物体A 对升降机地板的压力在数值上等于(A)M A g. (B) (M A +M B )g.(C) (M A +M B )(g +a ). (D) (M A +M B )(g -a ). ［ D ］14、如图，物体A 、B 质量相同，B 在光滑水平桌面上．滑轮与绳的质量以及空气阻力均不计，滑轮与其轴之间的摩擦也不计．系统无初速地释放，则物体A 下落的加速度是 (A) g. (B) 4g /5 .(C) g /2 . (D) g /3 . ［ B ］15、如图，滑轮、绳子质量及运动中的摩擦阻力都忽略不计，物体A 的质量m 1大于物体B 的质量m 2．在A 、B 运动过程中弹簧秤S 的读数是(A) .)(21g m m + (B) .)(21g m m -(C).22121g m m m m + (D) .42121g m m m m + ［ D ］16、如图所示，质量为m 的物体用细绳水平拉住，静止在倾角为θ的固定的光滑斜面上，则斜面给物体的支持力为(A) θcos mg . (B) θsin mg . (C)θcos mg . (D) θsin mg. [ C ]17、光滑的水平桌面上放有两块相互接触的滑块，质量分别为m 1和m 2，且m 1<m 2．今对两滑块施加相同的水平作用力，如图所示．设在运动过程中，两滑块不离开，则两滑块之间的相互作用力N 应有(A) N =0. (B) 0 < N < F . (C) F < N <2F . (D) N > 2F . ［ B ］18、用水平压力F 把一个物体压着靠在粗糙的竖直墙面上保持静止．当F逐渐增大时，物体所受的静摩擦力f(A) 恒为零．1(B) 不为零，但保持不变． (C) 随F 成正比地增大．(D) 开始随F 增大，达到某一最大值后，就保持不变［ B ］19、用水平压力F 把一个物体压着靠在粗糙的竖直墙面上保持静止．当F逐渐增大时，物体所受的静摩擦力f(A) 恒为零． (B) 不为零，但保持不变． (C) 随F 成正比地增大．(D) 开始随F 增大，达到某一最大值后，就保持不变［ B ］ 20、一光滑的内表面半径为10 cm 的半球形碗，以匀角速度ω绕其对称OC 旋转．已知放在碗内表面上的一个小球P 相对于碗静止，其位置高于碗底4 cm ，则由此可推知碗旋转的角速度约为 (A) 10 rad/s ． (B) 13 rad/s ．(C) 17 rad/s (D) 18 rad/s ．［ B ］21、竖立的圆筒形转笼，半径为R ，绕中心轴OO ＇转动，物块A 紧靠在圆筒的内壁上，物块与圆筒间的摩擦系数为μ，要使物块A 不下落，圆筒转动的角速度ω至少应为(A)Rgμ (B)g μ(C)Rgμ (D)R g ［ C ］22、已知水星的半径是地球半径的 0.4倍，质量为地球的0.04倍．设在地球上的重力加速度为g ，则水星表面上的重力加速度为： (A) 0.1 g (B) 0.25 g (C) 2.5 g (D) 4 g [ B ]23、如图所示，假设物体沿着竖直面上圆弧形轨道下滑，轨道是光滑的，在从A 至C 的下滑过程中，下面哪个说法是正确的？(A) 它的加速度大小不变，方向永远指向圆心．(B) 它的速率均匀增加． (C) 它的合外力大小变化，方向永远指向圆心． (D) 它的合外力大小不变．(E) 轨道支持力的大小不断增加．［ E ］24、一个圆锥摆的摆线长为l ，摆线与竖直方向的夹角恒为θ，如图所示．则摆锤转动的周期为ωPCOA ROθCAO O ′ ω(A)g l. (B) gl θcos . (C) g l π2. (D) gl θπcos 2 . ［ D ］25、一公路的水平弯道半径为R ，路面的外侧高出内侧，并与水平面夹角为θ．要使汽车通过该段路面时不引起侧向摩擦力，则汽车的速率为(A) Rg . (B) θtg Rg .(C)θθ2sin cos Rg . (D)θctg Rg ［ B ］26、一段路面水平的公路，转弯处轨道半径为R ，汽车轮胎与路面间的摩擦系数为μ，要使汽车不致于发生侧向打滑，汽车在该处的行驶速率 (A) 不得小于gR μ． (B) 不得大于gR μ．(C) 必须等于gR 2． (D) 还应由汽车的质量M 决定．［ B ］ 27、一小珠可在半径为R 竖直的圆环上无摩擦地滑动，且圆环能以其竖直直径为轴转动．当圆环以一适当的恒定角速度ω 转动，小珠偏离圆环转轴而且相对圆环静止时，小珠所在处圆环半径偏离竖直方向的角度为(A) π21=θ. (B) ).arccos(2ωθR g = (C) )arctg(2gR ωθ=. (D) 需由小珠的质量m 决定．［ B ］ 28、在作匀速转动的水平转台上，与转轴相距R 处有一体积很小的工件A ，如图所示．设工件与转台间静摩擦系数为μs ，若使工件在转台上无滑动，则转台的角速度ω应满足(A) Rgs μω≤.(B) Rgs 23μω≤. (C) R gs μω3≤. (D) Rg s μω2≤. ［ A ］二、填空题1、质量相等的两物体A 和B ，分别固定在弹簧的两端，竖直放在光滑水平面C 上，如图所示．弹簧的质量与物体A 、B 的质量相比，可以忽略不计．若把支持面C 迅速移走，则在移开的一瞬间，A 的加速度大小a A ＝_______．答案：02、质量相等的两物体A 和B ，分别固定在弹簧的两端，竖直放在光滑水平面C 上，如图所示．弹簧的质量与物体A 、B 的质量相比，可以忽略不计．若把支持面C 迅速移走，则在移开的一瞬间， B 的加速度的大小a B ＝_______ g ．答案：25、质量分别为m 1、m 2、m 3的三个物体A 、B 、C ，用一根细绳和两根轻弹簧连接并悬于固定点O ，如图．取向下为x 轴正向，开始时系统处于平衡状态，后将细绳剪断，则在刚剪断瞬时，物体A 的加速度A a＝______．答案：07、质量m =40 kg 的箱子放在卡车的车厢底板上，已知箱子与底板之间的静摩擦系数为μs ＝0.40，滑动摩擦系数为μk ＝0.25，试写出在下列情况下，作用在箱子上的摩擦力的大小和方向．卡车以a = 2 m/s 2的加速度行驶，f =____________ N 。

大学物理课件第2章,质点动力学

本章题头§2-1 牛顿运动定律英国物理学家, 经典物理学的奠基人.创立了经典力学的基本体系光学，牛顿致力于光的颜色和光的本性数学，建立了二项式定理，创立了微积分牛顿 Issac Newton （1643－1727）天文学，发现了万有引力定律，创制反射望远镜，初步观察到了行星运动的规律。

一、牛顿第一定律 (Newton first law)惯性定律任何物体都保持静止或匀速直线运动的状态，直到受到力的作用迫使它改变这种状态为止。

意义惯性以及力的概念 1、定义了物体（质点）的惯性；2、说明了力是物体运动状态改变的原因定义了惯性参考系二、牛顿第二定律 (Newton second law)质点加速度的大小与所受合力的大小成正比 , 与质点自身的质量成反比; 加速度方向与合力方向相同。

牛顿第二定律的数学形式为 Fma 原始形式：F dPd mv dmvm dvdtdtdtdt当 v c 时，m 为常量 Fm dvmadt宏观低速运动时1、瞬时性：之间一一对应（同生、同向、同变、同灭） n 2、力的叠加性：F F1 F2 Fi Fii =13、矢量性：具体运算时应写成分量式直角坐标系中： Fma maximay jmaz k Fxmaxmdv x dt Fyma ymdv y dt Fzmazmdvz dt 自然坐标系中： Fmam at anF mdv dtFnmv24、说明了质量是物体惯性的量度5、在一般情况下力， F是一个变力常见的几中变力形式：F F x kx常见的几中变力形式：F F t F F v kv弹性力打击力阻尼力6、适用对象:质点 7、成立的参考系：惯性系 8、成立的条件：宏观低速10＇T 三、牛顿第三定律(Newton third law)物体A 以力F AB 作用于物体B 时, 物体B 也必定同时以力F BA 作用于物体A , F AB 与F BA 大小相等, 方向相反, 并处于同一条直线上,（物体间相互作用规律）mmT P ＇P 地球F AB = F BA作用力与反作用力：1、它们总是成对出现。

大学物理第2章质点动力学

第2章质点动力学2.1 牛顿运动定律一、牛顿第一定律任何物体都保持静止或匀速直线运动状态，直到其他物体所作用的力迫使它改变这种状态为止。

二、牛顿第二定律物体所获得的加速度的大小与合外力的大小成正比，与物体的质量成反比, 方向与合外力的方向相同。

表示为f ma说明:⑵在直角坐标系中，牛顿方程可写成分量式f x ma *， f y ma y ， f z ma z 。

⑶ 在圆周运动中，牛顿方程沿切向和法向的分量式f t ma t f n ma n⑷ 动量：物体质量m 与运动速度v 的乘积，用p 表示。

p mv动量是矢量，方向与速度方向相同。

由于质量是衡量，引入动量后，牛顿方程可写成dv m 一 dt 当 f 0时，r 0，dp 常量，即物体的动量大小和方向均不改变。

此结论成为质点动量守恒定律三、牛顿第三定律：物体间的作用力和反作用力大小相等，方向相反，且在同一直线上。

物体同时受几个力f i ,f 2f n 的作用时，合力f 等于这些力的矢量和f n力的叠加原理d pdtf ma说明：作用力和反作用力是属于同一性质的力。

四、国际单位制量纲基本量与基本单位导出量与导出单位五、常见的力力是物体之间的相互作用。

力的基本类型：引力相互作用、电磁相互作用和核力相互作用。

按力的性质来分，常见的力可分为引力、弹性力和摩擦力。

六、牛顿运动定律的应用用牛顿运动定律解题时一般可分为以下几个步骤：隔离物体，受力分析。

建立坐标，列方程。

求解方程。

当力是变力时，用牛顿第二定律得微分方程形式求解。

例题例2-1如下图所示，在倾角为30°的光滑斜面（固定于水平面）上有两物体通过滑轮相连，已知叶3kg, m2 2kg，且滑轮和绳子的质量可忽略，试求每一物体的加速度a及绳子的张力F T（重力加速度g取9.80m • s 2）。

解分别取叶和m2为研究对象，受力分析如上图。

利用牛顿第二定律列方程:「m2g F TYL F T m1gsi n30o m1a绳子张力F T F T代入数据解方程组得加速度a 0.98m • s 2，张力F T 17.64N。

牛顿第二定律与质点运动方程

牛顿第二定律与质点运动方程牛顿第二定律是经典力学的基本定律之一，它描述了质点运动的原理和规律。

根据牛顿第二定律，质点的加速度与施加在质点上的合外力成正比，与质点的质量成反比。

这个定律是力学中非常重要的一个定律，能够帮助我们理解物体的运动和相互作用。

牛顿第二定律可以用一个简洁的数学公式来表示：F = ma其中，F代表合外力的大小和方向，m代表质点的质量，a代表质点的加速度。

这个公式告诉我们，当质量一定时，加速度与施加力成正比；当施加力一定时，加速度与质量成反比。

反过来说，如果我们知道施加在物体上的力和物体的质量，就可以计算出物体的加速度。

在这个公式中，加速度与净外力成正比，净外力是指作用于物体上的所有力的合力。

它可以是由多个力合成的结果，也可以是单个力的作用。

例如，当一个物体在水平表面上受到重力和摩擦力的作用时，净外力就是这两个力的合力。

根据牛顿第二定律，净外力与物体的质量成正比，加速度与净外力成正比。

牛顿第二定律还可以用来解释物体的运动方程。

运动方程是描述物体运动的数学方程。

对于一维运动（即沿着一条直线的运动），物体的运动方程可以写为：x = x0 + v0t + 1/2at^2其中，x代表物体的位移，x0代表物体的初始位移，v0代表物体的初始速度，t代表时间，a代表加速度。

这个方程包含了物体的初始条件（即初始位移和初始速度）以及物体的加速度。

根据牛顿第二定律，加速度与质量成反比，即a = F/m。

将这个表达式代入运动方程中可以得到：x = x0 + v0t + 1/2(F/m)t^2这个方程告诉我们，在给定初始条件和知道外力大小和方向的情况下，我们可以计算出物体的位移随时间的变化。

这是牛顿第二定律的一个重要应用。

牛顿第二定律适用于所有质点运动，并且在经典力学中具有普遍性。

它的简洁公式不仅方便了理论研究，也为我们解决实际问题提供了有力的工具。

例如，在工程中，我们可以利用牛顿第二定律来计算机械结构的受力和变形；在运动学中，我们可以利用牛顿第二定律来分析物体的运动轨迹和速度变化。

大学物理第二章习题质点力学的基本规律守恒定律

第2章质点力学的基本规律守恒定律
基本要求
掌握经典力学的基本原理及会应用其分析和处理质点动力学问题，理解力学量的单位和量纲。掌握动量、冲量、动量定理，动量守恒定律。并能分析和计算二维平面简单力学问题。理解惯性系概念及经典力学的基本原理的适用范围。掌握功与功率、动能、势能（重力势能、弹性势能、引力势能）概念，动能定理、功能原理、机械能守恒定律。
教学基本内容、基本公式
1.牛顿定律
解牛顿定律的问题可分为两类：第一类是已知质点的运动，求作用于质点的力；第二类是已知作用于质点的力，求质点的运动.
2.基本定理动量定理
动能定理

I
t2 t1
F (t )dt

mv

mv0
A12

2
F
(r)

dr

1
1 2
mv
2 2

1 2
解：根据牛顿第二定律
f

k x2
m dv dt
m dv d x dx dt
mv
dv dx

k x2
mv
dv dx
v
dv

k
dx mx2

v
v
0
dv

A/4

A
k mx2
d
x
1v2 k (4 1) 3 k 2 m A A mA
另解：根据动能定理
v 6k /(mA)
(2)写出初末态系统的动量
t 时刻水平方向动量
dm m
t+dt时刻水平方向动量
O
x
(3)求出系统水平方向动量的增量

大学物理习题册及解答(第二版)第二章质点的运动定律

mg ≤ f 摩 = µN = µmRω 2
ω≥
g µR
3．一单摆挂在木板的小钉上（摆球的质量<<木板的质量），木板可沿两根竖直且无摩擦的轨道下滑，如图．开始时木板被支撑物托住，且使单摆摆动．当摆球尚未摆到最高点时，移开支撑物，木板自由下落，则在下落过程中，摆球相对于板 (A) 作匀速率圆周运动 (C) 仍作周期性摆动 (B) 静止 (D) 作上述情况之外的运动
4 质量为m的小球在水平面内作半径为R的匀速圆周运动，圆周运动的角速度为 ω .试通过小球受到合外力的时间积分计算，小球在经过(1) 1/4圆周，(2) 1/2圆周，(3) 3/4圆周，(4) 整个圆周，几个的过程中向心力的冲量，以及由动量定理得出这几个 y 过程中的冲量． ωt O 解：方法1 小球所受合力作为它作圆周运动的向 R x 心力，合力的冲量表示为：
x
y
y
0
x
x
0
7．设作用在质量为1kg的物体上的力F＝6t＋3（SI）．如果物体在这一力的作用下，由静止开始沿直线运动，在 0到2.0 s的时间间隔内，这个力作用在物体上的冲量大小 18 N·s Ｉ＝____________． 8．一人站在质量（连人带船）为m1＝300 kg的静止的船上，他用F＝100 N的恒力拉一水平轻绳，绳的另一端系在岸边的一棵树上，则船开始运动后第三秒末的速率为 1 m/s __________；在这段时间内拉力对船所做的功为 ____________．（水的阻力不计） 150 J 分析：利用动量定理和动能定理求解
三、计算及证明
1．质量为m的木块放在质量为M倾角为θ的光滑斜劈上，斜劈与地面的摩擦不计，若使m相对斜面静止，需在斜劈上施加多大的 N θ y 水平外力？木块对斜劈的压力为多少？解：在 x方向和y方向分别应用牛顿第二定律

《大学物理》第2章质点动力学

TM
Tm
2Mm M m
g
a
ar
M M
m m
g
a
FM
TM
ar
F m
Tm m
a
M PM
ar
Pm
注：牛顿第二定律中的加速度是相对于惯性系而言的。
例2 在倾角 θ 30 的固定光滑斜面上放一质量为
M的楔形滑块，其上表面与水平面平行，在其上放一质量为m的小球， M 和m间无摩擦，
且 M 2m 。
解：以弹簧原长处为坐标原点。
Fx kx
F Bm A
元功：
O xB x
xA x
dW Fx dx kxdx
dx
弹力做功：W
xB xA
kxdx
1 2
kxA2
1 2
kxB2
2.3.4 势能 Ep
W保 Ep Ep0 Ep
Ep重 mgh
牛顿 Issac Newton（1643－1727）杰出的英国物理学家,经典物理学的奠基人.他的不朽巨著《自然哲学的数学原理》总结了前人和自己关于力学以及微积分学方面的研究成果. 他在光学、热学和天文学等学科都有重大发现.
第2章质点动力学
2.1 牛顿运动定律 2.1.1 牛顿运动定律
1 牛顿第一定律（惯性定律） • 内容：一切物体总保持静止状态或匀速直线运动状态，直到有外力迫使它改变这种状态为止。 • 内涵：任何物体都有保持静止或匀速直线运动状态的趋势。给出了力的定义。定义了一种参照系------惯性参照系。
非惯性参照系：相对于已知的惯性系作变速运动的参照系。
惯性定律在非惯性系中不成立。
2．2 动量定理动量守恒定律

大学物理第2章-质点动力学基本定律

②保守力作功。
势能的绝对值没有意义，只关心势能的相对值。势能是属于具有保守力相互作用的系统计算势能时必须规定零势能参考点。但是势能差是一定的，与零点的选择无关。如果把石头放在楼顶，并摇摇欲坠，你就不会不关心它。一块石头放在地面你对它并不关心。
重力势能：以地面为势能零点
01
万有引力势能：以无限远处为势能零点
m
o
θ
设：t 时刻质点的位矢
质点的动量
运动质点相对于参考原点O的角动量定义为：
大小：
方向：右手螺旋定则判定
若质点作圆周运动，则对圆心的角动量：
质点对轴的角动量:
质点系的角动量:
设各质点对O点的位矢分别为
动量分别为
二.角动量定理
对质点:
---外力对参考点O 的力矩
力矩的大小：
力矩的方向:由右手螺旋关系确定
为质点系的动能，
令
---质点系的动能定理
讨论
内力和为零,内力功的和是否为零？
不一定为零
A
B
A
B
S
L
例:炸弹爆炸，过程内力和为零，但内力所做的功转化为弹片的动能。
内力做功可以改变系统的总动能
例用铁锤将一只铁钉击入木板内,设木板对铁钉的阻力与铁钉进入木板之深度成正比,如果在击第一次时,能将钉击入木板内 1 cm, 再击第二次时（锤仍以第一次同样的速度击钉）,能击入多深？第一次的功第二次的功解：
（1）重力的功
重力做功仅取决于质点的始、末位置za和zb，与质点经过的具体路径无关。
（2）万有引力的功
*
设质量M的质点固定，另一质量m的质点在M 的引力场中从a运动到b。
M
a
b

大学物理A 练习题第2章《质点力学的运动定律守恒定律》

《第2章质点力学的运动定律守恒定律》一选择题1. 水平地面上放一物体A ，它与地面间的滑动摩擦系数为μ．现加一恒力F 如图所示．欲使物体A 有最大加速度，则恒力F 与水平方向夹角θ 应满足(A) sin θ ＝μ． (B) cos θ ＝μ． (C) tg θ ＝μ． (D) ctg θ ＝μ．[ ]2. 一质点在力F = 5m (5 - 2t ) (SI)的作用下，t =0时从静止开始作直线运动，式中m 为质点的质量，t 为时间，则当t = 5 s 时，质点的速率为(A) 50 m ·s -1． (B) 25 m ·s -1．(C) 0． (D) -50 m ·s -1．[ ]3. 体重、身高相同的甲乙两人，分别用双手握住跨过无摩擦轻滑轮的绳子各一端．他们从同一高度由初速为零向上爬，经过一定时间，甲相对绳子的速率是乙相对绳子速率的两倍，则到达顶点的情况是(A) 甲先到达． (B) 乙先到达．(C) 同时到达． (D) 谁先到达不能确定．[ ]4．一质点在如图所示的坐标平面内作圆周运动，有一力)(0j y i x F F+=作用在质点上．在该质点从坐标原点运动到(0，2R ）位置过程中，力F 对它所作的功为(A) 20R F ． (B) 202R F ． (C) 203R F ． (D) 204R F ．[ ]5. 对质点组有以下几种说法：(1) 质点组总动量的改变与内力无关． (2) 质点组总动能的改变与内力无关． (3) 质点组机械能的改变与保守内力无关．在上述说法中： (A) 只有(1)是正确的． (B) (1)、(3)是正确的．(C) (1)、(2)是正确的． (D) (2)、(3)是正确的．[ ] 6. 一火箭初质量为M 0，每秒喷出的质量(-d M /d t )恒定，喷气相对火箭的速率恒定为u．设火箭竖直向上发射，不计空气阻力，重力加速度g 恒定，则t = 0时火箭加速度a在竖直方向（向上为正）的投影式为 (A) g t M M u a --=)d d (0． (B) g tM M u a +=)d d (0．(C) d d (0t M M u a -=． (D) g tM M u a -=d d (0 [ ]7. 一竖直向上发射之火箭，原来静止时的初质量为m 0经时间t 燃料耗尽时的末质量为m ，喷气相对火箭的速率恒定为u ，不计空气阻力，重力加速度g 恒定．则燃料耗尽时火箭速率为(A) 2/ln0gt m m u -=v ． (B) gt m m u -=0ln v ． (C) gt m m u +=0ln v ． (D) gt mmu -=0ln v ．[ ]二填空题 1. 某质点在力F ＝(4＋5x )i(SI)的作用下沿x 轴作直线运动，在从x ＝0移动到x ＝10 m的过程中，力F所做的功为__________．2．质量为m ＝0.5kg 的质点，在Oxy 坐标平面内运动，其运动方程为x ＝5t ，y =0.5t 2（SI），从t =2s 到t =4s 这段时间内，外力对质点作的功为_____________.3. 设作用在质量为1 kg 的物体上的力F ＝6t ＋3（SI ）．如果物体在这一力的作用下，由静止开始沿直线运动，在0到2.0 s 的时间间隔内，这个力作用在物体上的冲量大小Ｉ＝__________．4. 质量m ＝1 kg 的物体，在坐标原点处从静止出发在水平面内沿x 轴运动，其所受合力方向与运动方向相同，合力大小为F ＝3＋2x (SI)，那么，物体在开始运动的3 m 内，合力所作的功W ＝_________；且x ＝3 m 时，其速率v ＝_________．5. 质量为0.05 kg 的小块物体，置于一光滑水平桌面上．有一绳一端连接此物，另一端穿过桌面中心的小孔（如图所示）．该物体原以3 rad/s 的角速度在距孔0.2 m 的圆周上转动．今将绳从小孔缓慢往下拉，使该物体之转动半径减为0.1 m ．则拉力所做的功为____________________．6. 粒子B 的质量是粒子A 的质量的4倍，开始时粒子A 的速度j i43+=0A v ,粒子B 的速度j i72-=0B v ；在无外力作用的情况下两者发生碰撞，碰后粒子A 的速度变为j i 47-=A v ，则此时粒子B 的速度B v＝____________________．7. 一维保守力的势能曲线如图所示，有一粒子自右向左运动，通过此保守力场区域时，在 _________________ 区间粒子所受的力F x > 0；在 _________________ 区间粒子所受的力F x < 0；在x = _______________ 时粒子所受的力F x = 0．三计算题1. 一质点沿x 轴运动，其加速度a 与位置坐标x 的关系为a ＝2＋6 x 2 (SI)，如果质点在原点处的速度为零，试求其在任意位置处的速度．2. 质点沿曲线 j t i t r22+= (SI) 运动，其所受摩擦力为 v 2-=f (SI)．求摩擦力在t = 1 s 到t = 2 s 时间内对质点所做的功．3. 一辆水平运动的装煤车，以速率v 0从煤斗下面通过，每单位时间内有质量为m 0的煤卸入煤车．如果煤车的速率保持不变，煤车与钢轨间摩擦忽略不计，试求： (1) 牵引煤车的力的大小； (2) 牵引煤车所需功率的大小；(3) 牵引煤车所提供的能量中有多少转化为煤的动能？其余部分用于何处？4. 一链条总长为l ，质量为m ，放在桌面上，并使其部分下垂，下垂一段的长度为a ．设链条与桌面之间的滑动摩擦系数为．令链条由静止开始运动，则(1)到链条刚离开桌面的过程中，(2)链条刚离开桌面时的速率是多少？a5. 如图所示，在中间有一小孔O 的水平光滑桌面上放置一个用绳子连结的、质量m = 4 kg 的小块物体．绳的另一端穿过小孔下垂且用手拉住．开始时物体以半径R 0 = 0.5 m 在桌面上转动，其线速度是4 m/s ．现将绳缓慢地匀速下拉以缩短物体的转动半径．而绳最多只能承受 600 N 的拉力．求绳刚被拉断时，物体的转动半径R 等于多少？6. 小球A ，自地球的北极点以速度0v 在质量为M 、半径为R 的地球表面水平切向向右飞出，如图所示，地心参考系中轴OO ＇与0v 平行，小球A 的运动轨道与轴OO ＇相交于距O 为3R 的C 点．不考虑空气阻力，求小球A 在C点的速度v 与0v 之间的夹角θ．7. 一个具有单位质量的质点在随时间 t 变化的力j t i t t F)612()43(2-+-= (SI) 作用下运动．设该质点在t = 0时位于原点，且速度为零．求t = 2秒时，该质点受到对原点的力矩和该质点对原点的角动量．四研讨题1. 汽车发动机内气体对活塞的推力以及各种传动部件之间的作用力能使汽车前进吗？使汽车前进的力是什么力？2. 在经典力学范围内，若某物体系对某一惯性系满足机械能守恒条件，则在相对于上述惯性系作匀速直线运动的其它参照系中，该物体系是否一定也满足机械能守恒条件？请举例说明．3. 在车窗都关好的行驶的汽车内，漂浮着一个氢气球，当汽车向左转弯时，氢气球在车内将向左运动还是向右运动？4. 为了避免门与墙壁的撞击，常常在门和墙上安装制动器，目前不少制动器安装在靠近地面的位置上（如图），在开关门的过程中，门与制动器发生碰撞，从而门受到撞击力的作用。

第二章质点的运动定理

物理学第五版第二章质点的运动定理
2-0 教学基本要求 2-1 牛顿运动定律 2-2 质点的动量定理 2-3 质点的动能定理 2-4 质点的角动量定理 -
§ 2-0 -
教学基本要求
掌握牛顿定律的基本内容及其适用条件牛顿定律的基本内容及其适用条件．一掌握牛顿定律的基本内容及其适用条件．熟练掌握用隔离物体法分析物体的受力情况，用隔离物体法分析物体的受力情况，能用微积分方法求变力作用下的简单质点动力学问题的简单质点动力学问题．解变力作用下的简单质点动力学问题．二理解动量、冲量概念，掌握质点动量定理理解动量、冲量概念，掌握质点动量定理动量
2 牛顿第二定律
v v 动量：动量： p = mυ v v v 的物体，动量为 p 的物体，在合外力 F ( = ∑ F ) 的作
i
用下，用下，其动量随时间的变化率应当等于作用于物体的合外力——牛顿第二定律． ——牛顿第二定律于物体的合外力——牛顿第二定律． v v v dp(t ) d(mv) 当v << c 时，数学表达式：数学表达式： F (t ) = = m为常量 dt dt
3 牛顿第三定律
v v 两个物体之间作用力 F 和反作用力 F＇，
沿同一直线，大小相等，方向相反，沿同一直线，大小相等，方向相反，分别作用在两个物体上．用在两个物体上．
数学表达式：数学表达式：
v v F12 = − F21 （物体间相互作用规律）物体间相互作用规律）
v F12
v F21
Fx = ma x F y = ma y Fz = ma z
自然坐标系中
2 v dv v v v v v F = ma = m(at + an ) = m et + m dt ρ 2 dv ds Ft = m = m 2 dt dt v a 2 v Fn = m v en ρ 注意：注意：ρ 为A处曲线处曲线 A

牛顿第二运动定律与质点

牛顿第二运动定律与质点牛顿第二运动定律是经典力学中的重要定律之一，描述了质点运动的原理和规律。

质点是一种理想化的物体，它可以看作是没有大小和形状的，只有质量的点。

在牛顿第二运动定律中，质点的加速度与作用在其上的力成正比，与质点的质量成反比。

下面将详细介绍牛顿第二运动定律与质点的理论和应用。

牛顿第二运动定律表述如下：质点的加速度等于作用在其上的合外力与质点质量的乘积的比值。

数学表达式为 F = ma，F 表示作用在质点上的合外力，a 表示质点的加速度，m 表示质点的质量。

这个定律说明了质点的加速度与合外力的大小成正比，与质点的质量成反比。

质点的加速度方向与作用力方向相同。

当合外力为零时，质点的加速度为零，即质点保持静止或匀速直线运动。

根据牛顿第二运动定律，我们可以推导出其他与质点运动相关的物理量。

例如，通过加速度求解力，我们可以得到 F = ma；通过力求解加速度，我们可以得到 a =F/m；通过力和加速度求解质量，我们可以得到 m = F/a。

这些关系式为我们分析和计算质点运动提供了基本的工具。

牛顿第二运动定律不仅适用于直线运动，也适用于曲线运动。

在曲线运动中，我们可以将曲线分解为一系列微小的直线段，对每个直线段分别应用牛顿第二运动定律，并求解其在各个方向上的分力。

通过这种方式，我们可以推导出质点在曲线上的运动规律。

牛顿第二运动定律还可以应用于力学系统的分析和计算。

通过对力学系统中各个质点的牛顿第二运动定律的求解，我们可以得到整个系统的运动规律。

这种方法被广泛应用于自然科学和工程领域的研究中，帮助我们更好地理解和掌握物体的运动。

值得注意的是，牛顿第二运动定律是在经典力学范畴内有效的。

在宏观物体和低速运动的情况下，牛顿第二运动定律是一个非常准确的描述。

然而，在极小尺度或高速运动的情况下，牛顿第二运动定律需要相对论力学的修正。

相对论力学揭示了高速运动和大能量情况下质点的运动规律，它与牛顿力学存在差异。

第02章__质点运动定律补充

1、一根长为l 、质量可以忽略的细棒可绕其端点O 在竖直平面内运动，棒的另一端附着一个质量为m 的小球。

已知小球在其轨道顶点A 处的速度v =gl ，设棒对小球的作用力T 以沿径向向外为正，则T 与θ函数关系为：(A) θcos 3mg ； (B) )cos 1(3θ-mg ；(C) )1(cos 3-θmg ； (D) θsin 3mg ；［ C ］难度：中2、质量相同的物体A 、B ，用一根细绳和一根轻弹簧连接并悬于固定点O ，如图。

开始时系统处于平衡状态，后将细绳剪断，则在刚剪断瞬时：(A) A 、B 的加速度均为g ； (B) A 、B 的加速度均为零；(C) A 的加速度均为零， B 的加速度均为2g ； (D) A 的加速度均为2g ；B 的加速度均为零；［ D ］难度：中3、用细绳系一小球使之在竖直平面内作圆周运动，则： (A)小球在任意位置都有切向加速度； (B)小球在任意位置都有法向加速度；(C)小球在任意位置绳子的拉力和重力是惯性离心力的反作用力；(D)当小球运动到最高点时，它将受到重力、绳的拉力和向心力的作用；［ B ］难度：中4、一质点在力F = 5m (5 - 2t ) (SI)的作用下，t =0时从静止开始作直线运动，式中m 为质点的质量，t 为时间，则当t = 5 s 时，质点的速率为(A) 50 m ·s -1．. (B) 25 m ·s -1．(C) 0．(D) -50 m ·s -1．［ C ］难度：中5、如图所示，在光滑平面上有一个运动物体P ，在P 的正前方有一个连有弹簧和挡板M 的静止物体Q ，弹簧和挡板M 的质量均不计，P 与Q 的质量相同．物体P 与Q 碰撞后P 停止，Q 以碰前P 的速度运动．在此碰撞过程中，弹簧压缩量最大的时刻是 (A) P 的速度正好变为零时． (B) P 与Q 速度相等时． (C) Q 正好开始运动时．(D) Q 正好达到原来P 的速度时．难度：难6、站在电梯内的一个人，看到用细线连结的质量不同的两个物体跨过电梯内的一个无摩擦的定滑轮而处于“平衡”状态．由此，他断定电梯作加速运动，其加速度为 (A) 大小为g ，方向向上． (B) 大小为g ，方向向下．(C) 大小为g 21，方向向上． (D) 大小为g 21，方向向下．［ B ］难度：中7、图示系统置于以g a 21=的加速度上升的升降机内，A 、B 两物体质量相同均为m ，A 所在的桌面是水平的，绳子和定滑轮质量均不计，若忽略滑轮轴上和桌面上的摩擦并不计空气阻力，则绳中张力为(A) mg ． (B) m g 21． (C) 2mg ． (D) 3mg / 4．［ D ］难度：中8、一根细绳跨过一光滑的定滑轮，一端挂一质量为M 的物体，另一端被人用双手拉着，人的质量M m 21=．若人相对于绳以加速度a 0向上爬，则人相对于地面的加速度（以竖直向上为正）是(A) 3/)2(0g a +． (B) )3(0a g --．(C) 3/)2(0g a +-． (D) 0a［ A ］难度：中9、设物体沿固定圆弧形光滑轨道由静止下滑，在下滑过程中，(A) 它的加速度方向永远指向圆心． (B) 它受到的轨道的作用力的大小不断增加． (C) 它受到的合外力大小变化，方向永远指向圆心．(D) 它受到的合外力大小不变．［ B ］难度：中10、质量相等的两个物体甲和乙，并排静止在光滑水平面上（如图所示）．现用一水平恒力F 作用在物体甲上，同时给物体乙一个与F同方向的瞬时冲量量I，使两物体沿同一方向运动，则两物体再次达到并排的位置所经过的时间为：(A) I / F ． (B) 2I / F ．(C) 2 F/ I ． (D) F/ I ．a俯视图F I难度：中11、竖直上抛一小球．若空气阻力的大小不变，则球上升到最高点所需用的时间，与从最高点下降到原位置所需用的时间相比(A) 前者长． (B) 前者短．(C) 两者相等． (D) 无法判断其长短．［ B ］难度：易12、一个质点，在力作用下从A 点出发经C 点运动到B 点，其运动轨迹如图所示．已知质点运动的速率是递增的，下面关于C 点加速度的方向的四个图示中正确的是：［ C ］难度：易13、一个质点，在力作用下从A 点出发经C 点运动到B 点，其运动轨迹如图所示．已知质点运动的速率是递减的，下面关于C 点加速度的方向的四个图示中正确的是：［ D ］难度：易aaaa14、两个形状、大小和质量相同的物体，一个从光滑的斜面上由静止开始下滑，另一个同时从同一高度由静止开始下落，则：(A) 两物体同时到达地面．(B) 自由下落的物体先到达地面． (C) 沿斜面下滑的物体先到达地面． (D) 哪个物体先到达，不一定．［ A ］难度：易15、如图所示装置开始处于平衡状态，当左边的细丝刚被剪断的瞬间，质量为3m 、2 m 、 m 的物体的加速度大小分别是：(A) g ，g ，g ．(B) 0，2g ，3g ． (C) 3g ，0，2g ． (D) g ，0，3g ．［ A ］难度：中16、如图所示，A 、B 、C 三木块质量均为M ，用轻绳连起来，现用力F 向右拉木块，使三木块一起作加速运动，设桌面是光滑的，则木块B 所受合外力的大小为：(A) F ．(B)2F． (C) 3F ．(D) 32F ．［ C ］难度：易17、水平地面上放一物体A ，它与地面间的滑动摩擦系数为μ．如图所示．欲使F 最省力，则力F与水平方向夹角θ 应满足：(A) 0． (B)4π． (C) tg θ ＝μ． (D) ctg θ ＝μ．［ C ］难度：易18、质量分别为m和M的滑块A和B，一起在水平面上向右作匀减速直线运动，加速度大小为a，如图所示。

第02章__质点运动定律

第二章质点运动定律一、选择题1、在升降机天花板上拴有轻绳，其下端系一重物，当升降机以加速度a 1上升时，绳中的张力正好等于绳子所能承受的最大张力的一半，问升降机以多大加速度上升时，绳子刚好被拉断？(A) 2a 1． (B) 2a 1＋g ．(C) 2(a 1+g )． (D) a 1＋g ．［ B ］2、质量为m 的小球，放在光滑的木板和光滑的墙壁之间，并保持平衡，如图所示．设木板和墙壁之间的夹角为α，当α逐渐增大时，小球对木板的压力将 (A) 增加．(B) 减少．(C) 不变． (D) 先是增加，后又减小．压力增减的分界角为α＝45°． [ B ]3、两个质量相等的小球由一轻弹簧相连接，再用一细绳悬挂于天花板上，处于静止状态，如图所示．将绳子剪断的瞬间，球1和球2的加速度分别为(A) a 1＝ｇ，a 2＝0． (B) a 1＝0，a 2＝ｇ． (C) a 1＝ｇ，a 2＝ｇ． (D) a 1＝2ｇ，a 2＝0．［ D ］4、水平地面上放一物体A ，它与地面间的滑动摩擦系数为μ．现加一恒力F如图所示．欲使物体A 有最大加速度，则恒力F 与水平方向夹角θ 应满足(A) sin θ ＝μ． (B) cos θ ＝μ．(C) tg θ ＝μ． (D) ctg θ ＝μ．［ C ］5、一只质量为m 的猴，原来抓住一根用绳吊在天花板上的质量为M 的直杆，悬线突然断开，小猴则沿杆子竖直向上爬以保持它离地面的高度不变，此时直杆下落的加速度为(A) g M m (B) g M m M - (C)g M m M +. (D) g mM mM -+ .[ C ]a 16、如图所示，质量为m 的物体A 用平行于斜面的细线连结置于光滑的斜面上，若斜面向左方作加速运动，当物体开始脱离斜面时，它的加速度的大小为(A) g sin θ． (B) g cos θ．(C) g ctg θ． (D) g tg θ．［ C ］7、如图所示，一轻绳跨过一个定滑轮，两端各系一质量分别为m 1和m 2的重物，且m 1>m 2．滑轮质量及轴上摩擦均不计，此时重物的加速度的大小为a ．今用一竖直向下的恒力gm F =代替质量为m 1的物体，可得质量为m 2的重物的加速度为的大小a ′，则(A) a ′= a (B) a ′> a(C) a ′< a (D) 不能确定. ［ B ］8、质量分别为m 1和m 2的两滑块A 和B 通过一轻弹簧水平连结后置于水平桌面上，滑块与桌面间的摩擦系数均为μ，系统在水平拉力F 作用下匀速运动，如图所示．如突然撤消拉力，则刚撤消后瞬间，二者的加速度a A 和a B 分别为(A) a A =0 , a B =0. (B) a A >0 , a B <0.(C) a A <0 , a B >0. (D) a A <0 , a B =0.［ D ］9、质量为m 的物体自空中落下，它除受重力外，还受到一个与速度平方成正比的阻力的作用，比例系数为k ，k 为正值常量．该下落物体的收尾速度(即最后物体作匀速运动时的速度)将是(A)kmg. (B) k g 2 .(C) gk . (D) gk . ［ A ］10、质量分别为m 和M 的滑块A 和B ，叠放在光滑水平桌面上，如图所示．A 、B 间静摩擦系数为μs ，滑动摩擦系数为μk ，系统原处于静止．今有一水平力作用于A 上，要使A 、B 不发生相对滑动，则应有(A) F ≤μs mg ． (B) F ≤μs (1+m /M )mg ． (C) F ≤μs (m+M )mg ． (D) F ≤MmM mgk +μ．［ B ］11、如图所示，用一斜向上的力F(与水平成30°角)，将一重为G 的木块压靠在竖直壁面上，如果不论用怎样大的力F ，都不能使木块向上滑动，则说明木块与壁面间的静摩擦系数μ的大小为(A) .21≥μ (B) 31≥μ. (C) 3≥μ. (D) 32≥μ. ［ B ］12、一辆汽车从静止出发，在平直公路上加速前进的过程中，如果发动机的功率一定，阻力大小不变，那么，下面哪一个说法是正确的？(A) 汽车的加速度是不变的． (B) 汽车的加速度不断减小． (C) 汽车的加速度与它的速度成正比．(D) 汽车的加速度与它的速度成反比．［ B ］13、升降机内地板上放有物体A ，其上再放另一物体B ，二者的质量分别为M A 、M B ．当升降机以加速度a 向下加速运动时(a <g )，物体A 对升降机地板的压力在数值上等于(A)M A g. (B) (M A +M B )g.(C) (M A +M B )(g +a ). (D) (M A +M B )(g -a ). ［ D ］14、如图，物体A 、B 质量相同，B 在光滑水平桌面上．滑轮与绳的质量以及空气阻力均不计，滑轮与其轴之间的摩擦也不计．系统无初速地释放，则物体A 下落的加速度是 (A) g. (B) 4g /5 .(C) g /2 . (D) g /3 . ［ B ］15、如图，滑轮、绳子质量及运动中的摩擦阻力都忽略不计，物体A 的质量m 1大于物体B 的质量m 2．在A 、B 运动过程中弹簧秤S 的读数是(A) .)(21g m m + (B) .)(21g m m -(C) .22121g m m m m + (D) .42121g m m m m + ［ D ］16、如图所示，质量为m 的物体用细绳水平拉住，静止在倾角为θ的固定的光滑斜面上，则斜面给物体的支持力为(A) θcos mg . (B) θsin mg . (C)θcos mg . (D) θsin mg. [ C ]17、光滑的水平桌面上放有两块相互接触的滑块，质量分别为m 1和m 2，且m 1<m 2．今对两滑块施加相同的水平作用力，如图所示．设在运动过程中，两滑块不离开，则两滑块之间的相互作用力N 应有(A) N =0. (B) 0 < N < F . (C) F < N <2F . (D) N > 2F . ［ B ］18、用水平压力F 把一个物体压着靠在粗糙的竖直墙面上保持静止．当F逐渐增大时，物体所受的静摩擦力f(A) 恒为零．1(B) 不为零，但保持不变． (C) 随F 成正比地增大．(D) 开始随F 增大，达到某一最大值后，就保持不变［ B ］19、用水平压力F 把一个物体压着靠在粗糙的竖直墙面上保持静止．当F逐渐增大时，物体所受的静摩擦力f(A) 恒为零． (B) 不为零，但保持不变． (C) 随F 成正比地增大．(D) 开始随F 增大，达到某一最大值后，就保持不变［ B ］ 20、一光滑的内表面半径为10 cm 的半球形碗，以匀角速度ω绕其对称OC 旋转．已知放在碗内表面上的一个小球P 相对于碗静止，其位置高于碗底4 cm ，则由此可推知碗旋转的角速度约为(A) 10 rad/s ． (B) 13 rad/s ．(C) 17 rad/s(D) 18 rad/s ．［ B ］21、竖立的圆筒形转笼，半径为R ，绕中心轴OO ＇转动，物块A 紧靠在圆筒的内壁上，物块与圆筒间的摩擦系数为μ，要使物块A 不下落，圆筒转动的角速度ω至少应为(A)R gμ (B)g μ (C) Rgμ (D)R g ［ C ］22、已知水星的半径是地球半径的 0.4倍，质量为地球的0.04倍．设在地球上的重力加速度为g ，则水星表面上的重力加速度为： (A) 0.1 g (B) 0.25 g (C) 2.5 g (D) 4 g [ B ]23、如图所示，假设物体沿着竖直面上圆弧形轨道下滑，轨道是光滑的，在从A 至C 的下滑过程中，下面哪个说法是正确的？(A) 它的加速度大小不变，方向永远指向圆心． (B) 它的速率均匀增加． (C) 它的合外力大小变化，方向永远指向圆心． (D) 它的合外力大小不变． (E) 轨道支持力的大小不断增加．［ E ］24、一个圆锥摆的摆线长为l ，摆线与竖直方向的夹角恒为θ，如图所示．则摆锤转动的周期为A R(A)g l. (B) gl θcos . (C) g l π2. (D) gl θπcos 2 . ［ D ］25、一公路的水平弯道半径为R ，路面的外侧高出内侧，并与水平面夹角为θ．要使汽车通过该段路面时不引起侧向摩擦力，则汽车的速率为(A) Rg . (B) θtg Rg .(C)θθ2sin cos Rg . (D)θctg Rg ［ B ］26、一段路面水平的公路，转弯处轨道半径为R ，汽车轮胎与路面间的摩擦系数为μ，要使汽车不致于发生侧向打滑，汽车在该处的行驶速率 (A) 不得小于gR μ． (B) 不得大于gR μ．(C) 必须等于gR 2． (D) 还应由汽车的质量M 决定．［ B ］ 27、一小珠可在半径为R 竖直的圆环上无摩擦地滑动，且圆环能以其竖直直径为轴转动．当圆环以一适当的恒定角速度ω 转动，小珠偏离圆环转轴而且相对圆环静止时，小珠所在处圆环半径偏离竖直方向的角度为(A) π21=θ. (B) ).arccos(2ωθR g = (C) )a r c t g (2gR ωθ=. (D) 需由小珠的质量m 决定．［ B ］28、在作匀速转动的水平转台上，与转轴相距R 处有一体积很小的工件A ，如图所示．设工件与转台间静摩擦系数为μs ，若使工件在转台上无滑动，则转台的角速度ω应满足(A)Rgs μω≤.(B)R gs 23μω≤. (C) R gs μω3≤. (D) Rg s μω2≤. ［ A ］二、填空题1、质量相等的两物体A 和B ，分别固定在弹簧的两端，竖直放在光滑水平面C 上，如图所示．弹簧的质量与物体A 、B 的质量相比，可以忽略不计．若把支持面C 迅速移走，则在移开的一瞬间，A 的加速度大小a A ＝_______．答案：02、质量相等的两物体A 和B ，分别固定在弹簧的两端，竖直放在光滑水平面C 上，如图所示．弹簧的质量与物体A 、B 的质量相比，可以忽略不计．若把支持面C 迅速移走，则在移开的一瞬间， B 的加速度的大小a B ＝_______ g ．答案：25、质量分别为m 1、m 2、m 3的三个物体A 、B 、C ，用一根细绳和两根轻弹簧连接并悬于固定点O ，如图．取向下为x 轴正向，开始时系统处于平衡状态，后将细绳剪断，则在刚剪断瞬时，物体A 的加速度A a＝______．答案：07、质量m =40 kg 的箱子放在卡车的车厢底板上，已知箱子与底板之间的静摩擦系数为μs ＝0.40，滑动摩擦系数为μk ＝0.25，试写出在下列情况下，作用在箱子上的摩擦力的大小和方向．卡车以a = 2 m/s 2的加速度行驶，f =____________ N 。

第2章质点系力学

现在来补充说明
∑F
i =1
n
(i ) i
= 0 这一条件。
①. 首先，我们这里不能根据牛顿第三定律来提供这一条件。因为如果承认牛顿第三定律，则当然可以由（A）式得到（B）式，但是这就违背了我们在这里进行注解的初衷：我们原本就是想撇开牛顿定律去得出（B）；其次，第一章中已指出，牛顿第三定律实际是一个关于力的性质的很强的假设，不是一个物理上普遍的定律,物理学中有些力并不符合这个定律（例如洛仑兹力）；另外，第一章中我们还指出，就现今物理学的观点看，牛顿第三定律所说的“相互作用是同时的”值得怀疑，它隐含着力的超距作用机制在内，这是第三定律用到近代物理中遇到的又一个困难。实际上力并不能即时跨越空间发生作用，而是以不大于光速的有限速率传递的。 ②. 迄今为止，人们发现对于一个孤立的系统（即没有受到外力作用的系统），动量都守恒。也就是说，一系统即使不服从牛顿定律，但只要是孤立的，动量守恒定律仍成立。所以，动量守恒定律可以不依赖于牛顿第三定律而独立存在，而且是比牛顿定律更为基本的（或说更为普遍的）物理规律。质点系的动量守恒律可以被表为：如果作用于质点系的总外力为零，则质点系的总动量不变，而不论内力是多么复杂地相互作用着（注意这里动量守恒是针对整个质点系来说的，至于组内各个质点的动量则因各自所受到的内力和外力之和未必也是零而不守恒）。这样就可以由动量守恒律得出上述内力之和为0即恒律
∑F
i =1
n
(i ) i
= 0 条件并由（A）推出（B）时已
看到，除了动量守恒律外还应用了单个质点的动量定理。实际上不论是正文还是刚才所注的推导都不是由一般到特殊的推理，推导过程中都临时插入了除前提以外的条件（如牛顿第三定律或动量守恒律等），因此严格意义上只是“引出”而不是“推出” 。反过来，牛顿第二定律及单个质点的动量定理却确实能作为质点系动量定理的特例。可见，相比起来，质点系动量定理最弱、最基本。引出式的“推出”只是出于教学上的考虑，动量定理作为更普遍的公理其实也不需要去推出。

(普通物理)第二章-2质点系的功能原理

14
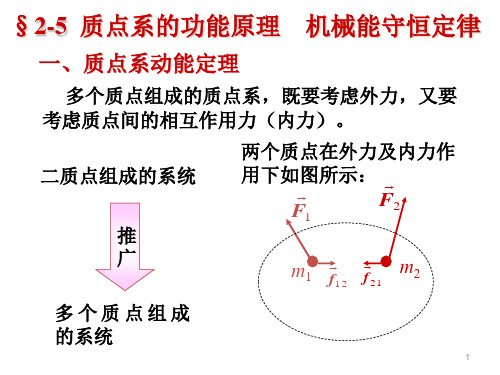
（2）参看图(b)，以加力F 时为初态，撤去力F 而弹簧伸长最大时为末态，则
初态末态
Ek1 0 Ek 2 0
x
E p1
1 2
kx12
Ep2
1 2
kx22
x0 x
F
x2
O
x1
15
根据能量守恒定律，应有
1 2
kx12
1 2
kx2 2
因恰好提起m2时，k(x2-x0)=m2g，而kx1=F, kx0=m1g
Aid
0
非保守内力不做功，系统内部不发生机械能和其他形式能量的交换
定律 E EK EP 常量
10
四、能量守恒定律
一个孤立系统经历任何变化时，该系统的所有能量的总和是不变的，能量只能从一种形式变化为另外一种形式，或从系统内一个物体传给另一个物体。这就是普遍的能量守恒定律.
例如：利用水位差推动水轮机转动，能使发电机发电，将机械能转换为电能。
4
注意：
(1)当我们取物体作为研究对象时，使用的是单个物体的动能定理，其中外力所作的功指的是作用在物体上的所有外力所作的总功，所以必须计算包括重力、弹性力的一切外力所作的功。
(2)当我们取系统作为研究对象时，由于应用了系统这个概念，关于保守内力所作的功，已为系统势能的变化所代替，因此在演算问题时，如果计算了保守内力所作的功，就不必再去考虑势能的变化；反之，考虑了势能的变化，就不必再计算保守内力的功。
代入解得
F m1 m2 g
这就是说F（m1+m2)g时，下板就能被拉起。
16
例 2 有一轻弹簧, 其一端系在铅直放置的圆环的顶点P, 另一端系一质量为m 的小球, 小球穿过圆环并在圆环上运动(不计摩擦) .开始小球静止于点 A, 弹簧处于自然状态,其长度为圆环半径R; 当小球运动到圆环的底端点B时,小球对圆环没有压力. 求弹簧的劲度系数.

力学第二章质点运动学

方向： 90， arccos vy 3342 '
v
arccos vz 5618'
v
二、平均加速度与瞬时加速度
1、平均加速度：速度矢量对时间的平均变化率。
a v v(t t) v(t)
t
t
v(t )

v

速度矢端曲线
v( t t )
§2.3 质点的直线运动(x vx ax )
一、运动学方程
x xt
二、速度和加速度
1、速度（瞬时速度）
vx

dx dt
大小表示质点在t时刻运动的快慢；
正负分别对应于质点沿Ox正向和负向运动。
2、加速度
ax

dvx dt

d2x dt 2
ax与vx同号，则加速；ax与vx反号，则减速。
4、质点的运动学轨迹方程
质点运动时描出的轨迹称为质点的轨迹。也就是位置矢量的矢端曲线。
质点在平面Oxy上运动，
轨迹方程： y y(x) 或者：f (x, y, z) 0
例题：r R cos tiˆ R sin tˆj, 求:轨迹方程。
y R
解： x2 y2 R2.
x
二、位移
v
v
v
4、注意：
（1）平均速度的大小不等于平均速率。（2）瞬时速度的大小等于瞬时速率。（3）即使位置矢量的大小不变，也可以有速度。
ΔS
r(t )
r
S
r(
t

t
)
o
dr / dt
r(t )
ΔS

S
r

r( t t )

大学物理(上)课件-第02章质点动力学3-2

(
)
50
� � � dL � 质点系角动量定理： M = ∑ ri × Fi = dt
质点系对某一参考点的角动量随时间的变化率等于系统所受各个外力对同一参考点力矩之矢量和。质点系角动量定理的积分式：
∫
t2
t1
� � � Mdt = L2 − L1
作用于质点系的冲量矩等于质点系在作用时间内的角动量的增量。
例6 宇宙飞船在宇宙尘埃中飞行，尘埃密度为ρ。如果质量为mo的飞船以初速vo穿过尘埃，由于尘埃粘在飞船上，致使飞船速度发生变化。求飞船的速度与其在尘埃中飞行的时间的关系。（设飞船为横截面面积为S的圆柱体）解：某时刻飞船速度： v，质量：m 动量守恒：质量增量：
m0v0 = mv
dm = ρ Sv dt
2.质点系的动量定理：
∫
t
t0
� � � � ∑ Fi dt = p − p0 = ∆p
� � dp ∑ Fi = dt
质点系统所受合外力的冲量等于系统总动量的增量。微分式：
注意：系统的内力不能改变整个系统的总动量。
31
设有n个质点构成一个系统第i个质点：质量
� � 内力 F 外力 Fi 内i
O
y
48
3. 质点的角动量定理
� � dL MO = dt
质点对某一参考点的角动量随时间的变化率等于质点所受的合外力对同一参考点的力矩。角动量定理的积分式：
∫
t2
t1
� � � M O dt = L2 − L1
∫
t2
t1
� M O dt
称为“冲量矩”
49
n � n � � � 质点系的角动量： L = ∑ Li = ∑ ( ri × pi ) i =1 i =1

《大学物理》第二章《质点动力学》课件

相对论中的质点动力学
相对论简介
01
相对论是由爱因斯坦提出的理论，包括特殊相对论和广义相对
论，对经典力学和电动力学进行了修正和发展。
质点动力学
02
在相对论中，质点的运动遵循质点动力学规律，需要考虑相对
论效应。
实际应用
03
相对论中的质点动力学在粒子物理、宇宙学和天文学等领域具
有重要意义，如解释宇宙射线、黑洞和宇宙膨胀等现象。
牛顿运动定律的应用
通过牛顿第二定律分析质点在各种力作用下的运动规律。
弹性碰撞和非弹性碰撞
碰撞的定义
两个物体在极短时间内相互作用的过程。
弹性碰撞
两个物体碰撞后，动能没有损失，只发生形状和速度方向的改变。
非弹性碰撞
两个物体碰撞后，动能有一定损失，不仅发生形状和速度方向的改变，还可能有物质交换。
01
运动分析
火箭发射过程中，需要分析火箭的加速度、速度和位移等运动参数，以确定最佳发射时间和条件。
02
03
实际应用
火箭发射的运动分析对于航天工程、军事和商业发射等领域具有重要意义。Fra bibliotek球自转的角动量守恒
1 2
地球自转
地球绕自身轴线旋转，具有角动量。
角动量守恒
在没有外力矩作用的情况下，地球自转的角动量保持不变。
相对论和量子力学
随着科学技术的不断发展，相对论和量子力学逐渐兴起，对质点动力学产生了深远的影响。相对论提出了新的时空观念和质能关系，而量子力学则揭示了微观世界的奇特性质。
牛顿时代
牛顿在《自然哲学的数学原理》中提出了三大运动定律和万有引力定律，奠定了经典力学的基础。
现代
现代物理学在继承经典理论的基础上，不断探索新的理论框架和实验手段，推动质点动力学的发展和完善。