社会统计学(卢淑华版)
社会统计学(卢淑华)_第六章

第一节 统计推论
一、统计推论:根据局部资料对总体特征进行推断 特点: 1、局部资料的特性在某种程度上能反映总体的特征 2、抽样结果不能恰好等于总体的结果
二、理论基础:概率论 三、内容:
1、通过样本对总体的未知参数进行估计(参数估计) 2、通过样本对总体的某种假设进行检验(假设检验)
第二节 名词解释
二、评价估计值的标准
1、无偏性:x 的均值等于待估参数μ
如果 Qˆ 是总体参数Q的估计值,且Qˆ 分布的均值有 E Qˆ 称 Qˆ 是Q的无偏估计。
Q,则
2、有效性:
1)方法:如果两个估计值Qˆ1 x1 x2 xn 及 Qˆ 2 x1 x2 xn ,它
都满足无偏性,那么当 Qˆ1 的方差比 Qˆ 2 的方差小时,则Q1 较 Q 2 更
有效。
2)增加样本容量可以有效的增加一次抽样接近待估参数的概率。
x 样本均值
2
的方差:Dx n
样本方差
S 2 的方差
:D2 S
4
n 2 1
3、一致性: 一个数的估计值要求随样本容量n的增大而以较
大的概率去接近被估计参数的值。
把样本容量为n时的估计值记作 Qˆ n ,如果 n
第五节 正态总体的区间估计
一、置信度、置信区间
如果用Qˆ x1 x2 xn 作为未知参数Q的估计值,那么区间
包含参数Q之概率为1
的关系表达式为
Q Q,
——置信区间(反映估计的准确性)
1
置信度(置信概率)(置信区间估计的可靠性)
显著性水平(置信区间不可靠的概率)
置信区间与置信度的关系:
社会统计学(卢淑华)-第三章

接上例。某天,随机抽出一份表格,发现有错 误,办公室主管想知道由第一、第二、第三个 工作人员所造成的概率是多少?
第二节 概率分布、均值不方差
一、概率分布:
随机现象一共有多少种结果,以及每种结果伴随的概率。
1、离散型随机变量及其概率分布——分布列
概率分布:P X i Pi
例1:10人中,女性3人,抽3人,女性人数的概率分布。
③ 求[ E()]2P·( =xi)
④ 2=
5、方差的性质
① 常数的方差为0
② D(+C)= D()
③ D(C·)=DC2 ·()
④ 两个独立变量
D(+ )= D()+D( )
推广n个
例题
12名学生,3女,9男。任抽一人,如为女 生,则不放回,再抽一人,直到抽到男生 为止,求,抽到男生以前已抽出的女生人 数的数学期望与方差。
PAB PA P B A 或 PAB PB P A B
推论: PA1 A2 An PA1 AP1 A2PAn A1 A2 An
例题1
某城市中,有60%的家庭订阅日报,有80% 的家庭有电视机,假定这两个事件是独立 的,随机抽出一个家庭,发现既订日报又 有电视机的概率?
答案
PAi
B
PAi
• PB PB
Ai
其中
n
PB
i 1
PAi • PB Ai
全概例:
有三个工作人员被指定复制某种表格。某一人 复制了这种表格的40%,第二人复制了35%, 第三人复制了23%,第一人的错误率为0.04, 第二人的错误率为0.06,第三人的错误率为 0.03。随机抽一份表格,这份表格有错误的概 率为多少?
集
社会统计学(卢淑华),第十章

调查过程不应给被调查者带来身体或心理 上的伤害,避免涉及敏感或隐私问题。
数据处理与分析中的伦理问题
数据真实性
在处理和分析数据时,应确保数 据的真实性和完整性,避免篡改
、伪造或选择性使用数据。
数据安全性
采取必要的技术和管理措施, 确保数据的安全存储和传输, 防止数据泄露、损坏或丢失。
数据分析的客观性
报告统计结果时,应提供足够的信息 和数据支持结论,避免选择性报告或 隐瞒不利结果。
避免过度解读
在解释统计结果时,应避免过度解读 或夸大其意义,以免误导读者或产生 不必要的恐慌。
尊重被调查者的权益
在报告统计结果时,应注意保护被调 查者的隐私和权益,避免泄露个人信 息或造成不必要的伤害。
THANK YOU
社会问题调查
通过问卷调查、访谈、观察等方 法收集数据,了解社会问题的现
状、原因和影响。
社会问题分析
运用统计分析方法对调查数据进 行处理和分析,揭示社会问题的
本质和规律。
社会问题解决方案
基于分析结果,提出针对性的解 决方案和建议,为政府和社会各
界提供参考。
社会政策的制定与评估
社会政策制定
01
运用统计数据和分析结果,为政府制定社会政策提供科学依据
04
因子分析
一种通过降维技术,将多个相关变量简化为少数几个 综合变量的统计分析方法。
05
聚类分析
一种根据样本或变量之间的相似性或距离,将其分为 不同类别的统计分析方法。
02
描述性统计方法
频数分布与图形表示
频数分布表
将数据进行分类,并统计各类别出现的次数,形成 频数分布表,以直观展示数据的分布情况。
SAS是一款高级统计分析软件 ,具有强大的数据处理、分析 和可视化功能,适用于大规模 数据处理和复杂统计分析。
(完整word版)卢淑华 《社会统计学》讲义

社会统计学讲义第一章导论一、社会统计学1、社会统计学是运用统计的一般原理,对社会各种静态结构与动态趋势进行定量描述或推断的一种专门方法和技术。
研究对象:概括而言是指社会现象的数量方面。
2、选择统计分析方法的原则是根据研究目的和资料本身的特点选择。
3、统计分析的作用:(1)可对资料进行简化和描述;(2)可对变量间的关系进行描述和深入地分析(统计分析通过事后解释使得探讨变量间复杂的因果联系成为可能);(3)可通过样本资料推断总体(通过参数估计和假设检验,将样本推论到总体并指出这种推论的误差及做出这种推论的把握有多大)。
4、社会统计的基本程序(1)制定计划;(2)统计调查;(3)统计整理;(4)统计分析;(5)统计报告。
5、几个基本概念(1)总体与单位总体又称母体,是作为统计研究对象的、由许多具有共性的单位构成的整体。
构成总体的每一个个体称为总体单位,简称单位或个体。
3个基本特征:大量性、同质性和变异性。
(2)标志与变量总体的每个单位都具有许多属性和特性,说明总体单位属性或数量特征的名称在统计上称为标志,分为数量标志和品质标志。
可变的品质标志无法用数值表示,我们称之为变项;可变的数量标志能够用数值表示,我们称之为变量。
(3)指标与指标体系统计指标是反映总体(或样本总体)的数量特征的概念或范畴。
一个完整的统计指标由两部分构成:指标名称和指标数值。
在社会统计中,如要全面把握对象总体情况,就不能单凭一个指标,而要靠一组相互联系的并与之相适应的指标来完整地反映对象总体。
指标体系就是一系列有内在联系的统计指标的集合体。
二、社会调查研究的程序社会学研究之阶段与步骤(1)确定课题:来源与社会学理论、当前社会现实和要解决的实际问题;具有强烈的时代感、为国家现代化服务;(2)了解情况:查阅文献和向有经验、有知识的人了解,运用个案调查、典型调查进行探索性研究;(3)提出一定的想法和建立假设:差异式、函数式;(4)建立概念和测量方法:采用适当的术语和概念;操作化定义;概念的表现形式往往具有多值性;(5)设计问卷:内容包括事实、态度与看法、行为趋向、理由;方式有固定答题式和自由答题式;(6)试填问卷:发现不周或遗漏之处在试填阶段予以纠正;(7)调查实施(抽样调查):从局部推论到全体(8)校核与登录(9)统计分析与命题的检验:检验最初研究阶段的命题或假设是否得到证实或部分证实,在此基础上对研究内容提出建议和确定进一步的研究方案。
社会统计学(卢淑华)PPT培训课件

例:
根据生命表,年龄为60岁的人,可望活 到下年的概率P=0.95。设某单位年龄为 60岁的人共有10人,问:
(1)其中有9人活到下年的概率为多少 (2)至少有9人活到下年的概率为多少 (3)至多有9人活到下年的概率为多少
第四节 多项分布
以三项分布作为研究对象,依此类推
三项分布: P x1 , x2 , x3 n! P P P 1 x1 2 2x 3 x3
x
x nx
n
xa
例:
教师中吸烟的比例为50%,随机抽查教 师10人,求概率:
1、全不吸烟 2、1人吸烟 3、至少2人吸烟 4、2-4人吸烟
三、二项分布的数学期望
E
n
x
P
n
x
x
x
Cp q x
n
nx
n
p
x 0
x 0
5、二项分布的方差等于
2
2
6、查表方法
3、二点分布----一次贝努里试验的概率分布; 二项分布----n次贝努里试验的概率分布;
4、二点分布是二项分布的特殊情况
5、二点分布 :
变量的取值只有两类 ;
x
0
p
q
代码:0、1 ;
1
p
分布列:
6、二点分布的性质 1)P(=0)>0 P(=1) >0 2)P(=0)+ P(=1)=q+p=1 3)二点分布的期望与方差
如:同一地点的交通事故。
例
某城市一交叉路口每年平均发生交通事 故5起,如果交通事故的发生服从泊松分 布,在指定的一年内以下交通事故发生 的概率是多少?
社会统计学(卢淑华),第五章

卡方分布性质
性质1 如果随机变量 1 , 2 ,…… k 相互独立,
2
量:
x
2
1
2
i
k 2 i 1
仍然服从自由度为k的 X2 的平方分布。
性质2:
如果随机变量 和 独立,并且分别服 从自由度为K1与K2的X2 分布,则其和 服从自由度为K1 + K2的X2分布。
,求
2)P 1.3 3)P1.3 2.3
2、ξ 满足N 0,1 ,P 0.05 ,求λ 值。 3、ξ 满足 N 50,52 ,求 P 61
第四节 常用统计分布
一、X2分布(卡方分布) 1、设随机变量 1,2, k 相互独立,且都服
三、切贝谢夫大数定理
1、定义:设随机变量 , …是相互独立服 从 同 一 分 布 , 并 且 有 数 学 期 望 E i 差 Di 2 ,那么对于任何一个正数 ,
1
2
有: n 为 1 , 2 …n个随即变量的平均值 2、含义:当实验次数n足够大时,n个随机变 量的平均值 与单个随机变量的数学期望 的 差可以任意的小,这个事实以接近于1的很大 概率来说是正确的,即 趋近于数学期望 3、实际:意义可以用抽样的均值 做为总体均
P 2 z 2 0.9546
P 3 z 3 0.9973
例:
例1:σ相同而µ 不同。学习成绩:甲位于一班, 乙位于二班。一班平均成绩80分,二班平均成绩 60分,甲成绩80分,乙成绩80分。σ相同,为 10,比较二者在班上的成绩。 例二: µ 相同而σ不同:如果 1 2 60
社会统计学(卢淑华)-第一章

资料的对象 3)要把握统计分析的前提是否满足:资料的信度和效度;
资料收集的科学性;资料在总体中的分布。
统计分析中常见的错误
社会统计学
社会统计学以德国为中心;克里斯首创 认为社会统计学是一门社会科学,研究
社会变动与规律性 研究对象是社会总体而不是个体,大量
观察、研究内在联系,才能揭示其规律 性。
社会统计学的两大流派
❖ 社会指标学派 ❖ 描述统计学派
社会指标
用来测定某一社会要素状态的统计量。 社会指标举例:
检验;定类-定距:方差分析;
定序变量
初级定量测定 除类别、属性之分外,还有等级、秩序
之分 如:教育程度;社会经济地位 定序-定序:等级相关
定距变量
除定类、定序外,取值之间有标准化的 量度
可进行加减运算,但不能进行乘除运算 典型例子:智商测定 定距-定距:回归与相关
定比变量
除定类、定序、定距之特征外,取值可 构成一个有意义的比例
有一个绝对固定的、非任意的零点 可进行乘除运算 绝大多数经济变量可进行定比测定 如:年龄;收入;
知识回顾 Knowledge Review
祝您成功!
联合国有关组织规定: 若低于0.2表示收入绝对平均; 0.2-0.3表示比较平均; 0.3-0.4表示相对合理; 0.4-0.5表示收入差距较大; 0.6以上表示收入差距悬殊。
二、社会学不社会统计学
1、社会学研究的重要环节 ▲课题---了解课题---假设---术语---问卷---调查---校核---统计
社会统计学(卢淑华),第一章资料

一、社会统计学的发展
统计学的两大流派:数理统计学派和社 会统计学派
数理统计学派的原创始人是比利时的A ·凯特靳, 其最大的贡献就是将法国的古典概率引入统计 学,用纯数学的方法对社会现象进行研究; 社会统计学派的首倡者是德国的K·克尼斯,他 认为统计研究的对象是社会现象,研究方法为 大量观察法。
例:中学升学率调查
课题确定:升学率差异较大;学生择校
初探:收集文献,前人研究;咨询相关人员; 典型个案观察(好坏各2-3所中学)
假设:构思影响因素:1、师资专业水平,2、 学生入学水平,3、父母教育水平;
师资水平高
升学率高
入学成绩好
升学率高
父母教育水平高
升学率高
续例
操作化定义:如,师资:学历、职称、 获奖等;学生水平:考分、地域、性别 等;父母水平:学历、职业、教育子女的 时间等(注意:每一个定义就是一个变量, 要注意变量的各种可能取值)
1、混淆统计联系与因果关系 根据观测数据得到的统计联系(如相关 关系)只是因果关系存在的必要条件, 而不是充分条件。
2、事后解释错误 将探测性研究或描述性研究得到的理论 假设反过来作为假设检验来看待。
统计分析中常见的错误
3、生态学错误 混淆宏观模式与微观模式。 如:教育、经济水平越高的地区生育水平 越低,不能引申为个人教育水平与生育 水平的关系。 4、还原论错误 根据较低层次研究单位的分析结果推断较 高层次单位的运行规律。
联合国有关组织规定: 若低于0.2表示收入绝对平均; 0.2-0.3表示比较平均; 0.3-0.4表示相对合理; 0.4-0.5表示收入差距较大; 0.6以上表示收入差距悬殊。
二、社会学不社会统计学
1、社会学研究的重要环节 ▲课题---了解课题---假设---术语---问卷---调查---校核---统计
社会统计学(卢淑华),第十一章

系数。
d yx
ns nd ns nd n y
d
xy
ns nd ns nd nx
d yx :仅考虑在y方向的同分对 d xy :仅考虑在x方向的同分对
.
三、s值检验
H0: s 0
H1: s 0
统计量:
S
z —N(0,1)
Se
s ns nd
Y\x
10
1
12
4
32
2
22
4
23
4
32
2
12
1
12
5
.
4、 Gamma系数的PRE性质:
PRE ns nd ns nd 与G系数相同
5、当定序变量只有两种等级 G
n1 n4 n3 n2
不计符号时(方向)与Q系数相同
.
三、 Gamma系数的检验
H0: r0
H1: r0
统计量:
z G 1 G2
ns nd n
.
例:在某地选取409名已婚男人,研究他们对 母亲的感情会否影响他们对婚姻的适应,并问 是否有总体推论价值。
婚姻适应
丈夫对母亲的感情
平淡 不错 良好 很好
差
32 41 26 28 127
一般
28 47 41 22 138
很好
15 69 61 59 204
75 157 128 109 409
.
每对父子(女)作为一个观测单元,将其等 级写成一个集合:如(1,2)
将等级差平方后求和 其极值会是怎样?
.
r 1、相关系数 s
以等级差的平方和为基础来讨论等级相关。
社会统计学(卢淑华),第二章

计量资料频数表的编制
计量资Байду номын сангаас频数表的编制
一般情况下,样本含量小于30的统计资料 无须编制频数表,但对于大样本含量的资料,
编制频数表有利于进一步的统计分析、且频
数表本身也具有统计描述的作用.
编制频数表的步骤
编制频数表的步骤
第一组段包括极小值,最后 一组段包括极大值,除最后 一组段可同时标出上下限,
续例
计量资料频数分布表
118 例 13 岁女孩身高(cm)资料频数表。 身高组段 (1) 129~ 132~ 135~ 138~ 141~ 144~ 147~ 150~ 153~ 156~ 159~162 合计 频数 (2) 2 2 8 20 26 25 20 9 3 2 1 118 组中值 (3) 130.5 133.5 136.5 139.5 142.5 145.5 148.5 151.5 154.5 157.5 160.5 —
*
144.9 145.5 139.3 146.2 145.2 155.2 148.7 148.7 137.5 146.7 152.3 149.5
152.2 149.5 144.8 146.8 146.8 138.9 139.5 153.2 143.5 139.2 141.8 147.5
145.0 141.1 147.5 142.3 148.9 140.9 140.6 146.5 150.0 142.6 150.8 140.3
%
20.0 27.6 52.4 100.0
干部 工人 农民 总数
二、统计表
统计表的制作 要注意的问题: 1、标题、内容简明 2、统计栏数多时,要加编号 3、数字填写要求:位数对准,同栏数字、小数位 要一致,相同数字不可以写“同上”,无数字栏 用 “—”,缺资料“…” 4、表中数字用同一单位时,标在右上角 5、表的左右两端不封闭 判断 练习:分别制作定类、定序、定距变量统计表 注意:统计表的分组科学性问题
社会统计学(卢淑华),第十章ppt课件

第十讲 列联表
第一节 概念 1、研究内容 1)研究两定类变量的关系 2)为研究y的分类是否与x之分类有关,将
可编辑课件
30
E1即为猜错人数之和。 推广:
E1 n*1 (1 n*1 ) n*2 (1 n*2 ) n*r (
n
n
n 1
n
r
2
n j1 * j
可编辑课件
31
知道x与y有关后:用y的条件分布来猜y值 当x=男生时 随机10人,猜对聊天的人数:10×10/50 猜错的人数:10-10×10/50 随机40人,猜对游戏的人数:40×40/50 猜错的人数:40-40×40/50 猜错二者相加:=(10-10×10/50)+(40-40×40/50)
在1,1之间。
可编辑课件
20
1、 系数
ad bc
a bc d a cb d
0 ——当两变量相互独立
1 —— b、c为零, 值最大1
a、d为零, 值最小-1
1 ——一般情况
前例中计算
可编辑课件
21
2、Q系数
Q ad - bc ad bc
当a、b、c、d中有一个是零时,则 Q 1
x2 i 1
ni Ei2 Ei
~
2
r 1
3、
4、比较
可编辑课件
16
例:以下是老、中、青三代对某影片的抽 样,能否认为三代人对该影片评价有显 著差异
老
中
青
很高
社会统计学(卢淑华),第十一章

当全为同序对时:
a 取值:
1 当全为异序对时: 1
1,1
2、
b
当出现同分对时:
b
n n 1 1 nn 1 T nn 1 T 2 2
s d x y
T :变量x方向的全部同分对数
x
T :变量y方向的全部同分对数
y
1 Tx C t i (t i 1) 2 t i Txi TXiyj
活动能力名次 1 2 3 4 5 6 7 8 9 10
智商 110 110 105 95 120 94 100 105 105 110
第二节 Gamma等级相关
一、名词 1、同序对:x的变化方向与y的变化方向相 同。 2、异序对:x的变化方向与y的变化方向相 反。
3、同分对:存在相同等级 变量x具有相同等级 x同分对 变量y具有相同等级 y同分对 变量x、y都具有相同等级 x、y同分对
:异序对数目
不考虑同分对时,当数据均为同序对 G 1
不考 1,1
3、利用列联表中频次计算
n和 n
s
d
已知列联表,求同序、异序对
Y\x 10 12 32 1 4 2 23 32 12 4 2 1
22
4
12
5
4、 Gamma系数的PRE性质: PRE 与G系数相同 5、当定序变量只有两种等级
6 d i2
n
等级差的平方和为: 2 d i2 xi yi
则: rs 1
n n 1
i 1 2
外貌等级:1;2;3; 4;5;6;恋爱的6对 男女学生配对如表:
社会统计学,卢淑华(第4版),第2章.pptx
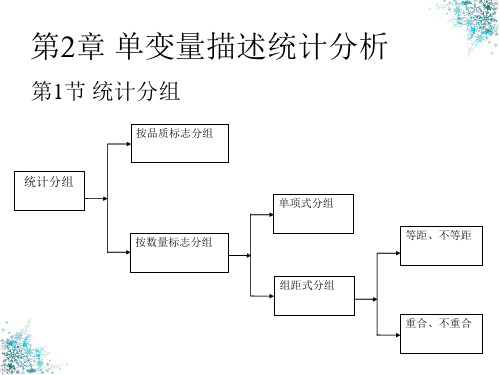
家庭结构 核心家庭
直系家庭 联合家庭
频次 1050
720 110
百分比(%) 49.30
33.80 5.16
其他
总数
250
2130
11.74
100.00
多选项二分法
a 样本1 样本2 样本3 样本4 样本5 √ × √ √ √ b √ × × √ √ c √ √ × × × d × √ √ × × e √ √ √ √ √
Me=“乙”
(三)组距式分组
• ①首先确定中位数组;②使用公式 • 下限公式: f S m 1 Me L 2 i fm
• 上限公式:
Me U
f
2
S m1 fm
i
公式中各字母含义
• • • • U:中位数组的上限; L:中位数组的下限; fm:中位数组的频数; Sm-1:向上累计时中位数组前一组的累计频数, 即中位数前一组所对应的向上累计频数; • Sm+1:向下累计时中位数组后一组的累计频数 即中位数后一组所对应的向下累计频数; • i:中位数组的组距。
(二)定距数据
1、未分组资料(spss版本)
Q1位置=(n+1)/4; Q2位置=(n+1)/2; Q3位置=3(n+1)/4 表2.10 Q1位置=(n+1)/4=25.25; Q2位置=(n+1)/2=50.5; Q3位置=3(n+1)/4=75.75
Q1=x(25)+0.25× [x(26)-x(25)]=1.37+0.25 ×[1.37-1.37]=1.37 Q2=x(50)+0.5× [x(51)-x(50)]=1.4+0. 5 ×[1.41-1.4]=1.405 Q3=x(75)+0.75× [x(76)-x(75)]=1.44+0.75 ×[1.44-1.44]=1.44
卢淑华讲义

社会统计学讲义(卢淑华)第一章社会学研究与统计分析一、社会调查资料的特点(随时掌握)随机性、统计规律性;二、统计学的作用:为社会研究提供数据分析和推论的方法三、统计分析的作用及其前提。
四、统计分析方法的选择1、全面调查和抽样调查的分析方法2、单变量和多变量的统计分析方法五、不同变量层次的比较;定类、定序、定距、定比定义、数学特征、运算特性、涵盖关系、等第二章单变量统计描述分析一、统计图表,熟悉不同层次变量对应的分析图表,不能混淆。
尤其是直方图的意义。
二、标明组限与真实组限的换算,重要。
三、集中趋势测量法1、定义、优缺点、注意事项;2、众值:定义、计算公式、解释、运用,注意事项;3、中位值:定义、计算公式(频数和比例两种公式)、解释、运用,注意事项;4、均值:定义、计算公式(分组与加权)、解释、运用,注意事项;5、众值、中位值和均值的关系及其相互比较,会用众值和中位值估算均值;四、离散趋势测量法1、定义、优缺点、注意事项,与集中趋势的关系;2、异众比例:定义、计算公式、解释、运用,注意事项;3、质异指数:定义、计算公式、解释、运用,注意事项;4、四分位差:定义、计算公式(频数和比例两种公式)、解释、运用,注意事项;要会举一反三,如求十分位差、以及根据数据求其在总体中的位置。
4、方差及标准差:定义、计算公式(分组与加权)、解释、运用,注意事项;第三章概率一、概率:就是指随机现象发生的可能性大小。
随机现象具有不确定性和随机性。
二、概率的性质:1、不可能事件的概率为0;2、必然事件的概率为1;3、随机事件的概率在0-1之间;三、概率的计算方法:1、古典法:计算等概率事件,P=有效样本点数/样本空间数;2、频率法:求随机事件在多次试验后的极限频率。
3、概率是理论值,只有一个,频率是试验值,不同的试验有不同的频率。
四、概率的运算:会画文氏图1、加法公式:两个或多个随机事件的求和概率‘2、乘法公式:两个或多个随机时间共同发生的概率。
社会统计学(卢淑华版)ppt课件

⑴自变量A的检验 检验统计量:
根据给定的显著性水平α,查出临界值 。如果
,
则不拒绝原假设。否则,拒绝原假设。
⑵自变量B的检验
检验统计量:
根据给定的显著性水平α,查出临界值 。如果
,
则不拒绝原假设。否则,拒绝原假设。 31
5、交互作用显著情况下,自变量A、B显著性的检验 交互作用显著情况下,自变量A、B的检验方法要根据变 量A和B的性质来确定。如果某变量的取值是固定的,则 该变量属于固定变量。如果变量所涉及的测试个体是随 机选择的,则该变量属于随机变量。根据A、B性质的不 同,可以分为三种模型: ⑴固定模型:A、B都是固定变量 对于固定模型,F检验分母项就用剩余误差项(RSS)的均方
• 若原假设(自变量对因变量没有影响)成立,组 间均方与组内均方的数值就应该很接近,它们的 比值就会接近1;若原假设不成立,组间均方会大 于组内均方,它们之间的比值就会大于1。当这个
比值大到某种程度时,就可以说不同水平之间存 在着显著差异,即自变量对因变量有影响。
• 三、方差分析的基本假定
• 1、每个总体都应服从正态分布
然后选择【确定】
第4步:当对话框出现时
在【输入区域 】方框内键入数据单元格区域
在【】方框内键入0.05(可根据需要确定) 在【输出选项 】中选择输出区域
22
• 例 三个地区家庭人口数的抽样调查如下表所示, 试问这三地区的平均家庭人口有没有显著差异?
家庭人口数
甲地
2 6 4 13 5 8 4 6
地区
5
第一节 方差分析的原理
• 对于因素的每一个水平,其观察值是来自服从正态 分布总体的简单随机样本。
• 2、各个总体的方差必须相同 • 各组观察数据是从具有相同方差的总体中抽取的。 • 3、观察值是独立的 • 四、问题的一般提法
社会统计学 卢淑华

社会统计学社会统计学是一门研究社会现象和问题的统计学科。
它通过收集、整理和分析大量社会数据,提供了对社会行为、社会关系和社会结构的科学视角。
社会统计学可以帮助我们理解社会的变迁和发展趋势,为社会科学研究和决策提供数据支持。
一、社会统计学的定义和作用社会统计学是统计学的一个重要分支,它关注社会领域的统计数据和现象。
社会统计学包括以下几个方面的研究内容:1.社会人口统计学:研究人口的数量、分布、结构和变动趋势等问题,包括人口普查、人口调查和人口统计分析等方法。
2.社会经济统计学:研究社会经济活动的数量、结构和变动趋势等问题,包括就业率、收入分配、消费水平等指标的统计分析。
3.社会调查统计学:研究社会问题和社会行为的数据收集和分析方法,包括问卷调查、面访调查和实地观察等技术手段。
4.社会健康统计学:研究社会健康问题的统计数据和分析方法,包括疾病发生率、医疗资源分布和保健水平等指标的统计分析。
5.社会环境统计学:研究社会环境问题的统计数据和分析方法,包括自然资源利用、环境污染和生态平衡等指标的统计分析。
社会统计学的作用主要体现在以下几个方面:1.揭示社会现象的特征:社会统计学通过大量统计数据的分析,能够揭示社会现象的数量、分布和变动趋势等特征,帮助我们更好地理解社会。
2.分析社会问题的原因:社会统计学可以对社会问题进行定量分析,帮助我们找到问题的原因和影响因素,为制定解决方案提供依据。
3.评估社会政策效果:社会统计学可以用于对社会政策的实施效果进行评估,了解政策对社会的影响程度和效果,为政策调整和优化提供参考。
4.提供决策支持:社会统计学可以为政府、企业和组织等提供科学的决策支持,帮助他们做出准确的决策,提高工作效率和决策的科学性。
二、社会统计学的方法和技术社会统计学主要依靠大量数据的收集、整理和分析来揭示社会现象和问题。
以下是一些常用的社会统计学方法和技术:1.问卷调查:通过编制调查问卷,对一定群体进行调查,收集社会数据和意见信息。
社会统计学(卢淑华),第十二章

y
104 115 124 131 132 145 158 172
建立回归方程,并进行F检验 0.05
第四节 相关
一、相关系数
(线性相关)
i i
1、协方差:
x x y y Covx, y n1
2 E i 0
D
5、处于检验的需要,要求y值的每一个子 总体都满足正态分布。
二、回归方程的检验 1、原假设:x与y不存在线性关系
H : 0
0
H : 0
1
2、线性回归的平方和分解 1)总偏差平方和:反映观察值 值 y 的总分散程度。
y 围绕均
i
TSS
它是总体线性回归方程 y x 的最佳 估计方程
例:妇女受教育的年限不家务劳劢时间调查资料
妇女 A B C D E F G H I
教育年限 2 2 3 3 4 4 4 6 8 36
劳动小时 5 4 4 3 1 1 0 0 0 18
xy 10 8 12 9 4 4 0 0 0 47
x
F
r n 2 1r
2
2
F 1, n 2
RSS r 即:RSS r 2TSS TSS 2 2 TSS ESS r TSS r F (n 2) 2 ESS (1 r )TSS 1 r2 n2 n2
2
6、相关与回归的比较 1)相同点:都是研究变量之间的非确定 性关系,而且都是研究其中的线性关 系。 2)不同点: ①回归是研究变量之间的因果关系,但 相关不一定具有因果关系。 ②相关系数是双向对称的,回归直线是 非对称的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 因变量y与自变量A、B之间的关系可以表达为以下 模型:
yijk i j ij ijk
K=1,2,…,r r为自变量A和B每种搭配的重复数
ijk εijk相互独立,并且服务正态分布:
~ N 0,
2
j
ij 及 2都是未知参数,且有: 、i、 j、
第二节:单因素方差分析 三、关系强度的测量 拒绝原假设表明因素(自变量)与观测值之间有显著关系,组间平 方和(BSS)度量了自变量(行业)对因变量(投诉次数)的影响效应。 只要组间平方和BSS不等于0,就表明两个变量之间有关系(只是 是否显著的问题) 。当组间平方和比组内平方和(SSE)大,而且 大到一定程度时,就意味着两个变量之间的关系显著,大得越 多,表明它们之间的关系就越强。反之,就意味着两个变量之 间的关系不显著,小得越多,表明它们之间的关系就越弱。 • 变量间关系的强度用自变量平方和(BSS) 占总平方和(TSS) 的比例大小来反映,自变量平方和占总平方和的比例记为 R2 ,即:
εij相互独立,并且服务正态分布: ij
~ N 0,
2
、i、 j 及 2都是未知参数,且有:
i 1
a
i
0
j 1
b
j
0
⒉有交互作用的二元方差分析模型 如果除了行因素和列因素对试验数据的单独影响外,两 个因素的搭配还会对结果产生一种新的影响,这时的双 因素方差分析称为有交互作用的双因素方差分析或可重 复双因素方差分析 (Two-factor with replication )。
i 1 j 1
a b
a
b
2
⑥ 总离差平方和 T SS TSS yij y
i 1 j 1
2
⑦ 剩余平方和RSS
a b i 1 j 1 a b
RSS yij y i. y . j y
2
2 [( yij y ) - ( y i. - y ) - ( y . j - y )] i 1 j 1
i 1
a
i
0
j 1
b
j
0
i 1
a
i
0
j 1
b
0
• 二、无交互作用的二元方差分析 • ⒈提出假设 H0 : i 0 i 1,2,, a j 0 j 1,2,, b
H1 : i不全为 0 i 1,2,, a
2、构造检验统计量
• 如果两个因素对试验结果的影响是相互独立的,分别 判断行因素和列因素对试验数据的影响,这时的二元 方差分析称为无交互作用的二元方差分析或无重复二 元方差分析(Two-factor without replication) 。
• 因变量y与自变量A、B之间的关系可以表达为以下 模型:
yij i j ij
例(参见教材376页例1、383页例2)为了研究职业对家庭赡养 人数的影响,研究者抽查了某企业41名员工的家庭赡养人数(如 下表),试判断职业对家庭赡养人数是否有影响。
家庭赡养人数 职 工人 业
管理人员 技术员
3 5 0 5 4 4 2 3 1 3 2 3 3 2 4 2 6 1 1 3 4 4 6 2 3 4 3 5 2 4 6 4 2 2 3 0 5 3 1 2 1
n
式中:n n1 n2 nm
第二节:单因素方差分析/一元方差分析
• ⑶计算总误差平方和TSS • 总误差平方和 TSS是全部观察值 x 与总平均值 的 离差平方和,反映全部观察值的离散状况,其计 算公式为:
TSS xij x
m ni i 1 j 1 2
⑷计算组间平方和BSS
组间平方和是各组平均值 x i与总平均值 的离差平方和, x 反映各总体的样本均值之间的差异程度,计算公式为:
BSS xi x ni xi x
组间平方和是各组平均值
第二节:单因素方差分析/一元方差分析
• ⑸计算组内平方和RSS • 组内平方和是每个水平或组的各样本数据与其组 平均值的离差平方和,该平方和反映的是随机误 差的大小,计算公式为:
⑷确定临界 值,并与检 验统计量进 行比较,得 出结论:
第八章 类别变量与尺度变量关系的假设检验——方差分析
• 8.1方差分析的原理 • 8.2一元方差分析 • 8.3二元方差分析
第一节 方差分析的原理
• 一、方差分析及其有关术语 • 1、什么是方差分析 • 方差分析通过分析数据的误差判断各总体均值是 否相等来检验多个总体均值是否相等,从而研究 分类型自变量对数值型因变量的影响。 • 根据自变量的多少,方差分析可分分为单因素方 差、双因素方差分析和多因素方差分析。 • 2、因素或因子 • 因素或因子是指所要检验的对象。 • 3、水平或处理 • 水平或处理是指因子的不同表现。
第一节 方差分析的原理
• 对于因素的每一个水平,其观察值是来自服从正态 分布总体的简单随机样本。 • 2、各个总体的方差必须相同 • 各组观察数据是从具有相同方差的总体中抽取的。 • 3、观察值是独立的 • 四、问题的一般提法 • 1、设因素有m个水平,每个水平的均值分别用1 , 2,, m表示 • 2、要检验m个水平(总体)的均值是否相等,需要提 出如下假设: • H0 : 1 2 … m H1 : 1 , 2 , ,m 不全相 等
1 a b 1 1 a 1 b y yij T.. y i. y. j ab i 1 j 1 ab a i 1 b j 1
④ 变量A的离差平方和BSSA
BSSA y i. y
i 1 j 1
a
b
2
⑤变量B的离差平方和BSSB
BSSB y . j y
xi
x ij j
1
ni
ni
(i 1, 2, ,k )
式中: ni为第 i 个总体的样本观察值个数,xij 为第 i 个总 体的第 j 个观察值。 ⑵计算全部观察值的总均值 用全部观察值的总和除以观察值的总个数,计算公式:
x
x
i 1 j 1
m
ni
ij
n
n x
i 1
m
i i
②列平均值y i.
1 b 1 y i. yij Ti. b j 1 b
由于列平均值是把观测 值按行加总求平均。 yi.是把
自变量yi1,yi2 , … ,yib,观测一次取平均的,因此可以认为 变量B的影响已经相互抵消,所以行平均值 反映的是自 变量A对因变量y的影响。 ③ 总平均值y
第二节:单因素方差分析/一元方差分析
• 一、数据结构
观察值 ( j ) 因素(A) i 水平A1 水平A2 … 水平Am
1 2 : : n
x11 x12 : : x1 n
x21 x22 : : x2n
… … : : …
xm1 xm2 : : xmn
第二节:单因素方差分析/一元方差分析
• • • •
BSS MSB 组间方差MSB: m 1
组内方差MSR: MSR
RSS nm
第二节:单因素方差分析/一元方差分析 3、计算检验统计量 F
BSS / m 1 MSB F ~ F (m 1, n m) MSR / n m MSR
4、统计决策 将统计量的值F与给定的显著性水平的临界值F进行比较, 作出对原假设H0的决策。
BSS(组间平方和 ) R TSS(总平方和)
2
其平方根R就可以用来测量两个变量之间的关系强度。
第三节 双因素方差分析/二元方差分析
• 一、二元方差分析的数学模型 • 二元方差又称双因素方差分析,用来分析两个因素 (行因素Row和列因素Column)对试验结果的影响。 • 设两个自变量A和B作用于总体,其中自变量A有a种 取值:A1,A2,…,Aa,自变量B有b种取值:B1, B2,…,Bb。变量A的取值为Ai 、变量B的取值为Bj 时因 变量y的取值为yij • ⒈无交互作用的二元方差分析模型
第一节 方差分析的原理
自变量对因变量没有 • ⑶均方—MS 影响,则没有系统性 误差,组间平方和中 • 均方是指平方和除以相应的自由度。 只有随机误差。 • ⑷基本原理
• 若原假设(自变量对因变量没有影响)成立,组 间均方与组内均方的数值就应该很接近,它们的 比值就会接近1;若原假设不成立,组间均方会大 于组内均方,它们之间的比值就会大于1。当这个 比值大到某种程度时,就可以说不同水平之间存 在着显著差异,即自变量对因变量有影响。 • 三、方差分析的基本假定 • 1、每个总体都应服从正态分布
二、分析步骤 1、提出假设 H0 :μ1 = μ2 =…= μm 自变量对因变量没有显著影响 H1 :μ1 ,μ2 ,… ,μk不全相等 自变量对因变量有 显著影响
• 注意:拒绝原假设,只表明至少有两个总体的均值 不相等,并不意味着所有的均值都不相等 • 2、构造检验的统计量 • ⑴水平的均值
第二节:单因素方差分析/一元方差分析 • 假定从第i个总体中抽取一个容量为ni的简单随机样本,第i 个总体的样本均值为该样本的全部观察值总和除以观察值 的个数。计算公式:
观测值y ij 的总误差
变量A解 释的误差
变量A解 释的误差
离差平方和之间的关系
TSS=BSSA+BSSB+RSS
⑧计算均方
变量A的平均离差平方和 BSS A
BSS A BSS A a 1 BSS B BSS B b 1
其中a-1是自由度
变量B的平均离差平方和 BSS B
其中a-1是自由度
其中(a-1)、(b-1) 是自由度
