半变异函数的求解
变异函数及结构分折

型也称块金效应型。这种类型说明变异函数 (h) 连续性差。当 h 增大时, (h) 又可逐渐变 得比较连续。
3 变异函数的功能
(2) 变异函数在原点处的性状反映变量的空间连续性
(d) 随机型 当 h 0 时, (h) C0 ,当 h 增大时, | h | 时, (h) 仍是在 C0 附 近摆动,无论 h 多么小,区域化变量 Z ( x) 与 Z ( x h) 总是不相关。这种类型称随机型,也 称纯块金效应型。 它反映了区域化变量完全不存在空间相关的情况、 或者说反映了变量是普 通的随机变量。这时 C0 等于先验方差, Var[Z ( x)] C0 。 (e) 过渡型 当 h 0 时, (h) C0 ,当 h=a(a 为变程) ,
h 0 h 0
1. 变异函数图结构分析
块金方差:主要来源于远小于抽样间距的空间尺度上
存在的差异。块金方差的大小直接限制了空间内插的精
度,如果实际的样本方差图主要表现为块金效应,即随 的增加变异函数的变化近似于一水平线,说明了在最小 抽样间距以上的空间尺度上不存在自相关性,这种结果 也意味着可能存在一个比抽样间距更加小的空间自相关
3 变异函数的功能
(4) 块金常数 的大小可反映区域化变量的随机性大小
C (0) 0 ,即先验方差不小于零。 C (h) C (h) ,即 C (h) 是对 h=0 的直线对称。
| C (h) | C (0) ,协方差函数绝对值小于等于先验方差。
| h | 时, C (h) 0 ,或写作 C () 0 。 C (h) 必须是一个非负定函数 (即由 C ( xi x j ) 构成的协方差函数矩阵必须是一个非
负定矩阵) 。
2 变异函数的性质
半方差函数

半方差半方差函数(Semi-variogram)及其模型半方差函数也称为半变异函数,它就是地统计学中研究土壤变异性的关键函数、2、1、1半方差函数的定义与参数如果随机函数Z(x)具有二阶平稳性,则半方差函数((h)可以用Z(x)的方差S2与空间协方差C(h)来定义:((h)= S2-C(h)((h)反映了Z(x)中的空间相关部分,它等于所有以给定间距h相隔的样点测值之差平方的数学期望:(1)实际可用:(2)式中N(h)就是以h为间距的所有观测点的成对数目、某个特定方向的半方差函数图通常就是由((h)对h作图而得、在通常情况下,半方差函数值都随着样点间距的增加而增大,并在一定的间距(称为变程,arrange)升大到一个基本稳定的常数(称为基台,sill)、土壤性质的半方差函数也可能持续增大,不表现出确定的基台与变程,这时无法定义空间方差,说明存在有趋势效应与非平稳性、另一些半方差函数则可能完全缺乏空间结构,在所用的采样尺度下,样品间没有可定量的空间相关性、从理论上讲,实验半方差函数应该通过坐标原点,但就是许多土壤性质的半方差函数在位置趋于零时并不为零、这时的非零值就称为"块金方差(Nugget variance)"或"块金效应"、它代表了无法解释的或随机的变异,通常由测定误差或土壤性质的微变异所造成、对于平稳性数据,基底方差与结构方差之与约等于基台值、2、1、2 方差函数的理论模型土壤在空间上就是连续变异的,所以土壤性质的半方差函数应该就是连续函数、但就是,样品半方差图却就是由一批间断点组成、可以用直线或曲线将这些点连接起来,用于拟合的曲线方程就称为半方差函数的理论模型、在土壤研究中常用的模型有:①线性有基台模型:式中C1/a就是直线的斜率、这就是一维数据拟合的最简单模型:((h)=C0 +C1·h/a 0在极限情况下,C1/a可以为0,这时就有纯块金效应模型:((h)=C0, h>0 (4)((0)=0 h=0②球状模型((h)= C0 +C1[1、5h/a-0、5(h/a)3] 0a (5)((0)=0 h=0③指数模型((h)=C0+C1[1-exp-h/a ] h>0 (6)((0)=0 h=0④双曲线模型(7)⑤高斯模型((h)=C0+C1[1-exp(-h2/a2)] h>0 (8)((0)=0 h=0选定了半方差函数的拟合模型后,通常就是以最小二乘法计算方程的参数,并应用Ross等的最大似然程序(MLP),得到效果最好的半方差方程、2、1、3 模型的检验(cross-validation,又称作jacknifing)为了检验所选模型三个参数的合理性,必须作一定的检验、但就是到现在为止还没有一个有效的方法检验参数的置信区间;同时,由于我们不知道半方差模型的确切形式,所选定的模型只就是半方差函数的近似式,故无法以确切的函数形式对模型参数进行统计检验、交叉验证法的检验方法,一种间接的结合普通克立格的方法,为检验所选模型的参数提供了一个途径、这个方法的优点就是在检验过程中对所选定的模型参数不断进行修改,直至达到一定的精度要求、交叉验证法的基本思路就是:依次假设每一个实测数据点未被测定,由所选定的半方差模型,根据n-1个其它测定点数据用普通克立格估算这个点的值、设测定点的实测值为,估算值为,通过分析误差,来检验模型的合理性、2、1、4半方差函数的模型的选取原则与参数的确定半方差函数的模型的选取原则就是:首先根据公式计算出((h)的散点图,然后分别用不同类型的模型来进行拟合,得到模型的参数值及离差平方与,首先考虑离差平方与较小的模型类型,其次,考虑块金值与独立间距,最后用交叉验证法来修正模型的参数、2、2 Kriging最优内插估值法如果区域化变量满足二阶平稳或本征假设,对点或块段的估计可直接采用点克立格法(Puctual Kriging )或者块段克立格法(Block Kriging)、这两种方法就是最基本的估计方法,也称普通克立格法(Origing Kriging,简称OK)、半方差图除用于分析土壤特性空间分布的方向性与相关距离外,还可用于对未测点的参数进行最优内插估值与成图,该法原理如下:Kriging最优内插法的原理设x0为未观测的需要估值的点,x1, x2,…, xN 为其周围的观测点,观测值相应为y(x1 ),y(x2),…,y(xN)、未测点的估值记为(x0),它由相邻观测点的已知观测值加权取与求得:(9)此处,(i为待定加权系数、与以往各种内插法不同,Kriging内插法就是根据无偏估计与方差最小两项要求来确定上式中的加权系数(i的,故称为最优内插法、1、无偏估计设估值点的真值为y(x0)、由于土壤特性空间变异性的存在,以及,•1。
半方差

半方差半方差函数(Semi-variogram)及其模型半方差函数也称为半变异函数,它是地统计学中研究土壤变异性的关键函数.2.1.1半方差函数的定义和参数如果随机函数Z(x)具有二阶平稳性,则半方差函数((h)可以用Z(x)的方差S2和空间协方差C(h)来定义:((h)= S2-C(h)((h)反映了Z(x)中的空间相关部分,它等于所有以给定间距h相隔的样点测值之差平方的数学期望:(1)实际可用:(2)式中N(h)是以h为间距的所有观测点的成对数目.某个特定方向的半方差函数图通常是由((h)对h作图而得.在通常情况下,半方差函数值都随着样点间距的增加而增大,并在一定的间距(称为变程,arrange)升大到一个基本稳定的常数(称为基台,sill).土壤性质的半方差函数也可能持续增大,不表现出确定的基台和变程,这时无法定义空间方差,说明存在有趋势效应和非平稳性.另一些半方差函数则可能完全缺乏空间结构,在所用的采样尺度下,样品间没有可定量的空间相关性.从理论上讲,实验半方差函数应该通过坐标原点,但是许多土壤性质的半方差函数在位置趋于零时并不为零.这时的非零值就称为"块金方差(Nugget variance)"或"块金效应".它代表了无法解释的或随机的变异,通常由测定误差或土壤性质的微变异所造成.对于平稳性数据,基底方差与结构方差之和约等于基台值.2.1.2 方差函数的理论模型土壤在空间上是连续变异的,所以土壤性质的半方差函数应该是连续函数.但是,样品半方差图却是由一批间断点组成.可以用直线或曲线将这些点连接起来,用于拟合的曲线方程就称为半方差函数的理论模型.在土壤研究中常用的模型有:①线性有基台模型:式中C1/a是直线的斜率.这是一维数据拟合的最简单模型:((h)=C0 +C1·h/a 0在极限情况下,C1/a可以为0,这时就有纯块金效应模型:((h)=C0, h>0 (4)((0)=0 h=0②球状模型((h)= C0 +C1[1.5h/a-0.5(h/a)3] 0a (5)((0)=0 h=0③指数模型((h)=C0+C1[1-exp-h/a ] h>0 (6)((0)=0 h=0④双曲线模型(7)⑤高斯模型((h)=C0+C1[1-exp(-h2/a2)] h>0 (8)((0)=0 h=0选定了半方差函数的拟合模型后,通常是以最小二乘法计算方程的参数,并应用Ross等的最大似然程序(MLP),得到效果最好的半方差方程.2.1.3 模型的检验(cross-validation,又称作jacknifing)为了检验所选模型三个参数的合理性,必须作一定的检验.但是到现在为止还没有一个有效的方法检验参数的置信区间;同时,由于我们不知道半方差模型的确切形式,所选定的模型只是半方差函数的近似式,故无法以确切的函数形式对模型参数进行统计检验.交叉验证法的检验方法,一种间接的结合普通克立格的方法,为检验所选模型的参数提供了一个途径.这个方法的优点是在检验过程中对所选定的模型参数不断进行修改,直至达到一定的精度要求.交叉验证法的基本思路是:依次假设每一个实测数据点未被测定,由所选定的半方差模型,根据n-1个其它测定点数据用普通克立格估算这个点的值.设测定点的实测值为,估算值为,通过分析误差,来检验模型的合理性.2.1.4半方差函数的模型的选取原则和参数的确定半方差函数的模型的选取原则是:首先根据公式计算出((h)的散点图,然后分别用不同类型的模型来进行拟合,得到模型的参数值及离差平方和,首先考虑离差平方和较小的模型类型,其次,考虑块金值和独立间距,最后用交叉验证法来修正模型的参数.2.2 Kriging最优内插估值法如果区域化变量满足二阶平稳或本征假设,对点或块段的估计可直接采用点克立格法(Puctual Kriging )或者块段克立格法(Block Kriging).这两种方法是最基本的估计方法,也称普通克立格法(Origing Kriging,简称OK).半方差图除用于分析土壤特性空间分布的方向性和相关距离外,还可用于对未测点的参数进行最优内插估值和成图,该法原理如下: Kriging最优内插法的原理设x0为未观测的需要估值的点,x1, x2,…, xN 为其周围的观测点,观测值相应为y(x1 ),y(x2),…,y(xN).未测点的估值记为(x0),它由相邻观测点的已知观测值加权取和求得:(9)此处,(i为待定加权系数.和以往各种内插法不同,Kriging内插法是根据无偏估计和方差最小两项要求来确定上式中的加权系数(i的,故称为最优内插法.1. 无偏估计设估值点的真值为y(x0).由于土壤特性空间变异性的存在,以及, y(x0)均可视为随机变量.当为无偏估计时,(10)将式(9)代入(10)式,应有(11)2. 估值和真值y(x0)之差的方差最小.即(12)利用式(3-10),经推导方差为(13)式中,((xi,xj)表示以xi和xj两点间的距离作为间距h时参数的半方差值,((xi, x0)则是以xi和x0两点之间的距离作为间距h时参数的半方差值.观测点和估值点的位置是已知的,相互间的距离业已知,只要有所求参数的半方差((h)图,便可求得各个((xi,xj)和((xi,x0)值.因此,确定式(9)中各加权系数的问题,就是在满足式(11)的约束条件下,求目标函数以式(13)表示的方差为最小值的优化问题.求解时可采用拉格朗日法,为此构造一函数,(为待定的拉格朗日算子.由此,可导出优化问题的解应满足:i=1,2,N (14)由式(14)和式(11)组成n+1阶线性方程组,求解此线性方程组便可得到n个加权系数(i和拉格朗日算子(.该线性方程组可用矩阵形式表示:(15)式中,( ij为((xi,xj)的简写.求得各(i值和(值后,由式(9)便可得出x0点的最优估值y(x0).而且还可由式(13)求出相应该估值的方差之最小值(2min.将式(14)代入式(13),最小方差值还可由下式方便地求出:(16)上述最优化问题求解还可用其他方法,在应用Kriging内插法时还有其他方面的问题,在此都不一一列举了.。
arcgis克里金插值无法估算半变异函数

arcgis克里金插值无法估算半变异函数以arcgis克里金插值无法估算半变异函数为标题克里金插值是一种常用的地理信息系统(GIS)插值方法,可用于估算未知位置的数值。
然而,克里金插值在一些情况下可能无法有效估算半变异函数,这是因为半变异函数的特性与克里金插值的假设之间存在不匹配。
半变异函数是地统计学中常用的工具,用于描述变量值在空间上的变化程度。
它可以通过计算不同距离下的半方差来确定。
半方差表示两个位置之间的变量值差异程度,距离越大,半方差值越大,说明变量值的差异越大。
半变异函数的形状和参数可以提供有关空间变量结构的重要信息,从而可以用于空间数据的插值和预测。
然而,克里金插值方法在估算半变异函数时存在一些限制。
首先,克里金插值假设数据是平稳的,即在空间上具有相似的统计特性。
然而,实际数据往往呈现出空间非平稳性,即在不同位置上具有不同的统计特性。
这导致克里金插值无法准确地估算半变异函数的形状和参数。
克里金插值假设数据的半变异函数是稳定的,即在不同距离下具有相似的半方差值。
然而,实际数据往往呈现出非稳定性,即半方差值在不同距离下发生明显变化。
这使得克里金插值无法准确地估算半变异函数的参数,从而影响插值结果的可靠性。
克里金插值还假设数据的半变异函数是光滑的,即在不同距离下具有连续的半方差值。
然而,实际数据往往呈现出非光滑性,即半方差值在不同距离下出现跳跃或断裂。
这使得克里金插值无法准确地估算半变异函数的形状,从而导致插值结果的不准确性。
为了解决克里金插值无法估算半变异函数的问题,可以尝试使用其他插值方法或改进的克里金插值方法。
例如,可以尝试使用反距离加权插值(IDW)方法,该方法在估算插值值时不需要假设数据的平稳性、稳定性和光滑性。
另外,也可以尝试使用基于样条函数的插值方法,该方法可以更好地拟合非光滑的半变异函数。
克里金插值在估算半变异函数时存在一些限制,特别是在数据呈现空间非平稳性、非稳定性和非光滑性的情况下。
第四章 变异函数的结构分析

(4)变异函数计算
• 考虑数据的结构
等间距规则网格数据 非等间距不规则网格数据
(4)变异函数计算
• 1)扇区分组
– 以笛卡尔坐标原点为原点,如 图4-17所示虚线为样点对距离h ,利用扇形分区进行不规则格 网数据分组。
• 2)格网分组
– 扇区分组虽然合理,但不适宜 计算机表示,为此采用格网分 组。
2、模型拟合评价及类型确定
• 模型拟合评 • 最优曲线的检验 价包括: • 即理论模型的检验。由于把最优理论模型的求解转化为一
元和二元线性方程来求解,显然就需要对回归方程参数及 • 最优曲线的 方程本身进行显著性检验。 检验和模型 比较 • 模型比较
•
即是通过平均误差、均方根误差、平均标准误差等统计指 标对不同的理论模型比较,从中选出最优拟合模型。一般 来说,人们总是希望预测误差是无偏且最优的。
带状异向性:当区域化变量在 不同方向上变异性差异不能用 简单几何变换得到时,就称为 带状异向性。此时,实验变异 函数具有不同的基台值,而变 程可以相同也可以不同。
2、不同方向上的套合
• (2)变换矩阵
• 为了便于计算,在克里格估算中所用的变异函数或协方差函数的理论模式要 求区域化变量是各向同性。
2、不同方向上的套合
第四章 变异函数结构分析
提
纲
• 一、变异函数的理论模型 • 二、变异函数理论模型的最优拟合 • 三、变异函数的套合结构
一、变异函数的理论模型
纯块金效应模型 球状模型 有基台值模型 指数模型 高斯模型 线性有基台值模型 无基台值模型 线性无基台值模型 幂函数模型 对数模型 孔穴效应模型(可有有基台或无基台模型)
1、有基台值模型
• (1)纯块金效应模型
克里金插值无法估算半变异函数

克里金插值无法估算半变异函数介绍克里金插值是一种常用的空间插值方法,用于估算未知位置的属性值。
它基于半变异函数的理论,通过已知点的属性值和位置信息,推断未知点的属性值。
然而,克里金插值在某些情况下无法准确估算半变异函数,这给插值结果的可靠性带来了挑战。
克里金插值原理克里金插值的基本原理是通过已知点的属性值和位置信息,建立一个半变异函数模型,然后利用该模型来估算未知点的属性值。
半变异函数描述了属性值在空间上的变异程度,它是克里金插值的核心。
克里金插值的限制克里金插值的主要限制在于对半变异函数的估算。
半变异函数通常用经验模型或理论模型来拟合,但在某些情况下,这些模型无法准确地描述属性值的变异特征。
以下是一些导致克里金插值无法估算半变异函数的情况:1. 非线性变异当属性值在空间上呈现非线性变异时,克里金插值无法准确估算半变异函数。
例如,当属性值在某个区域内呈现强烈的非线性变化趋势时,克里金插值很难找到一个合适的半变异函数来描述这种变异特征。
2. 异常值和离群点克里金插值对异常值和离群点非常敏感。
如果数据集中存在异常值或离群点,它们会对半变异函数的估算产生很大的影响。
在这种情况下,克里金插值往往无法准确估算半变异函数,从而导致插值结果的不可靠性。
3. 数据稀疏性当已知点的分布非常稀疏时,克里金插值无法有效地估算半变异函数。
数据稀疏性会导致半变异函数的估算不准确,从而影响插值结果的可靠性。
在这种情况下,需要考虑其他插值方法或增加更多的采样点来改善插值结果。
4. 多变量插值克里金插值通常用于单变量属性的插值,当存在多个属性时,克里金插值无法准确估算半变异函数。
多变量插值需要考虑不同属性之间的相互关系,而克里金插值无法捕捉这种关系。
在这种情况下,可以考虑使用其他的多变量插值方法。
克里金插值的改进方法为了克服克里金插值无法估算半变异函数的限制,可以采取以下改进方法:1. 引入其他插值方法在克里金插值无法估算半变异函数的情况下,可以考虑引入其他插值方法来改善插值结果。
变异函数

变异函数
马特隆(G?Matheron)的地质统计学中用以研究区域化变量空间变化特征和强度的手段和工具,它被定义为区域化变量增量平方的数学期望,即区域化变量增量的方差。
在以向量h相隔两点x、x+h处的两个区域化变量值Z(x)与Z(x+h)之间的变异,用变异函数2γ(x,h)表征:2γ(x,h)=E{〔Z(x+h) Z(x)〕2}=∫〔Z(x+h)-Z(x)〕2dx实际工作中只有有限个观测点,难以上式计算变异函数。
根据内蕴假设,增量〔Z(x+h) Z(x)〕只与h有关,而与x无关。
因此,实际计算的实验变异函数2γ*(h)是在以向量h相隔的N对点的两个观测值间增量平方的平均值,即2γ*(h)=1N(h)∑N(h)i=1〔Z(xi+h) Z(xi)〕22γ*(h)为增量方差之半,又叫半变异函数,简称变异函数。
利用上式对一系列间距h计算出一系列γ*(h),用以编制出经验半变异函数曲线,亦称半变差图(见图)。
该图中的一些特征值反映了矿体变化性。
变程a:经验半变异函数曲线及相应理论曲线图两点间距小于变程a时,两点变量有自相关性,大于变程a自相关性消失。
可以根据变程a确定工程或样品间距。
基台值C(o)反映区域化变量变异性大小,在满足平衡条件时等于数据的先验方差。
块金常数C0表示原点处变异函数的不连续性,代表了观测误差、矿化微观变化等导致的随机变化。
拱高C表示总变异中的空间变化。
典型变异函数曲线分为抛物线型(连续型)、线性型、间断型(块金型)、随机型(纯块金型)、转变型,它们代表了具有不同连续性和随机性的地质体参数的变化性特点。
变异函数结构分析

——地统计学的工具
第一节 协方差函数和变异函数的性质
一、协方差函数的计算公式
设区域化变量Z(x)满足(准)二阶平稳假设,h为两样 本点空间分隔距离,Z(xi)与Z(xi+h)分别是Z(x)在空间 位置xi和xi+h上的观测值(i=1,2,…N(h)),则计算协方差 的公式为:
n
(
0)非负定矩阵,或说函数 (h)为非负定
i
i 1
函数
区域化变量Z(x)的 变异函数γ(h)是有条件的,即 需满足条件非负定条件
五、协方差函数与变异函数的关系
(h) C(0) C(h) C(h) C(0) (h)
变异函数与协方差函数值变化相反
C(0) C(h) (h)
4、随机型(random type)
(h)
0, C0
h (
0 0) ,
h
0
此时,C0=C(0)
这种变异函数可看成具有基台值C0和无穷小变程a的 跃迁型变异函数,则无论h多小,h总大于a,故Z(x)与 Z(x+h)总是互不相关
又称纯块金效应型,反映了区域化变量完全不存在空 间相关的情况,则本质上此区域化变量为普通随机变 量
x x #
1 N(h)
2
(h)
[Z( ) Z( h)]
2N (h) i1
i
i
式中,N (h)是分隔距离为h时的样本对数
变异函数曲线图:以h为横坐标, γ #(h)为纵坐标 作图
变异函数计算实例
(1)一维变异函数的计算
以下为一研究对象在水平方向上的采样数据,满足 二阶平稳或本征假设,采样值如图所示,点间分隔 距离h=1米,计算 γ #(h) 43 4 5 7 9 7 8 7 7 x1 x2 x3 x4 x5 x6 x7 x8 x9 x10
克里金插值法的基本 做法

克里金插值法的基本做法
克里金插值法是一种空间插值方法,用于估计地理空间上某一点的未知数值。
其基本做法包括以下几个步骤:
1. 数据收集,首先,需要收集一定数量的已知数值点的数据,这些数据通常是在地理空间上具有坐标位置的点上观测得到的。
这些数据可以是地面测量、遥感获取、传感器监测等手段得到的。
2. 半变异函数的拟合,接下来,需要对所收集到的数据进行半变异函数的拟合。
半变异函数描述了地点之间的变异程度,是克里金插值法的关键。
通过拟合半变异函数,可以得到地点之间的空间相关性。
3. 克里金插值模型的建立,在获得半变异函数后,可以建立克里金插值模型。
这个模型可以根据已知点的数据和半变异函数的拟合结果,对未知点进行插值估计。
4. 插值估计,最后,利用建立的克里金插值模型,对未知点进行插值估计。
通过模型计算,可以得到未知点的估计数值,并且估计值的精度也可以通过模型得到。
需要注意的是,克里金插值法的基本做法是基于对空间数据的
模型化和空间相关性的分析,因此在实际应用中需要根据具体的数
据特点和空间变异性进行适当的调整和参数设定。
同时,对于较大
规模的数据集,也需要考虑计算效率和模型精度之间的平衡。
总之,克里金插值法是一种常用的空间插值方法,通过合理的数据处理和
模型建立,可以对地理空间上的未知数值进行较为准确的估计。
半变异函数拟合指数模型

半边也函数的应用半变异函数拟合指数模型程序(c++代码)#include <stdio.h>#include <time.h>#include<windows.h>#include <math.h>#include <stdlib.h>#define S 1 /*试验次数*/#define G 2000 /*混合迭代次数*/#define P 200 /*个体总数*/#define M 20 /*族群数*/#define I 10 /*因此,一个族群中的个体数是10*/#define V 3 /*个体维数*/#define N 10 /*族群内更新次数*/#define MAX 10#define MIN 0double DMAX=1.0; /*蛙跳的最大值*/double DMIN=0.4; /*蛙跳的最大值*/double D=MAX/1; /*蛙跳的最大值*/int i1,i2,i3,i4,ii;int try_number=0;int try_max=5;double C=1.0;#define R ((double)(rand()%10000)/10000)//0-1之间的随机数,精度为1/10000 //#define R1 rand()%100/100.0static int kk;double PI=3.14159265;double Tolerance=0.0000001;//收敛精度double c3=0.03;//扰动幅度double e=2.718281828459;//自然对数底数int sm=3;int bz=0;//扰动因子标志double aw[V];double nihe[17][2]={1115.658026,8.70628355,1915.362904,8.20840555,2467.305693,9.1856689,2952.330784,9.0543057,5095.207855,9.132906445,5418.830566,8.852431395,4146.89209,9.45153145,6037.806376,9.103558859,4818.459044,7.2313171,5143.558017,9.0538129,5459.844361,9.74985695,5762.570046,8.6310193,6060.453719,9.194387,6356.051127,10.398948,6651.015103,9.8449629,6941.254523,7.2279982,7223.868903,6.579128};typedef struct {double d[V];double fitness;}Individal;typedef struct {double h[V];}heli;Individal pw[M];/*族群中个体最差位置*/Individal pb[M];/*族群中个体最好位置*/Individal px;/*全体中最好位置*/Individal individual[P];/*全部个体*/Individal pop[M][I];/*排序后的群组*/Individal temp[M];Individal temp1[I];Individal tem;Individal temx[S];/*计算标准差*//*选择测试函数为Sphere*/double fitness(double a[]){int i;double sum=0.0;double sum1=0.0;double s1=0.0,h1=0.0;double x1[V+1];for(i=0;i<V;i++)x1[i]=a[i];for(i=0;i<V;i++)for(i=0;i<17;i++){if(nihe[i][0]>x1[2])sum1=x1[0]+x1[1];elsesum1=nihe[i][1]-(x1[0]+x1[1]*(1.5*nihe[i][0]-0.5*pow(nihe[i][0],3)/pow(x1[2],3)));sum=sum+sum1;}return sum;}/*对每一个个体初始化*/void init(){int i,j;srand((unsigned)time(NULL)+kk++);for(i=0;i<P;i++){for(j=0;j<V;j++){individual[i].d[j]=R*(MAX-MIN)+MIN;}individual[i].fitness=fitness(individual[i].d);px.fitness=individual[P-1].fitness;}}/*按照适应度降序对全部个体进行排序和族群划分*/void sort(){int i,j,k;for(i=1;i<P;i++){for(j=0;j<P-i;j++){if(individual[j].fitness<individual[j+1].fitness){tem=individual[j];individual[j]=individual[j+1];individual[j+1]=tem;}}}k=0;/*按照规则分组*/for(i=0;i<I;i++){for(j=0;j<M;j++){pop[j][i]=individual[k];k++;}}if (px.fitness>individual[P-1].fitness)px=individual[P-1];for(i=0;i<M;i++){pw[i]=pop[i][0];pb[i]=pop[i][I-1];}}/*对某个群组中的个体进行重新排序*/void sortPop(int b){int i,j;for(i=1;i<I;i++){for(j=0;j<I-i;j++){if(pop[b][j].fitness<pop[b][j+1].fitness){tem=pop[b][j];pop[b][j]=pop[b][j+1];pop[b][j+1]=tem;}}}}/*群组内更新*/void update(){int i,j,k,l,n;double a;double b;for(n=0;n<N;n++){for(i=0;i<M;i++){// temp1[I]=pop[i][];a=0.0;b=0.0;// fitnessFw(i);//D=DMIN+(DMAX-DMIN)*(G-i2)/G;//D=DMIN+(DMAX-DMIN)*pow(e,-30*pow(i2/G,sm));for(j=0;j<V;j++){// temp[i].d[j]=R*(pb[i].d[j]-pw[i].d[j])+aw[j];temp[i].d[j]=C*R*(pb[i].d[j]-pw[i].d[j]);if(fabs(temp[i].d[j])>D){if(temp[i].d[j]>0){temp[i].d[j]=D;}else{temp[i].d[j]=-D;}}temp[i].d[j]+=pw[i].d[j];if(temp[i].d[j]>MAX)temp[i].d[j]=MAX;if(temp[i].d[j]<MIN)temp[i].d[j]=MIN;}a=fitness(temp[i].d);temp[i].fitness=a;if(a<pw[i].fitness){pop[i][0]=temp[i];sortPop(i);pw[i]=pop[i][0];pb[i]=pop[i][I-1];}else//标志{for(k=0;k<V;k++){// temp[i].d[k]=R*(px.d[k]-pw[i].d[k])+aw[k];temp[i].d[k]=C*R*(px.d[k]-pw[i].d[k]);if(fabs(temp[i].d[k])>D){if(temp[i].d[k]>0.0){temp[i].d[k]=D;}else{temp[i].d[k]=-D;}}temp[i].d[k]+=pw[i].d[k];if(temp[i].d[k]>MAX)temp[i].d[k]=MAX;if(temp[i].d[k]<MIN)temp[i].d[k]=MIN;// a+=temp[i].d[k]*temp[i].d[k];//适应度值计算//z=z+(x1[i]*x1[i]-10*cos(2*PI*x1[i])+10);}a=fitness(temp[i].d);temp[i].fitness=a;if(a<pw[i].fitness){pop[i][0]=temp[i];sortPop(i);pw[i]=pop[i][0];pb[i]=pop[i][I-1];}else{for(l=0;l<V;l++){pop[i][0].d[l]=R*(MAX-MIN)+MIN;// b+=pop[i][0].d[l]*pop[i][0].d[l];//适应度值计算//pop[i][0].fitness=b;}pop[i][0].fitness=fitness(pop[i][0].d);sortPop(i);pw[i]=pop[i][0];pb[i]=pop[i][I-1];}}//标志}//****M循环for(ii=0;ii<M;ii++)if(px.fitness>pb[ii].fitness)px=pb[ii];}//***N循环}/*将pop[M][I]复制到individual*/void copy(){int i,j,k;i=0;for(j=0;j<M;j++){for(k=0;k<I;k++){individual[i]=pop[j][k];i++;}}}void report(){printf("第%d次试验极值为%.10e\n",i1+1,px.fitness);}double sigma(){int j;double f=0.0;double fitness_avg=0.0;for (j=0;j<S;j++){// printf("极值e为%16f\n",temx[j].fitness);fitness_avg=fitness_avg+temx[j].fitness;}fitness_avg=fitness_avg/S;printf("平均值为%.16e\n",fitness_avg);//printf("%d极值e为%.16f\n",j,temx[j].fitness);for (j=0;j<S;j++)f=f+fabs(temx[j].fitness-fitness_avg)*fabs(temx[j].fitness-fitness_avg);// printf("极值e为%.16f\n",f);f=sqrt(f/(S-1));return f;}void main(){clock_t start,end;double ave,sigmax;FILE *f=fopen("result(SFLA).txt","w");ave=0.0;start=clock();for(i1=0;i1<S;i1++){init();for(i2=0;i2<G;i2++){sort();update();copy();}temx[i1]=px;report();ave=ave+px.fitness;}sigmax=sigma();end=clock();ave=ave/S;//printf("平均极值为\n%.16f\nCompleted!",ave);printf("50次试验标准差为%.16e\n",sigmax);printf("50次试验平均运行时间=%.2fseconds\n",(double)(end-start)/(S*(double)CLOCKS_PER_SEC));printf("50次试验的平均极值为%.16e\n",ave);fprintf(f,"50次试验平均极值为%.16f\n",ave);fprintf(f,"50次试验标准差为%.16f\n",sigmax);fprintf(f,"50次试验平均运行时间=%.2fseconds\n",(double)(end-start)/(S*(double)CLOCKS_PER_SEC)); fprintf(f,"解为:%.3f %.3f %.3f \n",px.d[0],px.d[1],px.d[2]);。
arcgis克里金插值法原理

克里金插值法(Kriging Interpolation)是一种用于空间数据插值的地统计学方法,常用于地理信息系统(GIS)软件如ArcGIS中。
它基于统计学原理,根据已知点的空间分布和变量值,预测未知位置的变量值。
以下是克里金插值法的基本原理:
1. 空间自相关性:克里金插值法的核心思想是假设同一地理区域内的点之间存在空间自相关性,即相邻点之间的变量值具有一定的关联性。
这意味着离得越近的点之间的变化趋势可能更相似。
2. 半变异函数:插值过程中使用了半变异函数(Semi-Variogram Function)来描述点之间的变异性。
半变异函数展示了不同距离下变量值之间的相关性或协方差。
这个函数可以帮助确定变量值在不同方向上的变异性和相关性。
3. 权重计算:在插值过程中,为了预测未知点的变量值,需要根据已知点的位置、变量值以及它们之间的空间关系来计算权重。
与离目标点距离近且变异性较小的点会得到较大的权重,而距离远或变异性大的点则得到较小的权重。
4. 插值预测:通过计算权重,将已知点的变量值加权平均,从而预测未知点的变量值。
权重的计算基于半变异函数和点之间的距离。
5. 交叉验证:为了评估插值的精度,通常会采用交叉验证方法。
该方法将已知数据分成训练集和测试集,通过对测试集进行插值并与真实值比较,评估克里金插值法的预测能力。
总之,克里金插值法通过考虑空间自相关性和半变异函数,利用已知点之间的关系来预测未知点的变量值。
这使得它在GIS等领域中广泛用于空间数据插值和预测。
1/ 1。
半变异函数的求解

半变异函数的求解克里金差值首先需要求取半变异函数,它是矢量距离h的函数,但这个问题似乎一直是大家纠结的问题,我也很纠结。
实际工作中,采样点位并未位于正规网格节点上,甚至较为离散,所以在计算半变异函数值时,要考虑角度容差和距离容差;也就是说,在理论上,x+h数据是足够的,但实际上,x+h 数据极少,因此必须考虑容差。
在矢量h的角度容差和距离容差范围内,都可以看做是x+h,这样才能计算半变异函数值。
在半变异函数的求解中,最方便又常用的软件就是GS+和Surfer(不要提ArgGIS),两者区别在哪?个人认为主要在以下三个方面:(1)容差。
我们知道,在看各向异性时,一般都是以0度(即x轴正向)为始,45度为间隔,看8个方向上的各向异性。
在GS+中,默认角度容差为22.5度,这个数字化刚刚好(这个容易理解),而Surfer中默认为90度,那也就是说surfer中考虑各向异性仅仅考虑x轴正向和x轴负向两个方向,当然这个似乎可以改变。
(2)距离选择。
GS+中有两个距离,一个是最大滞后距离,一个是计算间隔,其中计算间隔才是决定半变异函数模型的主要参数;surfer中只有一个,是最大滞后距离。
最大滞后距离(是否也就是搜索半径呢?我个人认为是),GS+选择的是x、y轴两者最大距离的1/2,surfer选择的是对角线距离最大值的1/3。
但这个数值我个人认为影响不大(只要不是太离谱),它影响的仅仅是点对数的多少(因为在实际工作中,各自距离的1/2和1/3都应该超出了样品的相关性范围)。
不过对于搜索半径,我也看到一些资料说选择采样间隔的2.5倍到3倍。
(3)各向异性的整体考虑。
GS+中,在半变异函数计算中并未整体考虑各向异性(我个人认为,不知道是否对),而surfer考虑了,但是surfer中的自动拟合参数似乎有些问题;而且,模型得自己选择并进行比较得出最优结果,而GS+默认选择的已经是最优的。
不知道上述观点大家是否同意?大家一起讨论讨论。
ArcGIS教程:半变异函数与协方差函数
半变异函数和协方差函数将邻近事物比远处事物更相似这一假设加以量化。
半变异函数和协方差都将统计相关性的强度作为距离函数来测量。
对半变异函数和协方差函数建模的过程将半变异函数或协方差曲线与经验数据拟合。
目标是达到最佳拟合,并将对现象的认知纳入模型。
之后模型便可用于预测。
在拟合模型时,浏览数据中的方向自相关。
基台、变程和块金是模型的重要特征。
如果数据中有测量误差,请使用测量值误差模型。
跟踪这一链接来了解如何将模型与经验半变异函数拟合。
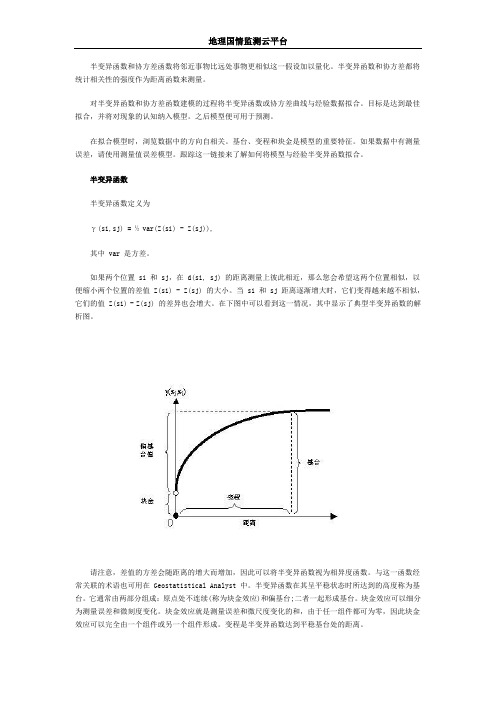
半变异函数半变异函数定义为γ(si,sj) = ½ var(Z(si) - Z(sj)),其中 var 是方差。
如果两个位置 si 和 sj,在 d(si, sj) 的距离测量上彼此相近,那么您会希望这两个位置相似,以便缩小两个位置的差值 Z(si) - Z(sj) 的大小。
当 si 和 sj 距离逐渐增大时,它们变得越来越不相似,它们的值 Z(si) - Z(sj) 的差异也会增大。
在下图中可以看到这一情况,其中显示了典型半变异函数的解析图。
请注意,差值的方差会随距离的增大而增加,因此可以将半变异函数视为相异度函数。
与这一函数经常关联的术语也可用在 Geostatistical Analyst 中。
半变异函数在其呈平稳状态时所达到的高度称为基台。
它通常由两部分组成:原点处不连续(称为块金效应)和偏基台;二者一起形成基台。
块金效应可以细分为测量误差和微刻度变化。
块金效应就是测量误差和微尺度变化的和,由于任一组件都可为零,因此块金效应可以完全由一个组件或另一个组件形成。
变程是半变异函数达到平稳基台处的距离。
协方差函数协方差函数定义为C(si, sj) = cov(Z(si), Z(sj)),其中 cov 是协方差。
协方差是相关性的缩放版。
因此当两个位置,si 和 sj 彼此相近时,您会希望这两个位置相似,而他们的协方差(相关性)会变大。
当 si 和 sj 距离逐渐增大时,它们变得越来越不相似,并且它们的协方差会变为零。
半变异函数分析共80页

66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做,明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生,以及整个命运 的,只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
半变异函数分析
16、人民应该为法律而战斗,就像为 了城墙 而战斗 一样。 ——赫 拉克利 特 17、人类对于不公正的行为ቤተ መጻሕፍቲ ባይዱ以指责 ,并非 因为他 们愿意 做出这 种行为 ,而是 惟恐自 己会成 为这种 行为的 牺牲者 。—— 柏拉图 18、制定法律法令,就是为了不让强 者做什 么事都 横行霸 道。— —奥维 德 19、法律是社会的习惯和思想的结晶 。—— 托·伍·威尔逊 20、人们嘴上挂着的法律,其真实含 义是财 富。— —爱献 生
变异函数参数的直接求解方法研究

变异函数参数的直接求解方法研究变异函数参数是数学建模中的一个重要概念,是一类解决特定问题所需参数的综合表达式。
它可以用来描述一个物体的大小、形状、空间分布、运动模式等,在工程设计、图形模拟等多个应用领域有重要意义。
本文针对变异函数参数求解问题,提出了一种基于直接算法的求解方法,以求解参数系统。
首先,针对变异函数参数求解问题,我们定义了变异函数参数的几何表达式,这与椭球参数的形式类似。
其次,我们利用坐标变换的方法,建立了一个变异函数参数的几何模型,以把变异函数从实际空间转换到参数化空间。
然后,我们利用变异函数参数的理论模型,提出了一种基于直接算法的求解方法,以求解参数系统。
最后,通过实验结果表明,该方法能够有效地求解变异函数参数。
变异函数参数是物体形状特征的重要描述依据,也是一种复杂的数学问题。
本文就其求解方法做了一些初步的研究,提出了一种基于直接算法的求解方法,以求解参数系统。
其方法能够有效求解变异函数参数,对于软件和硬件设计有一定参考价值。
但是,本文只是针对变异函数参数求解的初步研究,在实际应用中还有很多有待深入研究的问题。
例如,如何提高求解精度和准确性,如何降低算法的计算量和复杂性,如何更好地应用现有技术,如最优化方法等。
有些这些问题在本文初步提出,对于进一步的研究仍有待进一步深入的探讨,通过实际应用成果来反馈,努力实现更好的求解结果。
综上所述,本文探讨了变异函数参数求解问题,提出了一种基于直接算法的求解方法,以求解参数系统。
该方法能够有效地求解变异函数参数,对于软件和硬件设计有一定参考价值,但是求解精度和准确性仍有待提高,所以仍有很多有待深入研究的问题。
未来,我们将继续努力探索变异函数参数求解方法,提高求解精度和准确性,期望在现有技术的支持下取得更大的应用成果。
关于半整数维波动方程求解的几点注记

关于半整数维波动方程求解的几点注记
半整数维波动方程是数学中一种相对复杂的动力学系统,其关系及其求解方法
都被广泛应用于各行各业,特别是互联网领域。
在这里,我将给大家总结关于半整数维波动方程的几点注记。
首先,半整数维波动方程是一种类似于常微分方程的动力学系统,它能够定量
描述某个系统的变化过程,既可以表示总的物理模型,也可以作为理论的分析,以及实验结果的数学描述,用于描述信号波形和一阶线性连续时间系统。
其次,关于半整数维波动方程的求解,应该从曲线几何角度出发,根据定义,
其首先以特定方式对原始曲线进行加权处理,然后再将其表示为一元多项式,最后使用数值分析等分析方法来求解求解表达式。
此外,半整数维波动方程的实际应用日益普及,例如其在互联网领域的应用,
半整数维波动方程能够准确观测互联网流量与营销等方面,可以轻松掌控网站的访问信息,对网站的营销规划也能提供有力的支持。
最后,半整数维波动方程也在无线传感、音频处理、声学和图像处理等技术领
域发挥着重要作用,其中,最关键的在于有效地记录和提取信号波形,从而能够从视频图像中提取视觉信息,监控网络流动,以及对来自社会的音频信号进行处理等。
总之,半整数维波动方程是许多数学概念的综合体现,它的求解及应用都可谓
多才多艺,值得细细品味。
基于GA和PS的不同权重的半变异函数球状模型优化算法研究

基于GA和PS的不同权重的半变异函数球状模型优化算法研究舒彦军;曾令权;张立亭【摘要】In order to describe accurately space randomness and structural about natural phenomenon suited for regionalized variables theory, optimized spherical model for different weight by Genetic Algorithm and Pattern Search, compared distance with sample point number, the former got a more fit precision.%为了精确描述适用于区域化变量理论的自然现象的空间随机性和结构性,运用遗传算法和模式搜索法分另Il对不同权重的半变异函数球状模型进行了优化,并进行了对比分析,得到结论:权重基于滞后距倒数的优化算法比基于采样点对数的优化方法具有更好的拟合精度。
【期刊名称】《江西科学》【年(卷),期】2011(029)006【总页数】3页(P729-730,821)【关键词】权重;球状模型;遗传算法;模式搜索;半变异函数;地统计学【作者】舒彦军;曾令权;张立亭【作者单位】东华理工大学测绘工程学院,江西抚州344000;东华理工大学测绘工程学院,江西抚州344000;东华理工大学测绘工程学院,江西抚州344000【正文语种】中文【中图分类】P628.2目前一些成熟方法譬如多项式回归法[1]、线性规划法[2]和目标规划法[3]可通过加权对半变异函数理论模型进行优化,但是拟合精度并不十分理想,并且不同权重计算方式也会对优化结果产生影响。
对于不同权重的目标函数,笔者运用遗传算法进行优化,在得到球状模型近似最优参数值基础上,再把它作为模式搜索的起始点继续进行优化研究。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
半变异函数的求解
克里金差值首先需要求取半变异函数,它是矢量距离h的函数,但这个问题似乎一直是大家纠结的问题,我也很纠结。
实际工作中,采样点位并未位于正规网格节点上,甚至较为离散,所以在计算半变异函数值时,要考虑角度容差和距离容差;也就是说,在理论上,x+h数据是足够的,但实际上,x+h 数据极少,因此必须考虑容差。
在矢量h的角度容差和距离容差范围内,都可以看做是x+h,这样才能计算半变异函数值。
在半变异函数的求解中,最方便又常用的软件就是GS+和Surfer(不要提ArgGIS),两者区别在哪?个人认为主要在以下三个方面:
(1)容差。
我们知道,在看各向异性时,一般都是以0度(即x轴正向)为始,45度为间隔,看8个方向上的各向异性。
在GS+中,默认角度容差为22.5度,这个数字化刚刚好(这个容易理解),而Surfer中默认为90度,那也就是说surfer中考虑各向异性仅仅考虑x轴正向和x轴负向两个方向,当然这个似乎可以改变。
(2)距离选择。
GS+中有两个距离,一个是最大滞后距离,一个是计算间隔,其中计算间隔才是决定半变异函数模型的主要参数;surfer中只有一个,是最大滞后距离。
最大滞后距离(是否也就是搜索半径呢?我个人认为是),GS+选择的是x、y轴两者最大距离的1/2,surfer选择的是对角线距离最大值的1/3。
但这个数值我个人认为影响不大(只要不是太离谱),它影响的仅仅是点对数的多少(因为在实际工作中,各自距离的1/2和1/3都应该超出了样品的相关性范围)。
不过对于搜索半径,我也看到一些资料说选择采样间隔的2.5倍到3倍。
(3)各向异性的整体考虑。
GS+中,在半变异函数计算中并未整体考虑各向异性(我个人认为,不知道是否对),而surfer考虑了,但是surfer中的自动拟合参数似乎有些问题;而且,模型得自己选择并进行比较得出最优结果,而GS+默认选择的已经是最优的。
不知道上述观点大家是否同意?大家一起讨论讨论。
此外,我个人还有四点不懂:
(1)两者的距离容差是怎么规定的?
(2)surfer中的Angular Divisions和Radial Divisions具体代表什么意义?
(3)surfer中模型选择中似乎块金效应和常用的直线、球状、指数三种模型是并列的?(4)GS+中,h的选择是计算间隔的倍数,surfer中h是如何选择的?是最大滞后距离的25份(surfer默认好像是25个数据点对)?
其实,我常常想自己编程计算一下来验证这两个软件的结果,但这也是极为费力的事情。
不知道在此启开这个话题,大家一起讨论后,能否让大家真正的使用这两个软件进行正确的半变异函数计算和选择?
突然又想起一个问题,根据半变异函数理论,只有在一定范围内的数据才具有空间相关性,但我们在实际区域数据分析中,比如相关分析、因子分析等等,却并不考虑数据之间的距离,这不是矛盾了么???
2、GS+和Arcgis变异函数拟合
在GS+里对变异函数进行拟合,选择出最优的变异函数。
然后在Arcgis里进行克里格插值,比较了不同的变异函数,进行交叉验证。
验证结果发现,GS+里得到的最优的变异函数,交叉验证的结果并不是最好的。
这个时候该要怎么取舍和解决呢?
3、如何将GS+软件作出的半变异函数图表通过输出数据用Excel做出
来???急!已有1人参与
初始悬赏金币 5 个
由于要使用ArcGIS的Ordinary Kriging插值,所以需要先用GS+获得相应的参数。
在GS+做成半变异函数模型后,因为软件给出的图实在是太丑了(请原谅我没事找事)。
然后想用Excel做一下
初步探索后,可以点击list导出一个average distance,average semivariance和pair的一组数据点,然后在Excel中以average distance为X,average semivariance为Y 就得到experimental semivariogram(一些点)
然后关键就是怎么把模型的那条线弄出来了,以X=100,200,300.....20000 然后根据得出的最佳模型(线性、指数、高斯、球面),按照它的公式计算出相应的y值,然后这些密密麻麻的点就形成了一条线
但是我用Excel作出的图和GS+本身给出的图不大一样,主要就是Excel作出的图点和线的贴合度不是很好,那些试验点离那条线比较远,求大神指导到底怎么做,这样做对不对,Cd和Cr的图和原图差不多,Pb和Cu差的比较多
回复:可以用ISATIS软件做变差函数图。
