A 寻路算法模拟实现 C++ 可运行

合集下载

浅谈游戏中自动寻路算法的实现与应用

浅谈游戏中自动寻路算法的实现与应用作者：蒋恺来源：《中国新通信》 2018年第2期在信息技术的支持下，互联网进入了迅猛发展期，各种网游、页游大量出现，受到不同玩家的喜爱与青睐。

当然为了逐步扩大受众群，需要不断的优化游戏，满足玩家对游戏的需求，其中自动寻路算法就是十分关键的技术之一，提升了游戏角色在虚拟游戏环境中的灵活性，更利于对游戏角色的控制，是判断游戏质量的重要标准之一”1。

一、关于自动寻路算法的概述1.1自动寻路算法的原理在自动寻路算法中最常用的为A*算法，这属于启发式的算法，被广泛应用于游戏中的路径搜索【21。

主要是节点的设置，具有记录、搜索进度的功能，通过节点在游戏地图中移动，当搜寻到目标位置时就结算，否则会进一步搜索记录目标位置周围相邻的位置。

举例而言，游戏角色最初的位置就是开始节点，将要到达的目标位置设置为目标节点，在两者之间存在一定的障碍物和可以顺利通行的路径，黑色部分为障碍物，白色部分为可通行路径，具体如下图1所示：在设计A*算法时采用的基本原理，其实为最短路径算法，在整个游戏地图中，从起始节点到目标节点的路径多种多样，将这些全部读入到开放式列表中，再通过与目标节点距离最近的节点进行对比，从而找到最优路径”1。

将上图1中的起始节点设置为A，目标节点力B，在计算最优路径节点C时需要在考虑几何距离基础上使用计算公式：(A—C)2+fB—C)2在A*算法中通过对各个不同节点的计算，从而找出路径最短最优的节点，但这一算法具有一定的缺陷，很可能要将整个地图上的节点都计算完了才能得出结果，当游戏场景复杂且节点数量过多的话，会大大增加游戏设计制作中的寻路算法的费用。

为此，就要对A*算法进行优化改进，以便扩大应用范围，满足玩家的游戏需求。

1.2自动寻路算法的实现为了最快的找到游戏地图中的最优路径，需要将游戏场景进行网格划分，让每个网路成为大小相同的正方形，成为游戏中的导航网格，就可以选择一个节点起始位置，进行目标节点位置的广度搜索，在确定区域后在计算最佳路径。

C++DFS算法实现走迷宫自动寻路

C++DFS算法实现⾛迷宫⾃动寻路C++ DFS算法实现⾛迷宫⾃动寻路，供⼤家参考，具体内容如下深度优先搜索百度百科解释：事实上，深度优先搜索属于图算法的⼀种，英⽂缩写为DFS即Depth First Search.其过程简要来说是对每⼀个可能的分⽀路径深⼊到不能再深⼊为⽌，⽽且每个节点只能访问⼀次.运⾏效果：说明：深度优先搜索算法是在我在图的部分接触到的，后来才发现它也可以不⽤在图的遍历上，它是⼀个独⽴的算法，它也可以直接⽤在⼀个⼆维数组上。

其算法原理和实现步骤在代码中已经有了很好的体现了，这⾥就不再赘述。

在程序中实现了⼿动操控⾛迷宫和⾃动⾛迷宫两种模式，并且可在⾃动⾛完迷宫后显⽰⾏⾛的路径。

如果要修改程序使⽤的迷宫地图只需要修改map⼆维地图数组和两个地图宽⾼的常量值即可。

同样可以使⽤⾃动⾛迷宫的模式。

理论上这种算法可以对任意⼤⼩任意复杂的迷宫搜索路径，但是因为这种算法是⽤递归实现的，占⽤空间较⼤，地图⼤⼩增⼤也会多使⽤很多的空间，受限于堆栈空间的限制我在把地图⼤⼩增加到2020的时候运⾏⾃动寻路模式就会报堆栈溢出异常了。

我在代码准备了1818和15*15的两个迷宫地图⼆维数组⽤于测试。

编译环境：Windows VS2019代码：Game.h 游戏类#pragma once#include <iostream>#include <map>#include <conio.h>#include <vector>#include <windows.h>using namespace std;//地图宽⾼常量constexpr unsigned int mapWidth = 18;constexpr unsigned int mapHeight = 18;//游戏类class Game{private:map<int, string> cCMAEMap; //地图数组元素对应字符map<char, int*> movDistanceMap; //按键对应移动距离int px, py; //玩家坐标int dArr[4][2] = { {0, -1}, {0, 1}, {-1, 0}, {1, 0} }; //数值和移动⽅向对应数组vector<int*> tempPathVec; //路径向量vector<vector<int*>> allPathVec;//存储所有路径向量//检查参数位置是否可⾛bool check(int x, int y, int(*map)[mapWidth]){//判断修改后的玩家坐标是否越界、修改后的玩家坐标位置是否可⾛if (x < 0 || x >= mapWidth || y < 0 || y >= mapHeight || (map[y][x] != 0 && map[y][x] != 3)) return false;return true;}//控制玩家移动函数bool controlMove (int(*map)[mapWidth]){//键盘按下时if (!_kbhit()) return false;char key = _getch();if (key != 'w' && key != 's' && key != 'a' && key != 'd')return false;int temp_x = px, temp_y = py; //临时记录没有改变之前的玩家坐标px += movDistanceMap[key][0];py += movDistanceMap[key][1];//如果位置不可⾛则撤销移动并结束函数if (!check(px, py, map)){px = temp_x, py = temp_y;return false;}//判断是否已到达终点if (map[py][px] == 3){//打印信息并返回truecout << "胜利！" << endl;return true;}map[temp_y][temp_x] = 0; //玩家原本的位置重设为0路⾯map[py][px] = 2; //玩家移动后的位置设为玩家2//清屏并打印修改后地图system("cls");printMap(map);return false;}//⽤对应图形打印地图void printMap(int(*map)[mapWidth]){for (int i = 0; i < mapHeight; i++){for (int j = 0; j < mapWidth; j++)cout << cCMAEMap[map[i][j]];cout << endl;}}//初始化map容器void initMapContainer(){//数组元素和字符对应string cArr[4] = { " ", "■", "♀", "★" };for (int i = 0; i < 4; i++)cCMAEMap.insert(pair <int, string>(i, cArr[i]));//输⼊字符和移动距离对应char kArr[4] = { 'w', 's', 'a', 'd' };for (int i = 0; i < 4; i++)movDistanceMap.insert(pair <char, int*>(kArr[i], dArr[i]));}//找到玩家所在地图的位置void findPlayerPos(const int(*map)[mapWidth]){for (int i = 0; i < mapHeight; i++)for (int j = 0; j < mapWidth; j++)if (map[i][j] == 2){px = j, py = i;return;}}//深度优先搜索void dfs(int cx, int cy, int(*map)[mapWidth]){//把当前玩家位置插⼊到数组tempPathVec.push_back(new int[2] {cx, cy});//循环四个⽅向上下左右for (int i = 0; i < 4; i++){int x = cx + dArr[i][0]; //玩家下⼀个位置的坐标int y = cy + dArr[i][1];//检查下⼀个位置是否可⾛if (!check(x, y, map))continue;if (map[y][x] == 3) //已到达终点{tempPathVec.push_back(new int[2]{ x, y }); //把终点位置插⼊到向量中allPathVec.push_back(tempPathVec);return;}//为普通路径else{map[cy][cx] = -1; //当前位置临时设为-1，递归搜索时不可⾛原路，⾮0且⾮3的位置都不可⾛ dfs(x, y, map); //⽤下⼀个位置作为参数递归map[cy][cx] = 0; //递归完成后将当前位置重设为0，可⾛路径}}//最后没有找到可⾛的路径则删除向量最后⼀个元素，此时函数结束递归退回到上⼀层tempPathVec.pop_back();}//输出路径信息void printPathInformation(){//int minSizePathIndex = 0; //记录最短路径在路径向量中的下标//for (int i = 0; i < allPathVec.size(); i++)//{// cout << allPathVec.at(i).size() << " ";// if (allPathVec.at(i).size() < allPathVec.at(minSizePathIndex).size())// minSizePathIndex = i;//}//cout << endl << "最⼩长度：" << allPathVec.at(minSizePathIndex).size() << endl;输出最短路径信息//for (auto dArr2 : allPathVec.at(minSizePathIndex))// cout << dArr2[0] << "_" << dArr2[1] << " ";//输出所有路径信息//for (auto arr : allPathVec)//{// for (auto dArr2 : arr)// cout << dArr2[0] << "__" << dArr2[1] << " ";// cout << endl;//}}int findPath(int(*map)[mapWidth]){findPlayerPos(map); //找到玩家所在地图中的位置//如果多次调⽤findPaths函数，则需要先清除上⼀次调⽤时在向量中遗留下来的数据 tempPathVec.clear();allPathVec.clear();dfs(px, py, map); //找到所有路径插⼊到allPathVec//找到最短路径在allPathVec中的下标int minSizePathIndex = 0; //记录最短路径在路径向量中的下标for (int i = 0; i < allPathVec.size(); i++){if (allPathVec.at(i).size() < allPathVec.at(minSizePathIndex).size())minSizePathIndex = i;}return minSizePathIndex;}//显⽰路径void showPath(int(*map)[mapWidth], vector<int*> tempPathVec){//将能找到的最短的路径上的元素赋值全部赋值为2并输出for (auto tempDArr : tempPathVec)map[tempDArr[1]][tempDArr[0]] = 2;system("cls");printMap(map); //打印地图}//⼿动模式void manualMode(int(*map)[mapWidth]){while (!controlMove(map)) //游戏循环Sleep(10);}//⾃动模式void automaticMode(int(*map)[mapWidth]){//找到最短路径vector<int*> tempPathVec = allPathVec.at(findPath(map));for (int i = 1; i < tempPathVec.size(); i++){map[tempPathVec[i - 1][1]][tempPathVec[i - 1][0]] = 0;map[tempPathVec[i][1]][tempPathVec[i][0]] = 2;system("cls");printMap(map); //打印地图Sleep(200);}cout << "胜利！是否打印完整路径？（Y / N）" << endl;char key = _getch();if(key == 'Y' || key == 'y')showPath(map, tempPathVec);}public://构造Game(int(*map)[mapWidth], char mode){initMapContainer(); //初始化map容器findPlayerPos(map); //找到玩家所在地图中的位置system("cls");printMap(map); //先打印⼀遍地图♀■★(mode == '1') ? manualMode(map) : automaticMode(map);}//析构释放内存{for (auto it = tempPathVec.begin(); it != tempPathVec.end(); it++){delete* it;*it = nullptr;}tempPathVec.clear();//这⾥不会释放allPathVec了allPathVec.clear();}};迷宫.cpp main函数⽂件#include "Game.h"//光标隐藏void HideCursor(){CONSOLE_CURSOR_INFO cursor_info = { 1, 0 };SetConsoleCursorInfo(GetStdHandle(STD_OUTPUT_HANDLE), &cursor_info); }int main(){HideCursor(); //光标隐藏//0空地，1墙，2⼈， 3出⼝//int map[mapHeight][mapWidth] = {// 2, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1,// 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1,// 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0,// 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1,// 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0,// 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0,// 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0,// 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1,// 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0,// 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0,// 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1,// 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1,// 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0,// 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0,// 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 3,//};int map[mapHeight][mapWidth]{2, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1,0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1,1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0,1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0,1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1,0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1,0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1,0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0,0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1,1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0,1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0,0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1,1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1,1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0,0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1,0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1,1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0,1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 3,};//复制⼀个⼀样的数组以保证重新开始游戏时可以重置数组int mapCopy[mapHeight][mapWidth];memcpy(mapCopy, map, sizeof(mapCopy));while (true){cout << "选择模式：1，⼿动 2，⾃动" << endl;char key = _getch();Game game(mapCopy, key); //进⼊游戏cout << "输⼊r重新开始：" << endl;key = _getch();if (key != 'r' && key != 'R') //输⼊值不为r则结束程序break;memcpy(mapCopy, map, sizeof(mapCopy)); //重新赋值system("cls");}return 0;}以上就是本⽂的全部内容，希望对⼤家的学习有所帮助，也希望⼤家多多⽀持。

C++八方向Astar寻路算法大作业

#define col 27
using namespace std;
const int direction[8][2] = { { -1,-1 },{ -1,0 },{ -1,1 },{ 0,-1 },{ 0,1 },{ 1,-
1 },{ 1,0 },{ 1,1 } };// 方向
enum { virable, wall, inOpen, inClose, start, goal };
{
if (tempPoint->parent->r-tempPoint->r == 1 && tempPoint->parent->c == tempPoint->c)
map[tempPoint->parent->r][tempPoint->parent->c] = 4;
if (tempPoint->parent->r-tempPoint->r == -1 && tempPoint->parent->c == tempPoint->c)
1)
map[tempPoint->parent->r][tempPoint->parent->c] = 8;
if (tempPoint->parent->r-tempPoint->r == -1 && tempPoint->parent->c - tempPoint->c ==
1)
map[tempPoint->parent->r][tempPoint->parent->c] = 9;
temp->openPoint = point;

单源最短路径dijkstra算法c语言

单源最短路径dijkstra算法c语言单源最短路径问题是图论中的经典问题之一，指的是在图中给定一个起始节点，求出该节点到其余所有节点之间的最短路径的算法。

其中，Dijkstra 算法是一种常用且高效的解决方案，可以在有向图或无向图中找到起始节点到其余所有节点的最短路径。

本文将逐步介绍Dijkstra算法的思想、原理以及C语言实现。

一、Dijkstra算法的思想和原理Dijkstra算法的思想基于贪心算法，通过逐步扩展当前已知路径长度最短的节点来逐步构建最短路径。

算法维护一个集合S，初始时集合S只包含起始节点。

然后，选择起始节点到集合S之外的节点的路径中长度最小的节点加入到集合S中，并更新其他节点的路径长度。

具体来说，算法分为以下几个步骤：1. 初始化：设置起始节点的路径长度为0，其他节点的路径长度为无穷大。

2. 选择最小节点：从集合S之外的节点中选择当前路径长度最短的节点加入到集合S中。

3. 更新路径长度：对于新加入的节点，更新与其相邻节点的路径长度（即加入新节点后的路径长度可能更小）。

4. 重复步骤2和3，直到集合S包含所有节点。

二、Dijkstra算法的C语言实现下面我们将逐步讲解如何用C语言实现Dijkstra算法。

1. 数据结构准备首先，我们需要准备一些数据结构来表示图。

我们可以使用邻接矩阵或邻接表来表示图。

这里，我们选择使用邻接矩阵的方式来表示权重。

我们需要定义一个二维数组来表示图的边权重，以及一个一维数组来表示起始节点到各个节点的路径长度。

c#define MAX_NODES 100int graph[MAX_NODES][MAX_NODES];int dist[MAX_NODES];2. 初始化在使用Dijkstra算法之前，我们需要对数据进行初始化，包括路径长度、边权重等信息。

cvoid initialize(int start_node, int num_nodes) {for (int i = 0; i < num_nodes; i++) {dist[i] = INT_MAX; 将所有节点的路径长度初始化为无穷大}dist[start_node] = 0; 起始节点到自身的路径长度为0初始化边权重for (int i = 0; i < num_nodes; i++) {for (int j = 0; j < num_nodes; j++) {if (i == j) {graph[i][j] = 0; 自身到自身的边权重为0} else {graph[i][j] = INT_MAX; 其他边权重初始化为无穷大}}}}3. 主要算法接下来是Dijkstra算法的主要逻辑。

c语言最短路径搜寻算法

c语言最短路径搜寻算法
C 语言最短路径搜寻算法常用于在网图中寻找两点之间的最短路径，其中网图的最短路径分为单源最短路径和多源最短路径。

以下是两种常见的最短路径搜寻算法：- Dijkstra 算法：从一个起始点出发，到达一个终点，通过对路径权值的累加，找到最短路径。

- Floyd 算法：对于网中的任意两个顶点来说，之间的最短路径不外乎有两种情况。

一种是直接从一个顶点到另一个顶点的边的权值；另一种是先经过若干个顶点，最终达到另一个顶点，期间经过的边的权值和。

这两种算法都可以用 C 语言实现，你可以根据具体需求选择合适的算法。

若你想了解更多关于最短路径搜寻算法的内容，可以继续向我提问。

浅谈寻路A算法范文

浅谈寻路A算法范文寻路算法（Pathfinding）是计算机中常用的一种算法，通过图形结构中两个节点之间的最佳路径，解决了很多实际问题，如游戏中的NPC寻路、自动驾驶的路径规划等。

其中，A*算法（A-star algorithm）被广泛应用于寻路算法中，本文将对A*算法进行详细介绍。

A*算法是通过启发式算法（Heuristic Search）实现的一种寻路算法，根据估算函数（Heuristic Function）对节点进行评估，并选择具有最小开销的节点进行扩展。

A*算法的核心思想是综合考虑节点的实际开销（G 值）和预估的目标开销（H值），并选择最优节点进行。

在A*算法中，节点的开销是通过计算路径上节点的实际开销和预估开销得到的。

实际开销是指从起始节点到当前节点的移动开销，通常是节点间的距离或代价。

预估开销是通过估算函数对当前节点到目标节点的距离进行评估，常用的估算函数有欧几里得距离、曼哈顿距离等。

A*算法的具体步骤如下：1. 创建一个开启列表（Open List）和一个关闭列表（Closed List），起始节点放入开启列表。

2.从开启列表中选出具有最小开销的节点作为当前节点，并将其放入关闭列表中。

3.对当前节点的所有相邻节点进行遍历，如果该节点不可通过或者在关闭列表中，则忽略。

4.计算相邻节点的实际开销和预估开销，更新节点的G值和H值。

5.如果相邻节点不在开启列表中，将其加入开启列表，并将当前节点设置为该节点的父节点。

6.如果相邻节点已经在开启列表中，比较当前节点作为父节点时的G 值和之前的G值，如果小于之前的G值，更新节点的父节点为当前节点。

7.重复2-6步骤，直到达到目标节点或者开启列表为空。

8.如果达到目标节点，从目标节点开始回溯父节点，得到最佳路径。

A*算法的优势在于通过使用估算函数，能够快速找到目标节点，而且能够保证找到的路径是最佳路径。

同时，A*算法可以通过调整估算函数的权重来权衡的速度和路径的质量。

A算法的实现原理及应用

A算法的实现原理及应用算法是计算机科学中重要的概念，其本质是一种数学思想，是一系列求解问题的方法和步骤。

A算法，也称为A*算法，是一种常见的寻路算法，被广泛应用于游戏开发、人工智能、机器人控制等领域。

本文将介绍A算法的实现原理及其应用。

一、A算法的实现原理A算法是一种搜索算法，其目标是在搜索图中找到从起点到终点的最短路径。

A算法基于一种启发式搜索策略，即优先考虑最有可能通向终点的节点。

下面是A算法的基本实现步骤：1. 初始化开始节点和结束节点，并把开始节点加入到开启列表中。

2. 从开启列表中选出具有最小f值（f值是节点的启发值和代价值之和）的节点作为当前节点。

3. 把当前节点从开启列表中删除，并将其加入到关闭列表中。

4. 遍历当前节点的相邻节点，如果相邻节点不可通过或者已经在关闭列表中，就忽略。

5. 对于未被遍历过的相邻节点，计算它的f值、g值和h值。

其中，g值表示从起点到该节点的代价，h值表示该节点到终点的启发值，即估算到终点的实际代价。

6. 如果相邻节点已经在开启列表中，比较新的g值和原先的g值，如果新的g值更小，就更新g值和f值。

如果相邻节点不在开启列表中，将其加入到开启列表中，并计算其f、g、h值。

7. 重复步骤2到步骤6，直到找到终点或者开启列表为空。

二、A算法的应用A算法是一种高效的寻路算法，其应用非常广泛。

下面列举几个例子：1. 游戏开发在游戏开发中，A算法被广泛用于计算游戏场景中的敌人或角色行走的最佳路径。

游戏场景通常被表示为一个二维数组，A算法可以根据玩家角色的位置和目标位置，在场景图中寻找最短路径，并输出路径。

2. 人工智能A算法是人工智能领域中常用的算法之一，可以被用于求解最优路径问题。

例如，在机器人路径规划中，A算法可以根据机器人的当前位置和目标位置，搜索机器人的最短路径，并输出路径。

3. 网络路由A算法也被广泛应用于网络路由领域。

当网络中出现路由选择问题时，A算法可以根据网络拓扑结构和路由代价，寻找到源节点到目标节点的最短路径。

简单寻路算法

简单寻路算法在⽂中可能会出现⼀些专业术语或者是我信⼝雌黄的话语，未免看官不明⽩，前⾯我先加以注解，具体意思可以从⽂中体会到该寻路算法是在⼀个由很多⽅格组成的图像中，你操纵⼀个蓝⾊⼩⽅格进⾏寻路的环境下进⾏讲解，具体请看⽂章⼀开始的flash⽰例，或者是查看⽅格：⼀个⼀个的⼩⽅块障碍物：挡着去路的东西⽬标⽅格：你想到达的⽅格操控⽅格：你控制的寻路对象标记：临时为某⼀个⽅格做的标记⽗标记：除了操控⽅格所创建的临时标记，每个标记都有个⽗标记，但⽗标记不是随便乱定的，请看下⽂开启标记列表：当该标记还未进⾏过遍历，会先加⼊到开启标记列表中关闭标记列表：当该标记已经进⾏过遍历，会加⼊到关闭标记列表中路径评分：通过某种算法，计算当前所遍历的标记离⽬标⽅格的路径耗费估值（后⾯会讲⼀种通⽤的耗费算法）⾸先描述⼀个环境，在⼀望⽆际的⽅格中，我⾝处某某⽅格，如今我想去某某⽅格，接下来我开始寻路！在脑海中，先创建开启标记列表、关闭标记列表，然后把我的初始位置设置为开始标记进⾏遍历，同时因为开始标记已经遍历过了，因此把开始标记加⼊到关闭列表。

通过开始标记我们找出了相邻的⼋个⽅格，为它们创建相应的标记，加⼊到开启标记列表中，并把每个标记的⽗标记设置为开始标记，是因为开始标记才让我们这些⽅格创建了属于⾃⼰的标记，它就是我们的再⽣⽗母。

但不符合条件的我们就不加⼊开启标记列表（下⾯的条件符合任何⼀条都不要加⼊到开启标记列表中）： 1、它在我们的搜寻地图范围外，⽐如你地图的寻路范围是 0*0 - 50*50，那么但这个点在边缘的时候，那它相邻的⼋个⽅格，必定有⼏个是处在外⾯的！ 2、搜寻的这个⽅格是否有障碍物、或不可到达，⽐如河流，⽯头，⼭川等 3、判断它是否已经加⼊关闭标记列表，若已经加⼊表⽰该⽅格已经遍历过了，在遍历⼀次也⽆济于事，还会影响效率 4、判断它是否已经加⼊开启标记列表，若已经加⼊那么咋们就来判断⼀下该标记是否离开始标记更近⼀些 5、判断当斜着⾛的时候，它的上下或左右是否有障碍，如果有则表⽰你⽆法斜着⾛，需要先横⾛⼀下，再竖⾛⼀下或者是竖⾛⼀下，再横⾛⼀下如果想象不出来，可以看着这个进⾏学习和⽐较。

虚拟现实技术在数字图书馆中的应用

ｐｒｏｖｅｔｈｅｓｏｃｉａｌｓｔａｔｕｓｏｆｔｈｅｌｉｂｒａｒｙ．
【Ｋｅｙｗｏｒｄｓ】Ｖｉｒｔｕａｌｒｅａｌｉｔｙｔｅｃｈｎｏｌｏｙ；ｇＤｉｇｉｔａｌｌｉｂｒａｒｙ；Ａｕｔｏｍａｔｉｃｒｏｕｔｉｎｇ
刊等纸质范畴向数字化、虚拟化方向发展。虚拟图书馆作为一个全新的发展方向已成为图书馆数字化建设的一个重要方
图书馆领域，可以极大地提高图书馆资源建设水平和读者服务工作质量，给人带来无以伦比的体验效果，吸引更多的读
者。２．１核心技术
为了真实复现图书馆场景，显示画面采用以等角投影显
示的二维地图，把场景中的元素沿坐标轴旋转一定角度制作
并绘制到屏幕上，让用户能够看到物体的多个侧面，从而产成２．５Ｄ效果。这种手法在游戏界也成为 “ ２．５Ｄ ” 或者 “ Ｉｓｏ — ｍｅｔｒｉｃＧａｍｅ ” 。ＩｓｏｍｅｔｒｉｃＧａｍｅ中的ｉｓｏｍｅｔｒｉｃ，指的正是机械制图中，以等轴测投影法在投影平面上绘制三维物体平面图的一种测绘方法。等轴测图是一种单面投影图，在一个投影面上能同时反映出物体三个坐标面的形状，并接近于人们的
行为的人机交互技术，用户借助必要的设备与虚拟世界中的
物体进行交互，同时可以漫游、查询，甚至分析虚拟现实中的物体，可以产生身临其境的感受和体验［１－２］。虚拟现实技术的

dijkstra算法代码c语言

Dijkstra算法简介Dijkstra算法是一种用于在加权图中找到最短路径的算法。

它以荷兰计算机科学家Edsger Dijkstra的名字命名。

该算法从一个源节点开始，逐步找到离源节点最近的节点，直到找到目标节点或者遍历了所有节点。

Dijkstra算法在很多领域有着广泛的应用，例如路由器和网络通信。

算法原理Dijkstra算法通过动态规划的思想来解决最短路径问题。

它维护两个集合，一个是已被访问的节点集合，一个是待访问的节点集合。

同时，还维护一个长度数组，用来保存从源节点到各个节点的当前最短路径长度。

算法的运行过程如下：1.初始化起始节点的路径长度为0，其他节点的路径长度为无穷大。

2.将起始节点加入已被访问节点集合，并将其加入已访问节点集合。

3.更新所有与起始节点直接相连的节点的路径长度，如果某个节点的路径长度通过当前路径到达更短，则更新路径长度。

4.从待访问节点集合中选择路径长度最小的节点，将其加入已访问节点集合。

5.重复步骤3和步骤4，直到所有节点都被访问。

6.最终得到从起始节点到其他节点的最短路径长度。

伪代码下面是Dijkstra算法的伪代码：function Dijkstra(G, source):dist[source] := 0 // 初始化起始节点的路径长度为0for each vertex v in G:if v ≠ sourcedist[v] := infinity // 其他节点的路径长度为无穷大add v to Q // 将所有节点加入待访问集合while Q is not empty: // 当待访问集合不为空时u := vertex in Q with min dist[u] // 选择路径长度最小的节点remove u from Q // 将节点从待访问集合中移除for each neighbor v of u: // 遍历与节点u直接相连的节点alt := dist[u] + length(u, v) // 计算新的最短路径长度if alt < dist[v] // 如果新的路径较短dist[v] := alt // 更新路径长度return dist // 返回最短路径长度数组示例假设我们有一个有向图，每条边都有一个权重。

单源最短路径dijkstra算法c语言 -回复

单源最短路径dijkstra算法c语言-回复什么是单源最短路径问题？单源最短路径问题是图论中的一个重要问题，它可以用来寻找图中从一个给定节点到其他节点的最短路径。

其中，图由节点和边组成，节点之间的边代表节点之间的连接关系，边上可以带有权重，代表从一个节点到另一个节点的代价或距离。

单源最短路径问题需要找到从给定的源节点到其他所有节点的最短路径。

为什么需要单源最短路径算法？在实际应用中，我们经常会遇到需要找到一条最短路径的问题，比如计算导航时找到最短驾驶路线、网络路由器确定数据传输路径等等。

利用单源最短路径算法，我们可以高效地找到从一个节点到其他节点的最短路径，这样可以大大提高计算效率和节省资源。

Dijkstra算法是什么？Dijkstra算法是一种用于解决单源最短路径问题的经典算法，由荷兰计算机科学家Edsger Dijkstra于1956年提出。

该算法经过多次迭代，依次确定从源节点到其他节点的最短距离，并逐步生成最短路径。

Dijkstra算法的步骤有哪些？Dijkstra算法的步骤如下：1. 创建一个集合Q，用于保存图中所有的节点。

2. 初始化一个距离表dist，其中包括源节点到其他所有节点的距离。

将源节点的距离设为0，其他节点的距离设为无穷大。

3. 重复以下步骤，直到集合Q为空：a. 在集合Q中找到距离表dist中距离最小的节点u，并将其从集合Q 中移除。

b. 对节点u的所有邻接节点进行松弛操作，更新距离表dist中的距离值。

4. 距离表dist中保存了从源节点到其他所有节点的最短距离。

Dijkstra算法的详细实现步骤是什么？下面是Dijkstra算法的详细实现步骤：1. 首先，创建一个辅助数组prev，用于保存到达每个节点的前一个节点，用于生成最短路径。

2. 初始化距离数组dist，将源节点到其他所有节点的距离设为无穷大，源节点的距离设为0。

3. 创建一个优先队列Q，用于保存待处理的节点。

dijkstra算法代码c语言

dijkstra算法代码c语言Dijkstra算法代码C语言简介Dijkstra算法是一种用于寻找带权有向图中最短路径的经典算法。

它由荷兰计算机科学家Edsger Dijkstra于1956年发明。

本文将介绍Dijkstra算法的基本原理和用C语言实现的代码。

算法原理1.初始化：设定一个起始点，将起始点到其他所有点的距离初始为无穷大，将起始点到自身的距离设为0，创建一个空的集合用于存放已找到最短路径的点。

2.选取最短路径：从未找到最短路径的点中选择一个距离起始点最近的点，将其加入到已找到最短路径的点的集合中。

3.更新距离：对于新加入的点，更新它周围点到起始点的最短距离。

如果通过新加入的点到达某个点的距离比当前已知最短距离小，则更新该点的最短距离。

4.重复步骤2和步骤3，直到所有点都找到最短路径。

C语言实现下面是用C语言实现Dijkstra算法的代码：#include <>#include <>#define SIZE 10#define INFINITY 9999void dijkstra(int graph[SIZE][SIZE], int startNode) {int distance[SIZE];bool visited[SIZE];for (int i = 0; i < SIZE; i++) {distance[i] = INFINITY;visited[i] = false;}distance[startNode] = 0;for (int count = 0; count < SIZE - 1; count++) {int minDistance = INFINITY;int minIndex;for (int i = 0; i < SIZE; i++) {if (!visited[i] && distance[i] <= minDistanc e) {minDistance = distance[i];minIndex = i;}}visited[minIndex] = true;for (int i = 0; i < SIZE; i++) {if (!visited[i] && graph[minIndex][i] && dis tance[minIndex] != INFINITY &&distance[minIndex] + graph[minIndex][i] < distance[i]) {distance[i] = distance[minIndex] + graph [minIndex][i];}}}printf("最短路径为:\n");for (int i = 0; i < SIZE; i++) {printf("%d 到 %d 的距离: %d\n", startNode, i, di stance[i]);}}int main() {int graph[SIZE][SIZE] = {{0, 6, 0, 1, 0},{6, 0, 5, 2, 2},{0, 5, 0, 0, 5},{1, 2, 0, 0, 1},{0, 2, 5, 1, 0}};int startNode = 0; // 起始点的索引dijkstra(graph, startNode);return 0;}总结Dijkstra算法是解决最短路径问题的一种有效方法。

C++八方向Astar寻路算法大作业

{
insertToOpenList(open, startpoint_r, startpoint_c);// 起点
addPointToCloseList(close, open);
// 起点放到 close中
while (!insertToOpenList(open, open->openPoint->r, open->openPoint->c))
//定义方格点
struct point
{
int flag; //标志位 0 为可走， 1 为墙壁 2 在penlist 3 在 closelist中 4 为起点 5 为终点
unsigned int r;
unsigned int c;
unsigned int h;
unsigned int g;
unsigned int f;
if (tempPoint->parent->r-tempPoint->r == 0 && tempPoint->parent->c - tempPoint->c == -
1)
map[tempPoint->parent->r][tempPoint->parent->c] = 7;
if (tempPoint->parent->r-tempPoint->r == 1 && tempPoint->parent->c - tempPoint->c == -
#define col 27
using namespace std;
const int direction[8][2] = { { -1,-1 },{ -1,0 },{ -1,1 },{ 0,-1 },{ 0,1 },{ 1,-

迷宫寻路游戏编程

迷宫寻路游戏编程迷宫寻路游戏是一种常见的益智游戏，在这种游戏中，玩家需要通过思考和推理找到从迷宫入口到出口的最短路径。

虽然看似简单，但实际上需要运用图论和搜索算法来实现。

本文将介绍迷宫寻路游戏的基本原理以及一种实现方法。

一、迷宫寻路游戏的基本原理迷宫可以看作是一个由格子组成的二维矩阵，每个格子可以是墙壁或通道。

其中，墙壁表示不可通过的障碍物，而通道表示可以通过的路径。

寻路游戏的目标是从迷宫的入口到出口找到一条尽可能短的路径。

二、迷宫寻路游戏的编程思路为了实现迷宫寻路游戏，我们可以采用深度优先搜索（DFS）或广度优先搜索（BFS）算法。

其中，DFS算法以堆栈（栈）为基础，BFS 算法以队列为基础。

1. 深度优先搜索（DFS）DFS算法可以简单描述为以下步骤：（1）将迷宫的入口状态（起点）加入堆栈。

（2）从堆栈中取出一个状态，并将其标记为已访问。

（3）检查当前状态是否为出口状态，如果是则返回路径，游戏结束。

（4）如果当前状态不是出口状态，则扩展当前状态的邻居状态，并将未访问的邻居状态加入堆栈。

（5）重复步骤（2）至（4），直到堆栈为空或找到出口状态。

2. 广度优先搜索（BFS）BFS算法可以简单描述为以下步骤：（1）将迷宫的入口状态（起点）加入队列。

（2）从队列中取出一个状态，并将其标记为已访问。

（3）检查当前状态是否为出口状态，如果是则返回路径，游戏结束。

（4）如果当前状态不是出口状态，则扩展当前状态的邻居状态，并将未访问的邻居状态加入队列。

（5）重复步骤（2）至（4），直到队列为空或找到出口状态。

三、迷宫寻路游戏的编程实现下面是一种基于Python语言的迷宫寻路游戏编程实现示例：```python# 导入必要的模块import queue# 迷宫地图，0表示墙壁，1表示通道maze = [[0, 1, 0, 0, 0],[0, 1, 1, 1, 0],[0, 0, 0, 1, 0],[0, 1, 1, 1, 0],[0, 0, 0, 0, 0]]# 定义迷宫的行数和列数rows = len(maze)cols = len(maze[0])# 定义起点和终点坐标start = (0, 0)end = (rows - 1, cols - 1)# 定义方向数组，用于控制上下左右移动dirs = [(-1, 0), (1, 0), (0, -1), (0, 1)]# 定义BFS算法函数def BFS(maze, start, end):q = queue.Queue()q.put(start)# 使用visited数组记录已经访问过的状态visited = [[False] * cols for _ in range(rows)]visited[start[0]][start[1]] = Truewhile not q.empty():cur_pos = q.get()if cur_pos == end:return Truefor dir in dirs:next_pos = (cur_pos[0] + dir[0], cur_pos[1] + dir[1])# 如果下一个状态合法且未访问过，则加入队列并标记为已访问if isValid(next_pos) and not visited[next_pos[0]][next_pos[1]]: q.put(next_pos)visited[next_pos[0]][next_pos[1]] = Truereturn False# 判断状态是否合法def isValid(pos):x, y = pos[0], pos[1]return 0 <= x < rows and 0 <= y < cols and maze[x][y] == 1# 测试迷宫寻路游戏if BFS(maze, start, end):print("找到了一条路径")else:print("未找到路径")```以上是一个简单的迷宫寻路游戏编程实现示例，通过运行代码，即可在命令行中得到游戏结果。

一种3D网络游戏寻路方法的实现与优化的开题报告

一种3D网络游戏寻路方法的实现与优化的开题报告一、选题背景和意义随着互联网和计算机技术的不断发展，网络游戏得到了前所未有的发展，并成为当今年轻人最喜爱的娱乐方式之一。

在3D网络游戏中，寻路算法是非常关键的一环，如何使玩家在游戏中愉快地畅游而不受路径寻找的困扰，是游戏开发者需要解决的一个难题。

本选题旨在为3D网络游戏提供一种高效、可靠的寻路算法，以提高游戏体验。

二、选题研究内容和思路本文选用A*算法和Dijkstra算法作为网络游戏寻路算法的基础，进一步优化和改进这两种算法，提供更适合3D网络游戏的寻路算法。

本文研究的具体内容如下：（1）A*算法的优化A*算法是一种高效的寻路算法，但是在某些场景下会出现路径偏离的问题，本选题将研究如何优化算法，使其能够更精准地寻找最短路径。

（2）Dijkstra算法的优化Dijkstra算法是一种经典的单源最短路径算法，在许多场景下也有很好的应用效果。

但在3D网络游戏中，因为需要不断更新网络图的状态，所以需要对其进行优化。

本选题将研究如何对Dijkstra算法进行优化，使其能够适应网络游戏的场景。

（3）实现和比较为了验证优化后的算法效果，在选题中还将编写一个3D网络游戏，将优化前后的A*算法和Dijkstra算法与传统的算法进行比较。

通过游戏模拟的方式，验证提出的优化方法的有效性。

三、选题意义和预期目标本选题的意义在于提供一种更适合3D网络游戏的寻路算法。

首先，本选题将通过修改经典的寻路算法并引入新的技术，提高寻路算法的效率；其次，本选题将构建一个3D网络游戏，完成不同算法的比较和优化，从而验证提出的优化方案对网络游戏所形成的实践价值，以帮助游戏开发者提高游戏体验，为用户带来更好的享受。

最终的目标是提供一种更好的寻路算法，以改进具有实践意义的网络游戏开发。

寻路算法

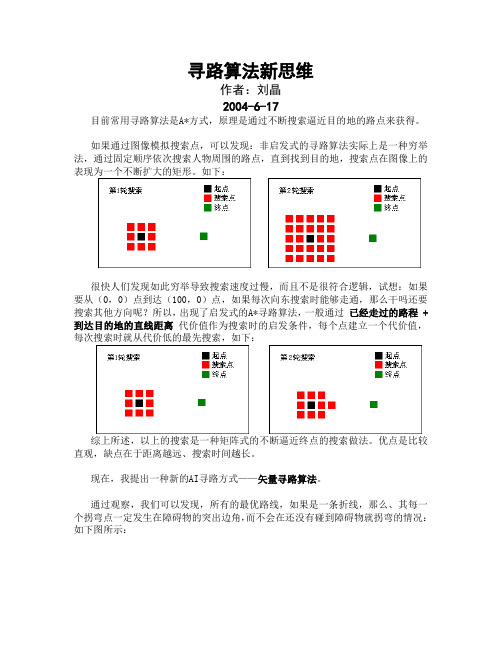
寻路算法新思维作者：刘晶2004-6-17目前常用寻路算法是A*方式，原理是通过不断搜索逼近目的地的路点来获得。

如果通过图像模拟搜索点，可以发现：非启发式的寻路算法实际上是一种穷举法，通过固定顺序依次搜索人物周围的路点，直到找到目的地，搜索点在图像上的表现为一个不断扩大的矩形。

如下：很快人们发现如此穷举导致搜索速度过慢，而且不是很符合逻辑，试想：如果要从（0，0）点到达（100，0）点，如果每次向东搜索时能够走通，那么干吗还要搜索其他方向呢？所以，出现了启发式的A*寻路算法，一般通过已经走过的路程 + 到达目的地的直线距离代价值作为搜索时的启发条件，每个点建立一个代价值，每次搜索时就从代价低的最先搜索，如下：综上所述，以上的搜索是一种矩阵式的不断逼近终点的搜索做法。

优点是比较直观，缺点在于距离越远、搜索时间越长。

现在，我提出一种新的AI寻路方式——矢量寻路算法。

通过观察，我们可以发现，所有的最优路线，如果是一条折线，那么、其每一个拐弯点一定发生在障碍物的突出边角，而不会在还没有碰到障碍物就拐弯的情况：如下图所示：我们可以发现，所有的红色拐弯点都是在障碍物（可以认为是一个凸多边形）的顶点处，所以，我们搜索路径时，其实只需要搜索这些凸多边形顶点不就可以了吗？如果将各个顶点连接成一条通路就找到了最优路线，而不需要每个点都检索一次，这样就大大减少了搜索次数，不会因为距离的增大而增大搜索时间。

这种思路我尚未将其演变为算法，姑且提出一个伪程序给各位参考：1．建立各个凸多边形顶点的通路表TAB，表示顶点A到顶点B是否可达，将可达的顶点分组保存下来。

如: ( (0,0) (100,0) ),这一步骤在程序刚开始时完成，不要放在搜索过程中空耗时间。

2．开始搜索A点到B点的路线3．检测A点可以直达凸多边形顶点中的哪一些，挑选出最合适的顶点X1。

4．检测与X1相连（能够接通）的有哪些顶点，挑出最合适的顶点X2。

5．X2是否是终点B？是的话结束，否则转步骤4（X2代入X1）如此下来，搜索只发生在凸多边形的顶点，节省了大量的搜索时间，而且找到的路线无需再修剪锯齿，保证了路线的最优性。

基于Leap Motion的机械臂手势控制研究

2019.06科学技术创新-85-基于Leap Motion的机械臂手势控制研究袁晨曹志强张永波唐齐鸿(西南科技大学信息工程学院，四川绵阳621010)摘要：本文提出了一种新颖的可通过手势控制的机械臂控制系统软硬件实现方案。

使用体感控制器Leap Motion采集手部信息，通过SDK接口在PC机上对信息进行处理，将指令主数据发送给uarm控制器，完成机械臂的运动。

实现了对机械臂的灵活高精度控制。

系统测试证明，Leap Motion设备提取的特征总体识别程度高、效果好，机械臂定位速度快、定位精度高。

关键词：Uarm机械臂；手势控制；Leap Motion中图分类号:TP241文献标识码:A文章编号:2096-4390(2019)06-0085-02近些年新出现的可穿戴式交互设备扩大了增强现实和虚拟现实技术的影响力，如Google眼镜、三维体感交互设备Kinect和Leap Motion等"。

与实体按键和触摸等传统控制方法相比,手势控制方法优点有:简单灵活、可简化交互过程、改善用户体验。

Leap Motion与机械手结合有很大发展空间,应用在军事中，拆弹人员远程操控机械手完成拆弹动作,保证拆弹人员安全;应用在医学中，利用手势控制机器手臂执行手术，可实现远程搜救。

B1uArm Metal机械臂1.1uArm Metal机械设计。

uArm Metal是一款桌面级开源机械臂,其特殊的机械结构使得末端的执行机构始终平行于水平面。

由图1进行分析可知：小臂和大臂各存在一个平行四边形,D点是平行四边形ABCD和DEFG和ADEF共有的点，是小臂和大臂的交点，也是小臂的关节点M3。

本机构中，当底座固定在水平面时，线AB固定，边AB平行于边DE,厶ABC=,DEF,BC为水平线，分析得边EF平行与线BC,即边EF始终保持水平。

同理，边DF平行于边GH.,DFE=ZHGL,EF为水平线，分析得末端执行器终端边常用的便是A*(A-Star)算法。

寻路算法实验报告

一、实验目的1. 熟悉和掌握寻路算法的基本原理和实现方法；2. 了解不同寻路算法的优缺点和应用场景；3. 通过实际编程实现寻路算法，提高算法设计能力。

二、实验原理寻路算法是指在一个给定图中，寻找从起点到终点的一条路径的算法。

常见的寻路算法有深度优先搜索（DFS）、广度优先搜索（BFS）、A搜索等。

本实验将重点介绍A搜索算法，并对其原理进行详细阐述。

A搜索算法是一种启发式搜索算法，其核心思想是利用启发式函数来评估路径的优劣，从而在搜索过程中优先选择最有希望的路径。

A搜索算法的估价函数f(n)由两部分组成：g(n)表示从起点到当前节点n的实际代价，h(n)表示从当前节点n到终点d的估计代价。

A搜索算法的流程如下：1. 初始化：将起点加入开放列表（Open List），将终点加入封闭列表（Closed List）；2. 循环：a. 从开放列表中选出f(n)最小的节点n；b. 将节点n从开放列表移除，加入封闭列表；c. 遍历节点n的邻居节点m；d. 如果m在封闭列表中，跳过；e. 如果m不在开放列表中，将m加入开放列表；f. 如果m在开放列表中，且新的g(n)小于原来的g(m)，则更新m的f(n)、g(n)和父节点；3. 当终点被加入开放列表时，搜索结束。

三、实验内容1. 实现A搜索算法，并验证其在不同迷宫中的搜索效果；2. 对比A搜索算法与DFS、BFS算法在搜索效果和效率上的差异；3. 尝试改进A搜索算法，提高搜索效率。

四、实验步骤1. 设计迷宫数据结构，包括起点、终点和迷宫的宽度和高度；2. 实现A搜索算法，包括初始化、搜索过程和路径输出；3. 实现DFS和BFS算法，并与A搜索算法进行对比；4. 改进A搜索算法，如使用不同的启发式函数或优化搜索策略。

五、实验结果与分析1. A搜索算法在迷宫中的搜索效果：通过实验发现，A搜索算法在迷宫中能够找到一条最短路径，并且搜索效率较高。

在较复杂的迷宫中，A搜索算法仍能较快地找到路径。