寻路算法 Transit Node Routing based on Highway Hierarchies
服务器 路点寻路算法

服务器路点寻路算法在当今信息技术迅猛发展的时代,服务器作为数据处理和存储的核心设备,其性能和效率对于整个信息系统的运行至关重要。
特别是在大规模网络应用、游戏、导航系统等领域,服务器需要处理大量的路径查询请求,如何实现高效、准确的路点寻路算法成为了一个亟待解决的问题。
路点寻路算法不仅要考虑服务器的计算能力,还要兼顾网络带宽、数据传输量以及用户体验等多个方面。
因此,本文旨在探讨服务器上路点寻路算法的设计原理、实现方法以及优化策略,以期为相关领域的研究和实践提供有益的参考。
一、路点寻路算法概述路点寻路算法是一种用于在图形或网络中寻找从起点到终点最优或次优路径的算法。
在服务器应用中,路点通常指的是网络中的节点或位置点,寻路则是指在这些节点之间找到一条符合特定条件的路径。
根据不同的应用场景和需求,路点寻路算法可以分为多种类型,如最短路径算法、最快路径算法、最少换乘算法等。
这些算法在服务器中的实现需要考虑到数据的存储结构、查询效率、并发处理能力等因素。
二、服务器路点寻路算法设计原理2.1 数据结构设计在服务器中实现路点寻路算法,首先需要设计一个合适的数据结构来存储路点和路径信息。
常用的数据结构包括邻接矩阵、邻接表、图等。
邻接矩阵适用于节点数量较少、关系密集的情况,而邻接表则更适合节点数量多、关系稀疏的场景。
图数据结构则可以灵活地表示节点和边的关系,并支持复杂的路径查询操作。
在实际应用中,可以根据路点数量、路径复杂度和查询需求来选择合适的数据结构。
2.2 算法选择与优化路点寻路算法的选择取决于具体的应用场景和需求。
例如,在游戏服务器中,可能需要使用A*算法或Dijkstra算法来寻找最短路径;在导航系统中,则可能需要考虑实时交通信息,使用基于时间的动态路径规划算法。
此外,还可以通过优化算法来提高寻路效率,如使用启发式搜索、剪枝技术、并行计算等方法。
2.3 并发处理与负载均衡服务器通常需要处理大量的并发路径查询请求,因此路点寻路算法的设计需要考虑到并发处理和负载均衡的问题。
寻路算法的理解

寻路算法的理解一、寻路算法是什么呢?哎呀,寻路算法这东西呀,就像是我们在一个超级大的迷宫里找出口的魔法一样。
你想想看,假如你在一个超级复杂的游戏地图里,周围全是弯弯曲曲的小道、高高的墙壁,你要从一个地方到另一个地方,要是没有个好办法,那可就只能像没头的苍蝇一样乱撞啦。
寻路算法就是这样一个超级聪明的办法,它能帮我们在这种超级复杂的环境里,找到一条从起点到终点的路。
比如说在那些超酷的角色扮演游戏里,我们的小角色要从村子跑到遥远的山洞去探险。
寻路算法就开始工作啦,它会把整个地图当成一个大拼图,一块一块地去看,哪些地方能走,哪些地方是走不通的。
它就像一个超级细心的小管家,把所有的路线都放在心里衡量一下,然后选出那条最棒的路线。
二、寻路算法的种类寻路算法可不是只有一种哦,就像世界上有各种各样的小宠物一样,每种都有自己的特点。
有A算法呢,这个算法就像是一个超级学霸,它总是能很快地找到一条看起来很不错的路线。
它是怎么做到的呢?它呀,会给每个可能的路线打分,就像老师给学生的作业打分一样。
分数高的路线,那肯定就是比较好的啦。
还有Dijkstra算法,这个算法就像是一个超级老实的小工人。
它会从起点开始,一点一点地去探索周围的路。
它不会像A算法那样那么聪明地去打分,但是它特别的踏实,一步一个脚印,最后也能找到到达终点的路。
三、寻路算法的重要性寻路算法在我们的生活里可重要啦。
在那些超级大的物流仓库里,有好多好多的货物要搬运。
寻路算法就能帮那些搬运机器人找到最快的路线,这样就能更快地把货物送到该去的地方。
如果没有寻路算法的话,那些机器人可能就会在仓库里绕来绕去,浪费好多好多的时间呢。
在导航软件里也离不开寻路算法呀。
当我们要开车从一个城市到另一个城市的时候,导航软件里的寻路算法就会根据实时的路况,给我们找出一条最不堵车、最快到达的路线。
要是没有它的话,我们可能就会被堵在路上,不停地抱怨啦。
四、寻路算法的小缺点不过呢,寻路算法也不是完美无缺的。
astar寻路算法原理

astar寻路算法原理
A(A星)寻路算法是一种常用的启发式搜索算法,用于在图中
找到从起点到终点的最短路径。
它结合了Dijkstra算法和启发式搜
索的优点,具有较高的搜索效率。
A算法基于图的搜索,其中每个节点表示一个状态,边表示从
一个状态到另一个状态的转移。
算法使用两个函数来评估每个节点
的重要性,g(n)表示从起点到节点n的实际代价,h(n)表示从节点
n到终点的估计代价。
A算法通过综合考虑这两个函数来选择下一个
要扩展的节点。
具体来说,A算法通过维护一个开放列表和一个关闭列表来进
行搜索。
它首先将起点加入开放列表,然后重复以下步骤直到找到
终点或者开放列表为空:
1. 从开放列表中选择f(n)=g(n)+h(n)最小的节点n进行扩展。
2. 将节点n从开放列表中移入关闭列表。
3. 对节点n的相邻节点进行检查,更新它们的g值和f值,并
将它们加入开放列表中。
A算法的关键在于如何选择合适的启发函数h(n)以及如何高效地维护开放列表和关闭列表。
合适的启发函数可以大大提高搜索效率,而高效的列表维护可以减少搜索时间。
总的来说,A算法是一种高效的寻路算法,能够在图中找到最短路径,并且可以通过调整启发函数来适应不同的问题。
浅谈寻路A算法范文

浅谈寻路A算法范文寻路算法(Pathfinding)是计算机中常用的一种算法,通过图形结构中两个节点之间的最佳路径,解决了很多实际问题,如游戏中的NPC寻路、自动驾驶的路径规划等。
其中,A*算法(A-star algorithm)被广泛应用于寻路算法中,本文将对A*算法进行详细介绍。
A*算法是通过启发式算法(Heuristic Search)实现的一种寻路算法,根据估算函数(Heuristic Function)对节点进行评估,并选择具有最小开销的节点进行扩展。
A*算法的核心思想是综合考虑节点的实际开销(G 值)和预估的目标开销(H值),并选择最优节点进行。
在A*算法中,节点的开销是通过计算路径上节点的实际开销和预估开销得到的。
实际开销是指从起始节点到当前节点的移动开销,通常是节点间的距离或代价。
预估开销是通过估算函数对当前节点到目标节点的距离进行评估,常用的估算函数有欧几里得距离、曼哈顿距离等。
A*算法的具体步骤如下:1. 创建一个开启列表(Open List)和一个关闭列表(Closed List),起始节点放入开启列表。
2.从开启列表中选出具有最小开销的节点作为当前节点,并将其放入关闭列表中。
3.对当前节点的所有相邻节点进行遍历,如果该节点不可通过或者在关闭列表中,则忽略。
4.计算相邻节点的实际开销和预估开销,更新节点的G值和H值。
5.如果相邻节点不在开启列表中,将其加入开启列表,并将当前节点设置为该节点的父节点。
6.如果相邻节点已经在开启列表中,比较当前节点作为父节点时的G 值和之前的G值,如果小于之前的G值,更新节点的父节点为当前节点。
7.重复2-6步骤,直到达到目标节点或者开启列表为空。
8.如果达到目标节点,从目标节点开始回溯父节点,得到最佳路径。
A*算法的优势在于通过使用估算函数,能够快速找到目标节点,而且能够保证找到的路径是最佳路径。
同时,A*算法可以通过调整估算函数的权重来权衡的速度和路径的质量。
寻路算法发展史

寻路算法发展史
寻路算法是一种常见的算法,在许多领域中都有应用,尤其是在游戏领域。
以下是寻路算法的发展史:
- 宽度优先搜索算法:这是一种简单的寻路算法,它会优先扩展距离起始点最近的节点,然后再扩展相邻的节点,以此类推,直到找到目标点为止。
- Dijkstra 算法:这是一种基于图的寻路算法,它可以找到从起始点到目标点的最短路径。
该算法通过不断更新每个节点的最短路径,最终找到最短路径。
- 贪心算法:这种算法基于贪心策略,每次选择当前状态下的最优解,从而逐步接近目标点。
- A*搜索算法:这是一种启发式寻路算法,它通过评估每个节点的启发值来指导搜索方向,从而更快地找到目标点。
- B*搜索算法:这是一种改进的 A*算法,它考虑了路径的弯曲程度,从而更加准确地预测搜索方向。
随着寻路算法的不断发展和改进,其应用范围也不断扩大,在游戏、机器人、导航等领域都有着广泛的应用。
Unity3D

Unity3D 官⽅⽂档 NavMesh三个组件的翻译与解释⾃动寻路需要知道的细节版本:unity 5.4.1 语⾔:C#总起:最近研究的ARPG游戏中,敌⼈AI的寻路就使⽤到了NavMesh,Unity该套组件倒也不复杂:三个组件和⼀个烘培的Map。
我这边不讲基础怎么使⽤,主要是翻译⼀下各个组件的属性,说说需要注意的事情。
主要参考就是官⽅⽂档和⾃⼰在Unity中的⼀些实践。
NavMesh中实现了A*算法作为底层的算法,使⽤NavMesh Agent可以作为⾓⾊的⽬标路径查找代理,⽽NavMesh Obstacle则是动态的⼀些障碍物,Off-Mesh Link作为特殊路径点的连接,并且可以与Animator动画组件实现经过特殊路径的动画,⽐如开门,连接门内门外的路径点,并执⾏Animator中的开门动画,这样的需求就可以⽤Off-Mesh Link来实现。
寻路三⼤组件:♦NavMesh Agent:NavMeshAgent⽤于⾓⾊的寻路代理,可以在预先烘培的NavMesh中找到⽬标的⼀条路线,并且尽可能的规避其他的Agent 和Obstacle。
(直接官⽅贴图拿来⽤了)Radius Radius of the agent, used to calculate collisions between obstacles and other agents.agent的半径,⽤于计算该agent和其他agent、obstacle的碰撞。
Height The height clearance the agent needs to pass below an obstacle overhead.agent的⾼度,agent可以通过的头顶障碍最⼩⾼度。
Base offset Offset of the collision cylinder in relation to the transform pivot point.agent圆柱碰撞体中⼼点的偏移值。
navmesh 寻路算法步骤

一、介绍navmesh寻路算法1.1 什么是navmesh1.2 navmesh寻路算法的作用1.3 navmesh寻路算法的应用领域二、navmesh寻路算法的基本原理2.1 基于图的路径规划2.2 navmesh网格的构建2.3 寻路算法的实现三、navmesh寻路算法的步骤3.1 准备工作3.2 寻路起点和终点的指定3.3 寻路算法的执行3.4 路径的优化和平滑四、常用的navmesh寻路算法4.1 A*算法4.2 Dijkstra算法4.3 Floyd-Warshall算法五、navmesh寻路算法的优缺点5.1 优点5.2 缺点六、navmesh寻路算法在游戏开发中的应用6.1 游戏场景中的角色移动6.2 路径规划和本人行为控制6.3 实际应用案例分析七、结语一、介绍navmesh寻路算法1.1 什么是navmeshnavmesh是一种用于游戏开发中角色寻路的网格数据结构,它以三角形网格的形式表示游戏场景中的可行走区域,可以用于快速、高效地进行路径规划和寻路。
1.2 navmesh寻路算法的作用navmesh寻路算法可以帮助游戏中的角色实现智能的移动和路径规划,使游戏中的NPC、玩家角色等能够根据场景的实时变化自动调整移动路径,提升游戏的真实感和趣味性。
1.3 navmesh寻路算法的应用领域navmesh寻路算法广泛应用于游戏开发中,特别是3D游戏中的角色移动、本人行为控制等方面,也被用于虚拟仿真、建筑规划等领域。
二、navmesh寻路算法的基本原理2.1 基于图的路径规划navmesh寻路算法基于图的路径规划原理,将游戏场景中的可行走区域表示为一个有向图,角色的移动路径即为在这个图中的一条最优路径。
2.2 navmesh网格的构建navmesh网格的构建是navmesh寻路算法的基础,它通过对游戏场景中的可行走区域进行采样、三角化等处理,生成一个表示可行走区域的三角形网格。
2.3 寻路算法的实现navmesh寻路算法的核心是寻路算法的实现,常用的寻路算法包括A*算法、Dijkstra算法、Floyd-Warshall算法等,它们通过对navmesh网格进行搜索和路径评估,找到从起点到终点的最短路径。
寻路算法实验报告

一、实验目的1. 熟悉和掌握寻路算法的基本原理和实现方法;2. 了解不同寻路算法的优缺点和应用场景;3. 通过实际编程实现寻路算法,提高算法设计能力。
二、实验原理寻路算法是指在一个给定图中,寻找从起点到终点的一条路径的算法。
常见的寻路算法有深度优先搜索(DFS)、广度优先搜索(BFS)、A搜索等。
本实验将重点介绍A搜索算法,并对其原理进行详细阐述。
A搜索算法是一种启发式搜索算法,其核心思想是利用启发式函数来评估路径的优劣,从而在搜索过程中优先选择最有希望的路径。
A搜索算法的估价函数f(n)由两部分组成:g(n)表示从起点到当前节点n的实际代价,h(n)表示从当前节点n到终点d的估计代价。
A搜索算法的流程如下:1. 初始化:将起点加入开放列表(Open List),将终点加入封闭列表(Closed List);2. 循环:a. 从开放列表中选出f(n)最小的节点n;b. 将节点n从开放列表移除,加入封闭列表;c. 遍历节点n的邻居节点m;d. 如果m在封闭列表中,跳过;e. 如果m不在开放列表中,将m加入开放列表;f. 如果m在开放列表中,且新的g(n)小于原来的g(m),则更新m的f(n)、g(n)和父节点;3. 当终点被加入开放列表时,搜索结束。
三、实验内容1. 实现A搜索算法,并验证其在不同迷宫中的搜索效果;2. 对比A搜索算法与DFS、BFS算法在搜索效果和效率上的差异;3. 尝试改进A搜索算法,提高搜索效率。
四、实验步骤1. 设计迷宫数据结构,包括起点、终点和迷宫的宽度和高度;2. 实现A搜索算法,包括初始化、搜索过程和路径输出;3. 实现DFS和BFS算法,并与A搜索算法进行对比;4. 改进A搜索算法,如使用不同的启发式函数或优化搜索策略。
五、实验结果与分析1. A搜索算法在迷宫中的搜索效果:通过实验发现,A搜索算法在迷宫中能够找到一条最短路径,并且搜索效率较高。
在较复杂的迷宫中,A搜索算法仍能较快地找到路径。
unity寻路线的实现方法

unity寻路线的实现方法
在Unity中实现寻路线有多种方法,其中最常用的是使用Unity内置的NavMesh系统或者寻路算法。
下面我将从两个方面来介绍这两种方法。
1. 使用Unity的NavMesh系统:
Unity的NavMesh系统是一种基于网格的寻路系统,它可以帮助游戏对象在场景中自动寻找路径。
要使用NavMesh系统,首先需要在场景中设置NavMesh面,然后在需要进行寻路的游戏对象上添加NavMeshAgent组件。
NavMeshAgent组件可以根据NavMesh面自动计算路径并移动游戏对象。
你可以通过代码控制NavMeshAgent 的目标位置,它会自动寻找最佳路径并移动到目标位置。
2. 使用寻路算法:
如果你需要更加灵活的寻路方式,可以考虑使用寻路算法,比如A算法。
A算法是一种常用的寻路算法,它可以在游戏场景中找到最佳路径并导航游戏对象移动。
要使用A算法,你可以使用Unity Asset Store中提供的一些寻路插件,比如A Pathfinding
Project。
这些插件提供了可视化的编辑器工具,可以帮助你在场景中设置障碍物、目标点等,并且提供了API接口,可以在代码中调用进行路径计算和移动控制。
总的来说,Unity的NavMesh系统适用于简单的场景寻路,而寻路算法适用于复杂的场景和更灵活的寻路需求。
你可以根据具体的游戏需求选择合适的方法来实现寻路线。
希望这些信息能够帮助到你。
astar寻路算法原理 -回复

astar寻路算法原理-回复A*寻路算法原理及步骤一、简介A*(A-Star)寻路算法是一种常用的路径规划算法,用于找到两个点之间的最短路径。
它综合了Dijkstra算法和贪心算法的优点,既考虑了每个节点的代价,也考虑了每个节点到目标节点的预估代价。
本文将一步一步详细介绍A*寻路算法的原理和步骤。
二、原理A*算法的核心思想是使用一个估算函数来预测从起始节点到目标节点的代价,并在遍历过程中选择最小代价节点来进行扩展。
该算法综合了代价函数和启发函数的信息,以更快地找到最短路径。
其具体步骤如下:1. 初始化将起始节点添加到一个开放列表(open list)中,开放列表存放待扩展的节点。
同时,创建一个空的闭合列表(closed list),用于存放已扩展过的节点。
2. 循环操作进入循环操作,直到开放列表为空或找到目标节点。
在每次循环中,选择开放列表中代价最小的节点进行扩展。
3. 节点扩展取开放列表中代价最小的节点,将其从开放列表中删除,并加入到闭合列表中。
然后,获取该节点的相邻节点,计算它们的代价和预估代价,并更新它们的代价值和路径。
4. 判断相邻节点对于每个相邻节点,判断它们是否在开放列表或闭合列表中。
若在闭合列表,则跳过该节点;若在开放列表,比较新路径与旧路径的代价,若新路径更好,则更新代价和路径;否则,不做任何操作。
5. 添加新节点对于不在开放列表中的相邻节点,将它们添加到开放列表中,并计算它们的代价和预估代价。
6. 重复操作重复步骤2至5,直到开放列表为空或找到目标节点。
若开放列表为空,则无法找到路径;若找到目标节点,则回溯路径,回到起始节点。
三、关键要点在上述步骤中,有几个关键要点需要注意:1. 代价函数代价函数用于计算节点到起始节点的实际代价,包括走过的距离、障碍物等影响因素。
根据具体情况,可以自定义代价函数。
2. 启发函数启发函数用于估算节点到目标节点的代价,即预测代价。
常见的启发函数有曼哈顿距离、欧几里得距离等,根据实际情况选择合适的启发函数。
寻路算法

A* 寻路算法2010-02-11 1:44施健泉1.概述虽然掌握了A* 算法的人认为它容易,但是对于初学者来说,A* 算法还是很复杂的。
2.搜索区域(The Search Area)我们假设某人要从A 点移动到B 点,但是这两点之间被一堵墙隔开。
如图1。
(绿色是A ,红色是B ,中间蓝色是墙)图 1你应该注意到了,我们把要搜寻的区域划分成了正方形的格子。
这是寻路的第一步,简化搜索区域,就像我们这里做的一样。
这个特殊的方法把我们的搜索区域简化为了2维数组。
数组的每一项代表一个格子,它的状态就是可走(walkable) 和不可走(unwalkable)两种。
通过计算出从 A 到 B 需要走过哪些方格,就找到了路径。
一旦路径找到了,人物便从一个方格的中心移动到另一个方格的中心,直至到达目的地。
方格的中心点我们成为“节点(nodes) ”。
如果你读过其他关于A* 寻路算法的文章,你会发现人们常常都在讨论节点。
为什么不直接描述为方格呢?因为我们有可能把搜索区域划为其他多边形而不是正方形,例如可以是六边形,矩形,甚至可以是任意多变形。
而节点可以放在任意多边形里面,可以放在多变形的中心,也可以放在多边形的边上。
我们使用这个系统,因为它最简单。
3.开始搜索(Starting the Search)一旦我们把搜寻区域简化为一组可以量化的节点后,就像上面做的一样,我们下一步要做的便是查找最短路径。
在A* 中,我们从起点开始,检查其相邻的方格,然后向四周扩展,直至找到目标。
我们这样开始我们的寻路旅途:3.1从起点A 开始,并把它就加入到一个由方格组成的open list( 开放列表) 中。
这个open list 有点像是一个购物单。
当然现在open list 里只有一项,它就是起点A ,后面会慢慢加入更多的项。
open list 里的格子是路径可能会是沿途经过的,也有可能不经过。
基本上open list 是一个待检查的方格列表。
寻路算法
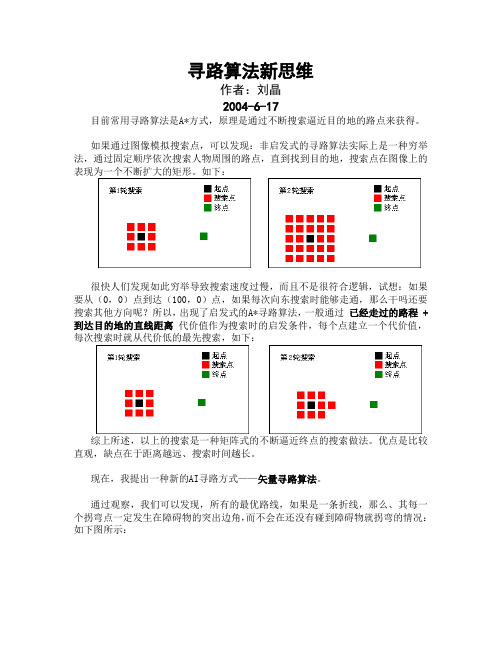
寻路算法新思维作者:刘晶2004-6-17目前常用寻路算法是A*方式,原理是通过不断搜索逼近目的地的路点来获得。
如果通过图像模拟搜索点,可以发现:非启发式的寻路算法实际上是一种穷举法,通过固定顺序依次搜索人物周围的路点,直到找到目的地,搜索点在图像上的表现为一个不断扩大的矩形。
如下:很快人们发现如此穷举导致搜索速度过慢,而且不是很符合逻辑,试想:如果要从(0,0)点到达(100,0)点,如果每次向东搜索时能够走通,那么干吗还要搜索其他方向呢?所以,出现了启发式的A*寻路算法,一般通过已经走过的路程 + 到达目的地的直线距离代价值作为搜索时的启发条件,每个点建立一个代价值,每次搜索时就从代价低的最先搜索,如下:综上所述,以上的搜索是一种矩阵式的不断逼近终点的搜索做法。
优点是比较直观,缺点在于距离越远、搜索时间越长。
现在,我提出一种新的AI寻路方式——矢量寻路算法。
通过观察,我们可以发现,所有的最优路线,如果是一条折线,那么、其每一个拐弯点一定发生在障碍物的突出边角,而不会在还没有碰到障碍物就拐弯的情况:如下图所示:我们可以发现,所有的红色拐弯点都是在障碍物(可以认为是一个凸多边形)的顶点处,所以,我们搜索路径时,其实只需要搜索这些凸多边形顶点不就可以了吗?如果将各个顶点连接成一条通路就找到了最优路线,而不需要每个点都检索一次,这样就大大减少了搜索次数,不会因为距离的增大而增大搜索时间。
这种思路我尚未将其演变为算法,姑且提出一个伪程序给各位参考:1.建立各个凸多边形顶点的通路表TAB,表示顶点A到顶点B是否可达,将可达的顶点分组保存下来。
如: ( (0,0) (100,0) ),这一步骤在程序刚开始时完成,不要放在搜索过程中空耗时间。
2.开始搜索A点到B点的路线3.检测A点可以直达凸多边形顶点中的哪一些,挑选出最合适的顶点X1。
4.检测与X1相连(能够接通)的有哪些顶点,挑出最合适的顶点X2。
5.X2是否是终点B?是的话结束,否则转步骤4(X2代入X1)如此下来,搜索只发生在凸多边形的顶点,节省了大量的搜索时间,而且找到的路线无需再修剪锯齿,保证了路线的最优性。
navmesh 寻路算法步骤 -回复

navmesh 寻路算法步骤-回复Navmesh寻路算法步骤导言:Navmesh(Navigation Mesh)是游戏开发中常用的寻路算法,它通过将场景网格化来实现寻路效果,其优点是可以处理复杂的场景以及障碍物,使得角色可以在场景中自由移动,提高游戏的可玩性。
本文将详细介绍Navmesh寻路算法的步骤。
1. 场景建模:Navmesh寻路算法需要基于地图的场景建模来进行寻路。
首先需要确定寻路的起点和终点,然后将场景的地形通过网格划分成一系列三角形,这些三角形就构成了Navmesh的基本单位,也称为导航网格。
2. 导航网格生成:根据场景的地形和导航需求,生成导航网格是Navmesh寻路算法的关键步骤。
在该步骤中,需要通过一系列的算法和规则来生成导航网格。
常见的生成方法有:手动生成、自动生成和混合方法。
手动生成方式是通过编辑器手动绘制三角形,然后连接起来形成导航网格。
自动生成方式是通过算法在地图上自动生成导航网格,常用的自动生成算法有Delaunay三角剖分算法、Voronoi图算法等。
混合方法是手动生成和自动生成的组合,即可以通过手动编辑一部分导航网格,然后通过算法自动生成其余部分。
3. 导航网格优化:生成导航网格后,需要进行优化处理,以提高寻路算法的效率和准确性。
常见的导航网格优化方法有:合并小三角形、合并共线三角形、三角化等。
合并小三角形是将面积过小的三角形合并成邻接的大三角形,减少导航网格的复杂度。
合并共线三角形是将共线的三角形合并成一个更大的三角形,以缩小导航网格的规模。
三角化是将导航网格中存在凹多边形的部分进行三角化,以确保寻路算法能够正确处理复杂的几何形状。
4. 寻路图生成:导航网格生成完成后,需要生成一个寻路图,以进行路径搜索。
寻路图主要包括节点和连接关系。
节点是导航网格的基本单位,连接关系表示两个节点之间是否存在通路。
生成寻路图的方式有多种,常见的方法有:A*算法、网格图优化等。
A*算法是一种常见的启发式搜索算法,通过评估启发式函数的值来选择最优的路径。
最优寻路算法公式

最优寻路算法公式寻路算法,这听起来是不是有点高大上?别急,让我慢慢给您讲讲这其中的门道。
您知道吗?就像我们每天出门找路去上班、上学或者去玩耍一样,在计算机的世界里,程序也得“找路”。
比如说,在一个游戏里,角色怎么从 A 点走到 B 点,走哪条路最快、最省事儿,这就得靠寻路算法来帮忙啦。
先来说说最简单的一种寻路算法,叫深度优先搜索。
这就好比您走进了一个迷宫,啥也不想,先一条道走到黑,走不通了再回头换条路。
听起来有点笨是不是?但有时候还真能管用。
我想起之前玩一个解谜游戏,里面的小角色就得靠这种简单的算法来找路。
那个场景是在一个古老的城堡里,到处都是弯弯绕绕的通道和紧闭的门。
我控制的小角色就这么闷着头往前走,有时候走进死胡同,那叫一个郁闷。
但当它终于找到出路的时候,那种惊喜感简直难以言表。
再说说广度优先搜索算法。
这个就像是您在探索迷宫的时候,一层一层地往外扩,把周围能走的路都先看一遍,再决定下一步往哪走。
这种算法相对更全面一些,不容易错过好的路线。
有一次我设计一个小程序,要让一个小机器人在一个虚拟的地图上找宝藏。
我一开始用了深度优先搜索,结果小机器人老是迷路。
后来换成广度优先搜索,嘿,它很快就找到了通往宝藏的最佳路径,那感觉就像我自己找到了宝藏一样兴奋。
然后咱们来聊聊 A* 算法。
这可是寻路算法里的大明星!它综合考虑了距离和预估的代价,就像是您出门前不仅知道距离有多远,还能大概猜到路上会不会堵车、好不好走。
我曾经参与过一个物流配送的项目,要给送货的车规划最优路线。
用了 A* 算法之后,送货的效率大大提高,司机师傅们都夸这个算法厉害,省了不少油钱和时间。
还有 Dijkstra 算法,它总是能找到从起点到所有点的最短路径。
这就像是您有一张超级详细的地图,能清楚地知道去任何地方的最短距离。
在实际应用中,选择哪种寻路算法可不是随便拍拍脑袋就能决定的。
得看具体的情况,像地图的大小、复杂程度,还有对时间和资源的限制等等。
从头理解JPS寻路算法

从头理解JPS寻路算法JPS(Jump Point Search)寻路算法是一种高效的路径算法,其核心思想是通过优化跳跃点来减少的节点数量,从而提高寻路效率。
本文将从头理解JPS寻路算法,并详细介绍其原理、流程和关键步骤。
一、JPS寻路算法原理JPS寻路算法基于A*(A star)算法,但通过引入跳跃点的概念来减少路径的节点数量。
跳跃点是一种特殊类型的节点,它们对路径具有重要的作用。
JPS算法通过识别和利用每个节点上的跳跃点,来跳过不必要的检查和,从而加速路径的查找。
二、JPS寻路算法流程1.初始化起始节点和目标节点,将起始节点加入开启列表。
2.当开启列表非空时,重复以下步骤:-从开启列表中选择最佳节点作为当前节点,并将其从开启列表中移出。
-将当前节点加入封闭列表。
-如果当前节点是目标节点,表示已找到路径,结束。
-否则,计算当前节点的所有邻居节点(包括跳跃点和普通节点)。
-对于每个邻居节点,进行以下处理:-如果邻居节点已在封闭列表中,跳过该节点。
-计算邻居节点的G值(从起始节点到邻居节点的实际代价)。
-如果邻居节点不在开启列表中,将其加入开启列表,并更新其G值和父节点。
-如果邻居节点已在开启列表中,检查是否通过当前节点到达该节点更短,如果是则更新其G值和父节点。
3.如果开启列表为空,表示未找到路径。
三、JPS寻路算法关键步骤1.节点的扩展方式:JPS算法通过事先查找每个节点的跳跃点来减少的节点数量。
节点的扩展方式有四种:水平、垂直、对角线和跳跃。
-水平扩展:从当前节点开始,沿着水平方向扩展,直到遇到障碍物或边界。
-垂直扩展:从当前节点开始,沿着垂直方向扩展,直到遇到障碍物或边界。
-对角线扩展:从当前节点开始,沿着对角线方向扩展,直到遇到障碍物、边界或对角线上的一个跳跃点。
-跳跃扩展:从当前节点开始,在每个扩展方向上,找到一个或多个跳跃点,并沿该跳跃点继续扩展,直到遇到障碍物、边界或目标节点。
2.跳跃点的确定:跳跃点是指在一些方向上可以直接跳过多个节点的特殊节点。
寻路算法 Transit Node Routing based on Highway Hierarchies

Transit Node Routing based on Highway Hierarchies Peter Sanders Dominik SchultesRoute PlanningGoals:exact shortest(i.e.fastest)paths in large road networks fast queriesfast preprocessinglow space consumptionApplications:route planning systems in the internetcar navigation systems···Motivation‘Problem’:existing solutions are already‘too fast’.Example:perform a query(using hwy.hierarchies):≈1msvisualise the path(using our Java application):≈400msCounter-Argument:applications that require a lot of queries(and only a few paths)massive traffic simulationsoptimisations in logistics systemsKarlsruhe→CopenhagenKarlsruhe→BerlinKarlsruhe→ViennaKarlsruhe→MunichKarlsruhe→RomeKarlsruhe→ParisKarlsruhe→LondonKarlsruhe→BrusselsKarlsruhe→CopenhagenKarlsruhe→BerlinKarlsruhe→ViennaKarlsruhe→MunichKarlsruhe→RomeKarlsruhe→ParisKarlsruhe→LondonKarlsruhe→BrusselsFirst ObservationFor long-distance travel:leave current locationvia one of only a few‘important’traffic junctions,called access points( we can afford to store all access points for each node) [in Europe:about10access points per node on average]Karlsruhe→BerlinKarlsruhe→BerlinKarlsruhe→BerlinSecond ObservationEach access point is relevant for several nodes.union of the access points of all nodes is small,called transit node set( we can afford to store the distances between all transit node pairs) [in Europe:about10000transit nodes]Transit Node RoutingPreprocessing:identify transit node set T⊆Vcompute complete|T|×|T|distance tablefor each node:identify its access points(mapping A:V→2T),store the distancesQuery(source s and target t given):computed top(s,t):=min{d(s,u)+d(u,v)+d(v,t):u∈A(s),v∈A(t)}Transit Node RoutingLocality Filter:local cases must befiltered( special treatment) L:V×V→{true,false}¬L(s,t)implies d(s,t)=d top(s,t)ExampleRelated Workseparator-based implementation[Müller et al.2006]–determine separator nodes(=transit nodes)–partition the graph into small components–access points of node u:border nodes of u’s component–localityfilter:“same component?”grid-based implementation[Bast,Funke,Matijevic2006]–compute geometric subdivision of the network into cells–access points:border nodes needed for‘long-distance’travel–transit nodes:union of all access points–localityfilter:“less than a certain number of grid cells apart?”Our Approach:Highway Hierarchies1complete search within a local areasearch in a (thinner )highway network =minimal graph that preserves all shortest pathscontract network,e.g.,iterate highway hierarchyExample:Karlsruhe123Local Areachoose neighbourhood radius r(s)(by a heuristic)define neighbourhood of sN(s):={v∈V|d(s,v)≤r(s)}Highway NetworkEdge(u,v)belongs to highway network iff there are nodes s and t s.t.(u,v)is on the“canonical”shortest path from s to tand(u,v)is not entirely within N(s)or N(t)ContractionDistance Table:Search Space ExampleDistance TableCompute an all-pairs distance tablefor the core of the topmost levelℓ.13465×13465entriesAbort the search when all entrance points in thecore of levelℓhave been encountered.≈55for each direction Use the distance table to bridge the gap.≈55×55entriesHH-based Transit Node RoutingCompute an all-pairs distance tablefor the core of the topmost levelℓ.13465×13465entries transit node set TAbort the search when all entrance points in thecore of levelℓhave been encountered.≈55for each direction do not‘search’,just perform look-upsUse the distance table to bridge the gap.≈55×55entriesMissing Pieces1.localityd(s,t)=d u(s,t)<d top(s,t) L(s,t):=“disks of s and t overlap”Missing Pieces2.too many‘entrance points’(55)solution:fall back on comparatively few‘access points’(10) (motivated by the observations from[Bast,Funke,Matijevic2006])Missing Piecespute top distance table in the original graphsolution:[Knopp,S,S,Schulz,Wagner2007]“Computing Many-to-Many Shortest PathsUsing Highway Hierarchies”(e.g.10000×10000table in one minute)for each t∈T,perform backward search up to top levelℓ,store search space entries(t,u,d(u,t))arrange search spaces:group entries by ufor each s∈T,perform forward search,at each node u,scan all entries(t,u,d(u,t))andcompute d(s,u)+d(u,t)Second Layer(to deal with medium range queries)secondary transit node set T2⊃Tsecondary access mapping A2:V→2T2d(u,v):u,v∈T2∧d(u,v)=d top(u,v) secondary dist.tablesecondary localityfilter L2¬L2(s,t)impliesd(s,t)=d top(s,t)ORd(s,t)=min{d(s,u)+d(u,v)+d(v,t):u∈A2(s),v∈A2(t)}Two Concrete VariantsPreprocessingfor each secondary transit node t∈T2:–perform backward highway search–stop at primary transit nodes( set of backward access points)–store search space entries(t,u,d(u,t))arrange search spacesPreprocessingfor each secondary transit node s∈T2:–perform forward highway search–stop at primary transit nodes( set of forward access points)–at each node u and for each search space entry(t,u,d(u,t)):∗compute distance d u(s,t):=d(s,u)+d(u,t)via u∗compute distance d top(s,t)via top layer∗if d u(s,t)<d top(s,t)then·add entry d u(s,t)to the secondary distance table·ensure that the disks around s and t contain u(use similar procedure for lower layers)ExperimentsW.Europe(PTV)USA(TIGER/Line)#nodes#directed edges#road categoriesspeed range[km/h]Preprocessinglayer2|T||A|space timeUSA timeeco184379 4.910674 5.72443:25 dist eco10235210.9EUR timeeco118356 5.5112939.92512:44 dist eco6977513.1Querylayer2[%]wrong cont’d time0.14 1.1311.5µs gen0.00140.01381.578.1087.5µs0.54 2.8713.4µs gen0.00150.01904.6818.32107.4µsDijkstra RankQ u e r y T i m e [µs ]2526272829210211212213214215216217218219220221222223224510204010030010005102040100300100Local Queries:USA,travel time metricDetermine Shortest Pathsfrom source s,look iteratively for the next adjacent node s′thatleads to fwd acc pnt ud(s,s′)+d(s′,u)=d(s,u)analogously,from target to bwd acc pntfrom fwd acc pnt u,look iteratively for the next adjacent node u′in the topmost level that leads to bwd acc pnt vd(u,u′)+d(u′,v)=d(u,v)(if necessary,use a hidden path instead)unpack shortcutsif path not through top layer,fall back on highway query。
寻路算法TransitNodeRoutingbasedonHighwayHierarchies

visualise the path(using our Java application):≈400ms
Counter-Argument:
applications that require a lot of queries(and only a few paths)
massive traf?c simulations
ystems
Karlsruhe→Copenhagen
Karlsruhe→Berlin
Karlsruhe→Vienna
Karlsruhe→Munich
Karlsruhe→Rome
Karlsruhe→Paris
寻路算法TransitNodeRoutingbasedonHighwayHierarchies
Transit Node Routing based on Highway Hierarchies Peter Sanders Dominik Schultes
Route Planning
Goals:
exact shortest(i.e.fastest)paths in large road networks fast queries
寻路算法 transit node routing based on highway hierarchies transit node routing based on highway hierarchies peter sanders dominik schultes route planning goals: exact shortest(i.e.fastest)paths in large road networks fast queries fast preprocessing low space consumption applications: route planning systems in the internet car navigation systems ··· motivation 'problem': existing solutions are already'too fast'. example:perform a query(using hwy.hierarchies):≈1ms visualise the path(using our java application):≈400ms counter-argument: applications that require a lot of queries(and only a few paths) massive traf?c simulations optimisations in logistics systems karlsruhe→copenhagen karlsruhe→berlin karlsruhe→vienna karlsruhe→munich karlsruhe→rome karlsruhe→paris karlsruhe→london karlsruhe→brussels karlsruhe→copenhagen karlsruhe→berlin karlsruhe→vienna karlsruhe→munich karlsruhe→rome karlsruhe→paris karlsruhe→london karlsruhe→brussels
基于打破对称性的快速寻路算法

基于打破对称性的快速寻路算法邱磊【期刊名称】《宁夏大学学报(自然科学版)》【年(卷),期】2014(000)003【摘要】Jump Point Search (JPS)algorithm is implemented in Java,and the implementation procedures of JPS algorithm is given.Experimental results show that an optimal path has been found by JPS algorithm from start node to goal node,which could identify and eliminate path symmetries on grid maps effectively, so it reduces nodes number expanded by a large paring JPS with A*,Breadth First Search, Best First Search and Dijkstra,the results show that JPS is faster over them more pronounced on condition of the path length being computed are uniform.For these reasons,JPS algorithm is fast and effective.%基于Java实现了跳点搜索算法,给出了算法实现的过程。
实验结果表明:跳点搜索算法找到了一条从起始节点到目标节点的最优路径,且能够有效地识别和消除网格地图上的路径对称性,大幅度减少了节点扩展的数量。
对比 A*、宽度优先搜索、最佳优先搜索和Dijkstra可知,在所求解的路径长度一致的情况下,跳点搜索在平均搜索时间上显著快于其他算法。
UE3导航网格寻路算法概述

目录:1,导航网格寻路 —— 导航寻路和传统路点寻路比较 2,导航网格寻路 —— 寻路方法3,导航网格寻路 —— 生成导航网格需要的几何知识 4,导航网格寻路 —— 生成导航网格5,导航网格寻路 —— 生成网格的一些补充6,导航网格寻路 —— A*寻路实现细节7,导航网格寻路 —— 一些优化1,导航网格寻路 -- 介绍传统路点寻路截图下图是一个寻路路点的截图导航网格寻路截图下图是一个导航网格截图路点寻路和导航网格的比较,具有的不足之处:1. 一些复杂的游戏地图需要的路点数量过于庞大,比如柱角拐弯较多的地方,这样将会大大降低寻路算法的效率。
而导航网格多边形数量对于同样的地形则能保持比较少的数量水平。
路点所需要路点数:导航网格所需要的多边形数:显然,导航网格需要的多边形数大大降低。
2. 路点寻路即使在直线线路上没有阻挡,有时也会使角色走折线路径。
而导航路径寻路,则可以保证直线行走。
如下图A点和B点之间的路径路点寻路如下图(产生了”Z”字型寻路路径)导航网格寻路如下图(产生了直线寻路路径)3. 路点寻路路径在拐弯处不能进行路径平滑,而导航网格则可以通过曲线来平滑路径,只要保证该曲线在导航网格内即可。
如下所示,红线是路径寻路的路线,蓝线是导航网格通过曲线平滑的路线。
4. 路点寻路数据不包含任何地形外的物体数据,所以路点寻路系统在处理动态阻挡的时候去修改路径是很困难的。
而导航网格包含地形信息,能够知道网格内哪些区域有动态阻挡物体,通过射线投射能够方便地动态修改行走路线。
路点寻路在遇到动态阻挡的情况导航网格遇到动态阻挡的情况,能够在导航网格内找到可通行的一条折线路径。
5. 路径点寻路不能根据不同的寻路角色来改变路径(例如不同角色有不同的包围盒),而导航网格则可以处理这种情况。
下图是寻路路点在拐角处的情形,该路径能够保证一个人顺利拐弯,但对于一辆坦克却无能为力,因为坦克的包围盒半径通过该路点时要撞上阻挡物。
下图是导航网格的情况,这时人和坦克能够根据包围盒信息,通过导航网格计算出两条符合对应角色的路径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Transit Node Routing based on Highway Hierarchies Peter Sanders Dominik SchultesRoute PlanningGoals:exact shortest(i.e.fastest)paths in large road networks fast queriesfast preprocessinglow space consumptionApplications:route planning systems in the internetcar navigation systems···Motivation‘Problem’:existing solutions are already‘too fast’.Example:perform a query(using hwy.hierarchies):≈1msvisualise the path(using our Java application):≈400msCounter-Argument:applications that require a lot of queries(and only a few paths)massive traffic simulationsoptimisations in logistics systemsKarlsruhe→CopenhagenKarlsruhe→BerlinKarlsruhe→ViennaKarlsruhe→MunichKarlsruhe→RomeKarlsruhe→ParisKarlsruhe→LondonKarlsruhe→BrusselsKarlsruhe→CopenhagenKarlsruhe→BerlinKarlsruhe→ViennaKarlsruhe→MunichKarlsruhe→RomeKarlsruhe→ParisKarlsruhe→LondonKarlsruhe→BrusselsFirst ObservationFor long-distance travel:leave current locationvia one of only a few‘important’traffic junctions,called access points( we can afford to store all access points for each node) [in Europe:about10access points per node on average]Karlsruhe→BerlinKarlsruhe→BerlinKarlsruhe→BerlinSecond ObservationEach access point is relevant for several nodes.union of the access points of all nodes is small,called transit node set( we can afford to store the distances between all transit node pairs) [in Europe:about10000transit nodes]Transit Node RoutingPreprocessing:identify transit node set T⊆Vcompute complete|T|×|T|distance tablefor each node:identify its access points(mapping A:V→2T),store the distancesQuery(source s and target t given):computed top(s,t):=min{d(s,u)+d(u,v)+d(v,t):u∈A(s),v∈A(t)}Transit Node RoutingLocality Filter:local cases must befiltered( special treatment) L:V×V→{true,false}¬L(s,t)implies d(s,t)=d top(s,t)ExampleRelated Workseparator-based implementation[Müller et al.2006]–determine separator nodes(=transit nodes)–partition the graph into small components–access points of node u:border nodes of u’s component–localityfilter:“same component?”grid-based implementation[Bast,Funke,Matijevic2006]–compute geometric subdivision of the network into cells–access points:border nodes needed for‘long-distance’travel–transit nodes:union of all access points–localityfilter:“less than a certain number of grid cells apart?”Our Approach:Highway Hierarchies1complete search within a local areasearch in a (thinner )highway network =minimal graph that preserves all shortest pathscontract network,e.g.,iterate highway hierarchyExample:Karlsruhe123Local Areachoose neighbourhood radius r(s)(by a heuristic)define neighbourhood of sN(s):={v∈V|d(s,v)≤r(s)}Highway NetworkEdge(u,v)belongs to highway network iff there are nodes s and t s.t.(u,v)is on the“canonical”shortest path from s to tand(u,v)is not entirely within N(s)or N(t)ContractionDistance Table:Search Space ExampleDistance TableCompute an all-pairs distance tablefor the core of the topmost levelℓ.13465×13465entriesAbort the search when all entrance points in thecore of levelℓhave been encountered.≈55for each direction Use the distance table to bridge the gap.≈55×55entriesHH-based Transit Node RoutingCompute an all-pairs distance tablefor the core of the topmost levelℓ.13465×13465entries transit node set TAbort the search when all entrance points in thecore of levelℓhave been encountered.≈55for each direction do not‘search’,just perform look-upsUse the distance table to bridge the gap.≈55×55entriesMissing Pieces1.localityd(s,t)=d u(s,t)<d top(s,t) L(s,t):=“disks of s and t overlap”Missing Pieces2.too many‘entrance points’(55)solution:fall back on comparatively few‘access points’(10) (motivated by the observations from[Bast,Funke,Matijevic2006])Missing Piecespute top distance table in the original graphsolution:[Knopp,S,S,Schulz,Wagner2007]“Computing Many-to-Many Shortest PathsUsing Highway Hierarchies”(e.g.10000×10000table in one minute)for each t∈T,perform backward search up to top levelℓ,store search space entries(t,u,d(u,t))arrange search spaces:group entries by ufor each s∈T,perform forward search,at each node u,scan all entries(t,u,d(u,t))andcompute d(s,u)+d(u,t)Second Layer(to deal with medium range queries)secondary transit node set T2⊃Tsecondary access mapping A2:V→2T2d(u,v):u,v∈T2∧d(u,v)=d top(u,v) secondary dist.tablesecondary localityfilter L2¬L2(s,t)impliesd(s,t)=d top(s,t)ORd(s,t)=min{d(s,u)+d(u,v)+d(v,t):u∈A2(s),v∈A2(t)}Two Concrete VariantsPreprocessingfor each secondary transit node t∈T2:–perform backward highway search–stop at primary transit nodes( set of backward access points)–store search space entries(t,u,d(u,t))arrange search spacesPreprocessingfor each secondary transit node s∈T2:–perform forward highway search–stop at primary transit nodes( set of forward access points)–at each node u and for each search space entry(t,u,d(u,t)):∗compute distance d u(s,t):=d(s,u)+d(u,t)via u∗compute distance d top(s,t)via top layer∗if d u(s,t)<d top(s,t)then·add entry d u(s,t)to the secondary distance table·ensure that the disks around s and t contain u(use similar procedure for lower layers)ExperimentsW.Europe(PTV)USA(TIGER/Line)#nodes#directed edges#road categoriesspeed range[km/h]Preprocessinglayer2|T||A|space timeUSA timeeco184379 4.910674 5.72443:25 dist eco10235210.9EUR timeeco118356 5.5112939.92512:44 dist eco6977513.1Querylayer2[%]wrong cont’d time0.14 1.1311.5µs gen0.00140.01381.578.1087.5µs0.54 2.8713.4µs gen0.00150.01904.6818.32107.4µsDijkstra RankQ u e r y T i m e [µs ]2526272829210211212213214215216217218219220221222223224510204010030010005102040100300100Local Queries:USA,travel time metricDetermine Shortest Pathsfrom source s,look iteratively for the next adjacent node s′thatleads to fwd acc pnt ud(s,s′)+d(s′,u)=d(s,u)analogously,from target to bwd acc pntfrom fwd acc pnt u,look iteratively for the next adjacent node u′in the topmost level that leads to bwd acc pnt vd(u,u′)+d(u′,v)=d(u,v)(if necessary,use a hidden path instead)unpack shortcutsif path not through top layer,fall back on highway query。
