C++八方向Astar寻路算法大作业
使用AStar算法实现自动寻路详解

使⽤AStar算法实现⾃动寻路详解@⽬录前些⽇⼦我有兄弟给我打电话,问我会不会⼈⼯智能,来实现⼀个机器⼈在仓库⾃动寻路的功能。
因为没有接触过这样的场景,但是⾃⼰⼜⽐较对此兴趣,所以就看了⼀些⾃动寻路的算法,⽐如:基于⼆叉树的深度优先遍历、D Star、A Star算法,其中我感觉A Star算法最好。
下⾯我给⼤家介绍⼀下,⾸次实现的语⾔是Java,但是Java不太直观,⼜不想使⽤Java的图形界⾯,所以就使⽤JS+HTML来实现的,⾸先展⽰⼀下效果图。
效果图如下:1、什么是A Start算法A*搜索算法是求出在⼀个⼆维平⾯中从起点到终点最低运算代价的算法,它可以算出A点到B点的最短距离,也就是最优路径。
常见的应有主要是在游戏中,⼈物的⾃动寻路;机器⼈探路;交通路线导航等。
2、A Star算法的原理和流程2.1 前提在讲述A Star算法之前,需要声明下列这些属性:(1)从起点开始扩散的节点;(2)最短距离计算公式:F = G + H;(3)欧⼏⾥得距离计算公式:p = $\sqrt (x_2 - x_1)^2+(y_2 - y_1)^2$(其实就是勾股定理);(4)OPENLIST 和 CLOSELIST;上⾯的属性和公式不懂没关系,下⾯我会对他们⼀⼀进⾏详细介绍。
⾮常简单!2.1.1 从起点开始扩散的节点我们在HTML页⾯上使⽤横和竖画出来的格⼦。
所谓扩散就是以起点为基点向上、下、左、右四个放向进⾏扩散,这些扩展的节点就是可以⾛的“路”。
如下图所⽰黄⾊的⽅格就是扩散的点:PS:A Star有四个⽅向和⼋个⽅向的扩散。
扩展四个⽅向的节点就是⽬前我们所说的;⼋个⽅向是还包含了,上左、上右、下左、下右四个⽅向的节点。
我们通篇使⽤的是四个⽅向的扩展。
2.1.2 最短距离计算公式:F = G + H如何在扩散的节点中找到最优也就是最短的⼀条路呢?就需要⽤到这个公式:F=G+H。
那么这个公式⾥⾯的属性都代表什么意识呢?下⾯我们就说明⼀下:(1)G:表⽰从起点到扩散的四个节点的距离,换句话说就是从起点到扩散的四个节点需要移动的格⼦。
八数码问题C语言A星算法详细实验报告含代码

一、实验内容和要求八数码问题:在3×3的方格棋盘上,摆放着1到8这八个数码,有1个方格是空的,其初始状态如图1所示,要求对空格执行空格左移、空格右移、空格上移和空格下移这四个操作使得棋盘从初始状态到目标状态。
例如:图1 八数码问题示意图请任选一种盲目搜索算法(广度优先搜索或深度优先搜索)或任选一种启发式搜索方法(全局择优搜索,加权状态图搜索,A 算法或A* 算法)编程求解八数码问题(初始状态任选)。
选择一个初始状态,画出搜索树,填写相应的OPEN 表和CLOSED表,给出解路径,对实验结果进行分析总结,得出结论。
二、实验目的1. 熟悉人工智能系统中的问题求解过程;2. 熟悉状态空间的盲目搜索和启发式搜索算法的应用;3. 熟悉对八数码问题的建模、求解及编程语言的应用。
三、实验算法A*算法是一种常用的启发式搜索算法。
在A*算法中,一个结点位置的好坏用估价函数来对它进行评估。
A*算法的估价函数可表示为:f'(n) = g'(n) + h'(n)这里,f'(n)是估价函数,g'(n)是起点到终点的最短路径值(也称为最小耗费或最小代价),h'(n)是n到目标的最短路经的启发值。
由于这个f'(n)其实是无法预先知道的,所以实际上使用的是下面的估价函数:f(n) = g(n) + h(n)其中g(n)是从初始结点到节点n的实际代价,h(n)是从结点n到目标结点的最佳路径的估计代价。
在这里主要是h(n)体现了搜索的启发信息,因为g(n)是已知的。
用f(n)作为f'(n)的近似,也就是用g(n)代替g'(n),h(n)代替h'(n)。
这样必须满足两个条件:(1)g(n)>=g'(n)(大多数情况下都是满足的,可以不用考虑),且f必须保持单调递增。
(2)h必须小于等于实际的从当前节点到达目标节点的最小耗费h(n)<=h'(n)。
astar(a星)算法(精)

A*算法原理简介A*(A-Star)算法是一种静态路网中求解最短路最有A star算法在静态路网中的应用效的方法。
公式表示为: f(n)=g(n)+h(n),其中f(n) 是节点n从初始点到目标点的估价函数,g(n) 是在状态空间中从初始节点到n节点的实际代价,h(n)是从n到目标节点最佳路径的估计代价。
保证找到最短路径(最优解的)条件,关键在于估价函数h(n)的选取:估价值h(n)<= n到目标节点的距离实际值,这种情况下,搜索的点数多,搜索范围大,效率低。
但能得到最优解。
如果估价值>实际值, 搜索的点数少,搜索范围小,效率高,但不能保证得到最优解。
估价值与实际值越接近估价函数取得就越好例如对于几何路网来说,可以取两节点间欧几理德距离(直线距离)做为估价值,即f=g(n)+sqrt((dx-nx)*(dx-nx)+(dy-ny)*(dy-ny));这样估价函数f在g值一定的情况下,会或多或少的受估价值h的制约,节点距目标点近,h值小,f值相对就小,能保证最短路的搜索向终点的方向进行。
明显优于Dijstra算法的毫无无方向的向四周搜索。
conditions of heuristicOptimistic (must be less than or equal to the real cost)As close to the real cost as possible详细内容主要搜索过程伪代码如下:创建两个表,OPEN表保存所有已生成而未考察的节点,CLOSED表中记录已访问过的节点。
算起点的估价值;将起点放入OPEN表;while(OPEN!=NULL){从OPEN表中取估价值f最小的节点n;if(n节点==目标节点){break;}for(当前节点n 的每个子节点X){算X的估价值;if(X in OPEN){if( X的估价值小于OPEN表的估价值 ){把n设置为X的父亲;更新OPEN表中的估价值; //取最小路径的估价值}}if(X inCLOSE) {if( X的估价值小于CLOSE表的估价值 ){把n设置为X的父亲;更新CLOSE表中的估价值;把X节点放入OPEN //取最小路径的估价值}}if(X not inboth){把n设置为X的父亲;求X的估价值;并将X插入OPEN表中; //还没有排序}}//end for将n节点插入CLOSE表中;按照估价值将OPEN表中的节点排序; //实际上是比较OPEN表内节点f的大小,从最小路径的节点向下进行。
A star 算法 八数码问题 C++ 报告+代码+详细注释
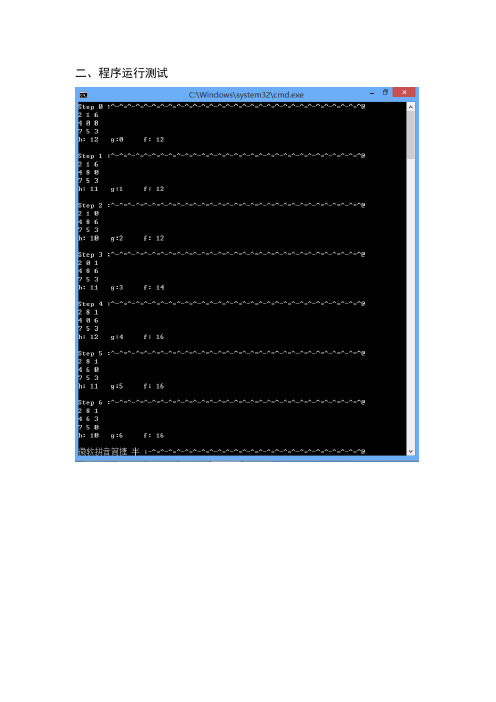
二、程序运行测试A*算法求解八数码问题一、详细设计说明1.评价函数以当前状态下各将牌到目标位置的距离之和作为节点的评价标准。
距离的定义为:“某将牌行下标与目标位置行下标之差的绝对值 + 列下标与目标位置列下标之差的绝对值”。
距离越小,该节点的效果越好。
某个状态所有将牌到目标位置的距离之和用“h值”表示。
2.主要函数2.1countH(state & st);countH函数功能是计算st状态的h值。
计算过程中将会用到rightPos数组,数组里记录的是目标状态下,0~9每个将牌在九宫格里的位置(位置 = 行下标 * 3 + 列下标)。
2.2f(state * p);f()=h()+level2.3look_up_dup(vector<state*> & vec, state * p);在open表或close表中,是否存在指定状态p,当找到与p完全相等的节点时,退出函数。
2.4search(state & start);在open表不为空时,按f值由小到大对open表中元素进行排序。
调用findZero()函数找到0值元素的位置。
空格可以向上下左右四个方向移动,前提是移动后不能越过九宫格的边界线。
确定某方向可走后,空格移动一步,生成状态p’。
此时,检查open表中是否已有p’,若有,更新p’数据;检查close表中是否已有p’,若有,将p’从close表中删除,添加到open表中。
重复的执行这个过程,直到某状态的h值为零。
2.5dump_solution(state * q);在终端输出解路径。
// A*算法八数码问题#include"stdafx.h"#include<iostream>#include<vector>#include<time.h>#include<algorithm>using namespace std;const int GRID = 3; //Grid表示表格的行数(列数),这是3*3的九宫格int rightPos[9] = { 4, 0, 1, 2, 5, 8, 7, 6, 3 };//目标状态时,若p[i][j]=OMG,那么3*i+j = rightPos[OMG]struct state{int panel[GRID][GRID];int level; //记录深度int h;state * parent;state(int level) :level(level){}bool operator == (state & q){//判断两个状态是否完全相等(对应位置元素相等),完全相等返回true,否则返回falsefor (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++){if (panel[i][j] != q.panel[i][j])return false;}}return true;}state & operator = (state & p){ //以状态p为当前状态赋值,对应位置元素相同for (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++){panel[i][j] = p.panel[i][j];}}return *this;}};void dump_panel(state * p){ //将八数码按3*3矩阵形式输出for (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++)cout << p->panel[i][j] << " ";cout << endl;}}int countH(state & st){ //给定状态st,计算它的h值。
AStar算法解决八数码问题

江南大学物联网工程学院实验报告课程名称人工智能实验名称A*算法解决8数码问题实验日期2018.3.20班级计科1501 姓名周启航学号1030415127一、实验目的:修改A*算法,使之能解决N*N矩阵八数码问题问题描述:八数码难题:在3×3方格棋盘上,分别放置了标有数字1,2,3,4,5,6,7,8的八张牌,初始状态S0可自己随机设定,使用的操作有:空格上移,空格左移,空格右移,空格下移。
二、算法描述:1.状态描述八数码的任何一种摆法就是一个状态,所有摆法即为状态集S,他们构成了一个状态空间,其大小为9包括8个数码和一个空格,每个数码就是一个分离的独立的子空间,其所在位置为x:i/3,y:i%3.相应的操作算子就是数码的移动即:将空格向上移UP、将空格向下移DOWN、将空格向左移LEFT、将空格向右移RIGHT,经过一些操作算子后达到目标状态。
2.启发函数设计启发函数为现在的状态中各位置与目标状态各位置数码值不同的个数,例如:现在状态:w=123456780,目标状态为:t=123456708,则h(n)=2.3.规则的判断条件把未扩展的状态存入open表,排序后取出优先状态扩展搜索,将扩展后的存入closed表,循环执行直到扩展出目标状态。
4.算法流程图5.核心代码操作算子:int solve() //搜索过程{P cur;P p;while(!open.empty()){cur=open.top(); //open表open.pop();if(cur.s==t) return cur.id; //达到目标状态,返回当前节点的idint x,y;int ops=0;while(cur.s[ops]!='0') ops++;x=ops/N,y=ops%N; //空格所在位置int r=cur.id;if(x>0){ //空格向上移p.s=cur.s;swap(p.s[ops],p.s[ops-3]);if(!mp[p.s]){p.d=cur.d+1,p.w=calw(p.s),p.id=top+1;open.push(p);stack[++top]=p.s;father[top]=r;mp[p.s]=1;}}if(x<N-1){ //空格向下移p.s=cur.s;swap(p.s[ops],p.s[ops+3]);if(!mp[p.s]){p.d=cur.d+1,p.w=calw(p.s),p.id=top+1;open.push(p);stack[++top]=p.s;father[top]=r;mp[p.s]=1;}}if(y>0){ //空格向左移p.s=cur.s;swap(p.s[ops],p.s[ops-1]);if(!mp[p.s]){p.d=cur.d+1,p.w=calw(p.s),p.id=top+1;open.push(p);stack[++top]=p.s;father[top]=r;mp[p.s]=1;}}if(y<N-1){ //空格向右移p.s=cur.s;swap(p.s[ops],p.s[ops+1]);if(!mp[p.s]){p.d=cur.d+1,p.w=calw(p.s),p.id=top+1;open.push(p);stack[++top]=p.s;father[top]=r;mp[p.s]=1;}}}return -1; //搜索失败}int main(){cout<<"请输入棋盘大小N*N\nN:";cin>>N;cout<<"请输入测试的组数:\n";int tt; //测试的组数cin>>tt;for(int k=1;k<=tt;k++){cout<<"Case "<<k<<":\n";int i,j;char a;cout<<"请输入目的状态:\n";cin>>t;p.s="";cout<<"请输入初始状态:\n";for(i=0;i<N;i++){for(j=0;j<N;j++){cin>>a; //输入0~8数码p.s+=a;}}p.d=0,p.w=calw(p.s),p.id=0;father[0]=-1;mp[p.s]=1;stack[0]=p.s;open.push(p); //往open表中加入初始状态节点int id=solve();//调用搜索过程if(id==-1){cout<<"无解!\n";}else{int c=-1;while(id>=0){ //把stack中存的节点按次序放入到record中record[++c]=stack[id];id=father[id];}cout<<"原图:"<<endl;print(c); //输出初始节点cout<<"移动过程: \n\n";for(i=c-1;i>=0;i--){cout<<"Step "<<c-i<<":\n";//输出当前搜索步骤print(i);//输出当前搜索的节点}cout<<"移动结束!\n";mp.clear();while(!open.empty()) open.pop();top=0;cout<<endl;}system("pause\n");return 0;}三、实验结果:四、实验心得:只是做了简单修改,只能解决些简单的问题,过于复杂的还不能实现,不过还是体会到了A*算法的厉害,也见识到了人工智能的神奇,会继续努力学习。
基于启发式搜索算法A星解决八数码问题

int statue[size][size]; //记录当前节点的状态 struct Node * Tparent; //用来构成搜索树,该树由搜索图的反向指针构成 struct Node * opennext; //用来构成 open 表,该指针指向该节点在 open 表中的下一个 节点 struct Node * closenext; //用来构成 open 表,该指针指向该节点在 close 表中的下一个 节点 struct Node * brothernext; //构成兄弟链表,该指针指向该节点在兄弟链表中的下一个节 点 int f; //记录当前节点的 f 函数值 int g; //记录当前节点的 g 函数的值 int h; //记录当前节点的 h 函数的值 };
5
get_bestroute (bestNode); return; }
2.2.7 生成 bestNode 所指节点的后继节点
定义一个后继节点链表,表头为 head_b,将 bestNode 所指节点的不是前驱节点的后继 节点,链接到后继及诶单链表中。getchild 函数可以实现这个功能。
//产生 bestNode 的一切后继节点。。 head head_b; //定义 bestNode 的后继节点表 head_b.next=NULL; getchild (&head_b,bestNode); //产生 bestNode 的子节点,将不是 bestNode 的父节点的
while (head_b.next!=NULL) { Node *tmp=getbrother (&head_b); //从后继节点表中取出一个节点记为 tmp,并从
基于A星算法的8数码问题求解方案设计(1)

基于A星算法的8数码问题求解⽅案设计(1)⼀、问题描述8数码问题⼜称9宫问题,与游戏“华容道”类似。
意在给定的33棋格的8个格⼦内分别放⼀个符号,符号之间互不相同,余下的⼀格为空格。
并且通常把8个符号在棋格上的排列顺序称作8数码的状态。
开始时,规则给定⼀个初始状态和⼀个⽬标状态,并要求被试者对棋格内的符号经过若⼲次移动由初始状态达到⽬标状态,这个过程中只有空格附近的符号可以朝空格的⽅向移动,且每次只能移动⼀个符号。
为⽅便编程和表⽰,本⽂中8个格⼦内的符号分别取1—8的8个数字表⽰,空格⽤0表⽰。
并给定8数码的初始状态和⽬标状态分别如图1、2所⽰。
图1 初始状态图2 ⽬标状态则要求以图1为初始状态,通过交换0和0的上、下、左、右四个⽅位的数字(每次只能和其中⼀个交换),达到图2所⽰⽬标状态。
⼆、实验⽬的熟悉和掌握启发式搜索的定义、估价函数和算法过程,并利⽤A*算法求解N数码难题,理解求解流程和搜索顺序。
三、实验任务1)实现类似于如图所⽰N数码难题演⽰程序。
2)⽤你所熟悉的程序语⾔实现,可以B/S实现,也可以C/S实现四、算法设计根据任务要求,本⽂采⽤A*搜索算法。
但要在计算机上通过编程解决该问题,还应当解决该问题在计算机上表⽰的⽅式,并设计合适的启发函数,以提⾼搜索效率。
①状态的表⽰在A*算法中,需要⽤到open表和closed表,特别是在open表中,待扩展节点间有很严格的扩展顺序。
因此在表⽰当前状态的变量中,必须要有能指向下⼀个扩展节点的指针,以完成对open表中元素的索引。
从这⼀点上看,open表中的元素相互间即构成了⼀个线性表,因此初步选定使⽤结构体表⽰问题的状态。
如图3所⽰,表⽰问题的结构体包括表⽰当前节点状态的DATA和指向open 表中下⼀个待扩展节点的指针NEXT。
图3 结构体现在进⼀步考虑DATA中包括的内容:如图1、2所⽰,8数码问题的提出是以⼀个33数表表⽰的,因此本⽂中采⽤⼀个33的⼆维数组s[3][3]表⽰当前状态的具体信息。
astar寻路算法原理

astar寻路算法原理
A(A星)寻路算法是一种常用的启发式搜索算法,用于在图中
找到从起点到终点的最短路径。
它结合了Dijkstra算法和启发式搜
索的优点,具有较高的搜索效率。
A算法基于图的搜索,其中每个节点表示一个状态,边表示从
一个状态到另一个状态的转移。
算法使用两个函数来评估每个节点
的重要性,g(n)表示从起点到节点n的实际代价,h(n)表示从节点
n到终点的估计代价。
A算法通过综合考虑这两个函数来选择下一个
要扩展的节点。
具体来说,A算法通过维护一个开放列表和一个关闭列表来进
行搜索。
它首先将起点加入开放列表,然后重复以下步骤直到找到
终点或者开放列表为空:
1. 从开放列表中选择f(n)=g(n)+h(n)最小的节点n进行扩展。
2. 将节点n从开放列表中移入关闭列表。
3. 对节点n的相邻节点进行检查,更新它们的g值和f值,并
将它们加入开放列表中。
A算法的关键在于如何选择合适的启发函数h(n)以及如何高效地维护开放列表和关闭列表。
合适的启发函数可以大大提高搜索效率,而高效的列表维护可以减少搜索时间。
总的来说,A算法是一种高效的寻路算法,能够在图中找到最短路径,并且可以通过调整启发函数来适应不同的问题。
scratch编程算法题

scratch编程算法题一、题目描述Scratch编程算法题是一个基于Scratch编程平台的趣味算法题目。
题目包括各种不同类型的算法问题,旨在锻炼学生的编程思维和解决问题的能力。
二、题目列表1.斐波那契数列求和:给定一个整数n,编写一个算法,使用递归或循环计算前n个斐波那契数的和。
2.寻找最长回文串:给定一个字符串,编写一个算法,找出其中的最长回文串。
3.快速排序:编写一个算法实现快速排序,并检查其性能。
4.八皇后问题:在一个8x8的棋盘上放置8个皇后,使得它们不能互相攻击(即在同一行、同一列或同一对角线上不能有两个皇后)。
编写一个算法找出所有解决方案。
5.汉明码校验:给定一组二进制数据和一个汉明码位数,编写一个算法验证数据的正确性。
三、解题思路1.斐波那契数列求和:可以使用递归或循环来计算斐波那契数列的和。
递归方法简单易懂,但效率较低;循环方法更常见,效率更高。
2.寻找最长回文串:可以使用双指针法,一左一右向中间移动,比较字符是否相同,当遇到不相同时就向后移动指针,直到指针相遇为止。
3.快速排序:快速排序是一种常用的排序算法,其核心思想是分而治之。
首先选取一个基准值,将数组分成两部分,一部分小于基准值,一部分大于基准值。
然后对这两部分继续进行快速排序,直到整个数组有序。
性能可以通过优化选择基准值的方式进行提高。
4.八皇后问题:这是一个经典的回溯算法问题。
首先在棋盘上放置一个皇后,检查是否会与其它皇后发生冲突。
如果不冲突,就将皇后向右下方移动一格。
如果冲突,则回溯到上一次放置的位置,并尝试另一种放置方式。
重复这个过程直到找到所有解决方案。
5.汉明码校验:汉明码是一种具有较强检错和纠错能力的编码方式。
首先根据给定的位数和二进制数据生成校验位,然后将数据和校验位一起传输。
在接收端,通过计算校验位是否正确来判断数据的正确性。
四、代码实现由于Scratch编程平台主要面向初学者,因此代码实现部分将主要以伪代码形式呈现,具体实现可以参考Scratch编程平台的官方文档和示例代码。
A星算法求解8数码问的题目某实验

A*算法求解8数码问题实验一、实验目的熟悉和掌握启发式搜索的定义、估价函数和算法过程,并利用A*算法求解N数码难题,理解求解流程和搜索顺序。
二、实验内容1、八数码问题描述所谓八数码问题起源于一种游戏:在一个3×3的方阵中放入八个数码1、2、3、4、5、6、7、8,其中一个单元格是空的。
将任意摆放的数码盘(城初始状态)逐步摆成某个指定的数码盘的排列(目标状态),如图1所示图1 八数码问题的某个初始状态和目标状态对于以上问题,我们可以把数码的移动等效城空格的移动。
如图1的初始排列,数码7右移等于空格左移。
那么对于每一个排列,可能的一次数码移动最多只有3中,即空格左移、空格右移、空格上移、空格下移。
最少有两种(当空格位于方阵的3个角时)。
所以,问题就转换成如何从初始状态开始,使空格经过最小的移动次数最后排列成目标状态。
2、八数码问题的求解算法2.1 盲目搜索宽度优先搜索算法、深度优先搜索算法2.2 启发式搜索启发式搜索算法的基本思想是:定义一个评价函数f,对当前的搜索状态进行评估,找出一个最有希望的节点来扩展。
先定义下面几个函数的含义:f*(n)=g*(n)+h*(n) (1)式中g*(n)表示从初始节点s到当前节点n的最短路径的耗散值;h*(n)表示从当前节点n到目标节点g的最短路径的耗散值,f*(n)表示从初始节点s经过n到目标节点g的最短路径的耗散值。
评价函数的形式可定义如(2)式所示:f(n)=g(n)+h(n) (2)其中n是被评价的当前节点。
f(n)、g(n)和h(n)分别表示是对f*(n)、g*(n)和h*(n)3个函数值的估计值。
利用评价函数f(n)=g(n)+h(n)来排列OPEN表节点顺序的图搜索算法称为算法A。
在A算法中,如果对所有的x,h(x)<=h*(x) (3)成立,则称好h(x)为h*(x)的下界,它表示某种偏于保守的估计。
采用h*(x)的下界h(x)为启发函数的A算法,称为A*算法。
astar寻路算法原理 -回复

astar寻路算法原理-回复A*寻路算法原理及步骤一、简介A*(A-Star)寻路算法是一种常用的路径规划算法,用于找到两个点之间的最短路径。
它综合了Dijkstra算法和贪心算法的优点,既考虑了每个节点的代价,也考虑了每个节点到目标节点的预估代价。
本文将一步一步详细介绍A*寻路算法的原理和步骤。
二、原理A*算法的核心思想是使用一个估算函数来预测从起始节点到目标节点的代价,并在遍历过程中选择最小代价节点来进行扩展。
该算法综合了代价函数和启发函数的信息,以更快地找到最短路径。
其具体步骤如下:1. 初始化将起始节点添加到一个开放列表(open list)中,开放列表存放待扩展的节点。
同时,创建一个空的闭合列表(closed list),用于存放已扩展过的节点。
2. 循环操作进入循环操作,直到开放列表为空或找到目标节点。
在每次循环中,选择开放列表中代价最小的节点进行扩展。
3. 节点扩展取开放列表中代价最小的节点,将其从开放列表中删除,并加入到闭合列表中。
然后,获取该节点的相邻节点,计算它们的代价和预估代价,并更新它们的代价值和路径。
4. 判断相邻节点对于每个相邻节点,判断它们是否在开放列表或闭合列表中。
若在闭合列表,则跳过该节点;若在开放列表,比较新路径与旧路径的代价,若新路径更好,则更新代价和路径;否则,不做任何操作。
5. 添加新节点对于不在开放列表中的相邻节点,将它们添加到开放列表中,并计算它们的代价和预估代价。
6. 重复操作重复步骤2至5,直到开放列表为空或找到目标节点。
若开放列表为空,则无法找到路径;若找到目标节点,则回溯路径,回到起始节点。
三、关键要点在上述步骤中,有几个关键要点需要注意:1. 代价函数代价函数用于计算节点到起始节点的实际代价,包括走过的距离、障碍物等影响因素。
根据具体情况,可以自定义代价函数。
2. 启发函数启发函数用于估算节点到目标节点的代价,即预测代价。
常见的启发函数有曼哈顿距离、欧几里得距离等,根据实际情况选择合适的启发函数。
人工智能结课作业-DFSBFSAstar解决八数码问题

⼈⼯智能结课作业-DFSBFSAstar解决⼋数码问题如果帮到你了,希望给个star⿎励⼀下1 深度优先遍历搜索(DFS)1.1算法介绍深度优先搜索算法(Depth-First-Search,DFS)是⼀种⽤于遍历或搜索树或图的算法。
沿着树的深度遍历树的节点,尽可能深的搜索树的分⽀。
当节点v的所在边都⼰被探寻过,搜索将回溯到发现节点v的那条边的起始节点。
这⼀过程⼀直进⾏到已发现从源节点可达的所有节点为⽌。
如果还存在未被发现的节点,则选择其中⼀个作为源节点并重复以上过程,整个进程反复进⾏直到所有节点都被访问为⽌。
属于盲⽬搜索。
以上图为例,简述DFS的过程。
⾸先从根节点"1"出发,按⼀定的顺序遍历其⼦节点,这⾥我们假设优先遍历左边的。
所以,在遍历"1"之后,我们到了节点"2",此时"2"仍有⼦节点,所以应继续向下遍历,下⼀个节点是"3",然后是"4"。
到了"4"之后,没有⼦节点了,说明我们已经将这⼀条路遍历完了,接着我们应该回溯,应该回到"4"的⽗节点,也就是"3"。
因为"3"还有⼀个⼦节点"5"没有遍历,所以下⼀个我们应该遍历的是"5"。
遍历完"5"之后⼜发现⼀条路到头了,再次回溯依然回溯到其⽗节点"3",此时"3"的所有⼦节点都已经遍历完了,因该接着回溯到"3"的⽗节点"2",然后检查"2"是否有没有遍历完的⼦节点。
按照这样的规则,完成所有节点的遍历。
最终得到的遍历顺序是"1-2-3-4-5-6-7-8-9-10-11-12"在介绍了DFS在遍历树的应⽤后,我们将其应⽤于⼋数码问题的解决。
A星寻路算法

此文档由网络搜集而来。
会者不难,A*(念作A星)算法对初学者来说的确有些难度。
这篇文章并不试图对这个话题作权威的陈述。
取而代之的是,它只是描述算法的原理,使你可以在进一步的阅读中理解其他相关的资料。
最后,这篇文章没有程序细节。
你尽可以用任意的计算机程序语言实现它。
如你所愿,我在文章的末尾包含了一个指向例子程序的链接。
压缩包包括C++和Blitz Basic两个语言的版本,如果你只是想看看它的运行效果,里面还包含了可执行文件。
我们正在提高自己。
让我们从头开始。
序:搜索区域假设有人想从A点移动到一墙之隔的B点,如下图,绿色的是起点A,红色是终点B,蓝色方块是中间的墙。
[图1]你首先注意到,搜索区域被我们划分成了方形网格。
像这样,简化搜索区域,是寻路的第一步。
这一方法把搜索区域简化成了一个二维数组。
数组的每一个元素是网格的一个方块,方块被标记为可通过的和不可通过的。
路径被描述为从A到B我们经过的方块的集合。
一旦路径被找到,我们的人就从一个方格的中心走向另一个,直到到达目的地。
这些中点被称为“节点”。
当你阅读其他的寻路资料时,你将经常会看到人们讨论节点。
为什么不把他们描述为方格呢?因为有可能你的路径被分割成其他不是方格的结构。
他们完全可以是矩形,六角形,或者其他任意形状。
节点能够被放置在形状的任意位置-可以在中心,或者沿着边界,或其他什么地方。
我们使用这种系统,无论如何,因为它是最简单的。
开始搜索正如我们处理上图网格的方法,一旦搜索区域被转化为容易处理的节点,下一步就是去引导一次找到最短路径的搜索。
在A*寻路算法中,我们通过从点A开始,检查相邻方格的方式,向外扩展直到找到目标。
我们做如下操作开始搜索:1,从点A开始,并且把它作为待处理点存入一个“开启列表”。
开启列表就像一张购物清单。
尽管现在列表里只有一个元素,但以后就会多起来。
你的路径可能会通过它包含的方格,也可能不会。
基本上,这是一个待检查方格的列表。
寻路算法

A* 寻路算法2010-02-11 1:44施健泉1.概述虽然掌握了A* 算法的人认为它容易,但是对于初学者来说,A* 算法还是很复杂的。
2.搜索区域(The Search Area)我们假设某人要从A 点移动到B 点,但是这两点之间被一堵墙隔开。
如图1。
(绿色是A ,红色是B ,中间蓝色是墙)图 1你应该注意到了,我们把要搜寻的区域划分成了正方形的格子。
这是寻路的第一步,简化搜索区域,就像我们这里做的一样。
这个特殊的方法把我们的搜索区域简化为了2维数组。
数组的每一项代表一个格子,它的状态就是可走(walkable) 和不可走(unwalkable)两种。
通过计算出从 A 到 B 需要走过哪些方格,就找到了路径。
一旦路径找到了,人物便从一个方格的中心移动到另一个方格的中心,直至到达目的地。
方格的中心点我们成为“节点(nodes) ”。
如果你读过其他关于A* 寻路算法的文章,你会发现人们常常都在讨论节点。
为什么不直接描述为方格呢?因为我们有可能把搜索区域划为其他多边形而不是正方形,例如可以是六边形,矩形,甚至可以是任意多变形。
而节点可以放在任意多边形里面,可以放在多变形的中心,也可以放在多边形的边上。
我们使用这个系统,因为它最简单。
3.开始搜索(Starting the Search)一旦我们把搜寻区域简化为一组可以量化的节点后,就像上面做的一样,我们下一步要做的便是查找最短路径。
在A* 中,我们从起点开始,检查其相邻的方格,然后向四周扩展,直至找到目标。
我们这样开始我们的寻路旅途:3.1从起点A 开始,并把它就加入到一个由方格组成的open list( 开放列表) 中。
这个open list 有点像是一个购物单。
当然现在open list 里只有一项,它就是起点A ,后面会慢慢加入更多的项。
open list 里的格子是路径可能会是沿途经过的,也有可能不经过。
基本上open list 是一个待检查的方格列表。
Astar算法

若附加值=启发函数h,A* 搜索的点会变少。
另一种附加函数是当前点到起点和终点的向量 的叉积的模。这种附加函数在没有障碍物时很 好,不过在有障碍物时看上去比较奇怪(但仍 是对的)。
OPEN = priority queue containing START CLOSED = empty set while lowest rank in OPEN is not the GOAL: current = remove lowest rank item from OPEN add current to CLOSED for neighbors of current: cost = g(current) + movementcost(current, neighbor) if neighbor in OPEN and cost less than g(neighbor): remove neighbor from OPEN, because new path is better if neighbor in CLOSED and cost less than g(neighbor):(shouldn’t happen) remove neighbor from CLOSED if neighbor not in OPEN and neighbor not in CLOSED: set g(neighbor) to cost add neighbor to OPEN set priority queue rank to g(neighbor) + h(neighbor) set neighbor's parent to current
《AStar算法详解》课件

AStar算法的应用实践
AStar算法在游戏中的应用
在游戏中,AStar算法被广泛用于实现自动行走和角色 动画平滑移动。
AStar算法在路径规划中的应用
在寻找城市中特定地点的最短路径等问题上,AStar算 法能够帮助我们找到最佳解决方案。
未来,我们可以看到更多的AStar变体出现,以处理更复杂的场景,并开发更多用于自学 习和重用的模型。
3 应用前景和展望
随着机器人模型的批量生产和自主驾驶汽车的普及,AStar算法将有很大的应用前景。我 们可以期待AStar的进一步改进和高效应用。
AStar算法的改进
算法名称 加权AStar算法 IDAStar算法 迭代加深AStar算法 结合其他算法的AStar算法
改进方法 在计算代价时考虑一些额外的因素,例如地形难度, 以此来提高路径的准确性。 基于DFS算法,将AStar算法转化为迭代加深搜索。这 个算法可以有效地解决内存不足的问题。 类似于IDAStar,但是它每次迭代的深度都是动态的。
应用场景
AStar算法在许多领域都有广泛 的应用,例如:游戏制作、机 器人自主导航、自动驾驶等。 可以应用于任何需要进行路径 规划的领域。
算法思想
AStar算法采用启发式函数来评 估每个搜索状态的价值,其中 评估价值的启发式函数包括已 花费的代价和剩余的代价。它 在搜索过程中扩展代价最小的 节点,目标是找到代价最小的 路径。
AStar算法在自动驾驶中的应用
自动驾驶汽车需要一种高效的路线规划算法,以使它
AStar算法在其他领域的应用
除了游戏、自动驾驶和路径规划之外,AStar算法还在
C++八方向Astar寻路算法大作业

{
insertToOpenList(open, startpoint_r, startpoint_c);// 起点
addPointToCloseList(close, open);
// 起点放到 close中
while (!insertToOpenList(open, open->openPoint->r, open->openPoint->c))
//定义方格点
struct point
{
int flag; //标志位 0 为可走, 1 为墙壁 2 在penlist 3 在 closelist中 4 为起点 5 为终点
unsigned int r;
unsigned int c;
unsigned int h;
unsigned int g;
unsigned int f;
if (tempPoint->parent->r-tempPoint->r == 0 && tempPoint->parent->c - tempPoint->c == -
1)
map[tempPoint->parent->r][tempPoint->parent->c] = 7;
if (tempPoint->parent->r-tempPoint->r == 1 && tempPoint->parent->c - tempPoint->c == -
#define col 27
using namespace std;
const int direction[8][2] = { { -1,-1 },{ -1,0 },{ -1,1 },{ 0,-1 },{ 0,1 },{ 1,-
Astar经典算法

牛刀小试 - A*寻路算法简介eidiot挂帅出征,携令牌一枚,率人马若干,编制如下:∙寻路元帅寻路总指挥,执“行动令牌”一枚和“开启士兵名录”、“关闭将军名录”各一册。
凭“行动令牌”调兵遣将。
∙预备士兵由元帅或预备将军派往未探索区域,完成探索任务后授“开启”军衔,晋为“开启士兵”。
发令派其出者为其“父将”。
∙开启士兵前线待命。
接到“行动令牌”后晋为“预备将军”执行探索任务。
∙预备将军凭“行动令牌”派出预备士兵至周围未探索区域,并考察周围“开启士兵”状态,以“父将”之名节制所派士兵。
归还“行动令牌”后授“关闭”军衔,晋为“关闭将军”。
∙关闭将军后方待命。
到达终点后依次报告“父将”直至元帅,寻路任务完成。
为协调行动,特颁军令如下:∙“预备士兵”只能由起点或“父将”所在格横、竖或斜向移动一格,直向(横、竖)移动一格走10步,斜向一格14步(斜向是直向1.414倍,取整数),抵达后不得再移动。
∙所有人员需记下派出自己的“父将”、从起点到所在位置所走步数(G)、预计到达终点共需步数(F)。
其中 F = G + H,F 是从起点经过该点到终点的总路程,G 为起点到该点的“已走路程”,H 为该点到终点的“预计路程”。
G 的计算是“父将”的 G 值加上“父将”位置到该位置所走步数,H 的计算是该点到终点“只走直路”所需路程。
看看战图更容易理解,从红色方格出发越过黄色障碍到达蓝色方格:图例:由图可形象看出何谓“开启士兵”、“关闭将军”:外围的绿色方格为“开启士兵”,“前线待命”,随时可向外继续探索。
内围的紫色方格是“关闭将军”,从终点开始沿箭头寻其“父将”直至起点即得最终路径。
战前会议结束,拔营出征。
∙首先派出编号为0的“预备士兵”侦查起点,然后升其为“开启士兵”,列入“开启士兵名录”。
∙检查“开启士兵名录”,找出F值最低的“开启士兵”(只有一名人员,当然是0号),发出“行动令牌”派其执行探索任务。
∙0号“开启士兵”接到“行动令牌”,晋为“预备将军”,探索周围格子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
#define col 27
using namespace std;
const int direction[8][2] = { { -1,-1 },{ -1,0 },{ -1,1 },{ 0,-1 },{ 0,1 },{ 1,-
1 },{ 1,0 },{ 1,1 } };// 方向
enum { virable, wall, inOpen, inClose, start, goal };
{
if (tempPoint->parent->r-tempPoint->r == 1 && tempPoint->parent->c == tempPoint->c)
map[tempPoint->parent->r][tempPoint->parent->c] = 4;
if (tempPoint->parent->r-tempPoint->r == -1 && tempPoint->parent->c == tempPoint->c)
1)
map[tempPoint->parent->r][tempPoint->parent->c] = 8;
if (tempPoint->parent->r-tempPoint->r == -1 && tempPoint->parent->c - tempPoint->c ==
1)
map[tempPoint->parent->r][tempPoint->parent->c] = 9;
temp->openPoint = point;
while (openList->next != NULL)
//按从小到大的顺序存储openList;
{
if (point->f < openList->next->openPoint->f)
{
OpenList* tempadd = openList->next;
作业上交时间:最后一节课前发送到课程邮箱。包括源代码,以及运行出来的效果图。
第 1 页,共 9 页
Homework3:
Solution:
1、算法分析: 地图的构建,需要定义一个整型二维数组,障碍位置为 1,可通过点为 0;同样定义坐标 点结构体,以存放每个点的行列 GHF 父结点等信息。 Astar 算法要用到两个表来存放将要搜索的结点和还未搜索的结点,分别是开放列表 openList 和封闭列表 openList,Astar 算法的计算步骤如下: ① S→openList ② S 邻居→openList openList→S→closeList ③ S 邻居有 8 个如何确定先检查哪个? G 移动成本(10/14) H Manhattan 距离 H=(|e_r-r|+|e_c-c|)*10 F=G+H S=F 最小的点 ④ 重复②③,openList=NULL 未到终点,说明无通路。当 endPoint 在开放表中的 时候,说明已经找到通路,根据每个结点的父结点信息,通过回溯可以找出通 路。 NOTE : 在第②步中检查邻居时,以下几点需要注意: ① 若邻居结点已经在封闭表 closeList 中,可以直接忽略。 ② 若邻居结点不在开放表 openList 和封闭表 closeList 中,计算 GHF 的值,并设置 该结点的父亲结点 ③ 若邻居结点已经在开放表 openList 中,若能得到更小的 G 值则重新计算 GHF 的值 并更新父结点
closeList->closePoint = openList->openPoint; OpenList*temp = openList; openList = openList->next; delete temp; return; } while (closeList->next != NULL) closeList = closeList->next; CloseList*t = new CloseList; t->closePoint = openList->openPoint; t->next = NULL; closeList->next = t;
{
addPointToCloseList(close, open);
if (open == NULL)
{
cout << "未找到出口!地图有误" << endl;
return;
}
}
point*tempPoint = &a[endpoint_r][endpoint_c];
while (tempPoint->parent->flag != start)
map[tempPoint->parent->r][tempPoint->parent->c] = 5;
if (tempPoint->parent->r-tempPoint->r == 0 && tempPoint->parent->c - tempPoint->c == 1)
map[tempPoint->parent->r][tempPoint->parent->c] = 6;
if (tempPoint->parent->r - tempPoint->r == 1&& tempPoint->parent->c - tempPoint->c ==
aStar::aStar() {
第 4 页,共 9 页
steps = 0; startpoint_r = -1; startpoint_c = -1; endpoint_c = -1; endpoint_r = -1; }
void aStar::findGoal(OpenList* open, CloseList* close, int map[row + 2][col + 2])
temp->next = tempadd;
break;
第 3 页,共 9 页
} else
openList = openList->next; } openList->next = temp; } //往封闭表中添加元素 void addPointToCloseList(CloseList*closeList, OpenList*&openList) { if (openList == NULL) { cout << "No data in the OpenList!\n"; return; } if (openList->openPoint->flag != start)openList->openPoint->flag = inClose; if (closeList->closePoint == NULL) {
{
insertToOpenList(open, startpoint_r, startpoint_c);// 起点
addPointToCloseList(close, open);
// 起点放到 close中
while (!insertToOpenList(open, open->openPoint->r, open->openPoint->c))
//定义方格点
struct point
{
int flag; //标志位 0 为可走, 1 为墙壁 2 在penlist 3 在 closelist中 4 为起点 5 为终点
unsigned int r;
unsigned int c;
unsigned int h;
unsigned int g;
unsigned int f;
OpenList*tempOpen = openList; openList = openList->next; delete tempOpen; } //定义aStar类 class aStar { public: point a[row][col]; aStar(); ~aStar() {}
void initPointMap(int map[row + 2][col + 2], OpenList *open); void findGoal(OpenList* open, CloseList* close, int map[row + 2][col + 2]); OpenList* minInOpen(OpenList* open); bool insertToOpenList(OpenList*, int r, int c); bool isInOpenList(OpenList*, int r, int c); bool isInCloseList(OpenList*, int r, int c); void isChangeParent(OpenList*, int r, int c); bool isValid(OpenList*, int r, int c); unsigned int Manhattan(int m_r, int m_c, int r, int c); void counter() { cout << "\n从起点走到终点至少需要" << steps+1 << "步!\n"; cout << endl; } private: unsigned int steps; int startpoint_r; int startpoint_c; int endpoint_r; int endpoint_c; };
