海淀试题及答案

合集下载

初三数学试题及答案海淀

初三数学试题及答案海淀一、选择题（每题3分，共30分）1. 下列哪个数是无理数？A. 0.33333…（循环）B. πC. √2D. √4答案：C2. 如果一个直角三角形的两条直角边分别为3和4，那么斜边的长度是：A. 5B. 6C. 7D. 8答案：A3. 一个数的平方根是2，那么这个数是：A. 2B. 4C. -4D. 8答案：B4. 一个圆的半径是5，那么它的面积是：A. 25πB. 50πC. 75πD. 100π答案：B5. 一个二次方程x² - 5x + 6 = 0的根是：A. x = 2, 3B. x = 1, 6C. x = -2, 3D. x = 2, -3答案：A6. 一个数的立方根是3，那么这个数是：A. 27B. 64C. 81D. 243答案：A7. 如果一个数的相反数是-7，那么这个数是：A. 7B. -7C. 0D. 14答案：A8. 一个数的绝对值是5，那么这个数可能是：A. 5B. -5C. 5或-5D. 都不是答案：C9. 一个多项式3x³ - 2x² + 5x - 7的首项是：A. 3x³B. -2x²C. 5xD. -7答案：A10. 一个分数的倒数是1/3，那么这个分数是：A. 3B. 1/2C. 1/3D. 3/1答案：D二、填空题（每题2分，共20分）1. 一个数的平方是16，这个数是______。

答案：±42. 一个圆的直径是10，那么它的周长是______。

答案：π×103. 如果一个三角形的三个内角分别是30°，60°，90°，那么这是一个______三角形。

答案：直角4. 一个数的立方是-27，这个数是______。

答案：-35. 一个数的平方根是-2或2，这个数是______。

答案：46. 如果一个数的绝对值是3，那么这个数是______。

答案：3或-37. 一个多项式x³ - 2x² + x - 2的常数项是______。

2024海淀高三语文期末试题答案

海淀区2023—2024高三年级第一学期期末练习语文一、（本大题共5小题，共18分）1．（3分）C 2．（3分）A 3．（3分）D 4．（3分）B5．（6分）答案要点：①传播方式由波动方程主导②引导光线绕过物体并按原路传播③引导背景热流避开物体④无法被声呐探测到⑤在红外探测视角中完全隐身【评分说明】②2分，其余一点1分。

二、（本大题共5小题，共18分）6．（3分）B 7．（3分）C 8．（3分）C 9．（3分）D10．（6分）参考答案：（1）（2分）【甲】吕公不动，语其仆曰：“醉者勿与较也。

”闭门谢之。

【乙】翼日，吕请棋处士他适，以束帛赆之。

（或“以他事俾去。

”）【评分说明】甲、乙各1分。

（2）（4分）品质：能包容不同的见解主张；尊重前辈；谦让，不贪功；实事求是分析：略。

【评分说明】从不同角度概括出两种品质，2分；结合内容分析合理，2分。

三、（本大题共5小题，共31分）11．（3分）C 12．（3分）B13．（6分）参考答案：①这四句诗写凉风骤起，月光皎洁，天宇空阔，江面平旷，呈现出开阔澄明的意境；②表现了诗人此刻内心与之相融为一的澄净肃穆（或：衬托了诗人因身负公务不得不夜间行路的无奈与孤独）；③承接开篇四句远离尘嚣的闲静意趣；④引出后文对弃官还乡、返璞归真的情志的抒写。

【评分标准】①②各2分；③④各1分。

14．（8分）①三顾频烦天下计②两朝开济老臣心③落木千山天远大④就有道而正焉⑤而臆断其有无⑥汩余若将不及兮⑦执敲扑而鞭笞天下⑧铁衣远戍辛勤久【评分说明】一句1分；句中有错别字、多字、少字，或字迹不清，该句不得分。

15.（11分）（1）（2分）黛玉与宝钗两姐妹情意投合（2）（3分）A（3）（6分）略四、（本大题共4小题，共17分）16．（3分）A 17．（3分）B18．（6分）参考答案：这个不动的“顷刻”指，当《梁祝》全曲进入总高潮，全乐队响起天泣地恸的高潮，演员却让舞蹈动作陡然刹住，屹立不动（2分）。

海淀区2024-4025学年第一学期期中七年级数学试题及答案

海淀区2024年七年级增值评价基线调研数学注意事项1. 本调研卷共 6 页，共3道大题，26道小题。

满分100分。

调研时间 90 分钟。

2. 在答题纸上准确填写姓名、学校名称和准考证号，并将条形码贴在指定区域。

3. 答案一律填涂或书写在答题纸上，在调研卷上作答无效。

4. 在答题纸上，选择题用2B铅笔作答，其他题目用黑色字迹的签字笔作答。

5. 调研结束，请将答题纸交回。

一、选择题（本题共30分，每小题3分）1．−12的相反数是A．12B．−12C．2 D．-22．稀土是钪、钇、镧系17种元素的总称，素有“工业味精”之美誉，是我国重要的战略矿产资源．2024年我国稀土勘探在四川凉山取得新突破，预期新增稀土资源量496万吨．将4 960 000用科学记数法表示为A．0.49610×7B．49.610×5C．4.9610×7D．4.9610×63．下列计算正确的是A．（-5） + （-2）＝7 B．（-5） - （-2）＝3C．（-5）×（-2）＝-10 D．（-5）÷（-2）＝5 24．若x和y成反比例关系，当x的值分别为2，3时，y的值如下表所示，则表中a的值是x23y a4A．2 B．4 C．6 D．85．将下列各数在数轴上表示，其中与原点距离最近的点表示的数是A．-3 B．-0.8 C．1 D．26．对于多项式2x xy−，下列说法正确的是A．次数是2 B．一次项是2C．二次项系数是1 D．其值不可能等于22024. 117．某文具原价为每件m 元，为迎接开学季，每件降5元，在此基础上新生还可以享受九折优惠. 一名新生购买一件该文具付款n 元，则n ＝A．0.9 （m -5） B．0.9m -5C．0.9mD．0.1 （m -5）8．若2s -4t ＝9，则s t −+212的值为A．10B．9.5C．5D．-49．若有理数a ，b 在数轴上的对应点的位置如图所示.下列结论中正确的是A．-a ＜b B．ab ＞1C．a b −＝b -aD．|2|a +＞|2|b −10．关于x ，y 的单项式，若x 的指数与y 的指数是相等的正整数，则称该单项式是“等次单项式”，如x 2y 2，-3xy .给出下面四个结论：①-2x 3y 3是“等次单项式”；②“等次单项式”的次数可能是奇数；③两个次数相等的“等次单项式”的和一定是“等次单项式”；④若五个“等次单项式”的次数均不高于8，则它们中必有同类项.上述结论中，所有正确结论的序号是A．①③ B．①④C．②③D．②④二、填空题（本大题共18分，每小题3分）11．在游乐场的“旋转茶杯”项目中，游客可以通过转动茶杯的方向盘自主控制茶杯的旋转方向.如果把逆时针旋转两圈记作+2，那么顺时针旋转三圈可以记作．12．比较大小：-1 −23．（填“＜”“＝”或“＞”）13．约1500年前，我国古代伟大的数学家和天文学家祖冲之计算出圆周率应在3.1415926和3.1415927之间，成为世界上第一个把圆周率的值精确到小数点后7位的人. 用四舍五入法将圆周率精确到千分位，所得到的近似数为．14．多项式x y xy 2+2与一个整式的和是单项式，则这个整式可以是．（写出一个整式即可）15．若有理数m ，n 满足||m +（2-n ）4＝ 0，则m -n ＝．16．A ，B ，C ，D ，E 是圆上的5个点，在这些点之间连接线段，规则如下：ABC DE如图，已连接线段AB ，BC ，CD ，DE .（1）若想增加一条新的线段，共有种连线方式；（2）至多可以增加条线段.三、解答题（本大题共52分，第17题3分，第18题12分，第19题6分，第20-24题，每小题4分，第25题5分，第26题6分）解答应写出文字说明、演算步骤或证明过程.17．如图，数轴上点A 表示的数是-4，点B 表示的数是3．（1）在图中所示的数轴上标出原点O ；（2）在图中所示的数轴上表示下列各数，并将它们按从小到大的顺序用“＜”连接起来．-3，0，-1，2.5.18．计算：（1）2 - （-1）+（-6）；（2）-12×4÷（-2）；（3）（-103）×（2.5 -52）；（4）（-2）3−−+÷|2|94（−23）2.19．化简：（1）−+−23m n nm m n 222；（2）5[52()]a a a a 22−+−.20．先化简，再求值：11312323x x y x y −−+−+2()()22，其中x ＝13，y ＝-1.21．如图，正方形ABCD 的边长为a .（1）根据图中数据，用含a ，b 的代数式表示阴影部分的面积S ；（2）当a ＝6，b ＝2时，求阴影部分的面积.22． A I（人工智能）技术有望为传统的教学方式带来新变化，如AI 解题. 某公司为测验其AI 产品的解题能力，尝试利用最新考试题进行全科目测试. 分数记录以60分为基准，超过基准的分数记为正数，少于基准的分数记为负数. 将测试的相对分数记录如下:科目语文数学英语道法地理历史物理化学生物相对分数+20-16+30+28+8-9-18-9已知该AI 产品的地理测试分数为81分.（1）请补全上表；（2）在本次测试的各科目中，该产品所得最高分为分，最低分为分；（3）求该产品在本次测试中全科目的总分.23． “圆楼之王”承启楼位于福建省龙岩市，始建于明崇祯年间，是永定客家土楼群的组成部分.整座楼造型奇特，三环主楼环环叠套. 如图，中心位置耸立着一座祠堂．第三环楼为单层，有m 间房间；第二环楼为两层，每层的房间数均比第三环楼的房间数多8间；外环楼为四层，每层的房间数均等于第二环楼每层的房间数与第三环楼的房间数之和．（1）第二环楼每层有间房间，外环楼共有间房间；（用含m 的式子表示）（2）民间流传一首顺口溜：“高四层，楼四圈，上上下下间；圈套圈，圆中圆，历经沧桑数百年”.“”处所填内容是三环主楼所有房间数之和，已知m ＝32，求“”处所填的数.24. 小云和小明参加了数学节活动的某游戏，一次玩法如下：若S 1＜S 2，则小云获胜；若S 1＞S 2，则小明获胜；若S 1＝S 2，则双方平局. （1）若给定的有理数是2，小云为了确保自己获胜，则a 的值应该是；（2）若给定的有理数是2，4，则小云确保自己获胜；（填“能”或“不能”）（3）若给定的有理数是-2，0，2，4.当a 是负数，且双方平局时，则b ＝ .（用含a的式子表示）25．对有理数a ，b 进行如下操作：第一次，将a ，b 中的一个数加1或者减1，另一个数加2或者减2，得到数a 1和b 1；第二次，将a 1和b 1中的一个数加1或者减1，另一个数加2或者减2，得到数a 2和b 2；…；第n 次，将a n -1和b n -1中的一个数加1或者减1，另一个数加2或者减2，得到数a n 和b n .（1）a ＝1，b ＝3.① 若a 1＝0，则b 1的值可以是； ② a b 22+所有可能的取值为；（2）若a n ＝a ，b n ＝b ，则n 的值是否可以是5？请说明理由.26．给定有理数a ，b ，对整式A ，B ，定义新运算“⊕”：A B ⊕＝aA + bB ；对正整数n （n ≥2）和整式A ，定义新运算“⊗”：n ⊗A ＝ A A A ⊕⊕⊕n A个（按从左到右的顺序依次做“⊕”运算），特别地，1⊗A ＝A .例如，当a ＝1，b ＝2时，若A ＝x ，B ＝-y ，则A B ⊕＝A + 2B ＝x - 2y ，2⊗A ＝A A ⊕＝3x .（1）当a ＝２，b ＝1时，若A ＝x + y ，B ＝x - 2y ，则A B ⊕＝，3⊗A ＝；（2）写出一组a ，b 的值，使得对每一个正整数n 和整式A ，均有n A ⊗＝A ，并说明理由；（3）当a ＝２，b ＝1时，若A ＝3x 2 + 7xy ，B ＝2x 2 - 30xy - y 2，p ，q 是正整数，令P ＝p A ⊗，Q ＝q B ⊗，且P Q ⊕不含xy 项，直接写出p 和q 的值.海淀区2024年七年级增值评价基线调研数学试题参考答案一、选择题（本题共30分，每小题3分）二、填空题（本大题共18分，每小题3分）11. 3− 12.<13. 3.14214.2xy −（答案不唯一）15. 2−16. 3; 2注：16题第一空1分，第二空2分三、解答题（本大题共52分，第17题3分，第18题12分，第19题6分，第20-24题，每小题4分，第25题5分，第26题6分） 17. 解：…………2分310 2.5−<−<< …………3分18. 解：（1）2(1)(6)−−+−21(6)=++− 3(6)=+−3=− …………3分（2）124(2)−⨯÷−48(2)=−÷−24=…………3分（3）法1：102()(2.5)35−⨯− 1052()()325=−⨯−105102()()()3235=−⨯+−⨯−25433=−+ 7=− …………3分法2：102()(2.5)35−⨯− 10()(2.50.4)3=−⨯− 10() 2.13=−⨯7=− …………3分（4）3242(2)|2|()93−−−+÷− 498294=−−+⨯821=−−+9=− …………3分19. 解：（1）n m nm n m 22232−+−n m 2132）（−+−=0= …………3分（2）225[52()]a a a a −+−)225522a a a a −+−=（)27522a a a −−=（22275a a a +−=a a 772−= …………3分20. 解：)3123()31(22122y x y x x +−+−− 22312332221y x y x x +−+−= ）（）（22313223221y y x x x ++−−= 23x y =−+ …………3分当13x =，1y =−时，原式21(3)(1)1103=−⨯+−=−+=. …………4分21. 解：（1）21143()22S a b a b =−⋅−⨯−=233222a b a b −−+=23122a ab −− …………3分（2）当6a =，2b =时, 23166222S =−⨯−⨯=3691−−=26 …………4分答：阴影部分的面积为26.22．解：（1）21+； …………1分（2）90；42； …………3分（3）609(20)(16)(30)(28)(21)(8)(9)(18)(9)595⨯+++−+++++++++−+−+−=．答：全科目的总分为595分. …………4分23. 解：（1）(8)m +；(832)m +； …………2分（2）2(8)4(28)1148m m m m ++++=+，当32m =时，原式=113248400⨯+=． …………4分答：“*”处所填的数为400.24. 解：（1）2； …………1分（2）不能； …………2分（3）2a −. …………4分25．解：（1）①1或5； ②2−，0，2，4，6，8，10； …………2分（2）n 不可能是5. 理由如下： …………3分由（1）②的分析知，每次操作，两个数的和的变化量只能是1±或3±，都是奇数. 5次操作后，和的变化量依然是奇数.若5a a =，5b b =，两个数的和不变，变化量为0，是偶数，矛盾. …………5分所以n 不可能是5.26. 解：（1）3x ，77x y +； …………2分（2）1a =，0b =（答案不唯一，满足a ，b 都是有理数，且1a b +=即可）． …………3分理由如下：首先1A A ⊗=成立．因为1a =，0b =，所以10A A A A A ⊕=⋅+⋅=，即2A A ⊗=．对每一个大于2的正整数n ，()1n An An A A A A A A AA A A−⊗=⊕⊕⊕=⊕⊕⊕==⊕=个个所以对每一个正整数n ，均有n A A ⊗=． …………4分（3）4p =，3q =． …………6分。

2024北京海淀区初一(下)期末语文试题及答案

海淀区七年级练习语文参考答案及评分标准2024.07一、基础·运用（共14分）1.A（2分）2.B（2分）3.（1）A（2分）（2）示例：岸上的观众激动万分，为自己心仪的龙舟呐喊助威，声浪一浪高过一浪。

（2分）4.③①②⑥或②⑥③①（2分）5.C（2分）6.示例：主题活动让我们了解了端午的历史习俗，理解了端午的人文精神。

（2分。

恰当运用所给词语1分，清楚表达1分）二、古诗文阅读（共21分）（一）（共7分）7.无案牍之劳形8.濯清涟而不妖9.烟笼寒水月笼沙10.山重水复疑无路柳暗花明又一村11.落红不是无情物化作春泥更护花（7分。

每空1分，有错则该空不得分）（二）（共6分）12.①神奇秀丽②会当③夸张④锐意变法的政治抱负（4分，每空1分）13.B（2分）（三）（共8分）14.C（2分）15.乙（2分）16.①制字②排版③还字④便（易）（4分。

每空1分）三、名著阅读（共5分）17.示例：在潜水艇遭到围攻时，尼摩船长用给铁栏杆通电的方法击退了土著人。

当时电还没有被大规模使用，电的使用让故事变得神奇，同时体现出船长的聪明、博学，让人物形象更加鲜明。

从中，我体会到科学幻想小说的魅力。

(5分。

概括出具有科幻色彩的情节2分，对故事呈现的作用分析1分，对人物形象的作用分析1分，语言表达1分)四、现代文阅读（共20分）（一）（共8分）18.A （2分）19.示例：①建设社区食堂②启用暖心车站③开展文体活动（3分。

每空1分）20.序号：乙理由：示例：在老年群体中开展体育活动，应强化健身主调，弱化竞技属性，降低安全风险，而手划船竞速比赛有较强的竞技属性，有一定安全风险，因此不适合面向老年群体开展。

（3分。

序号正确1分，运用信息“强化健身主调，弱化竞技属性”1分，说明手划船竞速比赛有竞技属性或安全风险1分）（二）（共12分）21.示例：①看到雄伟的人类建筑②“我”感到惊惶与恐惧③来到地下洞窟④看到起伏不绝的坟茔（4分。

2024北京海淀区初一(下)期末数学试题及答案

七年级期末练习数学参考答案一、选择题二、填空题 11. B 12. 128 13. 314. ∠1=∠5（答案不唯一） 15. 93,75x y y x −=⎧⎨−=⎩ 16. 2；52a ≥− 说明：第16题第一空2分，第二空1分.三、解答题17. 解：原式3(2)1)=−−+4=18. 解：2⨯−②①得，510y =−.得，2y =−.入②，得1x =. 以原方程组的为1,2.x y =⎧⎨=−⎩19. 解：解不等式①，得52x <.不等式②去分母，得2(2)3(13)x x −≤+. 去括号得2439x x −≤+.解得1x ≥−. 所以原不等式组的解为512x −≤<.20. 解：（1）画出线段11A B 如图．点1B 的坐标为(1,2)−．（2）点M 的坐标为(0,1)或(0,5)．21. 解：（1）补全图形如下图．（2）证明：∵DE ⊥AC ，∴∠DEA =90°．∵∠ACB =90°，∴∠DEA =∠ACB .∴DE ∥BC .∴∠ADE =∠B ．∵l ∥AB ，∴∠ADE =∠CFE ．∴∠B =∠CFE ．22．任务一：解：设精包装销售了x 盒，简包装销售了y 盒.2370025358500x y x y +=⎧⎨+=⎩①② 解这个方程组，得100,200.x y =⎧⎨=⎩答：精包装销售了100盒，简包装销售了200盒.任务二：解：设分装时使用精包装m 个，简包装n 个（m ，n 为正整数）.依题意可列出下列方程和不等式：7532=+n m ， ①.182<+n m ② 由①得.2375n m −= 将2375n m −=带入 ②，得519.n >因为m ，n 为正整数，所以n =21,m =6或n =23,m =3.分装方案1：精包装6个，简包装21个分装方案2：精包装3个，简包装23个说明：写出任意一个正确的分装方案，同时有合理的理由即可. 23. 解：（1）①如图② 45.注：答44或45均可（2） ① 多; ② ＞.24. 解：（1） 8（答案不唯一）；（2）∵12x =−，123x x +<−，∴21x −＜.∵21122x x x ≥=−，，∴24x ≥−∴241x −≤−＜.（3）8.25．解：（1）如图1所示，即为所求.图1150MDO ∠=︒.（2）①12m =.理由如下.如图2，过O 作射线AB 的平行线GH ，满足点G 在O 左侧，点H 在O 右侧.当12m =时， ∵COD m BAC ∠=∠，()1COF m CAE ∠=−∠， ∴12COD BAC ∠=∠，12COF CAE ∠=∠， ∴DOF COD COF ∠=∠+∠ 11221.2BAC CAE BAE =∠+∠=∠ ∵AE AB ⊥，∴90BAE ∠=︒，∴45DOF ∠=︒，∴180135DOG FOH DOF ∠+∠=︒−∠=︒.∵AB MN ∥，B 图 2∴GH MN ∥，∴ 180MDO DOG ∠=︒−∠， 180NFO FOH ∠=︒−∠， ∴180180MDO NFO DOG FOH ∠+∠=︒−∠+︒−∠()360DOG FOH =︒−∠+∠ 225=︒② m 的值为15或47或57. 26. （1）① 7；② (0,6)或(0,4)−.（2）①依题意，(6,0),(4,0)D E ，线段DE 经过t 秒后得到线段D 1E 1. 可知 11(6,0),(4,0)D t E t −−.设点(,0)P x 为线段D 1E 1上的任意一点，得 46t x t −≤≤−.由 F (2,4)，得242x x +−=−. 所以2x −的最大值为点F 与线段D 1E 1的特征值h . 由于08t <≤，所以6422t −≤−−<, 4624t −≤−−<.所以，当t ＝8时，h 取得最大值6.点(,0)P x 为线段D 1E 1上的任意一点，且D 1E 1的长度为2. 所以，当点D 1和点E 1关于（2, 0）对称时，即D 1(3,0)，E 1(1,0). 此时h 取得最小值1. 所以点F 与线段D 1E 1的特征值h 的取值范围为：16h ≤≤.② k 1；t 10t ≤。

2024北京海淀区高三(上)期末数学试题及答案

高三年级（数学）参考答案第 1 页（共 9 页）海淀区2023—2024学年第一学期期末练习高三数学参考答案一、选择题（共10小题，每小题4分，共40分）（1）A（2）D （3）B （4）D （5）C （6）A （7）D （8）B （9）B （10）D二、填空题（共5小题，每小题5分，共25分）（ 11 ）5-（12）2 （13）1-（14）1 1（答案不唯一）（15）②④三、解答题（共6小题，共85分）（16）（共13分）解：（Ⅰ）连接1AD .在四棱柱1111ABCD A B C D -中，侧面11CDD C 为平行四边形，所以11//C D CD ，11C D CD =.因为//AB CD ，12CD AB =，M 为AB 中点，所以//CD AM ，CD AM =.所以11//C D AM ，11C D AM =.所以四边形11MAD C 为平行四边形.所以11//MC AD .因为1C M ⊄平面11ADD A ，所以1//C M 平面11ADD A ．（Ⅱ）在正方形11ABB A 中，1AA AB ⊥.因为平面11ABB A ⊥平面ABCD ，所以1AA ⊥平面ABCD .所以1AA ⊥AD .因为1AD B M ⊥, 1B M ⊂平面11ABB A ，1B M 与1AA 相交，M D 1C 1B 1A 1D C B A高三年级（数学）参考答案第 2 页（共 9 页）所以AD ⊥平面11ABB A .所以AD ⊥AB .如图建立空间直角坐标系A xyz -.不妨设1AD =，则(0,0,0)A ，1(1,2,1)C ，1(0,2,2)B ，(0,0,1)M . 所以1(1,2,1)AC =，11(1,0,1)C B =-，1(1,2,0)MC =. 设平面11MB C 的法向量为 (,,)x y z =n ，则 1110,0,C B MC ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,20.x z x y -+=⎧⎨+=⎩ 令2x =，则1y =-，2z =.于是(2,1,2)=-n .因为111cos ,|||AC AC AC ⋅<>==⋅n n n |，所以直线1AC 与平面11MB C高三年级（数学）参考答案第 3 页（共 9 页）（17）（共14分）解：（Ⅰ）由正弦定理sin sin sin a b c A B C==及2cos 2c A b a =-，得 2sin cos 2sin sin C A B A =-. ①因为πA B C ++=，所以sin sin()sin cos cos sin B A C A C A C =+=+. ② 由①②得2sin cos sin 0A C A -=.因为(0,π)A ∈，所以sin 0A ≠. 所以1cos 2C =. 因为(0,π)C ∈，所以π3C =. （Ⅱ）选条件②：1sin sin 2B A -=. 由（Ⅰ）知，π2ππ33B A A ∠=--∠=-∠. 所以2πsin sin sin()sin 3B A A A -=--11sin sin sin 22A A A A A =+-- πsin()3A =-. 所以π1sin()32A -=. 因为2π(0,)3A ∈，所以πππ(,)333A -∈-. 所以ππ36A -=，即π6A =. 所以ABC △是以AC 为斜边的直角三角形.因为c =所以2sin sin 3AB AC C ==.高三年级（数学）参考答案第 4 页（共 9 页）所以AC 边上的中线的长为1.选条件③：2222b a -=.由余弦定理得223a b ab +-=.AC 设边上的中线长为d ，由余弦定理得 2222cos 42b ab d a C =+-⋅ 2242b ab a =+- 2222234a b b a =-+-+1=. 所以AC 边上的中线的长为1.（18）（共13分）解：（Ⅰ）根据三人投篮得分统计数据，在10场比赛中，甲共获胜3场，分别是第3场，第8场，第10场.设A 表示“从10场比赛中随机选择一场，甲获胜”，则 3()10P A =.（Ⅱ）根据三人投篮得分统计数据，在10场比赛中，甲得分不低于10分的场次有6场，分别是第2场，第3场，第5场，第8场，第9场，第10场，其中乙得分大于丙得分的场次有4场，分别是第2场、第5场、第8场、第9场. 所以X 的所有可能取值为0，1，2．2024261(0)15C C P X C ===，1124268(1)15C C P X C ⋅===，0224262(2)5C C P X C ===. 所以X 的分布列为所以()012151553E X =⨯+⨯+⨯=. （Ⅲ）213()()()D Y D Y D Y >>.高三年级（数学）参考答案第 5 页（共 9 页）（19）（共15分）解：（Ⅰ）由题意知3=a，2=c所以c 2224=-=b a c ．所以椭圆E 的方程为22194+=x y ，其短轴长为4．（Ⅱ）设直线CD 的方程为1=+x my ， 11(,)C x y ，22(,)D x y ，则11(,)--M x y .由221,941⎧+=⎪⎨⎪=+⎩x y x my 得22(49)8320m y my ++-=. 所以122849-+=+my y m .由(3,0)A 得直线AM 的方程为11(3)3=-+y y x x . 由11(3),31⎧=-⎪+⎨⎪=+⎩y y x x x my 得11123y y x my -=+-.因为111=+x my ，所以12y y =-，112()122y my x m -=-+=.所以112(,)22my yN --. 因为Q 为OD 的中点，且221=+x my ，所以221(,)22my y Q +. 所以直线NQ 的斜率21221222121288492212()1812912249m y y y y m m k my my m y y m m m -+++====+-+--+--+. 当0m ≤时，0k ≤.高三年级（数学）参考答案第 6 页（共 9 页）当0m >时，因为912m m +≥m .所以28129m k m =+.所以当m k（20）（共15分）解：（Ⅰ）①当1=a 时，2()sin (sin )f x x x x b x x x b =-+=-+.记()sin =-g x x x （0x ≥），则'()1cos 0=-≥g x x . 所以()g x 在[0,)+∞上是增函数. 所以当0>x 时，()(0)0>=g x g .所以当0>x 时，()(sin )f x x x x b b =-+>.②由2()sin =-+f x x x x b 得'()2sin cos f x x x x x =--，且'(0)0=f . 当0>x 时，'()(1cos )sin =-+-f x x x x x . 因为1cos 0-≥x ，sin 0->x x ，所以'()0>f x .因为'()'()-=-f x f x 对任意∈R x 恒成立，所以当0<x 时，'()0<f x . 所以0是()f x 的唯一极值点.（Ⅱ）设曲线()=y f x 与曲线cos =-y x 的两条互相垂直的“优切线”的切点的横坐标分别为1x ，2x ，其斜率分别为1k ，2k ，则121=-k k . 因为(cos )'sin x x -=，所以1212sin sin 1⋅==-x x k k . 所以12{sin ,sin }{1,1}=-x x . 不妨设1sin 1=x ，则122π=π+x k ，∈Z k . 因为111111'()2sin cos ==--k f x ax x x x ，由“优切线”的定义可知111112sin cos sin --=ax x x x x .高三年级（数学）参考答案第 7 页（共 9 页）所以1124==π+πa x k ，∈Z k . 由“优切线”的定义可知2111111sin cos x x x b x x ⋅-+=-，所以0=b . 当24=π+πa k ，∈Z k ，0=b 时，取122π=π+x k ，222π=-π-x k ，则11()cos 0=-=f x x ，22()cos 0=-=f x x ，11'()sin 1==f x x ，22'()sin 1==-f x x ，符合题意. 所以24=π+πa k ，∈Z k ，0=b .（21）（共15分）解：（Ⅰ）1()10f A =,1()12H A =； 2()12f A =，2()15H A =．由定义可知：将数表A 中的每个数变为其相反数，或交换两行（列），()H A ，()f A 的值不变. 因为m 为奇数，{1,1}ij a ∈-，所以(1),(2),,()r r r m ，(1),(2),,()c c c m 均不为0.（Ⅱ）当{0,}s m ∈或{0,}t m ∈时，不妨设0s =，即()0r i <，1,2,,i m =.若0t =，结论显然成立；若0t ≠，不妨设()0c j >，1,2,,j t =，则(,)i j H ∈，1,2,,i m =，1,2,,j t =.所以()H A mt ≥，结论成立.当{0,}s m ∉且{0,}t m ∉时，不妨设()0r i >，1,2,,i s =，()0c j >，1,2,,j t =，则当1s i m +≤≤时，()0r i <；当1t j m +≤≤时，()0c j <. 因为当1,2,,i s =，1,2,,j t t m =++时，()0r i >，()0c j <，所以2(())(())()()0ij ij ij a r i a c j a r i c j ⋅⋅⋅=⋅⋅<.高三年级（数学）参考答案第 8 页（共 9 页）所以(,)i j H ∈.同理可得：(,)i j H ∈，1,2,,i s s m =++，1,2,,j t =.所以()()()2H A s m t m s t mt ms st ≥-+-=+-. （Ⅲ）当5m =时，()()H A f A 的最小值为89. 对于如下的数表A ，()8()9H A f A =. 下面证明：()8()9H A f A ≥. 设(1)r ，(2)r ，…，()r m 中恰有s 个正数，(1)c ，(2)c ，…，()c m 中恰有t 个正数，,{0,1,2,3,4,5}s t ∈.①若{0,5}s ∈或{0,5}t ∈，不妨设0s =，即()0r i <，1,2,,5i =.所以当1ij a =时，(,)i j H ∈.由A 中所有数不全相同，记数表A 中1的个数为a ，则1a ≥，且25(1)(2)(5)25(25)()22r r r a a f A a +++++--===，()H A a ≥.所以()81()9H A f A ≥>. ②由①设{0,5}s ∉且{0,5}t ∉.若{2,3}s ∈或{2,3}t ∈，不妨设2s =，则由（Ⅱ）中结论知：()51041011H A t t t ≥+-=+≥.因为25|(1)(2)(5)|0()122r r r f A -+++<=≤，所以()118()129H A f A ≥>. ③由①②设{0,2,3,5}s ∉且{0,2,3,5}t ∉.若{,}{1,4}s t =，则由（Ⅱ）中结论知：()25817H A ≥-=. 因为0()12f A <≤，所以()178()129H A f A ≥>.高三年级（数学）参考答案第 9 页（共 9 页）若s t =，{1,4}s ∈，不妨设1s t ==，(1)0r >，(1)0c >，且()1()H A f A <，由（Ⅱ）中结论知：()8H A ≥.所以()()8f A H A >≥.若数表A 中存在ij a （,{2,3,4,5}i j ∈）为1，将其替换为1-后得到数表'A . 因为(')()1H A H A =-，(')()1f A f A ≥-，所以(')()1()(')()1()H A H A H A f A f A f A -≤<-. 所以将数表A 中第i 行第j 列（,2,3,4,5i j =）为1的数替换为1-后()()H A f A 值变小. 所以不妨设1ij a =-（,2,3,4,5i j =）. 因为()5528H A ≥+-=，()9f A ≤，所以()8()9H A f A ≥.。

2024北京海淀区高一(下)期末物理试题及答案

F N mgf 答图1海淀区高一年级练习物理2024.07一、单项选择题。

本题共10小题，在每小题给出的四个选项中，只有一个．．．．选项是符合题意的。

（每小题3分，共30分）题号12345678910答案B C C A D A D C A B二、多项选择题。

本题共4小题，在每小题给出的四个选项中，有多个．．．选项是符合题意的。

（每小题3分，共12分。

每小题全选对的得3分，选对但不全的得2分，只要有选错的该小题不得分）题号11121314答案BD BCD AC ABD三、实验题。

本题共2小题。

（共18分。

15题6分，16题12分）15.（1）B （2分）（2）A （2分）（3）1：2：3（2分）16.（1）AC （2分）（2）D （2分）（3）-mg h B （2分）；()2C A 28m h h T -（2分）（4）以托盘和砝码以及滑块和挡光条为系统，若机械能守恒，则应满足()222M m d mgl t +＝（4分）四、论述、计算题。

本题共4小题。

（17、18题各9分，19题10分，20题12分。

共40分）17．解：（1）见答图1（2）小物体受到的摩擦力大小为f ＝mrω02＝0.040N （3）当小物体与圆盘间的静摩擦力达到最大静摩擦力时，为使小物体不滑动，圆盘转动的角速度有最大值根据牛顿第二定律μmg ＝mrω2解得ω＝5.0rad/s18．解：（1）根据动能定理，有20132W m mgR ＝＝v （2）滑块从A 运动到B 的过程中，根据动能定理，有2201122B mgx m m μ--＝v v 根据牛顿第二定律，在B 点，对滑块有2B m F mg R -支＝v解得F 支＝5mg因为滑块对轨道的压力与其所受支持力为作用力与反作用力，根据牛顿第三定律，有F 压＝F 支＝5mg（3）设滑块恰能到达最高点C 点，且在C 点速度为v C ，此时轨道对滑块的压力为零，滑块只受重力根据牛顿第二定律2C mg m R ＝v解得C v 再假设滑块能够到达最高点C 点，且在C 点速度为v C ＇，由机械能守恒定律可得：22B C 11222m mgR m '+＝v v 解得v C ＇＝0＜gR 。

2024北京海淀区高一(下)期末语文试题及答案

海淀区2023—2024高一年级第二学期期末练习参考答案语文一、（本大题共4小题，共10分）1．（2分）D 2．（2分）C3．（2分）B4.（4分）参考答案：①共情可以使人获得愉悦体验。

②共情可以催生利他的行为。

③共情有助于建立和谐的人际关系。

④共情可以提升个体的幸福感。

【评分参考】答对3点可得满分，答对2点得2分，答对1点得1分，意思对即可给分二、（本大题共4小题，共10分）5．（2分）A 6．（2分）A 7．（2分）D8．（4分）①文章第一、二段运用对比论证，阐明奇才需急求，以应不测之变的道理；运用比喻论证，说明奇才应在平时蓄积。

②文章第三段通过举例论证和对比论证，阐明求取奇才需运用正确方法，且将人才放置到合适位置的道理。

【评分参考】答出内容要点，3分；答出论证方式，1分。

三、（本大题共4小题，共16分）9．（2分）B 10．（2分）C11．（6分）答案要点：彭词：①对明室倾覆（亡国）的悲痛之情；②对人们淡忘历史、不思荣辱的无奈之感王词：①对金陵胜景的赞叹之情；②对人们空谈荣辱兴亡的委婉批评③隐含着对统治者奋起变革、有所作为的期许【评分参考】彭词3分，①②各1分，结合词句1分；王词3分，三点答出其中两点，可得2分，结合词句1分；意思对即可得分。

12．（6分）①度义而后动是而不见可悔故也②罚所及则思无因怒而滥刑③悠然心会妙处难与君说④吴楚东南坼【评分说明】每空1分；如有错别字、多字、少字，或字迹不清的情况，该空不得分。

1四、（本大题共3小题，共14分）13．（2分）B14．（6分）参考答案：湘云认为宝钗体贴周到；黛玉好使小性儿，爱吃醋。

袭人认为宝钗让人敬重，有涵养，心地宽大；黛玉爱哭闹，气量狭小。

宝玉不满宝钗劝自己追求仕途经济，认为她不够理解自己；感念黛玉从不说类似的话，认为她与自己心意相通。

【评分参考】答出湘云、袭人、宝玉对钗黛的看法各给2分；意思对即可得分。

15.（6分）答案要点：①“诉肺腑”是宝黛彼此表露心迹、确认感情的重要事件（概括“诉肺腑”的内容，明确“诉肺腑”的性质）②“诉肺腑”意味着宝黛感情试探期的结束（此前的误解现已消除）③“诉肺腑”促进了宝黛感情进一步深化，二人关系由此更加亲密、默契【评分参考】每点2分，后两点需结合具体情节。

海淀区2024-2025学年第一学期期中高三英语试题答案

海淀区2024-2025学年第一学期期中练习高三英语参考答案第一部分知识运用（共两节，30分）第一节（共10小题；每小题1.5分，共15分）1. A2. C3. B4. D5. C6. D7. B8. D9. C 10. A第二节（共10小题；每小题1.5分，共15分）11. which 12. has been working/has worked 13. industries 14. for 15. creating16. were required 17. to progress 18. growth 19. what 20. invited第二部分阅读理解（共两节，38分）第一节（共14小题；每小题2分，共28分）21. C 22. D 23. A 24. D 25. B 26. C 27. D 28. A 29. B 30. C 31. B 32. D33. C 34. A第二节（共5小题；每小题2分，共10分）35. B 36. D 37. C 38. G 39. F第三部分书面表达（共两节，32分）第一节（共4小题；第40、41题各2分，第42题3分，第43题5分，共12分）40. It refers to the people you come into contact with daily, who you may not know well but can puta smile on your face.41. They not only help the author feel a stronger sense of belonging to the community but also helpwith loneliness.42. Having consequential strangers is well worth celebrating as they are going to become yourgood friends.Having consequential strangers is well worth celebrating as they are a valuable part of your life, able to make you smile and feel a sense of connection.43. Possible version 1:The librarian at my community library is an important consequential stranger to me. He always greets me with a smile and extends appropriate care. I remember when I was having problems adjusting to high school life, he spotted it and encouraged me to embrace the new life bravely.Possible version 2:My consequential stranger is a friendly delivery person who always waves and asks about my day. His cheerful manner and genuine interest make me feel valued and connected to my neighborhood. His simple act of kindness brightens my day and reminds me that small interactions can make a difference.第二节（20分）Possible version 1:一个方案（数字餐厅），两个理由（学生层面和学校层面）Dear Jim,I’m excited to hear about your interest in the Smart Campus Initiative at your school, and I’d like to share my advice.You may consider proposing a digital smart canteen system which enables students to ordertheir desired dishes and select their pick-up time in advance.This innovative method can help students save time during lunch, allowing them to collect their chosen meals at their convenience. Moreover, school kitchen staff can monitor food consumption accurately and adjust meal preparations based on actual orders so as to cut down on food waste.I hope my suggestions can be of help to you.Yours,Li HuaPossible version 2:两个方案建议（智能学习工具和虚拟现实教学），分别有各自的理由Dear Jim,I’m thrilled to receive your letter and eager to share with you my ideas for a smart school plan.Firstly, classrooms should be equipped with advanced digital tools, such as interactive smart boards, tablets for students and high-speed internet. These tools can support learning apps that tailor educational content to students’ individual needs, which can significantly enhance study efficiency.Moreover, incorporating virtual reality into the curriculum can transform the learning experience. Just imagine studying in a school where textbook concepts all comes to life! For example, when learning about gravity in physics, students can take a virtual spacewalk to experience the zero gravity firsthand. Isn’t that thrilling?What do you think of my suggestions? I hope they can inspire you and help your plan stand out.Yours,Li HuaPossible version 3:两个方案建议（校园生活和数字学习），分别有各自的理由Dear Jim,Knowing your interest in the Smart Campus Project at your school, I’m delighted to share my advice.You may focus on improving students’ life experience. For example, you can suggest building a digital smart canteen system or equipping the gym with AI devices. These systems will enable students to enjoy more personalized services, making their school life more convenient and enjoyable.When it comes to students’ learning, integrating virtual reality courses into the curriculum can be a great way to transform their learning experience. Also, a digital library will definitely provide students with access to more diverse and interactive materials, which will make learning more immersive and tailored to individual needs.I wish you all the best in your efforts!Yours,Li Hua。

2024-2025学年北京市海淀区高三上学期10月月考数学试题及答案

数学试题2024.10.06本试卷共4页，共150分.考试时长120分钟.考生务必将答案答在答题纸上，在试卷上作答无效.第一部分（选择题共40分）一、选择题（本大题共10小题，每小题4分，共40分）1. 设集合{}21,3M m m =--，若3M -∈，则实数m =（）A. 0B. 1- C. 0或1- D. 0或12. 记n S 为等差数列{}n a 的前n 项和．已知4505S a ==，，则A. 25n a n =- B. 310n a n =- C. 228n S n n=- D. 2122n S n n =-3. 已知 1.50.31.50.3,log 0.3, 1.5a b c ===，则（）A. a b c << B. b a c <<C. a c b<< D. b c a<<4. 设()()1i 21i z -=+，则z =（）A.B. 1C.D. 25. 下列函数中，既是偶函数又是区间(0,)+∞上的增函数的是（）A. y =B. 21y x =C. lg y x =D. 332x xy --=6. 已知向量()3,4a = ，()1,0b = ，c a tb =+ ，若,,a c b c = 则实数t =（）A. 6- B. 5- C. 5D. 67. 函数()()()cos sin f x x a x b =+++，则（）A. 若0a b +=，则()f x 为奇函数 B. 若π2a b +=，则()f x 为偶函数C. 若π2b a -=，则()f x 偶函数 D. 若πa b -=，则()f x 为奇函数8. 已知函数()0x f x x <=≥⎪⎩，若对任意的1x ≤有()()20f x m f x ++>恒成立，则实数m 的取值为范围是（）A. (),1∞-- B. (],1-∞- C. (),2-∞- D. (],2-∞-9. 已知a 、b 、e 是平面向量，e 是单位向量．若非零向量a 与e 的夹角为3π，向量b满足2430b e b -⋅+=，则a b - 的最小值是A1-B.1+ C. 2D. 2-10.已知函数()f x k =+，若存在区间[,]a b ，使得函数()f x 在区间[,]a b 上的值域为[1,1]a b ++则实数k 的取值范围为（）A. (1,)-+∞ B. (1,0]- C. 1,4⎛⎫-+∞ ⎪⎝⎭D. 1,04⎛⎤- ⎥⎝⎦第二部分（非选择题共110分）二、填空题共5小题，每小题5分，共25分.11. 已知角α的终边与单位圆交于点1,2⎛⎫⎪⎝⎭y P ，则πsin 2α⎛⎫+= ⎪⎝⎭__________.12. 记n S 为数列{}n a 的前n 项和，若21n n S a =+，则6S =_____________．13. 若命题“对任意2R,20x ax x a ∈++≥为假命题的a 的取值范围是______14. 若函数()()cos sin 0f x A x x A =->最大值为2，则A =________，()f x 的一个对称中心为_______15. 对于函数()y f x =，若在其定义域内存在0x ，使得()001x f x =成立，则称函数()f x 具有性质P .（1）下列函数中具有性质P 的有___________.①()2f x x =-+②()[]()sin 0,2πf x x x =∈③()1f x x x=+，（x ∈(0,+∞)）④()()ln 1f x x =+（2）若函数()ln f x a x =具有性质P ，则实数a 的取值范围是___________.三、解答题共6小题，共85分.解答应写出文字说明，演算步骤或证明过程.16. 在ABC V中，sin A B =，b =．再从条件①，条件②、条件③这三个条件中选择一个作.的为已知，使ABC V 存在且唯一确定，并解决下面的问题：（1）求角B 的大小；（2）求ABC V 的面积．条件①：4c =；条件②：222b a c -=；条件③：cos sin a B b A =．17. 已知n S 是等差数列{a n }的前n 项和，51120S a ==，数列{b n }是公比大于1的等比数列，且236b b =，4212b b -=.（1）求数列{a n }和{b n }的通项公式；（2）设nn nS c b =，求使n c 取得最大值时n 的值.18. 已知函数π3()6sin(62cos f x x x =-+．（1）求()f x 的最小正周期和单调增区间；（2）若函数()y f x a =-在π5π[,]1212x ∈存在零点，求实数a 的取值范围．19. 1.已知函数()21exax x f x +-=，0a ≥.（1）讨论函数()f x 的单调性；（2）当0a >时，求证：函数()f x 在区间()0,1上有且仅有一个零点.20. 已知函数()e sin 2xf x x x =-.（1）求曲线()y f x =在点(0,(0))f 处的切线方程；（2）求()f x 在区间[1,1]-上的最大值；（3）设实数a 使得()e xf x x a +>对R x ∈恒成立，写出a 最大整数值，并说明理由.21. 已知数列{a n }记集合()(){}*1,,,1,,i i j T S i j S i j a a a i j i j +==+++≤<∈N （1）对于数列{a n }：1,2,3，列出集合T 的所有元素；（2）若2n a n =是否存在*,i j ∈N ，使得(),1024S i j =？若存在，求出一组符合条件,i j ；若不存在，说明理由；（3）若22n a n =-把集合T 中的元素从小到大排列，得到的新数列为12:,,,,.m B b b b 若的的b m ≤0202，求m 的最大值数学试题2024.10.06本试卷共4页，共150分.考试时长120分钟.考生务必将答案答在答题纸上，在试卷上作答无效.第一部分（选择题共40分）一、选择题（本大题共10小题，每小题4分，共40分）1. 设集合{}21,3M m m =--，若3M -∈，则实数m =（）A. 0B. 1- C. 0或1- D. 0或1【答案】C 【解析】【分析】根据元素与集合的关系，分别讨论213-=-m 和33m -=-两种情况，求解m 并检验集合的互异性，可得到答案.【详解】设集合{}21,3M m m =--，若3M -∈，3M -∈ ，213m ∴-=-或33m -=-，当213-=-m 时，1m =-，此时{}3,4M =--；当33m -=-时，0m =，此时{}3,1M =--；所以1m =-或0.故选：C2. 记n S 为等差数列{}n a 的前n 项和．已知4505S a ==，，则A. 25n a n =- B. 310n a n =- C. 228n S n n=- D. 2122n S n n =-【答案】A 【解析】【分析】等差数列通项公式与前n 项和公式．本题还可用排除，对B ，55a =，44(72)1002S -+==-≠，排除B ，对C ，245540,25850105S a S S ==-=⨯-⨯-=≠，排除C ．对D ，24554150,5250522S a S S ==-=⨯-⨯-=≠，排除D ，故选A ．【详解】由题知，41514430245d S a a a d ⎧=+⨯⨯=⎪⎨⎪=+=⎩，解得132a d =-⎧⎨=⎩，∴25n a n =-，故选A ．【点睛】本题主要考查等差数列通项公式与前n 项和公式，渗透方程思想与数学计算等素养．利用等差数列通项公式与前n 项公式即可列出关于首项与公差的方程，解出首项与公差，在适当计算即可做了判断．3. 已知 1.50.31.50.3,log 0.3, 1.5a b c ===，则（）A. a b c << B. b a c <<C. a c b << D. b c a<<【答案】B 【解析】【分析】根据指对数的性质，分别求三个数的范围，再比较大小.【详解】由条件可知，()1.50.30,1a =∈， 1.5log 0.30b =<，0.31.51>，所以b a c <<.故选：B4. 设()()1i 21i z -=+，则z =（）A.B. 1C.D. 2【答案】D 【解析】【分析】利用复数除法法则计算出()21i 2i 1iz +==-，求出模长.【详解】()()22221i 21i 12i i 2i 1i 1iz ++===++=--，故2z =.故选：D5. 下列函数中，既是偶函数又是区间(0,)+∞上的增函数的是（）A. y =B. 21y x =C lg y x= D. 332x xy --=【答案】C 【解析】【分析】根据幂函数和指对函数的奇偶性和单调性，逐一检验选项，得出答案．【详解】选项A，y =(0,)+∞上的增函数，错误；.选项B ，21y x =是偶函数，是区间(0,)+∞上的减函数，错误；选项C ，lg y x =是偶函数，是区间(0,)+∞上的增函数，正确；选项D ，332x xy --=是奇函数，是区间(0,)+∞上的增函数，错误；故选：C6. 已知向量()3,4a = ，()1,0b = ，c a tb =+ ，若,,a c b c = 则实数t =（）A. 6-B. 5- C. 5D. 6【答案】C 【解析】【分析】由向量坐标的运算求出向量c的坐标，再根据,,a c b c = ，利用向量夹角余弦公式列方程，求出实数t 的值．【详解】由()3,4a = ，()1,0b = ，则()3,4c a tb t =+=+，又,,a c b c = ，则cos ,cos ,a c b c =，则a c b c a c b c ⋅⋅=⋅⋅ ，即a b a bc c⋅⋅=，31t+=，解得5t =，故选：C.7. 函数()()()cos sin f x x a x b =+++，则（）A. 若0a b +=，则()f x 为奇函数 B. 若π2a b +=，则()f x 为偶函数C. 若π2b a -=，则()f x 为偶函数 D. 若πa b -=，则()f x 为奇函数【答案】B 【解析】【分析】根据选项中,a b 的关系，代入()f x 的解析式，对AD 用特值说明()f x 不是奇函数，对BC 用奇偶性的定义验证即可.【详解】()f x 的定义域为R ，对A ：若0a b +=，()()()cos sin f x x a x a =++-，若()f x 为奇函数，则()00f =，而()0cos sin 0f a a =-=不恒成立，故()f x 不是奇函数；对B ：若π2a b +=，()()()()πcos sin cos cos 2f x x a x a x a x a ⎛⎫=+++-=++- ⎪⎝⎭，()()()()()cos cos cos cos ()f x x a x a x a x a f x -=-++--=-++=，故()f x 偶函数，B 正确；对C ：若π2b a -=，()()()πcos sin 2cos 2f x x a x a x a ⎛⎫=++++=+ ⎪⎝⎭，()()2cos ()f x x a f x -=-+≠，故()f x 不是偶函数，故C 错误；对D ：若πa b -=，()()()()()cos πsin cos sin f x x b x b x b x b =++++=-+++，若()f x 为奇函数，则()00f =，而()0cos sin 0f b b =-+=不恒成立，故()f x 不是奇函数；故选：B8. 已知函数()0x f x x <=≥⎪⎩，若对任意的1x ≤有()()20f x m f x ++>恒成立，则实数m 的取值范围是（）A. (),1∞-- B. (],1-∞- C. (),2-∞- D. (],2-∞-【答案】A 【解析】【分析】根据奇函数的定义证明()f x 为奇函数，再判断函数的单调性，利用函数的性质化简不等式可得m 的取值范围.【详解】当0x <时，0x ->，()f x =()()f x f x -==-，当0x >时，0x -<，()f x =()()f x f x -==-，当0x =时，()00f =，所以对任意的R x ∈，()()f x f x -=-，函数()f x 为奇函数，又当0x >时，()f x =为单调递减函数，所以函数()f x 在(),-∞+∞上为单调递减函数，所以不等式()()20f x m f x ++>可化为()()2f x m f x +>-，为所以2x m x +<-，所以x m <-，由已知对任意的1x ≤有x m <-恒成立，所以1m <-，即1m <-，故m 的取值范围是(),1∞--.故选：A.9. 已知a 、b 、e 是平面向量，e 是单位向量．若非零向量a 与e 的夹角为3π，向量b满足2430b e b -⋅+= ，则a b - 的最小值是A.1B.1+ C. 2D. 2-【答案】A 【解析】【分析】先确定向量a、b所表示的点的轨迹，一个为直线，一个为圆，再根据直线与圆的位置关系求最小值.【详解】设()()(),,1,0,,a x y e b m n ===r r r，则由π,3a e =r r得πcos ,3a e e x y a ⋅=⋅=∴=r r r r ，由2430b e b -⋅+=r r r 得()2222430,21,m n m m n +-+=-+=因此，a b -r r 的最小值为圆心()2,0到直线y =11.选A.【点睛】以向量为载体求相关变量的取值范围，是向量与函数、不等式、三角函数、曲线方程等相结合的一类综合问题.通过向量的坐标运算，将问题转化为解方程、解不等式、求函数值域或直线与曲线的位置关系，是解决这类问题的一般方法.10.已知函数()f x k =+，若存在区间[,]a b ，使得函数()f x 在区间[,]a b 上的值域为[1,1]a b ++则实数k 的取值范围为（）A. (1,)-+∞ B. (1,0]- C. 1,4⎛⎫-+∞ ⎪⎝⎭D. 1,04⎛⎤- ⎥⎝⎦【答案】D 【解析】【分析】根据函数的单调性可知，()()11f a a f b b ⎧=+⎪⎨=+⎪⎩，即得1010a kb k ⎧+--=⎪⎨+--=⎪⎩方程20x x k --=的两个不同非负实根，由根与系数的关系即可求出．【详解】根据函数的单调性可知，()()11f a a f b b ⎧=+⎪⎨=+⎪⎩，即可得到1010a kb k ⎧+--=⎪⎨+-=⎪⎩，20x x k --=两个不同非负实根，所以1400k k ∆=+>⎧⎪=-≥，解得104k -<≤．故选：D ．【点睛】关键点睛：利用函数的单调性以及一元二次方程的根与系数的关系是解决本题的关键.第二部分（非选择题共110分）二、填空题共5小题，每小题5分，共25分.11. 已知角α的终边与单位圆交于点1,2⎛⎫⎪⎝⎭y P ，则πsin 2α⎛⎫+= ⎪⎝⎭__________.【答案】12##0.5【解析】【分析】由三角函数定义得到1cos 2α=，再由诱导公式求出答案.【详解】由三角函数定义得1cos 2α=，由诱导公式得1cos 2πsin 2αα⎛⎫= ⎪⎭=+⎝.故答案为：1212. 记n S 为数列{}n a 的前n 项和，若21n n S a =+，则6S =_____________．【答案】63-【解析】【分析】首先根据题中所给的21n n S a =+，类比着写出1121n n S a ++=+，两式相减，整理得到12n n a a +=，从而确定出数列{}n a 为等比数列，再令1n =，结合11,a S 的关系，求得11a =-，之后应用等比数列的求和的公式求得6S 的值.【详解】根据21n n S a =+，可得1121n n S a ++=+，两式相减得1122n n n a a a ++=-，即12n n a a +=，当1n =时，11121S a a ==+，解得11a =-，所以数列{}n a 是以-1为首项，以2为公比的等比数列，所以66(12)6312S --==--，故答案是63-.点睛：该题考查的是有关数列的求和问题，在求解的过程中，需要先利用题中的条件，类比着往后写一个式子，之后两式相减，得到相邻两项之间的关系，从而确定出该数列是等比数列，之后令1n =，求得数列的首项，最后应用等比数列的求和公式求解即可，只要明确对既有项又有和的式子的变形方向即可得结果.13. 若命题“对任意2R,20x ax x a ∈++≥为假命题的a 的取值范围是______【答案】1a <【解析】【分析】写出全称量词命题的否定，2R,20x ax x a ∃∈++<为真命题，分0a =，0a <和0a >三种情况，得到不等式，求出答案.【详解】由题意得2R,20x ax x a ∃∈++<为真命题，当0a =时，不等式为20x <，有解，满足要求，当0a ≠时，若0a <，此时220ax x a ++<必有解，满足要求，若0a >，则2440a ∆=->，解得01a <<，综上，a 的取值范围为1a <.故答案为：1a <14. 若函数()()cos sin 0f x A x x A =->的最大值为2，则A =________，()f x 的一个对称中心为_______【答案】 ①. ②. π,03⎛⎫⎪⎝⎭（答案不唯一）【解析】【分析】根据辅助角公式对函数()f x 进行化简，再根据最大值求出A ，最后利用余弦型函数求出对称中心.【详解】由()cos sin f x A x x x ϕ=-=+（），其中1tan A ϕ=，又函数()f x 的最大值为22=，又0A >，则A =，tan ϕ=，不妨取π6ϕ=，故()π2cos 6f x x ⎛⎫=+ ⎪⎝⎭，则()f x 的对称中心满足πππ62x k +=+，k ∈Z ，解得ππ3x k =+，k ∈Z ，即()f x 的对称中心为ππ,03k ⎛⎫+ ⎪⎝⎭，k ∈Z ，则()f x 的一个对称中心可为：π,03⎛⎫⎪⎝⎭，π,03⎛⎫ ⎪⎝⎭（答案不唯一）15. 对于函数()y f x =，若在其定义域内存在0x ，使得()001x f x =成立，则称函数()f x 具有性质P .（1）下列函数中具有性质P 的有___________.①()2f x x =-+②()[]()sin 0,2πf x x x =∈③()1f x x x=+，（x ∈(0,+∞)）④()()ln 1f x x =+（2）若函数()ln f x a x =具有性质P ，则实数a 的取值范围是___________.【答案】①. ①②④ ②. 0a ＞或a e ≤-．【解析】【分析】（1）令12x x -=，由0∆=，可判断；由sin x =1x 有解，可判断是否具有性质P ；令1+x x=1x ，此方程无解，由此可判断；由()1ln 1,x x y y =+=两图象在()1，-+∞有交点可判断；（2）问题转化为方程1ln x x a =有根，令()ln g x x x =，求导函数，分析导函数的符号，得所令函数的单调性及最值，由此可求得实数a 的取值范围．【详解】解：（1）在0x ≠时， ()1f x x =有解，即函数具有性质P ，令12x x-= ，即2210x -+-=，∵880∆=-=，故方程有一个非0实根，故()2f x x =-+ 具有性质P ；()()sin ]02[f x x x π=∈，的图象与1y x=有交点，故sin x =1x有解，故()()sin ]02[f x x x π=∈，具有性质P ；令1+x x =1x ，此方程无解，故()1f x x x=+，（x ∈(0,+∞)）不具有性质P ；令()1ln 1x x +=，则由()1ln 1,x x y y =+=两图象在()1，-+∞有交点，所以()1ln 1x x +=有根，所以()()ln 1f x x =+具有性质P ；综上所述，具有性质P 的函数有：①②④；（2）()ln f x a x =具有性质P ，显然0a ≠，方程1ln x x a =有根，令()ln g x x x =，则()'ln +1g x x =，令()'ln +10g x x ==，解得1=x e ，当11x e -<<时，()'0g x <，所以()g x 在11e ⎛⎫- ⎪⎝⎭，上单调递减，当1>x e 时，()'>0g x ，所以()g x 在1e ⎛⎫+∞ ⎪⎝⎭，上单调递增，所以()1111ln g x g e e e e⎛⎫≥==- ⎪⎝⎭，所以()ln g x x x =的值域[1e -，+∞），∴11a e ≥-，解之可得：0a ＞或a e ≤-．故答案为：①②④；0a ＞或a e ≤-．【点睛】方法点评：解决本题的关键是审清题意，把方程的解转化为两个图象有交点，本题考查的是方程的根，新定义，函数的值域，是方程和函数的综合应用，难度比较大．三、解答题共6小题，共85分.解答应写出文字说明，演算步骤或证明过程.16. 在ABC V 中，sin A B =，b =．再从条件①，条件②、条件③这三个条件中选择一个作为已知，使ABC V 存在且唯一确定，并解决下面的问题：（1）求角B 的大小；（2）求ABC V 的面积．条件①：4c =；条件②：222b a c -=；条件③：cos sin a B b A =．【答案】（1）选②或③，4B π=；（2）ABC V 的面积为1.【解析】【分析】（1）选①，利用三边关系可判断ABC V 不存在；选②：利用余弦定理可求得角B 的值；选③：利用正弦定理可求得tan B 的值，结合角B 的取值范围可求得角B 的值；（2）利用余弦定理可求得c 的值，再利用三角形的面积公式可求得ABC V 的面积．【小问1详解】解：因为sin A B =，b =，则2a ==.选①：因为4c =，则a b c +<，则ABC V 不存在；选②：因为222b a c -=，则222a c b +-=，由余弦定理可得222cos 2a c b B ac +-==，()0,B π∈ ，则4B π=；选③：cos sin a B b A = ，则sin cos sin sin A B A B =，A 、()0,B π∈，则sin 0A >，sin cos 0B B =>，故tan 1B =，从而4B π=.【小问2详解】解：因为4B π=，2a =，b =，由余弦定理可得2222cos b a c ac B =+-，即220c -+=，解得c =，因此，11sin 2122ABC S ac B ==⨯=△.17. 已知n S 是等差数列{a n }的前n 项和，51120S a ==，数列{b n }是公比大于1的等比数列，且236b b =，4212b b -=.（1）求数列{a n }和{b n }的通项公式；（2）设n n nS c b =，求使n c 取得最大值时n 的值.【答案】（1）22n a n =-，2n n b =（2）3或4【解析】【分析】（1）根据等差数列的通项及前n 项和公式求出首项与公差，即可求出数列{a n }的通项公式，再求出数列{b n }的首项与公比，即可得{b n }的通项公式；（2）先求出{}n c 的通项，再利用作差法判断数列的单调性，根据单调性即可得出答案.【小问1详解】设等差数列{a n }的公差为d ，则511115452021020S a d a a d ⨯⎧=+=⎪⎨⎪=+=⎩，解得10,2a d ==，所以22n a n =-，设等比数列{b n }的公比为()1q q >，则()2251131112b q b q b q b q ⎧=⎪⎨-=⎪⎩，解得122b q =⎧⎨=⎩，所以2n n b =；【小问2详解】由（1）得()()2212n n n S n n -==-，则()12n n nn n n S c b -==，()()2111113222n n n n n n n n n n n c c ++++---=-=，当1,2n =时，11230,n n c c c c c +-><<，当3n =时，1340,n n c c c c +-==，当4n ≥时，1450,n n n c c c c c +->> ，所以当3n =或4时，n c 取得最大值.18. 已知函数π3()6sin(62cos f x x x =-+．（1）求()f x 的最小正周期和单调增区间；（2）若函数()y f x a =-在π5π[,]1212x ∈存在零点，求实数a 的取值范围．【答案】（1）π，()πππ,πZ 63k k k ⎡⎤-++∈⎢⎥⎣⎦（2）[]0,3【解析】【分析】（1）化简函数()π3sin 26f x x ⎛⎫=- ⎪⎝⎭，结合三角函数的图象与性质，即可求解；（2）根据题意转化为方程πsin 263a x ⎛⎫-= ⎪⎝⎭在π5π,1212x ⎡⎤∈⎢⎥⎣⎦上有解，以π26x -为整体，结合正弦函数图象运算求解.【小问1详解】对于函数π313()6cos sin 6cos cos 6222f x x x x x x ⎫⎛⎫=-+=-+⎪ ⎪⎪⎝⎭⎭()231cos 231π3sin cos 3cos 2332cos 23sin 222226x f x x x x x x x x ⎫+⎛⎫=-+-⨯+=-=-⎪ ⎪⎪⎝⎭⎭，所以函数()f x 的最小正周期为2ππ2T ==，令πππ2π22π,Z 262k x k k -+£-£+Î，则ππππ,Z 63k x k k -+££+Î，∴函数()f x 单调递增区间为()πππ,πZ 63k k k ⎡⎤-++∈⎢⎥⎣⎦.【小问2详解】令()0y f x a =-=，即π3sin 206x a ⎛⎫--= ⎪⎝⎭，则πsin 263a x ⎛⎫-= ⎪⎝⎭，∵()y f x a =-在π5π,1212x ⎡⎤∈⎢⎥⎣⎦存在零点，则方程πsin 263a x ⎛⎫-= ⎪⎝⎭在π5π,1212x ⎡⎤∈⎢⎥⎣⎦上有解，若π5π,1212x ⎡⎤∈⎢⎥⎣⎦时，则π2π20,63x ⎡⎤-∈⎢⎥⎣⎦，可得πsin 2[0,1]6x ⎛⎫-∈ ⎪⎝⎭，∴013a ≤≤，得03a ≤≤故实数a 的取值范围是[]0,3．的19. 1.已知函数()21ex ax x f x +-=，0a ≥.（1）讨论函数()f x 的单调性；（2）当0a >时，求证：函数()f x 在区间()0,1上有且仅有一个零点.【答案】（1）当0a =时，()f x 的单调递减区间为()2,∞+，单调递增区间为(),2∞-；当0a >时，()f x 的单调递减区间为1,a ⎛⎫-∞-⎪⎝⎭，()2,∞+，单调递增区间为1,2a ⎛⎫- ⎪⎝⎭. （2）证明过程见解析【解析】【分析】（1）求出导数，然后通过对a 分情况讨论，研究导数的符号研究函数的单调性；（2）结合第一问的结果，判断出函数在()0,1上的单调性，然后结合端点处的函数值的符合证明【小问1详解】()()()12e x ax xf x -+-'==，当0a =时，()()2e x x f x --'=，由()0f x '>得：2x <，由()0f x '<，得：2x >，故此时()f x 的单调递减区间为()2,∞+，单调递增区间为(),2∞-当0a >时，令()()()120g x ax x =-+-=得：x =−1a <0或2x =由()0g x >得：12x a-<<，此时()0f x '>由()0g x <得：1x a <-或2x >，此时()0f x '<故此时()f x 的单调递减区间为1,a ⎛⎫-∞- ⎪⎝⎭，()2,∞+，单调递增区间为1,2a ⎛⎫- ⎪⎝⎭综上：当0a =时，()f x 的单调递减区间为()2,∞+，单调递增区间为(),2∞-；当0a >时，()f x 的单调递减区间为1,a ⎛⎫-∞-⎪⎝⎭，()2,∞+，单调递增区间为1,2a ⎛⎫- ⎪⎝⎭.【小问2详解】由（1）可知，当0a >时，()f x 的单调递增区间为1,2a ⎛⎫- ⎪⎝⎭，而()1,20,1a ⎛-⊂⎫ ⎪⎝⎭，所以()f x 在()0,1上单调递增，又()010f =-<，()10ea f =>所以()()010f f ⋅<，由零点存在性定理可得：：函数()f x 在区间()0,1上有且仅有一个零点20. 已知函数()e sin 2xf x x x =-.（1）求曲线()y f x =在点(0,(0))f 处的切线方程；（2）求()f x 在区间[1,1]-上的最大值；（3）设实数a 使得()e xf x x a +>对R x ∈恒成立，写出a 的最大整数值，并说明理由.【答案】（1）y x =-（2）()max sin12ef x =- （3）2-，理由见解析【解析】【分析】（1）求出函数在0x =处的导数，即切线斜率，求出(0)f ，即可得出切线方程；（2）求出函数在区间[1,1]-上的单调性，求出最值即可；（3）将不等式等价转化为sin e x x a x <-在R x ∈上恒成立.构造函数()sin e xx x x ϕ=-，利用导数求出函数的单调性和最小值，进而得证.【小问1详解】因为()e sin 2x f x x x =-，所以()()e sin cos 2x f x x x =+-'，则(0)1f '=-，又(0)0f =，所以曲线()y f x =在点(0,(0))f 处的切线方程为y x =-.【小问2详解】令()()()esin cos 2x g x f x x x +'==-，则()2e cos x g x x '=，当[1,1]x ∈-时，()0g x '>，()g x 在[1,1]-上单调递增.因为(0)10g =-<，()()1e sin1cos120g =+->，所以0(0,1)x ∃∈，使得0()0g x =.所以当0(1,)x x ∈-时，()0f x '<，()f x 单调递减；当0(,1)x x ∈时，()0f x '>，()f x 单调递增，又()1esin12e 21f =-<-<，()sin1121e f -=->，所以()()max sin112ef x f =-=-.【小问3详解】满足条件的a 的最大整数值为2-.理由如下：不等式()e x f x x a +>恒成立等价于sin e xx a x <-恒成立.令()sin e x x x x ϕ=-，当0x ≤时，0e xx -≥，所以()1x ϕ>-恒成立.当0x >时，令()e x x h x =-，()0h x <，()1ex x h x '-=，()h x '与()h x 的情况如下：所以()()min 11eh x h ==-，当x 趋近正无穷大时，()0h x <，且()h x 无限趋近于0，所以()h x 的值域为1,0e ⎡⎫-⎪⎢⎣⎭，因为sin [1,1]x ∈-，所以()ϕx 的最小值小于1-且大于2-.所以a 的最大整数值为2-.21. 已知数列{a n }记集合()(){}*1,,,1,,i i j T S i j S i j a a a i j i j +==+++≤<∈N（1）对于数列{a n }：1,2,3，列出集合T 的所有元素；（2）若2n a n =是否存在*,i j ∈N ，使得(),1024S i j =？若存在，求出一组符合条件的,i j ；若不存在，说明理由；（3）若22n a n =-把集合T 中的元素从小到大排列，得到的新数列为12:,,,,.m B b b b 若2020m b ≤，求m 的最大值.【答案】（1）{}3,5,6T =；（2）不存在，理由见解析；（3）1001.【解析】【分析】（1）根据题目给出的集合T 的定义求解即可；（2）假设存在*,i j ∈N ，使得(),1024S i j =，则有()()()1102422121i i j a a a i i j j i i j +=+++=++++=-++ ，则i j +与j i -奇偶性相同，所以i j +与1j i -+奇偶性不同，进行分析即可得解；（3）由22n a n =-，根据题意给出的集合T 新定义可对()()()()22221212j i j i j i j i -+--+=+--+进行计算分析，讨论元素的奇偶情况，即可得出答案．【小问1详解】由题意可得123a a +=，1236a a a ++=，235a a +=，所以{}3,5,6T =.【小问2详解】假设存在*,i j ∈N ，使得(),1024S i j =，则有()()()1102422121i i j a a a i i j j i i j +=+++=++++=-++ ，由于i j +与j i -奇偶性相同，所以i j +与1j i -+奇偶性不同，又因为3,12i j j i +≥-+≥，所以1024必有大于等于3的奇数因子，这与1024无1以外的奇数因子矛盾.故不存在*,i j ∈N ，使得(),1024S i j =成立.小问3详解】由题意得()()()()22221212j i j i j i j i -+--+=+--+，当2j =，1i =时，12b =，除2j =，1i =外22j i +-≥，12j i -+≥，【其中2j i +-与1j i -+一奇一偶，则n b 能拆成奇数与偶数之乘积，在正偶数中，只有2n 无法拆成一个大于2的奇数与一个不小于2的偶数之乘积，又T 中的元素均为偶数，故{}**2,2,k T n n n k =∈≠∈N N ，故2至2024偶数中除去4，8，16，32，64，128，256，512，1024，2020910012m ∴=-=，故m 的最大值为1001．【点睛】关键点睛：求解新定义运算有关的题目，关键是理解和运用新定义的概念以及运算，利用化归和转化的数学思想方法，将不熟悉的数学问题，转化成熟悉的问题进行求解.对于新型集合，首先要了解集合的特性，抽象特性和计算特性，抽象特性是将集合可近似的当作数列或者函数分析.计算特性，将复杂的关系通过找规律即可利用已学相关知识求解.。

2024北京海淀区初一(下)期末英语试题及答案

more about Chinese culture and fine arts. I can’t wait to visit the museum again.
Yours,
Li Hua
题目 2 简单版：
I live in a quiet neighborhood. There is a shopping mall, a bank, a bookshop, and a post office in the neighborhood, but my favorite place is the park.
All in all, this trip was a good way for us to learn things outside the classroom. It was such
an unforgettable memory for me.
Yours,
Li Hua 丰富版：
Dear Jack,
dynasties. Thanks to the guide’s patient explanation, we learned about the stories behind each
exhibit and were amazed by the achievements our ancestors made in those times. After that, we
Because in sleep tourism, I can make the most of my time visiting places, experiencing new cultures
and tasting new types of food, and at the same time naturally catching up on much-needed sleep.

海淀试题及答案

海淀试题及答案一、单选题（每题2分，共10题）1. 下列哪个选项是正确的？A. 地球是平的B. 太阳围绕地球转C. 地球围绕太阳转D. 月球是地球的卫星答案：C2. 以下哪个是化学元素的符号？A. H2OB. CO2C. NaClD. Fe答案：D3. 以下哪个是计算机编程语言？A. HTMLB. CSSC. JavaScriptD. Python答案：D4. 以下哪个是人体最大的器官？A. 心脏B. 肺C. 皮肤D. 大脑答案：C5. 以下哪个是联合国的官方语言？A. 英语B. 法语C. 汉语D. 所有选项答案：D6. 下列哪个选项是正确的？A. 光速是宇宙中最快的速度B. 声音在真空中传播C. 地球的自转周期是24小时D. 以上都是答案：A7. 以下哪个是著名的物理学家？A. 爱因斯坦B. 牛顿C. 法拉第D. 所有选项答案：D8. 以下哪个是人体必需的微量元素？A. 钙B. 铁C. 锌D. 所有选项答案：D9. 下列哪个选项是正确的？A. 氧气是可燃的B. 氢气是不可燃的C. 二氧化碳是可燃的D. 氧气是助燃的答案：D10. 以下哪个是数学中的基本概念？A. 圆周率B. 勾股定理C. 斐波那契数列D. 所有选项答案：D二、多选题（每题3分，共5题）1. 以下哪些是计算机的组成部分？A. 中央处理器B. 显示器C. 键盘D. 鼠标答案：A, B, C, D2. 以下哪些是人体必需的维生素？A. 维生素AB. 维生素BC. 维生素CD. 维生素D答案：A, B, C, D3. 以下哪些是常见的编程语言？A. JavaB. C++C. PythonD. Ruby答案：A, B, C, D4. 以下哪些是人体的主要器官？A. 心脏B. 肝脏C. 肾脏D. 脾脏答案：A, B, C, D5. 以下哪些是联合国的五个常任理事国？A. 中国B. 法国C. 俄罗斯D. 美国答案：A, B, C, D三、判断题（每题1分，共5题）1. 地球是太阳系中唯一有生命的行星。

海淀区2024-2025学年第一学期期中高三化学试题答案

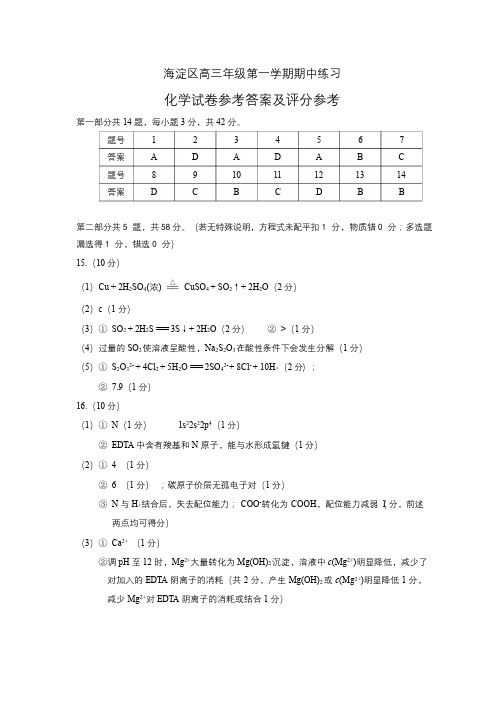
海淀区高三年级第一学期期中练习化学试卷参考答案及评分参考第一部分共 14 题，每小题 3 分，共 42 分。

题号 1 2 3 4 5 6 7答案 A D A D A B C题号8 9 10 11 12 13 14答案 D C B C D B B第二部分共5题，共58分。

（若无特殊说明，方程式未配平扣1分，物质错0分；多选题漏选得1分，错选0分）15.（10 分）（1）Cu + 2H2SO4(浓) CuSO4 + SO2↑+ 2H2O（2 分）（2）c（1 分）（3）①SO2 + 2H2S === 3S↓+ 2H2O（2 分）②>（1 分）（4）过量的 SO2 使溶液呈酸性，Na2S2O3 在酸性条件下会发生分解（1 分）（5）①S2O32-+ 4Cl2 + 5H2O === 2SO42-+ 8Cl-+ 10H+（2 分）；②7.9（1 分）16.（10 分）（1）①N（1 分）1s22s22p4（1 分）②EDTA 中含有羧基和 N 原子，能与水形成氢键（1 分）（2）①4 （1 分）②6 （1 分）；碳原子价层无孤电子对（1 分）③N 与 H+结合后，失去配位能力；-COO-转化为-COOH，配位能力减弱（1 分，前述两点均可得分）（3）①Ca2+ （1 分）②调 pH 至 12 时，Mg2+大量转化为 Mg(OH)2 沉淀，溶液中c(Mg2+)明显降低，减少了对加入的 EDT A 阴离子的消耗（共 2 分，产生 Mg(OH)2 或c(Mg2+)明显降低 1 分，减少 Mg2+对 EDT A 阴离子的消耗或结合 1 分）17.（12 分）（1）增大接触面积，加快浸出速率/使浸出更充分（1 分）（2）①Bi2S3 + 6Fe3+ === 2Bi3+ + 3S + 6Fe2+（共 2 分）②H+与 Bi2S3 中的 S2-结合，促进 Bi2S3 的沉淀溶解平衡正向移动；抑制 Fe3+水解平衡的正向移动（抑制 Bi3+水解平衡的正向移动）（共 2 分，每个平衡 1 分）（3）3Fe + 2Bi3+ === 2Bi + 3Fe2+ 2H+ + Fe === Fe2+ + H2↑（共 2 分，每个方程式 1 分，方程式有错即扣 1 分）（4）①盐酸（1 分）②在 Fe3+的催化作用下，H2O2 易分解（产生的 O2 快速脱离反应体系）（共 2 分）③取少量溶液于试管中，加入 K3[Fe(CN)6]溶液，观察溶液中是否产生蓝色沉淀（共 2分，试剂 1 分，写铁氰化钾也可给分，现象 1 分，必须是蓝色沉淀）18.（12 分）（1）2CO2(g) + 6H2(g) CH3OCH3(g) + 3H2O(g) △H= -122.5kJ·mol-1（共 2 分）c(CH3OCH3)c3(H2Oc2(CO2)c6(H2（1 分）（2）a b（2 分）（3）c（1 分）（4）①温度升高，I、III的化学反应速率增大（2分）②二甲醚选择性与甲醇选择性总和变化很小，CO选择性增大的空间有限（答案合理即可）（共2分）（5）增大空速减少了催化剂与 CO2 和 H2 原料气的接触时间，导致 CO2 和 H2 与催化剂不能充分接触，CO2 的转化率减小；空速增大，反应Ⅱ、Ⅲ的速率降低较多，甲醇的选择性增大。

海淀区2024-2025学年第一学期期中高三物理试题及答案

海淀区20242025学年第一学期期中练习参考答案及评分标准高三物理2024.11第一部分共 10 题，每题 3 分，共 30 分。

在每题给出的四个选项中，有的题只有一个选项是正确的，有的题有多个选项是正确的。

全部选对的得 3 分，选不全的得 2 分，有选错或不答的得 0 分。

题号 1 2 3 4 5 6 7 8 9 10答案BD D ABD AD BC CD AB AD B BCD第二部分共 8 题，共 20 分。

11.（5 分）（1）C（2）①平抛运动的下落高度一定，运动时间相同，水平射程与速度大小成正比②（3）AB12. （10 分）（1）乙（2）97.48~97.52（3）（4）9.86（5）（或其他正确答案均可得分）13．（8 分）（1）以沿斜面向上为正方向，设滑块的加速度为a，根据牛顿第二定律，有得根据运动学公式得x v22g sin（2）以沿斜面向上为正方向，滑块速度变化量为v2v1根据运动学公式2得0tvg sin（3）根据瞬时功率定义，得14．（8 分）（1）运动员在竖直方向下落高度根据运动的合成与分解，结合运动学公式，有竖直方向2h 220 得t s 2sg 10（2）根据动量定理，有I p合可知p mgt 1600kg m/s ，方向竖直向下（3）根据运动的合成与分解，结合运动学公式，有水平方向竖直方向得15．（8 分）（1）管口单位时间内喷出水的体积得（2）在喷水口处，设经过 Δt 的时间喷出水的质量为 Δm，有m=ρS v0t在 Δt 时间内动力装置做功转化为水的动能得2（3）选取刚要撞击到车身表面上的一段水柱为研究对象，设初速度方向为正，设水柱受到的作用力为F x，在水平方向由动量定理，有得由牛顿第三定律，可得16. （9 分）（1）设卫星的质量为m，万有引力提供卫星做圆周运动所需的向心力得（2）设小物体质量为m。

a．在北极地面在赤道地面根据向心力定义得b．如答图 1 所示，在纬度为 45°的地面F3小物体做圆周运动所需向心力F n45ºO得又有联立可得答图 1317．（10 分）（1）a．小物体被甩出时，静摩擦力达到最大值由牛顿第二定律，得得b．设小物体被甩出时的速度为v0有对于加速过程，由动能定理，有得（2）a．小物体所受摩擦力的示意图如答图 2 所示b．物体被甩出瞬间，静摩擦力达到最大值转速迅速增大即设f 与半径夹角为휃，在沿半径方向，由牛顿第二定律θOf 得物体被甩落后做平抛运动，两种情况下平抛的飞行时间t 相等答图 2由几何关系，可知转速缓慢增大转速迅速增大由于可得L1> L2418. （12 分）（1）运动员在离开地面之后做竖直上抛运动，满足02 2ghv，离开地面瞬间的速度v2gh（2）a. 设该模型弹簧的劲度系数为k，静止时弹簧的压缩量为x0根据受力分析可知mg= k x0得k mg xb. 当B 恰好能离开地面时，意味着A 的速度为 0，弹簧处于伸长状态。

2024年北京海淀中考数学试题及答案

2024年北京海淀中考数学试题及答案考生须知：1.本试卷共6页，共两部分.三道大题，28道小题。

满分100分。

考试时间120分钟。

2.在试卷和草稿纸上准确填写姓名、准考证号、考场号和座位号。

3.试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

4.在答题卡上.选择题、作图题用2B 铅笔作答，其他试题用黑色字迹签字笔作答。

5.考试结束，将本试卷、答题卡和草稿纸一并交回。

第一部分选择题一、选择题（共16分，每题2分）第1-8题均有四个选项，符合题意的选项只有一个1．下列图形中，既是轴对称图形又是中心对称图形的是（）A ．B ．C ．D．2．如图，直线AB 和CD 相交于点O ，OE OC ⊥，若58AOC ∠=︒，则EOB ∠的大小为（）A ．29︒B ．32︒C ．45︒D ．58︒3．实数a ，b 在数轴上的对应点的位置如图所示，下列结论中正确的是（）A ．1b >-B ．2b >C ．0a b +>D ．0ab >4．若关于x 的一元二次方程240x x c -+=有两个相等的实数根，则实数c 的值为（）A ．16-B ．4-C ．4D ．165．不透明的袋子中装有一个红色小球和一个白色小球，除颜色外两个小球无其他差别．从中随机取出一个小球后，放回并摇匀，再从中随机取出一个小球，则两次都取到白色小球的概率为（　）A ．34B ．12C ．13D ．146．为助力数字经济发展，北京积极推进多个公共算力中心的建设.北京数字经济算力中心日前已部署上架和调试的设备的算力为17410⨯Flops （Flops 是计算机系统算力的一种度量单位），整体投产后，累计实现的算力将是日前已部署上架和调试的设备的算力的5倍，达到m Flops ，则m 的值为（）A ．16810⨯B ．17210⨯C ．17510⨯D ．18210⨯7．下面是“作一个角使其等于AOB ”的尺规作图方法.（1）如图，以点O 为圆心，任意长为半径画弧，分别交OA ，OB 于点C ，D ；（2）作射线O A ''，以点O '为圆心，OC 长为半径画弧，交O A ''于点C '；以点C '为圆心，CD 长为半径画弧，两弧交于点D ¢；（3）过点D ¢作射线O B ''，则A O B AOB '''∠=∠.上述方法通过判定C O D COD '''△≌△得到A O B AOB '''∠=∠，其中判定C O D COD '''△≌△的依据是（）A ．三边分别相等的两个三角形全等B ．两边及其夹角分别相等的两个三角形全等C ．两角及其夹边分别相等的两个三角形全等D ．两角分别相等且其中一组等角的对边相等的两个三角形全等8．如图，在菱形ABCD 中，60BAD ∠=︒，O 为对角线的交点.将菱形ABCD 绕点O 逆时针旋转90︒得到菱形A B C D ''''，两个菱形的公共点为E ，F ，G ，H .对八边形BFB GDHD E ''给出下面四个结论：①该八边形各边长都相等；②该八边形各内角都相等；③点O 到该八边形各顶点的距离都相等；④点O 到该八边形各边所在直线的距离都相等。

海淀试题及答案

海淀试题及答案一、选择题（每题2分，共20分）1. 下列哪个选项不是中国的传统节日？A. 春节B. 清明节C. 圣诞节D. 端午节2. 以下哪个不是四大名著之一？A. 《红楼梦》B. 《西游记》C. 《水浒传》D. 《聊斋志异》3. 根据题目所给的数学公式，哪个选项是正确的？A. \( a + b = b + a \)（交换律）B. \( a * b = b * a \)（结合律）C. \( a / b = b / a \)（分配律）D. \( (a + b)^2 = a^2 + b^2 \)（平方差公式）4. 以下哪个国家不是联合国安全理事会常任理事国？A. 中国B. 法国C. 德国D. 俄罗斯5. 以下哪种植物不是被子植物？A. 松树B. 桃树C. 苹果树D. 梨树6. 以下哪个是元素周期表中的稀有气体？A. 氢B. 氦C. 氧D. 氮7. 以下哪个是牛顿三大定律中的第二定律？A. 物体的加速度与作用力成正比B. 物体的加速度与作用力成反比C. 物体的加速度与作用力无关D. 物体的加速度与作用力的平方成正比8. 以下哪个是计算机编程中的错误类型？A. 语法错误B. 逻辑错误C. 运行时错误D. 所有选项都是9. 以下哪个是经济学中的边际效用递减原理？A. 随着商品数量的增加，消费者对商品的需求逐渐减少B. 随着商品价格的增加，消费者对商品的需求逐渐减少C. 随着商品数量的增加，消费者从每增加一个单位商品中获得的满足感逐渐减少D. 随着商品价格的增加，消费者从每增加一个单位商品中获得的满足感逐渐增加10. 以下哪个是物理学中的电磁感应现象？A. 电流通过导线产生磁场B. 磁场通过导线产生电流C. 电流通过导线产生电场D. 磁场通过导线产生电场答案：1. C2. D3. A4. C5. A6. B7. A8. D9. C10. B二、填空题（每题2分，共20分）1. 地球的自转周期是________小时。

海淀初中试题及答案

海淀初中试题及答案一、选择题（每题2分，共10分）1. 下列词语中，没有错别字的一项是（）。

A. 张冠李戴B. 振耳欲聋C. 再接再励D. 黄梁美梦答案：A2. 下列句子中，标点符号使用正确的一项是（）。

A. 他问我：“你明天有空吗？”B. “你明天有空吗？”他问我。

C. 他问我：“你明天有空吗？”。

D. “你明天有空吗？”他问我。

答案：B3. 下列各句中，没有语病的一项是（）。

A. 通过这次活动，使我们认识到团结协作的重要性。

B. 他虽然学习成绩优异，但是性格内向。

C. 为了避免不再发生类似事故，我们必须加强安全教育。

D. 他不但学习刻苦，而且成绩优异。

答案：D4. 下列句子中，使用了比喻修辞手法的一项是（）。

A. 他像一只小鸟一样在操场上飞奔。

B. 他跑得像风一样快。

C. 他的声音像泉水一样清澈。

D. 他像一只猎豹一样敏捷。

答案：C5. 下列句子中，使用了排比修辞手法的一项是（）。

A. 春天的花开了，夏天的树绿了，秋天的果实熟了，冬天的雪白了。

B. 他不仅学习好，而且品德好，还乐于助人。

C. 他喜欢唱歌，喜欢跳舞，喜欢画画。

D. 他学习刻苦，成绩优异，品德高尚。

答案：A二、填空题（每空1分，共10分）1. 请填写下列诗句的下一句。

“春眠不觉晓，处处闻啼鸟。

”下一句是：__________。

答案：夜来风雨声，花落知多少。

2. 请填写下列成语的空缺部分。

“__________，必有近忧。

”“__________，必有远虑。

”答案：人无远虑，人无近忧。

3. 请填写下列句子中的空缺词语。

他__________地走进了教室，脸上洋溢着自信的微笑。

答案：从容不迫4. 请填写下列句子中的空缺词语。

在老师的__________下，我们顺利完成了这次实验。

答案：悉心指导5. 请填写下列句子中的空缺词语。

他__________地完成了作业，得到了老师的表扬。

答案：一丝不苟三、阅读理解（每题5分，共20分）阅读下面的短文，回答问题。

海淀初中试题及答案

海淀初中试题及答案一、选择题（每题2分，共10分）1. 以下哪个选项是正确的？A. 地球是平的B. 地球是圆的C. 地球是三角形的D. 地球是正方形的答案：B2. 光年是什么单位？A. 时间单位B. 距离单位C. 质量单位D. 速度单位答案：B3. 以下哪种植物属于被子植物？A. 苔藓B. 蕨类C. 裸子植物D. 被子植物答案：D4. 人体最大的器官是什么？A. 心脏B. 肝脏C. 皮肤D. 肺答案：C5. 以下哪个国家是位于南美洲的？A. 巴西B. 印度C. 澳大利亚D. 加拿大答案：A二、填空题（每题2分，共10分）1. 牛顿的第三定律指出，对于每一个______，都有一个大小相等、方向相反的______。

答案：作用力；反作用力2. 世界上最长的河流是______。

答案：尼罗河3. 人体中最大的淋巴器官是______。

答案：脾脏4. 地球的自转周期是______小时。

答案：245. 光的三原色是红、绿、______。

答案：蓝三、简答题（每题5分，共20分）1. 简述光合作用的过程。

答案：光合作用是植物、藻类和某些细菌通过叶绿素吸收光能，将二氧化碳和水转化为葡萄糖和氧气的过程。

2. 描述水循环的过程。

答案：水循环包括蒸发、凝结、降水和径流等过程，水分子在大气、地表和地下之间循环。

3. 为什么说地球是圆的？答案：地球是圆的，因为从太空中观察地球时，它呈现出球形；此外，地球的重力作用使得物质向中心聚集，形成球形。

4. 简述人体免疫系统的三大防线。

答案：人体免疫系统的三大防线包括物理屏障（如皮肤和粘膜）、化学屏障（如胃酸和酶）和生物屏障（如白细胞和抗体）。

四、计算题（每题10分，共20分）1. 一个物体的质量是5千克，如果它受到的重力是49牛顿，求地球表面的重力加速度。

答案：g = F/m = 49N / 5kg = 9.8m/s²2. 一个圆的直径是14厘米，求它的面积。

答案：A = πr² = π(7cm)² = 3.14 × 49cm² = 153.86cm²五、论述题（每题15分，共30分）1. 论述为什么说生物多样性对生态系统至关重要。