秘密比较
中德侵犯通信秘密犯罪之比较

宰 收稿 日期 : 21 -4 1 0 10 - 3
‘
作者简介 : 1朱华春( 8 - ) . 1 6 9 ,男 ,湖北公安人 。云南大学法学院 2 0 08级刑法学硕士研 究生 ,研 究方向 : 中国刑法与毒品犯罪 ;2 刘振华【 8- ) . 17 9 ,另。江西兴国人,云南大学法学院 20 级诉讼法学硕士研究生 ,研 究 08
此 ,德国刑法理论认为 , 侵害通信秘密罪并不
以行 为人 实际 知悉文 件 内容 为必要 ,即使行 为
德国刑法典中,犯罪对象除了信件以外 , 售 还
第2 1卷第 2期 21 年 6月 01
临沧师范高等专科学校学报
J un lo icn ah  ̄' l g o r a f Ln a g Te c e Col e e
V0 .2 NO 1 1 .2
J n .0 1 u e2 1
中德侵犯通信秘密犯罪之 比较
朱华春 ’ 刘振华 ( 云南大学法学院 ,云南 昆明 609) 501
可 罚性 ,与 实际上 是否 出现 危 险状态 无关 易
密 。 所以,似应认 为源自文件所载思想肉害
的法律权限 ,亦即排除他人而唯有特定 得知 人
悉该内容的权限 ,或是经 由封缄特别避免他人
任 意 知悉 内 容 的权 利 ,始 为本 罪 的保护 法
言之,即使一个被立法者认为有危险的行为, 在 实 际上 并 未惹 起 危 险状 态 ,依 然 是可 罚 的。”“ 可见 ,抽象危险犯并 不要求犯罪行 为 对法益造成侵害或危险 。其可罚性在于构成要
法 比较 。
年 刑法 19条 的规 定 ,并 未进 行任 何改 动 。但 4 值 得 注 意 的是 ,根 据 全 国人 大常 委 会 20 00年 1 2月 2 8日颁 布 的 < 国人 民代 表 大 会常 务 委 全 员 会 关 于 维 护 互 联 网 安全 的决 定 > ,非法 截
【免费下载】那些男生和女生的秘密未成年禁止进入

那些男生和女生的秘密,未成年禁止进入 1。
80%的男生都幻想过被爆菊的感觉 2。
男生经常用剪刀箭下面的毛,而且长毛时很痒 3。
男生做春梦是和不认识的女生,撸管是幻想认识的女生或者明星 4。
在路上,男生经常偷偷看路人的胸,或者是跟在女生后面看女生的屁股 5。
男生都有去女厕所的冲动 6。
男生都有幻想和老师××的经历,是男生都有 7。
大多数情况下,男生洗澡时喜欢撸管 8。
看到自己的兄弟有了新的兄弟,会很伤心 9。
如果男生极力夸一个女生,那么一定是喜欢这个女生 10。
如果晚上女生邀请男生出来,男生一定会出门前梳头,然后自恋的照镜子 11。
大多数男生在街上走路时会注意穿超短裙的女生,然后幻想有一阵风吹过 (台风) 12。
男生耳朵很灵敏,在家偷偷看岛国片时,如果父母突然回来,男生能根据脚步声马上关闭窗口 13。
女生们,如果男生在你面前突然很奇怪,别生气,他爱上你了。
14。
女生莫害羞,如果你来了大姨妈,男生一眼就能看出来。
15。
男生走到路上,前方是女神,男生往往不会追上去,因为害羞,最普遍的做法是默默跟在女生后面。
16。
男生发了短信给女神,会默默拿着手机等,如果等了很久还没收到回复,、管路敷设技术通过管线敷设技术,不仅可以解决吊顶层配置不规范问题,而且可保障各类管路习题到位。
在管路敷设过程中,要加强看护关于管路高中资料试卷连接管口处理高中资料试卷弯扁度固定盒位置保护层防腐跨接地线弯曲半径标高等,要求技术交底。
管线敷设技术中包含线槽、管架等多项方式,为解决高中语文电气课件中管壁薄、接口不严等问题,合理利用管线敷设技术。
线缆敷设原则:在分线盒处,当不同电压回路交叉时,应采用金属隔板进行隔开处理;同一线槽内,强电回路须同时切断习题电源,线缆敷设完毕,要进行检查和检测处理。
、电气课件中调试对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料试卷相互作用与相互关系,根据生产工艺高中资料试卷要求,对电气设备进行空载与带负荷下高中资料试卷调控试验;对设备进行调整使其在正常工况下与过度工作下都可以正常工作;对于继电保护进行整核对定值,审核与校对图纸,编写复杂设备与装置高中资料试卷调试方案,编写重要设备高中资料试卷试验方案以及系统启动方案;对整套启动过程中高中资料试卷电气设备进行调试工作并且进行过关运行高中资料试卷技术指导。
专利保护与商业秘密保护的比较

专利保护与商业秘密保护的比较在当今竞争激烈的商业环境下,企业对于知识产权的保护变得越来越重要。
专利保护和商业秘密保护是两种常见且有效的保护方式。
本文将比较专利保护和商业秘密保护,分析它们的优缺点,并探讨在不同情况下应选择何种保护方式。
一、专利保护专利是一种通过法律手段来保护发明技术的独占权。
专利保护是公开的、明确的,适用于那些可以被明确定义并满足专利法规定要求的技术创新。
主要优点如下:1. 法律保护:专利保护受法律保护,具备法律地位,可以有效地防止他人在专利权有效期内复制、制造、销售等侵权行为。
2. 可证明性:专利在申请和授予过程中需要进行公开和审查,可以通过专利权证书来证明专利权的合法性和有效性。
这为企业在法律纠纷中提供了有力的证据依据。
3. 直接权益:专利权利人可以以自己对发明的独占权为基础,拥有利用和转让权,从中获得经济利益。
然而,专利保护也存在一些缺点:1. 昂贵和繁琐:专利申请过程繁琐,需要进行专利搜索、撰写申请文件等多个步骤。
此外,专利费用也相对较高,包括申请费、年费等。
2. 时效性:专利保护有一定的有效期限,一般为20年。
在专利权期限到期后,创新技术将进入公有领域,其他人可以自由使用。
二、商业秘密保护商业秘密是指企业在商业活动中具有实际或潜在价值的信息,未公开并实施相应的保密措施。
商业秘密保护是一种隐秘的、实质性的保护方式,适用于那些不能通过专利保护或希望长期保持商业优势的创新。
商业秘密保护的优点如下:1. 灵活性:商业秘密保护没有严格的法定要求,企业可以自行决定保密范围和保密措施。
这种灵活性使得企业能够更好地保护商业机密,并根据需要进行调整。
2. 经济高效:相比专利保护,商业秘密保护过程更简单,费用更低。
企业可以集中精力和资源用于核心商业活动,而不需要花费在申请和维护专利上。
然而,商业秘密保护也存在一定的难点:1. 法律保护有限:商业秘密保护依赖于保密措施和非竞争协议等合同约束,如果这些合同受到侵犯,法律保护的效果将会受到影响。
关于中美两国对国家秘密界定的比较
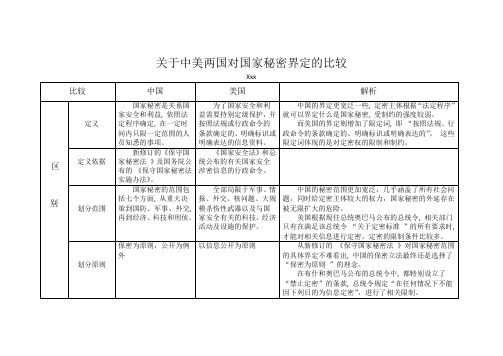
中国的秘密范围更加宽泛,几乎涵盖了所有社会问题,同时给定密主体较大的权力,国家秘密的外延存在被无限扩大的危险。
美国根据现任总统奥巴马公布的总统令,相关部门只有在满足该总统令“关于定密标准”的所有要求时,才能对相关信息进行定密。定密的限制条件比较多。
而美国的界定则增加了限定词,即“按照法规、行政命令的条款确定的、明确标识或明确表达的”,这些限定词体现的是对定密权的限制和制约。
定义依据
新修订的《保守国家秘密法》及国务院公布的《保守国家秘密法实施办法》。
《国家安全法》和总统公布的有关国家安全涉密信息的行政命令。
划分范围
国家秘密的范围包括七个方面,从重大决策到国防、军事、外交,再到经济、科技和刑侦。
划分原则
保密为原则,公开为例外
以信息公开为原则
从新修订的《保守国家秘密法》对国家秘密范围的具体界定不难看出,中国的保密立法最终还是选择了“保密为原则”的理念。
在布什和奥巴马公布的总统令中,都特别设立了“禁止定密”的条款,总统令规定“在任何情况下不能因下列目的为信息定密”,进行了相关限制。
表述方法
中国对国家秘密范围的表述使用的是抽象概括的方法。
美国对国家秘密范围的表述使用的是具体列举的方法。
中国对国家秘密的范围这一条款本身没有约束性限制。具体实施办法规定,在某一事项泄露后会造成所列后果之一的,应当列入国家秘密及其密级的具体范围。此外,某些划分依据很抽象隐晦、模糊不清,有些只是以后果的严重程度来划分,但是程度的判定也缺乏统一的标准。在保密管理的具体工作实践中很容易产生歧义和误判情况。
关于中美两国对国家秘密界定的比较
比较的奥秘教案幼儿园

比较的奥秘教案幼儿园简介比较是幼儿园教育中的重要内容之一,其基本本领是判断大小,区分轻重、长短、高低等。
通过比较活动,可以培养幼儿的分析判断能力和对事物的观察力。
教学目标1.能够正确区分事物的大小、形状、颜色、数量等差异;2.能够参与比较活动,提高观察能力和逻辑思维能力;3.培养幼儿的合作意识和团队精神。
教学步骤第一步:导入活动比较重要性的引入,教师向幼儿介绍比较,引导幼儿观察房间里的物品,让幼儿就其大小、颜色、形状、高低等不同特点进行比较。
示例:老师给孩子两个小球:一个大,一个小,让孩子比较它们的大小,然后问孩子哪个球更重。
第二步:比较智力游戏通过一些简单的比较游戏,激发幼儿的兴趣,提高幼儿观察力,培养幼儿的逻辑思维和判断能力。
示例:老师找来一些蔬菜水果,将它们放在一起让孩子找出相同物品和不同物品。
第三步:创意小制作在制作活动中,通过手工制作让幼儿能够更直观地理解大小、高低、轻重等差异。
让幼儿在制作中获得深入的体验,更深刻地理解比较活动。
示例:老师让孩子做两个不同大小的泡泡,然后让孩子根据大小粘贴到不同的位置上,让孩子发现大小的不同带来的位置上的区别。
教学方法在教学过程中,我们应该根据幼儿的认知水平,选择合适的比较对象,让幼儿体会比较的乐趣,激发幼儿的兴趣。
1.播放视频:通过播放适合幼儿的动画视频或绘本,让幼儿活动中亲自参与比较过程,不仅能够增加孩子的阅读兴趣,还能在趣味中潜移默化地让孩子学会比较。
2.奖励激励:适当使用奖励激励制度,鼓励幼儿尽力参与比较活动,引导幼儿发现事物中的差异和相似之处,促进幼儿匀称发展。
3.亲子互动:在比较活动中引导家长一起参与进来,让家庭、学校和社区形成合力,使幼儿在不同环境中学到知识,获取不同的体验。
教学评估1.对学生个体评估:记录每个孩子在比较活动中的表现,包括判断能力、观察力、逻辑思维能力等方面,对每个孩子进行分析评估,发现优点和不足,合理引导。
2.对教学过程的评估:教师需要在教学中进行教学结果评估,包括教学流程的优化、活动内容的设计、教学方法的选择、教学环境的布置等,为下一次教学做好指导或改进。
论秘密监听制度的比较与权衡

一
、
秘 密监 听之法理悖论
( )国家公权与个人私权的对立 一
监听是一种行使公权 力的表现 ,是一种基于诉讼实体 目的实现而采取 的有 效侦 查行为 , 别是在有组 特 织犯罪 、恐怖犯罪 、 品犯罪等 无被害人犯罪中更是如此。但是 ,由于监听是一种超常规 的特殊侦 查手 段 , 毒
宪法权利才具有无可置疑性 。
( )司法威信与侦查诡道之间 的对垒 二 国家在追诉犯罪中的威信和威严 ,并不完全是因为其打击的力度 ,也是因 为在道德 、伦理方 面也具有
合理 性。国家形象是集体道德 的总和 ,因此 ,作为国家机 器的侦查机 关而言,必须在维护社会秩序运 转中
保持一种正义之师 的风度 。 于国家来说 , 对 在利益衡量 的过程 中, 不能仅仅根据微观的利益标准进行衡量 , 有时候 ,通过卑鄙 的手段抓获犯罪人并不一定 比通过高 尚的手段释放犯罪人 的效果更好 这是 因为,前者 攻的是城 ,是个案 之城 ;后者 的 目的是攻心 ,是攻 的公众之心。“ 攻心 为上 ,攻城为下 ”既是 军事 学的哲 理,也是侦查 学的哲理 。监 听的本质就 是偷听 ,即使是 以国家的名义也是如此 。一个法治的国家,一个 以
其手段的有效性往往会带来侵犯公 民私权 的严重性 ,其秘密性会 导致对公 民私 权侵 害的无形性 。其主要表
现为对公 民隐私权、 言论 自由、通 讯 自由等 一系列宪法权利虽不是明 目张胆但 是根深蒂 固的侵 害 。
一
方面 ,监听是一种对 付一些特 定犯罪的利器,但它同时也是侵 犯个人权利 的锋利 凶器,为 了解 决因
① 【 国台湾】 舜 明: 《 听界 限与 证据 排除 》 ,载 《 中 江 监 法学 从刊 》第 1 1 ,第 9 页 。 7 期 8
“秘密”可否写成“密秘”

既然 “秘 ”和 “密 ”是 两个 不 同 的语素 ,那么它们之间肯定存在 不同之处 。首先探索它们的语源 , 分 为三个 方 面 :字音 、字 形 、字义 。
在字音方面 ,两者的古代读 音是有差异的。秘 ,《广韵》兵媚 切 ,帮部声母 ,声 调为去声 ;密 , 《广韵》美毕切 ,明部声母 ,声调为 入声。可见 ,“秘”和“密”的古音是 不 同 的 ,这一 点在 现在 的 方言 中 能够清晰地体现出来。例如 ,在客 家方言 中,“秘”音为 bi4或 bi5; “密 ”音 为 mid6,两 者 的 声母 不 同 ,声调 有差 异 ,“密 ”在 客家 方 言 中依 然保 留着 入声 的读 音 ,读 音 非 常短促 ;在粤方 言 中 ,“秘”音 为 bei3或 bitl;“密 ”音 为 mat6,两 者 的读 音 同样差 异很 大 。
在现 代 汉 语 中 ,“秘 ”和 “密 ” 的音 相 同 ,都 读 “m i”。再 者 “秘 ” 和 “密 ”的 字形 有 相 似 性 ,两 个 字 都 由一个 “必 ”和其他部件组成 。 最 重要 的是 ,“秘 ”和 “密 ”的义 项 有 交 集之 处 ,在 “秘密 ”一 词 中 ,两 者都含有 机密 、有所 隐蔽的意思 。 除此 之外 ,“秘史 ”、“隐秘 ”、“奥秘 ” 等词语 中的“秘”和“保密 ”、“密谋”、 “密使”等词语 中的“密”意思也是 一 样 ,都解释 为隐蔽 、不公 开。读音 相 同 、字形 相似 、意 义 又有 重合 的 地方,那 么,当“秘 ”和“密”连用合 成一个词 的时候 ,何者在先 ,何者 在后 ,阅读 量还没达 到一定程度 的 小学生难免会搞不清楚 。
在字 形 、字义 方 面 ,两者 亦 有 差异 。东汉许慎的《说文解字》并 没 有 收录 “秘 ”字 ,只 收 录 了 “秘 ” 的异体字“秘”:“神也 ,从示 ,必 声 ”,即不可预测 、不公开的意思 , 如张衡《西京赋》:“秘舞更奏”。而 “秘”的字形可追溯到小篆 ,从字 形 上看 ,可 知 “秘 ”的意 思 最初 是
关于秘密的句子

关于秘密的句子1、每个人都有自己的秘密,有秘密的女人是可爱的,那些秘而不宣的各种滋味只有自己清楚。
如果你想知道,就用心去找,用爱去感受,因为分享秘密就是分担彼此的命运,那种感觉,甘之如饴!2、曾经拥有的不要忘记,难以得到的更要珍惜,属于自己的不要放弃,已经失去的留作回忆。
3、有本事的男人,不会怀疑自己的女人在外面有外遇,因为他相信自己的人格魅力,会吸引住自己爱的人。
4、天气冷的很快,腐烂在心底的秘密,随着旧的一年安静的埋进心底。
我总说不愿意去怀念旧的东西,但安静下来的时候,还是会去翻翻旧时候写的日记簿。
5、只要不对别人说起,秘密就不算是秘密。
一个人的秘密,那还叫什么秘密,只是记忆而已。
6、有本事的男人,可以家庭事业双照顾,而不会把爱情当作自己的负荷,不会说,为了爱情失去了很多,因为他知道,一切都是为了家好。
7、如果你有一个秘密,就到深山里在树上挖个洞,然后对着这个洞说出你心中的秘密,这样秘密就不会被人知道。
8、爱情解释它即使被说出口还是一个秘密,因为只有真正的爱人才知道他是被爱着的。
9、女孩子要注意喜欢发誓的男人,绝无好人,只言不行,轻于言誓而必心存背叛。
10、曾经,我想和你分享我所有的秘密,但现在,你成了我心底的秘密。
——你要明白,你爱的不是那段时光,不是那个念念不忘的人,不是那段经历,你爱的只是当年那个羽翼未丰但依然执迷不悔的自己。
11、没本事的男人,天天和女人抱怨,为了你,我失去了很多,我放弃了很多,如果要靠失去和放弃换来的爱情,那只不过是昙花一现。
12、每个人都有不能说出口的秘密,这些秘密或许在多年之后才发现是如此雷同。
13、别人拼命想掩盖的,必然是你不希望看到的。
所以,追寻别人的秘密必然要承担知道秘密的后果14、爱是不能言说的秘密,那份默契和妥帖,最是那爱到骨子里的样子,一遍遍幸福着,回想着,是如此的美妙!倾了心、倾了城、倾了时光!最好的爱,不是轰轰烈烈之后的两败俱伤,而是平平淡淡的牵手把这一生走完。
secret变形词汇

secret词性变化
secret的词性变化包括:比较级more secret;最高级most secret,复数secrets。
一、secret的读音。
secret的英式发音为/ˈsiːkrət/,美式发音为/ˈsiːkrət/。
二、secret的基本释义。
1、作名词时:秘密;机密;秘诀;奥秘;诀窍;奥妙。
2、作形容词时:秘密的;保密的;神秘;(指行为与习惯)暗中进行的,未公开的,隐秘的;诡秘;外人不得而知的。
三、secret的短语搭配。
1、in secret:秘密地;暗中。
2、a guilty secret:见不得人的秘密。
3、be an open secret:是公开的秘密。
4、Victoria Secret:维多利亚的秘密;维多莉亚秘奥;维多莉亚的秘密。
secret的例句:
1、He's the last person I'd trust with a secret.
我要是有什么秘密,告诉谁也不能告诉他。
2、The secret number is my phone number in reverse.
这个密码是我的电话号码的逆序排列。
3、Shall we let him in on the secret?
我们要不要把秘密透露给他?
4、The donor's identity is a close secret. 捐赠人的身份是一个严加保守的秘密。
5、Can you keep a secret?
你能保守秘密吗?。
集成电路布图设计与商业秘密保护方式比较

集成电路布图设计与商业秘密保护方式比较集成电路布图设计是一种高科技的结晶,其中凝结了开发者大量创造性的脑力劳动,是智力成果的一种重要形式。
由于知识产权是人们基于自己的智力活动创造的成果和经营管理活动中的经验、知识的结晶而依法享有的民事权利。
因此,最初人们很自然地试图在各种已有的知识产权法律当中寻找合适的一种为集成电路布图设计提供保护。
商业秘密法保护:含有布图设计的集成电路虽然是一种科技产品,有一定的布图设计技术,但在通常情况下,该产品一旦出售,其布图设计就可能会公开了,从而丧失了商业秘密保护的前提之一:秘密性,因而无法再作为技术秘密予以保护。
因为无论采用何种封装技术,持有该集成电路产品的人都可用适当的方法了解和复制其内部的布图设计。
只有对于某些尚未公开或者不宜公开的集成电路芯片,商业秘密仍然可以在一定程度上提供保护。
但即使存在为集成电路布图设计提供商业秘密保护的可能性,同时也必须看到其困难:(1)商业秘密保护模式需要集成电路制作者在保密方面投入大量的精力和金钱,势必提高集成电路的成本,妨碍公众获得相对的廉价商品。
(2)商业秘密保护模式势必引导集成电路制作者将其制作的集成电路留做自用,而不是作为商品供公众使用,阻碍了整个社会的技术提升水平。
(3)即使集成电路制作者将其制作的集成电路投入市场,也很可能被竞争对手在短时间内将其布图设计反求出来。
因此,集成电路布图设计是兼备作品与技术成果特性的独立的知识产权客体,有着自己的特点。
根据TRIPS协议第35条的规定,对布图设计的保护适用《集成电路知识产权条约》第2至7条、第12条和第16条。
根据这些条款的规定,对布图设计的保护可以根据情况适用特别法、版权法、专利法、实用新型法、工业品外观设计法、不正当竞争法或其他法,或任何这类法的结合。
事实上,已颁布集成电路保护法的国家,基本上不引用著作权法或专利法等来保护它,而是依据其特点,制订单行法规,将之作为独立的客体予以保护。
国家保密法规定了各个密级

国家保密法规定了各个密级根据国家保密法规定,不同类型的信息和文件将根据其重要性和敏感性被分为不同的密级。
各个密级的定义和保护措施如下:1.机密级(Confidential):机密级信息和文件是指国家安全、国家利益和公共利益的需要程度比较高的信息。
这些信息和文件的泄露可能会对国家安全和利益产生较大的损害。
对于机密级信息和文件的保护措施包括:严格的访问控制措施,只有被授权人员才能查看和处理相关文件;加密和安全传输技术的使用,以防止信息在传输过程中被窃取或篡改;严格的存储管理,包括文档归档和定期更换媒体等。
2.秘密级(Secret):秘密级信息和文件是指对国家安全、国家利益和公共利益具有较大影响的信息。
这些信息和文件的泄露可能会导致一定程度上的损害。
对于秘密级信息和文件的保护措施包括:访问控制与权限管理,确保只有经过特定授权的人员才能接触相关信息;数据备份和恢复机制,以防止数据丢失或损坏;网络安全防护,包括防火墙和入侵检测系统等。
3.绝密级(Top Secret):绝密级信息和文件是指对国家安全、国家利益和公共利益产生严重威胁的信息。
这些信息和文件的泄露可能会导致重大损失或危害国家的安全而引发危机。
对于绝密级信息和文件的保护措施要求更加严格:严格的身份验证和审批流程,确保只有最高级别的授权人员才能处理相关文件;物理存储设备的保护,如冷库、防水、防火等设施;加密技术和网络隔离,确保绝密信息在传输和存储过程中不被泄露或篡改。
国家保密法还规定了对于不同密级信息的管理和处罚措施。
例如,泄露机密级信息可能会受到行政处罚,包括警告、记过、降级、撤职等;泄露秘密级信息可能会受到刑事责任追究,包括罚款、有期徒刑等;泄露绝密级信息可能会触犯国家安全法,被追究更为严厉的刑事责任,可能面临无期徒刑甚至死刑的惩罚。
总之,国家保密法对各个密级信息和文件进行了明确的分类和保护规定,旨在确保国家安全和保护国家利益。
对于机密级、秘密级和绝密级信息,国家要求相应的严格管理和保护措施,同时对违反保密规定的行为进行严厉处罚,以维护国家的机密信息不受泄露和篡改的威胁。
“秘密”可否写成“密秘”

“秘密”可否写成“密秘”作者:张德娴来源:《语文教学之友》2014年第04期笔者发现小学生容易混淆“秘密”的“秘”和“密”,常常误写为“密秘”。
教师纠正错误时,往往知其然而不知其所以然。
为此,本文试着辨析“秘”与“密”,以期使教学能更好地为学生服务。
一、误写的缘由在现代汉语中,“秘”和“密”的音相同,都读“mì”。
再者“秘”和“密”的字形有相似性,两个字都由一个“必”和其他部件组成。
最重要的是,“秘”和“密”的义项有交集之处,在“秘密”一词中,两者都含有机密、有所隐蔽的意思。
除此之外,“秘史”、“隐秘”、“奥秘”等词语中的“秘”和“保密”、“密谋”、“密使”等词语中的“密”意思也是一样,都解释为隐蔽、不公开。
读音相同、字形相似、意义又有重合的地方,那么,当“秘”和“密”连用合成一个词的时候,何者在先,何者在后,阅读量还没达到一定程度的小学生难免会搞不清楚。
二、“秘”与“密”的异同及其先后顺序既然“秘”和“密”是两个不同的语素,那么它们之间肯定存在不同之处。
首先探索它们的语源,分为三个方面:字音、字形、字义。
在字音方面,两者的古代读音是有差异的。
秘,《广韵》兵媚切,帮部声母,声调为去声;密,《广韵》美毕切,明部声母,声调为入声。
可见,“秘”和“密”的古音是不同的,这一点在现在的方言中能够清晰地体现出来。
例如,在客家方言中,“秘”音为bi4或bi5;“密”音为mid6,两者的声母不同,声调有差异,“密”在客家方言中依然保留着入声的读音,读音非常短促;在粤方言中,“秘”音为bei3 或bit1;“密”音为mat6,两者的读音同样差异很大。
在字形、字义方面,两者亦有差异。
东汉许慎的《说文解字》并没有收录“秘”字,只收录了“秘”的异体字“祕”:“ 神也,从示,必声”,即不可预测、不公开的意思,如张衡《西京赋》:“祕舞更奏”。
而“秘”的字形可追溯到小篆,从字形上看,可知“秘”的意思最初是和植物有关。
商业秘密和技术秘密的区别有哪些

一、商业秘密和技术秘密的区别有哪些商业秘密是一种特殊的知识产权。
《中华人民共和国刑法》第219条规定:所谓商业秘密,是指不为公众所知悉,能为权利人带来经济利益,具有实用性并经权利人采取保密措施的技术信息和经营信息。
商业秘密的"不为公众所知悉"即只要不是在本行业内众所周知的普通信息,能够与普通信息保持最低的秘密或新颖限度的差异的信息,都构成商业秘密。
相对于技术秘密就像是专利或者一些其他技术性的秘密,以专利为例。
专利是一项发明创造,即发明、实用新型或外观设计向国家专利局提出专利申请,经依法审查合格后,向专利申请人授予的在规定的时间内对该项发明创造享有的专有权。
二、技术秘密特点1、秘密性(新颖性的最低要求)技术秘密必须具有实质上的秘密性或秘密因素,也就是“不为公众所知悉”,技术秘密的核心只是由技术秘密的权利人或相关具有保密义务的人或组织才能知悉,其他组织或人员要想获得此技术秘密就只能花费相应劳动去探究(不违反社会道德的前提下)或付出足够的酬金去得到权利人的许可,要么就只能采取故意侵权的方法。
2、实用性技术秘密具有实用性,可以为技术秘密的拥有者带来相应的经济利益,没有实用性的技术不能成为技术秘密。
3、价值性技术秘密现在或将来的使用,可以给技术秘密的权利人带来现实的或潜在的竞争优势。
技术秘密可以是正在被权利人使用的,也可以是由权利人控制尚未使用的。
4、保密性技术秘密的合法控制者必须针对技术秘密本身采取相应的保护措施,技术秘密一旦公诸于世就失去了存在的价值,重要的是单位或组织能否对技术秘密采取保密措施,这是该技术秘密取得法律保护的前提要求。
三、技术秘密保护技术秘密保护的特点技术秘密权利人对技术取得的专有权或垄断权,并非法律确认和保护的“法定专有权”,而仅仅是一种“事实专有权”,它是通过合法持有人对技术的保密来实现的,通过与专利相比较,技术秘密保护有以下几个特点:①自主性。
专利有专门的《专利法》来保护。
专利保护与商业秘密保护的比较与选择

专利保护与商业秘密保护的比较与选择作者:李凡来源:《今日财富》2017年第05期专利保护是指利用法律和经济手段确认发明人对其发明享有专有权,以利于保护和促进技术发明的制度,这是国际上通行的一种做法。
商业秘密保护则是指通过采取保密措施对不为公众所知晓、具有实用性并能为权利人带来经济利益的技术、经营信息进行保护的措施。
一、专利保护与商业秘密保护的比较(一)专利保护与商业秘密保护的联系1.被保护对象均为无形资产。
专利权和商业秘密作为知识产权大体系中的两个小部分,均以无形财产的形式存在着。
尽管它们能够形成图案、文字等实际载体,但是它们本身看不见、摸不着,没有客观存在的实体,本质上依然是无形财产。
2.被保护对象均能够给权利人带来经济利益。
这一点在商业秘密的概念中已经有所体现,而专利保护的概念中虽未提及,但从实践中权利人利用专利许可获得经济利益的情况看是显而易见的。
(二)专利保护与商业秘密保护的区别1.产生方式不同。
专利必须通过申请,由国家授权后才受法律保护。
商业秘密则既不需申请,更无需授权。
权利人只要对其尚未公开的技术采取了保密措施,商业秘密便随即产生。
2.财产权性质不同。
专利是一种完全的财产权,具有独占性,首先申请专利的主体一旦获得批准,便享有对此技术的专有权,未经专利人许可,可排除权利人之外所有人的使用。
而商业秘密不是一种完全的财产权,其权利人不具有独占权,只要不是通过非正当手段获取,若干权利人可以同时享有同一项商业秘密。
3.受保护的时限不同。
根据我国《专利法》规定,专利保护有时间限制,其中发明专利权的保护期限为20年,实用新型和外观设计专利权的保护期限为10年。
期限届满,该项技术则不再受法律保护。
而商业秘密的保护没有时间限制,只要不被泄露或由权利人自行公开,可以一直受到法律保护。
4.保护方式不同。
专利主要通过技术公开和限制使用的方式对专利技术实施法律保护的。
商业秘密则是通过采取保密措施,严格控制知悉范围的方式对专有技术实施保护。
秘密拍摄的比较研究

的, 抑制了对 方 的反 侦察 , 惑 或者 欺 骗 了对 手 , 样 的 迷 这
“ 地下” 的行动效率更 高更快 。
4 现实 的急迫性。拍 照是短暂 的 , . 不像录像那 样可 以 不问断的抓捕信息 。有些关键 时机是稍 纵即逝 的, 比如 说 嫌疑人 暗地里会见他人并商讨价格 、 交付毒 品, 拍摄 记录下 这样 的场景 、 犯罪行 为 、 物品 , 是有利的证据 , 也是其他手段
21 0 2年第 2期 ( 总第 9 ) 5期
黑 龙 江 省 政 法 管 理 " 部 学 院 学 报 T-
No 2 2 2 . 01
Ju a o el g a gA m ns a v ar oபைடு நூலகம்eeo o t sA dLw or l f i nj n d iirt eC deC l g f li n a n H o i t i l P ic
(u o 5 SmN. ) 9
秘 密 拍摄 的 比较 研 究
杨 薇
( 安徽 大学 , 肥 200 ) 合 36 1
摘要 :刑事诉讼法修 正案( 《 草案) 中规定 了秘密侦查 , 实际上具体 的秘 密拍摄没 有得 到充 分重视。规定 》 但
原则抽 象, 也没有相关配套规 范, 其应有 的特性和功能没有体现 , 当通过对比国外的 法律 , 应 分析其的特点 、 状、 现
隐私权 的侵犯是却难 以抗拒的和躲 避的。在刑事 追诉 中 , 对个人 隐私权 的干预最明显。侦查机关试 图掌握哪些属于
公民个人 保 密 的信 息 , 这些 信 息 与 隐 私 权 必 然联 系。 而 《 民权利和政治权 利 国际公 约》 公 中明确 肯定 了保 障隐私 权对维护公民基本 价值 的重要意 义 , 第 1 其 7条 规定 , 任何
专利与技术秘密优劣分析及差异

专利与技术秘密优劣分析及差异1 专利或者不专利由于法律为发明创造的保护,提供了专利、商业秘密等多样化的选择,因此,在选择保护发明创造的专利类型之前,还必须解决一个前提问题,即是否需要采用专利的形式来保护发明创造。
作为法律赋予的一种垄断权,专利虽然享有独占的优势,但也存在固有的一些不足之处。
有时采用商业秘密,更准确地说是采用技术秘密来保护发明创造,可能更有意义。
专利还是不专利?这是一个问题。
1.1 专利与技术秘密的差异比较专利是国家知识产权局对申请专利的发明创造进行审查,认为符合专利法规定后,而授予的在一定期限内的独占性权利。
商业秘密则是不为公众所知悉、能为权利人带来经济利益、具有实用性并经权利人采取保密措施的技术信息和经营信息。
商业秘密分两种基本类型:技术秘密与经营秘密。
由于经营秘密的保护范围与发明创造关系不大,因此,从发明创造保护的角度,比较专利与商业秘密,实质上是比较专利与技术秘密。
比较专利与技术秘密的不同之处,可以简单归纳如下:由上可见,专利与技术秘密存在较大的差异,而且因其差异而各具优劣。
所以,尽管专利制度已经施行多年,但专利保护并不能取代技术秘密,两者相辅相成,有时还互为依靠。
企业在选择保护发明创造的权利形式时,需要斟酌各自取得方式、成本支出、保护时间、权利范围等因素,来综合衡量专利与技术秘密的优劣。
1.2 专利和技术秘密的优劣分析(1)专利的优劣分析1)专利的优势专利技术的明确性,专利授权的权威性,专利保护的垄断性,决定了专利在保护发明创造方面,拥有极大的优势:①可以垄断利用同样的发明创造,不能再向其他人授予专利权,为专利权人提供了垄断利用的竞争优势。
②权利相对稳定除非因为被宣告专利无效等原因,专利一旦授权即可持续占有,不像技术秘密随时可能因为被公开,或被他人专利化而失去权利。
③保护力度较强由于专利权利要求清晰,保护范围明确,便于确定专利侵权行为,也便于请求行政执法,因此有利于权利保护。
专利与商业秘密的比较与选择

专利与商业秘密的比较与选择专利和商业秘密是知识产权保护的两种主要方式。
它们各有优点和限制,企业在选择时需要考虑多种因素。
本文将对专利和商业秘密进行比较,并探讨在不同情况下的选择。
一、专利的优点和限制专利是一种法律保护的权利,授予发明者在一定期限内对其发明进行独占。
专利权利清晰明确,可以有效地保护技术创新和发明。
以下是专利的一些优点:1. 独占性:专利权利提供了对发明的独占权,可以防止他人在专利有效期内制造、使用或销售同样的发明。
这种保护可以为创造者带来经济回报,鼓励其进行更多的研发与创新。
2. 法律保护:获得专利后,专利持有人可以依法追究侵权行为,维护自己的权益。
一旦发现他人侵犯专利权,可以通过法律手段要求其停止侵权,以及获得经济赔偿。
然而,专利也存在一些限制和缺点:1. 披露要求:获得专利需要对发明进行充分的披露,包括技术细节、工艺、设计和功能等。
这意味着其他竞争对手可以获得这些信息并加以利用。
对于一些技术较为敏感的领域,披露可能是一种风险。
2. 有限期限:专利权的保护期限通常为20年,在此期限结束后,发明将进入公共领域,其他人可以自由使用。
这对于技术更新较快的行业来说可能是一个挑战。
二、商业秘密的优点和限制商业秘密是指企业拥有并对外保密的非公开信息,可以包括技术、工艺、客户列表、市场策略等。
以下是商业秘密的一些优点:1. 保密性:商业秘密可以完全保密,只有内部人员知晓。
这种保护使企业能够保持竞争优势,防止他人复制或利用其核心技术和经营模式。
2. 保持竞争优势:商业秘密可以为企业带来长期的竞争优势,因为无需公开披露,其他竞争对手难以获得相同的技术或市场信息。
然而,商业秘密也存在一些限制和挑战:1. 法律保护有限:商业秘密的法律保护范围相对较窄,侵权需要证明对商业秘密的非法获取和使用。
一旦商业秘密泄露,很难追溯和恢复。
2. 风险和成本:维护商业秘密需要企业投入一定的时间和资源,包括加强内部保密措施和监控机制等。
大小顺序的秘密学习整数小数和分数的大小比较

大小顺序的秘密学习整数小数和分数的大小比较大小顺序的秘密:学习整数、小数和分数的大小比较在数学学习过程中,了解和掌握整数、小数和分数的大小关系是非常重要的。
本文将介绍如何比较整数、小数和分数的大小,并揭示其中的秘密。
通过理解这些秘密,我们将能更好地运用这些知识。
一、整数的大小比较整数是没有小数部分的数字,可以是正数、负数或零。
在比较两个整数的大小时,可以通过以下几种方法判断:1. 比较符号:我们可以使用“<”、“>”或“=”符号来比较两个整数的大小。
例如,对于整数a和b,如果a<b,那么a就比b小;如果a>b,那么a就比b大;如果a=b,那么a就等于b。
2. 数轴法:我们可以在数轴上画出整数a和b,并比较它们的位置。
在数轴上,较大的整数将位于较小的整数的右侧。
3. 数值大小:我们可以直接比较两个整数的数值大小。
较大的整数将有更高的绝对值。
二、小数的大小比较小数是在整数部分后面加上小数部分的数字。
小数也可以通过比较符号、数轴法和数值大小来进行比较。
1. 比较符号:我们可以使用“<”、“>”或“=”符号来比较两个小数的大小。
比较小数时,先比较整数部分,如果整数部分相同,则继续比较小数部分。
例如,对于小数x和y,如果x<y,那么x就比y小;如果x>y,那么x就比y大;如果x=y,那么x就等于y。
2. 数轴法:我们可以在数轴上画出小数x和y,并比较它们的位置。
在数轴上,较大的小数将位于较小的小数的右侧。
3. 数值大小:我们可以将两个小数转换成分数进行比较。
将小数的位数扩大到相同的位数,然后进行比较。
例如,0.25可以表示为25/100,0.3可以表示为30/100。
通过比较分数大小,可以确定小数的大小关系。
三、分数的大小比较分数是由一个整数除以另一个整数得到的数。
分数的大小比较与整数和小数的大小比较有些不同,但同样可以使用比较符号、数轴法和数值大小来进行比较。
“秘”和“密”的区别

“秘”和“密”的区别新高考新问题2013-09-23 2044“秘”和“密”的区别●秘mìㄇㄧˋ1. 不公开的,不让大家知道的~密。
~藏(cáng )。
~方。
~诀。
~计。
~史。
神~。
奥~。
2. 保守秘密~而不宣。
3. 珍贵罕见~本。
~籍。
~宝。
~府。
4. 姓。
◎秘祕mì〈形〉(1) (形声。
从禾,必( bì)声。
本义一种香草)(2) 不可测知;不公开 [secret]祕,神也。
从示,必声。
——《》祕舞更奏。
——张衡《西京赋》祕器。
——《·袁安传》。
注“棺也。
”祕宝。
——《·班彪传》。
传“河图之属。
”祕经。
——《·苏竟传》。
注“图纬书也。
”其事秘,世莫知也。
——《·武帝本纪》(3) 又如秘箓(秘文);秘法(秘术,秘密的方法);秘狱(也称掖庭狱,汉代专指幽囚罪人于皇宫掖庭而不作公开审理的监狱)(4) 稀奇,世上少有 [rare]博学强记,多奇篇秘籍。
——《唐诗纪事·段成式》(5) 又如秘怪(神奇怪异);秘珍(罕见珍品);秘异(奇异);秘籍(珍贵罕见的书籍);秘宝(不常见的珍异宝物)(6) 深,深邃 [deep]。
如秘宇(深殿);秘典(含义深奥的典籍);秘义(深奥的意义)(7) 与皇帝有关的 [imperial]。
如秘驾(帝王的车驾);秘馆(即秘阁,帝王藏书之所);秘色(古代越州官窑所产瓷器的颜色,因为帝王所专用,故云)◎秘mì〈动〉(1) 隐藏;保守秘密 [hide;keep sth.secret;hold sth.back]丞相斯为上崩在外,恐诸公子及天下有变,乃秘之,不发表。
——《·秦始皇本纪》(2) 又如秘惜(隐藏珍惜,不以示人);秘郁(隐秘,隐藏);秘丘(山林之所,隐居之处)(3) 闭 [close]。
如秘固(犹密封,封固)◎秘mì〈名〉(1) 秘密、奥妙的事物 [secret thing]而此秘未睹。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011,ACM,安全两方计算公平性(被引68次); 2011,安全多方计算:从百万富翁问题到匿名者(被引3次) 2011,安全多方计算排序问题(被引4次),Science China Information Sciences 2013,Yao's millionaires' problem and decoy-based public key encryption by classical physics 通过经典物理学的姚氏百万富翁问题和诱捕式公钥加密 2013,Fair Two-Party Computations via the BitCoin Deposits( 被引2次)
1
协议三:保护私有信息的较小数的比较协议 协议四:保护私有信息的任意两数的比较协议
①长度函数 ②茫然传输
协议五:基于同态加密的百万富翁问题高效解决方案 • 协议思想:对保密输入进行0编码和1编码,将自然数编码成一个
集合从而把数据比较问题转化为集合的相交问题,并利用 ElGamal同态加密算法解决了这个问题,这是一个很有创意的协 议。 C类会议,ACNS, • 0-编码和1-编码 被引64次 • GT Protocol:
1
2
2006年,Damgard等人在无条件安全环境下,利用线性秘密 分享方案设计一个保护私有信息的数据比较协议。 2008年,Jin等人提出了一个百万富翁问题的扩展问题,即 向量优势问题。这个问题可以描述为两个参与方,各自拥 有向量A=(a1,a2,……, an),B = (b1,b2,…… ,bn),问题的输出 就是想知道是否对于所有的i,都有ai > bi,并且都不向对方 泄露自己的输入。作者在半诚实模型和恶意模型下都研 究了向量优势问题,并且给出了不同轮数的协议。
姚氏百万富翁问题
协议一:姚氏百万富翁协议
O(2n)
协议二:基于OT1 协议的保护私有信息的数据比较协议 假设Alice和Bob的数据都小于2d。 步骤1:Alice随机生成一个数据全为k比特的d×2阶矩阵A, 其中k为 OT 协议的密钥长度,然后随机选择r和足够大的S, 满足0≤r<2k,s<k。 步骤2:令Aijl表示元素Aij的第l比特值,Aij0表示最不重要 的比特。对于每个i (1≤i≤d),Alice进行以下操作: • 对每个j≥s,令Ai1j和Ai2j为随机比特; • 如果ai=1,则l=1,否则l=2;对每个(0≤j≤2i-1),令Ailj 为随机 比特位;
一个简洁、高效而且通用的解决方案,将两个数的保密比较问题 归约到向量的部分标量积(scalarproduct)的保密计算问题;
社会主义百万富翁问题
在姚氏百万富翁问题的研究屮,只是知道了两个数a和 b的大小关系:a≥b或a<b。而社会主义百万富翁问题主 要解决a与b是否相等。 —协议一:基于DL-DH-DDH假设的社会主义百万富翁协 议(2001年) —协议二:基于ϕ-隐藏假设的社会主义百万富翁协议 (2004年) —协议三:基于滑动窗口和交换加密函数的社会主义百 万富翁协议(半诚实模型下)(2007年) 总结:同时,目前现有数据比较协议中也大多是要么 只解决百万富翁问题,要么只解决社会主义百万富翁 问题。并且,目前存在的同时解决两个问题的方案也 是局限于整数范围内。
安全多方计算模型
• • 参与方:诚实参与方、半诚实参与方、恶意参与方 攻击者:被动攻击者、主动攻击者 恶意行为: 计算模型 开始时拒绝参与协议、 半诚实模型(The Semi-honest Model) 更换自己的输入、 在协议进行中终止协议。 恶意模型(The Malicious Model):此模型下 SMC研究是 难点 通信信道模型:同步模型、异步模型 —安全信道:点对点安全信道、带广播的安全信道(目前 主要) 安全性定义 保密性、正确性、独立输入性、保密输出、公平性
排序问题
保护私有信息的排序问题(百万富翁的扩展问题) — 保护私有信息的两方整数排序协议(2008) — 保护私有信息的多方排序协议(2008) — 基于ElGamal的保护私有信息的数据排序协议(2007) — 基于秘密共享的保护私有信息的排序协议(2011)
协议一:A Fair and Efficient Solution to the Socialist Millionaires' Problem, Discrete Applied Mathematics(2001被 引95次) 公平高效的社会主义百万富翁问题解决方案,O(k) 协议二:无信息泄露的比较协议(软件学报,2004) 协议三:刘文等人,基于滑动窗口和交换加密函数解决 SMP的新方案(计算机工程,2007)
2003年,Ioannidis等人,基于OT 协议;O(d2); ①同态加密体制 2004年,Blake等人使用Paillier加同态密码体制设计了一个秘密比较协议 ,其时 ②茫然传输协议 间复杂度和计算复杂度都为O(nlogN)。 ③不可信第三方 2004年,Schoenmakers等人利用同态门限ElGamal方案的安全乘法协议提出了 一个解决加密的输入输出的整数的安全比较的方案。他们的方案要求线性 轮O(m)和安全乘法门。 2005年,李顺东等人构造特殊函数,利用不经意传输协议;(电子学报) 2005年,Lin等人,对保密输入进行特殊0/1编码,并且基于ElGamal乘法同态 加密算法,比较问题→判断两个集合是否相交问题,从而设计了一个百万 富翁协议。(数据比较问题→区间之间比较)
姚氏百万富翁问题研究现状
1982年,姚氏百万富翁协议,O(2n)
Hale Waihona Puke ①不可信第三方 ②协议缺点:必须在双方 数据不相等的前提下
只适用于比较两个较小的数,针对较大秘密数据的比较问题: 1996年,Jakobsson,多轮迭代;该协议的复杂性是多项式级的,其幂次为O(k); 1999年,Cachin引入一个不可信第三方,提出了一个高效的秘密比较方案并用于 拍卖中;该方案基于ϕ-隐藏假设以及同态加密的语义安全性;对位长为l的数据进行 比较,通信复杂度为O(l); 2004年,秦静等人的改进,提出了两个高效的协议来完成秘密比较;
2 1
2
m m1 • 设m=2i,令 Ail = 1, Ail = a i; • 对于每个i(1≤i≤d),构造一个随机k比特数Si,构造一个除 了最高两位以外其余各位都是随机的数Sd,令
O(d2)
• 对于对l=1,2,令 Ail =leftrot(Ail Si, r),其中lefttrot(x,y)表示 用y比特对左边的数x进行旋转操作。 1 步骤3:对于每个i (1≤i≤d), Bob通过不经意传输 Ail ,其中 l=bi+1。 d 步骤4: Alice发送S=lefttrot(j1 Sj,r)给Bob。 步骤5: Bob用获得的数据和S进行异或运算,从左向右扫描 知道到达连续0的个数最大的数目。
(引用协议五的文献) • 2010,计算机工程,通过采用0编码与1编码,将百万 富翁问题转换为集合交集问题,提出一种基于可交换 加密函数的百万富翁问题高效解决方案,加解密O(n), 通信轮数为4 • 2011年,黄山学院,该协议在比较出“≤”的关系上增 加了比较“=”的关系同时还给出协议的正确性安全性 和效率的分析 • 2013年,电子学报,李顺东等人,基于同态加密的高 效多方保密计算 — 将保密的数据编码成一个向量,在加法同态加密算法基础上设计
SMC
安全多方计算
——秘密比较
报告人:唐璇 2014.03
目录 1 安全多方计算(SMC) ① 基本知识 ② 基本密码学工具 ③目前SMC研究问题 2 秘密比较问题研究进展 ① 姚氏百万富翁协议 ② 社会主义百万富翁协议 ③ 排序问题
1 安全多方计算
安全多方计算 • 安全多方计算的数学化定义如下: 假设有n个参与方P1,...,Pn,每一个参与方都有 一个秘密输入mi (i = 1,2,…… ,n)。这n个参与者共同执 行一个协议 来计算函数f(m1,...,mn) = (y1,...,yn)。计算 结束后,每个参与者Pi仅能得到自己的输出yi,除此以外 ,不知道其他的输入、输出信息。 • 如果存在一个可信的第三方,那么可信第三方通过收 集各个秘密输入来计算函数f,然后将输出yi秘密的传 给各个参与方,很容易的解决这个安全多方计算问题。 但是在现实中非常不容易找到满足条件的第三方。 • 安全多方计算的研究主要是针对在无可信第三方的情 况下设计一个安全的多方计算协议,让各个参与者进 行安全的合作计算。
SMC
茫然传输协议
2 秘密比较
保护私有信息的数据比较问题 问题的提出 姚氏百万富翁问题的提出打开了数据比较问题的 大门,后续又出现了社会主义的百万富翁问题以及一 些扩展问题。 对保护私有信息的数据比较问题也不仅仅局限于 数据大小的比较,还扩展到单个数据甚至向量的相等 性比较和排序问题的研究等等。 现在,保护私有数据的比较问题已经作为安全多 方计算解决方案的基本模块,引起人们对其广泛地关 注与研究。
安全多方计算基本密码学工具 安全多方计算协议的一个 同态加密、哈希函数、秘密共享、零知识证明、茫然 基础问题,基础协议模块 传输 目前主要研究的安全多方计算问题有 — 安全数据比较问题、安全多方计算几何问题、保护私 有信息的查询问题、安全多方集合计算问题 — 安全电子拍卖问题、保护私有信息的数据挖掘问题、 线性系统背景下安全多方计算问题等等。 著名密码学家Goldwasser曾经说过:"安全多方计算今天 所处的地位正是公开密钥密码10多年前所处的地位。它 是密码学研究中一个非常重要的工具,它在计算科学中 的应用才刚刚开始,丰富的理论将使它成为计算科学中 一个必不可少的组成部分。”
SMC
