(完整word版)模糊层次分析法的Matlab实现

模糊层次分析法FAHPma ab代码

for j=[2,3]
if sm(i)>=sm(j) v0=1;
elseif sm(i)<=sm(j)&su(i)>=sl(j) v0=(sl(j)-su(i))/((sm(i)-su(i))-(sm(j)-sl(j)));
else v0=0;
end j=j+1; V=[v1,v0];
v1=V; end end v2=[]; for i=2 for j=[1,3]
编程
clc,clear a1=[1 1 1;0.86 1.17 1.56;0.67 1 1.5;0.33 0.39 0.49]; b1=sum(a1); a2=[0.64 0.85 1.16;1 1 1;2.5 3 3.5;0.95 1.33 1.83]; b2=sum(a2); a3=[0.87 1 1.49;0.29 0.33 0.40;1 1 1;0.4 0.5 0.67]; b3=sum(a3); a4=[2.04 2.56 3.03;0.55 0.75 1.05;1.49 2 2.5;1 1 1]; b4=sum(a4); d1=b1(1)+b2(1)+b3(1)+b4(1); d2=b1(2)+b2(2)+b3(2)+b4(2); d3=b1(3)+b2(3)+b3(3)+b4(3); s1=[b1(1) b1(2) b1(3)].*[1/d3 1/d2 1/d1]; s2=[b2(1) b2(2) b2(3)].*[1/d3 1/d2 1/d1]; s3=[b3(1) b3(2) b3(3)].*[1/d3 1/d2 1/d1]; s4=[b4(1) b4(2) b4(3)].*[1/d3 1/d2 1/d1]; s=[s1;s2;s3;s4]; sl=s(:,1); sm=s(:,2); su=s(:,3); v1=[]; for i=1

层次分析法MATLAB编程

层次分析法机器期望获得信息和所获得的信息是多层次的，属于多目标问题，对于多目标问题，由于各目标重要程度不同，决策者对于目标重要程度所进行的比较及量化称为价值权衡，最终体现为各个目标的加权系数，那么确定权重系数，目前最广的使用方法为层次分析法。

层次分析法的步骤：①确定层次结构模型②构造判断矩阵A，决策者对多个属性的重要程度作比较，同时进行比较和判断的属性不能过多，最多不能超过七个因素。

比较法是在一个属性中只对两个属性进行比较，对i,j两个因素进行比较时做如下约定。

同时，矩阵A=（)mxn满足以下特征：(1) >0(2)=1/(3)=1③求矩阵A的最大特征根,然后求矩阵A的最大特征相应的特征向量W,AW=W。

④一致性检验。

为了检验矩阵的一致性，需要计算它的一致性指标CI，CI 的定义为显然，当判断矩阵具有完全一致性时，CI=0。

越大，CI越大，判断矩阵的一致性越差。

注意到矩阵A的n个特征值之和恰好等于n, 所以CI相当于除max外其余n-1个特征根的平均值。

为了检验判断矩阵是否具有满意的一致性，需要找出衡量矩阵A的一致性指标CI的标准，引入修正值CR概念。

当阶数大于2时，判断矩阵的一致性指标CI，与同阶平均随机一致性的指标RI之比。

取CR=CI/RI,当CR=<0.01时，就认为矩阵具有满意的一致性，否则就需对判断矩阵进行调整。

程序:A=[]; %矩阵自行输入[m,n]=size(A); %获取指标个数RI=[0 0 0.58 0.96 1.12 1.24 1.32 1.41 1.45 1.49 1.51];R=rank(A); %判断矩阵的秩[V,D]=eig(A); %判断矩阵的特征值和特征向量，V特征值，D特征向量；tz=max(D);B=max(tz); %最大特征值[row,col]=find(D==B); %查询最大特征值所在位置C=V(:,col); %求对应特征向量CI=(B-n)/(n-1);CR=CI/RI(1,n); %计算一致性检验指标CI，CRif CR<0.10disp('CT=');disp(CI);disp('对比矩阵A通过一致性检验，各向量权重向量Q为：');Q=zeros(n,1);for i=1:nQ(i,1)=C(i,1)/sum(C(i,1)); %特征向量标准化endQ %输出权重向量elsedisp('对比矩阵A未通过一致性检验，需重新构造');end。

利用Matlab进行模糊逻辑和模糊控制的基本原理

利用Matlab进行模糊逻辑和模糊控制的基本原理Matlab是一种强大的数学计算软件，广泛应用于各个领域的工程和科学研究。

在现实生活中，我们经常会遇到一些模糊不清、不确定的情况，而模糊逻辑和模糊控制正是用来处理这些模糊问题的有效工具。

本文将介绍利用Matlab进行模糊逻辑和模糊控制的基本原理，并通过一些具体案例来说明其在实际应用中的价值。

首先，我们需要了解模糊逻辑和模糊控制的基本概念和原理。

模糊逻辑是Lotfi Zadeh教授于1965年提出的一种处理模糊信息的形式化逻辑系统。

与传统的布尔逻辑只有两个取值（真和假）不同，模糊逻辑引入了模糊概念，可以处理多个取值范围内的逻辑判断。

其基本原理是将模糊的语言描述转化为数学上的模糊集合，然后通过模糊运算进行推理和决策。

在Matlab中，可以使用Fuzzy Logic Toolbox工具箱来进行模糊逻辑的建模和模拟。

该工具箱提供了一系列的函数和工具，可以帮助我们创建模糊逻辑系统、定义模糊集合和模糊规则，并进行输入输出的模糊化和去模糊化运算。

一个典型的模糊逻辑系统包括三个主要组成部分：模糊集合、模糊规则和模糊推理。

模糊集合用于描述模糊化的输入和输出变量，可以是三角形、梯形、高斯等形状。

模糊规则定义了模糊逻辑系统的推理过程，通常由一系列的if-then规则组成，如“如果温度较低，则输出加热”，其中“温度较低”和“加热”为模糊集合的标签。

模糊推理根据输入变量的模糊值和模糊规则，计算出输出变量的模糊值。

为了更好地理解模糊逻辑的原理和应用，我们以一个简单的案例来说明。

假设我们需要设计一个自动化灯光控制系统，使得灯光的亮度能够根据环境光线的强弱自动调节。

首先，我们需要收集一些实际的数据来建立模糊逻辑系统。

通过传感器测量到的环境光强度作为输入变量，设定的亮度值作为输出变量。

在Matlab中，可以使用Fuzzy Logic Designer来创建一个模糊逻辑系统。

首先，我们需要定义输入和输出变量，以及它们的模糊集合。

模糊聚类分析算法的MATLAB语言实现

0 . 3 0 . 3 0 . 2 l 97 97 94
0 . 8 0 . 8 0 . 8 0 . 8 l 88 88 88 88
R =
0.7 l 99
0 .2 0. 3 0 .8 l 94 97 88
0 . 8 0 . 8 0 . 8 0 . 8 0 . 5 0 . 8 l 65 65 65 65 68 65
m it g
r , 1
兰二= 量 ! l
j I 一 < I i <似 xk —j f xk in i N J ) ) j
其中 k=12 . m , ,. ,
1 2 建立模糊相似矩阵 .
应用数量积法求出被分类对象间相似程度的相似
0 . 8 0 . 8 0 . 03 65 93 3 0 . 8 0 . 03 65 3
0 . 03 3
0 . 7 0 . 7 0 . 7 0 . 7 0 .. 0 . 7 0 . 5 l 74 74 74 74 77 4 74 68
0 . 8 0 . 8 0 . 8 0 . 8 0 . 8 0 . 5 0 . 8 0 . 8 l 65 65 65 65 65 68 93 65
类结果略) .
4 讨论
Malb是专用的矩阵计算软件 , a t 对矩阵的计算又快又好 ,而且允许用户编程 ,将程序编制成函数和过程 ,随时对系统功能进行扩展 . Malb中已经将大量 t a 的, 复杂的数学运算编制成了各种函数 , 只要灵活地搭配, 就能较好地编写求解程序 ,而且能加快数据处理 ,
are a
--—
—
4 —— 5 - - —

基于Matlab的层次分析法(提供代码)

基于Matlab的层次分析法(提供代码)层次分析法是一种常用的决策分析方法，可以用来解决复杂决策问题。

在Matlab中，我们可以使用ahp函数来实现层次分析法，以下是具体实现方法和代码示例。

1. 构建层次结构模型在进行层次分析法之前，首先需要构建层次结构模型。

层次结构模型是由多个因素构成的层次结构，每个因素都对应有多个子因素或者指标，最终目标会在最底层的因素或指标进行判断。

在Matlab中，我们可以使用ahp函数中的输入参数来构建层次结构模型。

2. 对各因素进行比较接着我们需要对各因素进行比较，即两两之间构建比较矩阵。

比较矩阵的大小取值应该为1，3，5，7，9这几个数，分别代表相当于、稍微重要、中等重要、非常重要和绝对重要。

在Matlab中，我们可以使用ahp函数中的输入参数来进行比较矩阵的构建。

3. 计算权重计算权重即为计算每个因素在最终目标中所占的权重大小。

我们可以根据比较矩阵来计算每个因素的权值，这可以通过Matlab的ahp函数中的输出参数进行得到。

以下是一个具体的代码示例：% 定义层次结构模型hierarchy = {'目标' {'因素1' '因素2' '因素3'}};% 构建比较矩阵% 比较矩阵大小代表相当于、稍微重要、中等重要、非常重要和绝对重要% 1代表相等，3代表比较略微重要等等，9代表比较绝对重要cmpMat{1} = [1 3 5;1/3 1 2;1/5 1/2 1];cmpMat{2} = [1 1/5 1/3;5 1 3;3 1/3 1];cmpMat{3} = [1 1/3 2;3 1 4;1/2 1/4 1];% 计算权重，得到结果存储在results变量中 results = ahp(hierarchy, cmpMat);% 层次分析法计算结果的可视化disp('计算结果：');disp(results);。

Matlab中的模糊逻辑控制方法

Matlab中的模糊逻辑控制方法引言模糊逻辑控制（FLC）是一种常用的控制方法，在很多实际应用中得到了广泛的应用。

Matlab作为一种功能强大的数学计算和工程仿真软件，提供了丰富的工具和函数来支持模糊逻辑控制的设计和实现。

本文将介绍Matlab中的模糊逻辑控制方法及其应用。

一、模糊逻辑控制的基本概念模糊逻辑控制是一种基于模糊逻辑原理的控制方法，它可以处理不确定性信息和模糊概念，适用于那些难以建立精确数学模型的控制系统。

模糊逻辑控制系统由四个基本部分组成：模糊化、推理、解模糊和规则库。

1.1 模糊化模糊化是将输入量从实际值转化为模糊集合的过程。

在Matlab中，可以使用fuzzifier函数将实际输入映射到模糊集合上。

模糊集合可以通过一些参数来描述，如三角形型、梯形型、高斯型等。

1.2 推理推理是根据模糊集合的规则进行推导，得到系统的输出。

在Matlab中，可以使用inference函数进行推理。

推理的方法有三种：基于规则的推理、基于模糊集合的推理和基于模型的推理。

根据应用的需求和系统的复杂程度，可以选择不同的推理方法。

1.3 解模糊解模糊是将模糊输出转化为实际值的过程。

在Matlab中，可以使用defuzzifier 函数进行解模糊。

常用的解模糊方法有：最大值法、平均值法、面积法等。

1.4 规则库规则库是模糊逻辑控制系统的核心，它包含了一系列的模糊规则，用来描述输入和输出之间的关系。

在Matlab中，可以使用fuzzy规则对象来定义规则库。

规则库的设计是模糊逻辑控制系统设计中的关键一步，直接影响系统的性能和稳定性。

二、Matlab中的模糊逻辑控制工具箱Matlab提供了专门的工具箱，用于支持模糊逻辑控制系统的设计和实现。

这个工具箱包含了一些常用的函数和工具，能够帮助用户更加方便快捷地进行模糊逻辑控制系统的设计和仿真。

2.1 模糊逻辑控制系统设计工具Matlab的模糊逻辑控制系统设计工具提供了一种用户友好的可视化界面，用于设计和编辑模糊逻辑控制系统。

模糊层次分析法FAHPmatlab代码

j=j+1; V=[v2,v0]; v2=V; end end v3=[]; for i=3 for j=[1,2,4] if sm(i)>=sm(j) v0=1; elseif sm(i)<=sm(j)&su(i)>=sl(j) v0=(sl(j)-su(i))/((sm(i)-su(i))-(sm(j)-sl(j))); else v0=0; end j=j+1; V=[v3,v0]; v3=V; end end v4=[]; for i=4 for j=[1,2,3] if sm(i)>=sm(j) v0=1; elseif sm(i)<=sm(j)&su(i)>=sl(j) v0=(sl(j)-su(i))/((sm(i)-su(i))-(sm(j)-sl(j))); else v0=0; end j=j+1; V=[v4,v0]; v4=V; end end dc1=min(v1); dc2=min(v2); dc3=min(v3); dc4=min(v4); w=[dc1,dc2,dc3,dc4]' for ii=1:4 w0(ii,1)=w(ii,1)/sum(w);%对w归一化并输出 end w0
计算结果
w =
1.0000 0.9851 0.9701 w3 = 0.3384 0.3333 0.3283
编程
clc,clear a1=[1 1 1;;0.95 1.25 1.59]; b1=sum(a1); a2=[;1 1 1;1.5 2 2.5]; b2=sum(a2); a3=[0.95 1.25 1.59;0.4 0.5 0.67;1 1 1]; b3=sum(a3); d1=b1(1)+b2(1)+b3(1); d2=b1(2)+b2(2)+b3(2); d3=b1(3)+b2(3)+b3(3); s1=[b1(1) b1(2) b1(3)].*[1/d3 1/d2 1/d1]; s2=[b2(1) b2(2) b2(3)].*[1/d3 1/d2 1/d1]; s3=[b3(1) b3(2) b3(3)].*[1/d3 1/d2 1/d1]; s=[s1;s2;s3]; sl=s(:,1); sm=s(:,2); su=s(:,3); v1=[]; for i=1 for j=[2,3] if sm(i)>=sm(j) v0=1; elseif sm(i)<=sm(j)&su(i)>=sl(j) v0=(sl(j)-su(i))/((sm(i)-su(i))-(sm(j)-sl(j))); else v0=0; end j=j+1; V=[v1,v0];

Matlab中的模糊集合和模糊决策方法

Matlab中的模糊集合和模糊决策方法引言随着计算机科学的迅速发展，人工智能逐渐成为了当今的热门研究领域之一。

在人工智能领域中，模糊集合和模糊决策方法被广泛应用于解决实际问题。

Matlab 作为一种强大的数学计算和仿真工具，为研究人员提供了丰富的工具包，从而可以对模糊集合和模糊决策方法进行快速、高效的分析和开发。

本文将探讨在Matlab 中使用模糊集合和模糊决策方法的相关技术和应用。

第一部分：模糊集合的基本概念模糊集合是一类既有确定性又有不确定性特征的数学集合。

与传统的集合论不同，模糊集合中的元素具有一定的隶属度。

Matlab中提供了一系列用于处理模糊集合的函数和工具，可以方便地进行模糊集合的定义、运算和可视化。

在Matlab中，可以使用fuzzy工具箱来定义和操作模糊集合。

通过fuzzy工具箱提供的函数，可以定义模糊隶属函数、模糊集合的交、并、补运算等。

例如，可以使用fuzzmf函数定义一个具有三个隶属函数的模糊集合，然后使用fuzzymf函数将该模糊集合的隶属函数赋值给一个变量，进一步操作。

第二部分：模糊决策方法的基本原理模糊决策方法是一种以模糊集合理论为基础的决策方法。

在实际问题中，往往需要考虑到不确定性和模糊性因素。

模糊决策方法通过用模糊集合描述问题的不确定性和模糊性，从而提供了一种灵活且有效的决策方法。

在Matlab中，可以使用fuzzy工具箱提供的函数来实现模糊决策方法。

通过fuzzy工具箱，可以定义模糊规则和模糊推理方法，从而实现对模糊集合的有效决策。

例如，可以使用fuzzy工具箱中的fis工具来定义一个模糊规则集，然后使用evalfis函数进行模糊推理，得到最终的决策结果。

第三部分：Matlab中的模糊决策方法应用案例在实际应用中，模糊决策方法被广泛应用于各个领域，如金融、医疗、自动控制等。

在这一部分，以医疗领域为例，介绍模糊决策方法在Matlab中的具体应用。

在医疗领域中，模糊决策方法可以用于辅助医生进行疾病诊断。

层次分析法matlab实现

层次分析法matlab实现disp('请输入判断矩阵A(n阶)');A=input('A=');[n,n]=size(A);x=ones(n,100);y=ones(n,100);m=zeros(1,100);m(1)=max(x(:,1));y(:,1)=x(:,1);x(:,2)=A*y(:,1);m(2)=max(x(:,2));y(:,2)=x(:,2)/m(2);p=0.0001;i=2;k=abs(m(2)-m(1));while k>pi=i+1;x(:,i)=A*y(:,i-1);m(i)=max(x(:,i));y(:,i)=x(:,i)/m(i);k=abs(m(i)-m(i-1));enda=sum(y(:,i));w=y(:,i)/a;t=m(i);disp(w);disp(t);%以下是一致性检验CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]; CR=CI/RI(n);if CR<0.10disp('此矩阵的一致性可以接受!');disp('CI=');disp(CI);disp('CR=');disp(CR);endfunction AHPInit1(x,y)%层次分析的初始化%默认只有两层x为准则数，y为方案数%CToT为准则对目标生成的比较阵%EigOfCri为准则层的特征向量%EigOfOpt为选项层的特征向量EigOfCri=zeros(x,1);%准则层的特征向量EigOfOpt=zeros(y,x);dim=x;%维度RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51];%RI标准%生成成对比较阵for i=1:dimCToT(i,:)=input('请输入数据:');endCToT %输出pause,tempmatrix=zeros(x+1);tempmatrix=AHP1(dim,CToT); EigOfCri=tempmatrix(1:x);ci1=tempmatrix(1+x);EigOfCrici1pause,matrix=cell(x);%元胞数组ci=zeros(1,x);dim=y;for k=1:xmatrix{k}=zeros(dim,dim);%生成成对比较阵for i=1:dimmatrix{k}(i,:)=input('请输入数据:'); end%判断该比较阵是不是一致阵tempmatrix=zeros(y+1);tempmatrix=AHP1(dim,matrix{k}); EigOfOpt(:,k)=tempmatrix(1:y);ci(k)=tempmatrix(y+1);EigOfOpt(:,k)ci(k)pause,%下面进行组合一致性检查RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51]; CR=ci1/RI(x)+ci*EigOfCri/RI(y);CRif CR>0.1disp('组合一致性不通过，请重新评分')returnend%下面根据比较阵的结果进行组合result=EigOfOpt*EigOfCri;resultfunction f=AHP1(dim,CmpMatrix)RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51]; %判断该比较阵是不是一致阵%判断该比较阵是不是一致阵[V,D]=eig(CmpMatrix);%求得特征向量和特征值%求出最大特征值和它所对应的特征向量tempNum=D(1,1);pos=1;for h=1:dimif D(h,h)>tempNumtempNum=D(h,h);pos=h;endeigVector=V(:,pos);maxeig=D(pos,pos);maxeigdimCI=(maxeig-dim)/(dim-1);CR=CI/RI(dim);if CR>0.1disp('准则对目标影响度评分生成的矩阵不是一致阵，请重新评分') returnendCI%归一化sum=0;for h=1:dimsum=sum+eigVector(h);endsumpause,for h=1:dimeigVector(h)=eigVector(h)/sum;endf=[eigVector;CI];层次分析法的应用在应用层次分析法研究问题时，遇到的主要困难有两个：（i ）如何根据实际情况抽象出较为贴切的层次结构；（ii ）如何将某些定性的量作比较接近实际定量化处理。

层次分析法matlab实现

层次分析法matlab实现disp('请输入判断矩阵A(n阶)');A=input('A=');[n,n]=size(A);x=ones(n,100);y=ones(n,100);m=zeros(1,100);m(1)=max(x(:,1));y(:,1)=x(:,1);x(:,2)=A*y(:,1);m(2)=max(x(:,2));y(:,2)=x(:,2)/m(2);p=0.0001;i=2;k=abs(m(2)-m(1));while k>pi=i+1;x(:,i)=A*y(:,i-1);m(i)=max(x(:,i));y(:,i)=x(:,i)/m(i);k=abs(m(i)-m(i-1));enda=sum(y(:,i));w=y(:,i)/a;t=m(i);disp(w);disp(t);%以下是一致性检验CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]; CR=CI/RI(n);if CR<0.10disp('此矩阵的一致性可以接受!');disp('CI=');disp(CI);disp('CR=');disp(CR);endfunction AHPInit1(x,y)%层次分析的初始化%默认只有两层x为准则数，y为方案数%CToT为准则对目标生成的比较阵%EigOfCri为准则层的特征向量%EigOfOpt为选项层的特征向量EigOfCri=zeros(x,1);%准则层的特征向量EigOfOpt=zeros(y,x);dim=x;%维度RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51];%RI标准%生成成对比较阵for i=1:dimCToT(i,:)=input('请输入数据:');endCToT %输出pause,tempmatrix=zeros(x+1);tempmatrix=AHP1(dim,CToT); EigOfCri=tempmatrix(1:x);ci1=tempmatrix(1+x);EigOfCrici1pause,matrix=cell(x);%元胞数组ci=zeros(1,x);dim=y;for k=1:xmatrix{k}=zeros(dim,dim);%生成成对比较阵for i=1:dimmatrix{k}(i,:)=input('请输入数据:'); end%判断该比较阵是不是一致阵tempmatrix=zeros(y+1);tempmatrix=AHP1(dim,matrix{k}); EigOfOpt(:,k)=tempmatrix(1:y);ci(k)=tempmatrix(y+1);EigOfOpt(:,k)ci(k)pause,%下面进行组合一致性检查RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51]; CR=ci1/RI(x)+ci*EigOfCri/RI(y);CRif CR>0.1disp('组合一致性不通过，请重新评分')returnend%下面根据比较阵的结果进行组合result=EigOfOpt*EigOfCri;resultfunction f=AHP1(dim,CmpMatrix)RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51]; %判断该比较阵是不是一致阵%判断该比较阵是不是一致阵[V,D]=eig(CmpMatrix);%求得特征向量和特征值%求出最大特征值和它所对应的特征向量tempNum=D(1,1);pos=1;for h=1:dimif D(h,h)>tempNumtempNum=D(h,h);pos=h;endeigVector=V(:,pos);maxeig=D(pos,pos);maxeigdimCI=(maxeig-dim)/(dim-1);CR=CI/RI(dim);if CR>0.1disp('准则对目标影响度评分生成的矩阵不是一致阵，请重新评分') returnendCI%归一化sum=0;for h=1:dimsum=sum+eigVector(h);endsumpause,for h=1:dimeigVector(h)=eigVector(h)/sum;endf=[eigVector;CI];层次分析法的应用在应用层次分析法研究问题时，遇到的主要困难有两个：（i ）如何根据实际情况抽象出较为贴切的层次结构；（ii ）如何将某些定性的量作比较接近实际定量化处理。

使用Matlab进行模糊逻辑分析的技巧

使用Matlab进行模糊逻辑分析的技巧引言：在现代科学中，逻辑分析在决策、控制系统和模糊推理等领域发挥着重要的作用。

模糊逻辑是一种能够处理复杂和不确定的问题的有效工具。

而Matlab作为一种功能强大的数学软件，也提供了丰富的工具和函数来支持模糊逻辑的建模和分析。

本文将介绍使用Matlab进行模糊逻辑分析的一些技巧和实例。

一、安装模糊逻辑工具箱Matlab提供了自带的模糊逻辑工具箱，可以通过Matlab的插件管理器进行安装。

打开Matlab后，在工具栏中选择"Add-Ons"，然后在搜索框中输入"模糊逻辑工具箱"，点击搜索按钮，选择合适的版本进行安装。

安装完成后，即可在工具箱中找到并使用模糊逻辑相关的函数和工具。

二、建立模糊逻辑系统使用Matlab进行模糊逻辑分析的第一步是建立一个模糊逻辑系统。

可以使用命令"fuzzy"创建一个模糊逻辑系统对象，然后使用该对象进行后续的分析。

例如，创建一个简单的三角形隶属函数的模糊逻辑系统对象：```matlabfis = fuzzyfis = addInput(fis,[0 10],'Name','input1')fis = addOutput(fis,[0 20],'Name','output1')fis = addMF(fis,'input1','trimf',[2 5 7])fis = addMF(fis,'output1','trimf',[4 10 16])```上述代码创建了一个输入变量input1和一个输出变量output1，并添加了三角形隶属函数。

通过这种方式，可以根据实际问题的需求建立模糊逻辑系统。

三、设置模糊规则在模糊逻辑系统中，模糊规则是描述输入和输出之间关系的关键。

Matlab技术模糊控制方法

Matlab技术模糊控制方法随着科技的不断进步，控制系统在各个领域中起着至关重要的作用。

为了适应不同的应用场景，不同的控制方法也应运而生。

其中，模糊控制方法因其对系统非线性特性的适应性和可解释性而备受关注。

本文将详细介绍Matlab技术中的模糊控制方法，包括模糊集合的表示与运算、模糊推理规则的建立、模糊控制器的设计与优化。

第一部分：模糊集合与模糊运算在模糊控制中，首先需要将系统的输入和输出用模糊集合的形式表示。

模糊集合是用隶属度函数来描述的，隶属度函数表示了某个元素属于该模糊集的程度。

Matlab中提供了一些方便的工具和函数来实现模糊集合的表示和计算。

首先，我们需要定义模糊集合的隶属度函数。

常见的隶属度函数有三角形隶属度函数、梯形隶属度函数、高斯隶属度函数等。

可以使用Matlab中的fuzzify函数来定义这些函数，并通过plot函数来可视化。

接下来，我们可以使用Matlab中的模糊运算函数来进行模糊集合的运算，例如交集运算和并集运算。

这些函数包括min、max、prod等函数。

通过这些函数，我们可以方便地实现模糊集合的合并和比较。

第二部分：模糊推理规则的建立模糊推理规则是模糊控制中的核心部分，它将模糊集合的输入映射为输出。

在Matlab中，我们可以使用fuzzy规则编辑器来定义和管理模糊推理规则。

首先，我们需要确定输入和输出的模糊集合。

在fuzzy规则编辑器中，我们可以指定输入和输出变量，并为其分配模糊集合。

接着，我们可以添加模糊规则，每个模糊规则包括条件和结论两个部分。

条件部分是输入变量的模糊集合的组合，结论部分是输出变量的模糊集合。

在添加模糊规则之后，我们可以使用fuzzify函数将输入变量模糊化，并使用inference函数进行推理。

推理结果将以模糊集合的形式表示。

第三部分：模糊控制器的设计与优化在模糊控制中，模糊控制器是通过将输入模糊集合映射为输出模糊集合来实现控制目标的。

在Matlab中，我们可以使用fuzzy控制器编辑器来设计和优化模糊控制器。

MATLAB模糊逻辑与控制方法与实践

MATLAB模糊逻辑与控制方法与实践近年来，人工智能和机器学习技术得到了广泛的应用和发展。

其中，模糊逻辑和模糊控制是一种用来处理不确定性和模糊性信息的重要方法。

作为一种数学工具和计算工具，MATLAB在模糊逻辑与控制方法的研究和应用中发挥了重要的作用。

本文将以MATLAB为工具，系统全面地介绍模糊逻辑与控制的原理、方法和实践应用。

一、模糊逻辑的原理与方法模糊逻辑是一种处理模糊信息和模糊关系的数学理论和方法。

传统的逻辑只能处理清晰和确定的关系，而模糊逻辑则可以用来处理不确定和模糊的关系。

模糊集合、模糊关系和模糊推理是模糊逻辑的基本概念和方法。

在MATLAB中，可以利用模糊逻辑工具箱来实现模糊集合和模糊关系的定义和运算。

通过定义模糊集合的隶属函数，可以描述一个对象属于某个模糊集合的程度。

常见的隶属函数包括三角函数、高斯函数等，可以根据实际问题选择合适的隶属函数。

而模糊关系可以通过模糊矩阵来表示，矩阵中的元素表示不同模糊集合之间的关系。

模糊推理是模糊逻辑中的关键技术之一。

在MATLAB中，可以利用模糊规则推理引擎来实现模糊推理。

通过定义一组模糊规则，可以实现从输入到输出的模糊推理过程。

常见的模糊推理方法包括模糊逻辑控制和模糊推理系统。

模糊逻辑控制是一种基于模糊规则的控制方法，可以应用于各种系统的控制问题。

而模糊推理系统则是一种更加通用的模糊推理方法，可以应用于非控制问题的模糊推理和决策。

二、模糊控制的原理与方法模糊控制是一种基于模糊逻辑的控制方法，主要用于处理不确定和模糊的系统。

模糊控制包括模糊建模、模糊推理和模糊控制器设计三个主要步骤。

在MATLAB中，可以利用模糊逻辑工具箱来实现模糊控制的设计和仿真。

通过建立模糊模型，可以将系统的输入和输出用模糊集合表示，从而形成模糊规则。

模糊模型的建立可以基于系统的经验数据或者专家知识，可以采用最小二乘法、最大似然法等方法进行参数估计。

模糊推理是模糊控制的核心，通过模糊规则和模糊推理引擎，将模糊输入转化为模糊输出。

(完整word版)matlab下模糊控制器设计步骤

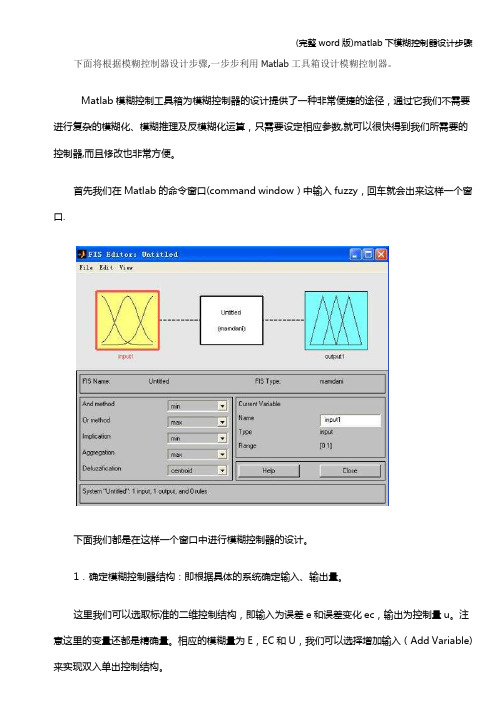
下面将根据模糊控制器设计步骤,一步步利用Matlab工具箱设计模糊控制器。

Matlab模糊控制工具箱为模糊控制器的设计提供了一种非常便捷的途径，通过它我们不需要进行复杂的模糊化、模糊推理及反模糊化运算，只需要设定相应参数,就可以很快得到我们所需要的控制器,而且修改也非常方便。

首先我们在Matlab的命令窗口(command window）中输入fuzzy，回车就会出来这样一个窗口.下面我们都是在这样一个窗口中进行模糊控制器的设计。

1．确定模糊控制器结构：即根据具体的系统确定输入、输出量。

这里我们可以选取标准的二维控制结构，即输入为误差e和误差变化ec，输出为控制量u。

注意这里的变量还都是精确量。

相应的模糊量为E，EC和U，我们可以选择增加输入（Add Variable)来实现双入单出控制结构。

2．输入输出变量的模糊化：即把输入输出的精确量转化为对应语言变量的模糊集合。

首先我们要确定描述输入输出变量语言值的模糊子集，如{NB，NM，NS，ZO，PS，PM，PB}，并设置输入输出变量的论域,例如我们可以设置误差E(此时为模糊量)、误差变化EC、控制量U的论域均为｛-3，—2，-1，0，1，2,3｝；然后我们为模糊语言变量选取相应的隶属度函数。

在模糊控制工具箱中,我们在Member Function Edit中即可完成这些步骤.首先我们打开Member Function Edit窗口.然后分别对输入输出变量定义论域范围，添加隶属函数，以E为例,设置论域范围为［—3 3］，添加隶属函数的个数为7。

然后根据设计要求分别对这些隶属函数进行修改，包括对应的语言变量,隶属函数类型。

3．模糊推理决策算法设计：即根据模糊控制规则进行模糊推理,并决策出模糊输出量。

首先要确定模糊规则,即专家经验。

对于我们这个二维控制结构以及相应的输入模糊集，我们可以制定49条模糊控制规则(一般来说，这些规则都是现成的,很多教科书上都有），如图。

模糊控制的MATLAB实现具体过程

在rulelist的每一行中，前m个数字表示各输入语言变量的语言值（隶属度函数的编号），随后的n个数字表示输出语言变量的语言值，第n+m+1个数字是该规则的权重，权重的值在0到1之间，一般设定为1；第n+m+2 个数字为0或1两者之一，为1表示模糊规则各输入语言变量之间是and关系，为0则表示是or关系。
PPT学习交流
16
例：a=newfis(‘tipper’); a=addvar(a,’input’,’service’,[0 10]); a=addmf(a,’input’,1,’poor’,’guassmf’,[1.5 0]); a=addmf(a,’input’,1,’good’,’guassmf’,[1.5 5]); a=addmf(a,’input’,1,’excellent’,’guassmf’,[1.5 10]); plot(a,’input’,1)
注意：对于添加到同一个模糊推理系统的语言变量，按先后顺序自动编号，编号从1开始，逐渐递增。对于分属于输入与输出的不同语言变量则独立地分别编号。
例：a=newfis(‘tipper’); //创建并返回一个新的FIS系统
a=addvar(a,’input’,’service’,[0 10]);
getfis(a,’input’,1) /P/P取T学习得交流FIS的部分或全部属性
如果输入U是M*N矩阵，则系统是N输入的，返回的Y是M*L矩阵，L是系统的输出的数目。
例：fis=readfis(‘tipper’);
PPT学习交流
11
③ 函数gaussmf 功能：建立高斯型隶属度函数。
格式：y=gaussmf(x,[sig c])
其中：参数x指定变量论域范围，参数c决定了函数的中心点，sig决定了函数曲线的宽度σ。

(完整word版)模糊聚类分析及matlab程序实现

模糊聚类分析及matlab 程序实现采用模糊数学语言对按一定的要求进行描述和分类的数学方法称为模糊聚类分析。

聚类分析主要经过标定和聚类两步骤。

【1】 1 标定（建立模糊相似矩阵）城市居民食品零售价格，第t 时刻第i 种食品的零售价记为),(t i x 。

相似矩阵R 的构建方法：NTV 法设时间序列),(j i A 表示食品i 在时间t 的价格，其中i=1，2…42；t=1，2…39。

∑∑==--=mk jk ik m k jk ik x xx x j i R 11),max (1),(（其中i,j,k=1,2…42,m=39） 42*42),(j i R R = 2 聚类2.1 计算R 的传递闭包：对模糊相似矩阵R,依次用平方法计算,2R ,4R ,…,t2R ,…,当第一次出现k k k R R R =*时，则称k R 为传递闭包。

【1】2.2 开始聚类：【2】（1）令T={1,2,3…42}，取)1(xi T ∈ ,令X 、Q 为空集；（2）令0=j ；（3）若λ>=),(j xi R 且X x j ∉，则令}{j X X ⋃=，}{j Q Q ⋃=；（4）1+=j j ；（5）若n j <，返回（1）；（6）若Q 为空集，怎输出聚类x,X -T T =；（7）)1(xi Q =,}{xi Q Q -=,返回（2）。

设置不同的置信水平λ值，就可以得到不同的分类。

Matlab 程序实现：A=data;[N M] = size(A);for i = 1:Nfor j = 1:NR(i,j)=abs(1-sum(abs(A(i,:)-A(j,:)))/sum(max([A(i,:);A(j,:)])));endendfor j=1:42for i=1:42y(i,j)=0;for k=1:42mn(k)=min(R(i,k),R(k,j));endy(i,j)=max(mn);endendnumda=[1 0.9 0.95 0.85 0.8 0.75 0.55 0.7 0.655 0.65 0.6 0.55 0.5 0.45 0.454 0.4 0.45 0.3 0.35 0.255 0.25 0.2 0.15 0.1];for i=1:42TT(i)=i;endfor i=1:length(numda)disp ('当分类系数是');disp(numda(i));a=numda(i);T=TT;disp ('分类为');while 1if ~isempty(T)xi=T(1);endX=[];Q=[];while 1for j=1:42if (y(xi,j)>=a)&isempty(intersect(X,j))X=union(X,j);Q(length(Q)+1)=j;endendif isempty(Q)disp(X);breakelsexi=Q(1);Q(1)=[];endendT=setdiff(T,X); if isempty(T) breakendendend。

MATLAB模糊聚类分析案例程序

3.数据标准化（1）数据矩阵设论域12345678910,1112U={,,,,,,,,,,}x x x x x x x x x x x x 为被分类的对象，每个对象又由指标1234567Y ={,,,,,,,,}y y y y y y y y y 表示其性状即1234567891x ={,,,,,,,,,,}i i i i i i i i i i i i ix x x x x x x x x x x x (i=1,2,…,12)于是得到原是数据矩阵7 5 2 5 0 1 3 4 2 12 17 8 21 9 2 38 4 37 83 29 59 65 37 20 54 13 26 53 13 31 36 21 A =23 12 18 14 178 69 112 78 104 36 94 31 47 23 25 36 11 12 11 24 6 16 101 32 53 52 86 52 41 38 94 28 6 7 8 8 2 0 3 29 169 51 58 72 49 30 48 37 146 327 91 126 92 89 69 79 29 49 93 27 54 64 24 17 23 11 49 18 7 9 5 1 2 18 3 8 ⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭（2）数据标准化将模糊矩阵的每一个数据压缩到[0,1]上，采用平移.极差变换进行数据标准化1i n1i n1i nA (i,k)-{A (i,k )}B (i,k)={A (i,k)}-{A (i,k)}m in m ax m in ≤≤≤≤≤≤ (k=1,2,…,m)运用matlab 编程由函数F_jisjbzh.m 【见附录3.4】的标准化矩阵是附录3.4function [X]=F_JISjBzh(cs,X) %模糊聚类分析数据标准化变换%X 原始数据矩阵；cs=0，不变换；cs=1，标准差变换 %cs=2,极差变换if(cs==0) return ;end[n,m]=size(X);% 获得矩阵的行列数 if(cs==1) % 平移极差变换 for(k=1:m) xk=0;for(i=1:n) xk=xk+X(i,k);end xk=xk/n;sk=0;for(i=1:n) sk=sk+(X(i,k)-xk)^2;end sk=sqrt(sk/n);for(i=1:n) X(i,k)=(X(i,k)-xk)/sk;end endelse %平移*极差变换for(k=1:m) xmin=X(1,k);xmax=X(1,k); for(i=1:n)if(xmin>X(i,k)) xmin=X(i,k);end if(xmax<X(i,k)) xmax=X(i,k);end endfor(i=1:n) X(i,k)=(X(i,k)-xmin)/(xmax-xmin);end endend0 0 0 0 0 0 0.0319 0.0286 0 0.0156 0.1395 0.0484 0.1839 0.0865 0.0147 0.4043 0.B=0286 0.2431 0.2375 0.2791 0.4597 0.6897 0.3558 0.2794 0.5745 0.2857 0.1667 0.1437 0.0930 0.2339 0.3563 0.2019 0.3235 0.1277 0.4286 0.0833 0.5344 0.7442 0.8871 0.8391 1.0000 0.5147 1.0000 0.8000 0.3125 0.0500 0.2326 0.2742 0.0690 0.1154 0.1471 0.2553 0.0857 0.0972 0.2938 0.3140 0.4113 0.5402 0.8269 0.7500 0.4362 1.0000 0.6389 0.0656 0.0116 0.0403 0.0345 0.0769 0.0147 0 0 0.1875 0.5062 0.5349 0.4516 0.7701 0.4712 0.4265 0.5106 0.9714 1.0000 1.0000 1.0000 1.0000 1.0000 0.8558 1.0000 0.8404 0.7429 0.3264 0.2687 0.2558 0.4194 0.6782 0.2308 0.2353 0.2447 0.2286 0.3264 0.0344 0.0233 0.0565 0 0.0096 0.0147 0.1915 0 0.0417⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭第二步：标定（建立模糊相似矩阵）对标定我们运用了直接欧几里得距离法：ij r 1c d(x ,x )i j =-⨯其中c 为任意选区的参数，它使得0≤ij r ≤1,d(x ,x )i j 表示i x 与j x 的距离，(,)i j d x x =运用matlab 软件编写F_jir.m 函数【见附录3.5】，取cs==8，的模糊相似矩阵附录3.5：（仅附录了一段用到的程序） function [R]=F_jir(cs,X) %cs==8，直接欧几里得距离法%cs==9，直接海明距离法（绝对值减数法） %cs==10，直接切比雪夫距离法elseif(cs<=10)C=0;for(i=1:n)for(j=i+1:n)d=0;%直接欧几里得距离法if(cs==8)for(k=1:m)d=d+(X(i,k)-X(j,k))^2;endd=sqrt(d);%直接海明距离法elseif(cs==9)for(k=1:m)d=d+abs(X(i,k)-X(j,k)); end%直接切比雪夫距离法elsefor(k=1:m)if(d<abs(X(i,k)-X(j,k))) d=abs(X(i,k)-X(j,k)); endendendif(C<d)C=d;endendendC=1/(1+C);for(i=1:n)for(j=1:n)d=0;%直接欧几里得距离法if(cs==8)for(k=1:m)d=d+(X(i,k)-X(j,k))^2;endd=sqrt(d);%直接海明距离法elseif(cs==9)for(k=1:m)d=d+abs(X(i,k)-X(j,k)); end%直接切比雪夫距离法 elsefor(k=1:m)if(d<abs(X(i,k)-X(j,k))) d=abs(X(i,k)-X(j,k)); end end endR(i,j)=1-C*d; end end1.0000 0.8596 0.6731 0.7995 0.3715 0.8668 0.4930 0.9383 0.4602 0.2745 0.7151 0.9499 0.8596 1.0000 0.7638 0.8150 0.4634 0.8973 0.5608 0.87R =46 0.5490 0.3541 0.7866 0.8972 0.6731 0.7638 1.0000 0.8140 0.6694 0.7736 0.6961 0.6907 0.6812 0.5618 0.8907 0.7016 0.7995 0.8150 0.8140 1.0000 0.5349 0.8534 0.6705 0.8105 0.6204 0.4449 0.8491 0.8063 0.3715 0.4634 0.6694 0.5349 1.0000 0.4863 0.7104 0.3928 0.6905 0.7863 0.5998 0.4001 0.8668 0.8973 0.7736 0.8534 0.4863 1.0000 0.5801 0.8755 0.5494 0.3881 0.7991 0.8972 0.4930 0.5608 0.6961 0.6705 0.7104 0.5801 1.0000 0.5216 0.8026 0.6199 0.6783 0.5091 0.9383 0.8746 0.6907 0.8105 0.3928 0.8755 0.5216 1.0000 0.4959 0.2979 0.7446 0.9300 0.4602 0.5490 0.6812 0.6204 0.6905 0.5494 0.8026 0.4959 1.0000 0.6214 0.6852 0.4802 0.2745 0.3541 0.5618 0.4449 0.7863 0.3881 0.6199 0.2979 0.6214 1.0000 0.5161 0.3002 0.7151 0.7866 0.8907 0.8491 0.5998 0.7991 0.6783 0.7446 0.6852 0.5161 1.0000 0.7343 0.9499 0.8972 0.7016 0.8063 0.4001 0.8972 0.5091 0.9300 0.4802 0.3002 0.7343 1.0000⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭（3）聚类（求动态聚类图） <1>传递闭包法根据标定所得的模糊矩阵，只是一个模糊相似矩阵R ，不一定具有传递性，即R 不一定是模糊等价矩阵，还需要对其改造成模糊等价矩阵R ’,根据定理，用二次方法求传递闭包t （R ），t （R ）就是所求模糊等价矩阵R ’,即：t （R ）=R ’,再让λ由大变到小，就可形成动态聚类图。

（完整word版）模糊层次分析法的Matlab实现

（完整word版）模糊层次分析法的Matlab实现一、引言层析分析法是将定量与定性相结合的多目标决策法,是一种使用频率很高的方法,在经济管理、城市规划等许多领域得到了广泛应用。

由于其结果受主观思维的影响较大,许多科研工作者对其进行了深入的研究,将模糊理论与层次分析法相结合,提出了模糊层次分析法。

为克服层次分析法中判断矩阵的一致性与人类思维的一致性存在的显著差异,文献[1-2]引入了模糊一致矩阵。

为解决解的精度及收敛问题,文献[3-4]引入幂法来求排序向量。

运用模糊层次分析法研究实际问题时,常采用迭代法来得到精度更高的排序向量,这就要求选择合适的初始值并通过大量的计算,为此,文中利用三种方法计算了初始排序向量,并给出了算法的Matlab程序,最后通过实例说明。

二、模糊层次分析法为解决AHP种所存在的问题,模糊层次分析法引入模糊一致矩阵,无需再进行一致性检验,同时使用幂法来计算排序向量,可以减少迭代齿数,提高收敛速度,满足计算精度的要求.具体步骤:1.构造优先关系矩阵采用0.1～0.9标度[2],建立优先判断矩阵2.将优先关系矩阵转化为模糊一致矩阵3.计算排序向量(1)和行归一法:(2)方根法:(3)利用排序法:(4)利用幂法[5-6]求精度更高的排序向量:否则,继续迭代。

三、模糊层次分析法的程序实现给出模糊层次分析法的Matlab程序。

clear;clc;E=input('输入计算精度e:')Max=input('输入最大迭代次数Max:')F=input('输入优先关系矩阵F:');%计算模糊一致矩阵N=size(F);r=sum(F');for i=1:N(1)for j=1:N(2)R(i,j)=(r(i)-r(j))/(2*N(1))+0.5;endendE=R./R';% 计算初始向量----------% W=sum(R')./sum(sum(R)); % 和行归一法%---------------------------------------------------------for i=1:N(1)S(i)=R(i,1);for j=2:N(2)S(i)=S(i)*R(i,j);endendS=S^(1/N(1));W = S./sum(S);%方根法%-------------------------------------------------------- % a=input('参数a=?');%W=sum(R')/(N(1)*a)-1/(2*a)+1/N(1); %排序法% 利用幂法计算排序向量----V(:,1)=W'/max(abs(W)); %归一化for i=1:MaxV(:,i+1)=E*V(:,i);V(:,i+1)=V(:,i+1)/max(abs(V(:,i+1)));if max(abs(V(:,i+1)-V(:,i)))k=i;A=V(:,i+1)./sum(V(:,i+1));breakElseEndEnd四、计算实例由优先关系矩阵得到模糊一致矩阵利用三种方法计算排序向量分别为:五、结束语模糊层次分析法广泛应用于许多领域,解决了判断矩阵的一致性与人类思维一致性的差异问题,同时还得到了计算精度较高的且与实际情况较吻合的排序向量,但是模糊一致矩阵的转换和排序向量的求解计算复杂,工作量大,本文运用Matlab程序实现了该方法,能够方便的解决方法的计算问题。

Matlab学习系列23. 模糊聚类分析报告原理及实现

23. 模糊聚类分析原理与实现聚类分析，就是用数学方法研究和处理所给定对象，按照事物间的相似性进展区分和分类的过程。

传统的聚类分析是一种硬划分，它把每个待识别的对象严格地划分到某个类中，具有非此即彼的性质，这种分类的类别界限是清楚的。

随着模糊理论的建立，人们开始用模糊的方法来处理聚类问题，称为模糊聚类分析。

由于模糊聚类得到了样本数与各个类别的不确定性程度，表达了样本类属的中介性，即建立起了样本对于类别的不确定性的描述，能更客观地反映现实世界。

本篇先介绍传统的两种〔适合数据量较小情形，与理解模糊聚类原理〕：基于择近原如此、模糊等价关系的模糊聚类方法。

〔一〕预备知识一、模糊等价矩阵定义1设R=(r ij)n×n为模糊矩阵，I为n阶单位矩阵，假如R满足i) 自反性：I≤R 〔等价于r ii =1〕；ii) 对称性：R T =R;如此称R 为模糊相似矩阵，假如再满足iii) 传递性：R 2≤R 〔等价于1()nik kj ij k r r r =∨∧≤〕如此称R 为模糊等价矩阵。

定理1 设R 为n 阶模糊相似矩阵，如此存在一个最小的自然数k 〔k <n 〕, 使得R k 为模糊等价矩阵，且对一切大于k 的自然数l ，恒有R l =R k . R k 称为R 的传递闭包矩阵，记为t(R). 二、模糊矩阵的λ-截矩阵定义2 设A =(a ij )n ×m 为模糊矩阵，对任意的λ∈[0,1], 作矩阵()()ij n mA a λλ⨯=其中，()1, 0, ij ijij a aa λλλ≥⎧=⎨<⎩称为模糊矩阵A 的λ-截矩阵。

显然，A λ为布尔矩阵，且其等价性与与A 一致。

意义：将模糊等价矩阵转化为等价的布尔矩阵，可以得到有限论域上的普通等价关系，而等价关系是可以分类的。

因此，当λ在[0,1]上变动时，由A λ得到不同的分类。

假如λ1＜λ2, 如此A λ1≥A λ2, 从而由A λ2确定的分类是由A λ1确定的分类的加细。