FLUENT多孔介质中平面面板(plane surface)工具的使用
FLUENT多孔介质数值模拟设置

FLUENT多孔介质数值模拟设置FLUEN■多孔介质数值模拟设置多孔介质条件多孔介质模型可以应用于很多问题,如通过充满介质的流动、通过过滤纸、穿孔圆盘、流量分配器以及管道堆的流动。
当你使用这一模型时,你就定义了一个具有多孔介质的单元区域,而且流动的压力损失由多孔介质的动量方程中所输入的内容来决定。
通过介质的热传导问题也可以得到描述,它服从介质和流体流动之间的热平衡假设,具体内容可以参考多孔介质中能量方程的处理一节。
多孔介质的一维化简模型,被称为多孔跳跃,可用于模拟具有已知速度/压降特征的薄膜。
多孔跳跃模型应用于表面区域而不是单元区域,并且在尽可能的情况下被使用(而不是完全的多孔介质模型),这是因为它具有更好的鲁棒性,并具有更好的收敛性。
详细内容请参阅多孔跳跃边界条件。
多孔介质模型的限制如下面各节所述,多孔介质模型结合模型区域所具有的阻力的经验公式被定义为“多孔”。
事实上多孔介质不过是在动量方程中具有了附加的动量损失而已。
因此,下面模型的限制就可以很容易的理解了。
—I 二流体通过介质时不会加速,因为事实上出现的体积的阻塞并没有在模型中出现。
这对于过渡流是有很大的影响的,因为它意味着FLUENT S 会正确的描述通过介质的过渡时间。
多孔介质对于湍流的影响只是近似的。
详细内容可以参阅湍流多孔介质的处理一节。
多孔介质的动量方程多孔介质的动量方程具有附加的动量源项。
源项由两部分组成,一部分是粘性损失项(Darcy),另一个是内部损失项:其中S_i是i向(x, y, or z) 动量源项,D和C是规定的矩阵。
在多孔介质单元中,动量损失对于压力梯度有贡献,压降和流体速度(或速度方阵)成比例。
对于简单的均匀多孔介质:其中a是渗透性,C_2时内部阻力因子,简单的指定D和C分别为对角阵1/a 和C_2其它项为零。
FLUENT?允许模拟的源项为速度的幕率:其中C_0和C_1为自定义经验系数。
注意:在幕律模型中,压降是各向同性的,C_0的单位为国际标准单位。
Fluent使用指南

Fluent使用指南第一步:网格1、读入网格(File→Read→Case)2、检查网格(Grid→Check)3、平滑网格(Grid→Smooth/Swap)4、更改网格的长度单位(Grid→Scale)5、显示网格(Display→Grid)第二步:建立求解模型1、保持求解器的默认设置不变(定常)2、开启标准K-ε湍流模型和标准壁面函数Define→Models→Viscous第三步:设置流体的物理属性ari→Density→viscosity→第四步:设置边界条件对outflow、velocity-inlet、wall 采用默认值第五步:求解1、Solv→Controls→Solution中,Discretitation→Pressure→standardPressure→ Momentum→2、Solution Initialization→ all zone3、Residual Monitors→Plot第六步:迭代第七步:进行后处理第八步:1、Define→Model→Evlerian2、在Vissous Model→K-epsilon Multiphase Model→Mixture 第九步:在Define Phase Model→Discrete phase ModelInteraction↓选中→Interaction With Continuous Phase Nomber of Continuous PhaseInteractions per DPM Interaction第十步:设置物理属性第十一步:Define→Operating →重力加速度Define→Boondary Conditionsflvid→Mixture→选中Sovrce Terms 其他默认Phase-1→选中Sovrce Terms 其他默认Phase-2→选中Sovrce Terms 其他默认inflow→Mixture→全部默认Phase-1→全部默认Phase-2→Multiphase→Volume Fraction→其他默认outflow→Mixture→默认Phase-1→默认Phase-2→默认wall→Mixture→全部默认Phase-1→默认Phase-2默认第十二步:Slove→Controls→Slution Controls→Pressure→ Momentum→其余默认第十三步:千万不能再使用初始化第十四步:进行迭代计算截Z轴上的图:在Surface→iso↓Surface of constant↓Grid↓然后选x、y、z轴(根据具体情况而定)↓在Iso-Values→选取位置C的设置在New Surface Name中输入新各字→点创建然后在Display→Grid→Edge type→Feature→选中刚创建的那个面,然后Display查看刚才那面是否创建对最后在Display→Contours→Options→Filled→Surface→选中面,然后Display。
史上Fluent最详细操作步骤 一看就懂
Fluent简单分析教程第1步双击运行Fluent,首先出现如下界面,对于二维模型我们可以选择2d(单精度)或2ddp(双精度)进行模拟,通常选择2d即可。
Mode选择缺省的Full Simulation即可。
点击“Run”。
然后进入如下图示意界面:第2步:与网格相关的操作1.读入网格文件car1.mesh操作如下图所示:打开的“Select File”对话框如图所示:(1)找到网格文件E:\gfiles\car1.mesh;(2)点击OK,完成输入网格文件的操作。
注意:FLUENT读入网格文件的同时,会在信息反馈窗口显示如下信息:其中包括节点数7590等,最后的Done表示读入网格文件成功。
2.网格检查:操作如下图所示:FLUENT在信息反馈窗口显示如下信息:注意:(1)网格检查列出了X,Y的最小和最大值;(2)网格检查还将报告出网格的其他特性,比如单元的最大体积和最小体积、最大面积和最小面积等;(3)网格检查还会报告出有关网格的任何错误,特别是要求确保最小体积不能是负值,否则FLUENT无法进行计算。
3.平滑(和交换)网格这一步是为确保网格质量的操作。
操作:→Smooth/Swap...打开“Smooth/Swap Grid”对话框如图所示:(1)点击Smooth按钮,再点击Swap,重复上述操作,直到FLUENT 报告没有需要交换的面为止。
如图所示:(2)点击Close按钮关闭对话框。
注意:这一功能对于三角形单元来说尤为重要。
4.确定长度单位操作如下图所示:打开“Scale Grid”对话框如图所示:(1)在单位转换(Units Conversion)栏中的(Grid Was Created In)网格长度单位右侧下拉列表中选择m;(2)看区域的范围是否正确,如果不正确,可以在Scale Factors 的X和Y中分别输入值10,然后点击“Scale”或“Unscale”即可;(3)点击Scale;(4)点击Close关闭对话框。
fluent软件功能操作--入门教程

二.算例介绍
2、计算结果
谢谢!
二.算例介绍
1、问题描述
一个圆形的突然扩张管道,假设工质是水,通常 当流动经过类似这种突然扩张或突然收缩的管道时, 流动与管壁分离,形成流动的漩涡,与此同时发生压 强的损失。现在介绍用FLUENT模拟水流在管道中的 速度场。
Hale Waihona Puke 二.算例介绍1、问题描述
二.算例介绍
2、计算结果
二.算例介绍
2、计算结果
一.软件简介
2、组成
Fluent主要包含三方面功能:前处理、 求解器、后处理。
其中前处理主要是几何建模,网格生 成。
求解器指求解控制方程的选取。 后处理是对计算结果进行显示,输出。
一.软件简介
3、工程应用背景
●定常/非定常问题。 ●可压/不可压问题。 ●无粘流、层流、湍流问题。 ●热传导问题。 ●化学组分的混合与反应问题。 ●基于精细流场解算的预测流体噪声声学模 拟。
一.软件简介
1、简介
Fluent针对二维问题支持三角形或四边 形网格;针对三位问题支持四面体,六面体, 棱锥,多面体网格;同时也支持混合网格。
一.软件简介
1、简介
Fluent由C语言开发,支持并行计算, 支持unix和windows多平台。计算结果可以 用云图,等值线图,矢量图,剖面图,xy散 点图,动画等多方式显示。
CFD仿真计算软件—FLUENT介绍
张鑫 2011年8月19日
主要介绍两项内容
• 软件简介
• 算例介绍
一.软件简介
1、简介
Fluent是一款目前处于世界领先地位的 CFD软件,最初由Fluent公司发行,2006年2 月被ansys公司收购,并发行新的版本。
fluent多孔介质简单操作
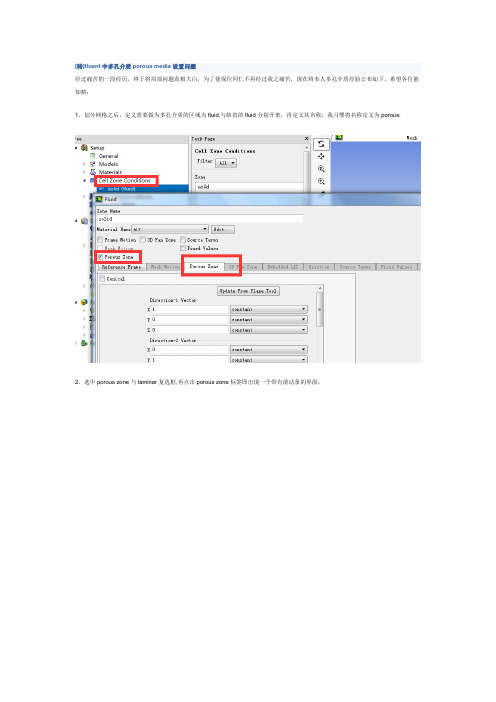
[转]fluent中多孔介质porous media设置问题
经过痛苦的一段经历,终于将局部问题真相大白,为了使保位同仁不再经过我之痛苦,现在将本人多孔介质经验公布如下,希望各位能加精:
1。
划分网格之后,定义需要做为多孔介质的区域为fluid,与缺省的fluid分别开来,再定义其名称,我习惯将名称定义为porous;
2。
选中porous zone与laminar复选框,再点击porous zone标签即出现一个带有滚动条的界面;
3。
porous zone设置方法:
1)定义矢量:二维定义一个矢量,第二个矢量方向不用定义,是与第一个矢量方向正交的;
三维定义二个矢量,第三个矢量方向不用定义,是与第一、二个矢量方向正交的;
(如何知道矢量的方向:打开grid图,看看X,Y,Z的方向,如果是X向,矢量为1,0,0,同理Y向为0,1,0,Z向为0,0,1,如果所需要的方向与坐标轴正向相反,则定义矢量为负)
圆锥坐标与球坐标请参考fluent帮助。
2)定义粘性阻力1/a与内部阻力C2:请参看本人上一篇博文“终于搞清fluent中多孔粘性阻力与内部阻力的计算方法”,此处不赘述;
3)如果了定义粘性阻力1/a与内部阻力C2,就不用定义C1与C0,因为这是两种不同的定义方法,C1与C0只在幂率模型中出现,该处保持默认就行了;
4)定义孔隙率porousity,默认值1表示全开放,此值按实验测值填写即可。
完了,其他设置与普通k-e或RSM相同。
总结一下,与君共享!。
Fluent软件的使用(2)

压力速度耦合方法
当使用压力基求解时,压力速度耦合算法(通过 连续方程和动量方程的组合推导出压力修正方程) 有四种。
Semi-Implicit Method for Pressure-Linked Equations (SIMPLE) 默认方法,鲁棒性很强。
速度入口Velocity Inlet
描述速度的三种方法
Magnitude, Normal to Boundary Components
Magnitude and Direction
除非使用UDF或者profile文件, 否则只能使用均匀的速度剖面。
通常用在不可压缩流动中,不推 荐在可压缩流动中使用。
Pressure-Based (coupled)
Density-Based (coupled)
压力基求解器包含两种算法:
解耦求解器,顺序求解压力修 正方程和动量方程 耦合求解器,同时求解压力修 正方程和动量方程
Solve Energy Solve Species Solve Turbulence Equation(s) Solve Other Transport Equations as required
速度大小可以是负的,表明正在 使用速度出口边界。
压力入口Pressure Inlet
对于可压与不可压流动均适用。
从驻点到入口的无损转换条件。
FLUENT计算入口处的静压和速度
通过边界的质量流率取决于内部的 求解和描述的流动方向
要求的信息
总的表压 超音速/初始化的表压
Yes
Check for accuracy
No
Stop
可用的求解器
Fluent提供两种求解器——压 力基的和密度基的。 压力基的求解器将速度和压 力(或者压力修正量)作为 基本变量
FLUENT软件使用说明

FLUENT软件使⽤说明FLUENT问题:⼀、计算思路建模流场⽹格分区、结构、尺⼨边界模型离散迭代处理分析⼆、求解问题⼆维三维理想⽓体层流湍流⼆相流化学反应三、学些⽅法典型实例具体问题学习⼩节:CFD 分析的基本步骤1. 定义⽬标模型2. 确定模型区域3.选择合适的求解器◆⼆者都可⽤于⼴泛的流体计算,但⼀般情况下发:●segregated :适⽤于不可压及微可压流。
只使⽤隐式格式。
●coupled :适⽤于⾼速可压流,有强体积⼒的耦合流以及密⽹格问题。
耦合求解流动和能量⽅程,可以快速收敛。
●coupled implicit 格式内存需要量⼤,如果内存不够可以使⽤coupled explicit,同样也是耦合求解流动和能量⽅程,但收敛速度较慢。
Segregated适⽤于不可压及微可压流,只使⽤隐式格式。
Coupled适⽤于⾼速可压流,有强体积⼒的耦合流以及流场密⽹较密的问题以上情况宜使⽤coupled implicit 格式,但需内存量⼤。
当内存不⾜时,可⽤segregated或coupled explicit (显式格式⽐隐式格式收敛慢)4. 选择并⽣成⽹格对简单的⼏何体,四边形/六⾯体⽹格⽐使⽤三⾓形/四⾯体⽹格⽤更少的单元数可以⽣成更好的⽹格。
对复杂的⼏何体,四边形/六⾯体⽹格⼰经没有数值精度上的优势,⽽使⽤三⾓形/四⾯体⽹格可以节省⼤量时间。
5.建⽴数值模型边界设定有处理6. 计算求解◆在FLUENT中可以选择控制⽅程中对流项的离散⽅法。
有四种⽅法可以选择:FirstOrder、Second Order、QUICK、Power。
●当流动⽅向与⽹格相⼀致时(如:使⽤四边形或六⾯体⽹格的管内层流问题),⼀阶迎风格式就可以了,但⼀阶格式会增加计算中的数值扩散错误。
●当流动⽅向不与⽹格相⼀致时(如:流动⽅向倾斜的穿过⽹格线),或使⽤三⾓形、四⾯体⽹格,应使⽤⼆阶格式以获得更⾼精度的解。
在使⽤四边形或六⾯体⽹格的复杂流场时,也可以使⽤⼆阶格式以获得更⾼精度的解。
多孔介质在fluent中的操作方法 网络上传版本

如何在Fluent中实现多孔介质双能量方程(LNTE)How to use Non-equilibrium Thermal equation (LNTE) model forPorous media in Fluent Software●请参照本人发表的文章:●Please refer to the following papers:1)Wang Fu–Qiang*,Shuai Yong*,Wang Zhi–Q iang,Leng Yu,Tan He–Ping.Thermal and chemical reaction performance analyses of steam methane reforming in porous media solar thermochemical reactor,International Journal of Hydrogen Energy,39(2):718-730,2014关键词:Porous, Solar, Hydrogen, Methane, Reforming, P1 approximation, radiative heat transfer2)Wang Fu–Qiang*,Shuai Yong*,Tan He–Ping,Zhang Xiao-Feng,MaoQian-Jun,Heat transfer analyses of porous media receiver with multi–dish collector by coupling MCRT and FVM method,Solar Energy,93:158–168,2013关键词:Solar, Porous, dish concentrator, Receiver, Monte Carlo3)Wang Fu–Qiang*,Shuai Yong*,Tan He–Ping,Yu Chun–Liang,ThermalPerformance Analysis of Porous Media Receiver with Concentrated Solar Irradiation,International Journal of Heat and Mass Transfer,62:247–254,2013关键词:Solar, Porous, dish concentrator, Receiver, Monte Carlo一、说明1、模型此例基于稳态、层流、对称模型。
3 Fluent软件的使用(2)

Translationally periodic planes
/mesh/modify-zones/make-periodic
2D Tube Heat Exchanger
内部面边界Internal Face Boundaries
仅仅能够在内部单元的面上定义
内部边界的厚度为零。 利用内部边界可以在流场属性中引入阶跃变化
减少网格数量 流场和几何必须包含旋转或者流动方向的周期性
旋转周期
在周期平面上的ΔP = 0
通过周期平面有压降ΔP 模拟流动完全发展的情况,或者 描述每个周期的平均压降
Flow
平移周期
Rotationally periodic planes
如果在网格中未事先定义 周期边界条件,也可以在 TUI中进行定义:
边界处所需的流动信息,取决于边界条件的类型 和计算采用的物理模型。
不恰当的边界条件对流场解具有显著的影响。
单元区域 – Fluid
Fluid单元区域是一组单元的组合, 激活的方程都将在这些单元上求解。 需要选择流体材料
对于多组分或者多相流,材料不显示, 取而代之,流体区域包含各相的混合
对称边界和轴边界 Symmetry and Axis Boundaries
对称边界
流场和几何必须是对称的
对称面处的法向速度为零 对称面处所有物理量的法向 梯度为零
轴边界
被用作轴对称问题的中心 不要求任何输入 必须与X轴方向一致
Symmetry Planes
Axis
周期边界Periodic Boundaries
出流边界被设计用于不可压缩流动。
只能够和速度入口边界联合使用 不能够用于变密度的非定常流动。
FLUENT教程

FLUENT教程FLUENT是一种流体动力学(CFD)软件,用于模拟各种流体行为和流体-结构相互作用。
它是由ANSYS开发的,并广泛应用于工程设计和科学研究领域。
本教程将介绍FLUENT的基本操作和一些常用的模拟技术。
首先,我们需要了解FLUENT的界面和主要功能。
FLUENT的界面包括几个主要的区域:预处理器、求解器和后处理器。
预处理器用于创建和修改模型,包括定义几何形状、边界条件和物理模型。
求解器用于执行模拟,并计算流体参数如速度、压力、温度等。
后处理器用于分析并可视化模拟结果。
开始使用FLUENT之前,我们需要准备一个几何模型。
FLUENT支持导入多种格式的几何模型,如.STL和.IGES。
一旦导入模型,我们可以使用预处理器进行一些几何操作,如修复几何错误、划分网格等。
划分网格是一个重要的步骤,它将模型分成多个小单元,用于计算流体参数。
在划分网格之后,我们可以设置边界条件。
边界条件定义了流体的入口、出口和固体表面的性质,如速度、压力、温度等。
根据实际情况,我们可以选择不同的边界条件类型,如强制入口、自由出口或壁面。
此外,我们还可以定义流体的物理属性,如密度、粘度、热传导系数等。
在准备工作完成后,我们可以开始进行模拟。
首先,我们需要选择一个求解器类型,如稳态模拟或非稳态模拟。
对于稳态模拟,我们需要定义求解器设置,如收敛标准、迭代次数等。
对于非稳态模拟,我们还需要定义时间步长和模拟时间。
在设置求解器后,我们可以执行模拟并观察结果。
FLUENT提供了多种可视化工具,如矢量图、剖面图和动画。
我们可以选择不同的参数进行可视化,并对结果进行分析。
此外,我们还可以导出结果数据,以便在其他软件中进行进一步处理。
除了基本的模拟技术,FLUENT还支持其他高级功能。
例如,我们可以使用多相流模型来模拟多个相的流体行为,如气-液两相流或骨料-流体两相流。
我们还可以使用动网格模型来模拟流体和结构的相互作用。
此外,FLUENT还支持耦合模拟,如流体-热传导耦合或流体-固体耦合。
Fluent_操作手册

Fluent_操作⼿册第01章fluent简单算例21FLUENT是⽤于模拟具有复杂外形的流体流动以及热传导的计算机程序。
对于⼤梯度区域,如⾃由剪切层和边界层,为了⾮常准确的预测流动,⾃适应⽹格是⾮常有⽤的。
FLUENT解算器有如下模拟能⼒:●⽤⾮结构⾃适应⽹格模拟2D或者3D流场,它所使⽤的⾮结构⽹格主要有三⾓形/五边形、四边形/五边形,或者混合⽹格,其中混合⽹格有棱柱形和⾦字塔形。
(⼀致⽹格和悬挂节点⽹格都可以)●不可压或可压流动●定常状态或者过渡分析●⽆粘,层流和湍流●⽜顿流或者⾮⽜顿流●对流热传导,包括⾃然对流和强迫对流●耦合热传导和对流●辐射热传导模型●惯性(静⽌)坐标系⾮惯性(旋转)坐标系模型●多重运动参考框架,包括滑动⽹格界⾯和rotor/stator interaction modeling的混合界⾯●化学组分混合和反应,包括燃烧⼦模型和表⾯沉积反应模型●热,质量,动量,湍流和化学组分的控制体源●粒⼦,液滴和⽓泡的离散相的拉格朗⽇轨迹的计算,包括了和连续相的耦合●多孔流动●⼀维风扇/热交换模型●两相流,包括⽓⽳现象●复杂外形的⾃由表⾯流动上述各功能使得FLUENT具有⼴泛的应⽤,主要有以下⼏个⽅⾯●Process and process equipment applications●油/⽓能量的产⽣和环境应⽤●航天和涡轮机械的应⽤●汽车⼯业的应⽤●热交换应⽤●电⼦/HV AC/应⽤●材料处理应⽤●建筑设计和⽕灾研究总⽽⾔之,对于模拟复杂流场结构的不可压缩/可压缩流动来说,FLUENT是很理想的软件。
当你决定使FLUENT解决某⼀问题时,⾸先要考虑如下⼏点问题:定义模型⽬标:从CFD模型中需要得到什么样的结果?从模型中需要得到什么样的精度;选择计算模型:你将如何隔绝所需要模拟的物理系统,计算区域的起点和终点是什么?在模型的边界处使⽤什么样的边界条件?⼆维问题还是三维问题?什么样的⽹格拓扑结构适合解决问题?物理模型的选取:⽆粘,层流还湍流?定常还是⾮定常?可压流还是不可压流?是否需要应⽤其它的物理模型?确定解的程序:问题可否简化?是否使⽤缺省的解的格式与参数值?采⽤哪种解格式可以加速收敛?使⽤多重⽹格计算机的内存是否够⽤?得到收敛解需要多久的时间?在使⽤CFD分析之前详细考虑这些问题,对你的模拟来说是很有意义的。
FLUENT软件实际操作

求解技术(Solve)Solve>Controls>Solution…计算格式的选择一阶迎风格式:适用于流动方向与网格方向基本一致,结构化网格。
具有稳定性高,计算速度快的优点。
在网格方向与流动方向不一致时,产生的数值误差比较大。
二阶格式:计算时间比较长,收敛性差。
合适的计算方式:在计算开始时先用一阶格式进行计算以获得一个相对粗糙的解,在计算收敛后再用二阶格式完成计算以提高解的精度。
避免二阶格式收敛性差、计算时间长的问题,也避免了一阶格式在复杂流场计算中数值误差大的问题。
QUICK格式:对于结构网格计算旋转流动问题时,计算精度高,但在其它情况下,QUCIK格式的精度与二阶格式相当。
指数律格式:与一阶格式精度基本相同。
中心差分:在LES湍流模型中使用,且应该在网格足够密集、局部Peclet数小于1的情况下使用。
压强插值格式的选择1在彻体力对流场有很大影响的情况下,应该选择彻体力加权(body-force-weighted)格式。
2 在流场中有涡量很大的集中涡、高雷诺数自然对流、高速旋转流、多孔介质,以及流线曲率很大时,应该选择PRESTO!格式。
3 对于可压流,应该使用二阶格式。
4 二阶格式不能用于多孔介质计算和多相流计算中的混合物模型及VOF 模型。
在其他情况下,为了提高精度可以选用二阶格式。
密度插值格式的选择在用分离算法计算单相可压流时,有三种密度插值格式可供选择,即一阶迎风格式、二阶格式和QUICK 格式。
一阶迎风格式具有良好的稳定性,但是在计算带激波的可压流时,会对激波解产生“抹平”作用,因此应该选用二阶格式或QUICK 格式。
在用四边形网格、六面体网格或混合网格计算带激波的流动时,最好使用QUICK 格式计算所有变量。
需要注意的是,在计算可压多项流时,只能用一阶迎风格式计算可压缩相的流动。
Solve>Controls>Solution…Discretization(离散)定义动量、能量、湍流动能等项目,有一阶迎风格式、二阶迎风格式、指数律格式、QUICK格式和中心差分格式(在LES湍流模式计算中),也可以在使用耦合求解器时,定义湍流动能、湍流耗散率等项目,并为这些项目选择一阶迎风格式、二阶迎风格式。
FLUENT中定义多孔介质的方法

FLUENT中定义多孔介质的方法多孔介质计算中需要输入的项目如下:(1)定义多孔介质区域。
(2)定义多孔介质速度函数形式。
(3)定义流过多孔介质区的流体属性。
(4)设定多孔区的化学反应。
(5)设定粘性阻力系数。
(6)设定多孔介质的多孔率。
(7)在计算热交换的过程中选择多孔介质的材料。
(8)设定多孔介质固体部分的体热生成率。
(9)设定流动区域上的任意固定值的流动参数。
(10)需要的话,将多孔区流动设为层流,或取消湍流计算。
(11)定义旋转轴或区域的运动。
经过痛苦的一段经历,终于将局部问题真相大白,为了使保位同仁不再经过我之痛苦,现在将本人多孔介质经验公布如下,希望各位能加精:1。
Gambit中划分网格之后,定义需要做为多孔介质的区域为fluid,与缺省的fluid 分别开来,再定义其名称,我习惯将名称定义为porous;2。
在fluent中定义边界条件define-boundary condition-porous(刚定义的名称),将其设置边界条件为fluid,点击set按钮即弹出与fluid边界条件一样的对话框,选中porous zone与laminar复选框,再点击porous zone标签即出现一个带有滚动条的界面;3。
porous zone设置方法:1)定义矢量:二维定义一个矢量,第二个矢量方向不用定义,是与第一个矢量方向正交的;三维定义二个矢量,第三个矢量方向不用定义,是与第一、二个矢量方向正交的;(如何知道矢量的方向:打开grid图,看看X,Y,Z的方向,如果是X向,矢量为1,0,0,同理Y向为0,1,0,Z向为0,0,1,如果所需要的方向与坐标轴正向相反,则定义矢量为负)圆锥坐标与球坐标请参考fluent帮助。
2)定义粘性阻力1/a与内部阻力C2:见附fluent中多孔粘性阻力系数与惯性阻力系数的方法:对比Darcy 定律v K J =⋅J 为水力坡度,即流经路径长度为L 的水头损失,m/m ;K 为比例系数,也称渗流系数,m/sg p v Kρ∆=- p μνα∆=- 这样可以得到,g K ρμα=,所以1g K ραμ= 其中: 1α为粘性阻力系数,1/m 2; K 为比例系数,也称渗流系数,m/s ;μ为动力粘度,Pa.s ;ρ为流体密度,kg/m 3;g 为重力加速度,m/s 2;采用20℃饱和水的物性参数:密度为998.2kg/m 3 ,运动粘度1.004×10-3Pa.s ;渗流速度取1.0×10-6m/s ,K 取1.0×10-4m/s ,水力坡度约为0.01m/m ; 10461998.29.89.74101.010100410g K ραμ--⨯===⨯⨯⨯⨯ 3)如果了定义粘性阻力1/a 与内部阻力C2,就不用定义C1与C0,因为这是两种不同的定义方法,C1与C0只在幂率模型中出现,该处保持默认就行了;4)定义孔隙率porousity ,默认值1表示全开放,此值按实验测值填写即可。
fluent中多孔介质模型的设置

7.19.6 User Inputs for Porous MediaWhen you are modeling a porous region, the only additional inputs for the problem setup are as follows. Optional inputs are indicated as such.1. Define the porous zone.2. Define the porous velocity formulation. (optional)3. Identify the fluid material flowing through the porous medium.4. Enable reactions for the porous zone, if appropriate, and select the reaction mechanism.5. Enable the Relative Velocity Resistance Formulation. By default, this option is already enabled and takes the moving porous media into consideration (as described in Section 7.19.6).6. Set the viscous resistance coefficients ( in Equation7.19-1,or in Equation 7.19-2) and the inertial resistance coefficients ( in Equation 7.19-1, or in Equation 7.19-2), and define the direction vectors for which they apply. Alternatively, specify the coefficients for the power-law model.7. Specify the porosity of the porous medium.8. Select the material contained in the porous medium (required only for models that include heat transfer). Note that the specific heat capacity, , for the selected material in the porous zone can only be entered as a constant value.9. Set the volumetric heat generation rate in the solid portion of the porous medium (or any other sources, such as mass or momentum). (optional) 10. Set any fixed values for solution variables in the fluid region (optional).11. Suppress the turbulent viscosity in the porous region, if appropriate.12. Specify the rotation axis and/or zone motion, if relevant.Methods for determining the resistance coefficients and/or permeability are presented below. If you choose to use the power-law approximation of the porous-media momentum source term, you will enter thecoefficients and in Equation 7.19-3 instead of the resistance coefficients and flow direction.You will set all parameters for the porous medium inthe Fluid panel (Figure 7.19.1), which is opened from the Boundary Conditions panel (as described in Section 7.1.4).Figure 7.19.1: The Fluid Panel for a Porous Zone Defining the Porous ZoneAs mentioned in Section 7.1, a porous zone is modeled as a special type of fluid zone. To indicate that the fluid zone is a porous region, enablethe Porous Zone option in the Fluid panel. The panel will expand to show the porous media inputs (as shown in Figure 7.19.1).Defining the Porous Velocity FormulationThe Solver panel contains a Porous Formulation region where you can instruct FLUENT to use either a superficial or physical velocity in the porous medium simulation. By default, the velocity is set to SuperficialVelocity. For details about using the Physical Velocity formulation, see Section 7.19.7.Defining the Fluid Passing Through the Porous MediumTo define the fluid that passes through the porous medium, select the appropriate fluid in the Material Name drop-down list in the Fluid panel. If you want to check or modify the properties of the selected material, you can click Edit... to open the Material panel; this panel contains just the properties of the selected material, not the full contents of thestandard Materials panel.If you are modeling species transport or multiphase flow,the Material Name list will not appear in the Fluid panel. Forspecies calculations, the mixture material for all fluid/porous zones will be the material you specified in the SpeciesModel panel. For multiphase flows, the materials are specified when you define the phases, as described in Section 23.10.3.Enabling Reactions in a Porous ZoneIf you are modeling species transport with reactions, you can enable reactions in a porous zone by turning on the Reaction option inthe Fluid panel and selecting a mechanism in the ReactionMechanism drop-down list.If your mechanism contains wall surface reactions, you will also need to specify a value for the Surface-to-Volume Ratio. This value is the surface area of the pore walls per unit volume ( ), and can be thought of as a measure of catalyst loading. With this value, FLUENT can calculate the total surface area on which the reaction takes place in each cell bymultiplying by the volume of the cell. See Section 14.1.4 for detailsabout defining reaction mechanisms. See Section 14.2for details about wall surface reactions.Including the Relative Velocity Resistance FormulationPrior to FLUENT 6.3, cases with moving reference frames used the absolute velocities in the source calculations for inertial and viscous resistance. This approach has been enhanced so that relative velocities are used for the porous source calculations (Section 7.19.2). Using the Relative Velocity Resistance Formulation option (turned on by default) allows you to better predict the source terms for cases involving moving meshes or moving reference frames (MRF). This option works well in cases withnon-moving and moving porous media. Note that FLUENT will use the appropriate velocities (relative or absolute), depending on your case setup. Defining the Viscous and Inertial Resistance CoefficientsThe viscous and inertial resistance coefficients are both defined in the same manner. The basic approach for defining the coefficients using a Cartesian coordinate system is to define one direction vector in 2D or two direction vectors in 3D, and then specify the viscous and/or inertial resistance coefficients in each direction. In 2D, the second direction, which is not explicitly defined, is normal to the plane defined by the specified direction vector and the direction vector. In 3D, the third direction is normal to the plane defined by the two specified direction vectors. For a 3D problem, the second direction must be normal to the first. If you fail to specify two normal directions, the solver will ensure that they are normal by ignoring any component of the second direction that is in the first direction. You should therefore be certain that the first direction is correctly specified. You can also define the viscous and/or inertial resistance coefficients in each direction using a user-defined function (UDF). The user-defined options become available in the corresponding drop-down list when the UDF has been created and loaded into FLUENT. Note that the coefficients defined in the UDF must utilize the DEFINE_PROFILE macro. For moreinformation on creating and using user-defined function, see the separate UDF Manual.If you are modeling axisymmetric swirling flows, you can specify an additional direction component for the viscous and/or inertial resistance coefficients. This direction component is always tangential to the other two specified directions. This option is available for both density-based and pressure-based solvers.In 3D, it is also possible to define the coefficients using a conical (or cylindrical) coordinate system, as described below.Note that the viscous and inertial resistance coefficients aregenerally based on the superficial velocity of the fluid in the porous media.The procedure for defining resistance coefficients is as follows:1. Define the direction vectors.To use a Cartesian coordinate system, simply specify the Direction-1 Vector and, for 3D, the Direction-2 Vector. The unspecifieddirection will be determined as described above. These directionvectors correspond to the principle axes of the porous media.For some problems in which the principal axes of the porous mediumare not aligned with the coordinate axes of the domain, you may notknow a priori the direction vectors of the porous medium. In suchcases, the plane tool in 3D (or the line tool in 2D) can help you todetermine these direction vectors.(a) "Snap'' the plane tool (or the line tool) onto the boundary of theporous region. (Follow the instructions inSection 27.6.1 or 27.5.1 for initializing the tool to a position on anexisting surface.)(b) Rotate the axes of the tool appropriately until they are alignedwith the porous medium.(c) Once the axes are aligned, click on the Update From PlaneTool or Update From Line Tool button inthe Fluid panel. FLUENT will automatically set the Direction-1Vector to the direction of the red arrow of the tool, and (in 3D)the Direction-2 Vector to the direction of the green arrow.To use a conical coordinate system (e.g., for an annular, conical filter element), follow the steps below. This option is available only in 3D cases.(a) Turn on the Conical option.(b) Specify the Cone Axis Vector and Point on Cone Axis. Thecone axis is specified as being in the direction of the Cone AxisVector (unit vector), and passing through the Point on Cone Axis.The cone axis may or may not pass through the origin of thecoordinate system.(c) Set the Cone Half Angle (the angle between the cone's axis andits surface, shown in Figure 7.19.2). To use a cylindrical coordinate system, set the Cone Half Angle to 0.Figure 7.19.2: Cone Half AngleFor some problems in which the axis of the conical filter element is not aligned with the coordinate axes of the domain, you may notknow a priori the direction vector of the cone axis and coordinates ofa point on the cone axis. In such cases, the plane tool can help you todetermine the cone axis vector and point coordinates. One method is as follows:(a) Select a boundary zone of the conical filter element that isnormal to the cone axis vector in the drop-down list next to the Snap to Zone button.(b) Click on the Snap to Zone button. FLUENT will automatically"snap'' the plane tool onto the boundary. It will also set the Cone Axis Vector and the Point on Cone Axis. (Note that you will still have to set the Cone Half Angle yourself.)An alternate method is as follows:(a) "Snap'' the plane tool onto the boundary of the porous region.(Follow the instructions in Section 27.6.1 for initializing the tool to a position on an existing surface.)(b) Rotate and translate the axes of the tool appropriately until thered arrow of the tool is pointing in the direction of the cone axisvector and the origin of the tool is on the cone axis.(c) Once the axes and origin of the tool are aligned, click onthe Update From Plane Tool button inthe Fluid panel. FLUENT will automatically set the Cone AxisVector and the Point on Cone Axis. (Note that you will still have toset the Cone Half Angle yourself.)2. Under Viscous Resistance, specify the viscous resistancecoefficient in each direction.Under Inertial Resistance, specify the inertial resistance coefficient in each direction. (You will need to scroll down with the scroll bar to view these inputs.)For porous media cases containing highly anisotropic inertial resistances, enable Alternative Formulation under Inertial Resistance.The Alternative Formulation option provides better stability to the calculation when your porous medium is anisotropic. The pressure loss through the medium depends on the magnitude of the velocity vector ofthe i th component in the medium. Using the formulation ofEquation 7.19-6 yields the expression below:(7.19-10) Whether or not you use the Alternative Formulation option depends on how well you can fit your experimentally determined pressure drop data to the FLUENT model. For example, if the flow through the medium is aligned with the grid in your FLUENT model, then it will not make a difference whether or not you use the formulation.For more infomation about simulations involving highly anisotropic porous media, see Section 7.19.8.Note that the alternative formulation is compatible only with the pressure-based solver.If you are using the Conical specification method, Direction-1 is the cone axis direction, Direction-2 is the normal to the cone surface (radial ( )direction for a cylinder), and Direction-3 is the circumferential ( ) direction.In 3D there are three possible categories of coefficients, and in 2D there are two:∙In the isotropic case, the resistance coefficients in all directions are the same (e.g., a sponge). For an isotropic case, you must explicitlyset the resistance coefficients in each direction to the same value.∙When (in 3D) the coefficients in two directions are the same and those in the third direction are different or (in 2D) the coefficients inthe two directions are different, you must be careful to specify thecoefficients properly for each direction. For example, if you had aporous region consisting of cylindrical straws with small holes inthem positioned parallel to the flow direction, the flow would passeasily through the straws, but the flow in the other two directions(through the small holes) would be very little. If you had a plane offlat plates perpendicular to the flow direction, the flow would notpass through them at all; it would instead move in the other twodirections.∙In 3D the third possible case is one in which all three coefficients are different. For example, if the porous region consisted of a plane ofirregularly-spaced objects (e.g., pins), the movement of flow between the blockages would be different in each direction. You wouldtherefore need to specify different coefficients in each direction. Methods for deriving viscous and inertial loss coefficients are described in the sections that follow.Deriving Porous Media Inputs Based on Superficial Velocity, Using a Known Pressure LossWhen you use the porous media model, you must keep in mind that the porous cells in FLUENT are 100% open, and that the values that you specify for and/or must be based on this assumption. Suppose, however, that you know how the pressure drop varies with the velocity through the actual device, which is only partially open to flow. The following exercise is designed to show you how to compute a valuefor which is appropriate for the FLUENT model.Consider a perforated plate which has 25% area open to flow. The pressure drop through the plate is known to be 0.5 times the dynamic head in the plate. The loss factor, , defined as(7.19-11)is therefore 0.5, based on the actual fluid velocity in the plate, i.e., the velocity through the 25% open area. To compute an appropriate valuefor , note that in the FLUENT model:1. The velocity through the perforated plate assumes that the plate is 100% open.2. The loss coefficient must be converted into dynamic head loss per unit length of the porous region.Noting item 1, the first step is to compute an adjusted loss factor, , which would be based on the velocity of a 100% open area:(7.19-12) or, noting that for the same flow rate, ,(7.19-13)The adjusted loss factor has a value of 8. Noting item 2, you must now convert this into a loss coefficient per unit thickness of the perforated plate. Assume that the plate has a thickness of 1.0 mm (10 m). The inertial loss factor would then be(7.19-14)Note that, for anisotropic media, this information must be computed for each of the 2 (or 3) coordinate directions.Using the Ergun Equation to Derive Porous Media Inputs for a Packed BedAs a second example, consider the modeling of a packed bed. In turbulent flows, packed beds are modeled using both a permeability and an inertial loss coefficient. One technique for deriving the appropriate constants involves the use of the Ergun equation [ 98], a semi-empirical correlation applicable over a wide range of Reynolds numbers and for many types of packing:(7.19-15)When modeling laminar flow through a packed bed, the second term in the above equation may be dropped, resulting in the Blake-Kozenyequation [ 98]:(7.19-16) In these equations, is the viscosity, is the mean particlediameter, is the bed depth, and is the void fraction, defined as the volume of voids divided by the volume of the packed bed region. Comparing Equations 7.19-4 and 7.19-6 with 7.19-15, the permeability and inertial loss coefficient in each component direction may be identified as(7.19-17) and(7.19-18) Using an Empirical Equation to Derive Porous Media Inputs for Turbulent Flow Through a Perforated PlateAs a third example we will take the equation of Van Winkle et al. [ 279, 339] and show how porous media inputs can be calculated for pressure loss through a perforated plate with square-edged holes.The expression, which is claimed by the authors to apply for turbulent flow through square-edged holes on an equilateral triangular spacing, is(7.19-19) where= mass flow rate through the plate= the free area or total area of the holes= the area of the plate (solid and holes)= a coefficient that has been tabulated for various Reynolds-numberrangesand for various= the ratio of hole diameter to plate thicknessfor and for the coefficient takes a value of approximately 0.98, where the Reynolds number is based on hole diameter and velocity in the holes.Rearranging Equation 7.19-19, making use of the relationship(7.19-20)and dividing by the plate thickness, , we obtain(7.19-21)where is the superficial velocity (not the velocity in the holes). Comparing with Equation 7.19-6 it is seen that, for the direction normal to the plate, the constant can be calculated from(7.19-22)Using Tabulated Data to Derive Porous Media Inputs for Laminar Flow Through a Fibrous MatConsider the problem of laminar flow through a mat or filter pad which is made up of randomly-oriented fibers of glass wool. As an alternative to the Blake-Kozeny equation (Equation 7.19-16) we might choose to employ tabulated experimental data. Such data is available for many types offiber [ 158].fraction of dimensionless permeability of glass woolwhere and is the fiber diameter. , for use inEquation 7.19-4, is easily computed for a given fiber diameter and volume fraction.Deriving the Porous Coefficients Based on Experimental Pressure and Velocity DataExperimental data that is available in the form of pressure drop against velocity through the porous component, can be extrapolated to determine the coefficients for the porous media. To effect a pressure drop across a porous medium of thickness, , the coefficients of the porous media are determined in the manner described below.If the experimental data is:then an curve can be plotted to create a trendline through these points yielding the following equationwhere is the pressure drop and is the velocity.Note that a simplified version of the momentum equation, relating the pressure drop to the source term, can be expressed as(7.19-24)or(7.19-25)Hence, comparing Equation 7.19-23 to Equation 7.19-2, yields the following curve coefficients:(7.19-26)with kg/m , and a porous media thickness, , assumed to be 1m in this example, the inertial resistance factor, .Likewise,with , the viscous inertial resistancefactor,.Note that this same technique can be applied to the porous jump boundary condition. Similar to the case of the porous media, you have to take into account the thickness of the medium . Your experimental data can be plotted in ancurve, yielding an equation that is equivalent to Equation 7.22-1. From there, you can determine the permeability and the pressure jumpcoefficient.Using the Power-Law ModelIf you choose to use the power-law approximation of the porous-media momentum source term (Equation 7.19-3), the only inputs required are the coefficients and . Under Power Law Model in the Fluid panel, enter the values for C0 and C1. Note that the power-law model can be used in conjunction with the Darcy and inertia models. C0 must be in SI units, consistent with the value of C1.Defining PorosityTo define the porosity, scroll down below the resistance inputs in the Fluid panel, and set the Porosity under Fluid Porosity .You can also define the porosity using a user-defined function (UDF). The user-defined option becomes available in the corresponding drop-down list when the UDF has been created and loaded into FLUENT. Note that the porosity defined in the UDF must utilize the DEFINE_PROFILE macro. For more information on creating and using user-defined function, see the separate UDF Manual.The porosity, , is the volume fraction of fluid within the porous region (i.e., the open volume fraction of the medium). The porosity is used in the prediction of heat transfer in the medium, as described in Section 7.19.3, and in the time-derivative term in the scalar transport equations for unsteady flow, as described in Section 7.19.5. It also impacts the calculation of reaction source terms and body forces in the medium. These sources will be proportional to the fluid volume in the medium. If you want to represent the medium as completely open (no effect of the solid medium), you should set the porosity equal to 1.0 (the default). When the porosity is equal to 1.0, the solid portion of the medium will have no impact on heat transfer or thermal/reaction source terms in the medium.Defining the Porous MaterialIf you choose to model heat transfer in the porous medium, you must specify the material contained in the porous medium.To define the material contained in the porous medium, scroll down below the resistance inputs in the Fluid panel, and select the appropriate solid in the Solid Material Name drop-down list under Fluid Porosity. If you want to check or modify the properties of the selected material, you canclick Edit... to open the Material panel; this panel contains just the properties of the selected material, not the full contents of thestandard Materials panel. In the Material panel, you can define thenon-isotropic thermal conductivity of the porous material using auser-defined function (UDF). The user-defined option becomes available in the corresponding drop-down list when the UDF has been created and loaded into FLUENT. Note that the non-isotropic thermal conductivity defined in the UDF must utilize the DEFINE_PROPERTY macro. For more information on creating and using user-defined function, see the separate UDF Manual.Defining SourcesIf you want to include effects of the heat generated by the porous medium in the energy equation, enable the Source Terms option and set anon-zero Energy source. The solver will compute the heat generated by the porous region by multiplying this value by the total volume of the cells comprising the porous zone. You may also define sources of mass, momentum, turbulence, species, or other scalar quantities, as described in Section 7.28.Defining Fixed ValuesIf you want to fix the value of one or more variables in the fluid region of the zone, rather than computing them during the calculation, you can do so by enabling the Fixed Values option. See Section 7.27 for details. Suppressing the Turbulent Viscosity in the Porous RegionAs discussed in Section 7.19.4, turbulence will be computed in the porous region just as in the bulk fluid flow. If you are using one of the turbulence models (with the exception of the Large Eddy Simulation (LES) Model), and you want the turbulence generation to be zero in the porous zone, turn on the Laminar Zone option in the Fluid panel. Refer to Section 7.17.1 for more information about suppressing turbulence generation.Specifying the Rotation Axis and Defining Zone MotionInputs for the rotation axis and zone motion are the same as for a standard fluid zone. See Section 7.17.1 for details.。
Fluent 使用指导

Fluent简介 (1)
目前国际主流的商用CFD软件之一
发展历程
• 1975年 在谢菲尔德大学(UK)开发的tempest (fluent的原形)
• 1983 creature公司开始销售fluent
• 1988 fluent Inc.成立 • 1995 收购最大对手FDI公司 • 1997 收购polyflow公司 • 2000 年归属Wills Stain&Partners财团
• 提供边界上的信息
边界条件类型和所采用的物理模型决定了边界上需要的数据 注意边界上的流体变量应该是已知的或可以合理预估的,不好的边界条 件对计算结果影响很大
流体域和固体域
Fluent的边界条件类型
外部边界 • 通用
• Pressure Inlet • Pressure Outlet
内部边界
• Fan
对湍流可以指定壁面粗糙度壁面可以设置平移或旋转速度热边界五类基本热边界条件对流模拟外部环境的对流定义换热系数辐射模拟外部环境的辐射定义外部发射率和辐射温度混合对流和辐射边界的结合耦合换热对称面必须和x轴正向重合对称边界和轴边界symmetryplanesaxis周期边界用来减少全局网格量流场和几何必须是旋转周期对称或平移周期对称模型是充分发展条件
压力出口
适用于压缩和不可压流动 • 如果流动在出口是超音速的,指定的压 力被忽略 • 在外流或非封闭区域流动,作为自由边 界条件
要求输入
• 表压– 流体流入环境的静压。 • 回流量 – 当有回流发生时,起到进口的 作用 对理想气体(可压缩)流动,可以使用无 反射出口边界条件
壁面边界
粘性流动中,壁面采用无滑移边 界条件 • 可以指定剪切应力. 热边界条件 • 有几种类型的热边界条件。 • 对一维或薄壳导热计算,可以 指定壁面材料和厚度。 对湍流可以指定壁面粗糙度 壁面可以设置平移或旋转速度
FLUENT使用步骤指南(新手参考)

Fluent 使用步骤指南(新手参考)步骤一:网格1.读入网格(*.Msh)File →Read →Case读入网格后,在窗口显示进程2.检查网格Grid →Check'Fluent对网格进行多种检查,并显示结果。
注意最小容积,确保最小容积值为正。
3.显示网格Display →Grid①以默认格式显示网格可以用鼠标右键检查边界区域、数量、名称、类型将在窗口显示,本操作对于同样类型的多个区域情况非常有用,以便快速区别它们。
4.网格显示操作Display →Views(a)在Mirror Planes面板下,axis(b)点击Apply,将显示整个网格(c)点击Auto scale, 自动调整比例,并放在视窗中间(d)点击Camera,调整目标物体位置(e)用鼠标左键拖动指标钟,使目标位置为正(f)点击Apply,并关闭Camera Parameters 和Views窗口步骤二:模型1. 定义瞬时、轴对称模型Define →models→Solver(a)保留默认的,Segregated解法设置,该项设置,在多相计算时使用。
(b)在Space面板下,选择Axisymmetric;(c)在Time面板下,选择Unsteady2. 采用欧拉多相模型Define→Models→Multiphase(a)选择Eulerian作为模型(b)如果两相速度差较大,则需解滑移速度方程(c)如果Body force比粘性力和对流力大得多,则需选择implicit body force 通过考虑压力梯度和体力,加快收敛(d)保留设置不变3. 采用K-ε湍流模型(采用标准壁面函数)Define →Models →Viscous(a) 选择K-ε ( 2 eqn模型)(b) 保留Near wall Treatment面板下的Standard Wall Function设置(c)在K-ε Multiphase Model面板下,采用Dispersed模型,dispersed湍流模型在一相为连续相,而材料密度较大情况下采用,而且Stocks数远小于1,颗粒动能意义不大。
fluent中多孔介质模型的设置

7.19.6 User Inputs for Porous MediaWhen you are modeling a porous region, the only additional inputs for the problem setup are as follows. Optional inputs are indicated as such.1. Define the porous zone.2. Define the porous velocity formulation. (optional)3. Identify the fluid material flowing through the porous medium.4. Enable reactions for the porous zone, if appropriate, and select the reaction mechanism.5. Enable the Relative Velocity Resistance Formulation. By default, this option is already enabled and takes the moving porous media into consideration (as described in Section 7.19.6).6. Set the viscous resistance coefficients ( in Equation7.19-1,or in Equation 7.19-2) and the inertial resistance coefficients ( in Equation 7.19-1, or in Equation 7.19-2), and define the direction vectors for which they apply. Alternatively, specify the coefficients for the power-law model.7. Specify the porosity of the porous medium.8. Select the material contained in the porous medium (required only for models that include heat transfer). Note that the specific heat capacity, , for the selected material in the porous zone can only be entered as a constant value.9. Set the volumetric heat generation rate in the solid portion of the porous medium (or any other sources, such as mass or momentum). (optional) 10. Set any fixed values for solution variables in the fluid region (optional).11. Suppress the turbulent viscosity in the porous region, if appropriate.12. Specify the rotation axis and/or zone motion, if relevant.Methods for determining the resistance coefficients and/or permeability are presented below. If you choose to use the power-law approximation of the porous-media momentum source term, you will enter thecoefficients and in Equation 7.19-3 instead of the resistance coefficients and flow direction.You will set all parameters for the porous medium inthe Fluid panel (Figure 7.19.1), which is opened from the Boundary Conditions panel (as described in Section 7.1.4).Figure 7.19.1: The Fluid Panel for a Porous Zone Defining the Porous ZoneAs mentioned in Section 7.1, a porous zone is modeled as a special type of fluid zone. To indicate that the fluid zone is a porous region, enablethe Porous Zone option in the Fluid panel. The panel will expand to show the porous media inputs (as shown in Figure 7.19.1).Defining the Porous Velocity FormulationThe Solver panel contains a Porous Formulation region where you can instruct FLUENT to use either a superficial or physical velocity in the porous medium simulation. By default, the velocity is set to SuperficialVelocity. For details about using the Physical Velocity formulation, see Section 7.19.7.Defining the Fluid Passing Through the Porous MediumTo define the fluid that passes through the porous medium, select the appropriate fluid in the Material Name drop-down list in the Fluid panel. If you want to check or modify the properties of the selected material, you can click Edit... to open the Material panel; this panel contains just the properties of the selected material, not the full contents of thestandard Materials panel.If you are modeling species transport or multiphase flow,the Material Name list will not appear in the Fluid panel. Forspecies calculations, the mixture material for all fluid/porous zones will be the material you specified in the SpeciesModel panel. For multiphase flows, the materials are specified when you define the phases, as described in Section 23.10.3.Enabling Reactions in a Porous ZoneIf you are modeling species transport with reactions, you can enable reactions in a porous zone by turning on the Reaction option inthe Fluid panel and selecting a mechanism in the ReactionMechanism drop-down list.If your mechanism contains wall surface reactions, you will also need to specify a value for the Surface-to-Volume Ratio. This value is the surface area of the pore walls per unit volume ( ), and can be thought of as a measure of catalyst loading. With this value, FLUENT can calculate the total surface area on which the reaction takes place in each cell bymultiplying by the volume of the cell. See Section 14.1.4 for detailsabout defining reaction mechanisms. See Section 14.2for details about wall surface reactions.Including the Relative Velocity Resistance FormulationPrior to FLUENT 6.3, cases with moving reference frames used the absolute velocities in the source calculations for inertial and viscous resistance. This approach has been enhanced so that relative velocities are used for the porous source calculations (Section 7.19.2). Using the Relative Velocity Resistance Formulation option (turned on by default) allows you to better predict the source terms for cases involving moving meshes or moving reference frames (MRF). This option works well in cases withnon-moving and moving porous media. Note that FLUENT will use the appropriate velocities (relative or absolute), depending on your case setup. Defining the Viscous and Inertial Resistance CoefficientsThe viscous and inertial resistance coefficients are both defined in the same manner. The basic approach for defining the coefficients using a Cartesian coordinate system is to define one direction vector in 2D or two direction vectors in 3D, and then specify the viscous and/or inertial resistance coefficients in each direction. In 2D, the second direction, which is not explicitly defined, is normal to the plane defined by the specified direction vector and the direction vector. In 3D, the third direction is normal to the plane defined by the two specified direction vectors. For a 3D problem, the second direction must be normal to the first. If you fail to specify two normal directions, the solver will ensure that they are normal by ignoring any component of the second direction that is in the first direction. You should therefore be certain that the first direction is correctly specified. You can also define the viscous and/or inertial resistance coefficients in each direction using a user-defined function (UDF). The user-defined options become available in the corresponding drop-down list when the UDF has been created and loaded into FLUENT. Note that the coefficients defined in the UDF must utilize the DEFINE_PROFILE macro. For moreinformation on creating and using user-defined function, see the separate UDF Manual.If you are modeling axisymmetric swirling flows, you can specify an additional direction component for the viscous and/or inertial resistance coefficients. This direction component is always tangential to the other two specified directions. This option is available for both density-based and pressure-based solvers.In 3D, it is also possible to define the coefficients using a conical (or cylindrical) coordinate system, as described below.Note that the viscous and inertial resistance coefficients aregenerally based on the superficial velocity of the fluid in the porous media.The procedure for defining resistance coefficients is as follows:1. Define the direction vectors.To use a Cartesian coordinate system, simply specify the Direction-1 Vector and, for 3D, the Direction-2 Vector. The unspecifieddirection will be determined as described above. These directionvectors correspond to the principle axes of the porous media.For some problems in which the principal axes of the porous mediumare not aligned with the coordinate axes of the domain, you may notknow a priori the direction vectors of the porous medium. In suchcases, the plane tool in 3D (or the line tool in 2D) can help you todetermine these direction vectors.(a) "Snap'' the plane tool (or the line tool) onto the boundary of theporous region. (Follow the instructions inSection 27.6.1 or 27.5.1 for initializing the tool to a position on anexisting surface.)(b) Rotate the axes of the tool appropriately until they are alignedwith the porous medium.(c) Once the axes are aligned, click on the Update From PlaneTool or Update From Line Tool button inthe Fluid panel. FLUENT will automatically set the Direction-1Vector to the direction of the red arrow of the tool, and (in 3D)the Direction-2 Vector to the direction of the green arrow.To use a conical coordinate system (e.g., for an annular, conical filter element), follow the steps below. This option is available only in 3D cases.(a) Turn on the Conical option.(b) Specify the Cone Axis Vector and Point on Cone Axis. Thecone axis is specified as being in the direction of the Cone AxisVector (unit vector), and passing through the Point on Cone Axis.The cone axis may or may not pass through the origin of thecoordinate system.(c) Set the Cone Half Angle (the angle between the cone's axis andits surface, shown in Figure 7.19.2). To use a cylindrical coordinate system, set the Cone Half Angle to 0.Figure 7.19.2: Cone Half AngleFor some problems in which the axis of the conical filter element is not aligned with the coordinate axes of the domain, you may notknow a priori the direction vector of the cone axis and coordinates ofa point on the cone axis. In such cases, the plane tool can help you todetermine the cone axis vector and point coordinates. One method is as follows:(a) Select a boundary zone of the conical filter element that isnormal to the cone axis vector in the drop-down list next to the Snap to Zone button.(b) Click on the Snap to Zone button. FLUENT will automatically"snap'' the plane tool onto the boundary. It will also set the Cone Axis Vector and the Point on Cone Axis. (Note that you will still have to set the Cone Half Angle yourself.)An alternate method is as follows:(a) "Snap'' the plane tool onto the boundary of the porous region.(Follow the instructions in Section 27.6.1 for initializing the tool to a position on an existing surface.)(b) Rotate and translate the axes of the tool appropriately until thered arrow of the tool is pointing in the direction of the cone axisvector and the origin of the tool is on the cone axis.(c) Once the axes and origin of the tool are aligned, click onthe Update From Plane Tool button inthe Fluid panel. FLUENT will automatically set the Cone AxisVector and the Point on Cone Axis. (Note that you will still have toset the Cone Half Angle yourself.)2. Under Viscous Resistance, specify the viscous resistancecoefficient in each direction.Under Inertial Resistance, specify the inertial resistance coefficient in each direction. (You will need to scroll down with the scroll bar to view these inputs.)For porous media cases containing highly anisotropic inertial resistances, enable Alternative Formulation under Inertial Resistance.The Alternative Formulation option provides better stability to the calculation when your porous medium is anisotropic. The pressure loss through the medium depends on the magnitude of the velocity vector ofthe i th component in the medium. Using the formulation ofEquation 7.19-6 yields the expression below:(7.19-10) Whether or not you use the Alternative Formulation option depends on how well you can fit your experimentally determined pressure drop data to the FLUENT model. For example, if the flow through the medium is aligned with the grid in your FLUENT model, then it will not make a difference whether or not you use the formulation.For more infomation about simulations involving highly anisotropic porous media, see Section 7.19.8.Note that the alternative formulation is compatible only with the pressure-based solver.If you are using the Conical specification method, Direction-1 is the cone axis direction, Direction-2 is the normal to the cone surface (radial ( )direction for a cylinder), and Direction-3 is the circumferential ( ) direction.In 3D there are three possible categories of coefficients, and in 2D there are two:∙In the isotropic case, the resistance coefficients in all directions are the same (e.g., a sponge). For an isotropic case, you must explicitlyset the resistance coefficients in each direction to the same value.∙When (in 3D) the coefficients in two directions are the same and those in the third direction are different or (in 2D) the coefficients inthe two directions are different, you must be careful to specify thecoefficients properly for each direction. For example, if you had aporous region consisting of cylindrical straws with small holes inthem positioned parallel to the flow direction, the flow would passeasily through the straws, but the flow in the other two directions(through the small holes) would be very little. If you had a plane offlat plates perpendicular to the flow direction, the flow would notpass through them at all; it would instead move in the other twodirections.∙In 3D the third possible case is one in which all three coefficients are different. For example, if the porous region consisted of a plane ofirregularly-spaced objects (e.g., pins), the movement of flow between the blockages would be different in each direction. You wouldtherefore need to specify different coefficients in each direction. Methods for deriving viscous and inertial loss coefficients are described in the sections that follow.Deriving Porous Media Inputs Based on Superficial Velocity, Using a Known Pressure LossWhen you use the porous media model, you must keep in mind that the porous cells in FLUENT are 100% open, and that the values that you specify for and/or must be based on this assumption. Suppose, however, that you know how the pressure drop varies with the velocity through the actual device, which is only partially open to flow. The following exercise is designed to show you how to compute a valuefor which is appropriate for the FLUENT model.Consider a perforated plate which has 25% area open to flow. The pressure drop through the plate is known to be 0.5 times the dynamic head in the plate. The loss factor, , defined as(7.19-11)is therefore 0.5, based on the actual fluid velocity in the plate, i.e., the velocity through the 25% open area. To compute an appropriate valuefor , note that in the FLUENT model:1. The velocity through the perforated plate assumes that the plate is 100% open.2. The loss coefficient must be converted into dynamic head loss per unit length of the porous region.Noting item 1, the first step is to compute an adjusted loss factor, , which would be based on the velocity of a 100% open area:(7.19-12) or, noting that for the same flow rate, ,(7.19-13)The adjusted loss factor has a value of 8. Noting item 2, you must now convert this into a loss coefficient per unit thickness of the perforated plate. Assume that the plate has a thickness of 1.0 mm (10 m). The inertial loss factor would then be(7.19-14)Note that, for anisotropic media, this information must be computed for each of the 2 (or 3) coordinate directions.Using the Ergun Equation to Derive Porous Media Inputs for a Packed BedAs a second example, consider the modeling of a packed bed. In turbulent flows, packed beds are modeled using both a permeability and an inertial loss coefficient. One technique for deriving the appropriate constants involves the use of the Ergun equation [ 98], a semi-empirical correlation applicable over a wide range of Reynolds numbers and for many types of packing:(7.19-15)When modeling laminar flow through a packed bed, the second term in the above equation may be dropped, resulting in the Blake-Kozenyequation [ 98]:(7.19-16) In these equations, is the viscosity, is the mean particlediameter, is the bed depth, and is the void fraction, defined as the volume of voids divided by the volume of the packed bed region. Comparing Equations 7.19-4 and 7.19-6 with 7.19-15, the permeability and inertial loss coefficient in each component direction may be identified as(7.19-17) and(7.19-18) Using an Empirical Equation to Derive Porous Media Inputs for Turbulent Flow Through a Perforated PlateAs a third example we will take the equation of Van Winkle et al. [ 279, 339] and show how porous media inputs can be calculated for pressure loss through a perforated plate with square-edged holes.The expression, which is claimed by the authors to apply for turbulent flow through square-edged holes on an equilateral triangular spacing, is(7.19-19) where= mass flow rate through the plate= the free area or total area of the holes= the area of the plate (solid and holes)= a coefficient that has been tabulated for various Reynolds-numberrangesand for various= the ratio of hole diameter to plate thicknessfor and for the coefficient takes a value of approximately 0.98, where the Reynolds number is based on hole diameter and velocity in the holes.Rearranging Equation 7.19-19, making use of the relationship(7.19-20)and dividing by the plate thickness, , we obtain(7.19-21)where is the superficial velocity (not the velocity in the holes). Comparing with Equation 7.19-6 it is seen that, for the direction normal to the plate, the constant can be calculated from(7.19-22)Using Tabulated Data to Derive Porous Media Inputs for Laminar Flow Through a Fibrous MatConsider the problem of laminar flow through a mat or filter pad which is made up of randomly-oriented fibers of glass wool. As an alternative to the Blake-Kozeny equation (Equation 7.19-16) we might choose to employ tabulated experimental data. Such data is available for many types offiber [ 158].fraction of dimensionless permeability of glass woolwhere and is the fiber diameter. , for use inEquation 7.19-4, is easily computed for a given fiber diameter and volume fraction.Deriving the Porous Coefficients Based on Experimental Pressure and Velocity DataExperimental data that is available in the form of pressure drop against velocity through the porous component, can be extrapolated to determine the coefficients for the porous media. To effect a pressure drop across a porous medium of thickness, , the coefficients of the porous media are determined in the manner described below.If the experimental data is:then an curve can be plotted to create a trendline through these points yielding the following equationwhere is the pressure drop and is the velocity.Note that a simplified version of the momentum equation, relating the pressure drop to the source term, can be expressed as(7.19-24)or(7.19-25)Hence, comparing Equation 7.19-23 to Equation 7.19-2, yields the following curve coefficients:(7.19-26)with kg/m , and a porous media thickness, , assumed to be 1m in this example, the inertial resistance factor, .Likewise,with , the viscous inertial resistancefactor,.Note that this same technique can be applied to the porous jump boundary condition. Similar to the case of the porous media, you have to take into account the thickness of the medium . Your experimental data can be plotted in ancurve, yielding an equation that is equivalent to Equation 7.22-1. From there, you can determine the permeability and the pressure jumpcoefficient.Using the Power-Law ModelIf you choose to use the power-law approximation of the porous-media momentum source term (Equation 7.19-3), the only inputs required are the coefficients and . Under Power Law Model in the Fluid panel, enter the values for C0 and C1. Note that the power-law model can be used in conjunction with the Darcy and inertia models. C0 must be in SI units, consistent with the value of C1.Defining PorosityTo define the porosity, scroll down below the resistance inputs in the Fluid panel, and set the Porosity under Fluid Porosity .You can also define the porosity using a user-defined function (UDF). The user-defined option becomes available in the corresponding drop-down list when the UDF has been created and loaded into FLUENT. Note that the porosity defined in the UDF must utilize the DEFINE_PROFILE macro. For more information on creating and using user-defined function, see the separate UDF Manual.The porosity, , is the volume fraction of fluid within the porous region (i.e., the open volume fraction of the medium). The porosity is used in the prediction of heat transfer in the medium, as described in Section 7.19.3, and in the time-derivative term in the scalar transport equations for unsteady flow, as described in Section 7.19.5. It also impacts the calculation of reaction source terms and body forces in the medium. These sources will be proportional to the fluid volume in the medium. If you want to represent the medium as completely open (no effect of the solid medium), you should set the porosity equal to 1.0 (the default). When the porosity is equal to 1.0, the solid portion of the medium will have no impact on heat transfer or thermal/reaction source terms in the medium.Defining the Porous MaterialIf you choose to model heat transfer in the porous medium, you must specify the material contained in the porous medium.To define the material contained in the porous medium, scroll down below the resistance inputs in the Fluid panel, and select the appropriate solid in the Solid Material Name drop-down list under Fluid Porosity. If you want to check or modify the properties of the selected material, you canclick Edit... to open the Material panel; this panel contains just the properties of the selected material, not the full contents of thestandard Materials panel. In the Material panel, you can define thenon-isotropic thermal conductivity of the porous material using auser-defined function (UDF). The user-defined option becomes available in the corresponding drop-down list when the UDF has been created and loaded into FLUENT. Note that the non-isotropic thermal conductivity defined in the UDF must utilize the DEFINE_PROPERTY macro. For more information on creating and using user-defined function, see the separate UDF Manual.Defining SourcesIf you want to include effects of the heat generated by the porous medium in the energy equation, enable the Source Terms option and set anon-zero Energy source. The solver will compute the heat generated by the porous region by multiplying this value by the total volume of the cells comprising the porous zone. You may also define sources of mass, momentum, turbulence, species, or other scalar quantities, as described in Section 7.28.Defining Fixed ValuesIf you want to fix the value of one or more variables in the fluid region of the zone, rather than computing them during the calculation, you can do so by enabling the Fixed Values option. See Section 7.27 for details. Suppressing the Turbulent Viscosity in the Porous RegionAs discussed in Section 7.19.4, turbulence will be computed in the porous region just as in the bulk fluid flow. If you are using one of the turbulence models (with the exception of the Large Eddy Simulation (LES) Model), and you want the turbulence generation to be zero in the porous zone, turn on the Laminar Zone option in the Fluid panel. Refer to Section 7.17.1 for more information about suppressing turbulence generation.Specifying the Rotation Axis and Defining Zone MotionInputs for the rotation axis and zone motion are the same as for a standard fluid zone. See Section 7.17.1 for details.。
[VIP专享]史上Fluent最详细操作步骤 一看就懂
![[VIP专享]史上Fluent最详细操作步骤 一看就懂](https://img.taocdn.com/s3/m/25d705bfcfc789eb162dc868.png)
Fluent简单分析教程第1步双击运行Fluent,首先出现如下界面,对于二维模型我们可以选择2d(单精度)或2ddp(双精度)进行模拟,通常选择2d即可。
Mode选择缺省的Full Simulation即可。
点击“Run”。
然后进入如下图示意界面:第2步:与网格相关的操作1.读入网格文件car1.mesh操作如下图所示:打开的“Select File”对话框如图所示:(1)找到网格文件E:\gfiles\car1.mesh;(2)点击OK,完成输入网格文件的操作。
注意:FLUENT读入网格文件的同时,会在信息反馈窗口显示如下信息:其中包括节点数7590等,最后的Done表示读入网格文件成功。
2.网格检查:操作如下图所示:FLUENT在信息反馈窗口显示如下信息:注意:(1)网格检查列出了X,Y的最小和最大值;(2)网格检查还将报告出网格的其他特性,比如单元的最大体积和最小体积、最大面积和最小面积等;(3)网格检查还会报告出有关网格的任何错误,特别是要求确保最小体积不能是负值,否则FLUENT无法进行计算。
3.平滑(和交换)网格这一步是为确保网格质量的操作。
操作:→Smooth/Swap...打开“Smooth/Swap Grid”对话框如图所示:(1)点击Smooth按钮,再点击Swap,重复上述操作,直到FLUENT报告没有需要交换的面为止。
如图所示:(2)点击Close按钮关闭对话框。
注意:这一功能对于三角形单元来说尤为重要。
4.确定长度单位操作如下图所示:打开“Scale Grid”对话框如图所示:(1)在单位转换(Units Conversion)栏中的(Grid Was Created In)网格长度单位右侧下拉列表中选择m;(2)看区域的范围是否正确,如果不正确,可以在Scale Factors 的X和Y中分别输入值10,然后点击“Scale”或“Unscale”即可;(3)点击Scale;(4)点击Close关闭对话框。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、输出grid图形
2、选择surface---plane,打开plane surface面板
3、通过确定三个点来确定平面位置。
单击slect point,出现提示,不点选cancel.在grid 图形的多孔介质区域任意位置右键点选3个点。
4、回到plane surface面板,勾选plane tool,则在grid图形的多孔介质区域出现一个平面。
若出现的平面与我们的预期相差比较大的话,可以单击reset points,可以获得一个特殊位置的平面。
5、打开多孔介质的控制面板,选择porou zone标签,点击update from plane tool按钮,获得方向矢量1,和方向矢量2的原始值,并与左下角的坐标系统比较,确定我们大概的旋转方向。
6、对比grid图形左下角的坐标系统,红线和红色箭头代表的是方向矢量1,绿线和绿色箭头代表的是方向矢量2
应该使红线和X正方向平行,绿线和Y正方向平行。
具体的操作应该是:
一:先单击白线的蓝色箭头,固定了该方向在旋转过程中不变,可以保证在旋转的过程比较有规律,然后右键点选白线的红色箭头旋转红线的红色箭头到X的正轴;
二: 接下来应该是单击白线的红色箭头,固定该方向不变,单击白线的蓝色箭头,旋转绿线的绿色箭头指向Y的正轴。
(所以多孔介质区域我们一般是设置在坐标系统里面,轴线等
与坐标系统无非直角角度关系)。
把平面移动到图形外有利于旋转,比较清楚。
平面
法线方向的移动是用鼠标右键单击平面阴影部分并拖动,横向移动则需按下shift并进行如上操作。
7、旋转到适当的位置后(鼠标右键拖动箭头),再次点击update from plane tool按钮,获得方向矢量1,和方向矢量2。
得到的数值很可能不是整数,这个时候我们可以把他简化为整数。
例如:0.9123可以简化为1,0.01245可以简化为0,以此类推。
