第二章 状态方程的解
2_状态方程求解

4) (t2 t1 ) (t1 t0 ) (t2 t0 )
e At e Bt e( A B )t 5)当且仅当AB=BA时
状态转移矩阵的基本性质
1) (t ) A (t ) (t ) A
2) (0) I
3)
(t )1 1 (t ) (t )
5 线性系统的脉冲响应矩阵
6 线性连续系统方程的离散化
7 线性离散系统的运动分析 8 用MATLAB求解系统方程
2.1
线性定常系统齐次状态方程的解
x (t ) Ax (t )
(1)
线性定常系统齐次状态方程为 这时系统的输入为零 先考察标量齐次微分方程的幂级数解法
x ax
假设其解为一幂级数
如果 [ sI A]为非奇异
[ sI A] x ( s) x (0)
1
x(s) [sI A]1 x(0) [sI A]1 x(0)
(10)
x (t ) L
1
{[sI A]1 x(0)} L
1
由微分方程解的唯一性
(t ) e At L
[sI A]1
而 b0 x(0) (4)
则解为 x(t ) (1 at 因为
1 2 2 1 a t a k t k ) x(0) e at x(0) 2! k!
1 2 2 1 a t akt k 2! k!
e at 1 at
模仿标量齐次微分方程的解法,假设线性定常系统齐次状态方程 (1)的解为 (5) x b0 b1t b2t 2 b3t 3 bk t k 将(5)式代入(1)式
e
Jt
现代控制理论第二章

= α n −1 (t ) An −1 + α n − 2 (t ) An − 2 + ⋯ + α1 (t ) A + α 0 (t ) I
【例2-5】见板书
(3)α i (t )的计算公式 A的特征值互异时 α 0 (t ) 1 λ1 α1 (t ) 1 λ2 ⋮ = ⋮ ⋮ α (t ) 1 λ n −1 n
λ λ λ
பைடு நூலகம்
2 1 2 2
⋮
2 n
⋯ λ e λ1t λ2 t ⋯ λ e ⋮ ⋮ λn t n −1 ⋯ λn e
At
2.变换A为约旦标准型 (1)A特征根互异 Λ = T −1 AT 有
例2-2 ,同例2-1
e At = Te ΛtT −1
(2)A特征值有重根
J = T AT e At = Te JtT −1
0 1 0 [例2 - 3]已知A = 0 0 1 , 求e At 2 - 5 4
若
σ ω A= −ω σ
则
cos ωt sin ωt σt e = Φ(t ) = e − sin ωt cos ωt
At
2.2.4 计算
1.根据 e At 或 Φ (t ) 的定义直接计算
1 2 2 1 33 1 n n e = I + At + A t + A t ⋯ A t + ⋯ 2! 3! k! 1 0 [例2 - 1]已知A = , 求e At − 2 − 3
现代控制理论基础第二章习题答案

第二章 状态空间表达式的解3-2-1 试求下列矩阵A 对应的状态转移矩阵φ(t )。
(1) ⎥⎦⎤⎢⎣⎡-=2010A (2) ⎥⎦⎤⎢⎣⎡-=0410A (3) ⎥⎦⎤⎢⎣⎡--=2110A (4) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=452100010A (5)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0000100001000010A (6)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=λλλλ000100010000A 【解】:(1) (2) (3) (4)特征值为:2,1321===λλλ。
由习题3-1-7(3)得将A 阵化成约当标准型的变换阵P 为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=421211101P ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=-1211321201P线性变换后的系统矩阵为:(5)为结构四重根的约旦标准型。
(6)虽然特征值相同,但对应着两个约当块。
或}0100010000{])[()(1111----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=-=Φλλλλs s s s L A sI L t 3-2-2 已知系统的状态方程和初始条件 (1)用laplace 法求状态转移矩阵; (2)用化标准型法求状态转移矩阵; (3)用化有限项法求状态转移矩阵; (4)求齐次状态方程的解。
【解】:(1) (2)特征方程为: 特征值为:2,1321===λλλ。
由于112==n n ,所以1λ对应的广义特征向量的阶数为1。
求满足0)(11=-P A I λ的解1P ,得:0110000000312111=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--P P P ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0011P 再根据0)(22=-P A I λ,且保证1P 、2P 线性无关,解得:对于当23=λ的特征向量,由0)(33=-P A I λ容易求得: 所以变换阵为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==110010001321P P P P ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-1100100011P 线性变换后的系统矩阵为:(3)特征值为:2,1321===λλλ。
第二章流体的P-V-T关系与状态方程

2.2.3 立方型状态方程
2.2.3.1 Van der Waals (vdW)范德华方程
RT a pVbV2
体积修正项, b为有效分子体 积,斥力参数
压力修正项, a为引力参数
vdW方程的优点:
1)1873年范德华在其著名的论文“关于气态和液态的连 续性”中提出,是第一个有实用意义的状态方程。1910年 曾获诺贝尔奖。
方程两边乘以 (V b ) P
得:
RT a(Vb)
VbPP1 T/2VVb
V k 1R P TbPa 1T /2 V V k k V b kb
初值取
1.875107
理想气体EOS只适合压力非常低的气体, 不适合真实气体。
2.2.2 气体的非理想性
真实气体分子有大小、分子间有相互作用力是造成气体非理 想性的原因。 真实气体对理想气体的偏离程度可以用压缩因子Z来表达:
Z PV V RT Vig
分子间吸引力促使Z<1; 分子间排斥力使Z>1; 吸引力和排斥力的平衡暗指Z=1。
方程在P →0 时,应变为:PV = RT
2. 低压下的气体(特别是难液化的N2,H2,CO,CH4,…), 在工程设计中,在几十个大气压(几个MPa)下,仍可按 理想气体状态方程计算P、V、T: 而对较易液化的气体,如NH3,CO2,C2H4(乙炔)等,在 较低压力下,也不能用理想气体状态方程计算。
对方程的引力项进行修正,以使计算的V减小, 提高计算的准确性,是真正实用的EOS。
R-K 方程中的常数a,b 的求取
•用同于vdW方程的方法得到常数a,b值, •即临界等温线在临界点的条件得到:
a 0 .42748
R
2T
2.5 c
第2章 控制系统状态空间表达式的解

其必满足方程(2-1),将上式代入方程(2-1)可得 比较可得:
b1 2b2 t 3b3t 2 A( b0 b1t b2 t 2 )
1 1 2 1 1 3 1 k b1 Ab0,b2 Ab1 A b0,b3 Ab2 A b0, ,bk A b0, 2 2 3 3! k!
1 k k 1 t 1 k k k! e1t 1 t k 0 k! 1 T 1 1 T T T T ( )T k 0 1 k k ent 1 k k k! nt nt k 0 k!
1 2 2 1 3 3 At x( t ) ( I At A t A t )x0 e x0 2! 3!
线性定常系统零输入响应的几点说明: l如果t取某个固定值,零输入响应就是状态空间中由初始状态 x0 经线性 变换阵 e At 所导出的一个变换点。系统的自由运动就是由初始状态 x0 出 发,并由各个时刻的变换点 x0 所组成的一条轨线。
§2-1 线性定常齐次状态方程的解(自由解)
而
e J it
1 k 1 J1 t k 1 k 0 k! k 0 k! i
i 1
tk
k
1 0 it e 0 0
1 2 1 t t t i 1 2! ( i 1)! 1 1 t t i 2 ( i 2)! 0 0 t 0 0 1
ቤተ መጻሕፍቲ ባይዱ
1 1 a 0 ( t ) a ( t ) 1 1 2 2 n 1 a n1 ( t ) 1 n n n
现代控制理论(第二章)讲解

sI
A 1
s 2
s3
1 1 s 3
(s
1)(s 2
2)
(s 1)(s 2)
1
(s
1)(s s
2)
(s 1)(s 2)
s3
e At
L1
(s
1)( s 2
2)
(s 1)(s 2)
EAST CHINA INSTITUTE OF TECHNOLOgy
第二章 控制系统状态空间表达式的解
2.1 线性定常齐次状态方程的解(自由解) 2.2 矩阵指数函数——状态转移矩阵 2.3 线性定常系统非齐次方程的解 2.4 * 线性时变系统的解 2.5 * 离散时间系统状态方程的解 2.6* 连续时间状态空间表达式的离散化
(s
1)( s 2
2)
(s 1)(s 2)
1
(s
1)( s s
2)
(s 1)(s 2)
eAt L1
sI A 1
2et e2t 2et 2e2t
et e2t
et
2e2t
et
2e2t
例2-6,利用凯莱-哈密顿定理— -----------------自学! 例2-3与例2-7也请注意自学!
EAST CHINA INSTITUTE OF TECHNOLOgy
2.3 线性定常系统非齐次方程的解
现在讨论线性定常系统在控制作用 方程为非齐次矩阵微分方程:
第二章 状态方程的解

例1:设系统的状态方程为 :
ɺ x1 0 1 x1 = ɺ x2 0 0 x2
试求状态转移矩阵. 试求状态转移矩阵
解:求状态转移矩阵为
1 22 1 k k Φ(t ) = e = I + At + A t + ⋯ + A t + ⋯ 2! k!
e
At
矩阵,称矩阵指数。 为n×n矩阵,称矩阵指数。
于是, 于是,齐次状态方程的解为
x(t ) = e x(0)
At
若初始时刻 t0 ≠0 ,对应的初始状态为 x(t0 ) ,则 齐次状态方程的解为
x(t ) = e
A ( t −t0 )
x(t0 )
Φ (t ) = e
At
状态转移矩阵具有以下性质: 状态转移矩阵具有以下性质:
λk +1 , λk + 2 ,⋯ , λn 互异,则 A 的 (n − k) 个互异特征值均满足系统方程,得到 (n − k) 个代数方程。
eλit = α0 (t ) + α1 (t )λi + ⋯ + αn−1 (t )λin−1 , i = k + 1, k + 2,⋯, n
对于 A 的 k 重特征根,则有下列 k 个代数方程。 将 λ1 代入系统方程,得
Φ(t ) = e At = I + At + 1 22 1 A t + ⋯ + Ak t k + ⋯ 2! k!
n −1
= α0 (t ) I + α1 (t ) A + ⋯ + αn−1 (t ) A
= ∑αk (t ) Ak
k =0
系统的状态空间模型
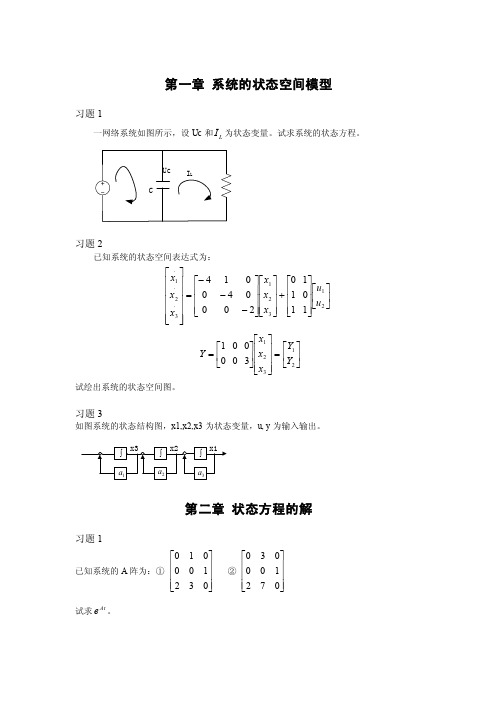
第一章 系统的状态空间模型习题1一网络系统如图所示,设Uc 和L I 为状态变量。
试求系统的状态方程。
习题2已知系统的状态空间表达式为:⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡21321.3.2.1101110200040014u u x x x x x x⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=21321300001Y Y x x x Y 试绘出系统的状态空间图。
习题3如图系统的状态结构图,x1,x2,x3为状态变量,u, y 为输入输出。
第二章 状态方程的解习题1已知系统的A 阵为:① ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡032100010 ②⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡072100030 试求At e 。
习题2F= ⎥⎦⎤⎢⎣⎡--5610 G=⎥⎦⎤⎢⎣⎡11 试求系统当u (k )=3的解。
第三章 能控性和能观性习题1能控且能观的两个系统1S ,2S : 1S :11111.u b x A x +=, 111x c y = 其中,⎥⎦⎤⎢⎣⎡--=43101A ,⎥⎦⎤⎢⎣⎡=101b ,[]121=c ,2S :22222.u b x A x +=,222x c y = 12-=A ,12=b ,12=c① 试求对于⎥⎦⎤⎢⎣⎡=21x x x 的状态方程。
② 考察图中系统得能控性及能观性。
③ 求关于1S ,2S 这两个子系统得传递函数,并验证②。
习题2直流电动机系统如下:RL① 以w 为输出时的状态能控性及输出能观性;② 以转角θ为输出时系统的能观性。
第四章 动态系统的确定性分析习题1⎪⎩⎪⎨⎧--==2.31.22.1x x x x x 试确定e x 的稳定性。
习题2⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡21.2.1211x x K x x试用李雅普诺夫理论求系统稳定时K 的取值范围 第五章 极点配置与观测器设计习题1试为下面系统设计一个全阶观测器,使闭环极点配置在-4和-5上。
第二章 流体的压力、体积、温度关系:状态方程讲解

Virial方程不同形式的关系
PV B C Z 1 2 RT V V 1 B ' P C ' P 2
二种形式的Virial方程是等价的,其系数之间也有相 互关系。
C '
CB ( RT )
2
2
B B' RT
如何证明?
——试试看
33
实际中常用Virial截断式
只能计算气体,不能同时用于汽、液两相 Virial方程的价值已超出PVT的应用,能描述气体的粘度、声速和热容
例2-1 P14
34
2.2.3 立方型方程式 2.2.3.1 范德华方程
理想气体 PV=RT ∴P=RT/V
van der Waals(vdW) EOS ①
(2)分子间力的修正项 a为引力参数。
Peng-Robinson方程
多参数 高次型
Virial(维里)方程 BWR方程、马丁——侯方程等等
30
Virial方程的形式
2.2.2 Virial (维里)方程
PV B C Z 1 2 RT V V
2
1 B' P C ' P
P 0,V
dG SdT VdP dA SdT PdV
S V - P T T P
S P V T T V
Maxwell关系式特点是将难测的量用易测的量代 S V P S 替。如 P T 用 T P 代; 用 V T 代 T V ; 建立了S=S(T,P)。
5
2.1 纯物质的PVT行为
现代控制理论--3控制系统的状态方程求解

7
小结:
1.齐次状态方程的解表示了系统在初始条件作用 下的自由运动,又称为零输入解;
2.系统状态的变化实质上是从初始状态开始的状
态转移,而转移规律取决于 eAt ,eA(t-t0) 故称其
为状态转移矩阵.一般用
x
(t) eAt (t t0) eA(tt0)
来表示。 x 0
2 ! 3 !
AA2t1A3t2L 2!
A(I At 1 A2t2 L ) 2!
AeAt eAt A
13
所以当 Φ(t)=eAt时, &(t)A(t) 又因为 Φ(t)=eAt (t=0时) eA0 =I+A0+...=I 所以 Φ(0)=I 故 eAt 是状态转移矩阵Φ(t)
(2)状态转移矩阵Φ(t)是A阵同阶的方阵,其元 素均为时间函数.
sX(s)-x0=AX(s)+BU(s)
即
X(s)=(sI-A)-1[x0+BU(s)]
其中X(s)和U(s)分别为x(t)和u(t)的拉氏变换。
对上式两边取拉氏反变换,并利用卷积分公式,则有
x ( t ) L 1 ( s A ) I 1 x 0 L 1 ( s A ) I 1 B ( s )U
1 0 3x1u
试求:x(0)=0,u(t)=1(t) 时的状态解。
解:1.求 eAt : 由前例得:
eAt
2et 2et
e2t 2e2t
et e2t et 2e2t
25
2. 求x(t)
x(t)eA tx00 teA (t )B u ()d
t2 e (t )e 2 (t ) e (t ) e 2 (t ) 0
由于状态空间表达式由两部分组成,即 x& Ax Bu y Cx Du
现代控制理论总结

现代控制理论总结第一章:控制系统的状态空间表达式1、状态变量,状态空间与状态轨迹的概念:在描述系统运动的所有变量中,必定可以找到数目最少的一组变量,他们足以描述系统的全部运动,这组变量就称为系统的状态变量。
以状态变量X1,,X2,X3,……X n为坐标轴所构成的n维欧式空间(实数域上的向量空间)称为状态空间。
随着时间的推移,x(t)在状态空间中描绘出一条轨迹,称为状态轨迹。
2、状态空间表达式:状态方程和输出方程合起来构成对一个系统完整的动态描述,称为系统的状态空间表达式。
3、实现问题:由描述系统输入输出关系的运动方程或传递函数建立系统的状态空间表达式,这样的问题称为实现问题单入单出系统传函:W(s)=,实现存在的条件是系统必须满足m<=n,否则是物理不可实现系统最小实现是在所有的实现形式中,其维数最低的实现。
即无零,极点对消的传函的实现。
三种常用最小实现:能控标准型实现,能观标准型实现,并联型实现(约旦型)4、能控标准型实现,能观标准型实现,并联型实现(约旦型)传函无零点系统矩阵A的主对角线上方元素为1,最后一行元素是传函特征多项式系数的负值,其余元素为0,A为友矩阵。
控制矩阵b除最后一个元素是1,其他为0,矩阵A,b具有上述特点的状态空间表达式称为能控标准型。
将b与c矩阵元素互换,另输出矩阵c除第一个元素为1外其他为0,矩阵A,c具有上述特点的状态空间表达式称为能观标准型。
传函有零点见书p17页……..5、建立空间状态表达式的方法:①由结构图建立②有系统分析基里建立③由系统外部描述建立(传函)6、子系统在各种连接时的传函矩阵:设子系统1为子系统2为1)并联:另u1=u2=u,y=y1+y2的系统的状态空间表达式所以系统的传递函数矩阵为:2)串联:由u1=u,u2=y1,y=y2得系统的状态空间表达式为:W(S)=W2(S)W1(S)注意不能写反,应为矩阵乘法不满足交换律3)反馈:系统状态空间表达式:第二章:状态空间表达式的解:1、状态方程解的结构特征:线性系统的一个基本属性是满足叠加原理,把系统同时在初始状态和输入u作用下的状态运动x(t)分解为由初始状态和输入u分别单独作用所产生的运动和的叠加。
2.线性系统的运动分析(第四讲)

第二章:线性系统的运动分析(第四讲)内容介绍:状态方程的解、离散系统的状态方程的解、离散化方法状态方程及其解一般P 个输入,m 个输出的线性定常系统x=Ax+Bu y=Cx (D=0时,称为严格的定常系统) 其中An×n 、Bn×p 、Cm×n 阵, 阵中各元素均为常数。
对此一般系统的分析,本质上为对状态空间表达式的分析。
如果已知x(t)、y(t),则系统运动一目了然。
问题归结为:求解方程 x=Ax+Bu 。
事实上,求解 x=Ax+Bu 完全可利用现成程序。
(但作为专业课了解并掌握状态方程解的求法十分重要,一并介绍常用术语。
)一、齐次方程的解 (输入u=0时)x=Ax 当初值为 x(t)|t=0 = x 0 其解为 x(t)=0x e At ⋅ At e ---A 为n×n 阵,为特定的矩阵函数 事实上,可设其解为 +++++=k k t b t b t b b )t (x 2210则 ++++='-1212k k t kb t b b )t (x 代入方程有:)t b t b t b b (A t kb t b b k k k k +++++=++++-22101212比较有:01Ab b =02122b A Ab b == 02!212b Ab =0323213b A Ab b == 033!31b Ab =011b A )!k (kb k k -=0)!(1b Ak bkk=且t 0=0时x(0) =b 0)0(e )( !1!21e )0(]!1!21[ )0(!1)0(!21)0(x(0) !1!21 x(t)At 22At 222220200x t x t A k t A At I x t A k t A At I t x A k t x A t Ax t b A k t b A t Ab b k k k k k k k k k =+++++=+++++=+++++=+++++=则且(因为 输入u=0 为零输入响应) 引入记号 )(Ate t =Φ 则 )0()()(x t t x ⋅Φ=视 )(Atet =Φ为将x(0)转移到x(t)的变换称其为状态转移阵。
2.状态方程的解

4
3
3
100
(sI
A) 1
1 s3
0 1 0 s2
001
010
0 0 1s 000
001 000 000
11 1 s s2 s3 01 1
s s2 00 1
s
11 1
次(u(t) 0 )状态方程的解
x(t) e At x0
At k 0 kk ! k x0
定义矩阵指数: e At
Akt k k 0 k!
I At 1 A2t 2 2
阵。
1
A t ,它仍是一个矩
kk
k!
若初始时间为t 0,则状态方程的解为
x(t ) e x A(t t0 ) 0
Ak (t t0 )k x0
幂零矩阵:存在某一正整数 k ,使得 A 0 称为 k 次“幂零矩阵”。 A 为幂零矩 阵的“充要条件”是 A 的所有特征值为k零: AX A , i 0 i 1,2, , n
特例: A 为数字矩阵,即 A
P31 例 2-1: A
010 0 0 1 , A2 000
001 0 0 0 , A3 000
(2) e0 I ; (3) e A]t 称e A为频e域A(t求)法;或(叫4)Lapl(aecAet )变1 换法e A;t
(5) 若矩阵 A、B 满足交换律 AB BA,则有e At e Bt ( A B)t (;A 、 B 可交换的 e
充要条件是 AB 为反称矩阵, A A 称为对称矩阵, A A 称为反称矩阵)
(9) 传递性:对任意满足t t t ,有e A(t2 t ) e A(t1 t )
1
0
2
1
0
e A(t2 t0 ) 。这表明状态
(哈工大)2.线性定常系统齐次状态方程的解 gai

对于1 -1 ,有 AP1 -P1 1 0 P11 0 P11 0 P P 0 1 21 21 6 11 6 P31 P31 P21 P11 P31 P21 - 6P 11P 6P P 21 31 31 11 解得
L (sI - A)
1
-1
te t t (1 t )e
1 s2 t 2 2 ( 1 t ) e (s 1) 1 (s 1) L t 1 s te 2 2 (s 1) (s 1) 1 -1 x(t) L (sI - A) x(0)
3.两种方法的关系
I A A2 Ak (sI - A)( 2 3 k 1 ) I s s s s 2 k I A A A -1 (sI - A) 2 3 k 1 s s s s 1 2 2 1 k k 1 -1 L (sI - A) I At A t A t 2! k! e At L1 (sI - A)-1
s - 1 sI A 1 s 2
sI A
Page 11
-1
s2 adj( sI A) (s 1)2 det(sI A) - 1 2 (s 1)
1 2 (s 1) s 2 (s 1)
t x ( t ) 1 (1 t )e x (t ) t 2 te
Page 12
x1 (0) te t (1 t )e x 2 (0)
t
MATLAB
>>a=[0 1;-1 -2] >> s=sym(‘s’) >>sa=inv(s*eye(2)-a) >>ilaplace(sa)
现代控制理论课后习题及答案
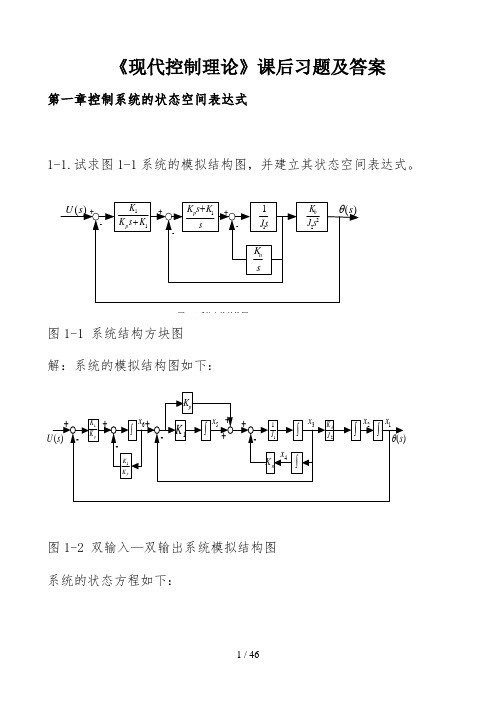
《现代控制理论》课后习题及答案第一章控制系统的状态空间表达式1-1.试求图1-1系统的模拟结构图,并建立其状态空间表达式。
图1-27系统方块结构图图1-1 系统结构方块图解:系统的模拟结构图如下:图1-30双输入--双输出系统模拟结构图图1-2 双输入—双输出系统模拟结构图系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••6543211654321111111126543210000010000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2.有电路如图1-3所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
U图1-28 电路图图1-3 电路图解:由图,令32211,,x u x i x i c===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
《状态方程的解》课件

解的误差分析
误差来源
主要来源于初始值选取、迭代过程和数值方法的近似误差。
误差传播
误差在迭代过程中会不断累积和放大,影响最终求解精度。
误差控制
通过收敛性分析和敏感性分析,控制误差在可接受范围内。
THANKS
感谢您的观看
03
状态方程的解的性 质
解的存在性
01
存在性定理
对于给定的状态方程,存在至少 一个解。
证明方法
02
03
应用场景
使用反证法,假设不存在解,然 后推导出矛盾,从而证明解的存 在性。
在控制工程、物理、化学等领域 ,经常需要求解状态方程,因此 解的存在性非常重要。
解的唯一性
1 2
唯一性定理
对于给定的初始条件和状态方程,解是唯一的。
《状态方程的解》 ppt课件
目录
CONTENTS
• 状态方程的基本概念 • 状态方程的解法 • 状态方程的解的性质 • 状态方程的解的实例 • 状态方程解的进一步研究
01
状态方程的基本概 念
定义与性质
定义
状态方程是描述系统状态随时间变化 的数学模型,通常表示为微分方程或 差分方程。
性质
状态方程具有非线性、时变性和不确 定性等特点,描述了系统内部状态与 外部输入之间的动态关系。
证明方法
通过数学推导和证明,证明解的唯一性。
3
应用场景
在很多实际问题中,我们需要找到唯一的解来解 决问题,因此解的唯一性非常重要。
解的稳定性
稳定性定义
如果一个解在微小扰动下仍然保持其性质,则称该解是稳定的。
稳定性分类
根据不同的标准,可以将稳定性分为多种类型,如局部稳定性和全 局稳定性、渐进稳定性和非渐进稳定性等。
线性控制系统状态方程求解

0 1
0 0
et
1
2
1
1 t2et 2
(1 t t 2 )et
t
1 2
t
2
et
t
1 2
t
2
et
3t t 2 et
(1
2t
1 2
t
2
)et
4、凯莱-哈密顿(以下简称C-H)定理法:将 e At 化为A的有限项多
项式来求解:
(1):设n×n维矩阵A的特征方程为:
f ( ) | I A | n a1n1 an1 an 0
2!
k!
P
1 P
P
1
ΛtP
P
1
1 2!
Λ2t
2
P
P 1
1 k!
Λkt k
P
P 1
I
Λt
1 2
Λ2t 2
1 Λkt k k!
P
P 1eΛt P
例2-5 已知
A
0 2
13, 求状态转移 矩阵1Φ(t)
解:系统特征方程式为
I A
2 3
2
3
2
0
可解出系统特征值为 1 1, 2 2
,
1 3 3
可解出系统特征值为 1,2,3 1
变换矩阵为
1 0 01 1 0 01 1 0 0
P
1
1
0 1 1 0 1 1 0
12 21 1 1 2 1 1 2 1
1 0 0 P 1 1 1 0
1 2 1
e1t
eJt
0
te1t e1t
1 t e2 1t 2 te1t
et 0
为约当形矩阵
1 1
第二章控制系统状态空间表达式的解

a(b0 b1t b2t 2 bkt k )
(1) (2) (3)
2.1 线性定常齐次状态方程的解(自由解)
等式两边t 的同次幂的系数相等,因此有
b1 ab0
b2 bk
1 2
1 k
ab1
abk
1 2!
a
2b0
1 k!
a
(5)
将(5)式代入(1)式
2.1 线性定常齐次状态方程的解(自由解)
b1 2b2t 3b3t 2 kbkt k 1
A(b0 b1t b2t 2 bkt k )
等式两边t 同次幂的系数相等,因此有
b1 Ab0
b2 bk
1 2
1 k
Ab1
Abk
1 2!
A2b0
1 k!
2.1 线性定常齐次状态方程的解(自由解)
1、线性定常系统的运动
1)、自由运动:线性定常系统在没有控制作用,即u=0时, 由初始状态引起的运动称自由运动。
u0
x
( A, B)
齐次状态方程的解: x Ax , x(t) |t0 x(0)
2)、强迫运动:线性定常系统在控制u作用下的运动,称
为强迫运动。
e1t
0
e At Te AtT1 T
T 1
0
ent
其中: T为使A化为对角线标准型的非奇异变换矩阵。
求状态转移矩阵的步骤:
1)先求得A阵的特征值 。i
2)求对应于 的i 特征向量 ,p并i 得到T阵及T的逆阵。
3)代入上式即可得到状态转移矩阵的值。
即:A det(I A) 0 i (i I A)pi 0 pi T
0 0 0 0 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
or y(t)= Cx(t) = Cϕ (t ) x(0) + C ∫ ϕ (t ) Bu(τ )dτ t ≥ 0
(a) 设 n × n 矩阵 A 的特征值 λ1 , λ 2 ,⋯ λ n 是两两相异的,则
eλit = α0 (t ) + α1 (t )λi + ⋯ + αn−1 (t )λin−1 , i = 1, 2,⋯, n
因而,计算 α i ( t ) 的关系式为:
α 0 (t ) 1 λ1 α (t ) 1 = 1 λ2 ⋮ ⋮ ⋮ α n −1 (t ) 1 λn
举例 P69
kλ1 ⋯
(n − 1)⋯ (n − k + 1) n − k λ1 α (t) (k − 1)! 0 ⋮ α1 (t) (n − 1)(n − 2) n −3 α 2 (t) λ1 2! ⋮ (n − 1)λ1n − 2 α k −1 (t) λ1n −1 α k (t) λkn+−11 ⋮ α n −1 (t) ⋮ n −1 λn
第二章 状态方程的解
本章重点讨论在给定系统的输入信号和初始状 态下状态空间表达式的求解, 态下状态空间表达式的求解,并在此基础上定 义状态转移矩阵, 义状态转移矩阵,讨论状态转移矩阵的性质和 计算方法。状态空间表达式的求解, 计算方法。状态空间表达式的求解,有助于直 观地了解和分析系统, 观地了解和分析系统,获得描述系统所需的全 部信息。 部信息。
Φ(t ) = e At = I + At + 1 22 1 A t + ⋯ + Ak t k + ⋯ 2! k!
n −1
= α0 (t ) I + α1 (t ) A + ⋯ + αn−1 (t ) A
= ∑αk (t ) Ak
k =0
n −1
式中α 0 ( t ),α 1 ( t ),α 2 ( t ),⋯ ,α n−1 ( t ) 为 t 的函数。
1. 线性定常系统状态方程的零输入响应
(1)齐次状态方程的解 (1)齐次状态方程的解
齐次微分方程
ɺ x = Ax
方程的解为
(1)
x (t ) = b0 + b1t + b2t 2 + ⋯ + bk t k + ⋯ (2)
b 式中, 均为列向量。 式中, i ( i = 0 ,1, 2 ⋯ ) 均为列向量。
由状态转移方程,代入系统的输出方程, 由状态转移方程,代入系统的输出方程, 就可以得到系统在初始状态x(t , 就可以得到系统在初始状态 0),输入 作用为u(t)时,系统输出响应: 作用为 时 系统输出响应:
y(t)= Cx(t) = Cϕ (t − t0 ) x(t0 ) + C ∫ ϕ (t − t0 ) Bu(τ )dτ t ≥ t0
At
可以写出方程解为
0 1 2 0 0 3 n 其中 A = , A = A = ⋯ = A = 0 0 0 0 1 0 0 t 1 t Φ (t ) = + 0 0 = 0 1 0 1
x1 ( t ) 1 = x2 (t ) 0
λ12 ⋯ λ1n −1 λ22 ⋯ λ2n −1
⋮ ⋯
−1
λn2
⋮ ⋯ λnn −1
eλ1t λ2t e ⋮ λnt e
, 其 余 (n − k) 个 特 征 值
(b)
设
n× n
的矩阵 A 有 k 重特征值
λ1 = λ2 = ⋯ = λk
−1
1 1 − s +1 s + 2 −1 2 + s +1 s + 2
将上式进行拉氏反变换
2e−t − e−2t e−t − e−2t eAt = L−1[(sI− A)−1] = −t −2t −t −2t − e + 2e − 2e + 2e
状态方程之解为
k Akt
= Φ ( kt )
(2) 状态转移矩阵的计算 一、根据定义计算 二、应用拉氏变换法求解
ɺ x (t ) = Ax (t )
sX (s) − x0 = AX (s)
(3) (4)
X ( s ) = ( sI − A) x0
拉氏反变换后得到
−1
−1
x (t ) = L [( sI − A) ] x0
e
At
矩阵,称矩阵指数。 为n×n矩阵,称矩阵指数。
于是, 于是,齐次状态方程的解为
x(t ) = e x(0)
At
若初始时刻 t0 ≠0 ,对应的初始状态为 x(t0 ) ,则 齐次状态方程的解为
x(t ) = e
A ( t −t0 )
x(t0 )
Φ (t ) = e
At
状态转移矩阵具有以下性质: 状态转移矩阵具有以下性质:
将 x ( t ) 代入方程(1),得
b1 + 2b2t +⋯+ kbkt
b1 = Ab0 =
k −1
+⋯= A(b0 + b1t +⋯+ bkt +⋯)
k
方程两边系数必相等, 即
1 Ab0 1! 1 1 2 1 2 b2 = Ab1 = A b0 = A b0 2 2 2! 1 1 3 1 b3 = Ab2 = A b0 = A3b0 3 3× 2 3! ⋮ bk = 1 k A b0 k!
(3) 非齐次状态方程的解
非齐次方程
ɺ x (t ) = Ax (t ) + Bu (t )
改写为
ɺ x ( t ) − Ax ( t ) = Bu ( t )
用e
−At
左乘等式两边
e
− At
d − At ɺ [ x (t ) − Ax (t )] = [e x (t )] = e − At Bu (t ) dt
ɺ 1. Φ (t ) = AΦ (t ) 2. Φ (0) = I 3. Φ ( −t ) = e
− At
= ( e ) = Φ (t )
At −1
−1
4. Φ (t 2 − t1 )Φ (t1 − t0 ) = Φ (t 2 − t0 ) 5. Φ (t1 + t 2 ) = Φ (t1 )Φ (t 2 ) 6. [Φ (t )] = e
−t −2t 2e−t − e−2t e − e x1 (0) At x(t) = e x(0) = −t −2t −t −2t x2 (0) − e + 2e − 2e + 2e
三、应用凯莱-哈密顿定理 应用凯莱-
1.Calay-Hamilton 定理 . 设 n × n 系统矩阵 A 的特征多项式为:
λk +1 , λk + 2 ,⋯ , λn 互异,则 A 的 (n − k) 个互异特征值均满足系统方程,得到 (n − k) 个代数方程。
eλit = α0 (t ) + α1 (t )λi + ⋯ + αn−1 (t )λin−1 , i = k + 1, k + 2,⋯, n
对于 A 的 k 重特征根,则有下列 k 个代数方程。 将 λ1 代入系统方程,得
将t=0代入(2)式得 t=0代入(2)式得 代入(2)
x (0) = b0
因此,齐次状态方程的解为 因此,
1 22 1 k k x(t ) = ( I + At + A t + ⋯ + A t + ⋯) x(0) 2! k!
仿照标量指数函数 exp( at ) ,我们定义
e
At
1 2 2 1 K k = I + At + A t + ⋯ + A t +⋯ 2! k!
t0 t
上式通常又称为线性定常系统的状态转移方程。 上式通常又称为线性定常系统的状态转移方程。 其中, 其中,等式右边第一项是输入作用为零时的状态 转移,称为系统零输入的状态转移 系统零输入的状态转移; 转移,称为系统零输入的状态转移;第二项是系 统初始状态为零对应输入作用的状态转移, 统初始状态为零对应输入作用的状态转移,称为 系统零状态的状态转移。 系统零状态的状态转移。
在区间[0 t]上积分,得
e − At x(t ) = x(0) + ∫ e − Aτ Bu (τ )dτ
0t x(0) + ∫ e A( t −τ ) Bu (τ )dτ
可改写为
0
t
t
x (t ) = Φ (t ) x (0) + ∫ Φ (t − τ ) Bu (τ ) dτ
(3)
总共 n 个代数方程,写成向量矩阵形式为:
1 0 1 t k −1eλ1t 0 ⋯ (k − 1)! ⋮ ⋮ 1 2 λ1t 0 0 1 3λ1 te 2! λ1t = 0 1 2λ1 te λ12 eλ1t 1 λ1 1 λ λk2+1 eλk+1t k +1 ⋮ ⋮ ⋮ ⋮ λn2 eλn t 1 λn
f (λ ) = λ n + a1λ n −1 + ⋯ + an −1λ + an = 0 ,则 A 满足它自身的特征方程,
即方阵 A 的特征多项式是 A 的零化多项式。
f ( A) = An + a1 An −1 + ⋯ + an −1 A + an I = 0
