聚类分析与判别分析区别
多元统计分析(聚类分析,判别分析,对应分析)

91.500
358.500
95.000
357.000
输出的第一部分对应表是由原始数据学号与科目 分类的列联表,可以看出观测总数n=40,说明原 始数据中没有记录缺失,有效边际为行列数的总 和。
维数 1 2 3 总计
汇总 惯量比例
置信奇异值
奇异值 .075 .052
惯量 .006 .003
解释 .548 .264
2 -.143 -.427 .065 -.013
概述列点a
惯量 .002 .003 .005 .000 .010
点对维惯量
1 .000
2 .099
.022
.880
.975
.021
.003
.001
1.000
1.000
贡献
1 .000 .047 .989 .039
维对点惯量 2 .135 .887 .010 .006
(列)的每一状态对每一维度(公共因子)特
征值的贡献及每一维度对行(列)各个状态的
特征值等贡献。如第一维度中,外语对应的数 值最大,为0.975,说明外语这一状态对第一维 度的贡献最大。
对应分析
由以上两张坐标表可以得出如下的叠加散点图,也是输出 的最后一部分,是学号各状态与科目各状态同时在一张二 维图上的投影。在图上既可以看到每一变量内部各状态之 间的相关关系,又可以同时考察两变量之间的相关关系。
对应分析
结果分析
学号 1 2 3 4
语文 82.000 81.000 83.000 72.000
对Байду номын сангаас表
数学 120.000 119.000 115.000 115.000
科目 外语 71.000 77.000 69.000 75.000
「聚类分析与判别分析」

「聚类分析与判别分析」聚类分析和判别分析是数据挖掘和统计学中常用的两种分析方法。
聚类分析是一种无监督学习方法,通过对数据进行聚类,将相似的样本归为一类,不同的样本归入不同的类别。
判别分析是一种有监督学习方法,通过学习已知类别的样本,构建分类模型,然后应用模型对未知样本进行分类预测。
本文将对聚类分析和判别分析进行详细介绍。
聚类分析是一种数据探索技术,其目标是在没有任何先验知识的情况下,将相似的样本聚集在一起,形成互相区别较大的样本群。
聚类算法根据样本的特征,将样本分为若干个簇。
常见的聚类算法有层次聚类、k-means聚类和密度聚类。
层次聚类是一种自下而上或自上而下的层次聚合方法,通过测量样本间的距离或相似性,不断合并或分裂簇,最终形成一个聚类树状结构。
k-means聚类将样本划分为k个簇,通过优化目标函数最小化每个样本点与其所在簇中心点的距离来确定簇中心。
密度聚类基于样本点的密度来判断是否属于同一簇,通过划定一个密度阈值来确定簇的分界。
聚类分析在很多领域中都有广泛的应用,例如市场分割、医学研究和社交网络分析。
在市场分割中,聚类分析可以将消费者按照其购买行为和偏好进行分组,有助于企业制定更精准的营销策略。
在医学研究中,聚类分析可以将不同患者分为不同的亚型,有助于个性化的治疗和药物开发。
在社交网络分析中,聚类分析可以将用户按照其兴趣和行为进行分组,有助于推荐系统和社交媒体分析。
相比之下,判别分析是一种有监督学习方法,其目标是通过学习已知类别的样本,构建分类模型,然后应用模型对未知样本进行分类预测。
判别分析的目标是找到一个决策边界,使得同一类别内的样本尽可能接近,不同类别之间的样本尽可能远离。
常见的判别分析算法有线性判别分析(LDA)和逻辑回归(Logistic Regression)。
LDA是一种经典的线性分类方法,它通过对数据进行投影,使得同类样本在投影空间中的方差最小,不同类样本的中心距离最大。
逻辑回归是一种常用的分类算法,通过构建一个概率模型,将未知样本划分为不同的类别。
聚类分析和判别分析

18
24 30 36 42 48 54 60 66 72
0.69
0.77 0.59 0.65 0.51 0.73 0.53 0.36 0.52 0.34
1.33
1.41 1.25 1.19 0.93 1.13 0.82 0.52 1.03 0.49
0.48
0.52 0.30 0.49 0.16 0.35 0.16 0.19 0.30 0.18
i i
( xi x ) 2 ( yi y ) 2
i i
i
当变量的测量值相差悬殊时,要先进行 标准化. 如R为极差, s 为标准差, 则标 准化的数据为每个观测值减去均值后 再除以R或s. 当观测值大于0时, 有人 采用Lance和Williams的距离
1 | xi yi | x y p i i i
Number of Cases in each Cluster Cluster 1 2 3 4 1.000 1.000 2.000 15.000 19.000 .000
Valid Missing
结果解释
参照专业知识,将儿童生长发育分期定为: 第一期,出生后至满月,增长率最高; 第二期,第2个月起至第3个月,增长率次之; 第三期,第3个月起至第8个月,增长率减缓; 第四期,第8个月后,增长率显著减缓。
k-均值聚类:案例
为研究儿童生长发育的分期,调查1253名1月至7岁儿 童的身高(cm)、体重(kg)、胸围(cm)和坐高(cm) 资料。资料作如下整理:先把1月至7岁划成19个月份段, 分月份算出各指标的平均值,将第1月的各指标平均值与出 生时的各指标平均值比较,求出月平均增长率(%),然后 第2月起的各月份指标平均值均与前一月比较,亦求出月平 均增长率(%),结果见下表。欲将儿童生长发育分为四期, 故指定聚类的类别数为4,请通过聚类分析确定四个儿童生 长发育期的起止区间。
聚类分析、判别分析、主成分分析、因子分析

聚类分析、判别分析、主成分分析、因子分析主成分分析与因子分析的区别1. 目的不同:因子分析把诸多变量看成由对每一个变量都有作用的一些公共因子和仅对某一个变量有作用的特殊因子线性组合而成,因此就是要从数据中控查出对变量起解释作用的公共因子和特殊因子以及其组合系数;主成分分析只是从空间生成的角度寻找能解释诸多变量变异的绝大部分的几组彼此不相关的新变量(主成分)。
2. 线性表示方向不同:因子分析是把变量表示成各公因子的线性组合;而主成分分析中则是把主成分表示成各变量的线性组合。
3. 假设条件不同:主成分分析中不需要有假设;因子分析的假设包括:各个公共因子之间不相关,特殊因子之间不相关,公共因子和特殊因子之间不相关。
4. 提取主因子的方法不同:因子分析抽取主因子不仅有主成分法,还有极大似然法,主轴因子法,基于这些方法得到的结果也不同;主成分只能用主成分法抽取。
5. 主成分与因子的变化:当给定的协方差矩阵或者相关矩阵的特征值唯一时,主成分一般是固定的;而因子分析中因子不是固定的,可以旋转得到不同的因子。
6. 因子数量与主成分的数量:在因子分析中,因子个数需要分析者指定(SPSS 根据一定的条件自动设定,只要是特征值大于1的因子主可进入分析),指定的因子数量不同而结果也不同;在主成分分析中,成分的数量是一定的,一般有几个变量就有几个主成分(只是主成分所解释的信息量不等)。
7. 功能:和主成分分析相比,由于因子分析可以使用旋转技术帮助解释因子,在解释方面更加有优势;而如果想把现有的变量变成少数几个新的变量(新的变量几乎带有原来所有变量的信息)来进入后续的分析,则可以使用主成分分析。
当然,这种情况也可以使用因子得分做到,所以这种区分不是绝对的。
1 、聚类分析基本原理:将个体(样品)或者对象(变量)按相似程度(距离远近)划分类别,使得同一类中的元素之间的相似性比其他类的元素的相似性更强。
目的在于使类间元素的同质性最大化和类与类间元素的异质性最大化。
聚类和判别分析

市场细分
在市场营销中,判别分析可用于 识别消费者群体的特征和行为模 式,以便进行更有效的市场细分 和定位。
04
判别分析算法
线性判别分析(LDA)
01
基本思想:通过找到一个投影方向,使得同类样本在该方 向上投影后尽可能接近,不同类样本在该方向上投影后尽 可能远离。
02
算法步骤
03
1. 计算各类样本均值。
04
2. 计算类间散度矩阵和类内散度矩阵。
05
3. 计算投影方向,使得类间散度矩阵最大,类内散度矩 阵最小。
06
4. 将样本投影到该方向上,得到判别结果。
支持向量机(SVM)
算法步骤
2. 计算支持向量所构成的法向量 。
基本思想:通过找到一个超平面 ,使得该超平面能够将不同类样 本尽可能分开,同时使得离超平 面最近的样本距离尽可能远。
目的
聚类分析的目的是揭示数据集中的内在结构,帮助我们更好地理解数据的分布 和特征,为进一步的数据分析和挖掘提供基础。
聚类方法分类
01
基于距离的聚类
根据对象之间的距离进行聚类,常见的算法有K-means 、层次聚类等。
02
基于密度的聚类
根据数据点的密度进行聚类,将密度较高的区域划分为 一类,常见的算法有DBSCAN、OPTICS等。
聚类和判别分析
目录
• 聚类分析概述 • 聚类分析算法 • 判别分析概述 • 判别分析算法 • 聚类与判别分析的比较与选择
01
聚类分析概述
定义与目的
定义
聚类分析是一种无监督学习方法,旨在将数据集中的对象按照它们的相似性或 差异性进行分组,使得同一组内的对象尽可能相似,不同组之间的对象尽可能 不同。
判别分析与聚类分析

判别分析与聚类分析判别分析与聚类分析是数据分析领域中常用的两种分析方法。
它们都在大量数据的基础上通过统计方法进行数据分类和归纳,从而帮助分析师或决策者提取有用信息并作出相应决策。
一、判别分析:判别分析是一种有监督学习的方法,常用于分类问题。
它通过寻找最佳的分类边界,将不同类别的样本数据分开。
判别分析可以帮助我们理解和解释不同变量之间的关系,并利用这些关系进行预测和决策。
判别分析的基本原理是根据已知分类的数据样本,建立一个判别函数,用来判断未知样本属于哪个分类。
常见的判别分析方法包括线性判别分析(LDA)和二次判别分析(QDA)。
线性判别分析假设各类别样本的协方差矩阵相同,而二次判别分析则放宽了这个假设。
判别分析的应用广泛,比如在医学领域可以通过患者的各种特征数据(如生理指标、疾病症状等)来预测患者是否患有某种疾病;在金融领域可以用来判断客户是否会违约等。
二、聚类分析:聚类分析是一种无监督学习的方法,常用于对数据进行分类和归纳。
相对于判别分析,聚类分析不需要预先知道样本的分类,而是根据数据之间的相似性进行聚类。
聚类分析的基本思想是将具有相似特征的个体归为一类,不同类别之间的个体则具有明显的差异。
聚类分析可以帮助我们发现数据中的潜在结构,识别相似的群组,并进一步进行深入分析。
常见的聚类分析方法包括层次聚类分析(HCA)和k-means聚类分析等。
层次聚类分析基于样本间的相似性,通过逐步合并或分割样本来构建聚类树。
而k-means聚类分析则是通过设定k个初始聚类中心,迭代更新样本的分类,直至达到最优状态。
聚类分析在市场细分、社交网络分析、图像处理等领域具有广泛应用。
例如,可以将客户按照他们的消费喜好进行分组,以便为不同群体提供有针对性的营销活动。
总结:判别分析和聚类分析是两种常用的数据分析方法。
判别分析适用于已知分类的问题,通过建立判别函数对未知样本进行分类;聚类分析适用于未知分类的问题,通过数据的相似性进行样本聚类。
聚类分析与判别分析的区别

武汉学刊 2006 年第 1 期
经济研究
聚类分析与判别分析的区别
邓海燕
上世纪 60 年代末到 70 年代初, 人们把大量 因变量的各个类别。
义如下:
m
"! 2
dij=
( Xik- Xjk)
k= 1
其中: Xik: 第 i 个样品的第 k 个指标的观测值
Xjk: 第 j 个样品的第 k 个指标的观测值
dij: 第 i 个样品与第 j 个样品之间的欧氏距离
依次求出任何两个点的距离系数 dij( i, j=1, 2,
…, n) 以后, 则可形成一个距离矩阵:
或“ 相 似 系 数 ”较 小 的 点 归 为 不 同 的 类 。
“距离”常用来度量样品之间的相似性 ,“相似
系 数 ”常 用 来 度 量 变 量 之 间 的 相 似 性 。
a、根 据 不 同 的 需 要 , 距 离 可 以 定 义 为 许 多 类
型, 最常见、最 直 观 的 距 离 是 欧 几 里 德 距 离 , 其 定
目的决定 , 一般 可 用 背 景 变 量 、生 活 形 态 变 量 、产 品使用变量或消费者行为变量等。
b 、研 究 消 费 者 行 为 同一类别的消费者或购买者可能有着相似的 购买行为, 通过对不同类别的消费者的研究, 可以 深入地探讨各类消费者的消费行为。 c 、设 计 抽 样 方 案 在大规模的抽样调查中, 常常采用分层抽样, 以提高抽样的精度。例如: 湖北省的消费者调查的 抽样方案, 首先将城市或地区按一些可能影响消 费水平和行为的变量分层, 然后在各层中再实行 多级抽样, 分层所采用的方法之一就是聚类分析。 d 、寻 找 新 的 潜 在 市 场 按照同一类的产品或品牌聚类, 可将竞争的 产 品 或 品 牌 分 类 。竞 争 更 为 激 烈 的 会 在 同 一 类 内 。 通过考察和比较目前自己的情况和竞争对手的情 况, 就有可能发现潜在的新产品机会。 e 、选 择 试 验 的 市 场 为了推出某项新的市场策略, 例如开发新的 产品、实行新的 促 销 方 式 、新 的 广 告 创 意 等 , 需 要 进行事先的实验。通过聚类分析, 可将实验的对象 ( 例如商店、城市、居民区等) 分成同质的几个组作 为实验组和控制组。 f、作 为 多 元 分 析 的 预 处 理 通过聚类分析可以达到简化数据的目的, 将 众多的样品先聚集成比较好处理的几个类别或子 集, 然后再进行后续的多元分析。比如在回归分析 中, 有时不对原始数据进行拟合, 而是对这些子集 的中心作拟合, 可能会更有意义。又比如, 为了研 究不同消费者群体的消费行为特征, 可以先聚类, 然后再利用判别分析进一步研究各个群体之间的 差异。 ( 2) 判别分析在市场研究中主要用于对一个 企业进行市场细分, 以选择目标市场, 有针对性地 进行广告、促销等活动。例如, 根据消费者的一些 背景资料如何判定他们中的哪些会是某种品牌的 忠诚用户, 哪些不是? 或者想要知道, 忠诚用户和 非忠诚用户在人口的基本特征方面到底有哪些不 同? 如何区分价格敏感型的顾客和非敏感型的顾 客? 哪些心里特征或生活形态特征可以用作判别 或区分的标准? 各种目标消费群体在媒介接触方 面是否有显著的差异? 等等这类均可以通过判别
聚类分析聚类分析和判别分析有相似的作用,都是起到分类的作用...

聚类分析聚类分析和判别分析有相似的作用,都是起到分类的作用。
但是,判别分析是已知分类然后总结出判别规则,是一种有指导的学习;而聚类分析则是有了一批样本,不知道它们的分类,甚至连分成几类也不知道,希望用某种方法把观测进行合理的分类,使得同一类的观测比较接近,不同类的观测相差较多,这是无指导的学习。
所以,聚类分析依赖于对观测间的接近程度(距离)或相似程度的理解,定义不同的距离量度和相似性量度就可以产生不同的聚类结果。
SAS/STAT中提供了谱系聚类、快速聚类、变量聚类等聚类过程。
谱系聚类方法介绍谱系聚类是一种逐次合并类的方法,最后得到一个聚类的二叉树聚类图。
其想法是,对于个观测,先计算其两两的距离得到一个距离矩阵,然后把离得最近的两个观测合并为一类,于是我们现在只剩了个类(每个单独的未合并的观测作为一个类)。
计算这个类两两之间的距离,找到离得最近的两个类将其合并,就只剩下了个类……直到剩下两个类,把它们合并为一个类为止。
当然,真的合并成一个类就失去了聚类的意义,所以上面的聚类过程应该在某个类水平数(即未合并的类数)停下来,最终的类就取这些未合并的类。
决定聚类个数是一个很复杂的问题。
设观测个数为,变量个数为,为在某一聚类水平上的类的个数,为第个观测,是当前(水平)的第类,为中的观测个数,为均值向量,为类中的均值向量(中心),为欧氏长度,为总离差平方和,为类的类内离差平方和,为聚类水平对应的各类的类内离差平方和的总和。
假设某一步聚类把类和类合并为下一水平的类,则定义为合并导致的类内离差平方和的增量。
用代表两个观测之间的距离或非相似性测度,为第水平的类和类之间的距离或非相似性测度。
进行谱系聚类时,类间距离可以直接计算,也可以从上一聚类水平的距离递推得到。
观测间的距离可以用欧氏距离或欧氏距离的平方,如果用其它距离或非相似性测度得到了一个观测间的距离矩阵也可以作为谱系聚类方法的输入。
根据类间距离的计算方法的不同,有多种不同的聚类方法。
聚类分析和判别分析

(5)重复上面(3)(4)两步计算过程,直到达到指 定的迭代次数或者终止迭代的判别要求为止。
例1:利用快速聚类分析对20家上市公司进行分类。
SPSS实现
(1)打开文件:上市 公司.sav。
常用的有快速( K-均值)聚类分析、系统聚 类分析。
1、快速聚类
快速聚类也称为逐步聚类,它先 对数据进行初始分类,然后系统采用标 准迭代算法进行运算,逐步调整,把所 有的个案归并在不同的类中,得到最终 分类。它适用于大容量样本的情形。
快速聚类的分析计算过程如下:
(1)用户确定聚类的类别数,如k类。
(2)SPSS系统确定k个类的初始中心点。 SPSS会根据样本数据的实际情况,选择 k个有代表性的样本数据作为初始中心。 初始类中心也可以由用户自行指定,需 要指定k组样本数据作为初始类中心点。
(3)计算所有样本数据点到k个类中心点的欧式 距离,SPSS按照距K个类中心点的聚类最短原 则,把所有样本分派到中心点所在的类中, 形成一个新的k类,完成一次迭代过程。
对话框中的2表示 京样本分为两类 时,各个样本的 归类情况。
提供了7种计算类间距离的方法。 区间:适合于连续型变量,提供了8 种计算样品距离的方法 计数:适用于顺序或名义变量 二分类:适用于二值变量
结果分析:
凝 聚 状 态 表
第一列表示聚类分析的步骤号,共进行了19次。第2列和第3列表示在聚类 分析时那两个样品或类进行了合并,合并后的类用第2列的样品号或类别标 志。第4列式聚类时两个样品或类间距离,可以看出最近的先聚类。第5列和 第6列表示某步聚类时,是样本还是类参与合并。第7列表示本步的聚类结果 在下面聚类的第几步用到。
现代地理学中的数学方法 (3)

聚类分析是根据样本之间的亲疏关系 (相似程度或差异程度)进行分类的,其 基本思想是:把相似度高的样本划归为同 一类,把差异程度大的样本划分到不同的 类。聚类分析的方法有:系统聚类法,K均值法,图论聚类法,模糊聚类法,等等 。本节主要介绍系统聚类法。
第3节
聚类分析与判别分析
聚类分析和判别分析,是定量化的研究分 类问题的统计学方法。这两种方法都是研究事 物分类的数学方法,但二者是有区别的。 聚类分析,事先并不知道样本有多少类, 也不知道每一个样本来自哪一类,而是根据样 本的自身属性确定亲疏关系,并按这种亲疏关 系程度对样本进行分类。 而判别分析,则是在事先已知样本分类的 前提下,对给定的新样本进行归类。它是根据 已知对象的观测指标和所属类别,判断未知对 象所属类别的方法。
12 13 14 15 16 17 18 19 20 21
51.274 68.831 77.301 76.948 99.265 118.505 141.473 137.761 117.612 122.781
1.041 0.836 0.623 1.022 0.654 0.661 0.737 0.598 1.245 0.731
64.609 62.804 60.102 68.001 60.702 63.304 54.206 55.901 54.503 49.102
968.33 957.14 824.37 1 255.42 1 251.03 1 246.47 814.21 1 124.05 805.67 1 313.11
181.38 194.04 188.09 211.55 220.91 242.16 193.46 228.44 175.23 236.29
表4.3.1 8种系统聚类方法的距离参数值(下页)
聚类分析与判别分析比较实证研究
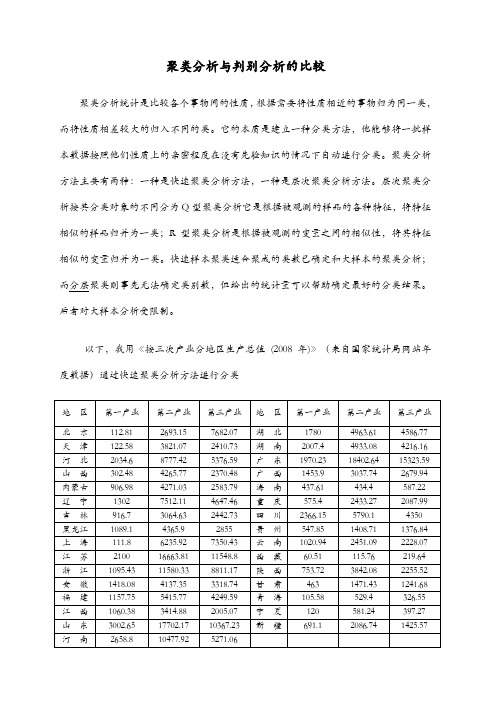
聚类分析与判别分析的比较聚类分析统计是比较各个事物间的性质,根据需要将性质相近的事物归为同一类,而将性质相差较大的归入不同的类。
它的本质是建立一种分类方法,他能够将一批样本数据按照他们性质上的亲密程度在没有先验知识的情况下自动进行分类。
聚类分析方法主要有两种:一种是快速聚类分析方法,一种是层次聚类分析方法。
层次聚类分析按其分类对象的不同分为Q型聚类分析它是根据被观测的样品的各种特征,将特征相似的样品归并为一类;R型聚类分析是根据被观测的变量之间的相似性,将其特征相似的变量归并为一类。
快速样本聚类适合聚成的类数已确定和大样本的聚类分析;而分层聚类则事先无法确定类别数,但给出的统计量可以帮助确定最好的分类结果。
后者对大样本分析受限制。
以下,我用《按三次产业分地区生产总值(2008年)》(来自国家统计局网站年度数据)通过快速聚类分析方法进行分类结果分析:从输出结果可以看出,当样本层次聚类分析成3个类时,样本的类归属情况:第一类包括7个省:北京、上海、安徽、福建、湖南、湖北、四川;第二类包含17个省:天津、山西、内蒙古、吉林、黑龙江、江西、广西、海南、重庆、贵州、云南、西藏、陕西、甘肃、青海、宁夏、新疆;第三类包含4省:河北、辽宁、浙江、河南;第四类包含3个省:江苏、山东、广东判别分析是另一种处理分类分体的统计方法。
它是先根据已知类别的事物的性质,建立函数式,然后对未知类别的新事物进行判断以将之归入已知的类别中。
判别分析的内容十分丰富,按照已知分类的多少,分成两组判别喝多组判别;按照判别方法分为逐步判别和序贯判别;按照判别则分为距离判别、贝叶斯判别和费歇判别等。
通过聚类分析我们已经知道以上31个省的分类情况,现在将福建、江西、山东、河南四个省的聚类结果删除掉。
然后进行判别分析。
得出结果如上图,福建,江西,山东,河南四省的判别结果与之前分类结果一样。
典型判别式函数系数函数1 2 3第一产业.000 .002 .001第二产业.001 -.001 .000第三产业.000 .001 .000(常量) -3.744 -1.017 -.516非标准化系数由此图得出三个函数(X1,X2,X3分别为第一产业、第二产业、第三产业)D1=-3.744+0.001X2D2==1.017+0.002X1-0.001X2+0.001X3D3=-0.516+0.001X1通过聚类分析和判别分析,我们得到了31省的分类结果。
聚类分析与判别分析

该例可以借用层次聚类Q型聚类的实例,分析某班级中语文成绩、数学成绩、化 学成绩和外语快速聚类分析的概念 Ø 快速聚类分析的计算过程及公式 Ø快速聚类分析应用实例
10.3.1 快速聚类分析的概念
快速聚类分析是由用户指定类别数的大样本资料的逐步聚类分析。它先对数据进 行初始分类,然后逐步调整,得到最终分类。快速聚类分析的实质是K-Mean聚类。
10.3.2 快速聚类分析的计算过程及公式
快速聚类分析的计算过程如下:
1.指定聚类的类数
在SPSS中确定 个类的初始类中心点。SPSS会根据样本数据的实际情况,选择 个 由代表性的样本数据作为初始类中心。初始类中心也可以由用户自行指定,需要指定 组样本数据作为初始类中心点。
2. 确定中心点
接着,SPSS重新确定 个类的中心点。SPSS计算每个变量的变量值均值, 并以均值点作的类中心点;最后重复上面的两步计算过程,直到达到指定的 迭代次数或终止迭代的判断要求为止。
10.3.3 快速聚类分析应用实例
本实例调查了全国10个学校的校风、校纪、领导角色和教师态度4个指标, 希望使用快速聚类分析将这10个学校按照其各自的特点分成4种类型。
10.4 判别分析
Ø 判别分析的概念 Ø 判别分析应用实例
10.4.1 判别分析的概念
判别分析先根据已知类别的事物的性质建立函数式,然后对未知类别的新事物进 行判断以将之归入已知的类别中。 在判别分析中有如下假定:
预测变量服从正态分布。 预测变量之间没有显著的相关。 观测变量的平均值和方差不相关。 预测变量之间的相关性在不同类中是一样的。
10.1.1 聚类分析的意义
聚类分析是一种探索性的分析,在分类的过程中,人们不必事先给出一个 分类的标准,聚类分析能够从样本数据出发,自动进行分类分析,所得到的聚 类数未必一致。因此,这里所说的聚类分析是一种探索性的分析方法。
聚类分析、判别分析、主成分分析、因子分析

聚类分析、判别分析、主成分分析、因子分析主成分分析与因子分析的区别1. 目的不同:因子分析把诸多变量看成由对每一个变量都有作用的一些公共因子和仅对某一个变量有作用的特殊因子线性组合而成,因此就是要从数据中控查出对变量起解释作用的公共因子和特殊因子以及其组合系数;主成分分析只是从空间生成的角度寻找能解释诸多变量变异的绝大部分的几组彼此不相关的新变量(主成分)。
2. 线性表示方向不同:因子分析是把变量表示成各公因子的线性组合;而主成分分析中则是把主成分表示成各变量的线性组合。
3. 假设条件不同:主成分分析中不需要有假设;因子分析的假设包括:各个公共因子之间不相关,特殊因子之间不相关,公共因子和特殊因子之间不相关。
4. 提取主因子的方法不同:因子分析抽取主因子不仅有主成分法,还有极大似然法,主轴因子法,基于这些方法得到的结果也不同;主成分只能用主成分法抽取。
5. 主成分与因子的变化:当给定的协方差矩阵或者相关矩阵的特征值唯一时,主成分一般是固定的;而因子分析中因子不是固定的,可以旋转得到不同的因子。
6. 因子数量与主成分的数量:在因子分析中,因子个数需要分析者指定(SPSS根据一定的条件自动设定,只要是特征值大于1的因子主可进入分析),指定的因子数量不同而结果也不同;在主成分分析中,成分的数量是一定的,一般有几个变量就有几个主成分(只是主成分所解释的信息量不等)。
7. 功能:和主成分分析相比,由于因子分析可以使用旋转技术帮助解释因子,在解释方面更加有优势;而如果想把现有的变量变成少数几个新的变量(新的变量几乎带有原来所有变量的信息)来进入后续的分析,则可以使用主成分分析。
当然,这种情况也可以使用因子得分做到,所以这种区分不是绝对的。
1 、聚类分析基本原理:将个体(样品)或者对象(变量)按相似程度(距离远近)划分类别,使得同一类中的元素之间的相似性比其他类的元素的相似性更强。
目的在于使类间元素的同质性最大化和类与类间元素的异质性最大化。
判别分析与聚类分析

判别分析(Discriminant Analysis)一、概述:判别问题又称识别问题,或者归类问题。
判别分析是由Pearson于1921年提出,1936年由Fisher首先提出根据不同类别所提取的特征变量来定量的建立待判样品归属于哪一个已知类别的数学模型。
根据对训练样本的观测值建立判别函数,借助判别函数式判断未知类别的个体。
所谓训练样本由已知明确类别的个体组成,并且都完整准确地测量个体的有关的判别变量。
训练样本的要求:类别明确,测量指标完整准确。
一般样本含量不宜过小,但不能为追求样本含量而牺牲类别的准确,如果类别不可靠、测量值不准确,即使样本含量再大,任何统计方法语法弥补这一缺陷。
判别分析的类别很多,常用的有:适用于定性指标或计数资料的有最大似然法、训练迭代法;适用于定量指标或计量资料的有:Fisher二类判别、Bayers多类判别以及逐步判别。
半定量指标界于二者之间,可根据不同情况分别采用以上方法。
类别(有的称之为总体,但应与population的区别)的含义——具有相同属性或者特征指标的个体(有的人称之为样品)的集合。
如何来表征相同属性、相同的特征指标呢?同一类别的个体之间距离小,不同总体的样本之间距离大。
距离是一个原则性的定义,只要满足对称性、非负性和三角不等式的函数就可以称为距绝对距离马氏距离:(Manhattan distance)设有两个个体(点)X与Y(假定为一维数据,即在数轴上)是来自均数为μ,协方差阵为∑的总体(类别)A的两个个体(点),则个体X与Y的马氏距离为(,)X与总体(类别)A的距离D X Y=(,)为D X A=明考斯基距离(Minkowski distance):明科夫斯基距离欧几里德距离(欧氏距离)二、Fisher两类判别一、训练样本的测量值A类训练样本编号 1x 2xm x1 11A x 12A x 1A m x 221A x22A x2A m xA n1A An x 2A An xA An m x 均数1A x2A xAm xB 类训练样本编号 1x 2x m x1 11B x 12B x 1B m x 221B x22B x2B m xB n1B Bn x 2B Bn x B Bn m x 均数1B x2B xBm x二、建立判别函数(Discriminant Analysis Function)为:1122m m Y C X C X C X =+++其中:1C 、2C 和m C 为判别系数(Discriminant Coefficient ) 可解如下方程组得判别系数。
聚类分析和判别分析

西安科技大学
数学建模
Mathematical Modeling
1. 系统聚类法核心思想
设有 n 个样品,每个样品测得 m 项指标。系统 聚类法的基本思想是:首先定义样品间的距离(或 相似系数)和类与类之间的距离。初始将 n 个样品 看成 n 类(每一类包含一个样品) ,这时类间的距离 与样品间的距离是等价的;然后将距离最近的两类 合并成为新类,并计算新类与其它类的类间距离, 再按最小距离准则并类。这样每次缩小一类,直到 所有的样品都并成一类为止。
聚类分析和判别分析 张守刚
西安科技大学
数学建模
Mathematical Modeling
• 总体来说,聚类分析就是把没有分类信息 的资料按照相似程度进行归类; • 两类:系统聚类法和非系统聚类法,系统 聚类法是应用最广泛的一种方法; • 聚类分析的核心是确定“度量==分类的准 则”;
聚类分析和判别分析
聚类分析和判别分析
张守刚
西安科技大学
数学建模
Mathematical Modeling
• 逐步判别法:与逐步回归法思想类似,都 是逐步引入变量,每引入一个“最重要” 的变量进入判别式,同时也考虑较早引入 判别式的某些变量,若其判别能力不显著 了,就剔除,知道判别式中没有不重要的 变量需要剔除,且没有重要的变量需要引 入为止。这个筛选过称的本质就是假设检 验。
聚类分析和判别分析
张守刚
西安科技大学
数学建模
Mathematical Modeling
案例1
• 中国统计年鉴,2005,主要城市日照时数。 变量有: City—城市名称; 月份—Jan、Feb、……、Dec。 注:聚类可分为变量聚类和观测量聚类, 本案例采用变量聚类方法。
应用多元统计分析习题解答-聚类分析

第五章 聚类分析5.1 判别分析和聚类分析有何区别?答:即根据一定的判别准则,判定一个样本归属于哪一类。
具体而言,设有n 个样本,对每个样本测得p 项指标(变量)的数据,已知每个样本属于k 个类别(或总体)中的某一类,通过找出一个最优的划分,使得不同类别的样本尽可能地区别开,并判别该样本属于哪个总体。
聚类分析是分析如何对样品(或变量)进行量化分类的问题。
在聚类之前,我们并不知道总体,而是通过一次次的聚类,使相近的样品(或变量)聚合形成总体。
通俗来讲,判别分析是在已知有多少类及是什么类的情况下进行分类,而聚类分析是在不知道类的情况下进行分类。
5.2 试述系统聚类的基本思想。
答:系统聚类的基本思想是:距离相近的样品(或变量)先聚成类,距离相远的后聚成类,过程一直进行下去,每个样品(或变量)总能聚到合适的类中。
5.3 对样品和变量进行聚类分析时, 所构造的统计量分别是什么?简要说明为什么这样构造?答:对样品进行聚类分析时,用距离来测定样品之间的相似程度。
因为我们把n 个样本看作p 维空间的n 个点。
点之间的距离即可代表样品间的相似度。
常用的距离为(一)闵可夫斯基距离:1/1()()pq qij ikjk k d q XX ==-∑q 取不同值,分为(1)绝对距离(1q =) (2)欧氏距离(2q =) 21/21(2)()pij ikjk k d XX ==-∑(3)切比雪夫距离(q =∞)1()max ij ik jk k pd X X ≤≤∞=-(二)马氏距离(三)兰氏距离对变量的相似性,我们更多地要了解变量的变化趋势或变化方向,因此用相关性进行衡量。
将变量看作p 维空间的向量,一般用 (一)夹角余弦(二)相关系数5.4 在进行系统聚类时,不同类间距离计算方法有何区别?选择距离公21()()()ij i j i j d M -'=--X X ΣX X 11()p ik jkij k ik jkX X d L p X X =-=+∑cos pikjkijXX θ=∑()()piki jk j ij XX X X r --=∑式应遵循哪些原则?答: 设d ij 表示样品X i 及X j 之间距离,用D ij 表示类G i 及G j 之间的距离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
表示
:
cos
!
ij
=
p
a
=
1
!
x
ia
x
ja
p
a
=
1
!
x
2
・
p
a
=
1
!
x
2
"
ia
ja
1
≤
cos
!
ij
≤
1
当
cos
!
ij
=1
,
说明两个样品
x
i
与
x
j
完全相似
;
cos
!
ij
接
近
1
,
说
明
两
个
样
品
x
i
与
x
j
相
似
密
切
;
cos
!
ij
=0
,
说明
x
i
与
x
j
完全不一样
;
cos
!
ij
接近
0
,
说
明
x
i
与
x
j
差别大。把所有两两样品的相似系数都
通过聚类分析可以达到简化数据的目的
,
将
众多的样品先聚集成比较好处理的几个类别或子
集
,
然后再进行后续的多元分析。
比如在回归分析
中
,
有时不对原始数据进行拟合
,
而是对这些子集
的中心作拟合
,
可能会更有意义。又比如
,
为了研
究不同消费者群体的消费行为特征
,
可以先聚类
,
然后再利用判别分析进一步研究各个群体之间的
差异。
算出
,
可排成相似系数矩阵
:
H=
cos
!
11
,
cos
!
12
,
…
cos
!
1n
cos
!
21
,
cos
!
22
,
…
cos
!
2n
…
cos
!
n1
,
cos
!
n2
,
…
cos
!
nn
#
*
*
*
*
*
*
*
*
*
*
*
*
%
&
’
’
’
’
’
’
’
’
’
’
’
’
(
其中
cos
!
11
=cos
!
22
=
…
=cos
!
nn
=1
。
H
是一个实
对
称
阵
,
只
须
计
算
上
三
角
可以把自变量
X
的取值空间
R
p
划分为
G
个区域
R
t
,
t=1
,
…
,
G
,
使得当
X
的取值
x
属于
R
t
时后验概率在第
t
组最大
,
即
p
(
t|x
)
=
max
p
(
s|x
)
,
+
x
∈
R
t
s=1
,
…
,
G
从上面的分析越来越清晰的看到
,
在实际应
用中
,
当已知了类别的判别问题时
,
我们应选择判
别分析
;
而当我们面对大量的数据
,
杂乱无章
,
而
又需要分类时
依据
判别类型的多少与方法不同
,
分为多类判别和逐
级判别。判别分析的过程是通过建立自变量的线
性
组
合
(
或
其
他
非
线
性
函
数
)
,
使
之
能
最
佳
地
区
分
因变量的各个类别。
二、
聚类分析与判别分析的区别
1
、
基本思想不同
(
1
)
聚类分析的基本思想
我们所研究的样品或指标
(
变量
)
之间存在程
度不同的相似性
(
亲疏关系
)
,
于是根据一批样品
而判别分析的前提是已经知道分类情况
,
判
定新的观测样
品
到
已
知
组
中
。
即
由
若
干
个
不
同
的
样
本
来
构
造
判
别
函
数
,
以
此
决
定
新
的
未
知
类
别的样品属于哪一类。例如
,
炼钢产品按化学成
分
分
为
非
合
金
钢
、
低
合
金
钢
、
合
金
钢
和
不
锈
钢
,
在
测
得
所
要
判
断
钢
坯
的
化
学
成
分
后
,
就
可
以
判
定
属
于
哪
一
类
钢
种
;
某
医
院
已
有
1000
个
分
别
患
有
胃
炎
、
肝
炎
、
合并协方差阵估计
,
t=1
,
…
,
G
为组的下
标
,
共有
G
个组。
S
t
:
第
t
组的协方差阵
q
t
:
第
t
组出现的先验概率
p
(
t|x
)
:
自变量为
x
的观测属于第
t
组的后验
概率
f
t
(
x
)
:
第
t
组的分布密度在
X=x
处的值
按照
Bayes
理论
,
自变量为
x
的观测属于第
t
组的后验概率
:
p
(
t|x
)
=q
t
f
t
(
x
)
/f
(
x
)
。
于是
,
判别分析都是多元统计中研究事物分类的基本方
法
,
但二者却存在着较大的差异。
一、
聚类分析与判别分析的基本概念
1
、
聚类分析
又称群分析、
点群分析。
根据研究对象特征对
研究对象进行分类的一种多元分析技术
,
把性质
相近的个体归为一类
,
使得同一类中的个体都具
有高度的同质性
,
不同类之间的个体具有高度的
异质性。
根据分类对象的不同分为样品聚类和变量聚类。
通过考察和比较目前自己的情况和竞争对手的情
况
,
就有可能发现潜在的新产品机会。
e
、
选择试验的市场
为了推出某项新的市场策略
,
例如开发新的
产品、
实行新的促销方式、
新的广告创意等
,
需要
进行事先的实验。
通过聚类分析
,
可将实验的对象
(
例如商店、
城市、
居民区等
)
分成同质的几个组作
为实验组和控制组。
f
、
作为多元分析的预处理
21
d
22
…
d
2n
…
…
…
…
d
n1
d
n2
…
d
nn
#
$
$
$
$
$
$
$
$
$
$
$
$
%
&
’
’
’
’
’
’
’
’
’
’
’
’
(
若
d
ij
越小
,
那么第
i
与
j
两个样品之间的性
质就越接近。性质接近的样品就可以划为一类。
b
、
常用的相似系数中如夹角余弦系数
:
将
任
何
两
个
样
品
x
i
与
x
j
看
成
维
p
空
间
的
两
个向量
,
这两个向量的夹角余弦用
cos
!
义如下
:
d
ij
=
m
k
=
1
!
(
X
ik
-
X
jk
)
2
"
其中
:
X
ik
:
第
i
个样品的第
k
个指标的观测值
X
jk
:
