力矩分配法习题解答.doc
力矩分配法例题及详解

力矩分配法例题及详解1. 引言嘿,大家好!今天我们来聊聊一个听起来有点复杂,但其实非常实用的概念——力矩分配法。
首先,别被这个名字吓到了,力矩听起来就像是一种神秘的力量,但其实它和我们日常生活息息相关,像是开门、搬家具,甚至是扔飞盘,都能用上哦!接下来,我们就从一些基础概念说起,慢慢让这个看似高深的东西变得简单易懂。
2. 力矩的基本概念2.1 力矩是什么?那么,力矩到底是什么呢?简单来说,力矩就是一个力在某个点上产生的转动效果。
你可以想象一下,你在转动一个门把手。
门把手离门铰链越远,你转动的效果就越明显。
也就是说,力矩=力×距离,这里的距离就是你施力的点到铰链的距离。
明白了吗?就像你拉开冰箱门的时候,越往边上拉,门就开得越大,没错吧?2.2 力矩的方向力矩不仅仅有大小,还有方向哦!通常我们用“顺时针”和“逆时针”来描述。
比如你在玩转盘游戏时,顺时针转动力矩可以让转盘指向某个数字,而逆时针则可能指向另一个数字。
方向的不同,有时候就能让你赢得游戏,没错,力矩在生活中可真是无处不在。
3. 力矩分配法的应用3.1 生活中的例子好了,咱们说了这么多,来点实际的例子吧!想象一下你和朋友们一起搬一个大沙发。
沙发很重,大家都想用力去推,但如果每个人都往同一个方向使劲,结果可能就是沙发半天也动不了。
这时候,你就需要用到力矩分配法!大家可以分成两组,一组在沙发一端推,另一组在另一端拉,利用力矩的原理,沙发就能轻松移动,简单又有效。
3.2 力矩分配法的步骤说到这儿,大家肯定好奇,具体怎么分配力矩呢?首先,得找到一个合适的支点。
然后,大家围绕这个支点站好,确定每个人施力的方向和位置。
最后,再开始施力,看看大家的默契如何!这个过程就像打篮球一样,配合得当才能得分;而力矩分配法就能让你在各种“搬运”中轻松获胜。
4. 小结最后,总结一下今天的内容。
力矩分配法听上去复杂,但其实它的原理就是利用每个人的力量,合理分配到不同的位置,达到最佳效果。
力矩分配

超静定结构计算——力矩分配法一、判断题:1、力矩分配法中的分配系数、传递系数与外来因素(荷载、温度变化等)有关。
2、若图示各杆件线刚度i相同,则各杆A端的转动刚度S分别为:4 i , 3 i , i。
AAA3、图示结构EI =常数,用力矩分配法计算时分配系数4Aμ= 4 / 11。
1234All l l4、图示结构用力矩分配法计算时分配系数μAB=12/,μAD=18/。
BCA DE=1i=1i=1i=1i5、用力矩分配法计算图示结构,各杆l相同,EI =常数。
其分配系数μBA=0.8,μBC=0.2,μBD=0。
A B CD6、在力矩分配法中反复进行力矩分配及传递,结点不平衡力矩愈来愈小,主要是因为分配系数及传递系数< 1。
7、若用力矩分配法计算图示刚架,则结点A 的不平衡力矩为 --M Pl 316。
l /2l二、计算题:8、用力矩分配法作图示结构的M 图。
已知:M BA BC 0153747=⋅==kN m,μμ/,/,P =24kN 。
9、用力矩分配法计算连续梁并求支座B 的反力。
D 20kN10、用力矩分配法作图示结构的M 图。
已知,571.0,429.0==BC BA μμ50.0==CD CB μμ。
(计算二轮)。
12、用力矩分配法作图示梁的弯矩图。
EI 为常数。
(计算两轮)。
第八章 力矩分配法

第八章 力矩分配法1. 图中结构中固定端弯矩 为: ( )2.在力矩分配中等截面杆的远端固定,杆传递系数C等于: ______3.图中结构中固定端弯矩 =_______4.在力矩分配法中杆端的转动刚度与杆另一端的支撑情况有关。
( )5.图中结构中力矩分配系数 =_______6.单独使用力矩分配法,只能解算连续梁和无侧移刚架。
( )7.图a和图b的A端转动刚度相同。
( )8.一个刚结点无论连接多少个杆件,这些杆件的力矩分配系数之和总等于( )9.在力矩分配法中已知某杆一端的分配力矩M,若该杆另端为滑动支座,则传递力矩为M。
( )10.力矩分配法中的传递系数等于传递力矩与分配力矩之比,它与荷载作用无关。
( )11.对图示结构,力矩分配系数 和固端弯矩 分别为:( )A.0.238, -41.67 KN·mB.0.238, 41.67 KN·mC.0.294, -41.67 KN·mD.0.294, 41.67 KN·m12.图示结构中,各杆i等于常数,欲使结点产生顺时针转角,即 =1,要在结点A上施加(顺时针)外力偶为:( )A.8iB.8iC. 11iD.9i13.用力矩分配法计算图示结构,结点A的不平衡力矩为:( )A.-16 KN·mB. 16 KN·mC. 0D.-64 KN·m14.图示连续梁,已知 =1/2,则杆端弯矩 为: ( )A.8 KN·mB.-8 KN·mC.16 KN·mD.-16 KN·m15.用力矩分配法计算图示结构,分配系数 和为4/7和3/7,则杆端弯矩分别为: ( )A.80 KN·m, 60 KN·mB.-80 KN·m,60 KN·mC.80 KN·m,-60 KN·mD.-80 KN·m,-60 KN·m16.AB杆的弯矩传递系数 与: ( )A.杆AB的A端支承情况有关B. 杆AB的两端支承情况有关C. 杆AB的B端支承情况有关D. 杆AB的两端支承情况无关17.在力矩分配法中,某杆端分配系数与该杆的转动刚度: ( )A.成正比B.有时成正比,有时成反比C.无关系D.成反比18.取左半部为如图示对称结构的等代结构,在等代结构中分配系数 等于:( )A.1/3B.4/11C.2/5D.2/719.用力矩分配法计算图示结构,分配系数 、分别等于: ( )A.0.5 0.333B.0.25 0.5C.0.25 0.333D.0.50.57120.如图连续梁中,已知 =4/7,则 等于: ( )A.4/7(-M+Pd/6)B. 4/7(M+Pd/8)C.4/7(-M+Pd/8)D. 4/7(M-Pd/8)。
《土木工程力学》-力矩分配法

土木工程力学辅导——力矩分配法1. 力矩分配法的基本运算● 三个基本概念转动刚度: 111z S M k k =k S 1:1k 杆的1用的弯矩。
分配系数: M SS M kkk )1(111=∑k 1μ:当结点1杆的1端的力矩。
传递系数: k k k M C M 111=k C 1矩的比值。
当单位力偶作用在结点1弯矩乘以传递系数。
● 一个基本运算如图1所示,各杆的转动刚度为:141413131212,4,3i S i S i S ===各杆的力矩分配系数为:∑∑∑===)1(11414)1(11313)1(11212,,kKkS S S S S S μμμ分配给各杆的分配力矩即近端弯矩为: M SS MM SS MM M SS Mkkk∑∑∑====)1(11414)1(1131312)1(11212,,μμμμ各杆的传递系数为:1,21,0141312-===C C C各杆的传递弯矩即远端弯矩为:144113131331121221,21,0M MM M C MM C MCCC -=====2.具有一个结点角位移结构的计算 步骤:●加约束:在刚结点i 处加一附加刚臂,求出固端弯矩,再求出附加刚臂给结点的约束力矩f i M 。
●放松约束:为消掉约束力矩f i M ,加-f i M ,求出各杆端弯矩。
分配系数固端弯矩分配及传递弯矩最后弯矩M图(单位:KN.m)附加刚臂对结点的约束力矩为:m KN MBf .7560135=-=● 放松结点:在结点B 上加外力偶Bf M-,求出分配弯矩和传递弯矩。
定义lEI i =转动刚度为:i i S i i S BC BC AB BA 44,33====分配系数为:57.043.0=+==+=BCAB BC BC BCBA BA BA S S S S S S μμ分配弯矩为: ()()mkN Mm kN M BCBA .25.327543.0.75.427557.0-=-⨯=-=-⨯=μμ传递弯矩为: ()mkN MM CBcABc .38.2175.42210-=-⨯==● 合并,固端弯矩+分配弯矩=近端弯矩,固端弯矩+传递弯矩=远端弯矩。
第十七章力矩分配法

M
F AB
ql2 12
1582 12
80kN m
M
F BA
ql 2 12
1582 12
80kN
m
M
F BC
Fl 8
100 6 8
75kN
m
M
F CD
ql 2 8
1582 8
120kN
M
M
F DC
0
2. 确定各刚节点处各杆的分配系数,(可令 EI = 1) B 节点处:
SBA
4iAB
由此可知,一个节点所连各杆的近端杆端分配弯矩总和在数值上等于节点不平衡力矩,
但符号相反,即:
M
BA
M
BC
M
BD
S BA SB
(
M
F B
)
S BC SB
(
M
F B
)
S BD SB
(
M
F B
)
(
M
F B
)
而各杆的近端分配弯矩是将不平衡力矩变号后按比例分配得到的。
3、远端传递弯矩的计算及传递系数 近端杆端分配弯矩可通过固端弯矩按比例分配得到,而远端传递 弯矩则可通过近端位移弯矩得到。 设
1、转动刚度(S)
定义:杆件固定端转动单位角位移所引起的力矩称为该杆的转动刚度,(转动刚度也可
定义为使杆件固定端转动单位角位移所需施加的力矩)。转动刚度与远端约束及线刚度有关
远端固定:
S=4i
远端铰支:
S = 3i
远端双滑动支座: S = i
远端自由:
S = 0 (i 为线刚度)
力矩分配法的基本思路
3. 通过列表方式计算分配弯矩与传递弯矩及杆端弯矩。 4. 叠加计算,得出最后的杆端弯矩,作弯矩图。
龙驭球《结构力学》笔记和课后习题(含真题)详解(渐近法及其他算法简述)

中的计算,进行二次分配传递。 (5)各点循环放松,每次产生的新约束力矩会越来越小,一般进行两三轮计算就能满
3 / 52
圣才电子书
足工程精度。
十万种考研考证电子书、题库视频学习平台
l 转动刚度可由位移法中的杆端弯矩公式导出,以下列出常用转动刚度: 远端固定,S=4i;远端简支,S=3i;远端滑动,S=i;远端自由,S=0。
2.分配系数
任一杆件在某结点的分配系数等于杆件的转动刚度不汇交于该结点的各杆转动刚度之
和的比值。它起到将作用于某结点的弯矩按比例分配到汇交于该结点各杆的近端的作用,用
三、无剪力分配法 1.应用条件 刚架中除杆端无相对线位移的杆件外,其余杆件都是剪力静定杆件。
2.剪力静定杆件的固端弯矩
4 / 52
圣才电子书 十万种考研考证电子书、题库视频学习平台
先根据静力条件求出杆端剪力,然后将杆端剪力看作杆端荷载。按该端滑动,另端固定 的杆件进行计算。
出附加刚臂给予结点的约束力矩,用 M 表示。约束力矩规定以顺时针转向为正。
(3)放松结点:将丌平衡弯矩(固端弯矩之和)反号后,按分配系数、传递系数进行 分配、传递。
2 / 52
圣才电子书 十万种考研考证电子书、题库视频学习平台
(4)结构的实际受力状态:将各杆的固端弯矩、分配弯矩和传递弯矩相加,即得各杆 的最后弯矩。
束力 M C 相反的力矩,由这个 M C 引起的固端弯矩,可利用力矩分配法进行计算。计算后 经过一次传递,B 点处的约束力矩变成了 M B M BC 。
(3)将结点 C 重新固定,放松结点 B,相当于在有一个反向力矩加到 B 点上,即为
第六章 力矩分配法

第六章 力矩分配法一 判 断 题1. 传递系数C 与杆件刚度和远端的支承情况有关.( √ )2. 力矩分配中的传递系数等于传递弯矩与分配弯矩之比,它与外因无关.( √ )3. 力矩分配法所得结果是否正确,仅需校核交于各结点的杆端弯矩是否平衡.( × )4. 力矩分配法经一个循环计算后,分配过程中的不平衡力矩(约束力矩)是传递弯矩的代数和.( √ )5. 用力矩分配法计算结构时,汇交与每一结点各杆端力矩分配系数总和为1,则表明力矩分配系数的计算绝对无错误.( × )6. 在力矩分配法中,分配与同一结点的杆端弯矩之和与结点不平衡力矩大小相等,方向相同.( × )7. 力矩分配法是以位移法为基础的渐进法,这种计算方法不但可以获得近似解,也可获得精确解.( √ )8. 在任何情况下,力矩分配法的计算结构都是近似的.( × )9. 力矩分配系数是杆件两端弯矩的比值.( × )10. 图示刚架用力矩分配法,求得杆端弯矩M CB =-16/2ql ( × )题10图 题11图 题12图11. 图示连续梁,用力矩分配法求得杆端弯矩M BC =—M/2.( × )12. 图示刚架可利用力矩分配法求解.( √ )13. 力矩分配法就是按分配系数分配结点不平衡力矩到各杆端的一种方法.(× )14. 在力矩分配法中,同一刚性结点处各杆端的力矩分配系数之和等于1.( √ )15. 转动刚度(杆端劲度)S 只与杆件线刚度和其远端的支承情况有关.( √ )16. 单结点结构的力矩分配法计算结果是精确的.( √ )17. 力矩分配法仅适用于解无线位移结构.( √ )18. 用力矩分配法计算图示结构时,杆端AC 的分配系数29/18=AC μ.(√ )题18图 题19图 题21图19. 图示杆AB 与CD 的EI,l 相等,但A 端的劲度系数(转动刚度)S AB 大于C 端的劲度系数(转动刚度) S CD .( √ )20. 力矩分配法计算荷载作用问题时,结点最初的不平衡力矩(约束力矩)仅是交于结点各杆端固端弯矩的代数和.( × )21. 若使图示刚架结点A 处三杆具有相同的力矩分配系数,应使三杆A 端的劲度系数(转动刚度)之比为:1:1:1.( √ )22. 有结点线位移的结构,一律不能用力矩分配法进行内力分析.( × )23. 计算有侧移刚架时,在一定条件下也可采用力矩分配法.( √ )24. 有结点线位移的结构,一律不能用力矩分配法进行内力分析.( × )二 选 择 题1. 图示结构汇交于A 的各杆件抗弯劲度系数之和为∑A S ,则AB 杆A 端的分配系数为: ( B )A.∑=S A AB AB i /4μB. ∑=S A AB AB i /3μC. ∑=S A AB AB i /2μD. ∑=S A AB ABi /μ题1图 题2图2. 图示结构EI=常数,用力矩分配法计算时,分配系数μ4A 为:( D )A.4/11 B.1/2 C.1/3 D. 4/93. 在图示连续梁中,对结点B进行力矩分配的物理意义表示( D )A. 同时放松结点B和结点CB. 同时固定结点B和结点CC. 固定结点B,放松结点CD. 固定结点C,放松结点B题3图题4图4.图示等截面杆件,B端为定向支座,A端发生单位角位移,其传递系数为( C )A. C AB=1B. C AB =1/2C. C AB =-1D. C AB =05. 等直杆件AB的转动刚度(劲度系数)S AB :(A)A 与B端支承条件及杆件刚度有关B 只与B端的支承条件有关C 与A、B两端的支承条件有关D 只与A端支承条件有关6. 等直杆件AB的弯矩传递系数C AB:(B)A 与B端支承条件及杆件刚度有关B 只与B端的支承条件有关C 与A、B两端的支承条件有关D 只与A端支承条件有关7.当杆件刚度(劲度)系数S AB =3i时,杆的B端为:(C)A 自由端B 固定端C 铰支承D 定向支承8.力矩分配法计算得出的结果(D)A 一定是近似解B 不是精确解C 是精确解D 可能为近似解,也可能是精确解。
钢结构力矩分配法习题

3、剪力静定杆的转动刚度和传递系数:
➢剪力静定杆的 S= i C=-1
2kN/m
↓↓↓↓↓↓↓↓
2kN/m
↓↓↓↓↓↓↓↓
Δ
A
θA
B
确定图示梁的转动刚度SAB,SBA 和传递系数CAB,CBA
B
E
0.4 0.6
1.5i - 0.6i - 0.9i - 0.6i 0.6i
C
2/3 1/3
- 1.5i 1.0i 0.5i
- 0.5i 0.5i
k11
DG
0.55i
0.6i
0.55i k11 8 4
0.5i
k11
1.1i 4
MCE 3(2i) l 1.5i
M BE
3(2)i
l
1.5i
0.762 0.238 33.3 -288
129141.1.7 60.6 -51.4
41.7 13
-9.1 288
1解,3 :
2
1,3
1) 求分配2.系7 2数.5: 2)M求1 固 7端8.弯1-矩100:.92
0.5 0.4
.0S121323A1A212-102M1..3430.32407(.i.i9k.357-,N61306M.5..339m256.,.3.,147)686,213,S323BS331B2.23300-.64.324261371i38i...789268830359..,24.462,85,4
0, SA4
4, 1A1
5 14
+
4-6、定性分析图示刚架结点B的水平位移的方向。
结构力学中的力矩分配法

B EI=3
3m
30kN/m C EI=4
6m
D
0.4 0.0
0.6 -225.0
0.5
0.5
+225.0 -135.0 +67.5 -78.8 -78.7 +11.8 -5.9 -5.9 +0.9 -0.5 -0.4 +220.0 -220.0 220 135
0.0 0.0 0.0 0.0
+90.0 +135.0 -39.4 +15.8 +23.6 -3.0 +1.2 +1.8 +107.0 -107.0 107 135
例6−4 用力矩分配法计算图9−8(a)所示的刚架,并绘M图。 用力矩分配法计算图 ( )所示的刚架,并绘 图
80kN A EI B EI EI C EI EI 30kN/m D
52.04 120 A
91.84 75.92 135 15.92 B B
62.33 26.72 D C C 35.63
6m
6.3 无剪力分配法
一、无剪力分配法的应用条件
P P P P/2 P/2 P/2 P/2 P/2 P/2 P/2 P/2 P/2 P/2 P/2 P/2
P/2 F P/2 D P/2 B A G
F P/2
E C
D P B 3P/2 A
刚架中除两端无相对线位移的杆件外,其余杆件都是剪力静定杆件。
二、无剪力分配法的解题步骤
= 4 i12 φ1 = S 12 ϕ 1 = 3 i13 φ1 = S 13 ϕ 1 = i14 φ1 = S 14 ϕ 1 = 4 i15 φ1 = S 15 ϕ 1 − − − (a)
第6章 章
典型例题分析第6章力矩分配法
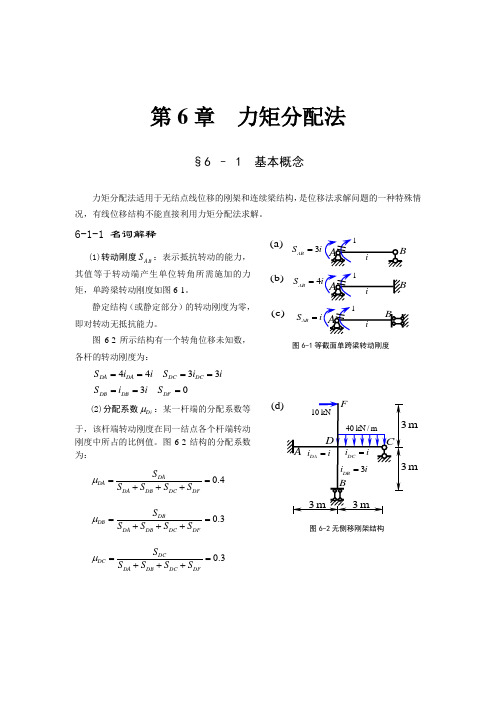
第6章 力矩分配法§6 – 1 基本概念力矩分配法适用于无结点线位移的刚架和连续梁结构,是位移法求解问题的一种特殊情况,有线位移结构不能直接利用力矩分配法求解。
6-1-1 名词解释(1)转动刚度A B S :表示抵抗转动的能力,其值等于转动端产生单位转角所需施加的力矩,单跨梁转动刚度如图6-1。
静定结构(或静定部分)的转动刚度为零,即对转动无抵抗能力。
图6-2所示结构有一个转角位移未知数,各杆的转动刚度为:4433DA DA DC DC S i i S i i ==== 30DB DB DF S i iS ===(2)分配系数Di μ:某一杆端的分配系数等于,该杆端转动刚度在同一结点各个杆端转动刚度中所占的比例值。
图6-2结构的分配系数为:0.4DADADA DB DC DFS S S S S μ==+++ 0.3DBDB DA DB DC DFS S S S S μ==+++0.3DCDC DA DB DC DFS S S S S μ==+++图6-2无侧移刚架结构)b ()c ((a)3AB S i =4AB S =AB S =(d)图6-1等截面单跨梁转动刚度mm0DFDF DA DB DC DFS S S S S μ==+++(3)弯矩符号规定:力矩分配法在计算过程中不需要画弯矩图,只是以数值形式进行计算,因此,需要事先对力矩和弯矩符号进行规定,具体规定如下:固端弯矩:顺时针为正。
结点外力偶:顺时针为正。
(4)固端弯矩F i j M :将转动结点固定变成位移法的基本体系,外荷载在基本体系上产生的杆端弯矩。
如图6-2结构的固端弯矩为:F F F F F F 0DA DA DB BD CD FD M M M M M M ======F 2145kN m 8DC M ql -==-⋅ F 30kN m DF M =-⋅(5)不平衡力矩u D M :不平衡力矩为转动结点所连杆端的固端弯矩之和,其值等于刚臂反力矩。
力矩分配法课后习题答案

力矩分配法课后习题答案力矩分配法课后习题答案力矩分配法是一种常用的力学分析方法,用于计算物体上的力矩分布。
在工程学和物理学中,力矩分配法被广泛应用于解决各种问题,包括结构力学、机械设计和静力学等。
下面将通过几个具体的习题来介绍和解答力矩分配法的应用。
习题1:一个均匀的杆AB长为L,质量为m,放置在两个支点A和B上。
支点A距离杆的左端点的距离为a,支点B距离杆的右端点的距离为b。
求支点A和B所受的力。
解答:根据力矩分配法,我们可以先计算出杆的重心位置。
重心位置可以通过以下公式计算得出:x = (m1 * x1 + m2 * x2) / (m1 + m2)其中,m1和m2分别是杆上两个质点的质量,x1和x2分别是这两个质点的位置。
在本题中,我们可以将杆分为两个部分:左侧的部分质量为m1,右侧的部分质量为m2。
左侧部分的质心位置为a/2,右侧部分的质心位置为L - b/2。
代入公式,我们可以得到:x = (m1 * a/2 + m2 * (L - b/2)) / (m1 + m2)接下来,我们可以计算出支点A和B所受的力。
根据平衡条件,支点A所受的力的大小应该等于杆上重心位置处的力矩与杆的重力矩之和。
支点B所受的力的大小应该等于杆上重心位置处的力矩与杆的重力矩之差。
因此,我们可以得到以下两个方程:Fa = (m1 + m2) * g - (m1 * a/2 + m2 * (L - b/2)) * gFb = (m1 + m2) * g + (m1 * a/2 + m2 * (L - b/2)) * g其中,g是重力加速度。
通过解这两个方程,我们可以求解出支点A和B所受的力。
习题2:一个悬挂在墙上的杆,杆的质量为m,长度为L。
杆的左端点与墙壁接触,右端点悬挂在墙上的钩子上。
求杆的重心位置和墙壁对杆的支持力。
解答:首先,我们可以计算出杆的重心位置。
由于杆是均匀的,重心位置就在杆的中点。
因此,杆的重心位置为L/2。
力矩分配法
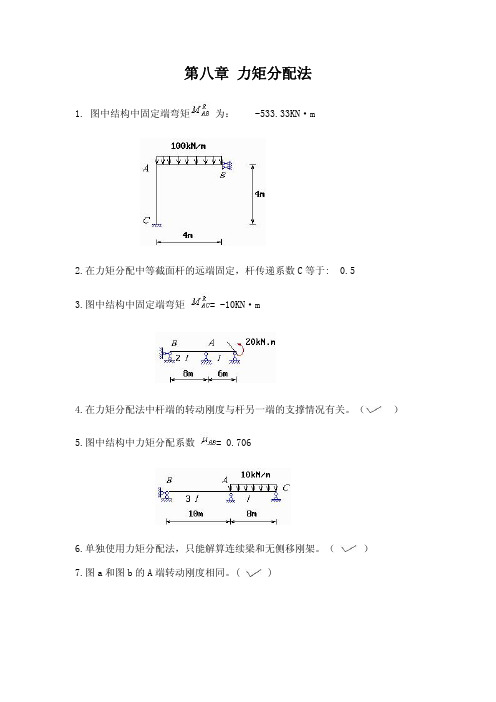
第八章 力矩分配法1. 图中结构中固定端弯矩 为: -533.33KN·m2.在力矩分配中等截面杆的远端固定,杆传递系数C等于: 0.53.图中结构中固定端弯矩 = -10KN·m4.在力矩分配法中杆端的转动刚度与杆另一端的支撑情况有关。
( )5.图中结构中力矩分配系数 = 0.7066.单独使用力矩分配法,只能解算连续梁和无侧移刚架。
( )7.图a和图b的A端转动刚度相同。
( )8.一个刚结点无论连接多少个杆件,这些杆件的力矩分配系数之和总等于( )9.在力矩分配法中已知某杆一端的分配力矩M,若该杆另端为滑动支座,则传递力矩为M。
( )10.力矩分配法中的传递系数等于传递力矩与分配力矩之比,它与荷载作用无关。
( )11.对图示结构,力矩分配系数 和固端弯矩 分别为:( A )A.0.238, -41.67 KN·mB.0.238, 41.67 KN·mC.0.294, -41.67 KN·mD.0.294, 41.67 KN·m12.图示结构中,各杆i等于常数,欲使结点产生顺时针转角,即 =1,要在结点A上施加(顺时针)外力偶为:( A )A.8iB.8iC. 11iD.9i13.用力矩分配法计算图示结构,结点A的不平衡力矩为:( A )A.-16 KN·mB. 16 KN·mC. 0D.-64 KN·m14.图示连续梁,已知 =1/2,则杆端弯矩 为: ( A )A.8 KN·mB.-8 KN·mC.16 KN·mD.-16 KN·m15.用力矩分配法计算图示结构,分配系数 和为4/7和3/7,则杆端弯矩分别为: ( A )A.80 KN·m, 60 KN·mB.-80 KN·m,60 KN·mC.80 KN·m,-60 KN·mD.-80 KN·m,-60 KN·m16.AB杆的弯矩传递系数 与: ( C )A.杆AB的A端支承情况有关B. 杆AB的两端支承情况有关C. 杆AB的B端支承情况有关D. 杆AB的两端支承情况无关17.在力矩分配法中,某杆端分配系数与该杆的转动刚度: ( A )A.成正比B.有时成正比,有时成反比C.无关系D.成反比18.取左半部为如图示对称结构的等代结构,在等代结构中分配系数 等于:( D )A.1/3B.4/11C.2/5D.2/719.用力矩分配法计算图示结构,分配系数 、分别等于: ( D )A.0.5 0.333B.0.25 0.5C.0.25 0.333D.0.50.57120.如图连续梁中,已知 =4/7,则 等于: ( D )A.4/7(-M+Pd/6)B. 4/7(M+Pd/8)C.4/7(-M+Pd/8)D. 4/7(M-Pd/8)。
第20章:力矩分配法

-ql
2/8
=
-10×8
2/8
=
-
80kN·m
F
MCB =0
将它们填入表中第二行相应杆端下面。
由表可求得B点的不平衡力矩。但因B点有 外力偶,故不平衡力矩等于:
MB = -80 +150 = 70 kN·m
3、计算分配弯矩与传递弯矩
将结点B的不平衡力矩反号乘以各杆分配系 数得各杆近端分配弯矩。将所得分配弯矩 乘以相应杆的传递系数即得远端传递弯矩。
Mjc C = Mij
远端固定端时,C = 1/2 远端铰支座时, C = 0 远端定向支座时, C = -1
三、最终弯矩
将第一步固定结点各杆端的固端弯矩与 第二步放松节点时相应杆端的分配弯矩 或传递弯矩相加即得出杆端的最终弯矩。
例20-1用力矩分配法计算图(a)所示的两 跨连续梁,画出弯矩图。
3、将杆端的固端弯矩与分配弯矩或 传递弯矩相加,得到杆端最终弯矩。
一、固定结点
在结点1上附加刚臂,限制结点1的转动,原刚 架被解体成三个单跨梁,此时单跨梁A1两端 产生的弯矩即是位移法中所提到的固端弯矩。
q
M1
A 1
C
M1
M1A 1
M1C
B
M1B
查表得:MAF1 = 0
M1FA = 1 ql 2 由于附加刚臂阻8止了结点1转动,附加
F
MBA=
Pa
2b/l
= 50×42×6/10
= 48 kN·m
F
MBC=-ql
2/12=-25×122
/12=-300
kN·m
F
MCB=
ql
2/12=
25×12
2/12=
力矩分配法(两个例题)

表示杆端对转动的抵抗能力。
在数值上 = 仅使杆端发生单位转动时需在杆端施加的力矩。
SAB与杆的i(材料的性质、横截面的形状和尺寸、杆长)及远端支承有关,
h
3
2. 传递系数C
对于单跨超静定梁而言,当一端发生转角而具 有弯矩时(称为近端弯矩),其另一端即远端一般也 将产生弯矩(称为远端弯矩),如图所示。通常将远 端弯矩同近端弯矩的比值,称为杆件由近端向远端的
(2)放松结点B,相当于在结点B加力矩-
M
F B
计算下列各项
分配系数
BK
SBK SB
分配弯矩 传递弯矩
M
BK
B(K-
M
BF)
M
C KB
CBKMBK
(3)叠加,计算各杆杆端最后弯矩
MBKMB FKMB K
h MKBMK FBMK CB
9
。 试用力矩分配法计算图所示的连续梁,并绘M图
{形常数(表22-2)}
•
h
20
感谢下 载
h
21
正向。梁的变形曲线如图中虚线所示。
约束力矩 称M为BF 结点B上的不平衡力矩。
将图b 和图 c所示两种情况相叠加,就 得到图a原结构的情况。
h
8
通过以上分析,我们将单结点结构力矩分配法的 计算步骤归纳如下:
(1)固定结点B,即在结点B加附加刚臂。计算各杆的固端弯矩
,并求出
结点不平衡力矩
M
F BK
MBF MBFK
M
S Ak
将所求得的φA代入前式,得
h
所以
6
M
A1
S A1 S Ak
M
M
A2
结构力学 力矩分配法题目大全

148第六章 力矩分配法一 判 断 题1. 传递系数C 与杆件刚度和远端的支承情况有关.( √ )2. 力矩分配中的传递系数等于传递弯矩与分配弯矩之比,它与外因无关.( √ )3. 力矩分配法所得结果是否正确,仅需校核交于各结点的杆端弯矩是否平衡.( × )4. 力矩分配法经一个循环计算后,分配过程中的不平衡力矩(约束力矩)是传递弯矩的代数和.( √ )5. 用力矩分配法计算结构时,汇交与每一结点各杆端力矩分配系数总和为1,则表明力矩分配系数的计算绝对无错误.( × )6. 在力矩分配法中,分配与同一结点的杆端弯矩之和与结点不平衡力矩大小相等,方向相同.( × )7. 力矩分配法是以位移法为基础的渐进法,这种计算方法不但可以获得近似解,也可获得精确解.( √ )8. 在任何情况下,力矩分配法的计算结构都是近似的.( × ) 9. 力矩分配系数是杆件两端弯矩的比值.( × )10. 图示刚架用力矩分配法,求得杆端弯矩M CB =-16/2ql ( ×)题10图 题11图 题12图11. 图示连续梁,用力矩分配法求得杆端弯矩M BC =—M/2.( × ) 12. 图示刚架可利用力矩分配法求解.( √ )13. 力矩分配法就是按分配系数分配结点不平衡力矩到各杆端的一种方法.(× ) 14. 在力矩分配法中,同一刚性结点处各杆端的力矩分配系数之和等于1.( √ ) 15. 转动刚度(杆端劲度)S 只与杆件线刚度和其远端的支承情况有关.( √ ) 16. 单结点结构的力矩分配法计算结果是精确的.( √ ) 17. 力矩分配法仅适用于解无线位移结构.( √ ) 18. 用力矩分配法计算图示结构时,杆端AC 的分配系数29/18=ACμ.(√ )149题18图 题19图 题21图 19. 图示杆AB 与CD 的EI,l 相等,但A 端的劲度系数(转动刚度)S AB 大于C 端的劲度系数(转动刚度) S CD .( √ )20. 力矩分配法计算荷载作用问题时,结点最初的不平衡力矩(约束力矩)仅是交于结点各杆端固端弯矩的代数和.( × )21. 若使图示刚架结点A 处三杆具有相同的力矩分配系数,应使三杆A 端的劲度系数(转动刚度)之比为:1:1:1.( √ )22. 有结点线位移的结构,一律不能用力矩分配法进行内力分析.( × ) 23. 计算有侧移刚架时,在一定条件下也可采用力矩分配法.( √ )24. 有结点线位移的结构,一律不能用力矩分配法进行内力分析.( × )二 选 择 题1. 图示结构汇交于A 的各杆件抗弯劲度系数之和为∑AS,则AB 杆A 端的分配系数为:( B ) A.∑=S A AB ABi /4μB. ∑=S A AB ABi /3μ C. ∑=S A AB ABi /2μD.∑=S A AB ABi /μ题1图 题2图 2. 图示结构EI=常数,用力矩分配法计算时,分配系数μ4A 为:( D )A. 4/11B. 1/2C. 1/3D.4/91503. 在图示连续梁中,对结点B 进行力矩分配的物理意义表示( D )A. 同时放松结点B 和结点CB. 同时固定结点B 和结点CC. 固定结点B,放松结点CD. 固定结点C,放松结点B题3图 题4图4. 图示等截面杆件,B 端为定向支座,A 端发生单位角位移,其传递系数为( C )A. C AB =1B. C AB =1/2C. C AB =-1D. C AB =05. 等直杆件AB 的转动刚度(劲度系数)S AB :(A )A 与B 端支承条件及杆件刚度有关 B 只与B 端的支承条件有关C 与A 、B 两端的支承条件有关D 只与A 端支承条件有关6. 等直杆件AB 的弯矩传递系数C AB :(B )A 与B 端支承条件及杆件刚度有关 B 只与B 端的支承条件有关C 与A 、B 两端的支承条件有关D 只与A 端支承条件有关7. 当杆件刚度(劲度)系数S AB =3i 时,杆的B 端为:(C )A 自由端B 固定端C 铰支承D 定向支承8. 力矩分配法计算得出的结果(D )A 一定是近似解B 不是精确解C 是精确解D 可能为近似解,也可能是精确解。
力矩分配法
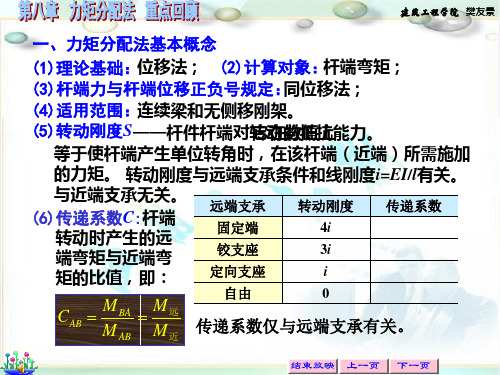
CAB
M BA M 远 M AB M 近
自由
0
无意义
传递系数仅与远端支承有关。
结束放映 上一页 下一页
建筑工程学院 樊友景
二、单结点结构在集中结点力偶作用下的力矩分配法
分配力矩计算
M1 j 1 j M , ( j A, B, C ) 分配系数1 j S1 j / S
5kN/m A 6m B 3m
32kN C 3m
-15 12 -3
4/7 3/7 21 15 -36 24 18 39 -18
(3)力矩的分配与传递 (4)计算杆端弯矩 (5)作M图
结束放映 上一页 下一页
建筑工程学院 樊友景
思考题1:等截面直杆的弯矩传递系数C与什么因素有关。 A 荷载 B 线刚度i C 材料的性质 D 远端支承 思考题2:等截面直杆的转动刚度与下列什么因素无关。 A 近端支承 B 远端支承 C 刚度 D 杆长 思考题3:力矩分配法的计算对象是 A 多余未知力 B 支座反力 C 结点位移 D 杆端弯矩 思考题4:欲使图示梁A端发生单位转动,需在A端施加的 力矩是 A MAB=4i B MAB=3i C MAB=i D 3i<MAB<4i
B
M 1
A
注意:①∑μ=1。 ②分配力矩是杆端转动时产生的 近端弯矩。 ③结点集中力偶顺时针为正。 传递力矩计算 M j1 C1 j M1jቤተ መጻሕፍቲ ባይዱ,
C
j A, B, C
注意:①传递力矩是杆端转动时产生的远端弯矩。 ②只有分配弯矩才能向远端传递。
结束放映 上一页 下一页
建筑工程学院 樊友景
建筑工程学院 樊友景
一、力矩分配法基本概念 (1)理论基础:位移法; (2)计算对象: 杆端弯矩; (3)杆端力与杆端位移正负号规定: 同位移法; (4)适用范围:连续梁和无侧移刚架。 (5)转动刚度S——杆件杆端对转动的抵抗能力。 它在数值上 等于使杆端产生单位转角时,在该杆端(近端)所需施加 的力矩。 转动刚度与远端支承条件和线刚度i=EI/l有关。 与近端支承无关。 远端支承 转动刚度 传递系数 (6)传递系数C:杆端 4i 0.5 固定端 转动时产生的远 3i 0 铰支座 端弯矩与近端弯 i 定向支座 -1 矩的比值,即:
力矩分配法)(选择题-已补充)

说明:(1) 总成绩构成:平时作业20分,机考20分,期末考试60分,合计共100分。
(2) 机考题型分二类,一、判断题(10分);二、选择题(10分)。
(3) 机考题库一为判断题已有120题,机考题库二为选择题已有110题。
(4) 机考时,每位学生从题库一、二中各随机抽取6题,共作12题,每小题2分,满分20分。
机考时间为一节课(30分钟)A、B、C、D四选一选择题(已有110题,待补充)八、力矩分配法(已有8题)1.力矩分配法中的分配系数μ、传递系数C,与外界因素(如荷载、温度变化等):( B )A . 均有关;B. 均无关;C . μ有关,C无关;D. μ无关,C有关。
2.力矩分配法中的传递弯矩等于:(B )A. 固端弯矩;B. 分配弯矩乘以传递系数;C. 固端弯矩乘以传递系数;D. 结点不平衡力矩乘以传递系数。
3.力矩分配法中的分配弯矩等于:( C )A. 固端弯矩;B. 远端弯矩;C. 结点不平衡力矩改变符号后乘以分配系数;D. 固端弯矩乘以分配系数。
4.图示结构,用力矩分配法计算时,分配系数μAB、μAD为:( C ) A. μAB = 1/2,μAD = 1/6;B. μAB = 4/11,μAD = 1/8;C. μAB = 1/2,μAD = 1/8;D. μAB = 4/11,μAD = 1/6。
5.图示结构用力矩分配法计算时:( D )A. μBC=1/8,C BC= -1;B. μBC=2/9,C BC= 1;C. μBC=1/8,C BC= 1;D. μBC=2/9,C BC= -1。
6.等截面直杆AB的A端转动刚度S AB:( D )A. 仅与杆件的线刚度有关;B. 与杆件的线刚度及荷载有关;C. 仅与杆件两端的约束情况有关;D. 与杆件的线刚度及两端的约束情况有关。
7.在力矩分配法中,AB杆的弯矩传递系数C AB与:( B )A. A端约束条件有关;B. B端约束条件有关;C. 杆AB两端的约束条件有关;D. 杆AB两端的约束条件无关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、清华 5-6试用力矩分配法计算图示连续梁,并画其弯矩图和剪力图。
kNkNA20·A55·Bi CBC清华2i题9-1b EIEI题5-635M 图15M 图(kN · m)(kN · m)59017.527.58.75V 图V 图32.5分配系数 0.6 0.4分配系数0.5 0.5固端弯矩 0(20) 0固端弯矩 0 (55) 0 67.5 0 45 0 分与传 0 -52.5 -35 -17.5 分与传 0 -50 -50 0 最后弯矩15 -35-17.5最后弯矩-5-50解:( 1)计算分配系数:sBA3 2i 0.6BAsBC3 2i 4sBAisBC4 i 0.4BCsBC3 2i 4sBAi( 2)计算固端弯矩: 固端弯矩仅由非结点荷载产生,结点外力偶不引起固端弯矩,结点外力偶逆时针为正直接进行分配。
M AB F 0M BA F 3Pl3606 67.5kN m16 16( 3)分配与传递,计算列如表格。
( 4)叠加固端弯矩和分配弯矩或传递弯矩,得各杆端的最后弯矩,作弯矩图如图所示。
( 5)根据弯矩图作剪力图如图所示。
V ABMABMBA300 155kNV ABl6 27.V BA 0M AB M BA30 0 15 5kNVBAl6 32.VBCVCBM BCMCB35 17.5kNl68.752、利用力矩分配法计算连续梁,并画其弯矩图和剪力图。
kNkN/m20kN M 图 15.7130 20(kN · m)7.14AEIB EIC D202m2m 4m1m题9-1b原结构28.93kN·m20NV 图 7.86kN/m 20kkNA(kN)EIBEICD12.1431.07kNkN/mA20kN ·mEIBEIC分配系数 0.571 0.429简化结构固端弯矩 -1010 -30+10 20 -20分与传2.865.71 4.29 0 0最后弯矩 -7.1415.71 -15.7120 -20解:( 1)计算分配系数: 令EI ,4 ,3i BAii BCS BAi S BCi4BAsBA4i0.429BCsBC3i 0.571s BA s BC 4i3is BA s BC4i 3i( 2)计算固端弯矩: CD 杆段剪力和弯矩是静定的,利用截面法将外伸段从C 处切开,让剪力直接通过支承链杆传给地基,而弯矩暴露成为BC 段的外力偶矩,将在远端引起 B 、C 固端弯矩。
FPl 20 4 kN m, F = 10 kN mMAB8 810 MBAM BC Fql 2 m 15 421020kN m,M CB F 20kN m828( 3)分配与传递,计算列如表格。
( 4)叠加固端弯矩和分配弯矩或传递弯矩,得各杆端的最后弯矩,作弯矩图如图所示。
( 5)根据弯矩图作剪力图如图所示。
VABMABMBA207.14 15.71 kNV ABl 247.86V BAV BA 0MABM BA20 7.14 15.71 12.14kNl 24 V BCV BC 0MBC MCB15 415.71 20 28.93 kNl24 VCBV CB 0M BCM CB15 4 15.71 20 31.07kNl243、 9-2a 利用力矩分配法计算连续梁,并画其弯矩图。
45kNq=15kN/m40kN解:( 1)计算分配系数:A0.75 EI B 1.5EICD令EI 4EI题9-2a 2m 4m 4m 4m3m 3m结点:B 0.75EIEI1.5EI 3EI 分配系数0.60.40.4 0.6SBA462 2 ,S BC43固端弯矩 -40 20-80 80 -4584分1224 3618sBA2 0.4-15.9 -31.8 -21.2BAsBAs BC2 3配3.186.36 9.544.77与sBC3-1.43 -2.86 -1.91 传0.6递0.290.57 0.860.43BCsBAsBC2 3-0.24 -0.16最后弯矩 -24.5350.93 -50.9368.28 -68.28结点:C68.281.5EI3EI,EI EIS CB4S CD 326050.938462M 图 24.5360sCB3 0.6(kN · m)CBsCBsCD3 2120sCD2 0.4CDsCBsCD3 2( 2)计算固端弯矩:固端弯矩仅由非结点荷载产生。
FPab 2 45 2 42kN m F Pba 245 4 22kN m M ABl 26240 , M ABl 26220Fql 2 15 82 10kN m, FkN mM BC1212 80M CB80F3Pl 3 40 6kN m ,FM CD161645M DC( 3)分配与传递,计算列如表格。
( 4)叠加固端弯矩和分配弯矩或传递弯矩,得各杆端的最后弯矩,作弯矩图如图所示。
4、 9-3c 利用力矩分配法计算刚架,并画其弯矩图。
10kN ·m 10kN·10kN·q =5kN/m q = 5kN/m q =5kN/m 40kN40kN40kNB C10kN · m10kN · mA 2EI2EIDA 2EIB 2EI CA 2EIB2EI Cm1.5EI1.5EI1.5EI 4(a )简化结构原结构E EE(题9-3 c4m 3m 3m 1mb)ABA BE BC2530100.375 0.375 0.25C10B(-10) -45+10/210A 15 C D10 06015 15 10E 7.50 25 15-30 10M 图( d)( c)(kN ·m)E7.57.5解:( 1)计算分配系数:SBA3 2EI1.5EI 3, S BC3 2EIEI 2, S BE4 1.5EIEI 2466令EI 2则, S BA 3, S BC2, S BE2 BAs BA30.375s BCSBE3 3 sBA2 BCs BC2 0.25 s BCS BE3 3 s BA 2BCsBE3 0.375sBCSBE3 3 sBA2( 2)计算固端弯矩:刚结点处力偶不引起固端弯矩,结点外力偶逆时针为正直接进行分配。
CD 杆段剪力和弯矩是静定的,利用截面法将外伸段从C 处切开,让剪力直接通过支承链杆传给地基,而弯矩暴露成为 BC 段的外力偶矩,将在远端引起B 、C 固端弯矩。
F, Fql 2 5 42 kN m F3Pl m 3 40 6 10kN m,M AB0 M BA8 810 M BC16 2 16 240FkN mF FkN m MAB10MEBMBE( 3)分配与传递,计算如图所示。
( 4)叠加固端弯矩和分配弯矩或传递弯矩,得各杆端的最后弯矩,作弯矩图如图所示。
9-3d 利用力矩分配法计算刚架,并画其弯矩图。
10kN10kN10kNGGGq= 10kN/m2.5EIm 20kN · m q= 2.5EI2.5kN20kN ·mq= 10kN/m2.5EI4EI310kN/m2.5kN4EIB4EIAB4EICD4EICD4EI CDm B4EI4EI4EI4EI 4EI4EI4题9-3 d简化结构EFE FE F2m4m 4m( a)( b)G20-0.5-0.558.50.5205.5CB CF CG CDD1B0.3 0.4 0.2 0.1210 0 0 -5 -5-204.5-1.5 -2 -1 -0.5 0.5M 图8.5-2-1-5.5-4.5(kN · m) 1( c)E0 F-1-1( d)解:( 1)计算分配系数:S3iCB 3 4EI3EI ,S4iCG4 2.5EI2EI ,CB4 CG5SCF4i CF4 4EI4EI , S CDiCD4EI EI44CBS CB3EI 0.3 sCBs CGSCFSCD3EI2EI 4EI EICGS CG2EI0.2 sCBsCGSCF SCD3EI2EI 4EI EICFSCF4EI0.4 sCBsCGSCFSCD3EI2EI4EI EICDSCDEI 0.1sCBsCGS CFSCD3EI2EI4EI EI( 2)计算固端弯矩: AB 杆段剪力和弯矩是静定的,利用截面法将外伸段从B 处切开,让剪力直接通过BE 杆传给地基,而弯矩暴露成为 BC 段的外力偶矩,将在远端 C 引起固端弯矩。
M BC F 20kN m M CB F m ql 2 20 10 42 10kN m2 8 2 8M CD F M DC F Pl 2.5 4 5kN m2 2M CG F M GC F 0(3)分配与传递,计算如图所示。
(4)叠加固端弯矩和分配弯矩或传递弯矩,得各杆端的最后弯矩,作弯矩图如图所示。
9-3e 利用力矩分配法计算刚架,并画其弯矩图。
36kN·m36kN·m48.5 55.5 42.25q=24kN/m 18kN q=24kN/m 18kN 18A A 108B C D B C 18kN·m42.25 37.5题9-3 eEI=常数mM 图6(kN · m)E F E F21.13 18.754.5m 6m 1m( a) ( b ) ( c)BA BE BC CB CF1/3 1/3 1/3 0.5 0.5(-36) (-18)0 0 -72 7236 36 36 18-18 -36 -366 6 6 3-0.75 -1.5 -1.50.25 0.25 0.2542.25 42.25 -48.50 018 -183 -0.750.13( d ) -18.7521.13解:( 1)计算分配系数:B刚结点:SBA 3 EI 2EI,S BC 4 EI2EI,S BE 4 EI2EI4.5 3 6 3 6 31BA BC BE3C刚结点:SCB 4 EI 2EI,S CF 4 EI2EI6 3 6 3CB CF 0.5( 2)计算固端弯矩:CD杆段剪力和弯矩是静定的,利用截面法将外伸段从 B 处切开,让剪力直接通过CF杆传给地基,而弯矩暴露成为作用于刚结点 B 的外力偶矩,将在远端C不引起固端弯矩。
M BC F ql 2 1 24 62 72kN m M BC F ql 2 1 24 62 72kN m12 12 12 12无荷载杆无固端弯矩。
(3)分配与传递,计算如图所示。
(4)叠加固端弯矩和分配弯矩或传递弯矩,得各杆端的最后弯矩,作弯矩图如图所示。
9-3h 利用力矩分配法计算刚架,并画其弯矩图。
53.31 40.05q=30kN/m 80kN 13.38 13.3760A B C D 26.68 80m题9-3 hEI=常数 4E F M 图(kN · m) ( b) 13.344m 4m 2m 2m( a)BA BC CB CF CD0.5 0.5 0.364 0.364 0.272-40 40 0 0 0 -6010.92 21.84 21.84 16.32-12.73 -25.46 -25.46 -12.732.32 4.63 4.633.47-0.58 -1.16 -1.16 -0.580.21 0.21 0.16-53.31 13.38 -13.38 13.37 26.68 -40.0510.92( c)2.320.10 13.34解:( 1)计算分配系数:B刚结点:S BAEIEI,S BC 4EI4 EI ,4 4EIBA BC 0.52EIC刚结点:SCD 3 EI 3EI, S CF 4 EI EI , S CB 4 EI EI4 4 4 4CF CBEI0.364 3EIEIEI43EICD 3EI 4 0.272 EI EI4( 2)计算固端弯矩:M BA F ql 2 1 30 42 40kN m M12 12M CD F 3Pl 3 80 4 60kN m16 16 Fql 2 1 240kN m AB1230 412M BC F M CB F M CF F0无荷载杆无固端弯矩。
