2006典型例题分析--第6章 力矩分配法
力矩分配法例题及详解

力矩分配法例题及详解1. 引言嘿,大家好!今天我们来聊聊一个听起来有点复杂,但其实非常实用的概念——力矩分配法。
首先,别被这个名字吓到了,力矩听起来就像是一种神秘的力量,但其实它和我们日常生活息息相关,像是开门、搬家具,甚至是扔飞盘,都能用上哦!接下来,我们就从一些基础概念说起,慢慢让这个看似高深的东西变得简单易懂。
2. 力矩的基本概念2.1 力矩是什么?那么,力矩到底是什么呢?简单来说,力矩就是一个力在某个点上产生的转动效果。
你可以想象一下,你在转动一个门把手。
门把手离门铰链越远,你转动的效果就越明显。
也就是说,力矩=力×距离,这里的距离就是你施力的点到铰链的距离。
明白了吗?就像你拉开冰箱门的时候,越往边上拉,门就开得越大,没错吧?2.2 力矩的方向力矩不仅仅有大小,还有方向哦!通常我们用“顺时针”和“逆时针”来描述。
比如你在玩转盘游戏时,顺时针转动力矩可以让转盘指向某个数字,而逆时针则可能指向另一个数字。
方向的不同,有时候就能让你赢得游戏,没错,力矩在生活中可真是无处不在。
3. 力矩分配法的应用3.1 生活中的例子好了,咱们说了这么多,来点实际的例子吧!想象一下你和朋友们一起搬一个大沙发。
沙发很重,大家都想用力去推,但如果每个人都往同一个方向使劲,结果可能就是沙发半天也动不了。
这时候,你就需要用到力矩分配法!大家可以分成两组,一组在沙发一端推,另一组在另一端拉,利用力矩的原理,沙发就能轻松移动,简单又有效。
3.2 力矩分配法的步骤说到这儿,大家肯定好奇,具体怎么分配力矩呢?首先,得找到一个合适的支点。
然后,大家围绕这个支点站好,确定每个人施力的方向和位置。
最后,再开始施力,看看大家的默契如何!这个过程就像打篮球一样,配合得当才能得分;而力矩分配法就能让你在各种“搬运”中轻松获胜。
4. 小结最后,总结一下今天的内容。
力矩分配法听上去复杂,但其实它的原理就是利用每个人的力量,合理分配到不同的位置,达到最佳效果。
力矩分配法剖析

力矩分配法剖析第六章力矩分配法一判断题1. 传递系数C与杆件刚度和远端的支承情况有关.( )2.力矩分配中的传递系数等于传递弯矩与分配弯矩之比,它与外因无关.( )3.力矩分配法所得结果是否正确,仅需校核交于各结点的杆端弯矩是否平衡.()4.力矩分配法经一个循环计算后,分配过程中的不平衡力矩(约束力矩)是传递弯矩的代数和.( )5.用力矩分配法计算结构时,汇交与每一结点各杆端力矩分配系数总和为1,则表明力矩分配系数的计算绝对无错误.( )6.在力矩分配法中,分配与同一结点的杆端弯矩之和与结点不平衡力矩大小相等,方向相同.( )7.力矩分配法是以位移法为基础的渐进法,这种计算方法不但可以获得近似解,也可获得精确解.( )8.在任何情况下,力矩分配法的计算结构都是16.单结点结构的力矩分配法计算结果是精确的.( )17.力矩分配法仅适用于解无线位移结构.( )18.用力矩分配法计算图示结构时,杆端AC的分配系数29/18μ.( )=AC题18图题19图题21图19.图示杆AB与CD的EI,l相等,但A端的劲度系数(转动刚度)S AB大于C端的劲度系数(转动刚度) S CD .( )20.力矩分配法计算荷载作用问题时,结点最初的不平衡力矩(约束力矩)仅是交于结点各杆端固端弯矩的代数和.( )21.若使图示刚架结点A处三杆具有相同的力矩分配系数,应使三杆A端的劲度系数(转动刚度)之比为:1:1:1.( )22. 有结点线位移的结构,一律不能用力矩分配法进行内力分析.( )23. 计算有侧移刚架时,在一定条件下也可采用力矩分配法.( )24. 有结点线位移的结构,一律不能用力矩分配法进行内力分析.( )二 选 择 题1. 图示结构汇交于A 的各杆件抗弯劲度系数之和为∑AS ,则AB 杆A 端的分配系数为: ( )A.∑=S AAB AB i /4μ B. ∑=S A AB AB i /3μC. ∑=S AAB AB i /2μD. ∑=S A AB AB i /μ题1图 题2图2. 图示结构EI=常数,用力矩分配法计算时,分配系数μ4A 为:( ) A. 4/11B.1/2C.1/3D.4/93. 在图示连续梁中,对结点B进行力矩分配的物理意义表示( )A. 同时放松结点B和结点CB. 同时固定结点B和结点CC. 固定结点B,放松结点CD. 固定结点C,放松结点B题3图题4图4.图示等截面杆件,B端为定向支座,A端发生单位角位移,其传递系数为( )A. C AB=1B. C AB =1/2C. C AB =-1D. C AB =05. 等直杆件AB的转动刚度(劲度系数)S AB :()A 与B端支承条件及杆件刚度有关B 只与B端的支承条件有关C 与A、B两端的支承条件有关D 只与A端支承条件有关6. 等直杆件AB的弯矩传递系数C AB:()A 与B端支承条件及杆件刚度有关B 只与B端的支承条件有关C 与A、B两端的支承条件有关D 只与A端支承条件有关7.当杆件刚度(劲度)系数S AB =3i时,杆的B 端为:()A 自由端B 固定端C 铰支承D 定向支承8.力矩分配法计算得出的结果()A 一定是近似解B 不是精确解C 是精确解D 可能为近似解,也可能是精确解。
结构力学——6位移法和力矩分配法

△ △
4、5、6 三个固定端都是不动的点,结点1 、2、3均无竖向位移。又因两根横梁其长 度不变,故三个结点均有相同的水平位移 FP △ 。
1
2
3
4
5
6
(a)
事实上,图(a)所示结构的独立线位移数 将结构的刚结点(包括固定支座)都变成 目,与图(b)所示铰结体系的线位移数目 铰结点(成为铰结体系),则使其成为几何 是相同的。因此,实用上为了能简捷地确 不变添加的最少链杆数,即为原结构的独 定出结构的独立线位移数目,可以 立线位移数目(见图b)。
4
5
6
(a)
共有四个刚结点,结点线位移数目为二 ,基本未知量为六个。基本结构如图所 示。
7
10 返回
5
6
(b)
例:确定图a所示连续梁的基本结构。 D B A C D B A C
(图a)
A A
B B
基本结构 基本结构
C C
D (图b) D
在确定基本结构的同时,也就确定了基本未知量及其数目。
EI
第六章
位移法和力矩分配法
§6—1 位移法的基本概念 §6—2 位移法基本未知量的确定 §6—3 位移法典型方程计算步骤和示例 §6—4 力矩分配法的基本概念 §6—5 用力矩分配法计算连续梁 §6—6 用力矩分配法计算无接点线位移刚架
1
§6—1
位移法的基本概念
一、位移法的提出(Displacement Method)
M
A
B
0
2i
r11 4i 4i 0
8EI r11 8i l
2i
M1
得
15
求自由项R1P,作出基本结构在荷载作用时的弯矩 图(MP图)。 取结点B为隔离体
《土木工程力学》-力矩分配法

土木工程力学辅导——力矩分配法1. 力矩分配法的基本运算● 三个基本概念转动刚度: 111z S M k k =k S 1:1k 杆的1用的弯矩。
分配系数: M SS M kkk )1(111=∑k 1μ:当结点1杆的1端的力矩。
传递系数: k k k M C M 111=k C 1矩的比值。
当单位力偶作用在结点1弯矩乘以传递系数。
● 一个基本运算如图1所示,各杆的转动刚度为:141413131212,4,3i S i S i S ===各杆的力矩分配系数为:∑∑∑===)1(11414)1(11313)1(11212,,kKkS S S S S S μμμ分配给各杆的分配力矩即近端弯矩为: M SS MM SS MM M SS Mkkk∑∑∑====)1(11414)1(1131312)1(11212,,μμμμ各杆的传递系数为:1,21,0141312-===C C C各杆的传递弯矩即远端弯矩为:144113131331121221,21,0M MM M C MM C MCCC -=====2.具有一个结点角位移结构的计算 步骤:●加约束:在刚结点i 处加一附加刚臂,求出固端弯矩,再求出附加刚臂给结点的约束力矩f i M 。
●放松约束:为消掉约束力矩f i M ,加-f i M ,求出各杆端弯矩。
分配系数固端弯矩分配及传递弯矩最后弯矩M图(单位:KN.m)附加刚臂对结点的约束力矩为:m KN MBf .7560135=-=● 放松结点:在结点B 上加外力偶Bf M-,求出分配弯矩和传递弯矩。
定义lEI i =转动刚度为:i i S i i S BC BC AB BA 44,33====分配系数为:57.043.0=+==+=BCAB BC BC BCBA BA BA S S S S S S μμ分配弯矩为: ()()mkN Mm kN M BCBA .25.327543.0.75.427557.0-=-⨯=-=-⨯=μμ传递弯矩为: ()mkN MM CBcABc .38.2175.42210-=-⨯==● 合并,固端弯矩+分配弯矩=近端弯矩,固端弯矩+传递弯矩=远端弯矩。
结构力学——力矩分配法分解

3 . 一般最终的杆端力矩与固端力矩是同量级的,要求精确 到三位有效数字,计算中取4位计算,以保证前三位的 精确度
第三节 多结点力矩分配法
计算的指导思想由两个步骤说明:
固定状态的计算(与单点固定一样)。
即刚臂→荷载→固端力矩→约束力矩;
100k0N
EI
1 EI
2 EI
0.43 0.57 0.57 0.43
-500 -1000
M3B=1000
例题:有支座移动(已知结点线位移)E=200GPa,I = 2500cm4
绘制弯矩图。
A
B
C
D
EI
EI
=1cm
10m
10m
10m
0.429 0.571
0.571 0.429
MF
3000
3000 -1500
2 . 不相邻 点可同时 释放.
例题:用力矩分配法求图示结构弯矩图(利用传递系数的概念) 。
A
EI
10m
1 EI
10m
100k0N 2 EI 3 B 3B是悬臂梁,
转动结点3 时,
10m 1m 悬臂可自由转
0.43 0.57 0.5 0.5 1 0
动,固其转动
MF
1000 刚度为零
或A
MF
100k0N
放松状态的计算(与单点放松不同)。
力矩的分配和传递是在远端约束已知的情况下进行的, 因此,分配单元的相邻结点不应同时放松。每次只能 放松一个结点,同时相邻结点保持固定,所以,整个 放松过程是轮流放松每一个结点来逐步完成的。
第三节 多结点力矩分配法
结构力学第六章超静定结构的计算——力矩分配法

《结构力学》习题集- 33 -第六章 超静定结构的计算——力矩分配法一、本章基本内容:1、基本概念:转动刚度、分配系数、传递系数、侧移刚度;(1)力矩分配法是以位移法为基础的一种渐进解法;(2)转动刚度与杆件的线刚度和远端支承情况有关;(3)杆件远端的支承情况不同,相应的传递系数也不同;(4)分配系数的值小于等于1,并且1=∑ik μ;(5)力矩分配法只适用于计算无结点线位移的结构。
2、固端力矩、结点不平衡力矩的计算;3、用力矩分配法计算多跨梁和无侧移刚架的一般步骤:(1)计算汇交于各结点的每一杆端的分配系数并确定传递系数;(2)求出各杆件的固端弯矩;(3)求出结点不平衡力矩,将其反号乘上各杆件的分配系数得到相应的分配弯矩。
然后,再将分配弯矩乘以传递系数,求出远端的传递弯矩。
按此步骤循环计算,直到不平衡力矩小到可以忽略不计为止。
(4)将每一杆端的固端弯矩、历次的分配弯矩和传递弯矩相加,求出最后杆端弯矩。
(5)校核最后杆端弯矩,作内力图。
二、习题:(一)、判断题(不作为考试题型):1、力矩分配法中的分配系数、传递系数与外来因素(荷载、温度变化等)有关。
2、若图示各杆件线刚度i 相同,则各杆A 端的转动刚度S 分别为:4 i , 3 i , i 。
AA A3、图示结构EI =常数,用力矩分配法计算时分配系数4 A μ= 4 / 11。
1l ll第六章 力矩分配法- 34 -4、图示结构用力矩分配法计算时分配系数μAB =12/,μAD =18/。
BCA D E =1i =1i =1i =1i5、用力矩分配法计算图示结构,各杆l 相同,EI =常数。
其分配系数μBA =0.8,μBC =0.2,μBD =0。
A B CD6、在力矩分配法中反复进行力矩分配及传递,结点不平衡力矩愈来愈小,主要是因为分配系数及传递系数< 1。
7、若用力矩分配法计算图示刚架,则结点A 的不平衡力矩为 −−M Pl 316。
结构力学中的力矩分配法

B EI=3
3m
30kN/m C EI=4
6m
D
0.4 0.0
0.6 -225.0
0.5
0.5
+225.0 -135.0 +67.5 -78.8 -78.7 +11.8 -5.9 -5.9 +0.9 -0.5 -0.4 +220.0 -220.0 220 135
0.0 0.0 0.0 0.0
+90.0 +135.0 -39.4 +15.8 +23.6 -3.0 +1.2 +1.8 +107.0 -107.0 107 135
例6−4 用力矩分配法计算图9−8(a)所示的刚架,并绘M图。 用力矩分配法计算图 ( )所示的刚架,并绘 图
80kN A EI B EI EI C EI EI 30kN/m D
52.04 120 A
91.84 75.92 135 15.92 B B
62.33 26.72 D C C 35.63
6m
6.3 无剪力分配法
一、无剪力分配法的应用条件
P P P P/2 P/2 P/2 P/2 P/2 P/2 P/2 P/2 P/2 P/2 P/2 P/2
P/2 F P/2 D P/2 B A G
F P/2
E C
D P B 3P/2 A
刚架中除两端无相对线位移的杆件外,其余杆件都是剪力静定杆件。
二、无剪力分配法的解题步骤
= 4 i12 φ1 = S 12 ϕ 1 = 3 i13 φ1 = S 13 ϕ 1 = i14 φ1 = S 14 ϕ 1 = 4 i15 φ1 = S 15 ϕ 1 − − − (a)
第6章 章
建筑力学讲义之力矩分配法

13 力矩分配法力法和位移法的优点是计算结果准确可靠。
力矩分配法,是一种渐近计算法。
简便。
只适合于连续梁及无侧移刚架的计算。
13.1 力矩分配法的基本原理1、名词解释(1)转动刚度: 111z S M k k =:1k 杆的1端产生单位转角时,在该端所需作用的弯矩。
(2)分配系数:MM S S M k kk k1)1(111μ==∑ k 1μ:当结点1处作用有单位力偶时,分配给1k 杆的1端的力矩。
(3)传递系数:k k k M C M 111=:当杆件近端发生转角时,远端弯矩与近端弯矩的比值。
当单位力偶作用在结点1时,按分配系数分配给各杆的近端为近端弯矩;远端弯矩等于近端弯矩乘以传递系数。
2、力矩分配法的基本原理(1)计算各杆的分配系数=(2)由分配系数计算近端的弯矩。
=M(3)计算各杆的远端弯矩。
= C A k3、非结点荷载作用下单结点结构的计算 力矩分配法的计算步骤如下:(1)固定结点B ,即在结点B 加附加刚臂。
计算各杆的固端弯矩,并求出结点不平衡力矩F BK F B M M ∑=。
(2)放松结点B ,相当于在结点B 加力矩-。
计算下列各项 分配系数B BKBKS S ∑=μ分配弯矩 BK μ=(-)传递弯矩 μBK BK M C =(3)叠加,计算各杆杆端最后弯矩μBK F BKBK M M M +=CKB F KB KB M M M +=13.2力矩分配法计算连续梁及无侧移刚架1.掌握力矩分配法中正负号规定。
理解转动刚度、分配系数、传递系数概念的物理意义;掌握它们的取值。
能够根据远端的不同支承条件熟练地写出各种情形的杆端转动刚度、向远端的传递系数,并计算分配系数。
2.通过单结点的力矩分配法,理解力矩分配法的物理意义,掌握力矩分配法的主要环节:(1) 固定刚结点。
对刚结点施加阻止转动的约束,根据荷载,计算各杆的固端弯矩和结点的约束力矩;(2) 放松刚结点。
根据各杆的转动刚度,计算分配系数,将结点的约束力矩相反值乘以分配系数,得各杆的分配弯矩;(3) 将各杆端的分配弯矩乘以传递系数,得各杆远端的传递弯矩。
力矩分配法计算超静定结构典型例题(附详细解题过程)

力矩分配法计算超静定结构——典型例题
【例1】用力矩分配法作如图1(a)所示连续梁的弯矩图。
已知EI 为常数。
【解】该连续梁为对称结构承受对称荷载作用,可取如图1(b)所示左半结构来分析。
此时,只有一个结点转角,可以采用力矩分配法进行分析,这里记线刚度。
计算结点B 处的分配系数:
,
, 在结点B 加入附加刚臂,计算由荷载单独作用时产生的各杆端固端弯矩值
, 附加刚臂中产生的约束力矩为:
放松结点B ,力矩分配和传递的过程如图1(c)所示。
根据最后的杆端弯矩可先绘制半结构的M 图,再根据对称性可绘出整个结构的M 图,如图1(d)所示。
/i EI l =3BA S i =4BC S i =BA 3
7μ=BC 47
μ=12F AB M Fl =-14
F BA M Fl =-14
B M Fl =
-
图1
【例2】用力矩分配法作如图2(a)所示刚架的弯矩图。
已知EI 为常数。
【解】该对称刚架承受对称荷载作用,可取如图2(b)所示半结构来分析,可采用力矩分配法分析,记线刚度。
计算结点A 处的分配系数:
,
在结点A 加入附加刚臂,各杆均无固端弯矩,附加刚臂中产生的约束力矩为:
放松结点B ,将约束力矩反号后进行分配和传递,可得各杆端的分配、传递弯矩分别为:
根据各杆端弯矩值可绘制结构构的M 图,如图2(c)所示,为对称的图形。
/i EI l =3AB S i =A 3C S i =AB AC 0.5μμ==A M Fl =-12
AC AB M M Fl μμ==0C C CA BA M M ==。
力矩分配法

注意:μ12+μ13+μ14=1 C13=1/2
C12=0
C14=-1 结论
计算简图
远端支承
转动刚度
传递系数
A MAB
θ=1
B MBA B MBA B
固定 铰支
SAB=4i
SAB=3i
CAB=1/2
θ=1 A M
AB
CAB=0
A MAB
θ=1
滑移
MBA
SAB=i
CAB=-1
A MAB
θ=1
B MBA
例2.如图连续梁,用力矩分配法计算并绘弯矩图。
2)加约束确定固端弯矩 和不平衡力矩
M M M
f BC
f
CB
f
CD
1 pl 60kNm 8 1 pl 60kNm 8 1 2 ql 90kNm 8
例2.如图12所示,用力矩分配法计算并绘弯矩图。
1)计算各结点的分配系数 结点B:
第6章 力矩分配法
学习目标
1.牢记力矩分配法的使用条件是没有结点 线位移。 2.掌握力矩分配法计算连续梁和无结点线 位移刚架。
学习重点
力矩分配法计算连续梁 1)计算转动刚度、分配系数和传递系 数; 2)计算各杆固端弯矩和不平衡力矩。 3)不平衡力矩的分配和传递 4)最后杆端弯矩的计算。
第一节 力矩分配法的基本概念
80kN A 3m 3m 80kN A
120 15
B 6m
C 6m
10kN D
10kN 120 120kNm
B C 6m
3m 分配系数 固端弯矩 分配弯矩
3m
单位:kNm
0.5 0 0 90 -75
0.5 60 -75 120 0
力矩分配法

例1 用力矩分配法计算图示连续梁。 结点。列表计 算如下: 分配系数µ 固端弯矩MF -300
结点1分配传递 +75 结点2分配传递 结点1分配传递 +16 结点2分配传递 结点1分配传递 +1 结点2分配传递
解:定1` 2 固
25kN/m
400kN
25kN/m
0
1
EI 12m EI 6m 6m
MAB =i
A
EI
L SAB=MAB=4i
B
MBA =2i
EI
SAB=MAB=3i
B
A
EI
SAB=MAB=i
B
1 A
MAB
MBA =-i
EI
SAB=MAB=0
B
4
远端滑动支撑: CAB=-1
杆端弯矩正负号规定
在力矩分配法中对杆端转角、杆端弯矩、固端弯矩的正负号规 定与位移法相同,即都假定对杆端顺时针转动为正号。作用于 结点上的外力偶荷载,约束力矩,也假定顺时针转动为正号, 而杆端弯矩作用于结点上时逆时针转动为正号。
2
EI 12m
3
0.5 0.5 -300 +300 -600 +150 +150 -64 +32 +32 -5 +2 +3 +484 -484
0.571 0.429 +150 +600 -450 +75 +225 -225 -129 -96 +16 -9 -7 +1 -1 0 +553 -553
8
0 0 0
MAB =o
力矩分配法的基本原理
1.劲度系数、传递系数
1
力矩分配法计算步骤

力矩分配法计算步骤
嘿,朋友们!今天咱就来好好唠唠力矩分配法的计算步骤。
你想想啊,这力矩分配法就像是搭积木,得一块一块稳稳地往上放。
第一步呢,就是要把结构拆分成一个个杆件,这就好比把一个大拼图
拆成小块,得拆得仔细,不能有遗漏。
然后呢,要计算各个杆件的转动刚度。
这可不能马虎,就像给每个
小积木标上它的重要性一样。
每个杆件都有它自己的“分量”呢!
接着呀,就是确定刚节点处的不平衡力矩。
这就好像是找到积木堆
里不平衡的地方,得想办法让它平衡起来。
之后呢,就开始分配力矩啦!把不平衡力矩按照转动刚度的比例分
配给各个杆件,这就像把多的积木往少的地方匀一匀。
分配完了还不算完哦,还得传递呢!就像是把匀过去的积木再传递
到其他地方,让整个结构都能稳稳当当的。
在这过程中,可别小看了每一步的计算和处理,稍有差错,那可就
像搭积木歪了一块,后面可能就全乱套啦!
你说这力矩分配法是不是很有意思?就像是在玩一个精细的游戏,
每一步都得小心翼翼,又得充满智慧。
咱再打个比方,这力矩分配法就如同做菜,杆件就是各种食材,转动刚度是调料的用量,不平衡力矩是食材搭配的不协调,分配和传递就是翻炒、搅拌的过程,最后得出一道完美的“结构大餐”。
所以啊,大家在学习力矩分配法计算步骤的时候,可一定要认真仔细,把每一个环节都搞清楚,弄明白。
这样才能在实际运用中游刃有余呀!
总之呢,力矩分配法的计算步骤虽然有些复杂,但只要我们用心去学,就一定能掌握好它。
就像攀登一座高峰,虽然过程艰难,但登顶后的风景绝对值得我们付出努力呀!加油吧,朋友们!让我们一起征服力矩分配法这座“山峰”!。
力矩分配法

M图(kN· m)
CBA 1
3
6.61
27
3.5
17kN B 5 C 4kN A 54 3.5 8.5kN B 54 5 C -6.6 4kN -6.6
3.5 27
5
7.05 0.0211 7.05 -6.6 -0.6 0.15 -6.6 -7.05 0.6 -0.15 0 -6.15
B
0.9501 0.0206 0.0293
M F -150
M -17.2 传 M
分
0.571 0.429 150
-34.3
-90
-25.7 0
M -167.2
167.2 300 A
115.7 -115.7 115.7 90 B M图(kN· m)
0
4i 0.571 4i 3i 3i BC 0.429 7i (2)计算固端弯矩 200 6 F 150 kN m MAB = 8 150 kN m MF BA = 2 20 6 90kN m MF BC = 8 (3)计算力矩分配与传递
Aj
S
A
S Aj
A
A
M Aj Aj ( M1不)
分配系数
1
五、传递系数 MAB = 4 iAB A
近端 A A l
MBA = 2 iAB A
远端 B
C AB
M BA 1 M AB 2
MAB = 3iABA
A
A
MAB= iABA
B
C AB
M BA 0 M AB
BA
C
(4)计算弯矩并作图
例2.用力矩分配法计算图示连续梁。 100kN 20kN/m A EI=1 6m B 0.4 0.6 60 -100 -33.4 29.4 44 -7.3 2.9 0.3 4.4 -0.7 0.4 EI=2 4m 4m 0.667 0.333 100 C EI=1 6m D
第6章 力矩分配法

§6-1 力矩分配法的基本概念
理论基础:位移法;
力矩分配法
计算对象:杆端弯矩; 计算方法:逐次渐近的方法; 适用范围:连续梁和无侧移刚架。
一、力矩分配法中的几个概念:
1.转动刚度Sij:使等截面直杆某杆端旋转单位角度=1时,在
该端所需施加的力矩。表示杆端对转动的抵抗能力
在数值上 = 仅使杆端发生单位转动时需在杆端施加的力矩。
B
0.4
CB 0.445 CD 0.333 0.222 CF
C
4m
5m
2m
mBA= 40kN· m mBC= - 41.7kN· m mCB= 41.7kN· m 0.3 B 40 3.3 0.445 41.7 -18.5 2.2 -1.0 -0.5 -0.7 24.4 -9.8 -14.6 -4.65 -0.25 -4.90
M ki M ik 1 2 远端为固定端 0 远端为铰支端 1 远端为平行支链杆
C ik
§6-1 力矩分配法的基本概念
B A MAB MBA MB A MFAB MFBA MFBC MBC C 固端弯矩带本身符号 MB MFBA MFBC
=
C
MFBC MB= MFBA+ -MB
例题
B q i A l i C l 0.8 0.2 ql2/12
C
-4ql2/60 ql2/60
-ql2/60 -ql2/60
ql2/60 ql2/60
ql2/60
M图
7ql2/60
-ql2/12 -2ql2/60 -7ql2/60
A
§6-2:单结点的力矩分配——基本运算
练习
i
k
典型例题分析第6章力矩分配法
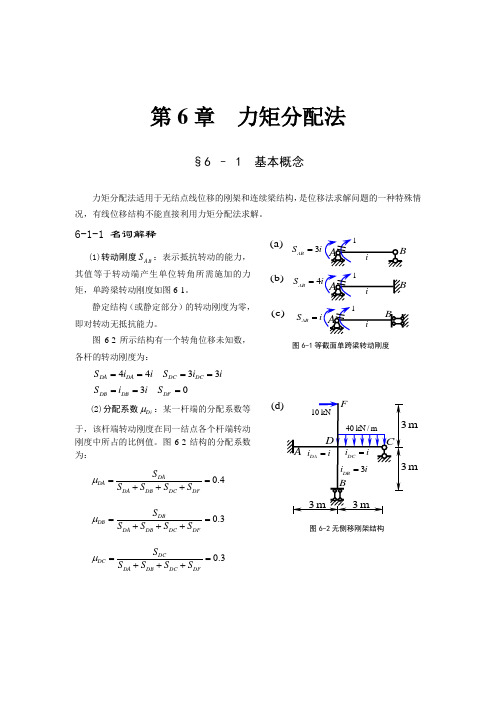
第6章 力矩分配法§6 – 1 基本概念力矩分配法适用于无结点线位移的刚架和连续梁结构,是位移法求解问题的一种特殊情况,有线位移结构不能直接利用力矩分配法求解。
6-1-1 名词解释(1)转动刚度A B S :表示抵抗转动的能力,其值等于转动端产生单位转角所需施加的力矩,单跨梁转动刚度如图6-1。
静定结构(或静定部分)的转动刚度为零,即对转动无抵抗能力。
图6-2所示结构有一个转角位移未知数,各杆的转动刚度为:4433DA DA DC DC S i i S i i ==== 30DB DB DF S i iS ===(2)分配系数Di μ:某一杆端的分配系数等于,该杆端转动刚度在同一结点各个杆端转动刚度中所占的比例值。
图6-2结构的分配系数为:0.4DADADA DB DC DFS S S S S μ==+++ 0.3DBDB DA DB DC DFS S S S S μ==+++0.3DCDC DA DB DC DFS S S S S μ==+++图6-2无侧移刚架结构)b ()c ((a)3AB S i =4AB S =AB S =(d)图6-1等截面单跨梁转动刚度mm0DFDF DA DB DC DFS S S S S μ==+++(3)弯矩符号规定:力矩分配法在计算过程中不需要画弯矩图,只是以数值形式进行计算,因此,需要事先对力矩和弯矩符号进行规定,具体规定如下:固端弯矩:顺时针为正。
结点外力偶:顺时针为正。
(4)固端弯矩F i j M :将转动结点固定变成位移法的基本体系,外荷载在基本体系上产生的杆端弯矩。
如图6-2结构的固端弯矩为:F F F F F F 0DA DA DB BD CD FD M M M M M M ======F 2145kN m 8DC M ql -==-⋅ F 30kN m DF M =-⋅(5)不平衡力矩u D M :不平衡力矩为转动结点所连杆端的固端弯矩之和,其值等于刚臂反力矩。
力矩分配法习题解答

1、清华5-6 试用力矩分配法计算图示连续梁,并画其弯矩图和剪力图。
C清华V图M(kN解:(1)计算分配系数:320.632440.4324BABABA BCBCBCBA BCs is s i is is s i iμμ⨯===+⨯+⨯⨯===+⨯+⨯(2)计算固端弯矩:固端弯矩仅由非结点荷载产生,结点外力偶不引起固端弯矩,结点外力偶逆时针为正直接进行分配。
3360667.51616FABFBAMPlM=⨯⨯===⋅kN m(3)分配与传递,计算列如表格。
(4)叠加固端弯矩和分配弯矩或传递弯矩,得各杆端的最后弯矩,作弯矩图如图所示。
(5)根据弯矩图作剪力图如图所示。
0153027.60153032.63517.58.756AB BA AB AB AB BA BA BA BC CB BC CB M M V V l M M V V l M M V V l ++=-=-=++=-=--=+--==-=-=5kN 5kN kN2、利用力矩分配法计算连续梁,并画其弯矩图和剪力图。
4m1m2m2m原结构简化结构·解:(1)计算分配系数:,4,34BA BC BA BC EIi i i S i S i =====令 430.4290.5714343BC BA BA BC BA BC BA BC s s iis s i is s i iμμ======++++(2)计算固端弯矩:CD 杆段剪力和弯矩是静定的,利用截面法将外伸段从C 处切开,让剪力直接通过支承链杆传给地基,而弯矩暴露成为BC 段的外力偶矩,将在远端引起B 、C 固端弯矩。
22204101088154102020828F FAB BA F F BCCB Pl M M ql m M M ⨯=-=-=-⋅⋅⨯=-+=-+=-⋅=⋅kN m,=kN m kN m,kN m(3)分配与传递,计算列如表格。
(4)叠加固端弯矩和分配弯矩或传递弯矩,得各杆端的最后弯矩,作弯矩图如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第6章 力矩分配法
§6 – 1 基本概念
力矩分配法适用于无结点线位移的刚架和连续梁结构,是位移法求解问题的一种特殊情况,有线位移结构不能直接利用力矩分配法求解。
6-1-1 名词解释
(1)转动刚度AB S :表示抵抗转动的能力,其值等于转动端产生单位转角所需施加的力矩,单跨梁转动刚度如图6-1。
静定结构(或静定部分)的转动刚度为零,即对转动无抵抗能力。
图6-2所示结构有一个转角位移未知数,各杆的转动刚度为:
4433DA DA DC DC S i i S i i ==== 30DB DB DF S i i S ===
(2)分配系数Di μ:某一杆端的分配系数等于,该杆端转动刚度在同一结点各个杆端转动刚度中所占的比例值。
图6-2结构的分配系数为:
0.4DA
DA DA DB DC DF
S S S S S μ==+++
0.3DB
DB DA DB DC DF
S S S S S μ=
=+++
0.3DC
DC DA DB DC DF
S S S S S μ=
=+++
图6-2无侧移刚架结构
)b ()
c (
(a)
3AB S i
=4AB S =AB S =(d)
图6-1等截面单跨梁转动刚度
2 结构力学典型例题解析
0DF
DF DA DB DC DF
S S S S S μ=
=+++
(3)弯矩符号规定:力矩分配法在计算过程中不需要画弯矩图,只是以数值形式进行计算,因此,需要事先对力矩和弯矩符号进行规定,具体规定如下:
固端弯矩:顺时针为正。
结点外力偶:顺时针为正。
(4)固端弯矩F i j M :将转动结点固定变成位移法的基本体系,外荷载在基本体系上产生的杆端弯矩。
如图6-2结构的固端弯矩为:
F F F F F F 0DA DA DB BD CD FD M M M M M M ====== F 2
145kN m 8
DC M ql -=
=-⋅ F 30kN m DF M =-⋅
(5)不平衡力矩u D M :不平衡力矩为转动结点所连杆端
的固端弯矩之和,其值等于刚臂反力矩。
如图6-3为荷载引起的不平衡力矩u
D M
,此时就是位移法典型方程的
1P R :
F F F F
1P u D DA DB DC DF M R M M M M ==+++ 75kN m u
D M =-⋅
(6)被分配力矩M :M 等于不平衡力矩u D M 的负值;
若该转动结点有外力矩,外力矩可以直接进行分配,此时外力矩是被分配力矩的一部分。
如图6-3被分配力矩为:
75kN m u D M M =-=⋅
(7)分配弯矩Di M :某一杆端的分配弯矩Di M 等于该杆端的分配系数Di μ乘以被分配力矩
M 。
如图6-3结构的分配弯矩为:
30kN m DA DA M M μ==⋅ 22.5k N m D B D B M M μ==⋅ 22.5kN m DC DC M M μ==⋅ 0D F D F
M M μ== (8)传递系数AB C :传递系数AB C 只与另一端(远端,即B 端)的支座情况有关,远端为定向支座时其值为-1,远端为固定支座时其值为0.5,远端为铰支座(包括自由端)时其值为0。
如图6-3结构的传递系数为:
0.5DA C = 1DB C =- 0DC C = 0DF C =
图6-3不平衡力矩
F DC F M DB
F
第6章 力矩分配法 3
(9)传递弯矩iD M :iD M 等于近端的分配弯矩Di M 乘以传递系数iD C 。
如图6-3结构的传递弯矩为:
15kN m AD DA DA M C M ==⋅ 22.5k N m B D D B D B M C M ==-
⋅ 0CD DC DC M C M == 0F D D F D F M C M ==
6-1-2 力矩分配法的解题步骤
●未知数分析:首先确定结构转角位移个数;力矩分配法只能计算无线位移的结构,若有线位移则不能利用常规力矩分配法进行计算。
●计算转动刚度:施加刚臂约束,得到位移法基本体系;利用形常数得到各个杆端的转动刚度。
●计算分配系数:每个可转动结点杆端的分配系数,由该结点各个杆端的转动刚度所占的比例求得。
●计算固端弯矩:利用位移法的基本体系,作荷载弯矩图,杆端弯矩即是所求的固端弯矩,固端弯矩以顺时针方向为正,逆时针方向为负。
●计算不平衡力矩:施加刚臂的结点存在不平衡力矩,其值等于刚臂所连结点的各杆端固端弯矩之和。
●计算被分配力矩:不平衡力矩的负值,外力矩可以直接分配,即外力矩按照顺时针方向为正直接加入被分配力矩。
●计算分配弯矩和传递弯矩:某个杆端的分配弯矩等于该杆端的分配系数乘以被分配力矩;该分配弯矩乘以传递系数就等于远端的传递弯矩。
●计算最终弯矩:利用叠加原理将同一杆端的固端弯矩与分配弯矩(或传递弯矩)相加即得到杆端的最终弯矩。
●求解注意:
单点分配:只有一个转角位移未知数的结构,经过一轮分配、传递完成求解,即所求结果为精确解。
多点分配:当有两个或两个以上转角位移未知数。
需要逐个放松刚臂约束分配每个结点,先分配不平衡力矩大的结点,且相邻结点不能同时分配,经过多轮分配与传递可以得到所需要精度的解,结果为近似解。
§6 – 2 典型例题
4结构力学典型例题解析
第6章力矩分配法5
6结构力学典型例题解析
第6章力矩分配法7
8结构力学典型例题解析
第6章力矩分配法9
10结构力学典型例题解析
第6章力矩分配法11
12结构力学典型例题解析。
