隐含圆的动点问题

合集下载

例谈几类常见的“隐藏圆”问题

为
常数
，犃，犅
为定
点．利
用
求
动
点
５２
微专题突破
轨迹方程的一般方法，可得动点犘的轨迹为圆．因此这也是一种形式的“隐藏圆”，不妨称之为“数量积圆”．
三、阿波罗尼斯圆
例３（２００８年江苏卷第１３题）在△犃犅犆中，已知犃犅＝２，犃犆＝槡２犅犆，则△犃犅犆面
积的最大值为．
●●分析本题表面上看是一个解三角形的问题，因此利用余弦定理、面积公式，将
的取值范围为．
●●分析类似于例３，建立平面直角坐标系后，用求轨迹方程的一般方法，可得（１）（２）中
（）（）点犆的轨迹均为圆，所以求面积最大值的方法与例３相同．（３）中，设犆（狓０，狔０），则
｜狓０－狔０＋１｜
槡２
２＋
｜狓０＋狔０－１｜
槡２
２＝４，化简得
狓２０＋（狔０－１）２＝４，即点
槡（）的最大值．而由弦长公式可得动点犇到圆心犆的距离犇犆＝狉２－犃２犅２＝１，由圆的定义
可得动点犇在以犆为圆心，１为半径的圆上．所以问题最终转化为圆上的动点犇到定点犗
的距离的最大值．由几何关系可得犇犗最大值为犆犗＋１＝４，所以答案为８．
●●评注本题可得出如下结论：若已知圆的一条弦长为定值（小于直径），则此弦的中点
知识可得犱的最大值为半径２槡２，所以面积最大值为２槡２．
●●评注由例３可得出，若动点犆到两定点犃，犅的距离之比犆犆犅犃＝λ（其中λ 为正常
数），则动点犆的轨迹为圆．这种“隐藏圆”最初是由古希腊数学家阿波罗尼斯发现，因此我们称之为“阿波罗尼斯圆”．
四、平方和（差）圆
例４（１）在△犃犅犆中，已知犃犅＝２，犆犃２＋犆犅２＝８，则△犃犅犆面积的最大值为

2024河南中考数学习微专题利用“隐形圆”解决动点问题课件

1
（3）的最小值为_ ________.
模型总结
1.知识依据：的圆周角所对的弦是直径（圆周角定理的推论）.
2.模型说明：（1）如图（1），在中，，若的长固定，则点的运动轨迹为以为直径的不含点， .
图（1）
图（2）
（2）如图（2），和共斜边，则，，，四点共圆，均在以为直径的上.（确定四点共圆后，可根据圆周角定理的推论得到角相等，完成角度的等量转化）
强化训练
7.[2023四川达州] 在中，，，在边上有一点，且，连接，则的最小值为__________．
▶▶ 完成练习册相关习题
作业：
提分技法圆上的点到，过点作于点，交优弧于点，交劣弧于点 ,则的长为上的点到的最大距离，的长为劣弧上的点到的最大距离._
如图，是外一条直线，过点作于点 ,交于点 , ，则上的点到的最大距离为的长，最小距离为的长._
强化训练
4.如图，在平行四边形中, ，，，点是平行四边形内部的一个动点,且 ,则线段的最小值为_ ________.
（第5题）
5.如图，正方形的边长为6，点 , 分别从点 , 同时出发，沿着射线 ,射线匀速运动（二者速度相等）.设直线与直线交于点，连接，则线段的长度的最小值为_ ________.
（1） _____ ；
120
（2）点在以线段为弦，且所对圆心角为_____ 的圆上运动，在图中画出该圆；
120
[答案] 图略.
（3）的最小值为_ ____.
模型总结
1.知识依据：在同圆或等圆中，同弧或等弧所对的圆周角相等（圆周角定理的推论）.如图（1）, .

数学隐形圆问题解题技巧

数学隐形圆问题解题技巧1. 嘿，你知道吗？遇到那种动点问题，别慌！比如有个点在一个图形上运动，这时候就要想到隐形圆啦。

就好像一只小老鼠在迷宫里乱跑，咱们得找到它的规律呀！比如在一个直角三角形里，斜边就是那个“隐形成员”，动点到斜边中点的距离始终不变，这不就是个隐形圆嘛。

2. 哇塞，还有一种情况也会有隐形圆哦！当几个固定的点到一个动点的距离相等时，这不就是圆的定义嘛。

就好比一群小朋友围着一个大哥哥，这个大哥哥就是圆心呀！比如四边形的四个顶点到某点距离相等，那隐形圆不就出来啦。

3. 嘿呀，你想想，要是给你一些角度条件呢？当固定的边所对的角是定值的时候，也能发现隐形圆呀！就像一部精彩的电影，有了关键情节就能猜到后面的发展，比如一个三角形，一条边固定，它所对的角一直是 60 度，这不就是隐形圆在向你招手嘛。

4. 还有呢！当有两个动点，它们到同一点的距离比值是定值时，也可能有隐形圆哦。

这就像两个小伙伴比赛跑步，速度有个固定比例，那就能找出其中的秘密啦！比如两个点到另一个点的距离一直是 2 比 1，那隐形圆可能就藏在里面哟。

5. 哎呀呀，再告诉你一个秘密哦。

要是有几条线段长度不变，互相垂直呢？对啦，隐形圆就藏在那里！就像一个神奇的魔法阵，只要发现了就能破解谜题啦。

比如三条线段组成一个直角三角形，那这个直角三角形的外接圆不就是隐形圆嘛。

6. 你可别小瞧这些隐形圆呀！它们就像隐藏在数学世界里的宝藏，等你去发现呢。

比如在一些几何图形中，乍一看没啥特别，但是仔细一分析，哇，隐形圆出现啦！就像突然找到了宝藏的入口一样兴奋。

7. 总之呀，数学隐形圆问题有很多技巧呢，只要多观察多思考，就能找到它们。

不要怕难题，就像爬山一样，一步步往上爬，总会看到美丽的风景呀！记住这些技巧，以后再遇到隐形圆问题，就不会头疼啦，可以轻松搞定它们！我的观点就是，只要用心去钻研，数学隐形圆问题并不难，反而会很有趣呢！。

初中数学冲刺重难点：隐圆问题的7种模型

初中数学冲刺重难点：隐圆问题的7种模型初中数学中的隐圆问题是一个较为复杂的概念，涉及多种模型。

以下是七种常见的隐圆模型：模型一：动点到定点的距离等于定长在这个模型中，一个动点到一个固定点的距离始终等于一个定长。

这个模型可以通过在圆上任意选择一个点，并连接该点和圆心，形成一个半径，然后通过旋转半径来寻找符合条件的点。

模型二：定点到动点的距离随动点的移动而变化在这个模型中，一个定点到另一个动点的距离会随着动点的移动而不断变化。

这个模型可以通过在圆上选择一个定点，并连接该点和圆心，形成一个半径，然后移动半径来寻找符合条件的点。

模型三：直角所对的直径在这个模型中，一个直径所对的圆周角必须是直角。

这个模型可以通过在圆上选择一个点，并连接该点和圆心，形成一个直径，然后通过旋转直径来寻找符合条件的点。

模型四：四点共圆在这个模型中，四个点都在同一个圆上。

这个模型可以通过在圆上选择四个点，并连接这四个点形成一个四边形，然后通过旋转四边形的边来寻找符合条件的点。

模型五：三角形外接圆在这个模型中，一个三角形有三个顶点，这三个顶点都在同一个圆上。

这个模型可以通过在圆上选择三个点，并连接这三个点形成一个三角形，然后通过旋转三角形的边来寻找符合条件的点。

模型六：圆与多边形的内切与外接在这个模型中，一个圆与一个多边形相切或相离。

这个模型可以通过在圆上选择一个点，并连接该点和圆心，形成一个半径，然后通过旋转半径来寻找符合条件的点。

模型七：两圆相交、相切、相离在这个模型中，两个圆相交、相切或相离。

这个模型可以通过在两个圆上分别选择两个点，并连接这两组对应点形成两个直径，然后通过旋转直径来寻找符合条件的点。

2020年九年级数学中考专题复习：隐形圆求最值问题(含答案)

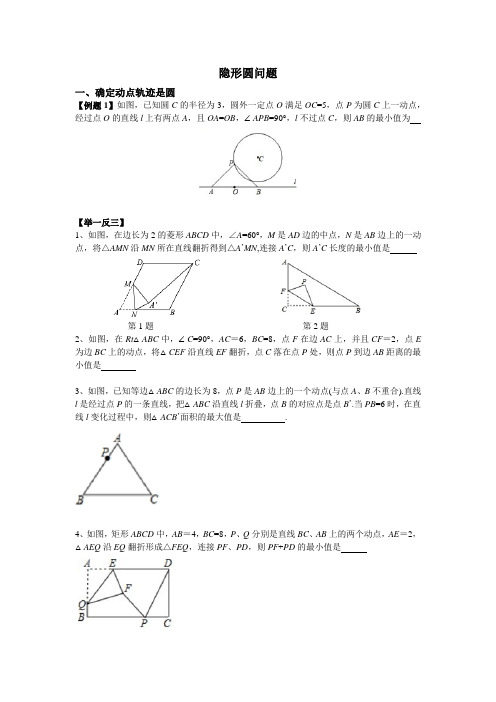
隐形圆问题一、确定动点轨迹是圆【例题1】如图，已知圆C的半径为3，圆外一定点O满足OC=5，点P为圆C上一动点，经过点O的直线l上有两点A，且OA=OB，∠APB=90°，l不过点C，则AB的最小值为【举一反三】1、如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A’MN,连接A’C，则A’C长度的最小值是第1题第2题2、如图，在Rt△ABC中，∠C=90°，AC＝6，BC=8，点F在边AC上，并且CF＝2，点E 为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是3、如图，已知等边△ABC的边长为8，点P是AB边上的一个动点(与点A、B不重合).直线l是经过点P的一条直线，把△ABC沿直线l折叠，点B的对应点是点B’.当PB=6时，在直线l变化过程中，则△ACB’面积的最大值是.4、如图，矩形ABCD中，AB＝4，BC=8，P、Q分別是直线BC、AB上的两个动点，AE＝2，△AEQ沿EQ翻折形成△FEQ，连接PF、PD，则PF+PD的最小值是二、定边对直角知识回顾:直径所对的圆周角是直角构造思路:一条定边所对的角始终为直角，则直角顶点轨迹是以定边为直径的圆或圆弧.图形释义:若AB是一条定线段，且∠APB-90°，则P点轨迹是以AB为直径的圆【例题1】已知正方形ABCD边长为2，E、F分别是BC、CD上的动点，且满足BE＝CF，连接AE、BF，交点为P点，则PC的最小值为【举一反三】1、如图，E、F是正方形ABCD的边AD上的两个动点，满足AE＝DF，连接CF交BD于点G，连接BE交AG于点H，若正方形边长为2，则线段DH长度的最小值是2、如图，Rt△ABC中，AB⊥BC，AB=6，BC＝4，P是△ABC内部的一个动点，且满足∠P AB ＝∠PBC，则线段CP长的最小值是3、如图，AB是半圆O的直径，点C在半圆O上，AB＝5，AC＝4.D是弧BC上的一个动点，连接AD，过点C作CE⊥AD于E，连接BE.在点D移动的过程中，BE的最小值为4、如图，在Rt△ABC中，∠BAC=90°，AC＝12，AB＝10，点D是AC上的一个动点，以AD为直径作圆O，连接BD交圆O于点E，则AE的最小值为5、如图，正方形ABCD的边长为4，动点E、F分別从点A、C同时出发，以相同的速度分别沿AB、CD向终点B、D移动，当点E到达点B时，运动停止，过点B作直线EF的垂线BG，垂足为点G，连接AG，则AG长的最小值为【辅助圆+将军饮马】如图，正方形ABCD的边长是4，点E是AD边上一动点，连接BE，过点A作AF⊥BE于点F，点P是AD边上另一动点，则PC+PF的最小值为【辅助圆+相切】如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AB＝4，D是BC上一动点，CE⊥AD于E，EF⊥AB交BC于点F，则CF的最大值是三、定边对定角在“定边对直角”问题中，依据“直径所对的圆周角是直角”，关键性在于寻找定边、直角，而根据圆周角定理:同圆或等圆中，同弧或等弧所対的圆周角都相.定边必不可少，而直角则可一般为定角.例如，AB为定值，∠P为定角，则P点轨迹是一个圆.当然，∠P度数也是特殊角，比如30°、45°、60°、120°，下面分别作对应的轨迹圆若∠P＝30°，以AB为边，同侧构造等边三角形AOB，O即为圆心若∠P＝45°，以AB为斜边，同侧构造等腰直角三角形AOB，O即为圆心.若∠P＝60°，以AB为底，同侧构造顶角为120°的等腰三角形AOB，O即为圆心.若∠P＝120°，以AB为底，异侧为边构造顶角为120°的等腰三角形AOB，O即为圆心.【例题1】如图，等边△ABC边长为2，E、F分別是BC、CA上两个动点，且BE=CF，连接AE、BF，交点为P点，则CP的最小值为【举一反三】1、如图，△ABC为等边三角形，AB=3，若P为△ABC内一动点，且满足∠P AB＝∠ACP，则线段PB长度的最小值为2、在△ABC中，AB＝4，∠C＝60°，∠A>∠B，则BC的长的取值范围是3、如图，AB是圆O的直径，M、N是弧AB(异于A、B)上两点，C是弧MN上一动点，∠ACB 的角平分线交圆O于点D，∠BAC的平分线交CD于点E，当点C从点M运动到点N时，则C、E两点的运动路径长的比是。

隐圆问题的十大类型：高考数学微专题

隐圆问题的十大类型：高考数学微专题隐圆问题是高中数学中难度较大的一个跨单元主题，它承接于初中的圆，融入了高中的平面向量，解三角形，解析几何等内容，综合性很高，更是学生学习的难点之一！当然，这部分内容在课本上也多有涉及，比如阿波罗尼斯圆，圆的参数方程等，基于此，本节将系统梳理相关内容，力争做成一份全面，完整的隐圆资料.类型1.利用圆的定义（到定点的距离等于定长的点的轨迹）确定隐形圆例1.如果圆4)3()2(22=--+-a y a x 上总存在两个点到原点的距离为1，则实数a 的取值范围为________.类型2.动点P 满足对两个定点B A ,的张角是90（1-=⋅PB P A k k 或者0=⋅→→PB P A ）确定隐形圆.该类型实质就是直径所对的圆周角为直角的应用.例2.已知点P 在圆O ：224x y +=上，点()30A -,，()0,4B ，满足AP BP ⊥的点P 的个数为（）A．3B．2C．1D．0例3.已知点()3,0P -在动直线()30mx ny m n +-+=上的投影为点M ，若点32,2N ⎛⎫ ⎪⎝⎭，则MN 的最大值为（）A．1B．32C．2D．1124．已知点P 是圆C ：222430x y x y +--+=的动点，直线l ：30x y --=上存在两点A ，B ，使得π2APB ∠=恒成立，则线段AB 长度的最小值是（）A．B．C．D．5．已知EF 是圆22:2430C x y x y +--+=的一条弦，且CE CF ⊥，P 是EF 的中点，当弦EF 在圆C 上运动时，直线:30l x y --=上存在两点,A B ，使得2APB π∠≥恒成立，则线段AB 长度的最小值是（）A．1B．C．D．2+6．若对于圆22:2220C x y x y +---=上任意的点A ，直线:4380l x y ++=上总存在不同两点M ，N ，使得90MAN ∠≥︒，则MN 的最小值为______.类型3.正弦定理对边对角模型.由正弦定理可知，当已知三角形任意一边和该边所对角大小时，即可得到外接圆半径，即AaR sin 2=.7.（2020年全国2卷）在ABC ∆中，C B C B A sin sin sin sin sin 222⋅=--（1）求A ；（2）若3=BC ，求ABC ∆周长的最大值.8．如图，正方形ABCD 的边长为6，点E ，F 分别在边AD ，BC 上，且2DE AE =，2CF BF =．点P 在正方形ABCD 的边AD 或BC 上运动，若1PE PF ⋅=，则满足条件的点P 的个数是（）A．0B．2C．4D．6类型5.动点P 满足对两个定点B A ,满足：)0(||||22>=+λλPB P A .类型6.阿波罗尼斯圆定义：已知平面上两点B A ,，则所有满足1,||||≠=λλPB P A 的动点P 的轨迹是一个以定比为n m :内分和外分定线段AB 的两个分点的连线为直径的圆.若)0,(),0,(b B a A ,则圆的半径为|||1|2AB ⋅-λλ，圆心为)0|,|11(22AB ⋅-+λλ.解析：设(,0),(,0),(,)A c B c P x y -．因为(0,0AP BP c λλ=>>且1)λ≠由两点间距离=，化简得2222221211x c y c λλλλ⎛⎫+⎛⎫-+= ⎪ ⎪--⎝⎭⎝⎭．所以点P 的轨迹是以221,01c λλ⎛⎫+ ⎪-⎝⎭为圆心，以221c λλ-为半径的圆．9.ABC ∆中，2=AB ，BC AC 2=，则ABC ∆的面积最大值为_______.类型7.“从动点圆”，若A 为定点，点P 在圆上运动，则线段AP 的中点也在一个圆上.10.已知线段AB 的端点B 的坐标是(4,3)，端点A 在圆22(1)4x y ++=上运动，则线段AB的中点M 的轨迹方程是__________.类型8.圆的内接四边形与托勒密定理若四边形ABCD 对角互补，或者BC AD CD AB DB AC ⋅+⋅=⋅，则D C B A ,,,四点共圆.11．在平面四边形ABCD 中，,AB AC AC ⊥=，AD =3，BD =则CD 的最小值为（）B．2C．2类型9.向量隐圆12.已知向量→→→c b a ,,满足12||,1||-=⋅==→→→→b a b a ，且向量→→→→--c b c a ,的夹角为4π，则||→c 的最大值为_________.13.（2018年浙江高考）已知a 、b 、e 是平面向量，e是单位向量．若非零向量a与e的夹角为3π，向量b 满足2430b e b -⋅+= ，则a b - 的最小值是（）11C．2D．214已知平面向量a 、b 、c 满足0a b ⋅= ，1a b == ，()()12c a c b -⋅-= ，则c a - 的最大值为（）B．12+C．32D．2类型10.米勒圆与最大视角米勒定理1：已知点B A ,是MON ∠的边ON 上的两个定点，点P 是边OM 上的动点，则当且仅当ABP ∆的外接圆与边OM 相切于点P 时，APB ∠最大.13.（2022南昌一模）已知点)0,3(),0,1(B A -.点P 为圆45:22=+y x O 上一个动点，则APB ∠sin 的最大值为__________.隐圆问题的十大类型（解析版）隐圆问题是高中数学中难度较大的一个跨单元主题，它承接于初中的圆，融入了高中的平面向量，解三角形，解析几何等内容，综合性很高，更是学生学习的难点之一！当然，这部分内容在课本上也多有涉及，比如阿波罗尼斯圆，圆的参数方程等，基于此，本节将系统梳理相关内容，力争做成一份全面，完整的隐圆资料.类型1.利用圆的定义（到定点的距离等于定长的点的轨迹）确定隐形圆例1.如果圆4)3()2(22=--+-a y a x 上总存在两个点到原点的距离为1，则实数a 的取值范围为________.解析：转化为4)3()2(22=--+-a y a x 与圆122=+y x 有两个交点，求a 的取值范围问题，由两圆相交的条件可知：)0,56(-∈a .类型2.动点P 满足对两个定点B A ,的张角是90（1-=⋅PB P A k k 或者0=⋅→→PB P A ）确定隐形圆.该类型实质就是直径所对的圆周角为直角的应用.例2.已知点P 在圆O ：224x y +=上，点()30A -,，()0,4B ，满足AP BP ⊥的点P 的个数为（）A．3B．2C．1D．0解析：设点(,)P x y ，则224x y +=，且(3,)(,4)AP x y BP x y =+=-，，由AP BP ⊥，得22(3)(4)340AP BP x x y y x y x y ⋅=++-=++-= ，即22325()(2)24x y ++-=，故点P 的轨迹为一个圆心为3(,2)2-，半径为52的圆，则两圆的圆心距为52，半径和为59222+=，半径差为51222-=，有159222<<，所以两圆相交，满足这样的点P 有2个.故选B.例3.已知点()3,0P -在动直线()30mx ny m n +-+=上的投影为点M ，若点32,2N ⎛⎫ ⎪⎝⎭，则MN 的最大值为（）A．1B．32C．2D．112解析：由动直线方程()30mx ny m n +-+=得()()130m x n y -+-=，所以该直线过定点Q（1,3），所以动点M 在以PQ 为直径的圆上，5,2=圆心的坐标为3(1,)2-，所以点N 3=，所以MN 的最大值为5113+22=.故选：D.4．已知点P 是圆C ：222430x y x y +--+=的动点，直线l ：30x y --=上存在两点A ，B ，使得π2APB ∠=恒成立，则线段AB 长度的最小值是（）A．B．C．D．解析：圆()()22:122C x y -+-=，圆心为()1,2C ，半径为1r 依题意，P 是圆C 上任意一点，直线l 上存在两点,A B ，使得π2APB ∠=恒成立，故以AB 为直径的圆D 始终与圆C 相切，即圆D 的半径2r 的最小值是P 到直线l 距离的最1r ==AB 的最小值是2⨯=.故选：A5．已知EF 是圆22:2430C x y x y +--+=的一条弦，且CE CF ⊥，P 是EF 的中点，当弦EF 在圆C 上运动时，直线:30l x y --=上存在两点,A B ，使得2APB π∠≥恒成立，则线段AB 长度的最小值是（）A．1B．C．D．2+解析：由题可知：22:(1)(2)2C x y -+-= ，圆心()1,2C ，半径r =又CE CF ⊥，P 是EF 的中点，所以112CP EF ==，所以点P 的轨迹方程22(1)(2)1x y -+-=，圆心为点()1,2C ，半径为1R =，若直线:30l x y --=上存在两点,A B ，使得2APB π∠≥恒成立，则以AB 为直径的圆要包括圆22(1)(2)1x y -+-=，点()1,2C 到直线l 的距离为d =，所以AB 长度的最小值为()212d +=+，故选：B．6．若对于圆22:2220C x y x y +---=上任意的点A ，直线:4380l x y ++=上总存在不同两点M ，N ，使得90MAN ∠≥︒，则MN 的最小值为______.解析：由题设圆22:(1)(1)4C x y -+-=，故圆心(1,1)C ，半径为2r =，所以C 到:4380l x y ++=的距离3d r ==>，故直线与圆相离，故圆C 上点到直线:4380l x y ++=的距离范围为[1,5]，圆C 上任意的点A ，直线:4380l x ++=上总存在不同两点M 、N ，使90MAN ∠≥︒，即以MN 为直径的圆包含圆C ，至少要保证直线上与圆C 最近的点，与圆上点距离最大值为半径的圆包含圆C ，所以10MN ≥.故答案为：10类型3.正弦定理对边对角模型.由正弦定理可知，当已知三角形任意一边和该边所对角大小时，即可得到外接圆半径，即AaR sin 2=.7.（2020年全国2卷）在ABC ∆中，C B C B A sin sin sin sin sin 222⋅=--（1）求A ；（2）若3=BC ，求ABC ∆周长的最大值.解析：（1）由正弦定理可得：222BC AC AB AC AB --=⋅，2221cos 22AC AB BC A AC AB +-∴==-⋅()0,A π∈ ，23A π∴=.（2）由余弦定理得：222222cos 9BC AC AB AC AB A AC AB AC AB =+-⋅=++⋅=，即()29AC AB AC AB +-⋅=.22AC AB AC AB +⎛⎫⋅≤ ⎪⎝⎭（当且仅当AC AB =时取等号），()()()22223924AC AB AC AB AC AB AC AB AC AB +⎛⎫∴=+-⋅≥+-=+ ⎪⎝⎭，解得：AC AB +≤（当且仅当AC AB =时取等号），ABC ∴ 周长3L AC AB BC =++≤+，ABC ∴ 周长的最大值为3+类型4.动点P 满足对两个定点B A ,满足：)0(≠=⋅→→λλPB P A .分析：由于||AB 定值，设AB 中点为M ，根据平面向量部分极化恒等式可得：222||41||)0(41AB PM AB PM PB P A +=⇒≠=-=⋅→→→→λλλ，故动点P 是以AB 中点M为圆心，半径为2||41AB +λ的圆.8．如图，正方形ABCD 的边长为6，点E ，F 分别在边AD ，BC 上，且2DE AE =，2CF BF =．点P 在正方形ABCD 的边AD 或BC 上运动，若1PE PF ⋅=，则满足条件的点P 的个数是（）A．0B．2C．4D．6解析：由上述分析可知，故动点P 是以EF 中点M 为圆心，半径为2||41EF +λ的圆.故此题中点P 以EF 中点M 为圆心，半径为10的圆，所以，共有4个点满足条件.故选：C类型5.动点P 满足对两个定点B A ,满足：)0(||||22>=+λλPB P A .解析：由于→→→→⋅-+=+PB P A PB P A PB P A 2)(||||222，设AB 中点为M ，则由向量关系与极化恒等式可知：λ=--=⋅-+→→→→→→→)41(242)(2222AB PM PM PB P A PB P A ，整理可得：→→+=22412AB PM λ，显然动点P 以M 为圆心，→+2412AB λ为半径的圆.类型6.阿波罗尼斯圆定义：已知平面上两点B A ,，则所有满足1,||||≠=λλPB P A 的动点P 的轨迹是一个以定比为n m :内分和外分定线段AB 的两个分点的连线为直径的圆.若)0,(),0,(b B a A ,则圆的半径为|||1|2AB ⋅-λλ，圆心为)0|,|11(22AB ⋅-+λλ.解析：设(,0),(,0),(,)A c B c P x y -．因为(0,0AP BP c λλ=>>且1)λ≠由两点间距离=，化简得2222221211x c y c λλλλ⎛⎫+⎛⎫-+= ⎪ ⎪--⎝⎭⎝⎭．所以点P 的轨迹是以221,01c λλ⎛⎫+ ⎪-⎝⎭为圆心，以221c λλ-为半径的圆．9.ABC ∆中，2=AB ，BC AC 2=，则ABC ∆的面积最大值为_______.解析：由2,AB AC ==，见系代入得22(3)8x y -+=．设圆心为M ，显然当CM x ⊥轴时，ABC 面积最大，此时||CM =．所以()122ABC mx S ∆=⋅⋅=．类型7.“从动点圆”，若A 为定点，点P 在圆上运动，则线段AP 的中点也在一个圆上.10.已知线段AB 的端点B 的坐标是(4,3)，端点A 在圆22(1)4x y ++=上运动，则线段AB 的中点M 的轨迹方程是__________.解析：设点M 的坐标为(,)x y ，点00(,)A x y ，M 为AB 的中点，B 的坐标为(4,3)，004232x x y y +⎧=⎪⎪⎨+⎪=⎪⎩，解得002423x x y y =-⎧⎨=-⎩，点00(,)A x y 满足2200(1)4x y ++=22(241)(23)4x y ∴-++-=，即2233122x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭，故点M 的轨迹是以33,22⎛⎫ ⎪⎝⎭为圆心，以1为半径的圆，点M 的轨迹方程为：2233122x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭．类型8.圆的内接四边形与托勒密定理若四边形ABCD 对角互补，或者BC AD CD AB DB AC ⋅+⋅=⋅，则D C B A ,,,四点共圆.11．在平面四边形ABCD中，,AB AC AC ⊥=，AD =3，BD=则CD 的最小值为（）解析：如图，可设x AB =，则x BC x AC 3,2==，则由托勒密不等式可得：BD AC AB CD BC AD ⋅≥⋅+⋅，代值可得：362233≥⇒⋅≥⋅+⋅CD x x CD ，等号成立当且仅当D C B A ,,,四点共圆.B．2C．2类型9.向量隐圆12.已知向量→→→c b a ,,满足12||,1||-=⋅==→→→→b a b a ，且向量→→→→--c b c a ,的夹角为4π，则||→c 的最大值为_________.解析：依题→→b a ,夹角为43π，而向量→→→→--c b c a ,的夹角为4π，故由四点共圆结论可知，向量→c 的终点C 与B A O ,,四点共圆，则||→c 的最大值即为圆的直径，由于5||||=-=→→b a AB 则由正弦定理：1043sin||||max ==→πAB c .13.（2018年浙江高考）已知a 、b 、e 是平面向量，e是单位向量．若非零向量a 与e 的夹角为3π，向量b 满足2430b e b -⋅+= ，则a b - 的最小值是（）11C．2D．2解析：设()()(),,1,0,,a x y e b m n ===，则由π,3a e =得πcos ,3a e e x y a ⋅=⋅=∴= ，由2430be b -⋅+= 得()2222430,21,m n m m n +-+=-+=因此，a b - 的最小值为圆心()2,0到直线y =的距离2321，为1.-选A.14已知平面向量a 、b 、c 满足0a b ⋅= ，1a b == ，()()12c a c b -⋅-= ，则c a - 的最大值为（）B．12+C．32D．2解析：在平面内一点O ，作OA a = ，OB b = ，OC c = ，则0a b OA OB ⋅=⋅=，则OA OB ⊥，因为1a b ==，则1== OA OB ，故AOB为等腰直角三角形，则AB =uu u r取AB 的中点E ，则()()()11112222OE OA AE OA AB OA OB OA OA OB a b =+=+=+-=+=+，所以，()22222a ba b a b +=++⋅=，所以，2122a b ⎛⎫+= ⎪⎝⎭，因为()()()212c a c b c c a b -⋅-=-⋅+= ，所以，()()()22222142a b a b c c a b c OC OE EC +⎛⎫+-⋅++=-=-== ⎝⎭，则1EC = ，所以，12c a OC OA AC AE EC AE EC -=-==+≤+=+.11当且仅当AE 、EC 同向时，等号成立，故c a -1.故选：B.类型10.米勒圆与最大视角米勒定理1：已知点B A ,是MON ∠的边ON 上的两个定点，点P 是边OM 上的动点，则当且仅当ABP ∆的外接圆与边OM 相切于点P 时，APB ∠最大.13.（2022南昌一模）已知点)0,3(),0,1(B A -.点P 为圆45:22=+y x O 上一个动点，则APB ∠sin 的最大值为__________.解析：如图，设D 是圆O 上不同于点P 的任意一点，连结DA 与圆O 交于点E ，连接EC ，由三角形外角的性质，可知ADC AEC ∠>∠，由圆周角定理：=∠APC AEC ∠，因此ADC APC ∠>∠，当且仅当ACP ∆的外接圆与圆O 相切于点P 时，APC ∠最大.此时，可设ACP ∆的外接圆圆心),1(t M ，由于此时P M O ,,三点共线且MP OM OP +=，而42+==t MC MP ，则531422=+++t t ，解得：5442=t ，于是58=M R ，由正弦定理，则APB ∠sin 的最大值为45.。

八种隐圆类最值问题,圆来如此简单(原卷版)

八种隐圆类最值问题，圆来如此简单在中考数学中，有一类高频率考题，几乎每年各地都会出现，明明图形中没有出现“圆”，但是解题中必须用到“圆”的知识点，像这样的题我们称之为“隐圆模型”。

正所谓：有“圆”千里来相会，无“圆”对面不相逢。

“隐圆模型”的题的关键突破口就在于能否看出这个“隐藏圆”。

一旦“圆”形毕露，则答案手到擒来！知识点梳理题型一定点定长得圆2023年湖北省鄂州市中考数学真题2023·邵阳市中考真题2023·广西南宁市二模2022·辽宁抚顺·中考真题2022·长春·中考真题题型二直角的对边是直径2023·菏泽市中考真题2022·通辽·中考真题2023·汕头市金平区一模2023·广州市天河区三模2022·成都市成华区二诊题型三对角互补得圆2023年·广元市一模题型四定弦定角得圆2023·成都市新都区二模2023·成都市金牛区二模2023·达州·中考真题题型五四点共圆题型六相切时取到最值2023·随州市中考真题2022·江苏无锡·中考真题2022扬州中考真题题型七定角定高面积最小、周长最小问题题型八米勒角（最大张角）模型徐州中考知识点梳理一、定点定长得圆在几何图形中，通过折叠、旋转，滑梯模型得到动点的轨迹为绕定点等于定长的圆，从而画出动点轨迹，并进行计算二、直角的对边是直径前世：在⊙O中，AB为直径，则始终有AB所对的∠C=90°今生：若有AB是固定线段，且总有∠ACB＝90°，则C在以AB为直径径的圆上．(此类型本来属于定弦定角，但是因为比较特殊，故单独分为一类)xB三、对角互补前世：在⊙O 上任意四点A ，B ，C ，D 所围成的四边形对角互补今生：若四边形ABCD 对角互补，则A ，B ，C ，D 四点共圆四、定弦定角模型定角模型是直角模型的一种变形形式，其依据是已知定角，则根据“同弧所对的圆周角相等”得到动点的轨迹为圆弧，再画出对应图形进行计算．前世：在⊙O 中，若弦AB 长度固定则弦AB 所对的圆周角都相等(注意：弦AB 在劣弧AB 上也有圆周角，需要根据题目灵活运用)今生：若有一固定线段AB 及线段AB 所对的∠C 大小固定，根据圆的知识可知C 点并不是唯一固定的点，C 在⊙O 的优弧ACB 上均可(至于是优弧还是劣弧取决于∠C 的大小，小于90°，则C 在优弧上运动；等于90°，则C 在半圆上运动；大于90°则C 在劣弧运动)五、四点共圆模型前世:在⊙O 中，ABCD 是圆的内接四边形，则有∠1=∠2，∠3=∠4，△BPC~△APD(同理△BPA~△CPD) 今生:若四边形ABCD 中有∠1=∠2(通常情况下∠5=∠6对顶角相等，故不需要∠3=∠4，实际应用中长用∠1=∠2，∠5=∠6)则ABCD 四点(某些不能直接使用四点共圆的地区，可以通过证明两次三角形相似也可)，选填题可以直接使用六、定角定高（探照灯模型）什么叫定角定高，如右图，直线BC 外一点A ，A 到直线BC 距离为定值（定高），∠BAC 为定角。

专题复习-“隐形圆”问题

12“隐形圆”问题江苏省通州高级中学一、问题概述江苏省高考考试说明中圆的方程是 C 级知识点，每年都考，但有些时候，在条件中没有直接给出圆方面的信息,而是隐藏在题目中的，要通过分析和转化，发现圆（或圆的方程)，从而最终可以利用圆的知识来求解，我们称这类问题为“隐形圆”问题．二、求解策略如何发现隐形圆（或圆的方程）是关键，常见的有以下策略．策略一利用圆的定义（到定点的距离等于定长的点的轨迹)确定隐形圆例 1（1）如果圆(x －2a ）2＋（y －a －3)2＝4 上总存在两个点到原点的距离为 1，则实数 a 的取值范围是．- 6 < a < 05略解：到原点的距离为 1 的点的轨迹是以原点为圆心的单位圆，转化到此单位圆与已知圆相交求解．（2）（2016 年南京二模）已知圆 O :x 2＋y 2＝1，圆 M :（x －a )2＋（y －a ＋4）2＝1．若圆 M上存在点 P ,过点 P 作圆 O 的两条切线,切点为 A ，B ，使得∠APB ＝60°，则 a 的取值范围为．解：由题意得 OP = 2 ，所以 P 在以 O 为圆心 2 为半径的圆上，即此圆与圆 M 有公共点,因此有 2 - 1 < OM < 2 + 1 ⇒ 1≤ a 2 + （a - 4)2 ≤9 ⇒ 2 a ≤ 2 + ．2 2（3）（2017 年苏北四市一模）已知 A 、B 是圆 C ： x 2 + y 2 = 1 上的动点，， P 是圆C ： (x - 3）2+ （ y - 4）2= 1 上的动点，则 PA + PB 的取值范围是．[7，13］1 略解：取 AB 的中点 M ，则 C 1M =2 1，所以 M 在以 C 1 圆心，半径为 2的圆上，且PA + PB = 2PM ，转化为两圆上动点的距离的最值．（4）若对任意α∈R ,直线 l :x cos α＋y sin α＝2sin （α＋ π)＋4 与圆 C ：（x －m ）2 3m ）26＝1 均无公共点，则实数 m 的取值范围是．（- 1 , 5）2 2略解：直线 l 的方程为：（x —1）cos α- 3 ）sin α＝1, 3 )到 l 距离为 4，所以 l 是以 M 为圆心半径为 4 的定圆的切线系，转化为圆 M 与圆 C 内含．0 0O2 ，⎪注：直线l：(x—x0)cosα＋（y- y0)sinα＝R 为圆M：（x -x ）2 +（x -y )2 =R2 的切线系．例2（2017 年南通市一模）在平面直角坐标系xOy 中，已知B，C 为圆x2 +y2 = 4 上两点, 点A（1，1) ，且AB⊥AC，则线段BC 的长的取值范围为．解：法一（标解）：设BC 的中点为M(x,y)，因为OB2 =OM 2 +BM 2 =OM 2 +AM 2 ，所以4 =x2 +y2 +(x-1)2+(y -1)2, B MC2 2化简得⎛x -1 ⎫ +⎛y -1 ⎫ =3 ，A2 ⎪ 2 ⎪2⎝⎭⎝⎭所以点M 的轨迹是以⎛1 1 ⎫为半径的2⎝⎭圆，所以AM 的取值范围是2，所2 2 例2⎣ ⎦以BC 的取值范围是．法二：以AB、AC 为邻边作矩形BACN，则BC＝AN ，由矩形的几何性质(矩形所在平面上的任意一点到其对角线上的两个顶点的距离的平方和相等），有OB2 +OC2 =OA2 +O N 2 ，所以ON＝故N 在以O 为圆心，半径为BC 的取值范围是．⎦变式1 （2014 年常州高三期末卷）在平面直角坐标系xOy 中，已知圆O : x2 +y2 =16 ，点P （1，2) ，M、N 为圆O 上两个不同的点，且PM ⋅PN = 0 ,若PQ =PM +PN ，则PQ 的最小值为．2 2 2 2变式2 已知圆C1: x +y= 9 ，圆C2：x +y= 4 ，定点P（1, 0），动点A, B 分别在圆C1和圆C2上，满足∠APB =则线段AB 的取值范围．-1 3 +1]变式3 已知向量a、b、c 满足a = 3, b = 2，c =1,（a -c）⋅（b -c）= 0 ，则a -b 范围为．- 3 +1］策略二动点P 对两定点A、B 张角是900 ( kPA⋅kPB=-1 ，或PA ⋅PB = 0）确定隐形圆例3 （1）（2014 年北京卷）已知圆C: (x - 3)2 +(y - 4)2 =1和两点A(-m， 0) ，B（m, 0），若圆上存在点P，使得∠APB = 90 ，则m 的取值范围是．[4, 6]略解：由已知以AB 为直径的圆与圆C 有公共点．（2）（海安2016 届高三上期末）在平面直角坐标系xOy 中，已知点P （−1，0) ，Q（2 ，1) ,直线l:ax +by +c = 0 其中实数a，b，c 成等差数列,若点P 在直线l 上的射影为H,则线段QH 的取值范围是．解：由题意,圆心C（1,－2）在直线ax＋by＋c＝0 上，可得a－2b＋c＝0,即c＝2b－a．直线l:（2a－b)x＋(2b－c)y＋（2c－a)＝0，即a（2x＋y－3)＋b(4－x)＝0,⎧2x +y - 3 = 0,由⎨⎩4 -x = 0,可得x＝4，y＝－5，即直线过定点M（4,－5）,由题意，H 在以PM 为直径的圆上,圆心为A（5，2)，方程为(x－5)2＋(y－2）2＝50，∵｜CA 2 ，∴CH 2 ，CH 2 2 2 ，∴线段CH ,．（3）（通州区2017 届高三下开学初检测）设m ∈R ，直线l1：x +my = 0 与直线l2：mx -y - 2m - 4 = 0 交于点P（x，y），则x2 +y 2 +2x的取值范围是．［12 ，]略解:l1 过定点O（0，0），l2 过定点A(2，—4)，则P 在以OA 为直径的圆上（除去一点)，变式（2017 年南京二模）在平面直角坐标系xOy 中，直线l1：kx－y＋2＝0 与直线l2：x＋ky－2＝0 相交于点P，则当实数k 变化时,点P 到直线x－y－4＝0 的距离的最大值为．策略三两定点A、B，动点P 满足PA⋅PB=λ确定隐形圆例4 (1）（2017 年南通密卷3）已知点A(2, 3），点B（6，-3),点P 在直线3x -4y+ 3 = 0 上,若满足等式AP ⋅BP + 2λ= 0 的点P 有两个,则实数λ的取值范围是．解：设P（x，y)，则AP = (x - 2，y - 3) , BP = ( x- 6，y + 3) ，根据AP⋅BP+2λ=0,有(x-4)2 +y2 =13-2λ⎛λ<13⎫.由题意2 ⎪⎝ ⎭心，圆： ( x - 4)2+ y 2 = 13 - 2λ ⎛λ <13 ⎫圆与直线 3x - 4 y + 3 = 0 相交， 2 ⎪ ⎝⎭圆心到直线的距离 d 3 <λ < 2 。

中考数学隐形圆专题含答案

类型一：定点到动点定长点A为定点，点B为动点，AB为定长，则点B的轨迹为圆心为点A，半径为AB的圆。

【经典例题1】如图，在矩形ABCD中，AB=4，AD=6，E是AB边的中点，F 是线段BC边上的动点，将△EBF沿EF所在直线折叠得到△EB′F，连接B′D，则B′D的最小值是___.【解析】如图所示：当∠BFE=∠B′EF，点B′在DE上时，此时B′D的值最小，根据折叠的性质，△EBF≌△EB′F，∴EB′⊥B′F，∴EB′=EB，∵E是AB边的中点，AB=4，∴AE=EB′=2，∵AD=6，∴DE=1022622=+，∴B′D=102−2.练习1-1如图③，矩形ABCD 中，AB=3，BC=4，点E 是AB 边上一点，且AE=2，点F 是BC 边上的任意一点，把△BEF 沿EF 翻折，点B 的对应点为G ，连接AG 、CG ，四边形AGCD 的面积是否存在最小值，若存在，求这个最小值及此时BF 的长度。

若不存在，请说明理由。

【解析】（3）如图3，△四边形ABCD 是矩形，△CD=AB=3，AD=BC=4，△ABC=△D=90°，根据勾股定理得，AC=5， △AB=3，AE=2，△点F 在BC 上的任何位置时，点G 始终在AC 的下方，设点G 到AC 的距离为h ，△S 四边形AGCD =S △ACD +S △ACG =21AD×CD+21AC×h=21×4×3+21×5×h=25h+6， △要四边形AGCD 的面积最小，即：h 最小，△点G 是以点E 为圆心，BE=1为半径的圆上在矩形ABCD 内部的一部分点， △EG△AC 时，h 最小，由折叠知△EGF=△ABC=90°，延长EG 交AC 于H ，则EH△AC ，在Rt△ABC 中，sin△BAC=AC BC =54，在Rt△AEH 中，AE=2，sin△BAC=AE EH =54， △EH=54AE=58，△h=EH -EG=58-1=53 △S 四边形AGCD 最小=25h+6=25×53+6=215．练习1-2如图，等边△ABC 的边AB=8，D 是AB 上一点，BD=3，P 是AC 边上一动点，将△ADP 沿直线DP 折叠，A 的对应点为A'，则CA'的长度最小值是 .【解析】2练习1-3如图，在平行四边形ABCD 中，△BCD =30°，BC =4，CD=M 是AD 边的中点，N 是AB 边上的一动点，将△AMN 沿MN 所在直线翻折得到△AMN ，连接A'C ，则A'C 长度的最小值是 .【解析】如图，连接MC ；过点M 作ME△CD ，交CD 的延长线于点E ；△四边形ABCD 为平行四边形，△AD△BC ，AD=BC=4，△点M 为AD 的中点，△BCD=30△，△DM=MA=2，△MDE=△BCD=30△， △ME=21DM=1，DE=3， △CE=CD+DE=43，由勾股定理得：CM 2=ME 2+CE 2，第4题图AB C DA'M N△CM=7;由翻折变换的性质得：MA′=MA=2，显然，当折线MA′C 与线段MC 重合时，线段A′C 的长度最短，此时A′C=7−2=5，故答案为5.练习1-4如图，在边长为2的菱形ABCD 中，∠A=60∘，点M 是AD 边的中点，点N 是AB 边上一动点，将△AMN 沿MN 所在的直线翻折得到△A′MN ，连结A′C ，则A′C 长度的最小值是( ) A. 7 B. 7−1 C. 3 D. 2【解析】如图所示：∵MA′是定值，A′C 长度取最小值时，即A′在MC 上时，过点M 作MF ⊥DC 于点F ，∵在边长为2的菱形ABCD 中，∠A=60∘，M 为AD 中点，∴2MD=AD=CD=2，∠FDM=60∘，∴∠FMD=30∘，∴FD=21MD=21，∴FM=DM×cos30∘=23， ∴MC=722=+CF FM ，∴A′C=MC−MA′=7−1.故选：B.变式：在Rt △ABC 中，∠C=90°，AC=6，BC=8，点F 在边AC 上，并且CF=2，点E 为边BC 上的动点，将△CEF 沿直线EF 翻折，点C 落在点P 处，则点P 到边AB 距离的最小值是_____解题思路：同上题，不难看出点P 的运动轨迹为以点F 为圆心，PF 为半径的圆上运动，求点P 到AB 的距离最小，可过点F 作AB 的垂线于点M ，交圆 F 于点P ，此时，最小值为PM 。

2019中考数学复习隐形圆问题大全(后有专题练习无答案)

2019中考数学复习隐形圆问题大全(后有专题练习无答案)2019中考数学复：隐形圆问题大全一定点+定长根据到定点的距离等于定长的点的集合是以定点为圆心定长为半径的圆的原理，可以应用到以下问题中：1.在四边形ABCD中，AB=AC=AD=2，BC=1，且AB∥CD，求BD的长度。

解析：因为AB=AC=AD=2，所以B、C、D在以A为圆心、2为半径的圆上。

又因为AB∥CD，所以DE=BC=1.根据勾股定理，易得BD=√15.2.在矩形ABCD中，AB=4，AD=6，E是AB边的中点，F是线段BC边上的动点，将△EBF沿EF所在直线折叠得到△EB′F，连接B′D，则B′D的最小值是多少？解析：因为E是定点，EB′是定长，所以B′点路径为以E为圆心、EB′为半径的圆。

作穿心线DE可得B′D的最小值为2√10.3.在ΔABC中，AB=4，AC=2，以BC为边在ΔABC外作正方形BCDE，BD、CE交于点O，则线段AO的最大值为多少？解析：首先确定A、B点的位置，因为AC=2，所以C点在以A为圆心、2为半径的圆上。

因为点O是点C以点B为中心顺时针旋转45度并1：√2缩小而得，所以将圆A旋转45度再1：2缩小即可得到O点路径。

转化为求定点A到定圆F的最长路径，即AF+FO=3+2√2.二定线+定角根据与一条定线的两端夹角一定的动点路径是以定线为弦，定角为圆周角的弧的原理，可以应用到以下问题中：1.在矩形ABCD中，AB=10，AD=4，点P是CD上的动点，当∠APB=90°时求DP的长度。

解析：因为AB为定线，∠APB为定角（90°），所以P点路径为以AB为弦（直径）的弧。

根据勾股定理，可得DP为2或8.2.在等边三角形ABC中，∠XOY = 45°，点A、B分别在OX、OY上移动，且AB = 2，那么OC的最大值为多少？解析：因为AB为定线，∠XOY为定角，所以O点路径为以AB为弦所含圆周角为45°的弧。

初中数学隐形圆问题

初中数学隐形圆问题
嘿呀，咱来说说初中数学里超级有趣的隐形圆问题呀！比如说，你看那图形里几个动点晃来晃去，怎么就突然发现有个隐形的圆藏在里面呢，神奇不神奇？就像变魔术一样！
比如说，给定几个点，它们到一个固定点的距离始终相等，这不就是在暗示有个圆嘛！这不就好比一群小伙伴围绕着一个中心人物，那可不就形成了个圈嘛！再比如，有个动点在某个轨迹上运动，突然发现它的运动轨迹能构成一个圆，哇塞，那种恍然大悟的感觉，太妙啦！像不像是你找了好久的东西突然出现在眼前一样惊喜！
还有呀，在一些几何问题里，看似毫无头绪，可一旦你发现了那个隐形的圆，一切都迎刃而解啦！就好像你在迷宫里突然找到了出口，兴奋不兴奋？哎呀，初中数学的隐形圆问题真的是充满了奥秘和乐趣，等你去探索和发现呢！你还在等啥，赶紧去和这些隐形圆来一场奇妙的邂逅吧！。

隐形圆_精品文档

隐形圆（引圆）最值问题：我们首先要知道圆上一动点到平面内一定点距离的何时取得最小值和最大值；1》当定点在圆外时，如图所示动点P是在圆o上运动，定点C在圆o外，连接CO并延长，连接OP；我们令OC=d，OP=r；（1）当P，O，C三点不共线时P，O，C三点围成三角形，OC-OP<PC<OC+OP；即d-r<PC<d+r;（2）当P，O，C三点共线时，①P在P’处时，OC-OP=PC,即d-r=PC；②P在P1处时，OC+OP=PC,即d+r=PC；综上可得d-r≤PC≤d+r，PC min=d-r，PC max=d+r.2》当定点在圆内时（不与圆心重合）如图所示：动点P是在圆o上运动，定点C在圆o内，连接CO并双向延长，连接OP；我们令OC=d，OP=r；（1）当P，O，C三点不共线时P，O，C三点围成三角形，OP-OC<PC<OC+OP；即r-d<PC<d+r;（2）当P，O，C三点共线时，①P在P’处时，OP-OC=PC,即r-d=PC；②P在P1处时，OC+OP=PC,即d+r=PC；综上可得r-d≤PC≤d+r，PC min=r-d，PC max=d+r.1.折叠引圆：如图所示在矩形ABCD中，AB=4，AD=6.点E为AB边中点，F为边BC上一动点，以EF为折痕将三角形BEF折叠点B落在B’处，求线段DB’最小值.解析：由题中条件可知折痕EF 满足一定一动的特点，所以满足折叠引圆，根据折叠的性质我们可得到EB=EB ’=21AB=2,根据圆的定义可知，动点B ’是以E 为圆心，2为半径的圆上运动，而B ’的运动又与动点F 有关，我们如果我们将F 看成是从点B →C 的运动可得到B ’的轨迹，如下图所示，B ’的运动并不是完整的圆，而是一部分圆弧。

根据圆上一动点到圆外一定点的最小值分析可知，B ’D 取得最小值时，B ’，D ，E 三点共线，B ’在G 处；所以B ’D min =DE-EG,在直角三角形ADE 中，DE=，因为EG=EB=2，所以B ’D min =-2例1. 如图所示，四边形ABCD 是菱形，∠A=60o，AB=6，点E 是边AD 中点，动点F 是在线段AB 上由A →B 运动,到达B 点停止运动，102AE AD 22=+102连接EF，以EF为折痕将△AEF折叠，点A落在A’处.(1)求A’C长度最小值.(2)求A’的路径长.例2.如图所示矩形ABCD中，AB=8，AD=6，点E是AD边上的中点，点F是AB边上的动点，连接EF，以EF为折痕将△AEF折叠，点A落在A’处，求△A’BC的面积最小值.定角定弦引圆（隐圆）：如图所示，在平面内存在定点A，B.点P是平面内的一动点，且点∠P=a.像这类动点处存在一个角度恒为定角，且该角能放在一个三角形内，所对边为定边，那么该动点就是在圆上运动；这个定角就可以理解为圆周角，它所对的定边就是该圆周角所对的弦.（1）直角类型：如图1所示，在平面内存在定点A，B.点P是平面内的一动点，且点∠P=90o，根据上面定角定弦可知，∠P是圆周角，AB是它所对弦，因为∠P=90o，图1 图2（2）锐角类型:如图1所示，在平面内存在定点A，B.点P是平面内的一动点，且点∠P=a,且a<90o，根据上面定角定弦可知，∠P是圆周角，AB是它所对弦，此时的AB并不是直径，我们知道想要画出这个P所在的圆我们需要圆心和半径，或者找到直径；因为A，P，B三点都是圆上的点，∠A，∠B也是圆周角，点P在运动的时候∠A，∠B的大小是会发生改变的，，如图2所示.图1 图2（3）钝角类型：如图1所示，在平面内存在定点A，B.点P是平面内的一动点，且点∠P=a,且a>90o，根据上面定角定弦可知，∠P是圆周角，AB是它所对弦,此时我们发现钝角是无法构造到直角三角形中去的，那么我们就要想办法去转化，我们可以通过四点共圆的特点去转化，我们可以图1 图2图3例1. 如图所示，在矩形ABCD 中AB=8，AD=6，点Q 是边AD 边上一动点，连接CQ ，过点D 作DP ⊥CQ ，交CQ 于点P .(1) 求线段BP 最小值.(2) 如图2所示，点M 也是边AD 上的动点，求BM+PM 最小值.(3) 如图2所示，点M 是边AD 上的动点，求AM+PM 最小值21图1 图2例2.在三角形ABP中，AB=6，∠P=60o，求AP+BP最大值.例3.在等边三角形ABC中，D、E分别为边AC，AB上的动点，且AD=BE；BC=6，连接CE、BD交于点F.（1）.求∠CFD.（2）.求AF最小值.2.瓜豆原理引圆：瓜豆原理：从动点的运动状态与主动点吻合（主动点在直线上运动，从动点就会在直线上运动；主动点在圆上运动，从动点就会在圆上运动）(1)如图所示点A 、B 都是定点，点D 是圆B 上一动点，连接AD ，取AD 上一点E ，使=k ，此时点D 在圆B 上运动的时候就会带着点E 一起运动，那么点D 就是主动点，点E 就是从动点；（圆B 大小不变，k 为定值）∵=k （主动点与从动点之间的关联所在）∵点A 是定点∴我们可以将点E 所在图形是点D 所在图形关于点A 位似得到的如下图：圆的位似可以对其半径进行位似，即取AB 上一点C ，使=k ∵∠A=∠A ，==k ，∴△ABD ∽△ACE ，∴==k∴CE=kBD 为定值；所以点E 就是以点C 为圆心CE 为半径的圆上运动AD AEAD AEAB ACAD AE AB AC BD CE ABAC(2).如图所示，点A 、B 是平面内定点，点D 是圆B 上一动点，∠DAE=a ，=k ，此时点D 在圆B 上运动的时候就会带着点E 一起运动，那么点D 就是主动点，点E 就是从动点；（圆B 大小不变，k 为定值，a 角度为定值）这个可以看成（1）中图形旋转得到的；取AB 上一点C ，使=k ，将AC 以点A 为旋转中心逆时针旋转a得到C ’,易证△ACE ’∽△ABD ，所以==k ，即C ’E=kBD 所以点E 为C ’为圆心C ’E 为半径的圆上运动例1．如图，点A ，B 的坐标分别为(60)(06)A B C ，，，，为坐标平面内一点，BC M 为线段AC 的中点，连接OM ，当OM 取最大值时，点M 的坐标为__________________． AD AEAB ACBD E C'ABAC2．如图，△ACB中，CA＝CB＝4，∠ACB＝90°，点P为CA上的动点，连BP，过点A作AM⊥BP于M．当点P从点C运动到点A 时，线段BM的中点N运动的路径长为。

中考数学复习指导：发现“隐形”圆巧求最小值

发现发现““隐形隐形””圆巧求最小值在近几年的中考数学试题中，常有一些涉及到求线段最小值的问题.这些题目入手较难，得分率很低，分析其原因不难发现，学生对题目中运动变化的本质没有搞清楚.在这些蕴含运动变化的问题中，并没有显性的圆，但是仔细分析题目的条件，如果能发现某个点的运动路径是一个圆(或是一段弧)，可谓是“山重水复疑无路，柳暗花明又一村”，将会对问题的解决起着重要的作用.下面举例说明.一、翻折中的“隐形”圆例1 如图1，在Rt ABC ∆中，90,6,8C AC BC ∠=°==，点F在边AC 上，并且2CF =，点E 为边BC 上的动点，将CEF ∆沿直线EF 翻折，点C 落在点P 处，则点P 到边AB 距离的最小值是 .解如图2，当点E 在BC 上运动时, PF 的长固定不变，即2PF CF ==.所以点P 在以点F 为圆心，以2为半径的圆上运动.过点F 作FH AB ⊥交⊙F 于点P ，垂足为H ，此时PH 最短.由AFH ABC ∆∆:，得FH FA BC AB=.又由已知易得4,10AF AB ==.所以4810FH =，即165FH =.所以P 到AB 距离的最小值166255PH FH FP =−=−=.点评本题关键的地方在于抓住无论点E 的位置在哪，翻折,FCE PF ∆的长度始终等于FC 的长度，即2PF =.也就是说动点P 到定点F 的距离是定值2，所以点F 的运动路径是以点F 为圆心，2为半径的圆(或部分).如此，这个问题就最终转化为在圆上找一个到定直线距离最短的点.我们可以利用图3的模型1来作出直观解释.模型1 如图3，直线m 与⊙O 相离，过D 点O 作直线m 的垂线，垂足为点H ，交⊙O 与点P 、点Q ，则⊙O 上点P 到直线m 的距离最短，点Q 到直线m 的距离最长理由简述在⊙O 上任意找一点P ′，过P ′作P H ′′⊥直线m ，垂足为点H ′.由三角形三边关系及直角三角形斜边大于直角边可得:OP P H OH OH ′′′′+>>，而OH OP PH =+,OP OP ′=，所以P H PH ′′>，所以点P 到直线m 的距离最短.类似的方法可以说明点P 到直线m 的距离最长.例2如图4，在边长为2的菱形ABCD 中，60,A M ∠=°对是AD 边的中点，N 是AB 边上一动点.将AMN ∆沿MN 所在的直线翻折得到A MN ′∆，连结A C ′，则A C ′长度的最小值是 .解当点N 在AB 边上运动时，MA ′的长度固定不变，即1MA MA ′==，所以点A ′在以点M 为圆心，1为半径的圆上运动，如图5，连接CM ，与⊙M 交于点A ′，此时CA ′最短.过点C 作CG AD ⊥交AD 的延长线于点G .因为2,60CD CDG A =∠=∠=°，所以1,DG CG ==，在Rt CMG ∆中，由勾股定理，得CM == 点评同例1，无论N 点在何处，沿MN 翻折后，线段MA ′的长度(1MA MA ′==)保持不变，而且点M 是定点，所以点A ′的运动轨迹是以M 为圆心，1为半径的圆(部分).要求A C ′的最小值，回归到模型1中，连结圆外定点C 与圆心M 与圆M 交于点A ′，此时A C ′的长度即为最小值.我们可以借助图6利用模型2来作出直观解释.模型2 如图6，点P 为⊙O 外一定点，连结PO 交⊙O 于点A ，延长线与⊙O 交于另一点B ，则PA 的长度为⊙O 外一点P 到⊙O 的最短距离，PB 的长度为⊙O 外一点P 到⊙O 的最长距离.理由简述在⊙O 上再任意找一点A ′ ,连接PA ′，由三角形三边关系，可得OA PA OP ′′+>.又,OP OA AP OA OA ′=+=，所以PA PA ′>.类似的方法可以说明PB 的长度为⊙O 外一点P 到⊙O 的最长距离.例3 如图7，菱形ABCD 的边8,60AB B =∠=°,P 是AB 上一点，3,BP Q =是CD 边上一动点，将梯形APQD 沿直线PQ 折叠, A 的对应点为A ′.当 CA ′的长度最小时，CQ 的长为 .解如图8，过C 作CE AB ⊥，连结AC .因为ABCD 是菱形，60B ∠=°，所以ABC ∆为等边三角形，所以84,3,12AE EB BP EP =====.要使CA ′的长度最小，则梯形APQD 沿直线PQ 折叠后A 的对应点A ′应落在CP 上，且对称轴PQ 应满足//PQ DE .由作图知，DEPQ 为平行四边形，所以1,817DQ EP CQ CD DQ ===−=−=.点评点Q 在线段CD 上无论运动到何处，梯形APQD 沿直线PQ 折叠后PA ′的长度始终保持不变，因此A ′点的运动路径就是以点P 为圆心，PA 长为半径的圆.借助模型2，可知，当点A ′落在线段CP 与⊙P 的交点时，CA ′的长度最小.由PQ 平分,//APC CD AB ∠，可得CQ CP =.作CE AB ⊥，构造Rt CEP ∆，从而可以求出CP 的长.二、直角中的“隐形”圆例4 如图9，在正方形ABCD 中，动点,E F 分别从,D C 两点同时出发，以相同的速度在直线,DC CB 上移动.连结AE 和DF 交于点P ,由于点,E F 的移动，使得点P 也随之运动，请你画出点P 运动路径的草图.若2AD =,试求出线段CP 的最小值.解由题意，可得DE CF =.又因为,90AD CD ADC DCB =∠=∠=°,所以ADE DCF ∆≅∆,所以DAE CDF ∠=∠.因为90ADP CDF ∠+∠=°，所以90DAE ADP ∠+∠=°.由于点P 在运动中保持90APD ∠=°.听以点P 的路径是一段以AD 为直径的弧.设AD 的中点为O ，连结OC 交弧于点P ，此时CP 的长度最小.在Rt ODC ∆中，OC ===，所以1CP OC OP =−=−. 点评此题的本质是抓住动点,E F 在运动过程中，始终保持AE DF ⊥，即90APD ∠=°,这样点P 的运动路径就确定了，即点P 在以AD 为直径的圆弧上，再根据模型2求解即可.例5如图10, Rt ABC ∆中，,6,4,AB BC AB BC P ⊥==是ABC ∆内部的一个动点，且满足PAB PBC ∠=∠，则线段CP 长的最小值为 .解因为90ABC ∠=°,所以90ABP PBC ∠+∠=°.又因为PAB PBC ∠=∠,所以90BAP ABP ∠+∠=°，即90APB ∠=°，所以点P 在以AB 为直径的⊙O 上.连结OC 交⊙O 于点P ，此时PC 最小，在Rt BCO ∆中，90,4,3OBC BC OB ∠=°==，可得5OC =,所以532PC OC OP =−=−=，即PC 最小值为2.点评首先，根据题目的条件不难得出90APB ∠=°，从而可以证明点P 在以AB 直径的⊙O 上.利用模型2，连结OC ，与⊙O 交于点P ，此时PC 最小，利用勾股定理求出OC即可解决问题.以上例题说明，在求一类线段最值问题中，如果遇到动点的运动路径是圆时，只需利用上面提到的模型1或模型2就可以解决.然而难点在于如何知道动点的运动路径是圆，如何将这个隐身“圆”找出来?从以上例子中可以得出以下两种方法:①观察到定点的距离，即圆是到定点距离等于定长的点的集合;②“定弦对定张角”，如例5中线段AB是定值，当动点P在运动过程中，APB∠的大小不变等于90°(当然不一定为直角)，点P的运动路径也是圆(或弧).因此，教师在教学时，要让学生理解概念的本质，还要培养学生对常见模型的敏感性，从而在有限的考试时间内，能快速获得破解难题的策略.。

隐圆问题最值问题 7种题型知识点+例题+练习(非常好分类全面)

4、如图，在Rt△ABC中，∠ACB=90∘，AC=4，BC=3，点D是平面内的一个动点，且AD=2，M为BD的中点，在D点运动过程中，线段CM长度的取值范围是_________.
3、过定点做折叠的可用圆
（定点为圆心，对应点到定点的距离为半径）
例1、如图，在△ABC中，∠ACB=90°，AB= 5，BC=3，P是AB边上的动点（不与点B重合），将△BCP沿CP所在的直线翻折，得到△B′CP，连接B′A，则B′A长度的最小值是．
例2、平面内有四个点A、O、B、C，其中∠AOB=120°，∠ACB=60°，AO=BO=2，则满足题意的OC长度为整数的值可以是___________
练习、如图，AB为直径，AB=4，C、D为圆上两个动点，N为CD中点，CM⊥AB于M，当C、D在圆上运动时保持∠CMN=30°，则CD的长（）
A．随C、D的运动位置而变化，且最大值为4
教学内容
隐圆问题
教学目标
掌握隐圆的题型
重点
隐圆
难点
隐圆
教学过程
隐圆专题
1、几个点到某个定点距离相等可用圆
（定点为圆心，相等距离为半径）
例1：如图，若AB＝OA＝OB＝OC，则∠ACB的大小是_______
练习：如图，已知AB=AC=AD，∠CBD=2∠BDC，∠BAC=44°，则∠CAD的度数为__________
B．随C、D的运动位置而变化，且最小值为2
C．随C、D的运动位置长度保持不变，等于2
D．随C、D的运动位置而变化，没有最值
6、一边固定及其所对角不变可用圆（定弦定角角）
（圆心在弦的垂直平分线上且和弦的两端点形成的圆心角等于圆周角的两倍）
例1：已知在中，，，则的最大面积为_____________

“隐形圆”问题

“隐形圆”问题有些时候，圆的信息在条件中没有直接给出，而是隐藏在题目中的，要通过分析和转化，发现圆(或圆的方程)，从而最终可以利用圆的知识来求解，我们称这类问题为“隐形圆”问题．如何发现圆(或圆的方程)是关键，常见的策略有以下几种：(1)利用圆的定义(到定点的距离等于定长的点的轨迹)确定隐形圆；(2)动点P 对两定点A ，B 张角为90∘(k PA ⋅k PB =-1)确定隐形圆；动点P 对两定点A ，B 中点的距离等于AB 距离的一半为确定隐形圆；(3)A ，B 是两个定点，动点P 满足PA PB =λ(λ>0且λ≠1)确定隐形圆(阿波罗尼斯圆)；(4)A ，B 是两个定点，动点P 满足PA 2+PB 2是定值确定隐形圆；(5)A ，B 是两个定点，动点P 满足PA ⋅PB =λ确定隐形圆.例1：圆O :x 2+y 2=1，直线l :ax +y =3，若直线上存在点P ，过点P 作圆O 的两条切线，切点是A ,B ，使得PA ⋅PB =23，则实数a 的取值范围是________．例2：直线l 1:kx −y +2=0与直线l 2:x +ky −2=0交于P 点，当k 变化时，点P 到直线x −y −4=0的距离的最大值是_________．例3：已知A (1,0)，B (4,0)，若直线x −y +m =0上存在点P ，使得PA =12PB ，则m 的取值范围是___．例4：已知点A -1,0 ，点B 1,0 ，点C 满足AC 2+BC 2=8，过点C 作圆D ：(x -3)2+(y -3)2=1的两条切线，切点分别为P ，Q ，则CP ⋅CQ 的最小值是．例5：已知点A 2,3 ，点B 6,-3 ，点P 在直线3x -4y +3=0上，若满足等式AP ⋅BP +2λ=0的点P 有两个，则实数λ的取值范围是________．例6：满足条件AB =2，AC 2−2BC 2=1的ΔABC 的面积的最大值是　．·1·。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

挖掘隐含条件破解动点问题
本文剖析一类隐含圆的动点问题，供同学们学习参考.
一、动点问题中可构建圆的基本结论
1.“定线定角”隐藏着外接圆
如图1，已知线段4AB =，点C 是直线AB 上方的一个动点，30ACB ∠=︒，动点C 的路径是什么?
想一想:在直线AB 上方找这样的点C ，能找到多少个?把这些点连起来成的图形是怎样的图形?
通过思考可知，在直线AB 上方可以找到无数个点C ，把这些点连结起来是一条圆弧. 再想一想:如何画出弧所在的圆?
根据条件，圆周角是30°，圆心角是60°,画等边三角形ABO ∆就可以了. O 点就是圆心，半径就是线段AB 的长，可以画出一个圆.
实际上，这个问题可以这样理解:如图1,因为点C 是动点，则,,A B C 三点构成的ABC ∆是一个动三角形，其中线段AB 是定长，C ∠是一个定角，且线段AB 所对的角是C ∠.由“同圆或等圆中相等的圆周角所对的弦相等”可知，点C 是在ABC ∆的外接圆上运动.画圆的关键是找圆心，定半径.因为AB 是弦，⊙O 的圆心是在AB 的垂直平分线上，C ∠是圆周角，所以在圆中C ∠所对的圆心角是60°，即60,AOB OA OB ∠=︒=，画等边三角形AOB ∆，圆的半径4R AB ==，动点C 构成⊙O 的一段优弧ACB ，即点C 的路径长就是优弧ACB 的长.
变式其它条件不变，C ∠的度数改为45°,60°, α(0°<α<90°)，求点C 路径.
如图2，线段4AB =是定值，当C α∠=时，C α∠=的大小确定，即“定线定角”，根据“同圆或等圆中相等的圆周角所对的弦相等”，可知这些问题中所求C 点应在某个圆上运动.构画出圆，从而使问题中原本隐含的条件和信息在圆中展现出来.
2.“公共料边的直角三角形”隐藏着外接圆
如图3，已知线段4AB =，画出平面内满足90ACB ∠=︒的所有动点C 组成的图形. 想一想，能画出的是什么图形?
经过分析思考可知，所有动点C 组成的图形是圆(图4).
再想一想:
圆心怎么找?半径是多少?⊙O 各点都是使90ACB ∠=︒的点C 吗?
通过画图可让我们联想到:直径所对的圆周角是90°直角，从而画出隐藏的圆.
再根据“90°的圆周角所对的弦是直径”可知，AB 是圆的直径，圆心是AB 的中点，所以半径是2.点C 在点A 、点B 处不能构成直角三角形，所以动点C 组成的图形是除,A B 两点的圆.
二、实际应用
例1 如图5，在平面直角坐标系中，点O 为坐标原点，,,A B C 三点的坐标分别为
，且60ADB ∠=︒，点D 在第一象限.求线段CD 的最小值.
解如图6，由60ADB ∠=︒，作等腰APB ∆,且120APB ∠=︒，则P 为圆心，过P 点作PE AB ⊥于E ，垂足为E .
(3,0),3,0)A B ，
(,0)E ∴,1,22PE PA PE ===,
(,1)P ∴. (0,5)
C ,
PC ∴==== 当,,P D C 三点共线时，CD 最短.
又2PD PA ==,
2C D P C P D
∴=--，
即CD 最小值为2.
注这道题中60ADB ∠=︒是定角，线段AB =在一个隐圆，圆的半径是定值，求最值的问题就转化成圆外一点到圆上一点的最值问题. 例2 如图7，正方形ABCD 的边长为2, P 是对角线BD 上的一个动点(不与,B D 重合)，连结AP ，过点B 作,BH AP H ⊥为垂足，连结DH ，求线段DH 的最小值.
解如图8，取AB 的中点O ，连结,OH OD ，则1OA =.
,B H A P A B H ⊥∴∆是直角三角形，
1
12O H A O A B ∴==
=, 在Rt AOD ∆中，
OD == 在OHD ∆中，OH DH OD +>,
∴当,,O D H 三点共线时,DH 的长度最小，此时，
1DH OD OH =-=.
注解题的关键是找到共斜边的直角三角形隐藏的外接圆.解题中要能自己创造图形，挖掘问题本质，就能知其然，也知其所以然，从而牢固建立系统的知识体系，而且能灵活应用所学的知识解决问题.
练一练
如图9，矩形ABCD 的边,OA OC 分别在x 轴、y 轴上，
点E 在边AB 上，且点E ，
点B .已知点P 为y 轴上一动点，连结EP ,过点O 作OH EP ⊥，垂足为点H .在点P 从点(0,2)F 运动到原点O 的过程中，点H 的运动路径长为 .
解如图9连结OE .
122
O F E S ∆=
⨯ 在Rt OEA ∆中，
OE
2=
==,
2FE =
=. 12
O F E S F E O H ∆=⋅,
即
122
OH OH ⨯=∴= ∴在Rt OEH ∆中，
s i n 2
OH OEH OE ∠==, 60OEH ∴∠=︒.
点H 的运动路径长是:
260121803
ππ⨯⨯=. 注通过这一类问题的分析，进一步掌握“有公共斜边的直角三角形”具有共圆的性质，体会了此类问题的证明思路和方法.
例3 如图10, AB 是半圆O 的直径，10AB =cm, 8AC =cm ，点C 在半圆上，D 是弧BC 上的一个动点(含端点B ，不含端点C )，连结,AC AD .过点C 作CE AD ⊥于,E E 为垂足，连接BE ，在点D 的运动过程中，BE 的取值范围是 .
解如图10，设⊙M 与AB 相交于点N ,连结BM 且与⊙M 交相交于点E '. C E A D ⊥,90AEC ∴∠=︒，
因为E 在以AC 为直径的⊙M 上(不含点C ，可含点N )，所以当,,M E B 三点共线时，BE '最短，此时点E 与E '重合，即为BE 最短.
10,8,6
A B A C B C ==∴=. 作MF AB ⊥于F ,
90AFM ACB ∴∠=∠=︒,FAM CAB ∠=∠,
A M F A
B C
∴∆∆. M F A M B C A B ∴
=,即426105
MF ==， 125
MF ∴=.
165
AF ∴==, 则345BF AB AF =-=.
BM ∴==,
BE ∴长度的最小值4BE BM ME =-=,
BE 最长时，即E 与C 重合.
6BC =，且点E 与点C 不重合，
6BE ∴<.
综上所述，46BE ≤≤.
三、反思
1.认真审题找突破口
近几年的中考试卷中常会出现动点问题，其中一类动点题，看似无圆，但其中隐藏着圆的模型.如“定线定角”、“有公共斜边的直角三角形”等.我们应通过去伪成真，让“圆”形显露，再利用圆的性质解决问题.
2.抓准延伸点思维持续生长
在审题时要寻找题目中的特征，挖掘隐含条件，抓准知识的延伸点，让自己的思维持续生长.平时要注意积累解题方法，它对你来说就是一种解题模式，当你碰到类似问题或求解其他问题时，就能起到指引作用.解题后要归纳、总结和反思，使思维品质不断提升.
3.找出数学模型求出正确结果
在平时的学习中，对基础知识、基本图形、基本方法、基本结论要进行深人研究，把解题的过程当作建立数学模型的过程，并在建模过程中培养自己的数学应用能力.变与不”都是相对的，变的是几何问题或图形，不变的是解题思路和数学本质.在解题过程中，要抓住图形的特点，从中发现解决该问题的数学模型，并快速求出正确结果.。