圆中动点问题2
圆中的动点问题学生版
初三数学
圆中的动点问题·邬平剑作品
Page 5 of 9
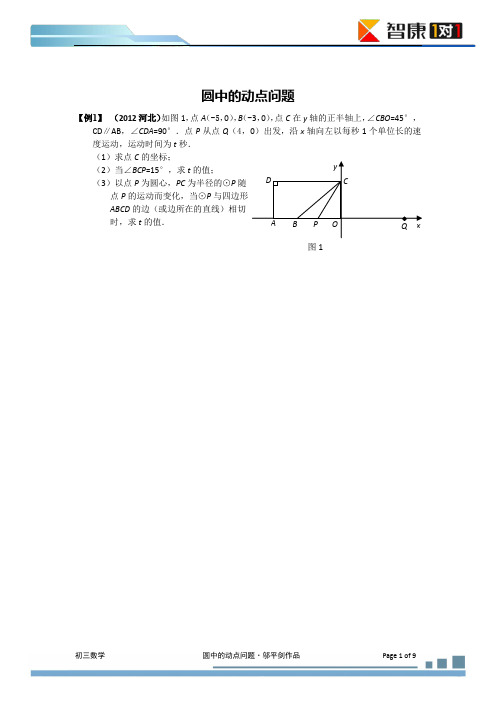
【例6】 (2012 上海模拟)如图,已知:正方形 ABCD 中,AB=8,点 O 为边 AB 上一动点,以 点 O 为圆心,OB 为半径的⊙O 交边 AD 于点 E(不与点 A、D 重合) ,EF⊥OE 交边 CD 于点 F。设 BO=x,AE=y。 (1) 求 y 关于 x 的函数关系式,并写出定义域; (2) 在点 O 运动的过程中,△EFD 的周长是否发生变化?如果发生变化,请用 x 的代数 式表示△EFD 的周长 ;如果不变化,请求出△EFD 的周长; (3) 以点 A 为圆心, OA 为半径作圆, 在点 O 运动的过程中, 讨论⊙O 与⊙A 的位置关系, 并写出相应的 x 的取值范围。 E A D D
初三数学Leabharlann 圆中的动点问题·邬平剑作品
Page 2 of 9
【例3】 (2011 江苏南京)如图,在 Rt△ABC 中,∠ACB=90°,AC=6 ㎝,BC=8 ㎝,P 为 BC 的 中点.动点 Q 从点 P 出发,沿射线 PC 方向以 2 ㎝/s 的速度运动,以 P 为圆心,PQ 长 为半径作圆.设点 Q 运动的时间为 t s. ⑴ 当 t=1.2 时,判断直线 AB 与⊙P 的位置关系,并说明理由; ⑵ 已知⊙O 为△ABC 的外接圆,若⊙P 与⊙O 相切,求 t 的值. A O C Q P B C Q P A O B C Q P A O B
2
1 O Q
第 28 题图
B
·
2 A l
1 x O B
·
2 A
x
第 28 题备用图
初三数学
圆中的动点问题·邬平剑作品
Page 9 of 9
圆中的动点问题
2023年中考数学高频考点训练——圆-动点问题

2023年中考数学高频考点训练——圆-动点问题一、综合题1.如图,四边形OBCD 中的三个顶点在⊙O 上,A 是优弧BD 上的一个动点(不与点B 、D 重合).(1)当圆心O 在BAD ∠内部,∠ABO +∠ADO=70°时,求∠BOD 的度数;(2)当点A 在优弧BD 上运动,四边形OBCD 为平行四边形时,探究ABO ∠与ADO ∠的数量关系.2.如图,在每个小正方形的边长为1的网格中,ABO 的顶点A ,B ,O 均落在格点上,OB 为⊙O 的半径.(1)AOB ∠的大小等于(度);(2)将ABO 绕点O 顺时针旋转,得A B O '' ,点A ,B 旋转后的对应点为A ',B '.连接AB ',设线段AB '的中点为M ,连接A M '.当A M '取得最大值时,请在如图所示的网格中,用无刻度的直尺画出点B ',并简要说明点B '的位置是如何找到的(不要求证明).3.如图,AB 是O 的直径,CD 是O 的切线,切点为C ,过B 作BE CD ⊥,垂足为点E ,直线BE 交O 于点F.(1)判断ABC ∠与EBC ∠的数量关系,并说明理由.(2)若点C 在直径AB 上方半圆弧上运动,O 的半径为4,则①当CB 的长为时,以B 、O 、E 、C 为顶点的四边形是正方形;②当BE 的长为时,以B 、O 、F 、C 为顶点的四边形是菱形.4.先阅读材料,再解答问题:已知点00(:)P x y 和直线y kx b =+,则点P 到直线y kx b =+的距离d 可用公式d =计算.例如:求点(2,1)P -到直线23y x =+的距离.解:由直线23y x =+可知:2,3k b ==.所以点(2,1)P -到直线23y x =+的距离为255d ==.求:(1)求点P (2,-1)到直线y=x+1的距离.(2)已知直线21y x =+与25y x =-平行,求这两条平行线之间的距离;(3)如图已知直线443y x =--分别交,x y 轴于,A B 两点,☉C 是以(2,2)C 为圆心,2为半径的圆,P 为☉C 上的动点,试求PAB ∆面积的最大值.5.如图,⊙O 的半径为1,点A 是⊙O 的直径BD 延长线上的一点,C 为⊙O 上的一点,AD =CD ,∠A =30°.(1)求证:直线AC 是⊙O 的切线;(2)求△ABC 的面积;(3)点E 在 BND 上运动(不与B 、D 重合),过点C 作CE 的垂线,与EB 的延长线交于点F.①当点E 运动到与点C 关于直径BD 对称时,求CF 的长;②当点E 运动到什么位置时,CF 取到最大值,并求出此时CF 的长.6.一块含有30︒角的三角板ABC 如图所示,其中90C ∠=︒,30A ∠=︒,3BC cm =.将此三角板在平面内绕顶点A 旋转一周.(1)画出边BC 旋转一周所形成的图形;(2)求出该图形的面积.7.如图,在ABE 中,BE AE >,延长BE 到点D ,使DE BE =,延长AE 到点C ,使CE AE =.以点E 为圆心,分别以BE 、AE 为半径作大小两个半圆,连结CD .(1)求证:AB CD =;(2)设小半圆与BD 相交于点M ,24BE AE ==.①当ABE S 取得最大值时,求其最大值以及CD 的长;②当AB 恰好与小半圆相切时,求弧AM 的长.8.如图,A 是半径为12cm 的O 上的定点,动点P 从A 出发,以2πcm /s 的速度沿圆周逆时针运动,当点P 回到A 地立即停止运动.(1)如果90POA ∠= ,求点P 运动的时间;(2)如果点B 是OA 延长线上的一点,AB OA =,那么当点P 运动的时间为2s 时,判断直线BP 与O 的位置关系,并说明理由.9.古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”。
教案_圆动点问题

圆上的动点例题1: 如图(1):已知⊙O 的半径为6cm , 射 线PM 经 过点O ,OP=10cm ,射线PN 经过点⊙O 相切于点Q 。
A ,B 两点同时从点P 出发,点A 以5cm/s 的速度沿射线PM 方向运动,点B 以4cm/s 的速度沿射线PN 方向运动,设运动时间为ts 。
求PQ 的长;(2)当为t 何值时,直线AB 与⊙O 相切。
练习:1.如图,⊙O 的半径为1,圆心O 在正三角形的边AB 上沿图示方向移动,当⊙O 移动到与AC边相切时,OA 的长是.2.在直角梯形ABCD 中,AD∥BC,∠B=90°,AD=13cm,BC=5cm,AB 为圆O 的直径,动点P 沿AD 从点A 开始向点D 以1m/s,的速度运动,动点Q 沿CB 从点C 开始向点B 以2cm/s 的速度运动,点P 、Q 分别从A 、C 两点同时出发,当其中一点停止时,另一点也随之停止运动。
是否存在某一时刻t,使直线PQ 与圆O 相切?若存在,求出t 的值,若不存在,说明理由。
A B Q O P N M例题2(2004年·上海)如图,在△ABC 中,∠BAC=90°,AB=AC=22,⊙A 的半径为1.若点O 在BC 边上运动(与点B 、C 不重合),设BO=x ,△AOC 的面积为y .(1)求y 关于x 的函数解析式,并写出函数的定义域.(2)以点O 为圆心,BO 长为半径作圆O,求当⊙O 与⊙A 相切时, △AOC 的面积.练习:如图,点A ,B 在直线MN 上,AB =11厘米,⊙A ,⊙B 的半径均为1厘米.⊙A 以每秒2厘米的速度自左向右运动,与此同时,⊙B 的半径也不断增大,其半径r (厘米)与时间t (秒)之间的关系式为r =1+t (t ≥0). (1)试写出点A ,B 之间的距离d (厘米) 与时间t (秒)之间的函数表达式;(2)问点A 出发后多少秒两圆相切?例题3如图,在平面直角坐标系中,点1O 的坐标为(40) ,,以点1O 为圆心,8为半径的圆与x 轴交于A B ,两点,过A 作直线l 与x 轴负方向相交成60°的角,且交y 轴于C 点,以A B CO 图8H A BNM点2(135)O ,为圆心的圆与x 轴相切于点D . (1)求直线l 的解析式;(2)将2O ⊙以每秒1个单位的速度沿x 轴向左平移,当2O ⊙第一次与1O ⊙外切时,求2O ⊙平移的时间.练习:已知:如图所示,直线l 的解析式为334y x =-,并且与x 轴、y 轴分别交于点A 、B 。
动点问题所有的题型

动点问题所有的题型
动点问题涉及的题型非常多,以下是一些常见的动点问题题型:
1. 直线运动中的动点问题:这类问题中,动点在直线上移动,需要求出动点的坐标或者轨迹方程。
2. 圆周运动中的动点问题:这类问题中,动点在圆周上运动,需要求出动点的轨迹方程或者运动时间。
3. 抛物线中的动点问题:这类问题中,动点在抛物线上运动,需要求出动点的坐标或者轨迹方程。
4. 双曲线中的动点问题:这类问题中,动点在双曲线上运动,需要求出动点的坐标或者轨迹方程。
5. 椭圆中的动点问题:这类问题中,动点在椭圆上运动,需要求出动点的坐标或者轨迹方程。
6. 多边形中的动点问题:这类问题中,动点在多边形边上运动,需要求出动点的坐标或者轨迹方程。
7. 函数图像中的动点问题:这类问题中,动点在函数图像上运动,需要求出动点的坐标或者函数解析式。
8. 行程问题中的动点问题:这类问题中,两个或多个动点在同一直线上运动,需要求出它们相遇的次数或者距离。
9. 工程问题中的动点问题:这类问题中,两个或多个动点在同一直线上运动,需要求出它们完成工程所需的时间或者距离。
10. 速度问题中的动点问题:这类问题中,动点在直线或曲线上运动,需要求出它的速度或者加速度。
以上仅是动点问题的一些常见题型,实际上还有很多其他类型的动点问题。
初一路程动点问题练习题

一、直线上的动点问题1. 已知直线l:y=2x+1,动点P在直线l上,且P到点A(1,3)的距离为2,求动点P的坐标。
2. 在直线l:x+y=3上,动点P的坐标为(t,3t),求点P到原点O的距离d的表达式。
3. 直线l:y=kx+b上,动点P的坐标为(x,kx+b),若点P到点A(a,b)的距离为定值,求k和b的取值范围。
二、圆上的动点问题1. 圆O的方程为x^2+y^2=16,动点P在圆上,且OP的长度为4,求动点P的坐标。
2. 圆O的方程为x^2+y^2=9,动点P在圆上,且OP的长度为3,求动点P到圆心O的距离的最大值和最小值。
3. 圆O的方程为x^2+y^2=4,动点P在圆上,且∠AOP=60°,求点P的坐标。
三、直线与圆的位置关系1. 圆O的方程为x^2+y^2=9,直线l:y=x+1与圆O相交于A、B两点,求AB的长度。
2. 圆O的方程为x^2+y^2=16,直线l:y=x+4与圆O相切于点P,求点P的坐标。
3. 圆O的方程为x^2+y^2=25,直线l:y=2x+3与圆O相交于A、B两点,求AB的中点坐标。
四、椭圆上的动点问题1. 椭圆的方程为x^2/4+y^2/9=1,动点P在椭圆上,且∠AOP=60°,求点P的坐标。
2. 椭圆的方程为x^2/9+y^2/16=1,动点P在椭圆上,且OP的长度为5,求动点P的坐标。
3. 椭圆的方程为x^2/25+y^2/16=1,动点P在椭圆上,且∠AOP=45°,求点P的坐标。
五、双曲线上的动点问题1. 双曲线的方程为x^2/9y^2/16=1,动点P在双曲线上,且∠AOP=30°,求点P的坐标。
2. 双曲线的方程为x^2/16y^2/9=1,动点P在双曲线上,且OP的长度为10,求动点P的坐标。
3. 双曲线的方程为x^2/25y^2/36=1,动点P在双曲线上,且∠AOP=90°,求点P的坐标。
圆形的动点问题

圆形的动点问题
简介
圆形的动点问题是一个经典的数学问题,涉及到在一个固定半径的圆上找到一个动点的运动轨迹。
本文将探讨在给定的圆上找到一个动点的运动轨迹的一种简单策略。
策略
我们可以将圆形的动点问题简化为一个平面几何问题。
设定一个固定半径的圆,我们需要找到一个动点,在圆的周长上运动。
为了简化问题,我们将动点的速度设定为相等和恒定。
步骤
以下是解决圆形的动点问题的简单策略的步骤:
1. 确定圆的半径:首先,我们需要确定给定圆的半径。
这将帮助我们计算动点的运动轨迹。
2. 计算圆的周长:根据圆的半径,我们可以计算出圆的周长。
周长是动点在圆上运动的路径。
3. 确定动点的速度:我们需要确定动点的速度。
假设动点的速
度是相等和恒定的,以便简化问题。
4. 计算动点的运动轨迹:根据动点的速度和圆的周长,我们可
以计算出动点在给定圆上的运动轨迹。
5. 图形化运动轨迹:为了更直观地理解动点在圆上的运动轨迹,可以图形化展示。
结论
通过简化圆形的动点问题,我们可以使用上述策略找到动点的
运动轨迹。
这个问题对几何学及其应用具有重要意义,并且可以帮
助我们理解运动轨迹的计算方法。
请注意,以上策略是一种简化的方法,可能不适用于所有情况。
特殊情况下可能涉及更复杂的数学问题和计算方法。
以上是关于圆形的动点问题的简要介绍和解决策略。
希望这能
为您提供有用的信息。
与圆有关的动点问题.doc题

动点问题(4)------与圆有关的动点直线与圆相切1.如图,⊙O 的半径为1,圆心O 在正三角形的边AB 上沿图示方向移动,当⊙O 移动到与AC 边相切时,OA 的长是 .2.如图,已知⊙O 的半径为6cm ,射线PM 经过点O ,10cm OP ,射线PN 与⊙O 相切于点Q .A B ,两点同时从点P 出发,点A 以5cm/s 的速度沿射线PM 方向运动,点B 以4cm/s 的速度沿射线PN 方向运动.设运动时间为t s .(1)求PQ 的长; (2)当t 为何值时,直线AB 与⊙O 相切?3如图,ABC ∆中,090C ∠=,4AC =,3BC =.半径为1的圆的圆心P 以1个单位/s 的速度由点A 沿AC 方向在AC 上移动,设移动时间为t (单位:s ). (1)当t 为何值时,⊙P 与AB 相切;(2)作PD AC ⊥交AB 于点D ,如果⊙P 和线段BC 交于点E ,证明:当165t s=时,四边形PDBE 为平行四边形.4.(2012河北中考25)如图14,(50)(30).A B --,,,点C 在y 轴的正半轴上,CBO∠=45,CD AB ∥,90CDA = ∠.点P 从点(40)Q ,出发,沿x 轴向左以每秒1个单位长的速度运动,运动时间为t 秒.(1) 求点C 的坐标;(2) 当15BCP =∠时,求t 的值;(3) 以点P 为圆心,PC 为半径的P ⊙随点P 的运动而变化,当P ⊙与四边形ABCD 的边(或边所在的直线)相切时,求t 的值.5.如图,形如量角器的半圆O的直径DE=12cm,形如三角板的⊿ABC中,∠ACB=90°,∠ABC= 30°,BC=12cm。
半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC 上。
设运动时间为t (s),当t=0s时,半圆O在⊿ABC的左侧,OC=8cm。
(1)当t为何值时,⊿ABC的一边所在直线与半圆O所在的圆相切?(2)当⊿ABC的一边所在直线与半圆O所在的圆相切时,如果半圆O与直线DE围成的区域与⊿ABC 三边围成的区域有重叠部分,求重叠部分的面积。
与圆有关的动点问题[下学期]--浙教版
![与圆有关的动点问题[下学期]--浙教版](https://img.taocdn.com/s3/m/d53cce990066f5335b81219f.png)
bbin电竞游戏 慢性肾衰竭尿毒症期一般不出现A.高镁血症B.高钾血症C.高钙血症D.高磷血症E.水潴留 防喷器组合的通径必须一致,其大小取决于井身结构设计中的套管尺寸,即必须略联结套管的直径。A、大于B、小于C、等于 设计单位的设计进度计划不包括。A.各类设计文件和图纸的预期完成时间B.各类设计文件和图纸的审核期限C.拟采用的设计方法的详细描述及主要原理D.各阶段设计评审、联络会的安排 [单选,共用题干题]某计算机的Cache采用相联映像,Cache容量为16KB,每块8个字,每个字32位,并且将Cache中每4块分为一组。若主存最大容量为4GB且按字节编址,则主存地址应为(1)位,组号应为(2)位。若Cache的命中率为0.95,且Cache的速度是主存的5倍, 那么与不采用Cache相比较,采用Cache后速度大致提高到(3)倍。空白(2)处应选择A.5B.6C.7D.8 CCU室,一患有急性心肌梗死3天的病人,突然感到呼吸困难,伴心悸,不能平卧。体检:口唇发绀,强迫端坐位,两肺中、下部可闻及中、小水泡音,心率120次/分,律齐,S1增强,以下哪项体征对合并乳头肌功能失调的诊断最有意义。A.血压下降B.胸骨左缘第三、四肋 间可闻及心包摩擦音C.心尖区收缩中、晚期喀喇音和收缩晚期杂音D.胸骨左缘第三、四肋间可触及收缩期震颤E.心浊音界向左扩大 根据白喉棒状杆菌在亚碲酸钾培养基上生长情况和生化反应特点,可将本菌分为三型A.危重型,重型,中间型B.危重型,中间型,轻型C.危重型,重型,轻型D.重型,中间型,轻型E.重型,过渡型,轻型 下列对骨质疏松描述错误的是A.骨质疏松症可分为原发性、继发性两类B.雌激素可抑制骨吸收,雌激素水平不足是病因之一C.多数患者为原发性骨质疏松症D.女性绝经期后发病率升高E.骨折是本病最为严重的后果 不属于半夏厚朴汤主治证候的是()A.咽中如有物阻B.咯吐不出C.吞咽不下D.脘腹疼痛E.或咳或呕 下列关于信息高速公路的描述正确的是。A.一条公路B.一条车流量很大的高速公路C.一条信息流通量很大的公路D.一个能够给用户提供大量信息,由通信网、计算机、数据库以及各种日用电子设备组成的完备网络 臭氧在大气中有什么作用?它与平流层温度的铅直分布有什么关系? 气胸破裂口较小,随肺萎陷而关闭,空气不再继续进入胸膜腔,称为。A.高压性气胸B.自发性气胸C.闭合性气胸D.张力性气胸E.交通性气胸 细胞因子生物活性测定法的主要特点是A.敏感性较高B.特异性不高C.操作繁琐D.易受干扰E.以上均是 患者,68岁,急性心肌梗死,一旦出现房颤。对于这个患者测量心率和脉率的正确方法是()A.一个人测心率另一个人测脉率同时测一分钟B.一个人先测心率后测脉率C.一人先测脉率后测心率D.报告医师由医师来测心率脉率E.一人发口令和计时,另一人测心率脉率 慢性支气管炎慢性迁延期是指有不同程度的咳、痰、喘症状迁延多长时间以上者。A.2周B.1个月C.2个月D.半年E.1年 下列哪项不是肺痨的别名A.尸疰B.劳疰C.伏连D.呷嗽首层发生火灾,其控制程序应先接通。A、本层B、地下各层C、二层D、所有层 精气生万物的机理是天地阴阳二气的A.互根互用B.对立制约C.交感合和D.消长平衡E.相互转化 已知某船Lbp=78,宽B=16.4m,水线面面积为921m2,则其水线面积系数为CW为。(小吨位船试题)A.0.77B.0.65C.0.68D.0.72 适用于金瓷冠也适用于铸瓷冠的肩台形式是A.135°肩台B.带斜面90°肩台C.刃状边缘D.90°肩台E.深凹形 确定某种传染病隔离期的根据是A.病程的长短B.潜伏期的长短C.前驱期的长短D.传染期的长短E.病情严重程度 离心铸造球墨铸铁管国家标准号是。 对于口腔教育不正确的认识是A.是口腔预防的保健项目B.是口腔公共卫生的基础C.是争取领导支持的方法D.是传递科学信息的途径E.是提高健康意识的手段 医患之间非技术关系的是A.同事关系B.道德关系C.上下级关系D.陌生人关系E.竞争关系 船舶随遇平衡的主要特征是。A.稳心与重心重合,复原力矩为零B.重心与漂心重合,复原力矩为零C.重心与浮心重合,复原力矩为零D.稳心与浮心重合,复原力矩为零 安全气囊的碰撞传感器一般安装在汽车。A.中部B.前部C.后部 骨性关节炎关节液特点不包括哪一项A.关节液黄色或草黄色B.白细胞数>2乘以十的六次方/LC.黏度正常D.凝固试验正常E.以上都不是 发生医疗事故争议时,在医患双方在场的情况下封存的病历资料是。A.门诊病历B.疑难病例讨论记录C.医嘱单D.特殊检查同意书E.住院志 当颅内压高于多少mmHg(1mmHg=O.133kPa)以上时,视网膜中央静脉血流将停止()A.15B.25C.35D.45E.55 铁缺乏时,供给骨髓造血用的铁是A.血红蛋白铁B.肌红蛋白铁C.易变池铁D.贮存铁E.运转中的铁 黄连在朱砂安神丸中的作用是()A.清热解毒B.清热燥湿C.清心泻火D.清热安神E.泻火解毒 下列各项不宜区分阴阳属性的是A.寒与热B.邪与正C.上与下D.左与右E.动与静 在对进度计划进行工期和时间安排的合理性审查时,应重点审查。A.施工总工期的安排应符合合同工期B.主要骨干人员及施工队伍的进场日期已经落实C.各项施工方案和施工方法应与施工经验和技术水平相适应D.所需主要材料和设备的运送日期已有保证E.对动员、清场、假 日及天气影响的时间,应有充分的考虑并留有余地 能测出梅毒螺旋体特异抗体的试验是A.荧光密螺旋体抗体吸收试验B.捕获ELISA法C.梅毒螺旋体制动试验D.非密螺旋体抗原试验E.梅毒螺旋体血凝试验 控制结核病流行的基本原则,以下哪项不正确。A.控制传染源B.切断传染途径C.增强免疫力D.预防性使用抗结核药E.降低易感性 演示紧急外科洗手的过程。 肾结核早期唯一重要的阳性发现为A.大量血尿和脓尿B.尿常规检查中有较多的红细胞、白细胞C.全身慢性消耗症状D.肾区疼痛E.发热 VHF/UHF频段,可以用较小的发射功率获得较好的。 下列药材不属于西北药的是A.五味子B.当归C.甘草D.秦艽E.大黄 患者,男,23岁,因上呼吸道感染,剧烈咳嗽,持续发热而就诊,测体温持续在39~40℃左右一周时间,且一天内体温波动幅度不超过1℃。其热型为()A.稽留热B.弛张热C.间歇热D.不规则热E.超高热 麦金瑟7S结构中的七种文化要素是____,____,____,____,____,_____,_____.
圆的动点问题方法总结

圆的动点问题方法总结
圆的动点问题涉及圆的运动轨迹和动点的位置变化。
在解决这类问题时,我们
可以采用以下方法:
1. 构建几何模型:首先,我们可以通过绘制几何图形来简化问题。
将圆和动点
在纸上画出来,有助于我们更清楚地理解问题。
2. 利用圆的性质:圆有很多重要的性质,我们可以利用这些性质来解决动点问题。
例如,圆的半径和直径之间的关系,圆的切线和切点的性质等。
3. 使用向量方法:在处理圆的动点问题时,向量方法很有用。
我们可以将动点
的位置表示为向量,并使用向量的运算规则来解决问题。
例如,我们可以用位置向量来表示动点的位置,并使用向量的加法和减法来计算动点的移动方向和距离。
4. 应用三角函数:如果涉及到角度的变化,我们可以使用三角函数来解决问题。
例如,如果动点绕圆心旋转,我们可以使用正弦和余弦函数来描述动点在不同位置的坐标变化。
5. 运用解析几何:解析几何是解决圆的动点问题的常用方法之一。
我们可以使
用坐标系和代数方程来描述圆和动点的运动轨迹。
通过求解方程组,我们可以得到动点的位置和移动方向。
总的来说,解决圆的动点问题需要充分利用圆的性质,运用几何、向量、三角
函数和解析几何等方法。
通过选择合适的方法,我们可以更好地理解问题并求解出准确的结果。
关于圆的动点问题常见解决方案[例谈圆中常见两解问题]
![关于圆的动点问题常见解决方案[例谈圆中常见两解问题]](https://img.taocdn.com/s3/m/3882bbf0960590c69ec376f9.png)
关于圆的动点问题常见解决方案[例谈圆中常见两解问题] 由于圆具有对称性,以及点、弦、角等元素在圆中位置的相对性.因此,在解答没有给出图形的圆的有关计算题时,就要仔细审题,周密思考,以防漏解. 一、有关点与圆的位置关系问题例1:点P到⊙O的最大距离是8cm,最小距离是4cm,则⊙O的半径是.分析:题中并没有说明点P与圆的位置关系,故需分点P在圆内与点P在圆外两种情况求解.(如图1)当点P在圆内时,由已知,得PA=4, PB=8.(如图2)当点P在圆外时,由已知,得PA=4,PB=8.综上所述,⊙O的半径为6cm或2cm.二、有关平行弦问题例2:已知四边形ABCD是⊙O的内接梯形,AB∥CD,AB=8,CD=6.⊙O的半径等于5,求梯形ABCD的高.分析:求圆内接梯形的高就是求圆中两条平行弦间的距离.(如图3)当AB、CD在圆心的两侧时,过圆心O作EF⊥AB于E,交CD于F.∵AB∥CD,∴EF⊥CD.连结OA、OD,则△OAE、△ODF都是直角三角形.∴梯形的高EF=OE+OF=3+4=7.(如图4)当AB、CD在圆心O的同侧时,作OF⊥CD于F,交AB于E,连结OA、OD.同理,求得OE=3,OF=4.∴梯形的高EF=OF-OE=4-3=1.综上所述,⊙O的内接梯形ABCD的高为7或1.三、有关公共弦问题例3:⊙O1和⊙O2相交于A、B两点,它们的半径AO1=20,AO2=15,公共弦AB=24,则△AO1O2的周长为 .分析:因为已知两圆的半径不等,所以,圆心可能在公共弦AB 的两侧(如图5),也可能在AB的同侧(如图6).分别在Rt△AO1C和Rt△AO2C中,由勾股定理求得O1C=16,O2C=9.∴O1O2=16+9=25.∴△AO1O2的周长为20+15+25=60.在图6中,同理求得O1C=16,O2C=9.∴O1O2=16-9=7.∴△AO1O2的周长为20+15+7=42.综上所述,△AO1O2的周长为60或42.四、有关两条弦的夹角问题分析:连结OA,则弦AC、AD可能在半径OA的两侧(如图7),也可能在OA的同侧(如图8).在图7中,连结OC.∴∠OAD=30°.∴∠CAD=∠CAO+∠OAD=45°+30°=75°.在图8中,同理求得∠OAD=30°,∠OAC=45°.∴∠CAD=∠OAC-∠OAD=45°-30°=15°.综上所述,∠CAD等于75°或15°.五、有关圆周角问题例5 :PA、PB是⊙O的切线,A、B是切点,∠APB=78°,点C是⊙O上异于A、B的任意一点,则∠ACB=.分析:如图9,因为C是⊙O上异于A、B的任意一点,所以点C可能在优弧AB上,也可能在劣弧 AB上.当点C在优弧AB上时,连结OA、OB,则OA⊥PA,OB⊥PB.又∠APB=78°,∴∠AOB=360°-90°-90°-78°=102°.当点C"在劣弧AB上时,四边形AC"BC是圆内接四边形.∴∠AC"B=180°-∠ACB=180°-51°=129°.综上所述,∠ACB等于51°或129°.六、有关圆的相切问题例6:以O为圆心的两个同心圆的半径分别9cm和5cm,若⊙A 与这两个圆都相切,则⊙A的半径为 .分析:因为相切分内切和外切两种,所以⊙A可能与大圆内切,与小圆外切(如图10),也可能与两个圆都内切(如图11).综上所述,⊙A的半径为2cm或7cm.本文为全文原貌未安装PDF浏览器用户请先下载安装原版全文内容仅供参考。
与圆有关的动点问题

与圆有关得动点问题1、如图,⊙O得直径AB=4,C为圆周上一点,AC=2,过点C作⊙O得切线DC,P点为优弧CBA上一动点(不与A.C重合).(1)求∠APC与∠ACD得度数;(2)当点P移动到CB弧得中点时,求证:四边形OBPC就是菱形.(3)P点移动到什么位置时,△APC与△ABC全等,请说明理由.2、如图,在菱形ABCD中,AB=23,∠A=60º,以点D为圆心得⊙D与边AB相切于点E.(1)求证:⊙D与边BC也相切;(2)设⊙D与BD相交于点H,与边CD相交于点F,连接HF,求图中阴影部分得面积(结果保留π);(3)⊙D上一动点M从点F出发,按逆时针方向运动半周,当S△HDF=3 S△MDF时,求动点M经过得弧长(结果保留π).3、半径为2cm得与⊙O边长为2cm得正方形ABCD在水平直线l得同侧,⊙O与l相切于点F,DC在l上.(1)过点B作得一条切线BE,E为切点.①填空:如图1,当点A在⊙O上时,∠EBA得度数就是;②如图2,当E,A,D三点在同一直线上时,求线段OA得长;(2)以正方形ABCD得边AD与OF重合得位置为初始位置,向左移动正方形(图3),至边BC与OF重合时结束移动,M,N分别就是边BC,AD与⊙O得公共点,求扇形MON得面积得范围.4、如图,Rt△ABC得内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P在射线AC上运动,过点P作PH⊥AB,垂足为H.(1)直接写出线段AC、AD及⊙O半径得长;(2)设PH=x,PC=y,求y关于x得函数关系式;(3)当PH与⊙O相切时,求相应得y值.5、如图1,正方形ABCD得边长为2,点M就是BC得中点,P就是线段MC上得一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O得切线,交AD于点F,切点为E.(1)求证:OF∥BE;(2)设BP=x,AF=y,求y关于x得函数解析式,并写出自变量x得取值范围;(3)延长DC、FP交于点G,连接OE并延长交直线DC与H(图2),问就是否存在点P,使△EFO∽△EHG(E、F、O与E、H、G为对应点)?如果存在,试求(2)中x与y得值;如果不存在,请说明理由.6、如图,⊙O得半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M就是直线CD上异于点C、O、D得一个动点,AM所在得直线交于⊙O于点N,点P就是直线CD上另一点,且PM=PN.(1)当点M在⊙O内部,如图一,试判断PN与⊙O得关系,并写出证明过程;(2)当点M在⊙O外部,如图二,其它条件不变时,(1)得结论就是否还成立?请说明理由;(3)当点M在⊙O外部,如图三,∠AMO=15°,求图中阴影部分得面积.答案:1、解:(1)连接AC,如图所示:∵AB=4,∴OA=OB=OC=12AB=2。
怎样运用分类讨论思想解答几何中的动点问题

数学篇几何动点问题一直是初中几何中的一个难点,因为点运动的位置不同,形成的图形就不同,符合结论的情况可能就不止一种.同学们在求解此类问题时常常因为考虑不周导致漏解而出错.因此,解答动点问题尤其要注意分类讨论.下面就如何运用分类讨论思想解答两类几何图形中的动点问题进行分析,以供参考.一、运用分类讨论思想解答等腰三角形中的动点问题等腰三角形具有两条边相等、底角相等的特点,在求解涉及等腰三角形的动点问题时,由于边的不确定性或角的不确定,需要运用分类讨论思想,从动态的角度逐一讨论三角形的三边两两相等的三种情况,或三角形的三个角为其顶角的三种可能性,然后综合所有分类的结果确定最终答案.例1如图1,在直角坐标系中,已知点P (-2,-1),点T (t ,0)是x 轴上的一个动点.(1)求点P 关于原点的对称点P ′的坐标;(2)当[t ]取何值时,△P ′TO是等腰三角形?图1图1-1分析:第(1)问求P 点的对称点P ′比较简单,利用对称性即可解答.第(2)问,T 是x 轴上的动点,它在运动的过程中△P ′TO 可能是等腰三角形但顶点未确定,需要分情况讨论.解:(1)∵P (-2,-1),∴P 关于原点的对称点P ′坐标为(2,-1),(2)由(1)知P ′(2,-1),作图如图1-1所示,①当△P ′TO 中,点P ′为顶点时,T 点为图1-1中T 4点,此时P ′T =P ′O ,T 坐标为T 4(4,0),②当△P ′TO 中,点T 为顶点时,T 点为图1-1中T 2点,此时TO =TP ′,又∵T (t ,0)且P ′(2,-1),∴(0-t )2+(0-0)2=(2-t )2+(-1-0)2解得,t =54,此时点T 坐标为T 2(54,0),③当△P ′TO 中,点O 为顶点时,T 点为图1-1中T 1和T 3点,此时TO =P ′O ,∵T (t ,0)且P ′(2,-1),∴(0-t )2+(0-0)2=(0-2)2+[0-(-1)]2,解得,t =±5,此时T 点坐标为T 1(-5,0)和T 3(5,0),综合①②③可知,当t 取-5、54、5、4时,△P ′TO 是等腰三角形.评注:本题看似简单,实则非常复杂.由于题目中没有明确等腰三角形的顶点,且T 为坐标轴上的一个动点,所以点T 、O 、P 均有可能为等腰三角形顶角的顶点,需要对此进怎样运用分类讨论思想解答几何中盐城市新洋初级中学吉华丽解法荟萃32数学篇行分类讨论.二、运用分类讨论思想解答圆中的动点问题圆既是轴对称图形,又是中心对称图形,还具有旋转不变性.圆的这些特性决定了与圆有关的动点问题可能存在多解.在解题时,我们可以根据题目要求初步绘制“圆”可能存在的位置,然后依据分类标准(比如x 轴、y 轴等)逐一分类讨论,做到不重不漏,最后综合所有情况得到完整答案.例2如图2,直线y =-43x +4与x 轴、y 轴分别交于点M ,N .(1)求M ,N 两点的坐标;(2)如果点P 在坐标轴上,以点P 为圆心,125为半径的圆与直线y=-43x +4相切,求点P 的坐标.图2图2-1分析:这是一个直线与圆相结合的题目.第(1)问,我们借助直线方程y=-43x +4可以直接求出M 、N 的坐标.第(2)问P 点在坐标轴上,到底在x 轴还是y 轴不确定,所以以P 点为圆心,半径为125的圆也具有不确定性,需要借助分类讨论思想加以讨论.解:(1)∵直线y =-43x +4与x 轴、y 轴分别交于点M ,N ,∴令x =0,y =4,即N (0,4).同理可得M (3,0).(2)经过分析发现P 点可能在x 轴上或y 轴上,通过作图发现可能有4种情况,如图2-1所示.①当P 在x 轴上时,设P (x 0,0),则圆P可能是图2-1中的两个虚线圆.125=43x ,解得x 0=0或6,此情况下P 点坐标为P 1(0,0)P 2(6,0);②当P 在y 轴上时,设P (0,y 0),则圆P可能是图2-1中的两个实线圆.125=|-43×0-y 0+4|4,解得y 0=0或8,此情况下P 坐标为P 3(0,0)和P 4(0,8),由此可见P 1和P 3重合,是同一个点.综合①②,符合条件的P 点一共有3个,分表为(0,0)、(6,0)、(0,8).评注:审题时一定要充分挖掘隐含条件,“点P 在坐标轴上”就是一个不确定的表述,可能存在多种情况.另外作图要准确,可以通过作图的方式大致确定点的位置,预估答案.此外,该题还有一个关键之处,即“点到直线的距离公式”.考试中常用的有两种公式,分别为:①设直线方程为一般式Ax +By +C =0,点P 的坐标为(x 0,y 0),则点P 到直线L 的距离为:d =|Ax 0+By 0+C |A 2+B2;②当P (x 0,y 0),直线L 的方程为截距式y =kx +b ,则P 点到直线的距离为d =|kx 0-y 0+b |1+k2.总之,动点问题常常要借助分类讨论思想辅助解题.一般涉及到与“直角三角形”“等腰三角形”“相似三角形”“圆”等相关的动点问题,往往具有不确定性,存在多解的情况.解法荟萃。
初三-圆中动点问题

个性化教学辅导教案例1.已知如图, 在平面直角坐标系中, 直线与轴、轴分别交于A, B两点, P是直线AB 上一动点, ⊙的半径为1.(1)判断原点O与⊙的位置关系, 并说明理由;(2)当⊙过点B时, 求⊙被轴所截得的劣弧的长;(3)当⊙与轴相切时, 求出切点的坐标.练习1: 平面上, 矩形ABCD与直径为QP的半圆K如图15-1摆放, 分别延长DA和QP交于点O, 且∠DOQ=60°, OQ=OD=3, OP=2, OA=AB=1, 让线段OD及矩形ABCD位置固定, 将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转, 设旋转角为.发现:(1)当, 即初始位置时, 点P 直线AB上.(填“在”或“不在”)求当是多少时, OQ经过点B?(2)在OQ旋转过程中, 简要说明是多少时, 点P, A间的距离最小?并指出这个最小值;如图15-2, 当点P恰好落在BC边上时, 求及.拓展: 如图15-3, 当线段OQ与CB边交于点M, 与BA边交于点N时, 设B M=x(x>0),用含x的代数式表示B N的长,并求x的取值范围.图15-2图15-3备用图探究: 当半圆K与矩形ABCD的边相切时, 求sin 的值.练习2: 如图1, 已知点A(8, 4), 点B(0, 4), 线段CD的长为3, 点C与原点O重合, 点D在x轴正半轴上. 线段CD沿x轴正方向以每秒1个单位长度的速度向右平移, 过点D作x轴的垂线交线段AB于点E, 交OA于点G, 连接CE交OA于点F(如图2), 设运动时间为t. 当E点与A点重合时停止运动.(1)求线段CE的长;(2)记△CDE与△ABO公共部分的面积为S, 求S关于t的函数关系式;(3)如图2, 连接DF.①当t取何值时, 以C、F、D为顶点的三角形为等腰三角形?②△CDF的外接圆能否与OA相切?如果能, 直接写出此时t的值;如果不能, 请说明理由。
图1图2最值问题例2.如图, 在△ACE 中, CA=CE, ∠CAE=30°, ⊙O 经过点C, 且圆的直径AB 在线段AE 上. (1)试说明CE 是⊙O 的切线;(2)若△ACE 中AE 边上的高为h, 试用含h 的代数式表示⊙O 的直径AB ;(3)设点D 是线段AC 上任意一点(不含端点), 连接OD, 当 CD+OD 的最小值为6时, 求⊙O 的直径AB 的长.练习1: 在△ 中, ,将△ 绕点 顺时针旋转, 得到△ .⑴.如图①, 当点 在线段 延长线上时.①.求证: ;②.求△ 的面积;⑵.如图②,点 是 上的中点,点 为线段 上的动点,在△ 绕点 顺时针旋转过程中,点 的对应点是 ,求线段 长度的最大值与最小值的差.练习2: 如图, 在平面直角坐标系中, 圆M 过原点o, 与x 轴交于A (4.0), 与y 轴交于B (0,3), 点C 为劣弧AO 的中点, 连接AC 并延长到D, 使DC=4CA,连接BD.(1)圆M 的半径;(2)证明:BD 为圆M 的切线;(3)在直线MC 上找一点p, 使|DP-AP |最大。
圆中的动点问题

圆中的动点问题教学目标:【知识与技能】:1.复习圆的基本知识,包括圆的定义,垂经定理,圆周角定理,切线定理。
2.运用圆的有关知识解决圆中的动点问题。
【过程与方法】:经历探究圆中的动点问题的解题过程,初步体会解决动点问题的思考方法。
【情感、态度与价值观】:培养学生分类讨论的数学方法,以静制动的解题策略。
教学重难点:【重点】:圆中的动点问题的解决方法。
【难点】:分类讨论的数学方法的运用。
教与学互动设计:(一)创设情境导入新课1.欣赏下列图片2. 复习圆的定义,与圆有关的角、线段。
CA B OMDENO ℓGO(1)圆周角与圆心角的关系:(2)复习垂径定理:(3)切线,切线的性质与切线的判定:(二)合作交流解读探究例1:已知:点A、B是⊙O上的两个定点,且∠AOB=70◦(1)点P是⊙O上不与A、B重合的一个动点,∠APB的度数是多少?讨论:采用了什么方法和技巧?(∠APB=35◦,145◦)①以静制动②分类讨论(2)过点O分别作OC⊥PA,OD⊥PB垂足分别为C、D。
连接CD,线段CD与AB的位置关系和数量关系会不会随点P的变化而改变,请说明理由。
例2:已知:AB 为⊙O 的直径,点C 为直径AB 上的一个动点,过C 作DE ⊥AB(1)连接OD ,作∠ODE 的角平分线交⊙O 于点P (如图2),请观察点P 的位置,你有什么发现吗?(2)点M 为线段CD 上不同于C ,D 的一动点,作直线AM 交O 于N ,过N 点作O 的切线NG ,直线NG 与直线CD 交于点G ,请你通过观察测量判断∆MNG(三) 总结反思 拓展升华总结:主要数学知识圆的有关知识以及与圆有关的动点问题。
主要数学方法分类讨论与以静制动。
BB。
八上圆形动点问题

八上圆形动点问题
圆形动点问题是初中数学中的重要知识点之一,让我们一起来了解一下吧。
问题描述
假设有一个圆形轨道,上面有一个动点P。
动点P在轨道上运动,每个位置的坐标都会发生变化。
我们需要研究动点P的运动规律和性质。
基本概念
在解决圆形动点问题时,我们需要了解以下几个基本概念:
1. 动点:动点是指在圆形轨道上运动的点。
在每个时刻,动点的位置和坐标都可能发生变化。
2. 圆心:圆心是圆形轨道的中心点,通常用字母O表示。
3. 圆心角:圆心角是指以圆心为顶点的角度。
在圆形动点问题中,我们常常通过圆心角来描述动点的位置和运动状态。
4. 弧长:弧长是指圆形轨道上两个点之间的弧的长度。
在解决圆形动点问题时,我们常常用弧长来表示动点在轨道上的位置。
问题解答
在解答圆形动点问题时,我们需要根据具体的问题描述,采取合适的方法和策略进行分析和计算。
注意事项
在研究圆形动点问题时,需要保持独立思考,不依赖于其他人的帮助。
我们应该利用自身的知识和经验,采用简单明了的策略,避免出现复杂的法律问题。
此外,在引用内容时,应确保能够进行确认,避免引用不可靠的信息。
以上是关于八上圆形动点问题的基本介绍和解答要点。
希望对你有所帮助!。
与圆有关的动点问题[下学期]--浙教版
![与圆有关的动点问题[下学期]--浙教版](https://img.taocdn.com/s3/m/76c2bba219e8b8f67c1cb988.png)
(2)当△ABC的一边与半圆O所在的圆相切时,如果半圆O与 直径DE围成的区域与△ABC的三边围成的区域有重叠部分, 求重叠部分的面积.
小结:
1.复习整理所学圆的知识,注意前后知识的衔接.
2.解题要注重审题.在了解所用知识和产生解题方 案过程中,适时关注数学思想方法运用.
与圆有关的动点 问题
初三数学组
1.如图,⊙ O的半径为1,圆心O在正三角形的边
AB上沿图示方向移动,当⊙ O移动到与AC边相
23
切时,OA的长是 3 .
2.如图,从⊙ O外一点A作⊙ O的切线AB,AC,切点 分别为B、C, ⊙ O的直径BD为6,连结CD,AO.
(1)求证:CD∥AO;
(2)设CD=x,AO=y,求y与x之间的函数关系式,并写 出x的取值范围;
(3)若AO+CD=11,求AB的长.
3.如图,在矩形ABCD中,AB=20cm,BC=4cm,点p从 A开始折线A——B——C——D以4cm/秒的 速度 移动, 点Q从C开始沿CD边以1cm/秒的速度移动,如果点P、Q 分别从A、C同时出发,当其中一点到达D时,另一点也 随之停止运动,设运动的时间t(秒)
OF FH 1 AE AB 2
∴AE与以CD为直径的圆F相 切.
如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=900, ∠ACBC=300.半圆O以每秒2个单位从左到右运动,在运动 过程中,点D,E始终在直线BC上,设运动时间为t秒.当t=0 时,半圆O在△ABC的左侧,OC=8.
y ( X 2 1) X 2
4
4
4
(2)作OF⊥CD,垂足为F,
圆中的动点问题

为!盯
() l Mz A 2过点 作M, / B  ̄O " / f
3
3
形 AB D 的 C
一
在 Rt HF中 。 H C △C 明 = +
F +
边 于 点 R,
C D :在 R AHF t D中 。 叫 HF 一
9
点 , 善
A ,M2易得 S : M2O , △
出 的值 盟
Q R
图4
图5
蕊
(当 R 边 时 1 点在 D 上 , )
Q. R 所以鱼 值为1 的 _
Q R
( ) 点R在 C 2当 D边 上 时 , 图5 如 所 示 , 易 证 △A P B △B R. 所 以 C
/ P _B A=/ C RB. R= 1 B A Q
数 譬公开 I翘 学 专数
蓠 研 点, 运 过 究 p的 动 程 尺
发现 , 随着 点9在 线段AP 上运 动 , R 点J 也在 四边 形AB D边 上运 动 ,即落在 C
四 边 形ABC D的 边 D或 边 C D上 . 画 可
出图 形 , 应 用 全 等 、 似 等知 识 求 再 相
10 — 2 : 8
订 .所 以 , 点 运 动 到 时 , 当
删 , 此 时 点 经 过 的 弧 长 为
所形半=角c ( 示0径, I一U ,黧A z 扇的 即一U 心 、 O 3 广 蠹 圆 J
所示
S
8
3
AO 9 。 B= 0 ,点 C 弧AB上异 于A, 是 日 的 动点 ,过 点C C 作 D上O A于 点D, 作 C E上O B于点 , 结DE, G, 线 连 点 H在 段D 上 ,且DG G E = 日 E 求证 : D C % 3 H2z 值. C  ̄定
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆中动点问题一、选择题【题1】如图,点P是等边三角形ABC外接圆⊙O上的点,在以下判断中,不正确...的是( C )A、当弦PB最长时,ΔAPC是等腰三角形。
B、当ΔAPC是等腰三角形时,PO⊥AC。
C、当PO⊥AC时,∠ACP=300.D、当∠ACP=300,ΔPBC是直角三角形【答案】【题2】如图,以M(-5,0)为圆心、4为半径的圆与x轴交于A、B两点,P是⊙M上异于A、B的一动点,直线PA、PB分别交y轴于C、D,以CD为直径的⊙N与x轴交于E、F两点,则EF的长( C )A.等于42B.等于43C.等于6D.随P点位置的变化而变化【答案】分析:连接NE,设圆N半径为r,ON=x,则OD=r﹣x,OC=r+x,证△OBD∽△OCA,推出OC:OB=OD:OA,即(r+x):1=9:(r﹣x),求出r2﹣x2=9,根据垂径定理和勾股定理可求出答案.解答:解:连接NE,设圆N半径为r,ON=x,则OD=r﹣x,OC=r+x,∵以M(﹣5,0)为圆心、4为半径的圆与x轴交于A.B两点,∴OA=4+5=9,0B=5﹣4=1,∵AB是直径,∴∠APB=90°,∵∠BOD=90°,∴∠PAB+∠PBA=90°,∠ODB+∠OBD=90°,∵∠PBA=∠OBD,∴∠PAB=∠ODB,∵∠APB=∠BOD=90°,∴△OBD∽△OCA,∴OC ODOB OA=,即91r xr x+=-解得:r2﹣x2=9,由垂径定理得:OE=OF,OE2=EN2﹣ON2=r2﹣x2=9,即OE=OF=3,∴EF=2OE=6,故选C.【题3】如图,已知⊙O1的半径为1cm,⊙O2的半径为2cm,将⊙O1,⊙O2放置在直线l上,如果⊙O1在直线l上任意滚动,那么圆心距O1O2的长不可能是0.5cm【答案】解:∵⊙O1的半径为1cm,⊙O2的半径为2cm,∴当两圆内切时,圆心距为1,∵⊙O1在直线l上任意滚动,∴两圆不可能内含,∴圆心距不能小于1,故选D.【题4】如图,⊙O的半径为4cm,直线l与⊙O相交于A、B两点,AB=4cm,P为直线l上一动点,以1cm为半径的⊙P与⊙O没有公共点.设PO=dcm,则d的范围是d>5cm或2cm≤d<3cm.【答案】解:连接OP、OA,∵⊙O的半径为4cm,1cm为半径的⊙P,⊙P与⊙O没有公共点,∴d>5时,两圆外离,当两圆内切时,过点O作OD⊥AB于点D,OP′=4-1=3cm,OD=2cm,∴以1cm为半径的⊙P与⊙O没有公共点时,2≤d<3,故答案为:d>5或2≤d<3.【题5】如图,在Rt△AOB中,OA=OB=32,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O 的一条切线PQ(点Q为切点),则切线PQ的最小值为22.【答案】解:连接OP、OQ.∵PQ是⊙O的切线,∴OQ⊥PQ;根据勾股定理知PQ2=OP2﹣OQ2,∴当PO⊥AB时,线段PQ最短,∵在Rt△AOB中,OA=OB=222OA=6,∴OP=·OA OBAB=3,∴PQ=2222【题6】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为7,则GE+FH的最大值为10.5 .【答案】当GH 为⊙O 的直径时,GE+FH 有最大值.当GH 为直径时,E 点与O 点重合,∴AC 也是直径,AC=14.∵∠ABC 是直径上的圆周角,∴∠ABC=90°,∵∠C=30°, ∴AC=7.∵点E 、F 分别为AC 、BC 的中点,∴EF=3.5, ∴GE+FH=GH-EF=14-3.5=10.5.故答案为10.5.【题7】如图,△ABC 中,∠BAC=600,∠ABC=450,AB=2 2 ,D 是线段BC 上的一个动点,以AD 为直径画⊙O分别交AB,AC 于E,F ,连接EF,则线段EF 长度的最小值为____ 3 ___【答案】∠ACB=60°,∠ABC=45°,那么,∠BAC=75°.∠EOF=2∠BAC=150°所以,∠OEF=∠OFE=30°所以,EF=√3×OE,∠ABC=√3×AO 所以,当直径AD 最小时,EF 最小;所以,EF 最小时,AD 与BC 垂直AB=2√2,,∠ABC=45°,所以,AD=2OA=1,所以,EF 最小值为√3【题8】如图,已知⊙O 是以坐标原点O 为圆心,1为半径的圆,∠AOB=45°,点P 在x 轴上运动,若过点P且与OA 平行的直线与⊙O 有公共点,设P (x ,0),则x 的取值范围是22x -≤≤【答案】解:连接OD ,由题意得,OD =1,∠DOP '=45°,∠ODP '=90°,故可得OP '=,即x 的极大值为,同理当点P 在x 轴左边时也有一个极值点,此时x 取得极小值,x =-,综上可得x 的范围为:-≤x ≤.【题9】射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值t=2或3≤t≤7或t=8(单位:秒)【答案】解:∵△ABC是等边三角形,∴AB=AC=BC=AM+MB=4cm,∠A=∠C=∠B=60°,∵QN∥AC,AM=BM.∴N为BC中点,∴MN=AC=2cm,∠BMN=∠BNM=∠C=∠A=60°,分为三种情况:①如图1,当⊙P切AB于M′时,连接PM′,则PM′=cm,∠PM′M=90°,∵∠PMM′=∠BMN=60°,∴M′M=1cm,PM=2MM′=2cm,∴QP=4cm﹣2cm=2cm,即t=2;②如图2,当⊙P于AC切于A点时,连接PA,则∠CAP=∠APM=90°,∠PMA=∠BMN=60°,AP=cm,∴PM=1cm,∴QP=4cm﹣1cm=3cm,即t=3,当⊙P于AC切于C点时,连接PC,则∠CP′N=∠ACP′=90°,∠P′NC=∠BNM=60°,CP′=cm,∴P′N=1cm,∴QP=4cm+2cm+1cm=7cm,即当3≤t≤7时,⊙P和AC边相切;③如图1,当⊙P切BC于N′时,连接PN′3则PN′=cm,∠PM\N′N=90°,∵∠PNN′=∠BNM=60°,∴N′N=1cm,PN=2NN′=2cm,∴QP=4cm+2cm+2cm=8cm,即t=8;故答案为:t=2或3≤t≤7或t=8.【题10】如图1,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.(1)求证:OF∥BE;(2)设BP=x,AF=y,求y关于x的函数解析式,并写出自变量x的取值范围;(3)延长DC、FP交于点G,连接OE并延长交直线DC与H(图2),问是否存在点P,使△EFO∽△EHG (E、F、O与E、H、G为对应点)?如果存在,试求(2)中x和y的值;如果不存在,请说明理由.分析:(1)首先证明Rt△FAO≌Rt△FEO进而得出∠AOF=∠ABE,即可得出答案;(2)过F作FQ⊥BC于Q,利用勾股定理求出y与x之间的函数关系,根据M是BC中点以及BC=2,即可得出BP的取值范围;(3)首先得出当∠EFO=∠EHG=2∠EOF时,即∠EOF=30°时,Rt△EFO∽Rt△EHG,求出y=AF=OA•tan30°,即可得出答案.解答:(1)证明:连接OE. FE、FA是⊙O的两条切线∴∠FAO=∠FEO=90°∴Rt△FAO≌Rt△FEO(HL),∴∠AOF=∠EOF=∠AOE,∴∠AOF=∠ABE,∴OF∥BE(2)解:过F作FQ⊥BC于Q ∴PQ=BP﹣BQ=x﹣yPF=EF+EP=FA+BP=x+y ∵在Rt△PFQ中∴FQ2+QP2=PF2∴22+(x﹣y)2=(x+y)2化简得:,(1<x<2);(3)存在这样的P点,理由:∵∠EOF=∠AOF,∴∠EHG=∠EOA=2∠EOF,当∠EFO=∠EHG=2∠EOF时,即∠EOF=30°时,Rt△EFO∽Rt△EHG,此时Rt△AFO中,y=AF=OA•tan30°=,∴∴当时,△EFO∽△EHG.点评:此题主要考查了圆的综合应用以及全等三角形的判定和性质以及相似三角形的判定与性质等知识,得出FQ2+QP2=PF2是解题关键.【题11】如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交于⊙O于点N,点P是直线CD上另一点,且PM=PN.(1)当点M在⊙O内部,如图一,试判断PN与⊙O的关系,并写出证明过程;(2)当点M在⊙O外部,如图二,其它条件不变时,(1)的结论是否还成立?请说明理由;(3)当点M在⊙O外部,如图三,∠AMO=15°,求图中阴影部分的面积.考点:圆的综合题.分析:(1)根据切线的判定得出∠PNO=∠PNM+∠ONA=∠AMO+∠ONA进而求出即可;(2)根据已知得出∠PNM+∠ONA=90°,进而得出∠PNO=180°﹣90°=90°即可得出答案;(3)首先根据外角的性质得出∠AON=30°进而利用扇形面积公式得出即可.解答:(1)PN与⊙O相切.证明:连接ON,则∠ONA=∠OAN,∵PM=PN,∴∠PNM=∠PMN.∵∠AMO=∠PMN,∴∠PNM=∠AMO.∴∠PNO=∠PNM+∠ONA=∠AMO+∠ONA=90°.即PN与⊙O相切.(2)成立.证明:连接ON,则∠ONA=∠OAN,∵PM=PN,∴∠PNM=∠PMN.在Rt△AOM中,∴∠OMA+∠OAM=90°,∴∠PNM+∠ONA=90°.∴∠PNO=180°﹣90°=90°.即PN与⊙O相切(3)解:连接ON,由(2)可知∠ONP=90°.∵∠AMO=15°,PM=PN,∴∠PNM=15°,∠OPN=30°,∵∠PON=60°,∠AON=30°.作NE⊥OD,垂足为点E,则NE=ON•sin60°=1×=.S阴影=S△AOC+S扇形AON﹣S△CON=OC•OA+CO•NE=×1×1+π﹣×1×=+π﹣.【题12】如图,△OAB 中,OA = OB = 10,∠AOB = 80°,以点O 为圆心,6为半径的优弧MN ⌒分别交OA ,OB 于点M ,N .(1)点P 在右半弧上(∠BOP 是锐角),将OP 绕点O 逆时针旋转80°得OP ′. 求证:AP = BP ′; (2)点T 在左半弧上,若AT 与弧相切,求点T 到OA 的距离;(3)设点Q 在优弧MN ⌒上,当△AOQ 的面积最大时,直接写出∠BOQ 的度数.【答案】(1)证明:∵∠AOP=∠AOB+∠BOP=80º+∠BOP.∠BOP ’=∠POP ’+∠BOP=80º+∠BOP ∴∠AOP=∠BOP’又∵OA=OB ,OP=OP’ ∴△AOP ≌△BOP’∴AP=BP’(2)解:连接OT ,过T 作TH ⊥OA 于点H,∵AT 与MN ⌒相切,∴∠ATO=90º∴22AT OA OT =-=22106-=8∵12OA TH ⨯⨯=12AT OT ⨯⨯,即1102TH ⨯⨯=1862⨯⨯ ∴TH=245,即为所求的距离(3)10º,170º【注:当OQ ⊥OA 时,△AOQ 的面积最大,且左右两半弧上各存在一点】【题13】如图,已知直线l 与⊙O 相离,OA ⊥l 于点A ,OA=5,OA 与⊙O 相交于点P ,AB 与⊙O 相切于点B ,BP 的延长线交直线l 于点C.(1)试判断线段AB 与AC 的数量关系,并说明理由; (2)若PC=25,求⊙O 的半径和线段PB 的长;(3)若在⊙O 上存在点Q ,使△QAC 是以AC 为底边的等腰三角形,求⊙O 的半径r 的取值范围.【解析】(1)由于AB 是⊙O 的切线,故连半径,利用切线性质,圆半径相等,对顶角相等,余角性质,推出AB ,AC 两底角相等;(2)设圆半径为r ,利用勾股定理列方程求半径,再利用三角形相似求PB(3)先作出线段AC 的垂直平分线MN ,作OD 垂直于MN ,再利用勾股定理计算即可【答案】(1)AB =AC ; 连接OB ,则OB ⊥AB ,所以∠CBA+∠OBP=900,又OP=OB ,所以∠OBP=∠OPB ,又∠OPB=∠CPA ,又OA ⊥l 于点A , 所以∠PCA+∠CPA=900,故∠PCA=∠CBA ,所以AB=AC (2)设圆半径为r ,则OP =OB =r ,PA =5-r;∴AB 2=OA 2-OB 2=52-r 2,AC 2=PC 2-AP 22-(5-r )2,从而建立等量关系,r=3,∵AB=AC ,∴AB 2= AC 2,利用相似,求出PB=4 (3)作出线段AC 的垂直平分线MN,作OD 垂直于MN ,则可推出OD =1122AC AB =; 由题意,圆O 要与直线MN 有交点,所以,OD r r =≤≥ 又因为圆O 与直线l 相离;所以r <5;5r <.【点评】本题主要考查了切线的性质、等角对等边、三角形相似的判定及其性质的运用以及勾股定理的应用等知识,知识点丰富;考查了学生综合运用知识以及转化思想来解决问题的能力,考查了圆的相关知识,圆的切线是圆中的重点,也是考试常考的部分;求线段的长常用勾股定理或相似等知识解答.【题14】如图,⊙O 是△ABC 外接圆,AB=AC=10,BC=12,P 是BC 弧上一动点,过点P 作BC 的平行线交AB 延长线与点D.(1)当点P 在什么位置时,DP 是⊙O 的切线?说明理由.(2)当DP 是⊙O 的切线时,求DP 的长.解析:(1)根据PD//BC ,可以天加辅助线由切线判定定理解题;(2)根据勾股定理与垂径定理求出⊙O 半径r ,再结合△ABE ∽△ADP 即可.解:(1)当P 是BC 中点时,DP 是⊙O 的切线.理由如下:∵AB=AC ,∴又∴PA 是⊙O 的直径.又AB=AC ,∴PA ⊥BC.∵DP//BC ,∴PD ⊥AP.∴DP 是⊙O 的切线.(2)连接OB ,设PA 交BC 于点E.由垂径定理得,BE=621=BC . 在Rt △ABE 中,据勾股定理,86102222=-=-=BE AB AE .设⊙O 的半径为r ,则OE=8-r. 在Rt △OBE 中,222)8(6r r -+=.解得r=425. (3)∵DP//BC ,∴∠ABE=∠D.又∵∠1=∠1,∴△ABE ≌△ADP AP AE DP BE =,即425286⨯=DP ,∴DP=875【题15】如图,菱形ABCD 的边长为2cm ,∠DAB=60°.点P 从A 点出发,以3cm/s 的速度,沿AC 向C 作匀速运动;与此同时,点Q 也从A 点出发,以1cm/s 的速度,沿射线AB 作匀速运动。
