2016年中考数学几何选择填空压轴题配答案

2016年中考数学试卷答案及解析与点评25

2016年中考数学试卷25一、选择题（下列各题的备选答案中，只有一个是正确的。

每小题3分，共30分）1．（3分）﹣23的相反数是（）A．﹣8 B．8 C．﹣6 D．62．（3分）如图所示的物体是由两个紧靠在一起的圆柱体组成，小明准备画出它的三视图，那么他所画的三视图中的主视图应该是（）A．B．C． D．3．（3分）若关于x的一元二次方程kx2+2x﹣1=0有实数根，则实数k的取值范围是（）A．k≥﹣1 B．k＞﹣1 C．k≥﹣1且k≠0 D．k＞﹣1且k≠04．（3分）如图，将一副三角板叠放在一起，使直角的顶点重合于点O，AB∥OC，DC与OB交于点E，则∠DEO的度数为（）A．85°B．70°C．75°D．60°5．（3分）化简+﹣的结果为（）A．0 B．2 C．﹣2D．26．（3分）如图，矩形ABCD的对角线交于点O，若∠ACB=30°，AB=2，则OC的长为（）A．2 B．3 C．2 D．47．（3分）为了解某市参加中考的25000名学生的身高情况，抽查了其中1200名学生的身高进行统计分析．下面叙述正确的是（）A．25000名学生是总体B．1200名学生的身高是总体的一个样本C．每名学生是总体的一个个体D．以上调查是全面调查8．（3分）如图，在△ABC中，∠ACB=90°，分别以点A和点C为圆心，以相同的长（大于AC）为半径作弧，两弧相交于点M和点N，作直线MN交AB于点D，交AC于点E，连接CD．下列结论错误的是（）A．AD=CD B．∠A=∠DCE C．∠ADE=∠DCB D．∠A=2∠DCB9．（3分）已知一次函数y=（a+1）x+b的图象如图所示，那么a的取值范围是（）A．a＞1 B．a＜﹣1 C．a＞﹣1 D．a＜010．（3分）如图，等腰直角三角形ABC的直角顶点C与平面直角坐标系的坐标原点O重合，AC，BC分别在坐标轴上，AC=BC=1，△ABC在x轴正半轴上沿顺时针方向作无滑动的滚动，在滚动过程中，当点C第一次落在x轴正半轴上时，点A的对应点A1的横坐标是（）A．2 B．3 C．1+D．2+二、填空题（每小题3分，共24分）11．（3分）在网络上搜索“奔跑吧，兄弟”，能搜索到与之相关的结果为35 800 000个，将35 800 000用科学记数法表示为．12．（3分）如图，AB是⊙O的直径，弦CD垂直平分OB，垂足为点E，连接OD、BC，若BC=1，则扇形OBD的面积为．13．（3分）已知一组数据：18，17，13，15，17，16，14，17，则这组数据的中位数与众数分别是．14．（3分）若分式有意义，则a的取值范围是．15．（3分）如图，在边长为1的小正方形组成的网格中，建立平面直角坐标系，△ABC的三个顶点均在格点（网格线的交点）上．以原点O为位似中心，画△A1B1C1，使它与△ABC的相似比为2，则点B的对应点B1的坐标是．16．（3分）如图，四边形ABCD为正方形，点A、B在y轴上，点C的坐标为（﹣3，1），反比例函数y=的图象经过点D，则k的值为．17．（3分）下列图形中：①圆；②等腰三角形；③正方形；④正五边形，既是轴对称图形又是中心对称图形的有个．18．（3分）如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于A、B两点，与y轴交于点C，对称轴是直线x=﹣1，点B的坐标为（1，0）．下面的四个结论：①AB=4；②b2﹣4ac＞0；③ab＜0；④a﹣b+c＜0，其中正确的结论是（填写序号）．三、解答题19．（10分）先化简，再求值：（﹣1）÷，其中x=2+．20．（10分）如图是一个转盘，转盘被平均分成4等份，即被分成4个大小相等的扇形，4个扇形分别标有数字1、2、3、4，指针的位置固定，转动转盘后任其自由停止，每次指针落在每一扇形的机会均等（若指针恰好落在分界线上则重转）．（1）图中标有“1”的扇形至少绕圆心旋转度能与标有“4”的扇形的起始位置重合；（2）现有一本故事书，姐妹俩商定通过转盘游戏定输赢（赢的一方先看）．游戏规则是：姐妹俩各转动一次转盘，两次转动后，若指针所指扇形上的数字之积为偶数，则姐姐赢；若指针所指扇形上的数字之积为奇数，则妹妹赢．这个游戏规则对双方公平吗？请利用树状图或列表法说明理由．21．（12分）学校为了了解全校1600名学生对“初中学生带手机上学”现象的看法，在全校随机抽取了若干名学生进行问卷调查．问卷给出了四种看法供学生选择，每人只能选一种，且不能不选．将调查结果整理后，绘制成如图①、图②所示的条形统计图与扇形统计图（均不完整）．（1）在这次调查中，一共抽取了多少名学生？（2）补全条形统计图和扇形统计图；（3）估计全校有多少名学生对“初中学生带手机上学”现象持“不赞同”的看法．22．（12分）某居民楼紧挨一座山坡AB，经过地质人员勘测，当坡度不超过45°时，可以确保山体不滑坡，如图所示，已知AE∥BD，斜坡AB的坡角∠ABD=60°，．为防止滑坡，现对山坡进行改造，改造后，斜坡BC与地面BD成45°角，AC=20米．求斜坡BC的长是多少米？（结果精确到0.1米，参考数据：≈1.41，≈1.73）23．（12分）如图，AB为⊙O的直径，CD切⊙O于点C，与BA的延长线交于点D，OE⊥AB交⊙O于点E，连接CA、CE、CB，过点A作AF⊥CE于点F，延长AF 交BC于点P．（1）求证：CA=CP；（2）连接OF，若AC=，∠D=30°，求线段OF的长．24．（12分）某花店准备购进甲、乙两种花卉，若购进甲种花卉20盆，乙种花卉50盆，需要720元；若购进甲种花卉40盆，乙种花卉30盆，需要880元．（1）求购进甲、乙两种花卉，每盆各需多少元？（2）该花店销售甲种花卉每盆可获利6元，销售乙种花卉每盆可获利1元，现该花店准备拿出800元全部用来购进这两种花卉，设购进甲种花卉x盆，全部销售后获得的利润为W元，求W与x之间的函数关系式；（3）在（2）的条件下，考虑到顾客需求，要求购进乙种花卉的数量不少于甲种花卉数量的6倍，且不超过甲种花卉数量的8倍，那么该花店共有几种购进方案？在所有的购进方案中，哪种方案获利最大？最大利润是多少元？25．（14分）已知：如图①，将∠D=60°的菱形ABCD沿对角线AC剪开，将△ADC 沿射线DC方向平移，得到△BCE，点M为边BC上一点（点M不与点B、点C 重合），将射线AM绕点A逆时针旋转60°，与EB的延长线交于点N，连接MN．（1）①求证：∠ANB=∠AMC；②探究△AMN的形状；（2）如图②，若菱形ABCD变为正方形ABCD，将射线AM绕点A逆时针旋转45°，原题其他条件不变，（1）中的①、②两个结论是否仍然成立？若成立，请直接写出结论；若不成立，请写出变化后的结论并证明．26．（14分）如图①，已知△ABC的三个顶点坐标分别为A（﹣1，0）、B（3，0）、C（0，3），直线BE交y轴正半轴于点E．（1）求经过A、B、C三点的抛物线解析式及顶点D的坐标；（2）连接BD、CD，设∠DBO=α，∠EBO=β，若tan （α﹣β）=1，求点E的坐标；（3）如图②，在（2）的条件下，动点M从点C出发以每秒个单位的速度在直线BC上移动（不考虑点M与点C、B重合的情况），点N为抛物线上一点，设点M移动的时间为t秒，在点M移动的过程中，以E、C、M、N四个点为顶点的四边形能否成为平行四边形？若能，直接写出所有满足条件的t值及点M 的个数；若不能，请说明理由．2016年辽宁省营口市中考数学试卷参考答案与试题解析一、选择题（下列各题的备选答案中，只有一个是正确的。

2016年中考数学压轴题70题精选(含答案及解析)

2016年中考数学压轴题70题精选（含答案）【001】如图13，二次函数)0(2<++=p q px x y 的图象与x 轴交于A 、B 两点，与y 轴交于点C （0，-1），ΔABC 的面积为45。

（1）求该二次函数的关系式；（2）过y 轴上的一点M （0，m ）作y 轴的垂线，若该垂线与ΔABC 的外接圆有公共点，求m 的取值范围；（3）在该二次函数的图象上是否存在点D ，使四边形ABCD 为直角梯形？若存在，求出点D 的坐标；若不存在，请说明理由。

【002】如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（4，0）、C（8，0）、D（8，8）.抛物线y=ax2+bx过A、C两点.(1)直接写出点A的坐标，并求出抛物线的解析式；(2)动点P从点A出发．沿线段AB向终点B运动，同时点Q从点C出发，沿线段CD向终点D运动．速度均为每秒1个单位长度，运动时间为t秒.过点P作PE⊥AB交AC 于点E，①过点E作EF⊥AD于点F，交抛物线于点G.当t为何值时，线段EG最长?②连接EQ．在点P、Q运动的过程中，判断有几个时刻使得△CEQ是等腰三角形? 请直接写出相应的t值。

【003】抛物线)0(2≠++=a c bx ax y 的顶点为M ，与x 轴的交点为A 、B （点B 在点A 的右侧），△ABM 的三个内角∠M 、∠A 、∠B 所对的边分别为m 、a 、b 。

若关于x 的一元二次方程0)(2)(2=+++-a m bx x a m 有两个相等的实数根。

（1）判断△ABM 的形状，并说明理由。

（2）当顶点M 的坐标为（－2，－1）时，求抛物线的解析式，并画出该抛物线的大致图形。

（3）若平行于x 轴的直线与抛物线交于C 、D 两点，以CD 为直径的圆恰好与x 轴相切，求该圆的圆心坐标。

【004】一次函数y ax b =+的图象分别与x 轴、y 轴交于点,M N ，与反比例函数ky x=的图象相交于点,A B ．过点A 分别作AC x ⊥轴，AE y ⊥轴，垂足分别为,C E ；过点B 分别作BF x ⊥轴，BD y ⊥轴，垂足分别为F D ，，AC 与BD 交于点K ，连接CD ．（1）若点A B ，在反比例函数ky x=的图象的同一分支上，如图1，试证明： ①AEDK CFBK S S =四边形四边形； ②AN BM =．（2）若点A B ，分别在反比例函数ky x=的图象的不同分支上，如图2，则AN 与BM 还相等吗？试证明你的结论．)【005】如图1，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A 的坐标为（－3，4），点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H．（1）求直线AC的解析式；（2）连接BM，如图2，动点P从点A出发，沿折线ABC方向以2个单位／秒的速度向终点C匀速运动，设△PMB的面积为S（S≠0），点P的运动时间为t秒，求S 与t之间的函数关系式（要求写出自变量t的取值范围）；（3）在（2）的条件下，当t为何值时，∠MPB与∠BCO互为余角，并求此时直线OP与直线AC所夹锐角的正切值．【006】如图，抛物线23y ax bx =+-与x 轴交于A B ，两点，与y 轴交于C 点，且经过点(23)a -，，对称轴是直线1x =，顶点是M ．（1）求抛物线对应的函数表达式；（2）经过C,M 两点作直线与x 轴交于点N ，在抛物线上是否存在这样的点P ，使以点P A C N ，，，为顶点的四边形为平行四边形？若存在，请求出点P 的坐标；若不存在，请说明理由；（3）设直线3y x =-+与y 轴的交点是D ，在线段BD 上任取一点E （不与B D ，重合），经过AB E ，，三点的圆交直线BC 于点F ，试判断AEF △的形状，并说明理由；（4）当E 是直线3y x =-+上任意一点时，（3）中的结论是否成立？（请直接写出结论）．【007】如图9，已知正比例函数和反比例函数的图象都经过点(33)A ，．（1）求正比例函数和反比例函数的解析式；（2）把直线O A 向下平移后与反比例函数的图象交于点(6)B m ，，求m 的值和这个一次函数的解析式；（3）第（2）问中的一次函数的图象与x 轴、y 轴分别交于C 、D ，求过A 、B 、D 三点的二次函数的解析式；（4）在第（3）问的条件下，二次函数的图象上是否存在点E ，使四边形O ECD 的面积1S 与四边形O ABD 的面积S 满足：123S S？若存在，求点E 的坐标；若不存在，请说明理由．【008】如图，在平面直角坐标系xOy 中，半径为1的圆的圆心O 在坐标原点，且与两坐标轴分别交于A B C D 、、、四点．抛物线2y ax bx c =++与y 轴交于点D ，与直线y x =交于点M N 、，且MA NC 、分别与圆O 相切于点A 和点C ．（1）求抛物线的解析式；（2）抛物线的对称轴交x 轴于点E ，连结DE ，并延长DE 交圆O 于F ，求EF 的长．（3）过点B 作圆O 的切线交DC 的延长线于点P ，判断点P 是否在抛物线上，说明理由．【009】如图，抛物线经过(40)(10)(02)A B C -，，，，，三点．（1）求出抛物线的解析式；（2）P 是抛物线上一动点，过P 作PM x ⊥轴，垂足为M ，是否存在P 点，使得以A ，P ，M 为顶点的三角形与OAC △相似？若存在，请求出符合条件的点P 的坐标；若不存在，请说明理由；（3）在直线AC 上方的抛物线上有一点D ，使得DCA △的面积最大，求出点D 的坐标．【010】如图，抛物线24y ax bx a =+-经过(10)A -，、(04)C ，两点，与x 轴交于另一点B ．（1）求抛物线的解析式；（2）已知点(1)D m m +，在第一象限的抛物线上，求点D 关于直线BC 对称的点的坐标；（3）在（2）的条件下，连接BD ，点P 为抛物线上一点，且45DBP ∠=°，求点P 的坐标．7)，且顶点C的横坐标为4，该图象在【011】如图，二次函数的图象经过点D(0，39x 轴上截得的线段AB的长为6.⑴求二次函数的解析式；⑵在该抛物线的对称轴上找一点P，使PA+PD最小，求出点P的坐标；⑶在抛物线上是否存在点Q，使△QAB与△ABC相似？如果存在，求出点Q的坐标；如果不存在，请说明理由．【012】如图，已知抛物线2y x bx c =++经过(10)A ，，(02)B ，两点，顶点为D ．（1）求抛物线的解析式；（2）将OAB △绕点A 顺时针旋转90°后，点B 落到点C 的位置，将抛物线沿y 轴平移后经过点C ，求平移后所得图象的函数关系式；（3）设（2）中平移后，所得抛物线与y 轴的交点为1B ，顶点为1D ，若点N 在平移后的抛物线上，且满足1NBB △的面积是1NDD △面积的2倍，求点N 的坐标．（第26【013】如图，点P 是双曲线11(00)k y k x x=<<，上一动点，过点P 作x 轴、y 轴的垂线，分别交x 轴、y 轴于A 、B 两点，交双曲线y =xk 2（0＜k 2＜|k 1|）于E 、F 两点．（1）图1中，四边形PEOF 的面积S 1= ▲ (用含k 1、k 2的式子表示)；（2）图2中，设P 点坐标为（－4，3）． ①判断EF 与AB 的位置关系，并证明你的结论；②记2PEF OEF S S S ∆∆=-，S 2是否有最小值？若有，求出其最小值；若没有，请说明理由。

浙江省中考数学《填空压轴题》专题练习含答案解析

2016年中考数学《填空压轴题》专题练习1. （2015年广东4分）如图，△ABC 三边的中线AD ，BE ，CF 的公共点G ，若12ABC S =△，则图中阴影部分面积是 . （第1题）（第2题）2. （2015年广东深圳3分）如图，已知点A 在反比例函数(0)k y x x=<上，作Rt ABC ∆，点D 为斜边AC 的中点，连DB 并延长交y 轴于点E ，若BCE ∆的面积为8，则k = .3. （2015年广东汕尾5分）（2015年广东梅州3分）若()()121212121a b n n n n =+-+-+，,对任意自然数n 都成立，则a = ，b = ；计算：11111335571921m =+++⋅⋅⋅+=⨯⨯⨯⨯ .. 4. （2015年广东广州3分）如图，四边形ABCD 中，∠A =90°，33AB =，AD =3，点M ，N 分别为线段BC ，AB 上的动点（含端点，但点M 不与点B 重合），点E ，F 分别为DM ，MN 的中点，则EF 长度的最大值为 .（第4题）（第6题）（第7题）5. （2015年广东佛山3分）各边长度都是整数，最大边长为8的三角形共有个.6. （2015年陕西3分）如图，AB 是⊙O 的弦，AB =6，点C 是⊙O 上的一个动点，且∠ACB =45°．若点M ，N 分别是AB ，BC 的中点，则MN 长的最大值是．7. （2015年浙江衢州4分）如图，已知直线334y x =-+分别交x 轴、y 轴于点A 、B ，P 是抛物线21252y x x =-++上的一个动点，其横坐标为a ，过点P 且平行于y 轴的直线交直线334y x =-+于点Q ，则当PQ BQ =时，a 的值是 .【 8. （2015年浙江绍兴5分）（2015年浙江义乌4分）实验室里，水平桌面上有甲、乙、丙三个圆柱形容器（容器足够高），底面半径之比为1：2：1，用两个相同的管子在容器的5cm 高度处连通（即管子底端离容器底5cm ），现三个容器中，只有甲中有水，水位高1cm ，如图所示. 若每分钟同时向乙和丙注入相同量的水，开始注水1分钟，乙的水位上升65cm ，则开始注入分钟的水量后，甲与乙的水位高度之差是0.5cm. （第8题）（第9题）9. （2015年浙江台州5分）如图，正方形ABCD 的边长为1，中心为点O ，有一边长大小不定的正六边形EFGHIJ 绕点O 可任意旋转，在旋转过程中，这个正六边形始终在正方形ABCD 内（包括正方形的边），当这个六边形的边长最大时，AE 的最小值为。

2016天津中考数学压轴题及答案解析

2016天津中考数学压轴题及答案解析
2016年天津中考数学压轴题及答案解析，更多2016中考真题答案、2016中考志愿填报、2016中考成绩查询、2016中考分数线等信息，请及时关注2016年中考真题及答案※中考作文※成绩查询
选择压轴题
今年的选择压轴题考查的内容沿用了2015天津中考数学试卷的最后一道大题，也就是区间最值问题，难度不大。

填空压轴题
今年的填空压轴题已经是连续第五年考察格点作图问题，同学们平日的练习以及各级各类考试中都会涉及到，难度还没有到想不出来的地步，如果用。

中考数学几何压轴题及答案及答案

中考数学几何压轴题及答案一、解答题（共30小题）1.观察猜想（1）如图①，在Rt△ABC中，∠BAC＝90°，AB＝AC＝3，点D与点A重合，点E在边BC上，连接DE，将线段DE绕点D顺时针旋转90°得到线段DF，连接BF，BE与BF的位置关系是，BE+BF＝；探究证明（2）在（1）中，如果将点D沿AB方向移动，使AD＝1，其余条件不变，如图②，判断BE与BF的位置关系，并求BE+BF的值，请写出你的理由或计算过程；拓展延伸（3）如图③，在△ABC中，AB＝AC，∠BAC＝α，点D在边BA的延长线上，BD＝n，连接DE，将线段DE绕着点D顺时针旋转，旋转角∠EDF＝α，连接BF，则BE+BF的值是多少？请用含有n，α的式子直接写出结论2.在△ABC的边BC上取B′、C′两点，使∠AB′B＝∠AC′C＝∠BAC（1）如图1中∠BAC为直角，∠BAC＝∠AB′B＝∠AC′C＝90°（点B′与点C′重合），则△ABC∽△B'BA∽△C'AC，，，进而可得AB2+AC2＝；（2）如图2中当∠BAC为锐角，图3中∠BAC为钝角时（1）中的结论还成立吗？若不成立，则AB2+AC2等于什么（用含用BC和B′C′的式子表示）？并说明理由（3）若在△ABC中，AB＝5，AC＝6，BC＝9，请你先判断出△ABC的类型，再求出B′C′的长3．（1）问题发现如图1，在Rt△ABC和Rt△CDE中，∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝45°，点D是线段AB上一动点，连接BE填空：①的值为；②∠DBE的度数为．（2）类比探究如图2，在Rt△ABC和Rt△CDE中，∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝60°，点D是线段AB上一动点，连接BE．请判断的值及∠DBE的度数，并说明理由；（3）拓展延伸如图3，在（2）的条件下，将点D改为直线AB上一动点，其余条件不变，取线段DE 的中点M，连接BM、CM，若AC＝2，则当△CBM是直角三角形时，线段BE的长是多少？请直接写出答案．4.（1）问题发现：如图①，在△ABC中，∠BAC＝90°，AB＝AC，点D是BC的中点，以点D为顶点作正方形DFGE，使点A、C分别在DE和DF上，连接BE、AF．则线段BE 和AF数量关系．（2）类比探究：如图②，保持△ABC固定不动，将正方形DFGE绕点D旋转α（0°＜α≤360°），则（1）中的结论是否成立？如果成立，请证明；如果不成立，请说明理由．（3）解决问题：若BC＝DF＝2，在（2）的旋转过程中，连接AE，请直接写出AE的最大值．5.如图，在平行四边形ABCD中，AC与BD交于点O，以点O为顶点的∠EOF的两边分别与边AB、AD交于点E、F，且∠EOF与∠BAD互补．（1）若四边形ABCD是正方形，则线段OE与OF有何数量关系？请直接写出结论；（2）若四边形ABCD是菱形，那么（1）中的结论是否成立？若成立，请画出图形并给出证明；若不成立，请说明理由；（3）若AB：AD＝m：n，探索线段OE与OF的数量关系，并证明你的结论.6.如图（1），已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F.（1）证明与推断：①求证：四边形CEGF是正方形；②推断：的值为：（2）探究与证明：将正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图（2）所示，试探究线段AG与BE之间的数量关系，并说明理由；（3）拓展与运用：正方形CEGF在旋转过程中，当B，E，F三点在一条直线上时，如图（3）所示，延长CG交AD于点H．若AG＝6，GH＝2，则BC＝．7.如图1，在△ABC中，AB＝AC＝2，∠BAC＝120°，点D、E分别是AC、BC的中点，连接DE.定理：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．探索发现：图1中，的值为；的值为．（2）拓展探完若将△CDE绕点C逆时针方向旋转一周，在旋转过程中的大小有无变化？请仅就图2的情形给出证明．（3）问题解决当△CDE旋转至A，D，E三点共线时，直接写出线段BE的长．8.已知△ABC是边长为4的等边三角形，边AB在射线OM上，且OA＝6，点D是射线OM上的动点，当点D不与点A重合时，将△ACD绕点C逆时针方向旋转60°得到△BCE，连接DE，设OD＝m．（1）问题发现如图1，△CDE的形状是三角形．（2）探究证明如图2，当6＜m＜10时，△BDE的周长是否存在最小值？若存在，求出△BDE周长的最小值；若不存在，请说明理由．（3）解决问题是否存在m的值，使△DEB是直角三角形？若存在，请直接写出m的值；若不存在，请说明理由．9.等腰直角三角形ABC和等腰直角三角形ADE中，∠BAC＝∠DAE＝90°，AB＝4，AE＝2，其中△ABC固定，△ADE绕点A作360°旋转，点F、M、N分别为线段BE、BC、CD 的中点，连接MN、NF．问题提出：（1）如图1，当AD在线段AC上时，则∠MNF的度数为，线段MN 和线段NF的数量关系为；深入讨论：（2）如图2，当AD不在线段AC上时，请求出∠MNF的度数及线段MN和线段NF的数量关系；拓展延伸：（3）如图3，△ADE持续旋转过程中，若CE与BD交点为P，则△BCP面积的最小值为．10．四边形是我们在学习和生活中常见的图形，而对角线互相垂直的四边形也比较常见，比如筝形、菱形、图1中的四边形ABCD等．它们给我们的学习和生活带来了很多的乐趣和美感．（1）如图2，在四边形ABCD中，AB＝AD，CB＝CD，则AC与BD的位置关系是，请说明理由．（2）试探究图1中四边形ABCD的两组对边AB，CD与BC，AD之间的数量关系，请写出证明过程．（3）问题解决：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE，连接CE，BG，GE，已知AC＝4，AB＝5，求GE的长．11．问题发现：如图（1）在Rt△ABC和Rt△BDE中，∠A＝∠DEB＝30°，BC＝BE＝6，Rt△BDE绕点B逆时针旋转，H为CD的中点，当点C与点E重合时，BH与AE的位置关系为，BH与AE的数量关系为；问题证明：在Rt△BDE绕点B旋转的过程中，（1）中的结论是否仍然成立？若成立，请就图（2）的情形给出证明若不成立，请说明理由；拓展应用：在Rt△BDE绕点B旋转的过程中，当DE∥BC时，请直接写出BH2的长．12．如图1，菱形ABCD与菱形GECF的顶点C重合，点G在对角线AC上，且∠BCD＝∠ECF＝60°，（1）问题发现的值为；（2）探究与证明将菱形GECF绕点C按顺时针方向旋转α角（0°＜α＜60°），如图2所示，试探究线段AG与BE之间的数量关系，并说明理由；（3）拓展与运用：菱形GECF在旋转过程中，当点A，G，F三点在一条直线上时，如图3所示连接CG并延长，交AD于点H，若CE＝2，GH＝，则AH的长为．13．如图，在Rt△ABC中，∠ACB＝90°，＝，CD⊥AB于点D，点E是直线AC上一动点，连接DE，过点D作FD⊥ED，交直线BC于点F．（1）探究发现：如图1，若m＝n，点E在线段AC上，则＝；（2）数学思考：①如图2，若点E在线段AC上，则＝（用含m，n的代数式表示）；②当点E在直线AC上运动时，①中的结论是否仍然成立？请仅就图3的情形给出证明；（3）拓展应用：若AC＝，BC＝2，DF＝4，请直接写出CE的长．14．如图，已知点E是射线BC上的一点，以BC、CE为边作正方形ABCD和正方形CEFG，连接AF，取AF的中点M，连接DM、MG（1）如图1，判断线段DM和GM的数量关系是，位置关系是；（2）如图2，在图中的正方形CEFG绕点C逆时针旋转的过程中，其他条件不变，（1）中的结论是否成立？说明理由；（3）已知BC＝10，CE＝2，正方形CEFG绕点C旋转的过程中，当A、F、E共线时，直接写出△DMG的面积．15.在Rt△ABC中，∠ACB＝90°，AB＝，AC＝2，过点B作直线m∥AC，将△ABC绕点C顺时针旋转得到△A′B′C（点A，B的对应点分别为A'，B′），射线CA′，CB′分别交直线m于点P，Q．（1）如图1，当P与A′重合时，求∠ACA′的度数；（2）如图2，设A′B′与BC的交点为M，当M为A′B′的中点时，求线段PQ的长；（3）在旋转过程中，当点P，Q分别在CA′，CB′的延长线上时，试探究四边形P A'B′Q的面积是否存在最小值．若存在，求出四边形P A′B′Q的最小面积；若不存在，请说明理由．16.如图（1），在等边三角形ABC中，点D，E分别在边AB，AC上，AD＝AE，连接BE，CD，点M，N，P分别是BE，CD，BC的中点，连接DE，PM，PN，MN．（1）观察猜想，图（1）中△PMN是（填特殊三角形的名称）（2）探究证明，如图（2），△ADE绕点A按逆时针方向旋转，则△PMN的形状是否发生改变？并就图（2）说明理由．（3）拓展延伸，若△ADE绕点A在平面内自由旋转，AD＝2，AB＝6，请直接写出△PMN 的周长的最大值．17.已知△ABC，AB＝AC，D为直线BC上一点，E为直线AC上一点，AD＝AE，设∠BAD＝α，∠CDE＝β，（1）如图1，若点D在线段BC上，点E在线段AC上．∠ABC＝60°，∠ADE＝70°，则α＝°；β＝°.（2）如图2，若点D在线段BC上，点E在线段AC上，则α，β之间有什么关系式？说明理由．（3）是否存在不同于（2）中的α，β之间的关系式？若存在，请写出这个关系式（写出一种即可），说明理由；若不存在，请说明理由.18.问题提出：（1）如图1，在四边形ABCD中，连接AC、BD，AB＝AD，∠BAD＝∠BCD＝90°，将△ABC绕点A逆时针旋转90°，得到△ADE，点B的对应点落在点D，点C的对应点为点E，可知点C、D、E在一条直线上，则△ACE为三角形，BC、CD、AC的数量关系为；探究发现：（2）如图2，在⊙O中，AB为直径，点C为的中点，点D为圆上一个点，连接AD、CD、AC、BC、BD，且AD＜BD，请求出CD、AD、BD间的数量关系.拓展延伸：（3）如图3，在等腰直角三角形ABC中，点P为AB的中点，若AC＝13，平面内存在一点E，且AE＝10，CE＝13，当点Q为AE中点时，PQ＝.19.已知△ABC中，CA＝CB，0°＜∠ACB≤90°，点M、N分别在边CA，CB上（不与端点重合），BN＝AM，射线AG∥BC交BM延长线于点D，点E在直线AN上，EA＝ED．（1）【观察猜想】如图1，点E在射线NA上，当∠ACB＝45°时，①线段BM与AN的数量关系是；②∠BDE的度数是；（2）【探究证明】如图2点E在射线AN上，当∠ACB＝30°时，判断并证明线段BM与AN的数量关系，求∠BDE的度数；（3）【拓展延伸】如图3，点E在直线AN上，当∠ACB＝60°时，AB＝3，点N是BC 边上的三等分点，直线ED与直线BC交于点F，请直接写出线段CF的长．20.如图①，在正方形ABCD和正方形AB'C'D'中，AB＝2，AB'＝，连接CC’（1）问题发现：．（2）拓展探究：将正方形AB'C'D'绕点A逆时针旋转，记旋转角为θ，连接BB'，试判断：当0°≤θ＜360°时，的值有无变化？请仅就图②中的情形给出你的证明；（3）问题解决：请直接写出在旋转过程中，当C，C′，D'三点共线时BB′的长．21.如图1，在正方形ABCD中，点O是对角线BD的中点．（1）观察猜想将图1中的△BCD绕点O逆时针旋转至图2中△ECF的位置，连接AC，DE，则线段AC与DE的数量关系是，直线AC与DE的位置关系是．（2）类比探究将图2中的△ECF绕点O逆时针旋转至图3的位置，（1）中的结论是否成立？并说明理由．（3）拓展延伸将图2中的△ECF在平面内旋转，设直线AC与DE的交点为M，若AB＝4，请直接写出BM的最大值与最小值．22.如图1，点B在直线l上，过点B构建等腰直角三角形ABC，使∠BAC＝90°，且AB＝AC，过点C作CD⊥直线l于点D，连接AD．（1）小亮在研究这个图形时发现，∠BAC＝∠BDC＝90°，点A，D应该在以BC为直径的圆上，则∠ADB的度数为°，将射线AD顺时针旋转90°交直线l于点E，可求出线段AD，BD，CD的数量关系为；（2）小亮将等腰直角三角形ABC绕点B在平面内旋转，当旋转到图2位置时，线段AD，BD，CD的数量关系是否变化，请说明理由；（3）在旋转过程中，若CD长为1，当△ABD面积取得最大值时，请直接写AD的长．23．如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合，三角板的一边交CD于点F．另一边交CB的延长线于点G．（1）观察猜想：线段EF与线段EG的数量关系是；（2）探究证明：如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变，（1）中的结论是否仍然成立？若成立，请给予证明：若不成立．请说明理由：（3）拓展延伸：如图3，将（2）中的“正方形ABCD”改为“矩形ABCD”，且使三角板的一边经过点B，其他条件不变，若AB＝a、BC＝b，求的值．24．如图1，在Rt△ABC中，∠B＝90°，AB＝2，BC＝1，点D，E分别是边BC，AC的中点，连接DE．将△EDC绕点C按顺时针方向旋转，记旋转角为α．（1）问题发现①当α＝0°时，＝；②当α＝180°时，＝．（2）拓展探究试判断：当0°≤α＜360°时，的大小有无变化？请仅就图2的情况给出证明．（3）问题解决当△EDC旋转至A、B、E三点共线时，直接写出线段BD的长．25.在△ABC中，AD为BC边上的中线，E为AD上一动点，设DE＝nEA，连接CE并延长，交AB于点F．（1）尝试探究如图（1），当∠BAC＝90°，∠B＝30°，DE＝EA时，BF，BA之间的数量关系是；（2）类比延伸如图（2），当△ABC为锐角三角形，DE＝EA时，（1）中的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由；（3）拓展迁移如图（3），当△ABC为锐角三角形，DE＝nEA时，请直接写出BF，BA之间的数量关系．26.古希腊数学家毕达哥拉斯认为：“一切平面图形中最美的是圆”．请研究如下美丽的圆．如图，线段AB是⊙O的直径，延长AB至点C，使BC＝OB，点E是线段OB的中点，DE ⊥AB交⊙O于点D，点P是⊙O上一动点（不与点A，B重合），连接CD，PE，PC．（1）求证：CD是⊙O的切线；（2）小明在研究的过程中发现是一个确定的值．回答这个确定的值是多少？并对小明发现的结论加以证明．27．定义：三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角．（1）如图1，∠E是△ABC中∠A的遥望角，若∠A＝α，请用含α的代数式表示∠E．（2）如图2，四边形ABCD内接于⊙O，＝，四边形ABCD的外角平分线DF交⊙O 于点F，连结BF并延长交CD的延长线于点E．求证：∠BEC是△ABC中∠BAC的遥望角．（3）如图3，在（2）的条件下，连结AE，AF，若AC是⊙O的直径．①求∠AED的度数；②若AB＝8，CD＝5，求△DEF的面积．28.【性质探究】如图，在矩形ABCD中，对角线AC，BD相交于点O，AE平分∠BAC，交BC于点E．作DF⊥AE于点H，分别交AB，AC于点F，G．（1）判断△AFG的形状并说明理由．（2）求证：BF＝2OG．【迁移应用】（3）记△DGO的面积为S1，△DBF的面积为S2，当＝时，求的值．【拓展延伸】（4）若DF交射线AB于点F，【性质探究】中的其余条件不变，连结EF，当△BEF的面积为矩形ABCD面积的时，请直接写出tan∠BAE的值．29．如图，已知AC为正方形ABCD的对角线，点P是平面内不与点A，B重合的任意一点，连接AP，将线段AP绕点P顺时针旋转90°得到线段PE，连接AE，BP，CE．（1）求证：△APE∽△ABC；（2）当线段BP与CE相交时，设交点为M，求的值以及∠BMC的度数；（3）若正方形ABCD的边长为3，AP＝1，当点P，C，E在同一直线上时，求线段BP 的长．30．如图1和图2，在△ABC中，AB＝AC，BC＝8，tan C＝．点K在AC边上，点M，N 分别在AB，BC上，且AM＝CN＝2．点P从点M出发沿折线MB﹣BN匀速移动，到达点N时停止；而点Q在AC边上随P移动，且始终保持∠APQ＝∠B．（1）当点P在BC上时，求点P与点A的最短距离；（2）若点P在MB上，且PQ将△ABC的面积分成上下4：5两部分时，求MP的长；（3）设点P移动的路程为x，当0≤x≤3及3＜x≤9时，分别求点P到直线AC的距离（用含x的式子表示）；（4）在点P处设计并安装一扫描器，按定角∠APQ扫描△APQ区域（含边界），扫描器随点P从M到B再到N共用时36秒．若AK＝，请直接写出点K被扫描到的总时长．参考答案与试题解析一．解答题（共30小题）1．【解答】解：（1）如图①中，∵∠EAF＝∠BAC＝90°，∴∠BAF＝∠CAE，∵AF＝AE，AB＝AC，∴△BAF≌△CAE，∴∠ABF＝∠C，BF＝CE，∵AB＝AC，∠BAC＝90°，∴∠ABC＝∠C＝45°，∴∠FBE＝∠ABF+∠ABC＝90°，BC＝BE+EC＝BE+BF，故答案为：BF⊥BE，BC．（2）如图②中，作DH∥AC交BC于H．∵DH∥AC，∴∠BDH＝∠A＝90°，△DBH是等腰直角三角形，由（1）可知，BF⊥BE，BF+BE＝BH，∵AB＝AC＝3，AD＝1，∴BD＝DH＝2，∴BH＝2，∴BF+BE＝BH＝2；（3）如图③中，作DH∥AC交BC的延长线于H，作DM⊥BC于M．∵AC∥DH，∴∠ACB＝∠H，∠BDH＝∠BAC＝α，∵AB＝AC，∴∠ABC＝∠ACB∴∠DBH＝∠H，∴DB＝DH，∵∠EDF＝∠BDH＝α，∴∠BDF＝∠HDE，∵DF＝DE，DB＝DH，∴△BDF≌△HDE，∴BF＝EH，∴BF+BE＝EH+BE＝BH，∵DB＝DH，DM⊥BH，∴BM＝MH，∠BDM＝∠HDM，∴BM＝MH＝BD•sin．∴BF+BE＝BH＝2n•sin．2．【解答】解：（1）如图1中，∵△ABC∽△B'BA∽△C'AC，∴＝，＝，∴AB2＝BB′×BC，AC2＝CC′×BC，∴AB2+AC2＝BC（BB′+CC′）＝BC×BC＝BC2，故答案为BC2．（2）不成立．理由：如图2中当∠BAC为锐角时，BB′+CC′﹣B′C′＝BC，且△ABC∽△B'BA∽△C'AC，∴∴＝，＝，∴AB2＝BB′×BC，AC2＝CC′×BC，∴AB2+AC2＝BC（BB′+CC′）＝BC2+BC•B′C′．图3中∠BAC为钝角时，BB′+CC′+B′C′＝BC．AB2+AC2＝BC（BB′+CC′）＝BC2﹣BC•B′C′．（3）当AB＝5，AC＝6，BC＝9时，则AB2+AC2＜BC2，可知△ABC为钝角三角形，由图3可知：AB2+AC2＝BC2﹣BC•B′C′，∴52+62＝92﹣9B′C′，∴B′C′＝．3．【解答】解：（1）∵∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝45°，∴∠ABC＝∠CAB＝45°＝∠CDE＝∠CED，∴AC＝BC，CD＝CE，∵∠ACB＝∠DCE＝90°，∴∠ACD＝∠BCE，在△ACD和△BCE中，，∴△ACD≌△BCE（SAS），∴BE＝AD，∠CAB＝∠CBE＝45°，∴∠DBE＝∠ABC+∠CBE＝90°，＝1，故答案为：1，90°（2），∠DBE＝90°理由如下：∵∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝60°，∴∠ACD＝∠BCE，∠CED＝∠ABC＝30°∴tan∠ABC＝tan30°＝＝∵∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝60°，∴Rt△ACB∽Rt△DCE∴∴，且∠ACD＝∠BCE∴△ACD∽△BCE∴＝，∠CBE＝∠CAD＝60°∴∠DBE＝∠ABC+∠CBE＝90°（3）若点D在线段AB上，如图，由（2）知：＝，∠ABE＝90°∴BE＝AD∵AC＝2，∠ACB＝90°，∠CAB＝90°∴AB＝4，BC＝2∵∠ECD＝∠ABE＝90°，且点M是DE中点，∴CM＝BM＝DE，∵△CBM是直角三角形∴CM2+BM2＝BC2＝（2）2，∴BM＝CM＝∴DE＝2∵DB2+BE2＝DE2，∴（4﹣AD）2+（AD）2＝24∴AD＝+1∴BE＝AD＝3+若点D在线段BA延长线上，如图同理可得：DE＝2，BE＝AD∵BD2+BE2＝DE2，∴（4+AD）2+（AD）2＝24，∴AD＝﹣1∴BE＝AD＝3﹣综上所述：BE的长为3+或3﹣4．【解答】解：（1）∵△ABC中，∠BAC＝90°，AB＝AC，点D是BC的中点，∴AD＝BD＝DC，∠BDA＝90°，∵四边形DFGE是正方形，∴DE＝DF，∠EDF＝90°，∴∠BDE＝∠ADF＝90°，在△BDE和△ADF中，，∴△BDE≌△ADF（SAS），∴BE＝AF故答案为：BE＝AF；（2）成立；理由如下：当正方形DFGE在BC的上方时，如图②所示，连接AD，∵在Rt△ABC中，AB＝AC，D为斜边BC的中点，∴AD＝BD，AD⊥BC，∴∠ADE+∠EDB＝90°，∵四边形DFGE为正方形，∴DE＝DF，且∠EDF＝90°，∴∠ADE+∠ADF＝90°，∴∠BDE＝∠ADF，在△BDE和△ADF中，，∴△BDE≌△ADF（SAS），∴BE＝AF；当正方形DFGE在BC的下方时，连接AD，如图③所示：∵∠BDE＝∠BDF+90°，∠ADF＝∠BDF+90°，∴∠BDE＝∠ADF，在△BDE和△ADF中，，∴△BDE≌△ADF（SAS），∴BE＝AF；综上所述，（1）中的结论BE＝AF成立；（3）在△ADE中，∵AE＜AD+DE，∴当点A、D、E共线时，AE取得最大值，最大值为AD+DE．如图④所示：则AD＝BC＝1，DE＝DF＝2，∴AE＝AD+DE＝3，即AE的最大值为3．5．【解答】解：（1）如图1，过点O作OM⊥AB于M，ON⊥AD于N，∴∠OME＝∠ONF＝90°，∴∠BAD+∠MON＝180°，∵∠BAD+∠EOF＝180°，∴∠MON＝∠EOF，∴∠EOM＝∠FON，∵O是正方形ABCD的对角线的交点，∴∠BAO＝∠DAO，∵OM⊥AB，ON⊥AD，∴OM＝ON，∴△OME≌△ONF（AAS）∴OE＝OF；（2）（1）的结论成立；理由：如图2，过点O作OM⊥AB于M，ON⊥AD于N，∴∠OME＝∠ONF＝90°，∴∠BAD+∠MON＝180°，∵∠BAD+∠EOF＝180°，∴∠MON＝∠EOF，∴∠EOM＝∠FON，∵O是菱形ABCD的对角线的交点，∴∠BAO＝∠DAO，∵OM⊥AB，ON⊥AD，∴OM＝ON，∴△OME≌△ONF（AAS）∴OE＝OF；（3）如图3，过点O作OG⊥AB于G，OH⊥AD于H，∴∠OGE＝∠OHF＝90°，∴∠BAD+∠GOH＝180°，∵∠BAD+∠EOF＝180°，∴∠GOH＝∠EOF，∴△EOG∽△FOH，∴，∵O是▱ABCD的对角线的交点，∴S△AOB＝S△AOD，∵S△AOB＝AB•OG，S△AOD＝AD•OH，∴AB•OG＝AD•OH，∴＝，∴．6．【解答】解：（1）①∵四边形ABCD是正方形，∴∠BCD＝90°，∠BCA＝45°，∵GE⊥BC、GF⊥CD，∴∠CEG＝∠CFG＝∠ECF＝90°，∴四边形CEGF是矩形，∠CGE＝∠ECG＝45°，∴EG＝EC，∴四边形CEGF是正方形；②由①知四边形CEGF是正方形，∴∠CEG＝∠B＝90°，∠ECG＝45°，∴＝，GE∥AB，∴＝＝，故答案为：；（2）连接CG，由旋转性质知∠BCE＝∠ACG＝α，在Rt△CEG和Rt△CBA中，＝cos45°＝、＝cos45°＝，∴＝＝，∴△ACG∽△BCE，∴＝＝，∴线段AG与BE之间的数量关系为AG＝BE；（3）∵∠CEF＝45°，点B、E、F三点共线，∴∠BEC＝135°，∵△ACG∽△BCE，∴∠AGC＝∠BEC＝135°，∴∠AGH＝∠CAH＝45°，∵∠CHA＝∠AHG，∴△AHG∽△CHA，∴＝＝，设BC＝CD＝AD＝a，则AC＝a，则由＝得＝，∴AH＝a，则DH＝AD﹣AH＝a，CH＝＝a，∴＝得＝，解得：a＝3，即BC＝3，故答案为：3．7．【解答】解：（1）如图1，连接AE，∵AB＝AC＝2，点E分别是BC的中点，∴AE⊥BC，∴∠BEC＝90°，∵AB＝AC＝2，∠BAC＝120°，∴∠B＝∠C＝30°，在Rt△ABE中，AE＝AB＝1，根据勾股定理得，BE＝∵点E是BC的中点，∴BC＝2BE＝2，∴＝＝，∵点D是AC的中点，∴AD＝CD＝AC＝1，∴＝＝，故答案为：，；（2）无变化，理由：由（1）知，CD＝1，CE＝BE＝，∴＝，，∴＝，由（1）知，∠ACB＝∠DCE＝30°，∴∠ACD＝∠BCE，∴△ACD∽△BCE，∴，（3）当点D在线段AE上时，如图2，过点C作CF⊥AE于F，∠CDF＝180°﹣∠CDE＝60°，∴∠DCF＝30°，∴DF＝CD＝，∴CF＝DF＝，在Rt△AFC中，AC＝2，根据勾股定理得，AF＝＝，∴AD＝AF+DF＝，由（2）知，，∴BE＝AD＝当点D在线段AE的延长线上时，如图3，过点C作CG⊥AD交AD的延长线于G，∵∠CDG＝60°，∴∠DCG＝30°，∴DG＝CD＝，∴CG＝DG＝，在Rt△ACG中，根据勾股定理得，AG＝，∴AD＝AG﹣DG＝，由（2）知，，∴BE＝AD＝即：线段BE的长为或．8．【解答】解：（1）证明：∵将△ACD绕点C逆时针方向旋转60°得到△BCE，∴∠DCE＝60°，DC＝EC，∴△CDE是等边三角形；故答案为：等边；（2）存在，当6＜t＜10时，由旋转的性质得，BE＝AD，∴C△DBE＝BE+DB+DE＝AB+DE＝4+DE，由（1）知，△CDE是等边三角形，∴DE＝CD，∴C△DBE＝CD+4，由垂线段最短可知，当CD⊥AB时，△BDE的周长最小，此时，CD＝2，∴△BDE的最小周长＝CD+4＝2+4；（3）存在，①∵当点D与点B重合时，D，B，E不能构成三角形，∴当点D与点B重合时，不符合题意，②当0≤m＜6时，由旋转可知，∠ABE＝60°，∠BDE＜60°，∴∠BED＝90°，由（1）可知，△CDE是等边三角形，∴∠DEB＝60°，∴∠CEB＝30°，∵∠CEB＝∠CDA，∴∠CDA＝30°，∵∠CAB＝60°，∴∠ACD＝∠ADC＝30°，∴DA＝CA＝4，∴OD＝OA﹣DA＝6﹣4＝2，∴m＝2；③当6＜m＜10时，由∠DBE＝120°＞90°，∴此时不存在；④当m＞10时，由旋转的性质可知，∠DBE＝60°，又由（1）知∠CDE＝60°，∴∠BDE＝∠CDE+∠BDC＝60°+∠BDC，而∠BDC＞0°，∴∠BDE＞60°，∴只能∠BDE＝90°，从而∠BCD＝30°，∴BD＝BC＝4，∴OD＝14，∴m＝14，综上所述：当m＝2或14时，以D、E、B为顶点的三角形是直角三角形．9．【解答】解：（1）如图1中，连接DB，MF，CE，延长BD交EC于H．∵AC＝AB，AE＝AD，∠BAD＝∠CAE＝90°，∴△BAD≌△CAE（SAS），∴BD＝EC，∠ACE＝∠ABD，∵∠ABD+∠ADB＝90°，∠ADB＝∠CDH，∴∠ADH+∠DCH＝90°，∴∠CHD＝90°，∴EC⊥BH，∵BM＝MC，BF＝FE，∴MF∥EC，MF＝EC，∵CM＝MB，CN＝ND，∴MN∥BD，MN＝BD，∴MN＝MF，MN⊥MF，∴∠NMF＝90°，∴∠MNF＝45°，NF＝MN．故答案为：45°（2）：如图2中，连接MF，EC，BD．设EC交AB于O，BD交EC于H．∵AC＝AB，AE＝AD，∠BAD＝∠CAE＝90°，∴∠BAD＝∠CAE，∴△BAD≌△CAE（SAS），∴BD＝EC，∠ACE＝∠ABD，∵∠AOC+∠ACO＝90°，∠AOC＝∠BOH，∴∠OBH+∠BOH＝90°，∴∠BHO＝90°，∴EC⊥BD，∵BM＝MC，BF＝FE，∴MF∥EC，MF＝EC，∵CM＝MB，CN＝ND，∴MN∥BD，MN＝BD，∴MN＝MF，MN⊥MF，∴∠NMF＝90°，∴∠MNF＝45°，NF＝MN．（3）：如图3中，如图以A为圆心AD为半径作⊙A．当直线PB与⊙A相切时，此时∠CBP的值最小，点P到BC的距离最小，即△BCP的面积最小，∵AD＝AE，AB＝AC，∠BAC＝∠DAE＝90°，∴∠BAD＝∠CAE，∴△BAD≌△CAE（SAS），∴∠ACE＝∠ABD，BD＝EC，∵∠ABD+∠AOB＝90°，∠AOB＝∠CPO，∴∠CPB＝90°，∵PB是⊙A的切线，∴∠ADP＝90°，∵∠DPE＝∠ADP＝∠DAE＝90°，∴四边形ADPE是矩形，∵AE＝AD，∴四边形ADPE是正方形，∴AD＝AE＝PD＝PE＝2，BD＝EC＝＝2，∴PC＝2﹣2，PB＝2+2，∴S△BCP的最小值＝×PC×PB＝（2﹣2）（2+2）＝4．10．【解答】（1）解：AC⊥BD，理由如下：连接AC、BD，如图2所示：∵AB＝AD，∴点A在线段BD的垂直平分线上，∵CB＝CD，∴点C在线段BD的垂直平分线上，∴直线AC是线段BD的垂直平分线，∴AC⊥BD，故答案为：AC⊥BD；（2）解：AD2+BC2＝AB2+CD2；理由如下：如图1，已知四边形ABCD中，AC⊥BD，设BD、AC相交于E，∵AC⊥BD，∴∠AED＝∠AEB＝∠BEC＝∠CED＝90°，由勾股定理得，AD2+BC2＝AE2+DE2+BE2+CE2，AB2+CD2＝AE2+BE2+CE2+DE2，∴AD2+BC2＝AB2+CD2；（3）解：如图3，连接CG、BE，∵四边形ACFG和四边形ABDE是正方形，∴AC＝AG，AB＝AE，∠CAG＝∠BAE＝90°，∴∠CAG+∠BAC＝∠BAE+∠BAC，即∠GAB＝∠CAE，在△GAB和△CAE中，，∴△GAB≌△CAE（SAS），∴∠ABG＝∠AEC，又∠AEC+∠AME＝90°，∴∠ABG+∠AME＝90°，即CE⊥BG，由（2）得，CG2+BE2＝CB2+GE2，在Rt△ABC中，AC＝4，AB＝5，根据勾股定理得，BC2＝52﹣42＝9，∵CG和BE分别是正方形ACFG和正方形ABDG的对角线，∴CG2＝42+42＝32，BE2＝52+52＝50，∴GE2＝CG2+BE2﹣CB2＝32+50﹣9＝73，∴GE＝．11．【解答】解：问题发现：如图1中，结论：AE＝2BH，AE⊥BH．理由：在Rt△ABC中，∵BC＝6，∠A＝30°，∴AE＝2BC＝12，在Rt△CDB中，∵∠DCB＝30°，∴CD＝＝4，∵CH＝DH，∴BH＝CD＝2，∴＝＝2，∴AE＝2BH．故答案为AE⊥BH，AE＝2BH．问题证明：如图2中，（1）中结论成立．理由：延长BH到F使得HF＝BH，连接CF．设AE交BF于O．∵CH＝DH，BH＝HF，∠CHF＝∠BHD，∴△CHF≌△DHB（SAS），∴BD＝CF，∠F＝∠DBH，∴CF∥BD，∵AB＝BC，BE＝BD，∴BE＝CF，∴＝＝，∵CF∥BD，∴∠BCF+∠CBD＝180°，∵∠ABC+∠DBE＝∠ABD+∠CBD+∠CBD+∠CBE＝∠CBD+∠ABE＝180°，∴∠BCF＝∠ABE，∴△ABE∽△BCF，∴∠CBF＝∠BAE，＝＝，∴AE＝BF＝2BH，∵∠CBF+∠ABF＝90°，∴∠ABF+∠BAE＝90°，∴∠AOB＝90°，∴BH⊥AE．拓展应用：如图3﹣1中，当DE在BC的下方时，延长AB交DE于F．∵DE∥BC∴∠ABC＝∠BFD＝90°，由题意BC＝BE＝6，AB＝6，BD＝2，DE＝4，∵•BD•BE＝•DE•BF，∴BF＝＝3，∴EF＝BF＝3，∴AF＝6+3，∴AE2＝AF2+EF2＝（6+3）2+（3）2＝144+36．∵AE＝2BH，∴AE2＝12BH2，∴BH2＝12+3如图3﹣2中，当DE在BC的上方时，同法可得AF＝6﹣3，EF＝3，∴BH2＝＝（＝12﹣3．12．【解答】解：（1）如图1中，作EH⊥CG于H．∵四边形ECFG是菱形，∠ECF＝60°，∴∠ECH＝∠ECF＝30°，EC＝EG，∵EH⊥CG，∴GH＝CG，∴＝cos30°＝，∴＝2•＝，∵EG∥CD，AB∥CD，∴GE∥AB，∴＝＝．故答案为．（2）结论：AG＝BE．理由：如图2中，连接CG．∵四边形ABCD，四边形ECFG都是菱形，∠ECF＝∠DCB＝60°，∴∠ECG＝∠EGC＝∠BCA＝∠BAC＝30°，∴△ECG∽△BCE，∴＝，∵∠ECB＝∠GCA，∴△ECB∽△GCA，∴＝＝，∴AG＝BE．（3）如图3中，∵∠AGH＝∠CGF＝30°．∠AGH＝∠GAC+∠GCA，又∵∠DAC＝∠HAG+∠GAC＝30°，∴∠HAG＝∠ACH，∵∠AHG＝∠AHC，∴△HAG∽△HCA，∴HA：HC＝GH：HA，∴AH2＝HG•HC，∴FC＝2，CG＝CF，∴GC＝2，∵HG＝，∴AH2＝HG•HC＝•3＝9，∵AH＞0，∴AH＝3．故答案为3．13．【解答】解：（1）当m＝n时，即：BC＝AC，∵∠ACB＝90°，∴∠A+∠ABC＝90°，∵CD⊥AB，∴∠DCB+∠ABC＝90°，∴∠A＝∠DCB，∵∠FDE＝∠ADC＝90°，∴∠FDE﹣∠CDE＝∠ADC﹣∠CDE，即∠ADE＝∠CDF，∴△ADE∽△CDF，∴，∵∠A＝∠DCB，∠ADC＝∠BDC＝90°，∴△ADC∽△CDB，∴＝1，∴＝1（2）①∵∠ACB＝90°，∴∠A+∠ABC＝90°，∵CD⊥AB，∴∠DCB+∠ABC＝90°，∴∠A＝∠DCB，∵∠FDE＝∠ADC＝90°，∴∠FDE﹣∠CDE＝∠ADC﹣∠CDE，即∠ADE＝∠CDF，∴△ADE∽△CDF，∴，∵∠A＝∠DCB，∠ADC＝∠BDC＝90°，∴△ADC∽△CDB，∴，∴②成立．如图，∵∠ACB＝90°，∴∠A+∠ABC＝90°，又∵CD⊥AB，∴∠DCB+∠ABC＝90°，∴∠A＝∠DCB，∵∠FDE＝∠ADC＝90°，∴∠FDE+∠CDE＝∠ADC+∠CDE，即∠ADE＝∠CDF，∴△ADE∽△CDF，∴，∵∠A＝∠DCB，∠ADC＝∠BDC＝90°，∴△ADC∽△CDB，∴，∴．（3）由（2）有，△ADE∽△CDF，∵＝，∴＝，∴CF＝2AE，在Rt△DEF中，DE＝2，DF＝4，∴EF＝2，①当E在线段AC上时，在Rt△CEF中，CF＝2AE＝2（AC﹣CE）＝2（﹣CE），EF＝2，根据勾股定理得，CE2+CF2＝EF2，∴CE2+[2（﹣CE）]2＝40∴CE＝2，或CE＝﹣（舍）而AC＝＜CE，∴此种情况不存在，②当E在AC延长线上时，在Rt△CEF中，CF＝2AE＝2（AC+CE）＝2（+CE），EF＝2，根据勾股定理得，CE2+CF2＝EF2，∴CE2+[2（+CE）]2＝40，∴CE＝，或CE＝﹣2（舍），③如图1，当点E在CA延长线上时，CF＝2AE＝2（CE﹣AC）＝2（CE﹣），EF＝2，根据勾股定理得，CE2+CF2＝EF2，∴CE2+[2（CE﹣）]2＝40，∴CE＝2，或CE＝﹣（舍）即：CE＝2或CE＝．14．【解答】解：（1）如图1，延长GM交AD于H，∵AD∥GF，∴∠GFM＝∠HAM，在△FMG和△AMH中，，∴△FMG≌△AMH（ASA），∴HM＝GM，AH＝FG，∵AD＝CD，AH＝FG＝CG，∴DH＝DG，∵∠HDG＝90°，HM＝GM，∴DM＝MG，DM⊥MG，故答案为DM＝MG，DM⊥MG．（2）结论成立：DM＝MG，DM⊥MG，理由：如图2中，延长GM使得MH＝GM，连接AH、DH、DG，延长AD交GF的延长线于N，交CD于O．∵AM＝MF，∠AMH＝∠FMG，MH＝MG，∴△AMH≌△FMG（SAS），∴AH＝GF＝CG，∠AHM＝∠FGM，∴AH∥GN，∴∠HAD＝∠N，∵∠ODN＝∠OGC＝90°，∠DON＝∠GOC，∴∠N＝∠OCG，∴∠HAD＝∠DCG，∵AH＝CG，AD＝CD，∴△HAD≌△GCD（SAS），∴DH＝DG，∠HDA＝∠CDG，∴∠HDG＝∠ADC＝90°，∴△HDG是等腰直角三角形，∵MH＝MG，∴DM⊥GH，DM＝MH＝MG，（3）①如图3﹣1中，连接AC．在Rt△ABC中，AC＝＝10，在Rt△ACE中，AE＝＝14，∴AF＝AE＝EF＝14﹣2＝12，∴FM＝AM＝AF＝6，在Rt△MGF中，MG＝＝2，∴S△DMG＝×2×2＝20，②如图3﹣2中，连接AC．同法可得AE＝14，AF＝16，FM＝8，MG＝＝2，∴S△DMG＝×2×2＝34，综上所述，满足条件的△DMG的面积为20或34．15．【解答】解：（1）由旋转可得：AC＝A'C＝2，∵∠ACB＝90°，AB＝，AC＝2，∴BC＝，∵∠ACB＝90°，m∥AC，∴∠A'BC＝90°，∴cos∠A'CB＝＝，∴∠A'CB＝30°，∴∠ACA'＝60°；（2）∵M为A'B'的中点，∴∠A'CM＝∠MA'C，由旋转可得，∠MA'C＝∠A，∴∠A＝∠A'CM，∴tan∠PCB＝tan∠A＝，∴PB＝BC＝，∵∠PCQ＝∠PBC＝90°，∴∠BQC+∠BPC＝∠BCP+∠BPC＝90°，∴∠BQC＝∠BCP＝∠A，∴tan∠BQC＝tan∠A＝，∴BQ＝BC×＝2，∴PQ＝PB+BQ＝；（3）∵S四边形P A'B′Q＝S△PCQ﹣S△A'CB'＝S△PCQ﹣，∴S四边形P A'B′Q最小，即S△PCQ最小，∴S△PCQ＝PQ×BC＝PQ，法一：（几何法）取PQ的中点G，∵∠PCQ＝90°，∴CG＝PQ，即PQ＝2CG，当CG最小时，PQ最小，∴CG⊥PQ，即CG与CB重合时，CG最小，∴CG min＝，PQ min＝2，∴S△PCQ的最小值＝3，S四边形P A'B′Q＝3﹣；法二（代数法）设PB＝x，BQ＝y，由射影定理得：xy＝3，∴当PQ最小时，x+y最小，∴（x+y）2＝x2+2xy+y2＝x2+6+y2≥2xy+6＝12，当x＝y＝时，“＝”成立，∴PQ＝+＝2，∴S△PCQ的最小值＝3，S四边形P A'B′Q＝3﹣．16．【解答】解：（1）结论：△PMN是等边三角形．理由：如图1中，∵△ABC是等边三角形，∴AB＝AC，∠ABC＝∠ACB＝60°，∵AD＝AE，∴BD＝EC，∵PB＝PC，CN＝ND，BM＝EM，∴PN∥BD，PM∥EC，PN＝BD，PM＝EC，∴PM＝PN，∠NPC＝∠ABC＝60°，∠MPB＝∠ACB＝60°，∴∠MPN＝60°，∴△PMN是等边三角形，故答案为等边三角形．（2）△PMN的形状不发生改变，仍为等边三角形，理由如下：如图2中，连接BD，CE．由旋转可得∠BAD＝∠CAE，∵△ABC是等边三角形，∴AB＝AC，∠ACB＝∠ABC＝60°又∵AD＝AE，∴△ABD≌△ACE（SAS），∴BD＝CE，∠ABD＝∠ACE，∵M是BE的中点，P是BC的中点，∴PM是△BCE的中位线，∴PM＝，且PM∥CE．同理可证PN＝BD且PN∥BD，∴PM＝PN，∠MPB＝∠ECB，∠NPC＝∠DBC，∴∠MPB+∠NPC＝∠ECB+∠DBC＝（∠ACB+∠ACE）+（∠ABC﹣∠ABD）＝∠ACB+∠ABC＝120°，∴∠MPN＝60°，∴△PMN是等边三角形．（3）∵PM＝EC，∴当EC最大时，等边△PMN的周长最大，∵EC≤AE+AC，∴EC≤8，∴PM≤4，∴PM的最大值为4，∴△PMN的周长的最大值为12．17．【解答】解：（1）∵AB＝AC，∠ABC＝60°，∴∠BAC＝60°，∵AD＝AE，∠ADE＝70°，∴∠DAE＝180°﹣2∠ADE＝40°，∴α＝∠BAD＝60°﹣40°＝20°，∴∠ADC＝∠BAD+∠ABD＝60°+20°＝80°，∴β＝∠CDE＝∠ADC﹣∠ADE＝10°，故答案为：20，10；（2）设∠ABC＝x，∠AED＝y，∴∠ACB＝x，∠AED＝y，在△DEC中，y＝β+x，在△ABD中，α+x＝y+β＝β+x+β，∴α＝2β；（3）①当点E在CA的延长线上，点D在线段BC上，如图1设∠ABC＝x，∠ADE＝y，∴∠ACB＝x，∠ACE＝y，在△ABD中，x+α＝β﹣y，在△DEC中，x+y+β＝180°，∴α＝2β﹣180°，②当点E在CA的延长线上，点D在CB的延长线上，如图2，同①的方法可得α＝180°﹣2β．18．【解答】解：（1）由旋转变换的性质可知，∠CAE＝90°，AC＝AE，∴△ACE为等腰直角三角形，∴CE＝AC，∵CE＝CD+DE＝CD+BC，∴BC+CD＝AC，故答案为：等腰直角；BC+CD＝AC；（2）延长CO交⊙O于E，连接AE、BE、DE，则∠CDE＝90°，∵点C为的中点，∴点E为的中点，∴EA＝EB，∵AB为⊙O的直径，∴∠ADB＝90°，由（1）得，DE＝（AD+BD），由勾股定理得，CD2＝CE2﹣DE2＝AD2+BD2﹣（AD+BD）2＝（AD﹣BD）2，∴CD＝（BD﹣AD）；（3）如图3，当点E在直线AC的左侧时，连接CQ、PC，∵CA＝CB，点P为AB的中点，∴CP⊥AB，∵CA＝CE，点Q为AE中点，∴CQ⊥AE，AQ＝QE＝AE＝5，∴由勾股定理得，CQ＝＝12，由（1）得，AQ+CQ＝PQ，。

(完整word版)2016年中考数学压轴题70题精选(含答案及解析),推荐文档

2016年中考数学压轴题70题精选(含答案)【001】如图13，二次函数y x px q( p 0)的图象与x轴交于A、B两点，与y轴交于点C( 0, -1),5A ABC的面积为4(1)求该二次函数的关系式；(2 )过y轴上的一点M (0, m)作y轴的垂线，若该垂线与A ABC的外接圆有公共点，求m的取值范围；(3)在该二次函数的图象上是否存在点D,使四边形ABCD为直角梯形？若存在，求出点D的坐标；若不存在，请说明理由。

【002】如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B ( 4, 0)、C (8 , 0)、D (8 , 8)抛物线y=ax2+bx过A、C两点.(1) 直接写出点A的坐标，并求出抛物线的解析式；(2) 动点P从点A出发•沿线段AB向终点B运动，同时点Q从点C出发，沿线段CD向终点D运动.速度均为每秒1个单位长度，运动时间为t秒•过点P作PE丄AB交AC于点E,①过点E作EF丄AD 于点F,交抛物线于点G当t为何值时，线段EG最长？②连接EQ.在点P、Q运动的过程中，判断有几个时刻使得厶CEQ是等腰三角形？请直接写出相应的t值。

【003】抛物线y ax2 bx c(a 0)的顶点为M，与x轴的交点为A、B (点B在点A的右侧)，△ ABM的三个内角/ M、/ A> Z B所对的边分别为m、a、b。

若关于x的一元二次方程(m a)x2 2bx (m a) 0 有两个相等的实数根。

(1)判断△ ABM的形状，并说明理由。

(2)当顶点M的坐标为(一2,—1)时，求抛物线的解析式，并画出该抛物线的大致图形。

(3)若平行于x轴的直线与抛物线交于C、D两点，以CD为直径的圆恰好与x轴相切，求该圆的圆心坐标。

k【004】一次函数y ax b的图象分别与x轴、y轴交于点M,N，与反比例函数y 的图象相交于点xA, B •过点A分别作AC x轴，AE y轴，垂足分别为C,E ;过点B分别作BF x轴，BD y轴，垂足分别为F， D, AC与BD交于点K，连接CD •k(1 )若点A , B 在反比例函数y 仝的图象的同一分支上，如图1，试证明:x① S 四边形AEDKS 四边形CFBK ；② AN BM •k-的图象的不同分支上，如图 2,则AN 与BM 还相等吗？试证 x明你的结论.(2) 连接BM ，如图2,动点P 从点第A2出题图沿折线ABC 方向第25个单位/秒的速度向终点 C 匀速运动，设△ PMB 的面积为S(S 工0)，点P 的运动时间为t 秒，求S 与t 之间的函数关系式(要求写出自变量 t 的取值范围)；(3) 在(2)的条件下，当t 为何值时，/ MPB 与/ BCO 互为余角，并求此时直线 OP 与直线AC 所夹锐角的正切值.【006】如图，抛物线y ax 2 bx 3与x 轴交于A, B 两点，与y 轴交于C 点，且经过点(2, 3a)，对称轴是直线x 1，顶点是M . (1 )求抛物线对应的函数表达式； (2)经过C,M 两点作直线与x 轴交于点N ，在抛物线上是否存在这样的点 P ，使以点P , A, C , N 为顶点的四边形为平行四边形？若存在，请求出点P 的坐标；若不存在，请说明理由；(3) 设直线y x 3与y 轴的交点是D ，在线段BD 上任取一点E (不与B , D 重合)，经过 A, B, E 三点的圆交直线BC 于点F ，试判断△ AEF 的形状，并说明理由；(2)若点A ，B 分别在反比例函数S MK C F【005】如图1 ,在平面直角坐标系中，点点C 在x 轴的正半轴上，直线 AC 交y 轴于点(1)求直线AC 的解析式; y+ Ny，点A 的坐标为(一3, 4), O仝标原点，四边形ABCqE 校y 轴于点x ~ D K(4) 当E 是直线y x 3上任意一点时，(3)中的结论是否成立？(请直接写出结论).如图9，已知正比例函数和反比例函数的图象都经过点I{(第26题A(3,3).x函数和反比例函数的解析式;OA 向下平移m)，求m 的值和这个一次函数的解析式;y I【007】(2 )把A O (1 )求 M(3)第(2)问中的一次函数的图象与x轴、y轴分别交于C、D,求过A、B、D三点的二次函数的解析式;(4)在第(3)问的条件下，二次函数的图象上是否存在点E,使四边形OECD的面积S与四边形OABD过点B作圆0的切线交DC的延长线于点P，判断点P是否在抛物线上，说明理由. NC分(3)yA(4,0, B(1,0, C(0, 2)三点.(1 )A(2三角形与F .-动点，过【009】如图,P作PM x轴，垂足为M，是否存在P点，使得以A, P, M为顶点的△OAC 相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由；(3)在直线AC上方的抛物线上有一点D,使得△ DCA的面积最大，求出点D的坐标.【010】如图，抛物线y ax2 bx 4a经过A( (1)求抛物线的解析式; B •(2)已知点D(m, m 1)在第一象限的抛物线上，求点D关于直线BC对称的点的坐标;⑴求二次函数的解析式；⑵在该抛物线的对称轴上找一点 P ,使PA+PD 最小，求出点P 的坐标；⑶在抛物线上是否存在点 0,使厶QAB 与厶ABC 相似？如果存在，求出点 Q 的坐标；如果不存在，请说明理由.【012】如图，已知抛物线y x 2 bx c 经过A(1,0) , B(0,2)两点，顶点为D . (1) 求抛物线的解析式；(2) 将厶OAB 绕点A 顺时针旋转90。

上海市2016年中考数学试卷及答案解析

上海市2016年中考数学试卷参考答案与试题解析一、选择题：本大题共6小题，每小题4分，共24分1．如果a与3互为倒数，那么a是（）A．﹣3 B．3 C．﹣ D．【考点】倒数．【解析】根据乘积为1的两个数互为倒数，可得答案．【解答】解：由a与3互为倒数，得a是，故选：D．【点评】本题考查了倒数，分子分母交换位置是求一个数的倒数的关键．2．下列单项式中，与a2b是同类项的是（）A．2a2b B．a2b2C．ab2D．3ab【考点】同类项．【解析】根据同类项的概念：所含字母相同，并且相同字母的指数也相同，结合选项解答即可．【解答】解：A、2a2b与a2b所含字母相同，且相同字母的指数也相同，是同类项，故本选项正确；B、a2b2与a2b所含字母相同，但相同字母b的指数不相同，不是同类项，故本选项错误；C、ab2与a2b所含字母相同，但相同字母a的指数不相同，不是同类项，本选项错误；D、3ab与a2b所含字母相同，但相同字母a的指数不相同，不是同类项，本选项错误．故选A．【点评】本题考查了同类项的知识，解答本题的关键是掌握同类项中相同字母的指数相同的概念．3．如果将抛物线y=x2+2向下平移1个单位，那么所得新抛物线的表达式是（）A．y=（x﹣1）2+2 B．y=（x+1）2+2 C．y=x2+1 D．y=x2+3【考点】二次函数图象与几何变换．【解析】根据向下平移，纵坐标相减，即可得到答案．【解答】解：∵抛物线y=x2+2向下平移1个单位，∴抛物线的解析式为y=x2+2﹣1，即y=x2+1．故选C．【点评】本题考查了二次函数的图象与几何变换，向下平移|a|个单位长度纵坐标要减|a|．4．某校调查了20名男生某一周参加篮球运动的次数，调查结果如表所示，那么这20名男生该周参加篮球运动次数的平均数是（）A．3次 B．3.5次 C．4次 D．4.5次【考点】加权平均数．【解析】加权平均数：若n个数x1，x2，x3，…，xn的权分别是w1，w2，w3，…，wn，则x1w1+x2w2+…+xnwnw1+w2+…+wn叫做这n个数的加权平均数，依此列式计算即可求解．【解答】解：（2×2+3×2+4×10+5×6）÷20=（4+6+40+30）÷2080÷20=4（次）．答：这20名男生该周参加篮球运动次数的平均数是4次．【点评】本题考查的是加权平均数的求法．本题易出现的错误是求2，3，4，5这四个数的平均数，对平均数的理解不正确．5．已知在△ABC中，AB=AC，AD是角平分线，点D在边BC上，设=， =，那么向量用向量、表示为（）A．+B．﹣C．﹣+D．﹣﹣【考点】*平面向量．【解析】由△ABC中，AD是角平分线，结合等腰三角形的性质得出BD=DC，可求得的值，然后利用三角形法则，求得答案．【解答】解：如图所示：∵在△ABC中，AB=AC，AD是角平分线，∴BD=DC，∵=，∴=，∵=，∴=+=+．故选：A．【点评】此题考查了平面向量的知识，注意掌握三角形法则的应用是解题关键．6．如图，在Rt△ABC中，∠C=90°，AC=4，BC=7，点D在边BC上，CD=3，⊙A的半径长为3，⊙D与⊙A相交，且点B在⊙D外，那么⊙D的半径长r的取值范围是（）A．1＜r＜4 B．2＜r＜4 C．1＜r＜8 D．2＜r＜8【考点】圆与圆的位置关系；点与圆的位置关系．【解析】连接AD，根据勾股定理得到AD=5，根据圆与圆的位置关系得到r＞5﹣3=2，由点B在⊙D外，于是得到r＜4，即可得到结论．【解答】解：连接AD，∵AC=4，CD=3，∠C=90°，∴AD=5，∵⊙A的半径长为3，⊙D与⊙A相交，∴r＞5﹣3=2，∵BC=7，∴BD=4，∵点B在⊙D外，∴r＜4，∴⊙D的半径长r的取值范围是2＜r＜4，故选B．【点评】本题考查了圆与圆的位置关系，点与圆的位置关系，设点到圆心的距离为d，则当d=r时，点在圆上；当d＞r时，点在圆外；当d＜r时，点在圆内．二、填空题：本大题共12小题，每小题4分，共48分7．计算：a3÷a= a2．【考点】同底数幂的除法．【专题】计算题．【解析】根据同底数幂相除，底数不变指数相减进行计算即可求解．【解答】解：a3÷a=a3﹣1=a2．故答案为：a2．【点评】本题考查了同底数幂的除法的运算性质，熟记运算性质是解题的关键．8．函数y=的定义域是x≠2 ．【考点】函数自变量的取值范围．【解析】直接利用分式有意义的条件得出答案．【解答】解：函数y=的定义域是：x≠2．故答案为：x≠2．【点评】此题主要考查了函数自变量的取值范围，正确把握相关性质是解题关键．9．方程=2的解是x=5 ．【考点】无理方程．【解析】利用两边平方的方法解出方程，检验即可．【解答】解：方程两边平方得，x﹣1=4，解得，x=5，把x=5代入方程，左边=2，右边=2，左边=右边，则x=5是原方程的解，故答案为：x=5．【点评】本题考查的是无理方程的解法，正确利用两边平方的方法解出方程，并正确进行验根是解题的关键．10．如果a=，b=﹣3，那么代数式2a+b的值为﹣2 ．【考点】代数式求值．【专题】计算题；实数．【解析】把a与b的值代入原式计算即可得到结果．【解答】解：当a=，b=﹣3时，2a+b=1﹣3=﹣2，故答案为：﹣2【点评】此题考查了代数式求值，熟练掌握运算法则是解本题的关键．11．不等式组的解集是x＜1 ．【考点】解一元一次不等式组．【解析】首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集．【解答】解：，解①得x＜，解②得x＜1，则不等式组的解集是x＜1．故答案是：x＜1．【点评】本题考查了一元一次不等式组的解法：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．12．如果关于x的方程x2﹣3x+k=0有两个相等的实数根，那么实数k的值是．【考点】根的判别式；解一元一次方程．【解析】根据方程有两个相等的实数根结合根的判别式，即可得出关于k的一元一次方程，解方程即可得出结论．【解答】解：∵关于x的方程x2﹣3x+k=0有两个相等的实数根，∴△=（﹣3）2﹣4×1×k=9﹣4k=0，解得：k=．故答案为：．【点评】本题考查了根的判别式以及解一元一次方程，解题的关键是找出9﹣4k=0．本题属于基础题，难度不大，解决该题型题目时，根据方程解的情况结合根的判别式得出方程（不等式或不等式组）是关键．13．已知反比例函数y=（k≠0），如果在这个函数图象所在的每一个象限内，y的值随着x 的值增大而减小，那么k的取值范围是k＞0 ．【考点】反比例函数的性质．【解析】直接利用当k＞0，双曲线的两支分别位于第一、第三象限，在每一象限内y随x的增大而减小；当k＜0，双曲线的两支分别位于第二、第四象限，在每一象限内y随x的增大而增大，进而得出答案．【解答】解：∵反比例函数y=（k≠0），如果在这个函数图象所在的每一个象限内，y的值随着x的值增大而减小，∴k的取值范围是：k＞0．故答案为：k＞0．【点评】此题主要考查了反比例函数的性质，正确记忆增减性是解题关键．14．有一枚材质均匀的正方体骰子，它的六个面上分别有1点、2点、…6点的标记，掷一次骰子，向上的一面出现的点数是3的倍数的概率是．【考点】概率公式．【专题】计算题．【解析】共有6种等可能的结果数，其中点数是3的倍数有3和6，从而利用概率公式可求出向上的一面出现的点数是3的倍数的概率．【解答】解：掷一次骰子，向上的一面出现的点数是3的倍数的概率==．故答案为．【点评】本题考查了概率公式：随机事件A的概率P（A）=事件A可能出现的结果数除以所有可能出现的结果数．15．在△ABC中，点D、E分别是边AB、AC的中点，那么△ADE的面积与△ABC的面积的比是．【考点】三角形中位线定理．【解析】构建三角形中位线定理得DE∥BC，推出△ADE∽△ABC，所以=（）2，由此即可证明．【解答】解：如图，∵AD=DB，AE=EC，∴DE∥BC．DE=BC，∴△ADE∽△ABC，∴=（）2=，故答案为．【点评】本题考查三角形中位线定理，相似三角形的判定和性质，解题的关键是记住相似三角形的面积比等于相似比的平方，属于中考常考题型．16．今年5月份有关部门对计划去上海迪士尼乐园的部分市民的前往方式进行调查，图1和图2是收集数据后绘制的两幅不完整统计图．根据图中提供的信息，那么本次调查的对象中选择公交前往的人数是6000 ．【考点】条形统计图；扇形统计图．【解析】根据自驾车人数除以百分比，可得答案．【解答】解：由题意，得4800÷40%=12000，公交12000×50%=6000，故答案为：6000．【点评】本题考查了条形统计图，读懂统计图，从统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据．17．如图，航拍无人机从A处测得一幢建筑物顶部B的仰角为30°，测得底部C的俯角为60°，此时航拍无人机与该建筑物的水平距离AD为90米，那么该建筑物的高度BC约为208米．（精确到1米，参考数据：≈1.73）【考点】解直角三角形的应用-仰角俯角问题．【解析】分别利用锐角三角函数关系得出BD ，DC 的长，进而求出该建筑物的高度．【解答】解：由题意可得：tan30°===，解得：BD=30， tan60°===，解得：DC=90，故该建筑物的高度为：BC=BD+DC=120≈208（m ），故答案为：208．【点评】此题主要考查了解直角三角形的应用，熟练应用锐角三角函数关系是解题关键．18．如图，矩形ABCD 中，BC=2，将矩形ABCD 绕点D 顺时针旋转90°，点A 、C 分别落在点A ′、C ′处．如果点A ′、C ′、B 在同一条直线上，那么tan ∠ABA ′的值为．【考点】旋转的性质；矩形的性质；锐角三角函数的定义．【解析】设AB=x ，根据平行线的性质列出比例式求出x 的值，根据正切的定义求出tan ∠BA ′C ，根据∠ABA ′=∠BA ′C 解答即可．【解答】解：设AB=x ，则CD=x ，A ′C=x+2， ∵AD ∥BC ， ∴=，即=，解得，x 1=﹣1，x 2=﹣﹣1（舍去），∵AB ∥CD ，∴∠ABA ′=∠BA ′C ， tan ∠BA ′C===，∴tan∠ABA′=，故答案为：．【点评】本题考查的是旋转的性质、矩形的性质以及锐角三角函数的定义，掌握旋转前、后的图形全等以及锐角三角函数的定义是解题的关键．三、解答题：本大题共7小题，共78分19．计算：|﹣1|﹣﹣+．【考点】实数的运算；负整数指数幂．【解析】利用绝对值的求法、分数指数幂、负整数指数幂分别化简后再加减即可求解．【解答】解：原式=﹣1﹣2﹣2+9=6﹣【点评】本题考查了实数的运算及负整数指数幂的知识，解题的关键是了解相关的运算性质及运算法则，难度不大．20．解方程：﹣=1．【考点】解分式方程．【解析】根据解分式方程的步骤：去分母、去括号、移项、合并同类项、系数化为1进行计算即可．【解答】解：去分母得，x+2﹣4=x2﹣4，移项、合并同类项得，x2﹣x﹣2=0，解得x1=2，x2=﹣1，经检验x=2是增根，舍去；x=﹣1是原方程的根，所以原方程的根是x=﹣1．【点评】本题考查了解分式方程，熟记解分式方程的步骤：去分母、去括号、移项、合并同类项、系数化为1是解题的关键，注意验根．21．如图，在Rt△ABC中，∠ACB=90°，AC=BC=3，点D在边AC上，且AD=2CD，DE⊥AB，垂足为点E，联结CE，求：（1）线段BE的长；（2）∠ECB的余切值．【考点】解直角三角形；勾股定理．【解析】（1）由等腰直角三角形的性质得出∠A=∠B=45°，由勾股定理求出AB=3，求出∠ADE=∠A=45°，由三角函数得出AE=，即可得出BE的长；（2）过点E作EH⊥BC，垂足为点H，由三角函数求出EH=BH=BE•cos45°=2，得出CH=1，在Rt△CHE中，由三角函数求出cot∠ECB==即可．【解答】解：（1）∵AD=2CD，AC=3，∴AD=2，∵在Rt△ABC中，∠ACB=90°，AC=BC=3，∴∠A=∠B=45°，AB===3，∵DE⊥AB，∴∠AED=90°，∠ADE=∠A=45°，∴AE=AD•cos45°=2×=，∴BE=AB﹣AE=3﹣=2，即线段BE的长为2；（2）过点E作EH⊥BC，垂足为点H，如图所示：∵在Rt△BEH中，∠EHB=90°，∠B=45°，∴EH=BH=BE•cos45°=2×=2，∵BC=3，∴CH=1，在Rt△CHE中，cot∠ECB==，即∠ECB的余切值为．【点评】本题考查了解直角三角形、勾股定理、等腰直角三角形的性质、三角函数；熟练掌握等腰直角三角形的性质，通过作辅助线求出CH是解决问题（2）的关键．22．某物流公司引进A、B两种机器人用来搬运某种货物，这两种机器人充满电后可以连续搬运5小时，A种机器人于某日0时开始搬运，过了1小时，B种机器人也开始搬运，如图，线段OG表示A种机器人的搬运量yA（千克）与时间x（时）的函数图象，根据图象提供的信息，解答下列问题：（1）求yB关于x的函数解析式；（2）如果A、B两种机器人连续搬运5个小时，那么B种机器人比A种机器人多搬运了多少千克？【考点】一次函数的应用．【解析】（1）设设yB 关于x的函数解析式为yB=kx+b（k≠0），将点（1，0）、（3，180）代入一次函数函数的解析式得到关于k，b的方程组，从而可求得函数的解析式；（2）设yA 关于x的解析式为yA=k1x．将（3，180）代入可求得yA关于x的解析式，然后将x=6，x=5代入一次函数和正比例函数的解析式求得yA ，yB的值，最后求得yA与yB的差即可．【解答】解：（1）设yB 关于x的函数解析式为yB=kx+b（k≠0）．将点（1，0）、（3，180）代入得：，解得：k=90，b=﹣90．所以yB 关于x的函数解析式为yB=90x﹣90（1≤x≤6）．（2）设yA 关于x的解析式为yA=k1x．根据题意得：3k1=180．解得：k1=60．所以yA=60x．当x=5时，yA=60×5=300（千克）；x=6时，yB=90×6﹣90=450（千克）．450﹣300=150（千克）．答：若果A、B两种机器人各连续搬运5小时，B种机器人比A种机器人多搬运了150千克．【点评】本题主要考查的是一次函数的应用，依据待定系数法求得一次函数的解析式是解题的关键．23．已知：如图，⊙O是△ABC的外接圆， =，点D在边BC上，AE∥BC，AE=BD．（1）求证：AD=CE；（2）如果点G在线段DC上（不与点D重合），且AG=AD，求证：四边形AGCE是平行四边形．【考点】三角形的外接圆与外心；全等三角形的判定与性质；平行四边形的判定；圆心角、弧、弦的关系．【解析】（1）根据等弧所对的圆周角相等，得出∠B=∠ACB，再根据全等三角形的判定得△ABD≌△CAE，即可得出AD=CE；（2）连接AO并延长，交边BC于点H，由等腰三角形的性质和外心的性质得出AH⊥BC，再由垂径定理得BH=CH，得出CG与AE平行且相等．【解答】证明：（1）在⊙O中，∵=，∴AB=AC，∴∠B=∠ACB，∵AE∥BC，∴∠EAC=∠ACB，∴∠B=∠EAC，在△ABD和△CAE中，，∴△ABD≌△CAE（SAS），∴AD=CE；（2）连接AO并延长，交边BC于点H，∵=，OA为半径，∴AH⊥BC，∴BH=CH，∵AD=AG，∴DH=HG，∴BH﹣DH=CH﹣GH，即BD=CG，∵BD=AE，∴CG=AE，∵CG∥AE，∴四边形AGCE是平行四边形．【点评】本题考查了三角形的外接圆与外心以及全等三角形的判定和性质，平行四边形的判定，圆心角、弧、弦之间的关系，把这几个知识点综合运用是解题的关键．24．如图，抛物线y=ax2+bx﹣5（a≠0）经过点A（4，﹣5），与x轴的负半轴交于点B，与y轴交于点C，且OC=5OB，抛物线的顶点为点D．（1）求这条抛物线的表达式；（2）联结AB、BC、CD、DA，求四边形ABCD的面积；（3）如果点E在y轴的正半轴上，且∠BEO=∠ABC，求点E的坐标．【考点】二次函数综合题．【解析】（1）先得出C点坐标，再由OC=5BO，得出B点坐标，将A、B两点坐标代入解析式求出a，b；（2）分别算出△ABC和△ACD的面积，相加即得四边形ABCD的面积；（3）由∠BEO=∠ABC可知，tan∠BEO=tan∠ABC，过C作AB边上的高CH，利用等面积法求出CH，从而算出tan∠ABC，而BO是已知的，从而利用tan∠BEO=tan∠ABC可求出EO长度，也就求出了E点坐标．【解答】解：（1）∵抛物线y=ax2+bx﹣5与y轴交于点C，∴C（0，﹣5），∴OC=5．∵OC=5OB，∴OB=1，又点B在x轴的负半轴上，∴B（﹣1，0）．∵抛物线经过点A（4，﹣5）和点B（﹣1，0），∴，解得，∴这条抛物线的表达式为y=x2﹣4x﹣5．（2）由y=x 2﹣4x ﹣5，得顶点D 的坐标为（2，﹣9）．连接AC ，∵点A 的坐标是（4，﹣5），点C 的坐标是（0，﹣5），又S △ABC =×4×5=10，S △ACD =×4×4=8， ∴S 四边形ABCD =S △ABC +S △ACD =18．（3）过点C 作CH ⊥AB ，垂足为点H ． ∵S △ABC =×AB ×CH=10，AB=5，∴CH=2，在RT △BCH 中，∠BHC=90°，BC=，BH==3，∴tan ∠CBH==．∵在RT △BOE 中，∠BOE=90°，tan ∠BEO=，∵∠BEO=∠ABC ， ∴，得EO=，∴点E 的坐标为（0，）．【点评】本题为二次函数综合题，主要考查了待定系数法求二次函数解析式、三角形面积求法、等积变换、勾股定理、正切函数等知识点，难度适中．第（3）问，将角度相等转化为对应的正切函数值相等是解答关键．25．如图所示，梯形ABCD 中，AB ∥DC ，∠B=90°，AD=15，AB=16，BC=12，点E 是边AB 上的动点，点F 是射线CD 上一点，射线ED 和射线AF 交于点G ，且∠AGE=∠DAB ．（1）求线段CD的长；（2）如果△AEC是以EG为腰的等腰三角形，求线段AE的长；（3）如果点F在边CD上（不与点C、D重合），设AE=x，DF=y，求y关于x的函数解析式，并写出x的取值范围．【考点】四边形综合题．【专题】综合题．【解析】（1）作DH⊥AB于H，如图1，易得四边形BCDH为矩形，则DH=BC=12，CD=BH，再利用勾股定理计算出AH，从而得到BH和CD的长；（2）分类讨论：当EA=EG时，则∠AGE=∠GAE，则判断G点与D点重合，即ED=EA，作EM⊥AD于M，如图1，则AM=AD=，通过证明Rt△AME∽Rt△AHD，利用相似比可计算出此时的AE长；当GA=GE时，则∠AGE=∠AEG，可证明AE=AD=15，（3）作DH⊥AB于H，如图2，则AH=9，HE=AE﹣AH=x﹣9，先利用勾股定理表示出DE=，再证明△EAG∽△EDA，则利用相似比可表示出EG=，则可表示出DG，然后证明△DGF∽△EGA，于是利用相似比可表示出x和y的关系．【解答】解：（1）作DH⊥AB于H，如图1，易得四边形BCDH为矩形，∴DH=BC=12，CD=BH，在Rt△ADH中，AH===9，∴BH=AB﹣AH=16﹣9=7，∴CD=7；（2）当EA=EG时，则∠AGE=∠GAE，∵∠AGE=∠DAB，∴∠GAE=∠DAB，∴G点与D点重合，即ED=EA，作EM⊥AD于M，如图1，则AM=AD=，∵∠MAE=∠HAD，∴Rt△AME∽Rt△AHD，∴AE：AD=AM：AH，即AE：15=：9，解得AE=；当GA=GE时，则∠AGE=∠AEG，∵∠AGE=∠DAB，而∠AGE=∠ADG+∠DAG，∠DAB=∠GAE+∠DAG，∴∠GAE=∠ADG，∴∠AEG=∠ADG，∴AE=AD=15，综上所述，△AEC是以EG为腰的等腰三角形时，线段AE的长为或15；（3）作DH⊥AB于H，如图2，则AH=9，HE=AE﹣AH=x﹣9，在Rt△ADE中，DE==，∵∠AGE=∠DAB，∠AEG=∠DEA，∴△EAG∽△EDA，∴EG：AE=AE：ED，即EG：x=x：，∴EG=，∴DG=DE﹣EG=﹣，∵DF∥AE，∴△DGF∽△EGA，∴DF：AE=DG：EG，即y：x=（﹣）：，∴y=（9＜x＜）．【点评】本题考查了四边形的综合题：熟练掌握梯形的性质等等腰三角形的性质；常把直角梯形化为一个直角三角形和一个矩形解决问题；会利用勾股定理和相似比计算线段的长；会运用分类讨论的思想解决数学问题．上海市2016年中考数学试卷一、选择题：本大题共6小题，每小题4分，共24分1．如果a与3互为倒数，那么a是（）A．﹣3 B．3 C．﹣ D．2．下列单项式中，与a2b是同类项的是（）A．2a2b B．a2b2C．ab2D．3ab3．如果将抛物线y=x2+2向下平移1个单位，那么所得新抛物线的表达式是（）A．y=（x﹣1）2+2 B．y=（x+1）2+2 C．y=x2+1 D．y=x2+34．某校调查了20名男生某一周参加篮球运动的次数，调查结果如表所示，那么这20名男生该周参加篮球运动次数的平均数是（）A．3次 B．3.5次 C．4次 D．4.5次5．已知在△ABC中，AB=AC，AD是角平分线，点D在边BC上，设=， =，那么向量用向量、表示为（）A．+B．﹣C．﹣+D．﹣﹣6．如图，在Rt△ABC中，∠C=90°，AC=4，BC=7，点D在边BC上，CD=3，⊙A的半径长为3，⊙D与⊙A相交，且点B在⊙D外，那么⊙D的半径长r的取值范围是（）A．1＜r＜4 B．2＜r＜4 C．1＜r＜8 D．2＜r＜8二、填空题：本大题共12小题，每小题4分，共48分7．计算：a3÷a= ．8．函数y=的定义域是．9．方程=2的解是．10．如果a=，b=﹣3，那么代数式2a+b的值为．11．不等式组的解集是．12．如果关于x的方程x2﹣3x+k=0有两个相等的实数根，那么实数k的值是．13．已知反比例函数y=（k≠0），如果在这个函数图象所在的每一个象限内，y的值随着x 的值增大而减小，那么k的取值范围是．14．有一枚材质均匀的正方体骰子，它的六个面上分别有1点、2点、…6点的标记，掷一次骰子，向上的一面出现的点数是3的倍数的概率是．15．在△ABC中，点D、E分别是边AB、AC的中点，那么△ADE的面积与△ABC的面积的比是．16．今年5月份有关部门对计划去上海迪士尼乐园的部分市民的前往方式进行调查，图1和图2是收集数据后绘制的两幅不完整统计图．根据图中提供的信息，那么本次调查的对象中选择公交前往的人数是．17．如图，航拍无人机从A处测得一幢建筑物顶部B的仰角为30°，测得底部C的俯角为60°，此时航拍无人机与该建筑物的水平距离AD为90米，那么该建筑物的高度BC约为米．（精确到1米，参考数据：≈1.73）18．如图，矩形ABCD中，BC=2，将矩形ABCD绕点D顺时针旋转90°，点A、C分别落在点A′、C′处．如果点A′、C′、B在同一条直线上，那么tan∠ABA′的值为．三、解答题：本大题共7小题，共78分19．计算：|﹣1|﹣﹣+．20．解方程：﹣=1．21．如图，在Rt△ABC中，∠ACB=90°，AC=BC=3，点D在边AC上，且AD=2CD，DE⊥AB，垂足为点E，联结CE，求：（1）线段BE的长；（2）∠ECB的余切值．22．某物流公司引进A、B两种机器人用来搬运某种货物，这两种机器人充满电后可以连续搬运5小时，A种机器人于某日0时开始搬运，过了1小时，B种机器人也开始搬运，如图，线（千克）与时间x（时）的函数图象，根据图象提供的信息，段OG表示A种机器人的搬运量yA解答下列问题：关于x的函数解析式；（1）求yB（2）如果A、B两种机器人连续搬运5个小时，那么B种机器人比A种机器人多搬运了多少千克？23．已知：如图，⊙O是△ABC的外接圆， =，点D在边BC上，AE∥BC，AE=BD．（1）求证：AD=CE；（2）如果点G在线段DC上（不与点D重合），且AG=AD，求证：四边形AGCE是平行四边形．24．如图，抛物线y=ax2+bx﹣5（a≠0）经过点A（4，﹣5），与x轴的负半轴交于点B，与y轴交于点C，且OC=5OB，抛物线的顶点为点D．（1）求这条抛物线的表达式；（2）联结AB、BC、CD、DA，求四边形ABCD的面积；（3）如果点E在y轴的正半轴上，且∠BEO=∠ABC，求点E的坐标．25．如图所示，梯形ABCD中，AB∥DC，∠B=90°，AD=15，AB=16，BC=12，点E是边AB上的动点，点F是射线CD上一点，射线ED和射线AF交于点G，且∠AGE=∠DAB．（1）求线段CD的长；（2）如果△AEC是以EG为腰的等腰三角形，求线段AE的长；（3）如果点F在边CD上（不与点C、D重合），设AE=x，DF=y，求y关于x的函数解析式，并写出x的取值范围．。

(完整版)中考数学几何综合压轴题初三难题训练(真题附答案)

中考数学几何综合压轴题初三难题训练1. （2015金华中考）如图，正方形 ABCD 和正三角形 AEF 都内接于eO , EF 与BC , CD 分别相交于点G ， H ，则-EF 的值是（）GHA.——B. 2C. . 3D. 222.（2015遵义中考）将正方形 ABCD 绕点A 按逆时针方向旋转 30°，得正方形 AB 1GD 1，B^!交CD 于点E ， AB 3，则四边形A^ED 的内切圆半径为（）D ，E 分别是OA ，OB 的中点，则图中影阴部分的面积为 ___________ cm 2 .A. D.3. （2015遵义中考）如图，在圆心角为90°的扇形OAB 中，半径 OA 2cm ，C 为弧AB 的中点,6Di到E ，且有 EBD CAB • (1) 求证：BE 是eO 的切线；(2 )若BC 3 , AC 5，求圆的直径 AD 及切线BE 的长.5. (2016岳阳中考)数学活动旋转变换(1) 如图①，在 VABC 中， ABC 130°，将VABC 绕点C 逆时针旋转500得到VABC ，连接 BB ，求ABB 的大小；(2) 如图②，在 VABC 中， ABC 150° , AB 3, BC 5，将VABC 绕点C 逆时针旋转 60° 得到VABC ，连接BB ，以A 为圆心，AB 长为半径作圆.(I)猜想：直线 BB 与e A 的位置关系，并证明你的结论； (H)连接AB ，求线段AB 的长度；(3)如图③，在 VABC 中， ABC 90° 180° , AB m , BC n ，将VABC 绕点 C 逆180°得到VABC ，连接AB 和BB ，以A 为圆心，AB 长为半与角满足什么条件时，直线 BB 与e A 相切，请说明理由，并求此条件下线段AB 的长度(结果用角或角的三角函数及字母 m , n 所组成的式子表示)时针旋转2角度0° 2径作圆，问：角6. (2016成都中考)如图，在RtVABC中，ABC 90°，以CB为半径作eC，交AC于点D，交AC 的延长线于点E，连接BD , BE .(1)求证：VABD s VAEB ;AB 4(2)当一—时，求tanE ；BC 3BE父于点F .(3 )在(2 )的条件下，作BAC的平分线，与7. （2016苏州中考）如图，在矩形ABCD中，AB 6cm , AD 8cm •点P从点B出发，沿对角线BD向点D匀速运动，速度为4cm/s，过点P作PQ BD交BC于点Q，以PQ为一边作正方形PQMN，使得点N落在射线PD上，点O从点D出发，沿DC向点C匀速运动，速度为3cm/s，以O为圆心，0.8cm为半径作圆O,点P与点O同时出发，设它们的运动时间为t （单位：s）（0 t 8）•3（1）如图，连接DQ，当DQ平分BDC时，t的值为.（2）如图，连接CM，若VCMQ是以CQ为底的等腰三角形，求t的值；（3）请你继续连行探究，并解答下列问题：①证明：在运动过程中，点O始终在QM所在直线的左侧；②如图3,在运动过程中，当QM与圆O相切时，求t的值；并判断此时PM与圆O是否也相切？说明理由.8. （2015扬州中考）如图，已知 eO 的直径AB 12cm , AC 是eO 的弦，过点延长线于点P ，连接BC •（1）求证： PCA B ；（2）已知 P 400 ,点Q 在优弧ABC 上，从点A 开始逆时针运动到点重合），当VABQ 与VABC 的面积相等时，求动点 Q 所经过的弧长.C 作eO 的切线交BA 的C 停止（点Q 与点C 不9. （ 2015大庆中考）如图，四边形ABCD 内接于eO ,ADPBC P 为BD 上一点，APB BAD . (1) 证明：AB CD ;(2) 证明：DP BD AD BC ； (3) 证明：BD 2 AB 2 AD BC .10. （2015武汉中考）如图，AB是eO的直径，ABT 4^ , AT AB •（1）求证：AT是eO的切线；（2）连接OT交e O于点C，连接AC，求tan TAC的值.11. （2016随州中考）如图，AB是eO的弦，点C为半径OA的中点，过点C作CD OA交弦AB 于点E，连接BD，且DE DB •（1）判断BD与eO的位置关系，并说明理由；5(2)若CD 15 , BE 10 , ta nA -，求eO 的直径.1212. (2015德州中考)如图，eO的半径为1 , A, P , B , C是eO上的四个点, APC CPB 60°•(1) 判断VABC的形状：；(2) 试探究线段PA，PB，PC之间的数量关系，并证明你的结论；(3) 当点P位于的什么位置时，四边形APBC的面积最大？求出最大面积.13. (2016淮安中考)问题背景：如图1，在四边形 ADBC 中， ACB形，所以CE . 2CD ，从而得出结论：AC BC . 2CD •(1) 简单应用：在图1中，若AC 2 , BC 2 2，则CD •(2) 如图3, AB 是eO 的直径，点 C 、D 在e 上，AD BD ，若AB 13, BC 12，求CD 的长. (3) 拓展规律：如图 4 , ACB ADB 90° , AD BD ，若 AC m , BC n m n ，求 CD 的长(用含m , n 的代数式表示)1(4 )如图5 , ACB 90° , AC BC ,点P 为AB 的中点，若点E 满足AE 1AC ,3CE CA ，点Q 为AE 的中点，则线段 PQ 与AC 的数量关系是.ADB 90° , A D BD ，探究线段 AC,BC,CD 之间的数量关系•小吴同学探究此问题的思路是：将 VBCD 绕点D ，逆时针旋转 90°到 VAED 处，点 B,C 分别落在点 A,E 处(如图2)，易证点 C,A,E 在同一条直线上，并且VCDE 是等腰直角三角li14. (2015宜昌中考)如图，四边形ABCD为菱形，对角线AC , BD相交于点E , F是边BA延长线上一点，连接EF，以EF为直径作eO，交边DC于D，G两点，AD分别与EF，GF交于I , H两占八、、♦(1)求FDE的度数；(2)试判断四边形FACD的形状，并证明你的结论；(3)当G为线段DC的中点时，(i)求证：FD FI ;(ii)设AC 2m, BD 2n，求eO的面积与菱形ABCD的面积之比.15. （2015株洲中考）已知AB是圆O的切线，切点为B，直线AO交圆O于C , D两点，CD 2 , DAB 30°，动点P在直线AB上运动，PC交圆O于另一点Q .（1）当点P运动到使Q , C两点重合时（如图1），求AP的长;（2）点P在运动过程中，有几个位置（几种情况）使VCQD的面积为丄?（直接写出答案）21（3）当使VCQD的面积为丄，且Q位于以CD为直径的的上半圆上，CQ QD时（如图2）,2求AP的长.第11页（共29页）第12页(共29页)第一部分 1.C【解析】如图，连接 AC 、BD 、OF ,其中AC 与EF 交于点I . QAO 是EAF 的角平分线,OAF 60o 2 30o .QOA OF ,OFA OAF 30° ,COF 60° ,BD CO 2 1 1 GH BD 2r r , 2 2竺3 3 .GH r作 DAB 1与 AB 1C 1的角平分线交于点 O ，过O 作OF AB 1 , 则 OAF 30° , AB 1O 4^ ,答案EF 3 o r 2 23r . QAO 2OI ,OI -r , CI 21 r r2 FI r sin60°GH CI 11 r , 22.B 【解析】设eO 的半径为r ,则 OF r ，第13页（共29页）故B i FOF 〔OA , 2 设B i Fx , 则AF ：丄3 x , 故 3 2 x 2 2 x 2 2x ,解得x3 -，负值舍去. 2 四边形AB iE D 的内切圆半径为宁-第二部分3. n 1二2 2 2 【解析】连接0C ，过C 点作CF OA 于F •Q 半径OA 2cm , C 为A B 的中点，D 、E 分别是OA 、OB 的中点, OD OE 1cm , OC 2cm , AOC 4^ •CF . 2 • 鸟白图形ACDS 扇形OACS VOCD 2 45 n 221 2 1 23601 n2 2 cm . 2 2Q S VODE 〔OD 2 1 OE cm 2 2S 阴影S 扇形OAB S 空白图形ACD S VODE90 n 221 2 1—n ------ —360 2 2 21 —n _! 12 cm . 2 2 2第三部分4. (1)如图，连接OB .第14页(共29页)QBD BC ,CAB BAD .Q EBD CAB ,BAD EBD .QAD 是eO 的直径，ABD 90o , OA BO .BAD ABO .EBD ABO .OBE EBD OBD ABD OBD ABD 90°.Q 点B 在e O 上，BE 是eO 的切线.(2)如图，设圆的半径为 R ，连接CD .QAD 为eO 的直径，ACCD 90° .QBC BD ,OB CD .OB PAC .QOA OD ,1 5 OF AC .2 2Q 四边形ACBD 是圆内接四边形,BDE ACB .Q DBE ACB ,VDBE s VCAB . DB DEAC BC .3DE 5 3 .DEQ OBE OFD 90 ,DF PBE .QR 0 ,R 3.QBE 是eO 的切线,5. (1)如图①中， QVA BC 是由VABC 旋转得到，ABC ABC 130°，CB CBCBB CBB ，Q BCB 50o ，CBB CB B 650，ABB ABC BB C 65° .(2 )(1)结论：直线 BB ，是e A 的切线. 理由：如图②中，150°,CB CB ,Q ABC ABC CBB CBB ,Q BCB 60° ,CBB CB B 60° ,ABB ABC BBC 90° .AB BB ,直线BB ，是e A 的切线.(H) Q 在 RtVABB 中，Q AB B 90° , BB BC 5 , AB AB 3,AB AB 2 BB 2 34 .(3 )如图③中，当 180°时，直线BB ，是e A 的切线理由：Q ABC ABC ,CB CB ,OF OB ODOEBE JDE AE * 2 3 3\5 5 3 115(3)解法一：在 RtVABC 中, -AC 2 BG -AB 2 11BG 即 5x BG 4x 3x ，解得BG 2 2 12 x . 590°.AB BB ,直线BB ，是e A 的切线.在VCBB 中QCB CB n , BCB 2 ,BB 2 nsin ,在 RtVA BB 中,AB . BB 2 AB 2 ,m 2 4n 2si n 26. (1) QDE 为e C 的直径，DBE 90° . 又 Q ABC 90° ,DBE DBC 90° , CBE DBC 90° ,ABD CBE .又QCB CE ,CBE E , ABD E .又 Q BAD EAB ,VABD ^VAEB .(2 )由(1)知，VABD s VAEB 在 RtVDBE 中,BD 1 tanEBE 2CBB CBB ,Q BCB 2 ,CBB ABB CB B 180° 2-------------? 2ABC BBC90°180° 90°BD BE ABAEABQ - BC设 AB 4x ，贝U CE 在 RtVABC 中，AB CB 3x .5x ,AE AC CE 5x 3x 8x BD BE AB AE 4x8xQAF 是 BAC 的平分线, BF AB 4x 1 FHEF 2BG BE 32 2 12 8FH BG一x x3 3 5 5 1又 Qta nE2EH 2FH 16 x ,5AM AE EM24 x ・ 5 在 RtVAHF 中, 2 2 AH HF AF 1 2 3即 224 x5e C 的半径是3xQAF 平分 BAC ， FE AE 8x 2AE 于 H , 【解析】解法二：如图 2过点A 作EB 延长线的垂线，垂足为点在 VBAE 中，有 1 2 3 E 180°90° 90° , 4 2 E 45 ,VGAF 为等腰直角三角形8.5 L ，AFeC 的半径是NG BN a ，CG 3 a ，4 NC BC 9 a，4BH 9a， 5AB 3a ， AC AG 3a ，tan NAC NG AG sin NAC 10105a ，4 15 a，4 13由( 2) 可知, AE 8x , tanEAG AE 于点M ，解法三:AE 于点G ，FM BAC 的平分线,QAF 是AE 10 .在 RtVDBE 中,设 BP 4t ，则 PQ 3t , BQ 5t .Q DQ 平分 BDC , QC CD , QP BD .CQ PQ 3t .QCQ 8 5t.3t 8 5t ，即 t 1.(2)如图，过点M 作ME BC 于点E .在 RtVAFM 中, FM AF sin NAC 2 卫互,AM 10 5 3 10 5 在 RtVEFM 中, EM FM tanE2 10 QBH a,5 EH 18 a, 5 DE 9 a ,2 DC 9 a ,4 AD 3 a,2 又QAE DE3 a 2 9 a2 9a,10 106DC 3.1087. (1)【解析】由题意可VBPQ s VBCD .DH AE10 ,a在 RtVABD 中，AB 6cm , AD 8cm ,BD 10cm .由 BPQ BCD , QBP DBC ，得 VPBQ ^VCBD .PB PQ BQBC CD BD .Q PB 4t ,PQ 3t , BQ 5t .Q MQ MC ,1 1 QE CE —QC - 8 5t2 2Q VMEQ s VDCB , EQ BCMQ BD1 -8 5t 23t40t 49(3)如图1，设QM 所在直线交CD 于点F . ① Q VQCF s VBCD , CF CDCQ CB CF 68 5t 8E15 -t , DF 4 又DO 3t , DO DF CF 6 ，即点O 始终在QM 所在直线的左侧.②如图，设MQ与eO相切时，切点我G，连接OG ,OG BCOF BD，0.88吗3t 10，4丄4t3当t -时，正方形PQMN的边长为3解法一：连接MO并延长交PQ于点贝U VMOG s VMHQ ,OG MGHQ MQ，260.815HQ4，HQ241328PH13 °HK14 213HK HQ .点O不在PMQ的平分线上，当QM1与eO相切时，PM与eO【解析】解法二：连接OM , OP ,Q SVMPQ SVMOQ S VPOQ S VPOM ，则VOGF s VBCD ,534 , QF-,FG3 5 .H，过点H作HK PM于点K不相切.OQ，设点O到MP的距离为h ,1 4 0.8 1 344142 h 8 .2 2 152h7 20.8 .15当QM与eO相切时，PM与eO不相切QAB是eO的直径，ACB 1 2 90o,又PC是eO的切线，PCO PCA 1 90°,2 PCA.又OC OB .2 B,PCA B .(2) Q P 40°,AOC 50°.QAB 12，AO 6 .AOQ 130°时，VABQ与VABC的面积相等,优弧ABQ所对的圆心角为230°时，VABQ与VABC的面积相等,13n31803180当BOQ 50°时，即9. (1) Q AD PBC ,ADB DBC ,AB DC ,AB CD .(2) Q APB BAD , BAD BCD 180° , APBBCD APD ,Q ADB CBD .VADPWDBC ,AD DPBD BC ，DP BD AD BC .QBD 2DE 2 BE 2, DE 2 CD 2 CE 2 ,2 BD 2CD 2 BE 2 CE 2AB 2 BE CE BE CEAB 2 AD BC.10. (1) QAB AT ,ATB B 45°.BAT 90° .AT 是eO 的切线.(2 )设eO 半径为r ，延长TO 交eO 于D ，连接AD .点Q 所经过的弧长 230 n 6 180 23 n3AAPD 180° , (3)如图，过点D 作DE BC 交BC 于E .QCD是直径，CAD BAT 90°.TAC OAD D . 又ATC DTA,VTAC s VTDA.TA TCTD AT .TA2TC TD , 即4r2 TC TC 2r 解得TC 5 1r.tan TAC tan DACADTCAT.5 1 r2r51211. (1)连接OB .QOB OA, DE DB ,A OBA, DEB ABD.QCD OA,A AEC A DEB 90°,OBA ABD 90°,OB BD ,BD是eO的切线；(2)如图，过点D作DG BE于G .QDE DB,1EG -BE 5,2GDE A,VACE s VDGE,QVACE s VDGE12. (1)等边三角形(2) PA PB PC .证明：如图，在PC上截取PD PA，连接AD .PA AD , PAD 60o.Q BAC 60o,PAB DAC .Q APC 60o,VPAD是等边三角形.Q ACE DGE 90°, AEC GED ,tan EDG tanAEGDG5—，即DG 12 .12在RtVEDG 中，DE .DG2 EG213. QCD 15, DECE 2 .13 ,ACDGCEGE，AC CE DGGE245e O的直径2OA 4AD96QAB AC ,VPAB 也VDAC .PB DC .QPD DC PC ,PA PB PC .(3)当点P 为A B 的中点时，四边形 APBC 面积最大.理由如下：如图，过点 P 作PE AB ，垂足为E , 过点C 作CF AB ，垂足为F ，四边形APBC 面积最大. Qe O 的半径为1,其内接正三角形的边长AB 31S 四边形APBC 匚 2 32 3 . 13. (1) CD 3(2)连接 AC 、BD 、AD ,Q AB 是eO 的直径，ADB ACB 90° ,Q A D B D ,AD BD ,将VBCD 绕点D ，逆时针旋转90°到VAED 处，如图3 ,EADDBC , Q DBCDAC 180° , EADDAC 180° , E 、A 、C 三点共线，Q AB 13,BC 12,由勾股定理可求得： AC 5 ,Q BC AE ,CE AE AC 17,2 AB PE ，S VABC 1AB CF . 2S 四边形APBC 1 — AB PE 2 Q 当点P 为A B 的中点时, CF . PE CF PC , PC 为eO 直径, Q S VPABQ EDA CDB ,EDA ADC CDB ADC ,即 EDCADB 90° ,Q CD ED , VEDC 是等腰直角三角形，CE 2CD ,17近 CD 2(3)以AB 为直径作eO ,连接OD 并延长交eO 于点D 1 , 连接D 1A ，D 1B ， D 1C ，如图D 1C又Q 0D 是eO 的直径,DCD 1 90o ,Q AC m ， BC n由勾股定理可求得: 2 2 DQ AB2 n22PQ = -^」AC • 614.( 1)QEF 为eO 的直径,FDE 90° .(2)四边形FACD 为平行四边形•理由如下:QABCD 为菱形，AB PCD , AC BD ,AEB 90° • 又 FDE 90o ,AC PFD •四边形FACD 为平行四边形.(3)(i )如图，连接GE •由(2)的证明过程可知： ACBC ■ 2D 1C ，ABm 2 2 Q D 1C 2 CD 2 2 D 1D 2CD m 2 n 2CD (4)Q 在RtVDEC 中，G 为CD 的中点,EG DG ,弧DG 弧EG ,1 2.又EF 为eO 的直径,FGE 90° ,FG EG .QG 为DC 中点，E 为AC 中点,GE 为VDAC 的中位线，EG PAD . FGADF l HDFHI 90o . 1 3 24 90o , 3 4 ,FD FI .(ii ) Q 菱形ABCD , AE CE m , BE DE nQ 四边形FACD 为平行四边形,FD AC 2m FIQ FD PAC , 3 8 .又34 7, 78 , EI EA m . 在 RtVFDE 中，FE 2 FD 2 DE 2 ,3m $ 2m $ n 2，解得，n 5m .2 3m9 2 1 S eo n 测，S 菱形ABCD — 2m 2n 2mn 2 4 2 S e O : S 菱形ABCD 9 n m 2:2 5m 2葺5. 4 4015. (1) QAB 是圆O 的切线，OBA 90o .2 5m 2 ,QRtVOBA中，CD 2, DAB 30°,OB 1 ,OB OC AC 1 .Q当点P , C运动到Q , C两点重合时,PC为圆O的切线，PCA 90°,Q DAB 30°, AC 1 ,AP -A/3•3(2)有4个位置使VCQD的面积为-•21【解析】由于CD的长度2，而S VCQD1, 故CD上的高的长度为-，从而如下图，我们可得到答案.2(3)过点Q作QN AD于点N，过点P作PM AD于点M •QNQCD是圆O的直径,CQD 90°• 易证VQCN s VDQN •QN CNDN QNQN2 CN DN .1x 2 x4解得X i 2 3, x22QCQ QD ,CNCNQN易证VPMC s VQNC .易得列空2 3MP QNCM 2 3 MP .在RtVAMP中易得AM 3MP , QAM CM AC 1,2,3 MP . 3MP 1 ,MP 3 14 ，薦1AP2MP21 2.又QCB CE,3 E .。

中考数学几何压轴题(有关三角形、四边形)的综合专题(含答案解析)

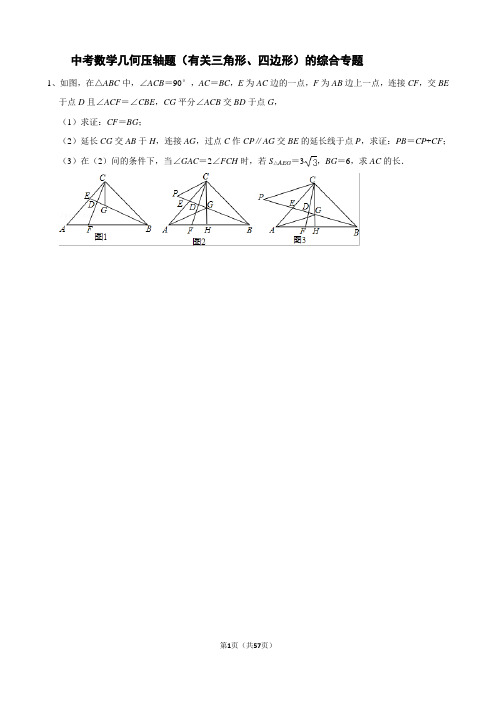
中考数学几何压轴题（有关三角形、四边形）的综合专题1、如图，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的一点，F为AB边上一点，连接CF，交BE于点D且∠ACF＝∠CBE，CG平分∠ACB交BD于点G，（1）求证：CF＝BG；（2）延长CG交AB于H，连接AG，过点C作CP∥AG交BE的延长线于点P，求证：PB＝CP+CF；（3）在（2）问的条件下，当∠GAC＝2∠FCH时，若S△AEG＝3，BG＝6，求AC的长．2、[问题背景]如图1所示，在△ABC中，AB＝BC，∠ABC＝90°，点D为直线BC上的一个动点（不与B、C重合），连结AD，将线段AD绕点D按顺时针方向旋转90°，使点A旋转到点E，连结EC．[问题初探]如果点D在线段BC上运动，通过观察、交流，小明形成了以下的解题思路：过点E作EF⊥BC 交直线BC于F，如图2所示，通过证明△DEF≌△，可推证△CEF是三角形，从而求得∠DCE＝．[继续探究]如果点D在线段CB的延长线上运动，如图3所示，求出∠DCE的度数．[拓展延伸]连接BE，当点D在直线BC上运动时，若AB＝，请直接写出BE的最小值．3、（2019秋•锦江区校级期末）在Rt△ABC中，∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线．（1）如图1，求证：AD＝2DC．（2）如图2，作∠CBD的角平分线交线段CD于点M，若CM＝1，求△DBM的面积；（3）如图3，过点D作DE⊥AB于点E，点N是线段AC上一点（不与C、D重合），以BN为一边，在BN的下方作∠BNG＝60°，NG交DE延长线于点G，试探究线段ND，DG与AD之间的数量关系，并说明理由．4、（2019•镇平县三模）如图1，已知直角三角形ABC，∠ACB＝90°，∠BAC＝30°，点D是AC边上一点，过D作DE⊥AB于点E，连接BD，点F是BD中点，连接EF，CF．（1）发现问题：线段EF，CF之间的数量关系为；∠EFC的度数为；（2）拓展与探究：若将△AED绕点A按顺时针方向旋转α角（0°＜α＜30°），如图2所示，（1）中的结论还成立吗？请说明理由；（3）拓展与运用：如图3所示，若△AED绕点A旋转的过程中，当点D落到AB边上时，AB边上另有一点G，AD＝DG＝GB，BC＝3，连接EG，请直接写出EG的长度．5、（2017春•西城区校级期末）如图1，在等腰△ABC中，AB＝AC，∠BAC＝a，点P是线段AB的中点，点E是线段CB延长线上一点，且PE＝PC，将线段PC绕点P顺时针旋转α得到PD，连接BD．（1）如图2，若α＝60°，其他条件不变，先补全图形，然后探究线段BD和BC之间的数量关系，并说明理由．（2）如图3，若α＝90°，其他条件不变，探究线段BP、BD和BC之间的等量关系，并说明理由．6、【发现问题】如图1，已知△ABC，以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE．请你以A为直角顶点、AC为腰，向△ABC外作等腰直角△ACD（不写作法，保留作图痕迹）．连接BD、CE．那么BD与CE的数量关系是BD＝CE．【拓展探究】如图2，已知△ABC，以AB、AC为边向外作正方形AEFB和正方形ACGD，连接BD、CE，试判断BD与CE之间的数量关系，并说明理由．【解决问题】如图3，有一个四边形场地ABCD，∠ADC＝60°，BC＝15，AB＝8，AD＝CD，求BD的最大值．7、（1）如图1，点C为线段AB外一个动点，已知AB＝a，AC＝b．当点C位于BA的延长线上时，线段BC取得最大值，则最大值为（用含a，b的式子表示）；（2）如图2，点C为线段AB外一个动点，若AB＝10，AC＝3，分别以AC，BC为边，作等边三角形ACD和等边三角形BCE，连接AE，DB．①求证：AE＝DB；②请直接写出线段AE的最大值；（3）如图3，AB＝6，点M为线段AB外一个动点，且AM＝2，MB＝MN，∠BMN＝90°，请直接写出线段AN的最大值．8、【初步探索】（1）如图1：在四边形ABC中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF ＝BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是；【灵活运用】（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；【拓展延伸】（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．9、（2018•大东区一模）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB中点，点P为直线BC上的动点（不与点B、点C重合），连接OC、OP，将线段OP绕点P逆时针旋转60°，得到线段PQ，连接BQ．（1）如图1，当点P在线段BC上时，请直接写出线段BQ与CP的数量关系．（2）如图2，当点P在CB延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；（3）如图3，当点P在BC延长线上时，若∠BPO＝45°，AC＝，请直接写出BQ的长．10、模型发现：同学们知道，三角形的两边之和大于第三边，即如图1，在△ABC中，AB+AC＞BC．对于图1，若把点C看作是线段AB外一动点，且AB＝c，AC＝b，则线段BC的长会因为点C的位置的不同而发生变化．因为AB、AC的长度固定，所以当∠BAC越大时，BC边越长．特别的，当点C位于时，线段BC的长取得最大值，且最大值为（用含b，c的式子表示）（直接填空）.模型应用：点C为线段AB外一动点，且AB＝3，AC＝2，如图2所示，分别以AC，BC为边，作等边三角形ACD 和等边三角形BCE，连接BD，AE．（1）求证：BD＝AE．（2）线段AE长的最大值为．模型拓展：如图3，在平面直角坐标系中，点A是y轴正半轴上的一动点，点B是x轴正半轴上的一动点，且AB ＝8．若AC⊥AB，AC＝3，试求OC长的最大值．11、已知：△ABC中，∠ACB＝90°，AC＝BC．（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD＝BF；（2）如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE＝AD，连BE交AC于F，连DE，问BD与CF有何数量关系，并加以证明；（3）如图3，点D在CB延长线上，AE＝AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC ＝3MC，请直接写出的值．12、已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求的值．13、已知，△ABC中，AB＝AC，∠BAC＝90°，E为边AC任意一点，连接BE．（1）如图1，若∠ABE＝15°，O为BE中点，连接AO，且AO＝1，求BC的长；（2）如图2，F也为AC上一点，且满足AE＝CF，过A作AD⊥BE交BE于点H，交BC于点D，连接DF交BE于点G，连接AG；①若AG平分∠CAD，求证：AH＝AC；②如图3，当G落在△ABC外时，若将△EFG沿EF边翻折，点G刚好落在AB边上点P，直接写出AG与EF的数量关系．14、如图所示，Rt△ABC中，∠ACB＝90°，E为AC中点，作ED⊥AC交AB于D，连接CD；（1）如图1，求证：AB＝2CD；（2）如图2，作CF⊥AB交AB于F，点G为CF上一点，点H为DE延长线上一点，分别连接AH、GH，若∠AHG＝2∠B，求证：AH＝GH；（3）如图3，在（2）的条件下，连接DG，且有DE＝BF，∠EDG＝90°，若AC＝6，求AH的长度．15、【问题情境】一节数学课后，老师布置了一道课后练习题：如图：已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1＝∠2，FG⊥AB于点G，求证：△CDE≌△EGF．（1）阅读理解，完成解答本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写这道练习题的证明过程；（2）特殊位置，证明结论若CE平分∠ACD，其余条件不变，求证：AE＝BF；（3）知识迁移，探究发现如图，已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC＝EF，请直接写出AE与BF的数量关系．（不必写解答过程）16、在正方形ABCD和等腰直角△BGF中，∠BGF＝90°，P是DF的中点，连接PG、PC．（1）如图1，当点G在BC边上时，延长GP交DC于点E．求证：PG＝PC；（2）如图2，当点F在AB的延长线上时，（1）中的结论是否成立？请证明你的结论；（3）如图3，若四边形ABCD为菱形，且∠ABC＝60°，△BGF为等边三角形，点F在CB的延长线上时，线段PC、PG又有怎样的数量关系，请直接写出你的结论，并画出论证过程中需要添加的辅助线．17、在△ABC中，∠BAC＝60°，点D、E分别在边AC、AB上，AD＝AE，连接CE、BD相交于点F，且∠BEC＝∠ADF，连接AF．（1）如图1，连接ED，求证：∠ABD＝∠CED；（2）如图2，求证：EF+FD＝AF；（3）如图3，取BC的中点G，连接AG交BD于点H，若∠GAC＝3∠ABD，BH＝7，求△ABH的面积．18、点D，E分别在△ABC的边AC，BD上，BD，CE交于点F，连接AF，∠F AE＝∠F AD，FE＝FD．（1）如图1，若∠AEF＝∠ADF，求证：AE＝AD；（2）如图2，若∠AEF≠∠ADF，FB平分∠ABC，求∠BAC的度数；（3）在（2）的条件下，如图3，点G在BE上，∠CFG＝∠AFB若AG＝6，△ABC的周长为20，求BC长．中考数学几何压轴题（有关三角形、四边形）的综合专题参考答案1、如图，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的一点，F为AB边上一点，连接CF，交BE于点D且∠ACF＝∠CBE，CG平分∠ACB交BD于点G，（1）求证：CF＝BG；（2）延长CG交AB于H，连接AG，过点C作CP∥AG交BE的延长线于点P，求证：PB＝CP+CF；（3）在（2）问的条件下，当∠GAC＝2∠FCH时，若S△AEG＝3，BG＝6，求AC的长．证明：（1）如图1，∵∠ACB＝90°，AC＝BC，∴∠A＝45°，∵CG平分∠ACB，∴∠ACG＝∠BCG＝45°，∴∠A＝∠BCG，在△BCG和△CAF中，∵，∴△BCG≌△CAF（ASA），∴CF＝BG；（2）如图2，∵PC∥AG，∴∠PCA＝∠CAG，∵AC＝BC，∠ACG＝∠BCG，CG＝CG，∴△ACG≌△BCG，∴∠CAG＝∠CBE，∵∠PCG＝∠PCA+∠ACG＝∠CAG+45°＝∠CBE+45°，∠PGC＝∠GCB+∠CBE＝∠CBE+45°，∴∠PCG＝∠PGC，∴PC＝PG，∵PB＝BG+PG，BG＝CF，∴PB＝CF+CP；（3）解法一：如图3，过E作EM⊥AG，交AG于M，∵S△AEG＝AG•EM＝3，由（2）得：△ACG≌△BCG，∴BG＝AG＝6，∴×6×EM＝3，EM＝，设∠FCH＝x°，则∠GAC＝2x°，∴∠ACF＝∠EBC＝∠GAC＝2x°，∵∠ACH＝45°，∴2x+x＝45，x＝15，∴∠ACF＝∠GAC＝30°，在Rt△AEM中，AE＝2EM＝2，AM＝＝3，∴M是AG的中点，∴AE＝EG＝2，∴BE＝BG+EG＝6+2，在Rt△ECB中，∠EBC＝30°，∴CE＝BE＝3+，∴AC＝AE+EC＝2+3+＝3+3．解法二：同理得：∠CAG＝30°，AG＝BG＝6，如图4，过G作GM⊥AC于M，在Rt△AGM中，GM＝3，AM＝＝＝3，∵∠ACG＝45°，∠MGC＝90°，∴GM＝CM＝3，∴AC＝AM+CM＝3+3．2、[问题背景]如图1所示，在△ABC中，AB＝BC，∠ABC＝90°，点D为直线BC上的一个动点（不与B、C重合），连结AD，将线段AD绕点D按顺时针方向旋转90°，使点A旋转到点E，连结EC．[问题初探]如果点D在线段BC上运动，通过观察、交流，小明形成了以下的解题思路：过点E作EF⊥BC 交直线BC于F，如图2所示，通过证明△DEF≌△ADB，可推证△CEF是等腰直角三角形，从而求得∠DCE＝135°．[继续探究]如果点D在线段CB的延长线上运动，如图3所示，求出∠DCE的度数．[拓展延伸]连接BE，当点D在直线BC上运动时，若AB＝，请直接写出BE的最小值．解：[问题初探]如图2，过点E作EF⊥BC交直线BC于F，∴∠DFE＝90°＝∠ABD，∴∠EDF+∠DEF＝90°，由旋转知，AD＝DE，∠ADE＝90°，∴∠ADB+∠EDF＝90°，∴∠ADB＝∠DEF，∴△ABD≌△DFE（AAS），∴BD＝EF，DF＝AB，∵AB＝BC，∴BC＝DF，∴BD＝CF，∴EF＝CF，∴△CEG是等腰直角三角形，∴∠ECF＝45°，∴∠DCE＝135°，故答案为：ADB，等腰直角，135；[继续探究]如图3，过点E作EF⊥BC于F，∴∠DFE＝90°＝∠ABD，∴∠EDF+∠DEF＝90°，由旋转知，AD＝DE，∠ADE＝90°，∴∠ADB+∠EDF＝90°，∴∠ADB＝∠DEF，∴△ABD≌△DFE（AAS），∴BD＝EF，DF＝AB，∵AB＝BC，∴BC＝DF，∴BD＝CF，∴EF＝CF，∴△CEG是等腰直角三角形，∴∠ECF＝45°，∴∠DCE＝45°；[拓展延伸]如图4，在△ABC中，∠ABC＝90°，AB＝BC＝，∴∠ACB＝45°当点D在射线BC上时，由[问题初探]知，∠BCM＝135°，∴∠ACM＝∠BCM﹣∠ACB＝90°，当点D在线段CB的延长线上时，由[继续探究]知，∠BCE＝45°，∴∠ACN＝∠ACB+∠BCM＝90°，∴点E是过点C垂直于AC的直线上的点，∴当BE⊥MN时，BE最小，∵∠BCE＝45°，∴∠CBE＝45°＝∠BCE，∴BE＝CE，∴BE最小＝BC＝，即：BE的最小值为．3、在Rt△ABC中，∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线．（1）如图1，求证：AD＝2DC．（2）如图2，作∠CBD的角平分线交线段CD于点M，若CM＝1，求△DBM的面积；（3）如图3，过点D作DE⊥AB于点E，点N是线段AC上一点（不与C、D重合），以BN为一边，在BN的下方作∠BNG＝60°，NG交DE延长线于点G，试探究线段ND，DG与AD之间的数量关系，并说明理由．证明：（1）如图1，过点D作DE⊥AB，∵BD是△ABC的角平分线，DE⊥AB，∠ACB＝90°，∴DC＝DE，∵∠A＝30°，DE⊥AB，∴AD＝2DE，∴AD＝2DC；（2）如图2，过点M作ME∥BD，∵∠ACB＝90°，∠A＝30°，∴∠ABC＝60°，∵BD是△ABC的角平分线，∴∠ABD＝∠DBC＝30°，∵BM平分∠CBD，∴∠CBM＝15°＝∠DBM，∵ME∥BD，∴∠MEC＝∠CBD＝30°，∠EMB＝∠DBM＝∠MBE，∴ME＝BE，∵∠MEC＝30°，∠C＝90°∴CE＝MC＝，ME＝2MC＝2＝BE，∴BC＝+2，∵∠CBD＝30°，∠C＝90°，∴BC＝CD，∴CD＝1+，∴DM＝，∴△DBM的面积＝××（+2）＝1+；（3）若点N在CD上时，AD＝DG+DN，理由如下：如图3所示：延长ED使得DW＝DN，连接NW，∵∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线，DE⊥AB于点E，∴∠ADE＝∠BDE＝60°，AD＝BD，∵DN＝DW，且∠WDN＝60°∴△WDN是等边三角形，∴NW＝DN，∠W＝∠WND＝∠BNG＝∠BDN＝60°，∴∠WNG＝∠BND，在△WGN和△DBN中，∴△WGN≌△DBN（SAS），∴BD＝WG＝DG+DN，∴AD＝DG+DN．（3）若点N在AD上时，AD＝DG﹣DN，理由如下：如图4，延长BD至H，使得DH＝DN，连接HN，由（1）得DA＝DB，∠A＝30°．∵DE⊥AB于点E．∴∠2＝∠3＝60°．∴∠4＝∠5＝60°．∴△NDH是等边三角形．∴NH＝ND，∠H＝∠6＝60°．∴∠H＝∠2．∵∠BNG＝60°，∴∠BNG+∠7＝∠6+∠7．即∠DNG＝∠HNB．在△DNG和△HNB中，∴△DNG≌△HNB（ASA）．∴DG＝HB．∵HB＝HD+DB＝ND+AD，∴DG＝ND+AD．∴AD＝DG﹣ND．4、如图1，已知直角三角形ABC，∠ACB＝90°，∠BAC＝30°，点D是AC边上一点，过D作DE⊥AB于点E，连接BD，点F是BD中点，连接EF，CF．（1）发现问题：线段EF，CF之间的数量关系为EF＝CF；∠EFC的度数为120°；（2）拓展与探究：若将△AED绕点A按顺时针方向旋转α角（0°＜α＜30°），如图2所示，（1）中的结论还成立吗？请说明理由；（3）拓展与运用：如图3所示，若△AED绕点A旋转的过程中，当点D落到AB边上时，AB边上另有一点G，AD＝DG＝GB，BC＝3，连接EG，请直接写出EG的长度．解：（1）如图1中，∵DE⊥AB，∴∠BED＝90°，∵∠BCD＝90°，BF＝DF，∴FE＝FB＝FD＝CF，∴∠FBE＝∠FEB，∠FBC＝∠FCB，∴∠EFC＝∠EFD+∠CFD＝∠FBE+∠FEB+∠FBC+∠FCB＝2（∠FBE+∠FBC）＝2∠ABC＝120°，故答案为：EF＝CF，120°．（2）结论成立．理由：如图2中，取AB的中点M，AD的中点N，连接MC，MF，ED，EN，FN．∵BM＝MA，BF＝FD，∴MF∥AD，MF＝AD，∵AN＝ND，∴MF＝AN，MF∥AN，∴四边形MFNA是平行四边形，∴NF＝AM，∠FMA＝∠ANF，在Rt△ADE中，∵AN＝ND，∠AED＝90°，∴EN＝AD＝AN＝ND，同理CM＝AB＝AM＝MB，在△AEN和△ACM中，∠AEN＝∠EAN，∠MCA＝∠MAC，∵∠MAC＝∠EAN，∴∠AMC＝∠ANE，又∵∠FMA＝∠ANF，∴∠ENF＝∠FMC，在△MFC和△NEF中，，∴△MFC≌△NEF（SAS），∴FE＝FC，∠NFE＝∠MCF，∵NF∥AB，∴∠NFD＝∠ABD，∵∠ACB＝90°，∠BAC＝30°，∴∠ABC＝60°，△BMC是等边三角形，∠MCB＝60°∴∠EFC＝∠EFN+∠NFD+∠DFC＝∠MCF+∠ABD+∠FBC+∠FCB＝∠ABC+∠MCB＝60°+60°＝120°．（3）如图3中，作EH⊥AB于H．在Rt△ABC中，∵∠BAC＝30°，BC＝3，∴AB＝2BC＝6，在Rt△AED中，∠DAE＝30°，AD＝2，∴DE＝AD＝1，在Rt△DEH中，∵∠EDH＝60°，DE＝1，∴EH＝ED•sin60°＝，DH＝ED•cos60°＝，在Rt△EHG中，EG＝＝．5、如图1，在等腰△ABC中，AB＝AC，∠BAC＝a，点P是线段AB的中点，点E是线段CB延长线上一点，且PE＝PC，将线段PC绕点P顺时针旋转α得到PD，连接BD．（1）如图2，若α＝60°，其他条件不变，先补全图形，然后探究线段BD和BC之间的数量关系，并说明理由．（2）如图3，若α＝90°，其他条件不变，探究线段BP、BD和BC之间的等量关系，并说明理由．解：（1）BC＝2BD，理由：如图2，连接CD，由旋转可得，CP＝DP，∠CPD＝60°，∴△CDP是等边三角形，∴∠CDP＝60°＝∠PCD，又∵P是AB的中点，AB＝AC，∠A＝60°，∴等边三角形ABC中，∠PCB＝30°，CP⊥AB，∴∠BCD＝30°，即BC平分∠PCD，∴BC垂直平分PD，∴∠BDC＝∠BPC＝90°，∴Rt△BCD中，BC＝2BD．（2）如图3，取BC中点F，连接PF，∵∠A＝90°，AB＝AC，∴△ABC是等腰直角三角形，∵P是AB的中点，F是BC的中点，∴PF是△ABC的中位线，∴PF∥AC，∴∠PFB＝∠ACB＝45°，∠BPF＝∠A＝90°，∴△BPF是等腰直角三角形，∴BF＝BP，BP＝PF，∵∠DPC＝∠BPF＝90°，∴∠BPD＝∠FPC，又∵PD＝PC，∴△BDP≌△FCP，∴BD＝CF，∵BC＝BF+FC，∴BC＝BD+BP．6、【发现问题】如图1，已知△ABC，以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE．请你以A为直角顶点、AC为腰，向△ABC外作等腰直角△ACD（不写作法，保留作图痕迹）．连接BD、CE．那么BD与CE的数量关系是BD＝CE．【拓展探究】如图2，已知△ABC，以AB、AC为边向外作正方形AEFB和正方形ACGD，连接BD、CE，试判断BD与CE之间的数量关系，并说明理由．【解决问题】如图3，有一个四边形场地ABCD，∠ADC＝60°，BC＝15，AB＝8，AD＝CD，求BD的最大值．【发现问题】解：延长CA到M，作∠MAC的平分线AN，在AN上截取AD＝AC，连接CD，即可得到等腰直角△ACD；连接BD、CE，如图1所示：∵△ABE与△ACD都是等腰直角三角形，∴AB＝AE，AD＝AC，∠BAE＝∠CAD＝90°，∴∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE，【拓展探究】解：BD＝CE；理由如下：∵四边形AEFB与四边形ACGD都是正方形，∴AB＝AE，AD＝AC，∠BAE＝∠CAD＝90°，∴∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE；【解决问题】解：以AB为边向外作等边三角形ABE，连接CE，如图3所示：则∠BAE＝60°，BE＝AB＝AE＝8，∵AD＝CD，∠ADC＝60°，∴△ACD是等边三角形，∴∠CAD＝60°，AC＝AD，∴∠CAD+∠BAC＝∠BAE+∠BAC，即∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE；当C、B、E三点共线时，CE最大＝BC+BE＝15+8＝23，∴BD的最大值为23．7、如图1，点C为线段AB外一个动点，已知AB＝a，AC＝b．当点C位于BA的延长线上时，线段BC取得最大值，则最大值为a+b（用含a，b的式子表示）；（2）如图2，点C为线段AB外一个动点，若AB＝10，AC＝3，分别以AC，BC为边，作等边三角形ACD和等边三角形BCE，连接AE，DB．①求证：AE＝DB；②请直接写出线段AE的最大值；（3）如图3，AB＝6，点M为线段AB外一个动点，且AM＝2，MB＝MN，∠BMN＝90°，请直接写出线段AN的最大值．（1）解：∵点C为线段AB外一动点，且AC＝b，AB＝a，∴当点C位于BA的延长线上时，线段BC的长取得最大值，且最大值为AC+AB＝a+b，（2）①证明：如图2中，∵△ACD与△BCE是等边三角形，∴CD＝AC，CB＝CE，∠ACD＝∠BCE＝60°，∴∠DCB＝∠ACE，在△CAD与△EAB中，，∴△CAD≌△EAB（SAS），∴AE＝BD．②∵线段AE长的最大值＝线段BD的最大值，由（1）知，当线段BD的长取得最大值时，点D在BA的延长线上，∴最大值为AD+AB＝3+10＝13；（3）如图3中，连接BN，∵将△AMN绕着点M顺时针旋转90°得到△PBM，连接AP，则△APM是等腰直角三角形，∴MA＝MP＝2，BP＝AN，∴P A＝2，∵AB＝6，∴线段AN长的最大值＝线段BP长的最大值，∴当P在线段BA的延长线时，线段BP取得最大值最大值＝AB+AP＝6+2．8、【初步探索】（1）如图1：在四边形ABC中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF ＝BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是∠BAE+∠F AD＝∠EAF；【灵活运用】（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；【拓展延伸】（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．解：（1）∠BAE+∠F AD＝∠EAF．理由：如图1，延长FD到点G，使DG＝BE，连接AG，根据SAS可判定△ABE≌△ADG，进而得出∠BAE＝∠DAG，AE＝AG，再根据SSS可判定△AEF≌△AGF，可得出∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF．故答案为：∠BAE+∠F AD＝∠EAF；（2）仍成立，理由：如图2，延长FD到点G，使DG＝BE，连接AG，∵∠B+∠ADF＝180°，∠ADG+∠ADF＝180°，∴∠B＝∠ADG，又∵AB＝AD，∴△ABE≌△ADG（SAS），∴∠BAE＝∠DAG，AE＝AG，∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，∴△AEF≌△AGF（SSS），∴∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF；（3）∠EAF＝180°﹣∠DAB．证明：如图3，在DC延长线上取一点G，使得DG＝BE，连接AG，∵∠ABC+∠ADC＝180°，∠ABC+∠ABE＝180°，∴∠ADC＝∠ABE，又∵AB＝AD，∴△ADG≌△ABE（SAS），∴AG＝AE，∠DAG＝∠BAE，∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，∴△AEF≌△AGF（SSS），∴∠F AE＝∠F AG，∵∠F AE+∠F AG+∠GAE＝360°，∴2∠F AE+（∠GAB+∠BAE）＝360°，∴2∠F AE+（∠GAB+∠DAG）＝360°，即2∠F AE+∠DAB＝360°，∴∠EAF＝180°﹣∠DAB．9、如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB中点，点P为直线BC上的动点（不与点B、点C重合），连接OC、OP，将线段OP绕点P逆时针旋转60°，得到线段PQ，连接BQ．（1）如图1，当点P在线段BC上时，请直接写出线段BQ与CP的数量关系．（2）如图2，当点P在CB延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；（3）如图3，当点P在BC延长线上时，若∠BPO＝45°，AC＝，请直接写出BQ的长．解：（1）CP＝BQ，理由：如图1，连接OQ，由旋转知，PQ＝OP，∠OPQ＝60°⊅∴△POQ是等边三角形，∴OP＝OQ，∠POQ＝60°，在Rt△ABC中，O是AB中点，∴OC＝OA＝OB，∴∠BOC＝2∠A＝60°＝∠POQ，∴∠COP＝∠BOQ，在△COP和△BOQ中，，∴△COP≌△BOQ（SAS），∴CP＝BQ，（2）CP＝BQ，理由：如图2，连接OQ，由旋转知，PQ＝OP，∠OPQ＝60°∴△POQ是等边三角形，∴OP＝OQ，∠POQ＝60°，在Rt△ABC中，O是AB中点，∴OC＝OA＝OB，∴∠BOC＝2∠A＝60°＝∠POQ，∴∠COP＝∠BOQ，在△COP和△BOQ中，，∴△COP≌△BOQ（SAS），∴CP＝BQ，（3）如图3，在Rt△ABC中，∠A＝30°，AC＝，∴BC＝AC•tan∠A＝，过点O作OH⊥BC，∴∠OHB＝90°＝∠BCA，∴OH∥AB，∵O是AB中点，∴CH＝BC＝，OH＝AC＝，∵∠BPQ＝45°，∠OHP＝90°，∴∠BPQ＝∠PQH，∴PH＝OH＝，∴CP＝PH﹣CH＝﹣＝，连接BQ，同（1）的方法得，BQ＝CP＝．10、模型发现：同学们知道，三角形的两边之和大于第三边，即如图1，在△ABC中，AB+AC＞BC．对于图1，若把点C看作是线段AB外一动点，且AB＝c，AC＝b，则线段BC的长会因为点C的位置的不同而发生变化．因为AB、AC的长度固定，所以当∠BAC越大时，BC边越长．特别的，当点C位于线段BA的延长线上时，线段BC的长取得最大值，且最大值为b+c（用含b，c的式子表示）（直接填空）模型应用：点C为线段AB外一动点，且AB＝3，AC＝2，如图2所示，分别以AC，BC为边，作等边三角形ACD 和等边三角形BCE，连接BD，AE．（1）求证：BD＝AE．（2）线段AE长的最大值为5．模型拓展：如图3，在平面直角坐标系中，点A是y轴正半轴上的一动点，点B是x轴正半轴上的一动点，且AB ＝8．若AC⊥AB，AC＝3，试求OC长的最大值．解：当点C位于线段BA的延长线上时，线段BC的长取得最大值，最大值为b+c，故答案为：线段BA的延长线上；b+c；模型应用：（1）证明：∵△ACD、△BCE都是等边三角形，∴CD＝CA＝AD，CB＝CE，∠ACD＝60°，∠BCE＝60°，∴∠DCB＝∠ACE，在△DCB和△ACE中，，∴△DCB≌△ACE（SAS）∴BD＝AE；（2）当点D位于线段BA的延长线上时，线段BD的长取得最大值，最大值为AB+AD＝AB+AC＝3+2＝5，∵AE＝BD，∴线段AE长的最大值为5，模型拓展：取AB的中点G，连接OG、CG，在Rt△AOB中，G为AB的中点，∴OG＝AB＝4，在Rt△CAG中，CG＝＝＝5，当点O、G、C在同一条直线上时，OC最大，最大值为4+5＝9．11、已知：△ABC中，∠ACB＝90°，AC＝BC．（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD＝BF；（2）如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE＝AD，连BE交AC于F，连DE，问BD与CF有何数量关系，并加以证明；（3）如图3，点D在CB延长线上，AE＝AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC ＝3MC，请直接写出的值．（1）证明：如图1中，∵BE⊥AD于E，∴∠AEF＝∠BCF＝90°，∵∠AFE＝∠CFB，∴∠DAC＝∠CBF，∵BC＝CA，∴△BCF≌△ACD，∴BF＝AD．（2）结论：BD＝2CF．理由：如图2中，作EH⊥AC于H．∵∠AHE＝∠ACD＝∠DAE＝90°，∴∠DAC+∠ADC＝90°，∠DAC+∠EAH＝90°，∴∠DAC＝∠AEH，∵AD＝AE，∴△ACD≌△EHA，∴CD＝AH，EH＝AC＝BC，∵CB＝CA，∴BD＝CH，∵∠EHF＝∠BCF＝90°，∠EFH＝∠BFC，EH＝BC，∴△EHF≌△BCF，∴FH＝CF，∴BD＝CH＝2CF．（3）如图3中，同法可证BD＝2CM．∵AC＝3CM，设CM＝a，则AC＝CB＝3a，BD＝2a，∴＝＝．12、已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求的值．（1）①证明：如图1中，∵AB＝AC，∠ABC＝60°∴△ABC是等边三角形，∴∠BAC＝60°，∵AD⊥BN，∴∠ADB＝90°，∵∠MBN＝30°，∠BFD＝60°＝∠1+∠BAF＝∠2+∠BAF，∴∠1＝∠2②证明：如图2中，在Rt△BFD中，∵∠FBD＝30°，∴BF＝2DF，∵BF＝2AF，∴BF＝AD，∵∠BAE＝∠FBC，AB＝BC，∴△BFC≌△ADB，∴∠BFC＝∠ADB＝90°，∴BF⊥CF（2）在BF上截取BK＝AF，连接AK．∵∠BFE＝∠2+∠BAF，∠CFE＝∠4+∠1，∴∠CFB＝∠2+∠4+∠BAC，∵∠BFE＝∠BAC＝2∠EFC，∴∠1+∠4＝∠2+∠4∴∠1＝∠2，∵AB＝AC，∴△ABK≌CAF，∴∠3＝∠4，S△ABK＝S△AFC，∵∠1+∠3＝∠2+∠3＝∠CFE＝∠AKB，∠BAC＝2∠CEF，∴∠KAF＝∠1+∠3＝∠AKF，∴AF＝FK＝BK，∴S△ABK＝S△AFK，∴＝2．13、已知，△ABC中，AB＝AC，∠BAC＝90°，E为边AC任意一点，连接BE．（1）如图1，若∠ABE＝15°，O为BE中点，连接AO，且AO＝1，求BC的长；（2）如图2，F也为AC上一点，且满足AE＝CF，过A作AD⊥BE交BE于点H，交BC于点D，连接DF交BE于点G，连接AG；①若AG平分∠CAD，求证：AH＝AC；②如图3，当G落在△ABC外时，若将△EFG沿EF边翻折，点G刚好落在AB边上点P，直接写出AG与EF的数量关系．（1）解：如图1中，在AB上取一点M，使得BM＝ME，连接ME．在Rt△ABE中，∵OB＝OE，∴BE＝2OA＝2，∵MB＝ME，∴∠MBE＝∠MEB＝15°，∴∠AME＝∠MBE+∠MEB＝30°，设AE＝x，则ME＝BM＝2x，AM＝x，∵AB2+AE2＝BE2，∴（2x+x）2+x2＝22，∴x＝（负根已经舍弃），∴AB＝AC＝（2+）•，∴BC＝AB＝+1．方法二：作EH⊥BC于H，求出BH，CH即可解决问题．（2）证明：如图2中，作CP⊥AC，交AD的延长线于P，GM⊥AC于M．∵BE⊥AP，∴∠AHB＝90°，∴∠ABH+∠BAH＝90°，∵∠BAH+∠P AC＝90°，∴∠ABE＝∠P AC，在△ABE和△CAP中，，∴△ABE≌△CAP，∴AE＝CP＝CF，∠AEB＝∠P，在△DCF和△DCP中，，∴△DCF≌△DCP，∴∠DFC＝∠P，∴∠GFE＝∠GEF，∴GE＝GF，∵GM⊥EF，∴FM＝ME，∵AE＝CF，∴AF＝CE，∴AM＝CM，在△GAH和△GAM中，，∴△AGH≌△AGM，∴AH＝AM＝CM＝AC（3）解：结论：AG＝EF．理由：如图3中，作CM⊥AC交AD的延长线于M，连接PG交AC于点O．由（2）可知△ACM≌△BAE，△CDF≌△CDM，∴∠AEB＝∠M＝∠GEF，∠M＝∠CFD＝∠GFE，AE＝CM＝CF，∴∠GEF＝∠GFE，∴GE＝GF，∵△EFP是由△EFG翻折得到，∴EG＝EP＝GF＝PF，∴四边形EGFP是菱形，∴PG⊥AC，OE＝OF，∵AE＝CF，∴AO＝OC，∵AB∥OP，∴BP＝PC，∵PF∥BE，∴EF＝CF＝AE，∵PB＝PC，AO＝OC，∴PO＝OG＝AB，∴AB＝PG，AB∥PG，∴四边形ABPG是平行四边形，∴AG∥BC，∴∠GAO＝∠ACB＝45°，设EO＝OF＝a，则OA＝OG＝3a，AG＝3a，∴＝＝，∴AG＝EF14、如图所示，Rt△ABC中，∠ACB＝90°，E为AC中点，作ED⊥AC交AB于D，连接CD；（1）如图1，求证：AB＝2CD；（2）如图2，作CF⊥AB交AB于F，点G为CF上一点，点H为DE延长线上一点，分别连接AH、GH，若∠AHG＝2∠B，求证：AH＝GH；（3）如图3，在（2）的条件下，连接DG，且有DE＝BF，∠EDG＝90°，若AC＝6，求AH的长度．解：（1）∵E为AC中点，作ED⊥AC交AB于D，∴AD＝CD，∵∠ACB＝90°，∴BC∥DE，∴AD＝BD，∴CD＝BD，∴AB＝2CD；（2）如图2，连接CH，∵点E是AC的中点，∴AE＝CE，∵DE⊥AC，∴CH＝AH，∴∠ACH＝∠CAH，∵∠ACB＝90°，∴∠B+∠BAC＝90°，∵CF⊥AB，∴∠BAC+∠ACF＝90°，∴∠ACF＝∠B，∴∠HCG＝∠ACH+∠ACF＝∠CAH+∠B，∠AHG＝2∠B∴在四边形AHGF中，∠AFG+∠FGH+∠AHG+∠F AH＝360°，∴∠FGH＝360°﹣（∠AFG+∠AHG+∠F AH）＝360°﹣（90°+2∠B+∠CAH+∠BAC）＝360°﹣（90°+2∠B+∠CAH+90°﹣∠B）＝360°﹣（180°+∠B+∠CAH）＝180°﹣（∠B+∠CAH），∵∠CGH＝180°﹣∠FGH＝∠B+∠CAH＝∠HCG，∴CH＝GH，∵CH＝AH，∴AH＝GH；（3）如图3，由（1）知，DE∥BC，∴∠B＝∠ADE，在△BFC和△DEA中，，∴△BFC≌△DEA，∴BC＝AD，∵AD＝BD＝CD，∴BC＝BD＝CD，∴△BCD是等边三角形，∴∠B＝60°，在Rt△ABC中，AC＝6，∴BC＝2，AB＝4，∵CF⊥BD，∴DF＝，CF＝3，∵∠BAC＝30°，∴∠ADE＝60°，∵∠EDG＝90°，∠FDG＝30°，在Rt△DFG中，DF＝，∴FG＝1，DG＝2，∴CG＝CF﹣FG＝2过点H作HN⊥CF，由（2）知，CH＝GH，∴NG＝CG＝1，∴FN＝NG+FG＝2，过点H作HM⊥AB，∴∠FMH＝∠NFM＝∠HNF＝90°，∴四边形NFMH是矩形，∴HM＝FN＝2，在Rt△DMH中，∠ADE＝60°，HM＝2，∴DH＝，在Rt△HDG中，根据勾股定理得，HG＝＝．15、【问题情境】一节数学课后，老师布置了一道课后练习题：如图：已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1＝∠2，FG⊥AB于点G，求证：△CDE≌△EGF．（1）阅读理解，完成解答本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写这道练习题的证明过程；（2）特殊位置，证明结论若CE平分∠ACD，其余条件不变，求证：AE＝BF；（3）知识迁移，探究发现如图，已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC＝EF，请直接写出AE与BF的数量关系．（不必写解答过程）（1）证明：∵AC＝BC，∠ACB＝90°，∴∠A＝∠B＝45°，∵CD⊥AB，∴∠CDB＝90°，∴∠DCB＝45°，∵∠ECF＝∠DCB+∠1＝45°+∠1，∠EFC＝∠B+∠2＝45°+∠2，∠1＝∠2，∴∠ECF＝∠EFC，∴CE＝EF，∵CD⊥AB，FG⊥AB，∴∠CDE＝∠EGF＝90°，在△CDE和△EGF中，，∴△CDE≌△EGF（AAS）；（2）证明：由（1）得：CE＝EF，∠A＝∠B，∵CE平分∠ACD，∴∠ACE＝∠1，∵∠1＝∠2，∴∠ACE＝∠2，在△ACE和△BEF中，，∴△ACE≌△BEF（AAS），∴AE＝BF；（3）AE＝BF，作EH⊥BC与H，如图3所示：设DE＝x，根据题意得：BE＝DE＝x，AD＝BD＝2x，CD＝AD＝2x，AE＝3x，根据勾股定理得：BC＝AC＝2x，∵∠ABC＝45°，EH⊥BC，∴BH＝x，∴CH＝BC﹣BH＝x，∵EC＝EF，∴FH＝CH＝x，∴BF＝x﹣x＝x，∴＝，∴AE＝．16、在正方形ABCD和等腰直角△BGF中，∠BGF＝90°，P是DF的中点，连接PG、PC．（1）如图1，当点G在BC边上时，延长GP交DC于点E．求证：PG＝PC；（2）如图2，当点F在AB的延长线上时，（1）中的结论是否成立？请证明你的结论；（3）如图3，若四边形ABCD为菱形，且∠ABC＝60°，△BGF为等边三角形，点F在CB的延长线。

北京市2016年中考数学试题含答案解析

2016年北京市高级中等学校招生考试数学试卷一、选择题（本题共30分，每小题3分）第1-10题均有四个选项，符合题意的选项只有．．一个。

1. 如图所示，用量角器度量∠AOB，可以读出∠AOB的度数为（A） 45°（B） 55°（C） 125°（D） 135°答案：B考点：用量角器度量角。

解析：由生活知识可知这个角小于90度，排除C、D，又OB 边在50与60之间，所以，度数应为55°。

2. 神舟十号飞船是我国“神舟”系列飞船之一，每小时飞行约28 000公里。

将28 000用科学计数法表示应为（A）错误！未找到引用源。

（B） 28错误！未找到引用源。

（C）错误！未找到引用源。

（D）错误！未找到引用源。

答案：C考点：本题考查科学记数法。

解析：科学记数的表示形式为10na⨯形式，其中1||10≤<，n为整数，28000＝。

故选C。

a3. 实数a，b在数轴上的对应点的位置如图所示，则正确的结论是（A）a错误！未找到引用源。

（B）错误！未找到引用源。

（C）错误！未找到引用源。

（D）错误！未找到引用源。

答案：D考点：数轴，由数轴比较数的大小。

解析：由数轴可知，－3＜a错误！未找到引用源。

＜－2，故A、B错误；1＜b＜2，－2＜－b＜－1，即－b在－2与－1之间，所以，错误！未找到引用源。

4. 内角和为540错误！未找到引用源。

的多边形是答案：ｃ考点：多边形的内角和。

n-⨯︒，当n＝5时，内角和为540°，所以，选C。

解析：多边形的内角和为(2)1805. 右图是某个几何体的三视图，该几何体是（A）圆锥（B）三棱锥（C）圆柱（D）三棱柱答案：D考点：三视图，由三视图还原几何体。

解析：该三视图的俯视为三角形，正视图和侧视图都是矩形，所以，这个几何体是三棱柱。

6. 如果错误！未找到引用源。

,那么代数错误！未找到引用源。

的值是（A） 2 （B）-2 （C）错误！未找到引用源。

中考数学几何选择填空压轴题四边形难题(含答案))

1、《求长度》（答案）1、（容易）如图1的矩形ABCD 中，有一点E 在AD 上，今以BE 为折线将A 点往右折，如图2所示，再作过A 点且与CD 垂直的直线，交CD 于F 点，如图3所示，若AB= 36，BC=13，∠BEA=60°，则图3中AF 的长度为 4【解】作AH ⊥BC 于H2、（难）如图，矩形ABCD 与菱形EFGH 的对角线均交于点O ，且EG ∥BC ，将矩形折叠，使点C 与点O 重合，折痕MN 恰好过点G 若AB=6，EF=2，∠H=120°，则DN 的长为36-【解】长EG 交DC 于P 点，连接GC 、FH ；如图所示：则CP=DP=21CD=26，△GCP 为直角三角形，∵四边形EFGH 是菱形，∠EHG=120°，∴GH=EF=2，∠OHG=60°，EG ⊥FH ，∴OG=GH•sin60°=2×23=3，由折叠的性质得：CG=OG=3，OM=CM ，∠MOG=∠MCG ，∴PG==26，∵OG ∥CM ，∴∠MOG+∠OMC=180°，∴∠MCG+∠OMC=180°，∴OM ∥CG ，∴四边形OGCM 为平行四边形，∵OM=CM ，∴四边形OGCM 为菱形，∴CM=OG=3，根据题意得：PG 是梯形MCDN 的中位线，∴DN+CM=2PG=6，∴DN=36-3、（中等）如图，△ABC 的周长为19，点D ，E 在边BC 上，∠ABC 的平分线垂直于AE ，垂足为N ，∠ACB 的平分线垂直于AD ，垂足为M ，若BC=7，则MN 的长度为25【解】△BNA ≅△BNE∴BA=BE ，∴△BAE 是等腰三角形，同理△CAD 是等腰三角形，∴点N 是AE 中点，点M 是AD 中点（三线合一），∴MN 是△ADE 的中位线， ∵BE+CD=AB+AC=19-BC=19-7=12，∴DE=BE+CD-BC=5，∴MN=21DE=25．4、（难度）如图，在菱形ABCD 中，∠ABC=120°，将菱形折叠，使点A 恰好落在对角线BD 上的点G 处（不与B 、D 重合），折痕为EF ，若DG=2，BG=6，则BE 的长为______2.8【解】作EH ⊥BD ，设BE=x在Rt △EHG 中，EG 2=EH 2+GH 2，即(8－x )2=(23x )2+(6－21x )2，解得，x =2.8，即BE=2.8，故答案为：2.85、如图，▱ABCD 中，AB=7，BC=3，连接AC ，分别以点A 和点C 为圆心，大于21AC 的长为半径作弧，两弧相交于点M ，N ，作直线MN ，交CD 于点E ，连接AE ，则△AED 的周长是_____ 10．6、（容易）如图，ABCD 的对角线相交于点O ，且AD CD ，过点O 作OM AC ，交AD 于点M ．如果CDM 的周长为8，那么ABCD 的周长是_ 16【解】∵四边形ABCD 是平行四边形，∴OA=OC ，∵OM ⊥AC ，∴AM=CM ，∵△CDM 的周长为8， ∴CM+DM+CD=AM+DM+CD=AD+CD=8，∴平行四边形ABCD 的周长是：2×8=16.7、（中等）如图，正方形ABCD 的边长为12，点E 在边AB 上，BE=8，过点E 作EF ∥BC ，分别交BD 、CD 于G 、F 两点．若点P 、Q 分别为DG 、CE 的中点，则PQ 的长为_____ 1328、（难度）如图，在平行四边形ABCD 中，对角线AC 、BD 相交于点O ，AB=OB ，点E 、点F 分别是OA 、OD 的中点，连接EF ，∠CEF=45°，EM ⊥BC 于点M ，EM 交BD 于点N ，FN=，则线段BC 的长为_____249、（难度）如图，平行四边形ABCD 中，AM ⊥BC 于M ，AN ⊥CD 于N ，已知AB ＝10，BM ＝6，MC ＝3，则MN 的长为___________5734【方法】将目标量置入直角三角形中10、（容易）如上图，在矩形ABCD 中，AB =6，BC =8，点E 是BC 中点，点F 是边CD 上的任意一点，当△AEF 的周长最小时，则DF 的长为 4【解】以CD 为对称轴作对称变换11、如图，在矩形ABCD 中，E 是BC 边上的点，连接AE 、DE ，将△DEC 沿线段DE 翻折，点C 恰好落在线段AE 上的点F 处．若AB ＝6，BE : EC ＝4 : 1，则线段DE 的长为 ____102_______．【方法】AD = AE=10；勾股定理12、如图，矩形ABCD 中，AB ＝8，BC ＝4．点E 在边AB 上，点F 在边CD 上，点G 、H 在对角线AC 上．若四边形EGFH 是菱形，则AE 的长是 [5【解】连接EF 交AC 于O ，∵四边形EGFH 是菱形，∴EF ⊥AC ，OE =OF ， ∵四边形ABCD 是矩形，∴∠B =∠D =90°，AB ∥CD ，∴∠ACD =∠CAB ，在△CFO 与△AOE 中，，∴△CFO ≌△AOE ，∴AO =CO ，A BDCM NAE BDC F∵AC ==4，∴AO =21AC =2，∵∠CAB =∠CAB ，∠AOE =∠B =90°，∴△AOE ∽△ABC ，∴，∴，∴AE =5．13、（难度）如图，矩形ABCD 中，AB ＝2，AD ＝2．点E 是BC 边上的一个动点，连接AE ，过点D 作DF ⊥AE 于点F ．当△CDF 是等腰三角形时，BE 的长为 1、2、22-【解】①CF ＝CD 时，过点C 作CM ⊥DF ，垂足为点M ，则CM ∥AE ，DM ＝MF ，延长CM 交AD 于点G ，∴AG ＝GD ＝1，∴CE ＝1， ∵CG ∥AE ，AD ∥BC ，∴四边形AGCE 是平行四边形，∴CE ＝AG ＝1，∴BE ＝1 ∴当BE ＝1时，△CDF 是等腰三角形；②DF ＝DC 时，则DC ＝DF ＝2，∵DF ⊥AE ，AD ＝2，∴∠DAE ＝45°，则BE ＝2， ∴当BE ＝2时，△CDF 是等腰三角形；③FD ＝FC 时，则点F 在CD 的垂直平分线上，故F 为AE 中点． ∵AB ＝2，BE ＝x ，∴AE ＝，AF ＝，∵△ADF ∽△EAB ，∴＝，，x 2﹣4x +2＝0，解得：x ＝2±2，∴当BE ＝22-时，△CDF 是等腰三角形．综上，当BE ＝1、2、22-时，△CDF 是等腰三角形．14、如图，边长为1的菱形ABCD 中，∠DAB=60度．连接对角线AC ，以AC 为边作第二个菱形ACC 1D 1，使∠D 1AC=60°；连接AC 1，再以AC 1为边作第三个菱形AC 1C 2D 2，使∠D 2AC 1=60°；…，按此规律所作的第n 个菱形的边长为 1)3(-n ．解：连接DB ，∵四边形ABCD 是菱形，∴AD=AB ．AC ⊥DB ， ∵∠DAB=60°，∴△ADB 是等边三角形，∴DB=AD=1，∴BM=21， ∴AM==23，∴AC=3，同理AC 1=3AC=（3）2，AC 2=3AC 1=33=（3）3，按此规律所作的第n 个菱形的边长为1)3(-n15、如图，以Rt △ABC 的斜边BC 为一边在△ABC 的同侧作正方形BCEF ，设正方形的中心为O ，连接AO ，如果AB=4，AO=26，那么AC 的长等于 16 ．【解】如图，过O 点作OG 垂直AC ，G 点是垂足．∵∠BAC=∠BOC=90°，∴ABCO 四点共圆，∴∠OAG=∠OBC=45° ∴△AGO 是等腰直角三角形，∴2AG 2=2GO 2=AO 2=2)26(=72， ∴OG=AG=6，∵∠BAH=∠OGH=90°，∠AHB=∠OHG ，∴△ABH ∽△GOH ，∴AB/OG=AH/（AG ﹣AH ），∵AB=4，OG=AG=6，∴AH=2.4 在直角△OHC 中，∵HG=AG ﹣AH=6﹣2.4=3.6，OG 又是斜边HC 上的高， ∴OG 2=HG×GC ，而OG=6，GH=3.6，∴GC=10．∴AC=AG+GC=6+10=16．故AC 边的长是16．16、如图，在梯形ABCD 中，AD ∥BC ，∠B=90°，AD=2，BC=5，E 为DC 中点，tanC=34．则AE 的长度为265【解】过点E 作BC 的垂线交BC 于点F ，交AD 的延长线于点M ，在梯形ABCD 中，AD ∥BC ，E 是DC 的中点，∴∠M=∠MFC ，DE=CE ；在△MDE 和△FCE 中，∠M=∠MFC ，∠DEM=∠CEF ，DE=CE ；∴△MDE ≌△FCE ，∴EF=ME ，DM=CF ． ∵AD=2，BC=5，∴DM=CF=23，在Rt △FCE 中，tanC=CFEF =34，∴EF=ME=2，在Rt △AME 中，AE=265)232(222=++ 17、如图，平行四边形ABCD 中，AE 平分∠BAD 交BC 边于E ，EF ⊥AE 交CD 边于F ，延长BA 到点G ，使AG = CF ，连接GF ．若BC = 7，DF = 3，tan ∠AEB =3 ，则GF 的长为 23【解】连接AC ，羊场AE 与DC 延长线交于一点H18、（容易）如图，梯形ABCD 中，AD ∥BC ，AB = 3，BC=4，连结BD ，∠BAD 的平分线交BD 于点E ，且AE ∥CD ，则AD 的长为1DG ABCDEMABC DEF【解】构造平行四边形。

2016年中考数学选择压轴题专题练习及解析

2016年中考数学《选择压轴题》专题练习1. （2015年广东3分）如图，已知正ΔABC 的边长为2，E ，F ，G 分别是AB ，BC ，CA 上的点，且AE =BF =CG ，设ΔEFG 的面积为y ，AE 的长为x ，则y 关于x 的函数图象大致是【】A. B.C. D.2. （2015年广东深圳3分）如图，已知正方形ABCD 的边长为12，BE =EC ，将正方形边CD 沿DE 折叠到DF ，延长EF 交AB 于G ，连接DG ，现在有如下4个结论：①ADG FDG ∆∆≌；②2GB AG =；③GDE BEF ∆∆∽；④725BEF S ∆=.在以上4个结论中，正确的有【】 A. 1 B. 2 C.3D. 43. （2015年广东汕尾4分）对于二次函数2 2y x x =-+有下列四个结论：①它的对称轴是直线1x =；②设22111222 2 2y x x y x x =-+=-+，，则当21>x x 时，有21>y y ；③它的图象与x 轴的两个交点是（0，0）和（2，0）；④当0<<2x 时，>0y .其中正确结论的个数为【】 A. 1 B.2 C. 3 D. 44. （2015年广东广州3分）已知2是关于x 的方程2230x mx m -+=的一个根，并且这个方程的两个根恰好是等腰三角形ABC 的两条边长，则三角形ABC 的周长为【】A. 10B. 14C. 10或14D. 8或10 5. （2015年广东佛山3分）下列给出5个命题：①对角线互相垂直且相等的四边形是正方形；②六边形的内角和等于720°； ③相等的圆心角所对的弧相等； ④顺次连结菱形各边中点所得的四边形是矩形；⑤三角形的内心到三角形三个顶点的距离相等.其中正确命题的个数是【】A. 2个B. 3个C. 4个D. 5个 6. （2015年广东梅州3分）对于二次函数2 2y x x =-+有下列四个结论：①它的对称轴是直线1x =；②设22111222 2 2y x x y x x =-+=-+，，则当21>x x 时，有21>y y ；③它的图象与x 轴的两个交点是（0，0）和（2，0）；④当0<<2x 时，>0y .其中正确结论的个数为【】 A. 1 B.2 C. 3 D. 47. （2015年浙江衢州）如图，已知等腰,ABC AB BC ∆= ，以AB 为直径的圆交AC 于点D ，过点D 的O e 的切线交BC 于点E ，若5,4CD CE == ，则O e 的半径是【】 A. 3 B. 4 C.256 D. 2588. （2015年浙江绍兴4分）挑游戏棒是一种好玩的游戏，游戏规则：当一根棒条没有被其它棒条压着时，就可以把它往上拿走. 如图中，按照这一规则，第1次应拿走⑨号棒，第2次应拿走⑤号棒，…，则第6次应拿走【】 A. ②号棒 B. ⑦号棒 C. ⑧号棒 D. ⑩号棒 9. （2015年浙江台州4分）（2015年浙江义乌3分）某班有20位同学参加围棋、象棋比赛，甲说：“只参加一项的人数大于14人” ；乙说：“两项都参加的人数小于5人” .对于甲、乙两人的说法，有下列四个命题，其中真命题的是【】A.若甲对，则乙对B.若乙对，则甲对C.若乙错，则甲错D.若甲粗，则乙对10. （2015年浙江温州4分）如图，C 是以AB 为直径的半圆O 上一点，连结AC ，BC ，分别以AC ，BC 为边向外作正方形ACDE ，BCFG ，DE ，FG ，»»AC BC，的中点分别是M ，N ，P ，Q. 若MP+NQ=14，AC+BC=18，则AB 的长是【】 A.29 B.790C. 13D. 16 11. （2015年浙江舟山3分）（2015年浙江嘉兴4分）如图，抛物线221y x x m =-+++交x 轴于点A （a ，0）和B （b ， 0），交y 轴于点C ，抛物线的顶点为D .下列四个命题：①当>0x 时，>0y ；②若1a =-，则4b =；③抛物线上有两点P （1x ，1y ）和Q （2x ，2y ），若12<1<x x ，且12>2x x +，则12>y y ；④点C 关于抛物线对称轴的对称点为E ，点G ，F 分别在x 轴和y 轴上，当2m =时，四边形EDFG周长的最小值为. 其中真命题的序号是【】A. ①B. ②C. ③D. ④ 12.（2015年浙江杭州3分）设二次函数11212())0(()y a x x x x a x x =--≠≠，的图象与一次函数()20y dx e d =+≠的图象交于点1(0)x ，，若函数21y y y =+的图象与x 轴仅有一个交点，则【】A. 12()a x x d -=；B. 21()a x x d -=； C. 212()a x x d -=；D. ()212a x x d +=（第11题）（第13题）（第14题） 13.（2015年浙江湖州3分）如图，已知在平面直角坐标系xOy 中，O 是坐标原点，点A 是函数1y x=(x <0)图象上一点，AO 的延长线交函数2k y x=（x >0，k 是不等于0的常数)的图象于点C ，点A 关于y 轴的对称点为A ′，点C 关于x 轴的对称点为C ′，连接CC ′，交x 轴于点B ，连结AB ，AA ′，A ′C ′，若ΔABC 的面积等于6，则由线段AC ，CC ′，C ′A ′，A ′A 所围成的图形的面积等于【】【来A.8B.10C.D.14.（2015年浙江金华3分）如图，正方形ABCD 和正三角形AEF 都内接于⊙O ，EF 与BC ，CD 分别相交于点G ，H ，则EFGH的值是【】【 A.26B. 2C. 3D. 215.（2015年浙江丽水3分）如图，在方格纸中，线段a ，b ，c ，d 的端点在格点上，通过平移其中两条线段，使得和第三条线段首尾相接组成三角形，则能组成三角形的不同平移方法有【】A. 3种B. 6种C. 8种D. 12种（第15题）（第16题）16.（2015年浙江宁波4分）如图，小明家的住房平面图呈长方形，被分割成3个正方形和2个长方形后仍是中心对称图形. 若只知道原住房平面图长方形的周长，则分割后不用测量就能知道周长的图形标号为【】A. ①②B. ②③C. ①③D. ①②③ 17. （2015年安徽4分）如图，一次函数y 1＝x 与二次函数y 2＝ax 2＋bx ＋c 图象相交于P 、Q 两点，则函数y ＝ax 2＋(b －1)x ＋c 的图象可能是【】A．B ．C ．D ．18. （2015年北京3分）一个寻宝游戏的寻宝通道如图1所示，通道由在同一平面内的AB ，BC ，CA ，OA ，OB ，OC 组成. 为记录寻宝者的进行路线，在BC 的中点M 处放置了一台定位仪器，设寻宝者行进的时间为x ，寻宝者与定位仪器之间的距离为y ，若寻宝者匀速行进，且表示y 与x 的函数关系的图象大致如图2所示，则寻宝者的行进路线可能为【】A 、A→O→B B 、B→A→CB 、C 、B→O→CD 、C→B→O19. （2015年上海4分）如图，已知在⊙O 中，AB 是弦，半径OC ⊥AB ，垂足为点D ，要使四边形OACB 为菱形，还需要添加一个条件，这个条件可以是【】A 、AD BD =B 、OD CD =C 、CAD CBD ∠=∠ D 、OCA OCB ∠=∠ 20. （2015年重庆A4分）如图，在平面直角坐标系中，菱形ABCD 在第一象限内，边BC 与x 轴平行，A ，B 两点的纵坐标分别为3，1，反比例函数3y x=的图像经过A ，B 两点，则菱形ABCD 的面积为【】A. 2 B. 4C.D.（第19题）（第20题）（第21题）21. （2015年重庆B4分）如图，在平面直角坐标系中，菱形ABOC 的顶点O 在坐标原点，边BO 在x 轴的负半轴上，∠BOC =60°，顶点C 的坐标为(m,，反比例函数ky x=的图像与菱形对角线AO 交于D 点，连接BD ，当BD ⊥x 轴时，k 的值是【】A.B. -C.D. -22. （2015年江苏苏州3分）如图，在一笔直的海岸线l 上有A 、B 两个观测站，AB =2km ，从A 测得船C 在北偏东45°的方向，从B 测得船C 在北偏东22.5°的方向，则船C 离海岸线l 的距离（即CD 的长）为【】A ．4km B．(2+km C． D．(4km（第22题）（第23题）23. （2015年江苏无锡3分）如图，Rt △ABC 中，∠ACB ＝90º，AC ＝3，BC ＝4，将边AC 沿CE 翻折，使点A 落在AB 上的点D 处；再将边BC 沿CF 翻折，使点B 落在CD 的延长线上的点B ′处，两条折痕与斜边AB 分别交于点E 、F ，则线段B ′F 的长为【】A.35 B. 45 C. 23D. 24. （2015年福建福州3分）已知一个函数图像经过()()1422-- ，，，两点，在自变量x 的某个取值范围内，都有函数值y 随x 的增大而减小，则符合上述条件的函数可能是【】A. 正比例函数B. 一次函数C. 反比例函数D. 二次函数25. （2015年福建泉州3分）在同一平面直角坐标系中，函数2y ax bx =+与y bx a =+的图象可能是【】A.B.C.D.26. （2015年福建厦门4分）如图，在ΔABC 中，AB ＝AC ，D 是边BC 的中点，一个圆过点A ，交边AB 于点E ，且与BC 相切于点D ，则该圆的圆心是【】A ．线段AE 的中垂线与线段AC 的中垂线的交点B ．线段AB 的中垂线与线段AC 的中垂线的交点 C ．线段AE 的中垂线与线段BC 的中垂线的交点D ．线段AB 的中垂线与线段BC 的中垂线的交点（第26题）（第28题）27. （2015年内蒙古呼和浩特3分）函数22x xy x+=的图象为【】A.B.C.D.28. （2015年江苏徐州3分）若函数y kx b =-的图像如图所示，则关于x 的不等式()3>0kx b --的解集为【】A. <2xB. >2xC. <5xD. >5x 29.（2015年福建漳州4分）在数学活动课上，同学们利用如图的程序进行计算，发现无论x 取任何正整数，结果都会进入循环，下面选项一定不是该循环的是【】A. 4，2，1B. 2，1，4C. 1，4，2D. 2，4，1 30. （2015年湖南株洲3分）有两个一元二次方程：M ：20ax bx c ++=N ：20cx bx a ++=，其中0a c +=，以下列四个结论中，错误的是【】A 、如果方程M 有两个不相等的实数根，那么方程N 也有两个不相等的实数根；B 、如果方程M 有两根符号相同，那么方程N 的两根符号也相同；C 、如果5是方程M 的一个根，那么15是方程N 的一个根； D 、如果方程M 和方程N 有一个相同的根，那么这个根必是1x =.31. （2015年江西南昌3分）如图，在ΔABC 中，AB ＝BC ＝4，AO ＝BO ，P 是射线CO 上的一个动点，∠AOC ＝60°，则当ΔP AB 为直角三角形时，AP 的长为 ▲ ．（第31题）（第32题）32. （2015年江西3分）已知抛物线()20y ax bx c a ++>=过()()2023- ，，，两点，那么抛物线的对称轴【】A. 只能是x ＝－1B. 可能是y 轴C. 在y 轴右侧且在直线x ＝2的左侧D. 在y 轴左侧 33. （2015年四川成都3分）如图，正六边形ABCDEF 内接于圆O ，半径为4，则这个正六边形的边心距OM 和弧BC 的长分别为【】A.2、3πB. 32、π C. 3、23π D. 32、43π34. （2015年四川宜宾3分）在平面直角坐标系中，任意两点()()1122,,，A x y B x y 规定运算：①()1212,⊕=++A B x x y y ；②1212=⊗+A B x x y y ；③当x 1= x 2且y 1= y 2时，A =B.有下列四个命题：（1）若A (1，2)，B (2，–1)，则(),31⊕= A B ，0=⊗A B ；（2）若⊕=⊕A B B C ，则A =C ；（3）若=⊗⊗A B B C ，则A =C ；（4）对任意点A 、B 、C ，均有()()⊕⊕=⊕⊕A B C A B C 成立.其中正确命题的个数为【】A. 1个B. 2个C. 3个D. 4个 35. （2015年四川资阳3分）如图，在ΔABC 中，∠ACB =90º，AC =BC =1，E 、F 为线段AB 上两动点，且∠ECF =45°，过点E 、F 分别作BC 、AC 的垂线相交于点M ，垂足分别为H 、G ．现有以下结论：①AB =②当点E 与点B 重合时，12MH =；③AF BE EF +=；④MG•MH =12，其中正确结论为【】A. ①②③B. ①③④C. ①②④D. ①②③④ 36. （2015年四川泸州3分）在平面直角坐标系中，点A ，B ，动点C 在x 轴上，若以A 、B 、C 三点为顶点的三角形是等腰三角形，则点C 的个数为【】A.2B.3C.4D.537. （2015年广东茂名3分）张三和李四两人加工同一种零件，每小时张三比李四多加工5个零件，张三加工120个这种零件与李四加工100个这种零件所用时间相等，求张三和李四每小时各加工多少个这种零件？若设张三每小时加工这种零件x 个，则下面列出的方程正确的是【】A. 1201005x x =- B. 1201005x x =-C.1201005x x=+ D. 1201005x x =+（第35题）（第38题）38. （2015年广东珠海3分）如图，在⊙O 中，直径CD 垂直于弦AB ，若∠C=25°，则∠BOD 的度数是（） A. 25° B. 30° C. 40° D. 50°39. （2015年贵州铜仁4分）如图，在平面直角坐标系系中，直线12y k x =+与x 轴交于点A ，与y 轴交于点C ，与反比例函数2k y x=在第一象限内的图象交于点B ，连接BO ．若113OBCS tan BOC =∠=V ，，则k 2的值是【】A. 3-B. 1C. 2D. 340. （2015年河南3分）如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O 1，O 2，O 3，… 组成一条平滑的曲线，点P 从原点O 出发，沿这条曲线向右运动，速度为每秒2π个单位长度，则第2015秒时，点P 的坐标是【】A. （2014，0）B. （2015，-1）C. （2015，1）D. （2016，0）41. （2015年湖北黄冈3分）货车和小汽车同时从甲地出发，以各自的速度匀速向乙地行驶，小汽车到达乙地后，立即以相同的速度沿原路返回甲地，已知甲、乙两地相距180千米，货车的速度为60千米/小时，小汽车的速度为90千米/小时，则下图中能分别反映出货车、小汽车离乙地的距离y （千米）与各自行驶时间t （小时）之间的函数图象是【】A. B. C. D. 42. （2015年湖北黄石3分）如图是自行车骑行训练场地的一部分，半圆O 的直径AB =100，在半圆弧上有一运动员C 从B 点沿半圆周匀速运动到M （最高点），此时由于自行车故障原地停留了一段时间，修理好继续以相同的速度运动到A 点停止．设运动时间为t ，点B 到直线OC 的距离为d ，则下列图象能大致刻画d 与t 之间的关系是【】A.B.C.D.43. （2015年江苏连云港3分）如图是本地区一种产品30天的销售图象，图①是产品日销售量y （单位：件）与时间t （单位；天）的函数关系，图②是一件产品的销售利润z （单位：元）与时间t （单位：天）的函数关系，已知日销售利润=日销售量×一件产品的销售利润，下列结论错误的是【】A. 第24天的销售量为200件；B. 第10天销售一件产品的利润是15元；C. 第12天与第30天这两天的日销售利润相等；D. 第30天的日销售利润是750元44. （2015年江苏南京2分）如图，在矩形ABCD 中，AB =4，AD =5，AD 、AB 、BC 分别与⊙O 相切于E 、F 、G 三点，过点D 作⊙O 的切线交BC 于点M ，则DM 的长为【】 A.133 B. 92C.D.（第44题）（第45题）45. （2015年江苏泰州3分）如图，ΔABC 中，AB =AC ，D 是BC 的中点，AC 的垂直平分线分别交 AC 、AD 、AB 于点E 、O 、F ，则图中全等的三角形的对数是【】 A. 1对 B. 2对 C. 3对 D. 4对 46. （2015年陕西3分）下列关于二次函数()2211y ax ax a =-+＞的图象与x 轴交点的判断，正确的是【】A. 没有交点B. 只有一个交点，且它位于y 轴右侧C. 有两个交点，且它们均位于y 轴左侧D. 有两个交点，且它们均位于y 轴右侧 47. （梅州市2015年3分）对于二次函数x x y 22+-=.有下列四个结论：①它的对称轴是直线1=x；②设12112x x y +-=，22222x x y +-=，则当12x x >时，有12y y >；③它的图象与x 轴的两个交点是（0，0）和（2，0）；④当20<<x 时，0>y .其中正确的结论的个数为（）A ．1B ．2C ．3D ．4 48. （3分）（2015•济南）如图，抛物线y=﹣2x 2+8x ﹣6与x 轴交于点A 、B ，把抛物线在x 轴及其上方的部分记作C 1，将C 1向右平移得C 2，C 2与x 轴交于点B ，D ．若直线y=x+m与C1、C2共有3个不同的交点，则m的取值范围是（）A．﹣2＜m＜B．﹣3＜m＜﹣C．﹣3＜m＜﹣2 D．﹣3＜m＜﹣49.（2015•菏泽3分）如图，在平面直角坐标系xOy中，直线y=x经过点A，作AB⊥x轴于点B，将△ABO绕点B逆时针旋转60°得到△CB D．若点B的坐标为（2，0），则点C的坐标为（）A．（﹣1，）B．（﹣2，）C．（﹣，1）D．（﹣，2）50.（2015年四川省自贡市3分）如图，在矩形ABCD中，AB＝4，AD＝6，E是AB边的中点，F是线段BC上的动点，将△EBF沿EF所在直线折叠得到△EB′F，连接B′D，则B′D的小值是（）A、2102-B、6 C、2132-D、4参考答案1.【答案】D.【考点】由实际问题列函数关系式（几何问题）；二次函数的性质和图象.【分析】根据题意，有AE=BF=CG，且正三角形ABC的边长为2，∴2===-BE CF AG x. ∴△AEG、△BEF、△CFG三个三角形全等．在△AEG 中，2==-，A E x A G x ，∴()1224=⋅⋅⋅=-V AEGS AE AG sinA x x .∴()2332442=-=-=-+V V ABC AEGy S S x x x x ．∴其图象为开口向上的二次函数.故选D. 2. 【答案】C.【考点】折叠问题；正方形的性质；全等、相似三角形的判定和性质；勾股定理.【分析】由折叠和正方形的性质可知，0,90D F D C D A D F C C ==∠=∠=， ∴090DFG A ∠=∠=.又∵DG DG =，∴()ADG FDG HL ∆∆≌. 故结论①正确.∵正方形ABCD的边长为12，BE =EC ，∴6BE EC EF ===.设AG FG x ==，则6,12E G x B G x =+=-，在Rt BEG ∆中，由勾股定理，得222EG BE BG =+，即()()222662x x +=+-，解得，4x =.∴4,8AG GF BG === .∴2GB AG =. 故结论②正确.∵6BE EF ==，∴BEF ∆是等腰三角形.易知GDE ∆不是等腰三角形，∴GDE ∆和BEF ∆不相似. 故结论③错误. ∵11682422BEG S BE BG ∆=⋅⋅=⋅⋅=，∴67224105BEFBEG EF S S EG ∆∆=⋅=⋅=.故结论④正确. 综上所述，4个结论中，正确的有①②④三个.故选C. 3. 【答案】C.【考点】二次函数的图象和性质.【分析】∵()22211y x x x =-+=--+，∴二次函数图象的对称轴是直线1x =.故结论①正确.∴当1x ≥时，y 随x 的增大而减小，此时，当21>x x 时，有21<y y .故结论②错误.∵2 20y x x =-+=的解为120,2x x == ，∴二次函数x 轴的两个交点是（0，0）和（2，0） .故结论③正确.∵二次函数图象与x 轴的两个交点是（0，0）和（2，0），且有最大值1，∴当0<<2x 时，>0y .故结论④正确. 综上所述，正确结论有①③④三个.故选C. 4. 【答案】B.【考点】一元二次方程的解和解一元二次方程；确定三角形的条件.【分析】∵2是关于x 的方程2230x mx m -+=的一个根，∴4430m m -+=，解得4m =. ∴方程为28120x x -+=，解得122,6x x == .∵这个方程的两个根恰好是等腰三角形ABC 的两条边长， ∴根据三角形三边关系，只能是6，6，2.∴三角形ABC 的周长为14.故选B.5.【答案】A.【考点】命题和定理；正方形的判定；多边形内角和定理；圆周角定理；三角形中位线定理；菱形的性质；矩形的判定；三角形的内心性质.【分析】根据相关知识对各选项进行分析，判作出断： ①对角线互相垂直且相等的平行四边形才是正方形，命题不正确.②根据多边形内角和公式，得六边形的内角和等于()62180720-⨯︒=︒，命题正确.③同圆或等圆满中，相等的圆心角所对的弧才相等，命题不正确.④根据三角形中位线定理、菱形的性质和矩形的判定可知：顺次连结菱形各边中点所得的四边形是矩形，命题正确. ⑤三角形的内心到三角形三边的距离相等，命题不正确.其中正确命题的个数是2个.故选A.6. 【答案】C.【考点】二次函数的图象和性质.【分析】∵()22211y x x x =-+=--+，∴二次函数图象的对称轴是直线1x =.故结论①正确. ∴当1x ≥时，y 随x 的增大而减小，此时，当21>x x 时，有21<y y .故结论②错误.∵220y x x =-+=的解为120,2x x == ，∴二次函数图象与x 轴的两个交点是（0，0）和（2，0） .故结论③正确.∵二次函数图象与x 轴的两个交点是（0，0）和（2，0），且有最大值1，∴当0<<2x 时，>0y .故结论④正确.综上所述，正确结论有①③④三个.故选C. 7. 【答案】D ．【考点】等腰三角形的性质；切线的性质；平行的判定和性质；矩形的判定和性质；勾股定理；方程思想的应用．【分析】如答图，连接OD ，过点B 作BF OD ⊥于点F ， ∵AB BC =，∴A C ∠=∠.∵AO DO =，∴A ADO ∠=∠.∴C ADO ∠=∠.∴//OD BC .∵DE 是O e 的切线，∴DE OD ⊥.∴DE BC ⊥. ∴90CED ∠=︒，且四边形DEBF 是矩形. ∵5,4CD CE == ，∴由勾股定理，得3DE =. 设O e 的半径是x ，则(),3,244OB x BF OF x BE x x x ===-=--=- .∴由勾股定理，得222OB OF BF =+，即()22234x x =+-，解得258x =.∴O e 的半径是258.故选D ． 8. 【答案】D.【考点】探索规律题（图形变化类）.【分析】当一根棒条没有被其它棒条压着时，就可以把它往上拿走. 如图中，按照这一规则，第1次应拿走⑨号棒，第2次应拿走⑤号棒，第3次应拿走⑥号棒，第4次应拿走②号棒，第5次应拿走⑧号棒，第6次应拿走⑩号棒，故选D.9. 【答案】B.【考点】逻辑判断推理题型问题；真假命题的判定. 【分析】针对逻辑判断问题逐一分析作出判断：A.若甲对，即只参加一项的人数大于14人，等价于等于15或16或17或18或19人，则两项都参加的人数为5或4或3或2或1人，故乙不对；B.若乙对，即两项都参加的人数小于5人，等价于等于4或3或2或1人，则只参加一项的人数为等于16或17或18或19人，故甲对；C.若乙错，即两项都参加的人数大于或等于5人，则只参加一项的人数小于或等于15人，故甲可能对可能错；D.若甲粗，即只参加一项的人数\小于或等于14人，则两项都参加的人数大于或等于6人，故乙错.综上所述，四个命题中，其中真命题是“若乙对，则甲对”. 故选B.10. 【答案】C.【考点】正方形的性质；垂径定理；梯形的中位线定理；方程思想、转换思想和整体思想的应用.【分析】如答图，连接OP 、OQ ，∵DE ，FG ，»»AC BC，的中点分别是M ，N ，P ，Q ， ∴点O 、P 、M 三点共线，点O 、Q 、N 三点共线. ∵ACDE ，BCFG 是正方形， ∴AE=CD=AC ，BG=CF=BC.设AB=2r ，则,OM MP r ON NQ r =+=+ . ∵点O 、M 分别是AB 、ED 的中点， ∴OM是梯形ABDE的中位线.∴()()()1112222OM AE BD AE CD BC AC BC =+=++=+，即()122M P r A CB C +=+.同理，得()122NQ r BC AC +=+.两式相加，得()322MP NQ r AC BC ++=+.∵MP+NQ=14，AC+BC=18，∴3142182132r r +=⨯⇒=.故选C. 11. 【答案】C.【考点】真假命题的判断；二次函数的图象和性质；曲线上点的坐标与方程的关系；轴对称的应用（最短线路问题）；勾股定理.【分析】根据二次函数的图象和性质对各结论进行分析作出判断：①从图象可知当>>0x b 时，<0y ，故命题“当>0x 时，>0y ”不是真命题；②∵抛物线221y x x m =-+++的对称轴为212x =-=-，点A 和B 关于轴对称，∴若1a =-，则3b =，故命题“若1a =-，则4b =”不是真命题；③∵故抛物线上两点P （1x ，1y ）和Q （2x ，2y ）有12<1<x x ，且12>2x x +，∴211>1x x --，又∵抛物线221y x x m =-+++的对称轴为1x =，∴12>y y ，故命题“抛物线上有两点P （1x ，1y ）和Q （2x ，2y ），若12<1<x x ，且12>2x x +，则12>y y ” 是真命题；④如答图，作点E 关于x 轴的对称点M ，作点D 关于y 轴的对称点N ，连接MN ，ME 和ND 的延长线交于点P ，则MN 与x 轴和y 轴的交点G ，F 即为使四边形EDFG 周长最小的点.2∵2m =， ∴223y x x =-++的顶点D 的坐标为（1，4），点C 的坐标为（0，3）.∵点C 关于抛物线对称轴的对称点为E ，∴点E 的坐标为（2，3）.∴点M 的坐标为()2,3- ，点N 的坐标为()1,4- ，点P 的坐标为（2，4）.∴DE MN ==∴当2m =时，四边形EDFG 周长的最小值为DE MN +=故命题“点C 关于抛物线对称轴的对称点为E ，点G ，F 分别在x 轴和y 轴上，当2m =时，四边形EDFG 周长的最小值为不是真命题. 综上所述，真命题的序号是③.故选C.12. 【答案】B.【考点】一次函数与二次函数综合问题；曲线上点的坐标与方程的关系.【分析】∵一次函数()20y dx e d =+≠的图象经过点1(0)x ，，∴110dx e e dx =+⇒=-.∴()211y dx dx d x x =-=-.∴()()[]2112112()()()y y y a x x x x d x x x x a x x d =+=--+-=--+.又∵二次函数112()()(0)y ax x x x a x x =--≠≠，的图象与一次函数()20y dx e d =+≠的图象交于点1(0)x ，，函数21y y y =+的图象与x 轴仅有一个交点，∴函数21y y y =+是二次函数，且它的顶点在x 轴上，即()2211y y y a x x =+=-.∴()[]()()212121()()x x a x x d a x x a x x d a x x --+=-⇒-+=-.. 令1x x =，得()1211()a x x d a x x -+=-，即1221()0()0a xx d ax x d -+=⇒--=.故选B. 13. 【答案】B.【考点】反比例函数综合题；曲线上点的坐标与方程的关系；轴对称的性质；特殊元素法和转换思想的应用. 【分析】如答图，连接A ′C ， ∵点A 是函数1y x= (x <0)图象上一点，∴不妨取点A ()1,1-- . ∴直线AB ：y x =.∵点C 在直线AB 上，∴设点C (),x x .∵△ABC 的面积等于6，∴()1162x x ⋅⋅+=，解得123,4x x ==- （舍去）.∴点C ()3,3 .∵点A 关于y 轴的对称点为A ′，点C 关于x 轴的对称点为C ′，∴点A ′()1,1- ，点C ′()3,3- .∴由线段AC ，CC ′，C ′A ′，A ′A 所围成的图形的面积等于'''1124621022AA C CA C S S ∆∆+=⨯⨯+⨯⨯=.故选B.14. 【答案】C.【考点】正方形和等边三角形的性质；圆周角定理；锐角三角函数定义；特殊角的三角函数值；等腰直角三角形的判定和性质，特殊元素法的应用.【分析】如答图，连接AC,EC ，AC 与EF 交于点M .则根据对称性质，AC 经过圆心O ，∴AC 垂直平分EF ，01EAC FAC EAF 302∠=∠=∠=.不妨设正方形ABCD 的边长为2，则A C =∵AC 是⊙O 的直径，∴0AEC 90∠=. 在Rt ACE ∆中，A E c o=⋅=1CE AC sin EAC 2=⋅∠=在Rt MCE ∆中，∵0FEC FAC 30∠=∠=，∴1CM CE sin EAC 2=⋅∠=易知G C H ∆是等腰直角三角形，∴GF 2CM ==又∵A EF ∆是等边三角形，∴EF AE ==.∴EF GH ==故选C. 15. 【答案】B ．【考点】网格问题；勾股定理；三角形构成条件；无理数的大小比较；平移的性质；分类思想的应用. 【分析】由图示，根据勾股定理可得：a b c d =∵<,<,,<<a b c a d c b d c b a d b d +++=-+ ，∴根据三角形构成条件，只有,,a b d 三条线段首尾相接能组成三角形.如答图所示，通过平移,,a b d 其中两条线段，使得和第三条线段首尾相接组成三角形，能组成三角形的不同平移方法有6种.故选B ．16. 【答案】A.【考点】多元方程组的应用（几何问题）.【分析】如答图，设原住房平面图长方形的周长为2l ，①的长和宽分别为,a b ，②③的边长分别为,c d .根据题意，得2a c d c b d a b c l =+⎧⎪=+⎨⎪++=⎩ ①②③，-①②，得2a c c b a b c -=-⇒+=，将2a b c +=代入③，得1422c l c l =⇒=（定值），将122c l =代入2a b c +=，得()122a b l a b l+=⇒+=（定值），而由已列方程组得不到d .∴分割后不用测量就能知道周长的图形标号为①②.故选A. 17. 【答案】A ．【考点】一次函数和二次函数综合问题；曲线上点的坐标与方程的关系；数形结合思想的应用．【分析】∵y ＝ax 2＋(b －1)x ＋c ＝ax 2＋bx ＋c －x ，∴函数y ＝ax 2＋(b －1)x ＋c 的图象上点的纵坐标是二次函数y 2＝ax 2＋bx ＋c 图象上点的纵坐标与一次函数y 1＝x 图象上点的纵坐标之差．∵一次函数y 1＝x 与二次函数y 2＝ax 2＋bx ＋c 图象相交于P 、Q 两点，而P 、Q 两点都在第一象限，∴函数y ＝ax 2＋(b －1)x ＋c 的图象与x 轴相交于两点，且这两点都在x 轴的正方向．故选A ． 18. 【答案】C【考点】单动点问题；函数图象的识别；垂线段最短的性质；排他法的应用.【分析】从图2可知，寻宝者与定位仪器之间的距离开始和结束时是相同的，因此，可排除A 、D 选项；从图2可知，寻宝者与定位仪器之间的距离的最近点，相对于开始和结束时位置离中点更近，因此，如答图，过点M分别作,,,OB OC AB AC 的垂线，垂足分别为点,,,E F P Q ，此时，根据垂线段最短的性质，点,,,E F P Q 是寻宝者与定位仪器之间的距离的最近点. 显然，,OE OF BE CF AP =<==，即点,E F离中点的距离小于开始和结束时的距离；点,P Q离中点的距离大于开始和结束时的距离.∴寻宝者的行进路线可能为B→O→C. 故选C.19.【答案】B.【考点】菱形的判定；垂径定理；平行四边形的判定.【分析】要判定四边形OACB为菱形，根据菱形的判定可知，一组邻边相等的平行四边形是菱形，由于OA OB=，且半径OC⊥AB，根据垂径定理有AD BD=，从而根据对角线互相平分的四边形是平行四边形的判定，只要另一条对角线也平分即可，从而只要添加条件OD CD=即可. 因此，这个条件可以是OD CD=.故选B.20.【答案】D．【考点】反比例函数综合题；曲线上点的坐标与方程的关系；菱形的性质；勾股定理.【分析】∵A，B两点的纵坐标分别为3，1，反比例函数3 yx =的图像经过A，B两点，∴A（1，3），B（3，1）.∴AB=∵四边形ABCD是菱形，∴AD AB==AD 与BC的距离为2.∴菱形ABCD的面积为2=故选D．21.【答案】D．【考点】反比例函数综合题；曲线上点的坐标与方程的关系；菱形的性质；锐角三角函数定义；特殊角的三角函数值.【分析】如答图，AC交y轴于点H，则CH⊥y轴.∵∠BOC=60°，∴∠COH=30°，∵点C的坐标为(m,)，∴,CH m OH==∴6cosOHOCCOH===∠.∵四边形ABOC是菱形，∴6OB OC==，∠BOD=30°.∵BD⊥x轴，∴6BD OB tan BOD=⋅∠==∴点D的坐标为(6,-.∵点D在反比例函数kyx=的图像上，∴()6-⋅=-故选D．22.【答案】B．【考点】解直角三角形的应用（方向角问题）；矩形的判定和性质；等腰直角三角形的判定和性质.【分析】如答图，过点B作BE⊥AC交AC于点E，过点E作EF⊥CD交CD于点F，则根据题意，四边形BDEF是矩形，△ABE、△EFC和△ADC都是等腰直角三角形，∵AB=2，∴DF=BF= AB=2，AE=∵∠EBC=∠BCE=22.5°，∴CE=BE=2.∴CF==∴2CD DF CF=+=km）.∴船C离海岸线l的距离为(2+km.故选B．23.【答案】B．【考点】翻折变换（折叠问题）；折叠的性质；等腰直角三角形的判定和性质；勾股定理．【分析】根据折叠的性质可知34CD AC B C BC ACE DCE BCF B CF CE A=='==∠=∠∠=∠'⊥，，，，，∴431B D DCE B CF ACE BCF '=-=∠+∠'=∠+∠，.∵90ACB ∠=︒，∴45ECF ∠=︒. ∴ECF V 是等腰直角三角形. ∴45EF CE EFC =∠=︒，.∴135BFC B FC ∠=∠'=︒. ∴90B FD ∠'=︒. ∵1122ABC S AC BC AB CE =⋅⋅=⋅⋅V ，∴AC BC AB CE ⋅=⋅.在Rt ABC V 中，根据勾股定理，得A B=5，∴123455CE CE ⋅=⋅⇒=.∴125EF CE ==. 在Rt AECV 中，根据勾股定理，得95AE ==，∴95ED AE ==.∴35DF EF ED =-=.在Rt B FD 'V 中，根据勾股定理，得45B F '==.故选B ．24. 【答案】D.【考点】正比例函数、一次函数、反比例函数、二次函数的图象和性质.【分析】∵函数图像经过()()1422-- ，，，两点，∴该函数不可能是正比例函数.∵若一次函数的图像经过()()1422-- ，，，两点，则函数值y 随x 的增大而增大， ∴该函数不可能是一次函数.∵若反比例函数的图像经过()()1422-- ，，，两点，则函<0和>0x 两个范围内，函数值y 随x的增大而增大，∴该函数不可能是反比例函数.∵若二次函数的图像经过()()1422-- ，，，两点，则当图像开口向下，对称轴在2x =右侧时，在对称轴右侧，函数值y 随x 的增大而减小；当图像开口向上，对称轴在1x =左侧时，在对称轴左侧，函数值y 随x 的增大而减小.2∴该函数可能是二次函数.故选D. 25. 【答案】C ．【考点】一次函数、二次函数图象与系数的关系. 【分析】根据一次函数、二次函数图象与系数的关系对各选项逐一分析，作出判断：A 、对于直线y bx a =+来说，由图象可以判断，00a b ＞，＞；而当00a b ＞，＞时，对于抛物线2y ax bx=+来说，对称轴02bx a=-＜，应在y 轴的左侧，故不合题意，图形错误．B 、对于直线y bx a =+来说，由图象可以判断，00a b ＜，＜；而当0a ＜时，对于抛物线2y ax bx =+来说，图象应开口向下，故不合题意，图形错误．C 、对于直线y bx a =+来说，由图象可以判断，00a b ＜，＞；而当00a b ＜，＞时，对于抛物线2y ax bx=+来说，图象开口向下，对称轴>02bx a=-位于y 轴的右侧，故符合题意.D 、对于直线y bx a =+来说，由图象可以判断，00a b ＞，＞；而当0a ＞时，对于抛物线2y ax bx =+来说，图象开口向下，故不合题意，图形错误．故选C ．26. 【答案】C.【考点】线段中垂线的性质；切线的性质；垂径定理. 【分析】根据线段中垂线的性质、切线的性质和垂径定理，该圆的圆心是线段AE 的中垂线与线段BC 的中垂线的交点. 故选C. 27. 【答案】D.【考点】代数式化简；一次函数的图象；分类思想的应用.【分析】∵()()22>022<0x x x x y x x x ⎧++⎪==⎨--⎪⎩，∴当>0x 时，函数的图象为直线2y x =+的一部分；当<0x 时，函数的图象为直线2y x =--的一部分.符合此条件的是图象D.故选D.。

2016年中考数学试题(含答案)

XX ★启用前 [考试时间：6月13日上午9:00～11:00]2016年高中阶段教育学校招生统一考试数学本试题卷分第一部分（选择题）和第二部分（非选择题）．第一部分1至2页，第二部分3至6页，共6页．考生作答时，须将答案答在答题卡上，在本试题卷、草稿纸上答题无效．满分120分．考试时间120分钟．考试结束后，将本试题卷和答题卡一并交回．第一部分（选择题共30分）注意事项：1．选择题必须使用2B 铅笔将答案标号填涂在答题卡上对应题目标号的位置上． 2．本部分共10小题，每小题3分，共30分．一、选择题：本大题共10个小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．下列各数中，不是负数的是（）A ．2-B ． 3C ．58-D ．0.10- 2. 计算()32ab的结果，正确的是（）A ．36a b B ．35a b C ．6ab D ．5ab3.下列图形中，既是轴对称图形又是中心对称图形的是（）A ．B ．C ．D ．4.下列说法中正确的是()A ．“打开电视，正在播放《新闻联播》”是必然事件B ．“20x <（x 是实数）”是随机事件C ．掷一枚质地均匀的硬币10次，可能有5次正面向上D ．为了了解夏季冷饮市场上冰淇淋的质量情况，宜采用普查方式调查5.化简22m n m n n m+--的结果是（） A ．m n +B ．n m -C ．m n -D ．m n -- 6.下列关于矩形的说法中正确的是（）A ．对角线相等的四边形是矩形B ．矩形的对角线相等且互相平分C ．对角线互相平分的四边形是矩形D ．矩形的对角线互相垂直且平分2图7.若2x =-是关于x 的一元二次方程22302x ax a +-=的一个根，则a 的值为（） A ．1-或4 B ．1-或4- C ．1或4- D ．1或48.如图1，点(0,3)D ，(0,0)O ，(4,0)C 在A 上，BD 是A 的一条弦，则sin OBD ∠=（）A ．12B ．34C ．45D ．359．如图2，二次函数2(0)y ax bx c a =++>图象的顶点为D ，其图象与x 轴的交点A 、B 的横坐标分别为1-和3，则下列结论正确的是（）A . 20a b -=B . 0a b c ++>C . 30a c -=D . 当12a =时，ABD ∆是等腰直角三角形10.如图3，正方形纸片ABCD 中，对角线AC 、BD 交于点O ，折叠正方形纸片ABCD ，使AD 落在BD 上，点A 恰好与BD 上的点F 重合，展开后折痕DE 分别交AB 、AC 于点E 、G ，连结GF ．给出下列结论：①22.5ADG ∠=；②tan 2AED ∠=；③AGD OGD S S ∆∆=；④四边形AEFG 是菱形；⑤2BE OG =；⑥若1OGF S ∆=，则正方形ABCD 的面积是642+．其中正确的结论个数为（）A ．2B ．3C ．4D ．5第二部分（非选择题共90分）注意事项：1．必须使用0.5毫米的黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答．作图题可先用铅笔绘出，确认后再用0.5毫米的黑色墨迹签字笔描清楚．答在试题卷上无效．2．本部分共14小题，共90分．二、填空题：本大题共6小题，每小题4分，共24分．11.月球的半径约为1 738 000米，1 738 000这个数用科学记数法表示为．3图BCxy DOA1图12.对部分参加夏令营的中学生的年龄（单位：岁）进行统计，结果如表：年龄 13 14 15 16 17 18 人数 4 5 6 6 7 2则这些学生年龄的众数是．13.如果一个正多边形的每个外角都是30，那么这个多边形的内角和为． 14.设12x x 、是方程25320x x --=的两个实数根，则1211x x +的值为． 15.已知关于x 的分式方程111k x k x x ++=+-的解为负数，则k 的取值范围是． 16. 如图4，ABC ∆中，90C ∠=，3AC =，5AB =，D 为BC 边的中点，以AD 上一点O 为圆心的O和AB 、BC 均相切，则O 的半径为．三、解答题：本大题共8小题，共66分．解答应写出文字说明、证明过程或演算步骤． 17.（本小题满分60201621+18.（本小题满分6分）如图5，在平面直角坐标系中，直角ABC ∆的三个顶点分别是(3,1)A -，(0,3)B ，(0,1)C .（1）将ABC ∆以点C 为旋转中心旋转180（2）分别连结1AB 、1BA 后，求四边形11AB A B5图AO4图19.（本小题满分6分）中秋佳节我国有赏月和吃月饼的传统，某校数学兴趣小组为了了解本校学生喜爱月饼的情况，随机抽取了60名同学进行问卷调查，经过统计后绘制了两幅尚不完整的统计图（图6）.(注：参与问卷调查的每一位同学在任何一种分类统计中只有一种选择)请根据统计图完成下列问题: （1）在扇形统计图中，“很喜欢”的部分所对应的扇形圆心角为度；在条形统计图中，喜欢“豆沙”月饼的学生有人；（2）若该校共有学生900人，请根据上述调查结果，估计该校学生中“很喜欢”和“比较喜欢”月饼的共有人；（3）甲同学最爱吃云腿月饼，乙同学最爱吃豆沙月饼.现有重量、包装完全一样的云腿、豆沙、莲蓉、蛋黄四种月饼各一个，让甲、乙每人各选一个，请用画树状图法或列表法求出甲、乙两人中有且只有一人选中自己最爱吃的月饼的概率.20.（本小题满分8分）如图7，在平面直角坐标系中，O 为坐标原点，ABO ∆的边AB 垂直于x 轴，垂足为点B ，反比例函数(0)ky x x =>的图象经过AO 的中点C ，且与AB 相交于点D ,4OB =,3AD =.（1）求反比例函数ky x=的解析式；（2）求cos OAB ∠的值；（3）求经过C 、D 两点的一次函数解析式.喜爱月饼情况扇形统计图很喜欢不喜欢25%40%比较喜欢“很喜欢”月饼的同学最爱吃的月饼品种条形统计图6图21.（本小题满分8分）某市为了鼓励居民节约用水，决定实行两级收费制度.若每月用水量不超过14吨（含14吨），则每吨按政府补贴优惠价m 元收费；若每月用水量超过14吨，则超过部分每吨按市场价n 元收费.小明家3月份用水20吨，交水费49元；4月份用水18吨，交水费42元.（1）求每吨水的政府补贴优惠价和市场价分别是多少？（2）设每月用水量为x 吨，应交水费为y 元，请写出y 与x 之间的函数关系式；（3）小明家5月份用水26吨，则他家应交水费多少元？22.（本小题满分8分）如图8，在矩形ABCD 中，点F 在边BC 上，且AF AD =，过点D 作DE AF ⊥，垂足为点E . （1）求证：DE AB =；（2）以A 为圆心，AB 长为半径作圆弧交AF 于点G . 若1BF FC ==，求扇形ABG 的面积.（结果保留π）23.（本小题满分12分）如图9，在AOB ∆中，AOB ∠为直角，6OA =，8OB =.半径为2的动圆圆心Q 从点O 出发，沿着OA 方向以1个单位长度/秒的速度匀速运动，同时动点P 从点A 出发，沿着AB 方向也以1个单位长度/秒的速度匀速运动，设运动时间为t 秒(05)t <≤.以P 为圆心，PA 长为半径的P 与AB 、OA 的另一个交点分别为C 、D ，连结CD 、QC .（1）当t 为何值时，点Q 与点D 重合？（2）当Q 经过点A 时，求P 被OB 截得的弦长；（3）若P 与线段QC 只有一个公共点，求t 的取值范围.QP9图A D 8图24.（本小题满分12分）如图10，抛物线2y x bx c =++与x 轴交于A 、B 两点，B 点坐标为(3,0)，与y 轴交于点(0,3)C -．（1）求抛物线的解析式；（2）点P 在抛物线位于第四象限的部分上运动，当四边形ABPC 的面积最大时，求点P 的坐标和四边形ABPC 的最大面积；（3）直线l 经过A 、C 两点，点Q 在抛物线位于y 轴左侧的部分上运动，直线m 经过点B 和点Q ．是否存在直线m ，使得直线l 、m 与x 轴围成的三角形和直线l 、m 与y 轴围成的三角形相似？若存在，求出直线m 的解析式；若不存在，请说明理由．2016年高中阶段教育学校招生统一考试数学参考答案与评分意见一、选择题（每题3分，共30分）1、B2、A3、D4、C5、A6、B7、C8、D9、D 10、B 二、填空题（每小题4分，共24分） 11、61.73810⨯；12、17；13、1800； 14、32-；15、102k k >-≠且；16、67三、解答题（本大题共8个小题，共66分）以下各题只提供参考解法，使用其它方法求解，按步骤相应给分．17、（6分）解：原式21(21=+--+…………………………3分（注：分项给分）42=-+5分10图2=+6分18、（6分）解：（1 (3)分（2）111111641222AB A B S AA BB =⋅⋅=⨯⨯=四．…………………………6分19、（6分）解：（1）126 ，4．…………………………………………2分（2）675…………………………………………3分（3）甲云腿莲蓉豆沙蛋黄乙莲蓉豆沙蛋黄云腿豆沙黄云腿莲蓉蛋黄云腿莲蓉豆沙…………………5分41123P ==.………………………6分 20、（8分）解：（1）设(4,)D a ，3AB a =+过点C 作CE x ⊥轴，垂足为E ，∵C 是AO 的中点， ∴CE 是AOB ∆的中位线,……………1分∴点3(2,)2aC +， ……………2由点C 和点D 都在反比例函数图象上得：3242aa +⨯=解得：1a =，点(4,1)D ……………3分反比例函数：4y x=……………4分（2）由4OB AB ==得，∴45OAB ∠=, cos 2OAB ∠=……………5分（3）设直线CD 的函数关系式：11(0)y k x b k =+≠∵(2,2)C ,(4,1)D 在直线上，得112214k bk b=+⎧⎨=+⎩………………………6分解得：1123k b ⎧=-⎪⎨⎪=⎩………………………7分直线CD 的函数关系式：132y x =-+………………………8分21、（8分）解：（1）由题意得：14(2014)4914(1814)42m n m n +-=⎧⎨+-=⎩………………………2分解得：23.5m n =⎧⎨=⎩………………………4分（2）当014x <≤时，2y x =；当14x >时，28(14) 3.5 3.521y x x =+-⨯=-所以2,0143.521,14x x y x x <≤⎧=⎨->⎩……………………7分（3）当26x =时， 3.5262170y =⨯-=（元） ……………………8分22、（8分）（1）证明：∵DE AF ⊥，∴90AED ∠=，又∵四边形ABCD 是矩形， ∴90ABF ∠=， ∴90ABF AED ∠=∠=，……………………1分又∵//AD BC∴DAE AFB ∠=∠，……………………2分又∵AF AD =，∴ADE ∆≌()FAB AAS ∆，……………………3分∴DE AB =……………………4分（2）∵1BF FC ==，∴2AD BC BF FC ==+=，又∵ADE ∆≌FAB ∆，∴2AF AD ==，……………………5分 ∴在Rt ABF ∆中，12BF AF =，∴30BAF ∠=，……………………6分又∵AB== ……………………7分∴扇形ABG 的面积230313603604n r πππ⨯===……………………8分A8图23、（12分）解：（1）在直角ABO ∆中，6AO =,8BO =,∴10AB =63cos 105AO BAO AB ∠===……………………1分 ∵AC P 是的直径， ∴90CDA ∠=在直角ACD ∆中，3cos 5AD CAD AC ∠== ∵OQ AP t ==，2AC t =， ∴65AD t =……………………2分∵点Q 与点D 重合，∴6OQ AD OA +==665t t +=，解得：3011t =当3011t =时，点Q 与点D 重合.……………………3分（2）∵Q 经过点A ，Q 的半径是2∴2AQ =,624OQ =-=,4t =∴4AP =,1046BP =-=……………………4分设P 被OB 截得的弦为线段EF ,过点P 作PM EF M ⊥于点,//PM OA ,BPM ∆∽BAO ∆,BP PMBA OA=∴6106PM =,185PM =……………………5分连结PE ,4PE =在直角PEM ∆中，EM ===……………………6分∴2EF EM ==7分（3）当QC P 与相切时，AC QC ⊥在直角ACQ ∆中，3cos 5CAQ ∠=2AC t =，51033AQ AC t ==， ……………………8分 ∵6AQ OA OQ t =-=-∴1063t t =-，得：1813t =……………………9分 ∴当18013t <≤时，P 与线段QC 只有一个公共点 (10)分又∵当3011t =时，点Q 与点D 重合，P 与线段QC 有两个公共点 ∴当30511t <≤时，P 与线段QC 只有一个公共点 ……………………11分综上，当18013t <≤或30511t <≤时，P 与线段QC 只有一个公共点 ……………………12分24、（12分）解：（1）∵抛物线2y x bx c =++与x 轴交于B 点(3,0)，与y 轴交于(0,3)C -． ∴9303b c c ++=⎧⎨=-⎩，∴2b =-……………………1分∴抛物线的解析式：223y x x =--……………………2分（2）抛物线223y x x =--与x 轴的交点(1,0)A -，4AB = 连结BC ,ABC BCP ABPC S S S ∆∆=+四, 1143622ABC S AB OC ∆=⋅=⨯⨯= 当BCP S ∆最大时，四边形ABPC 的面积最大求出直线BC 的函数关系式：3y x =-……………………3分平移直线BC ，当平移后直线与抛物线223y x x =--相切时，BC 边上的高最大，BCP S ∆最大.设平移后直线关系式为：3y x m =--联立2323y x m y x x =--⎧⎨=--⎩， 2233x x x m --=-- 当0∆=时，94m =∴平移后直线关系式为：214y x =-……………………4分 221423y x y x x ⎧=-⎪⎨⎪=--⎩ ，解得：32154x y ⎧=⎪⎪⎨⎪=-⎪⎩ ∴点315(,)24P -……………………5分过点P 向x 轴作垂线，与线段BC 交于点D 点33(,)22D -，3159()244PD =---= ∴BCP S ∆最大值91273428=⨯⨯=， ∴四边形ABPC 的最大面积2775688=+=……………………6分（3）存在，设直线m 与y 轴交于点N ，与直线l 交于点M ，设点N 的坐标为(0,)t ① 当l m ⊥时， 90NOB NMC ∠=∠=∴90MCN MNC ∠+∠=, 90ONB OBN ∠+∠=又∵ONB MNC ∠=∠∴MCN OBN ∠=∠∵90AMB NMC ∠=∠=∴AMB ∆∽NMC ∆求出直线l 的函数关系式：33l y x =--∵l m ⊥，设直线m 的函数关系式：13m y x b =+ ∵直线m 经过点(3,0)B∴直线m 的函数关系式：113m y x =-，此时1t =-……………………7分 ② 当31t -<<-时，90,90AMB CMB ∠<∠>AMB ∆是一个锐角三角形，CMN ∆却是一个钝角三角形∴AMB ∆与CMN ∆不相似∴符合条件的直线m 不存在 ……………………8分③ 当10t -<<时，90,90AMB CMB ∠>∠< AMB ∆是一个钝角三角形，CMN ∆却是一个锐角三角形∴AMB ∆与CMN ∆不相似∴符合条件的直线m 不存在 ……………………9分④当01t <<时，1ON < ∴OA ON OC OB>, MCN MBA ∠>∠ 又∵CMN BMA ∠=∠（公共角）∴AMB ∆与CMN ∆不相似∴符合条件的直线m 不存在 (10)分⑤当1t =时，1ON = ∴13OAONOC OB ==， MCN MBA ∠=∠又∵CMN BMA ∠=∠（公共角）∴AMB ∆∽NMC ∆∵直线m 经过点(3,0)B 和(0,1)N∴直线m 的函数关系式：113m y x =-+……………………11分⑥当1t >时，1ON > ∴OA ONOC OB <, MCN MBA ∠<∠又∵CMN BMA ∠=∠（公共角）∴AMB ∆与CMN ∆不相似∴符合条件的直线m 不存在 ……………………12分综上，直线m 的函数关系式为：113m y x =-+或113m y x =-。

中考数学几何压轴题及答案及答案

中考数学几何压轴题及答案一、解答题（共30小题）1.观察猜想（1）如图①，在Rt△ABC中，∠BAC＝90°，AB＝AC＝3，点D与点A重合，点E在边BC上，连接DE，将线段DE绕点D顺时针旋转90°得到线段DF，连接BF，BE与BF的位置关系是，BE+BF＝；探究证明（2）在（1）中，如果将点D沿AB方向移动，使AD＝1，其余条件不变，如图②，判断BE与BF的位置关系，并求BE+BF的值，请写出你的理由或计算过程；拓展延伸（3）如图③，在△ABC中，AB＝AC，∠BAC＝α，点D在边BA的延长线上，BD＝n，连接DE，将线段DE绕着点D顺时针旋转，旋转角∠EDF＝α，连接BF，则BE+BF的值是多少？请用含有n，α的式子直接写出结论2.在△ABC的边BC上取B′、C′两点，使∠AB′B＝∠AC′C＝∠BAC（1）如图1中∠BAC为直角，∠BAC＝∠AB′B＝∠AC′C＝90°（点B′与点C′重合），则△ABC∽△B'BA∽△C'AC，，，进而可得AB2+AC2＝；（2）如图2中当∠BAC为锐角，图3中∠BAC为钝角时（1）中的结论还成立吗？若不成立，则AB2+AC2等于什么（用含用BC和B′C′的式子表示）？并说明理由（3）若在△ABC中，AB＝5，AC＝6，BC＝9，请你先判断出△ABC的类型，再求出B′C′的长3．（1）问题发现如图1，在Rt△ABC和Rt△CDE中，∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝45°，点D是线段AB上一动点，连接BE填空：①的值为；②∠DBE的度数为．（2）类比探究如图2，在Rt△ABC和Rt△CDE中，∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝60°，点D是线段AB上一动点，连接BE．请判断的值及∠DBE的度数，并说明理由；（3）拓展延伸如图3，在（2）的条件下，将点D改为直线AB上一动点，其余条件不变，取线段DE 的中点M，连接BM、CM，若AC＝2，则当△CBM是直角三角形时，线段BE的长是多少？请直接写出答案．4.（1）问题发现：如图①，在△ABC中，∠BAC＝90°，AB＝AC，点D是BC的中点，以点D为顶点作正方形DFGE，使点A、C分别在DE和DF上，连接BE、AF．则线段BE 和AF数量关系．（2）类比探究：如图②，保持△ABC固定不动，将正方形DFGE绕点D旋转α（0°＜α≤360°），则（1）中的结论是否成立？如果成立，请证明；如果不成立，请说明理由．（3）解决问题：若BC＝DF＝2，在（2）的旋转过程中，连接AE，请直接写出AE的最大值．5.如图，在平行四边形ABCD中，AC与BD交于点O，以点O为顶点的∠EOF的两边分别与边AB、AD交于点E、F，且∠EOF与∠BAD互补．（1）若四边形ABCD是正方形，则线段OE与OF有何数量关系？请直接写出结论；（2）若四边形ABCD是菱形，那么（1）中的结论是否成立？若成立，请画出图形并给出证明；若不成立，请说明理由；（3）若AB：AD＝m：n，探索线段OE与OF的数量关系，并证明你的结论.6.如图（1），已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F.（1）证明与推断：①求证：四边形CEGF是正方形；②推断：的值为：（2）探究与证明：将正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图（2）所示，试探究线段AG与BE之间的数量关系，并说明理由；（3）拓展与运用：正方形CEGF在旋转过程中，当B，E，F三点在一条直线上时，如图（3）所示，延长CG交AD于点H．若AG＝6，GH＝2，则BC＝．7.如图1，在△ABC中，AB＝AC＝2，∠BAC＝120°，点D、E分别是AC、BC的中点，连接DE.定理：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．探索发现：图1中，的值为；的值为．（2）拓展探完若将△CDE绕点C逆时针方向旋转一周，在旋转过程中的大小有无变化？请仅就图2的情形给出证明．（3）问题解决当△CDE旋转至A，D，E三点共线时，直接写出线段BE的长．8.已知△ABC是边长为4的等边三角形，边AB在射线OM上，且OA＝6，点D是射线OM上的动点，当点D不与点A重合时，将△ACD绕点C逆时针方向旋转60°得到△BCE，连接DE，设OD＝m．（1）问题发现如图1，△CDE的形状是三角形．（2）探究证明如图2，当6＜m＜10时，△BDE的周长是否存在最小值？若存在，求出△BDE周长的最小值；若不存在，请说明理由．（3）解决问题是否存在m的值，使△DEB是直角三角形？若存在，请直接写出m的值；若不存在，请说明理由．9.等腰直角三角形ABC和等腰直角三角形ADE中，∠BAC＝∠DAE＝90°，AB＝4，AE＝2，其中△ABC固定，△ADE绕点A作360°旋转，点F、M、N分别为线段BE、BC、CD 的中点，连接MN、NF．问题提出：（1）如图1，当AD在线段AC上时，则∠MNF的度数为，线段MN 和线段NF的数量关系为；深入讨论：（2）如图2，当AD不在线段AC上时，请求出∠MNF的度数及线段MN和线段NF的数量关系；拓展延伸：（3）如图3，△ADE持续旋转过程中，若CE与BD交点为P，则△BCP面积的最小值为．10．四边形是我们在学习和生活中常见的图形，而对角线互相垂直的四边形也比较常见，比如筝形、菱形、图1中的四边形ABCD等．它们给我们的学习和生活带来了很多的乐趣和美感．（1）如图2，在四边形ABCD中，AB＝AD，CB＝CD，则AC与BD的位置关系是，请说明理由．（2）试探究图1中四边形ABCD的两组对边AB，CD与BC，AD之间的数量关系，请写出证明过程．（3）问题解决：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE，连接CE，BG，GE，已知AC＝4，AB＝5，求GE的长．11．问题发现：如图（1）在Rt△ABC和Rt△BDE中，∠A＝∠DEB＝30°，BC＝BE＝6，Rt△BDE绕点B逆时针旋转，H为CD的中点，当点C与点E重合时，BH与AE的位置关系为，BH与AE的数量关系为；问题证明：在Rt△BDE绕点B旋转的过程中，（1）中的结论是否仍然成立？若成立，请就图（2）的情形给出证明若不成立，请说明理由；拓展应用：在Rt△BDE绕点B旋转的过程中，当DE∥BC时，请直接写出BH2的长．12．如图1，菱形ABCD与菱形GECF的顶点C重合，点G在对角线AC上，且∠BCD＝∠ECF＝60°，（1）问题发现的值为；（2）探究与证明将菱形GECF绕点C按顺时针方向旋转α角（0°＜α＜60°），如图2所示，试探究线段AG与BE之间的数量关系，并说明理由；（3）拓展与运用：菱形GECF在旋转过程中，当点A，G，F三点在一条直线上时，如图3所示连接CG并延长，交AD于点H，若CE＝2，GH＝，则AH的长为．13．如图，在Rt△ABC中，∠ACB＝90°，＝，CD⊥AB于点D，点E是直线AC上一动点，连接DE，过点D作FD⊥ED，交直线BC于点F．（1）探究发现：如图1，若m＝n，点E在线段AC上，则＝；（2）数学思考：①如图2，若点E在线段AC上，则＝（用含m，n的代数式表示）；②当点E在直线AC上运动时，①中的结论是否仍然成立？请仅就图3的情形给出证明；（3）拓展应用：若AC＝，BC＝2，DF＝4，请直接写出CE的长．14．如图，已知点E是射线BC上的一点，以BC、CE为边作正方形ABCD和正方形CEFG，连接AF，取AF的中点M，连接DM、MG（1）如图1，判断线段DM和GM的数量关系是，位置关系是；（2）如图2，在图中的正方形CEFG绕点C逆时针旋转的过程中，其他条件不变，（1）中的结论是否成立？说明理由；（3）已知BC＝10，CE＝2，正方形CEFG绕点C旋转的过程中，当A、F、E共线时，直接写出△DMG的面积．15.在Rt△ABC中，∠ACB＝90°，AB＝，AC＝2，过点B作直线m∥AC，将△ABC绕点C顺时针旋转得到△A′B′C（点A，B的对应点分别为A'，B′），射线CA′，CB′分别交直线m于点P，Q．（1）如图1，当P与A′重合时，求∠ACA′的度数；（2）如图2，设A′B′与BC的交点为M，当M为A′B′的中点时，求线段PQ的长；（3）在旋转过程中，当点P，Q分别在CA′，CB′的延长线上时，试探究四边形P A'B′Q的面积是否存在最小值．若存在，求出四边形P A′B′Q的最小面积；若不存在，请说明理由．16.如图（1），在等边三角形ABC中，点D，E分别在边AB，AC上，AD＝AE，连接BE，CD，点M，N，P分别是BE，CD，BC的中点，连接DE，PM，PN，MN．（1）观察猜想，图（1）中△PMN是（填特殊三角形的名称）（2）探究证明，如图（2），△ADE绕点A按逆时针方向旋转，则△PMN的形状是否发生改变？并就图（2）说明理由．（3）拓展延伸，若△ADE绕点A在平面内自由旋转，AD＝2，AB＝6，请直接写出△PMN 的周长的最大值．17.已知△ABC，AB＝AC，D为直线BC上一点，E为直线AC上一点，AD＝AE，设∠BAD＝α，∠CDE＝β，（1）如图1，若点D在线段BC上，点E在线段AC上．∠ABC＝60°，∠ADE＝70°，则α＝°；β＝°.（2）如图2，若点D在线段BC上，点E在线段AC上，则α，β之间有什么关系式？说明理由．（3）是否存在不同于（2）中的α，β之间的关系式？若存在，请写出这个关系式（写出一种即可），说明理由；若不存在，请说明理由.18.问题提出：（1）如图1，在四边形ABCD中，连接AC、BD，AB＝AD，∠BAD＝∠BCD＝90°，将△ABC绕点A逆时针旋转90°，得到△ADE，点B的对应点落在点D，点C的对应点为点E，可知点C、D、E在一条直线上，则△ACE为三角形，BC、CD、AC的数量关系为；探究发现：（2）如图2，在⊙O中，AB为直径，点C为的中点，点D为圆上一个点，连接AD、CD、AC、BC、BD，且AD＜BD，请求出CD、AD、BD间的数量关系.拓展延伸：（3）如图3，在等腰直角三角形ABC中，点P为AB的中点，若AC＝13，平面内存在一点E，且AE＝10，CE＝13，当点Q为AE中点时，PQ＝.19.已知△ABC中，CA＝CB，0°＜∠ACB≤90°，点M、N分别在边CA，CB上（不与端点重合），BN＝AM，射线AG∥BC交BM延长线于点D，点E在直线AN上，EA＝ED．（1）【观察猜想】如图1，点E在射线NA上，当∠ACB＝45°时，①线段BM与AN的数量关系是；②∠BDE的度数是；（2）【探究证明】如图2点E在射线AN上，当∠ACB＝30°时，判断并证明线段BM与AN的数量关系，求∠BDE的度数；（3）【拓展延伸】如图3，点E在直线AN上，当∠ACB＝60°时，AB＝3，点N是BC 边上的三等分点，直线ED与直线BC交于点F，请直接写出线段CF的长．20.如图①，在正方形ABCD和正方形AB'C'D'中，AB＝2，AB'＝，连接CC’（1）问题发现：．（2）拓展探究：将正方形AB'C'D'绕点A逆时针旋转，记旋转角为θ，连接BB'，试判断：当0°≤θ＜360°时，的值有无变化？请仅就图②中的情形给出你的证明；（3）问题解决：请直接写出在旋转过程中，当C，C′，D'三点共线时BB′的长．21.如图1，在正方形ABCD中，点O是对角线BD的中点．（1）观察猜想将图1中的△BCD绕点O逆时针旋转至图2中△ECF的位置，连接AC，DE，则线段AC与DE的数量关系是，直线AC与DE的位置关系是．（2）类比探究将图2中的△ECF绕点O逆时针旋转至图3的位置，（1）中的结论是否成立？并说明理由．（3）拓展延伸将图2中的△ECF在平面内旋转，设直线AC与DE的交点为M，若AB＝4，请直接写出BM的最大值与最小值．22.如图1，点B在直线l上，过点B构建等腰直角三角形ABC，使∠BAC＝90°，且AB＝AC，过点C作CD⊥直线l于点D，连接AD．（1）小亮在研究这个图形时发现，∠BAC＝∠BDC＝90°，点A，D应该在以BC为直径的圆上，则∠ADB的度数为°，将射线AD顺时针旋转90°交直线l于点E，可求出线段AD，BD，CD的数量关系为；（2）小亮将等腰直角三角形ABC绕点B在平面内旋转，当旋转到图2位置时，线段AD，BD，CD的数量关系是否变化，请说明理由；（3）在旋转过程中，若CD长为1，当△ABD面积取得最大值时，请直接写AD的长．23．如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合，三角板的一边交CD于点F．另一边交CB的延长线于点G．（1）观察猜想：线段EF与线段EG的数量关系是；（2）探究证明：如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变，（1）中的结论是否仍然成立？若成立，请给予证明：若不成立．请说明理由：（3）拓展延伸：如图3，将（2）中的“正方形ABCD”改为“矩形ABCD”，且使三角板的一边经过点B，其他条件不变，若AB＝a、BC＝b，求的值．24．如图1，在Rt△ABC中，∠B＝90°，AB＝2，BC＝1，点D，E分别是边BC，AC的中点，连接DE．将△EDC绕点C按顺时针方向旋转，记旋转角为α．（1）问题发现①当α＝0°时，＝；②当α＝180°时，＝．（2）拓展探究试判断：当0°≤α＜360°时，的大小有无变化？请仅就图2的情况给出证明．（3）问题解决当△EDC旋转至A、B、E三点共线时，直接写出线段BD的长．25.在△ABC中，AD为BC边上的中线，E为AD上一动点，设DE＝nEA，连接CE并延长，交AB于点F．（1）尝试探究如图（1），当∠BAC＝90°，∠B＝30°，DE＝EA时，BF，BA之间的数量关系是；（2）类比延伸如图（2），当△ABC为锐角三角形，DE＝EA时，（1）中的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由；（3）拓展迁移如图（3），当△ABC为锐角三角形，DE＝nEA时，请直接写出BF，BA之间的数量关系．26.古希腊数学家毕达哥拉斯认为：“一切平面图形中最美的是圆”．请研究如下美丽的圆．如图，线段AB是⊙O的直径，延长AB至点C，使BC＝OB，点E是线段OB的中点，DE ⊥AB交⊙O于点D，点P是⊙O上一动点（不与点A，B重合），连接CD，PE，PC．（1）求证：CD是⊙O的切线；（2）小明在研究的过程中发现是一个确定的值．回答这个确定的值是多少？并对小明发现的结论加以证明．27．定义：三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角．（1）如图1，∠E是△ABC中∠A的遥望角，若∠A＝α，请用含α的代数式表示∠E．（2）如图2，四边形ABCD内接于⊙O，＝，四边形ABCD的外角平分线DF交⊙O 于点F，连结BF并延长交CD的延长线于点E．求证：∠BEC是△ABC中∠BAC的遥望角．（3）如图3，在（2）的条件下，连结AE，AF，若AC是⊙O的直径．①求∠AED的度数；②若AB＝8，CD＝5，求△DEF的面积．28.【性质探究】如图，在矩形ABCD中，对角线AC，BD相交于点O，AE平分∠BAC，交BC于点E．作DF⊥AE于点H，分别交AB，AC于点F，G．（1）判断△AFG的形状并说明理由．（2）求证：BF＝2OG．【迁移应用】（3）记△DGO的面积为S1，△DBF的面积为S2，当＝时，求的值．【拓展延伸】（4）若DF交射线AB于点F，【性质探究】中的其余条件不变，连结EF，当△BEF的面积为矩形ABCD面积的时，请直接写出tan∠BAE的值．29．如图，已知AC为正方形ABCD的对角线，点P是平面内不与点A，B重合的任意一点，连接AP，将线段AP绕点P顺时针旋转90°得到线段PE，连接AE，BP，CE．（1）求证：△APE∽△ABC；（2）当线段BP与CE相交时，设交点为M，求的值以及∠BMC的度数；（3）若正方形ABCD的边长为3，AP＝1，当点P，C，E在同一直线上时，求线段BP 的长．30．如图1和图2，在△ABC中，AB＝AC，BC＝8，tan C＝．点K在AC边上，点M，N 分别在AB，BC上，且AM＝CN＝2．点P从点M出发沿折线MB﹣BN匀速移动，到达点N时停止；而点Q在AC边上随P移动，且始终保持∠APQ＝∠B．（1）当点P在BC上时，求点P与点A的最短距离；（2）若点P在MB上，且PQ将△ABC的面积分成上下4：5两部分时，求MP的长；（3）设点P移动的路程为x，当0≤x≤3及3＜x≤9时，分别求点P到直线AC的距离（用含x的式子表示）；（4）在点P处设计并安装一扫描器，按定角∠APQ扫描△APQ区域（含边界），扫描器随点P从M到B再到N共用时36秒．若AK＝，请直接写出点K被扫描到的总时长．参考答案与试题解析一．解答题（共30小题）1．【解答】解：（1）如图①中，∵∠EAF＝∠BAC＝90°，∴∠BAF＝∠CAE，∵AF＝AE，AB＝AC，∴△BAF≌△CAE，∴∠ABF＝∠C，BF＝CE，∵AB＝AC，∠BAC＝90°，∴∠ABC＝∠C＝45°，∴∠FBE＝∠ABF+∠ABC＝90°，BC＝BE+EC＝BE+BF，故答案为：BF⊥BE，BC．（2）如图②中，作DH∥AC交BC于H．∵DH∥AC，∴∠BDH＝∠A＝90°，△DBH是等腰直角三角形，由（1）可知，BF⊥BE，BF+BE＝BH，∵AB＝AC＝3，AD＝1，∴BD＝DH＝2，∴BH＝2，∴BF+BE＝BH＝2；（3）如图③中，作DH∥AC交BC的延长线于H，作DM⊥BC于M．∵AC∥DH，∴∠ACB＝∠H，∠BDH＝∠BAC＝α，∵AB＝AC，∴∠ABC＝∠ACB∴∠DBH＝∠H，∴DB＝DH，∵∠EDF＝∠BDH＝α，∴∠BDF＝∠HDE，∵DF＝DE，DB＝DH，∴△BDF≌△HDE，∴BF＝EH，∴BF+BE＝EH+BE＝BH，∵DB＝DH，DM⊥BH，∴BM＝MH，∠BDM＝∠HDM，∴BM＝MH＝BD•sin．∴BF+BE＝BH＝2n•sin．2．【解答】解：（1）如图1中，∵△ABC∽△B'BA∽△C'AC，∴＝，＝，∴AB2＝BB′×BC，AC2＝CC′×BC，∴AB2+AC2＝BC（BB′+CC′）＝BC×BC＝BC2，故答案为BC2．（2）不成立．理由：如图2中当∠BAC为锐角时，BB′+CC′﹣B′C′＝BC，且△ABC∽△B'BA∽△C'AC，∴∴＝，＝，∴AB2＝BB′×BC，AC2＝CC′×BC，∴AB2+AC2＝BC（BB′+CC′）＝BC2+BC•B′C′．图3中∠BAC为钝角时，BB′+CC′+B′C′＝BC．AB2+AC2＝BC（BB′+CC′）＝BC2﹣BC•B′C′．（3）当AB＝5，AC＝6，BC＝9时，则AB2+AC2＜BC2，可知△ABC为钝角三角形，由图3可知：AB2+AC2＝BC2﹣BC•B′C′，∴52+62＝92﹣9B′C′，∴B′C′＝．3．【解答】解：（1）∵∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝45°，∴∠ABC＝∠CAB＝45°＝∠CDE＝∠CED，∴AC＝BC，CD＝CE，∵∠ACB＝∠DCE＝90°，∴∠ACD＝∠BCE，在△ACD和△BCE中，，∴△ACD≌△BCE（SAS），∴BE＝AD，∠CAB＝∠CBE＝45°，∴∠DBE＝∠ABC+∠CBE＝90°，＝1，故答案为：1，90°（2），∠DBE＝90°理由如下：∵∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝60°，∴∠ACD＝∠BCE，∠CED＝∠ABC＝30°∴tan∠ABC＝tan30°＝＝∵∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝60°，∴Rt△ACB∽Rt△DCE∴∴，且∠ACD＝∠BCE∴△ACD∽△BCE∴＝，∠CBE＝∠CAD＝60°∴∠DBE＝∠ABC+∠CBE＝90°（3）若点D在线段AB上，如图，由（2）知：＝，∠ABE＝90°∴BE＝AD∵AC＝2，∠ACB＝90°，∠CAB＝90°∴AB＝4，BC＝2∵∠ECD＝∠ABE＝90°，且点M是DE中点，∴CM＝BM＝DE，∵△CBM是直角三角形∴CM2+BM2＝BC2＝（2）2，∴BM＝CM＝∴DE＝2∵DB2+BE2＝DE2，∴（4﹣AD）2+（AD）2＝24∴AD＝+1∴BE＝AD＝3+若点D在线段BA延长线上，如图同理可得：DE＝2，BE＝AD∵BD2+BE2＝DE2，∴（4+AD）2+（AD）2＝24，∴AD＝﹣1∴BE＝AD＝3﹣综上所述：BE的长为3+或3﹣4．【解答】解：（1）∵△ABC中，∠BAC＝90°，AB＝AC，点D是BC的中点，∴AD＝BD＝DC，∠BDA＝90°，∵四边形DFGE是正方形，∴DE＝DF，∠EDF＝90°，∴∠BDE＝∠ADF＝90°，在△BDE和△ADF中，，∴△BDE≌△ADF（SAS），∴BE＝AF故答案为：BE＝AF；（2）成立；理由如下：当正方形DFGE在BC的上方时，如图②所示，连接AD，∵在Rt△ABC中，AB＝AC，D为斜边BC的中点，∴AD＝BD，AD⊥BC，∴∠ADE+∠EDB＝90°，∵四边形DFGE为正方形，∴DE＝DF，且∠EDF＝90°，∴∠ADE+∠ADF＝90°，∴∠BDE＝∠ADF，在△BDE和△ADF中，，∴△BDE≌△ADF（SAS），∴BE＝AF；当正方形DFGE在BC的下方时，连接AD，如图③所示：∵∠BDE＝∠BDF+90°，∠ADF＝∠BDF+90°，∴∠BDE＝∠ADF，在△BDE和△ADF中，，∴△BDE≌△ADF（SAS），∴BE＝AF；综上所述，（1）中的结论BE＝AF成立；（3）在△ADE中，∵AE＜AD+DE，∴当点A、D、E共线时，AE取得最大值，最大值为AD+DE．如图④所示：则AD＝BC＝1，DE＝DF＝2，∴AE＝AD+DE＝3，即AE的最大值为3．5．【解答】解：（1）如图1，过点O作OM⊥AB于M，ON⊥AD于N，∴∠OME＝∠ONF＝90°，∴∠BAD+∠MON＝180°，∵∠BAD+∠EOF＝180°，∴∠MON＝∠EOF，∴∠EOM＝∠FON，∵O是正方形ABCD的对角线的交点，∴∠BAO＝∠DAO，∵OM⊥AB，ON⊥AD，∴OM＝ON，∴△OME≌△ONF（AAS）∴OE＝OF；（2）（1）的结论成立；理由：如图2，过点O作OM⊥AB于M，ON⊥AD于N，∴∠OME＝∠ONF＝90°，∴∠BAD+∠MON＝180°，∵∠BAD+∠EOF＝180°，∴∠MON＝∠EOF，∴∠EOM＝∠FON，∵O是菱形ABCD的对角线的交点，∴∠BAO＝∠DAO，∵OM⊥AB，ON⊥AD，∴OM＝ON，∴△OME≌△ONF（AAS）∴OE＝OF；（3）如图3，过点O作OG⊥AB于G，OH⊥AD于H，∴∠OGE＝∠OHF＝90°，∴∠BAD+∠GOH＝180°，∵∠BAD+∠EOF＝180°，∴∠GOH＝∠EOF，∴△EOG∽△FOH，∴，∵O是▱ABCD的对角线的交点，∴S△AOB＝S△AOD，∵S△AOB＝AB•OG，S△AOD＝AD•OH，∴AB•OG＝AD•OH，∴＝，∴．6．【解答】解：（1）①∵四边形ABCD是正方形，∴∠BCD＝90°，∠BCA＝45°，∵GE⊥BC、GF⊥CD，∴∠CEG＝∠CFG＝∠ECF＝90°，∴四边形CEGF是矩形，∠CGE＝∠ECG＝45°，∴EG＝EC，∴四边形CEGF是正方形；②由①知四边形CEGF是正方形，∴∠CEG＝∠B＝90°，∠ECG＝45°，∴＝，GE∥AB，∴＝＝，故答案为：；（2）连接CG，由旋转性质知∠BCE＝∠ACG＝α，在Rt△CEG和Rt△CBA中，＝cos45°＝、＝cos45°＝，∴＝＝，∴△ACG∽△BCE，∴＝＝，∴线段AG与BE之间的数量关系为AG＝BE；（3）∵∠CEF＝45°，点B、E、F三点共线，∴∠BEC＝135°，∵△ACG∽△BCE，∴∠AGC＝∠BEC＝135°，∴∠AGH＝∠CAH＝45°，∵∠CHA＝∠AHG，∴△AHG∽△CHA，∴＝＝，设BC＝CD＝AD＝a，则AC＝a，则由＝得＝，∴AH＝a，则DH＝AD﹣AH＝a，CH＝＝a，∴＝得＝，解得：a＝3，即BC＝3，故答案为：3．7．【解答】解：（1）如图1，连接AE，∵AB＝AC＝2，点E分别是BC的中点，∴AE⊥BC，∴∠BEC＝90°，∵AB＝AC＝2，∠BAC＝120°，∴∠B＝∠C＝30°，在Rt△ABE中，AE＝AB＝1，根据勾股定理得，BE＝∵点E是BC的中点，∴BC＝2BE＝2，∴＝＝，∵点D是AC的中点，∴AD＝CD＝AC＝1，∴＝＝，故答案为：，；（2）无变化，理由：由（1）知，CD＝1，CE＝BE＝，∴＝，，∴＝，由（1）知，∠ACB＝∠DCE＝30°，∴∠ACD＝∠BCE，∴△ACD∽△BCE，∴，（3）当点D在线段AE上时，如图2，过点C作CF⊥AE于F，∠CDF＝180°﹣∠CDE＝60°，∴∠DCF＝30°，∴DF＝CD＝，∴CF＝DF＝，在Rt△AFC中，AC＝2，根据勾股定理得，AF＝＝，∴AD＝AF+DF＝，由（2）知，，∴BE＝AD＝当点D在线段AE的延长线上时，如图3，过点C作CG⊥AD交AD的延长线于G，∵∠CDG＝60°，∴∠DCG＝30°，∴DG＝CD＝，∴CG＝DG＝，在Rt△ACG中，根据勾股定理得，AG＝，∴AD＝AG﹣DG＝，由（2）知，，∴BE＝AD＝即：线段BE的长为或．8．【解答】解：（1）证明：∵将△ACD绕点C逆时针方向旋转60°得到△BCE，∴∠DCE＝60°，DC＝EC，∴△CDE是等边三角形；故答案为：等边；（2）存在，当6＜t＜10时，由旋转的性质得，BE＝AD，∴C△DBE＝BE+DB+DE＝AB+DE＝4+DE，由（1）知，△CDE是等边三角形，∴DE＝CD，∴C△DBE＝CD+4，由垂线段最短可知，当CD⊥AB时，△BDE的周长最小，此时，CD＝2，∴△BDE的最小周长＝CD+4＝2+4；（3）存在，①∵当点D与点B重合时，D，B，E不能构成三角形，∴当点D与点B重合时，不符合题意，②当0≤m＜6时，由旋转可知，∠ABE＝60°，∠BDE＜60°，∴∠BED＝90°，由（1）可知，△CDE是等边三角形，∴∠DEB＝60°，∴∠CEB＝30°，∵∠CEB＝∠CDA，∴∠CDA＝30°，∵∠CAB＝60°，∴∠ACD＝∠ADC＝30°，∴DA＝CA＝4，∴OD＝OA﹣DA＝6﹣4＝2，∴m＝2；③当6＜m＜10时，由∠DBE＝120°＞90°，∴此时不存在；④当m＞10时，由旋转的性质可知，∠DBE＝60°，又由（1）知∠CDE＝60°，∴∠BDE＝∠CDE+∠BDC＝60°+∠BDC，而∠BDC＞0°，∴∠BDE＞60°，∴只能∠BDE＝90°，从而∠BCD＝30°，∴BD＝BC＝4，∴OD＝14，∴m＝14，综上所述：当m＝2或14时，以D、E、B为顶点的三角形是直角三角形．9．【解答】解：（1）如图1中，连接DB，MF，CE，延长BD交EC于H．∵AC＝AB，AE＝AD，∠BAD＝∠CAE＝90°，∴△BAD≌△CAE（SAS），∴BD＝EC，∠ACE＝∠ABD，∵∠ABD+∠ADB＝90°，∠ADB＝∠CDH，∴∠ADH+∠DCH＝90°，∴∠CHD＝90°，∴EC⊥BH，∵BM＝MC，BF＝FE，∴MF∥EC，MF＝EC，∵CM＝MB，CN＝ND，∴MN∥BD，MN＝BD，∴MN＝MF，MN⊥MF，∴∠NMF＝90°，∴∠MNF＝45°，NF＝MN．故答案为：45°（2）：如图2中，连接MF，EC，BD．设EC交AB于O，BD交EC于H．∵AC＝AB，AE＝AD，∠BAD＝∠CAE＝90°，∴∠BAD＝∠CAE，∴△BAD≌△CAE（SAS），∴BD＝EC，∠ACE＝∠ABD，∵∠AOC+∠ACO＝90°，∠AOC＝∠BOH，∴∠OBH+∠BOH＝90°，∴∠BHO＝90°，∴EC⊥BD，∵BM＝MC，BF＝FE，∴MF∥EC，MF＝EC，∵CM＝MB，CN＝ND，∴MN∥BD，MN＝BD，∴MN＝MF，MN⊥MF，∴∠NMF＝90°，∴∠MNF＝45°，NF＝MN．（3）：如图3中，如图以A为圆心AD为半径作⊙A．当直线PB与⊙A相切时，此时∠CBP的值最小，点P到BC的距离最小，即△BCP的面积最小，∵AD＝AE，AB＝AC，∠BAC＝∠DAE＝90°，∴∠BAD＝∠CAE，∴△BAD≌△CAE（SAS），∴∠ACE＝∠ABD，BD＝EC，∵∠ABD+∠AOB＝90°，∠AOB＝∠CPO，∴∠CPB＝90°，∵PB是⊙A的切线，∴∠ADP＝90°，∵∠DPE＝∠ADP＝∠DAE＝90°，∴四边形ADPE是矩形，∵AE＝AD，∴四边形ADPE是正方形，∴AD＝AE＝PD＝PE＝2，BD＝EC＝＝2，∴PC＝2﹣2，PB＝2+2，∴S△BCP的最小值＝×PC×PB＝（2﹣2）（2+2）＝4．10．【解答】（1）解：AC⊥BD，理由如下：连接AC、BD，如图2所示：∵AB＝AD，∴点A在线段BD的垂直平分线上，∵CB＝CD，∴点C在线段BD的垂直平分线上，∴直线AC是线段BD的垂直平分线，∴AC⊥BD，故答案为：AC⊥BD；（2）解：AD2+BC2＝AB2+CD2；理由如下：如图1，已知四边形ABCD中，AC⊥BD，设BD、AC相交于E，∵AC⊥BD，∴∠AED＝∠AEB＝∠BEC＝∠CED＝90°，由勾股定理得，AD2+BC2＝AE2+DE2+BE2+CE2，AB2+CD2＝AE2+BE2+CE2+DE2，∴AD2+BC2＝AB2+CD2；（3）解：如图3，连接CG、BE，∵四边形ACFG和四边形ABDE是正方形，∴AC＝AG，AB＝AE，∠CAG＝∠BAE＝90°，∴∠CAG+∠BAC＝∠BAE+∠BAC，即∠GAB＝∠CAE，在△GAB和△CAE中，，∴△GAB≌△CAE（SAS），∴∠ABG＝∠AEC，又∠AEC+∠AME＝90°，∴∠ABG+∠AME＝90°，即CE⊥BG，由（2）得，CG2+BE2＝CB2+GE2，在Rt△ABC中，AC＝4，AB＝5，根据勾股定理得，BC2＝52﹣42＝9，∵CG和BE分别是正方形ACFG和正方形ABDG的对角线，∴CG2＝42+42＝32，BE2＝52+52＝50，∴GE2＝CG2+BE2﹣CB2＝32+50﹣9＝73，∴GE＝．11．【解答】解：问题发现：如图1中，结论：AE＝2BH，AE⊥BH．理由：在Rt△ABC中，∵BC＝6，∠A＝30°，∴AE＝2BC＝12，在Rt△CDB中，∵∠DCB＝30°，∴CD＝＝4，∵CH＝DH，∴BH＝CD＝2，∴＝＝2，∴AE＝2BH．故答案为AE⊥BH，AE＝2BH．问题证明：如图2中，（1）中结论成立．理由：延长BH到F使得HF＝BH，连接CF．设AE交BF于O．∵CH＝DH，BH＝HF，∠CHF＝∠BHD，∴△CHF≌△DHB（SAS），∴BD＝CF，∠F＝∠DBH，∴CF∥BD，∵AB＝BC，BE＝BD，∴BE＝CF，∴＝＝，∵CF∥BD，∴∠BCF+∠CBD＝180°，∵∠ABC+∠DBE＝∠ABD+∠CBD+∠CBD+∠CBE＝∠CBD+∠ABE＝180°，∴∠BCF＝∠ABE，∴△ABE∽△BCF，∴∠CBF＝∠BAE，＝＝，∴AE＝BF＝2BH，∵∠CBF+∠ABF＝90°，∴∠ABF+∠BAE＝90°，∴∠AOB＝90°，∴BH⊥AE．拓展应用：如图3﹣1中，当DE在BC的下方时，延长AB交DE于F．∵DE∥BC∴∠ABC＝∠BFD＝90°，由题意BC＝BE＝6，AB＝6，BD＝2，DE＝4，∵•BD•BE＝•DE•BF，∴BF＝＝3，∴EF＝BF＝3，∴AF＝6+3，∴AE2＝AF2+EF2＝（6+3）2+（3）2＝144+36．∵AE＝2BH，∴AE2＝12BH2，∴BH2＝12+3如图3﹣2中，当DE在BC的上方时，同法可得AF＝6﹣3，EF＝3，∴BH2＝＝（＝12﹣3．12．【解答】解：（1）如图1中，作EH⊥CG于H．∵四边形ECFG是菱形，∠ECF＝60°，∴∠ECH＝∠ECF＝30°，EC＝EG，∵EH⊥CG，∴GH＝CG，∴＝cos30°＝，∴＝2•＝，∵EG∥CD，AB∥CD，∴GE∥AB，∴＝＝．故答案为．（2）结论：AG＝BE．理由：如图2中，连接CG．∵四边形ABCD，四边形ECFG都是菱形，∠ECF＝∠DCB＝60°，∴∠ECG＝∠EGC＝∠BCA＝∠BAC＝30°，∴△ECG∽△BCE，∴＝，∵∠ECB＝∠GCA，∴△ECB∽△GCA，∴＝＝，∴AG＝BE．（3）如图3中，∵∠AGH＝∠CGF＝30°．∠AGH＝∠GAC+∠GCA，又∵∠DAC＝∠HAG+∠GAC＝30°，∴∠HAG＝∠ACH，∵∠AHG＝∠AHC，∴△HAG∽△HCA，∴HA：HC＝GH：HA，∴AH2＝HG•HC，∴FC＝2，CG＝CF，∴GC＝2，∵HG＝，∴AH2＝HG•HC＝•3＝9，∵AH＞0，∴AH＝3．故答案为3．13．【解答】解：（1）当m＝n时，即：BC＝AC，∵∠ACB＝90°，∴∠A+∠ABC＝90°，∵CD⊥AB，∴∠DCB+∠ABC＝90°，∴∠A＝∠DCB，∵∠FDE＝∠ADC＝90°，∴∠FDE﹣∠CDE＝∠ADC﹣∠CDE，即∠ADE＝∠CDF，∴△ADE∽△CDF，∴，∵∠A＝∠DCB，∠ADC＝∠BDC＝90°，∴△ADC∽△CDB，∴＝1，∴＝1（2）①∵∠ACB＝90°，∴∠A+∠ABC＝90°，∵CD⊥AB，∴∠DCB+∠ABC＝90°，∴∠A＝∠DCB，∵∠FDE＝∠ADC＝90°，∴∠FDE﹣∠CDE＝∠ADC﹣∠CDE，即∠ADE＝∠CDF，∴△ADE∽△CDF，∴，∵∠A＝∠DCB，∠ADC＝∠BDC＝90°，∴△ADC∽△CDB，∴，∴②成立．如图，∵∠ACB＝90°，∴∠A+∠ABC＝90°，又∵CD⊥AB，∴∠DCB+∠ABC＝90°，∴∠A＝∠DCB，∵∠FDE＝∠ADC＝90°，∴∠FDE+∠CDE＝∠ADC+∠CDE，即∠ADE＝∠CDF，∴△ADE∽△CDF，∴，∵∠A＝∠DCB，∠ADC＝∠BDC＝90°，∴△ADC∽△CDB，∴，∴．（3）由（2）有，△ADE∽△CDF，∵＝，∴＝，∴CF＝2AE，在Rt△DEF中，DE＝2，DF＝4，∴EF＝2，①当E在线段AC上时，在Rt△CEF中，CF＝2AE＝2（AC﹣CE）＝2（﹣CE），EF＝2，根据勾股定理得，CE2+CF2＝EF2，∴CE2+[2（﹣CE）]2＝40∴CE＝2，或CE＝﹣（舍）而AC＝＜CE，∴此种情况不存在，②当E在AC延长线上时，在Rt△CEF中，CF＝2AE＝2（AC+CE）＝2（+CE），EF＝2，根据勾股定理得，CE2+CF2＝EF2，∴CE2+[2（+CE）]2＝40，∴CE＝，或CE＝﹣2（舍），③如图1，当点E在CA延长线上时，CF＝2AE＝2（CE﹣AC）＝2（CE﹣），EF＝2，根据勾股定理得，CE2+CF2＝EF2，∴CE2+[2（CE﹣）]2＝40，∴CE＝2，或CE＝﹣（舍）即：CE＝2或CE＝．14．【解答】解：（1）如图1，延长GM交AD于H，∵AD∥GF，∴∠GFM＝∠HAM，在△FMG和△AMH中，，∴△FMG≌△AMH（ASA），∴HM＝GM，AH＝FG，∵AD＝CD，AH＝FG＝CG，∴DH＝DG，∵∠HDG＝90°，HM＝GM，∴DM＝MG，DM⊥MG，故答案为DM＝MG，DM⊥MG．（2）结论成立：DM＝MG，DM⊥MG，理由：如图2中，延长GM使得MH＝GM，连接AH、DH、DG，延长AD交GF的延长线于N，交CD于O．∵AM＝MF，∠AMH＝∠FMG，MH＝MG，∴△AMH≌△FMG（SAS），∴AH＝GF＝CG，∠AHM＝∠FGM，∴AH∥GN，∴∠HAD＝∠N，∵∠ODN＝∠OGC＝90°，∠DON＝∠GOC，∴∠N＝∠OCG，∴∠HAD＝∠DCG，∵AH＝CG，AD＝CD，∴△HAD≌△GCD（SAS），∴DH＝DG，∠HDA＝∠CDG，∴∠HDG＝∠ADC＝90°，∴△HDG是等腰直角三角形，∵MH＝MG，∴DM⊥GH，DM＝MH＝MG，（3）①如图3﹣1中，连接AC．在Rt△ABC中，AC＝＝10，在Rt△ACE中，AE＝＝14，∴AF＝AE＝EF＝14﹣2＝12，∴FM＝AM＝AF＝6，在Rt△MGF中，MG＝＝2，∴S△DMG＝×2×2＝20，②如图3﹣2中，连接AC．同法可得AE＝14，AF＝16，FM＝8，MG＝＝2，∴S△DMG＝×2×2＝34，综上所述，满足条件的△DMG的面积为20或34．15．【解答】解：（1）由旋转可得：AC＝A'C＝2，∵∠ACB＝90°，AB＝，AC＝2，∴BC＝，∵∠ACB＝90°，m∥AC，∴∠A'BC＝90°，∴cos∠A'CB＝＝，∴∠A'CB＝30°，∴∠ACA'＝60°；（2）∵M为A'B'的中点，∴∠A'CM＝∠MA'C，由旋转可得，∠MA'C＝∠A，∴∠A＝∠A'CM，∴tan∠PCB＝tan∠A＝，∴PB＝BC＝，∵∠PCQ＝∠PBC＝90°，∴∠BQC+∠BPC＝∠BCP+∠BPC＝90°，∴∠BQC＝∠BCP＝∠A，∴tan∠BQC＝tan∠A＝，∴BQ＝BC×＝2，∴PQ＝PB+BQ＝；（3）∵S四边形P A'B′Q＝S△PCQ﹣S△A'CB'＝S△PCQ﹣，∴S四边形P A'B′Q最小，即S△PCQ最小，∴S△PCQ＝PQ×BC＝PQ，法一：（几何法）取PQ的中点G，∵∠PCQ＝90°，∴CG＝PQ，即PQ＝2CG，当CG最小时，PQ最小，∴CG⊥PQ，即CG与CB重合时，CG最小，∴CG min＝，PQ min＝2，∴S△PCQ的最小值＝3，S四边形P A'B′Q＝3﹣；法二（代数法）设PB＝x，BQ＝y，由射影定理得：xy＝3，∴当PQ最小时，x+y最小，∴（x+y）2＝x2+2xy+y2＝x2+6+y2≥2xy+6＝12，当x＝y＝时，“＝”成立，∴PQ＝+＝2，∴S△PCQ的最小值＝3，S四边形P A'B′Q＝3﹣．16．【解答】解：（1）结论：△PMN是等边三角形．理由：如图1中，∵△ABC是等边三角形，∴AB＝AC，∠ABC＝∠ACB＝60°，∵AD＝AE，∴BD＝EC，∵PB＝PC，CN＝ND，BM＝EM，∴PN∥BD，PM∥EC，PN＝BD，PM＝EC，∴PM＝PN，∠NPC＝∠ABC＝60°，∠MPB＝∠ACB＝60°，∴∠MPN＝60°，∴△PMN是等边三角形，故答案为等边三角形．（2）△PMN的形状不发生改变，仍为等边三角形，理由如下：如图2中，连接BD，CE．由旋转可得∠BAD＝∠CAE，∵△ABC是等边三角形，∴AB＝AC，∠ACB＝∠ABC＝60°又∵AD＝AE，∴△ABD≌△ACE（SAS），∴BD＝CE，∠ABD＝∠ACE，∵M是BE的中点，P是BC的中点，∴PM是△BCE的中位线，∴PM＝，且PM∥CE．同理可证PN＝BD且PN∥BD，∴PM＝PN，∠MPB＝∠ECB，∠NPC＝∠DBC，∴∠MPB+∠NPC＝∠ECB+∠DBC＝（∠ACB+∠ACE）+（∠ABC﹣∠ABD）＝∠ACB+∠ABC＝120°，∴∠MPN＝60°，∴△PMN是等边三角形．（3）∵PM＝EC，∴当EC最大时，等边△PMN的周长最大，∵EC≤AE+AC，∴EC≤8，∴PM≤4，∴PM的最大值为4，∴△PMN的周长的最大值为12．17．【解答】解：（1）∵AB＝AC，∠ABC＝60°，∴∠BAC＝60°，∵AD＝AE，∠ADE＝70°，∴∠DAE＝180°﹣2∠ADE＝40°，∴α＝∠BAD＝60°﹣40°＝20°，∴∠ADC＝∠BAD+∠ABD＝60°+20°＝80°，∴β＝∠CDE＝∠ADC﹣∠ADE＝10°，故答案为：20，10；（2）设∠ABC＝x，∠AED＝y，∴∠ACB＝x，∠AED＝y，在△DEC中，y＝β+x，在△ABD中，α+x＝y+β＝β+x+β，∴α＝2β；（3）①当点E在CA的延长线上，点D在线段BC上，如图1设∠ABC＝x，∠ADE＝y，∴∠ACB＝x，∠ACE＝y，在△ABD中，x+α＝β﹣y，在△DEC中，x+y+β＝180°，∴α＝2β﹣180°，②当点E在CA的延长线上，点D在CB的延长线上，如图2，同①的方法可得α＝180°﹣2β．18．【解答】解：（1）由旋转变换的性质可知，∠CAE＝90°，AC＝AE，∴△ACE为等腰直角三角形，∴CE＝AC，∵CE＝CD+DE＝CD+BC，∴BC+CD＝AC，故答案为：等腰直角；BC+CD＝AC；（2）延长CO交⊙O于E，连接AE、BE、DE，则∠CDE＝90°，∵点C为的中点，∴点E为的中点，∴EA＝EB，∵AB为⊙O的直径，∴∠ADB＝90°，由（1）得，DE＝（AD+BD），由勾股定理得，CD2＝CE2﹣DE2＝AD2+BD2﹣（AD+BD）2＝（AD﹣BD）2，∴CD＝（BD﹣AD）；（3）如图3，当点E在直线AC的左侧时，连接CQ、PC，∵CA＝CB，点P为AB的中点，∴CP⊥AB，∵CA＝CE，点Q为AE中点，∴CQ⊥AE，AQ＝QE＝AE＝5，∴由勾股定理得，CQ＝＝12，由（1）得，AQ+CQ＝PQ，。

2016年中考数学试题分项版解析(第02期)专题16 压轴题

专题16 压轴题一、选择题1．（2016四川省凉山州）已知，一元二次方程28150x x -+=的两根分别是⊙O 1和⊙O 2的半径，当⊙O 1和⊙O 2相切时，O 1O 2的长度是（）A ．2B ．8C ．2或8D ．2＜O 2O 2＜8 【答案】C ．考点：1．圆与圆的位置关系；2．根与系数的关系；3．分类讨论．2．（2016四川省宜宾市）如图，点P 是矩形ABCD 的边AD 上的一动点，矩形的两条边AB 、BC 的长分别是6和8，则点P 到矩形的两条对角线AC 和BD 的距离之和是（）A ．4.8B ．5C ．6D ．7.2 【答案】A ．【解析】试题分析：首先连接OP ，由矩形的两条边AB 、BC 的长分别为3和4，可求得OA =OD =5，△AOD 的面积，然后由S △A O D =S △A O P +S △D O P =12OA •PE +OD •PF 求得答案．试题解析：连接OP ，∵矩形的两条边AB 、BC 的长分别为6和8，∴S 矩形A B C D=AB •BC =48，OA =OC ，OB =OD ，AC =BD =10，∴OA =OD =5，∴S △A C D =12S 矩形A B C D=24，∴S △A O D =12S △A C D =12，∵S △A O D =S △A O P +S △D O P =12OA •PE +12OD •PF =12×5×PE +12×5×PF =52（PE +PF ）=12，解得：PE +PF =4.8．故选A ．考点：1．矩形的性质；2．和差倍分；3．定值问题．3．（2016四川省宜宾市）宜宾市某化工厂，现有A种原料52千克，B种原料64千克，现用这些原料生产甲、乙两种产品共20件．已知生产1件甲种产品需要A种原料3千克，B种原料2千克；生产1件乙种产品需要A种原料2千克，B种原料4千克，则生产方案的种数为（）A．4 B．5 C．6 D．7【答案】B．故选B．考点：1．二元一次方程组的应用；2．方案型．4．（2016四川省泸州市）以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是（）A B C．D【答案】D ．考点：1．正多边形和圆；2．分类讨论．5．（2016四川省自贡市）圆锥的底面半径为4cm ，高为5cm ，则它的表面积为（）A ．12πcm 2B ．26πcm 2C cm 2D ．16)πcm 2【答案】D ．【解析】试题分析：利用勾股定理求得圆锥的母线长，则圆锥表面积=底面积+侧面积=π×底面半径2+底面周长×母线长÷2．试题解析：底面半径为4cm ，则底面周长=8πcm ，底面面积=16πcm 2；由勾股定理得，母线长cm ，圆锥的侧面面积=182π⨯=cm 2，∴它的表面积=16π+=16)π cm 2，故选D ．考点：1．圆锥的计算；2．压轴题．6．（2016甘肃省白银市）如图，△ABC是等腰直角三角形，∠A=90°，BC=4，点P是△ABC边上一动点，沿B→A→C的路径移动，过点P作PD⊥BC于点D，设BD=x，△BDP的面积为y，则下列能大致反映y与x函数关系的图象是（）A．B．C．D．【答案】A．当2＜x≤4时，如图2，∵∠C=45°，∴PD=CD=4﹣x，∴y=12•（4﹣x）•x=2122x x-+，故选A．考点：1．动点问题的函数图象；2．分类讨论．二、填空题7．（2016四川省凉山州）如图，四边形ABCD中，∠BAD=∠ADC=90°，AB=AD=CD=P是四边形ABCD四条边上的一个动点，若P到BD的距离为52，则满足条件的点P有个．【答案】2．考点：1．点到直线的距离；2．分类讨论．8．（2016四川省宜宾市）如图，在边长为4的正方形ABCD中，P是BC边上一动点（不含B、C两点），将△ABP沿直线AP翻折，点B落在点E处；在CD上有一点M，使得将△CMP沿直线MP翻折后，点C落在直线PE上的点F处，直线PE交CD于点N，连接MA，NA．则以下结论中正确的有（写出所有正确结论的序号）①△CMP∽△BPA；②四边形AMCB的面积最大值为10；③当P为BC中点时，AE为线段NP的中垂线；④线段AM的最小值为⑤当△ABP≌△ADN时，BP=4．【答案】①②⑤．考点：相似形综合题．9．（2016四川省自贡市）如图，把Rt△ABC放在直角坐标系内，其中∠CAB=90°，BC=5，点A、B的坐标分别为（1，0）、（4，0），将△ABC沿x轴向右平移，当点C落在直线y=2x﹣6上时，线段BC扫过的面积为cm2．【答案】16．考点：1．一次函数综合题；2．压轴题．10．（2016江苏省宿迁市）如图，在矩形ABCD中，AD=4，点P是直线AD上一动点，若满足△PBC是等腰三角形的点P有且只有3个，则AB的长为．【答案】4．考点：1．矩形的性质；2．等腰三角形的性质；3．勾股定理；4．分类讨论．11．（2016江西省）如图是一张长方形纸片ABCD，已知AB=8，AD=7，E为AB上一点，AE=5，现要剪下一张等腰三角形纸片（△AEP），使点P落在长方形ABCD的某一条边上，则等腰三角形AEP的底边长是．【答案】5．【解析】试题分析：分情况讨论：①当AP=AE=5时，则△AEP是等腰直角三角形，得出底边PE AE=②当PE=AE=5时，求出BE，由勾股定理求出PB，再由勾股定理求出等边AP即可；③当PA=PE时，底边AE=5；即可得出结论．试题解析：如图所示：①当AP=AE=5时，∵∠BAD=90°，∴△AEP是等腰直角三角形，∴底边PE AE=②当PE=AE=5时，∵BE=AB﹣AE=8﹣5=3，∠B=90°，∴PB==4，∴底边考点：1．矩形的性质；2．等腰三角形的性质；3．勾股定理；4．分类讨论．12．（2016甘肃省兰州市）对于一个矩形ABCD 及⊙M 给出如下定义：在同一平面内，如果矩形ABCD 的四个顶点到⊙M 上一点的距离相等，那么称这个矩形ABCD 是⊙M 的“伴侣矩形”．如图，在平面直角坐标系xOy 中，直线l ：3y =-交x 轴于点M ，⊙M 的半径为2，矩形ABC D 沿直线运动（BD 在直线l 上），BD =2，AB ∥y 轴，当矩形ABCD 是⊙M 的“伴侣矩形”时，点C 的坐标为．【答案】（12，2-）或（32，2）．【解析】试题分析：根据“伴侣矩形”的定义可知：圆上的点一定在矩形的对角线交点上，因为只有对角线交点到四个顶点的距离相等，由此画出图形，先求出直线与x 轴和y 轴两交点的坐标，和矩形的长和宽；有两种情况：①矩形在x 轴下方时，作辅助线构建相似三角形得比例式，分别求出DG 和DH 的长，从而求出CG 的长，根据坐标特点写出点C 的坐标；②矩形在x 轴上方时，也分别过C 、B 两点向两坐标轴作垂线，利用平行相似得比例式，求出C 的坐标．考点：1．圆的综合题；2．新定义；3．分类讨论．三、解答题13．（2016上海市）如图，抛物线25y ax bx =+-（a ≠0）经过点A （4，﹣5），与x 轴的负半轴交于点B ，与y 轴交于点C ，且OC =5OB ，抛物线的顶点为点D ．（1）求这条抛物线的表达式；（2）联结AB 、BC 、CD 、DA ，求四边形ABCD 的面积；（3）如果点E 在y 轴的正半轴上，且∠BEO =∠ABC ，求点E 的坐标．【答案】（1）245y x x =--；（2）18；（3）E （0，32）．（2）由245y x x =--，得顶点D 的坐标为（2，﹣9）．连接AC ，∵点A 的坐标是（4，﹣5），点C 的坐标是（0，﹣5），又S △ABC =12×4×5=10，S △ACD =12×4×4=8，∴S 四边形ABCD =S △ABC +S △ACD =18；（3）过点C 作CH ⊥AB ，垂足为点H ．∵S △ABC =12×AB ×CH =10，AB =，∴CH =，在RT △BCH 中，∠BHC =90°，BC =，BH ==，∴tan ∠CBH =23CH BH =．∵在RT △BOE 中，∠BOE =90°，tan ∠BEO =BO EO，∵∠BEO =∠ABC ，∴BO EO =23，得EO =32，∴点E 的坐标为（0，32）．考点：二次函数综合题．14．（2016上海市）如图所示，梯形ABCD 中，AB ∥DC ，∠B =90°，AD =15，AB =16，BC =12，点E 是边AB 上的动点，点F 是射线CD 上一点，射线ED 和射线AF 交于点G ，且∠AGE =∠DAB ．（1）求线段CD 的长；（2）如果△AEC 是以EG 为腰的等腰三角形，求线段AE 的长；（3）如果点F 在边CD 上（不与点C 、D 重合），设AE =x ，DF =y ，求y 关于x 的函数解析式，并写出x 的取值范围．【答案】（1）7；（2）15或252；（3）22518x y x -=（2592x <<）．考点：1．四边形综合题；2．相似三角形综合题；3．分类讨论；4．压轴题．15．（2016北京市）在等边△ABC中：（1）如图1，P，Q是BC边上的两点，AP=AQ，∠BAP=20°，求∠AQB的度数；（2）点P，Q是BC边上的两个动点（不与点B，C重合），点P在点Q的左侧，且AP=AQ，点Q关于直线AC 的对称点为M，连接AM，PM．①依题意将图2补全；②小茹通过观察、实验提出猜想：在点P，Q运动的过程中，始终有PA=PM，小茹把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：想法1：要证明PA=PM，只需证△APM是等边三角形；想法2：在BA上取一点N，使得BN=BP，要证明PA=PM，只需证△ANP≌△PCM；想法3：将线段BP绕点B顺时针旋转60°，得到线段BK，要证PA=PM，只需证PA=CK，PM=CK…请你参考上面的想法，帮助小茹证明PA=PM（一种方法即可）．【答案】（1）40°；（2）①作图见解析；②证明见解析．考点：三角形综合题．16．（2016北京市）在平面直角坐标系xOy 中，点P 的坐标为（1x ，1y ），点Q 的坐标为（2x ，2y ），且12x x ≠，12y y ≠，若P ，Q 为某个矩形的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为点P ，Q 的“相关矩形”．下图为点P ，Q 的“相关矩形”的示意图．（1）已知点A 的坐标为（1，0）．①若点B 的坐标为（3，1）求点A ，B 的“相关矩形”的面积；②点C 在直线x =3上，若点A ，C 的“相关矩形”为正方形，求直线AC 的表达式；（2）⊙O M 的坐标为（m ，3）．若在⊙O 上存在一点N ，使得点M ，N 的“相关矩形”为正方形，求m 的取值范围．【答案】（1）①2；②1y x =- 或 1y x =-+；（2）1≤m ≤5 或者51m -≤≤-．考点：1．圆的综合题；2．新定义．17．（2016吉林省长春市）如图，在菱形ABCD中，对角线AC与BD相交于点O，AB=8，∠BAD=60°，点E从点A出发，沿AB以每秒2个单位长度的速度向终点B运动，当点E不与点A重合时，过点E作EF⊥AD于点F，作EG∥AD交AC于点G，过点G作GH⊥AD交AD（或AD的延长线）于点H，得到矩形EFHG，设点E运动的时间为t秒（1）求线段EF的长（用含t的代数式表示）；（2）求点H与点D重合时t的值；（3）设矩形EFHG与菱形ABCD重叠部分图形的面积与S平方单位，求S与t之间的函数关系式；（4）矩形EFHG的对角线EH与FG相交于点O′，当OO′∥AD时，t的值为；当OO′⊥AD时，t的值为．【答案】（1）EF=t；（2）t=83；（3）228(0)383 (4)3tSt⎧≤≤⎪⎪=⎨⎪+-<≤⎪⎩；（4）t=4；t=3．考点：1．四边形综合题；2．动点型；3．分类讨论；4．分段函数；5．压轴题．18．（2016吉林省长春市）如图，在平面直角坐标系中．有抛物线2(3)4y a x =-+和2()y a x h =-.抛物线2(3)4y a x =-+经过原点，与x 轴正半轴交于点A ，与其对称轴交于点B ．P 是抛物线2(3)4y a x =-+上一点，且在x 轴上方．过点P 作x 轴的垂线交抛物线2()y a x h =-于点Q ．过点Q 作PQ 的垂线交抛物线2()y a x h =-于点'Q （不与点Q 重合），连结'PQ .设点P 的横坐标为m ．（1）求a 的值；（2）当抛物线2()y a x h =-经过原点时，设△'PQQ 与△OAB 重叠部分图形的周长为l ．②求l 与m 之间的函数关系式；（3）当h 为何值时，存在点P ，使以点O 、A 、Q 、'Q 为顶点的四边形是轴对称图形？直接写出h 的值．【答案】（1）49a =-；（2）①43；②24 (03)1171010(36)163m m l m m m <≤⎧⎪=⎨-++<<⎪⎩；（3）h =3或3-3+考点：1．二次函数综合题；2．分类讨论；3．压轴题．19．（2016四川省凉山州）为了更好的保护美丽图画的邛海湿地，西昌市污水处理厂决定先购买A、B两型污水处理设备共20台，对邛海湿地周边污水进行处理，每台A型污水处理设备12万元，每台B型污水处理设备10万元．已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640吨，2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1080吨．（1）求A、B两型污水处理设备每周分别可以处理污水多少吨？（2）经预算，市污水处理厂购买设备的资金不超过230万元，每周处理污水的量不低于4500吨，请你列举出所有购买方案，并指出哪种方案所需资金最少？最少是多少？【答案】（1）A型污水处理设备每周每台可以处理污水240吨，B型污水处理设备每周每台可以处理污水200吨；（2）共有三种方案，详见解析，购买A型污水处理设备13台，则购买B型污水处理设备7台时，所需购买资金最少，最少是226万元．即A型污水处理设备每周每台可以处理污水240吨，B型污水处理设备每周每台可以处理污水200吨；考点：1．一元一次不等式组的应用；2．二元一次方程组的应用；3．最值问题；4．方案型．20．（2016四川省凉山州）如图，已知抛物线2y ax bx c =++（a ≠0）经过A （﹣1，0）、B （3，0）、C （0，﹣3）三点，直线l 是抛物线的对称轴．（1）求抛物线的函数关系式；（2）设点P 是直线l 上的一个动点，当点P 到点A 、点B 的距离之和最短时，求点P 的坐标；（3）点M 也是直线l 上的动点，且△MAC 为等腰三角形，请直接写出所有符合条件的点M 的坐标．【答案】（1）223y x x =--；（2）P （1，0）；（3）．【解析】试题分析：（1）直接将A 、B 、C 三点坐标代入抛物线的解析式中求出待定系数即可；（2）由图知：A ．B 点关于抛物线的对称轴对称，那么根据抛物线的对称性以及两点之间线段最短可知，直线l 与x 轴的交点，即为符合条件的P 点；（3）由于△MAC 的腰和底没有明确，因此要分三种情况来讨论：①MA =AC 、②MA =MC 、③AC =MC ；可先设出M 点的坐标，然后用M 点纵坐标表示△MAC 的三边长，再按上面的三种情况列式求解．试题解析：（1）将A （﹣1，0）、B （3，0）、C （0，﹣3）代入抛物线2y ax bx c =++中，得：09303a b c a b c c -+=⎧⎪++=⎨⎪=-⎩考点：1．二次函数综合题；2．分类讨论；3．综合题；4．动点型．21．（2016四川省宜宾市）如图，已知二次函数21y a x b x =+过（﹣2，4），（﹣4，4）两点．（1）求二次函数1y 的解析式；（2）将1y 沿x 轴翻折，再向右平移2个单位，得到抛物线2y ，直线y =m （m ＞0）交2y 于M 、N 两点，求线段MN 的长度（用含m 的代数式表示）；（3）在（2）的条件下，1y 、2y 交于A 、B 两点，如果直线y =m 与1y 、2y 的图象形成的封闭曲线交于C 、D 两点（C 在左侧），直线y =﹣m 与1y 、2y 的图象形成的封闭曲线交于E 、F 两点（E 在左侧），求证：四边形CEFD 是平行四边形．【答案】（1）21132y x x =--；（2）（3）证明见解析．CD =12x x -==，由219(1)22y m y x =-⎧⎪⎨=+-⎪⎩，消去y 得到22820x x m +-+=，设两个根为1x ，2x ，则EF =12x x -==∴EF =CD ，EF ∥CD ，∴四边形CEFD 是平行四边形．考点：二次函数综合题．22．（2016四川省巴中市）已知：如图，四边形ABCD 是平行四边形，延长BA 至点E ，使AE +CD =AD ．连结CE ，求证：C E 平分∠BCD ．【答案】证明见解析．考点：1．平行四边形的性质；2．和差倍分．23．（2016四川省巴中市）如图，在平面直角坐标系中，抛物线245y mx mx m =+-（m ＜0）与x 轴交于点A 、B （点A 在点B 的左侧），该抛物线的对称轴与直线3y x =相交于点E ，与x 轴相交于点D ，点P 在直线y x =上（不与原点重合），连接PD ，过点P 作PF ⊥PD 交y 轴于点F ，连接DF ．（1）如图①所示，若抛物线顶点的纵坐标为（2）求A 、B 两点的坐标；（3）如图②所示，小红在探究点P 的位置发现：当点P 与点E 重合时，∠PDF 的大小为定值，进而猜想：对于直线3y x =上任意一点P （不与原点重合），∠PDF 的大小为定值．请你判断该猜想是否正确，并说明理由．【答案】（1）2333y x x =--+；（2）A （﹣5，0）、B （1，0）；（3）∠PDF =60°．考点：1．二次函数综合题；2．定值问题．24．（2016四川省广安市）如图，抛物线2y x bx c =++与直线132y x =-交于A 、B 两点，其中点A 在y 轴上，点B 坐标为（﹣4，﹣5），点P 为y 轴左侧的抛物线上一动点，过点P 作PC ⊥x 轴于点C ，交AB 于点D ．（1）求抛物线的解析式；（2）以O ，A ，P ，D 为顶点的平行四边形是否存在？如存在，求点P 的坐标；若不存在，说明理由．（3）当点P 运动到直线AB 下方某一处时，过点P 作PM ⊥AB ，垂足为M ，连接PA 使△PAM 为等腰直角三角形，请直接写出此时点P 的坐标．【答案】（1）2932y x x =+-；（2）P （2-1--，（﹣1，132-），（﹣3，152-）；（3）P （32-，152-）．【解析】试题分析：（1）先确定出点A 坐标，然后用待定系数法求抛物线解析式；（2）先用m 表示出PD ，当PD =OA =3，故存在以O ，A ，P ，D 为顶点的平行四边形，得到243m m +=，分两种情况进行讨论计算即可；（3）由△PAM 为等腰直角三角形，得到∠BAP =45°，从而求出直线AP 的解析式，最后求出直线AP 和抛物线的交点坐标即可．试题解析：（1）∵直线132y x =-交于A 、B 两点，其中点A 在y 轴上，∴A （0，﹣3），∵B （﹣4，﹣5），考点：1．二次函数综合题；2．动点型；3．存在型；4．分类讨论；5．压轴题．25．（2016四川省成都市）如图，在Rt △ABC 中，∠ABC =90°，以CB 为半径作⊙C ，交AC 于点D ，交AC 的延长线于点E ，连接ED ，BE ．（1）求证：△ABD ∽△AEB ；（2）当43AB BC 时，求tanE ；（3）在（2）的条件下，作∠BAC 的平分线，与BE 交于点F ，若AF =2，求⊙C 的半径．【答案】（1）证明见解析；（2）12；（3）8．考点：圆的综合题．26．（2016四川省成都市）如图，在平面直角坐标系xOy 中，抛物线2(1)3y a x =+-与x 轴交于A ，B 两点（点A 在点B 的左侧），与y 轴交于点C （0，83-），顶点为D ，对称轴与x 轴交于点H ，过点H 的直线l 交抛物线于P ，Q 两点，点Q 在y 轴的右侧．（1）求a 的值及点A ，B 的坐标；（2）当直线l 将四边形ABCD 分为面积比为3：7的两部分时，求直线l 的函数表达式；（3）当点P 位于第二象限时，设PQ 的中点为M ，点N 在抛物线上，则以DP 为对角线的四边形DMPN 能否为菱形？若能，求出点N 的坐标；若不能，请说明理由．【答案】（1）13a =，A （－4，0），B （2，0）；（2）y ＝2x ＋2或4433y x =--；（3）存在，N （－132-， 1）．【解析】由⎪⎩⎪⎨⎧-+=+=3832312x x y k kx y ，∴038)32(312=---+k x k x ，∴1223x x k+=-+，212123y y kx k kx k k +=+++=，∵点M 是线段PQ 的中点，∴由中点坐标公式的点M （312k -，232k ）．假设存在这样的N 点如图，直线DN ∥PQ ，设直线DN 的解析式为y =kx +k ﹣3，由⎪⎩⎪⎨⎧-+=-+=38323132x x y k kx y ，解考点：1．二次函数综合题；2．压轴题．27．（2016四川省攀枝花市）如图，在△AOB中，∠AOB为直角，OA=6，OB=8，半径为2的动圆圆心Q从点O出发，沿着OA方向以1个单位长度/秒的速度匀速运动，同时动点P从点A出发，沿着AB方向也以1个单位长度/秒的速度匀速运动，设运动时间为t秒（0＜t≤5）以P为圆心，PA长为半径的⊙P与AB、OA的另一个交点分别为C、D，连结CD、QC．（1）当t为何值时，点Q与点D重合？（2）当⊙Q经过点A时，求⊙P被OB截得的弦长．（3）若⊙P与线段QC只有一个公共点，求t的取值范围．【答案】（1）3011；（2；（3）0＜t ≤1813或3011＜t ≤5．考点：1．圆的综合题；2．分类讨论；3．动点型；4．压轴题．28．（2016四川省攀枝花市）如图，抛物线2y x bx c =++与x 轴交于A 、B 两点，B 点坐标为（3，0），与y 轴交于点C （0，﹣3）（1）求抛物线的解析式；（2）点P 在抛物线位于第四象限的部分上运动，当四边形ABPC 的面积最大时，求点P 的坐标和四边形ABPC 的最大面积．（3）直线l 经过A 、C 两点，点Q 在抛物线位于y 轴左侧的部分上运动，直线m 经过点B 和点Q ，是否存在直线m ，使得直线l 、m 与x 轴围成的三角形和直线l 、m 与y 轴围成的三角形相似？若存在，求出直线m 的解析式，若不存在，请说明理由．【答案】（1）223y x x =--；（2）P 点坐标为（32，154-）时，四边形ABPC 的面积最大，最大面积为758；（3）存在，113y x =-．在223y x x =--中，令y =0可得2023x x =--，解得x =﹣1或x =3，∴A 点坐标为（﹣1，0），∴AB =3﹣（﹣1）=4，且OC =3，∴S △ABC =12AB •OC =12×4×3=6，∵B （3，0），C （0，﹣3），∴直线BC 解析式为y =x ﹣3，设P 点坐标为（x ，223x x --），则M 点坐标为（x ，x ﹣3），∵P 点在第四限，∴PM =23(23)x x x ----=23x x -+，∴S △PBC =12PM •OH +12PM •HB =12PM •（OH +HB ）=12PM •OB =32PM ，∴当PM 有最大值时，△PBC 的面积最大，则四边形ABPC 的面积最大，∵PM =23x x -+=239()24x --+，∴当x =32时，PM max =94，则S △PBC =3924⨯=278，此时P 点坐标为（32，154-），S 四边形ABPC =S △ABC +S △PBC =6+278=758，即当P 点坐标为（32，154-）时，四边形ABPC 的面积最大，最大面积为758；考点：1．二次函数综合题；2．存在型；3．最值问题；4．二次函数的最值；5．动点型；6．压轴题．29．（2016四川省泸州市）如图，△ABC内接于⊙O，BD为⊙O的直径，BD与AC相交于点H，AC的延长线与过点B的直线相交于点E，且∠A=∠EBC．（1）求证：B E是⊙O的切线；（2）已知CG∥EB，且CG与BD、BA分别相交于点F、G，若BG•BA=48，FG=，DF=2BF，求AH的值．【答案】（1）证明见解析；（2）考点：1．圆的综合题；2．三角形的外接圆与外心；3．切线的判定．30．（2016四川省泸州市）如图，在平面直角坐标系中，点O为坐标原点，直线l与抛物线2=+相交于A（1，，B（4，0）两点．y mx nx（1）求出抛物线的解析式；（2）在坐标轴上是否存在点D，使得△ABD是以线段AB为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；（3）点P是线段AB上一动点，（点P不与点A、B重合），过点P作PM∥OA，交第一象限内的抛物线于点M，过点M作MC⊥x轴于点C，交AB于点N，若△BCN、△PMN的面积S△B C N、S△P M N满足S△B C N=2S△P M N，求出MNNC的值，并求出此时点M的坐标．【答案】（1）2y=+；（2）D（1，0）或（0）或（0）；（3），M（1，）．综上可知存在满足条件的D 点，其坐标为（1，0）或（0，2）或（0，2）；（3）如图2，过P 作PF ⊥CM 于点F ，∵PM ∥OA ，∴Rt △ADO ∽Rt △MFP ，∴MF ADPF OD==∴MF =，在Rt △ABD 中，BD =3，AD =∴tan ∠ABD =∴∠ABD =60°，设BC =a ，则CN =a ，在Rt △PFN 中，∠PNF =∠BNC =30°，∴tan ∠PNF =3PF PN =，∴FN =，∴MN =MF +FN =PF ，∵S △B C N =2S △P M N ，∴22122=⨯⨯，∴a =PF ，∴NC =a =PF ，∴MNNC ==，∴MN =NC ==a ，∴MC =MN +NC =（）a ，∴M 点坐标为（4﹣a ，（）a ），又M 点在抛物线上，代入可得2))a a -+-=（）a ，解得a =3或a =0（舍去），OC =4﹣a =1，MC =，∴点M 的坐标为（1，）．考点：1．二次函数综合题；2．分类讨论；3．动点型；4．存在型；5．压轴题． 31．（2016四川省资阳市）已知抛物线与x 轴交于A （6，0）、B （54-，0）两点，与y 轴交于点C ，过抛物线上点M （1，3）作MN ⊥x 轴于点N ，连接OM ．（1）求此抛物线的解析式；（2）如图1，将△OMN 沿x 轴向右平移t 个单位（0≤t ≤5）到△O ′M ′N ′的位置，MN ′、M ′O ′与直线AC 分别交于点E 、F ．①当点F 为M ′O ′的中点时，求t 的值；②如图2，若直线M ′N ′与抛物线相交于点G ，过点G 作GH ∥M ′O ′交AC 于点H ，试确定线段EH 是否存在最大值？若存在，求出它的最大值及此时t 的值；若不存在，请说明理由．【答案】（1）241921515y x x =-++；（2）①1；②t =2时，EH 最大值为考点：1．二次函数综合题；2．最值问题；3．二次函数的最值；4．存在型；5．平移的性质；6．压轴题．32．（2016山东省临沂市）现代互联网技术的广泛应用，催生了快递行业的高速发展．小明计划给朋友快递一部分物品，经了解有甲、乙两家快递公司比较合适．甲公司表示：快递物品不超过1千克的，按每千克22元收费；超过1千克，超过的部分按每千克15元收费．乙公司表示：按每千克16元收费，另加包装费3元．设小明快递物品x千克．（1）请分别写出甲、乙两家快递公司快递该物品的费用y（元）与x（千克）之间的函数关系式；（2）小明选择哪家快递公司更省钱？【答案】（1）22 (01)157 (1)x xyx x<<⎧=⎨+>⎩甲，=163y x+乙；（2）当12＜x＜4时，选乙快递公司省钱；当x=4或x=12时，选甲、乙两家快递公司快递费一样多；当0＜x＜12或x＞4时，选甲快递公司省钱．当0＜x ＜12或x ＞4时，选甲快递公司省钱．考点：1．一次函数的应用；2．分段函数；3．方案型．33．（2016山东省临沂市）如图，在平面直角坐标系中，直线y =﹣2x +10与x 轴，y 轴相交于A ，B 两点，点C 的坐标是（8，4），连接AC ，BC ．（1）求过O ，A ，C 三点的抛物线的解析式，并判断△ABC 的形状；（2）动点P 从点O 出发，沿OB 以每秒2个单位长度的速度向点B 运动；同时，动点Q 从点B 出发，沿BC 以每秒1个单位长度的速度向点C 运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．设运动时间为t 秒，当t 为何值时，PA =QA ？（3）在抛物线的对称轴上，是否存在点M ，使以A ，B ，M 为顶点的三角形是等腰三角形？若存在，求出点M 的坐标；若不存在，请说明理由．【答案】（1）21566y x x =-，直角三角形；（2）103；（3）M 1（52），M 2（52，M 3（52，2），M 4（52，2-）．（3）存在，∵21566y x x =-，∴抛物线的对称轴为x =52，∵A （5，0），B （0，10），∴AB = 设点M （52，m ）；①若BM =BA 时，∴225()(10)1252m +-=，∴m 1=202+，m 2=202-M 1（52，202+），M 2（52②若AM =AB 时，∴225()1252m +=，∴m 3=2，m 4=2-，∴M 3（52，2），M 4（52，2-）； ③若MA =MB 时，∴222255(5)()(10)22m m -+=+-，∴m =5，∴M （52，5），此时点M 恰好是线段AB 的中点，构不成三角形，舍去；∴点M 的坐标为：M 1（52，202+），M 2（52，202-），M 3（52，2），M 4（52，2-）．考点：1．二次函数综合题；2．动点型；3．存在型；4．分类讨论；5．压轴题．34．（2016山东省德州市）如图，⊙O 是△ABC 的外接圆，AE 平分∠BAC 交⊙O 于点E ，交BC 于点D ，过点E做直线l∥BC．（1）判断直线l与⊙O的位置关系，并说明理由；（2）若∠ABC的平分线BF交AD于点F，求证：B E=EF；（3）在（2）的条件下，若DE=4，DF=3，求AF的长．【答案】（1）直线l与⊙O相切；（2）证明见解析；（3）214．∵AE平分∠BAC，∴∠BAE=∠CAE，∴BE CE，∴∠BOE=∠COE．又∵OB=OC，∴OE⊥BC．∵l∥BC，∴OE⊥l，∴直线l与⊙O相切．（2）∵BF平分∠ABC，∴∠ABF=∠CBF．又∵∠CBE=∠CAE=∠BAE，∴∠CBE+∠CBF=∠BAE+∠ABF．又∵∠EFB =∠BAE +∠ABF ，∴∠EBF =∠EFB ，∴BE =EF ．（3）由（2）得BE =EF =DE +DF =7．∵∠DBE =∠BAE ，∠DEB =∠BEA ，∴△BED ∽△AEB ，∴DE BE BE AE =，即477AE=，解得；AE =494，∴AF =AE ﹣EF =494﹣7=214．考点：圆的综合题．35．（2016山东省德州市）已知，m ，n 是一元二次方程2+430x x +=的两个实数根，且|m |＜|n |，抛物线2y x bx c =++的图象经过点A （m ，0），B （0，n ），如图所示．（1）求这个抛物线的解析式；（2）设（1）中的抛物线与x 轴的另一个交点为抛物线的顶点为D ，试求出点C ，D 的坐标，并判断△BCD 的形状；（3）点P 是直线BC 上的一个动点（点P 不与点B 和点C 重合），过点P 作x 轴的垂线，交抛物线于点M ，点Q 在直线BC 上，距离点P个单位长度，设点P 的横坐标为t ，△PMQ 的面积为S ，求出S 与t 之间的函数关系式．【答案】（1）223y x x =--；（2）△BCD 是直角三角形；（3）S =2213(03)2213 (03)22t t t t t t t ⎧-+<<⎪⎪⎨⎪-<>⎪⎩或．考点：1．二次函数综合题；2．分类讨论．36．（2016江苏省宿迁市）如图，在平面直角坐标系xOy 中，将二次函数21y x =-的图象M 沿x 轴翻折，把所得到的图象向右平移2个单位长度后再向上平移8个单位长度，得到二次函数图象N ．（1）求N 的函数表达式；（2）设点P （m ，n ）是以点C （1，4）为圆心、1为半径的圆上一动点，二次函数的图象M 与x 轴相交于两点A 、B ，求22PA PB +的最大值；（3）若一个点的横坐标与纵坐标均为整数，则该点称为整点．求M 与N 所围成封闭图形内（包括边界）整点的个数．【答案】（1）245y x x =-++；（2）38+（3）25．。

成都市2016年中考数学试题及全解析(精编word版,一题多解)

l1 l2 2 1 3
l1 l2 2 3
1
l1 3 l2 2
1
解析：（法 1，左图），由对顶角性质，∠3=∠1=56° ，由��1 ∥ ��2 得∠2 + ∠3 = 180° ，故∠1=180°− 56°= 124° 。（法 2，中图），由��1 ∥ ��2 得∠3 = ∠1 = 56° ；由补角概念，∠2+∠3=180° ，故∠2=180°− 56°= 124° 。（法 3，右图），由补角概念，∠1+∠3=180° ，故∠3=180°− 56°= 124° 。由��1 ∥ ��2 得∠2 = ∠3 = 124° ；答案：C 6.考点：平面直角坐标系，点的坐标，轴对称。解析：关于 x 轴对称，横坐标不变，纵坐标变为相反数，P(−2,3) → P′(−2, −3)。答案：A 7.考点：解分式方程。解析：方程两边乘以（x − 3），变为2x = x − 3，移项，合并同类项得x = −3。答案：B 8.考点：平均数、方差，好坏比较与稳定性估计。解析：用平均数判断成绩好坏，因为乙和丙的平均数相同且比甲和丁大，先选乙或丙；用方差估计稳定性，因为甲和丙的方差相同且比乙和丁小，应选乙和丙；综合两者选丙。答案：C 9.考点：二次函数基本概念、图像和性质。解析：由y = 2x 2 − 3知，二次项系数为 2，开口向上，A 错；当 x=2 时，y=5，B 错；
学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛,各组
的平时成绩的平均数x (单位:分)及方差s 2 如下表所示：甲 x s2 7 1 乙 8 1.2 丙 8 1 丁 7 1.8
如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是（） (A)甲 (B)乙 (C)丙 (D)丁

2016年全国中考数学真题分类锐角三角函数(习题解析)

2016年全国中考数学真题分类锐角三角函数一、选择题1.（2016江苏无锡，3，3分）sin30°的值为（） A ．12 B ．32 C ．22 D ．33【答案】A ．2．（2016江苏无锡，7，3分）tan45º的值为（）A ．12B ．1C ．22 D ． 2【答案】B3、（2016广东，8，3分）如图，在平面直角坐标系中，点A 那么cos 的值是（） A 、34 B 、43 C 、35 D 、45答案：D4．（2016山东烟台，5，3分）如图，是我们数学课本上采用的科学计算器面板，利用该型号计算器计算cos55°，按键顺序正确的是（）A ．B ．C ．D ．【答案】CαoxyAABCD图35. （2016兰州，4，4分）在Rt ΔABC 中，∠C=900，sinA=53,BC=6,则AB=（）A. 4B. 6C. 8D. 10 【答案】D6.(2016四川乐山，5,3分）如图3，在Rt ABC ∆中，90BAC ∠=，AD BC ⊥于点D ，则下列结论不正确．．．的是 ()A sin ADB AB =()B sin ACB BC =()C sin ADB AC =()D sin CDB AC=答案：C7.（2016，浙江金华，8,3分）一座楼梯的示意图如图所示，BC 是铅垂线，CA 是水平线，BA 与CA 的夹角为θ.现要在楼梯上铺一条地毯，已知CA =4米，楼梯宽度1米，则地毯的面积至少需要（ )A.4sin θ米2 B. 4cos θ米2 C. 44tan θ+（）米2 D. 44tan θ+（）米2 【答案】D8.(2016福州，9，3分)如图，以O 为圆心，半径为1的弧交坐标轴于A ，B 两点，P 是AB 上一点(不与A ，B 重合)，连接设∠POB ＝α，则点P 的坐标是( )A ．(sin α，sin α)B ．(cos α，cos α)C ．(cos α，sin α)D ．(sin α，cos α)CBA4 θ1单位：米【答案】C9．（2016，山东淄博，4，4分）如图是由边长相同的小正方形组成的网格，A，B，P，Q四点均在正方形网格的格点上，线段AB，PQ相交于点M，则图中∠QMB的正切值是（）A．B．1 C．D．2【答案】A5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39. 二、填空题1.(2016年甘肃白银、张掖，13，4分)如图，点A (3，t )在第一象限，射线OA 与x 轴所夹的锐角为α，tan α＝32，则t 的值是______．[答案]9216．（2016湖北孝感，16，3分）如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”，图中的四个直角三角形是全等的，如果大正方形ABCD 的面积是小正方形EFGH 面积的13倍，那么tan ADE 的值为 ☆ ．第13题图ABCDEF GH【答案】322.(2016福州，18，4分)如图，6个形状、大小完全相同的菱形组成网格，菱形的顶点称为格点．已知菱形的一个角(∠O)为60°，A，B，C都在格点上，则tan∠ABC的值是．【答案】32【思路分析】要求三角函数，必须有直角三角形，构造直角三角形，如图延长BC到下一格交点处D，连接AD，△BDA即是直角三角形．因为∠O＝60°，小网格是菱形，所以∠ADE＝30°，∠BDE＝60°．在Rt△ADC中ADDC＝3，所以tan∠ABC＝ADBD＝2ADDC＝32．（2016山东菏泽，13，3分）如图，在正方形ABCD外作等腰直角△CDE，DE=CE，连接BE，则tan ∠EBC= ．【答案】313.（2016山东临沂， 19，3分）一般地，当α、β为任意角时，sin（α+β）与sin（α—β）的值可以用下面的公式求得：sin （α+β）=sin αcos β+cos αsin β；sin （α—β）= sin αcos β—cos αsin β . 例如sin 90°=sin （60°+30°）= sin 60°cos 30°+cos 60°sin 30°=21212323⨯+⨯=1 . 类似地，可以求得sin 15°的值是 . 【答案】624.5．（2016四川自贡，15，4分）如图，在边长相同的小正方形网格中，点A 、B 、C 、D 都在这些小正方形的顶点上，AB ，CD 相交于点P ，则的值= 3 ，tan ∠APD 的值= 2 ．【答案】3，2．5.14．（2016山东青岛，14，3分）如图，以边长为20cm 的正三角形纸板的各顶点为端点，在各边上分别截取4cm 长的六条线段，过截得的六个端点作所在边的垂线，形成三个有两个直角的四边形．把它们沿图中虛线剪掉，用剩下的纸板折成一个底为正三角形的无盖柱形盒子，则它的容积为 cm 3．【答案】448﹣4806. 7. 8. 9. 10. 11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.三、解答题21、（2016广东，21，7分）如图，Rt△ABC中，∠B=30°，∠ACB=90°，CD ⊥AB 交AB于D ，以CD 为较短的直角边向 △CDB 的同侧作Rt △DEC ，满足∠E=30°， ∠DCE=90°，再用同样的方法作Rt △FGC ， ∠FCG=90°，继续用同样的方法作Rt △HCI ，∠HCI=90°，若AC=a ，求CI 的长.解析：由题意，知：∠A ＝∠EDC ＝∠GFC ＝∠IHC ＝60°，因为AC ＝a ，故DC ＝ACsin60°＝3a ，同理：CF ＝DCsin60°＝34a ，CH ＝CFsin60°＝33a ， CI ＝CHsin60°＝98a 。

2016年中考数学几何选择填空压轴题配答案

2016年中考数学试卷答案及解析与点评25

2016年中考数学压轴题70题精选(含答案及解析)

浙江省中考数学《填空压轴题》专题练习含答案解析

2016天津中考数学压轴题及答案解析

中考数学几何压轴题及答案及答案

(完整word版)2016年中考数学压轴题70题精选(含答案及解析),推荐文档

上海市2016年中考数学试卷及答案解析

(完整版)中考数学几何综合压轴题初三难题训练(真题附答案)

中考数学几何压轴题(有关三角形、四边形)的综合专题(含答案解析)

北京市2016年中考数学试题含答案解析

中考数学几何选择填空压轴题四边形难题(含答案))

2016年中考数学选择压轴题专题练习及解析

2016年中考数学试题(含答案)

中考数学几何压轴题及答案及答案

2016年中考数学试题分项版解析(第02期)专题16 压轴题

成都市2016年中考数学试题及全解析(精编word版,一题多解)

2016年全国中考数学真题分类 锐角三角函数(习题解析)

2016年全国中考数学真题分类锐角三角函数(习题解析)