统计学
什么是统计学?

什么是统计学?作为一门综合性学科,统计学在现代社会中发挥着越来越重要的作用。
那么,在具体了解它的实际应用之前,让我们先来探讨一下,什么是统计学?1. 统计学的定义统计学是研究如何收集、分析、解释和展示数据的学科。
简单来说,它是一种用于从数据中提取有关事物的定量信息的方法。
统计学从根本上来说就是一种科学,其研究对象是数据,它应用数学、概率论、逻辑学等多种工具,旨在通过分析数据来分析现象、发现规律。
2. 统计学的应用领域统计学作为一门应用型学科,广泛应用于众多领域。
2.1 生物学在生物学中,统计学被用于解释生命现象,如遗传和进化的机制、药物治疗的有效性等等。
例如,在生物医学研究中,统计学的应用包括临床试验、药物疗效研究等等。
2.2 经济学统计学在经济学中也有重要的应用,可以用来衡量经济上的数据,如国民生产总值、物价指数、就业率等。
它可以分析消费者的购买习惯、市场需求及供应情况,从而为经济决策提供参考意见。
此外,公司能够使用统计学来进行预测和财务计划。
2.3 市场营销在市场营销中,统计学可用于分析消费者行为和市场趋势,帮助企业制定营销战略,提高广告效益等等。
3. 统计学方法了解了统计学的定义和应用领域之后,接下来就是探讨统计学的方法。
3.1 描述性统计学描述性统计学是一种可以帮助我们理解数据的方法,它涵盖了我们可以从数据中获取的所有信息,包括中心趋势、变异程度和分布形状等指标。
3.2 推断性统计学推断性统计学是一种可以通过采样同一群体的某些因素来了解整体群体的方法。
它涉及到估计、假设检验和置信度间隔等内容。
4. 统计学的局限性统计学虽然可以用于对数据进行分析和解释,但是它并不是万能的。
它受到所使用数据的质量和数量限制,也受到分析人员的限制。
另外,一个很重要的问题是统计学并不能直接证明因果关系,它只能通过相关性来证明两个变量之间的关系。
综上所述,统计学是一门关于数据管理和分析的学科,它以数据为基础,运用多种工具和方法帮助人们解答各种问题。
第一章 统计学概述

二、统计学的发展
• (一)古典统计学时期 • 1、国势学派 • 国势学派产生于17世纪的德国,其创始人是海 尔曼·康令(Hermann Conring,1606-1681) 教授。 • 2、政治算术学派 • 治算术学派产生于17世纪中叶的英国,主要代 表人物是威廉· 配第(William Petty,1623-1687) 和约翰· 格朗特(Johan Graunt,1620-1674)。
一、总体和样本
• (一)总体 • 统计总体简称总体,是指由特定的研究目 的确定的一定范围内的所有单位构成的集 合体。 • (二)样本 • 广义而言,样本是指从总体中抽取的部分 单位构成的集合体;但为了符合统计理论 的需要,统计中所指的样本特指从总体中 按照随机原则抽取的部分单位构成的集合。
二、统计标志
三、统计学在我国的应用
• 第一,对系统性及系统复杂性的认识为统 计学的未来发展增加了新的思路。
• 第二,定性与定量相结合的综合集成法将 为统计分析方法的发展提供新的思想。 • 第三,统计科学与其他科学渗透将为统计 学的应用开辟新的领域。
第二节 统计学的特点和分类
• 一、统计学的特点 • 二、统计学的类别
标志与指标的区别和联系。
• 它们的主要区别是:
• 第一、标志是说明总体单位特征的,指标 是说明总体特征的。例如,一个工人的工 资是数量标志,全体工人的工资总额是统 计指标。 • 第二、标志有用文字表示的品质标志和用 数值表示的数量标志,指标则都是用数值 表区别和联系。
• 在该时期,为现代统计学的发展作出重大 贡献的主要统计学家和理论有:20世纪初 英国的戈赛特(W.S. Gosset,1876-1937)的T 分布理论;20年代英国的费雪(R.A. Fisher, 1890-1962)的F分布理论;30年代波兰的尼 曼(J.S. Neyman,1894-1981)等人的假设检验 理论及置信区间估计等理论;40年代美国 的瓦尔德(A. Wasld, 1902-1950)等学者的统 计决策理论,多元分布理论等。
统计学

统计学一、定义:统计学是一门对群体现象数量特征进行计量、描述、分析和推论的科学。
二、:一)统计的含义1、统计工作:资料的搜集、整理和分析这一系列的工作。
2、统计资料:统计工作的成果。
3、统计学:统计工作的理论概括。
二)统计的性质1、统计是调查研究社会的方法之一2、统计是核算的工具之一(会计核算、统计核算、业务核算)3、统计是国家或企业管理、监督的工具三、统计的特点四、统计学的理论基础五、统计学的研究方法(一)数量性(一)历史唯物论(一)大量观察法(二)工具性(二)辨证唯物主义(二)综合指标法(三)广泛性(三)政治经济学(三)归纳推断法(四)总体性(四)数学和计算机(四)大数定律(五)社会性总体:统计总体就是根据一定的目的和要求所确定的研究事物的全体,它是由客观存在的、具有某种相同性质的许多单位组成的集体。
总体单位:总体单位是指构成总体的每一个单位。
关系:统计总体和总体单位并不是固定不变的。
两者可以相互转换。
标志:标志是说明总体单位的属性和特征的名称。
品质标志(用文字表示),如中的性别、籍贯、政治面貌等;数量标志(用数字表示)。
数量标志的具体数值表现称为标志值,如某同学年龄为21岁,21岁就是标志值。
指标:是说明总体的属性和特征的。
任何一个统计指标必须用数字说明。
(标志和指标也是可以相互转换的。
)统计总体中各单位之间的差异称为变异。
正由于总体中各单位之间存在差异,才需要进行统计,也才有各种各样的统计方法。
如果总体各单位之间没有差异,也就没有统计。
在数量标志中,不变的数量标志称为常量或参数。
可变的数量标志称为变量。
变量取值又称为变量值,也就是标志值。
变量按其取值的连续性又分为离散变量和连续变量两种。
统计调查是根据统计的研究目的和任务,有组织、有计划地向客观实际搜集资料的工作过程。
统计调查是搜集资料获得感性认识的阶段,它既是对现象总体认识的开始,也是进行资料整理和分析的基础环节。
搜集统计资料的方式:一种是对原始资料的搜集。
统计学知识点(完整)

基本统计方法第一章概论1•总体(Population ):根据研究目的确定的同质对象的全体(集合) ;样本(Sample ):从总体中随机抽取的部分具有代表性的研究对象。
2.参数(Parameter ):反映总体特征的统计指标,如总体均数、标准差等,用希腊字母表示,是固定的常数;统计量(Statistic ):反映样本特征的统计指标,如样本均数、标准差等,采用拉丁字字母表示,是在参数附近波动的随机变量。
3.统计资料分类:定量(计量)资料、定性(计数)资料、等级资料。
第二章计量资料统计描述1.集中趋势:均数(算术、几何)、中位数、众数2.离散趋势:极差、四分位间距( QR=P75-P25)、标准差(或方差)、变异系数(CV)3.正态分布特征:①X轴上方关于X= 对称的钟形曲线;②X= 时,f(X)取得最大值;③ 有两个参数,位置参数和形态参数;④曲线下面积为1,区间土的面积为68.27% ,区间±1.96 的面积为95.00%,区间±2.58 的面积为99.00%。
4.医学参考值范围的制定方法:正态近似法:X U /2 S ;百分位数法:P2.5-P 97.5。
第三章总体均数估计和假设检验1.抽样误差(Sampling Error ):由个体变异产生、随机抽样造成的样本统计量与总体参数的差异。
抽样误差不可避免,产生的根本原因是生物个体的变异性。
2.均数的标准误(Standard error of Mean, SEM):样本均数的标准差,计算公式:八n。
反映样本均数间的离散程度,说明抽样误差的大小。
3.降低抽样误差的途径有:①通过增加样本含量n;②通过设计减少S。
4.t分布特征:①单峰分布,以0为中心,左右对称;②形态取决于自由度,越小,t值越分散,t分布的峰部越矮而尾部翘得越高;③当逼近a ,S X逼近X, t分布逼近u分布,故标准正态分布是t分布的特例。
5.置信区间(Con fide nee In terval , CI ):按预先给定的概率(1-)确定的包含总体参数的一个范围,计算公式:X t /2, S X或X U /2, S X。
统计学的含义、研究对象、特点和基本方法

统计学的含义、研究对象、特点以及基本方法一、统计学的含义统计学是一门通过搜集、整理、分析数据等手段,以达到推断所测对象的本质,甚至预测对象未来的一门综合性科学。
它是应用数学的一个分支,其研究领域包括数据的收集、分析、解释和呈现,以及通过这些数据来做出决策和预测。
统计学的核心在于收集和分析数据,从而提取出有用的信息,为决策提供科学依据。
二、统计学的研究对象统计学的研究对象十分广泛,包括社会、经济、自然现象等各个领域的数量关系。
其主要研究对象可以概括为以下几个方面:社会经济统计:研究社会经济现象的数量方面,如人口、就业、收入、消费等。
通过对这些数据的收集和分析,可以了解社会经济的运行状态和发展趋势,为政府和企业提供决策支持。
自然科学统计:研究自然现象的数量规律,如物理、化学、生物等领域的实验数据。
通过对这些数据的统计分析,可以发现自然现象的内在规律,推动科学研究的进步。
工程统计:研究工程技术的数量问题,如产品质量控制、可靠性分析、优化设计等。
工程统计可以帮助提高产品质量、降低生产成本,推动工程技术的发展。
医学统计:研究人体健康与疾病的数量关系,如疾病发病率、药物疗效等。
医学统计可以为医学研究提供科学依据,推动医学事业的进步。
三、统计学的特点数量性:统计学是通过数据来揭示事物本质和规律的,因此具有数量性的特点。
它通过对数据的收集、整理和分析,提取出有用的数量信息,为决策提供科学依据。
总体性:统计学研究的是总体而非个体,它通过对总体数据的分析来推断总体的特征。
这种总体性的特点使得统计学能够更全面地反映事物的本质和规律。
具体性:统计学研究的是具体事物的数量关系,而不是抽象的概念。
它通过对具体事物的数据分析,揭示事物的内在规律和联系。
社会性:统计学研究的对象广泛涉及社会、经济、自然现象等各个领域,因此具有社会性的特点。
它通过对这些领域的数据分析,为政府、企业和社会提供决策支持。
四、统计学的基本方法描述性统计:描述性统计是通过对数据进行整理和描述,以揭示数据的分布特征、集中趋势和离散程度等。
统计学

2、社会统计学派
代表人物:德国的克尼斯(K. G. A. Knies)、恩格尔 (C. L. E. Engel)、梅尔(G. V. Mayr)等。 他们强调统计学是研究社会现象 的社会科学,包括统计资料的搜集、 整理和分析研究,目的是要揭示社会 现象内部的联系。
1、统计学的研究对象 “统计学是一门研究客观事物数量方面的方法论 科学,其研究对象是客观现象总体的数量方面,即 现象总体的数量特征和数量关系。” ——刘德智主编的《统计学》教材 “统计学的研究对象是统计工作的规律。” ——暨南大学韩启南、韩兆洲所编的《统计学》教材
2、统计学的学科体系
a、理论统计学与应用统计学(P6~8)
1.数量性
统计工作的目的是从数量上认识事物的 性质和规律,在统计工作过程中始终要 求用数据说话。
原始社会后期: 统计萌芽于计数活动; 奴隶制国家产生:使统计日显重要;
封建社会时期: 统计已具规模;
资本主义的兴起: 统计扩展到社会经济各方面。
目前,人们一般认为统计学作为一门系统的科学, 产生于17世纪中叶 ,距今只有300多年的历史。
可分为三个时期:
古典统计学时期
(17世纪中叶-18世纪中叶)
与统计教育的现状,特别是统计学完全成为一级学科后面对的大好发展机遇,以
及在做大的基础上如何做强统计学科需要我们重视、研究和解决的主要问题。
http://202.195.176.39/showart.asp?id=265
第二节 统计工作的特点和方法
一、统计工作的基本特点(统计学的基本特点)
见P11年)
07 理学 0701 0702 0703 0704 0705 0706 0707 数学 物理学 化学 天文学 地理学 大气科学 海洋科学 0708 0709 0710 0711 0712 0713 0714 地球物理学 地质学 生物学 系统科学 科学技术史 生态学 统计学
统计学

1.统计学的含义:统计学是研究统计工作的理论与方法的一份方法论学科。
2.统计学研究的对象:统计是研究如何搜索、整理和分析社会经济现象的数量方面的方法和方法体系。
3.统计研究的基本程序:①统计设计②统计调查③统计整理④统计分析⑤统计预测⑥统计决策4.统计研究的基本方法:①大量观察法②统计分组法③综合分析法④归纳推断法5.统计的作用:①反馈信息②支持决策③提供咨询④实施监督6.总体:它是由若干个具有共同性质的个体构成的集合,即研究对象的全体。
总体中所含的每个个体称为总体单位。
7.总体中所含的总体单位数称为总体容量。
8.样本:总体中抽出的一部分总体单位构成的集合叫样本。
样本中的每一个总体单位又叫样本单位或调查单位。
9.标志:是说明总体单位属性或特征的名称,有品质标志和数量标志之分,品质标志是说明总体单位质的属性或特征的名称。
品质标志在总体单位上的表现是不能用数值来表达的。
数量标志是说明总体单位量的特征的名称,数量标志在总体单位上的表现必须用数值表示。
10.指标:是用来说明统计总体数量特征的,有两重含义:1总体现象数量化的概念或范畴,如人口数、国内生产总值、商品销售额等。
2总体现象数量特征的概念和具体数值。
11.指标应包括的三要素:指标名称、计量单位、计算方法。
12.指标和标志存在的区别:⑪统计指标是说明总体数量特征的,而标志是说明总体单位特征的⑫标志有不能用数量表示的品质标志和能用数量表示的数量标志之分,而指标都是用数值表示的。
13.指标和标志的联系:⑪统计指标的数值是从个体的数量标志值直接进行汇总或间接计算分析而来的⑫指标和数量标志之间存在着互变关系14.变异:是指在选定的标志下,总体单位的表现不是完全相同,而是存在差异的,这种差异就叫变异。
15.变量:即为可变的数量标志。
16.统计设计:就是根据统计研究的对象的性质和研究目的,对统计工作各个方面和各个环节的通盘考虑和安排。
17.统计设计的作用:①统计设计是对总体的定性认识和定量认识过渡的桥梁②统计设计是保证统计工作顺利进行的必要条件。
统计学

一、名词解释1、定性数据是指只能用文字或数字代码来表现事物的品质特征或属性特征的数据,具体又分为定类数据与定序数据。
(定类数据是对事物进行分类的结果,表现为类别,由定类尺度计量而成。
定序数据是对事物按照一定的排序进行分类的结果,表现为有顺序的类别,由定序尺度计量而成。
)2、定量数据是指用数值来表现事物数量特征的数据,具体又分为定距数据与定比数据两种。
(定距数据是一种不仅能反映事物所属的类别和顺序,还能反映事物类别或顺序之间数量差距的数据,由定距尺度计量而成。
定比数据是一种不仅能体现事物之间数量差距,还能通过对比运算,即计算两个测度值之间的比值来体现相对程度的数据,由定比尺度计量而成。
)3、长期趋势是指时间数列中指标值在较长一段时间内,由于受普遍的、持续的、决定性的基本因素的作用,使发展水平沿着一个方向持续向上或向下发展或持续不变的基本态势。
4、季节变动是指数列中各期指标值随着季节交替而出现周期性的、有规则的重复变动,这里的时间通常指一年。
5、循环变动是指时间数列中各项指标值随着时间变动发生周期性的重复变化,但循环变动所需的时间更长,重复变动的规律性、变动周期和时间也不像季节变动来得稳定、可以预测。
6、不规则变动是由未能得到解释的一些短期波动所组成的,常指时间数列由于受偶然因素或意外条件影响,在一段时间内(通常指短期内)呈现不规则的或自然不可预测的变动。
7、相关关系,也称统计相关,是指现象之间存在的非确定性的数量依存关系。
8、点估计也称定值估计,就是以样本观测数据为依据,对总体参数做出确定值的估计,也就是用一个样本的具体统计值去估计总体的未知参数。
9、区间估计,就是指用一个具有一定可靠程度的区间范围来估计总体参数,即对于未知的总体参数θ,想办法找出两个数值θ1和θ2(θ1<θ2),使θ处于区间(θ1,θ2)内的概率为1-α,即π(θ1<θ<θ2)=1-α。
区间(θ1,θ2)为总体参数的估计区间或置信区间,θ1为估计下限或置信下限,θ2为估计上限或置信上限。
统计学概述

(一)统计学按统计方法的构成分为描述统计学和推断统计学
描述统计学主要是对现象的某一特征的变化加以记录、整理 和反映,统计数据是对总体的描述和观测结果的表现。
推断统计学主要是研究随机现象数量特征的,即从现象总体 中随机抽取一部分个体构成样本,并根据样本数据对现象总体作 出估计。
(二)统计学按研究领域分为理论统计学和应用统计学
根据样本来推断总体数量特征的方法称为统计推断法。
1 -8
第三节 统计学中的几个基本概念
一、统计总体与总体单位 1、什么是统计总体(简称总体)
凡是客观存在的,在同一性质基础上由许许多多个别事物构 成的整体,称为统计总体。 2、什么是总体单位
构成总体的每一个个别事物,称为总体单位。 3、统计总体的分类
按照某种标志把总体划分为若干性质不同的组成部分的一 种统1计-方7 法。
第二节 统计的工作过程及研究方法
(三)综合指标法 运用各种统计指标来反映总体的一般数量特征和数量关系的
研究方法。 (四)统计模型法
用适当的数学模型去拟合现实经济现象相互关系的一种研究 方法,借以反映社会经济现象之间的数量关系和数量特征,从而 揭示其发展变化规律。 (五)归纳推断法
离散型变量是指其变量值在变动过程中呈跳跃式变化,用整 数表示而不能以带小数表示的变量。
连续型变量是指其变量值在变动过程中呈连续不断地变化, 在任意小的两个数值之间可以作无限次分割,能以带小数表示的 变量1 。- 12
第三节 统计学中的几个基本概念
四、统计指标与统计指标体系 (一)统计指标的分类
1.根据统计指标的表现形式不同,可以分为总量指标、相对 指标与平均指标
联系: (1)在统计中有许多统计指标的数值是由单位标志值直接汇 总而1 来- 11;
《统计学》完整ppt课件

适用于等级资料或无法精确测量的数据,如医学 领域的疗效评价、心理学中的量表评分等。
3
秩和检验的优缺点
优点在于对数据分布的假设较为宽松,适用范围 广;缺点是当样本量较大时,检验效率可能降低 。
符号检验
符号检验的基本原理
通过比较样本数据的中位数或均值与某个参考值的大小关 系,判断总体分布是否存在显著差异。
推论性统计分析
介绍如何在Excel中进行推论性统计分析, 如假设检验、方差分析等。
Python编程实现统计分析案例展示
Python统计分析库介绍
数据处理与可视化
简要介绍Python中常用的统计分析库,如 NumPy、Pandas、SciPy等。
演示如何使用Python进行数据清洗、处理 及可视化,包括缺失值处理、异常值检测 等。
相关分析与回归分析
相关分析
研究两个或多个变量之间相关关系的统计分析方法,通过计算相关系数来衡量变量之间 的相关程度。
回归分析
研究因变量与一个或多个自变量之间关系的统计分析方法,通过建立回归模型来预测因 变量的取值。
04
CATALOGUE
非参数统计方法
卡方检验
卡方检验的基本原理
通过比较实际观测值与理论期望值之间的差异,判断两个或多个分 类变量之间是否存在显著关联。
03
CATALOGUE
推论性统计方法
参数估计方法
点估计
用样本统计量直接作为总体参数的估计值。
区间估计
根据样本统计量和抽样分布,构造一个包含总体参数的真值的置信区间,并给出该区间被总体参数真值覆盖的概 率。
假设检验原理及步骤
假设检验的基本原理
先对总体参数提出一个假设,然后利用样本信息判断这一假设是否合理,即判断总体参数与假设值是 否有显著差异。
统计学
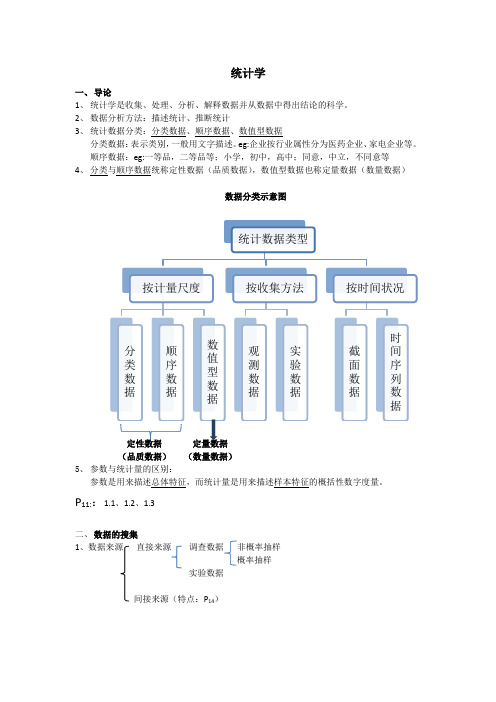
统计学一、导论1、统计学是收集、处理、分析、解释数据并从数据中得出结论的科学。
2、数据分析方法:描述统计、推断统计3、统计数据分类:分类数据、顺序数据、数值型数据分类数据:表示类别,一般用文字描述。
eg:企业按行业属性分为医药企业、家电企业等。
顺序数据:eg:一等品,二等品等;小学,初中,高中;同意,中立,不同意等4、分类与顺序数据统称定性数据(品质数据),数值型数据也称定量数据(数量数据)数据分类示意图(品质数据)(数量数据)5、参数与统计量的区别:参数是用来描述总体特征,而统计量是用来描述样本特征的概括性数字度量。
P11::1.1、1.2、1.3二、数据的搜集1、数据来源直接来源调查数据非概率抽样概率抽样实验数据间接来源(特点:P14)茎叶图箱线图直方图累积频数分布表条形图、帕累托图、饼图、环形图、频数分布表三、 数据的图表展示1、 数据的预处理包括:审核、筛选、排序。
2、 品质数据(包括分类与顺序数据)主要进行分类整理,数值型数据进行分组整理。
图形展示分类数据:条形图、帕累托图、饼图、环形图、频数分布表顺序数据:条形图、帕累托图、饼图、环形图、频数分布表、累积频数分布表数据类型原始数据:茎叶图、箱线图条形图数值型数据分组数据:直方图帕累托图 +以上 时间序列数据线图+饼图、环形图多变量数据:散点图、气泡图、雷达图频数分布表即:(图表展示金字塔)3、 比例与比率比例=各个部分的数据全部数据(<1)比率=类别数据1类别数据2(可能>1,<1, =1)4、 条形图与直方图的区别1、 条形图宽度固定(无意义),用长度表示频数;直方图宽度表示组距,高度表示频数(或频数/组距),用面积表示频数。
2、 条形图各矩形分开,直方图则连续。
3、 条形图用来表示分类数据,直方图表示数值型数据。
单变量值分组:离散变量或变量值较少 5组距分组:连续变量或变量值较多5、 组距分组步骤:确定组数(5-15组)确定组距(5或10的倍数)频数分布表(上组限不在内a ≤X <b ) 6、 组中值=上限值+ 下限值2(为反映各组数据的一般水平,可以用组中值代表)前提:各组数据在本组内呈均匀分布或在组中值两侧呈对称分布。
统计学

统计学1.1统计有三种含义,即统计活动、统计数据和统计学。
1. 统计活动又称统计工作,是指收集、整理和分析统计数据,并探索数据的内在数量规律性的活动过程。
2. 统计数据统计资料,即统计活动过程所获得的各种数字资料和其他资料的总称。
3. 统计学统计学是指阐述统计工作基本理论和基本方法的科学,是对统计工作实践的理论概括和经验总结。
1.2数据的计量尺度①定类尺度:对事物进行平行的分类只能区分事物之间的类别,但不能比较类别间的大小;使用时必须符合类别穷尽和互斥的要求;主要表现为频数或频率。
②定序尺度:对事物分类的同时给出各类别的顺序。
不仅能区分事物类型,还能比较类间的优劣和顺序;使用时必须符合类别穷尽和互斥的要求;统计量主要是频数和累计频数。
③定距尺度:是对事物类别或次序之间间距的测度。
不仅能区分事物类型,进行排序、比较大小,还可以精确地计量大小的差异;没有绝对零点。
④定比尺度:对事物之间比值的一种测度。
不仅能区分事物类型,进行排序、比较大小,计量大小的差异,还能计算两个测度值之间的比值;具有绝对零点。
1.3统计调查组织方式普查是为某一特定目的而专门组织的一次性全面调查方式。
抽样调查从总体中随机抽取一部分单位作为样本进行调查,并根据样本调查结果来推断总体特征的数据收集方法。
统计报表是按照国家有关法规规定,自上而下统一布置,自下而上逐级填报的一种调查组织方式。
重点调查是从全部总体中选择少数重点单位进行调查,尽管在全部总体单位中出现的频数极少,但其某一数量标志在所要研究的数量标志值总量中却占有很大的比重。
典型调查是从全部总体单位中选择一个或几个有代表性的单位进行深入细致的调查。
1.4描述统计:研究如何取得反映客观现象的数据,并通过图表形式对所搜集的数据进行加工处理和显示,进而通过综合、概括与分析得出反映客观现象的规律性数量特征。
推断统计:研究如何根据样本数据去推断总体数量特征。
2.1数据审核:准确性审核、全面性审核、及时性审核2.3频数分布分组方法:1)单变量值分组:将一个变量值作为一组;适合于离散变量且变量值较少的情况。
统计学

一、名词解释1、统计学:收集、处理、分析、解释数据并从数据中得出结论的科学。
2、总体:包含所研究的全部个体的集合。
3、样本:从总体中抽取的一部分元素的集合。
4、统计量:描述样本特征的概括性数字度量。
5、描述统计:研究的是数据收集、处理、汇总、图表描述、概括与分析等统计方法。
6、推断统计:研究如何利用样本数据来推断总体特征的统计方法。
7、相关系数:根据样本数据计算的度量两个变量之间线性关系强度的统计量。
8、参数估计:用样本统计量估计总体参数。
9、点估计:用样本统计量的某个取值直接作为总体参数的估计值.10、区间估计:在点估计基础上,给出总体参数估计的一个区间范围,该区间常由样本统计量加减估计误差得到。
11、简单随机抽样:从总体N个单位的抽样框中随机地、一个个地抽取n个单位作为样本,每个单位入样概率相等。
12、分层抽样:将抽样单位按某种特征或某种规则划分为不同的层,从不同层中独立随机地抽取样本。
13、整群抽样:抽样时直接抽取群,然后对中选群中的所有单位全部实施调查。
14、系统抽样:将总体中的所有单位按一定顺序排列,在规定的范围内随机地抽取一个单位作为初始单位,然后按事先规定好的规则确定其他样本单位。
15、概率抽样(随机抽样):遵循随机原则进行的抽样,总体中每个单位都有一定的机会被选入样本。
16、非概率抽样:根据研究目的对数据的要求,采用某种方式从总体中抽出部分单位对其实施调查。
17、参数:描述总体特征的概括性数字度量。
18、估计量:在参数估计中,用来估计总体参数的统计量称为估计量。
19、抽样误差:由抽样的随机性引起的样本结果于总体真值之间的误差。
20、非抽样误差:除抽样误差之外,由其他原因引起的样本观察结果与总体真值之间的差异。
21、频数:落在某一特定类别或组中的数据个数。
22、频数分布:把各个类别及落在其中的相应频数全部列出,并用表格形式表现出来。
23、列联表:由两个或两个以上变量交叉分类的频数分布表称为列联表。
统计学ppt(全)

概率沦研究起源于17世纪中叶意大利文艺复兴时代,代表人物主要有法国的拉普拉斯和比利时的凯特勒 古典统计时期的概率论基本上是独立发展的,最开始的概率论是从对赌博的研究开始。它与统计学(主要是指政治算术)没有太多的联系 从19世纪中叶到20世纪中叶,概率论的进一步发展为数理统计学的形成和发展奠定了基础。主流从描述性统计学向推断统计学发展 本世纪50年代以后,统计理论、方法和应用进入了一个全面发展的阶段
统计指标体系
由若干个相互联系相互制约的统计指标组成的一个统计指标系统 基本统计指标体系 专题统计指标体系
几种常用的统计软件 (Software)
典型的统计软件 SAS SPSS MINITAB STATISTICA Excel
第一章 绪论
第一节 统计与统计学 第二节 统计学的产生与发展 第三节 统计学的研究对象与方法 第四节 统计学的要素和指标
学习目标
1. 理解统计与统计学的含义 2. 理解统计学的对象和方法 了解统计学的产生与发展过程
第一节 统计与统计学
一. 统计与统计学的含义 二. 统计学的性质和作用
统计数据的内在规律 (一些例子)
正常条件下新生婴儿的性别比为107:100 投掷一枚均匀的硬币,出现正面和反面的频率各为1/2;投掷一枚骰子出现1~6点的频率各为1/6 农作物的产量与施肥量之间存在相关关系
统计学的应用领域
统计学
经济学
管理学
医学
工程学
社会学
…
应用统计的领域
actuarial work (精算) agriculture (农业) animal science (动物学) anthropology (人类学) archaeology (考古学) auditing (审计学) crystallography (晶体学) demography (人口统计学) dentistry (牙医学) ecology (生态学) econometrics (经济计量学) education (教育学) election forecasting and projection (选举预测和策划) engineering (工程) epidemiology (流行病学) finance (金融) fisheries research (水产渔业研究) gambling (赌博) genetics (遗传学) geography (地理学) geology (地质学) historical research (历史研究) human genetics (人类遗传学)
统计学

统计学概述统计学是一门通过搜索、整理、分析数据等手段,以达到推断所测对象的本质,甚至预测对象未来的一门综合性科学。
其中用到了大量的数学及其它学科的专业知识,它的使用范围几乎覆盖了社会科学和自然科学的各个领域。
统计学主要分为描述统计学和推断统计学。
给定一组数据,统计学可以摘要并且描述这份数据,这个用法称作为描述统计学。
另外,观察者以数据的形态建立出一个用以解释其随机性和不确定性的数学模型,以之来推论研究中的步骤及母体,这种用法被称作推断统计学。
这两种用法都可以被称为应用统计学。
另外还有数理统计学专门讨论这门科目背后的理论基础。
统计学,英文Statistics,最早源于现代拉丁文statisticum collegium (国会)以及意大利文statista (国民或政治家)。
德文Statistik,代表对国家的资料进行分析的学问,也就是“研究国家的科学”。
统计学是一门很古老的科学,一般认为其学理研究始于古希腊的亚里斯多德时代,迄今已有两千三百多年的历史。
它起源于研究社会经济问题,在两千多年的发展过程中,统计学至少经历了“城邦政情”,“政治算数”和“统计分析科学”三个发展阶段。
所谓“数理统计”并非独立于统计学的新学科,确切地说:它是统计学在第三个发展阶段所形成的所有收集和分析数据的新方法的一个综合性名词。
概率论是数理统计方法的理论基础,但是它不属于统计学的范畴,而属于数学的范畴。
统计学的发展过程的三个阶段:1).城邦政情(Matters of state)“城邦政情”阶段始于古希腊的亚里斯多德撰写“城邦政情”或“城邦纪要”。
他一共撰写了一百五十余种纪要,其内容包括各城邦的历史、行政、科学、艺术、人口、资源和财富等社会和经济情况的比较、分析,具有社会科学特点。
“城邦政情”式的统计研究延续了一两千年,直至十七世纪中叶才逐渐被“政治算数”这个名词所替代,并且很快被演化为“统计学”(Statistics)。
什么是统计学?统计学对我们的生活有哪些影响?

什么是统计学?统计学对我们的生活有哪些影响?
统计学作为一门研究数据收集、分析与解释的学科,涉及各个领域。
统计学在经济学、社会学、医学、科学研究等方面都有广泛应用,对我们的生活产生深远影响。
一、什么是统计学?
统计学是一门涉及搜集、整理、分析、解释和表示数据的学科。
它用于收集运算和解析数据,帮助我们发现并理解事件之间的联系。
二、统计学对我们的生活有哪些影响?
1.数据分析
统计学可以通过数学建模和数据分析解释各种事件之间的联系。
它为政府、企业和个人进行决策提供了重要支持。
2.医学研究
统计学在医学研究中的应用越来越广泛。
通过对数据的分析,可以对新药物、疫苗和治疗方法进行临床试验,这对预防和治疗各种疾病非常有帮助。
3.财务决策
统计学的应用使得我们能够进行复杂的财务决策,例如预算制定、项
目选择、股票投资和风险管理等。
4.社会学研究
社会学研究涵盖了诸如人口学、家庭结构、教育、收入和职业等方面。
统计学在这些方面的应用有助于研究不同群体间的差异和变化,了解
并改善社会现象。
5.科学研究
统计学在科学研究中广泛应用,例如物理学、化学、地理和气象学等
领域。
它有助于提炼数据模型,分析数据趋势,预测和解释自然现象。
总之,统计学是一门非常重要的学科,广泛应用于各个领域,对我们
的生活产生了深远影响。
通过掌握统计学的基本原理和技能,我们可
以更好地理解并应对各种挑战。
什么是统计学?

什么是统计学?统计学是一门研究如何收集、分类、分析和解释数据的科学。
它的诞生可以追溯到19世纪初,最初目的是在天文学和管理学领域中支持决策制定。
随着科技的发展和数据的大量产生,统计学逐渐被应用于更广泛的领域,如医学、经济学、社会学、心理学等。
下面,我们将逐一揭开统计学的奥秘。
一、基本概念统计学的基本概念包括总体、样本、变量、统计量和假设检验等。
1. 总体和样本总体是指研究对象的全体,而样本是从总体中随机抽取的一部分。
样本可以代表总体,但不一定完全准确。
研究中,我们经常需要对总体进行推断,但由于无法对总体进行直接观察和测量,因此必须通过样本进行推断。
2. 变量变量是指研究对象的某些属性或特征,可以是数值型或非数值型。
数值型变量可以进一步分为离散型和连续型,非数值型变量可以分为名义型和有序型。
变量是统计学中最基本的概念之一,因为所有的统计分析都依赖于变量。
3. 统计量和假设检验统计量是对样本数据加以计算后得出的指标,如均值、标准差、相关系数等。
假设检验是一种统计方法,用于检查一个假设是否成立。
通常会设立一个零假设和一个备择假设,然后通过检验统计量与临界值的大小关系,来判断零假设是否成立。
二、统计学的方法统计学的方法可以分为描述统计和推论统计。
1. 描述统计描述统计是对数据进行描述、总结和展示的方法,主要包括频数分布表、直方图、饼图、条形图、箱线图等。
这些图表可以直观地反映数据的分布情况、中心位置和离散程度等。
2. 推论统计推论统计是从小样本数据中推断总体参数的方法,主要包括参数估计和假设检验。
在参数估计中,通过样本数据对总体某个参数的取值进行估计,并给出相应的置信区间。
在假设检验中,通过样本数据对某个假设的真伪进行检验。
三、应用领域统计学广泛应用于各个领域,下面我们来看看其中几个典型的应用领域。
1. 医学在医学研究中,统计学的应用非常广泛。
例如,通过对临床试验数据进行分析,可以确定药物的疗效和副作用;通过对流行病学数据进行分析,可以揭示疾病的流行规律和影响因素。
统计学

方差分析
(二)应用方塞分析条件 二 应用方塞分析条件
方差分析是通过对误差的分析来判断多个正态总体均值是否相等的一种方法,它与前面所 方差分析是通过对误差的分析来判断多个正态总体均值是否相等的一种方法 它与前面所 讲述的比较两组平均值的T检验法一样 有基本的假定条件: 检验法一样,有基本的假定条件 讲述的比较两组平均值的 检验法一样 有基本的假定条件 (1)设检验的因孖有 种水平 1,x2,…xr,是r个相互独立的正态总体 分别服从于 设检验的因孖有r种水平 个相互独立的正态总体,分别服从于 设检验的因孖有 种水平,x 是 个相互独立的正态总体 分 个总体的均值, 为方差. 布,i=1,2,…,R.ui,第i个总体的均值 第 个总体的均值 为方差. (2)Xi j(i=1,2…,r;j=1,2…,n)是分别从总体 i中抽得的简单随机样本 是分别从总体x 是分别从总体 中抽得的简单随机样本. 这就是说,应用方差分析时要求符合下面两个条件 应用方差分析时要求符合下面两个条件: 这就是说 应用方差分析时要求符合下面两个条件 各个水平的测量观察数据,要能够被年作是从服从正态分布的总体中随机抽得的样本 要能够被年作是从服从正态分布的总体中随机抽得的样本. ①各个水平的测量观察数据 要能够被年作是从服从正态分布的总体中随机抽得的样本 各组测量观察数据,是从具有相同方差的相互独立的总体中抽得的 是从具有相同方差的相互独立的总体中抽得的. ②各组测量观察数据 是从具有相同方差的相互独立的总体中抽得的 通常,对第一个条件的要求并不苛刻 而第三个条件则要求必须满足. 对第一个条件的要求并不苛刻,而第三个条件则要求必须满足 通常 对第一个条件的要求并不苛刻 而第三个条件则要求必须满足
(1)统计方法处理的数据必须是受到偶然性的影响而产生差异的 数据. (2)在方法上数学常常是用演绎的方法,即在作结论时,是从一些 假设命题,已知的事实出发,按一定的逻辑推理去得到有关 的结论
统计学

一:统计学(statistics)是应用数学的一个分支,主要通过利用概率论建立数学模型,收集所观察系统的数据,进行量化的分析、总结,并进而进行推断和预测,为相关决策提供依据和参考。
它被广泛的应用在各门学科之上,从物理和社会科学到人文科学,甚至被用来工商业及政府的情报决策之上。
二:统计学是一门关于研究客观事务数量方面和数量关系的方法论科学。
三:统计学是收集处理分析解释数据并从数据中得出结论的科学四:统计学是“对用数字表示的事实或数据进行收集、分类、分析,以及解释的科学”简而言之,统计学就是数据的科学。
五:统计学是一门收集、整理、分析和解释,统计数据的方法科学,其目的是探索数据的内在数量规律性以达到对客观事物的科学认识,也可以说统计学是关于数据的科学,其内容包括数据的收集、分类、汇总、组织、分析、推断和解释。
统计学研究的过程是:收集数据→整理数据→分析数据→解释数据六:统计科学史指导人们进行收集、整理和分析实际资料的一门方法论,它是统计工作的理论概括和总结,是阐述统计工作的基本理论和基本方法。
目前,统计学已经发展成了一个涉及范围广泛,内容丰富多彩的学科体系。
七:统计学是关于统计理论和方法的科学,是研究如何对社会总体的数量特征和规律进行描述,推断,认识的一么办学科。
统计学是统计实践活动经验的科学总结,从理论上和方法上指导统计实践活动。
广义的统计学内涵较宽是指横跨自然科学和社会科学的统计科学理论的综合,既包括运用梳理统计对各种自然现象及其规律进行研究的自然科学统计学,如生物统计、医学统计、气象统计等。
也包括以社会经济现象为研究对象的社会经济统计学及其分支科学,如经济统计学、工业统计学、农业统计学等。
八:根据有关文献记载,英语“statistics”语源出自拉丁语“status”和“statista”是表示国家的概念以及关于各国国家结构和国情方面的只是的总称。
实际上英文statistics这个词有两个含义:当它一单数名词出现时表示统计学,当它一复数名词出现时表示统计资料或统计数据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
统计基础知识与统计务实第一章总论1、统计学产生于17世纪中叶的欧洲2、统计的发展阶段(1)古典统计学:政治算数派(威廉·配第)国势学派(海尔曼·康令、阿哼尔华)(2)近代统计学:数理统计学派(创始人是比利时的阿道夫·凯特勒)社会经济统计学派(德国学者克尼斯创始,梅尔和恩格尔)(3)现代统计学:1907年3、统计的涵义:统计工作:即统计实践活动,指利用科学的方法,对社会经济现象的数量方面的信息资料进行搜集、整理和分析的工作过程。
统计资料:是在统计工作中取得的,反映社会现象的各项数据资料以及与之相关的其他实际资料的总称。
统计学:是指研究如何对统计资料进行搜集、整理、和分析的理论与方法的科学。
4、统计工作、统计资料和统计学的关系第一,统计工作与统计资料的关系是统计活动与统计成果的关系;第二,统计工作与统计学的关系是统计实践和统计理论的关系;第三,统计工作是先于统计学发展起来的。
5、个体又称总体单位6、样本室从总体中抽取出来,作为这一总体的代表的部分个体组成的集合体。
构成样本的每一个个体称为样本单位。
样本单位的数目称为样本量。
7、指标是说明总体数量特征的概念,还可以反映总体现象数量特征的概念及具体数值。
如,2012年我国国内生产总值(GDP)达到518942.1亿元等。
8、标志是说明个体特征的名称:(1)品质标志:表示事物的品质属性特征,是不能用数值表示的,如,性别,工种等。
(2)数量标志:表示事物的数量特征,是可以用数值表示的,如年龄,工资等特别提醒:标志的具体表现是在标志名称之后所表明的属性或数值。
9、指标和标志的关系:区别:标志是说明总体特征的,而标志说明个体特征的。
标志可以分为不能用数值表示的品质标志和能用数值表示的数量标志两种,而指标都是用数值表示的,没有不能用数值表示的指标。
联系:有许多指标的数值是从个体的数量标志值汇总而来。
指标与数量标志之间存在着变换关系。
10、标志按其个体的表现不同,分为不变标志和变异标志。
11、变异标志可以分为品质变异标志和数量变异标志。
12、总体的基本特征:同质性、大量性、差异性。
13、变量:习惯将数量变异标志称为变量。
数量变异标志的表现形式是具体的数值,称为变量值。
14、按变量值的的连续性可把变量分为连续变量与离散变量。
15、连续变量的数值是连续不断的,相邻的两个值之间可做无线分割,即可取无限个值,如,人的身高和体重等。
16、离散变量的两个变量值之间只能取有限个变量值,在社会经济统计中,一般将表现为只能取整数的变量称为离散变量,如,职工人数、工业企业个数等。
特别提醒:有些连续变量如“年龄”,我们通常习惯用整数表示。
17、统计的过程:统计设计(前提)、统计调查(基础)、统计整理(过程)、统计 分析(系统、完善的资料是统计分析的必要条件)18、统计分析的认识过程:从定性认识(统计设计)到定量认识(统计调查和统 计整理),再到定量认识与定性认识相结合(统计分 析)。
第二章 统计调查1、统计调查的定义:根据统计设计方案对调查的要求,运用科学的调查方法,有组织、有计划地、系统地向客观实际搜集统计资料的过程。
2、搜集统计资料的工作一般分为两种:(1)对原始资料的搜集(2)对次级资料的搜集:次级资料指已经经过加工整理的资料,能够在一定程度上说明总体现象。
它包括原来用于其他研究目的,但本次研究仍可利用的资料。
3、统计调查的基本要求是:准确性、及时性和全面性。
准确性是统计调查的基础,及时性是统计调查的关键,全面性是统计调查的保障。
4统计调查的分类:(1)按照调查对象包括的范围划分:全面调查和非全面调查(又称抽样调查,是指对调查对象的一部分单位进行调查,包括非全面统计报表。
重点调查、典型调查等。
非全面调查依据被调查单位的选择是否按随机原则分为概率抽样和非概率抽样。
)(2)按照调查登记的时间是否连续划分:连续调查:一定时期内(通常一年)如,工厂的产品生产,原材料的投入,能源的消耗,人口的出生、死亡等。
不连续调查:间隔一定时期(通常一年以上)如,生产设备拥有量、耕地面积等。
说明数量标志 数量变异标志 变量 具体表现 变量值指标 总体 汇总 说明组成 个体标志 品质标志(3)按照调查的组织形式:常规调查和专项调查4、一个完整的统计调查方案应包括:(1)调查目的:是关键,衡量一个调查方案是否科学的标准,主要是看方案的设计是否体现调查目的的要求,是否符合客观实际。
(2)调查对象:调查的总体(3)调查单位:所要调查的的对象总体中的个体。
(4)报告单位:负责向统计调查机关提交调查资料的单位。
提别提醒:调查单位和报告单位有时一致有时不一致,如,在对全市百货商场进行调查中,每个百货商场是调查单位也是报告单位,又如,在某单位台式计算机使用状况调查时,某单位所有的计算机是调查对象,某单位死亡每一台计算机都是一个调查单位,而每一个使用者都是报告单位。
(5)调查方式和调查方法(6)调查项目(7)调查表:单一表:每张只登记一个调查单位的资料,它的优点是可以容纳较多的调查内容,且便于分类和管理。
一览表:一张表上可以登记多个调查单位的资料,它的优点是便于汇总,但不足是调查内容不能过多。
(8)调查时间:指调查资料所属的时间。
(9)调查期限:指调查工作进行的时间,即规定调查登记工作的开始时间和结束时间。
(10)调查空间(11)调查的组织形式5、统计的调查方式:普查、概率抽查、重点抽查、典型抽查(1)普查:是专门组织的一次性的全面调查,用来调查属于一定时点上或时期内的现象的总量。
普查比任何其他调查方式所搜集的资料都更全面、更系统。
普查的组织工作很重要,必须统一领导,统一要求和统一行动。
(2)概率抽样调查:又称随机抽样调查,简称概率抽样。
方法有四种:A简单随机抽样:优点,简单直观,便于对总体进行推断,缺点是在总体包含的个数比较多时不便进行抽样,且后期调查不便操作。
如:要从10000名职工中抽出200名组成一个样本,则10000名职工的名册,就是抽样框。
B系统抽样:也称机械抽样或等距抽样。
优点是操作简单,对总体的推断误差较小。
如,某小区居住着4000名居民,为调查居民食盐摄入量,需抽取40户居民调查,平均每100户抽取1户,为此,将居民资料从1到4000编号号码,先在1到100号中间随机抽取1个号码,再将这个号码加上100的整数倍,共40户构成样本,如,第一组中抽取的是5号,于是5,105,205····3805,3905共四十户被抽取出来做样本。
C分层抽样:又称类型随进抽样、分类随机抽样。
如,某地区有三种地形:平原、丘陵和山区,统计粮食产量,先将该地区分为平原、丘陵、山区三个组,然后每个组内按简单随机抽样的方法抽取调查地块,构成样本。
优点:分层抽样对总体推断的误差是四种基本方法最小的。
D整群抽样:以群为单位进行简单随机抽样,然后到抽到的每个单位都进行调查,而对为抽中的群不做调查。
优点:减少抽样工作量,节省调查成本,便于实施。
它的不足是对总体的推断误差较大。
友情提醒:影响概率抽样误差的因素:A样本单位:抽取数越多,误差越小B个体标志变动程度:个体变异标志程度越大,误差越大 C抽样方法:分层抽样误差最小,整群抽样最大(3)重点调查:一种非全面调查,属于非概率调查。
所选择的重点单位虽然只是全部单位的一小部分,但就调查的标志值来说在总体中占绝大比重。
如,为了及时了解全国房价的变动趋势,就可以对全国70个大中型城市进行调查。
重点调查能以投入少,较快的速度取得某些现象主要标志的基本情况或变动趋势,如国家统计局今年来积极推进的企业一套表联网直报制度。
(4)典型调查:有意识的选择若干具有典型意义的或是有代表性的单位进行的调查。
具有机动灵活性,主要作用是弥补全面调查的不足、验证全面调查数据的真实性。
6、统计资料搜集方法原始资料搜集方法:(1)直接观察法:如对农作物产量进行实割实测;(2)报告法:报表法;(3)面谈访问法:入户和上街截访(4)邮寄访问法;(5)电话访问法;(6)互联网访问法;次级资料搜集方法:对次级资料搜集方法一般称作文案调查。
优点是获取资料较为方便,容易,调查费用低。
缺点是具有一定的局限性。
企业、事业单位统计资料的搜集:(1)原始记录(2)统计台账:根据编制统计报表、满足经营管理需要而设置,按照时间的顺序进行登记、汇总或积累资料的账册,其特点表现在:A按照时间的顺序对统计资料进行登记。
B随着时间的进程不断循序地汇总或累计资料。
统计台账一般分为进度台账和历史台账。
统计台账的设置:在企业中,厂部(公司)、车间、班组都担负有分级管理的责任,因此,这三级应该分别设置与管辖范围相适应的统计台账。
(3)企业内部报表7统计资料报送的形式:传统的报送方式(邮寄、电话、磁介质)网络远程报送。
8、统计调查误差:(1)登记误差:由于调查环节上的工作不准确而产生的误差,登记误差是可以避免,是不可测的。
(2)代表性误差:是可测,但是不可避免的。
9、控制误差的途径:(1)控制登记误差:A加强对统计人员的培训;B做好统计基础工作;C加强对统计调查过程中数据填报质量的检查。
(2)控制代表性误差第三章统计整理一、统计整理的定义:按照统计研究任务的要求,根据统计对象的特点,对统计调查所搜集到的大量原始资料进行分类、汇总或对已加工过的资料进行在加工,使其条理化、系统化、科学化,最后形成能够反映现象总体特征的统计资料的过二、统计整理的意义:统计整理作为统计工作过程的中心环节,是人们对社会现象从感性认识上升到理性认识的过渡阶段,在统计工作中起着承前启后的作用。
三、统计整理的步奏:1、设计和编制统计整理方案2、对原始资料进行审核与检查(1)完整性审核;(2)准确性审核;(3)适用性审核;(4)时效性审核。
3、对原始资料进行统计分组和统计汇总4、编制统计表或绘制统计图设计统计整理方案和审核原始资料是统计整理的前提,统计分组是统计整理的基础,统计汇总是统计整理的中心,统计表或统计图则是统计整理的结果。
其中,统计分组、统计汇总和编制统计图表是统计整理的基本方法。
四、统计分组的定义:第一,对总体而言,是“分”;第二,对个体而言,是“合”。
五、统计分组的作用:1、凸显社会经济现象的规律;2、划分社会经济现象的类型;3、反映社会经济现象的内部结构;4、分析现象之间的相互依存关系六:统计分组的原则:1、科学性原则;2、完整性原则;3、互斥性原则。
七、统计分组的方法:统计分组的关键是选择分组标志和划分各组界限。
1、选择分组变量:(1)根据研究目的的选择分组标志;(2)选择最能够反映现象本质特征的标志作为分组标志;(3)根据事物所处的具体条件选择分组标志。
