卫星姿态动力学与控制(1)

合集下载

自动控制原理实验-卫星三轴姿态控制系统

自动控制理论实验报告人：赵振根02020802班2008300597卫星三轴姿态飞轮控制系统设计一：概述1.1．坐标系选择与坐标变换在讨论卫星姿态时，首先要选定空间坐标系，不规定参考坐标系就无从描述卫星的姿态，至少要建立两个坐标系，一个是空间参考坐标系，一个是固连在卫星本体的星体坐标系。

在描述三轴稳定对地定向卫星的姿态运动时，一般以轨道坐标系为参考坐标系，还有星体坐标系。

（1）轨道坐标系o o o O X Y Z -，原点位于卫星的质心O ，o OX 轴在轨道平面上与o OZ 轴垂直，与轨道速度方向一致，o OZ 轴指向地心，o OY 轴垂直于轨道平面并构成右手直角坐标系（2）星体坐标系b b b O X Y Z -，原点位于卫星的质心O ，b OX ，b OY ，bOZ 固连在星体上，为卫星的三个惯性主轴。

其中b OX 为滚动轴，b OY为俯仰轴，OZ为偏航轴。

b1.2 飞轮控制系统在卫星三轴姿态控制中的应用与特点长寿命，高精度的三轴姿态稳定卫星，在轨道上正常工作时，普遍采用角动量交换装置作为姿态控制系统的执行机构。

与喷气推力器三轴姿态稳定系统相比，飞轮三轴姿态稳定系统具有多方面的有点：(1)飞轮可以给出较为精确地连续变化的控制力矩，可以进行线性控制，而喷气推力器只能作为非线性开关控制，因此轮控系统的精度比喷气推力器的精度高一个数量级，而姿态误差速率也比喷气控制小。

(2)飞轮所需要的能源是电能可以不断地通过太阳能电池在轨得到补充，因而适用于长寿命工作，喷气推力器需要消耗工质或燃料，在轨无法补充，因而寿命大大受限。

(3)轮控系统特别适用于克服周期性扰动。

(4)轮控系统能够避免热推力器对光学仪器的污染。

然而，轮控系统在具有以上优越性的同时，也存在两个主要问题，一是飞轮会发生速度饱和。

当飞轮朝着一个方向加速或偏转以克服某一方面的非周期性扰动时，飞轮终究要达到其最大允许转速。

二是由于转速部件的存在，特别是轴承寿命和可靠性受到限制。

第10章航天器姿态与轨道控制分系统(1)

24
3. 航天器轨道控制系统
3.2 航天器的轨道机动与轨道保持
航天器在控制系统作用下使其轨道发生有意的改变称为轨道机动。轨道机动方式一般有两种：无线电指令控制系统或称遥控系统；惯性控制系统。变轨控制分为轨道改变和轨道转移。轨道保持是对在轨航天器受到外界干扰的作用下偏离预定轨道的修正。
8
1. 航天器控制的基本概念
1.6 姿态控制与轨道控制的关系
航天器是一个比较复杂的控制对象，一般来说轨道控制与姿态控制密切相关。为实现轨道控制，航天器姿态必须符合要求。即当需要对航天器进行轨道控制时，同时也要求进行姿态控制。在某些具体情况或某些飞行过程中，可以把姿态控制和轨道控制分开来考虑。有些应用任务对轨道没有严格要求，如空间环境探测卫星，则只有姿态控制系统。
3
1. 航天器控制的基本概念
1.2.航天器的控制
航天器在轨道上运动将受到各种力矩的作用。从刚体力学的角度来说，力使航天器的轨道产生摄动，力矩使航天器姿态产生扰动。航天器的控制可以分为两大类：轨道控制和姿态控制。 1.对航天器的质心施加外力，以有目的地改变其运动轨迹的技术，称为轨道控制。 2.对航天器绕质心施加力矩，以保持或按需要改变其在空间的定向技术，称为姿态控制。
11
1. 航天器控制的基本概念
星上自主控制框图星—地大回路控制框图
轨道运动
星载控制器
执行机构
星体姿态和轨道动力学
姿态运动
卫星动力学
⊗
给定
敏感器
姿态轨道控制器
敏感器
执行机构
跟踪
遥测
遥控
跟踪
遥测
遥控
数据处理测定轨道
控制参数计算
12

卫星姿态动力学与控制2

功率计和功率传感器
USB 和局域网功率传感器
通过即插即用的 USB 连通性，您可以快速和轻松地对功率传感器进行设置。只需将传感器连接到 PC 上，便可使用捆绑软件立即执行功率测量。Keysight USB 功率传感器可以让您梦想成真 ― 简单的设置，发挥远超传感器的功能。
功率计和功率传感器
USB 和局域网功率传感器
2.4 自旋稳定卫星消旋系统：
消旋控制系统是一个锁相控制系统，以装在卫星自旋体上的红外地平仪的地中脉冲为输入信号，通过调整消旋电机的转速，使天线脉冲和地中脉冲重合，即此时天线波束指向地心，且在相位锁定时，天线相对于自旋卫星反方向旋转，且转速与卫星相同。
电子消旋消旋方式机械消旋
敏感器
消旋控制系统组成
2.1 自旋、双旋卫星姿态信息测量
自旋卫星的姿态指的是卫星自旋轴在惯性空间的方位。
自旋卫星通常使用以下姿态敏感器：红外地球敏感器、太阳敏感器、星敏感器、陆标敏感器。
2.1 自旋、双旋卫星姿态姿态确定的精度
自旋卫星的姿态确定可看成在天球上由观测量求出两条以上姿态轨迹的交点。实际测量中，由于误差，单个测量将给出一个轨迹带而不是一条线，贷款依赖于观测误差，两条测量带交出一个姿态区。
V3500A 手持式射频功率计是一款紧凑型手持式仪器，在现场和制造应用中均可精确地测量射频功率。V3500A 拥有 ±0.21 dB 的绝对精度、10 MHz 至 6 GHz的广泛频率范围及-63 dBm 至 +20 dBm 的测量范围，适用于各种射频测量应用。
功率计和功率传感器
53140 系列微波计数器/功率计/DVM
卫星姿态动力学与控制2
汇报人：薛梦轩
目

哈工大航天学院课程-空间飞行器动力学与控制-第1课-绪论

“礼炮1号”空间站
空间飞行器动力学与控制第一课绪论
1981年4月，世界上第一架垂直起飞、水平着陆、可重复使用的美国航天飞机 “哥伦比亚号”试飞成功，标志着航天运载器由一次性使用的运载火箭转向重复使用的航天运载器的新阶段，标志着人类在空间时代又上了一层楼，进入了航天飞机时代。
美国“哥伦比亚号”航天飞机
空间飞行器动力学与控制第一课绪论
人类自20世纪60年代开始探测火星的尝试。大约半数火星探测任务成功。 2008年05月25日，美国“凤凰”号火星探测器成功降落在火星北极区域，其核心任务是寻找水和生命痕迹。 2008年11月，凤凰号与地面控制中心失去联络。
“凤凰”号挖掘臂挖掘火星土壤的情景
空间飞行器动力学与控制第一课绪论
1988年11月15日，前苏联的暴风雪号航天飞机从拜科努尔航天中心首次发射升空，47分钟后进入距地面 250公里的圆形轨道。它绕地球飞行两圈，在太空遨游三小时后，按预定计划于 9时25分安全返航，准确降落在离发射点12公里外的混凝土跑道上，完成了一次无人驾驶的试验飞行。
“水手2号”探测器
空间飞行器动力学与控制第一课绪论
1966年1月，前苏联两艘载人飞船第一次在轨道上成功交会对接，并实现了两位航天员从一艘飞船向另一艘飞船的转移。
前苏联“联盟号”载人飞船
前苏联“上升号”载人飞船
空间飞行器动力学与控制第一课绪论
1971年4月19日，前苏联“礼炮1号”空间站入轨成功，其质量约18t，总长14m，轨道高度200～ 250 km，轨道倾角51.6º ，成为人类第一个空间站。
空间飞行器动力学与控制第一课绪论
13～14世纪，中国的火箭技术与其他火药兵器一同传到阿拉伯国家和印度，后又传入欧洲。至18世纪后期，印度军队在抗击英国和法国军队的多次战争中就曾大量使用火药火箭并取得了成功结果，由此推动了欧洲火箭技术的发展。曾在印度作战的英国人康格里夫(William Congreve)在19世纪初对印度火箭作了改进，他确定了黑火药的多种配方，改善了制造方法并使火箭系列化，最大射程可达3km。这些初期火箭的原理都成为了近代火箭技术的最初基础。

航天器姿态确定与姿态控制

光敏元件阵列是由一排相互平行且独立的
光电池条组成，其数量决定了太阳敏感器输出
编码的位数，从而在一定程度上影响到敏感器
的分辨率。
图4.3 两轴模拟式太阳敏感器
航天器姿态确定
红外地平仪
红外地平仪就是利用地球自身的红外辐射来测量航天器相对于当地垂线或者当地地平方位的姿态敏感器，简称地平仪。
目前红外地平仪主要有3种形式：地平穿越式、边界跟踪式和辐射热平衡式。
磁矩与地球磁场相互作用就可产生控制力矩，实现姿态控制。
航天器姿态控制
利用环境场产生控制力矩，最常用的除了磁力矩以外，还有重力梯度力矩等。
磁力矩与轨道高度的3次方成反比，轨道高度越低，磁力矩越大。所以磁力矩作为控制力矩比较适用于低轨道航天器。
重力梯度力矩适用于中高度轨道航天器。太阳辐射力矩适用于同步轨道卫星等高轨道航天器。气动力矩也适用于低轨道。但是最后两种力矩较少用来作为控制力矩。利用环境力矩产生控制力矩的装置可称为环境型执行机构。
单脉冲比相干涉仪是由光的干涉原理引伸而来，至少要采用两个接收天线，其间矩为d，称为基线长度。当天线与地面距离比基线长度d大得多时，有如下关系式：
cos 2 d
式中，为两个天线接收电波的相位差，A为波长。由式可见，是预先确定的，因此只要测出两个天线接收信号的相位差，便可确定方向角。
➢ 被动式
被动控制系统是用自然环境力矩源或物理力矩源，如自旋、重力梯度、地磁场、太阳辐射力矩或气动力矩等以及它们之间的组合来控制航天器的姿态。
其中地平穿越式地平仪扫描视场大，其余两种地平仪的工作视场较小，只能适用于小范围的姿态测量，但精度较高。
航天器姿态确定
➢ 地平穿越式地平仪
地平穿越式地平仪的视场相对于地球作扫描运动。当视场穿越地平线时，也就是说扫到地球和空间交界时，地平仪接收到的红外辐射能量发生跃变，经过热敏元件探测器把这种辐射能量的跃变转变成电信号，形成地球波形。然后通过放大和处理电路，把它转变成为前后沿脉冲。最后通过计算电路，把前后沿脉冲与姿态基准信号进行比较，得出姿态角信息，也就是滚动角或俯仰角。

卫星磁姿态控制方法与算法综述

第２２卷第１期２０２４年１月动力学与控制学报J O U R N A L O FD Y N AM I C SA N DC O N T R O LV o l ．２２N o ．１J a n ．２０２４文章编号:１６７２Ｇ６５５３Ｇ２０２４Ｇ２２(１)Ｇ００１Ｇ０２１D O I :１０．６０５２/１６７２Ｇ６５５３Ｇ２０２３Ｇ０１１㊀２０２２Ｇ１２Ｇ０２收到第１稿,２０２３Ｇ０１Ｇ１４收到修改稿．∗国家自然科学基金资助项目(U ２１B ２０５０),N a t i o n a lN a t u r a l S c i e n c eF o u n d a t i o no fC h i n a (U ２１B ２０５０)．†通信作者E Ｇm a i l :１１１９７６３４５＠i m u ．e d u ．c n卫星磁姿态控制方法与算法综述∗穆硕１㊀占英２†㊀宝音贺西１(１．清华大学航天航空学院,北京㊀１０００８４)(２．内蒙古大学电子信息工程学院,呼和浩特㊀０１００２１)摘要㊀自太空探索之初,姿态控制磁控系统便因其体积小㊁质量轻㊁成本低㊁可靠性高等优点被广泛应用于各类轨道卫星．近些年,随着微小卫星技术的迅猛发展,姿态控制磁控系统满足了微小卫星对质量㊁空间等资源的限制,成为了学者们研究的热点．本文综述了自２０世纪６０年代以来卫星尤其是微小卫星所采用的主要磁姿态控制方法和算法,包括飞轮起旋与卸载算法㊁被动以及主动磁姿态控制算法等．其中主动磁姿态控制算法包括主动磁阻尼算法㊁磁控与自旋㊁定转速飞轮㊁重力梯度力矩结合的算法以及纯磁控算法．最后对该研究进行了总结与展望．关键词㊀卫星磁控,㊀飞轮起旋与卸载,㊀被动磁控,㊀主动磁阻尼,㊀磁控与其他方式结合,㊀纯磁控中图分类号:V ４１２．４＋２文献标志码:AA nO v e r v i e wo fM a g n e t i cA t t i t u d eC o n t r o lA l go r i t h m s f o r S a t e l l i t e s ∗M uS h u o １㊀Z h a nY i n g ２†㊀B a o yi nH e x i １(１．S c h o o l o fA e r o s p a c eE n g i n e e r i n g ,T s i n g h u aU n i v e r s i t y ,B e i j i n g㊀１０００８４,C h i n a )(２．S c h o o l o fE l e c t r o n i c I n f o r m a t i o nE n g i n e e r i n g ,I n n e rM o n g o l i aU n i v e r s i t y,H u h h o t ㊀０１００２１,C h i n a )A b s t r a c t ㊀M a g n e t i c a t t i t u d e c o n t r o l s y s t e m s h a v e b e e nw i d e l y us e d f o r l o we a r t h o r b i t s a t e l l i t e s s i n c e t h e b e g i n n i n g o f s p a c e e r a b e c a u s e o f t h e i r r e l i a b i l i t y ,l i g h t w e i g h t ,l o wc o s t a n d e n e r g y e f f i c i e n c y ．R e c e n t l y,s m a l l s a t e l l i t e sa r e i n c r e a s i n g l y a t t r a c t i v e ．M a gn e t i cc o n t r o l l e r s m e e t t h e l i m i t a t i o n so f s m a l l s a t e l l i t e s a n d a r e c o n s i d e r e da s f a v o r a b l e c a n d i d a t e s f o r s m a l l s a t e l l i t e s ．I n t h i s p a p e r ,t h e s a t e l l i t em a gn e t i c a t t i Ｇt u d e c o n t r o l a l g o r i t h m s ,i n c l u d i n g a l g o r i t h m s f o r r e a c t i o nw h e e l s t a r t Ｇu p a n du n l o a d i n g ,pa s s i v e a n d a c Ｇt i v em a g n e t i c a t t i t u d e c o n t r o l a l g o r i t h m s ,a r e c o v e r e d ．T h e a l g o r i t h m s h e r e i n a r e e s p e c i a l l y f o r s m a l l s a t Ｇe l l i t e s ．A s f o r a c t i v em a g n e t i c a t t i t u d e c o n t r o l a l g o r i t h m s ,m a g n e t i c d a m p i n g a l g o r i t h m s ,t h e a l g o r i t h m s c o mb i n i n g m a g n e t ic c o n t r o lw i t hs p i n ,c o n s t a n t s p e ed f l y w he e l a n d g r a v i t yg r a d i e n t t o r q u e ,a n d p u r e l y m a g n e t i c c o n t r o l a l g o r i t h m s a r e c o v e r e d ．F i n a l l y,t h e r e s e a r c h i s s u mm a r i z e d ．K e y wo r d s ㊀s a t e l l i t em a g n e t i c c o n t r o l ,㊀r e a c t i o nw h e e l s t a r t Ｇu p a n du n l o a d i n g ,㊀p a s s i v em a g n e t i c c o n Ｇt r o l ,㊀a c t i v em a g n e t i c a n g u l a r v e l o c i t y d a m p i n g ,㊀m a gn e t i c c o n t r o l w i t h o t h e r a c t u a t o r s ,㊀p u r e l y m a gn e t i c c o n t r o l动㊀力㊀学㊀与㊀控㊀制㊀学㊀报２０２４年第２２卷引言自探索太空之初,磁姿态控制系统便因其轻便,可靠等诸多优点受到卫星设计者的青睐．第一颗成功使用磁姿态控制系统的卫星是T r a n s i t１B,由美国约翰霍普金斯大学应用物理实验室(A P L)设计．该卫星于１９６０年４月发射,采用被动磁控,进行了８９天在轨操作[１]．１９６０年１１月,第一颗采用主动磁姿态控制的卫星T i r o s I I成功发射[２]．相比于其他控制方式,磁姿态控制系统具有质量轻㊁体积小㊁成本低㊁可靠性高,使用寿命长等诸多优点,是低轨近地卫星尤其是微小卫星实现稳定控制的首选．磁姿态控制系统依靠卫星自身磁矩m与地磁场强度矢量B相互作用,产生控制力矩T．被动磁控卫星主要通过永磁体与磁滞棒产生磁矩;主动磁控卫星则需要通过电流驱动磁力矩器产生所需磁矩．磁控力矩计算公式为:T＝mˑB(１)从公式(１)中可看出,磁姿态控制系统的主要缺点是无法施加独立的三轴控制力矩,在每一瞬时只能产生垂直于卫星所处地磁场的控制力矩,这会大幅降低姿态控制效果,甚至出现瞬时不可控．磁姿态控制卫星的可控性一直困扰着学者们．直到２００３年,B h a t与D h a m[３]基于周期性地磁场假设,证明了磁控卫星的可控性:当卫星沿非赤道轨道运行时,地磁场方向会随卫星位置改变而不断发生变化．这种变化使得磁控系统不可控方向也在不断变化,确保了磁控卫星的可控性．随后, S m i r n o v等[４]证明了在偏离平衡点较小时,可利用两轴磁控实现卫星稳定姿态控制．Y a n g[５]基于线性时变系统理论,证明了在卫星惯量满足一定条件时,可实现磁控卫星稳定姿态控制．地磁场模型精度是决定所设计磁姿态控制系统能否成功实施的另一个关键因素．目前,最精确的地磁场模型为国际地磁参考场(I G R F模型),由国际地磁与气象学协会(I A G A)于１９６８年提出,此后每五年更新一次,目前为第１３代[６]．I G R FＧ１３采用１３阶球谐函数模型,结构复杂,通常适用于数值仿真过程．而对磁控算法的理论分析,学界通常采用偶极子假设．常用的偶极子模型有倾斜偶极子模型㊁直接偶极子模型以及简化偶极子模型[７]．基于偶极子假设并忽略地球自转的影响,卫星所处地磁场会随卫星轨道运动而周期性变化．同时,也可采用更高阶球谐函数进行更精确的理论分析[８,９]．本文参考了前人的综述文章[１０Ｇ１３],沿用了文献[１１]的分类结构,整理综述了自２０世纪６０年代以来卫星尤其是微小卫星所采用的主要磁姿态控制方法和算法,包括飞轮起旋㊁卸载,被动以及主动磁姿态控制算法,重点关注主动磁姿态控制算法的发展．其中主动磁姿态控制算法包括BＧd o t等主动磁阻尼算法,磁控与自旋㊁定转速飞轮㊁重力梯度力矩结合的算法以及纯磁控算法．最后,本文对各类磁控算法进行了总结与展望．１㊀飞轮起旋与卸载１．１㊀飞轮起旋根据动量矩守恒原理,当飞轮的动量矩变化时会改变卫星的动量矩．目前主要有两类磁控算法用于飞轮起旋问题[１４]．第一种方法首先利用磁力矩器与飞轮实现卫星稳定控制．此阶段磁控制律可采用P D控制律．卫星稳定后加速飞轮至目标转速,利用磁力矩器维持卫星姿态稳定[１４,１５]．另一种方法是在卫星实现稳定控制前起旋飞轮,再利用磁力矩器与定转速飞轮稳定卫星．C h a n g等人在姿态获取阶段起旋俯仰轴飞轮,并使用BＧd o t控制律阻尼卫星角速度[１４]．该方案可更快实现稳定控制．研究表明,在BＧd o t控制律下,卫星姿态误差会以指数形式进行收敛[１６]．M e n g 等人设计了两种用于飞轮起旋的磁控律[１７]: m＝Bˑ(－k１h )B ２(２)m＝Bˑ(－k１h －k２θ )B ２(３)其中m为卫星本体系下磁力矩器产生的磁矩,B为本体系下的地磁场强度矢量,h 为飞轮起旋产生的干扰力矩,θ 为三轴姿态误差的时间导数,k１,k２为控制增益．上述控制律均可在姿态稳定前使用．当角速度信息可知时,卫星采用控制律(３)进行控制．１．２㊀飞轮卸载工程中磁控制系统常用于飞轮角动量卸载．飞轮可抵抗环境干扰力矩的影响,实现卫星高精度姿２第１期穆硕等:卫星磁姿态控制方法与算法综述态控制．但同时,由于一些常值干扰力矩的影响,如气动力矩,飞轮的转速可能会持续增加．当上升至最高转速时,飞轮将不能提供有效的控制力矩．需在飞轮转速达到其上限值前进行角动量卸载．常用的卸载方法有喷气卸载,磁卸载等．但喷气卸载需消耗卫星燃料．而磁卸载可利用电能进行卸载,且使用寿命长．１９６１年,W h i t e等人[１８]提出了叉乘磁卸载控制律,在磁控卫星中应用广泛[１９Ｇ２１],具体形式为:m＝kΔh wˑB(４)其中k为控制增益,Δh w为飞轮角动量与目标角动量差值.通过该控制律,磁控力矩可卸载垂直于地磁场强度矢量B的角动量分量．通常,当Δh w与地磁场矢量的夹角足够大时(如夹角处于４５~１３５度之间),才启动磁力矩器卸载,以防止垂直于Δh w的磁力矩分量过大对卫星产生不利影响．该控制律也可采用b a n gＧb a n g控制形式计算所需磁矩[２２]．针对叉乘控制律,后续文献进行了大量研究．C a m i l l o与M a r k l e y[２２]推导了叉乘控制律解析分析公式．该公式可用于增益系数k的初步选取．N iＧn o m i y a等人[２３]对叉乘控制律进行了改进,使得控制律可同时实现飞轮角动量卸载与卫星章动阻尼．H a b l a n i[２４]使用线性极点配置方法,对叉乘控制律增益系数进行设计．针对冗余配置的飞轮系统,L e b e d e v[２５],H o g a n与S c h a u b[２６]设计的叉乘控制律可确保每个飞轮的转速都卸载到零值附近．T rég o uët等人[２７]与A v a n z i n i等人[２８]改进的叉乘控制律可在磁卸载的同时保证姿态控制律的渐进稳定．一些优化方法也被用于飞轮磁卸载控制律设计．G l a e s e等人[２９]设计了能量最优磁卸载控制律．F l a s h n e r与B u r n s[３０]提出了一种基于单元映射方法的离散磁卸载控制律．该控制律基于周期性磁场假设,可离线设计优化方案．S t e y n[３１]基于L Q R方法,通过最小化目标函数J＝ʏt f t０(h T w Q h w＋m T R m)d t(５)实现了磁卸载控制律的优化．其中h w为飞轮角动量,Q,R为权重矩阵．G i u l i e t t i等人[３２]构建了结合时间最优与能量最优的目标函数,即:J＝－aΔt－(１－a)２ʏt f t０(m２x＋m２y)d t(６)其中a为调节机动时间与能量消耗比例的权重系数．通过最大化目标函数,文献[３２]给出了包含参数a的磁卸载控制律．此外,Hɕ方法也被用于磁卸载控制律优化[３３]．磁卸载也可结合其他卸载方法提高效果．C h e n等人[３４]将磁卸载与喷气卸载组合,节省了喷气卸载的燃料消耗,同时提高了卸载速度．B u r n s与F l a s h n e r[３５]利用重力梯度力矩㊁磁力矩㊁气动力矩三种环境力矩,设计了具有自适应特性的磁卸载控制律．其他方案如模型预测方法[３６],被动阻尼方法[３７],点映射技术[３８,３９]等均可应用于磁卸载控制律设计．２㊀被动磁姿态控制被动磁姿态控制系统结构简单,性能可靠,不消耗卫星能源,常应用于设备有限且控制精度要求较低的卫星．其通常包括永磁体与磁滞棒两个组件．其中永磁体用于控制卫星指向,使其大致沿所处地磁场方向．磁滞棒通过磁化作用,可起到角速度阻尼作用．二者结合可实现低精度稳定姿态控制．被动磁姿态控制系统最早于１９６０年应用于美国海军通讯试验星[４０]．通过被动磁控与机械消旋设备,该卫星成功实现了角速度阻尼与稳定指向．１９６０年６月,该项目另一颗试验星T r a n s i t２A成功发射．该卫星仅凭借被动磁姿态控制系统实现了稳定控制[４０]．第一颗由大学自主研发的被动磁控卫星I n j u n３于１９６２年成功发射入轨[４１]．此后,更多被动磁控卫星任务成功实施,如E S R OＧ１A(１９６８),E S R OＧ１B(１９６９),A z u r(１９６９),E x o s(１９７８),M a g i o n(１９７８)[４２]．随着星载计算机与控制设备的发展,被动磁姿态控制系统已不能满足卫星任务高精度与多样化需求．至２０世纪７０年代中期,被动磁姿态控制系统逐渐被主动控制方法替代．直到微小卫星技术的兴起,被动磁姿态控制系统再次受到学者关注．其满足了微小卫星质量㊁空间以及设备成本的限制,在一些大学自主研发的试验星或演示卫星中应用广泛．１９９０年,四颗采用被动磁控的微小卫星被送入太空[４３]．此后,更多应用被动磁控的微小卫星相继发射[４２,４４Ｇ５０]．被动磁姿态控制原理简单,无需设计复杂的控３动㊀力㊀学㊀与㊀控㊀制㊀学㊀报２０２４年第２２卷制算法．目前学者更多关注主动磁姿态控制算法设计．３㊀主动磁姿态控制３．１㊀主动磁阻尼控制当卫星角速度过大时,部分星载仪器如星敏感器无法正常使用,需使用星载设备降低卫星角速度至一定阈值．与运载器分离㊁执行变轨等机动操作或是设备故障均可能使角速度过大,因此,角速度阻尼是卫星姿态控制的必需过程．虽然喷气控制,飞轮控制等方法均可阻尼角速度,但喷气控制会消耗卫星燃料,飞轮控制易饱和．相比之下,磁阻尼控制不仅节省能源,还具备性能可靠,成本低廉等优势,在各类卫星中应用广泛．S t i c k l e r与A l f r i e n d[１９]提出了著名的主动磁阻尼算法 BＧd o t 控制律．该控制律最早出现在１９７２年[５１],利用地磁场导数信息进行角速度阻尼,具体表达式为:m＝－k B (７)其中k为正增益系数,B 为地磁场强度矢量相对于卫星本体系的导数．利用绝对导数与相对导数的关系,即:d Bd t＝B ＋ωˑB(８)其中d B/d t为地磁场强度矢量相对于惯性系的导数,式(７)可表示为:m＝－k d B d t＋k ωˑB(９)由于地磁场强度矢量在惯性系中变化的角频率仅为轨道角速度两倍,而通常在阻尼过程中卫星角速度较大,因此式(９)右侧第一项可近似为零．故式(９)可进一步简化为:m＝k ωˑB(１０)卫星转动动能E的时间导数可表达为:d Ed t＝T ω＝(mˑB) ω＝－k(ωˑB)２ɤ０(１１)从上式可看出,采用BＧd o t控制律可有效减小卫星转动动能,实现角速度阻尼．BＧd o t控制律具有很强的鲁棒性,通常利用当前时刻与前一时刻磁强计测量数据进行差分便可有效阻尼角速度．同时,BＧd o t控制律可转化为b a n gＧb a n g控制形式,适用于实际工程问题[５２]．基于等式(９)的假设,BＧd o t控制律可以指数形式进行收敛[５３,５４],具体收敛速度受轨道倾角等因素影响[５４]．BＧd o t也存在缺点．首先在阻尼精度方面,由于在上述分析中忽略了地磁场矢量相对于惯性系的时间变化率,即地磁场变化项,该项会对最终阻尼精度产生较大影响．研究发现,BＧd o t控制律最终会有约二倍轨道角速度的误差[５５]．同时,剩磁等干扰力矩会进一步降低阻尼精度．为克服地磁场变化项等带来的不利影响,学者们对BＧd o t控制律进行了改进[５６Ｇ６１],其中大部分变形基于等式(９)．该变形可阻尼卫星角速度至零,但同时需要角速度测量数据,提高了测量设备需求．为减少测量设备,D e s o u k y与A b d e l k h a l i k[６２]基于地磁场数据对角速度进行等效计算,给出了改进的BＧd o t控制律．该控制律可保证磁力矩器需产生的磁矩m时刻垂直于卫星所处地磁场,提高了磁利用效率．蒙特卡罗仿真实验验证了该控制律的有效性．同时,该控制律可在一定程度上减少收敛时间,降低能源消耗．J i n等人为惯量缺陷卫星(z轴惯量大于其他两轴)提出了垂直消旋控制律[６３]:m＝k BˑBB ３(１２)该控制律可避免z轴长时间指向太阳而造成仪器损坏．一些学者研究了增益系数k的选取方法．A v a n z i n i与G i u l i e t t i[５７]基于卫星轨道与形状特征,提出了一种增益系数调整方法,具体表达式为: k＝２ω０(１＋s i nζm)J m i n/ B ２(１３)其中ζm为卫星轨道倾角,ω０为轨道角速度,J m i n 为卫星最小惯量矩．W i sᶄn i e w s k i与B l a n k e[５６]利用正定矩阵替换标量增益系数k,增强了阻尼效果,同时为后续优化提供了更多空间．需要注意的是,文献[５６]中关于被动重力梯度稳定性的证明在文献[６４]中进行了更正．随着仪器设备与微小卫星技术的发展,BＧd o t 控制律也发展出了适用于纳卫星㊁立方星的方案[６５Ｇ７０],如嵌入式磁线圈控制等．同时,新型磁阻尼方案如反馈阻尼控制律[７１]也相继提出．但由于BＧ４第１期穆硕等:卫星磁姿态控制方法与算法综述d o t 的简便性与鲁棒性,其仍是目前乃至未来很长一段时间磁阻尼算法的首选．目前磁阻尼算法体系已较为完备,要取得较大研究进展十分困难．３．２㊀组合磁姿态控制系统由于磁姿态控制系统无法施加独立的三轴控制力矩,其通常结合其他设备与方法实现高精度稳定控制,如自旋㊁飞轮㊁重力梯度力矩等．３．２．１㊀磁控与自旋结合磁控与自旋结合克服了磁控的固有缺陷,同时具有低功耗㊁低成本㊁高控制精度等优点,因此应用广泛,也是目前磁控卫星的主要控制方案之一．通过围绕最大惯量主轴旋转,自旋卫星可获得自旋稳定性．若无外界干扰,自旋卫星可在惯性空间中维持稳定．但由于太阳光压力矩等的影响,自旋卫星会发生章动,需采用其他控制方法对自旋卫星的旋转轴指向与转速进行控制,而磁控则是首选．第一颗磁控与自旋相结合的卫星发射于１９６０年[２]．此后,该方案被广泛应用于各类卫星任务．其中由S h i g e h a r a [７２]提出的b a n g Ｇb a n g 控制律应用广泛．该控制律采用特定开关函数实现磁力矩器磁矩的正负控制,具体公式如下:m j ＝m ０,Δh (e j ˑB )＞０－m ０,Δh (e j ˑB )＜０{(１４)其中m j 为沿卫星本体系坐标轴e j 的磁矩大小;j ＝１,２,３;m j 的幅值为m ０;Δh 为当前卫星角动量与目标角动量差值．该控制律可使卫星沿特定轴自旋,并调整自旋轴的惯性空间指向．该方案也广泛应用于立方星等微小卫星[７３]．C r o c k e r 与V r a b l i k[７４]提出了可使卫星自旋轴z 轴垂直于太阳矢量的b a n g Ｇb a n g 控制,即:m z ＝m ０,㊀㊀e s ＞０－m ０,㊀e s ＜０{(１５)其中e 为卫星自旋轴,s 为本体系下太阳方向矢量．b a n g Ｇb a n g 控制还可与BＧd o t 控制律结合解决自旋卫星章动问题．H o l d e n 与L a w r e n c e [７５]基于李雅普诺夫方法设计了章动控制律,该控制律仅使用自转轴方向磁力矩器进行控制:m z ＝m ０s i g n [(C －A )B y ωx －(C －B )B x ωy ](１６)其中A ,B ,C 为卫星三轴转动惯量;ωx ,ωy 及B x ,B y 分别为卫星角速度与地磁场强度矢量沿卫星本体系x ,y 轴的分量．该控制律不仅适用于轴对称卫星,对非轴对称卫星也有较好控制表现．O v c h i n n i Ｇk o v 等人[７６,７７],R o l d u gi n 与T e s t a n i [７８]基于B Ｇd o t 提出了简化控制律,利用磁场导数信息即可完成章动阻尼:m z ＝－k (Be )e(１７)该控制律可使用一轴磁力矩器完成控制．Z a v o l i 等人[７９]分析了控制律(１７)的具体性质,包括全局渐近收敛性质与自旋轴指向等．需要注意的是,由于该控制律所施加的控制力矩垂直于自旋轴,因此不能使卫星起旋．O v c h i n n i k o v 等人[７６]提供了一种卫星起旋控制律:m ＝k (B y ,－B x ,０)(１８)该控制律可产生沿自转轴方向的控制力矩,但同时会引入沿其他两轴的干扰力矩,需通过控制律(１７)消除．针对自旋卫星起旋问题,T h o m s o n [８０]提出了 Y ＧT h o m s o n 控制律,利用当前转速与目标转速差值对卫星转速进行控制．C r e a m e r [８１]基于B Ｇd o t控制律提出了另一种自旋卫星控制方法,具体形式为:m ＝－k (B＋ωd ˑB )(１９)其中ωd 为卫星期望转速．该控制律可有效阻尼卫星初始角速度,使得卫星按照所设定角速度旋转．C u b a s 等人[８２]对该控制律的稳定性,收敛时间,自转轴指向以及控制精度进行了详细分析,并在考虑实际工程限制条件下进行了仿真,验证了控制律的可靠性．可利用卫星当前角动量与目标角动量差值进行控制律设计．A v a n z i n i 等人[８３]利用本体系与惯性系下的角动量差值,分别控制卫星角速度与自旋轴指向．此外,A v a n z i n i 等人[８４]利用投影方法,即将角动量差值投影至与地磁场矢量垂直的平面,设计了另一种控制律:T ＝k (I －B B T )Δh (２０)基于文献[５７]的分析方法,文中提供了增益系数k 的选取方法．D eR u i t e r [８５]同样利用投影方法,融合了章动阻尼㊁起旋以及自转轴指向等多个控制律,设计了应用于纳卫星的磁控方案．文中利用李雅普诺夫方法,证明了即使在两轴磁力矩器失效以及磁力矩器饱和等限制下,控制律也可保证渐进稳定．在考虑各种扰动以及设备故障等情况下,控制系统５动㊀力㊀学㊀与㊀控㊀制㊀学㊀报２０２４年第２２卷表现均能满足任务需求[８６]．该控制律已被成功应用于纳卫星E S T C u b eＧ１[８７]．卫星可携带的能源有限,对于装备太阳能帆板的卫星,需尽快将电池板对准太阳．Y o u等人[８８]基于投影方法提出了一种太阳获取控制律,具体形式如下:T＝－k(ω－ωd),|l z|ɤ０．８－k(ω－ωd)－k１|L z|θ[lˑ(s ˑl)]－㊀k２s ˑe３,|l z|＞０．８ìîíïïïï(２１)其中L为卫星角动量,l为其单位矢量,k１,k２为相关增益系数,θ＝a r c c o s(－s z),下标z表示该矢量沿本体系z轴的分量(z轴为其自旋轴)．卫星首先进行角速度阻尼,然后切换至指向控制律,利用太阳敏感器读数实现太阳指向．C h a s s e t等人[８９]介绍了太阳获取控制律在具体卫星任务中的应用．利用太阳矢量与卫星本体系z轴夹角以及目标转速,文中构建了包含指向信息与转速信息的目标转速,通过投影方法实现了太阳获取．A l f r i e n d[９０]利用地磁场信息以及卫星滚转角构建闭环控制律:m２＝k１B xφ－k２B y(２２)其中φ为１Ｇ２Ｇ３转序下相对于轨道坐标系的卫星滚转角．使用多时间尺度方法,文中对控制律的渐进稳定性进行了分析,通过与数值仿真以及F l oＧq u e t理论对比,对控制律进行了验证．同时,文中分析了控制律对干扰力矩的鲁棒性．W h e e l e r[９１]使用沿自旋轴方向的单轴磁线圈,利用卫星姿态㊁角速度与磁场信息构建反馈函数,实现了卫星稳定控制．O v c h i n n i k o v与R o l d u g i n[９２]使用单轴磁力矩器,设计了可使小卫星在轨道平面内任意方向旋转的控制律．E r g i n与W h e e l e r[９３]利用卫星姿态误差与地磁场信息,使用固定时间间隔内的恒定控制力矩设计了磁控制律．R e n a r d[９４]比较了在轨道偏心率,地球自转等影响下,仅使用沿自旋轴方向单轴磁线圈,不同控制律的表现．结果表明,基于轨道周期进行磁矩极性转换可实现较好鲁棒性．C h e o n等人[９５]利用星载地磁场模型,设计了仅使用磁强计与G P S信息的磁控制律,其具体形式为:m＝１|b m|[－１２Kb^p－D(b^ p－b^ m)－㊀Λd(ω~z－Ψz)(b^mˑe)](２３)其中b m为磁强计测量的磁场矢量;K,D为正定增益矩阵;Λd为矩阵D对角元素;ω~z为通过磁强计测量值估计得到的当前卫星沿自转轴方向角速度,Ψz为目标角速度;上标 ^ 表示该矢量的单位矢量;b p为通过特殊优化方法得到的期望磁场矢量,其具体计算方式如下．通过星载磁场模型,计算出当卫星达到目标姿态时地磁场矢量在本体系下所有可能的表示,这些矢量在空间中构成一个圆锥,而b p则是圆锥与b m㊁e所确定平面的交线．控制律通过减小b p与b m之间夹角,使得卫星自旋轴指向目标方向．文中使用线性估计模型与李雅普诺夫方法对控制律稳定性进行了分析,通过仿真验证了控制律的可行性．需要注意的是,只有当卫星自旋速度足够大时,该控制律才可保证卫星稳定控制．J u n k i n s等人[９６]基于庞特里亚金最值原理,给出了控制自旋轴指向的时间最优机动设计方法．S o r e n s e n[９７]使用L Q R方法对所需磁矩进行设计．自旋卫星磁控制律时至今日仍在推陈出新[９８,９９]．但自旋卫星的高速旋转特性不利于实施优化方法,同时相关研究也较为成熟,难以实现大突破．３．２．２㊀磁控与定转速飞轮结合当一轴飞轮以一定转速旋转时,会为卫星提供陀螺稳定性,使飞轮轴向保持在轨道法向方向,该类卫星称为偏置动量卫星．此类卫星无需高速旋转,降低了设备及卫星惯量要求．加入磁控可进一步提高偏置动量卫星控制精度,使卫星姿态误差渐近收敛．由于飞轮在轨道法向提供了足够的稳定性,磁控偏置动量卫星甚至可在赤道轨道实现稳定控制．偏置动量卫星也需进行章动阻尼．S t i c k l e r与A l f r i e n d[１９]使用控制律(２２)进行章动与进动控制．G o e l与R a j a r a m[１００]对该控制律进行改进,应用于近赤道轨道卫星,并给出了时间响应表达式．H aＧb l a n i[１０１]改进了控制律(２２),提供了增益系数选取方法．同时,H a b l a n i[１０２]还考虑了非圆轨道下章动与进动控制,给出了控制律进一步改进形式．P u l e cＧc h i等人[１０３]对H a b l a n i改进的控制律进行了详细的性能分析．T s u c h i y a与I n o u e[１０４]在控制律中添加积分项,提高了控制力对干扰力矩的鲁棒性．６第１期穆硕等:卫星磁姿态控制方法与算法综述P D 控制是偏置动量卫星常用的磁姿态控制方案之一．其基本形式为[１０５]:m ＝B ˑ(－k ωωe －k q q ңe ) B ２(２４)其中k ω与k q 为增益矩阵,ωe 为误差角速度,q ңe 为误差四元数矢量部分．Z h a n g 等人[１０６]利用滚转与偏航两轴P D 控制及俯仰轴飞轮实现了小卫星稳定控制．同时,通过调节增益系数,文中对收敛时间及控制误差进行了优化．D o r o s h i n [１０７,１０８]研究了偏置动量卫星在控制律m ＝k ω(２５)下的运动问题．O v c h i n n i k o v 等人[１６]提出了可使卫星在轨道平面内实现任意指向的磁控制律,具体形式为:T ＝０k s i n (α０－α)－k s i n (α０－α)B y B z éëêêùûúú(２６)其中α为３Ｇ１Ｇ２转序下第一个姿态角,α０为其目标值．文中分析了重力梯度力矩干扰下卫星的运动,并给了运动形式．W a n g 与Sh t e s s e l [１０９]基于滑模控制提出了偏置动量卫星磁控制律．通过解耦俯仰轴运动方程,设计了针对滚转偏航轴及俯仰轴两种滑模控制律,通过开关转换函数,实现了b a n g Ｇb a n g 控制．基于L Q R 方法的优化方案也可用于偏置动量卫星控制律设计．早在１９９３年,P i t t e l k a u[１１０]就基于L Q R 方法,提出了针对极轨道卫星的最优控制律．文中建立了干扰力矩周期模型,通过求解R i c Ｇc a t i 方程得到了最优控制增益．此后,L a gr a s t a 与B o r d i n [１１１]同样使用L Q R 方法设计了磁控制律,该控制律可抵抗恒定干扰力矩．G u e l m a n 等人[１１２]介绍了应用于小卫星G u r w i n ＧT e c h S A T 的优化控制律．同时,文中提到了一种类似于控制律(２２)的b a n g Ｇb a n g 控制,具体形式为m ＝－k １(Bm e a s －Be x p )－k ２(B m e a s －B e x p )(２７)其中B m e a s 与B e x p 分别为磁强计测量与星载磁场模型计算得到的地磁场强度矢量．P u l e c c h i 等人[１１３]提出了适用于星载计算机的离散L Q R 方法．偏置动量卫星磁控制律的另一种优化方法为H ２与H ɕ方法．W i s ᶄn i e w s k i [１１４]等人使用H ２方法设计了小卫星磁控制律,T r égo u ët [１１５]等人将H ２方法应用于偏置动量卫星．H ɕ方法则可提高控制律对干扰力矩及参数不确定性等因素[１１６Ｇ１１８]的鲁棒性．偏置动量卫星的陀螺稳定性质克服了磁控固有缺陷,同时其设备简单,控制精度高,自上个世纪以来应用广泛,并不断与新技术融合[１１９Ｇ１２２]．后续关于磁控偏置动量卫星的研究会多集中于优化方法应用,如时间最优机动方案设计等．但偏置动量轮体积较大,应用于纳卫星,皮卫星等存在一定局限性,需做进一步研究．３．２．３㊀磁控与重力梯度力矩结合重力梯度力矩也可为卫星提供被动稳定．通过重力梯度杆等装置,地球重力可为卫星提供一轴稳定力矩．该方式在上个世纪卫星任务中应用广泛．同时,为防止卫星绕重力梯度杆旋转等,需利用磁力矩对卫星进行姿态控制．M a r t e l 等人[１２３]将主动磁姿态控制应用于重力梯度卫星,解决了卫星重力梯度杆稳定指向及热量处理问题．文中提出了两种主动磁控制律．控制律(２７)在姿态获取阶段进行角速度阻尼控制．三轴稳定控制阶段则采用P D 控制,通过投影方法,实现高精度稳定．G r a s s i [１２４]同样利用控制律(２７)及基于误差矢量e ң的P D 控制实现了重力梯度小卫星稳定控制,其P D 误差控制律为:m ＝k １e ң＋k ２eң(２８)同时,文中还设计了控制律(２７)的实施阈值,即当误差大于一定阈值时该控制律才会施加于卫星,以防止卫星因仪器测量与执行误差在平衡点附近发生摆动．L o v e r a 与A s t o l f i [１２５]证明了P D 控制律的稳定性．同时,基于磁场平均化理论以及小角速度假设,L o v e r a 与A s t o l f i [１２５]证明了P D 控制可指数收敛．通常控制律得到的理想控制力矩T d 会使用投影方法计算所需磁矩m ．此时施加于卫星的实际力矩T 根据式(１)进行计算．由于T 须垂直于地磁场矢量,因此与理想控制力矩T d 存在一定误差．A r Ｇd u i n i 与B a i o c c o [１２６]针对重力梯度卫星,提出了两种可使T d 与T 误差最小化的方法．其中一种是最小化二者欧拉二范数,另一种则是使T 两轴分量与T d 一致,在满足T 垂直于地磁场矢量的限制下,设计其第三轴力矩分量．B a k 等人[１２７]基于滑模控制提出了姿态阻尼控７。

卫星姿态控制

M sgn(U ) 0
(6.14a)
U (1 h)1或 sgn(UU ) 0 (6.14b) U 1或 sgn(UU ) 0
系统框图见图6.10。图中k为微分系数，θ c为给定的姿态角。
当θ c=0时，系统由初始条件逐渐向里收敛，最后停留在一个稳定振荡上面，即为极限环(见图6.11)。显然该控制系统也是稳定的，有阻尼存在，且阻尼的大小取决于超前网络参数k的大小。过渡过程的最大角度超调发生在点“2”处，从分析式(6.12)得知，发生在处，其大小可以表示为
对于一般的n维控制任务，由上述分析方法可以证明以下结论：
(1)n维任务的最小结构要求推力器数目m为
m=n+1
(2)n 维任务如果要求冗余度为 R ，则最小冗余结构的推力器数目m为
m=n+1+2R
6.3.2 推力器系统的操作航天器推力器系统的正确操作包含许多方面的正确选择。其中有： (1)任务字 (2)指令矢量 (3)档次字 (4)推力器组合 (5)组合体
最小冗余结构可用作图法确定。以图6.17所示的二维控制任务为例，图6.18为各种推力器配置方案的推力矢量图。图中的每一个矢量代表配置的一个推力器的推力矢量或力矩矢量。
过矢量的交点作任一直线aa’，把二维控制平面分为两半。如果每一个半平面内至少含i个推力或力矩矢量，则系统有冗余度R=I-1。依此方法可以判定，图6.18所示中由左至右4种推力器配置方案的冗余度分别为R=1，l，2，2。
从该理想化的极限环工作状态可知，在死区负极限 ( R )和正极限( R )之间存在一个常值角速度 R ，见式(6.18)。尽量减小这个常值角速度有利于节省工质消耗量。若推力器的推力为F，相对航天器质心的力臂为l，比冲(比推力)为 I sp ，推力器的最小脉宽为△t，则容易证明航天器继电控制的理想平均工质消耗量为

第四章航天器的姿态动力学与控制

在设计飞轮控制系统时，第一需要考虑卸载（磁卸载或喷气卸载），这也就不可避免地增加了系统的复杂性。第二需要考虑飞轮的使用寿命。我国自主研发的飞轮工作寿命在 10年以上，而且可靠性也很高。在某些精度非常高的控制系统中，可以采用磁浮轴承的飞轮。
11.3.6 姿态敏感器
姿态就是航天器在空间的方位，而姿态敏感器用来测量航天器本体坐标系相对于某个基准坐标系的相对角位置和角速度，以确定航天器的姿态。要完全确定一个航天器的姿态，需要3个轴的角度信息。由于从一个方位基准最多只能得到两个轴的角度信息（俯仰和偏航），为此要确定航天器的三轴姿态至少要有两个方位基准。姿态敏感器按不同的基准方位，可分为下列5类：1、以地球为基准方位：红外地平仪，地球反照敏感器；2、以天体为基准方位：太阳敏感器，星敏感器；3、以惯性空间为基准方位：陀螺，加速度计；4、以地面站为基准方位：射频敏感器；5、其他：例如磁强计（以地磁场为基准方位），陆标敏感器（以地貌为基准方位）。
单轴
与喷气推力器三轴姿态稳定系统相比，飞轮三轴姿态稳定系统具有多方面的优点。
1、飞轮可以给出较精确的连续变化的控制力矩，可以进行线性控制，而喷气推力器只能作非线性开关控制。因此飞轮的控制精度一般比喷气推力器的高一个数量级，而且姿态误差速率也比喷气控制小。
2、飞轮所需要的能源是电能，可以不断通过太阳能电池在轨得到补充，因而适合于长寿命工作。喷气推力器需要消耗工质或燃料，在轨无法补充，因此其使用寿命大大受限，基本上与航天器携带的工质或燃料质量成正比，而且还有长期密封问题。
11.3.3 自旋稳定
自旋稳定的原理：是利用航天器绕自旋轴旋转所获得的陀螺定轴性，使航天器的自旋轴方向在惯性空间定向。它的主要优点首先是为航天器获得规则的姿态运动提供了一种简单的手段。自旋卫星利用非常简单的仪器便可提供姿态信息，而且因为运载工具通常是以自旋方式入轨的，所以航天器很容易达到完全无源的惯性定向，并且有一定的精度。其次，由于自旋运动具有比较大的动量矩，因此航天器抵抗外干扰的能力很强，因为当自旋航天器受到恒定干扰力矩作用时，其自旋轴是以速度漂移，而不是以加速度漂移。加之自旋稳定能使航天器发动机的推力偏心影响减至最小，因此自旋稳定方式在航天器，特别是在早期发射的航天器中得到了广泛的应用。

卫星姿态动力学2

参考矢量：地心方向矢量太阳方向矢量姿态确定方法：首先利用地球敏感器的测量值确定卫星的滚动角和俯仰角，其后再由太阳敏感器的测量时局，结合卫星的轨道参数和太阳星历数据确定卫星偏航角。敏感器的安装形式：地球敏感器太阳敏感器扫描自旋轴沿滚动轴滚动太阳敏感器扫描自旋轴沿俯仰轴偏航太阳敏感器偏航太阳敏感器姿态测量误差 ●敏感器测量误差 ●敏感器安装误差
手
持
示
波
器
手持式示波器具有： ★三位一体的双通道手持式示波器，内置数字万用表和数据记录仪功能； ★符合CAT III 600V通道间隔离度标准，能够安全地执行大功率信号分析； ★高达200MSa/s采样率和2Mpts深存储器，让您对信号细节一览无余； ★双窗口缩放功能支持您轻松识别并放大问题区域，以进行更详细的分析； ★提供三种显示模式（室内、室外或夜间），使用户可在任何光线条件下进行信号调试； ★ 10种本地化用户界面任选； ★ USB2.0全速I/O接口； ★使用在阳光直射条件下也能清晰显示的 5.7 英寸 VGA TFT LCD 显示屏（色彩强度增强），波形细节纤毫可辨； ★更高的分辨率和更宽的视角让用户可以更精确地查看信号； ★在时域和频域中进行更快速的波形分析。
用途：姿态初值确定姿态修正
误差源：敏感器测量误差计算误差分类：单参考矢量法双参考矢量法多参考矢量法
惯
测量敏感器：高速旋转的陀螺
性
测
量
优点： ★可星上自主测量 ★具有较高的精度缺点： ★需要已知初始姿态 ★陀螺偏移引起误差 ★参考系不为惯性参考系时，需要转换坐标系
空间基准场
重
力
梯
度
杆
重力梯度力矩的大小与航天器惯量分布有关。重力梯度伸缩杆就是为重力梯度稳定航天器提供所要求的结构形状和惯量分布，以产生较大的稳定力矩。重力梯度伸缩杆在发射前收卷在伸缩杆机构中，入轨后由伸杆机构将重力梯度杆伸展出来。目前可作为伸杆机构的形式很多，如卷伸式，套筒式和电机控制伸展等形式。

卫星姿态动力学与控制

沿本体锥运动
由于ωy和 ωz周期性变化，所以在本体坐标系Oyz平面内， ω绕Ox轴以速率Ω旋转，而幅值ω恒定。由此可见，星体的瞬时转速ω绕自旋轴Ox 作圆锥运动。
Ox沿H动量矩空间锥运动
考虑到在无外力矩作用下，航天器动量矩H守恒，即在空间中固定不变，
由于ω绕Ox轴旋转，因此Ox也必然作圆锥运动，才可能使得它们的合矢量H在空间定向
推进剂的消耗对卫星具有反作用力和力矩
模态截断和溢出
模态阶段：为了方便起见，在工程设计中，对动力学方程进一步降阶，截区对系统影响较小的模态，保留影响较大的模态坐标。
模态溢出：在实际情况中，任然会激发被截取的模态坐标，被称为控制溢出。
测量与分析时，留有足够的增益裕量或相位裕量，使得被截去的模态不会影响系统的稳定性和性能。
频谱分析仪（信号分析仪）
通过使用行业领先的分析工具，查看器件的真实性能，这些频谱分析仪工具能够帮助您: 使用各种硬件平台满足不断变化的测试需求—无论是研发领域追求的最高性能，还是制造环节恰到好处的性能利用业界最广泛的特定频谱分析软件，实施更深入的故障诊断或一键式测量在您优化测试以提升测量性能或吞吐量时，可以利用经过证明的测量科学以及能够保证测量完整性的深厚技术来获得可靠的测量结果通过升级功能特性和性能，延长测试资产的使用寿命
基础频谱分析仪（BSA）
基础频谱分析仪（BSA）执行简单有效的操作 •在高达 7 GHz 的频率上提供可靠的性能，可以提高生产效率、避免不必要的开支 •经过优化的测量速度和增值特性可以提高您的测试效率 •仪器的可用性得到改善，可以缩短您的学习时间和提高测试效率 •覆盖了频谱分析、信号监测和传输/反射测量等多种功能，能够满足更广泛的、严苛的射频测试需求

卫星姿态控制的现状及发展方向

优点简单，方便质量小，功耗小
缺点受轨道影响大，无法测量
偏航轴有阴影区，间断使用
星敏感器 0.001°
3
精度高
复杂，成本高，昂贵
陀螺仪 0.01°/h
3
带宽大，精度较高成本高，偏移随时间累积
根据目前对高精度卫星的要求，姿态确定系统中一般将各种敏感器进行组合使用。下面介绍几种比较典型的敏感器组合方式[1]：
或机动时,易引起章动,且偏航轴无主动控制,因此控制精度比零动量方式低。
（3）零动量轮和偏置动量轮的混合系统
采用 RW 和 MW 的多种组合方案,以进一步改变动量轮系统的性能,提高精度。
例如美国 Seasat 卫星,俯仰轴安装偏置动量轮,滚动和偏航轴由反作用轮主动控
制。
一般而言,零动量轮控方式控制精度最高,偏置动量轮控方式或偏置动量轮
（1）确定性算法确定性算法针对具体的姿态参数设计优化方法，它要求结果有明确的物理或几何上的意义，对参考矢量的测量精度要求较高，无法克服如敏感器的安装误差等参考矢量的不确定性，最早出现的确定性算法是 Wahba 提出的求解姿态矩阵的最小二乘性能指标[3-5]。通过最小化包含矢量测量信息的性能指标，得到姿态矩阵最优解，TRIAD[6-7]方法根据两个非平行矢量测量值确定姿态矩阵，但是丢失部分测量信息，只能处理两个矢量，另外还有四元数估计法(QUAST) [7]、快速最优矩阵估计法(FOAM) [5]、欧拉轴/角估计法(Euler-q) [8]等。（2）状态估计法状态估计法与确定性算法的不同之处在于，它将状态空间表达式运用于系统模型中，不仅仅限于估计姿态参数，还可以对系统观测中的一些不确定性参数进行估计。状态估计法提供被估计量的统计最优解，尽可能的减少一些不确定性因素所造成的影响。从而提高姿态确定的精度[9]。在卫星姿态确定中，在卫星姿态动力学或运动学模型基础上，建立星体姿态方程，只需要一个时变的矢量来对星体姿态进行估计[10]。文献[11]首次在航天器的姿态估计中应用卡尔曼滤波技术，建立基于陀螺仪和矢量姿态敏感器的数学模型，应用卡尔曼滤波进行状态估计，文献[12]给出了仅采用星敏感器和滤波算法的卫星姿态参数和角速度参数的估计方法，文献[13]在陀螺仪和星敏感器组合下采用最小方差估计，用高精度的星敏感器校正陀螺仪常值漂移，文献[14]较为全面的给出了多种非线性姿态估计方法。由于扩展卡尔曼滤波(EKF)算法的局限性，导致基于卡尔曼滤波的估计方法只能解决小角度情况下的姿态确定问题，另外还有粒子滤波(Particle Filters, PF)，正交姿态滤波(Orthogonal Attitude Filter, OAF)，预测滤波(Predictive Filtering, PF)，自适应方法(Adaptive Methods, AM)等，采用这些基于卡尔曼滤波的状态估计法，估计精度能够满足系统要求[15]。不论系统的测量值有几个，状态估计法都适用，并且还能够对某些系统误差进行最优估计。因此，状态估计法一般用于对姿态精度要求很高的情况。但估计法估计器需求较高的稳定性和和较强的实时性。即在建立准确的估计模型和误差模型的同时，还要求估计算法简单，易于实时计算。

航天器姿态动力学与控制

姿态参数 – 欧拉轴/角
e
v
u' b
a
u
欧拉轴/角坐标变换示意图
姿态参数 – 欧拉轴/角
zb
za
e
z
x xa
xb
yb
y
ya
姿态参数 – 欧拉参数(姿态四元数)
欧拉参数与方向余弦矩阵的关系
Cbaq02qTqE32qqT2q0q
q202qq1q122qq223q0q32 2q1q3q2q0
2q1q2q3q0
q02q12q22q32
2q2q3q1q0
2q1q3q2q0 2q2q3q1q0
q02q12q22q32
q0
1 2
1 C 11 C 22 C 33
q1
1 4q0
C 23
C 3 2
q2
1 4q0
C 31
C 1 3
q3
1 4q0
C 12
C 2 1
q1
1 2
1 C 11 C 22 C 33
b 细长体航天器的空间锥和本体锥
第4章自旋、双自旋航天器姿态动力学
z
自旋航天器在惯性空间的运动
y
x
第4章自旋、双自旋航天器姿态动力学
能量椭球和角动量椭球的交线(本体极迹)
第4章自旋、双自旋航天器姿态动力学
一般刚体自由姿态运动的本体极迹
第4章自旋、双自旋航天器姿态动力学
不变平面和不变线的定义 Poinsot椭圆在不变平面上的无滑动滚动
绪论
章节安排
第一部分航天器姿态动力学
绪论第1章航天器姿态运动学第2章航天器姿态动力学基本方程 ➢ 第3章空间环境力矩 ➢ 第4章自旋、双自旋航天器的姿态动力学 ➢ 第5章重力梯度稳定航天器的姿态动力学 ➢ 第6章三轴稳定航天器的姿态动力学

卫星轨姿动力学及控制方法_图文

– 特征模型与高阶系统的降阶模型不同,它是把高阶模型的有关信息都压缩到几个特征参量之中,并不丢失信息,一般情况下特征模型用慢时变差分方程描述.
挠性结构航天器飞行控制
大型挠性结构的运动形式
1 系统整体运动 2 柔性部件的弹性振动
大型挠性结构姿态控制特点
1 控制对象无限维，控制器有限维 2 挠性附件有限阶振型
卫星轨姿动力学及控制方法_图文.ppt
航天器（卫星）基本知识卫星轨姿控制挠性卫星姿态控制
航天器（卫星）分类
地球观测站：侦察卫星、气象卫星、地球资源卫星
中继站：通信卫星、广播卫星、跟踪和数据中继卫星
基准站：导航卫星、测地卫星
轨道拦截（或攻击）武器：拦截摧毁敌方卫星的反卫星和攻击地面目标的卫星
姿态敏感器： 1 利用地球物理特性 2 利用天体位置 3 利用惯性器件 4 利用无线电信标 5 其他
姿态确定软件算法：
姿态稳定控制
被动控制：利用自然环境力矩或物理力矩源。
主动控制：三自由度的姿态闭环控制系统。
组合控制
姿态控制系统设计理念
敏感功能确定航天器的姿态。逻辑单元让电信号以正确顺序送到力矩产生单元，使航天器绕其质心转动。然后运动(动力学)再由敏感器监视，形成航天器姿态控制系统的闭合回路
特征建模
特征建模
传统建模方式和控制存在缺点
– 建模方式缺点
• 分布参数和偏微分建模 • 模态分析
– 控制方法缺点
• 高阶控制器 • 现场调试 • 模型降阶
特征建模
特征建模概念：
– 结合对象的动力学特征和控制性能要求进行建模。不是仅以对象精确的动力学分析来建模。
– 针对高阶线性定常系统，可以采用二阶时变差分方程形式描述。

第二章姿态运动学与动力学

A被称为方向余弦阵或姿态矩阵
方向余弦阵的性质及特点
方向余弦阵只有三个独立参数 xa⋅ xa=1, ya⋅ ya=1, za⋅ za=1 xa⋅ ya=0, xa⋅ za=0, ya⋅ za=0 方向余弦阵是正交矩阵方向余弦阵的行列式为1 方向余弦阵可作为坐标变换矩阵
Fa=CabFb, Fb=CbcFc, Fa=CacFc Cac=CabCbc
yp o zp xp 太阳
2.1.7 太阳-黄道坐标系oxsyszs
太阳黄道平面为坐标平面 xs轴指向太阳圆盘中心 zs轴指向黄极 ys轴与xs、 zs右手正交三轴稳定的科学卫星
ϒ
PN C
zs ys o xs 黄道 S 赤道
§2.2 姿态描述
2.2.1 2.2.2 2.2.3 2.2.4 2.2.5 2.2.6 姿态描述初步方向余弦式姿态描述 Euler轴/角式姿态描述 Euler角式姿态描述 Euler四元素式姿态描述 Rodrigues参数式姿态描述
yb
坐标轴的相对关系
ya
xa =Axxxb+Axyyb+Axzzb ya =Ayxxb+Ayyyb+Ayzzb za =Azxxb+Azyyb+Azzzb
方向余弦阵(姿态矩阵)的引入
将两个坐标系坐标轴之间的关系写成紧凑形式
Fa = AFb
⎡ Axx ⎢ A = ⎢ A yx ⎢ Azx ⎣ Axy A yy Azy Axz ⎤ ⎥ A yz ⎥ Azz ⎥ ⎦
2.2.4.1 Euler角基本理论依据
出发点
希望三个姿态参数具有简便、明显的几何意义，并能用姿态敏感器直接测量，且可方便求解动力学方程
理论依据(Euler定理)

飞行器的运动学和动力学分析

飞行器的运动学和动力学分析飞行器运动学和动力学分析随着科技的发展和人类探索空间的越来越深入，飞行器作为空间探索的重要工具和交通工具，得到了越来越广泛的应用。

对于飞行器的运动学和动力学分析是飞行器设计和控制的基础，也是飞行器性能的重要指标之一。

本文将从运动学和动力学两个方面对飞行器进行分析。

一、运动学分析运动学是研究物体运动的位置、速度、加速度等变化过程的物理学分支。

在飞行器设计和控制中，运动学分析主要包括三个方面：1、姿态控制飞行器的姿态控制涉及到飞行器的姿态稳定性和姿态调整能力。

在飞行器运动过程中，由于外部环境的影响和内部器件的失效等原因，飞行器可能会出现不稳定的姿态，影响飞行器的性能和安全性。

因此，姿态控制是飞行器设计和控制的重要问题。

姿态控制的基本原理是通过飞行器内置的传感器感知飞行器的动态姿态，再通过控制器对飞行器的控制面进行调整，最终使飞行器保持稳定的姿态状态。

姿态控制的技术难点在于如何快速、精确地感知飞行器的姿态变化，并做出相应的调整。

2、飞行轨迹规划飞行器的飞行轨迹规划主要包括确定飞行器的起点、终点和中间路径，以及确定飞行器在不同时间段内的飞行速度和飞行方向等。

飞行轨迹规划是飞行器飞行过程中的重要问题，直接关系到飞行器的航行安全和性能。

在飞行轨迹规划中，需要考虑到各种环境因素的影响，如风力、气压、温度、湿度等，以及地形地貌的变化。

飞行轨迹规划的目的是使飞行器在最短时间内达到目标点，并尽量避免遭受损失。

3、动力系统分析飞行器的动力系统是飞行器能够运行的重要部件，在设计和控制中需要对其进行分析和优化。

动力系统分析主要包括飞行器的动力来源、动力输出能力以及能量转换效率等方面。

在动力系统分析中，需要综合考虑动力系统的质量、功率和效率等因素，以及飞行器的运动学特性，选定合适的动力系统，实现飞行器的高效、稳定和可靠运行。

二、动力学分析动力学是研究物体受力作用下运动状态的变化过程的物理学分支。

在飞行器设计和控制中，动力学分析主要包括四个方面：1、空气动力学分析飞行器在空气中运动时，会受到空气的阻力、升力、侧向力和剪切力等作用力。

航天器姿态的描述与姿态动力学

航天器姿态运动学
x
y
z
x ' cos 1 cos 2
cos 3
y ' cos 1 cos 2
z ' cos 1 cos 2
cos 3
cos 3
方向余弦矩阵(Direction
Cosine Matrix) 为正交矩
阵，有时以表格形式给出
➢ 直接求取方向余弦矩阵比较困难，因此引入内框架坐标系oxyz和
的本体坐标系Oxyz。变换矩阵为
x cos

y sin
z 0

sin
cos
0
0

0

1

15
航天器姿态运动学
综合以上变换，坐标系OXYZ与Oxyz之间的直接转换关系即为
系 O 中的分量分别为：
O 轴为，
O 轴为 sin ， O 轴为
cos 。再将
O 轴和 O 轴分量按Ox和Oy轴分解，其结果表示如下：
x sin sin cos

y sin cos sin
标轴保持平行。
质心轨道坐标系
简称轨道坐标系。这是一个以航天器质心为原点的正
交坐标系，如图所示。
卫星轨道平面为坐标平面，O为卫星质心，z
轴由质心指向地心（当地垂线），x轴在轨道
平面内与z轴垂直并指向卫星速度方向，y轴与
x、z轴右手正交且与轨道平面法线平行
3
航天器姿态运动学
本体坐标系Oxyz
又称为星体坐标系。在此坐标系中，原点0在航天器质心，Ox，

空间飞行器飞行动力学(工大教纲)

《空间飞行器飞行动力学》课程教学大纲课程编码： T1180230课程中文名称：空间飞行器飞行动力学课程英文名称：SPACECRAFT DYNAMICS总学时：50 讲课学时：50 实验学时：0习题学时：0 上机学时：0学分：3授课对象：飞行器设计专业、空间环境专业本科生先修课程：高等数学、普通物理、理论力学、自动控制理论教材及参考书：《空间飞行器动力学》，刘暾. 赵钧，哈尔滨工业大学出版社《空间飞行器动力学与控制》，M．H．卡普兰一、课程教学目的《空间飞行器动力学》是一门航天工程专业学生的专业基础课。

本课程主要研究空间飞行器动力学的基本概念、原理和应用，包括轨道动力学和姿态动力学两大部分，其主要任务是培养学生：建立空间飞行器动力学的基本概念，理解飞行器的运动与受力之间的关系，掌握空间飞行器动力学问题的基本分析方法；掌握应用空间飞行器动力学的基本理论，解决一般的空间飞行器动力学应用问题的基本技能；了解空间飞行器动力学理论、方法及其应用的最新发展；掌握使用相关的参考文献、计算机应用软件进行动力学问题研究分析的能力；《空间飞行器动力学》是高等工科院校中航天工程类专业的一门主要课程。

通过该课程的学习，学生可以初步掌握解决空间飞行器动力学问题的基本方法和技能，并了解其他空间飞行器应用问题的动力学依据，为日后从事空间飞行器的动力学及其他的空间飞行器应用专业的研究工作奠定初步的理论基础。

二、教学内容及基本要求轨道动力学部分(上篇)第一章绪论（1学时）概论，齐奥尔科夫斯基公式，单级火箭的极限速度。

第二章空间飞行器的入轨（1学时）运载火箭的运动方程式，纵向平面内的动力学方程，运载火箭导引规律。

第三章空间飞行器的轨道（4学时）两体运动方程的建立、求解，中心引力场中的运动，四种基本轨道的轨道方程、特性及时间方程。

第四章轨道的建立和星下点轨迹（2学时）空间飞行器轨道建立的方法，轨道要素与发射参数的关系，星下点轨迹的描述。

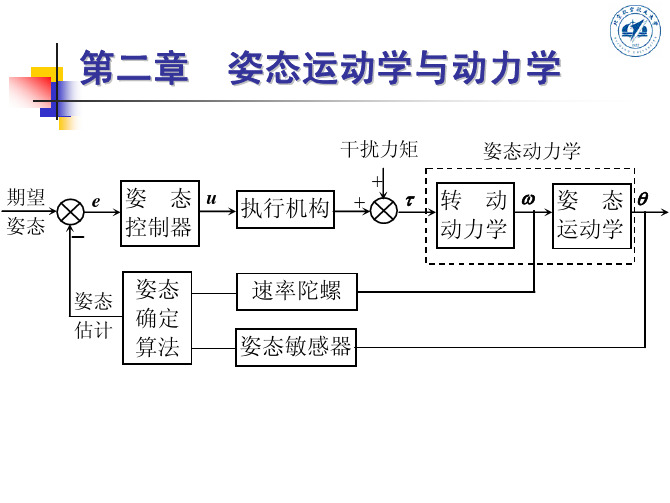
SimuLink卫星姿态控制_动力学模块的建立

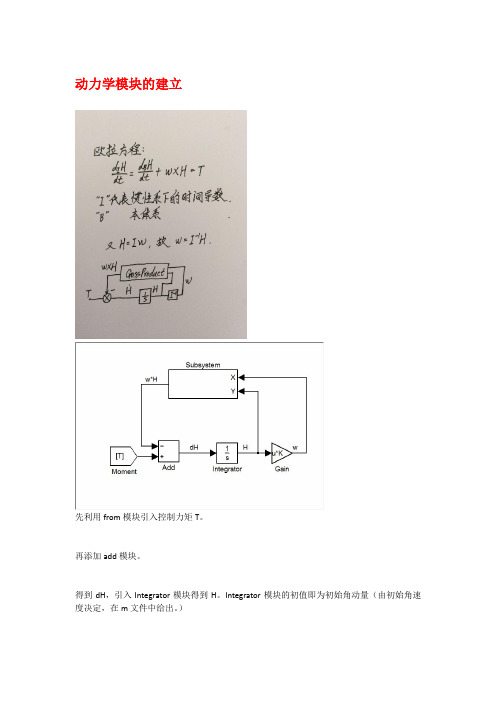
动力学模块的建立
先利用from模块引入控制力矩T。

再添加add模块。

得到dH，引入Integrator模块得到H。

Integrator模块的初值即为初始角动量（由初始角速度决定，在m文件中给出。

）
利用Gain模块得到转动惯量矩阵I的逆来得到w。

修改gain模式为Matrix(u*K)。

I的逆Inv(I)最好在m文件中计算出来（SimuLink从Workspace中调用），这样减少计算量。

将H与w引入Subsystem模块（叉乘模块）。

右键Subsystem模块-“Create Mask”来修改模块的外貌。

（为模块起名Cross Product，为输入输出起名，以防止叉乘顺序出错）
建立叉乘模块。

在模块里面添加两个in，一个out。

添加两个Mux，三个Fuc，模型如下：
计算叉乘结果如下：
按照计算结果填写Fcn模块：
叉乘模块即建立完成。

将叉乘结果w*H引至add模块即完成动力学模块。