第11章 轮系(OK)
第十一章 轮系

第十一章 轮系一、学习指导与提示工程中实际应用的齿轮机构经常以齿轮系(简称轮系)的形式出现,它用来获得大传动比、变速和换向、合成或分解运动以及距离较远的传动。
轮系可分为定轴轮系和周转轮系两大类,所谓复合轮系只不过是既包含定轴轮系又包含周转轮系,或几部分周转轮系组成的复杂轮系。
因此,首要的是弄清定轴轮系和周转轮系的本质属性,并掌握它们各自的传动比计算方法,在此基础上,只要注意正确区分轮系,就可以将一个复杂的复合轮系分解为若干个单一周转轮系和定轴轮系,这是学习轮系传动比计算的一个总体原则,应当牢牢把握。
本章的主要内容是:(1)轮系的应用和分类;(2)定轴轮系及其传动比;(3)周转轮系及其传动比;(4)复合轮系及其传动比;(5)特殊行星传动简介。
1.定轴轮系一个轮系,若运动过程中,所有齿轮的几何轴线的位置都是固定不变的,则可判定该轮系为定轴轮系(亦称普通轮系)。
注意:这里指的是几何轴线位置固定,并不是该轴不能转动,无论该轴是转动的,或不转动的(与机架相联),只要几何轴线位置不变,就是定轴的。
定轴轮系传动比计算公式:()各主动轮齿数连乘积各从动轮齿数连乘积J G J G n n i mJ G GJ →→-==1 (11.1) 上述公式包含两方面的问题:传动比GJ i 的大小,以及主从动转速 n G 、n J 之间的转向关系(即传动比的正负号),m 为外啮合齿轮对数。
但需注意:① 只有在J G →传动路线中无空间齿轮,各轮几何轴线均互相平行的情况下,公式中()m 1-才有其特定意义,可以用其来表示n G 、n J 之间的转向关系。
若计算结果GJ i 为正,说明G 、J 两轮转向相同;若为负,则说明G 、J 两轮转向相反。
② J G →传动路线中有空间齿轮(如锥齿轮、蜗轮蜗杆),如图11.1所示,各轮转向只能用标注箭头法确定,()m 1-没有意义。
图11.12.周转轮系轮系中至少有一齿轮的几何轴线不固定,而是绕另一轴线位置固定的齿轮回转,这样的轮系,就是周转轮系。
机械原理第11章 轮系

2 H 1
ω1 ω2 ω3 ωH
ω = ω1 −ωH ω = ω2 −ωH ω = ω3 −ωH H ωH = ωH −ωH = 0
H 1 H 2 H 3
3 转化轮系传动比计算
H z2z3 z3 ω1 ω1 −ωH H =− =− i13 = H = ω3 ω3 −ωH z2z1 z1
2 H 1 3
z2z4 ⋅ ⋅ ⋅ zn ω1 −ωH i = =± ωn −ωH z1z3 ⋅ ⋅ ⋅ zn−1
H 1n
4 真实轮系传动比计算 1)差动轮系 差动轮系(F=2) 差动轮系
ω1 、ωn和ωH中有 个量已知,未知量可求; 中有2个量已知 未知量可求; 个量已知,
z2z4 ⋅ ⋅ ⋅ zn ω1 −ωH i = =± ωn −ωH z1z3 ⋅ ⋅ ⋅ zn−1
i16< 0,1与6转向相反。 转向相反。 , 与 转向相反
(2)封闭型复合轮系 ) 封闭型复合轮系 ●结构特点 单自由度基本轮系的首尾分别与双自由 度差动轮系的两个基本构件固连。 度差动轮系的两个基本构件固连。
●解题方法步骤 1)区分基本轮系 (1)区分基本轮系 从行星轮入手,找出所有周转轮系; 从行星轮入手,找出所有周转轮系; 其余则为定轴轮系。 其余则为定轴轮系。 (2)列传动比方程 2)列传动比方程 3)联立求解 (3)联立求解 系杆 支 承 行星轮 啮合 太阳轮
n4 4 (90)
【解】
z2z3z4 n1 − nH i = =− n4 − nH z1z2' z3'
H 14
3(30) 2 (30) 3'(20)
30⋅ 30⋅ 90 =− = −6.48 25⋅ 25⋅ 20 1− nH 1− nH = −6.48 = −6.48 2 2 nn − −−H
第11章-轮系习题答案

一、填空题:1.轮系可以分为:定轴轮系和 周转轮系 。
2.定轴轮系是指:当轮系运动时,各轮轴线位置固定不动的轮系;周转轮系是指:轮系运动时,凡至少有一个齿轮的轴线是绕另一齿轮的轴线转动的轮系。
3.周转轮系的组成部分包括: 太阳轮 、 行星轮 和 行星架 。
4.行星轮系具有 1个自由度,差动轮系有 2自由度。
5、行星轮系的同心条件是指:要使行星轮系能正常运转,其基本构件的回转线必须在同一直线上。
6、确定行星轮系中各轮齿数的条件包括:传动比条件、同心条件、均布条件、邻接条件。
7、正号机构和负号机构分别是指:转化轮系的传动比H 1n i 为正号或者负号的周转轮系。
动力传动中多采用 负号 机构。
二、分析计算题 1、在图示的车床变速箱中,移动三联齿轮a 使3’和4’啮合。
双移动双联齿轮b 使齿轮5’和6’啮合。
已知各轮的齿数为z 1=42,582=z ,38'3=z ,42'4=z ,48'5=z ,48'6=z 电动机的转速为n 1=1445r/min ,求带轮转速的大小和方向。
解:3858483842484258'5'31'6'426116-=⨯⨯⨯⨯=-==z z z z z z n n i min /9466r n -=(与电动机转动方向相反)2、在图示的轮系中,已知各轮齿数为20z z z z z 65321=====, 已知齿轮1、4、5、7为同轴线,试求该轮系的传动比17i 。
(1)z z z z z 41231225520100=++==⨯=z z z z 75612332060=+==⨯=(2)iz z z z zz z z z z17323467123561=-()=-⨯⨯=-100602020153、在图示轮系中,已知:蜗杆为单头且右旋,转速n11440= r/min,转动方向如图示,其余各轮齿数为:402=z,20'2=z,303=z,18'3=z,544=z,试:(1)说明轮系属于何种类型;(2)计算齿轮4得转速n4;(3)在图中标出齿轮4的转动方向。
机械原理 轮系

i= 14
z2z3z4 z1z2' 3' z
传动比方向判断: 传动比方向判断:画箭头 传动比大小表示: 传动比大小表示:在传动比大小前加正负号
§11-3 周转轮系的传动比 11一、周转轮系传动比计算原理 1.反转法 1.反转法——转化轮系 反转法 转化轮系
给整个轮系加上一个假想的公共角速度(-wH),据相对 的公共角速度( 运动原理,各构件之间的相对运动关系并不改变,但此 运动原理,各构件之间的相对运动关系并不改变, 时系杆的角速度就变成了wH-wH=0,即系杆可视为静止不 =0, 动。于是,周转轮系就转化成了一个假想的定轴轮系— 于是,周转轮系就转化成了一个假想的定轴轮系— —周转轮系的转化机构。 周转轮系的转化机构。
z5 L ⇒ω3 = − ω5 L (2) z3′
3)联立(1)、(2)求解 联立(1)、(2)求解 (1)
z ω1 z2 z3 1 + 5 + 1 ⇒ i15 = = ω5 z1 z2′ z3′
33× 78 78 = 1+ +1 = 28.24 24 × 21 18
-ω H
ωH
ω H - ω H=0
周转轮系 假想定轴轮系
转化轮系
指给整个 周转轮系加上 一个“ 的 一个“-wH”的 公共角速度, 公共角速度, 使系杆H变为 相对固定后, 相对固定后,
原轮系
所得到的假想 转化轮系 的定轴轮系。 的定轴轮系。
2. 转化轮系中各构件的角速度
3. 转化轮系的传动比
在运动简图上用箭头标明两轮的转向关 在运动简图上用箭头标明两轮的转向关 箭头标明 系。
大小: 大小:
ω 从动齿轮齿数连乘积 1 = i1k = ωk 主动齿轮齿数连乘积
第11章 轮系-复合轮系

例6:图示为一电动卷扬机的减速器运动简图, 已知:z1=24,z2=33,z’2=21,z3=78,z’3=18, z4=30,z5=78,试求传动比 i15。
解: 1)齿轮 1 - 2 - 2’ - 3 - H
(齿轮5)组成差动轮系;
2 4
z2 z3 1 H 1 5 i 3 H 3 5 z1 z 2
动画1 动画2 动画3
本章结束
返回
A
D
B C
5
4
P
2 H
3
1
车轮
H 2L
33 78 78 1 1 28.24 24 21 18
§11-5
轮系的功用
一、实现分路传动:
利用轮系可以使一个主 动轴带动若干个从动轴
同时旋转,并获得不同ຫໍສະໝຸດ 的转速。二、获得较大的传动比
采用周转轮系,可以在使用很 少的齿轮并且也很紧凑的条件 下,得到很大的传动比。
例5: 如图所示的轮系中,设已知各轮齿数,
试求其传动比。 解:1) 齿轮123H1组成行 星轮系:
i1 H 1 1 i
H1 13
z3 1 z1
z6 1 z4
2) 齿轮456H2组成行 星轮系:
i4 H 2 1 i
H2 46
i1 H 2
z3 z6 i1 H1 i4 H 2 1 1 z1 z4
汽车后桥的差动器能根据汽车不同的行驶状态,
自动将主轴的转速分解为两后轮的不同转动。
n1 r L n3 r L
图片
z1=z3 , nH=n4
动画1 动画2 动画3 动画4
机械基础 轮系传动——第十一章

解:利用公式: 利用公式:
n1 Z 2 Z3 Z 4 Z5 Z 6 Z7 i17 = = n7 Z1Z 2' Z3' Z 4 Z5' Z6' 36 * 80 *18 * 30 * 30 * 60 = 18 * 20 * 20 *18 *15 * 2 = 720 ,逆时针方向) (↑
变速器
差速器
第一节
二、轮系分类
轮系的类型
根据齿轮系运转时齿轮的轴线位置相对于机架是否固定, 根据齿轮系运转时齿轮的轴线位置相对于机架是否固定,可将齿 轮系分为三大类:定轴齿轮系、周转轮系和复合轮系。 轮系分为三大类:定轴齿轮系、周转轮系和复合轮系。 平面定轴轮系 定轴轮系(轴线固定) 定轴轮系(轴线固定) 空间定轴轮系 差动轮系(F=2) 差动轮系(F=2) 轮系分类 周转轮系(轴有公转) 周转轮系(轴有公转) 行星轮系(F=1) 行星轮系(F=1) 复合轮系(两者混合) 复合轮系(两者混合)
2)画箭头表示首末两轮的转向关系
a.圆柱齿轮: 圆柱齿轮: 圆柱齿轮
b.圆锥齿轮: 圆锥齿轮: 圆锥齿轮
b.蜗杆传动: 蜗杆传动: 蜗杆传动 2 1
2 1
右旋蜗杆
例题1. 图所示空间定轴轮系中, =15, 例题1. 图所示空间定轴轮系中,已知各轮的齿数为z1=15, z2=25,z3=14,z4=20,z5=14,z6=20,z7=30,z8=40,z9=2(右 =25, =14, =20, =14, =20, =30, =40, =2( =60。试求:( :(1 ;(2 r/min, 旋),z10=60。试求:(1)传动比i1 10;(2)若n1=200 r/min, 向看去,齿轮1顺时针转动, 从A向看去,齿轮1顺时针转动,求n7和n10。
第11章 混合轮系

第十一章 轮系及其设计
第四节 混合轮系传动比的计算
一、串联式混合轮系 二、封闭组合式混合轮系 三、叠加组合式混合轮系
混合轮系传动比计算步骤:
1.判别该轮系由几种轮系组成的,各轮系如何连接 2.列出各轮系的传动比计算式 3.根据各基本轮系间的连接关系,将各计算式联立
求解
第四节 混合轮系传动比的计算
一、串联式混合轮系
基本思路 前一个轮系的输出构件与后一基本轮系的输入构件固 接组合而成的混合轮系。 整个混合轮系传动比,等于所串联的各轮系传动比的 连乘积。
第四节 混合轮系传动比的计算
一、串联式混合轮系
例11-4
已知:各轮齿数,n1 = 300 r min 求:系杆H的转速nH的大小和转向 解:
= −4
3.联立求解 nH = −30 r min
第四节 混合轮系传动比的计算
一、串联式混合轮系
二、封闭组合式混合轮系
差动轮系的两个构件和自由度为1的轮系封闭联接,形成一个自 由度为1的混合轮系。 被联接的两个构件间始终保持一定的运动约束关系。 例11-5 已知:各轮齿数
z1 = 24, z2 = 52, z2′ = 21, z3 = 78, z3′ = 18, z4 = 30, z5 = 78
运动合成
iH
13
= n1H n3H
= n1 − nH n3 − nH
= − z3 z1
= −1
z1 = z3
nH = (n1 + n3 ) / 2
应用实例:机床、计算机构和补偿装置等。
第五节 轮系的功能及其应用
三、实现运动的合成与分解 运动分解
nH = (n1 + n3 ) / 2
轮系

H-5、3-3′
B、应选转速已知的轮轴。
C、应选与要求传动比或转速有关
的轮轴。 (3)解方程 应注意解法技巧 已知:z1=24, 求:i1H? z2=52,z2′=21, z3=78,z3′=18, z4=21, z5=78
′ —3 —H中 解:在周转轮系: 1 — 22 将(1)变形得
(-nH)
反转法
(定轴轮系) 转化轮系
z2 z3 n n1 nH i () n n3 nH z1 z2
轮2:n2
轮3:n3
H nH nH nH 0 H n1 n1 nH (定轴) H n2 n2 nH (定轴) H n3 n3 nH (定轴 )
m
①、当I、N之间所有的轴线都平行
B、当I、N两轴不平行时:不 能用符号表示转向关系,只能用 画箭头和文字说明。
§5—2
解定轴轮系
定轴轮系传动比计算公式 Ⅰ 所 有 啮 合 对 中 从 动 轮数 齿之 积 iⅠN ( 符 号 )所 有 啮 合 对 中 主 动 轮 数 齿之 积 N
A、当I、N两轴平行时:在表 达式的( )里用“+”、“-” 号表示两轴的转向关系。
教、学目标
轮系
解轮系
一、掌握定轴轮系的解法; 二、掌握周转轮系的解法; 三、掌握复合轮系的解法;
认识轮系机构运动简图
Ⅱ 2
2
Ⅲ 3' 4' Ⅳ 5 Ⅴ
Ⅰ
1
1
3' 4'
3
3
4
4 5
D
认识轮系机构运动简图
Ⅱ 2
Ⅰ
1
Ⅲ 3' 4' Ⅳ 5 Ⅴ
11-第11章-轮系PPT课件

即:imH 1 imHn
4. 主从关系视传递路线不同而不同。
绝对传动比
公转
5. 平面轮系中行星轮的运动: 自转
H
H m
绝对转速 m
例二 轮系中, z1=z2=20, z3=60
2
1)轮3固定。求i1H 。
轮1逆转1圈,轮3顺转1圈
H
2)n1=1, n3=-1, 求nH 及i1H 的值。
1
3)n1=-1, n3=1, 求nH 及i1H 的值。 轮1、轮3各逆转1圈
解: 1)划分轮系 ✓齿轮1-2组成定轴轮系部分; ✓齿轮2-3-4-H组成周转轮系部分。
2)计算各轮系传动比
➢定轴轮系部分
i1 2
n1 n2
z2 z1
40 20
2
n 1 2 n 2 (1)
➢周转轮系部分
i
H 24
n2 nH n4 nH
z4 z2
z1=20
H z4=80
z3=30
z2=40 z2=20
定轴轮系 周转轮系
i2H4
n2 nH n4 nH
z4 z2
由 n4 0 , n2 n2 , z2 2 0 , z4 8 0
n2 nH nH
4
z1=20 z3=30
H z4=80
z2=40 z2=20
n 2 = 5 n H (2)
3)将(1)、(2)联立求解
n 1 = - 2 n 2 (1)
其它构件:行星轮。其运动有自转和绕中心轮的公转,类似行星运动,故得名。
由于轮2既有自转又有公转,故不
ω 能直接求传动比 3
2
-ωH
2 ω2
H
3
H
ωH
轮系

1 实现分路传动
图示为机械式钟表机构。 在同一主动轴的带动下, 利用定轴轮系可实现几个 从动轴多分路输出传动。 动力源(发条盘N)直接 带动分针M,同时又通过 另外定轴轮系分别带动时 针H、秒针S,实现多路 传动。iMH=12,iSM=60.
5. 6.
4 获得较大的传动比
5 实现运动的分解和合成
汽车后桥差速器
汽车动力传动路线: 汽车动力传动路线: 发动机-曲轴- 发动机-曲轴- 飞轮-离合器- 飞轮-离合器-变 速器- 速器-万向联轴节 传动轴- -传动轴-万向联 轴节- 轴节-主减速器 锥齿轮i=4.111) (锥齿轮 ) 差速器-半轴- -差速器-半轴- 驱动轮
2. 当汽车转弯时,两轮行驶的距离不相等,其 转速比为 n1 r − L = n3 r + L
又因为:
z 2 ∗ z3 n1 − n4 i = =− = −1( z1 = z3 ) n3 − n4 z1 ∗ z 2
H 13
2n4 = n1 + n3
方向判断如图(锥齿轮为空间齿轮,用箭头表示 方向),联解得两轮的转速为:
动力源(发条盘N)经由定轴轮系1-2直 接带动分针M,同时又分成两路:一路通 过定轴轮系9-10-11-12带动时针H, 另一路通过定轴轮系3-4-5-6一方面 直接带动秒针S,另一方面又通过定轴轮 系7-8带动擒纵轮E。由图可见,M与H 7 8 E M H 之间的传动比iMH 、S与M之间的传动比 iSM :
H AB H iAH =1−iAB
2、图示行星轮系中, 各轮的齿数为: z1=27,z2=17,z3=61, 已知n1=6000r/min, 求传动比i1H和行星架H 的转速nH.
第11章 轮系(OK)——机械原理学习指导资料文档

解
1. 根据同心条件
z7 z5 2z6 18 218 54
15
2. (1)划分基本轮系 差动轮系:1、2-3、4和5 定轴轮系:5、6、7
因为:n4=n7
(2)列方程
i154
n1 n4
n5 n5
z2z4 z1 z 3
18 63 24 21
9 4
i57
n5 n7
z7 z5
54 18
12
(2)快速退回时,齿轮1、4组成定轴轮系
i14
n1 n4
z4 z1
1
手轮转动一周,砂轮横向移动量为:
l sn4 sn1 41 4mm
2. 如手轮圆周刻度为200格,则根 据1(1),慢速 进给时,每格砂 轮架的移动量为
11
1
l sn4 4 sn1 4 4 200 0.005mm
17
解
齿轮1、2、3、4和H组成行星轮系
n1 0
i1H4
n1 nH n4 nH
z2z4 z1 z 3
19 20 10 1918 9
手轮转动一周时,工作台的进给量为:
l
Pn4
1 10
P
nH
1 51 0.2mm 10
i4 H
n4 nH
1 10
18
2.图示为行星搅拌机的机构简图,已知:
13
例3 图示为一电动卷扬机简图,所有齿轮均为标准齿轮,模数 m=4mm,各轮齿数为:
z1 24, z2 z2' 18, z3 z3' 21, z4 63, z5 z6 z6' 18
试求: 1. 齿数z7=? 2. 传动比i17=?
14
分析
利用同心条件可以计算出z7,然后按照复合轮系 的“三步走”即可求解出i17。
最新11-第11章-轮系课件PPT

本章要解决的问题:
1.轮系传动比 i 的计算;
2.从动轮转向的判断。
1. 定轴轮系 各齿轮轴线的位置都相对机架固定不动的齿轮传动系统。
2. 周转轮系
至少有一个齿轮的轴线(位置不固定)绕另一齿轮的轴线 转动的齿轮传动系统。
➢周转轮系的组成:
太阳轮 —— 周转轮系中轴线位置固定不动的齿轮
行星轮 —— 周转轮系中轴线不固定的齿轮
——由定轴—动轴或多个动轴轮系组成的轮系
1 2
3H
2' 4
11.2 定轴轮系及其传动比
一、传动比大小的计算
一对齿轮: i12 =ω1 /ω2 =z2 /z1
可直接得出
对于齿轮系,设输入轴的角速度为ω1,输出轴的 角速度为ωm ,按定义有:
i1m=ω1 /ωm
强调下标记法
当i1m>1时为减速, i1m<1时为增速。
i1m
==ωω 11*ω 2*ω 3....* ..ω .m .-1
ωω m2 ω 3 ω 4
ω m
=zz12**zz23**zz34 ....* .* .z. z m . m -1
所有从动轮齿数的乘积 =
所有主动轮齿数的乘积
二、首、末轮转向的确定
转向相反
两种方法:
ω1
ω2
1
1)用“+” “-”表示
p 2
vp
适用于平面定轴轮系(轴线平行,
2
转向相同
p vp
ω1
1
ω2
两轮转向不是相同就是相反)。
外啮合齿轮:两轮转向相反,用“-”表示; 内啮合齿轮:两轮转向相同,用“+”表示。每虑一方对向外时齿有轮反向一次考 设轮系中有m对外啮合齿轮,则末轮转向为(-1)m
机械原理课后答案第11章

第11章作业11-1在给定轮系主动轮的转向后,可用什么方法来确定定轴轮系从动轮的转向?周转轮系中主、从动件的转向关系又用什么方法来确定?答:参考教材216~218页。
11-2如何划分一个复合轮系的定轴轮系部分和各基本周转轮系部分?在图示的轮系中,既然构件5作为行星架被划归在周转轮系部分中,在计算周转轮系部分的传动比时,是否应把齿轮5的齿数,Z5计入?答:划分一个复合轮系的定轴轮系部分和各基本周转轮系部分关键是要把其中的周转轮系部分划出来,周转轮糸的特点是具有行星轮和行星架,所以要先找到轮系中的行星轮,然后找出行星架。
每一行星架,连同行星架上的行星轮和与行星轮相啮合的太阳轮就组成一个基本周转轮糸。
在一个复合轮系中可能包括有几个基本周转轮系(一般每一个行星架就对应一个基本周转轮系),当将这些周转轮一一找出之后.剩下的便是定轴轮糸部分了。
在图示的轮系中.虽然构件5作为行星架被划归在周转轮系部分中,但在计算周转轮系部分的传动比时.不应把齿轮5的齿数计入。
11-3在计算行星轮系的传动比时,式i mH=1-i H mn只有在什么情况下才是正确的?答在行星轮系,设固定轮为n, 即ωn=0时, i mH=1-i H mn公式才是正确的。
11-4在计算周转轮系的传动比时,式i H mn=(n m-n H)/(n n-n H)中的i H mn是什么传动比,如何确定其大小和“±”号?答: i H mn是在根据相对运动原理,设给原周转轮系加上一个公共角速度“-ωH”。
使之绕行星架的固定轴线回转,这时各构件之间的相对运动仍将保持不变,而行星架的角速度为0,即行星架“静止不动”了.于是周转轮系转化成了定轴轮系,这个转化轮系的传动比,其大小可以用i H mn=(n m-n H)/(n n-n H)中的i H mn公式计算;方向由“±”号确定,但注意,它由在转化轮系中m. n两轮的转向关系来确定。
11-5用转化轮系法计算行星轮系效率的理论基础是什么?为什么说当行星轮系为高速时,用它来计算行星轮系的效率会带来较大的误差?答: 用转化轮系法计算行星轮系效率的理论基础是行星轮系的转化轮系和原行星轮系的差别,仅在于给整个行星轮系附加了一个公共角速度“-ωH”。
第11章知识资料轮系(OK)(6)

i143
n1 n3
n4 n4
z3 z1
48 16
3
n1 4 n4
手轮转动一周,砂轮横向移动量为:
l
sn4
1 4
sn1
1 4
41 1mm
(2)快速退回时,齿轮1、4组成定轴轮系
i14
n1 n4
z4 z1
1
手轮转动一周,砂轮横向移动量为:
l sn4 sn1 41 4mm
2. 如手轮圆周刻度为200格,则根 据1(1),慢速 进给时,每格砂 轮架的移动量为
i1k
1 k
n1 nk
z2 zk z1 zk1
所有从动轮齿数的连乘积 所有主动轮齿数的连乘积
➢ 计算结果的绝对值表示传动比的大小
结 论
➢ 计算结果前面的“+”、“-”号表示首、末轮的转 向关系,“+”为相同,“-”为相反
注意
1. 对于平面轮系,“+、-”号由(-1)m确定,m为外啮合的次数
2. 对于首、末轮轴线平行的空间轮系,“+、-”号由标注方 向箭头确定,相同为“+”,相反为“-”
试计算当手柄转动一周时工作台的进给量?
解
齿轮1、2、3、4和H组成行星轮系
n1 0
i1H4
n1 nH n4 nH
z2z4 z1 z 3
19 20 10 1918 9
手轮转动一周时,工作台的进给量为:
l
Pn4
1 10
P
nH
1 51 0.2mm 10
i4 H
n4 nH
1 10
2.图示为行星搅拌机的机构简图,已知:
11
1
l sn4 4 sn1 4 4 200 0.005mm
例3 图示为一电动卷扬机简图,所有齿轮均为标准齿轮,模数 m=4mm,各轮齿数为:
轮系

(2)机床丝杠的反向传动
五、运动合成和分解
合成运动是将两个输入运动合成为一个输出运动;分解运动
是把一个输入运动按可变的比例分解成两个输出运动。合成 运动和分解运动都可用差动轮系实现。
如图所示的轮系,若z1=z3,z2 = z2’ ,则
H 13
z 2 z3 n1 n H i 1 n3 n H z1 z 2'
解 该轮系是由齿轮1、2所组成的
定轴轮系部分有
n1 z2 40 i12 2 n2 z1 20
得 周转轮系部分有
n2 150
H i 2; 4
r
min
n2 ' n H z 80 4 4 n4 n H z 2' 20
因 为 2 与 2′ 两 轮 为 同 一 构 件 , 所 以 n2′ = n2 = 150r/min,而齿轮4固定不动,故n4=0,将以上数 值代入上式求得: nH=-30r/min
转化轮系是定轴轮系,可按定轴轮系传动比计算方法对转
化轮系进行求解。
在任一周转轮系中,当任意两轮G、K及行星架H回转轴线
平行时,则其转化轮系传动比的一般计算式为
H iGK H nG nG n H H nK nK nH
转化轮系从G至齿轮K所有从动轮齿数的乘积 转化轮系从G至齿轮K所有主动轮齿数的乘积
三、周转轮系分析 (1)找行星架 (2)找行星齿轮 (3)找中心轮 (4)判断中心轮的运动情况
四、周转轮系传动比的计算
(一)周转轮系和定轴轮系的本质区别
( 二)、周转轮系的转化轮系
求解周转轮系传动比,常用的方法是转化轮系法。 假定给图a所示整个周转轮系加上一个绕O轴线回转、并与行星架
机械原理 11-3周转轮系的传动比
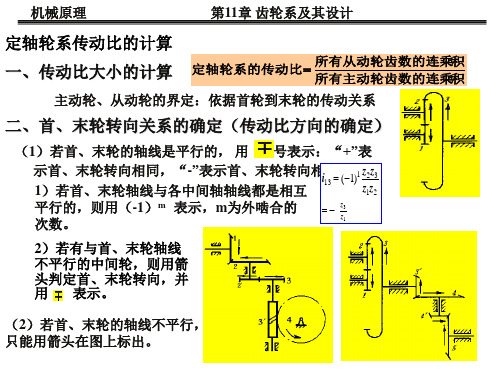
(1)转化轮系传动比中的
此符号表示在转化轮系中m、n轮的转向关系,但这个符号却直接 影响周转轮系的转速 m、n、H 之间的数值关系。
另外,此符号仅代表在转化轮系中m、n轮的转向关系,并不代表 在周转轮系中m、n轮的转向关系(在转化轮系中m、n轮转向相同, 在周转轮系中m、n轮转向可能相反,也可能相同)。
机械原理
第11章 齿轮系及其设计
(3)此公式适用于周转轮系中任意两个轴线与H轴线平行的齿轮,不仅仅限于 两个太阳轮m、n,若行星轮的轴线与基本构件的轴线平行,也可用此公式求 行星轮与基本构件的角速度关系,但若行星轮的轴线与基本构件的轴线不平 行,则不能用此公式。
例如:在左图2K-H差动轮系中
i1H2
机械原理
第11章 齿轮系及其设计
定轴轮系传动比的计算 一、传动比大小的计算
定轴轮系的传动比
所有从动轮齿数的连乘积 所有主动轮齿数的连乘积
主动轮、从动轮的界定:依据首轮到末轮的传动关系
二、首、末轮转向关系的确定(传动比方向的确定)
(1)若首、末轮的轴线是平行的, 用 号表示:“+”表
示1)首若、首末、轮末转轮向轴相线同与,各“中-”间表轴示轴首线、都末是轮相转互向相i1反3 。(1)1
(2)计算公式中,m、n、H 均为代数量,需将其代数量的符 号代入公式中参加运算,计算时,可假定一个方向为正(顺时针
或逆时针),另一个方向则为负。
(3)此公式适用于周转轮系中任意两个轴线与H轴线平行的齿轮,不 仅仅限于两个太阳轮m、n,若行星轮的轴线与基本构件的轴线平行, 也可用此公式求行星轮与基本构件的角速度关系,但若行星轮的轴线 与基本构件的轴线不平行,则不能用此公式。
左图是一复合轮系,
第11章 轮系

i 解:
H 13
z 2 z3 z3 n1 − n H = =− =− n3 − n H z1 z 2 z1
n1 − n H 80 =− = −4 0 − nH 20 n1 i1H = = 1 − (−4) = 5 nH
1 n4 z5 i45 = =− =− 2 n5 z4
n1 1 i15 = = i14i45 = 5 × (− ) = −2.5 n5 2
解:(1). 1,2,3,4为行星轮系,4, 为行星轮系, 和机架为定轴轮系。 5和机架为定轴轮系。
4 i13 =
z z n1 − n4 60 =− 2 3 =− = −3 z1 z 2 20 0 − n4
n4 z 5 40 = = = 40 n5 z 4 1
4 ∴ i14 = 1 − i13 = 4
知识提炼与精讲
1.轮系的分类
(1) 定轴轮系:各个齿轮的轴线位置相对于机架都是固定的轮系。 定轴轮系:各个齿轮的轴线位置相对于机架都是固定的轮系。 定轴轮系又可分为平面定轴轮系和空间定轴轮系。 定轴轮系又可分为平面定轴轮系和空间定轴轮系。 (2) 周转轮系(基本周转轮系):各齿轮中有一个或几个齿轮轴 周转轮系(基本周转轮系) 线的位置是绕着其他齿轮的固定轴线回转的轮系。 线的位置是绕着其他齿轮的固定轴线回转的轮系 。 周转轮系按 其自由度的数目分为:差动轮系——自由度为 自由度为2 其自由度的数目分为:差动轮系——自由度为2的周转轮系和行 星轮系——自由度为 的周转轮系。 自由度为1 星轮系——自由度为1的周转轮系。 (3) 复合轮系:既包含有定轴轮系又包含有周转轮系或由几个 复合轮系: 基本周转轮系组成的复杂轮系。 基本周转轮系组成的复杂轮系。
5.轮系的主要功用 5.轮系的主要功用
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复合轮系的传动比计算
三步走
1.划分基本轮系 1.划分基本轮系 2.列方程 2.列方程——基本轮系的传动比计算式 列方程 基本轮系的传动比计算式 3.解方程 3.解方程——各基本轮系的传动比计算方程联立求解 解方程 各基本轮系的传动比计算方程联立求解
三、学习重点及难点
学习重点 轮系的传动比计算 定轴轮系 周转轮系 复合轮系 学习难点 计算复合轮系传动比时基本轮系的正确划分
B i12 =
ω1 − ωB z 20 1 =− 2 =− =− ω2 − ωB z1 40 2
ω2 i2 B = =3 ωB
ω2 = i2 BωB = 3 × 31 = 93rad / s
3. 图示为龙门刨床工作台的变速机构,J、K为 图示为龙门刨床工作台的变速机构, 、 为 K 电磁制动器,设已知各轮的齿数, 电磁制动器,设已知各轮的齿数,求J、K分别 、 分别 刹车时的传动比i 刹车时的传动比 1B。 解:(1)刹住 时 :( )刹住J 1、2、3为定轴轮系 i13 = 、 、 为定轴轮系
周转轮系的传动比计算
ω1H ω1 − ω H z2 L zk 所有从动轮齿数的连乘 积 H i1k = H = =± =± ωk ωk − ωH z1 L z k −1 所有主动轮齿数的连乘 积
注意
几何轴线O 几何轴线 1、Ok和OH必须互相重合 “+”、“−”号由转化轮系按定轴轮系确定 + 、
ω1、ωk、ωH均为代数值
l = sn4 = 1 1 1 sn1 = × 4 × = 0.005mm 4 4 200
例3 图示为一电动卷扬机简图,所有齿轮均为标准齿轮,模数 图示为一电动卷扬机简图,所有齿轮均为标准齿轮, m=4mm,各轮齿数为: =4mm,各轮齿数为:
z1 = 24, z2 = z2' = 18, z3 = z3' = 21, z4 = 63, z5 = z6 = z6' = 18
齿轮1、 齿轮 、2-2’、3和4组成行星轮系 和 组成行星轮系
4 i13 =
n3 = 0
25 × 63 105 n1 − n4 z z =− 2 3 =− =− n3 − n4 z1 z 2 ' 15 × 23 23
i14 =
128 23
齿轮4、 组成定轴轮系 齿轮 、5组成定轴轮系
i45 = −
z1 = z2 = 19, z3 = 18, z4 = 20
试计算当手柄转动一周时工作台的进给量? 试计算当手柄转动一周时工作台的进给量?
解
齿轮1、 、 、 和 组成行星轮系 齿轮 、2、3、4和H组成行星轮系
n1 = 0
n − nH z z 19 × 20 10 i = 1 =+ 2 4 =+ =+ n4 − nH z1 z 3 19 × 18 9
试计算: 试计算: (1)机构的自由度 ? )机构的自由度F? (2)搅拌轴的角速度及转向? )搅拌轴的角速度及转向?
解
(1) )
F = 3n − 2 PL − PH = 3 × 2 − 2 × 2 − 1 = 1
ω1 = 0
(2)齿轮 、2、3、4和H组成行星轮系 )齿轮1、 、 、 和 组成行星轮系
z5 40 4 =− =− z4 30 3
iI,II
128 4 512 = i14 ⋅ i45 = × (− ) = − 23 3 69
(2) Ⅰ轴转速 )
nI = nII ⋅ iI,II
512 v ⋅ iI,II 69 = 17.71 r/min = = 2πR 2 × π × 0.2 3×
(2)列方程 列方程
5 i14 =
n1 − n5 z z 18 × 63 9 =− 2 4 =− =− n4 − n5 z1 z3 24 × 21 4
i57 =
n5 z 54 = − 7 = − = −3 n7 z5 18
因为: 因为:n4=n7 (3)联立求解 联立求解
n1 i17 = = −12 n7
4 i13 =
n1 − n4 z 48 =− 3 =− = −3 n3 − n4 z1 16
n1 =4 n4
手轮转动一周,砂轮横向移动量为: 手轮转动一周,砂轮横向移动量为:
1 1 l = sn4 = sn1 = × 4 ×1 = 1mm 4 4
(2)组成定轴轮系
z n1 =− 3 n3 z1
B
3’ 4 5
3 2 1
J A
3’、4、5和B为周转轮系 i3B'5 = n3' − nB = − z5 、 、 和 为周转轮系 n5 − nB z3' 因为: 因为:
n3 = n3' , n5 = 0
联立解得: 联立解得:
i1 B =
z z n1 = − 3 (1 + 5 ) nB z1 z 3'
试题自测及答案( 五、试题自测及答案(1、2、3、4、5)
1. 图示为万能刀具磨床工作台横向微动进给装置,运动经手柄输入, 图示为万能刀具磨床工作台横向微动进给装置,运动经手柄输入, 再由丝杠传给工作台。现已知:丝杠螺距P= 单头), 再由丝杠传给工作台。现已知:丝杠螺距 =50mm(单头 ,各齿轮齿 单头 数为: 数为:
第十一章
一、基本要求
轮系
二、基本概念和基础知识 三、学习重点及难点 四、例题精选 五、试题自测及答案
一、基本要求
1 . 了解轮系的定义、分类和用途。 了解轮系的定义、分类和用途。 2 . 熟练掌握定轴轮系、周转轮系和混合轮系的 熟练掌握定轴轮系、 传动比计算方法。 传动比计算方法。 3 . 能计算行星轮系的效率,并了解行星轮系设计 能计算行星轮系的效率, 的基础知识。 的基础知识。 4 . 了解其他行星轮系的特点及用途。 了解其他行星轮系的特点及用途。
试求: 试求: 1. 齿数z7=? 齿数z 2. 传动比i17=? 传动比i
分析 解
利用同心条件可以计算出z 利用同心条件可以计算出 7,然后按照复合轮系的 三步走”即可求解出i “三步走”即可求解出 17。
1. 根据同心条件
z7 = z5 + 2 z6 = 18 + 2 × 18 = 54
2. (1)划分基本轮系 划分基本轮系 差动轮系: 、 、 和 差动轮系:1、2-3、4和5 定轴轮系:5、6、7 定轴轮系: 、 、
n1 = 500r / min
求:齿条6的线速度v 的大小 齿条6的线速度v 和方向
分析
由于5’和 为齿轮齿条机构 齿条6为移动 为齿轮齿条机构, 为移动, 由于 和6为齿轮齿条机构,齿条 为移动,无法 计算齿轮1与齿条 之间的传动比,因此, 与齿条6之间的传动比 计算齿轮 与齿条 之间的传动比,因此,可以先计 之间的传动比, 算1与5之间的传动比,然后利用 与5’同轴同向等速 与 之间的传动比 然后利用5与 同轴同向等速 的特点,即可求出齿条6的速度 的速度。 的特点,即可求出齿条 的速度。
例2 如图所示为磨床砂轮架微动进给机构中,z1=z2=z4=16, z3= 如图所示为磨床砂轮架微动进给机构中, 16, 48,丝杠导程s=4mm,慢速进给时,齿轮1和2啮合;快速退回时, 48,丝杠导程s=4mm,慢速进给时,齿轮1 啮合;快速退回时, 齿轮1与内齿轮4啮合。 齿轮1与内齿轮4啮合。 求: 1. 慢速进给过程和快速退回过程中, 慢速进给过程和快速退回过程中, 手轮转一圈时, 手轮转一圈时,砂轮横向移动的距 离各为多少? 离各为多少? 2. 如手轮圆周刻度为200格,慢速 如手轮圆周刻度为200格 进给时,每格砂轮架移动量为多少? 进给时,每格砂轮架移动量为多少?
1. 对于平面轮系,“+、-”号由(-1)m确定,m为外啮合的次数 对于平面轮系, +、-”号由( 确定, 2. 对于首、末轮轴线平行的空间轮系,“+、-”号由标注 对于首、末轮轴线平行的空间轮系, +、-” 方向箭头确定,相同为“ 相反为“ 方向箭头确定,相同为“+”,相反为“-” 3. 对于首、末轮轴线不平行的空间轮系,“+、-”号无意 对于首、末轮轴线不平行的空间轮系, +、-” 只能用标注的方向箭头表示首、 义,只能用标注的方向箭头表示首、末轮的转向关系
n1 z4 i14 = = =1 n4 z1
手轮转动一周,砂轮横向移动量为: 手轮转动一周,砂轮横向移动量为:
l = sn4 = sn1 = 4 ×1 = 4mm
2. 如手轮圆周刻度为200格,则根 如手轮圆周刻度为 格 ),慢速 进给时, 据1(1),慢速 进给时,每格砂 ( ), 轮架的移动量为
例题精选( 四、例题精选(例1、例2、例3)
例1 如图所示为具有空间齿轮机构的定轴轮系,已知 如图所示为具有空间齿轮机构的定轴轮系,
z1 = 15, z 2 = 25, z 2' = 15 z 3 = 30, z 3' = 15, z4 = 30, z4' = 2 右旋) (右旋)
z5 = 60, z5' = 20(m = 4mm)
分析 解
问题的关键是计算丝杠即齿轮4的转速。齿轮 、 问题的关键是计算丝杠即齿轮 的转速。齿轮1、2 的转速 啮合时为行星轮系,齿轮1、 啮合时为定轴轮系 啮合时为定轴轮系。 啮合时为行星轮系,齿轮 、4啮合时为定轴轮系。
1. (1)慢速进给时,齿轮 、2、3和4组成行星轮系 )慢速进给时,齿轮1、 、 和 组成行星轮系
z1 = 15, z2 = 25, z2' = 23, z4 = 30, z5 = 40
试求: 试求: (1)机械的总传动比 ⅠⅡ? )机械的总传动比i (2)Ⅰ轴的转速 Ⅰ和转向? ) 轴的转速n (3)Ⅰ轴的输入功率 Ⅰ? ) 轴的输入功率N
解
(1)根据同心条件 )
z3 = z1 + z2 + z2 ' = 15 + 25 + 23 = 63
