MATLAB实验程序
高等数学:MATLAB实验

MATLAB实验
2.fplot绘图命令 fplot绘图命令专门用于绘制一元函数曲线,格式为:
fplot('fun',[a,b]) 用于绘制区间[a,b]上的函数y=fun的图像.
MATLAB实验 【实验内容】
MATLAB实验
由此可知,函数在点x=3处的二阶导数为6,所以f(3)=3为 极小值;函数在点x= 1处的二阶导数为-6,所以f(1)=7为极大值.
MATLAB实验
例12-10 假设某种商品的需求量q 是单价p(单位:元)的函 数q=12000-80p,商 品的总成本C 是需求量q 的函数 C=25000+50q.每单位商品需要纳税2元,试求使销售 利润达 到最大的商品单价和最大利润额.
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验 实验九 用 MATLAB求解二重积分
【实验目的】 熟悉LAB中的int命令,会用int命令求解简单的二重积分.
MATLAB实验
【实验M步A骤T】 由于二重积分可以化成二次积分来进行计算,因此只要
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
实验七 应用 MATLAB绘制三维曲线图
【实验目的】 (1)熟悉 MATLAB软件的绘图功能; (2)熟悉常见空间曲线的作图方法.
【实验要求】 (1)掌握 MATLAB中绘图命令plot3和 mesh的使用; (2)会用plot3和 mesh函数绘制出某区间的三维曲线,线型
MATLAB全部实验及答案

MATLAB全部实验及答案实验一、MATLAB基本操作实验内容及步骤1、命令窗口的简单使用(1)简单矩阵的输入(2)求[12+2×(7-4)]÷32的算术运算结果2、有关向量、矩阵或数组的一些运算(1)设A=15;B=20;求C=A+B与c=a+b?(2)设A=[1 2 3;4 5 6;7 8 9],B=[9 8 7;6 5 4;3 2 1];求A*B与A.*B?A*B就是线代里面的矩阵相乘 A.*B是对应位置的元素相乘(3)设a=10,b=20;求i=a/b=0.5与j=a\b=2?(4)设a=[1 -2 3;4 5 -4;5 -6 7]请设计出程序,分别找出小于0的矩阵元素及其位置(单下标、全下标的形式),并将其单下标转换成全下标。
clear,clca=[1 -2 3;4 5 -4;5 -6 7];[x,y]=find(a<0);c=[];for i=1:length(x)c(i,1)=a(x(i),y(i));c(i,2)=x(i);c(i,3)=y(i);c(i,4)=(y(i)-1)*size(a,2)+x(i);endc(5)在MATLAB命令行窗口运行A=[1,2;3,4]+i*[5,6;7,8];看结果如何?如果改成运行A=[1,2;3,4]+i[5,6;7,8],结果又如何?前面那个是虚数矩阵,后面那个出错(6)请写出完成下列计算的指令:a=[1 2 3;3 4 2;5 2 3],求a^2=?,a.^2=?a^2= 22 16 1625 26 2326 24 28a.^2=1 4 99 16 425 4 9(7)有一段指令如下,请思考并说明运行结果及其原因clearX=[1 2;8 9;3 6];X( : ) 转化为列向量(8)使用三元组方法,创建下列稀疏矩阵2 0 8 00 0 0 10 4 0 06 0 0 0方法一:clear,clcdata=[2 8 1 4 6];ir=[1 1 2 3 4 ];jc=[1 3 4 2 1];s=sparse(ir,jc,data,4,4);full(s)方法二:不用三元组法clear,clca=zeros(4,4);a(1,[1,3])=[2,8];a(2,4)=1;a(3,2)=4;a(4,1)=6;a(9) 写出下列指令的运行结果>> A = [ 1 2 3 ]; B = [ 4 5 6 ];>> C = 3.^A>> D = A.^B3、 已知⎪⎭⎫ ⎝⎛+⋅=-334sin 234πt e y t 若需要计算t ∈[-1,1],取间隔为0.01,试计算出相对应的y 值。
MATLAB实验教程
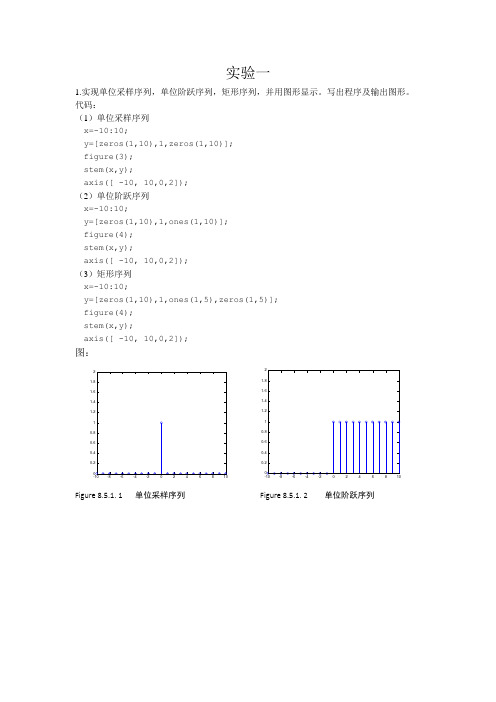
实验一1.实现单位采样序列,单位阶跃序列,矩形序列,并用图形显示。
写出程序及输出图形。
代码:(1)单位采样序列x=-10:10;y=[zeros(1,10),1,zeros(1,10)];figure(3);stem(x,y);axis([ -10, 10,0,2]);(2)单位阶跃序列x=-10:10;y=[zeros(1,10),1,ones(1,10)];figure(4);stem(x,y);axis([ -10, 10,0,2]);(3)矩形序列x=-10:10;y=[zeros(1,10),1,ones(1,5),zeros(1,5)];figure(4);stem(x,y);axis([ -10, 10,0,2]);图:Figure 8.5.1. 1 单位采样序列Figure 8.5.1. 2 单位阶跃序列Figure 8.5.1. 3 矩形序列实验心得:实验二1.模拟信号x(t)=2sin(4*pi*t)+5cos(8*pi*t),以t=0.01n(n=0:N-1)进行采样,求:(1)N=40点FFT的幅度频谱,从图中能否观察出信号的2个频谱分量?(2)提高采样点数,如N=128,再求该信号的频谱幅度,此时幅度频谱发生了什么变化?代码:N=40;n=0:N-1;t=0.01*n;x=2*sin(4*pi*t)+5*cos(8*pi*t);k=0:N/2;w=2*pi/N*k;X=fft(x,N);magX=abs(X(1:N/2+1));subplot(2,1,1);stem(n,x,'.');title('signal x(n)');subplot(2,1,2);plot(w/pi,magX);title('FFT N=40');xlabel('f (unit :pi)');ylabel('|X|');gridN=128;n=0:N-1;t=0.01*n;x=2*sin(4*pi*t)+5*cos(8*pi*t);k=0:N/2;w=2*pi/N*k;X=fft(x,N);magX=abs(X(1:N/2+1));subplot(2,1,1);stem(n,x,'.');title('signal x(n)');subplot(2,1,2);plot(w/pi,magX);title('FFT N=128');xlabel('f (unit :pi)');ylabel('|X|');grid图:510152025303540signal x(n)50100FFT N=40Figure 8.2.1. 1 N=40 的FFT 频谱图20406080100120140signal x(n)0.10.20.30.40.50.60.70.80.91010*******400FFT N=128f (unit :pi)|X |Figure 8.2.1. 2 N=128 的FFT 频谱图实验心得: 实验六双线性变换法 代码%Filter clc;%clear;%digital filter specifications; lfp=100; lfs=300;ws=2*pi*lfs;wp=2*pi*lfp;Rp=1;Rs=25;fs=1000;[n,Wn]=buttord(wp,ws,Rp,Rs,'s');[z,p,k] = buttap(n);[b,a]=zp2tf(z,p,k);x=[-4,-2,0,-4,-6,-4,-2,-4,-6,-6,-4,-4,-6,-6,-2,6,12,8,0,-16,-38,-60,-84,-90,-66,-32,-4,2,-4,8,12,12,10,6,6,6,4,0,0,0,0,0,-2,-4,0,0,0,-2,-2 ,0,0,-2,-2,-2,-2,0];Y=filter(b,a,x);N=56;n=0:N-1;subplot(2,1,1);plot(n,x);subplot(2,1,2);plot(n,Y);[bt,at]=lp2lp(b,a,Wn);[bbs,abs]=bilinear(bt,at,fs);[dB,mag,pha,grd,w]=freqz_m(bbs,abs);Ripple=10^(-Rp/20);Attn=10^(-Rs/20);%»-ͼsubplot(2,2,1);plot(w/pi,mag);title('·ùƵÏìÓ¦');xlabel('¹éÒ»»¯ÆµÂÊ');axis([0,1,0,1.1]);set(gca,'XTickMode','manual','XTick',[0,2*lfp/fs,2*lfs/fs,1]);set(gca,'XTickMode','manual','XTick',[Attn,Ripple,1]);grid;subplot(2,2,2);plot(w/pi,pha/pi);title('ÏàƵÏìÓ¦');xlabel('¹éÒ»»¯ÆµÂÊ');ylabel('µ¥Î»:pi');axis([0,1,-1.1,1.1]);set(gca,'XTickMode','manual','XTick',[0,2*lfp/fs,2*lfs/fs,1]);set(gca,'XTickMode','manual','XTick',[-1,-0.5,0,0.5,1]);grid;subplot(2,2,3);plot(w/pi,dB,'red');title('·ùƵÏìÓ¦:dB');xlabel('¹éÒ»»¯ÆµÂÊ');axis([0,1,-60,5]);set(gca,'XTickMode','manual','XTick',[0,2*lfp/fs,2*lfs/fs,1]);set(gca,'XTickMode','manual','XTick',[-60,-40,-20,5]);grid;subplot(2,2,4); plot(w/pi,grd,'red'); title('ȺʱÑÓ'); xlabel('¹éÒ»»¯ÆµÂÊ') axis([0,1,0,6]);set(gca,'XtickMode','manual','Xtick',[0,2*lfp/fs,2*lfs/fs,1]); set(gca,'YtickMode','manual','Ytick',[0,1,2,4,6]); grid;%²ÉÓÃÊý×ÖÓòƵÂʱ任·¨Éè¼ÆÊý×Ö´ø×èÂ˲¨Æ÷(using bilinear and Chebyshev-I)x=[-4,-2,0,-4,-6,-4,-2,-4,-6,-6,-4,-4,-6,-6,-2,6,12,8,0,-16,-38,-60,-84,-90,-66,-32,-4,2,-4,8,12,12,10,6,6,6,4,0,0,0,0,0,-2,-4,0,0,0,-2,-2,0,0,-2,-2,-2,-2,0]; Y=filter(b,a,x); N=56;n=0:N-1;figure(2)subplot(2,1,1);plot(n,x);grid on ; subplot(2,1,2);plot(n,Y);grid on ;图双线性变换法设计的滤波器特性0.05620.891310.20.40.60.81幅频响应归一化频率00.51-1-0.500.51相频响应归一化频率单位:p i-60-40-200幅频响应:dB归一化频率0.20.6101246群时延归一化频率原始心电图信号和经过滤波后的心电图信号0102030405060-100-5050102030405060-30-20-1001020实验心得:脉冲响应不变法代码:%Âö³åÏìÓ¦²»±ä·¨% digital filter specifications: lfp=100; lfs=300; ws=2*pi*lfs; wp=2*pi*lfp; Rp=1; Rs=25; fs=1000;%Êý×ÖÖ¸±êµ½Ä£ÄâÖ¸±êµÄ±ä»¯¡ªË«ÏßÐԱ任 %¼ÆËã½×ÊýºÍ½ØֹƵÂÊ[n,Wn]=buttord(wp,ws,Rp,Rs,'s'); %Éè¼ÆÄ£ÄâµÍͨÔ-ÐÍ [z,p,k]=buttap(n); [b,a]=zp2tf(z,p,k);x=[-4,-2,0,-4,-6,-4,-2,-4,-6,-69,-4,-4,-6,-6,-2,6,12,8,0,-16,-38,-60,-84,-90,-66,-32,-4,2,-4,8,12,12,10,6,6,6,4,0,0,0,0,0,-2,-4,0,0,0,-2,-2,0,0,-2,-2,-2,-2,0];Y=filter(b,a,x);%ÓÉÄ£ÄâµÍͨÔ-Ð;-ƵÂʱ任»ñµÃÄ£ÄâµÍͨ¡¢¸ßͨ¡¢´øͨ»ò´ø×èÂ˲¨Æ÷[bt,at]=lp2lp(b,a,Wn);%ÀûÓÃÂö³åÏìÓ¦²»±ä·¨»òË«ÏßÐÔ²»±ä·¨£¬ÊµÏÖÄ£ÄâÂ˲¨Æ÷µ½Êý×ÖÂ˲¨Æ÷µÄÓ³Éä[bbs,abs]=impinvar(bt,at,fs);%Â˲¨Æ÷ƵÂÊÏìÓ¦[dB,mag,pha,grd,w]=freqz_m(bbs,abs);Ripple=10^(-Rp/20);Attn=10^(-Rs/20);%»-ͼsubplot(2,2,1);plot(w/pi,mag) %Êý×ÖÂ˲¨Æ÷·ù¶ÈÏìÓ¦title('·ùƵÏìÓ¦');xlabel('¹éÒ»»¯ÆµÂÊ');axis([0,1,0,1.1]);set(gca,'XTickMode','manual','XTick',[0,2*lfp/fs,2*lfs/fs,1]);set(gca,'YTickMode','manual','YTick',[Attn,Ripple,1]);grid;subplot(2,2,2);plot(w/pi,pha/pi); %Êý×ÖÂ˲¨Æ÷ÏàλÏìÓ¦title('ÏàƵÏìÓ¦');xlabel('¹éÒ»»¯ÆµÂÊ');ylabel('µ¥Î»£ºpi');axis([0,1,-1.1,1.1]);set(gca,'XTickMode','manual','XTick',[0,2*lfp/fs,2*lfs/fs,1]);set(gca,'YTickMode','manual','YTick',[-1,-0.5,0,0.5,1]);grid;subplot(2,2,3);plot(w/pi,dB,'red');%Êý×ÖÂ˲¨Æ÷·ù¶ÈÏìÓ¦£¨dB£©title('·ùƵÏìÓ¦£ºdB');xlabel('¹éÒ»»¯ÆµÂÊ');axis([0,1,-60,5]);set(gca,'XTickMode','manual','XTick',[0,2*lfp/fs,2*lfs/fs,1]);set(gca,'YTickMode','manual','YTick',[-60,-40,-20,5]);grid;subplot(2,2,4);plot(w/pi,grd,'red');%Êý×ÖÂ˲¨Æ÷ÑÓʱtitle('ȺÑÓʱ');xlabel('¹éÒ»»¯ÆµÂÊ');axis([0,1,0,6]);set(gca,'XTickMode','manual','XTick',[0,2*lfp/fs,2*lfs/fs,1]);set(gca,'YTickMode','manual','YTick',[0,1,2,4,6]);grid;%²ÉÓÃÊý×ÖÓòƵÂʱ任·¨Éè¼ÆÊý×Ö´ø×èÂ˲¨Æ÷£¨using bilinear and Chebyshev-1£©x=[-4,-2,0,-4,-6,-4,-2,-4,-6,-6,-4,-4,-6,-6,-2,6,12,8,0,-16,-38,-60,-84,-90,-66,-32,-4,2,-4,8,12,12,10,6,6,6,4,0,0,0,0,-2,-4,0,0,0,-2,-2,0 ,0,-2,-2,-2,-2,0]Y =filter(b,a,x);N=56;n=0:N-1;figure(2)subplot(2,1,1);plot(n,x);grid on; subplot(2,1,2);plot(n,Y);grid on;子函数:function[dB,mag,pha,grd,w]=freqz_m(b,a)%computation of s-domain frequency response:modified version%---------------------------------------------------------%[dB,mag,pha,grd,w]=freqz_m(b,a);% dB=Relative magintude in dB over [0 to 2pi]% mag=Absolute magintude over [0 to 2pi]% pha=Phase response in radians over [0 to 2pi]% w=array of 500 frequency samples between [0 to 2pi]% b=numerator polynomial coefficients of H(z)% a=denominator polynomial coefficients of H(z)[H,w]=freqz(b,a,1000,'whole');%w ranging from 0 to 2pi radians per sample.%uses 1000 sample points around the entire unit circle to calculate the %frequency responseH=(H(1:501))';w=(w(1:501))';mag=abs(H);dB=20*log10((mag+eps)/max(mag));pha=angle(H);grd=grpdelay(b,a,w);图:0.20.610.05620.89131幅频响应归一化频率00.20.61-1-0.500.51相频响应归一化频率单位:p i00.20.61-60-40-205幅频响应:dB归一化频率00.20.611246群延时归一化频率0102030405060-100-5050102030405060-30-20-1001020实验七代码:主程序:% design a digital FIR lowpass filter with Hamming windowwp=0.3*pi;ws=0.5*pi;tr_width=ws-wp;N=ceil(6.6*pi/tr_width)+1; % N=34n=[0:1:N-1];wc=(ws-wp)/2;hd = ideal_lp(wc,N);w_ham=(hamming(N))';h=hd.*w_ham;[dB,mag,pha,grd,w]=freqz_m(h,[1]);delta_w=2*pi/1000;Rp=-(min(dB(1:1:wp/delta_w+1)));As=-round(max(dB(ws/delta_w+1:1:501)));%plotssubplot(2,2,1);stem(n,hd);title('ÀíÏëÂö³åÏìÓ¦');axis([0,N-1,-0.09,0.5]);xlabel('n');set(gcr,'YTickMode','manual','YTick',[0,0.1,0.2,0.3]);subplot(2,2,2);stem(n,w_ham);title('hamming´°');axis([0,N-1,0,1.1]);xlabel('n');subplot(2,2,3);stem(n,h);title('ʵ¼ÊÂö³åÏìÓ¦');axis([0,N-1,-0.09,0.5]);xlabel('n');set(gcr,'YTickMode','manual','YTick',[0,0.1,0.2,0.3]);subplot(2,2,4);plot(w/pi,dB);title('·ùƵÏìÓ¦:dB');grid;axis([0,1,-100,0]);xlabel('pi');ylabel('dB');set(gcr,'YTickMode','manual','YTick',[0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0 .8,0.9,1.0]);set(gcr,'YTickMode','manual','YTick',[-100,-90,-80,-70,-60,-50,-40,-3 0,-20,-10,0]);子程序:function[dB,mag,pha,grd,w]=freqz_m(b,a)%computation of s-domain frequency response:modified version%---------------------------------------------------------%[dB,mag,pha,grd,w]=freqz_m(b,a);% dB=Relative magintude in dB over [0 to 2pi]% mag=Absolute magintude over [0 to 2pi]% pha=Phase response in radians over [0 to 2pi]% w=array of 500 frequency samples between [0 to 2pi]% b=numerator polynomial coefficients of H(z)% a=denominator polynomial coefficients of H(z)[H,w]=freqz(b,a,1000,'whole');%w ranging from 0 to 2pi radians per sample.%uses 1000 sample points around the entire unit circle to calculate the %frequency responseH=(H(1:501))';w=(w(1:501))';mag=abs(H);dB=20*log10((mag+eps)/max(mag));pha=angle(H);grd=grpdelay(b,a,w);函数ideal_lp;function hd=ideal_lp(wc,N);alpha=(N-1)/2;n=0:1:N-1;m=n-alpha+eps;hd=sin(wc*m)./(pi*m);汉明窗法设计滤波器的102030理想脉冲响应n0102030hamming 窗n102030实际脉冲响应n 00.51-100-50幅频响应:dBpid B。
MATLAB实验及程序

实验一a=[1,2,3;4,5,6;7,8,9] b= repmat(a,2,2)B(24)=9实验二1、使用matlab命令统计randn(5)生成的矩阵里,有多少个元素小于0,将小于0元素个数存变量c中并将这些小于零元素存变量d中。
(实验报告要求:写出命令)a=randn(5)b=find(a<0);c=length(find(a<0))d=a(b)2、建立一个字符数组,内容如下所示:(实验报告要求:写出命令)A B C DE F G Ha b c da=['A B C D''E F G H''a b c d']3、已知有一个矩阵A(假如不知道其具体信息),请计算其元素个数(请先用实际矩阵来验证计算方法是否正确)。
(实验报告要求:写出正确计算方法的命令)A=randn(3,4)B=numel(A)4、已知有一个元胞数组B=[{ones(2,3,2)},{'Hello, Matlab'};{[4 5 6]},{1:100}],想获取字符串'Matlab',应输入什么命令?(实验报告要求:写出命令)f=B{1,2}(7:end)5、要从上题所建元胞数组B中获取列向量[4;5;6],可以有哪几种方法?(实验报告要求:写出命令及结果)方法1: i=B{2,1}(:)方法2: j=reshape(B{2,1},3,1)6、已知有两个学生的信息如下,请在matlab中创建结构对其进行存储,并算=['姓名''张三''李四']student.shuxue=[8778]student.yuwen=[7581 ]student.yingyu=[5560]实验三实验四:二维绘图(1)在同一个窗体(figure1)中画出正弦函数和余弦函数的图象。
要求如下:◆正弦图象用蓝色实线,时标用方格;◆余弦图象用黄色虚线,时标选向下三角形;◆为整个图像加中文标题;◆为x和y轴加轴标题;◆改x轴的单位为pi/2的倍数;◆增加图例;◆在图中合适的位置增加“正弦曲线”和“余弦曲线”两处文本信息。
matlab实验

实验一 MATLAB基本操作一、实验目的1、了解MATLAB应用程序环境2、掌握MATLAB语言程序的书写格式和MATLAB语言程序的结构。
3、掌握在MATLAB应用环境下编写程序4、掌握MATALB调试过程,帮助文件5、掌握MATLAB语言上机步骤,了解运行一个MATLAB程序的方法。
6、本实验可在学习完教材第一章后进行。
二、主要仪器及耗材PC电脑,MATLAB6.5软件三、实验内容和步骤1、MATLAB语言上机步骤:(1)、进入系统在C盘或其他盘上找到MATLAB或MATLAB6.5,然后双击其图标打开文件夹。
然后进行编辑源程序->编译->连接->执行程序->显示结果(2)、常用命令编辑切换(F6),编译(F9),运行(CTRL+F9),显示结果(ALT+F5)其它常用命令见“附录一”。
2、有下面的MATLAB程序。
(1)数值计算功能:如,求方程 3x4+7x3 +9x2-23=0的全部根p=[3,7,9,0,-23]; %建立多项式系数向量x=roots(p) %求根(2)绘图功能:如,绘制正弦曲线和余弦曲线x=[0:0.5:360]*pi/180;plot(x,sin(x),x,cos(x));(3)仿真功能:如,请调试上述程序。
3、熟悉MATLAB环境下的编辑命令,具体见附录一。
三、实验步骤1、静态地检查上述程序,改正程序中的错误。
2、在编辑状态下照原样键入上述程序。
3、编译并运行上述程序,记下所给出的出错信息。
4、按照事先静态检查后所改正的情况,进行纠错。
5、再编译执行纠错后的程序。
如还有错误,再编辑改正,直到不出现语法错误为止。
四、实验注意事项1、记下在调试过程中所发现的错误、系统给出的出错信息和对策。
分析讨论对策成功或失败的原因。
2、总结MATLAB程序的结构和书写规则。
五、思考题1、matlab到底有多少功能?2、MATLAB的搜索路径3、掌握使用MATLAB帮助文件实验二 MATLAB 矩阵及其运算一、 实验目的1、了解矩阵的操作,包括矩阵的建立、矩阵的拆分、矩阵分析等2、了解MATLAB 运算,包括算术运算、关系运算、逻辑运算等3、掌握字符串的操作,了解结构数据和单元数据。
MATLAB实验

MATLAB实验一:MATLAB语言基本概念实验实验目的:1. 熟悉MATLAB语言及使用环境;2.掌握MATLAB的常用命令;3.掌握MATLAB的工作空间的使用;4.掌握MATLAB的获得帮助的途径。
5.掌握科学计算的有关方法,熟悉MATLAB语言及其在科学计算中的运用;6.掌握MATLAB的命令运行方式和M文件运行方式;7.掌握矩阵在MATLAB中的运用。
实验方案分析及设计:本次实验主要目的是了解MATLAB的使用环境,以及常用的一些命令的使用;了解矩阵在MATLAB实验中的具体运用,以及相关的一些符号命令的使用。
实验器材:电脑一台,MATLAB软件实验步骤:打开MATLAB程序,将实验内容中的题目依次输入MATLAB中,运行得到并记录结果,最后再对所得结果进行验证。
实验内容及要求:1.熟悉MATLAB的菜单和快捷键的功能2.熟悉MATLAB的命令窗口的使用3.熟悉常用指令的使用format clc clear help lookfor who whos 4.熟悉命令历史窗口的使用5. 熟悉MATLAB工作空间的功能将工作空间中的变量保存为M文件,并提取该文件中的变量6.熟悉MATLAB获取帮助的途径将所有plot开头的函数列出来,并详细给出plotfis函数的使用方法1. 输入 A=[7 1 5;2 5 6;3 1 5],B=[1 1 1; 2 2 2;3 3 3],在命令窗口中执行下列表达式,掌握其含义:A(2, 3) A(:,2) A(3,:) A(:,1:2:3)A(:,3).*B(:,2) A(:,3)*B(2,:) A*BA.*BA^2 A.^2 B/A B./AA=[7 1 5;2 5 6;3 1 5]7 1 52 5 63 1 5>> B=[1 1 1; 2 2 2;3 3 3]1 1 12 2 23 3 3>> A(2, 3)6>> A(:,2)151>> A(3,:)3 1 5>> A(:,1:2:3)7 52 63 5>> A(:,3).*B(:,2)51215>> A(:,3)*B(2,:)10 10 1012 12 1210 10 10>> A*B24 24 2430 30 3020 20 20>> A.*B7 1 54 10 129 3 15>> A^266 17 6642 33 7038 13 46>> A.^249 1 254 25 369 1 25>> B/A0.1842 0.2105 -0.23680.3684 0.4211 -0.47370.5526 0.6316 -0.7105>> B./A0.1429 1.0000 0.20001.0000 0.4000 0.33331.0000 3.0000 0.60002.输入 C=1:2:20,则 C (i )表示什么?其中 i=1,2,3, (10)1到19差为2,i 代表公差3. 试用 help 命令理解下面程序各指令的含义:cleart =0:0.001:2*pi;subplot(2,2,1);polar(t, 1+cos(t))subplot(2,2,2);plot(cos(t).^3,sin(t).^3)subplot(2,2,3);polar(t,abs(sin(t).*cos(t)))subplot(2,2,4);polar(t,(cos(2*t)).^0.5)4计算矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡897473535与⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡638976242之和。
MATLAB实验指导书

MATLAB实验指导书皖西学院信息工程学院实验一 MATLAB编程环境及简单命令的执行一、实验目的1.熟悉MATLAB编程环境二、实验环境1.计算机2.MATLAB7.0集成环境三、实验说明1.首先应熟悉MATLAB7.0运行环境,正确操作2.实验学时:2学时四、实验内容和步骤1.实验内容(1)命令窗口的使用。
(2)工作空间窗口的使用。
(3)工作目录、搜索路径的设置。
(4)命令历史记录窗口的使用。
(5)帮助系统的使用。
(6)了解各菜单的功能。
2.实验步骤(1)启动MATLAB,熟悉MATLAB的桌面。
(2)进入MATLAB7.0集成环境。
(3)在命令窗口执行命令完成以下运算,观察workspace的变化,记录运算结果。
1) (365-52⨯2-70)÷3 2) >>area=pi*2.5^23) 已知x=3,y=4,在MATLAB 中求z :()232y x y x z -= 4) 将下面的矩阵赋值给变量m1,在workspace 中察看m1在内存中占用的字节数。
m1=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡11514412679810115133216 执行以下命令 >>m1( 2 , 3 ) >>m1( 11 ) >>m1( : , 3 )>>m1( 2 : 3 , 1 : 3 )>>m1( 1 ,4 ) + m1( 2 ,3 ) + m1( 3 ,2 ) + m1( 4 ,1) 5) 执行命令>>help abs查看函数abs 的用法及用途,计算abs( 3 + 4i ) 6) 执行命令>>x=0:0.1:6*pi; >>y=5*sin(x); >>plot(x,y)7) 运行MATLAB 的演示程序,>>demo ,以便对MATLAB 有一个总体了解。
五、思考题1、以下变量名是否合法?为什么? (1)x2 (2)3col (3)_row (4)for2、求以下变量的值,并在MATLAB 中验证。
实验matlab程序(exp1,2)

正弦信号%产生一个幅度为2,频率为4Hz,相位为pi/6的正弦信号A=2;f0=4;phi=pi/6;w0=2*pi*f0;t=0:.0001:1;x=A*sin(w0*t+phi);plot(t,x);ylabel('x(t)');xlabel('Time(s)');title('sinusoidal signal');周期方波%产生一个幅度为1,基频为3Hz,占空比为20%的周期方波A=1; %幅度为1f0=3; %基频为3Hzt=0:.0001:2.5;w0=2*pi*f0;y=A*square(w0*t,20);plot(t,y);axis([0,2.5,-1.5,1.5]);ylabel('y');xlabel('time(s)');title('square signal');阶跃信号%非周期信号:阶跃信号t=-2:0.02:6;x=(t>=0);plot(t,x);axis([-2,6,0,1.2]);ylabel('x(t)');xlabel('Time(s)');title('step signal');指数信号产生随机衰减的指数信号A=1;a=-1;t=0:.001:2.5;y=A*exp(a*t);plot(t,y);axis([0,2.5,0,1]);ylabel('x(t)');xlabel('Time(s)');title('exponential signal');矩形脉冲信号%rectpulse(t): 产生高度为1、宽度为1、关于t=0对称的矩形脉冲信号%rectpulse(t,w): 产生高度为1、宽度为w、关于t=0对称的矩形脉冲信号%产生高度为1、宽度为3、延时为2s的矩形脉冲信号t=-2:.02:6;plot(t,rectpuls(t-2,3));axis([-2,6,0,1.5]);ylabel('x(t)');xlabel('Time(s)');title('rectangular pulse');取样函数取样函数:Sa(x)=sin(x)/x。
实验二MATLAB程序设计含实验报告

实验二 MATLAB 程序设计一、 实验目的1.掌握利用if 语句实现选择结构的方法。
2.掌握利用switch 语句实现多分支选择结构的方法。
3.掌握利用for 语句实现循环结构的方法。
4.掌握利用while 语句实现循环结构的方法。
5.掌握MATLAB 函数的编写及调试方法。
二、 实验的设备及条件计算机一台(带有MATLAB7.0以上的软件环境)。
M 文件的编写:启动MATLAB 后,点击File|New|M-File ,启动MATLAB 的程序编辑及调试器(Editor/Debugger ),编辑以下程序,点击File|Save 保存程序,注意文件名最好用英文字符。
点击Debug|Run 运行程序,在命令窗口查看运行结果,程序如有错误则改正三、 实验内容1.编写求解方程02=++c bx ax 的根的函数(这个方程不一定为一元二次方程,因c b a 、、的不同取值而定),这里应根据c b a 、、的不同取值分别处理,有输入参数提示,当0~,0,0===c b a 时应提示“为恒不等式!”。
并输入几组典型值加以检验。
(提示:提示输入使用input 函数)2.输入一个百分制成绩,要求输出成绩等级A+、A 、B 、C 、D 、E 。
其中100分为A+,90分~99分为A ,80分~89分为B ,70分~79分为C ,60分~69分为D ,60分以下为E 。
要求:(1)用switch 语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
(提示:注意单元矩阵的用法)3.数论中一个有趣的题目:任意一个正整数,若为偶数,则用2除之,若为奇数,则与3相乘再加上1。
重复此过程,最终得到的结果为1。
如:2?13?10?5?16?8?4?2?16?3?10?5?16?8?4?2?1运行下面的程序,按程序提示输入n=1,2,3,5,7等数来验证这一结论。
请为关键的Matlab 语句填写上相关注释,说明其含义或功能。
matlab实验8综合程序

主函数:MAINclc;clear all;close all;echo ont0=3;%信号时长3dt=0.02; % 系统时域采样间隔fs=1/dt;%系统采样频率df=0.2; %所需的频率分辨率t=0:dt:t0;Lt=length(t);%仿真过程中,信号长度% 产生模拟信号m=[ones(1,t0/(3*dt)),-2*ones(1,t0/(3*dt )),zeros(1,t0/(3*dt)+1)];pausefigure(1);subplot(211);plot(t,m(1:length(t)));% 画出信号波形axis([0 3 -2.5 1.5]);xlabel('t');ylabel('模拟信号');subplot(212);[M,m,df1,f]=T2F(m,dt,df,fs);%求出信号频谱plot(f,fftshift(abs(M)))% 画出信号频谱axis([-15 15 0 3]);xlabel('f');ylabel('模拟信号频谱'); pause%..............抽样模块............. fs=50;sdt=1/fs;t1=0:sdt:t0;sm=[ones(1,t0/(3*sdt)),-2*ones(1,t0/(3* sdt)),zeros(1,t0/(3*sdt)+1)];figure(2);subplot(211);stem(t1,sm(1:length(t1)));title('抽样信号');axis([0 t0 -2.1 1.1]);subplot(212);[SM,sm,df1,f]=T2F(sm,sdt,df,fs);plot(f,10*log10(abs(fftshift(SM).^2/len gth(f))))% 画出抽样信号功率xlabel('f');ylabel('抽样信号PDF');% ··········模拟信号数字化·············guiyihua=2/2048;pcm_bianma=pcm_encode(m/guiyihua);figure(3);huitu(pcm_bianma);%***************加密**************q=length(pcm_bianma);out=reshape(pcm_bianma',8,q/8)';for i=1:q/8out(i,:)=jiami(out(i,:));endout=reshape(out',1,q);pause%``````````信道编码调制解调译码``````` r=3n=2^r-1k=n-rif rem(length(out),k)==0 %判断A的长度是否能被k整除BL=reshape(out,k,length(out)/k);BL=BL';for i=1:length(out)/khammc_out(i,:)=hamming_code(n,k,r,BL(i, :)) ;%将A进行(n,k)汉明编码endhamming_bianma=reshape(hammc_out',1,(le ngth(out)/k)*n )%串行输出编码结果figure(4);pausehuitu(hamming_bianma);[jietiao_out,numoferr]=bpsk(hamming_bia nma) %调制,解调,串行输出hammd_out1=zeros(length(jietiao_out)/n, k);out1=reshape(jietiao_out,n,length(jieti ao_out)/n)' ; %将串转换成n列矩阵for i=1:length(jietiao_out)/nhammd_out1(i,:)=hamming_decode(n,k,r,ou t1(i,:));%汉明译码endhamming_yima=reshape(hammd_out1',1,leng th(out)) %串行输出译码结果elseD=zeros(1,ceil(length(out)/k)*k); num=ceil(length(out)/k)*k-length(out);for i=1:length(out)D(i)=out(i);endF=reshape(D,k,(length(D)/k));F=F';for i=1:length(D)/khammc_out1(i,:)=hamming_code(n,k,r,F(i, :)) ;endhamming_bianma=reshape(hammc_out1',1,(l ength(D)/k)*n)figure(9);pauseboxing_tu(hamming_bianma);[jietiao_out,numoferr]=bpsk( hamming_bi anma)hammd_out2=zeros(length(jietiao_out)/n, k);out1=reshape(jietiao_out,n,length(jieti ao_out)/n)';for i=1:length(jietiao_out)/n hammd_out2(i,:)=hamming_decode(n,k,r,out1(i,:));endhammd_out1=reshape(hammd_out2',1,length (D));hamming_yima=hammd_out1(1,1:length(D)-n um)endzhuhanshu2(hamming_yima);%******************解密***************p=length(hamming_yima);st=reshape(hamming_yima',8,p/8)';for i=1:q/8st(i,:)=jiami(st(i,:));endst=reshape(st',1,p);%****************信源译码*************pcm_yima=pcm_decode(st,2)pausefigure(13)subplot(211)plot(t,pcm_yima(1:length(t)))axis([0 3.1 -2.5 1.5])t2=-50:dt:50;gt=sinc(fs*t2);stt=sigexpand(pcm_yima,0.1/dt);xt_t=conv(stt,gt);subplot(212)[M,m,df1,f]=T2F(m,dt,df,fs);%求出恢复信号频谱plot(f,fftshift(abs(M)))% 画出恢复信号频谱axis([-15 15 0 3]);xlabel('f');ylabel('恢复信号频谱');子函数:误码率:function zhuhanshu2(bianma)SNRindB1=-5:1:12; % 信噪比取值向量,dB 为单位SNRindB2=-5:0.2:12; % 信噪比取值向量,dB为单位simu_err_prb=zeros(1,length(SNRindB1)); %理论误码率for i=1:length(SNRindB2)% 计算信噪比值SNR=10^(SNRindB2(i)/10);% 计算普通接收机的理论误码率。
《MATLAB程序设计》实验指导书

三、
实验仪器和设备
1、 计算机一台。 2、 MATLAB7.0 以上集成环境。
四、
预习要求
2
《MATLAB 程序设计》实验指导书
1、 复习 MATLAB 的启动与Байду номын сангаас出,熟悉 MATLAB 运行环境。 2、 复习 MATLAB 中矩阵的生成以及矩阵运算的基本原理。
五、
实验内容及步骤
实验内容:
1、 求下列表达式的值 1) z1
5
《MATLAB 程序设计》实验指导书
2) 函数调用 函数文件编制好后,就可调用函数进行计算了。函数调用的一般格式为 [输出实参表]=函数名(输入实参表) 注意:函数调用时各实参出现的顺序、个数,应与函数定义时形参的顺序、个 数一致,否则会出错。函数调用时,实参先传递给形参,然后再执行函数功能。 5、 选择结构 1) if 语句 a) 单分支 if 语句 if 条件 语句块 end b) 双分支 if 语句 if 条件 语句块 1 else 语句块 2 end c) 多分支 if 语句 if 条件 1 语句块 1 elseif 条件 2 语句块 2 …… elseif 条件 n 语句块 n else 语句块 n+1 end 2) switch 语句 switch 表达式 case 结果表 1 语句块 1 case 结果表 2 语句块 2 ……
二、
实验原理
1、 M 文件 用 MATLAB 语言编写的程序,称为 M 文件,它们的扩展名均为.m。M 文件根据 调用方式的不同分为两类,命令文件(Script file)和函数文件(Function file) 。 2、 建立新的 M 文件 启动 MATLAB 文本编辑器有 3 种方法: 1) 单击工具栏上的“New M-File”命令按钮。 2) 从 MATLAB 主窗口的“File”菜单中选择“New”菜单项,再选择“M-file”命令。 3) 在 MATLAB 命令窗口输入命令“edit”。 3、 打开已有的 M 文件 1) 在当前目录窗口选中要打开的 M 文件,双击鼠标左键。 2) 单击 MATLAB 主窗口工具栏上的“Open File”命令按钮,再从弹出的对话框中 选择所需打开的 M 文件。 3) 从 MATLAB 主窗口的“File”菜单中选择“Open”命令,在“Open”对话框中选中 所需打开的文件。 4) 在 MATLAB 命令窗口输入命令“edit 文件名” 。 4、 函数文件 1) 函数文件的基本结构 函数文件由 function 语句引导,其基本结构为: function 输出形参表=函数名(输入形参表) 注释说明部分 函数体语句 注意:函数名的命名规则与变量名相同。当输出形参多于一个时,应用方括号 括起来。
实验4Matlab程序设计1

实验4 Matlab程序设计1实验目的:1、掌握建立和执行M文件的方法;2、掌握实现选择结构的方法;3、掌握实现循环结构的方法。
实验内容:1. 从键盘输入一个4位整数,按如下规则加密后输出。
加密规则:每位数字都加上7,然后用和除以10的余数取代该数字;再把第一位与第三位交换,第二位与第四位交换。
2. 求分段函数的值。
2x +x-6, x <0且x式-3y = *x2—5x + 6 0Wxc 5 且x 式2及x 式3X2 _ X -1 其他用if语句实现,分别输出x=-5,-3,0,1,2,2.5,3,5时的y值。
3. 输入一个百分制成绩,要求输出成绩等级A、B、C、D、E,其中90~100分为A,80~89分为B,70~79分为C,60~69分为D,60分以下为E。
要求:(1)分别用if语句和swich语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
4. 硅谷公司员工的工资计算方法如下:(1)工作时数超过120小时者,超过部分加发15% ;(2)工作时数低于60小时者,扣发700元;(3)其余按每小时84元计发。
试编程按输入的工号和该号员工的工时数,计算应发工资。
5. 设计程序,完成两位数的加、减、乘、除四则运算。
即:输入两个两位随机整数,再输入一个运算符号,做相应的运算,并显示相应的结果。
6. 建立5X 6矩阵,要求输出矩阵的第n行元素。
当n值超过矩阵的行数时,自动转为输出矩阵的最后一行元素,并给出出错信息。
7. 产生20 个两位随机整数,输出其中小于平均数的偶数。
实验代码及实验结果1.>> a=input(' 请输入一个四位整数:');请输入一个四位整数:9988>> a1=fix(a/1000);>> a2=rem(fix(a/100),10);>> a3=rem(fix(a/10),10);>> a4=rem(a,10);>> a1=rem(a1+7,10);>> a2=rem(a2+7,10);>> a3=rem(a3+7,10);>> a4=rem(a4+7,10);>> b=a1;a1=a3;a3=b;>> b=a2;a2=a4;a4=b;>> c=a1*1000+a2*100+a3*10+a4;>> disp(c)3.>> a=input C请输入一个四位整数:一); 请输人一个四f立整數:3988 »(a/1000);>> a2=ren(fix(a/100), 10);>> a3=ren(fiK(a/10)?10);>> 血(a, ID);» al=re&(al+^ 10);>> a^rsB(a2+7f 10);>> a3=rem(a3+7? 10):>> 丑"“血(M+C 10);>> b=al:a1=a3:a3=b;» b=a2:a2=a4:a4=b,» c-al *100(Hai2*l 0(H-a3*l 0+ttl;>> disp(c)55662.x=input('请输入x的值:');if x<0 & x~=-3y=x92+x-6;elseif x>=0 & x<5 & x~=2 & x~=3y=x.A2+5.*x+6elsey=x.A2-x-1;end请输入孟的値:[-瓦-亠0,1, 2t2. E f 3, 5]7 =29. 0000 IL ODDO -I. 0000 -1.0000 1. OODO 2.7500 5. QOOD(1) if语句:a=i nput('请输入成绩:');ig.ooooif a>=90 & a<=100disp('A');elseif a>=80 & a<90disp('B');elseif a>=70 & a<80disp('C');elseif a>=60 & a<70disp('D');elseif a<60 &a>=0disp('E');elsedisp('输入有误!'); end( 2) switch 语句:a=input(' 请输入成绩:'); switch fix(a/10)case{9}disp('A');case{8}disp('B');case{7}disp('C');case{6}disp('D');case nu m2cell(2:5)disp('E')otherwisedisp('输入有误!');end请输入咸绩:80E请输入咸绩;5E请输入成绩:1212输入有误I»4.n=i nput('请输入工号:’);a=i nput('请输入工作小时数:'); if a>=120 y=a*84+a*84*0.15;elseif a<120 & a>=60y=a*84;elsey=a*84-700;disp(y);end请输入工号:30请输入工作小时数:231232。
matlab实验

实验一1、计算y=x^3+(x-0.98)^2/(x+1.35)^3-5*(x+1/x)当x=2,x=4的值。
2、计算cos(pi/3)-(9-2^(1/2))^(1/3)。
3、已知a=3,A=4,b=a^2,B=b^2-1,c=a+2*B+c,求C。
4、创建一个3*3矩阵,然后用矩阵编辑器将其扩充为4*5矩阵。
5、创建一个4*4矩阵魔方阵和相应的随机矩阵,将两个矩阵并接起来,然后提取任意两个列向量。
7设A=[1,4,8,13;-3,6,-5,-9;2,-7,-12,-8],B=[5,4,3,-2;6,-2,3,-8;-1,3,-9,7],求C=A*B’,D=A.*B。
8、求(s^2+2)(s+4)(s+1)/(s^3+s+1)的“商”及“余”多项式。
9、建立矩阵A,然后找出在[10,20]q区间的元素的位置。
10、创建一个有7个元素的一维数组,并做如下处理:1)直接访问一位数组的第6个元素;2)寻访一维数组的第1、3、5个元素;3)寻访一维数组中的第4个至最后1个元素;4)寻访一维数组中大于70的元素。
三、实验程序:NO.1>> x=[2,4]x = 2 4>> y=x.^3+(x-0.98).^2/(x+1.35).^3-5*(x+1./x)y =-4.4423 42.8077>>NO.2>> cos(pi/3)-(9-sqrt(2))^(1/3) ans =-1.4649>>3>> a=3a =NO. 3>> A=4A =4>> b=a^2b =9>> B=b^2-1B =80>> c=a+A-2*Bc =-153>> C=a+2*B+cC =10NO..4A=rand(3)A =0.5341 0.8385 0.70270.7271 0.5681 0.54660.3093 0.3704 0.4449>> B=rand(3,2)B =0.6946 0.95680.6213 0.52260.7948 0.8801>> C=rand(1,5)C =0.1730 0.9797 0.2714 0.2523 0.8757 >> F=[A,B;C]F =0.5341 0.8385 0.7027 0.6946 0.95680.7271 0.5681 0.5466 0.6213 0.52260.3093 0.3704 0.4449 0.7948 0.88010.1730 0.9797 0.2714 0.2523 0.8757 NO.5>> A=magic(4)A =16 2 3 135 11 10 89 7 6 124 14 15 1>> B=rand(3,4)B =0.7373 0.8939 0.6614 0.06480.1365 0.1991 0.2844 0.98830.0118 0.2987 0.4692 0.5828 >> C=[A;B]C =16.0000 2.0000 3.0000 13.00005.0000 11.0000 10.0000 8.00009.0000 7.0000 6.0000 12.00004.0000 14.0000 15.0000 1.00000.7373 0.8939 0.6614 0.06480.1365 0.1991 0.2844 0.98830.0118 0.2987 0.4692 0.5828 >> C(:,[1,2])ans =NO.6>> A=[-4,-2,0,2,4;-3,-1,1,3,5]A =-4 -2 0 2 4-3 -1 1 3 5>> LA=abs(A)>3LA =1 0 0 0 10 0 0 0 1>> A(LA)ans =-445>>NO.7>> A=[1,4,8,13;-3,6,-5,-9;2,-7,-12,-8]A =1 4 8 13-3 6 -5 -92 -7 -12 -8>> B=[5,4,3,-2;6,-2,3,-8;-1,3,-9,7]B =5 4 3 -26 -2 3 -8-1 3 -9 7>> C=A*B'C =19 -82 3012 27 3-38 54 29>> D=A.*BD =5 16 24 -26-18 -12 -15 72-2 -21 108 -56>>NO.8>> den=conv([1,0,2],conv([1,4],[1,2])) den =1 6 10 12 16 num=[1,0,1,1];>> [q,r]=deconv(den,num)q =1 6r =0 0 9 5 10>>NO.9>> A=[10,15,8;5,16,35;16,8,26]A =10 15 85 16 3516 8 26>> (A>=10)&(A<=20)ans =1 1 00 1 01 0 0>>NO.10x =1 2 3 4 5 6 7 >> x(1)ans =1>> x(3)ans =3>> x(5)ans = 5>> x(4:end)ans = 4 5 6 7>> x(x>70)ans =Empty matrix: 1-by-0>>实验二1. 设()23sin cos 0.51x y x x ⎡⎤⎢⎥=++⎢⎥⎣⎦,把0~2x π=区间分为125点,画出以x 为横坐标,y 为纵坐标的曲线。
MATLAB程序设计实验1

测试数据:
b3= linspace(0,10,5)
4)定数对数采样的方法(logspace(a,b,n)):
n为数组的总个数,a为第一个元素,b为数组的最后一个元素。经过常用对数采样生成一维数组。
测试数据:
b4=logspace(-1,1,4)
[px,py] = gradient(z,.2,.2);
contour(v,v,z), hold on, quiver(v,v,px,py), hold off
4)fminbnd、fminsearch、fminunc极值
x1 = 0;
x2 =2*pi;
[x,y] = fminbnd(@func,x1,x2)
a5=tril(a)
a6=triu(a,1)
5.字符串数组的创建和操作实验
1)字符串的创建
a.直接输入的方法创建字符串数组
在直接创建数组的时候,可以直接用单引号将字符串括起来作为一个字符串数组,字符窗中如果有单引号,可以利用转义的方法,在单引号前面在加一个单引号。一个字符串的数组还可以由其他的字符串数组拼接而成。
e./f
11)克罗内克张量积
kron(a,b)表示利用a的每一个元素和b矩阵相乘,乘后分别作为结果矩阵的一块.
a=[1,2,3;4,5,6];
b=[1,0,0;0,1,0;0,0,1];
kron(a,b)
kron(b,a)
12)逻辑与&
当数组中的元素数字不为0,均表示逻辑1。
a=[1,2,3];
b=[3,4,5];
a.cat函数
cat函数用于连接数组,标准形式为c=cat(dim,A1,A2,A3,…)其中,dim表示传见数组的维数,A1,A2,A3表示各个维度上的数组。
MATLAB实验指导书

实验一:MATLAB的基本操作一、实验目的:1.熟悉MATLAB操作环境2.熟悉MATLAB的帮助3.熟悉MATLAB矩阵的操作4.熟悉MATLAB基本运算二、实验内容:1.自行设计试题,说明三角函数是按弧度还是按角度计算。
2.找出取整的函数,并自行设计试题,说明它们的区别。
3.自行设计试题,说明如何给矩阵按列符值。
4.自行设计试题,建一个5X5矩阵,然后将第一行乘1,第二行乘2,第三行乘3,第四行乘4,第五行乘5。
5.设计编写程序(命令),解方程3x5-7x4+5x2+2x-18=0。
6.自行设计试题,说明eval()函数的功能。
三、实验原理:ceil(x)= -4 -2 0 2 5 7fix(x) = -4 -2 0 1 4 6floor(x) = -5 -3 -1 1 4 6round(x) = -5 -2 0 1 5 72、系统的在线帮助help 命令:(1).当不知系统有何帮助内容时,可直接输入help以寻求帮助:>> help(回车)(2).当想了解某一主题的内容时,如输入:>> help syntax(了解Matlab的语法规定)(3).当想了解某一具体的函数或命令的帮助信息时,如输入:>> help sqrt (了解函数sqrt的相关信息)lookfor命令现需要完成某一具体操作,不知有何命令或函数可以完成,如输入:>> lookfor line (查找与直线、线性问题有关的函数)3、常量与变量系统的变量命名规则:变量名区分字母大小写;变量名必须以字母打头,其后可以是任意字母,数字,或下划线的组合。
此外,系统内部预先定义了几个有特殊意义和用途的变量,见下表:数值型向量(矩阵)的输入(1).任何矩阵(向量),可以直接按行方式...输入每个元素:同一行中的元素用逗号(,)或者用空格符来分隔;行与行之间用分号(;)分隔。
所有元素处于一方括号([ ])内;例1-1:>> Time = [11 12 1 2 3 4 5 6 7 8 9 10]>> X_Data = [2.32 3.43;4.37 5.98](2).系统中提供了多个命令用于输入特殊的矩阵:上面函数的具体用法,可以用帮助命令help得到。
MATLAB实验指导书(第一次实验)

************************ MATLAB上机指导书************************昆明理工大学机电学院刘孝保2013年3月实验一 MATLAB 工作环境熟悉及简单命令的执行一、实验目的:熟悉MATLAB 的工作环境,学会使用MATLAB 进行一些简单的运算。
二、实验内容:MATLAB 的启动和退出,熟悉MATLAB 的桌面(Desktop ),包括菜单(Menu )、工具条 (Toolbar )、命令窗口(Command Window)、历史命令窗口、工作空间(Workspace)等;完成一些基本的矩阵操作;学习使用在线帮助系统。
三、实验步骤:1、启动MATLAB ,熟悉MATLAB 的桌面。
2、在命令窗口执行命令完成以下运算,观察workspace 的变化,记录运算结果。
(1)(365-52⨯2-70)÷3 (2)>>area=pi*2.5^2(3)已知x=3,y=4,在MATLAB 中求z :()232y x y x z -= (4)将下面的矩阵赋值给变量m1,在workspace 中察看m1在内存中占用的字节数。
m1=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡11514412679810115133216 执行以下命令 >>m1( 2 , 3 ) >>m1( 11 ) >>m1( : , 3 )>>m1( 2 : 3 , 1 : 3 )>>m1( 1 ,4 ) + m1( 2 ,3 ) + m1( 3 ,2 ) + m1( 4 ,1) (5)执行命令>>help abs查看函数abs 的用法及用途,计算abs( 3 + 4i ) (6)执行命令>>x=0:0.1:6*pi; >>y=5*sin(x); >>plot(x,y)(6)运行MATLAB 的演示程序,>>demo ,以便对MATLAB 有一个总体了解。
实验三MATLAB的程序设计

end
ifk==0
Y=1;
elseifk==1&&n==1
Y=1;
elseifk<=n
Y=(n/k)*c(k-1,n-1);
end
程序测试:
>> c(0,0)
ans =
1
>> c(0,1)
ans =
1
>> c(3,4)
ans =
4
7,计算以下和式,并估计其求和公式以及验证:
functionY=s(n)
Y=0;
fork=1:n
Y=Y+k;
end
测试:
>> s(3)
ans =
6
functionY=s(n)
Y=0;
fork=1:n
Y=Y+k^2;
end
测试:
>> s(3)
ans =
14
functionY=s(n)
Y=0;
fork=1:n
Y=Y+k^3;
end
测试:
>> s(2)
4
>> Joseph0(7,4)
2
11,求出 之间的所有素数;
M函数文件:
functionout = nprimes(N)
A= [1:N];
A(1)=0;
i=2;
whilei<= floor(sqrt(N));
forj= 2:fix(N/i)
A(i*j) = 0;
end;
i = A(find(A>i,1));
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一要求: 查看matlab 的版本代码:version结果:ans =7.1.0.246 (R14) Service Pack 31.先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1)z 1=2185sin 2e+z1=(2*sin(85*pi/180))/(1+exp(2))z =0.2375(2)z 2=⎥⎦⎤⎢⎣⎡+=++545.0-i 212其中),1ln(212x x x x=[2,1+2*i;-0.45,5]x =2.0000 1.0000 + 2.0000i-0.4500 5.0000>> z2=1/2*log(x+sqrt(1+x*x))z2 =0.7114 - 0.0253i 0.8968 + 0.3658i0.2139 + 0.9343i 1.1541 - 0.0044i(3)z 3=23.0ln )3.0sin(23.03.0a a e e aa +++--,a=-3.0,-2.9,-2.8, …3.0 提示:用冒号表达式生成a 向量,求各点的函数值时用点乘计算。
a=[-3.0:0.1:3.0]z3=1/2.*((exp(0.3.*a)-exp(-0.3.*a))).*sin(a+0.3)+log((0.3+a).*1/2)(4)z 4=⎪⎩⎪⎨⎧<≤+-<≤-<≤32,12,21,110,222t t t t t t t 其中t=0:0.5:2.5提示:用逻辑表达式求分段函数值。
t=0:0.5:2.5t =0 0.5000 1.0000 1.5000 2.0000 2.5000>> z4=t.^2.*(t>=0&t<1)+(t.^2-1).*(t>=1&t<2)+(t.^2-2*t+1).*(t>=2&t<3) z4 =0 0.2500 0 1.2500 1.0000 2.25002.已知:A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡7653877344-3412,B=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡72-3321-31求下列表达式的值:(1)A+6*B和A-B+I(其中I为单位矩阵) A=[12,34,-4;34,7,87;3,65,7]A =12 34 -434 7 873 65 7>> B=[1,3,-1;2,0,3;3,-2,7]B =1 3 -12 0 33 -2 7>> A+6*Bans =18 52 -1046 7 10521 53 49>> I=eye(size(A))I =1 0 00 1 00 0 1>> A-B+Ians =12 31 -332 8 840 67 1(2)A*B和A.*BA*Bans =68 44 62309 -72 596154 -5 241>> A.*Bans =12 102 468 0 2619 -130 49(3)A^3和A.^3A^3ans =37226 233824 48604247370 149188 60076678688 454142 118820>> A.^3ans =1728 39304 -6439304 343 65850327 274625 343(4)A/B和B\AA/Bans =16.4000 -13.6000 7.600035.8000 -76.2000 50.200067.0000 -134.0000 68.0000>> B/Aans =0.1027 -0.0062 -0.00690.0617 0.0403 -0.03660.0205 0.0855 -0.0507(5)[A,B]和[A([1,3],:);B^2][A,B]ans =12 34 -4 1 3 -134 7 87 2 0 33 65 7 3 -2 7>> [A([1,3],:);B^2]ans =12 34 -43 65 74 5 111 0 1920 -5 403.设有矩阵A和BA=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡25242322212019181716151413121110987654321,B=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡111340794-23096-171603 (1) 求它们的乘积C 。
A=[1 2 3 4 5;6 7 8 9 10;11 12 13 14 15;16 17 18 19 20;21 22 23 24 25]A =1 2 3 4 56 7 8 9 1011 12 13 14 1516 17 18 19 2021 22 23 24 25>> B=[3 0 6;17 -6 9;0 23 -4;9 7 0; 4 13 11]B =3 0 617 -6 90 23 -49 7 04 13 11C=A*BC =93 150 67258 335 177423 520 287588 705 397753 890 507(2) 将矩阵C 的左下角3×2子矩阵赋给D 。
(2)D=C([3,4,5],2:end)D =520 287705 397890 507(3) 查看MATLAB 工作空间的使用情况。
4.完成下列操作:(1)求[100,999]之间能被21整除的数的个数。
提示:先利用冒号表达式,再利用find 和length 函数。
A=100:999P=rem(A,21)==0Q=find(P)>> length(Q)ans =43(2)建立一个字符串向量,删除其中的大写字母。
提示:利用find 函数和空矩阵 。
ch='MmAaTtLlAaBb'ch =MmAaTtLlAaBb>> k=find(ch>='A'&ch<='Z')k =1 3 5 7 9 11ch(k)=[]ch =matlab实验二、1. 设有分块矩阵A=⎥⎦⎤⎢⎣⎡⨯⨯⨯⨯23322333E S O R ,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角矩阵,试通过数值计算验证A=⎥⎦⎤⎢⎣⎡+2E S O RS R 。
E=eye(3), R=rand([3,2]),O=zeros(2,3),S=diag([1,1]);A=[E,R;O,S]E =1 0 00 1 00 0 1R =0.9218 0.40570.7382 0.93550.1763 0.9169O =0 0 00 0 0A =1.0000 0 0 0.9218 0.40570 1.0000 0 0.7382 0.93550 0 1.0000 0.1763 0.91690 0 0 1.0000 00 0 0 0 1.00002.产生5阶希尔伯特矩阵H和5阶帕斯卡矩阵P,且求其行列式的值Hh和Hp以及它们的条件数Th和Tp,判断哪个矩阵的性能更好。
为什么?H=hilb(5),P=pascal(5)H =1.0000 0.5000 0.3333 0.2500 0.20000.5000 0.3333 0.2500 0.2000 0.16670.3333 0.2500 0.2000 0.1667 0.14290.2500 0.2000 0.1667 0.1429 0.12500.2000 0.1667 0.1429 0.1250 0.1111P =1 1 1 1 11 2 3 4 51 3 6 10 151 4 10 20 351 5 15 35 70>> Hh=det(H),Pp=det(P)Hh =3.7493e-012Pp =1>> Th=cond(H),Tp=cond(P)Th =4.7661e+005Tp =8.5175e+003矩阵T 条件数比矩阵H 的条件数更接近1,因此,矩阵T 的性能要好于矩阵H 。
3. 建立一个5×5矩阵,求它的行列式值、迹、秩和范数。
A=[1 4 7 10 10;2 5 8 11 7;3 6 9 4 8;11 12 3 2 1;5 6 9 8 7]A =1 4 7 10 102 5 8 11 73 6 94 811 12 3 2 15 6 9 8 7>> a1=det(A),a2=trace(A),a3=rank(A),a4=norm(A)a1 =5376a2 =24a3 =5a4 =32.39474. 已知A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡588-1252018629-求A 的特征值及特征向量,并分析其数学意义。
A=[-29 6 18;20 5 12;-8 8 5]A =-29 6 1820 5 12-8 8 5>> [V,D]=eig(A)V =0.7130 0.2803 0.2733-0.6084 -0.7867 0.87250.3487 0.5501 0.4050D =-25.3169 0 00 -10.5182 00 0 16.8351数学意义:求得的3个特征值是-25.3169、-10.5182、16.8351,各特征值对应的特征向量为V 的各列构成的向量。
5.下面是一个线性方程组:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡52.067.095.06/15/14/15/14/13/14/13/12/1321x x x (1) 求方程的解。
A=[1/2 1/3 1/4;1/3 1/4 1/5;1/4 1/5 1/6]A =0.5000 0.3333 0.25000.3333 0.2500 0.20000.2500 0.2000 0.1667B=[0.95;0.67;0.52]B =0.95000.67000.5200x=inv(A)*Bx =1.20000.60000.6000(2)将方程右边向量元素b 3改为0.53,再求解,并比较b 3的变化和解的相对变化。
B=[0.95;0.67;0.53]B =0.95000.67000.5300>> x=inv(A)*Bx =3.0000-6.60006.6000(4) 计算系数矩阵A 的条件数并分析结论。
cond(A)ans =1.3533e+0036.建立A 矩阵,试比较sqrtm(A)和sqrt(A),并分析它们的区别。
A=rand(3)A =0.4103 0.3529 0.13890.8936 0.8132 0.20280.0579 0.0099 0.1987>> sqrtm(A)ans =0.4248 0.2963 0.13140.7418 0.7709 0.08730.0764 -0.0106 0.4354>> sqrt(A)ans =0.6405 0.5940 0.37270.9453 0.9018 0.45030.2406 0.0993 0.4458实验三、1. 求分段函数的值。
