机械优化设计一维搜索实验报告
机械优化设计实验报告

《机械优化设计》课程实验报告M a t l a b优化工具箱一、实验目的和要求熟悉Matlab7.0软件的界面和基本功能,了解Matlab优化工具箱的常用算法;使用Matlab优化工具箱的f m i n u n c/f m i n s e a r c h函数求解多变量非线性无约束优化问题;使用Matlab优化工具箱的f m i n c o n函数求解多变量非线性约束优化问题。
二、实验设备和软件台式计算机,Matlab7.0软件。
三、实验内容求解下列优化问题的最优解。
要求:(1)编写求解优化问题的M文件,(2)在命令窗口输入求解优化问题的命令,并得出计算结果。
1、标量优化问题1) f=x2-10x+362) f=x4-5x3+4x2-6x+603) f=(x+1)(x-2)22、多变量非线性无约束优化问题1) f=4(x1-5) 2+( x2-6) 2初始点:x0=[8,9]T;2) f=(x12+x2-11)2+( x1+ x22-7)2初始点:x0=[1,1]T;3) f=[1.5- x1(1- x2)]2+[2.25- x1(1- x22)]2+[2.625- x1(1- x23)]2初始点:x0=[2,0.2]T;4) f=( x12+12 x2-1)2+(49 x1+49 x2+84 x1+2324 x2-681)2初始点:x0=[1,1]T;5) f=( x1+10 x2)2+5(x3- x4)2+( x2-2 x3)4+10(x1- x4)4初始点:x0=[3,-1,0,1]T;3、多变量非线性约束优化问题1) f=( x1-2)2+( x2-1)2g1= x12-x2≤0g2= x1+x2-2≤0初始点:x0=[3,3]T;2) f= x23[( x1-3)2-9]/273≤0g1=x2-x1/3≤0g2=-x1+x2/3≤0g3=x1+x2/3-6≤0g4=-x1≤0g5=-x2≤0初始点:x0=[1,5]T;3) f=1000- x12-2x2 2-x32-x1x2-x1x3g1=-x1≤0g2=-x2≤0g3=-x3≤0g4=x12+x22+x3 2-25=0g5=8x1+14x2+7x3-56=0初始点:x0=[2,2,2]T4)f=100(x2-x12)2+(1-x1)2+90(x4-x32)2+(1-x3)2+10[(x2-1)2+(x4-1)2]+19.8(x2-1)(x4-1)-10≤x1≤10-10≤x2≤10-10≤x3≤10-10≤0x4≤10初始点:x0=[-3,-1,-3,-1]T;四、M文件、在命令窗口输入的求解命令清单及计算结果记录>>1、(1)目标函数的M文件function f=fun1(x)f=x^2-10*x+36调用求解命令x0=0;options=optimset('LargeScale','off');lb=-10;ub=10;[x,fval]=fminbnd(@fun1,lb,ub,options)或{ x0=0; [x,fval]=fminbnd(@fun1,-10,10)} x =5.0000fval =11.00002、(2)目标函数的M文件function f=fun2(x)f=x^4-5*x^3+4*x^2-6*x+60调用求解命令x0=0;options=optimset('LargeScale','off');lb=0;ub=10;[x,fval]=fminbnd(@fun2,lb,ub,options)x =3.2796fval =22.65902、(3)目标函数的M文件function f=fun3(x)f=(x+1)*(x-2)^2调用求解命令> x0=0;options=optimset('LargeScale','off');lb=0;ub=10;[x,fval]=fminbnd(@fun3,lb,ub,options)x =2.0000fval =1.9953e-0113(1)目标函数的M文件function f=fun4(x)f=4*(x(1)-5)^2+(x(2)-6)^2调用求解命令x0=[8,9];options=optimset('LargeScale','off');[x,fval]=fminunc(@fun4,x0,options)Optimization terminated: relative infinity-norm of gradient less than options.TolFun. x =5.00006.0000fval =1.7876e-0123(2)目标函数的M文件function f=fun5(x)f=(x(1)^2+x(2)-11)^2+(x(1)+x(2)^2-7)^2调用求解命令>> x0=[1,1];options=optimset('LargeScale','off');[x,fval]=fminunc(@fun5,x0,options)Optimization terminated: relative infinity-norm of gradient less than options.TolFun. x =3.0000 2.0000fval =5.2125e-0123(3)目标函数的M文件function f=fun6(x)f=[1.5-x(1)*(1-x(2))]^2+[2.25-x(1)*(1-x(2)^2)]^2+[2.625-x(1)*(1-x(2)^3)]^2调用求解命令x0=[2,0.2];options=optimset('LargeScale','off');[x,fval]=fminunc(@fun6,x0,options)Optimization terminated: relative infinity-norm of gradient less than options.TolFun. x =3.0000 0.5000fval =3.9195e-0143(4)目标函数的M文件function f=fun7(x)f=(x(1)^2+12*x(2)-1)^2+(49*x(1)+49*x(2)+84*x(1)+2324*x(2)-681)^2调用求解命令x0=[1,1];options=optimset('LargeScale','off');[x,fval]=fminunc(@fun7,x0,options)Optimization terminated: relative infinity-norm of gradient less than options.TolFun. x =0.9570 0.2333fval =7.37643(5)目标函数的M文件function f=fun8(x)f=(x(1)+10*x(2))^2+5*(x(3)-x(4))^2+(x(2)-2*x(3))^4+10*(x(1)-x(4))^4调用求解命令>> x0=[3,-1,0,1];options=optimset('LargeScale','off');[x,fval]=fminunc(@fun8,x0,options)Optimization terminated: relative infinity-norm of gradient less than options.TolFun.x =0.0015 -0.0002 -0.0031 -0.0031fval =6.3890e-009三、3、(1)目标函数的M文件function f=fun9(x)f=(x(1)-2)^2+(x(2)-1)^2约束函数的M文件function [c,cep]=con1(x)c=[x(1)^2-x(2);x(1)+x(2)-2];cep=[]当前窗口条用求解命令x0=[3,3];options=optimset('LargeScale','off');[x,fval]=fmincon(@fun9,x0,[],[],[],[],[],[],@con1,options)Optimization terminated: first-order optimality measure less than options.TolFun and maximum constraint violation is less than options.TolCon.Active inequalities (to within options.TolCon = 1e-006):lower upper ineqlin ineqnonlin12x =1.0000 1.0000fval =1.00003、(2)目标函数的M文件function f=fun10(x)f=x(2)^3*[(x(1)-3)^2-9]/27*3^(1/2)约束函数的M文件function [c,cep]=con2(x)c=[x(2)-x(1)/3^(1/2);-x(1)+x(2)/3^(1/2);x(1)+x(2)/3^(1/2)-6];cep=[]当前窗口条用求解命令x0=[1,5];lb=[0,0];options=optimset('LargeScale','off');[x,fval]=fmincon(@fun10,x0,[],[],[],[],lb,ub,@con2,options)Optimization terminated: first-order optimality measure lessthan options.TolFun and maximum constraint violation is lessthan options.TolCon.Active inequalities (to within options.TolCon = 1e-006):lower upper ineqlin ineqnonlin13x =4.5000 2.5981fval =-7.59383、(3)目标函数的M文件function f=fun11(x)f=1000-x(1)^2-2*x(2)^2-x(3)^2-x(1)*x(2)-x(1)*x(3)约束函数的M文件function [c,cep]=con3(x)c=[];cep=[x(1)^2+x(2)^2+x(3)^2-25;8*x(1)+14*x(2)+7*x(3)-56];当前窗口条用求解命令x0=[2,2,2];lb=[0,0,0];ub=[];options=optimset('LargeScale','off');[x,fval]=fmincon(@fun11,x0,[],[],[],[],lb,ub,@con3,options)Optimization terminated: first-order optimality measure lessthan options.TolFun and maximum constraint violation is lessthan options.TolCon.No active inequalitiesx =3.5121 0.2170 3.5522fval =961.71523、(4)目标函数的M文件function f=fun12(x)f=100*(x(2)-x(1)^2)^2+(1-x(1))^2+90*(x(4)-x(3)^2)^2+(1-x(3))^2+10*[(x(2)-1) ^2+(x(4)-1)^2]+19.8*(x(2)-1)*(x(4)-1)约束函数的M文件function [c,cep]=con4(x)cep=[];当前窗口条用求解命令x0=[-3,-1,-3,-1,];lb=[-10,-10,-10,-10];ub=[10,10,10,10];options=optimset('LargeScale','off');[x,fval]=fmincon(@fun12,x0,[],[],[],[],lb,ub,@con4,options)Optimization terminated: Magnitude of directional derivative in searchdirection less than 2*options.TolFun and maximum constraint violationis less than options.TolCon.No active inequalitiesx =1.0001 1.0002 0.9999 0.9997fval =2.3989e-007五、质疑和建议对于一维标量优化问题搜索,在当前窗口中调用求解命令时,[x,fval]=fminbnd(@fun1,lb,ub,options)可以改成[x,fval]=fminbnd(@fun1,-10,10)如下:function f=fun1(x)f=x^2-10*x+36调用求解命令x0=0;options=optimset('LargeScale','off');lb=-10;ub=10;[x,fval]=fminbnd(@fun1,lb,ub,options)或{ x0=0; [x,fval]=fminbnd(@fun1,-10,10)}x =5.0000fval =11.0000。
《机械优化设计》课程实践报告

合肥工业大学《机械优化设计》课程实践研究报告班级:学号:姓名:授课教师:日期: 2016年 11月 12 日目录1。
λ=0。
618的证明、一维搜索程序作业2。
单位矩阵程序作业3. 注释最佳再现给定运动规律连杆机构优化设计问题模型子程序4. 连杆机构问题+自行选择小型机械设计问题或其他工程优化问题(1)分析优化对象,根据设计问题的要求,选择设计变量,确立约束条件,建立目标函数,建立优化设计的数学模型并编制问题程序;(2)选择适当的优化方法,简述方法原理,进行优化计算;(3)进行结果分析,并加以说明。
5。
课程实践心得体会1。
λ=0.618的证明、一维搜索程序作业1.1证明:a α1 α2 ba α3 α1 α2黄金分割法要求插入点α1,α2的位置相对于区间[a,b]两端点具有对称性,即α1=b-λ(b-a)α2=b+λ(b-a)其中λ为待定常数.除了对称要求外,黄金分割法还要求在保留下来的区间内再插入一点,所形成的新三段与原来区间的三段具有相同的比例分布,故有1-λ=λ2取方程正数解,得≈0.618λ=√5−121.2一维搜索C语言程序:(以正弦函数y=sinx为例)#include〈stdio.h>#include<math.h>int main(){double a,b,c=0。
618,x[3],y[3],d;printf(”请输入区间[a,b]的值以及精度:\n”);scanf(”%lf,%lf,%lf”,&a,&b,&d);x[1]=b—c*(b—a);x[2]=a+c*(b—a);y[1]=sin(x[1]);y[2]=sin(x[2]);do{ if(y[1]>y[2]){ a=x[1];x[1]=x[2];y[1]=y[2];x[2]=a+c*(b—a);y[2]=sin(x[2]);}else{ b=x[2];x[2]=x[1];y[2]=y[1];x[1]=b—c*(b—a);y[1]=sin(x[1]);}}while(fabs((b-a)/b)>d);x[0]=(a+b)/2;y[0]=sin(x[0]);printf("极小点x*=%lf\n”,x[0]);printf("极小值y=%lf\n”,y[0]);}C语言程序运行结果:2. 单位矩阵程序作业2。
机械优化设计上机实践报告【精编版】

机械优化设计上机实践报告【精编版】机械优化设计上机实践报告班级:机械(茅以升)101姓名:学号: 1004010510成绩:指导教师: 张迎辉日期: 2013.11.201 《一维搜索方法》上机实践报告1、写出所选择的一维搜索算法的基本过程、原理(可附流程图说明)。
(一)进退法1. 算法原理进退法是用来确定搜索区间(包含极小值点的区间)的算法,其理论依据是:()f x 为单谷函数(只有一个极值点),且[,]a b 为其极小值点的一个搜索区间,对于任意12,[,]x x a b ∈,如果()()12f x f x <,则2[,]a x 为极小值的搜索区间,如果()()12f x f x >,则1[,]x b 为极小值的搜索区间。
因此,在给定初始点0x ,及初始搜索步长h 的情况下,首先以初始步长向前搜索一步,计算()0f x h +。
(1) 如果()()00f x f x h <+则可知搜索区间为0[,]xx h +%,其中x %待求,为确定x %,后退一步计算0()f x h λ-,λ为缩小系数,且01λ<<,直接找到合适的*λ,使得()*00()f x h f x λ->,从而确定搜索区间*00[,]x h x h λ-+。
(2) 如果()()00f x f x h >+则可知搜索区间为0[,]x x %,其中x %待求,为确定x %,前进一步计算0()f x h λ+,λ为放大系数,且1λ>,知道找到合适的*λ,使得()*00()f x h f x h λ+<+,从而确定搜索区间*00[,]x x h λ+。
2. 算法步骤用进退法求一维无约束问题min (),f x x R ∈的搜索区间(包含极小值点的区间)的基本算法步骤如下:(1) 给定初始点(0)x ,初始步长0h ,令0h h =,(1)(0)x x =,0k =;(2) 令(4)(1)x x h =+,置1k k =+;(3) 若()()(4)(1)f x f x <,则转步骤(4),否则转步骤(5);(4) 令(2)(1)(1)(4),x x x x ==,()()(2)(1)f x f x =,()()(1)(4)f x f x =,令2h h =,转步骤(2);(5) 若1k =,则转步骤(6)否则转步骤(7);(6) 令h h =-,(2)(4)x x =,()()(2)(4)f x f x =,转步骤(2);(7) 令(3)(2)(2)(1)(1)(4),,x x x x x x ===,停止计算,极小值点包含于区间(1)(3)(3)(1)[,][,]x x x x 或(二)黄金分割法1、黄金分割法基本思路:黄金分割法适用于[a ,b]区间上的任何单股函数求极小值问题,对函数除要求“单谷”外不做其他要求,甚至可以不连续。
机械优化设计_第三章一维搜索方法

机械优化设计_第三章一维搜索方法一维方法是一种常用的优化方法,适用于在一个单变量的空间中寻找最优解或近似最优解的问题。
在机械优化设计中,一维方法可以用来寻找最佳的设计参数值,以优化机械系统的性能。
一维方法包括了多种常用的算法,如二分法、黄金分割法、斐波那契法等。
下面将介绍其中的二分法和黄金分割法这两种常用的一维方法。
二分法是一种简单而常用的方法,基本思想是不断将空间划分为两部分,直到找到最优解或接近最优解的区间。
具体步骤如下:1.初始化区间[a,b],其中a和b分别是空间的下界和上界。
2.计算区间的中点x=(a+b)/23.根据目标函数的取值情况,确定最优解或接近最优解所在的子区间。
4.更新区间为[a,x]或[x,b],继续步骤2和3,直到区间足够小或找到了最优解。
二分法的优点是简单易实现,但其收敛速度相对较慢,特别是对于空间为初值范围较大的问题。
黄金分割法是一种相对高效的一维方法,其基本思想是通过黄金分割点来确定区间的缩减比例。
具体步骤如下:1.初始化区间[a,b],其中a和b分别是空间的下界和上界。
2.计算区间的两个黄金分割点,即x1=a+(1-φ)(b-a)和x2=a+φ(b-a),其中φ是黄金分割比例,其取值约为0.6183.根据目标函数的取值情况,确定最优解或接近最优解所在的子区间。
4.更新区间为[x1,b]或[a,x2],同时更新黄金分割点,继续步骤2和3,直到区间足够小或找到了最优解。
黄金分割法的优点是收敛速度相对较快,通常比二分法更有效。
然而,其实现相对复杂一些,需要额外的计算和判断步骤。
除了二分法和黄金分割法,还有其他一维方法,如斐波那契法、插值法等。
这些方法可以根据具体问题的特点选择适合的方法进行优化设计。
总结起来,一维方法是机械优化设计中常用的方法之一,用于在一个单变量的空间中寻找最优解或近似最优解的问题。
通过选择适当的方法,可以有效地优化机械系统的性能。
机械优化设计第三章一维搜索方法

(b a),故
Fn
b
a 。由Fn即可从斐波那契数列表或按F0
F1
1, Fn
Fn1
Fn2 (n
2, 3,
)
推算出相应的n。
3)确定试点并计算相应的函数值,在区间a, b内的两个试点:
x2
a
Fn1 Fn
(b
a),
x1
b
Fn1 Fn
(b
a),
f1 f (x1),
f2 f (x2 )
第三章 一维搜索方法
1.若f (a1) f (b1),则取[a,b1]为缩短后的搜索区间; 2.若f (a1) f (b1),则取[a1,b]为缩短后的搜索区间。
第三章 一维搜索方法
第二节 搜索区间的确定与区间消去法原理
间 接
假定在搜索区间[a, b]内取一点x, 并计算它的导数值 f '(x),可能出现三种情况:
x2 a b x1, f2 f (x2 )
5)检查迭代终止条件:bn1 an1
,若满足,则输出最优解x*
1 (a b), 2
ห้องสมุดไป่ตู้
f*
f (x*),
若不满足,则转入(4),继续进行迭代。
1. f (a1) f (b1),由于函数的单峰性, 极小点一定在[a, b1 ]内; 2. f (a1) f (b1),极小点一定在[a1,b]内; 3. f (a1) f (b1),极小点一定在[a1,b1]内。
第三章 一维搜索方法
第二节 搜索区间的确定与区间消去法原理
直 接 法
假定在搜索区间[a,b]内任取两点a1和b1,且a1 b1, 并计算f (a1)和f (b1),可能出现三种情况:
f (x1) f (x) f (x2)
机械优化设计上机报告

机械优化设计上机实践报告班级:机械(茅以升)101姓名:学号: 1004010510成绩:指导教师: 张迎辉日期: 2013.11.201 《一维搜索方法》上机实践报告1、写出所选择的一维搜索算法的基本过程、原理(可附流程图说明)。
(一)进退法 1. 算法原理进退法是用来确定搜索区间(包含极小值点的区间)的算法,其理论依据是:()f x 为单谷函数(只有一个极值点),且[,]a b 为其极小值点的一个搜索区间,对于任意12,[,]x x a b ∈,如果()()12f x f x <,则2[,]a x 为极小值的搜索区间,如果()()12f x f x >,则1[,]x b 为极小值的搜索区间。
因此,在给定初始点0x ,及初始搜索步长h 的情况下,首先以初始步长向前搜索一步,计算()0f x h +。
(1) 如果()()00f x f x h <+则可知搜索区间为0[,]x x h +,其中x 待求,为确定x ,后退一步计算0()f x h λ-,λ为缩小系数,且01λ<<,直接找到合适的*λ,使得()*00()f x h f x λ->,从而确定搜索区间*00[,]x h x h λ-+。
(2) 如果()()00f x f x h >+则可知搜索区间为0[,]x x ,其中x 待求,为确定x ,前进一步计算0()f x h λ+,λ为放大系数,且1λ>,知道找到合适的*λ,使得()*00()f x h f x h λ+<+,从而确定搜索区间*00[,]x x h λ+。
2. 算法步骤用进退法求一维无约束问题min (),f x x R ∈的搜索区间(包含极小值点的区间)的基本算法步骤如下:(1) 给定初始点(0)x ,初始步长0h ,令0h h =,(1)(0)x x =,0k =; (2) 令(4)(1)x x h =+,置1k k =+;(3) 若()()(4)(1)f x f x <,则转步骤(4),否则转步骤(5);(4) 令(2)(1)(1)(4),x x x x ==,()()(2)(1)f x f x =,()()(1)(4)f x f x =,令2h h =,转步骤(2); (5) 若1k =,则转步骤(6)否则转步骤(7);(6) 令h h =-,(2)(4)x x =,()()(2)(4)f x f x =,转步骤(2);(7) 令(3)(2)(2)(1)(1)(4),,x x x x x x ===,停止计算,极小值点包含于区间(1)(3)(3)(1)[,][,]x x x x 或(二)黄金分割法1、黄金分割法基本思路:黄金分割法适用于[a ,b]区间上的任何单股函数求极小值问题,对函数除要求“单谷”外不做其他要求,甚至可以不连续。
机械优化设计实验
§1 综合性编程的上机实验一实验目的无约束坐标轮换优化方法调用一维最优化方法,一维最优化方法(0。
618法)又调用区间搜索法(进退法),综合性编制程序的上机实验。
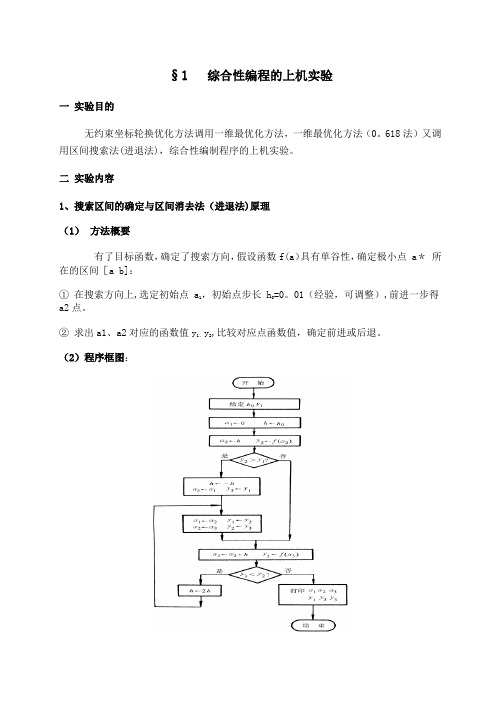
二实验内容1、搜索区间的确定与区间消去法(进退法)原理(1)方法概要有了目标函数,确定了搜索方向,假设函数f(a)具有单谷性,确定极小点 a*所在的区间[a b]:①在搜索方向上,选定初始点 a1,初始点步长 h=0。
01(经验,可调整),前进一步得a2点。
②求出a1、a2对应的函数值y1、y2,比较对应点函数值,确定前进或后退。
(2)程序框图:3、一维搜索黄金分割法(0.618法)(1)基本思想前提:已通过进退法确定了符合函数值高低高规律的搜索区间[a,b]即,函数的极小点必在[a,b]内.所以要调用搜索区间的进退法(2)程序框图①初始区间[a,b],由进退法确定。
收敛精度ε(ε=10—4~ 10-5),缩短率λ=0。
618②计算a1、a2,f (a1)、 f (a2),③根据区间消去法原理缩短区间,进行区间名称的代换,并保留区间中计算的一个新试验点及函数值。
④检查区间是否短到足够小和函数值收敛到足够近。
若条件不满足,则返回到②⑤若条件满足,则取最后两个试验点的平均值作为极小点数值的近似解。
4、多维无约束坐标轮换法(1)基本思想把多维问题转化为一系列一维搜索问题.沿设计变量的各个分量形成的坐标轴依次进行一维搜索(固定其它分量,仅对一个分量优选,轮番搜索),即调用一维最优化方法(0.618法),而一维最优化方法(0。
618法)又调用区间搜索法(进退法)。
重复进行,直至找出满足精度的极小点。
(2)程序框图(3)具体要求①注意数组的应用,便于设计过程中沿各坐标轴迭代时的数据处理;②注意子程序和子函数的调用,简化设计过程,便于数据的计算机处理;③设计结果在界面上显示,并进行数据分析。
④写出上机实验报告§2有约束优化方法应用编制程序的上机实验一、实验目的使学生能用有约束优化设计方法解决简单工程问题的优化设计,对所设计的问题建立数学模型,并确定设计变量、目标函数和约束条件;调用有约束问题的最优化方法(惩罚函数法)编制程序,进而在计算机上求解并对优化的计算结果进行正确的分析和处理。
机械优化设计上机实践报告书

机械优化设计上机实践报告班级:机械(茅以升)101姓名:学号: 1004010510成绩:指导教师: 张迎辉日期: 2013.11.201 《一维搜索方法》上机实践报告1、写出所选择的一维搜索算法的基本过程、原理(可附流程图说明)。
(一)进退法1.算法原理进退法是用来确定搜索区间(包含极小值点的区间)的算法,其理论依据是:()f x 为单谷函数(只有一个极值点),且[,]a b 为其极小值点的一个搜索区间,对于任意12,[,]x x a b ∈,如果()()12f x f x <,则2[,]a x 为极小值的搜索区间,如果()()12f x f x >,则1[,]x b 为极小值的搜索区间。
因此,在给定初始点0x ,及初始搜索步长h 的情况下,首先以初始步长向前搜索一步,计算()0f x h +。
(1) 如果()()00f x f x h <+则可知搜索区间为0[,]x x h +,其中x 待求,为确定x ,后退一步计算0()f x h λ-,λ为缩小系数,且01λ<<,直接找到合适的*λ,使得()*00()f x h f x λ->,从而确定搜索区间*00[,]x h x h λ-+。
(2) 如果()()00f x f x h >+则可知搜索区间为0[,]x x ,其中x 待求,为确定x ,前进一步计算0()f x h λ+,λ为放大系数,且1λ>,知道找到合适的*λ,使得()*00()f x h f x h λ+<+,从而确定搜索区间*00[,]x x h λ+。
2. 算法步骤用进退法求一维无约束问题min (),f x x R ∈的搜索区间(包含极小值点的区间)的基本算法步骤如下:(1) 给定初始点(0)x ,初始步长0h ,令0h h =,(1)(0)x x =,0k =; (2) 令(4)(1)x x h =+,置1k k =+;(3) 若()()(4)(1)f x f x <,则转步骤(4),否则转步骤(5);(4) 令(2)(1)(1)(4),x x x x ==,()()(2)(1)f x f x =,()()(1)(4)f x f x =,令2h h =,转步骤(2); (5) 若1k =,则转步骤(6)否则转步骤(7);(6) 令h h =-,(2)(4)x x =,()()(2)(4)f x f x =,转步骤(2);(7) 令(3)(2)(2)(1)(1)(4),,x x x x x x ===,停止计算,极小值点包含于区间(1)(3)(3)(1)或x x x x[,][,](二)黄金分割法1、黄金分割法基本思路:黄金分割法适用于[a,b]区间上的任何单股函数求极小值问题,对函数除要求“单谷”外不做其他要求,甚至可以不连续。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《机械优化设计》
实验报告
班级: 机械设计(2)班
姓名:邓传淮
学号:0901102008
1 实验名称:一维搜索黄金分割法求最佳步长
2 实验目的:通过上机编程,理解一维搜索黄金分割法的原理,了解计算机在优化设计中的应用。
3 黄金分割法的基本原理
黄金分割法是用于一元函数f(x)在给定初始区间[a,b]内搜索极小点α*的一种方法。
它是优化计算中的经典算法,以算法简单、收敛速度均匀、效果较好而著称,是许多优化算法的基础,但它只适用于一维区间上的凸函数[6],即只在单峰区间内才能进行一维寻优,其收敛效率较低。
其基本原理是:依照“去劣存优”原则、对称原则、以及等比收缩原则来逐步缩小搜索区间[7]。
具体步骤是:在区间[a,b]内取点:a1 ,a2 把[a,b]分为三段。
如果f(a1)>f(a2),令a=a1,a1=a2,a2=a+r*(b-a);如果f(a1)<f(a2) ,令b=a2,a2=a1,a1=b-r*(b-a),如果|(b-a)/b|和|(y1-y2)/y2|都大于收敛精度ε重新开始。
因为[a,b]为单峰区间,这样每次可将搜索区间缩小0.618倍或0.382倍,处理后的区间都将包含极小点的区间缩小,然后在保留下来的区间上作同样的处理,如此迭代下去,将使搜索区[a,b]逐步缩小,直到满足预先给定的精度时,即获得一维优化问题的近似最优解。
黄金分割法原理如图所示,
4实验所编程序框图(1)进退发确定单峰区间的计算框图
(2)黄金分割法计算框图
5 程序源代码
(1)进退发确定单峰区间的程序源代码
#include<stdio.h>
#include<math.h>
#define f(x) pow(x,4)-3*pow(x,3)-5*pow(x,2)-14*x+46 main()
{
int k;
double x,h,x1,x2,x3;
double f1,f2,f3,f;
double a,b;
x1=0;
h=1;
x2=x1+h;
f1=f(x1);
f2=f(x2);
if (f1>f2)
{
h=2*h;
x3=x2+h;
f3=f(x3);
. }
else
{
h=-h;
x1=x2;
f1=f2;
x3=x2+h;
f3=f(x3);
}
printf("x1=%lf,x2=%lf\0",x1,x2);
do
{
x1=x2;
x2=x3;
f1=f2;
f2=f3;
x3=x2+h;
f3=f(x3);
}while(f3<f2);
if (h>0)
{
a=x1;
b=x3;
}
else
{
a=x3;
b=x1;
}
printf("a=%lf,b=%lf\n",a,b);
}
(2)黄金分割法的程序源代码
#include<stdio.h>
#include<math.h>
#define f(x)=pow(x,4)-3*pow(x,3)-5*pow(x,2)-14*x+46 main()
{
int k;
double x,h,x1,x2,x3,c;
double f1,f2,f3,f;
double a,b;
printf("input c:\n");
scanf("%lf",&c);
a=1;
b=5;
x1=b-0.618*(b-a);printf("x1=%lf ",x1);
f1=f(x1);printf("f1=%lf ",f1);
x2=a+0.618*(b-a);printf("x2=%lf ",x2);
f2=f(x2);printf("f2=%lf ",f2);
k=0;
loop:
{
if(f1<f2)
{
b=x2;printf("b=%lf ",b);
x2=x1;printf("x2=%lf ",x2);
f2=f1;printf("f2=%lf ",f2);
x1=a+0.382*(b-a);printf("x1=%lf ",x1);
f1=f(x1);printf("f1=%lf ",f1);
}
else
{
a=x1;printf("a=%lf ",a);
x1=x2;printf("x1=%lf ",x1);
f1=f2;printf("f1=%lf ",f1);
x2=a+0.618*(b-a);printf("x2=%lf ",x2);
f2=f(x2);printf("f2=%lf ",f2);
}
k=k+1;
printf("k=%d\n",k);
}
if(fabs(b-a<c))
{
x=0.5*(b+a);printf("x=%lf ",x);
f=f(x);printf("f=%lf ",f);
}
else
{
goto loop;
}
getchar();
}
6 程序运行截图。
