材料力学公式汇总完全版
(完整版)材料力学常用公式

材料力学常用公式1.外力偶矩计算公式(P功率,n转速)2.弯矩、剪力和荷载集度之间的关系式3.轴向拉压杆横截面上正应力的计算公式(杆件横截面轴力F N,横截面面积A,拉应力为正)4.轴向拉压杆斜截面上的正应力与切应力计算公式(夹角a 从x轴正方向逆时针转至外法线的方位角为正)5.纵向变形和横向变形(拉伸前试样标距l,拉伸后试样标距l1;拉伸前试样直径d,拉伸后试样直径d1)6.纵向线应变和横向线应变7.泊松比8.胡克定律9.受多个力作用的杆件纵向变形计算公式?10.承受轴向分布力或变截面的杆件,纵向变形计算公式11.轴向拉压杆的强度计算公式12.许用应力,脆性材料,塑性材料13.延伸率14.截面收缩率15.剪切胡克定律(切变模量G,切应变g )16.拉压弹性模量E、泊松比和切变模量G之间关系式17.圆截面对圆心的极惯性矩(a)实心圆(b)空心圆18.圆轴扭转时横截面上任一点切应力计算公式(扭矩T,所求点到圆心距离r)19.圆截面周边各点处最大切应力计算公式20.扭转截面系数,(a)实心圆(b)空心圆21.薄壁圆管(壁厚δ≤ R0 /10 ,R0为圆管的平均半径)扭转切应力计算公式22.圆轴扭转角与扭矩T、杆长l、扭转刚度GH p的关系式23.同一材料制成的圆轴各段内的扭矩不同或各段的直径不同(如阶梯轴)时或24.等直圆轴强度条件25.塑性材料;脆性材料26.扭转圆轴的刚度条件? 或27.受内压圆筒形薄壁容器横截面和纵截面上的应力计算公式,28.平面应力状态下斜截面应力的一般公式,29.平面应力状态的三个主应力,,30.主平面方位的计算公式31.面内最大切应力32.受扭圆轴表面某点的三个主应力,,33.三向应力状态最大与最小正应力 ,34.三向应力状态最大切应力35.广义胡克定律36.四种强度理论的相当应力37.一种常见的应力状态的强度条件,38.组合图形的形心坐标计算公式,39.任意截面图形对一点的极惯性矩与以该点为原点的任意两正交坐标轴的惯性矩之和的关系式40.截面图形对轴z和轴y的惯性半径? ,41.平行移轴公式(形心轴z c与平行轴z1的距离为a,图形面积为A)42.纯弯曲梁的正应力计算公式43.横力弯曲最大正应力计算公式44.矩形、圆形、空心圆形的弯曲截面系数? ,,45.几种常见截面的最大弯曲切应力计算公式(为中性轴一侧的横截面对中性轴z的静矩,b为横截面在中性轴处的宽度)46.矩形截面梁最大弯曲切应力发生在中性轴处47.工字形截面梁腹板上的弯曲切应力近似公式48.轧制工字钢梁最大弯曲切应力计算公式49.圆形截面梁最大弯曲切应力发生在中性轴处50.圆环形薄壁截面梁最大弯曲切应力发生在中性轴处51.弯曲正应力强度条件52.几种常见截面梁的弯曲切应力强度条件53.弯曲梁危险点上既有正应力σ又有切应力τ作用时的强度条件或,54.梁的挠曲线近似微分方程55.梁的转角方程56.梁的挠曲线方程?57.轴向荷载与横向均布荷载联合作用时杆件截面底部边缘和顶部边缘处的正应力计算公式58.偏心拉伸(压缩)59.弯扭组合变形时圆截面杆按第三和第四强度理论建立的强度条件表达式,60.圆截面杆横截面上有两个弯矩和同时作用时,合成弯矩为61.圆截面杆横截面上有两个弯矩和同时作用时强度计算公式62.63.弯拉扭或弯压扭组合作用时强度计算公式64.剪切实用计算的强度条件65.挤压实用计算的强度条件66.等截面细长压杆在四种杆端约束情况下的临界力计算公式67.压杆的约束条件:(a)两端铰支μ=l(b)一端固定、一端自由μ=2(c)一端固定、一端铰支μ=0.7(d)两端固定μ=0.568.压杆的长细比或柔度计算公式,69.细长压杆临界应力的欧拉公式70.欧拉公式的适用范围71.压杆稳定性计算的安全系数法72.压杆稳定性计算的折减系数法73.关系需查表求得。
(word完整版)材料力学常用公式

材料力学常用公式1外力偶矩计算公式(P功率,n转速)2弯矩、剪力和荷载集度之间的关系式3轴向拉压杆横截面上正应力的计算公式 (杆件横截面轴力F N,横截面面积A,拉应力为正)4轴向拉压杆斜截面上的正应力与切应力计算公式(夹角a从x轴正方向逆时针转至外法线的方位角为正)5纵向变形和横向变形(拉伸前试样标距l,拉伸后试样标距l1;拉伸前试样直径d,拉伸后试样直径d1)6纵向线应变和横向线应变7泊松比8胡克定律9受多个力作用的杆件纵向变形计算公式?10承受轴向分布力或变截面的杆件,纵向变形计算公式11轴向拉压杆的强度计算公式12许用应力, 脆性材料,塑性材料13延伸率14截面收缩率15剪切胡克定律(切变模量G,切应变g)16拉压弹性模量E、泊松比和切变模量G之间关系式17圆截面对圆心的极惯性矩(a)实心圆(b)空心圆18圆轴扭转时横截面上任一点切应力计算公式(扭矩T,所求点到圆心距离r)19圆截面周边各点处最大切应力计算公式20扭转截面系数,(a)实心圆(b)空心圆21薄壁圆管(壁厚δ≤ R0 /10 ,R0为圆管的平均半径)扭转切应力计算公式22圆轴扭转角与扭矩T、杆长l、扭转刚度GH p的关系式23同一材料制成的圆轴各段内的扭矩不同或各段的直径不同(如阶梯轴)时或24等直圆轴强度条件25塑性材料;脆性材料26扭转圆轴的刚度条件? 或27受内压圆筒形薄壁容器横截面和纵截面上的应力计算公式,28平面应力状态下斜截面应力的一般公式,29平面应力状态的三个主应力 ,,30主平面方位的计算公式31面内最大切应力32受扭圆轴表面某点的三个主应力,,33三向应力状态最大与最小正应力,34三向应力状态最大切应力35广义胡克定律36四种强度理论的相当应力37一种常见的应力状态的强度条件,38组合图形的形心坐标计算公式,39任意截面图形对一点的极惯性矩与以该点为原点的任意两正交坐标轴的惯性矩之和的关系式40截面图形对轴z和轴y的惯性半径?,41平行移轴公式(形心轴z c与平行轴z1的距离为a,图形面积为A)42纯弯曲梁的正应力计算公式43横力弯曲最大正应力计算公式44矩形、圆形、空心圆形的弯曲截面系数?,,45几种常见截面的最大弯曲切应力计算公式(为中性轴一侧的横截面对中性轴z的静矩,b为横截面在中性轴处的宽度)46矩形截面梁最大弯曲切应力发生在中性轴处47工字形截面梁腹板上的弯曲切应力近似公式48轧制工字钢梁最大弯曲切应力计算公式49圆形截面梁最大弯曲切应力发生在中性轴处50圆环形薄壁截面梁最大弯曲切应力发生在中性轴处51弯曲正应力强度条件52几种常见截面梁的弯曲切应力强度条件53弯曲梁危险点上既有正应力σ又有切应力τ作用时的强度条件或,54梁的挠曲线近似微分方程55梁的转角方程56梁的挠曲线方程?57轴向荷载与横向均布荷载联合作用时杆件截面底部边缘和顶部边缘处的正应力计算公式58偏心拉伸(压缩)59弯扭组合变形时圆截面杆按第三和第四强度理论建立的强度条件表达式,60圆截面杆横截面上有两个弯矩和同时作用时,合成弯矩为61圆截面杆横截面上有两个弯矩和同时作用时强度计算公式6263弯拉扭或弯压扭组合作用时强度计算公式64剪切实用计算的强度条件65挤压实用计算的强度条件66等截面细长压杆在四种杆端约束情况下的临界力计算公式67压杆的约束条件:(a)两端铰支μ=l(b)一端固定、一端自由μ=2(c)一端固定、一端铰支μ=0.7(d)两端固定μ=0.568压杆的长细比或柔度计算公式,69细长压杆临界应力的欧拉公式70欧拉公式的适用范围71压杆稳定性计算的安全系数法72压杆稳定性计算的折减系数法。
材料力学公式超级大汇总

材料力学公式超级大汇总(总29页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除材料力学公式超级大汇总1.外力偶矩计算公式(P功率,n转速)2.弯矩、剪力和荷载集度之间的关系式3.轴向拉压杆横截面上正应力的计算公式(杆件横截面轴力F N,横截面面积A,拉应力为正)4.轴向拉压杆斜截面上的正应力与切应力计算公式(夹角a 从x轴正方向逆时针转至外法线的方位角为正)5.纵向变形和横向变形(拉伸前试样标距l,拉伸后试样标距l1;拉伸前试样直径d,拉伸后试样直径d1)6.7.纵向线应变和横向线应变8.9.泊松比110.胡克定律11.受多个力作用的杆件纵向变形计算公式12.承受轴向分布力或变截面的杆件,纵向变形计算公式13.轴向拉压杆的强度计算公式14.许用应力,脆性材料,塑性材料15.延伸率16.截面收缩率17.剪切胡克定律(切变模量G,切应变g )18.拉压弹性模量E、泊松比和切变模量G之间关系式19.圆截面对圆心的极惯性矩(a)实心圆20. (b)空心圆221.圆轴扭转时横截面上任一点切应力计算公式(扭矩T,所求点到圆心距离r)22.圆截面周边各点处最大切应力计算公式23.扭转截面系数,(a)实心圆24. (b)空心圆25.薄壁圆管(壁厚δ≤ R0 /10 ,R为圆管的平均半径)扭转切应力计算公式26.圆轴扭转角与扭矩T、杆长l、扭转刚度GH p的关系式27.同一材料制成的圆轴各段内的扭矩不同或各段的直径不同(如阶梯轴)时或28.等直圆轴强度条件29.塑性材料;脆性材料330.扭转圆轴的刚度条件或31.受内压圆筒形薄壁容器横截面和纵截面上的应力计算公式,32.平面应力状态下斜截面应力的一般公式,33.平面应力状态的三个主应力,,34.主平面方位的计算公式35.面内最大切应力36.受扭圆轴表面某点的三个主应力,,437.三向应力状态最大与最小正应力 ,38.三向应力状态最大切应力39.广义胡克定律40.41.四种强度理论的相当应力42.一种常见的应力状态的强度条件,43.组合图形的形心坐标计算公式,44.任意截面图形对一点的极惯性矩与以该点为原点的任意两正交坐标轴的惯性矩之和的关系式45.截面图形对轴z和轴y的惯性半径546.,47.平行移轴公式(形心轴z c与平行轴z1的距离为a,图形面积为A)48.纯弯曲梁的正应力计算公式49.横力弯曲最大正应力计算公式50.矩形、圆形、空心圆形的弯曲截面系数,,51.几种常见截面的最大弯曲切应力计算公式(为中性轴一侧的横截面对中性轴z的静矩,b为横截面在中性轴处的宽度)52.矩形截面梁最大弯曲切应力发生在中性轴处53.工字形截面梁腹板上的弯曲切应力近似公式654.轧制工字钢梁最大弯曲切应力计算公式55.圆形截面梁最大弯曲切应力发生在中性轴处56.圆环形薄壁截面梁最大弯曲切应力发生在中性轴处57.弯曲正应力强度条件58.几种常见截面梁的弯曲切应力强度条件59.弯曲梁危险点上既有正应力σ又有切应力τ作用时的强度条件或,60.梁的挠曲线近似微分方程61.梁的转角方程62.梁的挠曲线方程63.轴向荷载与横向均布荷载联合作用时杆件截面底部边缘和顶部边缘处的正应力计算公式764.偏心拉伸(压缩)65.弯扭组合变形时圆截面杆按第三和第四强度理论建立的强度条件表达式,66.圆截面杆横截面上有两个弯矩和同时作用时,合成弯矩为67.圆截面杆横截面上有两个弯矩和同时作用时强度计算公式68.69.弯拉扭或弯压扭组合作用时强度计算公式70.剪切实用计算的强度条件71.挤压实用计算的强度条件72.等截面细长压杆在四种杆端约束情况下的临界力计算公式873.压杆的约束条件:(a)两端铰支μ=l74. (b)一端固定、一端自由μ=275. (c)一端固定、一端铰支μ=76. (d)两端固定μ=77.压杆的长细比或柔度计算公式,78.细长压杆临界应力的欧拉公式79.欧拉公式的适用范围80.压杆稳定性计算的安全系数法81.压杆稳定性计算的折减系数法82.关系需查表求得95 应力状态分析2 内力和内力图6 强度计算9 能量法和简单超静定问题材料力学公式汇总一、应力与强度条件 1、 拉压 []σσ≤=maxmax AN2、 剪切 []ττ≤=AQmax 挤压 []挤压挤压挤压σσ≤=AP3、 圆轴扭转 []ττ≤=W tTmax 4、平面弯曲 ①[]σσ≤=maxz max W M②[]max t max t max max σσ≤=y I Mz tmax c max max y I Mzc =σ[]cnax σ≤③[]ττ≤⋅=bI S Q z *max z max max5、斜弯曲 []σσ≤+=maxyyz z max W M W M6、拉(压)弯组合 []σσ≤+=maxmax zW M A N[]t max t zmax t σσ≤+=y I M A N z[]c max c z z max c σσ≤-=A N y I M 注意:“5”与“6”两式仅供参考 7、圆轴弯扭组合:①第三强度理论 []στσσ≤+=+=z 2n2w 2n2wr34W M M ②第四强度理论 []στσσ≤+=+=z2n2w 2n2w r475.03W M M二、变形及刚度条件 1、 拉压 ∑⎰===∆LEAx x N EAL N EANLL d )(ii2、 扭转 ()⎰=∑==Φpp i i p GI dx x T GI L T GI TLπφ0180⋅=Φ=p GI T L (m / )3、 弯曲(1)积分法:)()(''x M x EIy = C x x M x EI x EIy +==⎰d )()()('θ D Cx x x x M x EIy ++=⎰⎰d ]d )([)((2)叠加法:()21,P P f …=()()21P f P f ++…, ()21,P P θ=()()++21P P θθ…(3)基本变形表(注意:以下各公式均指绝对值,使用时要根据具体情况赋予正负号)EI ML B =θ EI PL B 22=θ EIqL B 63=θEIML f B 22=EI PL f B 33= EI qL f B 84=EI ML B 3=θ,EI ML A 6=θ EI PL A B 162==θθ EIqL A B 243==θθEI ML f c 162=EI PLf c 483= EIqL f c 3844= (4)弹性变形能(注:以下只给出弯曲构件的变形能,并忽略剪力影响,其他变形与此相似,不予写出)EIL M U 22==i i i EI L M 22∑=()⎰EI dx x M 22 (5)卡氏第二定理(注:只给出线性弹性弯曲梁的公式)P A B MA B A B q LL LLL=∂∂=∆i i P U ()()⎰∂∂∑dx P x M EI x M i三、应力状态与强度理论1、 二向应力状态斜截面应力ατασσσσσα2sin 2cos 22xy yx yx --++=ατασστα2cos 2sin 2xy yx +-=2、 二向应力状态极值正应力及所在截面方位角22min max )2(2xy y x y x τσσσσσσ+-±+= yx xy σστα--=22tg 0 3、 二向应力状态的极值剪应力22max )2(xyyx τσστ+-=注:极值正应力所在截面与极值剪应力所在截面夹角为450 4、 三向应力状态的主应力:321σσσ≥≥最大剪应力:231max σστ-=5、二向应力状态的广义胡克定律(1)、表达形式之一(用应力表示应变))(1y x x E μσσε-=)(1x y y E μσσε-= )(y x z E σσμε+-= Gxy xy τγ=(2)、表达形式之二(用应变表示应力))(12y x x E μεεμσ+-=)(12x y y E μεεμσ+-=0=z σ xy xy G γτ=6、三向应力状态的广义胡克定律()[]z y x x Eσσμσε+-=1()z y x ,, Gxy xy τγ= ()zx yz xy ,,7、强度理论(1)[]111σσσ≤=r ()3212σσμσσ+-=r []σ≤ []bb n σσ=(2)[]σσσσ≤-=313r ()()()[]213232221421σσσσσσσ-+-+-=r []σ≤ []s s n σσ=8、平面应力状态下的应变分析 (1)αγαεεεεεα2sin 22cos 22⎪⎪⎭⎫⎝⎛---++=xyyx yx+-=⎪⎭⎫ ⎝⎛-αεεγα2sin 22yx αγ2cos 2⎪⎪⎭⎫ ⎝⎛-xy (2)22min max 222⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛-±+=xy y x y x γεεεεεεyx xyεεγα-=02tg四、压杆稳定1、临界压力与临界应力公式(若把直杆分为三类)①细长受压杆 p λλ≥ ()2min2cr L EI P μπ=22crλπσE =②中长受压杆 s p λλλ≥≥ λσb a -=cr③短粗受压杆 s λλ≤ “cr σ”=s σ 或 b σ2、关于柔度的几个公式 i Lμλ= p 2p σπλE= ba s s σλ-=3、惯性半径公式AI i z= (圆截面 4d i z =,矩形截面12min b i =(b 为短边长度))五、动载荷(只给出冲击问题的有关公式) 能量方程 U V T ∆=∆+∆冲击系数 std 211∆++=hK (自由落体冲击) st20d ∆=g v K (水平冲击) 六、截面几何性质1、惯性矩(以下只给出公式,不注明截面的形状)⎰=dA I P 2ρ=324d π()44132απ-D Dd =α ⎰==6442d dA y I z π ()44164απ-D 123bh 123hb 323max d y I W z z π== ()43132απ-D62bh 62hb 2、惯性矩平移轴公式A a I I 2zc z +=。
材料力学公式大全(值得收藏)

材料⼒学公式⼤全(值得收藏)
1、轴向拉伸与压缩强度条件
2、切应⼒强度条件
3、泊松⽐
4、轴向拉伸和压缩的胡克定律
5、挤压强度条件
6、外⼒偶矩
7、薄壁圆筒横截⾯上的切应⼒
8、剪切胡克定律
9、弹性模量、泊松⽐、剪切弹性模量的关系
10、圆轴扭转的切应⼒
Ip为极惯性矩
11、圆轴扭转的最⼤切应⼒(Wt抗扭截⾯系数)
12、扭转强度条件
13、圆轴扭转时的变形及刚度计算
14、载荷集度、剪⼒和弯矩关系
15、弯曲正应⼒公式
Iz为惯性矩(常⽤型钢查表可得)
16、最⼤弯曲正应⼒
Wz为抗弯截⾯模量。
17、常见截⾯的I Z 和WZ
18、梁在弯曲变形下的微分⽅程
19、⼴义胡克定律的⼀般形式
20、最⼤拉应⼒理论(第⼀强度理论)
21、最⼤伸长线应变理论(第⼆强度理论)
22、最⼤切应⼒理论(第三强度理论)
23、畸变能密度理论(第四强度理论)
24、欧拉公式的普遍形式(适⽤于细长杆)
临界应⼒
25、细长杆稳定的临界压⼒
26、压杆柔度
27、中⼩柔度杆临界应⼒经验公式(系数a、b查表)
28、平⾯图形形⼼坐标
29、静矩
30、惯性积
31、平⾏移轴公式
32、转轴公式
33、主惯性矩公式。
材料力学公式汇总

材料力学公式汇总一、轴向拉压。
1. 轴力计算。
- 截面法:F_N=∑ F_i(F_N为轴力,F_i为截面一侧外力的代数和,拉力为正,压力为负)2. 正应力计算。
- σ=(F_N)/(A)(σ为正应力,A为横截面面积)3. 胡克定律。
- Δ L=(F_NL)/(EA)(Δ L为轴向变形量,L为杆件原长,E为弹性模量)4. 泊松比。
- ν =-(varepsilon')/(varepsilon)(ν为泊松比,varepsilon为轴向线应变,varepsilon'为横向线应变)二、扭转。
1. 扭矩计算。
- 截面法:T=∑ M_i(T为扭矩,M_i为截面一侧外力偶矩的代数和,右手螺旋法则确定正负,拇指指向截面外法线方向时,扭矩为正)2. 切应力计算(圆轴扭转)- τ=(Tρ)/(I_p)(τ为切应力,ρ为所求点到圆心的距离,I_p为极惯性矩)- 对于圆轴最大切应力:τ_max=(T)/(W_t)(W_t=(I_p)/(R),R为圆轴半径)- 对于实心圆轴:I_p=(π D^4)/(32),W_t=(π D^3)/(16)(D为圆轴直径)- 对于空心圆轴:I_p=(π)/(32)(D^4 - d^4),W_t=(π)/(16D)(D^4 - d^4)(d为空心圆轴内径)3. 扭转角计算(圆轴扭转)- φ=(TL)/(GI_p)(φ为扭转角,L为轴长,G为切变模量)三、弯曲内力。
1. 剪力和弯矩计算。
- 截面法:F_Q=∑ F_i(F_Q为剪力,截面左侧向上的外力或右侧向下的外力为正)- M=∑ M_i(M为弯矩,使梁下侧受拉的弯矩为正)2. 剪力图和弯矩图绘制。
- 利用载荷、剪力、弯矩之间的微分关系:(dF_Q)/(dx)=q(x),(dM)/(dx)=F_Q,frac{d^2M}{dx^2} = q(x)(q(x)为分布载荷集度)四、弯曲应力。
1. 正应力计算(梁的纯弯曲)- σ=(My)/(I_z)(σ为正应力,M为弯矩,y为所求点到中性轴的距离,I_z为截面对中性轴的惯性矩)- 最大正应力:σ_max=(M)/(W_z)(W_z=(I_z)/(y_max))- 对于矩形截面:I_z=frac{bh^3}{12},W_z=frac{bh^2}{6}(b为截面宽度,h 为截面高度)- 对于圆形截面:I_z=(π D^4)/(64),W_z=(π D^3)/(32)2. 切应力计算(矩形截面梁)- τ=frac{F_QS_z^*}{bI_z}(S_z^*为所求点以上(或以下)部分截面对中性轴的静矩,b为截面宽度)- 最大切应力(矩形截面):τ_max=(3F_Q)/(2bh)(发生在中性轴上)五、弯曲变形。
材料力学公式大全pdf

材料力学公式大全pdf
材料力学公式大全pdf
本文主要介绍材料力学中的相关公式,方便学习和应用。
以下是材料力学公式大全pdf:
1. 应力公式:
应力(σ)=受力(F)/截面积(A)
2. 应变公式:
应变(ε)=变形(ΔL)/初始长度(L)
3. 餘弦定理:
c² = a² + b² - 2ab cosC
4. 正弦定理:
a / sinA =
b / sinB =
c / sinC
其中A,B,C为三角形的内角。
5. 费马原理:
任何在保持稳定的条件下遵循最短路线的点在路线最短。
6. 钢材强度公式:
σs = Fs / A
其中,σs表示钢材的强度,Fs表示钢材的极限拉力,A表示截面积。
7. 钢材弹性模量公式:
Es = σs / εs
其中,Es表示钢材的弹性模量,σs表示钢材的强度,εs表示钢材的应变。
8. 抗弯公式:
M = σ x I / y
其中,M表示悬臂梁的弯矩,σ表示应力,I表示截面惯性矩,y 为距截面中性轴的距离。
9. 泊松比公式:
ν = -ε₂ / ε₁
其中,ν为泊松比,ε₁为轴向应变,ε₂为横向应变。
10. 拉力公式:
F = A x ε x E
其中,F表示拉力,A表示截面积,ε表示应变,E为材料的弹性模量。
以上就是材料力学公式大全pdf。
希望能对大家学习和应用材料力学有所帮助。
材料力学公式最全总汇分析

外力偶矩计算公式(P功率,n转速)弯矩、剪力和荷载集度之间的关系式轴向拉压杆横截面上正应力的计算公式(杆件横截面轴力FN,横截面面积A,拉应力为正)轴向拉压杆斜截面上的正应力与切应力计算公式(夹角a 从x轴正方向逆时针转至外法线的方位角为正)纵向变形和横向变形(拉伸前试样标距l,拉伸后试样标距l1;拉伸前试样直径d,拉伸后试样直径d1)纵向线应变和横向线应变泊松比胡克定律受多个力作用的杆件纵向变形计算公式?承受轴向分布力或变截面的杆件,纵向变形计算公式轴向拉压杆的强度计算公式许用应力,脆性材料,塑性材料延伸率截面收缩率剪切胡克定律(切变模量G,切应变g )拉压弹性模量E、泊松比和切变模量G之间关系式圆截面对圆心的极惯性矩(a)实心圆(b)空心圆圆轴扭转时横截面上任一点切应力计算公式(扭矩T,所求点到圆心距离r )圆截面周边各点处最大切应力计算公式扭转截面系数,(a)实心圆(b)空心圆薄壁圆管(壁厚δ≤ R0 /10 ,R0 为圆管的平均半径)扭转切应力计算公式圆轴扭转角与扭矩T、杆长l、扭转刚度GHp的关系式同一材料制成的圆轴各段内的扭矩不同或各段的直径不同(如阶梯轴)时或等直圆轴强度条件塑性材料;脆性材料扭转圆轴的刚度条件? 或受内压圆筒形薄壁容器横截面和纵截面上的应力计算公式,平面应力状态下斜截面应力的一般公式,平面应力状态的三个主应力,,主平面方位的计算公式面内最大切应力受扭圆轴表面某点的三个主应力,,三向应力状态最大与最小正应力,三向应力状态最大切应力广义胡克定律四种强度理论的相当应力一种常见的应力状态的强度条件,组合图形的形心坐标计算公式,任意截面图形对一点的极惯性矩与以该点为原点的任意两正交坐标轴的惯性矩之和的关系式截面图形对轴z和轴y的惯性半径? ,平行移轴公式(形心轴zc与平行轴z1的距离为a,图形面积为A)纯弯曲梁的正应力计算公式横力弯曲最大正应力计算公式矩形、圆形、空心圆形的弯曲截面系数? ,,几种常见截面的最大弯曲切应力计算公式(为中性轴一侧的横截面对中性轴z的静矩,b为横截面在中性轴处的宽度)矩形截面梁最大弯曲切应力发生在中性轴处工字形截面梁腹板上的弯曲切应力近似公式轧制工字钢梁最大弯曲切应力计算公式圆形截面梁最大弯曲切应力发生在中性轴处圆环形薄壁截面梁最大弯曲切应力发生在中性轴处弯曲正应力强度条件几种常见截面梁的弯曲切应力强度条件弯曲梁危险点上既有正应力σ又有切应力τ作用时的强度条件或,梁的挠曲线近似微分方程梁的转角方程梁的挠曲线方程?轴向荷载与横向均布荷载联合作用时杆件截面底部边缘和顶部边缘处的正应力计算公式偏心拉伸(压缩)弯扭组合变形时圆截面杆按第三和第四强度理论建立的强度条件表达式,圆截面杆横截面上有两个弯矩和同时作用时,合成弯矩为圆截面杆横截面上有两个弯矩和同时作用时强度计算公式弯拉扭或弯压扭组合作用时强度计算公式剪切实用计算的强度条件挤压实用计算的强度条件等截面细长压杆在四种杆端约束情况下的临界力计算公式压杆的约束条件:(a)两端铰支μ=l(b)一端固定、一端自由μ=2(c)一端固定、一端铰支μ=0.7(d)两端固定μ=0.5压杆的长细比或柔度计算公式,细长压杆临界应力的欧拉公式欧拉公式的适用范围压杆稳定性计算的安全系数法压杆稳定性计算的折减系数法关系需查表求得3 截面的几何参数4 应力和应变5 应力状态分析2 内力和内力图6 强度计算7 刚度校核8 压杆稳定性校核10 动荷载9 能量法和简单超静定问题材料力学公式汇总一、应力与强度条件1、拉压 []σσ≤=maxmax AN2、剪切 []ττ≤=AQmax 挤压 []挤压挤压挤压σσ≤=AP3、圆轴扭转 []ττ≤=W tTmax 4、平面弯曲 ①[]σσ≤=maxz max W M②[]max t max t max max σσ≤=y I Mz tmax c max max y I Mzc =σ[]cnax σ≤③[]ττ≤⋅=bI S Q z *max z max max5、斜弯曲 []σσ≤+=maxyyz z max W M W M6、拉(压)弯组合 []σσ≤+=maxmax zW M A N[]t max t zmax t σσ≤+=y I M A N z[]c max c z z max c σσ≤-=A N y I M 注意:“5”与“6”两式仅供参考 7、圆轴弯扭组合:①第三强度理论 []στσσ≤+=+=z 2n2w 2n 2w r34W M M②第四强度理论 []στσσ≤+=+=z2n2w 2n2wr475.03W M M二、变形及刚度条件 1、拉压 ∑⎰===∆LEAxx N EAL N EANLL d )(ii 2、扭转 ()⎰=∑==Φpp i i p GI dx x T GI L T GI TLπφ0180⋅=Φ=p GI T L (m / ) 3、弯曲(1)积分法:)()(''x M x EIy = C x x M x EI x EIy +==⎰d )()()('θ D Cx x x x M x EIy ++=⎰⎰d ]d )([)( (2)叠加法:()21,P P f …=()()21P f P f ++…, ()21,P P θ=()()++21P P θθ…(3)基本变形表(注意:以下各公式均指绝对值,使用时要根据具体情况赋予正负号)EI ML B =θ EI PL B 22=θ EIqL B 63=θEIML f B 22=EI PL f B 33= EI qL f B 84=EI ML B 3=θ,EI ML A 6=θ EIPL A B 162==θθ EI qL A B 243==θθEI ML f c 162=EI PL f c 483= EIqL f c 3844= (4)弹性变形能(注:以下只给出弯曲构件的变形能,并忽略剪力影响,其他变形与此相似,不予写出)EIL M U 22==i i i EI L M 22∑=()⎰EI dxx M 22 (5)卡氏第二定理(注:只给出线性弹性弯曲梁的公式)=∂∂=∆ii P U()()⎰∂∂∑dx P x M EI x M i PAB MAB A BqL LLLL三、应力状态与强度理论 1、二向应力状态斜截面应力ατασσσσσα2sin 2cos 22xy yx yx --++=ατασστα2cos 2sin 2xy yx +-=2、二向应力状态极值正应力及所在截面方位角22min max )2(2xy y x y x τσσσσσσ+-±+= yx xy σστα--=22tg 0 3、二向应力状态的极值剪应力22max )2(xyyx τσστ+-= 注:极值正应力所在截面与极值剪应力所在截面夹角为4504、三向应力状态的主应力:321σσσ≥≥ 最大剪应力:231max σστ-=5、二向应力状态的广义胡克定律(1)、表达形式之一(用应力表示应变))(1y x x E μσσε-=)(1x y y E μσσε-= )(y x z E σσμε+-= Gxy xy τγ= (2)、表达形式之二(用应变表示应力) )(12y x x E μεεμσ+-= )(12x y yEμεεμσ+-= 0=z σ xy xy G γτ= 6、三向应力状态的广义胡克定律()[]z y x x E σσμσε+-=1()z y x ,, Gxy xy τγ= ()zx yz xy ,,7、强度理论(1)[]111σσσ≤=r ()3212σσμσσ+-=r []σ≤ []bb n σσ=(2)[]σσσσ≤-=313r ()()()[]213232221421σσσσσσσ-+-+-=r []σ≤ []s s n σσ=8、平面应力状态下的应变分析 (1)αγαεεεεεα2sin 22cos 22⎪⎪⎭⎫ ⎝⎛---++=xyyx yx +-=⎪⎭⎫ ⎝⎛-αεεγα2sin 22y x αγ2cos 2⎪⎪⎭⎫⎝⎛-xy(2)22min max 222⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛-±+=xy y x y x γεεεεεεyx xyεεγα-=02tg四、压杆稳定1、临界压力与临界应力公式(若把直杆分为三类)①细长受压杆 p λλ≥ ()2min 2cr L EI P μπ= 22cr λπσE=②中长受压杆 s p λλλ≥≥ λσb a -=cr ③短粗受压杆 s λλ≤ “cr σ”=s σ 或 b σ2、关于柔度的几个公式 i Lμλ= p 2p σπλE= ba s s σλ-=3、惯性半径公式AI i z =(圆截面 4di z =,矩形截面12min b i =(b 为短边长度))五、动载荷(只给出冲击问题的有关公式) 能量方程 U V T ∆=∆+∆冲击系数 std 211∆++=hK (自由落体冲击) st20d ∆=g v K (水平冲击) 六、截面几何性质1、 惯性矩(以下只给出公式,不注明截面的形状)⎰=dA I P 2ρ=324d π()44132απ-D Dd =α ⎰==6442d dA y I z π ()44164απ-D 123bh 123hb323maxd y I W zz π==()43132απ-D 62bh 62hb2、惯性矩平移轴公式A a I I 2zc z +=。
材料力学公式汇总完全版

1截面几何参数【2】2应力与应变3应力状况剖析4内力和内力争5强度盘算序号公式b* = bT(5.11a)(5.11b)(5.11c)(5.11d)=T = ---- < [b ]max七'(实用于脆性材料)b* = b -V( b +b ) _-v (0-T )= (1 +V)T < [b ] T莅] max '< - 一(实用于脆性材料)-(-TmaxL2Tmax](5.11e)(5.12a)(5.12b)(5.13)(5.14a)(5.14b)(5.15a)(5.15a)由强度理论树立的扭转轴的强度前提由扭转实验树立的强度前提平面曲折梁的正应力强度前提平面曲折梁的剪应力强度前提平面曲折梁的主应力强度前提圆截面弯扭组合变形构件的相当弯矩max J WT1 +v=b -b=T1 3maxT/ [b ]T =——-< -_-max ]W2Tb *3max(实用于塑性材料)Y 2 〜-b l + (b -b l + (b -b=1=\: 2=t 3T<[b ]max-0、+ G +Tmax max+Q T -Tmax maxT = T < 风max W T "(实用于塑性材料)T r _ T = <[T ]max WTbt maxbcmaxM r [ 祈Vb tZ|M 用< [b c ]ZVS * r .T = -- Z max <[T ]Zfb * = v'b 2 + 4T 2 <[b ]3b* = ■,:b 2 + 3T 2 <[b ]■M 2 + M 2 + T 2 M=b -b =——Z W y------- = ~W-b》+ G -b》+ G -bJ M2 + M 2 + 0.75T 2 M *~W6刚度校核7压杆稳固性校核8动荷载9能量法和简略超静定问题。
材料力学公式超级大汇总
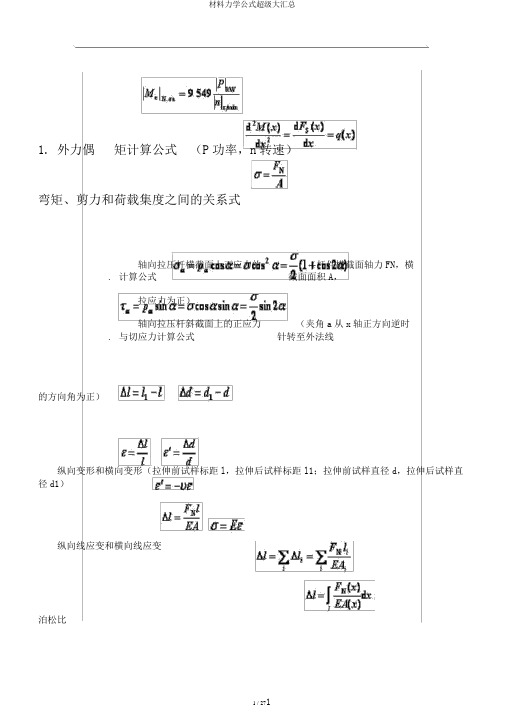
1. 外力偶矩计算公式(P功率,n转速)弯矩、剪力和荷载集度之间的关系式3 .轴向拉压杆横截面上正应力的计算公式(杆件横截面轴力FN,横截面面积A,拉应力为正)4 .轴向拉压杆斜截面上的正应力与切应力计算公式(夹角a从x轴正方向逆时针转至外法线的方向角为正)纵向变形和横向变形(拉伸前试样标距l,拉伸后试样标距l1;拉伸前试样直径d,拉伸后试样直径d1)纵向线应变和横向线应变泊松比胡克定律受多个力作用的杆件纵向变形计算公式?7.蒙受轴向散布力或变截面的杆件,纵向变形计算公式O(∩_∩)O轴向拉压杆的强度计算公式12.许用应力,脆性资料,塑性资料延长率截面缩短率剪切胡克定律(切变模量G,切应变g)拉压弹性模量E、泊松比和切变模量G之间关系式圆截面对圆心的极惯性矩(a)实心圆(b)空心圆18.圆轴扭转时横截面上任一点切应力计算公式(扭矩,所求点到圆心距离r )T圆截面周边各点处最大切应力计算公式20.扭转截面系数,(a)实心圆b)空心圆20.薄壁圆管(壁厚δ≤R0/10,R0为圆管的均匀半径)扭转切应力计算公式O(∩_∩)O22.圆轴扭转角与扭矩、杆长l、扭转刚度GH p的关系式T同一资料制成的圆轴各段内的扭矩不一样或各段的直径不一样(如阶梯轴)时或等直圆轴强度条件25.塑性资料;脆性资料26.扭转圆轴的刚度条件?或27.受内压圆筒形薄壁容器横截面和纵截面上的应力计算公式,平面应力状态下斜截面应力的一般公式,29.平面应力状态的三个主应力,,主平面方向的计算公式面内最大切应力32.受扭圆轴表面某点的三个主应力,,O(∩_∩)O33.三向应力状态最大与最小正应力,三向应力状态最大切应力广义胡克定律四种强度理论的相当应力37.一种常有的应力状态的强度条件,38.组合图形的形心坐标计算公式,随意截面图形对一点的极惯性矩与以该点为原点的随意两正交坐标轴的惯性矩之和的关系式40.截面图形对轴z和轴y的惯性半径?,平行移轴公式(形心轴z c与平行轴z1的距离为a,图形面积为A)41.纯曲折梁的正应力计算公式O(∩_∩)O横力曲折最大正应力计算公式44.矩形、圆形、空心圆形的曲折截面系数?,,45.几种常有截面的最大曲折切应力计算公式(为中性轴一侧的横截面对中性轴z的静矩,b为横截面在中性轴处的宽度)矩形截面梁最大曲折切应力发生在中性轴处工字形截面梁腹板上的曲折切应力近似公式轧制工字钢梁最大曲折切应力计算公式圆形截面梁最大曲折切应力发生在中性轴处圆环形薄壁截面梁最大曲折切应力发生在中性轴处曲折正应力强度条件几种常有截面梁的曲折切应力强度条件53.曲折梁危险点上既有正应力σ又有切应力τ作用时的强度条件或,O(∩_∩)O梁的挠曲线近似微分方程梁的转角方程梁的挠曲线方程?轴向荷载与横向均布荷载结合作用时杆件截面底部边沿和顶部边沿处的正应力计算公式偏爱拉伸(压缩)弯扭组合变形时圆截面杆按第三和第四强度理论成立的强度条件表达式,60.圆截面杆横截面上有两个弯矩和同时作用时,合成弯矩为61.圆截面杆横截面上有两个弯矩和同时作用时强度计算公式62.弯拉扭或弯压扭组合作用时强度计算公式64.剪确适用计算的强度条件O(∩_∩)O挤压适用计算的强度条件等截面修长压杆在四种杆端拘束状况下的临界力计算公式压杆的拘束条件:(a)两头铰支μ=lb)一端固定、一端自由μ=2c)一端固定、一端铰支μd)两头固定μ68.压杆的长细比或柔度计算公式,修长压杆临界应力的欧拉公式欧拉公式的合用范围压杆稳固性计算的安全系数法压杆稳固性计算的折减系数法关系需查表求得截面的几何参数序号公式名称公式符号说明()截面形心地点zdA Z为水平方向z c ydAA,y c A Y为竖直方向A A()截面形心地点z i A i,y c y i A iz cA i A iO(∩_∩)O()面积矩()面积矩()截面形心地点()面积矩()轴惯性矩()极惯必矩()极惯必矩)惯性积)轴惯性矩)惯性半径(展转半径))面积矩轴惯性矩极惯性矩惯性积()平行移轴公式S Z ydA,S y zdAA AS z A i y i,S y A i z i z cS y S zA,y c AS y Az c,S z Ay cI z y2dA,I y z2dAA AI2dAAI I z I yIzy zydAAI z i z2A,I y i y2Ai z I z,i y I yAAS z S zi,S ySyi I zIzi,I yIyiI I i,I zyIzyiI z I zc a2AI yIyc b2AIzyIzcyc abA4应力和应变序号公式名称公式符号说明()轴心拉压杆横N截面上的应力A()危险截面上危max N险点上的应力A ()轴心拉压杆的l纵向线应变lO(∩_∩)O()轴心拉压杆的纵向绝对应变()虎克定理(()虎克定理()虎克定理()横向线应变()泊松比(横向变形系数)()剪力双生互等定理()剪切虎克定理()实心圆截面扭转轴横截面上的应力()实心圆截面扭转轴横截面的圆周上的应力()抗扭截面模量(扭转抵挡矩)()实心圆截面扭转轴横截面的圆周上的应力()圆截面扭转轴的变形()圆截面扭转轴的变形l l l1.lEElN.lEAl iliNiilEA i 'b b1bb b''x yGTITRmaxIIW TRTmaxW T.lGITiil i()单位长度的扭转角,GI i Tl GI O(∩_∩)O()矩形截面扭转轴长边中点上的剪应力()矩形截面扭转轴短边中点上的剪应力()矩形截面扭转轴单位长度的扭转角()矩形截面扭转轴全轴的扭转角()平面曲折梁上任一点上的线应变()平面曲折梁上任一点上的线应力()平面曲折梁的曲率()纯曲折梁横截面上任一点的正应力()离中性轴最远的截面边沿各点上的最大正应力T Tmax W T b31maxT TGI T Gb4T.l.lG b4yEyMEI zMyI zM.y maxmaxI zW T是矩形截面W T的扭转抵抗矩I T是矩形截面的I T相当极惯性矩,与截面高宽比h/b相关的参数()抗弯截面模量(截面对曲折的抵挡矩)()离中性轴最远的W zIymaxM截面边沿各点上的最大正应力()横力曲折梁横截面上的剪应力maxW zVS*zI z b*S z被切割面O(∩_∩)O()中性轴各点的剪应力()矩形截面中性轴各点的剪应力)工字形和T形截面的面积矩)平面曲折梁的挠曲线近似微分方程)平面曲折梁的挠曲线上任一截面的转角方程)平面曲折梁的挠曲线上任一点挠度方程)双向曲折梁的合成弯矩)拉(压)弯组合矩形截面的中性轴在Z轴上的截距()拉(压)弯组合矩形截面的中性轴在Y轴上的截距的面积矩。
材料力学公式汇总.doc

材料力学常用公式1.外力偶矩计算公式(P功率,n转速)2.弯矩、剪力和荷载集度之间的关系式3.轴向拉压杆横截面上正应力的计算公式(杆件横截面轴力F N,横截面面积A,拉应力为正)4.轴向拉压杆斜截面上的正应力与切应力计算公式(夹角a 从x轴正方向逆时针转至外法线的方位角为正)5.纵向变形和横向变形(拉伸前试样标距l,拉伸后试样标距l1;拉伸前试样直径d,拉伸后试样直径d1)6.纵向线应变和横向线应变7.泊松比8.胡克定律9.受多个力作用的杆件纵向变形计算公式?10.承受轴向分布力或变截面的杆件,纵向变形计算公式11.轴向拉压杆的强度计算公式12.许用应力,脆性材料,塑性材料13.延伸率14.截面收缩率15.剪切胡克定律(切变模量G,切应变g )16.拉压弹性模量E、泊松比和切变模量G之间关系式17.圆截面对圆心的极惯性矩(a)实心圆(b)空心圆18.圆轴扭转时横截面上任一点切应力计算公式(扭矩T,所求点到圆心距离r)19.圆截面周边各点处最大切应力计算公式20.扭转截面系数,(a)实心圆(b)空心圆21.薄壁圆管(壁厚δ≤ R0 /10 ,R0为圆管的平均半径)扭转切应力计算公式22.圆轴扭转角与扭矩T、杆长l、扭转刚度GH p的关系式23.同一材料制成的圆轴各段内的扭矩不同或各段的直径不同(如阶梯轴)时或24.等直圆轴强度条件25.塑性材料;脆性材料26.扭转圆轴的刚度条件? 或27.受内压圆筒形薄壁容器横截面和纵截面上的应力计算公式,28.平面应力状态下斜截面应力的一般公式,29.平面应力状态的三个主应力, ,30.主平面方位的计算公式31.面内最大切应力32.受扭圆轴表面某点的三个主应力,,33.三向应力状态最大与最小正应力,34.三向应力状态最大切应力35.广义胡克定律36.四种强度理论的相当应力37.一种常见的应力状态的强度条件,38.组合图形的形心坐标计算公式,39.任意截面图形对一点的极惯性矩与以该点为原点的任意两正交坐标轴的惯性矩之和的关系式40.截面图形对轴z和轴y的惯性半径? ,41.平行移轴公式(形心轴z c与平行轴z1的距离为a,图形面积为A)42.纯弯曲梁的正应力计算公式43.横力弯曲最大正应力计算公式44.矩形、圆形、空心圆形的弯曲截面系数?,,45.几种常见截面的最大弯曲切应力计算公式(为中性轴一侧的横截面对中性轴z的静矩,b为横截面在中性轴处的宽度)46.矩形截面梁最大弯曲切应力发生在中性轴处47.工字形截面梁腹板上的弯曲切应力近似公式48.轧制工字钢梁最大弯曲切应力计算公式49.圆形截面梁最大弯曲切应力发生在中性轴处50.圆环形薄壁截面梁最大弯曲切应力发生在中性轴处51.弯曲正应力强度条件52.几种常见截面梁的弯曲切应力强度条件53.弯曲梁危险点上既有正应力σ又有切应力τ作用时的强度条件或,54.梁的挠曲线近似微分方程55.梁的转角方程56.梁的挠曲线方程?57.轴向荷载与横向均布荷载联合作用时杆件截面底部边缘和顶部边缘处的正应力计算公式58.偏心拉伸(压缩)59.弯扭组合变形时圆截面杆按第三和第四强度理论建立的强度条件表达式,60.圆截面杆横截面上有两个弯矩和同时作用时,合成弯矩为61.圆截面杆横截面上有两个弯矩和同时作用时强度计算公式62.63.弯拉扭或弯压扭组合作用时强度计算公式64.剪切实用计算的强度条件65.挤压实用计算的强度条件66.等截面细长压杆在四种杆端约束情况下的临界力计算公式67.压杆的约束条件:(a)两端铰支μ=l(b)一端固定、一端自由μ=2(c)一端固定、一端铰支μ=0.7(d)两端固定μ=0.568.压杆的长细比或柔度计算公式,69.细长压杆临界应力的欧拉公式70.欧拉公式的适用范围71.压杆稳定性计算的安全系数法72.压杆稳定性计算的折减系数法73.关系需查表求得。
材料力学公式汇总完全版

:y
(2.23
平面弯曲梁上任
一点上的线应力
旦
(2.24
平面弯曲梁的曲
率
1 M
Elz
(2.25)
纯弯曲梁横截面
上任一点的正应
力
My
77
(2.26
离中性轴最远的
截面边缘各点上
的最大正应力
M.ymax
max
1z
(2.27)
抗弯截面模量
(截面对弯曲
的抵抗矩)
Wz1
ymax
(2.28)
离中性轴最远的
截面边缘各点上
的最大正应力
M
max
Wz
(2.29)
横力弯曲梁横截
面上的剪应力
*
VSz
Izb
S;被切割面 积对中性轴 的
面积矩。
(2.30
中性轴各点的剪
应力
*
VSz max max..
Izb
(2.31)
矩形截面中性
轴各点的剪应力
3V
max小..
2bh
(2.32)
工字形和T形截
面的面积矩
* * *
SzAYci
l l l,」
(2.4a
(2.4b)
胡克定律
E
E
(2.5)
胡克定律
l皿
EA
(2.6)
胡克定律
l丄如
iiea
(2.7)
横向线应变
bb]b
bb
(2.8)
泊松比(横向
1
变形系数)
1
(2.9)
剪力双生互等
定理
xy
(2.10
剪切虎克定理
G
材料力学公式大全

材料力学公式大全1. 应力(stress)公式:应力是单位面积上的力,常用符号表示为σ。
在一维情况下,应力公式可以表示为:σ=F/A其中,σ是应力,F是作用力,A是力作用的面积。
2. 应变(strain)公式:应变是用于描述物体形变的量,常用符号表示为ε。
在一维情况下,应变公式可以表示为:ε=ΔL/L0其中,ε是应变,ΔL是变形长度,L0是原始长度。
3. 弹性模量(elastic modulus)公式:弹性模量是衡量材料对外力作用下变形能力的指标,常用符号表示为E。
在一维情况下,弹性模量公式可以表示为:E=σ/ε其中,E是弹性模量,σ是应力,ε是应变。
4. 屈服强度(yield strength)公式:屈服强度是材料在变形过程中开始发生塑性变形的临界应力,常用符号表示为σy。
屈服强度公式可以表示为:σy=Fy/A其中,σy是屈服强度,Fy是屈服点的作用力,A是力作用的面积。
5. 拉伸强度(tensile strength)公式:拉伸强度是材料在拉伸过程中最大的抗拉应力,常用符号表示为σts。
拉伸强度公式可以表示为:σts = Fmax / A其中,σts是拉伸强度,Fmax是最大作用力,A是力作用的面积。
6. 断裂强度(fracture strength)公式:断裂强度是材料在破坏前的最大抗拉应力,常用符号表示为σf。
断裂强度公式可以表示为:σf=Ff/A其中,σf是断裂强度,Ff是破坏点的作用力,A是力作用的面积。
以上是一些常用的材料力学公式,这些公式在材料力学的研究和实际应用中有着重要的作用。
通过对这些公式的使用和理解,我们可以更好地了解材料在受力下的性能和行为,对于材料的设计和实际应用有着重要的指导意义。
材料力学公式大全

材料力学公式大全材料力学是研究材料在各种外力作用下产生的应变、应力、强度、刚度和稳定性的学科。
在工程设计和分析中,材料力学公式起着至关重要的作用。
下面为大家详细介绍一些常见的材料力学公式。
一、应力与应变1、正应力公式:轴向拉伸与压缩时,正应力$\sigma =\frac{F}{A}$,其中$F$ 是轴力,$A$ 是横截面面积。
圆轴扭转时,横截面上的切应力$\tau =\frac{T}{Ip}$,$T$ 是扭矩,$Ip$ 是极惯性矩。
2、线应变公式:轴向拉伸与压缩时,线应变$\epsilon =\frac{\Delta L}{L}$,$\Delta L$ 是长度的改变量,$L$ 是原长。
3、切应变公式:圆轴扭转时,切应变$\gamma =\frac{r\theta}{L}$,$r$ 是半径,$\theta$ 是扭转角,$L$ 是轴的长度。
二、胡克定律1、轴向拉伸与压缩时:$\sigma = E\epsilon$ ,其中$E$ 是弹性模量。
2、剪切胡克定律:$\tau = G\gamma$ ,$G$ 是剪切模量。
三、杆件的内力1、轴力$F_N$ :通过截面法求解,沿杆件轴线方向的内力。
2、扭矩$T$ :外力偶矩对杆件产生的内力。
3、剪力$F_Q$ 和弯矩$M$ :在梁的弯曲分析中,通过截面法求解。
四、梁的弯曲应力1、纯弯曲时的正应力:$\sigma =\frac{M y}{I_z}$,$y$ 是所求应力点到中性轴的距离,$I_z$ 是横截面对于中性轴的惯性矩。
2、横力弯曲时的正应力:需要考虑切应力的影响,进行修正。
五、梁的弯曲变形1、挠度$y$ 和转角$\theta$ 的计算公式:通过积分法或叠加法求解。
2、挠曲线近似微分方程:$EIz''= M(x)$。
六、组合变形1、拉(压)弯组合:分别计算拉伸(压缩)应力和弯曲应力,然后叠加。
2、弯扭组合:先计算弯曲应力和扭转切应力,然后根据强度理论进行强度校核。
材料力学公式汇总完全版(完整资料).doc
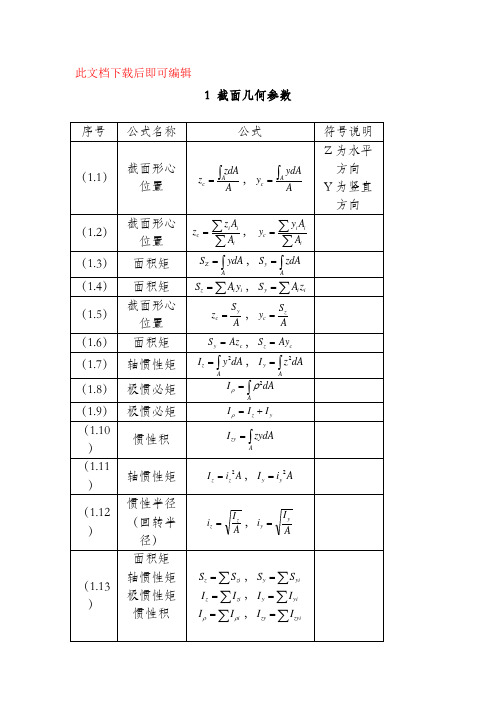
1 截面几何参数
序号
公式名称
公式
符号说明
(1.1)
截面形心位置
,
Z为水平方向
Y为竖直方向
(1.2)
截面形心位置
,
(1.3)
面积矩
,
(1.4)
面积矩
,
(1.5)
截面形心位置
,
(1.6)
面积矩
,
(1.7)
轴惯性矩
,
(1.8)
极惯必矩
(1.9)
极惯必矩
(1.10)
惯性积
(1.11)
轴惯性矩
I取最小值
(7.2)
细长压杆在不同支承情
况下的临界力公式
—计算长度。
—长度系数;
一端固定,一端自由:
一端固定,一端铰支:
两端固定:
(7.3)
压杆的柔度
是截面的惯性半径
(回转半径)
(7.4)
压杆的临界应力
(7.5)
欧拉公式的适用范围
(7.6)
抛物线公式
当 时,
—压杆材料的屈服极限;
—常数,一般取
(7.7)
(5.16)
螺栓的抗剪强度条件
(5.17)
螺栓的抗挤压强度条件
(5.18)
贴角焊缝的剪切强度条件
6 刚度校核
序号
公式名称
公式
符号说明
(6.1)
构件的刚度条件
(6.2)
扭转轴的刚度条件
(6.3)
平面弯曲梁的刚度条件
7 压杆稳定性校核
序号
公式名称
公式
符号说明
(7.1)
两端铰支的、细长压杆
的、临界力的欧拉公式
材料力学公式汇总完全版.pdf
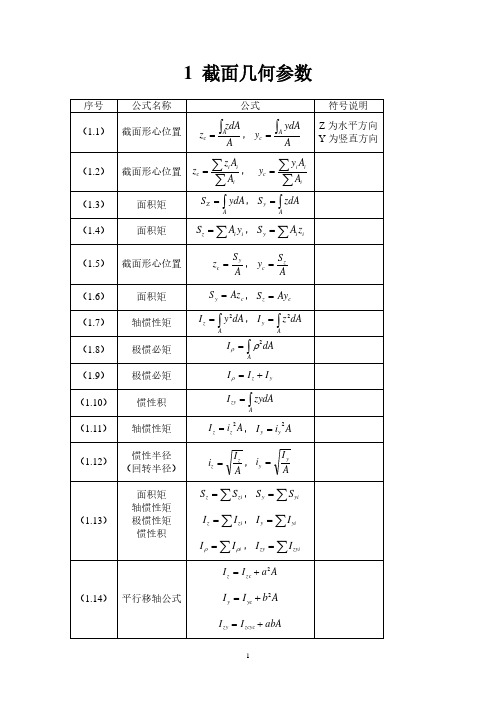
平面弯曲梁上任 一点上的线应变
平面弯曲梁上任 一点上的线应力
平面弯曲梁的曲 率
纯弯曲梁横截面 上任一点的正应
力
max
=
T WT
= T.l GI
=
i =
Tiil GI i
= , = T
l
GI
max
=T WT
=
T b3
1 = max
=T GIT
=
T Gb4
=
.l
=
T.l Gb4
= y
面上的线 应变
面与
(3.9)
+ 90o 面之 间的角应变
(3.10)
主应变方向 公式
(3.11) 最大主应变
(3.12) 最小主应变
(3.13) xy 的替代公 式
公式
=
x
+y 2
+ x
−y 2
cos 2
− x sin 2
=
x
−y 2
sin
2
+ x cos 2
tan 20
xy x −y
max
=
x
+y 2
+
x
− 2
y
2
+
2 xy
4
max
=
x
+y 2
−
x
− 2
y
2
+
2 xy
4
xy = 2 450 − x − y
符号说明
5
(3.14)
A
A
I = 2dA A
I = Iz + Iy
Izy = zydA A
Iz = iz2 A, I y = iy2 A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
面咼宽 比h/b有关
的参数
(2.22)
平面弯曲梁上任 一点上的线应变
(2.23)
平面弯曲梁上任 一点上的线应力
(2.24)
平面弯曲梁的曲 率
(2.25)
纯弯曲梁横截面 上任一点的正应
力
(2.26)
离中性轴最远的 截面边缘各点上 的最大正应力
(2.27)
抗弯截面模量 (截面对弯曲 的抵公式
符号说明
(6.1)
—构件的刚度条件
)
条件
(5.12a
)
平面弯曲梁的正应力强
(5.12b
)
度条件
(5.13)
平面弯曲梁的剪应力强 度条件
(5.14a
)
平面弯曲梁的主应力强
(5.14b
)
度条件
(5.15a
)
圆截面弯扭组合变形构
(5.15a
)
件的相当弯矩
(5.16)
螺栓的抗剪强度条件
(5.17)
螺栓的抗挤压强度条件
(5.18)
贴角焊缝的剪切强度条 件
(1.7)
轴惯性矩
Izy2dA, Iyz2dA
AA
(1.8)
极惯必矩
(1.9)
极惯必矩
(1.10)
惯性积
(1.11)
轴惯性矩
2 2
IzizA,IyiyA
(1.12)
惯性半径
(回转半径)
|'lzi帀iz1 _,iyj—\AA
(1.13)
面积矩 轴惯性矩 极惯性矩
惯性积
SzSzi,SySyi
1z1zi,1y1yi
11i,1zy1zyi
(1.14)
平行移轴公式
2
序号
公式名称
公式
符号说明
(2.1)
轴心拉压杆横 截面上的应力
(2.2)
危险截面上危 险点上的应力
(2.3a)
轴心拉压杆的
纵向线应变
(2.3b)
轴心拉压杆的 纵向绝对应变
(2.4a)
(2.4b)
胡克定律
(2.5)
胡克定律
(2.6)
胡克定律
(2.7)
横向线应变
(2.16)
圆截面扭转轴的 变形
(2.17)
单位长度的扭转 角
T l,GI
(2.18)
矩形截面扭转轴 长边中点上的剪 应力
W是矩形截 面
W的扭转抵 抗矩
(2.19)
矩形截面扭转轴 短边中点上的剪 应力
(2.20)
矩形截面扭转轴 单位长度的扭转 角
IT是矩形截
面的
It相当极惯
性矩
(2.21)
矩形截面扭转轴 全轴的扭转 角
符号说明
(3.1)
单元体上任 意截面上的 正应力
(3.2)
单元体上任 意截面上的 剪应力
(3.3)
主平面方位 角
2
tan2o—(o与x反号)
xy
(3.4)
最大主应力 的计算公式
(3.5)
最小主应力 的计算公式
(3.6)
单元体中的 最大剪应力
(3.7)
主单元体的 八面体面上 的剪应力
(3.8)
面上的线
平面弯曲梁的挠曲 线上任一截面 的转角方程
(2.35)
平面弯曲梁的挠曲 线上任一点挠度方 程
(2.36)
双向弯曲梁的合成 弯矩
(2.37a)
拉(压)弯组合矩形 截面的中性轴在Z轴 上的截距
zp, yp是集中
力作用点的 标
(2.37b)
拉(压)弯组合矩形 截面的中性轴在Y轴 上的截距
3
序号
公式名称
公式
(5.5)
第一强度理论相当应力
(5.6)
第二强度理论相当应力「
(5.7)
第三强度理论相当应力
(5.8)
第四强度理论相当应力
(5.9a)
由强度理论建立的强度 条件
(5.9b)
(5.9c)
(5.9d)
由直接试验建立的强度 条件
(5.10a
)
(5.10b
)
轴心拉压杆的强度条件
*
11max
T
WT
[t](适用于脆性材料)
应变
(3.9)
面与
+90°面之
间的角应变
(3.10)
主应变方向
公式
(3.11)
最大主应变
(3.12)
最小主应变
(3.13)
xy的替代公
式
(3.14)
主应变方向 公式
(3.15)
取大主应变
(3.16)
最小主应变
(3.17)
简单应力状 态下的虎克 定理
XXX
x,y,z
EyEE
(3.18)
空间应和状 态下的虎克 定理
1
序号
公式名称
公式
符号说明
(1.1)
截面形心位置
AzdAAydA
ZcA,ycA
AA
Z为水平方向丫为竖直方向
(1.2)
截面形心位置
乙AyiA
ZcA,%A
(1.3)
面积矩
SZydA, SyzdA
AA
(1.4)
面积矩
SZA yi,SyAz
(1.5)
截面形心位置
SySz
Z^—,yc
AA
(1.6)
面积矩
SyAzc,SzAyc
(5.11a
*
2
1
(23)=
)
(5.11b
max(0
max
)(1)max[t]
)
(5.11c
)
由强度理论建立的扭转 轴的强度条件
T
max77""
Wr
[t]
1
(适用于脆性材料)
(5.11d
)
T
maxt A f
Wr
[]
2
(适用于塑性材料)
T
m ax
Wt
[]
v3
(适用于塑性材料)
(5.11e
由扭转试验建立的强度
(2.8)
泊松比(横向 变形系数)
(2.9)
剪力双生互等 定理
(2.10)
剪切虎克定理
(2.11)
实心圆截面扭 转轴横截面上
的应力
(2.12)
实心圆截面扭 转轴横截面的 圆周上的应力
(2.13)
抗扭截面模量 (扭转抵抗矩)
(2.14)
实心圆截面扭 转轴横截面的 圆周上的应力
(2.15)
圆截面扭转轴的 变形
(4.1b)
外力偶的 换算公式
(4.2)
分布何载集度 剪力、弯矩之 间的关系
q(x)向上
为正
(4.3)—
(4.4)
5
序号
公式名称
公式
(5.1)
第一强度理论:最大拉 应力理论。
当!fut(脆性材料)时
!fu*.(塑性材料)时
材料发生脆性断裂破坏。
(5.2)
第二强度理论:最大伸 长线应变理论。
当1(23)fut(脆性材料)时
离中性轴最远的 截面边缘各点上 的最大正应力
(2.29)
横力弯曲梁横截 面上的剪应力
S;被切割面 积对中性轴
的
面积矩。
(2.30)
中性轴各点的剪 应力
(2.31)
矩形截面中性 轴各点的剪应力
(2.32)
工字形和T形截 面的面积矩
(2.33)
平面弯曲梁的挠 曲线近似微分方
程
V向下为正
X向右为正
(2.34)
1(23)fu*(塑性材料)时
材料发生脆性断裂破坏。
(5.3)
第三强度理论:最大剪 应力理论。
当13fy(塑性材料)时
13fuc(脆性材料)' '
材料发生剪切破坏。
(5.4)
第四强度理论:八面体 面剪切理论。
当
£122132232fy(塑性材料)
j1122132232fuc(脆性材料)
\2
时,材料发生剪切破坏。
(3.19)
平面应力状 态下的虎克 定理(应变形 式)
(3.20)
平面应力状 态下的虎克 定理(应力形 式)
(3.21)
按主应力、主 应变形式写 出广义虎克
定理
(3.22)
二向应力状 态的广义虎 克定理
(3.23)
二向应力状 态的广义虎 克定理
(3.24)
剪切虎克定 理
4
序号
公式名称
公式
符号说明
(4.1a)
